If you feel your practice session is incomplete then you just need this one particular & useful material ie., Big Ideas Math Algebra 1 Answers Chapter 10 Radical Functions and Equations. This is one of the best study resources available on the internet for international students who want to become pro in mathematics.
Kids will discover more preparation sections in this Big Ideas Math book Ch 10 Answer Key of Algebra 1 such as Exercises 10.1 to 10.4 Questions, Chapter Test, Review Tests, Cumulative Practice, Quizzes, etc. Therefore, go through this article and gain more subject knowledge and also enhance your math skills by concerning the Chapter 10 Radical Functions and Equations BIM Algebra 1 Answer Key.
Topic-wise Big Ideas Math Book Algebra 1 Solution Key Chapter 10 Radical Functions and Equations
The solutions of BIM Algebra 1 Chapter 10 Radical Functions and Equations are explained by the expert professionals as per the common core standards. So, students can trust this ch 10 Radical Functions and Equations Big Ideas math book Answers and make use of them at their preparation. It helps to improve your math knowledge and also clarify your queries on algebra 1 ch 1o Radical Functions and Equations complex topics. Download the Chapter 10 Big Ideas Math Algebra 1 Radical Functions and Equations Answer key from the links without a single penny and ace up your preparation.
- Radical Functions and Equations Maintaining Mathematical Proficiency – Page 541
- Radical Functions and Equations Mathematical Practices – Page 542
- Lesson 10.1 Graphing Square Root Functions – Page(543-550)
- Graphing Square Root Functions 10.1 Exercises – Page(548-550)
- Lesson 10.2 Graphing Cube Roots Functions – Page(551-556)
- Graphing Cube Roots Functions 10.2 Exercises – Page(555-556)
- Radical Functions and Equations Study Skills: Making Note Cards – Page 557
- Study Skills: Making Note Cards
- Radical Functions and Equations 10.1–10.2 Quiz – Page 558
- Lesson 10.3 Solving Radical Equations – Page(559-566)
- Solving Radical Equations 10.3 Exercises – Page(564-566)
- Lesson 10.4 Inverse of a Function – Page(567-574)
- Inverse of a Function 10.4 Exercises – Page(572-574)
- Radical Functions and Equations Performance Task: Medication and the Mosteller Formula – Page 575
- Radical Functions and Equations Chapter Review – Page (576-578)
- Radical Functions and Equations Chapter Test – Page 579
- Radical Functions and Equations Cumulative Assessment – Page(580-581)
Radical Functions and Equations Maintaining Mathematical Proficiency
Evaluate the expression.
Question 1.
7\(\sqrt{25}\) + 10
Answer:
Question 2.
-8 – \(\sqrt{\frac{64}{16}}\)
Answer:
Question 3.
\(5\left(\frac{\sqrt{81}}{3}-7\right)\)
Answer:
Question 4.
-2(3\(\sqrt{9}\) + 13)
Answer:
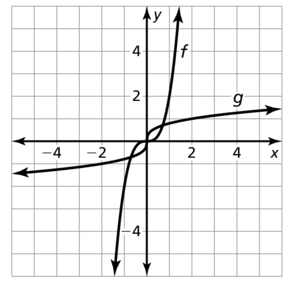
Graph f and g. Describe the transformations from the graph of f to the graph of g.
Question 5.
f(x) = x; g(x) = 2x – 2
Answer:
Question 6.
f(x) = x; g(x) = \(\frac{1}{3}\)x + 5
Answer:
Question 7.
f(x) = x; g(x) = -x + 3
Answer:
Question 8.
ABSTRACT REASONING
Let a and b represent constants, where b ≥ 0. Describe the transformations from the graph of m(x) = ax + b to the graph of n(x) = -2ax – 4b.
Answer:
Radical Functions and Equations Mathematical Practices
Mathematically proficient students distinguish correct reasoning from flawed reasoning.
Monitoring Progress
Question 1.
Which of the following square roots are rational numbers? Explain your reasoning.
\(\sqrt{0}, \sqrt{1}, \sqrt{3}, \sqrt{4}, \sqrt{5}, \sqrt{6}, \sqrt{7}, \sqrt{8}, \sqrt{9}\)
Answer:
Question 2.
The sequence of steps shown appears to prove that 1 = 0. What is wrong with this argument?

Answer:
Lesson 10.1 Graphing Square Root Functions
Essential Question What are some of the characteristics of the graph of a square root function?
EXPLORATION 1
Graphing Square Root Functions
Work with a partner.
- Make a table of values for each function.
- Use the table to sketch the graph of each function.
- Describe the domain of each function.
- Describe the range of each function.
Answer:
EXPLORATION 2
Writing Square Root Functions
Work with a partner. Write a square root function, y = f (x), that has the given values. Then use the function to complete the table.

Answer:
Communicate Your Answer
Question 3.
What are some of the characteristics of the graph of a square root function?
Answer:
Question 4.
Graph each function. Then compare the graph to the graph of f(x) = \(\sqrt{x}\).
a. g(x) = \(\sqrt{x-1}\)
b. g(x) = \(\sqrt{x-1}\)
c. g(x) = 2\(\sqrt{x}\)
d. g(x) = -2 \(\sqrt{x}\)
Answer:
Monitoring Progress
Describe the domain of the function.
Question 1.
f(x) = 10 \(\sqrt{x}\)
Answer:
Question 2.
y = \(\sqrt{2x}\) + 7
Answer:
Question 3.
h(x) = \(\sqrt{-x+1}\)
Answer:
Graph the function. Describe the range.
Question 4.
g(x) = \(\sqrt{x}\) – 4
Answer:
Question 5.
y = \(\sqrt{2x}\) + 5
Answer:
Question 6.
n(x) = 5\(\sqrt{x}\)
Answer:
Graph the function. Compare the graph to the graph of f(x) = \(\sqrt{x}\) .
Question 7.
h(x) = \(\sqrt{\frac{1}{4} x}\)
Answer:
Question 8.
g(x) = \(\sqrt{x}\) – 6
Answer:
Question 9.
m(x) = -3\(\sqrt{x}\)
Answer:
Question 10.
Let g(x) = \(\frac{1}{2} \sqrt{x+4}+1\). Describe the transformations from the graph of f(x) = \(\sqrt{x}\) to the graph of g. Then graph g.
Answer:
Question 11.
In Example 5, compare the velocities by finding and interpreting their average rates of change over the interval d = 30 to d = 40.
Answer:
Question 12.
WHAT IF?
At what depth does the velocity of the tsunami exceed 100 meters per second?
Answer:
Graphing Square Root Functions 10.1 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A ________ is a function that contains a radical expression with the independent variable in the radicand.
Answer:

Question 2.
VOCABULARY
Is y = 2x\(\sqrt{5}\) a square root function? Explain.
Answer:
Question 3.
WRITING
How do you describe the domain of a square root function?
Answer:
Question 4.
REASONING
Is the graph of g(x) = 1.25\(\sqrt{x}\) a vertical stretch or a vertical shrink of the graph of f(x) = \(\sqrt{x}\)? Explain.
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 5–14, describe the domain of the function.
Question 5.
y = 8\(\sqrt{x}\)
Answer:
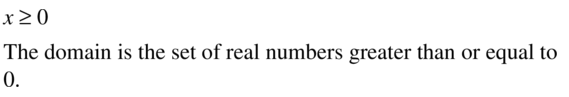
Question 6.
y = \(\sqrt{4x}\)
Answer:
Question 7.
y = 4 + \(\sqrt{-x}\)
Answer:

Question 8.
y = \(\sqrt{-\frac{1}{2^{x}}}\) + 1
Answer:
Question 9.
h(x) = \(\sqrt{x-4}\)
Answer:
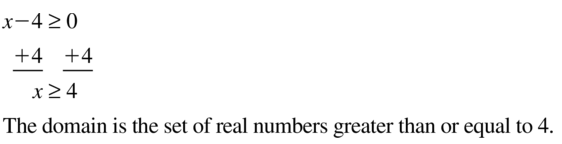
Question 10.
p(x) = \(\sqrt{x+7}\)
Answer:
Question 11.
f(x) = \(\sqrt{-x+8}\)
Answer:

Question 12.
g(x) = \(\sqrt{-x-1}\)
Answer:
Question 13.
m(x) = 2\(\sqrt{x+4}\)
Answer:
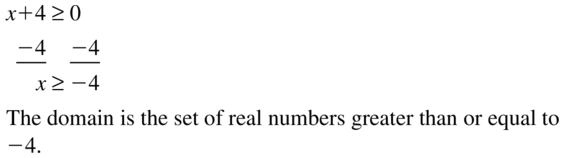
Question 14.
n(x) = \(\frac{1}{2} \sqrt{-x}-2\)
Answer:
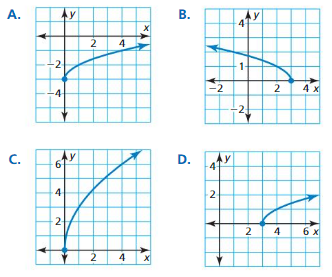
In Exercises 15–18, match the function with its graph. Describe the range.
Question 15.
y = \(\sqrt{x-3}\)
Answer:

Question 16.
y = 3\(\sqrt{x}\)
Answer:
Question 17.
y = \(\sqrt{x}\) – 3
Answer:

Question 18.
y = \(\sqrt{-x+3}\)
Answer:
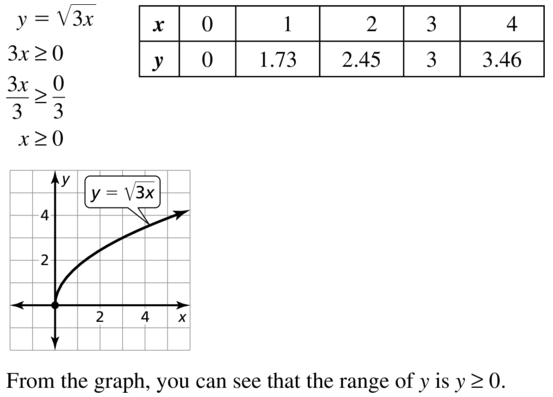
In Exercises 19–26, graph the function. Describe the range.
Question 19.
y = \(\sqrt{3x}\)
Answer:
Question 20.
y = 4\(\sqrt{-x}\)
Answer:
Question 21.
y = \(\sqrt{x}\) + 5
Answer:
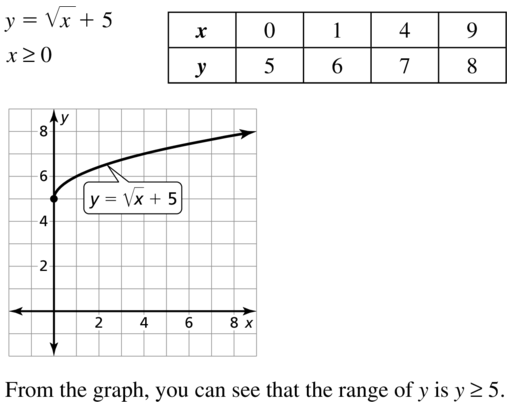
Question 22.
y = -2 + \(\sqrt{x}\)
Answer:
Question 23.
f(x) = – \(\sqrt{x-3}\)
Answer:
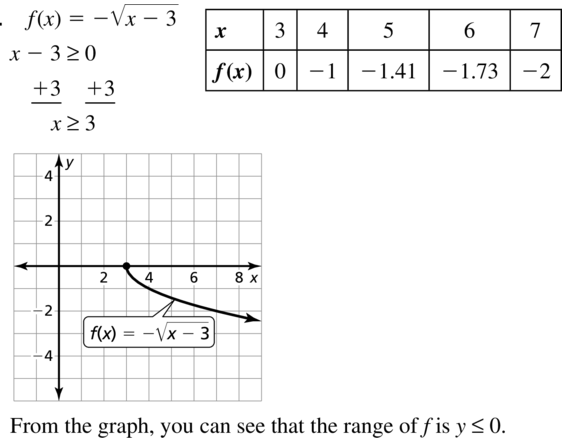
Question 24.
g(x) = \(\sqrt{x+4}\)
Answer:
Question 25.
h(x) = \(\sqrt{x+2}\) – 2
Answer:
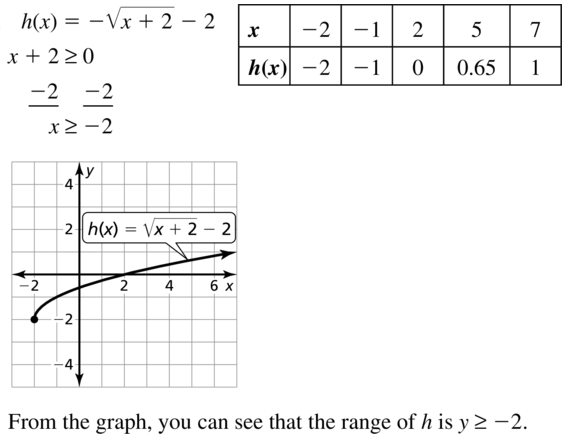
Question 26.
f(x) = –\(\sqrt{x-1}\) + 3
Answer:
In Exercises 27–34, graph the function. Compare the graph to the graph of f (x) = \(\sqrt{x}\).
Question 27.
g(x) = \(\frac{1}{4} \sqrt{x}\)
Answer:
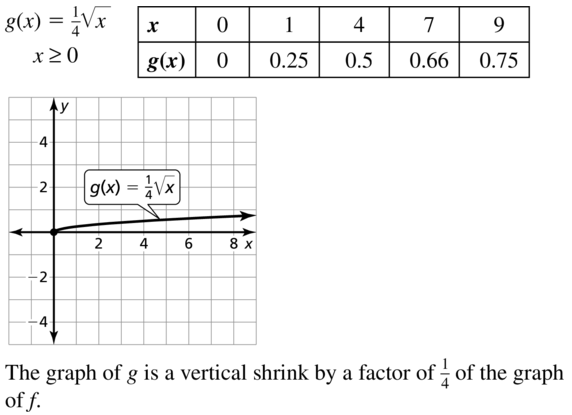
Question 28.
r(x) = \(\sqrt{2x}\)
Answer:
Question 29.
h(x) = \(\sqrt{x+3}\)
Answer:
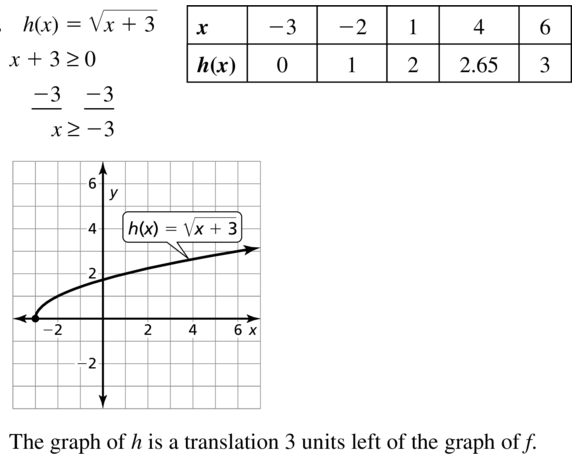
Question 30.
q(x) = \(\sqrt{x}\) + 8
Answer:
Question 31.
p(x) = \(\sqrt{-\frac{1}{3} x}\)x
Answer:
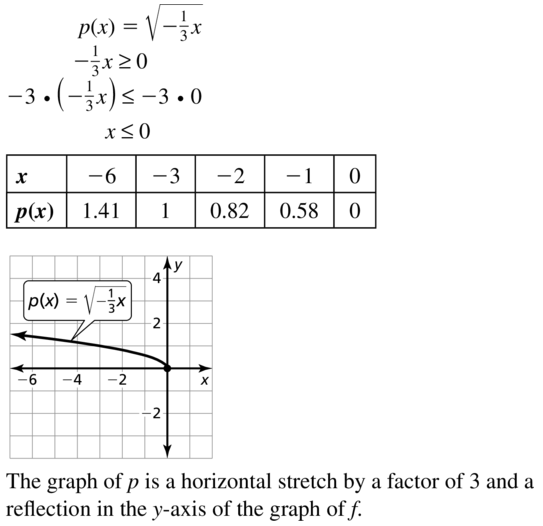
Question 32.
g(x) = -5\(\sqrt{x}\)
Answer:
Question 33.
m(x) = –\(\sqrt{x}\) – 6
Answer:
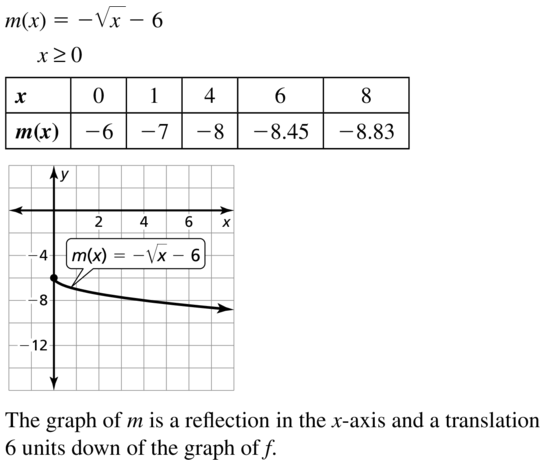
Question 34.
n(x) = –\(\sqrt{x}\) – 4
Answer:
Question 35.
ERROR ANALYSIS
Describe and correct the error in graphing the function y = \(\sqrt{x}\) + 1 .
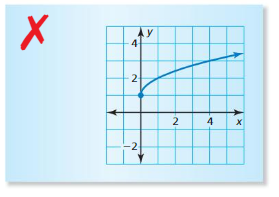
Answer:
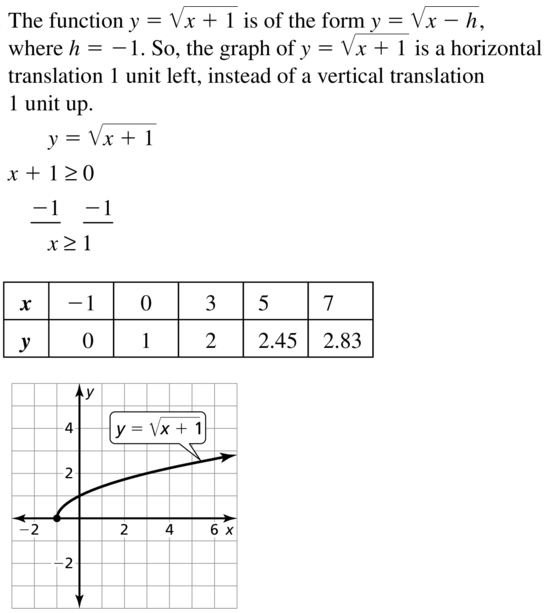
Question 36.
ERROR ANALYSIS
Describe and correct the error in comparing the graph of g(x) = \(-\frac{1}{4} \sqrt{x}\) to the graph of f (x) = \(\sqrt{x}\).
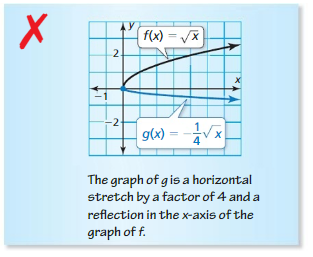
Answer:
In Exercises 37–44, describe the transformations from the graph of f (x) = \(\sqrt{x}\) to the graph of h. Then graph h.
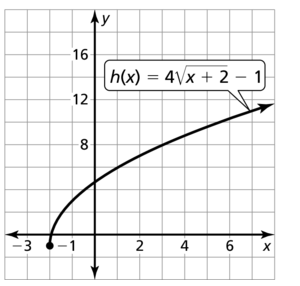
Question 37.
h(x) = 4\(\sqrt{x+2}\) – 1
Answer:

Question 38.
h(x) = \(\frac{1}{2} \sqrt{x-6}\)+ 3
Answer:
Question 39.
h(x) = 2\(\sqrt{-x}\) – 6
Answer:

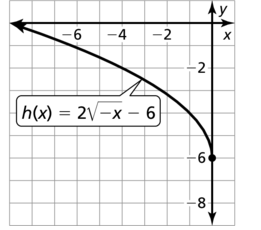
Question 40.
h(x) = –\(\sqrt{x-3}\) – 2
Answer:
Question 41.
h(x) = \(\frac{1}{3} \sqrt{x+3}\) + 3
Answer:

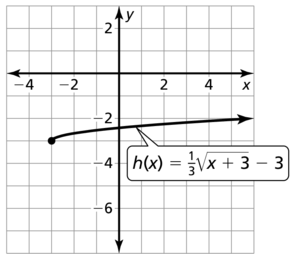
Question 42.
h(x) = 2\(\sqrt{x-1}\) + 4
Answer:
Question 43.
h(x) = -2\(\sqrt{x-1}\) + 5
Answer:

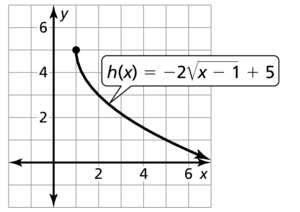
Question 44.
h(x) = -5\(\sqrt{x+2}\) – 1
Answer:
Question 45.
COMPARING FUNCTIONS
The model S(d ) = \(\sqrt{30df}\) represents the speed S (in miles per hour) of a van before it skids to a stop, where f is the drag factor of the road surface and d is the length (in feet) of the skid marks. The drag factor of Road Surface A is 0.75. The graph shows the speed of the van on Road Surface B. Compare the speeds by finding and interpreting their average rates of change over the interval d = 0 to d = 15.
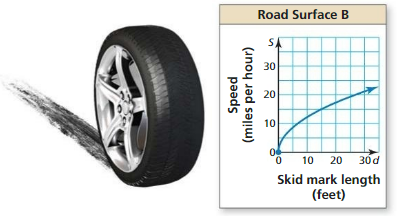
Answer:

Question 46.
COMPARING FUNCTIONS
The velocity v (in meters per second) of an object in motion is given by v(E ) = \(\sqrt{\frac{2 E}{m}}\), where E is the kinetic energy of the object (in joules) and m is the mass of the object (in kilograms). The mass of Object A is 4 kilograms. The graph shows the velocity of Object B. Compare the velocities of the objects by finding and interpreting the average rates of change over the interval E = 0 to E = 6.
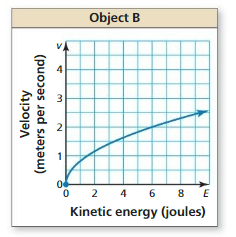
Answer:
Question 47.
OPEN-ENDED
Consider the graph of y = \(\sqrt{x}\).
a. Write a function that is a vertical translation of the graph of y = \(\sqrt{x}\).
b. Write a function that is a reflection of the graph of y = \(\sqrt{x}\).
Answer:

Question 48.
REASONING
Can the domain of a square root function include negative numbers? Can the range include negative numbers? Explain your reasoning.
Answer:
Question 49.
PROBLEM SOLVING
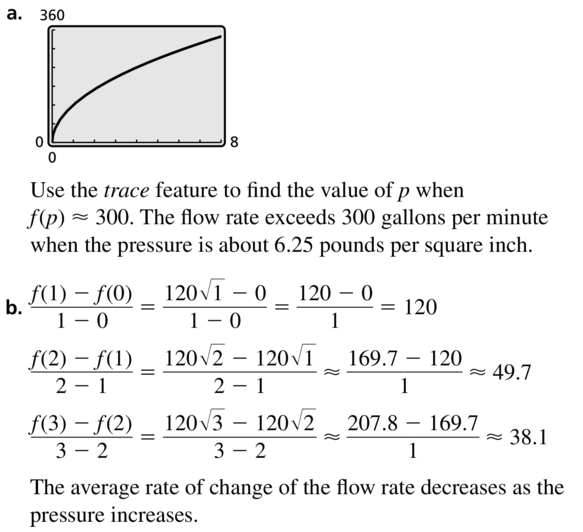
The nozzle pressure of a fire hose allows firefighters to control the amount of water they spray on a fire. The flow rate f(in gallons per minute) can be modeled by the function f = 12\(\sqrt{p}\), where p is the nozzle pressure (in pounds per square inch).

a. Use a graphing calculator to graph the function. At what pressure does the flow rate exceed 300 gallons per minute?
b. What happens to the average rate of change of the flow rate as the pressure increases?
Answer:
Question 50
PROBLEM SOLVING
The speed s (in meters per second) of a long jumper before jumping can be modeled by the function s = 10.9\(\sqrt{h}\), where h is the maximum height (in meters from the ground) of the jumper.

a. Use a graphing calculator to graph the function. A jumper is running 9.2 meters per second. Estimate the maximum height of the jumper.
b. Suppose the runway and pit are raised on a platform slightly higher than the ground. How would the graph of the function be transformed?
Answer:
Question 51.
MATHEMATICAL CONNECTIONS
The radius r of a circle is given by r = \(\sqrt{\frac{A}{\pi}}\), where A is the area of the circle.
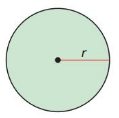
a. Describe the domain of the function. Use a graphing calculator to graph the function.
b. Use the trace feature to approximate the area of a circle with a radius of 5.4 inches.
Answer:

Question 52.
REASONING
Consider the function f(x) = 8a\(\sqrt{x}\).
a. For what value of a will the graph of f be identical to the graph of the parent square root function?
b. For what values of a will the graph of f be a vertical stretch of the graph of the parent square root function?
c. For what values of a will the graph of f be a vertical shrink and a reflection of the graph of the parent square root function?
Answer:
Question 53.
REASONING
The graph represents the function f(x) = \(\sqrt{x}\).
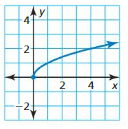
a. What is the minimum value of the function?
b. Does the function have a maximum value? Explain.
c. Write a square root function that has a maximum value. Does the function have a minimum value? Explain.
d. Write a square root function that has a minimum value of -4.
Answer:

Question 54.
HOW DO YOU SEE IT?
Match each function with its graph. Explain your reasoning.
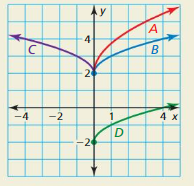
Answer:
Question 55.
REASONING
Without graphing, determine which function’s graph rises more steeply, f(x) = 5\(\sqrt{x}\) or g(x) = \(\sqrt{5x}\). Explain your reasoning.
Answer:

Question 56.
THOUGHT PROVOKING
Use a graphical approach to find the solutions of x – 1 = \(\sqrt{5x-9}\). Show your work. Verify your solutions algebraically.
Answer:
Question 57.
OPEN-ENDED
Write a radical function that has a domain of all real numbers greater than or equal to -5 and a range of all real numbers less than or equal to 3.
Answer:

Maintaining Mathematical Proficiency
Evaluate the expression.(Section 6.2)
Question 58.
\(\sqrt [ 3]{ 343 }\)
Answer:
Question 59.
\(\sqrt [ 3]{ -64 }\)
Answer:
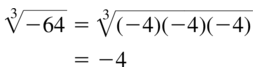
Question 60.
\(-\sqrt[3]{-\frac{1}{27}}\)
Answer:
Factor the polynomial.(Section 7.5)
Question 61.
x2 + 7x + 6
Answer:

Question 62.
d2 – 11d + 28
Answer:
Question 63.
y2 – 3y – 40
Answer:

Lesson 10.2 Graphing Cube Roots Functions
Essential Question What are some of the characteristics of the graph of a cube root function?
EXPLORATION 1
Graphing Cube Root Functions
Work with a partner.
- Make a table of values for each function. Use positive and negative values of x.
- Use the table to sketch the graph of each function.• Describe the domain of each function.
- Describe the range of each function.
Answer:
EXPLORATION 2
Writing Cube Root Functions
Work with a partner. Write a cube root function, y = f(x), that has the given values. Then use the function to complete the table.

Answer:
Communicate Your Answer
Question 3.
What are some of the characteristics of the graph of a cube root function?
Answer:
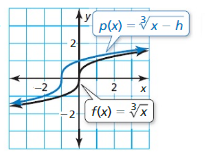
Question 4.
Graph each function. Then compare the graph to the graph of f (x) = \(\sqrt [ 3]{ x }\) .
a. g(x) = \(\sqrt [ 3]{ x-1 }\)
b. g(x) = \(\sqrt [ 3]{ x-1 }\)
c. g(x) = 2 \(\sqrt [ 3]{ x }\)
d. g(x) = -2\(\sqrt [ 3]{ x }\)
Answer:
Monitoring Progress
Graph the function. Compare the graph to the graph of f(x) = \(\sqrt [ 3]{ x }\).
Question 1.
h(x) = \(\sqrt [ 3]{ x }\) + 3
Answer:
Question 2.
m(x) = \(\sqrt [ 3]{ x }\) – 5
Answer:
Question 3.
g(x) = 4\(\sqrt [ 3]{ x }\)
Answer:
Graph the function. Compare the graph to the graph of f(x) = \(\sqrt [ 3]{ x }\).
Question 4.
g(x) =\(\sqrt [3]{ 0.5x+5 }\) + 5
Answer:
Question 5.
h(x) = 4\(\sqrt [3]{ x }\) – 1
Answer:
Question 6.
n(x) = \(\sqrt [ 3]{ 4-x }\)
Answer:
Question 7.
Let g(x) = \(-\frac{1}{2} \sqrt[3]{x+2}\) – 4. Describe the transformations from the graph of f (x) = \(\sqrt [ 3]{ x }\) to the graph of g. Then graph g.
Answer:
Question 8.
In Example 4, compare the average rates of change over the interval x = 2 to x = 10.
Answer:
Question 9.
WHAT IF?
Estimate the age of an elephant whose shoulder height is 175 centimeters.
Answer:
Graphing Cube Roots Functions 10.2 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The __________ of the radical in a cube root function is 3.
Answer:
![]()
Question 2.
WRITING
Describe the domain and range of the function f(x) = \(\sqrt [3]{ x-4 }\) + 1.
Answer:
Monitoring Progress and Modeling with Mathematics
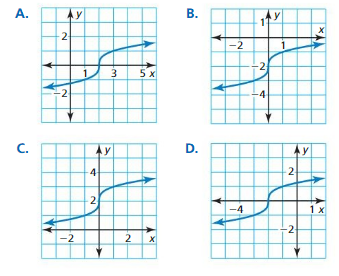
In Exercises 3–6, match the function with its graph.
Question 3.
y = 3\(\sqrt [3]{ x+2 }\)
Answer:
Question 4.
y = 3\(\sqrt [3]{ x-2 }\)
Answer:
Question 5.
y = 3\(\sqrt [3]{ x+2 }\)
Answer:
Question 6.
y = \(\sqrt [3]{ x }\) – 2
Answer:
In Exercises 7–12, graph the function. Compare the graph to the graph of f(x) = \(\sqrt [ 3]{ x }\).
Question 7.
h(x) = \(\sqrt [3]{ x-4 }\)
Answer:
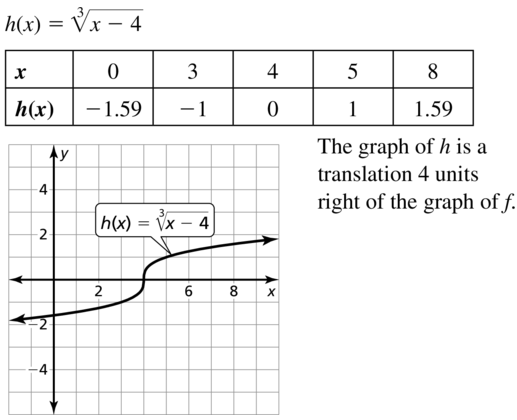
Question 8.
g(x) = \(\sqrt [3]{ x+1 }\)
Answer:
Question 9.
m(x) = \(\sqrt [3]{ x+5 }\)
Answer:

Question 10.
q(x) = \(\sqrt [3]{ x }\) – 3
Answer:
Question 11.
p(x) = 6\(\sqrt [3]{ x }\)
Answer:
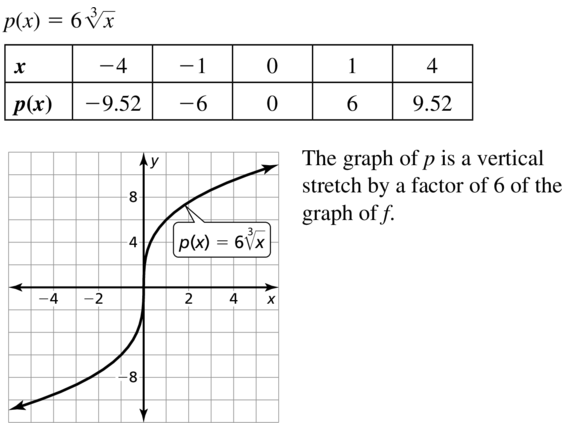
Question 12.
j(x) = \(\sqrt[3]{\frac{1}{2} x}\)
Answer:
In Exercises 13–16, compare the graphs. Find the value of h, k, or a.
Question 13.
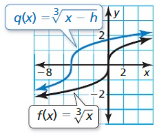
Answer:
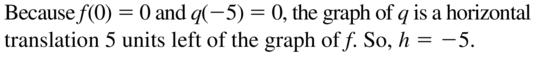
Question 14.
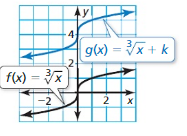
Answer:
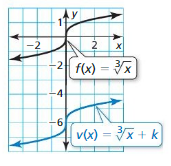
Question 15.
Answer:
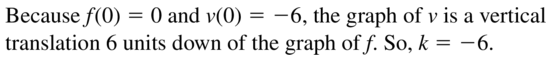
Question 16.
Answer:
In Exercises 17–26, graph the function. Compare the graph to the graph of f(x) = \(\sqrt [3]{ x }\).
Question 17.
r(x) = – \(\sqrt [3]{ x-2 }\)
Answer:
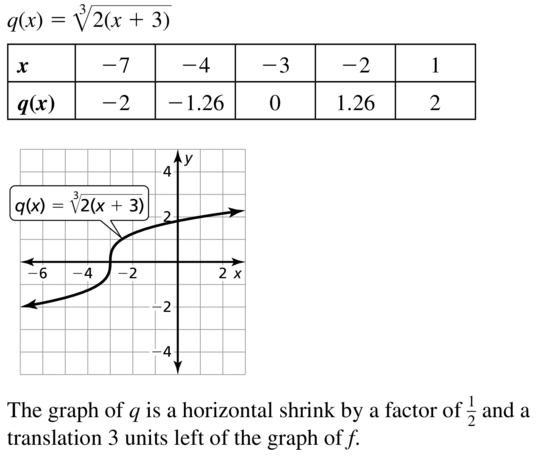
Question 18.
h(x) = – 3\(\sqrt [3]{ x+3 }\)
Answer:
Question 19.
k(x) = 5\(\sqrt [3]{ x+1 }\)
Answer:
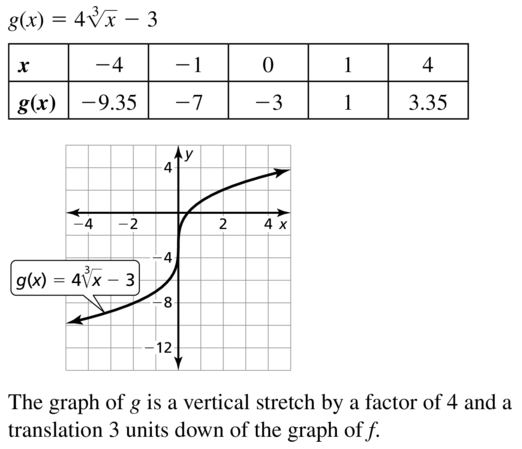
Question 20.
j(x) = 0.5\(\sqrt [3]{ x-4 }\)
Answer:
Question 21.
g(x) = 4\(\sqrt [3]{ x }\) – 3
Answer:
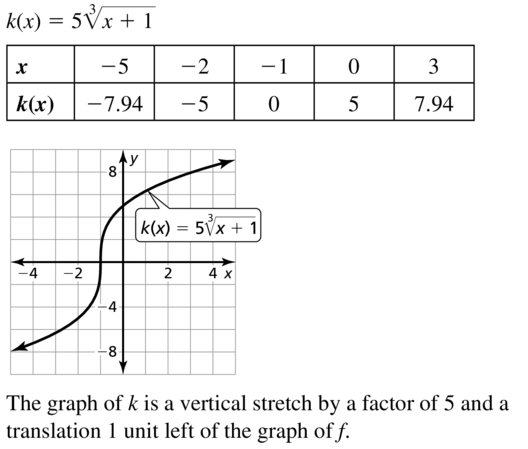
Question 22.
m(x) = 3\(\sqrt [3]{ x }\) + 7
Answer:
Question 23.
n(x) = \(\sqrt [3]{ -8x }\) – 1
Answer:

Question 24.
v(x) =\(\sqrt [3]{ 5x }\) + 2
Answer:
Question 25.
q(x) = \(\sqrt[3]{2(x+3)}\)
Answer:
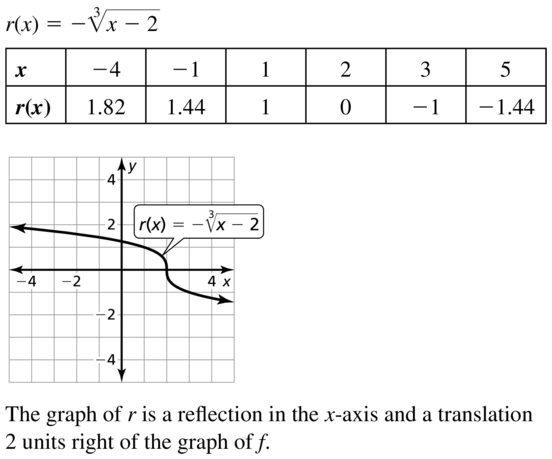
Question 26.
p(x) = \(\sqrt[3]{3(1-x)}\)
Answer:
In Exercises 27–32, describe the transformations from the graph of f(x) = \(\sqrt [3]{ x }\) to the graph of the given function. Then graph the given function.
Question 27.
g(x) = \(\sqrt [3]{ x-4 }\) + 2
Answer:

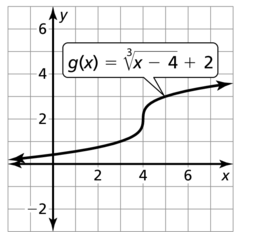
Question 28.
n(x) = \(\sqrt [3]{ x+1 }\) – 3
Answer:
Question 29.
j(x) = -5\(\sqrt [3]{ x+3 }\) + 2
Answer:

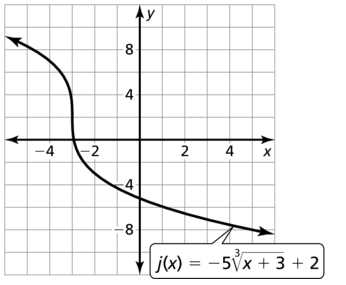
Question 30.
k(x) = 6\(\sqrt [3]{ x-9 }\) – 5
Answer:
Question 31.
v(x) = \(\frac{1}{3} \sqrt[3]{x-1}\) + 7
Answer:

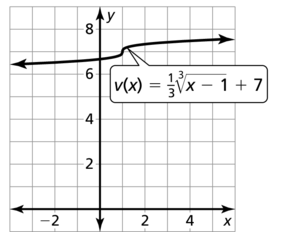
Question 32.
h(x) = -\frac{3}{2} \sqrt[3]{x+4} – 3
Answer:
Question 33.
ERROR ANALYSIS
Describe and correct the error in graphing the function f(x) = \(\sqrt [3]{ x-3 }\).
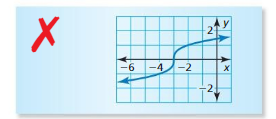
Answer:
Question 34.
ERROR ANALYSIS
Describe and correct the error in graphing the function h(x) = \(\sqrt [3]{ x }\) + 1.
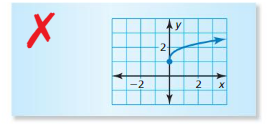
Answer:
Question 35.
COMPARING FUNCTIONS
The graph of cube root function q is shown. Compare the average rate of change of q to the average rate of change of f(x) = 3\(\sqrt [3]{ x }\) over the interval x = 0 to x = 6.
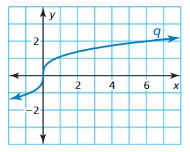
Answer:

Question 36.
COMPARING FUNCTIONS
The graphs of two cube root functions are shown. Compare the average rates of change of the two functions over the interval x = -2 to x = 2.
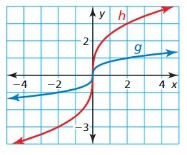
Answer:
Question 37.
MODELING WITH MATHEMATICS
For a drag race car that weighs 1600 kilograms, the velocity v (in kilometers per hour) reached by the end of a drag race can be modeled by the function v = 23.8\(\sqrt [3]{ p }\), where p is the car’s power (in horsepower). Use a graphing calculator to graph the function. Estimate the power of a 1600-kilogram car that reaches a velocity of 220 kilometers per hour.
Answer:
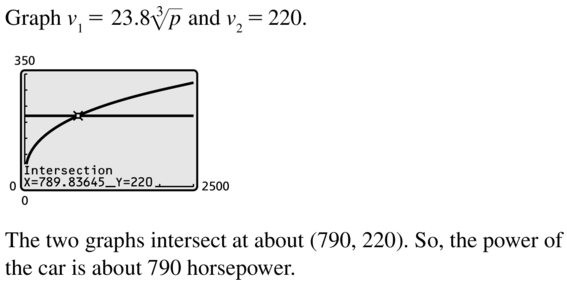
Question 38.
MODELING WITH MATHEMATICS
The radius r of a sphere is given by the function r = \(\sqrt[3]{\frac{3}{4 \pi}} V\), where V is the volume of the sphere. Use a graphing calculator to graph the function. Estimate the volume of a spherical beach ball with a radius of 13 inches.
Answer:
Question 39.
MAKING AN ARGUMENT
Your friend says that all cube root functions are odd functions. Is your friend correct? Explain.
Answer:

Question 40.
HOW DO YOU SEE IT?
The graph represents the cube root function f(x) = \(\sqrt [3]{ x }\).
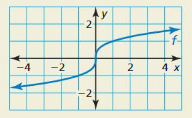
a. On what interval is f negative? positive?
b. On what interval, if any, is f decreasing? increasing?
c. Does f have a maximum or minimum value? Explain.
d. Find the average rate of change of f over the interval x = -1 to x = 1.
Answer:
Question 41.
PROBLEM SOLVING
Write a cube root function that passes through the point (3, 4) and has an average rate of change of -1 over the interval x = -5 to x = 2.
Answer:

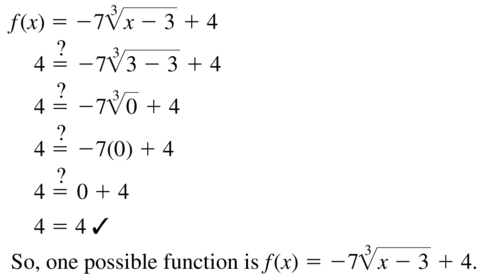
Question 42.
THOUGHT PROVOKING
Write the cube root function represented by the graph. Use a graphing calculator to check your answer.
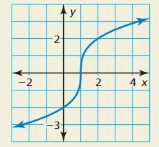
Answer:
Maintaining Mathematical Proficiency
Factor the polynomial.(Section 7.6)
Question 43.
3x2 + 12x – 36
Answer:

Question 44.
2x2 – 11x + 9
Answer:
Question 45.
4x2 + 7x – 15
Answer:

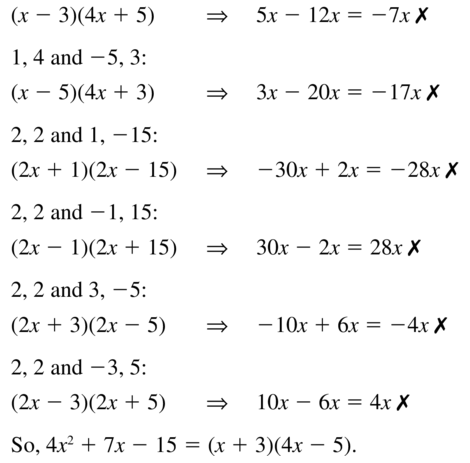
Solve the equation using square roots.(Section 9.3)
Question 46.
x2 – 36 = 0
Answer:
Question 47.
5x2 + 20 = 0
Answer:

Question 48.
(x + 4)2 – 81
Answer:
Question 49.
25(x – 2)2 = 9
Answer:
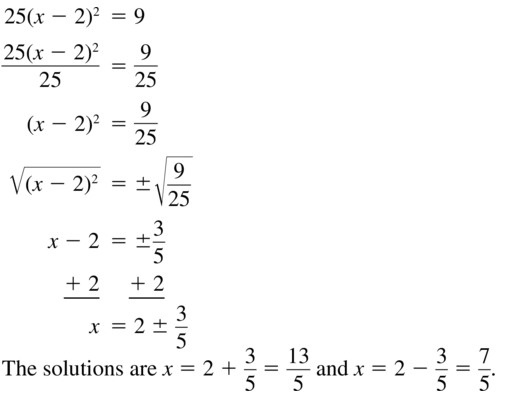
Radical Functions and Equations Study Skills: Making Note Cards
10.1–10.2 What Did YouLearn?
Core Vocabulary
square root function, p. 544
radical function, p. 545
cube root function, p. 552
Core Concepts
Lesson 10.1
Square Root Functions, p. 544
Transformations of Square Root Functions, p. 545
Comparing Square Root Functions Using Average Rates of Change, p. 546
Lesson 10.2
Cube Root Functions, p. 552
Comparing Cube Root Functions
Using Average Rates of Change, p. 554
Mathematical Practices
Question 1.
In Exercise 45 on page 549, what information are you given? What relationships are present? What is your goal?
Answer:
Question 2.
What units of measure did you use in your answer to Exercise 38 on page 556? Explain your reasoning.
Answer:
Study Skills: Making Note Cards
Invest in three different colors of note cards. Use one color for each of the following: vocabulary words, rules, and calculator keystrokes.
- Using the first color of note cards, write a vocabulary word on one side of a card. On the other side, write the definition and an example. If possible, put the definition in your own words.
- Using the second color of note cards, write a rule on one side of a card. On the other side, write an explanation and an example.
- Using the third color of note cards, write a calculation on one side of a card. On the other side, write the keystrokes required to perform the calculation.
Use the note cards as references while completing your homework. Quiz yourself once a day.

Radical Functions and Equations 10.1–10.2 Quiz
Describe the domain of the function.(Lesson 10.1)
Question 1.
y = \(\sqrt{x-3}\)
Answer:
Question 2.
f(x) = 15\(\sqrt{x}\)
Answer:
Question 3.
y = \(\sqrt{3-x}\)
Answer:
Graph the function. Describe the range. Compare the graph to the graph of f(x) = \(\sqrt{x}\). (Lesson 10.1)
Question 4.
g(x) = \(\sqrt{x}\) + 5
Answer:
Question 5.
n(x) = \(\sqrt{x-4}\)
Answer:
Question 6.
r(x) = –\(\sqrt{x-1}\) + 1
Answer:
Graph the function. Compare the graph to the graph of f(x) = \(\sqrt [3]{ x }\). (Lesson 10.2)
Question 7.
b(x) = \(\sqrt [3]{ x+2 }\)
Answer:
Question 8.
h(x) = -3\(\sqrt [3]{ x-6 }\)
Answer:
Question 9.
q(x) = \(\sqrt [3]{ -4-x }\)
Answer:
Compare the graphs. Find the value of h, k, or a. (Lesson 10.1 and Lesson 10.2)
Question 10.
Answer:
Question 11.
Answer:
Question 12.
Answer:
Describe the transformations from the graph of f to the graph of h. Then graph h. (Section 10.1 and Section 10.2)
Question 13.
f(x) = \(\sqrt{x}\); h(x) = -3 \(\sqrt{x+2}\) + 6
Answer:
Question 14.
f(x) = \(\sqrt[3]{x}\); h(x) = \(\frac{1}{2} \sqrt[3]{x}-3\)
Answer:
Question 15.
The time t (in seconds) it takes a dropped object to fall h feet is given by t = \(\frac{1}{4} \sqrt{h}\). (Section 10.1)

a. Use a graphing calculator to graph the function. Describe the domain and range.
b. It takes about 7.4 seconds for a stone dropped from the New River Gorge Bridge in West Virginia to reach the water below. About how high is the bridge above the New River?
Answer:
Question 16.
The radius r of a sphere is given by the function r = \(\sqrt[3]{\frac{3}{4 \pi} V}\), where V is the volume of the sphere. Spaceship Earth is a spherical structure at Walt Disney World that has an inner radius of about 25 meters. Use a graphing calculator to graph the function. Estimate the volume of Spaceship Earth. (Section 10.2)
Answer:
Question 17.
The graph of square root function g is shown. Compare the average rate of change of g to the average rate of change of h(x) = \(\sqrt[3]{\frac{3}{2} x}\)x over the interval x = 0 to x = 3.
Answer:
Lesson 10.3 Solving Radical Equations
Essential Question How can you solve an equation that contains square roots?
EXPLORATION 1
Analyzing a Free-Falling Object
Work with a partner. The table shows the time t (in seconds) that it takes a free-falling object (with no air resistance) to fall d feet.
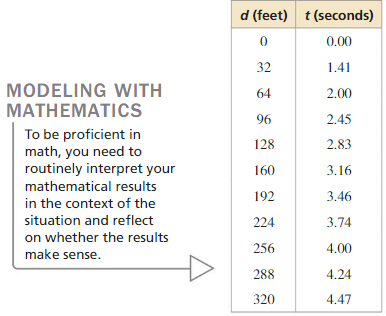
a. Use the data in the table to sketch the graph of t as a function of d. Use the coordinate plane below.
b. Use your graph to estimate the time it takes the object to fall 240 feet.
c. The relationship between d and t is given by the function t = \(\sqrt{\frac{d}{16}}\).
Use this function to check your estimate in part (b).
d. It takes 5 seconds for the object to hit the ground. How far did it fall? Explain your reasoning.

EXPLORATION 2
Solving a Square Root Equation
Work with a partner. The speed s (in feet per second) of the free-falling object in Exploration 1 is given by the functions
s = \(\sqrt{64d}\).
Find the distance the object has fallen when it reaches each speed.
a. s = 8 ft/sec
b. s = 16 ft/sec
c. s = 24 ft/sec
Communicate Your Answer
Question 3.
How can you solve an equation that contains square roots?
Answer:
Question 4.
Use your answer to Question 3 to solve each equation.
a. 5 = \(\sqrt{x}\) + 20
b. 4 = \(\sqrt{x-18}\)
c. \(\sqrt{x}\) + 2 = 3
d. -3 = -2\(\sqrt{x}\)
Answer:
Monitoring Progress
Solve the equation. Check your solution.
Question 1.
\(\sqrt{x}\) = 6
Answer:
Question 2.
\(\sqrt{x}\) – 7 = 3
Answer:
Question 3.
\(\sqrt{y}\) + 15 = 22
Answer:
Question 4.
1 – \(\sqrt{c}\) = -2
Answer:
Solve the equation. Check your solution.
Question 5.
\(\sqrt{x+4}\) + 7 = 11
Answer:
Question 6.
15 = 6 + \(\sqrt{3w-9}\)
Answer:
Question 7.
\(\sqrt{3x+1}\) = \(\sqrt{4x-7}\)
Answer:
Question 8.
\(\sqrt{n}\) = \(\sqrt{5n-1}\)
Answer:
Question 9.
\(\sqrt [3]{ y }\) = 4 = 1
Answer:
Question 10.
\(\sqrt [3]{ 3c+7 }\) = 10
Answer:
Solve the equation. Check your solution(s).
Question 11.
\(\sqrt{4-3x}\) = x
Answer:
Question 12.
\(\sqrt{3m}\) + 10 = 1
Answer:
Question 13.
p + 1 = \(\sqrt{7p+15}\)
Answer:
Question 14.
What is the length of a pendulum that has a period of 2.5 seconds?
Answer:
Solving Radical Equations 10.3 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Why should you check every solution of a radical equation?
Answer:

Question 2.
WHICH ONE DOESN’T BELONG?
Which equation does not belong with the other three? Explain your reasoning.
![]()
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3–12, solve the equation. Check your solution.
Question 3.
\(\sqrt{x}\) = 9
Answer:

Question 4.
\(\sqrt{x}\) = 4
Answer:
Question 5.
7 = \(\sqrt{x}\) – 5
Answer:

Question 6.
\(\sqrt{p}\) – 7 = -1
Answer:
Question 7.
\(\sqrt{c}\) + 12 = 23
Answer:

Question 8.
\(\sqrt{x}\) + 6 = 8
Answer:
Question 9.
4 – \(\sqrt{x}\) = 2
Answer:

Question 10.
-8 = 7 = \(\sqrt{r}\)
Answer:
Question 11.
3\(\sqrt{y}\) – 18 = -3
Answer:

Question 12.
2\(\sqrt{q}\) + 5 = 11
Answer:
In Exercises 13–20, solve the equation. Check your solution.
Question 13.
\(\sqrt{a-3}\) + 5 = 9
Answer:

Question 14.
\(\sqrt{b+7}\) – 5 = -2
Answer:
Question 15.
2 \(\sqrt{x+4}\) = 16
Answer:

Question 16.
5\(\sqrt{y-2}\) = 10
Answer:
Question 17.
-1 = \(\sqrt{5r+1}\) – 7
Answer:

Question 18.
2 = \(\sqrt{4s-4}\) – 4
Answer:
Question 19.
7 + 3\(\sqrt{3p-9}\) = 25
Answer:

Question 20.
19 – 4\(\sqrt{3c-11}\) = 11
Answer:
Question 21.
MODELING WITH MATHEMATICS
The Cave of Swallows is a natural open-air pit cave in the state of San Luis Potosí, Mexico. The 1220-foot- deep cave was a popular destination for BASE jumpers. The function t = \(\frac{1}{4} \sqrt{d}\) represents the time t (in seconds) that it takes a BASE jumper to fall d feet. How far does a BASE jumper fall in 3 seconds?

Answer:

Question 22.
MODELING WITH MATHEMATICS
The edge length s of a cube with a surface area of A is given by s = \(\sqrt{\frac{A}{6}}\). What is the surface area of a cube with an edge length of 4 inches?
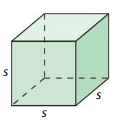
Answer:
In Exercises 23–26, use the graph to solve the equation.
Question 23.
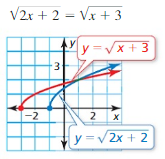
Answer:
Question 24.
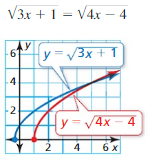
Answer:
Question 25.
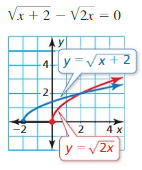
Answer:
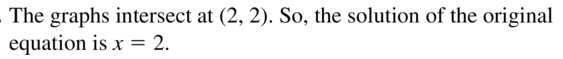
Question 26.
Answer:
In Exercises 27–34, solve the equation. Check your solution. (See Example 3.)
Question 27.
\(\sqrt{2x-9}\) = \(\sqrt{x}\)
Answer:

Question 28.
\(\sqrt{y+1}\) = \(\sqrt{4y-8}\)
Answer:
Question 29.
\(\sqrt{3g+1}\) = \(\sqrt{7g-19}\)
Answer:

Question 30.
\(\sqrt{8h-7}\) = \(\sqrt{6h+7}\)
Answer:
Question 31.
\(\sqrt{\frac{p}{2}-2}\) = \(\sqrt{p-8}\)
Answer:

Question 32.
\(\sqrt{2v-5}\) = \(\sqrt{\frac{v}{3}+5}\)
Answer:
Question 33.
\(\sqrt{2c+1}\) = \(\sqrt{4c}\) = 0
Answer:

Question 34.
\(\sqrt{5r}\) – \(\sqrt{8r-2}\) = 0
Answer:
MATHEMATICAL CONNECTIONS In Exercises 35 and 36, find the value of x.
Question 35.
Perimeter = 22 cm
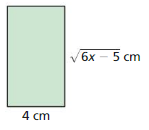
Answer:

Question 36.
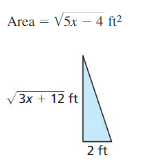
Answer:
In Exercises 37–44, solve the equation. Check your solution.
Question 37.
\(\sqrt [3]{ x }\) = 4
Answer:

Question 38.
\(\sqrt [3]{ y }\) = 2
Answer:
Question 39.
6 = 3\(\sqrt [3]{ 8g }\)
Answer:

Question 40.
\(\sqrt [3]{ r+19 }\) = 3
Answer:
Question 41.
\(\sqrt [3]{ 2x+9 }\) = -3
Answer:

Question 42.
-5 = \(\sqrt [3]{ 10x+15 }\)
Answer:
Question 43.
\(\sqrt [3]{ y+6 }\) = \(\sqrt [3]{ 5y-2 }\)
Answer:
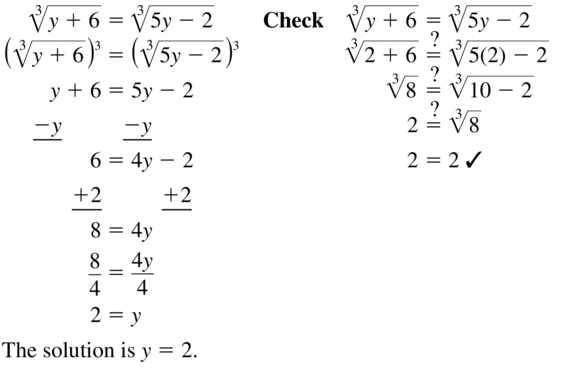
Question 44.
\(\sqrt [3]{ 7j-2 }\) = \(\sqrt [3]{ j+4 }\)
Answer:
In Exercises 45–48, determine which solution, if any, is an extraneous solution.
Question 45.
\(\sqrt{6x-5}\) = x; x = 5, x = 1
Answer:
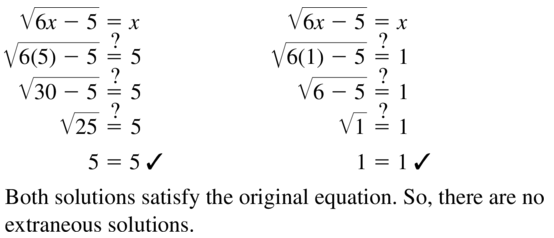
Question 46.
\(\sqrt{2y+3}\) = y; y = -1, y = 3
Answer:
Question 47.
\(\sqrt{12p+16}\) = -2p; p = -1, p = 4
Answer:
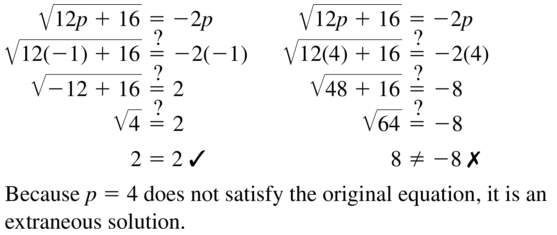
Question 48.
-3g = \(\sqrt{-18-27}\); g = -2, g = -1
Answer:
In Exercises 49–58, solve the equation. Check your solution(s).
Question 49.
y = \(\sqrt{5y-4}\)
Answer:

Question 50.
\(\sqrt{-14x-9x}\) = x
Answer:
Question 51.
\(\sqrt{1-3a}\) = 2a
Answer:
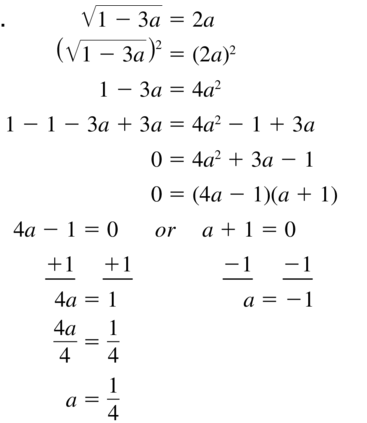

Question 52.
2q = \(\sqrt{10q-6}\)
Answer:
Question 53.
9 + \(\sqrt{5p}\) = 4
Answer:

Question 54.
\(\sqrt{3n}\) – 11 = -5
Answer:
Question 55.
\(\sqrt{2m+2}\) – 3 = 1
Answer:

Question 56.
15 + \(\sqrt{4b-8}\) = 13
Answer:
Question 57.
r + 4 = \(\sqrt{-4r-19}\)
Answer:

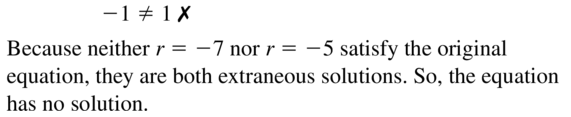
Question 58.
\(\sqrt{3-s}\) = s – 1
Answer:
ERROR ANALYSIS In Exercises 59 and 60, describe and correct the error in solving the equation.
Question 59.
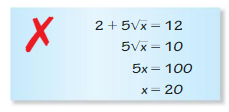
Answer:

Question 60.
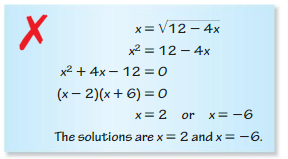
Answer:
Question 61.
REASONING
Explain how to use mental math to solve \(\sqrt{2x}\) + 5 = 1.
Answer:

Question 62.
WRITING
Explain how you would solve \(\sqrt [4]{ m+4 }\) – \(\sqrt [4]{ 3m }\) = 0.
Answer:
Question 63.
MODELING WITH MATHEMATICS
The formula V = \(\sqrt{PR}\) relates the voltage V (in volts), power P (in watts), and resistance R (in ohms) of an electrical circuit. The hair dryer shown is on a 120-volt circuit. Is the resistance of the hair dryer half as much as the resistance of the same hair dryer on a 240-volt circuit? Explain your reasoning.

Answer:

Question 64.
MODELING WITH MATHEMATICS
The time t (in seconds) it takes a trapeze artist to swing back and forth is represented by the function t = 2π \(\sqrt{\frac{r}{32}}\), where r is the rope length (in feet). It takes the trapeze artist 6 seconds to swing back and forth. Is this rope \(\frac{3}{2}\) as long as the rope used when it takes the trapeze artist 4 seconds to swing back and forth? Explain your reasoning.

Answer:
REASONING In Exercises 65–68, determine whether the statement is true or false. If it is false, explain why.
Question 65.
If \(\sqrt{a}\) = b, then (\(\sqrt{a}\))2 = b2.
Answer:

Question 66.
If \(\sqrt{a}\) = \(\sqrt{b}\), then a = b.
Answer:
Question 67.
If a2 = b2, then a = b.
Answer:

Question 68.
If a2 = \(\sqrt{b}\), then a4 = (\(\sqrt{b}\))2
Answer:
Question 69.
COMPARING METHODS
Consider the equation x + 2 = \(\sqrt{2x-3}\).
a. Solve the equation by graphing. Describe the process.
b. Solve the equation algebraically. Describe the process.
c. Which method do you prefer? Explain your reasoning.
Answer:
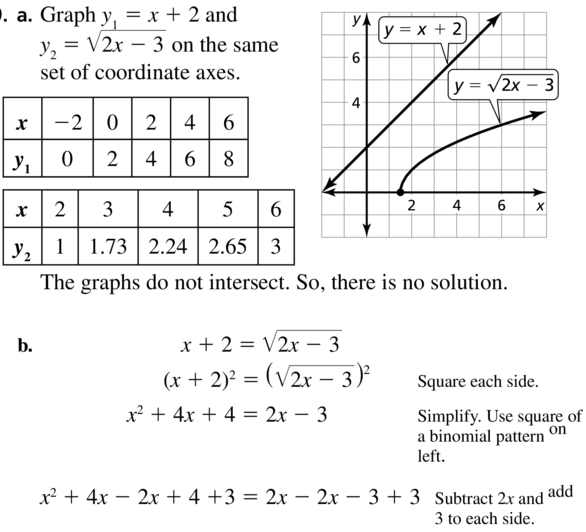

Question 70.
HOW DO YOU SEE IT?
The graph shows two radical functions.
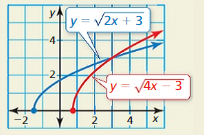
a. Write an equation whose solution is the x-coordinate of the point of intersection of the graphs.
b. Use the graph to solve the equation.
Answer:
Question 71.
MATHEMATICAL CONNECTIONS
The slant height s of a cone with a radius of r and a height of h is given by s = \(\sqrt{r^{2}+h^{2}}\). The slant heights of the two cones are equal. Find the radius of each cone.
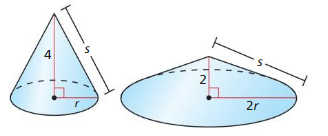
Answer:

Question 72.
CRITICAL THINKING
How is squaring \(\sqrt{x+2}\) different from squaring \(\sqrt{x}\) + 2?
Answer:
USING STRUCTURE In Exercises 73–78, solve the equation. Check your solution.
Question 73.
\(\sqrt{m+15}\) = \(\sqrt{m}\) + \(\sqrt{5}\)
Answer:
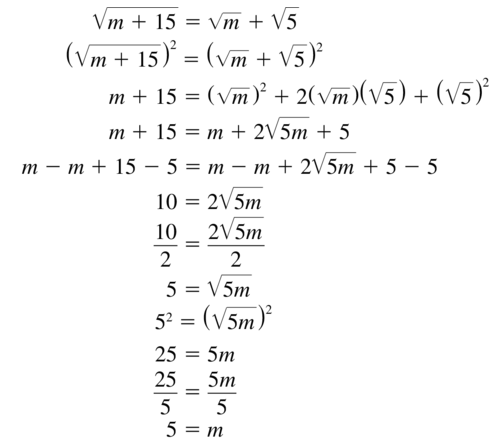
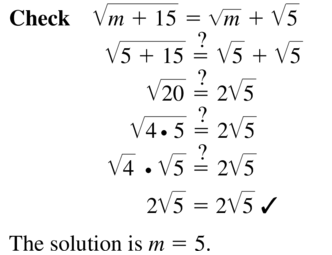
Question 74.
2 = \(\sqrt{x+1}\) = \(\sqrt{x+2}\)
Answer:
Question 75.
\(\sqrt{5y+9}\) + \(\sqrt{5y}\) = 9
Answer:
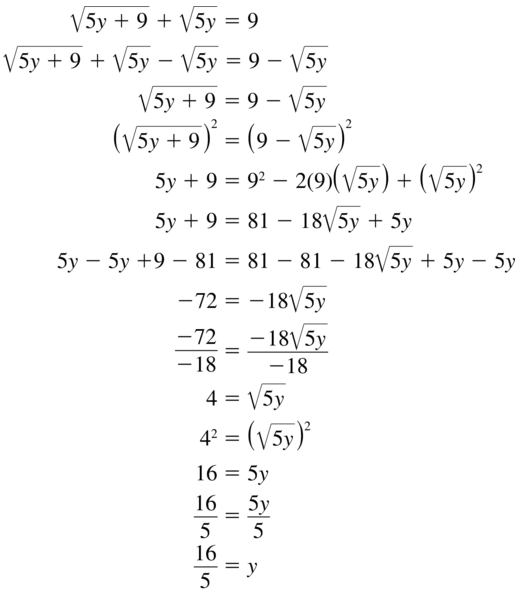
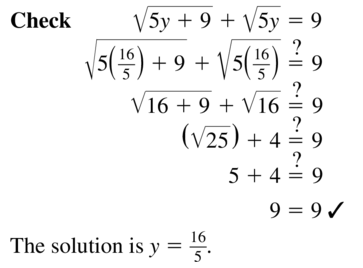
Question 76.
\(\sqrt{2c-8}\) – \(\sqrt{2c}\) – 4 = 0
Answer:
Question 77.
2\(\sqrt{1+4h}\) – 4\(\sqrt{h}\) – 2 = 0
Answer:
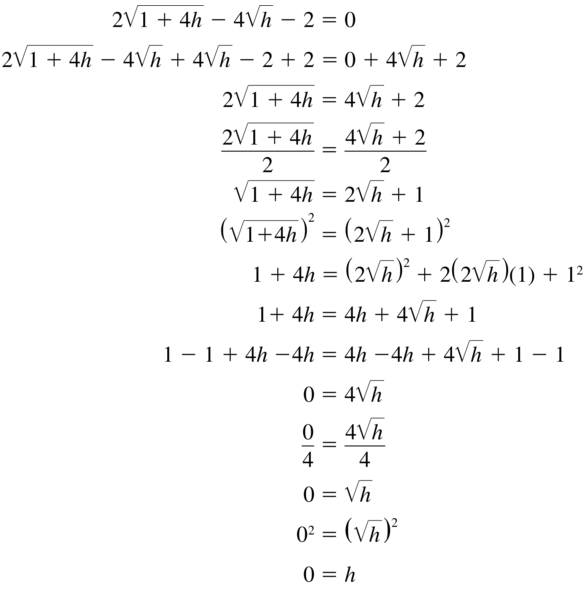

Question 78.
\(\sqrt{20-4z}\) + 2\(\sqrt{-z}\) = 10
Answer:
Question 79.
OPEN-ENDED
Write a radical equation that has a solution of x = 5.
Answer:
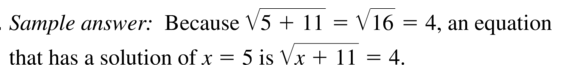
Question 80.
OPEN-ENDED
Write a radical equation that has x = 3 and x = 4 as solutions.
Answer:
Question 81.
MAKING AN ARGUMENT
Your friend says the equation \(\sqrt{(2 x+5)^{2}}\) = 2x + 5 is always true, because after simplifying the left side of the equation, the result is an equation with infinitely many solutions. Is your friend correct? Explain.
Answer:

Question 82.
THOUGHT PROVOKING
Solve the equation \(\sqrt [3]{ x+1 }\) = \(\sqrt{x-3}\). Show your work and explain your steps.
Answer:
Question 83.
MODELING WITH MATHEMATICS
The frequency f (in cycles per second) of a string of an electric guitar is given by the equation f = \(\frac{1}{2 \ell} \sqrt{\frac{T}{m}}\), where ℓ is the length of the string (in meters), T is the string’s tension (in newtons), and m is the string’s mass per unit length (in kilograms per meter). The high E string of an electric guitar is 0.64 meter long with a mass per unit length of 0.000401 kilogram per meter.

a. How much tension is required to produce a frequency of about 330 cycles per second?
b. Would you need more or less tension to create the same frequency on a string with greater mass per unit length? Explain.
Answer:

Maintaining Mathematical Proficiency
Find the product.(Section 7.2)
Question 84.
(x + 8)(x – 2)
Answer:
Question 85.
(3p – 1)(4p + 5)
Answer:
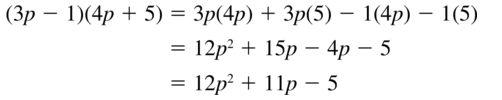
Question 86.
(s + 2)(s2 + 3s – 4)
Answer:
Graph the function. Compare the graph to the graph of f(x) = x2.(Section 8.1)
Question 87.
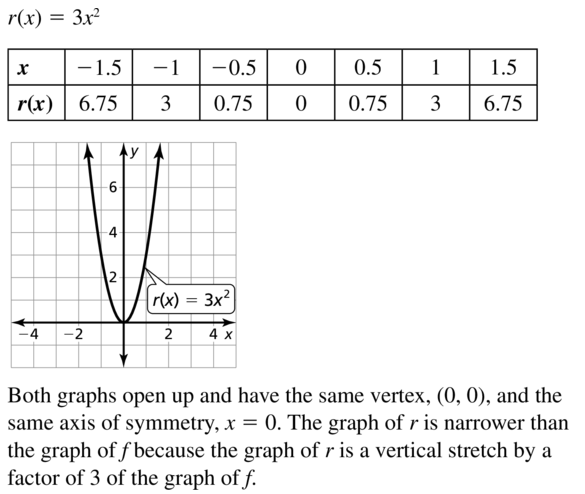
r(x) = 3x2
Answer:
Question 88.
g(x) = \(\frac{3}{4}\)x2
Answer:
Question 89.
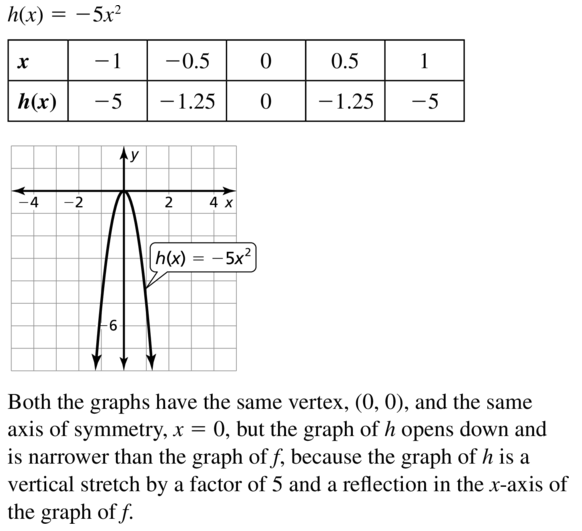
h(x) = -5x2
Answer:
Lesson 10.4 Inverse of a Function
Essential Question How are a function and its inverse related?
EXPLORATION 1
Exploring Inverse Functions
Work with a partner. The functions f and g are inverses of each other. Compare the tables of values of the two functions. How are the functions related?
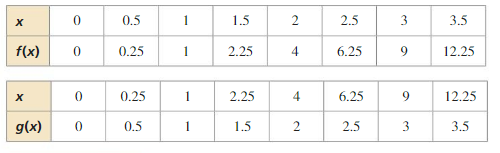
EXPLORATION 2
Exploring Inverse Functions
Work with a partner.
a. Plot the two sets of points represented by the tables in Exploration 1. Use the coordinate plane below.
b. Connect each set of points with a smooth curve.
c. Describe the relationship between the two graphs.
d. Write an equation for each function.
Communicate Your Answer
Question 3.
How are a function and its inverse related?
Answer:
Question 4.
A table of values for a function f is given. Create a table of values for a function g, the inverse of f.

Answer:
Question 5.
Sketch the graphs of f(x) = x + 4 and its inverse in the same coordinate plane. Then write an equation of the inverse of f. Explain your reasoning.

Answer:
Monitoring Progress
Find the inverse of the relation.
Question 1.
(-3, -4), (-2, 0), (-1, 4), (0, 8), (1, 12), (2, 16), (3, 20)
Answer:
Question 2.
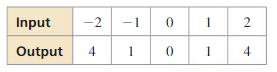
Answer:
Solve y = f(x) for x. Then find the input when the output is 4.
Question 3.
f(x) = x – 6
Answer:
Question 4.
f(x) = \(\frac{1}{2}\)x + 3
Answer:
Question 5.
f(x) = 4x2
Answer:
Find the inverse of the function. Then graph the function and its inverse.
Question 6.
f(x) = 6x
Answer:
Question 7.
f(x) = -x + 5
Answer:
Question 8.
f(x) = \(\frac{1}{4}\)x – 1
Answer:
Find the inverse of the function. Then graph the function and its inverse.
Question 9.
f(x) = -x2, x ≤ 0
Answer:
Question 10.
f(x) = 4x2 + 3, x ≥ 0
Answer:
Question 11.
Is the inverse of f(x) = \(\sqrt{2x-1}\) a function? Find the inverse.
Answer:
Inverse of a Function 10.4 Exercises
Vocabulary and Core ConceptCheck
Question 1.
COMPLETE THE SENTENCE
A relation contains the point (-3, 10). The ____________ contains the point (10, -3).
Answer:
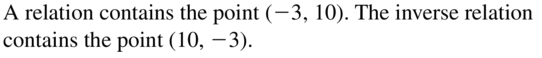
Question 2.
DIFFERENT WORDS, SAME QUESTION
Consider the function f represented by the graph. Which is different? Find “both” answers.

Answer:
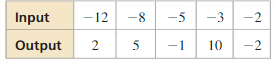
In Exercises 3–8, find the inverse of the relation.
Question 3.
(1, 0), (3, -8), (4, -3), (7, -5), (9, -1)
Answer:
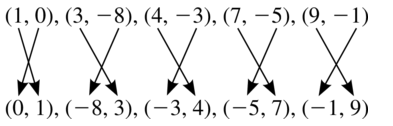
Question 4.
(2, 1), (4, -3), (6, 7), (8, 1), (10, -4)
Answer:
Question 5.
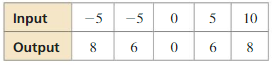
Answer:
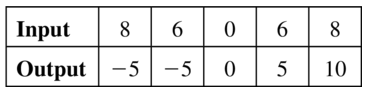
Question 6.
Answer:
Question 7.
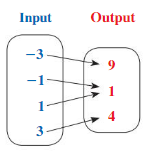
Answer:
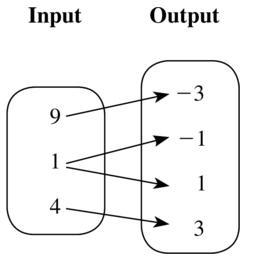
Question 8.
Answer:
In Exercises 9–14, solve y = f(x) for x. Then find the input when the output is 2.
Question 9.
f(x) = x + 5
Answer:

Question 10.
f(x) = 2x – 3
Answer:
Question 11.
f(x) = \(\frac{1}{4}\)x – 1
Answer:
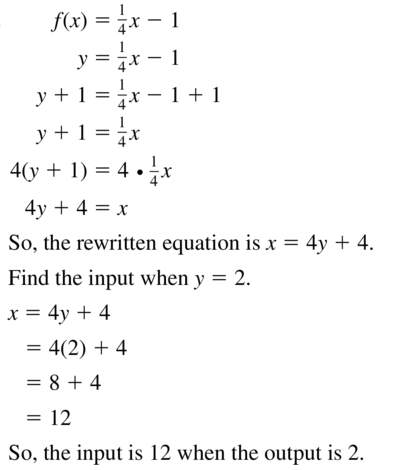
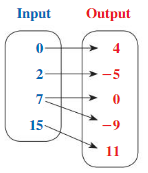
Question 12.
f(x) = \(\frac{2}{3}\)x + 4
Answer:
Question 13.
f(x) = 9x2
Answer:

Question 14.
f(x) = \(\frac{1}{2}\)x2 – 7
Answer:
In Exercises 15 and 16, graph the inverse of the function by reflecting the graph in the line y = x. Describe the domain and range of the inverse.
Question 15.
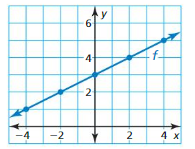
Answer:

Question 16.
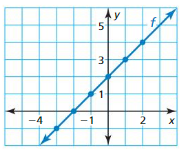
Answer:
In Exercises 17–22, find the inverse of the function. Then graph the function and its inverse.
Question 17.
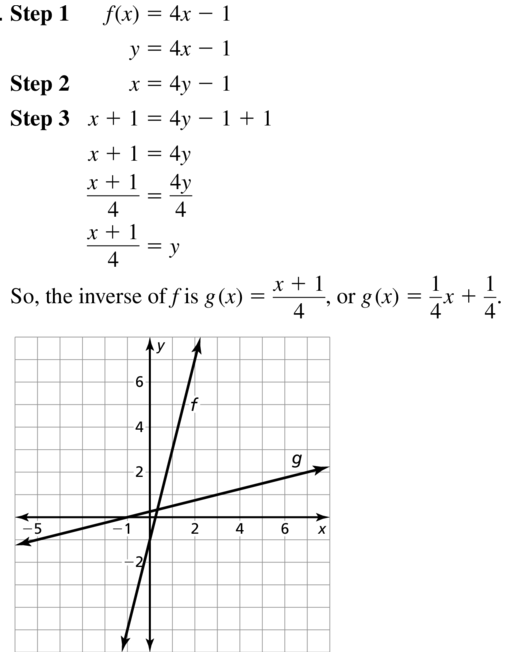
f(x) = 4x – 1
Answer:
Question 18.
f(x) = -2x + 5
Answer:
Question 19.
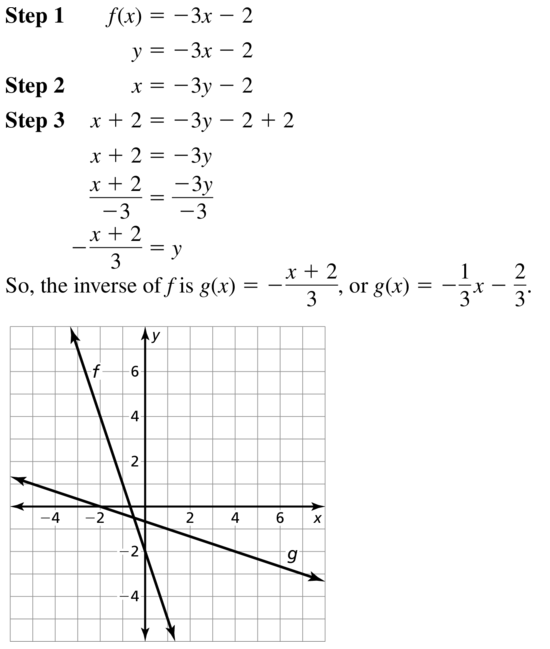
f(x) = -3x – 2
Answer:
Question 20.
f(x) = 2x + 3
Answer:
Question 21.
f(x) =\(\frac{1}{3}\)x + 8
Answer:
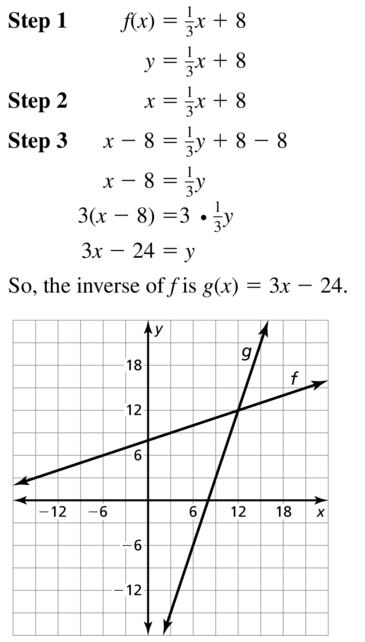
Question 22.
f(x) = – \(\frac{3}{2}\)x + \(\frac{7}{2}\)
Answer:
In Exercises 23–28, find the inverse of the function. Then graph the function and its inverse.
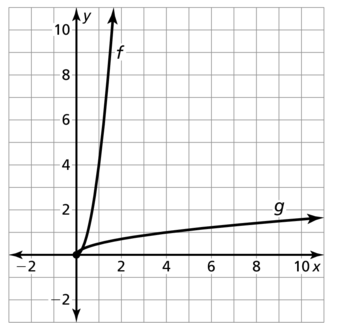
Question 23.
f(x) = 4x2, x ≥ 0
Answer:

Question 24.
f(x) = \(\frac{2}{25}\)x2, x ≤ 0
Answer:
Question 25.
f(x) = -x2 + 10, x ≤ 0
Answer:

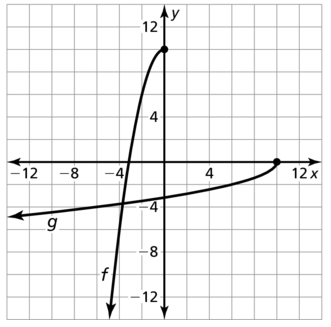
Question 26.
f(x) = 2x2 + 6, x ≥ 0
Answer:
Question 27.
f(x) = \(\frac{1}{9}\)x2 + 2, x ≥ 0
Answer:

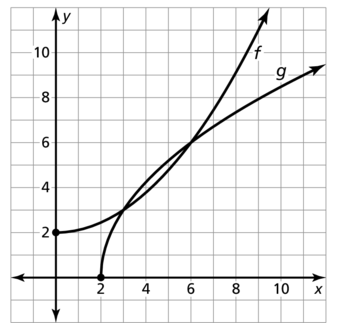
Question 28.
f(x) = -4x2 – 8, x ≤ 0
Answer:
In Exercises 29–32, use the Horizontal Line Test to determine whether the inverse of f is a function.
Question 29.
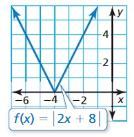
Answer:
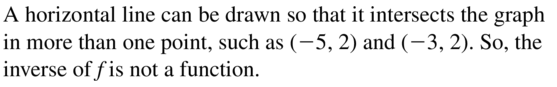
Question 30.
Answer:
Question 31.
Answer:

Question 32.
Answer:
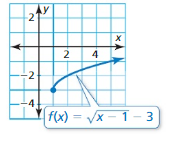
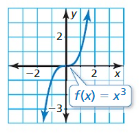
In Exercises 33–42, determine whether the inverse of f is a function. Then find the inverse.
Question 33.
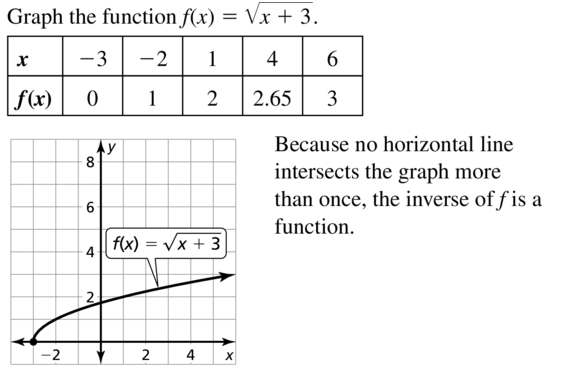
f(x) = \(\sqrt{x+3}\)
Answer:

Question 34.
f(x) = \(\sqrt{x-5}\)
Answer:
Question 35.
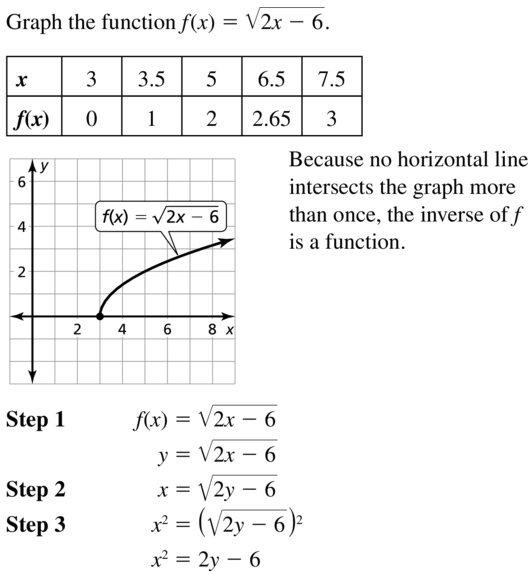
f(x) = \(\sqrt{2x-6}\)
Answer:

Question 36.
f(x) = \(\sqrt{4x+1}\)
Answer:
Question 37.
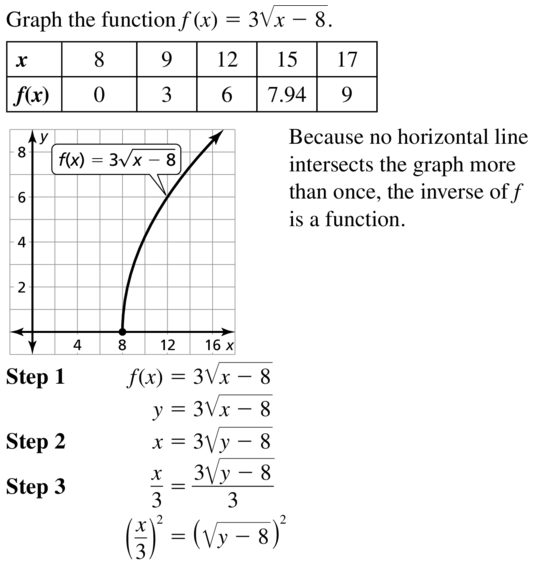
f(x) = 3\(\sqrt{x-8}\)
Answer:

Question 38.
f(x) = –\(\frac{1}{4} \sqrt{5 x+2}\)
Answer:
Question 39.
f(x) = –\(\sqrt{3x+5}\) – 2
Answer:
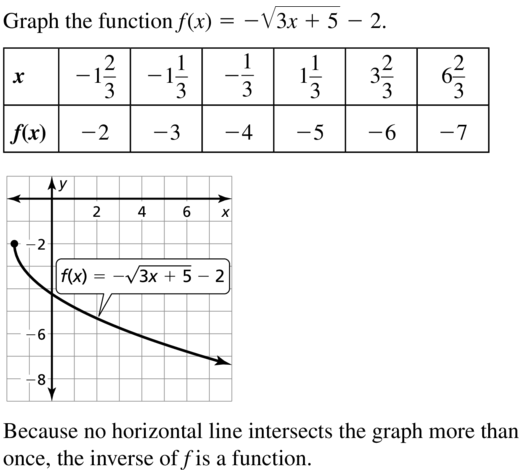
Question 40.
f(x) = 2\(\sqrt{x-7}\) + 6
Answer:
Question 41.
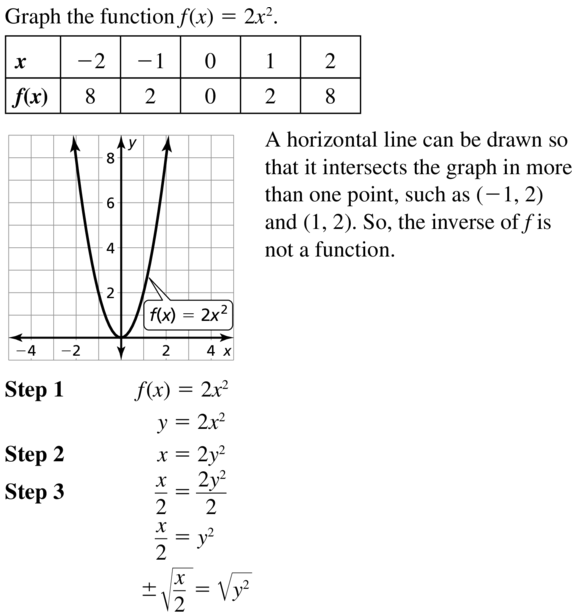
f(x) = 2x2
Answer:
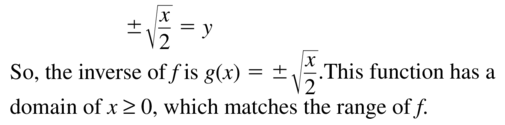
Question 42.
f(x) = |x|
Answer:
Question 43.
ERROR ANALYSIS
Describe and correct the error in finding the inverse of the function f(x) = – 3x + 5.
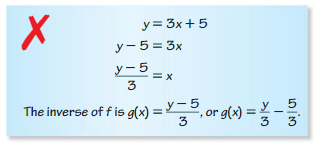
Answer:
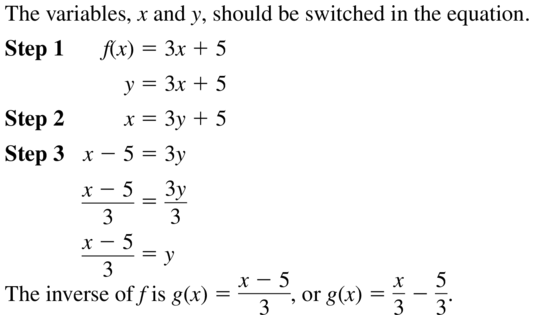
Question 44.
ERROR ANALYSIS
Describe and correct the error in finding and graphing the inverse of the function f(x) = \(\sqrt{x-3}\).
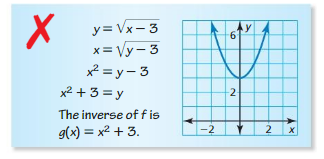
Answer:
Question 45.
MODELING WITH MATHEMATICS
The euro is the unit of currency for the European Union. On a certain day, the number E of euros that could be obtained for D U.S. dollars was represented by the formula shown.
E = 0.74683D
Solve the formula for D. Then find the number of U.S. dollars that could be obtained for 250 euros on that day.
Answer:

Question 46.
MODELING WITH MATHEMATICS
A crow is flying at a height of 50 feet when it drops a walnut to break it open. The height h (in feet) of the walnut above ground can be modeled by h = -16t2 + 50, where t is the time (in seconds) since the crow dropped the walnut. Solve the equation for t. After how many seconds will the walnut be 15 feet above the ground?

Answer:
MATHEMATICAL CONNECTIONS In Exercises 47 and 48, s is the side length of an equilateral triangle. Solve the formula for s. Then evaluate the new formula for the given value.
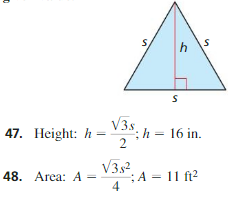
Answer:
47.
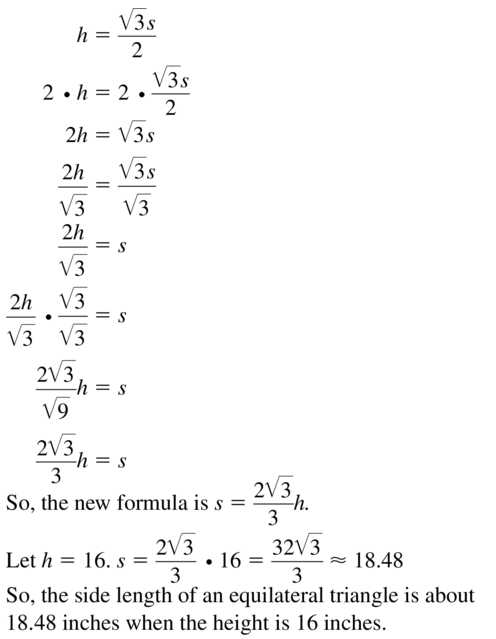
In Exercises 49–54, find the inverse of the function. Then graph the function and its inverse.
Question 49.
f(x) = 2x3
Answer:

Question 50.
f(x) = x3 – 4
Answer:
Question 51.
f(x) = (x – 5)3
Answer:

Question 52.
f(x) = 8(x + 2)3
Answer:
Question 53.
f(x) = 4\(\sqrt [3]{ x }\)
Answer:

Question 54.
f(x) = –\(\sqrt [3]{ x-1 }\)
Answer:
Question 55.
MAKING AN ARGUMENT
Your friend says that the inverse of the function f(x) = 3 is a function because all linear functions pass the Horizontal Line Test. Is your friend correct? Explain.
Answer:

Question 56.
HOW DO YOU SEE IT?
Pair the graph of each function with the graph of its inverse.
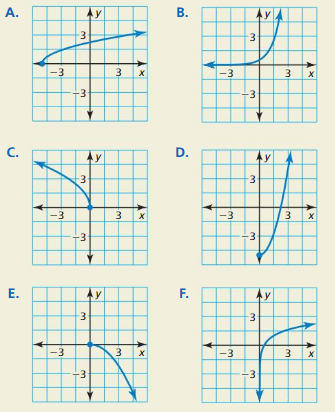
Answer:
Question 57.
WRITING
Describe changes you could make to the function f(x) = x2 – 5 so that its inverse is a function. Describe the domain and range of the new function and its inverse.
Answer:

Question 58.
CRITICAL THINKING
Can an even function with at least two values in its domain have an inverse that is a function? Explain.
Answer:
Question 59.
OPEN-ENDED
Write a function such that the graph of its inverse is a line with a slope of 4.
Answer:

Question 60.
CRITICAL THINKING
Consider the function g(x) = -x.
a. Graph g(x) = -x and explain why it is its own inverse.
b. Graph other linear functions that are their own inverses. Write equations of the lines you graph.
c. Use your results from part (b) to write a general equation that describes the family of linear functions that are their own inverses.
Answer:
Question 61.
REASONING
Show that the inverse of any linear function f(x) = mx + b, where m ≠ 0, is also a linear function. Write the slope and y-intercept of the graph of the inverse in terms of m and b.
Answer:

Question 62.
THOUGHT PROVOKING
The graphs of f(x) = x3 – 3x and its inverse are shown. Find the greatest interval -a ≤ x ≤ a for which the inverse of f is a function. Write an equation of the inverse function.
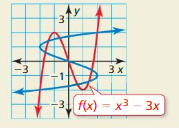
Answer:
Question 63.
REASONING
Is the inverse of f(x) = 2|x + 1|a function? Are there any values of a, h, and k for which the inverse of f(x) = a |x – h| + k is a function? Explain your reasoning.
Answer:

Maintaining Mathematical Proficiency
Find the sum or difference.(Section 7.1)
Question 64.
(2x – 9) – (6x + 5)
Answer:
Question 65.
(8y + 1) + (-y – 12)
Answer:
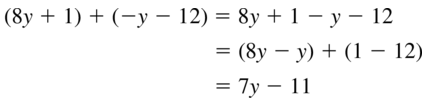
Question 66.
(t2 – 4t – 4) + (7t2 + 12t + 3)
Answer:
Question 67.
(-3d2 + 10d – 8) – (7d2 – d – 6)
Answer:
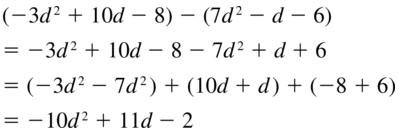
Graph the function. Compare the graph to the graph of f(x) = x2. (Section 8.2)
Question 68.
g(x) = x2 + 6
Answer:
Question 69.
h(x) = -x2 – 2
Answer:
Question 70.
p(x) = -4x2 + 5
Answer:
Question 71.
q(x) = \(\frac{1}{3}\)x2 – 1
Answer:
Radical Functions and Equations Performance Task: Medication and the Mosteller Formula
10.3–10.4What Did YouLearn?
Core Vocabulary
radical equation, p. 560
inverse relation, p. 568
inverse function, p. 569
Core Concepts
Lesson 10.3
Squaring Each Side of an Equation, p. 560
Identifying Extraneous Solutions, p. 562
Lesson 10.4
Inverse Relation, p. 568
Finding Inverses of Functions Algebraically, p. 570
Finding Inverses of Nonlinear Functions, p. 570
Horizontal Line Test, p. 571
Mathematical Practices
Question 1.
Could you also solve Exercises 37–44 on page 565 by graphing? Explain.
Answer:
Question 2.
What external resources could you use to check the reasonableness of your answer in Exercise 45 on page 573?
Answer:
Performance Task: Medication and the Mosteller Formula
When taking medication, it is critical to take the correct dosage. For children in particular, body surface area (BSA) is a key component in calculating that dosage. The Mosteller Formula is commonly used to approximate body surface area. How will you use this formula to calculate BSA for the optimum dosage?
To explore the answers to this question and more, go to

Radical Functions and Equations Chapter Review
10.1 Graphing Square Root Functions (pp. 543–550)
Graph the function. Describe the domain and range. Compare the graph to the graph of f(x) = \(\sqrt{x}\).
Question 1.
g(x) = \(\sqrt{x}\) + 7
Answer:
Question 2.
h(x) = \(\sqrt{x-6}\)
Answer:
Question 3.
r(x) = –\(\sqrt{x+3}\) – 1
Answer:
Question 4.
Let g(x) = \(\frac{1}{4} \sqrt{x-6}\) + 2. Describe the transformations from the graph of f(x) = \(\sqrt{x}\) to the graph of g. Then graph g.
Answer:
10.2 Graphing Cube Root Functions (pp. 551–556)
Graph the function. Compare the graph to the graph of f(x) = \(\sqrt [3]{ x }\).
Question 5.
g(x) = \(\sqrt [3]{ x }\) + 4
Answer:
Question 6.
h(x) = -8\(\sqrt [3]{ x }\)
Answer:
Question 7.
s(x) = \(\sqrt[3]{-2(x-3)}\)
Answer:
Question 8.
Let g(x) = -3\(\sqrt [3]{ x+2 }\) – 1. Describe the transformations from the graph of f(x) = \(\sqrt [3]{ x }\) to the graph of g. Then graph g.
Answer:
Question 9.
The graph of cube root function r is shown. Compare the average rate of change of r to the average rate of change of p(x) = \(\sqrt[3]{\frac{1}{2} x}\) over the interval x = 0 to x = 8.
Answer:
10.3 Solving Radical Equations (pp. 559-566)
Solve the equation. Check your solution(s).
Question 10.
8 + \(\sqrt{x}\) = 18
Answer:
Question 11.
\(\sqrt [3]{ x-1 }\) = 3
Answer:
Question 12.
\(\sqrt{5x-9}\) = \(\sqrt{4x}\)
Answer:
Question 13.
x = \(\sqrt{3x+4}\)
Answer:
Question 14.
8\(\sqrt{x-5}\) + 34 = 58
Answer:
Question 15.
\(\sqrt{5x}\) + 6 = 5
Answer:
Question 16.
The radius r of a cylinder is represented by the function r = \(\sqrt{\frac{V}{\pi h}}\), where V is the volume and h is the height of the cylinder. What is the volume of the cylindrical can?

Answer:
10.4 Inverse of a Function (pp. 567–574)
Find the inverse of the relation.
Question 17.
(1, -10), (3, -4), (5, 4), (7, 14), (9, 26)
Answer:
Question 18.
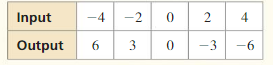
Answer:
Find the inverse of the function. Then graph the function and its inverse.
Question 19.
f(x) = -5x + 10
Answer:
Question 20.
f(x) = 3x2 – 1, x ≥ 0
Answer:
Question 21.
f(x) = \(\frac{1}{2} \sqrt{2 x+6}\)
Answer:
Question 22.
Consider the function f(x) = x2 + 4. Use the Horizontal Line Test to determine whether the inverse of f is a function.
Answer:
Question 23.
In bowling, a handicap is an adjustment to a bowler’s score to even out differences in ability levels. In a particular league, you can find a bowler’s handicap h by using the formula h = 0.8(210 – a), where a is the bowler’s average. Solve the formula for a. Then find a bowler’s average when the bowler’s handicap is 28.

Answer:
Radical Functions and Equations Chapter Test
Find the inverse of the function.
Question 1.
f(x) = 5x – 8 2.
Answer:
Question 2.
f(x) = 2\(\sqrt{x+3}\) – 1
Answer:
Question 3.
f(x) = –\(\frac{1}{3}\)x2 + 4, x ≥ 0
Answer:
Graph the function f. Describe the domain and range. Compare the graph of f to the graph of g.
Question 4.
f(x) = –\(\sqrt{x+6}\); g(x) = \(\sqrt{x}\)
Answer:
Question 5.
f(x) = \(\sqrt{x-3}\) + 2; g(x) = \(\sqrt{x}\)
Answer:
Question 6.
f(x) = \(\sqrt [3]{ x }\) – 5; g(x) = \(\sqrt [3]{ x }\)
Answer:
Question 7.
f(x) = -2\(\sqrt [3]{ x+1 }\); g(x) = \(\sqrt [3]{ x }\)
Answer:
Solve the equation. Check your solution(s).
Question 8.
9 – \(\sqrt{x}\) = 3
Answer:
Question 9.
\(\sqrt{2x-7}\) – 3 = 6
Answer:
Question 10.
\(\sqrt{8x-21}\) = \(\sqrt{18-5x}\)
Answer:
Question 11.
x + 5 = \(\sqrt{7x+53}\)
Answer:
Question 12.
When solving the equation x – 5 = \(\sqrt{ax+b}\), you obtain x = 2 and x = 8. Explain why at least one of these solutions must be extraneous.
Answer:
Describe the transformations from the graph of f(x) = \(\sqrt [3]{ x }\) to the graph of the given function. Then graph the given function.
Question 13.
h(x) = 4\(\sqrt [3]{ x-1 }\) + 5
Answer:
Question 14.
w(x) = –\(\sqrt [3]{ x+7 }\) – 2
Answer:
Question 15.
The velocity v (in meters per second) of a roller coaster at the bottom of a hill is given by v = \(\sqrt{19.6h}\), where h is the height (in meters) of the hill. (a) Use a graphing calculator to graph the function. Describe the domain and range. (b) How tall must the hill be for the velocity of the roller coaster at the bottom of the hill to be at least 28 meters per second? (c) What happens to the average rate of change of the velocity as the height of the hill increases?
Answer:
Question 16.
The speed s (in meters per second) of sound through air is given by s = 2\(\sqrt{T+273}\), where T is the temperature (in degrees Celsius).
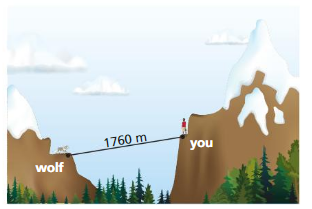
a. What is the temperature when the speed of sound through air is 340 meters per second?
b. How long does it take you to hear the wolf howl when the temperature is -17°C?
Answer:
Question 17.
How can you restrict the domain of the function f(x) = (x – 3)2 so that the inverse of f is a function?
Answer:
Question 18.
Write a radical function that has a domain of all real numbers less than or equal to 0 and a range of all real numbers greater than or equal to 9.
Answer:
Radical Functions and Equations Cumulative Assessment
Question 1.
Fill in the function so that it is represented by the graph.
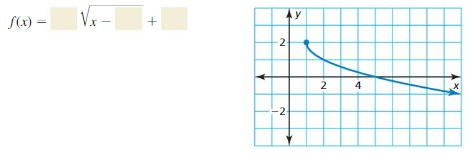
Answer:
Question 2.
Consider the equation y = mx + b. Fill in values for m and b so that each statement is true.
a. When m = ______ and b = ______, the graph of the equation passes through the point (-1, 4).
b. When m = ______ and b = ______, the graph of the equation has a positive slope and passes through the point (-2, -5).
c. When m = ______ and b = ______, the graph of the equation is perpendicular to the graph of y = 4x – 3 and passes through the point (1, 6).
Answer:
Question 3.
Which graph represents the inverse of the function f(x) = 2x + 4?
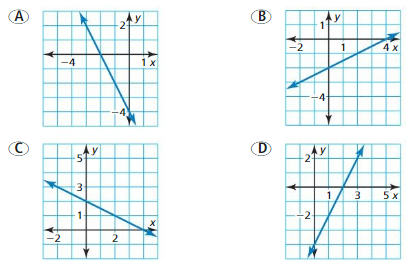
Answer:
Question 4.
Consider the equation x = \(\sqrt{ax+b}\). Student A claims this equation has one real solution. Student B claims this equation has two real solutions. Use the numbers to answer parts (a)–(c).

a. Choose values for a and b to create an equation that supports Student A’s claim.
b. Choose values for a and b to create an equation that supports Student B’s claim.
c. Choose values for a and b to create an equation that does not support either student’s claim.
Answer:
Question 5.
Which equation represents the nth term of the sequence 3, 12, 48, 192, . . .?
A. an = 3(4)n-1
B. an = 3(9)n-1
C. an = 9n – 6
D. an = 9n + 3
Answer:
Question 6.
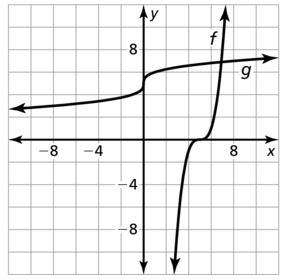
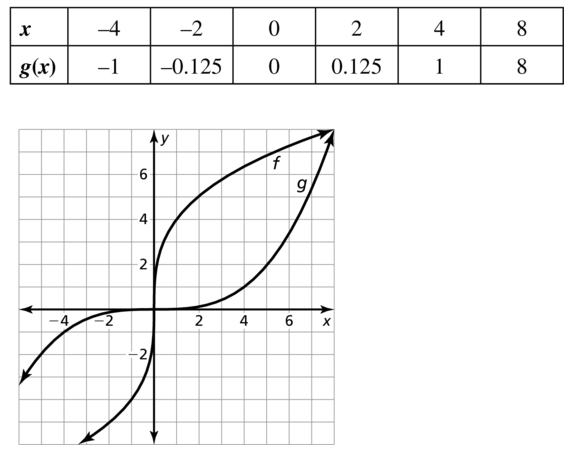
Consider the function f(x) = \(\frac{1}{2} \sqrt[3]{x+3}\). The graph represents function g. Select all the statements that are true.

Answer:
Question 7.
Place each function into one of the three categories.

Answer:
Question 8.
You are making a tabletop with a tiled center and a uniform mosaic border.
a. Write the polynomial in standard form that represents the perimeter of the tabletop.
b. Write the polynomial in standard form that represents the area of the tabletop.
c. The perimeter of the tabletop is less than 80 inches, and the area of tabletop is at least 252 square inches. Select all the possible values of x.

Answer:
