Here, on this page, we have shared the ultimate preparation guide for high school students on algebra 2 math concepts. The given material is Big Ideas Math Algebra 2 Answers Chapter 7 Rational Functions. You can access and download BIM Algebra 2 Ch 7 Answer key for free of cost. So, it helps you to practice efficiently and gain more subject knowledge. Get the exercise wise chapter 7 rational functions Big Ideas Math Algebra 2 Answers from the below pdf links and start your preparation by solving the questions from various given sources covered in the BIM Algebra 2 Chapter 7 Solution Key.
Big Ideas Math Book Algebra 2 Answer Key Chapter 7 Rational Functions
In the Big Ideas Math textbook solutions algebra 2 ch 7, you can find basic & strong fundamentals of Rational functons like inverse variation, graphing rational functions, adding, subtracting, mutliplying, and dividing rational expressions, and solving rational equations. By referring, practicing, and solving all the questions presented in the BigIdeas Math Book Algegra 2 Chapter 7 Answer Key, you can quickly learn the concepts and score highest rank in the exams. For students who are passionate about math skills should solve the problems in Topic-wise BIM Algebra 2 Rational functions solution key.
- Rational Functions Maintaining Mathematical Proficiency – Page 357
- Rational Functions Mathematical Practices – Page 358
- Lesson 7.1 Inverse Variation – Page(359-364)
- Inverse Variation 7.1 Exercises – Page(363-364)
- Lesson 7.2 Graphing Rational Functions – Page(365-372)
- Graphing Rational Functions 7.2 Exercises – Page(370-372)
- Rational Functions Study Skills: Analyzing Your Errors – Page 373
- Rational Functions 7.1–7.2 Quiz – Page 374
- Lesson 7.3 Multiplying and Dividing Rational Expressions – Page(375-382)
- Multiplying and Dividing Rational Expressions 7.3 Exercises – Page(380-382)
- Lesson 7.4 Adding and Subtracting Rational Expressions – Page(383-390)
- Adding and Subtracting Rational Expressions 7.4 Exercises – Page(388-390)
- Lesson 7.5 Solving Rational Equations – Page(391-398)
- Solving Rational Equations 7.5 Exercises – Page(396-398)
- Rational Functions Performance Task: Circuit Design – Page 399
- Rational Functions Chapter Review – Page(400-402)
- Rational Functions Chapter Test – Page 403
- Rational Functions Cumulative Assessment – Page(404-405)
Rational Functions Maintaining Mathematical Proficiency
Evaluate.
Question 1.
\(\frac{3}{5}+\frac{2}{3}\)
Answer:
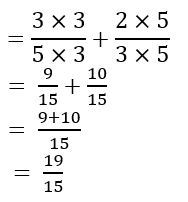
Question 2.
–\(\frac{4}{7}+\frac{1}{6}\)
Answer:
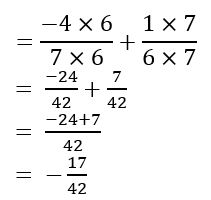
Question 3.
\(\frac{7}{9}-\frac{4}{9}\)
Answer:
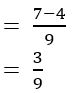
Question 4.
\(\frac{5}{12}-\left(-\frac{1}{2}\right)\)
Answer:
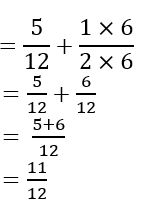
Question 5.
\(\frac{2}{7}+\frac{1}{7}-\frac{6}{7}\)
Answer:
![]()
Question 6.
\(\frac{3}{10}-\frac{3}{4}+\frac{2}{5}\)
Answer:
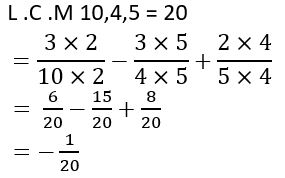
Simplify.
Question 7.
\(\frac{\frac{3}{8}}{\frac{5}{6}}\)
Answer:
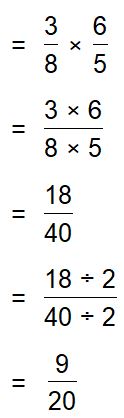
Question 8.
\(\frac{\frac{1}{4}}{-\frac{5}{7}}\)
Answer:
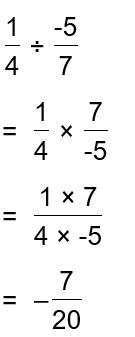
Question 9.
\(\frac{\frac{2}{3}}{\frac{2}{3}+\frac{1}{4}}\)
Answer:

Question 10.
ABSTRACT REASONING
For what value of x is the expression \(\frac{1}{x}\) undefined? Explain your reasoning.
Answer:
When a function is undefined there denominator would be equal to 0.
f(x) = 1/x
f(0) = 1/0 = undefined
Rational Functions Mathematical Practices
Mathematically proficient students are careful about specifying units of measure and clarifying the relationship between quantities in a problem.
Monitoring Progress
Question 1.
You drive a car at a speed of 60 miles per hour. What is the speed in meters per second?
Answer: 60 miles per hour to Meters per second is 26,8224.
Question 2.
A hose carries a pressure of 200 pounds per square inch. What is the pressure in kilograms per square centimeter?
Answer: 200 pounds per square inch to kilograms per square centimeter = 14.06139 kilograms per square centimeter
Question 3.
A concrete truck pours concrete at the rate of 1 cubic yard per minute. What is the rate in cubic feet per hour?
Answer:
A concrete truck pours concrete at the rate of 1 cubic yard per minute.
1 yard = 3 feet
3 cubic feet per minute
1 hour = 60 minute
3 × 60 = 180
So, the rate in cubic feet per hour is 180.
Question 4.
Water in a pipe flows at a rate of 10 gallons per minute. What is the rate in liters per second?
Answer:
Given,
Water in a pipe flows at a rate of 10 gallons per minute.
1 minute = 60 sec
1 sec = 1/60 min
10/60 = 1/6
Thus the rate in liters per second is 1/6.
Lesson 7.1 Inverse Variation
Essential Question How can you recognize when two quantities vary directly or inversely?
EXPLORATION 1
Recognizing Direct VariationWork with a partner. You hang different weights from the same spring.
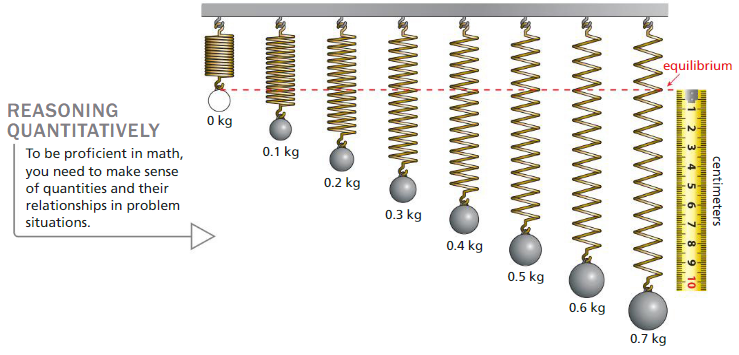
a. Describe the relationship between the weight x and the distance d the spring stretches from equilibrium. Explain why the distance is said to vary directly with the weight.
b. Estimate the values of d from the figure. Then draw a scatter plot of the data. What are the characteristics of the graph?
c. Write an equation that represents d as a function of x.
d. In physics, the relationship between d and x is described by Hooke’s Law. How would you describe Hooke’s Law?
EXPLORATION 2
Recognizing Inverse Variation
Work with a partner. The table shows the length x (in inches) and the width y (in inches) of a rectangle. The area of each rectangle is 64 square inches.

a. Copy and complete the table.
b. Describe the relationship between x and y. Explain why y is said to vary inversely with x.
c. Draw a scatter plot of the data. What are the characteristics of the graph?
d. Write an equation that represents y as a function of x.
Answer:
a. The area of each rectangle is 64 square inches.
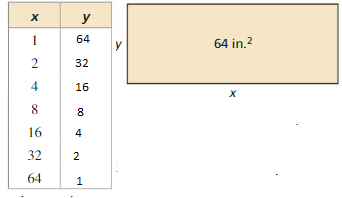
b. With the increase in the value of x the corresponding value of y decreases.
When two variables show this type of change they are termed as inversely proportional to each other.
The inverse variation is represented by equation xy = k
where x and y are non zero variables
k is non zero constant
Therefore we can say that the relationship between x and y is of inverse variation.
c.

The graph of inverse variation is a hyperbola.
The inverse variation hyperbola never pass through origin.
The inverse variation hyperbola do not cross x or y axis.
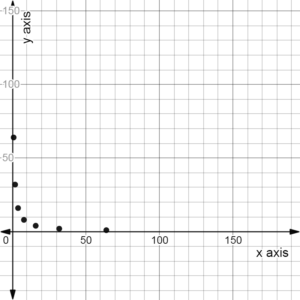
d. Equation that represents y as the function of x is given by y = kx
where k is non-zero constant
x ≠ 0
y ≠ 0
Communicate Your Answer
Question 3.
How can you recognize when two quantities vary directly or inversely?
Answer:
In the direct variation, the variables are said to be directly proportional. When one variables value increases, the other variables value increases as well. A direct variation can be expressed as y = kx assuming k as constant.
In the inverse variation, the variables are said to be inversely proportional. When one variables value increases the value of the other variable decreases. If k is constant, the inverse variation can be written as
xy = k
or
y = k/x
Question 4.
Does the mapping rate of the wings of a bird vary directly or inversely with the length of its wings? Explain your reasoning.
Answer:
As the length of the birds wing increases, the mapping rate of the wing decreases.
Thus it is inversely proportional to the length of its wings.
Monitoring Progress
Tell whether x and y show direct variation, inverse variation, or neither.
Question 1.
6x = y
Answer:
The equation is solved for y=6x
The type of variation is DIRECT
Question 2.
x y = −0.25
Answer:
Given equation x y=-0.25
y=-0.25/x
The type of variation is INVERSE
Question 3.
y + x = 10
Answer:
Given equation y + x=10
y=10-x
The type of variation is NEITHER direct , nor inverse
Tell whether x and y show direct variation, inverse variation, or neither.
Question 4.
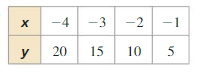
Answer:

Question 5.
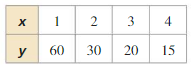
Answer:

The variables x and y vary inversely. Use the given values to write an equation relating x and y. Then find y when x = 2.
Question 6.
x = 4, y = 5
Answer:
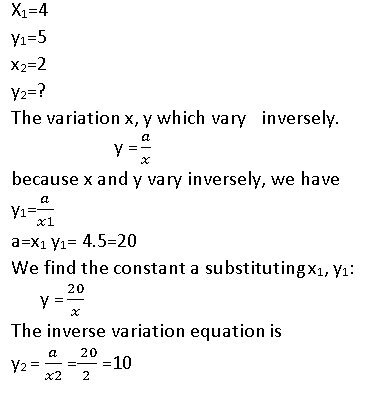
Question 7.
x = 6, y = −1
Answer:

Question 8.
x = \(\frac{1}{2}\), y = 16
Answer:

Question 9.
WHAT IF?
In Example 4, it takes a group of 10 volunteers 12 hours to build the playground. How long would it take a group of 15 volunteers?
Answer:

Inverse Variation 7.1 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Explain how direct variation equations and inverse variation equations are different.
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
(1): From definition of inverse variation we have that y=a/x where in our case a=4.This implies that inverse variation equation is
Y=4/x.
(2): Let now ration be constant a= 4. Then we get
y/x=4 => y =4x.
This implies that x and y show direct variation.
(3): From equation y=a/x and a=4 we have that
Y= 4/x
It implies that x and y show inverse variation.
(4): By equation x y =4 it implies that y=4/x
This equation means that x and y show inverse variation.
The different question is (2): where x and y show direct variation
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, tell whether x and y show direct variation, inverse variation, or neither.
Question 3.
y = \(\frac{2}{x}\)
Answer:
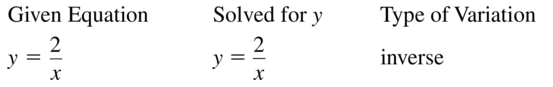
Question 4.
xy = 12
Answer:
Given equation Solved for y Type of variation
xy=12 Y=12/x inverse variation
Question 5.
\(\frac{y}{x}\) = 8
Answer:
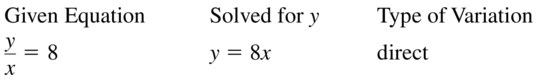
Question 6.
4x = y
Answer:
By definition ,x and y show direct variation
Question 7.
y = x + 4
Answer:
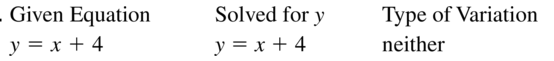
Question 8.
x + y = 6
Answer:
Given Equation Solved for y Types of variation
x+y=6 Add -x to both sides X and y shows no variation
Y= -x+6
Question 9.
8y = x
Answer:
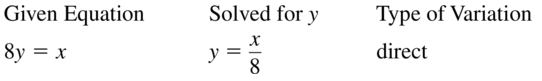
Question 10.
xy = \(\frac{1}{5}\)
Answer:
Solve for y . Divide equation with x
Xy = 1/5
Y=1/5x=( 1/5)/x
inverse variation
In Exercises 11–14, tell whether x and y show direct variation, inverse variation, or neither.
Question 11.
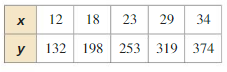
Answer:
y/x 132/12=11 198/18 =11 235/23 =11 319/29 =11 374/34=11
The products are not constant , and the rations are constant .
X and y show direct variation .
Question 12.
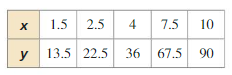
Answer:
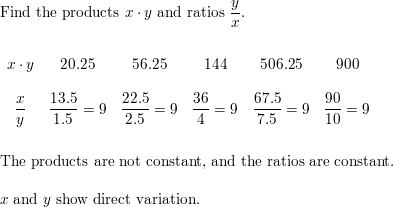
Question 13.
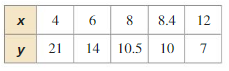
Answer:

Question 14.
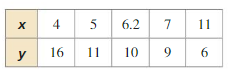
Answer:
| xy | 64 | 55 | 62 | 63 | 66 |
| y/ x | 16/4=4 | 11/5=2.2 | 10/6.2=1.612 | 9/7=1.285 | 6/11=0.545 |
The products are not constant, and the ratios are not constant.
X and y show no variation
In Exercises 15–22, the variables x and y vary inversely. Use the given values to write an equation relating x and y. Then find y when x = 3.
Question 15.
x = 5, y =−4
Answer:
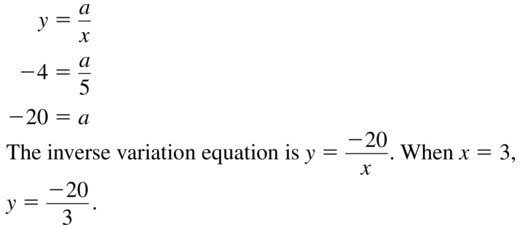
Question 16.
x = 1, y = 9
Answer:
Y=a/x
Plug x=1, y=9 into equation to determine a.
9=a/1
a =9.1=9
The inverse variation equation is y= 9/x
When x=3,
Y=9/3=3
Question 17.
x =−3, y = 8
Answer:
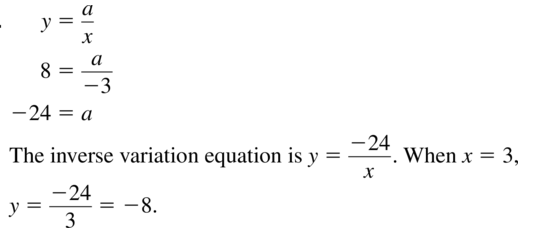
Question 18.
x = 7, y = 2
Answer:
Y=a/x
Plug x=7, y=2 into equation to determine a.
7=a/2
a=7. 2=14
The inverse variation equation is y=14/x
When x=3
Y=14/3
Question 19.
x = \(\frac{3}{4}\), y = 28
Answer:
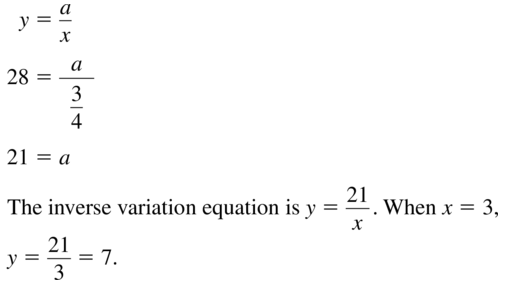
Question 20.
x = −4, y = –\(\frac{5}{4}\)
Answer:
Y=a/x
Plug x= -4 , y=-5/4 into equation to determine a.
-5/4 = a/-4
a =-5/4 . (-4)=5
The inverse variation equation is y=5/x
When x=3
Y=5/3
Question 21.
x = −12, y = −\(\frac{6}{2}\)
Answer:
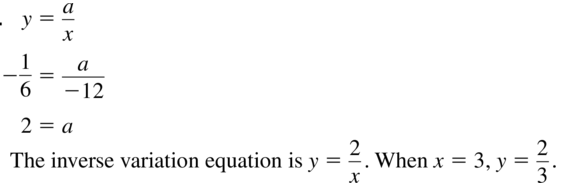
Question 22.
x = \(\frac{5}{3}\), y = −7
Answer:
Y=a/x
Plug x= 5/3 , y=-7 into equation to determine a.
-7 =a/5/3
A=-7 . 5/3 = – 35/3
The inverse variation equation is y=-35/3/x
When x=3
Y=-35/3/3=-35/9
ERROR ANALYSIS In Exercises 23 and 24, the variables x and y vary inversely. Describe and correct the error in writing an equation relating x and y.
Question 23.
x = 8, y = 5

Answer:

Question 24.
x = 5, y = 2
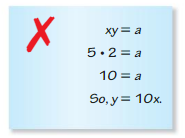
Answer:
Every thing is correct except last row when they plug a = 10 into starting equation . it shoulds be like this
a=10
Xy=a
Xy=10, divide with x
Y=10/x
Question 25.
MODELING WITH MATHEMATICS
The number y of songs that can be stored on an MP3 player varies inversely with the average size x of a song. A certain MP3 player can store 2500 songs when the average size of a song is 4 megabytes (MB).
a. Make a table showing the numbers of songs that will fit on the MP3 player when the average size of a song is 2 MB, 2.5 MB, 3 MB, and 5 MB.
b. What happens to the number of songs as the average song size increases?
Answer:

Question 26.
MODELING WITH MATHEMATICS
When you stand on snow, the average pressure P (in pounds per square inch) that you exert on the snow varies inversely with the total area A (in square inches) of the soles of your footwear. Suppose the pressure is 0.43 pound per square inch when you wear the snowshoes shown. Write an equation that gives P as a function of A. Then find the pressure when you wear the boots shown.

Answer:
The general equation for inverse variation is
Y=a/x
Let y=P where P is the average pressure on snow and x =A is the total area .
If we wear the snowshoes then the P is 0.43 and A=360. Using the equation about we have that
P=a/A
0.43=a/360
A=0.43.360=154.8
It implies that P=154.8/A
Now , if you boots then A=60. Using the equation about we have that
P=a/A
0.43=a/60
A=0.43.60=25.8
It implies that
P=25.8/A
Question 27.
PROBLEM SOLVING
Computer chips are etched onto silicon wafers. The table compares the area A (in square millimeters) of a computer chip with the number c of chips that can be obtained from a siliconwafer. Write a model that gives c as a function of A. Then predict the number of chips per wafer when the area of a chip is 81 square millimeters.
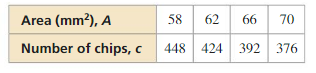
Answer:

Question 28.
HOW DO YOU SEE IT?
Does the graph of f represent inverse variation or direct variation? Explain your reasoning.
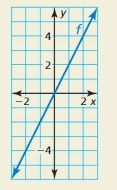
Answer:
As x increases, y increases as well, so product x. y cannot possibly be constant.
This means that x and y show direct variation.
Question 29.
MAKING AN ARGUMENT
You have enough money to buy 5 hats for $10 each or 10 hats for $5 each. Your friend says this situation represents inverse variation. Is your friend correct? Explain your reasoning.
Answer:

Question 30.
THOUGHT PROVOKING
The weight w (in pounds) of an object varies inversely with the square of the distance d (in miles) of the object from the center of Earth. At sea level (3978 miles from the center of theEarth), an astronaut weighs 210 pounds. How much does the astronaut weigh 200 miles above sea level?
Answer:
Write the equation that represents given variation :
W=a/d2 – there is d2 in denominator because w varies inversely with square of the distance .
Plug d=3978 and w=210 into equation to determine a.
210 = a/39782
A=210. 39782 = 3,323,141,640
Equation :
W = 3,323,141,640/d2
When d = 3978+200 = 4178:
W = 3,323,141,640/41782 = 190
Question 31.
OPEN-ENDED
Describe a real-life situation that can be modeled by an inverse variation equation.
Answer:

Question 32.
CRITICAL THINKING
Suppose x varies inversely with y and y varies inversely with z. How does x vary with z? Justify your answer.
Answer:
Y=b/z
From first equation:
X=a/y, multiply with y
X y= a, divide with x
Y=a/x
Substitute this y with y in equation with z:
Y=b/z
a/x = b/z, multiply with x z
a z=b z
x=a/b z
x varies directly with z.
Question 33.
USING STRUCTURE
To balance the board in the diagram, the distance (in feet) of each animal from the center of the board must vary inversely with its weight (in pounds). What is the distance of each animal from the fulcrum? Justify your answer.
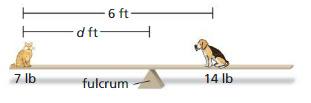
Answer:

Maintaining Mathematical Proficiency Divide.
Question 34.
(x2 + 2x − 99) ÷ (x + 11)
Answer:
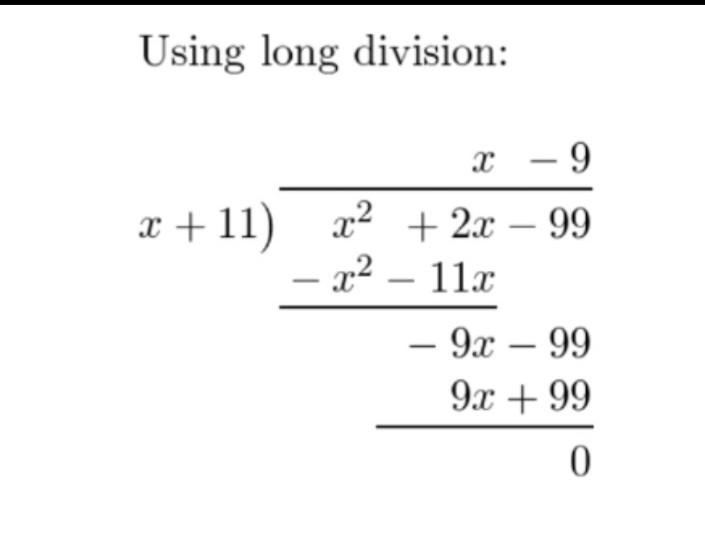
Question 35.
(3x4 − 13x2 − x3 + 6x − 30) ÷ (3x2 − x + 5)
Answer:
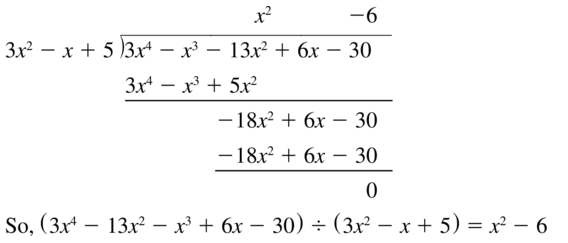
Graph the function. Then state the domain and range.
Question 36.
f(x) = 5x + 4
Answer:
First graph g(x)= 5x. Then translate it 4 units up to obtain f(x).
On graph :
Red – g(x)
Blue – f(x)
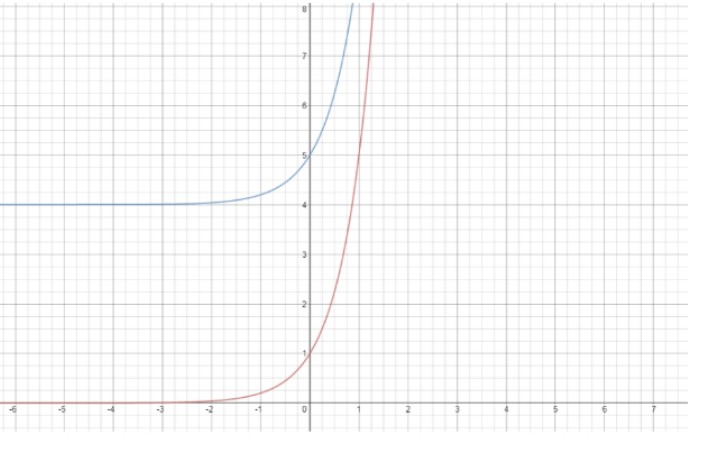
Domain of f is all real number and range of f is (4, ∞)
Question 37.
g(x) = ex-1
Answer:
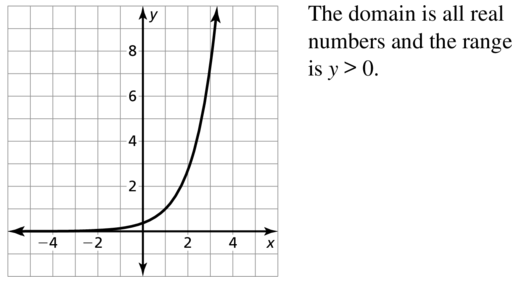
Question 38.
y = ln 3x – 6
Answer:
First graph g(x)=In 3x. Then translate it six units down to obtain f(x).
On graph :
Red – g(x)
Blue – f(x)
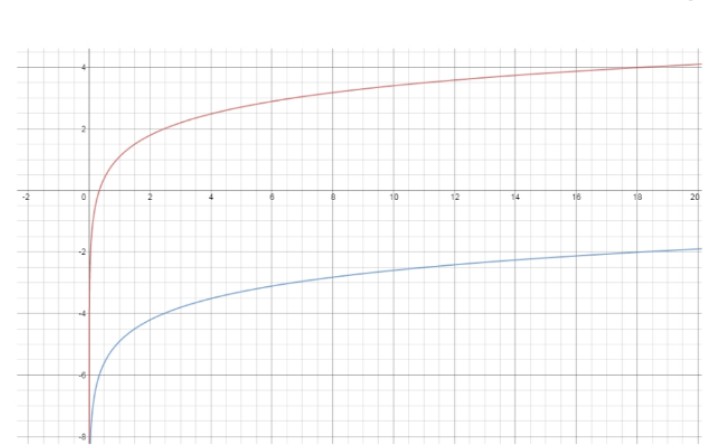
Domain of f is all positive number real numbers,(0, ∞) and range of f is (-∞, ∞)- all real numbers.
Question 39.
ln(x) = 2 ln (x + 9)
Answer:
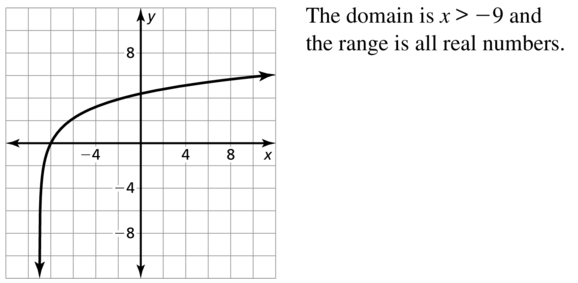
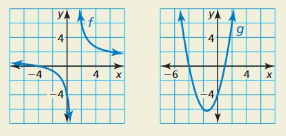
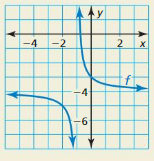
Lesson 7.2 Graphing Rational Functions
Essential Question What are some of the characteristics of the graph of a rational function?
The parent function for rational functions with a linear numerator and a linear denominator is
f(x) = \(\frac{1}{x}\). Parent function
The graph of this function, shown at the right, is a hyperbola.
EXPLORATION 1
Identifying Graphs of Rational Functions
Work with a partner. Each function is a transformation of the graph of the parent function f(x) = \(\frac{1}{x}\). Match the function with its graph. Explain your reasoning. Then describe the transformation.
Communicate Your Answer
Question 2.
What are some of the characteristics of the graph of a rational function?
Answer: One of the main characteristics of rational functions is the existence of asymptotes. An asymptote is a straight line to which the graph of the function gets arbitrarily close.
Question 3.
Determine the intercepts, asymptotes, domain, and range of the rational function g(x) = \(\frac{x-a}{x-b}\).

Answer:
Monitoring Progress
Question 1.
Graph g(x) = \(\frac{-6}{x}\). Compare the graph with the graph of f(x) = \(\frac{1}{x}\).
Answer:
Graph the function. State the domain and range.
Question 2.
y = \(\frac{3}{x}\) – 2
Answer:
Question 3.
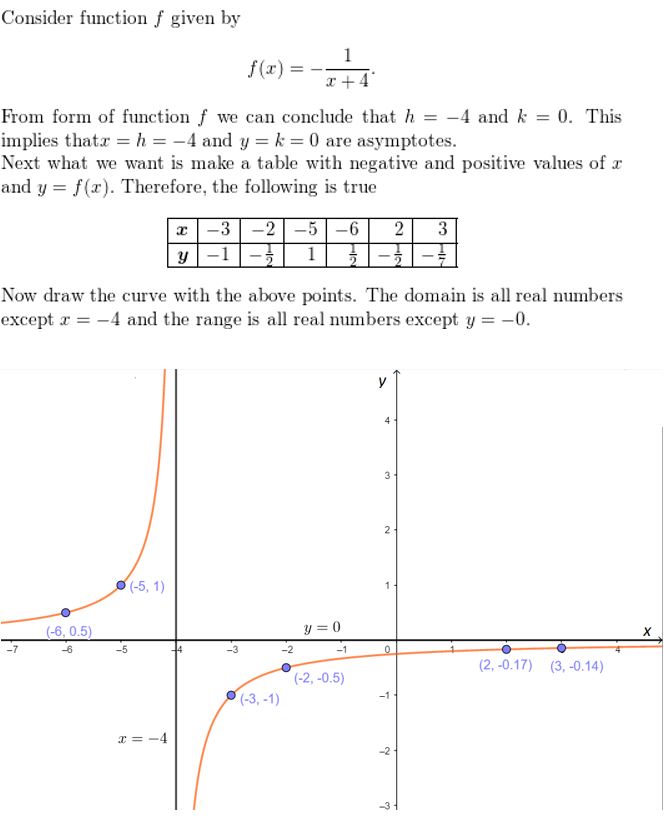
y = \(\frac{-1}{x + 4}\)
Answer:
Question 4.
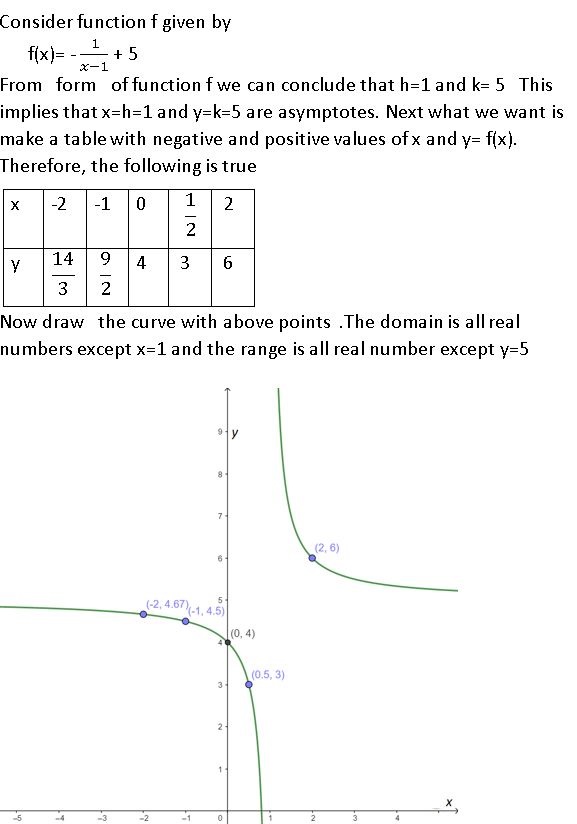
y = \(\frac{1}{x – 1}\) + 5
Answer:
Graph the function. State the domain and range.
Question 5.
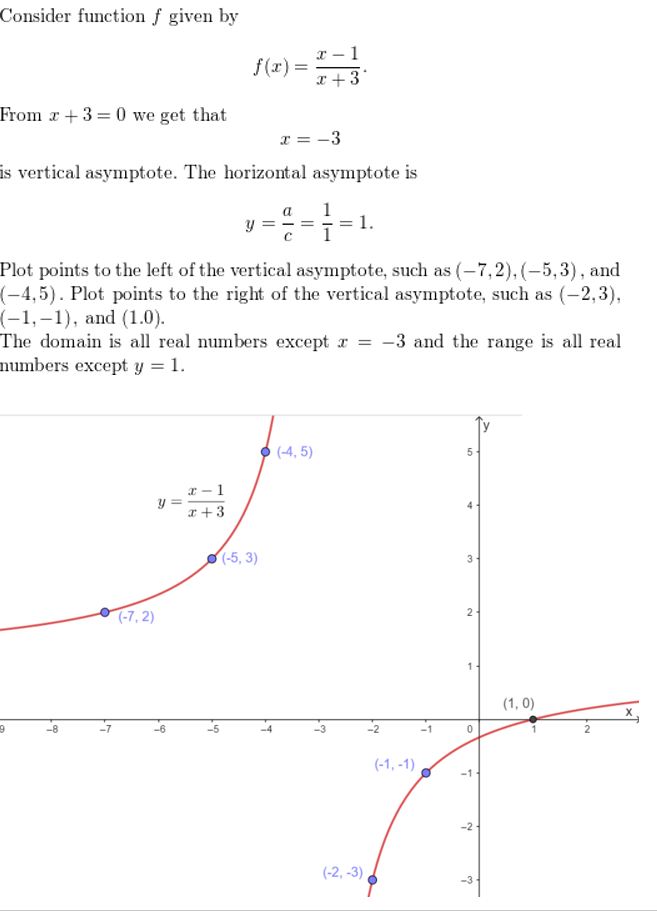
f(x) = \(\frac{x-1}{x+3}\)
Answer:
Question 6.
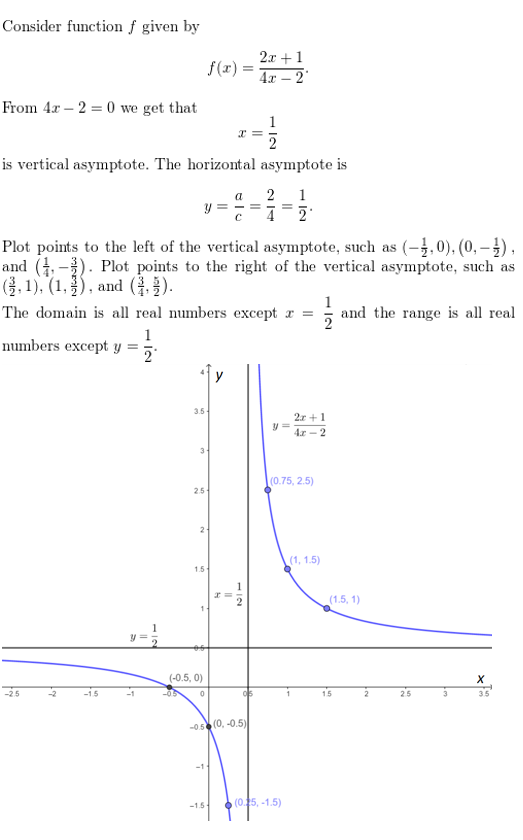
f(x) = \(\frac{2x+1}{4x-2}\)
Answer:
Question 7.
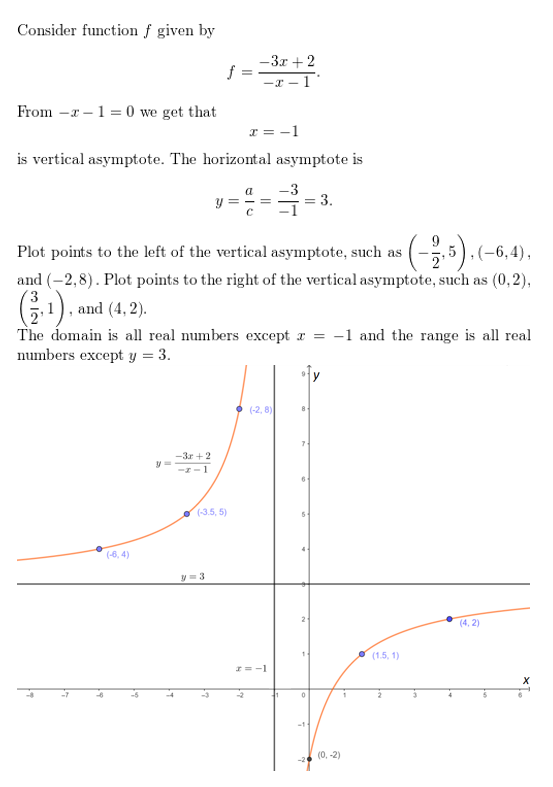
f(x) = \(\frac{-3x+2}{-x-1}\)
Answer:
Question 8.
Rewrite g(x) = \(\frac{2x+3}{x+1}\) in the form g(x) = \(\frac{a}{x-h}\). Graph the function.
Describe the graph of g as a transformation of the graph of f(x) = \(\frac{a}{x}\).
Answer:
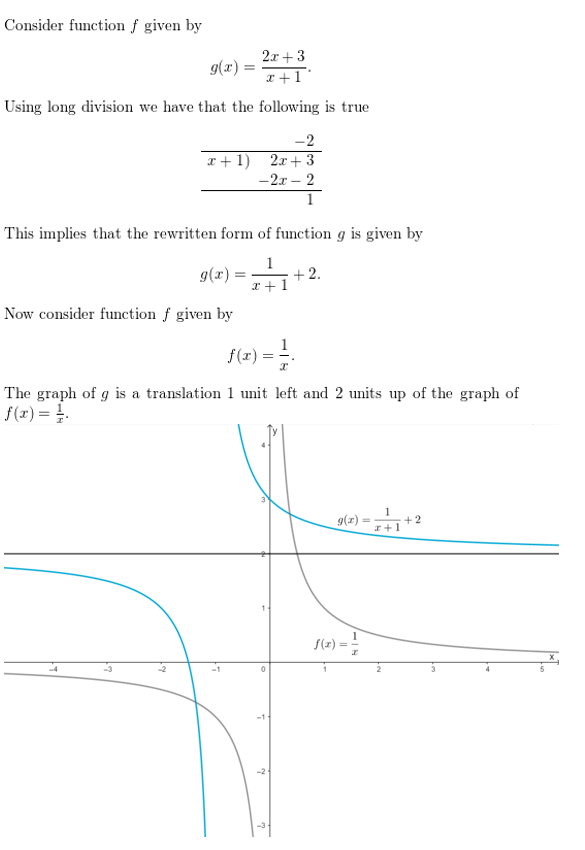
Question 9.
WHAT IF?
How do the answers in Example 5 change when the cost of the 3-D printer is $800?
Answer:
Graphing Rational Functions 7.2 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The function y = \(\frac{7}{x+2}\) has a(n) __________ of all real numbers except 3 and a(n) __________ of all real numbers except −4.
Answer:

Question 2.
WRITING
Is f(x) = \(\frac{-3 x+5}{2^{x}+1}\) a rational function? Explain your reasoning.
Answer:
Consider function f given by
f(x) =-3x+5/2x +1
know that the rational function has form
Y=a x +b/ c x +d
Where a, b, c, d are constant such that c x +d ≠ 0
Since 2x is exponential function then the given function is not rational
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, graph the function. Compare the graph with the graph of f(x) = \(\frac{1}{x}\).
Question 3.
g(x) = \(\frac{3}{x}\)
Answer:
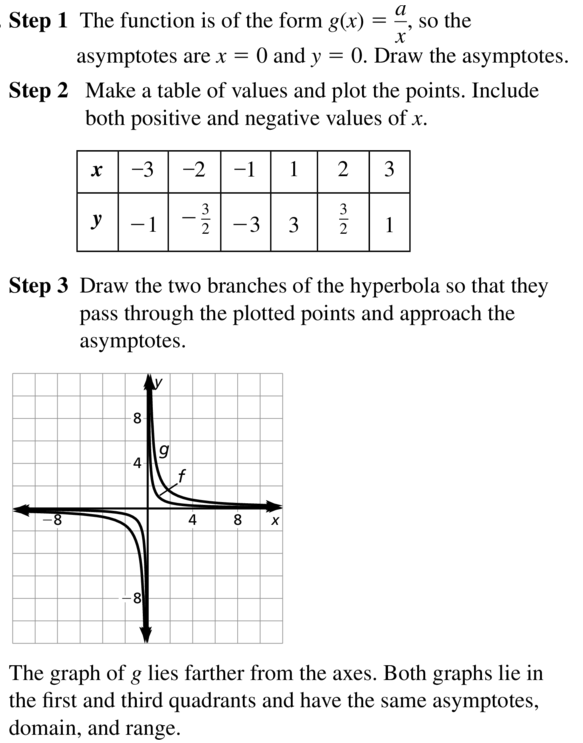
Question 4.
g(x) = \(\frac{10}{x}\)
Answer:
Step:1
The function is of form g(x)= a/x, so the asymptotes are x=0 and y=0
Step:2
Make a table of value and plot the points.
Include both positive and negative values of x.
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y | -10/3 | -5 | -10 | 10 | 5 | 10/3 |
Step=3
On graph :
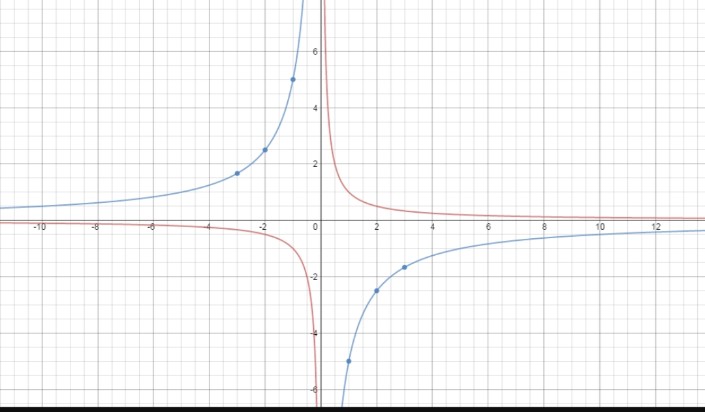
Red – f(x)= 1/x
Blue – g(x) = 10/x
Question 5.
g(x) = \(\frac{-5}{x}\)
Answer:
Question 6.
g(x) = \(\frac{-9}{x}\)
Answer:
Step:1
The function is of form g(x)= a/x, so the asymptotes are x=0 and y=0
Step:2
Make a table of value and plot the points.
Include both positive and negative values of x.
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y | 3 | 9/2 | 9 | -9 | -9/2 | -3 |
Step=3
On graph :
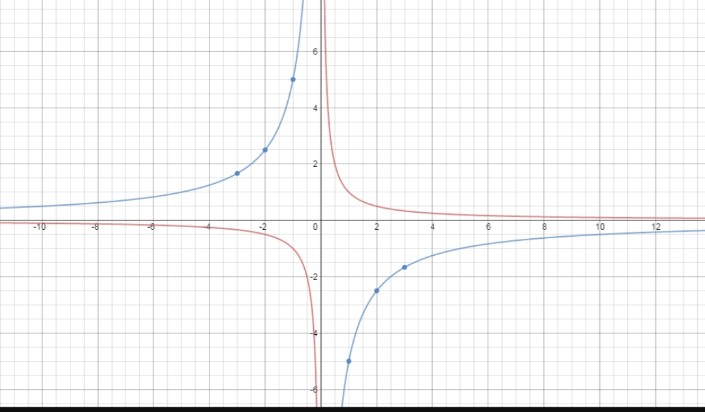
Red – f(x)= 1/x
Blue – g(x) = -9/x
The graph of g lies further from axes than the graph of f. Both have the same asymptotes, domain and range . Graph of g lies in second and fourth quadrants , and graph of f lies and third quadrants
Question 7.
g(x) = \(\frac{15}{x}\)
Answer:
Question 8.
g(x) = \(\frac{-12}{x}\)
Answer:
Step 1
The function is of form g(x)= a/x, so the asymptotes are x=0 and y=0
Step 2
Make a table of value and plot the points.
Include both positive and negative values of x.
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y | 4 | 6 | 12 | -12 | -6 | -4 |
Step 3
On graph :
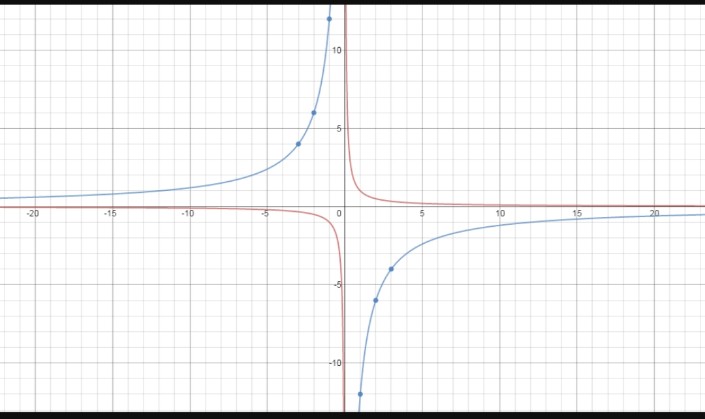
Red – f(x)= 1/x
Blue – g(x) = -12/x
The graph of g lies further from axes than the graph of f. Both have the same asymptotes, domain and range . Graph of g lies in second and fourth quadrants , and graph of f lies and third quadrants.
Question 9.
g(x) = \(\frac{-0.5}{x}\)
Answer:
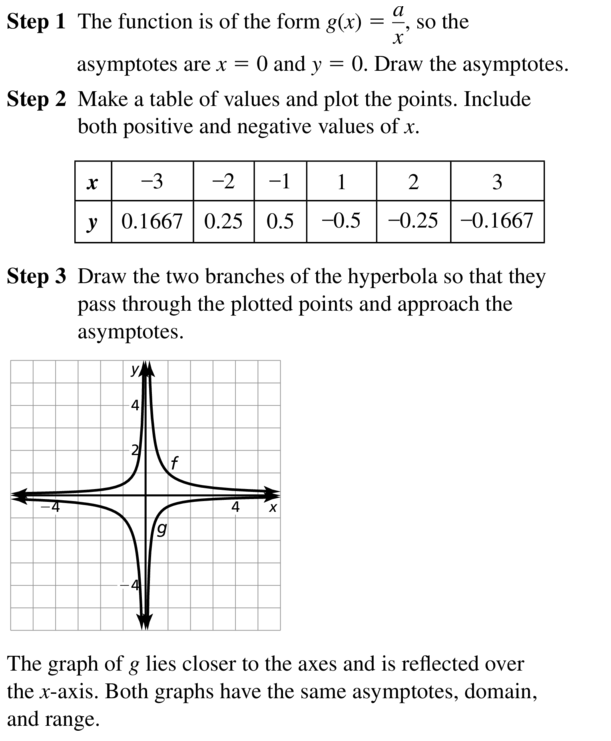
Question 10.
g(x) = \(\frac{0.1}{x}\)
Answer:
Step 1
The function is of form g(x)= a/x, so the asymptotes are x=0 and y=0
step 2
Make a table of value and plot the points.
Include both positive and negative values of x.
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y | -0.033 | -0.05 | -0.1 | 0.1 | 0.05 | 0.033 |
Step 3
On graph :
Red – f(x)= 1/x
Blue – g(x) = -0.1/x
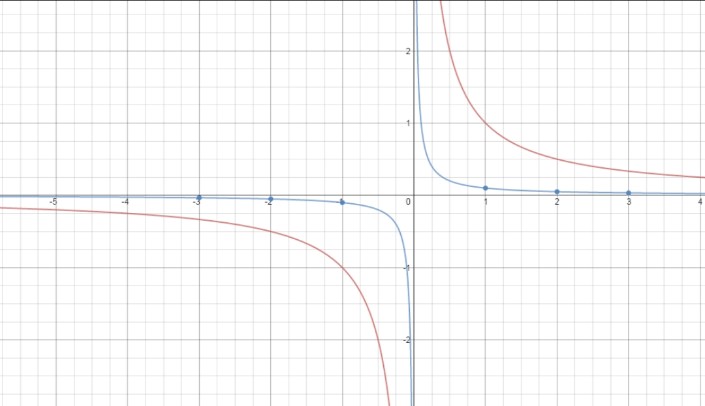
The graph of g lies closer to axes than the graph of f . Both graphs lie in first and third quadrants and have the same asymptotes, domain and range
In Exercises 11–18, graph the function. State the domain and range.
Question 11.
g(x) = \(\frac{4}{x}\)+ 3
Answer:
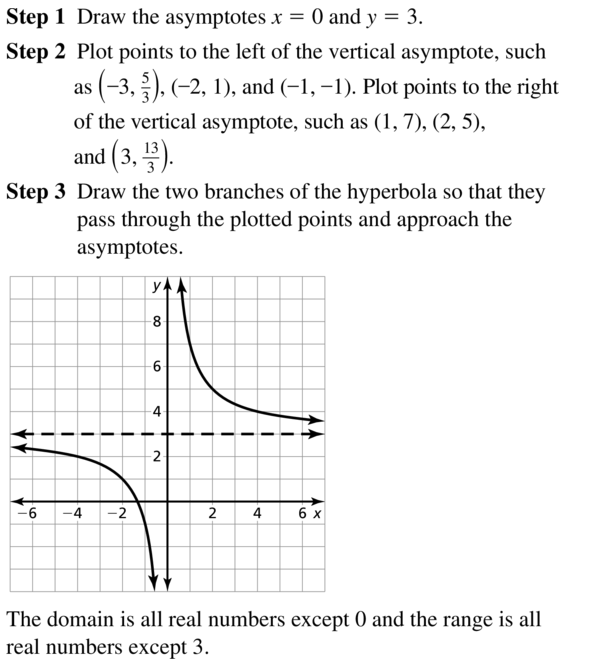
Question 12.
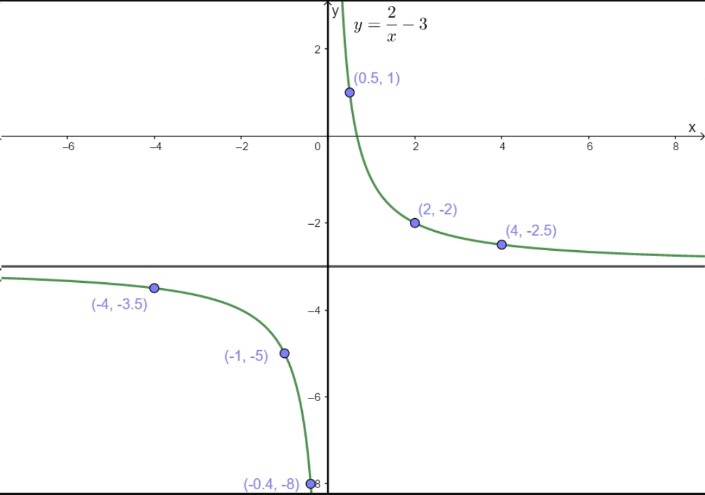
y = \(\frac{2}{x}\) − 3
Answer:
Consider function f given by
F(x)=2/x -3
We have that x=0
Is vertical asymptote .The horizontal asymptote is
Y=-3
Plot point to the left of the vertical asymptote, such as (-1,-5),(-4,-7/2),
And (-2/5, -8 ).Plot points to the right of the vertical asymptote, such as (2,-2),(1/2,1) and
(4,-5/2).
The domain is all real number except x=0 and the range is all real numbers except y=-3
Question 13.
h(x) = \(\frac{6}{x-1}\)
Answer:
Question 14.
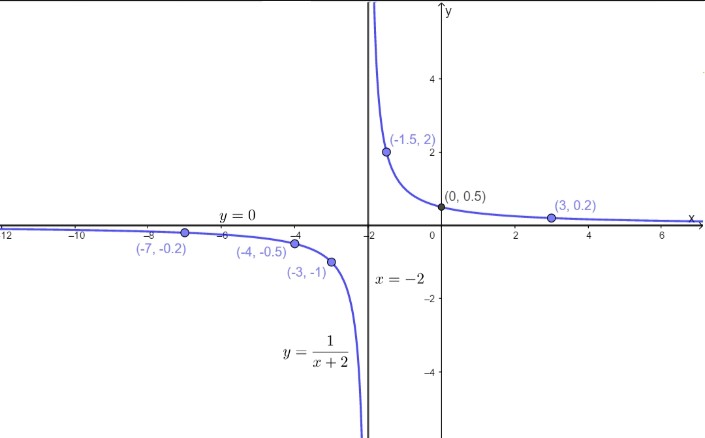
y = \(\frac{1}{x+2}\)
Answer:
Consider function f given by
f(x)=1/x+2
From x+2 =0 we get that x =-2
is vertical asymptote .The horizontal asymptote is
Y=0
Plot point to the left of the vertical asymptote, such as (-3,-1),(-4,-1/2),
And (-7 , -1/5).Plot points to the right of the vertical asymptote, such as (-1/2,-2),(0,1/2) and (3,1/5).
The domain is all real number except x= -2 and the range is all real numbers except y=0
Question 15.
h(x) = \(\frac{-3}{x+2}\)
Answer:
Question 16.
f(x) = \(\frac{-2}{x-7}\)
Answer:
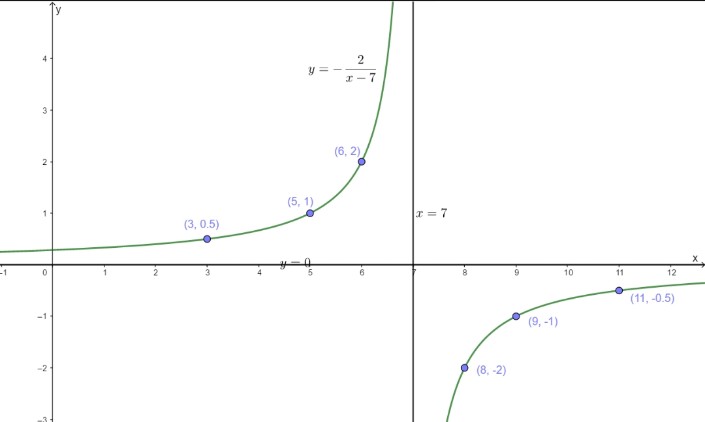
Consider function f given by
f(x)=-2/x-7
From x+2 =0 we get that x = 7 is vertical asymptote .The horizontal asymptote is
Y=0
Plot point to the left of the vertical asymptote, such as (5,1),(3,1/2),
And (6 , 2).Plot points to the right of the vertical asymptote, such as (8,-2),(9,1) and (11,-1/2).
The domain is all real number except x= 7and the range is all real numbers except y=0
Question 17.
g(x) = \(\frac{-3}{x-4}\) − 1
Answer:
Question 18.
y = \(\frac{10}{x+7}\) − 5
Answer:
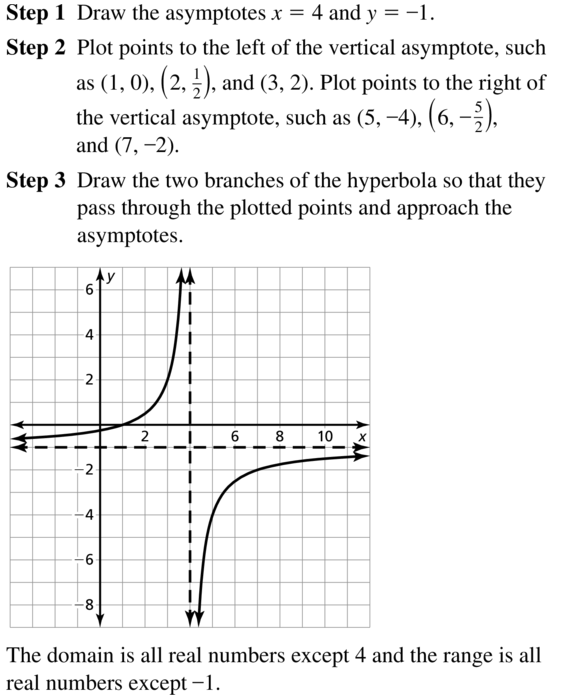
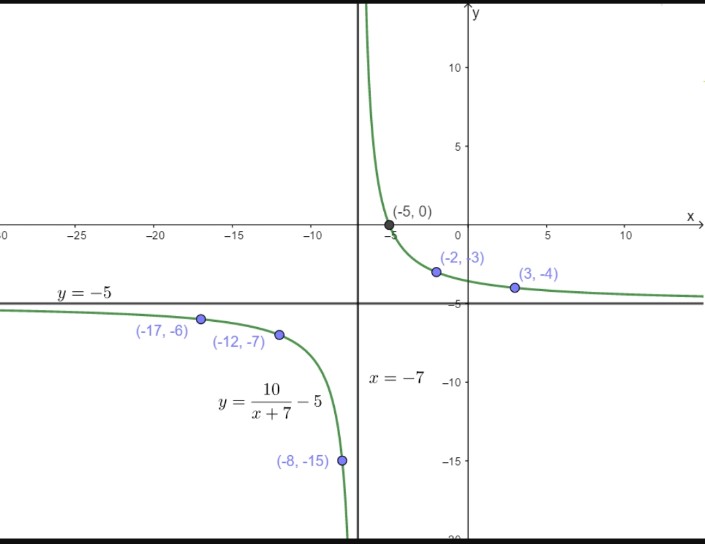
Consider function f given by
f(x)=10/x+7 – 5
From x+2 =0 we get that x = -7
is vertical asymptote .The horizontal asymptote is
Y=-5
Plot point to the left of the vertical asymptote, such as (-17,-6),(-12,-7),
And (-8 , -15).Plot points to the right of the vertical asymptote, such as (-5,0),(-2,-3) and (3,-4).
The domain is all real number except x= -7and the range is all real numbers except y=-5
ERROR ANALYSIS In Exercises 19 and 20, describe and correct the error in graphing the rational function.
Question 19.
y = \(\frac{-8}{x}\)
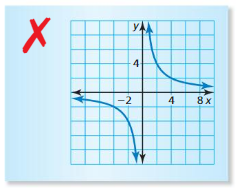
Answer:
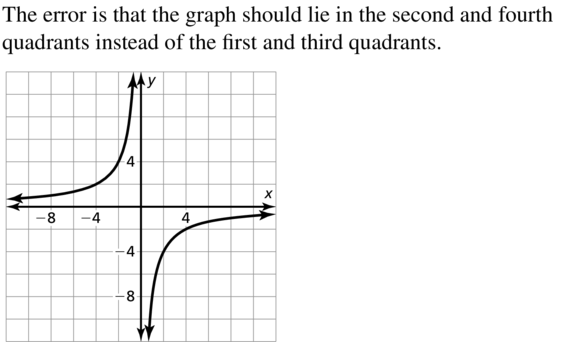
Question 20.
y = \(\frac{2}{x-1}\) – 2
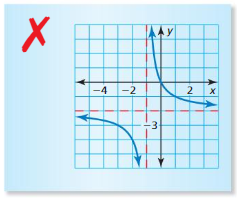
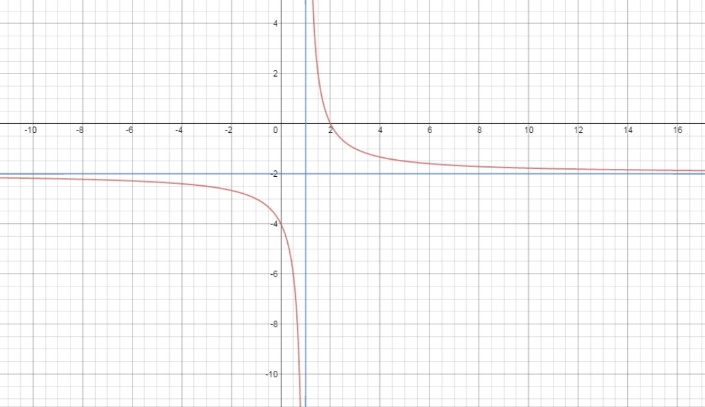
Answer:
Vertical asymptote is incorrect.
It should be x-1=0
X=1
Correct graph :
ANALYZING RELATIONSHIPS In Exercises 21–24, match the function with its graph. Explain your reasoning.
Question 21.
g(x) = \(\frac{2}{x-3}\) + 1
Answer:
![]()
Question 22.
h(x) = \(\frac{2}{x+3}\) + 1
Answer:
The graph is A because the asymptotes are x=-3 and y=1
Question 23.
f(x) = \(\frac{2}{x-3}\) − 1
Answer:
![]()
Question 24.
y = \(\frac{2}{x+3}\) − 1
Answer:
The graph is D because the asymptotes are x=-3 and y=1
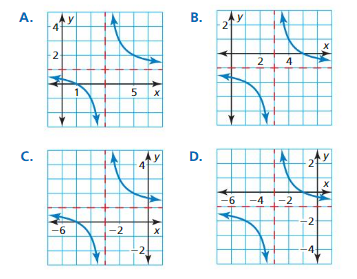
In Exercises 25–32, graph the function. State the domain and range.
Question 25.
f(x) = \(\frac{x+4}{x-3}\)
Answer:

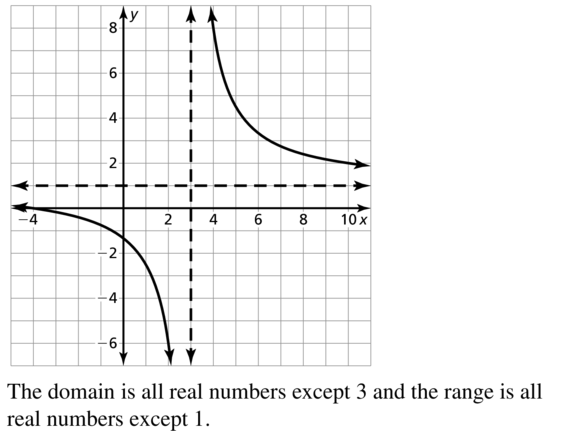
Question 26.
y = \(\frac{x-1}{x+5}\)
Answer:
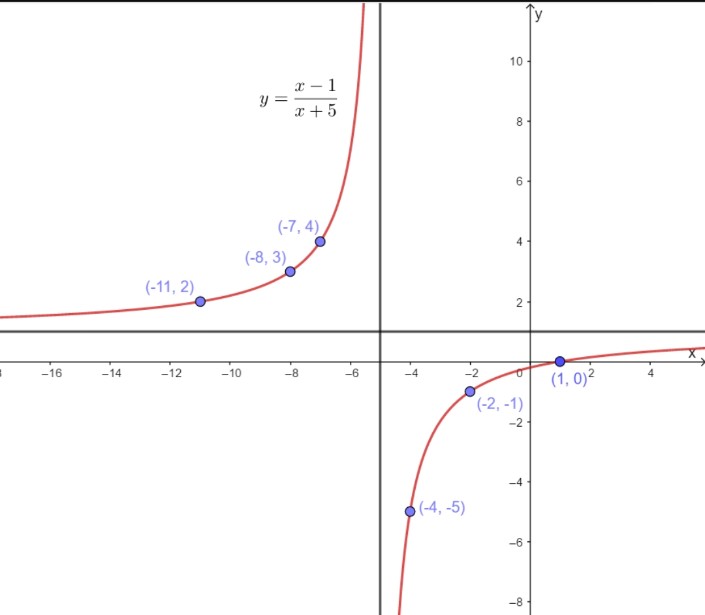
Consider function f given by
Y=x-1/x+5
We know that the rational function has form y= a x+ b/cx +d
Where a,b,c,d are constant such that cx+d 0 .
From x+5 =0 we get that x = -5 is vertical asymptote .The horizontal asymptote is
Y=a/c = 1/1 =1
Plot point to the left of the vertical asymptote, such as (-11,2),(-8,3),
And(-7 , -4).Plot points to the right of the vertical asymptote, such as (-4,-5),(-2,-1) and (1,0).
The domain is all real number except x= -5and the range is all real numbers except y=1
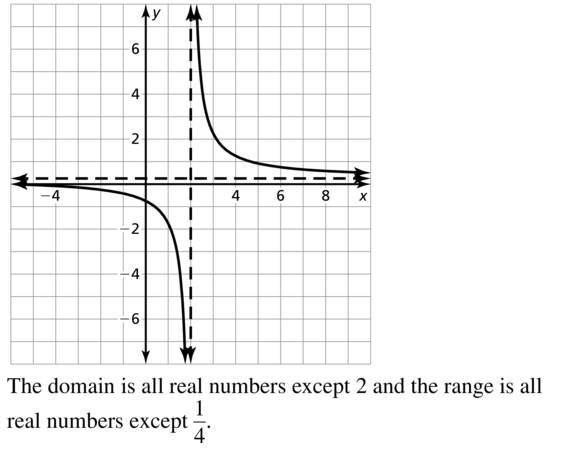
Question 27.
y = \(\frac{x+6}{4x-8}\)
Answer:

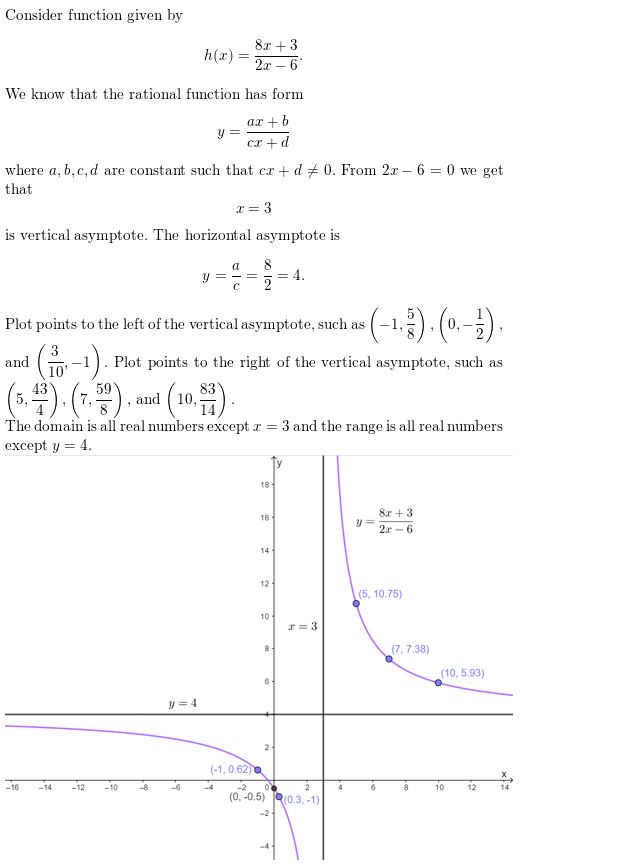
Question 28.
h(x) = \(\frac{8x+3}{2x-6}\)
Answer:
Question 29.
f(x) = \(\frac{-5x+2}{4x+5}\)
Answer:

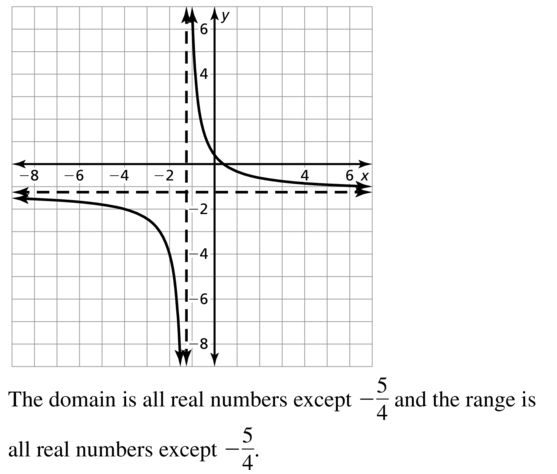
Question 30.
g(x) = \(\frac{6x-1}{3x-1}\)
Answer:
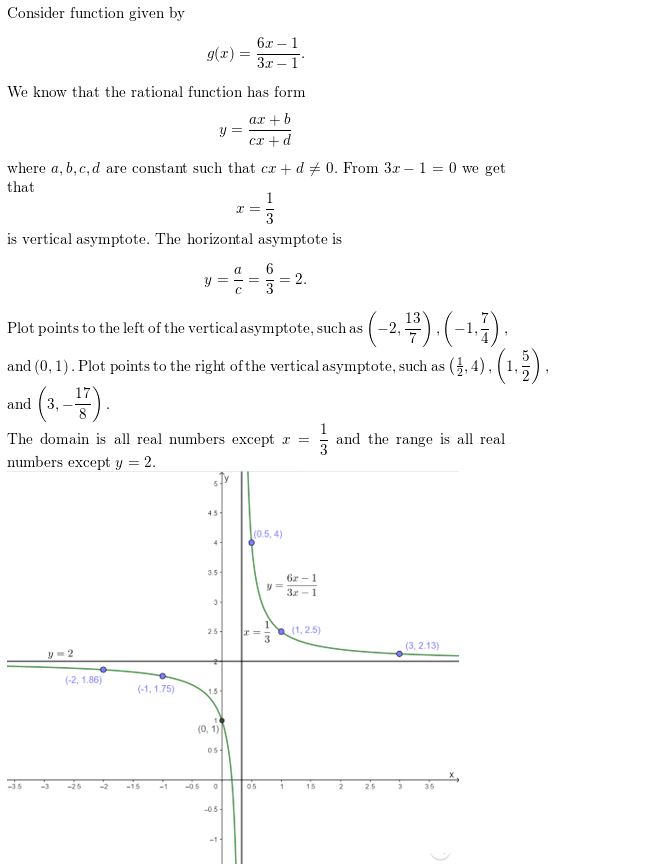
Question 31.
h(x) = \(\frac{-5x}{-2x-3}\)
Answer:


Question 32.
y = \(\frac{-2x+1}{-x+10}\)
Answer:
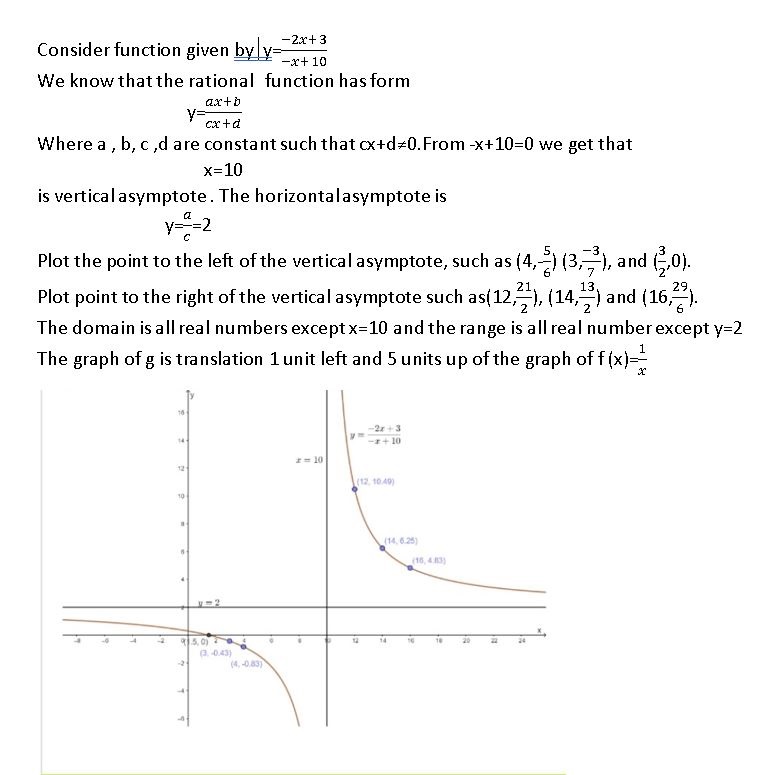
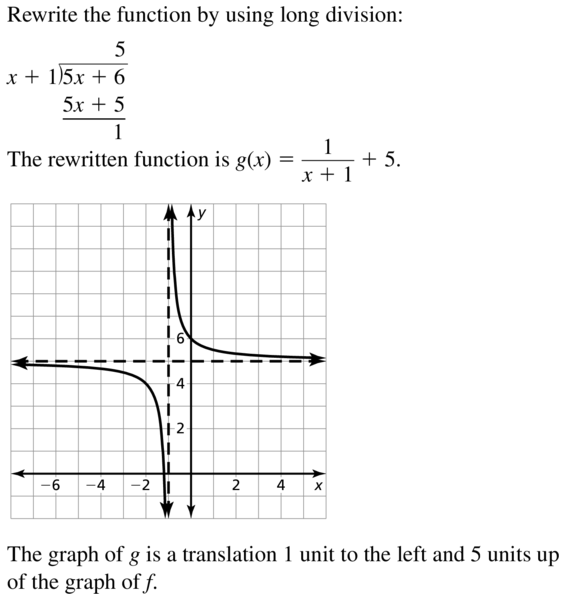
In Exercises 33–40, rewrite the function in the form g(x) = \(\frac{a}{x-h}\) + k. Graph the function. Describe the graph of g as a transformation of the graph of f(x) = \(\frac{a}{x}\).
Question 33.
g(x) = \(\frac{5x+6}{x+1}\)
Answer:
Question 34.
g(x) = \(\frac{7x+4}{x-3}\)
Answer:
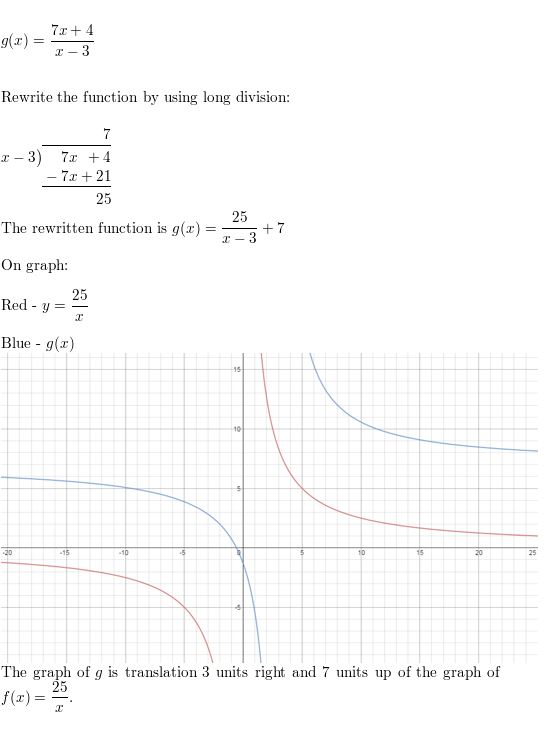
Question 35.
g(x) = \(\frac{2x-4}{x-5}\)
Answer:
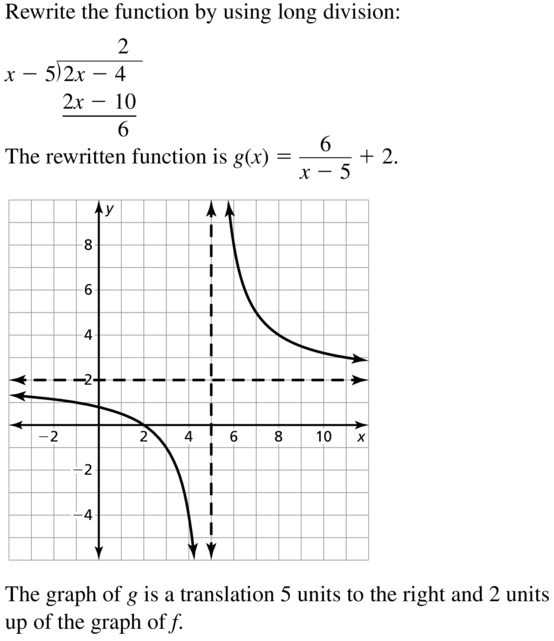
Question 36.
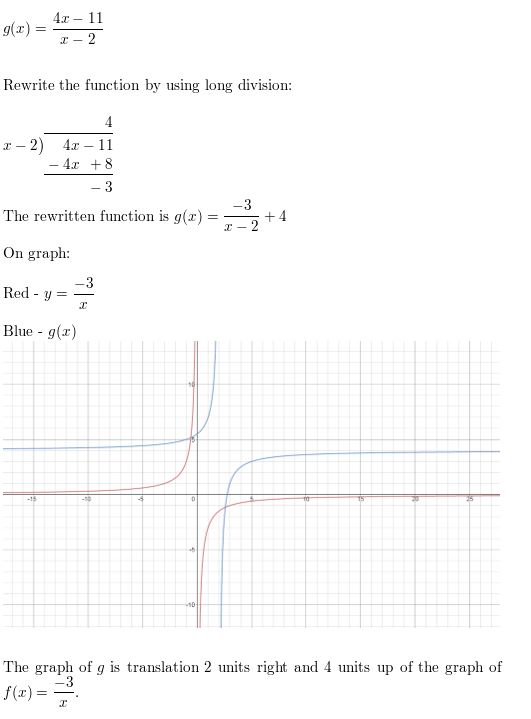
g(x) = \(\frac{4x-11}{x-2}\)
Answer:
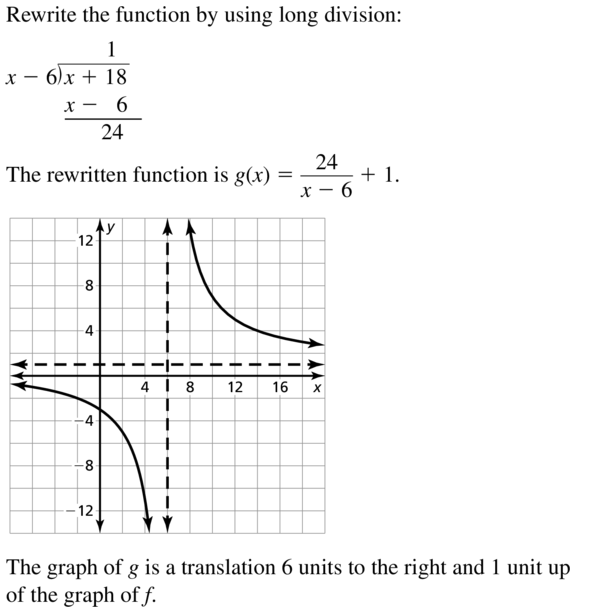
Question 37.
g(x) = \(\frac{x+18}{x-6}\)
Answer:
Question 38.
g(x) = \(\frac{x+2}{x-8}\)
Answer:
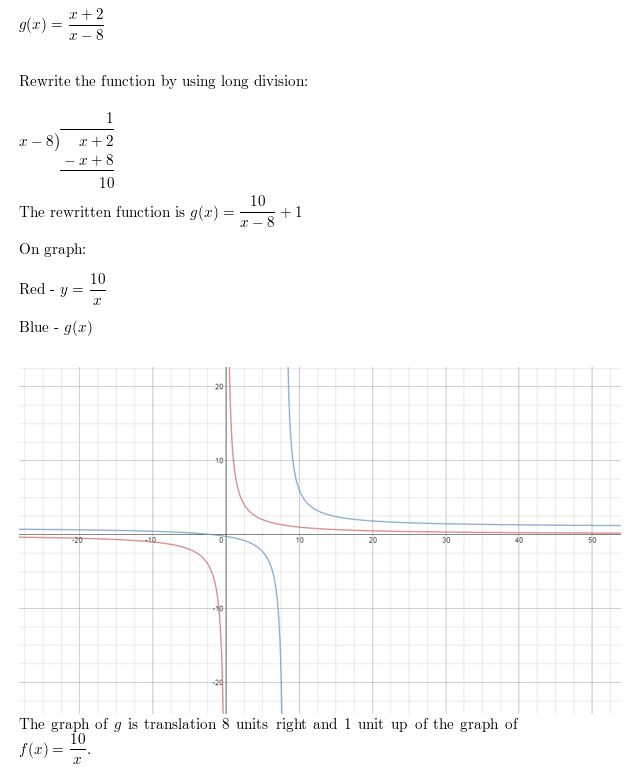
Question 39.
g(x) = \(\frac{7x-20}{x+13}\)
Answer:
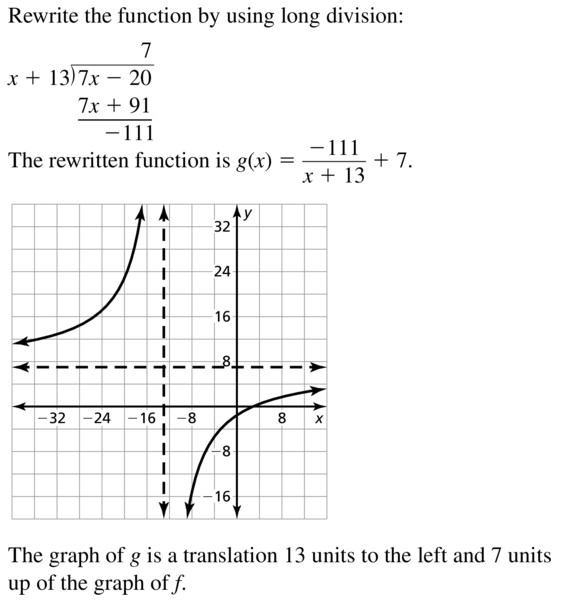
Question 40.
g(x) = \(\frac{9x-3}{x+7}\)
Answer:
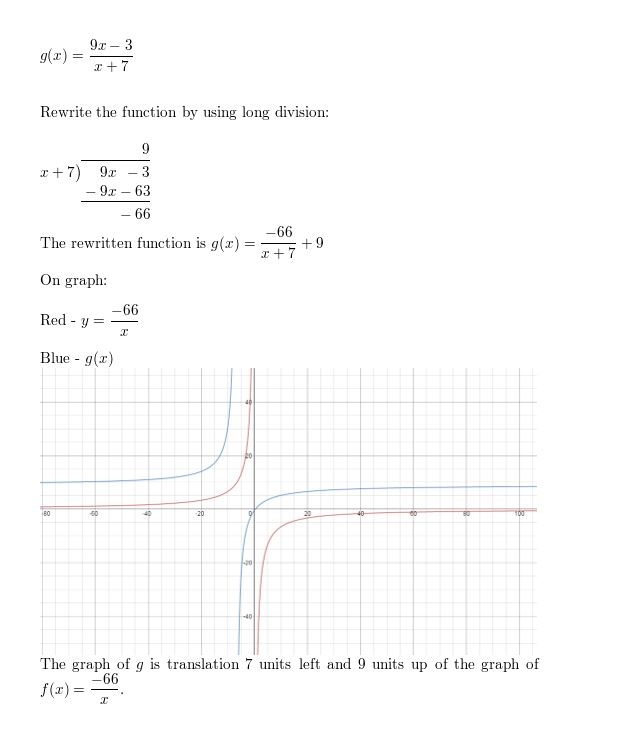
Question 41.
PROBLEM SOLVING
Your school purchases a math software program. The program has an initial cost of $500 plus $20 for each student that uses the program.
a. Estimate how many students must use the program for the average cost per student to fall to $30.
b. What happens to the average cost as more students use the program?
Answer:

Question 42.
PROBLEM SOLVING
To join a rock climbing gym, you must pay an initial fee of $100 and a monthly fee of $59.
a. Estimate how many months you must purchase a membership for the average cost per month to fall to $69.
b. What happens to the average cost as the number of months that you are a member increases?
Answer:

Question 43.
USING STRUCTURE
What is the vertical asymptote of the graph of the function y = \(\frac{2}{x+4}\) + 7?
A. x =−7
B. x = −4
C. x = 4
D. x = 7
Answer:
![]()
Question 44.
REASONING
What are the x-intercept(s) of the graph of the function y = \(\frac{x-5}{x^{2}-1}\)?
A. 1, −1
B. 5
C. 1
D. −5
Answer:

Question 45.
USING TOOLS
The time t (in seconds) it takes for sound to travel 1 kilometer can be modeled by
t = \(\frac{1000}{06T+331}\)
where T is the air temperature (in degrees Celsius).

a. You are 1 kilometer from a lightning strike. You hear the thunder 2.9 seconds later. Use a graph to fund the approximate air temperature.
b. Find the average rate of change in the time it takes sound to travel 1 kilometer as the air temperature increases from 0°C to 10°C.
Answer:

Question 46.
MODELING WITH MATHEMATICS
A business is studying the cost to remove a pollutant from the ground at its site. The function y = \(\frac{15x}{1.1-x}\) models the estimated cost y (in thousands of dollars) to remove x percent (expressed as a decimal) of the pollutant.
a. Graph the function. Describe a reasonable domain and range.
b. How much does it cost to remove 20% of the pollutant? 40% of the pollutant? 80% of the pollutant? Does doubling the percentage of the pollutant removed double the cost? Explain.
Answer:

USING TOOLS In Exercises 47–50, use a graphing calculator to graph the function. Then determine whether the function is even, odd, or neither.
Question 47.
h(x) = \(\frac{6}{x^{2}+1}\)
Answer:
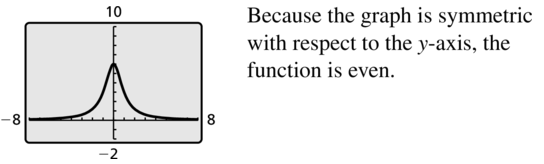
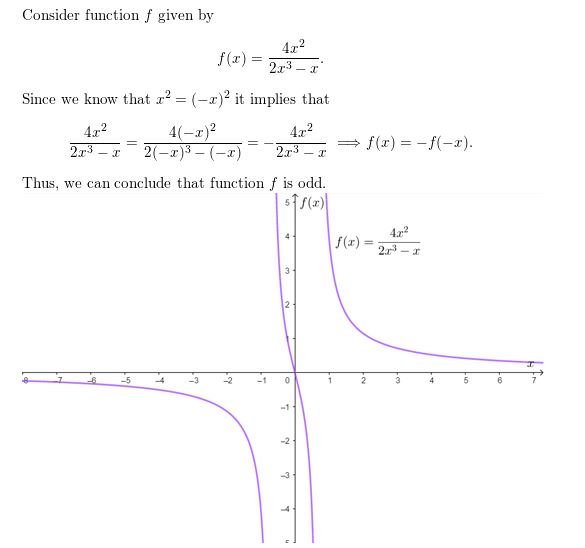
Question 48.
f(x) = \(\frac{2 x^{2}}{x^{2}-9}\)
Answer:
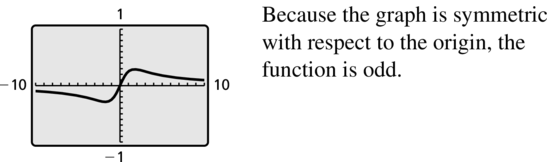
Question 49.
y = \(\frac{x^{3}}{3 x^{2}+x^{4}}\)
Answer:
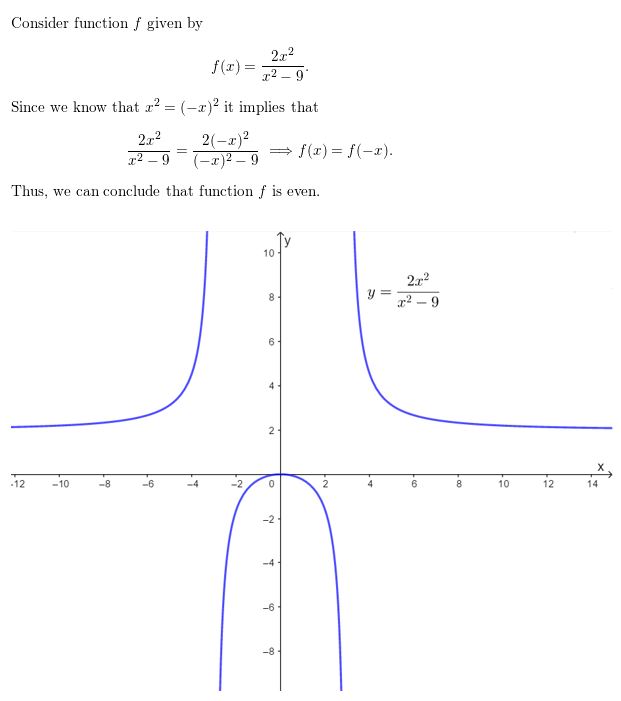
Question 50.
f(x) = \(\frac{4 x^{2}}{2 x^{3}-x}\)
Answer:
Question 51.
MAKING AN ARGUMENT
Your friend claims it is possible for a rational function to have two vertical asymptotes. Is your friend correct? Justify your answer.
Answer:

Question 52.
HOW DO YOU SEE IT?
Use the graph of f to determine the equations of the asymptotes. Explain.
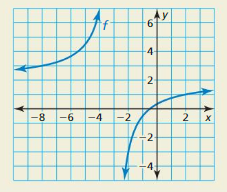
Answer:

Question 53.
DRAWING CONCLUSIONS
In what line(s) is the graph of y = \(\frac{1}{x}\) symmetric? What does this symmetry tell you about the inverse of the function f(x) = \(\frac{1}{x}\)?
Answer:

Question 54.
THOUGHT PROVOKING
There are four basic types of conic sections: parabola, circle, ellipse, and hyperbola. Each of these can be represented by the intersection of a double-napped cone and a plane. The intersections for a parabola, circle, and ellipse are shown below.Sketch the intersection for a hyperbola.
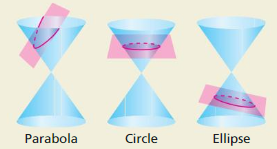
Answer:

Question 55.
REASONING
The graph of the rational function f is a hyperbola. The asymptotes of the graph of f intersect at (3, 2). The point (2, 1) is on the graph. Find another point on the graph. Explain your reasoning.
Answer:

Question 56.
ABSTRACT REASONING
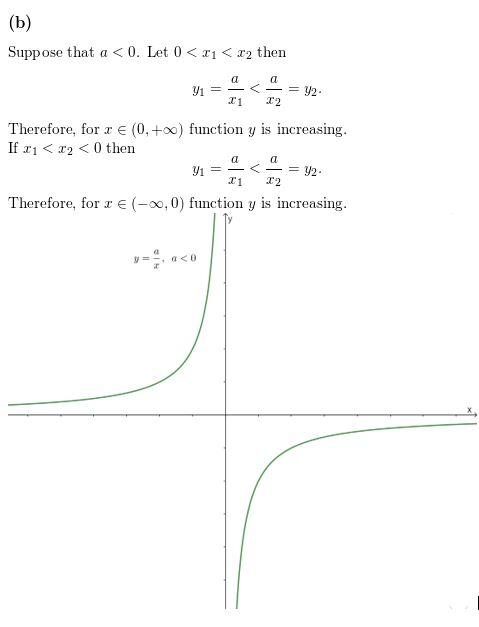
Describe the intervals where the graph of y = \(\frac{a}{x}\) is increasing or decreasing when (a) a > 0 and (b) a < 0. Explain your reasoning.
Answer:
Question 57.
PROBLEM SOLVING
An Internet service provider charges a $50 installation fee and a monthly fee of $43. The table shows the average monthly costs y of a competing provider for x months of service. Under what conditions would a person choose one provider over the other? Explain your reasoning.
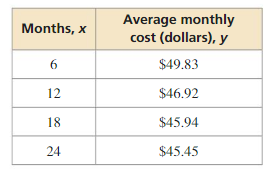
Answer:

Question 58.
MODELING WITH MATHEMATICS
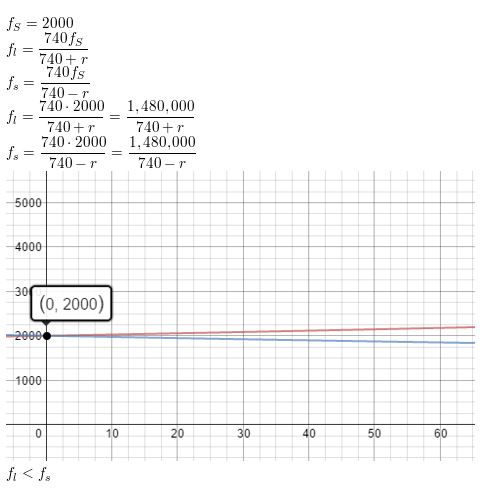
The Doppler effect occurs when the source of a sound is moving relative to a listener, so that the frequency fℓ(in hertz) heard by the listener is different from the frequency fs(in hertz) at the source. In both equations below, r is the speed (in miles per hour) of the sound source.
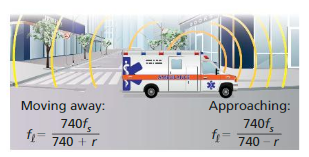
a. An ambulance siren has a frequency of 2000 hertz. Write two equations modeling the frequencies heard when the ambulance is approaching and when the ambulance is moving away.
b. Graph the equations in part (a) using the domain 0 ≤ r ≤ 60.
c. For any speed r, how does the frequency heard for an approaching sound source compare with the frequency heard when the source moves away?
Answer:
Maintaining Mathematical Proficiency
Factor the polynomial.
Question 59.
4x2 − 4x− 80
Answer:
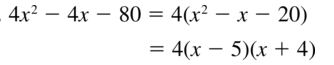
Question 60.
3x2 − 3x − 6
Answer:
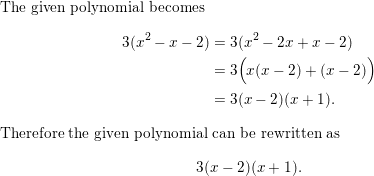
Question 61.
2x2 − 2x − 12
Answer:
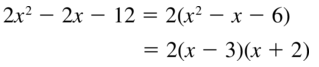
Question 62.
10x2 + 31x − 14
Answer:
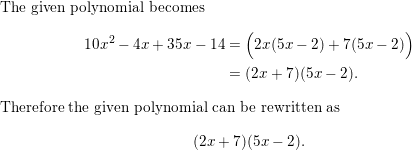
Simplify the expression.
Question 63.
32 • 34
Answer:
![]()
Question 64.
21/2 • 23/5
Answer:
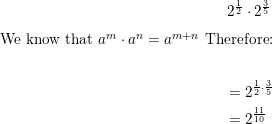
Question 65.
\(\frac{6^{5 / 6}}{6^{1 / 6}}\)
Answer:
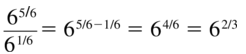
Question 66.
\(\frac{6^{8}}{6^{10}}\)
Answer:
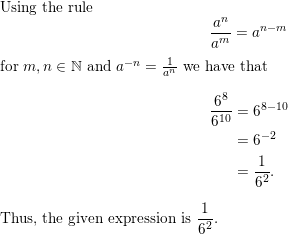
Rational Functions Study Skills: Analyzing Your Errors
7.1–7.2 What Did You Learn?
Core Vocabulary
inverse variation, p. 360
constant of variation, p. 360
rational function, p. 366
Core Concepts
Section 7.1
Inverse Variation, p. 360
Writing Inverse Variation Equations, p. 361
Section 7.2
Parent Function for Simple Rational Functions, p. 366
Graphing Translations of Simple Rational Functions, p. 367
Mathematical Practices
Question 1.
Explain the meaning of the given information in Exercise 25 on page 364.
Answer:
Question 2.
How are you able to recognize whether the logic used in Exercise 29 on page 364 is correct or flawed?
Answer:
Question 3.
How can you evaluate the reasonableness of your answer in part (b) of Exercise 41 on page 371?
Answer:
Question 4.
How did the context allow you to determine a reasonable domain and range for the function in Exercise 46 on page 371?
Answer:
Study Skills: AnalyzingYour Errors
Study Errors
What Happens: You do not study the right material or you do not learn it well enough to remember it on a test without resources such as notes.
How to Avoid This Error: Take a practice test. Work with a study group. Discuss the topics on the test with your teacher. Do not try to learn a whole chapter’s worth of material in one night.

Rational Functions 7.1–7.2 Quiz
Tell whether x and y show direct variation, inverse variation, or neither. Explain your reasoning.
Question 1.
x + y = 7
Answer:

Question 2.
\(\frac{2}{5}\)x = y
Answer:

Question 3.
xy = 0.45′
Answer:

Question 4.
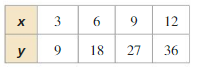
Answer:
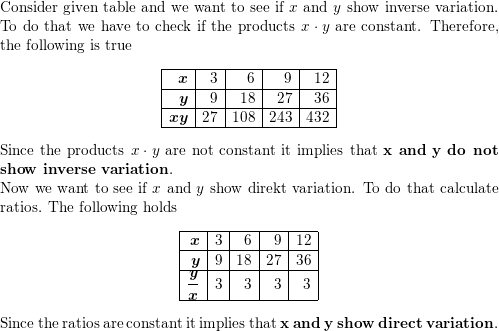
Question 5.
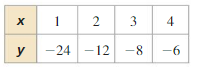
Answer:
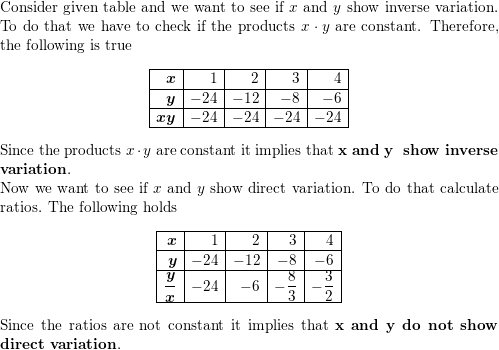
Question 6.
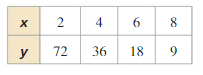
Answer:

Question 7.
The variables x and y vary inversely, and y= 10 when x= 5. Write an equation that relates x and y. Then find y when x = −2.
Answer:
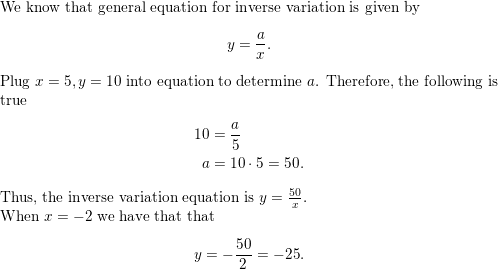
Match the equation with the correct graph. Explain your reasoning.
Question 8.
f(x) = \(\frac{3}{x}\) + 2
Answer:
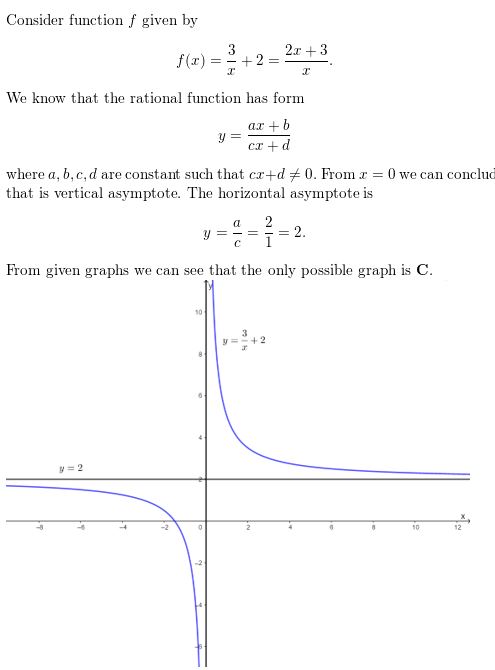
Question 9.
y = \(\frac{-2}{x+3}\) − 2
Answer:
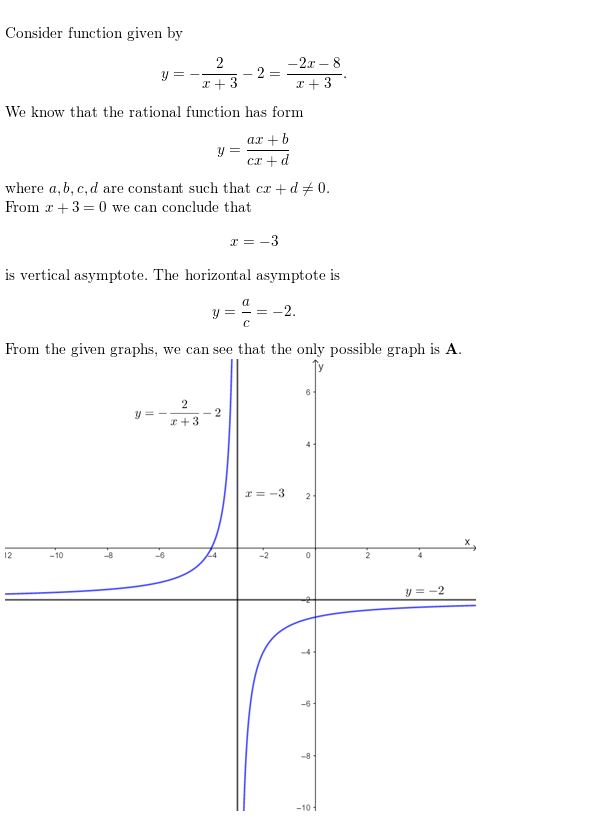
Question 10.
h(x) = \(\frac{2x+2}{3x+1}\)
Answer:
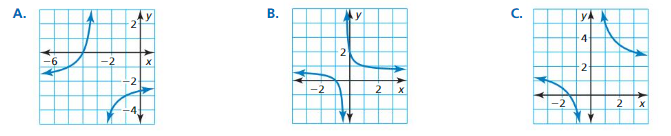
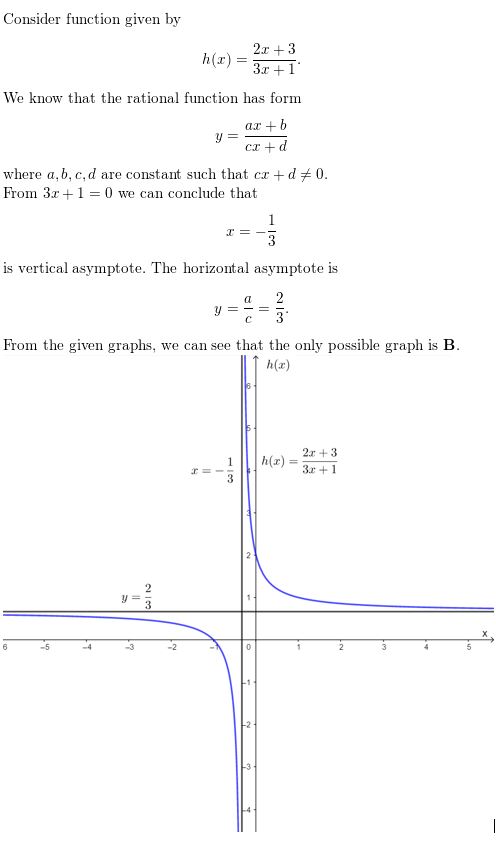
Question 11.
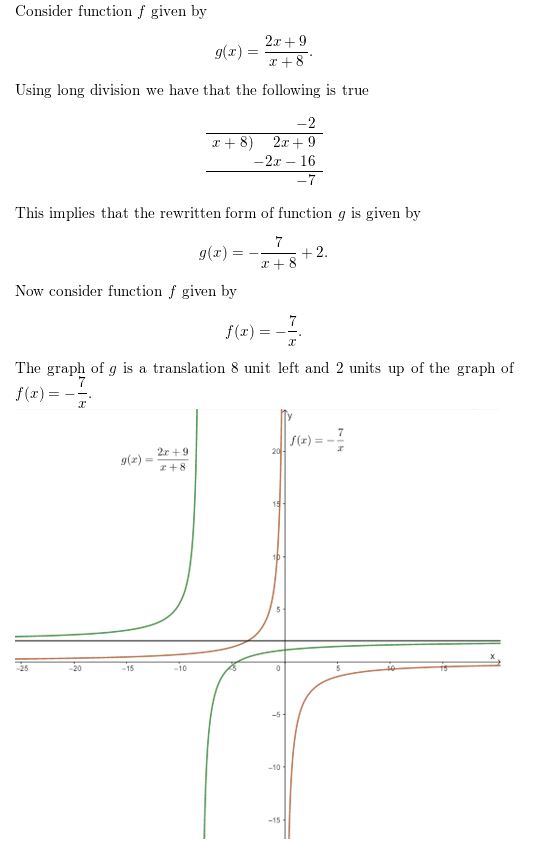
Rewrite g(x) = \(\frac{2x+9}{x+8}\) in the form g(x) = \(\frac{a}{x-h}\). Graph the function. Describe the graph of g as a transformation of the graph of f(x) = \(\frac{a}{x}\).
Answer:
Question 12.
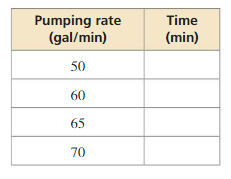
The time t (in minutes) required to empty a tank varies inversely with the pumping rate r (in gallons per minute). The rate of a certain pump is 70 gallons per minute. It takes the pump 20 minutes to empty the tank. Complete the table for the times it takes the pump to empty a tank for the given pumping rates.
Answer:
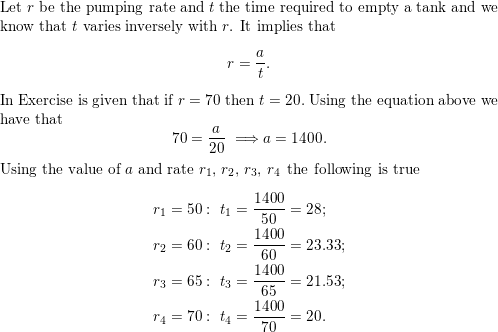
Question 13.
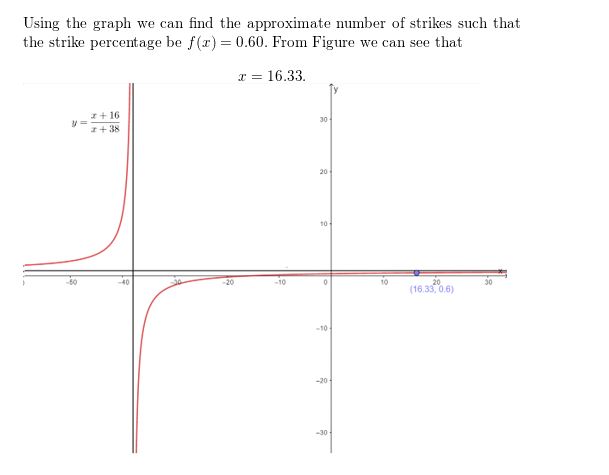
A pitcher throws 16 strikes in the first 38 pitches. The table shows how a pitcher’s strike percentage changes when the pitcher throws x consecutive strikes after the first 38 pitches. Write a rational function for the strike percentage in terms of x. Graph the function. How many consecutive strikes must the pitcher throw to reach a strike percentage of 0.60?
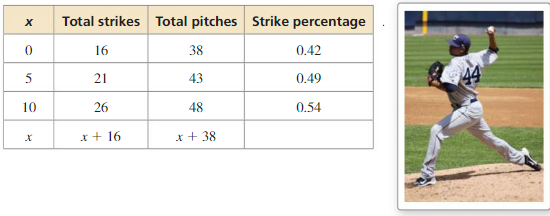
Answer:
Lesson 7.3 Multiplying and Dividing Rational Expressions
Essential Question How can you determine the excluded values in a product or quotient of two rational expressions?
You can multiply and divide rational expressions in much the same way that you multiply and divide fractions. Values that make the denominator of an expression zero are excluded values
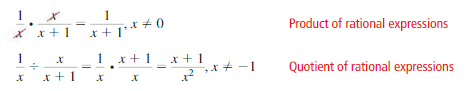
EXPLORATION 1
Multiplying and Dividing Rational Expressions
Work with a partner. Find the product or quotient of the two rational expressions. Then match the product or quotient with its excluded values. Explain your reasoning.
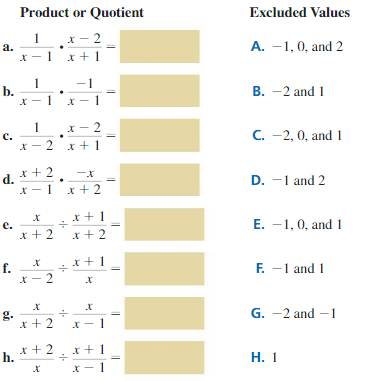
EXPLORATION 2
Writing a Product or Quotient

Work with a partner. Write a product or quotient of rational expressions that has the given excluded values. Justify your answer.
a. −1
b. −1 and 3
c. −1, 0, and 3
Communicate Your Answer
Question 3.
How can you determine the excluded values in a product or quotient of two rational expressions?
Answer:
It can multiply and divide rational expressions in much the same way that you multiply and divide fractions. Values that make the denominator of an expression zero are excluded values.
Question 4.
Is it possible for the product or quotient of two rational expressions to have no excluded values? Explain your reasoning. If it is possible, give an example.
Answer: yes
Example:2²+1. (x²+) will never =0.
Monitoring Progress
Simplify the rational expression, if possible.
Question 1.
\(\frac{2(x+1)}{(x+1)(x+3)}\)
Answer:

Question 2.
\(\frac{x+4}{x^{2}-16}\)
Answer:

Question 3.
\(\frac{4}{x(x+2)}\)
Answer:

Question 4.
\(\frac{x^{2}-2 x-3}{x^{2}-x-6}\)
Answer:
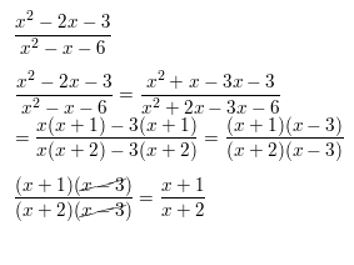
Find the product.
Question 5.
\(\frac{3 x^{5} y^{2}}{8 x y} \cdot \frac{6 x y^{2}}{9 x^{3} y}\)
Answer:

Question 6.
\(\frac{2 x^{2}-10 x}{x^{2}-25} \cdot \frac{x+3}{2 x^{2}}\)
Answer:

Question 7.
\(\frac{x+5}{x^{3}-1}\)
Answer:
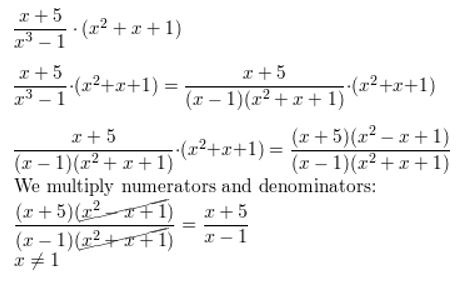
Question 8.
\(\) • (x2 + x + 1)
Answer:
Find the quotient.
Question 9.
\(\frac{4 x}{5 x-20} \div \frac{x^{2}-2 x}{x^{2}-6 x+8}\)
Answer:
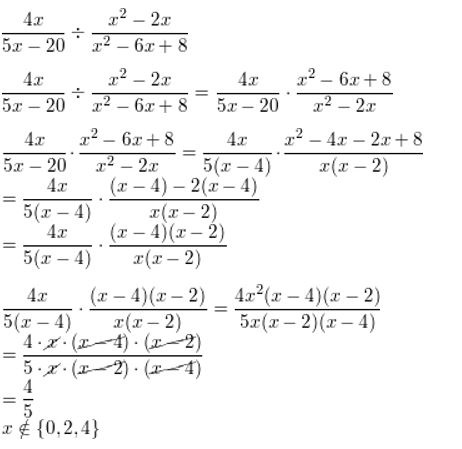
Question 10.
\(\frac{2 x^{2}+3 x-5}{6 x}\) ÷ (2x2 + 5x)
Answer:
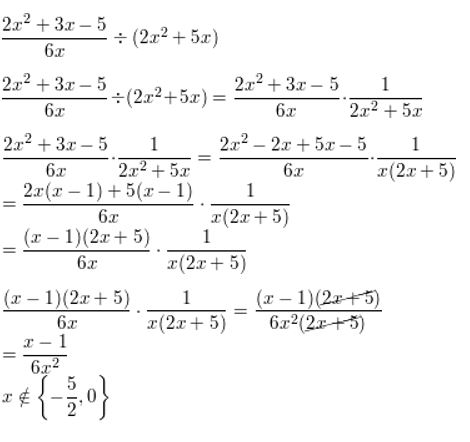
Multiplying and Dividing Rational Expressions 7.3 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Describe how to multiply and divide two rational expressions.
Answer:

Question 2.
WHICH ONE DOESN’T BELONG?
Which rational expression does not belong with the other three? Explain your reasoning.

Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, simplify the expression, if possible.
Question 3.
\(\frac{2 x^{2}}{3 x^{2}-4 x}\)
Answer:
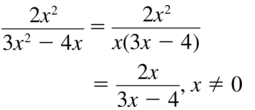
Question 4.
\(\frac{7 x^{3}-x^{2}}{2 x^{3}}\)
Answer:

Question 5.
\(\frac{x^{2}-3 x-18}{x^{2}-7 x+6}\)
Answer:
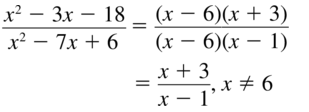
Question 6.
\(\frac{x^{2}+13 x+36}{x^{2}-7 x+10}\)
Answer:

Question 7.
\(\frac{x^{2}+11 x+18}{x^{3}+8}\)
Answer:
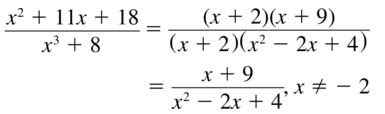
Question 8.
\(\frac{x^{2}-7 x+12}{x^{3}-27}\)
Answer:

Question 9.
\(\frac{32 x^{4}-50}{4 x^{3}-12 x^{2}-5 x+15}\)
Answer:
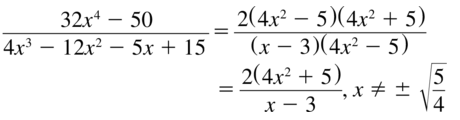
Question 10.
\(\frac{3 x^{3}-3 x^{2}+7 x-7}{27 x^{4}-147}\)
Answer:

In Exercises 11–20, find the product.
Question 11.
\(\frac{4 x y^{3}}{x^{2} y} \cdot \frac{y}{8 x}\)
Answer:
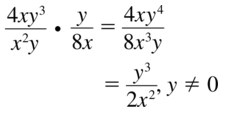
Question 12.
\(\frac{48 x^{5} y^{3}}{y^{4}} \cdot \frac{x^{2} y}{6 x^{3} y^{2}}\)
Answer:

Question 13.
\(\frac{x^{2}(x-4)}{x-3} \cdot \frac{(x-3)(x+6)}{x^{3}}\)
Answer:
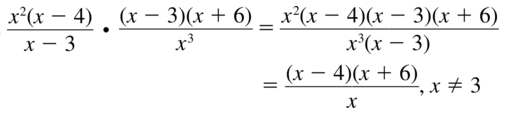
Question 14.
\(\frac{x^{3}(x+5)}{x-9} \cdot \frac{(x-9)(x+8)}{3 x^{3}}\)
Answer:

Question 15.
\(\frac{x^{2}-3 x}{x-2} \cdot \frac{x^{2}+x-6}{x}\)
Answer:
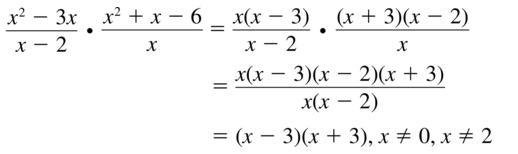
Question 16.
\(\frac{x^{2}-4 x}{x-1} \cdot \frac{x^{2}+3 x-4}{2 x}\)
Answer:

Question 17.
\(\frac{x^{2}+3 x-4}{x^{2}+4 x+4} \cdot \frac{2 x^{2}+4 x}{x^{2}-4 x+3}\)
Answer:
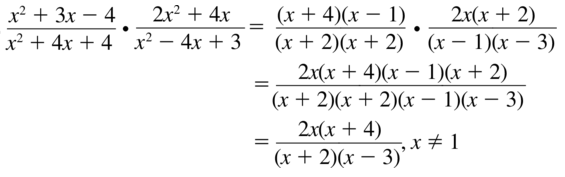
Question 18.
\(\frac{x^{2}-x-6}{4 x^{3}} \cdot \frac{2 x^{2}+2 x}{x^{2}+5 x+6}\)
Answer:

Question 19.
\(\frac{x^{2}+5 x-36}{x^{2}-49}\) • (x2 – 11x + 28)
Answer:
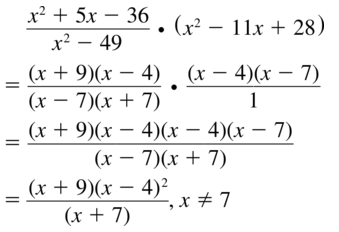
Question 20.
\(\frac{x^{2}-x-12}{x^{2}-16}\) • (x2 – 2x + 8)
Answer:

Question 21.
ERROR ANALYSIS
Describe and correct the error in simplifying the rational expression.
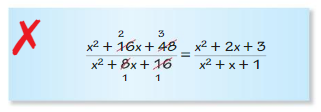
Answer:
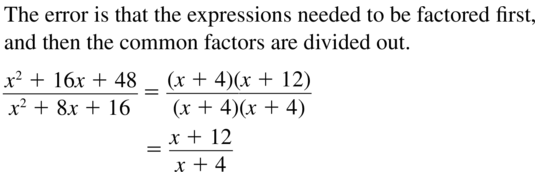
Question 22.
ERROR ANALYSIS
Describe and correct the error in finding the product.
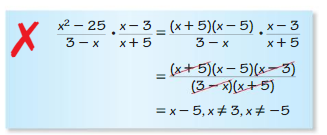
Answer:

Question 23.
USING STRUCTURE
Which rational expression is in simplified form?
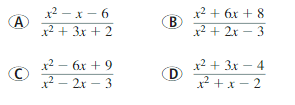
Answer:
![]()
Question 24.
COMPARING METHODS
Find the product below by multiplying the numerators and denominators, then simplifying. Then find the product by simplifying each expression, then multiplying. Which method do you prefer? Explain.
\(\frac{4 x^{2} y}{2 x^{3}} \cdot \frac{12 y^{4}}{24 x^{2}}\)
Answer:

Question 25.
WRITING
Compare the function f(x) = \(\frac{(3 x-7)(x+6)}{(3 x-7)}\) to the function g(x) = x + 6.
Answer:

Question 26.
MODELING WITH MATHEMATICS
Write a model in terms of x for the total area of the base of the building.
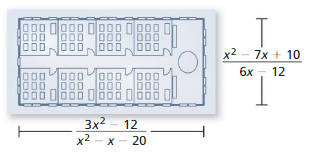
Answer:

In Exercises 27–34, find the quotient.
Question 27.
\(\frac{32 x^{3} y}{y^{8}} \div \frac{y^{7}}{8 x^{4}}\)
Answer:
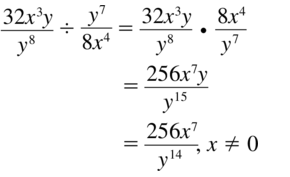
Question 28.
\(\frac{2 x y z}{x^{3} z^{3}} \div \frac{6 y^{4}}{2 x^{2} z^{2}}\)
Answer:

Question 29.
\(\frac{x^{2}-x-6}{2 x^{4}-6 x^{3}} \div \frac{x+2}{4 x^{3}}\)
Answer:
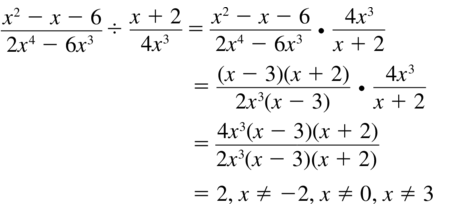
Question 30.
\(\frac{2 x^{2}-12 x}{x^{2}-7 x+6} \div \frac{2 x}{3 x-3}\)
Answer:

Question 31.
\(\frac{x^{2}-x-6}{x+4}\) ÷ (x2 – 6x + 9)
Answer:
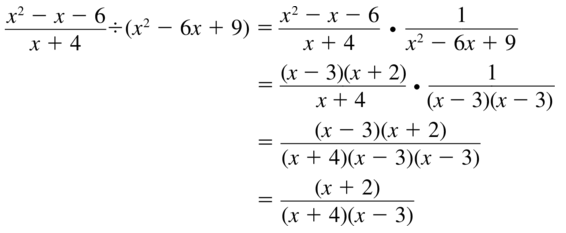
Question 32.
\(\frac{x^{2}-5 x-36}{x+2}\) ÷ (x2 – 18x + 81)
Answer:

Question 33.
\(\frac{x^{2}+9 x+18}{x^{2}+6 x+8} \div \frac{x^{2}-3 x-18}{x^{2}+2 x-8}\)
Answer:
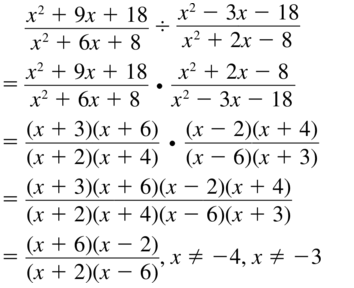
Question 34.
\(\frac{x^{2}-3 x-40}{x^{2}+8 x-20} \div \frac{x^{2}+13 x+40}{x^{2}+12 x+20}\)
Answer:

In Exercises 35 and 36, use the following information. Manufacturers often package products in a way that uses the least amount of material. One measure of the efficiency of a package is the ratio of its surface area S to its volume V. The smaller the ratio, the more efficient the packaging.
Question 35.
You are examining three cylindrical containers.
a. Write an expression for the efficiency ratio \(\frac{S}{V}\) of a cylinder.
b. Find the efficiency ratio for each cylindrical can listed in the table. Rank the three cans according to efficiency.
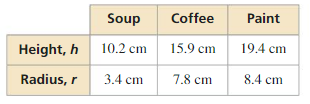
Answer:

Question 36.
PROBLEM SOLVING
A popcorn company is designing a new tin with the same square base and twice the height of the old tin.

a. Write an expression for the efficiency ratio \(\frac{S}{V}\) of each tin.
b. Did the company make a good decision by creating the new tin? Explain.
Answer:

Question 37.
MODELING WITH MATHEMATICS
The total amount I (in millions of dollars) of healthcare expenditures and the residential population P (in millions) in the United States can be modeled by
I = \(\frac{171,000 t+1,361,000}{1+0.018 t}\) and P = 2.96t + 278.649
where t is the number of years since 2000. Find a model M for the annual healthcare expenditures per resident. Estimate the annual healthcare expenditures per resident in 2010.
Answer:

Question 38.
MODELING WITH MATHEMATICS
The total amount I (in millions of dollars) of school expenditures from prekindergarten to a college level and the enrollment P(in millions) in prekindergarten through college in the United States can be modeled by
I = \(\frac{17.913 t+709,569}{1-0.028 t}\) and P = 0.5906t + 70.219
where t is the number of years since 2001. Find a model M for the annual education expenditures per student. Estimate the annual education expenditures per student in 2009.

Answer:

Question 39.
USING EQUATIONS
Refer to the population model P in Exercise 37.
a. Interpret the meaning of the coefficient of t.
b. Interpret the meaning of the constant term.
Answer:

Question 40.
HOW DO YOU SEE IT?
Use the graphs of f and g to determine the excluded values of the functions h(x) = (fg)(x) and k(x) = (\(\frac{f}{g}\)) (x). Explain your reasoning.
Answer:

Question 41.
DRAWING CONCLUSIONS
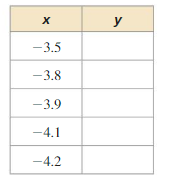
Complete the table for the function y = \(\frac{x+4}{x^{2}-16}\) . Then use the trace feature of a graphing calculator to explain the behavior of the function at x = −4.
Answer:

Question 42.
MAKING AN ARGUMENT
You and your friend are asked to state the domain of the expression below.
\(\frac{x^{2}+6 x-27}{x^{2}+4 x-45}\)
Your friend claims the domain is all real numbers except 5. You claim the domain is all real numbers except −9 and 5. Who is correct? Explain.
Answer:

Question 43.
MATHEMATICAL CONNECTIONS
Find the ratio of the perimeter to the area of the triangle shown.
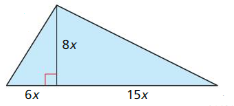
Answer:

Question 44.
CRITICAL THINKING
Find the expression that makes the following statement true. Assume x ≠ −2 and x ≠ 5.
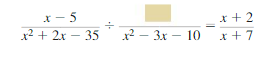
Answer:

USING STRUCTURE In Exercises 45 and 46, perform the indicated operations.
Question 45.
\(\frac{2 x^{2}+x-15}{2 x^{2}-11 x-21}\) • (6x + 9) ÷ \(\frac{2 x-5}{3 x-21}\)
Answer:
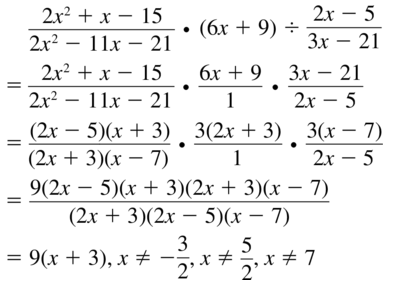
Question 46.
(x3 + 8) • \(\frac{x-2}{x^{2}-2 x+4} \div \frac{x^{2}-4}{x-6}\)
Answer:

Question 47.
REASONING
Animals that live in temperatures several degrees colder than their bodies must avoid losing heat to survive. Animals can better conserve body heat as their surface area to volume ratios decrease. Find the surface area to volume ratio of each penguin shown by using cylinders to approximate their shapes. Which penguin is better equipped to live in a colder environment? Explain your reasoning.
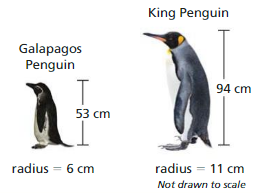
Answer:
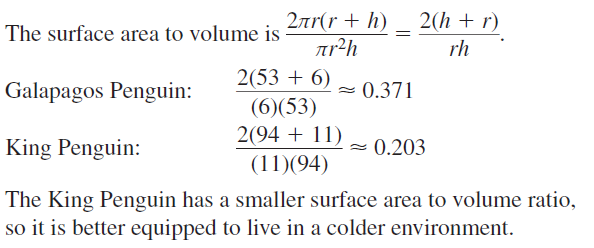
Question 48.
THOUGHT PROVOKING
Is it possible to write two radical functions whose product when graphed is a parabola and whose quotient when graphed is a hyperbola? Justify your answer.
Answer: Yes it is possible.
Question 49.
REASONING
Find two rational functions f and g that have the stated product and quotient.
(fg)(x) = x2, (\(\left(\frac{f}{g}\right)\)) (x) = \(\frac{(x-1)^{2}}{(x+2)^{2}}\)
Answer:
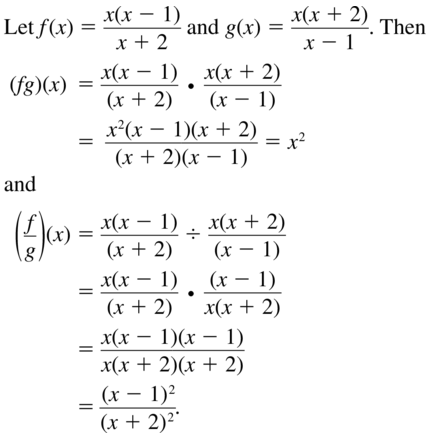
Maintaining Mathematical Proficiency
Solve the equation. Check your solution.
Question 50.
\(\frac{1}{2}\)x + 4 = \(\frac{3}{2}\)x + 5
Answer:
\(\frac{1}{2}\)x + 4 = \(\frac{3}{2}\)x + 5
\(\frac{1}{2}\)x – \(\frac{3}{2}\)x = 5 – 4
-1x = 1
x = -1
Question 51.
\(\frac{1}{3}\)x − 2 = \(\frac{3}{4}\)x
Answer:
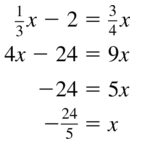
Question 52.
\(\frac{1}{4}\)x − \(\frac{3}{5}\) = \(\frac{9}{2}\)x − \(\frac{4}{5}\)
Answer:

Question 53.
\(\frac{1}{2}\)x + \(\frac{1}{3}\) = \(\frac{3}{4}\)x − \(\frac{1}{5}\)
Answer:
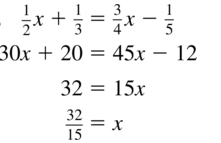
Write the prime factorization of the number. If the number is prime, then write prime.
Question 54.
42
Answer:

Question 55.
91
Answer:
![]()
Question 56.
72
Answer:
72 = 2 × 2 × 2 × 3 × 3
Question 57.
79
Answer:
![]()
Lesson 7.4 Adding and Subtracting Rational Expressions
Essential Question
How can you determine the domain of the sum or difference of two rational expressions?
You can add and subtract rational expressions in much the same way that you add and subtract fractions.
\(\frac{x}{x+1}+\frac{2}{x+1}=\frac{x+2}{x+1}\) Sum of rational expressions
\(\frac{1}{x}-\frac{1}{2 x}=\frac{2}{2 x}-\frac{1}{2 x}=\frac{1}{2 x}\) Difference of rational expressions
EXPLORATION 1
Adding and Subtracting Rational Expressions
Work with a partner. Find the sum or difference of the two rational expressions. Then match the sum or difference with its domain. Explain your reasoning.

EXPLORATION 2
Writing a Sum or Difference

Work with a partner. Write a sum or difference of rational expressions that has the given domain. Justify your answer.
a. all real numbers except −1
b. all real numbers except −1 and 3
c. all real numbers except −1, 0, and 3
Communicate Your Answer
Question 3.
How can you determine the domain of the sum or difference of two rational expressions?
Answer:
We need to simplify the given sum or difference of two rational expressions by finding LCM.
Then find out the values of x simplified expression for which denominator becomes zero.
Then domain is all real numbers except values of x for which denominator becomes 0.
Question 4.
Your friend found a sum as follows. Describe and correct the error(s).
\(\frac{x}{x+4}+\frac{3}{x-4}=\frac{x+3}{2 x}\)
Answer:
Monitoring Progress
Find the sum or difference.
Question 1.
\(\frac{8}{12 x}-\frac{5}{12 x}\)
Answer:

Question 2.
\(\frac{2}{3 x^{2}}+\frac{1}{3 x^{2}}\)
Answer:
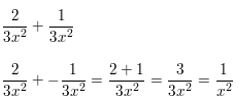
Question 3.
\(\frac{4 x}{x-2}-\frac{x}{x-2}\)
Answer:

Question 4.
\(\frac{2 x^{2}}{x^{2}+1}+\frac{2}{x^{2}+1}\)
Answer:
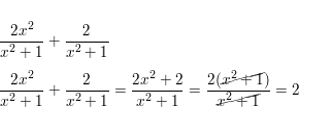
Question 5.
Find the least common multiple of 5x3 and 10x2 − 15x.
Answer:
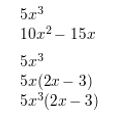
Find the sum or difference.
Question 6.
\(\frac{3}{4 x}-\frac{1}{7}\)
Answer:
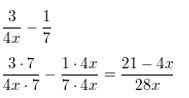
Question 7.
\(\frac{1}{3 x^{2}}+\frac{x}{9 x^{2}-12}\)
Answer:
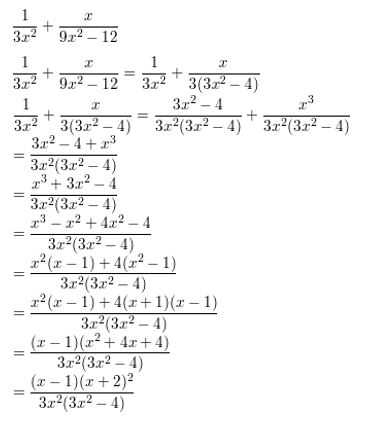
Question 8.
\(\frac{x}{x^{2}-x-12}+\frac{5}{12 x-48}\)
Answer:
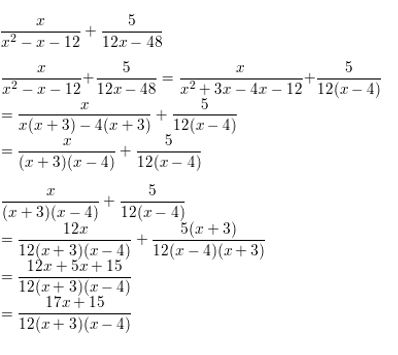
Question 9.
Rewrite g(x) = \(\frac{2 x-4}{x-3}\) in the form g(x) = \(\frac{a}{x-h}\) + k. Graph the function. Describe the graph of g as a transformation of the graph of f(x) = \(\frac{a}{x}\).
Answer:
Simplify the complex fraction.
Question 10.
\(\frac{\frac{x}{6}-\frac{x}{3}}{\frac{x}{5}-\frac{7}{10}}\)
Answer:

Question 11.
\(\frac{\frac{2}{x}-4}{\frac{2}{x}+3}\)
Answer:
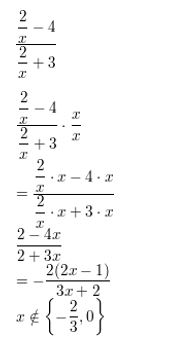
Question 12.
\(\frac{\frac{3}{x+5}}{\frac{2}{x-3}+\frac{1}{x+5}}\)
Answer:

Adding and Subtracting Rational Expressions 7.4 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A fraction that contains a fraction in its numerator or denominator is called a(n) __________.
Answer:

Question 2.
WRITING
Explain how adding and subtracting rational expressions is similar to adding and subtracting numerical fractions.
Answer: Both expressions require a common denominator before adding and subtracting the numerators.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, find the sum or difference.
Question 3.
\(\frac{15}{4 x}+\frac{5}{4 x}\)
Answer:
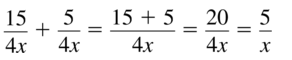
Question 4.
\(\frac{x}{16 x^{2}}-\frac{4}{16 x^{2}}\)
Answer:
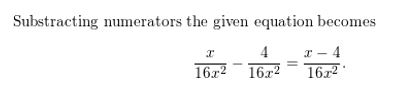
Question 5.
\(\frac{9}{x+1}-\frac{2 x}{x+1}\)
Answer:
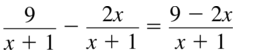
Question 6.
\(\frac{3 x^{2}}{x-8}+\frac{6 x}{x-8}\)
Answer:
Given that,
3x²/x – 8 + 6x/x – 8
= 3x² + 6x/(x – 8)
= 3x(x + 2)/x – 8.
Question 7.
\(\frac{5 x}{x+3}+\frac{15}{x+3}\)
Answer:
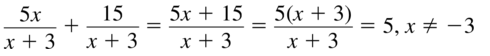
Question 8.
\(\frac{4 x^{2}}{2 x-1}-\frac{1}{2 x-1}\)
Answer:

In Exercises 9–16, find the least common multiple of the expressions.
Question 9.
3x, 3(x − 2)
Answer:
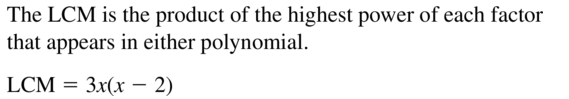
Question 10.
2x2, 4x+ 12
Answer:

Question 11.
2x, 2x(x − 5)
Answer:
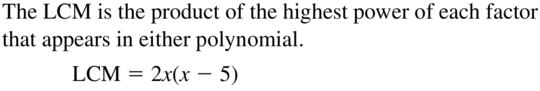
Question 12.
24x2, 8x2 − 16x
Answer:

Question 13.
x2 − 25, x − 5
Answer:
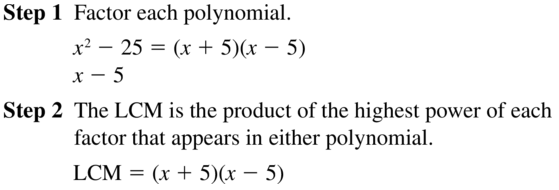
Question 14.
9x2 − 16, 3x2 + x − 4
Answer:

Question 15.
x2 + 3x − 40, x − 8
Answer:
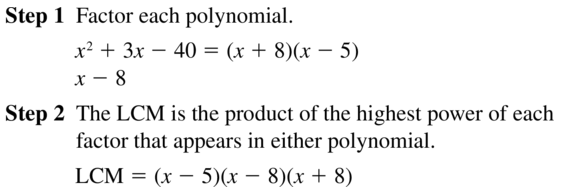
Question 16.
x2 − 2x − 63, x + 7
Answer:

ERROR ANALYSIS In Exercises 17 and 18, describe and correct the error in finding the sum.
Question 17.
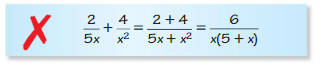
Answer:

Question 18.
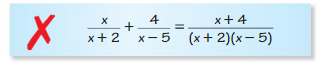
Answer:

In Exercises 19–26, find the sum or difference.
Question 19.
\(\frac{12}{5 x}-\frac{7}{6 x}\)
Answer:
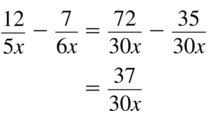
Question 20.
\(\frac{8}{3 x^{2}}+\frac{5}{4 x}\)
Answer:

Question 21.
\(\frac{3}{x+4}-\frac{1}{x+6}\)
Answer:
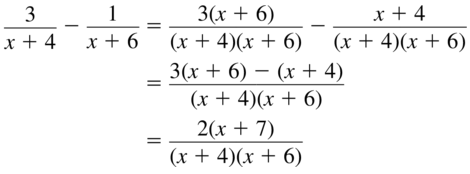
Question 22.
\(\frac{9}{x-3}+\frac{2 x}{x+1}\)
Answer:

Question 23.
\(\frac{12}{x^{2}+5 x-24}+\frac{3}{x-3}\)
Answer:
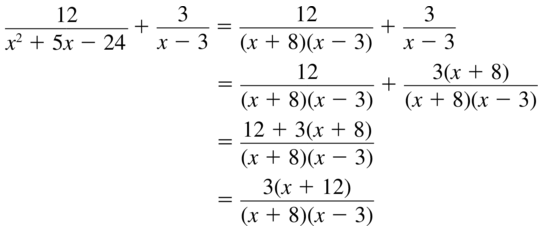
Question 24.
\(\frac{x^{2}-5}{x^{2}+5 x-14}-\frac{x+3}{x+7}\)
Answer:

Question 25.
\(\frac{x+2}{x-4}+\frac{2}{x}+\frac{5 x}{3 x-1}\)
Answer:
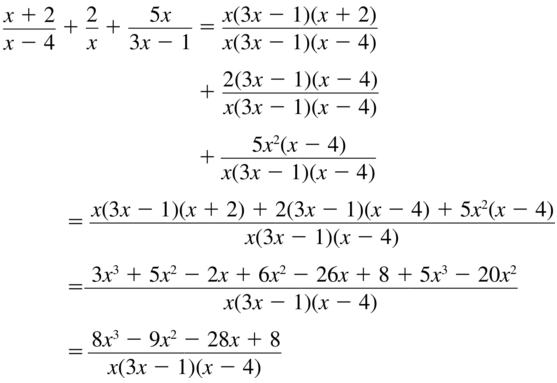
Question 26.
\(\frac{x+3}{x^{2}-25}-\frac{x-1}{x-5}+\frac{3}{x+3}\)
Answer:

REASONING In Exercises 27 and 28, tell whether the statement is always, sometimes, or never true. Explain.
Question 27.
The LCD of two rational expressions is the product of the denominators.
Answer:

Question 28.
The LCD of two rational expressions will have a degree greater than or equal to that of the denominator with the higher degree.
Answer: The LCD of two rational expressions will have a degree greater than are equal to that of the denominator with the higher degree always.
Question 29.
ANALYZING EQUATIONS
How would you begin to rewrite the function g(x) = \(\frac{4 x+1}{x+2}\) to obtain the form g(x) = a \(\frac{a}{x-h}\) + k?
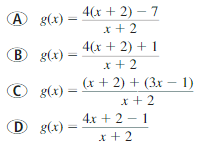
Answer:
![]()
Question 30.
ANALYZING EQUATIONS
How would you begin to rewrite the function g(x) = \(\frac{x}{x-5}\) to obtain the form g(x) = \(\frac{a}{x-h}\) + k?
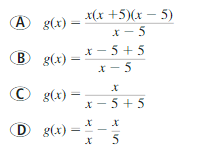
Answer:

In Exercises 31–38, rewrite the function g in the form g(x) = \(\frac{a}{x-h}\) + k. Graph the function. Describe the graph of g as a transformation of the graph of f(x) = \(\frac{a}{x}\).
Question 31.
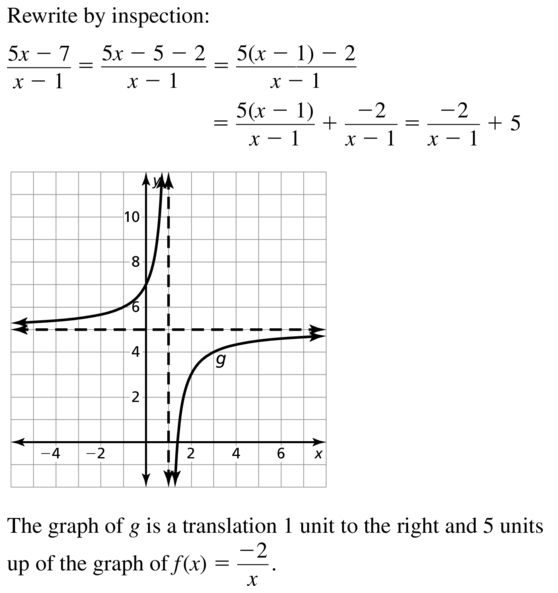
g(x) = \(\frac{5 x-7}{x-1}\)
Answer:
Question 32.
g(x) = \(\frac{6 x+4}{x+5}\)
Answer:
Question 33.
g(x) = \(\frac{12 x}{x-5}\)
Answer:

Question 34.
g(x) = \(\frac{8 x}{x+13}\)
Answer:
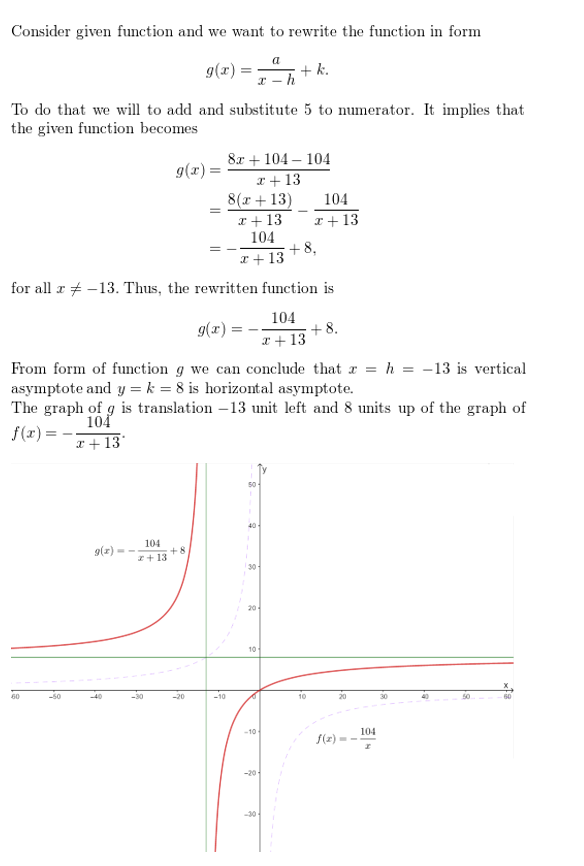
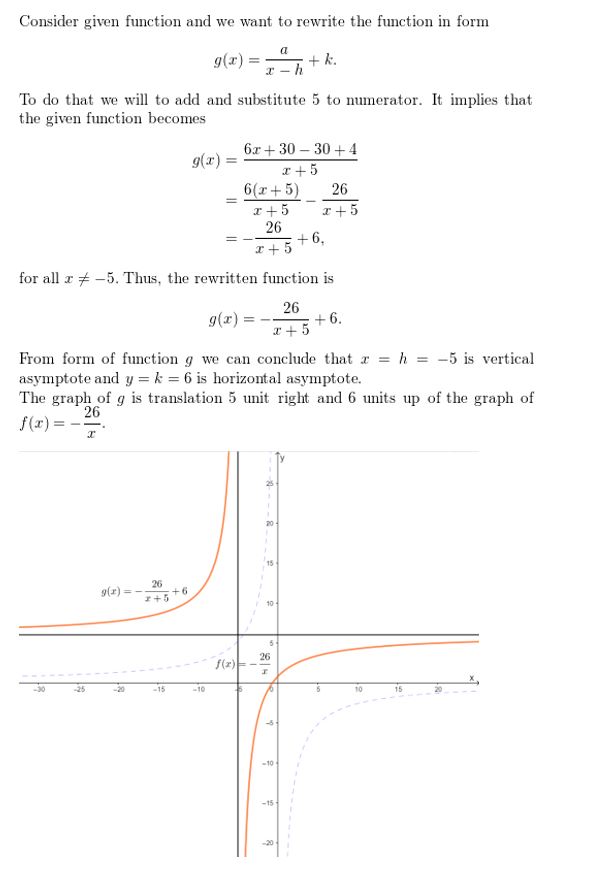
Question 35.
g(x) = \(\frac{2 x+3}{x}\)
Answer:
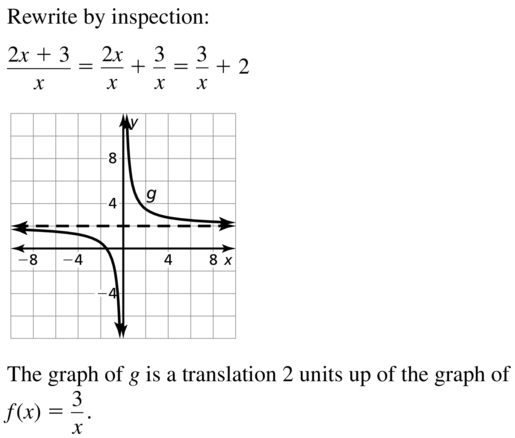
Question 36.
g(x) = \(\frac{4 x-6}{x}\)
Answer:
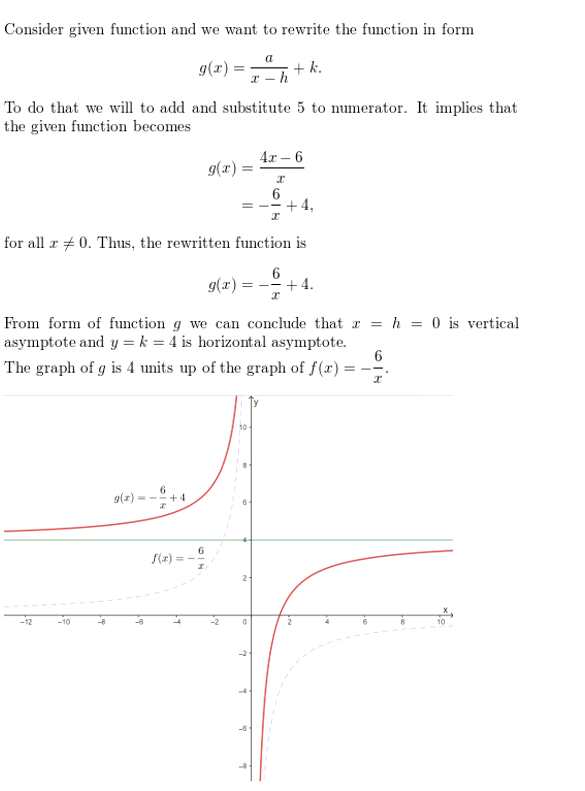
Question 37.
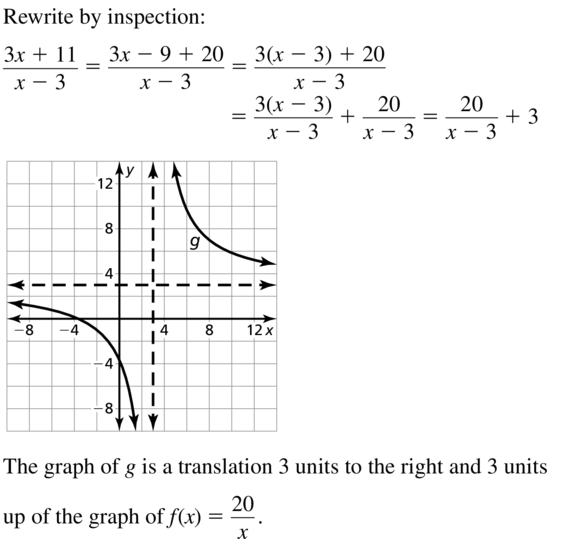
g(x) = \(\frac{3 x+11}{x-3}\)
Answer:
Question 38.
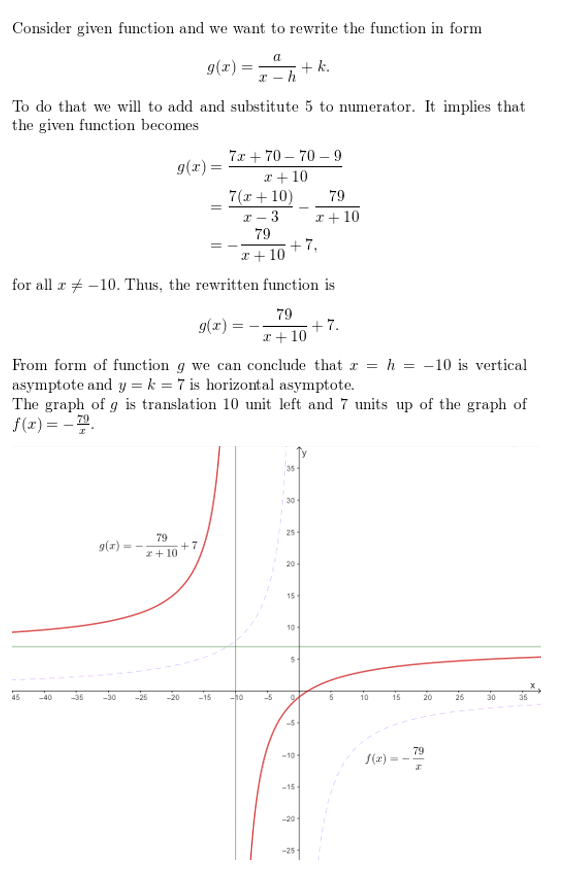
g(x) = \(\frac{7 x-9}{x+10}\)
Answer:
In Exercises 39–44, simplify the complex fraction.
Question 39.
\(\frac{\frac{x}{3}-6}{10+\frac{4}{x}}\)
Answer:
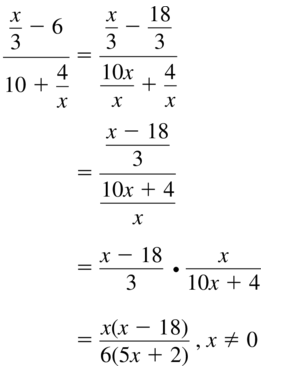
Question 40.
\(\frac{15-\frac{2}{x}}{\frac{x}{5}+4}\)
Answer:

Question 41.
\(\frac{\frac{1}{2 x-5}-\frac{7}{8 x-20}}{\frac{x}{2 x-5}}\)
Answer:

Question 42.
\(\frac{\frac{16}{x-2}}{\frac{4}{x+1}+\frac{6}{x}}\)
Answer:

Question 43.
\(\frac{\frac{1}{3 x^{2}-3}}{\frac{5}{x+1}-\frac{x+4}{x^{2}-3 x-4}}\)
Answer:
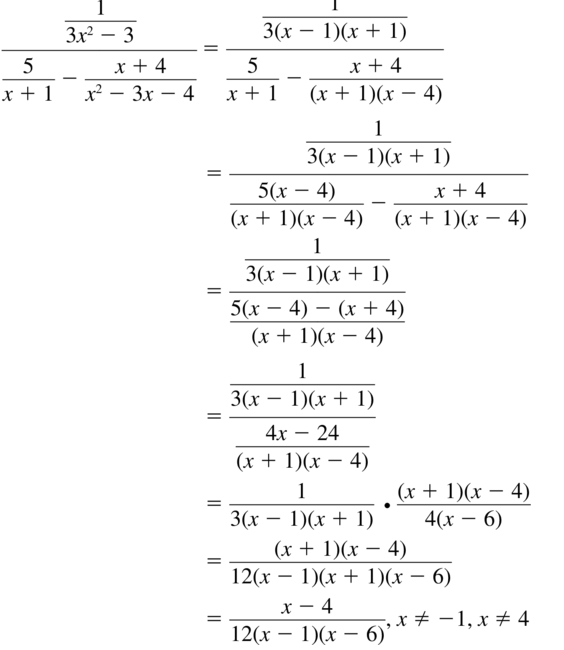
Question 44.
\(\frac{\frac{3}{x-2}-\frac{6}{x^{2}-4}}{\frac{3}{x+2}+\frac{1}{x-2}}\)
Answer:

Question 45.
PROBLEM SOLVING
The total time T (in hours) needed to fly from New York to Los Angeles and back can be modeled by the equation below, where dis the distance (in miles) each way, a is the average airplane speed (in miles per hour), and j is the average speed (in miles per hour) of the jet stream. Simplify the equation. Then find the total time it takes to fly 2468 miles when a= 510 miles per hour and j = 115 miles per hour.
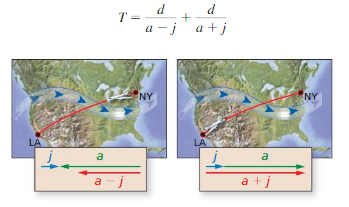
Answer:
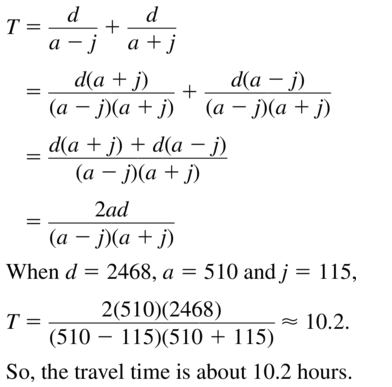
Question 46.
REWRITING A FORMULA
The total resistance Rt of two resistors in a parallel circuit with resistances R1 and R2 (in ohms) is given by the equation shown. Simplify the complex fraction. Then find the total resistance when R1 = 2000 ohms and R2 = 5600 ohms.
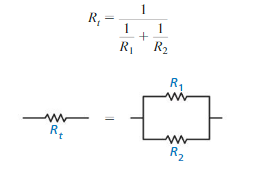
Answer:

Question 47.
PROBLEM SOLVING
You plan a trip that involves a 40-mile bus ride and a train ride. The entire trip is 140 miles. The time (in hours) the bus travels is y1 = \(\frac{40}{x}\), where x is the average speed (in miles per hour) of the bus. The time (in hours) the train travels is y2= \(\frac{100}{x+30}\).Write and simplify a model that shows the total time y of the trip.
Answer:
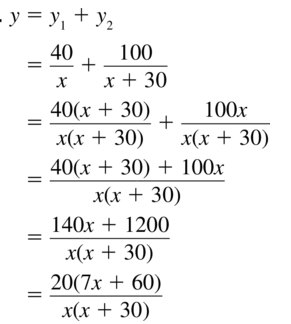
Question 48.
PROBLEM SOLVING
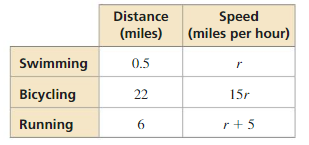
You participate in a sprint triathlon that involves swimming, bicycling, and running. The table shows the distances (in miles) and your average speed for each portion of the race.
a. Write a model in simplified form for the total time (in hours) it takes to complete the race.
b. How long does it take to complete the race if you can swim at an average speed of 2 miles per hour? Justify your answer.
Answer:
Given that,
The distance of swimming is 0.5 miles and its speed is r.
Distance of Bicycling is 22 miles and its speed is 15r.
The distance of running is 6 miles and its speed is r + 5.
The formula for the time is distance/speed.
a)
Time was taken during the swimming = 0.5/r
The taken during the bicycling = 22/15r
Time taken during the running = 6/r + 5
Total time taken
Time taken = swimming taken + bicycling taken + running taken
= 0.5/r + 22/15r + 6/r + 5
= 0.5(15r)(r+5) + 22(r)(r+5) + 6(15r)(r)/r(15r)(r+5)
= 7.5r² + 37.5r + 22(r)(r+5) + 6(15r)(r)/15r³ + 75r²
= 119.5r² + 147.5r/15r³ + 75r²
Time taken = 119.5r + 147.5/15r² + 75r.
b)
Time was taken during the swimming = 0.5/2 = 1/4
Time was taken during bicycling = 22/15r.
Time taken during Running = 6/r + 5.
Time taken = swimming taken + bicycling taken + running taken
= ¼ + 22/15r + 6/5+r
= 1/4 + 22(5 + r)+6(15r)/(15r)(5+r)
= 1/4 + 110+22r+90r/75r + 15r²
= 1/4 + 110+112r/75r + 15r²
= 440+523r+15r²/300r + 60r²
The total time taken by the participant in a sprint triathlon is 440+523r+15r²/300r + 60r².
Question 49.
MAKING AN ARGUMENT
Your friend claims that the least common multiple of two numbers is always greater than each of the numbers. Is your friend correct? Justify your answer.
Answer:
Question 50.
HOW DO YOU SEE IT?
Use the graph of the function f(x) = \(\frac{a}{x-h}\) + k to determine the values of h and k.
Answer: h is a vertical
Question 51.
REWRITING A FORMULA
You borrow P dollars to buy a car and agree to repay the loan over t years at a monthly interest rate of i (expressed as a decimal). Your monthly payment M is given by either formula below.
M = \(\frac{P i}{1-\left(\frac{1}{1+i}\right)^{12 t}}\) or M = \(\frac{P i(1+i)^{12 t}}{(1+i)^{12 t}-1}\)
a. Show that the formulas are equivalent by simplifying the first formula.
b. Find your monthly payment when you borrow$15,500 at a monthly interest rate of 0.5% and repay the loan over 4 years.
Answer:

Question 52.
THOUGHT PROVOKING
Is it possible to write two rational functions whose sum is a quadratic function? Justify your answer.
Answer:
Consider two rational functions to be added are x³-3/x-1 and 3x-x²/x-1
Add
x³-3/x-1 + 3x-x²/x-1
(x³-3 + 3x – x²)/x-1
x³ – x² + 3x – 3/x-1
x²(x-1) + 3(x-1)/x-1 = (x²+3)(x-1)/x-1
x² + 3
Thus the equation obtained is quadratic in nature.
Question 53.
USING TOOLS
Use technology to rewrite the function g(x) = \(\frac{(97.6)(0.024)+x(0.003)}{12.2+x}\) in the form g(x) = \(\frac{a}{x-h}\) + k. Describe the graph of g as a transformation of the graph of f(x) = \(\frac{a}{x}\).
Answer:

Question 54.
MATHEMATICAL CONNECTIONS
Find an expression for the surface area of the box.
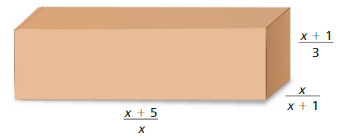
Answer:
Given that,
The length of the box = x+5/x
The width of the box = x/x+1
The height of the box = x+⅓
The formula for the surface of the box = SA = 2(lw) + 2(lh) + 2(hw)
= (2(x+5/x)(x/x+1)) + 2(x+5/x)(x+1/3) + 2(x+1/3)(x/x+1)
= (2x³ + 8x² + 52/3(x) + 10/3) /x² + x
= 2(3x³ + 12x² + 26x +5)/3x(x+1)
Therefore the surface of the box = 6x² + 24x² + 52x + 10/3x² + 3x
Question 55.
PROBLEM SOLVING
You are hired to wash the new cars at a car dealership with two other employees. You take an average of 40 minutes to wash a car (R1 = 1/40 car per minute). The second employee washes a car in x minutes. The third employee washes a car in x + 10 minutes.
a. Write expressions for the rates that each employee can wash a car.
b. Write a single expression R for the combined rate of cars washed per minute by the group.
c. Evaluate your expression in part (b) when the second employee washes a car in 35 minutes. How many cars per hour does this represent? Explain your reasoning.
Answer:

Question 56.
MODELING WITH MATHEMATICS
The amount A(in milligrams) of aspirin in a person’s bloodstream can be modeled by
A = \(\frac{391 t^{2}+0.112}{0.218 t^{4}+0.991 t^{2}+1}\)
where t is the time (in hours) after one dose is taken.
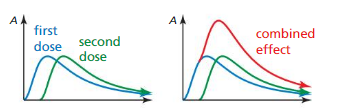
a. A second dose is taken 1 hour after the first dose. Write an equation to model the amount of the second dose in the bloodstream.
b. Write a model for the total amount of aspirin in the bloodstream after the second dose is taken.
Answer:

Question 57.
FINDING A PATTERN
Find the next two expressions in the pattern shown. Then simplify all five expressions. What value do the expressions approach?
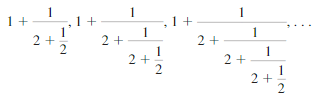
Answer:

Maintaining Mathematical Proficiency
Solve the system by graphing.
Question 58.
y = x2 + 6
y = 3x + 4
Answer:
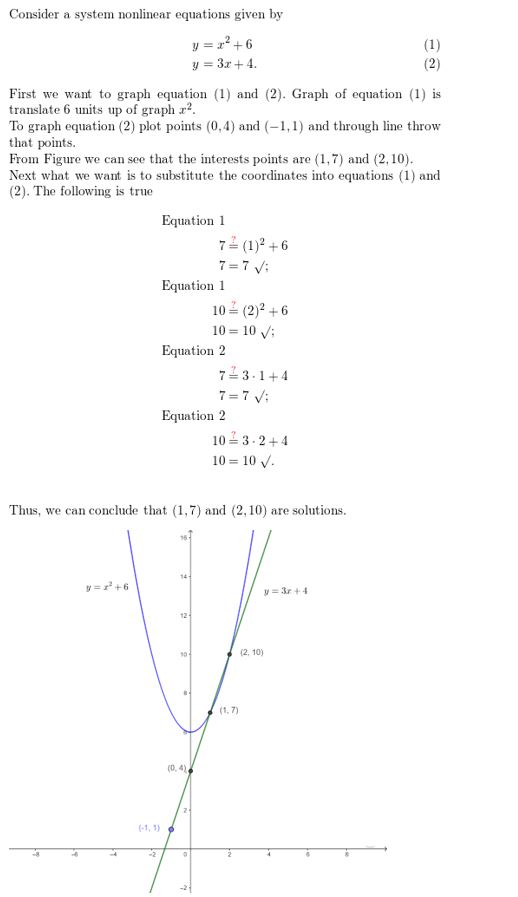
Question 59.
2x2 − 3x − y = 0
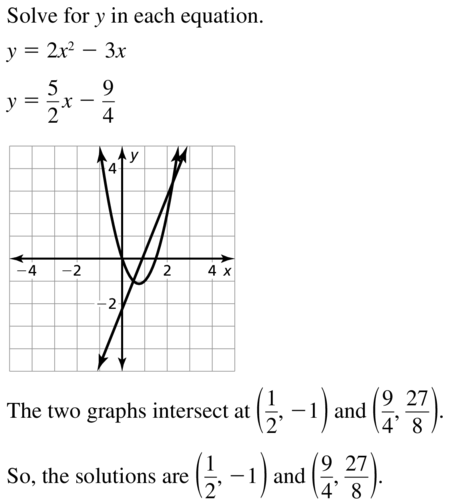
\(\frac{5}{2}\)x − y = \(\frac{9}{4}\)
Answer:
Question 60.
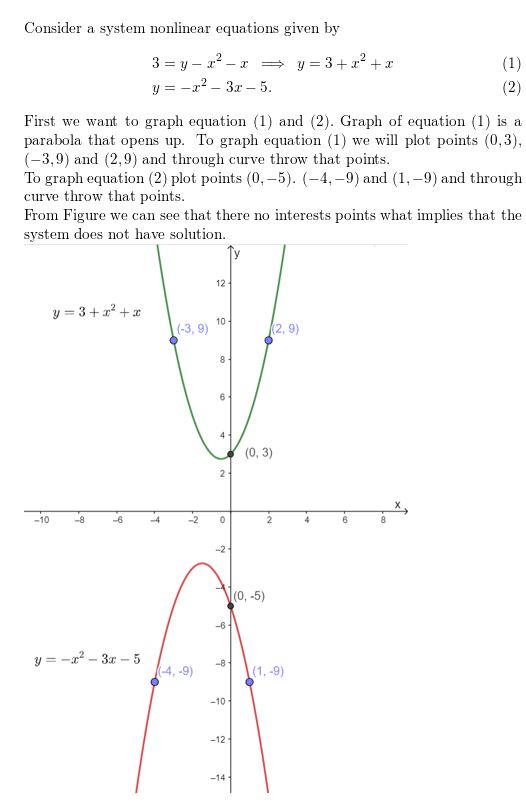
3 = y − x2 − x
y = −x2 − 3x − 5
Answer:
Question 61.
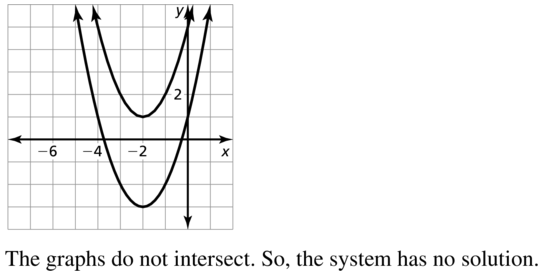
y= (x + 2)2 − 3
y = x2 + 4x + 5
Answer:
Lesson 7.5 Solving Rational Equations
Essential Question How can you solve a rational equation?
EXPLORATION 1
Solving Rational Equations
Work with a partner. Match each equation with the graph of its related system of equations. Explain your reasoning. Then use the graph to solve the equation.
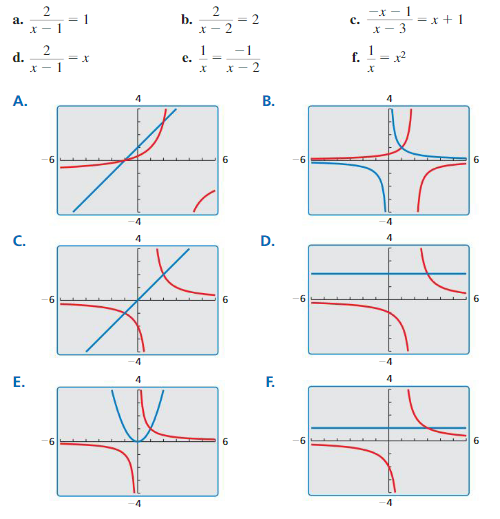
EXPLORATION 2
Solving Rational Equations
Work with a partner. Look back at the equations in Explorations 1(d) and 1(e). Suppose you want a more accurate way to solve the equations than using a graphical approach.
a. Show how you could use a numerical approach by creating a table. For instance, you might use a spreadsheet to solve the equations.

b. Show how you could use an analytical approach. For instance, you might use the method you used to solve proportions.
Communicate Your Answer
Question 3.
How can you solve a rational equation?
Answer:
To figure out the common denominator for these fractions, I’ll first need to factor that quadratic in the denominator on the right-hand side of the rational equation. This will also allow me to find the disallowed values for this equation. Factoring gives me:
x² – 6x + 8 = (x – 4)(x – 2)
Question 4.
Use the method in either Exploration 1 or 2 to solve each equation.
a. \(\frac{x+1}{x-1}=\frac{x-1}{x+1}\)
b. \(\frac{1}{x+1}=\frac{1}{x^{2}+1}\)
c. \(\frac{1}{x^{2}-1}=\frac{1}{x-1}\)
Answer:
Monitoring Progress
Solve the equation by cross multiplying. Check your solution(s).
Question 1.
\(\frac{3}{5 x}=\frac{2}{x-7}\)
Answer:

Question 2.
\(\frac{-4}{x+3}=\frac{5}{x-3}\)
Answer:

Question 3.
\(\frac{1}{2 x+5}=\frac{x}{11 x+8}\)
Answer:

Solve the equation by using the LCD. Check your solution(s).
Question 4.
\(\frac{15}{x}+\frac{4}{5}=\frac{7}{x}\)
Answer:

Question 5.
\(\frac{3 x}{x+1}-\frac{5}{2 x}=\frac{3}{2 x}\)
Answer:

Question 6.
\(\frac{4 x+1}{x+1}=\frac{12}{x^{2}-1}+3\)
Answer:

Solve the equation. Check your solution(s).
Question 7.
\(\frac{9}{x-2}+\frac{6 x}{x+2}=\frac{9 x^{2}}{x^{2}-4}\)
Answer:

Question 8.
\(\frac{7}{x-1}-5=\frac{6}{x^{2}-1}\)
Answer:

Question 9.
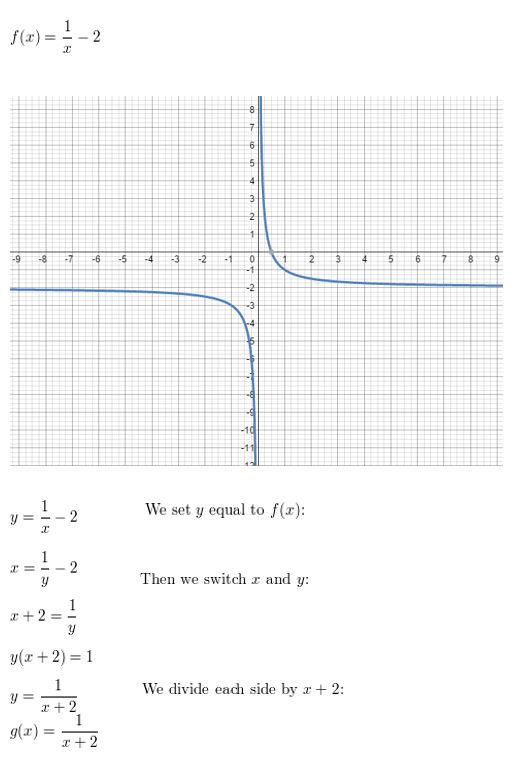
Consider the function f(x) = \(\frac{1}{x}\) − 2. Determine whether the inverse of f is a function. Then find the inverse.
Answer:
Question 10.
WHAT IF?
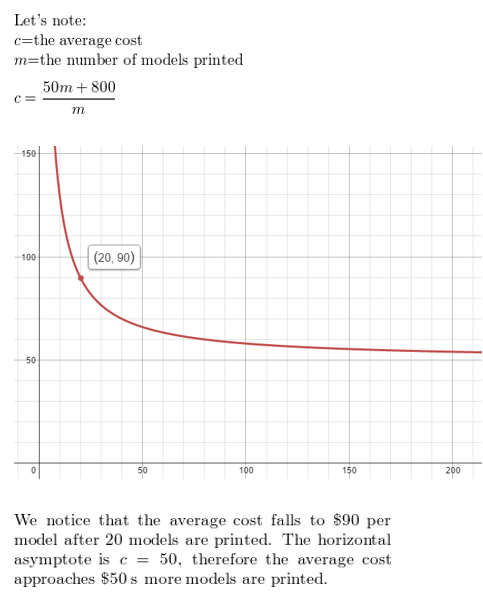
How do the answers in Example 6 change when c = \(\frac{50 m+800}{m}\)?
Answer:

Solving Rational Equations 7.5 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
When can you solve a rational equation by cross multiplying? Explain.
Answer:

Question 2.
WRITING
A student solves the equation \(\frac{4}{x-3}=\frac{x}{x-3}\) and obtains the solutions 3 and 4. Are either of these extraneous solutions? Explain.
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, solve the equation by cross multiplying. Check your solution(s).
Question 3.
\(\frac{4}{2 x}=\frac{5}{x+6}\)
Answer:

Question 4.
\(\frac{9}{3 x}=\frac{4}{x+2}\)
Answer:

Question 5.
\(\frac{6}{x-1}=\frac{9}{x+1}\)
Answer:

Question 6.
\(\frac{8}{3 x-2}=\frac{2}{x-1}\)
Answer:

Question 7.
\(\frac{x}{2 x+7}=\frac{x-5}{x-1}\)
Answer:

Question 8.
\(\frac{-2}{x-1}=\frac{x-8}{x+1}\)
Answer:

Question 9.
\(\frac{x^{2}-3}{x+2}=\frac{x-3}{2}\)
Answer:

Question 10.
\(\frac{-1}{x-3}=\frac{x-4}{x^{2}-27}\)
Answer:

Question 11.
USING EQUATIONS
So far in your volleyball practice, you have put into play 37 of the 44 serves you have attempted. Solve the equation \(\frac{90}{100}=\frac{37+x}{44+x}\) to find the number of consecutive serves you need to put into play in order to raise your serve percentage to 90%.

Answer:
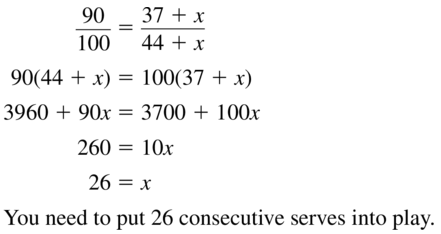
Question 12.
USING EQUATIONS
So far this baseball season, you have 12 hits out of 60 times at-bat. Solve the equation 0.360 = \(\frac{12+x}{60+x}\) to find the number of consecutive hits you need to raise your batting average to 0.360.
Answer:

Question 13.
MODELING WITH MATHEMATICS
Brass is an alloy composed of 55% copper and 45% zinc by weight. You have 25 ounces of copper. How many ounces of zinc do you need to make brass?
Answer:
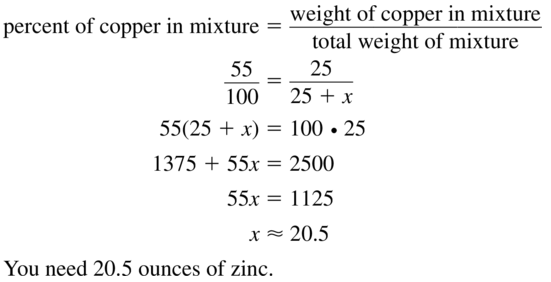
Question 14.
MODELING WITH MATHEMATICS
You have 0.2 liter of an acid solution whose acid concentration is 16 moles per liter. You want to dilute the solution with water so that its acid concentration is only 12 moles per liter. Use the given model to determine how many liters of water you should add to the solution.

Answer:

USING STRUCTURE In Exercises 15–18, identify the LCD of the rational expressions in the equation.
Question 15.
\(\frac{x}{x+3}+\frac{1}{x}=\frac{3}{x}\)
Answer:
![]()
Question 16.
\(\frac{5 x}{x-1}-\frac{7}{x}=\frac{9}{x}\)
Answer:

Question 17.
\(\frac{2}{x+1}+\frac{x}{x+4}=\frac{1}{2}\)
Answer:
![]()
Question 18.
\(\frac{4}{x+9}+\frac{3 x}{2 x-1}=\frac{10}{3}\)
Answer:

In Exercises 19–30, solvethe equation by using the LCD. Check your solution(s).
Question 19.
\(\frac{3}{2}+\frac{1}{x}\) = 2
Answer:

Question 20.
\(\frac{2}{3 x}+\frac{1}{6}=\frac{4}{3 x}\)
Answer:

Question 21.
\(\frac{x-3}{x-4}\) + 4 = \(\frac{3 x}{x}\)
Answer:

Question 22.
\(\frac{2}{x-3}+\frac{1}{x}=\frac{x-1}{x-3}\)
Answer:

Question 23.
\(\frac{6 x}{x+4}\) + 4 = \(\frac{2 x+2}{x-1}\)
Answer:

Question 24.
\(\frac{10}{x}\) + 3 = \(\frac{x+9}{x-4}\)
Answer:

Question 25.
\(\frac{18}{x^{2}-3 x}-\frac{6}{x-3}=\frac{5}{x}\)
Answer:

Question 26.
\(\frac{10}{x^{2}-2 x}+\frac{4}{x}=\frac{5}{x-2}\)
Answer:

Question 27.
\(\frac{x+1}{x+6}+\frac{1}{x}=\frac{2 x+1}{x+6}\)
Answer:

Question 28.
\(\frac{x+3}{x-3}+\frac{x}{x-5}=\frac{x+5}{x-5}\)
Answer:

Question 29.
\(\frac{5}{x}\) – 2 = \(\frac{2}{x+3}\)
Answer:
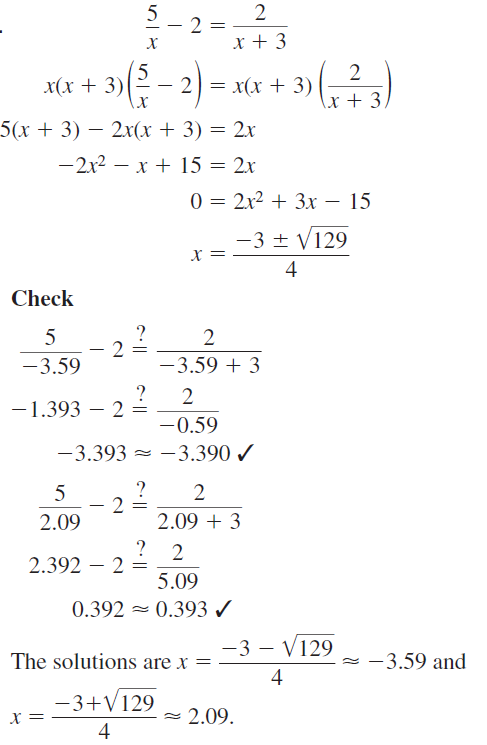
Question 30.
\(\frac{5}{x^{2}+x-6}\) = 2 + \(\frac{x-3}{x-2}\)
Answer:
Given that,
5/x² + 6 = 2 + x-3/x-2
5(x-2) = 2x² + 2x -12 + x³ + x² – 6x – 3x² + 3x + 18.
5x – 10 = x³ – x + 6
5x – 10 – x³ + x – 6 = 0
-x³ + 4x – 16 = 0
ERROR ANALYSIS In Exercises 31 and 32, describe and correct the error in the first step of solving the equation.
Question 31.

Answer:
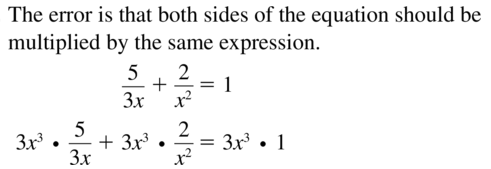
Question 32.
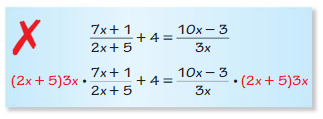
Answer:

Question 33.
PROBLEM SOLVING
You can paint a room in 8 hours. Working together, you and your friend can paint the room in just 5 hours.
a. Let t be the time (in hours) your friend would take to paint the room when working alone. Copy and complete the table.
(Hint: (Work done) = (Work rate) × (Time))
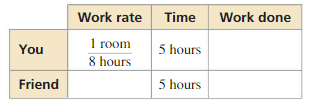
b. Explain what the sum of the expressions represents in the last column. Write and solve an equation to find how long your friend would take to paint the room when working alone.
Answer:
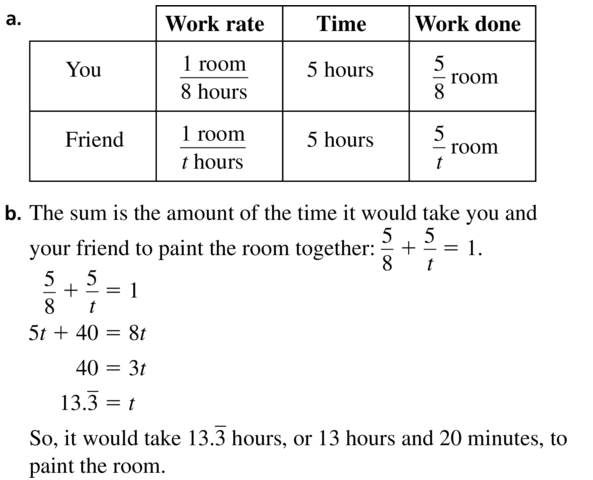
Question 34.
PROBLEM SOLVING
You can clean a park in 2 hours. Working together, you and your friend can clean the park in just 1.2 hours.a. Let t be the time (in hours) your friend would take to clean the park when working alone. Copy and complete the table.
(Hint: (Work done) = (Work rate) × (Time))
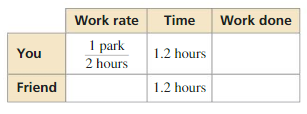
b. Explain what the sum of the expressions represents in the last column. Write and solve an equation to find how long your friend would take to clean the park when working alone.
Answer:

Question 35.
OPEN-ENDED
Give an example of a rational equation that you would solve using cross multiplication and one that you would solve using the LCD. Explain your reasoning.
Answer:
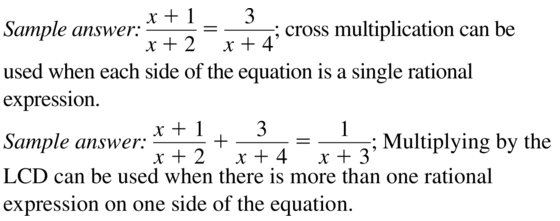
Question 36.
OPEN-ENDED
Describe a real-life situation that can be modeled by a rational equation. Justify your answer.
Answer:
In Exercises 37–44, determine whether the inverse of f is a function. Then find the inverse.
Question 37.
f(x) = \(\frac{2}{x-4}\)
Answer:
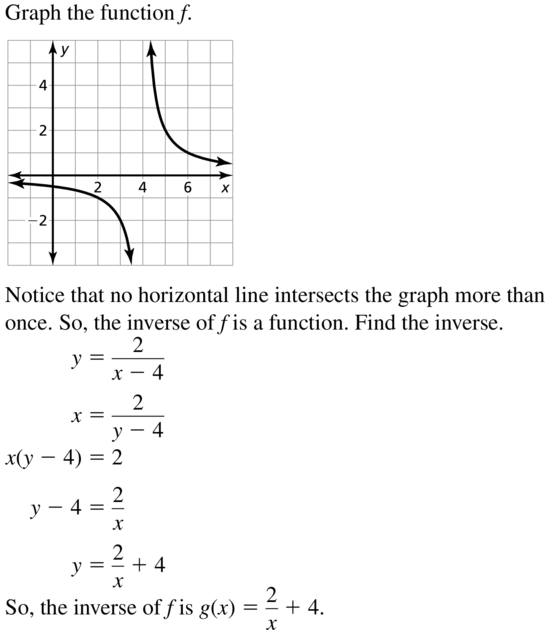
Question 38.
f(x) = \(\frac{7}{x+6}\)
Answer:
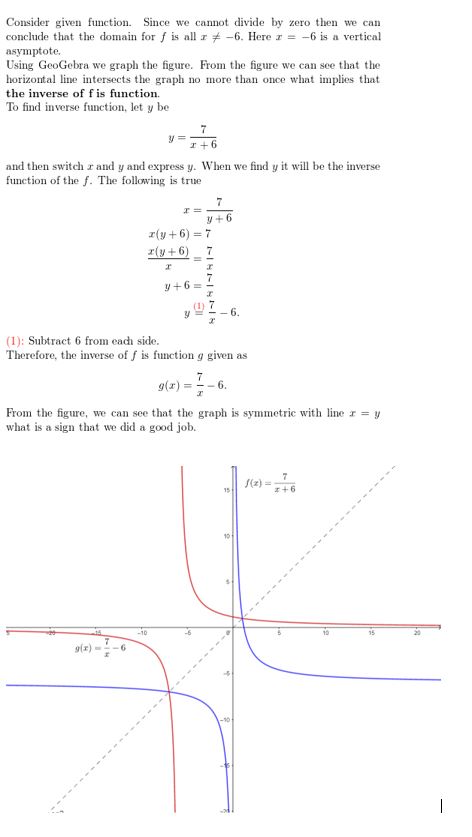
Question 39.
f(x) = \(\frac{3}{x}\) – 2
Answer:
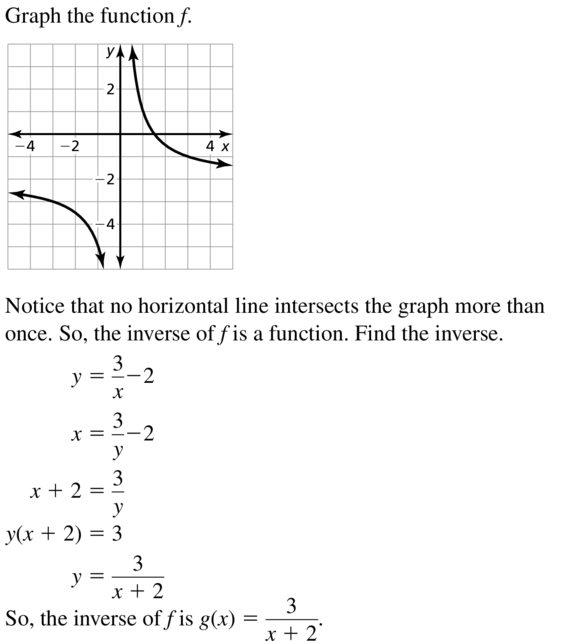
Question 40.
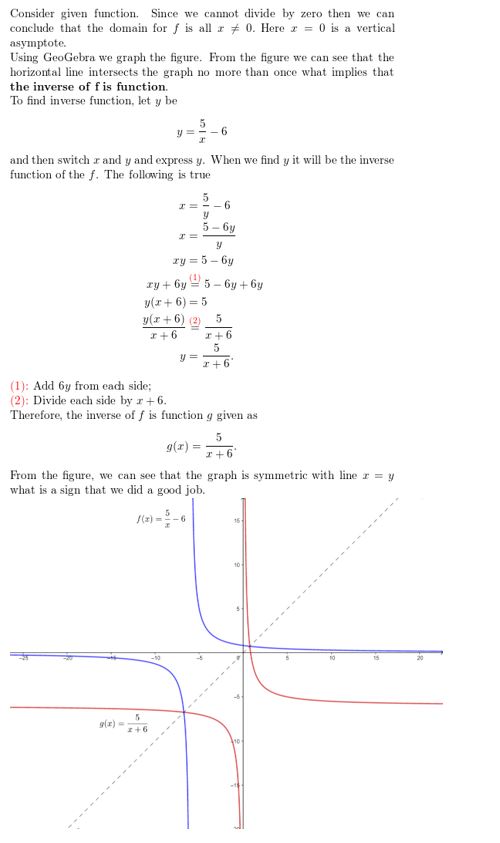
f(x) = \(\frac{5}{x}\) – 6
Answer:
Question 41.
f(x) = \(\frac{4}{11-2 x}\)
Answer:
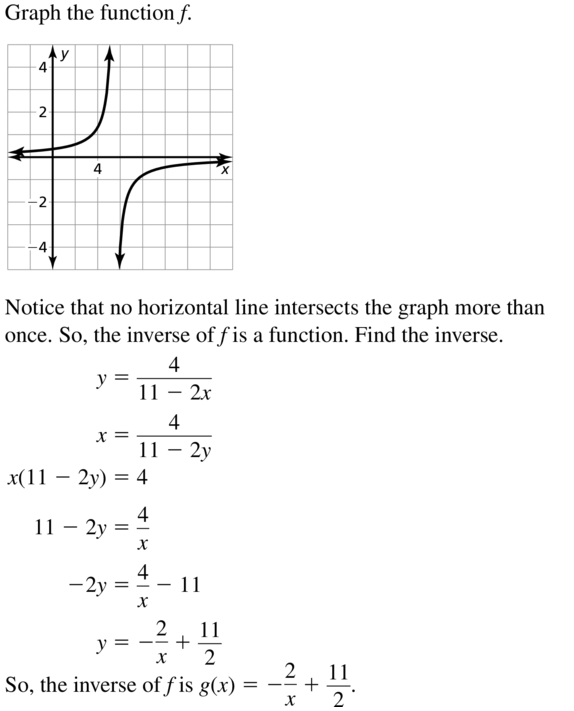
Question 42.
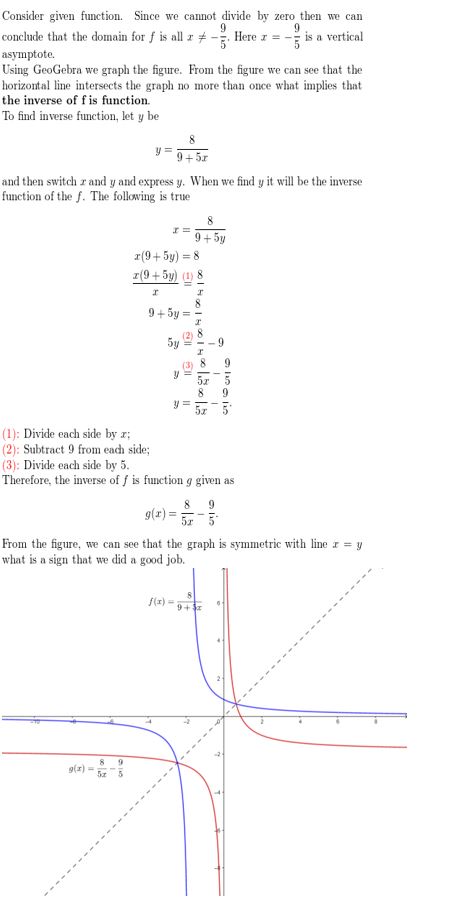
f(x) = \(\frac{8}{9+5 x}\)
Answer:
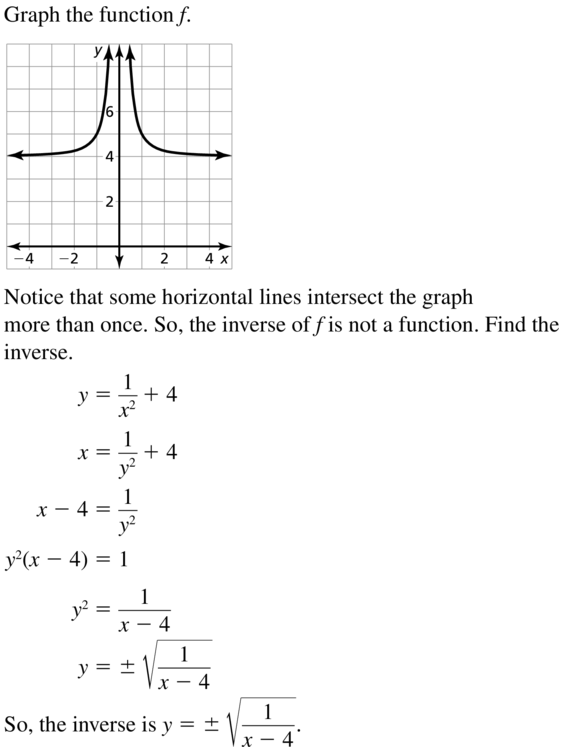
Question 43.
f(x) = \(\frac{1}{x^{2}}\) + 4
Answer:
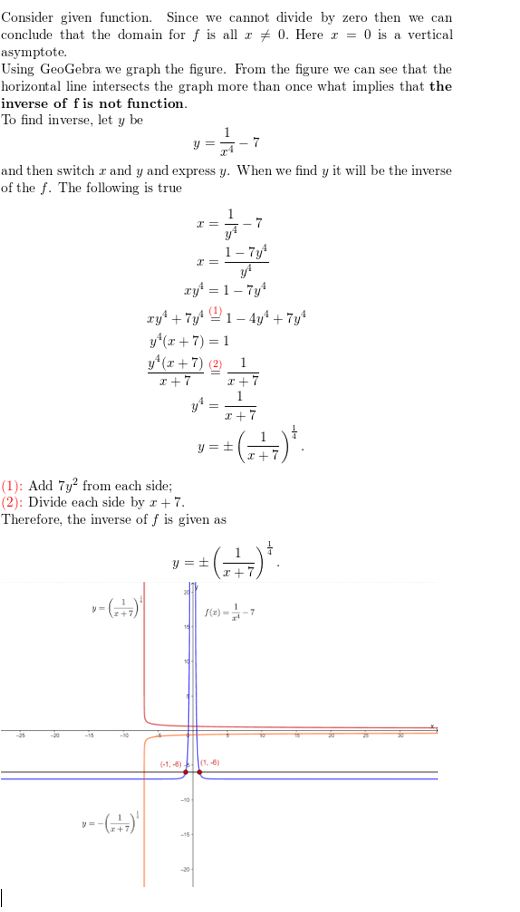
Question 44.
f(x) = \(\frac{1}{x^{4}}\) – 7
Answer:
Question 45.
PROBLEM SOLVING
The cost of fueling your car for 1 year can be calculated using this equation:

Last year you drove9000 miles, paid $3.24 per gallon of gasoline, and spent a total of $1389 on gasoline. Find the fuel-efficiency rate of your car by (a) solving an equation, and (b) using the inverse of the function.

Answer:

Question 46.
PROBLEM SOLVING
The recommended percent p (in decimal form) of nitrogen (by volume) in the air that a diver breathes is given by p = \(\frac{105.07}{d+33}\), where d is the depth (in feet) of the diver. Find the depth when the air contains 47% recommended nitrogen by (a) solving an equation, and (b) using the inverse of the function.
Answer:

USING TOOLS In Exercises 47–50, use a graphing calculator to solve the equation f(x) = g(x).
Question 47.
f(x) = \(\frac{2}{3}\)x, g(x) = x
Answer:
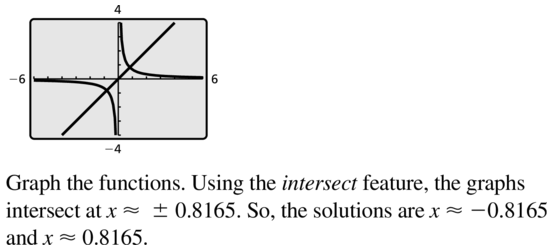
Question 48.
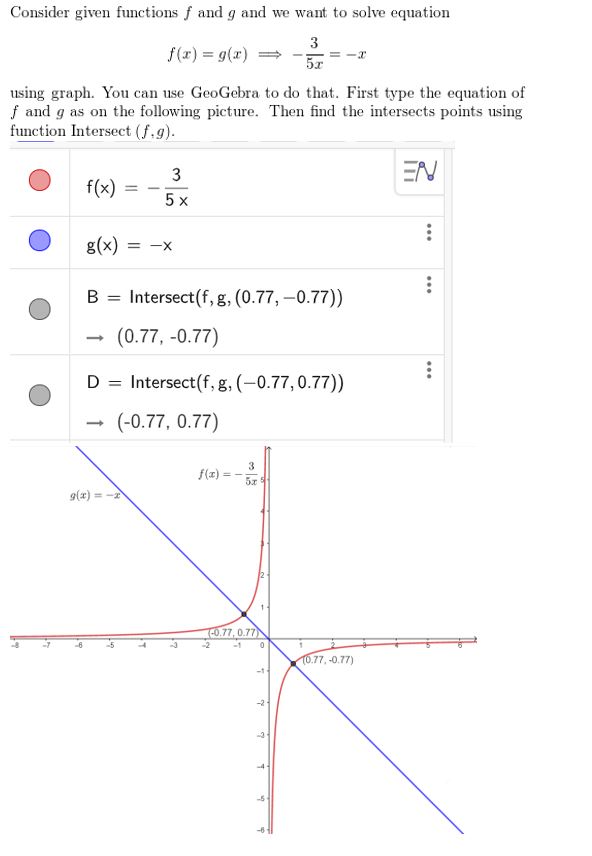
f(x) = −\(\frac{3}{5x}\), g(x) = −x
Answer:
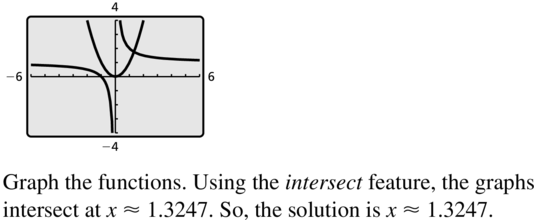
Question 49.
f(x) = \(\frac{1}{x}\) + 1, g(x) = x2
Answer:
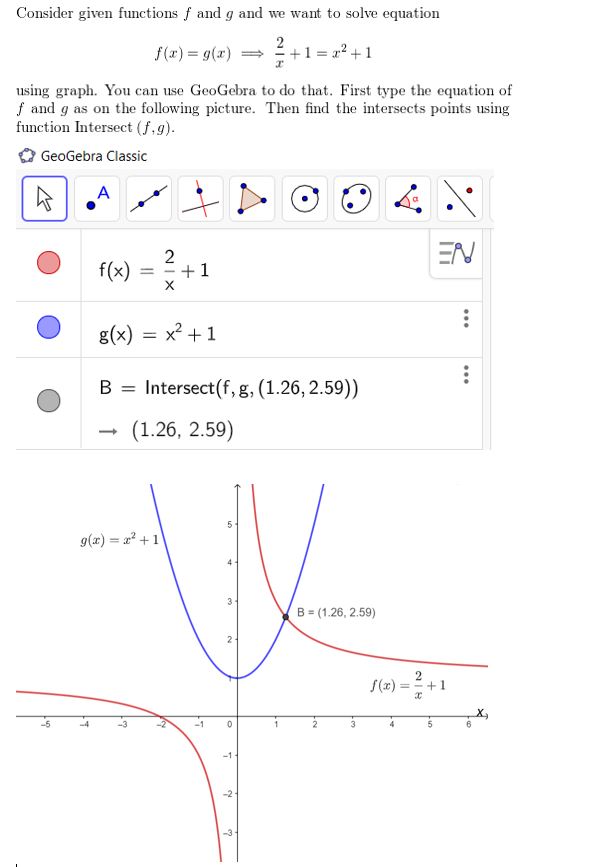
Question 50.
f(x) = \(\frac{2}{x}\) + 1, g(x) = x2 + 1
Answer:
Question 51.
MATHEMATICAL CONNECTIONS
Golden rectangles are rectangles for which the ratio of the width w to the length ℓ is equal to the ratio of ℓ to ℓ+w. The ratio of the length to the width for these rectangles is called the golden ratio. Find the value of the golden ratio using a rectangle with a width of 1 unit.
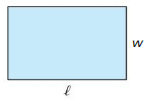
Answer:

Question 52.
HOW DO YOU SEE IT?
Use the graph to identify the solution(s) of the rational equation \(\frac{4(x-1)}{x-1}=\frac{2 x-2}{x+1}\). Explain your reasoning.
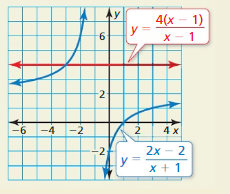
Answer:

USING STRUCTURE In Exercises 53 and 54, find the inverse of the function. (Hint: Try rewriting the function by using either inspection or long division.)
Question 53.
f(x) = \(\frac{3 x+1}{x-4}\)
Answer:
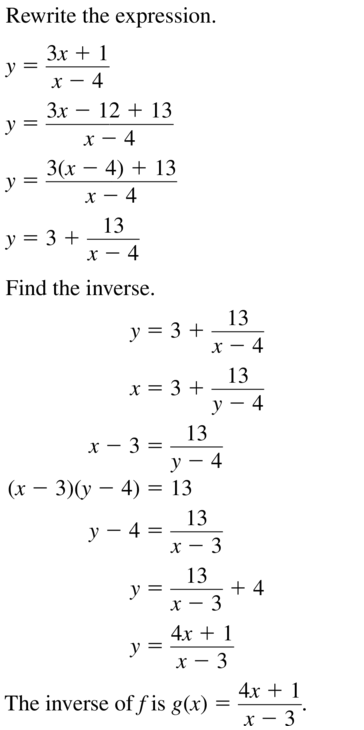
Question 54.
f(x) = \(\frac{4 x-7}{2 x+3}\)
Answer:

Question 55.
ABSTRACT REASONING
Find the inverse of rational functions of the form y = \(\frac{a x+b}{c x+d}\). Verify your answer is correct by using it to find the inverses in Exercises 53 and 54.
Answer:
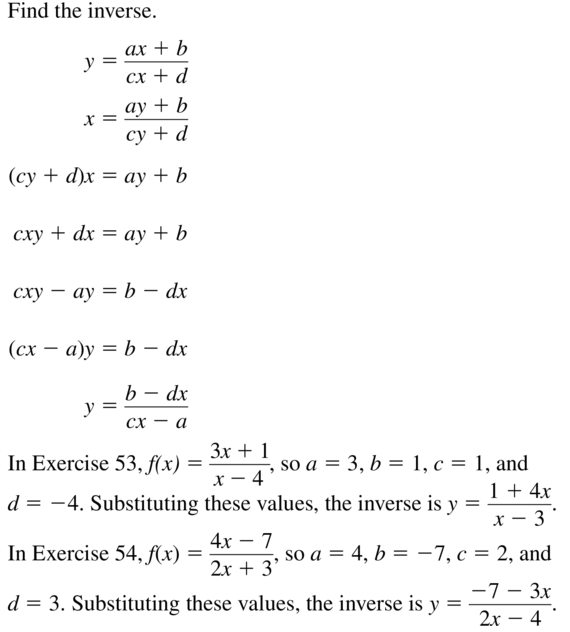
Question 56.
THOUGHT PROVOKING
Is it possible to write a rational equation that has the following number of solutions? Justify your answers.
a. no solution
b. exactly one solution
c. exactly two solutions
d. infinitely many solutions
Answer:

Question 57.
CRITICAL THINKING
Let a be a nonzero real number. Tell whether each statement is always true, sometimes true, or never true. Explain your reasoning.
a. For the equation \(\frac{1}{x-a}=\frac{x}{x-a}\), x=a is an extraneous solution.
b. The equation \(\frac{3}{x-a}=\frac{x}{x-a}\) has exactly one solution.
c. The equation \(\frac{1}{x-a}=\frac{2}{x+a}+\frac{2 a}{x^{2}-a^{2}}\) has no solution.
Answer:

Question 58.
MAKING AN ARGUMENT
Your friend claims that it is not possible for a rational equation of the form \(\frac{x-a}{b}=\frac{x-c}{d}\), where b≠ 0 and d≠ 0, to have extraneous solutions. Is your friend correct? Explain your reasoning.
Answer:

Maintaining Mathematical Proficiency
Is the domain discrete or continuous? Explain. Graph the function using its domain.
Question 59.
The linear function y = 0.25x represents the amount of money y (in dollars) of x quarters in your pocket. You have a maximum of eight quarters in your pocket.
Answer:

Question 60.
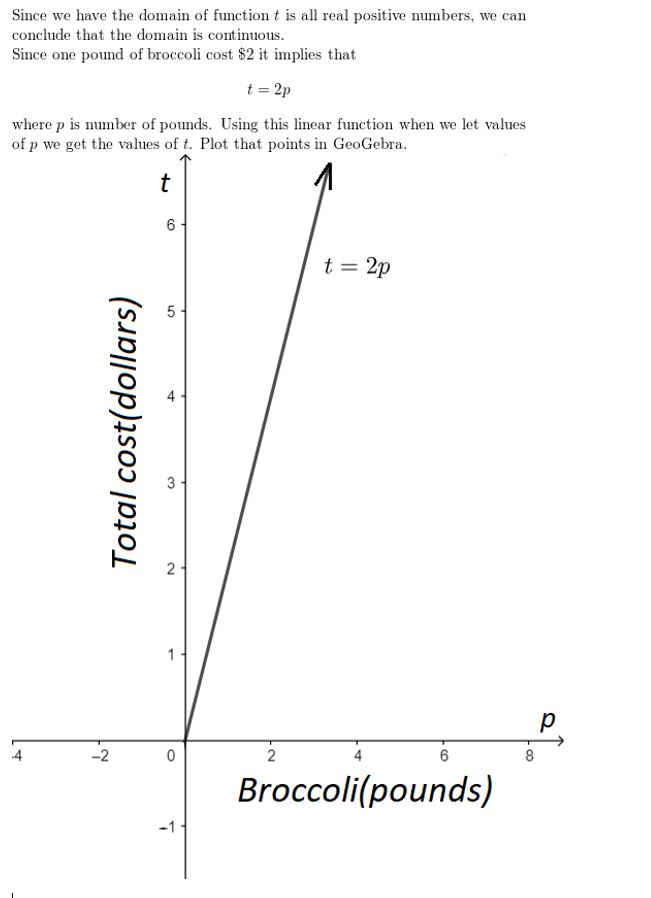
A store sells broccoli for $2 per pound. The total cost t of the broccoli is a function of the number of pounds p you buy.
Answer:
Evaluate the function for the given value of x.
Question 61.
f(x) = x3 − 2x + 7; x = −2
Answer:
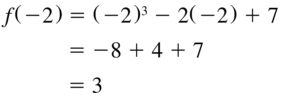
Question 62.
g(x) = −2x4 + 7x3 + x − 2; x = 3
Answer:
g(x) = −2x4 + 7x3 + x − 2; x = 3
g(3) = −2(3)4 + 7(3)3 + 3 − 2
g(3) = -2(81) + 7(27) + 1
g(3) = -162 + 189 + 1
g(3) = 28
Question 63.
h(x) = −x3 + 3x2 + 5x; x = 3
Answer:
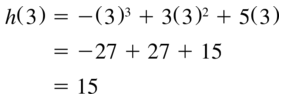
Question 64.
k(x) = −2x3 − 4x2 + 12x − 5; x = −5
Answer:
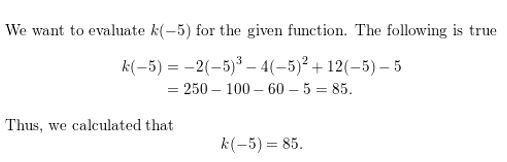
Rational Functions Performance Task: Circuit Design
7.3–7.5 What Did You Learn?
Core Vocabulary
Core Concepts
Section 7.3
Simplifying Rational Expressions, p. 376
Multiplying Rational Expressions, p. 377
Dividing Rational Expressions, p. 378
Section 7.4
Adding or Subtracting with Like Denominators, p. 384
Adding or Subtracting with Unlike Denominators, p. 384
Simplifying Complex Fractions, p. 387
Section 7.5
Solving Rational Equations by Cross Multiplying, p. 392
Solving Rational Equations by Using the Least Common Denominator, p. 393
Using Inverses of Functions, p. 395
Mathematical Practices
Question 1.
In Exercise 37 on page 381, what type of equation did you expect to get as your solution? Explain why this type of equation is appropriate in the context of this situation.
Answer:
Question 2.
Write a simpler problem that is similar to Exercise 44 on page 382. Describe how to use the simpler problem to gain insight into the solution of the more complicated problem in Exercise 44.
Answer:
Question 3.
In Exercise 57 on page 390, what conjecture did you make about the value the given expressions were approaching? What logical progression led you to determine whether your conjecture was correct?
Answer:
Question 4.
Compare the methods for solving Exercise 45 on page 397. Be sure to discuss the similarities and differences between the methods as precisely as possible.
Answer:
Performance Task: Circuit Design
A thermistor is a resistor whose resistance varies with temperature. Thermistors are an engineer’s dream because they are inexpensive, small, rugged, and accurate. The one problem with thermistors is their responses to temperature are not linear. How would you design a circuit that corrects this problem?
To explore the answers to these questions and more, go to BigIdeasMath.com.

Rational Functions Chapter Review
7.1 Inverse Variation (pp. 359–364)
Tell whether x and y show direct variation, inverse variation, or neither.
Question 1.
xy = 5
Answer:
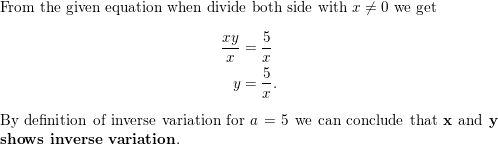
Question 2.
5y = 6x
Answer:

Question 3.
15 = \(\frac{x}{y}\)
Answer:
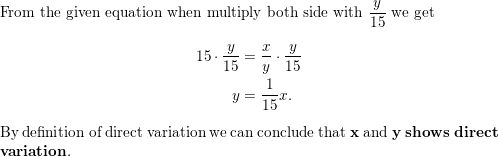
Question 4.
y − 3 = 2x
Answer:
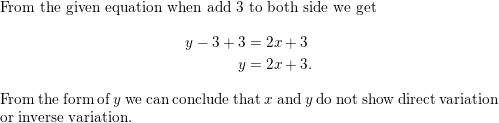
Question 5.
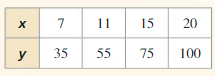
Answer:

Question 6.
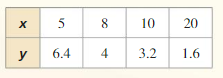
Answer:

The variables x and y vary inversely. Use the given values to write an equation relating x and y. Then find y when x = -3.
Question 7.
x = 1, y = 5
Answer:
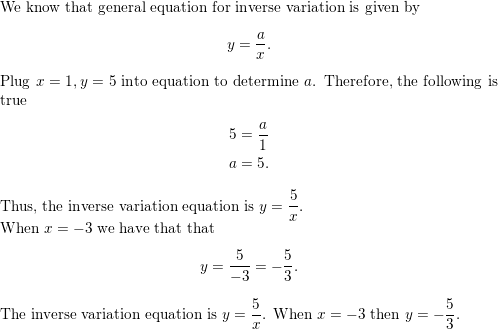
Question 8.
x = −4, y =−6
Answer:
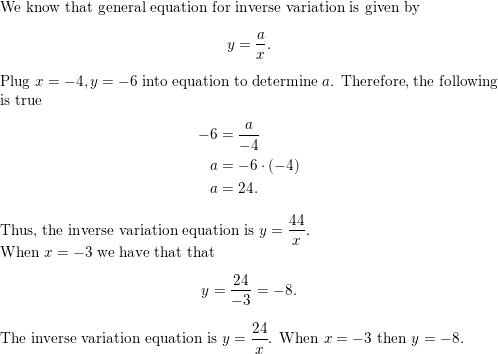
Question 9.
x = \(\frac{5}{2}\),y = 18
Answer:

Question 10.
x = −12, y = \(\frac{2}{3}\)
Answer:
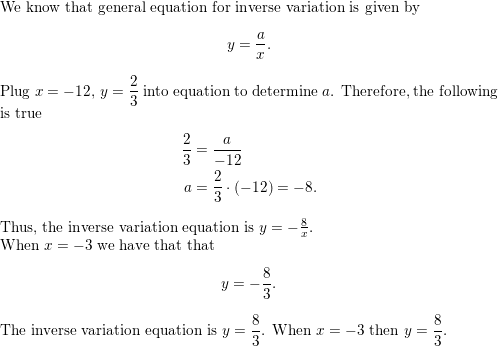
7.2 Graphing Rational Functions (pp. 365–372)
Graph the function. State the domain and range.
Question 11.
y = \(\frac{4}{x-3}\)
Answer:
Question 12.
y = \(\frac{1}{x+5}\) + 2
Answer:
Question 13.
f(x) = \(\frac{3 x-2}{x-4}\)
Answer:
7.3 Multiplying and Dividing Rational Expressions (pp. 375–382)
Find the product or quotient.
Question 14.
\(\frac{80 x^{4}}{y^{3}} \cdot \frac{x y}{5 x^{2}}\)
Answer:
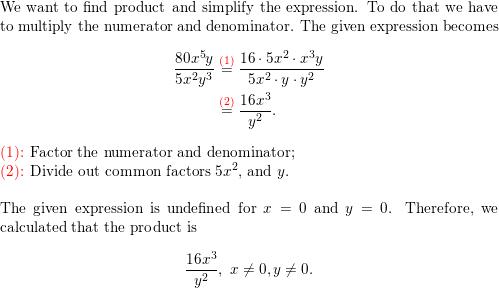
Question 15.
\(\frac{x-3}{2 x-8} \cdot \frac{6 x^{2}-96}{x^{2}-9}\)
Answer:

Question 16.
\(\frac{16 x^{2}-8 x+1}{x^{3}-7 x^{2}+12 x} \div \frac{20 x^{2}-5 x}{15 x^{3}}\)
Answer:

Question 17.
\(\frac{x^{2}-13 x+40}{x^{2}-2 x-15}\) ÷ (x2 – 5x – 24)
Answer:
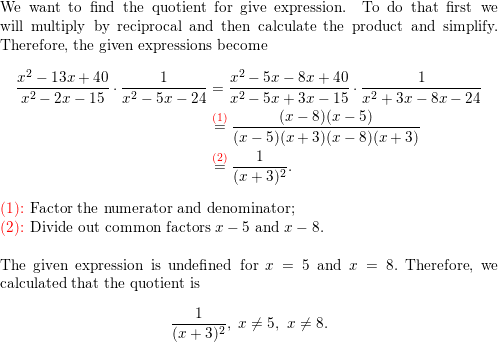
7.4 Adding and Subtracting Rational Expressions (pp. 383–390)
Find the sum or difference.
Question 18.
\(\frac{5}{6(x+3)}+\frac{x+4}{2 x}\)
Answer:
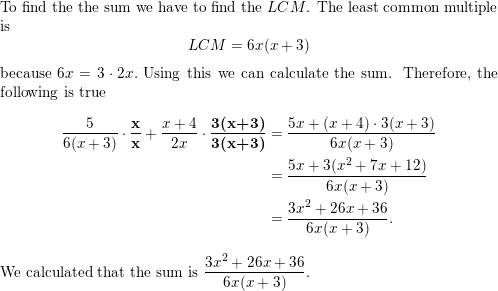
Question 19.
\(\frac{5 x}{x+8}+\frac{4 x-9}{x^{2}+5 x-24}\)
Answer:

Question 20.
\(\frac{x+2}{x^{2}+4 x+3}-\frac{5 x}{x^{2}-9}\)
Answer:

Rewrite the function in the form g(x) = \(\frac{a}{x-h}\) h + k. Graph the function. Describe the graph of gas a transformation of the graph of f(x) = \(\frac{a}{x}\).
Question 21.
g(x) = \(\frac{5 x+1}{x-3}\)
Answer:
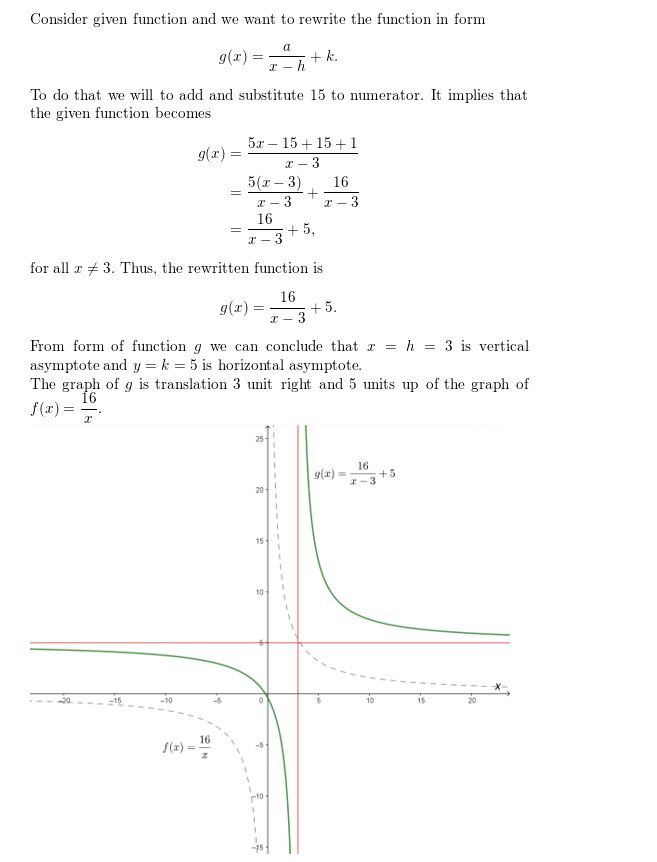
Question 22.
g(x) = \(\frac{4 x+2}{x+7}\)
Answer:
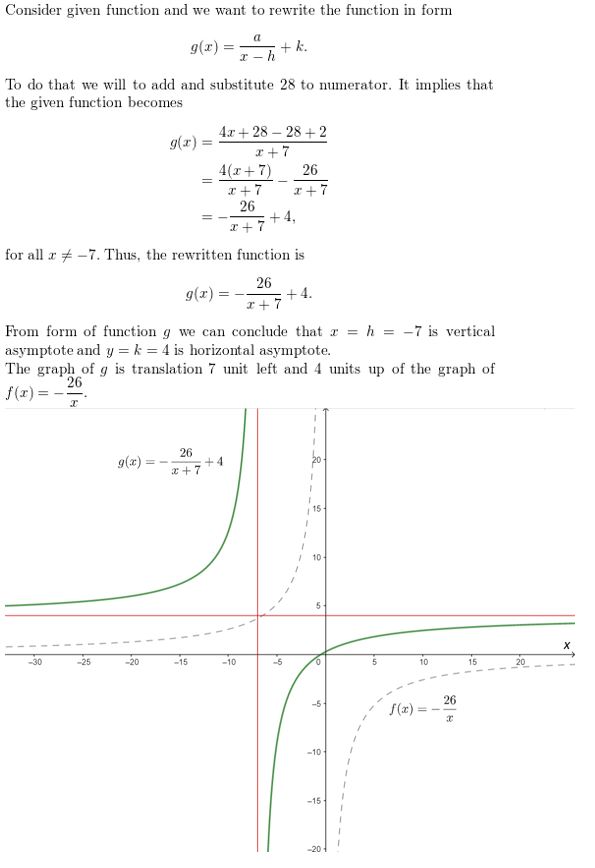
Question 23.
g(x) = \(\frac{9 x-10}{x-1}\)
Answer:
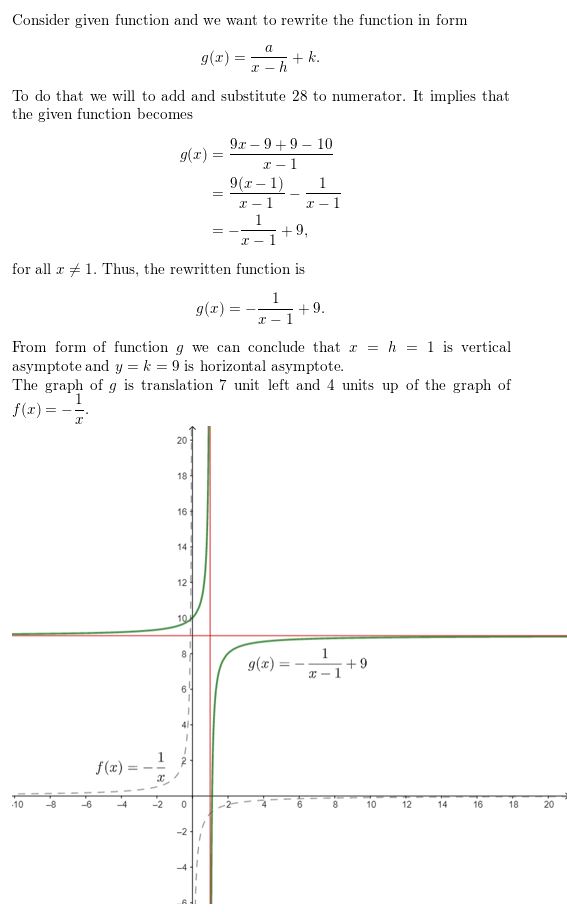
Question 24.
Let f be the focal length of a thin camera lens, p be the distance between the lens and an object being photographed, and q be the distance between the lens and the film. For the photograph to be in focus, the variables should satisfy the lens equation to the right. Simplify the complex fraction.
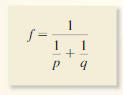
Answer:
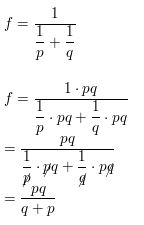
7.5 Solving Rational Equations (pp. 391–398)
Solve the equation. Check your solution(s).
Question 25.
\(\frac{5}{x}=\frac{7}{x+2}\)
Answer:
\(\frac{5}{x}=\frac{7}{x+2}\)
5(x + 2) = 7x
5x + 10 = 7x
7x – 5x = 10
2x = 10
x = 10/2
x = 5
Question 26.
\(\frac{8(x-1)}{x^{2}-4}=\frac{4}{x+2}\)
Answer:
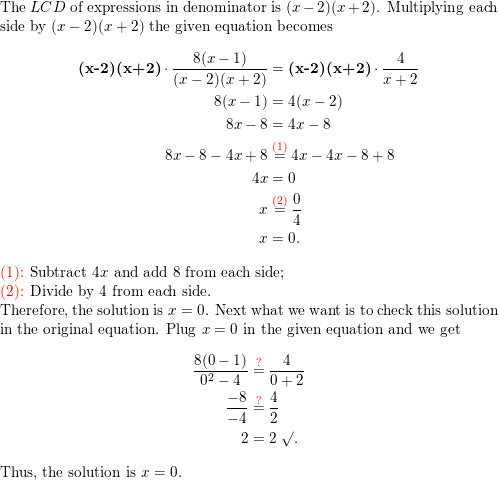
Question 27.
\(\frac{2(x+7)}{x+4}\) – 2 = \(\frac{2 x+20}{2 x+8}\)
Answer:
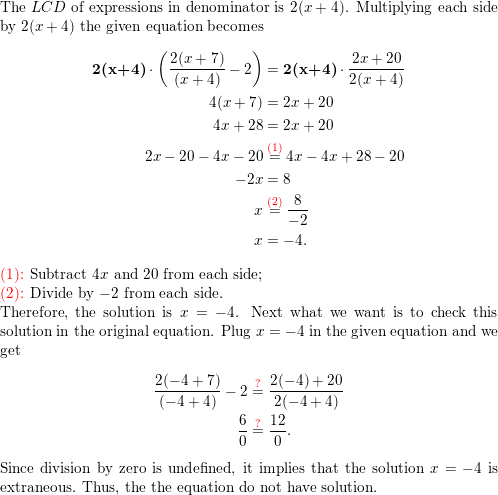
Determine whether the inverse of f is a function. Then find the inverse.
Question 28.
f(x) = \(\frac{3}{x+6}\)
Answer:
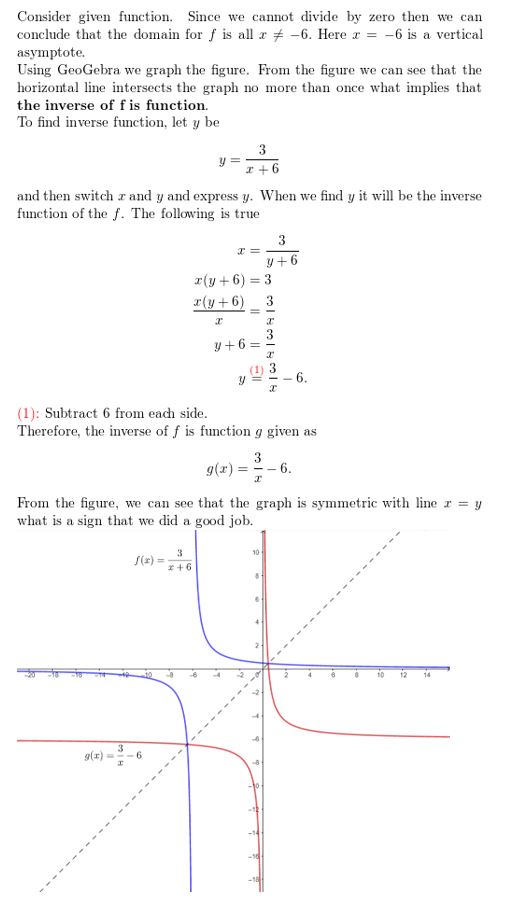
Question 29.
f(x) = \(\frac{10}{x-7}\)
Answer:
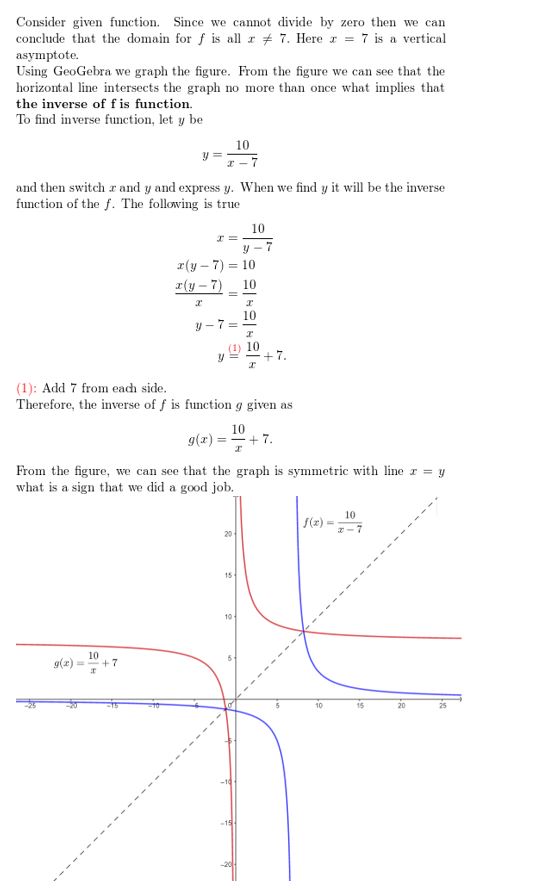
Question 30.
f(x) = \(\frac{1}{x}\) + 8
Answer:
Question 31.
At a bowling alley, shoe rentals cost $3 and each game costs $4. The average cost c (in dollars) of bowlingn games is given by c = \(\frac{4 n+3}{n}\). Find how many games you must bowl for the average cost to fall to $4.75 by (a) solving an equation, and (b) using the inverse of a function.
Answer:

Rational Functions Chapter Test
The variables x and y vary inversely. Use the given values to write an equation relating x and y. Then find y when x = 4.
Question 1.
x = 5, y = 2
Answer:
y = a/x
2 = a/5
a = 10
y = 10/x
x = 4
y = 10/4
y = 5/2
Question 2.
x = −4, y = \(\frac{7}{2}\)
Answer:
y = a/x
\(\frac{7}{2}\) = a/-4
\(\frac{7}{2}\) × -4 = a
-14 = a
y = a/x
x = 4
y = -14/4
y = –\(\frac{7}{2}\)
Question 3.
x = \(\frac{3}{4}\), y = \(\frac{5}{8}\)
Answer:
y = a/x
\(\frac{5}{8}\) = a/\(\frac{3}{4}\)
a = \(\frac{5}{8}\) × \(\frac{4}{3}\) = 20/24 = 5/6
y = a/x
x = 4
y = 5/6/4 = 5/24
The graph shows the function y = \(\frac{1}{x-h}\) + k. Determine whether the value of each constant h and k is positive, negative, or zero. Explain your reasoning.
Question 4.
Answer: Both h and are negative.
Question 5.
Answer: Both the values h and k are positive
Question 6.
Answer: Here h is negative and k is positive.
Perform the indicated operation.
Question 7.
\(\frac{3 x^{2} y}{4 x^{3} y^{5}} \div \frac{6 y^{2}}{2 x y^{3}}\)
Answer:
Question 8.
\(\frac{3 x}{x^{2}+x-12}-\frac{6}{x+4}\)
Answer:
Given that,
(3x/x² + x – 12) – (6/x+4)
= -3x² + 6x + 72/ x³ + 5x² – 8x – 48
= 3(-x-4)(x-6)/(x-3)(x-4)(x+4)
= -3x + 18/x² + x – 12.
Question 9.
\(\frac{x^{2}-3 x-4}{x^{2}-3 x-18} \cdot \frac{x-6}{x+1}\)
Answer:
Given that,
(x² – 3x – 4/x² – 3x – 18) x (x-6/x+1)
= x³ – 9x² + 14x + 24/x³ -2x² – 21x – 18
= (x+1)(x-4)(x-6)/(x-1)(x-3)(x-6)
= x-4/x+3
Question 10.
\(\frac{4}{x+5}+\frac{2 x}{x^{2}-25}\)
Answer:
Given that,
4/(x + 5) + 2x/(x² – 25)
= 6x² + 10x – 100/ x³ + 5x² – 25x – 125
= 2(3x – 10)(x+5)/(x+5)(x+5)(x-5)
= 6x-20/x² – 25
Question 11.
Let g(x) = \(\frac{(x+3)(x-2)}{x+3}\). Simplify g(x). Determine whether the graph of f(x) =x− 2 and the graph of g are different. Explain your reasoning.
Answer:
Question 12.
You start a small beekeeping business. Your initial costs are $500 for equipment and bees. You estimate it will cost $1.25 per pound to collect, clean, bottle, and label the honey. How many pounds of honey must you produce before your average cost per pound is $1.79? Justify your answer.
Answer:
C = 500 + 1.25x/x
1.79 = 500 + 1.25x/x
1.79x = 500 + 1.25x
0.54x = 500
x = 925.9 lbs
x = 926 lbs
Question 13.
You can use a simple lever to lift a 300-pound rock. The force F (in foot-pounds) needed to lift the rock is inversely related to the distance d (in feet) from the pivot point of the lever. To lift the rock, you need 60 pounds of force applied to a lever with a distance of 10 feet from the pivot point. What force is needed when you increase the distance to 15feet from the pivot point? Justify your answer.
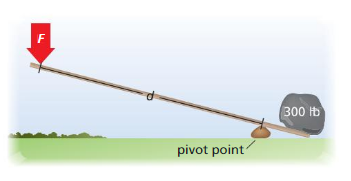
Answer:
Question 14.
Three tennis balls fit tightly in a can as shown.
a. Write an expression for the height h of the can in terms of its radius r. Then rewrite the formula for the volume of a cylinder in terms of r only.
b. Find the percent of the can’s volume that is not occupied by tennis balls.

Answer:
a. As there are 3 tightly fit tennis balls
The diameter d of three tennis balls will be equal to the height of the cylindrical can
3d = h
d = 2r
3 × 2r = h
h = 6r
Volume of cylinder = πr²h
h = 6r
v= πr².6r
v = 6πr³
b. Vs = 4/3πr³
Vb = 4πr³
V = Vc – VB
Percentage of empty volume = Vc-Vb/Vc × 100
= 6π . r³ – 4πr³/6π . r³ × 100
= 100/3%
= 33.33%
Rational Functions Cumulative Assessment
Question 1.
Which of the following functions are shown in the graph? Select all that apply. Justify your answers.
Answer:
The graph has two zeros at (0, 1) and its vertex is at (3, 8).
These points must satisfy the function of the graph.

Option A and C are correct.
Question 2.
You step onto an escalator and begin descending. After riding for 12 feet, you realize that you dropped your keys on the upper floor and walk back up the escalator to retrieve them. The total time T of your trip down and up the escalator is given by
T = \(\frac{12}{s}+\frac{12}{w-s}\)
where s is the speed of the escalator and w is your walking speed. The trip took 9 seconds, and you walk at a speed of 6 feet per second. Find two possible speeds of the escalator.
Answer:
T = \(\frac{12}{s}+\frac{12}{w-s}\)
w = 6
T = \(\frac{12}{s}+\frac{12}{6-s}\)
T = 12(6 – s) + 12s/s(6 -s)
T = 72 – 12s + 12s/s(6 – s)
T = 72/s(6 – s)
T = 9
9 = 72/s(6 – s)
s(6 – s) = 72/9
6s – s² = 8
s² – 6s + 8 = 0
s² – 4s – 2s + 8 = 0
s(s – 4) – 2(s – 4) = 0
(s – 4) (s – 2) = 0
s = 4 or s = 2
Possible speeds of the escalator are s = 2, 4
Question 3.
The graph of a rational function has asymptotes that intersect at the point (4, 3). Choose the correct values to complete the equation of the function.
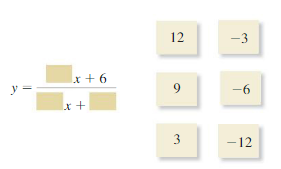
Answer:
y = a/c
4 = -d/c
4c = -d
3 = a/c
3c = a
y = 9x + 6/3x + (-12) = 9x + 6/3x – 12
To graph this function, plot points to the left of vertical asymptote, such as (-10, 2), (-3, -1) and (2, -4)
Next we have to plot points to the right of vertical asymptote, such as (5, 17), (6, 10) and (18, 4)
Question 4.
The tables below give the amounts A (in dollars) of money in two different bank accounts over time t (in years).

a. Determine the type of function represented by the data in each table.
b. Provide an explanation for the type of growth of each function.
c. Which account has a greater value after 10 years? after 15 years? Justify your answers.
Answer:
a. The x-values increase by the same amount of each time, we can begin by examining the first difference between the y-values.
5000 + 110 = 5110
5110 + 110 = 5220
5220 + 110 = 5330
The first difference is the same value, so the model is linear.
Again the x-values increase by the same amount over regular intervals.
It seems like neither the first difference nor the second difference will be the same value because after 4 years, the amount in the account is $5306.04.
5000 × 1.02 = 5100
5100 × 1.02 = 5202
5202 × 1.02 = 5306.04
b. The amount in the checking account grows by the same amount in each time, so it is a linear growth. On the other hand, the amount in the savings account grows by a fixed percent in each time. Therefore, it is exponential growth.
Question 5.
Order the expressions from least to greatest. Justify your answer. (HSN-RN.A.1)

Answer:
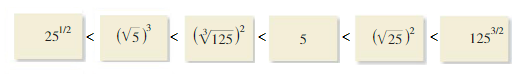
Question 6.
A movie grosses $37 million after the first week of release. The weekly gross sales y decreases by 30% each week. Write an exponential decay function that represents the weekly gross sales in week x. What is a reasonable domain and range in this situation? Explain your reasoning.(HSF-LE.A.2)
Answer:
Given that.
The movie grossed $37 million after the first week of release.
The weekly gross sales are y decreased by 30%.
The exponential function of the given data is
y = 37 x 30% x X.
y = 37 x 0.3x
Therefore Domain = (-∞,∞)
Range = (0, ∞).
Question 7.
Choose the correct relationship among the variables in the table. Justify your answer by writing an equation that relates p, q, and r. (HSA-CED.A.2)
A. The variable p varies directly with the difference of q and r.
B. The variable r varies inversely with the difference of p and q.
C. The variable q varies inversely with the sum of p and r.
D. The variable p varies directly with the sum of q and r.
Answer:
Question 8.
You have taken five quizzes in your history class, and your average score is 83 points. You think you can score 95 points on each remaining quiz. How many quizzes do you need to take to raise your average quiz score to 90 points? Justify your answer. (HSA-REI.A.2)
Answer:
Average score of 5 quizzes = 83
Total score by 5 quizzes = 83.5
T5 = 415
Total score required = 90 . n
Total score = 415 + 95(n – 5)
90n = 95n – 60
5n = 60
n = 12
Total score = 5 × 83 + 7 × 95
Total score = 415 + 665
Total score = 1080
Average score = Total score/no. of quizzes
= 1080/12 = 90
The remaining quizzes needed to take are 7 to bring the average score to 90 points.
