Big Ideas Math Answers Grade 4 Chapter 14

Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes

/ By

Understand the concept of Two-Dimensional Shapes with the help of Big Ideas Math Grade 4 Answer Key Chapter 14. The lesson Identify Symmetry and Two-Dimensional Shapes involves line symmetry, symmetric shapes, Classify Quadrilaterals, Classify Triangles, and so on. We have provided a clear cut explanation for all the questions topic wise. Thus Download Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes pdf for free.

Big Ideas Math Book 4th Grade Answer Key Chapter 14 Identify Symmetry and Two-Dimensional Shapes

Quick learning is possible with the clear explanations of Grade 4 Chapter 14 Answer Key. So, instantly start your practicing now and strengthen the knowledge. Complete concepts are solved with simple steps included in the Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes. Tap the below-attached links and improve your math skills.

Lesson: 1 Line Symmetry

Lesson: 2 Draw Symmetric Shapes

Lesson: 3 Classify Triangles by Sides

Lesson: 4 Classify Triangles by Angles

Lesson: 5 Classify Quadrilaterals

Performance Task

Lesson 14.1 Line Symmetry

Explore and Grow

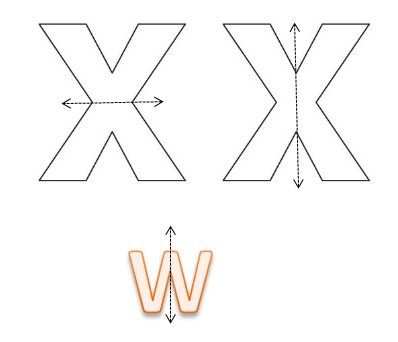
How many ways can you fold the Letter X so that the two parts match exactly? Draw models to support your Answer:
2 ways as shown in the below diagram.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 1

Structure
What other letters can you fold so that the two parts match exactly? Draw models to support your answer. Compare your models with a partner.
Answer:
The letter W can be folded. Both the letters formed after folding will be the same.

Think and Grow:

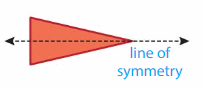
A shape has line symmetry when it can be folded on a line so that two parts match exactly. The fold line is called a line of symmetry.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 2
Example
Determine whether the shape has line symmetry.

The shape can be folded so that two parts match exactly.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 3
The shape has __4_ lines of symmetry.
So, the shape ___ line symmetry.

Example
Determine whether the shape has line symmetry.
The shape cannot be folded so that two parts match exactly.
The shape has ___ lines of symmetry.
So, the shape ___ line symmetry.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 4

Show and Grow

Determine whether the line is a line of symmetry.
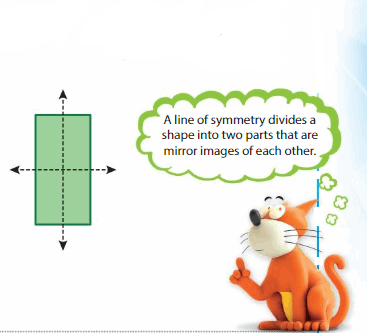
We say there is symmetry when the exact reflection or mirror image of a line, shape or object gets created.

Question 1.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 5
Answer:
No, because it’s not dividing the figure into identical Halves.

Question 2.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 6
Answer:
Yes, divides it into identical halves.

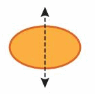
Question 3.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 7
Answer:
Yes, divides it into identical halves.

Determine whether the shape has line symmetry. Draw each line of symmetry

Question 4.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 8
Answer:
Yes, divides it into identical halves.

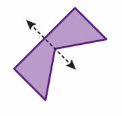
Question 5.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 9
Answer:
Yes,divides it into identical halves.

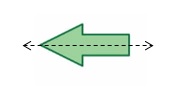
Question 6.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 10
Answer:
No, As it cannot divide the shape into identical halves.

Apply and Grow: Practice

Determine whether the shape has line symmetry. Draw each line of symmetry.

Question 7.
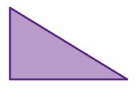
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 11
Answer:
No, as it is a scalene triangle with different sides.

Question 8.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 12
Answer:
Yes, as the line of symmetry divides it into identical halves.

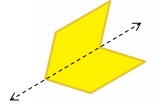
Question 9.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 13
Answer:
Yes, as the line of symmetry divides it into identical halves.

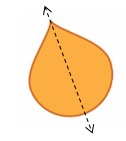
Question 10.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 14
Answer:
Yes, as the line of symmetry divides it into identical halves.

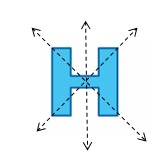
Question 11.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 15
Answer:
Yes, as the line of symmetry divides it into identical halves.

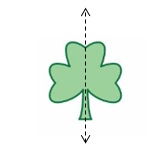
Question 12.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 16
Answer:
Yes, as the line of symmetry divides it into identical halves.

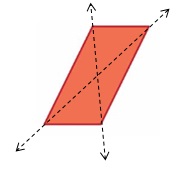
Question 13.
Structure
Create a three-digit number that has a line of symmetry.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 17
Answer:

Question 14.
Writing
How can you tell when a line is not a line of symmetry?
Answer:
The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
When the line of symmetry doesn’t divide the shape into identical halves then it is not a line of symmetry.

Question 15.q
DIG DEEPER!
Draw four lines of symmetry for the circle. Can you draw more lines of symmetry? Explain.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 18
Answer:
Yes.Circle has infinite lines of symmetry.
Since there are an infinite number of lines through the center, the circle has an infinite number of lines of symmetry. … This means that the parts of the circle on each side of the line  must  have the same area. So a line of symmetry divides the circle into two parts with equal area.

Think and Grow:Modeling Real Life

Example
Divide the archery target into multiple sections using each of its lines of symmetry. An archer gets 2 arrows in each section. How many arrows does the archer get on the target? Draw each line of symmetry on the target.
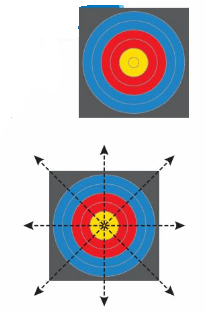
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 19
The target has _4__ lines of symmetry.
Count the sections.
The lines of symmetry divide the target into _8__ sections.
The archer gets 2 arrows in each section, so multiply the number of sections by 2.
_8__ × _2_ = 16
So, the archer gets _16__ arrows on the target.
Answer:
16.

Show and Grow

Question 16.
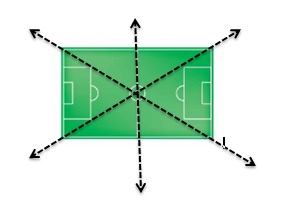
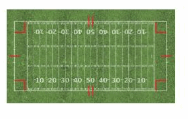
Divide the soccer field into multiple sections using each of its lines of symmetry. At the start of the game, there are 3 players in each section. How many players are on the field?
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 20
Answer:
Number of players in each section = 3
Number of sections = 6.
Total number of players = Number of sections x Number of players in each section
= 3 X 6. = 18 players.

Question 17.
DIG DEEPER!
Your friend folds a rectangular sheet of paper in half horizontally, and then in half again vertically. She then draws the shape shown on the folded paper, cuts it out, and then unfolds it. How many lines of symmetry does your friend’s cutout have? Explain.
Answer:
The rectangle paper is folded into 4 small rectangle.
Then the rectangle is cut it out. it means 2 side edges cuts.
Two rectangles with adjacent are left.
lines of symmetry does your friend’s cutout = 2.

Line Symmetry Homework & Practice 14.1

Determine whether the shape has line symmetry.

Question 1.
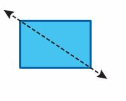
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 21
Answer:
Yes, as the line of symmetry divides it into identical halves.

Question 2.
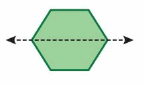
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 22
Answer:
Yes, as the line of symmetry divides it into identical halves.

Question 3.
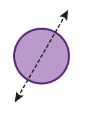
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 23
Answer:
Yes, as the line of symmetry divides it into identical halves.

Determine whether the line is a line of symmetry. Draw each line of symmetry.

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 24
Answer:
Yes, as the line of symmetry divides it into identical halves.

Question 5.
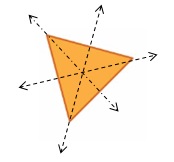
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 25
Answer:
NO, as the line of symmetry cannot divide it into identical halves.

Question 6.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 26
Answer:
Yes, as the line of symmetry divides it into identical halves.

Question 7.
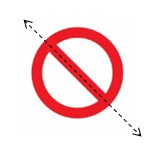
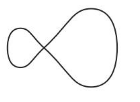
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 27
Answer:
No, as the line of symmetry cannot divide it into identical halves.

Question 8.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 28
Answer:
Yes, as the line of symmetry divides it into identical halves.

Question 9.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 29
Answer:
Yes, as the line of symmetry divides it into identical halves.

Question 10.
Precision
Which figure correctly shows all the lines of symmetry of a square?
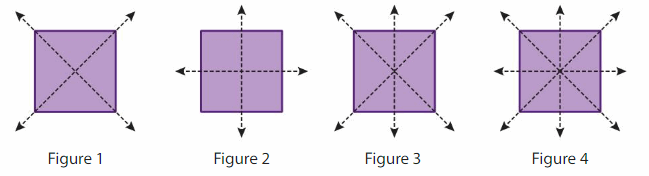
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 30
Answer:
Figure 4

Question 11.
YOU BE THE TEACHER
Your friend says the shape has exactly three lines of symmetry. Is your friend correct? Explain.
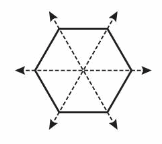
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 31
Answer:
No
Explanation:
A regular hexagon with six equal sides has six lines of symmetry.
For all regular polygons, the number of lines of symmetry is equal to the number of sides.

Question 12.
Modeling Real Life
Divide the tennis court into multiple sections using each of its lines of symmetry. There are 4 players on the court with an equal number of players in each section. How many players are in each section?
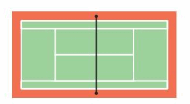
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 32
Answer:
Number of players = 4.
Number of sections= 2.
Number of players in each section = 4 /2=2.

Question 13.
DIG DEEPER!
In art class, you are making a black and white art piece. Your teacher says it has to have exactly 1 line of diagonal symmetry. Shade the square below to show what the art piece could look like.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 33
Answer:

Review & Refresh

Question 14.
\(\frac{8}{12}\)
Answer:
8/12=2/3=0.66

Question 15.
\(\frac{5}{100}\)
Answer:
5/100=0.05

Lesson 14.2 Draw Symmetric Shapes

Explore and Grow

You want to create a mask that has at least 1 line of symmetry. Does either mask meet your requirement? Explain.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 34
Answer:

Complete the mask below so that it has 1 line of symmetry.
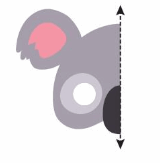
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 35
Answer:

Reasoning
When given one half of a figure and a line of symmetry, how can you draw the other half of the figure? Explain.
Answer:
Line symmetry and mirror reflection are naturally related and linked to each other.Mirror image of the given image helps to draw the other half of the figure.

Think and Grow: Draw Symmetric Shapes

Example
One half of a symmetric shape is shown. Draw the rest of the shape.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 36

One way: Draw a line of Symmetry.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 37
Draw the other half of the shape on the opposite side of the line of symmetry.
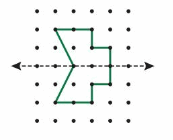
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 38

Another Way: Draw a different line of symmetry
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 39
Draw the other half of the shape on the opposite side of the line of symmetry.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 40
Answer:

Show and Grow

Question 1.
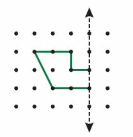
One half of a shape and a line of symmetry are shown. Draw the rest of the shape.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 400
Answer:

Question 2.
One half of a symmetric shape is shown. Draw the rest of the shape.
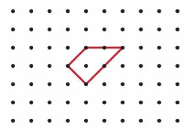
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 41
Answer:

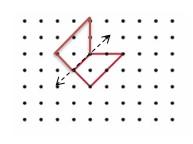
Apply and Grow: Practice

One half of a symmetric shape is shown. Draw the rest of the shape.

Question 3.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 42
Answer:

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 43
Answer:

Question 5.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 44
Answer:

Question 6.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 45
Answer:

Question 7.
Reasoning
Draw a shape that has exactly one line symmetry. Draw the line of symmetry.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 46
Answer:

Question 8.

YOU BE THE TEACHER
Your friend draws the other half of the shape on the opposite side of the line of symmetry. Is your friend correct? Explain.
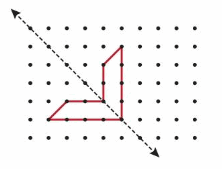
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 47
Answer:
Yes,The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves.
As per above figure both are two identical halves.

Think and Grow: Modeling Real Life

Example
A rokkaku is a six-sided Japanese kite. One half of a symmetric rokkaku and a line of symmetry are shown. Draw the rest of the kite. Then draw each additional line of symmetry, if any.
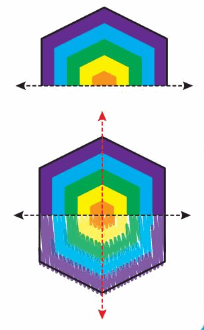
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 48
Draw the other half of the rokkaku on the opposite side of the line of symmetry.
The rokkaku can also be folded in half vertically so that two parts match exactly. So, draw a vertical line of symmetry.

Show and Grow

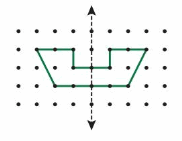
Question 9.
The Jamaican flag is symmetric. One half of the flag and a line of symmetry are shown. Draw the rest of the flag. Then draw each additional line of symmetry, if any.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 49
Answer:

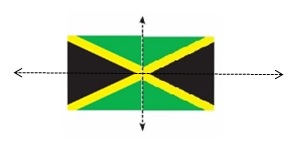
Question 10.
DIG DEEPER!
A symmetric quilt is folded in half horizontally, and then in half again vertically. The folded quilt and fold lines are shown. Draw the unfolded quilt. Then draw each line of symmetry.
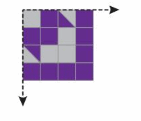
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 50
Answer:

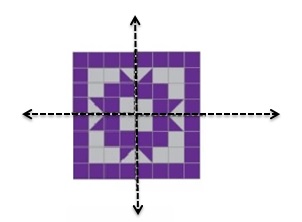
Draw Symmetric Shapes Homework & Practice 14.2

Example
One half of a symmetric shape is shown. Draw the rest of the shape.
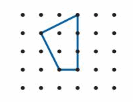
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 51

One Way: Draw a line symmetry.
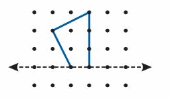
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 52
Draw the other half of the shape on the opposite side of the line of symmetry.
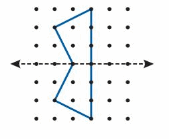
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 53
Another Way: Draw a different line of symmetry.
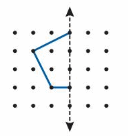
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 54
Drawthe other half of the shape on the opposite side of the line of symmetry.
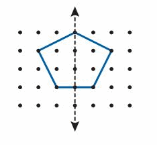
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 55

Question 1.
One half of a shape and a line of symmetry are shown. Draw the rest of the shape.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 56
Answer:

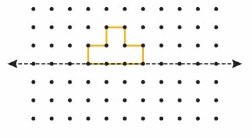
Question 2.
One half of a symmetric shape is shown. Draw the rest of the shape.
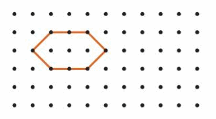
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 57
Answer:

One half of a symmetric shape is shown. Draw the rest of the shape.

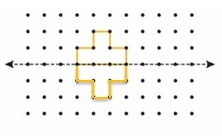
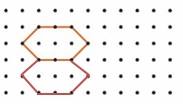
Question 3.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 58
Answer:

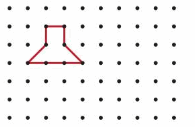
Question 4.
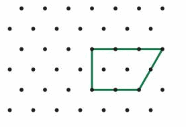
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 59
Answer:

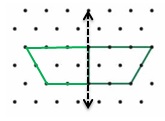
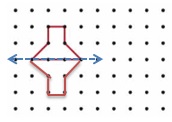
Question 5.
Structure
Draw a shape that has 5 sides and exactly 1 line of symmetry.
Answer:

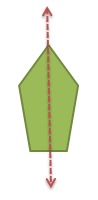
Question 6.
One fourth of a shape and two lines of symmetry are shown. Draw the rest of the shape.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 60
Answer:

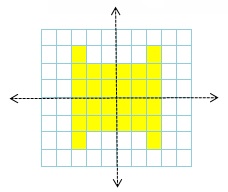
Question 7.
Modeling Real Life
The flag of the Bahamas is symmetric. One half of the flag and a line of symmetry are shown. Draw the rest of the flag. Then draw each additional line of symmetry, if any.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 61
Answer:
No other line of symmetry is possible.

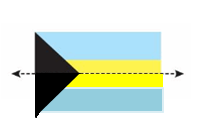
Question 8.
DIG DEEPER!
Snowflakes are symmetric. One half of a snowflake and a line of symmetry are shown. Draw the rest of the snowflake. Then draw each additional line of symmetry, if any.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 62
Answer:

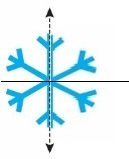
Review & Refresh

Find the equivalent weight.

Question 9.
2T = lb
Answer:
1Ton =2,000 pounds
2Ton =4,000 pounds

Question 10.
15lb = ___oz
Answer:
1pound = 16 ounce
15lb = 240 oz

Lesson 4.3 Classify Triangles by Sides

Explore and Grow

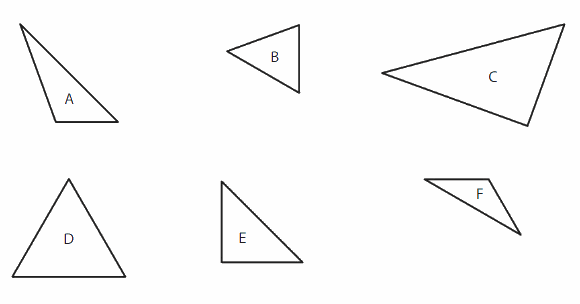
Sort the triangles into two or more groups using their side lengths. Explain how you sorted the triangles.
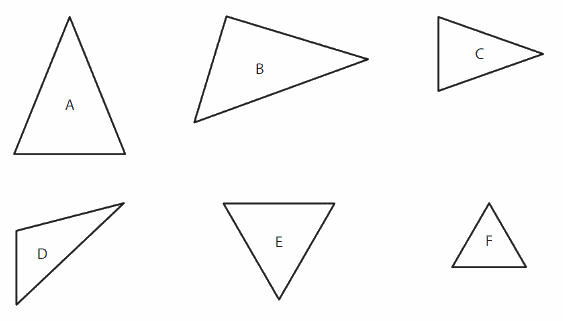
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 63
Answer:
Triangle A = Isosceles Triangle -An isosceles triangle has both two equal sides.
Triangle B = Scalene Triangle- no sides with same length
Triangle C -Isosceles Triangle -An isosceles triangle has both two equal sides.
Triangle D-Scalene Triangle- no sides with same length
Triangle E – Equilateral Triangle – All sides equal.
Triangle F – Equilateral Triangle – All sides equal.

Structure
Can you draw a triangle that does belong in any of your groups above? Explain.

Think and Grow: Classify Triangles by Sides

Triangles can be classified by their sides.
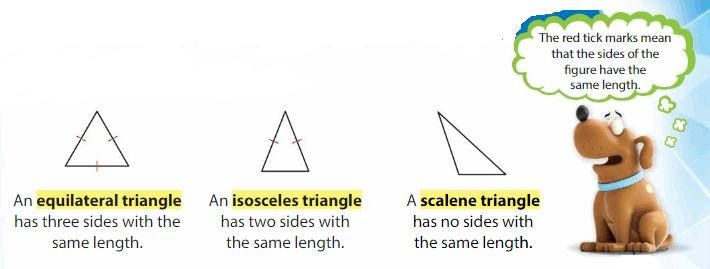
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 64
Answer:

Example
Classify the triangle by its sides.
The triangle has _2_ sides with the same length.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 66
So, it is an ___ triangle.
Answer:
Isosceles Triangle.

Show and Grow

Classify the triangle by its sides.

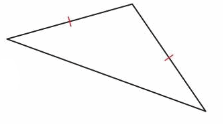
Question 1.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 401

Answer:
Scalene Triangle-no sides with same length

Question 2.
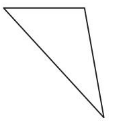
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 402

Answer:
Equilateral Triangle – All sides equal.

Question 3.
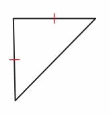
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 403

Answer:
Isosceles Triangle -An isosceles triangle has both two equal sides.

Question 4.
Use the triangular grid to draw any triangle. Classify the triangle by its sides
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 67
Answer:
It is Equilateral triangle with all sides equal.

Apply and Grow: Practice

Classify the triangle by its sides.

Question 5.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 68
Answer:
Isosceles Triangle -An isosceles triangle has both two equal sides.

Question 6.
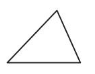
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 69
Answer:
Scalene Triangle-no sides with same length

Question 7.
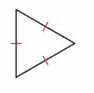
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 70
Answer:
Equilateral Triangle – All sides equal.

Question 8.
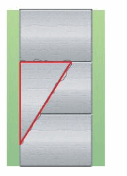
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 71
Answer:
Scalene Triangle-no sides with same length

Question 9.
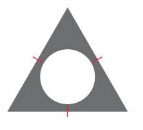
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 72
Answer:
Equilateral Triangle – All sides equal.

Question 10.
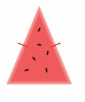
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 73
Answer:
Isosceles Triangle -An isosceles triangle has both two equal sides.

Question 11.
Draw a triangle that has three lines of symmetry. Classify the triangle by its sides.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 74
Answer:
Equilateral Triangle – All sides equal.It has 3 lines of symmentry.

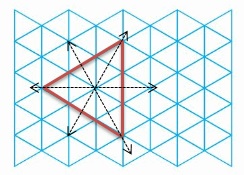
Question 12.
Draw a triangle that has no sides with the same length. Classify the triangle by its sides.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 75
Answer:

Question 13.
Reasoning
How many lines of symmetry does a scalene triangle have? Explain.
Answer:
A scalene triangle have is zero lines of symmetry
Explanation:
It has no equal sides and no equal angles.

Question 14.
DIG DEEPER!
Write an addition equation and a multiplication equation for the perimeter, P, of the triangle
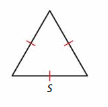
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 76
Answer:
if a triangle has sides a, b, and c, then the perimeter of that triangle will be P = a + b + c.
As the above Triangle given is an Equilateral Triangle then perimeter = s +s+s=3s.

Think and Grow: Modeling Real Life

Example
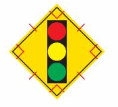
Classify the yield sign by its sides. Then find the perimeter of the sign.
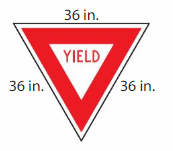
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 77
The yield sign is a triangle that has 3 sides with the same length.
So, it is an _Equilateral__ triangle.
To find the perimeter of the yield sign, find the sum of all of its side lengths.
36 + 36 + 36 = _108__
So, the perimeter of the yield sign is _108__ inches.
Answer:
108 inches.

Show and Grow

Question 15.
Classify the sports pennant by its sides. Then find the perimeter of the pennant.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 78
Answer:
Perimeter of triangle = a + b+ c (Where a,b,c are 3 sides of triangle).
P=  30(5/10) +77(7/10) + 77(7/10)
P=(305+777+777)/10
P=1859/10=185.9cms.

Question 16.
DIG DEEPER!
The perimeter of the canoe sail is 29.75 feet. Find the unknown side length. Then classify the sail by its sides.
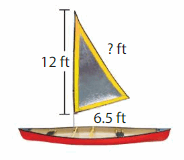
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 79
Answer:
Perimeter of triangle = a + b+ c (Where a,b,c are 3 sides of triangle).
P=29.75feet
29.75=12+6.5+c
c=29.75-18.5=11.25 feet.

Question 17.
DIG DEEPER!
An emergency warning triangle is an equilateral triangle. It has a perimeter of 51 inches. What are the side lengths of the warning triangle?
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 410
Answer:
Perimeter of Equilateral Triangle= s +s+s=3s.(s=side of the triangle)
P = 51 inches.
51=3s.
s=51/3=17 inches.

Classify Triangles by Sides Homework & Practice 14.3

Classify the triangle by its sides.

Question 1.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 80
Answer:
Equilateral Triangle – All sides equal.

Question 2.
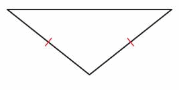
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 81
Answer:
Isosceles Triangle -An isosceles triangle has both two equal sides.

Question 3.
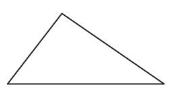
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 82
Answer:
Scalene Triangle-no sides with same length

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 83
Answer:
Isosceles Triangle -An isosceles triangle has both two equal sides.

Question 5.
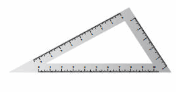
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 84
Answer:
Scalene Triangle-no sides with same length

Question 6.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 85
Answer:
Equilateral Triangle – All sides equal.

Question 7.
Draw a triangle that has exactly 2 sides with the same length. Classify the triangle by its sides.
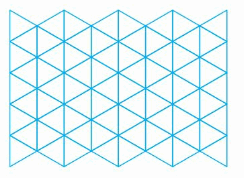
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 86
Answer:
Isosceles Triangle -An isosceles triangle has both two equal sides.

Question 8.
Draw a triangle that has exactly 1 line of symmetry. Classify the triangle by its sides.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 87
Answer:
Isosceles Triangle -An isosceles triangle has two equal sides.

Question 9.
Draw a triangle that has no lines of symmetry. Classify the triangle by its sides.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 88
Answer:

A scalene triangle have is zero lines of symmetry
Explanation:
It has no equal sides and no equal angles.

Question 10.
Structure
Classify the triangle pattern block by its sides.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 89
Answer:
It is a Equilateral Triangle as it has 3 equal sides.

Question 11.
Reasoning
Can the triangle have 3 lines of symmetry? Explain.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 90
Answer:
The above given Triangle is the Isosceles triangle it have only one line of symmentry.
Isosceles Triangle -An isosceles triangle has both two equal sides.
Only an equilateral triangle has three lines of symmetry.

Question 12.
Reasoning
Your friend draws a triangle with side lengths of 25.3 centimeters, 15.2 centimeters, and 12.6 centimeters. Classify your friend’s triangle.
Answer:
Scalene Triangle have 3 different sides, none of the side is equal.

Question 13.
Modeling Real Life
Classify the roof truss by its sides. Then find the perimeter of the roof truss.
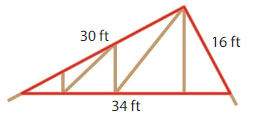
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 91
Answer:
P=a+b+c where a,b and c are sides.
P=30+16+34=80ft.

Review & Refresh

Find the perimeter of the rectangle

Question 14.
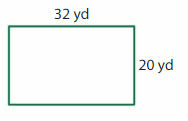
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 92
Answer:
Perimeter of a rectangle= 2(l+b) (where l=length and b=breadth of the rectangle).
Perimeter=2(32+20)=2(52)
Perimeter=104 yd.

Question 15.
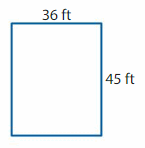
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 93
Answer:
Perimeter of a rectangle= 2(l+b) (where l=length and b=breadth of the rectangle).
Perimeter=2(36+45)=2(81)
Perimeter=162ft.

Lesson 14.4 Classify Triangles by Angles

Explore and Grow

Sort the triangles into two or more groups using their angle measures. Explain how you sorted the triangles.
Big Ideas Math Answers 4th Grade Chapter 14 Identify Symmetry and Two-Dimensional Shapes 94

Construct Arguments
Your friend saysa triangle that has three angles with the same measure also has three sides with the same length. Is your friend correct? Explain.

Think and Grow: Classify Triangles by Angles

Triangles can be classified by their angles.
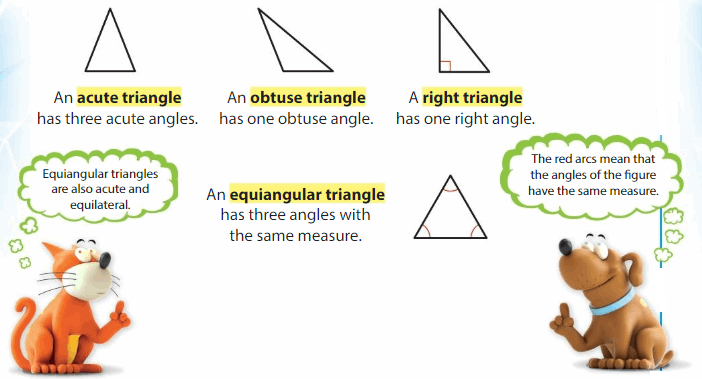
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 95
Example
Classify the triangle by its angles.
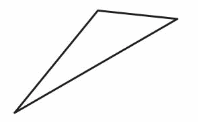
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 96
The triangle has one _obtuse_ angle.
So, it is an _obtuse__ triangle.
Answer:
Obtuse Triangle

Example
Classify the triangle by its angles and its sides.
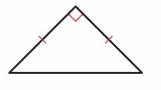
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 97
The triangle has one _right_ angle.
and _2_ sides with the same length.
So, it is an _right angled_ ___ triangle.
Answer:
Right angled triangle.

Show and Grow

Question 1.
Classify the triangle by its angles.
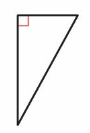
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 98
Answer:
Right-angled triangle-it have one right angle.

Question 2.
Classify the triangle by its angles and its sides
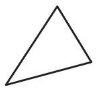
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 99
Answer:
Acute triangle.
Isosceles Triangle – 2 equal sides.

Apply and Grow: Practice

Classify the triangle by its angles.

Question 3.
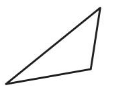
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 100
Answer:
Right angle triangle.

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 101
Answer:
Acute triangle

Question 5.
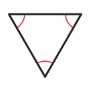
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 102
Answer:
Equiangular Triangle.

Classify the triangle by its angles and its sides.

Question 6.
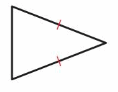
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 103
Answer:
Acute triangle-angles
Isosceles triangle-sides

Question 7.
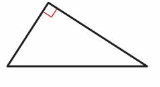
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 104
Answer:
Right angle triangle-angle
Scalene triangle-sides

Question 8.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 105
Answer:
Obtuse triangle-angle
Scalene triangle-side

Question 9.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 106
Answer:
Right angle triangle -angle
Isosceles triangle – side

Question 10.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 107
Answer:
Equiangular triangle-angles
Equilateral triangle – sides

Question 11.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 108
Answer:
Acute triangle-angle
Isosceles triangle-side

Question 12.
Precision
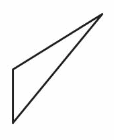
Draw an acute scalene triangle.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 109
Answer:

Question 13.
Can an obtuse triangle also be an equilateral triangle? Explain.
Answer:
An equilateral triangle can never be obtuse. Since an equilateral triangle has equal sides and angles, each angle measures 60°, which is acute.
Therefore, an equilateral angle can never be obtuse-angled.

Think and Grow: Modeling Real Life

Example
Classify the large triangle on the shuffleboard court by its angles. Verify your answer by finding the measure of each angle.
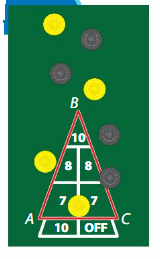
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 110
The triangle does not have a right angle or an obtuse angle.
So, it is an _Acute__ triangle.
Verify: Use a protractor to find the measure of each angle.
The measure of ∠ABC is ___.
The measure of ∠BCA is ___.
The measure of ∠CAB is ___.
Because each angle measure is less than 90°, you can conclude that the triangle is a ___ triangle.
Answer:
Acute triangle
The measure of ∠CAB is 70°.
The measure of ∠BCA is 70°.
The measure of ∠ABC is 40°.


Show and Grow

Question 14.
Classify the triangle in the clothes hanger by its angles. Verify your answer by finding the measure of each angle.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 111
Answer:
Obtuse angle triangle.

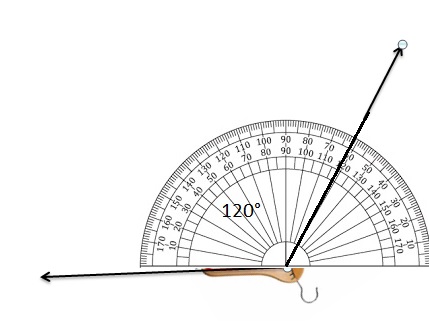
Question 15.
DIG DEEPER!
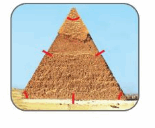
In the picture, the tree is perpendicular to the ground. Draw the triangle formed by the tree, the wire, and the ground. Classify the triangle by its angles. Explain.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 112
Answer:
It is right angles triangle. As the angled formed here is 90°.

Classify Triangles by Angles Homework & Practice 14.4

Classify the triangle by its angles.

Question 1.
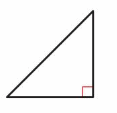
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 113
Answer:
Right angle triangle

Question 2.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 114
Answer:
Acute triangle

Question 3.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 115
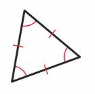
Answer:
Acute triangle

Classify the triangle by its angles and its sides

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 116
Answer:
Equiangular triangle-angles
Equilateral triangle – sides

Question 5.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 117
Answer:
Acute triangle- angles
Scalene triangle-sides

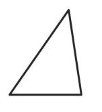
Question 6.
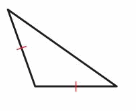
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 118
Answer:
Obtuse triangle-angle
Isosceles triangle-side

Question 7.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 119
Answer:
Right angle triangle-angle
Scalene triangle – side

Question 8.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 120
Answer:
Equiangular triangle-angles
Equilateral triangle – sides

Question 9.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 121
Answer:
Acute triangle – angles
Isosceles triangle – sides

Question 10.
Precision
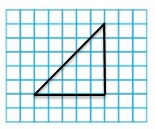
Draw a right isosceles triangle.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 122
Answer:

Question 11.
Reasoning
Can a triangle have more than one right angle? Explain.
Answer:
No a triangle cannot have more than one right angle as if there are 2 right angles the their sum will be 180° and the third angle will exceed the sum.
Therefore the construction is not possible.

Question 12.
Which One Doesn’t Belong? Which triangle does not belong with the other three?
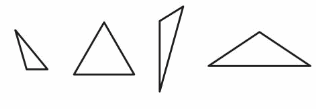
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 123
Answer:
Figure 2

Question 13.
DIG DEEPER!
Draw \(\overline{B D}\). Then classify each triangle by its angles and its sides.
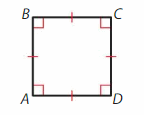
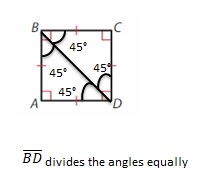
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 124
Answer:

â–³BAD and â–³BDC form Isosceles triangle and acute angle triangle.

Question 14.
Modeling Real Life
Classify the face of the bird house by its angles. Verify your answer by finding the measure of each angle.
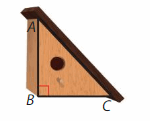
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 125
Answer:
It is a Right angled triangle. As the angle formed is 90°.

Question 15.
Modeling Real Life
A construction worker measures a triangle formed by the supports on a bridge. The angle measures are 120°, 36°, and 24°. The side lengths are 12.65 meters, 8.61 meters, and 5.91 meters. Classify the triangle by its angles and its sides.
Answer:
It is a Obtuse angle Triangle and Scalene Triangle (all different sides).

Review & Refresh

Add.

Question 16.
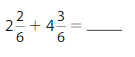
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 126
Answer:
(14/6)+(27/6)=(14+27)/6
=41/6=6.833

Question 17.
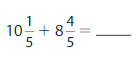
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 127
Answer:
=(51/5)+(44/5)=(51+44)/5
=95/5=19.

Question 18.
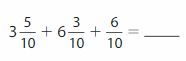
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 128
Answer:
(35/10)+(63/10)+(6/10)
=(35+63+6)/10
=104/10
=10.4

Lesson 14.5 Classify Quadrilaterals

Explore and Grow

Sort the quadrilaterals into two or more groups. Explain how you sorted the quadrilaterals.
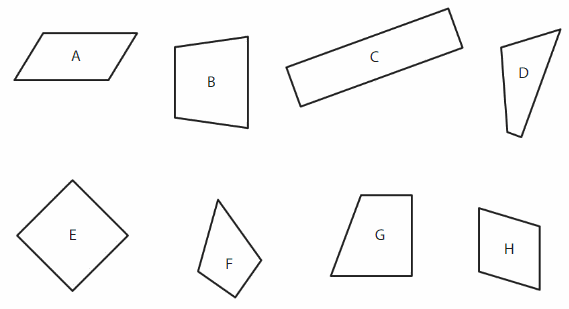
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 129
Answer:
G and A are Trapezoids – one pair of parallel lines.
E and H are rhombus – all sides equal.
C is a Rectangle parallelogram – 2 pairs of parallel sides and 4 right angles.

Precision
You draw a quadrilateral with four right angles. Your friend draws a quadrilateral with two pairs of parallel sides. Did you and your friend draw the same type of quadrilateral? Explain.
Answer:
Figure can be drawn indifferent many ways. The figure can be Square , Rectangle as they too have with two pairs of parallel sides and four right angles.

Think and Grow: Classify Quadrilaterals

Quadrilaterals can be classified by their angles and sides.

A trapezoid is a quadrilateral that has exactly one pair of parallel sides.
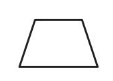
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 130

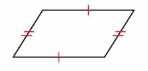
A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 131

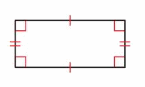
A rectangle is a parallelogram that has four right angles.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 132
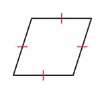
A rhombus is a parallelogram that has four sides with the same length.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 133
A square is a parallelogram that has four right angles and four sides with the same length.
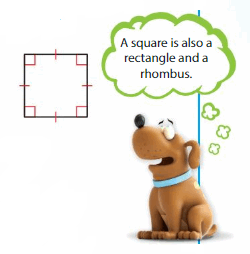
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 134
Answer:
No square is not a rectangle because rectangle have only opposite sides equal. square cannot be rhombus because it does not have right angles.

Example
Classify the quadrilateral in as many ways as possible.
The quadrilateral has __ right angles,
___ pairs of parallel sides, and
___ pairs of opposite sides with the same length.
So, it is a ___ and a ___.
Answer:

Show and Grow

Classify the quadrilateral in as many ways as possible.

Question 1.
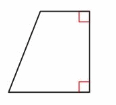
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 135
Answer:
It is a Trapezoid
A trapezoid is a quadrilateral that has exactly one pair of parallel sides.

Question 2.
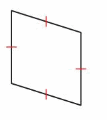
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 136
Answer:
It is a Rhombus
A rhombus is a parallelogram that has four sides with the same length.

Apply and Grow: Practice

Classify the quadrilateral in as many ways as possible.

Question 3.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 137
Answer:
It is a rectangle
A rectangle is a parallelogram that has four right angles.

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 138
Answer:
It is a trapezoid.
A trapezoid is a quadrilateral that has exactly one pair of parallel sides.

Question 5.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 139
Answer:
It is a Square.
A square is a parallelogram that has four right angles and four sides with the same length.

Question 6.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 140
Answer:
It is a parallelogram.
A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length.

Question 7.
The formula for the perimeter of a square with side length of s is P = 4 × s. Can you use this formula to find the perimeter of any other type of quadrilateral? If so, name the type of quadrilateral.
Answer:
It can be used to find the perimeter of a Rhombus.
A rhombus is a parallelogram that has four sides with the same length.

Question 8.
Structure
How many lines of symmetry can a parallelogram have?
Answer:
lines of symmetry can a parallelogram have is 2.

Question 9.
DIG DEEPER!
Write All, Some, or No for each statement
___ parallelograms are rectangles.
___ squares are rectangles.
___ trapezoids are parallelograms.
___ rectangles are squares.
___ trapezoids have four sides with the same length.
Answer:
_Some__ parallelograms are rectangles.
_All__ squares are rectangles.
__No_ trapezoids are parallelograms.
__No_ rectangles are squares.
_No__ trapezoids have four sides with the same length.

Think and Grow: Modeling Real Life

Example
Two artists each want to paint an identical half of a painting, like the one shown. Classify the shape of the painting in as many ways as possible. Then identify and show how many different ways the artists can divide the painting, if any.
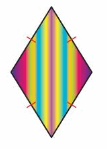
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 141
Classify the shape of the painting in as many ways as possible.
The painting has _4__ sides,
_2__ pairs of parallel sides,
_0__ right angles, and
_4__ sides with the same length.
So, it is a Rhombus.
Determine whether the painting has line symmetry. If so, find how many different ways the artists can divide the painting.
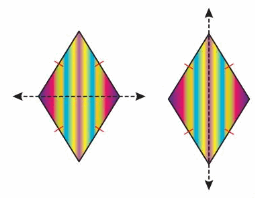
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 142
The rhombus-shaped painting has __ lines of symmetry.
So, the artists can divide the painting __ different ways.
Answer:
The rhombus-shaped painting has _2_ lines of symmetry.
So, the artists can divide the painting _2_ different ways.

Show and Grow

Question 10.
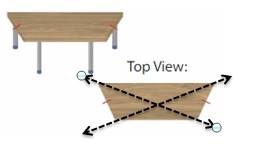
You and your friend each want to share an identical half of the tabletop. Classify the shape of the tabletop in as many ways as possible. Then identify and show how many different ways you and your friend can divide the tabletop, if any.
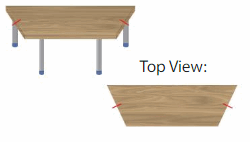
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 143
Answer:
The given shape is a Trapezoid.

Question 11.
A horse needs at least 4,046 square meters of pasture. Classify the shape of the pasture in as many ways as possible. Is the pasture large enough for the horse? Explain.
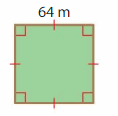
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 144
Answer:
The side of the square = 64m
Area of the Square = side x side=64m x 64 m =4096sqmtrs.
Area required by horse = 4046 sqmtrs.
Therefore area of square is more than pasture of horse.

Classify Quadrilaterals Homework & Practice 14.5

Classify the quadrilateral in as many ways as possible.

Question 1.
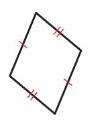
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 145
Answer:
It is a parallelogram
A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length.

Question 2.
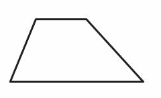
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 146
Answer:
It is a Trapezoid.
A trapezoid is a quadrilateral that has exactly one pair of parallel sides.

Question 3.
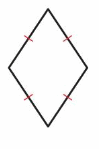
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 147
Answer:
It is a rhombus.
A rhombus is a parallelogram that has four sides with the same length.

Question 4.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 148
Answer:
It is a Rectangle.
A rectangle is a parallelogram that has four right angles.

Question 5.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 149
Answer:
It is a Trapezoid.
A trapezoid is a quadrilateral that has exactly one pair of parallel sides.

Question 6.
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 150
Answer:
It is a Square.
A square is a parallelogram that has four right angles and four sides with the same length.

Question 7.
Structure
Your friend sorts the shapes into two different groups. How do you think she sorted? Where does the shape below belong? Explain.
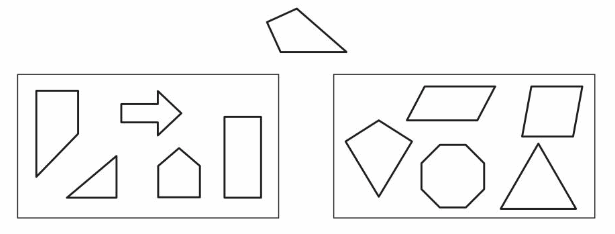
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 151
Answer:
The above belong to the group 2 . The group 2 images have 2 pairs of sides equal.

Question 8.
Reasoning
All of the sides of an equilateral triangle have the same length. Is an equilateral triangle a rhombus? Explain.
Answer:
A Rhombus have all sides equal. 2 equilateral triangles form a rhombus.

Question 9.
DIG DEEPER!
Within the star, trace at least two different examples of trapezoids and parallelograms. Explain how you found each quadrilateral.
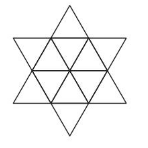
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 152
Answer:

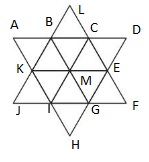
A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length. BJGD and CAIF are two parallelograms.
A trapezoid is a quadrilateral that has exactly one pair of parallel sides. LEGJ and KLFI are two trapezoids.

A Quadilateral can be defined as a closed, two-dimensional shape which has four straight sides.

Question 10.
Modeling Real Life
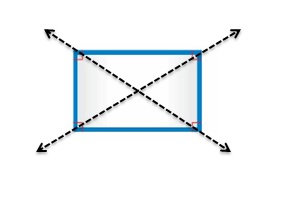
You and your friend each want to share an identical half of the whiteboard shown. Classify the shape of the whiteboard in as many ways as possible. Then identify and show how many different ways you and your friend can divide the whiteboard, if any.
Big Ideas Math Answers Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 153
Answer:
The image is divided into four identical parts with two lines of symmetry.

Review & Refresh

Question 11.
Write \(\frac{7}{10}\) as hundredths in fraction form and decimal form.
Answer:
7/10=0.7

Question 12.
Write \(\frac{50}{100}\) as tenths in fraction form and decimal form.
Answer:
50/100=0.5

Identify Symmetry and Two-Dimensional Shapes Performance Task 14

Roof trusses are wooden structures that support the roof of a building. They come in many different shapes and sizes.
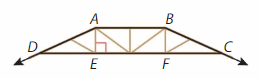
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 154
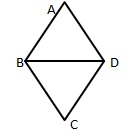
1. The truss has exactly one pair of parallel sides.
a. What polygon describes the shape of the truss?
Answer:   ABCD.
b. Does the truss have line symmetry? Explain.
Answer:
The line of symmetry divide the given truss into identical halves.

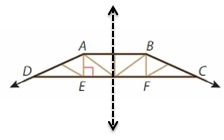
c. Name an acute angle, a right angle, and an obtuse angle.
Answer:
Right angle = ∠AED
Acute angle =∠DAE.
Obtuse angle =∠ABC.
d. Name a ray.
Answer: AD.

Question 2.
Most trusses are built in the shape of a triangle.
a. Classify each triangle by its sides. Identify any lines of symmetry.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 156
Answer:

b. Why do you think roof trusses come in different shapes and sizes?
Answer:
Roof trusses come in all shapes and sizes depending on your build project.

Question 3.
You see a truss in the shape of an obtuse isosceles triangle. The perimeter of the triangle is 36 feet. The length of the side opposite the obtuse angle is 16 feet. What are the lengths of the other two sides?
Answer:
An Isosceles triangle have 2 sides equal.
side of Isosceles triangle=16 feet.
Perimeter of isosceles triangle = s1+s2+s3. = s+s+16
36 feet =2s +16
2s=36-16
2s=20
s=10feet.
The other two sides lengths are 10 feet each.

Question 4.
Draw a triangular roof truss that has line symmetry. Include a few support lines inside the truss. Classify your triangle by its sides. What types of angles are on the inside of the truss?
Answer:

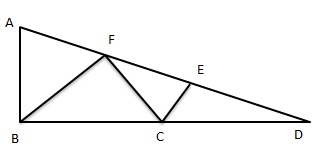
△ABF  = Isosceles triangle.
â–³BFC= Scalene Triangle.
â–³FEC = Isosceles Triangle.
â–³EDC=Scalene Triangle.

Identify Symmetry and Two-Dimensional Shapes Activity

Pyramid Climb and Slide

Directions:
1. Players take turns spinning the spinner.
2. On your turn, move your counter to the next triangle that best matches your spin.
3. If you land at the bottom of a ladder, climb to the top of the ladder. If you land at the top of a slide, slide down to the bottom of the slide.
4. The first player to reach the top of the pyramid wins!
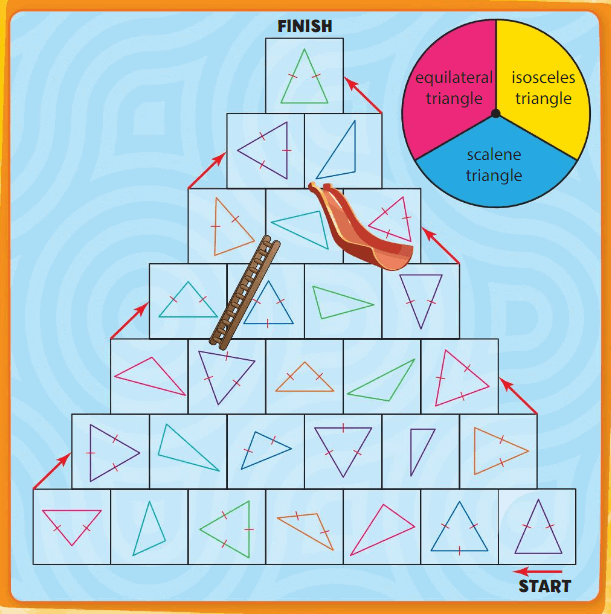
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 157
Answer:

Identify Symmetry and Two-Dimensional Shapes Chapter Practice

14.1 Line Symmetry

Determine whether the line is a line of symmetry.

Question 1.
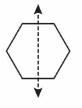
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 158
Answer:
Yes it is a line of Symmetry .It divides the given shape into two identical halves.

Question 2.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 159
Answer:
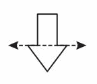
No, it is not a line of symmetry it doesnot divide the given shape into two identical halves.

Question 3.
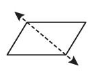
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 160
Answer:
Yes it is a line of Symmetry .It divides the given shape into two identical halves.

Determine whether the shape has line symmetry. Draw each line of symmetry.

Question 4.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 161
Answer:
Yes it is a line of Symmetry .It divides the given shape into two identical halves.

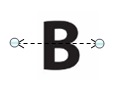
Question 5.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 162
Answer:
Yes it is a line of Symmetry .It divides the given shape into two identical halves.

Question 6.
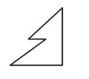
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 163
Answer:
No, It doesnot divides the given shape into two identical halves.

Question 7.
Modeling Real Life
Divide the parking lot shown into multiple sections using each of its lines of symmetry. When there are 4 cars in each section, how many cars are in the parking lot?
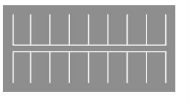
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 164
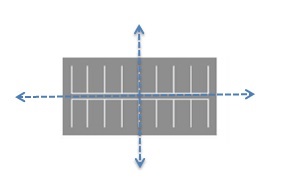
Answer:
Number of sections=4
Number of car parking slots in each section=4.
Total car parking slots in all sections = 4 x 4 =16 cars.

14.2 Draw Symmetric Shapes

Question 8.
One half of a shape and a line of symmetry are shown. Draw the rest of the shape.
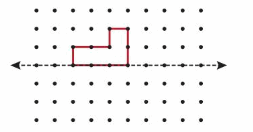
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 165
Answer:

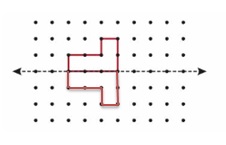
Question 9.
One half of a symmetric shape is shown. Draw the rest of the shape.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 166
Answer:

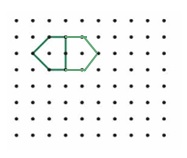
14.3 Classify Triangles by Sides

Classify the triangles by its sides.

Question 10.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 167
Answer:
Scalene triangle

Question 11.
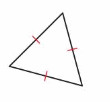
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 168
Answer:
Equilateral triangle

Question 12.
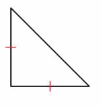
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 169
Answer:
Isosceles triangle

14.4 Classify Triangles by Angles

Classify the triangle by its angles and its sides.

Question 13.
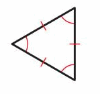
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 170
Answer:
Equiangular -Angles
Equilateral-Sides

Question 14.
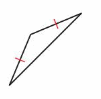
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 171
Answer:
Obtuse triangle -Angle
Isosceles triangle- Sides

Question 15.
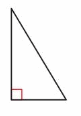
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 172
Answer:
Right angled Triangle-Angle
Scalene Triangle-Sides.

Question 16.
Which One Doesn’t Belong?
Which triangle does not belong with the other three? Explain.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 173
Answer:
First triangle is obtuse angle triangle. where other 3 triangles are acute triangles.

14.5 Classify Quadrilaterals

Classify the quadrilateral in as many ways as possible

Question 17.
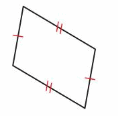
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 174
Answer:
It is parallelogram.
A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length.

Question 18.
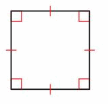
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 175
Answer:
It is a Square.
A square is a parallelogram that has four right angles and four sides with the same length.

Identify Symmetry and Two-Dimensional Shapes Cumulative Practice 1-14

Question 1.
What is the difference of 10 and 4\(\frac{7}{8}\) ?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 176
Answer:
C – 5(1/8)

Question 2.
Which letters have at least one line of symmetry?
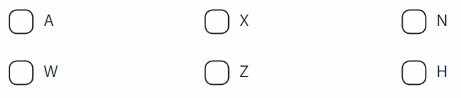
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 177
Answer:
W,Z AND H

Question 3.
The table shows the amount of rain that falls in each city in 1 day. Which city has more rainfall than Detroit and less rainfall than Seattle?
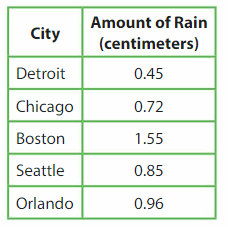
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 178
Answer:
Chicago – 0.72

Question 4.
Which shapes have four sides with the same length?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 179
Answer:
Rhombus and Square.

Question 5.
A movie starts at 2:55 P.M. and ends at 4:45 P.M. How long was the movie?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 180
Answer:
1 Hour 50 Mins

Question 6.
Which are equivalent to \(3 \times \frac{5}{6}\) ?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 181
Answer:
Expect 8/6 all the options are equal to \(3 \times \frac{5}{6}\) .

Question 7.
The rectangle has a perimeter of 48 centimeters. What is the width of the rectangle?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 182
Answer:
Perimeter of Rectangle = width + length.
48 = w + 15.
w=48-15
w=33cms.

Question 8.
Which two lines appear to be parallel?
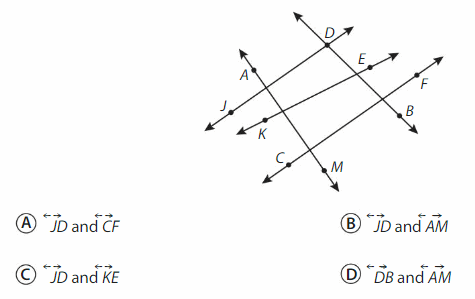
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 183
Answer:
Option A.

Question 9.
Your friend draws a triangle with side lengths of 10 centimeters,12 centimeters, and 10 centimeters. What type of triangle did your friend draw?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 184
Answer:
It is a Isosceles Triangle. It has 2 sides equal.

Question 10.
What is the quotient of 846 and 3?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 185
Answer:
282

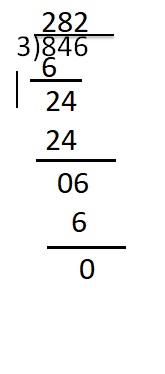
Question 11.
Which rectangular dimensions have an area of 3,600 square miles?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 186
Answer:
72 miles long and 50 miles wide.

Question 12.
The angle measures of a triangle are 57°, 60°, and 63°. How can you classify the triangle?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 187
Answer:
An acute-angled triangle is a type of triangle in which all the three internal angles of the triangle are acute, that is, they measure less than 90°.

Question 13.
Newton is walking on Path X that continues straight ahead. He turns onto Path Y.
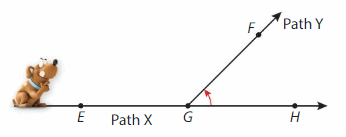
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 188
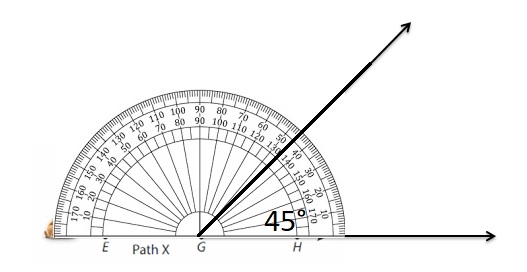
Using a protractor, which statement is true about ∠FGH
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 189
Answer:
The angle is 45°, and is acute.

Question 14.
You jump 3\(\frac{1}{2}\) feet. How far do you jump in inches?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 190
Answer:
3(1/2)=7/2=3.5feet.

Question 15.
Which of the following shows \(\overrightarrow{D E}\) ?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 191
Answer:
Option DE.

Question 16.
A rectangular backyard has a perimeter of 280 feet. The length of the backyard is 75 feet. What is the area of the backyard?
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 192
Answer:
The perimeter of the backyard =280 feet.
length of the backyard =75 feet
The breadth of the backyard = b feet.
280=75 + b
b=280-75
b=205.
Area of the backyard= l x b.
Area = 205 x 75.
Area=15375 sq feet.

Question 17.
Your friend makes a banner by taping the edges of 10 pieces of paper together. Each piece of paper is 28 centimeters long and 22 centimeters wide.
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 193
Part A What is the length of the entire banner? Explain.
Answer:
28 centimeters long and 22 centimeters wide. As the tapping is done for the edges only.
Part B Your friend wants to place ribbon along the outside of the entire banner. How much ribbon will she need?
Answer:
Perimeter = length + breadth.
P= 28 + 22= 50 cms.

Identify Symmetry and Two-Dimensional Shapes Steam Performance Task 1-14

In computer graphic design, polygons are connected at the vertices and edges to create a two-dimensional image that appears three-dimensional. This is called polygon mesh.
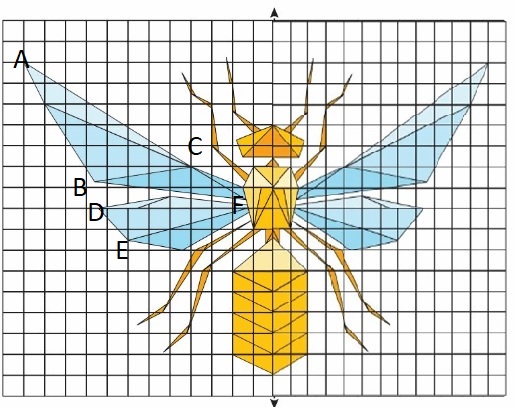
1. The elephant graphic is made from different polygons. Do the polygons have the same number of sides? Why do you think that is?
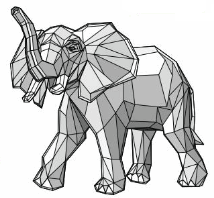
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 194
2. Use the quadrilateral shown from the elephant graphic.
a. Exactly one pair of sides are parallel. Classify the quadrilateral.
Answer:
It is a Trapezoid.
b. Which two lines are parallel?
Answer:
BC ll AD.
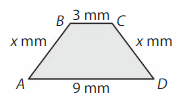
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 195
c. Which angles are acute?
Answer:
∠ADC.
d. The perimeter is 22 millimeters. Find the missing side lengths.
Answer:
Perimeter = 22 mm.
P= x +3 + x + 9 mm.
22= 2x + 12.
2x=10.
x=5 mm.

Question 3.
There are many different triangles in the elephant graphic. Use the side lengths and angle measures to classify two of the triangles. Trace your triangles in the elephant graphic
Answer:

Question 4.
In a polygon mesh, each polygon is shaded differently to make the object appear more three-dimensional. In the drawing, two polygons still need to be shaded. Which one should be darker, the triangle or the quadrilateral? Why?
Big Ideas Math Answer Key Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 600
Answer:
One should be darker is the triangle.A Triangle is a polygon with three edges and three vertices.

Question 5.
Triangle mesh is when a three-dimensional design is created using only triangles. The triangle mesh design below has line symmetry.
a. Use the line of symmetry to finish the design.
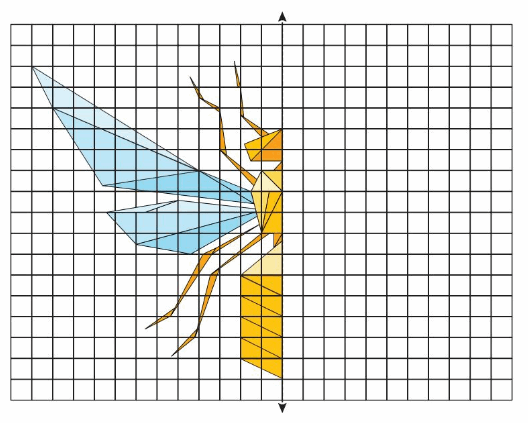
Big Ideas Math Solutions Grade 4 Chapter 14 Identify Symmetry and Two-Dimensional Shapes 196

b. Name two types of triangles you see in the design. Trace your triangles above. Explain.
Answer:
∆ DFE is Isosceles triangle.
∆ ABC is Scalene triangle.

Question 6.
Use the Internet or some other resource to find out more about polygon mesh and how it is used in graphic design. Write one thing that you learn.
Answer:
A polygon mesh is a collection of vertices, edges and faces that defines the shape of a polyhedral object.
In graphic design, it is used to make up a 3D object, 3D animated film, advertising, or video games.
We learn in making different animated pictures, videos.

Conclusion:

Enhance your performance by practicing the problems from Big Ideas Math Grade 4 Solution Key Chapter 14 Identify Symmetry and Two-Dimensional Shapes. Understand the concepts of symmetry and 2-D shapes and apply them to the real-time problems. Solving the problems of math is fun. Enjoy it by solving the questions given at the end of the chapter. So that you can know at which topic who were lagging. We are here to clarify your doubts. For any doubts, you can post the comments in the below section.

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top