Big Ideas Math Answers Grade 4 Chapter 9 Multiply Whole Numbers and Fractions is an essential study material for students. Basic concepts of Multiplication of Whole Numbers and Fractions are clearly explained to score good marks for students. Also, in-depth knowledge of Chapter 9 Multiplies Whole Numbers and Fractions Big Ideas Grade 4 Math Answer Key mentioned with a clear explanation. Furthermore, BIM Grade 4 Multiply Whole Numbers and Fractions Answer Key is very convenient for students who are struggling to learn that concept. We have also given extra practice in small groups for the best practice of the students.
Big Ideas 4th Grade Chapter 9 Multiply Whole Numbers and Fractions Math Book Answer Key
Every problem is solved and given with a detailed explanation to help the students while their preparation. We have included the BIM Grade 4 Chapter 9 Solution Key in all the ways such as quiz, formative assessment, homework, or extra practice, etc. Practice in all the ways to get a complete grip on the concept. Provide a bright future for students, by giving the Chapter 9 Multiplies Whole Numbers and Fractions Big Ideas Grade 4 Math Answers as a reference.
Lesson: 1 Understand Multiples of Unit Fractions
- Lesson 9.1 Understand Multiples of Unit Fractions
- Understand Multiples of Unit Fractions Homework & practice 9.1
Lesson: 2 Understand Multiples of Fractions
- Lesson 9.2 Understand Multiples of Fractions
- Understand Multiples of Fractions Homework & Practice 9.2
Lesson: 3 Multiply Whole Numbers and Fractions
- Lesson 9.3 Multiply Whole Numbers and Fractions
- Multiply Whole Numbers and Fractions Homework & practice 9.3
Lesson: 4 Multiply Whole Numbers and Mixed Numbers
- Lesson 9.4 Multiply Whole Numbers and Mixed Numbers
- Multiply Whole Numbers and Mixed Numbers Homework & Practice 9.4
Lesson: 5 Problem Solving: Fraction Operations
- Lesson 9.5 Problem Solving: Fraction Operations
- Problem Solving: Fraction Operations Homework & Practice 9.5
Performance Task
- Multiply Whole Numbers and Fractions Performance Task
- Multiply Whole Numbers and Fractions Activity
- Multiply Whole Numbers and Fractions Chapter Practice
Lesson 9.1 Understand Multiples of Unit Fractions
Explore and Grow
Draw a model of any fraction using unit fractions. Then write an addition equation to represent your model.
Reasoning
How can you rewrite the equation using multiplication? Explain.
Answer:
Let us take the fraction as \(\frac{3}{5}\) we draw a model using fractions as below
Addition equation to represent \(\frac{3}{5}\) model is \(\frac{3}{5}\) = \(\frac{1}{5}\) +
\(\frac{1}{5}\) +\(\frac{1}{5}\) to rewrite the equation using multiplication,
We write the equation as \(\frac{3}{5}\) = \(\frac{1}{5}\) +\(\frac{1}{5}\) +
\(\frac{1}{5}\) = 3 X \(\frac{1}{5}\) as the fraction \(\frac{3}{5}\)
represents 3 parts that are each \(\frac{1}{5}\) of the whole.
Think and Grow: Multiples of Unit Fractions
Any fraction can be written as a multiple of a unit fraction with a like denominator.
Example
Write \(\frac{5}{8}\) as a multiple of a unit fraction.
The fraction \(\frac{5}{8}\) represents 5 parts that are each \(\frac{1}{8}\) of the whole.
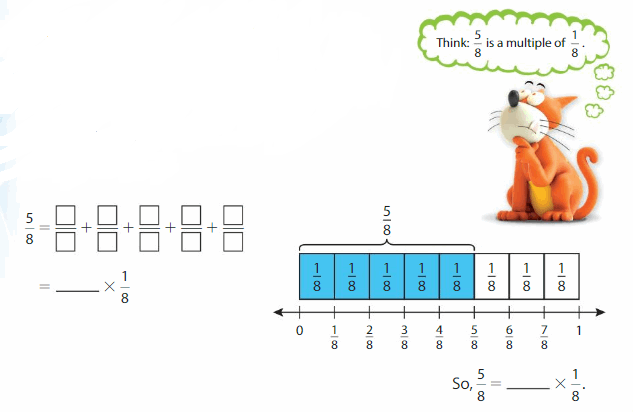
Answer:
Show and Grow
Write the fraction as a multiple of a unit fraction.
Question 1.
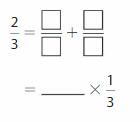
Answer:
\(\frac{2}{3}\) = \(\frac{1}{3}\) +\(\frac{1}{3}\)
= 2 X \(\frac{1}{3}\).
Explanation:
We write \(\frac{2}{3}\) in addition equation as \(\frac{2}{3}\) =\(\frac{1}{3}\) +
\(\frac{1}{3}\) and multiplication as fraction \(\frac{2}{3}\) represents 2 parts that are each
\(\frac{1}{3}\) of the whole, \(\frac{2}{3}\) =2 X \(\frac{1}{3}\).
Question 2.
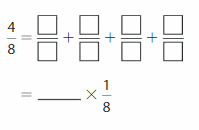
Answer:
\(\frac{4}{8}\) = \(\frac{1}{8}\) +\(\frac{1}{8}\) + \(\frac{1}{8}\) +
\(\frac{1}{8}\) = 4 X \(\frac{1}{8}\).
Explanation:
We write \(\frac{4}{8}\) in addition equation as \(\frac{4}{8}\) = \(\frac{1}{8}\) +
\(\frac{1}{8}\) + \(\frac{1}{8}\) +\(\frac{1}{8}\) and multiplication as
fraction \(\frac{4}{8}\) represents 4 parts that are each \(\frac{1}{8}\) of the whole,
\(\frac{4}{8}\) =4 X \(\frac{1}{8}\).
Question 3.
\(\frac{6}{5}\)
Answer:
\(\frac{6}{5}\) = \(\frac{1}{5}\)+\(\frac{1}{5}\) +\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\) = 6 X \(\frac{1}{5}\).
Explanation:
We write \(\frac{6}{5}\) in addition equation as \(\frac{6}{5}\)= \(\frac{1}{5}\)+
\(\frac{1}{5}\) +\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\) and multiplication as fraction \(\frac{6}{5}\) represents 6 parts
that are \(\frac{1}{5}\) of the whole \(\frac{6}{5}\) = 6 X \(\frac{1}{5}\).
Question 4.
\(\frac{7}{100}\)
Answer:
\(\frac{7}{100}\) = \(\frac{1}{100}\) + \(\frac{1}{100}\) + \(\frac{1}{100}\) +
\(\frac{1}{100}\)+ \(\frac{1}{100}\)+ \(\frac{1}{100}\)+ \(\frac{1}{100}\)
= 7 X \(\frac{1}{100}\).
Explanation:
We write \(\frac{7}{100}\) in addition equation as \(\frac{7}{100}\)= \(\frac{1}{100}\) +
\(\frac{1}{100}\) + \(\frac{1}{100}\) + \(\frac{1}{100}\)+ \(\frac{1}{100}\)+
\(\frac{1}{100}\)+ \(\frac{1}{100}\) and multiplication as fraction \(\frac{7}{100}\) represents
7 parts that are \(\frac{1}{100}\) of the whole, \(\frac{7}{100}\)= 7 X \(\frac{1}{100}\).
Apply and Grow: Practice
Write the fraction as a multiple of a unit fraction.
Question 5.
\(\frac{2}{6}\)
Answer:
\(\frac{2}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\)
= 2 X \(\frac{1}{6}\).
Explanation:
We write \(\frac{2}{6}\) in addition equation as \(\frac{2}{6}\)= \(\frac{1}{6}\) +
\(\frac{1}{6}\) and multiplication as fraction \(\frac{2}{6}\) represents 2 parts that are
\(\frac{1}{6}\) of the whole,\(\frac{2}{6}\) = 2 X \(\frac{1}{6}\).
Question 6.
\(\frac{6}{8}\)
Answer:
\(\frac{6}{8}\) = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)+
\(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\) = 6 X \(\frac{1}{8}\).
Explanation:
We write \(\frac{6}{8}\) in addition equation as \(\frac{6}{8}\) = \(\frac{1}{8}\) +
\(\frac{1}{8}\) + \(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\)+
\(\frac{1}{8}\) and multiplication as fraction \(\frac{6}{8}\) represents 6 parts that are
\(\frac{1}{8}\) of the whole, \(\frac{6}{8}\) =6 X \(\frac{1}{8}\).
Question 7.
\(\frac{5}{4}\)
Answer:
\(\frac{5}{4}\) = \(\frac{1}{4}\) + \(\frac{1}{4}\) +\(\frac{1}{4}\) +
\(\frac{1}{4}\) +\(\frac{1}{4}\) = 5 X \(\frac{1}{4}\).
Explanation:
We write \(\frac{5}{4}\) in addition equation as \(\frac{5}{4}\)=\(\frac{1}{4}\) +
\(\frac{1}{4}\) +\(\frac{1}{4}\) +\(\frac{1}{4}\) + \(\frac{1}{4}\)
and multiplication as fraction \(\frac{5}{4}\) represents 5 parts that are \(\frac{1}{4}\)
of the whole, \(\frac{5}{4}\) = 5 X \(\frac{1}{4}\).
Question 8.
\(\frac{3}{12}\)
Answer:
\(\frac{3}{12}\)= \(\frac{1}{12}\) + \(\frac{1}{12}\) +\(\frac{1}{12}\) =
3 X \(\frac{1}{12}\)
Explanation :
We write \(\frac{3}{12}\) in addition equation as \(\frac{3}{12}\)= \(\frac{1}{12}\) +
\(\frac{1}{12}\) + \(\frac{1}{12}\) and multiplication as fraction \(\frac{3}{12}\)
represents 3 parts that are \(\frac{1}{12}\) of the whole, \(\frac{3}{12}\) =
3 X \(\frac{1}{12}\).
Question 9.
\(\frac{8}{100}\)
Answer:
\(\frac{8}{100}\) = \(\frac{1}{100}\) + \(\frac{1}{100}\)+\(\frac{1}{100}\)+
\(\frac{1}{100}\)+\(\frac{1}{100}\)+\(\frac{1}{100}\)+\(\frac{1}{100}\)+
\(\frac{1}{100}\) = 8 X \(\frac{1}{100}\).
Explanation :
We write \(\frac{8}{100}\) in addition equation as \(\frac{8}{100}\) =
\(\frac{1}{100}\) + \(\frac{1}{100}\)+\(\frac{1}{100}\)+
\(\frac{1}{100}\)+\(\frac{1}{100}\)+ \(\frac{1}{100}\)+
\(\frac{1}{100}\)+\(\frac{1}{100}\) and multiplication as fraction
\(\frac{8}{100}\) represents 8 parts that are \(\frac{1}{100}\) of the whole,
\(\frac{8}{100}\)= 8 X \(\frac{1}{100}\).
Question 10.
\(\frac{7}{10}\)
Answer:
\(\frac{7}{10}\) = \(\frac{1}{10}\) +\(\frac{1}{10}\) +\(\frac{1}{10}\) +
\(\frac{1}{10}\) +\(\frac{1}{10}\) +\(\frac{1}{10}\) +\(\frac{1}{10}\)
= 7 X \(\frac{1}{10}\).
Explanation:
We write \(\frac{7}{10}\) in addition equation as \(\frac{7}{10}\) = \(\frac{1}{10}\) +
\(\frac{1}{10}\) +\(\frac{1}{10}\) +\(\frac{1}{10}\) +\(\frac{1}{10}\) +
\(\frac{1}{10}\) +\(\frac{1}{10}\) and multiplication as fraction \(\frac{7}{10}\)
represents 7 parts that are \(\frac{1}{10}\) of the whole,\(\frac{7}{10}\) = 7 X \(\frac{1}{10}\).
Question 11.
Structure
When a fraction is written as a multiple of a unit fraction, what is the relationship between the numerator of the
fraction and the number that is multiplied by the unit fraction?
Answer:
When a fraction is written as a multiple of a unit fraction, the relationship between the numerator of the fraction
and the number that is multiplied by the unit fraction, is the whole number times the unit fraction.
Explanation : We know that the numerator of a unit fraction is always one. So When a fraction is
written as a multiple of a unit fraction the number will be always the whole number (whole number of times the unit fraction)
and is multiplied by unit fraction. For example \(\frac{3}{8}\) we write it as 3 X \(\frac{1}{8}\)
here it is 3 and this 3 is multiplied by unit fraction.
DIG DEEPER!
Write the mixed number as a multiple of a unit fraction.
Question 12.
1\(\frac{1}{8}\)
Answer:
1\(\frac{1}{8}\) = \(\frac{9}{8}\) = \(\frac{1}{8}\)+\(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)= 9 X \(\frac{1}{8}\) .
Explanation:
First we convert a mixed number to an improper fraction, It is to multiply the bottom number 8 by the
“regular” number 1, add in the top number 1, and then put this on top of the original bottom number as 9 by 8.
1\(\frac{1}{8}\) = 1+\(\frac{1}{8}\) = \(\frac{9}{8}\)
We write \(\frac{9}{8}\) in addition equation as \(\frac{9}{8}\)= \(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\) +\(\frac{1}{8}\)
and multiplication as fraction \(\frac{9}{8}\) represents 9 parts that are \(\frac{1}{10}\)
of the whole, \(\frac{9}{8}\) = 9 X \(\frac{1}{8}\).
Question 13.
3\(\frac{4}{5}\)
Answer:
3\(\frac{4}{5}\) = \(\frac{19}{5}\)=\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\) +\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)= 19 X \(\frac{1}{5}\).
Explanation:
First we convert a mixed number to an improper fraction, It is to multiply the bottom number 5 by the “regular”
number 3, add in the top number 4, and then put this on top of the original bottom number as 19 by 5.
3\(\frac{4}{5}\)=3+\(\frac{4}{5}\) = \(\frac{19}{5}\)
We write \(\frac{19}{5}\) in addition equation as \(\frac{19}{5}\) = \(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\) +\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\) and multiplication as fraction \(\frac{19}{5}\)
represents 19 parts that are \(\frac{1}{5}\) of the whole,\(\frac{19}{5}\)= 19 X \(\frac{1}{5}\).
Question 13.
Think and Grow: Modeling Real Life
Example
A juice stand worker uses \(\frac{1}{2}\) of an orange to garnish each drink.
The worker has \(\frac{7}{12}\) of an orange left. How many more drinks can the worker garnish?
Write the fraction of orange left as a multiple of \(\frac{1}{12}\).

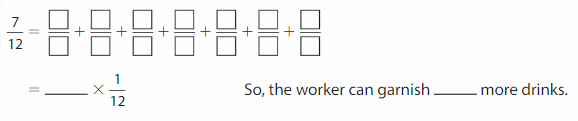
Answer:
The worker can garnish \(\frac{1}{12}\) more drinks,
\(\frac{7}{12}\) minus \(\frac{1}{2}\) means \(\frac{7}{12}\) – \(\frac{1}{2}\)
= \(\frac{1}{12}\), Orange left is 7 X \(\frac{1}{12}\).
Explanation:
Given a juice stand worker uses \(\frac{1}{2}\) of an orange to garnish each drink.
The worker has \(\frac{7}{12}\) of an orange left. So the worker can garnish more \(\frac{7}{12}\)
minus \(\frac{1}{2}\) means \(\frac{7}{12}\) – \(\frac{1}{2}\) = \(\frac{1}{12}\),
Given \(\frac{7}{12}\) of an orange is left , to write orange left as a multiple of \(\frac{1}{12}\)
we have orange left as \(\frac{7}{12}\) so write it as 7 parts that are \(\frac{1}{12}\) of the whole,
\(\frac{7}{12}\)= 7 X \(\frac{1}{12}\).
Show and Grow
Question 14.
A piece of rope is \(\frac{8}{5}\) meters long. You cut the rope into \(\frac{1}{5}\) meter long pieces.
How many pieces do you cut?
Answer:
8 pieces I have cut.
Explanation:
Given a piece of rope is \(\frac{8}{5}\) meters long and it has been cut into \(\frac{1}{5}\)
meter long pieces, therefore pieces of rope cut is \(\frac{8}{5}\) divided by \(\frac{1}{5}\)
= \(\frac{8}{5}\) X latex]\frac{5}{1}[/latex] = 8.
Question 15.
A restaurant serves \(\frac{4}{10}\) of a meatloaf to 4 customers. Each customer receives
the same amount of meatloaf. What fraction of the meatloaf does each customer receive?
Answer:
The fraction of the meatloaf each customer receives is \(\frac{1}{10}\)
Explanation:
Given a restaurant serves \(\frac{4}{10}\) of a meatloaf to 4 customers and each customer receives the same
amount of meatloaf so fraction of the meatloaf each customer receives is \(\frac{4}{10}\) divided by 4 =
\(\frac{4}{10}\) x \(\frac{1}{4}\) = \(\frac{1}{10}\).
Question 16.
You use 3\(\frac{3}{4}\) pounds of trail mix to make treat bags. You put \(\frac{1}{4}\)
pound of trail mix into each bag. How many treat bags do you make?

Answer:
Total number of treat bags made are 15
Explanation:
I use 3\(\frac{3}{4}\) pounds of trail mix to make treat bags, We convert a mixed number to an
improper fraction,It is to multiply the bottom number 4 by the “regular” number 3, add in the top number 3,
and then put this on top of the original bottom number as 15 by 4, it becomes \(\frac{15}{4}\),Each bag i kept
\(\frac{1}{4}\) pound of trail mix so total number of treat bags required to make are \(\frac{15}{4}\)
divided by \(\frac{1}{4}\)=\(\frac{15}{4}\) X \(\frac{4}{1}\)=15 treat bags.
Question 17.
DIG DEEPER!
You walk from home to school and then back home again each day for 5 days. Altogether, you walk \(\frac{10}{8}\) miles. What is the distance from your home to school? Explain.
Answer:
The distance from home to school is \(\frac{1}{8}\) miles
Explanation:
Total number of miles walked is \(\frac{10}{8}\) in 5 days that to from home to school and
then back home again means it is twice a day , Let us take X as the distance from home to school is,
Given 2X x 5=\(\frac{10}{8}\) miles, X = Then each day number of miles walked is \(\frac{10}{8}\)
divided by 10 which is equal to \(\frac{10}{8}\) x \(\frac{1}{10}\) =\(\frac{1}{8}\),
Therefore X = \(\frac{1}{8}\) miles.
Understand Multiples of Unit Fractions Homework & practice 9.1
Write the fraction as a multiple of a unit fraction.
Question 1.
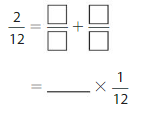
Answer:
\(\frac{2}{12}\)= \(\frac{1}{12}\)+\(\frac{1}{12}\) = 2 X \(\frac{1}{12}\)
Explanation:
We write \(\frac{2}{12}\) in addition equation as \(\frac{2}{12}\)= \(\frac{1}{12}\) +
\(\frac{1}{12}\) and multiplication as fraction \(\frac{2}{12}\) represents 2 parts that are
\(\frac{1}{12}\) of the whole, \(\frac{2}{12}\)= 2 X \(\frac{1}{12}\).
Question 2.
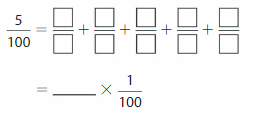
Answer:
\(\frac{5}{100}\)= \(\frac{1}{100}\)+\(\frac{1}{100}\)+\(\frac{1}{100}\)+
\(\frac{1}{100}\)+\(\frac{1}{100}\) = 5 X \(\frac{1}{100}\).
Explanation:
We write \(\frac{5}{100}\) in addition equation as \(\frac{5}{100}\)= \(\frac{1}{100}\)+
\(\frac{1}{100}\)+\(\frac{1}{100}\)+\(\frac{1}{100}\)+\(\frac{1}{100}\)
and multiplication as fraction \(\frac{5}{100}\) represents 5 parts that are \(\frac{1}{100}\) of the whole, \(\frac{5}{100}\) = 5 X \(\frac{1}{100}\).
Question 3.
\(\frac{3}{6}\)
Answer:
\(\frac{3}{6}\)=\(\frac{1}{6}\)+\(\frac{1}{6}\)+\(\frac{1}{6}\)
= 3 X \(\frac{1}{6}\).
Explanation:
We write \(\frac{3}{6}\) in addition equation as \(\frac{3}{6}\)=\(\frac{1}{6}\)+
\(\frac{1}{6}\)+\(\frac{1}{6}\) and multiplication as fraction \(\frac{3}{6}\)
represents 3 parts that are \(\frac{1}{6}\) of the whole,\(\frac{3}{6}\) = 3 X \(\frac{1}{6}\).
Question 4.
\(\frac{7}{10}\)
Answer:
\(\frac{7}{10}\) =\(\frac{1}{10}\)+\(\frac{1}{10}\)+\(\frac{1}{10}\)+
\(\frac{1}{10}\)+\(\frac{1}{10}\)+\(\frac{1}{10}\)+\(\frac{1}{10}\)
= 7 X \(\frac{1}{10}\)
Explanation:
We write \(\frac{7}{10}\) in addition equation as \(\frac{7}{10}\)= \(\frac{1}{10}\)+
\(\frac{1}{10}\)+\(\frac{1}{10}\)+\(\frac{1}{10}\)+\(\frac{1}{10}\)+
\(\frac{1}{10}\)+\(\frac{1}{10}\) and multiplication as \(\frac{7}{10}\) represents
7 parts that are \(\frac{1}{10}\) of the whole,\(\frac{7}{10}\) = 7 X \(\frac{1}{10}\).
Question 5.
\(\frac{4}{5}\)
Answer:
\(\frac{4}{5}\) = \(\frac{1}{5}\)+\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\) = 4 X \(\frac{1}{5}\).
Explanation:
We write \(\frac{4}{5}\) in addition equation as \(\frac{4}{5}\)=\(\frac{1}{5}\)+
\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\) and multiplication as \(\frac{4}{5}\)
represents 4 parts that are \(\frac{1}{5}\) of the whole,\(\frac{4}{5}\)= 4 X \(\frac{1}{5}\).
Question 6.
\(\frac{9}{2}\)
Answer:
\(\frac{9}{2}\) = \(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+
\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+
\(\frac{1}{2}\)+\(\frac{1}{2}\) = 9 X \(\frac{1}{2}\).
Explanation:
We write \(\frac{9}{2}\) in addition equation as \(\frac{9}{2}\) = \(\frac{1}{2}\)+
\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+
\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)
and multiplication as \(\frac{9}{2}\) represents 9 parts that are \(\frac{1}{2}\) of the whole,
\(\frac{9}{2}\)= 9 X \(\frac{1}{2}\).
Question 7.
\(\frac{8}{8}\)
Answer:
\(\frac{8}{8}\)=1=\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+
\(\frac{1}{8}\) = \(\frac{8}{8}\) = 8 X \(\frac{1}{8}\).
Explanation:
\(\frac{8}{8}\)= 1 ,but we write the fraction as a addition of a unit fraction and multiple of a unit fraction,
We write \(\frac{8}{8}\) in addition equation as \(\frac{8}{8}\) = \(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)+
\(\frac{1}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\) and multiplication as \(\frac{8}{8}\)
represents 8 parts that are \(\frac{1}{8}\) of the whole,\(\frac{8}{8}\)= 8 X \(\frac{1}{8}\).
Question 8.
\(\frac{6}{3}\)
Answer:
\(\frac{6}{3}\)=2,\(\frac{6}{3}\)= \(\frac{1}{3}\)+\(\frac{1}{3}\)+
\(\frac{1}{3}\)+\(\frac{1}{3}\)+\(\frac{1}{3}\)+\(\frac{1}{3}\)
= 6 X \(\frac{1}{3}\).
Explanantion:
\(\frac{6}{3}\)= 2 ,but we write the fraction as a addition of a unit fraction and multiple of a unit fraction,
We write \(\frac{6}{3}\) in addition equation as \(\frac{6}{3}\)= \(\frac{1}{3}\)+
\(\frac{1}{3}\)+\(\frac{1}{3}\)+\(\frac{1}{3}\)+\(\frac{1}{3}\)+
\(\frac{1}{3}\) and multiplication as \(\frac{6}{3}\) represents 6 parts that are
\(\frac{1}{3}\) of the whole,\(\frac{6}{3}\)= 6 X \(\frac{1}{3}\).
Question 9.
Logic
What is Newton’s fraction? Write the fraction as a multiple of a unit fraction.

Answer:
Newton’s fraction = \(\frac{9}{12}\)=\(\frac{1}{12}\) +\(\frac{1}{12}\) +
\(\frac{1}{12}\) +\(\frac{1}{12}\) +\(\frac{1}{12}\) +\(\frac{1}{12}\) +
\(\frac{1}{12}\) +\(\frac{1}{12}\) +\(\frac{1}{12}\) = 9 X \(\frac{1}{12}\).
Explanation:
Given that Newton’s fraction as sum of 9 unit fractions and each unit fraction is one twelfth of a whole.
So Newton’s fraction is \(\frac{9}{12}\) we write \(\frac{9}{12}\) in addition equation as
\(\frac{9}{12}\)= \(\frac{1}{12}\) +\(\frac{1}{12}\) +\(\frac{1}{12}\) +
\(\frac{1}{12}\) +\(\frac{1}{12}\) +\(\frac{1}{12}\) +\(\frac{1}{12}\) +
\(\frac{1}{12}\) +\(\frac{1}{12}\) and multiplication as \(\frac{9}{12}\) represents 9 parts
that are \(\frac{1}{12}\) of the whole,\(\frac{9}{12}\)= 9 X \(\frac{1}{12}\).
Question 10
Structure
Write a multiplication equation that represents the grapefruit halves.

Answer:
\(\frac{6}{2}\)=\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+
\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)
= 6 X \(\frac{1}{2}\).
Explanation:
Given 6 number of grapefruit halves so there are total grapefruit as \(\frac{6}{2}\) we write
\(\frac{6}{2}\) in addition equation as \(\frac{6}{2}\)=\(\frac{1}{2}\)+
\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+\(\frac{1}{2}\)+
\(\frac{1}{2}\),so the multiplication equation is \(\frac{6}{2}\) represents 6 parts that are
\(\frac{1}{2}\) of the whole,\(\frac{6}{2}\)= 6 X \(\frac{1}{2}\).
Question 11.
Which One Doesn’t Belong?
Which expression does not belong with the other three?

Answer:
4 X \(\frac{1}{5}\) expression does not belong with the other three, as all the other expressions values results are same =\(\frac{5}{4}\) only 4 X \(\frac{1}{5}\) expression is not.
Explanation:
1. 5 X \(\frac{1}{4}\) = \(\frac{5}{4}\)
2. \(\frac{1}{4}\)+\(\frac{1}{4}\)+\(\frac{1}{4}\)+\(\frac{1}{4}\)=
5 X \(\frac{1}{4}\)= \(\frac{5}{4}\)
3. \(\frac{5}{4}\) =\(\frac{5}{4}\)
4. 4 X \(\frac{1}{5}\)= \(\frac{4}{5}\)≠ \(\frac{5}{4}\)
So in the above expressions only 4 X \(\frac{1}{5}\) does not belong with the other three expressions.
Question 12.
Modeling Real Life
You are making blueberry pancakes. You have \(\frac{6}{8}\) cup of blueberries. You put \(\frac{1}{8}\) cup of blueberries in each pancake. How many pancakes do you make?

Answer:
6 pancakes i can make.
Explanation:
I have \(\frac{6}{8}\) cup of blueberries and i can put \(\frac{1}{8}\) cup of blueberries
in each pan cake so total number of pancakes made are \(\frac{6}{8}\) divided by \(\frac{1}{8}\) =
\(\frac{6}{8}\) X \(\frac{8}{1}\)= 6 pancakes.
Question 13.
DIG DEEPER!
You cut a loaf of zucchini bread into 20 equal slices. You and your friends eat \(\frac{3}{10}\) of the slices.
You want to put each leftover slice into its own bag. How many bags do you need?
Answer:
14 bags are needed.
Explanation :
Given a loaf of zucchini bread is cut into 20 equal slices and i ,friend eat \(\frac{3}{10}\) of the slices,
Total number of slices of zucchini bread =20, Number of slices ate = \(\frac{3}{10}\) means it says
out of 10 slices 3 were ate, so out of 20 slices 2 x 3= 6 slices were eaten. Number of slices left = 20 – 6 =14 slices
and one bag contains only one slice. Therefore number of bags needed are 14.
Question 14.
Is 46 a multiple of 45.
Answer:
No 46 is not a multiple of 45.
Explanation:
A multiple is a number that can be divided by another number a certain number of times without a remainder.
45 when divided by 46 a certain times will leave a remainder, So 46 is not a multiple of 45
or a factor is one of two or more numbers that divides a given number without a remainder.
As factors of 45 are 1,3,5,9,15 and factors of 46 are 1,2,23, both do not have common factors so 46 is not a multiple of 45.
Question 15.
Is 3 a factor of 75?
Answer:
Yes 3 is a factor of 75
Explanation:
We know that a factor is one that divides a given number without a remainder and 75 when divided by 3
leaves no remainder, So 3 is a factor of 75.
Lesson 9.2 Understand Multiples of Fractions
Draw a model for each expression. Then write a multiplication expression to represent each model.
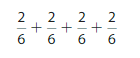
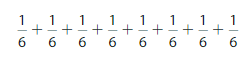
Answer:
The multiplication expression is \(\frac{2}{6}\) +\(\frac{2}{6}\) +\(\frac{2}{6}\) +
\(\frac{2}{6}\) = 4 X \(\frac{2}{6}\) =
\(\frac{1}{6}\) +\(\frac{1}{6}\)+ \(\frac{1}{6}\) +\(\frac{1}{6}\)+
\(\frac{1}{6}\) +\(\frac{1}{6}\)+ \(\frac{1}{6}\) +\(\frac{1}{6}\) =
8 X \(\frac{1}{6}\).
Explanation:
\(\frac{2}{6}\) +\(\frac{2}{6}\) +\(\frac{2}{6}\) +\(\frac{2}{6}\)
the multiplication equation is 4 parts that are \(\frac{2}{6}\) of the whole as 4 X \(\frac{2}{6}\)
\(\frac{1}{6}\) +\(\frac{1}{6}\)+ \(\frac{1}{6}\) +\(\frac{1}{6}\)+
\(\frac{1}{6}\) +\(\frac{1}{6}\)+ \(\frac{1}{6}\) +\(\frac{1}{6}\) =
8 X \(\frac{1}{6}\) the multiplication equation is 8 parts that are \(\frac{1}{6}\) of the whole as
8 X \(\frac{1}{6}\).
Structure
Compare your expressions. How are they the same? How are they different?
Same means the result of both expressions is same = \(\frac{8}{6}\)
Different means in one expression we take value of \(\frac{2}{6}\) 4 times and in another
expression we take \(\frac{1}{6}\) 8 times.
Explanation:
Same means \(\frac{2}{6}\) +\(\frac{2}{6}\) +\(\frac{2}{6}\) +\(\frac{2}{6}\) =
4 X \(\frac{2}{6}\) = \(\frac{8}{6}\) and \(\frac{1}{6}\) +\(\frac{1}{6}\)+
\(\frac{1}{6}\) +\(\frac{1}{6}\)+\(\frac{1}{6}\) +\(\frac{1}{6}\)+
\(\frac{1}{6}\) +\(\frac{1}{6}\) = 8 X \(\frac{1}{6}\) =\(\frac{8}{6}\) ,
both have results similar as \(\frac{8}{6}\), Different means here we are taking expressions as addition values of \(\frac{2}{6}\) by 4 times and in other expression we are taking addition values of \(\frac{1}{6}\) by 8 times.
Think and Grow: Multiples of Fractions
A multiple of any fraction can be written as a multiple of a unit fraction with a like denominator.
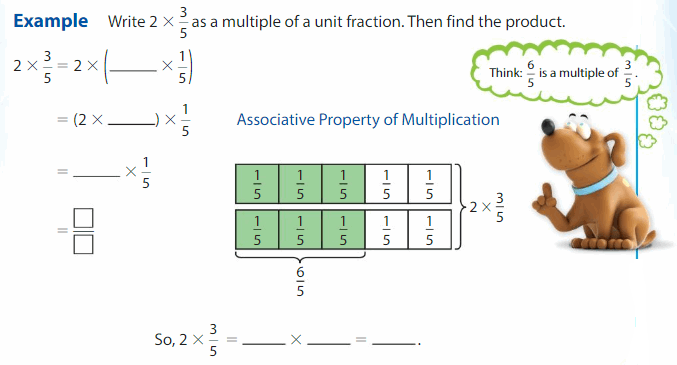
Answer:

Explanation:
To write 2 X \(\frac{3}{5}\) multiple of unit fraction first we write \(\frac{3}{5}\) as multiple of
3 X \(\frac{1}{5}\) then we multiply it by 2 as 2 X 3 X \(\frac{1}{5}\)=6 X \(\frac{1}{5}\).
Show and Grow
Write the product as a multiple of a unit fraction. Then find the product.
Question 1.
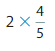
Answer:
2 X \(\frac{4}{5}\) = 2 X 4 X \(\frac{1}{5}\) = 8 X \(\frac{1}{5}\) = \(\frac{8}{5}\).
Explanation:
First we write \(\frac{4}{5}\) as \(\frac{1}{5}\) + \(\frac{1}{5}\) +
\(\frac{1}{5}\) + \(\frac{1}{5}\) = 4 X \(\frac{1}{5}\) then multiply it by 2
which is 2 X 4 X \(\frac{1}{5}\) = 8 X \(\frac{1}{5}\) = \(\frac{8}{5}\).
Question 2.
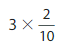
Answer:
3 X \(\frac{2}{10}\) = 3 X 2 X \(\frac{1}{10}\) = 6 X \(\frac{1}{10}\) =\(\frac{6}{10}\).
Explanation:
First we write \(\frac{2}{10}\) as \(\frac{1}{10}\) +\(\frac{1}{10}\) = 2 X \(\frac{1}{10}\)
then multiply it by 3 which is 3 X 2 X \(\frac{1}{10}\) = 6 X \(\frac{1}{10}\) =\(\frac{6}{10}\).
Question 3.
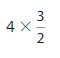
Answer:
4 X \(\frac{3}{2}\) = 4 X 3 X \(\frac{1}{2}\) = 12 X \(\frac{1}{2}\) = \(\frac{12}{2}\) = 6.
Explanation:
First we write \(\frac{3}{2}\) as \(\frac{1}{2}\) +\(\frac{1}{2}\) + \(\frac{1}{2}\) = 3 X \(\frac{1}{2}\) then we multiply it by 4 which is 4 X 3 X \(\frac{1}{2}\)= 12 X \(\frac{1}{2}\)= \(\frac{12}{2}\)=6.
Apply and Grow: Practice
Write the product as a multiple of a unit fraction. Then find the product.
Question 4.
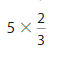
Answer:
5 X \(\frac{2}{3}\) = 5 X 2 X \(\frac{1}{3}\) = 10 X \(\frac{1}{3}\)=
\(\frac{10}{3}\).
Explanation:
First we write \(\frac{2}{3}\) as \(\frac{1}{3}\)+\(\frac{1}{3}\)=
2 X \(\frac{1}{3}\) then multiply it by 5 which is 5 X 2 X \(\frac{1}{3}\)=
10 X \(\frac{1}{3}\)= \(\frac{10}{3}\).
Question 5.
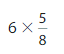
Answer:
6 X \(\frac{5}{8}\)= 6 X 5 X \(\frac{1}{8}\)= 30 X \(\frac{1}{8}\) =
\(\frac{30}{8}\).
Explanation:
First we write \(\frac{5}{8}\) as \(\frac{1}{8}\)+ \(\frac{1}{8}\)+
\(\frac{1}{8}\) + \(\frac{1}{8}\)+ \(\frac{1}{8}\) = 5 X \(\frac{1}{8}\)
then multiply it by 6 which is 6 X 5 X \(\frac{1}{8}\)=30 X \(\frac{1}{8}\)= \(\frac{30}{8}\).
Question 6.
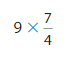
Answer:
9 X \(\frac{7}{4}\) = 9 X 7 X\(\frac{1}{4}\)= 63 X \(\frac{1}{4}\) =
\(\frac{63}{4}\).
Explanation:
First we write \(\frac{7}{4}\) as \(\frac{1}{4}\)+\(\frac{1}{4}\)+
\(\frac{1}{4}\)+ \(\frac{1}{4}\)+\(\frac{1}{4}\)+\(\frac{1}{4}\)+
\(\frac{1}{4}\) = 7 x \(\frac{1}{4}\)
then we multiply it by 9 which is 9 X 7 X \(\frac{1}{4}\)= 63 X \(\frac{1}{4}\) =
\(\frac{63}{4}\).
Question 7.
![]()
Answer:
7 X \(\frac{4}{12}\)=7 X 4 X \(\frac{1}{12}\)= 28 X \(\frac{1}{12}\)=
\(\frac{28}{12}\) also 7 X \(\frac{4}{12}\)= 7 X \(\frac{1}{3}\)= \(\frac{7}{3}\).
Explanation:
First we write \(\frac{4}{12}\) as \(\frac{1}{12}\)+ \(\frac{1}{12}\)+
\(\frac{1}{12}\)+\(\frac{1}{12}\)= 4 X \(\frac{1}{12}\) then we multiply it by 7
which is 7 X 4 X \(\frac{1}{12}\)= 28 X \(\frac{1}{12}\)=\(\frac{28}{12}\)
we can also simplify 7 X \(\frac{4}{12}\) as 4,12 can be divided by 4 we can also write
7 X \(\frac{4}{12}\) as 7 X \(\frac{1}{3}\)= \(\frac{7}{3}\).
Question 8.
![]()
Answer:
\(\frac{9}{6}\) X 8 = 9 X \(\frac{1}{6}\) X 8 = 72 X \(\frac{1}{6}\) =
\(\frac{72}{6}\) =12.
Explanation:
First we write \(\frac{9}{6}\) as \(\frac{1}{6}\) +\(\frac{1}{6}\) +
\(\frac{1}{6}\) + \(\frac{1}{6}\) +\(\frac{1}{6}\) +\(\frac{1}{6}\) +
\(\frac{1}{6}\) + \(\frac{1}{6}\) +\(\frac{1}{6}\) =9 X \(\frac{1}{6}\)
then we multiply it by 8 which is 9 X 8 X \(\frac{1}{6}\) = 72 X \(\frac{1}{6}\) =
\(\frac{72}{6}\) further as 6 can divide 72 and leaving no remainder we write \(\frac{72}{6}\) =12.
Question 9.
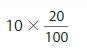
Answer:
10 X \(\frac{20}{100}\) = 10 X \(\frac{2}{10}\)=2 X 10 X \(\frac{1}{10}\)=
20 \(\frac{1}{10}\)=\(\frac{20}{10}\)=2.
Explanation:
First we write \(\frac{20}{100}\) = \(\frac{2}{10}\) as \(\frac{1}{10}\) +
\(\frac{1}{10}\) = 2 X \(\frac{1}{10}\) then multiply it by 10 which is
2 X 10 X \(\frac{1}{10}\)= 20 X \(\frac{1}{10}\)=\(\frac{20}{10}\)
and 10 can divide 20 leaving no remainder further we can write \(\frac{20}{10}\) as 2.
Number Sense
Find the unknown number.
Question 10.
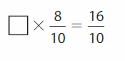
Answer:
The unknown number is 2.
Explanation:
___ X \(\frac{8}{10}\) = \(\frac{16}{10}\)= to get the unknown number we take it as P,
P X \(\frac{8}{10}\) = \(\frac{16}{10}\) means P = \(\frac{16}{10}\) X
\(\frac{10}{8}\) we get 2 , so P=2.
Question 11.
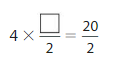
Answer:
The unknown number is 5.
Explanation:
Let us take unknown letter as P so 4 X \(\frac{P}{2}\) = \(\frac{20}{2}\) ,
4 X P= 2 X \(\frac{20}{2}\) to get value of P we take 4 to other side ,
Therefore P=20 X \(\frac{1}{4}\) = 5, so the unknown number is 5.
Question 12.
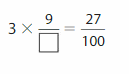
Answer:
The unknown number is 100.
Explanation:
Let us take unknown number as P given 3 X \(\frac{9}{P}\) = \(\frac{27}{100}\) ,
27 X[ latex]\frac{1}{P}[/latex] = \(\frac{27}{100}\), Therefore P= 27 X \(\frac{100}{27}\)=100.
Question 13.
Reasoning
Without calculating, would you plot the product of 5 and \(\frac{3}{6}\) to the left or to the right of 5 on a number line? Explain.
Answer:
Yes , without calculating we can plot 5 and \(\frac{3}{6}\) to the left of 5
Explanation:
5 X \(\frac{3}{6}\)= 5 X \(\frac{1}{2}\) since the denominator of each given fraction is 2
divide the space between every pairs of two consecutive integers (on the number line) in 2 equal parts each part
so obtained will represent the fraction \(\frac{1}{2}\) , so on the number line we move 5 parts on the
right-side of zero as shown in the figure.
Question 14.
Patterns
Describe and complete the pattern.
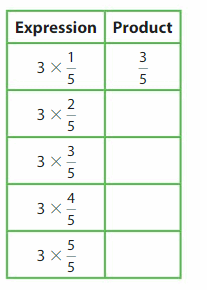
Answer:

Explanation:
We first write the expressions as multiple of unit fraction and find the product so
1. 3 X \(\frac{1}{5}\) can be written as product of 3 X 1 X \(\frac{1}{5}\)=
3 X \(\frac{1}{5}\) = \(\frac{3}{5}\)
2. 3 X \(\frac{2}{5}\) can be written as product of 3 X 2 X \(\frac{1}{5}\) =
6 X \(\frac{1}{5}\) = \(\frac{6}{5}\)
3. 3 X \(\frac{3}{5}\) can be written as product of 3 X 3 X \(\frac{1}{5}\) =
9 X \(\frac{1}{5}\) = \(\frac{9}{5}\)
4. 3 X \(\frac{4}{5}\) can be written as product of 3 X 4 X \(\frac{1}{5}\) =
12 X \(\frac{1}{5}\) = \(\frac{12}{5}\)
5. 3 X \(\frac{5}{5}\) can be written as product of 3 X 5 X \(\frac{1}{5}\) =
15 X \(\frac{1}{5}\) = \(\frac{15}{5}\) further can be simplified as 15,5 goes in 5,
so dividing by 5 we get \(\frac{15}{5}\) = 3.
Think and Grow: Modeling Real Life
A bird keeper uses a \(\frac{1}{3}\) cup scoop to feed 3 birds. He feeds each bird \(\frac{2}{3}\) cup of birdseed. How many times does he fill the scoop?
Three birds each need \(\frac{2}{3}\) cup of birdseed, so find 3 × \(\frac{2}{3}\).


Answer:

Explanation :
Given A bird keeper uses a \(\frac{1}{3}\) cup scoop to feed 3 birds each bird he feeds
\(\frac{2}{3}\) cup of birdseed, Three birds each need \(\frac{2}{3}\) cup of birdseed
so the bird keeper fills the scoop as 3 X \(\frac{2}{3}\) = 3 X _____P______ X \(\frac{1}{3}\) here
P is the number of times the bird keeper fills the cup scoop.
3 X 2 X \(\frac{1}{3}\) = 3 X P X \(\frac{1}{3}\) , when we equate both sides,
we get 3 X 2 = 3 X P , therefore P = 2.
Show and Grow
Question 15.
A chef makes 4 servings of honey1oatmeal. She uses a \(\frac{1}{2}\) tablespoon measuring spoon to measure \(\frac{3}{2}\) tablespoons of honey for each serving. How many times does she fill the measuring spoon?
Answer:
3 times the chef fill the measuring spoon.
Explanation:
Chef uses a \(\frac{1}{2}\) table spoon as measuring spoon, To measure honey for each serving
she needed for each serving is \(\frac{3}{2}\) , so 4 X \(\frac{3}{2}\) ,
Let us take P as number of times of measuring spoon , Given 4 X \(\frac{3}{2}\) =
4 X _P_ X \(\frac{1}{2}\), 4 X ___3___ X \(\frac{1}{2}\)= 4 X _P_ X \(\frac{1}{2}\) ,
we equate both sides we get value of P as 3 , therefore 3 times the chef fill the measuring spoon.
Question 16.
You have 7 magnetic blocks that are each \(\frac{9}{100}\) meter long. You connect the ends of the blocks to make a snake. What fraction of a meter is the block snake?
Answer:
\(\frac{63}{100}\) meter is the block snake.
Explanation:
Given 7 magnetic blocks and each are \(\frac{9}{100}\) meter long. After connecting the ends
of the blocks to make a snake is 7 X \(\frac{9}{100}\) = 7 X 9 X \(\frac{1}{100}\) =
63 X \(\frac{1}{100}\) = \(\frac{63}{100}\) meter.
Question 17.
Your friend roller-skates \(\frac{15}{10}\) miles each day for 5 days. How many miles does your friend roller-skate in all?

Answer:
My friend roller skate \(\frac{15}{2}\) miles in all.
Explanation:
Given friend roller-skates \(\frac{15}{10}\) miles each day means \(\frac{3}{2}\) miles
each day so for 5 days it is 5 X \(\frac{3}{2}\) = 5 X 3 X \(\frac{1}{2}\) =
15 X \(\frac{1}{2}\) = \(\frac{15}{2}\) miles.
Understand Multiples of Fractions Homework & Practice 9.2
Write the product as a multiple of a unit fraction. Then find the product.
Question 1.
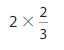
Answer:
2 X \(\frac{2}{3}\) = 2 X 2 X \(\frac{1}{3}\) = 4 X (\(\frac{1}{3}\)) =
\(\frac{4}{3}\)
Explanation:
To write the product as a multiple of a unit fraction we write it \(\frac{2}{3}\)
as 2 X \(\frac{1}{3}\) and multiply by 2 = 2 X 2 X \(\frac{1}{3}\) =
4 X \(\frac{1}{3}\) = \(\frac{4}{3}\)
Question 2.
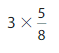
Answer:
3 X \(\frac{5}{8}\) = 3 X 5 X \(\frac{1}{8}\) = 15 X (\(\frac{1}{8}\)) =
\(\frac{15}{8}\).
Explanation:
To write the product as a multiple of a unit fraction we write it \(\frac{5}{8}\) as
5 X \(\frac{1}{8}\) and multiply by 3 = 3 X 5 X \(\frac{1}{8}\) = 15 X \(\frac{1}{8}\)
= \(\frac{15}{8}\)
Question 3.
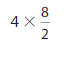
Answer:
4 X \(\frac{8}{2}\) = 4 X 8 X \(\frac{1}{2}\) = 32 X (\(\frac{1}{2}\)) =
\(\frac{32}{2}\) =16.
Explanation:
To write the product as a multiple of a unit fraction we write it \(\frac{8}{2}\) as
8 X \(\frac{1}{2}\) and multiply by 4 = 4 X 8 X \(\frac{1}{2}\) =
32 X \(\frac{1}{2}\) = \(\frac{32}{2}\) = 16.
Question 4.
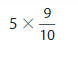
Answer:
5 X \(\frac{9}{10}\) = 5 X 9 X \(\frac{1}{10}\) = 45 X (\(\frac{1}{10}\)) =
\(\frac{45}{10}\) = \(\frac{9}{2}\)
Explanation:
To write the product as a multiple of a unit fraction we write it \(\frac{9}{10}\) as
9 X \(\frac{1}{10}\) and multiply by 5 = 5 X 9 X \(\frac{1}{10}\) =
45 X \(\frac{1}{10}\) = \(\frac{45}{10}\) = \(\frac{9}{2}\).
Question 5.
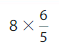
Answer:
8 X \(\frac{6}{5}\) = 8 X 6 X \(\frac{1}{5}\) = 48X (\(\frac{1}{5}\)) =
\(\frac{48}{5}\)
Explanation:
To write the product as a multiple of a unit fraction we write it \(\frac{6}{5}\) as
6 X \(\frac{1}{5}\) and multiply by 8 = 8 X 6 X \(\frac{1}{5}\) =
48 X \(\frac{1}{5}\) = \(\frac{48}{5}\).
Question 6.
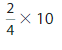
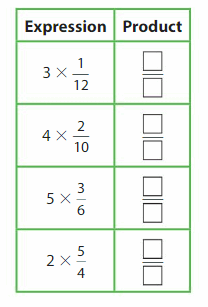
Answer:
10 X \(\frac{2}{4}\) = 10 X 2 X \(\frac{1}{4}\) = 20 X (\(\frac{1}{4}\)) =
\(\frac{20}{4}\) = \(\frac{10}{2}\).
Explanation:
To write the product as a multiple of a unit fraction we write it \(\frac{2}{4}\) as 2 X \(\frac{1}{4}\)
and multiply by 10 = 2 X 10 X \(\frac{1}{4}\) = 20 X \(\frac{1}{4}\) = \(\frac{20}{4}\) =
\(\frac{10}{2}\).
Question 7.
Number Sense
Which expression are equivalent to ![]() ?
?
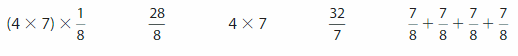
Answer:
The expressions equivalent to 4 X \(\frac{7}{8}\) are (4 X 7) x \(\frac{1}{8}\) ,
\(\frac{28}{8}\),\(\frac{7}{8}\)+\(\frac{7}{8}\)+\(\frac{7}{8}\) +
\(\frac{7}{8}\).
Explanation:
We have the value of expression of 4 X \(\frac{7}{8}\) as \(\frac{28}{8}\) So
1.(4 X 7) x \(\frac{1}{8}\)= \(\frac{28}{8}\)
2. \(\frac{28}{8}\)=\(\frac{28}{8}\)
3. 4 X 7 ≠ \(\frac{28}{8}\)
4. \(\frac{32}{7}\) ≠ \(\frac{28}{8}\)
5. \(\frac{7}{8}\)+\(\frac{7}{8}\)+\(\frac{7}{8}\)+\(\frac{7}{8}\) =
\(\frac{28}{8}\), Therefore expressions 1,2,5 are equivalent to \(\frac{28}{8}\).
The expressions equivalent to 4 X \(\frac{7}{8}\) are (4 X 7) x \(\frac{1}{8}\) , \(\frac{28}{8}\),\(\frac{7}{8}\)+\(\frac{7}{8}\)+\(\frac{7}{8}\)+\(\frac{7}{8}\)
Question 8.
Which is greater, ![]() ? Explain.
? Explain.
Answer:
6 X \(\frac{6}{2}\) is greater
Explanation:
6 X \(\frac{6}{2}\)= 6 X 6 X \(\frac{1}{2}\)=36 X \(\frac{1}{2}\)=
\(\frac{36}{2}\) and 5 X \(\frac{7}{2}\) =5 X 7 X \(\frac{1}{2}\)=
35 X \(\frac{1}{2}\), Now comparing both sides 36 X \(\frac{1}{2}\) and
35 X \(\frac{1}{2}\) we see 36 X \(\frac{1}{2}\) > 35 X \(\frac{1}{2}\)
so 6 X \(\frac{6}{2}\) is greater.
Question 9.
Structure
Your friend fills a \(\frac{3}{4}\) – cup measuring cup with rice 2 times.
Write an equation to show how much rice she uses.
Answer:
Friend uses \(\frac{3}{2}\) cups.
Explanation:
Friend fills a \(\frac{3}{4}\) – cup with rice 2 times, so she uses 2 X \(\frac{3}{4}\) =
2 X 3 x \(\frac{1}{4}\) = 6 X \(\frac{1}{4}\)= \(\frac{6}{4}\)=
\(\frac{3}{2}\).
Question 10.
Modeling Real Life
You are making a tornado in each of 2 bottles. Each bottle needs to contain \(\frac{20}{4}\) cups of water.
You only have a \(\frac{1}{4}\) – cup measuring cup. How many times do you need to fill the measuring cup?

Answer:
To make a tornado we require 40 cups of water.
Explanation:
Each bottle needs \(\frac{20}{4}\) cups of water and have a \(\frac{1}{4}\) – cup
measuring cup, Now we take P as number of times for filling so \(\frac{20}{4}\) =
P X \(\frac{1}{4}\), 20 X \(\frac{1}{4}\)=P X \(\frac{1}{4}\),
Equating both sides we get P = 20, so it is 20 times to fill the measuring cups of water
for one bottle, Given that to make a tornado we require 2 bottles, 2 X 20 cups of water = 40 cups of water.
Question 11.
DIG DEEPER!
You and your friend are each selling 12 coupon books. So far, you have sold \(\frac{2}{6}\)
of your books. Your friend has sold 3 times as many as you. What fraction of your friend’s coupon books has she sold?
Answer:
We will get the fraction as whole 1 so friend has sold all the 12 coupon books.
Explanation:
So far i sold \(\frac{2}{6}\) books out of 12 coupon books. Lets us take P number of books,
i have sold P out of 12 coupon books, P= 12 X \(\frac{2}{6}\) =12 X 2 X \(\frac{1}{6}\) =
24 X \(\frac{1}{6}\) = \(\frac{24}{6}\) =4 , So i have sold 4 coupon books,
Given friend has sold 3 times as many as I, Means 3 X 4 =12 means friend has sold all the coupon books
Review & Refresh
Find the product.
Question 12.
12 × 47 = ___
Answer:
12 X 47 = 564
Explanation:
When 12 is multiplied by 47 we get the product as 564.
Question 13.
35 × 31 = ___
Answer:
35 X 31 =1,085
Explanation:
When 35 is multiplied by 31 we get the product as 1,085.
Question 14.
58 × 49 = ___
Answer:
58 X 49 = 2,842
Explanation:
When 58 is multiplied by 49 we get the product as 2,842.
Lesson 9.3 Multiply Whole Numbers and Fractions
Explore and Grow
Use models to help you complete the table. What do you notice about each expression and its product?
Construct Arguments
Explain how to find the product of a whole number and a fraction without using models.
Answer:

Explanation:
We notice that each expression can be written as the product as a multiple of a unit fraction,
The product of a number and a counting number is a multiple of the number. We can find multiples
of unit fractions. To find the product of a whole number and a fraction without using models,
First we multiply the numerator by the whole number, then rewrite the expression as a multiple
of a unit fraction and denominator stays the same we get the product results.
Think and Grow: Multiply Whole Numbers and Fractions
You can find the product of a whole number and a fraction by multiplying the numerator by the whole number.
The denominator stays the same.
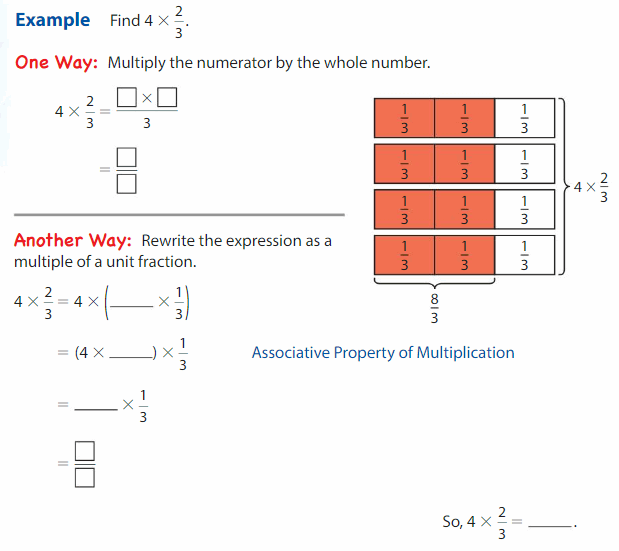
Answer:
Explanation:
To find 4 X \(\frac{2}{3}\)
Method 1: Multiply the numerator by the whole number as 4 X 2 and divide by 3= \(\frac{8}{3}\)
Method 2 : Then writing the expression as a multiple of unit fraction \(\frac{2}{3}\)=
4 X ( 2 X \(\frac{1}{3}\) ) applying associative property of multiplication
(4 X 2) X \(\frac{1}{3}\)= 8 X \(\frac{1}{3}\)=\(\frac{8}{3}\)
Show and Grow
Multiply.
Question 1.
![]()
Answer:
4 X \(\frac{1}{6}\) = \(\frac{4}{6}\) also equals to \(\frac{2}{3}\)
Explanation :
Already the expression is in multiple of unit fraction so 4 X \(\frac{1}{6}\) = \(\frac{4}{6}\) and further simplification it is equal to \(\frac{2}{3}\)
Question 2.
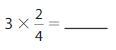
Answer:
3 X \(\frac{2}{4}\) = 3 X \(\frac{1}{2}\) = \(\frac{3}{2}\).
Explanation:
3 X \(\frac{2}{4}\) can be simplified as 3 X \(\frac{1}{2}\) now the expression is in
multiple of unit fraction so 3 X \(\frac{1}{2}\) =\(\frac{3}{2}\).
Question 3.
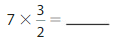
Answer:
7 X \(\frac{3}{2}\) = 7 x 3 X \(\frac{1}{2}\) = 21 X \(\frac{1}{2}\) =
\(\frac{21}{2}\).
Explanation:
7 X \(\frac{3}{2}\) first we write the expression as multiple of unit fraction so
7 X ( 3 X \(\frac{1}{2}\) ) applying associative property of multiplication
( 7 X 3) X \(\frac{1}{2}\) ) = 21 X \(\frac{1}{2}\) = \(\frac{21}{2}\)
Apply and Grow: Practice
Multiply.
Question 4.
![]()
Answer:
2 X \(\frac{1}{5}\) = \(\frac{2}{5}\).
Explanation :
Already the expression 2 X \(\frac{1}{5}\) is a multiple of unit fraction so we multiply
the whole with the numerator and numerator is being same, 2 X \(\frac{1}{5}\) =
\(\frac{2}{5}\).
Question 5.
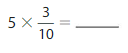
Answer:
5 X \(\frac{3}{10}\) = \(\frac{15}{10}\)=\(\frac{3}{2}\).
Explanation:
5 X \(\frac{3}{10}\), we write the expression as multiple of unit fraction so
5 X 3 X \(\frac{1}{10}\)= 15 X \(\frac{1}{10}\)= \(\frac{15}{10}\)
further it can be simplified, as both numerator and denominator can be divided by 5 so
\(\frac{15}{10}\)=\(\frac{3}{2}\).
Question 6.
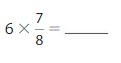
Answer:
6 X \(\frac{7}{8}\)= \(\frac{42}{8}\)= \(\frac{21}{4}\).
Explanation:
6 X \(\frac{7}{8}\), we write the expression as multiple of unit fraction so
6 X 7 X \(\frac{1}{8}\) applying associative property of multiplication
6 X ( 7 X \(\frac{1}{8}\) )= ( 6 X 7 ) X \(\frac{1}{8}\)= 42 X \(\frac{1}{8}\)=
\(\frac{42}{8}\) and further also the fraction can be simplified, as both numerator and denominator
can be divided by 2, making \(\frac{42}{8}\) as \(\frac{21}{4}\).
Question 7.
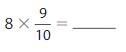
Answer:
8 X \(\frac{9}{10}\)= \(\frac{72}{10}\)=\(\frac{36}{5}\).
Explanation:
8 X \(\frac{9}{10}\), we write the expression as multiple of unit fraction
so 8 X 9 X \(\frac{1}{10}\) applying associative property of multiplication
8 X ( 9 X \(\frac{1}{10}\) )= (8 X 9 ) X \(\frac{1}{10}\)=
72 X \(\frac{1}{10}\)= \(\frac{72}{10}\) and further also the fraction can be simplified,
as both numerator and denominator can be divided by 2, making \(\frac{72}{10}\) as \(\frac{36}{5}\).
Question 8.
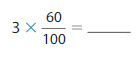
Answer:
3 X \(\frac{60}{100}\) =\(\frac{180}{100}\) =\(\frac{18}{10}\).
Explanation:
3 X \(\frac{60}{100}\), we write the expression as multiple of unit fraction,
So 3 X 60 X \(\frac{1}{100}\) applying associative property of multiplication
3 X (60 X \(\frac{1}{100}\) )= (3 X 60 ) X \(\frac{1}{100}\)= 180 X \(\frac{1}{100}\)=
\(\frac{180}{100}\) and further also the fraction can be simplified,
as both numerator and denominator can be divided by 10, making \(\frac{180}{100}\)
as \(\frac{18}{10}\).
Question 9.
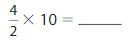
Answer:
\(\frac{4}{2}\) X 10 = 20.
Explanation :
\(\frac{4}{2}\) X 10 , we write the expression as multiple of unit fraction,
So 4 X \(\frac{1}{2}\) X 10= 40 X \(\frac{1}{2}\)=\(\frac{40}{2}\)
as the fraction can be further simplified as both numerator and denominator can be divided by 2, making it as 20.
Compare.
Question 10.
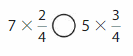
Answer:
7 X \(\frac{2}{4}\) =\(\frac{14}{4}\) is smaller < 5 X \(\frac{3}{4}\)=
\(\frac{15}{4}\).
Explanation:
7 X \(\frac{2}{4}\), First we write expression as a multiple of unit fraction
7 X 2 X \(\frac{1}{4}\) =14 X \(\frac{1}{4}\) = \(\frac{14}{4}\)
Now 5 X \(\frac{3}{4}\) is also written as a multiple of unit fraction 5 X 3 X \(\frac{1}{4}\) =
15 X \(\frac{1}{4}\) =\(\frac{15}{4}\) comparing \(\frac{14}{4}\) and
\(\frac{15}{4}\) as the denominators are same same 4 and in numerators 15 is great than 14,
So \(\frac{14}{4}\) is less than or smaller or < \(\frac{15}{4}\) ,
7 X \(\frac{2}{4}\) is smaller < 5 X \(\frac{3}{4}\)
Question 11.
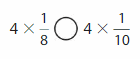
Answer:
4 X \(\frac{1}{8}\) is greater than > 4 X \(\frac{1}{10}\).
Explanation:
4 X \(\frac{1}{8}\) already the expression is in multiple of unit fraction,
we write as \(\frac{4}{8}\) and even the expression 4 X \(\frac{1}{10}\)
is in multiple of unit fraction we write as \(\frac{4}{10}\) because in order to compare
the fractions we must first turn their different denominators into the same denominators to make
denominators same we multiply 4 X \(\frac{1}{8}\) by 10 /10 the value will not change =
4 X 10 X \(\frac{1}{80}\)=40 X \(\frac{1}{80}\) = \(\frac{40}{80}\)
now other expression 4 X \(\frac{1}{10}\) by 8/8 so that the value = 4 X 8 X \(\frac{1}{80}\) =
32 X \(\frac{1}{80}\) now as denominator are same we can compare only numerators
\(\frac{40}{80}\) with \(\frac{32}{80}\) as 40 is greater than 32,
So \(\frac{4}{8}\) is greater than > \(\frac{4}{10}\) ,
4 X \(\frac{1}{8}\) is greater than > 4 X \(\frac{1}{10}\).
Question 12.
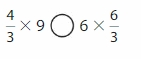
Answer:
\(\frac{4}{3}\) X 9 = 6 X \(\frac{6}{3}\) both are equal.
Explanation:
First we write expressions as a multiple of unit fraction \(\frac{4}{3}\) X 9 =
9 X 4 X \(\frac{1}{3}\) =36 X \(\frac{1}{3}\) =\(\frac{36}{3}\)
now other expression 6 X \(\frac{6}{3}\) as = 6 X 6 X \(\frac{1}{3}\) =
36 X \(\frac{1}{3}\) = \(\frac{36}{3}\) ,
As denominator is same in the both expression we compare numerators and even
the numerators are same in both the expression so given both products are equal .
Therefore \(\frac{4}{3}\) X 9 =, is equal to 6 X \(\frac{6}{3}\).
Question 13.
YOU BE THE TEACHER
Your friend says the product of 6 and \(\frac{5}{8}\) is \(\frac{5}{48}\). Is your friend correct? Explain.
Answer:
No she is not correct as the product of 6 X \(\frac{5}{8}\) ≠ \(\frac{5}{48}\).
Explanation:
We write the expression as a product 6 and \(\frac{5}{8}\) = 6 X \(\frac{5}{8}\)
to find the product of a whole number and a fraction we multiply the numerator by the whole number.
The denominator stays the same. 6 X 5 X \(\frac{1}{8}\) =30 X \(\frac{1}{8}\) =
\(\frac{30}{8}\) now comparing with \(\frac{5}{48}\) as denominators are different in order
to compare the fractions we must first turn their different denominators into the same denominators
to make denominators same we multiply \(\frac{30}{8}\) with numerator and denominator
as 6= \(\frac{30}{8}\) X \(\frac{6}{6}\) we get \(\frac{180}{48}\),
now comparing with \(\frac{5}{48}\) being denominators same, now numerators 180,5 both are
not same so friend is not correct as the product of 6 X \(\frac{5}{8}\) ≠ \(\frac{5}{48}\).
Question 14.
Open-Ended
The product of a whole number and a fraction is \(\frac{24}{10}\). What could the two factors be?
Answer:
The product is given as \(\frac{24}{10}\) and the two factors can be (1,24) or (2,12) or (3,8) or (4,6)
with multiple of \(\frac{1}{10}\).
Explanation:
Given the product of a whole number and a fraction is \(\frac{24}{10}\) to find the two factors,
we first write the product as whole with multiple of unit fraction,\(\frac{24}{10}\),
we write as 24 X \(\frac{1}{10}\), now the whole part is 24 we find the factors for 24,
two more numbers that multiply to make 24 are 1 x 24 = 2 x 12 = 3 x 8 = 4 x 6 = 24.
This means the factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24 so the two factors can be
(1,24) X \(\frac{1}{10}\) or (2,12) X \(\frac{1}{10}\) or (3,8) X \(\frac{1}{10}\)
or (4,6) X \(\frac{1}{10}\) = 24 X \(\frac{1}{10}\) = \(\frac{24}{10}\).
Think and Grow: Modeling Real Life
Example
A short roller-coaster track is \(\frac{3}{10}\) mile long. A longer roller-coaster track is about 4 times as long as the short track. About how long is the longer roller-coaster track?
Multiply the shorter roller-coaster track length by 4.

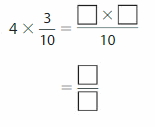
So, the longer roller-coaster track is about _\(\frac{12}{10}\) _ miles long or \(\frac{6}{5}\) miles long
Answer:
The longer roller-coaster track is about \(\frac{12}{10}\) miles long or \(\frac{6}{5}\).
Explanation:
Given a short roller-coaster track is \(\frac{3}{10}\) mile long and longer roller-coaster
track is about 4 times as long as the short track to find how long is the longer roller-coaster track
we multiply short roller-coaster track \(\frac{3}{10}\) mile by 4, 4 X \(\frac{3}{10}\)
now we write expression as a multiple of unit fraction so 4 X 3 X \(\frac{1}{10}\) =
12 X \(\frac{1}{10}\) =\(\frac{12}{10}\) as numerator and denominator
can be further simplified as both can be divided by 2 making it as \(\frac{6}{5}\).
Show and Grow
Question 15.
The Renaissance Tower in Dallas, Texas is \(\frac{27}{100}\) kilometer tall. The Burj Khalifa is about 3 times as tall as the Renaissance Tower. About how tall is the Burj Khalifa?

Answer:
The Burj Khalifa is \(\frac{81}{100}\) kilometers tall.
Explanation:
Given the Renaissance Tower in Dallas, Texas is \(\frac{27}{100}\) kilometer tall and
The Burj Khalifa is about 3 times as tall as the Renaissance Tower, To find how tall is the Burj Khalifa
we multiply the Renaissance Tower in Dallas, Texas length by 3,
3 X \(\frac{27}{100}\) we write expression as a multiple of unit fraction
3 X 27 X \(\frac{1}{100}\) = 81 X \(\frac{1}{100}\) =\(\frac{81}{100}\),
So the Burj Khalifa is \(\frac{81}{100}\) kilometers tall.
Question 16.
You water 6 plants using \(\frac{3}{5}\) liter of water for each. How many liters of water do you use?
Between which two whole numbers does your answer lie?
Answer:
\(\frac{18}{5}\) liters of water is used, The answer will lie in between 3 and 4.
Explanation:
Given \(\frac{3}{5}\) liter of water for each is watered, for 6 plants total number of liters of water
used is 6 X \(\frac{3}{5},now we write as multiple of unit fraction as 6 X 3 X [latex]\frac{1}{5}\) =
18 X \(\frac{1}{5}\)= \(\frac{18}{5}\) liters of water is used.
Now we divide \(\frac{18}{5}\) we get the value as 3.6,means between 3 and 4 whole numbers our answer will lie.
Question 17.
DIG DEEPER!
You have 6 cups of strawberries. You want to make 4 strawberry-banana smoothies and 4 strawberry-kiwi smoothies. Each smoothie needs \(\frac{2}{3}\) cup of strawberries. Do you have enough? If not, how many more cups of strawberries do you need?
Answer:
Yes we have enough cups of strawberries, we dont require more cups of strawberries.
Explanation:
Given to make each smoothie we need \(\frac{2}{3}\) cup of strawberries
first to make 4 strawberry-banana smoothies we need 4 X \(\frac{2}{3}\) cup of strawberries
= 4 X 2 X \(\frac{1}{3}\)= 8 X \(\frac{1}{3}\) =\(\frac{8}{3}\),
Now similarly for making 4 strawberry-kiwi smoothies we need 4 X \(\frac{2}{3}\)
cup of strawberries = 4 X 2 X \(\frac{1}{3}\)= 8 X \(\frac{1}{3}\) =
\(\frac{8}{3}\),Now total cups of strawberries requried to make smoothie is
\(\frac{8}{3}\) + \(\frac{8}{3}\) = 2 X \(\frac{8}{3}\)=
2 X 8 X \(\frac{1}{3}\)=16 X \(\frac{1}{3}\)= \(\frac{16}{3}\) totals cups
of strawberries required to make smoothies. Now we compare \(\frac{16}{3}\) with 6,
To compare first we make both denominators same so we multiply 6 with \(\frac{3}{3}\)=
6 X \(\frac{3}{3}\)= 6 X 3 X \(\frac{1}{3}\)= 18 X \(\frac{1}{3}\)=
\(\frac{18}{3}\) as both the denominators are same we compare
\(\frac{16}{3}\) and \(\frac{18}{3}\) by seeing numerator
16 is less than 18 means we have enough cups of strawberries.
Multiply Whole Numbers and Fractions Homework & practice 9.3
Multiply
Question 1.
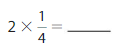
Answer:
2 X \(\frac{1}{4}\) = \(\frac{2}{4}\)=\(\frac{1}{2}\)
Explanation:
As the given expression is already a unit fraction we multiply it as 2 X \(\frac{1}{4} =
\)\(\frac{2}{4}\) and further both numerator and denominator can be divided by 2
making it as \(\frac{1}{2}\)
Question 2.
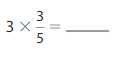
Answer:
3 X \(\frac{3}{5}\)= \(\frac{9}{5}\).
Explanation:
3 X \(\frac{3}{5}\) can be written as multiple of unit fraction as
3 X (3 X \(\frac{1}{5}\)) applying associative property of multiplication
( 3 X 3 ) X \(\frac{1}{5}\)= 9 X \(\frac{1}{5}\) = \(\frac{9}{5}\).
Question 3.
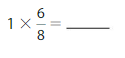
Answer:
1 X \(\frac{6}{8}\)= \(\frac{6}{8}\)= \(\frac{3}{4}\).
Explanation:
1 X \(\frac{6}{8}\) can be written as multiple of unit fraction as 1 X ( 6 X \(\frac{1}{8}\))
applying associative property of multiplication ( 1 X 6 ) X \(\frac{1}{8}\) = 6 X \(\frac{1}{8}\)=
\(\frac{6}{8}\) as numerator and denominator can be further simplified as both can be divided by 2
making as \(\frac{6}{8}\)= \(\frac{3}{4}\)X \(\frac{2}{2}\)=\(\frac{3}{4}\).
Question 4.
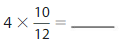
Answer:
4 X \(\frac{10}{12}\)= \(\frac{40}{12}\)= \(\frac{10}{3}\)
Explanation:
4 X \(\frac{10}{12}\) can be written as multiple of unit fraction as 4 X ( 10 X \(\frac{1}{12}\))
applying associative property of multiplication ( 4 X 10 ) X \(\frac{1}{12}\) = 40 X \(\frac{1}{12}\)=
\(\frac{40}{12}\) as numerator and denominator can be further simplified as both can be divided by 4
as \(\frac{40}{12}\)= \(\frac{10}{3}\) X \(\frac{4}{4}\)=\(\frac{10}{3}\) X 1 =
\(\frac{10}{3}\).
Question 5.
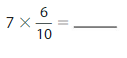
Answer:
7 X \(\frac{6}{10}\) = \(\frac{42}{10}\)= \(\frac{21}{5}\)
Explanation:
7 X \(\frac{6}{10}\) can be written as multiple of unit fraction as 7 X ( 6 X \(\frac{1}{10}\))
applying associative property of multiplication ( 7 X 6 ) X \(\frac{1}{10}\) =
42 X \(\frac{1}{10}\)= \(\frac{42}{10}\) as numerator and denominator
can be further simplified as both can be divided by 2 as \(\frac{42}{10}\)=
\(\frac{21}{5}\) X \(\frac{2}{2}\)=\(\frac{21}{5}\) X 1 = \(\frac{21}{5}\).
Question 6.
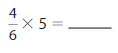
Answer:
\(\frac{4}{6}\) X 5 =\(\frac{20}{6}\) =\(\frac{10}{3}\).
Explanation:
\(\frac{4}{6}\) X 5 can be written as multiple of unit fraction as 5 X ( 4 X \(\frac{1}{6}\))
applying associative property of multiplication ( 5 X 4 ) X \(\frac{1}{6}\) =
20 X \(\frac{1}{6}\)= \(\frac{20}{6}\) as numerator and denominator
can be further simplified as both can be divided by 2 as \(\frac{20}{6}\) =
\(\frac{10}{3}\) X \(\frac{2}{2}\)=\(\frac{10}{3}\) X 1 =\(\frac{10}{3}\).
Question 7.
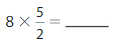
Answer:
8 X \(\frac{5}{2}\) = \(\frac{40}{2}\) =20.
Explanation:
8 X \(\frac{5}{2}\) can be written as multiple of unit fraction as
8 X ( 5 X \(\frac{1}{2}\)) applying associative property of multiplication
( 8 X 5 ) X \(\frac{1}{2}\) = 40 X \(\frac{1}{2}\) = \(\frac{40}{2}\)
further it can be simplified as \(\frac{40}{2}\)=20
Question 8.
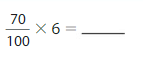
Answer:
\(\frac{70}{100}\) X 6 = \(\frac{420}{100}\) = \(\frac{42}{10}\).
Explanation:
\(\frac{70}{100}\) X 6 can be written as multiple of unit fraction as
6 X ( 70 X \(\frac{1}{100}\)) applying associative property of multiplication
( 6 X 70 ) X \(\frac{1}{100}\) = 420 X \(\frac{1}{100}\)= \(\frac{420}{100}\)
as numerator and denominator can be further simplified as both can be divided by 10 as \(\frac{420}{100}\)= \(\frac{42}{10}\) X \(\frac{10}{10}\)=\(\frac{42}{10}\) X 1 =\(\frac{42}{10}\).
Question 9.
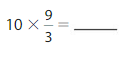
Answer:
10 X \(\frac{9}{3}\)=\(\frac{90}{3}\)=30.
Explanation:
10 X \(\frac{9}{3}\) can be written as multiple of unit fraction as
10 X ( 9 X \(\frac{1}{3}\)) applying associative property of multiplication
( 10 X 9 ) X \(\frac{1}{3}\) = 90 X \(\frac{1}{3}\)= \(\frac{90}{3}\)
further it can be simplified because 90 can be divided by 3 without leaving remainder making
\(\frac{90}{3}\) as 30.
Compare.
Question 10.
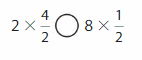
Answer:
2 X \(\frac{4}{2}\) = 8 X \(\frac{1}{2}\).
Explanation:
2 X \(\frac{4}{2}\) we write as multiple of unit fraction 2 X 4 X \(\frac{1}{2}\) =
8 X \(\frac{1}{2}\) = \(\frac{8}{2}\) and
8 X \(\frac{1}{2}\) is already multiple of unit fraction = latex]\frac{8}{2}[/latex]
now we can compare both sides as the denominators are same and numerators are same
both the expressions are equal 2 X \(\frac{4}{2}\) = 8 X \(\frac{1}{2}\).
Question 11.
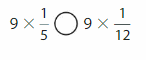
Answer:
9 X \(\frac{1}{5}\) > \(\frac{9}{12}\)
Explanation:
9 X \(\frac{1}{5}\) already it is multiple of unit fraction we write it as \(\frac{9}{5}\)
and 9 X \(\frac{1}{12}\) is also a multiple of unit fraction we write it as \(\frac{9}{12}\)
now comparing first we make both denominators same so the multiples of 5 are 5,10,15,20,25,30,35,40,45,50,55,60,65
and multiples of 12 are 12,24,36,48,60,72 so the least common multiple of both 5 and 12 is 60 ,
So to get denominator 60 we multiply top and bottom by 12 for \(\frac{9}{5}\) =
\(\frac{9}{5}\) X \(\frac{12}{12}\)= \(\frac{108}{60}\) ,
So to get denominator 60 we multiply top and bottom by 5 for \(\frac{9}{12}\)=
\(\frac{9}{12}\) X \(\frac{5}{5}\)= \(\frac{45}{60}\)
Now comparing \(\frac{108}{60}\) with \(\frac{45}{60}\) as both denominator are same,
As we see numerator it is clear that 108 is more than 45 so \(\frac{108}{60}\) > \(\frac{45}{60}\) ,
9 X \(\frac{1}{5}\) > \(\frac{9}{12}\).
Question 12.
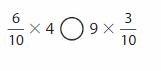
Answer:
\(\frac{6}{10}\)X 4 < 9 X \(\frac{3}{10}\).
Explanation:
\(\frac{6}{10}\)X 4 we write as multiple of unit fraction 4 X 6 X \(\frac{1}{10}\)=
24 X \(\frac{1}{10}\) =\(\frac{24}{10}\) and 9 X \(\frac{3}{10}\) as
9 X 3 X \(\frac{1}{10}\)= 27 X \(\frac{1}{10}\)=\(\frac{27}{10}\),
We can compare both as denominators of both are 10 we compare numerators as 24 with 27
as 27 is great,\(\frac{24}{10}\) < \(\frac{27}{10}\),
\(\frac{6}{10}\) X 4 < 9 X \(\frac{3}{10}\).
Question 13.
Writing
Explain one way to multiply a whole number by a fraction.
Answer:
First we write fraction as multiple of unit fraction then applying associative property of multiplication
we multiply the whole numbers first then with the unit fraction,later writing product.
Explanation:
Let us take the whole number as 2 and fraction as \(\frac{3}{5}\),Here first we write fraction as
multiple of unit fraction as 2 X 3 X \(\frac{1}{5}\) now applying associative property of multiplication,
we multiply the whole numbers first then with the unit fraction,
6 X \(\frac{1}{5}\) as \(\frac{6}{5}\).
Question 14.
Number Sense
Between which two whole numbers does the product of 10 and \(\frac{5}{6}\) lie ?
Answer:
In between 8 and 9 whole numbers the product of 10 and \(\frac{5}{6}\) lies.
Explanation:
10 X \(\frac{5}{6}\) we first write it as multiple of unit fraction as
10 X ( 5 X \(\frac{1}{6}\)) applying associative property of multiplication,
We write (10 X 5) X \(\frac{1}{6}\)= 50 X \(\frac{1}{6}\) = \(\frac{50}{6}\)
if we divide \(\frac{50}{6}\)) we get 8.333 which is in between 8 and 9 whole numbers.
Question 15.
Modeling Real Life
A seamstress makes fabric dog collars. An extra small dog collar is \(\frac{1}{3}\) yard long.
A large dog collar is 2 times as long as the extra small dog collar. How long is the large dog collar?
Answer:
The large dog collar is \(\frac{2}{3}\) yards long.
Explanation:
Given the extra small dog collar is \(\frac{1}{3}\) yard long and a large dog collar is
2 times as long as the extra small dog collar, so the large dog collar = 2 X \(\frac{1}{3}\)
as the fraction is multiple of unit fraction we write as \(\frac{2}{3}\) ,
therefore the large dog collar is \(\frac{2}{3}\) yards long.
Question 16.
DIG DEEPER!
Newton has 16 baseball cards. Descartes has \(\frac{1}{4}\) as many cards as Newton, and your friend has \(\frac{1}{2}\) as many cards as Descartes. How many baseball cards do Newton, Descartes, and your friend have in all?

Answer:
Newton has 16 baseball cards, Descartes has 4 baseball cards and my friend has 2 baseball cards,
over all there are total 22 baseball cards.
Explanation:
Given Newton has 16 baseball cards and Descartes has \(\frac{1}{4}\) as many cards as
Newton so\(\frac{1}{4}\) of 16 = 16 X \(\frac{1}{4}\) cards it is already
as multiple of unit fraction we can write as \(\frac{16}{4}\) further can be simplified
because 16 can be divide by 4 so we get as 4 means Descartes has 4 cards.Now my friend has
\(\frac{1}{2}\) as many cards as Descartes So Descartes has 4 cards means my friend has
\(\frac{1}{2}\) out of 4= 4 X \(\frac{1}{2}\) as it is already a multiple of unit fracrtion,
we take it as \(\frac{4}{2}\) further we can simplify as 4 is divisiblle by 2 we get 2 cards.
Newton has 16 baseball cards,Descartes has 4 baseball cards and my friend has 2 baseball cards,
over all there are total 22 baseball cards.
Review & Refresh
Divide
Question 17.
![]()
Answer:
![]() = 19.
= 19.
Explanation:

Question 18.
![]()
Answer:
![]() =81 with 4 as remainder.
=81 with 4 as remainder.
Explanation:
Step 1:Start by setting it up with the divisor 7 on the left side and the dividend 571 on the right side,
![]()
Step 2: The divisor (7) does not goes into the first digit of the dividend (5), So we take second digit also , The divisor (7) goes into the two digits of the dividend (57) by 8 time(s),there fore put 8 on the top
8
![]()
Step 3: Multiply the divisor by the result in the previous step. Therefore, put 8 on top (7 x 9 = 56) and write that answer below the dividend.
8
![]()
56
Step 4: Subtract the result in the previous step from the two digits of the dividend (57 -56 = 1) and write the answer below.
8
![]()
56
1
Step 5: Move down the 3rd digit of the dividend (1)
8
![]()
56
11
Step 6:The divisor (7) goes into the bottom number (11), time(s). Therefore, put 1 on top:
81
![]()
56
11
Step 7 : Multiply the divisor by the result in the previous step (7 x 1 = 7) and write that answer at the bottom:
81
![]()
56
11
07
Step 8 : Subtract the result in the previous step from the number written above it. (11 – 7 = 04) and write the answer at the bottom
81
![]()
56
11
07
4
We stop here as 4 is less than 7 and further we get in decimals , So ![]() =81 with 4 as remainder
=81 with 4 as remainder
Question 19.
![]()
Answer:
![]() = 184 with 3 as remainder.
= 184 with 3 as remainder.
Explanation:
Step 1:Start by setting it up with the divisor 5 on the left side and the dividend 923 on the right side,
![]()
Step 2: The divisor (5) goes into the first digit of the dividend (9) by 8 time there fore put 1 on the top
1
![]()
Step 3: Multiply the divisor by the result in the previous step (5 x 1 = 5) and write that answer below the dividend.
1
![]()
5
Step 4: Subtract the result in the previous step from the first digit of the dividend (9 -5 = 4) and write the answer below.
1
![]()
5
4
Step 5: Move down the 2nd digit of the dividend (2),like below
1
![]()
5
42
Step 6:The divisor (5) goes into the bottom number (40), 8 time(s). Therefore, put 8 on top:
18
![]()
5
42
Step 7 : Multiply the divisor by the result in the previous step (5 x 8 = 40) and write that answer at the bottom:
18
![]()
5
42
40
Step 8: Subtract the result in the previous step from the number written above it. (42 – 40 = 04) and write the answer at the bottom
18
![]()
5
42
40
2
Step 9 :Move down the 3nd digit of the dividend (3),like below
18
![]()
5
42
40
23
Step 10 : The divisor (5) goes into the bottom number (20), 4 time(s). Therefore, put 4 on top:
184
![]()
5
42
40
23
20
Step 11 : Subtract the result in the previous step from the number written above it. (23 – 20 = 03) and write the answer at the bottom
184
![]()
5
42
40
23
20
03
We stop here as 3 is less than 5 and further we get in decimals , So ![]() = 184 with 3 as remainder.
= 184 with 3 as remainder.
Lesson 9.4 Multiply Whole Numbers and Mixed Numbers
Explore and Grow
Use models to help you complete the table.
Structure
How does the Distributive Property relate to your models? Explain.
Answer:
Explanation:
According to the distributive property, multiplying the sum of two or more addends by a number
will give the same result as multiplying each addend individually by the number and then adding the products together.
We use distribute property while relating the models first we draw each multiplying addend individually and
then add the products together to give the result.
Example : 2 X 1 \(\frac{3}{8}\) using the distributive property we write
2 X 1 \(\frac{3}{8}\) as 2 X ( 1 + \(\frac{3}{8}\) )here first we draw model of
2 X 1 then we draw model of 2 X \(\frac{3}{8}\) then we add the products together as
2 + \(\frac{6}{8}\)= 2 + \(\frac{3}{4}\)=\(\frac{11}{4}\).
Think and Grow: Multiply Whole Numbers and Mixed Numbers
You can find the product of a whole number and a mixed number by writing the mixed number as a fraction or by using the Distributive Property

One Way: Write the mixed number as a fraction, then multiply.
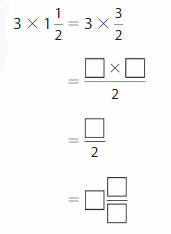
Another Way: Use the Distributive Property.
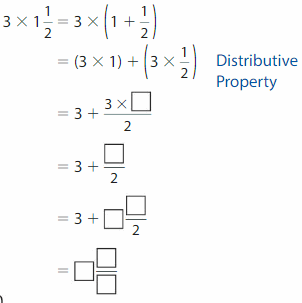
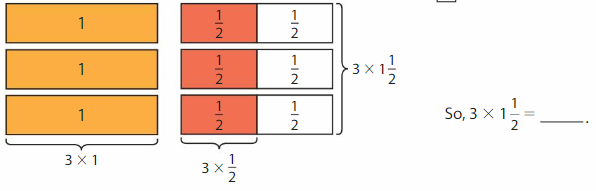
Answer:
3 X 1 \(\frac{1}{2}\) = \(\frac{9}{2}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 1 \(\frac{1}{2}\) =
1+ \(\frac{1}{2}\) = 2 x 1+1 by 2= \(\frac{3}{2}\) now we multiply it with the whole ,
3 X \(\frac{3}{2}\) now we write in unit fraction and multiply 3 X 3 X \(\frac{1}{2}\)=
9 X \(\frac{1}{2}\)= \(\frac{9}{2}\).
Show and Grow
Multiply
Question 1.
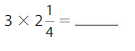
Answer:
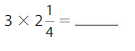 = \(\frac{27}{4}\)=6 \(\frac{3}{4}\)
= \(\frac{27}{4}\)=6 \(\frac{3}{4}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 2 \(\frac{1}{4}\) =
2 + \(\frac{1}{4}\)=(2 X 4 + 1) by 4 = \(\frac{9}{4}\) now we multiply it with the whole,
3 X \(\frac{9}{4}\) now we write in unit fraction and multiply 3 X 9 X \(\frac{1}{4}\) =
27 X \(\frac{1}{4}\) = \(\frac{27}{4}\), we can write the product as mixed fraction as
4 goes in 6 times. 6 will be our whole number 4 X 6 is 24 and we have 3 left over (27−24),
3 will be our numerator and our denominator will stay the same 4= \(\frac{27}{4}\)=
6 \(\frac{3}{4}\).
Question 2.
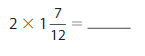
Answer:
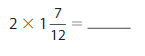 \(\frac{38}{12}\)= 3 \(\frac{2}{12}\).
\(\frac{38}{12}\)= 3 \(\frac{2}{12}\).
Explanation:
First we write the mixed number as a fraction then multiply, so 1 \(\frac{7}{12}\)=
1 + \(\frac{7}{12}\)= (1 X 12 + 7 ) by 12 = \(\frac{19}{12}\)
now we multiply it with the whole, 2 X \(\frac{19}{12}\) now we write in unit fraction and
multiply 2 X 19 X \(\frac{1}{12}\)= 38 X \(\frac{1}{12}\) = \(\frac{38}{12}\),
we can write the product as mixed fraction as 12 goes in 3 times. 3 will be our whole number 12 X 3 is 36 and
we have 2 left over (38−36). 2 will be our numerator and our denominator will be the same 12
= \(\frac{38}{12}\)= 3 \(\frac{2}{12}\).
Question 3.
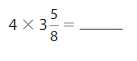
Answer:
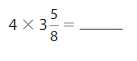 = \(\frac{116}{8}\)= 14 \(\frac{4}{8}\)
= \(\frac{116}{8}\)= 14 \(\frac{4}{8}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 3 \(\frac{5}{8}\)=
3 + \(\frac{5}{8}\)= (3 X 8 + 5) by 8 = \(\frac{29}{8}\) now we multiply it with the whole,
4 X \(\frac{29}{8}\) now we write in unit fraction and multiply 4 X 29 X \(\frac{1}{8}\)=
116 X \(\frac{1}{8}\) = \(\frac{116}{8}\), we can write the product as mixed fraction as
8 goes in 14 times. 14 will be our whole number 8 X 14 is 112 and we have 4 left over (116−112).
4 will be our numerator and our denominator will be the same 8= \(\frac{116}{8}\)=
14 \(\frac{4}{8}\).
Apply and Grow: Practice
Multiply.
Question 4.
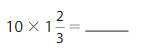
Answer:
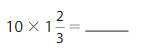 = \(\frac{50}{3}\)=16 \(\frac{2}{3}\)
= \(\frac{50}{3}\)=16 \(\frac{2}{3}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 1 \(\frac{2}{3}\)=
1 + \(\frac{2}{3}\)= (1 X 3 + 2) by 3 = \(\frac{5}{3}\) now we multiply it with the whole,
10 X \(\frac{5}{3}\) now we write in unit fraction and multiply 10 X 5 X \(\frac{1}{3}\)=
50 X \(\frac{1}{3}\) = \(\frac{50}{3}\), we can write the product as mixed fraction as
3 goes in 16 times. 16 will be our whole number 3 X 16 is 48 and we have 2 left over (50−48).
2 will be our numerator and our denominator will be the same 3= \(\frac{50}{3}\)= 16 \(\frac{2}{3}\).
Question 5.
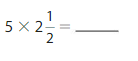
Answer:
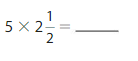 = \(\frac{25}{2}\)=12 \(\frac{1}{2}\)
= \(\frac{25}{2}\)=12 \(\frac{1}{2}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 2 \(\frac{1}{2}\)=
2 + \(\frac{1}{2}\)= (2 X 2 + 1) by 2 = \(\frac{5}{2}\)
now we multiply it with the whole, 5 X \(\frac{5}{2}\) .
We write in unit fraction and multiply 5 X 5 X \(\frac{1}{2}\)=
25 X \(\frac{1}{2}\) = \(\frac{25}{2}\), we can write the product as mixed fraction
as 2 goes in 12 times. 12 will be our whole number 2 X 12 is 24 and we have 1 left over (25−24).
1 will be our numerator and our denominator will be the same 2= \(\frac{25}{2}\)=
12 \(\frac{1}{2}\)
Question 6.
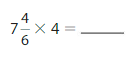
Answer:
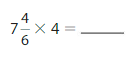 = \(\frac{184}{6}\)=\(\frac{92}{3}\)=30 \(\frac{4}{6}\).
= \(\frac{184}{6}\)=\(\frac{92}{3}\)=30 \(\frac{4}{6}\).
Explanation:
First we write the mixed number as a fraction then multiply, so 7 \(\frac{4}{6}\)=
7 + \(\frac{4}{6}\)=(7 X 6 + 4) by 6 = \(\frac{46}{6}\) now we multiply it with the whole,
4 X \(\frac{46}{6}\) now we write in unit fraction and multiply 4 X 46 X \(\frac{1}{6}\)=
184 X \(\frac{1}{6}\) = \(\frac{184}{6}\), we can write the product as mixed fraction as
6 goes in 30 times. 30 will be our whole number 6 X 30 is 180 and we have 4 left over (184−180).
4 will be our numerator and our denominator will be the same 6= \(\frac{184}{6}\)=
30 \(\frac{4}{6}\) and \(\frac{184}{6}\) can also written as \(\frac{92}{3}\)
because both 184 and 6 can also be further divided by 2.
Question 7.
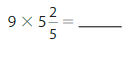
Answer:
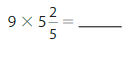 = \(\frac{243}{5}\)= 48 \(\frac{3}{5}\)
= \(\frac{243}{5}\)= 48 \(\frac{3}{5}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 5 \(\frac{2}{5}\)=
5 + \(\frac{2}{5}\)= (5 X 5 + 2) by 5 = \(\frac{27}{5}\) now we multiply it with the whole,
9 X \(\frac{27}{5}\) now we write in unit fraction and multiply 9 X 27 X \(\frac{1}{5}\)=
243 X \(\frac{1}{5}\) = \(\frac{243}{5}\), we can write the product as mixed fraction as
5 goes in 48 times. 48 will be our whole number 5 X 48 is 240 and we have 3 left over (243−240).
3 will be our numerator and our denominator will be the same 5= \(\frac{243}{5}\)=
48 \(\frac{3}{5}\).
Question 8.
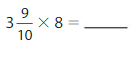
Answer:
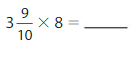 = \(\frac{312}{10}\)= 31 \(\frac{2}{10}\)
= \(\frac{312}{10}\)= 31 \(\frac{2}{10}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 3 \(\frac{9}{10}\)=
3 + \(\frac{9}{10}\)= (3 X 10 + 9) by 10 = \(\frac{39}{10}\)
now we multiply it with the whole, 8 X \(\frac{39}{10}\) now we write in unit fraction
and multiply 8 X 39 X \(\frac{1}{10}\)= 312 X \(\frac{1}{10}\) =
\(\frac{312}{10}\), we can write the product as mixed fraction as 10 goes in 31 times.
31 will be our whole number 10 X 31 is 310 and we have 2 left over (312−310).
2 will be our numerator and our denominator will be the same 10= \(\frac{312}{10}\)=
31 \(\frac{2}{10}\).
Question 9.
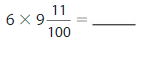
Answer:
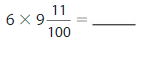 = \(\frac{5466}{100}\)=54 \(\frac{66}{100}\).
= \(\frac{5466}{100}\)=54 \(\frac{66}{100}\).
Explanation:
First we write the mixed number as a fraction then multiply, so 9 \(\frac{11}{100}\)=
9 + \(\frac{11}{100}\)= (9 X 100 + 11) by 100 = \(\frac{911}{100}\)
now we multiply it with the whole, 6 X \(\frac{911}{100}\) now we write in unit fraction
and multiply 6 X 911 X \(\frac{1}{100}\)= 5466 X \(\frac{1}{100}\) =
\(\frac{5466}{100}\), we can write the product as mixed fraction as 100 goes in 54 times.
54 will be our whole number 100 X 54 is 5400 and we have 66 left over (5466−5400).
66 will be our numerator and our denominator will be the same 100= \(\frac{5466}{100}\)=
54 \(\frac{66}{100}\).
Question 10.
Reasoning
How can you check whether your answer in Exercise 9 is reasonable?
Answer:
Exercise 9 is reasonable.
Explanation:
In the above problem 6 X 9 \(\frac{11}{100}\) we got product as
\(\frac{5466}{100}\) =54 \(\frac{66}{100}\) we can write the product as mixed fraction
as 100 goes in 54 times. 54 will be our whole number 100 X 54 is 5400 and 5466-5400,
leaving 66 as remainder so we consider the whole part 54,As 54 is reasonable close to 100.
Question 11.
YOU BE THE TEACHER
Your friend finds the product of 9 and 6\(\frac{1}{3}\). Is your friend correct? Explain.
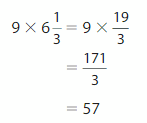
Answer:
Yes friend is correct.
Explanation:
First we write the mixed number as a fraction then multiply, so 6 \(\frac{1}{3}\)= 6 + \(\frac{1}{3}\)= (6 X 3 + 1) by 3 = \(\frac{19}{3}\) now we multiply it with the whole, 9 X \(\frac{19}{3}\) now we write in unit fraction and multiply 9 X 19 X \(\frac{1}{3}\)= 171 X \(\frac{1}{3}\) = \(\frac{171}{3}\), As 3 goes 57 times leaving no remainder so we get 9 X 6 \(\frac{1}{3}\)=57 which matches with the friend’s product so friend is correct.
Question 12.
DIG DEEPER!
Without multiplying, can you tell which expression is greater, ![]() ? Explain.
? Explain.
Answer:
5 X 6 \(\frac{1}{4}\) < 6 X 5 \(\frac{1}{4}\)
Explanation:
By drawing models also we can say
If the denominators are the same, then the fraction with the greater numerator is the greater fraction.
The fraction with the lesser numerator is the lesser fraction, But first we write the mixed number as a fraction
so in 5 X 6 \(\frac{1}{4}\), 6 \(\frac{1}{4}\)= 6+ \(\frac{1}{4}\)=
(6 X 4 +1) by 4 = \(\frac{25}{4}\) now we multiply it with the whole as
5 X \(\frac{25}{4}\) now we write the mixed fraction 5 \(\frac{1}{4}\)
as 5+ \(\frac{1}{4}\) = 5 x 4 +1 by 4=5 \(\frac{21}{4}\)
now we multiply it with the whole as 6 X \(\frac{21}{4}\) ,
Now comparing 5 X \(\frac{25}{4}\) and 6 X \(\frac{21}{4}\)
in both denominators are same and numerators 5 X \(\frac{25}{4}\) is less than
6 X \(\frac{21}{4}\) so 5 X 6 \(\frac{1}{4}\) < 6 X 5 \(\frac{1}{4}\)
Think and Grow: Modeling Real Life
Example
An elephant sleeps 2\(\frac{1}{2}\) hours in 1 day. A koala sleeps 6 times as long as the elephant in the same day. How many hours does the koala sleep that day?

Multiply the number of hours the elephant sleeps by 6.

Answer:
The koala sleeps 5 hours that day.
Explanation:
First we write mixed fraction as fraction so 2 \(\frac{1}{2}\) =( 2 X 2 + 1 ) by 2
= \(\frac{5}{2}\) , now we multiply with whole number 2 = 2 X \(\frac{5}{2}\) =
2 X 5 X \(\frac{1}{2}\) = 10 X \(\frac{1}{2}\) = \(\frac{10}{2}\)
further it can be simplified as both 10,2 can be divided by 2 so \(\frac{10}{2}\) = 5 hours that day.
Show and Grow
Question 13.
A small bag of popcorn has 1\(\frac{7}{8}\) cups of popcorn. A large bag has 7 times as many cups of popcorn as the small bag. How many cups of popcorn are in the large bag?
Answer:
The large bag has \(\frac{105}{8}\) cups of popcorn or 13 \(\frac{1}{8}\) cups of popcorn.
Explanation:
Given A small bag of popcorn has 1\(\frac{7}{8}\) cups of popcorn so first we write mixed fraction
as fraction as 1 \(\frac{7}{8}\)= ( 1 X 8 + 7 ) by 8 =\(\frac{15}{8}\) ,as a large bag has
7 times as many cups of popcorn as the small bag so 7 times \(\frac{15}{8}\)=
7 X 15 X \(\frac{1}{8}\)=105 X \(\frac{1}{8}\)=\(\frac{105}{8}\) cups of popcorn.
We can write the product as mixed fraction as 8 goes in 13 times.
13 will be our whole number 8 X 13 is 104 and we have 1 left over (105−104).
1 will be our numerator and our denominator will be the same 8= \(\frac{105}{8}\)=
13 \(\frac{1}{8}\) cups of popcorn.
Question 14.
DIG DEEPER!
A deli worker prepares 4 packages of meat. Each package contains 3\(\frac{1}{3}\) pounds of meat.
Your friend says the deli worker uses between 12 and 13 pounds of meat. Is your friend correct? Explain.
Answer:
No, friend is not correct as deli worker uses between 13 and 14 pounds of meat,
not between 12 and 13 pounds of meat.
Explanation:
Given each package contains 3\(\frac{1}{3}\) pounds of meat.
First we write mixed fraction as fraction as ( 3 X 3 +1 ) by 3= \(\frac{10}{3}\)
now deli worker prepares 4 packages of meat so 4 times \(\frac{10}{3}\)=
4 X 10 X \(\frac{1}{3}\)= 40 X \(\frac{1}{3}\)=\(\frac{40}{3}\) ,
we will write the product as mixed fraction as 3 goes in 13 times. 13 will be our whole number
3 X 13 is 39 and we have 1 left over (40−39). 1 will be our numerator and our denominator
will be the same 3= \(\frac{105}{8}\)= 13 \(\frac{1}{3}\),
so the whole number is greater than 13 means deli worker uses between 13 and 14 pounds of meat
not between 12 and 13 pounds of meat.
Question 15.
DIG DEEPER!
An athlete’s goal is to run at least 80 miles in 1 week. He runs 5\(\frac{3}{4}\) miles 2 times each day for 1 week. Does the athlete meet his goal? Explain.

Answer:
Athlete runs more than 80 miles in 1 week so he meets his goal.
Explanation:
Given an athlete runs 5\(\frac{3}{4}\) miles 2 times each day, First we write mixed fraction
as fraction as ( 5 X 4 +3) by 4 =\(\frac{23}{4}\) now we multiply by 2 ,
2 X \(\frac{23}{4}\)= 2 X 23 X \(\frac{1}{4}\)=46 x \(\frac{1}{4}\)=
\(\frac{46}{4}\), Now for 1 week it is 7 X \(\frac{46}{4}\)= 7 X 46 X \(\frac{1}{4}\)=
322 X \(\frac{1}{4}\)= \(\frac{322}{4}\) now we will write the product as mixed fraction
as 4 goes in 80 times. 80 will be our whole number 4 X 80 is 320 and we have 2 left over (322−320).
2 will be our numerator and our denominator will be the same 4= \(\frac{322}{4}\)= 80 \(\frac{2}{4}\) ,
As 80 \(\frac{2}{4}\) is greater than 80, athlete runs more than 80 miles in 1 week he meets his goal.
Multiply Whole Numbers and Mixed Numbers Homework & Practice 9.4
Multiply
Question 1.
![]()
Answer:
2 X 1 \(\frac{1}{12}\) = \(\frac{26}{12}\) = \(\frac{13}{6}\)=
2 \(\frac{1}{6}\).
Explanation:
First we write the mixed number as a fraction then multiply, so 1 \(\frac{1}{12}\) =
1 + \(\frac{1}{12}\) = ( 1 X 12 + 1 )by 12 = \(\frac{13}{12}\) now we multiply it with the whole,
2 X \(\frac{13}{12}\) now we write in unit fraction and multiply 2 X 13 X \(\frac{1}{12}\)=
26 X \(\frac{1}{12}\) = \(\frac{26}{6}\), Now the fraction can be further divided by 2
as 26,6 both goes in 2 after dividing it becomes as \(\frac{13}{6}\) now we can write the product
as mixed fraction as 6 goes in 2 times. 2 will be our whole number 6 X 2 is 12 and we have 1 left over (13−12).
1 will be our numerator and our denominator will be the same 6= \(\frac{13}{6}\)=
2 \(\frac{1}{6}\).
Question 2.
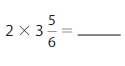
Answer:
2 X 3\(\frac{5}{6}\)=\(\frac{46}{6}\) = \(\frac{23}{3}\)= 7 \(\frac{2}{3}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 3 \(\frac{5}{6}\) =
3 + \(\frac{5}{6}\) =(3 X 6 + 5) by 6 = \(\frac{23}{6}\) now we multiply it with the whole,
2 X \(\frac{23}{6}\) now we write in unit fraction and multiply 2 X 23 X \(\frac{1}{6}\)=
46 X \(\frac{1}{6}\) = \(\frac{46}{6}\), Now the fraction can be further divided by 2
as 46,6 both goes in 2 after dividing it becomes as 23,3 = \(\frac{23}{3}\)
now we can write the product as mixed fraction as 3 goes in 7 times. 3 X 7 is 21 ,
7 will be our whole number and (23−21) we have 2 left over. 2 will be our numerator and
our denominator will be the same 3= \(\frac{23}{3}\)= 7 \(\frac{2}{3}\).
Question 3.

Answer:
4 X 3 \(\frac{6}{10}\) = \(\frac{144}{10}\) = \(\frac{72}{5}\) = 14 \(\frac{2}{5}\).
Explanation:
First we write the mixed number as a fraction then multiply, so 3 \(\frac{6}{10}\) =
3 + \(\frac{6}{10}\) =( 3 X 10 + 6 ) by 10 = \(\frac{36}{10}\) now we multiply it with the whole,
4 X \(\frac{36}{10}\) now we write in unit fraction and multiply 4 X 36 X \(\frac{1}{10}\)=
144 X \(\frac{1}{10}\) = \(\frac{144}{10}\), Now the fraction can be further divided by 2
as 144,10 both goes in 2 after dividing it becomes as 72,5 = \(\frac{72}{5}\)
now we can write the product as mixed fraction as 5 goes in 14 times. 5 X 14 is 70 ,14 will be our whole number
and (72−70) we have 2 left over. 2 will be our numerator and our denominator will be the same 5
= \(\frac{72}{5}\)= 14 \(\frac{2}{5}\).
Question 4.
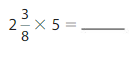
Answer:
2 \(\frac{3}{8}\) X 5 = \(\frac{95}{8}\) =11 \(\frac{7}{8}\).
Explanation:
First we write the mixed number as a fraction then multiply, so 2 \(\frac{3}{8}\) =
2 + \(\frac{3}{8}\) =(2 X 8 + 3) by 8 = \(\frac{19}{8}\) now we multiply it with the whole,
5 X \(\frac{19}{8}\) now we write in unit fraction and multiply 5 X 19 X \(\frac{1}{8}\)=
95 X \(\frac{1}{8}\) = \(\frac{95}{8}\), Now we can write the product as mixed fraction as
8 goes in 11 times. 8 X 11 is 88 ,11 will be our whole number and (95−88) we have 7 left over.
7 will be our numerator and our denominator will be the same 8= \(\frac{95}{8}\)=
11 \(\frac{7}{8}\).
Question 5.
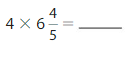
Answer:
4 X 6 \(\frac{4}{5}\) = \(\frac{136}{5}\) = 27 \(\frac{1}{5}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 6 \(\frac{4}{5}\) =
6 + \(\frac{4}{5}\) =(6 X 5 + 4) by 5 = \(\frac{34}{5}\) now we multiply it with the whole,
4 X \(\frac{34}{5}\) now we write in unit fraction and multiply 4 X 34 X \(\frac{1}{5}\) =
136 X \(\frac{1}{5}\) = \(\frac{136}{5}\), now we can write the product as mixed fraction as
5 goes in 27 times. 5 X 27 is 135 , 27 will be our whole number and (136−135) we have 1 left over.
1 will be our numerator and our denominator will be the same 5 = \(\frac{136}{5}\)=
27 \(\frac{1}{5}\).
Question 6.
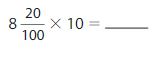
Answer:
8 \(\frac{20}{100}\) X 10 = \(\frac{8200}{100}\) = 82.
Explanation:
First we write the mixed number as a fraction then multiply, so 8 \(\frac{20}{100}\) =
8 + \(\frac{20}{100}\) = ( 8 X 100 + 20 ) by 100 = \(\frac{820}{100}\)
now we multiply it with the whole, 100 X \(\frac{820}{100}\) now we write in unit fraction
and multiply 10 X 820 X \(\frac{1}{100}\) = 8200 X \(\frac{1}{100}\) =
\(\frac{8200}{100}\), Now the fraction can be further divided by 100 as 8200,100
both goes in 100 after dividing by 100 it becomes as 82.
Question 7.
Reasoning
Without calculating, is the product of 7 and 5\(\frac{3}{4}\) greater than or less than 35? Explain.
Answer:
7 X 5 \(\frac{3}{4}\) is greater than ( > ) 35.
Explanation:
Given to compare between 7 X 5 \(\frac{3}{4}\) and 35, first we take 7 X 5 \(\frac{3}{4}\)
to this expression if we apply distributive property means if multiplying the sum of two or more addends
by a number will give the same result as multiplying each addend individually by the number and
then adding the products together. example a X b \(\frac{c}{d}\) = a X b + a X \(\frac{c}{d}\)
So 7 X 5 \(\frac{3}{4}\) = 7 X 5 + 7 X \(\frac{3}{4}\) means 35 + 7 X \(\frac{3}{4}\)
So by comparing left side it is addition of 35 plus some value ,it will be more than 35 only and right hand side
it it 35 so obiviously 7 X 5 \(\frac{3}{4}\) is greater than ( > ) 35.
Question 8.
YOU BE THE TEACHER
Your friend finds the product of 4 and 2\(\frac{8}{10}\). Is your friend correct? Explain.
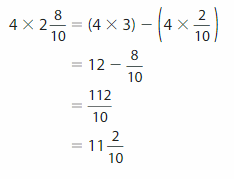
Answer:
Yes friend is correct, because the value is same as 11 \(\frac{2}{10}\) .
Explanation:
To caluculate the value of 4 X 2 \(\frac{8}{10}\) , First we write the mixed number as a
fraction then multiply, so 2 \(\frac{8}{10}\) = 2 + \(\frac{8}{10}\) =
( 2 X 10 + 8 ) by 10 = \(\frac{28}{10}\) now we multiply it with the whole,
4 X \(\frac{28}{10}\) now we write in unit fraction and multiply 4 X 28 X \(\frac{1}{10}\)=
112 X \(\frac{1}{10}\) = \(\frac{112}{10}\), now we can write the product as mixed fraction
as 10 goes in 11 times. 10 X 11 is 110 , 11 will be our whole number and (112−110) we have 2 left over.
2 will be our numerator and our denominator will be the same 10= \(\frac{112}{10}\)=
11 \(\frac{2}{10}\) is same as friend, So friend is correct.
Question 9.
Number Sense
Between which two whole numbers does the product of 9 and 7 \(\frac{1}{8}\) lie?
Answer:
The product of 9 and 7 \(\frac{1}{8}\) lies in between 64 and 65.
Explanation:
First we write the mixed number 7 \(\frac{1}{8}\) as a fraction then multiply, so 7 \(\frac{1}{8}\) =
7 + \(\frac{1}{8}\) = 7 X 8 + 1 by 8 = \(\frac{57}{8}\) now we multiply it with the whole,
9 X \(\frac{57}{8}\) now we write in unit fraction and multiply 9 X 57 X \(\frac{1}{8}\) =
513 X \(\frac{1}{8}\) = \(\frac{513}{8}\), now we can write the product as mixed fraction as
8 goes in 64 times. 8 X 64 is 512 , 64 will be our whole number and (513−512) we have 1 left over.
1 will be our numerator and our denominator will be the same 8 = \(\frac{513}{8}\)= 64
\(\frac{1}{8}\). Any how we got 64 whole number and next whole number is 65 means
the product of 9 and 7 \(\frac{1}{8}\) lies in between 64 and 65.
Question 10.
Modeling Real Life
Athlete A holds a 2\(\frac{1}{2}\) – kilogram plate while doing squats. Athlete B holds a plate that is 4 times heavier than Athlete A’s. How many kilograms is the plate held by Athlete B?

Answer:
Athlete B holds 10 kilograms of plate while doing squats.
Explanation:
Given Athlete A hold a 2 \(\frac{1}{2}\) kilogram plate while doing squats,
Athlete B holds a plate that is 4 times heavier than Athlete A’s, So Athlete B holds
4 X 2 \(\frac{1}{2}\), First we write the mixed number as a fraction then multiply,
so 2 \(\frac{1}{2}\) = 2 + \(\frac{1}{2}\) = ( 2 X 2 + 1 ) by 2 = \(\frac{5}{2}\)
now we multiply it with the whole, 4 X \(\frac{5}{2}\) now we write in unit fraction and
multiply 4 X 5 X \(\frac{1}{2}\) = 20 X \(\frac{1}{2}\) = \(\frac{20}{2}\)
as 20,2 goes by 2 we further divide both by 2 we get 10,1 = \(\frac{20}{2}\) = 10,
therefore Athlete B holds 10 kilograms of plate while doing squats.
Question 11.
DIG DEEPER!
A zoo nutritionist orders 5 \(\frac{1}{4}\) tons of apples and 7\(\frac{2}{4}\)tons of bananas each year to feed the animals. She orders 6 times as many tons of herbivore pellets than tons of fruit. How many tons of herbivore pellets does the nutritionist order?
Answer:
Explanation:
Review & Refresh
Subtract.
Question 12.
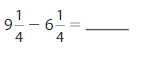
Answer:
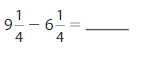 = \(\frac{12}{4}\) = 3
= \(\frac{12}{4}\) = 3
Explanation:
First we write the mixed numbers into fractions and subtract, So 9 \(\frac{1}{4}\) =
9 +\(\frac{1}{4}\) = (9 x 4 + 1) by 4 = \(\frac{37}{4}\) and 6 \(\frac{1}{4}\) =
6 + \(\frac{1}{4}\) = 6 X 4 + 1 by 4 = \(\frac{25}{4}\) now subtracting
\(\frac{37}{4}\) – \(\frac{25}{4}\) to subtract a fraction from another
we need to first make sure both fractions have the same denominator as both denominators
have same value 4 now we can subtract one numerator from the other to make one fraction as 37 – 25 by 4 = \(\frac{12}{4}\) as 12, 4 goes by 4 we further can divide both by 4 we get 12,1 = \(\frac{12}{4}\) = 3 .
Question 13.
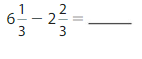
Answer:
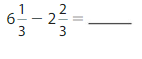 = \(\frac{11}{3}\) = 3 \(\frac{2}{3}\)
= \(\frac{11}{3}\) = 3 \(\frac{2}{3}\)
Explanation:
First we write the mixed numbers into fractions and subtract, So 6 \(\frac{1}{3}\) =
6 +\(\frac{1}{3}\) =(6 x 3 + 1) by 3 = \(\frac{19}{3}\) and 2 \(\frac{2}{3}\) =
2 + \(\frac{2}{3}\) = 2 X 3 + 2 by 3 = \(\frac{8}{3}\) now subtracting
\(\frac{19}{3}\) – \(\frac{8}{3}\) to subtract a fraction from another
we need to first make sure both fractions have the same denominator as both denominators
have same value 3 now we can subtract one numerator from the other to make one fraction as 19 – 8 by 3
= \(\frac{11}{3}\) since the numerator is greater than the denominator,
we can further simplify it into a mixed fraction as 3 goes in 3 times. 3 X 3 is 9 , 3 will be our
whole number and (11−9) we have 2 left over. 2 will be our numerator and our denominator will be the same 3
= \(\frac{11}{3}\) = 3 \(\frac{2}{3}\) .
Question 14.
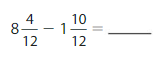
Answer:
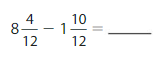 = \(\frac{78}{12}\) = 6 \(\frac{6}{12}\) or
= \(\frac{78}{12}\) = 6 \(\frac{6}{12}\) or
\(\frac{78}{12}\) = \(\frac{39}{6}\) = \(\frac{13}{2}\) = 6 \(\frac{1}{2}\).
Explanation:
First we write the mixed numbers into fractions and subtract, So 8 \(\frac{4}{12}\) =
8 +\(\frac{4}{12}\) = ( 8 x 12 + 4 ) by 12 = \(\frac{100}{12}\) and 1 \(\frac{10}{12}\) = 1 + \(\frac{10}{12}\) = 1 X 12 + 10 by 12 = \(\frac{22}{12}\) now subtracting \(\frac{100}{12}\) – \(\frac{22}{12}\) to subtract a fraction from another we need to first make sure both fractions
have the same denominator as both denominators have same value 3 now we can subtract one numerator
from the other to make one fraction as 100 – 22 by 12 = \(\frac{78}{12}\) since the numerator
is greater than the denominator , we can further simplify it into a mixed fraction as 12 goes in 6 times.
12 X 6 is 72 , 6 will be our whole number and (78−12) we have 6 left over. 6 will be our numerator and
our denominator will be the same 12, 6 \(\frac{6}{12}\) , Further \(\frac{78}{12}\)
can be simplified as 78,12 both goes by 2 making them as 39, 6=\(\frac{39}{6}\),
even further \(\frac{39}{6}\) can be simplified as 39,6 both goes by 3 making them as 13,2
=\(\frac{13}{2}\), Since the numerator is greater than the denominator , we can further simplify
it into a mixed fraction as 2 goes in 6 times. 6 X 2 is 12 , 6 will be our whole number and (13−12) we have 1 left over.
1 will be our numerator and our denominator will be the same 3 = \(\frac{78}{12}\) =
6 \(\frac{6}{12}\) or \(\frac{78}{12}\) = \(\frac{39}{6}\) = \(\frac{13}{2}\) =
6 \(\frac{1}{2}\).
Lesson 9.5 Problem Solving: Fraction Operations
Explore and Grow
You want to make 3 batches of the recipe. Explain how to find how much of each ingredient you need.

Reasoning
Explain how you can tell whether you need more than or less than 6 cups of blueberries without calculating
Answer:
To make 3 batches of recipe we require \(\frac{21}{4}\) pounds of strawberries or
5 \(\frac{1}{4}\) pounds of strawberries required,
\(\frac{3}{2}\) cups of orange juice or 1 \(\frac{1}{2}\) cups of orange juice,
12 tablespoons of lemon juice,12 tablespoons of honey and
\(\frac{27}{4}\) cups of blue berries are required or 6 \(\frac{3}{4}\) cups of blueberries are required.
We require more than 6 cups of blueberries why because if we see product required is
3 X 2 \(\frac{1}{4}\) cups of blue berries without calculating , Applying distributive property
we get (3 X 2 ) + ( 3 X \(\frac{1}{4}\) ) = 6 + ( 3 X \(\frac{1}{4}\) ) it clearly shows that
we require more than 6 cups of blueberries.
Explanation:
Given to make 1 batch of Recipe Ladybug Ice pops we require 1 \(\frac{3}{4}\) pounds of strawberries ,
\(\frac{1}{2}\) cup of orange juice , 4 tablespoons of lemon juice, 4 tablespoons of honey,
2 \(\frac{1}{4}\) cups of blue berries.
To find out how much of each ingredient needed to make 3 batches of recipe we multiply each ingredient with 3.
Strawberries needed are 3 X 1 \(\frac{3}{4}\), First we write the mixed number as a
fraction then multiply so 1 \(\frac{3}{4}\) = ( 1 X 4 + 3 ) by 4 = \(\frac{7}{4}\) ,
so 3 X \(\frac{7}{4}\) now we write in unit fraction and multiply 3 X 7 X \(\frac{1}{4}\) =
21 X \(\frac{1}{4}\) = \(\frac{21}{4}\) pounds of strawberries required,
Since the numerator is greater than the denominator , we can further simplify it into a mixed fraction as
4 goes in 5 times. 5 X 4 is 20 , 5 will be our whole number and (21−20) we have 1 left over.
1 will be our numerator and our denominator will be the same 4 =5 \(\frac{1}{4}\)
pounds of strawberries required,
Orange juice required 3 X \(\frac{1}{2}\) already it is in unit fraction
so we require \(\frac{3}{2}\) cups of orange juice Since the numerator is greater than the denominator ,
we can further simplify it into a mixed fraction as 2 goes in 1 times. 1 X 2 is 2, 1 will be our whole number and (3-2),
we have 1 left over. 1 will be our numerator and our denominator will be the same
2 = 1 \(\frac{1}{2}\) cups of orange juice.
Lemon juice required is 3 X 4 = 12 tablespoons of lemon juice, 3 X 4 = 12 tablespoons of honey,
now blue berries required are 3 X 2 \(\frac{1}{4}\) cups, First we write the mixed number as a
fraction then multiply so 2 \(\frac{1}{4}\) = ( 2 X 4 + 1 ) by 4 = \(\frac{9}{4}\) ,
now 3 X \(\frac{9}{4}\) now we write in unit fraction and multiply 3 X 9 X \(\frac{1}{4}\) =
27 X \(\frac{1}{4}\) = \(\frac{27}{4}\) cups of blue berries are required,
Since the numerator is greater than the denominator , we can further simplify it into a mixed fraction as
4 goes in 6 times. 6 X 4 is 24, 6 will be our whole number and (27-24) we have 3 left over.
3 will be our numerator and our denominator will be the same 4 = 6 \(\frac{3}{4}\) cups of blueberries are required.
Now comparing blueberries we require more than 6 cups of blueberries why because we use is
3 X 2 \(\frac{1}{4}\) cups of blue berries are required without calculating,
Applying distributive property we get (3 X 2 ) +( 3 X \(\frac{1}{4}\) )=
6 +( 3 X \(\frac{1}{4}\)), it clearly shows that we require more than 6 cups of blueberries.
Think and Grow: Problem Solving: Fraction Operations
Example
To convert a temperature from degrees Celsius to degrees Fahrenheit, multiply the Celsius temperature by \(\frac{9}{5}\), then add 32. What is the temperature shown by the thermometer in degrees Fahrenheit?

Answer:
The temperature shown by the thermometer is 500 Fahrenheit.
Explanation:
We know to convert a temperature from degrees Celsius to degrees Fahrenheit is Fahrenheit =
Celsius temperature X \(\frac{9}{5}\) + 32 .
So multiply the Celsius temperature by \(\frac{9}{5}\), then add 32,
Given the Celsius temperature as 100 in the figure above, First we write \(\frac{9}{5}\) in unit fraction and
multiply by Celsius temperature so \(\frac{9}{5}\)=9 X \(\frac{1}{5}\)
now we multiply by 10 as 10 X 9 X \(\frac{1}{5}\) = 90 X \(\frac{1}{5}\) =
\(\frac{90}{5}\) this value can be further simplified as 90,5 both goes by 5 making them as 18,1,
Now we got result as 18 , We add 18 + 32 we will get 500 Fahrenheit.
Understand the Problem
What do you know?
- To convert a temperature from degrees Celsius to degrees Fahrenheit, multiply the Celsius temperature by \(\frac{9}{5}\), then add 32.
- The thermometer shows 10 degrees Celsius.
What do you need to find? - You need to find the temperature shown by the thermometer in degrees Fahrenheit.
Make a Plan
How will you solve?
- First, multiply the Celsius temperature, 10 degrees, by \(\frac{9}{5}\).
- Then add 32 to the product.
Solve
So, the temperature shown by the thermometer is _500_ degrees Fahrenheit.
Answer:
The temperature shown by the thermometer is 500 Fahrenheit.
Explanation :
To convert a temperature from degrees Celsius to degrees Fahrenheit, Let us take p as multiply of
Celsius temperature by \(\frac{9}{5}\), Now we take f as p+32,
First we write \(\frac{9}{5}\) in unit fraction and multiply by Celsius temperature,
so \(\frac{9}{5}\)=9 X \(\frac{1}{5}\) now multiply by 10 = 10 X 9 X \(\frac{1}{5}\) =
90 X \(\frac{1}{5}\) = \(\frac{90}{5}\) this value we take as p this can be further simplified
as 90,5 both goes by 5 making them as 18, Now we got p as 18 we add 32 to p ,
we get f, So f = 18 + 32 = 500
So the temperature shown by the thermometer is 500 Fahrenheit.
Show and Grow
Question 1.
Show how to solve the example above using one equation.
Answer:
F= C X \(\frac{9}{5}\) + 32 degrees.
Explanation:
To solve the example above using one equation, Let us take Fahrenheit as F ,
Celsius as C so to convert a temperature from degrees Celsius to degrees Fahrenheit we multiply
C with \(\frac{9}{5}\) and add 32.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Answer:
We know Celsius temperature, We need to find the temperature shown by the thermometer in degrees Fahrenheit.
Explanation:
Given the temperature in Celsius and we know the formula to convert from Celsius temperature to
Fahrenheit as F= C X \(\frac{9}{5}\) + 32 degrees so we substitute the values and find the temperature.
Question 2.
You make a friendship bracelet with 3 pink strings and 2 blue strings. Each string is 3\(\frac{3}{4}\) feet long.
How many feet of string do you use?
Answer:
\(\frac{75}{4}\) feet long strings is used or 18 \(\frac{3}{4}\) feet long strings is used.
Explanation:
Given to make a friendship bracelet we use 3 pink strings , 2 blue strings means total 5 strings are needed
and each string is 3\(\frac{3}{4}\) feet long, First we convert mixed fraction into fraction as
( 3 X 4 + 3 ) by 4 = \(\frac{15}{4}\) ,Now we will convert into unit fraction as 15 X \(\frac{1}{4}\)
now we multiply with 5 , 5 X 15 X \(\frac{1}{4}\) =\(\frac{75}{4}\),
since the numerator is greater than the denominator , we can further simplify it into a mixed fraction as
4 goes in 18 times. 18 X 4 is 72, 18 will be our whole number and (75-72) we have 3 left over.
3 will be our numerator and our denominator will be the same 4 = 18 \(\frac{3}{4}\),
So \(\frac{75}{4}\) feet long strings is used or 18 \(\frac{3}{4}\) feet long strings is used.
Question 3.
A smoothie store worker makes 4 peanut butter banana smoothies and 2 fruit smoothies. The worker uses \(\frac{2}{3}\) cup of bananas in each smoothie. How many cups of bananas does the worker need?
Answer:
The worker needed \(\frac{12}{3}\) cups of bananas or 4 cups of bananas are needed to make smoothie.
Explanation:
Given a smoothie store worker makes 4 peanut butter banana smoothies and 2 fruit smoothies.
The worker uses \(\frac{2}{3}\) cup of bananas in each smoothie so the number of cups of bananas
the worker needed are 4 X latex]\frac{2}{3}[/latex] plus 2 X \(\frac{2}{3}\) first we convert
both into unit fractions and multiply 4 X 2 X \(\frac{1}{3}\) = 8 X \(\frac{1}{3}\) =
\(\frac{8}{3}\) of peanut butter banana smoothies and 2 X 2 X \(\frac{1}{3}\) =
4 X \(\frac{1}{3}\) = \(\frac{4}{3}\) fruit smoothies, now we add both \(\frac{8}{3}\) +
\(\frac{4}{3}\) as both denominators are same we add numerators as 8 + 4 =12 as numerator and
denominator as 3 = \(\frac{12}{3}\) as numerator is greater than denominator further can be simplified and
12 divides by 3 gives 4 with 0 remainder so the worker needed \(\frac{12}{3}\) cups of bananas or
4 cups of bananas are needed to make smoothie.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
Your friend walks her dog for \(\frac{1}{4}\) mile each day. She then runs 2\(\frac{3}{4}\) miles each day.
How many total miles does she walk her dog and run in 1 week?
Answer:
Total 21 miles my friend walks her dog and run in 1 week.
Explanation:
Given my friend walks her dog for \(\frac{1}{4}\) mile each day , She then runs
2\(\frac{3}{4}\) miles each day. So in each day she walk her dog and run is
\(\frac{1}{4}\) mile + 2\(\frac{3}{4}\) miles, Then we multiply with
7 because we have to calculate for 1 week. First we convert mixed fraction into fraction
2 \(\frac{3}{4}\) , ( 2 X 4 + 3 ) by 4 = \(\frac{11}{4}\), Now we add with
\(\frac{1}{4}\) + \(\frac{11}{4}\) = \(\frac{12}{4}\)
as numerator is greater than denominator further can be simplified and 12 divides by 4
gives 3 with 0 remainder, so 3 miles for each day, Now for 1 week it is 7 X 3 = 21 miles.
My friend walks 21 miles her dog and run in 1 week.
Question 5.
Hair donations must be 12 inches longer. Your friend’s hair is 7 inches long. Her hair grows
about \(\frac{1}{2}\) inch each month. Can she donate her hair in 8 months?
Answer:
No friend cannot donate her hair in 8 months as in 8 months it grows to 11 inches long and for
hair donations it must be 12 inches longer.
Explanation:
Given friend’s hair is 7 inches long. Her hair grows about \(\frac{1}{2}\) inch each month.
In 8 months it grows 8 X \(\frac{1}{2}\) = \(\frac{8}{2}\) as numerator is
greater than denominator further can be simplified and 8 divides by 2 gives 4 with 0 remainder,
in 8 months it will grow 4 inches , So after 8 months it will be 7 + 4 =11 inches long as 11 is less than 12
and hair donations must be 12 inches longer so friend cannot donate her hair in 8 months.
Question 6.
Today you walk \(\frac{6}{10}\) mile from the Martin Luther King Jr. Memorial to the Washington Monument. Tomorrow you will walk about 4 times as far from the Washington Monument to the White House. About how much farther will you walk tomorrow?
Answer:
Tomorrow i will walk father \(\frac{18}{10}\) miles or \(\frac{9}{5}\) miles or 1 \(\frac{4}{5}\) .
Explanation:
Given today i walked \(\frac{6}{10}\) mile from the Martin Luther King Jr. Memorial
to the Washington Monument, Tomorrow i will walk about 4 times as far from the Washington Monument
to the White House , So number of miles walked tomorrow will be 4 X \(\frac{6}{10}\)
first we write in unit fraction 4 X 6 X \(\frac{1}{10}\) = 24 X \(\frac{1}{10}\) =
\(\frac{24}{10}\) as numerator is greater than denominator further can be simplified as
24,10 both can be divided by 2 gives 12,5 so \(\frac{24}{10}\) = \(\frac{12}{5}\)
now farther i will walk tomorrow will be \(\frac{24}{10}\) – \(\frac{6}{10}\) as denominator
of both are same we substract numerators , 24 – 6 =18 and denominator will remain same 10 =
\(\frac{18}{10}\) miles or further can be simplified and 18,10 both can be divided by by 2
gives 9, 5 = \(\frac{18}{10}\) miles = \(\frac{9}{5}\) miles as numerator is greater than
denominator we can write it in mixed fraction as 5 goes in 1 times. 5 X 1 is 5 , 1 will be our whole number and
(9−5) we have 4 left over. 4 will be our numerator and our denominator will be the same 5 = 1 \(\frac{4}{5}\) .
Think and Grow: Modeling Real Life
Example
A 20-pound dog and a 60-pound dog eat the recommended amounts of dog food each day. How much more food does the 60-pound dog eat in 1 week than the 20-pound dog?
Think: What do you know? What do you need to find? How will you solve?
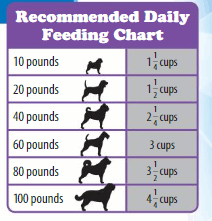


So, the 60-pound dog eats 10 \(\frac{1}{2}\) more cups of food than the 20-pound dog in 1 week.
Answer:
The 60-pound dog eats 10 \(\frac{1}{2}\) more cups of food than the 20-pound dog in 1 week.
Explanation:
Given A 20-pound dog eats 1 \(\frac{1}{2}\) cups and a 60-pound dog eats 3 cups,
the recommended amount of food each day. Now we need to calculate how much more food does
the 60-pound dog eat in 1 week than the 20-pound dog,
So Step 1 : First we find how much food the 20-pound dog eats in 1 week,
let us take it as b = 7 X 1 \(\frac{1}{2}\) we write mixed fraction as fraction
1 \(\frac{1}{2}\) = ( 1 X 2 + 1 )by 2 = \(\frac{3}{2}\) now multiply by 7 =
7 X \(\frac{3}{2}\) we write into unit fraction 7 X 3 X \(\frac{1}{2}\) =
21 X \(\frac{1}{2}\) = \(\frac{21}{2}\) cups,
Step 2: Now we find how much food the 60-pound dog eats in 1 week let us take it as c = 7 X 3 = 21 cups,
Step 3: Subtract b from c to find how much more food the 60-pound dog eats in 1 week.
c- b = 21 – \(\frac{21}{2}\) to subtract first we make both denominators same,
we multiply and divide 21 by 2 making as (21 x 2) by 2 = \(\frac{42}{2}\) –\(\frac{21}{2}\)
as denominators are same we subtarct numerators 42-21=21 will be numerator and denominator is same 2
=\(\frac{21}{2}\) as numerator is greater than denominator and 2 goes 10 times, 2 X 10 is 20 ,
10 will be our whole number and (21−20) we have 1 left over. 1 will be our numerator and our denominator
will be the same 2 = 10 \(\frac{1}{2}\) . Therefore the 60-pound dog eats 10 \(\frac{1}{2}\)
more cups of food than the 20-pound dog in 1 week.
Show and Grow
Question 7.
Use the table above. A 40-pound dog and a 100-pound dog eat the recommended amounts of dog food each day. How much food is needed to feed both dogs for 1 week?

Answer:
To feed the food for both dogs for 1 week we require \(\frac{182}{4}\) cups or \(\frac{91}{2}\) or 45 \(\frac{1}{2}\) cups.
Explanation:
From the table 40-pound dog eats 2 \(\frac{1}{4}\) and 100-pound dog eats
4 \(\frac{1}{4}\) the recommended amounts of dog food each day,
to find how much food is needed to feed both dogs for 1 week first we calculate for
40-pound dog= 7 X 2 \(\frac{1}{4}\) we write the mixed fraction as a fraction
2 x 4 + 1 by 4 = \(\frac{9}{4}\) and multiply by 7 , 7 X \(\frac{9}{4}\)
now we write in unit fraction 7 X 9 X \(\frac{1}{4}\) = 63 X \(\frac{1}{4}\) =
\(\frac{63}{4}\) now we calculate for 100-pound dog eats 4 \(\frac{1}{4}\) in 1 week is
7 X 4 \(\frac{1}{4}\) we write the mixed fraction as a fraction ( 4 X 4 + 1 )by 4 =
\(\frac{17}{4}\) and multiply by 7 , 7 X \(\frac{17}{4}\) now we write in unit fraction
7 X 17 X \(\frac{1}{4}\) = 119 X \(\frac{1}{4}\) = \(\frac{119}{4}\).
Now to feed the food for both dogs for 1 week is \(\frac{63}{4}\) + \(\frac{119}{4}\)
as denominators are same we add numerators we get 63 + 119 = 182 as numerator, \(\frac{182}{4}\)
further can be simplifed as 182 and 4 goes by 2 we write as \(\frac{91}{2}\) numerator is greater
we can write in mixed fraction as 2 goes 45 times, 2 X 45 is 90 , 45 will be our whole number and
(91−90) we have 1 left over. 1 will be our numerator and our denominator will be the same 2,
making as 45 \(\frac{1}{2}\) cups.
Problem Solving: Fraction Operations Homework & Practice 9.5
Understand the problem. Then make a plan. How will you solve? Explain.
Question 1.
Your friend makes strawberry jam and raspberry jam. He makes enough strawberry jam to fill \(\frac{1}{2}\) of a jar. He makes 5 times as much raspberry jam as strawberry jam. How many full jars of raspberry jam does he make?

Answer:
Friend makes \(\frac{5}{2}\) jars= 2 \(\frac{1}{2}\) jars in that full jars are 2,
So 2 jars of raspberry jam he makes.
Explanation:
Given friend makes strawberry jam to fill \(\frac{1}{2}\) of a jar and makes 5 times as
much raspberry jam as strawberry jam means he makes 5 X \(\frac{1}{2}\) of jars of
raspberry jam now we write as fraction \(\frac{5}{2}\) as numerator is greater,
we can write in mixed fraction as 2 goes 2 times, 2 X 2 is 4 , 2 will be our whole number and
(5−4) we have 1 left over. 1 will be our numerator and our denominator will be the same 2,
making as 2 \(\frac{1}{2}\) ,here 2 is whole there fore full jars of raspberry jam is 2.
So friend makes \(\frac{5}{2}\) jars= 2 \(\frac{1}{2}\) jars in that full jars are 2,
So 2 jars of raspberry jam he makes.
Question 2.
You buy a pair of jeans that originally cost $22. The pair of jeans is \(\frac{1}{2}\) off the original price.
You pay with a $20 bill. How much change do you receive?
Answer:
I receive $9 as change.
Explanation:
The pair of jeans is \(\frac{1}{2}\) off the original price and original cost is $ 22,
So the cost to be paid is $22 X \(\frac{1}{2}\) = \(\frac{22}{2}\)
further this can be simplified as both can be divided by 2 numerator becomes 11 and denominator as 1 = 11,
therefore the original cost for the pair of jeans is $ 11, Now i have paid $ 20bill,
i will receive a change that is $20 – $11= $9, i receive $9 as a change.
Question 3.
The observation deck of the Space Needle in Seattle is 520 feet above ground.
The tip of the Space Needle is 85 feet above the observation deck.
An artist makes a replica that is \(\frac{1}{100}\) the height of the entire Space Needle. How tall is the replica?

Answer:
The height of replica is \(\frac{605}{100}\) =\(\frac{121}{20}\) or
6 \(\frac{1}{20}\) feet.
Explanation:
Given the observation deck of the Space Needle in Seattle is 520 feet above ground and
the tip of the Space Needle is 85 feet above the observation deck means the height of
the entire Space Needle is 520 + 85 = 605 feet above the ground to tip,
now an artist makes a replica that is \(\frac{1}{100}\)
the height of the entire Space Needle. So the height of the replica is
605 X \(\frac{1}{100}\) = \(\frac{605}{100}\)
further can be simplifed as 605 and 100 goes by 5 we get numerator as 121 and denominator as 20 =
\(\frac{121}{20}\) as numerator is greater we can write in mixed fraction as 20 goes
6 times, 20 X 6 is 120 , 6 will be our whole number and (121−120) we have 1 left over.
1 will be our numerator and our denominator will be the same 20, making as 6 \(\frac{1}{20}\) feet tall.
Question 4.
Modeling Real Life
How many sheets of orange and black paper does a teacher need so that 30 students can each complete the art project?

Answer:
For 30 students to complete the Art Project orange sheets required are 11 \(\frac{2}{8}\) and
18 \(\frac{6}{8}\) black sheets of paper is required.
Explanation:
Given paper needed for Art Project orange is \(\frac{3}{8}\) and for 30 students it is
30 X \(\frac{3}{8}\) we write in unit fraction as 30 X 3 X \(\frac{1}{8}\) =
90 X \(\frac{1}{8}\) = \(\frac{90}{8}\) as numerator is greater we can write in mixed fraction
as 8 goes 11 times, 8 X 11 is 88, 11 will be our whole number and (90−88) we have 2 left over.
2 will be our numerator and our denominator will be the same 8, making as
11 \(\frac{2}{8}\) sheets of orange is required, given black paper needed for
Art Project is \(\frac{5}{8}\) and for 30 students it is 30 X \(\frac{5}{8}\)
we write in unit fraction as 30 X 5 X \(\frac{1}{8}\) = 150 X \(\frac{1}{8}\) =
\(\frac{150}{8}\) as numerator is greater we can write in mixed fraction as 8 goes 18 times,
8 X 18 is 144, 18 will be our whole number and (150−144) we have 6 left over.
6 will be our numerator and our denominator will be the same 8, making as
18 \(\frac{6}{8}\) black sheets are required.
Therefore for 30 students to complete the Art Project orange sheets required are
11 \(\frac{2}{8}\) and 18 \(\frac{6}{8}\) black sheets of paper is required.
Question 5.
Writing
Write and solve a two-step word problem with mixed numbers that can be solved using multiplication.
Answer:
A two-step problem is a word problem that requires two operations to solve it.
We take two mixed numbers and slove using multiplication. In step one
we use multiplication and add and in another step we use addition and again use multiplication
as explained below with an example,
Explanation:
For example: Percy walks 2 \(\frac{5}{4}\) kilometers for 2 days and
1 \(\frac{1}{4}\) kilometers for 5 days , how many kilometers does Percy walks in 1 week?
Given in first 2 days Percy walks 2 \(\frac{5}{4}\) kilometers so In first step
we change mixed fraction to fraction by using multiplication and then add 2 X 4 + 5 by 4 =
\(\frac{13}{4}\) kilometers for 1 day for 2 days it is 2 X \(\frac{13}{4}\) =
2 X 13 X \(\frac{1}{4}\) = 26 X \(\frac{1}{4}\) = \(\frac{26}{4}\) kilometers for 2 days ,
Now for rest of 5 days we calculate. Here 1 \(\frac{1}{4}\) we change the mixed fraction to fraction as
( 1 X 4 + 1 ) by 4 = \(\frac{5}{4}\) for 1 day, For 5 days it will be 5 X \(\frac{5}{4}\),
5 X 5 X \(\frac{1}{4}\) = 25 X \(\frac{1}{4}\) = \(\frac{25}{4}\) kilometers for rest 5 days ,
Now total number of kilometers Percy walks is \(\frac{26}{4}\) + \(\frac{25}{4}\) as denominators
are same we add numerators we get 26 + 25 as 51 and denominator being same as 4 = \(\frac{51}{4}\) kilometers
Percy walks in 1 week and further can be simplified as numerator is greater we can write in mixed fraction as
4 goes 12 times, 4 X 12 is 48, 12 will be our whole number and (51−48) we have 3 left over.
3 will be our numerator and our denominator will be the same 4, making as
12 \(\frac{3}{4}\) kilometers Percy walks in 1 week.
Question 6.
Modeling Real Life
In science class, you test how many grams different-sized bundles of spaghetti can hold. You predict that a bundle of 5 spaghetti noodles can hold 10 quarters before breaking. You predict that a bundle of 10 spaghetti noodles can hold 20 quarters before breaking. Each quarter 5\(\frac{67}{100}\) grams. According to your predictions, how many more grams can the bundle of 10 noodles hold than the bundle of 5 noodles?

Answer:
\(\frac{970}{100}\) grams more the bundle of 10 noodles hold than the bundle of 5 noodles
or \(\frac{97}{10}\) grams more the bundle of 10 noodles hold than the bundle of 5 noodles
or 9 \(\frac{7}{10}\) grams more the bundle of 10 noodles hold than the bundle of 5 noodles.
Explanation:
Given that bundle of 5 noodles can hold 10 quarters means 5 noodles can hold
10 X 5 \(\frac{67}{100}\) grams first we change mixed fraction to fraction by
using multiplication and then add as 5 \(\frac{67}{100}\) = 5 X 6 + 67 by 100 =
\(\frac{97}{100}\) now we multiply by 10, 10 X \(\frac{97}{100}\) =
10 X 97 X \(\frac{1}{100}\) = 970 X \(\frac{1}{100}\) = \(\frac{970}{100}\) grams ,
so 5 spaghetti noodles can hold \(\frac{970}{100}\) grams before breaking,
Now given 10 spaghetti noodles can hold 20 quarters means 10 spaghetti noodles can hold
20 X 5 \(\frac{67}{100}\) grams again first we change mixed fraction to fraction
by using multiplication and then add as 5 \(\frac{67}{100}\) = ( 5 X 6 + 67 ) by 100 =
\(\frac{97}{100}\) now we multiply by 20, 20 X \(\frac{97}{100}\) =
20 X 97 X \(\frac{1}{100}\) = 1940 X \(\frac{1}{100}\) = \(\frac{1940}{100}\) grams ,
so 10 spaghetti noodles can hold \(\frac{1940}{100}\) grams before breaking now to calculate
how many more grams can the bundle of 10 noodles hold than the bundle of 5 noodles we subtract
\(\frac{1940}{100}\) grams – \(\frac{970}{100}\) grams as denominators are same first
we substract numerators as 1940 – 970 = 970 as numerator and denominator being same 100
we get \(\frac{970}{100}\) grams more the bundle of 10 noodles hold than the bundle of 5 noodles,
further can be simplified as 970 and 100 both can be divided by 10 making it as \(\frac{97}{10}\) grams
more the bundle of 10 noodles hold than the bundle of 5 noodles and as numerator is greater ,
we can write in mixed fraction as 10 goes 9 times, 10 X 9 is 90, 9 will be our whole number and (97−90)
we have 7 left over. 7 will be our numerator and our denominator will be the same 10,
making as 9 \(\frac{7}{10}\) grams more the bundle of 10 noodles hold than the bundle of 5 noodles.
Review & Refresh
Compare
Question 7.
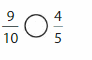
Answer:
\(\frac{9}{10}\) is greater than > \(\frac{4}{5}\) or
\(\frac{9}{10}\) is greater than > \(\frac{8}{10}\)
Explanation:
In order to compare the fractions we must first turn their different denominators into
the same denominators to make denominators same we multiply \(\frac{4}{5}\)
with both numerator and denominator by 2 the value will not change =
\(\frac{4}{5}\) X \(\frac{2}{2}\)= \(\frac{8}{10}\)
now as denominators are same 10 we can compare only numerators
\(\frac{9}{10}\) with \(\frac{8}{10}\) as 9 is greater than 8,
So \(\frac{9}{10}\) is greater than > \(\frac{8}{10}\) or
\(\frac{9}{10}\) is greater than > \(\frac{4}{5}\)
Question 8.
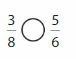
Answer:
\(\frac{3}{8}\) < is less than \(\frac{5}{6}\) or
\(\frac{9}{24}\) < is less than \(\frac{20}{24}\).
Explanation:
In order to compare the fractions we must first turn their different denominators into
the same denominators to make denominators same ,
we find the least common multiplier of 8 ,6 as ( 2 X 2 X 2 X 3 ) = 24,
Now convert each one of \(\frac{3}{8}\) and \(\frac{5}{6}\)
into an equivalent fraction having as denominator,
\(\frac{3}{8}\) = \(\frac{3}{8}\) X \(\frac{3}{3}\) =
\(\frac{9}{24}\) and \(\frac{5}{6}\) = \(\frac{5}{6}\) X \(\frac{4}{4}\) =
\(\frac{20}{24}\) now as denominators are same 24 we can compare only numerators
\(\frac{9}{24}\) with \(\frac{20}{24}\) as 9 is less than 20,
so \(\frac{9}{24}\) < is less than \(\frac{20}{24}\) or
\(\frac{3}{8}\) < is less than \(\frac{5}{6}\)
Question 9.
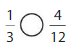
Answer:
\(\frac{1}{3}\) = is equal to \(\frac{4}{12}\) or
\(\frac{1}{3}\) = is equal to \(\frac{1}{3}\)
Explanation:
Here first we simplify \(\frac{4}{12}\) as both can be divided by 4 if we dividey
both numerator and denominator by 4 we get numerator as 1 and denominator as 4 =
\(\frac{1}{3}\) now comparing both sides, as values are same
so \(\frac{1}{3}\) = is equal to \(\frac{4}{12}\) or
\(\frac{1}{3}\) = is equal to \(\frac{1}{3}\).
Multiply Whole Numbers and Fractions Performance Task
Question 1.
You use identical glass jars, colored water, and a spoon to learn about sounds. When you tap a spoon on a jar, the vibrations make a sound. The jar that has the least amount of water makes the lowest sound.

a. You fill each glass using a \(\frac{3}{4}\)-cup measuring cup. Complete the table to find the total amount of water in each jar.
b. How much more water is in the purple jar than the green jar?
c. How many cups of water are used in all?
d. Each jar can hold 4 cups of water. Is it possible to add another \(\frac{3}{4}\) cup of water to the purple jar? Explain.
e. Which jars are more than half full?
f. You add another \(\frac{3}{4}\) cup of water to the green jar. How does that affect the sound?
Answer:
a. 
b. Purple jar is 3 cups more than the Green jar or Purple jar is \(\frac{12}{4}\) cups more than the Green jar.
c. Total number of cups of water used in all is \(\frac{45}{4}\) cups or 11 \(\frac{1}{4}\) cups.
d. No, it is not possible to add another \(\frac{3}{4}\) cup of water to the purple jar as if we add it will become \(\frac{18}{4}\) cups = 4 \(\frac{2}{4}\) = 4 + \(\frac{2}{4}\) cups of water
to the purple jar cups which is more than 4 cups it will overflow so it is not possible to add another
\(\frac{3}{4}\) cup of water to the purple jar.
e. Jars which are more than half full are Orange, Red and Purple.
f. After adding add another \(\frac{3}{4}\) cup of water to the green jar it becomes
\(\frac{6}{4}\) which is equal to blue color jar, we know the jar that has the least amount of water
makes the lowest sound before it was the green jar which had least amount of water so it had lowest sound,
so now after adding \(\frac{3}{4}\) cup of water to green jar it has become equal to blue jar
so now both green and blue jar has least amount of water so they both make the lowest sound.
Explanantion:
a. Given we fill each glass \(\frac{3}{4}\)-cup measuring cup so total water cups used for each color are
Green 1 means 1 X \(\frac{3}{4}\) cup = \(\frac{3}{4}\) cup
Blue 2 of \(\frac{3}{4}\) = 2 X \(\frac{3}{4}\) = 2 X 3 X \(\frac{1}{4}\) =
6 X \(\frac{1}{4}\)= \(\frac{6}{4}\) cups , as both numerator and denominator
can be divided by 2 we get \(\frac{3}{2}\) cups
Orange 3 of \(\frac{3}{4}\) = 3 X \(\frac{3}{4}\) = 3 X 3 X \(\frac{1}{4}\) =
9 X \(\frac{1}{4}\) = \(\frac{9}{4}\) cups
Red 4 of \(\frac{3}{4}\) = 4 X \(\frac{3}{4}\) = 4 X 3 X \(\frac{1}{4}\) =
12 X \(\frac{1}{4}\) = \(\frac{12}{4}\) as both numerator and denominator can be divided by 4
we get numerator as 3 and denominator 1 making Red 4 of \(\frac{3}{4}\) = 3 cups.
Purple 5 of \(\frac{3}{4}\) = 5 X \(\frac{3}{4}\) = 5 X 3 X \(\frac{1}{4}\) =
15 X \(\frac{1}{4}\) =
\(\frac{15}{4}\) cups.
b. To calculate how much more water is in the Purple jar than the Green jar we subtract
the quantity of purple jar minus quantity in green jar as \(\frac{15}{4}\) cups – \(\frac{3}{4}\) cup,
as denominators are same for the both we will sustract numerators 15-3 = 12 and
denominator remains the same as 4, \(\frac{12}{4}\) as both numerator and
denominator can be divided by 4 we get numerator as 3 and denominator 1 so Purple Jar is 3 cups
more than the Green jar.
c. Total number of cups of water are used in all is adding Green, Blue, Orange, Red,
Purple – \(\frac{3}{4}\) + \(\frac{6}{4}\) + \(\frac{9}{4}\) + \(\frac{12}{4}\) +
\(\frac{15}{4}\) as denominators are same we add numerators as 3 + 6 + 9 + 12 + 15 = 45 and
denominator being same as 4 = \(\frac{45}{4}\) as numerator is greater we can also write in mixed fraction
as 4 goes 11 , 4 X 11 is 44, 11 will be our whole number and (45−44) we have 1 left over.
1 will be our numerator and our denominator will be the same 4, making as 11 \(\frac{1}{4}\),
therfore total number of cups of water used in all is \(\frac{45}{4}\) cups or 11 \(\frac{1}{4}\) cups.
d. We got Purple jar contains \(\frac{15}{4}\) cups to this we will add another
\(\frac{3}{4}\) cup of water = \(\frac{15}{4}\) + \(\frac{3}{4}\) as denominator is
same we add numerators as 15 + 3 = 18 and denominator is same 4 so now the Purple jar contains
\(\frac{18}{4}\) cups , to find the whole value we write in mixed fraction as 4 goes , 4 X 4 is 16, 4
will be our whole number and (18−16) we have 2 left over. 2 will be our numerator and our denominator
will be the same 4, making as 4 \(\frac{2}{4}\) = 4 + \(\frac{2}{4}\) and
given that each jar can hold 4 cups of water but as we are getting more than 4 it will overflow,
so it is not possible to add another \(\frac{3}{4}\) cup of water to the purple jar.
e. Jars more than half full means each jars should be above 2 cups means to check we need
denominator to be same that is 4 so we multiply denominator and numerator by 4,
we get \(\frac{8}{4}\) to be more than half full means each jars numerators should be more than 8 and all jars denominators being same as 4, now we check with green jar, \(\frac{8}{4}\) and
\(\frac{3}{4}\) as 3 is not greater than 8 so not green jar, blue jar we have \(\frac{6}{4}\) cups
here also numerator 6 is not more than 8 so even we will not conside blue jar,
orange jar \(\frac{9}{4}\) now here numerator 8 is less than 9 so we will consider orange jar,
Now red jar as red jar has 3 cups which is above 2 cups we consider red jar and we have purple jar as
\(\frac{15}{4}\) here numerator 15 is more than numerator 8 so we consider purple jar,
therefore jars with more than half full are Orange, Red and Purple.
f. Now we will add another \(\frac{3}{4}\) cup of water to the green jar means
\(\frac{3}{4}\) + \(\frac{3}{4}\) as denominators as same we add numerators
we get \(\frac{6}{4}\) which is equal to blue color jar, we know the jar that has the
least amount of water makes the lowest sound before it was the green jar which had least amount of water,
so it had lowest sound, so now after adding \(\frac{3}{4}\) cup of water to green jar it has become equal
to blue jar so now both green and blue jar has least amount of water so they both make the lowest sound.
Multiply Whole Numbers and Fractions Activity
Three In a Row: Fraction Multiplication
Directions:
- Players take turns.
- On your turn, spin both spinners.
- Multiply the whole number and the fraction or mixed number. Cover the product.
- If the product is already covered, you lose your turn.
- The first player to get three in a row wins!
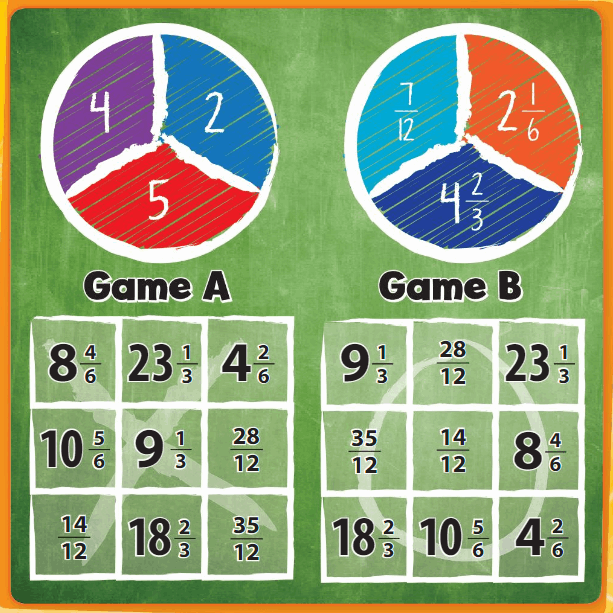
Answer:
Multiply Whole Numbers and Fractions Chapter Practice
9.1 Understand Multiples of Unit Fractions
Write the fraction as a multiple of a unit fraction.
Question 1.
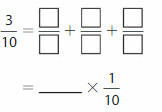
Answer:
\(\frac{3}{10}\)= \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
= 3 X \(\frac{1}{10}\).
Explanation:
We write \(\frac{3}{10}\) in addition equation as \(\frac{3}{100}\)=
\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) and
multiplication as unit fraction \(\frac{3}{10}\) represents 3 parts that are \(\frac{1}{10}\) of the whole, \(\frac{3}{10}\) = 3 X \(\frac{1}{10}\)
Question 2.
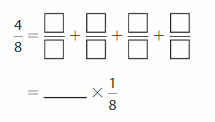
Answer:
\(\frac{4}{8}\)= \(\frac{1}{8}\) + \(\frac{1}{8}\) +
\(\frac{1}{8}\) + \(\frac{1}{8}\) = 4 X \(\frac{1}{8}\).
Explanation:
We write \(\frac{4}{8}\) in addition equation as \(\frac{4}{8}\)=
\(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) +
\(\frac{1}{8}\) and multiplication as unit fraction \(\frac{4}{8}\) represents 4 parts
that are \(\frac{1}{8}\) of the whole, \(\frac{4}{8}\) = 4 X \(\frac{1}{8}\)
Question 3.
\(\frac{7}{2}\)
Answer:
\(\frac{7}{2}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) +
\(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) +
\(\frac{1}{2}\) + \(\frac{1}{2}\) = 7 X \(\frac{1}{2}\).
Explanation:
we write \(\frac{7}{2}\) in addition equation as \(\frac{7}{2}\) =
\(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
+ \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) = 7 X \(\frac{1}{2}\)
and multiplication as unit fraction \(\frac{7}{2}\) represents 7 parts that are
\(\frac{1}{2}\) of the whole, \(\frac{7}{2}\) = 7 X \(\frac{1}{2}\).
Question 4.
\(\frac{56}{100}\)
Answer:
\(\frac{56}{100}\) = \(\frac{14}{25}\) = \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) = 14 X \(\frac{1}{25}\)
Explanation:
\(\frac{56}{100}\) first we simplify as both numerator and denominator can be
divided by 4 we get numerator as 14 and denominatior as 25 = \(\frac{14}{25}\)
now we write \(\frac{14}{25}\) in addition equation as \(\frac{14}{25}\) =
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) + \(\frac{1}{25}\) +
\(\frac{1}{25}\) + \(\frac{1}{25}\) = 14 X \(\frac{1}{25}\) and multiplication as unit fraction \(\frac{14}{25}\) represents 14 parts that are \(\frac{1}{25}\) of the whole,
\(\frac{14}{25}\) = 14 X \(\frac{1}{25}\) .
Question 5.
Logic
What is Newton’s fraction? Write the fraction as a multiple of a unit fraction.

Answer:
Newton’s fraction is 5 X \(\frac{1}{6}\), The fraction is already a multiple of a unit fraction =
5 X \(\frac{1}{6}\) , 5 is multiple and \(\frac{1}{6}\) is a unit fraction.
Explanation:
Given unit fraction is one sixth of a whole is \(\frac{1}{6}\) and Newton’s fraction is 5 unit fractions
means it is equal to \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) +
\(\frac{1}{6}\) + \(\frac{1}{6}\) = 5 X \(\frac{1}{6}\) already the
fraction is a multiple of a unit fraction = 5 X \(\frac{1}{6}\) , 5 is multiple and
\(\frac{1}{6}\) is a unit fraction.
9.2 Understand Multiples of Fractions
Write the product as a multiple of a unit fraction. Then find the product.
Question 6.
![]()
Answer:
2 X \(\frac{2}{4}\) = 2 X 2 X \(\frac{1}{4}\) = 4 X \(\frac{1}{4}\) = \(\frac{4}{4}\)= 1
Explanation:
First we write \(\frac{2}{4}\) as \(\frac{1}{4}\) + \(\frac{1}{4}\) =
2 X \(\frac{1}{4}\) then multiply it by 2 which is 2 X 2 X \(\frac{1}{4}\) =
4 X \(\frac{1}{4}\) = \(\frac{4}{4}\) as numerator and denominator are same
both get cancelled so we get 1 , \(\frac{4}{4}\) = 1.
Question 7.
![]()
Answer:
3 X \(\frac{9}{12}\) = 3 X \(\frac{3}{4}\) = 9 X \(\frac{1}{4}\) =
\(\frac{9}{4}\)
Explanantion:
As \(\frac{9}{12}\) can be simplified as both 9,12 can go with 3 leaving numerator as
3 and denominator as 4= \(\frac{3}{4}\), First we write \(\frac{3}{4}\) as \(\frac{1}{4}\) +
\(\frac{1}{4}\) + \(\frac{1}{4}\) = 3 X \(\frac{1}{4}\) then multiply it by 3
which is 3 X 3 X \(\frac{1}{4}\) = 9 X \(\frac{1}{4}\) is multiple of unit fraction,
The product is \(\frac{9}{4}\) .
Question 8.
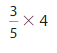
Answer:
\(\frac{3}{5}\) X 4 = 12 X \(\frac{1}{5}\) = \(\frac{12}{5}\).
Explanation:
First we write \(\frac{3}{5}\) as \(\frac{1}{5}\) + \(\frac{1}{5}\) +
\(\frac{1}{5}\) = 3 X \(\frac{1}{5}\) then multiply it by 4 which is
4 X 3 X \(\frac{1}{5}\) = 12 X \(\frac{1}{5}\) = \(\frac{12}{5}\).
Question 9.
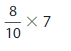
Answer:
\(\frac{8}{10}\) X 7= \(\frac{4}{5}\) X 7 = 28 X \(\frac{1}{5}\) is
multiple of unit fraction, The product is \(\frac{28}{5}\).
Explanantion:
As \(\frac{8}{10}\) can be simplified as both 8,10 can go with 2, leaving numerator as 4
and denominator as 5 = \(\frac{4}{5}\), First we write \(\frac{4}{5}\) as
\(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) =
4 X \(\frac{1}{5}\) then multiply it by 7 which is 7 X 4 X \(\frac{1}{5}\) =
28 X \(\frac{1}{5}\) is multiple of unit fraction, The product is \(\frac{28}{5}\).
Question 10.
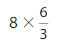
Answer:
8 X \(\frac{6}{3}\) = 8 X 2 = 16 as we got \(\frac{6}{3}\) =2,
So we get results as whole not in fraction.
Explanation:
As \(\frac{6}{3}\) can be simplified as both can be divided by 2, leaving numerator as 2 and denominator as 1 , \(\frac{6}{3}\) = 2 , now it is 8 X 2 = 16 as we got \(\frac{6}{3}\) =2, so we get results as whole not in fraction.
Question 11.
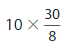
Answer:
10 X \(\frac{30}{8}\) = 10 X \(\frac{15}{4}\) = 150 X \(\frac{1}{4}\) =
\(\frac{150}{4}\) = \(\frac{75}{2}\).
Explanation:
As \(\frac{30}{8}\) can be simplified as both can be divided by 2 , we get numerator as 15 and denominator as 4, \(\frac{30}{8}\) = \(\frac{15}{4}\) = \(\frac{1}{4}\) + \(\frac{1}{4}\) +
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) +
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) +
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) +
\(\frac{1}{4}\) = 15 X \(\frac{1}{4}\) now multiply with 10 X 15 X \(\frac{1}{4}\)
= 150 X \(\frac{1}{4}\) = \(\frac{150}{4}\) this can be further simplified as 150 and 4 both
can be further divided by 2 making numerator as 75 and denominator as 2 = \(\frac{75}{2}\) .
9.3 Multiply Whole Numbers and Fractions
Multiply
Question 12.
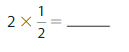
Answer:
2 X \(\frac{1}{2}\) = \(\frac{2}{2}\) = 1
Explanation:
Already it is in unit fraction so 2 X \(\frac{1}{2}\) = \(\frac{2}{2}\) = 1.
Question 13.
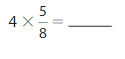
Answer:
4 X \(\frac{5}{8}\) = \(\frac{20}{8}\) = \(\frac{10}{4}\) =
\(\frac{5}{2}\).
Explanation :
First we write \(\frac{5}{8}\) in unit fraction as 5 X \(\frac{1}{8}\)
now we multiply with whole 4 X 5 X \(\frac{1}{8}\) = \(\frac{20}{8}\)
further can be simplifed as 20,8 both can be divided by 4 we get numerator as 5 and denominator 2,
therefore 4 X \(\frac{5}{8}\) = \(\frac{5}{2}\) .
Question 14.
Answer:
3 X \(\frac{9}{6}\) = \(\frac{9}{2}\).
Explanantion:
We can simplify \(\frac{9}{6}\) as both goes by 3 giving numerator as 3 and
denominator as 2 so we get \(\frac{9}{6}\) = \(\frac{3}{2}\) now we write in unit fraction
as 3 X \(\frac{1}{2}\) now we multiply by 3, 3 X 3 X \(\frac{1}{2}\) =
9 X \(\frac{1}{2}\) = \(\frac{9}{2}\).
Question 15.
Answer:
5 X \(\frac{7}{12}\) = \(\frac{35}{12}\).
Explanation:
first we write \(\frac{7}{12}\) as unit fraction = 7 X \(\frac{1}{12}\),
now we multiply with 5 as 5 X 7 X \(\frac{1}{12}\) = 35 X \(\frac{1}{12}\) =
\(\frac{35}{12}\) .
Question 16.
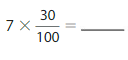
Answer:
7 X \(\frac{30}{100}\) = 7 X \(\frac{3}{10}\) = \(\frac{21}{10}\).
Explanation:
We can simplify \(\frac{30}{100}\) as both goes by 10 giving numerator as 3 and
denominator as 10 so we get \(\frac{3}{10}\) now we write in unit fraction as
3 X \(\frac{1}{10}\) and multiply by 7 , 7 X 3 X \(\frac{1}{10}\) = 21 X \(\frac{1}{10}\)
= \(\frac{21}{10}\) .
Question 17.
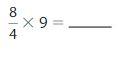
Answer:
\(\frac{8}{4}\) X 9 = 2 X 9 = 18.
Explanantion:
We can simplify \(\frac{8}{4}\) as both goes by 4 giving numerator as 2 and denominator
as 1 so we get 2 as whole, now we multiply with 9 we get 2 X 9 = 18.
9.4 Multiply Whole Numbers and Mixed Numbers
Multiply
Question 18.

Answer:
 = \(\frac{5}{2}\)= 2 \(\frac{1}{2}\)
= \(\frac{5}{2}\)= 2 \(\frac{1}{2}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 1 \(\frac{1}{4}\)=
1 + \(\frac{1}{4}\)= (1 X 4 + 1) by 4 = \(\frac{5}{4}\) now we multiply it with the whole,
2 X \(\frac{5}{4}\) now we write in unit fraction and multiply 2 X 5 X \(\frac{1}{4}\)=
10 X \(\frac{1}{4}\) = \(\frac{10}{4}\) further we can simplify as 10,4
both can be divided by 2 we get numerator as 5 and denominator as 2, \(\frac{5}{2}\)
as numerator is greater than denominator we can write in mixed fraction as 2 goes in 2 times.
2 will be our whole number 2 X 2 is 4 and we have 1 left over (5−4), 1 will be our numerator and our
denominator will stay the same 2, \(\frac{5}{2}\)= 2 \(\frac{1}{2}\).
Question 19.
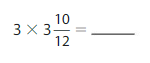
Answer:
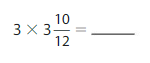 = \(\frac{69}{6}\) = \(\frac{23}{2}\) = 11 \(\frac{1}{2}\)
= \(\frac{69}{6}\) = \(\frac{23}{2}\) = 11 \(\frac{1}{2}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 3 \(\frac{10}{12}\)=
( 3 X 12 + 10 ) by 12 = \(\frac{46}{12}\) this can be further simplified as both 46,12 goes by 2
we get numerator as 23 and denominator as 6 , \(\frac{23}{6}\) now we multiply by 3 =
3 X \(\frac{23}{6}\) = \(\frac{69}{6}\) it can be more simplified as both 69,6 goes by 3
we get numerator as 23 and denominator as 2 making \(\frac{69}{6}\) as \(\frac{23}{2}\)
as numerator is greater than denominator we can write in mixed fraction as 2 goes in 11 times.
11 will be our whole number 2 X 11 is 22 and we have 1 left over (23−22), 1 will be our numerator
and our denominator will stay the same 2, \(\frac{23}{2}\) = 11 \(\frac{1}{2}\).
Question 20.
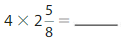
Answer:
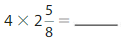 = \(\frac{84}{8}\) = \(\frac{21}{2}\) = 10 \(\frac{1}{2}\).
= \(\frac{84}{8}\) = \(\frac{21}{2}\) = 10 \(\frac{1}{2}\).
Explanantion:
First we write the mixed number as a fraction then multiply, so 2 \(\frac{5}{8}\) =
( 2 X 8 + 5 ) by 8 = \(\frac{21}{8}\) now we multiply by 4 we get 4 X \(\frac{21}{8}\) =
4 X 21 X \(\frac{1}{8}\) = 84 X \(\frac{1}{8}\) =\(\frac{84}{8}\)
further can be simplified as both 84,8 goes by 4 we get numerator as 21 and denominator as 2
=\(\frac{21}{2}\) as numerator is greater than denominator we can write in mixed fraction
as 2 goes in 10 times. 10 will be our whole number 2 X 10 is 20 and we have 1 left over (21−20),
1 will be our numerator and our denominator will stay the same 2,
\(\frac{21}{2}\) = 10 \(\frac{1}{2}\).
Question 21.
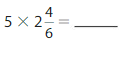
Answer:
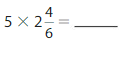 = \(\frac{40}{3}\) = 13 \(\frac{1}{3}\)
= \(\frac{40}{3}\) = 13 \(\frac{1}{3}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 2 \(\frac{4}{6}\) =
( 2 X 6 + 4 ) by 6 = \(\frac{16}{6}\) this can be simplified as 16,6 both goes by 2
we get numerator as 8 and denominator as 3 we get \(\frac{8}{3}\)
now we multiply by 5 we get 5 X \(\frac{8}{3}\) = 5 X 8 X \(\frac{1}{3}\) =
40 X \(\frac{1}{3}\) = \(\frac{40}{3}\) as numerator is greater than denominator
we can write in mixed fraction as 3 goes in 13 times. 13 will be our whole number 3 X 13 is 39 and
we have 1 left over (40−39), 1 will be our numerator and our denominator will stay the same 3,
we get mixed fraction as 13 \(\frac{1}{3}\) .
Question 22.
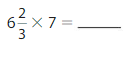
Answer:
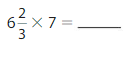 = \(\frac{140}{3}\) = 46 \(\frac{2}{3}\)
= \(\frac{140}{3}\) = 46 \(\frac{2}{3}\)
Explanation:
First we write the mixed number as a fraction then multiply, so 6 \(\frac{2}{3}\) =
( 6 X 3 + 2 ) by 3 = \(\frac{20}{3}\) now we multiply by 7 X \(\frac{20}{3}\) =
7 X 20 x \(\frac{1}{3}\) = 140 X \(\frac{1}{3}\) =\(\frac{140}{3}\)
as numerator is greater than denominator we can write in mixed fraction as 3 goes in 46 times.
46 will be our whole number 3 X 46 is 138 and we have 2 left over (140−138), 2 will be our numerator
and our denominator will stay the same 3, we get mixed fraction as 46 \(\frac{2}{3}\) .
Question 23.
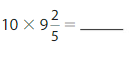
Answer:
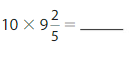 = \(\frac{470}{5}\) = 94
= \(\frac{470}{5}\) = 94
Explanation:
First we write the mixed number as a fraction then multiply, so 9 \(\frac{2}{5}\) =
( 9 X 5 + 2 ) by 5 = \(\frac{47}{5}\) now we multiply by 10 = 10 X \(\frac{47}{5}\) =
\(\frac{470}{5}\) this can be further simplified as both can be divided by 5 we get numerator as
94 and denominator as 1 so we get only whole number 94.
9.5 Problem Solving: Fraction Operations
Question 24.
Modeling Real Life
Your friend rides her bike \(\frac{2}{6}\) mile to your house and \(\frac{2}{6}\)
mile back home 4 times in 1 week. How far does she bike in all?
Answer:
My friend rides her bike by \(\frac{8}{3}\) miles or 2 \(\frac{2}{3}\) miles.
Explanation:
Given friend rides her bike \(\frac{2}{6}\) mile to your house and \(\frac{2}{6}\) mile
back home, first we calculate for 1 time, so first we will add \(\frac{2}{6}\) + \(\frac{2}{6}\)
as both have same denominators we will add numerators as ( 2 + 2 = 4 ).
So we get \(\frac{4}{6}\) miles for 1 time , now she rides 4 times means 4 X \(\frac{4}{6}\) =
\(\frac{16}{6}\) this can be further simplified as 16,6 both goes by 2 we get numerator as 8 and
denominator as 3 = \(\frac{8}{3}\) as numerator is greater than denominator we can write in
mixed fraction as 3 goes in 2 times. 2 will be our whole number 3 X 2 is 6 and
we have 2 left over (8−6), 2 will be our numerator and our denominator will stay the same 3,
we get mixed fraction as 2 \(\frac{2}{3}\) miles.
Conclusion:
Access the links given in the Big Ideas Math Book 4th Grade Answer Key Chapter 9 Multiply Whole Numbers and Fractions and practice well for the exams. We have solved all the questions in an easy and simple manner. We hope the information provided in this article has brought a smile to your face. Share Big Ideas Math Grade 4 Answer Key Chapter 9 Multiply Whole Numbers and Fractions.

