Download Big Ideas Math Book 7th Grade Answer Key Chapter 6 Percents Pdf for free of cost. If you are willing to be perfect in all concepts and math skills, then you must follow the syllabus given here. To score the best marks in the exam, students must learn all the conceptualized lessons on Simple Interest, Discounts, and also the Subject knowledge which will be helpful to improve practical skills.
Big Ideas Math Answers Grade 7 Chapter 6 Percents helps you to cross all the hurdle times while studying. You can easily grasp various concepts and problems on all the concepts given below. Get all the skills and different methods of solving problems easily and quickly. It helps to solve real-life calculations in a very dignified and smooth manner. Follow the below sections to get BIM Grade 7 Chapter 6 Percents problems and solutions.
Big Ideas Math Book 7th Grade Answer Key Chapter 6 Percents
Big ideas Math Book 7th Grade Answer Key Chapter 6 percents pdf is given here. It gives the most accurate answers to all the problems which are related to the given chapter. This chapter of percents contains various topics like Fractions, Decimals and Percents, The Percent Proportion, The Percent Equation, Percents of Increase and Decrease, Discounts and Markups, Simple Interest, and so on.
With the help of Big Ideas Math Book 7th Grade Solution Key Chapter 6 Percents, you can prepare the timetable. With the help of the timetable prepared, you can easily manage your syllabus and include all the topics into it as per the time remaining. In the further sections, you will know all the concepts that are present in Grade 7 Chapter 6 Percents. Check out all the information and kickstart your preparation.
STEAM Video/Performance Task
Getting Ready for Chapter 6
Lesson 1 : Fractions, Decimals, and Percents
- Lesson 6.1 Fractions, Decimals, and Percents
- Fractions, Decimals, and Percents Homework & practice 6.1
Lesson 2 : The Percent Proportion
Lesson 3 : The Percent Equation
Lesson 4 : Percents of Increase and Decrease
- Lesson 6.4 Percents of Increase and Decrease
- Percents of Increase and Decrease Homework & practice 6.4
Lesson 5 : Discounts and Markups
Lesson 6 : Simple Interest
Percents Connecting Concepts
- Percents Connecting Concept
- Percents Chapter Review
- Percents Practice Test
- Percents Cumulative Practice
STEAM Video/Performance Task
STEAM Video
Tornado!
More tornadoes occur each year in the United States than in any other country. How can you use a percent to describe the portion of tornadoes in the United States that occur in your state?

Watch the STEAM Video “Tornado!” Then answer the following questions.
1. The map below shows the average annual number of tornadoes in each state. Which regions have the most tornadoes? the fewest tornadoes?
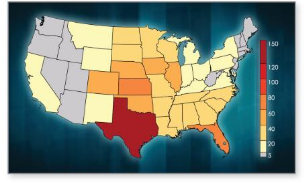
2. Robert says that only Alaska, Hawaii, and Rhode Island average less than 1 tornado per year. What percent of states average more than 1 tornado per year?
Performance Task
Tornado Alley
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given information about the average annual numbers of tornadoes in several states over a 25-year period. For example:

You will be asked to solve various percent problems about tornadoes. Why is it helpful to know the percent of tornadoes that occur in each state?
Getting Ready for Chapter 6
Chapter Exploration
Work with a partner. Write the percent of the model that is shaded. Then write the percent as a decimal.
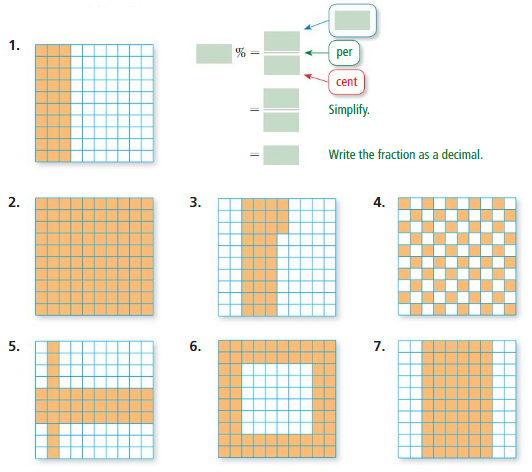
Answer : The Percent and decimal for the given models are
1. percent = 30%, decimal = 0.3
2. percent = 100%, decimal = 1
3. percent = 33%, decimal = 0.33
4. percent = 50%, decimal = 0.5
5. percent = 40%, decimal = 0.4
6. percent = 64%, decimal = 0.64
7. percent = 60%, decimal = 0.6
Explanation:
All the models given here are 10 by 10 grid forming a Square of 100 equal sections.
This entire square represents a whole and the shaded part is fraction.
Each of these shaded squares represents 1/100. So by using this data we have ,
1.  =
= 
From the shaded part and the whole, we have the fraction of \(\frac{30}{100}\),
Then the percent will be \(\frac{30}{100}\) = 30%,
By rewriting it in decimal form we have 0.3
2. =
= 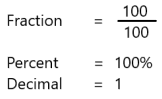
From the shaded part and the whole, we have the fraction of \(\frac{100}{100}\),
Then the percent will be \(\frac{100}{100}\) = 100%,
By rewriting it in decimal form we have 1
3. =
= 
From the shaded part and the whole, we have the fraction of \(\frac{33}{100}\),
Then the percent will be \(\frac{33}{100}\) = 33%,
By rewriting it in decimal form we have 0.33
4. =
= 
From the shaded part and the whole, we have the fraction of \(\frac{50}{100}\),
Then the percent will be \(\frac{50}{100}\) = 50%,
By rewriting it in decimal form we have 0.5
5. =
= 
From the shaded part and the whole, we have the fraction of \(\frac{40}{100}\),
Then the percent will be \(\frac{40}{100}\) = 40%,
By rewriting it in decimal form we have 0.4
6. =
= 
From the shaded part and the whole, we have the fraction of \(\frac{64}{100}\),
Then the percent will be \(\frac{64}{100}\) = 64%,
By rewriting it in decimal form we have 0.64
7. =
= 
From the shaded part and the whole, we have the fraction of \(\frac{60}{100}\),
Then the percent will be \(\frac{60}{100}\) = 60%,
By rewriting it in decimal form we have 0.6
8. WRITE A PROCEDURE Work with a partner. Write a procedure for rewriting a percent as a decimal. Use examples to justify your procedure.
Answer:
Let us say that the fraction be \(\frac{44}{100}\),
Then its percentage will be 44%,
To rewrite it as decimal, we divide 44 by 100 we get 0.44 (a decimal number). So, to convert from percent to decimal divide by 100 and remove the “%” sign.
We get 0.44 as decimal of 44%.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
percent of change
percent of decrease
discount
percent of increase
percent error
markup
Answer:
percent of change:
Percentage Change is all about comparing old values to new values.
percent of decrease:
percent of decrease is a measure of percent change, which is the extent to which something loses value. or
A negative percent of change indicates a decrease from the original value to the second value.
discount: A reduction of price is known as discount .Sometimes discounts are in percent, such as a 10% discount, and then you need to do a calculation to find the price reduction.
percent of increase :
Percent increase is a measure of percent change, which is the extent to which something gains value. or
A positive percent of change indicates an increase from the original value to the second value.
percent error :
Percent error is the difference between estimated value and the actual value in comparison to the actual value and is expressed as a percentage.
markup:
Markup is all about how much a retailer increases the price over what they paid for it to buy the product or item in order to which is how they make money to pay for all their costs and hopefully make a profit.
Lesson 6.1 Fractions, Decimals, and Percents
EXPLORATION 1
Comparing Numbers in Different Forms
Work with a partner. Determine which number is greater. Explain your method.

Answer:
a. 7% sales tax is greater than 5% sales tax
b. 0.37 cup of flour is greater than 0.33 cup of flour
c. 0.625 inch wrench is greater than 0.375 inch wrench
d. 12.6 dollars are greater than 12.56 dollars
e. 5.83 fluid ounces is greater than 5.6 fluid ounces
Explanation:
a. 7% sales tax or \(\frac{1}{20}\) sales tax
By using the method of converting fraction into Percent and comparing ,
We can rewrite \(\frac{1}{20}\) as 0.05 in decimal form,
To get get the percent , multiply 100 to 0.05, then we get 5%.
So, \(\frac{1}{20}\) can be write as 5%,
Finally, by comparing two values 7% sales tax is greater than 5% sales tax
b. 0.37 cup of flour or \(\frac{1}{3}\) cup for flour
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{1}{3}\) as 0.33 in decimal form
Finally, by comparing two values 0.37 cup of flour is greater than 0.33 cup of flour.
c. \(\frac{5}{8}\) inch wrench or 0.375 inch wrench
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{5}{8}\) by dividing 5 by 8, we have 0.625 in decimal form
Finally, by comparing two values 0.625 inch wrench is greater than 0.375 inch wrench.
d. \(12\) \({\Large\frac{3}{5}}\) dollars or 12.56 dollars
By using the method of converting fraction into decimal and comparing ,
We can rewrite fraction\(\frac{63}{5}\) by dividing 63 by 5, we have 12.6 in decimal form
Finally, by comparing two values 12.6 dollars are greater than 12.56 dollars
e. \(5\) \({\Large\frac{5}{6}}\) fluid ounces or 5.6 fluid ounces
By using the method of converting fraction into decimal and comparing ,
We can rewrite fraction \(\frac{35}{6}\) by dividing 35 by 6, we have 5.83 in decimal form
Finally, by comparing two values 5.83 fluid ounces is greater than 5.6 fluid ounces
EXPLORATION 2
Work with a partner and follow the steps below.

- Write five different numbers on individual slips of paper. Include at least one decimal, one fraction, and one percent.
- On a separate sheet of paper, create an answer key that shows your numbers written from least to greatest.
- Exchange slips of paper with another group and race to order the numbers from least to greatest. Then exchange answer keys to check your orders.
Answer: 78%, 0.95, \(\frac{83}{45}\), 6, 21
Explanation:
Let the numbers be 6, 21, 0.95, \(\frac{83}{45}\), 78%
In order to put them in an ascending order we have to calculate the fraction, percent, decimal in their respective form, So Fraction \(\frac{83}{45}\) can be rewrite as 1.84 in decimal form
Then 78% can be rewrite as 0.78 in decimal form,
As we can see 0.78 is less than 0.95 , 0.95 is less than \(\frac{83}{45}\),\(\frac{83}{45}\) is less than 6, 6 is less than 21,
Finally, we have the ascending order as 78%, 0.95, \(\frac{83}{45}\), 6, 21.
Try It
Write the percent as a decimal or the decimal as a percent. Use a model to represent the number.
Question 1.
39%
Answer: 0.39
Explanation: 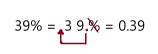
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 39% in decimal form is 0.39
Question 2.
12. 6 %
Answer: 0.126
Explanation: 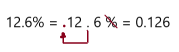
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 12.6% in decimal form is 0.126
Question 3.
0.05
Answer: 5%
Explanation: ![]()
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.05 can be rewrite as 5%
Question 4.
1.25
Answer: 125%
Explanation: ![]()
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 1.25 can be rewrite as 125%
Write the fraction as a decimal and a percent.
Question 5.
\(\frac{5}{8}\)
Answer: 0.625 or 62.5%
Explanation:
To get the percent or decimal from fraction \(\frac{5}{8}\) we have to divide 5 by 8 ,
Then, we get 0.625,
To get the percent of 0.625 multiply by 100 , it will be 62.5%
So, \(\frac{5}{8}\) can be written as 0.625 or 62.5%
Question 6.
\(\frac{1}{6}\)
Answer: 0.166 or 16.6%
Explanation:
To get the percent or decimal from fraction \(\frac{1}{6}\) we have to divide 1 by 6 ,
Then, we get 0.166,
To get the percent of 0.166 multiply by 100 , it will be 16.6%
So, \(\frac{1}{6}\) can be written as 0.166 or 16.6%
Question 7.
\(\frac{11}{3}\)
Answer: 3.66 or 366%
Explanation:
To get the percent or decimal from fraction \(\frac{11}{3}\) we have to divide 11 by 3 ,
Then, we get 3.66,
To get the percent of 3.66 multiply by 100 , it will be 366%
So, \(\frac{11}{3}\) can be written as 3.66 or 366%
Question 8.
\(\frac{3}{1000}\)
Answer: 0.003 or 0.3%
Explanation:
To get the percent or decimal from fraction \(\frac{3}{1000}\) we have to divide 3 by 1000 ,
Then, we get 0.003,
To get the percent of 0.003 multiply by 100 , it will be 0.3%
So, \(\frac{3}{1000}\) can be written as 0.003 or 0.3%
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
CONVERTING BETWEEN PERCENTS AND DECIMALS Write the percent as a decimal or the decimal as a percent. Use a model to represent the number.
Question 9.
46%
Answer: 0.46
Explanation: 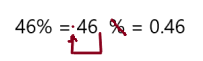
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 46% in decimal form is 0.46
Question 10.
\(66 . \overline{6} \%\)
Answer: \(0 .66 \overline{6}\)
Explanation: 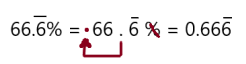
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, \(66 . \overline{6} \%\) in decimal form is \(0 .66 \overline{6}\)
Question 11.
0.18
Answer: 18%
Explanation: 
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.18 can be rewrite as 18%
Question 12.
\(2 . \overline{3}\)
Answer: \(233 . \overline{3} \%\)
Explanation: 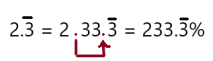
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, \(2 . \overline{3}\) can be rewrite as \(233 . \overline{3} \%\)
WRITING FRACTIONS AS DECIMALS AND PERCENTS Write the fraction as a decimal and a percent.
Question 13.
\(\frac{7}{10}\)
Answer: decimal = 0.7, percent = 70%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{7}{10}\) as 0.7 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.7 can be rewrite as 70%
So, \(\frac{7}{10}\) in decimal = 0.7, percent = 70%
Question 14.
\(\frac{5}{9}\)
Answer: decimal = \(0 .\overline{5}\), percent = \(55 . \overline{5} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{5}{9}\) as \(0 .\overline{5}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then \(0 .\overline{5}\) can be rewrite as \(55 . \overline{5} \%\)
So, \(\frac{5}{9}\) in decimal = \(0 .\overline{5}\), percent = \(55 . \overline{5} \%\)
Question 15.
\(\frac{7}{2000}\)
Answer: decimal = 0.0035, percent = 0.35%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{7}{2000}\) as 0.0035 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.0035 can be rewrite as 0.35%
So, \(\frac{7}{2000}\) in decimal = 0.0035, percent = 0.35%
Question 16.
\(\frac{17}{15}\)
Answer: decimal = \(1.1 \overline{3}\) , percent = \(113 . \overline{3} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{17}{15}\) as \(1.1 \overline{3}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then \(1.1 \overline{3}\) can be rewrite as \(113 . \overline{3} \%\)
So, \(\frac{17}{15}\) in decimal = \(1.1 \overline{3}\), percent = \(113 . \overline{3} \%\)
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
An astronaut spends 53% of the day working, 0.1 of the day eating, \(\frac{3}{10}\) of the day sleeping, and the rest of the day exercising. Order the events by duration from least to greatest. Justify your answer.

Answer: An astronaut spends the day 7% by exercising, 10% by eating, 30% by sleeping, 53% by working.
Explanation:
An astronaut spends 53% of the day working,
0.1 of the day eating, in terms of percent we can write it as 10%,
\(\frac{3}{10}\) of the day sleeping, in decimals we ca rewrite as 0.3 and in percent it will be 30%,
Let us say that the whole day be 100% , The sum of the works he is doing in percent we get,
53% + 10% + 30% = 93%, and
Given that the rest of the day exercising, so 100% – 93% = 7%, A whole day is completed with these works.
To put them in Order the events by duration from least to greatest, we have , 7%, 10%, 30%, 53%.
An astronaut spends the day 7% by exercising, 10% by eating, 30% by sleeping, 53% by working.
Question 18.
DIG DEEPER!
A band plays one concert in Arizona, one concert in California, and one concert in Georgia. In California, the band earned \(\frac{3}{2}\) the profit that they earned in Arizona. Of the total profit earned by the band, 32% is earned in Arizona. How many times more money did the band earn at the most profitable concert than at the least profitable concert? Justify your answer.
Answer:
Explanation:
Fractions, Decimals, and Percents Homework & Practice 6.1
Review & Refresh
Find the missing dimension. Use the scale 1 : 15.
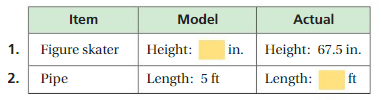
Answer: The model height of the Figure skater is 4.5inches and The Actual length of pipe is 75 feet .
Explanation:
Given , to use the scale oof 1 : 15 , Let the model height be x
The model height of Figure skater is \(\frac{1}{15}\) = \(\frac{x}{67.5}\)
15x = 67.5
x = \(\frac{67.5}{15}\)
x = 4.5
So , The model height of the Figure skater is 4.5inches
Let the Actual length is y
The Actual length of pipe is \(\frac{1}{15}\) = \(\frac{5}{y}\)
y = 15 × 5 = 75
So , The Actual length of pipe is 75 feet .
Simplify the expression.
Question 3.
2(3p – 6) + 4p
Answer: p = 1.2
Explanation:
Let us say that whole expression is equal to 0
2(3p – 6) + 4p = 0
[2(3p) – 2(6)] + 4p = 0
6p – 12 + 4p = 0
10p – 12 = 0
p = 12/10 = 1.2
So, p = 1.2
Question 4.
5n – 3(4n + 1)
Answer: n = -0.42
Explanation:
Let us say that whole expression is equal to 0
5n – 3(4n + 1) = 0
5n – [ 3(4n) + 3(1) ] = 0
5n – 12n – 3 = 0
– 3 – 7n = 0
7n = – 3
n = -3/7 = -0.42
So, n = -0.42
Question 5.
What is the solution of 2n – 4 > – 12?
A. n < – 10
B. n < – 4
C. n > – 2
D. n > – 4
Answer: D . n > -4
Explanation:
Given, 2n – 4 > – 12
add 4 in both sides,
2n – 4 + 4 > – 12 + 4
2n > – 8
divide both sides by 2
2n/2 > -8/2
n > – 4 .
Concepts, Skills, & Problem Solving
COMPARING NUMBERS IN DIFFERENT FORMS Determine which number is greater. Explain your method. (See Exploration 1, p. 235.)
Question 6.
4\(\frac{2}{5}\) tons or 4.3 tons
Answer: 4\(\frac{2}{5}\) tons is greater than 4.3 tons
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite fraction \(\frac{22}{5}\) by dividing 22 by 5, we have 4.4 in decimal form
Finally, by comparing two values 4\(\frac{2}{5}\) tons is greater than 4.3 tons
Question 7.
82% success rate or \(\frac{5}{6}\) success rate
Answer: \(\frac{5}{6}\) success rate is greater than 82% success rate
Explanation:
By using the method of converting fraction into Percent and comparing ,
We can rewrite \(\frac{5}{6}\) as 0.833 in decimal form,
To get get the percent , multiply 100 to 0.833, then we get 83.3%.
So, \(\frac{5}{6}\) can be write as 83.3%,
Finally, by comparing two values \(\frac{5}{6}\) success rate is greater than 82% success rate
CONVERTING BETWEEN PERCENTS AND DECIMALS Write the percent as a decimal or the decimal as a percent. Use a model to represent the number.
Question 8.
26%
Answer: 0.26
Explanation: 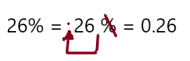
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 26% in decimal form is 0.26
Question 9.
0.63
Answer: 63%
Explanation: 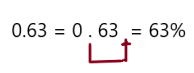
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.63 can be rewrite as 63%
Question 10.
9%
Answer: 0.09
Explanation: 
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 9% in decimal form is 0.09
Question 11.
0.6
Answer: 60%
Explanation: 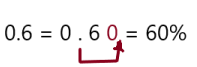
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.6 can be rewrite as 60%
Question 12.
44.7%
Answer: 0.447
Explanation: 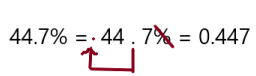
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 44.7% in decimal form is 0.447
Question 13.
55%
Answer: 0.55
Explanation: 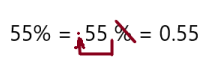
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 55% in decimal form is 0.55
Question 14.
\(39 . \overline{2} \%\)
Answer: \(0.39 \overline{2}\)
Explanation: 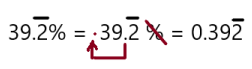
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, \(39 . \overline{2} \%\) in decimal form is \(0.39 \overline{2}\)
Question 15.
3.554
Answer: 355.4%
Explanation: 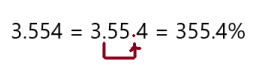
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 3.554 can be rewrite as 355.4%
Question 16.
123%
Answer: 1.23
Explanation: 
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 123% in decimal form is 1.23
Question 17.
0.041
Answer: 4.1%
Explanation: 
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.041 can be rewrite as 4.1%
Question 18.
0.122
Answer: 12.2%
Explanation: 
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.122 can be rewrite as 12.2%
Question 19.
\(49 . \overline{92} \%\)
Answer: \(0.49 \overline{92}\)
Explanation: 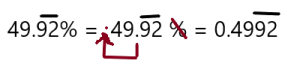
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, \(49 . \overline{92} \%\) in decimal form is \(0.49 \overline{92}\)
Question 20.
YOU BE THE TEACHER
Your friend writes \(49 . \overline{8} \%\) as a decimal. Is your friend correct? Explain your reasoning.
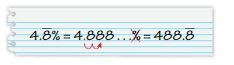
Answer: He wrote the decimal for \(4. \overline{8} \%\) instead of \(49 . \overline{8} \%\)
Explanation: 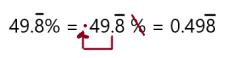
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, \(49 . \overline{8} \%\) in decimal form is \(0.49 \overline{8}\)
WRITING FRACTIONS AS DECIMALS AND PERCENTS Write the fraction as a decimal and a percent.
Question 21.
\(\frac{29}{100}\)
Answer: decimal = 0.29, percent = 29%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{29}{100}\) as 0.29 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.29 can be rewrite as 29%
So, \(\frac{29}{100}\) in decimal = 0.29, percent = 29%
Question 22.
\(\frac{3}{4}\)
Answer: decimal = 0.75, percent = 75%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite\(\frac{3}{4}\) as 0.75 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.75 can be rewrite as 75%
So, \(\frac{3}{4}\) in decimal = 0.75, percent = 75%
Question 23.
\(\frac{7}{8}\)
Answer: decimal = 0.875, percent = 87.5%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{7}{8}\) as 0.875 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.875 can be rewrite as 87.5%
So, \(\frac{7}{8}\) in decimal = 0.875, percent = 87.5%
Question 24.
\(\frac{2}{3}\)
Answer: decimal = \(0. \overline{6}\), percent = \(66. \overline{6} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{2}{3}\) as \(0. \overline{6}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then\(0. \overline{6}\) can be rewrite as \(66. \overline{6} \%\)
So, \(\frac{2}{3}\) in decimal =\(0. \overline{6}\), percent = \(66. \overline{6} \%\)
Question 25.
\(\frac{7}{9}\)
Answer: decimal = 0.77, percent = 77.7%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite\(\frac{7}{9}\) as 0.77 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.77 can be rewrite as 77.7%
So, \(\frac{7}{9}\) in decimal = 0.77, percent = 77.7%
Question 26.
\(\frac{12}{5}\)
Answer: decimal = 2.4, percent = 240%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{12}{5}\) as 2.4 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 2.4 can be rewrite as 240%
So, \(\frac{12}{5}\) in decimal =2.4, percent = 240%
Question 27.
\(\frac{9}{2}\)
Answer: decimal = 4.5, percent = 450%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite\(\frac{9}{2}\) as 4.5 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 4.5 can be rewrite as 450%
So, \(\frac{9}{2}\) in decimal = 4.5, percent = 450%
Question 28.
\(\frac{1}{1000}\)
Answer: decimal = 0.0010, percent = 0.10%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{1}{1000}\) as 0.0010 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.0010 can be rewrite as 0.10%
So, \(\frac{1}{1000}\) in decimal = 0.0010, percent = 0.10%
Question 29.
\(\frac{17}{6}\)
Answer: decimal = \(2.8 \overline{3}\), percent = \(283 . \overline{3} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{17}{6}\) as \(2.8 \overline{3}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then\(2.8 \overline{3}\) can be rewrite as \(283 . \overline{3} \%\)
So, \(\frac{17}{6}\) in decimal = \(2.8 \overline{3}\), percent = \(283 . \overline{3} \%\)
Question 30.
\(\frac{3}{11}\)
Answer: decimal = 0.27, percent = 27%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{3}{11}\) as 0.27 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.27 can be rewrite as 27%
So, \(\frac{3}{11}\) in decimal = 0.27, percent = 27%
Question 31.
\(\frac{1}{750}\)
Answer: decimal = \(0.001 \overline{3}\), percent =\(0.1 \overline{3} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{1}{750}\) as \(0.001 \overline{3}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then \(0.001 \overline{3}\) can be rewrite as \(0.1 \overline{3} \%\)
So, \(\frac{1}{750}\) in decimal = \(0.001 \overline{3}\), percent = \(0.1 \overline{3} \%\)
Question 32.
\(\frac{22}{9}\)
Answer: decimal = \(2. \overline{4}\), percent = \(244 . \overline{4} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{22}{9}\) as \(2. \overline{4}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then \(2. \overline{4}\) can be rewrite as \(244 . \overline{4} \%\)
So, \(\frac{22}{9}\) in decimal = \(2. \overline{4}\), percent = \(244 . \overline{4} \%\)
PRECISION Order the numbers from least to greatest.
Question 33.
66.1%, 0.66, \(\frac{2}{3}\), 0.667
Answer: 0.66, 66.1%, \(\frac{2}{3}\), 0.667
Explanation:
In order to put them in an ascending order we have to calculate the fraction, percent, decimal in their respective form, So Fraction \(\frac{2}{3}\) can be rewrite as \(0. \overline{6}\) in decimal form
Then 66.1% can be rewrite as 0.661 in decimal form,
As we can see 0.66 is less than 66.1% , 66.1% is less than \(\frac{2}{3}\), \(\frac{2}{3}\) is less than 0.667,
Finally, we have the ascending order as 0.66, 66.1%, \(\frac{2}{3}\), 0.667.
Question 34.
\(\frac{2}{9}\), 21%, \(0.2 \overline{1}\), \(\frac{11}{50}\)
Answer: 21%, \(0.2 \overline{1}\), \(\frac{11}{50}\), \(\frac{2}{9}\)
Explanation:
In order to put them in an ascending order we have to calculate the fraction, percent, decimal in their respective form, So Fraction \(\frac{11}{50}\) can be rewrite as 0.22 in decimal form,
\(\frac{2}{9}\) can be rewrite as \(0.22 \overline{2}\)in decimal form,
Then 21% can be rewrite as 0.21 in decimal form,
As we can see 21% is less than \(0.2 \overline{1}\) ,\(0.2 \overline{1}\) is less than \(\frac{11}{50}\), \(\frac{11}{50}\) is less than \(\frac{2}{9}\),
Finally, we have the ascending order as 21%, \(0.2 \overline{1}\), \(\frac{11}{50}\), \(\frac{2}{9}\)
MATCHING Tell which letter shows the graph of the number.
Question 35.
\(\frac{7}{9}\)
Answer: decimal = 0.777 , it is in the graph at the point A
Explanation:
By using the method of converting fraction into decimal ,
We can rewrite \(\frac{7}{9}\) as 0.777 in decimal form,
So, looking at the graph given, it is at point A.
Question 36.
0.812
Answer: it is at the point C in the given graph.
Question 37.
\(\frac{5}{6}\)
Answer: decimal = 0.833 , it is in the graph at the point D
Explanation:
By using the method of converting fraction into decimal ,
We can rewrite \(\frac{5}{6}\) as 0.833 in decimal form,
So, looking at the graph given, it is at point D.
Question 38.
79.5%
Answer: 0.795, it is in the graph at the point B
Explanation:
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 79.5% in decimal form is 0.795
0.795 is in the graph given , at the point B vb

Question 39.
PROBLEM SOLVING
The table shows the portion of students in each grade that participate in School Spirit Week. Order the grades by portion of participation from least to greatest.
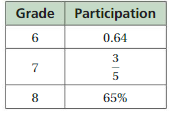
Answer: The grades by portion of participation from least to greatest are 7 , 6 , 8.
Explanation:
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left. So, 65% in decimal form is 0.65.
By using the method of converting fraction into Percent ,
We can rewrite \(\frac{5}{6}\) as 0.6 in decimal form,
Then grade 6 = 0.64 , grade 7 = 0.6 , grade 8 = 0.65 ,
So, The grades by portion of participation from least to greatest are 7 , 6 , 8.
Question 40.
MODELING REAL LIFE
The table shows the portion of gold medals that were won by the United States in five summer Olympic games. In what year did the United States win the least portion of gold medals? the greatest portion? Justify your answers.

Answer: The United States win the least portion of gold medals in the year 2004 and the greatest portion of gold medals won in the year 2012
Explanation:
By using the method of converting fraction into Percent and comparing ,
We can rewrite \(\frac{36}{301}\) as 0.119 in decimal form,
\(\frac{23}{150}\) as 0.153 in decimal form,
\(\frac{46}{307}\) as 0.149 in decimal form,
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
\(12. \overline{3} \%\) as \(0.12 \overline{3}\) in decimal form.
So, according to their years and portions of gold medals we have ,
year 2000 – \(0.12 \overline{3}\),
year 2004 – 0.119,
year 2008 – \(0. \overline{12}\),
year 2012 – 0.153,
year 2016 – 0.149,
Finally, The United States win the least portion of gold medals in the year 2004 and the greatest portion of gold medals won in the year 2012.
Question 41.
PROBLEM SOLVING
You, your friend, and your cousin have a basketball competition where each person attempts the same number of shots. You make 70% of your shots, your friend makes of her shots, \(\frac{7}{9}\) and your cousin makes \(0.7 \overline{2}\) of his shots. How many times more shots are made by the first place finisher than the third place finisher?

Answer: The first place finisher made 0.077 more shorts than the third place finisher.
Explanation:
The shorts made by 1st person are 70%, that is 0.7 in decimal,
The shorts made by 2nd person are \(\frac{7}{9}\) rewriting as 0.777 in decimal,
The shorts made by 3rd person are \(0.7 \overline{2}\)
The shorts made by the first place finisher is 0.777 and by the Third place finisher is 0.7,
To know how many more shorts are made by first place finisher than third place finisher is the difference between 0.777 and 0.7 , that is 0.777 – 0.7 = 0.077.
So, the first place finisher made 0.077 more shorts than the third place finisher.
Question 42.
DIG DEEPER!
Three different mixtures contain small amounts of acetic acid. Mixture A is 0.036 acetic acid, Mixture B is 4.2% acetic acid, and Mixture C is \(\frac{1}{22}\) acetic acid. Explain how to use this information to determine which mixture contains the greatest amount of acetic acid.

Answer: 0.045 , Mixture C has more amount of acetic acid as compared to Mixture A and Mixture B.
Explanation:
Mixture A is 0.036 acetic acid,
Mixture B is 4.2% acetic acid, in decimal we can write it as 0.042,
Mixture C is \(\frac{1}{22}\) acetic acid, rewriting as 0.045 in decimal form,
So, 0.036 is less than 0.042 , 0.042 is less than 0.045,
Finally, 0.045 Mixture c has the more amount of acetic acid as compared to Mixture A and Mixture B.
Question 43.
MODELING REAL LIFE
Over 44% of the 30 students in a class read a book last month. What are the possible numbers of students in the class who read a book last month? Justify your answer.
Answer: 13 number of students in the class read the book last month.
Explanation:
Given, 44% of 30 students
=(44%) × 30
= \(\frac{44}{100}\) × 30
= \(\frac{44 × 30}{100}\)
= \(\frac{1320}{100}\)
=13.2
So, 13 number of students in the class read the book last month.
Question 44.
NUMBER SENSE
Fill in the blanks using each of the numbers 0 – 7 exactly once, so that the percent, decimal, and fraction below are ordered from least to greatest. Justify your answer.

Answer: The percent, decimal, and fraction are ordered from least to greatest are 12.3%, 0.57, \(\frac{4}{6}\) by using 0 – 7 numbers only once .
Explanation:
Given , using each of the numbers 0 – 7 exactly once,
Estimating on the numbes
Using numbers 1 , 2 , 3 for percent gives 12.3% as shown and can be writen as 0.123
Using numbers 0 , 5 , 7 for decimal gives 0.57 as shown
Using numbers 4 and 6 for fraction gives \(\frac{4}{6}\) and can be writen as 0.66
The order from least to greatest is 0.123 , 0.57 , 0.66 .
So , The percent, decimal, and fraction are ordered from least to greatest are 12.3%, 0.57, \(\frac{4}{6}\)
Lesson 6.2 The Percent Proportion
EXPLORATION 1
Using Percent Models
Work with a partner.
a. Complete each model. Explain what each model represents.
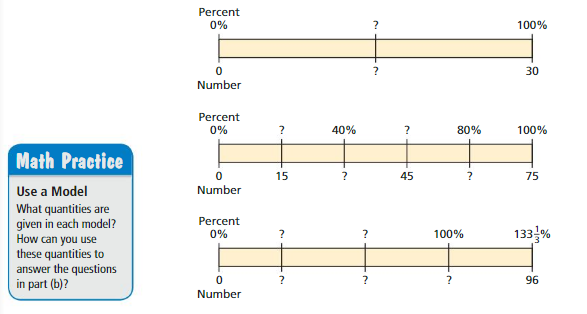
b. Use the models in part (a) to answer each question.
- What number is 50% of 30?
- 15 is what percent of 75?
- 96 is 133\(\frac{1}{3}\)% of what number?
c. How can you use ratio tables to check your answers in part(b)? How can you use proportions? Provide examples to support your reasoning.
d. Write a question different from those in part (b) that can be answered using one of the models in part(a). Trade questions with another group and find the solution.
Answer: All the answers are given below the explanation.
Explanation:
a. 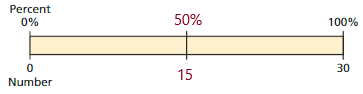
This model represents the number 30 which is divided in to two equal halves ,which can be represented in percent and numbers,
that is 50% of 30 is 15.
50 percent × 30 =
(50:100) × 30 =
(50 × 30):100 =
1500:100 = 15
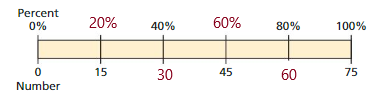
This model represents the number 75 which is divided in to five equal halves, which can be represented in percent and numbers ,That is
20% of 75 is 15,
40% of 75 is 30,
60% of 75 is 45,
80% of 75 is 60.
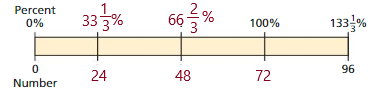
This model represents the number 96 which is divided in to four equal halves, which can be represented in percent and numbers ,That is
33\(\frac{1}{3}\%\) of 96 is 24,
66\(\frac{2}{3}\%\) of 96 is 48,
100% of 96 is 72.
b. As shown in the models in part (a) 15 is the number which is 50% of 30,
From the figure 2 of part (a) we know, 15 is the number which is 20% of 75,
From the figure 3 of part (a) we know, 96 is the number which is 133\(\frac{1}{3}\%\) of 96.
c. The models provided in the part (a) are representing the each of the number individually which are divided in to equal number of parts in respective of their numbers , Also the divided parts can be represented as percent and number form
Since the divided equal parts are equally represents the whole number given ,So that the ratios of the parts can be easily combined in to the whole number .
Thus, the proportion can be used to calculate the percent of each ratio and have the unchanged output .
For example, 
In the picture shown The number 30 is divided into 1:1 ratio equally which is exactly the half of the number and percent that is 15 is 50% of 30.
d. From the figure 2 of part (a), we can assume the question as
What number is 80% of 75?
Answer: 60 is the number which is 80% of 75 , as shown in the model above.
Try It
Write and solve a proportion to answer the question.
Question 1.
What percent of 5 is 3?
Answer: 60%
Explanation:
3 : 5 × 100 =
(3 × 100): 5
300 : 5 = 60
So, 5 is 60% of 3.
Question 2.
24 is what percent of 20?
Answer: 120%
Explanation:
24 : 20 × 100 =
(24 × 100) : 20 =
2400 : 20 = 120
So, 24 is the 120% of 20.
Write and solve a proportion to answer the question.
Question 3.
What number is 80% of 60?
Answer: 48
Explanation:
80 % × 60 =
(80 :100) × 60 =
(80 × 60) :100 =
4800 : 100 = 48
So, 48 is 80% of 60.
Question 4.
10% of 40.5 is what number?
Answer: 4.05
Explanation:
10 % × 40.5 =
(10 : 100) × 40.5 =
(10 × 40.5) : 100 =
4.05 : 100 = 4.05
So, 4.05 is the 10% of 40.5
Write and solve a proportion to answer the question.
Question 5.
0.1% of what number is 4?
Answer: 4,000
Explanation:
Let the number be X
0.1% × X = 4
X = 4 ÷ 0.1%
= 4 ÷ (0.1 ÷ 100)
= (100 × 4 ) ÷ 0.1
= 400 ÷ 0.1
=4,000
So, 4 is the 0.1% of 4,000.
Question 6.
\(\frac{1}{2}\) is 25% of what number?
Answer: 2
Explanation:
To make calculation easier we can rewrite \(\frac{1}{2}\) as 0.5
let the number be X
25% × X = 0.5
X = 0.5 ÷ 25%
= 0.5 ÷ (25 ÷ 100)
= (100 × 0.5 ) ÷ 25
= 50 ÷ 25
=2
So, 0.5 is the 25% of 2.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
USING THE PERCENT PROPORTION
Write and solve a proportion to determine what percent of 120 is 54.
Answer: 45%
Explanation:
By using percent proportion, we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{54}{120}\) = \(\frac{p}{100}\)
\(\frac{54 × 100}{120}\) = p
p = \(\frac{5400}{120}\)
p = 45%
so, 54 is the 45% of 120.
Question 8.
CHOOSE TOOLS
Use a model to find 60% of 30.
Answer: 18
Explanation: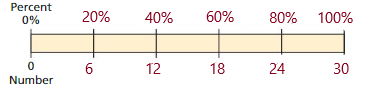
60% × 30
= (60 : 100) × 30
= (60 × 30) : 100
= 1800 : 100
= 18
So, 60% of 30 is 18.
Question 9.
WHICH ONE DOESN’T BELONG?
Which proportion at the left does not belong with the other three? Explain your reasoning.

Answer: second proportion doesn’t belong to other three
Explanation:
second proportion: 15/50 = p /100
p = (15 × 100) ÷50
p = 150 ÷ 5
p = 30
Here we got 30% , as the p values of the other three proportions are 50%
So, second proportion does not fit in to the other three proportions.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
An arctic woolly-bear caterpillar lives for 7 years and spends 90% of its life frozen. How many days of its life is the arctic woolly-bear frozen?

Answer: The arctic woolly-bear frozen for 6.3 years in their life time.
Explanation:
Given, An arctic woolly-bear caterpillar lives for 7 years and spends 90% of its life frozen
We have, 90% × 7
= (90 : 100 ) × 7
= (90 × 7) : 100
= 630 : 100
= 6.3 years
So, The arctic woolly-bear frozen for 6.3 years in their life time.
Question 11.
DIG DEEPER!
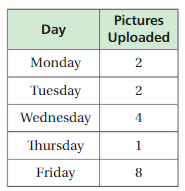
The table shows the numbers of pictures you upload to a social media website for 5 days in a row. How many total pictures do you upload during the week when 32% of the total pictures are uploaded on Saturday and Sunday?
Answer: The total pictures uploaded during the week are 53.
Explanation:
Given, 32% of the total pictures are uploaded on Saturday and Sunday
And adding the photos that we uploaded during the 5 days are 2 + 2 + 4 + 1 + 8 = 17
Let the number we should find be X
32% × X = 17
X = 17 ÷ 32%
= 17 ÷ (32 ÷ 100)
= (100 × 17 ) ÷ 32
= 1700 ÷ 32
= 53.12
So, 17 is the 32% of 53.
Finally we have, The total pictures uploaded during the week are 53.
The Percent Proportion Homework & Practice 6.2
Review & Refresh
Write the fraction as a decimal and a percent.
Question 1.
\(\frac{42}{100}\)
Answer: decimal = 0.42 , percent = 42%
Explanation:
To get the percent or decimal from fraction \(\frac{42}{100}\) we have to divide 42 by 100 ,
Then, we get 0.42,
To get the percent of 0.42 multiply by 100 , it will be 42%
So, \(\frac{42}{100}\) can be written as 0.42 or 42%
Question 2.
\(\frac{7}{1000}\)
Answer: decimal = 0.007 , percent = 0.7%
Explanation:
To get the percent or decimal from fraction \(\frac{7}{1000}\) we have to divide 7 by 1000 ,
Then, we get 0.007,
To get the percent of 0.007 multiply by 100 , it will be 0.7%
So, \(\frac{7}{1000}\) can be written as 0.007 or 0.7%
Question 3.
\(\frac{13}{9}\)
Answer: decimal = 1.444 , percent = 144.4%
Explanation:
To get the percent or decimal from \(\frac{13}{9}\) fraction we have to divide 13 by 9 ,
Then, we get 1.444,
To get the percent of 1.444 multiply by 100 , it will be 144.4%
So, \(\frac{13}{9}\) can be written as 1.444 or 144.4%
Question 4.
\(\frac{41}{66}\)
Answer: decimal = \(0.62 \overline{12}\) , percent = \(62. \overline{12} \%\)
Explanation:
To get the percent or decimal from fraction \(\frac{41}{66}\) we have to divide 41 by 66 ,
Then, we get \(0.62 \overline{12}\),
To get the percent of \(0.62 \overline{12}\) multiply by 100 , it will be \(62. \overline{12} \%\)
So, \(\frac{41}{66}\) can be written as \(0.62 \overline{12}\) or \(62. \overline{12} \%\)
Evaluate the expression when a = – 15 and b = – 5.
Question 5.
a ÷ 5
Answer: -3
Explanation:
Given , a = – 15
Then , – 15 ÷ 5
= \(\frac{-15}{5}\)
= – 3.
so, a ÷ 5 = – 3.
Question 6.
\(\frac{b+14}{a}\)
Answer: \(\frac{9}{-15}\)
Explanation:
Given , a = -15 , b = -5 , by substituting the given values in the expression, we get
= \(\frac{(- 5)+14}{-15}\)
= \(\frac{9}{-15}\)
So, \(\frac{b+14}{a}\) = \(\frac{9}{-15}\)
Question 7.
\(\frac{b^{2}}{a+5}\)
Answer: \(\frac{25}{-10}\)
Explanation:
Given , a = -15 , b = -5, by substituting the given values in the expression, we get
= \(\frac{(-5)^{2}}{(-15)+5}\)
= \(\frac{25}{-10}\)
So, \(\frac{b^{2}}{a+5}\) = \(\frac{25}{-10}\)
What is the solution of 9x = 1.8?
A. x = – 5
B. x = – 0.2
C. x = 0.2
D. x = 5
Answer: C . x = 0.2
Explanation:
Given, 9x = 1.8
x = \(\frac{1.8}{9}\)
x = 0.2.
Concepts, Skills, &Problem Solving
CHOOSE TOOLS Use a model to answer the question. Use a proportion to check your answer. (See Exploration 1, p. 241.)
Question 9.
What number is 20% of 80?
Answer: 16
Explanation: 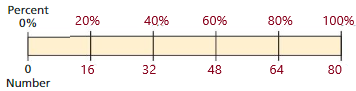
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{80}\) = \(\frac{20}{100}\)
\(\frac{a}{80}\) = \(\frac{1}{5}\)
a = \(\frac{80}{5}\)
a = 16.
So, 16 is 20% of 80.
Question 10.
10 is what percent of 40?
Answer: 25%
Explanation: 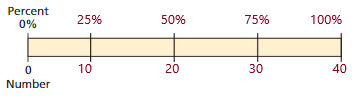
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{10}{40}\) = \(\frac{p}{100}\)
\(\frac{1}{4}\) = \(\frac{p}{100}\)
p = \(\frac{100}{4}\)
p = 25
So, 10 is 25% of 40.
Question 11.
15 is 30% of what number?
Answer: 50
Explanation: 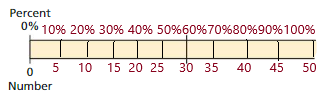
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{15}{w}\) = \(\frac{30}{100}\)
by cross multiplication we get,
30 × w = 15 × 100
w = \(\frac{1500}{30}\)
w = \(\frac{150}{30}\)
w = 50.
So, 15 is 30% of 50.
Question 12.
What number is 120% of 70?
Answer: 84
Explanation: 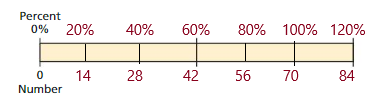
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{70}\) = \(\frac{120}{100}\)
\(\frac{a}{70}\) = \(\frac{6}{5}\)
a = \(\frac{70 × 6}{5}\)
a = \(\frac{420}{5}\)
a = 84
So, 84 is 120% of 70.
Question 13.
20 is what percent of 50?
Answer: 40%
Explanation: 
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{20}{50}\) = \(\frac{p}{100}\)
p = \(\frac{20 × 100}{50}\)
p = \(\frac{200}{5}\)
p = 40
So, 20 is 40% of 50.
Question 14.
48 is 75% of what number?
Answer: 64
Explanation: 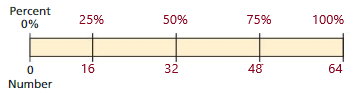
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{48}{w}\) = \(\frac{75}{100}\)
w =\(\frac{48 × 100}{75}\)
w = \(\frac{4800}{75}\)
w = 64
So, 48 is 75% of 64.
USING THE PERCENT PROPORTION Write and solve a proportion to answer the question.
Question 15.
What percent of 25 is 12?
Answer: 48%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{12}{25}\) = \(\frac{p}{100}\)
p = \(\frac{12 × 100}{25}\)
p = \(\frac{1200}{25}\)
p = 48
So, 12 is 48% of 25.
Question 16.
14 is what percent of 56?
Answer: 25%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{14}{56}\) = \(\frac{p}{100}\)
p = \(\frac{14 × 100}{56}\)
p = \(\frac{1400}{56}\)
p = 25
So, 14 is 25% of 56.
Question 17.
25% of what number is 9?
Answer: 36
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{9}{w}\) = \(\frac{25}{100}\)
\(\frac{9}{w}\) = \(\frac{1}{4}\)
w = 9 × 4
w = 36.
So, 9 is 25% of 36.
Question 18.
36 is 0.9% of what number?
Answer: 4,000
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{36}{w}\) = \(\frac{0.9}{100}\)
w = \(\frac{36 × 100}{0.9}\)
w = \(\frac{3600}{0.9}\)
w = \(\frac{36,000}{9}\)
w = 4,000
So, 36 is 0.9% of 4,000.
Question 19.
75% of 124 is what number?
Answer: 93
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{124}\) = \(\frac{75}{100}\)
a = \(\frac{75 × 124}{100}\)
a = \(\frac{9,300}{100}\)
a = 93
So, 93 is 75% of 124.
Question 20.
110% of 90 is what number?
Answer: 99
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{90}\) = \(\frac{110}{100}\)
a = \(\frac{110 × 90}{100}\)
a = \(\frac{9900}{100}\)
a = 99
So, 99 is 110% of 90.
Question 21.
What number is 0.4% of 40?
Answer: 0.16
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{40}\) = \(\frac{0.4}{100}\)
a = \(\frac{0.4 × 40}{100}\)
a = \(\frac{16}{100}\)
a = 0.16
So, 0.16 is 0.4% of 40.
Question 22.
72 is what percent of 45?
Answer: 160%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{72}{45}\) = \(\frac{p}{100}\)
p = \(\frac{72 × 100}{45}\)
p = \(\frac{7200}{45}\)
p = 160
So, 72 is 160% of 45.
Question 23.
YOU BE THE TEACHER
Your friend uses the percent proportion to answer the question below. Is your friend correct? Explain your reasoning.
“40%of what number is 34?”

Answer: yes, he used the correct percent proportion.
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{34}{w}\) = \(\frac{40}{100}\)
w = \(\frac{34 × 100}{40}\)
w = \(\frac{3400}{40}\)
w = 85
So, 34 is 40% of 85.
Question 24.
MODELING REAL LIFE
Of 140 seventh-grade students, 15% earn the Presidential Youth Fitness Award. How many students earn the award?

Answer: 21 students earn the Presidential Youth Fitness Award.
Explanation:
Given, Of 140 seventh-grade students, 15% earn the Presidential Youth Fitness Award.
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{140}\) = \(\frac{15}{100}\)
a = \(\frac{15 × 140}{100}\)
a = \(\frac{2100}{100}\)
a = 21
So, 21 is 15% of 140.
Totally ,21 students earn the Presidential Youth Fitness Award.
Question 25.
MODELING REAL LIFE
A salesperson receives a 3% commission on sales. The salesperson receives $180 in commission. What is the amount of sales?
Answer: The total amount of sale is $6,000.
Explanation:
Given, A salesperson receives a 3% commission on sales, The salesperson receives $180 in commission.
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{180}{w}\) = \(\frac{3}{100}\)
w = \(\frac{180 × 100}{3}\)
w = \(\frac{18,000}{3}\)
w = 6,000
So, $180 is 3% of $6,000.
Total amount of sale is $6,000.
USING THE PERCENT PROPORTION Write and solve a proportion to answer the question.
Question 26.
0.5 is what percent of 20?
Answer: 2.5%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{0.5}{20}\) = \(\frac{p}{100}\)
p = \(\frac{0.5 × 100}{20}\)
p = 0.5 × 5
p = 2.5
So, 0.5 is 2.5% of 20.
Question 27.
14.2 is 35.5% of what number?
Answer: 40
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{14.2}{w}\) = \(\frac{35.5}{100}\)
w = \(\frac{14.2 × 100}{35.5}\)
w = \(\frac{142 × 10}{35.5}\)
w = 40
So, 14.2 is 35.5% of 40.
Question 28.
\(\frac{3}{4}\) is 60% of what number?
Answer: 1.25
Explanation:
\(\frac{3}{4}\) can be rewrite as 0.75 in decimal,
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{0.75}{w}\) = \(\frac{60}{100}\)
w = \(\frac{0.75 × 100}{60}\)
w = \(\frac{75}{60}\)
w = 1.25
So, 0.75 is 60% of 1.25.
Question 29.
What number is 25% of \(\frac{7}{8}\)?
Answer: 0.218
Explanation:
\(\frac{7}{8}\) can be rewrite as 0.875 in decimal,
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{0.875}\) = \(\frac{25}{100}\)
a = \(\frac{0.875 × 25}{100}\)
a = \(\frac{21.87}{100}\)
a = 0.218
So, 0.218 is 25% of 0.875.
Question 30.
MODELING REAL LIFE
You are assigned 32 math exercises for homework. You complete 75% of the exercises before dinner. How many exercises do you have left to do after dinner?
Answer: 24 exercises are left .
Explanation:
You are assigned 32 math exercises for homework. You complete 75% of the exercises before dinner.
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{32}\) = \(\frac{75}{100}\)
a = \(\frac{32 × 75}{100}\)
a = \(\frac{2,400}{100}\)
a = 24
So, 24 is 75% of 32.
Totally, 24 exercise are left .
Question 31.
MODELING REAL LIFE
Your friend earns $10.50 per hour, which is 125% of her hourly wage last year. How much did your friend earn per hour last year?
Answer: Friend earned $8.4 per hour last year
Explanation:
Your friend earns $10.50 per hour, which is 125% of her hourly wage last year,
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{10.5}{w}\) = \(\frac{125}{100}\)
w = \(\frac{10.5 × 100}{125}\)
w = \(\frac{1050}{125}\)
w = 8.4
So, 8.4 is 125% of 10.5.
Question 32.
MODELING REAL LIFE
The bar graph shows the numbers of reserved campsites at a campground for one week. What percent of the reservations were for Friday or Saturday?
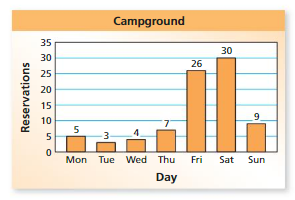
Answer: The percent of reservations For Friday is 74.2% and for Saturday is 85%
Explanation:
As per the graph shown, The reservations made for the week are 35 ,
Friday reservations are 26, so
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{26}{35}\) = \(\frac{p}{100}\)
p = \(\frac{26 × 100}{35}\)
p = \(\frac{2600}{35}\)
p = 74.2
So, 26 is 74.2% of 35.
Saturday reservations are 30, so
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{30}{35}\) = \(\frac{p}{100}\)
p = \(\frac{30 × 100}{35}\)
p = \(\frac{3,000}{35}\)
p = 85
So, 30 is 85% of 35.
Totally, The percent of reservations For Friday is 74.2% and for Saturday is 85%.
Question 33.
PROBLEM SOLVING
Your friend displays the results of a survey that asks several people to vote on a new school mascot.
a. What is missing from the bar graph?
b. What percent of the votes does the least popular mascot receive? Explain your reasoning.
c. There are 124 votes total. How many votes does tiger receive?
Answer: a. The numerical values for the votes are missing from the graph
b. In order to calculate the percent of the votes does the least popular mascot received will be halted due to lack of clear mentioning of of the proportion of the votes or the ratio of the votes.
c. The votes acquired by the tiger are cannot be determined because of figure which does not contain proper information.
Question 34.
DIG DEEPER!
A quarterback completes 18 of 33 passes during the first three quarters of a football game. He completes every pass in the fourth quarter and 62.5% of his passes for the entire game. How many passes does the quarterback throw in the fourth quarter? Justify your answer.

Answer: Quarterback throw 20.6 passes in the fourth quarter
Explanation:
A quarterback completes 18 of 33 passes during the first three quarters of a football game,
He completes every pass in the fourth quarter and 62.5% of his passes for the entire game.
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{33}\) = \(\frac{62.5}{100}\)
a = \(\frac{33 × 62.5}{100}\)
a = \(\frac{2,062.5}{100}\)
a = 20.6
So, 20.6 is 62.5% of 33.
Hence, Quarterback thrown 20.6 passes in the fourth quarter
Question 35.
REASONING
20% of a number is x. What is 100% of the number? Assume x > 0.
Answer: 5x
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
substitute a = x and p = 20
\(\frac{x}{w}\) = \(\frac{20}{100}\)
by cross multiplication , we get
w × 20 = x × 100
20w = 100x
Divide both sides by 20,
\(\frac{20w}{20}\) = \(\frac{100x}{20}\)
w = 5x
So, 100% of the number is 5x.
Question 36.
STRUCTURE
Answer each question. Assume x > 0.
a. What percent of 8x is 5x?
b. What is 65% of 80x?
Answer: a. 62.5% , b. 52x
Explanation:
a. percent of 8x is 5x
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{5x}{8x}\) = \(\frac{p}{100}\)
\(\frac{5}{8}\) = \(\frac{p}{100}\)
by cross multiplying
8p = 500
p = \(\frac{500}{8}\)
p = 62.5
So, 5x is 62.5% of 8x.
b. By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{8x}\) = \(\frac{65}{100}\)
a = \(\frac{8x × 65}{100}\)
a = \(\frac{520x}{100}\)
a = 52x
So, 52x is 65% of 80x.
Lesson 6.3 The Percent Equation
EXPLORATION 1
Using Percent Equations
Work with a partner.
a. The circle graph shows the number of votes received by each candidate during a school election. So far, only half of the students have voted. Find the percent of students who voted for each candidate. Explain your method.
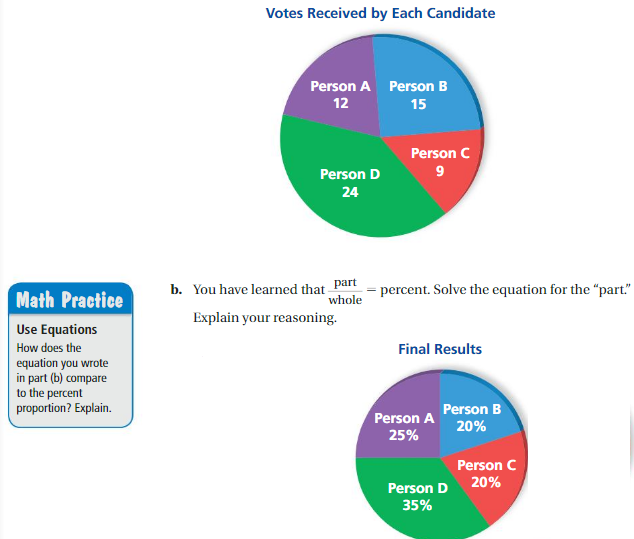
c. The circle graph shows the final results of the election after every student voted. Use the equation you wrote in part(b) to find the number of students who voted for each candidate.
d. Use a different method to check your answers in part(c). Which method do you prefer? Explain.
Answer:
a. The percent of students who voted for each candidate are
For Person A = 20% ,
For Person B = 25%
For Person C = 15%
For Person D = 40%
b. The equation is a = \(\frac{w × p}{100}\)
c. The number of students who voted for each candidate are
For Person A = 30
For Person B = 24
For Person C = 24
For Person D = 42
d. ratio proportion is used as another method.
Explanation:
a. Given, The circle graph shows the number of votes received by each candidate during a school election. So far, only half of the students have voted.
The number of votes received till now are 12 + 15 + 9 + 24 = 60,
To know the percent of students who voted for each candidate we have ,
For person A, w = 60 , a = 12 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{12}{60}\) = \(\frac{p}{100}\)
p = \(\frac{12 × 100}{60}\)
p = \(\frac{1200}{60}\)
p = 20
So, 12 is 20% of 60.
The percent of students who voted for person A is 20%
For person B , w = 60 , a = 15 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{15}{60}\) = \(\frac{p}{100}\)
p = \(\frac{15 × 100}{60}\)
p = \(\frac{1500}{60}\)
p = 25
So, 15 is 25% of 60.
The percent of students who voted for person B is 25%
For person C , w = 60 , a = 9 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{9}{60}\) = \(\frac{p}{100}\)
p = \(\frac{9 × 100}{60}\)
p = \(\frac{900}{60}\)
p = 15
So, 9 is 15% of 60.
The percent of students who voted for person C is 15%
For person D , w = 60 , a = 24 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{24}{60}\) = \(\frac{p}{100}\)
p = \(\frac{24 × 100}{60}\)
p = \(\frac{2400}{60}\)
p = 40
So, 24 is 40% of 60.
The percent of students who voted for person D is 40%
b. we know that percent proportion is \(\frac{a}{w}\) = \(\frac{p}{100}\)
where as a = part , w= whole , p = percent ,
To solve for a , we can write it as a = \(\frac{w × p}{100}\)
c. The figure showing the percent of all the candidates individually are after the final results ,
as shown in part (a) half of the students are 60 ,
The half of the students voted in all the students are 60 and total strength of students are 60 + 60 = 120
To calculate the number of voting acquired by each candidate we have,
For person A , w = 120 , p = 25 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{120}\) = \(\frac{25}{100}\)
a = \(\frac{120 × 25}{100}\)
a = \(\frac{120}{4}\)
a = 30
So, 30 is 25% of 120.
The number of students who voted for person A after final results are 30
For person B , w = 120 , p = 20 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{120}\) = \(\frac{20}{100}\)
a = \(\frac{120 × 20}{100}\)
a = \(\frac{120}{5}\)
a = 24
So, 24 is 20% of 120.
The number of students who voted for person B after final results are 24
For person C , w = 120 , p = 20 , a = ?
By using percent proportion , we have
same as for person B ,
So, 24 is 20% of 120.
The number of students who voted for person C after final results are 24
For person D , w = 120 , p = 35 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{120}\) = \(\frac{35}{100}\)
a = \(\frac{120 × 35}{100}\)
a = \(\frac{4,200}{100}\)
a = 42
So, 42 is 35% of 120.
The number of students who voted for person D after final results are 42.
d. We are using ratio proportion method , To check the answers of part (c),
For person A , 25 % × 120 =
(25 : 100) × 120 =
(25 × 120) : 100 =
3,000 : 100 = 30
So, 30 is the 25% of 120.
For person B , 20 % × 120 =
(20 : 100) × 120 =
(20 × 120) : 100 =
2,400 : 100 = 24
So, 24 is the 20% of 120.
For person C , 20% × 120 is same as person B
So, 24 is the 20% of 120.
For person D , 35 % × 120 =
(35 : 100) × 120 =
(35 × 120) : 100 =
4,200 : 100 = 42
So, 42 is the 35% of 120.
All the answers are verified with ratio proportion method.
Try It
Write and solve an equation to answer the question.
Question 1.
What number is 10% of 20?
Answer: 2
Explanation:
10 % × 20 =
(10 : 100) × 20 =
(10 × 20) : 100 =
200 : 100 = 2
So, 2 is the 10% of 20.
Question 2.
What number is 150% of 40?
Answer: 60
Explanation:
150 % × 40 =
(150 : 100) × 40 =
(150 × 40) : 100 =
6,000 : 100 = 60
So, 60 is the 150% of 40.
Write and solve an equation to answer the question.
Question 3.
3 is what percent of 600?
Answer: 0.5%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{3}{600}\) = \(\frac{p}{100}\)
p = \(\frac{3 × 100}{600}\)
p = \(\frac{300}{600}\)
p = \(\frac{1}{2}\)
p = 0.5
So, 3 is 0.5% of 600.
Question 4.
18 is what percent of 20?
Answer:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{18}{20}\) = \(\frac{p}{100}\)
p = \(\frac{18 × 100}{20}\)
p = \(\frac{1800}{20}\)
p = \(\frac{180}{2}\)
p = 90
So, 18 is 90% of 20.
Write and solve an equation to answer the question.
Question 5.
8 is 80% of what number?
Answer: 10
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{8}{w}\) = \(\frac{80}{100}\)
w = \(\frac{8 × 100}{80}\)
w = \(\frac{800}{80}\)
w = 10
So, 8 is 80% of 10.
Question 6.
90 is 180% of what number?
Answer: 50
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{90}{w}\) = \(\frac{180}{100}\)
w = \(\frac{90 × 100}{180}\)
w = \(\frac{9,000}{180}\)
w = 50
So, 90 is 180% of 50.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
VOCABULARY
Write the percent equation in words.
Answer:
Percent Equation:
In this equation, the whole is the number of which we are taking a percentage and the part is the value that results from taking the percent of the whole. This means that in any percent problem, there are three basic values to be concerned about: the percent, the whole, and the resulting part.
we can represent percent = p , whole = w , part = a
So, we have the percent equation as,
\(\frac{a}{w}\) = \(\frac{p}{100}\).
USING THE PERCENT EQUATION Write and solve an equation to answer the question.
Question 8.
14 is what percent of 70?
Answer: 20%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{14}{70}\) = \(\frac{p}{100}\)
p = \(\frac{14 × 100}{70}\)
p = \(\frac{1400}{70}\)
p = 20
So, 14 is 20% of 70.
Question 9.
What number is 36% of 85?
Answer: 30.6
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{85}\) = \(\frac{36}{100}\)
a = \(\frac{85 × 36}{100}\)
a = \(\frac{3,060}{100}\)
a = 30.6
So, 30.6 is 36% of 85.
Question 10.
9 is 12% of what number?
Answer: 75
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{9}{w}\) = \(\frac{12}{100}\)
w = \(\frac{9 × 100}{12}\)
w = \(\frac{900}{12}\)
w = 75
So, 9 is 12% of 75.
Question 11.
108 is what percent of 72?
Answer: 150%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{108}{72}\) = \(\frac{p}{100}\)
p = \(\frac{108 × 100}{72}\)
p = \(\frac{10,800}{72}\)
p = 150
So, 108 is 150% of 72.
Question 12.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer: 55 is 20% of what number ? , is different from other three questions.
Explanation:
Given , 20% of 55 , we have to find the part of whole number
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{55}\) = \(\frac{20}{100}\)
a = \(\frac{55 × 20}{100}\)
a = \(\frac{1,100}{100}\)
a = 11
So, 11 is 20% of 55.
But this 55 is 20% of what number ? is different from other three, because here we have to find out the whole number
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{55}{w}\) = \(\frac{20}{100}\)
w = \(\frac{55 × 100}{20}\)
w = \(\frac{5500}{20}\)
w = 275
So, 55 is 20% of 275.
Hence , 55 is 20% of what number ? , is different from other three questions.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
DIG DEEPER!
A school offers band and chorus classes. The table shows the percents of the 1200 students in the school who are enrolled in band, chorus, or neither class. How many students are enrolled in both classes? Explain.

Answer: The total number of students enrolled for both classes are 744.
Explanation:
Given, The table shows the percent of the 1200 students in the school who are enrolled in band, chorus, or neither class.
For Band , w = 1200 , p = 34 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{1200}\) = \(\frac{34}{100}\)
a = \(\frac{1200 × 34}{100}\)
a = 12 × 34
a = 408
So, 408 is 34% of 1200.
The number of students enrolled for the Band are 408.
For Band , w = 1200 , p = 28 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{1200}\) = \(\frac{28}{100}\)
a = \(\frac{1200 × 28}{100}\)
a = 12 × 28
a = 336
So, 336 is 28% of 1200.
The number of students enrolled for the chorus are 336.
The total number of students enrolled for both classes are 408 + 336 = 744.
Question 14.
Water Tank A has a capacity of 550 gallons and is 66% full. Water Tank B is 53% full. The ratio of the capacity of Water Tank A to Water Tank B is 11:15.
a. How much water is in each tank?
b. What percent of the total volume of both tanks is filled with water?
Answer:
a. The water tank A is filled with 363 gallons of water.
The water tank B is filled with 397.5 gallons of water.
b. The percent of the total volume of both tanks is filled with water is 58.5%.
Explanation:
a. Given , Water Tank A has a capacity of 550 gallons and is 66% full.
w = 550 gallons , p = 66% , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{550}\) = \(\frac{66}{100}\)
a = \(\frac{550 × 66}{100}\)
a = 550 × 0.66
a = 363
So, 363 is 66% of 550.
The water tank A is filled with 363 gallons of water.
Given, Water Tank B is 53% full.
The ratio of the capacity of Water Tank A to Water Tank B is 11:15.
The capacity of Water Tank A is 550 gallons
Let the capacity of tank B is x gallons
\(\frac{550}{x}\) = \(\frac{11}{15}\)
x = \(\frac{550 × 15}{11}\)
x = \(\frac{8,250}{11}\)
x = 750.
The capacity of the water Tank B is 750 gallons,
To know the amount of water filled in the tank we have,
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{750}\) = \(\frac{53}{100}\)
a = \(\frac{750 × 53}{100}\)
a = 7.5 × 53
a = 397.5
So, 397.5 is 53% of 750.
The water tank B is filled with 397.5 gallons of water.
b. To know the percent of the total volume of both tanks is filled with water, we have
The total capacity of Water tank A and Water tank B = 550 + 750 = 1,300 gallons
The total amount of water filled in both tanks are 363 + 397.5 = 760.5 gallons
So, w = 1,300 , a = 760.5 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{760.5}{1,300}\) = \(\frac{p}{100}\)
p = \(\frac{760.5 × 100}{1,300}\)
p = \(\frac{760.5}{13}\)
p = 58.5
So, 760.5 is 58.5% of 1,300.
The percent of the total volume of both tanks is filled with water is 58.5%.
The Percent Equation Homework & Practice 6.3
Review & Refresh
Write and solve a proportion to answer the question.
Question 1.
30% of what number is 9?
Answer: 30
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{9}{w}\) = \(\frac{30}{100}\)
w = \(\frac{9 × 100}{30}\)
w = \(\frac{900}{30}\)
w = 30
So, 9 is 30% of 30.
Question 2.
42 is what percent of 80?
Answer: 52.5%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{42}{80}\) = \(\frac{p}{100}\)
p = \(\frac{42 × 100}{80}\)
p = \(\frac{420}{8}\)
p = 52.5
So, 42 is 52.5% of 80.
Question 3.
What percent of 36 is 20?
Answer:
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{20}{36}\) = \(\frac{p}{100}\)
p = \(\frac{20 × 100}{36}\)
p = \(\frac{2,000}{36}\)
p = 5.55
So, 20 is55.5% of 36.
Question 4.
What number is 120% of 80?
Answer: 96
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{80}\) = \(\frac{120}{100}\)
a = \(\frac{80 × 120}{100}\)
a = 8 × 12
a = 96
So, 96 is 120% of 80.
Find the distance between the two numbers on a number line.
Question 5.
– 4 and 10
Answer: The distance between the two numbers – 4 and 10 on a number line is 14 .
Explanation: 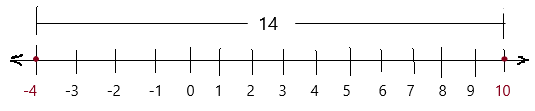
For the number line above we have divided each segment in to equal parts ,
So, The distance between the two numbers – 4 and 10 on a number line is 14 .
Question 6.
–\(\frac{2}{3}\) and \(\frac{4}{3}\)
Answer: The distance between the two numbers –\(\frac{2}{3}\) and \(\frac{4}{3}\) on a number line is 6 .
Explanation: 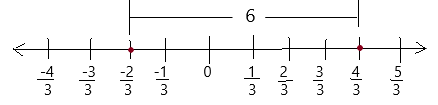
For the number line above we have divided each segment in to equal parts ,
So, The distance between the two numbers –\(\frac{2}{3}\) and \(\frac{4}{3}\) on a number line is 6 .
Question 7.
– 5\(\frac{2}{3}\) and – 1 \(\frac{3}{10}\)
Answer: The distance between the two numbers – 5\(\frac{2}{3}\) and – 1 \(\frac{3}{10}\) on a number line is 6.
Explanation: 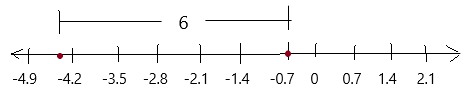
Given , – 5\(\frac{2}{3}\) and – 1 \(\frac{3}{10}\)
can be written as \(\frac{-13}{3}\) and \(\frac{-7}{10}\)
converting into decimal form we get , -4.3 and -0.7
For the number line above we have divided each segment in to equal parts ,
So, The distance between the two numbers – 5\(\frac{2}{3}\) and – 1 \(\frac{3}{10}\) on a number line is 6.
Question 8.
– 4.3 and 7.5
Answer: The distance between the two numbers – 4.3 and 7.5 on a number line is 8 .
Explanation: 
For the number line above we have divided each segment in to equal parts ,
So, The distance between the two numbers – 4.3 and 7.5 on a number line is 8 .
Question 9.
There are 160 people in a grade. The ratio of boys to girls is 3 to 5. Which proportion can you use to find the number x of boys?
![]()
Answer: A. \(\frac{3}{8}\) = \(\frac{x}{160}\)
Explanation:
Given, The ratio of boys to girls is\(\frac{3}{5}\)
The ratio of boys to the grade is \(\frac{3}{8}\)
to find the number of x boys, we have to
\(\frac{3}{8}\) = \(\frac{x}{160}\)
x = \(\frac{3 × 160}{8}\)
x = \(\frac{480}{8}\)
x = 60.
So, A = \(\frac{3}{8}\) = \(\frac{x}{160}\) is the correct answer.
Concepts, Skills, & Problem Solving
USING PERCENT EQUATIONS The circle graph shows the number of votes received by each candidate during a school election. Find the percent of students who voted for the indicated candidate. Each Candidate(See Exploration 1, p. 247.)
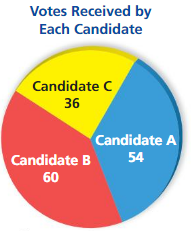
Question 10.
Candidate A
Answer: The percent of students who voted for the candidate A is 36%
Explanation:
Given, the circle graph shows the number of votes received by each candidate during a school election.
The total number of students voted are 54 + 60 + 36 = 150
For candidate A we have , w = 150 , a = 54 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{54}{150}\) = \(\frac{p}{100}\)
p = \(\frac{54 × 100}{150}\)
p = \(\frac{540}{15}\)
p = 36
So, 54 is 36% of 150.
The percent of students who voted for the candidate A is 36%.
Question 11.
Candidate B
Answer: The percent of students who voted for the candidate B is 40%.
Explanation:
For candidate B we have , w = 150 , a = 60 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{60}{150}\) = \(\frac{p}{100}\)
p = \(\frac{60 × 100}{150}\)
p = \(\frac{600}{15}\)
p = 40
So, 60 is 40% of 150.
The percent of students who voted for the candidate B is 40%.
Question 12.
Candidate C
Answer: The percent of students who voted for the candidate C is 24%.
Explanation:
For candidate C we have , w = 150 , a = 36 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{36}{150}\) = \(\frac{p}{100}\)
p = \(\frac{36 × 100}{150}\)
p = \(\frac{360}{15}\)
p = 24
So, 36 is 24% of 150.
The percent of students who voted for the candidate C is 24%.
USING THE PERCENT EQUATION Write and solve an equation to answer the question.
Question 13.
20% of 150 is what number?
Answer: 30
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{150}\) = \(\frac{20}{100}\)
a = \(\frac{150 × 20}{100}\)
a = 15 × 2
a = 30
So, 30 is 20% of 150.
Question 14.
45 is what percent of 60?
Answer: 75%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{45}{60}\) = \(\frac{p}{100}\)
p = \(\frac{45 × 100}{60}\)
p = \(\frac{4,500}{60}\)
p = 75
So, 45 is 75% of 60.
Question 15.
35% of what number is 35?
Answer: 35 is 35% of 100.
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{35}{w}\) = \(\frac{35}{100}\)
w = \(\frac{35 × 100}{35}\)
w = \(\frac{3500}{35}\)
w = 100
So, 35 is 35% of 100.
Question 16.
0.8% of 150 is what number?
Answer: 1.2 .
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{150}\) = \(\frac{0.8}{100}\)
a = \(\frac{150 × 0.8}{100}\)
a = \(\frac{120}{100}\)
a = 1.2
So, 1.2 is 0.8% of 150.
Question 17.
29 is what percent of 20?
Answer: 145%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{29}{20}\) = \(\frac{p}{100}\)
p = \(\frac{29 × 100}{20}\)
p = \(\frac{2,900}{20}\)
p = \(\frac{2,90}{2}\)
p = 145
So, 29 is 145% of 20.
Question 18.
0.5% of what number is 12?
Answer:
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{12}{w}\) = \(\frac{0.5}{100}\)
w = \(\frac{12 × 100}{0.5}\)
w = \(\frac{1200}{0.5}\)
w = 2,400.
So, 12 is 0.5% of 2,400.
Question 19.
What percent of 300 is 51?
Answer: 17%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{51}{300}\) = \(\frac{p}{100}\)
p = \(\frac{51 × 100}{300}\)
p = \(\frac{51}{3}\)
p = 17
So, 51 is 17% of 300.
Question 20.
120% of what number is 102?
Answer: 85
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{102}{w}\) = \(\frac{120}{100}\)
w = \(\frac{102 × 100}{120}\)
w = \(\frac{1020}{12}\)
w = 85
So, 102 is 120% of 85.
YOU BE THE TEACHER Your friend uses the percent equation to answer the question. Is your friend correct? Explain your reasoning.
Question 21.
What number is 35% of 20?

Answer: yes , He is correct .
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{20}\) = \(\frac{35}{100}\)
a = \(\frac{20 × 35}{100}\)
a = \(\frac{700}{100}\)
a = 7
So, 7 is 35% of 20.
Question 22.
30 is 60% of what number?

Answer: 30 is 60% of 50.
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{30}{w}\) = \(\frac{60}{100}\)
w = \(\frac{30 × 100}{60}\)
w = \(\frac{300}{6}\)
w = 50
So, 30 is 60% of 50.
Question 23.
MODELING REAL LIFE
A salesperson receives a 2.5% commission on sales. What commission does the salesperson receive for $8000 in sales?
Answer: He receives $200 for commission of the sale.
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{8000}\) = \(\frac{2.5}{100}\)
a = \(\frac{8000 × 2.5}{100}\)
a = 80 × 2.5
a = $200
So, $200 is 2.5% of $8000.
He receives $200 for commission of the sale.
Question 24.
MODELING REAL LIFE
Your school raised 125% of its fundraising goal. The school raised $6750. What was the goal?
Answer: The fundraising goal of the school is $5,400.
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{6750}{w}\) = \(\frac{125}{100}\)
w = \(\frac{6750 × 100}{125}\)
w =54 × 100
w = $5,400
So, $6750 is 125% of $5,400.
The fundraising goal of the school is $5,400.
Question 25.
MODELING REAL LIFE
The sales tax on the model rocket shown is $1.92. What is the percent of sales tax?

Answer: The percent of sales tax on the rocket model is 8%.
Explanation:
Given, The sales tax on the model rocket shown is $1.92.
The tax on the rocket is $24 , we have ,
w = 24 , a = 1.92 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{1.92}{24}\) = \(\frac{p}{100}\)
p = \(\frac{1.92 × 100}{24}\)
p = \(\frac{192}{24}\)
p = 8
So, $1.92 is 8% of $24.
The percent of sales tax on the rocket model is 8%.
PUZZLE There were n signers of the Declaration of Independence. The youngest was Edward Rutledge, who was x years old. The oldest was Benjamin Franklin, who was y years old.

Question 26.
x is 25% of 104. What was Rutledge’s age?
Answer: The age of Rutledge is 26.
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{104}\) = \(\frac{25}{100}\)
a = \(\frac{104 × 25}{100}\)
a = \(\frac{104}{4}\)
a = 26
x = 26.
So, 26 is 25% of 104.
Question 27.
7 is 10% of y. What was Franklin’s age?
Answer: The Franklin’s age is 70.
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{7}{w}\) = \(\frac{10}{100}\)
w = \(\frac{7 × 100}{10}\)
w = \(\frac{700}{10}\)
w = 70
y = 70.
So, 7 is 10% of 70.
The Franklin’s age is 70.
Question 28.
n is 80% of y. How many signers were there?
Answer: There are n = 56 members signers.
Explanation:
y = 70 , p = 80 ,
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{70}\) = \(\frac{80}{100}\)
a = \(\frac{70 × 80}{100}\)
a = 7 × 8
a =56
n = 56
So, 56 is 80% of 70.
There are n = 56 members signers.
Question 29.
LOGIC
How can you tell whether a percent of a number will be greater than, less than, or equal to the number? Give examples to support your answer.
Answer: The percent of a number is less than 100% , Then the percent of the number will be less than the number.
The percent of a number is 100% , Then the percent of the number will be equal the number.
The percent of a number is greater than 100% , Then the percent of the number will be greater than the number.
Explanation:
If the percent of a number is less than 100% , Then the percent of the number will be less than the number.
For example , 80% of 50
= 0.8 × 50
= 40
80% < 100% , so 40 < 50.
If the percent of a number is 100% , Then the percent of the number will be equal the number.
For example , 100% of 50
= 1 × 50
= 50.
100% = 100% , So, 50 = 50.
If the percent of a number is greater than 100% , Then the percent of the number will be greater than the number.
For example , 120% of 50
= 1.2 × 50
= 60.
120% > 100% , So, 60 > 50.
Question 30.
PROBLEM SOLVING
In a survey, a group of students is asked their favorite sport. Eighteen students choose “other” sports.
a. How many students participate in the survey?
b. How many choose football?
Answer: a. The number of students participated are 80.
b. The number of students chose football are 30.
Explanation:
a. 18 students chose ” other” sports So, a = 18 ,
The percent of the “other” sport = 100% – (40% + 37.5%) = 22.5%
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{18}{w}\) = \(\frac{22.5}{100}\)
w = \(\frac{18 × 100}{22.5}\)
w = \(\frac{1800}{22.5}\)
w = 80
So, 18 is 22.5% of 80.
The number of students participated are 80.
b. 80 students are participated , so w = 80
The percent of the students who chose football is 37.5%
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{80}\) = \(\frac{37.5}{100}\)
a = \(\frac{80 × 37.5}{100}\)
a = \(\frac{3,000}{100}\)
a = 30
So, 30 is 37.5% of 80.
The number of students chose football are 30.
Question 31.
TRUE OR FALSE?
Tell whether the statement is true or false. Explain your reasoning.
If W is 25% of Z, then Z : W is 75 : 25.
Answer: The statement is False.
Explanation:
Given , W is 25% of Z
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{W}{Z}\) = \(\frac{25}{100}\)
So, \(\frac{Z}{W}\) = \(\frac{100}{25}\)
But given that Z : W is 75 : 25
So, The statement is False.
Question 32.
DIG DEEPER!
At a restaurant, the amount of your bill before taxes and tip is $19.83. A 6% sales tax is applied to your bill, and you leave a tip equal to 19% of the original amount. Use mental math to estimate the total amount of money you pay. Explain your reasoning. (Hint: Use 10% of the original amount.)
Answer: The total amount of the money to be paid is $22.18.
Explanation:
Given ,The amount of your bill before taxes and tip is $19.83.
A 6% sales tax is applied to your bill, and you leave a tip equal to 19% of the original amount.
bill before the tax = $19.83
sales tax = 6%
So, $19.83 – 6%
= $19.83 – 0.06
= $18.64
Tip = 19%
So, $18.64 + 19%
= $18.64 + 0.19
= $22.18
The total amount of the money to be paid is $22.18.
Question 33
REASONING
The table shows your test results in a math class. What score do you need on the last test to earn 90% of the total points on the tests?
Answer: Of all the total test points you need 720 points to earn 90%
Explanation:
Total point value = 100 + 250 + 150 + 300 = 800
Given p = 90% , w = 800 , a= ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{800}\) = \(\frac{90}{100}\)
a = \(\frac{800 × 90}{100}\)
a = 8 × 90
a = 720
So, 720 is 90% of 800.
Finally, of all the total test points you need 720 points to earn 90%
Lesson 6.4 Percents of Increase and Decrease
EXPLORATION 1
Exploring Percent of Change
Work with a partner. Each year in the Columbia River Basin, adult salmon swim upriver to streams to lay eggs.
To go up the river, the adult salmon use fish ladders. But to go down the river, the young salmon must pass through several dams.
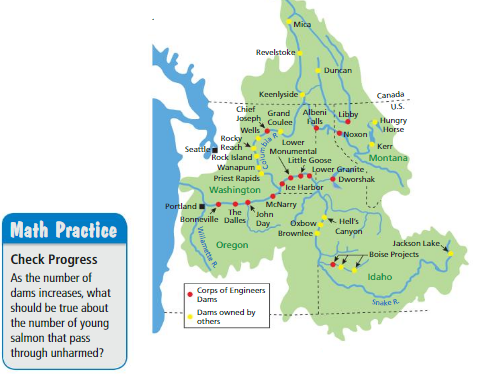
At one time, there were electric turbines at each of the eight dams on the main stem of the Columbia and Snake Rivers. About 88% of the young salmon pass through a single dam unharmed.
a. One thousand young salmon pass through a dam. How many pass through unharmed?
b. One thousand young salmon pass through the river basin. How many pass through all 8 dams unharmed?
c. By what percent does the number of young salmon decrease when passing through a single dam?
d. Describe a similar real-life situation in which a quantity increases by a constant percent each time an event occurs.
Answer: a. 880 salmon passed through single dam unharmed.
b. Totally , 358 salmon pass through all 8 dams unharmed.
c. The percent of the number of young salmon decrease when passing through a single dam is 12%
d. An example for, real-life situation in which a quantity increases by a constant percent each time an event occurs. is given below in explanation.
Explanation:
a. Given , One thousand young salmon pass through a dam. 88% of the young salmon pass through a single dam unharmed.
To know the number of salmon passed through unharmed we have,
88% of 1,000
= 88% × 1,000
= 0.88 × 1,000
= 880.
So, 880 salmon passed through single dam unharmed.
b. Given , One thousand young salmon pass through a dam. 88% of the young salmon pass through a single dam unharmed. To calculate number of salmon pass through all 8 dams unharmed are
number of salmon passed through dam 1 , unharmed are 880 (as shown in part a)
number of salmon passed through dam 2 , unharmed = 88% of 880
= 0.88 × 880
= 774
number of salmon passed through dam 3 , unharmed = 88% of 774
= 0.88 × 774
= 681
number of salmon passed through dam 4 , unharmed = 88% of 681
= 0.88 × 681
= 599
number of salmon passed through dam 5 , unharmed = 88% of 599
= 0.88 × 599
= 527
number of salmon passed through dam 6 , unharmed = 88% of 527
= 0.88 × 527
= 463
number of salmon passed through dam 7 , unharmed = 88% of 463
= 0.88 × 463
= 407
number of salmon passed through dam 8 , unharmed = 88% of 407
= 0.88 × 407
= 358
Totally , 358 salmon pass through all 8 dams unharmed.
c. To calculate The percent of the number of young salmon decrease when passing through a single dam is
The total percent of salmon is 100%, The percent of salmon pass through a single dam is 88%
So, 100% – 88% = 12%
Finally , The percent of the number of young salmon decrease when passing through a single dam is 12%
d. An Example of real-life situation in which a quantity increases by a constant percent each time an event occurs. is , while we are filling the tank with water , The amount of water ingoing increases constantly with the speed of the motor power running the water , water levels in the tank increases by a constant percent each time until the tank is filled up with the water fully.

Try It
Find the percent of change. Round to the nearest tenth of a percent if necessary.
Question 1.
10 inches to 25 inches
Answer: percent of change is 150%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 25 and old value = 10 , because a change of 10 to 25 is a positive (increase) change
So, percent change = \(\frac{25 – 10}{10}\)
= \(\frac{15}{10}\)
= \(\frac{15}{10}\) × 100
= 150%
So, percent of change is 150%
Question 2.
57 people to 65 people
Answer: percent of change is 14%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 65 and old value = 57 , because a change of 57 to 65 is a positive (increase) change
So, percent change = \(\frac{65 – 57}{57}\)
= \(\frac{8}{57}\)
= \(\frac{8}{57}\) × 100
= 14.03 %
Approximately We can write it as 14 %
So, percent of change is 14%
Question 3.
In Example 2, what was the percent of change from 2014 to 2015?
Answer: percent of change is – 44%
Explanation:
In Example 2, change from 2014 to 2015 , that is 18 to 10
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 10 and old value = 18 , because a change of 18 to 10 is a negative (decrease) change
So, percent change = \(\frac{10 – 18}{18}\)
= \(\frac{-8}{18}\)
= – 0.444
= – 0.444 × 100
= – 44.4 %
Approximately We can write it as – 44 %
So, percent of change is – 44%
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
VOCABULARY
What does it mean for a quantity to change by n%?
Answer: The meaning of a quantity to change is given by, which the amount of quantity increases or decreases of its original value to new value is called percent of change,
Then percent of change can be in positive or negative depending on the value of change , if it is for n% then it can be increase or decrease in the quantity of change.
Question 5.
NUMBER SENSE
Without calculating, determine which situation has a greater percent of change. Explain.
- 5 bonus points added to 50 points
- 5 bonus points added to 100 points
Answer: 5 bonus points added to 50 points has the greater percent of change.
Explanation:
5 bonus points added to 50 points
Then 50 points to 55 points
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 55 and old value = 50 , because a change of 50 to 55 is a positive (increase) change
So, percent change = \(\frac{55 – 50}{50}\)
= \(\frac{5}{50}\)
= \(\frac{1}{10}\) × 100
= 10%
So, percent of change is 10%
5 bonus points added to 100 points
Then 100 points to 105 points
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 105 and old value = 100 , because a change of 100 to 105 is a positive (increase) change
So, percent change = \(\frac{105 – 100}{100}\)
= \(\frac{5}{100}\)
= \(\frac{1}{20}\) × 100
= 5%
So, percent of change is 5%
Percent of change of 5 bonus points added to 50 points is 10%
Percent of change of 5 bonus points added to 100 points is 5%
So, 5 bonus points added to 50 points has the greater percent of change.
FINDING A PERCENT OF CHANGE Identify the percent of change as an increase or a decrease. Then find the percent of change.
Question 6.
8 feet to 24 feet
Answer: percent of change is increased that is 200%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 24 and old value = 8 , because a change of 8 to 24 is a positive (increase) change
So, percent change = \(\frac{24 -8}{8}\)
= \(\frac{16}{8}\)
= 2 × 100
= 200%
So, percent of change is 200%
Question 7.
300 miles to 210 miles
Answer: percent of change is decreased that is -30%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 210 and old value = 300 , because a change of300 to 210 is a negative (decrease) change
So, percent change = \(\frac{210 – 300}{300}\)
= \(\frac{-90}{300}\)
= \(\frac{-9}{30}\) × 100
= -0.3 × 100
= -30%
So, percent of change is -30%
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
In one round of a game, you are asked how many bones are in a human body. If the percent error of your answer is at most 5%, you earn two points. If the percent error is at most 10%, but greater than 5%, you earn one point. You guess 195 bones. The correct answer is 206 bones. How many points do you earn?
Answer: The percent Error we calculated is at most of 5% so points we earned is 2 points
Explanation:
Given, You guess 195 bones. The correct answer is 206 bones.
The amount of error is 206 – 195 = 11
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 11 and Actual value = 206 ,
So, percent Error = \(\frac{11}{206}\)
= 0.053
= 0.053 × 100
= 5.3%
Approximately we can write as 5%
So, percent Error is 5%
Then , the percent Error we calculated is at most of 5% so points we earned is 2 points
Question 9.
DIG DEEPER!
The manager of a restaurant offers a 20% decrease in price to tennis teams. A cashier applies a 10% decrease and then another 10% decrease. Is this the same as applying a 20% decrease? Justify your answer.
Answer: There is slight difference between these two methods but are approximately equal.
Explanation:
Given, The manager of a restaurant offers a 20% decrease in price to tennis teams.
Let the total price be 100
So, 100 decrease 20%
= 100 × (1 – 20%)
= 100 × (1 – 0.2)
= 80.
Given, A cashier applies a 10% decrease and then another 10% decrease.
Let the total price be 100
So, 100 decrease 10%
= 100 × (1 – 10%)
= 100 × (1 – 0.1)
= 90.
Again applying 10% decrease
90 decrease 10%
= 90 × (1 – 10%)
= 90 × (1 – 0.1)
= 81.
So, There is slight difference between these two methods but are approximately equal
Percents of Increase and Decrease Homework & Practice 6.4
Review & Refresh
Write and solve an equation to answer the question.
Question 1.
What number is 25% of 64?
Answer: 16
Explanation:
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{64}\) = \(\frac{25}{100}\)
a = \(\frac{64 × 25}{100}\)
a = \(\frac{64}{4}\)
a = 16
So, 16 is 25% of 64.
Question 2.
39.2 is what percent of 112?
Answer: 35%
Explanation:
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{39.2}{112}\) = \(\frac{p}{100}\)
p = \(\frac{39.2 × 100}{112}\)
p = \(\frac{3,920}{112}\)
p = 35
So, 39.2 is 35% of 112.
Find the sum. Write fractions in simplest form.
Question 5.
\(\frac{4}{7}\) + (- \(\frac{6}{7}\))
Answer: – \(\frac{2}{7}\)
Explanation:
To find the sum of the fractions given, we have to do addition, that is
\(\frac{4}{7}\) + (- \(\frac{6}{7}\))
= \(\frac{4 – 6}{7}\)
= – \(\frac{2}{7}\)
So, The sum of \(\frac{4}{7}\) + (- \(\frac{6}{7}\)) is – \(\frac{2}{7}\)
Question 6.
– 4.621 + 3.925
Answer: – 0.696
Explanation:
To find the sum we have to add the given numbers , that is
– 4.621 + 3.925
= 3.925 – 4.621
= – 0.696
So, the sum of – 4.621 + 3.925 is – 0.696.
Question 7.
–\(\frac{5}{12}\) + \(\frac{3}{4}\)
Answer: \(\frac{1}{3}\)
Explanation:
To find the sum of the fractions given, we have to do addition, that is
Given , –\(\frac{5}{12}\) + \(\frac{3}{4}\)
\(\frac{3}{4}\) – \(\frac{5}{12}\)
Expand the fraction , multilpy the numerator and denominator by 3
We get , \(\frac{3 × 3}{3 × 4}\)
= \(\frac{3 × 3}{3 × 4}\) – \(\frac{5}{12}\)
= \(\frac{9}{12}\) – \(\frac{5}{12}\)
= \(\frac{9 – 5}{12}\)
= \(\frac{4}{12}\)
The simplest form of \(\frac{4}{12}\) is \(\frac{1}{3}\)
So, The sum of –\(\frac{5}{12}\) + \(\frac{3}{4}\) is \(\frac{1}{3}\)
Concepts, Skills, & Problem Solving
EXPLORING PERCENT CHANGE You are given the percent of salmon that pass through a single dam unharmed. By what percent does the number of salmon decrease when passing through a single dam? (See Exploration 1, p. 253.)
Question 8.
75%
Answer: The percent of the number of salmon decrease when passing through a single dam is 25%
Explanation:
The percent of salmon that pass through a single dam unharmed is 75%
Let the percent of salmon coming to the dam are 100%
The percent of the number of salmon decrease when passing through a single dam is
100% – 75% = 25%
So, The percent of the number of salmon decrease when passing through a single dam is 25%
Question 9.
80%
Answer: The percent of the number of salmon decrease when passing through a single dam is 20%
Explanation:
The percent of salmon that pass through a single dam unharmed is 80%
Let the percent of salmon coming to the dam are 100%
The percent of the number of salmon decrease when passing through a single dam is
100% – 80% = 20%
So, The percent of the number of salmon decrease when passing through a single dam is 20%
Question 10.
62%
Answer: The percent of the number of salmon decrease when passing through a single dam is 38%
Explanation:
The percent of salmon that pass through a single dam unharmed is 62%
Let the percent of salmon coming to the dam are 100%
The percent of the number of salmon decrease when passing through a single dam is
100% – 62% = 38%
So, The percent of the number of salmon decrease when passing through a single dam is 38%
Question 11.
94%
Answer: The percent of the number of salmon decrease when passing through a single dam is 6%
Explanation:
The percent of salmon that pass through a single dam unharmed is 94%
Let the percent of salmon coming to the dam are 100%
The percent of the number of salmon decrease when passing through a single dam is
100% – 94% = 6%
So, The percent of the number of salmon decrease when passing through a single dam is 6%
FINDING A PERCENT OF CHANGE Identify the percent of change as an increase or a decrease. Then find the percent of change. Round to the nearest tenth of a percent if necessary.
Question 12.
12 inches to 36 inches
Answer: percent of change is 200%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 36 and old value = 12 , because a change of 12 to 36 is a positive (increase) change
So, percent change = \(\frac{36 – 12}{12}\)
= \(\frac{24}{12}\)
= 2 × 100
= 200%
So, percent of change is 200%
Question 13.
75 people to 25 people
Answer: percent of change is 66%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 25 and old value = 75 , because a change of 75 to 25 is a negative (decrease) change
So, percent change = \(\frac{25 – 75}{75}\)
= \(\frac{- 50}{75}\)
= – 0.666
= – 0.666 × 100
= – 66.6%
Approximately we can write it as – 66%
So, percent of change is – 66%
Question 14.
50 pounds to 35 pounds
Answer: percent of change is – 30%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 35 and old value = 50 , because a change of 35 to 50 is a negative (decrease) change
So, percent change = \(\frac{35 – 50}{50}\)
= \(\frac{- 15}{50}\)
= – 0.3
= – 0.3 × 100
= – 30%
So, percent of change is – 30%
Question 15.
24 songs to 78 songs
Answer: percent of change is 225%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 78 and old value = 24 , because a change of 24 to 78 is a positive (increase) change
So, percent change = \(\frac{78 – 24}{24}\)
= \(\frac{54}{24}\)
= 2.25 × 100
= 225%
So, percent of change is 225%
Question 16.
10 gallons to 24 gallons
Answer: percent of change is 140%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 24 and old value = 10 , because a change of 10 to 24 is a positive (increase) change
So, percent change = \(\frac{24 – 10}{10}\)
= \(\frac{14}{10}\)
= 1.4
= 1.4 × 100
= 140%
So, percent of change is 140%
Question 17.
72 paper clips to 63 paper clips
Answer: percent of change is – 12.5%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 63 and old value = 72 , because a change of 72 to 63 is a negative (decrease) change
So, percent change = \(\frac{63 – 72}{72}\)
= \(\frac{- 9}{72}\)
= \(\frac{- 1}{8}\)
= – 0.125
= – 0.125 × 100
= – 12.5%
So, percent of change is – 12.5%
Question 18.
16 centimeters to 44.2 centimeters
Answer: percent of change is 176%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 44.2 and old value = 16 , because a change of 16 to 44.2 is a positive (increase) change
So, percent change = \(\frac{44.2 – 16}{16}\)
= \(\frac{28.2}{16}\)
= 1.76
= 1.76 × 100
= 176%
So, percent of change is 176%
Question 19.
68 miles to 42.5 miles
Answer: percent of change is – 37.5%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 42.5 and old value = 68 , because a change of 68 to 42.5 is a negative (decrease) change
So, percent change = \(\frac{42.5 – 68}{68}\)
= \(\frac{- 25.5}{68}\)
= – 0.375
= – 0.375 × 100
= – 37.5%
So, percent of change is – 37.5%
Question 20.
YOU BE THE TEACHER
Your friend finds the percent increase from 18 to 26. Is your friend correct? Explain your reasoning.

Answer: No , The percent of change of 18 to 26 is positive (increase) that is 44.4%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 26 and old value = 18 , because a change of 18 to 26 is a positive (increase) change
So, percent change = \(\frac{26 – 18}{18}\)
= \(\frac{8}{18}\)
= 0.444
= 0.444 × 100
= 44.4%
So, percent of change is 44.4%
Question 21.
MODELING REAL LIFE
Last week, you finished Level 2 of a video game in 32 minutes. Today, you finish Level 2 in 28 minutes. What is the percent of change?
Answer: The percent of change from last week to today is – 12.5%
Explanation:
Given, you finished Level 2 of a video game in 32 minutes. Today, you finish Level 2 in 28 minutes.
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 28 and old value = 32 , because a change of 32 to 28 is a negative (decrease) change
So, percent change = \(\frac{28 – 32}{32}\)
= \(\frac{- 4}{32}\)
= \(\frac{- 1}{8}\)
= – 0.125
= – 0.125 × 100
= – 12.5%
So, percent of change is – 12.5%
Question 22.
MODELING REAL LIFE
You estimate that a baby pig weighs 20 pounds. The actual weight of the baby pig is 16 pounds. Find the percent error.

Answer: The percent Error is 20%.
Explanation:
Given , You estimate that a baby pig weighs 20 pounds. The actual weight of the baby pig is 16 pounds.
The amount of error is 20 – 16 = 4
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 4 and Actual value = 20 ,
So, percent Error = \(\frac{4}{20}\)
= \(\frac{1}{5}\)
= 0.2
= 0.2 × 100
= 20%
So, percent Error is 20% .
Question 23.
PRECISION
A researcher estimates that a fossil is 3200 years old. Using carbon-14 dating, a procedure used to determine the age of an object, the researcher discovers that the fossil is 3600 years old.

a. Find the percent error.
b. What other estimate gives the same percent error? Explain your reasoning.
Answer: a. The percent Error is 11.1%
b. The other estimate that gives the same percent error is 3,199 years old.
Explanation:
a. Given, A researcher estimates that a fossil is 3200 years old the researcher discovers that the fossil is 3600 years old.
The amount of error is 3600 – 3200 = 400
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 400 and Actual value = 3600 ,
So, percent Error = \(\frac{400}{3600}\)
= \(\frac{1}{9}\)
= 0.111
= 0.111 × 100
= 11.1%
So, percent Error is 11.1% .
b. If The other estimate that gives the same percent error is 3,199 years old.
The amount of error is 3600 – 3199 = 401
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 401 and Actual value = 3600 ,
So, percent Error = \(\frac{401}{3600}\)
= 0.111
= 0.111 × 100
= 11.1%
So, percent Error is 11.1% .
So , The other estimate that gives the same percent error is 3,199 years old.
FINDING A PERCENT OF CHANGE Identify the percent of change as an increase or a decrease. Then find the percent of change. Round to the nearest tenth of a percent if necessary.
Question 24.
\(\frac{1}{4}\) to \(\frac{1}{2}\)
Answer: percent of change is 100%
Explanation:
The given fractions can be written in decimal form then we have,
\(\frac{1}{4}\) as 0.25
\(\frac{1}{2}\) as 0.5 , so , 0.25 to 0.5
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 0.5 and old value = 0.25 , because a change of 0.25 to 0.5 is a positive (increase) change
So, percent change = \(\frac{0.5 – 0.25}{0.25}\)
= \(\frac{0.25}{0.25}\)
= 1 × 100
= 100%
So, percent of change is 100%
Question 25.
\(\frac{4}{5}\) to \(\frac{3}{5}\)
Answer: percent of change is – 25%
Explanation:
The given fractions can be written in decimal form then we have,
\(\frac{4}{5}\) as 0.8
\(\frac{3}{5}\) as 0.6 , so , 0.8 to 0.6
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 0.6 and old value = 0.8 , because a change of 0.8 to 0.6 is a negative (decrease) change
So, percent change = \(\frac{0.6 – 0.8}{0.8}\)
= \(\frac{-0.2}{0.8}\)
= – 0.25
= – 0.25 × 100
= – 25%
So, percent of change is – 25%
Question 26.
\(\frac{3}{8}\) to \(\frac{7}{8}\)
Answer: percent of change is 135%
Explanation:
The given fractions can be written in decimal form then we have,
\(\frac{3}{8}\) as 0.37
\(\frac{7}{8}\) as 0.87 , So 0.37 to 0.87
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 0.87 and old value = 0.37 , because a change of 0.37 to 0.87 is a positive (increase) change
So, percent change = \(\frac{0.87 – 0.37}{0.37}\)
= \(\frac{0.5}{0.37}\)
= 1.35
= 1.35 × 100
= 135%
So, percent of change is 135%
Question 27.
\(\frac{5}{4}\) to \(\frac{3}{8}\)
Answer: percent of change is – 70.4%
Explanation:
The given fractions can be written in decimal form then we have,
\(\frac{5}{4}\) as 1.25
\(\frac{3}{8}\) as 0.37 , So, 1.25 to 0.37
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 0.37 and old value = 1.25 , because a change of 1.25 to 0.37 is a negative (decrease) change
So, percent change = \(\frac{0.37 – 1.25}{1.25}\)
= \(\frac{- 0.88}{1.25}\)
= – 0.704
= – 0.704 × 100
= – 70.4%
So, percent of change is – 70.4%
Question 28.
CRITICAL THINKING
Explain why a change from 20 to 40 is a 100% increase, but a change from 40 to 20 is a 50% decrease.
Answer: From 20 to 40 is a 100% increase because of increase in number value and from 40 to 20 is a 50% decrease because of decrease in number value.
Explanation:
Given , 20 to 40
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 40 and old value = 20 , because a change of 20 to 40 is a positive (increase) change
So, percent change = \(\frac{40 – 20}{20}\)
= \(\frac{20}{20}\)
= 1 × 100
= 100%
Then , percent of change is 100%
So, The percent of change from 20 to 40 is a 100% increase
Given , 40 to 20
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 20 and old value = 40 , because a change of 40 to 20 is a negative (decrease) change
So, percent change = \(\frac{20 – 40}{40}\)
= \(\frac{- 20}{40}\)
= \(\frac{- 1}{2}\)
= – 0.5
= – 0.5 × 100
= – 50%
Then , percent of change is – 50%
So , The percent of change from 40 to 20 is a 50% decrease.
Finally , From 20 to 40 is a 100% increase because of increase in number value and from 40 to 20 is a 50% decrease because of decrease in number value.
Question 29.
MODELING REAL LIFE
The table shows population data for a community.
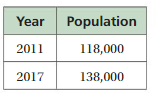
a. What is the percent of change from 2011 to 2017?
b. Predict the population in 2023. Explain your reasoning.
Answer: a. The percent of change from 2011 to 2017 is 169%
b. The estimated population of 2023 will be 158,000.
Explanation:
a. Given 2011 to 2017 , so from the table we know it as , 118,000 to 138,000
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 138,000 and old value = 118,000 , because a change of 118,000 to 138,000 is a positive (increase) change
So, percent change = \(\frac{138,000 – 118,000}{118,000}\)
= \(\frac{20,000}{118,000\)
= 0.169
=0.169 × 100
= 169%
So, percent of change is 169%
b. The population from 2011 to 2017 increased from 118,000 to 138,000,
The difference between 2011 to 2017 is 6 years ,So the population increase in numbers are
138,000 – 118,000 = 20,000.
If the population in 6 years is increased by 20,000.
Then from 2017 to 2023 is 6 years , So increase in population is 20,000
Then for 2023 The population will be 138,000 + 20,000 = 158,000
finally, The estimated population of 2023 will be 158,000.
Question 30.
GEOMETRY
Suppose the length and the width of the sandbox are doubled.
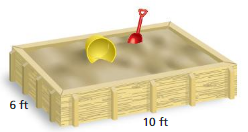
a. Find the percent of change in the perimeter.
b. Find the percent of change in the area.
Answer: a. the percent of change in the perimeter of sandbox is 100%
b. the percent of change in the area of sandbox is
Explanation:
a. Given , length of sandbox = 10 ft , width of sandbox = 6 ft
The sandbox is in the form of a rectangle , So the perimeter of a rectangle is P = 2 ( l + w) , where l = length of the rectangle and w = width of the rectangle,
Then P = 2( l + w )
= 2 ( 10 + 6 )
= 2 × 16
=18
So, the perimeter of sandbox is 32 ft
Given that , the length and the width of the sandbox are doubled.
Then l = 20 ft and w = 12 ft ,
P = 2( l + w )
= 2 ( 20 + 12 )
= 2 × 32
= 64
So, the perimeter of sandbox after the length and the width are doubled. is 64 ft .
The perimeter of sandbox changed from 32 ft to 64 ft , Then
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 64 and old value = 32 , because a change of 32 to 64 is a positive (increase) change
So, percent change = \(\frac{64 – 32}{32}\)
= \(\frac{32}{32}\)
= 1 × 100
= 100%
So, percent of change is 100%
Finally , the percent of change in the perimeter of sandbox is 100%
b. Given , length of sandbox = 10 ft , width of sandbox = 6 ft
The sandbox is in the form of a rectangle , So the area of a rectangle is A = l × w ,
Then A = l × w
= 10 × 6 = 60
So , The Area of Sandbox is 60 ft
Given that , the length and the width of the sandbox are doubled.
Then , l = 20 ft and w = 12 ft ,
Then A = l × w
= 20 × 12 = 240
So , The Area of Sandbox after the length and the width are doubled is 240 ft
The area of sandbox changed from 60 ft to 240 ft
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 240 and old value = 60 , because a change of 60 to 240 is a positive (increase) change
So, percent change = \(\frac{240 – 60}{60}\)
= \(\frac{180}{60}\)
= 3
= 3 × 100
= 300%
So, percent of change is 300%
Finally , the percent of change in the area of sandbox is 300%.
Question 31.
MODELING REAL LIFE
A company fills boxes with about 21 ounces of cereal. The acceptable percent error in filling a box is 2.5%. Box A contains 20.4 ounces of cereal and Box B contains 21.5 ounces of cereal. Tell whether each box is an acceptable weight.
Answer: The percent error of Box A is greater than acceptable percent error that is 2.8% and The percent error of Box B is less than acceptable percent error that is 2.3%.
Explanation:
For Box A , Given , A company fills boxes with about 21 ounces of cereal and Box A contains 20.4 ounces of cereal
The amount of error is 21 – 20.4 = 0.6
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 0.6 and Actual value = 21 ,
So, percent Error = \(\frac{0.6}{21}\)
= 0.028
= 0.028 × 100
= 2.8%
So, percent Error is 2.8%
The percent error of Box A is greater than acceptable percent error that is 2.8%
For Box B A company fills boxes with about 21 ounces of cereal and Box B contains 21.5 ounces of cereal.
The amount of error is 21.5 – 21 = 0.5
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 0.5 and Actual value = 21 ,
So, percent Error = \(\frac{0.5}{21}\)
= 0.023
= 0.023 × 100
= 2.3%
So, percent Error is 2.3%
The percent error of Box B is less than acceptable percent error that is 2.3%
Question 32.
PRECISION
Find the percent of change from June to September in the mile-run times shown.

Answer: The percent of change from June to September in the mile-run times is -26%.
Explanation:
Given , change from 7.45 to 5.51
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 5.51 and old value = 7.45 , because a change of 7.45 to 5.51 is a negative (decrease) change
So, percent change = \(\frac{5.51 – 7.45}{7.45}\)
= \(\frac{- 1.94}{7.45}\)
= – 0.26
= – 0.26 × 100
= – 26%
So, percent of change is – 26%
Finally , The percent of change from June to September in the mile-run times is -26%.
Question 33.
CRITICAL THINKING
A number increases by 10% and then decreases by 10%. Will the result be greater than, less than or equal to, the original number? Explain.
Answer: A number increases by 10% and then decreases by 10% , the result will be less than the original number.
Explanation:
Let original number is 100
Given ,The original number increases by 10%
The new number = original number + The original number increases by 10%
= 100 + ( 100 × 10%)
= 100 + ( 100 × 0.1)
= 100 + 10
= 110
So, The new number is 110.
Let the original number is 110
Given ,The original number decreases by 10%
The new number = original number – The original number decreases by 10%
= 110 – ( 110 × 10%)
= 110 – ( 110 × 0.1)
= 110 – 11
= 99
So, The new number is 99
99 < 100 .
So , A number increases by 10% and then decreases by 10% , the result will be less than the original number.
Question 34.
PROBLEM SOLVING
You want to reduce your daily calorie consumption by about 9%. You currently consume about 2100 calories per day. Use mental math to estimate the number of calories you should consume in one week to meet your goal. Explain.
Answer: The estimated calories you should consume per week is 13,377.
Explanation:
Given ,You currently consume about 2100 calories per day, reduce your daily calorie consumption by about 9%.
so, The calories you have to consume after reduction of 9% is
The new number = original number – The original number decreases by 9%
= 2100 – ( 2100 × 9%)
= 2100 – (2100 × 0.09)
= 2100 – 189
= 1,911 .
The calories you have to consume after reduction of 9% is 1,911
The calories you should consume per day is 1,911.
The calories you should consume per week (7 days) = 1,911 × 7 = 13,377.
Finally , The estimated calories you should consume per week is 13,377.
Question 35.
DIG DEEPER!
Donations to an annual fundraiser are 15% greater this year than last year. Last year, donations were10% greater than the year before. The amount raised this year is $10,120. How much was raised two years ago?
Answer: The amount raised 2 years ago is $7,741.8.
Explanation:
Given , The amount raised this year is $10,120.
Let the amount raised last year = x
Donations are 15% greater than last year
The amount raised last year = The amount raised this year – ((The amount raised this year .15%)
x = 10,120 – ( 10,120 × 0.15)
x = 10,120 – 1,518
x = 8,602
The amount raised last year = $8,602.
We know that , The amount raised last year = $8,602.
Let the amount raised the year before = x
Donations are 10% greater than the year before
The amount raised the year before = The amount raised last year – ((The amount raised last year .10%)
x = 8,602 – ( 8,602 × 0.1)
x = 8,602 – 860.2
x = 7,741.8
The amount raised the year before = $7,741.8.
So, The amount raised 2 years ago is $7,741.8.
Question 36.
REASONING
Forty students are in the science club. Of those, 45% are girls. This percent increases to 56% after more girls join the club. How many more girls join?
Answer: The number of new girls join the club is 10.
Explanation:
Let the number of new girls = x
The number of girls = x + 18
The number of students = x + 40
So, the number of girls = 56% The number of students
x + 18 = 0.56( x + 40 )
x + 18 = 0.56x + 22.4
0.56x – x = 22.4 – 18
0.44x = 4.4
x = \(\frac{4.4}{0.44}\)
x = 10.
So , The number of new girls is 10.
Lesson 6.5 Discounts and Markups
EXPLORATION 1
Comparing Discounts
Work with a partner.
a. The same pair of earrings is on sale at three stores. Which store has the best price? Use the percent models to justify your answer.
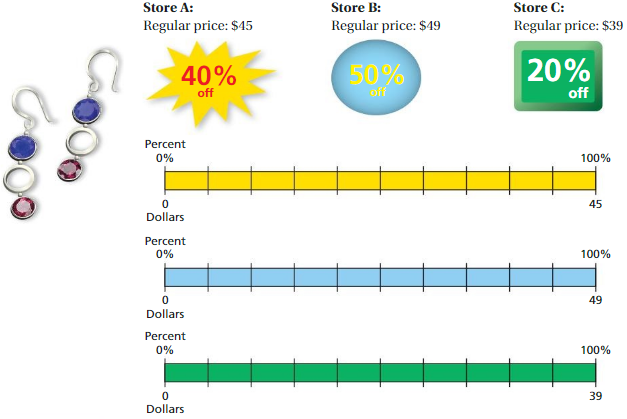
b. You buy the earrings on sale for 30% off at a different store. You pay $22.40. What was the original price of the earrings? Use the percent model to justify your answer.
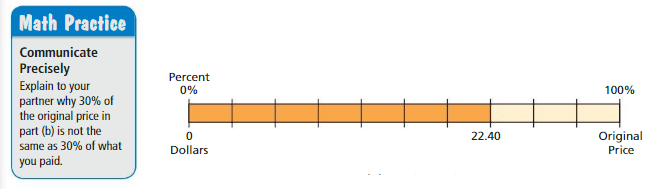
c. You sell the earrings in part(b) to a friend for 60% more than what you paid. What is the selling price? Use a percent model to justify your answer.
Answer:
a. For store A ,The sales price is $27
For store B ,The sales price is $24.5
For store C ,The sales price is $31.2
b. the original price of the earrings is $32
c. the selling price is $35.84.
Explanation:
a. Given store A = $45 with 40% off

We know , The sales price be 100% – 40% = 60% of the original price
sales price = 60% of 45
= 0.6 × 45 = 27
So, The sales price is $27
For store B = $49 with 50% off

We know , The sales price be 100% – 50% = 50% of the original price
sales price = 50% of 49
= 0.5 × 49 = 24.5
So, The sales price is $24.5
For store c = $39 with 20% off
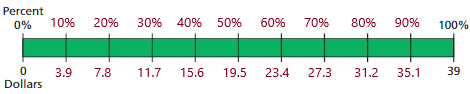
We know , The sales price be 100% – 20% = 80% of the original price
sales price = 80% of 39
= 0.8 × 39 = 31.2
So, The sales price is $31.2
b. Given , You buy the earrings on sale for 30% off at a different store. You pay $22.40
The saples price = 100% – 30% = 70%

we know a = 22.4 , p = 70% , w = ?
a = p% × w
22.4 = 0.7 × w
w = \(\frac{22.4}{0.7}\)
w = 32.
So , the original price of the earrings is $32
c. Given , You sell the earrings in part(b) to a friend for 60% more than what you paid.
If the selling price is more than the buying price then it is called markup

Here , the markup is 60% of $22.4
a = p% × w
a = 0.6 × 22.4
a = 13.44
So, the markup is $13.44
We know that selling price = cost of buying + markup
= 22.4 + 13.44
= 35.84
So , the selling price is $35.84.

Try It
Question 1.
The original price of a skateboard is $50. The skateboard is on sale for 20% off. What is the sale price?
Answer: The sales price of skateboard is $40
Explanation:
Given , skateboard is $50 with 20% off
We know , The sales price be 100% – 20% = 80% of the original price
sales price = 80% of 50
= 0.8 × 50 = 40
So, The sales price is $40
Question 2.
The discount on a DVD is 50%. It is on sale for $10. What is the original price of the DVD?
Answer: The original price of DVD is $20.
Explanation:
Given , discount on a DVD is 50%. , It is on sale for $10
We know , The sales price be 100% – 50% = 50%
a = p% × w
10 = 0.5 × w
w = \(\frac{10}{0.5}\)
w = 20
So, The original price is $20.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
WRITING
Describe how to find the sale price of an item that has a 15% discount.
Answer: To get the sales price , The discount percent must be cleared from the total percent of sales price , it gives the sales percentage of the original price , which is used to find the sales price.
So, The sales price = original price minus discount.
Explanation:
Let the original price be $50 with 15% off
We know , The sales price be 100% – 15% = 85% of the original price
sales price = 85% of 50
= 0.85 × 50 = 42.5
So, The sales price is $42.5
FINDING A SALE PRICE Find the sale price. Use a percent model to check your answer.
Question 4.
A portable table tennis set costs $30 before a 30% discount.
Answer: The sales price of portable table tennis set is $21.
Explanation: 
Given , tennis set is $30 with 30% off
We know , The sales price be 100% – 30% = 70% of the original price
sales price = 70% of 30
= 0.7 × 30 = 21
So, The sales price is $21.
Question 5.
The original price of an easel is $70. The easel is on sale for 20% off.
Answer: The sales price of an easel is $56.
Explanation: 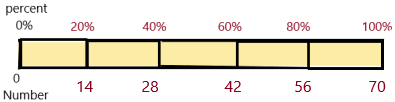
Given , easel is $70 with 20% off
We know , The sales price be 100% – 20% = 80% of the original price
sales price = 80% of 70
= 0.8 × 70 = 56
So, The sales price is $56.
FINDING AN ORIGINAL PRICE Find the original price. Use a percent model to check your answer.
Question 6.
A bracelet costs $36 after a 25% discount.

Answer: The original price of bracelet is $48.
Explanation: 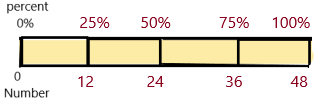
Given , discount on a bracelet is 25%. , It is cost $36 after discount
We know , The sales price be 100% – 25% = 75%
a = p% × w
36 = 0.75 × w
w = \(\frac{36}{0.75}\)
w = 48
So, The original price is $48.
Question 7.
The discount on a toy robot is 40%. The toy robot is on sale for $54.
Answer: The sale price toy robot is $32.4 .
Explanation: 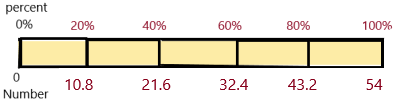
Given , discount on a toy robot is 40%. The toy robot is on sale for $54.
We know , The sales price be 100% – 40% = 60%
a = p% × w
a = 0.6 × 54
a = 32.4
So, The sale price is $32.4 .
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
DIG DEEPER!
You have two coupons for a store. The first coupon applies a $15 discount to a single purchase, and the second coupon applies a 10% discount to a single purchase. You can only use one coupon on a purchase. When should you use each coupon? Explain.
Answer: The first coupon of $15 discount is to be used on your highest cost of purchase and the second coupon with 10% off is to be used on your least cost of purchase .
Explanation:
Given , The first coupon applies a $15 discount to a single purchase,
Let the purchase be $50
Then the first coupon applies = $50 – $15 = $35.
So, when the first coupon applies price will be $35.
Given , the second coupon applies a 10% discount to a single purchase
Let the original price be $50 and with 10% off
We know , The sales price be 100% – 10% = 90% of the original price
sales price = 90% of 50
= 0.9 × 50 = 45
So, The sales price is $45.
Here , we can see that $15 discount is offering the reduction of the original price and discount with 10% of is offering to pay the 90% of its original price.
Finally , The first coupon of $15 discount is to be used on your highest cost of purchase and the second coupon with 10% off is to be used on your least cost of purchase .
Question 9.
A store sells memory cards for $25 each.

a. The markup for each memory card is 25%. How much did the store pay for 50 memory cards?
b. The store offers a discount when a customer buys two or more memory cards. A customer pays $47.50 for two memory cards. What is the percent of discount?
c. How much does a customer pay for three memory cards if the store increases the percent of discount in part (b) by 2%?
Answer: a. The store pay $937.5 for 50 memory cards
b. The discount offered by the store is 5%
c. The customer paid $69.75 for 3 memory cards.
Explanation:
a. The markup is 25% of $25
a = p% × w
= 25% × 25
= 0.25 × 25
= 6.25
So , the markup is $6.25.
To , find the cost to store , we have
cost to store = selling price – markup
= $25 – $6.25
= $18.75.
The cost to store for each memory card is $18.75.
Then for 50 memory cards = 50 × $18.75 = $937.5
b. A customer pays $47.50 for two memory cards.
Then for one memory card \(\frac{47.5}{2}\) = $23.75
we have , a = $23.75 , w = $25 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{23.75}{25}\) = \(\frac{p}{100}\)
p = \(\frac{23.75 × 100}{25}\)
p = \(\frac{2375}{25}\)
p = 95
So, 23.75 is 95% of 25.
To find the discount , = The percent of original price – the percent of selling price
= 100% – 95% = 5%
So, The discount offered by the store is 5%
c. If the discount is increased by 2% , Then the discount offered by store is 5% + 2% = 7%
The amount of selling price = 100% – 7% = 93%
So , 93% of $25
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{25}\) = \(\frac{93}{100}\)
a = \(\frac{25 × 93}{100}\)
a = \(\frac{2325}{100}\)
a = 23.25
So, The amount after the discount is $23.25
Then for 3 memory cards = $23.25 × 3 = $69.75
The customer paid $69.75 for 3 memory cards.
Discounts and Markups Homework & Practice 6.5
Review & Refresh
Identify the percent of change as an increase or decrease. Then find the percent of change. Round to the nearest tenth of a percent if necessary.
Question 1.
16 meters to 20 meters
Answer: The percent of change is 25%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 20 and old value = 16 , because a change of 16 to 20 is a positive (increase) change
So, percent change = \(\frac{20 – 16}{16}\)
= \(\frac{4}{16}\)
= \(\frac{1}{4}\)
= 0.25
= 0.25 × 100
= 25%
So, percent of change is 25%
Question 2.
9 points to 4 points
Answer: The percent of change is – 55.5%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 4 and old value = 9 , because a change of 9 to 4 is a negative (decrease) change
So, percent change = \(\frac{4 – 9}{9}\)
= \(\frac{- 5}{9}\)
= – 0.555
= – 0.555 × 100
= – 55.5%
So, percent of change is – 55.5%
Question 3.
15 ounces to 5 ounces
Answer: The percent of change is – 66.6%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 5 and old value = 15 , because a change of 15 to 5 is a negative (decrease) change
So, percent change = \(\frac{5 – 15}{15}\)
= \(\frac{- 10}{15}\)
= – 0.666
= – 0.666 × 100
= – 66.6%
So, percent of change is – 66.6%
Question 4.
38 staples to 55 staples
Answer:
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 55 and old value = 38 , because a change of 38 to 55 is a positive (increase) change
So, percent change = \(\frac{55 – 38}{38}\)
= \(\frac{17}{38}\)
= 0.447
= 0.447 × 100
= 44.7%
So, percent of change is 44.7%
Find the product. Write fractions in simplest form.
Question 5.
\(\frac{4}{7}\left(-\frac{1}{6}\right)\)
Answer: The product of \(\frac{4}{7}\left(-\frac{1}{6}\right)\) is 0.094.
Explanation:
The given fractions can be written in decimal form then we have,
\(\frac{4}{7}\left(-\frac{1}{6}\right)\) as 0.571 ( – 0.166)
To find the product we have to multiply the two numbers
= 0.571 × ( – 0.166)
= 0.094
So, The product of \(\frac{4}{7}\left(-\frac{1}{6}\right)\) is 0.094.
Question 6.
– 1.58(6.02)
Answer: The product of – 1.58(6.02) is – 9.51.
Explanation:
To find the product we have to multiply the two numbers
= – 1.58 × (6.02)
= – 9.51
So, The product of – 1.58(6.02) is – 9.51.
Question 7.
– 3(- 2\(\frac{1}{8}\))
Answer:
Explanation:
The given fractions can be written in decimal form then we have,
– 3(- 2\(\frac{1}{8}\)) as – 3 ( – 2.12)
To find the product we have to multiply the two numbers
= – 3 × ( – 2.12)
= 6.36
So, The product of – 3 ( – 2.12) is 6.36
Concepts, Skills, & Problem Solving
COMPARING DISCOUNTS The same item is on sale at two stores. Which one is the better price? Use percent models to justify your answer. (See Exploration 1, p. 259.)
Question 8.
60% off $60 or 55% off $50
Answer: The item has better price at 55% off $50 .
Explanation: 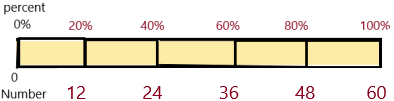
a. Given , 60% off $60.
We know , The sales price be 100% – 60% = 40% of the original price
sales price = 40% of 60
= 0.4 × 60 = 24
So, The sales price is $24
b. Given , 55% off $50

We know , The sales price be 100% – 55% = 45% of the original price
sales price = 45% of 50
= 0.45 × 50 = 22.5
So, The sales price is $22.5
Question 9.
85% off $90 or 70% off $65
Answer: The item has better price at 85% off $90 .
Explanation:

a. Given , 85% off $90
We know , The sales price be 100% –85% = 15% of the original price
sales price = 15% of 90
= 0.15 × 90 = 13.5
So, The sales price is $13.5 .
b. Given , 70% off $65

We know , The sales price be 100% –70% = 30% of the original price
sales price = 30% of 65
= 0.3 × 65 = 19.5
So, The sales price is $19.5.
USING TOOLS Copy and complete the table.

Answer: 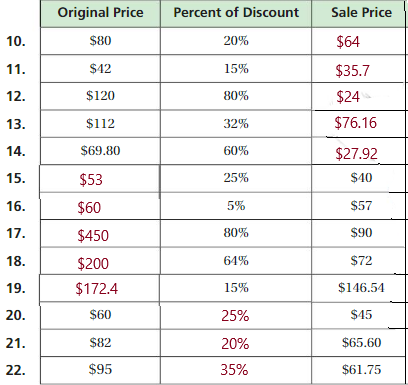
10. Given , Original price of the item is $ 80 , percent of discount is 20% , Find sales price ?
Answer: The sales price of the is $64.
Explanation:
We know , The sales price be 100% – 20% = 80% of the original price
sales price = 80% of 80
= 0.8 × 80 = 64
So, The sales price is $64.
11. Given , Original price of the item is $42 , percent of discount is 15% , Find sales price ?
Answer: The sales price of the is $35.7.
Explanation:
We know , The sales price be 100% – 15% = 85% of the original price
sales price = 85% of 42
= 0.85 × 42 = 35.7
So, The sales price is $35.7.
12. Given , Original price of the item is $120 , percent of discount is 80% , Find sales price ?
Answer: The sales price of the is $24.
Explanation:
We know , The sales price be 100% – 80% = 20% of the original price
sales price = 20% of 120
= 0.2 × 120 = 24
So, The sales price is $24.
13. Given , Original price of the item is $112 , percent of discount is 32% , Find sales price ?
Answer: The sales price of the is $76.16.
Explanation:
We know , The sales price be 100% – 32% = 68% of the original price
sales price = 68% of 112
= 0.68 × 112 = 76.16
So, The sales price is $76.16.
14. Given , Original price of the item is $69.8 , percent of discount is 60% , Find sales price ?
Answer: The sales price of the is $27.92.
Explanation:
We know , The sales price be 100% – 60% = 40% of the original price
sales price = 40% of 69.8
= 0.4 × 69.8 = 27.92
So, The sales price is $27.92.
15. Given , sales price of the item is $40 , percent of discount is 25% , Find original price ?
Answer: The Original price of the is $53.
Explanation:
The sales price be 100% – 25% = 75%
we know a = 40 , p = 75% , w = ?
a = p% × w
a = 75% × w
40 = 0.75 × w
w = \(\frac{40}{0.75}\)
w = 53
So , the original price of the earrings is $53.
16. Given , sales price of the item is $57 , percent of discount is 5% , Find original price ?
Answer: The Original price of the is $60.
Explanation:
The sales price be 100% – 5% = 95%
we know a = 57 , p = 95% , w = ?
a = p% × w
a = 95% × w
57 = 0.95 × w
w = \(\frac{57}{0.95}\)
w = 60
So , the original price of the earrings is $60.
17. Given , sales price of the item is $90 , percent of discount is 80% , Find original price ?
Answer: The Original price of the is $450.
Explanation:
The sales price be 100% – 80% = 20%
we know a = 90 , p = 20% , w = ?
a = p% × w
a = 20% × w
90 = 0.2 × w
w = \(\frac{90}{0.2}\)
w = 450
So , the original price of the earrings is $450.
18. Given , sales price of the item is $72 , percent of discount is 64% , Find original price ?
Answer: The Original price of the is $200.
Explanation:
The sales price be 100% – 64% = 36%
we know a = 72 , p = 36% , w = ?
a = p% × w
a = 36% × w
72 = 0.36 × w
w = \(\frac{72}{0.36}\)
w = 200
So , the original price of the earrings is $200.
19. Given , sales price of the item is $146.54 , percent of discount is 15% , Find original price ?
Answer: The Original price of the is $172.4.
Explanation:
The sales price be 100% – 15% = 85%
we know a = 146.54 , p = 85% , w = ?
a = p% × w
a = 85% × w
146.54 = 0.85 × w
w = \(\frac{146.54}{0.85}\)
w = 172.4
So , the original price of the earrings is $172.4.
20. Given , original price of the item is $60 , sales price of the item is $45 , Find percent of discount ?
Answer: The percent of discount is 25% .
Explanation:
We have a = 45 , w = 60 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{45}{60}\) = \(\frac{p}{100}\)
p = \(\frac{45 × 100}{60}\)
p = \(\frac{4,500}{60}\)
p = 75
So, 45 is 75% of 60.
To get the percent of discount we have ,
The percent of discount = The percent of original price – the percent of sales price
= 100% – 75%
= 25%.
So, The percent of discount is 25% .
21. Given , original price of the item is $82 , sales price of the item is $65.6 , Find percent of discount ?
Answer: The percent of discount is 20% .
Explanation:
We have a = 65.6 , w = 82 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{65.6}{82}\) = \(\frac{p}{100}\)
p = \(\frac{65.6 × 100}{82}\)
p = \(\frac{6,560}{82}\)
p = 80
So, 65.6 is 80% of 82.
To get the percent of discount we have ,
The percent of discount = The percent of original price – the percent of sales price
= 100% – 80%
= 20%.
So, The percent of discount is 20% .
22. Given , original price of the item is $95 , sales price of the item is $61.75 , Find percent of discount ?
Answer: The percent of discount is 35% .
Explanation:
We have a = 61.75 , w = 95 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{61.75}{95}\) = \(\frac{p}{100}\)
p = \(\frac{61.75 × 100}{95}\)
p = \(\frac{6,175}{95}\)
p = 65
So, 61.75 is 65% of 90.
To get the percent of discount we have ,
The percent of discount = The percent of original price – the percent of sales price
= 100% – 65%
= 35%.
So, The percent of discount is 35% .
FINDING A SELLING PRICE .
Question 23.
Cost to store: $50
Markup: 10%
Answer: The selling price is $55.
Explanation:
The markup is 10% of $50
a = p% × w
= 10% × 50
= 0.1 × 50
= 5
So , the markup is $5.
To , find the selling price , we have
selling price = cost to store + markup
= $50 + $5
= $55.
The selling price is $55.
Question 24.
Cost to store: $80
Markup: 60%
Answer: The selling price is $128.
Explanation:
The markup is 60% of $80
a = p% × w
= 60% × 80
= 0.6 × 80
= 48
So , the markup is $48.
To , find the selling price , we have
selling price = cost to store + markup
= $80 + $48
= $128.
The selling price is $128.
Question 25.
Cost to store: $140
Markup: 25%
Answer: The selling price is $175.
Explanation:
The markup is 25% of $140
a = p% × w
= 25% × 140
= 0.25 × 140
= 35
So , the markup is $35.
To , find the selling price , we have
selling price = cost to store + markup
= $140 + $35
= $175.
The selling price is $175.
Question 26.
YOU BE THE TEACHER
A store pays $60 for an item. Your friend finds the selling price when the markup is 20%. Is your friend correct? Explain your reasoning.
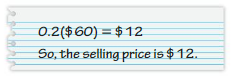
Answer: No , The selling price is $72.
Explanation:
Given , The markup is 20% of $60
a = p% × w
= 20% × 60
= 0.2 × 60
= 12
So , the markup is $12.
To , find the selling price , we have
selling price = cost to store + markup
= $60 + $12
= $72.
The selling price is $72.
Question 27.
STRUCTURE
The scooter is being sold at a 10% discount. The original price is shown. Which methods can you use to find the new sale price? Which method do you prefer? Explain.

Answer: The sales price is $37.8. Used the method of Multiplying $42 by 0.9.
Explanation:
By Using the method of Multiplying $42 by 0.9
We know , The sales price be 100% – 10% = 90% of the original price
sales price = 90% of 42
= 0.9 × 42 = 37.8
So, The sales price is $37.8.
Question 28.
NUMBER SENSE
The original price of an item is P dollars. Is the price of the item with an 18% markup the same as multiplying the original price by 1.18? Use two expressions to justify your answer.
Answer: The selling price is $1.18P and it is same as multiplying the original price by 1.18 .
Explanation:
Given , The original price of an item is P dollars.
The markup is 18% of $P
a = p% × w
= 18% × P
= 0.18 × P
= $0.18P
So , the markup is $0.18P.
To , find the selling price , we have
selling price = cost to store + markup
= $P + $0.18P
= $P ( 1 + 0.18 )
= $1.18P.
The selling price is $1.18P.
The given method is multiplying the original price by 1.18,
The original price is $P = $P × 1018.
So , The selling price is $1.18P.
Finally , The selling price is $1.18P and it is same as multiplying the original price by 1.18 .
Question 29.
PROBLEM SOLVING
You are shopping for a video game system.
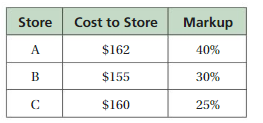
a. At which store should you buy the system?
b. Store A has a weekend sale. What discount must Store A offer for you to buy the system there?
Answer: a. you should buy the system at store C has The selling price is $200.
b. To buy the system at store A , it should have the discount of 28.6%.
a. Given , For store A cost to store is $162 , Markup is 40%
Then , The markup is 40% of $162
a = p% × w
= 40% × 162
= 0.4 × 162
= 64.8
So , the markup is $64.8.
To , find the selling price , we have
selling price = cost to store + markup
= $162 + $64.8
= $226.8.
So , For store A , The selling price is $226.8.
Given , For store B cost to store is $155 , Markup is 30%
Then , The markup is 30% of $155
a = p% × w
= 30% × 155
= 0.3 × 155
= 46.5
So , the markup is $46.5.
To , find the selling price , we have
selling price = cost to store + markup
= $155 + $46.5
= $201.5.
So , For store B , The selling price is $201.5.
Given , For store C cost to store is $160 , Markup is 25%
Then , The markup is 25% of $160
a = p% × w
= 25% × 160
= 0.25 × 160
= 40
So , the markup is $40.
To , find the selling price , we have
selling price = cost to store + markup
= $160 + $40
= $200.
So , For store C , The selling price is $200.
you should buy the system at store C has The selling price is $200.
b. Given , Store A has a weekend sale, to buy the system there , it should have the discount of ,
For store A , The selling price is $226.8 , cost to store is $162
We know a = $162 , w = $226.8
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{162}{226.8}\) = \(\frac{p}{100}\)
p = \(\frac{162 × 100}{226.8}\)
p = \(\frac{16,200}{226.8}\)
p = 71.4%
So, 162 is 71.4% of 226.8.
To get the percent of discount we have ,
The percent of discount = The percent of original price – the percent of sales price
= 100% – 71.4%
= 28.6%.
So, The percent of discount is 28.6% .
Hence , To buy the system at store A , it should have the discount of 28.6%.
Question 30.
DIG DEEPER!
A pool manager balances the pH level of a pool. The price of a bucket of chlorine tablets is $90, and the price of a pH test kit is $11. The manager uses a coupon that applies a 40% discount to the total cost of the two items. How much money does the pool manager pay for each item?
Answer: The pool manager pays for each item $60.6.
Explanation:
Now, to find the money the pool manager pay for each item
The price of a bucket of chlorine tablets is = $90.
The price of a pH test kit = $11.
So, to get the total price of both items we add both prices:
$90 + $11 = $101.
Total cost of two items = $101.
As, given a coupon that applies a 40% discount to the total cost of the two items.
Now, to get the total cost by applying discount:
101 – (40% of 101)
= 101 – (0.4 × 101)
= 101 – 40.4
= 60.6
So, The pool manager pays for each item $60.6
Question 31.
PRECISION
You buy a pair of jeans at a department store.

a. What is the percent of discount to the nearest percent?
b. What is the percent of sales tax to the nearest tenth of a percent?
c. The price of the jeans includes a 60% markup. After the discount, what is the percent of markup to the nearest percent?
Answer: a. The percent of discount is to the nearest percent 25% .
b. The percent of sales tax to the nearest percent is 7%.
c. The percent of markup to the nearest percent is 54%
Explanation:
a. To find the percent of discount to the nearest percent , we have
a = 29.99 , w = 39.99 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{29.99}{39.99}\) = \(\frac{p}{100}\)
p = \(\frac{29.99 × 100}{39.99}\)
p = 0.749 × 100
p = 74.9
So, 29.99 is 74.9% of 39.99.
To get the percent of discount we have ,
The percent of discount = The percent of original price – the percent of sales price
= 100% – 74.9%
= 24.9%.
So, The percent of discount is 25% .
b. To find the percent of sales tax to the nearest tenth of a percent we have
sales tax = 1.95 , price = 29.99 , so , a = 1.95 , w = 29.99 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{1.95}{29.99}\) = \(\frac{p}{100}\)
p = \(\frac{1.95 × 100}{29.99}\)
p = 0.065 × 100
p = 6.5
So, 1.95 is 6.5% of 29.99.
Thus , The percent of sales tax is 7%
c. Given , The price of the jeans includes a 60% markup.
The markup is 60% of $39.99
a = p% × w
= 60% × 39.99
= 0.6 × 39.99
= 23.99
So , the markup is $23.99.
To , find the original price , we have
selling price = cost to store + markup
cost to store = selling price – markup
= $39.99 – $23.99
= $15.99.
The selling price is $15.99.
After the discount, The amount is $29.99
To know the mark up we have , a = 15.99 , w = 29.99
a = p% × w
p% = \(\frac{a}{w}\)
p% = \(\frac{15.99}{29.99}\)
p% = 0.533
p = 0.533 × 100
p = 53.3 .%
So , The percent of markup to the nearest percent is 54%
Question 32.
CRITICAL THINKING
You buy a bicycle helmet for $22.26, which includes 6% sales tax. The helmet is discounted 30% off the selling price. What is the original price?
Answer: The original price of the helmet is $30.
Explanation:
Given , You buy a bicycle helmet for $22.26, which includes 6% sales tax.
Then , 6% of $22.26 is $1.33 , by decreasing the tax amount from the buying price we get $20.93
The helmet is discounted 30% off the selling price.
The sales price be 100% – 30% = 70%
we know a = 20.93 , p = 70% , w = ?
a = p% × w
a = 70% × w
20.93 = 0.7 × w
w = \(\frac{20.93}{0.7}\)
w = 29.9 , approximately equal to 30
So , the original price of the helmet is $30.
Question 33.
REASONING
A drone that costs $129.50 is discounted 40%. The next month, the sale price is discounted an additional 60%. Is the drone now “free”? If so, explain. If not, find the sale price.
Answer: The sales price of the next month is $31.8 , The drone not for free.
Explanation:
Given , A drone that costs $129.50 is discounted 40%.
We know , The sales price be 100% – 40% = 60% of the original price
sales price = 60% of 129.50
= 0.6 × 129.5 = $77.7
So, The sales price is $77.7.
Given , The next month, the sale price is discounted an additional 60%.
The original price this time is $77.7
We know , The sales price be 100% – 60% = 40% of the original price
sales price = 40% of 77.7
= 0.4 × 77.7 = $31.8
So, The sales price of the next month is $31.8 .
Thus , The drone not for free.
Lesson 6.6 Simple Interest
EXPLORATION 1
Understanding Simple Interest
Work with a partner. You deposit $150 in an account that earns 6% simple interest per year. You do not make any other deposits or withdrawals. The table shows the balance of the account at the end of each year.
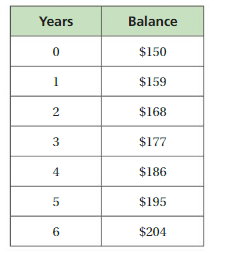
a. Describe any patterns you see in the account balance.
b. How is the amount of interest determined each year?
c. How can you find the amount of simple interest earned when you are given an initial amount, an interest rate, and a period of time?
d. You deposit $150 in a different account that earns simple interest. The table shows the balance of the account each year. What is the interest rate of the account? What is the balance after 10 years?
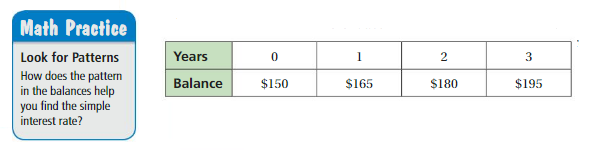
Answer: a. we observe the pattern of $9 increment in each year of the deposited amount.
b. the amount of interest each year is ,
For 0 years = $0
For 1 years I = $9.54
For 2 years I = $20.16
For 3 years I = $31.86
For 4 years I = $44.64
For 5 years I = $58.5
For 6 years I = $73.44
c. Formula for simple interest is I = Prt
d. The annual rate of interest is $ 2.60 .
Explanation:
a. As the table shows , we have a series of pattern among the years of amount deposited.
that is , For 0 years = $150
For 1 years = $150 + $9 = $159
For 2 years = $159 + $9 = $168
For 3 years = $168 + $9 = $177
For 4 years = $177 + $9 = $186
For 5 years = $186 + $9 = $195
For 6 years = $195 + $9 = $204 ,
Here, we observe the pattern of $9 increment in each year of the deposited amount.
b. From the table, we have , simple interest for each year as,
Principal = P , t = time in years , r = Annual interest rate
That is P = $150 , t = 0 years , r = 0.06
To find the simple interest I we know , I = Prt ,
For 0 years I = 150 × 0 × 0.06 = $0 .
For 1 years , P = $159 , t = 1 year , r = 0.06
I = 159 × 1 × 0.06 = $9.54
For 2 years , P = $168 , t = 2 year , r = 0.06
I = 168 × 2 × 0.06 = $20.16
For 3 years , P = $177 , t = 3 year , r = 0.06
I = 177 × 3 × 0.06 = $31.86
For 4 years , P = $186 , t = 4 year , r = 0.06
I = 186 × 4 × 0.06 = $44.64
For 5 years , P = $195 , t = 5 year , r = 0.06
I = 195 × 5 × 0.06 = $58.5
For 6 years , P = $204 , t = 6 year , r = 0.06
I = 204 × 6 × 0.06 = $73.44
C. To find the simple interest , we have Principal = P , t = time in years , r = Annual interest rate ,
Formula for simple interest is I = Prt , So by using this formula we can find the simple interest of the deposit .
d. From the table given , we have the pattern of increment of $5 in each year ,
in this case the deposit in the 10 year will be $230 .
To find the interest rate of the account ,
r = \(\frac{I}{pt}\)
r = \(\frac{0.06}{230 × 10}\)
r = 2.60
So , the annual rate of interest is $ 2.60 .
Interest principal is money paid or earned for using or lending money. The is the amount of money borrowed or deposited.

Try It
Question 1.
What is the balance of the account after 9 months?
Answer: The balance after 9 months = $500 + $1.66 = $501.66 .
Explanation:
From the example given , we know P = $500 , r = 0.03 , t = 9 months
I = prt
I = \(\frac{500 × 0.03}{9}\)
I = \(\frac{15}{9}\)
I = 1.66
The interest earned is $1.66 after 9 months ,
The balance after 9 months = $500 + $1.66 = $501.66 .
Question 2.
You deposit $350 in an account. The account earns $17.50 simple interest in 2.5 years. What is the annual interest rate?
Answer: The annual interest rate is 2%
Explanation:
Given , P = $350 , I = $17.5 , t = 2.5 ,
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{17.5}{350 × 2.5}\)
= \(\frac{17.5}{875}\)
= 0.02
we can write in percent as 2%
So , The annual interest rate is 2% .
Question 3.
In Example 3, how long does it take an account with a principal of $10,000 to earn $750 in interest?
Answer: It takes 3.75years to an account with a principal of $10,000 to earn $750 in interest .
Explanation:
Given , P = $10,000 , I = $750 , r = 0.02 , t = ? ,
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{750}{10,000 × 0.02}\)
= \(\frac{750}{200}\)
= 3.75
So, It takes 3.75years to an account with a principal of $10,000 to earn $750 in interest .
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
VOCABULARY
Explain the meaning of simple interest.
Answer:
Simple interest is interest calculated on the principal portion of a loan or the original contribution to a savings account. Simple interest does not compound, meaning that an account holder will only gain interest on the principal, and a borrower will never have to pay interest on interest already accrued.
So , To put in simplest form we can say that , simple interest money paid or earned only on the principal .
USING THE SIMPLE INTEREST FORMULA Use the simple interest formula.
Question 5.
You deposit $20 in a savings account. The account earns 4% simple interest per year. What is the balance after 4 years?
Answer: The balance of after 4 years is $23.2 .
Explanation:
To fin the principal , Given , P = $20 , r = 0.04 , t = 4 ,
We know that I = Prt
I = 20 × 0.04 × 4
= 3.2
Simple interest I = $3.2
To find the balance after 4 years we have to add the simple interest to principal amount = $20 + $3.2 = $23.2 .
The balance of after 4 years is $23.2 .
Question 6.
You deposit $800 in an account. The account earns $360 simple interest in 3 years. What is the annual interest rate?
Answer: The annual interest rate is 15% .
Explanation:
Given , P = $800 , I = $360 , t = 3 years ,
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{360}{800 × 3}\)
= \(\frac{360}{2400}\)
= 0.15
we can write in percent as 15%
So , The annual interest rate is 15% .
Question 7.
You deposit $650 in a savings account. How long does it take an account with an annual interest rate of 5% to earn $178.25 in interest?
Answer: It takes 7.13 years an account with an annual interest rate of 5% to earn $178.25 in interest .
Explanation:
Given , P = $650 , I = $178.25 , r = 0.05 , t = ? ,
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{178.25}{650 × 0.05}\)
= \(\frac{178.25}{32.5}\)
= 7.13
So, It takes 7.13 years an account with an annual interest rate of 5% to earn $178.25 in interest .
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
You want to deposit $1000 in a savings account for 3 years. One bank adds a $100 bonus to your principal and offers a 2% simple annual interest rate. Another bank does not add a bonus, but offers 6% simple interest per year. Which bank should you choose? Explain.
Answer: Second bank offers the best deal .
Explanation:
Given , we know P = $1000 , t = 3 years ,
And one bank adds $100 bonus and offers a 2% simple annual interest rate.
Then p = $1000 + $100 = $1100 , r = 0.02 ,
I = Prt
I = 1100 × 0.02 × 3
I = 11 × 2 × 3
I = 66
The simple interest of one bank = $66 .
The balance of the account will be = $1100 + $66 = $1166 .
Another bank offers no bonus, but 6% simple interest per year , r = 0.06 , p = $1000 , t = 3 years
I = prt
I = 1000 × 0.06 × 3
I = 10 × 6 × 3
I = 180
The simple interest of Another bank = $180 .
The balance of the account will be = $1000 + $180 = $1180 .
So, Second bank offers the best deal .
Question 9.
Your cousin borrows $1125 to repair her car. The simple annual interest rate is 10%. She makes equal monthly payments of $25. How many years will it take to pay off the loan?
Answer: It takes 2.2 years to pay off the loan.
Explanation:
Given , P = $1125 , r = 0.01 , I = $25 , t = ?
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{25}{1125 × 0.01}\)
= \(\frac{25}{11.25}\)
= 2.2
So, It takes 2.2 years to pay off the loan.
Question 10.
DIG DEEPER!
You borrow$900 to buy a laptop. You plan to pay off the loan after 5 years of equal monthly payments. After 10 payments, you have $1200 left to pay. What is the simple annual interest rate of your loan?
Answer: The annual interest rate is 15% .
Explanation:
Given , P = $900 , I = $1200 , t = 5 years ,
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{900}{1200 × 5}\)
= \(\frac{900}{6000}\)
= 0.15
we can write in percent as 15%
So , The annual interest rate is 15% .
Simple Interest Homework & Practice 6.6
Review & Refresh
Find the selling price.
Question 1.
A store pays $8 for a pool noodle. The markup is 20%.
Answer: The selling price is $9.6
Explanation:
Then , The markup is 20% of $8
a = p% × w
= 20% × 8
= 0.2 × 8
= 1.6
So , the markup is $1.6 .
To , find the selling price , we have
selling price = cost to store + markup
= $8 + $1.6
= $9.6.
So ,The selling price is $9.6 .
Question 2.
A store pays $3 for a magazine. The markup is 5%.
Answer: The selling price is $3.15
Explanation:
Then , The markup is 5% of $3
a = p% × w
= 5% × 3
= 0.05 × 3
= 0.15
So , the markup is $0.15 .
To , find the selling price , we have
selling price = cost to store + markup
= $3 + $0.15
= $3.15.
So ,The selling price is $3.15 .
Solve the inequality. Graph the solution.
Question 3.
x + 5 < 2
Answer: x < -3
Explanation:
Given , x + 5 < 2
add – 5 on both sides ,
x + 5 – 5 < 2 – 5
x < -3
Question 4.
b – 2 ≥ – 1
Answer: b ≥ 1
Explanation:
Given , b – 2 ≥ – 1
add 2 on both sides
b – 2 + 2 ≥ – 1 + 2
b ≥ 1
Question 5.
w + 6 ≤ – 3
Answer: w ≤ – 9
Explanation:
Given , w + 6 ≤ – 3
add -6 on both sides
w + 6 – 6 ≤ – 3 – 6
w ≤ – 9
Concepts, Skills, & Problem Solving
UNDERSTANDING SIMPLE INTEREST The table shows the balance of an account each year. What is the interest rate of the account? What is the balance after 10 years? (See Exploration 1, p. 265.)
Question 6.
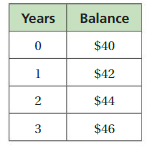
Answer: The annual interest rate is 3% .
Explanation:
Given , There is an increment of $2 each year , for 10 years it will be $60 .
Now we have , P = $60 , t = 10 years , I = $2 , r = ?
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{2}{60 × 10}\)
= \(\frac{2}{60}\)
= 0.03
we can write in percent as 3%
So , The annual interest rate is 3% .
Question 7.
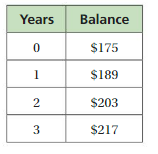
Answer: The annual interest rate is 0.4% .
Explanation:
Given , There is an increment of $14 each year , for 10 years it will be $315 .
Now we have , P = $315 , t = 10 years , I = $14 , r = ?
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{14}{315 × 10}\)
= 0.004
we can write in percent as 0.4%
So , The annual interest rate is 0.4% .
FINDING INTEREST EARNED An account earns simple annual interest. (a) Find the interest earned. (b) Find the balance of the account.
Question 8.
$600 at 5% for 2 years
Answer: The simple interest of bank is $60 .
The balance of the account will be $660 .
Explanation:
Given , P = $600 , t = 2 years , r = 0.05
I = prt
I = 600 × 0.05 × 2
I = 6 × 5 × 2
I = 60
The simple interest of bank is $60 .
The balance of the account will be = $600 + $60 = $660 .
Question 9.
$1500 at 4% for 5 years
Answer: The simple interest is $300 .
The balance of the account will be $1800 .
Explanation:
Given , P = $1500 , t = 5 years , r = 0.04
I = prt
I = 1500 × 0.04 × 5
I = 15 × 4 × 5
I = 300
The simple interest of bank = $300 .
The balance of the account will be $1500 + $300 = $1800 .
Question 10.
$350 at 3 % for 10 years
Answer: The simple interest of bank is $105 .
The balance of the account will be $455 .
Explanation:
Given , P = $350 , t = 10 years , r = 0.03
I = prt
I = 350 × 0.03 × 10
I = 35 × 3
I = 105
The simple interest of bank is $105 .
The balance of the account will be $350 + $105 = $455 .
Question 11.
$1800 at 6.5% for 30 months
Answer: The interest earned is $3.9 ,
The balance of the account will be $1,803.9 .
Explanation:
Given , P = $1800 , t = 30 months , r = 0.065
I = prt
I = \(\frac{1800 × 0.065}{30}\)
I = \(\frac{117}{30}\)
I = 3.9
The interest earned is $3.9 ,
The balance of the account will be $1800 + $3.9 = $1,803.9 .
Question 12.
$925 at2.3% for 2.4 years
Answer: The interest earned is $638.1 ,
The balance of the account will be $1,563.1 .
Explanation:
Given , P = $925 , t = 28 months , r = 0.023
I = prt
I = \(\frac{925 × 0.023}{28}\)
I = \(\frac{21.27}{30}\)
I = 638.1
The interest earned is $638.1 ,
The balance of the account will be $925 + $638.1 = $1,563.1 .
Question 13.
$5200 at 7.36% for 54 months
Answer: The interest earned is $7.08 ,
The balance of the account will be $5,207.
Explanation:
Given , P = $5200 , t = 54 months , r = 0.0736
I = prt
I = \(\frac{5200 × 0.0736}{54}\)
I = \(\frac{382.72}{54}\)
I = 7.08
The interest earned is $7.08 ,
The balance of the account will be $5200 + $7.08 = $5,207.
Question 14.
YOU BE THE TEACHER
Your friend finds the simple interest earned on $500 at 6% for 18 months. Is your friend correct? Explain your reasoning.
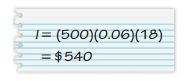
Answer: No , The simple interest is $1.6 .
Explanation:
Given , P = $500 , t = 18 months , r = 0.06
I = prt
I = \(\frac{500 × 0.06}{18}\)
I = \(\frac{30}{18}\)
I = 1.6
The simple interest is $1.6 .
FINDING AN ANNUAL INTEREST RATE Find the annual interest rate.
Question 15.
I = $24, P = $400, t = 2 years
Answer: The annual interest rate is 3% .
Explanation:
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{24}{400 × 2}\)
= \(\frac{24}{800}\)
= 0.03
we can write in percent as 3%
So , The annual interest rate is 3% .
Question 16.
I = $562.50, P = $1500, t = 5 years
Answer: The annual interest rate is 7.5% .
Explanation:
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{562.5}{1500 × 5}\)
= \(\frac{562.5}{7500}\)
= 0.075
we can write in percent as 7.5%
So , The annual interest rate is 7.5% .
Question 17.
I = $54, P = $900, t = 18 months
Answer: The annual interest rate is 108% .
Explanation:
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{54 × 18 }{900 }\)
= \(\frac{972}{900}\)
= 1.08
we can write in percent as 108%
So , The annual interest rate is 108% .
Question 18.
I = $160, P = $2000, t = 8 months
Answer: The annual interest rate is 64% .
Explanation:
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{160 × 8 }{2000 }\)
= \(\frac{1,280}{2,000}\)
= 0.64
we can write in percent as 64%
So , The annual interest rate is 64% .
FINDING AN AMOUNT OF TIME Find the amount of time.
Question 19.
I $30, P = $500, r = 3%
Answer: The amount of time is 1.6 years .
Explanation:
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac30}{500 × 0.03}\)
= \(\frac{30}{18}\)
=1.6
So , The amount of time is 1.6 years .
Question 20.
I = $720, P = $1000, r = 9%
Answer: The amount of time is 8 years .
Explanation:
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{720}{1000 × 0.09}\)
= \(\frac{720}{90}\)
= 8
So , The amount of time is 8 years .
Question 21.
I = $54, P = $800, r = 4.5%
Answer: The amount of time is 1.5 years .
Explanation:
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{54}{800 × 0.045}\)
= \(\frac{54}{36}\)
= 1.5
So , The amount of time is 1.5 years .
Question 22.
I = $450, P = $2400, r = 7.5%
Answer: The amount of time is 2.5 years .
Explanation:
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{450}{2400 × 0.075}\)
= \(\frac{450}{180}\)
= 2.5
So , The amount of time is 2.5 years .
Question 23.
FINDING AN ACCOUNT BALANCE
A savings account earns 5% simple interest per year. The principal is $1200. What is the balance after 4 years?
Answer: The bank balance is $1440 .
Explanation:
Given , P = $1200 , t = 4 years , r = 0.05
I = prt
I = 1200 × 0.05 × 4
I = 12 × 5 × 4
I = 240
The simple interest of bank is $240 .
The bank balance is $1200 + $240 = $1440 .
Question 24.
FINDING AN ANNUAL INTEREST RATE
You deposit $400 in an account. The account earns $18 simple interest in 9 months. What is the annual interest rate?
Answer: The annual interest rate is 40.5% .
Explanation:
Given , P = $400 , I = $18 , t = 9 months ,
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{18 × 9}{400}\)
= \(\frac{162}{400}\)
= 0.405
we can write in percent as 40.5%
So , The annual interest rate is 40.5% .
Question 25.
FINDING AN AMOUNT OF TIME
You deposit $3000 in a CD (certificate of deposit) that earns 5.6% simple annual interest. How long will it take to earn $336 in interest?
Answer: It takes 2 years to earn $336 in interest .
Explanation:
Given , P = $3000 , r = 0.056 , I = $336
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{336}{3000 × 0.056}\)
= \(\frac{336}{168}\)
= 2
So , It takes 2 years to earn $336 in interest .
FINDING AN AMOUNT PAID Find the amount paid for the loan.
Question 26.
$1500 at 9% for 2 years
Answer: The amount paid for the loan is $270 .
Explanation:
Given , P = $1500 , t = 2 years , r = 0.09
I = prt
I = 1500 × 0.09 × 2
I = 15 × 9 × 2
I = 270
So , The amount paid for the loan is $270 .
Question 27.
$2000 at 12% for 3 years
Answer: The amount paid for the loan is $72 .
Explanation:
Given , P = $2000 , t = 3 years , r = 0.012
I = prt
I = 2000 × 0.012 × 3
I = 2 × 12 × 3
I = 72
So , The amount paid for the loan is $72 .
Question 28.
$2400 at 10.5% for 5 years
Answer: The amount paid for the loan is $1,260 .
Explanation:
Given , P = $2400 , t = 5 years , r = 0.105
I = prt
I = 2400 × 0.105 × 5
I = 252 × 5
I = 1,260
So , The amount paid for the loan is $1,260 .
Question 29.
$4800 at 9.9% for 4 years
Answer: The amount paid for the loan is $1,900 .
Explanation:
Given , P = $4800 , t = 4 years , r = 0.099
I = prt
I = 4800 × 0.099 × 4
I = 475.2 × 4
I = 1,900
So , The amount paid for the loan is $1,900 .
USING THE SIMPLE INTEREST FORMULA Copy and complete the table.
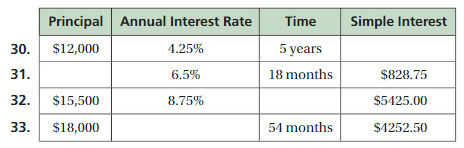
Answer: 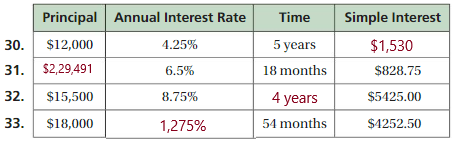
30. The simple interest is $1,530 .
31. The principal amount is $2,29,491 .
32. The time required is 4 years .
33. The annual interest rate is 1,275% .
30. Explanation:
Given , P = $12,000 , t = 5 years , r = 0.0425
I = prt
I = 12,000 × 0.0425 × 5
I = 510 ×
I = 1,530
So , The simple interest is $1,530 .
31. Explanation:
Given , I = $828.75 , t = 18 months , r = 0.065
I = Prt
P = \(\frac{I}{rt}\)
= \(\frac{828.75 × 18}{0.065}\)
= \(\frac{14,916.96}{0.065}\)
= 2,29,491
So , The principal amount is $2,29,491 .
32. Explanation:
Given , P = $15,500 , I = $5425 , r = 0.0875
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{5425}{15,500 × 0.0875}\)
= \(\frac{5425}{1,356.25}\)
= 4
So , The time required is 4 years .
33. Explanation:
Given , P = $18,000 , I = $4252.5 , t = 54 months ,
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{4252.5 × 54}{18,000}\)
= \(\frac{2,29,635}{18,000}\)
= 12.75
we can write in percent as 1,275%
So , The annual interest rate is 1,275% .
Question 34.
MODELING REAL LIFE
A family borrows money for a rainforest tour. The simple annual interest rate is 12%. The loan is paid after 3 months. What is the total amount paid for the tour?

Answer: The total amount paid for the tour will be $1,230 + $49.2 = $1,279.2 .
Explanation:
Given , P = $940 + $170 + $120 = 1,230
P = $1,230 , t = 3 months , r = 0.12
I = prt
I = \(\frac{1,230 × 0.12}{3}\)
I = \(\frac{147.6}{3}\)
I = 49.2
The simple interest is $49.2 .
So , The total amount paid for the tour will be $1,230 + $49.2 = $1,279.2 .
Question 35.
MODELING REAL LIFE
You deposit $5000 in an account earning 7.5% simple interest per year. How long will it take for the balance of the account to be $6500?
Answer: It takes 4 years for the balance of the account to be $6500.
Explanation:
Given , the balance of the account be $6500 , You deposit $5000
We know that . The total balance = deposit + simple interest
So, To get simple interest we have = The total balance – deposit = $6500 – $5000 = $1500 ,
P = $5000 , r = 0.075 , I = $1500 , t = ?
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{1500}{5000 × 0.075}\)
= \(\frac{1500}{375}\)
= 4
So , It takes 4 years for the balance of the account to be $6500.
Question 36.
MODELING REAL LIFE
You borrow$1300 to buy a telescope. What is the monthly payment?

Answer: The monthly payment is $66.95 .
Explanation:
Given , P = $1300 , t = 2 years , r = 0.118
I = prt
I = 1300 × 0.118 × 2
I = 153.4 × 2
I = 306.8
The simple interest of bank is $306.8 .
The balance of the account will be $1300 + $306.8 = $1,606.8 .
To get the monthly payment , convert 2 years into 24 months then , \(\frac{1,606.8}{24}\) = 66.95
So , The monthly payment is $66.95 .
Question 37.
REASONING
How many years will it take for $2000 to double at a simple annual interest rate of 8%? Explain how you found your answer.
Answer: It will take 12.5 years to make the principal amount double .
Explanation:
Given , it take for $2000 to double , so the total balance will be $2000 + $2000 = $4000
We know that . The total balance = deposit + simple interest
So, To get simple interest we have = The total balance – deposit = $4000 – $2000 = $2000
P = $2000 , r = 0.08 , I = $2000 , t = ?
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{2000}{2000 × 0.08}\)
= \(\frac{2000}{160}\)
= 12.5
So , It will take 12.5 years to make the principal amount double .
Question 38.
DIG DEEPER!
You take out two loans. After 2 years, the total interest for the loans is $138. On the first loan, you pay 7.5% simple annual interest on a principal of $800. On the second loan, you pay 3% simple annual interest. What is the principal for the second loan?
Answer: The principal amount of the second loan is $300 .
Explanation:
Given , For first loan , P = $800 , t = 2 years , r = 0.075
I = prt
I = 800 × 0.075 × 2
I = 120
The simple interest of bank is $120 .
For Second loan , Given , the total interest for the loans is $138
So , I = $138 – $120 = $18 ,
Given r = 0.03 , t = 2 years , I = $18
I = Prt
p = \(\frac{I}{rt}\)
= \(\frac{18}{0.03 × 2}\)
= \(\frac{18}{0.06}\)
= 300
So, The principal amount of the second loan is $300 .
Question 39.
REPEATED REASONING
You deposit $500 in an account that earns 4% simple annual interest. The interest earned each year is added to the principal to create a new principal. Find the total amount in your account after each year for 3 years.
Answer: The balance of the account for the first year will be $500 + $20 = $520
The balance of the account for the 2 year will be $520 + $41.6 = $561.6 .
The balance of the account for the 3 year will be $561.6 + $67.3 = $5683.9.
Explanation:
Given , P = $500 , t = 1 years , r = 0.04
I = prt
I = 500 × 0.04 × 1
I = 5 × 4
I = 20
The simple interest of bank is $20 .
The balance of the account for the first year will be $500 + $20 = $520 .
For 2 years , p = $520 , t = 2 , r = 0.04
I = prt
I = 520 × 0.04 × 2
I = 20.8 × 2
I = 41.6
The simple interest of bank is $41.6 .
The balance of the account for the 2 year will be $520 + $41.6 = $561.6 .
For 3 years , p = $561.6 , t = 3 , r = 0.04
I = prt
I = 561.6 × 0.04 × 3
I = 22.46× 3
I = 67.3
The simple interest of bank is $67.3 .
The balance of the account for the 3 year will be $561.6 + $67.3 = $5683.9.
Question 40.
NUMBER SENSE
An account earns r% simple interest per year. Does doubling the initial principal have the same effect on the total interest earned as doubling the amount of time? Justify your answer.
Answer: Yes ,Doubling the initial principal have the same effect on the total interest earned as doubling the amount of time
Explanation:
Given , An account earns r% simple interest per year. Does doubling the initial principal
Let us say P = 2P , t = t years , r = r%
we know I = Prt ,
I = 2P × t × r
I = 2Prt
The simple interest of the doubling initial principal is 2Prt .
Now , doubling the amount of time , t = 2t years
we know I = Prt ,
I = P × 2t × r
I = 2Prt
The simple interest of the doubling the amount is 2Prt .
So, Doubling the initial principal have the same effect on the total interest earned as doubling the amount of time
Percents Connecting Concepts
Using the Problem-Solving Plan
Question 1.
The table shows the percent of successful shots for each team in a hockey game. A total of 55 shots are taken in the game. The ratio of shots taken by the Blazers to shots taken by the Hawks is 6 : 5. How many goals does each team score?
Understand the problem.
You know that 55 shots are taken in a hockey game and that the Blazers take 6 shots for every 5 shots taken by the Hawks. You also know the percent of successful shots for each team.
Make a plan.
Use a ratio table to determine the number of shots taken by each team. Then use the percent equation to determine the number of successful shots for each team.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer: The goals made by Hawks are 50. and The goals made by Blazers are 60
Explanation:
Given , The ratio of shots taken by the Blazers to shots taken by the Hawks is 6 : 5
the percent of successful shots for each team in a hockey game is Blazers is 10% , Hawks is 16% ,
The goals made by Blazers are w = ? , a = 6 , p = 10%
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{6}{w}\) = \(\frac{10}{100}\)
w = \(\frac{6 × 100}{10}\)
w = \(\frac{600}{10}\)
w = 60
So, The goals made by Blazers are 60
The goals made by Hawks are w= ? , a = 5 , p = 16%
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{5}{w}\) = \(\frac{10}{100}\)
w = \(\frac{5 × 100}{10}\)
w = \(\frac{500}{10}\)
w = 50
So , The goals made by Hawks are 50.
Question 2.
Fill in the blanks with positive numbers so that the sum of the fractions is 37.5% of the first fraction. Justify your answer.
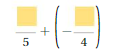
Answer: \(\frac{2}{5}\) + (- \(\frac{0.1}{4}\)) = 37.5%
Explanation:
Let us say that missing values be x and y
we have ,\(\frac{x}{5}\) + (- \(\frac{y}{4}\))
To get the simplified answer cross check the values of x and y
If x = 2 and y = 0.1 ,then
\(\frac{2}{5}\) + (- \(\frac{0.1}{4}\))
0.4 – 0.025 = 0.375
0.375 can be written as 37.5%
So , \(\frac{2}{5}\) + (- \(\frac{0.1}{4}\)) = 37.5%
Question 3.
The graph shows the distance traveled by a motorcycle on a dirt road. After turning onto a paved road, the motorcycle travels \(\frac{1}{5}\) mile every \(\frac{1}{4}\) minute. Find the percent of change in the speed of the motorcycle. Round to the nearest tenth of a percent if necessary.
Answer: The percent of change in the speed of the bike is 38%
Explanation:
speed of the bike on the dirty road is \(\frac{2.33}{4}\) = 0.58
speed of the bike on the paved road is \(\frac{0.2}{0.25}\) = 0.8
old value = 0.58 , new value = 0.8 ,
The amount of change = 0.8 – 0.58 = 0.22
So , percent of change is \(\frac{amount of change }{original amount}\)
= \(\frac{ 0.22}{0.58}\)
= 0.379
= 0.379 × 100
= 37.9 = 38%
So, the percent of change is 38%
Performance Task
Tornado Alley
At the beginning of this chapter, you watched a STEAM Video called “Tornado!” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Answer:
Percents Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

percent of change : It is the percent that a quantity changes from the original amount = \(\frac{amount of change }{original amount}\)
Example:
2 feet to 6 feet
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 6 and old value = 2 , because a change of 2 to 6 is a positive (increase) change
So, percent change = \(\frac{6 – 2}{2}\)
= \(\frac{4}{2}\)
= 2 × 100
= 200%
So, percent of change is 200%
percent of increase: When the original amount increases then the percent of change is called percent of increase = \(\frac{New value – old value}{old value}\)
Example:
5 cups to 10 cups
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 10 and old value = 5 , because a change of 5 to 10 is a positive (increase) change
So, percent change = \(\frac{10 – 5}{5}\)
= \(\frac{5}{5}\)
= 1 × 100
= 100%
So, percent of increase is 100%
percent of decrease: When the original amount decrease then the percent of change is called percent of decrease =\(\frac{old value – New value}{old value}\)
Example:
15 inches to 12 inches
We know that , formula for percent change = \(\frac{old value – new value}{old value}\)
where New value = 12 and old value = 15 , because a change of 15 to 12 is a negative (decrease) change
So, percent change = \(\frac{15 – 12}{15}\)
= \(\frac{3}{15}\)
= 0.2 × 100
= 20%
So, percent of decrease is 20%
percent error: It is the percent that estimated value differs from Actual value \(\frac{Error value}{Actual value}\)
Example:
Estimated value = 40 , Actual value = 30
The amount of error is 40 – 30 = 10
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 10 and Actual value = 30 ,
So, percent Error = \(\frac{10}{30}\)
= 0.333
= 0.333 × 100
= 33.3%
So, percent Error is 33.3%
Discount: It is a decrease in amount of original price of an item
Example:
A box is $5 with 20% off
We know , The sales price be 100% – 20% = 80% of the original price
sales price = 80% of 5
= 0.8 × 5 = 4
So, The sales price is $4.
Markup: The increase from what the stores pays to the selling price is called as Markup
Example:
The markup is 15% of $40
a = p% × w
= 15% × 40
= 0.15 × 40
= 6
So , the markup is $6.
To , find the selling price , we have
selling price = cost to store + markup
= $40 + $6
= $46.
The selling price is $46.
Interest: A money paid or earned for using or lending money is called interest
Example:
A bank offers a loan of $500 with an interest of $10 .
Here $10 is the interest amount to be paid for the loan
Principal: The amount of money borrowed or deposited
Example:
A bank offers a loan of $500 with an interest of $10 .
here the loan amount is the principal amount
Simple Interest: It is the money paid or earned only on the principal I = Prt , where I = simple interest , P = principal , r = rate of interest , t = time in years
Example:
A bank offers a loan of $500 with an interest rate of 3% for 2 years . the simple interest is
p = $500 , r = 0.03 , t = 2
I = 500 × 0.03 × 2
I = 30
So , The simple interest is $15 .
Graphic Organizers
You can use a Summary Triangle to explain a concept. Here is an example of writing a percent as a decimal a Summary Triangle for Writing a percent as a decimal.
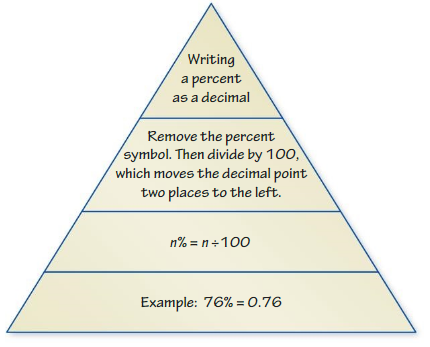
Answer: Summary triangle for writing a decimal into percent is 
Choose and complete a graphic organizer to help you study the concept.

1. writing a decimal as a percent
2. comparing and ordering fractions, decimals, and percents
3. the percent proportion
4. the percent equation
5. percent of change
6. discount
7. markup
Writing a decimal as a percent 
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

6.1 Fractions, Decimals, and Percents (pp. 235–240)
Learning Target: Rewrite fractions, decimals, and percents using different representations.
Write the percent as a decimal or the decimal as a percent. Use a model to represent the number.
Question 1.
74%
Answer: decimal form is 0.74
Explanation: 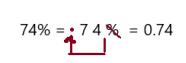
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 74% in decimal form is 0.74
Question 2.
2%
Answer: decimal form is 0.02
Explanation: 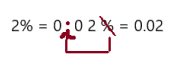
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 2% in decimal form is 0.02
Question 3.
221%
Answer: decimal form is 2.21
Explanation: 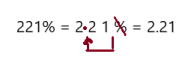
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 221% in decimal form is 2.21
Question 4.
0.17
Answer: 17%
Explanation: 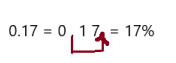
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.17 can be rewrite as 17%
Question 5.
\(4 . \overline{3}\)
Answer: \(433. \overline{3} \%\)
Explanation: 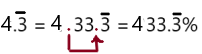
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, \(4 . \overline{3}\) can be rewrite as \(433. \overline{3} \%\)
Question 6.
0.079
Answer: 7.9%
Explanation: 
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.079 can be rewrite as 7.9%
Write the fraction as a decimal and a percent.
Question 7.
\(\frac{17}{20}\)
Answer: decimal = 0.85, percent = 85%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{17}{20}\) as 0.85 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.85 can be rewrite as 85%
So,\(\frac{17}{20}\) in decimal = 0.85, percent = 85%
Question 8.
\(\frac{3}{8}\)
Answer: decimal = 0.375, percent = 37.5%
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{3}{8}\) as 0.375 in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then 0.375 can be rewrite as 37.5%
So, \(\frac{3}{8}\) in decimal = 0.375, percent = 37.5%
Question 9.
\(\frac{14}{9}\)
Answer: decimal = \(1 . \overline{5}\), percent = \(155. \overline{5} \%\)
Explanation:
By using the method of converting fraction into decimal and comparing ,
We can rewrite \(\frac{14}{9}\) as \(1. \overline{5}\) in decimal form,
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol , then \(1 . \overline{5}\)can be rewrite as \(155. \overline{5} \%\)
So, \(\frac{14}{9}\) in decimal = \(1 . \overline{5}\), percent = \(155. \overline{5} \%\)
Question 10.
For school spirit day, 11.875% of your class wears orange shirts, \(\frac{5}{8}\) of your class wears blue shirts, 0.15625 of your class wears white shirts, and the rest of your class wears gold shirts. Order the portions of shirts of each color from least to greatest. Justify your answer.
Answer: In ascending order we have 10.1% , 15.6% , 62.5% , 11.875%
Explanation:
Given , 11.875% of your class wears orange shirts,
\(\frac{5}{8}\) of your class wears blue shirts,
It can be written as 0.625 in decimals and 62.5% in percent
0.15625 of your class wears white shirts,
it can be written as 15.6%
And the rest of your class wears gold shirts.
Let the total be 100% , The percent in all colors is 11.875% + 62.5% + 15.6% = 89.9%
So , the rest of the girls wears 100% – 89.9% = 10.1% ,
In ascending order we have 10.1% , 15.6% , 62.5% , 11.875%
6.2 The Percent Proportion (pp. 241–246)
Learning Target: Use the percent proportion to find missing quantities.
Write and solve a proportion to answer the question.
Question 11.
What percent of 60 is 18?
Answer: 18 is 30% of 60.
Explanation:
Given , a = 18 , w = 60 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{18}{60}\) = \(\frac{p}{100}\)
p = \(\frac{18 × 100}{60}\)
p = \(\frac{1800}{60}\)
p = 30
So, 18 is 30% of 60.
Question 12.
40 is what percent of 32?
Answer: 40 is 125% of 32.
Explanation:
Given , a = 40 , w = 32 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{40}{32}\) = \(\frac{p}{100}\)
p = \(\frac{40 × 100}{32}\)
p = \(\frac{4,000}{32}\)
p = 125
So, 40 is 125% of 32.
Question 13.
What number is 70% of 70?
Answer: 49 is 70% of 70.
Explanation:
Given , a = ? , w = 70 , p = 70%
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{70}\) = \(\frac{70}{100}\)
a = \(\frac{70 × 70}{100}\)
a = \(\frac{4900}{100}\)
a = 49
So, 49 is 70% of 70.
Question 14.
\(\frac{3}{4}\) is 75% of what number?
Answer: 0.75 is 755% of 1.
Explanation:
we can write \(\frac{3}{4}\) as 0.75 in decimal
Given , a = 0.75 , w = ? , p = 75%
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{0.75}{w}\) = \(\frac{75}{100}\)
w = \(\frac{0.75 × 100}{75}\)
w = \(\frac{75}{755}\)
w = 1
So, 0.75 is 755% of 1.
Question 15.
About 29% of the Earth’s surface is covered by land. The total surface area of the Earth is about 510 million square kilometers. What is the area of the Earth’s surface covered by land?

Answer: The area of the Earth’s surface covered by land is 147.9 million square kilometers .
Explanation:
Given , p = 29% , w = 510 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{510}\) = \(\frac{29}{100}\)
a = \(\frac{510 × 29}{100}\)
a = \(\frac{14,790}{100}\)
a = 147.9
So, 147.9 is 29% of 510.
The area of the Earth’s surface covered by land is 147.9 million square kilometers .
6.3 The Percent Equation (pp. 247–252)
Learning Target: Use the percent equation to find missing quantities. Write and solve an equation to answer the question.
Question 16.
What number is 24% of 25?
Answer: 6 is 24% of 25.
Explanation:
Given p = 24% , w = 25 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{25}\) = \(\frac{24}{100}\)
a = \(\frac{25 × 24}{100}\)
a = \(\frac{600}{100}\)
a = 6
So, 6 is 24% of 25.
Question 17.
9 is what percent of 20?
Answer: 9 is 45% of 20.
Explanation:
Given p = ? , w = 20 , a = 9
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{9}{20}\) = \(\frac{p}{100}\)
p = \(\frac{9 × 100}{20}\)
p = \(\frac{900}{20}\)
p = 45
So, 9 is 45% of 20.
Question 18.
60.8 is what percent of 32?
Answer: 60.8 is 190% of 32.
Explanation:
Given p = ? , w = 32, a = 60.8
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{60.8}{32}\) = \(\frac{p}{100}\)
p = \(\frac{60.8 × 100}{32}\)
p = \(\frac{6080}{32}\)
p = 190
So, 60.8 is 190% of 32.
Question 19.
91 is 130% of what number?
Answer: 91 is 130% of 70.
Explanation:
Given p = 130% , w = ? , a = 91
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{91}{w}\) = \(\frac{130}{100}\)
w = \(\frac{91 × 100}{130}\)
w = \(\frac{9100{130}\)
w = 70
So, 91 is 130% of 70.
Question 20.
85% of what number is 10.2?
Answer: 10.2 is 85% of 12.
Explanation:
Given p = 85% , w = ? , a = 10.2
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{10.2}{w}\) = \(\frac{85}{100}\)
w = \(\frac{10.2 × 100}{85}\)
w = \(\frac{1020}{85}\)
w = 12
So, 10.2 is 85% of 12.
Question 21.
83% of 20 is what number?
Answer: 16.6 is 83% of 20.
Explanation:
Given p = 83% , w = 20 , a = ?
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{20}\) = \(\frac{83}{100}\)
a = \(\frac{20 × 83}{100}\)
a = \(\frac{1,660}{100}\)
a = 16.6
So, 16.6 is 83% of 20.
Question 22.
15% of the parking spaces at a school are handicap spaces. The school has 18 handicap spaces. How many parking spaces are there in total?

Answer: Totally , there are 120 parking spaces .
Explanation:
Given , p = 15% , a = 18 , w = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{18}{w}\) = \(\frac{15}{100}\)
w = \(\frac{18 × 100}{15}\)
w = \(\frac{1800}{15}\)
w = 120
So, 18 is 15% of 120.
Totally , there are 120 parking spaces .
Question 23.
Of the 25 students on a field trip, 16 bring cameras. What percent of the students bring cameras?
Answer: 64% of students brought the cameras .
Explanation:
Given , a = 16 , w = 25 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{16}{25}\) = \(\frac{p}{100}\)
p = \(\frac{16 × 100}{25}\)
p = \(\frac{1600}{25}\)
p = 64
So, 16 is 64% of 25.
Thus, 64% of students brought the cameras .
6.4 Percents of Increase and Decrease (pp. 253–258)
Learning Target: Find percents of change in quantities.
Identify the percent of change as an increase or a decrease. Then find the percent of change. Round to the nearest tenth of a percent if necessary.
Question 24.
6 yards to 36 yards
Answer: percent of change is 500%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 36 and old value = 6 , because a change of 6 to 36 is a positive (increase) change
So, percent change = \(\frac{36 – 6}{6}\)
= \(\frac{30}{6}\)
= 5× 100
= 500%
So, percent of change is 500%
Question 25.
120 meals to 52 meals
Answer: percent of change is – 56.6%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 52 and old value = 120 , because a change of 120 to 52 is a negative (decrease) change
So, percent change = \(\frac{52 – 120}{120}\)
= \(\frac{- 68}{120}\)
= – 0.566
= – 0.566 × 100
= – 56.6%
So, percent of change is – 56.6%
Question 26.
You estimate that a jar contains 68 marbles. The actual number of marbles is 60. Find the percent error.
Answer: percent Error is 13%
Explanation:
The amount of error is 68 – 60 = 8
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 8 and Actual value = 60 ,
So, percent Error = \(\frac{8}{60}\)
= 0.133
= 0.133 × 100
= 13.3%
Approximately we can write as 13%
So, percent Error is 13%
Question 27.
The table shows the numbers of skim boarders at a beach on Saturday and Sunday. What was the percent of change in boarders from Saturday to Sunday?

Answer: percent of change is – 12.5%
Explanation:
Given , 12 to 9
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 63 and old value = 72 , because a change of 72 to 63 is a negative (decrease) change
So, percent change = \(\frac{63 – 72}{72}\)
= \(\frac{- 9}{72}\)
= \(\frac{- 1}{8}\)
= – 0.125
= – 0.125 × 100
= – 12.5%
So, percent of change is – 12.5%
6.5 Discounts and Markups (pp. 259–264)
Learning Target: Solve percent problems involving discounts and markups.
Find the sale price or original price.
Question 28.
Original price: $50
Discount: 15%
Sale price: ?
Answer: The sales price is $42.5
Explanation:
We know , The sales price be 100% – 15% = 85% of the original price
sales price = 85% of 50
= 0.85 × 50 = 42.5
So, The sales price is $42.5
Question 29.
Original price: ?
Discount: 20%
Sale price: $75
Answer: The original price is $93.75.
Explanation:
We know , The sales price be 100% – 20% = 80%
a = p% × w
75 = 0.8 × w
w = \(\frac{75}{0.8}\)
w = 93.75
So, The original price is $93.75.
Question 30.
What is the original price of the tennis racquet?

Answer: The original price is $30.
Explanation:
We know , The sales price be 100% – 30% = 70%
a = p% × w
21 = 0.7 × w
w = \(\frac{21}{0.7}\)
w = 30
So, The original price is $30.
Question 31.
A store pays $50 for a pair of shoes. The markup is 25%.
a. What is the selling price for the shoes?
b. What is the total cost for a person to buy the shoes including a 6% sales tax?
Answer: a. The selling price is $62.5.
b. Total cost for a person is $66.25 .
Explanation:
The markup is 25% of $50
a = p% × w
= 25% × 50
= 0.25 × 50
= 12.5
So , the markup is $12.5.
To , find the selling price , we have
selling price = cost to store + markup
= $50 + $12.5
= $62.5.
The selling price is $62.5.
b. with 6% sales tax we have ,
6% of $62.5
= 0.06 × 62.5
= 3.75 , it is the tax rate
So , total cost for a person is $62.5 + $3.75 = $66.25
6.6 Simple Interest (pp. 265–270)
Learning Target: Understand and apply the simple interest formula.
An account earns simple interest. (a) Find the interest earned. (b) Find the balance of the account.
Question 32.
$300 at 4% for 3 years
Answer: a. The interest earned is $36
b. The balance of the account is $336 .
Explanation:
we know P = $300 , r = 0.04 , t = 3 years
I = prt
I = 300 × 0.04 × 3
I = 3 × 4 × 3
I = $36
The interest earned is $36
The balance of the account = $300 + $36 = $336 .
Question 33.
$2000 at 3.5% for 4 years
Answer: a. The interest earned is $280
b. The balance of the account is $2,280 .
Explanation:
we know P = $2000 , r = 0.035 , t = 4 years
I = prt
I = 2000 × 0.035 × 4
I = 2 × 35 × 4
I = $280
The interest earned is $280
The balance of the account = $2000 + $280 = $2,280 .
Find the annual interest rate.
Question 34.
I = $17, P = $500, t = 2 years
Answer: The annual interest rate is 1.7% .
Explanation:
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{17}{500 × 2}\)
= \(\frac{17}{1000}\)
= 0.017
we can write in percent as 1.7%
So , The annual interest rate is 1.7% .
Question 35.
I = $426, P = $1200, t = 5 years
Answer: The annual interest rate is 7.1% .
Explanation:
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{426}{1200 × 5}\)
= \(\frac{426}{6000}\)
= 0.071
we can write in percent as 7.1%
So , The annual interest rate is 7.1% .
Find the amount of time.
Question 36.
I = $60, P = $400, r = 5%
Answer: The amount of time is 3 years .
Explanation:
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{60}{400 × 0.05}\)
= \(\frac{60}{20}\)
= 3
So, The amount of time is 3 years .
Question 37.
I = $237.90, P = $1525, r = 2.6%
Answer: The amount of time is 6 years .
Explanation:
We know that I = Prt
t = \(\frac{I}{Pr}\)
= \(\frac{237.9}{1525 × 0.026}\)
= \(\frac{237.9}{39.65}\)
= 6
So, The amount of time is 6 years .
Question 38.
You deposit $100 in an account. The account earns $2 simple interest in 6 months. What is the annual interest rate?
Answer: The annual interest rate is 12%
Explanation:
Given , p = $100 , I = $2 , t = 6 months ,
We know that I = Prt
So , r = \(\frac{I}{Pt}\)
r = \(\frac{2 × 6}{100}\)
= \(\frac{12}{100}\)
= 0.12
we can write in percent as 12%
So , The annual interest rate is 12%
Question 39.
Bank A is offering a loan with a simple interest rate of 8% for 2 years. Bank B is offering a loan with a simple interest rate of 6.5% for 3 years.

a. Assuming the monthly payments are equal, what is the monthly payment for the four wheeler from Bank A? from Bank B?
b. Give reasons for why a person might choose Bank A and why a person might choose Bank B for a loan to buy the four wheeler. Explain your reasoning.
Answer: a. The monthly payment for bank A is $261 and for Bank B is $179.25 .
b. If a person chooses Bank A , it will be high in monthly payment but within 2 years loan will be cleared .
If a person chooses Bank B , it will be low monthly payment and can pay the loan a year extra in small amounts.
Explanation:
For bank A , Then p = $5400 , r = 0.08 , t = 2 years
I = Prt
I = 5400 × 0.08 × 2
I = 54 × 8 × 2
I = 864
The simple interest of one bank = $864 .
The balance of the account will be = $5400 + $864 = $6,264 .
The monthly payment = \(\frac{6,264}{24}\) = $261 .
For bank B, Then p = $5400 , r = 0.065 , t = 3 years
I = Prt
I = 5400 × 0.065 × 3
I = 54 × 6.5 × 3
I = 1,053
The simple interest of one bank = $1,053 .
The balance of the account will be = $5400 + $1,053 = $6,453 .
The monthly payment = \(\frac{6,453}{36}\) = $179.25 .
b. If a person chooses Bank A , it will be high in monthly payment but within 2 years loan will be cleared .
If a person chooses Bank B , it will be low monthly payment and can pay the loan a year extra in small amounts.
Percents Practice Test
Write the percent as a decimal, or the decimal as a percent. Use a model to represent the number.
Question 1.
0.96%
Answer: 0.0096
Explanation: 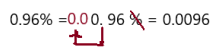
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 0.96% in decimal form is 0.0096
Question 2.
3%
Answer: 0.03
Explanation: ![]()
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, 3% in decimal form is 0.03
Question 3.
\(25 . \overline{5} \%\)
Answer: \(0 .25 \overline{5}\)
Explanation: 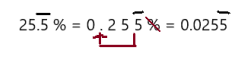
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, \(25 . \overline{5} \%\) in decimal form is \(0 .25 \overline{5}\)
Question 4.
\(0 . \overline{6} \%\)
Answer: \(0 .006\overline{6}\)
Explanation: 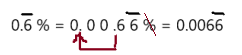
To write percent into decimal we have to remove percent symbol and divide by 100, which moves the decimal point two places to the left.
So, \(0 . \overline{6} \%\) in decimal form is\(0 .006 \overline{6}\)
Question 5.
7.88
Answer: 788%
Explanation: 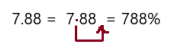
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 7.88 can be rewrite as 788%
Question 6.
0.58
Answer: 58%
Explanation: 
To write decimal into percent we should multiply the number by 100, which moves the decimal point two places to the right and add a percent symbol.
So, 0.58 can be rewrite as 58%
Order the numbers from least to greatest.
Question 7.
86%, \(\frac{15}{18}\), 0.84, \(\frac{8}{9}\), \(0 . \overline{86} \%\)
Answer: The numbers from least to greatest are \(0 .00 \overline{86}\) , \(0 .8 \overline{3}\) , 0.84 , 0.86 , \(0 .\overline{8}\)
Explanation:
86%, in decimals as 0.86
\(\frac{15}{18}\), can be \(0 .8 \overline{3}\)
\(\frac{8}{9}\), can be \(0 .\overline{8}\)
\(0 . \overline{86} \%\) can be written as \(0 .00 \overline{86}\)
So, The numbers from least to greatest are \(0 .00 \overline{86}\) , \(0 .8 \overline{3}\) , 0.84 , 0.86 , \(0 .\overline{8}\)
Question 8.
91.6%, 0.91, \(\frac{11}{12}\), 0.917, 9.2%
Answer: The numbers from least to greatest are 0.092 , 0.91 , 0.916 , \(0 .91\overline{6}\) , 0.917 .
Explanation:
91.6%, can be written as 0.916
\(\frac{11}{12}\), ca be written as \(0 .91\overline{6}\)
9.2% can be written as 0.092
So, The numbers from least to greatest are 0.092 , 0.91 , 0.916 , \(0 .91\overline{6}\) , 0.917 .
Write and solve a proportion or equation to answer the question.
Question 9.
What percent of 28 is 21?
Answer: 21 is 75% of 28.
Explanation:
Given , a = 21 , w = 28 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{21}{28}\) = \(\frac{p}{100}\)
p = \(\frac{21 × 100}{28}\)
p = \(\frac{2100}{28}\)
p = 75
So, 21 is 75% of 28.
Question 10.
64 is what percent of 40?
Answer: 64 is 160% of 40.
Explanation:
Given , a = 64 , w = 40 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{64}{40}\) = \(\frac{p}{100}\)
p = \(\frac{64 × 100}{40}\)
p = \(\frac{6400}{40}\)
p = 160
So, 64 is 160% of 40.
Question 11.
What number is 80% of 45?
Answer: 36 is 80% of 45.
Explanation:
Given , a = ? , w = 45 , p = 80%
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{45}\) = \(\frac{80}{100}\)
a = \(\frac{45 × 80}{100}\)
a = \(\frac{3600}{100}\)
a = 36
So, 36 is 80% of 45.
Question 12.
0.8% of what number is 6?
Answer: 6 is 0.8% of 750.
Explanation:
Given , a = 6 , w = ? , p = 0.8%
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{6}{w}\) = \(\frac{0.8}{100}\)
w = \(\frac{6 × 100}{0.8}\)
w = \(\frac{600}{0.8}\)
w = 750
So, 6 is 0.8% of 750.
Identify the percent of change as an increase or a decrease. Then find the percent of change. Round to the nearest tenth of a percent if necessary.
Question 13.
4 strikeouts to 10 strikeouts
Answer: percent of change is 150%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 10 and old value = 4 , because a change of 4 to 10 is a positive (increase) change
So, percent change = \(\frac{10 – 4}{4}\)
= \(\frac{6}{4}\)
= 1.5 × 100
= 150%
So, percent of change is 150%
Question 14.
$24 to $18
Answer: percent of change is – 25%
Explanation:
We know that , formula for percent change = \(\frac{New value – old value}{old value}\)
where New value = 18 and old value = 24 , because a change of 24 to 18 is a negative (decrease) change
So, percent change = \(\frac{18 – 24}{24}\)
= \(\frac{- 6}{24}\)
= – 0.25
= – 0.25 × 100
= – 25%
So, percent of change is – 25%
Find the sale price or selling price.
Question 15.
Original price: $15
Discount: 5%
Sale price: ?
Answer: The sales price is $14.25
Explanation:
We know , The sales price be 100% – 5% = 95% of the original price
sales price = 95% of 15
= 0.95 × 15 = 14.25
So, The sales price is $14.25
Question 16.
Cost to store: $5.50
Markup: 75%
Selling price: ?
Answer: The selling price is $9.625.
Explanation:
The markup is 75% of $5.50
a = p% × w
= 75% × 5.5
= 0.75 × 5.5
= 4.125
So , the markup is $4.125.
To , find the selling price , we have
selling price = cost to store + markup
= $5.5 + $4.125
= $9.625.
The selling price is $9.625.
An account earns simple interest. Find the interest earned or the principal.
Question 17.
Interest earned: ?
Principal: $450
Interest rate: 6%
Time: 8 years
Answer: The interest earned is $216 .
Explanation:
we know P = $450 , r = 0.06 , t = 8 years
I = prt
I = 450 × 0.06 × 8
I = 27 × 8
I = $216
The interest earned is $216 .
Question 18.
Interest earned: $27
Principal: ?
Interest rate: 1.5%
Time: 2 years
Answer: The principal is $900 .
Explanation:
Given , P = ? , I = $27 , t = 2 years , r = 0.015
We know that I = Prt
So , p = \(\frac{I}{rt}\)
p = \(\frac{27}{0.015 × 2}\)
= \(\frac{27}{0.03}\)
= 900
So, The principal is $900 .
Question 19.
You spend 8 hours each weekday at school. (a) Write the portion of a weekday spent at school as a fraction, a decimal, and a percent. (b) What percent of a week is spent at school if you go to school 4 days that week? Round to the nearest tenth.
Answer: a. the portion of a weekday spent at school is 33% , It can be written as \(\frac{100}{3}\) and in decimal as 0.333
b . The 9% of a week is spent at school if you go to school 4 days that week.
Explanation:
Given , You spend 8 hours each weekday at school.
a. In a day we have 24 hours so , The percent of 8 hours in 24 hours is
a = 8 , w = 24 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{8}{24}\) = \(\frac{p}{100}\)
p = \(\frac{8 × 100}{24}\)
p = \(\frac{800}{24}\)
p = 33.3 %
It can be written as \(\frac{100}{3}\) and in decimal as 0.333
So, 8 is 33% of 24.
b. The number of hours in a week , that is 7 days are 168 hours
The number of hours in 4 days to school are 32
So , we have a = 32 , w = 168 , p = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{32}{168}\) = \(\frac{p}{100}\)
p = \(\frac{32 × 100}{168}\)
p = \(\frac{3200}{168}\)
p = 9.04 %
p = 9%
So , The 9% of a week is spent at school if you go to school 4 days that week.
Question 20.
Research indicates that90% of the volume of an iceberg is below water. The volume of the iceberg above the water is 160,000 cubic feet. What is the volume of the iceberg below water?

Answer: The volume of the iceberg below water is 1,77,777 cubic feet
Explanation:
Given , p = 90% , a = 160,000 , w = ?
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{160,000}{w}\) = \(\frac{90}{100}\)
w = \(\frac{160,000 × 100}{90}\)
w = \(\frac{1050}{125}\)
w = 1,77,777.7
So, the volume of the iceberg below water is 1,77,777 cubic feet
Question 21.
You estimate that there are 66 cars in a parking lot. The actual number of cars is 75.
a. Find the percent error.
b. What other estimate gives the same percent error? Explain your reasoning.
Answer: a. percent Error is 12%
b, If the estimated number is 66.1 then percent error will be 12%
Explanation:
The amount of error is 75 – 66 = 9
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 9 and Actual value = 75 ,
So, percent Error = \(\frac{9}{75}\)
= 0.12
= 0.12 × 100
= 12%
So, percent Error is 12%
b. if the estimation is 66.1
The amount of error is 75 – 66.1 = 8.9
We know that , formula for percent error = \(\frac{Error value}{Actual value}\)
where Error value = 8.9 and Actual value = 75 ,
So, percent Error = \(\frac{8.9}{75}\)
= 0.1198
= 0.1198 × 100
= 11.9%
Apporximately 12%
So, percent Error is 12%
Percents Cumulative Practice

Question 1.
A movie theater offers 30% a movie ticket to students from your school. The regular price of a movie ticket is $8.50. What is the discounted price that you pay for a ticket?
A. $2.55
B. $5.50
C. $5.95
D. $8.20
Answer: C. $5.95
Explanation:
Given , original price = $8.5 , with 30% off
We know , The sales price be 100% – 30% = 70% of the original price
sales price = 70% of 8.5
= 0.7 × 8.5 = 5.95
So, The sales price is $5.95.
Question 2.
What is the least value of x for which the inequality is true?

16 ≥ – 2x
Answer: x = 1
Explanation:
Let us say X = 1
16 ≥ – 2(1)
16 ≥ – 2
So , x = 1 , for 16 ≥ – 2x
Question 3.
You are building a scale model of a park that is planned for a city. The model uses the scale 1 centimeter = 2 meters. The park will have a rectangular reflecting pool with a length of 20 meters and a width of 12 meters. In your scale model, what will be the area of the reflecting pool?
F. 60 cm2
G. 120 cm2
H. 480 cm2
I. 960 cm2
Answer: F . 60 cm2
Explanation:
Given ,actual l = 20 meters , The model uses the scale 1 centimeter = 2 meters. let the model length be x
The model length x will be , \(\frac{1cm}{2m}\) = \(\frac{x cm}{20m}\)
2x = 20
x = 10 ,
Let the model width be y , The model width y will be \(\frac{1 cm}{2m}\) = \(\frac{y}{12}\)
y= 6 ,
So The model area of the reflecting pool , Area of rectangle = l × w
l = 10 , y = 6 , then A = 10 × 6 = 60 cm2
The model area of the reflecting pool is 60 cm2
Question 4.
Which proportion represents the problem?
Answer: D . \(\frac{43}{n}\) = \(\frac{17}{100}\)
Explanation:
Given , p = 17% , a = 43
By using proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{43}{w}\) = \(\frac{17}{100}\)
w = \(\frac{43 × 100}{17}\)
w = \(\frac{4300}{17}\)
w = 252.9
So, 43 is 17% of 252.9.
Question 5.
Which list of numbers is in order from least to greatest?
F. 0.8, \(\frac{5}{8}\), 70%, 0.09
G. 0.09, \(\frac{5}{8}\), 0.8, 70%
H. \(\frac{5}{8}\), 70%, 0.8, 0.09
I. 0.09, \(\frac{5}{8}\), 70%, 0.8
Answer: H. \(\frac{5}{8}\), 70%, 0.8, 0.09
Explanation:
Given,
\(\frac{5}{8}\) can be written as 0.625 ,
70% can be written as 0.7
The order from least to greatest is \(\frac{5}{8}\) , 70% , 0.8 , 0.9
Question 6.
What is the value of \(\frac{9}{8}\) ÷ (-\(\frac{11}{4}\))?

Answer: the value of \(\frac{9}{8}\) ÷ (-\(\frac{11}{4}\)) is – 0.413
Explanation:
\(\frac{9}{8}\) can be written as 1.125
–\(\frac{11}{4}\) can be written as – 2.75
then , \(\frac{1.125}{-2.75}\) = – 0.413
Question 7.
The number of calories you burn by playing basketball is proportional to the number of minutes you play. Which of the following is a valid interpretation of the graph?
A. The unit rate is \(\frac{1}{9}\) calorie per minute.
B. You burn 5 calories by playing basketball for 45 minutes.
C. You do not burn any calories if you do not play basketball for at least 1 minute.
D. You burn an additional 9 calories for each minute of basketball you play.
Answer: C. You do not burn any calories if you do not play basketball for at least 1 minute.
Explanation:
As , the graph shows the coordinates of the minutes to calories by (0,0) at the initial stage of playing basketball for at least a minute .
So , the graph represents , You do not burn any calories if you do not play basketball for at least 1 minute.
Question 8.
A softball team is ordering uniforms. Each player receives one of each of the items shown in the table.

Which expression represents the total cost (in dollars) when there are 15 players on the team?
F. x + 24.86
G. 15x + 372.90
H. x + 372.90
I. x + 387.90
Answer: G. 15x + 372.90
Explanation:
Given , jersey = x
So , the only option in the options with an x for 15 members is 15x ,
So, G. 15x + 372.90 is the correct option
Question 9.
Your friend solves the equation. What should your friend do to correct the error that he made?
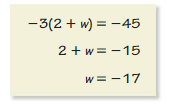
A. Multiply – 45 by – 3.
B. Add 3 to – 45.
C. Add 2 to – 15.
D. Divide – 45 by – 3.
Answer: A. Multiply – 45 by – 3.
Explanation:
Given , – 3(2 + w) = -45
By , Multiply – 45 by – 3.
we get 2 + w = 15
w = 15 – 2
w = 13.
Question 10.
You are comparing the costs of a certain model of ladder at a hardware store and at an online store.

Part A What is the total cost of buying the ladder at each of the stores? Show your work and explain your reasoning.
Part B Suppose that the hardware store is offering 10% off the price of the ladder and that the online store is offering free shipping and handling. Which store offers the lower total cost for the ladder? by how much? Show your work and explain your reasoning.
Answer: Part A , The total cost at hardware store is $371 and The total cost at online store is $355.2
Part B ,The hardware store offers the best price $336 by $3.2 less than the online store $339.2
Explanation:
Part A , The ladder cost at hardware store is $350 , with 6% tax ,
So, 6% of 350
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{350}\) = \(\frac{6}{100}\)
a = \(\frac{350 × 6}{100}\)
a = \(\frac{2100}{100}\)
a = 21
So, 21 is 6% of 350.
The total cost at hardware store is $350 + $ 21 = $371
The ladder cost at online store is $320 , with 6% tax ,
So, 6% of 320
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{320}\) = \(\frac{6}{100}\)
a = \(\frac{320 × 6}{100}\)
a = \(\frac{1920}{100}\)
a = 19.2
So,19.2 is 6% of 320.
Additionally shipping cost is 5% of $320
By using percent proportion , we have
\(\frac{a}{w}\) = \(\frac{p}{100}\)
\(\frac{a}{320}\) = \(\frac{5}{100}\)
a = \(\frac{320 × 5}{100}\)
a = \(\frac{1600}{100}\)
a = 16
So,16 is 5% of 320.
The total cost at online store is $320 + $ 19.2 + $16 = $355.2
Part B, If the hardware store offers 10% off
Then , We know , The sales price be 100% – 10% = 90% of the original price
sales price = 90% of 350
= 0.9 × 350 = 315
So, The sales price is $315 .
The 6% of 320 is $21
The total cost in hardware store after 10% off is $315 + $ 21 = $336
The online store offers free shipping and handling then the price will be $320 and 6% tax
So , 6% of 320 is $19.2
The total cost online store is $320 + $ 19.2 = $339.2
The hardware store offers the best price $336 by $3.2 less than the online store $339.2
Question 11.
Which graph represents the inequality – 5 – 3x ≥ – 11.
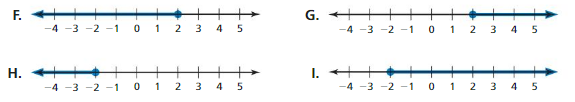
Answer: ![]()
Explanation:11
Option F represents the x value from -4 to 2
So , if x = -4 ,
Then – 5 – 3(-4) ≥ – 11
-5 + 12 ≥ – 11
7 ≥ – 11
if x = 2
– 5 – 3(2) ≥ – 11
-5 – 6 ≥ – 11
-11 ≥ – 11
So, option F represents the inequality – 5 – 3x ≥ – 11.
Final Conclusion:
We have given Big Ideas Math Answers Grade 7 Chapter 6 Percents Pdf free links here. Download BIM Grade 7 Chapter 6 Pdf from the direct links given in the above section. We wish you make use of the given information and score better marks in the exam. If you have any doubts you can easily clear them within the below-given comment section. All the best to all the candidates!!
