To enhance your knowledge you have to practice all the problems of Big Ideas Math Answers Grade 7 Chapter 8 Statistics. You can get the pdf’s of Big Ideas Math Book 7th Grade Answer Key Chapter 8 Statistics from bigideasmathanswers.com for free of cost. Refer to the Big Ideas Math Answers Grade 7 Chapter 8 Statistics book and score the maximum marks in the exam. Follow the reference problems and attend the exam with good preparation.
It is necessary to know the important questions according to the latest syllabus. Follow the complete article and you will come to know the various important points regarding Statistics. You can find the complete syllabus in one pdf of Big Ideas Math Book 7th Grade Solutions Chapter 8 Statistics. Maximize your scores with the help of the given information in the below sections.
Big Ideas Math Book 7th Grade Answer Key Chapter 8 Statistics
We provide the weightage key of each topic by which you can figure out the important topics and prepare a schedule according to it. The schedule helps you to prepare each topic within the time period. Know the various methods of solving each problem. Become perfect in the concept of statistics with the given solved examples, guide, exploration, and also the formulae, etc.
There are various topics involved in Statistics like Samples and Populations, Using Random Samples to Describe Populations, Comparing Populations, Using Random Samples to Compare Populations, Statistics, etc. Big Ideas Math Book 7th Grade Answer Key Chapter 8 Statistics pdf download link is available in the next sections. You can also get the video links to understand the concept more clearly.
Performance Task
Lesson: 1 Samples and Populations
Lesson: 2 Using Random Samples to Describe Populations
- Lesson 8.2 Using Random Samples to Describe Populations
- Using Random Samples to Describe Populations Homework & Practice 8.2
Lesson: 3 Comparing Populations
Lesson: 4 Using Random Samples to Compare Populations
- Lesson 8.4 Using Random Samples to Compare Populations
- Using Random Samples to Compare Populations Homework & Practice 8.4
Chapter: 8 – Statistics
Statistics STEAM Video/Performance Task
STEAM Video
Comparing Dogs
Although dogs and wolves are the same species, they can have very different characteristics. How are dogs and wolves similar?
Watch the STEAM Video “Comparing Dogs.” Then answer the following questions.

1. In the video, the dogs Devo and Etta are walking in a population park. Describe the of the dogs shown in the sample video. Then describe a of the dogs shown in the video. Explain your reasoning.
2. Dogs, wolves, and dingos are all the same species. This species is called Canis lupus
a. Describe one possible sample of the species. Explain your reasoning.
b. You want to know the average height of an animal in the Canis lupus species. Would you use the entire population of the species or would you use a sample to gather data? Explain.
c. The entire Canis lupus species is a sample of what population? Explain.
Answer:
1. In the video, the dogs Devo and Etta are walking in a population park. The population of the dogs is very big. They may differ from color, size, hair, size and skin yet they all are the same species. Here they have shown Canis Lupus bread dogs. They all are the same bone body structured dogs yet are differently living for their specification of work performance.
2. Dogs, wolves, and Dingo’s are all the same species. This species is called Canis lupus.
a. A wolf with a grey coat living in forested northern regions of North America is one possible sample of the species for Canis Lupus because they resemble like wolfs yet they match to dogs bone structure and near to dogs D.N.A.
b. If you want to know the average height of an animal in the Canis lupus species you should use a sample to gather data because they are grand children of extinct dogs species having same D.N.A yet different in color, shapes, hair because they having been changing from one generation to another.
c. The entire Canis lupus species is a sample of what population of mammals and under this genus he listed the dog-like carnivores including domestic dogs, wolves, and jackals.
Performance Task
Estimating Animal Populations
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given a double box-and-whisker plot that represents the weights of male and female gray wolves.
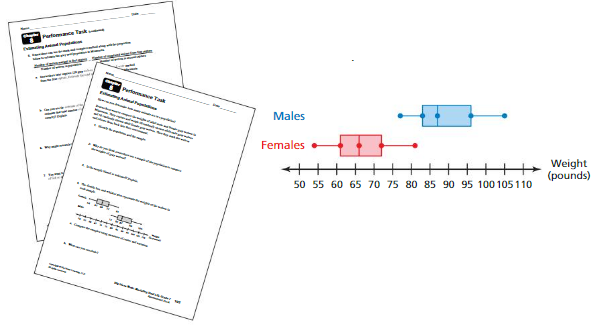
You will be asked to compare the weights of male and female gray wolves. Why might a researcher want to compare data from two different groups of wildlife?
Statistics Getting Ready for Chapter 8
Chapter Exploration
A population is an entire group of people or objects. A sample is a part of the population. You can use a sample to make an inference, or conclusion about a population.

1. Work with a partner. Identify the population and the sample in each pair.

Answer:
A population is an entire group of people or objects. A sample is a part of the population.
a) In the given picture, the school bus students is the population and the class room students is sample because individual class strength is used for collecting total school population.
b) In the given picture, the grizzly bear with GPS collars in a park is used as sample to collect the population of grizzly bear in a park.
c) In the given picture, 150 quarters coins are used as sample for the calculating all the total collection in all quarters circulation .
d) In the given picture, 10 fiction books in the library are used as sample to get the total count of all fiction books present in the library.
2. Work with a partner. When a sample is random, each member of the population is equally likely to be selected. You want to know the favorite activity of students at your school. Tell whether each sample is random. Explain your reasoning.
a. members of the school band
b. students in your math class
c. students who enter your school in a morning
d. school newspaper readers
Answer:
c) Students who enter your school in a morning is a random sample because every student data entering into the school is collected and can help to know the favorite activity of them.
Explanation:
2. a) Members of the school band is a not random sample because it gives only the data of the students in the school band not others.
b) Students in your math class is a not random sample because it gives the data of the students who like math.
c) Students who enter your school in a morning is a random sample because every student data entering into the school is collected and can help to know the favorite activity of them.
d) School newspaper readers is not a random sample because here it only collects the data of the students who are in that respective activity of newspaper readers not other students.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
population
unbiased sample
sample
biased sample
Lesson 8.1 Samples and Populations
A population is an entire group of people or objects. A sample is a part of a population. You can gain information about a population by examining samples of the population.
EXPLORATION 1
Using Samples of Populations
Work with a partner. You want to make conclusions about the favorite extracurricular activities of students at your school.

a. Identify the population. Then identify five samples of the population.
b. When a sample is selected at random, each member of the population is equally likely to be selected. Are any of the samples in part (a) selected at random? Explain your reasoning.
c. How are the samples below different? Is each conclusion valid? Explain your reasoning.

d. Write a survey question about a topic that interests you. How can you choose people to survey so that you can use the results to make a valid conclusion?
Answer:
Option B is correct to make conclusions about the favorite extracurricular activities of students at your school.
Explanation:
Option B is correct because the information is collected randomly and gives the accurate result conclusions about the favorite extracurricular activities of students at your school.
An unbiased sample is representative of a population. It is selected at random unbiased sample and is large enough to provide accurate data. A biased sample is not representative of a population. One or more parts of the population are favored over others

Try It
Question 1.
WHAT IF?
You want to estimate the number of twelfth-grade students in a high school who ride a bus to school. Which sample is unbiased? Explain.
Answer:
Option A is correct.
Explanation:
Option A is correct to collect the twelfth- grade population. Then identity five samples of the population n make a conclusion of the students who come in bus to school.
Question 2.
You want to estimate the number of eighth-grade students in your school who find it relaxing to listen to music. You consider two samples.
- fifteen randomly selected members of the band
- every fifth student whose name appears on an alphabetical list of eighth-grade students
Which sample is unbiased? Explain.
Answer:
Every fifth student whose name appears on an alphabetical list of eighth-grade students.
Explanation:
Every fifth student whose name appears on an alphabetical list of eighth-grade students is a unbiased sample because here it covers large data n gives us the correct data about the students who are relaxed while listening to music.
Question 3.
Four out of five randomly chosen teenagers support the new land fill. So, you conclude that 80% of the residents of your town support the new land fill. Is the conclusion valid? Explain.
Answer:
Yes, its a valid conclusion.
Explanation:
Yes, its a valid conclusion because 4 out of 5 people in the town means 80% of the people are supporting the new land bill mathematically.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
WRITING
You want to estimate the number of students in your school who play a school sport. You ask 40 honors students at random whether they play a school sport. Is this sample biased or unbiased? Explain.
Answer:
Yea, its a unbiased sample.
Explanation:
Yes, its a unbiased sample because it gives the information about the number of students who play a school sport in the school randomly and accurate data.
Question 5.
ANALYZING A CONCLUSION
You survey 50 randomly chosen audience members at a theater about whether the theater should produce a new musical. The diagram shows the results. You conclude that 80% of the audience members support production of a new musical. Is your conclusion valid? Explain.
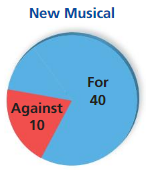
Answer:
Yes, its a valid conclusion.
Explanation:
Yes, its a valid conclusion because 80% of 50 people in the audience members at a theater is equal to 40 people, they support production of a new musical. Out of which 20% of 50 people is equal to 10 people, who are against the production of a new musical.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
You want to estimate the mean photo size on your cell phone. You choose 30 photos at random from your phone. The total size of the sample is 186 megabytes. Explain whether you can use the sample to estimate the mean size of photos on your cell phone. If so, what is your estimate?

Answer:
Yes, we can use it for sample to estimate the mean size of photos on your cell phone.
Explanation:
Yes, we can use it for sample to estimate the mean size of photos on your cell phone because it allows to estimate the size of the cell phone.
Mean size of photos = total size of the sample / photos chose
= 186 × 30
= 6.2 bytes.
Question 7.
DIG DEEPER!
You ask 50 randomly chosen employees of a company how many books they read each month. The diagram shows the results. There are 600 people employed by the company. Estimate the number of employees who read at least one book each month.
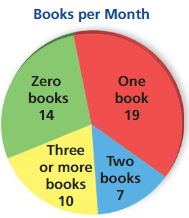
Answer:
Number of employees who read at least one book each month = 12
Explanation:
Total number of chosen employee = 50
Total number of people employed = 600
Number of employees who read at least one book each month = Total number of chosen employee / Total number of people employed
= 600 × 50
= 12.
Samples and Populations Homework & Practice 8.1
Review & Refresh
Design a simulation that you can use to model the situation. Then use your simulation to find the experimental probability.

Question 1.
The probability that a meal at a restaurant is overcooked is 10%. Estimate the probability that exactly 1 of the next 2 meals is overcooked.
Answer:
The probability that exactly 1 of the next 2 meals is overcooked = 3.34%
Explanation:
The probability that a meal at a restaurant is overcooked is 10%
The probability that exactly 1 of the next 2 meals is overcooked = out of 3 meals 1 meal is overcooked of 10%
= 1 × 3 × 10%
= 10 × 3 %
= 3.34 %
Question 2.
The probability that you see a butterfly during a nature center tour is 80%. The probability that you see a turtle is 40%. What is the probability of seeing both?
Answer:
The probability of seeing both = 60%
Explanation:
The probability that you see a butterfly during a nature center tour = 80%.
The probability that you see a turtle = 40%
The probability of seeing both = 80 % + 40%/2
= 120 × 2%
= 60%
Solve the inequality. Graph the solution.
Question 3.
2x – 5 < 9
Answer:
Graph:

Explanation:
2x – 5 < 9
add 5 on both sides
=> 2x – 5 + 5 < 9 + 5
=>2x < 14
=> Divide both sides by 2
=> 2x ÷ 2 < 14 ÷ 2
=> x < 7.
Question 4.
5q + 2 ≥ – 13
Answer:
Graph:

Explanation:
5q + 2 ≥ – 13
Subtract 2 from both sides
=> 5q + 2 – 2 ≥ – 13 – 2
=> 5q ≥ – 15
Divide both sides by 5
=> 5q ÷ 5 ≥ – 15 ÷ 5
=> q ≥ – 3
Question 5.
2 > 6 – 3r
Answer:
Graph :
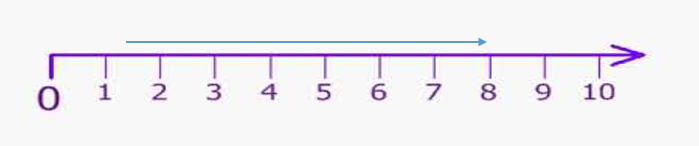
Explanation:
2 > 6 – 3r
subtract 6 from both sides.
2 – 6 > 6 – 3r – 6
=> -4 > -3r
=> -4 ÷ -3 > r
=> 1. 333 > r
Concepts, Skills, & Problem Solving
USING SAMPLES OF POPULATIONS You ask 50 randomly chosen artists in your town about their favorite art form. Determine whether your conclusion is valid. Justify your answer. Favorite Art Form(See Exploration 1, p. 325.)

Question 6.
You conclude that drawing is the favorite art form of 60% of artists in your town.
Answer:
The conclusion made is not valid that drawing is the favorite art form of 60% of artists in your town.
Explanation:
Total strength of town people = 50
Number of people interested in drawing = 20
Percentage of people interested in drawing = Total strength of town people \times Number of people interested in drawing
= 20 × 50 ×100
= 40%
Hence, the conclusion made is not valid that drawing is the favorite art form of 60% of artists in your town.
Question 7.
You conclude that ceramics is the favorite art form of 10% of people in your town.
Answer:
The conclusion made is valid that ceramics is the favorite art form of 10% of people in your town.
Explanation:
Total strength of town people = 50
Number of people interested in ceramics = 5
Percentage of people interested in drawing = Total strength of town people / Number of people interested in ceramics
= 5 × 50 × 100
= 10%
Hence, the conclusion made is valid that ceramics is the favorite art form of 10% of people in your town.
IDENTIFYING POPULATIONS AND SAMPLES Identify the population and the sample.
Question 8.
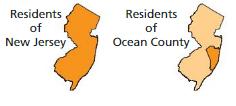
Answer:
Residents of New Jersey is the population.
Residents of Ocean Country is the sample.
Question 9.

Answer:
4 cards is the sample.
All cards in a desk is the population.
IDENTIFYING BIASED AND UNBIASED SAMPLES Determine whether the sample is biased or unbiased. Explain.
Question 10.
You want to estimate the number of books students in your school read over the summer. You survey every fourth student who enters the school.
Answer:
Its a unbiased sample.
Explanation:
You can estimate the number of students who are reading books over the summer by the survey every fourth student who enters the school because its a unbiased sample which gives you the accurate rate of information.
Question 11.
You want to estimate the number of people in a town who think that a park needs to be remodeled. You survey every 10th person who enters the park.
Answer:
Its a biased sample.
Explanation:
You cannot estimate the number of people in a town who think that a park needs to be remodeled by the survey asking every 10th person who enters the park because its a biased sample as every person entering into the park would like it to be remodeled and its not going to be accurate.
Question 12.
MODELING REAL LIFE
You want to determine the number of students in your school who have visited a science museum. You survey 50 students at random. Twenty have visited a science museum, and thirty have not. So, you conclude that40% of the students in your school have visited a science museum. Is your conclusion valid? Explain.

Answer:
Its a valid Conclusion that 40% of the students in your school have visited a science museum.
Explanation:
Total number of students the survey taken = 50
Number of students in visited science museum = 20
Number of students who did not visit science museum = 30
Percentage of students visited a science museum = Total number of students the survey taken – Number of students in visited science museum
= 20 ×50 × 100
= 40%
Question 13.
USING A SAMPLE
Which sample is better for making an estimate? Explain.

Answer:
Sample B -A random sample of 500 pencils from 1 machines is better than Sample A – A random sample of 500 pencils from 20 machines
Explanation:
Sample A = A random sample of 500 pencils from 20 machines.
Sample B = A random sample of 500 pencils from 1 machines.
Sample B -A random sample of 500 pencils from 1 machines is better than Sample A – A random sample of 500 pencils from 20 machines because its gives us the accurate and sufficient data of pencils produced and how many are defective among them. Its a biased sample with correct data.
CONDUCTING SURVEYS Determine whether you should survey the population or a sample. Explain.
Question 14.
You want to know the average height of seventh graders in the United States.
Answer:
Survey on sample of the seventh graders should be taken.
Explanation:
Survey on sample of the seventh graders should be taken because the total population in United States is very large and its very difficult to survey on the population. Sample survey will be easy and we can get the information regarding the average height of seventh graders in the United States accurately.
Question 15.
You want to know the favorite types of music of students in your homeroom.
Answer:
Survey on Population should be taken.
Explanation:
Survey on the population in your homeroom should be taken because its a very small area of some limited people and its better to take than sample survey to know the favorite types of music of students.
Question 16.
CRITICAL THINKING
Does increasing the size of a sample necessarily make the sample more representative of a population? Give an example to support your explanation.
Answer:
Yes, increasing the size of the sample necessarily makes the sample more representative of a population. A representative sample is a group or set chosen from a larger statistical population according to specified characteristics. A random sample is a group or set chosen in a random manner from a larger population.
Explanation:
Yes, increasing the size of the sample necessarily makes the sample more representative of a population lead to more accurate or representative results at the same time when it comes to surveying large populations, bigger isn’t always better.
For Example:
You want to know the average height of students in the UK .
Question 17.
LOGIC
A person surveys residents of a town to determine whether a skateboarding ban should be overturned. Describe how the person can conduct the survey so that the sample is biased toward overturning the ban.
Answer:
Yes, the sample is biased toward overturning the ban.
Explanation:
If the person takes the survey on a skateboarding ban should be overturned from every tenth person living in a town then the person surveys is going to be a biased sample toward overturning the ban because every tenth person wishes to overturning on the ban.
Question 18.
MODELING REAL LIFE
You ask 20 randomly chosen environmental scientists from your state to name their favorite way to eliminate waste. There are 200 environmental scientists in your state. Estimate the number of environmental scientists in your state whose favorite way to eliminate waste is recycling.

Answer:
Number of environmental scientists in your state whose favorite way to eliminate waste is recycling = 20
Explanation:
Total number of scientists in your state = 200
Number of scientists randomly ask in your state = 20
Out of 20 randomly asked scientists whose favorite way to eliminate waste is recycling = 2
=> 2 × 20 = 10%
Number of environmental scientists in your state whose favorite way to eliminate waste is recycling = Total number of scientists in your state x Out of 20 randomly asked scientists whose favorite way to eliminate waste is recycling \times100
= 200 × 10 × 100 = 20.
Question 19.
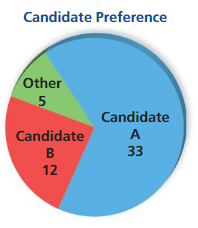
MODELING REAL LIFE
To predict the result of a mayoral election, you survey 50 likely voters at random. The diagram shows the results. Describe whether the sample can be used to predict the outcome of the election. If so, what is your prediction for the number of votes received by the winner assuming that500 people vote?
Answer:
Yes, the sample can be used to predict the outcome of the election because it lets us know how voters are going to vote and whose going to be the winner.
Number of votes candidate A gets = 330
Explanation:
Number of voters randomly taken in the survey = 50
Total number of people voting = 500
Yes, the sample can be used to predict the outcome of the election because it lets us know how voters are going to vote and whose going to be the winner.
According to survey candidate A gets 33 out of 50.
=> 33 ÷ 50 ×100 = 66 %
According to survey candidate B gets 12 out of 50.
=> 12 ÷ 50 ×100 = 24%
According to survey others gets 5 out of 50.
=> 5 ÷ 50 ×100 = 10%
So, the winner according to survey prediction is candidate A.
Number of votes candidate A gets = 66% of 500
=> 330 votes.
Question 20.
DIG DEEPER!
You ask 100 randomly chosen dog owners in your town how many dogs they own. The results are shown in the table. There are 500 dog owners in your town.
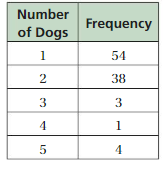
a. Estimate the median number of dogs per dog owner in your town. Justify your answer.
b. Estimate the mean number of dogs per dog owner in your town. Justify your answer.
Answer:
a) The median number of dogs per dog owner in your town = 4.
b) The mean number of dogs per dog owner in your town = 20.
Explanation:
a) The median is the middle number in a sorted, ascending or descending, list of numbers and can be more descriptive of that data set than the average.
The sorted order of the frequency = 1 3 4 38 54
The median number of dogs per dog owner in your town = 4
b) Explanation:
The mean is the average of the numbers.
Number of listed dogs = 5
Total sum of the frequency of the dogs listed = 54 + 38 + 3 + 1 + 4 = 100
The mean number of dogs per dog owner in your town = 100 ÷ 5 = 20
Lesson 8.2 Using Random Samples to Describe Populations
EXPLORATION 1
Exploring Variability in Samples
Work with a partner. Sixty percent of all seventh graders have visited a planetarium.
a. Design a simulation using packing peanuts. Mark 60% of the packing peanuts and put them in a paper bag. What does choosing a marked peanut represent?

b. Simulate a sample of 25 students by choosing peanuts from the bag, replacing the peanut each time. Record the results.
c. Find the percent of students in the sample who have visited a planetarium. Compare this value to the actual percent of all seventh graders who have visited a planetarium.
d. Record the percent in part(c) from each pair in the class. Use a dot plot to display the data. Describe the variation in the data.

Try It
Question 1.
Use each sample to make an estimate for the number of students in your school who prefer rap music. Describe the center and the variation of the estimates.
Answer:
The Variance is defined as the average of the squared differences from the Mean.
The center of the estimates = 2
The variation of the estimates = 0.64
The Standard Deviation of the estimates = 0.8
Explanation:
Survey randomly took in the school = 20
Total number of students in the school = 840
Number of students who choose rap music by me = 1
Number of students who choose rap music by friend A = 2
Number of students who choose rap music by friend B = 1
Number of students who choose rap music by friend C = 1
Number of students who choose rap music by friend D = 3
The center of the estimates = 1 2 3 = 2
Mean of the estimates = 1+ 2 + 1 + 1 + 3 ÷5= 8 ÷ 5 = 1.6
The variation of the estimates = (1- 1.6)^2 + (2 – 1.6)^2 +(1- 1.6)^2 + (1- 1.6)^2 + (3 – 1.6)^2 ÷ 5
= (-0.6)^2 + (0.4)^2 + (-0.6)^2 + (-0.6)^2 + (1.4)^2 ÷ 5
= 0.36 + 0.16 + 0.36 + 0.36 + 1.96 ÷ 5
= 3.20 ÷ 5
= 0.64
The Standard Deviation of the estimates = \sqrt{0.64} = 0.8
Question 2.
Repeat Example 2, but estimate the medians instead of the means.
Answer:
Median of the students who choose pop music = 5
Explanation:
The six estimates are that students with part time jobs work = 5 7 7 3 7 7
8 and 9 hours per week. The estimates have an average range from 9 – 5 = 4 hours.
Sorted estimates that students with part time jobs work = 3 5 7
Median of the students who choose pop music = 5
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
USING MULTIPLE RANDOM SAMPLES
Use each sample in Example 1 to make an estimate for the number of students in your school who prefer rock music. Describe the variation of the estimates.
Answer:
The variation of the estimates = 1.84
Explanation:
Estimate for the number of students in your school who prefer rock music = 4 7 5 4 3
Sorted estimate for the number of students in your school who prefer rock music = 3 4 5 7
Mean of the estimate for the number of students in your school who prefer rock music = 4 +7 +5 +4 +3 ÷ 5
= 4.6
The variation of the estimates = (4-4.6)^2 + ( 7-4.6)^2 + ( 5 – 4.6)^2 + ( 4-4.6)^2 + ( 3 – 4.6)^2 ÷ 5
= (-0.6)^2 + ( 2.4)^2 + ( 0.4)^2 + (-0.6)^2 + (- 1.6)^2 ÷ 5
= 0.36 + 5.76 + 0.16 + 0.36 + 2.56 ÷ 5
= 9.2 ÷ 5
= 1.84
Question 4.
ESTIMATING AN AVERAGE OF A POPULATION
You want to know the mean number of hours music students at your school practice each week. At each of three music classes you randomly survey 10 students. Your results are shown. Use all three samples to make one estimate for the mean number of hours music students practice each week.

Answer:
Mean value of hours for number of students practiced for each week for all three classes A,B,C
= 4.93
Explanation:
Mean value of hours for number of students practiced for each week of class A
= 6 + 5 + 5 + 6 + 4 + 6 + 8 + 5 + 5 + 2+ 6 \div 10
= 58 ÷ 10
= 5.8
Mean value of hours for number of students practiced for each week of class B
= 0 + 6 + 6 + 5 + 4 + 5 + 6 + 3 + 4 + 9 ÷ 10
= 48 ÷ 10
=4.8
Mean value of hours for number of students practiced for each week of class C
= 4 + 5 + 6 + 4 + 3 + 2 + 2 + 3 + 12 + 1 ÷ 10
= 42 ÷10
= 4.2
Mean value of hours for number of students practiced for each week for all three classes A,B,C
= 5.8 + 4.8 + 4.2 ÷3
= 14.8 ÷ 3
= 4.93
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
Repeat Example 3 with the assumption that 50% of all seventh graders have visited a planetarium.
Answer:
So, most of the samples are within 10% of the actual population that of all seventh graders have visited a planetarium.
Explanation:
The actual percentage of 60% , the number of samples is 200 and the sample size is 50.
The estimates are clustered around 50% , most are between 45 and 60.
So, most of the samples are within 10% of the actual population.
Question 6.
Forty percent of all seventh graders have visited a state park. How closely do 200 random samples of 50 students estimate the percent of seventh graders who have visited a state park? Use a simulation to support your answer.

Answer:
Its a biased sample of 200 random samples of 50 students for estimating the percent of seventh graders who have visited a state park.
Explanation:
40% of the all seventh graders have visited a state park.
Total samples taken = 200
Number of students randomly taken = 50
Its a biased sample of 200 random samples of 50 students for estimating the percent of seventh graders who have visited a state park because it does not gives the correct information of the seventh graders and they may or may not be the visitors of the park.
Using Random Samples to Describe Populations Homework & Practice 8.2
Review & Refresh
You ask 100 randomly chosen high school students whether they support a new college in your town. Determine whether your conclusion is valid.
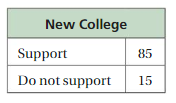
Question 1.
You conclude that 85% of high school students in your town support the new college.
Answer:
No, its not a valid conclusion.
Explanation:
Because it is randomly chosen for only 100 people for one set.
It can be 85 do not support for another set of 100 people who are randomly chosen.
You support the statement if total 85 % of the people in the town support the new college .
Question 2.
You conclude that 15% of residents in your town do not support the new college.
Answer:
No, its not a valid conclusion.
Explanation:
No, its not a valid conclusion because this percentage which is taken is only for respected chosen students not on the total population of the town who does not prefer new colleges in the town.
Write and solve a proportion to answer the question.
Question 3.
What percent of 30 is 12?
Answer:
3.6 is the percent of 30 is 12.
Explanation:
30 = 100 %
X = 12
Cross multiply the equation
=> X × 100 = 30 × 12
=> X × 100 = 360
=> X = 360 × 100
=> X = 3.6
Question 4.
17 is what percent of 68?
Answer:
25 percent of 68 is 17.
Explanation:
68 = 100%
17 = X%
Cross multiply the equation
X × 68 = 17 × 100
=> X × 68 = 1700
=> X = 1700 ÷ 68
=> X = 25
Concepts, Skills, & Problem Solving
EXPLORING VARIABILITY IN SAMPLES Thirty percent of all seventh graders own a bracelet. Explain whether the sample closely estimates the percentage of seventh graders who own a bracelet. (See Exploration 1, p. 331.)

Question 5.
50 seventh graders, 14 own a bracelet
Answer:
Its not a valid conclusion that 50 seventh graders 14 own a bracelet.
Explanation:
Thirty percent of all seventh graders own a bracelet.
30 percent of 50 seventh graders.
=> 30 × 50 ÷ 100
=> 1500 ÷ 100
=> 15.
Its not a valid conclusion that 50 seventh graders 14 own a bracelet because 15 out of 30 own a bracelet.
Question 6.
30 seventh graders, 3 own a bracelet
Answer:
Its not a valid conclusion that 30 seventh graders 3 own a bracelet.
Explanation:
30 percent of 30 seventh graders.
30 × 30 ÷ 100
=> 900 ÷ 100
=> 9.
Question 7.
USING MULTIPLE RANDOM SAMPLES
A store owner wants to know how many of her 600 regular customers prefer canned vegetables. Each of her three cashiers randomly surveys 20 regular customers. The table shows the results.
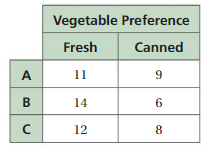
a. Use each sample to make an estimate for the number of regular customers of the store who prefer fresh vegetables.
b. Describe the variation of the estimates.
Answer:
a) The Estimation for the number of regular customers of the store who prefer fresh
vegetables = 47.
b) The variation of the estimates = 12.6889.
Explanation:
a) Total number of regular customers to the store = 600
Total number of cashier who takes the survey = 3
Number of customers they have taken survey = 3 × 20 = 60
According to the three survey, number of customers who willing to take fresh vegetables
= (11 + 14 + 12) = 47
b. Describe the variation of the estimates.
Mean of estimates = (11 + 14 + 12) ÷ 3 = 47 ÷ 3 = 15.67
Variation of the estimates = (11 – 15.67)^2 + (14 – 15.67)^2 + (12 – 15.67)^2 ÷ 3
= ( -4.67)^2 + (-1.67)^2 + (-3.67)^2 ÷ 3
= 21.8089 + 2.7889 + 13.4689 ÷ 3
= 38.0667 ÷ 3
= 12.6889
Question 8.
USING MULTIPLE RANDOM SAMPLES
An arcade manager wants to know how many of his 750 regular customers prefer to visit in the winter. Each of five state members randomly surveys 25 regular customers. The table shows the results.
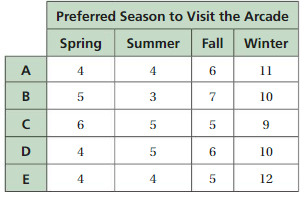
a. Use each sample to make an estimate for the number of regular customers who prefer to visit in the winter.
b. Describe the variation of the estimates.
Answer:
a) An estimate for the number of regular customers who prefer to visit in the winter according to survey sample = 52.
b) Variation of the estimates = 1.04
Explanation:
a) Total number of regular customers who prefer to visit in the winter taken in the five survey sample = 25 × 5 = 125
An estimate for the number of regular customers who prefer to visit in the winter according to survey sample = 11 + 10 +9 + 10 +12
= 52
b) Mean of estimates = 11 + 10 +9 + 10 +12 ÷ 5 = 52 ÷ 5 = 10.4
Variation of the estimates = (11 – 10.4)^2 + ( 10 -10.4)^2 + (9 – 10.4)^2 + ( 10 – 10.4)^2 + ( 12 -10.4)^ 2 ÷5
= ( 0.6)^2 + ( -0.4)^2 + ( -1.4)^2 + ( -0.4)^2 + (1.6)^2 ÷5
= 0.36 + 0.16 + 1.96 + 0.16 + 2.56 ÷5
= 5.2 ÷5
= 1.04
Question 9.
ESTIMATING A MEAN OF A POPULATION
A park ranger wants to know the mean number of nights students in your school plan to camp next summer. The park ranger randomly surveys 10 students from each class. The results are shown.
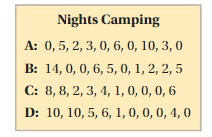
a. Use each sample to make an estimate for the mean number of nights students in your school plan to camp next summer. Describe the variation of the estimates.
b. Use all four samples to make one estimate for the mean number of nights students plan to camp next summer.
Answer:
a) The variation of the estimates is quite increasing from one to other sample.
b) One estimate for the mean number of nights students plan to camp next summer = 3.3.
Explanation:
a) Mean value of Sample A= 0+5+2+3+0+6+0+10+3+0 ÷ 10 = 29 ÷ 10 = 2.9
Variation of Sample A= (0-2.9)^2 + (5-2.9)^2 + (2-2.9)^2 + (3-2.9)^2 + (0-2.9)^2 + (6-2.9)^2 + (0-2.9)^2 + (10-2.9)^2 + (3-2.9)^2 + (0-2.9)^2 ÷ 10
= (-2.9)^2 + (2.1)^2 + (-0.9)^2 + (0.1)^2 + (-2.9)^2 + (3.1)^2 + (-2.9)^2 + (3.1)^2 + (0.1)^2 + (-2.9)^2 ÷ 10
= 8.41 + 4.41 + 0.81 + 0.01 + 8.41 + 9.61 + 8.41 + 9.61 +0.01 + 8.41 ÷ 10
= 58.1 ÷ 10
=5.81
Mean value of Sample B= 14+0+0+6+5+0+1+2+2+5 ÷ 10 = 35 ÷ 10 = 3.5
Variation of Sample B= (14-3.5)^2 + (0-3.5)^2 + (0-3.5)^2 + (6-3.5)^2 + (5-3.5)^2 + (0-3.5)^2 + (1-3.5)^2 + (2-3.5)^2 + (2-3.5)^2 + (5-3.5)^2 ÷ 10
= (10.5)^2 + (-3.5)^2 + (-3.5)^2 + (2.5)^2 + (1.5)^2 + (-3.5)^2 + (-2.5)^2 + (-1.5)^2 + (-1.5)^2 + (1.5)^2 ÷ 10
= 110.25 + 12.25 + 12.25 + 6.25 + 2.25 + 12.25 + 6.25 +2.25 + 2.25 +2.25 ÷ 10
= 168.5 ÷ 10
= 16.85
Mean value of Sample C = 8+8+2+3+4+1+0+0+0+6 ÷ 10 = 32 ÷ 10 = 3.2
Variation of Sample C= (8-3.2)^2 + (8-3.2)^2 + (2-3.2)^2 + (3-3.2)^2 + (4-3.2)^2 + (1-3.2)^2 + (0-3.2)^2 + (0-3.2)^2 + (0-3.2)^2 + (6-3.2)^2 ÷ 10
= (4.8)^2 + (4.8)^2 + (-1.2)^2 + (-0.2)^2 + (0.8)^2 + (-2.2)^2 + (-2.2)^2 + (-2.2)^2 + (-3.2)^2 + (2.8)^2 ÷ 10
= 23.04 + 23.04 + 1.44 + 0.04 + 0.64 + 4.84 + 4.84 + 4.84 + 10.24 + 7.84 ÷ 10
= 80.8 ÷ 10
= 8.08
Mean value = 10+10+5+6+1+0+0+0+4+0 ÷ 10 = 36 ÷ 10 = 3.6
Variation of Sample D= (10-3.6)^2 + (10-3.6)^2 + (5-3.6)^2 + (6-3.6)^2 + (1-3.6)^2 + (0-3.6)^2 + (0-3.6)^2 + (0-3.6)^2 + (4-3.6)^2 + (0-3.6)^2 ÷ 10
= (6.4)^2 + (6.4)^2 + (1.4)^2 + (2.4)^2 + (-2.6)^2 + (-3.6)^2 + (-3.6)^2 + (-3.6)^2 + (0.4)^2 + (-3.6)^2 ÷ 10
= 40.96 + 40.96 + 1.96 + 5.76 + 6.76 + 12.96 + 12.96 + 12.96 + 0.16 +12.96 ÷ 10
= 148.4 ÷ 10
= 14.84
b) One estimate for the mean number of nights students plan to camp next summer
= 2.9 +3.5+3.2+3.6 ÷ 4
= 13.2 ÷ 4
= 3.3
Question 10.
ESTIMATING A MEDIAN OF A POPULATION
Repeat Exercise 9, but estimate the medians instead of the means.
Answer:
Median value of Sample A = 3 + 5 ÷2 = 8 ÷ 2 = 4.
Median value of Sample B = 2 + 5 ÷2 = 7 ÷ 2 = 3.5.
Median value of Sample C = 3 + 4 ÷ 2 = 7 ÷ 2 = 3.5.
Median value of Sample C = 4 + 5 ÷ 2 = 9 ÷ 2 = 4.5.
Explanation:
Sample A= 0+5+2+3+0+6+0+10+3+0
Ascending order of Sample A= 0 2 3 5 6 10
Median value of Sample A = 3 + 5 ÷2 = 8 ÷ 2 = 4
Sample B = 14+0+0+6+5+0+1+2+2+5
Ascending order of Sample B = 0 1 2 5 6 14
Median value of Sample B = 2 + 5 ÷2 = 7 ÷ 2 = 3.5
Sample C = 8+8+2+3+4+1+0+0+0+6
Ascending order of Sample C = 0 1 2 3 4 6 8
Median value of Sample C = 3 + 4 ÷ 2 = 7 ÷ 2 = 3.5
Sample D = 10+10+5+6+1+0+0+0+4+0
Ascending order of Sample D = 0 1 4 5 6 10
Median value of Sample C = 4 + 5 ÷ 2 = 9 ÷ 2 = 4.5
Question 11.
DESCRIBING SAMPLE VARIATION
Fifty-five percent of doctors at a hospital prescribe a particular medication. A simulation with 200 random samples of 50 doctors each is shown. Describe how the sample percentages vary.
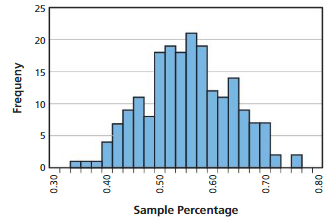
Answer:
There is a lot of change in the range of the sample percentages with respective to the frequency. The graph increases from 0 range and reaches to the highest range and later it declines to zero in the last.
Explanation:
The range of sample variation of frequency from 0.30 to 0.50 is from 0 to 18, here the graph range constantly increases from low to some extent.
The range of the sample variation of frequency from 0.50 to 0.60 is from 18 to 22, here the graph range continuously increased and reached to the highest range and declines to middle range.
The range of the sample variation of frequency from 0.60 to 0.80 is from 18 to 0 , here the graph declines and in between its increases and in the last it declines to zero completely.
Question 12.
MODELING REAL LIFE
Sixty percent of vacationers enjoy water parks. Use technology to generate 20 samples of size 100. How closely do the samples estimate the percent of all vacationers who enjoy water parks?
Answer:
Samples vary slightly in terms of their estimation of the percent of all vacationers who enjoy water parks compared to the people who does not enjoy the water parks. Out of 2000 total vacationers, 50.65% of people loves the water parks that compared to 49.35% of the people who does not like water parks.
Explanation:
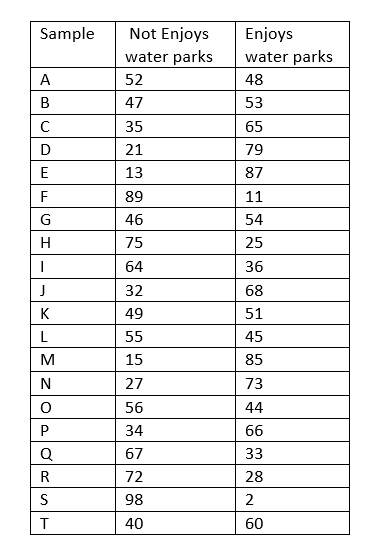
Total number of vacationers = 20 × 100 = 2000
Total number of vacationers who enjoys the water parks = 48 + 53+ 65 + 79+ 87 +11 + 54 + 25 + 36 + 68 + 51 + 45 + 85 + 73 + 44 + 66 + 33 + 28 + 2 + 60 = 1013
Percent of Total number of vacationers who enjoys the water parks = 1013 ÷2000 ×100
= 50. 65 %
Total number of vacationers who enjoys the water parks = 52 + 47 + 35 + 21 + 13 + 89 + 46 + 75 + 64 + 32 + 49 + 55 + 15 + 27 + 56 + 34 + 67 + 72 + 98 + 40 = 987.
Percent of Total number of vacationers who enjoys the water parks = 987 ÷2000 ×100
= 49.35%
Question 13.
MODELING REAL LIFE
Thirty percent of all new wooden benches have a patch of chipped paint. Use technology to simulate 100 random samples of 10 wooden benches. How closely do the samples estimate the percent of all wooden benches with a patch of chipped paint?

Answer:
The samples estimate the percent of all wooden benches with a patch of chipped paint are completely differ because almost 79 % are having chipped paint on the wooden bench and 21 % does not have chipped paint on the wooden bench. Majority goes with yes.
Explanation:

This means 79% of the students are having patch of chipped paint and 21% of the students are not having patch of chipped paint.
Question 14.
DIG DEEPER!
You want to predict whether a proposal will be accepted by likely voters. You randomly sample 3 different groups of 100 likely voters. The results are shown. Do you expect the proposal to be accepted? Justify your answer.

Answer:
No, I think proposal is not to be accepted because out of 300 people opposing people strength is more than supporting people the proposal.
Explanation:
Number of people in the each group = 100
Total number of people in the three groups = 3 × 100 = 300
Number of people who are supporting the proposal in three samples A, B and C
= 48 + 52 +47 = 147
Number of people who are opposing the proposal in three samples A, B and C
= 52 + 48 + 53 = 153
No, I think proposal is not to be accepted because out of 300 people opposing people strength is more than supporting people the proposal.
Question 15.
CRITICAL THINKING
Explain why public opinion polls use sample sizes of more than 1000 people instead of using a smaller sample size.
Answer:
Public opinion polls use sample sizes of more than 1000 people instead of using a smaller sample size because sampling more than 1000 people normally wont add much to the accuracy given the extra time an money it would cost.
Explanation:
Opinion polls are usually designed to represent the opinions of a population by conducting a series of questions and then extrapolating generalities in ratio or within confidence intervals.
Public opinion polls use sample sizes of more than 1000 people instead of using a smaller sample size because sampling more than 1000 people normally wont add much to the accuracy given the extra time an money it would cost.
For example, in a population of 5000, 10% would be 500. In a population of 200,000, 10% would be 20,000. This exceeds 1000, so in this case the maximum would be 1000. Even in a population of 200,000, sampling 1000 people will normally give a fairly accurate result.
Lesson 8.3 Comparing Populations
EXPLORATION 1
Comparing Two Data Distributions
Work with a partner.
a. Does each data display show? Explain.
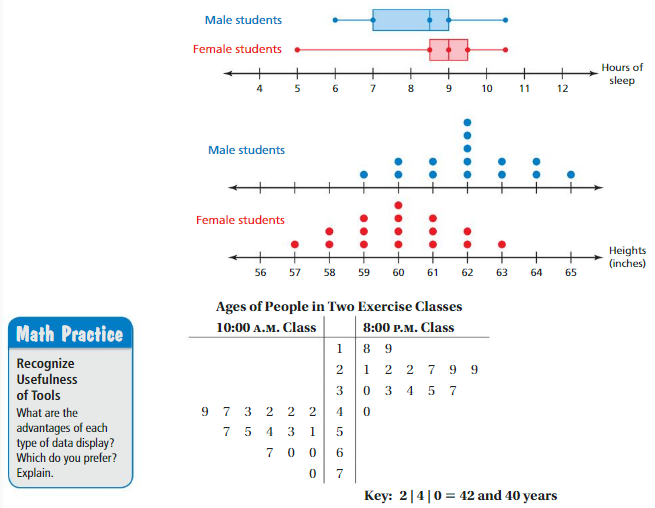
b. How can you describe the overlap of two data distributions using words? How can you describe the overlap numerically?
c. In which pair of data sets is the difference in the measures of center the most significant? Explain your reasoning.
Answer:
a) Yes, the female students and male students data is overlapping as they are having same common sleeping hours in them from 8.5 to 10.5 hours and other data distribution gets overlapping from 59 to 63 inches.
b) The data distribution hours for sleeping for both female and male students is commonly same and in the heights both of them are completely different as they is no common height point in them as same. The female students and male students data is overlapping as they are having same common sleeping hours in them from 8.5 to 10.5 hours. Here, the data distribution gets overlapping from 59 to 63 inches.
c) There is a lot of difference in the graph of age chart data distribution that of the first and second data distribution because in the center of 4, there is a big difference of 25 in this set.
Explanation:
a) Overlap means to have something in common with. Female students sleeping hours starts from 5 to 10.5 hours, whereas male students sleeping hours starts from 6 to 10.5 hours. The female students and male students data is overlapping as they are having same common sleeping hours in them from 8.5 to 10.5 hours.
b) In the first data distribution, Female students and male students maximum sleep for 4 hours. Female students sleeping hours are maximum from 5 to 9 hours and male students sleeping hours are maximum from 6 to 8.5 hours. In the second distribution, Female students height starts from 57 to 63 inches. Male students height starts from 59 to 65 inches. Here, the data distribution gets overlapping from 59 to 63 inches. Maximum height of male students is 62 inches whereas female students is 60 inches.
c) The data distribution in the center is more significant because it shows almost same difference. the center difference in data set 1 of 9.5 – 8.5 = 1hour for female students and male students 9 – 7 = 2hours. And maximum height of the both female and male students and who attended the class more. In the chart, the center of difference of exercises at the center of 4, class of 10am has total 9+7+3+2+2+2= 25 and the 8pm class strength is zero, which is a big difference in this set.
Try It
Question 1.
Which data set is more likely to contain a value of 70?
Answer:
No data sets has more likely to contain a value of 70 in them.
Explanation:
About 25% in the data set A data values are between 80 to 130.
About 50% in the data set B data values are between 80 to 100.
Question 2.
Which data set is more likely to contain a value that differs from the center by no more than 3?
Answer:
Data set B has more likely to contain a value that differs from the center by no more than 3.
Explanation:
Data set A center is 60.
Data set B center is 90.
Difference in the intervals from center of set A = 60 to 30 = 3
Difference in the intervals from center of set B = 90 to 80=1
Question 3.
WHAT IF?
Each value in the dot plot for Data set A increases by 30. How does this affect your answers? Explain.
Answer:
If each value in the dot plot for Data set A increases by 30 there is going to be a difference of 2 increased value in the mean value and MAD Value of both the Data Sets.
Explanation:
Data Set A Data Set B
Mean = 810 ÷ 15 = 54 Mean = 420 ÷ 15 = 28
MAD = 244 ÷ 15 = 16 MAD = 236 ÷ 15 = 16
Difference in Mean ÷ MAD = 26 ÷ 16 = 1.6
If 30 increased in Data Set A:
=> Mean = 810+30 ÷ 15 = 840 ÷ 15 = 56
=> MAD = 244 + 30 ÷ 15 = 274 ÷ 15 = 18.267
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
COMPARING POPULATIONS
The double dot plot shows two data sets. Compare the data sets using measures of center and variation. Then express the difference in the measures of center as a multiple of the measure of variation.
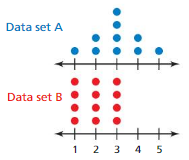
Answer:
So, the difference in the means is about 1.25 times the MAD.
Explanation:
Total value of Data Set A = 1 +2+2+3+3+3+3+4+4+5 = 30
Mean of Data Set A = 30 ÷ 10 = 3
MAD of Data Set A = |∣−3∣ + |2−3∣ +|2−3∣ +|3−3∣ +|3−3∣ + |3−3∣ + |3−3∣ + |4−3∣ + |4−3∣ + |5−3∣ ÷ 10
= 2 + 1 + 1 + 0 + 0 + 0 + 0 + 0+ 1 + 1 +2 ÷ 10
= 8 ÷ 10
= 0.8
Variance of Data Set A :
= (1 – 3 )^2 + (2 – 3 )^2 + (2 – 3)^2 + (3 – 3)^2 + (3 – 3)^2 + (3 – 3)^2 + (3 – 3)^2 + (4 – 3)^2 + (4 – 3)^2 +
(5 -3)^2 ÷10
= (-2)^2 + (-1)^2 + (-1)^2 + (0)^2 + (0)^2 + (0)^2 + (0)^2 + (1)^2 + (1)^2 + (2)^2 ÷10
= 4 + 1 + 1 + 0 + 0 + 0 + 0 + 1 +1 + 4 ÷10
= 12 ÷10
= 1.2
Total value of Data Set B = 1+1+1+1+2+2+2+2+3+3+3+3 = 24
Mean of Data Set B = 24 ÷ 12 = 2
MAD of Data Set B = |∣−2∣ + |1−2∣ +|1−2∣ +|1−2∣ +|2−2∣ + |2−2∣ + |2−2∣ + |2−2∣ + |3−2∣ + |3−2∣ + |3−2∣ + |3−2∣ ÷ 12
= 1 + 1 + 1 + 1 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1
= 8
= 0.8
Variance of Data Set B :
(1 -2)^2 + (1 -2)^2 + (1 -2)^2 + (1 -2)^2 + (2 – 2)^2 + (2 – 2)^2 + (2 – 2)^2 + (2 – 2)^2 + (3 -2)^2 +
(3 -2)^2 + (3 -2)^2 + (3 -2)^2 ÷12
= (-1)^2 + (-1)^2 + (-1)^2 + (-1)^2 + (0)^2 + (0)^2 + (0)^2 + (0)^2 + (1)^2 + (1)^2 + (1)^2 + (1)^2 ÷12
= 1 + 1 + 1 + 1 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1 ÷ 12
= 8 ÷ 12
= 0.67
Difference in mean ÷ MAD = 3 – 2 ÷ 0.8 = 1 ÷ 0.8 = 1.25
So, the difference in the means is about 1.25 times the MAD.
Question 5.
WHICH ONE DOESN’T BELONG?
You want to compare two populations represented by skewed distributions. Which measure not does belong with the other three? Explain your reasoning.

Answer:
IQR of first data set does not belong to the other three measurements because its the difference between the first and third quartiles, whereas median is related to the center value of the data and MAD of a data set is the average distance between each data value and the mean.
Explanation:
Data of first set = 1 2 4
Median of first data = 2
Data of second set = 3
Median of second data = 3
MAD of second data set = 0.8
IQR of first data set = 4 – 1 = 3
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
The double box-and-whisker plot represents the weights of cats at two shelters. Are the cats significantly heavier at one shelter than at the other? Explain.
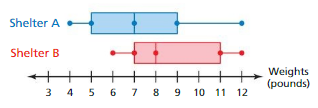
Answer:
The cats are not significantly heavier at one shelter than at the other.
Explanation:
Data of cats weights in shelter A = 4 5 7 9 12 pounds
Data of cats weights in shelter B = 6 7 8 11 12 pounds
Median of shelter A cats = 7 Median of shelter B cats = 8
IQR of shelter A cats = 9 – 5 = 4 IQR of shelter B cats =11 – 7 = 4
Because the variables are same, you can describe the vision overlap by the expression of the difference in the medians as a multiple of the IQR .
Difference in Median ÷ IQR = 8 – 7 ÷ 4 = 1 ÷ 4 = 0.25
Because the quotient is less than 2, the difference in the medians is not significant.
The cats are not significantly heavier at one shelter than at the other.
Question 7.
DIG DEEPER!
Tornadoes in Region A travel significantly farther than tornadoes in Region B. The tornadoes in Region A travel a median of 10 miles. Create a double box-and-whisker plot that can represent the distances traveled by the tornadoes in the two regions.
Answer:
Double box-and-whisker plot that can represent the distances traveled by the tornadoes in the two regions.
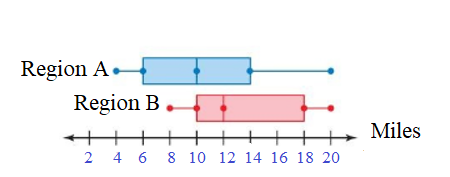
Explanation:
Data of Tornadoes in Region A = 4 6 10 14 20
Median of Tornadoes in Region A = 10 miles
Data of Tornadoes in Region B = 8 10 12 18 20
Median of Tornadoes in Region B =12
Comparing Populations Homework & Practice 8.3
Review & Refresh
Twenty percent of all seventh graders have watched a horse race. Explain whether the sample closely estimates the percentage of seventh graders who have watched a horse race.

Question 1.
In a sample of 15 seventh graders, 4 have watched a horse race.
Answer:
No, the sample estimation of the percentage of 15 seventh graders who have watched a horse race is not valid.
Explanation:
Number of seventh graders = 15
Twenty percent of all seventh graders have watched a horse race.
=> 20 % of the number of seventh graders = 20 % × 15 = 3
Hence, 3 only watched the horse race not 4.
Question 2.
In a sample of 10 seventh graders, 6 have watched a horse race.
Answer:
No, the sample estimation of the percentage of 10 seventh graders who have watched a horse race is not valid.
Explanation:
Number of seventh graders = 10
Twenty percent of all seventh graders have watched a horse race.
=> 20 % of the number of seventh graders = 20 % × 10 = 2
Hence, 2 only watched the horse race not 6.
Find the unit rate.
Question 3.
60 kilometers in 2 hours
Answer:
60 kilometers in 2 hours = 30 kilometer per hour.
Explanation:
Time taken to cover 60 kilometers = 2 hours
Time taken to cover 1 kilometer = 60kilometers ÷ 2 hours
= 30 kilometer per hour
Question 4.
$11.40 for 5 cans
Answer:
Cost for 1 can = $2.28.
Explanation:
Cost for 5 cans = $11.40
Cost for 1 can = $11.40 ÷ 5
= $2.28
Concepts, Skills, & Problem Solving
COMPARING TWO DATA DISTRIBUTIONS The double box-and-whisker plot represents the values in two data sets. (See Exploration 1, p. 337.)
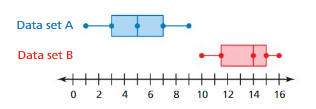
Question 5.
Does the data display show overlap? Explain.
Answer:18.2
Yes, the data display show overlap.
Explanation:
Data of set A = 1 3 5 7 9
Mean of set A = 1 + 3 + 5 + 7 + 9 ÷ 5
= 25 ÷ 5 = 5
MAD of set A = |∣−5∣ + |3−5∣ +|5−5∣ +|7−5∣ + |9−5∣ ÷ 5
= 4 + 2 + 0 + 2 + 4 = 20 ÷ 5
= 20 ÷ 5 =4
Data of set B = 10 11 14 15 16
Mean of set B = 8.2 + 6.7 + 4.2 + 3.2 + 2.2 ÷ 5
= 24.5 ÷ 5 = 4.9
MAD of set B = |∣0−18.2∣ + |11.5−18.2∣ +|14−18.2∣ +|15−18.2∣ + |16−18.2∣ ÷ 5
= 8.2 + 6.7 + 4.2 + 3.2 + 2.2 ÷ 5
= 24.5 ÷ 5 = 4.9
Differences in means ÷ MAD = 18.2 – 4.9 ÷ 5
= 13.3 ÷ 5 = 2.66
So, the differences in means is about 2.66 times the MAD.
Question 6.
Is there a significant difference in the measures of center for the pair of data sets? Explain.
Answer:
No, there is no significant difference in the measures of center for the pair of data sets because the quotient is less than 2, the difference in the medians is not significant.
Explanation:
Data of set A = 1 3 5 7 9 Data of set B = 10 11 14 15 16
Median of set A = 5 Median of set B = 14
IQR of set A = 7 – 3 = 4 IQR of set B = 15 – 11.5 = 3.5
Differences in Median ÷ IQR of set A = 5 – 4 ÷ 4 = 1 ÷ 4 = 0.25
Differences in Median ÷ IQR of set B = 5 – 4 ÷ 3.5 = 0.286
COMPARING POPULATIONS Two data sets contain an equal number of values. The double box-and-whisker plot represents the values in the data sets.
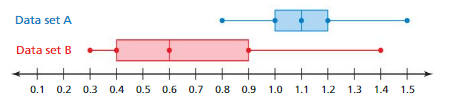
Question 7.
Compare the data sets using measures of center and variation.
Answer:
Comparison:
Variation of set A and Variation of set B
=> 0.5432 is greater than 0.1576.
Explanation:
Data of set A = 0.8 1.0 1.1 1.2 1.5
Mean of set A = 0.8 + 1.0 + 1.1 + 1.2 + 1.5 ÷ 5 = 5.6 ÷ 5 = 1.12
Variation of set A = (0.8 -1.12)^2 + (1.0-1.12)^2 + (1.1 -1.12)^2 + (1.2 – 1.12)^2 + (1.5 – 1.12)^2 ÷ 5
= (-0.32)^2 + (-0.12)^2 + (-0.02)^2 + (0.08)^2 + (0.38)^2 ÷ 5
= 0.1024 + 0.0144 + 0.004 + 0.0064 + 0.1444 ÷ 5
= 0.2716 ÷ 5
= 0.5432
Data of set B = 0.3 0.4 0.6 0.9 1.4
Mean of set B = 0.3 + 0.4 + 0.6 + 0.9 + 1.4 ÷ 5 = 3.6 ÷ 5 = 0.72
Variation of set B = (0.3 -0.72)^2 + (0.4 – 0.72)^2 + (0.6 -0.72)^2 + (0.9 – 0.72)^2 + (1.4 – 0.72)^2 ÷ 5
= (-0.42)^2 + (-0.32)^2 + (-0.12)^2 + (0.18)^2 + (0.68)^2 ÷ 5
= 0.1764 + 0.1024 + 0.0144 + 0.0324 + 0.4624 ÷ 5
= 0.788 ÷ 5
= 0.1576
Comparison:
Variation of set A and Variation of set B
=> 0.5432 is greater than 0.1576.
Question 8.
Which data set is more likely to contain a value of 1.1?
Answer:
Data of set A is more likely to contain a value of 1.1.
Explanation:
Data of set A = 0.8 1.0 1.1 1.2 1.5 Data of set B = 0.3 0.4 0.6 0.9 1.4
Median of set A = 1.1 Median of set B = 0.6
Question 9.
Which data set is more likely to contain a value that differs from the center by 0.3?
Answer:
No, data set is more likely to contain a value that differs from the center by 0.3.
Explanation:
Data of set A = 0.8 1.0 1.1 1.2 1.5 Data of set B = 0.3 0.4 0.6 0.9 1.4
Median of set A = 1.1 Median of set B = 0.6
Question 10.
DESCRIBING VISUAL OVERLAP
The double dot plot shows the values in two data sets. Express the difference in the measures of center as a multiple of the measure of variation.
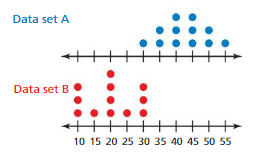
Answer:
Because the quotient is less than 2, the difference in the median is not significant of data set A.
Because the quotient is more than 2, the difference in the median is significant of data set B.
Explanation:
Data of set A = 30 35 40 45 50 55 Data of set B = 10 15 20 25 30
Median of set A = 40 +45 ÷ 2 = 85 ÷ 2 = 42.5 Median of set B = 20
IQR of set A = 50 – 35 = 15 IQR of set B = 30 – 10 = 20
Differences in medians ÷ IQR of set A = 42.5 – 20 ÷ 15 = 22.5 ÷ 15 = 1.5
Because the quotient is less than 2, the difference in the median is not significant of data set A.
Differences in medians ÷ IQR of set B = 42.5 – 20 ÷ 10 = 22.5 ÷ 10 = 2.25
Because the quotient is more than 2, the difference in the median is significant of data set B.
Question 11.
The distributions of attendance at basketball games and volleyball games at your school are symmetric. Your friend makes a conclusion based on the calculations shown below. Is your friend correct? Explain your reasoning.

Answer:
No, my friend is not correct.
Explanation:
Volleyball Game attendance:
Mean = 80
MAD = 20
Basketball Game attendance:
Mean = 160
MAD = 20
The difference in means is 4 times the MAD, so attendance at basketball games is significantly greater than the attendance at volleyball games. Since the MAD is “large”, it implies that the mean of 160 is not a reliable indicator of the other values within the data set.
Question 12.
MODELING REAL LIFE
The double box-and-whisker plot represents the goals scored per game by two hockey teams during a 20-game season. Is the number of goals scored per game significantly greater for one team than the other? Explain.

Answer:
Yes, the number of goals scored per game significantly greater for one team than the other.
Explanation:
Data of Team A = 0 2 3 4 6 Data of Team B = 0 6 7 8 10
Median of data Team A = 3 Median of data Team B = 7
IQR of Team A = 4 – 2 = 2 IQR of Team B = 8 – 6 = 2
Differences in medians ÷ IQR = 7 – 3 ÷ 2 = 4 ÷ 2 = 2
So, the quotient is equal to 2 the difference in the medians is significant.
Question 13.
MODELING REAL LIFE
The dot plots show the test scores for two classes taught by the same teacher. Are the test scores significantly greater for one class than the other? Explain.
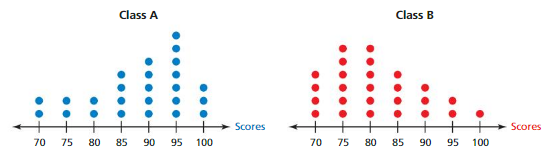
Answer:
No, the test scores are not significantly greater for one class than the other.
Explanation:
Data of Class A = 70 75 80 85 90 95 100 Data of Class B = 70 75 80 85 90 95 100
Median of data Class A = 85 Median of data Class B = 85
IQR of Class A = 95 – 85 = 10 IQR of Class B = 80 – 70 = 10
Both the variables and the center are similar. So, it is not significant.
Question 14.
PROBLEM SOLVING
A scientist experiments with mold colonies of equal area. She adds a treatment to half of the colonies. After a week, she measures the area of each colony. If the areas are significantly different, the scientist will repeat the experiment. The results are shown. Should the scientist repeat the experiment? Justify your answer.
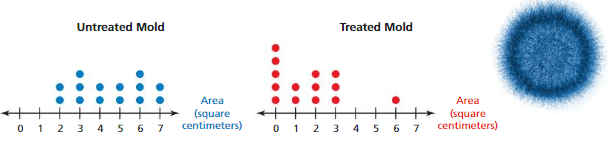
Answer:
Yes, the scientist should repeat the experiment because areas are significantly different from one to other.
Explanation:
Order of Data of untreated Mold = 2 3 4 5 6 7 Order of Data of treated Mold = 0 1 2 3 6
Median of untreated Mold = 4 + 5 ÷ 2 = 9 ÷ 2 = 4.5 Median of treated Mold = 2
IQR of untreated Mold = 4 – 2 = 2 IQR of treated Mold = 2 – 0 = 2
Because the variables are same, you can describe the overlap in areas by expressing the difference in the medians as a multiple of the IQR.
Difference in Medians ÷ IQR = 4.5 – 2 ÷ 2
= 2.5 ÷ 2 = 1.25
Because the quotient is less than 2, the differences in the medians is not significant.
The areas are not significantly greater than one and other colony.
Lesson 8.4 Using Random Samples to Compare Populations
EXPLORATION 1
Using Random Samples
Work with a partner. You want to compare the numbers of hours spent on homework each week by male and female students in your state. You take a random sample of 15 male students and 15 female students throughout the state.
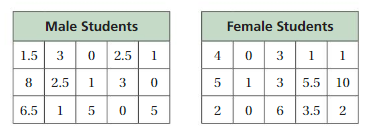
a. Compare the data in each sample.
b. Are the samples likely to be representative of all male and female students in your state? Explain.
c. You take 100 random samples of 15 male students in your state and 100 random samples of 15 female students in your state and record the median of each sample. The double box-and-whisker plot shows the distributions of the sample medians. Compare the distributions in the double box-and-whisker plot with the distributions of the data in the tables.
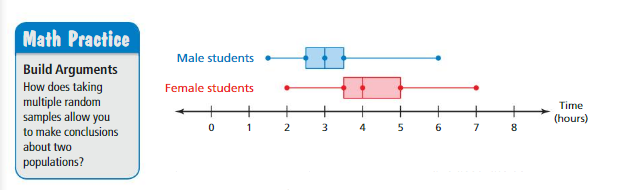
d. What can you conclude from the double box-and-whisker plot? Explain. d. How can you use random samples to make accurate comparisons of two populations?
Answer:
a) According to the given data in the table, the center of the Female students is greater than the center of the Male students.
b) Yes, the samples likely to be representative of all male and female students in your state because they are randomly selected students allover the state.
c) The data given in the table and the data given in the double box-and-whisker plot are both completely different and there is a lot of variation in the values. The double box-and-whisker plot has greater values than in the table.
d) According to the data in double box-and-whisker plot, the medians of male students is less than female students. So, the hours of male students spent are less than female students.
Explanation:
a)Data of Male students = 1.5 3 0 2.5 1 8 2.5 1 3 0 6.5 1 5 0 5
Arrange the data in order : 0 1 1.5 2.5 3 5 6.5 8
Median of Male students = 2.5 + 3 ÷ 2 = 5.5 ÷ 2 = 2.75
Data of Female students = 4 0 3 1 1 5 1 3 5.5 10 2 0 6 3.5 2
Arrange the data in order : 0 1 2 3 3.5 4 5.5 6
Median of Female students = 3 + 3.5 ÷ 2 = 6.5 ÷ 2 = 3.25
b) Data of Male students = 1.5 3 0 2.5 1 8 2.5 1 3 0 6.5 1 5 0 5
Data of Female students = 4 0 3 1 1 5 1 3 5.5 10 2 0 6 3.5 2
Yes, the samples likely to be representative of all male and female students in your state because they are randomly selected students allover the state.
c) Data in the Table:
Data of Male students = 1.5 3 0 2.5 1 8 2.5 1 3 0 6.5 1 5 0 5
Median of Male students = 2.5 + 3 ÷ 2 = 5.5 ÷ 2 = 2.75
Mean of Male students = 1.5 + 3 + 0 + 2.5 + 1 + 8 + 2.5 + 1 + 3 + 0 + 6.5 + 1 + 5 + 0 + 5 ÷ 15
= 40 ÷ 15
= 2.67
Data of Female students = 4 0 3 1 1 5 1 3 5.5 10 2 0 6 3.5 2
Median of Female students = 3 + 3.5 ÷ 2 = 6.5 ÷ 2 = 3.25
Mean of Female students = 4 + 0 + 3 + 1 + 1 + 5 + 1 + 3 + 5.5 + 10 + 2 + 0 + 6 + 3.5 + 2 ÷ 15
= 47 ÷ 15
= 3.13
Data in the double box-and-whisker plot:
Data of Male students = 1.5 2.5 3 3.5 6 Data of Female students = 2 3.5 4 5 7
Mean of Male students = 1.5 + 2.5 + 3 + 3.5 + 6 ÷ 5 Mean of Female students = 2 + 3.5 + 4 + 5 + 7 ÷ 5
= 16.5 ÷ 5 = 3.3 = 21.5 ÷ 5 = 4.3
d) Data in the double box-and-whisker plot:
Data of Male students = 1.5 2.5 3 3.5 6 Data of Female students = 2 3.5 4 5 7
Median of Male students = 3 Median of Female students = 4
Try It
Question 1.
The double dot plot shows the weekly reading habits of a random sample of 10 students in each of two schools. Compare the samples using measures of center and variation. Can you determine which school’s students read less? Explain.
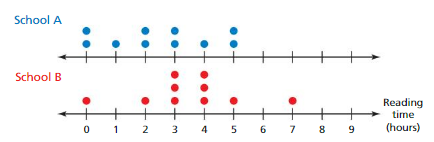
Answer:
According to the data of distribution, school A students are reading less compared to that of school B students.
Explanation:
Data of school A = 0 0 1 2 2 3 3 4 5 5
Mean of school A = 0 + 0 + 1 + 2 + 2 +3 + 3 + 4 + 5 + 5 ÷ 10
= 25 ÷ 10 = 2.5
Variation of school A = (0-2.5)^2 + (0-2.5)^2 + (1-2.5)^2 + (2-2.5)^2 + (2-2.5)^2 + (3-2.5)^2 + (3-2.5)^2 + (4-2.5)^2 + (5-2.5)^2 + (5-2.5)^2 ÷ 10
= (-2.5)^2 + (-2.5)^2 + (-1.5)^2 + (-0.5)^2 + (-0.5)^2 + (0.5)^2 + (0.5)^2 + (-1.5)^2 + (2.5)^2 + (2.5)^2 ÷ 10
= 6.25 + 6.25 + 2.25 + 0.25 + 0.25 + 0.25 + 0.25 + 2.25 + 6.25 + 6.25 ÷ 10
= 30.5 ÷ 10
= 3.05
Data of school B = 0 2 3 3 3 4 4 4 5 7
Mean of school B = 0 + 2 + 3 + 3 + 3 + 4 + 4 + 4+ 5 +7 ÷ 10
= 60 ÷ 10 = 6
Variation of school A = (0-6)^2 + (2-6)^2 + (3-6)^2 + (3-6)^2 + (3-6)^2 + (4-6)^2 + (4-6)^2 + (4-6)^2 + (5-6)^2 + (7-6)^2 ÷ 10
= (-6)^2 + (-4)^2 + (-3)^2 + (-3)^2 + (-3)^2 + (-2)^2 + (-2)^2 + (-2)^2 + (-1)^2 + (1)^2 ÷ 10
= 36 + 16 + 9 + 9+ 9 + 4 + 4 + 4 + 1 + 1÷ 10
= 93 ÷ 10
= 9.3
Question 2.
WHAT IF?
Each value in the box-and-whisker plot of the sample medians for Bag A decreases by2. Does this change your answer?
Answer:
Yes, this changes the answer because which makes the medians of Bag A and Bag B same.
Explanation:
Data of bag A = 4 5 5.5 6 6.5 Data of bag B = 2.5 3 3.5 4 5
Median of bag A = 5.5 Median of bag B = 3.5
IQR of bag A = 6 – 5 = 1 IQR of bag B = 4 – 3 = 1
If the sample medians for Bag A decreases by 2:
Median of bag A = 5.5 – 2 = 3.5
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
COMPARING RANDOM SAMPLES
Two boxes each contain 600 numbered tiles. The double dot plot shows a random sample of 8 numbers from each box. Compare the samples using measures of center and variation. Can you determine which box contains tiles with greater numbers? Explain.
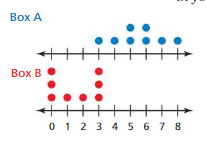
Answer:
Box A contains greater numbers more than Box B because its has greater median and also in variation.
Explanation:
Data of Box A = 3 4 5 5 6 6 7 8
Order of Box A =3 4 5 6 7 8
Median of Box A = 5 + 6 ÷ 2 = 11 ÷ 2 =5.5
Mean of Box A = 3 + 4 + 5 + 5 + 6 + 6 + 7 + 8 ÷ 8
= 44 ÷ 8
= 5.5
Variation of Box A = (3 -5.5)^2 + (4-5.5)^2 + (5-5.5)^2 + (5-5.5)^2 + (6-5.5)^2 + (6-5.5)^2 + (7-5.5)^2 + (8-5.5)^2 ÷ 8
= (-2.5)^2 + (-1.5)^2 + (-0.5)^2 + (-0.5)^2 + (0.5)^2 + (1.5)^2 + (1.5)^2 + (2.5)^2 ÷ 8
= 6.25 + 2.25 + 0.25 + 0.25 + 0.25 + 2.25 + 2.25 + 6.25 ÷ 8
= 20 ÷ 8
= 2.5
Data of Box B = 0 0 0 1 2 3 3 3
Order of Box B = 0 1 2 3
Median of Box B = 1 +2 ÷ 2 = 3 ÷ 2 =1.5
Mean of Box B = 0 + 0 + 0 + 1 + 2 + 3 + 3 + 3 ÷ 8
= 12 ÷ 8
= 1.5
Variation of Box B = (0-1.5)^2 + (0-1.5)^2 + (0-1.5)^2 + (1-1.5)^2 + (2-1.5)^2 + (3-1.5)^2 + (3-1.5)^2 + (3-1.5)^2 ÷ 8
= (-1.5)^2 + (-1.5)^2 + (-1.5)^2 + (-0.5)^2 + (0.5)^2 + (1.5)^2 + (1.5)^2 + (1.5)^2 ÷ 8
= 2.25 + 2.25 +2.25 + 0.25 +0.25 + 2.25 + 2.25 + 2.25 ÷ 8
= 14 ÷ 8
= 1.75
Question 4.
USING MULTIPLE RANDOM SAMPLES
Two crates each contain 750 objects. The double box-and-whisker plot shows the median weights of 50 random samples of 10 objects from each crate. Can you determine which crate weighs more? Explain.
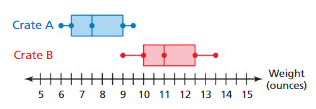
Answer:
Crate B weighs more than Crate A.
Explanation:
Data of crate A = 6 6.5 7.5 9 9.5
Median of crate A = 7.5
Mean of crate A = 6 + 6.5 + 7.5 + 9 + 9.5 ÷ 5 = 38.5 ÷5 = 7.7
IQR = 9 – 6.5 = 2.5
Data of crate B = 9 10 11 12.5 13.5
Median of crate B = 11
IQR = 12.5 – 10 = 2.5
Mean of crate B = 9 + 10 + 11 + 12.5 + 13.5 ÷ 5 = 56 ÷ 5 = 11.2
The variation in the center of crate B is greater than the measure of crate A. The variation of crate A is similar to the variation of crate B.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
The double box-and-whisker plot represents the medians of 100 random samples of 20 battery lives for two cell phone brands. Compare the battery lives of the two brands.
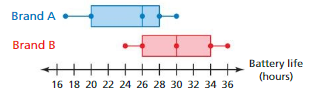
Answer:
The variation in the center of Brand B batteries is greater than the measure of Brand A batteries and the variation of Brand A batteries is similar to the variation of Brand B batteries.
Explanation:
Data of Brand A = 16.5 20 26 28 30 Data of Brand B = 24 26 30 34 36
Median of Brand A = 26 Median of Brand B = 30
IQR of Brand A = 28 – 20 = 8 IQR of Brand B = 34 – 28 = 6
Question 6.
DIG DEEPER!
The double box-and-whisker plot represents the medians of 50 random samples of 10 wait times at two patient care facilities. Which facility should you choose? Explain your reasoning.
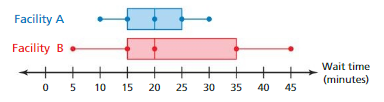
Answer:
Facility B should be chosen than the Facility A.
Explanation:
Data of Facility A = 10 15 20 25 30 Data of Facility B = 5 15 20 35 45
Median of Facility A = 20 Median of Facility B = 20
IQR of Facility A = 25 – 15 = 10 IQR of Facility B = 35 – 15 = 20
The variation in the center of Facility A is similar to the measure of Facility B and the variation of Facility B is greater than the variation of Facility A .
Using Random Samples to Compare Populations Homework & Practice 8.4
Review & Refresh
The double dot plot shows the values in two data sets.
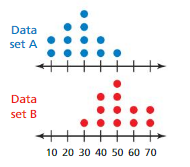
Question 1.
Compare the data sets using measures of center and variation.
Answer:
The measures of center of set B is greater and the variation of it greater than that of the variation of set A.
Explanation:
Data of Set A = 10 10 20 20 20 30 30 30 30 40 40 50 Data of set B = 30 40 40 40 50 50 50 50 60 60 70 70
Order: 10 20 30 40 50 Order: 30 40 50 60 70
Median of set A = 30 Median of set B = 50
Mean of set A = 10+10 + 20 + 20 + 20 + 30 + 30 + 30 + 30 + 40 + 40 + 50 ÷ 12
= 330 ÷ 12
= 27.5
Variation of set A = (10 -27.5)^2 + (10-27.5)^2 + (20-27.5)^2 + (20-27.5)^2 + (20-27.5)^2 + (30-27.5)^2 + (30-27.5)^2 + (30-27.5)^2 + (30-27.5)^2 + (40-27.5)^2 + (40-27.5)^2 + (50-27.5)^2 ÷ 12
= (-17.5)^2 + (-17.5)^2 + (-7.5)^2 + (-7.5)^2 + (-7.5)^2 + (2.5)^2 + (2.5)^2 + (2.5)^2 + (2.5)^2 + (12.5)^2 + (12.5)^2 + (22.5)^2 ÷ 12
= 306. 25 + 306.25 + 56.25 + 56.25 + 56.25 + 6.25 + 6.25 +6.25 + 6.25 + 156.25 + 156.25 + 506.25 ÷ 12
= 1625 ÷ 12
= 135.42
Mean of set B= 30 + 40 + 40 + 40 + 50 + 50 + 50 + 50 + 60 + 60 + 70 + 70 ÷ 12
= 610 ÷ 12
= 50.83
Variation of set B = (30-50.83)^2 + (40-50.83)^2 + (40-50.83)^2 + (40-50.83)^2 + (50-50.83)^2 + (50-50.83)^2 + (50-50.83)^2 + (50-50.83)^2 + (60-50.83)^2 + (60-50.83)^2 + (70-50.83)^2 + (70-50.83)^2 ÷ 12
= (-20.83)^2 + (-10.83)^2 + (-10.83)^2 + (-10.83)^2 + (-0.83)^2 + (-0.83)^2 + (-0.83)^2 + (-0.83)^2 + (10.83)^2 + (10.83)^2 + (20.83)^2 + (20.83)^2 ÷ 12
= 433.89 + 117.29 + 117.29 + 117.29 + 0.6889 + 0.6889 + 0.6889 + 0.6889 + 117.29 + 117.29 + 433.89 + 433.89 ÷ 12
= 1890.8756 ÷ 12
= 157.57
Question 2.
Are the values of one data set significantly greater than the values of the other data set? Explain.
Answer:
Yes, the variation of center of set B is greater than the measure of set A and the variation of set B is greater than the variation of set A.
Explanation:
Median of set A = 30 Median of set B = 50
Variation of set A = 135.42 Variation of set B = 157.57
Solve the equation. Check your solution.
Question 3.
5b – 3 = 22
Answer:
b= 5.
Explanation:
5b – 3 = 22
5b = 22 + 3
5b = 25
b = 25/5
b= 5.
Check: substitute b = 5 in 5b – 3 = 22.
LHS => 5b – 3 = 22.
=> (5 x 5) -3 = 22
=> 25 – 3 = 22 = RHS
Question 4.
1.5d + + 3 = – 4.5
Answer:
d = -5
Explanation:
1.5d + 3 = – 4.5
=>1.5d = -4.5 -3
=> 1.5d = -7.5
=> d = -7.5 ÷ 1.5
=> d = – 5
Checking:
Substitute d = – 5 in Equation:
LHS: 1.5d + 3
=> (1.5 × -5) + 3
=> -7.5 + 3
=> -4.5 = RHS
Question 5.
4 = 9z – 2
Answer:
z = 0.67
Explanation:
4 = 9z – 2
=> 4 + 2 = 9z
=> 6 = 9z
=>6 ÷ 9 = z
=> 0.67 = z
Checking:
Substitute z = 0.67 in Equation:
RHS: 9z – 2
=> (9 × 0.67) – 2
=> 6 – 2
= 4 = LHS
Concepts, Skills, & Problem Solving
USING RANDOM SAMPLES You want to compare the numbers of hours spent on recreation each week by teachers and non-teachers in your state. You take100 random samples of 15 teachers and 100 random samples of 15 non-teachers throughout the state and record the median value of each sample. The double box-and-whisker plot shows the distributions of sample medians. (See Exploration 1, p. 343.)
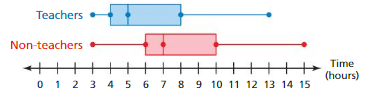
Question 6.
Are the samples likely to be representative of all teachers and non-teachers in your state?
Answer:
Yes, the samples are likely to be representative of all teachers and non-teachers in your state because it has been given in the question.
Question 7.
What can you conclude from the double box-and-whisker plot? Explain.
Answer:
The number of hours spent by Non-teachers is more than the teachers.
Explanation:
Median of Non-Teachers = 7
Median of Teachers = 5
Question 8.
COMPARING RANDOM SAMPLES
The double dot plot shows the weekly running habits of athletes at two colleges. Compare the samples using measures of center and variation. Can you determine which college’s athletes spend more time running? Explain.
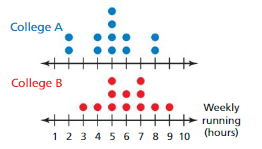
Answer:
Data of College B has the greater measure of center and in the measure of variation that of data of college B.
College B athletes spend more time running than college A.
Explanation:
Data of College A = 2 2 4 4 5 5 5 5 6 6 8 8
Order : 2 4 5 6 8
Median of Data A = 5
Variation of Data A = (2-5)^2 + (2-5)^2 + (4-5)^2 + (4-5)^2 + (5-5)^2 + (5-5)^2 + (5-5)^2 + (5-5)^2 + (6-5)^2 + (6-5)^2 + (8-5)^2 + (8-5)^2 ÷ 12
= (-3)^2 + (-3)^2 + (-1)^2 + (-1)^2 + (0)^2 + (0)^2 + (0)^2 + (0)^2 + (1)^2 + (1)^2 + (3)^2 + (3)^2 ÷ 12
= 9 + 9 + 1 + 1 + 0+ 0 + 0 + 0 + 1 + 1 + 9 + 9 ÷ 12
= 40 ÷ 12
= 3.33
Data of College B = 3 4 5 5 5 6 6 7 7 7 8 9
Order : 3 4 5 6 7 8
Median of Data A = 5 + 6 ÷ 2 = 11 ÷ 2 = 5.5
Variation of Data A = (3-5.5)^2 + (4-5.5)^2 + (5-5.5)^2 + (5-5.5)^2 + (5-5.5)^2 + (6-5.5)^2 + (6-5.5)^2 + (7-5.5)^2 + (7-5.5)^2 + (7-5.5)^2 + (8-5.5)^2 + (9-5.5)^2 ÷ 12
= (-2.5)^2 + (-1.5)^2 + (0)^2 + (0)^2 + (0)^2 + (1.5)^2 + (1.5)^2 + (2.5)^2 + (2.5)^2 + (2.5)^2 + (3.5)^2 + (4.5)^2 ÷ 12
= 6.25 + 2.25 + 0 + 0 + 0 + 2.25 + 2.25 + 6.25 + 6.25 + 6.25 + 12.25 + 20.25 ÷ 12
= 64.25 ÷ 12
= 5.35
Question 9.
USING MULTIPLE RANDOM SAMPLES
Two lakes each contain about 2000 fish. The double box-and-whisker plot shows the medians of 50 random samples of 14 fish lengths from each lake. Can you determine which lake contains longer fish? Explain.
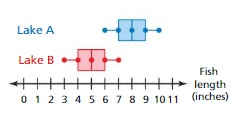
Answer:
Lake A is the Lake contains longer fish because the measure in the variation is comparatively greater than the measure of variation of Lake B.
Explanation:
Data of Lake A = 6 7 8 9 10 Data of Lake B = 3 4 5 6 7
Median of Lake A = 8 Median of Lake B = 5
IQR of Lake A = 9 – 7 = 2 IQR of Lake B = 6 – 4 = 2
Question 10.
MODELING REAL LIFE
Two laboratories each produce 800 chemicals. A chemist takes 10 samples of 15 chemicals from each lab, and records the number that pass an inspection. Are the samples likely to be representative of all the chemicals for each lab? If so, which lab has more chemicals that will pass the inspection? Justify your answer.
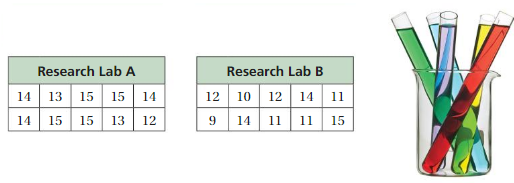
Answer:
Yes, the samples are likely to be representative of all the chemicals for each lab.
Research Lab B is having the more chemicals that will pass the inspection.
Explanation:
Data of Research Lab A = 14 14 13 15 1515 15 13 14 12
Order : 12 13 14 15
Median of Research Lab A =13 +14 ÷ 2=27 ÷ 2 = 3.5
Mean of Research Lab A = 14 +14 +13+ 15 +15 +15 + 15 + 13 + 14 + 12 ÷ 10
= 140 ÷ 10
= 14
Data of Research Lab B = 12 9 10 14 12 11 14 11 11 15
Order : 9 10 11 12 14 15
Median of Research Lab B = 11+12 ÷ 2 = 23 ÷ 2 = 11.5
Mean of Research Lab B = 12 + 9 + 10 +14 + 12 +11 + 14 + 11 + 11 + 15 ÷ 10
= 119 ÷ 10
= 11.9
So, the variation of Research Lab A is having greater values and the measure of the center Research Lab B is greater than the center of the Research Lab A.
Question 11.
MODELING REAL LIFE
A farmer grows two types of corn seedlings. There are 1000 seedlings of each type. The double box-and-whisker plot represents the median growths of 50 random samples of 7 corn seedlings of each type. Compare the growths of each type of corn seedling. Justify your result.
Answer:
The growth of Type B type of corn seedling is more that of growth of Type B of corn seedling.
Explanation:
Data of Type A = 1.5 3 3.5 4 5.5 Data of Type B = 2.5 5 6.5 7 9
Median of Type A = 3.5 Median of Type B = 6.5
IQR of Type A = 4 – 3 = 1 IQR of Type B = 7 – 5 = 2
So, the Variation of Type B is having greater than the measure of Variation of Type A . The measure of the center of Type B is greater than the center of the Type A.
Question 12.
DIG DEEPER!
You want to compare the number of words per sentence in a sports magazine to the number of words per sentence in a political magazine.
a. The data represent random samples of the number of words in 10 sentences from each magazine. Compare the samples using measures of center and variation. Can you use the data to make a valid comparison about the magazines? Explain.
Sports magazine: 9, 21, 15, 14, 25, 26, 9, 19, 22, 30
Political magazine: 31, 22, 17, 5, 23, 15, 10, 20, 20, 17
b. The double box-and-whisker plot represents the means of 200 random samples of 20 sentences from each magazine. Compare the variability of the sample means to the variability of the sample numbers of words in part(a).
c. Make a conclusion about the numbers of words per sentence in each magazine.
Answer:
a) Variation of Sports magazine is having greater measure in variation and Median of Sports magazine is having greater value of center.
b) The variability of the sample is similar to the variability of the sample numbers of words in part(a).
c) Number of words per sentence in political magazine are more than the number of words per sentence in sports magazine.
Explanation:
a)
Data of Sports magazine = 9, 21, 15, 14, 25, 26, 9, 19, 22, 30
Order : 9 14 15 19 21 22 25 26 30
Median of Sports magazine = 21
Mean of Sports magazine = 9 + 21 + 15 + 14 + 25 + 26 + 9 + 19 + 22 + 30 ÷ 10 = 190 ÷ 10 = 19
Variation of Sports magazine = (9-19)^2 + (21-19)^2 + (15-19)^2 + (14-19)^2 + (25-19)^2 + (26-19)^2 + (9-19)^2 + (19-19)^2 + (22-19)^2 + (30-19)^2 ÷ 10
= (-10)^2 + (2)^2 + (-4)^2 + (-5)^2 + (6)^2 + (7)^2 + (-10)^2 + (0)^2 + (3)^2 + (11)^2 ÷ 10
= 100 + 4 + 16 + 25 + 36 + 49 + 100 + 0 + 9 +121 ÷ 10
= 460 ÷ 10
= 46
Data of Political magazine = 31, 22, 17, 5, 23, 15, 10, 20, 20, 17
Order : 5 10 15 17 20 22 23 31
Median of Political magazine = 17 + 20 ÷ 2 = 37 ÷ 2 = 13.5
Mean of Political magazine = 31+ 22 +17 + 5 +23 + 15 +10 + 20 + 20 + 17 ÷ 10
= 180÷ 10
= 18
Variation of Sports magazine = (31-18)^2 + (22-18)^2 + (17-18)^2 + (5-18)^2 + (23-18)^2 + (15-18)^2 + (10-18)^2 + (20-18)^2 + (20-18)^2 + (17-18)^2 ÷ 10
= (13)^2 + (4)^2 + (-1)^2 + (-13)^2 + (5)^2 + (-3)^2 + (-8)^2 + (2)^2 + (2)^2 + (-1)^2 ÷ 10
= 169 + 16 + 1 + 169 + 25 + 9 + 64 + 4 + 4 + 1 ÷ 10
= 462 ÷ 10
= 46.2
b)
Data of Sports magazine = 16 19 20 21 23 Data of Political magazine = 18 22 23 24 26
Median of Sports magazine = 20 Median of Political magazine = 23
IQR of Sports magazine = 21 – 9 = 2 IQR of Political magazine = 24 -22 = 2
Mean of Sports magazine = 16 + 19 + 20 + 21 + 23 ÷ 5
= 99 ÷ 5 = 19.8
Mean of Political magazine = 18 + 22 + 23 + 24 + 26 ÷ 5
= 113 ÷ 5 = 22.6
c)
Data of Sports magazine = 16 19 20 21 23
Maximum used words in Political magazine = 16 to 23
=> 23 – 16 = 7
Data of Political magazine = 18 22 23 24 26
Maximum used words in Political magazine = 18 to 26.
=> 26 – 18 = 8
Question 13.
PROJECT
You want to compare the average amounts of time students in sixth, seventh, and eighth grade spend on homework each week.
a. Design an experiment involving random sampling that can help you make a comparison.
b. Perform the experiment. Can you make a conclusion about which grade spends the most time on homework? Explain your reasoning.
Answer:
a)Number of hours :
Total number of students of sixth spent = 26 + 33 +30 = 89
Total number of students of seventh spent = 32 + 46 + 40 = 118
Total number of students of Eighth spent = 42 +21 +25 = 88
b) Number of students who spent most time on homework are the seventh grades students.
Explanation:
a) In a school, randomly chosen students are asked about amounts of time students in sixth, seventh, and eighth grade spend on homework each week. The school has 1000 students. Randomly 100 students are asked and three different sampling is taken.
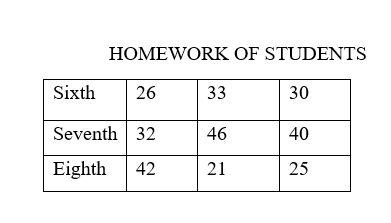
b) Average of students spent on homework of sixth grades = 26 + 33 +30 ÷ 3 = 89 ÷ 3= 29.67
Average of students spent on homework of seventh grades = 32 + 46 + 40 ÷ 3 = 118 ÷ 3 = 39.33
Average of students spent on homework of eighth grades = 42 +21 +25 ÷ 3 = 88 ÷ 3 = 29.33
Statistics Connecting Concepts
Using the Problem-Solving Plan
Question 1.
In a city, 1500 randomly chosen residents are asked how many sporting events they attend each month. The city has 80,000 residents. Estimate the number of residents in the city who attend at least one sporting event each month.
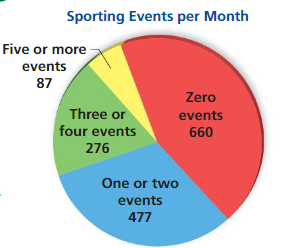
Understand the problem.
You are given the numbers of sporting events attended each month by a sample of 1500 residents. You are asked to make an estimate about the population, all residents of the city.
Make a plan.
The sample is representative of the population because it is selected at random and is large enough to provide accurate data. So, find the percent of people in the survey that attend at least one sporting event each month, and use the percent equation to make an estimate.
Solve and .check.
Use the plan to solve the problem. Then check your solution
Answer:
Number of residents attended one sports events = 30
Number of residents in the city who attend at least one sporting event each month = 30÷ 1500 × 80000
= 0.02 × 80000 = 1600
Explanation:
Number of residents attended zero sports events = 660
Number of residents attended zero sports events in the city = 660 ÷ 1500 = 0.44 × 80000 = 35200
Number of residents attended one or two sports events = 447
Number of residents attended one or two sports events in the city = 447 ÷ 1500 = 0.298 × 80000 =23840
Number of residents attended three or four sports events = 276
Number of residents attended three or four sports events in the city= 276 ÷ 1500 = 0.184 × 80000 = 14720
Number of residents attended five or more sports events = 87
Number of residents attended five or more sports events in the city= 87 ÷ 1500 = 0.058 × 80000 =4640
Total number of residents sample taken = Number of residents attended zero sports events + Number of residents attended one or two sports events + Number of residents attended three or four sports events + Number of residents attended five or more sports events + Number of residents attended one sports events
=>1500 = 660 + 447 + 276 + 87 + Number of residents attended one sports events
=> 1500 = 1470 + Number of residents attended one sports events
=> 1500 – 1470 = Number of residents attended one sports events
=> 30 = Number of residents attended one sports events
Check :
Total number of all events add = Total population in the city
LHS:
=> 35200 + 23840 + 14720 + 4640 + 1600
=> 80000
= RHS
Hence, LHS = RHS
Question 2.
The dot plots show the values in two data sets. Is the difference in the measures of center for the data sets significant?
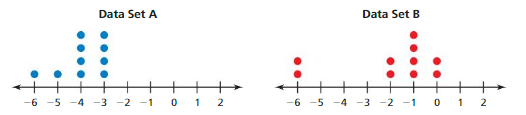
Answer:
Yes, the difference in the measures of center for the data set of A is not significant because the quotient is not less than 2.
No, the difference in the measures of center for the data set of B is significant because the quotient is less than 2.
Explanation:
Data of set A= – 6 – 5 -4 -4 – 4 -4 -3 -3 -3 -3
Order: -3 -4 -5 -6
Median of set A = -4 + – 5 ÷ 2 = -9 ÷ 2 = -4.5
Mean of set A = – 6 + -5 + -4 + -4 + -4 + -4 + -3 + -3 + -3 + -3 ÷10
= 35 ÷10 = 3.5
IQR of set A = -6 – (-4) = -6 + 4 = -2
Data of set B = -6 -6 -2 -2 -1 -1 -1 -1 0 0
Order : 0 -1 -2 -6
Median of set B = -1 + -2 ÷ 2 = -3 ÷ 2 = -1.5
Mean of set B = -6 + -6 + -2 + -2 + -1 + -1 + -1 + -1 + 0 + 0 ÷10
= 20 ÷10 = 2.0
IQR of set B = -6 – (-1) = -6 +1 = -5
Differences in medians ÷ IQR = -4.5 – (-1.5) ÷ -2 = -4.5 + 1.5 ÷ -2 = -3.0 ÷ -2 = 1.5
Differences in medians ÷ IQR = -4.5 – (-1.5) ÷ -5 = -4.5 + 1.5 ÷ -5 = -3.0 ÷ -5 = 0.6
Question 3.
You ask 60 randomly chosen students whether they support a later starting time for school. The table shows the results. Estimate the probability that at least two out of four randomly chosen students do not support a later starting time.
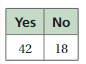
Answer:
Explanation:
Performance Task
Estimating Animal Populations
At the beginning of the this chapter, you watched a STEAM Video called “Comparing Dogs.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Statistics Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Answer:
Population: Population is an entire group of objects or people.
Sample: A Sample is a part of the population.
Unbiased Sample: Unbiased Sample is a representative of a population. It is selected random and is a large enough to provide accurate data.
Biased Sample: Biased Sample is a not representative of a population. One or more parts of the population are favored over others.
Graphic Organizers
You can use a Definition and Example Chart to organize information about a concept. Here is an example of a Definition and Example Chart for the vocabulary term sample.
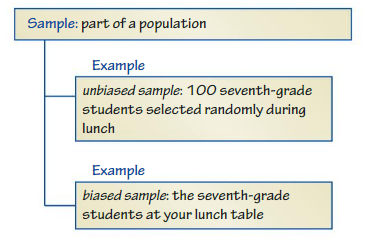
Choose and complete a graphic organizer to help you study each topic.

1. population
2. shape of a distribution
3. mean absolute deviation (MAD)
4. interquartile range
5. double box-and-whisker plot
6. double dot plot
Answer: Its a double box-and-whisker plot.

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

8.1 Samples and Populations (pp. 325–330)
Learning Target: Understand how to use random samples to make conclusions about a population.
Question 1.
You want to estimate the number of students in your school whose favorite subject is biology. You survey the first 10 students who arrive at biology club. Determine whether the sample is biased or unbiased. Explain.
Answer:
The sample is a Biased Sample because the students in the biology club are not representative of a population. One or more parts of the students are favored over others.
Question 2.
You want to estimate the number of athletes who play soccer. Give an example of a biased sample. Give an example of an unbiased sample.

Answer:
Example of Biased sample :
What is your favorite sport? Sample is chosen from people attending a soccer game.
Example of Unbiased sample :
What is your favorite sport? Sample is chosen by picking names out of a register of school.
Question 3.
You want to know how the residents of your town feel about building a new baseball stadium. You randomly survey 100 people who enter the current stadium. Eighty support building a new stadium, and twenty do not. So, you conclude that80% of the residents of your town support building a new baseball stadium. Is your conclusion valid? Explain.
Answer:
The conclusion is valid.
Explanation:
Number of randomly chosen = 100
Number of people support new stadium = 80
Number of people does not support new stadium = 20
Percentage of people support new stadium = 80 ÷100 × 100= 80%
Question 4.
Which sample is better for making an estimate? Explain.

Answer:
Sample B is better for making an estimate about predicting the number of students in a school who like gym class because its a unbiased sample and we get accurate data out of it.
Question 5.
You ask 125 randomly chosen students to name their favorite beverage. There are 1500 students in the school. Predict the number of students in the school whose favorite beverage is a sports drink.
Answer:
Number of students in the school whose favorite beverage is a sports drink = 696.
Explanation:
Number of students in the school whose favorite beverage is a sports drink = Favorite Beverage sport drink ÷ randomly chosen students × students in the school.
= 58 ÷ 125 ×1500
= 0.464 ×1500
= 696.
Question 6.
You want to know the number of students in your state who have summer jobs. Determine whether you should survey the population or a sample. Explain.
Answer:
You should survey the sample.
Explanation:
You should survey the sample because a sample is the representation of population and selected at random and is a large which gives you the accurate data.
8.2 Using Random Samples to Describe Populations (pp. 331–336)
Learning Target: Understand variability in samples of a population.
Question 7.
To pass a quality control inspection, the products at a factory must contain no critical defects, no more than 2.5% of products can contain major defects, and no more than 4% of products can contain minor defects. There are 40,000 products being shipped from a factory. Each inspector randomly samples 125 products. The table shows the results.
a. Use each sample to make an estimate for the number of products with minor defects at the factory. Describe the center and the variation of the estimates.
b. Use the samples to make an estimate for the percent of products with minor defects, with major defects, and with critical defects at the factory. Does the factory pass inspection? Explain.
Answer:
a. The median of major defect is greater than the median of minor defect in the factory. The variation of major defects is greater than the measure of variation of minor defects in the factory.
b. Yes, the factory pass inspection because not more than 2.5% of products can contain major defects, and not more than 4% of products can contain minor defects.
Explanation:
a. Number of products with minor defects at the factory = 5 6 3 6
Order: 3 5 6
Median of minor defects= 5
Mean of minor defects= 5+6+3+6 ÷ 4 = 20 ÷ 4 =5
Variation of minor defects= (5-5)^2 + (6-5)^2 + (3-5)^2 + (6-5)^2 ÷ 4
= (0)^2 + (1)^2 + (-2)^2 + (1)^2 ÷ 4
= 0 + 1 + 4 +1 ÷ 4
= 6÷ 4
= 1.5
Number of products with major defects at the factory = 2 1 3 5
Order: 1 2 3 5
Median of major defects= 2 + 3 ÷ 2 = 5 ÷ 2 = 2.5
Mean of major defects= 2 + 1+ 3 +5 ÷ 4 = 11 ÷ 4 = 2.75
Variation of major defects = (2-2.75)^2 + (1-2.75)^2 + (3-2.75)^2 + (5-2.75)^2 ÷ 4
= (-0.75)^2 + (-1.75)^2 + (0.25)^2 + (2.25)^2 ÷ 4
= 0.5625 + 3.0625 +0.625 + 5.0625 ÷ 4
= 9.3125 ÷ 4
= 2.33
Number of products with critical defects at the factory = 0 0 0 0
Median critical defects = 0
Mean critical defects = 0
Variation critical defects = 0
b. Percent of minor defects in the factory = 20 ÷ 125 = 0.16
Percent of major defects in the factory = 11 ÷125 = 0.088
Percent of critical defects in the factory = 0 ÷ 125 = 0
Question 8.
A scientist determines that 35% of packages of a food product contain a specific bacteria. Use technology to simulate choosing 100 random samples of 20 packages. How closely do the samples estimate the percent of all packages with the specific bacteria?
Answer:
Percent of bacteria in rice food product = 74 × 35 ÷ 100 = 2590 ÷ 100 = 25.9
Percent of bacteria in Wheat food product = 91 × 35 ÷ 100 = 3185 ÷ 100 = 31.85
Percent of bacteria in Milk food product = 78 × 35 ÷ 100 = 2730 ÷ 100 = 27.30
Percent of bacteria in Cereals food product = 57 × 35 ÷ 100 = 1995 ÷ 100 = 19.95
Explanation:
Total number of Rice food product = 12 + 30 +32 = 74
Percent of bacteria in rice food product = 74 × 35 ÷ 100 = 2590 ÷ 100 = 25.9
Total number of Wheat food product = 34 + 29 + 28 = 91
Percent of bacteria in Wheat food product = 91 × 35 ÷ 100 = 3185 ÷ 100 = 31.85
Total number of Milk food product = 32 + 21 +25 = 78
Percent of bacteria in Milk food product = 78 × 35 ÷ 100 = 2730 ÷ 100 = 27.30
Total number of Cereals food product = 22 +20 +15 =
Percent of bacteria in Cereals food product = 57 × 35 ÷ 100 = 1995 ÷ 100 = 19.95
8.3 Comparing Populations (pp. 337–342)
Learning Target: Compare populations using measures of center and variation.
Question 9.
The double box-and-whisker plot represents the points scored per game by two football teams during the regular season.
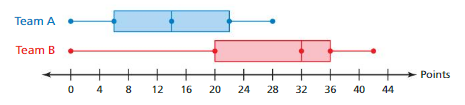
a. Compare the data sets using measures of center and variation.
b. Which team is more likely to score 28 points in a game?
Answer:
a. Team B has greater measures of center and both the team have same measures of variation.
b. Team A is most likely to score 28 points in a game.
Explanation:
a. Data of Team A = 0 6 14 22 28
Median of Team A = 14
IQR of Team A = 22 – 6 = 16
Data of Team B = 0 20 32 36 42
Median of Team B = 32
IQR of Team B = 36 – 20 = 16
b. In the data given, 28 points are given in team A not in Team B.
Question 10.
The dot plots show the ages of campers at two summer camps.
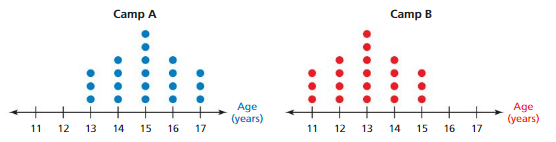
a. Express the difference in the measures of center as a multiple of the measure of variation.
b. Are the ages of campers a tone camp significantly greater than at the other? Explain.
Answer:
a. Differences in medians ÷ IQR = 15 – 13 ÷ 2 = 2 ÷ 2 = 1
b. No, the ages of campers are significantly greater than at the other.
Explanation:
a. Data of Camp A = 13 13 13 14 14 14 14 15 15 15 15 15 15 16 16 16 16 17 17 17
Order: 13 14 15 16 17
Median of Camp A = 15
IQR of Camp A = 16 – 14 = 2
Data of Camp B = 11 11 11 12 12 12 12 13 13 13 13 13 13 14 14 14 14 15 15 15
Order: 11 12 13 14 15
Median of Camp B = 13
IQR of Camp B = 14 – 12 = 2
Differences in medians ÷ IQR = 15 – 13 ÷ 2 = 2 ÷ 2 = 1
b. Because the quotient is less than 2, the difference in the medians is not significant.
8.4 Using Random Samples to Compare Populations (pp. 343–348)
Learning Target: Use random samples to compare populations.
Question 11.
The double dot plot shows the median gas mileages of 10 random samples of 50 vehicles for two car models. Compare the samples using measures of center and variation. Can you determine which car model has a better gas mileage? Explain.
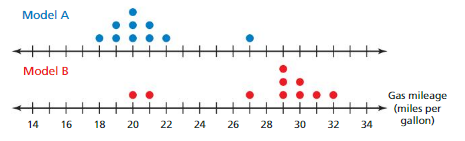
Answer:
The Variation of Model B measures are greater compared to the measures of the Variation of Model A.
The measures of center of Model B is greater than the measures of Model A.
Model B cars has a better gas mileage than that of Model A cars.
Explanation:
Data of Model A = 18 19 19 20 20 20 21 21 22 27
Order: 18 19 20 21 22 27
Median of Model A = 20 + 21 ÷ 2 =41 ÷ 2 = 20.5
Mean of Model A = 18 + 19 + 19 + 20 + 20 + 20 + 21 + 21 +22 +27 ÷ 10
= 207 ÷ 10
= 20.7
Variation of Model A = (18-20.7)^2 + (19-20.7)^2 + (19-20.7)^2 + (20-20.7)^2 + (20-20.7)^2 + (20-20.7)^2 + (21-20.7)^2 + (21-20.7)^2 +(22-20.7)^2 + (27-20.7)^2 ÷ 10
= (-2.7)^2 + (-1.7)^2 + (-1.7)^2 + (-0.7)^2 + (-0.7)^2 + (-0.7)^2 + (0.3)^2 + (0.3)^2 +(1.3)^2 + (6.3)^2 ÷ 10
= 7.29 + 2.89 + 2.89 + 0.49 + 0.49 + 0.49 + 0.09 +0.09 + 1.69 + 39.69 ÷ 10
= 56.37 ÷ 10
= 5.637
Data of Model B = 20 21 27 29 29 29 30 30 31 32
Order: 20 21 27 29 30 31 32
Median of Model B = 29
Mean of Model B = 20 + 21 + 27 + 29 + 29 + 29 + 30 + 30 + 31 + 32 ÷ 10
= 278 ÷ 10
= 27.8
Variation of Model B = (20-27.8)^2 + (21-27.8)^2 + (27-27.8)^2 + (29-27.8)^2 + (29-27.8)^2 + (30-27.8)^2 + (30-27.8)^2 + (31-27.8)^2 +(31-27.8)^2 + (32-27.8)^2 ÷ 10
= (-7.8)^2 + (-6.8)^2 + (-0.8)^2 + (1.2)^2 + (1.2)^2 + (2.2)^2 + (2.2)^2 + (3.2)^2 +(3.2)^2 + (4.2)^2 ÷ 10
= 60.84 + 46.24 + 0.64 + 1.44 + 1.44 + 4.84 + 4.84 + 10.24 + 10.24 + 17.64 ÷ 10
= 158.4 ÷ 10
= 15.84
Question 12.
You compare the average amounts of time people in their twenties and thirties spend driving each week. The double box-and-whisker plot represents the medians of 100 random samples of 8 people from each age group. Can you determine whether one age group drives more than the other? Explain.
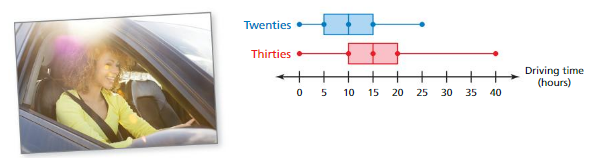
Answer:
Because the variables are same, you can determine the one age group drives more than the other visual overlap by expressing the differences in the medians as the multiples of IQR.
Explanation:
Data of Twenties = 0 5 10 15 25
Median of Twenties = 10
IQR of Twenties = 15 – 5 = 10
Data of Thirties = 0 10 15 20 40
Median of Thirties = 15
IQR of Thirties = 20 – 10 =10
Differences in medians ÷ IQR = 15- 10 ÷10 = 5 ÷10 =0.5
Because the quotient is less than 2, the difference is not significant.
Statistics Practice Test
Question 1.
You want to estimate the number of students in your school who prefer to bring a lunch from home rather than buy one at school. You survey five students who are standing in the lunch line. Determine whether the sample biased or unbiased. Explain.
Answer:
The sample is biased.
Explanation:
The sample taken is biased because it does not gives you the accurate information of the number of students in your school prefer to bring a lunch from home rather than buy one at school. The sample size chosen is incorrect as taking the students in the lunch line..
Question 2.
You want to predict which candidate will likely be voted Seventh Grade Class President. There are 560 students in the seventh grade class. You randomly sample 3 different groups of 50 seventh-grade students. The results are shown.
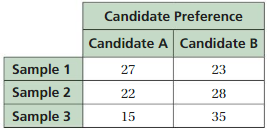
a. Use each sample to make an estimate for the number of students in seventh grade that vote for Candidate A.
b. Who do you expect to be voted Seventh Grade Class President? Explain.
Answer:
a. Estimation for the number of students who vote for Candidate A = 64.
b. Candidate B is to be expected to be voted Seventh Grade Class President.
Explanation:
a. Estimation for the number of students who vote for Candidate A = 27 + 22 +15 = 64.
Estimation for the number of students who vote for Candidate B = 23 + 28 + 35 = 86.
b. Candidate B is to be expected to be voted Seventh Grade Class President.
Question 3.
Of 60 randomly chosen students from a school surveyed, 16 chose the aquarium as their favorite field trip. There are 720 students in the school. Predict the number of students in the school who choose the aquarium as their favorite field trip.
Answer:
Number of students in the school who choose the aquarium as their favorite field trip = 192.
Explanation:
Number of students who chose the aquarium as their favorite field trip = 16
Number of students chosen students from a school surveyed = 60
Total number of students in the school = 720
Number of students in the school who choose the aquarium as their favorite field trip = 720/60 × 16 = 192
Question 4.
The double box-and-whisker plot shows the ages of the viewers of two television shows in a small town.
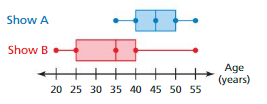
a. Compare the data sets using measures of center and variation.
b. Which show is more likely to have a 44-year-old viewer?
Answer:
a. The Show A center is likely to be greater than the measures of the center of Show B. Variation of show B is greater than Variation of show A.
b. Show A is more likely to have a 44-year-old viewer.
Explanation:
Data of Show A = 35 40 45 50 55
Median of Show A = 45
Mean of Show A = 35 + 40 + 45 + 50 + 55 ÷ 5 = 225 ÷ 5 = 45
Variation of Show A = (35-45)^2 + (40-45)^2 + (45-45)^2 + (50-45)^2 + (55-45)^2 ÷ 5
= (-10)^2 + (-5)^2 + (0)^2 + (5)^2 + (10)^2 ÷ 5
= 100 + 25 + 0 + 25 +100 ÷ 5
= 250 ÷ 5
= 50.
Data of Show B = 20 25 35 40 55
Median of Show B = 35
Mean of Show B = 20 + 25 + 35 + 40 + 55 ÷ 5 = 175 ÷ 5 = 35.
Variation of show B = (20-35)^2 + (25-35)^2 + (35-35)^2 + (40-35)^2 + (55-35)^2 ÷ 5
= (-15)^2 + (-10)^2 + (0)^2 + (5)^2 + (5)^2 ÷ 5
= 225 + 100 + 0 + 25 + 25 ÷ 5
= 375 ÷ 5
= 75.
Question 5.
The double box-and-whisker plot shows the test scores for two French classes taught by the same teacher.
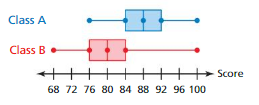
a. Express the difference in the measures of center as a multiple of the measure of variation.
b. Are the scores for one class significantly greater than for the other? Explain.
Answer:
a. The difference of the Variation of Class A is similar to the Variation of Class A and the measures of the center of Class A is comparably greater than the measures of the center of Class B.
b. Yes, the scores for one class significantly greater than for the other.
Explanation:
Data of Class A = 76 84 88 92 100 Data of Class B = 68 76 80 84 100
Median of Class A = 76 + 84 + 88 + 92 + 100 ÷ 5 Median of Class B = 68 + 76 + 80 + 84 + 100 ÷ 5
= 440 ÷ 5 = 88 = 408 ÷ 5 = 81.6
IQR of Class A = 92 – 84 = 8 IQR of Class B = 84 – 76 = 8
Question 6.
Two airplanes each hold about 400 pieces of luggage. The double dot plot shows a random sample of 8 pieces of luggage from each plane. Compare the samples using measures of center and variation. Can you determine which plane has heavier luggage? Explain.
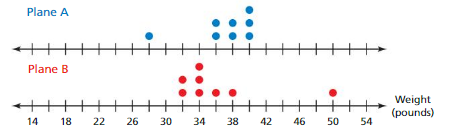
Answer:
The measures of center of Plane A is greater than the measure of center of Plane B.
Plane A is likely to have heavier luggage than Plane B. The Variation of Plane A is greater than Variation of Plane B.
Explanation:
Data of Plane A = 28 36 36 38 38 40 40 40 Data of plane B = 32 32 34 34 34 36 38 50
Order = 28 36 38 40 Order = 32 34 36 38 50
Median of Plane A = 36 + 38 ÷ 2 = 74 ÷ 2 = 37 Median of Plane B = 36
Variation of Plane A = (28-37)^2 + (36-37)^2 + (36-37)^2 + (38-37)^2 + (38-37)^2 + (40-37)^2 + (40-37)^2 + (40-37)^2 ÷ 8
=(-9)^2 + (-1)^2 + (-1)^2 + (1)^2 + (1)^2 + (3)^2 + (3)^2 + (3)^2 ÷ 8
= 81 + 1 +1 +1 +1 +9 +9 +9 ÷ 8
= 112 ÷ 8
= 14.
Variation of Plane B = (32-36)^2 + (32-36)^2 + (34-36)^2 + (34-36)^2 + (34-36)^2 + (36-36)^2 + (38-36)^2 + (50-36)^2 ÷ 8
= (-4)^2 + (-4)^2 + (-2)^2 + (-2)^2 + (-2)^2 + (0)^2 + (2)^2 + (4)^2 ÷ 8
= 16 + 16 + 4+ 4+ 4+ 0 +4 + 16 ÷ 8
= 64 ÷ 8
= 8.
Statistics Cumulative Practice

Question 1.
Which of the ratios form a proportion?
A. 5 to 2 and 4 to 10
B. 2 : 3 and 7 : 8
C. 3 to 2 and 15 to 10
D. 12 : 8 and 8 : 42.
Answer:
C. 3 to 2 and 15 to 10 is the ratios form a proportion
Explanation:
A) 5 to 2 and 4 to 10
B) 2 : 3 and 7 : 8
C) 3 to 2 and 15 to 10
=> 3 : 2 and 15 : 10
=> Divide by 5 on both sides
=> 3 : 2 and 3 : 2
D) 12 : 8 and 8 : 42.
=> Divide by 2 on both sides
=> 6 : 4 and 4 : 21
=> Divide by 2 on both sides
=> 3 : 2 and 2 :21
Question 2.
A student scored 600 the first time. she took the mathematics portion of a college entrance exam. The next time she took the exam, she scored 660. Her second score represents what percent increase over her first score?
F. 9.1%
G. 10%
H. 39.6%
I. 60%
Answer:
F = 9.1 % is the Percentage increase in her second score over her first score.
Explanation:
Number of marks she scored in first attempt in the exam = 600
Number of marks she scored in second attempt in the exam = 660
Difference in the score = 660 – 600 = 60
Percentage increase in her second score over her first score = 60 ÷ 660 × 100
= 0.9090 × 100 = 9.1%
Question 3.
You ask 100 randomly chosen students to name their favorite food. There are 1250 students in the school. Based on this sample, what is the number of students in the school whose favorite food is chicken?
A. 100
B. 225
C. 450
D. 475
Answer:
Number of students in the school whose favorite food is chicken = 100.
Explanation:
Total number of students in the school = 1250
Number of students randomly chosen = 100
Number of students in the school whose favorite food is chicken = 8 ÷ 100 × 1250
= 0.08 × 1250 = 100.
Question 4.
Which value of makes the equation p + 6 = 5 true?
F. – 1
G. 1
H. 11
I. 30
Answer:
F. – 1
p = -1 makes the equation p + 6 = 5 true.
Explanation:
F) Substitute p = -1 in Equation:
p + 6 = 5 = -1 + 6 = 5
G) Substitute p = 1 in Equation:
p + 6 = 5 = 1 + 6 = 7
H ) Substitute p = 11 in Equation:
p + 6 = 5 = 11 + 6 = 17
I) Substitute p = 30 in Equation:
p + 6 = 5 = 30 + 6 = 36
Question 5.
The table shows the costs for four cans of tomato soup. Which can has the lowest cost per ounce?
A. Can A
B. Can B
C. Can C
D. Can D
Answer:
The lowest cost per ounce has D. Can D.
Explanation:
Cost of Can A cost per ounce= 1.95 ÷ 26 = 0.075
Cost of Can B cost per ounce= 0.72 ÷ 8 = 0.09
Cost of Can C cost per ounce=0.86 ÷ 10.75 = 0.08
Cost of Can D cost per ounce= 2.32 ÷ 23.2 = 0.1
Question 6.
What value of y makes the equation – 3y = – 18 true?

Answer:
y = 6 makes the equation – 3y = – 18 true.
Explanation:
Equation – 3y = – 18
=> y = -18 ÷ -3
Divide by 3 both sides.
=> y = 6
Question 7.
The double dot plot shows the values in two data sets. Which sentence best represents the difference in the measures of center as a multiple of the measure of variation?
F. The difference of the means is about 3.3 times the MAD.
G. The difference of the means is about 3.8 times the MAD.
H. The difference of the means is 36 times the MAD.
I. The difference of the means is 48.7 times the MAD.
Answer:
G. The difference of the means is about 3.8 times the MAD.
Explanation:
Data of set A = 42 43 46 48 48 51 51 51 52 55
Mean of set A = 42 + 43 + 46 + 48 + 48 + 51 + 51 + 51 + 52 + 55 ÷ 10
= 487 ÷ 10
= 48.7
MAD of set A = |42−48.7∣ + |43−48.7∣ +|46−48.7∣ +|48−48.7∣ + |48-48.7∣ + |51-48.7∣ + |51-48.7∣ +|51-48.7∣ +|52-48.7∣ + |55-48.7∣ ÷ 10
= |-6.7∣ + |-5.7∣ +|-2.7∣ +|-0.7∣ + |-0.7∣ + |2.3∣ + |2.3∣ +|2.3∣ +|3.3∣ + |6.3 ∣ ÷ 10
= 33 ÷ 10
= 3.3
Data of set B = 30 31 33 34 36 36 38 40 41 41
Mean of set B = 30 + 31 + 33 + 34 + 36 + 36 + 38 + 40 + 41 + 41 ÷ 10
= 360÷ 10
= 36.0
MAD of set B = |30-36∣ + |31-36∣ +|33-36∣ +|34-36∣ + |36-36∣ + |36-36∣ + |38-36∣ +|40-36∣ +|41-36∣ + |41-36∣ ÷ 10
= |-6∣ + |-5∣ +|-3∣ +|-2∣ + |0∣ + |0∣ + |2∣ +|4∣ +|5∣ + |5∣ ÷ 10
= 32 ÷ 10
= 3.2
Difference in Means ÷ MAD of set A= 48.7 – 36 ÷ 3.3 = 12.7 ÷ 3.3= 3.85
Difference in Means ÷ MAD of set B= 48.7 – 36 ÷ 3.2 = 12.7 ÷ 3.2 =3.97
Question 8.
What is the missing value in the ratio table?
Answer:
The missing value in the ratio table is 20.
Explanation:
a) 2/3 = 5
=> 2 = 5 × 3
=> 2 = 15
b) 8/3 = X
8 = 3 × = 60
=> 60 ÷ 3
=> 20
Question 9.
You are selling tomatoes. What is the minimum number of 4pounds of tomatoes you need to sell to earn at least $44?

A. 11
B. 12
C. 40
D. 176
Answer:
A. 11 is the minimum number of tomatoes needed to sell to earn at least $44.
Explanation:
Cost of the tomatoes = $44
cost of the tomatoes per pound = $4
The minimum number of tomatoes needed to sell to earn at least $44 = 44 ÷ 4 = 11.
Question 10.
You and a group of friends want to know how many students in your school prefer science. There are 900 students in your school. Each person randomly surveys 20 students. The table shows the results. Which subject do students at your school prefer?
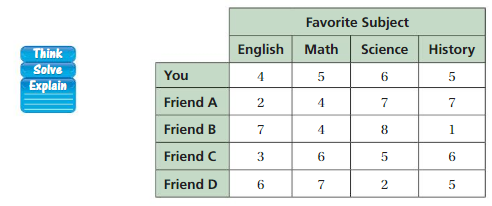
Part A Use each sample to make an estimate for the number of students in your school who prefer science.
Part B Describe the variation of the estimates.
Part C Use the samples to make one estimate for the number of students who prefer science in your school.
Answer:
Number of students who prefer science = 28
Mean = 5.6
Variation of the estimate = 4.24
Explanation:
Number of students who prefer science = 6 + 7 + 8 +5 + 2 = 28
Mean of number of students who prefer science = 6 + 7 + 8 +5 + 2 ÷ 5 = 28 ÷ 5 = 5.6
Variation of the estimate = (6-5.6)^2 + (7-5.6)^2 + (8-5.6)^2 + (5-5.6)^2 + (2-5.6)^2 ÷ 5
= (-0.4)^2 + (1.4)^2 + (2.4)^2 + (0.6)^2 + (-3.6)^2 ÷ 5
= 0.16 +1.96 + 5.76 + 0.36 + 12.96 ÷ 5
= 21.2 ÷ 5
= 4.24
Conclusion:
We hope that the information given about Big Ideas Math Answers Grade 7 Chapter 8 Statistics satisfies you. You can compare all the questions in real-time and can understand the concept easily. Stick to our website to get the solution key for all chapters of BIM Grade 7 Chapter 8. Clear all your doubts from the below-given comment section and share the article with your friends.
