Big Ideas Math Answers 8th Grade Ch 10 Volume and Similar Solids helps you to have strong fundamentals of concepts underlying. Learn the associated lessons of Volume and Similar Solids easily and quickly taking the help of the BIM Book Grade 8 Chapter 10 Answers. All the Big Ideas Math Grade 8 Answers Chapter 10 Concepts are sequenced as per the BIM Textbooks. Resolve all your queries taking the help of the Step by Step Solutions provided for Big Ideas Math 8th Grade Questions and attempt the exam with utmost confidence.
Big Ideas Math Book 8th Grade Answer Key Chapter 10 Volume and Similar Solids
Big Ideas Math Book Grade 8 Answer Key Chapter 10 Volume and Similar Solids is given by subject experts after extensive research and meets the Common Core State Standards Curriculum. Refer to the below links available for BIM Textbook 8th Grade Ch 10 Volume and Similar Solids Solution Key and clear all your concerns in no time. Download the Volume and Similar Solids Big Ideas Math 8th Grade Answers for free of cost.
Performance Task
- Volume and Similar Solids STEAM Video/Performance Task
- Volume and Similar Solids Getting Ready for Chapter 10
Lesson: 1 Volumes of Cylinders
Lesson: 2 Volumes of Cones
Lesson: 3 Volumes of Spheres
Lesson: 4 Surface Areas and Volumes of Similar Solids
- Lesson 10.4 Surface Areas and Volumes of Similar Solids
- Surface Areas and Volumes of Similar Solids Homework & Practice 10.4
Chapter: 10 – Volume and Similar Solids
- Volume and Similar Solids Connecting Concepts
- Volume and Similar Solids Chapter Review
- Volume and Similar Solids Practice Test
- Volume and Similar Solids Cumulative Practice
Volume and Similar Solids STEAM Video/Performance Task
STEAM Video
Canning Salsa
You can estimate the volumes of ingredients to predict the total volume of a finished recipe. In what other real-life situations is it helpful to know the volumes of objects?

Watch the STEAM Video “Canning Salsa.” Then answer the following questions.
1. You can approximate the volumes of foods by comparing them to common solids. A cube of cheese has side lengths of 3 centimeters. What is the volume of the cheese?
2. The table shows the amounts x (in cubic inches) of tomato used to make y cubic inches of salsa.
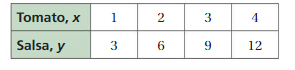
a. Is there a proportional relationship between x and y? Justify your answer.
b. How much tomato do you need to make 15 cubic inches of salsa?
Answer:
1. The volume of the cheese = 27 cubic centimeters.
2. a = 1: 3 relationship.
b. 5 tomatoes are used to make 15 cubic inches of salsa.
Explanation:
1. Given that a cube of cheese has a side length of 3 centimeters.
the volume of cube = s³
volume = side x side x side
volume = 3 x 3 x 3
volume = 27 cubic centimeters.
2. The relationship given in the above table is a 1: 3 ratio.
1 x 3 = 3
2 x 3 = 6
3 x 3 = 9
4 x 3 = 12.
b. The tomatoes used to make 15 cubic inches of salsa = 5
5 x 3 = 15
Performance Task
Packaging Salsa
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the dimensions of a jar and a shipping box.
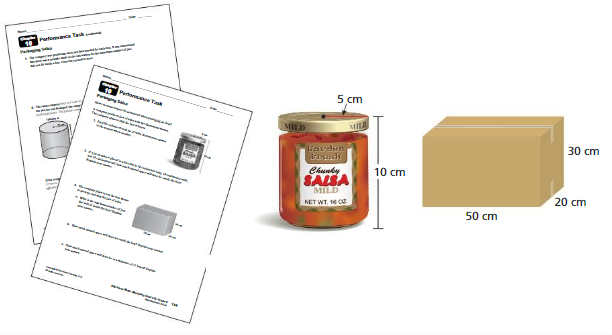
You will be asked questions about how to package jars of salsa. Why is it helpful to know how many jars of salsa fit in one box?
Volume and Similar Solids Getting Ready for Chapter 10
Chapter Exploration
1. Work with a partner.

a. How does the volume of the stack of dimes compare to the volume of a single dime?
b. How does the volume of the stack of nickels compare to the volume of the stack of dimes? Explain your reasoning. (The height of each stack is identical.)
c. How does the volume of each stack change when you double the number of coins?
d. LOGIC Your friend adds coins to both stacks so that the volume of the stack of dimes is greater than the volume of the stack of nickels. What can you conclude about the number of coins added to each stack? Explain your reasoning.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
cone
hemisphere
sphere
similar solids
Answer:
cone = A solid or hollow object which tapers from a circular or roughly circular base to a point.
hemisphere = a half of the celestial sphere as divided into two halves by the horizon.
sphere = a round solid figure, or its surface, with every point on its surface equidistant from its center.
similar solids = two solids are similar if they are the same type of solid and their corresponding radii, heights, base lengths, widths, etc. are proportional.
Lesson 10.1 Volumes of Cylinders
EXPLORATION 1
Exploring Volume
Work with a partner.
a. Each prism shown has a height of h units and bases with areas of B square units. Write a formula that you can use to find the volume of each prism.
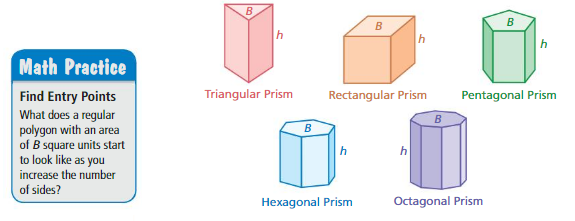
b. How can you find the volume of a prism with bases that each have 100 sides?
c. Make a conjecture about how to find the volume of a cylinder. Explain your reasoning.
Answer:
a. Volume of triangular prism = (bhl/2)
rectangular prism = lwh
pentagonal prism =(1/2)(5 s x a) h
Hexagonal prism = BH
octagonal prism = (A x H)/2
b. volume of prism = 5,00,000
c. volume of cylinder = πr² h
Explanation:
a. volume of traingular prism = (bhl/2)
where b = base, h = height, l= length.
rectangular prism = lwh
where l = length, w= width, h= height.
pentagonal prism = (1/2) x (5 s x a) h
where s = side , a= area , h= height.
hexagonal prism = BH
where b = base h = height
octagonal prism = (A X H)/2
A = area , H = height
volume of triangular prism = (bhl/2)
volume = (100 x 100 x 100/2)
volume = (100x 100 x 50)
volume = 5,00,000
volume of cylinder =πr² h
where r = radius and h = height.
EXPLORATION 2
Finding Volume Experimentally
Work with a partner. Draw a net for a cylinder. Then cut out the net and use tape to form an open cylinder. Repeat this process to form an open cube. The edge length of the cube should be greater than the diameter and the height of the cylinder.

a.Use your conjecture in Exploration 1 to find the volume of the cylinder.
b. Fill the cylinder with rice. Then pour the rice into the open cube. Find the volume of rice in the cube. Does this support your answer in part(a)? Explain your reasoning.
Answer:
a. volume of cylinder = πr² h
b. we did not find the volume of rice in the cube.
Explanation:
a. volume of cylinder = πr² h
where r = radius , h = height
b. we did not find the volume of rice in the cube because they did not give the value for the volume of rice.
Try It
Question 1.
Find the volume of a cylinder with a radius of 4 feet and a height of 15 feet. Round your answer to the nearest tenth.
Answer:
volume of cylinder = 753.6 cubic feet.
Explanation:
volume of cylinder =πr² h
where r = radius and h = height.
r = 4 feet , h = 15 feet π = 3.14 given.
v = π x 4 x 4 x 15
v = 3.14 x 16 x 15
v = 753.6 cubic feet.
Question 2.
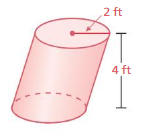
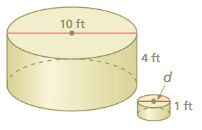
Find the height of the cylinder at the left. Round your answer to the nearest tenth.
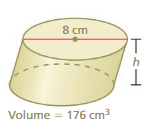
Answer:
height of the cylinder =0.28545 cm
Explanation:
volume of cylinder =πr² h
where r = radius and h = height.
r = 4 cm , v = 176 π = 3.14 given.
176= π x 4 x 4 x h
176= 3.14 x 16 h
176 = 50.24 h
h = (50.24/176)
h = 0.28545 cm
Find the radius of the cylinder. Round your answer to the nearest tenth.
Question 3.
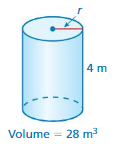
Answer:
radius of the cylinder = 0.2242 m²
Explanation:
volume of cylinder =πr² h
where r = radius and h = height.
h = 4 m , v = 28 π = 3.14 given.
28= π x r x r x 4
28= 3.14 x 4 r²
28 = 12.56 r²
r² = (12.56/28)
r² = 0.44857143 m⁴
r = 0.2242 m²
Question 4.
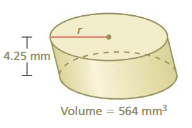
Answer:
radius of the cylinder =0.01183067 mm²
Explanation:
volume of cylinder =πr² h
where r = radius and h = height.
h = 4.25mm , v = 564 π = 3.14 given.
564= π x r x r x 4.25
564= 3.14 x 4.25 r²
564= 13.345 r²
r² = (13.345/564)
r² = 0.02366135.
r = 0.01183067 mm²
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
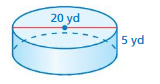
Question 5.
FINDING THE VOLUME OF A CYLINDER
Find the volume of the cylinder at the left. Round your answer to the nearest tenth.
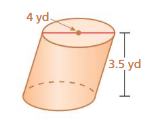
Answer:
volume of cylinder = 43.96 cu yds
Explanation:
volume of cylinder = πr² h
where π = 3.14 diameter = 4 given
so radius = (d/2)
r = (4/2)
r = 2 , h = 3.5
v = 3.14 x 2 x 2 x 3.5
v = 6.28 x 2 x 3.5
v = 12.56 x 3.5
v = 43.96 cu yds
Question 6.
FINDING THE HEIGHT OF A CYLINDER
Find the height of the cylinder at the right. Round your answer to the nearest tenth.
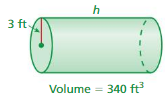
Answer:
volume of cylinder = 43.96 cu yds
Explanation:
volume of cylinder = πr² h
where π = 3.14 diameter = 4 given
so radius = (d/2)
r = (4/2)
r = 2 , h = 3.5
v = 3.14 x 2 x 2 x 3.5
v = 6.28 x 2 x 3.5
v = 12.56 x 3.5
v = 43.96 cu yds
Question 7.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
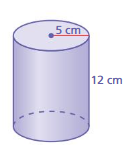
Answer:
volume of cylinder = 942 cu cm
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 5 cm
r = 5 , h = 12 given
v = 3.14 x 5 x 5 x 12
v = 3.14 x 25 x 12
v = 78.5 x 12
v = 942 cu cm
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
How much salsa is missing from the jar? Explain your reasoning.

Answer:
The salsa missing from the jar = 6 cm
Explanation:
Given that the jar height = 10 cm
salsa filled is 4 cm
salsa missing from the jar = 10 – 4
salsa missing from the jar = 6 cm
Question 9.
A cylindrical swimming pool has a circumference of 18π feet and a height of 4 feet. About how many liters of water are needed to fill the swimming pool to 85% of its total volume? Justify your answer. (1 ft3 ≈ 28.3 L)

Answer:
The total amount of water needed to fill the swimming pool = 9 feet
Explanation:
No of liters of water = volume of cylinder = πr² h
h = 4 feet given,
circumference = 18 π feet given
2 πr = 18 π
π get canceled on both sides.
2r = 18
r = 9 feet
Question 10.
DIG DEEPER!
A company creates two designs for a cylindrical soup can. Can A has a diameter of 3.5 inches and a height of 3.6 inches. Can B has a height of 4.9 inches. Each can holds the same amount of soup. Which can requires less material to make? Explain your reasoning.
Answer:
can B requires less material to make.
Explanation:
volume of the cylinder = πr² h
volume of can A = πr² h
h = 3.6 in,diameter = 3.5 in given where r = (d/2)
r = (3.5/2) = 1.75 in
v = 3.14 x 1.75 x 1.75 x 3.6
v = 3.14 x 3.0625 x 3.6
v = 3.14 x 11.025
v = 34.6185 cu in
volume of can B = πr² h
h = 4.9 in,diameter = 3.5 in given where r = (d/2)
r = (3.5/2) = 1.75 in
v = 3.14 x 3.5 x 3.5 x 3.6
v = 3.14 x 12.25 x 3.6
v = 3.14 x 44.1
v = 138.474 cu in
Volumes of Cylinders Homework & Practice 10.1
Review & Refresh
Tell whether the triangle with the given side lengths is a right triangle.
Question 1.
20 m, 21 m, 29 m
Answer:
Yes, the given side lengths form a right triangle.
Explanation:
The length of any sides of right triangle = a² + b² = c²
a² + b² = c² = a² + 2b= c²
a = 20 , b = 21, c = 29
400 + 441 = 841
841 is equal to 841
Question 2.
1 in., 2.4 in., 2.6 in.
Answer:
the given side lengths is not a right triangle.
Explanation:
The length of any sides of right triangle = a² + b² = c²
a² + b² = c² = a² + 2b= c²
a = 1 , b = 2.4, c = 2.6
1+ 2.4 x 2 = 6.76
5.8 = 6.76
5.8 is not equal to 6.76
Question 3.
5.6 ft, 8 ft, 10.6 ft
Answer:
the given side lengths is not a right triangle.
Explanation:
The length of any sides of right triangle = a² + b² = c²
a² + b² = c² = a² + 2b= c²
a = 5.6 , b = 8, c = 10.6
5.6 x 5.6 + 8 x 2 = 10.6 x 10.6
31.36 + 16 = 112.36
47.36 = 112.36
47.36 is not equal to 112.36
Write the number in standard form.
Question 4.
3.9 × 106
Answer:
3.9000000
Explanation:
3.9 x 10⁶
3.9 x (10⁵ x 10⁶)
3.9 x (10 ⁵⁺⁶)
using aᵐx aᵑ = aᵐ⁺ᵑ
3.9 x (10 ¹¹)
3.9 x 10¹¹
3.900000000000
Question 5.
6.7 × 10-5
Answer:
0.000067
Explanation:
6.7x 10-5
6.7 x 10-⁴ x 10-5
6.7 x (10-⁴- ⁵)
6.7 x 10-⁹
0.000067
Question 6.
6.24 × 1010
Answer:
6.240000000000
Explanation:
6.24 x 10¹⁰
6.24 x (10⁹ x 10¹⁰)
6.24 x (10⁹ ⁺¹⁰)
using aᵐx aᵑ = aᵐ⁺ᵑ
6.24 x (10 ¹⁹ )
6.24 x 10¹⁹
6.240000000000000000000
Question 7.
Which ordered pair is the solution of the linear system 3x + 4y = -10 and 2x – 4y = 0?
A. (6, 2)
B. (2, 6)
C. (2, 1)
D. (1, 2)
Answer:
option c is correct.
Explanation:
3x + 4y = -10
3 (2) + 4 (1) = -10
6 + 4 = -10
2x – 4y = 0
2 (2) – 4 (1) = 0
4 – 4 = 0
Concepts, Skills, &Problem Solving
FINDING VOLUME The height h and the base area B of a cylinder are given. Find the volume of the cylinder. Write your answer in terms of π. (See Explorations 1 and 2, p. 427.)
Question 8.
h = 5 units
B = 4π square units
Answer:
volume of cylinder = 251.2 π cubic units
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 4π
r = 4π , h = 5 given
v = 3.14 x 4 x 4 x 5
v = 3.14 x 16 x 5
v = 251.2
v = 251.2 π cubic units
Question 9.
h = 2 units
B = 25π square units
Answer:
volume of cylinder = 50 π cubic units
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 25π
r = 25π , h = 2 given
v = 3.14 x 25x 25 x 2
v = 3.14 x 25 x 2
v = 3.14 x 50
v = 50 π cu. units
Question 10.
h = 4.5 units
B = 16π square units
Answer:
volume of cylinder = 3,617.28 π cu. units
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 16π
r = 16π , h = 4.5 given
v = 3.14 x 16 x 16 x 4.5
v = 3.14 x 256 x 4.5
v = 3.14 x 1152
v = 3,617.28 π cu. units
FINDING THE VOLUME OF A CYLINDER Find the volume of the cylinder. Round your answer to the nearest tenth.
Question 11.
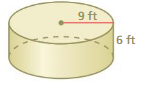
Answer:
volume of cylinder = 1,526.04 cu. feet
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 9
r = 9 , h = 6 given
v = 3.14 x 9 x 9 x 6
v = 3.14 x 81 x 6
v = 3.14 x 486
v = 1,526.04 cu. feet
Question 12.
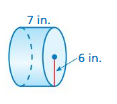
Answer:
volume of cylinder = 791.28 cu. in
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 6
r = 6 , h = 7 given
v = 3.14 x 6 x 6 x 7
v = 3.14 x 36 x 7
v = 3.14 x 252
v = 791.28 cu. in
Question 13.
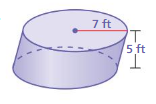
Answer:
volume of cylinder = 769.3 cu feet
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 7
r = 7 , h = 5 given
v = 3.14 x 7 x 7 x 5
v = 3.14 x 49 x 5
v = 3.14 x 245
v = 769.3 cu feet
Question 14.
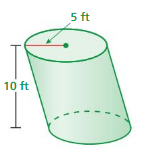
Answer:
volume of cylinder = 785 cu. feet
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 5 ft
r = 5 , h = 10 given
v = 3.14 x 5 x 5 x 10
v = 3.14 x 25 x 10
v = 3.14 x 250
v = 785 cu. feet
Question 15.
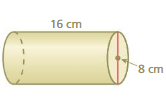
Answer:
volume of cylinder = 804.2 cu. cm
Explanation:
volume of cylinder = πr² h
where π = 3.14 r = 8 cm
r = 8 , h = 16 given
v = 3.14 x 8 x 8 x 16
v = 3.14 x 64 x 16
v = 3.14 x 1,024
v = 804.2 cu. cm
Question 16.
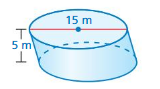
Answer:
volume of cylinder = 883.125 cu. m
Explanation:
volume of cylinder = πr² h
where π = 3.14 d = 15 r = (d/2)
r = 7.5 , h = 5 given
v = 3.14 x 7.5 x 7.5 x 5
v = 3.14 x 56.25 x 5
v = 3.14 x 281.25
v = 883.125 cu. m
Question 17.
REASONING
Without calculating, which of the solids has the greater volume? Explain.
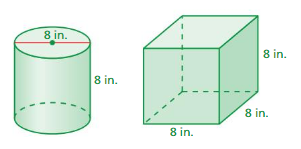
Answer:
the cube has a greater volume.
Explanation:
the volume of square prism = s³
v = side x side x side
v = 8 x 8 x 8
v = 64 x 8
v = 512 cubic inches
volume of cylinder = πr² h
where π = 3.14 r = 4 cm
r = 4 , h = 8 given
v = 3.14 x 4 x 4 x 8
v = 3.14 x 16 x 8
v = 3.14 x 128
v = 401.92 cu. in
FINDING A MISSING DIMENSION Find the missing dimension of the cylinder. Round your answer to the nearest whole number.
Question 18.
Volume = 10,000 π in.3
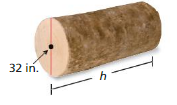
Answer:
height of cylinder = 0.080384 in
Explanation:
volume of cylinder = πr² h
where π = 3.14 d = 32 r = (d/2)
r = 16 , v = 10,000
10,000 = 3.14 x 16 x 16 x h
10,000 = 3.14 x 256 h
10,000= 803.84 h
h = (803.84/10,000)
h = 0.080384 in
Question 19.
Volume = 3785 cm3

Answer:
radius of cylinder = 8 cm
Explanation:
volume of cylinder = πr² h
where π = 3.14 h = 19
v = 3785
3785 = 3.14 x r x r x 19
3785 = 3.14 x 19r²
3785= 59.66 r²
r² = (3785/59.66)
r² =64
r = 8 cm
Question 20.
Volume = 600,000 cm3

Answer:
Radius of cylinder = 0.00198867 cm
Explanation:
Volume of cylinder = πr² h
where π = 3.14 h = 76 cm given
, v = 600,000
600,000 = 3.14 x r x r x 76
600,000 = 3.14 x 76r²
600,000= 238.64r²
r² = (238.64/600,000)
r² = 0.00397733
r = 0.00198867 cm
Question 21.
MODELING REAL LIFE
A cylindrical hazardous waste container has a diameter of 1.5 feet and a height of 1.6 feet. About how many gallons of hazardous waste can the container hold? (1 ft3 ≈ 7.5 gal)
Answer:
Hazardous waste can hold the container = 21.195 gal
Explanation:
volume of cylinder = πr² h
where π = 3.14 d = 1.5 r = (d/2)
r = 0.75 , h = 1.6 feet
v = 3.14 x 0.75 x 0.75 x 1.6
v = 3.14 x 0.5625 x 1.6
v= 3.14 x 0.9
h = 2.826
h = 2.826 x 7.5
h = 21.195 gal
Question 22.
CRITICAL THINKING
How does the volume of a cylinder change when its diameter is halved? Explain.
Answer:
the volume of the cylinder change when its diameter is halved.
Explanation:
If the diameter is halved it is the same as a radius.
d = (r/2)
(d/2)
so the volume of the cylinder change when its diameter is halved.
Question 23.
PROBLEM SOLVING
A traditional “square” bale of hay is actually in the shape of a rectangular prism. Its dimensions are 2 feet by 2 feet by4 feet. How many square bales contain the same amount of hay as one large “round” bale?

Answer:
The square bales contain the same amount of hay as one large round bale = 4 squares bale
Explanation:
The surface area of rectangular prism = 2(lw + lh +wh)
given that l = 2, w=2 h = 4
area = 2(2 x 2 + 2 x 4 +4 x 2)
area = 2(4 + 8 + 8)
area = 2(2)
area = 4 sq ft
Question 24.
MODELING REAL LIFE
A tank on a road roller is filled with water to make the roller heavy. The tank is a cylinder that has a height of 6 feet and a radius of 2 feet. About how many pounds of water can the tank hold? (One cubic foot of water weighs about 62.5 pounds.)

Answer:
The pounds of water can hold the tank = 4,710 pounds
Explanation:
Volume of cylinder = πr² h
where π = 3.14 h = 6 ft given
r = 2 ft
v = 3.14 x 2 x 2 x 6
v = 3.14 x 4 x 6
v= 3.14 x 24
v = 75.36 cu. feet
v = 75.36 x 62.5
v = 4,710 pounds
Question 25.
REASONING
A cylinder has a surface area of 1850 square meters and a radius of 9 meters. Estimate the volume of the cylinder to the nearest whole number.
Answer:
Volume of the cylinder = 6035 cubic meters.
Explanation:
volume of the cylinder= πr²h
volume = 3.14 x 9 x 9 x 1850
volume = 8325 – 729 π
v = 8325 – 729 x 3.14
v = 8325 – 102.06
v = 8222.94
the nearest whole number to the 8222.94 is 6035 cubic meters.
Question 26.
DIG DEEPER!
Water flows at 2 feet per second through a cylindrical pipe with a diameter of 8 inches. A cylindrical tank with a diameter of 15 feet and a height of 6 feet collects the water.
a. What is the volume (in cubic inches) of water flowing out of the pipe every second?
b. What is the height (in inches) of the water in the tank after 5 minutes?
c. How many minutes will it take to fill 75% of the tank?
Answer:
a. Volume of water flowing out of the pipe every second = 100.48 cu. in
b. The height of the water in tank after 5 minutes = 1,059.75 sq ft
c. 75% of water to fill tank = 25
Explanation:
a. Volume of cylinder = πr² h
where π = 3.14 h = 2 ft given
r = 4
v = 3.14 x 4 x 4 x 2
v = 3.14 x 16 x 2
v= 3.14 x 32
v = 100.48 cu. in
b. Volume of cylinder = πr² h
where π = 3.14 h = 6 ft given
r = 7.5
v = 3.14 x 7.5 x 7.5 x 6
v = 3.14 x 56.25 x 6
v= 3.14 x 337.5
v = 1,059.75 cu. ft
c. 100 – 75
25 %
Question 27.
PROJECT
You want to make and sell three different sizes of cylindrical candles. You buy 1 cubic foot of candle wax for $20 to make 8 candles of each size.

a. Design the candles. What are the dimensions of each size of candle?
b. You want to make a profit of $100. Decide on a price for each size of candle. Explain how you set your prices.
Answer:
a. The dimensions of each size of candle = 20cm
b. price for each size of candle = $ 30
Explanation:
$ x 80 candles given
20 x 3 = 60
each candle has a dimension of 20 cm
b. price for each side = $ 30
Lesson 10.2 Volumes of Cones
You already learned how the volume of a pyramid relates to the volume of a cone prism. In this exploration, you will discover how the volume of a relates to the volume of a cylinder.
A cone is a solid that has one circular base and one vertex.
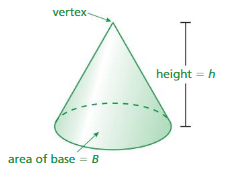
EXPLORATION 1
Finding a Formula Experimentally
Work with a partner.Use a paper cup that is shaped like a cone. Measure the height of the cup and the diameter of the circular base. Use these measurements to draw a net for a cylinder with the same base and height as the paper cup. Then cut out the net and use tape to form an open cylinder.

a. Find the volume of the cylinder.
b. Fill the paper cup with rice. Then pour the rice into the cylinder. Repeat this until the cylinder is full. How many cones does it take to fill the cylinder?
c. Use your result to write a formula for the volume of a cone.
d. Use your formula in part(c) to find the volume of the cone. How can you tell whether your answer is correct?
e. Do you think your formula for the volume of a cone oblique is also true for cones? Explain your reasoning.
Answer:
a. volume of cylinder = πr² h
b. 2 cones will take to fill the cylinder.
c. volume of cone = πr²( h/3)
d. yes the answer is correct.
e. volume of cone oblique is true for cones.
Explanation:
a.volume of cylinder = πr² h
where r = radius , h= height
b. 2 cones = 1 cylinder
c. . volume of cone = πr²( h/3)
where r = radius , h= height
d. Yes the answer is correct.

Try It
Question 1.
Find the volume of a cone with a radius of 6 centimeters and a height of 15 centimeters. Round your answer to the nearest tenth.
Answer:
volume of cone = 565.2 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r = 6 ,h=15
v = 3.14 x 6 x 6 x (15/3)
v = 3.14 x 36 x 5
v=3.14 x 180
v= 565.2 cu. cm
Question 2.
Find the height of the cone at the left. Round your answer to the nearest tenth.
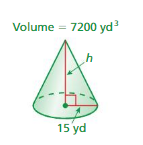
Answer:
height of cone = 0.03270833 yd
Explanation:
volume of cone =πr² (h/3)
given that r = 15 ,v = 7200
7200 = 3.14 x 15 x 15 x (h/3)
7200 = 3.14 x 15 x 5h
7200=3.14 x 75h
7200= 235.5 h
h = (235.5/7200)
h = 0.03270833
Find the radius of the cone. Round your answer to the nearest whole number.
Question 3.
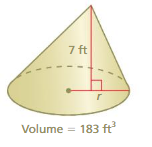
Answer:
radius of cone = 12.4887397 feet
Explanation:
volume of cone =πr² (h/3)
given that h = 7 ,v = 183
183 = 3.14 x r x r x (7/3)
183 = 3.14 x r² x 2.33
183=3.14 x 2.33 r²
183= 7.32666 r²
r² = (183/7.32666)
r² = 24.97747
r=12.4887397 feet
Question 4.
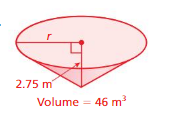
Answer:
radius of cone = 1.78594585 meter
Explanation:
volume of cone =πr² (h/3)
given that h = 2.75 ,v = 46
46 = 3.14 x r x r x (2.75/3)
46 = 3.14 x r² x 0.9166
46 = 12.87833 r²
r² = (46/12.87833)
r² = 3.57189
r=1.78594585 meter
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
FINDING THE VOLUME OF A CONE
Find the volume of a cone with a diameter of 10 yards and a height of 12 yards. Round your answer to the nearest tenth.
Answer:
volume of cone = 314 cu. yards.
Explanation:
volume of cone =πr² (h/3)
given that d = 10 r=(d/2) r = (10/2) r = 5 ,h=12
v = 3.14 x 5 x 5 x (12/3)
v = 3.14 x 25 x 4
v=3.14 x 100
v= 314 cu. yards
FINDING A MISSING DIMENSION OF A CONE Find the missing dimension of the cone. Round your answer to the nearest tenth.
Question 6.
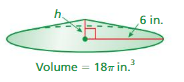
Answer:
height of cone = 66.6666 in
Explanation:
volume of cone =πr² (h/3)
given that r = 6 ,v = 2,512
2512 = 3.14 x 6 x 6 x (h/3)
2512 = 3.14 x 6 x 2h
2512 =3.14 x 12h
2512= 37.68h
h = (2512/37.68)
h = 66.6666 in
Question 7.
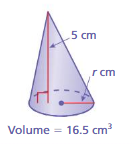
Answer:
radius of cone = 25.12 centimeter
Explanation:
volume of cone =πr² (h/3)
given that h = 5 ,v = 16.5
16.5 = 3.14 x r x r x (5/3)
16.5 = 3.14 x r² x 1.666
16.5 = 5.23333 r²
r² = (16.5/5.23333)
r² = 3.152868
r= 8π centimeter
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
A stalactite is a mineral formation that hangs from the ceiling of a cave. A cone-shaped stalactite has a height of 48 centimeters and a base circumference of 3.5π centimeters. What is the volume of the stalactite?

Answer:
volume of cone = 615.44 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r =3.5 ,h=48
v = 3.14 x 3.5 x 3.5 x (48/3)
v = 3.14 x 12.25 x 16
v=3.14 x 196
v= 615.44 cu. cm
Question 9.
A store sells two cone-shaped funnels. What is the height of each funnel? (1 pt = 28.875 in.3)

Answer:
height of ist funnel =2.72469922 in
height of 2nd funnel = 3.06528662 in
Explanation:
volume of 1st cone =πr² (h/3)
given that r= (d/2)r = (4.5/2) r = 2.25 ,v = 0.5
0.5 = 3.14 x 2.25 x 2.25 x (h/3)
0.5 = 3.14 x 5.0625 x (h/3)
0.5 =3.14 x 1.6875h
0.5= 5.29875 h
h = (0.5/5.29875)
h = 0.09436188
h = 0.09436188 x 28.875
h = 2.72469922
volume of 2nd cone =πr² (h/3)
given that r= (d/2)r = (6/2) r=3 ,v = 1
1 = 3.14 x 3 x 3 x (h/3)
1 = 3.14 x 3x h
1 =3.14 x 3h
1= 9.42 h
h = (1/9.42)
h = 0.10615711 x 28.875
h = 3.0652866
Question 10.
You fill cone-shaped pastry bags with icing to a height of 1 foot and a diameter of 3.5 inches. You use about 1.35 cubic inches of icing per cupcake. About how many cupcakes can you decorate with 2 bags of icing?
Answer:
Cupcakes can decorate with 2 bags of icing = 6.410833 sq in
Explanation:
volume of cone =πr² (h/3)
given that r= (d/2)r = (3.5/2) r=1.75 ,h = 1
v = 3.14 x 1.75 x 1.75 x (1/3)
v = 3.14 x 3.0625 x (1/3)
v =3.14 x 3.0625 x 0.333
v= 3.14 x 1.0208333
v = 3.20541667 inches
for 2 bags of icing = 6.4108333
Volumes of Cones Homework & Practice 10.2
Review & Refresh
Find the volume of the cylinder. Round your answer to the nearest tenth.
Question 1.
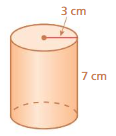
Answer:
volume of cone = 65.94 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r=3 ,h = 7
v = 3.14 x 3 x 3 x (7/3)
v = 3.14 x 9 x (7/3)
v =3.14 x 9 x 2.33
v= 3.14 x 21
v = 65.94 cu. cm
Question 2.
Answer:
volume of cone = 16.7466 cu. ft
Explanation:
volume of cone =πr² (h/3)
given that r=2 ,h = 4
v = 3.14 x 2 x 2 x (4/3)
v = 3.14 x 4 x (4/3)
v =3.14 x 4 x 1.33
v= 3.14 x 5.333
v = 16.7466 cu. ft
Question 3.
Answer:
volume of cone = 523.333 cu. yds
Explanation:
volume of cone =πr² (h/3)
given that r=10 ,h = 5
v = 3.14 x 10 x 10 x (5/3)
v = 3.14 x 100 x (5/3)
v =3.14 x 100 x 1.666
v= 3.14 x 166.66
v = 523.333 cu. yds
Solve the equation.
Question 4.
x3 = 27
Answer:
x = 3
Explanation:
x³ = 27
x³ = 3³
when power are equal exponents must be equal.
x = 3
Question 5.
– 6 = y3 + 2
Answer:
y = – 2
Explanation:
-6 = y³ + 2
y³ = 2 + 6
y³ = 8
y³ = 2³
y = -2
Question 6.
2h3 – 33 = 95
Answer:
h = 4
Explanation:
2h³ – 33 = 95
2h³ = 95 + 33
2h³ = 128
h³ = (128/2)
h³ = 64
h³ = 4³
h = 4
Concepts, Skills, & Problem Solving
FINDING A VOLUME The height h and the base B area of a cone are given. Find the volume of the cone. Write your answer in terms of π. (See Exploration 1, p. 433.)
Question 7.
h = 6 units
B = 4π square units
Answer:
volume of cone = 8 π cubic units
Explanation:
volume of cone =πr² (h/3)
given that r=4 ,h = 6
v = 3.14 x 4 x 4 x (6/3)
v = 3.14 x 16 x (6/3)
v =3.14 x 4 x 2
v= 8 x π
v = 25.12 cubic units
Question 8.
h = 9 units
B = 5π square units
Answer:
volume of cone = 235.5 cubic units
Explanation:
volume of cone =πr² (h/3)
given that r=5 ,h = 9
v = 3.14 x 5 x 5 x (9/3)
v = 3.14 x 25 x (9/3)
v =3.14 x 25 x 3
v= 3.14 x 75
v = 235.5 cubic units
FINDING THE VOLUME OF A CONE Find the volume of the cone. Round your answer to the nearest tenth.
Question 9.
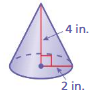
Answer:
volume of cone = 16.7466 cu. in
Explanation:
volume of cone =πr² (h/3)
given that r=2 ,h = 4
v = 3.14 x 2 x 2 x (4/3)
v = 3.14 x 4 x (4/3)
v =3.14 x 4 x 1.33
v= 3.14 x 5.33
v = 16.7466 cu. in
Question 10.
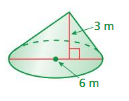
Answer:
volume of cone = 28.26 cu. m
Explanation:
volume of cone =πr² (h/3)
given that r=(d/2) (6/2)=3 ,h = 3
v = 3.14 x 3 x 3 x (3/3)
v = 3.14 x 9 x (3/3)
v =3.14 x 9 x 1
v= 3.14 x 9
v = 28.26 cu. m
Question 11.
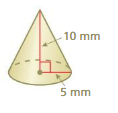
Answer:
volume of cone =261.66 cu. mm
Explanation:
volume of cone =πr² (h/3)
given that r = 5 ,h = 10
v = 3.14 x 5 x 5 x (10/3)
v = 3.14 x 25 x (10/3)
v =3.14 x 25 x 3.33
v= 3.14 x 83.333
v = 261.66 cu. mm
Question 12.
Answer:
volume of cone =2.093333 cu. ft
Explanation:
volume of cone =πr² (h/3)
given that r = 1 ,h = 2
v = 3.14 x 1 x 1 x (2/3)
v = 3.14 x 1 x (2/3)
v =3.14 x 1 x 0.6666
v= 3.14 x 0.666
v = 2.093333 cu. ft
Question 13.
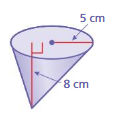
Answer:
volume of cone = 804.2 cubic cm
Explanation:
volume of cone =πr² (h/3)
given that r = 5 ,h = 8
v = 3.14 x 5 x 5 x (8/3)
v = 3.14 x 25 x (8/3)
v =3.14 x 25 x 2.6666
v= 3.14 x 256
v = 804.2 cubic cm
Question 14.
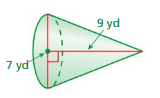
Answer:
volume of cone = 115.395 cu. yd
Explanation:
volume of cone =πr² (h/3)
given that r =(d/2) = (7/2) = 3. 5 ,h = 9
v = 3.14 x 3.5 x 3.5 x (9/3)
v = 3.14 x 12.25 x (9/3)
v =3.14 x 12.25 x 3
v= 3.14 x 36.75
v = 115.395 cu. yd
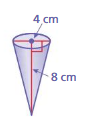
Question 15.
Answer:
volume of cone =117.226667 cu. ft
Explanation:
volume of cone =πr² (h/3)
given that r = 4 ,h = 7
v = 3.14 x 4 x 4 x (7/3)
v = 3.14 x 16 x (7/3)
v =3.14 x 16 x 2.3333
v= 3.14 x 37.33333
v = 117.226667 cu. ft
Question 16.
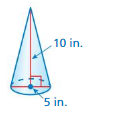
Answer:
volume of cone =65.416666 cu. in
Explanation:
volume of cone =πr² (h/3)
given that r = 2.5 ,h = 10
v = 3.14 x 2.5 x 2.5 x (10/3)
v = 3.14 x 6.25 x (10/3)
v =3.14 x 6.25 x 3.33
v= 3.14 x 20.8333
v = 65.416666 cu. in
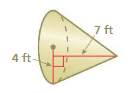
Question 17.
Answer:
volume of cone =1.5 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r = 2 ,h = 8
v = 3.14 x 2 x 2x (8/3)
v = 3.14 x 4 x (8/3)
v =3.14 x 4 x 2.666
v= 3.14 x 10.6666
v = 1.5 cu. cm
Question 18.
STRUCTURE
The inside of each glass is shaped like a cone. Which glass can hold more liquid? How much more?
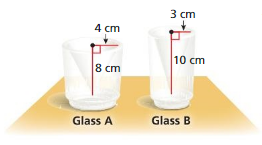
Answer:
Glass A can hold more liquid than glass B.
Explanation:
volume of Glass A =πr² (h/3)
given that r = 4 ,h = 8
v = 3.14 x 4 x 4 x (8/3)
v = 3.14 x 16 x (8/3)
v =3.14 x 16 x 2.666
v= 3.14 x 42.656
v = 42.656 cu. cm
volume of Glass A =πr² (h/3)
given that r = 3 ,h = 10
v = 3.14 x 3 x 3 x (10/3)
v = 3.14 x 9 x (10/3)
v =3.14 x 9 x 3.33
v= 3.14 x 30
v = 94.2 cu. cm
FINDING A MISSING DIMENSION OF A CONE Find the missing dimension of the cone. Round your answer to the nearest tenth.
Question 19.
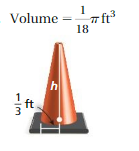
Answer:
volume of cone = 9203 cubic cm
Explanation:
volume of cone =πr² (h/3)
given that r=0.33 ,v = (1/18) ,v = 0.055
0.055 = 3.14 x 0.33 x 0.33 x (h/3)
0.055 = 3.14 x 0.1089h
0.055 =0.341946 h
h =(8788/3) x 3.14
h = 2929.33 x 3.14
h = 9203 cubic cm
Question 20.
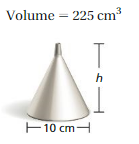
Answer:
volume of cone = 0.1162963 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r=5 ,v = 225
225 = 3.14 x 5 x 5 x (h/3)
225 = 3.14 x 5 x 1.666 h
225 =8.3333 x 3.14 h
225 = 26.1666666 h
h = (26.1666666/225)
h = 0.1162963 sq cm
Question 21.

Answer:
radius of cone = 3.15 cubic in
Explanation:
volume of cone =πr² (h/3)
given that h= 4.2 ,v = 3.6
3.6 = 3.14 x r x r x (4.2/3)
3.6 = 3.14 x r² x 1.4
3.6 =( 4.396 / r² )
r² = 3/4 x h
r = 0.75 x 4.12
r = 3.15 cubic in
Question 22.
FINDING A MISSING DIMENSION OF A CONE
The volume of a cone with a height of 10 meters is 20π cubic meters. What is the diameter of the cone?
Answer:
diameter of cone = 0.333 meters
Explanation:
volume of cone =πr² (h/3)
given that h= 10 ,v = 20
20 = 3.14 x r x r x (10/3)
20 = 3.14 x r² x3.33
20 = 10.46666 r²
r² = 0.1665 x 2
r = 0.333 meters.
Question 23.
MODELING REAL LIFE
Water leaks from a crack in a cone-shaped vase at a rate of 0.5 cubic inch per minute. The vase has a height of 10 inches and a diameter of 4.8 inches. How long does it take for 20% of the water to leak from the vase when it is full of water?
Answer:
20% of water to leak from the vase when it is full of water = 1206.4
Explanation:
volume of cone =πr² (h/3)
given that r = 2.4 ,h = 10
v = 3.14 x 2.4 x 2.4 x (10/3)
v = 3.14 x 5.76 x (10/3)
v =3.14 x 5.76 x 3.33
v= 3.14 x 384
v = 1206.4
20% of water to leak from the vase when it was full of water
1206.4
Question 24.
DIG DEEPER!
You have 10 gallons of lemonade to sell. (1 gal ≈ 3785 cm3)

a. Each customer uses 1 paper cup. The cups are sold in packages of 50. How many packages should you buy?
b. How many cups will be left over if you sell 80% of the lemonade?
Answer:
a. the no of packages should buy = 25
b. 20 cups will be left over if we sell 80% of lemonade.
Explanation:
a. the no of packages = 25
In the question given that the cups are sold in the packages of 50
b. 80% of cups will be left in the lemonade = 20
100 – 80 = 20
Question 25.
STRUCTURE
The cylinder and the cone have the same volume. What is the height of the cone?
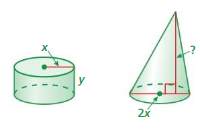
Answer:
The height of the cone = 54 π
Explanation:
Given that the cone and the cylinder have the same volume.
The height of the cone = 54 π
54 x 3.14
169.56
170 cubic cm
Question 26.
CRITICAL THINKING
In Example 4, you use a different timer with the same dimensions. The sand in this timer has a height of 30 millimeters. How much time do you have to answer the question?
Answer:
300 minutes will take to answer the question.
Explanation:
The sand in this timer has a height of 30 mm
time to answer the question = 5 x 6
5 hrs
300 minutes will take to answer the question.
Question 27.
REASONING
A vapor cone is a cloud of condensed water that forms when an aircraft breaks the sound barrier. How does doubling both the diameter and the height affect the volume of the vapor cone?

Answer:
The volume of the vapor cone is changed.
Explanation:
the volume of the cone = 4/3 πr³
v =4/3 πr³
r = 3√ 435,750,000
3200 + 3√ 435,750,000
3958
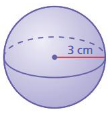
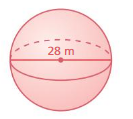
Lesson 10.3 Volumes of Spheres
A sphere is the set of all points in space that are the same distance from a point called the center. The radius r is the distance from the center to any point on the sphere. A sphere is different from the other solids you have studied so far because it does not have a base.
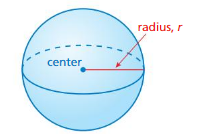
EXPLORATION 1
Finding a Formula Experimentally
Work with a partner. Use a plastic ball similar to the one shown. Draw a net for a cylinder with a diameter and a height equal to the diameter of the ball. Then cut out the net and use tape to form an open cylinder.

a. How is the height h of the cylinder related to the radius r of the ball?
b. Cover the ball with aluminum foil or tape. Leave one hole open. Fill the ball with rice. Then pour the rice into the cylinder. What fraction of the cylinder is filled with rice?

c. Use your result in part(b) and the formula for the volume of a cylinder to write a formula for the volume of a sphere. Explain your reasoning.
Answer:
a. Height of the cylinder is proportional to the radius of the ball.
c. volume of cylinder = πr²h
volume of sphere = (4/3) πr² x r

Try It
Find the volume of the sphere. Round your answer to the nearest tenth.
Question 1.
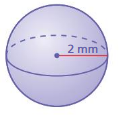
Answer:
volume of the sphere = 33.49333 cubic mm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x 2 x 2 x2
where r = 2 given
v = 1.33 x 3.14 x 8
v= 4.18666 x 8
v = 33.49333 cubic mm
Question 2.
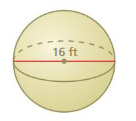
Answer:
volume of the sphere =2,138.2144 sq ft
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x 8 x 8 x8
where r = 8 given
v = 1.33 x 3.14 x 512
v= 1.33 x 1,607.68
v = 2,138.2144 cu. ft
Find the radius of the sphere. Round your answer to the nearest tenth if necessary.
Question 3.
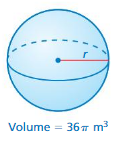
Answer:
radius of the sphere=0.333055310396 m
Explanation:
volume of sphere = (4/3) πr² x r
36 = (4/3) x 3.14 x r³
where v = 36
36 = 1.33r³
r³ = (1.33/36)
r³ = 0.036944
r =0.333055310396 m
Question 4.

Answer:
radius of the sphere= 0.6681660696 in
Explanation:
volume of sphere = (4/3) πr² x r
14 = (4/3) x 3.14 x r³
where v = 14
14 = 1.33 x 3.14 r³
14 = 4.1762 r³
r³ = (4.1762/14)
r³ = 0.2983 cubic in
r = 0.6681660696 in
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
FINDING THE VOLUME OF A SPHERE
Find the volume of the sphere. Round your answer to the nearest tenth.
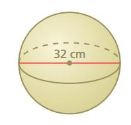
Answer:
volume of the sphere =17,105.7552 cu. cm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x 16 x 16 x 16
where r = 16 given
v = 1.33 x 3.14 x 4,096
v= 1.33 x 12,861.44
v = 17,105.7552 cu. cm
Question 6.
FINDING THE RADIUS OF A SPHERE
Find the radius of a sphere with a volume of 4500π cubic yards.
Answer:
radius of the sphere= 0.00029556 sq yds
Explanation:
volume of sphere = (4/3) πr² x r
4500 = (4/3) x 3.14 x r³
where v = 4500
4500 = 1.33 x 3.14 r³
4500 = 1.33 r³
r³ = (1.33/4500)
r³ = 0.00029556
Question 7.
WHICH ONE DOESN’T BELONG?
Which figure does not belong with the other three? Explain your reasoning.
Answer:
sphere does not belong with the other three.
Explanation:
pyramid, prism, cylinder have bases.
sphere does not have a base.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
In sphering, a person is secured inside a small, hollow sphere that is surrounded by a larger sphere. The space between the spheres is inflated with air. What is the volume of the inflated space? Explain.

Answer:
The volume of the inflated surface = 79.54649 cu. m
Explanation:
The volume of larger sphere = (4/3) πr³
v = (4/3) x 3.14 x 3³
v = 1.333 x 3.14 x 27
v = 4.18666 x 27
v = 113.03982 cu. m
The volume of hollow sphere = (4/3) πr³
v = (4/3) x 3.14 x 2³
v = 1.333 x 3.14 x 8
v = 4.18666 x 8
v = 33.49333 cu. m
inflated space = larger sphere – hollow sphere
inflated space = 79.54649
Question 9.
DIG DEEPER!
A vendor sells cones filled with frozen yogurt, as shown. The vendor has 4 cylindrical containers of frozen yogurt, each with a diameter of 18 centimeters and a height of 15 centimeters. About how much money will the vendor make when all of the frozen yogurt is sold? Justify your answer.

Answer:
volume of cone= 113.04 cu. cm
Explanation:
the volume of cone =πr² (h/3)
given that r = 3 ,h = 12
v = 3.14 x 3 x 3 x (12/3)
v = 3.14 x 9 x (12/3)
v =3.14 x 9 x 4
v= 3.14 x 36
v = 113.04 cu. cm
Volumes of Spheres Homework & Practice 10.3
Review & Refresh
Find the volume of the cone. Round your answer to the nearest tenth.
Question 1.
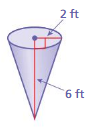
Answer:
volume of cone= 25.12 cu. ft
Explanation:
volume of cone =πr² (h/3)
given that r = 2 ,h = 6
v = 3.14 x 2 x 2 x (6/3)
v = 3.14 x 4 x (6/3)
v =3.14 x 4 x 2
v= 3.14 x 8
v = 25.12 cu. ft
Question 2.
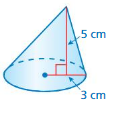
Answer:
volume of cone= 47.1 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r = 3 ,h = 5
v = 3.14 x 3 x 3 x (5/3)
v = 3.14 x 9 x (5/3)
v =3.14 x 9 x 1.666
v= 3.14 x 15
v = 47.1 cu. cm
Question 3.
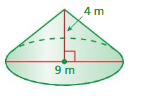
Answer:
volume of cone=84.78 cu. m
Explanation:
volume of cone =πr² (h/3)
given that r = 4.5 ,h = 4
v = 3.14 x 4.5 x 4.5 x (4/3)
v = 3.14 x 20.25 x (4/3)
v =3.14 x 20.25 x 1.333
v= 3.14 x 27
v = 84.78 cu. m
Evaluate the expression. Write your answer in scientific notation.
Question 4.
(4.6 × 109) + (3.9 × 109)
Answer:
85,00,00,00000
Explanation:
(4.6 × 109) + (3.9 × 109)
4.6 x 1000000000 + 3.9 x 1000000000
85,00,00,00000
Question 5.
(1.4 × 10-4) ÷ (2.8 × 106)
Answer:
5e – 12
Explanation:
0.00014 / 28000000
5e – 12
Question 6.
A person who is 5 feet tall casts a 6-foot-long shadow. A nearby flag pole casts a 30-foot-long shadow. What is the height of the flagpole?
A. 25 ft
B. 29 ft
C. 36 ft
D. 40 ft
Answer:
Option B is correct.
Explanation:
Given that person who is 5 feet tall casts a 6-foot-long shadow.
A nearby flag pole casts a 30-foot-long shadow.
the height of the flagpole is 29 ft
Concepts, Skills, &Problem Solving
FINDING VOLUME The radius of a sphere is given. Find the volume of the sphere. Write your answer in terms of π. (See Exploration 1, p. 439.)
Question 7.
r = 6 units
Answer:
volume of the sphere= 902.0592 units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =6
v = 1.33 x 3.14 x 6 x 6 x 6
v = 1.33 x 3.14 x 216
v = 1.33 x 678.24
v = 902.0592 units
Question 8.
r = 12 units
Answer:
volume of the sphere= 7,216.4736 units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =12
v = 1.33 x 3.14 x 12 x 12 x 12
v = 1.33 x 3.14 x 1,728
v = 1.33 x 5,425.92
v = 7,216.4736 units
Question 9.
r = 10 units
Answer:
volume of the sphere=4,176.2 units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =10
v = 1.33 x 3.14 x 10 x 10 x 10
v = 1.33 x 3.14 x 1000
v = 1.33 x 3140
v = 4,176.2 units
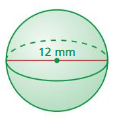
FINDING THE VOLUME OF A SPHERE Find the volume of the sphere. Round your answer to the nearest tenth.
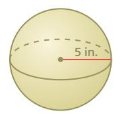
Question 10.
Answer:
volume of the sphere= 522.025 cu. units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =5
v = 1.33 x 3.14 x 5 x 5 x 5
v = 1.33 x 3.14 x 125
v = 1.33 x 3.92.5
v = 522.025 cu. units
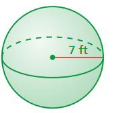
Question 11.
Answer:
volume of the sphere=1,432.4366 cu. units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =7
v = 1.33 x 3.14 x 7 x 7 x 7
v = 1.33 x 3.14 x 343
v = 1.33 x 1,077.02
v = 1,432.4366 cu. units
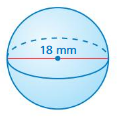
Question 12.
Answer:
volume of the sphere= 3,044.4498 units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =9
v = 1.33 x 3.14 x 9 x 9 x 9
v = 1.33 x 3.14 x 729
v = 1.33 x 2,289.06
v = 3,044.4498 cu. units
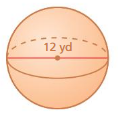
Question 13.
Answer:
volume of the sphere= 300.6864 cu. units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =6
v = 1.33 x 3.14 x 6 x 6 x 6
v = 1.33 x 3.14 x 72
v = 1.33 x 226.08
v = 300.6864 cu. units
Question 14.
Answer:
volume of the sphere= 112.7574 cu. units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =3
v = 1.33 x 3.14 x 3 x 3 x 3
v = 1.33 x 3.14 x 27
v = 1.33 x 84.78
v = 112.7574 cu. units
Question 15.
Answer:
volume of the sphere=11,459.4928 cu. units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =14
v = 1.33 x 3.14 x 14 x 14 x 14
v = 1.33 x 3.14 x 2744
v = 1.33 x 8,616.16
v = 11,459.4928 cu. units
FINDING THE RADIUS OF A SPHERE Find the radius of a sphere with the given volume. Round your answer to the nearest tenth if necessary.
Question 16.
Volume = 972π mm3
Answer:
radius of the sphere= 0.0004561 cubic mm
Explanation:
volume of sphere = (4/3) πr² x r
972 = (4/3) x 3.14 x r³
where v = 972
972 = 1.33 x 3.14 r³
972 = 1.33 r³
r³ = (1.33/972)
r³ = 0.00136831 cubic mm
r = 0.0004561
Question 17.
Volume = 4.5π cm3
Answer:
radius of the sphere= 0.09851852 cubic cm
Explanation:
volume of sphere = (4/3) πr² x r
4.5 = (4/3) x 3.14 x r³
where v = 4.5
4.5 = 1.33 x 3.14 r³
4.5 = 1.33 r³
r³ = (1.33/4.5)
r³ = 0.29555555 cubic mm
r = 0.09851852 cubic cm
Question 18.
Volume = 180 ft3
Answer:
radius of the sphere=0.0077337 cubic ft
Explanation:
volume of sphere = (4/3) πr² x r
180 = (4/3) x 3.14 x r³
where v = 180
180 = 1.33 x 3.14 r³
180 = 1.33 x 3.14r³
180 = 4.1762 r³
r³ = (4.1762/180)
r³ = 0.02320111 cubic ft
r = 0.0077337 cubic ft
Question 19.
MODELING REAL LIFE
The globe of the moon has a radius of 13 centimeters. Find the volume of the globe. Round your answer to the nearest whole number.

Answer:
Volume of the globe =9,175.1114 cu. cm
Explanation:
volume of the globe=11,459.4928 units
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =13
v = 1.33 x 3.14 x 13 x 13 x 13
v = 1.33 x 3.14 x 2,197
v = 1.33 x 6,898.58
v = 9,175.1114 cu. cm
Question 20.
MODELING REAL LIFE
A softball has a volume of about 29 cubic inches. Find the radius of the softball. Round your answer to the nearest tenth.
Answer:
radius of the softball= 0.0480023 ft
Explanation:
volume of sphere = (4/3) πr² x r
29= (4/3) x 3.14 x r³
where v = 29
29 = 1.33 x 3.14 r³
29 = 1.33 x 3.14r³
29 = 4.1762 r³
r³ = (4.1762/29)
r³ = 0.1440069 cubic ft
r = 0.0480023 ft
Question 21.
REASONING
A sphere and a right cylinder have the same radius and volume. Find the radius r in terms of the height h of the cylinder.
Answer:
The volume of sphere = (4/3) π h³
the volume of cylinder = πr² r
Explanation:
volume of sphere = (4/3) π r³
They said to find the radius r in terms of height h.
the volume of sphere = (4/3) π h³
the volume of cylinder = πr² r
FINDING VOLUME Find the volume of the composite solid. Round your answer to the nearest tenth.
Question 22.
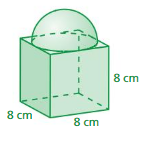
Answer:
volume = 256 cubic cm
Explanation:
volume of rectangular prism = lwh
where l= length, w = weight, h= height
l = 8 ,w = 8 , h = 8 given
v= 8 x 8 x 8
v = 64 x 4
v = 256 cubic cm
Question 23.
Answer:
volume = 192 cubic feet
Explanation:
volume of triangular prism = (bhl/2)
b = 16 , h = 6 , l = 4 given
v = (16 x 6 x 4/2)
v = (16 x 24/2)
v = 16 x 12
v = 192 cubic feet
Question 24.
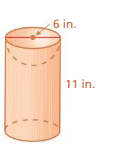
Answer:
volume of cylinder = 310.86 cu. in
Explanation:
volume of cylinder = πr² h
v = 3.14 x 3 x 3 x 11
v = 3.14 x 9 x 11
v = 3.14 x 99
v = 310.86 cu. in
Question 25.
PROBLEM SOLVING
A cylindrical container of three rubber balls has a height of 18 centimeters and a diameter of 6 centimeters. Each ball in the container has a radius of 3 centimeters. Find the amount of space in the container that is not occupied by rubber balls. Round your answer to the nearest whole number.

Answer:
The amount of space in the container that is not occupied by the rubber balls = 2,034.72 cu. cm
Explanation:
volume of cylinder = πr² h
v = 3.14 x 6 x 6 x 18
v = 3.14 x 36 x 18
v = 3.14 x 648
v =2,034.72 cu. cm
Question 26.
DIG DEEPER!
The basketball shown is packaged in a box that is in the shape of a cube. The edge length of the box is equal to the diameter of the basketball. What are the surface area and the volume of the box?

Answer:
The volume of sph0.01646091 cubic in
Explanation:
the volume of sphere = 4 πr²
121.5 π = 4 π r²
121.5 = 4 r²
r² = (4/121.5)
r² = 0.03292181
r = 0.01646091 cubic in
Question 27.
PROBLEM SOLVING
The inner core of Earth begins about 3200 miles below the surface of Earth and has a volume of about 581,000,000π cubic miles. Approximate the radius of Earth. Justify your answer.
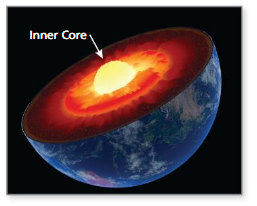
Answer:
radius of earth = 0.00240199 miles.
Explanation:
volume of sphere = (4/3) π r³
581,000,000 π = (4/3) x 3.14 x r³
581,000,000= 1.3333 x 3.14 x r³
581,000,000= 4.18666667 r³
r³ = (4.18666667/581.000,000)
r³ = 0.00720597
r = 0.00240199 miles,
Question 28.
LOGIC
Your friend says that the volume of a sphere with radius r is four times the volume of a cone with radius r. When is this true? Justify your answer.
Answer:
No my friend is wrong.
Explanation:
volume of cone = πr² (h/3)
volume of sphere = (4/3) πr² x r
when the radius is equal to the height h
then the volume of a sphere with radius r is four times the volume of a cone with a radius r.
Lesson 10.4 Surface Areas and Volumes of Similar Solids
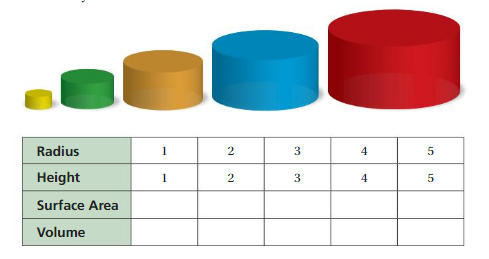
EXPLORATION 1
Comparing Similar Solids
Work with a partner.
a.You multiply the dimensions of the smallest cylinder by different factors to create the other four cylinders. Complete the table. Compare the surface area and volume of each cylinder with the surface area and volume of the smallest cylinder.
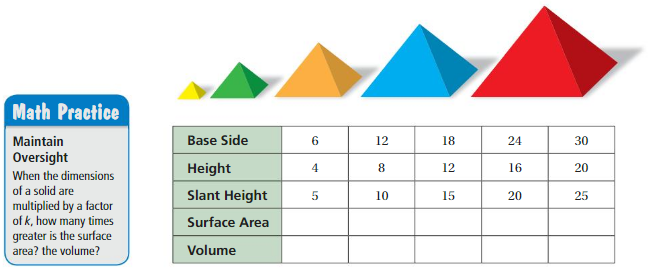
b. Repeat part(a) using the square pyramids and table below.
Answer:
a. surface area of cylinder 1 = 12.56
b. surface area of cylinder 2 = 50.24
c. surface area of cylinder 3 = 113.04
d. surface area of cylinder 4 = 200.96
e.. surface area of cylinder 5 = 314
Explanation:
a. surface area of cylinder 1 = 2 πr² + 2 πrh
A = 2 x 3.14 x 1 + 2 x 3.14 x 1 x 1
A = 6.28 + 6.28
A = 12.56
volume of cylinder = πr²h
v = 3.14 x 1 x 1
v = 3.14
b. surface area of cylinder 2 = 2 πr² + 2 πrh
A = 2 x 3.14 x 2 x 2 + 2 x 3.14 x 2 x 2
A = 6.28 x 4 + 6.28 x 4
A = 25.12 + 25.12
A = 50.24
volume of cylinder = πr²h
v = 3.14 x 2 x 2
v = 3.14 x 4
v = 12.56
c. surface area of cylinder 1 = 2 πr² + 2 πrh
A = 2 x 3.14 x 3 x 3 + 2 x 3.14 x 3 x 3
A = 6.28 x 9 + 6.28 x 9
A = 56.52 +56.52
A = 113.04
volume of cylinder = πr²h
v = 3.14 x 3 x 3
v = 3.14 x 9
v = 28.26
d. surface area of cylinder 1 = 2 πr² + 2 πrh
A = 2 x 3.14 x 4 x 4 + 2 x 3.14 x 4 x 4
A = 6.28 x 16 + 6.28 x 16
A = 100.48 + 100.48
A = 200.96
volume of cylinder = πr²h
v = 3.14 x 4 x 4
v = 3.14 x 16
v = 50.24
e. surface area of cylinder 1 = 2 πr² + 2 πrh
A = 2 x 3.14 x 5 x 5 + 2 x 3.14 x 5 x 5
A = 6.28 x 25 + 6.28 x 25
A = 157 + 157
A = 314
volume of cylinder = πr²h
v = 3.14 x 5 x 5
v = 3.14 x 25
v = 78.5

Try It
Question 1.
Cylinder D has a radius of 7.5 meters and a height of 4.5 meters. Which cylinder in Example 1 is similar to Cylinder D?
Answer:
volume of cylinder = 794.8125 cu. meters.
Explanation:
volume of cylinder = πr²h
v = 3.14 x 7.5 x 7.5 x 4.5
v = 3.14 x 56.25 x 4.5
v = 3.14 x 253.125
v = 794.8125 cu. meters.
Question 2.
The prisms at the right are similar. Find the missing width and length.
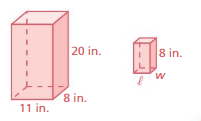
Answer:
volume = 1760 cubic in
Explanation:
the volume of rectangular prism = lwh
where l= length, w = weight, h= height
l = 11,w = 8 , h = 20 given
v= 11 x 8 x 20
v = 88 x 20
v = 1760 cubic in
The solids are similar. Find the surface area of the red solid. Round your answer to the nearest tenth.
Question 3.
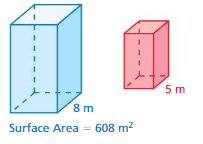
Answer:
volume = 440 cubic m
Explanation:
volume of rectangular prism = lwh
where l= length, w = weight, h= height
l = 11,w = 8 , h = 5 given
v= 11 x 8x 5
v = 11 x 40
v = 440 cubic m
Question 4.
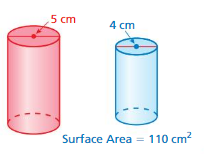
Answer:
Volume of cylinder= 0.17840909 cu. cm
Explanation:
Volume of cylinder = πr² h
where π = 3.14
r = 2.5
110 = 3.14 x 2.5 x 2.5 x h
110 = 3.14 x 6.25 h
110= 19.625 h
h = (19.625/110)
h = 0.17840909 sq cm
Question 5.
The pyramids at the left are similar. Find the volume of the red pyramid. Round your answer to the nearest tenth.
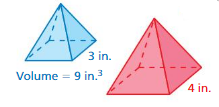
Answer:
volume of red pyramid = 0.444 cubic in
Explanation:
the volume of the pyramid =( l x w x h/3)
v = 9 given, width = 4 h = 3
9=( 4 x 3h /3)
9 = 4h
h = (4/9)
h = 0.444 cubic in
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
IDENTIFYING SIMILAR SOLIDS
Cone A and Cone B are right cones. Cone B has a radius of 1.25 feet and a height of 3 feet. Are the cones similar?
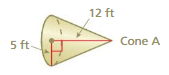
Answer:
No the cones are not similar.
Explanation:
volume of cone A =πr² (h/3)
given that r = 5 ,h = 12
v = 3.14 x 5 x 5 x (12/3)
v = 3.14 x 25 x (12/3)
v =3.14 x 25 x 4
v= 3.14 x100
v = 314 cu. ft
volume of cone B =πr² (h/3)
given that r = 1.25 ,h = 3
v = 3.14 x 1.25 x 1.25 x (3/3)
v = 3.14 x 1.5625 x (3/3)
v =3.14 x 1.5625 x 1
v= 3.14 x1.5625
v = 4.90625 cu. ft
Question 7.
FINDING A MISSING MEASURE
A cylinder with a radius of 4 inches r and a height of 6 inches is similar to a cylinder with a radius of r inches and a height of 9 inches. What is the value of r?
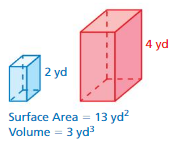
Answer:
The value of r = 3 yds
Explanation:
volume of cylinder =πr² (h/3)
given that r = 4 ,h = 6
v = 3.14 x 4 x 4 x (6/3)
v = 3.14 x 16 x (6/3)
v =3.14 x 16 x 2
v= 3.14 x 32
v = 100.48
Question 8.
FINDING SURFACE AREA AND VOLUME
The rectangular prisms shown are similar. Find the surface area and volume of the red rectangular prism .
Answer:
The surface area of rectangular prism =2(lw +lh +wh)
the volume of rectangular prism = lwh
Explanation:
The surface area of rectangular prism =2(lw +lh +wh)
where h = height, w = width, l = length
the volume of rectangular prism = lwh
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
Two snails have shells that are similar in shape. The younger snail has a shell with a height of 3.9 centimeters and a volume of 3 cubic centimeters. The older snail has a shell with a volume of 10 cubic centimeters. Estimate the height of the older snail’s shell.

Answer:
The height of the older snails shell = 0.942 cm
Explanation:
the volume of cylinder =πr² (h/3)
given that r = 3 ,v = 10
10 = 3.14 x 3 x 3 x (h/3)
10 = 3.14 x 3 x h
10 =3.14 x 3h
10= 9.42 h
h = (9.42/10)
h = 0.942 cm
Question 10.
Two barrels filled with sand are similar in shape. The smaller barrel has a height of 4 feet and a volume of 4.5 cubic feet. The larger barrel has a height of 6 feet. What is the weight of the sand in the larger barrel? Round your answer to the nearest tenth.(One cubic foot of sand weighs about 110 pounds.)
Answer:
The weight of the sand in the larger barrel = 18 cubic feet
Explanation:
Given that the smaller barrel h = 4 ft and v = 4.5 cubic ft
weight = 4 x 4.5
weight = 18 cubic feet
larger barrel h = 6feet, v= 3 cubic feet,
weight = 3 x 6
weight = 18 cubic feet
1 cubic ft = 110 pounds
Question 11.
Two trunks are similar in shape. The larger trunk has a length of 6 feet and a surface area of 164.25 square feet. The smaller trunk has a length of 4 feet. The materials needed to manufacture each trunk cost $0.60 per square foot. What is the total cost of the materials needed to manufacture the smaller trunk?
Answer:
Surface Areas and Volumes of Similar Solids Homework & Practice 10.4
Review & Refresh
Find the volume of the sphere. Round your answer to the nearest tenth.
Question 1.
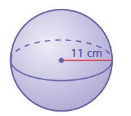
Answer:
volume of the sphere= 5,558.52222 cubic cm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =11
v = 1.33 x 3.14 x 11 x 11 x 11
v = 1.33 x 3.14 x 1,331
v = 1.33 x 4,179.34
v = 5,558.52222 cubic cm
Question 2.
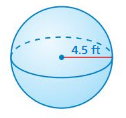
Answer:
volume of the sphere= 380.556225 cubic ft
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =4.5
v = 1.33 x 3.14 x 4.5 x 4.5 x 4.5
v = 1.33 x 3.14 x 91.125
v = 1.33 x 286.1325
v = 380.556225 cubic ft
Question 3.
Answer:
volume of the sphere=902.0592 cubic mm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =6
v = 1.33 x 3.14 x 6 x 6 x 6
v = 1.33 x 3.14 x 216
v = 1.33 x 678.24
v = 902.0592 cubic mm
Question 4.
Which system of linear equations has no solution?
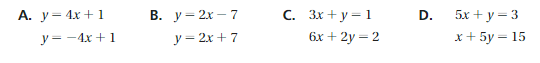
Answer:
Option c has no solution.
Explanation:
if we take x = 2
A. y = 4x + 1 = 4(2) + 1= 9 , y = – 4x + 1 = -8 + 1= -7
b. Y = 2x – 7 = 4 – 7 = -3 , y = 2x + 7 = 4 + 7 = 11
c. 3x + y = 1 , y = 1 – 6 y = -5 , 6x + 2y = 2 = 12 + 2y = 2,2y =- 10 y = -5
Concepts, Skills, & Problem Solving
COMPARING SIMILAR SOLIDS All of the dimensions of the solid are multiplied by a factor of k. How many times greater is the surface area of the new solid? How many times greater is the volume of the new solid? (See Exploration 1, p. 445.)
Question 5.
k = 5
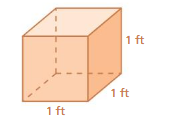
Answer:
25 times greater.
volume of new solid = 125 cubic ft
Explanation:
volume of prism = lwh
where l= length, w = weight, h= height
l = 5 ,w = 5 , h = 5 given
v= 5 x 5 x 5
v = 5 x 25
v = 125 cubic ft
Question 6.
k = 10
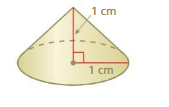
Answer:
volume of new cone= 1,046.666 cubic cm
Explanation:
volume of cone =πr² (h/3)
given that r = 10 ,h = 10
v = 3.14 x 10 x 10 x (10/3)
v = 3.14 x 100 x (10/3)
v =3.14 x 100 x 3.33
v= 3.14 x 333.33
v = 1,046.666 cubic cm
IDENTIFYING SIMILAR SOLIDS Determine whether the solids are similar.
Question 7.
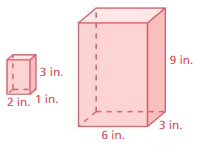
Answer:
The solida are similar
Explanation:
volume of small prism = lwh
where l= length, w = weight, h= height
l = 2 ,w = 1 , h = 3 given
v= 2 x 1 x 3
v = 2 x 3
v = 6 cubic in
volume of large prism = lwh
where l= length, w = weight, h= height
l = 6 ,w = 3 , h = 9 given
v= 6 x 3 x 9
v = 2 x 27
v = 54 cubic in
Question 8.
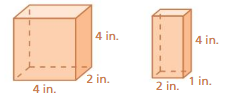
Answer:
The solida are not similar
Explanation:
surface area of large prism =2 (lw + wh +1h)
where l= length, w = weight, h= height
l = 4 ,w = 2 , h = 4 given
v=2( 4 x 2 + 2 x 4 + 4 x 4)
v = 2 (8 + 8+ 16)
v = 2( 32)
v = 64 cubic in
surface area of small prism =2 (lw + wh +1h)
where l= length, w = weight, h= height
l = 2 ,w = 1 , h = 4 given
v=2( 2 x 1 + 1 x 4 + 2 x 4)
v = 2 (2 + 4+ 8)
v = 2( 16)
v = 32 cubic in
Question 9.
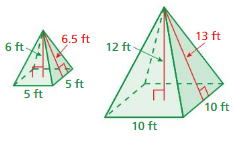
Answer:
The pyramids are similar.
Explanation:
surface area of triangular pyramid 1 = area of faces + base
area of face 1 = 5
area of face 2 = 5
area of face 3 = 6.5
area of face 4 = 6
area of base = 5
A= 5 + 5 + 6.5 + 6 + 5
A = 10 + 6.5 + 11
A = 21 + 6.5
A = 27.5
surface area of triangular pyramid 2 = area of faces + base
area of face 1 = 10
area of face 2 = 10
area of face 3 = 13
area of face 4 = 12
area of base = 10
A= 10 + 10 + 13 + 12 + 10
A = 20 + 13 + 22
A = 42 + 13
A = 55
Question 10.
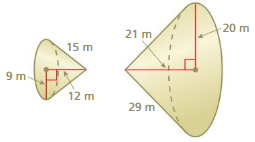
Answer:
Two solids are not similar.
Explanation:
volume of cone 1 =πr² (h/3)
given that r=9 ,h = 12
v = 3.14 x 9 x 9 x (12/3)
v = 3.14 x 9 x9 x 4
v =3.14 x 81 x 4
v = 3.14 x 324
h = 1,017.36sq m
volume of cone 2 =πr² (h/3)
given that r=20 ,h = 21
v = 3.14 x 20 x 20 x (21/3)
v = 3.14 x20 x 20 x 7
v =3.14 x 400 x 7
v = 3.14 x 2800
h = 8,792 sq m
FINDING MISSING MEASURES IN SIMILAR SOLIDS The solids are similar. Find the missing measure(s).
Question 11.
Answer:
volume of the sphere=2.5 cu. feet
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =5
v = 1.33 x 3.14 x 5 x 5 x 5
v = 1.33 x 3.14 x 125
v = 1.33 x 392.5
v = 2.5 cu. feet
Question 12.
Answer:
surface area of triangular pyramid = 54 cubic m
Explanation:
surface area of triangular pyramid = area of faces + base
area of face 1 = 12
area of face 2 = 6
area of face 3 = 13
area of face 4 = 5
area of base = 18
A= 12 + 6 + 13 + 5 + 18
A = 18 + 13 + 23
A = 18 + 36
A = 54 cubic m
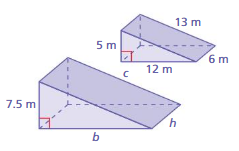
Question 13.
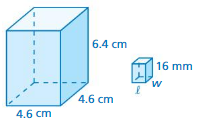
Answer:
volume = 11.5 cu. mm
Explanation:
volume of triangular prism = (bhl/2)
b = 4.6 , h = 4.6 , l = 6.4 given
v = (4.6 x 4.6 x 6.4/2)
v = (21.16 x 6.4/2)
v = (135.424/2)
v = 11.5 cu. mm
Question 14.
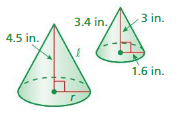
Answer:
volume of cone = 8.0384 cu. in
Explanation:
volume of cone =πr² (h/3)
given that r=1.6 ,h = 3
v = 3.14 x 1.6 x 1.6 x (3/3)
v = 3.14 x 1.6 x1.6 x 1
v =3.14 x 2.56 x 1
v = 3.14 x 2.56
v = 8.0384 cu. in
FINDING SURFACE AREA The solids are similar. Find the surface area of the red solid. Round your answer to the nearest tenth if necessary.
Question 15.
Answer:
The surface area of the red solid = 90 sq m
Explanation:
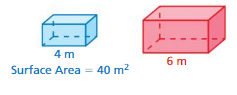
Given that the surface area of blue solid = 40 sq m
s0 the surface area of the red solid = 60 sq m
4 x 10 = 40
9 x 10 = 90 sq m
Question 16.
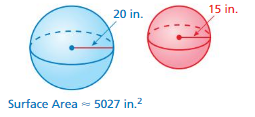
Answer:
volume of the sphere= 14,094 cu. in
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =15
v = 1.33 x 3.14 x 15 x 15 x 15
v = 1.33 x 3.14 x 3375
v = 1.33 x 10,597.5
v = 14,094.675 cu. in
Question 17.
FINDING SURFACE AREA
The ratio of the corresponding linear measures of two similar cans is 4 to 7. The smaller can has a surface area of 220 square centimeters. Find the surface area of the larger can.
Answer:
The surface area of larger can = 55 sq cm
Explanation:
Given that the smaller can has a surface area of 220 sq cm
The ratio of two similar cans is 4: 7
(220/5) = 55 sq cm
FINDING VOLUME The solids are similar. Find the volume of the red solid.
Question 18.
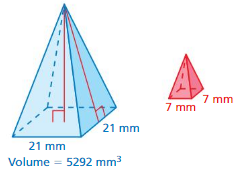
Answer:
The volume of red soil = 70 cu. mm
Explanation:
surface area of triangular pyramid = area of faces + base
area of face 1 = 21
area of face 2 = 21
area of face 3 = 7
area of face 4 = 7
area of base = 14
A= 21 + 21 + 7 + 7 + 14
A = 42 + 14 + 14
A = 42 + 28
A = 70 cu. mm
Question 19.
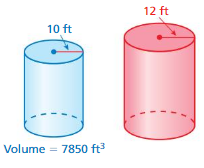
Answer:
height of cylinder=13,564.8 ft
Explanation:
Volume of cylinder = πr² h
where π = 3.14
r = 12
v = 3.14 x 12 x 12 x h
7850 = 3.14 x 144 h
7850= 452.16 h
h = (452.16/7850)
h = 13,564.8 sq ft
Question 20.
YOU BE THE TEACHER
The ratio of the corresponding linear measures of two similar solids is 3:5. The volume of the smaller solid is 108 cubic inches. Your friend finds the volume of the larger solid. Is your friend correct? Explain your reasoning.

Answer:
Yes my friend is correct.
Explanation:
the volume of smaller solid is 108 cubic inches.
(108/v) = (3/5) x (3/5)
(108/v) = (9/25)
v = 300 cubic in
Question 21.
MODELING REAL LIFE
A hemisphere-shaped mole has a diameter of 5.7 millimeters and a surface area of about 51 square millimeters. The radius of the mole doubles. Estimate the new surface area of the mole.

Answer:
The new surface area of the mole = 19.742 sq. mm
Explanation:
surface area of sphere = (4/3) πr² x r
A = (4/3) x 3.14 x r³
where r = 2.85
A = 1.33 x 3.14 x 2.85 x 2.85
A= 1.33 x 3.14 x 8.1225
A = 1.33 x 25.50465
A = 19.742 sq. mm
Question 22.
REASONING
The volume of a 1968 Ford Mustang GT engine is 390 cubic inches. Which scale model of the Mustang has the greater engine volume, a 1 : 18 scale model or a 1 : 24 scale model? How much greater is it?

Answer:
Question 23.
DIG DEEPER!
You have a small marble statue of Wolfgang Mozart. It is 10 inches tall and weighs 16 pounds. The original marble statue is 7 feet tall.

a. Estimate the weight of the original statue. Explain your reasoning.
b. If the original statue were 20 feet tall, how much would it weigh?
Answer:
a. The weight of the original statue = 84/10 cubic pounds
b. The original statue weight = 221 lb
Explanation:
a. The weight of the original statue = 7 ft
1 ft = 12 pounds
7 x 12 / 10 = 84/10 cubic pounds.
b. given that the original statue was 20 ft
221,184 lb
Question 24.
REPEATED REASONING
The nesting dolls are similar. The largest doll is 7 inches tall. Each of the other dolls is 1 inch shorter than the next larger doll. Make a table that compares the surface areas and the volumes of the seven dolls.

Answer:

Explanation:
In the above given figure the larger doll is 7 inches tall.
Each of the other doll is 1 inch shorter than the next larger doll.
Question 25.
PRECISION
You and a friend make paper cones to collect beach glass. You cut out the largest possible three-fourths circle from each piece of paper.

a. Are the cones similar? Explain your reasoning.
b. Your friend says that because your sheet of paper is twice as large, your cone will hold exactly twice the volume of beach glass. Is this true? Explain your reasoning.
Answer:
a. Yes, the cones are similar.
b.No my friend is correct.
Explanation:
a. all circles are similar, the slant height and the circumference of the base of the cones are proportional .
b. my cone holds about 2 times as much my friend cone.
Volume and Similar Solids Connecting Concepts
Using the Problem-Solving Plan
Question 1.
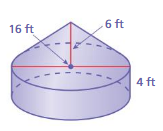
A yurt is a dwelling traditionally used in Mongolia and surrounding regions. The yurt shown is made of a cylinder and a cone. What is the volume of the yurt?

Understand the problem
You know that the yurt is made of a cylinder and a cone. You also know several dimensions. You are asked to find the volume of the yurt.
Make a plan.
Use the Pythagorean Theorem to find the height of the cone. Then use the formulas for the volume of a cylinder and the volume of a cone to find the volume of the yurt.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
volume of hurt = 4855 cu. ft
Explanation:
volume of cone =πr² (h/3)
given that r = 15 ,h = 7
v = 3.14 x 15 x 15 x (17/3)
v = 3.14 x 225 x (17/3)
v =3.14 x 225 x 5.666
v = 3.14 x 1275
v = 4,003
volume of cylinder = πr² h
where π = 3.14 d =
r = 3 , h = 30
v = 3.14 x 3 x 3 x 30
v = 3.14 x 9 x 30
v= 3.14 x 270
h = 847.8
4008 +847 =4855
Question 2.
supervoidA spherical , a region in space that is unusually empty, has a diameter of 1.8 × 19 0light-years. What is the volume of the supervoid? Use 3.14 for π. Write your answer in scientific notation.
Answer:
volume of supervoid =3.75858000000000 light years
Explanation:
volume of sphere = (4/3) πr³
v = (4/3) x 3.14 x r³
v = 1.33 x 3.14 x 0.9
v = 2.826 x 1.33
v = 3.75858000000000 light years
Question 3.
The cylinders are similar. The volume of Cylinder A is \(\frac{8}{27}\) times the volume of Cylinder B. Find the volume of each cylinder. Round your answers to the nearest tenth.
Answer:
volume of cylinder = 452.16 cu. cm
Explanation:
the volume of cylinder = πr² h
where π = 3.14
r = 4 , h = 9
v = 3.14 x 4 x 4 x 9
v = 3.14 x 16 x 9
v= 3.14 x 144
h = 452.16 sq cm
Performance Task
Packaging Salsa
At the beginning of this chapter, you watched a STEAM Video called “Canning Salsa.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Volume and Similar Solids Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use a Summary Triangle to explain a concept. Here is an example of a Summary Triangle for volume of a cylinder.
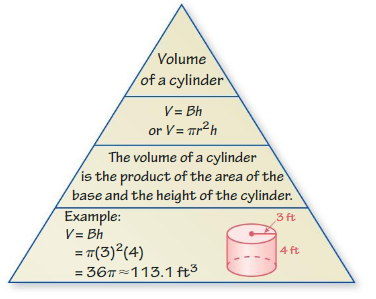
Choose and complete a graphic organizer to help you study the concept.

1. volume of a cone
2. volume of a sphere
3. volume of a composite solid
4. surface areas of similar solids
5. volumes of similar solids
Answer:
cone = A solid or hollow object which tapers from a circular or roughly circular base to a point.
hemisphere = a half of the celestial sphere as divided into two halves by the horizon.
sphere = a round solid figure, or its surface, with every point on its surface equidistant from its center.
similar solids = two solids are similar if they are the same type of solid and their corresponding radii, heights, base lengths, widths, etc. are proportional.
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

10.1 Volumes of Cylinders (pp. 427–432)
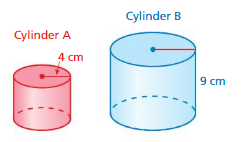
Learning Target: Find the volume of a cylinder. Find the volume of the cylinder. Round your answer to the nearest tenth.
Question 1.
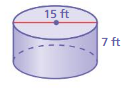
Answer:
volume of cylinder =1,236.375 cu. ft
Explanation:
volume of cylinder = πr² h
where π = 3.14 d = 15 r = (d/2)
r = 7.5 , h = 7 given
v = 3.14 x 7.5 x 7.5 x 7
v = 3.14 x 56.25 x 7
v = 3.14 x 393.75
v = 1,236.375 cu. ft
Question 2.
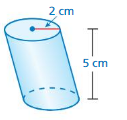
Answer:
volume of cylinder =62.8 cu. cm
Explanation:
volume of cylinder = πr² h
where π = 3.14
r = 2 , h = 5 given
v = 3.14 x 2 x 2 x 5
v = 3.14 x 4 x 5
v = 3.14 x 20
v = 62.8 cu. cm
Find the missing dimension of the cylinder. Round your answer to the nearest whole number.
Question 3.
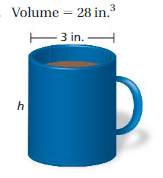
Answer:
height of cylinder = 0.25232143 sq in
Explanation:
volume of cylinder = πr² h
where π = 3.14
r = 1.5 , v = 28 given
28 = 3.14 x 1.5 x 1.5 x h
28= 3.14 x 2.25h
28 = 7.065 h
h = 7.065/28
h = 0.25232143 sq in
Question 4.
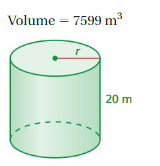
Answer:
radius of cylinder =60.501 sq m
Explanation:
volume of cylinder = πr² h
where π = 3.14
h = 20 m, v = 7599 given
7599= 3.14 x r x r x 20
7599= 3.14 x 20 r²
7599 = 62.8 r²
r² = 7599/62.8
r² = 121.00 m
r = 60.501 sq m
Question 5.
You are buying two cylindrical cans of juice. Each can holds the same amount of juice.
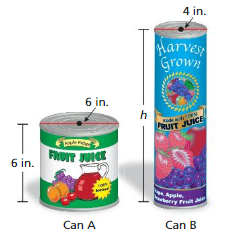
a. What is the height of Can B?
b. About how many cups of juice does 3≈each can hold? (1 in.3 ≈ 0.07 cup)
Answer:
a.The height of can B = 0.074 in
b. The cups of juice does 3 each can hold = 21 cups
Explanation:
volume of cylinder = πr² h
where π = 3.14
h = 6, r = 3given
v = 3.14 x 3 x 3 x 6
v= 3.14 x 9 x 6
v = 3.14 x 54
v = 169.56 sq in
volume of cylinder = πr² h
where π = 3.14
v = 169.56, r = 2given
169.56 = 3.14 x 2 x 2 h
169.56= 3.14 x 4 h
169.56= 12.56 h
h = 0.074 in
b. 3 x 0.07
0.21
21 cups.
Question 6.
You triple the radius of a cylinder. How many times greater is the volume of the new cylinder? Explain.
Answer:
3 times greater than the volume of the new cylinder.
Explanation:
Given that the radius is tripled.
volume of cylinder = πr⁵ h
10.2 Volumes of Cones (pp. 433–438)
Learning Target: Find the volume of a cone.
Find the volume of the cone. Round your answer to the nearest tenth.
Question 7.
Answer:
volume of cone= 803.84 cu. m
Explanation:
volume of cone =πr² (h/3)
given that r = 8 ,h = 12
v = 3.14 x 8 x 8 x (12/3)
v = 3.14 x 64 x (12/3)
v =3.14 x 64 x 4
v= 3.14 x 256
v = 803.84 cu. m
Question 8.
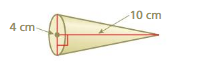
Answer:
volume of cone= 41.8666 cu. cm
Explanation:
volume of cone =πr² (h/3)
given that r = 2 ,h = 10
v = 3.14 x 2 x 2 x (10/3)
v = 3.14 x 4 x (10/3)
v =3.14 x 4 x 3.33
v= 3.14 x 13.33
v = 41.8666 cu. cm
Find the missing dimension of the cone. Round your answer to the nearest tenth.
Question 9.
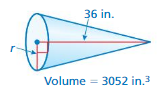
Answer:
radius of cone= 0.006173 in
Explanation:
volume of cone =πr² (h/3)
given that ,h = 36
3052= 3.14 x r x r (36/3)
3052 = 3.14 x 12 r²
3052 =37.68 r²
r²= 0.012346
v = 0.006173 cu. in
Question 10.
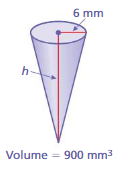
Answer:
height of cone=0.041866 sq mm
Explanation:
volume of cone =πr² (h/3)
given that ,r =6
900= 3.14 x 6 x 6 (h/3)
900 = 3.14 x 12 h
900 =37.68 h
h= (37.68/900)
h = 0.041866 sq mm
Question 11.
The paper cup can hold 84.78 cubic centimeters of water. What is the height of the cup?
Answer:
height of cone= 0.111111 cm
Explanation:
volume of cone =πr² (h/3)
given that ,r =3
84.78= 3.14 x 3 x 3 (h/3)
84.78 = 3.14 x 3 h
84.78 =9.42 h
h= (9.42/84.78)
h = 0.111111 cm
10.3 Volumes of Spheres (pp. 439–444)
Learning Target: Find the volume of a sphere.
Find the volume of the sphere. Round your answer to the nearest tenth.
Question 12.
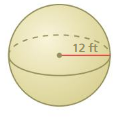
Answer:
volume of the sphere=7,216.4736 cubic ft
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =12
v = 1.33 x 12 x 12 x 12 x 3.14
v = 1.33 x 3.14 x 1728
v = 1.33 x 5,425.92
v = 7,216.4736 cubic ft
Question 13.
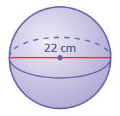
Answer:
volume of the sphere= 5,558.52222 cu. cm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =11
v = 1.33 x 11 x 11 x 11 x 3.14
v = 1.33 x 3.14 x 1331
v = 1.33 x 4,179.34
v = 5,558.52222 cu. cm
Question 14.
The volume of a water walking ball is \(\frac{4}{3}\)π cubic meters. Find the diameter of the water walking ball.

Answer:
Find the volume of the composite solid. Round your answer to the nearest tenth if necessary.
Question 15.
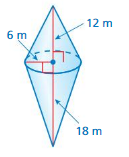
Answer:
volume of cone= 452.16 cu. m
Explanation:
volume of cone =πr² (h/3)
given that ,r = 6, h = 12
v= 3.14 x 6 x 6 (12/3)
v = 3.14 x 36 x (12/3)
v =3.14 x 36 x 4
v= 3.14 x 144
v = 452.16 cu. m
Question 16.
Answer:
The volume of solid= 31 cu. ft
Explanation:
surface area of triangular pyramid = area of faces + base
area of face 1 = 6
area of face 2 = 6
area of face 3 = 2
area of face 4 = 5
area of base = 12
A= 6 + 6 + 2 + 5 + 12
A = 12 + 7 + 12
A = 24 + 7
A = 31 sq ft
Question 17.
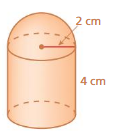
Answer:
volume of cylinder =50.24 cu. cm
Explanation:
volume of cylinder = πr² h
where π = 3.14
r = 2 , h = 4 given
v = 3.14 x 2 x 2 x 4
v = 3.14 x 16
v= 50.24 cu. cm
Question 18.
The volume of water that a submerged object displaces is equal to the volume of the object. Find the radius of the sphere. Round your answer to the nearest tenth.(1 mL = 1 cm3)

Answer:
10.4 Surface Areas and Volumes of Similar Solids (pp. 445–452)
Learning Target: Find the surface areas and volumes of similar solids.
Question 19.
Determine whether the solids are similar.
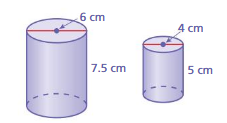
Answer:
Volume of cylinder= 0.17840909 cu. cm
Explanation:
Volume of cylinder = πr² h
where π = 3.14
r = 2.5
110 = 3.14 x 2.5 x 2.5 x h
110 = 3.14 x 6.25 h
110= 19.625 h
h = (19.625/110)
h = 0.17840909 sq cm
Question 20
The prisms are similar. Find the missing measures.
Answer:
Question 21.
The prisms are similar. Find the surface area of the red prism. Round your answer to the nearest tenth.
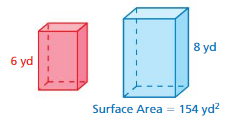
Answer:
volume = 67.712 cubic cm
Explanation:
volume of triangular prism = (bhl/2)
b = 4.6 , h = 4.6 , l = 6.4 given
v = (4.6 x 4.6 x 6.4/2)
v = (21.16 x 6.4/2)
v = (135.424/2)
v = 67.712 cubic cm
Question 22.
The pyramids are similar. Find the volume of the red pyramid.
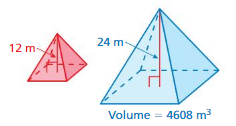
Answer:
The volume of red soil = 70 cu. mm
Explanation:
surface area of triangular pyramid = area of faces + base
area of face 1 = 21
area of face 2 = 21
area of face 3 = 7
area of face 4 = 7
area of base = 14
A= 21 + 21 + 7 + 7 + 14
A = 42 + 14 + 14
A = 42 + 28
A = 70 sqmm
Question 23.
The ratio of the corresponding linear measures of two similar jewelry boxes is 2 to 3. The larger jewelry box has a volume of 162 cubic inches. Find the volume of the smaller jewelry box.
Answer:
volume of the jewelry box = 36.4 cubics in
Explanation:
given that 2: 3 ratio
(162/v) = (2/3) x (2/3)
(162/v) = (4/9)
4v = 1458
v = (1458/4)
v = 36.4 cubic in
Volume and Similar Solids Practice Test
Find the volume of the solid. Round your answer to the nearest tenth.
Question 1.
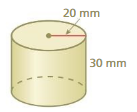
Answer:
volume of the sphere=33,409.6 cu. mm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =20
v = 1.33 x 20 x 20 x 20 x 3.14
v = 1.33 x 3.14 x 8000
v = 1.33 x 25,120
v = 33,409.6 cu. mm
Question 2.
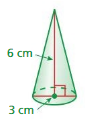
Answer:
volume of cone= 452.16 cu. m
Explanation:
volume of cone =πr² (h/3)
given that ,r = 6, h = 12
v= 3.14 x 6 x 6 (12/3)
v = 3.14 x 36 x (12/3)
v =3.14 x 36 x 4
v= 3.14 x 144
v = 452.16 cu. m
Question 3.
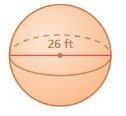
Answer:
volume of the sphere=33,409.6 cu. mm
Explanation:
volume of sphere = (4/3) πr² x r
v = (4/3) x 3.14 x r³
where r =20
v = 1.33 x 20 x 20 x 20 x 3.14
v = 1.33 x 3.14 x 8000
v = 1.33 x 25,120
v = 33,409.6 cu. mm
Question 4.
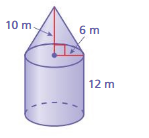
Answer:
volume of cone= 452.16 cu. m
Explanation:
volume of cone =πr² (h/3)
given that ,r = 6, h = 12
v= 3.14 x 6 x 6 (12/3)
v = 3.14 x 36 x (12/3)
v =3.14 x 36 x 4
v= 3.14 x 144
v = 452.16 cu. m
Question 5.
The pyramids are similar.
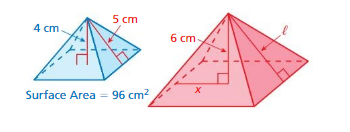
a. Find the missing measures.
b. Find the surface area of the red pyramid.
Answer:
The volume of red soil = 70 cu. mm
Explanation:
surface area of triangular pyramid = area of faces + base
area of face 1 = 21
area of face 2 = 21
area of face 3 = 7
area of face 4 = 7
area of base = 14
A= 21 + 21 + 7 + 7 + 14
A = 42 + 14 + 14
A = 42 + 28
Question 6.
You are making smoothies. You will use either the cone-shaped glass or the cylindrical glass. Which glass holds more? About how much more?
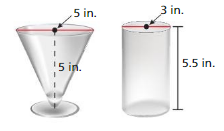
Answer:
volume of cone= 452.16 cu. m
Explanation:
volume of cone =πr² (h/3)
given that ,r = 6, h = 12
v= 3.14 x 6 x 6 (12/3)
v = 3.14 x 36 x (12/3)
v =3.14 x 36 x 4
v= 3.14 x 144
v = 452.16 cu. m
Question 7.
The ratio of the corresponding linear measures of two similar waffle cones is 3 to 4. The smaller cone has a volume of about 18 cubic inches. Find the volume of the larger cone. Round your answer to the nearest tenth.
Answer: 24 cubic inches.
Explanation:
(18/v) = (3/4)
3v = 18 x 4
3v = 72
v = 24 cubic in
Question 8.
Draw two different composite solids that have the same volume but different surface areas.Explain your reasoning.
Answer:
Question 9.
There are 13.5π cubic inches of blue sand and 9π cubic inches of red sand in the cylindrical container. How many cubic inches of white sand are in the container? Round your answer to the nearest tenth.
Answer:
v = 169.56 cu. in
Explanation:
volume of cylinder = πr² h
where π = 3.14
h = 6, r = 3given
v = 3.14 x 3 x 3 x 6
v= 3.14 x 9 x 6
v = 3.14 x 54
v = 169.56 cu. in
Question 10.
Without calculating, determine which solid has the greater volume. Explain your reasoning.
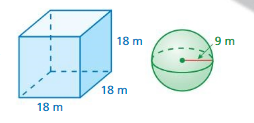
Answer:
prism has great volume.
Explanation:
the volume of the sphere is less than the volume of a prism.
Volume and Similar Solids Cumulative Practice

Question 1.
What is the value of 14 – 2\(\sqrt [ 3 ]{ 64 } \) ?
A. – 50
B. – 2
C. 6
D. 48
Answer:
option A Is correct
Explanation:
14 – 2 (3/64 x 100)
12 (150/32)
12 x (75/16)
-50
Question 2.
What is the volume of the cone? (Use \(\frac{22}{7}\) for π.)
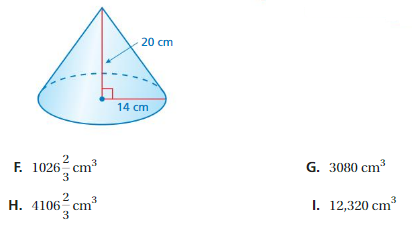
Answer:
volume of cone= 4098. 8304 cubic cm
Explanation:
volume of cone =πr² (h/3)
given that ,r = 14, h = 20
v= 3.14 x 14 x 14 (20/3)
v = 3.14 x196 x (20/3)
v =3.14 x 196 x 6.66
v= 3.14 x 1305.36
v = 4098. 8304
Question 3.
The cylinders are similar. What is the volume of the red cylinder?
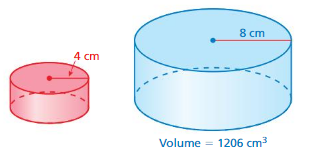
A. 6 cm
B. 150.75 cm3
C. 301.5 cm3
D. 603 cm3
Answer:
option D is correct.
Explanation:
(1206/2 ) = 603
large cylinder is 2 times greater than small cylinder.
Question 4.
A rectangle is graphed in the coordinate plane.
Which of the following shows Rectangle E’F’G’H’, the image of Rectangle EFGH after it is reflected in the -axis?
Answer:
option I is correct.
Explanation:
EFGH is reflected in the -ve axis.
Question 5.
What are the ordered pairs shown in the mapping diagram?
A. (2, 5), (4, – 2), (6, – 7), (8, 1)
B. (2, – 7), (4, – 2), (6, 1), (8, 5)
C. (2, 5), (4, 1), (6, – 2), (8, – 7)
D. (5, 2), (- 2, 4), (- 7, 6), (1, 8)
Answer:
option A is correct.
Explanation:
(2, 5)
(4, -2)
(6, -7)
(8, 1)
Question 6.
What is \(0 . \overline{75}\) written as a fraction?

Answer:
Question 7.
Solve the formula A = P + PI for I.

Answer:
option I is correct.
Explanation:
A = P + PI
I = (A – P/P)
A = P + P (A – P/P)
A = A.
Question 8.
A cylinder has a volume of 1296 cubic inches. If you divide the radius of the cylinder by 12, what is the volume (in cubic inches) of the smaller cylinder?

Answer:
The volume =0.1162963 cubic in
Explanation:
volume of cylinder =πr² (h/3)
given that r = 12 , v = 1296
1296 = 3.14 x 12 x 12 x (h/3)
1296 = 3.14 x 12x 4h
1296 =3.14 x 48 h
1296= 150.72 h
h =(150.72/1296)
h = 0.1162963 cubic in
Question 9.
The cost y (in dollars) for pounds of grapes is represented by y = 2x. Which graph represents the equation?
Answer:
Option c is correct.
Explanation:
y = 2x
on the x axis the graph represents the straight line on x – axis.
Question 10.
You are making a giant crayon. What is the volume (in cubic centimeters) of the entire crayon? Show your work and explain your reasoning. (Use 3.14 for π.)
Answer:
The volume = =75.34116 cubic cm
Explanation:
the volume of cylinder =πr² (h/3)
given that r = 3 ,h = 8
v = 3.14 x 3 x 3 x (8/3)
v = 3.14 x 9 x (8/3)
v =3.14 x 9 x 2.666
v= 3.14 x 23.994
v = 75.34116 cubic cm
Conclusion
We wish the knowledge shared regarding the Big Ideas Math Answers Grade 8 Ch 10 Volume and Similar Solids has helped you in your preparation. In case of any queries, do leave us your suggestions via the comment section and we will get back to you.
