Redefine your true self using the Big Ideas Math Answers Grade 8 Ch 9 Real Numbers and the Pythagorean Theorem. Shed the inhibitions that are holding you back and begin your practice using the BIM Grade 8 Chapter 9 Solutions and clear the exam with better grades. Big Ideas Math Grade 8 Answers Chapter 9 Real Numbers and the Pythagorean Theorem is given as per the latest syllabus guidelines. Enhance your math skills by making the most out of the BIM Book Grade 8 Chapter 9 Real Numbers and the Pythagorean Theorem Solutions.
Big Ideas Math Book 8th Grade Answer Key Chapter 9 Real Numbers and the Pythagorean Theorem
Access the Topicwise Big Ideas Math Grade 8 Chapter 9 Real Numbers and Pythagorean Theorem Answers provided below via quick links. Help your child with the homework help he might need right after class and master the concepts. Kickstart your preparation taking the help of the BIM 8th Grade Ch 9 Real Numbers and Pythagorean Theorem Answer Key and identify the areas of need and allot time accordingly.
Performance Task
- Real Numbers and the Pythagorean Theorem STEAM Video/Performance Task
- Real Numbers and the Pythagorean Theorem Getting Ready for Chapter 9
Lesson: 1 Finding Square Roots
Lesson: 2 The Pythagorean Theorem
Lesson: 3 Finding Cube Roots
Lesson: 4 Rational Numbers
Lesson: 5 Irrational Numbers
Lesson: 6 The Converse of the Pythagorean Theorem
- Lesson 9.6 The Converse of the Pythagorean Theorem
- The Converse of the Pythagorean Theorem Homework & Practice 9.6
Chapter: 9 – Real Numbers and the Pythagorean Theorem
- Real Numbers and the Pythagorean Theorem Connecting Concepts
- Real Numbers and the Pythagorean Theorem Chapter Review
- Real Numbers and the Pythagorean Theorem Practice Test
- Real Numbers and the Pythagorean Theorem Cumulative Practice
Real Numbers and the Pythagorean Theorem STEAM Video/Performance Task
STEAM Video
Metronome Design
A metronome is a device that ticks at a constant rate. A metronome includes a pendulum, which swings back and forth in a precise time called a period. Why do musicians use metronomes?
Watch the STEAM Video “Metronome Design.” Then answer the following questions. The equation T = 0.2√L relates the period T (in seconds) and the length L (in centimeters) of a pendulum, where √L is the square root of L.
1. The table shows the square roots of several values of L. Use the pattern to find the values of √36 , √49 , and √64 .
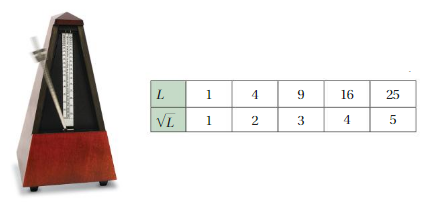
2. What is the period of a pendulum that is 100 centimeters long? Justify your answer.
Answer:
1. √36 = 6
√49 = 7
√64 = 8
2. √100 = 10
Explanation:
In the above given table the square roots of 1,2, 3,4,5 are given
square root of 36 = 6
6 x 6 = 36
square root of 49 = 7
7 x 7 =49
square root of 64 = 8
8 x 8 =64
2. given that period of the pendulum is 100 centimeters.
square root of 100 =10
10 x 10 = 100
Performance Task
Identify and Correct the Error!
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the lengths of several pendulums.

You will be asked to identify and correct errors in calculations of periods. Why is it important to pay attention to units when substituting values into a formula?
Answer:
0.438 sec, 1.219 sec, 1.612sec.
Explanation:
1 feet = 0.3048 seconds
so in the question given that the length of 1.44= 1.44 x 0.3048 sec
0.438 sec
4 x 0.3048 = 1.219 sec
5.29 x 0.3048 = 1.612 sec.
Real Numbers and the Pythagorean Theorem Getting Ready for Chapter 9
Chapter Exploration
When you multiply a number by itself, you square the number.
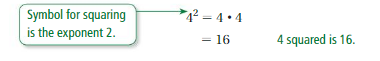
To“undo” this, take the square root of the number.
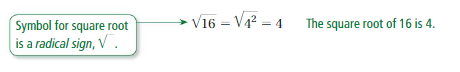
1. Work with a partner. Find the radius of each circle.
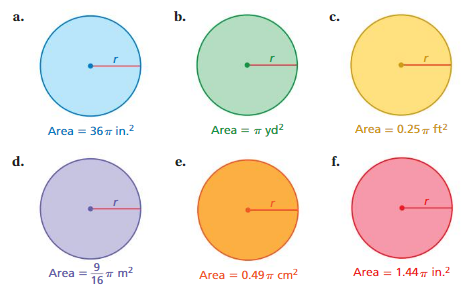
Answer:
a. 6 in
b. 1 yd
c. 0.5 ft
d. (3/9) m
e. 0.7 cm
f. 1.2 in
Explanation:
a. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = 36 π in²
radius = (√ 36 π / π )
both in the numerator and denominator π get canclled.
radius = ( √ 36)
square root of 36 is 6 x 6
√ 36 = √ 6²
where square and square root get cancelled.
radius = 6 in
b. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = π yd²
radius = (√ π / π )
both in the numerator and denominator π get canceled.
radius = ( √ 1)
the square root of 1 is 1 x 1
√ 1= √ 1²
where square and square root get canceled.
radius =1 yd
c. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = 0.25 π ft
radius = (√ 0.25π / π )
both in the numerator and denominator π get canceled.
radius = ( √ 0.25)
the square root of 0.25 is 0.5 x 0.5
√ 0.25 = √ 0.5²
where square and square root get canceled.
radius = 0.5 ft
c. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = 0.25 π ft
radius = (√ 0.25π / π )
both in the numerator and denominator π get canceled.
radius = ( √ 0.25)
the square root of 0.25 is 0.5 x 0.5
√ 0.25 = √ 0.5²
where square and square root get canceled.
radius = 0.5 ft
d. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = (9/16) π m²
radius = (√ (9/16)π / π )
both in the numerator and denominator π get canceled.
radius = ( √ (9/16)
the square root of (9/16) is (3/4) x (3/4)
√ (9/16) = √ (3/4)²
where square and square root get canceled.
radius = (3/4) m
e. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = (0.49) πcm²
radius = (√ (0.49)π / π )
both in the numerator and denominator π get canceled.
radius = ( √ (0.49)
the square root of (0.49) is (0.7) x (0.7)
√ (0.49) = √ (0.7)²
where square and square root get canceled.
radius = (0.7) cm
f. The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
given that area = (1.44) π in²
radius = (√ (1.44)π / π )
both in the numerator and denominator π get canceled.
radius = ( √ (1.44)
the square root of (1.44) is (1.2) x (1.2)
√ (1.44) = √ (1.2)²
where square and square root get canceled.
radius = (1.2) in
2. WRITING GUIDELINES Work with a partner. Explain how you can find the radius and diameter of a circular object when you are given its area. Justify your answer using an example that is different from those in Exercise 1.
Answer:
The radius of circle = 8 cm
The diameter of circle = 16 cm
Explanation:
for example, we have to consider the area of a circle is 64π cm² given.
we have to find the radius and diameter of the circle.
The radius of circle = (√A/π)
where A = area of a circle, π = 3.14
the radius of circle = (√64π/π)
both in the numerator and denominator π get canceled.
radius = ( √ (64)
the square root of (64) is (8) x (8)
√ (64) = √ (8)²
where square and square root get canceled.
radius = 8 cm
The radius of circle = (2√A/π)
where A = area of a circle, π = 3.14
the radius of circle = (2√64π/π)
both in the numerator and denominator π get canceled.
diameter = ( 2√ (64)
the square root of (64) is (8) x (8)
√ (64) = 2√ (8)²
where square and square root get canceled.
diameter = 2 x 8 cm
diameter = 16 cm
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what the terms might mean and record your thoughts.
square root
cube root
irrational number
perfect square
perfect cube
Answer:
square root = a number that produces a specified quantity when multiplied by itself.
cube root = the number which produces a given number when cubed.
irrational number = an irrational number is a number that cannot be expressed as a fraction for any integers.
perfect square = perfect square is another term for square number.
perfect cube = a perfect cube is an integer that is equal to some other integer raised to the third power
square root of 36
Explanation:
36 = 6 x 6
√ 36 = √ 6 ²
where square and square root get canceled.
36 = 6
cube root of 343
343 = 7 x 7 x 7
3√ 343 = √ 7 ³
where cube and cube root get canceled.
343 = 7
irrational number
Example : √ 2, √ 3, √ 5, √ 11, √ 12, π (pi) are all irrational.
perfect square
9 = 3 x 3
perfect cube
125 = 5 x 5 x 5
Lesson 9.1 Finding Square Roots
EXPLORATION 1
Finding Side Lengths
Work with a partner. Find the side length of each square. Explain your method.
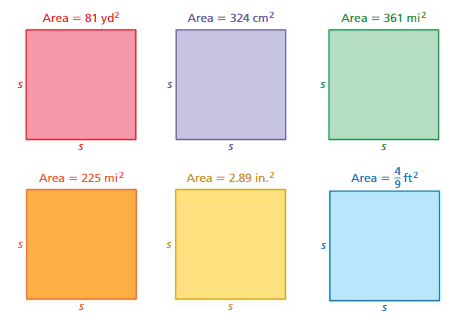
Answer:
a. 9yd
b. 18 cm
c. 19 mi
d. 15 mi
e. 1.7 in
f. 0.2 ft
Explanation:
Area of a square = a ²
where a = side
Given that A = 81yd ²
A = s x s
A = 9 x 9
a = 9
b.Given that A =324cm ²
A = s x s
A = 18 x 18
a = 18 cm
c. Given that A =361 mi ²
A = s x s
A = 19 x 19
a = 19 mi
d. Given that A =225 mi²
A = s x s
A = 15 x 15
a = 15 mi
e. Given that A =2.89in ²
A = s x s
A = 1.7 x 1.7
a = 1.7 in
f. Given that A =(4/9) ft ²
A = s x s
A = (2/3) x (2/3)
a = (2/3) ft
EXPLORATION 2
Finding Solutions of Equations
Work with a partner. Use mental math to solve each equation. How many solutions are there for each equation? Explain your reasoning.
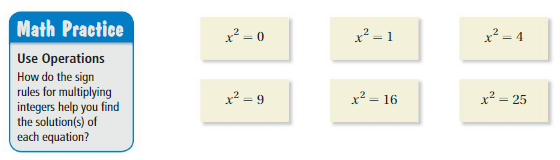
Answer:
x = +0, -0
x = +1, -1
x = +2, -2
x = +3, -3
x = +4, -4
x = +5, -5
Explanation:
x² = 0, x = +0, -0
x² = 1, x =+1, -1
x² = 4, x = +2, -2
x² = 9, x = +3, -3
x² = 16, x = +4, -4
x² = 25, x = +5, -5

Try It
Find the two square roots of the number.
Question 1.
36
Answer:
6 , -6
Explanation:
square root of 36 = 6x 6
6 and -6
Question 2.
100
Answer:
10 , – 10
Explanation:
square root of 100 = 10 x 10
10 and – 10
Question 3.
121
Answer:
11, – 11
Explanation:
square root of 121 = 11 x 11
11 and – 11
Find the square root(s).
Question 4.
\(\sqrt{4}\)
Answer:
2
Explanation:
square root of 4 = 2 x 2
2
Question 5.
– \(\sqrt{81}\)
Answer:
9
Explanation:
square root of 81 = 9 x 9
9
Question 6.
± \(\sqrt{64}\)
Answer:
8
Explanation:
square root of 64 = 8 x 8
8
Find the square root(s).
Question 7.
– \(\sqrt{\frac{1}{100}}\)
Answer:
– 0.1
Explanation:
square root of (1/100) = (1/10 x 10)
(1/10) = 0.1
– 0.1
Question 8.
± \(\sqrt{\frac{4}{25}}\)
Answer:
± 0.4
Explanation:
square root of (4/25) = 0.16
0.16 = 0.4 x 0.4
Question 9.
\(\sqrt{12.25}\)
Answer:
3.5
Explanation:
square root of (12.25) = 3.5
12.25 = 3.5 x 3.5
Evaluate the expression.
Question 10.
12 – 3\(\sqrt{25}\)
Answer:
-3
Explanation:
square root of 25 = 5
12 – 3 (5)
12 – 15
-3
Question 11.
\(\sqrt{\frac{28}{7}}\) + 2.4
Answer:
4.4
Explanation:
(28/7) = 4
square root of 4 = 2
2 + 2.4
4.4
Question 12.
15 – (√4)2
Answer:
11
Explanation:
square root of 16 = 4
15 – 4
11
Solve the equation.
Question 13.
k2 = 169
Answer:
k = 13
Explanation:
square root of 169 = 13 x 13
k = 13
Question 14.
7n2 = 175
Answer:
n = 5
Explanation:
n² = (175/7)
n = 25
square root of 25 = 5 x 5
n = 5
Question 15.
190 = 4b2 – 6
Answer:
b = 7
Explanation:
190 = 4b2 – 6
4b² = 190 + 6
4b²=196
b² = (196/4)
b² = 49
b = 7
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING SQUARE ROOTS Find the square root(s).
Question 16.
\(\sqrt{256}\)
Answer:
16
Explanation:
square root of 256 = 16 x 16
16
Question 17.
– \(\sqrt{\frac{1}{9}}\)
Answer:
– (1/3)
Explanation:
square root of (1/9) = (1/3)
square root of 9 = 3 x 3
given in – ve symbol
– (1/3)
Question 18.
± \(\sqrt{1.44}\)
Answer:
± 1.2
Explanation:
square root of 1.44 = 1.2
square root of 1.44 = 1.2 x 1.2
given in ± symbol
± 1.2
EVALUATING EXPRESSIONS Evaluate the expression.
Question 19.
\(\sqrt{\frac{81}{9}}\) – 7
Answer:
– 4
Explanation:
square root of 81 = 9 x 9
square root of 9 = 3x 3
(9/3) = 3
3 – 7 = -4
Question 20.
– 1 – \(\sqrt{121}\)
Answer:
-12
Explanation:
square root of 121 = 11 x 11
– 1 – 11
– 12
Question 21.
5 + (\(\sqrt{2}\))2
Answer:
7
Explanation:
square root of 4 = 2 x 2
5 + 2
7
SOLVING EQUATIONS Solve the equation.
Question 22.
2r2 = 162
Answer:
r = 9
Explanation:
2r2 = 162
r ² = (162/2)
r² = 81
square root of 81 = 9 x 9
r = 9
Question 23.
d2 + 5 = 41
Answer:
d = 6
Explanation:
d2 + 5 = 41
d ² = 41 – 5
d ² = 36
square root of 36 = 6 x 6
d = 6
Question 24.
– 42 = 7b2 – 385
Answer:
b = – 7
Explanation:
– 42 = 7b2 – 385
7b ² = – 385 + 42
7b ² = – 343
b ² = (- 343/7)
b ² = – 49
square root of – 49 = 7 x 7
b = – 7
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 25.
Your distance d (in miles) from the horizon can be approximated by d = 1.22√h, where h is your eye level (in feet above ground level). What is your eye level when you are 9.76 miles from the horizon?
Answer:
The eye level when you are 9.76 miles from the horizon = 11.907 ft
Explanation:
Given that the horizon can be approximated by 1.22 feet
so 1.22 x 11.907
11.907 ft
the eye level when you are 9.76 miles from the horizon = 11.907 ft.
Question 26.
DIG DEEPER!
The speed s (in meters per second) of a tsunami can be modeled by the function s = √9.8d, where d is the water depth (in meters).

a.What is the speed of the tsunami when the water depth is 500 meters?
b. What happens to the speed of the tsunami as the depth decreases? Explain.
Answer:
a. The speed of tsunami = 4,900 sq meters.
b. if the speed of the tsunami as depth decreases it has low flow.
Explanation:
a. Given that the speed of the tsunami = √9.8d
√9.8 x 500 where d = 500 given
4,900 sq meters
b. if the speed of the tsunami as depth decreases the flow of the water is also less.
Finding Square Roots Homework & Practice 9.1
Review & Refresh
Evaluate the expression. Write your answer in scientific notation.
Question 1.
(4.3 × 103) + (2.4 × 103)
Answer
6.7 x 10 ³
Explanation:
(4.3 × 103) + (2.4 × 103)
(4.3 + 2.4) x 10³
6.7 x 10 ³
Question 2.
(1.5 × 10-2) – (3.5 × 10-3)
Answer:
2 × 10-2
Explanation:
(1.5 × 10-2) – (3.5 × 10-3)
(1.5 – 3.5) x 10-2
2 × 10-2
Question 3.
9 × (7 × 10-2)
Answer:
6.3 x 10 ⁻¹
Explanation:
9 × (7 × 10-2)
(9 x 10) x 10-2
6.3 x 10 ⁻¹
Question 4.
(6.6 × 10-5) ÷ (1.1 × 104)
Answer:
6 x 10-5
Explanation:
(6.6 × 10-5) ÷ (1.1 × 104)
(6.6/ 1.1) x 10-5
6 x 10-5
Make a scatter plot of the data. Identify any outliers, gaps, or clusters.
Question 5.

Answer:
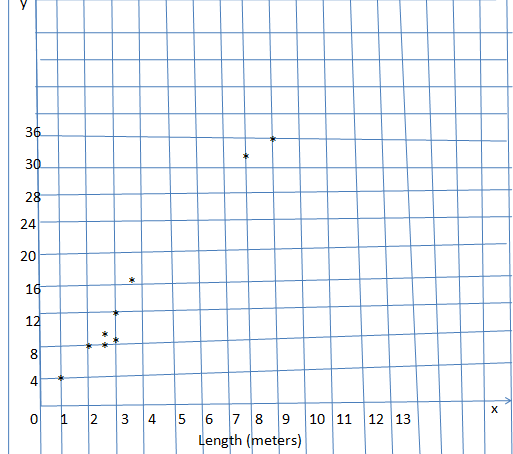
Explanation:
outliers = (8,33) and (9,36)
gap = 3.5 meters to 8 meters.
fillers=2 meters to 3 meters.
Question 6.

Answer:
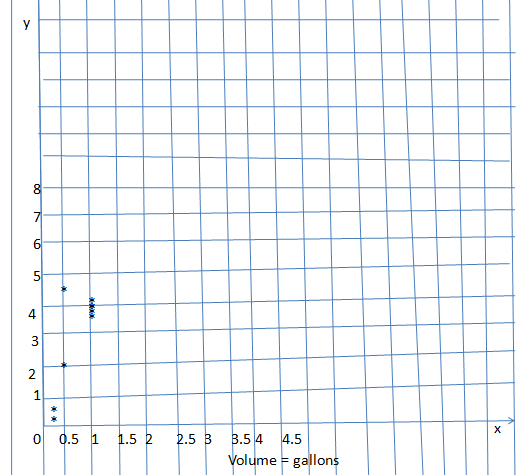
Explanation:
outliers = (1,4.05) and (1, 4.00)
gap = 0.5 gallons to 1 gallon
fillers =1meter to 1.5 meters.
Concepts, Skills, &Problem Solving
FINDING SIDE LENGTHS Find the side length s of the square. (See Exploration 1, p. 373.)
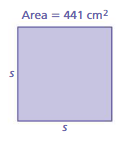
Question 7.
Answer:
S = 21 cm
Explanation:
Area = 441 cm²
Area of square = a ²
where a = side
square root of 441 = 21 x 21
side length = 21
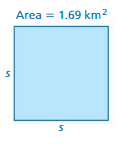
Question 8.
Answer:
S = 1.3 km
Explanation:
Area = 1.69 km²
Area of square = a ²
where a = side
square root of 1.69 = 1.3 x 1.3
side length = 1.3km
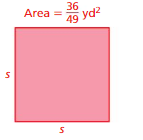
Question 9.
Answer:
S = (6/7) yd
Explanation:
Area = (36/49)²
Area of square = a ²
where a = side
square root of (36/49) = (6/7) x (6/7)
side length =(6/7) yd
FINDING SQUARE ROOTS OF A PERFECT SQUARE Find the two square roots of the number.
Question 10.
9
Answer:
3, – 3
Explanation:
square root of 9 = 3 x 3
3
given that two square roots
3, -3
Question 11.
64
Answer:
8, – 8
Explanation:
square root of 64 = 8 x 8
8
given that two square roots
8, -8
Question 12.
4
Answer:
2, -2
Explanation:
square root of 4 = 2 x 2
2
given that two square roots
2, -2
Question 13.
144
Answer:
12, -12
Explanation:
square root of 144 = 12 x 12
12
given that two square roots
12, -12
FINDING SQUARE ROOTS Find the square root(s).
Question 14.
√625
Answer:
25
Explanation:
√625
√25² therefore square and square root get canceled.
the square root of 625 is 25
Question 15.
± √196
Answer:
± 14
Explanation:
± √196
√14² therefore square and square root get canceled.
the square root of 196 is 14
Question 16.
– √1600
Answer:
– 40
Explanation:
– √1600
√40² therefore square and square root get canceled.
the square root of 1600 is 40
Question 17.
± √2500
Answer:
± 50
Explanation:
± √2500
√50² therefore square and square root get canceled.
the square root of 2500 is 50
Question 18.
\(\sqrt{\frac{1}{16}}\)
Answer:
(1/4)
Explanation:
√(1/16)
√(1/4)² therefore square and square root get canceled.
the square root of (1/16) is (1/4)
Question 19.
\(\sqrt{\frac{49}{576}}\)
Answer:
(7/24)
Explanation:
√(49/576)
√(7/24)² therefore square and square root get canceled.
the square root of (49/576) is (7/24)
Question 20.
± \(\sqrt{\frac{1}{961}}\)
Answer:
±(1/31)
Explanation:
√(1/961)
√(1/31)² therefore square and square root get canceled.
the square root of (1/961) is (1/31)
Question 21.
– \(\sqrt{\frac{9}{100}}\)
Answer:
– (3/10)
Explanation:
√(9/100)
√(3/10)² therefore square and square root get canceled.
the square root of (9/100) is (3/10)
Question 22.
± √4.84
Answer:
± 2.2
Explanation:
√4.84
√2.2² therefore square and square root get canceled.
the square root of 4.84 is 2.2
Question 23.
√7.29
Answer:
2.7
Explanation:
√7.29
√27² therefore square and square root get canceled.
the square root of 7.29 is 2.7
Question 24.
– √361
Answer:
– 19
Explanation:
-√361
√19² therefore square and square root get canceled.
the square root of 361 is 19
Question 25.
– √2.25
Answer:
– 1.5
Explanation:
– √2.25
√15² therefore square and square root get canceled.
the square root of 2.25 is 1.5
Question 26.
YOU BE THE TEACHER
Your friend finds ± \(\sqrt{\frac{1}{4}}\). Is your friend correct? Explain your reasoning.

Answer:
± (1/2)
Explanation:
±√(1/4)
√(1/2)² therefore square and square root get canceled.
the square root of (1/4) is (1/2)
Question 27.
MODELING REAL LIFE
The area of a square patch of fabric is 2.25 square inches. What is the side length of the patch?
Answer:
1.5 inch
Explanation:
Area of a square patch of fabric is 2.25
area of a square is s²
area = 1.5 x 1.5
side = 1.5 inch
Question 28.
CRITICAL THINKING
There are two square roots of 25. Why is there only one answer for the radius of the button?

Answer:
The radius of the button = 5 mm
Explanation:
Given that the area of a circle = πr²
25π = πr²
where π get canceled on both sides.
25 = r²
r = 5
NUMBER SENSE Copy and complete the statement with <, >, or =.
Question 29.
![]()
Answer:
√81 > 8
Explanation:
square root of 81 = 9 x 9
9 is greater then 8
Question 30.
![]()
Answer:
0.5 = √0.25
Explanation:
square root of 0.25 = 0.5 x 0.5
0.5 is equal to 0.5
Question 31.
![]()
Answer:
(3/2) < √(25/4)
Explanation:
square root of (25/4) = (5/2) x (5/2)
(3/2) is less than (5/2)
(3/2) = 1.5
(5/2) = 3.5
EVALUATING EXPRESSIONS Evaluate the expression.
Question 32.
(√9)2 + 5
Answer:
14
Explanation:
square and square root get canceled.
9 + 5
14
Question 33.
28 – (√144)2
Answer:
-116
Explanation:
square and square root get canceled.
28 – 144
-116
Question 34.
3√16 – 5
Answer:
7
Explanation:
the square root of 16 is 4
16 = 4 x 4
3 x 4 – 5
12 – 5
7
Question 35.
10 – 4\(\sqrt{\frac{1}{16}}\)
Answer:
9
Explanation:
the square root of 16 is 4
16 = 4 x 4
10 – 4 (1/4)
10 – 4 (0.25)
10 – 1
9
Question 36.
√6.76 + 5.4
Answer:
12.56
Explanation:
square and square root get canceled
6.76 + 5.4
12.16
Question 37.
8√8.41 + 1.8
Answer:
25
Explanation:
square and square root get canceled
8 x 8.41 + 1.8
67.28 + 1.8
69.08
Question 38.
2(\(\sqrt{\frac{80}{5}}\) – 5)
Answer:
3
Explanation:
the square root of 16 is 4 x 4
(80/5) = 16
2 x 4 -5
8 – 5
3
Question 39.
4(\(\sqrt{\frac{147}{3}}\) + 3
Answer:
40
Explanation:
the square root of 49 is 7 x 7
(147/3) = 49
4 x 7 + 3
37 + 3
40
Question 40.
NUMBER SENSE
Without calculating, describe how the value of \(\sqrt{\frac{1}{a}}\) changes as a increases. Assume a > 0.
Answer:
0.5
Explanation:
Assuming a > 0
a = 4
the square root of 4 is 2
4 = 2 x 2
(1/2) = 0.5
SOLVING EQUATIONS Solve the equation.
Question 41.
x2 = 100
Answer:
x = 10 , x = -10
Explanation:
x2 = 100
x² = 10²
when powers are equal exponents must be equal.
x = 10
Question 42.
42 = d2 – 22
Answer:
d = 8 , d = 8
Explanation:
42 = d2 – 22
d² = 42 + 22
d² = 64
d² = 8²
when powers are equal exponents must be equal.
d = 8
Question 43.
4z2 = 144
Answer:
z = 6, z = -6
Explanation:
4z2 = 144
z² = (144/4)
z² = 36
z² = 6²
when powers are equal exponents must be equal.
z = 6
Question 44.
\(\sqrt{\frac{136}{9}}\) = \(\frac{1}{3}\) m2 – 10
Answer:
m = 4.8335, m = -4.8335
Explanation:
(136/9) = 45.33
(1/3) = 0.333
0.3333 m2 – 10
m2 = 10 – 0.33
m2 = 9.67
m = 4.835
Question 45.
0.25r2 = 49
Answer:
r = 14, r = -14
Explanation:
0.25r2 = 49
r² = (49/0.25)
r² = 196
r² = 14²
when powers are equal exponents must be equal.
r = 14
Question 46.
3h2 = h2 + 18
Answer:
h = 3, h = -3
Explanation:
3h2 = h2 + 18
3h² – h² = 18
2h² = 18
h² = (18/2)
h² = 9
h² = 3²
when powers are equal exponents must be equal.
h = 3
Question 47.
YOU BE THE TEACHER
Your friend solves the equation 9x2 = 36. Is your friend correct? Explain your reasoning.

Answer:
Yes, my friend is correct.
Explanation:
9x2 = 36
x² = (36/9)
x² = 4
x² = 2²
when powers are equal exponents must be equal.
x =2
Question 48.
PROBLEM SOLVING
The period of a pendulum is the time the pendulum takes to complete one back-and-forth T swing. The period T (in seconds) can be modeled by the function T = 1.1√L, where L is the length (in feet) of the pendulum. Estimate the length of a pendulum with a period of 1.65 seconds.

Answer:
The length of the pendulum with a period of 1.65 seconds = 0.50292 sec
Explanation:
Given that the period (in seconds) is 1.1
1.65 x 0.3048
1 feet = 0.3048 sec
0.50292
Question 49.
MODELING REAL LIFE
The area of a sail is 40\(\frac{1}{2}\) square feet. The base and the height of the sail are equal. What is the height of the sail?

Answer:
The height of the sail = 9 ft
Explanation:
Area of triangle = (b h/2)
area = 40 x (1/2)
40 x 0.5 = 20
h = 9 , b = 4
(9 x 4/2) = (36/2)
18 = area
Question 50.
REASONING
Is the product of two perfect squares always a perfect square? Explain your reasoning.
Answer:
Yes, the product of two perfect squares always a perfect square.
Explanation:
for example, we take 9
the square root of 9 = 3 x 3
3 is also a perfect square.
Question 51.
PROBLEM SOLVING
The kinetic energy (in joules) of a falling apple is represented byK = \(\frac{v^{2}}{2}\), where v is the speed of the apple (in meters per second). How fast is the apple traveling when the kinetic energy is 32 joules?
Answer:
The apple traveling when the kinetic energy is 32 joules = 8 meter per second.
Explanation:
Given that the apple is represented by k
k = 2 x 2
k = 4
also given that 32 joules.
32 / 4 = 8 meter per sec.
Question 52.
PRECISION
The areas of the two watch faces have a ratio of 16:25.

a. What is the ratio of the radius of the smaller watch face to the radius of the larger watch face?
b. What is the radius of the larger watch face?
Answer:
a. The ratio of the radius of the smaller watch face to the radius of the larger watch face = 4: 5
b. the radius of the larger watch face = 25
Explanation:
a. square root of (16/25) = (4/5)
ratio = 4: 5
b. the radius of the larger watch = 25
Question 53.
PROBLEM SOLVING
The cost (in dollars) of making a square window with a side length of n inches is represented by C = \(\frac{n^{2}}{2}\) + 175. A window costs $355. What is the side length (in feet) of the window? Justify your answer.
Answer:
The side length of the window = 2.5 feet
Explanation:
Given that the window costs = 355$
the side length of n inches is represented by c
the side length of the window 355 = n x n /5+ 175
n = 30
(30/12)
2.5 ft
Question 54.
DIG DEEPER!
Albert Einstein’s most famous equation is E = mc2, where E is the energy of an object (in joules), is the mass of the object (in kilograms), and c is the speed of light (in meters per second). A hydrogen atom has 15.066 × 10-7 joule of energy and a mass of 1.674 × 10-27 kilogram. What is the speed of light? Write your answer in scientific notation.
Answer:
The speed of the light =3 x 10²⁰ meters per second.
Explanation:
Given that mass of the object = 1.674 x 10-27
energy of the object = 15.066 x 10-7
Albert Einsteins equation = E = mc2
where m = mass , e = energy, c = speed
c² = (E/M)
c² = (15.066/1.674)
c² = 9 x 10²⁰
c² = 3²
c = 3 x 10²⁰
Question 55.
GEOMETRY
The area of the triangle is represented by the formula A = \(\sqrt{s(s-21)(s-17)(s-10)}\), where s is equal to half the perimeter. What is the height of the triangle?
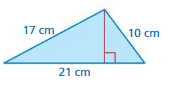
Answer:
The height of the triangle = 8 cm
Explanation:
Area of the triangle = 2 (A/b)
where b = base A = area
area = 2 x 4
area = 8 cubic cm
Question 56.
WRITING
Can you find the square root of a negative number? Explain.
Answer:
Yes, we can find the square root of a negative number.
Explanation:
The square root of – 144 is – 12 x 12
the square root of – ve number is also a + ve.
REASONING Without solving, determine the number of solutions of the equation.
Question 57.
x2 = 1
Answer:
2 solutions
x = 1, x = -1
Explanation:
x² = 1²
when powers are equal exponents must be equal.
x = 1
Question 58.
b2 = – \(\sqrt{\frac{1}{9}}\)
Answer:
b = -0.16, b = 0.16
Explanation:
b2 = – \(\sqrt{\frac{1}{9}}\)
square root of (1/9) = (1/3)
b² = – (1/3)
b² = – 0.33
b = 0.16
Question 59.
z = √-144
Answer:
z = 0
Explanation:
√-144 = √(12 x 12 )²
√-144 = 12
square and square root get cancelled.
z = -12
Lesson 9.2 The Pythagorean Theorem
Pythagoras was a Greek mathematician and philosopher who proved one of the most famous rules in mathematics. In mathematics, a rule is called a theorem. So, the rule that Pythagoras proved is called the Pythagorean Theorem.

EXPLORATION 1
Discovering the Pythagorean Theorem
Work with a partner.
- On grid paper,draw a right triangle with one horizontal side and one vertical side.
- Label the lengths of the two shorter sides a and b. Label the length of the longest side c.
- Draw three squares that each share a side with your triangle. Label the areas of the squares a2, b2, and c2.
- Cut out each square. Then make eight copies of the right triangle and cut them out.
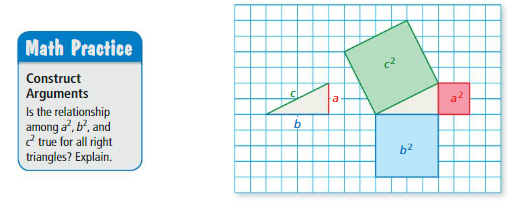
a. Arrange the figures to show how a2 and b2 relate to c2. Use an equation to represent this relationship.
b. Estimate the side length of your triangle. Then use the relationship in part(a) to find c. Compare the values.
Answer:
a. a² + b² = c²
b. 9 + 16 = 25
Explanation:
a. a² + b² = c²
b. we are estimating a = 3 , b = 4 , c =5
a² + b² = c²
3² + 4² = 5²
9 + 16 = 25

Try It
Find the length of the hypotenuse of the triangle.
Question 1.
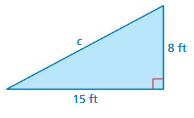
Answer:
Length = -6, 6
Explanation:
a² + b² = c²
15 – 8 = 6
Question 2.
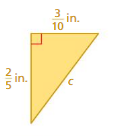
Answer:
Length = 0.7
Explanation:
a² + b² = c²
0.4² + 0.3² =0.7²
length = 0.7
Find the missing length of the triangle.
Question 3.
Answer:
Length of the triangle = 8 , -8
Explanation:
a² + b² = c²
16² -8 =8²
length = 8yd
Question 4.
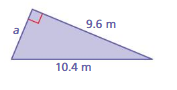
Answer:
Length of the triangle = 0.8 m
Explanation:
a² + b² = c²
0.8² + 9.6² =10.4²
length = 0.8 m
Find x
Question 5.
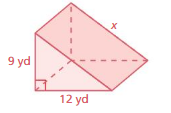
Answer:
x = 10 yd
Explanation:
a² + b² = x²
9² + 1² =10²
length = 10 yd
Question 6.
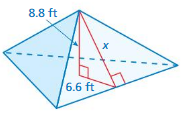
Answer:
x = 15.4 ft
Explanation:
a² + b² = x²
6.6² + 8.8² =15.4²
length = 15.4 ft
Find the distance between the points.
Question 7.
(3, 6) and (7, 9)
Answer:
3, 2
Explanation:
(3,6) = (6- 3) = 3
(7 , 9) = (9 – 7) = 2
Question 8.
(- 3, – 4) and (2, 8)
Answer:
-7 , 6
Explanation:
(-3 ,-4) = (-4- -3) = -7
(2 , 8) = (8 – 2) = 6
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING A MISSING LENGTH Find x.
Question 9.
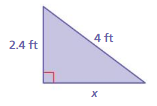
Answer:
The missing length = 1.6 ft
Explanation:
a² + x² = c²
2.4² + 1.6² =4²
length = 1. 6 ft
Question 10.
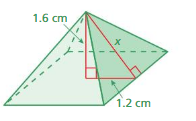
Answer:
The missing length = 2.8 cm
Explanation:
a² + x² = c²
1.6² + 1.2² =2.8²
length = 2.8 cm
Question 11.
FINDING A DISTANCE
Find the distance between (- 5, 2) and (7, – 7).
Answer:
– 3 , 0
Explanation:
(-5 ,2) = (-4 -2) = -3
(7 , -7) = (7 – 7) = 0
-3 , 0
Question 12.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
The hypotenuse = c
longest side = c
leg = c
opposite to right angle = c
Explanation:
By using Pythagoras theorem
a² + x² = c²
The hypotenuse = c
longest side = c
leg = c
opposite to right angle = c
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
A zoo keeper knows that an escaped red panda is hiding somewhere in the triangular region shown. What is the area (in square miles) that the zoo keeper needs to search? Explain.
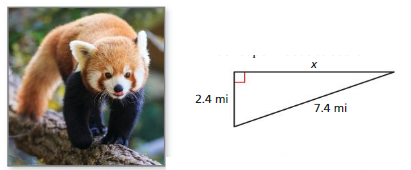
Answer:
The area that zoo keeper needs to search = 9.8 sq m
Explanation:
By using Pythagoras theorem
a² + b² = c²
2.4 + 7.4 = 9.8 sq m
c² = a² + b²
Question 14.
DIG DEEPER!
Objects detected by radar are plotted in a coordinate plane where each unit represents 1 mile. The point (0, 0) represents the location of a shipyard. A cargo ship is traveling at a constant speed and in a constant direction parallel to the coastline. At9 A.M., the radar shows the cargo ship at(0, 15). At 10 A.M., the radar shows the cargo ship at(16, 15). How far is the cargo ship from the shipyard at 4 P.M.? Explain.
Answer:
The cargo ship from the shipyard at 4 p.m = (16, 0)
Explanation:
Given that cargo ship at (0, 15) 9 a.m
cargo ship at (16, 15) 10 a.m
(16 – 0) , (15 – 15)
(16, 0) at 4 p.m
The Pythagorean Theorem Homework & Practice 9.2
Review & Refresh
Solve the equation.
Question 1.
7z2 = 252
Answer:
z = 6
Explanation:
7z2 = 252
z² = (252/7)
z² = 36
z² = 6²
when powers are equal exponents must be equal.
z = 6
Question 2.
0.75 q2 = 108
Answer:
q = 12
Explanation:
0.75 q2 = 108
q² = (108/0.75)
q² = 144
q² = 12²
when powers are equal exponents must be equal.
q = 12
Question 3.
\(\sqrt{\frac{1000}{10}}\) = n2 – 54
Answer:
n = 8
Explanation:
(1000/10) = 100
square root of 100 = 10 x 10
10 = n² – 54
n² = 10 + 54
n² = 64
n² = 8²
when powers are equal exponents must be equal.
n = 8
Question 4.
What is the solution of the system of linear equations y = 4x + 1 and 2x + y = 13?
A. (1, 5)
B. (5, 3)
C. (2, 9)
D. (9, 2)
Answer:
option c is correct.
Explanation:
y = 4x + 1, 2x + y = 13
if we consider x = 2 and y = 9 the values are equal.
9 = 4(2) + 1 , 2 (2) + 9 = 13
9 = 8 + 1, 4 + 9 = 13
9 = 9 , 13 = 13.
Concepts, Skills, &Problem Solving
USING GRID PAPER Find c. (See Exploration 1, p. 381.)
Question 5.
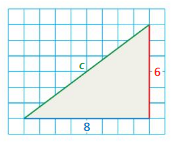
Answer:
The value of c = 13
Explanation:
given that grid paper
a = 6 ( 6 boxes touching.)
b = 6 ( 8 boxes touching.)
c = 13 (13 boxes touching.)
Question 6.
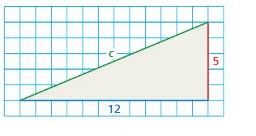
Answer:
The value of c = 15
Explanation:
given that grid paper
a = 5 ( 5 boxes touching.)
b = 12 ( 12 boxes touching.)
c = 15 (15 boxes touching.)
FINDING A MISSING LENGTH Find the missing length of the triangle.
Question 7.
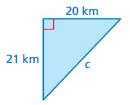
Answer:
The missing length = 41km
Explanation:
By using Pythagoras theorem
a² + b² = c²
20² + 21² =41²
length = 41 km
Question 8.
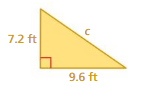
Answer:
The missing length = 16.8 sq ft
Explanation:
By using Pythagoras theorem
a² + b² = c²
7.2² + 9.6² =16.8²
length = 16.8 sq ft
Question 9.
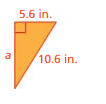
Answer:
The missing length = 5.0 sq in
Explanation:
By using Pythagoras theorem
a² + b² = c²
5.0² + 5.6² =10.6²
length = 10.6 sq in
Question 10.
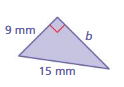
Answer:
The missing length = 6 mm
Explanation:
By using Pythagoras theorem
a² + b² = c²
9² + 6² =15²
length = 6 mm
Question 11.
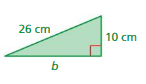
Answer:
The missing length = 16 cm
Explanation:
By using Pythagoras theorem
a² + b² = c²
10² + 16² =26²
length = 16 cm
Question 12.
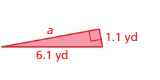
Answer:
The missing length = 5.0 yd
Explanation:
By using Pythagoras theorem
a² + b² = c²
5.0² + 1.1² = 6.1²
length = 5.0 yd
Question 13.
YOU BE THE TEACHER
Your friend finds the missing length of the triangle. Is your friend correct? Explain your reasoning.

Answer:
No my friend is not correct.
Explanation:
By using Pythagoras theorem
a² + b² = c²
7² + 18² = 25²
length = 18 ft
FINDING LENGTHS OF THREE-DIMENSIONAL FIGURES Find x.
Question 14.
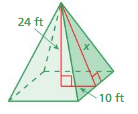
Answer:
The missing length = 14 ft
Explanation:
By using Pythagoras theorem
a² + b² = c²
10² + 14² = 24²
length = 14 ft
Question 15.
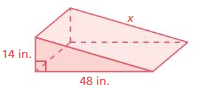
Answer:
The missing length = 50 in
Explanation:
By using Pythagoras theorem
a² + b² = c²
14² + 48² = 50²
length = 50 in
Question 16.
Answer:
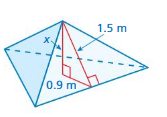
The missing length = 0.6 m
Explanation:
By using Pythagoras theorem
a² + b² = c²
0.6² + 0.9² = 1.5²
length = 0.6 m
Question 17.
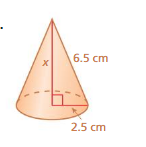
Answer:
The missing length = 6 cm
Explanation:
By using Pythagoras theorem
a² + b² = c²
4.5² + 2.5² = 6²
length = 6 cm
FINDING DISTANCES IN THE COORDINATE PLANE Find the distance between the points.
Question 18.
(0, 0), (9, 12)
Answer:
(9,12)
Explanation:
(0, 0), (9, 12)
(9-0) = 9
(12 – 0) = 12
Question 19.
(1, 2), (- 3, 5)
Answer:
5 units
Explanation:
(1, 2), (-3, 5)
(-3-1) = -4
(5- 2) = 5
Question 20.
(—18, 9), (22, 0)
Answer:
(4,9)
Explanation:
(—18, 9), (22, 0)
(22-18) = 4
(9- 0) = 9
Question 21.
(- 7, – 2), (13, – 23)
Answer:
29 units
Explanation:
(- 7, – 2), (13, – 23)
(13-7) = 6
(-23- 2) = -25
Question 22.
(15, – 17), (- 20, – 5)
Answer:
(-35, -22)
Explanation:
(15, – 17), (- 20, – 5)
(-20-15) = -35
(-5- 17) = -22
Question 23.
(- 13, – 3.5), (17, 2)
Answer:
(30, 18.5)
Explanation:
(- 13, – 3.5), (17, 2)
(17+13) = 30
(15+ 3.5) = 18.5
FINDING A MISSING LENGTH Find x.
Question 24.
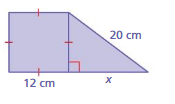
Answer:
The missing length = 8 cm
Explanation:
By using Pythagoras theorem
a² + b² = c²
8² + 12² = 20²
length = 8 cm
Question 25.
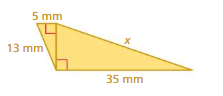
Answer:
The missing length = 37 mm
Explanation:
By using Pythagoras theorem
a² + b² = c²
13² + 22² = 37²
length = 37 mm
Question 26.
MODELING REAL LIFE
The figure shows the location of a golf ball after a tee shot. How many feet from the hole is the ball?
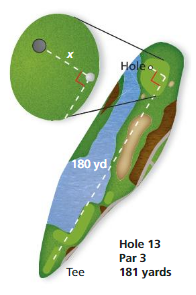
Answer:
The ball from the hole = 540 feet
Explanation:
Given that the hole and ball is
180 x 3
540 feet
1 yd = 3 ft
Question 27.
MODELING REAL LIFE
A tennis player asks the referee a question. The sound of the player’s voice travels 30 feet. Can the referee hear the question? Explain.
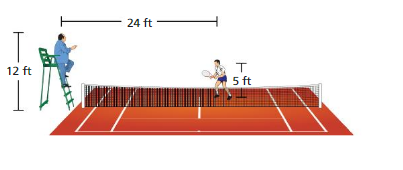
Answer:
Yes, the referee hears the voice.
Explanation:
In the question given that the sound of the player’s voice travels 30 feet.
in the figure given that 24 feet.
so the referee can hear the voice.
Question 28.
PROBLEM SOLVING
You are cutting a rectangular piece of fabric in half along a diagonal. The fabric measures 28 inches wide and 1\(\frac{1}{4}\) yards long. What is the length (in inches) of the diagonal?
Answer:
The length of the diagonal = 28.25 in
Explanation:
Given that the fabric wides = 28 inches.
(1/4) = 0.25 in
The length of the diagonal = 28 x 0.25
28.25 in
Question 29.
PROJECT
Measure the length, width, and height of a rectangular room. Use the Pythagorean Theorem to find the distance from B to C and the distance from A to B.
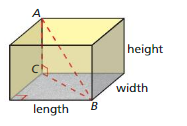
Answer:
a² + b² = c²
Explanation:
By using Pythagoras theorem
a² + b² = c²
length + width = height
Question 30.
STRUCTURE
The legs of a right triangle have lengths of 28 meters and 21 meters. The hypotenuse has a length of 5x meters. What is the value of x?
Answer:
The value of x = 9.8 meters.
Explanation:
Given that the right triangle has length = 28 meters and 21 meters.
the hypotenuse = 5x
28 + 21 = 5x
49 = 5x
x = (49/5)
x = 9.8 meters.
Question 31.
PRECISION
You and a friend stand back-to-back. You run 20 feet forward, then 15 feet to your right. At the same time, your friend runs 16 feet forward, then 12 feet to her right. She stops and hits you with a snowball.
a. Draw the situation in a coordinate plane.
b. How far does your friend throw the snowball?
Answer:
Question 32.
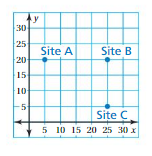
MODELING REAL LIFE
The coordinate plane shows dig sites for archaeological research. Each unit on the grid represents 1 square foot. What is the distance from Site A to Site C?
Answer:
7 square feet.
Explanation:
Given that each grid represents 1 sq feet.
in the below figure shows that the distance.
distance from site A to site C is 7 sq ft.
the boxes 7 are touching the edges of the site A to B
Question 33.
PRECISION
A box has a length of 30 inches, a width of 40 inches, and a height of 120 inches. Can a cylindrical rod with a length of 342.9 centimeters fit in the box? Explain your reasoning.
Answer:
No, the cylindrical rod with a length of 135 cm will fit in the box.
Explanation:
Given that the box has a length = 30 in
width = 40 in
height = 120 in
area = l x w x h
area = 30 x 40 x 120
area = 1,44,000 cm
Question 34.
MODELING REAL LIFE
A green roof is like a traditional roof but covered with plants. Plants used for a green roof cost $0.75 per square foot. The roof at the right is 40 feet long. How much does it cost to cover both sides of the roof? Justify your answer.
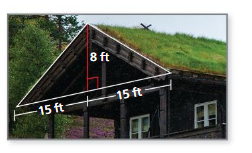
Answer:
The cost to cover both sides of the roof = 60 sq ft
Explanation:
Given that the plants used for a green roof cost = $0.75 sq ft.
the roof at the right = 40 ft long
the roof at both sides = 40 + 40 =80
1 sq feet = 0.75 $
80 x $0.75 = 60 sq ft
Question 35.
CRITICAL THINKING
A triangle has coordinates A(2, 1), B(2, 4), and C(5, 1). Write an expression for the length of \(\overline{B C}\). Use a calculator to find the length of \(\overline{B C}\) to the nearest hundredth.
Answer:
4.24 units
Question 36.
DIG DEEPER!
Write an equation for the distance d between the points (x1, y1) and (x2, y2). Explain how you found the equation.
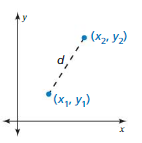
Answer:
x1 + y1 = x2 + y2
Explanation:
Given that the points (x1, y1) and (x2 , y2)
the equation is
x1 + y1 = x2 + y2
Lesson 9.3 Finding Cube Roots
EXPLORATION 1
Finding Edge Lengths
Work with a partner. Find the edge length of each cube. Explain your method.
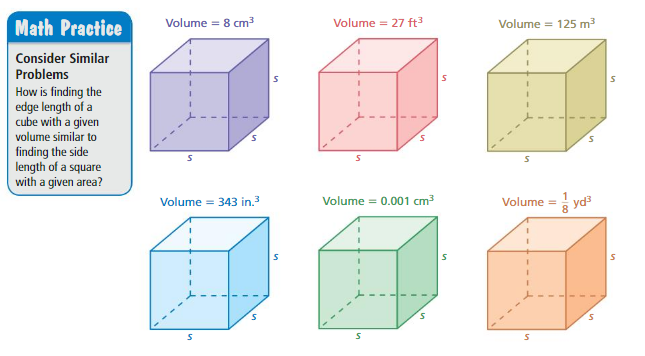
Answer:
a. 2 cm
b. 3 ft
c. 5m
d. 7 in
e. 0.1 cm
f. 0.5 yd
Explanation:
a. volume = 8 = 2 x 2 x 2
b. 27 = 3 x 3 x 3
c. 125 = 5 x 5 x 5
d. 343 = 7 x 7 x 7
e. 0.001 = 0.1 x 0.1 x 0.1
f. (1/8) = 0.5 x 0.5 x 0.5
EXPLORATION 2
Finding Solutions of Equations
Work with a partner. Use mental math to solve each equation. How many solutions are there for each equation? Explain your reasoning.
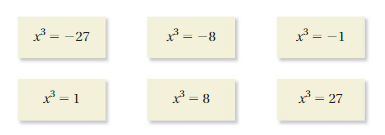
Answer:
x = -3
x = -2
x = -1
x = 1
x = 2
x = 3
Explanation:
x³ = -27
x³ = -3³
when powers are equal exponents must be equal.
x = -3
x³ = -8
x³ = -2³
when powers are equal exponents must be equal.
x = -2
x³ = -1
x³ = -1³
when powers are equal exponents must be equal.
x = -1
x³ = 27
x³ = 3³
when powers are equal exponents must be equal.
x = 3
x³ = 8
x³ = 2³
when powers are equal exponents must be equal
x = 2
x³ = 1
x³ =1³
when powers are equal exponents must be equal
x = 1

Try It
Find the cube root.
Question 1.
\(\sqrt [ 3 ]{ 1 } \)
Answer:
1
Explanation:
cube root of 1 is 1
3√1 = 1
Question 2.
\(\sqrt [ 3 ]{ -343 } \)
Answer:
-7
Explanation:
cube root of -343 is -7
3√ -343= 7 x 7 x 7
(-343)³ = 7³
when powers are equal exponents must be equal.
-343 = 7
Question 3.
\(\sqrt[3]{-\frac{27}{1000}}\)
Answer:
(-3/10)
Explanation:
cube root of -27 is -3
3√ -27= 3 x 3 x 3
(-27)³ = 3³
when powers are equal exponents must be equal.
-27 = 3
cube root of -1000 is -10
3√ -1000= 10 x 10 x 10
(-1000)³ = 10³
when powers are equal exponents must be equal.
-1000= 10
Evaluate the expression.
Question 4.
18 – 4 \(\sqrt [ 3 ]{ 8 } \)
Answer:
10
Explanation:
cube root of 8 is 2
3√ 8 = 2 x 2 x 2
(8)³ = 2³
when powers are equal exponents must be equal.
8= 2
18 – 4 (2)
18 – 8
10
Question 5.
(\(\sqrt[3]{-64})^{3}\)) + 43
Answer:
44.333
Explanation:
cube root of -64 is -4
3√ -64 = 4 x 4 x 4
(-64)³ = 4³
when powers are equal exponents must be equal.
-64= 4
1.333 + 43
44.333
Question 6.
5\(\sqrt [ 3 ]{ 512 } \) – 19
Answer:
21
Explanation:
cube root of 512 is 8
3√512 = 8 x 8 x 8
(512)³ = 8³
when powers are equal exponents must be equal.
512= 8
5 x 8 -19
40 – 19
21
Solve the equation.
Question 7.
z3 = – 1000
Answer:
z = -10
Explanation:
cube root of -1000 is -10
3√-1000 = 10 x 10 x 10
z3 = 10³
when powers are equal exponents must be equal.
z= -10
Question 8.
3b3 = 1029
Answer:
b = 7
Explanation:
3b3 = 1029
b³ = (1029/3)
b³ = 343
cube root of 343 is 7
3√343 = 7 x 7 x 7
b³ = 7³
when powers are equal exponents must be equal.
b = 7
Question 9.
33 = – \(\frac{1}{5}\) m3 + 8
Answer:
m³ = 25.8
Explanation:
33 = – 0.2 m³ + 8
m³ = 33+0.2 -8
m³ = 25.8
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING CUBE ROOTS Find the cube root.
Question 10.
\(\sqrt [ 3 ]{ 64 } \)
Answer:
4
Explanation:
cube root of 64 is 4
3√64 = 4 x 4 x 4
64³ = 4³
when powers are equal exponents must be equal.
64 = 4
Question 11.
\(\sqrt [ 3 ]{ -216 } \)
Answer:
-6
Explanation:
cube root of -216 is -6
3√-216 = 6 x 6 x 6
216³ = 6³
when powers are equal exponents must be equal.
216 = 6
Question 12.
\(\sqrt[3]{-\frac{343}{100}}\)
Answer:
– 7
Explanation:
cube root of -343 is -7
3√-343 = 7 x 7 x 7
-343³ = 7³
when powers are equal exponents must be equal.
-343 = 7
EVALUATING EXPRESSIONS Evaluate the expression.
Question 13.
\((\sqrt[3]{-27})^{3}\) + 61
Answer:
52
Explanation:
cube root of -27 is -3
3√-27 = 3 x 3 x 3
-27³ = 3³
when powers are equal exponents must be equal.
-27 = -3
-3 x 3 + 61
-9 + 61
52
Question 14.
15 + 3\(\sqrt[3]{125}\)
Answer:
30
Explanation:
cube root of 125 is 5
3√125 = 5 x 5 x 5
125³ = 5³
when powers are equal exponents must be equal.
125 = 5
15 + 3 (5)
15 + 15
30
Question 15.
z\(\sqrt[3]{-729}\) – 5
Answer:
-14
Explanation:
cube root of -729 is -9
3√-729 = 9 x 9 x 9
729³ = 9³
when powers are equal exponents must be equal.
729 = 9
-9 -5 = -14
SOLVING EQUATIONS Solve the equation.
Question 16.
d3 = 512
Answer:
d = 8
Explanation:
cube root of 512 is 8
3√512 = 8 x 8 x 8
512³ = 8³
when powers are equal exponents must be equal.
d³ = 8³
d = 8
Question 17.
w3 – 12 = – 76
Answer:
w = -4
Explanation:
w3 – 12 = – 76
w³ = -76 + 12
w³ = -64
cube root of -64 is -4
3√-64 = 4 x 4 x 4
w³ = 4³
when powers are equal exponents must be equal.
w = 4
Question 18.
– \(\frac{1}{3}\)m3 + 13 = 4
Answer:
-8.67
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 19.
You have 275 square inches of wrapping paper. Do you have enough wrapping paper to wrap the gift box shown? Explain.
Answer:
Yes i have enough wrapping paper to wrap the gift box.
Explanation:
Given that 275 sq in of wrapping paper.
6.5 x 6.5 x 6.5 = 274.6
275 sq in
Question 20.
A cube-shaped end table has a volume of 16,000 cubic centimeters. Does the end table fit in the corner shown? Justify your answer.
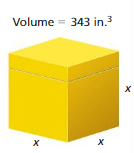
Answer:
No the end table does not fit in the corner.
Explanation:
volume = 343
343³ = 7³
when powers are equal exponents must be equal.
343 = 7
Question 21.
DIG DEEPER!
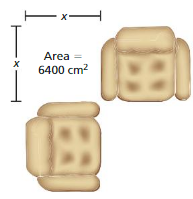
The relationship between the volumes and the lengths of two cereal boxes is represented by
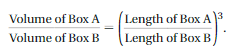
Box A has a volume of 192 cubic inches and a length of 8 inches. Box B has a volume of 375 cubic inches. What is the length of Box B? Justify your answer.
Answer:
The length of the box B = 1.6 inches.
Explanation:
(v of A/ v of B ) = ( l of A / l of B) ³
B³ = (192/375) x 8
b³ = 0.512 x 8
b³ = 4.096
b ³ = 1.6³
when powers are equal exponents must be equal.
b = 1.6
Finding Cube Roots Homework & Practice 9.3
Review & Refresh
Find the missing length of the triangle.
Question 1
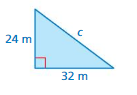
Answer:
The missing length = 40 m
Explanation:
By using Pythagoras theorem
a² + b² = c²
24² + 32² = 40²
576 + 1024 = 1600
1600 = 1600
length = 56m
Question 2.
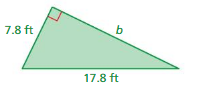
Answer:
The missing length = 10 ft
Explanation:
By using Pythagoras theorem
a² + b² = c²
7.8² + 10² = 17.8²
length = 10 ft
Question 3.
Which linear function is shown by the table?
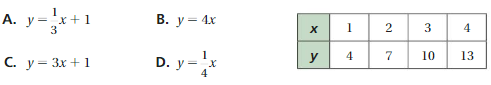
Answer:
option C is correct.
Explanation:
y = 3x + 1
x = 1, y = 4
4 = 3(1) + 1
y= 4
Concepts, Skills, &Problem Solving
FINDING EDGE LENGTHS Find the edge length s of the cube. (See Exploration 1, p. 389.)
Question 4.
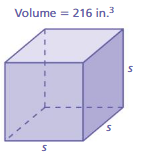
Answer:
The edge length of the cube = 6
Explanation:
cube root of 216 is 6
3√216 = 6 x 6 x 6
216³ = 6³
when powers are equal exponents must be equal.
s³ = 6³
s = 6
Question 5.
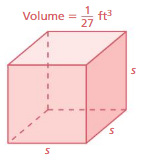
Answer:
The edge length of the cube = (1/3) ft
Explanation:
cube root of (1/27) is (1/3)
3√(1/27) = (1/3)x (1/3) x (1/3)
(1/27)³ = (1/3)³
when powers are equal exponents must be equal.
s³ = (1/3)³
s = (1/3)
Question 6.
Answer:
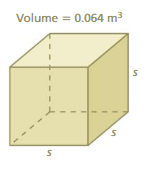
The edge length of the cube = 0.4
Explanation:
cube root of 0.064 is 0.4
3√0.064 = 0.4 x 0.4 x 0.4
0.064³ = 0.4³
when powers are equal exponents must be equal.
s³ = 0.4³
s = 0.4
FINDING CUBE ROOTS Find the cube root.
Question 7.
\(\sqrt [ 3 ]{ 729 } \)
Answer:
9
Explanation:
cube root of 729 is 9
3√729 = 9 x 9 x 9
729³ = 9³
when powers are equal exponents must be equal.
729 = 9
Question 8.
\(\sqrt [ 3 ]{ -125 } \)
Answer:
-5
Explanation:
cube root of -125 is -5
3√-125 = 5 x 5 x 5
-125³ = -5³
when powers are equal exponents must be equal.
125 = -5
Question 9.
\(\sqrt [ 3 ]{ -1000} \)
Answer:
-10
Explanation:
cube root of -1000 is -10
3√-1000 = 10 x 10 x 10
-1000³ = -10³
when powers are equal exponents must be equal.
-1000 = -10
Question 10.
\(\sqrt [ 3 ]{ 1728 } \)
Answer:
12
Explanation:
cube root of 1728 is 12
3√1728 = 12 x 12 x 12
1728³ = 12³
when powers are equal exponents must be equal.
1728 = 12
Question 11.
\(\sqrt[3]{-\frac{1}{512}}\)
Answer:
(-1/6)
Explanation:
cube root of – 512 is -(1/6)
3√-512 = (1/6) x (1/6) x (1/6)
-512³ = -(1/6)³
when powers are equal exponents must be equal.
-512 = (-1/6)
Question 12.
\(\sqrt[3]{\frac{343}{64}}\)
Answer:
(7/4)
Explanation:
cube root of (343/64) is (7/4)
3√343 = (7/4) x (7/4) x (7/4)
343³ = (7/4)³
when powers are equal exponents must be equal.
343 = (7/4)
EVALUATING EXPRESSIONS Evaluate the expression.
Question 13.
18 – (\(\sqrt [ 3 ]{ 27 }\))3
Answer:
-9
Explanation:
3√27³ = 27
where cube and cube root get cancelled.
18 – 27
-9
Question 14.
\(\left(\sqrt[3]{-\frac{1}{8}}\right)^{3}\) + 3\(\frac{3}{4}\)
Answer:
1.75
Explanation:
cube root of (1/18) is -(1/2)
3√(1/18) = (1/2) x (1/2) x (1/2)
(1/18)³ = (1/2)³
when powers are equal exponents must be equal.
(1/18) =- (1/2)
-(1/2) + 3(3/4)
– 0.5 + 3 (0.75)
-0.5 + 2.25
1.75
Question 15.
5\(\sqrt[3]{729}\) – 24
Answer:
21
Explanation:
cube root of (729) is (9)
3√729 = (9) x (9) x (9)
729³ = (9)³
when powers are equal exponents must be equal.
729 = 9
5 x 9 -24
45 – 24
21
Question 16.
\(\frac{1}{4}-2 \sqrt[3]{\frac{1}{216}}\)
Answer:
-11.75
Explanation:
cube root of (216) is (6)
3√216 = (6) x (6) x (6)
216³ = (6)³
when powers are equal exponents must be equal.
216 = 6
(1/4) -2 (6)
(1/4) – 12
0.25 – 12
-11.75
Question 17.
54 + \(\sqrt[3]{-4096}\)
Answer:
38
Explanation:
cube root of (-4096) is (-16)
3√-4096 = (-16) x (-16) x (-16)
-4096³ = (-16)³
when powers are equal exponents must be equal.
4096 = -16
54 +(-16)
54 – 16
38
Question 18.
4\(\sqrt[3]{8000}\) – 6
Answer:
166
Explanation:
cube root of (8000) is (43)
3√8000 = (43) x (43) x (43)
8000³ = (43)³
when powers are equal exponents must be equal.
8000 = 43
4 x 43 -6
172 – 6
166
EVALUATING EXPRESSIONS Evaluate the expression for the given value of the variable.
Question 19.
\(\sqrt[3]{\frac{n}{4}}+\frac{n}{10}\), n = 500
Answer:
55
Explanation:
(500/4) = 125
(500/10) = 50
cube root of (125) is (5)
3√125 = (5) x (5) x (5)
125³ = (5)³
when powers are equal exponents must be equal.
125 = 5
5 + 50
55
Question 20.
\(\sqrt[3]{6 w}\) – w, w = 288
Answer:
276
Explanation:
w = 288 given
6 x 288 = 1728
Question 21.
2d + \(\sqrt[3]{-45 d}\), d = 75
Answer:
165
Explanation:
d = 75 given
-45 x 75 = -3375
cube root of (-3375) is (-15)
3√-3375 = (-15) x (15) x (15)
(-3375)³ = (-15)³
when powers are equal exponents must be equal.
3375 = 15
2x 75 + 15
150 +15
165
SOLVING EQUATIONS Solve the equation.
Question 22.
x3 = 8
Answer:
x = 2
Explanation:
x³= 8
x³ = 2³
when powers are equal exponents must be equal.
x = 2
Question 23.
t3 = – 343
Answer:
t = – 7
Explanation:
t³ = -343
t³ = -7³
when powers are equal exponents must be equal.
t = -7
Question 24.
– 75 = y3 + 50
Answer:
y = -5
Explanation:
– 75 = y3 + 50
y³ = -75 – 50
y³ = -125
y³ = -5³
when powers are equal exponents must be equal.
y = -5
Question 25.
– \(\frac{1}{2}\)z3 = – 108
Answer:
z = 6
Explanation:
-(1/2)z³ = -108
(1/2) = 0.5
-0.5z³ = -108
z³ = (-108 /-0.5)
z³ = 216
z³ = 6³
when powers are equal exponents must be equal.
z = 6
Question 26.
2h3 – 11 = 43
Answer:
h = 17
Explanation:
2h3 – 11 = 43
2h³ = 43 + 11
2h³ = 54
h³ = (54/2)
h³ = 17
h = 17
Question 27.
– 600 = \(\frac{2}{5}\)k3 + 750
Answer:
k = -15
Explanation:
(2/5) = 0.4
-600 = 0.4 k³ + 750
0.4 k³ = -600 -750
0.4k³ = -1350
k³ = -(1350/0.4)
k³ = -3375
k³ = -15³
when powers are equal exponents must be equal.
k = -15
Question 28.
MODELING REAL LIFE
The volume of a cube-shaped compost bin is 27 cubic feet. What is the edge length of the compost bin?
Answer:
The edge length of the compost bin = 3 feet.
Explanation:
Given that the volume of a cube-shaped compost bin = 27 cubic ft.
volume of cube = s x sx s
volume = 3 x 3 x3
volume = 27
Question 29.
MODELING REAL LIFE
The volume of a cube of ice for an ice sculpture is 64,000 cubic inches.

a. What is the edge length of the cube of ice?
b. What is the surface area of the cube of ice?
Answer:
a. The edge length of the cube of ice = 40 inches.
b. The surface area of the cube of ice = 9600 sq in
Explanation:
a. The edge length of the cube of ice = 40 in
volume = s x s x s
v = 40 x 40 x 40
v = 40 in
b. The surface area of cube = 6a²
area = 6 x 40 x 40
where a = edge
area = 6 x 1600
area = 9600 sq in
Question 30.
NUMBER SENSE
There are three numbers that are their own cube roots. What are the numbers?
Answer:
-1, 1 , 0
Explanation:
cube root of -1 = -1
cube root of 1 = 1
cube root of 0 = 0
The 3 numbers have their own cube roots.
REASONING Copy and complete the statement with <, >, or =.
Question 31.
![]()
Answer:
-(1/4) < 3√(-8/125)
Explanation:
(1/4) = -0.25
(8/125) = (-2/5)
(-2/5) = 0.4
Question 32.
![]()
Answer:
3√ 0.001 > 0.01
Explanation:
3√ 0.001 = 0.1
0.1 > 0.01
Question 33.

Answer:
3√64 < √64
Explanation:
3√64 = 4 x 4 x4
3√64 = 4
√64 = 8 x 8
√64 = 8
4 < 8
Question 34.
DIG DEEPER!
You bake a dessert in the baking pan shown. You cut the dessert into cube-shaped pieces of equal size. Each piece has a volume of 8 cubic inches. How many pieces do you get from one pan? Justify your answer.

Answer:
24 pieces.
Explanation:
Given that volume = 8 cubic inches
s = 2 in
Area = 64 sq in given
area = 6 x a²
area = 6 x 2 x2
area = 6 x 4
area = 24 sq in
Question 35.
LOGIC
Determine whether each statement is true for square roots. Then determine whether each statement is true for cube roots. Explain your reasoning.
a. You cannot find the square root of a negative number.
b. Every positive number has a positive square root and a negative square root.
Answer:
a.Yes
b. yes
Explanation:
a. we can find the square root of a negative number.
for example -2
the square root of -2 = -4
b. yes, every positive number has a positive square root and a negative square root.
for example = 4
-2 and 2 are the square roots of 4
Question 36.
GEOMETRY
The pyramid has a volume of 972 cubic inches. What are the dimensions of the pyramid?
Answer:
The dimensions of the pyramid = 14 in
Explanation:
Given that volume of pyramid = 972 cubic in
volume = ( l w h/3)
volume = (14 x 14 x 14/3)
v = 972 cubic in
Question 37.
REASONING
The ratio 125 : x is equivalent to the ratio x2 :125. What is the value of x?
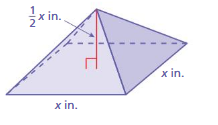
Answer:
The value of x = 25
Explanation:
Given that the ratio = 125 : x
x ² : 125 = x = 25
when powers are equal exponents must be equal.
x = 25
CRITICAL THINKING Solve the equation.
Question 38.
(3x + 4)3 = 2197
Answer:
x = 6
Explanation:
(3x + 4)3 = 2197
9x³+ 64 = 2197
9x³ = 2197 – 64
9 x³ = 2133
x³ = (2133/9)
x³ = 237
x = 6
Question 39.
(8x3 – 9)3 = 5832
Answer:
x³ = 11.86
x = 3/2
Explanation:
512 x³ – 243 = 5832
512 x³ = 5832 + 243
512 x³ = 6075
x³ = 6075/512
x³ = 11.86
Question 40.
((5x – 16)3 – 4)3 = 216,000
Answer:
x = 56
Explanation:
125 x³ – 4096 – 64 = 216000
125 x³ – 4096 = 216000 + 64
125 x³ = 216064 + 4096
125 x³ = 220160
x³ = 1761.28
x = 56
Lesson 9.4 Rational Numbers
EXPLORATION 1
Work with a partner.
a. Complete the table.

b. For each row of the table, use the two equations and what you know about solving systems of equations to write a third equation that does not involve a repeating decimal. Then solve the equation. What does your solution represent?
c. Write each repeating decimal below as a fraction. How is your procedure similar to parts (a) and (b)? How is it different?
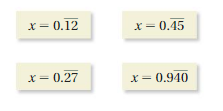
d. Explain how to write a repeating decimal with n repeating digits as a fraction.
Answer:
a. x = 0.666 , 10 x = 10 x 0.666 = 6.666
x = 0.111, 10 x = 10 x0.111 = 1.111
x = 0.2444, 10 x = 10 x 0.24444 = 2.4444
c. x = (12/100)
x = (0.45/100)
x = (0.27/100)
x = (0.940/1000)
Explanation:
Given that x = 0.333
10 x = 10 x 0.333 = 3.3333
x = 0.666
10 x = 10 x 0.666 = 6.6666
x = 0.111
10 x = 10 x 0.111 = 1.111
x = 0.244
10 x = 10 x 0.244 = 2.444
Try It
Write the fraction or mixed number as a decimal.
Question 1.
\(\frac{3}{15}\)
Answer:
0.2
Explanation:
(3/15) = 0.2
Question 2.
–\(\frac{2}{9}\)
Answer:
-0.222
Explanation:
(-2/9) = -0.222
Question 3.
4\(\frac{3}{8}\)
Answer:
1.5
Explanation:
(3/8) = 0.375
4 x 0.375 = 1.5
Question 4.
2\(\frac{6}{11}\)
Answer:
1.09
Explanation:
(6/11) = 0.5454
2 x 0.5454 = 1.0909
Write the decimal as a fraction or a mixed number.
Question 5.
0.888 …..
Answer:
(111/125)
Explanation:
0.888
(888/1000)
(444/500)
(222/250)
(111/125)
Question 6.
\(2.0 \overline{6}\)
Answer:
(33/100)
Explanation:
(2.0 /6)
0.333
(33/100)
Question 7.
\(0 . \overline{64}\)
Answer:
0
Explanation:
(0/64)
64
Question 8.
\(-4 . \overline{50}\)
Answer:
-(8/100)
Explanation:
-4 /50
– 0.08
-8/100
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
VOCABULARY
How can you identify a rational number?
Answer:
A rational number is a number that can be written as a ratio, which means it can be written as a fraction, in which both the numerator and denominator are whole numbers.
Explanation:
8
(8/1)
the number 8 is a rational number because the number written as a fraction.
WRITING FRACTIONS OR MIXED NUMBERS AS DECIMALS Write the fraction or mixed number as a decimal.
Question 10.
\(\frac{9}{50}\)
Answer:
0.18
Explanation:
(9/50)
(9/50) = 0.18
Question 11.
– \(\frac{7}{18}\)
Answer:
-0.388
Explanation:
-(7/18)
-(7/18) = -0.388
Question 12.
3\(\frac{4}{9}\)
Answer:
1.333
Explanation:
(4/9)
4/9 = 0.444
3 x 0.444
1.333
Question 13.
– 12 \(\frac{1}{6}\)
Answer:
– 1.9992
Explanation:
(1/6)
(1/6) = 0.1666
0.1666 x -12
-1.9992
WRITING A REPEATING DECIMAL AS A FRACTION Write the repeating decimal as a fraction or a mixed number.
Question 14.
\(-1 . \overline{7}\)
Answer:
(-1/7)
Explanation:
-1: 7
-(1/7)
Question 15.
\(0 . \overline{2}\)
Answer:
(0/2)
Explanation:
0 : 2
(0/2)
Question 16.
\(8 . \overline{93}\)
Answer:
(8 /93)
Explanation:
8 : 93
(8/93)
Question 17.
\(-6 . \overline{235}\)
Answer:
-(6/235)
Explanation:
-6 : 235
-(6 /235)
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
A fun house mirror distorts the image it reflects. Objects reflected in the mirror appear \(1 . \overline{3}\) times taller. When a five-foot-tall person looks in the mirror, how tall does he appear?

Answer:
He appears in the mirror = 5 feet.
Explanation:
1 x 3 = 3 given that
1 x 5 = 5
Question 19.
An exchange rate represents the value of one currency relative to another. Your friend visits a country that uses a local currency with an exchange rate of \(1 . \overline{265}\) units of the local currency to $1. If a bank charges $2 to change currency, how many units of the local currency does your friend receive when she gives the bank $200?
Answer:
Friend receive local currency = 1,06,000 units.
Explanation:
Given that local currency of $1 = 265 units.
if a bank charges to $ 2
265 + 265 = 530
the local currency of the friend receive when she gives the bank $ 200
200 x 530
1,06,000 units.
Question 20.
DIG DEEPER!
A low fuel warning appears when a particular car has \(0.014 \overline{6}\) 6 of a tank of gas remaining. The car holds 18.5 gallons of gas and can travel 36 miles for each gallon used. How many miles can the car travel after the low fuel warning appears?
Answer:
9.324 gallons.
Explanation:
(0.014/6) = 0.0023
0.0023 x 6
0.014
Given that car holds 18.5 gallons of gas can travel 36 miles for each gallon.
36 x 0.014
0.504
0.504 x 18.5 gallons
9.324 gallons.
Rational Numbers Homework & Practice 9.4
Review & Refresh
Evaluate the expression.
Question 1.
2 + \(\sqrt [ 3 ]{ 27 } \)
Answer:
5
Explanation:
cube root of (27) is (3)
3√27 = (3) x (3) x (3)
27³ = (3)³
when powers are equal exponents must be equal.
27 = 3
2 + 3
5
Question 2.
1 – \(\sqrt [ 3 ]{ 8 } \)
Answer:
-1
Explanation:
cube root of (8) is (2)
3√8 = (2) x (2) x (2)
8³ = (2)³
when powers are equal exponents must be equal.
8 = 2
1- 2
-1
Question 3.
7\(\sqrt [ 3 ]{ 125 } \) – 12
Answer:
23
Explanation:
cube root of (125) is (5)
3√125 = (5) x (5) x (5)
125³ = (5)³
when powers are equal exponents must be equal.
125 = 5
7 x 5 -12
35 -12
23
Find the measures of the interior angles of the triangle.
Question 4.

Answer:
x = 75⁰
Explanation:
Right angle triangle = 90⁰
x = 90⁰ – 15⁰
given that 75⁰
x = 75⁰
Question 5.
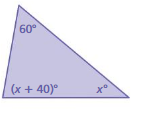
Answer:
x = 80⁰
Explanation:
x + 40⁰ = 60⁰
x = 60⁰ +40⁰ +80
x = 80⁰
Question 6.
Answer:
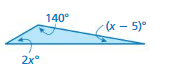
Explanation:
given that (x – 5)⁰ = 140⁰
x – 5⁰ = 140⁰
x = 140⁰ + 5⁰
x = 145⁰
2x = 145⁰ x 2
2x = 290⁰
x = 290⁰/2
x = 145⁰
Concepts, Skills, &Problem Solving
WRITING REPEATING DECIMALS AS FRACTIONS Write the repeating decimal as a fraction. (See Exploration 1, p. 395.)
Question 7.
0.777 . . .
Answer:
(7/9)
Explanation:
0.7777. . .
(7/9)
Question 8.
0.858585 . . .
Answer:
(85/99)
Explanation:
0.858585 . . .
(85/99)
Question 9.
0.232323 . . .
Answer:
(23/99)
Explanation:
0.232323 . . .
(23/99)
it is a repeating decimal
WRITING FRACTIONS OR MIXED NUMBERS AS DECIMALS Write the fraction or mixed number as a decimal.
Question 10.
–\(\frac{3}{20}\)
Answer:
-0.15
Explanation:
(3/20) = 0.15
Question 11.
9\(\frac{1}{12}\)
Answer:
9.083
Explanation:
(1/12) = 0.833
0.833 x 9 = 9.083
Question 12.
\(\frac{5}{36}\)
Answer:
0.1388
Explanation:
(5/36) = 0.1388
Question 13.
6\(\frac{1}{40}\)
Answer:
6.025
Explanation:
(1/40) = 0.025
6 x 0.025
6.025
Question 14.
\(\frac{11}{75}\)
Answer:
0.1466
Explanation:
(11/75)
0.1466
Question 15.
– 2\(\frac{7}{18}\)
Answer:
-2.38
Explanation:
(17/18)
0.3888
-2 x 0.3888
-2.38
Question 16.
PRECISION
Your hair is \(\frac{5}{16}\) inch long. Write this length as a decimal.
Answer:
0.3125 in
Explanation:
(5/16)
0.3125
WRITING A REPEATING DECIMAL AS A FRACTION Write the repeating decimal as a fraction or a mixed number.
Question 17.
\(-0 . \overline{5}\)
Answer:
-5/9
Explanation:
-5/9
Question 18.
\(4 . \overline{1}\)
Answer:
4
Explanation:
4 x 1
4
Question 19.
\(-0.3 \overline{56}\)
Answer:
-353/990
Explanation:
-0.3 x 56
-26.7
-(353/990)
Question 20.
\(6.0 \overline{89}\)
Answer:
(674/1000)
Explanation:
(6/89)
0.0674
(674/1000)
Question 21.
\(0.18 \overline{72}\)
Answer:
103/550
Explanation:
(0.18/72)
103/550
Question 22.
\(11 . \overline{510}\)
Answer:
(2156/10000)
Explanation:
(11/510)
0.02156
(2156/10000)
Question 23.
STRUCTURE
A forecast cone defines the probable path of a tropical cyclone. The probability that the center of a particular tropical cyclone remains within the forecast cone is \(0 . \overline{8}\). Write this probability as a fraction.
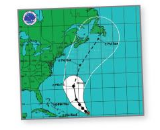
Answer:
8 : 9
Explanation:
Given that cone is 8 x 9
they said to write it in the fraction.
Question 24.
STRUCTURE
Describe how to write a decimal with 12 repeating digitsas a fraction.
Answer:
12: 0
Explanation:
given that 12 is a decimal
and they said to write in decimal.
12 : 0
Question 25.
STRUCTURE
An approximation for the value of π is \(\frac{22}{7}\). Write this number as a repeating decimal.
Answer:
3.14 2857
Explanation:
π = (22/7)
(22/7) = 3.14
3.142857
Question 26.
MODELING REAL LIFE
The density of iodine is about \(6.28 \overline{1}\) times the density of acetone. The density of acetone is about 785 kilograms per cubic meter. What is the density of iodine? Write your answer as a repeating decimal.
Answer:
4929.8. . .
Explanation:
The density of iodine = 6.28 given
the density of acetone is 785 kg for cubic meter.
6.28 x 785
4,929.8
Question 27.
MODELING REAL LIFE
A disinfectant manufacturer suggests that its product kills \(99.9 \overline{8}\) % of germs. Write this percent as a repeating decimal and then as a fraction. How many germs would survive when the disinfectant is applied to an object with 18,000 germs?

Answer:
Fraction = (8999/9000)
2 germs
Explanation:
Given that the product kills (99.9/8)%
8999/9000
2 germs
Question 28.
MODELING REAL LIFE
You and your friend are making pear tarts for a bake sale. Your recipe uses \(\frac{7}{6}\) times the weight of the diced pears used in your friend’s recipe. Your friend’s recipe calls for 0.3 pound of diced pears. How many pounds of pears should you buy to have enough for both recipes?

Answer:
0.35 pounds of pears should buy to have enough for both recipes.
Explanation:
Given that my recipe uses (7/6) times the weight of the diced pears used in friends recipe.
my friends recipie calls for 0.3 pounds of diced pears.
(7/6) x 0.3
1.16666 x 0.3
0.35 pounds
Question 29.
PROBLEM SOLVING
The table shows the principal and interest earned per year for each of three savings accounts with simple annual interest. Which account has the greatest interest rate? Justify your answer.

Answer:
Account c has the greatest interest rate.
Explanation:
Simple interest = (px r x t /100)
where p = principal amount, rate of interest, and time = t
Account A = $ 4/$90 =0.04 = 4.4 %
Account B = $5.50/$120.00 = 0.04583 = 4.583%
Account C = $4.80/$100.00 = 0.048 = 4.8%
Question 30.
DIG DEEPER!
The probability that an athlete makes a half-court basketball shot is 22 times the probability that the athlete makes a three-quarter-court shot. The probability that the athlete makes three-quarter-court shot is \(0.00 \overline{9}\). What is the probability that the athlete makes a half-court shot? Write your answer as a percent.

Answer:
1.98 %
Explanation:
Given that the athlete makes three-quarter-court shot is 0.00 x 9
basketball shot is 22 times the probability that the athlete makes 3 -quarter-court shot.
0.00 x 9
0
22 x 9
198 writing it as decimal
1.98%
NUMBER SENSE Determine whether the numbers are equal. Justify your answer.
Question 31.
\(\frac{9}{22}\) and \(0.4 \overline{09}\)
Answer:
The numbers are not equal.
Explanation:
(9/22) = 0.4090
(0.4/9) = 0.0444
Question 32.
\(\frac{1}{999}\) and 0
Answer:
The numbers are not equal.
Explanation:
(1/999) = 0.001
0 = 0.001
Question 33.
\(\frac{135}{90}\) and 1.5
Answer:
The numbers are not equal.
Explanation:
(35/90) = 1.5
1.5 = 1.5
ADDING AND SUBTRACTING RATIONAL NUMBERS Add or subtract.
Question 34.
\(0.4 \overline{09}+0.6 \overline{81}\)
Answer:
0.45180
Explanation:
(0.4/9) = .04444
(0.6/81) = 0.0074
0.0074 +0.444
Question 35.
\(-0 . \overline{63}+\frac{5}{99}\)
Answer:
-58/99
Explanation:
(5/99) = 0.0505
63 + 0.0505
Question 36.
\(\frac{11}{6}-0 . \overline{27}\)
Answer:
-25.1666
Explanation:
(11/6) = 1.833333
27
1.83333 – 27
-25.1666
Question 37.
\(0 . \overline{03}-0 . \overline{04}\)
Answer:
-1/99
Question 38.
STRUCTURE
Write a repeating decimal that is between \(\frac{9}{7}\) and \(\frac{10}{7}\). Justify your answer.
Answer:
1.3546
Explanation:
(9/7)
1.2857
(10/7)
1.4285
The number between 1.2857 and 1.4285 is 1.3546
Lesson 9.5 Irrational Numbers
EXPLORATION 1
Approximating Square Roots
Work with a partner. Use the square shown.

a. Find the exact length x of the diagonal. Is this number a number a rational number or an irrational number? Explain.
b. The value of x is between which two whole numbers? Explain your reasoning.
c. Use the diagram below to approximate the length of the diagonal to the nearest tenth.Explain your method.
d. Which of the following is the closest approximation of the length of the diagonal? Justify your answer using inverse operations.

Answer:
a. The length of x = √2
a number is an irrational number.
d. 1.412 is the closest approximation of the length of the diagonal.
Try It
Classify the real number.
Question 1.
0.121221222 ……
Answer:
Irrational number.
Explanation:
Irrational number : the decimal form neither terminates nor repeats.
so the given number is a irrational number.
Question 2.
– √196
Answer:
The number is real number
Explanation:
the real number are the numbers which includes both rational and irrational numbers.
Question 3.
\(\sqrt [ 3 ]{ 2 } \)
Answer:
The number is real number
Explanation:
cube root of 3 is 2
where cube and cube root get cancelled.
Approximate the number to the nearest (a) integer and (b) tenth.
Question 4.
√8
Answer:
Integer = 3
tenth = 3 .0
Explanation:
square root of 8 = 2 x 2 x2
2 x2 = 4
3 is nearest integer to the 2
Question 5.
– √13
Answer:
-14
Question 6.
– √24
Answer:
13
Question 7.
√20
Answer:
11
Which number is greater? Explain.
Question 8.
√8, π
Answer:
√8 is greater.
Explanation:
√8 = 8
π = 3.14
so 8 is greater.
Question 9.
\(\sqrt [ 3 ]{ 65 }\), √26
Answer:
√26 is greater.
Explanation:
cube root of 65 = 4 x 4 x4
square root of 26 = 26
26 is greater.
Question 10.
– √2, – \(\sqrt [ 3 ]{ 10 }\)
Answer:
10 is greater.
Explanation:
cube root of 10 = 10
square root of -2 = -2
soo 10 is greater.
Approximate the distance between the points to the nearest tenth.
Question 11.
(- 3, – 1) and (- 2, – 2)
Answer:
Question 12.
(1, – 1) and (5, 4)
Answer:
Question 13.
(5, 4) and (9, 8)
Answer:
Question 14.
(- 7, 10) and (3, – 5)
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 15.
VOCABULARY
How are rational numbers and irrational numbers different?
Answer:
rational number: a rational number is a number such as -3/7 that can be expressed as the quotient or fractionp/q of two integers, a numerator p, and non zero denominator q. Every integer is a rational number.
irrational number: irrational numbers are all the real numbers that are not rational numbers.
Explanation:
rational number: a rational number is a number such as -3/7 that can be expressed as the quotient or fractionp/q of two integers, a numerator p, and non zero denominator q. Every integer is a rational number.
irrational number: irrational numbers are all the real numbers that are not rational numbers.
CLASSIFYING REAL NUMBERS Classify the real number.
Question 16.
\(\frac{48}{16}\)
Answer:
Real number
Explanation:
(48/16) = 3
3 is a real number.
Question 17.
– √76
Answer:
Irrational numbers
Explanation:
76 is irrational number
irrational numbers are real numbers.
Question 18.
\(\sqrt [ 3 ]{ -216 }\)
Answer:
-6 is a rational number.
Explanation:
cube root of 216 = -6
APPROXIMATING AN IRRATIONAL NUMBER Approximate the number to the nearest (a) integer and (b) tenth.
Question 19.
√51
Answer:
26
Question 20.
– √87
Answer:
44
Question 21.
\(\sqrt [ 3 ]{ 60 }\)
Answer:
5
Question 22.
WHICH ONE DOESN’T BELONG?
Which number does not belong with the other three? Explain your reasoning.

Answer:
-3.3 is different from the three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 23.
The equation 3600b2 = hw represents the relationship among the body surface area b (in square meters), height h (in centimeters), and weight w (in kilograms) of a person. To the nearest tenth, approximate the body surface area of a person who is 168 centimeters tall and weighs 60 kilograms.
Answer:
2.8 cm
Explanation:
Given that the surface area of a person = 168 cm
w = 60
3600 b² = 168 x 60
3600 b² = 10080
b² = (10080/3600)
b² = 2.8
Question 24.
Which plane is closer to the base of the airport tower? Justify your answer.
Answer:
Plane B is closer to the base of the airport tower.
Irrational Numbers Homework & Practice 9.5
Review & Refresh
Write the repeating decimal as a fraction or a mixed number.
Question 1.
\(0 . \overline{4}\)
Answer:
Question 2.
\(1.0 \overline{3}\)
Answer:
Question 3.
\(0 . \overline{75}\)
Answer:
Question 4.
\(2 . \overline{36}\)
Answer:
Simplify the expression. Write your answer as a power.
Question 5.
(54)2
Answer:
5 ⁸
Explanation:
(54)2
5 ⁸ = 5 x 5 x 5 x 5 x5 x5 x5
5⁸
Question 6.
(- 9)4 . (- 9)7
Answer:
(-9)¹¹
Explanation:
(-9)⁴ . (-9)⁷
when exponents are equal powers must be added.
(-9)⁴ +⁷
(-9)¹¹
Question 7.
a8 . a
Answer:
a⁹
Explanation:
(a)⁸ . (a)¹
when exponents are equal powers must be added.
(a)⁸ +¹
(a)⁹
Question 8.
(y3)6
Answer:
y ⁶
Explanation:
cube root of y = y x y x y
y ⁶
Concepts, Skills, &Problem Solving
APPROXIMATING SQUARE ROOTS Find the exact length x of the diagonal of the square or rectangle. The value of x is between which two whole numbers? (See Exploration 1, p. 401.)
Question 9.
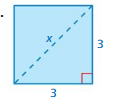
Answer:
x = 18
Explanation:
Given that the sides of a square = s x s
square =2 3 x 3
s = 18
Question 10.
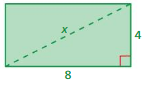
Answer:
x = 24
Explanation:
Given that the sides of a rectangle = 2 (l + b)
rectangle = 2( 8 + 4)
rectangle = 2(12)
rectangle = 24
CLASSIFYING REAL NUMBERS Classify the real number.
Question 11.
0
Answer:
whole
integer
rational
Question 12.
\(\sqrt [ 3 ]{ 343 }\)
Answer:
7
Explanation:
cube root of 343 = 7 x 7 x 7
7
Question 13.
\(\frac{π}{6}\)
Answer:
18.84
irrational number.
Question 14.
– √81
Answer:
-9
Explanation:
square root of -81 = -9 x -9
Question 15.
– 1.125
Answer:
rational number
Question 16.
\(\frac{52}{13}\)
Answer:
676
Explanation:
(52/13)
676
Question 17.
\(\sqrt [ 3 ]{ -49 }\)
Answer:
-7
irrational
Question 18.
√15
Answer:
15
Question 19.
YOU BE THE TEACHER
Your friend classifies √144. Is your friend correct? Explain your reasoning.
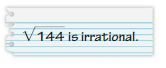
Answer:
No
Explanation:
144 is a perfect square.
square root of 144 is rational number.
Question 20.
MODELING REAL LIFE
You cut a photograph into a right triangle for a scrapbook. The lengths of the legs of the triangle are 4 inches and 6 inches. Is the length of the hypotenuse a rational number? Explain.
Answer:
√52
Explanation:
By using Pythagoras theorem
a² + b² = c²
4² + 6² = c²
16 + 36 = c²
52 = c²
c =√52
Question 21.
REASONING
Place each number in the correct area of the Venn diagram.
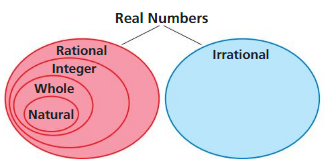
a. the last digit of your phone number
b. the square root of any prime number
c. the quotient of the circumference of a circle and its diameter
Answer:
b. irrational number.
c. irrational number.
APPROXIMATING AN IRRATIONAL NUMBER Approximate the number to the nearest (a) integer and (b) tenth.
Question 22.
√46
Answer:
a. 46
b.√36
Explanation:
square root of 46 = 46
nearest tenth = 36
46 – 10 = 36
Question 23.
– √105
Answer:
a.-10
b.-10 .2
Explanation:
square root of -105 = -10
nearest tenth = -10.2
Question 24.
\(\sqrt [ 3 ]{ -12 }\)
Answer:
a.³√-12
b..³√-2
Explanation:
square root of -12= -12
nearest tenth = -2
12 – 10 = 2
Question 25.
\(\sqrt [ 3 ]{ 310 }\)
Answer:
a. 7
b. 6.8
Explanation:
cube root of 310 = 7
nearest tenth = 7
6.8
Question 26.
\(\sqrt{\frac{27}{4}}\)
Answer:
6.75
6.65
Explanation:
(27/4)
6.75
6.75 – 10 = 6.65
Question 27.
\(-\sqrt{\frac{335}{2}}\)
Answer:
-13
12.9
Explanation:
(335/2)
-13
-13 – 10
-12.9
COMPARING IRRATIONAL NUMBERS Which number is greater? Explain.
Question 28.
√125, √135
Answer:
√135
Explanation:
135 is greater than 125
Question 29.
√22, \(\sqrt [ 3 ]{ 34 }\)
Answer:
34
Explanation:
34 is greater then 22
Question 30.
– \(\sqrt [ 3 ]{ 100 }\), – √42
Answer:
-42
Explanation:
-42 is greater than -100
Question 31.
√5, π
Answer:
√5
Explanation:
5 is greater than 3.14
Question 32.
\(\sqrt [ 3 ]{ 130 }\), √28
Answer:
130
Explanation:
130 is greater than 28
Question 33.
– √38, \(\sqrt [ 3 ]{ -250 }\)
Answer:
-250
Explanation:
250 is greater than 38
USING TOOLS Use the graphing calculator screen to determine whether the statement is true or false.
Question 34.
To the nearest tenth, √10 = 3.1.
Answer:
3.16227766
Question 35.
The value of √14 is between 3.74 and 3.75.
Answer:
True
Explanation:
Given that the √14 = 3.74165
Question 36.
√10 lies between 3.1 and 3.16 on a number line.
Answer:
True
Explanation:
Given that the √10 = 3.1622
USING THE PYTHAGOREAN THEOREM Approximate the distance between the points to the nearest tenth.
Question 37.
(1, 2), (7, 6)
Answer:
7.2 units.
Question 38.
(2, 4), (7, 2)
Answer:
Question 39.
(- 1, – 3), (1, 3)
Answer:
6.3 units.
Question 40.
(- 6, – 7), (0, 0)
Answer:
Question 41.
(- 1, 1), (7, 4)
Answer:
8.5 units.
Explanation:
7 + 1 = 8
4 + 1 = 5
8.5 units
Question 42.
(- 6, 5), (- 4, – 6)
Answer:
Question 43.
MODELING REAL LIFE
The locations of several sites in a forest are shown in the coordinate plane. Approximate each distance to the nearest tenth.
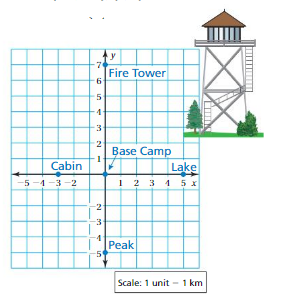
a. How far is the cabin from the peak?
b. How far is the fire tower from the lake?
c. How far is the lake from the peak?
d. You are standing at(- 5, – 6). How far are you from the lake?
Answer:
a. 5.8 km
b. 8.6 km
c. 7.1 km
d. 11.7 km
Question 44.
WRITING
Explain how to continue the method in Example 2 to approximate √71 to the nearest hundredth.
Answer:
29
Question 45.
MODELING REAL LIFE
The area of a four square court is 66 square feet. Approximate the side length s of the four square court to the nearest whole number.
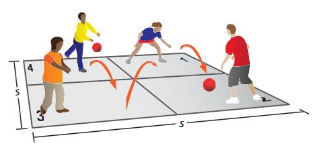
Answer:
The side length = 8 ft
Explanation:
The area of a four square court is 66 square feet given.
the side lengths = 8 x 8
s = 8 ft
Question 46.
MODELING REAL LIFE
A checker board is 8 squares long and 8 squares wide. The area of each square is 14 square centimeters. Approximate the perimeter (in centimeters) of the checker board to the nearest tenth.
Answer:
The perimeter of the checker board = 384
Explanation:
Given that the checker board is 8 squares long and 8 squares wide.
perimeter = 6 x side x side
perimeter = 6 x 8 x 8
p= 6 x 64
p = 384 cm
Question 47.
GEOMETRY
The cube has a volume of 340 cubic inches. Approximate the length d of the diagonal to the nearest whole number. Justify your answer.
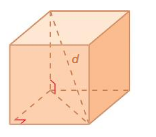
Answer:
The length of the diagonal = 12 in
Explanation:
Given that the volume of cube = 340 cubic inches.
v = s x s
v = 7 x 7
d = 7 x 7 + 10 x 10 = 149
12 in
Question 48.
CRITICAL THINKING
Ona number line, π is between 3 and 4.
a. Use this information to draw a number line and shade a region that represents the location of π2. Explain your reasoning.
b. Repeat part(a) using the fact that π is between 3.1 and 3.
c. Repeat part(a) using the fact that π is between 3.14 and 3.15.
Answer:
NUMBER SENSE Approximate the square root to the nearest tenth.
Question 49.
√0.39
Answer:
0.6
Explanation:
√0.39²
where square and square root get cancelled.
0.39 – 10
0.6
Question 50.
√1.19
Answer:
1.09
Explanation:
√1.19²
where square and square root get cancelled.
1.19 – 10
1.09
Question 51.
√1.52
Answer:
1.2
Explanation:
√1.52²
where square and square root get cancelled.
1.52 – 10
1.2
Question 52.
STRUCTURE
Is \(\sqrt{\frac{1}{4}}\) a rational number? Is \(\sqrt{\frac{3}{16}}\) a rational number? Explain.
Answer:
Question 53.
MODELING REAL LIFE
The equation s2 = 54r represents the relationship between the speed s (in meters per second) of a roller-coaster car and the radius r (in meters) of the loop. Approximate the speed of a roller-coaster car going around the loop shown to the nearest tenth.

Answer:
s = 30.1 meters per second.
Explanation:
s2 = 54r
where r = 16.764 m
s² = 54 x 16.764 m
s² = 905.256
s =30.1
Question 54.
OPEN-ENDED
Find two numbers a and b that satisfy the diagram.

Answer:
√a = 9.3
√b = 9.8
Explanation:
Given that a = 9
b = 10
√a = 9.3
√b = 9.8
the distance between the two points is 1 inch
Question 55.
DIG DEEPER!
The equation d3 = t3 represents the relationship between the mean distance d (in astronomical units) of a planet from the Sun and the t time (in years) it takes the planet to orbit the Sun.
a. Jupiter takes about 11.9 years to orbit the Sun. Approximate the mean distance of Jupiter from the Sun to the nearest tenth.
b. The mean distance of Saturn from the Sun is about 9.5 astronomical units. Approximate the time it takes Saturn to orbit the Sun to the nearest tenth.
Answer:
a. d = 5.2 astronomical units
b. 29.3 years
Explanation:
Given that the
a. Jupiter takes about 11.9 years to orbit the sun.
b. the mean distance of Saturn from the sun is about 9.5 astronomical units.
Question 56.
MODELING REAL LIFE
The equation h = – 16t2 + 26 represents the height h (in feet) of a water balloon t seconds after it is dropped. Approximate the time it takes the water balloon to reach the ground to the nearest tenth. Justify your answer.

Answer:
– 28 feet.
Explanation:
Given that the equation h = – 16t2 + 26
we assuming t = 2
h = -16 x 4 + 26
h = -64 + 26
h = -38
nearest tenth = 38 – 10
– 28 feet
Question 57.
NUMBER SENSE
Determine whether the statement is sometimes, always, or never true. Explain your reasoning.
a. A rational number multiplied by a rational number is rational.
b. A rational number multiplied by an irrational number is rational.
c. An irrational number multiplied by an irrational number is rational.
Answer:
a. always.
b. sometimes.
c. sometimes.
Explanation:
a. if a/b and c/d are rational numbers, then ac and bd are integers and bd not equal to zero. so ac/bd is rational.
b. for example, π . 0 = 0 is rational, but 2. √3 is irrational.
c. for example, √2 . π is irrational, but π . 1/ π is rational.
Lesson 9.6 The Converse of the Pythagorean Theorem
The converse of a statement switches the hypothesis and the conclusion.

EXPLORATION 1
Analyzing the Converse of a Statement
Work with a partner.
a.Write the converse of each statement. Then determine whether each statement and its converse are true or false.

- If I live in California,then I live in the United States.
- If my heart is beating, then I am alive.
- If one figure is a translation of another figure,then the figures are congruent.
b. Write your own statement whose converse is true. en write your own statement whose converse is false.
EXPLORATION 2
The Converse of the Pythagorean Theorem
Work with a partner.
a.Write the converse of the Pythagorean Theorem. Do you think the converse is true or false?
b. Consider △DEFwith side lengths a, b, and c such that a2 + b2 = c2. Also consider △JKL with leg lengths a and b, where the measure of ∠K is 90°. Use the two triangles and the Pythagorean Theorem to show that the converse of the Pythagorean Theorem is true.
Try It
Tell whether the triangle with the given side lengths is a right triangle.
Question 1.
28 in., 21 in., 20 in.
Answer:
The given sides does not form a right triangle.
Explanation:
20² + 21² = 28²
400 + 441 = 784
841 = 784
the given sides does not form a right triangle.
Question 2.
1.25 mm, 1 mm, 0.75 mm
Answer:
The given sides form a right triangle.
Explanation:
1² + 0.75² = 1.25²
1 + 0.5625= 1.5623
1.5625 = 784
the given sides form a right triangle.
Tell whether the points form a right triangle.
Question 4.
D (- 4, 0), E (- 2, 3), F (1, 0)
Answer:
Yes the given points form a right triangle.
Question 5.
J (4, 1), K (1, – 3), L (- 3, 0)
Answer:
Yes the given points form a right triangle.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
WRITING
Explain the converse of the Pythagorean Theorem.
Answer:
a² + b² ≠ c²
Explanation:
a² + b² = c²
where a, b and c are side lengths of a triangle.
converse of pythagoras theorem
a² + b² ≠ c²
Question 6.
IDENTIFYING A RIGHT TRIANGLE
Is a triangle with side lengths of 2 millimeters, 2.5 millimeters, and 3 millimeters a right triangle?
Answer:
No the side lengths does not form a right triangle.
Explanation:
2 ² + 2.5² = 3²
4 + 6.25 = 9
10.25 = 9
Question 7.
IDENTIFYING A RIGHT TRIANGLE
Do the points (- 1, 1), (- 3, 5), and (0, 8) form a right triangle?
Answer:
No the given points does not form a right triangle.
Question 8.
WHICH ONE DOESN’T BELONG?
Which set of numbers does not belong with the other three? Explain your reasoning.
![]()
Answer:
3, 6, 8 set does not belong with the other 3 sets.
Explanation:
3 ² + 6² = 8²
9 + 36 = 64
45 = 64
the given sides does not form a right triangle.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
You practice archery as shown. Determine whether the arrow is perpendicular to the vertical support. Justify your answer.
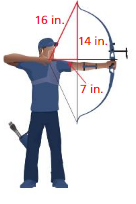
Answer:
Yes the archery is perpendicular to vertical support.
Explanation:
2 times of 7 is 14.
so archery is perpendicular to vertical support.
Question 10.
DIG DEEPER!
Three fire hydrants in a neighborhood are represented on a map. The coordinates of the fire hydrants are (0, 0), (2, 5), and (7, y). The fire hydrants are arranged in a right triangle, where y is a natural number less than 10. Find y.

Answer:
y = 5
Explanation:
Given that the coordinates of the fire hydrants are (0, 0), (2, 5), and (7, y).
y can meet the y-axis on 5
y = 5
7 -2 = 5
The Converse of the Pythagorean Theorem Homework & Practice 9.6
Review & Refresh
Approximate the number to the nearest (a) integer and (b) tenth.
Question 1.
√31
Answer:
a. 6
b. 5.6
Explanation:
square root of 31 = 31
√31 ² = 6
where square and square root get cancelled.
nearest tenth = it is decreased by 10
5.6
Question 2.
– √7
Answer:
a. 7
b. -3
Explanation:
square root of 7 = 7
√7 ² = 7
where square and square root get cancelled.
nearest tenth = it is decreased by 10
7 -10
-3
Question 3.
\(\sqrt [ 3 ]{ 25 }\)
Answer:
a. 3
b. 2.9
Explanation:
cube root of 25 = 25
3√25 = 3
where square and square root get cancelled.
nearest tenth = it is decreased by 10
2.9
The figures are similar. Find x.
Question 4.
The ratio of the perimeters is 2 : 5.
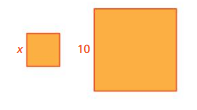
Answer:
x = 2
Explanation:
Given that the ratio of perimeters = 2 : 5
x = 2
5 x 2 = 10
Question 5.
The ratio of the perimeters is 4 : 3.
Answer:
x = 4.5
Explanation:
Given that the ratio of perimeters = 4 : 3
x = 4.5
3 x 2 = 4.5
Concepts, Skills, &Problem Solving
ANALYZING THE CONVERSE OF A STATEMENT Write the converse of the statement. Then determine whether the statement and its converse are true or false. Explain. (See Exploration 1, p. 409.)
Question 6.
If a is an odd number, then a2 is odd.
Answer:
False.
if a is not an odd number, then square of a is not odd.
Explanation:
The given statement is true.
converse of a given statement is false.
Question 7.
If ABCD is a square, then ABCD is a parallelogram.
Answer:
True.
If ABCD is not a square, then ABCD is not a parallelogram.
Explanation:
The given statement is false.
converse of a given statement is true.
IDENTIFYING A RIGHT TRIANGLE Tell whether the triangle with the given side lengths is a right triangle.
Question 8.
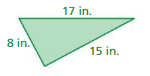
Answer:
Yes the given side lengths is a right triangle.
Explanation:
8 ² + 15² = 17²
64 + 225 = 289
289 = 625
Question 9.
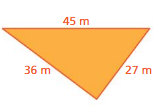
Answer:
Yes the given side lengths is a right triangle.
Explanation:
27 ² + 36² = 45²
729 + 1296 = 2025
2025 = 625
Question 10.
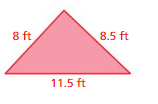
Answer:c
Question 11.
14 mm, 19 mm, 23 mm
Answer:
No the given side lengths is not a right triangle.
Explanation:
14 ² + 19² = 23²
196 + 361 = 529
557 = 625
Question 12.
\(\frac{9}{10}\) mi, 1 \(\frac{1}{5}\) mi, 1 \(\frac{1}{2}\) mi
Answer:
Question 13.
1.4 m, 4.8 m, 5 m
Answer:
Yes the given side lengths is a right triangle.
Explanation:
1.4 ² + 4.8² = 5²
1.96 + 23.04 = 25
25 = 25
Question 14.
MODELING REAL LIFE
A post-and-beam frame for a shed is shown in the diagram. Does the brace form a right triangle with the post and beam? Explain.
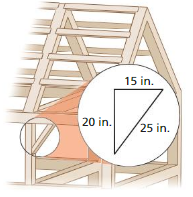
Answer:
Yes the given side lengths is a right triangle.
Explanation:
15 ² + 20² = 25²
225 + 400 = 625
625 = 625
Question 15.
MODELING REAL LIFE
A traffic sign has side lengths of 12.6 inches, 12.6 inches, and 12.6 inches. Is the sign a right triangle? Explain.
Answer:
No the given side lengths is not a right triangle.
Explanation:
12.6 ² + 12.6² = 12.6²
158.76 + 158.76 = 158.76
317.52 = 158.76
IDENTIFYING A RIGHT TRIANGLE Tell whether a triangle with the given side lengths is a right triangle.
Question 16.
√63, 9, 12
Answer:
Yes the given side lengths is a right triangle.
Explanation:
√63 ² + 9² = 12²
63 + 81 = 144
144 = 144
Question 17.
4, √15, 6
Answer:
No the given side lengths is not a right triangle.
Explanation:
√15 ² + 4² = 6²
15 + 16 = 36
31 = 36
Question 18.
√18, √24, √42
Answer:
Yes the given side lengths is a right triangle.
Explanation:
√18 ² + √24² = √42²
18 +24 = 42
42= 42
Question 19.
YOU BE THE TEACHER
Your friend determines whether a triangle with side lengths of 3, √58, and 7 is a right triangle. Is your friend correct? Explain your reasoning.

Answer:
No my friend is not correct.
Explanation:
By using Pythagoras theorem
a² + b² = c²
13² + 58² = 7²
9 + 58 is not equal to 49
IDENTIFYING A RIGHT TRIANGLE Tell whether the points form a right triangle.
Question 20.
(0, 0), (0, 5), (2, 0)
Answer:
Yes the points forms a right triangle
Explanation:
the above given points are all positive
Question 21.
(0, 8), (2, 2), (11, 6)
Answer:
No the points not forms a right triangle
Explanation:
the above given points are all positive.
Question 22.
(- 1, 0), (5, 0), (2, – 3)
Answer:
No the points not forms a right triangle
Explanation:
the above given points are all positive and negative.
Question 23.
(- 1, – 2), (2, 6), (4, – 1)
Answer:
No the points does not forms a right triangle
Explanation:
the above given points are all positive
Question 24.
(- 8, 6), (7, 9), (0, – 13)
Answer:
Yes the points forms a right triangle
Explanation:
the above given points are all positive and negative
Question 25.
(0.5, 1.5), (7.5, 5.5), (9.5, 0.5)
Answer:
No the points does not forms a right triangle
Explanation:
the above given points are all positive and negative
Question 26.
LOGIC
The equation a2 + b2 = c2 is not true for a particular triangle with side lengths of a, b, and c. What can you conclude about the type of triangle?
Answer:
If the triangle is right triangle the above condition satisfies.
Explanation:
The equation a2 + b2 = c2 is a pythagoras theroem.
it satisfies for only right triangle.
where a,b, c are side lengths.
Question 27.
MODELING REAL LIFE
You spend the day looking for hidden containers in a wooded area using a Global Positioning System (GPS). You park your bike on the side of the road, and then locate Container 1 and Container 2 before going back to your bike. Does your path form a right triangle? Explain. Each grid line represents 10 yards.
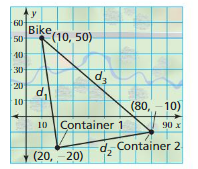
Answer:
No path does not forms a right triangle.
Explanation:
(10, 50) , (20, -20) and (80, -10)
the given points form a right triangle.
Question 28.
DIG DEEPER!
The locations of a fishing boat, buoy, and kayak are represented by the points (0, 0), (16, 12), and (10, – 5). Each unit represents 1 nautical mile

a. Do the boat, kayak, and buoy form a right triangle?
b. The boattravels at8 nautical miles per hour. How long does the boat take to reach the buoy if the boat travels directly toward it?
Answer:
a. yes the boat, kayak, buoy form a right triangle.
b. the boat travels at 8 nautical miles per hr= 80 miles per hr
Explanation:
a.yes the boat, kayak, buoy form a right triangle.
b. the boat travels at 8 nautical miles per hr.
8 x 10
80 miles per hr
Question 29.
The vertices of a quadrilateral are (1, 2), (5, 4), (6, 2), and (2, 0). Use the converse of the Pythagorean Theorem to determine whether the quadrilateral is a rectangle.
Answer:
Yes the given points forms a rectangle.
Real Numbers and the Pythagorean Theorem Connecting Concepts
Using the Problem-Solving Plan
Question 1.
The scale drawing of a baseball field has a scale factor of \(\frac{1}{270}\). Approximate the distance from home plate to second base on the actual baseball field to the nearest tenth.
Understand the problem.
You know several measurements and the scale factor in a scale drawing of a baseball field. You are asked to approximate the distance from home plate to second base on the actual baseball field.
Make a plan.
The distance from home plate to second base is the hypotenuse of a right triangle. Approximate the distance in the scale drawing to the nearest tenth. Then use the scale factor to approximate the distance on the actual field.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
0.048 sq in
Explanation:
Given that the scale factor of (1/270)
(1/270) = 0.003
from home plate to second base
4 x 4
16 x 0.003
0.048
Question 2.
You cut the wood cube shown into two identical triangular prisms. Approximate the surface area of each triangular prism to the nearest tenth. Justify your answer.

Answer:
The surface area of triangular prism = 64 cm
Explanation:
the volume of the cube
v = s x s x
v = 8 x 8 x 8
v = 64 x 8
v = 512
Question 3.
Complete the mapping diagram representing the relationship between the lengths of the hypotenuse and the legs of an isosceles right triangle. Is the relationship linear? Explain.
Answer:
a√2
Performance Task
Identify and Correct the Error!
At the beginning of this chapter, you watched a STEAM Video called “Metronome Design.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Answer:
Real Numbers and the Pythagorean Theorem Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use a Four Square to organize information about a concept. Each of the four squares can be a category, such as definition, vocabulary, example, non-example, words, algebra, table, numbers, visual, graph, or equation. Here is an example of a Four Square for Pythagorean Theorem.
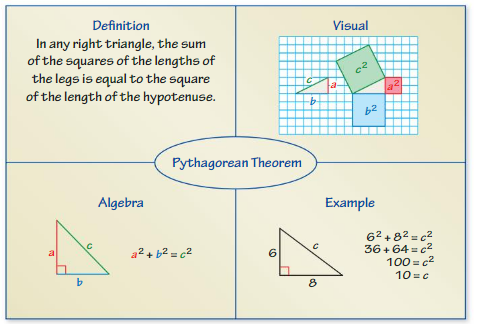
Choose and complete a graphic organizer to help you study the concept.

1. square roots
2. cube roots
3. rational numbers
4. irrational numbers
5. real numbers
6. converse of the Pythagorean Theorem
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

9.1 Finding Square Roots (pp. 373–380)
Learning Target: Understand the concept of a square root of a number.
Find the square root(s).
Question 1.
√1
Answer:
1
Explanation:
square root of 1 = 1 x 1
Question 2.
– \(\sqrt{\frac{9}{25}}\)
Answer:
-(3/5)
Explanation:
square root of 9 = 3x 3
square root of 25 = 5 x 5
Question 3.
± √1.69
Answer:
± 1.3
Explanation:
square root of 1.69 = 1.3 x 1.3
Evaluate the expression.
Question 4.
15 – 4 √36
Answer:
-9
Explanation:
15 – 4 √36
square root of 36 = 6 x 6
15 – 4 x 6
15 – 24
-9
Question 5.
\(\sqrt{\frac{54}{6}}+\frac{2}{3}\)
Answer:
9.66
Explanation:
(54/6) = 9
(2/3) = 0.66
9 + 0.66
9.66
Question 6.
\((\sqrt{9})^{2}\) – 12
Answer:
-7.5
Explanation:
(9/2) = 4.5
4.5 – 12
-7.5
Question 7.
The total area of a checker board is 256 square inches. What is the side length (in inches) of one of the small squares?

Answer:
The side length = 16 in
Explanation:
Given that total area = 256 sq in
area of square = s x s
area = 16 x 16
side = 16 in
9.2 The Pythagorean Theorem (pp. 381–388)
Learning Target: Understand the Pythagorean Theorem.
Find the missing length of the triangle.
Question 8.
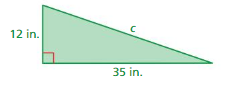
Answer:
The missing length = 47 in
Explanation:
By using Pythagoras theorem
a² + b² = c²
12² + 35² = 47²
length = 47 in
Question 9.
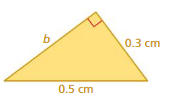
Answer:
The missing length = 0.2 cm
Explanation:
By using Pythagoras theorem
a² + b² = c²
0.3² + 0.2² = 0.5²
length = 0.2 cm
Question 10.
You lean a 13-foot ladder on a house so the bottom of the ladder is 5 feet from the house. From the top of the ladder, you can safely reach another 4 feet higher. Can you reach a window that is located 13 feet above the ground? Explain.

Answer:
No we cannot reach a window.
Explanation:
Given that we lean a 13-foot ladder on a house
so that the bottom of the ladder is 5 feetfrom the house.
from the top of ladder, we can reach safely another 4 feet higher.
5 + 4
we can reach 9 feet.
Question 11.
Find the distance between (- 6, 8) and (10, – 4).
Answer:
9.3 FindingCube Roots (pp. 389–394)
Learning Target: Understand the concept of a cube root of a number.
Find the cube root.
Question 12.
\(\sqrt [ 3 ]{ -2197 }\)
Answer:
-13
Explanation:
cube root of (-2197) is (-13)
3√-2197= (-13) x (-13) x (-13)
-2197³ = (-13)³
when powers are equal exponents must be equal.
-2197 = -13
Question 13.
\(\sqrt[3]{\frac{64}{343}}\)
Answer:-
(4/7)
Explanation:
cube root of (64/343) is (4/7)
3√(64/343)= (4/7) x (4/7) x (4/7)
(64/343)³ = (4/7)³
when powers are equal exponents must be equal.
(64/343)= (4/7)
Question 14.
\(\sqrt[3]{-\frac{8}{27}}\)
Answer:
-2/3
Explanation:
cube root of (8/27) is (2/3)
3√(8/27)= (2/3) x (2/3) x (2/3)
(8/27)³ = (2/3)³
when powers are equal exponents must be equal.
(8/27)= (2/3)
Question 15.
Evaluate the expression 25 + 2\(\sqrt [ 3 ]{ -64 }\).
Answer:
17
Explanation:
cube root of (-64) is (-4)
3√(64)= (4) x (4) x (4)
(64)³ = (4)³
when powers are equal exponents must be equal.
(64)= 4
25 + 2(-4)
25 -8
17
Question 16.
Solve the equation – 55 = \(\frac{1}{4}\)x3 + 73.
Answer:
x =8
Explanation:
-55 = 0.25 x ³ + 73
0.25 x³ = -55 -73
0.25 x³ = -128
x³ = -(128/0.25)
x³ = 512
x = 8
Question 17.
You are shipping a puzzle cube to your friend using the cube-shaped box shown. What is the difference between the height of the puzzle cube and the top of the box when you place the cube in the box?

Answer:
The height of the puzzle cube = 6 cm
Explanation:
Given that the volume of the cube-shaped box = 216 cubic cm
volume of cube = s x s x s
v = 6 x 6 x 6
v = 36 x 6
v = 216
the height of puzzle cube= 6 cm
9.4 Rational Numbers (pp. 395–400)
Learning Target: Convert between different forms of rational numbers.
Write the fraction or mixed number as a decimal.
Question 18.
– 2\(\frac{5}{6}\)
Answer:
-1.66
Explanation:
(5/6) = 0.83
-1.66
Question 19.
\(\frac{27}{80}\)
Answer:
0.33
Explanation:
(27/80)
0.3375
Question 20.
3\(\frac{8}{9}\)
Answer:
2.66
Explanation:
(8/9) = 0.888
3 x 8/9
3 x 0.88
2.66
Question 21.
Write \(1 . \overline{36}\) as a mixed number.
Answer:
Question 22.
The gas mileage of a hybrid car is \(3.0 \overline{3}\) times the gas mileage of a regular car. The regular car averages 24 miles per gallon. Find the gas mileage of the hybrid car.

Answer:
The gas mileage of the hybrid car is 72 miles
Explanation:
Given that the mileage of the hybrid car is 3
the regular car averages 24 miles per gallon.
the gas mileage of the hybrid car is
24 x 3
72 miles
Question 23.
Your friend’s cat weighs 0.8 3 times the weight of your cat. Your friend’s cat weighs 10 pounds. How much more does your cat weigh than your friend’s cat?
Answer:
2 pounds
Explanation:
Given that the my friend’s cat weighs = 0.8
3 times the weight of my cat.
my friend cat weighs = 10 pounds
10 x 0.2 = 2 pounds.
Question 23.
An apple dessert recipe makes \(2 . \overline{3}\) pounds of dessert and serves 6 people. What is the serving size (in pounds)?
Answer:
The serving size is 18 pounds.
Explanation:
given that an apple dessert recipe makes 3 pounds.
the serving size is
6 x 3
18 pounds.
9.5 Irrational Numbers (pp. 401–408)
Learning Target: Understand the concept of irrational numbers.
Classify the real number.
Question 24.
\(0.81 \overline{5}\)
Answer:
real number
Explanation:
given expression is a real number.
Question 25.
√101
Answer:
no
Explanation:
square root of 101 is real algebraic number
so it is not a real number.
Question 26.
√4
Answer:
no
Explanation:
square root of 4 is real algebraic number
so it is not a real number.
Approximate the number to the nearest (a) integer and (b) tenth.
Question 27.
√14
Answer:
a. 3
b. 4
Explanation:
3 is a integer for square root of 14
4 is the nearest tenth for 14
Question 28.
√90
Answer:
89
80
Explanation:
89 is a integer for square root of 90
80 is the nearest tenth for 90
Question 29.
√175
Answer:
174
165
Explanation:
174 is a integer for square root of 175
165 is the nearest tenth for 175
Question 31.
Which is greater, √48 or \(\sqrt [ 3 ]{ 127 }\) ? Explain.
Answer:
cube root of 127 is greater.
Explanation:
cube root of 127 = 127
cube root of 48 = 48
Question 32.
Approximate the distance between (- 2, – 5) and (3, 5) to the nearest tenth.
Answer:
Question 33.
The equation d = \(\frac{v^{2}}{15.68}\)represents the relationship between the distance d (in meters) needed to stop a vehicle and the velocity v (in meters per second) of the vehicle. Approximate the velocity of the vehicle when it takes 40 meters to stop.

Answer:
The velocity of vehicle = 5.102 meters
Explanation:
given that the equation d = (2/15.68)
(2/15.68 = 0.12755
the velocity of the vehicle when it takes 40 meters
0.12755 x 40
5.102 meters.
9.6 The Converse of the Pythagorean Theorem (pp. 409–414)
Learning Target: Understand the converse of the Pythagorean Theorem.
Tell whether the triangle with the given side lengths is a right triangle.
Question 34.
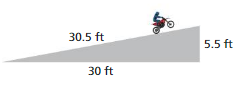
Answer:
yes.
Explanation:
the given triangle is a right triangle.
Question 35.
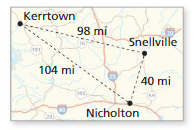
Answer:
no
Explanation:
the given measures not forming a right triangle.
Question 36.
Tell whether the points A (1, – 1), B (3, – 4), and C (4, 1) form a right triangle.
Answer:
no
Explanation:
given that the points
A(1, -1) B(3, -4) and C(4, 1)
the given measures does not form the right triangle.
Question 37.
You want to make a wooden border around a flower bed in the shape of a right triangle. You have three pieces of wood that measure 3.5 meters, 1.2 meters, and 3.9 meters. Do these pieces of wood form a right triangle? If not, explain how you can cut the longest piece of wood to make a right triangle.

Answer:
Yes these pieces of wood form a right triangle.
Explanation:
Given that the length of wooden pieces have measures of 3.5 m, 1.2 m, 3.9 m
so it can cut the wooden border in the shape of right triangle.
Real Numbers and the Pythagorean Theorem Practice Test
Question 1.
Find − √1600 .
Answer:
-40
Explanation:
square root of 1600 = 40 x 40
√1600 = 40²
when powers are equal exponents must be equal.
40
Question 2.
Find \(\sqrt[3]{-\frac{729}{64}}\).
Answer:
(-9/4)
Explanation:
cube root of -729 = 9
cube root of -64 = 4
-(9/4)
Evaluate the expression.
Question 3.
12 + 8√16
Answer:
80
Explanation:
12 + 8√16
square root of 16 is 4
12 + 8 x 4
20 x 4
80
Question 4.
\((\sqrt[3]{-125})^{3}+75\)
Answer:
60
Explanation:
cube root of -125 is -5
-5 x 3 + 75
-15 + 75
60
Question 5.
Find the missing length of the triangle.
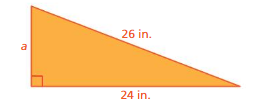
Answer:
The missing length = 2 in
Explanation:
By using Pythagoras theorem
a² + b² = c²
2² + 24² = 26²
length = 2 in
Classify the real number.
Question 6.
16 π
Answer:
4π
Explanation:
square root of 16 = 4 x 4
square root of 16 = 4
Question 7.
– √49
Answer:
7
Explanation:
square root of 49 = 7 x 7
square root of 49 = 7
Question 8.
Approximate √83 to the nearest (a) integer and (b) tenth.
Answer:
83
Question 9.
Write \(1 . \overline{24}\) as a mixed number.
Answer:
23
Question 10.
Tell whether the triangle is a right triangle.
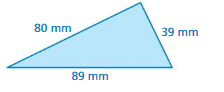
Answer:
The given triangle is not a right triangle.
Explanation:
The above given triangle is not a right triangle,
right triangle = 90 degrees.
Approximate the distance between the points to the nearest tenth, if necessary.
Question 11.
(- 2, 3), (6, 9)
Answer:
(4, 6)
Explanation:
(- 2, 3), (6, 9)
(6-2, 9-3)
(4, 6)
Question 12.
(0, – 5), (4, 1)
Answer:
Question 13.
How high is the hand of the superhero balloon above the ground?
Answer:
The hand of superhero ballon above the ground = 78 cubic feet.
Explanation:
The height of the ground = 6 ft
height from the man hand = 11ft
the distance from super hero to hand of the man is
6 + 11 + 61
17 + 61
78 cubic feet
Question 14.
The area of a circular pool cover is 314 square feet. Write and solve an equation to find the diameter of the pool cover. Use 3.14 for π.
Answer:
46,735.76
Explanation:
Area of the circle = π x r x r
Area = 3.14 x 122 x 122
Area = 46,735.76 ft
Question 15.
Five roads form two triangles. What is the value of x? Justify your answer.
Answer:
Real Numbers and the Pythagorean Theorem Cumulative Practice

Question 1.
The period T of a pendulum is the time (in seconds) it takes the pendulum to swing back and forth once. The period can be found using the formula T = 1.1 √L, where is the length (in feet) of the pendulum. A pendulum has a length of 4 feet. What is the period of the pendulum?
A. 2.2 sec
B. 3.1 sec
C. 4.4 sec
D. 5.1 sec
Answer:
option C is correct.
Explanation:
given that the pendulum has a length of 4 feet.
T = 1.1 l
where t = time and l = length
T = 4.4 sec
Question 2.
Whatis the value of y = 5 – 2x when x = – 3?
F. – 1
G. 1
H. 4
I. 11
Answer:
option F is correct.
Explanation:
given that x = -3
y = 5 -2 x
y = 5- 2 (-3)
y = 5 -6
y = -1
Question 3.
Which graph represents the linear equation 3x + 2y = 12?
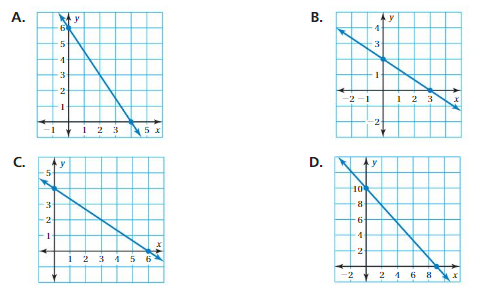
Answer:
option B is correct.
Explanation:
In the above 4 graphs option B is correct.
3x + 2y = 12
x = 2 and y= 3
3 x 2 + 2 x 3
6 + 6 = 12
Question 4.
Which expression is equivalent to \(\frac{(-3)^{12}}{(-3)^{3}}\)?
F. (- 3)4
G. (- 3)9
H. 09
I. 19
Answer:
option F is correct.
Explanation:
given that -3 x -3 x -3 x -3
(-3)⁴
Question 5.
A football field is 40 yards wide and 120 yards long. Approximate the distance between opposite corners of the football field to the nearest tenth. Show your work and explain your reasoning.

Answer:
The distance between opposite corners of the football field is 80 yards
Explanation:
Given that the football field is 40 yards and 120 yards long.
the distance between opposite corners = 120 – 40
120 – 40 = 80 yards
Question 6.
A computer consultant charges $50 plus $40 for each hour she works. The consultant charged $650 for one job. This can be represented by the equation below, where h represents the number of hours worked.

40h + 50 = 650
How many hours did the consultant work?
Answer:
The consultant work = 7 hours.
Explanation:
Given that the consultant charges $ 50 + $ 40
for 1 hour the consultant charges $ 90
The consultant charged = 650$
seven hours worked = 650
9 x 7 = 63
Question 7.
Which triangle is not a right triangle?

Answer:
option D is not a right triangle.
Explanation:
Given that the three triangles are right triangle.
right triangle = 90 degree.
Question 8.
What is the distance between (- 3,- 1) and (- 1, – 5)?
F. \(\sqrt{12}\)
G. \(\sqrt{20}\)
H. \(\sqrt{40}\)
I. \(\sqrt{52}\)
Answer:
option F is correct.
Explanation:
given that the distance is (-3, -1) and (-1, -5)
(-3, -1) and (-1, -5)
(-4 , -6)
Question 9.
An airplane flies from City 1 at (0, 0) to City 2 at (33, 56) and then to City 3 at (23, 32). Whatis the total number of miles it flies? Each unit represents 1 mile.
Answer:
The total number of miles it flies = 56 miles
Explanation:
given that city 1 at (0, 0)
city 2 at (33, 56)
city 3 at (23, 32)
33 + 23
56
Question 10.
The national debt of Country A is $398,038,013,519. The national debt of Country B is $2,137,348,918. Approximately how many times greater is the debt of Country A than the debt of Country B?
A. 2 times greater
B. 20 times greater
C. 133 times greater
D. 200 times greater
Answer:
option B is correct.
Explanation:
country A = $398,038,013,519
country B = $2,137,348,918.
Question 11.
What is the solution of the system?
F.(2, 4)
G. (3, 0)
H.(4, 2)
I. (5, 0)
Answer:
option H is correct.
Explanation:
In the given graph
the line x-axis meets on 4 and y-axis meet on 2
(4, 2)
Question 12.
In the diagram, lines ℓ and m are parallel. Which angle has the same measure as ∠1?
A. ∠2
B. ∠5
C. ∠7
D. ∠8
Answer:
option D
Explanation:
given that l and m are parallel lines.
˂ 1 is equal to ˂8
Question 12.
Which graph represents the linear equation y = – 2x – 2?
Answer:
option F is correct.
Explanation:
graph F represents the linear equation.
y = -2x -2
Conclusion
Hope the information shared regarding the Big Ideas Math Answers Grade 8 Ch 9 Real Numbers and Pythagorean Theorem has shed some light on you. For any further clarifications on the same do leave us your suggestions and we will look into them and respond on the same.
