Big Ideas Math Book Geometry Answer Key Ch 12 Probability is aligned as per the BIM Geometry Textbooks. Refer to the BIM Geometry Solutions for quick guidance on the Topicwise Concepts of Probability. Big Ideas Math Geometry Solution Key can be downloaded for free of cost. Access the Big Ideas Math Geometry Chapter 12 Probability Answers created by subject experts adhering to the latest Common Core State Standards guidelines. Download the handy resources for Big Ideas Math Geometry Chapter 12 Probability Solutions and begin your preparation.
Big Ideas Math Book Geometry Answer Key Chapter 12 Probability
Make the most out of the Big Ideas Math Geometry Answer Key for Cha 12 Probability and score better grades in the exams. Simply tap on the quick links available and prepare the respective topics available as and when you need them. Big Ideas Math Geometry Answers Chapter 12 Probability available here covers questions from the Topics Sample Spaces, Independent and Dependent Events, Disjoint and Overlapping Events, Binomial Distributions, Probability Test, etc.
Lesson: 1 Sample Spaces and Probability
- 12.1 Sample Spaces and Probability
- Lesson 12.1 Sample Spaces and Probability
- Exercise 12.1 Sample Spaces and Probability
Lesson: 2 Independent and Dependent Events
- 12.2 Independent and Dependent Events
- Lesson 12.2 Independent and Dependent Events
- Exercise 12.2 Independent and Dependent Events
Lesson: 3 Two-Way Tables and Probability
- 12.3 Two-Way Tables and Probability
- Lesson 12.3 Two-Way Tables and Probability
- Exercise 12.3 Two-Way Tables and Probability
Quiz
Lesson: 4 Probability of Disjoint and Overlapping Events
- 12.4 Probability of Disjoint and Overlapping Events
- Lesson 12.4 Probability of Disjoint and Overlapping Events
- Exercise 12.4 Probability of Disjoint and Overlapping Events
Lesson: 5 Permutations and Combinations
- 12.5 Permutations and Combinations
- Lesson 12.5 Permutations and Combinations
- Exercise 12.5 Permutations and Combinations
Lesson: 6 Binomial Distributions
Chapter: 12 – Probability
Probability Maintaining Mathematical Proficiency
Write and solve a proportion to answer the question.
Question 1.
What percent of 30 is 6?
Answer: 20
Explanation:
100% = 30
x% = 6
100% = 30(1)
x% = 6(2)
100%/x% = 30/6
Taking the inverse of both sides
x%/100% = 6/30
x = 20%
Thus 6 is 20% of 30.
Question 2.
What number is 68% of 25?
Answer: 17
Explanation:
68% × 25
(68 ÷ 100) × 25
(68 × 25) ÷ 100
1700 ÷ 100 = 17
Question 3.
34.4 is what percent of 86?
Answer: 40
Explanation:
100% = 86
x% = 34.4
100% = 86(1)
x% = 34.4(2)
100%/x% = 86/34.4
Taking the inverse of both sides
x%/100% = 34.4/86
x = 40%
Therefore, 34.4 is 40% of 86.
Display the data in a histogram.
Question 4.
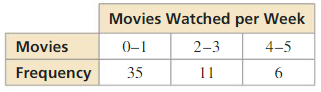
Answer:
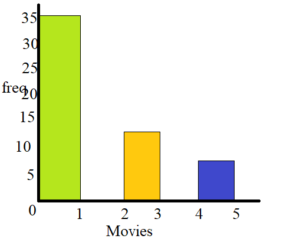
Question 5.
ABSTRACT REASONING
You want to purchase either a sofa or an arm chair at a furniture store. Each item has the same retail price. The sofa is 20% off. The arm chair is 10% off. and you have a coupon to get an additional 10% off the discounted price of the chair. Are the items equally priced after the discounts arc applied? Explain.
Answer: Yes
Explanation:
You want to purchase either a sofa or an armchair at a furniture store.
Each item has the same retail price. The sofa is 20% off. The armchair is 10% off. and you have a coupon to get an additional 10% off the discounted price of the chair.
The price of armchair and sofa are the same.
If you add 10% to chair the discount for the chair and sofa will be the same.
10% + 10% = 20%
Probability Monitoring Progress
In Exercises 1 and 2, describe the event as unlikely, equally likely to happen or not happen, or likely. Explain your reasoning.
Question 1.
The oldest child in a family is a girl.
Answer: equally likely to happen
Question 2.
The two oldest children in a family with three children are girls.
Answer: Unlikely
Question 3.
Give an example of an event that is certain to occur.
Answer:
If A and B are independent event
P(A) = 1/2
P(B) = 1/5
P(A and B) = P(A) × P(B)
= 1/2 × 1/5
= 1/10
12.1 Sample Spaces and Probability
Exploration 1
Finding the Sample Space of an Experiment
Work with a partner: In an experiment, three coins are flipped. List the possible outcomes in the sample space of the experiment.

Answer:
The number of different outcomes when three coins are tossed is 2 × 2 × 2 = 8.
All 8 possible outcomes are HHH, HHT, HTH, HTT, THH, THT, TTH and TTT.
Exploration 2
Finding the Sample Space of an Experiment
Work with a partner: List the possible outcomes in the sample space of the experiment.
a. One six-sided die is rolled.

Answer: 6 possible outcomes
b. Two six-sided die is rolled.

Answer:
Rolling two six-sided dice: Each die has 6 equally likely outcomes, so the sample space is 6 . 6 or 36 equally likely outcomes.
Exploration 3
Finding the Sample Space of an Experiment
Work with a partner: In an experiment, a spinner is spun.
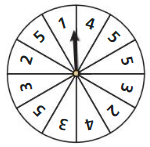
a. How many ways can you spin a 1? 2? 3? 4? 5?
Answer: 1, 2, 3, 2, 4
b. List the sample space.
Answer: 1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5
c. What is the total number of outcomes?
Answer: 12
Exploration 4
Finding the Sample Space of an Experiment
Work with a partner: In an experiment, a bag contains 2 blue marbles and 5 red marbles. Two marbles arc drawn from the bag.

a. How many ways can you choose two blue? a red then blue? a blue then red? two red?
Answer: BB – 2, RB – 10, BR – 10, RR – 20
b. List the sample space.
Answer:
c. What is the total number of outcomes?
Answer: 42
Communicate Your Answer
Question 5.
How can you list the possible outcomes in the sample space of an experiment?
Answer:
There are four possible outcomes for each spin: red, blue, yellow, green. Then, multiply the number of outcomes by the number of spins. June flipped the coin three times. The answer is there are 12 outcomes in the sample space.
Question 6.
For Exploration 3, find the ratio of the number of each possible outcome to the total number of outcomes. Then find the sum of these ratios. Repeat for Exploration 4. What do you observe?
LOOKING FOR A PATTERN
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
Number 1 could be spun in 1 way, out of a total of 12 ways
r1 = 1/12
Number 2 could be spun in 2 way, out of a total of 12 ways
r2 = 2/12
Number 3 could be spun in 3 way, out of a total of 12 ways
r3 = 3/12
Number 4 could be spun in 2 way, out of a total of 12 ways
r4 = 2/12
Number 5 could be spun in 4 way, out of a total of 12 ways
r5 = 4/12
The sum of the ratios r1, r2, r3, r4 and r5 is
1/12 + 2/12 + 3/12 + 2/12 + 4/12 = 1
Two red balls can be drawn in 20 ways, out of a total of 42 ways
rBB = 20/42
Red then Blue can be drawn in 10 ways, out of a total of 42 ways
rRB = 10/42
Blue then Red can be drawn in 10 ways, out of a total of 42 ways
rRB = 10/42
Two Red balls can be drawn in 2 ways, out of a total of 42 ways
rRR = 2/42
20/42 + 10/42 + 10/42 + 2/42 = 1
Thus the sum of both explorations are same.
Lesson 12.1 Sample Spaces and Probability
Monitoring Progress
Find the number of possible outcomes in the sample space. Then list the possible outcomes.
Question 1.
You flip two coins.
Answer: 4
Explanation:
When we flip two coins simultaneoulsy then the possible outcomes will be (H, H), (T, T), (T, H), (H, T)
where H represents heads
T represents tails.
Thus the possible outcomes are 2² = 4
Question 2.
You flip two Coins and roll a six-sided die.
Answer: 6 × 2² = 24
Explanation:
We roll a die and flip two coins. We have to find the number of possible outcomes in this space. Also we have to list the possible outcomes.
1 = {When rolling the dice, the number 1 fell};
2 = {When rolling the dice, the number 2 fell};
3 = {When rolling the dice, the number 3 fell};
4 = {When rolling the dice, the number 4 fell};
5 = {When rolling the dice, the number 5 fell};
6 = {When rolling the dice, the number 6 fell};
On the other hand, using H for Heads and T for Tails we can list the outcomes.
(1, H, H), (2, H, H), (3, H, H), (4, H, H), (5, H, H), (6, H, H)
(1, T, H), (2, T, H), (3, T, H), (4, T, H), (5, T, H), (6, T, H)
(1, H, T), (2, H, T), (3, H, T), (4, H, T), (5, H, T), (6, H, T)
(1, T, T), (2, T, T), (3, T, T), (4, T, T), (5, T, T), (6, T, T)
Therefore, we can conclude that the number of all possible outcomes is
6 × 2² = 24
Question 3.
You flip a coin and roll a six-sided die. What is the probability that the coin shows tails and the die shows 4?
Answer:
The sample space has 12 possible outcomes.
Heads, 1
Heads, 2
Heads, 3
Heads, 4
Heads, 5
Heads, 6
Tails, 1
Tails, 2
Tails, 3
Tails, 4
Tails, 5
Tails, 6
Probability that the coin shows tails and the die shows 4 is 4/12 = 1/3
Find P(\(\bar{A}\)).
Question 4.
P(A) = 0.45
Answer:
P(\(\bar{A}\)) = 1 – P(A)
P(A) = 0.45
P(\(\bar{A}\)) = 1 – 0.45
P(\(\bar{A}\)) = 0.55
Question 5.
P(A) = \(\frac{1}{4}\)
Answer:
P(\(\bar{A}\)) = 1 – P(A)
P(A) = \(\frac{1}{4}\)
P(\(\bar{A}\)) = 1 – \(\frac{1}{4}\)
P(\(\bar{A}\)) = \(\frac{3}{4}\)
Question 6.
P(A) = 1
Answer:
P(\(\bar{A}\)) = 1 – P(A)
P(A) = 1
P(\(\bar{A}\)) = 1 – 1
P(\(\bar{A}\)) = 0
Question 7.
P(A) = 0.03
Answer:
P(\(\bar{A}\)) = 1 – P(A)
P(A) = 0.03
P(\(\bar{A}\)) = 1 – 0.03
P(\(\bar{A}\)) = 0.97
Question 8.
In Example 4, are you more likely to get 10 points or 5 points?
Answer:
10: 0.09
5: (5 – 10)/324
= (36π – 9π)/324
= 27π/324
= 0.26
Question 9.
In Example 4, are you more likely to score points (10, 5, or 2) or get 0 points?
Answer:
2: (2 – 5)/324
= (81π – 36π)/324
= 45π/324
= 0.43
0.09 + 0.26 + 0.43 = 0.78
More likely to get 2 points.
Question 10.
In Example 5, for which color is the experimental probability of stopping on the color greater than the theoretical probability?
Answer:
9/20 = 0.45
Question 11.
In Example 6, what is the probability that a pet-owning adult chosen at random owns a fish?
Answer:
146/1328 = 73/664 = 0.11
Exercise 12.1 Sample Spaces and Probability
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A number that describes the likelihood of an event is the ___________ of the event.
Answer:
A number that describes the likelihood of an event is the probability of the event.
Question 2.
WRITING
Describe the difference between theoretical probability and experimental probability.
Answer: Experimental probability is the result of an experiment. Theoretical probability is what is expected to happen.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6. find the number of possible outcomes in the sample space. Then list the possible outcomes.
Question 3.
You roll a die and flip three coins.
Answer:
![]()

Question 4.
You flip a coin and draw a marble at random from a hag containing two purple marbles and one while marble.
Answer:
Given data,
You flip a coin and draw a marble at random from a hag containing two purple marbles and one while marble.
the probability of getting a purple marble = 2/3
the probability of getting a white marble = 1/3
Question 5.
A bag contains four red cards numbered 1 through 4, four white cards numbered 1 through 4, and four black cards numbered 1 through 4. You choose a card at random.
Answer:

Question 6.
You draw two marbles without replacement from a bag containing three green marbles and four black marbles.
Answer:
In all there are 7 marbles when you first grab a marble, after that you take one marble away then you have 6 marbles to choose.
7 × 6 = 42
42 possible outcomes: GG, GG, GB, GB, GB, GB, GG, GG, GB, GB, GB, GB, GG, GG, GB, GB, GB, GB, BG, BG, BG, BB, BB, BB, BG, BG, BG, BB, BB, BB, BG, BG, BG, BB, BB, BB, BG, BG, BG, BB, BB, BB, BB.
Question 7.
PROBLEM SOLVING
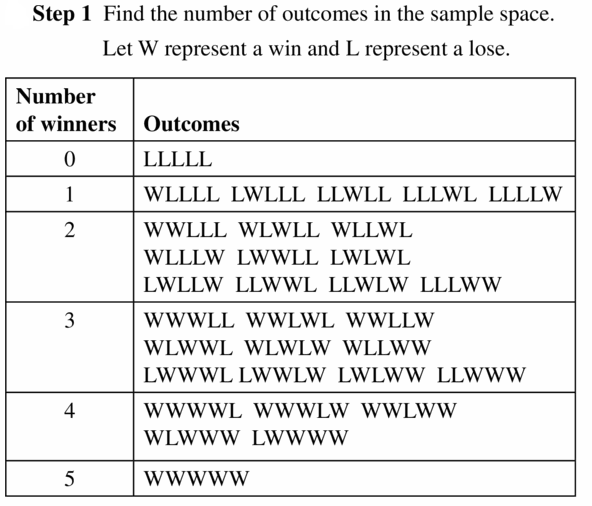
A game show airs on television five days per week. Each day, a prize is randomly placed behind one of two doors. The contestant wins the prize by selecting the correct door. What is the probability that exactly two of the five contestants win a prize during a week?

Answer:

Question 8.
PROBLEM SOLVING
Your friend has two standard decks of 52 playing cards and asks you to randomly draw one card from each deck. What is the probability that you will draw two spades?
Answer:
You have two decks of 52 cards and in a normal deck, there are 13 cards of each suit.
So there are 13 spades in the deck.
Therefore the probability of you drawing a spade is 13 out of all the 52 cards or \(\frac{13}{52}\), which can be reduced to \(\frac{1}{4}\). You do this two times with different decks that are exactly the same so you multiply \(\frac{1}{4}\) times \(\frac{1}{4}\). 1 times 1 is 1 and 4 times 4 is 16, so it is \(\frac{1}{16}\).
You can turn this into a percentage by dividing 1 by 16 and moving the decimal place to places to the right.
6.25% is the probability that you will draw two spades.
Question 9.
PROBLEM SOLVING
When two six-sided dice are rolled, there are 36 possible outcomes. Find the probability that
(a) the sum is not 4 and
(b) the sum is greater than 5.
Answer:

Question 10.
PROBLEM SOLVING
The age distribution of a population is shown. Find the probability of each event.
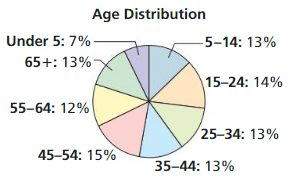
a. A person chosen at random is at least 15 years old.
Answer: 80%
b. A person chosen at random is from 25 to 44 years old.
Answer: 13% + 13% = 26%
Question 11.
ERROR ANALYSIS
A student randomly, guesses the answers to two true-false questions. Describe and correct the error in finding the probability of the student guessing both answers correctly.

Answer:

Question 12.
ERROR ANALYSIS
A student randomly draws a number between 1 and 30. Describe and correct the error in finding the probability that the number drawn is greater than 4.

Answer:
The error is that the probability of the complement of the event is 4/30, not 3/30, because if you are looking for a sum greater than 4, than you subtract 1 by numbers less than or equal to 4 by the total amount of numbers, which is 30.
P(Sum is greater than 4)=1-P(Sum is less than or equal to 4)
1 – 2/15
= 13/15
Question 13.
MATHEMATICAL CONNECTIONS
You throw a dart at the board shown. Your dart is equally likely to hit any point inside the square board. What is the probability your dart lands in the yellow region?

Answer:

Question 14.
MATHEMATICAL CONNECTIONS
The map shows the length (in miles) of shoreline along the Gulf of Mexico for each state that borders the body of water. What is the probability that a ship coming ashore at a random point in the Gulf of Mexico lands in the given state?
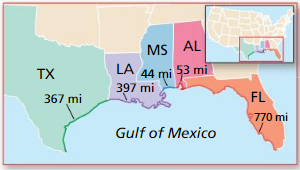
a. Texas
Answer:
By using the above map we can solve the problem
Total length of the shoreline: 367 + 397 + 44 + 53 + 770 = 1631 miles
The probability of the ship landing in Texas: 367/1631 = 0.23
b. Alabama
Answer:
The probability of the ship landing in Alabama: 53/1631 = 0.03
c. Florida
Answer:
The probability of the ship landing in Florida: 770/1631 = 0.47
d. Louisiana
Answer:
The probability of the ship landing in Louisiana: 397/1631 = 0.24
Question 15.
DRAWING CONCLUSIONS
You roll a six-sided die 60 times. The table shows the results. For which number is the experimental probability of rolling the number the same as the theoretical probability?
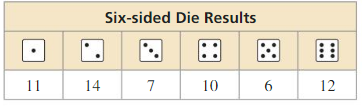
Answer:

Question 16.
DRAWING CONCLUSIONS
A bag contains 5 marbles that are each a different color. A marble is drawn, its color is recorded, and then the marble is placed back in the hag. This process is repeated until 30 marbles have been drawn. The table shows the results. For which marble is the experimental probability of drawing the marble the same as the theoretical probability?
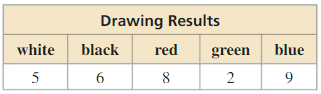
Answer:
Total number of marbles = 30
6/30 = 1/5
For black marble the experimental probability of drawing the marble the same as the theoretical probability.
Question 17.
REASONING
Refer to the spinner shown. The spinner is divided into sections with the same area.
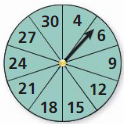
a. What is the theoretical probability that the spinner stops on a multiple of 3?
b. You spin the spinner 30 times. If stops on a multiple of 3 twenty times. What is the experimental probability of Stopping on a multiple of 3?
c. Explain why the probability you found in part (b) is different than the probability you found in part (a).
Answer:
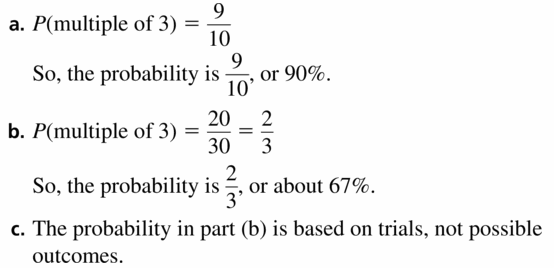
Question 18.
OPEN-ENDED
Describe a real-life event that has a probability of 0. Then describe a real-life event that has a probability of 1.
Answer:
The probability of rolling a 7 with a standard 6-sided die = 0
The probability of rolling a natural number with a standard 6-sided die = 1
Question 19.
DRAWING CONCLUSIONS
A survey of 2237 adults ages 18 and over asked which Sport 15 their favorite. The results are shown in the figure. What is the probability that an adult chosen at random prefers auto racing?
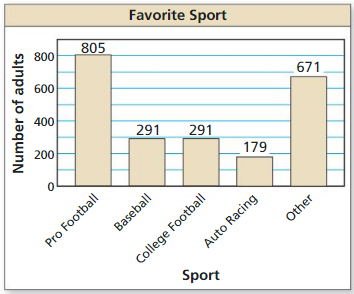
Answer:

Question 20.
DRAWING CONCLUSIONS
A survey of 2392 adults ages 18 and over asked what type of food they Would be most likely to choose at a restaurant. The results are shown in the figure. What is the probability that an adult chosen at random prefers Italian food?
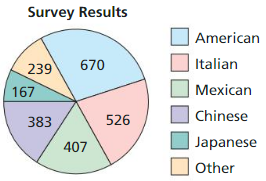
Answer:
P(Italian) = 526/1196
= 263/1196
P(Italian) ≈ 22%
Question 21.
ANALYZING RELATIONSHIPS
Refer to the board in Exercise 13. Order the likelihoods that the dart lands in the given region from least likely to most likely.
A. green
B. not blue
C. red
D. not yellow
Answer:


Question 22.
ANALYZING RELATIONSHIPS
Refer to the chart below. Order the following events from least likely to most likely.

A. It rains on Sunday.
Answer:
80%
= 80/20 = 4/1
The ratio is 4:1
B. It does not rain on Saturday.
Answer:
100 – 30 = 70%
= 30/70 = 3 : 7
C. It rains on Monday.
Answer: 90%
= 90/10 = 9/1
= 9 : 1
D. It does not rain on Friday.
Answer:
100 – 5 = 95%
= 5/95 = 1/19
= 1 : 19
Question 23.
USING TOOLS
Use the figure in Example 3 to answer each question.
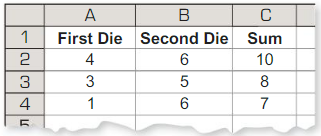
a. List the possible sums that result from rolling two six-sided dice.
b. Find the theoretical probability of rolling each sum.
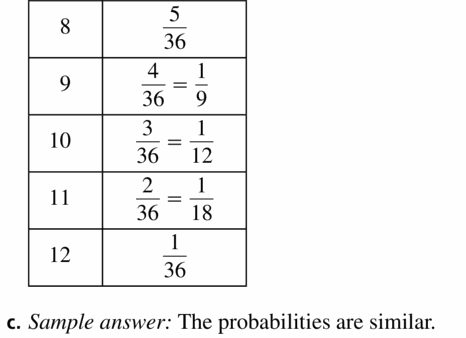
c. The table below shows a simulation of rolling two six-sided dice three times. Use a random number generator to simulate rolling two six-sided dice 50 times. Compare the experimental probabilities of rolling each sum with the theoretical probabilities.
Answer:

Question 24.
MAKING AN ARGUMENT
You flip a coin three times. It lands on heads twice and on tails once. Your friend concludes that the theoretical probability of the coin landing heads up is P(heads up) = \(\frac{2}{3}\). Is your friend correct? Explain your reasoning.
Answer:
The friend is incorrect because the probability of heads here is \(\frac{2}{3}\), is the experimental probabiility of heads for this particular case, while its theoretical probability will always be \(\frac{1}{2}\).
Question 25.
MATHEMATICAL CONNECTIONS
A sphere fits inside a cube so that it touches each side, as shown. What is the probability a point chosen at random inside the cube is also inside the sphere ?
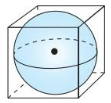
Answer:
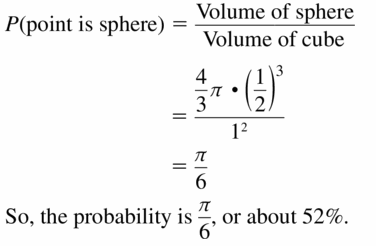
Question 26.
HOW DO YOU SEE IT?
Consider the graph of f shown. What is the probability that the graph of y = f(x) + c intersects the x-axis when c is a randomly chosen integer from 1 to 6? Explain.
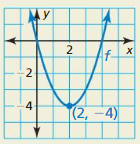
Answer:
Given that y=f(x)+c intersect x- axis
Explanation
The graph will intersect the x-axis if c is either 1,2,3, or 4, These are 4 events out of six, therefore the possible is 4/6 = 2/3
Question 27.
DRAWING CONCLUSIONS
A manufacturer tests 1200 computers and finds that 9 of them have defects. Find the probability that a computer chosen at random has a defect. Predict the number of computers with defects in a shipment of 15,000 computers. Explain your reasoning.
Answer:
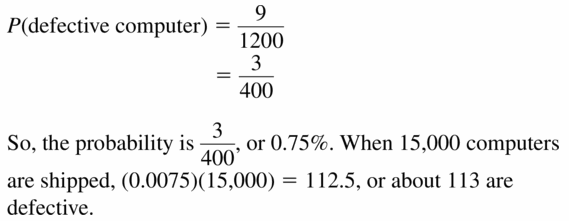
Question 28.
THOUGHT PROVOKING
The tree diagram shows a sample space. Write a probability problem that can be represented by the sample space. Then write the answer(s) to the problem.
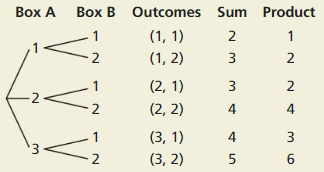
Answer:
Maintaining Mathematical Proficiency
Simplify the expression. Write your answer using only positive exponents.
Question 29.
\(\frac{2 x^{3}}{x^{2}}\)
Answer:
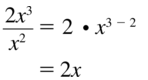
Question 30.
\(\frac{2 x y}{8 y^{2}}\)
Answer:
\(\frac{2y}{8 y^{2}}\)
= \(\frac{2}{8y}\)
= \(\frac{1}{4y}\)
Question 31.
\(\frac{4 x^{9} y}{3 x^{3} y}\)
Answer:
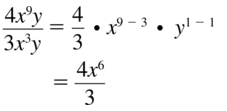
Question 32.
\(\frac{6 y^{0}}{3 x^{-6}}\)
Answer:
Given,
\(\frac{6 y^{0}}{3 x^{-6}}\)
= 6 . 1/3x-6
= 2 . x6
Question 33.
(3Pq)4
Answer:
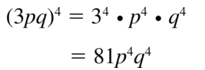
Question 34.
\(\left(\frac{y^{2}}{x}\right)^{-2}\)
Answer: (\(\frac{y}{x}\))²
12.2 Independent and Dependent Events
Exploration 1
Identifying Independent and Dependent Events
Work with a partner: Determine whether the events are independent or dependent. Explain your reasoning.
REASONING ABSTRACTLY
To be proficient in math, you need to make sense of quantities and their relationships in problem situations.
a. Two six-sided dice are rolled.

Answer:
P = Number of outcomes that satisfy the requirements/Total number of possible outcomes
Probability for rolling two dice with the six sided dots such as 1, 2, 3, 4, 5 and 6 dots in each die.
When two dice are thrown simultaneously, thus the number of event can be 62 = 36 because each die has 1 to 6 number on its faces.
This is independent event
b. Six pieces of paper, numbered 1 through 6, are in a bag, Two pieces of paper are selected one at a time without replacement.

Answer:
P = Number of outcomes that satisfy the requirements/Total number of possible outcomes
When we pick up any paper the probability result is equal of 1/6
This is dependent event
Exploration 2
Work with a partner:
a. In Exploration 1(a), experimentally estimate the probability that the sum of the two numbers rolled is 7. Describe your experiment.
Answer:
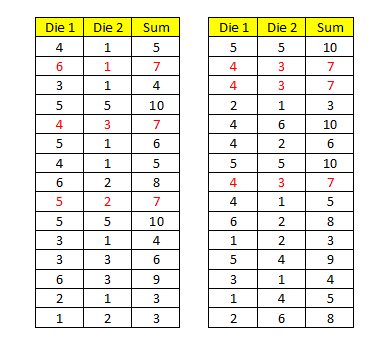
The experimental probability that the sum of two number rolled is 7
P(sum = 7) = 3/30 = 1/10 = 10%
(b). In Exploration 1 (b), experimentally estimate the probability that the sum of the two numbers selected is 7. Describe your experiment.
Answer:
One possible experiment is, that the numbers 1 to 6, were written on pieces of paper and placed in a box or container. One event means selecting a number followed by another, and add them. I tried the experiment 30 times and the results are listed below.
| Paper 1 | Paper 2 | Sum |
| 1 | 2 | 3 |
| 1 | 3 | 4 |
| 1 | 4 | 5 |
| 1 | 5 | 6 |
| 1 | 6 | 7 |
| 2 | 1 | 3 |
| 2 | 3 | 5 |
| 2 | 4 | 6 |
| 2 | 5 | 7 |
| 2 | 6 | 8 |
| 3 | 1 | 4 |
| 3 | 2 | 5 |
| 3 | 4 | 7 |
| 3 | 5 | 8 |
| 3 | 6 | 9 |
| 4 | 1 | 5 |
| 4 | 2 | 6 |
| 4 | 3 | 7 |
| 4 | 5 | 9 |
| 4 | 6 | 10 |
| 5 | 1 | 6 |
| 5 | 2 | 7 |
| 5 | 3 | 8 |
| 5 | 4 | 9 |
| 5 | 6 | 11 |
| 6 | 1 | 7 |
| 6 | 2 | 8 |
| 6 | 3 | 9 |
| 6 | 4 | 10 |
| 6 | 5 | 11 |
The experimental probability that the sum of the two numbers selected is 7,
P(Sum = 7) = 6/30 = 1/5 = 20%
Exploration 3
Finding Theoretical Probabilities
Work with a partner:
a. In Exploration 1(a), find the theoretical probability that the sum of the two numbers rolled is 7. Then compare your answer with the experimental probability you found in Exploration 2(a).
b. In Exploration 1(b). find the theoretical probability that the sum of the two numbers selected is 7. Then compare your answer with the experimental probability you found in Exploration 2(b).
C. Compare the probabilities you obtained in parts (a) and (b).
Answer:
For each of the possible outcomes add the numbers on the two dice and count how many times this sum is 7. If you do so you will find that the sum is 7 for 6 of the possible outcomes. Thus the sum is a 7 in 6 of the 36 outcomes and hence the probability of rolling a 7 is 6/36 = 1/6.
Communicate Your Answer
Question 4.
How can you determine whether two events are independent or dependent?
Answer:
Two events A and B are said to be independent if the fact that one event has occurred does not affect the probability that the other event will occur.
If whether or not one event occurs does affect the probability that the other event will occur, then the two events are said to be dependent.
Question 5.
Determine whether the events are independent or dependent. Explain your reasoning.
a. You roil a 4 on a six-sided die and spin red on a spinner.
Answer: Independent
b. Your teacher chooses a student to lead a group. chooses another student to lead a second group. and chooses a third student to lead a third group.
Answer: Dependent
Lesson 12.2 Independent and Dependent Events
Monitoring progress
Question 1.
In Example 1, determine whether guessing Question 1 incorrectly and guessing Question 2 correctly are independent events.
Answer:
In example 1 it makes sense that the events are independent because the second guess should not affected by the first guess.
Question 2.
In Example 2, determine whether randomly selecting a girl first and randomly selecting a boy second are independent events.
Answer:
In example 2, the selection of the second person depends on the selection of the first person because the same person cannot be selected twice.
Question 3.
In Example 3, what is the probability that you spin an even number and then an odd number?
Answer:
Let be A be “5 on first spin” and B be greater than 3 on second spin.
Total outcomes = 8
P(even number) = 4/8 = 1/2
P(odd number) = 4/8 = 1/2
P(E and O) = P(E) . P(O) = 1/2 × 1/2 = 1/4
Question 4.
In Example 4, what is the probability that both hills are $1 hills?
Answer:
Question 5.
In Example 5, what is the probability that none of the cards drawn are hearts when (a) you replace each card, and (b) you do not replace each card? Compare the probabilities.
Answer:
(a) you replace each card,
P(A and B and C) = P(A) P(B) P(C)
= 13/52 . 13/52 . 13/52 = 1/4 . 1/4 . 1/4 = 1/64 = 0.016
Question 6.
In Example 6, find (a) the probability that a non-defective part “passes” and (b) the probability that a defective part “fails.”
Answer:
(a) the probability that a non-defective part “passes”
P(P/D) = 3/39 = 1/13 = 0.077
(b) the probability that a defective part “fails.”
P(F/N) = 11/461 = 0.024
Question 7.
At a coffee shop. 80% of customers order coffee. Only 15% of customers order coffee and a bagel. What is the probability that a customer who orders coffee also orders a bagel?
Answer:
A: Customer order coffee
B: Customer order a bagel
P(B/A) = P(A and B)/P(A)
80% of customers order coffee and Only 15% of customers order coffee and a bagel.
P(A) = 80/100 = 0.8
P(A and B) = 15/100 = 0.15
P(B/A) = P(A and B)/P(A) = 0.15/0.8 = 0.1875 = 18.75%
Exercise 12.2 Independent and Dependent Events
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain the difference between dependent events and independent events, and give an example of each.
Answer:
When two events are dependent, the occurrence of one event affects the other. When two events are independent, the occurrence of one event does not affect the other.
Question 2.
COMPLETE THE SENTENCE
The probability that event B will occur given that event A has occurred is called the _____________ of B given A and is written as _____________ .
Answer:
The probability that event B will occur given that event A has occurred is called the conditional probability of B given A and is written as P(B/A).
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, tell whether the events are independent or dependent. Explain your reasoning.
Question 3.
A box of granola bars contains an assortment of flavors. You randomly choose a granola bar and eat it. Then you randomly choose another bar.
Event A: You choose a coconut almond bar first.
Event B: You choose a cranberry almond bar second.
Answer:
The two events, which considered in this experiment are an example of dependent events.
Question 4.
You roll a six-sided die and flip a coin.
Event A: You get a 4 when rolling the die.
Event B: You get tails when flipping the coin

Answer: Independent, the events do not influence each other.
Question 5.
Your MP3 player contains hip-hop and rock songs. You randomly choose a song. Then you randomly choose another song without repeating song choices.
Event A: You choose a hip-hop song first.
Event B: You choose a rock song second.

Answer:
The events are dependent because the occurrence of event A affects the occurrence of event B.
Question 6.
There are 22 novels of various genres on a shell. You randomly choose a novel and put it back. Then you randomly choose another novel.
Event A: You choose a mystery novel.
Event B: You choose a science fiction novel.
Answer:
The 1st book chosen is put back so the second book picked has the same probability of being chosen a if the 1st book was never chosen to begin with the events are independent.
In Exercises 7 – 10. determine whether the events are independent.
Question 7.
You play a game that involves spinning a wheel. Each section of the wheel shown has the same area. Use a sample space to determine whether randomly spinning blue and then green are independent events.
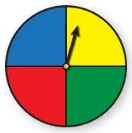
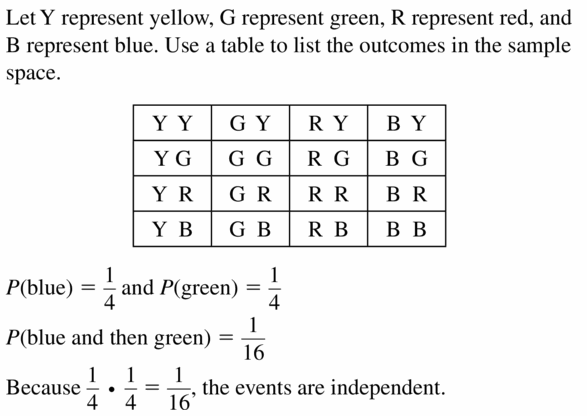
Answer:
Question 8.
You have one red apple and three green apples in a bowl. You randomly select one apple to eat now and another apple for your lunch. Use a sample space to determine whether randomly selecting a green apple first and randomly selecting a green apple second are independent events.
Answer:
Let R represent the red apple.
Let G1, G2, G3 represent the 3 green apples.
P(G first) = P(green apple first) = 9/12 = 3/4 = 0.75
P(G second) = P(green apple second) = 9/12 = 3/4 = 0.75
P(green apple first and second) = 6/12 = 1/2 = 0.5
Events are not independent.
Question 9.
A student is taking a multiple-choice test where each question has four choices. The student randomly guesses the answers to the five-question test. Use a sample space to determine whether guessing Question 1 correctly and Question 2 correctly are independent events.
Answer:

Question 10.
A vase contains four white roses and one red rose. You randomly select two roses to take home. Use a sample space to determine whether randomly selecting a white rose first and randomly selecting a white rose second are independent events.
Answer:
P(A and B) = P(A) and P(B)
A = {First randomly selected roses is white}
B = {Second randomly selected roses is white}
P(A) = Number of favorable outcomes/Total number of outcomes = 4/5
P(B) = 4/5
P(A) . P(B) = 4/5 . 4/5 = 16/25
Question 11.
PROBLEM SOLVING
You play a game that involves spinning the money wheel shown. You spin the wheel twice. Find the probability that you get more than $500 on your first spin and then go bankrupt on your second spin.

Answer:

Question 12.
PROBLEM SOLVING
You play a game that involves drawing two numbers from a hat. There are 25 pieces of paper numbered from 1 to 25 in the hat. Each number is replaced after it is drawn. Find the probability that you will draw the 3 on your first draw and a number greater than 10 on your second draw.
Answer:
P(A) = 1/25
P(B) = 15/25
P(A and B) = P(A) . P(B)
= 1/25 . 15/25 = 3/125
Thus P(A and B) = 3/125
Question 13.
PROBLEM SOLVING
A drawer contains 12 white socks and 8 black socks. You randomly choose 1 sock and do not replace it. Then you randomly choose another sock. Find the probability that both events A and B will occur.
Event A: The first sock is white.
Event B: The second sock is white.
Answer:

Question 14.
PROBLEM SOLVING
A word game has 100 tiles. 98 of which are letters and 2 of which are blank. The numbers of tiles of each letter are shown. You randomly draw 1 tile, set it aside, and then randomly draw another tile. Find the probability that both events A and B will occur.

Answer:
P(A) = 56/100 = 0.56
P(B) = 42/(100 – 1) = 0.424
P(A) . P(B) = 0.56 × 0.424 = 0.2376
Question 15.
ERROR ANALYSIS
Events A and B are independent. Describe and correct the error in finding P(A and B).
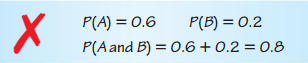
Answer:
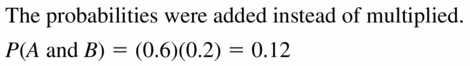
Question 16.
ERROR ANALYSIS
A shelf contains 3 fashion magazines and 4 health magazines. You randomly choose one to read, set it aside, and randomly choose another for your friend to read. Describe and correct the error in finding the probability that both events A and B occur.
Event A: The first magazine is fashion.
Event B: The second magazine is health.
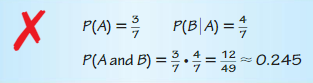
Answer:
P(A) = 3/7
P(B/A) = 4/(7 – 1) = 4/6
P(A and B) = P(A) × P(B/A)
P(A and B) = 3/7 × 4/6 = 2/7
Question 17.
NUMBER SENSE
Events A and B are independent. Suppose P(B) = 0.4 and P(A and B) = 0.13. Find P(A).
Answer:
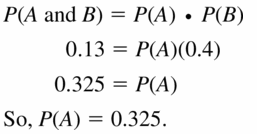
Question 18.
NUMBER SENSE
Events A and B are dependent. Suppose P(B/A) = 0.6 and P(A and B) = 0.15. Find P(A).
Answer:
P(A) = x
P(B/A) = 0.6
P(A and B) = 0.15
P(A and B) = P(A) × P(B/A)
0.15 = x × 0.6
x = 0.15/0.6
x = 0.25
Question 19.
ANALYZING RELATIONSHIPS
You randomly select three cards from a standard deck of 52 playing cards. What is the probability that all three cards are face cards when (a) you replace each card before selecting the next card, and (b) you do not replace each card before selecting the next card? Compare the probabilities.
Answer:

Question 20.
A bag contains 9 red marbles. 4 blue marbles, and 7 yellow marbles. You randomly select three marbles from the hag. what is the probability that all three marbles are red when (a) you replace each marble before selecting the next marble, and (b) you do not replace each marble before selecting the next marble? Compare the probabilities.
Answer:
a. There are a total of 9 + 4 + 7= 20 marbles.
Therefore, the probability of selecting a red marble in each attempt is 9/20 when the marble is replaced.
Therefore the probability of selecting a red marble in each of 3 of the attempt is
9/20 × 9/20 × 9/20 = 0.09125
The replacement makes these independent events.
b. There are total of 9 + 4 + 7 = 20 marbles.
The probability of selecting a red marble in the first attempt is 9/20, second attempt is 8/19 and the third attempt is 7/18 when the marbles are not replaced.
Therefore the probability of selecting a red marble in each of 3 of the attempts is 9/20 × 8/19 × 7/18 = 0.0737
Question 21.
ATTEND TO PRECISION
The table shows the number of species in the United States listed as endangered and threatened. Find (a) the probability that a randomly selected endangered species is a bird, and (b) the probability that a randomly selected mammal is endangered.
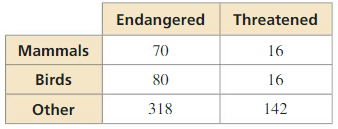
Answer:

Question 22.
ATTEND TO PRECISION
The table shows the number of tropical cyclones that formed during the hurricane seasons over a 12-year period. Find (a) the probability to predict whether a Future tropical cyclone in the Northern Hemisphere is a hurricane, and (b) the probability to predict whether a hurricane is in the Southern Hemisphere.
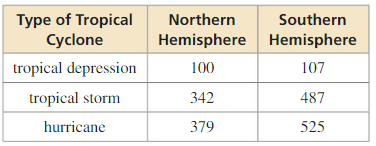
Answer:
a. Norther hemisphere = 100 + 342 + 379 = 821
P = Hurricane/northern hemisphere = 379/821
b. Southern hemisphere = 107 + 487 + 525 = 904
P = Hurricane/southern hemisphere = 525/904
Question 23.
PROBLEM SOLVING
At a school, 43% of students attend the homecoming football game. Only 23% of students go to the game and the homecoming dance. What is the probability that a student who attends the football game also attends the dance?
Answer:

Question 24.
PROBLEM SOLVING
At a gas station. 84% of customers buy gasoline. Only 5% of customers buy gasoline and a beverage. What is the probability that a customer who buys gasoline also buys a beverage?
Answer:
Given,
P(A) = 84% = 0.84
P(A and B) = 5% = 0.05
P(A and B) = P(A) × P(B/A)
P(B/A) = 0.05/0.84
P(B/A) = 0.0595
Question 25.
PROBLEM SOLVING
You and 19 other students volunteer to present the “Best Teacher” award at a school banquet. One student volunteer will be chosen to present the award. Each student worked at least 1 hour in preparation for the banquet. You worked for 4 hours, and the group worked a combined total of 45 hours. For each situation, describe a process that gives you a “fair” chance to be chosen. and find the probability that you are chosen.
a. “Fair” means equally likely.
b. “Fair” means proportional to the number of hours each student worked in preparation.
Answer:

Question 26.
HOW DO YOU SEE IT?
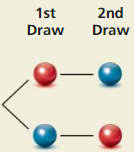
A bag contains one red marble and one blue marble. The diagrams show the possible outcomes of randomly choosing two marbles using different methods. For each method. determine whether the marbles were selected with or without replacement.
a.
Answer:
It is given that a bag contains one red marble and one blue marble. The diagrams show the possible outcomes of randomly choosing two marbles using different methods.
As per the diagram, we observe that
If firstly red marble is drawn randomly, then we get blue marble on the 2nd draw.
Blue marble is drawn randomly, then we get red marble on the 2nd draw.
That means after choosing red marble we then get the blue marble only.
After choosing blue marble we then get the red marble only.
It means that red marble was not put back in the bag after getting selected.
Blue marble was not put back in the bag after getting selected.
b.
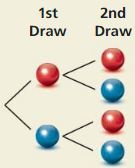
Answer:
We have to determine whether the marbles were selected with or without replacement, for each method.
“Without replacement ” means that you don’t put the ball or balls back in the box so that the number of balls in the box gets less as each ball is removed.
“With replacement ” means that you put the ball or balls back in the box.
According to the diagram, we can see that
If firstly, red marble is drawn randomly, then we get either red marble or blue marble on the 2nd draw.
If firstly, blue marble is drawn randomly, then we get also get either red marble or blue marble on the 2nd draw.
That means, after choosing red marble, we then get any of the marbles, either red or blue.
And, after choosing blue marble, we then also get any of the marbles, either red or blue.
That means red marble was put back in the bag after getting selected.
Similarly, blue marble was put back in the bag after getting selected.
This shows that marbles were selected “With Replacement” in each method.
Question 27.
MAKING AN ARGUMENT
A meteorologist claims that there is a 70% chance of rain. When it rains. there is a 75% chance that your softball game will be rescheduled. Your friend believes the game is more likely to be rescheduled than played. Is your friend correct? Explain your reasoning.
Answer:
The chance that the game will be rescheduled is (0.7)(0.75) = 0.525
which is 52.5 percent
making it greater than 50 percent.
Question 28.
THOUGHT PROVOKING
Two six-sided dice are rolled once. Events A and B are represented by the diagram. Describe each event. Are the two events dependent or independent? Justify your reasoning.
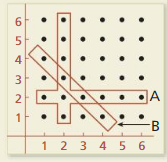
Answer:
Event A: “Two dice are rolled, and number 2 is on one of them”.
Event B: “Two dice are rolled, and the sum of the numbers on them is 5 “.
Events A and B are independent if and only if
P(A and B) =P(A) . P(B)
There are 11 favorable outcomes for event A out of total 36 outcomes so the probability is
P(A) = 11/36
There are 4 favorable outcomes for event B out of 36 outcimes
P(B) = 1/9
There are 2 favorable outcomes for event A and B out of 36 outcomes
P(A and B) = 1/18
P(A and B) = 1/18, P(A) = 11/36
P(B) = 1/9
1/18 = 11/36 × 1/9
1/18 ≠ 11/324
So, the equality is false so the events are dependent.
Question 29.
MODELING WITH MATHEMATICS
A football team is losing by 14 points near the end of a game. The team scores two touchdowns (worth 6 points each) before the end of the game. After each touchdown, the coach must decide whether to go for 1 point with a kick (which is successful 99% of the time) or 2 points with a run or pass (which is successful 45% of the time).

a. If the team goes for 1 point after each touchdown, what is the probability that the team wins? loses? ties?
b. If the team goes for 2 points after each touchdown. what is the probability that the team wins? loses? ties?
c. Can you develop a strategy so that the coach’s team has a probability of winning the game that is greater than the probability of losing? If so, explain your strategy and calculate the probabilities of winning and losing the game.
Answer:

Question 30.
ABSTRACT REASONING
Assume that A and B are independent events.
a. Explain why P(B) = P(B/A) and P(A) = P(A/B).
Answer:
P(B) = P(B/A)
P(B) = P(A) . P(B/A)
P(A) = P(A/B).
P(A) = P(B) . P(A/B)
b. Can P(A and B) also be defined as P(B) • P(A/B)? Justify your reasoning.
Answer:
P(A/B) = P(A)
P(A and B) = P(A) . P(B) = P(B) . P(A/B)
So, yes P(A and B) = P(B) . P(A/B)
Maintaining Mathematical Proficiency
Solve the equation. Check your solution.
Question 31.
\(\frac{9}{10}\) x = 0.18
Answer:

Question 32.
\(\frac{1}{4}\)x + 0.5x = 1.5
Answer:
Given,
\(\frac{1}{4}\)x + 0.5x = 1.5
0.25x + 0.50x = 1.5
0.75x = 1.5
x = 1.5/0.75
x = 2
Question 33.
0.3x – \(\frac{3}{5}\)x + 1.6 = 1.555
Answer:
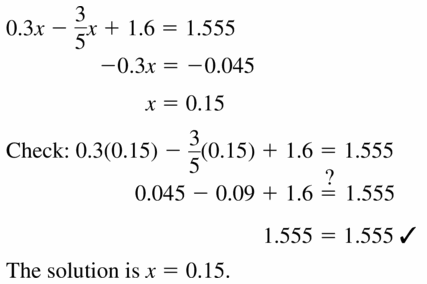
12.3 Two-Way Tables and Probability
Exploration 1
Completing and Using a Two-Way Table
Work with a partner: A two-way table displays the same information as a Venn diagram. In a two-way table, one category is represented by the rows and the other category is represented by the columns.
The Venn diagram shows the results of a survey in which 80 students were asked whether they play a musical instrument and whether they speak a foreign language. Use the Venn diagram to complete the two-way table. Then use the two-way table to answer each question.

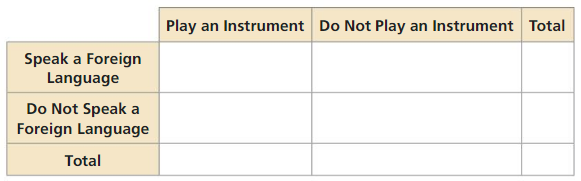
a. How many students play an instrument?
Answer: 41
b. How many students speak a foreign language?
Answer: 46
c. How many students play an instrument and speak a foreign language?
Answer: 16
d. How many students do not play an instrument and do not speak a foreign language?
Answer: 9
e. How many students play an instrument and do not speak a foreign language?
Answer: 25
Exploration 2
Two – Way Tables and Probability
Work with a partner. In Exploration 1, one student is selected at random from the 80 students who took the survey. Find the probability that the student
a. plays an instrument.
Answer: 41/80
b. speaks a foreign language.
Answer: 46/80
c. plays an instrument and speaks a foreign language.
Answer: 16/80
d. does not play an instrument and does not speak a foreign language.
Answer: 9/80
e. plays an instrument and does not speak a foreign language.
Answer:
P = number of students plays an instrument and not speak a foreign language/number of students
P = 25/80 = 5/16
Exploration 3
Conducting a Survey
Work with your class. Conduct a survey of the students in your class. Choose two categories that are different from those given in Explorations 1 and 2. Then summarize the results in both a Venn diagram and a two-way table. Discuss the results.
MODELING WITH MATHEMATICS
To be proficient in math, you need to identify important quantities in a practical situation and map their relationships using such tools as diagrams and two-way tables.
Answer:
On conducting survey of 50 students whether they like mathematics and whether they like history.
Out of 50 students, 12 students like math, 10 students like history, 16 students like both and 12 sudents neither like math nor history.
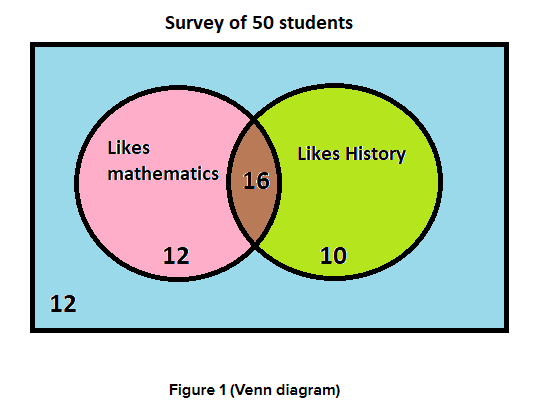
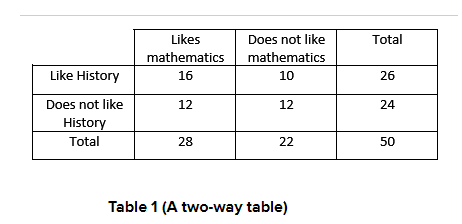
Now the Venn diagram and two-way table interpret that out of 50 students surveyed, 28 students like maths 22 does not like maths, 26 students like history and 24 do not like history.
Communicate Your Answer
Question 4.
How can you construct and interpret a two-way table?
Answer:
Identify the variables. There are two variables of interest here: the commercial viewed and opinion.
Determine the possible values of each variable. For the two variables, we can identify the following possible values
Set up the table
Fill in the frequencies
Question 5.
How can you use a two-way table to determine probabilities?
Answer:
- Count how many possible outcomes the first event has.
- Count how many possible outcomes the second event has.
- Draw a table with the appropriate number of rows and columns.
- Label the columns
- Label the rows.
Lesson 12.3 Two-Way Tables and Probability
Monitoring Progress
Question 1.
You randomly survey students about whether they are in favor of planting a community garden at school. of 96 boys surveyed, 61 are in favor. 0f 88 girls surveyed, 17 are against. Organize the results in a two-way table. Then find and interpret the marginal frequencies.
Answer:
In order to find out how many boys are against you do 96 – 61. In order to find out how many girls are in favor you do 88 – 17.
In order to find the probability you make a proportion. It will be:
P/100 = number of girls against/total number of students
17/184 = p/100
17 × 100 = 184p
1700 = 184p
p = 9.23
Question 2.
Use the survey results in Monitoring Progress Question 1 to make a two-way table that shows the joint and marginal relative frequencies.
Answer:
Given,
Total boys = 96
Number of boys favored in survey = 61
Total girls = 88
Number of girls against for survey = 17
| Favor | No. | Total | |
| Girls | 71/184 = 0.39 | 17/184 = 0.09 | 0.48 |
| Boys | 61/184 = 0.33 | 35/184 = 0.19 | 0.52 |
| Total | 0.72 | 0.28 | 1 |
Question 3.
Use the survey results in Example 1 to make a two-way table that shows the conditional relative frequencies based on the column totals. Interpret the conditional relative frequencies in the context of the problem.
Answer:
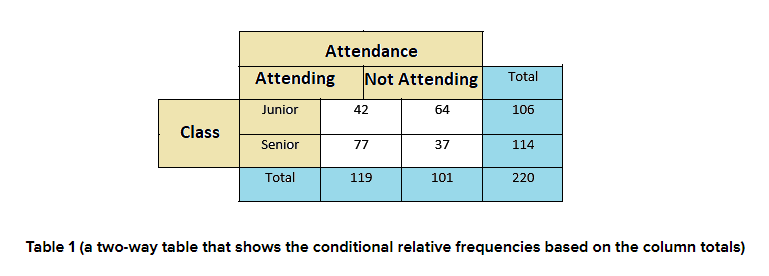
Now we will find the joint relative frequencies. By dividing each frequency by 220 because the total number of juniors and seniors are 220.
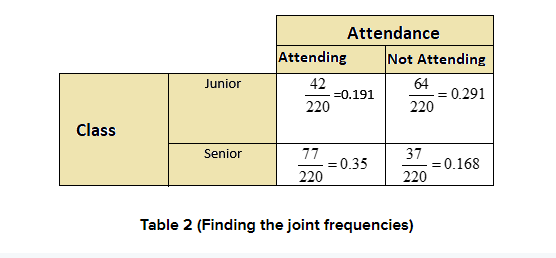
Find the marginal relative frequencies
It is given by the sum of each row and each column.
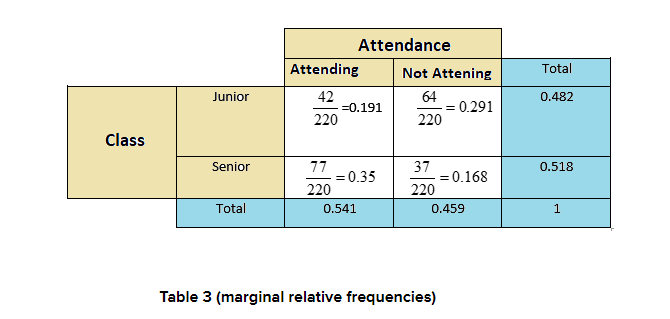
Question 4.
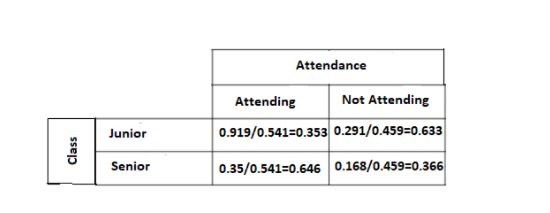
Use the survey results in Monitoring Progress Question 1 to make a two-way table that shows the conditional relative frequencies based on the row totals. Interpret the conditional relative frequencies in the context of the problem.
Answer:
We have to create a two-way table that shows the conditional relative frequencies based on the row totals.
Joint relative frequency is the ratio of the frequency in a particular category and the total number of data values.
Marginal relative frequency is the ratio of the sum of the joint frequency in a row or column and the total number of data values.
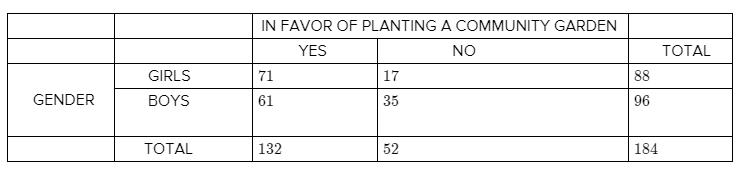
Divide each joint frequency by the grand total to obtain the joint relative frequencies.
We will divide each marginal frequency by the grand total to obtain the marginal relative frequencies.
| GENDER | IN FAVOR OF PLANTING A COMMUNITY GARDEN | |||
| YES | NO | TOTAL | ||
| GIRLS | 71/184 = 0.386 | 17/184 = 0.092 | 88/184 = 0.478 | |
| BOYS | 61/184 = 0.332 | 35/184 = 0.19 | 96/184 = 0.522 | |
| TOTAL | 132/184 = 0.717 | 52/184 = 0.283 | 184/184 = 1 | |
Question 5.
In Example 4, what is the probability that a randomly selected customer who is located in Santa Monica will not recommend the provider to a friend?
Answer:
Given that a satellite provider does a survey of customers in three cities and asks whether they would recommend it to a friend. The given two-way table gives joint relative frequencies.
Calculate the probability that the customer is located in Santa Monica
P(Customer located in Santa Monica) = 0.03 + 0.27
P(Customer located in Santa Monica) = 0.30
Calculate the probability that the customers in Santa Monica a No.
P(Santa Monica and customers in Santa Monica respond No) = 0.03
P(Customer in Santa Monica respond No| Customer located in Santa Monica) = P(Customer located in Santa Monica and Customer responding No)/P(Customer located in Santa Monica)
= 0.03/(0.03+0.27)
= 0.03/0.3 = 0.1
The probability that a randomly selected customer living in Santa Monica will not recommend the provider to a friend is about 10%.
Question 6.
In Example 4, determine whether recommending the provider to a friend and living in Santa Monica are independent events. Explain your reasoning.
Answer:

Question 7.
A manager is assessing three employees in order to offer one of them a promotion. Over a period of time, the manager records whether the employees meet or exceed expectations on their assigned tasks. The table shows the managers results. Which employee should be offered the promotion? Explain.
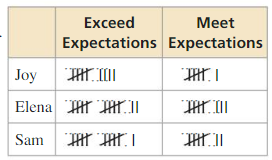
Answer:

Exercise 12.3 Two-Way Tables and Probability
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A(n) ______________ displays data collected from the same source that belongs to two different categories.
Answer:
A two-way table displays data collected from the same source that belongs to two different categories.
Question 2.
WRITING
Compare the definitions of joint relative frequency, marginal relative frequency, and conditional relative frequency.
Answer:
Joint relative frequency: joint relative frequency is the ratio of a frequency that is not in the total row or the total column to the total number of values.
Marginal relative frequency: marginal relative frequency is the sum of the joint relative frequencies in a given row or column.
Conditional relative frequency: It is the ratio of joint relative frequency to the marginal relative frequency.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, complete the two-way table.
Question 3.
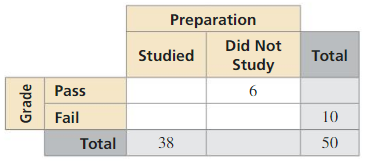
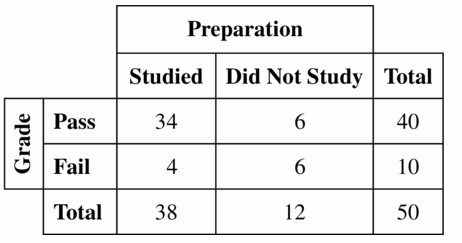
Answer:
Number of students who have passed the exam is 50 – 10 = 40
Of those 40 students, 6 did not study for the exam,
Number of the students who studied and have passed the exam is 40 – 6 = 34
Number of the students who did not study and did not pass the exam is 10 – 4 = 6
Question 4.
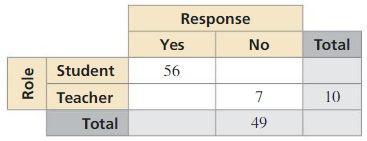
Answer:
Number of students who said no is 49 – 7 = 42
Total number of students is 56 + 42 = 98
Total number of people is 98 + 10 = 108
Out of the total number of people, 49 of them said no,
Total number of people who said yes is 108 – 49 = 59
Number of teachers who said yes is 59 – 56 = 3
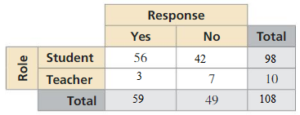
Question 5.
MODELING WITH MATHEMATICS
You survey 171 males and 180 females at Grand Central Station in New York City. Of those, 132 males and 151 females wash their hands after using the public rest rooms. Organize these results in a two-way table. Then find and interpret the marginal frequencies.

Answer:


Question 6.
MODELING WITH MATHEMATICS
A survey asks 60 teachers and 48 parents whether school uniforms reduce distractions in school. Of those, 49 teachers and 18 parents say uniforms reduce distractions in school, Organize these results in a two-way table. Then find and interpret the marginal frequencies.
Answer:
Given,
A survey asks 60 teachers and 48 parents whether school uniforms reduce distractions in school. Of those, 49 teachers and 18 parents say uniforms reduce distractions in school
Number of teacher who said no is 60 – 49 = 11
Number of parents who said no = 48 – 18 = 30
Total number of people who said yes = 49 + 18 = 67
Total number of people who said no = 11 + 30 = 41
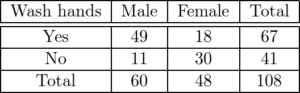
USING STRUCTURE
In Exercises 7 and 8, use the two-way table to create a two-way table that shows the joint and marginal relative frequencies.
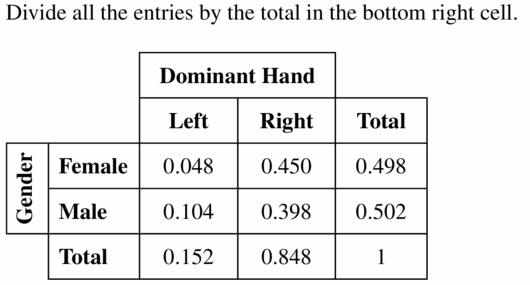
Question 7.
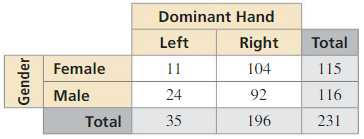
Answer:
P1,1 = Number of favorable outcomes/Total number of outcomes
= 11/231 = 0.0476
P2,1 = 24/231 = 0.1039
P1,2 = 104/231 = 0.4502
P2,2 = 92/231 = 0.3983
The marginal relative frequencies we find as the sum of each row and each column.
P(A randomly chosen person is male) = 115/231 = 0.4978
P(A randomly chosen person is female) = 116/231 = 0.5022
P(A randomly chosen person have left dominant hand) = 35/231 = 0.1515
P(A randomly chosen person have left dominant hand) = 196/231 = 0.8484
Question 8.
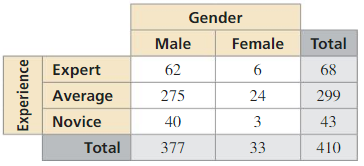
Answer:
P1,1 = Number of favorable outcomes/Total number of outcomes
= 62/410 = 0.1513
The marginal relative frequencies we find as the sum of each row and each column.
P(A randomly chosen person is male) = 377/410 = 0.9195
P(A randomly chosen person is female) = 33/410 = 0.0805
Question 9.
MODELING WITH MATHEMATICS
Use the survey results from Exercise 5 to make a two-way table that shows the joint and marginal relative frequencies.
Answer:
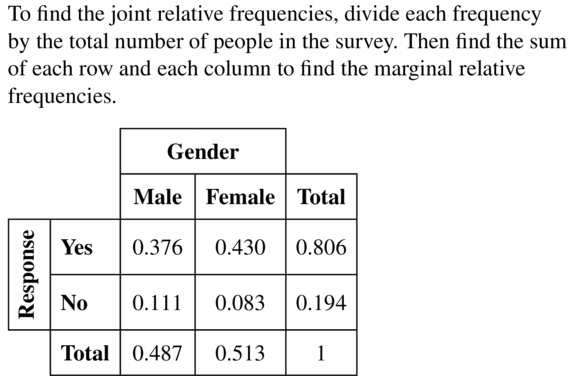
Question 10.
MODELING WITH MATHEMATICS
In a survey, 49 people received a flu vaccine before the flu season and 63 people did not receive the vaccine. Of those who receive the flu vaccine, 16 people got the flu. Of those who did not receive the vaccine, 17 got the flu. Make a two-way table that shows the joint and marginal relative frequencies.
Answer:
We see that the total no. of people who received the vaccine is 49, of which 16 got a fly.
Number of people who received the vaccine and did not get a fly is 49 – 16 = 33
Number of people who did not received the vaccine and did not get a fly is 63 – 17 = 46
Total number of people who got a fly is 16 + 17 = 33
Total Number of people who did not get a fly is 33 + 46 = 79
We also know that the total number of people who were surveyed is 49 + 63 = 112
P1,1 = Number of favorable outcomes/Total number of outcomes
= 16/112 = 0.1428
The marginal relative frequencies we find as the sum of each row and each column.
P(A randomly chosen person got a fly) = 33/112 = 0.2946
P(A randomly chosen person did not get a fly) = 79/112 = 0.7053
Question 11.
MODELING WITH MATHEMATICS
A survey finds that 110 people ate breakfast and 30 people skipped breakfast. Of those who ate breakfast. 10 people felt tired. Of those who skipped breakfast. 10 people felt tired. Make a two-way table that shows the conditional relative frequencies based on the breakfast totals.
Answer:
Given,
A survey finds that 110 people ate breakfast and 30 people skipped breakfast.
Of those who ate breakfast. 10 people felt tired. Of those who skipped breakfast. 10 people felt tired.
Number of people who ate breakfast and not tired is 110 – 10 = 100
Number of people who did not eat breakfast and not tired is 30 – 10 = 20
Total number of people who felt tired is 10 + 10 = 20
Total number of people who did not get tired is 100 + 20 = 120
120 +20 = 140
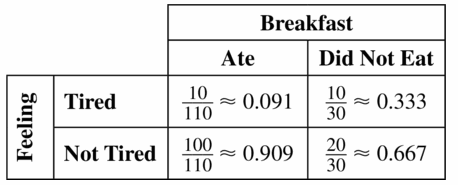
Question 12.
MODELING WITH MATHEMATICS
Use the survey results from Exercise 10 to make a two-way table that shows the conditional relative frequencies based on the flu vaccine totals.
Answer:
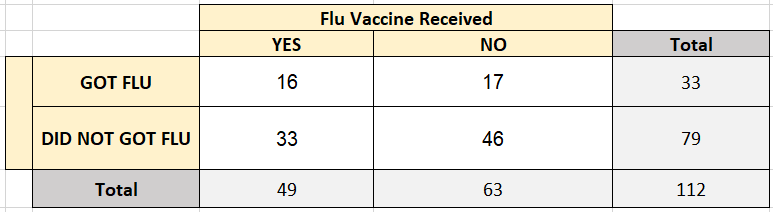
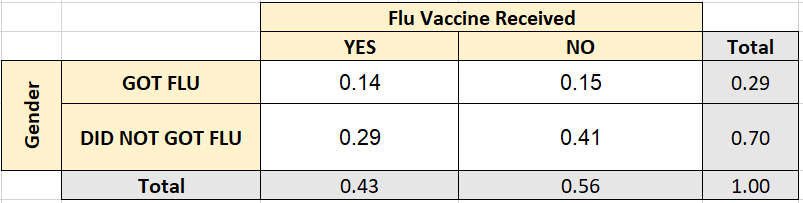
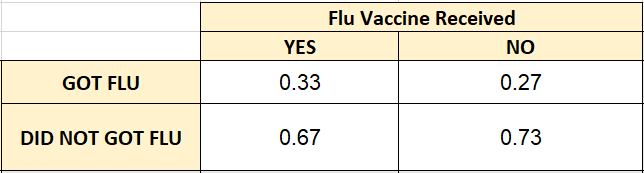
Question 13.
PROBLEM SOLVING
Three different local hospitals in New York surveyed their patients. The survey asked whether the patients physician communicated efficiently. The results, given as joint relative frequencies. are shown in the two-way table.
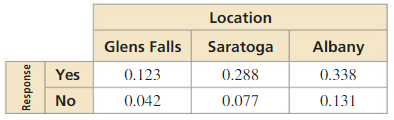
a. What is the probability that a randomly selected patient located in Saratoga was satisfied with the communication of the physician?
b. What is the probability that a randomly selected patient who was not satisfied with the physician’s communication is located in Glens Falls?
c. Determine whether being satisfied with the Communication of the physician and living in Saratoga are independent events.
Answer:

Question 14.
PROBLEM SOLVING
A researcher surveys a random sample of high school students in seven states. The survey asks whether students plan to stay in their home state after graduation. The results, given as joint relative frequencies, are shown in the two-way table.
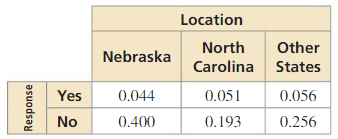
a. What is the probability that a randomly selected student who lives in Nebraska plans to stay in his or her home state after graduation?
Answer:
In this case we consider a event A = {arandomly chosen student lives in Nebraska}
B = {a randomly chosen student plans to stay in his or her home state after graduation}
P(A) = 0.044 + 0.4 = 0.444
P(B/A) = P(A and B)/P(A) = 0.044/0.444 = 0.099
About 1% students who lives Nebraska plans to stay in his or her home state after graduation.
b. What is the probability that a randomly selected student who does not plan to stay in his or her home state after graduation lives in North Carolina?
Answer:
C = {a randomly chosen student does not plan to stay in his or her home state after graduation}
D = {a randomly chosen student lives in North Carolina}
P(C) = 0.4 + 0.193 + 0.256 = 0.849
P(D/C) = P(C and D)/P(C)
= 0.193/0.849 = 0.227
Therefore about 22.7% students who does not plan to stay in his or her home state after graduation lives in North Carolina.
c. Determine whether planning to stay in their home state and living in Nebraska are independent events.
Answer:
P(B/A) = 0.099
P(B) = 0.044 + 0.05
1 + 0.056 = 0.151
P(B/A) ≠ P(B)
This events are independent.
ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error in finding the given conditional probability.
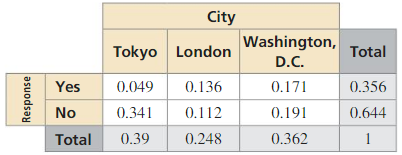
Question 15.
P(yes|Tokyo)
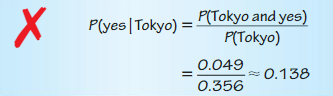
Answer:
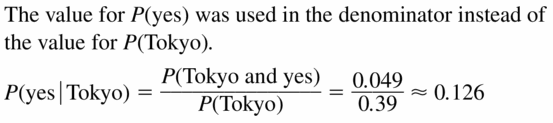
Question 16.
P(London|No)
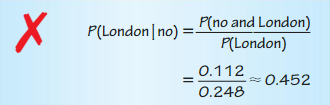
Answer:
P(A and B) = P(A)P(B/A)
P(A) = 0.341 + 0.112+ 0.191 = 0.644
P(B/A) = P(A and B)/P(A) = 0.112/0.644 = 0.1739
In the denominator the probability P(B) = 0.248 is used instead of P(A), where P(B) is probability that a randomly chosen person live in London.
Question 17.
PROBLEM SOLVING
You want to find the quickest route to school. You map out three routes. Before school, you randomly select a route and record whether you are late or on time. The table shows your findings. Assuming you leave at the same time each morning, which route should you use? Explain.
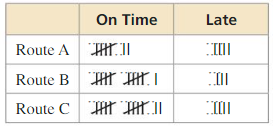
Answer:
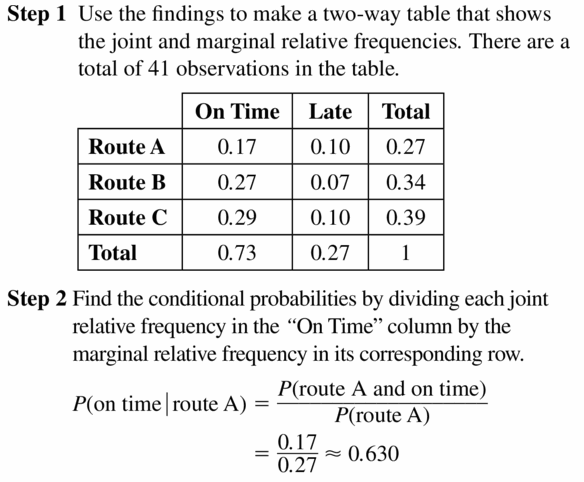

Question 18.
PROBLEM SOLVING
A teacher is assessing three groups of students in order to offer one group a prize. Over a period of time, the teacher records whether the groups meet or exceed expectations on their assigned tasks. The table shows the teacher’s results. Which group should be awarded the prize? Explain.
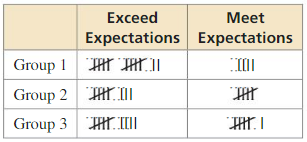
Answer: Group 1 exceeded expectations 12 out of 16 times or 75% of the time.
Question 19.
OPEN-ENDED
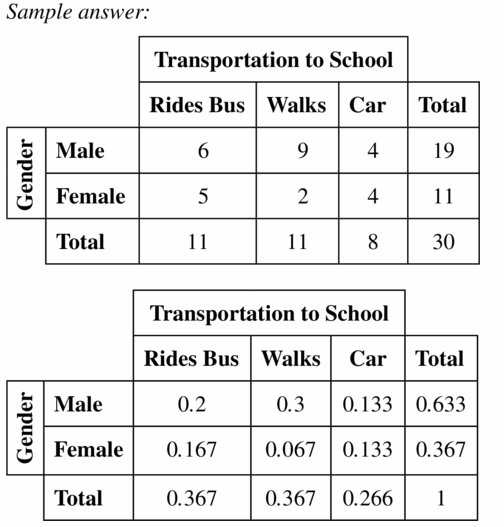
Create and conduct a survey in your class. Organize the results in a two-way table. Then create a two-way table that shows the joint and marginal frequencies.
Answer:
Question 20.
HOW DO YOU SEE IT?
A research group surveys parents and Coaches of high school students about whether competitive sports are important in school. The two-way table shows the results of the survey.
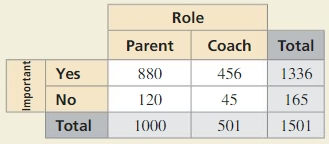
a. What does 120 represent?
Answer: 120 parents said that competitive sports are not important in school.
b. What does 1336 represent?
Answer: 1336 is the sum of parents and coaches who agree that competitive sports are important in school.
c. What does 1501 represent?
Answer: 1501 is the total number of people surveyed. Here is the sum of the parents and the coaches who participated in the survey.
Question 21.
MAKING AN ARGUMENT
Your friend uses the table below to determine which workout routine is the best. Your friend decides that Routine B is the best option because it has the fewest tally marks in the “Docs Not Reach Goal” column. Is your friend correct? Explain your reasoning.

Answer:

Question 22.
MODELING WITH MATHEMATICS
A survey asks students whether they prefer math class or science class. Of the 150 male students surveyed, 62% prefer math class over science class. Of the female students surveyed, 74% prefer math. Construct a two-way table to show the number of students in each category if 350 students were surveyed.
Answer:
The survey asks students whether they prefer math class or science class. Of the 150 male students surveyed, 62% prefer math class over science class.
62% = 0.62
0.62 = P(Math/Male)
= P(Math and Male)/P(Male)
= Number of male students who prefer math/150
Number of male students who prefer math = 0.62 × 150 = 93
0.74 = P(Math/Female)
= P(Math and Female)/P(Female)
= Number of female students who prefer math/200
Number of female students who prefer math = 0.74 × 200 = 148
So, the total number of students who prefer math class is 148 + 93 = 241
Number of male students who prefer science class = 150 -93 = 57
Number of female students who prefer science class = 200 – 148 = 52
Number of students who prefer science class = 57 + 52 = 109
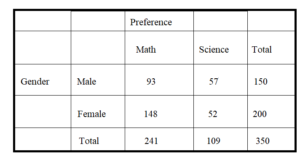
Question 23.
MULTIPLE REPRESENTATIONS
Use the Venn diagram to construct a two-way table. Then use your table to answer the questions.
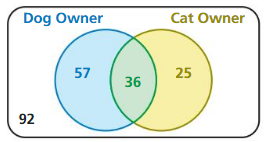
a. What is the probability that a randomly selected person does not own either pet?
b. What is the probability that a randomly selected person who owns a dog also owns a cat?
Answer:
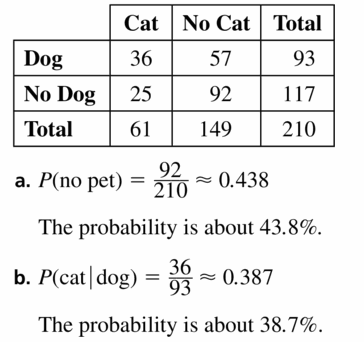
Question 24.
WRITING
Compare two-way tables and Venn diagrams. Then describe the advantages and disadvantages of each.
Answer:
To compare two-way tables and Venn diagrams.
A two-way table is a frequency table that displays data collected from one source that belongs to two different categories. One category of data is represented by rows and the other is represented by columns.
A venn diagram is an illustration that uses a circle to show the relationships among things or finite groups of things. Circle that overlaps do not share those traits.
The difference between two way tables and venn diagrams is that two-way tables have two different categories while venn diagrams have only one category.
Advantages and disadvantages of two-way table
→ Helpful to discover the overlap between two different categories.
→ But there cannot be overlap in the same category. If one category has the option of yes and no, a member cannot be the part of yes group and no group simultaneously.
Advantages and disadvantages of venn diagram
→ Venn diagrams are helpful when discovering overlap within the same category.
→ Only one category of data is represented by venn diagram.
Question 25.
PROBLEM SOLVING
A company creates a new snack, N, and tests it against its current leader, L. The table shows the results.
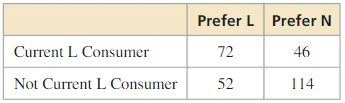
The company is deciding whether it should try to improve the snack before marketing it, and to whom the snack should be marketed. Use probability to explain the decisions the company should make when the total size of the snack’s market is expected to (a) change very little, and (b) expand very rapidly.
Answer:

Question 26.
THOUGHT PROVOKING
Baye’s Theorem is given by
![]()
Use a two-way table to write an example of Baye’s Theorem.
Answer:
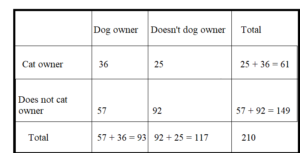
P(Cat owner) = 61/210 = 0.29
P(Dog owner) = 93/210 = 0.442
P(Cat Owner/Dog owner) = P(Dog owner and cat owner)/P(Dog owner) = 0.387
P(Dog owner/Cat owner) = P(Cat owner/Dog owner)P(Dog owner)/P(Cat owner)
= 0.387 × 0.442/0.29
= 0.5898
Maintaining Mathematical Proficiency
Draw a Venn diagram of the sets described.
Question 27.
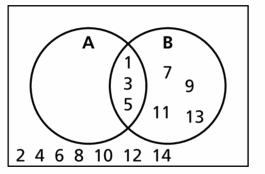
Of the positive integers less than 15, set A consists of the factors of 15 and set B consists of all odd numbers.
Answer:
Question 28.
Of the positive integers less than 14, set A consists of all prime numbers and set B consists of all even numbers.
Answer:
Set A = {2. 3, 5, 7, 11, 13}
Set B = {2, 4, 6, 8, 10, 12}
It can be seen that here A and B are overlapping sets.
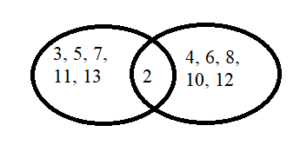
Question 29.
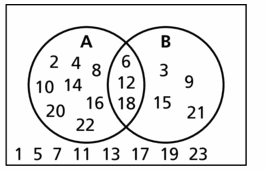
Of the positive integers less than 24, set A consists of the multiples of 2 and set B consists of all the multiples of 3.
Answer:
12.1 – 12.3 Quiz
Question 1.
You randomly draw a marble out of a bag containing 8 green marbles, 4 blue marbles 12 yellow marbles, and 10 red marbles. Find the probability of drawing a marble that is not yellow.
Answer:
Given,
You randomly draw a marble out of a bag containing 8 green marbles, 4 blue marbles 12 yellow marbles, and 10 red marbles.
Total number of outcomes here are 8 + 4 + 12 + 10 = 34
Thus the probability of obtaining a marble that is not yellow is (8 + 4 + 10)/34
= 22/34
= 11/17
= 0.647
= 64.7%
Thus the probability of obtaining a marble that is not yellow is 64.7%
Find P(\(\)(\bar{A}))
Question 2.
P(A) = 0.32
Answer:
P(\(\)(\bar{A}) = 1 – P(A)
1 – 0.32
= 0.68
P(\(\)(\bar{A}) = 0.68
Question 3.
P(A) = \(\frac{8}{9}\)
Answer:
P(\(\)(\bar{A}) = 1 – P(A)
1 – \(\frac{8}{9}\)
= \(\frac{1}{9}\)
P(\(\)(\bar{A}) = \(\frac{1}{9}\)
Question 4.
P(A) = 0.01
Answer:
P(\(\)(\bar{A}) = 1 – P(A)
1 – 0.01 = 0.99
Question 5.
You roll a six-sided die 30 times. A 5 is rolled 8 times. What is the theoretical probability of rolling a 5? What is the experimental probability of rolling a 5?
Answer:
Given,
You roll a six-sided die 30 times. A 5 is rolled 8 times.
The theoretical probability of rolling a 5 on a number cube is \(\frac{1}{6}\) while the experimental probability of rolling a 5 on a number cube is \(\frac{8}{30}\) = \(\frac{4}{15}\)
Question 6.
Events A and B are independent. Find the missing probability.
P(A) = 0.25
P(B) = ____
P(A and B) = 0.05
Answer:
Given,
P(A) = 0.25
P(A and B) = 0.05
P(A and B) = P(A) × P(B)
P(B) = P(A and B)/P(A)
P(B) = 0.05/0.25 = 0.2
P(B) = 0.2
Question 7.
Events A and B are dependent. Find the missing probability.
P(A) = 0.6
P(B/A) = 0.2
P(A and B) = ____
Answer:
Given,
P(A) = 0.6
P(B/A) = 0.2
P(A and B) = P(A) × P(B/A)
P(A and B) = 0.6 × 0.2
= 0.12
P(A and B) = 0.12
Question 8.
Find the probability that a dart thrown at the circular target Shown will hit the given region.
Assume the dart is equally likely to hit any point inside the target.
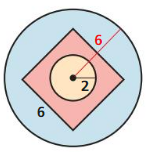
a. the center circle
Answer:
Total area of the given region is π × r² = π × 6² = 36π = 113.112 sq. units
Area of the center circle is π × r² = π × 2² = 4π sq. units.
Therefore the probability of hitting the center circle is 4π/36π = 1/9 = 0.11…
b. outside the square
Answer:
Area of the square is 6² = 36
So the region outside of it is equal to 36π – 36 = 77.112 sq. units
Thus the probability of hitting the region outside the square is 77.112/113.112 = 0.682
c. inside the square but outside the center circle
Answer:
Area of the center circle is π × r² = π × 2² = 4π sq. units.
Area of the square is 6² = 36
Thus the probability of hitting the region outside the center circle but inside the square is 36 – 4π = 23.432 sq. units
Thus the probability of hitting the region is 23.432/113.112 = 0.207
Question 9.
A survey asks 13-year-old and 15-year-old students about their eating habits. Four hundred students are surveyed, 100 male students and 100 female students from each age group. The bar graph shows the number of students who said they eat fruit every day.
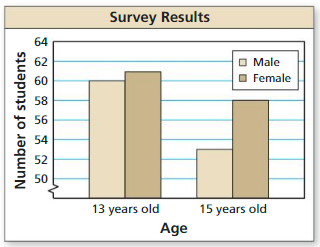
a. Find the probability that a female student, chosen at random from the students surveyed, eats fruit every day.
Answer:
Total number of females who eat a fruit everyday are 61 + 58 = 119
Therefore the probability of randomly choosing a female who eats a fruit everyday is 119/400= 0.2975
b. Find the probability that a 15 – year – old student. chosen at random from the students surveyed, eats fruit every day.
Answer:
Total number of 15 year old student who eat a fruit everyday are 53 + 58 = 111
Therefore the probability of randomly choosing a 15 year old student who eats a fruit everyday is 111/200 = 0.555
Question 10.
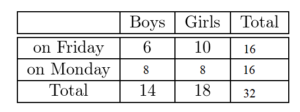
There are 14 boys and 18 girls in a class. The teacher allows the students to vote whether they want to take a test on Friday or on Monday. A total of 6 boys and 10 girls vote to take the test on Friday. Organize the information in a two-way table. Then find and interpret the marginal frequencies.
Answer:
Given,
There are 14 boys and 18 girls in a class. The teacher allows the students to vote whether they want to take a test on Friday or on Monday.
14 + 18 = 32
Number of boys who vote to take the test on Monday is 14 – 6 = 8
Number of girls who vote to take the test on monday is 18 – 10 = 8
A total of 6 boys and 10 girls vote to take the test on Friday.
The total number of students who take the test on Friday is 10 + 6 = 16
The total number of students who vote to take the test on Friday is 8 + 8 = 16
Question 11.
Three schools compete in a cross country invitational. Of the 15 athletes on your team. 9 achieve their goal times. Of the 20 athletes on the home team. 6 achieve their goal times. On your rival’s team, 8 of the 13 athletes achieve their goal times. Organize the information in a two-way table. Then determine the probability that a randomly elected runner who achieves his or her goal time is from your school.
Answer:
Three schools compete in a cross country invitational. Of the 15 athletes on your team. 9 achieve their goal times.
Number of runners in your team who do not achieve their goal team is 15 – 9 = 6
Number of runners in home team who do not achieve their goal team is 20 – 6 = 14
Number of runners in rival’s team who do not achieve their goal team is 13 – 8 = 5
Total number of runners who achieve their goal team is 9 + 6 + 8 = 23
Total number of runners who do not achieve their goal team is 6 + 14 + 5 = 25
The total number of rubbers who was surveyed is 23 + 25 = 48
P = Your team ans achieve their goal team/P(Archive their goal team)
P = 9/23
P = 0.39
12.4 Probability of Disjoint and Overlapping Events
Exploration 1
Work with a partner: A six-sided die is rolled. Draw a Venn diagram that relates the two events. Then decide whether the cents are disjoint or overlapping.
MODELING WITH MATHEMATICS
To be proficient in math, you need to map the relationships between important quantities in a practical situation using such tools as diagrams.

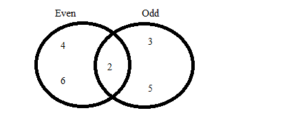
a. Event A: The result is an even number.
Event B: The result is a prime number.
Answer:
b. Event A: The result is 2 or 4.
Event B: The result is an odd number
Answer:
Exploration 2
Finding the Probability that Two Events Occur
Work with a partner: A six-sided die is roiled. For each pair of events. find (a) P(A), (b) P(B). (C) P(A) and (B). and (d) P(A or B).

a. Event A: The result is an even number.
Event B: The result is a Prime number.
Answer:
P(A) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P(B) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P(A or B) = P(A) + P(B) – P(A and B)
P(A and B) = \(\frac{1}{6}\)
P(A or B) = \(\frac{5}{6}\)
b. Event A: The result is 2 or 4.
Event B: The result is an odd number.
Answer:
P(A) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
P(B) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P(A or B) = P(A) + P(B) – P(A and B)
P(A and B) = 0
P(A or B) = \(\frac{5}{6}\)
Exploration 3
Discovering Probability Formulas
Work with a partner:
a. In general, if event A and event B arc disjoint, then what is the probability that event A or event B will occur? Use a Venn diagram to justify your conclusion.
Answer:
If event A and B are disjoint, there are no common outcomes.
So we add the probabilities that each event occurs:
P(A or B) = P(A) + P(B)
b. In general, if event A and event B are overlapping, then what is the probability that event A or event B will occur? Use a Venn diagram to justify your conclusion.
Answer:
If event A and event B are overlapping, there are common outcomes.
So, we add the probabilities that each event occurs then subtract the probability of the common outcomes.
P(A or B) = P(A) + P(B) – P(A and B)
c. Conduct an experiment using a six-sided die. Roll the die 50 times and record the results. Then use the results to find the probabilities described in Exploration 2. How closely do your experimental probabilities compare to the theoretical probabilities you found in Exploration 2?
Answer:
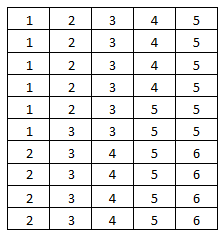
a. P(A) = \(\frac{1}{2}\) = 50%
P(A) = \(\frac{21}{50}\) = 42%
P(B) = \(\frac{1}{2}\) = 50%
P(B) = \(\frac{32}{50}\) = 64%
P(A and B) = \(\frac{1}{6}\) ≈ 16.7%
P(A and B) = \(\frac{9}{50}\) ≈ 18%
P(A or B) = \(\frac{5}{6}\) ≈ 83.3%
P(A or B) = \(\frac{44}{50}\) ≈ 88%
P(A) = \(\frac{1}{3}\) ≈ 33.3%
P(A) = \(\frac{17}{50}\) = 34%
P(B) = \(\frac{1}{2}\) = 50%
P(B) = \(\frac{29}{50}\) = 58%
P(A and B) = 0 = 0%
P(A and B) = \(\frac{0}{50}\) = 0%
P(A or B) = \(\frac{5}{6}\) ≈ 83.3%
P(A or B) = \(\frac{46}{50}\) = 92%
Communicate Your Answer
Question 4.
How can you find probabilities of disjoint and overlapping events?
Answer:
If A and B are disjoint events, then the probability of A or B is P(A or B) = P(A) + P(B). If two events A and B are overlapping, then the outcomes in the intersection of A and B are counted twice when P(A) and P(B) are added.
P(A or B) = P(A) + P(B) – P(A and B)
Question 5.
Give examples of disjoint events and overlapping events that do not involve dice.
Answer:
a. Event A: The result is an even number.
Event B: The result is a prime number.
Answer:

b. Event A: The result is 2 or 4.
Event B: The result is an odd number
Answer:

Lesson 12.4 Probability of Disjoint and Overlapping Events
Monitoring Progress
A card is randomly selected from a standard deck of 52 playing cards. Find the probability of the event.
Question 1.
selecting an ace or an 8
Answer:
A: Selecting an ace
B: You select 8
We know that A has 4 outcomes and B also has 4 outcomes.
P(A or B) = P(A) + P(B)
= 4/52 + 4/52
= 8/52
= 2/13 ≈ 0.15
Question 2.
selecting a 10 or a diamond
Answer:
A: Selecting a 10
B: You select diamond
P(A or B) = P(A) + P(B) – P(A and B)
= 4/52 + 13/52 – 1/52
= 16/52
= 4/13
Question 3.
WHAT IF?
In Example 3, suppose 32 seniors are in the band and 64 seniors are in the band or on the honor roll. What is the Probability that a randomly selected senior is both in the band and on the honor roll?
Answer:
Number of seniors = 200
Number of seniors in the band = 32
Number of seniors on the honor roll = 51
Number of seniors in the band or the honor roll = 64
Let us consider there are two events
A: Number of seniors in the band
B: Number of seniors in the honor roll
P(A or B) = P(A) + P(B) – P(A and B)
64/200 = 32/200 + 51/200 – P(A and B)
P(A and B) = 19/200
P(A and B) = 0.0095
Question 4.
In Example 4, what is the probability that the diagnosis is incorrect?
Answer:
Percentage of people who have diabetes = 8.3%
The test is 98% accurate for people who have a disease and 95% for people who do not have the disease.
P(X) = P(A)P(\(\bar{B}\)) + P(\(\bar{A}\))P(\(\bar{B}\))
P(X) = (0.083)(0.02) + (0.917)(0.05)
P(X) = 0.04751
So, the probability that the diagnosis is incorrect is 0.04751
Question 5.
A high school basketball team leads at halftime in 60% of the games in a season. The team wins 80% of the time when the have the halftime lead, but only 10% of the time when the do not. What is the probability that the team wins a particular game during the season?
Answer:
Given,
A high school basketball team leads at halftime in 60% of the games in a season. The team wins 80% of the time when the have the halftime lead, but only 10% of the time when the do not.
Let event A be team leads on the halftime and event B be win.
When A occurs, P(B) = 0.8
When A does not occur, P(B) = 0.1
P(B) = P(A and B) + P(\(\bar{A}\) and B)
P(A) . P(B | A) + P(\(\bar{A}\)) . P(B | \(\bar{A}\))
= 0.6 × 0.8 + 0.4 × 0.1
= 0.52
Exercise 12.4 Probability of Disjoint and Overlapping Events
Vocabulary and Core Concept Check
Question 1.
WRITING
Are the events A and \(\bar{A}\) disjoint? Explain. Then give an example of a real-life event and its complement.
Answer:
Yes A and \(\bar{A}\) are disjoint events because they are the complement of one another and so can not occur together and hence the name disjoint.
Example:
We flip a coin.
So, A = (the head fell)
\(\bar{A}\) = {the tail falls} are disjoint events.
Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
How many outcomes are in the intersection of A and B?
Answer: There are 2 outcomes in the intersection of A and B.
How many outcomes are shared by both A and B?
Answer: 2 outcomes are shared by both A and B.
How many outcomes are in the union of A and B?
Answer: There are 4 + 2 + 3 = 9 outcomes in the union of A and B.
How many outcomes in B are also in A?
Answer: There are 2 outcomes in B that are also in A.
Monitoring progress and Modeling with Mathematics
In Exercises 3 – 6, events A and B are disjoint. Find P(A or B)
Question 3.
p(A) = 0.3, P(B) = 0.1
Answer:
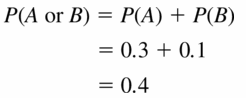
Question 4.
p(A) = 0.55, P(B) = 0.2
Answer:
Given,
p(A) = 0.55, P(B) = 0.2
P(A or B) = P(A) + P(B)
P(A or B) = 0.55 + 0.2 = 0.75
Question 5.
P(A) = \(\frac{1}{3}\), P(B) = \(\frac{1}{4}\)
Answer:
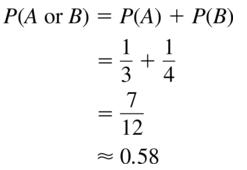
Question 6.
p(A) = \(\frac{2}{3}\), P(B) = \(\frac{1}{5}\)
Answer:
Given,
p(A) = \(\frac{2}{3}\), P(B) = \(\frac{1}{5}\)
P(A or B) = P(A) + P(B)
P(A or B) = \(\frac{2}{3}\) + \(\frac{1}{5}\)
P(A or B) = \(\frac{13}{15}\)
Question 7.
PROBLEM SOLVING
Your dart is equally likely to hit any point inside the board Shown. You throw a dart and pop a balloon. What is the probability that the balloon is red or blue?

Answer:

Question 8.
PROBLEM SOLVING
You and your friend are among several candidates running for class president. You estimate that there is a 45% chance you will win and a 25% chance your friend will win. What is the probability that you or your friend win the election?
Answer:
Let A be the event of you winning the election and B be of your friend winning the election
P(A) = 45% = 0.45
P(B) = 25% = 0.25
P(A or B) = P(A) + P(B)
P(A or B) = 0.45 + 0.25 = 0.70
Therefore the probability of you or your friend winning the election is 0.7
Question 9.
PROBLEM SOLVING
You are performing an experiment to determine how well plants grow under different light sources. 0f the 30 Plants in the experiment, 12 receive visible light, 15 receive ultraviolet light, and 6 receive both visible and ultraviolet light. What is the probability that a plant in the experiment receives visible or ultraviolet light?
Answer:

Question 10.
PROBLEM SOLVING
Of 162 students honored at an academic awards banquet, 48 won awards for mathematics and 78 won awards for English. There are 14 students who won awards for both mathematics and English. A newspaper chooses a student at random for an interview. What is the probability that the student interviewed won an award for English or mathematics?
Answer:
Given,
There are 162 students honored at an academic awards banquet, 48 won awards for mathematics and 78 won awards for English.
There are 14 students who won awards for both mathematics and English. A newspaper chooses a student at random for an interview.
P(A) = 48/162
P(B) = 78/162
P(A and B) = 14/162
P(A or B) = P(A) + P(B) – P(A and B)
P(A or B) = 48/162 + 78/162 – 14/162
P(A or B) = 112/162 = 56/81 = 0.691
ERROR ANALYSIS
In Exercises 11 and 12, describe and correct the error in finding the probability of randomly drawing the given card from a standard deck of 52 playing cards.
Question 11.

Answer:

Question 12.

Answer:
These 2 events are overlapping events as there is 1 card that is both a club and 9, therefore write equation of P(A or B) for overlapping events
P(A or B) = P(A) + P(B) – P(A and B)
= 13/52 + 4/52 – 1/52
= 4/13
In Exercises 13 and 14, you roll a six-sided die. Find P(A or B).
Question 13.
Event A: Roll a 6.
Event B: Roll a prime number.
Answer:
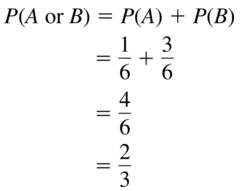
Question 14.
Event A: Roll an odd number.
Event B: Roll a number less than 5.
Answer:
P(A) = 3/6
1, 3, 5 out of 6 possible outcomes
P(B) = 4/6
1, 2, 3, 4 out of 6 possible outcomes
P(A and B) = 2/6
3/4 + 4/6 – 2/6 = 5/6
Question 15.
DRAWING CONCLUSIONS
A group of 40 trees in a forest are not growing properly. A botanist determines that 34 of the trees have a disease or are being damaged by insects, with 18 trees having a disease and 20 being damaged by insects. What is the probability that a randomly selected tree has both a disease and is being damaged by insects?

Answer:

Question 16.
DRAWING CONCLUSIONS
A company paid overtime wages or hired temporary help during 9 months of the year. Overtime wages were paid during 7 months. and temporary help was hired during 4 months. At the end of the year, an auditor examines the accounting records and randomly selects one month to check the payroll. What is the probability that the auditor will select a month in which the company paid overtime wages and hired temporary help?
Answer:
P(A) = 7/12
P(B) = 4/12
P(A or B) = 9/12
P(A and B) = P(A) + P(B) – P(A or B)
P(A and B) = 7/12 + 4/12 – 9/12
P(A and B) = 2/12 = 1/6
The probability of randomly selecting a month in which overtime was paid and temporary help was hired is 1/6 = 0.166…
Question 17.
DRAWING CONCLUSIONS
A company is focus testing a new type of fruit drink. The focus group is 47% male. 0f the responses, 40% of the males and 54% of the females said they would buy the fruit drink. What is the probability that a randomly selected person would buy the fruit drink?
Answer:

Question 18.
DRAWING CONCLUSIONS
The Redbirds trail the Bluebirds by one goal with 1 minute left in the hockey game. The Redbirds coach must decide whether to remove the goalie and add a frontline player. The probabilities of each team scoring are shown in the table.
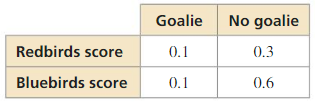
a. Find the probability that the Redbirds score and the Bluebirds do not score when the coach leaves the goalie in.
Answer:
Redbirds 10% x Bluebirds 90% = 9%
b. Find the probability that the Redbirds score and the Bluebirds do not score when the coach takes the goalie out.
Answer:
Redbirds 30% x Bluebirds 40% = 12%
c. Based on parts (a) and (b), what should the coach do?
Answer: Looks to be a 3% better chance to tie it up in B – pull the goalie
Question 19.
PROBLEM SOLVING
You can win concert tickets from a radio station if you are the first person to call when the song of the day is played. or if you are the first person to correctly answer the trivia question. The song of the day is announced at a random time between 7:00 and 7:30 A.M. The trivia question is asked at a random Lime between 7:15 and 7:45 A.M. You begin listening to the radio station at 7:20. Find the probability that you miss the announcement of the song of the day or the trivia question.
Answer:

Question 20.
HOW DO YOU SEE IT?
Are events A and B disjoint events? Explain your reasoning.
Answer:
A and B are not disjoint events and in fact they are overlapping events with 1 overlapping outcome.
Disjoint events do not have any overlap and they are mutually exclusive from one another.
Question 21.
PROBLEM SOLVING
You take a bus from sour neighborhood to your school. The express bus arrives at your neighborhood at a random time between 7:30 and 7:36 AM. The local bus arrives at your neighborhood at a random time between 7:30 and 7:40 A.M. You arrive at the bus stop at 7:33 A.M. Find the probability that you missed both the express bus and the local bus.

Answer:
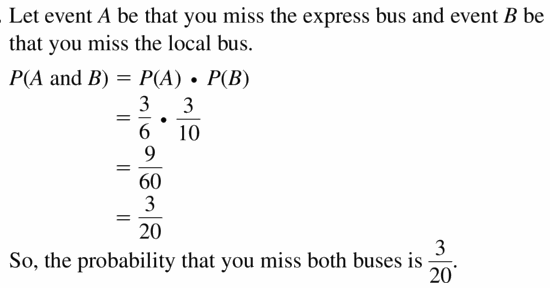
Question 22.
THOUGHT PROVOKING
Write a general rule for finding P(A or B or C) for (a) disjoint and (b) overlapping events A, B, and C.
Answer:
For 2 disjoint events, the equation becomes:
P(A or B) = P(A) + P(B), based on this it can be said that the equation of P(A or B or C) will be
P(A or B or C) = P(A) + P(B) + P(C)
For 2 overlapping events, the equation becomes:
P(A or B) = P(A) + P(B) – P(A and B)
P(A or B or C) = P(A) + P(B) + P(C) – P(A and B) – P(A and C) – P(B and C) + P(A and B and C)
Question 23.
MAKING AN ARGUMENT
A bag contains 40 cards numbered 1 through 40 that are either red or blue. A card is drawn at random and placed back in the bag. This is done four times. Two red cards are drawn. numbered 31 and 19, and two blue cards are drawn. numbered 22 and 7. Your friend concludes that red cards and even numbers must be mutually exclusive. Is your friend correct? Explain.
Answer:
Your friend is incorrect because we do not know all the number of cards. Also, from the given data we do not know all colors for cards. Therefore we can not conclude that red cards and even numbers be mutually exclusive.
Maintaining Mathematical Proficiency
Find the Product.
Question 24.
(n – 12)2
Answer:
We can solve the product by using the formula
(a – b)² = a² – 2ab + b²
(n – 12)2 = (n)² – 2(n)(12) + (12)²
n² – 24n + 144
Question 25.
(2x + 9)2
Answer:
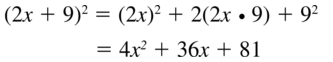
Question 26.
(- 5z + 6)2
Answer:
(- 5z + 6)2 = (6 – 5z)2
We can solve the product by using the formula
(a – b)² = a² + 2ab + b²
(6 – 5z)2 = (6)² – 2(6)(5z) + (5z)²
36 – 24n + 25z²
Question 27.
(3a – 7b)2
Answer:
We can solve the product by using the formula
(a – b)² = a² + 2ab + b²
(3a – 7b)2 = (3a)² – 2(3a)(7b) + (7b)²
9a² – 42ab + 49b²
12.5 Permutations and Combinations
Exploration 1
Reading a Tree Diagram
Work with a partner. Two coins are flipped and the spinner is spun. The tree diagram shows the possible outcomes.
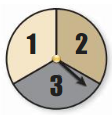
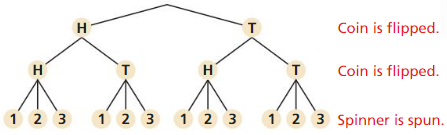
a. How many outcomes are possible?
Answer:
There are 4 possible outcomes when two coins are flipped.
There are three possible outcomes for the spinner.
Therefore the possible number of outcomes are,
4 × 3 = 12
b. List the possible outcomes.
Answer:
The possible outcomes when two coins are flipped are HH, HT, TH, TT.
Since the numbers on the spinner are 1, 2 and 3.
Therefore the possible outcomes when the spinner is spun are 1, 2, 3.
The possible outcomes are
(H, H, 1), (H, H, 2), (H, H, 3)
(H, T, 1), (H, T, 2), (H, T, 3)
(T, H, 1), (T, H, 2), (T, H, 3)
(T, T, 1), (T, T, 2), (T, T, 3)
Exploration 2
Reading a Tree Diagram
Work with a partner: Consider the tree diagram below.
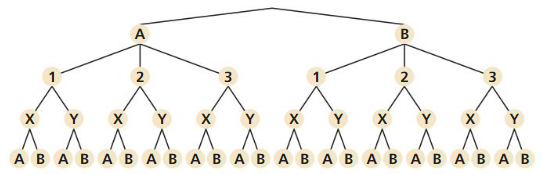
a. How many events are shown?
Answer:
In the given tree diagram, there is an initial event having two branches and its each branch is followed by the second event having three branches.
Further, each of the three branches of the second event are followed by the third event having two branches.
Lastly, these two branches are followed by a fourth event having two branches.
Thus there are total of four branches in a given tree diagram.
b. What outcomes are possible for each event?
Answer:
We know that the number of nodes at the end of the branch(s) representing an event in a tree diagram gives the number of its possible outcomes.
Number of possible outcomes of a first event =2
Number of possible outcomes of a second event =3
Number of possible outcomes of a third event =2
Number of possible outcomes of a fourth event =2
Thus the number of possible outcomes in first, second, third and fourth event are 2, 3, 2 and 2.
c. How many outcomes are possible?
Answer:
The number of nodes at the end of the tree diagram gives the number of its possible outcomes
Number of final nodes = Number of possible outcomes
Number of possible outcomes =24
d. List the possible outcomes.
Answer:
There are four events.
The first event has 2 outcomes which are A and B.
The second event has 3 outcomes which are1,2 and3.
The third event has 2 outcomes which are X and Y.
The fourth event has 2 outcomes which are A and B.The number of possible outcomes =24
All the possible outcomes are given by {A1, XA, A1XB, A1YA, A1YB, A2XA, A2XB, A2YA, A2YB, A3XA, A3XB, A3YA, A3YB, B1XA, B1XB, B1YB, B1YB, B2XA, B2XB, B2YA, B2YB, B3XA, B3XB, B3YA, B3YB}
Exploration 3
Writing a Conjecture
Work with a partner:
a. Consider the following general problem: Event 1 can occur in in ways and event 2 can occur in n ways. Write a conjecture about the number of ways the two events can occur. Explain your reasoning.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures.
Answer:
b. Use the conjecture you wrote in part (a) to write a conjecture about the number of ways more than two events can occur. Explain your reasoning.
Answer:
c. Use the results of Explorations 1(a) and 2(c) to verify your conjectures.
Answer:
Communicate Your Answer
Question 4.
How can a tree diagram help you visualize the number of ways in which two or more events can occur?
Answer:
Question 5.
In Exploration 1, the spinner is spun a second time. How many outcomes are possible?
Answer:
Lesson 12.5 Permutations and Combinations
Monitoring Progress
Question 1.
In how many ways can you arrange the letters in the word HOUSE?
Answer:
We have 5 slots
Assign H to a slot
Assign O to a slot
Assign U to a slot
Assign S to a slot
Assign E to a slot
The number of arrangments of the word HOUSE is 5! = 5 × 4 × 3 × 2 × 1 = 120
Question 2.
In how many ways can you arrange 3 of the letters in the word MARCH?
Answer:
MARCH = M, A, R, C, H = 5
Number of permutations = 5! = 5 × 4 × 3 × 2 × 1 = 120
There are 120 ways you can arrange all of the letters in the word MARCH.
When arranging 3 of the letters in the word MARCH, you have 5 choices for the first letter, 4 choices for the second letter.
Number of permutations = 5 × 4 × 3 = 60
There are 60 ways you can arrange 3 of the letters in the word MARCH.
Question 3.
WHAT IF
In Example 2, suppose there are 8 horses in the race. In how many different ways can the horses finish first, second, and third? (Assume there are no ties.)
Answer:
8P3 = 8!/(8 – 3)!
= 8!/5!
= 8 × 7 × 6 × 5!/5!
= 8 × 7 × 6
= 336
Thus there are 336 ways for the horses to finish first, second and third.
Question 4.
WHAT IF?
In Example 3, suppose there are 14 floats in the parade. Find the probability that the soccer team is first and the chorus is second.
Answer:
Write the number of possible outcomes as the number of permutations of the 14 floats in the parade.
14P14 = 14!
= 12!/14!
= 12!/14 × 13 × 12!
= 1/14 × 13
= 1/182
Question 5.
Count the possible combinations of 3 letters chosen from the list A, B, C, D, E.
Answer:
There are 10 possible combinations of 3 letters from the list A, B, C, D, E.
Question 6.
WHAT IF?
In Example 5, suppose you can choose 3 side dishes out of the list of 8 side dishes. How many combinations are possible?
Answer:
8C3 = 8!/(8 – 3)!3!
= 8!/5! × 3!
= (8 × 7 × 6 × 5!)/5! × 3!
= 8 × 7 × 6/3 × 2
= 56
There are 56 different combinations of side dishes you can order.
Question 7.
WHAT IF?
In Example 6, suppose there are 20 photos in the collage. Find the probability that your photo and your friend’s photo are the 2 placed at the top of the page.
Answer:
Write the number of possible outcomes as the number of combinations of 20 photos taken 2 at a time or 20C2, because the order in which the photos are chosen is not important.
20C2 = 20!/(20 – 2)! × 2!
= 20!/18! × 2!
= 20 × 19 × 18!/18! × 2!
= 20 × 19/2
= 10 × 19 = 190
The probability that your photo and your friend’s photo are the 2 placed at the top of the page is 1/190
Exercise 12.5 Permutations and Combinations
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
An arrangement of objects in which order is important is called a(n) _________ .
Answer:
An arrangement of objects in which order is important is called a Permutation.
Question 2.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.
\(\frac{7 !}{2 ! \cdot 5 !}\) 7C5 7C2 \(\frac{7 !}{(7-2) !}\)
Answer:
7C2 \(\frac{7 !}{(7-2) !}\) = \(\frac{7 !}{5!}\)
= 7C2
The expression \(\frac{7 !}{(7-2) !}\) does not belong with other three.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 8, find the number of ways you can arrange (a) all of the letters and (b) 2 of the letters in the given word.
Question 3.
AT
Answer:

Question 4.
TRY
Answer:
a. In this case, we have to find the number of permutations all of the letters in a given word that will consist of 3 letters.
Number of permutations = (1st place can be one of three letters) × (2nd can be one of two letters that is left) × (3rd can be one letter that is left)
= 3 . 2 . 1 = 6
Therefore we have 6 ways for arrange all of the letters in given word, that is TRY, TYR, YTR, YRT, RTY and RYT.
Now, we have to find the number of permutation 2 of the letters in a given word that will consists of 3 letters
Number of permutations = (1st place can be one of three letters) × (2nd can be one of two letters that is left)
= 3 . 2 = 6
We have 6 ways for arrange 2 of the letters in given word, tthat is TR, TY, YT, YR, RT and RY.
Question 5.
ROCK
Answer:

Question 6.
WATER
Answer:
In this case, we have to find the number of permutation all of the letters in a given word that will consist of 5 letters.
Number of permutations = (1st can be one of 5 letters) × (2nd place can be one of 4 letters that is left) × (3rd can be one of 3 letters that is left) × (4th can be two letters that is left) × (5th can be one letter that is left)
= 5 .4 . 3 . 2 . 1 = 120
Thus we have 120 ways to arrange all of the letters in given word, that WATER, WATRE, WARTE,…, RETAW.
Number of permutations = (1st can be one of 5 letters) × (2nd place can be one of 4 letters that is left)
= 5 . 4
= 20
Thus we have 20 ways to arrange 2 of the letters in given word, that WA, WT, WR, WE …, ER, RE.
Question 7.
FAMILY
Answer:

Question 8.
FLOWERS
Answer:
We have to find the number of permutation all of the letters in a given word that will consist of 7 letters.
Number of permutations = (1st place can be one of 7 letters) × (2nd place can be one of 6 letters that is left) × (3rd place can be one of 5 letters that is left) × (4th place can be one of 4 letters that is left) × (5th place can be one of 3 letters that is left) × (6th place can be one of 2 letters that is left) × (7th place can be one of 1 letters that is left)
= 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040
Thus we have 5040 ways to arrange all of the letters in given word, that is FLOWERS, FLOWERS, FLOWSER… SREWOLF
Now we have to find the number of permutation 2 of the letters in a given word that will consist of 7 letters.
Number of permutations = (1st place can be one of 7 letters) × (2nd place can be one of 6 letters that is left)
= 7 . 6
= 42
Thus we have 42 ways to arrange all of the letters in given word, that is FL, FO, FW, FE…RS, RE.
In Exercises 9 – 16, evaluate the expression.
Question 9.
5P2
Answer:
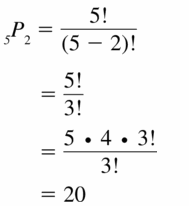
Question 10.
7P3
Answer:
7P3 = \(\frac{7 !}{(7-3) !}\) = \(\frac{7 !}{4!}\)
= 7 . 6 . 5 . 4 . 3 . 2 . 1/4 . 3 . 2 . 1
= 7 . 6 . 5
= 210
7P3 = 210
Question 11.
9P1
Answer:
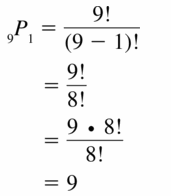
Question 12.
6P5
Answer:
6P5 = \(\frac{6 !}{(6-5) !}\) = \(\frac{6 !}{1!}\)
= 6 . 5 . 4 . 3 . 2 . 1/1
= 6 . 5 . 4 . 3 . 2
= 720
6P5 = 720
Question 13.
8P6
Answer:
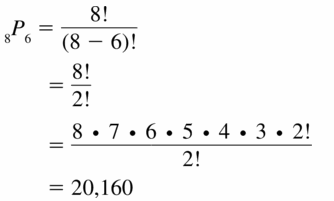
Question 14.
12P0
Answer:
12P0 = \(\frac{12 !}{(12-0) !}\)
= \(\frac{12 !}{12!}\)
= 1
12P0 = 1
Question 15.
30P2
Answer:
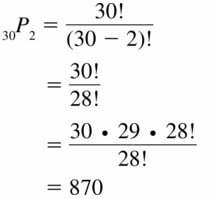
Question 16.
25P5
Answer:
25P5 = \(\frac{25 !}{(25-5) !}\) = \(\frac{25 !}{20!}\)
= 25 . 24 . 23 . 22 . 21 . 20 . 19 . 18 . …. 6 . 5 . 4 . 3 . 2 . 1/20 . 19 . 18 . … 3 . 2 . 1
= 25 . 24 . 23 . 22 . 21
= 720
25P5 = 6375600
Question 17.
PROBLEM SOLVING
Eleven students are competing in an art contest. In how many different ways can the students finish first, second, and third?
Answer:

Question 18.
PROBLEM SOLVING
Six Friends go to a movie theater. In how many different ways can they sit together in a row of 6 empty seats?
Answer:
Given,
Six Friends go to a movie theater.
6P6 = \(\frac{6!}{(6-6) !}\)
= \(\frac{6!}{0!}\)
= 6!
= 6 . 5 . 4 . 3 . 2 . 1
6P6 = 720
Question 19.
PROBLEM SOLVING
You and your friend are 2 of 8 servers working a shill in a restaurant. At the beginning of the shill. the manager randomly assigns 0ne section to each server. Find the probability that you are assigned Section 1 and your friend is assigned Section 2.
Answer:

Question 20.
PROBLEM SOLVING
You make 6 posters to hold up at a basketball game. Each poster has a letter of the word TIGERS. You and 5 friends sit next to each other in a row. The posters are distributed at random. Find the probability that TIGERS is spelled correctly when you hold up the posters.

Answer:
Number of favorable outcomes = 1 (TIGERS)
Total number of outcomes = 6!
= 6 . 5 . 4 . 3 . 2 . 1
= 720
Number of favorable outcomes/Total number of outcomes = 1/720
In Exercises 21 – 24, count the possible combinations of r letters chosen from the given list.
Question 21.
A, B, C, D; r = 3
Answer:

Question 22.
L, M, N, O; r = 2
Answer:
4P2 = \(\frac{4!}{(4-2) !}\)
= \(\frac{4!}{2!}\)
= 4 . 3 . 2 . 1/2 . 1
= 12
4P2 = 12
So, the possible permutations of two letters in the given list L, M, N, O is
LM, ML
LN, NL
LO, OL
MN, NM
MO, MO
NO, ON
Thus the number of possible combination of a = 2 letters chosen from the list L, M, N, O
4P2 = 12/2 = 6
Question 23.
U , V, W, X, Y, Z; r = 3
Answer:
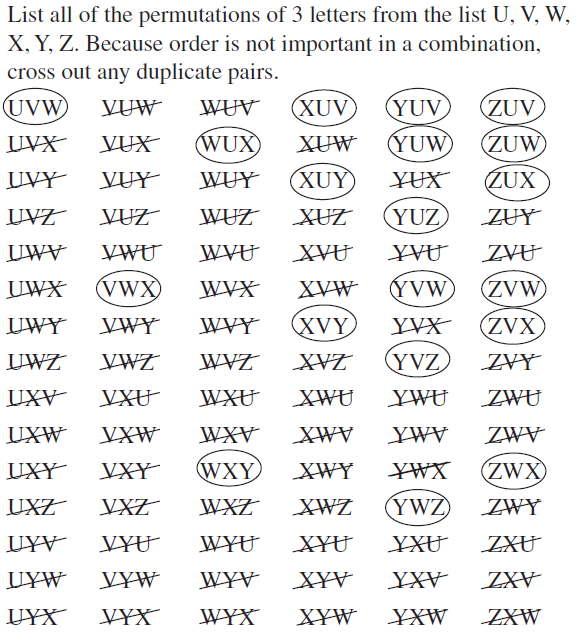
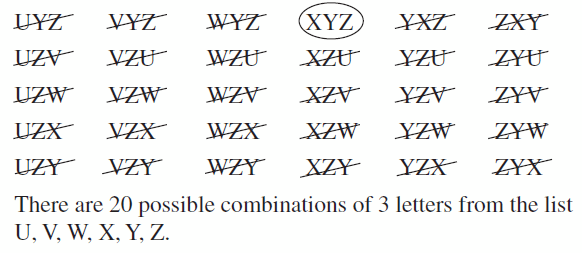
Question 24.
D, E, F, G, H; R = 4
Answer:
5P4 = \(\frac{5!}{(5-4) !}\)
= \(\frac{5!}{1!}\)
=5 . 4 . 3 . 2 . 1
= 120
5P4 = 120
Thus the possible permutations of four letters in the given list D, E, F, G, H is
DEFG, DEGF, DGEF, DGFE, DFGD…HEFG, EHFG, EHGF, FGEH.
Thus we conclude that the number of possible combination of a = 4 letters chosen from the list D, E, F, G, H is
5C4 = \(\frac{120}{(24) !}\) = 5
In Exercise 25 – 32, evaluate the expression
Question 25.
5C1
Answer:
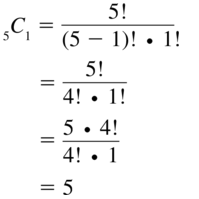
Question 26.
8C5
Answer:
8C5 = \(\frac{8!}{(8-5) !}\)
= \(\frac{8!}{3!}\) . \(\frac{1}{5!}\)
= 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(5 . 4 . 3 . 2 . 1) (3 . 2 . 1)
= 8 . 7
8C5 = 56
Question 27.
9C9
Answer:
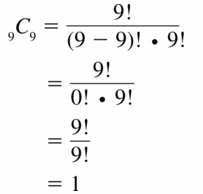
Question 28.
8C6
Answer:
8C6 = \(\frac{8!}{(8-6) !}\)
= \(\frac{8!}{2!}\) . \(\frac{1}{6!}\)
= 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(6. 5 . 4 . 3 . 2 . 1) (3 . 2 . 1)
= 8 . 7
8C5 = 56
Question 29.
12C3
Answer:
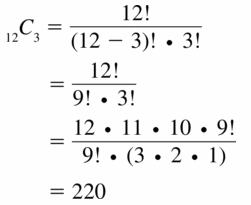
Question 30.
11C4
Answer:
11C4 = \(\frac{11!}{(11-4) !}\)
= \(\frac{11!}{7!}\) . \(\frac{1}{4!}\)
= 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(7 . 6. 5 . 4 . 3 . 2 . 1) (4 . 3 . 2 . 1)
= 11 . 10 . 3
11C4 = 330
Question 31.
15C8
Answer:
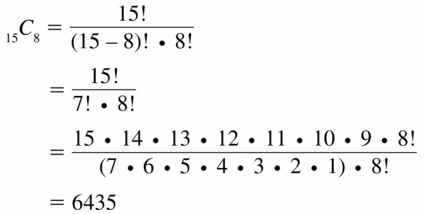
Question 32.
20C5
Answer:
20C5 = \(\frac{20!}{(20-5) !}\)
= \(\frac{20!}{5!}\) . \(\frac{1}{5!}\)
= 20 . 19 . 18 . 17 . 16 . 15 . … 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(5 . 4 . 3 . 2 . 1) (5 . 4 . 3 . 2 . 1)
= 19 . 3 . 17 . 16
20C5 = 15504
Question 33.
PROBLEM SOLVING
Each year, 64 golfers participate in a golf tournament. The golfers play in groups of 4. How many groups of 4 golfers are possible?
Answer:
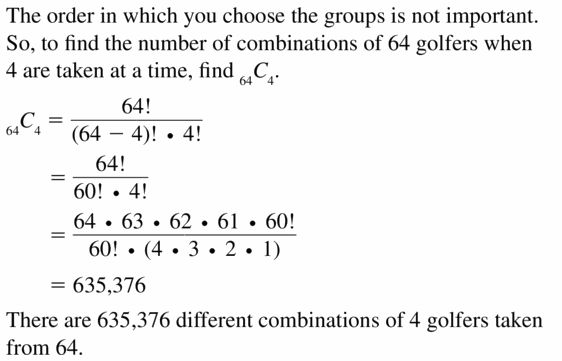
Question 34.
PROBLEM SOLVING
You want to purchase vegetable dip for a party. A grocery store sells 7 different flavors of vegetable dip. You have enough money to purchase 2 flavors. How many combinations of 2 flavors of vegetable dip are possible?
Answer:
given that,
You want to purchase vegetable dip for a party. A grocery store sells 7 different flavors of vegetable dip. You have enough money to purchase 2 flavors.
7C2 = \(\frac{7!}{(7-2) !}\)
= \(\frac{7!}{5!}\) . \(\frac{1}{2!}\)
= 7 . 6 . 5 . 4 . 3 . 2 . 1/(5 . 4 . 3 . 2 . 1) (2 . 1)
= 7 . 3
7C2 = 21
ERROR ANALYSIS
In Exercises 35 and 36, describe and correct the error in evaluating the expression.
Question 35.
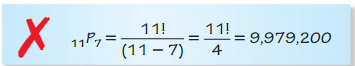
Answer:
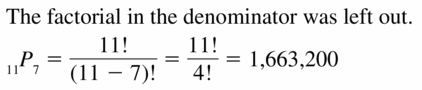
Question 36.
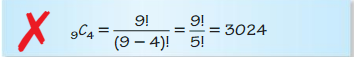
Answer:
The permutation formula was used instead of the combination formula.
REASONING
In Exercises 37 – 40, tell whether the question can be answered using permutations or combinations. Explain your reasoning. Then answer the question.
Question 37.
To complete an exam. u must answer 8 questions from a list of 10 questions. In how many ways can you complete the exam?
Answer:
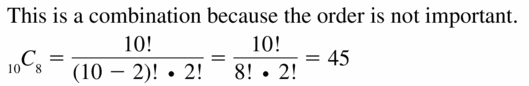
Question 38.
Ten students are auditioning for 3 different roles in a play. In how many ways can the 3 roles be filled?
Answer:
As 10 students are auditioning for 3 roles, which are different from each other, the order in which the roles are assigned to the students is important and should be taken into account.
As the Permutations formula takes into account the order of distribution. Hence the number of ways to fill the 3 roles can be found by using the permutations formula in the chapter.
So, the number of permutations of assigning the 3 roles to 3 students chosen from 10, using the permutations formula
10P3 = \(\frac{10!}{(10-3) !}\)
= \(\frac{10!}{7!}\)
= 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(7 . 6 . 5 . 4 . 3 . 2 . 1)
=10 . 9 . 8
10P3 = 720
Question 39.
Fifty-two athletes arc competing in a bicycle race. In how many orders can the bicyclists finish first, second, and third? (Assume there are no ties.)
Answer:
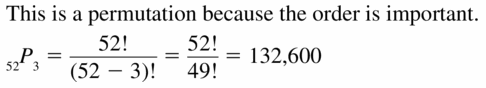
Question 40.
An employee at a pet store needs to catch 5 tetras in an aquarium containing 27 tetras. In how many groupings can the employee capture 5 tetras?
Answer:
Given,
An employee at a pet store needs to catch 5 tetras in an aquarium containing 27 tetras.
27C5 = \(\frac{27!}{(27-5) !}\)
= \(\frac{27!}{22!}\) . \(\frac{1}{5!}\)
= 27. 26 . 25 . 24 . … 7 . 6 . 5 . 4 . 3 . 2 . 1/(22 . 21. … 7 . 6 . 5 . 4 . 3 . 2 . 1)(5 . 4 . 3 . 2 . 1)
= 27 . 26 . 5 . 23
27C5 = 80730
Thus the number of combinations of 27 tetras taken 5 at the time is 80730.
Question 41.
CRITICAL THINKING
Compare the quantities 50C9 and 50C41 without performing an calculations. Explain your reasoning.
Answer:

Question 42.
CRITICAL THINKING
Show that each identity is true for any whole numbers r and n, where 0 ≤ r ≤ n.
a. nCn = 1
Answer:
nCn = n!/n!(n – n)!
nCn = n!/n!0!
= 1/0!
We know that,
0! = 1
= 1/1 = 1
Thus nCn = 1
b. nCr = nCn – r
Answer:
nCn-a= n!/a!(n – a)!
nCn-a = n!/a!(n-a)! = nCn-a
c. n + 1Cr = nCr + nCr – 1
Answer:
n+1Ca = n+1!/a!(n+1-a)!
nCr + nCa-1 = n!/a!(n – a)! + n!/(n – (a – 1))! (a – 1)!
= \(\frac{(n+1)!}{(n-a+1) !}\) . \(\frac{1}{a!}\)
Thus n + 1Ca = nCa + nCa – 1
Question 43.
REASONING
Complete the table for each given value of r. Then write an inequality relating nPr and nCr. Explain your reasoning.
Answer:

Question 44.
REASONING
Write an equation that relates nPr and nCr. Then use your equation to find and interpret the Value of \(\frac{182 P_{4}}{182 C_{4}}\).
Answer:
\(\frac{n P_{a}}{n C_{a}}\) = n!/(n – a)!/n!/a!(n – a)! = a!
\(\frac{182 P_{4}}{182 C_{4}}\) = 4! = 24
Question 45.
PROBLEM SOLVING
You and your friend are in the studio audience on a television game show. From an audience of 300 people, 2 people are randomly selected as contestants. What is the probability that you and your friend are chosen?
Answer:

Question 46.
PROBLEM SOLVING
You work 5 evenings each week at a bookstore. Your supervisor assigns you 5 evenings at random from the 7 possibilities. What is the probability that your schedule does not include working on the weekend?
Answer:
nCa = n!/a!(n – a)!
7C5 = \(\frac{7!}{(7-5) !}\)
= \(\frac{7!}{2!}\) . \(\frac{1}{5!}\)
=7 . 6 . 5 . 4 . 3 . 2 . 1/(2 . 1)(5 . 4 . 3 . 2 . 1)
= 7 . 3
7C5 = 21
Thus we see that there are 21 possible combinations of five days formed from 7 days.
Hence we see that one of 21 possible combination of 5 days does not contain saturday and sunday.
P = P(Are chosen one combination of 21 possible)
= Number of favorable outcomes/Number of possible outcomes
= 1/21
REASONING
In Exercises 47 and 48, find the probability of winning a lottery using the given rules. Assume that lottery numbers are selected at random.
Question 47.
You must correctly select 6 numbers, each an integer from 0 to 49. The order is not important.
Answer:

Question 48.
You must correctly select 4 numbers, each an integer from 0 to 9. The order is important.
Answer:
nCa = n!/a!(n – a)!
10C4 = \(\frac{10!}{(10-4) !}\)
= \(\frac{10!}{6!}\) . \(\frac{1}{4!}\)
=10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(6 . 5 . 4 . 3 . 2 . 1)(4 . 3 . 2 . 1)
= 10 . 3 . 7
10C4 = 210
There are 210 possible combination of 10 numbers taken 4 at a time.
P (You winning a lottery) = P(Are chosen one combination 210 possible)
= Number of favorable outcomes/Number of possible outcomes
= 1/210
Question 49.
MATHEMATICAL CONNECTIONS
A polygon is convex when no line that contains a side of the polygon contains a point in the interior of the polygon. Consider a convex polygon with n sides.
a. Use the combinations formula to write an expression for the number of diagonals in an n-sided polygon.
b. Use your result from part (a) to write a formula for the number of diagonals of an n-sided convex polygon.
Answer:

Question 50.
PROBLEM SOLVING
You are ordering a burrito with 2 main ingredients and 3 toppings. The menu below shows the possible choices. How many different burritos are possible

Answer:
You are ordering a burrito with 2 main ingredients and 3 toppings.
Total number of main ingredients = 6
As the order in which the ingredients are chosen is not important, the total number of ways to select 2 main ingredients out of 6 can be found by using the combinations formula.
nCa = n!/a!(n – a)!
6C2 = \(\frac{6!}{(6-2) !}\)
= \(\frac{6!}{4!}\) . \(\frac{1}{2!}\)
=6 . 5 . 4 . 3 . 2 . 1/(4 . 3 . 2 . 1)(2 . 1)
= 3 . 5
6C2 = 15
Total number of toppings = 8
Number of toppings to be chosen = 3
nCa = n!/a!(n – a)!
8C3 = \(\frac{8!}{(8-3) !}\)
= \(\frac{8!}{5!}\) . \(\frac{1}{3!}\)
=8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(5 . 4 . 3 . 2 . 1)(3 . 2 . 1)
= 8 . 7
8C3 = 56
Total possible selections = ways to select main ingredients × Ways to select toppings
= 15 × 56
= 840
Question 51.
PROBLEM SOLVING
You want to purchase 2 different types of contemporary music CDs and 1 classical music CD from the music collection shown. How many different sets of music types can you choose for your purchase?
a. How many combinations of three marbles can be drawn from the bag? Explain.
b. How many permutations of three marbles can be drawn from the bag? Explain.
Answer:

Question 52.
HOW DO YOU SEE IT?
A bag contains one green marble, one red marble, and one blue marble. The diagram shows the possible outcomes of randomly drawing three marbles from the hag without replacement.
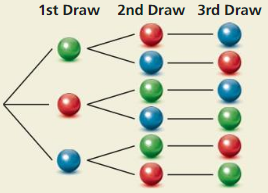
a. How many combinations of three marbles can be drawn from the bag? Explain.
Answer:
nCa = n!/a!(n – a)!
3C3 = \(\frac{3!}{(3-3) !}\)
= \(\frac{3!}{0!}\) . \(\frac{1}{3!}\)
=3 . 2 . 1/(1)(3 . 2 . 1)
= 1
3C3 = 1
b. How many permutations of three marbles can be drawn from the bag? Explain.
Answer:
nPa = n!/(n – a)!
3P3 = \(\frac{3!}{(3-3) !}\)
= \(\frac{3!}{0!}\)
=3 . 2 . 1/1
= 6
3P3 = 3
There are 6 possible combinations.
Question 53.
PROBLEM SOLVING
Every student in your history class is required to present a project in front of the class. Each day, 4 students make their presentations in an order chosen at random by the teacher. you make your presentation on the first day.
a. What is the probability that you are chosen to be the first or second presenter on the first day ?
b. What is the probability that you are chosen to be the second or third presenter on the first day? Compare your answer with that in part (a).
Answer:

Question 54.
PROBLEM SOLVING
The organizer of a cast party for a drama club asks each of the 6 cast members to bring 1 food item From a list of 10 items. Assuming each member randomly chooses a food item to bring. what is the probability that at least 2 of the 6 cast members bring the same item?
Answer:
Given,
The organizer of a cast party for a drama club asks each of the 6 cast members to bring 1 food item From a list of 10 items.
Assuming each member randomly chooses a food item to bring.
A = {At least 2 of the 6 cast members bring the same item}
\(\bar{A}\) = {All members bring different items}
First member can choose one of the 10 different products, the second can choose one of the 9 possible ways, and so on until the 6th member can choose one of the remaining 5 items.
10 . 9 . 8 . 7 . 6 . 5 = 151200
nPa = n!/(n – a)!
10P6 = \(\frac{10!}{(10-6) !}\)
= \(\frac{10!}{4!}\)
=10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/4 . 3 . 2 . 1
= 10 . 9 . 8 . 7 . 6 . 5 = 151200
10P6 = 151200
10 . 10 . 10 . 10 . 10 . 10 = 1000000
P(\(\bar{A}\)) = Number of favorable outcomes/Number of possible outcomes
= 151200/1000000
= 0.1512
P(A) = 1 – P(\(\bar{A}\))
P(A) = 1 – 0.1512 = 0.8488
The probability that at least 2 of the 6 members bring the same items is about 85%
Question 55.
PROBLEM SOLVING
You are one of 10 students performing in a school talent show. The order of the performances is determined at random. The first 5 performers go on stage before the intermission.
a. What is the probability that you are the last performer before the intermission and your rival performs immediately before you?
b. What is the probability that you are not the first performer?
Answer:

Question 56.
THOUGHT PROVOKING
How many integers, greater than 999 but not greater than 4000, can be formed with the digits 0, 1, 2, 3, and 4? Repetition of digits is allowed.
Answer:
Let fixed number 1 on the first place and in the second place can be one of 5 digits 0, 1, 2, 3 or 4. Because repetition of digits is allowed. In third and fourth place it can also be one of five digits.
Therefore we see that 5 . 5 . 5 = 125 integers which begin with 1, can be formed.
Second, If we fixed 2 on the first place, by the same logic as in the first part, we get that 5³ = 125 integers which begin with 2.
Next, if we fixed number 3 on the first place, we obtain 5³ = 125 integers which begin with 2.
5³ + 5³ + 5³ = 375
375 integers greater than 999 but not greater than 4000, can be formed with the digits 0, 1, 2, 3, 4.
Question 57.
PROBLEM SOLVING
There are 30 students in your class. Your science teacher chooses 5 students at random to complete a group project. Find the probability that you and your 2 best friends in the science class are chosen to work in the group. Explain how you found your answer.
Answer:
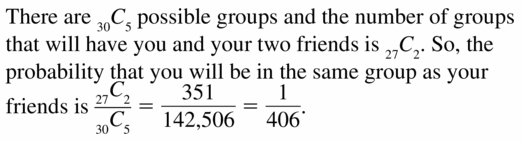
Question 58.
PROBLEM SOLVING
Follow the steps below to explore a famous probability problem called the birthday problem. (Assume there are 365 equally likely birthdays possible.)
a. What is the probability that at least 2 people share the same birthday in a group of 6 randomly chosen people? in a group of 10 randomly chosen people?
Answer:
nPa = n!/(n – a)!
A = {At least people share the same birthday in a group of 6 people}
So, we see that complement of event A is
\(\bar{A}\) = {All 6 people were born on different days}
nPa = n!/(n – a)!
365P6 = \(\frac{365!}{(365-6)!}\)
= \(\frac{365!}{(359)!}\)
= 365. 364 . 363 . 362 . 361 . 360 . 359 . 358 . ……. 2 . 1/(359 . 358. …. 2 . 1)
= 365. 364 . 363 . 362 . 361 . 360
For the first day we can also choose one of 365 possible for the second dat we can also choose one of 365 ways and so on.
For each of the 6 days we have the option to choose one day from 365 possible ways.
So, the number of possible outcomes is
365 . 365 . 365 . 365 . 365 . 365
P(\(\bar{A}\)) = Number of favorable outcomes/Number of possible outcomes
= 365. 364 . 363 . 362 . 361 . 360/365 . 365 . 365 . 365 . 365 . 365
= 0.959
P(A) = 1 – P(\(\bar{A}\))
P(A) = 1 – 0.959 = 0.04
P = 1 – 365P10/36510
1 – 0.883 = 0.117
b. Generalize the results from part (a) by writing a formula for the probability P(n) that at least 2 people in a group of n people share the same birthday. (Hint: Use nPr notation in your formula.)
Answer:
Based on the explanation in the part under a) we can conclude that the probability that at least two people share the same birthday in a group of n people is
P = 1 – 365Pn/365n
c. Enter the formula from part (b) into a graphing calculator. Use the table feature to make a table of values. For what group size does the probability that at least 2 people share the same birthday first exceed 50%?
Answer:

Based on the above table we see that for a group of 23 people and more, the probability that at least tweople share the same birthday exceed 50%
Maintaining Mathematical Proficiency
Question 59.
A bag contains 12 white marbles and 3 black marbles. You pick 1 marble at random. What is the probability that you pick a black marble?
Answer:
Given,
A bag contains 12 white marbles and 3 black marbles. You pick 1 marble at random
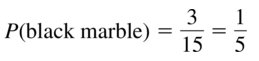
Question 60.
The table shows the result of flipping two coins 12 times. For what outcome is the experimental probability the same as the theoretical probability?
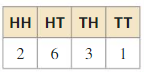
Answer:
The table shows the result of flipping two coins 12 times
P(HH) = P(HT) = P(TH) = P(TT) = 1/2 . 1/2 = 1/4
P(HH) = Number of favorable outcomes/Number of possible outcomes
= 2/12 = 1/6
P(HT) = 6/12 = 1/2
P(TH) = 3/12 = 1/4
P(TT) = 1/12
The most likely fell first heads, and second tails. Also, with the least probability fell twice tails.
12.6 Binomial Distributions
Exploration 1
Analyzing Histograms
Work with a partner: The histograms show the results when n coins are flipped.
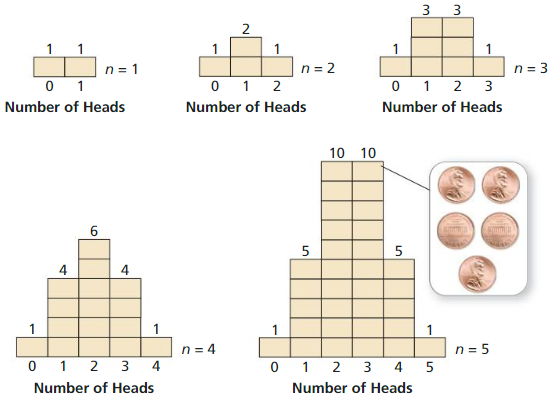
STUDY TIP
When 4 coins are flipped (n = 4), the possible outcomes are
TTTT TTTH TTHT TTHH
THTT THTH THHT THHH
HTTT HTTH HTHT HTHH
HHTT HHTH HHHT HHHH.
The histogram shows the numbers of outcomes having 0, 1, 2, 3, and 4 heads.
a. In how many ways can 3 heads occur when 5 coins are flipped?
Answer:
By the above histogram,
Combination of “0 Head” willl be 1 ,
A combination of “1 Head” will be 5,
A combination of “2 Heads” will be 10,
A combination of “3 Heads” will be 10,
A combination of “4 Heads” will be 5,
A combination of “5 Heads” will be 1.
Hence by using the Histogram, combinations of “3 Heads” will be 10
You can verify that by selecting this list from the sample space:
“HHHTT”, “HHTHT”, “HTHHT”, “THHHT”, “THHTH”. “THTHH”, “TTHHH”, “HTHTH”, “HTTHH” and “HHTTH”.
All have three Heads (and two Tail).
So 10 of the outcomes produce “Three Heads”.
b. Draw a histogram that shows the numbers of heads that can occur when 6 coins are flipped.
Answer:
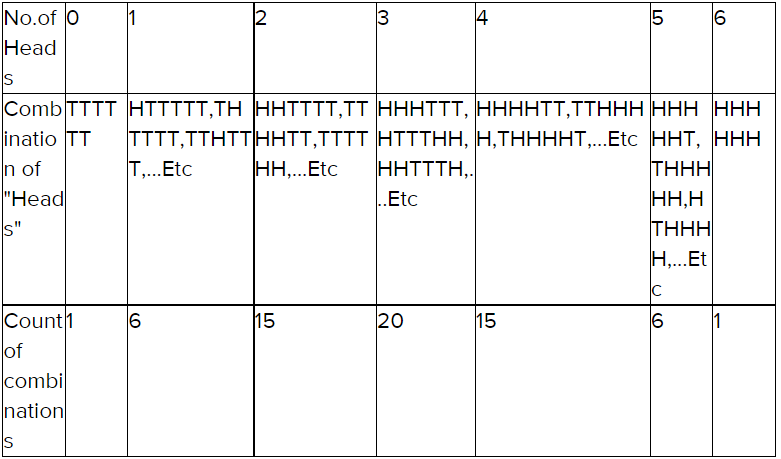
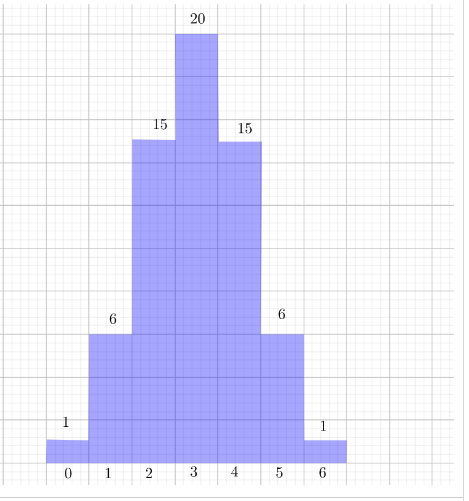
c. In how many ways can 3 heads occur when 6 coins are flipped?
Answer:
- Combination of 0 head will be 1.
- Combination of 1 head will be 6.
- Combination of 2 heads will be 15.
- Combination of 3 heads will be 20.
- Combination of 4 heads will be 15.
- Combination of 5 heads will be 6.
- Combination of 6 head will be 1.
6C3 = (6×5×4)/(1×2×3)
The possible outcome for 3 heads is 20.
Exploration 2
Determining the Number of Occurrences
Work with a partner:
a. Complete the table showing the numbers of ways in which 2 heads can occur when n coins are flipped.

Answer:
Let X be the number of occurrences of 2 heads.
Occurences of 2 heads when n = 3
X3 = 3C2
X3 = 3
Occurences of 2 heads when n = 4
X4 = 4C2
X4 = 6
Occurences of 2 heads when n = 5
X5 = 5C2
X5 = 10
Occurences of 2 heads when n = 6
X6 = 6C2
X6 = 15
Occurences of 2 heads when n = 7
X7 = 7C2
X7 = 21

b. Determine the pattern shown in the table. Use your result to find the number of ways in which 2 heads can occur when 8 coins are flipped.
LOOKING FOR A PATTERN
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
X3 = 3
X4 = 6
X5 = 10
X6 = 15
X7 = 21
X4 – X3 = 3
X5 – X4 = 4
X6 – X5 = 5
X7 – X6 = 6
X8 = X7 + 7
The number of occurrences of 2 heads when 8 coins are flipped will be 28.
Communicate Your Answer
Question 3.
How can you determine the frequency of each outcome of an event?
Answer:
The frequency of each outcome of an event is determined by f = p/t
Question 4.
How can you use a histogram to find the probability of an event?
Answer: By checking the variables in the x-axis and its measurement of height, the probability of an event can be obtained.
Lesson 12.6 Binomial Distributions
Monitoring Progress
An octahedral die has eight sides numbered 1 through 8. Let x be a random variable that represents the sum when two such dice are rolled.

Question 1.
Make a table and draw a histogram showing the probability distribution tor x.
Answer
The below table shows how many outcomes of rolling two dice produce each value of x.
| X(sum) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Outcomes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| P(x) | 1/64 | 1/32 | 3/64 | 1/16 | 5/64 | 6/64 | 7/64 | 1/8 | 7/64 | 6/64 | 5/64 | 4/64 | 3/64 | 2/64 | 1/64 |
Question 2.
What is the most likely sum when rolling the two dice?
Answer:
9 is the most common roll with two eight-sided dice.
Question 3.
What is the probability that the sum of the two dice is at most 3?
Answer:
According to a survey, about 85% of people ages 18 and older in the U.S. use the Internet or e-mail. You ask 4 randomly chosen people (ages 18 and older) whether they use the Internet or email.
Question 4.
Draw a histogram of the binomial distribution for your survey.
Answer:
It is given that in a survey about 85 % of people ages 18 and older in the U.S. use the Internet or e-mail.
It is required to draw a histogram of the binomial distribution for your survey.
p = 85/100 = 0.85
The value of n = 4, because the survey 4 people.
P(0) = 4C0 . 1 . (1 – 0.85)^4-0
P(0) = 4C0 . 1 . (1 – 0.85)^4
P(0) = 4C0 . 1 . (0.15)^4
P(0) = 0.0005
n = 4 and 0.85 for p
P(1) = 4C1(0.85) (1 – 0.85)^4-1
P(1) = 4C1(0.85) (1 – 0.85)^3
P(1) = 4C1(0.85) (0.15)^3
P(1) = 4!/(4-1)! (1!) × (0.85) (0.15)^3
P(1) = 4(0.85)(0.15)³
P(1) = 4 × 0.0028
P(1) = 0.0114
P(2) = 4C2 . (0.85)² . (1 – 0.85)²
P(2) = 4!/(4-2)!2! . (0.85)² . (1 – 0.85)²
P(2) = 4!/(2)!2! . (0.85)² . (1 – 0.85)²
P(2) = 12/2 . (0.85)² . (0.15)²
P(2) = 6 × 0.7225 × 0.0225
P(2) = 6 × 0.0162
P(2) = 0.0975
P(3) = 4C3(0.85)³ (1 – 0.85)^4-3
P(3) = 4C3(0.85)³ (1 – 0.85)¹
P(3) = 4C3(0.85)³ (0.15)
P(3) = 4 × (0.85)³ (0.15)
P(3) = 4 × 0.6141 × 0.15
P(3) = 4(0.0921)
P(3) = 0.3684
P(4) = 4C4(0.85)^4
P(4) = 1(0.85)^4 (0.15)
P(4) = 0.522 × 0.15
P(4) = 0.0783
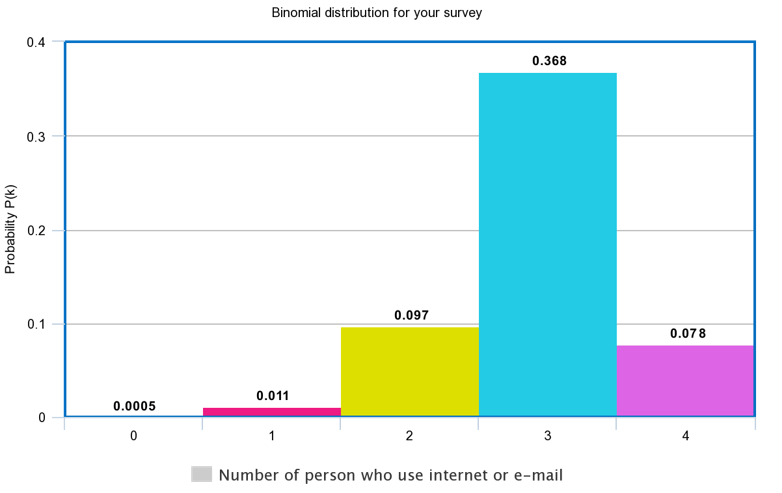
Question 5.
What is the most likely outcome of your survey?
Answer:
In the histogram from 4th question of the binomial distribution for your survey, clearly shows that when k = 3 the probability of P(3) is the highest
So, the most likely outcome is that 3 of the 4 people use the internet or e-mail.
Question 6.
What is the probability that at most 2 people you survey use the Internet or e-mail?
Answer:
Given,
85% of people ages 18 and older in the U.S. use the internet or e-mail.
The probability that at most 2 people you survey use the internet or e-mail
P(K≤2)
P(K≤2) = P(K = 0) + P(K = 1) + P(K = 2)
P(K = 0) = 0.0005
P(K = 1) = 0.0114
P(K = 2) = 0.0975
P(K≤2) = P(K = 0) + P(K = 1) + P(K = 2)
P(K≤2) = 0.0005 + 0.0114 + 0.0975
= 0.1094
Exercise 12.6 Binomial Distributions
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What is a random variable?
Answer:
A random variable is a variable whose value is determined by the outcomes of a probability experiment.
Question 2.
WRITING
Give an example of a binomial experiment and describe how it meets the conditions of a binomial experiment.
Answer:
We flipping a coin 10 times and register what fell.
We know that events, coin toss are independent.
Each trial has only two possible outcomes: H and T
The probabilities are P(H) = P(T) = 1/2 and are the same for each trial.
We can conclude that this experiment is a binomial experiment.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6. make a table and draw a histogram showing the probability distribution for the random variable.
Question 3.
x = the number on a table tennis ball randomly chosen from a bag that contains 5 balls labeled “1,” 3 halls labeled “2,” and 2 balls labeled “3.”
Answer:

Question 4.
c = 1 when a randomly chosen card out of a standard deck of 52 playing cards is a heart and c = 2 otherwise.
Answer:
Let C be a random variable that represents the randomly chosen card.
Standard desk have 52 playing cards.
P(C = 1) = Number of favorable outcomes/Total number of outcomes
= A randomly chosen card is a hard/Total number of cards
= 13/52
On the other hand,
P(C = 2) = A randomly chosen card is not a hard/Total number of cards
= 39/52
Question 5.
w = 1 when a randomly chosen letter from the English alphabet is a vowel and w = 2 otherwise.
Answer:

Question 6.
n = the number of digits in a random integer from O through 999.
Answer:
There are 10 outcomes for value 1, 90 outcomes for value 2, and 900 values for value 3.
P(N = 1) = Number of favorable outcomes/Total number of outcomes
= A randomly chosen integers in a one-digit number/Total number of integers
= 10/1000
= 1/100
P(N = 2) = 90/1000 = 9/100
P(N = 3) = 900/1000 = 9/10
In Exercises 7 and 8, use the probability distribution to determine (a) the number that is most likely to be spun on a spinner, and (b) the probability of spinning an even number.
Question 7.
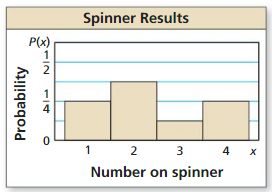
Answer:

Question 8.
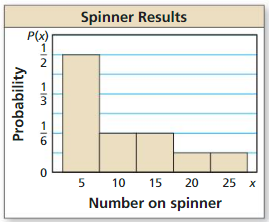
Answer:
The most likely number to be spun on the spinner is the value of random variable X(Number of spinner) of which P(X) is greatest.
From given histogram we see that this probability is greatest for X = 5.
Hence the most likely number to be spun on the spinner is 5.
P(Spinning an even number) = P(X = 10) + P(X = 20) = 1/6 + 1/12 = 1/4
USING EQUATIONS
In Exercises 9 – 12, calculate the probability of flipping a coin 20 times and getting the given number of heads.
Question 9.
1
Answer:
![]()
Question 10.
4
Answer:
P(Four success) = 20C4(1/2)4(1/2)20-4
= 20!/4!(20 – 4)!(1/2)20
= 20!/4!(16)!(1/2)20
= 0.0046
We see that the obtained probability is small, which is logical.
Question 11.
18
Answer:
![]()
Question 12.
20
Answer:
P(Four success) = 20C20(1/2)20(1/2)20-20
= 20!/20!(20 – 20)!(1/2)20
=(1/2)20
= 0.00000095
Question 13.
MODELING WITH MATHEMATICS
According to a survey, 27% of high school students in the United States buy a class ring. You ask 6 randomly chosen high school students whether they own a class ring.

a. Draw a histogram of the binomial distribution for your survey.
b. What is the most likely outcome of your survey?
c. What is the probability that at most 2 people have a class ring?
Answer:


Question 14.
MODELING WITH MATHEMATICS
According to a survey, 48% of adults in the United States believe that Unidentified Flying Objects (UFOs) are observing our planet. You ask 8 randomly chosen adults whether they believe UFOs are watching Earth.
a. Draw a histogram of the binomial distribution for your survey.
Answer:
p = P(the American is a sports fan) = 48% = 0.48
1 – p = P(the American is not a sports fan) = 1 – 0.48= 0.52
P (0 success) = 0C8 p0(1 – p)8-0
= 8!/0!(8 – 0)! 1 . 0.528
= 0.528
= 0.1513
P (One person believe that UFOs are watching Earth) =8C1 p¹(1 – p)8-1
=0.03948
P (Two person believe that UFOs are watching Earth) =8C2 p2(1 – p)8-2
=0.1275
P (Three person believe that UFOs are watching Earth) =8C3 p3(1 – p)8-3
=0.2355
P (Four person believe that UFOs are watching Earth) =8C4 p4(1 – p)8-4
=0.2717
P (Five person believe that UFOs are watching Earth) =8C5 p5(1 – p)8-5
=0.2006
P (Six person believe that UFOs are watching Earth) =8C6 p6(1 – p)8-6
=0.0926
P (Seven person believe that UFOs are watching Earth) =8C7 p7(1 – p)8-7
=0.0244
P (Eight person believe that UFOs are watching Earth) =8C8 p8(1 – p)8-8
=0.0028
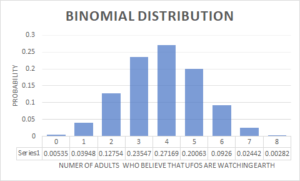
b. What is the most likely outcome of your survey?
Answer:
P (Four person believe that UFOs are watching Earth) = 0.2717
This probability has the highest, so we conclude that the most likely outcome is that four of the eight adults believe that UFOs are watching Earth.
c. What is the probability that at most 3 people believe UFOs are watching Earth?
Answer:
P (At most 3 persons believe that UFOs are watching Earth) = P (One person believe that UFOs are watching Earth) + P (Two person believe that UFOs are watching Earth) + P (Three person believe that UFOs are watching Earth)
= 0.0053 + 0.0395 + 0.1275 + 0.2355
= 0.4078
ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error in calculating the probability of rolling a 1 exactly 3 times in 5 rolls of a six-sided die.
Question 15.
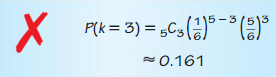
Answer:
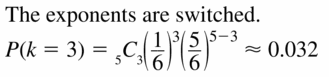
Question 16.
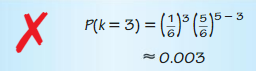
Answer:
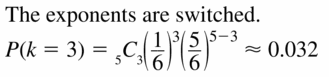
Question 17.
MATHEMATICAL CONNECTIONS
At most 7 gopher holes appear each week on the farm shown. Let x represent how many of the gopher holes appear in the carrot patch. Assume that a gopher hole has an equal chance of appearing at any point on the farm.
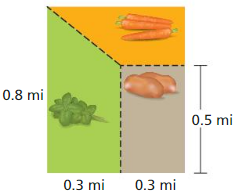
a. Find P(x) for x = 0, 1, 2 ….., 7.
Answer:
p = P(the gopher holes appear in the carrot patch)
= Area marked for carrot/Area of the whole farm
= Area of a square + Area of a triangle/Area of the whole farm
= 0.28125
1 – p = P(The gopher holes do not appear in the carrot patch)
= 1 – 0.28125
= 0.71875
P (0 success) = 0C7 p0(1 – p)7-0
= 7!/0!(7 – 0)! 1 . 0.727
= 0.727
= 0.099
P (There is one gopher hole in the carrot patch) =7C1 p¹(1 – p)7-1
=0.27143
P (There is two gopher hole in the carrot patch) =7C2 p¹(1 – p)7-2
=0.31863
P (There is three gopher hole in the carrot patch) =7C3 p¹(1 – p)7-3
=0.20781
P (There is four gopher hole in the carrot patch) =7C4 p¹(1 – p)7-4
=0.08131
P (There is five gopher hole in the carrot patch) =7C5 p¹(1 – p)7-5
=0.01909
P (There is six gopher hole in the carrot patch) =7C6 p¹(1 – p)7-6
=0.00249
P (There is seven gopher hole in the carrot patch) =7C7 p¹(1 – p)7-7
=0.00012
b. Make a table showing the probability distribution for x.
c. Make a histogram showing the probability distribution for x.
Answer:
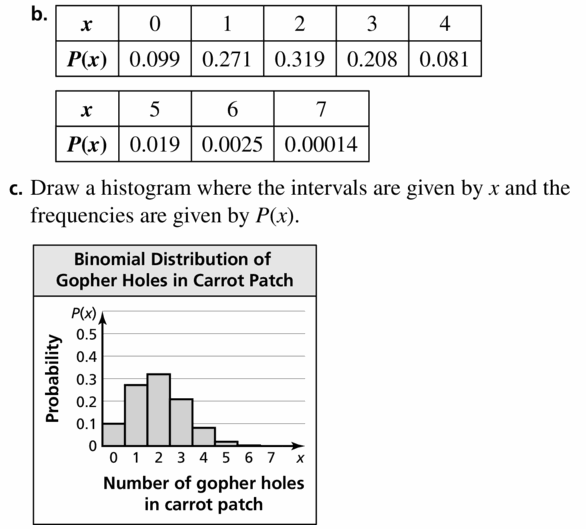
Question 18.
HOW DO YOU SEE IT?
Complete the probability distribution for the random variable x. What is the probability the value of x is greater than 2?
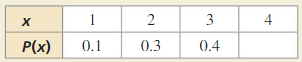
Answer:
P(X = 1) + P(X = 2) + … + P(X = n) = 1
P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = 0.1 + 0.3 + 0.4 + P(X = 4)
= 1
P(X = 4) = 1 – 0.8 = 0.2
Now lets find a probability that value of X is greater then two, as
P(X ≥ 2) = P(X = 2) + P(X = 3) + P(X = 4)
= 0.3 + 0.4 + 0.2
= 0.9
It is very likely that the random variable k will take a value greater than 2.
Question 19.
MAKING AN ARGUMENT
The binomial distribution Shows the results of a binomial experiment. Your friend claims that the probability p of a success must be greater than the probability 1 – p of a failure. Is your friend correct? Explain your reasoning.
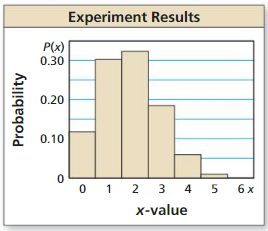
Answer:

Question 20.
THOUGHT PROVOKING
There are 100 coins in a bag. Only one of them has a date of 2010. You choose a coin at random, check the date, and then put the coin back in the bag. You repeat this 100 times. Are you certain of choosing the 2010 coin at least once? Explain your reasoning.
Answer:
Given,
There are 100 coins in a bag. Only one of them has a date of 2010. You choose a coin at random, check the date, and then put the coin back in the bag. You repeat this 100 times
p = P(Selected coin has a date of 2010)
= Number of favorable outcomes/Total number of outcomes
= 1/100
1 – p = 1 – 1/100 = 99/100
P (0 success) = 100C0 p0(1 – p)100-0
= 100!/0!(100 – 0)! 1 . (99/100)100
= (99/100)100
= 0.366
P(1 or more success) = 1 – P(0 success) = 1 – 0.366 = 0.634
Hence with a probability of 0.634, we will choose a coin which has a date of 2010.
We are not certain of choosing the 2010 coin at least once.
Question 21.
MODELING WITH MATHEMATICS
Assume that having a male and having a female child are independent events, and that the probability of each is 0.5.
a. A couple has 4 male children. Evaluate the validity of this statement: “The first 4 kids were all boys, so the next one will probably be a girl.”
b. What is the probability of having 4 male children and then a female child?
c. Let x be a random variable that represents the number of children a couple already has when they have their first female child. Draw a histogram of the distribution of P(x) for 0 ≤ x ≤ 10. Describe the shape of the histogram.
Answer:

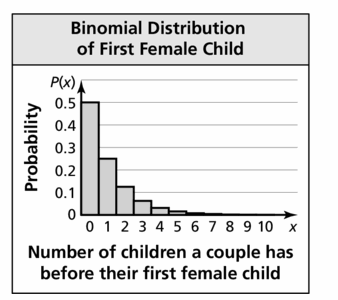
Question 22.
CRITICAL THINKING
An entertainment system has n speakers. Each speaker will function properly with probability p. independent of whether the other speakers are functioning. The system will operate effectively when at least 50% of its speakers are functioning. For what values of p is a 5-speaker system more likely to operate than a 3-speaker system?
Answer:
Given,
An entertainment system has n speakers. Each speaker will function properly with probability p. independent of whether the other speakers are functioning.
The system will operate effectively when at least 50% of its speakers are functioning.
p = P(Speaker will function properly)
1 – 9 = P(Speaker will not function properly)
P(5-speaker system operate) = P(X = 3) + P(X = 4) + P(X = 5)
P(5-Speaker system operate) = P (0 success) = 5C3 p3(1 – p)5-3 + 5C4 p4(1 – p)5-4 + 5C5 p5(1 – p)5-5 = 10p3(1 – p)5-4 + 5p4(1 – p)5
P = P(X = 2) + P(X = 3)
= 5C2 p2(1 – p)5-2 + 5C3 p3(1 – p)5-3
= 10p2(1 – p)5-3 + 10p3(1 – p)2
10p3(1 – p)5-4 + 5p4(1 – p)5 + p5 > 10p2(1 – p)3 + 10p3(1 – p)2
5p2 – 4p3 – 10 + 30p – 30p2 + 10p3 > 0
A 5-speaker system operate more likely to operate than 3-speaker system when p ∈ (0.558, 1]
Maintaining Mathematical Proficiency
List the possible outcomes for the situation.
Question 23.
guessing the gender of three children
Answer:
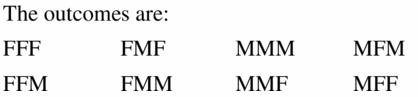
Question 24.
picking one of two doors and one of three curtains
Answer:
If we denote by D1 and D2 first and second door and with C1, C2, C3 first, second and third curtain, then the possible outcomes are
D1C1, D1C2, D1C3, D2C1, D2C2, D2C3
Thus there are six possible outcomes.
Probability Review
12.1 Sample Spaces and Probability
Question 1.
A bag contains 9 tiles. one for each letter in the word HAPPINESS. You choose a tile at random. What is the probability that you choose a tile with the letter S? What is the probability that you choose a tile with a letter other than P?
Answer:
Let X be a random variable that represent the letter on tile.
We know that a bag contains tiles labeled with “H”, “A”, “P”, “I”, “N”, “E” and “S”
So we can conclude that the possible values for X are letters “H”, “A”, “P”, “I”, “N”, “E” and “S” and total number of outcomes is 9.
Question 2.
You throw a dart at the board shown. Your dart is equally likely to hit any point inside the square board. Are you most likely to get 5 points, 10 points, or 20 points?
Answer: It is the most likely to get 20 points.
Explanation:
From given board, we can conclude that the probability that we get 5 points is
P(5 points) = Surface of red area/Surface of board = 4/36 = 1/9
On the other hand, we see that the probability we get 10 points is
P(10 points) = Surface of yellow area/Surface of board = (16 – 4)/36 = 1/3
and the probability that we get 20 points is
P(20 points) = Surface of blue area/Surface of board = (36 – 16)/36 = 5/9
From the obtained results we get that it is the most likely to get 20 points, which is logical because the surface of the blue area is the largest.
12.2 Independent and Dependent Events
Find the probability of randomly selecting the given marbles from a bag of 5 red, 8 green, and 3 blue marbles when (a) you replace the first marble before drawing the second, and (b) you do not replace the first marble. Compare the probabilities.
Question 3.
red, then green
Answer:
We selected two marbles from a bag of 5 red, 8 green and 3 blue. With R denote the event that the red marble is drawn, with P blue, and with G green. The draws are independent because we replace the first marble before drawing the second. Therefore, the probability that we selected first red marble and then green is
P(RG) = P(R)P(G) = 5/16 . 8/16 = k5/36 = 0.15625
b. In this case, we do not replace the first marble before drawing the second. So, the draws are not independent.
P(RG) = P(R)P(G|R) = 5/16 . 8/15 = 1/6 = 0.16667
It is more likely that we selected first red marble and then green when we not replace the first marble before drawing the second.
Question 4.
blue, then red
Answer:
We selected two marbles from a bag of 5 red, 8 green and 3 blue. With R denote the event that the red marble is drawn, with P blue, and with G green. The draws are independent because we replace the first marble before drawing the second. Therefore, the probability that we selected first red marble and then green is
P(BR) = P(B)P(R) = 3/16 . 5/16 = 15/256 = 0.05859
b. In this case, we do not replace the first marble before drawing the second. So, the draws are not independent.
P(BR) = P(B)P(R|B) = 3/16 . 5/15 = 1/16 = 0.0625
It is more likely that we selected first blue marble and then red when we not replace the first marble before drawing the second.
Question 5.
green, then green
Answer:
We selected two marbles from a bag of 5 red, 8 green and 3 blue. With R denote the event that the red marble is drawn, with P blue, and with G green. The draws are independent because we replace the first marble before drawing the second. Therefore, the probability that we selected first red marble and then green is
P(GG) = P(G)P(G) = 8/16 . 8/16 = 1/4 = 0.25
b. In this case, we do not replace the first marble before drawing the second. So, the draws are not independent.
P(GG) = P(G)P(G|G) = 8/16 . 7/15 = 0.23333
It is more likely that we selected first blue marble and then red when we not replace the first marble before drawing the second.
12.3 Two-Way Tables and Probability
Question 6.
What is the probability that a randomly selected resident who does not support the project in the example above is from the west side?
Answer:
P(West side|Does not support the project) = P(West side and Does not support the project)/P(Does not support the project)
= 0.09/(0.08 + 0.09)
= 0.529
The probability that random selected resident who does not support the project is from the west side is about 0.529
Question 7.
After a conference, 220 men and 270 women respond to a survey. Of those, 200 men and 230 women say the conference was impactful. Organize these results in a two-way table. Then find and interpret the marginal frequencies.
Answer:
After a conference, 220 men and 270 women respond to a survey. Of those, 200 men and 230 women say the conference was impactful.
Number of men who say the conference had not impact = 220 – 200 = 20
By the same method we come to the conclusion
Number of women who say the conference had not impact = 270 – 230 = 40
Now, we will find the marginal frequencies.
Total number of people who say the conference was impact is 200 + 230 = 430
Total Number of people who say the conference had not impact = 20 + 40 = 60
Also from given information we know that total number of people who was surveyed is 220 + 270 = 490
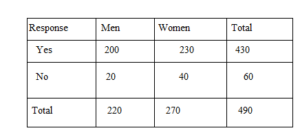
12.4 Probability of Disjoint and Overlapping Events
Question 8.
Let A and B be events such that P(A) = 0.32, P(B) = 0.48, and P(A and B) = 0.12. Find P(A or B).
Answer:
P(A or B) = P(A) + P(B) – P(A and B)
Given,
P(A) = 0.32, P(B) = 0.48, and P(A and B) = 0.12
P(A or B) = 0.32 + 0.48 – 0.12 = 0.68
Question 9.
Out of 100 employees at a company, 92 employees either work part time or work 5 days each week. There are 14 employees who work part time and 80 employees who work 5 days each week. What is the probability that a randomly selected employee works both part time and 5 days each week?
Answer:
A = {Employees either work part time},
B = {Employees either work 5 days}
Based on the given information we see that
P(A) = Number of favorable outcomes/Total Number of outcomes
= Number of Employees either work part time/Total number of employees
= 14/100
= 0.14
P(B) = Number of favorable outcomes/Total Number of outcomes
= Number of Employees either work 5 days/Total number of employees
= 80/100
= 0.8
Also, we know that 92 employees either work part time or 5 days each week
P(A or B) = Number of favorable outcomes/Total Number of outcomes
= 92/100 = 0.92
For given events A and B the probability of A or B is
P(A or B) = P(A) + P(B) – P(A and B)
P(A or B) = 0.14 + 0.8 – 0.92 = 0.02
Hence the probability that a randomly selected employee works part time and 5 days each week is 0.02
12.5 Permutations and Combinations
Evaluate the expression.
Question 10.
7P6
Answer:
We know that number of permutations of n objects taken at a time (a ≤ n)
nPa = n!/(n – a)!
= 7!/(7 – 6)!
= 7 . 6 . 5 . 4 . 3 . 2 . 1
= 5040
7P6 = 7! = 5040
Question 11.
13P10
Answer:
We know that number of permutations of n objects taken at a time (a ≤ n)
nPa = n!/(n – a)!
= 13!/(13 – 10)!
= 13!/3!
= 13. 12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 = 94348800
13P10 = 94348800
Question 12.
6C2
Answer:
nCa = n!/a!(n – a)!
6C2 = 6!/2!(6 – 2)!
= 6!/2!(4)!
= 6 . 5 . 4 . 3 . 2 . 1/(2 . 1)(4 . 3 . 2 . 1)
15
6C2 = 15
nC2 = n(n – 1)/2
6C2 = 15
Question 13.
8C4
Answer:
nCa = n!/a!(n – a)!
8C4 = 8!/4!(8 – 4)!
= 68!/4!(4)!
= 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(4 . 3 . 2 . 1)(4 . 3 . 2 . 1)
= 2 . 7 . 5
6C2 = 70
Question 14.
Eight sprinters are competing in a race. How many different ways can they finish the race? (Assume there are no ties.)
Answer:
nPn = n!
We know thata 8 sprinters are participating in a race. It is important to us in what order each of them will reach the goal. This tells us that it is necessary to calculate the number of permutations of 8 sprinters.
8P8 = 8! = 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 40320
Eight sprinters can finish a race in 40320 ways.
Question 15.
A random drawing will determine which 3 people in a group of 9 will win concert tickets. What is the probability that you and your 2 friends will win the tickets?
Answer:
nCa = n!/a!(n – a)!
9C3 = 9!/3!(9 – 3)!
= 9!/3!(6)!
= 9 . 8 . 7 6 . 5 . 4 . 3 . 2 . 1/(3 . 2 . 1)(6 . 5 . 4 . 3 . 2 . 1)
= 84
9C3 = 84
The probability that you and your 2 friends will win the tickets is equal to the probability that out of 84 possibilities, the trio in which you and your friend are in will be chosen.
P = Number of favorable outcomes/ Total number of outcomes = 1/84
12.6 Binomial Distributions
Question 16.
Find the Probability of flipping a coin 12 times and getting exactly 4 heads.
Answer:
The probabilities are P(H) = P(T) = 1/2, that is p = p – 1 = 1/2 and are the same for each trial.
n = 12
P = 12!/4!(12 – 4)! . (1/2)12
= 0.1208
Therefore the probability of flipping a coin 12 times and getting exactly 4 heads is about 0.12
Question 17.
A basketball player makes a free throw 82.6% of the time. The player attempts 5 free throws. Draw a histogram of the binomial distribution of the number of successful free throws. What is the most likely outcome?
Answer:
Given,
A basketball player makes a free throw 82.6% of the time. The player attempts 5 free throws.
p = P(Successful free throw) = 82.6% = 0.826
1 – p = P(Unsuccessful free throw) = 1 – 0.826 = 0.174
P (Out of 5 free throws one was successful) = 5C1 p¹(1 – p)5-1
P (Out of 5 free throws two was successful) =5C2 p²(1 – p)5-2
P(Out of 5 free throws three was successful) = 5C3p³(1 – p)5-3
P (Out of 5 free throws four was successful) =5C4 p4(1 – p)5-4
P (All 5 throws one was successful) = 5C5(1 – p)5-5
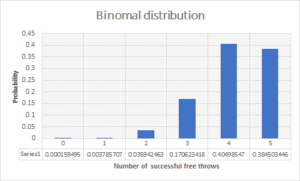
Probability Test
You roll a six-sided die. Find the probability of the event described. Explain your reasoning.
Question 1.
You roll a number less than 5.
Answer:
The die has 6 sides, thus the total number of possible outcomes is 6.
The favorable outcomes are
P(n<5) = Number of favorable outcomes/Total number of outcomes
Thus there are 4 favorable outcomes.
The probability to roll a number less than 5 is
= 4/6
= 2/3
Question 2.
You roll a multiple of 3.
Answer:
The die has 6 sides, thus the total number of possible outcomes is 6.
The favorable outcomes are
P(n = 3k) = Number of favorable outcomes/Total number of outcomes
Thus there are 2 favorable outcomes.
The probability to roll a number less than 3 is
= 2/6
= 1/3
Evaluate the expression.
Question 3.
7P2
Answer:
We know that number of permutations of n objects taken at a time (a ≤ n)
nPa = n!/(n – a)!
7P2 = 7!/(7 – 2)!
= 7!/5!
= (7 . 6 . 5 . 4 . 3 . 2 . 1)/(5 . 4 . 3 . 2 . 1)
= 7 . 6
= 42
7P2 = 42
Question 4.
8P3
Answer:
We know that number of permutations of n objects taken at a time (a ≤ n)
nPa = n!/(n – a)!
8P3 = 8!/(8 – 3)!
= 8!/5!
= (8 . 7 . 6 . 5 . 4 . 3 . 2 . 1)/(5 . 4 . 3 . 2 . 1)
= 8 . 7 . 6
= 336
8P3 = 336
Question 5.
6C3
Answer:
nCa = n!/a!(n – a)!
6C3 = 6!/3!(6 – 3)!
= 6!/3!(3)!
= 6 . 5 . 4 . 3 . 2 . 1/(3 . 2 . 1)(3 . 2 . 1)
= 2 . 5 . 2
= 20
6C3 = 20
Question 6.
12C7
Answer:
nCa = n!/a!(n – a)!
12C7 = 12!/7!(12 – 7)!
= 12!/7!(5)!
= 12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(7 . 6 . 5 . 4 . 3 . 2 . 1)(5 . 4 . 3 . 2 . 1)
= 11 . 2 . 9 . 4 = 792
12C7 = 792
Question 7.
In the word PYRAMID, how many ways can you arrange
(a) all of the letters and
Answer:
We have to find the number of permutation all of the letters in a given word that will consist of 7 letters. We see that it matters that order of letters are important.
Number of permutations = (In the 1st place can be one of 7 letters) × (In the 2nd place can be one of 6 letters that is left)
(In the 3rd can be one of 5 letters that is left) × (In the 4th can be 4 letters that is left)
(In the 5th can be three letter that is left) × (In the 6th can be two letters that is left)
(In the 7th can be one letter that is left)
= 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040
Therefore, we have 5040 ways for arrange all of the letters in given word, that is PYRAMID, PYRAMDI, PYRADMI, ……., DIMARYP.
(b) 5 of the letters?
Answer:
We have to find the number of permutation all of the letters in a given word that will consist of 3 letters. We see that it matters that order of letters are important.
Number of permutations = (In the 1st place can be one of 7 letters) × (In the 2nd place can be one of 6 letters that is left)
(In the 3rd can be one of 5 letters that is left) × (In the 4th can be 4 letters that is left)
(In the 5th can be three letter that is left)
= 7 . 6 . 5 . 4 . 3
= 2520
Therefore, we have 2520 ways for arrange 5 of the letters in given word, that is PYRAM, PYRAI, PYRAD….
Question 8.
You find the probability P(A or B) by using hie equation P(A or B) = P(A) + P(B) – P(A and B). Describe why it is necessary to subtract P(A and B) when the events A and B are overlapping. Then describe why it is not necessary to subtract P(A and B) when the events A and B are disjoint.
Answer:
When the events are overlapping then P(A and B) ≠ 0. This means that the expression P(A) + P(B) already contains the probability P(A and B) and so P(A and B) is subtracted from their sum to evaluate P(A or B)
When the events are overlapping then P(A and B) = 0 and so the equation of P(A or B reduces to P(A) + P(B))
Question 9.
Is it possible to use the formula P(A and B) = P(A) • P(B/A) when events A and B are independent? Explain your reasoning.
Answer:
If events A and B are independent events, then
P(A and B) = P(A) . P(B)
Also, because event B is independent of event A then P(B|A) = P(A)
P(A and B) = P(A) . P(B) = P(A) . P(B|A)
where A and B are the independent events.
Question 10.
According to a survey, about 58% of families sit down tor a family dinner at least four times per week. You ask 5 randomly chosen families whether the have a family dinner at least four times per week.
a. Draw a histogram of the binomial distribution for the survey.
Answer:
p = P(Family have dinner four times per week) = 58% = 0.58
1 – p = P(Family have no dinner dour times per week) = 1 – 0.58 = 0.42
P (One Family have dinner four times per week) = 5C1 p¹(1 – p)5-1
= 0.09024
P (Two Family have dinner four times per week) =5C2 p²(1 – p)5-2
= 0.24923
P(Three Family have dinner four times per week) = 5C3p³(1 – p)5-3
= 0.34418
P (Four Family have dinner four times per week) =5C4 p4(1 – p)5-4
= 0.23765
P (Family have dinner four times per week) = 5C5(1 – p)5-5 = 0.06563
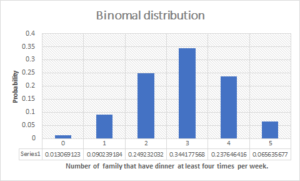
b. What is the most likely outcome of the survey?
Answer:
P(Three families have dinner four times per week) = 0.34418
This probability is the highest, so we can conclude that the most likely outcome is that three of the five families have dinner four times per week.
c. What is the probability that at least 3 families have a family dinner four times per week?
Answer:
In this part we have to find the probability that,
P(At least 3 families have dinner four times per week)
= P(Three families have dinner four times per week) + P(Four families have dinner four times per week) + P(Five families have dinner four times per week)
= 0.34418 + 0.23765 + 0.06563
= 0.64746
Question 11.
You are choosing a cell phone company to sign with for the next 2 years. The three plans you consider are equally priced. You ask several of your neighbors whether they are satisfied with their current cell phone company. The table shows the results. According to this survey, which company should you choose?
Answer:
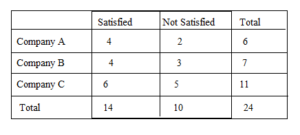
To find the joint relative frequencies we divide each frequency by the total number of people in the survey. Also the marginal relative frequencies we find as the sum of each row and each column.
So, we can present a two way table that shows the joint and marginal relative frequencies.
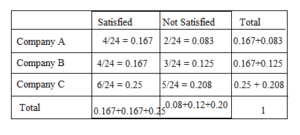
Finally, to get conditional relative frequencies we use the previous the marginal relative frequency of each row.
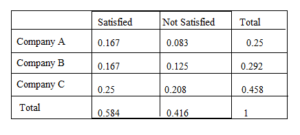
Therefore we should choose company A.
Question 12.
The surface area of Earth is about 196.9 million square miles. The land area is about 57.5 million square miles, and the rest is water. What is the probability that a meteorite that reaches the surface of Earth will hit land? What is the probability that it will hit water?
Answer:
From the formula for geometric probability we get the probability that a meteorite that reaches the surface of Earth will hit lend is
P = The lend area/ The surface area of Earth = 57.5/196.9 = 0.292
Alos we know that the probability for complement of event A is
P(\(\bar{A}\)) = 1 – P(A)
In this case, complement of event {A meteorite will hit lend} is {A meteorite will hit water}.
P = 1 – 0.292 = 0.708
Question 13.
Consider a bag that contains all the chess pieces in a set, as shown in the diagram.
a. You choose one piece at random. Find the probability that you choose a black piece or a queen.
Answer:
The total number of pieces is 2 + 2 + 4 + 4 + 4 + 16 = 32.
Also we see that the number of black and white pieces are the same, 16 and there are one black queen.
A = {We choose a black piece}
B = {We choose a queen}
P(A) = Number of favorable outcomes/Total number of outcomes = Number of black pieces/Total number of pieces = 16/32 = 1/2
P(B) = Number of queens/Total number of pieces = 2/32 = 1/16
P(A and B) = Number of black queens/Total number of pieces = 1/32
P(A or B) = P(A) + P(B) – P(A and B)
= 1/2 + 1/16 – 1/32 = 17/32
b. You choose one piece at random, do not replace it, then choose a second piece at random. Find the probability that you choose a king, then a pawn.
Answer:
C = {We choose a king} and D = {We choose a pawn}
P(C) = Number of pawns/Total number of pieces = 16/32 = 1/2
P(C and D) = Number of pawns and king/Total number of pieces = (16 + 2)/32 = 9/16
We know that for two dependent events A and B probability that both occur is
P(A and B) = P(A)P(B|A)
P(D|C) = P(C and D)/P(C) = 1/2 × 16/9 = 8/9
Question 14.
Three volunteers are chosen at random from a group of 12 to help at a summer camp.
a. What is the probability that you, your brother, and your friend are chosen?
Answer:
nCa = n!/a!(n – a)!
12C3 = 12!/3!(12 – 3)!
= 12!/3!(9)!
= 12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1/(3 . 2 . 1)(9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1)
= 12 . 11 . 10/3 . 2 . 1
= 2 . 11 . 10
12C3 = 220
P = Number of favorable outcomes/Total number of outcomes = 1/220
b. The first person chosen will be a counselor, the second will be a lifeguard, and the third will be a cook. What is the probability that you are the cook, your brother is the lifeguard, and your friend is the counselor?
Answer:
We know that number of permutations of n objects taken at a time (a ≤ n)
nPa = n!/(n – a)!
12P3 = 12!/(12 – 3)!
= 12!/9!
= (12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1)/(9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1)
= 12 . 11 . 10
= 1320
12P3 = 1320
P = 1/1320
Probability Cumulative Assessment
Question 1.
According to a survey, 63% of Americans consider themselves sports fans. You randomly select 14 Americans to survey.
a. Draw a histogram of the binomial distribution of your survey.
Answer:
p = P(the American is a sports fan) = 63% = 0.63
1 – p = P(the American is not a sports fan) = 1 – 0.63= 0.37
P (0 success) = 12C0 p0(1 – p)12-0
= 12!/0!(12 – 0)! 1 . 0.3712
= 0.3712
P (One American is a sports fans) =12C1 p¹(1 – p)12-1
=0.000134506
P (Two Americans are sports fans) =12C2 p2(1 – p)12-2
=0.001259628
P (Three Americans are sports fans) =12C3 p3(1 – p)12-3
=0.007149239
P (Four American is a sports fans) =12C4 p4(1 – p)12-4
=0.027389316
P (Five American is a sports fans) =12C5 p5(1 – p)12-5
=0.07461738
P (Six American is a sports fans) =12C6 p6(1 – p)12-6
=0.148226418
P (Seven American is a sports fans) =12C7 p7(1 – p)12-7
=0.216330447
P (Eight American is a sports fans) =12C8 p8(1 – p)12-8
=0.230216523
P (Nine American is a sports fans) =12C9 p9(1 – p)12-9
=0.174217909
P (Ten American is a sports fans) =12C10p10(1 – p)12-10
=0.088992392
P (Eleven American is a sports fans) =12C11 p11(1 – p)12-11
=0.023755047
P (Twelve American is a sports fans) =12C1 p12(1 – p)12-12
=0.003909188
b. What is the most likely number of Americans who consider themselves Sports fans?
Answer:
From histogram in part a and based on the calculations in the first part
We know that,
P(Eight Americans are sports fans) = 0.23
This probability is highest, so we can conclude that the most likley outcome is that eight of the 12 selected Americans consider themselves sports fans.
c. What is the probability at least 7 Americans consider themselves sports fans?
Answer:
In this part we have to find dthe probability that
P(At least 7 Americans consider themselves sports fans)
= P(Seven American is a sports fans) + P(Eight American is a sports fans) + P(Nine American is a sports fans) + P(Ten American is a sports fans) + P(Eleven American is a sports fans) + P(Twelve American is a sports fans)
= 0.2163 + 0.2302 + 0.1742 + 0.08899 + 0.0275 + 0.0039
= 0.7412
Therefore, we can conclude that the probability that at least 7 Americans consider themselves sports fans is 0.7412
Question 2.
What is the arc length of \(\widehat{A B}\) ?
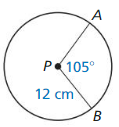
(A) 3.5 π cm
(B) 7 π cm
(C) 21 π cm
(D) 42 π cm
Answer:
Arc length of \(\widehat{A B}\) = 105/360 × 2π × 12 = 7π cm
Question 3.
you order a fruit smoothie made with 2 liquid ingredients and 3 fruit ingredients from the menu shown. How many different fruit smoothies can you order?

Answer:
Question 4.
The point (4, 3) is on a circle with center (- 2, – 5), What is the standard equation of the circle?
Answer:
Given,
The point (4, 3) is on a circle with center (- 2, – 5)
(x – h)² + (y – k)² = r²
Substitute the values in the given equation
(4 – (-2))² + (3 – (-5))² = r²
100 = r²
r = √100 = 10
General equation of circle
(x – h)² + (y – k)² = r²
Substitute the values in the given equation
(x – (-2))² + (y – (-5))² = 10²
(x + 2)² + (y + 5)² = 100
Question 5.
Find the length of each line segment with the given endpoints. Then order the line segments from shortest to longest.
a. A(1, – 5), B(4, 0)
Answer:
The general equation of distance between 2 points is
d = √(x2 – x1)² + (y2 – y1)²
dAB = √(4 – 1)² + (0 – (-5))²
= √34
= 5.83
b. C(- 4, 2), D(1, 4)
Answer:
The general equation of distance between 2 points is
d = √(x2 – x1)² + (y2 – y1)²
dCD = √(1 – (-4))² + (4 – 2)²
= √29
= 5.39
c. E(- 1, 1), F(- 2, 7)
Answer:
The general equation of distance between 2 points is
d = √(x2 – x1)² + (y2 – y1)²
dEF = √(-2 – (-1))² + (7 – 1)²
= √37
= 6.083
d. G(- 1.5, 0), H(4.5, 0)
Answer:
The general equation of distance between 2 points is
d = √(x2 – x1)² + (y2 – y1)²
dGH = √(4.5 – (-1.5))² + (0 – 0)²
= √36
= 6
e. J(- 7, – 8), K(- 3, – 5)
Answer:
The general equation of distance between 2 points is
d = √(x2 – x1)² + (y2 – y1)²
dJK = √(-3 – (-7))² + (-5 – (-8))²
= √25
= 5
f. L(10, – 2), M(9, 6)
Answer:
The general equation of distance between 2 points is
d = √(x2 – x1)² + (y2 – y1)²
dLM = √(9 – 10)² + (6 – (-2))²
= √65
= 8.06
Therefore, the line segments in ascending order are JK < CD < AB < GH < EF < LM
Question 6.
Use the diagram to explain why the equation is true.
P(A) + P(B) = P(A or B) + P(A and B)
Answer:
Given,
P(A) = 8/12
P(B) = 7/12
P(A or B) = 12/12
P(A and B) = 3/12
P(A) + P(B) = P(A or B) + P(A and B)
8/12 + 7/12 = 12/12 + 3/12
5/4 = 5/4
Question 7.
A plane intersects a cylinder. Which of the following cross sections cannot be formed by this intersection?
(A) line
(B) triangle
(C) rectangle
(D) circle
Answer:
If the plane is tangent to the curved surface of the cylinder, then the intersection is a line.
If the plane is cuts the cylinder parallel to its circular base, then the intersection is a circle.
If the plane cuts the cylinder perpendicular to its circular base and parallel to its curved surface, then the intersection is a rectangle.
The correct answer is option B.
Question 8.
A survey asked male and female students about whether the prefer to take gym class or choir. The table shows the results of the survey,
a. Complete the two-way table.
Answer:
From the given table we first find the joint frequencies.
Number of people who prefer gym class = 106 – 49 = 57
On the other hand, we know that 57 people prefer gym class, of which 23 was female.
Number of male who prefer the gym class = 57 – 23 = 34
Number of male who prefer the choir class = 50 – 34 = 16
Number of female who prefer the choir class = 49 – 16 = 33
Now, we will find the remaining marginal frequencies. Hence we know that 23 female prefer gym class and 33 female prefer choir class.
Total number of female is 23 + 33 = 56
b. What is the probability that a randomly selected student is female and prefers choir?
Answer:
P = Number of female who prefer choir class/Total number of students
= 33/106
= 0.31
c. What is the probability that a randomly selected male student prefers gym class?
Answer:
P(Prefer gym class|Male) = P(Male and prefer gym class)/P(Male)
= Number of male who prefer gym class/Number of male students
= 34/50
= 0.68
Question 9.
The owner of a lawn-mowing business has three mowers. As long as one of the mowers is working. the owner can stay productive. One of the mowers is unusable 10% of the time, one is unusable 8% of the time, and one is unusable 18% of the time.
a. Find the probability that all three mowers are unusable on a given day.
Answer:
P(A) = 10% = 0.1
P(B) = 8% = 0.08
P(C) = 18% = 0.18
\(\bar{A}\) = {The first mower is usable}
\(\bar{B}\) = {The second mower is usable}
\(\bar{C}\) = {The third mower is usable}
P(\(\bar{A}\)) = 1 – 0.1 = 0.9
P(\(\bar{B}\)) = 1 – 0.08 = 0.92
P(\(\bar{C}\)) = 1 – 0.18 = 0.82
Event that all three mowers are unusable on a given day is A and B and C. If we assume that the operation of the mowers are independent, then we get the probability that all three mowers are unusable on a given day as
P(A and B and C) = P(A) . P(B) . P(C) = 0.1 × 0.08 × 0.18 = 0.00144
b. Find the probability that at least one of the mowers is unusable on a given day.
Answer:
Event at least one of mowers is unusable on a given day is equivalent to event one of mowers is unusable on a given day or two of mowers is unusable on a given day.
A and \(\bar{B}\) and \(\bar{C}\) or \(\bar{A}\) and B and \(\bar{C}\) or \(\bar{A}\) and \(\bar{B}\) and C
On the other hand, event two of mowers is unusable on a given day is
A and B and \(\bar{C}\) or \(\bar{A}\) and B and C or A and \(\bar{B}\) and C
P(A and \(\bar{B}\) and \(\bar{C}\)) + P(\(\bar{A}\) and B and \(\bar{C}\)) + P(\(\bar{A}\) and \(\bar{B}\) and C)
= 0.1 × 0.92 × 0.82 + 0.9 × 0.08 × 0.82 + 0.9 × 0.92 × 0.18
= 0.28352
P(A and \(\bar{B}\) and \(\bar{C}\)) + P(\(\bar{A}\) and B and \(\bar{C}\)) + P(\(\bar{A}\) and \(\bar{B}\) and C)
= 0.1 × 0.08 × 0.82 + 0.9 × 0.08 × 0.18 + 0.1 × 0.92 × 0.18
= 0.03608
P(At least one of mowers is unusable) = P(One of mowers is unusable) + P(two of mowers is unusable)
= 0.28352 + 0.03608
= 0.3196
c. Suppose the least-reliable mower stops working completely. How does this affect the probability that the lawn-moving business can be productive on a given day?
Answer:
If the least-reliable mower stops working completely, this will not affect the probability that the lawn mowing business can be productive on a given day, because we know that as long as one of the mowers is working, the owner can stay productive.
Question 10.
You throw a dart at the board shown. Your dart is equally likely to hit any point inside the square board. What is the probability your dart lands in the yellow region?
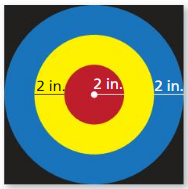
(A) \(\frac{\pi}{36}\)
(B) \(\frac{\pi}{12}\)
(C) \(\frac{\pi}{9}\)
(D) \(\frac{\pi}{4}\)
Answer:
The total area of the given figure is (6(2))² = 144 sq. units
Area of the red circle = π × 2² = 4π
The area of the yellow ring is π × (4² – 2²) = 12π
The area of the blue ring is π × (6² – 4²) = 20π
Therefore, the probability of hitting the blue region is 12π/144 = π/12
Thus the correct answer is option B.
Conclusion:
Hope you are all satisfied with the given solutions. You can get free access to Download Big Ideas Math Geometry Answers Chapter 12 Probability pdf from here. Bookmark our Big Ideas Math Answers to get detailed solutions for all Geometry Chapters.
