Give your kid the right assistance he/she needs regarding the Big Ideas Math Geometry Chapter 6 Relationships within Triangles concepts. Practicing from the Big Ideas Math Geometry Answers Ch 6 Relationships within Triangles on a frequent basis help you to attempt the exam with confidence. You can avail these handy resources for BIM Book Geometry Chapter 6 Relationships within Triangles Solution Key and clear the exams with high scores. In fact, you can download the BIM Book Geometry Ch 6 Relationships within Triangles Answers for free of cost and prepare them offline too.
Big Ideas Math Book Geometry Answer Key Chapter 6 Relationships Within Triangles
Have a deeper understanding of concepts from the surface level by making the most out of these BIM Geometry Solutions for Chapter 6. Solve the Questions within the BigIdeas Math Geometry Textbook Answer Key PDF on a frequent basis and answer any kind of question in the exam easily. Just click on the Topicwise Big Ideas Math Geometry Ch 6 Relationships within Triangles Answers and kickstart your preparation.
- Relationships Within Triangles Maintaining Mathematical Proficiency – Page 299
- Relationships Within Triangles Mathematical Practices – Page 300
- 6.1 Perpendicular And Angle Bisectors – Page 301
- Lesson 6.1 Perpendicular And Angle Bisectors – Page(302-308)
- Exercise 6.1 Perpendicular And Angle Bisectors – Page(306-308)
- 6.2 Bisectors of Triangles – Page 309
- Lesson 6.2 Bisectors of Triangles – Page(310-318)
- Exercise 6.2 Bisectors of Triangles – Page(315-318)
- 6.3 Medians and Altitudes of Triangles – Page 319
- Lesson 6.3 Medians and Altitudes of Triangles – Page(320-326)
- Exercise 6.3 Medians and Altitudes of Triangles – Page(324-326)
- 6.1 and 6.3 Quiz – Page 328
- 6.4 The Triangle Midsegment Theorem – Page 329
- Lesson 6.4 The Triangle Midsegment Theorem – Page (330-334)
- Exercise 6.4 The Triangle Midsegment Theorem – Page(333-334)
- 6.5 Indirect Proof and Inequalities in One Triangle – Page 335
- Lesson 6.5 Indirect Proof and Inequalities in One Triangle – Page(336-342)
- Exercise 6.5 Indirect Proof and Inequalities in One Triangle – Page(340-342)
- 6.6 Inequalities in Two Triangles – Page 343
- Lesson 6.6 Inequalities in Two Triangles – Page(344-348)
- Exercise 6.6 Inequalities in Two Triangles – Page(347-348)
- Relationships Within Triangles Chapter Review – Page(350-352)
- Relationships Within Triangles Chapter Test – Page 353
- Relationships Within Triangles Cumulative Assessment – Page(354-355)
Relationships Within Triangles Maintaining Mathematical Proficiency
Write an equation of the line passing through point P that is perpendicular to the given line.
Question 1.
P(3, 1), y = \(\frac{1}{3}\)x – 5
Answer:
y = -3x + 10
Explanation:
The slope of the given line is \(\frac { 1 }{ 3 } \). Since the slope of the perpendicular line must be the negative reciprocal of the slope of the given line.
The slope of the perpendicular line = -3
Substitute the values in y = mx + c
1 = -3(3) + c
1 = -9 + c
c = 1 + 9
c = 10
use the slope intercept form of a linear equation again substitute m, c
y = -3x + 10
Question 2.
P(4, – 3), y = – x – 5
Answer:
y = \(\frac { 1 }{ 3 } \)x – \(\frac { 5 }{ 3 } \)
Explanation:
The slope of the given line is -3. Since the slope of the perpendicular line must be the negative reciprocal of the slope of the given line.
The slope of the perpendicular line = \(\frac { 1 }{ 3 } \)
Substitute the values in y = mx + c
-3 = –\(\frac { 1 }{ 3 } \)(4) + c
c = -3 + \(\frac { 4 }{ 3 } \) = \(\frac { -9 + 4 }{ 3 } \) = \(\frac { -5 }{ 3 } \)
use the slope intercept form of a linear equation again substitute m, c
y = \(\frac { 1 }{ 3 } \)x + \(\frac { -5 }{ 3 } \)
y = \(\frac { 1 }{ 3 } \)x – \(\frac { 5 }{ 3 } \)
Question 3.
P(- 1, – 2), y = – 4x + 13
Answer:
y = \(\frac { 1 }{ 4 } \)x – \(\frac { 7 }{ 4 } \)
Explanation:
The slope of the given line is -4. Since the slope of the perpendicular line must be the negative reciprocal of the slope of the given line.
The slope of the perpendicular line = \(\frac { 1 }{ 4 } \)
Substitute the values in y = mx + c
-2 = \(\frac { 1 }{ 4 } \)(-1) + c
c = -2 + \(\frac { 1 }{ 4 } \) = \(\frac { -8 + 1 }{ 4 } \) = \(\frac { -7 }{ 4 } \)
use the slope intercept form of a linear equation again substitute m, c
y = \(\frac { 1 }{ 4 } \)x + \(\frac { -7 }{ 4 } \)
y = \(\frac { 1 }{ 4 } \)x – \(\frac { 7 }{ 4 } \)
Write the sentence as an inequality.
Question 4.
A number w is at least – 3 and no more than 8.
Answer:
-3 ≤ w < 8
Explanation:
At least means ≥ and no more than means <
w ≥ -3 and w < 8
-3 ≤ w < 8
Question 5.
A number m is more than 0 and less than 11.
Answer:
0 < m < 11
Explanation:
more than means > and less than means <
m > 0 and m < 11
0 < m < 11
Question 6.
A number s is less than or equal to 5 or greater than 2.
Answer:
2 < s ≤ 5
Explanation:
less than or equal to means ≤ and greater than means >
s ≤ 5 or s > 2
2 < s ≤ 5
Question 7.
A number d is fewer than 12 or no less than – 7.
Answer:
-7 < d < 12
Explanation:
fewer than means < no less than means >
d < 12 or d > -7
-7 < d < 12
Question 8.
ABSTRACT REASONING
Is it possible for the solution of a compound inequality to be all real numbers? Explain your reasoning.
Answer:
Yes
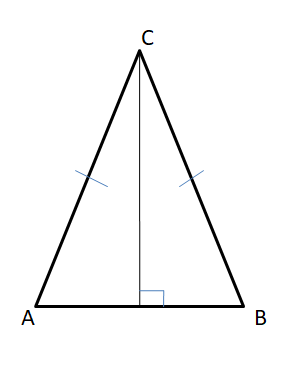
Relationships Within Triangles Mathematical Practices
Monitoring Progress
Refer to the figures at the top of the page to describe each type of line, ray, or segment in a triangle.
Question 1.
perpendicular bisector
Answer:
The perpendicular bisector of a side of a triangle is a line perpendicular to the side and passes through its midpoint. Three perpendicular bisectors of sides meet at a point in a triangle.
Question 2.
angle bisector
Answer:
The angle bisector of an angle in a triangle is a straight line that divides the angle into two congruent angles.
Question 3.
median
Answer:
It is a line segment from a vertex to the midpoint of the opposite side.
Question 4.
altitude
Answer:
It is a segment from a vertex of the triangle, perpendicular to the side opposite that vertex of the triangle.
Question 5.
midsegment
Answer:
It is a segment that connects the mid points of two sides in a triangle.
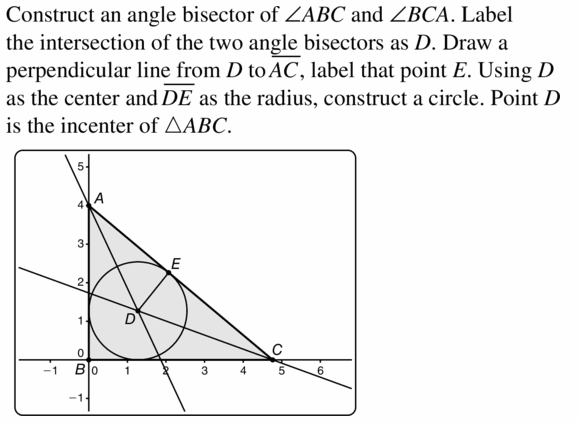
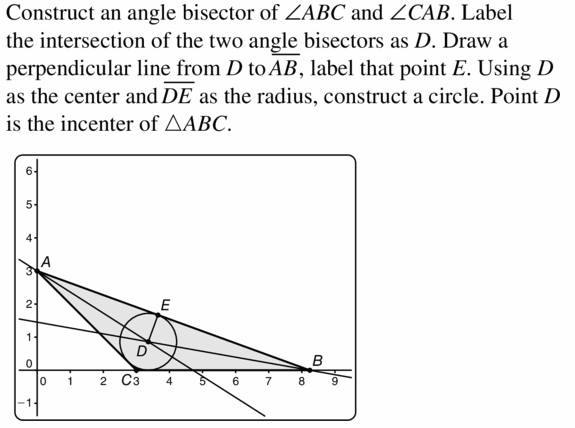
6.1 Perpendicular and Angle Bisectors
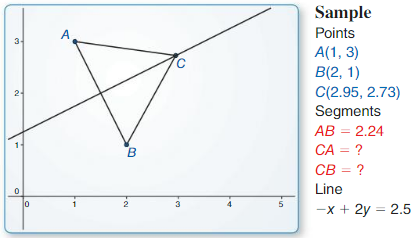
Exploration 1
Points on a Perpendicular Bisector
Work with a partner. Use dynamic geometry software.
a. Draw any segment and label it \(\overline{A B}\). ConStruct the perpendicular bisector of \(\overline{A B}\).
Answer:
b. Label a point C that is on the perpendicular bisector of \(\overline{A B}\) but is not on \(\overline{A B}\).
Answer:
c. Draw \(\overline{C A}\) and \(\overline{C B}\) and find their lengths. Then move point C to other locations on the perpendicular bisector and note the lengths of \(\overline{C A}\) and \(\overline{C B}\).
Answer:
d. Repeat parts (a) – (c) with other segments. Describe any relationships(s) you notice.
Answer:
Exploration 2
Points on an Angle Bisector
Work with a partner. Use dynamic geometry software.
a. Draw two rays \(\vec{A}\)B and \(\vec{A}\)C to form ∠BAC. Construct the bisector of ∠BAC.
Answer:
b. Label a point D on the bisector of ∠BAC.
Answer:
c. Construct and find the lengths of the perpendicular segments from D to the sides of ∠BAC. Move point D along the angle bisector and note how the lengths change.
Answer:
d. Repeat parts (a)-(c) with other angles. Describe an relationship(s) you notice.
USING TOOLS STRATEGICALLY
To be proficient in math, you need to visualize the results of varying assumptions, explore consequences, and compare predictions with data.
Answer:
Communicate Your Answer
Question 3.
What conjectures can you make about a point on the perpendicular bisector of a segment and a point on the bisector of an angle?
Answer:
It is given a point on the perpendicular bisector of a segment and a point on the bisector of an angle.
It is required to give conjectures about a point on the perpendicular bisector of a segment and a point on the bisector of an angle.
To do these use the perpendicular bisector and angle bisector theorem.
- By the perpendicular bisector theorem, a perpendicular bisector divides the line into two equal halves and makes a right angle with it. So, it can be said that every point on the perpendicular bisector will be equidistant from both the ends of the line it is bisecting.
- By the angle bisector theorem, a point is equidistant from the sides of the angle if a point is on the bisector of an angle.
Question 4.
In Exploration 2. what is the distance from point D to \(\vec{A}\)B when the distance from D to \(\vec{A}\)C is 5 units? Justify your answer.
Answer:
Lesson 6.1 Perpendicular and Angle Bisectors
Use the diagram and tile given information to find the indicated measure.
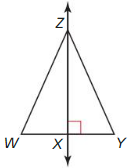
Question 1.
![]() is the perpendicular bisector of \(\overline{W Y}\), and \(\overline{y Z}\) = 13.75. Find WZ.
is the perpendicular bisector of \(\overline{W Y}\), and \(\overline{y Z}\) = 13.75. Find WZ.
Answer:
WZ = 13.75
Explanation:
Using the perpendicular bisector theorem YZ = WZ
13.75 = WZ
Question 2.
![]() is the perpendicular bisector of \(\overline{W Y}\), WZ = 4n – 13, and YZ = n + 17. Find YZ.
is the perpendicular bisector of \(\overline{W Y}\), WZ = 4n – 13, and YZ = n + 17. Find YZ.
Answer:
YZ = 27
Explanation:
Using the perpendicular bisector theorem YZ = WZ
n + 17 = 4n – 13
4n – n = 17 + 13
3n = 30
n = 10
YZ = 10 + 17 = 27
Question 3.
Find WX when WZ = 20.5. WY = 14.8. and YZ = 20.5.
Answer:
WX = 7.4
Explanation:
Because WZ = ZY and ZX is the perpendicular bisector of WY by the converse of perpendicular bisector theorem. By the definition of segment sector, WY = 2WX
14.8 = 2WX
WX = 7.4
Use the diagram and the given information to find the indicated measure.
Question 4.
\(\vec{B}\)D bisects ∠ABC, and DC = 6.9, Find DA.
Answer:
DA = 6.9
Explanation:
By using the angle bisector theorem
DC = DA
DA = 6.9
Question 5.
\(\vec{B}\)D bisects ∠ABC, AD = 3z + 7, and CD = 2z + 11. Find CD.
Answer:
z = 4
Explanation:
By using the angle bisector theorem
DC = DA
2z + 11 = 3z + 7
3z – 2z = 11 – 7
z = 4
Question 6.
Find m∠ABC when AD = 3.2, CD = 3.2, and m∠DBC = 39°.
Answer:
m∠DBC = 78°
Explanation:
m∠DBC = 39 = m∠DBA
m∠ABC = m∠DBC + m∠DBA
= 39 + 39 = 78°
Question 7.
Do you have enough information to conclude that \(\vec{Q}\)S bisects ∠PQR? Explain.
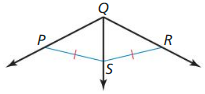
Answer:
Yes,
Because PS = SR.
Question 8.
Write an equation of the perpendicular bisector of the segment with endpoints (- 1, – 5) and (3, – 1).
Answer:
y + 5 = 0
Explanation:
Midpoint = (\(\frac { -1 + 3 }{ 2 } \), \(\frac { -5 – 1 }{ 2 } \))
= (\(\frac { 2 }{ 2 } \), \(\frac { -6 }{ 2 } \)) = (1, -3)
Slope of the line = \(\frac { -1 + 1 }{ 3 + 5 } \) = 0
Slope of the perpendicular line = 0
Equation of the perpendicular bisector is (y + 5) = 0(x + 1)
y + 5 = 0
Exercise 6.1 Perpendicular and Angle Bisectors
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Point C is in the interior of ∠DEF. If ∠DEC and ∠CEF are congruent, then \(\vec{E}\)C is the ________ of ∠DEF.
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
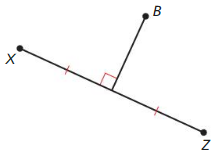
Is point B the same distance from both X and Z?
Answer:
Yes.
Is point B equidistant from X and Z?
Answer:
Yes
Is point B collinear with X and Z?
Answer:
No.
Is point B on the perpendicular bisector of \(\overline{X Z}\)?
Answer:
Yes
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, find the indicated measure. Explain your reasoning.
Question 3.
GH
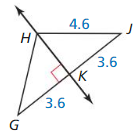
Answer:
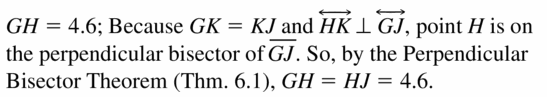
Question 4.
QR
Answer:
QR = RS
So, QR = 1.3
Question 5.
AB
Answer:

Question 6.
UW
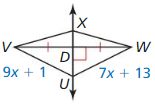
Answer:
UW = 55
Explanation:
UV = WU
9x + 1 = 7x + 13
9x – 7x = 13 – 1
2x = 12
x = 6
UW = 7(6) + 13 = 42 + 13 = 55
In Exercises 7-10. tell whether the information in the diagram allows you to conclude that point P lies on the perpendicular bisector of \(\overline{L M}\). Explain your reasoning.
Question 7.
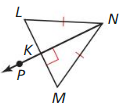
Answer:

Question 8.
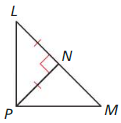
Answer:
PN ⊥ LM. So, LN – MN
Therefore, point P lies on the LM.
Question 9.
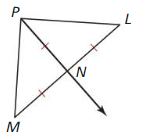
Answer:
![]()
Question 10.
Answer:
Yes.
In Exercises 11-14. find the indicated measure. Explain your reasoning.
Question 11.
m∠ABD
Answer:
Question 12.
Answer:
PS = RS
PS = 12
Question 13.
m∠KJL
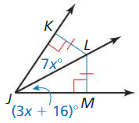
Answer:
Question 14.
FG
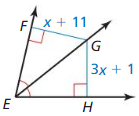
Answer:
FG = 16
Explanation:
FG = GH
x + 11 = 3x + 1
3x – x = 11 – 1
2x = 10
x = 5
FG = 5 + 11 = 16
In Exercises 15 and 16, tell whether the information in the diagram allows you to conclude that \(\vec{E}\)H bisects ∠FEG. Explain your reasoning.
Question 15.
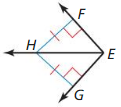
Answer:

Question 16.
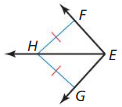
Answer:
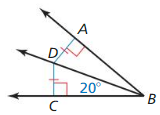
Yes, because H is equidistant from EF and EG, EH bisects ∠FEG by the Angle Bisector Theorem.
In Exercises 17 and 18, tell whether the information in the diagram allows you to conclude that DB = DC. Explain your reasoning.
Question 17.
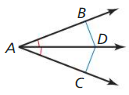
Answer:
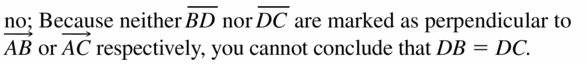
Question 18.
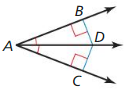
Answer:
Yes, because AD is perpendicular to BD and DC. using perpendicular bisector theorem DB = DC.
In Exercises 19-22, write an equation of the perpendicular bisector of the segment with the given endpoints.
Question 19.
M(1, 5), N(7, – 1)
Answer:

Question 20.
Q(- 2, 0), R(6, 12)
Answer:
An equation of the perpendicular bisector is y = –\(\frac { 3 }{ 7 } \)x + \(\frac { 36 }{ 7 } \)
Explanation:
Slope of QR = \(\frac { 12 + 2 }{ 6 – 0 } \) = \(\frac { 7 }{ 3 } \)
The slope of the perpendicular line m = –\(\frac { 3 }{ 7 } \)
Midpoint of QR = (\(\frac { -2 + 6 }{ 2 } \), \(\frac { 0 + 12 }{ 2 } \)
= (-2, 6)
y = mx + b
6 = –\(\frac { 3 }{ 7 } \)(-2) + b
6 = \(\frac { 6 }{ 7 } \) + b
b = \(\frac { 36 }{ 7 } \)
An equation of the perpendicular bisector is y = –\(\frac { 3 }{ 7 } \)x + \(\frac { 36 }{ 7 } \)
Question 21.
U(- 3, 4), V(9, 8)
Answer:

Question 22.
Y( 10, – 7), Z(- 4, 1)
Answer:
An equation of the perpendicular bisector is y = \(\frac { 7 }{ 4 } \)x – \(\frac { 33 }{ 4 } \)
Explanation:
Slope of YZ = \(\frac { 1 + 7 }{ -4 – 10 } \) = \(\frac { -4 }{ 7 } \)
The slope of the perpendicular line m = \(\frac { 7 }{ 4 } \)
Midpoint of YZ = (\(\frac { 10 – 4 }{ 2 } \), \(\frac { -7 + 1 }{ 2 } \))
= (3, -3)
y = mx + b
-3 = \(\frac { 7 }{ 4 } \)(3) + b
b = -3 – \(\frac { 21 }{ 4 } \) = \(\frac { -12 – 21 }{ 4 } \) = \(\frac { -33 }{ 4 } \)
An equation of the perpendicular bisector is y = \(\frac { 7 }{ 4 } \)x – \(\frac { 33 }{ 4 } \)
ERROR ANALYSIS
In Exercises 23 and 24, describe and correct the error in the student’s reasoning.
Question 23.
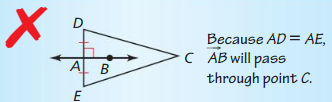
Answer:

Question 24.
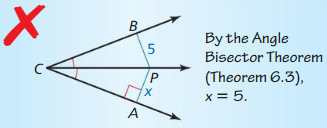
Answer:
CP is not perpendicular to BP. So, x = 5 is wrong.
Question 25.
MODELING MATHEMATICS
In the photo, the road is perpendicular to the support beam and \(\overline{A B} \cong \overline{C B}\). Which theorem allows you to conclude that \(\overline{A D} \cong \overline{C D}\)?
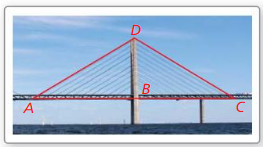
Answer:

Question 26.
MODELING WITH MATHEMATICS
The diagram shows the position of the goalie and the puck during a hockey game. The goalie is at point G. and the puck is at point P.
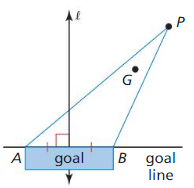
a. What should be the relationship between \(\vec{P}\)G and ∠APB to give the goalie equal distances to travel on each side of \(\vec{P}\)G?
Answer:
PG should be the perpendicular bisector of ∠APB.
b. How does m∠APB change as the puck gets closer to the goal? Does this change make it easier or more difficult for the goalie to defend the goal? Explain your reasoning.
Answer:
Question 27.
CONSTRUCTION
Use a compass and straightedge to construct a copy of \(\overline{X Y}\). Construct a perpendicular bisector and plot a point Z on the bisector so that the distance between point Z and \(\overline{X Y}\) is 3 centimeters. Measure \(\overline{X Z}\) and \(\overline{Y Z}\). Which theorem does this construction demonstrate?
![]()
Answer:
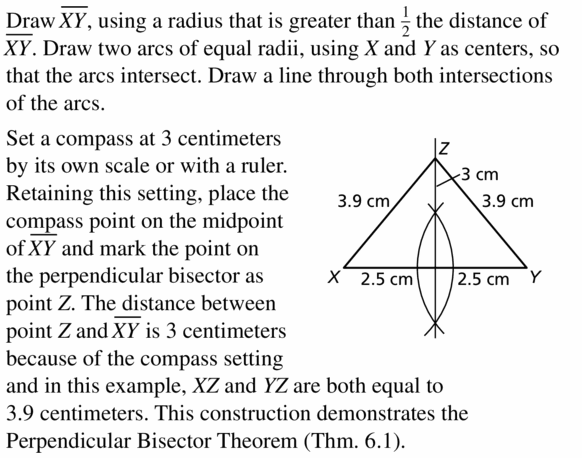
Question 28.
WRITING
Explain how the Converse of the Perpendicular Bisector Theorem (Theorem 6.2) is related to the construction of a perpendicular bisector.
Answer:
The converse of the perpendicular bisector theorem states if a point is equidistant from both the endpoints of the line segments in the same plane, then that point is on the perpendicular bisector of the line segment.
Question 29.
REASONING
What is the value of x in the diagram?
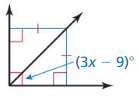
(A) 13
(B) 18
(C) 33
(D) not enough information
Answer:
Question 30.
REASONING
Which point lies on the perpendicular bisector of the segment with endpoints M(7, 5) and m(- 1, 5)?
(A) (2, 0)
(B) (3, 9)
(C) (4, 1)
(D) (1, 3)
Answer:
(B) (3, 9)
Explanation:
The distance from M to (3, 9) is = √(7 – 3)² + (5 – 9)² = √16 + 16 = √32
The distance from m to (3, 9) = √(-1 – 3)² + (5 – 9)² = √16 + 16 = √32
Question 31.
MAKING AN ARGUMENT
Your friend says it is impossible for an angle bisector of a triangle to be the same line as the perpendicular bisector of the opposite side. Is your friend correct? Explain your reasoning.
Answer:

Question 32.
PROVING A THEOREM
Prove the Converse of the Perpendicular Bisector Theorem (Thm. 6.2). (Hint: Construct a line through point C perpendicular to \(\overline{A B}\) at point P.)
Given CA = CB
Prove Point C lies on the perpendicular bisector of \(\overline{A B}\).
Answer:
Compare △ACP, △CPB
AP = BP
CP = CP
∠APC = ∠BPC = 90°
So, △ACP ≅ △CPB using SAS congruence theorem
So, CA = CB
Question 33.
PROVING A THEOREM
Use a congruence theorem to prove each theorem.
a. Angle Bisector Theorem (Thin. 6.3)
b. Converse of the Angle Bisector Theorem (Thm. 6.4)
Answer:


Question 34.
HOW DO YOU SEE IT?
The figure shows a map of a city. The city is arranged so each block north to south is the same length and each block east to west is the same length.
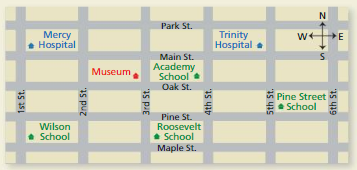
a. Which school is approximately equidistant from both hospitals? Explain your reasoning.
Answer:
Given,
The figure shows a map of a city. The city is arranged so each block north to south is the same length and each block east to west is the same length.
Roosevelt school is equidistant from both the hospitals.
It’s location is two blocks east of Wilson school.
Approximately two blocks west of a point three units vertically of thrifty hospital.
Thus Roosevelt school is approximately equidistant from both the hospitals.
b. Is the museum approximately equidistant from Wilson School and Roosevelt School? Explain your reasoning.
Answer:
The museum is closer to the Roosevelt school, while for Wilson school it is two blocks north and then two blocks east.
Question 35.
MATHEMATICAL CONNECTIONS
Write an equation whose graph consists of all the points in the given quadrants that are equidistant from the x- and y-axes.
a. I and III
b. II and IV
c. I and II
Answer:
![]()
Question 36.
THOUGHT PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry, is it possible for two lines to be perpendicular but not bisect each other? Explain your reasoning.
Answer:
- A line is a great circle that divides the sphere into two equal halves in spherical geometry.
- Any two lines intersecting in two points represent two poles of the spherical lines.
- So, it is not possible for two spherical lines to be perpendicular without bisecting each other.
Question 37.
PROOF
Use the information in the diagram to prove that \(\overline{A B} \cong \overline{C B}\) if and onI if points D, E, and B are collinear.
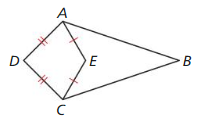
Answer:

Question 38.
PROOF
prove the statement in parts (a) – (c)
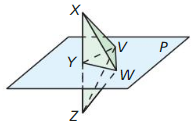
Given Plane P is a perpendicular bisector of \(\overline{X Z}\) at point Y.
Prove
a. \(\overline{X W} \cong \overline{Z W}\)
b. \(\overline{X V} \cong \overline{Z V}\)
c. ∠VXW ≅ ∠VZW
Answer:
a. By using the perpendicular bisector theorem \(\overline{X W} \cong \overline{Z W}\)
b. By using the perpendicular bisector theorem \(\overline{X V} \cong \overline{Z V}\)
Maintaining Mathematical Proficiency
Classify the triangle by its sides.
Question 39.
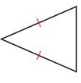
Answer:
![]()
Question 40.
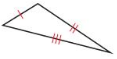
Answer:
The triangle is scalene as all the sides have different lengths.
Question 41.
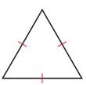
Answer:
![]()
Classify the triangles by its angles.
Question 42.
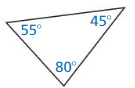
Answer:
The triangle is scalene as all angles are different.
Question 43.
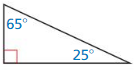
Answer:
![]()
Question 44.
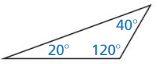
Answer:
The trinagle is an obtuse triangle.
6.2 Bisectors of Triangles
Exploration 1
Properties of the Perpendicular Bisectors of a Triangle
Work with a partner: Use dynamic geometry software. Draw any ∆ABC.
a. Construct the perpendicular bisectors of all three sides of ∆ABC. Then drag the vertices to change ∆ABC. ‘What do you notice about the perpendicular bisectors?
Answer:
b. Label a point D at the intersection of the perpendicular bisectors.
Answer:
c. Draw the circle with center D through vertex A of ∆ABC. Then drag the vertices to change ∆ABC. What do you notice?
Answer:
Exploration 2
Properties of the Angle Bisectors of a Triangle
Work with a partner. Use dynamic geometry software. Draw any ∆ABC.
a. Construct the angle bisectors of all three angles of ∆ABC, Then drag the vertices to change ∆ABC. What do you notice about the angle bisectors?
Answer:
b. Label a point D at the intersection of the angle bisectors.
Answer:
c. Find the distance between D and \(\overline{A B}\). Draw the circle with center D and this distance as a radius. Then drag the vertices to change ∆ABC. What do you notice?
LOOKING FOR STRUCTURE
To be proficient in math, you need to see complicated things as single objects or as being composed of several objects.
Answer:
Communicate Your Answer
Question 3.
What conjectures can you make about the perpendicular bisectors and the angle bisectors of a triangle?
Answer:
Lesson 6.2 Bisectors of Triangles
Monitoring Progress
Question 1.
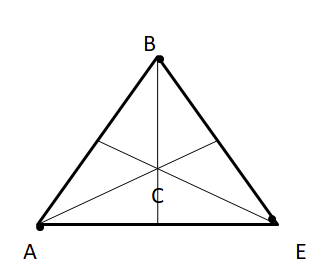
Three snack carts sell hot pretzels horn points A, B, and E. What is the location of the pretzel distributor if it is equidistant from the three carts? Sketch the triangle and show the location.

Answer:
The location is the circumcenter
Find the coordinates of the circumcenter of the triangle with the given vertices.
Question 2.
R(- 2, 5), S(- 6, 5), T(- 2, – 1)
Answer:
The circumcenter is (4, 7.33)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let R(- 2, 5), S(- 6, 5), T(- 2, – 1) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PR = PS = PT
PR² = PS² = PT²
PR² = PS²
(x + 2)² + (y – 5)² = (x + 6)² + (y – 5)²
x² + 4x + 4 + y² – 10x + 25 = x² + 12x + 36 + y² -10y + 25
4x + 4 = 12x + 36
12x – 4x = 36 – 4
8x = 32
x = 4
PS² = PT²
(x + 6)² + (y – 5)² = (x + 2)² + (y + 1)²
x² + 12x + 36 + y² -10y + 25 = x² + 4x + 4 + y² + 2y + 1
12x – 4x – 10y – 2y + 61 = 5
8x – 12y = -56
8(4) – 12y = -56
32 – 12y = -56
-12y = -56 – 32
-12y = -88
y = 7.33
The circumcenter is (4, 7.33)
Question 3.
W(- 1, 4), X(1, 4), Y( 1, – 6)
Answer:
The circumcenter is (0.25, -1)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let W(- 1, 4), X(1, 4), Y( 1, – 6) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PW = PX = PY
PW² = PY² = PX²
PX² = PY²
(x – 1)² + (y – 4)² = (x – 1)² + (y + 6)²
x² -2x + 1 + y² – 8y + 16 = x² -2x + 1 + y² + 12y + 36
-8y – 12y = 36 – 16
-20y = 20
y = -1
PW² = PX²
(x + 1)² + (y – 4)² = (x – 1)² + (y – 4)²
x² + 2x + 4 + y² – 8y + 16 = x² – 2x + 1 + y² – 8y + 16
4x = 1
x = 0.25
The circumcenter is (0.25, -1)
Question 4.
In the figure shown, QM = 3x + 8 and QN = 7x + 2. Find QP.
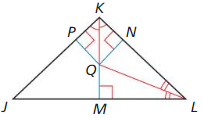
Answer:
QP = \(\frac { 23 }{ 2 } \)
Explanation:
QM = QN
3x + 8 = 7x + 2
7x – 3x = 8 – 2
4x = 6
x = \(\frac { 3 }{ 2 } \)
QP = QN
= 7(\(\frac { 3 }{ 2 } \)) + 2
= \(\frac { 23 }{ 2 } \)
Question 5.
Draw a sketch to show the location L of the lamppost in Example 4.
Answer:
Exercise 6.2 Bisectors of Triangles
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
When three or more lines, rays, or segments intersect in the same Point. they are called _____________ lines, rays, or segments.
Answer:
Question 2.
WHICH ONE DOESNT BELONG?
Which triangle does not belong with the other three? Explain your reasoning.

Answer:
The third triangle does not belong with the other three. Because the point P in the remaining triangles is the circumcenter. But P is not circumcenter in the third triangle.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, the perpendicular bisectors of ∆ABC intersect at point G and are shown in blue. Find the indicated measure.
Question 3.
Find BG
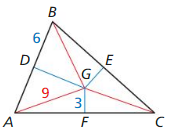
Answer:
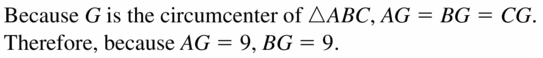
Question 4.
Find GA
Answer:
Because G is the circumcenter of ∆ABC, AG = BG = CG
AG = BG = 11
So, AG = 11
In Exercises 5 and 6, the angle bisectors of ∆XYZ intersect at point P and are shown in red. Find the indicated measure.
Question 5.
Find PB.
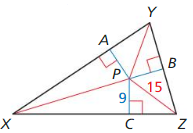
Answer:
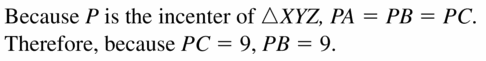
Question 6.
Find HP.
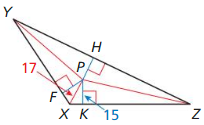
Answer:
Because P is the incenter of ∆XYZ, PH = PF = PK
Therefore, PK = 15
HP = 15
In Exercises 7-10. find the coordinates of the circumcenter of the triangle with the given vertice
Question 7.
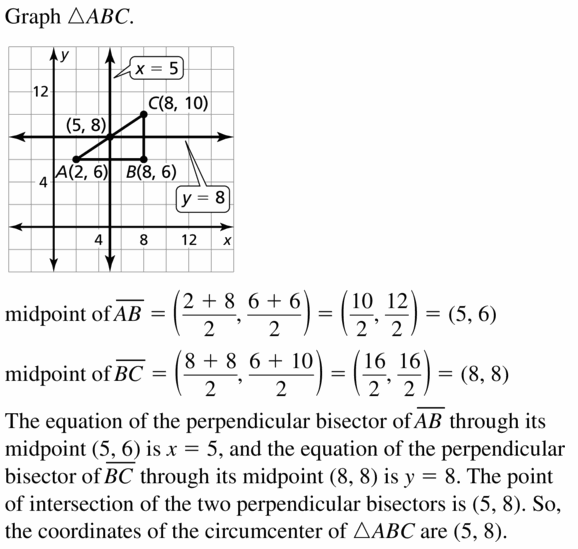
A(2, 6), B(8, 6), C(8, 10)
Answer:
Question 8.
D(- 7, – 1), E(- 1, – 1), F(- 7, – 9)
Answer:
The circumcenter is (-4, -5)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let D(- 7, – 1), E(- 1, – 1), F(- 7, – 9) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PD = PE = PF
PD² = PE² = PF²
PD² = PE²
(x + 7)² + (y + 1)² = (x + 1)² + (y + 1)²
x² + 14x + 49 + y² + 2y +1 = x² + 2x + 1 + y² + 2y + 1
14x – 2x = 1 – 49
12x = -48
x = -4
PD² = PF²
(x + 7)² + (y + 1)² = (x + 7)² + (y + 9)²
x² + 14x + 49 + y² + 2y + 1 = x² + 14x + 49 + y² + 18y + 81
18y – 2y = 1 – 81
16y = -80
y = -5
The circumcenter is (-4, -5)
Question 9.
H(- 10, 7), J(- 6, 3), K(- 2, 3)
Answer:
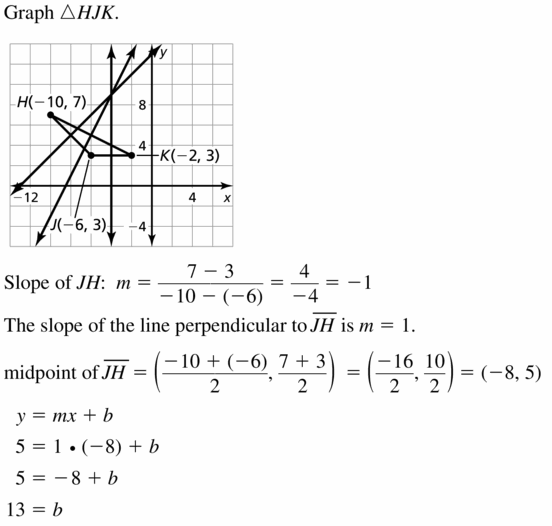

Question 10.
L(3, – 6), M(5, – 3) , N (8, – 6)
Answer:
The circumcenter is (5.5, -5.5)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let L(3, – 6), M(5, – 3) , N (8, – 6) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PL = PM = PN
PL² = PM² = PN²
PL² = PN²
(x – 3)² + (y + 6)² = (x – 8)² + (y + 6)²
x² – 6x + 9 + y² + 12y + 36 = x² -16x + 64 + y² + 12y + 36
-16x + 6x = 9 – 64
-10x = -55
x = 5.5
PL² = PM²
(x – 3)² + (y + 6)² = (x – 5)² + (y + 3)²
x² – 6x + 9 + y² + 12y + 36 = x² – 10x + 25 + y² + 6y + 9
-6x + 10x + 45 = 6y – 12y + 34
4x = -6y -11
4(5.5) = -6y – 11
22 + 11 = -6y
33 = -6y
y = -5.5
The circumcenter is (5.5, -5.5)
In Exercises 11-14, N is the incenter of ∆ABC. Use the given information to find the indicated measure.
Question 11.
ND = 6x – 2
NE = 3x + 7
Find NF.
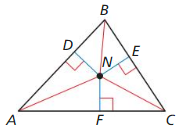
Answer:
Question 12.
NG = x + 3
NH = 2x – 3
Find NJ.
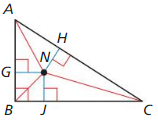
Answer:
NJ = 9
Explanation:
NG = NH = NJ
x + 3 = 2x – 3
2x – x = 3 + 3
x = 6
By Incenter theorem, NG = NH = NJ
NJ = 6 + 3 = 9
Question 13.
NK = 2x – 2
NL = – x + 10
Find NM
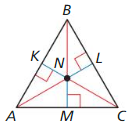
Answer:
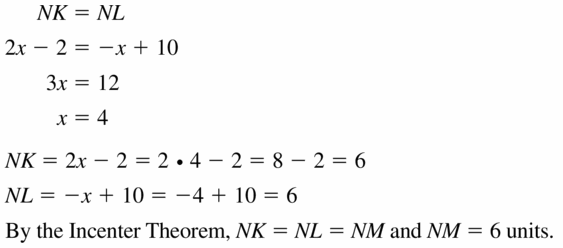
Question 14.
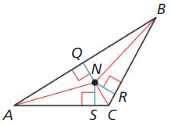
NQ = 2x
NR = 3x – 2
Find NS.
Answer:
NS = 4
Explanation:
NQ = NR
2x = 3x – 2
3x – 2x = 2
x = 2
NQ = 2 (2) = 4
By Incenter theorem NS = NR = NQ
So, NS = 4
Question 15.
P is the circumcenter of ∆XYZ. Use the given information to find PZ.
PX = 3x + 2
PY = 4x – 8
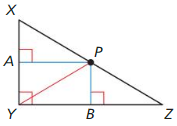
Answer:

Question 16.
P is the circumcenter of ∆XYZ. Use the given information to find PY.
PX = 4x + 3
PZ = 6x – 11
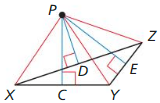
Answer:
PY = 31
Explanation:
PX = PZ
4x + 3 = 6x – 11
6x – 4x = 3 + 11
2x = 14
x = 7
PZ = 6(7) – 11 = 42 – 11 = 31
By the incenter theorem, PX = PZ = PY
PY = 31
CONSTRUCTION
In Exercises 17-20. draw a triangle of the given type. Find the circumcenter. Then construct the circumscribed circle.
Question 17.
right
Answer:
Question 18.
obtuse
Answer:
Question 19.
acute isosceles
Answer:
Question 20.
equilateral
Answer:
CONSTRUCTION
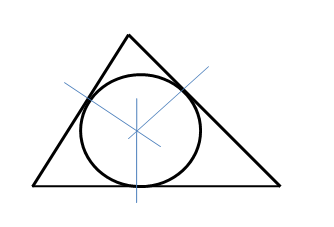
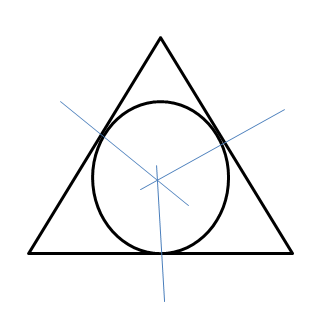
In Exercises 21-24, copy the triangle with the given angle measures. Find the incenter. Then construct the inscribed circle.
Question 21.
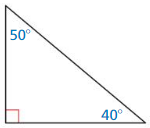
Answer:
Question 22.
Answer:
Question 23.
Answer:
Question 24.
Answer:
ERROR ANALYSIS
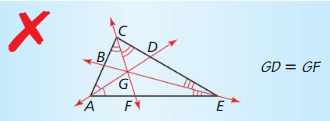
In Exercises 25 and 26. describe and correct the error in identifying equal distances inside the triangle.
Question 25.
Answer:

Question 26.
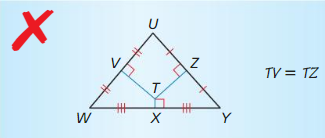
Answer:
Because point T is the intersection of the angle bisectors, it is the incenter. But, because TV and TF are not necessarily perpendicular to a side of the trinagle, there is not sufficient evidence to conclude that TV and TZ are congruent. Point T is equidistance from the sides of the triangle.
Question 27.
MODELING WITH MATHEMATICS
You and two friends plan to meet to walk your dogs together. You want the meeting place to be the same distance from each person’s house. Explain how you can use the diagram to locate the meeting place.

Answer:

Question 28.
MODELING WITH MATHEMATICS
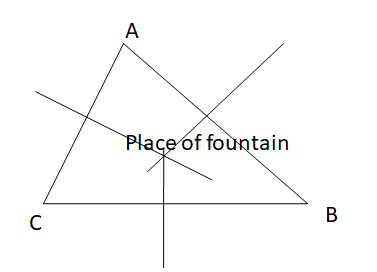
You are placing a fountain in a triangular koi pond. YOU want the foutain to be the same distance from each edge of the Pond. Where should you place the fountain? Explain your reasoning. Use a sketch to support your answer.

Answer:
A, B, C are edges of the pond.
Foutain to be the same distance from each edge of the Pond
Then, you need to find the circumcenter of the triangle.
Place the fountain at the circumcenter.
CRITICAL THINKING
In Exercises 29-32, complete the statement with always, sometimes, or never. Explain your reasoning.
Question 29.
The circumenter of a scalene triangle is ______________ inside the triangle.
Answer:

Question 30.
If the perpendicular bisector of one side of a triangle intersects the opposite vertex. then the triangle is ______________ isosceles.
Answer:
If the perpendicular bisector of one side of a triangle intersects the opposite vertex. then the triangle is always isosceles.
Explanation:
The Vertex is equidistant to other vertices then.
Question 31.
The perpendicular bisectors of a triangle intersect at a point that is ______________ equidistant from the midpoints of the sides of the triangle.
Answer:

Question 32.
The angle bisectors of a triangle intersect at a point that is ______________ equidistant from the sides of the triangle.
Answer:
The angle bisectors of a triangle intersect at a point that is circumcenter equidistant from the sides of the triangle.
CRITICAL THINKING
In Exercises 33 and 34, find the coordinates of the circumcenter of the triangle with the given vertices.
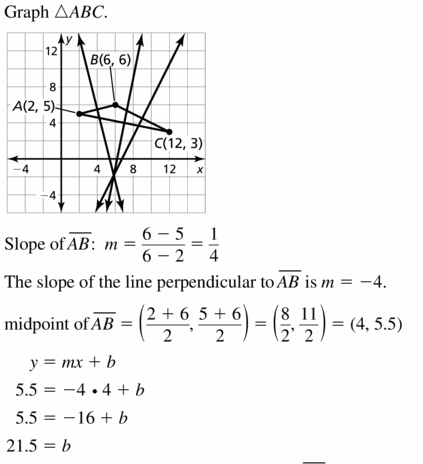
Question 33.
A(2, 5), B(6, 6). C( 12. 3)
Answer:


Question 34.
D(- 9, – 5), E(- 5, – 9), F(- 2, – 2)
Answer:
The circumcenter is (4.45, 4.45)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let D(- 9, – 5), E(- 5, – 9), F(- 2, – 2) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PD = PE = PF
PD² = PE² = PF²
PD² = PE²
(x + 9)² + (y + 5)² = (x + 5)² + (y + 9)²
x² + 18x + 81 + y² + 10y + 25 = x² + 10x + 25 + y² + 18y + 81
18x – 10x = 18y – 10y
8x = 8y
x = y
PE² = PF²
(x + 5)² + (y + 9)² = (x + 2)² + (y + 2)²
x² + 10x + 25 + y² + 18y + 81 = x² + 4x + 4 + y² + 2y + 4
10x – 4x + 106 = 8 + 2y – 18y
6x + 106 = 8 – 16y
6x + 98 = -16x
22x = -98
x = 4.45
y = 4.45
The circumcenter is (4.45, 4.45)
MATHEMATICAL CONNECTIONS
In Exercises 35 and 36. find the a1ue of x that makes N the incenter of the triangle.
Question 35.
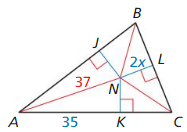
Answer:
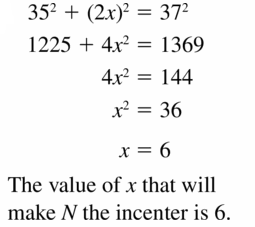
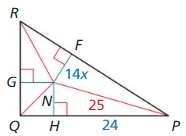
Question 36.
Answer:
N the incenter is \(\frac { 12 }{ 2 } \).
Explanation:
25² = 24² + (14x)²
625 = 576 + 196x²
49 = 196x²
x = \(\frac { 7 }{ 14 } \) = \(\frac { 1 }{ 2 } \)
The value of x will make N the incenter is \(\frac { 12 }{ 2 } \).
Question 37.
PROOF
Where is the circumcenter located in any right triangle? Write a coordinate proof of this result.
Answer:

Question 38.
PROVING A THEOREM
Write a proof of the Incenter Theorem (Theorem 6.6).
Given ∆ABC, \(\overline{A D}\) bisects∠CAB,
\(\overline{B D}\) bisects ∠CBA, \(\overline{D E}\) ⊥ \(\overline{A B}\), \(\overline{D F}\) ⊥ \(\overline{B C}\), and \(\overline{D G}\) ⊥ \(\overline{C A}\)
Prove The angle bisectors intersect at D, which is equidistant from \(\overline{A B}\), \(\overline{B C}\), and \(\overline{C A}\)
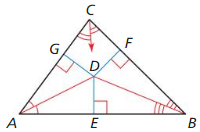
Answer:
Given ∆ABC, \(\overline{A D}\) bisects∠CAB,
\(\overline{B D}\) bisects ∠CBA, \(\overline{D E}\) ⊥ \(\overline{A B}\), \(\overline{D F}\) ⊥ \(\overline{B C}\), and \(\overline{D G}\) ⊥ \(\overline{C A}\)
To Prove: The angle bisectors intersect at D, which is equidistant from \(\overline{A B}\), \(\overline{B C}\), and \(\overline{C A}\)
It is also given that, AD bisects ∠CAD. So according to the definition of an angle bisector, we can write that∠CAD≅∠BAD.
∠ADP≅∠AFP [Corresponding right angles]
And, AP is the common side
Thus according to the AAS congruence theorem, we have that,
ΔAED≅ΔAGD
And, DE≅DG [corresponding parts of congruent triangles]
Also, we can write that DE≅DF
From the above result, we obtain that the point D is equidistant from the sides AB, BC and CA
Question 39.
WRITING
Explain the difference between the circumcenter and the incenter of a triangle.
Answer:

Question 40.
REASONING
Is the incenter of a triangle ever located outside the triangle? Explain your reasoning.
Answer:
No
Explanation:
Because the incenter is the center of an inscribed circle, it must always be inside the triangle.
Question 41.
MODELING WITH MATHEMATICS
You are installing a circular pool in the triangular courtyard shown. You want to have the largest pool possible on the site without extending into the walkway.
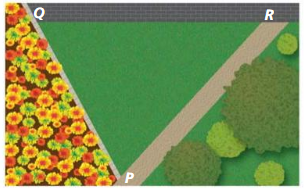
a. Copy the triangle and show how to install the pool so that it just touches each edge. Then explain how you can he sure that you could not fit a larger pool on the site.
b. You want to have the largest pool possible while leaving at least I foot of space around the pool. Would the center of the pool be in the same position as in part (a)? Justify your answer.
Answer:

Question 42.
MODELING WITH MATHEMATICS
Archaeologists find three stones. They believe that the stones were once pail of a circle of stones with a community fire pit at its center. They mark the locations of stones A, B, and C on a graph. where distances are measured in feet.
a. Explain how archaeologists can use a sketch to estimate the center of the circle of stones.
b. Copy the diagram and find the approximate coordinates of the point at which the archaeologists should look for the fire pit.
Answer:
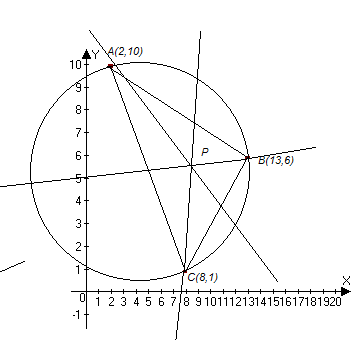
To get the centre of the circle P, we need to find the circumcenter of the triangle ABC.
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let A(2, 10), B(13, 6), C(6, 1) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PA = PB = PC
PA² = PB² = PC²
PA² = PB²
(x – 2)² + (y – 10)² = (x – 13)² + (y – 6)²
x² – 4x + 4 + y² – 20y + 100 = x² – 26x + 169 + y² – 12y + 36
-4x + 26x – 20y + 12y = 205 – 104
22x – 8y = 101 —- (i)
PB² = PC²
(x – 13)² + (y – 6)² = (x – 8)² + (y – 1)²
x² – 26x + 169 + y² – 12y + 36 = x² – 16x + 64 + y² – 2y + 1
-26x + 16x – 12y + 2y = 65 – 205
-10x – 10y = -140
x + y = 14
x = 14 – y — (ii)
Substitute (ii) in (i)
22(14 – y) – 8y = 101
308 – 22y – 8y = 101
308 – 101 = 30y
207 = 30y
y = 6.9
Substitute y = 6.9 in (ii)
x = 14 – 6.9
x = 7.1
The circumcenter is (7.1, 6.9)
Question 43.
REASONING
Point P is inside ∆ABC and is equidistant from points A and B. On which of the following segments must P be located?
(A) \(\overline{A B}\)
(B) the perpendicular bisector of \(\overline{A B}\)
(C) \(\overline{A C}\)
(D) the perpendicular bisector of \(\overline{A C}\)
Answer:
![]()
Question 44.
CRITICAL THINKING
A high school is being built for the four towns shown on the map. Each town agrees that the school should be an equal distance from each of the tourist towns. Is there a single point where they could agree to build the school? If so, find it. If not, explain why not. Justify your answer with a diagram.
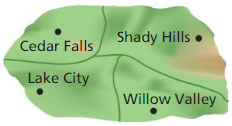
Answer:
It is given that a high school is being built for four towns shown on the map. Each town agrees that the school should be equidistant to each town.
To build such a school all the towns should be in a circle.
A circle is defined by three points when a circle passing three towns can be constructed. It will not pass through the fourth town as shown below.
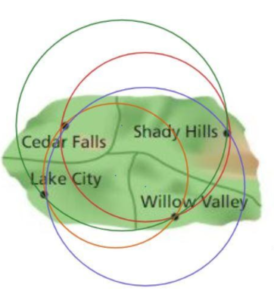
Hence it is not possible to build such a school that is equidistant from all the towns.
Question 45.
MAKING AN ARGUMENT
Your friend says that the circumcenter of an equilateral triangle is also the incenter of the triangle. Is your friend correct? Explain in your reasoning.
Answer:

Question 46.
HOW DO YOU SEE IT?
The arms of the windmill are the angle bisectors of the red triangle. What point of concurrency is the point that Connects the three arms?

Answer:
It is given in the Figure that the arms of the windmill are the angle bisectors of the red triangle. We have to find the point of concurrency.
The arms of a windmill are equal. So, this means that the incenter is equidistant from the vertices of the red triangle.
A point that is equidistant from the vertices of a triangle is known as the circumcenter of the triangle.
The only case where incenter and circumcenter coincide is the case of the equilateral triangle.
Question 47.
ABSTRACT REASONING
You are asked to draw a triangle and all its perpendicular bisectors and angle bisectors.
a. For which type of triangle would you need the fewest segments? What is the minimum number of segments you would need? Explain.
b. For which type of triangle would you need the most segments? What is the maximum number of segments you would need? Explain.
Answer:

Question 48.
THOUGHT PROVOKING
The diagram shows an official hockey rink used by the National Hockey League. Create a triangle using hockey players as vertices in which the center circle is inscribed in the triangle. The center dot should he the incenter of your triangle. Sketch a drawing of the locations of your hockey players. Then label the actual lengths of the sides and the angle measures in your triangle.
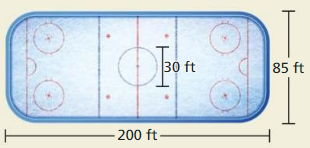
Answer:
Given,
The diagram shows an official hockey rink used by the National Hockey League. Create a triangle using hockey players as vertices in which the center circle is inscribed in the triangle. The center dot should he the incenter of your triangle.
Draw a circle
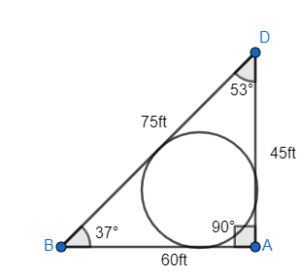
AD = 45 ft
AB = 60 ft
BD = 75 ft
∠A = 90°
∠B = 37°
∠D = 53°
COMPARING METHODS
In Exercises 49 and 50. state whether you would use perpendicular bisectors or angle bisectors. Then solve the problem.
Question 49.
You need to cut the largest circle possible from an isosceles triangle made of paper whose sides are 8 inches, 12 inches, and 12 inches. Find the radius of the circle.
Answer:
Question 50.
On a map of a camp. You need to create a circular walking path that connects the pool at (10, 20), the nature center at (16, 2). and the tennis court at (2, 4). Find the coordinates of the center of the circle and the radius of the circle.
Answer:
The center of the circular path is located at (10, 10) and the radius of the circular path is 10 units.
Explanation:
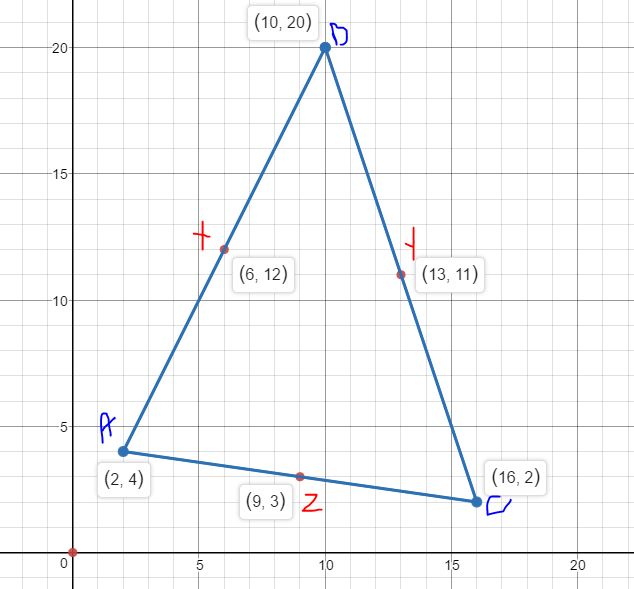
Let the centre of the circle be at O (x, y)
Slope of AB = \(\frac { 20 – 4 }{ 10 – 2 } \) = 2
The slope of XO must be \(\frac { -1}{ 2 } \) the negative reciprocal of the slope of AB as the 2 lines are perpendicular
Slope of XO = \(\frac { y – 12 }{ x – 6 } \) = \(\frac { -1 }{ 2 } \)
y – 12 = -0.5x + 3
0.5x + y = 12 + 3 = 15
x + 2y = 30
The slope of BC = \(\frac { 2 – 20 }{ 16 – 10 } \) = -3
The slope of XO must be \(\frac { 1 }{ 3 } \) = \(\frac { 11 – y }{ 13 – x } \)
33 – 3y = 13 – x
x – 3y = -33 + 13 = -20
Subtrcat two equations
x + 2y – x + 3y = 30 + 20
y = 10
x – 30 = -20
x = 10
r = √(10 – 2)² + (10 – 4)²
r = 10
Question 51.
CRITICAL THINKING
Point D is the incenter of ∆ABC. Write an expression for the length x in terms of the three side lengths AB, AC, and BC.
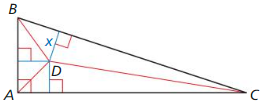
Answer:

Maintaining Mathematical Proficiency
The endpoints of \(\overline{A B}\) are given. Find the coordinates of the midpoint M. Then find AB.
Question 52.
A(- 3, 5), B(3, 5)
Answer:
AB = 6
Explanation:
Midpoint of AB = (\(\frac { -3 + 3 }{ 2 } \), \(\frac { 5 + 5 }{ 2 } \)) = (0, 5)
AB = √(3 + 3)² + (5 – 5)² = 6
Question 53.
A(2, – 1), B(10, 7)
Answer:
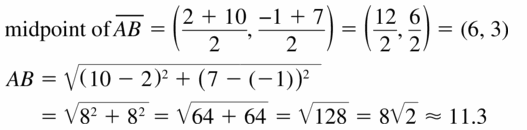
Question 54.
A(- 5, 1), B(4, – 5)
Answer:
AB = 10.81
Explanation:
Midpoint of AB = (\(\frac { -5 + 4 }{ 2 } \), \(\frac { 1 – 5 }{ 2 } \)) = (\(\frac { -1 }{ 2 } \), -2)
AB = √(4 + 5)² + (-5 – 1)² = √81 + 36 = 10.81
Question 55.
A(- 7, 5), B(5, 9)
Answer:
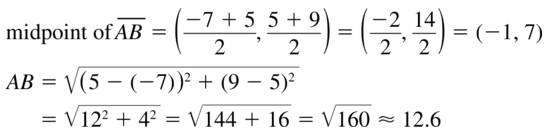
Write an equation of the line passing through point P that is perpendicular to the given line.
Graph the equations of the lines to check that they are perpendicular.
Question 56.
P(2, 8), y = 2x + 1
Answer:
y = \(\frac { -1 }{ 2 } \)x + 9
Explanation:
The slope of the given line m = 2
The slope of the perpendicular line M = \(\frac { -1 }{ 2 } \)
The perpendicular line passes through the given point P(2, 8) is
8 = \(\frac { -1 }{ 2 } \)(2) + b
b = 9
So, y = \(\frac { -1 }{ 2 } \)x + 9
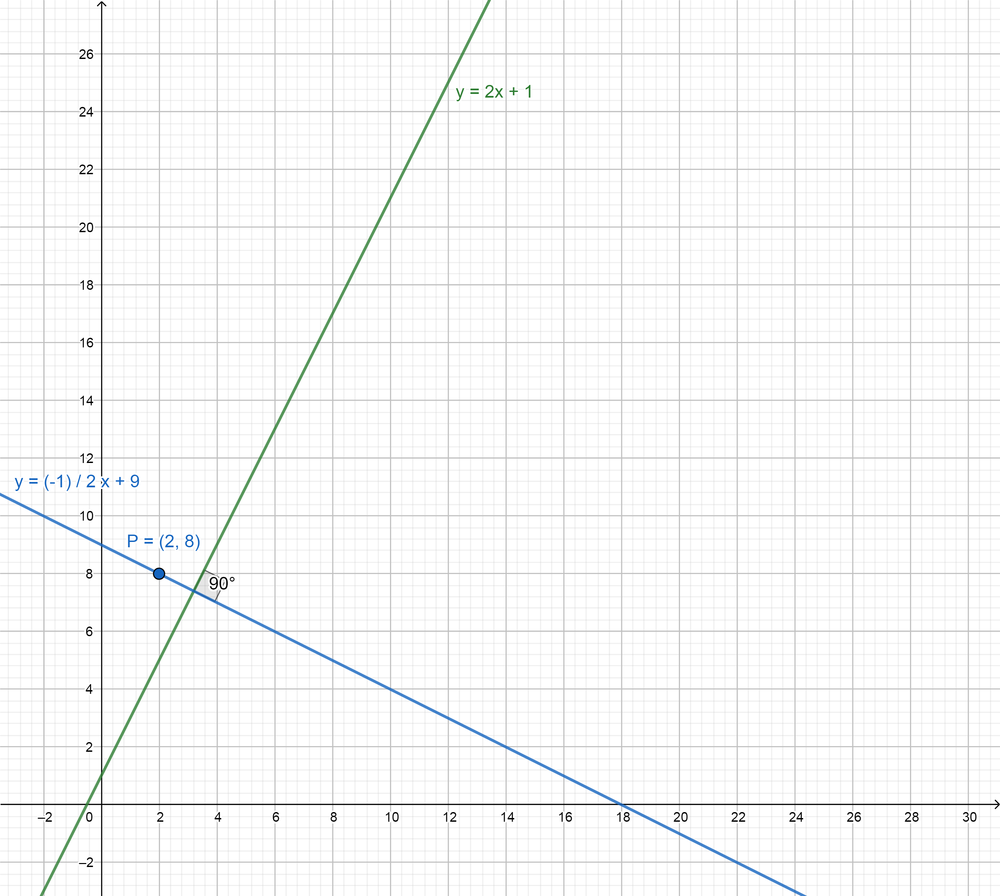
Question 57.
P(6, -3), y = – 5
Answer:
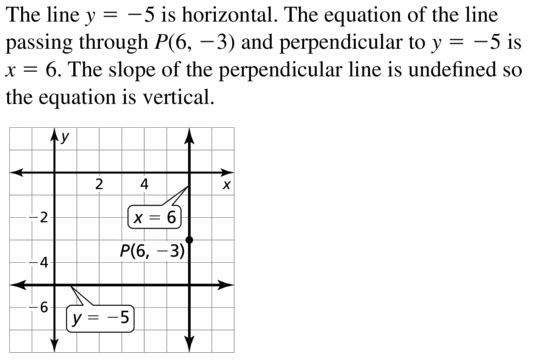
Question 58.
P(- 8, – 6), 2x + 3y = 18
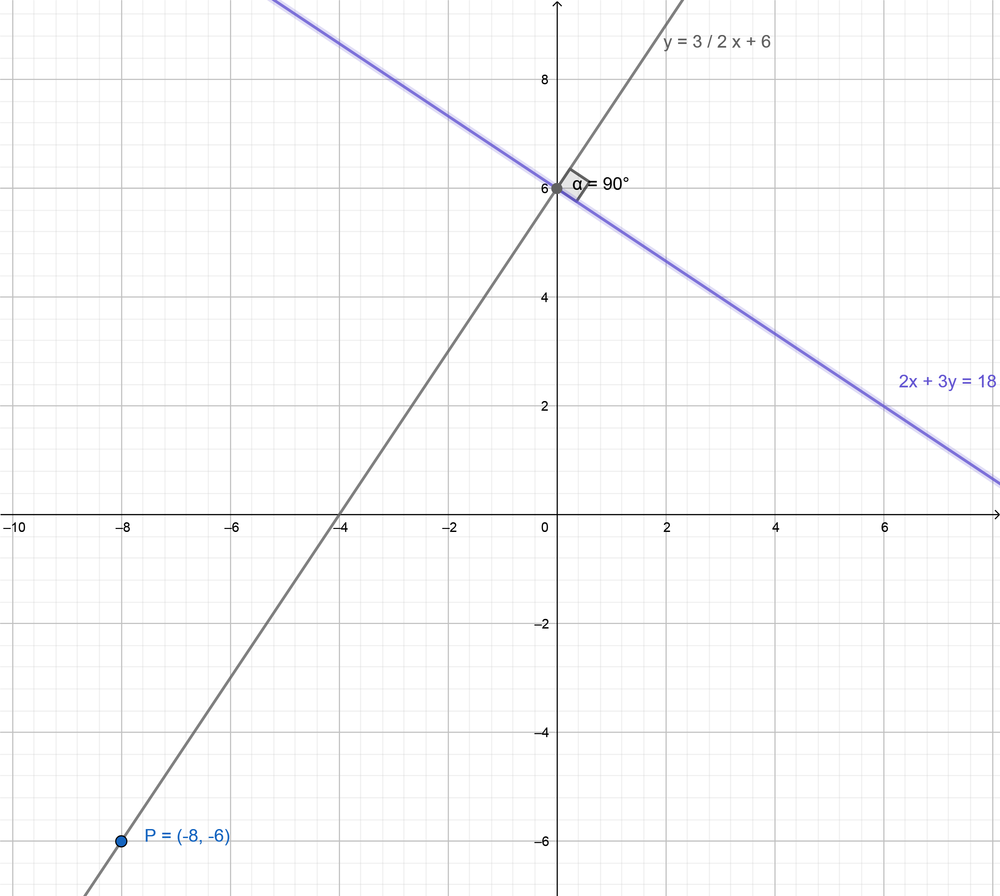
Answer:
The perpendicular equation is y = \(\frac { 3 }{ 2 } \)x + 6
Explanation:
The given line is 2x + 3y = 18
y = \(\frac { -2 }{ 3 } \)x + 6
The slope of the given line m = \(\frac { -2 }{ 3 } \)
The slope of the perpendicular line is M = \(\frac { 3 }{ 2 } \)
The perpendicular line passing through the point P(-8, -6) is
-6 = \(\frac { 3 }{ 2 } \)(-8) + b
b = 6
The perpendicular equation is y = \(\frac { 3 }{ 2 } \)x + 6
Question 59.
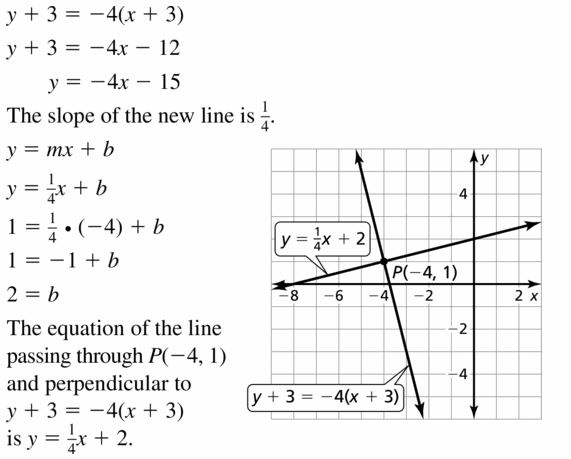
P(- 4, 1), y + 3 = – 4(x + 3)
Answer:
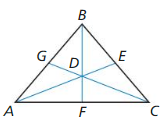
6.3 Medians and Altitudes of Triangles
Exploration 1
Finding Properties of the Medians of a Triangle
Work with a partner. Use dynamic geometry software. Draw any ∆ABC.
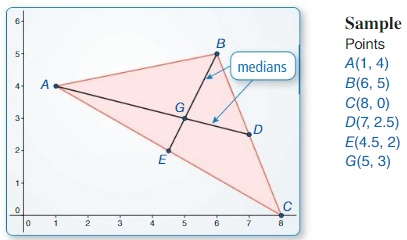
a. Plot the midpoint of \(\overline{B C}\) and label it D, Draw \(\overline{A D}\), which is a median of ABC. Construct the medians to the other two sides of ∆ABC.
Answer:
b. What do you notice about the medians? Drag the vertices to change ∆ABC. Use your observations to write a conjecture about the medians of a triangle.
Answer:
c. In the figure above, point G divides each median into a shorter segment and a longer segment. Find the ratio of the length of each longer segment to the length of the whole median. Is this ratio always the same? Justify your answer.
Answer:
Exploration 2
Finding Properties of the Altitudes of a Triangle
Work with a partner. Use dynamic geometry software. Draw any ∆ABC.
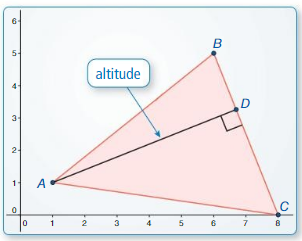
a. Construct the perpendicular segment from vertex A to \(\overline{B C}\). Label the endpoint D. \(\overline{A D}\) is an altitude of ∆ABC.
Answer:
b. Construct the altitudes to the other two sides of ∆ABC. What do you notice?
Answer:
c. Write a conjecture about the altitudes of a triangle. Test your conjecture by dragging the vertices to change ∆ABC.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
Communicate Your Answer
Question 3.
What conjectures can you make about the medians and altitudes of a triangle?
Answer:
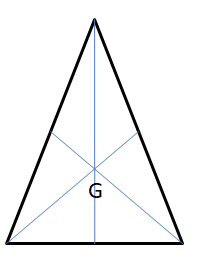
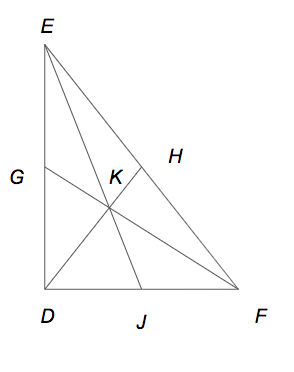
Median of the triangle is a line segment that joins the vertex and the midpoint of the opposite side of the triangle.
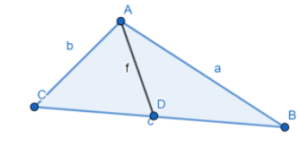
Here f is the medain of ∆ABC.
The altitude of the triangle is a line segment that perpendicularly joins the vertex and the opposite side of the triangle.
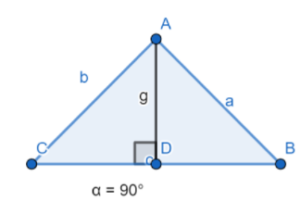
In this figure g is the altitude of ∆ABC.
Question 4.
The length of median \(\overline{R U}\) in ∆RST is 3 inches. The point 0f concurrency of the three medians of ∆RST divides \(\overline{R U}\) into two segments. What are the lengths of these two segments?
Answer:
The length of median \(\overline{R U}\) in ∆RST is 3 inches. The point of concurrency of the three medians of ∆RST divides \(\overline{R U}\) into two segments.
Let us draw the medians from each of the vertices of ∆RST and name them \(\overline{R U}\), \(\overline{S V}\), \(\overline{T W}\) respectively.
Also, let the point of concurrency of these three medians be named as O.
So, we get, SU = UT
RW = WS
RV = VT
Draw a line from U to VT such that it is parallel to OV and name it UX.
UT/SU = TX/VX
SU = UT
UT = TX
TX = VX
Also VT = 2XT
RO/OU = RV/VX
RV = 2XT
RO/OU = 2VX/VX
= 1/2
RU = RO + OU
RU = 2OU + OU = 3OU
So, OU = RU/3
OU = 3/3 = 1 inch.
RO = RU – OU
= 3 – 1 = 2 inches
So, RO = 2 inches and OU = 1 inch
Lesson 6.3 Medians and Altitudes of Triangles
Monitoring Progress
There are three paths through a triangular park. Each path goes from the midpoint of one edge to the opposite corner. The paths meet at point P.
Question 1.
Find PS and PC when SC = 2100 feet.
Answer:
PS = 700, PC = 2100
Explanation:
PC = \(\frac { 2 }{ 3 } \)SC
SC = PS + PC
SC = PS + \(\frac { 2 }{ 3 } \)SC
PS = \(\frac { 1 }{ 3 } \)SC
So, PS = \(\frac { 1 }{ 3 } \)(2100) = 700
PC = \(\frac { 2 }{ 3 } \)(2100) = 1400
Question 2.
Find TC and BC when BT = 1000 feet.
Answer:
BC = 2000 ft, TC = 1000 ft
Explanation:
BT = TC
So, TC = 1000 ft
BC = BT + TC
BC = 1000 + 1000 = 2000 ft
Question 3.
Find PA and TA when PT = 800 feet.
Answer:
PA = 2400 ft, TA = 1600 ft
Explanation:
PT = \(\frac { 1 }{ 3 } \)PA
PA = 3PT
= 3 • 800 = 2400
TA = \(\frac { 2 }{ 3 } \)PA
TA = \(\frac { 2 }{ 3 } \)(2400)
= 1600
Find the coordinates of the centroid of the triangle with the given vertices.
Question 4.
F(2, 5), G(4, 9), H(6, 1)
Answer:
The centroid is (4, 5).
Explanation:
The centroid of the triangle FGH is O = (\(\frac { 2 + 4 + 6 }{ 3 } \), \(\frac { 5 + 9 + 1 }{ 3 } \))
= (\(\frac { 12 }{ 3 } \), \(\frac { 15 }{ 3 } \))
= (4, 5)
Question 5.
X(- 3, 3), Y(1, 5), Z(- 1, – 2)
Answer:
The centriod of given triangle is (-1, 2)
Explanation:
The centroid of the triangle XYZ is O = (\(\frac { -3 + 1 – 1 }{ 3 } \), \(\frac { 3 + 5 – 2 }{ 3 } \))
= (\(\frac { -3 }{ 3 } \), \(\frac { 6 }{ 3 } \))
= (-1, 2)
Tell whether the orthocenter of the triangle with the given vertices is inside, on, or outside the triangle. Then find the coordinates of the orthocenter.
Question 6.
A(0, 3), B(0, – 2), C(6, -3)
Answer:
The orthocenter lies outside the triangle.
Explanation:
The slope of the line BC = \(\frac { -3 + 2 }{ 6 – 0 } \) = \(\frac { -1 }{ 6 } \)
The slope of the perpendicular line = 6
The perpendicular line is (y – 3) = 6(x – 0)
y – 3 = 6x
y = 6x + 3
The slope of AC = \(\frac { -3 – 3 }{ 6 – 0 } \) = \(\frac { -6 }{ 6 } \) = -1
The slope of the perpendicular line = 1
The equation of perpendicular line (y + 2) = 1(x – 0)
y + 2 = x
Substitute y = 6x + 3 in above equation
6x + 3 + 2 = x
5x = -5
x = -1
Put x = -1 in y + 2 = x
y + 2 = -1
y = -3
The orthocenter is (-1, -3)
The orthocenter lies outside the triangle.
Question 7.
J(- 3, – 4), K(- 3, 4), L(5, 4)
Answer:
The orthocenter lies on the vertex of the triangle.
Explanation:
The slope of JL = \(\frac { 4 + 4 }{ 5 + 3 } \) = 2
The slope of perpendicular line is \(\frac { -1 }{ 2 } \)
The equation of perpendicular line is (y – 4) = \(\frac { -1 }{ 2 } \)(x + 3)
2y – 8 = -x – 3
x + 2y – 5 = 0
The slope of JK = \(\frac { 4 + 4 }{ -3 + 3 } \) = 0
The slope of the perpendicular line is 0
the equation of perpendicular line is (y – 4) = 0
y = 4
Substitute y = 4 in x + 2y – 5 = 0
x + 2(4) – 5 = 0
x + 3 = 0
x = -3
So, the ortho center is (-3, 4)
It lies on the vertex of the triangle.
Question 8.
WHAT IF?
In Example 4, you want to show that median \(\overline{B D}\) is also an angle bisector. How would your proof be different?
Answer:
Given ABC is an isosceles triangle and BD is the median.
AB = BC
AD = CD
BD is the common sides
ΔABD ≅ ΔBDC
∠ABD = ∠CBD
So BD bisects ∠ABC
BD is the angle bisector.
Exercise 6.3 Medians and Altitudes of Triangles
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Name the four types of points of concurrency. Which lines intersect to form each of the points?
Answer:

Question 2.
COMPLETE THE SENTENCE
The length of a segment from a vertex to the centroid is ______________ the length of the median from that vertex.
Answer:
The length of a segment from a vertex to the centroid is one-third of the length of the median from that vertex.
Monitoring progress and Modeling with Mathematics
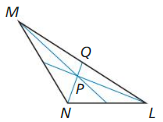
In Exercises 3-6, point P is the centroid of ∆LMN. Find PN and QP.
Question 3.
QN = 9
Answer:
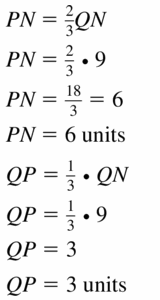
Question 4.
QN = 21
Answer:
PN = 14 units, QP = 7 units
Explanation:
PN = \(\frac { 2 }{ 3 } \)QN
PN = \(\frac { 2 }{ 3 } \)(21)
PN = 14
QP = \(\frac { 1 }{ 3 } \)QN
= \(\frac { 1 }{ 3 } \)(21)
= 7
Question 5.
QN = 30
Answer:
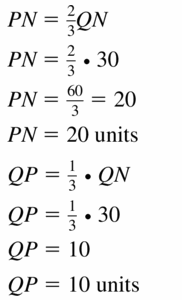
Question 6.
QN = 42
Answer:
PN = 28 units, QP = 14 units
Explanation:
PN = \(\frac { 2 }{ 3 } \)QN
PN = \(\frac { 2 }{ 3 } \)(42)
PN = 28
QP = \(\frac { 1 }{ 3 } \)QN
= \(\frac { 1 }{ 3 } \)(42)
= 14
In Exercises 7-10. point D is the centroid of ∆ ABC. Find CD and CE.
Question 7.
DE = 5
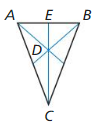
Answer:
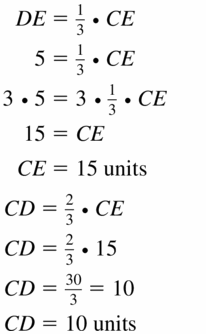
Question 8.
DE = 11
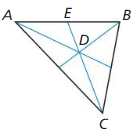
Answer:
CD = 22 units, CE = 33 units
Explanation:
DE = \(\frac { 1 }{ 3 } \)CE
11 = \(\frac { 1 }{ 3 } \) CE
CE = 33
CD = \(\frac { 2 }{ 3 } \) CE
CD = \(\frac { 2 }{ 3 } \)(33)
CD = 22
Question 9.
DE = 9
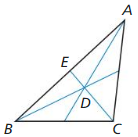
Answer:
Question 10.
DE = 15
Answer:
CE = 45 units, CD = 30
Explanation:
DE = \(\frac { 1 }{ 3 } \)CE
15 = \(\frac { 1 }{ 3 } \) CE
CE = 45
CD = \(\frac { 2 }{ 3 } \) CE
CD = \(\frac { 2 }{ 3 } \)(45)
CD = 30
In Exercises 11-14. point G is the centroid of ∆ABC. BG = 6, AF = 12, and AE = 15. Find the length of the segment.
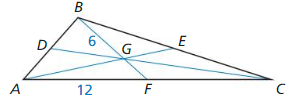
Question 11.
\(\overline{F C}\)
Answer:
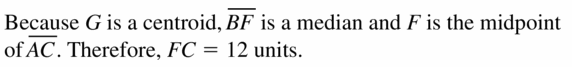
Question 12.
\(\overline{B F}\)
Answer:
\(\overline{B F}\) = 15
Explanation:
All the medians have same length.
so, AE = 15 = BF
Question 13.
\(\overline{A G}\)
Answer:

Question 14.
\(\overline{G E}\)
Answer:
\(\overline{G E}\) = 5 units
Explanation:
AE = AG + GE
15 = 10 + GE
GE = 5
In Exercises 15-18. find the coordinates of the centroid of the triangle with the given vertices.
Question 15.
A(2, 3), B(8, 1), C(5, 7)
Answer:

Question 16.
F(1, 5), G( – 2, 7), H(- 6, 3)
Answer:
The centroid is (\(\frac { -7 }{ 3 } \), 5)
Explanation:
The centroid of the trinagle = (\(\frac { 1 – 2 – 6 }{ 3 } \), \(\frac { 5 + 7 + 3 }{ 3 } \))
= (\(\frac { -7 }{ 3 } \), 5)
Question 17.
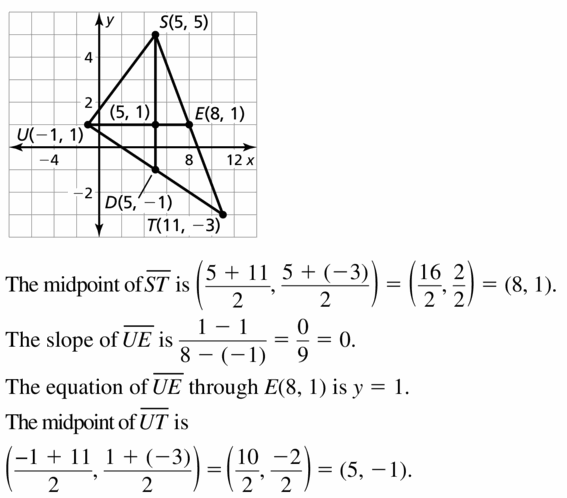
S(5, 5), T(11, – 3), U(- 1, I)
Answer:
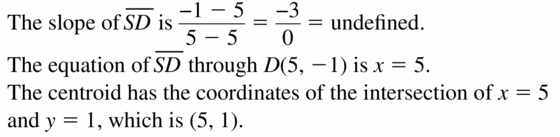
Question 18.
X(1, 4), Y(7, 2), Z(2, 3)
Answer:
The centroid of the triangle is (\(\frac { 10 }{ 2 } \), 3)
Explanation:
The centroid of the trinagle = (\(\frac { 1 + 7 + 2 }{ 3 } \), \(\frac { 4 + 2 + 3 }{ 3 } \))
= (\(\frac { 10 }{ 2 } \), 3)
In Exercises 19-22. tell whether the orthocenter is inside, on, or outside the triangle. Then find the coordinates of the orthocenter.
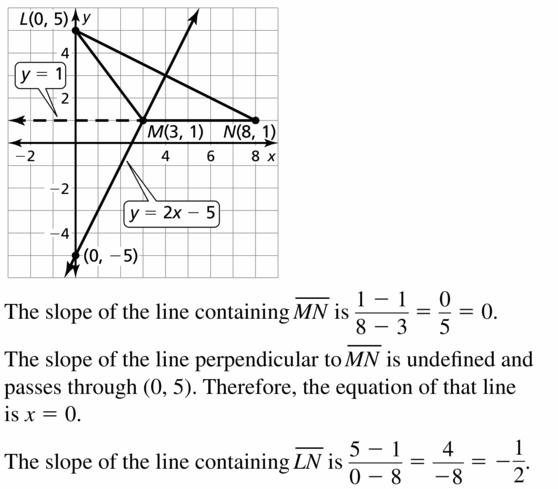
Question 19.
L(0, 5), M(3, 1), N(8, 1)
Answer:

Question 20.
X(- 3, 2), Y(5, 2), Z(- 3, 6)
Answer:
The orthocenter lies on the vertex of the triangle.
Explanation:
The slope of YZ = \(\frac { 6 – 2 }{ -3 – 5 } \) = \(\frac { -1 }{ 2 } \)
The slope of the perpendicular line is 2
The equation of perpendicular line is (y – 2) = 2(x + 3)
y – 2 = 2x + 6
2x – y + 8 = 0
The slope of XZ = \(\frac { 6 – 2 }{ -3 + 3 } \) = 0
The equation of perpendicular line is (y – 2) = 0
y = 2
Substitute y = 2 in 2x – y + 8 = 0
2x – 2 + 8 = 0
2x + 6 = 0
x = -3
the orthocenter is (-3, 2)
The orthocenter lies on the vertex of the triangle.
Question 21.
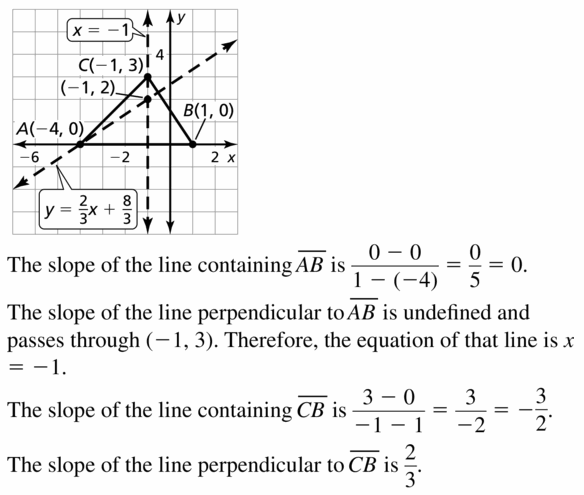
A(- 4, 0), B(1, 0), C(- 1, 3)
Answer:

Question 22.
T(-2, 1), U( 2, 1), V(0, 4)
Answer:
The orthocenter lies inside the triangle ABC.
Explanation:
The slope of UV = \(\frac { 4 – 1 }{ 0 – 2 } \) = \(\frac { -3 }{ 2 } \)
The slope of the perpendicular line is \(\frac { 2 }{ 3 } \)
The equation of the perpendicular line is (y – 1) = \(\frac { 2 }{ 3 } \)(x + 2)
3(y – 1) = 2(x + 2)
3y – 3 = 2x + 2
2x – 3y + 5 = 0 — (i)
The slope of TV = \(\frac { 4 – 1 }{ 0 + 2 } \) = \(\frac { 3 }{ 2 } \)
The slope of the perpendicular line is \(\frac { -2 }{ 3 } \)
The equation of the perpendicular line is (y – 1) = \(\frac { -2 }{ 3 } \)(x – 2)
3(y – 1) = -2(x – 2)
3y – 3 = -2x + 4
2x + 3y – 7 = 0 —(ii)
Add two equations
2x – 3y + 5 + 2x + 3y – 7 = 0
4x – 2 = 0
x = 0.5
2x – 1.5 + 5 = 0
x = -1.75
So, the orthocenter is (0, 2.33)
The orthocenter lies inside the triangle ABC.
CONSTRUCTION
In Exercises 23-26, draw the indicated triangle and find its centroid and orthocenter.
Question 23.
isosceles right triangle
Answer:

Question 24.
obtuse scalene triangle
Answer:
Construct the medians for all the sides of the trinagle by finding the midpoint. The point where all medians intersect is centroid. The orthocenter lies outside the triangle for an obtuse triangle.
Question 25.
right scalene triangle
Answer:

Question 26.
acute isosceles triangle
Answer:
ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in finding DE. Point D is the centroid of ∆ABC.
Question 27.
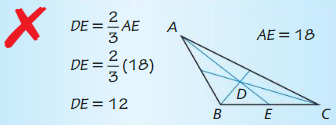
Answer:

Question 28.
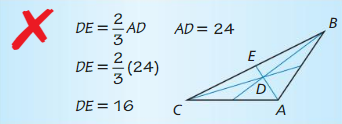
Answer:
The length of DE should be 1/3 of length of AE because it is the shorter segment from the centroid
DE = \(\frac { 1 }{ 3 } \)AE
= \(\frac { 1 }{ 3 } \)(24)
= 8
DE = 8
PROOF
In Exercises 29 and 30, write a proof of the statement.
Question 29.
The angle bisector from the vertex angle to the base of an isosceles triangle is also a median.
Answer:


Question 30.
The altitude from the vertex angle to the base of an isosceles triangle is also a perpendicular bisector.
Answer:
CRITICAL THINKING
In Exercises 31-36, complete the statement with always, sometimes, or never. Explain your reasoning.
Question 31.
The centroid is _____________ on the triangle.
Answer:

Question 32.
The orthocenter is _____________ outside the triangle.
Answer:
The orthocenter is always outside the triangle opposite the longest leg, on the same side as the largest angle. The only time all three of these centers fall in the same spot is in the case of an equilateral triangle. In fact, in this case, the incenter falls in the same place as well.
Question 33.
A median is _____________ the same line segment as a perpendicular bisector.
Answer:

Question 34.
An altitude is ______________ the same line segment as an angle bisector.
Answer: An altitude is sometimes the same line segment as an angle bisector.
Question 35.
The centroid and orthocenter are _____________ the same point.
Answer:

Question 36.
The centroid is ______________ formed by the intersection oÍ the three medians.
Answer:
The centroid is a point formed by the intersection oÍ the three medians.
Question 37.
WRITING
Compare an altitude of a triangle with a perpendicular bisector of a triangle.
Answer:

Question 38.
WRITING
Compare a median. an altitude, and an angle bisector of a triangle.
Answer:
Median is a line segment joining a vertex of a triangle with the midoint of the opposite side. Angle bisector is a line segment joining a vertex of a trianglr with the opposite side such that the angle at the vertex split into two equal parts. While altitude is also a line segment joining a vertex of a triangle with an opposite side such that the segment is perpendicular to the opposite side. In general, medians, angle bisectors and altitudes drawn from the same vertex of a triangle are different line segments. In an equilateral triangle, altitude, median, and angle bisector is drawn from the same vertex overlap. In an isosceles triangle, the altitude drawn to the base is the median and the angle bisector, the median drawn to the base is the altitude and the angle bisector, the bisector of the angle opposite to the base is the altitude and the median.
Question 39.
MODELING WITH MATHEMATICS
Find the area of the triangular part of the paper airplane wing that is outlined in red. Which special segment of the triangle did you use?
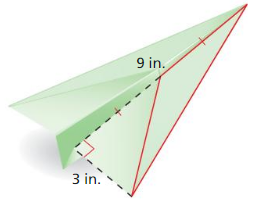
Answer:

Question 40.
ANALYZING RELATIONSHIPS
Copy and complete the statement for ∆DEF with centroid K and medians
\(\overline{D H}\), \(\overline{E J}\), and \(\overline{F G}\).
a. EJ = ____ KJ
Answer:
EJ = 2KJ
Explanation:
Since KJ is the shorter distance between the two parts of the median, its length is 1/3 of the EJ.
b. DK = ____ KH
Answer:
DK = 2 KH
Since KH is the shorter distance between the two parts of the median, its length is 1/3 of the DH.
c. FG = ___ KF
Answer:
FG = \(\frac { 2 }{ 3 } \)KF
Since KF is the longest distance between two parts, its length is \(\frac { 2 }{ 3 } \) of FG
d. KG = ___ FG
Answer:
KG = 2FG
Since KG is the shorter distance between the two parts of the median, its length is 1/3 of the FG.
MATHEMATCAL CONNETIONS
In Exercises 41-44, point D is the centroid of ∆ABC. Use the given information to find the value of x.
Question 41.
BD = 4x + 5 and BF = 9x
Answer:
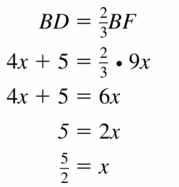
Question 42.
GD = 2x – 8 and GC = 3x + 3
Answer:
x = 9
Explanation:
GD = \(\frac { 1 }{ 3 } \)GC
2x – 8 = \(\frac { 1 }{ 3 } \)(3x + 3)
2x – 8 = x + 1
x = 9
Question 43.
AD = 5x and DE = 3x – 2
Answer:
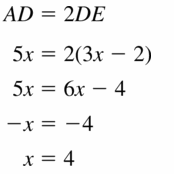
Question 44.
DF = 4x – 1 and BD = 6x + 4
Answer:
x = 3
Explanation:
BD = 2DF
6x + 4 = 2(4x – 1)
6x + 4 = 8x – 2
2x = 6
x = 3
Question 45.
MATHEMATICAL CONNECTIONS
Graph the lines on the same coordinate plane. Find the centroid of the triangle formed by their intersections.
y1 = 3x – 4
y2 = \(\frac{3}{4}\)x + 5
y2 = – \(\frac{3}{2}\)x – 4
Answer:
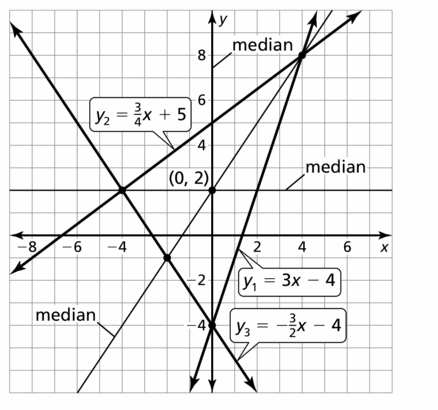

Question 46.
CRITICAL THINKING
In what types of triangles can a vertex be one of the points of concurrency of the triangle? Explain your reasoning.
Answer:
In right angles, the orthocenter forms at the 90 degrees angle.
Question 47.
WRITING EQUATIONS
Use the numbers and symbols to write three different equations for PE.

Answer:
![]()
Question 48.
HOW DO YOU SEE IT?
Use the figure.
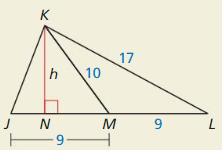
a. What type of segment is \(\overline{K M}\)? Which point of concurrency lies on \(\overline{K M}\)?
Answer:
KM is the median drawn from K to JL.
b. What type of segments is \(\overline{K N}\)? Which point of concurrency lies on \(\overline{K N}\)?
Answer:
KN is the altitude drawn from K to JL.
c. Compare the areas of ∆JKM and ∆KLM. Do you think the areas of the triangles formed by the median of any triangle will always compare this way? Explain your reasoning.
Answer:
Question 49.
MAKING AN ARGUMENT
Your friend claims that it is possible for the circumcenter, incenter, centroid, and orthocenter to all be the same point. Do you agree? Explain your reasoning.
Answer:

Question 50.
DRAWING CONCLUSIONS
The center of gravity of
a triangle, the point where a triangle can balance on the tip of a pencil, is one of the four points of concurrency. Draw and cut out a large scalene triangle on a piece of cardboard. Which of the four points of concurrency is the center of gravity? Explain.
Answer:
The median is the balancing line of the triangle
The centroid is the point of concurrency of three medians
The centroid is the center of gravity of the triangle.
Explanation:
The median is the balancing line of the triangle i.e median divides the triangle into two triangles of equal areas.
Assuming triangle ABC
The area of ABC = 0.5bh
The median divides the base into two equal parts, each forming a smaller triangle with the same height of the original one.
AD is the median of base BC
So, bD = CD = \(\frac { 1 }{ 2 } \) BC
The area of ABC = \(\frac { 1 }{ 2 } \) x BC x h
Area of ABD = \(\frac { 1 }{ 2 } \) x BD x h = \(\frac { 1 }{ 2 } \) x ABC area
Area of ACD = \(\frac { 1 }{ 2 } \) x CD x h = \(\frac { 1 }{ 2 } \) x ABC area
The centroid is the concurrency point of three medians.
So, the centroid is the gravity centre of the triangle.
Question 51.
PROOF
Prose that a median of an equilateral triangle is also an angle bisector, perpendicular bisector, and altitude.
Answer:


Question 52.
THOUGHT PROVOKING
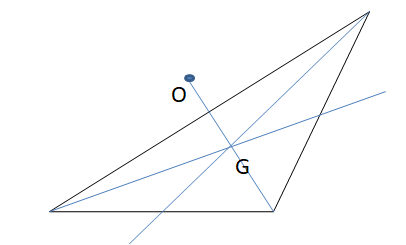
Construct an acute scalene triangle. Find the orthocenter, centroid, and circumcenter. What can you conclude about the three points of concurrency?
Answer:
The centroid, orthocenter and circumcenter are collinear.
Explanation:
Below is the scalene triangle with the centroid, orthocenter and circumcenter
Point G is the centroid, H is the orthocenter and J is the circumcenter.
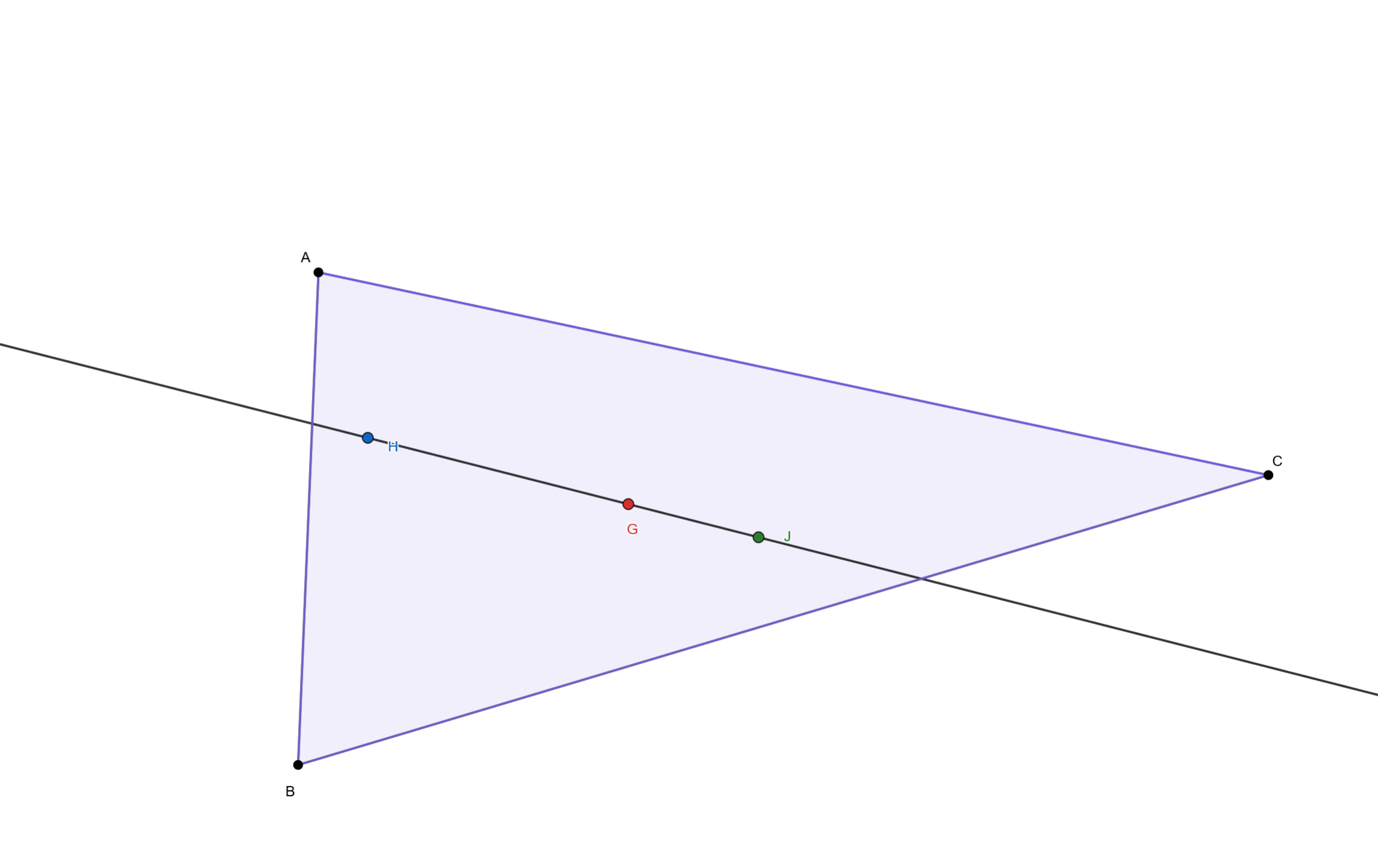
If we draw a line through these points, we can see all the points lie on the same line.
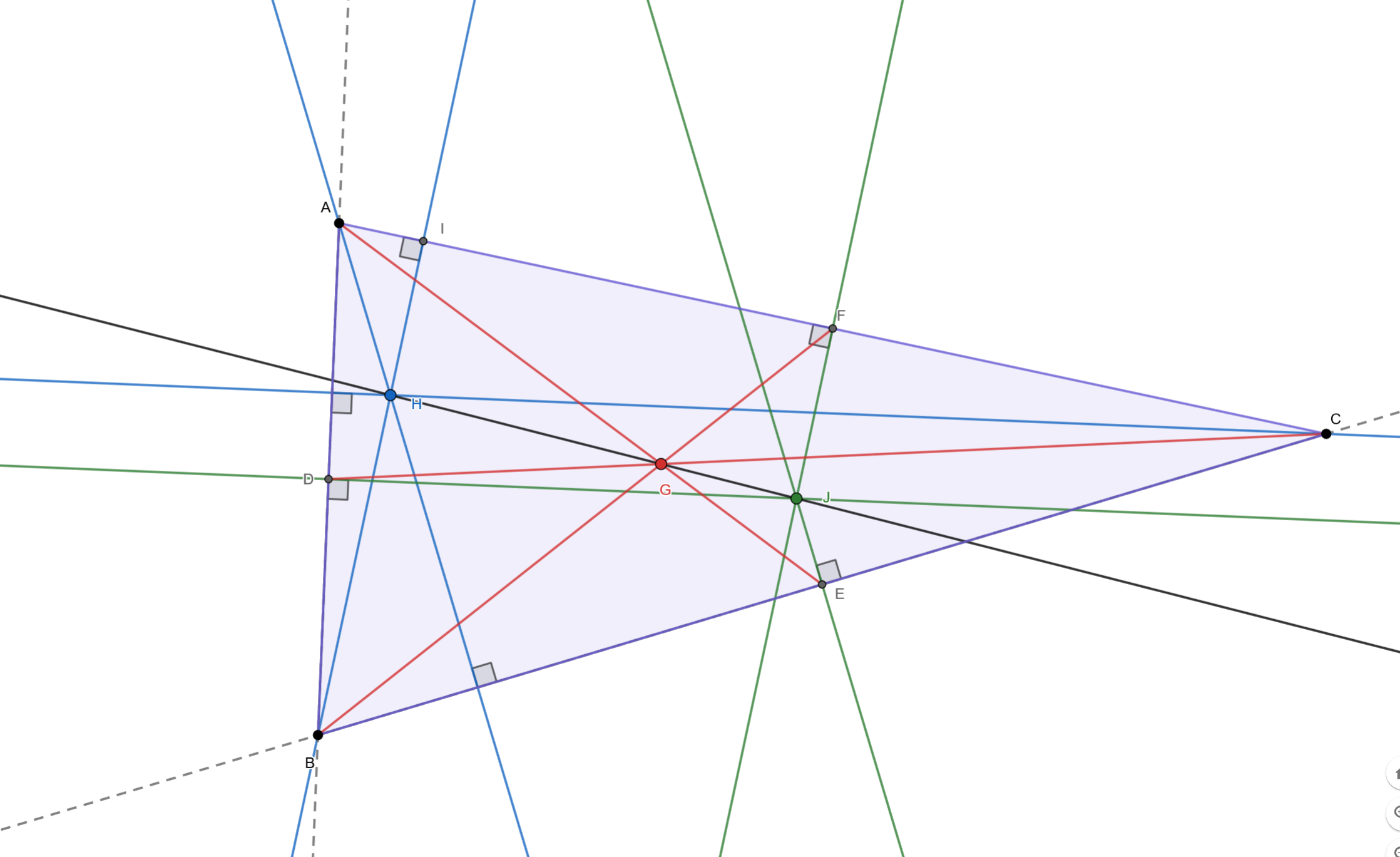
Therefore, we can conclude that the centroid, orthocenter and circumcenter are collinear.
Below mentioned is the construction part.
Question 53.
CONSTRUCTION
Follow the steps to construct a nine-point circle. Why is it called a nine-point circle?
Step 1 Construct a large acute scalene triangle.
Step 2 Find the orthocenter and circumcenter of the triangle.
Step 3 Find the midpoint between the orthocenter and circumcenter.
Step 4 Find the midpoint between each vertex and the orthocenter.
Step 5 Construct a circle. Use the midpoint in Step 3 as the center of the circle, and the distance from the center to the midpoint of a side of the triangle as the radius.
Answer:

Question 54.
PROOF
Prove the statements in parts (a)-(c).
Given \(\overline{L P}\) and \(\overline{M Q}\) are medians of scalenc ∆LMN.
Point R is on \(\vec{L}\)P such that \(\overline{L P} \cong \overline{P R}\). Point S is on \(\vec{M}\)Q such that \(\overline{M Q} \cong \overline{Q S}\).
Prove
a. \(\overline{N S} \cong \overline{N R}\)
b. \(\overline{N S}\) and \(\overline{N R}\) are both parallel to \(\overline{L M}\).
c. R, N, and S are collinear.
Answer:
Maintaining Mathematical Proficiency
Determine whether \(\overline{A B}\) is parallel to \(\overline{C D}\).
Question 55.
A(5, 6), B (- 1, 3), C(- 4, 9), D(- 16, 3)
Answer:
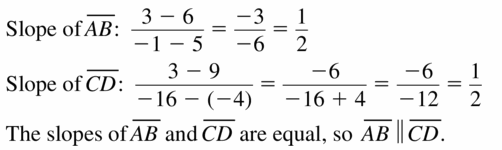
Question 56.
A(- 3, 6), B(5, 4), C(- 14, – 10), D(- 2, – 7)
Answer:
AB is not parallel to CD.
Explanation:
Slope of AB = \(\frac { 4 – 6 }{ 5 + 3 } \) = \(\frac { -1 }{ 4 } \)
Slopeof CD = \(\frac { -7 + 10 }{ -2 + 14 } \) = \(\frac { 1 }{ 4 } \)
The slopes of AB and CD are not equal. So AB and CD are not parallel.
Question 57.
A (6, – 3), B(5, 2), C(- 4, – 4), D(- 5, 2)
Answer:
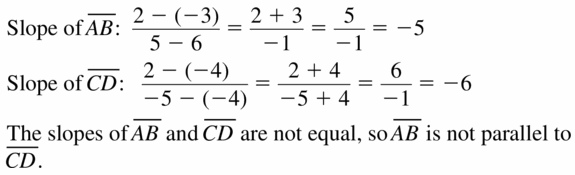
Question 58.
A(- 5, 6), B(- 7, 2), C(7, 1), D(4, – 5)
Answer:
AB is parallel to CD.
Explanation:
Slope of AB = \(\frac { 2 – 6 }{ -7 + 5 } \) = 2
Slopeof CD = \(\frac { -5 – 1 }{ 4 – 7 } \) = 2
The slopes of AB and CD are equal. So, AB is parallel to CD.
6.1 and 6.3 Quiz
Find the indicated measure. Explain your reasoning.
Question 1.
UV
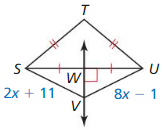
Answer:
UV = 15
Explanation:
SV = VU
2x + 11 = 8x – 1
8x – 2x = 11 + 1
6x = 12
x = 2
UV = 8(2) – 1 = 15
Question 2.
QP
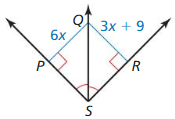
Answer:
QP = 18
Explanation:
QP = QR
6x = 3x + 9
3x = 9
x = 3
QP = 6(3) = 18
Question 3.
m∠GJK
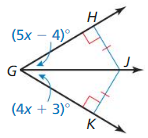
Answer:
m∠GJK = 59°
Explanation:
5x – 4 = 4x + 3
x = 7
∠JGK = 4(7) + 3 = 31
m∠GJK = 180 – (31 + 90) = 180 – 121 = 59
Find the coordinates of the circumcenter of the triangle with the given vertices.
Question 4.
A(- 4, 2), B(- 4, – 4), C(0, – 4)
Answer:
The circumcenter is (-2, -1)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let A(- 4, 2), B(- 4, – 4), C(0, – 4) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PA = PB = PC
PA² = PB² = PC²
PA² = PB²
(x + 4)² + (y – 2)² = (x + 4)² + (y + 4)²
x² + 8x + 16 + y² – 4y + 4 = x² + 8x + 16 + y² + 8y + 16
12y = -12
y = -1
PB² = PC²
(x + 4)² + (y + 4)² = (x – 0)² + (y + 4)²
x² + 8x + 16 + y² + 8y + 16 = x² + y² + 8y + 16
8x = -16
x = -2
The circumcenter is (-2, -1)
Question 5.
D(3, 5), E(7, 9), F(11, 5)
Answer:
The circumcenter is (7, 5)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let D(3, 5), E(7, 9), F(11, 5) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PD = PE = PF
PD² = PE² = PF²
PD² = PE²
(x – 3)² + (y – 5)² = (x – 7)² + (y – 9)²
x² – 6x + 9 + y² – 10y + 25 = x² – 14x + 49 + y² – 18y + 81
-6x + 14x – 10y + 18y = 130 – 34
8x + 8y = 96
x + y = 12 — (i)
PE² = PF²
(x – 7)² + (y – 9)² = (x – 11)² + (y – 5)²
x² – 14x + 49 + y² – 18y + 81 = x² – 22x + 121 + y² – 10y + 25
-14x + 22x – 18y + 10y = 146 – 130
8x – 8y = 16
x – y = 2 — (ii)
Add (i) & (ii)
x + y + x – y = 12 + 2
2x = 14
x = 7
Put x = 7 in (i)
7 + y = 12
y = 5
The circumcenter is (7, 5)
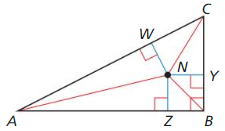
The incenter of ∆ABC is point N. Use the given information to find the indicated measure.
Question 6.
NQ = 2x + 1, NR = 4x – 9
Find NS.
Answer:
NS = 11
Explanation:
NQ = NR = NS
2x + 1 = 4x – 9
4x – 2x = 10
2x = 10
x = 5
NQ = 10 + 1 = 11
NS = 11
Question 7.
NU = – 3x + 6, NV = – 5x
Find NT.
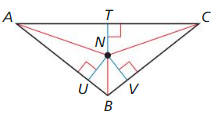
Answer:
NT = 15
Explanation:
NU = NV = NT
-3x + 6 = -5x
-3x + 5x = -6
2x = -6
x = -3
NT = -5(-3) = 15
Question 8.
NZ = 4x – 10, NY = 3x – 1
Find NW.
Answer:
NW = 26
Explanation:
NZ = NY = NW
4x – 10 = 3x – 1
x = 9
NZ = 4(9) – 10 = 36 – 10 = 26
NW = 26
Find the coordinates of the centroid of the triangle wilt the given vertices.
Question 9.
J(- 1, 2), K(5, 6), L(5, – 2)
Answer:
Centroid of the triangle is (3, 2)
Explanation:
Centroid of the triangle = (\(\frac { -1 + 5 + 5 }{ 3 } \), \(\frac { 2 + 6 – 2 }{ 3 } \))
= (3, 2)
Question 10.
M(- 8, – 6), N(- 4, – 2), P(0, – 4)
Answer:
Centroid of the triangle is (-4, -4)
Explanation:
Centroid of the triangle = (\(\frac { -8 – 4 + 0 }{ 3 } \), \(\frac { -6 – 2 – 4 }{ 3 } \))
= (-4, -4)
Tell whether the orthocenter is inside, on, or outside the triangle. Then find its coordinates.
Question 11.
T(- 2, 5), U(0, 1), V(2, 5)
Answer:
The orthocenter lies inside the triangle TUV
Explanation:
The slope of TU = \(\frac { 1 – 5 }{ 0 + 2 } \) = -2
The slope of the perpendicular line is \(\frac { 1 }{ 2 } \)
The perpendicular line is y – 5 = \(\frac { 1 }{ 2 } \)(x – 2)
2y – 10 = x – 2
x – 2y + 8 = 0
The slope of UV = \(\frac { 5 – 1 }{ 2 – 0 } \) = 2
The slope of the perpendicular line is \(\frac { -1 }{ 2 } \)
The perpendicular line is y – 5 = \(\frac { -1 }{ 2 } \)(x + 2)
2y – 10 = -x – 2
x + 2y – 8 = 0
equate both equations
x – 2y + 8 = x + 2y – 8
-4y = -16
y = 4
x – 2(4) + 8 = 0
x = 0
So, the orthocenter is (0, 4)
The orthocenter lies inside the triangle TUV
Question 12.
X(- 1, – 4), Y(7, – 4), Z(7, 4)
Answer:
The orthocenter lies on the vertex.
Explanation:
The slope of XY = \(\frac { -4 + 4 }{ 7 + 1 } \) = 0
The slope of the perpendicular line is 0
The perpendicular line is y – 4 = 0
y = 4
The slope of XZ =\(\frac { 4 + 4 }{ 7 + 1} \) = 1
The slope of the perpendicular line is -1
The perpendicular line is y + 4 = -1(x – 7)
y + 4 = -x + 7
x + y – 3 = 0
x + 4 – 3 = 0
x = -1
So, the orthocenter is (-1, 4)
The orthocenter lies on the vertex.
Question 13.
A woodworker is culling the largest wheel possible from a triangular scrap of wood. The wheel just touches each side of the triangle, as shown.
Answer:
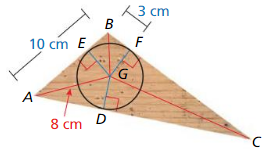
a. Which point of concurrency is the center of the circle? What type
of segments are \(\overline{B G}\), \(\overline{C G}\), and \(\overline{A G}\)?
Answer:
- The incircle of a triangle touches all sides of the triangle and has the incentre of the triangle as its center. Therefore, it is the largest possible circle that can be fitted inside a triangle.
- So, the wheel is the incircle of the triangle and its center is the incentre of the triangle.
- We know that the point of intersection of the angle bisectors of a triangle is called the incenter of the triangle.
- Since, BG, CG, and AG intersect at the center of the circle which is the incenter of the triangle. So, BG, CG, and AG are the angle bisectors of the triangle ABC.
b. Which theorem can you use to prove that ∆BGF ≅ ∆BGE?
Answer:
AG, BG, and CG are the angle bisectors of the triangle.
As BG is the angle bisector of ∠EBF.
∠FBG = ∠EBG—-(1)
∠GFC = ∠GEA = 90 degrees
As ∠GFC forms a linear pair with ∠GFB and ∠GEA forms a linear pair with ∠GEB
∠GFB = 180 – ∠GFC
∠GEB = 180 – ∠GEA
∠GFB = ∠GEB = 90 degrees —-(2)
In ΔBGF and ΔBGE
∠GFB ≅ ∠GEB
∠FBG ≅ ∠EBG
BG ≅ BG
c. Find the radius of the wheel to the nearest tenth of a centimeter. Justify your answer.
Answer:
ΔBGF ≅ ΔBGE
BF = BE
the length of BE is also 3 cm
BE + EA = 10
3 + EA = 10
EA = 10 – 3
EA = 7
Apply the Pythagoras theorem in ΔAEG
EA² + GE² = AG²
7² + GE² = 8²
GE² = 8² – 7²
GE² = 64 – 49
GE² = 15
GE = √15 = 3.88
So, the length of GE is 3.88 cm.
So, the radius of the wheel to the nearest tenth of cm is 3.9
Question 14.
The Deer County Parks Committee plans to build a park at point P, equidistant from the three largest cities labeled X, Y, and Z. The map shown was created b the committee.
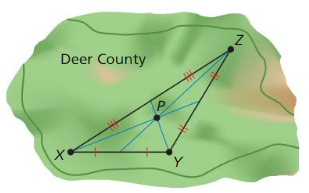
a. Which point of concurrency did the commIttee use as the location of the Park?
Answer:
- Given that committee plans to build a park at point P such that it is at an equal distance from three big cities. We were asked to find which point of concurrency the committee used to locate the park.
- As the three big cities are vertices X, Y, and Z, and point P is equidistance to them, point P must be the point where the perpendicular bisectors of the triangle meet.
- There the committee used the point of concurrency of the perpendicular bisectors.
b. Did the committee use the best point of concurrency for the location of the park? Ii not, which point would be better to use? Explain.
Answer:
- Give is to check whether the committee used the best point of concurrency for the location of the park.
- A point of intersection of perpendicular bisectors is the only point that is at equidistance from all three vertices.
- It is the best point for the location of the park.
6.4 The Triangle Midsegment Theorem
Exploration 1
Midsegments of a Triangle
Work with a partner. Use dynamic geometry software. Draw any ∆ABC.
a. Plot midpoint D of \(\overline{A B}\) and midpoint E of \(\overline{B C}\). Draw \(\overline{D E}\), which is a midsegment of ∆ABC.
Answer:
b. Compare the slope and length of \(\overline{D E}\) with the slope and length of \(\overline{A C}\).
Answer:
c. Write a conjecture about the relationships between the midsegments and sides of a triangle. Test your conjecture by drawing the other midsegments of ∆ABC, dragging vertices to change ∆ABC. and noting whether the relationships hold.
Answer:
Exploration 2
Midsegments of a Triangle
Work with a partner. Use dynamic geometry software. Draw any ∆ABC.
a. Draw all three midsegments of ∆ABC.
Answer:
b. Use the drawing to write a Conjecture about the triangle formed by the midsegments of the original triangle.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures.
Answer:
Communicate Your Answer
Question 3.
How are the midsegments of a triangle related to the sides of the triangle?
Answer:
Question 4.
In ∆RST. \(\overline{U V}\) is the rnidsegrnent connecting the midpoints of \(\overline{R S}\) and \(\overline{S T}\). Given
UV = 12, find RT.
Answer:
Lesson 6.4 The Triangle Midsegment Theorem
Monitoring progress
Use the graph of △ABC.
Question 1.
In △ABC, show that midsegments \(\overline{D E}\) is parallel to \(\overline{A C}\) and that DE = \(\frac { 1 }{ 2 }\)AC.
Answer:
Find the coordinates of D and E by getting the midpoints of AB, BC
AB midpoint = D(\(\frac { 1 – 1 }{ 2 } \), \(\frac { 4 – 6 }{ 2 } \)) = D(0, -1)
Midpoint of BC = E(\(\frac { 5 – 1 }{ 2 } \), \(\frac { 4 + 0 }{ 2 } \)) = E(2, 2)
Slope of AC = \(\frac { 0 + 6 }{ 5 – 1 } \) =\(\frac { 3 }{ 2 } \)
Slope of DE = \(\frac { 2 + 1 }{ 2 – 0 } \) = \(\frac { 3 }{ 2 } \)
The slopes are same, so the lines are not parallel.
DE = √(2 – 0)² + (2 + 1)² = √13
AC = √(5 – 1)² + (0 + 6)² = √16 + 36 = √52
So, DE = \(\frac { 1 }{ 2 }\)AC
Question 2.
Find the coordinates of the endpoints of midsegments \(\overline{E F}\), Which opposite \(\overline{A B}\). show that \(\overline{E F}\) is parallel to \(\overline{A B}\) and that EF = \(\frac { 1 }{ 2 }\)AB.
Answer:
The coordinates of E = (\(\frac { -1 + 5 }{ 2 } \), \(\frac { 0 + 4 }{ 2 } \)) = (2, 2)
The coordinates of F = (\(\frac { 1 + 5 }{ 2 } \), \(\frac { 0 + 6 }{ 2 } \)) = (3, 3)
The slope of AB = \(\frac { 4 + 6 }{ -1 – 1 } \) = -5
The slope of EF = \(\frac { 3 – 2 }{ 3 – 2 } \) = 1
The slopes are different. So the lines are not parallel
EF = √(3 – 2)² + (3 – 2)² = √2
AB = √(-1 – 1)² + (4 + 6)² = √4 + 100 = √104
Question 3.
In Example 2, find the coordinates of F, the midpoint of \(\overline{O C}\). Show that \(\overline{F E}\) || \(\overline{O B}\) and FE = \(\frac { 1 }{ 2 }\)OB.
Answer:
The coordinates of F = (\(\frac { 0 + 2p }{ 2 } \), \(\frac { 0 + 0 }{ 2 } \))
= (p, 0)
The slope of OB = \(\frac { 2r – 0 }{ 2q – 0 } \) = \(\frac { r }{ q } \)
The slope of FE = \(\frac { r – 0 }{ q + p – p }\) = \(\frac { r }{ q }\)
The slopes are equal. So, the lines are parallel.
FE = √(q + p – p)² + (r – 0)² = √q² + r²
OB = √(2q – 0)² + (2r – 0)² = √4q² + 4r² = 2√q² + r²
OB = 2(FE)
FE = \(\frac { 1 }{ 2 }\)OB.
Question 4.
Copy the diagram in Example 3. Draw and name the third midsegment.
Then find the length of \(\overline{V S}\) when the length of the third midsegment is 81 inches.
Answer:
The length of third midsegment = 81 in
The length of VS = \(\frac { 81 }{ 2 } \) = 40.5
Question 5.
In Example 4. if F is the midpoint of \(\overline{C B}\), what do you know about \(\overline{D F}\)?
Answer:
DF is parallel to AE.
Question 6.
WHAT IF?
In Example 5, you jog down Peach Street to Plum Street, over Plum Street to Cherry Street. up Cherry Street to Pear Street. over Pear Street to Peach Street. and then back home up Peach Street. Do you jog more miles in Example 5? Explain.
Answer:
The distance you jog = 2.25 + 1.4 + 1.3 + .65 = 5.6
Exercise 6.4 The Triangle Midsegment Theorem
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
The ___________ of a triangle is a segment that connects the midpoints of two sides of the triangle.
Answer:

Question 2.
COMPLETE THE SENTENCE
If \(\overline{D E}\) is the midsegment opposile \(\overline{A C}\) in ∆ABC, then \(\overline{D E}\) || \(\overline{A C}\) and DE = ________ AC by the Triangle Midsegrnent Theorem
Answer:
If \(\overline{D E}\) is the midsegment opposile \(\overline{A C}\) in ∆ABC, then \(\overline{D E}\) || \(\overline{A C}\) and DE = \(\frac { 1 }{ 2 } \) AC by the Triangle Midsegrnent Theorem (Theorem 6.8).
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, use the graph of ∆ABC with midsegments \(\overline{D E}\), \(\overline{E F}\), and \(\overline{D F}\).
Question 3.
Find the coordinates of points D, E, and F.
Answer:
![]()
Question 4.
Show that \(\overline{D E}\) is parallel to \(\overline{C B}\) and that DE = \(\frac{1}{2}\)CB.
Answer:
The slope of DE = \(\frac { 0 + 2 }{ -2 + 4 } \) = 1
The slope of CB = \(\frac { -2 + 6 }{ 1 + 3 } \) = 1
The slopes are same. So \(\overline{D E}\) is parallel to \(\overline{C B}\)
DE = √(-2 + 4)² + (0 + 2)² = √4 + 4 = √8
CB = √(1 + 3)² + (-2 + 6)² = √16 + 16 = √32
So, DE = \(\frac{1}{2}\)CB
Question 5.
Show that \(\overline{E F}\) is parallel to \(\overline{A C}\) and that EF = \(\frac{1}{2}\)AC.
Answer:
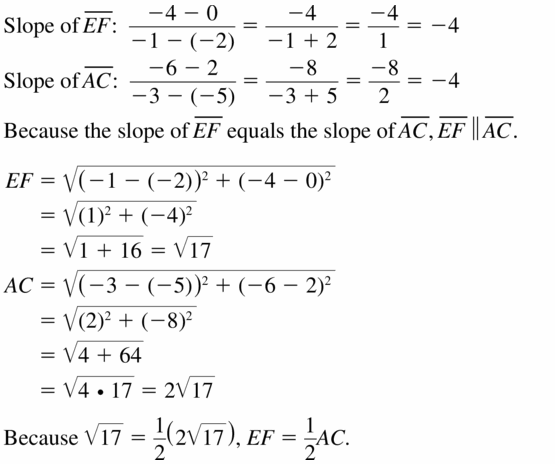
Question 6.
Show that \(\overline{D F}\) is parallel to \(\overline{A B}\) and that DF = \(\frac{1}{2}\)AB.
Answer:
The slope of DF = \(\frac { -4 + 2 }{ -1 + 4 } \) = \(\frac { -2 }{ 3 } \)
The slope of AB = \(\frac { -2 – 2 }{ 1 + 5 } \) = \(\frac { -4 }{ 6 } \) = \(\frac { -2 }{ 3 } \)
The slopes are equal. So, the lines are parallel.
DF = √(-1 + 4)² + (-4 + 2)² = √9 + 4 = √13
AB = √(1 + 5)² + (-2 – 2)² = √36 + 16 = √52
So, DF = \(\frac{1}{2}\)AB.
In Exercises 7-10, \(\overline{D E}\) is a midsegment of ∆ABC Find the value of x.
Question 7.
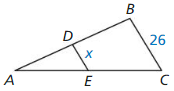
Answer:
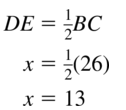
Question 8.
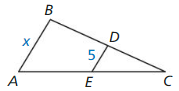
Answer:
x = 10
Explanation:
DE = \(\frac { 1 }{ 2 } \)AB
5 = \(\frac { 1 }{ 2 } \)x
x = 10
Question 9.
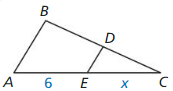
Answer:
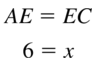
Question 10.
Answer:
x = 8
Explanation:
BE = EC
x = 8
In Exercise 11-16, \(\overline{X J} \cong \overline{J Y}\), \(\overline{Y L} \cong \overline{L Z}\), and \(\overline{X K} \cong \overline{K Z}\). Copy and complete the statement.
Question 11.
\(\overline{J K}\) || __________
Answer:
![]()
Question 12.
\(\overline{X Y}\) || __________
Answer:
\(\overline{X Y}\) || KL
Question 13.
\(\overline{J L}\) || __________
Answer:
![]()
Question 14.
\(\overline{J L}\) ≅ __________ ≅ __________
Answer:
\(\overline{J L}\) ≅ JK ≅ KL
Question 15.
\(\overline{J Y}\) ≅ __________ ≅ __________
Answer:
![]()
Question 16.
\(\overline{J K}\) ≅ __________ ≅ __________
Answer:
\(\overline{J K}\) ≅ JL ≅ KL
MATHEMATICAL CONNECTIONS
In Exercises 17-19. use ∆GHJ, where A, B, and C are midpoints of the sides.
Question 17.
When AB = 3x + 8 and GJ = 2x + 24, what is AB?
Answer:
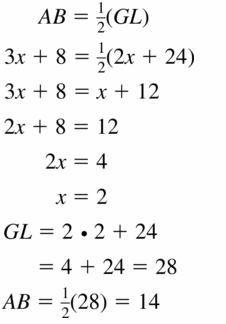
Question 18.
When AC = 3y – 5 and HJ = 4y + 2, what is HB?
Answer:
HB = 13
Explanation:
AC = 0.5(HJ)
3y – 5 = 0.5(4y + 2)
3y – 5 = 2y + 1
3y – 2y = 1 + 5
y = 6
HB = 0.5(HJ)
= 0.5(4(6) + 2) = 0.5(26) = 13
Question 19.
When GH = 7 – 1 and CB = 4z – 3. what is GA?
Answer:
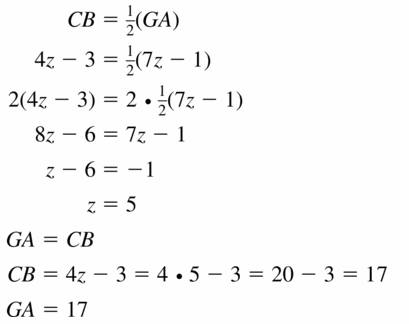
Question 20.
ERROR ANALYSIS
Describe and correct the error.
Answer:
BC = \(\frac { 1 }{ 2 } \)DE
10 = \(\frac { 12 }{ 2 } \)(5)
According to triangle midsegment theorem, AD = DB and AE = EC.
Question 21.
MODELING WITH MATHEMATICS
The distance between consecutive bases on a baseball held is 90 feet. A second baseman stands halfway between first base and second base, a shortstop stands hallway between second base and third base, and a pitcher stands halfway between first base and third base. Find the distance between the shortstop and the pitcher.
Answer:

Question 22.
PROVING A THEOREM
Use the figure from Example 2 to prose the Triangle Midsegment Theorem (Theorem 6.8) for midsegment \(\overline{D F}\), where F is the midpoint of \(\overline{O C}\).
Answer:
Question 23.
CRITICAL THINKING
\(\overline{X Y}\) is a midsegment of ∆LMN. Suppose \(\overline{D E}\) is called a “quarter segment” of ∆LMN. What do you think an “eighth segment” would be? Make conjectures about the properties of a quarter segment and an eighth segment. Use variable coordinates to verify your conjectures.
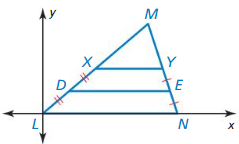
Answer:

Question 24.
THOUGHT PROVOKING
Find a real-life object that uses midsegments as part of its structure. Print a photograph of the object and identify the midsegments of one of the triangles in the structure.
Answer:
- We have to look for an object which has midsegments in our surroundings. Then identify the midsegment in one of the triangles present in it.
- When we look around, we will see that many structures like swings, rooftops of house, bridges etc, use midsegments in their design.
- One such structure is the swing.
Question 25.
ABSTRACT REASONING
To create the design shown. shade the triangle formed by the three midsegments of the triangle. Then repeat the process for each unshaded triangle.
a. What is the perimeter of the shaded triangle in Stage 1?
b. What is the total perimeter of all the shaded triangles in Stage 2?
c. What is the total perimeter of all the shaded triangles in Stage 3?
Answer:
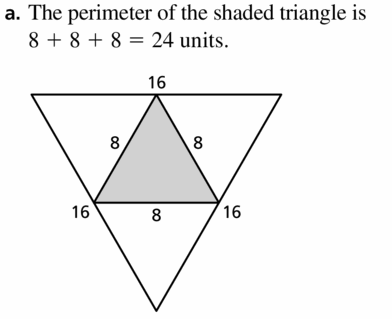
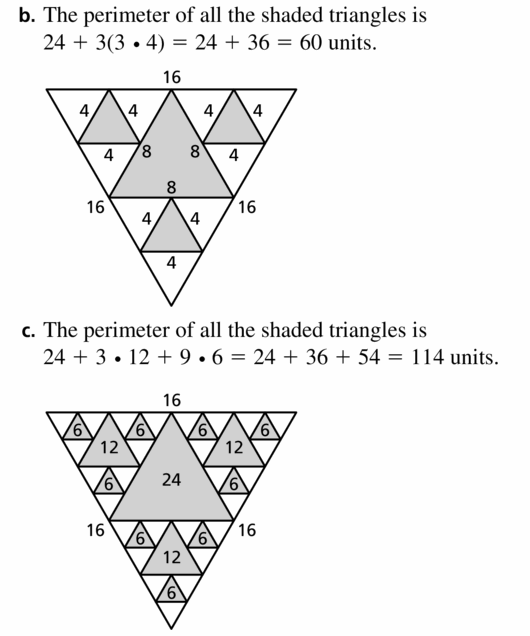
Question 26.
HOW DO YOU SEE IT?
Explain how you know that the yellow triangle is the midsegment triangle of the red triangle in the pattern of floor tiles shown.
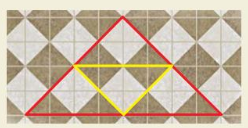
Answer:
Because the yellow triangle vertices are located at the midpoints of the red triangle sides.
Question 27.
ATTENDING TO PRECISION
The points P(2, 1), Q(4, 5), and R(7, 4) are the midpoints of the sides of a triangle. Graph the three midsegments. Then show how to use your graph and the properties of midsemeriLs to draw the original triangle. Give the coordinates of each vertex.
Answer:
Maintaining Mathematical Proficiency
Find a counter example to show that the conjecture is false.
Question 28.
The difference of two numbers is always less than the greater number.
Answer:
When we subtract -3 from 4 i.e 4 -(-3) = 7. The number is greater than the individual integers. So, the subtraction of a negative number from a positive number gives an answer greater than both numbers.
Question 29.
An isosceles triangle is always equilateral.
Answer:

6.5 Indirect Proof and Inequalities in One Triangle
Exploration 1
Comparing Angle Measures and Side Lengths
Work with a partner: Use dynamic geometry software. Draw any scalene ∆ABC
a. Find the side lengths and angle measures of the triangle.
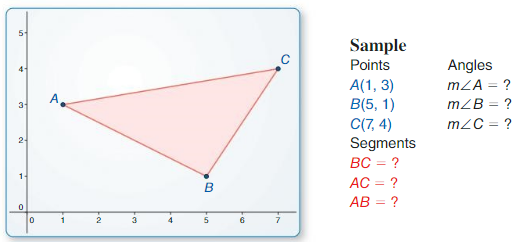
Answer:
b. Order the side lengths. Order the angle measures. What do you observe?
Answer:
c. Drug the vertices of ∆ABC to form new triangles. Record the side lengths and angle measures in a table. Write a conjecture about your findings.
Answer:
Exploration 2
A Relationship of the Side Lengths of a Triangle
Work with a partner. Use dynamic geometry software. Draw any ∆ABC.
a. Find the side lengths of the triangle.
Answer:
b. Compare each side length with the sum of the other two side lengths.
ATTENDING TO PRECISION
To be proficient in math, you need to express numerical answers with a degree of precision appropriate for the content.
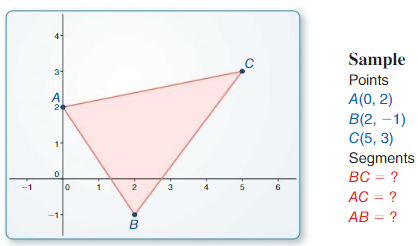
Answer:
c. Drag the vertices of ∆ABC to form new triangles and repeat parts (a) and (b). Organize your results in a table. Write a conjecture about your findings.
Answer:
Communicate Your Answer
Question 3.
How are the sides related to the angles of a triangle? How are any two sides of a triangle related to the third side?
Answer: The relation between the sides and the angles of the triangle is that in any triangle the largest side and the largest angle of the triangle are always opposite to each other and the shortest side and the shortest angle are always opposite to each other.
The relation of the two sides of a triangle to the third side is that the sum of the lengths of any two sides of a triangle is greater than the length of its third side.
Question 4.
Is it possible for a triangle to have side lengths of 3, 4, and 10? Explain.
Answer:
Given side lengths are 3, 4 and 10.
3 + 4 > 10
7 > 10
So, it is not possible to construct a triangle.
Lesson 6.5 Indirect Proof and Inequalities in One Triangle
Monitoring Progress
Question 1.
Write in indirect proof that a scalene triangle cannot have two congruent angles.
Answer:
- Let us consider the contradiction that a scalene triangle has two congruent angles and no congruent sides. This means that if two angles of a scalene triangle are congruent, then the two sides opposite two these congruent angles also congruent. But this is a contradiction to the above assumption that the triangle has no congruent sides.
- So, we can conclude that a scalene triangle cannot have two congruent angles.
Question 2.
List the angle of ∆PQR in order from smallest to largest.
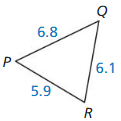
Answer:
The sides from the largest to smallest are PQ, QR, PR
The angles opposite to sides are ∠R, ∠P, ∠Q
The angles from smallest to the largest are ∠Q, ∠P, ∠R
Question 3.
List the sides of ∆RST in order from shortest to longest.
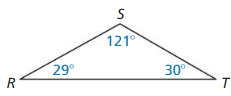
Answer:
The angles from shortest to longest are ∠R, ∠T, ∠S
Question 4.
A triangle has one side of length 12 inches and another side of length 20 inches. Describe the possible lengths of the third side.
Answer:
The length of the third side must be greater than 8 and lesser than 32.
Explanation:
Let x represent the length of the third side. Draw diagrams to help visualize the small and large values of x. Then use the Triangle Inequality Theorem to write and solve inequalities.
The smallest value of x is x + 12 > 20. So, x > 8
The largest value of x is 12 + 20 > x
32 > x
So, 32 > x or 32 < x
The length of the third side must be greater than 8 and lesser than 32.
Decide Whether it is possible to construct a triangle with the given side lengths. Explain your reasoning.
Question 5.
4 ft, 9 ft, 10 ft
Answer:
It is not possible to construct a triangle.
Explanation:
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
So, 9 + 4 = 13
13 is not greater than 10.
So, it is not possible to construct a triangle.
Question 6.
8 ft, 9 ft, 18 ft
Answer:
It is possible to construct a triangle.
Explanation:
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
8 + 9 = 17 > 18
So, it is possible to construct a triangle.
Question 7.
5 cm, 7 cm, 12 cm
Answer:
It is not possible to construct a triangle.
Explanation:
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
7 + 5 = 12
12 is not greater than 12
so, it is not possible to construct a triangle.
Exercise 6.5 Indirect Proof and Inequalities in One Triangle
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Why is an indirect proof also called a proof by contradiction?
Answer:

Question 2.
WRITING
How can you tell which side of a triangle is the longest Irom the angle measures of the
triangle? How can you tell which side is the shortest?
Answer:
The angle which is opposite to the longest side is the longest angle.
Monitoring progress and Modeling with Mathematics
In Exercises 3-6, write the first step in an indirect proof of the statement.
Question 3.
If WV + VU ≠ 12 inches and VU = 5 inches, then WV ≠ 7 inches.
Answer:
![]()
Question 4.
If x and y are odd integers. then xy is odd.
Answer:
Assume x = 1, y = 3
xy = 3
Question 5.
In ∆ABC. if m∠A = 100°, then ∠B is not a right angle.
Answer:
![]()
Question 6.
In ∆JKL, if M is the midpoint of \(\overline{K L}\), then \(\overline{J M}\) is a median.
Answer:
Assume temporarily JM is a median.
In Exercises 7 and 8, determine which two statements contradict each other. Explain your reasoning.
Question 7.
(A) ∆LMN is a right triangle.
(B) ∠L ≅∠V
(C) ∆LMN is equilateral.
Answer:
Question 8.
(A) Both ∠X and ∠Y have measures greater than 20°.
(B) Both ∠X and ∠Y have measures less than 30°.
(C) m∠X + m∠Y = 62°
Answer:
B and C. If ∠X and ∠Y are less than 30, then m∠X + m∠Y is not equal to 62.
In Exercises 9 and 10, use a ruler and protractor to draw the given type of triangle. Mark the largest angle and longest side in red and the smallest angle and shortest side in blue. What do you notice?
Question 9.
acute scalene
Answer:

Question 10.
right scalene
Answer:
To construct a scalene triangle draw a segment and label it AB. Assuring that three sides have different lengths. Draw an arc with center A and AC as radius draw an arc and draw another arc taking BC as radius and B as centre. Label the point of intersection of two arcs as C.
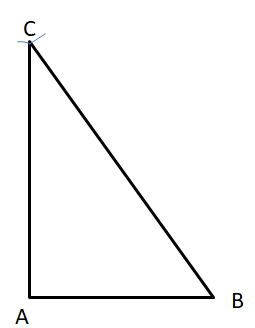
The largest side is BC. So, the largest angle is ∠A. The smallest side is AB and the smallest angle is ∠C.
In Exercises 11 and 12, list the angles of the given triangle from smallest to largest.
Question 11.
Answer:
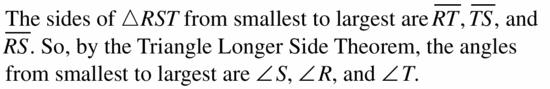
Question 12.
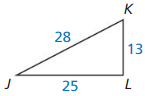
Answer:
The sides of △JKL from smallest to largest are KL, JL, JK. So by the triangle, longer side theorem, the angles from smallest to largest are ∠J, ∠K, ∠L.
In Exercises 13-16, list the sides of the given triangle from shortest to longest.
Question 13.
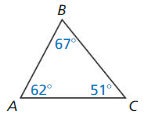
Answer:
Question 14.
Answer:
The angles of the triangle from smallest to largest are ∠Z, ∠X, ∠Y. So by the trinagle larger angle theorem, the sides from shortest to largest are XY, YZ, and XZ.
Question 15.
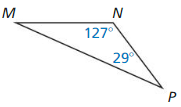
Answer:
Question 16.
Answer:
∠D = 180 – (90 + 33) = 180 – 57
The angles from smallest to largest are ∠G, ∠D, ∠F. So by the triangle larger angle theorem, the sides from shortest to longest are FD, FG, and DG.
In Exercises 17-20, describe the possible lengths of the third side of the triangle given the lengths of the other to sides.
Question 17.
5 inches, 12 inches
Answer:

Question 18.
12 feet, 18 feet
Answer:
The possible lengths of the third side are greater than 6 and less than 30 ft
Explanation:
x + 12 > 18
x > 6
12 + 18 > x
30 > x or x < 30
The possible lengths of the third side are greater than 6 and less than 30 ft
Question 19.
2 feet, 40 inches
Answer:

Question 20.
25 meters, 25 meters
Answer:
The possible lengths of the third side are greater than 0 and less than 50 m.
Explanation:
x + 25 > 25
x > 0
25 + 25 > x
50 > x or x < 50
The possible lengths of the third side are greater than 0 and less than 50 m.
In Exercises 21-23, is it possible to construct a triangle with the given side lengths? If not, explain why not.
Question 21.
6, 7, 11
Answer:

Question 22.
3, 6, 9
Answer:
No
Explanation:
3 + 6 = 9 → 9 = 9
6 + 9 = 15 → 15 < 9
9 + 3 = 12 → 12 < 9
No, the sum of any two side lengths of a triangle is less than the length of the third side.
Question 23.
28, 17, 46
Answer:
![]()
Question 24.
35, 120, 125
Answer:
35 + 120 = 155 → 155 < 125
So, No.
Question 25.
ERROR ANALYSIS
Describe and correct the error in writing the first step of an indirect proof.

Answer:

Question 26.
ERROR ANALYSIS
Describe and correct the error in labeling the side lengths 1, 2, and √3 on the triangle.
Answer:
Number 1 is opposite to 90 degrees and 2 is opposite to 60 degrees and the remaining is √3 on the triangle.
Question 27.
REASONING
You are a lawyer representing a client who has been accused of a crime. The crime took place in Los Angeles, California. Security footage shows your client in New York at the time of the crime. Explain how to use indirect reasoning to prove your client is innocent.
Answer:

Question 28.
REASONING
Your class has fewer than 30 students. The teacher divides your class into two groups. The first group has 15 students. Use indirect reasoning to show that the second group must have fewer than 15 students.
Answer:
The assumption that N2 ≥ 15 is false.
Explanation:
The number of students in a class N < 30
The number of students in the first group N1 = 15
The number of students in the second group N2
N = N1 + N2
Assume temporarily that the number of student in the second group has 15 or more students
N2 ≥ 15
N1 + N2 ≥ 15 + 15
30 ≥ 30
So, the assumption that N2 ≥ 15 is false.
Question 29.
PROBLEM SOLVING
Which statement about ∆TUV is false?
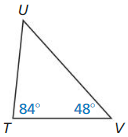
(A) UV > TU
(B) UV + TV > TU
(C) UV < TV
(D) ∆TUV is isosceles.
Answer:
Question 30.
PROBLEM SOLVING
In ∆RST. which is a possible side length for ST? Select all that apply.
(A) 7
(B) 8
(C) 9
(D) 10
Answer:
A.
Explanation:
∠R = 180 – (65 + 56) = 180 – 121 = 59, which indicates that ∆RST i isosceles. By the trinagle longer side theorem, ST is 7
Question 31.
PROOF
Write an indirect proof that an odd number is not divisible by 4.
Answer:

Question 32.
PROOF
Write an indirect proof of the statement
“In ∆QRS, if m∠Q + m∠R = 90°, then m∠S = 90°.”
Answer:
Question 33.
WRITING
Explain why the hypotenuse of a right triangle must always be longer than either leg.
Answer:

Question 34.
CRITICAL THINKING
Is it possible to decide if three side lengths form a triangle without checking all three inequalities shown in the Triangle Inequality Theorem (Theorem 6. 11)? Explain your reasoning.
Answer:
Given,
Is it possible to decide if three side lengths form a triangle without checking all three inequalities shown in the Triangle Inequality Theorem.
Yes, it is possible to decide if three side lengths form a triangle without checking all three inequalities shown in the Triangle Inequality Theorem.
If the sum of the lengths of the two shortest sides is greater than the length of the longest side. then the other two inequalities will also be true.
Question 35.
MODELING WITH MATHEMATICS
You can estimate the width of the river from point A to the tree at point B by measuring the angle to the tree at several locations along the riverbank. The diagram shows the results for locations C and D.
a. Using ∆BCA and ∆BDA, determine the possible widths of the river. Explain your reasoning.
b. What could you do if you wanted a closer estimate?
Answer:

Question 36.
MODELING WITH MATHEMATICS
You travel from Fort Peck Lake to Glacier National Park and from Glacier National Park to Granite Peak.
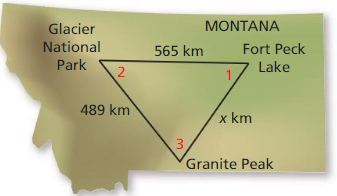
a. Write two inequalities to represent the possible distances from Granite Peak back to Fort Peck Lake.
Answer:
x < 565 + 489
x < 1054
x + 489 > 565
x > 565 – 489
x > 76
x + 489 > 565
x > 565 – 489
x > 76
Combining these two inequalities to find the possible distance from Granite Peak back to Fork Peck Lake
x < 1054
x > 76
76 < x < 1054
b. How is your answer to part (a) affected if you know that m∠2 < m∠1 and m∠2 < m∠3?
Answer: ∠WXY is smaller than ∠YXZ, ∠YXZ is smaller than ∠WYX, ∠WYX is smaller than ∠XZY and ∠XZY is smaller than ∠XYZ.
Question 37.
REASONING
In the figure. \(\overline{X Y}\) bisects ∠WYZ. List all six angles of ∆XYZ and ∆WXY in order from smallest to largest. Explain ‘our reasoning.
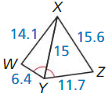
Answer:
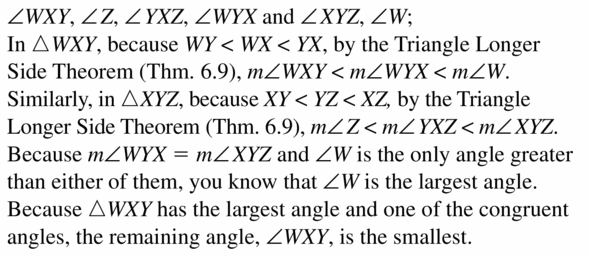
Question 38.
MATHEMATICAL CONNECTIONS
In ∆DEF, m∠D = (x + 25)°. m∠E = (2x – 4)°, and in m∠F = 63°. List the side lengths and angle measures of the triangle in order from least to greatest.
Answer:
sum of angles is 180 degrees
x + 25 + 2x – 4 + 63 = 180
3x + 84 = 180
3x = 96
x = 32
m∠D = 32 + 25 = 57
m∠E = 2(32) – 4 = 60
m∠F = 63
The angles from least to greatest are m∠D, m∠E, m∠F and the side lengths are EF, DF, DE.
Question 39.
ANALYZING RELATIONSHIPS
Another triangle inequality relationship is given by the Exterior Angle Inequality Theorem. It states:
The measures of an exterior angle of a triangle is greater than the measure of either of the nonadjacent interior angles.
Explain how you know that m∠1 > m∠A and m∠1 > m∠B in ∆ABC with exterior angle ∠1.
Answer:

MATHEMATICAL CONNECTIONS
In Exercises 40 and 41, describe the possible values of x.
Question 40.
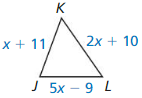
Answer:
The possible values of x are x > \(\frac { 5 }{ 3 } \) and x < 15
Explanation:
JK + JL > KL
x + 11 + 5x – 9 > 2x +10
6x + 2 > 2x + 10
4x > 8
x > 2
JK + KL > JL
x + 11 + 2x + 10 > 5x – 9
3x + 21 > 5x – 9
30 > 2x
15 > x
JL + KL > JK
5x – 9 + 2x + 10 > x + 11
7x + 1 > x + 11
6x > 10
x > \(\frac { 5 }{ 3 } \)
The possible values of x are x > \(\frac { 5 }{ 3 } \) and x < 15
Question 41.
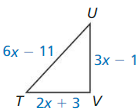
Answer:
Question 42.
HOW DO YOU SEE IT?
Your house is on the corner of Hill Street and Eighth Street. The library is on the corner of View Street and Seventh Street. What is the shortest route to et from your house to the library? Explain your reasoning.

Answer:
Through Washington ave is the shortest route to reach from house to the library.
Question 43.
PROVING A THEOREM
Use the diagram to prove the Triangle Longer Side Theorem (Theorem 6.9).
Given BC > AB, BD = BA
Prove m∠BAC > m∠C
Answer:

Question 44.
USING STRUCTURE
The length of the base of an isosceles triangle is l. Describe the possible lengths for each leg. Explain our reasoning.
Answer:
If other lengths are x and x
Then, x + x > l
2x > l
x > l/2
x + l > x
The possible lengths of each leg are l are l/2.
Question 45.
MAKING AN ARGUMENT
Your classmate claims to have drawn a triangle with one side length of 13 inches and a perimeter of 2 feet. Is this possible? Explain your reasoning.
Answer:

Question 46.
THOUGHT PROVOKING
Cut two pieces of string that are each 24 centimeters long. Construct an isosceles triangle out of one string and a scalene triangle out of the other. Measure and record the side lengths. Then classify each triangle by its angles.
Answer:
Given,
Cut two pieces of string that are each 24 centimeters long.
An isosceles triangle has two sides of the same length. One possible isosceles triangle is then a triangle with lengths of 9, 9, 6 (since 9 + 9 + 6 = 24) as shown below. This triangle has all acute angles so it is an acute isosceles triangle.
A scalene triangle has no sides of the same length. A possible scalene triangle could be a triangle with side lengths of 6, 8, 10 (6 + 8 + 10 = 24) as shown below.
This triangle has a right angle. So, it is a right scalene triangle.
Question 47.
PROVING A THEOREM
Prove the Triangle Inequality Theorem (Theorem 6. 11).
Given ∆ABC
Prove AB + BC > AC, AC + BC > AB, and AB + AC > BC
Answer:


Question 48.
ATTENDING TO PRECISION
The perimeter of ∆HGF must be between what two integers? Explain your reasoning.
Answer:
By the triangle inequality theorem, the sum of two sides of a triangle is always greater than the third side and the difference of two sides of a triangle is always smaller than the third side.
1 < GH < 7
1 < FH > 9
2 < GF < 8
4 < GH + FH + GF < 24
4 < Δ GHF < 24
Question 49.
PROOF
Write an indirect proof that a perpendicular segment is the shortest segment from a point to a plane.
Given \(\overline{P C}\) ⊥ palne M
Prove \(\overline{P C}\) is the shortest from P to plane M.
Answer:

Maintaining Mathematical Proficiency
Name the indicated angle between the pair of sides given.
Question 50.
\(\overline{A E}\) and \(\overline{B E}\)
Answer:
The included angle is \(\overline{A E}\) and \(\overline{B E}\) is ∠AEB
Question 51.
\(\overline{A C}\) and \(\overline{D C}\)
Answer:
![]()
Question 52.
\(\overline{A D}\) and \(\overline{D C}\)
Answer:
The included angle is \(\overline{A D}\) and \(\overline{D C}\) is ∠ADC
Question 53.
\(\overline{C E}\) and \(\overline{B E}\)
Answer:
![]()
6.6 Inequalities in Two Triangles
Exploration 1
Comparing Measures in Triangles
Work with a partner. Use dynamic geometry software.
a. Draw ∆ABC, as shown below.
Answer:
b. Draw the circle with center C(3, 3) through the point A(1, 3).
Answer:
c. Draw ∆DBC so that D is a point on the circle.
Answer:
d. Which two sides of ∆ABC are congruent to two sides of ∆DBC? Justify your answer.
Answer:
e. Compare the lengths of \(\overline{A B}\) and \(\overline{D B}\). Then compare the measures of ∠ACB and ∠DCB. Are the results what you expected? Explain.
Answer:
f. Drag point D to several locations on the circle. At each location, repeat part (e). Copy and record your results in the table below.
Answer:
g. Look for a pattern of the measures in our table. Then write a conjecture that summarizes your observations.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures.
Answer:
Communicate Your Answer
Question 2.
If two sides of one triangle are congruent to two sides of another triangle, what can you say about the third sides of the triangles?

Answer:
If three sides of a triangle are congruent to three sides of another triangle, the triangles are congruent. If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent
Question 3.
Explain how you can use the hinge shown at the left to model the concept described in Question 2.
Answer:
Lesson 6.6 Inequalities in Two Triangles
Monitoring Progress
Use the diagram
Question 1.
If PR = PS and m∠QPR > m∠QPS, which is longer, \(\overline{S Q}\) or \(\overline{R Q}\)?
Answer:
Given that,
PR = PS and PQ ≅ PQ by the reflexive property of congruence.
m∠QPR > m∠QPS.
So, two sides of △PSQ are congruent to two sides of △PRQ and included angle in △PRQ is larger.
By the hinge theorem RQ > SQ.
Question 2.
If PR = PS and RQ < SQ, which is larger, ∠RPQ or ∠SPQ?
Answer:
Given that,
PR = PS, RQ < SQ
PQ ≅ PQ by the reflexive property of congruence theorem.
So, two sides of △PSQ are congruent to two sides of △PRQ and third side of △PSQ is longer.
By the converse of the hinge theorem, ∠SPQ > ∠RPQ.
Question 3.
Write a temporary assumption you can make to prove the Hinge Theorem indirectly. What two cases does that assumption lead to?
Answer:
Hinge theorem states that if two sides of the triangle are congruent to two sides of another triangle and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle.
Question 4.
WHAT IF?
In Example 5, Group C leaves camp and travels 2 miles due north. then turns 40° towards east and travels 1.2 miles. Compare the distances from camp for all three groups.
Answer:
group A = 180 – 45 = 135
group B = 180 – 30 = 150
Group C = 180 – 40 = 140
Because 150 > 140 > 135, the distance Group B from the camp is greater than the distance Group C, A. by the hinge theorem.
The distances are Group B > group C > group A.
Exercise 6.6 Inequalities in Two Triangles
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain why Theorem 6.12 is named the “Hinge Theorem.”
Answer:

Question 2.
COMPLETE THE SENTENCE
In ∆ABC and ∆DEF, \(\overline{A B} \cong \overline{D E}\), \(\overline{B C} \cong \overline{E F}\). and AC < DF. So m∠_______ > m ∠ _______ by the Converse of the Hinge Theorem
Answer:
In ∆ABC and ∆DEF, \(\overline{A B} \cong \overline{D E}\), \(\overline{B C} \cong \overline{E F}\). and AC < DF. So m∠E > m ∠B by the Converse of the Hinge Theorem
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, copy and complete the statement with <, >, or = Explain your reasoning.
Question 3.
m∠1 ________ m∠2
Answer:

Question 4.
m∠1 ________ m∠2
Answer:
m∠1 < m∠2 by the converse of the hinge theorem.
Question 5.
m∠1 ________ m∠2
Answer:

Question 6.
m∠1 ________ m∠2
Answer:
m∠1 > m∠2 by the converse of the hinge theorem.
In Exercises 7-10. copy and complete the statement with <, >, or =. Explain your reasoning.
Question 7.
AD ________ CD
Answer:

Question 8.
MN ________ LK
Answer:
MN < KL by the converse of the hinge theorem.
Question 9.
TR ________ UR
Answer:

Question 10.
AC ________ DC
Answer:
AC > Dc by the converse of the hinge theorem.
PROOF
In Exercises 11 and 12, write a proof.
Question 11.
Given \(\overline{X Y} \cong \overline{Y Z}\), m∠WYZ > m∠WYX
Prove WZ > WX
Answer:

Question 12.
Given \(\overline{B C} \cong \overline{D A}\), DC < AB
Prove m∠BCA > m∠DAC
Answer:
Given that, AD ≅ BC
AC ≅ AC by the reflexive property of congruence theorem
DC < AB is given
So, m∠BCA > m∠DAC by the hinge theorem.
In Exercises 13 and 14, you and your friend leave on different flights from the same airport. Determine which flight is farther from the airport. Explain your reasoning.
Question 13.
Your flight: Flies 100 miles due west, then turns 20° toward north and flies 50 miles.
Friend’s flight: Flies 100 miles due north, then turns 30° toward east and flies 50 miles.
Answer:
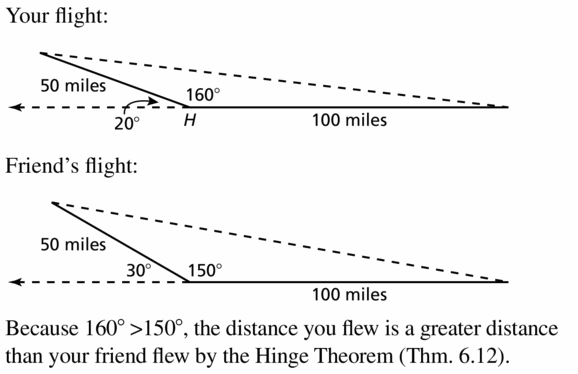
Question 14.
Your flight: Flies 21omiles due south, then turns 70° toward west and flies 80 miles.
Friend’s flight: Flies 80 miles due north, then turns 50° toward east and flies 210 miles.
Answer:
My friend flight is farther from the airport.
Explanation:
The figure below represents the situation.
I flew 210 miles north to point B then runed 70° to the west and flew 80 miles to point C.
My friend flew 80 miles north to point D then turned 50° east and flew 210 miles to point F.
We should take into consideration that 70° to west means 110° and 50° to east means 130°
AB = DF
BC = AD
m∠ABC < m∠ADF
So, AC < AF
My friend flight is farther from the airport.
Question 15.
ERROR ANALYSIS
Describe and correct the error in using the Hinge Theorem (Theorem 6.12).
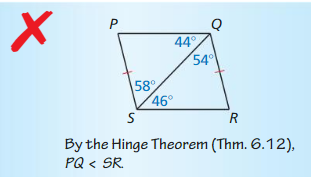
Answer:
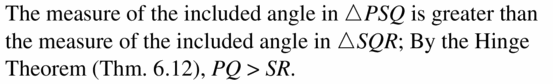
Question 16.
REPEATED REASONING
Which is possible measure for ∠JKM? Select all that apply.
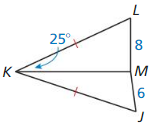
(A) 15°
(B) 22°
(C) 25°
(D) 35°
Answer:
(D) 35°
Explanation:
KL ≅ KJ is given
KM ≅ KM by the reflexive property of congruence
LM > MJ
So, m∠LKM > m∠MKJ
25 > 35
Question 17.
DRAWING CONCLUSIONS
The path from E to F is longer than the path from E to D. The path from G to D is the same length as the path from G to F. What can you conclude about the angles of the paths? Explain your reasoning.
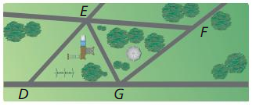
Answer:
Question 18.
ABSTRACT REASONING
In ∆EFG, the bisector of ∠F intersects the bisector of ∠G at point H. Explain why \(\overline{F G}\) must be longer than \(\overline{F H}\) or \(\overline{H G}\).
Answer:
The sum of interior angles of a triangle is 180 degrees
The sum of angles F and G cannot be larger than 180 degrees
∠HFG is half of the measurement of ∠F. ∠HGF is half of the measurement of ∠G. thus, ∠HFG + ∠HGF < 90°
∠FHG = 180° – ∠HGF – ∠HFG > 90°
Question 19.
ABSTRACT REASONING
\(\overline{N R}\) is a median of ∆NPQ, and NQ > NP Explain why ∠NRQ is obtuse.
Answer:

MATHEMATICAL CONNECTIONS
In Exercises 20 and 21, write and solve an inequality for the possible values of x.
Question 20.
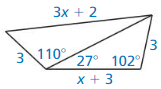
Answer:
3x + 2 = x + 3
3x – x = 3 – 2
2x = 1
x = \(\frac { 1 }{ 2 } \)
Question 21.
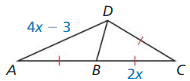
Answer:
Question 22.
HOW DO YOU SEE IT?
In the diagram, triangles are formed by the locations of the players on the basketball court. The dashed lines represent the possible paths of the basketball as the players pass. How does m∠ACB compare with m∠ACD?
Answer:
BC ≅ CD
AC ≅ AC by the reflexive property of congruence theorem
AB < AD
So, m∠ACB < m∠ACD by the converse of the hinge theorem.
Question 23.
CRITICAL THINKING
In ∆ABC, the altitudes from B and C meet at point D, and m∠BDC. What is true about ∆ABC? Justify your answer.
Answer:

Question 24.
THOUGHT PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry, state an inequality involving the sum of the angles of a triangle. Find a formula for the area of a triangle in spherical geometry.
Answer:
We know that, in the Euclidean Geometry, the sum of interior angles of a three-sided polygon (triangle) is equal to 180 degrees. If we include in the spherical geometry i.e., we will connect the vertices of the triangle that is created by the arcs of the great circles.
As we can see, the angle measures of the spherical triangle are greater than the angle measures of the Euclidean Triangle. This tells us that the sum ‘S’ of the angle measures of a triangle in spherical geometry is greater than 180 degrees.
L(x)/x = 4πr²/360
L(x) = xπr²/90
Let x, y, z be the interior angles of the spherical triangles
L(y) = yπr²/90
L(z) = zπr²/90
2L(x) + 2L(y) + 2L(z) – 4 = 4πr²
2(xπr²/90) + 2(yπr²/90) + 2(zπr²/90) – 4A = 4πr²
A = (x/180 + y/180 + z/180 – 1)πr²
Maintaining Mathematical proficiency
Find the value of x.
Question 25.
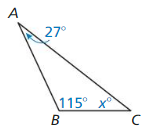
Answer:
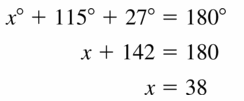
Question 26.
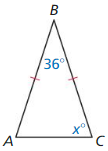
Answer:
As two sides are congruent, two angles opposite to the congruent sides are also congruent by the converse of the isosceles trinagle theorem.
36 + x + x = 180
36 + 2x = 180
2x = 144
x = 72
Question 27.
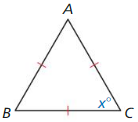
Answer:
Question 28.
Answer:
The sum of interior angles in a triangle are 180 degrees
44 + 64 + y = 180
y = 180 – 108
y = 72
x + y = 180
x + 72 = 180
x = 108
Relationships Within Triangles Chapter Review
6.1 Perpendicular and Angle Bisectors
Find the indicated measure. Explain your reasoning.
Question 1.
DC
Answer:
DC = 20
Explanation:
AD = CD
20 = 7x – 15
7x = 35
x = 5
DC = 7(5) – 15 = 20
Question 2.
RS
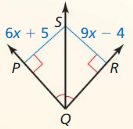
Answer:
RS = 23
Explanation:
PS = SR
6x + 5 = 9x – 4
9x – 6x = 9
3x = 9
x = 3
RS = 9(3) – 4 = 23
Question 3.
m∠JFH
Answer:
m∠JFH = 47°
Explanation:
m∠JFH = m∠JFG
So, m∠JFH = 47°
6.2 Bisectors of Triangles
Find the coordinates of the circumcenter of the triangle with the given vertices.
Question 4.
T(- 6, – 5), U(0, – 1), V(0, – 5)
Answer:
The circumcenter is (-3, -3)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let T(- 6, – 5), U(0, – 1), V(0, – 5) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then
PT = PU = PV
PT² = PU² = PV²
PT² = PU²
(x + 6)² + (y + 5)² = (x – 0)² + (y + 1)²
x² + 12x + 36 + y² + 10y + 25 = x² + y² + 2y + 1
12x + 8y + 61 = 1
12x + 8y + 60 = 0
3x + 2y + 15 = 0
PU² = PV²
(x – 0)² + (y + 1)² = (x – 0)² + (y + 5)²
x² + y² + 2y + 1 = x² + y² + 10y + 25
8y + 24 = 0
8y = -24
y = -3
Substitute y = -3 in 3x + 2y + 15 = 0
3x + 2(-3) + 15 = 0
3x – 6 + 15 = 0
3x = -9
x = -3
The circumcenter is (-3, -3)
Question 5.
X(- 2, 1), Y(2, – 3), Z(6, – 3)
Answer:
The circumcenter is (4, 3)
Explanation:
Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let X(- 2, 1), Y(2, – 3), Z(6, – 3) be the vertices of the given triangle and let P(x, y) be the circumcentre of this triangle. Then
PX = PY = PZ
PX² = PY² = PZ²
PX² = PY²
(x + 2)² + (y – 1)² = (x – 2)² + (y + 3)²
x² + 4x + 4 + y² – 2y + 1 = x² – 4x + 4 + y² + 6y + 9
8x – 8y + 5 = 13
8x – 8y – 8 = 0
x – y = 1
PY² = PZ²
(x – 2)² + (y + 3)² = (x – 6)² + (y + 3)²
x² – 4x + 4 + y² + 6y + 9 = x² – 12x + 36 + y² + 6y + 9
8x = 32
x = 4
Substitue x = 4 in x – y = 1
4 – y = 1
-y = -3
y = 3
The circumcenter is (4, 3)
Question 6.
Point D is the incenter of ∆LMN. Find the value of x.
Answer:
x = 13
6.3 Medians and Altitudes of Triangles
Find the coordinates of the centroid of the triangle with the given vertices.
Question 7.
A(- 10, 3), B(- 4, 5), C(- 4, 1)
Answer:
The centroid is (-6, 3)
Explanation:
The centroid = (\(\frac { -10 – 4 – 4 }{ 3 } \), \(\frac { 3 + 5 + 1 }{ 3 } \))
= (-6, 3)
Question 8.
D(2, – 8), E(2, – 2), F(8, – 2)
Answer:
The centroid is (4, -4)
Explanation:
The centroid = (\(\frac { 2 + 2 + 8 }{ 3 } \), \(\frac { -8 – 2 – 2 }{ 3 } \))
= (4, -4)
Tell whether the orthocenter of the triangle with the given vertices is inside, on, or outside the triangle. Then find the coordinates of the orthocenter.
Question 9.
G(1, 6), H(5, 6), J(3, 1)
Answer:
The orthocenter is (3, 5.2)
The orthocenter lies inside the triangle.
Explanation:
The slope of the line HJ = \(\frac { 1 – 6 }{ 3 – 5} \) = \(\frac { 5 }{ 2 } \)
The slope of the perpendicular line = \(\frac { -2 }{ 5 } \)
The perpendicular line is (y – 6) = \(\frac { -2 }{ 5 } \)(x – 1)
5(y – 6) = -2(x – 1)
5y – 30 = -2x + 2
2x + 5y – 32 = 0 — (i)
The slope of GJ = \(\frac { 1 – 6 }{ 3 – 1 } \) = \(\frac { -5 }{ 2 } \)
The slope of the perpendicular line = \(\frac { 2 }{ 5 } \)
The equation of perpendicular line (y – 6) = \(\frac { 2 }{ 5 } \)(x – 5)
5(y – 6) = 2(x – 5)
5y – 30 = 2x – 10
2x – 5y + 20 = 0 — (ii)
Equate both equations
2x + 5y – 32 = 2x – 5y + 20
10y = 52
y = 5.2
Substitute y = 5.2 in (i)
2x + 5(5.2) – 32 = 0
2x + 26 – 32 = 0
2x = 6
x = 3
The orthocenter is (3, 5.2)
The orthocenter lies inside the triangle.
Question 10.
K(-8, 5), L(- 6, 3), M(0, 5)
Answer:
The othrocenter is (-6, -1)
The orthocenter lies outside of the triangle
Explanation:
The slope of LM = \(\frac { 5 – 3}{ 0 + 6} \) = \(\frac { 1 }{ 3 } \)
The slope of the perpendicular line = -3
The perpendicular line is (y – 5) = -3(x + 8)
y – 5 = -3x – 24
3x + y + 19 = 0 —- (ii)
The slope of KL = \(\frac { 3 – 5 }{ -6 + 8 } \) = -1
The slope of the perpendicular line = \(\frac { 1 }{ 2 } \)
The equation of perpendicular line (y – 5) = \(\frac { 1 }{ 2 } \)(x – 0)
2y – 10 = x —- (ii)
Substitute (ii) in (i)
3(2y – 10) + y + 19 = 0
6y – 30 + y + 19 = 0
7y – 11 = 0
y = \(\frac { 11 }{ 7 } \)
x = -6
The othrocenter is (-6, -1)
The orthocenter lies outside of the triangle
6.4 The Triangle Midsegment Theorem
Find the coordinates of the vertices of the midsegment triangle for the triangle with the given vertices.
Question 11.
A(- 6, 8), B(- 6, 4), C(0, 4)
Answer:
The midsegment of AB = (-6, 6)
The midsegment of BC = (-3, 4)
The midsegment of AC = (-3, 6)
Explanation:
The midsegment of AB = (\(\frac { -6 – 6 }{ 2 } \), \(\frac { 8 + 4 }{ 2 } \))
= (-6, 6)
The midsegment of BC = (\(\frac { -6 + 0 }{ 2 } \), \(\frac { 4 + 4 }{ 2 } \))
= (-3, 4)
The midsegment of AC = (\(\frac { -6 + 0 }{ 2 } \), \(\frac { 8 + 4 }{ 2 } \))
= (-3, 6)
Question 12.
D(- 3, 1), E(3, 5), F(1, – 5)
Answer:
The midsegment of DE = (0, 3)
The midsegment of EF = (2, 0)
The midsegment of DF = (-1, -2)
Explanation:
The midsegment of DE = (\(\frac { -3 + 3 }{ 2 } \), \(\frac { 1 + 5 }{ 2 } \))
= (0, 3)
The midsegment of EF = (\(\frac { 3 + 1 }{ 2 } \), \(\frac { 5 – 5 }{ 2 } \))
= (2, 0)
The midsegment of DF = (\(\frac { -3 + 1 }{ 2 } \), \(\frac { 1 – 5 }{ 2 } \))
= (-1, -2)
6.5 Indirect Proof and Inequalities in One Triangle
Describe the possible lengths of the third side of the triangle given the lengths of the other two sides.
Question 13.
4 inches, 8 inches
Answer:
4 < x < 12
Explanation:
4 + 8 > x
12 > x
4 + x > 8
x > 4
8 + x > 4
x > -4
4 < x < 12
Question 14.
6 meters, 9 meters
Answer:
3 < x < 15
Explanation:
6 + 9 > x
15 > x
6 + x > 9
x > 3
9 + x > 6
x > -3
3 < x < 15
Question 15.
11 feet, 18 feet
Answer:
7 < x < 29
Explanation:
11 + 18 > x
29 > x
11 + x > 18
x > 7
18 + x > 11
x > -7
7 < x < 29
Question 16.
Write an indirect proof 0f the statement “In ∆XYZ, if XY = 4 and XZ = 8. then YZ > 4.”
Answer:
4 + 8 > x
12 > x
4 + x > 8
x > 4
8 + x > 4
x > -4
So, 12 > x > 4
Therefore, YZ > 4
6.6 Inequalities in Two Triangles
Use the diagram.
Question 17.
If RQ = RS and m∠QRT > m∠SRT, then how does \(\overline{Q T}\) Compare to \(\overline{S T}\)?
Answer:
TQ > ST
Explanation:
Given that,
RQ = RS and m∠QRT > m∠SRT
RT = RT by the reflexive property of congruence theorem
TQ > ST by the converse of the hinge theorem.
Question 18.
If RQ = RS and QT > ST, then how does ∠QRT compare to ∠SRT?
Answer:
Given that,
RQ = RS and QT > ST
RT = RT by the reflexive property of congruence theorem
So, m∠QRT > m∠SRT by the converse of the hinge theorem.
Relationships Within Triangles Chapter Test
In Exercise 1 and 2, \(\overline{M N}\) is a midsegment of ∆JKL. Find the value of x.
Question 1.
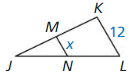
Answer:
x = 6
Explanation:
KL = 0.5(MN)
12 = 0.5x
x = 6
Question 2.
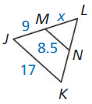
Answer:
x = 9
Explanation:
JM = ML
x = 9
Find the indicated measure. Identify the theorem you use.
Question 3.
ST
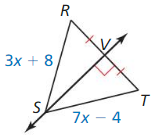
Answer:
ST = 17
Explanation:
RS = ST by the perpendicular bisector theorem
3x + 8 = 7x – 4
7x – 3x = 12
4x = 12
x = 3
ST = 7(3) – 4 = 21 – 4 = 17
Question 4.
WY
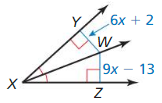
Answer:
WY = 32
Explanation:
6x + 2 = 9x – 13 by the angle bisector theorem
3x = 15
x = 5
WY = 6(5) + 2 = 32
Question 5.
BW
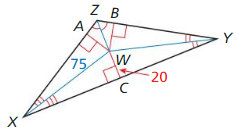
Answer:
BW = 20
Explanation:
WC = BW = AW by the incenter theorem
BW = 20
Copy and complete the statement with <, >, or =.
Question 6.
AB _____ CB
Answer:
AB > CB
Question 7.
m∠1 _____ m∠2
Answer:
m∠1 < m∠2 by the converse of the hinge theorem
Question 8.
m∠MNP ________ m∠NPM
Answer:
m∠MNP < m∠NPM
Question 9.
Find the coordinates of the circumcenter, orthocenter, and centroid of the triangle with vertices A(0, – 2), B(4, – 2), and C(0, 6).
Answer:
Circumcenter is (1.5, -0.5)
orthoceter is (0, -2)
centroid is (1.3, 0.7)
Explanation:
Graph the triangle
Draw the bisector of every angle and their intersection to get the circumcenter
Draw the altitudes and their intersections to get orthocenter
Find the midpoint of all sides and then connect it with the opposite vertex. The intersection of these medians is the centroid.
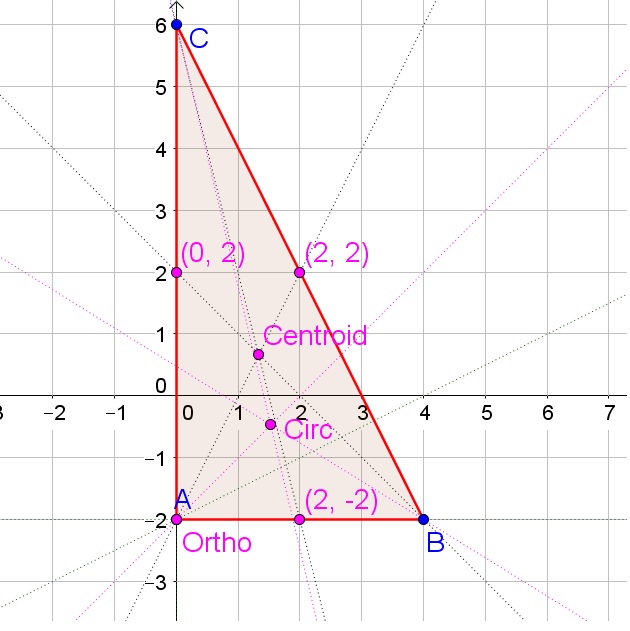
Circumcenter is (1.5, -0.5)
orthoceter is (0, -2)
centroid is (1.3, 0.7)
Question 10.
Write an indirect proof of the Corollary to the Base Angles Theorem (Corollary 5.2): If ∆PQR is equilateral, then it is equiangular.
Answer:
Assume for contradiction that there is an equilateral triangle namely △ABC. So, AB = BC = AC. According to the base angles theorem, if two sides of a triangle are congruent, then the angles opposite them are congruent.
Since AB = AC, the base angle theorem tells that m∠B = m∠C
Since AB = BC, the base angle theorem tells that m∠A = m∠C
By the transitive property of equality m∠A = m∠B = m∠C, which contradicts the assumption that triangle ABC is equiangular. Thus, the corollary is true.
Question 11.
∆DEF is a right triangle with area A. Use the area for ∆DEF to write an expression for the area of ∆GEH. Justify your answer.
Answer:
The area of ∆DEF = A
As HG is the midsegment of ∆DEF.
Area of ∆GEH = A/2
Question 12.
Two hikers start at a visitor center. The first hikes 4 miles hikes due west, then turns 40° toward south and hikes 1.8 miles. The second hikes 4 miles due east, then turns 52° toward north and hikes 1 .8 miles. Which hiker is farther from the visitor center? Explain how you know.
Answer:
The second hiker is farther away from the visitor center as all things being equal cos 128 < cos 140 from distance² = 4² + 1.8² — 2 x 4 x 1.8 cos (angle turned)
In Exercises 13-15, use the map.
Question 13.
Describe the possible lengths of Pine Avenue.
Answer:
The possible lengths of pine avenue are between 2 and 16.
Explanation:
7 + 9 > x
16 > x
7 + x > 9
x > 2
9 + x > 7
x > -2
2 < x < 16
The possible lengths of pine avenue are between 2 and 16.
Question 14.
You ride your bike along a trail that represents the shortest distance from the beach to Main Street. You end up exactly halfway between your house and the movie theatre. How long is Pine Avenue? Explain.
Answer:
halfway between your house and the movie theatre = 7/2 = 3.5
Pine Avenue is 3.5 mi
Question 15.
A market is the same distance from your house, the movie theater, and the beach. Copy the map and locate the market.
Answer:
Centroid is the market.
Relationships Within Triangles Cumulative Assessment
Question 1.
Which definitions(s) and/or theorem(s) do you need to use to prove the Converse of the Perpendicular Bisector Theorem (Theorem 6.2)? Select all that apply.
Given CA = CB
Prove Point C lies on the perpendicular bisector of AB.
| Definition of perpendicular bisector | Definition of angle bisector |
| Definition of segment congruence | Definition of angle congruence |
| Base Angles Theorem (Theorem 5.6) | Converse of the Base Angles Theorem (Theorem 5.7) |
| ASA Congruence Theorem (Theorem 5.10) | AAS Congruence Theorem (Theorem 5.11) |
Answer:
Definition of perpendicular bisector is used to prove the Converse of the Perpendicular Bisector Theorem.
Question 2.
Use the given information to write a two-column proof.
Given \(\overline{Y G}\) is the perpendicular bisector of \(\overline{D F}\).
Prove ∆DEY ≅ ∆FEY
Answer:
Question 3.
What are the coordinates of the centroid of ∆LMN?
(A) (2, 5)
(B) (3, 5)
(C) (4, 5)
(D) (5, 5)
Answer:
(B) (3, 5)
Explanation:
The coordinates of L(3, 8), M (1, 5), N(5, 2)
Centroid = (\(\frac { 3 + 1 + 5 }{ 3 } \), \(\frac { 8 + 5 + 2 }{ 3 } \))
= (3, 5)
Question 4.
Use the steps in the construction to explain how you know that the circle is circumscribed about ∆ABC.
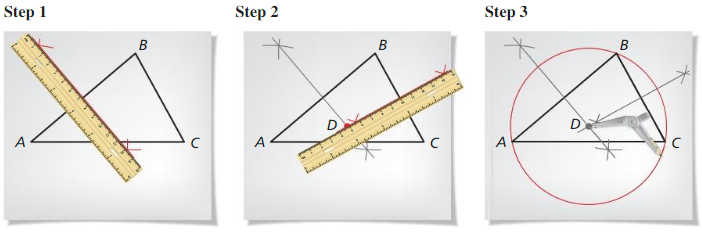
Answer:
Draw a perpendicular bisector for AB
Draw a perpendicular bisector for BC
Extend those bisectors to meet at one point.
By taking the point of intersection of perpendicular bisectors as radius, draw a circle that connects three vertices of the triangle.
Question 5.
Enter the missing reasons in the proof of the Base Angles Theorem (Theorem 5.6).
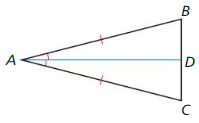
Given \(\overline{A B} \cong \overline{\Lambda C}\)
Prove ∠B = ∠C
| Statements | Reasons |
| 1. Draw \(\overline{A D}\), the angle bisector of ∠CAB | 1. Construction of angle bisector |
| 2. ∠CAD ≅ ∠BAD | 2. ________________________ |
| 3. \( \overline{\Lambda B} \cong \overline{A C} \) | 3. ________________________ |
| 4. \( \overline{D A} \cong \overline{D A} \) | 4. ________________________ |
| 5. ∆ADB ≅ ∆ADC | 5. ________________________ |
| 6. ∠B ≅ ∠C | 6. ________________________ |
Answer:
| Statements | Reasons |
| 1. Draw \(\overline{A D}\), the angle bisector of ∠CAB | 1. Construction of angle bisector |
| 2. ∠CAD ≅ ∠BAD | 2. Angle Bisector Congruence Theorem |
| 3. \( \overline{\Lambda B} \cong \overline{A C} \) | 3. Given |
| 4. \( \overline{D A} \cong \overline{D A} \) | 4. Reflexive property of congruence theorem |
| 5. ∆ADB ≅ ∆ADC | 5. SAS congruence theorem |
| 6. ∠B ≅ ∠C | 6. Angle congruence theorem |
Question 6.
Use the graph of ∆QRS.
a. Find the coordinates of the vertices of the midsegment triangle. Label the vertices T, U, and V.
Answer:
T(0, 7), U(2, 4), V(-1, 5)
Explanation:
The coordinates of Q(-3, 8), R(3, 6), S(1, 2)
The midpoint of QR = T = (\(\frac { -3 +3 }{ 2 } \), \(\frac { 8 + 6 }{ 2 } \)) = (0, 7)
Midpoint of RS = U = (\(\frac { 3 + 1 }{ 2 } \), \(\frac { 6 + 2 }{ 2 } \)) = (2, 4)
Midpoint of SR = V = (\(\frac { 1 – 3 }{ 2 } \), \(\frac { 2 + 8 }{ 2 } \)) = (-1, 5)
b. Show that each midsegment joining the midpoints of two sides is parallel to the third side and is equal to half the length of the third side.
Answer:
The slope of RS = \(\frac { 2 – 6 }{ 1 – 3 } \) = 2
The slope of TV = \(\frac { 5 – 7 }{ -1 – 0 } \) = 2
As the slopes are same. The lines are parallel.
TV = √(-1 – 0)² + (5 – 7)² = √1 + 4 = √5
RS = √(1 – 3)² + (2 – 6)² = √4 + 16 = √20
TV = 0.5(RS)
Question 7.
A triangle has vertices X(- 2, 2), Y(1, 4), and Z(2, – 2). Your friend claims that a translation of (x, y) → (x + 2, y – 3) and a translation by a scale factor of 3 will produce a similarity transformation. Do you support our friend’s claim? Explain our reasoning.
Answer:
A triangle has vertices X(- 2, 2), Y(1, 4), and Z(2, – 2).
The slope of XY
m1 = 1-(-2)/4-2 = 3/2
The slope of the side AB,
m2 = 3-0/(1-(-1)
m2 = 3/2 = 3/2
The slope of the side YZ,
m3 = 2-1/(-2-4) = -1/6
The slope of the side BC
m4 = 4-3/-5-1 = -1/6
The slope of the side XZ
m5 = 4-(-2)/(-2-2) = 4/-4 = -1
The slope of the side AC
m6 = 4-0/-5-(-1) = 4/-4 = -1
m1 = m2
m3 = m4
m5 = m6
XY || AB, YZ || BC and XZ || AC
Hence ΔABC is a similar transformation of the triangle ΔXYZ.
Question 8.
The graph shows a dilation of quadrilateral ABCD b a scale factor of 2. Show that the line containing points B and D is parallel to the line Containing points B’ and D’.
Answer:
The coordinates of B(4, 1), D(1, -1), B'(8, 2), D'(2, -2)
The slope of BD = \(\frac { -1 – 1 }{ 1 – 4 } \) = \(\frac { 2 }{ 3 } \)
The slope of B’D’ = \(\frac { -2 – 2 }{ 2 – 8 } \) = \(\frac { -4 }{ -6 } \) = \(\frac { 2 }{ 3 } \)
The slopes are equal. So, BD is parallel to B’D’.
