Practice with the help of enVision Math Common Core Grade 3 Answer Key Topic 10 Multiply by Multiples of 10 regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 10 Multiply by Multiples of 10

enVision STEM Project: Animal and Plant Characteristics
Do Research Use the Internet or other sources to find information about how the characteristics of some plants and animals help them survive. Think about how characteristics can be different among members of the same species.
Journal: Write a Report Include what you found. Also in your report:
- Tell about an insect that uses camouflage.
- Describe an example of how a plant’s thorns help it survive.
- Make up and solve multiplication problems about the animals or plants you research. Use multiples of 10.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
• multiplication
• factor
• equation
• Zero Property of Multiplication
Question 1.
A number sentence where the value on the left and right of the equal sign (=) is the same is called a(n) ___
Answer:
A number sentence where the value on the left and right of the equal sign (=) is the same is called a(n) = Equation .
Question 2.
The ___ states that any number multiplied by zero has a product of zero.
Answer:
The Zero Property of Multiplication states that any number multiplied by zero has a product of zero.
Question 3.
___ is an operation that gives the total number that results when you join equal groups.
Answer:
Multiplication is an operation that gives the total number that results when you join equal groups.
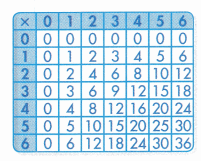
Multiplication Table
Find the value that makes the equations true. Use the multiplication table to help.
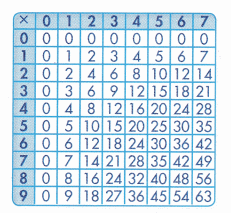 .
.
21 ÷ 7 = ___
7×__= 21
Answer:
21 ÷ 7 = 3
7× 3= 21
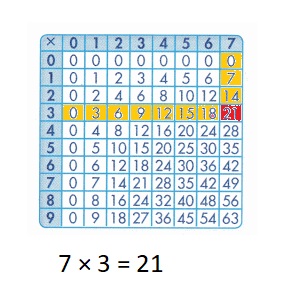
Explanation :
Step 1: Choose the first number from the numbers listed in the left-most column and the second number from the top-most row.
Step 2: Starting from the 3 move towards the right and starting from the 7 move towards down. The square where the two numbers meet gives the product 21 .
Question 5.
45 ÷ 5 = ___
5 × __ = 45
Answer:
45 ÷ 5 = 9
5 × 9 = 45
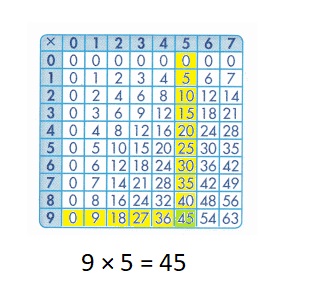
Explanation :
Step 1: Choose the first number from the numbers listed in the left-most column and the second number from the top-most row.
Step 2: Starting from the 9 move towards the right and starting from the 5 move towards down. The square where the two numbers meet gives the product 45 .
Question 6.
48 ÷ 6 = ___
6 × __ = 48
Answer:
48 ÷ 6 = 8
6 × 8 = 48

Explanation :
Step 1: Choose the first number from the numbers listed in the left-most column and the second number from the top-most row.
Step 2: Starting from the 8 move towards the right and starting from the 7 move towards down. The square where the two numbers meet gives the product 56 .
Question 7.
56 ÷ 8 = ___
8 × __= 56
Answer:
56 ÷ 8 = 7
8 × 7 = 56

Explanation :
Step 1: Choose the first number from the numbers listed in the left-most column and the second number from the top-most row.
Step 2: Starting from the 3 move towards the right and starting from the 7 move towards down. The square where the two numbers meet gives the product 21 .
Multiplication Properties
Find each product.
Question 8.
3 × 3 × 2 =___
Answer:
3 × 3 × 2 = 9 × 2 = 18
Question 9.
5 × 1 × 3 = ___
Answer:
5 × 1 × 3 = 5 × 3 = 15
Question 10.
4 × 2 × 4 = ___
Answer:
4 × 2 × 4 = 8 × 4 = 24
Question 11.
2 × 2 × 4 = ___
Answer:
2 × 2 × 4 =4 × 4 = 16
Question 12.
4 × 0 × 2 = ___
Answer:
4 × 0 × 2 = 0 × 2 =0
Question 13.
2 × 5 × 3 = ___
Answer:
2 × 5 × 3 = 10 × 3 =30
Multiplication on the Number Line
Question 14.
Which equation does the number line show?

A. 1 × 10 = 10
B. 3 × 10 × 1 = 30
C. 4 × 5 = 20
D. 5 × 10 = 50
Answer :
Option D. 5 × 10 = 50
Explanation:
Each jump represents + 10 .
Number of jumps made = 5
so, 5 × 10 = 50 .
from 0 to 50 the equation is represented .
Pick a Project
PROJECT 10A
What do you need to do to plan a trip?
Project: Research the Distance Between Two Cities
PROJECT 10B
How do stores make sure they have enough of an item to sell?
Project: Create Your Own Store

PROJECT 10C
How do trees help our environment?
Project: Design a Park and Sing a Song

PROJECT 10D
How many items can you fit in a box?
Project: Make a Product Game

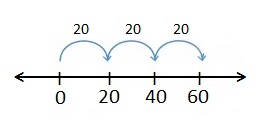
Lesson 10.1 Use Patterns to Multiply
Activity
Solve & Share
Companies package their goods in a variety of ways. One company packages a case of water as 2 rows of 10 bottles. How many bottles are in each of the cases shown in the table below? Explain your thinking.
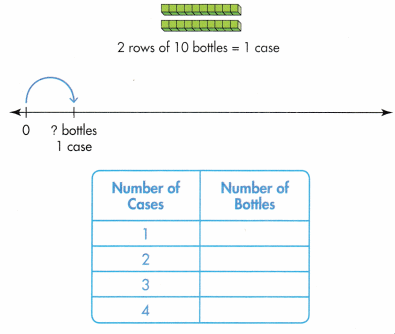
You can use appropriate tools. Place-value blocks or a number line can help you apply the math you know.

Look Back! How can place-value patterns help you when multiplying by 20?
Answer :
Number of bottles in 1 case = 2 rows of 10 bottles = 2 × 10 = 20 bottles .
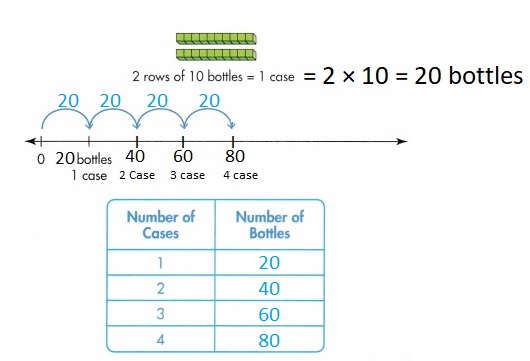
Explanation :
Number of bottles in 1 case = 1 jump of 20 is 20. 1 × 20 = 20
Number of bottles in 2 case = 2 jumps of 20 are 40. 2 × 20 = 40
Number of bottles in 3 case = 3 jumps of 20 are 60. 3 × 20 = 60
Number of bottles in 4 case = 4 jumps of 20 are 80. 4 × 20 = 80
Visual Learning Bridge
Glossary
Essential Question
How Can You Use Patterns to Multiply?
A.
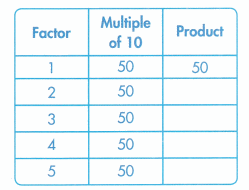
A half-century is a period of 50 years. Find the number of years in 5 half-centuries.

You can use place-value blocks or an open number line to multiply.
B.
One Way
Find 5 × 50. Use place-value blocks.

1 × 50 is 1 group of 5 tens = 5 tens or 50
2 × 50 is 2 groups of 5 tens = 10 tens or 100
3 × 50 is 3 groups of 5 tens = 15 tens or 150
4 × 50 is 4 groups of 5 tens = 20 tens or 200
5 × 50 is 5 groups of 5 tens = 25 tens or 250
You can skip count to find the number of years in 5 half-centuries.

There are 250 years in 5 half-centuries.
C.
Another Way
Find 5 × 50. Use an open number line.
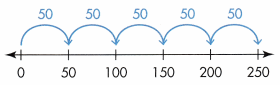
1 jump of 50 is 50. 1 × 50 = 50
2 jumps of 50 are 100. 2 × 50 = 100
3 jumps of 50 are 150. 3 × 50 = 150
4 jumps of 50 are 200. 4 × 50 = 200
5 jumps of 50 are 250. 5 × 50 = 250
There are place-value patterns when multiplying by multiples of 10.

There are 250 years in 5 half-centuries.
Convince Me! Use Structure Suppose the multiple of 10 in the table above was 40 years instead of 50. Explain how you can use place-value patterns to find each product.
Answer :
Find 5 × 50. Use place-value blocks.
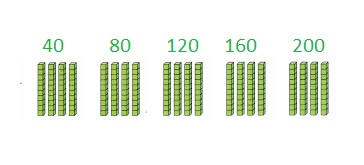
1 × 40 is 1 group of 4 tens = 4 tens or 40
2 × 40 is 2 groups of 4 tens = 80 tens or 80
3 × 40 is 3 groups of 4 tens = 12 tens or 120
4 × 40 is 4 groups of 4 tens = 16 tens or 160
5 × 40 is 5 groups of 4 tens = 20 tens or 200
There are 200 years in 5 half-centuries.
Guided Practice
Do You Understand?
Question 1.
Explain how to use place-value patterns to multiply 9 × 50.
Answer:
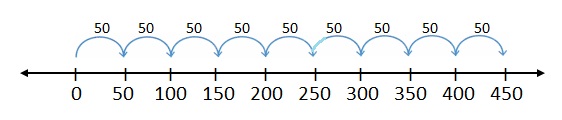
1 jump of 50 is 50. 1 × 50 = 50
2 jumps of 50 are 100. 2 × 50 = 100
3 jumps of 50 are 150. 3 × 50 = 150
4 jumps of 50 are 200. 4 × 50 = 200
5 jumps of 50 are 250. 5 × 50 = 250
6 jumps of 50 are 250. 6 × 50 = 300
7 jumps of 50 are 350. 7 × 50 = 350
8 jumps of 50 are 400. 8 × 50 = 400
9 jumps of 50 are 450. 9 × 50 = 450
There are place-value patterns when multiplying by multiples of 10.
Question 2.
How are the products in Box B on the previous page like skip counting by 5?
Answer:
Do You Know How?
Question 3.
Draw or use place-value blocks to show 3 × 60. Then find the product.
Answer:

1 × 60 is 1 group of 6 tens = 6 tens or 60
2 × 60 is 2 groups of 6 tens = 12 tens or 120
3 × 60 is 3 groups of 6 tens = 18 tens or 180
This are place value blocks of 3 × 60 = 180 .
Question 4.
Use the open number line to multiply 4 × 60.

Answer:
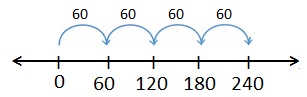
1 jump of 60 is 60. 1 × 60 = 60
2 jumps of 60 are 120. 2 × 60 = 120
3 jumps of 60 are 180. 3 × 60 = 180
4 jumps of 60 are 240. 4 × 60 = 240
Independent Practice
Leveled Practice In 5-10, use an open number line or draw place-value blocks to find each product.
Question 5.
3 × 70

Answer:
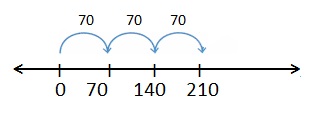
1 jump of 70 is 70. 1 × 70 = 70
2 jumps of 70 are 140. 2 × 70 = 140
3 jumps of 70 are 210. 3 × 70 = 210
4 jumps of 70 are 280. 4 × 70 = 280
Question 6.
8 × 20

Answer:

1 × 20 is 1 group of 2 tens = 2 tens or 20
2 × 20 is 2 groups of 2 tens = 4 tens or 40
3 × 20 is 3 groups of 2 tens = 6 tens or 60
4 × 20 is 4 groups of 2 tens = 8 tens or 80
5 × 20 is 5 groups of 2 tens = 10 tens or 100
6 × 20 is 6 groups of 2 tens = 12 tens or 120
7 × 20 is 7 groups of 2 tens = 14 tens or 140
8 × 20 is 8 groups of 2 tens = 16 tens or 160
This are place value blocks of 8 × 20 = 160 .
Question 7.
9 × 30
Answer:
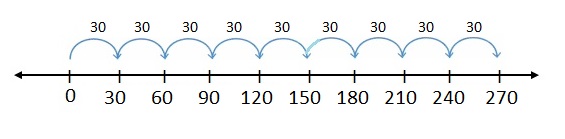
1 jump of 30 is 30. 1 × 30 = 30
2 jumps of 30 are 90. 2 × 30 = 90
3 jumps of 30 are 120. 3 × 30 = 120
4 jumps of 30 are 120. 4 × 30 = 120
5 jumps of 30 are 150. 5 × 30 = 150
6 jumps of 30 are 180. 6 × 30 = 180
7 jumps of 30 are 210. 7 × 30 = 210
8 jumps of 30 are 240. 8 × 30 = 240
9 jumps of 30 are 270. 9 × 30 = 270
There are place-value patterns when multiplying by multiples of 10.
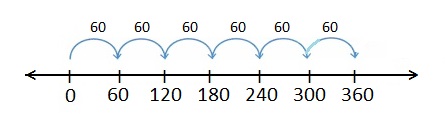
Question 8.
5 × 60
Answer:
1 jump of 60 is 60. 1 × 60 = 60
2 jumps of 60 are 120. 2 × 60 = 120
3 jumps of 60 are 180. 3 × 60 = 180
4 jumps of 60 are 240. 4 × 60 = 240
5 jumps of 60 are 300. 5 × 60 = 300
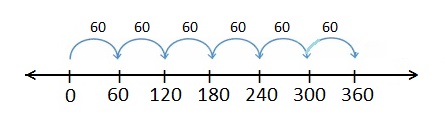
Question 9.
6 × 60
Answer:
1 jump of 60 is 60. 1 × 60 = 60
2 jumps of 60 are 120. 2 × 60 = 120
3 jumps of 60 are 180. 3 × 60 = 180
4 jumps of 60 are 240. 4 × 60 = 240
5 jumps of 60 are 300. 5 × 60 = 300
6 jumps of 60 are 360. 6 × 60 = 360
Question 10.
2 × 30
Answer:
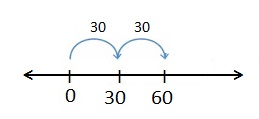
1 jump of 30 is 30. 1 × 30 = 30
2 jumps of 30 are 90. 2 × 30 = 60
There are place-value patterns when multiplying by multiples of 10.
Problem Solving
Question 11.
The Aztecs had a solar calendar. How many days are in 7 of the longer months in all? Show how to use place value to solve.

Answer:
Question 12.
Higher Order Thinking On one open number line, show 4 × 30. On the other open number line, show 3 × 40. How are the problems alike? How are they different?

Answer:

1 jump of 30 is 30. 1 × 30 = 30
2 jumps of 30 are 90. 2 × 30 = 60
3 jump of 30 is 30. 3 × 30 = 90
4 jumps of 30 are 120. 4 × 30 = 120 .
1 jump of 40 is 40. 1 × 40 = 40
2 jumps of 40 are 80. 2 × 40 = 80
3 jumps of 40 are 120. 3 × 40 = 120
jump of both number lines are different but the product is same .
Question 13.
Reasoning Martina has $504. She spends $199 on new computer software. Use mental math to find how much money Martina has left.
Answer:
Total Money with Martina = $504 .
Cost of New computer software = $199 .
Money left with Martina = $504 – $199 = 500 + 4 – (200 – 1) = 300 + 5 = 305$ .
Question 14.
Use place-value blocks to find 1 × 40, 2 × 40,3 × 40, and 4 × 40. What is the same in each of the products you listed?
Answer:
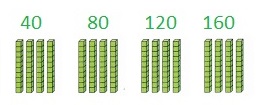
1 × 40 is 1 group of 4 tens = 4 tens or 40
2 × 40 is 2 groups of 4 tens = 80 tens or 80
3 × 40 is 3 groups of 4 tens = 12 tens or 120
4 × 40 is 4 groups of 4 tens = 16 tens or 160
All products end with 0 and all are even numbers .
Question 15.
A package of crepe paper streamers has 2 rolls. Yen bought 3 packages. How many inches of crepe paper did Yen get?
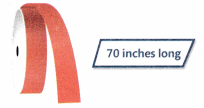
Answer:
Number of rolls in each package = 2
Number of packages = 3
Number of inches of crepe paper in 3 = 3 × 2 = 6 rolls .
Assessment Practice
Question 16.
Select all the expressions that have a product of 300.
![]() 3 × 10
3 × 10
![]() 5 × 60
5 × 60
![]() 5 × 600
5 × 600
![]() 6 × 50
6 × 50
![]() 6 × 500
6 × 500
Answer:

Explanation :
3 × 10 = 30
5 × 60 = 300
5 × 600 = 3000
6 × 50 = 300
6 × 500 = 3000
Question 17.
Select all the expressions that have a product of 240.
![]() 3 × 80
3 × 80
![]() 4 × 60
4 × 60
![]() 6 × 40
6 × 40
![]() 8 × 30
8 × 30
![]() 9 × 30
9 × 30
Answer:

Explanation :
3 × 80 = 240
4 × 60 = 240
6 × 40 = 240
8 × 30 = 240
9 × 30 = 270
Lesson 10.2 Use Mental Math to Multiply
Activity
Solve & Share
Find the products of 4 × 50, 3 × 40, and 9 × 20. Describe the patterns you find.
You can look for relationships. Think about how place-value patterns can help you solve the problems.

Look Back! How can you use place value to describe the patterns in the products?
Answer :
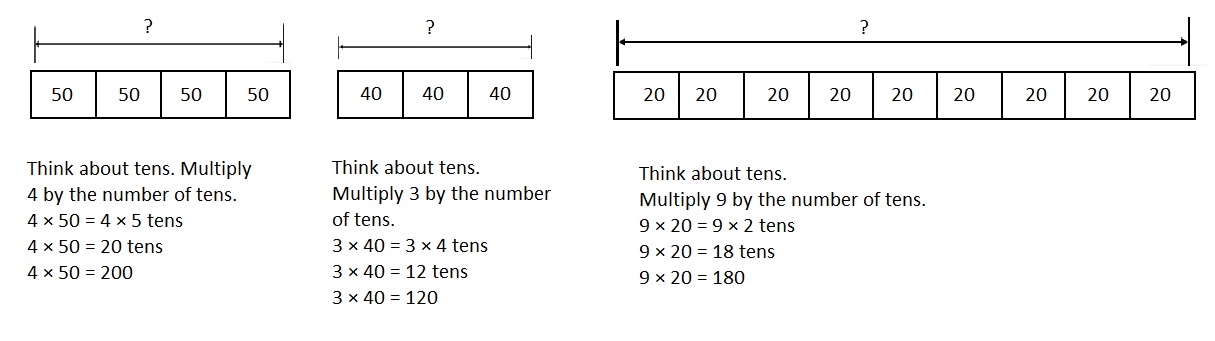
Visual Learning Bridge
Essential Question
How Can Place Value Help You Use Mental Math to Multiply by a Multiple of 10?
A.
A regular box of crayons has 30 crayons. A jumbo box holds 60 crayons. There are 5 boxes of regular crayons on one shelf and 5 boxes of jumbo crayons on another shelf. How many crayons are on each shelf?

You can use basic multiplication facts to multiply by multiples of 10.

B.
Find 5 × 30.
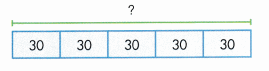
Think about tens. Multiply 5 by the number of tens.
5 × 30 = 5 × 3 tens
5 × 30 = 15 tens
5 × 30 = 150
There are 150 crayons on one shelf.
C.
Find 5 × 60.
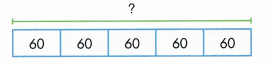
Sometimes the basic multiplication fact makes the product look different.
5 × 60 = 5 × 6 tens
5 × 60 = 30 tens
5 × 60 = 300
There are 300 crayons on the other shelf.
Convince Me! Make Sense and Persevere Suppose there are 50 crayons in each of the 5 boxes. Use mental math to find 5 × 50. How many crayons are in 5 boxes?
Answer :
Number of crayons in each box = 50
Number of boxes = 5
Number of crayons in 5 boxes = 5 × 50
5 × 50 = 5 × 5 tens
5 × 50 = 25 tens
5 × 50 = 250 crayons.
Therefore, Number of crayons in 5 boxes = 250 crayons .
Guided Practice
Do You Understand?
Question 1.
How can you find the product of 9 × 80? explain.
Answer:

Question 2.
Jon says, “4 × 6 is 4 groups of 6 ones. 4 times 6 equals 24.”
Complete the sentences to describe 4 × 60 in a similar way.
4 × 60 is 4 groups of 6 ___
4 times 60 equals ___
Answer:
4 × 60 is 4 groups of 6 = 4 × 6 = 24 .
4 times 60 equals = 4 × 60 = 240 .
Do You Know How?
In 3-8, complete each equation.
Question 3.
6 × 6 = ___
6 × 60 = ___
Answer:
6 × 6 = 36
6 × 60 =36 tens = 360 .
Question 4.
3 × 2 = ___
3 × 20 = ___
Answer:
3 × 2 = 6
3 × 20 = 60 = 6 tens
Question 5.
5 × 4 = ___
5 × 40 = ___
Answer:
5 × 4 = 20
5 × 40 = 20 tens = 200 .
Question 6.
8 × 2 = ___
80 × 2 = ___
Answer:
8 × 2 = 16
80 × 2 = 16 tens = 160 .
Question 7.
4 × 9 = ___
40 × 9 = ___
Answer:
4 × 9 = 36
40 × 9 = 36 tens = 360 .
Question 8.
7 × 8 = ___
70 × 8 = ___
Answer:
7 × 8 = 56
70 × 8 =56 tens = 560 .
Independent Practice
Leveled Practice In 9-19, complete each equation.
Question 9.
6 × 70 = (6 × __ ) tens
6 × 70 = __ tens
6 × 70 = __
Answer:
6 × 70 = (6 × 7 ) tens
6 × 70 = 42 tens
6 × 70 = 420
Question 10.
9 × 50 = (9 × __) tens
9 × 50 = __ tens
9 × 50 = ___
Answer:
9 × 50 = (9 × 5 ) tens
9 × 50 = 45 tens
9 × 50 = 450
Question 11.
2 × 6 = ___
2 × 60 = __
Answer:
2 × 6 = 12
2 × 60 = 12 tens
2 × 60 = 120
Question 12.
5 × 8 = ___
5 × 80 = __
Answer:
5 × 8 = 40
5 × 80 = 40 tens
5 × 80 = 400
Question 13.
9 × 4 = ___
9 × 40 = ___
Answer:
9 × 4 = 36
9 × 40 = 36 tens
9 × 40 = 360
Question 14.
2 × 30 = ___
Answer:
2 × 3 = 6
2 × 30 = 6 tens
2 × 30 = 60
Question 15.
60 × 9 = ___
Answer:
6 × 9 = 54
60 × 9 = 54 tens
60 × 9 = 540
Question 16.
___ = 8 × 20
Answer:
8 × 2 = 16
8 × 20 = 16 tens
8 × 20 = 160
Question 17.
80 × 5 = ___
Answer:
8 × 5 = 40
80 × 5 = 40 tens
80 × 5 = 400
Question 18.
___ = 90 × 2
Answer:
9 × 2 = 18
90 × 2 = 18 tens
90 × 2 = 180
Question 19.
30 × 4 = ___
Answer:
3 × 4 = 12
30 × 4 = 12 tens
30 × 4 = 120 .
Problem Solving
Question 20.
The horse conch can reach a length of 24 inches. Use multiplication to write 2 different equations that represent the conch’s length.

Answer:
Length of the horse conch = 24 inches .
The two different equations that represent length of horse conch =
24 = 6 × 4
24 = 3 × 8
Question 21.
Model with Math Juanita buys 7 sheets of postage stamps at the post office. Each sheet has 20 stamps. How many stamps does she buy in all? Explain how you solved the problem. Tell why you chose that method.
Answer:
Number of sheets of postage stamps = 7
Number of postage stamps for each sheet = 20 .
Number of postage stamps for 7 sheets = 7 × 20
7 × 2 = 14
7 × 20 = 4 tens
7 × 20 = 140 .
Therefore, Number of postage stamps for 7 sheets = 140 stamps .
This method is chosen because where 7 × 2 = 14 is the simply calculation steps are used to calculate the products .
Question 22.
Algebra What value makes the equation below true?
9 × ? = 630
Answer:
9 × ? = 630
9 × ? = 63 Tens
9 × 7 = 63
9 × 70 = 630
Question 23.
Janet bought 137 green beads. Now she has 349 beads. How many beads did Janet have before?
Answer:
Number of green beads = 137 .
Number of beads now = 349 .
Number of beads Janet have before = 349 – 137 = 212 beads .
Therefore, Number of beads Janet have before = 212 beads
Question 24.
Higher Order Thinking Ali and his family are going to the amusement park. If there are 2 adults and 5 children, how much will the tickets cost?

Answer:
Ticket cost for adult = $30 .
Number of Adults = 2
Tickets cost for adults = 2 × $30 = $60 .
Ticket cost for child = $20 .
Number of children = 5
Tickets cost for children’s = 5 × $20 = $100 .
Total Tickets cost = $60 + $ 100 = $160 .
Assessment Practice
Question 25.
Mr. Ridley owns a clothing store. The table at the right shows the number of racks and the number of pieces of clothing on each rack. Match each equation with its product to find the number of pieces of each type of clothing that are on the racks.
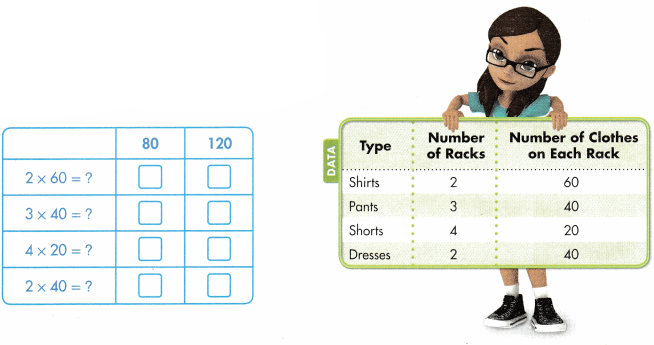
Answer:

2 × 60 = 120 .
3 × 40 = 120 .
4 × 20 = 80 .
2 × 40 = 80 .
Lesson 10.3 Use Properties to Multiply
Activity
Solve & Share
Three students found 5 × 30 in different ways. Which student is correct? Explain.

Properties can help you critique reasoning.

Look Back! What property of multiplication did Earl use in his reasoning?
Answer :
Property used is Associative property
Associative property :
For all real numbers a, b and c .
(a⋅b)⋅c=a⋅(b⋅c)
When you multiply any three real numbers, the grouping (or association) of the numbers does not change the result.
Visual Learning Bridge
Essential Question
How Can You Use Properties to Multiply by Multiples of 10?
A.
How can you find the product of 4 × 20?
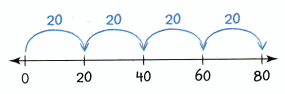
Remember the 10s facts pattern. Think about the product of a number and 10. The product has a zero in the ones place. The other factor is written to the left of the zero.

You know how to use an open number line to model multiplication.
You can use properties to explain a rule for finding a product when one factor is a multiple of 10.
B.
One Way
You can use the Associative Property of Multiplication to group the factors.

Think of 20 as 2 × 10
4 × 20 = 4 × (2 × 10)
4 × 20 = (4 × 2) × 10
4 × 20 = 8 × 10
4 × 20 = 80
C.
Another Way
You can use the Distributive Property to decompose a factor.
4 × 20 = (2 + 2) × 20
4 × 20 = (2 × 20) + (2 × 20)
4 × 20 = 40 + 40
4 × 20 = 80
Convince Me! Be Precise Use properties of multiplication to explain why 3 × 60 = 18 × 10.
Answer :
3 × 60 =
You can use the Associative Property of Multiplication to group the factors.
Think of 60 as 6 × 10
3 × 60 = 3 × (6 × 10)
3 × 60 = (3 × 6) × 10
3 × 60 = 18 × 10
3 × 60 = 180
3 × 60 = 18 × 10 = 180 .
Guided Practice
Do You Understand?
Question 1.
Why can you say that 3 × 20 = (2 × 20) + 20?
Answer:
Yes, 3 × 20 = (2 × 20) + 20 because
3 × 20 = 20 + 20 + 20 = (2 × 20 )+ 20 .
Question 2.
Why can you say that 3 × 20 = (3 × 2) × 10?
Answer:
3 × 20 =
You can use the Distributive Property to decompose a factor.
20 = 2 × 10
so , 3 × 20 = (3 × 2) × 10 = 6 × 10 = 60 .
Do You Know How?
In 3 and 4, find each product using properties of multiplication.
Question 3.
9 × 60 = 9 × (__ × 10)
9 × 60 = (9 × __) × 10
9 × 60 = ___ × 10 = ___
Answer:
You can use the Associative Property of Multiplication to group the factors.
9 × 60 = 9 × ( 6 × 10)
9 × 60 = (9 × 6) × 10
9 × 60 = 54 × 10 = 540
Question 4.
4 × 90 = (___ + 2) × 90
4 × 90 = (__ × 90) + ( ___ × 90)
4 × 90 = ___ + __ = ___
Answer:
You can use the Distributive Property to decompose a factor.
4 × 90 = (2 + 2) × 90
4 × 90 = (2 × 90) + ( 2 × 90)
4 × 90 = 180 + 180 = 360 .
Independent Practice
Leveled Practice In 5-12, show how to find each product using properties of multiplication.
Question 5.
7 × 60 = 7 × (___ × 10)
7 × 60 = (7 × __ ) × 10
7 × 60 = __ × 10 = ___
Answer:
You can use the Associative Property of Multiplication to group the factors
7 × 60 = 7 × ( 6 × 10)
7 × 60 = (7 × 6 ) × 10
7 × 60 = 42 × 10 = 420
Question 6.
5 × 40 = __ × (__ × 10)
5 × 40 = (__ × __) × 10
5 × 40 = ___ × ___ = __
Answer:
You can use the Associative Property of Multiplication to group the factors
5 × 40 = 5 × ( 4 × 10)
5 × 40 = (5 × 4) × 10
5 × 40 = 20 × 10 = 200
Question 7.
8 × 30
Answer:
8 × 30 = 8 × ( 3 × 10)
8 × 30 = (8 × 3) × 10
8 × 30 = 24 × 10 = 240
Question 8.
4 × 70
Answer:
You can use the Distributive Property to decompose a factor.
4 × 70 = (2 + 2) × 70
4 × 70 = (2 × 70) + ( 2 × 70)
4 × 70 = 140 + 140 = 280 .
Question 9.
5 × 90
Answer:
You can use the Associative Property of Multiplication to group the factors
5 × 90 = 5 × ( 9 × 10)
5 × 90 = (5 × 9) × 10
5 × 90 = 45 × 10 = 450
Question 10.
8 × 80
Answer:
You can use the Distributive Property to decompose a factor.
8 × 80 = (4 + 4) × 80
8 × 80 = (4 × 80) + ( 4 × 80)
8 × 80 = 320 + 320 = 640 .
Question 11.
6 × 40
Answer:
You can use the Associative Property of Multiplication to group the factors
6 × 40 = 6 × ( 4 × 10)
6 × 40 = (6 × 4) × 10
6 × 40 = 24 × 10 = 240 .
Question 12.
9 × 80
Answer:
You can use the Associative Property of Multiplication to group the factors
9 × 80 = 9 × ( 8 × 10)
9 × 80 = (9 × 8) × 10
9 × 80 = 72 × 10 = 720 .
Problem Solving
Question 13.
Look at the picture graph at the right. How many pounds of newspaper did Grade 3 collect?

Answer:
Each rectangle represents 30 pounds .
Number of pounds of newspaper in Grade 3 = 4 rectangles = 4 × 30 = 120 pounds .
Question 14.
How many pounds of newspaper did Grade 3 and Grade 4 collect together? Explain your plan for solving.
Answer:
Each rectangle represents 30 pounds .
Number of pounds of newspaper in Grade 3 = 4 rectangles = 4 × 30 = 120 pounds .
Number of pounds of newspaper in Grade 4 = 3 rectangles = 3 × 30 = 90 pounds .
Total pounds of newspaper did Grade 3 and Grade 4 collect together = 120 + 90 = 210 pounds .
Question 15.
Higher Order Thinking Grade 5 collected 150 pounds of newspaper. How many more symbols would be in the row for Grade 5 than for Grade 2?
Answer:
Number of pounds of newspapers Grade 5 collected = 150 pounds .
Each rectangle represents 30 pounds .
Number of rectangles symbol in grade 5 = 150 pounds ÷ 30 = 5 rectangles .
Number of rectangles in grade 2 = 2 rectangles.
Number of more symbols would be in the row for Grade 5 than for Grade 2 = 5 – 2 = 3 more symbols .
Question 16.
Generalize Without finding the products, how can you tell whether 4 × 60 or 7 × 40 is greater?
Answer:
4 × 60 or 7 × 40 is greater 7 × 40 .
4 × 60 = 4 × 6 × 10 .
7 × 40 = 4 × 7 × 10 .
we notice 4 × 10 is common so, greater than number greater the product. we notice 7 is greater than 6 so , 7 × 40 = 280 is greater than 4 × 60
Question 17.
Explain how to use mental math to add 521 + 104.
Answer:
521 + 104 = 625 .
add ones values numbers 1 + 4 = 5 .
add tens value numbers = 2 + 0 = 2
Add hundred value numbers = 5 + 1 = 6
so, the sum = 625 .
Question 18.
Tikie said that it is easy to count by 50s. Explain how she could use counting by 50s to find 5 × 60.
You can use properties and equations to help construct an argument!

Answer:
You can use the Associative Property of Multiplication to group the factors
5 × 60 = 5 × ( 6 × 10)
5 × 60 = (5 × 6) × 10
5 × 60 = 30 × 10 = 300 .
Assessment Practice
Question 19.
Which products are equal to 180? Select all that apply.
![]() 1 × 80
1 × 80
![]() 6× (3 × 10)
6× (3 × 10)
![]() 6× 30
6× 30
![]() 3 × (6 × 10)
3 × (6 × 10)
![]() 3 × 60
3 × 60
Answer:
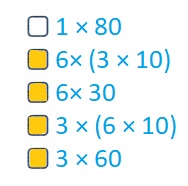
Explanation :
1 × 80 =80
6× (3 × 10) = 180
6× 30 = 180
3 × (6 × 10) = 180
3 × 60 = 180
Question 20.
Which products are equal to 200? Select all that apply.
![]() 2 × 10
2 × 10
![]() 5 × (4 × 10)
5 × (4 × 10)
![]() 5 × 40
5 × 40
![]() 2 × (1 × 10)
2 × (1 × 10)
![]() 4 × 50
4 × 50
Answer:
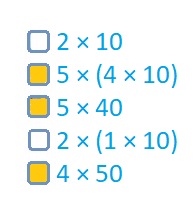
Explanation :
2 × 10 = 20
5 × (4 × 10) = 200
5 × 40 = 200
2 × (1 × 10) = 20
4 × 50 = 200
Lesson 10.4 Look For and Use Structure
Problem Solving
Activity
Solve & Share
Stefan says that he could use this multiplication table to help multiply 3 × 40 to get 120. Explain Stefan’s strategy.
Thinking Habits
Be a good thinker! These questions can help you.
• What patterns can I see and describe?
• How can I use the patterns to solve the problem?
• Can I see expressions and objects in different ways?

Answer :
3 × 40 = 120 .
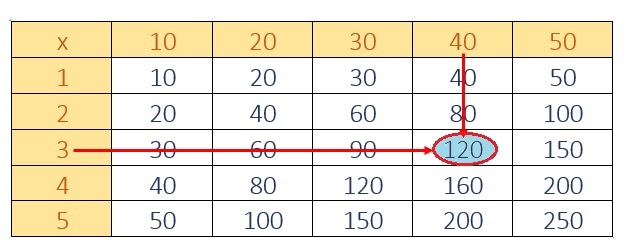
Explanation :
Reading a multiplication chart
Step 1: Choose the first number 3 from the numbers listed in the left-most column and the second number 40 from the top-most row.
Step 2: Starting from the first number 3 move towards the right and starting from the second number 40 move towards down. The square where the two numbers meet gives the product 120 !
The multiplication tables of 1, 2, 5, and 10 are easier to remember as they follow a pattern. The product of any number with 1 is the number itself whereas the product of any number with 2 is double the number. The ones digits of the multiplication table of 5 alternates between 0 and 5 and it is easy to remember the table of 10 as well because the digit at the ones place is always zero. These parts of the multiplication chart which are easy to remember are called lower times table.
One important property of multiplication is that the order in which you multiply any two numbers does not affect the product.
So, in a multiplication chart, for any product, you can find the identical number with the numbers reversed in the statement.
Look Back! Use Structure Could Stefan also use the multiplication table to solve 4 × 40 in the same way? explain how you decided.
Answer :
Yes, it is explained in the same way .
4 × 40 = 160 .

Explanation :
Reading a multiplication chart
Step 1: Choose the first number 4 from the numbers listed in the left-most column and the second number 40 from the top-most row.
Step 2: Starting from the first number 4 move towards the right and starting from the second number 40 move towards down. The square where the two numbers meet gives the product 160 !
Visual Learning Bridge
Essential Question
How Can I Use Structure to Multiply with Multiples of 10?
A.
Find the missing products in the multiplication table.
You can look for relationships in the multiplication table.

B.
How can I make use of structure to solve this problem?
I can
• look for patterns to help solve a problem.
• describe the patterns that i find.
• identify how numbers are organized.
C.
Here’s my thinking

As I move down the columns, the numbers increase by the value of the column.
As I move across the rows, the numbers increase by the value in the column where 10 is a factor.
I used patterns I know for multiplying by multiples of 10.
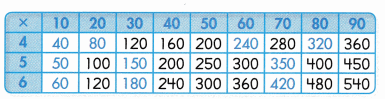
Convince Me! Use Structure The ones digit never changes in the products in the multiplication table above. Explain why.
Guided Practice
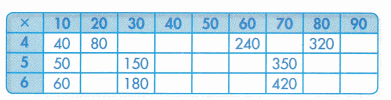
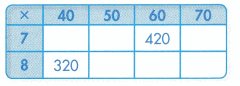
Use Structure Sean is making muffins. He is choosing to make either 7 or 8 batches. He is also choosing whether to use 40, 50, 60, or 70 raisins for each batch. Sean starts this table to show the total number of raisins he will need for each choice.
You can use the structure of the products and factors to find a pattern.

Question 1.
Find the missing products in the table to show how many raisins Sean will use for each batch. Think about patterns or properties you know.
Answer:
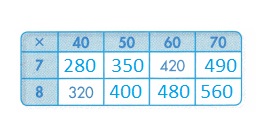
Explanation :
As I move down the columns, the numbers increase by the value of the column that is 40, 50, 60 and 70 respectively .
As I move across the rows, the numbers increase by the value in the column where 10 is a factor.
Question 2.
Sean uses 480 raisins in total. How many batches does he make? How many raisins does he use for each batch?
Answer:
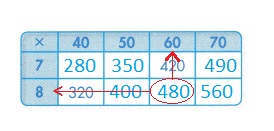
Explanation :
Total Raisins used = 480
The column represents the number of batches that is 8 .
The Row represents the number of raisins in each batch = 60 raisins.
8 × 60 = 480 .
Independent Practice
Use Structure
Jolene is making a display with equal rows of stickers. She is choosing whether to use 20, 30, 40, or 50 stickers in each row. She is also choosing whether to have 2, 3, or 4 rows. Jolene starts this table to show the total number of stickers she will need for each choice.
Question 3.
Find the missing products in the table to show how many stickers Jolene will need for each choice. Think about patterns or properties you know.

Answer:

Explanation :
As I move down the columns, the numbers increase by the value of the column that is 20, 30, 40 and 50 respectively .
As I move across the rows, the numbers increase by the value in the column where 10 is a factor.
Question 4.
Jolene uses 150 stickers in total. How many rows does she have in her display? How many stickers does she put in each row?
Answer:
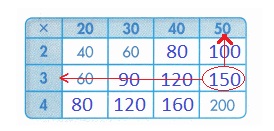
Explanation :
Number of stickers used = 150 .
Number of rows used represents the row value that is 3 .
Number of stickers in each row represents the column value that is 50 .
3 × 50 = 150 stickers .
Problem Solving
Performance Task
Music Lessons
Four students each took music lessons for different instruments this month. They want to know who spent the most money on music lessons.
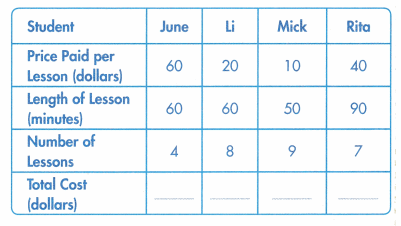
Question 5.
Make Sense and Persevere What do you need to do to solve the problem?
Answer:
To calculate the problem we need .
Price paid for 1 lesson and Number of lessons .
Total cost = Price paid for 1 lesson × Number of lessons .
June = 60 × 4 = 240 dollars
Li = 20 × 8 = 160 dollars .
Mick = 10 × 9 = 90 dollars .
Rita = 40 × 7 = 280 dollars
Question 6.
Use Structure How can you find the total amount for each student? Think about properties or patterns you know.
Answer:
Think about and look for relationships to help solve problems.

Answer :
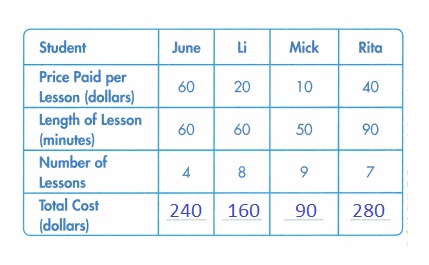
Explanation :
To calculate the problem we need .
Price paid for 1 lesson and Number of lessons .
Total cost = Price paid for 1 lesson × Number of lessons .
June = 60 × 4 = 240 dollars
Li = 20 × 8 = 160 dollars .
Mick = 10 × 9 = 90 dollars .
Rita = 40 × 7 = 280 dollars
Question 7.
Model with Math Use math you know to complete the table. Circle the name of the student who spent the greatest amount.
Answer:
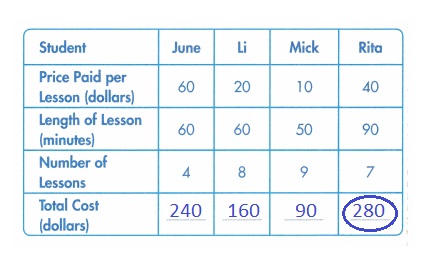
Explanation :
Total cost = Price paid for 1 lesson × Number of lessons .
June = 60 × 4 = 240 dollars
Li = 20 × 8 = 160 dollars .
Mick = 10 × 9 = 90 dollars .
Rita = 40 × 7 = 280 dollars
Among all Rita spends more money than all .
280 > 240 >160 > 90 .
Question 8.
Construct Arguments Did the student who spent the most per lesson also spend the greatest amount in total? explain why or why not.
Answer:
No, the student who spent the most per lesson did not spend the greatest amount in total because the student attends only 4 classes .
The Student spend the greatest amount in total attends 7 classes for 40 dollars for each class spends 280 dollars in total .
That means it depends on number of classes and cost of each class
Topic 10 Fluency Practice Activity
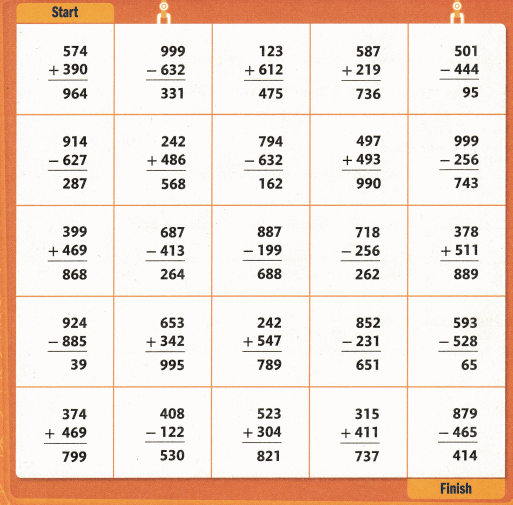
Shade a path from START to FINISH. Follow the sums or differences that are correct. You can only move up, down, right, or left.

Answer :

Topic 10 Vocabulary Review
Glossary
Understand Vocabulary
Word List
• Associative Property of Multiplication
• Distributive Property
• equal groups
• factor
• open number line
• product
• skip count
Question 1.
Skip count by 20s. Cross out any numbers that you do NOT say
when skip counting by 20s.
20 30 40 50 90
Answer:
Question 2.
Cross out any equations below in which 10 is NOT a factor.
3 × 10 = 30 10 = 5 × 2 50 = 10 × 5 10 × 0 = 0
Answer:
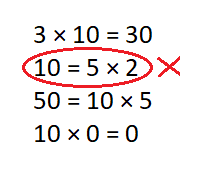
Explanation :
10 is the sum of factors 5 and 2 . so it doesn’t have 10 factor .
Question 3.
Cross out any equations below that do NOT show the Associative Property of Multiplication.
(4 × 6) × 7 = 4 (6 × 7) 4 × 3 = 3 × 4 0 = 2 × 0
Answer:
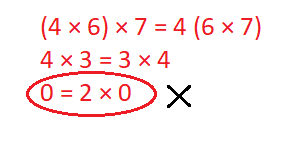
Explanation :
Associative property :
For all real numbers a, b and c .
(a⋅b)⋅c=a⋅(b⋅c)
When you multiply any three real numbers, the grouping (or association) of the numbers does not change the result.
Question 4.
Cross out any equations below in which 8 is NOT the product.
8 = 2 × 4 8 × 8 = 64 2 × (4 × 1) = 8 2 × 8 = 16
Answer:
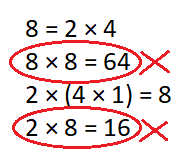
Write T for true or F for false.
____
Question 5.
An example of the Distributive Property is 6 × 0 = 0.
Answer:
False .
Explanation :
1.Simplify the numbers. In this example, 101 = 100 + 1, so . . . . . .
2.Split the problem into two easier problems. Take the number outside the parentheses, and multiply it by each number inside the parentheses, one at a time.
3.Add the products.
Question 6.
Equal groups have the same amount in each group.
Answer:
True.
Question 7.
An open number line is a plain line that can be used to help you multiply.
Answer:
True .
Explanation :
Multiplying on the number line works no matter what number you count off by.
For example, the number line in the following figure counts off by 5s. This time, the only numbers marked are the multiples of 5, so you can use this number line to multiply any number by 5.
Use Vocabulary in Writing
Question 8.
Use at least 2 terms from the Word List to explain how to solve 3 × 30.
Answer:
Distributive property
open number line .
Topic 10 Reteaching
Set A
pages 381-384
Find 5 × 70.
Show 5 jumps of 70 on the number line.

1 jump of 70 is 70. 1 × 70 = 70
2 jumps of 70 are 140. 2 × 70 = 140
3 jumps of 70 are 210. 3 × 70 = 210
4 jumps of 70 are 280. 4 × 70 = 280
5 jumps of 70 are 350. 5 × 70 = 350
There are place-value patterns when multiplying by 10.

Remember that you can skip count to show multiplication.
In 1-3, use an open number line to solve.
Question 1.
4 × 80

Answer:
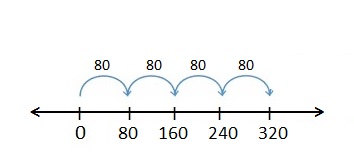
Explanation:
1 jump of 80 is 80. 1 × 80 = 80
2 jumps of 80 are 160. 2 × 80 = 160
3 jumps of 80 are 240. 3 × 80 = 240
4 jumps of 80 are 320. 4 × 80 = 320
There are place-value patterns when multiplying by 10.
Question 2.
7 × 20

Answer:
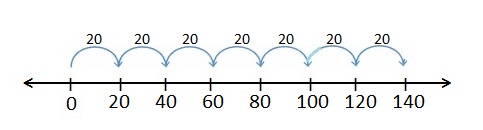
Explanation :
1 jump of 20 is 20. 1 × 20 = 20
2 jumps of 20 are 40. 2 × 20 = 40
3 jumps of 20 are 60. 3 × 20 = 60
4 jumps of 20 are 80. 4 × 20 = 80
5 jumps of 20 are 100. 5 × 20 = 100
6 jumps of 20 are 120. 5 × 20 = 120
7 jumps of 20 are 140. 5 × 20 = 140
There are place-value patterns when multiplying by 10.
Question 3.
3 × 50

Answer:
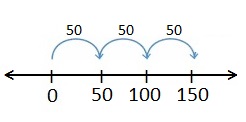
Explanation :
1 jump of 50 is 50. 1 × 50 = 50
2 jumps of 50 are 100. 2 × 50 = 100
3 jumps of 50 are 150. 3 × 50 = 150
here are place-value patterns when multiplying by 10.
Set B
pages 385-388
You can use basic multiplication facts to multiply by multiples of 10.
Find 6 × 30
Multiply the number of tens by 6.
6 × 30 = 6 × 3 tens
6 × 30 = 18 tens
6 × 30 = 180

Place-value patterns can help you learn a shortcut!
Remember to think about basic facts.
In 1-10, find each product.
Question 1.
3 × 30
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
3 × 30
Multiply the number of tens by 3.
3 × 30 = 3 × 3 tens
3 × 30 = 9 tens
3 × 30 = 90
Question 2.
50 × 9
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
9 × 50
Multiply the number of tens by 9.
9 × 50 = 9 × 5 tens
9 × 50 = 45 tens
9 × 50 = 450
Question 3.
6 × 60
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
6 × 60
Multiply the number of tens by 6.
6 × 60 = 6 × 6 tens
6 × 60 = 36 tens
6 × 60 = 360
Question 4.
5 × 80
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
5 × 80
Multiply the number of tens by 5.
5 × 80 = 5 × 8 tens
5 × 80 = 40 tens
5 × 80 = 400
Question 5.
8 × 40
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
8 × 40
Multiply the number of tens by 8.
8 × 40 = 8 × 4 tens
8 × 40 = 32 tens
8 × 40 = 320
Question 6.
80 × 7
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
7 × 80
Multiply the number of tens by 7.
7 × 80 = 7 × 8 tens
7 × 80 = 56 tens
7 × 80 = 560
Question 7.
70 × 4
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
4 × 70
Multiply the number of tens by 4.
4 × 70 = 4 × 7 tens
4 × 70 = 28 tens
4 × 70 = 280
Question 8.
8 × 30
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
8 × 30
Multiply the number of tens by 8.
8 × 30 = 8 × 3 tens
8 × 30 = 24 tens
8 × 30 = 240
Question 9.
7 × 70
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
7 × 70
Multiply the number of tens by 7.
7 × 70 = 7 × 7 tens
7 × 70 = 49 tens
7 × 70 = 490
Question 10.
60 × 5
Answer:
You can use basic multiplication facts to multiply by multiples of 10.
5 × 60
Multiply the number of tens by 5.
5 × 60 = 5 × 6 tens
5 × 60 = 30 tens
5 × 60 = 300
Set C
pages 389-392
Find 7 × 80.
Think of 80 as 8 × 10. Then use the Associative Property of Multiplication.
7 × 80 = 7 × (8 × 10)
7 × 80 = (7 × 8) × 10)
7 × 80 = 56 × 10
7 × 80 = 560
You can use properties of operations, such as the Associative Property and the Distributive Property, to help multiply.

Remember that the Associative Property of Multiplication lets you regroup factors. In 1 and 2, find the product using properties.
Question 1.
5 × 80 = 5 × (__× 10)
5 × 80 = (5 × __ ) × 10
5 × 80 = __ × 10 = __
Answer:
Write 80 as 8 × 10. Then use the Associative Property of Multiplication.
5 × 80 = 5 × ( 8 × 10)
5 × 80 = (5 × 8 ) × 10
5 × 80 = 40 × 10 = 400
Question 2.
7 × 40 = ___ × (__× 10)
7 × 40 = (__ × __) × 10
7 × 40 = ___ × 10 = ___
Answer :
Write 40 as 4 × 10. Then use the Associative Property of Multiplication.
7 × 40 = 7 × ( 4 × 10)
7 × 40 = ( 7 × 4 ) × 10
7 × 40 = 28 × 10 = 280
Set D
pages 393-396
Think about these questions to help you make use of structure.
Thinking Habits
• What patterns can I see and describe?
• How can I use the patterns to solve the problem?
• Can I see expressions and objects in different ways?

Remember to use patterns or properties to multiply by multiples of 10.
Christy is making a savings plan. She wants to know how much she will save if she saves $40 for 6, 7, 8, or 9 weeks.
Question 1.
How can you use patterns to help solve this problem?
Answer:
As I move down the columns, the numbers increase by the value of the column.
As I move across the rows, the numbers increase by the value in the column where 10 is a factor.
I used patterns I know for multiplying by multiples of 10.
Question 2.
Find the total amount Christy would save after 6, 7, 8, or 9 weeks. Think about patterns or properties you know.
Answer:
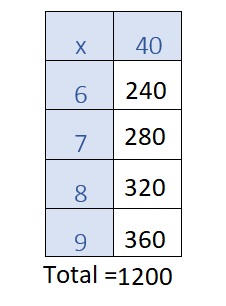
As I move down the columns, the numbers increase by the value of the column.
As I move across the rows, the numbers increase by the value in the column where 10 is a factor.
I used patterns I know for multiplying by multiples of 10.
Topic 10 Assessment Practice
Question 1.
Julia gives each of her 4 friends a sheet of stickers. Each sheet has 20 stickers. How many stickers do her friends have in all?
Answer:
Number of friends = 4
Number of stickers = 20 .
Number of stickers with each friend = 20 ÷ 4 = 5 stickers .
Question 2.
Select all of the expressions equal to 8 × 60.
![]() 48 × 10
48 × 10
![]() 6 × 80
6 × 80
![]() (8 × 6) × 10
(8 × 6) × 10
![]() 8 × (8 × 10)
8 × (8 × 10)
![]() 60 × 80
60 × 80
Answer:
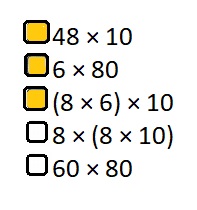
Explanation :
48 × 10 = 480
6 × 80 = 480
(8 × 6) × 10 = 480
8 × (8 × 10) = 640
60 × 80 = 4800
Question 3.
Mrs. Rode bought 80 packs of juice boxes for her school’s party. The juice boxes came in packs of 8. How many juice boxes did Mrs. Rode buy? explain how to solve.
Answer:
Number of juice boxes = 80 packs.
Number of packs = 8 .
Total Number of juices = 8 × 80
Write 80 as 8 × 10. Then use the Associative Property of Multiplication.
8 × 80 = 8 × ( 8 × 10)
8 × 80 = (8 × 8 ) × 10
8 × 80 = 64 × 10 = 640 Juices .
Question 4.
The third-grade teachers at Jenny’s school need 5 boxes of yellow folders and 4 boxes of red folders. Each box has 40 folders. How many folders do the teachers need?
A. 160
B. 320
C. 200
D. 360
Answer:
Option D – 360 folders
Explanation :
Number of Yellow folders = 5 boxes .
Number of Red folders = 4 boxes .
Number of folders in each box = 40 folders .
Total Folders Teacher needs = ( 5 × 40 ) + ( 4 × 40 ) = ( 5 + 4 ) 40 = 9 × 40 = 360 folders
Question 5..
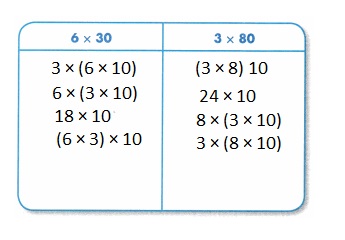
Write each expression in the correct answer space to show expressions equal to 6 × 30 and 3 × 80.
(3 × 8) 10
3 × (6 × 10)
24 × 10
8 × (3 × 10)
6 × (3 × 10)
18 × 10
3 × (8 × 10)
(6 × 3) × 10
Answer:
Question 6.
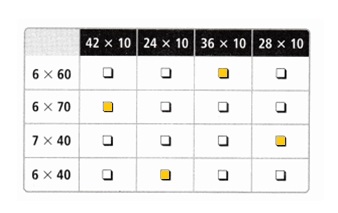
Match each expression on the left to an equal expression.
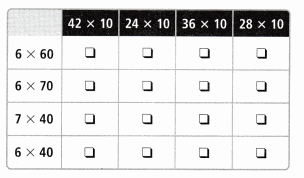
Answer:
Question 7.
What is 4 × 30?
A. 22
B. 34
C. 120
D. 160
Answer:
Option C – 120
Explanation :
4 × 30
Write 80 as 8 × 10. Then use the Associative Property of Multiplication.
4 × 30 = 4 × ( 3 × 10)
4 × 30 = (4 × 3 ) × 10
4 × 30 = 12 × 10 = 120
Question 8.
Tyler does 40 pushups each day. How many pushups does he do in 5 days?
Answer:
Number of pushups done in each day = 40
Number of days = 5
Number of pushups done in 5 days = 5 × 40 = 200 pushups.
Question 9.
The family membership to a children’s museum is $90 for a year. On Friday 5 families bought memberships. How much did the museum receive for the new memberships?
Answer:
Cost of Family membership = $90 for a year
Cost of 5 Families membership = 5 × 90 = 450 $ .
Therefore, the museum receive for the new memberships is 450 $ .
Question 10.
Select all of the expressions that are equal to 7 × 50.
![]() 7 × (5 × 10)
7 × (5 × 10)
![]() 35 × 10
35 × 10
![]() 7 × 5
7 × 5
![]() 75 × 10
75 × 10
![]() (7 × 5) × 10
(7 × 5) × 10
Answer:

Explanation :
7 × (5 × 10) = 350
35 × 10 =350
7 × 5 = 35
75 × 10 =750
(7 × 5) × 10 = 350
Question 11.
Tyrone drives 30 miles every day. How many miles does Tyrone drive in 7 days?
A. Use a number line to solve the problem.
B. Describe another way to solve the problem.
Answer:
Number of miles Tyrone every day = 30 miles .
Number of days Tyrone drives = 7 days.
Number of miles Tyrone drive for 7 days = 7 × 30 = 210 miles .
A .
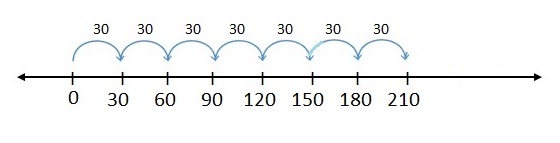
B.
Write 30 as 3 × 10. Then use the Associative Property of Multiplication.
7 × 30 = 7 × ( 3 × 10)
7 × 30 = (7 × 3 ) × 10
7 × 30 = 21 × 10 = 210 miles.
Topic 10 Performance Task
Pet Adoption
Carson and Adriana volunteer at a local animal rescue center. The adoption fee is different based on the animal and its age.
Carson made an Adoption Fee graph to show the fees for adult dogs, puppies, adult cats, and kittens. Adriana recorded the number of each animal adopted during the summer in the Animals Adopted table.
Use the Adoption Fee graph and the Animals Adopted table to answer Questions 1-3.
Question 1.
Carson wants to find the total adoption fees the rescue center received for adopted adult dogs. Show how Carson can use a number line to do this.
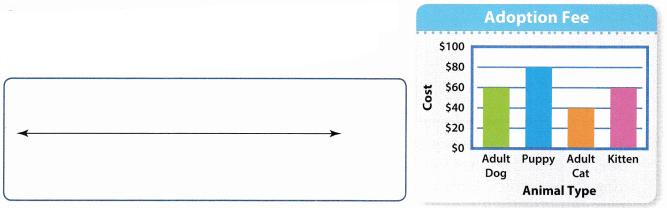
Answer:
Total Adoption fees the rescue center received for adopted adult dogs = $ 60 .
The cost is divided in increase of $20 .
It is represented on a number line is shown below .
Question 2.
Adriana says that she can use (4 × 8) × 10 to find the total adoption fees for adopted puppies. Is she correct? explain why or why not. Then find the total.

Answer:
Yes she is right .
Explanation :
Adoption fee for puppy = $80 .
Number of puppies adopted = 4
Total Fee for adopting puppies = 4 × 80 = 320$ .
Write 80 as 8 × 10. Then use the Associative Property of Multiplication.
4 × 80 = 4 × ( 8 × 10)
4 × 80 = (4 × 8 ) × 10
4 × 80 = 32 × 10 = 320$ .
Question 3.
Find the adoption fees the rescue center received for kittens. Think about patterns or properties you know. Show your work.
Answer:
Adoption fee for kittens = $60 .
Number of kittens adopted = 3
Total Fee for adopting kittens = 3 × 60 = 180$ .
Write 60 as 6 × 10. Then use the Associative Property of Multiplication.
3 × 60 = 3 × ( 6 × 10)
3 × 60 = (3 × 6 ) × 10
3 × 60 = 18 × 10 = 180$ .
Therefore, the adoption fees the rescue center received for kittens = 180$
The animal rescue center sells toy packages for pets.
The Toy Packages graph shows the amount earned for different types of packages. The Toy Packages Sold table shows how many packages were sold in the summer.
Use the Toy Packages graph and the Toy Packages Sold table to answer Questions 4 and 5.

Question 4.
How much money did the animal rescue center earn from toys for large dogs? Show your work.

Answer:
Cost of toy packages of large dogs = $50
Number of packages sold = 5
Money earned for selling 5 large dogs packages = 5 × 50
Write 50 as 5 × 10. Then use the Associative Property of Multiplication.
5 × 50 = 5 × ( 5 × 10)
5 × 50 = (5 × 5 ) × 10
5 × 50 = 25 × 10 = 250$ .
Therefore, Money earned for selling 5 large dogs packages = $250 .
Question 5.
Carson says that the center earned more money selling toys for small dogs than from selling toys for large dogs. Is he correct? explain why or why not.
Use the Toy Packages graph to answer Question 6.
Answer:
No he is wrong , More money is received by selling Large dog packages than small dog packages .
Explanation :
Cost of toy packages of large dogs = $50
Number of packages sold = 5
Money earned for selling 5 large dogs packages = 5 × 50 = $250 .
Cost of toy packages of small dogs = $30
Number of packages sold = 7
Money earned for selling 7 small dogs packages = 7 × 30 = $210 .
$250 >$210
Question 6.
Adriana forgot to record the number of packages of cat toys that were sold. She knows that the center earned a total of $140 from the toys for cats. How many packages of cat toys did they sell?
Answer:
Total Money earned from toys of cats = $140 .
Cost of toy packages of cats = $20 .
Number of toy cats packages sold = 140 ÷ 20 = 7 packages .
Therefore, packages of cat toys sold = 7 packages .