Practice with the help of enVision Math Common Core Grade 5 Answer Key Topic 9 Apply Understanding of Division to Divide Fractions regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 9 Apply Understanding of Division to Divide Fractions

enVision STEM Project: Thermal Energy
Do Research Use the Internet or other sources to learn about thermal energy. Make a list of 3 ways you use thermal energy in your home and at school. Which use is most important to you? Why?
Journal: Write a Report Include what you found. Also in your report:
• Ask each member of your household 3 ways they use thermal energy. Organize your data in a table.
• Draw conclusions from your data. How does your household use thermal energy?
• Make up and solve problems with fraction division.
Review What You Know
A-Z Vocabulary
Choose the best term from the list at the right. Write it on the blank.
• common factor
• equivalent fractions
• estimate
• like denominators
• mixed number
• quotient
Question 1.
To find an approximate answer or solution is to ______
Answer:
To find an approximate answer or solution is to estimate
Question 2.
The fractions \(\frac{3}{4}\) and \(\frac{17}{4}\) are fractions with
Answer:
The fractions \(\frac{3}{4}\) and \(\frac{17}{4}\) are fractions with common factor.
Question 3.
The fractions that name the same amount are ______
Answer:
The fractions that name the same amount are equivalent fractions.
Question 4.
The answer to a division problem is the ______
Answer:
The answer to a division problem is the quotient.
Question 5.
A number that has a whole-number part and a fraction part is called a _____
Answer:
A number that has a whole-number part and a fraction part is called a mixed number.
Meaning of Fractions Each rectangle represents one whole. Write the shaded part of each rectangle as a fraction.
Question 6.
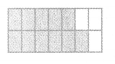
Answer:
The shaded part of each rectangle as a fraction is \(\frac{11}{7}\).
Explanation:
We can see that above rectangle shaded part is \(\frac{5}{7}\) and below rectangle shaded part is \(\frac{6}{7}\), so the total shaded part of each rectangle as a fraction is \(\frac{5}{7}\) + \(\frac{6}{7}\) which is \(\frac{11}{7}\).
Question 7.
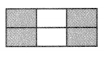
Answer:
The shaded part of each rectangle as a fraction is \(\frac{4}{3}\).
Explanation:
We can see that above rectangle shaded part is \(\frac{2}{3}\) and below rectangle shaded part is \(\frac{2}{3}\), so the total shaded part of each rectangle as a fraction is \(\frac{2}{3}\) + \(\frac{2}{3}\) which is \(\frac{4}{3}\).
Fraction Computation
Find each sum, difference, or product.
Question 8.
\(\frac{2}{5}\) + \(\frac{1}{4}\)
Answer:
\(\frac{2}{5}\) + \(\frac{1}{4}\) = \(\frac{13}{20}\).
Explanation:
The addition of \(\frac{2}{5}\) + \(\frac{1}{4}\)
= \(\frac{8+5}{20}\)
= \(\frac{13}{20}\).
Question 9.
\(\frac{5}{6}\) – \(\frac{1}{4}\)
Answer:
\(\frac{5}{6}\) – \(\frac{1}{4}\) = \(\frac{7}{12}\).
Explanation:
The subtraction of \(\frac{5}{6}\) – \(\frac{1}{4}\)
= \(\frac{10-3}{12}\)
= \(\frac{7}{12}\).
Question 10.
2\(\frac{5}{8}\) + 7\(\frac{1}{4}\) is 9\(\frac{7}{8}\).
Answer:
The addition of 2\(\frac{5}{8}\) + 7\(\frac{1}{4}\) is
Explanation:
The addition of 2\(\frac{5}{8}\) + 7\(\frac{1}{4}\) is
= \(\frac{21}{8}\) + \(\frac{29}{4}\)
= \(\frac{21+58}{8}\)
= \(\frac{79}{8}\)
= 9\(\frac{7}{8}\).
Question 11.
14 – 3\(\frac{5}{8}\)
Answer:
The subtraction of 14 – 3\(\frac{5}{8}\) is 10\(\frac{3}{8}\).
Explanation:
The subtraction of 14 – 3\(\frac{5}{8}\) is
= 14 – \(\frac{29}{8}\)
= \(\frac{112-29}{8}\)
= \(\frac{83}{8}\)
= 10\(\frac{3}{8}\).
Question 12.
3\(\frac{2}{3}\) + 4\(\frac{1}{2}\)
Answer:
The addition of 3\(\frac{2}{3}\) + 4\(\frac{1}{2}\) is 8\(\frac{1}{6}\).
Explanation:
The addition of 3\(\frac{2}{3}\) + 4\(\frac{1}{2}\) is
= \(\frac{11}{3}\) + \(\frac{9}{2}\)
= \(\frac{22+27}{6}\)
= \(\frac{49}{6}\)
= 8\(\frac{1}{6}\).
Question 13.
\(\frac{3}{8}\) × 2
Answer:
The multiplication of \(\frac{3}{8}\) × 2 is \(\frac{3}{4}\).
Explanation:
The multiplication of \(\frac{3}{8}\) × 2 is
= \(\frac{3}{4}\).
Question 14.
\(\frac{1}{4}\) × \(\frac{3}{5}\)
Answer:
The multiplication of \(\frac{1}{4}\) × \(\frac{3}{5}\) is \(\frac{3}{20}\).
Explanation:
The multiplication of \(\frac{1}{4}\) × \(\frac{3}{5}\) is
\(\frac{3}{20}\).
Question 15.
8 × \(\frac{9}{10}\)
Answer:
The multiplication of 8 × \(\frac{9}{10}\) is 7\(\frac{1}{5}\).
Explanation:
The multiplication of 8 × \(\frac{9}{10}\) is
= \(\frac{36}{5}\)
= 7\(\frac{1}{5}\).
Question 16.
3\(\frac{1}{2}\) × 2\(\frac{3}{5}\)
Answer:
The multiplication of 3\(\frac{1}{2}\) × 2\(\frac{3}{5}\) is 9\(\frac{1}{10}\).
Explanation:
The multiplication of 3\(\frac{1}{2}\) × 2\(\frac{3}{5}\) is
= \(\frac{7}{2}\) × \(\frac{13}{5}\)
= \(\frac{91}{10}\)
= 9\(\frac{1}{10}\).
Pick a Project
PROJECT 9A
Will your prototype make you rich and famous?
Project: Build a FractionDivision Prototype

PROJECT 9B
Why do so many math problems use pizza?
Project: Write a Skit About Pizza

PROJECT 9C
Would you like to improve your memory?
Project: Create a Mnemonic Device
3-ACT MATH PREVIEW
Math Modeling
Video
Slime Time

Before watching the video, think:
Slime is so much fun it makes me giggle. And the best part about slime is you can make it yourself with simple ingredients, including school glue.
Lesson 9.1 Fractions and Division
Solve & Share
Four people want waffles for breakfast. There are 6 waffles left. How can 6 waffles be shared equally among 4 people? How much does each person get? Draw a picture and write a division expression to model the problem.
You can use a circle to represent each whole waffle.

Answer:
Each person will get 1\(\frac{1}{2}\) waffle.
Explanation:
Given that four people want waffles for breakfast and there are 6 waffles left. So the number of waffles did each people get is 6 ÷ 4 which is 1\(\frac{1}{2}\).
Look Back! Construct Arguments One of the waffles was burnt. Explain how they can share 5 waffles equally.
Visual Learning Bridge
Essential Question
How Are Fractions Related to Division?
A.
Tom, Joe, and Sam each made a clay pot in his favorite color. They were given a total of two rolls of clay. If they shared the clay equally, how much clay did each friend use?

Divide 2 by 3 to find what fraction of the clay each person used.

B.
One Way
Think about sharing 2 rolls of clay equally among 3 people. Partition each roll into 3 equal parts. Each part is of \(\frac{1}{3}\) one roll.
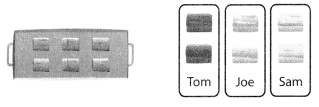
Each person colored one part from each roll of clay for a total of 2 parts. So, 2 ÷ 3 = 2 × \(\frac{1}{3}\) = \(\frac{2}{3}\). Each friend used \(\frac{2}{3}\) of a roll of clay.
C.
Another Way
Place the rolls end-to-end and divide the 2 rolls among 3 people. Each person gets \(\frac{1}{3}\) of 2 wholes. You can see this with shading on a number line.

S0, 2 ÷ 3 = 2 × \(\frac{1}{3}\) = \(\frac{2}{3}\). Each friend used \(\frac{2}{3}\) of a roll of clay.
Convince Me! Reasoning Amelia is sharing 4 slices of cheese with 5 friends. How much cheese will each person get? Explain how you decided.
Guided Practice
Do You Understand?
Question 1.
Explain how to write \(\frac{3}{10}\) as a division expression.
Answer:
The division expression is 3 ÷ 10.
Explanation:
Given the expression is \(\frac{3}{10}\), so to division expression will be 3 ÷ 10.
Question 2.
Explain how to write 2 ÷ 5 as a fraction.
Answer:
The expression as a fraction will be \(\frac{2}{5}\).
Explanation:
Given the expression is 2 ÷ 5, so the expression as a fraction will be \(\frac{2}{5}\).
Question 3.
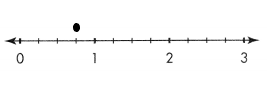
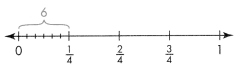
Use the number line below to show 3 ÷ 4
![]()
Answer:
The number line for 3 ÷ 4 is
Do You Know How?
In 4 and 5, write a division expression for each fraction.
Question 4.
\(\frac{1}{9}\)
Answer:
The division expression will be 1 ÷ 9.
Explanation:
Given that the expression is \(\frac{1}{9}\), so the division expression will be 1 ÷ 9.
Question 5.
\(\frac{7}{8}\)
Answer:
The division expression will be 7 ÷ 8.
Explanation:
Given that the expression is \(\frac{7}{8}\), so the division expression will be 7 ÷ 8.
In 6 and 7, tell what fraction each person gets when they share equally.
Question 6.
Five friends share 8 apples.
Answer:
The fraction will be \(\frac{5}{8}\).
Explanation:
Given that five friends share 8 apples, so the fraction will be \(\frac{5}{8}\).
Question 7.
Two friends share 1 bagel.
Answer:
The fraction will be \(\frac{1}{2}\).
Explanation:
Given that two friends share 1 bagel, so the fraction will be \(\frac{1}{2}\).
Independent Practice
In 8-12, write a division expression for each fraction.
Question 8.
\(\frac{6}{7}\)
Answer:
The division expression is 6 ÷ 7.
Explanation:
Given that the expression is \(\frac{6}{7}\), so the division expression is 6 ÷ 7.
Question 9.
\(\frac{1}{4}\)
Answer:
The division expression is 1 ÷ 4.
Explanation:
Given that the expression is \(\frac{1}{4}\), so the division expression is 1 ÷ 4.
Question 10.
\(\frac{6}{11}\)
Answer:
The division expression is 6 ÷ 11.
Explanation:
Given that the expression is \(\frac{6}{11}\), so the division expression is 6 ÷ 11.
Question 11.
\(\frac{4}{9}\)
Answer:
The division expression is 4 ÷ 9.
Explanation:
Given that the expression is \(\frac{4}{9}\), so the division expression is 4 ÷ 9.
Question 12.
\(\frac{8}{12}\)
Answer:
The division expression is 8 ÷ 12.
Explanation:
Given that the expression is \(\frac{8}{12}\), so the division expression is 8 ÷ 12.
In 13-17, write each division expression as a fraction.
Question 13.
9 ÷ 11
Answer:
The expression as a fraction will be \(\frac{9}{11}\).
Explanation:
Given the expression is 9 ÷ 11, so the expression as a fraction will be \(\frac{9}{11}\).
Question 14.
1 ÷ 10
Answer:
The expression as a fraction will be \(\frac{1}{10}\).
Explanation:
Given the expression is 1 ÷ 10, so the expression as a fraction will be \(\frac{1}{10}\).
Question 15.
7 ÷ 13
Answer:
The expression as a fraction will be \(\frac{7}{13}\).
Explanation:
Given the expression is 7 ÷ 13, so the expression as a fraction will be \(\frac{7}{13}\).
Question 16.
11 ÷ 17
Answer:
The expression as a fraction will be \(\frac{11}{17}\).
Explanation:
Given the expression is 11 ÷ 17, so the expression as a fraction will be \(\frac{11}{17}\).
Question 17.
25 ÷ 75
Answer:
The expression as a fraction will be \(\frac{25}{75}\).
Explanation:
Given the expression is 25 ÷ 75, so the expression as a fraction will be \(\frac{25}{75}\).
In 18-21, tell what fraction each person gets when they share equally.
Question 18.
8 students share 6 breakfast bars.
Answer:
The fraction will be \(\frac{8}{6}\).
Explanation:
Given that 8 students share 6 breakfast bars, so the fraction will be \(\frac{8}{6}\).
Question 19.
6 soccer players share 5 oranges.
Answer:
The fraction will be \(\frac{6}{5}\).
Explanation:
Given that 6 soccer players share 5 oranges, so the fraction will be \(\frac{6}{5}\).
Question 20.
10 friends share 7 dollars.
Answer:
The fraction will be \(\frac{10}{7}\).
Explanation:
Given that 10 friends share 7 dollars, so the fraction will be \(\frac{10}{7}\).
Question 21.
8 friends share 8 muffins.
Answer:
The fraction will be \(\frac{8}{8}\).
Explanation:
Given that 8 friends share 8 muffins, so the fraction will be \(\frac{8}{8}\).
Problem Solving
Question 22.
Four friends are baking bread. They equally share 3 sticks of butter. Write an equation to find the fraction of a stick of butter that each friend uses.
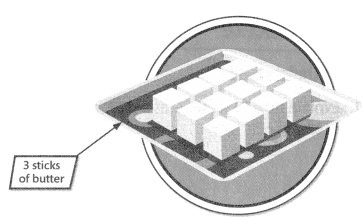
Answer:
The equation to find the fraction of a stick of butter that each friend uses is \(\frac{4}{3}\).
Explanation:
Given that four friends are baking bread and they equally share 3 sticks of butter, so the equation to find the fraction of a stick of butter that each friend uses is \(\frac{4}{3}\).
Question 23.
A group of friends went to the movies. They shared 2 bags of popcorn equally. If each person got \(\frac{2}{3}\) of a bag of popcorn, how many people were in the group?
Answer:
The number of people in the group is 3 people.
Explanation:
Given that a group of friends went to the movies and they shared 2 bags of popcorn equally and each person got \(\frac{2}{3}\) of a bag of popcorn, so the number of people were in the group is 3 people.
Question 24.
Higher Order Thinking Missy says that \(\frac{5}{6}\) equals 6 ÷ 5. Is she correct? Why or why not?
Answer:
Missy is not correct.
Explanation:
Given that Missy says that \(\frac{5}{6}\) which is equal to 5 ÷ 6, so she is not correct.
Question 25.
Make Sense and Persevere
The table shows the food and drinks Tabitha bought for herself and 4 friends for her party. How much did Tabitha spend for each person? Show your work.

Answer:
Assessment Practice
Question 26.
Which equation is made true with the number 5?

Answer:
The equation is 3 ÷ 5.
Explanation:
The equation that made true with the number 5 is 3 ÷ 5.
Question 27.
Which equation is made true with the number 3?

Answer:
The equation is 1 ÷ 3 and 3 ÷ 8.
Explanation:
The equation that made true with the number 3 is 1 ÷ 3 and 3 ÷ 8.
Lesson 9.2 Fractions and Mixed Numbers as Quotients
Solve & Share
Jonah has an 8-pound bag of potting soil. He divides it evenly among 5 flowerpots. How much soil is in each pot? Show your answer as a fraction or mixed number. Solve this problem any way you choose.
You can write an equation or draw a picture to help find the answer.

Look Back! Be Precise Suppose one of the pots breaks, so Jonah has to divide the soil evenly among 4 pots. How much soil is in each pot then?
Visual Learning Bridge
Essential Question
How Can You Show a Quotient Using estion a Fraction or Mixed Number?
A.
Three friends are going hiking. They bought a tub of trail mix to share equally. How much will each friend get?
You can divide to share 4 pounds among 3 people: 4 ÷ 3.

B.
Divide each pound into 3 equal parts. Each part is 1 ÷ 3 or \(\frac{1}{3}\)
Each friend gets 1 pound plus \(\frac{1}{3}\) of a pound, or 1 + \(\frac{1}{3}\) = 1\(\frac{1}{3}\) pounds of trail mix in all.
So, 4 ÷ 3 = \(\frac{4}{3}\) = 1\(\frac{1}{3}\)
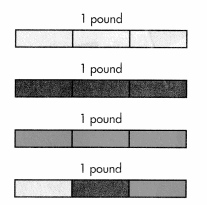
Convince Me! Construct Arguments Kate shares a 64-ounce bottle of apple cider with 5 friends. Each person’s serving will be the same number of ounces. Between what two whole number of ounces will each person’s serving be? Explain using division.
Guided Practice
Do You Understand?
Question 1.
How can you write \(\frac{10}{3}\) to as a division expression and as a mixed number?
Answer:
The division expression is 10 ÷ 3 and as a mixed number, it will be 3\(\frac{1}{3}\).
Explanation:
Given that the equation is \(\frac{10}{3}\), so the division expression is 10 ÷ 3 and as a mixed number it will be 3\(\frac{1}{3}\).
Question 2.
Suppose 3 friends want to share 16 posters equally. For this situation, why does the quotient 5 R1 make more sense than the quotient 5\(\frac{1}{3}\)?
Answer:
Here, each friend gets 5 posters and 1 1 is left over and \(\frac{1}{3}\) poster does not make sense.
Do You Know How?
Question 3.
Find 11 ÷ 10 and 10 ÷ 11. Write each quotient as a fraction or mixed number.
Answer:
The quotient is 1\(\frac{1}{10}\).
Explanation:
The quotient of 11 ÷ 10 is 1\(\frac{1}{10}\) and the fraction of 10 ÷ 11 is \(\frac{10}{11}\)
In 4 and 5, tell how much each person gets when they share equally.
Question 4.
2 friends share 3 apples.
Answer:
Each person will get \(\frac{3}{2}\) share.
Explanation:
Given that 2 friends share 3 apples, so each person will get \(\frac{3}{2}\) share.
Question 5.
3 students share 5 breakfast bars.
Answer:
Each student will get \(\frac{5}{3}\) breakfast bars.
Explanation:
Given that 3 students share 5 breakfast bars, so each student will get \(\frac{5}{3}\) breakfast bars.
Independent Practice
In 6-13, find each quotient. Write each answer as either a fraction or mixed number.
Question 6.
11 ÷ 6
Answer:
The quotient will be 1\(\frac{5}{6}\).
Explanation:
Given the division expression is 11 ÷ 6, so the quotient will be 1\(\frac{5}{6}\).
Question 7.
1 ÷ 5
Answer:
The quotient will be 0.2.
Explanation:
Given the division expression is 1 ÷ 5, so the quotient will be 0.2.
Question 8.
18 ÷ 4
Answer:
The fraction will be 4\(\frac{1}{2}\).
Explanation:
Given the division expression is 18 ÷ 4, so the fraction will be 4\(\frac{1}{2}\).
Question 9.
5 ÷ 9
Answer:
The quotient will be 0.56.
Explanation:
Given the division expression is 5 ÷ 9, so the quotient will be 0.56.
Question 10.
9 ÷ 8
Answer:
The fraction will be 1\(\frac{1}{8}\).
Explanation:
Given the division expression is 9 ÷ 8, so the fraction will be 1\(\frac{1}{8}\).
Question 11.
23 ÷ 10
Answer:
The fraction will be 2\(\frac{3}{10}\).
Explanation:
Given the division expression is 23 ÷ 10, so the fraction will be 2\(\frac{3}{10}\).
Question 12.
12 ÷ 17
Answer:
The quotient will be 0.70.
Explanation:
Given the division expression is 12 ÷ 17, so the quotient will be 0.70.
Question 13.
28 ÷ 20
Answer:
The fraction will be 1\(\frac{2}{5}\).
Explanation:
Given the division expression is 28 ÷ 20, so the fraction will be 1\(\frac{2}{5}\).
In 14-17, tell how much each person gets when they share equally.
Question 14.
2 girls share 7 yards of ribbon.
Answer:
Each girl will get \(\frac{7}{2}\).
Explanation:
Given that 2 girls share 7 yards of ribbon, so each girl will get \(\frac{7}{2}\).
Question 15.
4 friends share 7 bagels.
Answer:
Each friend will get \(\frac{7}{4}\).
Explanation:
Given that 4 friends share 7 bagels, so each friend will get \(\frac{7}{4}\).
Question 16.
4 cousins share 3 pies.
Answer:
Each cousin will get \(\frac{3}{4}\).
Explanation:
Given that 4 cousins share 3 pies, so each cousin will get \(\frac{3}{4}\).
Question 17.
8 soccer players share 12 oranges.
Answer:
Each player will get \(\frac{12}{8}\).
Explanation:
Given that 8 soccer players share 12 oranges, so each player will get \(\frac{12}{8}\).
Problem Solving
Question 18.
Daniella made gift bows from 8 yards of ribbon. The bows are all the same size. If she made 16 bows, how much ribbon did she use for each one? Give the answer as a fraction or mixed number.
Answer:
The ribbon did she uses is \(\frac{1}{2}\) yard.
Explanation:
Given that Daniella made gift bows from 8 yards of ribbon and the bows are all the same size and she made 16 bows. So the number of ribbons did she use for each one gets is 8 ÷ 16 which is \(\frac{1}{2}\) yard.
Question 19.
Be Precise Tammi has 4 pounds of gala apples and 3\(\frac{1}{2}\) pounds of red delicious apples. If she uses 1\(\frac{3}{4}\) pounds of gala apples in a recipe, how many pounds of apples does she have left?
Answer:
The number of pounds of apples does she have left is 5\(\frac{1}{4}\).
Explanation:
Given that Tammi has 4 pounds of gala apples and 3\(\frac{1}{2}\) pounds of red delicious apples and she uses 1\(\frac{3}{4}\) pounds of gala apples in a recipe, so the number of pounds of apples does she have left is 3\(\frac{1}{2}\) + 1\(\frac{3}{4}\) which is
= \(\frac{7}{2}\) + \(\frac{7}{4}\)
= \(\frac{14+7}{4}\)
= \(\frac{21}{4}\)
= 5\(\frac{1}{4}\).
Question 20.
Casey bought a 100-pound bag of dog food. He gave his dogs the same amount of dog food each week. The dog food lasted 8 weeks. How much dog food did Casey give his dogs each week? Give the answer as a fraction or mixed number.
Answer:
The number of pounds of food did Casey give his dogs each week is 12\(\frac{1}{2}\) pounds.
Explanation:
Given that Casey bought a 100-pound bag of dog food and he gave his dogs the same amount of dog food each week and the dog food lasted 8 weeks. So the number of pounds of food did Casey give his dogs each week is 100 ÷ 8 which is 12\(\frac{1}{2}\) pounds.
Question 21.
Higher Order Thinking Write a word problem that can be solved by dividing 6 by 5.
Answer:
Question 22.
The amount of fabric needed for an adult and a baby scarecrow costume is shown at the right. The amount of fabric for an adult scarecrow costume is how many times the amount of fabric for a baby scarecrow costume? Give the answer as a fraction or mixed number.

Answer:
The fraction will be 3\(\frac{1}{2}\).
Explanation:
Given that the amount of fabric needed for an adult 7 yards and the amount of fabric needed for baby is 2 yards. So the fraction will be \(\frac{7}{2}\) which is 3\(\frac{1}{2}\).
Assessment Practice
Question 23.
Jamal had 37 feet of decorative tape to share with 5 friends and himself. How much tape does each person get?
A. \(\frac{6}{37}\) feet
B. 6\(\frac{1}{6}\) feet
C. 6\(\frac{5}{6}\) feet
D. 6\(\frac{1}{37}\) feet
Answer:
6\(\frac{1}{6}\) feet.
Explanation:
Given that Jamal had 37 feet of decorative tape to share with 5 friends and himself, so how much tape does each person get is 37 ÷ 6 which is 6\(\frac{1}{6}\) feet.
Question 24.
Lindsay divides 40 by 9. Between what two whole numbers is her answer?
A. 2 and 3
B. 3 and 4
C. 4 and 5
D. 5 and 6
Answer:
4 and 5.
Explanation:
Given that Lindsay divides 40 by 9, so the whole numbers in her answer is 4 and 5.
Lesson 9.3 Use Multiplication to Divide
Activity
Solve&Share
A sandwich shop prepares large wraps and cuts them into fourths. Each fourth is one serving. William buys 5 whole wraps for a party. How many servings in all does he get? Solve this problem any way you choose.
How could fraction strips, bar diagrams, or other models help you visualize the problem?

Look Back! Model with Math Write an equation that represents the problem about the wraps.
Visual Learning Bridge
Essential Question How Is Dividing by a Fraction Related to Multiplication?
A.
If a bottle of liquid plant food contains 3 cups, how many plants will you be able to feed? Explain why your answer makes sense.

You need to find how many eighths are in 3 cups. 3 ÷ \(\frac{1}{8}\) = ?

B.
How many \(\frac{1}{8}\)s are in 3?

Use a model and multiplication to solve.
Since there are 8 eighths in each whole, there are 3 × 8 = 24 eighths in 3 wholes.
S0, 3 ÷ \(\frac{1}{8}\) = 24.
The plant food can feed 24 plants.
C.
Does the answer make sense?
Do 24 eighths equal 3?
Use multiplication to check.
24 × \(\frac{1}{8}\) = \(\frac{24}{8}\) = 3
Yes, 24 eighths equals 3, so the answer makes sense.
The inverse relationship between multiplication and division applies to fraction computation, too!

The division equation 3 ÷ \(\frac{1}{8}\) = 24 is true because the multiplication equation
24 × \(\frac{1}{8}\) = 3 is true.
Convince Me! Use Structure Use the same numbers in the multiplication equation 15 × \(\frac{1}{3}\) = 5 to write a division equation. Draw a diagram to show that your division equation makes sense.
Guided Practice
Do You Understand?
Question 1.
Explain how to use multiplication to find 4 ÷ \(\frac{1}{5}\).
Answer:
The multiplication is 4 × 5 = 20.
Explanation:
Here, we can use multiplication to the given expression 4 ÷ \(\frac{1}{5}\) as 4 × 5 which is 20.
Question 2.
Show how to use multiplication to check your answer to Exercise 1.
Answer:
Do You Know How?
Question 3.
Find 3 ÷ \(\frac{1}{10}\).
Answer:
3 ÷ \(\frac{1}{10}\) = 30.
Explanation:
Given the expression is 3 ÷ \(\frac{1}{10}\) which is 3 × 10 which is 30.
Question 4.
Draw a model to find 2 ÷ \(\frac{1}{6}\).
Answer:
2 ÷ \(\frac{1}{6}\) = 12.
Explanation:
Given the expression is 2 ÷ \(\frac{1}{6}\) which is 12.
Question 5.
Use a multiplication equation to check your answer to Exercise 4.
Answer:
Independent Practice
In 6-9, use the model to find each quotient. Use multiplication to check your answer.
Question 6.
3 ÷ \(\frac{1}{4}\)
Answer:
The multiplication will be 12.
Explanation:
Given the expression is 3 ÷ \(\frac{1}{4}\), so the multiplication will be 3 × 4 which is 12.
Question 7.
2 ÷ \(\frac{1}{12}\)
Answer:
The multiplication will be 24.
Explanation:
Given the expression is 2 ÷ \(\frac{1}{12}\), so the multiplication will be 2 × 12 which is 24.
Question 8.
4 ÷ \(\frac{1}{9}\)

Answer:
The multiplication will be 36.
Explanation:
Given the expression is 4 ÷ \(\frac{1}{9}\), so the multiplication will be 4 × 9 which is 36.
Question 9.
3 ÷ \(\frac{1}{6}\)
Answer:
The multiplication will be 18.
Explanation:
Given the expression is 3 ÷ \(\frac{1}{6}\), so the multiplication will be 3 × 6 which is 18.
In 10-12, draw a model to find each quotient. Use multiplication to check your answer.
Question 10.
5 ÷ \(\frac{1}{6}\)
Answer:
The multiplication will be 30.
Explanation:
Given the expression is 5 ÷ \(\frac{1}{6}\), so the multiplication will be 5 × 6 which is 30.
Question 11.
4÷ \(\frac{1}{8}\)
Answer:
The multiplication will be 32.
Explanation:
Given the expression is 4÷ \(\frac{1}{8}\), so the multiplication will be 4 × 8 which is 32.
Question 12.
3 ÷ \(\frac{1}{3}\)
Answer:
The multiplication will be 9.
Explanation:
Given the expression is 3 ÷ \(\frac{1}{3}\), so the multiplication will be 3 × 3 which is 9.
Problem Solving
Question 13.
Model with Math Write and solve a division equation to find the number of \(\frac{1}{3}\) pound hamburger patties that can be made from 4 pounds of ground beef.

Answer:
The number of patties will be 12 patties.
Explanation:
Given that there are \(\frac{1}{3}\) pound hamburger patties that can be made from 4 pounds of ground beef, so the number of patties will be 4 × 3 which is 12 patties.
Question 14.
Write and solve a word problem for the expression 8 ÷ \(\frac{1}{2}\).
Answer:
How many half-hour chess classes can a chess teacher give in 8 hours?
Explanation:
The number of classes will be 8 ÷ \(\frac{1}{2}\) which is 16 classes.
Question 15.
Use the numbers in the multiplication equation 28 × \(\frac{1}{7}\) = 4 to write a division equation involving division by a fraction.
Answer:
The division equation will be 4 ÷ \(\frac{1}{7}\) = 28.
Explanation:
Given the multiplication equation 28 × \(\frac{1}{7}\) = 4, so the division equation involving division by a fraction is 4 ÷ \(\frac{1}{7}\) = 28.
Question 16.
Number Sense Sally and Timothy have two different answers for 1,785 ÷ 35. Without dividing, how can you tell whose answer is wrong?
Sally: 1,785 ÷ 35 = 51
Timothy: 1,785 ÷ 35 = 501
Answer:
Timothy’s answer is wrong.
Explanation:
Given that Sally and Timothy have two different answers for 1,785 ÷ 35, here Timothy’s answer is wrong. Because when we multiply factors, the product with a certain number of place values and the product should have the sum of the number of place values. So without dividing, we can say as 35 has 2 digits and 51 has 2 digits, so 2 + 2 = 4, and 1785 has 4 digits.
Question 17.
Higher Order Thinking A restaurant charges $3.50 for a slice of pie that is one sixth of a pie and $3.00 for a slice that is one eighth of a pie. One day they baked 5 pies, all the same size. If they sell all the slices, would they make more money by slicing each pie into sixths or eighths? How much more? Explain.
Answer:
They make $15 more money by slicing each pie into sixths or eighths.
Explanation:
Given that a restaurant charges $3.50 for a slice of pie that is one-sixth of a pie and $3.00 for a slice that is one-eighth of a pie and they baked 5 pies all the same size. So if they sell all the slices, would they make more money by slicing each pie into sixths or eighths. So one-sixth of a pie will be 5 ÷ \(\frac{1}{6}\) which is 30 slices and they would make $3.50 × 30 which is $105. And for one-eighth of a pie 5 ÷ \(\frac{1}{8}\) which is 40 slices and they would make $3.00 × 40 which is $120. So $120 – $105 = $15.
Assessment Practice
Question 18.
Javier drew a model to determine how many fifths are in 6 wholes.

Part A
Describe Javier’s work by writing a division equation that includes a fraction.
Answer:
The division equation will be 6 ÷ \(\frac{1}{5}\) = 30.
Explanation:
Javier’s work by writing a division equation will be 6 ÷ \(\frac{1}{5}\) which will be 30.
Part B
Check your answer by using the numbers in your division equation to write a multiplication equation.
Answer:
The multiplication equation is 30 × \(\frac{1}{5}\) = 6.
Explanation:
The multiplication equation will be 30 × \(\frac{1}{5}\) which is 6.
Lesson 9.4 Divide Whole Numbers by Unit Fractions
Activity
Solve & Share
One ball of dough can be stretched into a circle to make a pizza. After the pizza is cooked, it is cut into 8 equal slices. How many slices of pizza can you make with 3 balls of dough? Solve this problem any way you choose.
You can use appropriate tools to help find the answer. Show your work!

Look Back! Into how many slices of pizza will each ball of dough be divided? What fraction of a whole pizza does 1 slice represent?
Visual Learning Bridge
Essential Question How Can You Divide by a Unit Fraction?
A.
Joyce is making sushi rolls. She needs \(\frac{1}{4}\) cup of rice for each sushi roll. How many sushi rolls can she make if she has 3 cups of rice?
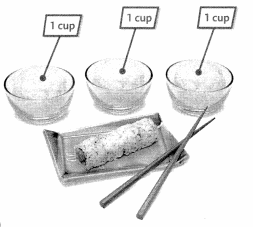
\(\frac{1}{4}\) is a unit fraction. A unit fraction is a fraction that describes one part of the whole. So, it has a numerator of 1.

B.
One Way Use an area model to find how many \(\frac{1}{4}\)s are in 3.

There are four \(\frac{1}{4}\)s in 1 whole cup. So, there are twelve \(\frac{1}{4}\)s in three whole cups. So, Joyce can make 12 sushi rolls.
You can use multiplication to check your answer.
3 × 4 = 12
C.
Another Way Use a number line to find how many \(\frac{1}{4}\)s are in 3.
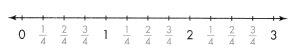
You can see that there are four \(\frac{1}{4}\)s in between each whole number.
There are four \(\frac{1}{4}\)s in 1 whole, eights in \(\frac{1}{4}\)s in 2 wholes, and twelve \(\frac{1}{4}\)s in 3 wholes.
So, 3 ÷ \(\frac{1}{4}\) = 12.
Joyce can make 12 sushi rolls.
Convince Me! Use Structure Use the diagram below to find 4 ÷ \(\frac{1}{3 }\).

Answer:
The multiplication equation will be 4 × 3 = 12.
Explanation:
Given that the expression is 4 ÷ \(\frac{1}{3 }\), so the multiplication equation will be 4 × 3 which is 12.
Guided Practice
Do You Understand?
Question 1.
In the example at the top of page 398, if Joyce had 4 cups of rice, how many rolls could she make?
Answer:
There will be 16 sushi rolls.
Explanation:
If Joyce had 4 cups of rice, then there will be 4 × 4 which will be 16 sushi rolls.
Question 2.
In the example at the top of page 398, how does the number line help to show that 3 ÷ \(\frac{1}{4}\) is equal to 3 × 4?
Answer:
Do You Know How?

In 3 and 4, use the picture below to find each quotient.
Question 3.
How many \(\frac{1}{3}\)s are in 3?
3 ÷ \(\frac{1}{3}\) = _____
Answer:
3 ÷ \(\frac{1}{3}\) = 3.
Explanation:
Here, we need to find \(\frac{1}{3}\)s in 3. So there will be 3 × 3 which is 9.
Question 4.
How many \(\frac{1}{3}\)s are in 6?
6 ÷ \(\frac{1}{3}\) = _____
Answer:
6 ÷ \(\frac{1}{3}\) = 18.
Explanation:
Here, we need to find \(\frac{1}{3}\)s in 6. So there will be 3 × 6 which is 18.
Independent Practice
Leveled Practice in 5 and 6, use the picture to find each quotient.
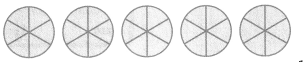
Question 5.
How many \(\frac{1}{6}\)s are in 1?
1 ÷ 6\(\frac{1}{3}\) = ___
Answer:
Question 6.
How many \(\frac{1}{6}\)s are in 5?
5 ÷ \(\frac{1}{6}\) = _____
Answer:
In 7-14, draw a picture or use a number line to find each quotient. Then use multiplication to check your answer.
Question 7.
4 ÷ \(\frac{1}{2}\)
Answer:
The multiplication equation will be 4 × 2 = 8.
Explanation:
Given that the expression is 4 ÷ \(\frac{1}{2}\), so the multiplication equation will be 4 × 2 which is 8.
Question 8.
2 ÷ \(\frac{1}{8}\)
Answer:
The multiplication equation will be 2 × 8 = 16.
Explanation:
Given that the expression is 2 ÷ \(\frac{1}{8}\), so the multiplication equation will be 2 × 8 which is 16.
Question 9.
2 ÷ \(\frac{1}{3}\)
Answer:
The multiplication equation will be 2 × 3 = 6.
Explanation:
Given that the expression is 2 ÷ \(\frac{1}{3}\), so the multiplication equation will be 2 × 3 which is 6.
Question 10.
6 ÷ \(\frac{1}{4}\)
Answer:
The multiplication equation will be 6 × 4 = 24.
Explanation:
Given that the expression is 2 ÷ \(\frac{1}{8}\), so the multiplication equation will be 2 × 8 which is 16.
Question 11.
8 ÷ \(\frac{1}{3}\)
Answer:
The multiplication equation will be 3 × 8 = 24.
Explanation:
Given that the expression is 8 ÷ \(\frac{1}{3}\), so the multiplication equation will be 3 × 8 which is 24.
Question 12.
3 ÷ \(\frac{1}{10}\)
Answer:
The multiplication equation will be 3 × 10 = 30.
Explanation:
Given that the expression is 3 ÷ \(\frac{1}{10}\), so the multiplication equation will be 3 × 10 which is 30.
Question 13.
9 ÷ \(\frac{1}{10}\)
Answer:
The multiplication equation will be 9 × 10 = 90.
Explanation:
Given that the expression is 9 ÷ \(\frac{1}{10}\), so the multiplication equation will be 9 × 10 which is 90.
Question 14.
15 ÷ \(\frac{1}{5}\)
Answer:
The multiplication equation will be 15 × 5 = 75.
Explanation:
Given that the expression is 15 ÷ \(\frac{1}{5}\), so the multiplication equation will be 15 × 5 which is 75.
Problem Solving
Question 15.
Dan has 4 cartons of juice. He pours \(\frac{1}{8}\) carton for each person on a camping trip. How many people can he serve? Draw a picture to help you answer the question.
Answer:
The number of people can he serve is 32 people.
Explanation:
Given that Dan has 4 cartons of juice and he pours \(\frac{1}{8}\) carton for each person on a camping trip, so the number of people can he serve is 4 ÷ \(\frac{1}{8}\) which is 4 × 8 = 32 people.
Question 16.
Higher Order Thinking Write a word problem that can be solved by dividing 10 by \(\frac{1}{3}\). Then answer the problem.
Answer:
Question 17.
Number Sense The Nile River is the longest river in the world. It is 4,160 miles long. You want to spend three weeks traveling the entire length of the river, traveling about the same number of miles each day. Estimate the number of miles you should travel each day.
Answer:
The number of miles you should travel each day is 198.09 miles per day.
Explanation:
Given that the Nile River is 4,160 miles long and if we are going to calculate the length for each day. And we need to multiply the number of weeks by the amount for each week is 3 × 7 which is 21 days. So to find the distance we should travel per day, divide the total distance by the number of days. So 4,160 ÷ 21 which is 198.09 miles per day.
Question 18.
Make Sense and Persevere
Maria used one bag of flour. She baked two loaves of bread. Then she used the remaining flour to make 48 muffins. How much flour was in the bag when Maria began?

Answer:
Assessment Practice
Question 19.
Deron is making light switch plates from pieces of wood. He starts with a board that is 18 feet long. How many light switch plates can he make?

A. 9 light switch plates
B. 24 light switch plates
C. 27 light switch plates
D. 54 light switch plates
Answer:
Lesson 9.5 Divide Unit Fractions by Non-Zero Whole Numbers
Activity
Solve & Share
Yesterday, the cooking club made a pan of lasagna. They left half of the lasagna for 4 members of the photography club to share equally. What fraction of the pan of lasagna did each photography club member get? Solve this problem any way you choose.

You can use appropriate tools to show how to divide what is left. Show your work!

Look Back! What equation can you write to model this problem?
Visual Learning Bridge
Essential Question How Can You Model Dividing a Unit Question Fraction by a Whole Number?
A.
Half of a pan of cornbread is left over. Ann, Beth, and Chuck are sharing the leftovers equally. What fraction of the original cornbread does each person get?

You can make a drawing to show \(\frac{1}{2}\) of the cornbread.

B.
One Way On an area model, divide \(\frac{1}{2}\) into 3 equal parts.

Each part contains \(\frac{1}{6}\) of the whole.
\(\frac{1}{2}\) ÷ 3 = \(\frac{1}{6}\)
Each person gets \(\frac{1}{6}\) of the cornbread.
C.
Another Way Use a number line. Shades \(\frac{1}{2}\) on the number line. Partition \(\frac{1}{2}\) into 3 equal parts.
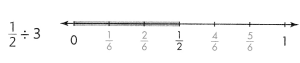
Each part is \(\frac{1}{6}\).
\(\frac{1}{2}\) ÷ 3 = \(\frac{1}{6}\)
Each person gets \(\frac{1}{6}\) of the cornbread.
Convince Me! Reasoning in the example above, how is dividing by 3 the same as multiplying by \(\frac{1}{3}\)?
Guided Practice
Do You Understand?
Question 1.
In the example at the top of page 402, suppose that 4 people were sharing half of the cornbread equally. What fraction of the original cornbread would each person get? Draw a picture or use objects to help.
Answer:
Question 2.
When you divide a unit fraction by a non-zero whole number greater than 1, will the quotient be greater than or less than the unit fraction?
Answer:
Do You Know How?
In 3-6, find each quotient. Use the picture or objects to help.

Qestion 3.
\(\frac{1}{4}\) ÷ 2
Answer:
The quotient will be \(\frac{1}{8}\).
Explanation:
Given that the expression is \(\frac{1}{4}\) ÷ 2, so the quotient will be \(\frac{1}{8}\).
Question 4.
\(\frac{1}{4}\) ÷ 4
Answer:
The quotient will be \(\frac{1}{16}\).
Explanation:
Given that the expression is \(\frac{1}{4}\) ÷ 4, so the quotient will be \(\frac{1}{16}\).
Question 5.
\(\frac{1}{2}\) ÷ 2
Answer:
The quotient will be \(\frac{1}{4}\).
Explanation:
Given that the expression is \(\frac{1}{2}\) ÷ 2, so the quotient will be \(\frac{1}{4}\).
Question 6.
\(\frac{1}{2}\) ÷ 4
Answer:
The quotient will be \(\frac{1}{8}\).
Explanation:
Given that the expression is \(\frac{1}{2}\) ÷ 4, so the quotient will be \(\frac{1}{8}\).
Independent Practice
Leveled Practice In 7 and 8, find each quotient. Use a picture or objects to help.
Question 7.
\(\frac{1}{2}\) ÷ 5
![]()
Answer:
The quotient will be \(\frac{1}{10}\).
Explanation:
Given that the expression is \(\frac{1}{2}\) ÷ 5, so the quotient will be \(\frac{1}{10}\).
Question 8.
\(\frac{1}{5}\) ÷ 2
![]()
Answer:
The quotient will be \(\frac{1}{10}\).
Explanation:
Given that the expression is \(\frac{1}{5}\) ÷ 2, so the quotient will be \(\frac{1}{10}\).
Partitioning pictures or objects can help when dividing fractions by a whole number.

In 9-14, find each quotient.
Question 9.
\(\frac{1}{2}\) ÷ 7
Answer:
The quotient will be \(\frac{1}{14}\).
Explanation:
Given that the expression is \(\frac{1}{2}\) ÷ 7, so the quotient will be \(\frac{1}{14}\).
Question 10.
\(\frac{1}{4}\) ÷ 3
Answer:
The quotient will be \(\frac{1}{12}\).
Explanation:
Given that the expression is \(\frac{1}{4}\) ÷ 3, so the quotient will be \(\frac{1}{12}\).
Question 11.
\(\frac{1}{6}\) ÷ 2
Answer:
The quotient will be \(\frac{1}{10}\).
Explanation:
Given that the expression is \(\frac{1}{2}\) ÷ 5, so the quotient will be \(\frac{1}{10}\).
Question 12.
\(\frac{1}{3}\) ÷ 4
Answer:
The quotient will be \(\frac{1}{12}\).
Explanation:
Given that the expression is \(\frac{1}{3}\) ÷ 4, so the quotient will be \(\frac{1}{12}\).
Question 13.
\(\frac{1}{4}\) ÷ 5
Answer:
The quotient will be \(\frac{1}{20}\).
Explanation:
Given that the expression is \(\frac{1}{4}\) ÷ 5, so the quotient will be \(\frac{1}{20}\).
Question 14.
\(\frac{1}{5}\) ÷ 3
Answer:
The quotient will be \(\frac{1}{15}\).
Explanation:
Given that the expression is \(\frac{1}{5}\) ÷ 3, so the quotient will be \(\frac{1}{15}\).
Problem Solving
Question 15.
Vin, Corrie, Alexa, and Joe equally shared one fourth of a submarine sandwich. What fraction of the original sandwich did each friend get? Use the number line to help you find the answer.

Answer:
Each person gets is \(\frac{1}{4}\).
Explanation:
Given that Vin, Corrie, Alexa, and Joe equally shared one fourth of a submarine sandwich, so the fraction of the original sandwich did each friend get is, as the sandwich a whole is \(\frac{4}{4}\) and there is 4 people, so each person gets is \(\frac{1}{4}\).
Question 16.
Sue has \(\frac{1}{2}\) gallon of milk to share evenly among four people. How much milk, in gallons, should she give each person?
Answer:
Sue gave \(\frac{1}{8}\) gallons of milk.
Explanation:
Given that Sue has \(\frac{1}{2}\) gallon of milk to share evenly among four people, so she gave each person \(\frac{1}{2}\) ÷ 4 which is \(\frac{1}{8}\) gallons.
Question 17.
Critique Reasoning Taryn says that \(\frac{1}{4}\) of a cereal bar is larger than \(\frac{1}{3}\) of the cereal bar. Is she correct? Explain.
Answer:
Taryn is not correct.
Explanation:
Given that Taryn says that \(\frac{1}{4}\) of a cereal bar is larger than \(\frac{1}{3}\) of the cereal bar. Here, Taryn is not correct. As it’s \(\frac{1}{4}\) is getting smaller than \(\frac{1}{3}\).
Question 18.
Algebra On Saturday, Amir ran 1\(\frac{3}{4}\) miles, and Janie ran 2\(\frac{1}{2}\) miles. Who ran farther? How much farther? Write an equation to find d, the difference of the two distances.
Answer:
The difference of the two distances is \(\frac{3}{4}\).
Explanation:
Given that on Saturday, Amir ran 1\(\frac{3}{4}\) miles, and Janie ran 2\(\frac{1}{2}\) miles. And the equation to find d is
d = Janie – Amir
= 2\(\frac{1}{2}\) – 1\(\frac{3}{4}\)
= \(\frac{5}{2}\) – \(\frac{7}{4}\)
= \(\frac{10-7}{4}\)
= \(\frac{3}{4}\).
Question 19.
Higher Order Thinking Five friends equally shared half of one large pizza and \(\frac{1}{4}\) of another large pizza. What fraction of each pizza did each friend get? How do the two amounts compare to each other?
Answer:
Each friend gets \(\frac{1}{20}\) of pizza.
Explanation:
Given that five friends equally shared half of one large pizza and \(\frac{1}{4}\) of another large pizza, so the fraction of each pizza did each friend get is \(\frac{1}{4}\) ÷ 5 which is \(\frac{1}{20}\).
Assessment Practice
Question 20.
Jamie cut a rope into thirds. He used two of the pieces to make a swing. He used equal lengths of the leftover rope on four picture frames. What fraction of the original rope did he use for each picture frame?
A. \(\frac{1}{4}\)
B. \(\frac{1}{12}\)
C.\(\frac{1}{16}\)
D. \(\frac{3}{4}\)
Answer:
The fraction of the original rope did he use for each picture frame \(\frac{3}{4}\).
Explanation:
Given that Jamie cut a rope into thirds and he used two of the pieces to make a swing and he used equal lengths of the leftover rope on four picture frames. So the fraction of the original rope did he use for each picture frame \(\frac{3}{4}\).
Question 21.
One half of an apple pie is left for 5 family members to share equally. What fraction of the original pie will each member get?
A. \(\frac{1}{10}\)
B.\(\frac{1}{7}\)
C. \(\frac{1}{3}\)
D. \(\frac{2}{5}\)
Answer:
The fraction of the original pie will each member get is \(\frac{1}{10}\).
Explanation:
Given that One half of an apple pie is left for 5 family members to share equally. So the fraction of the original pie will each member get is \(\frac{1}{2}\) ÷ 5 which is \(\frac{1}{10}\).
Lesson 9.6 Divide Whole Numbers and Unit Fractions
Activity
Solve&Share
The Brown family is planting \(\frac{1}{3}\) of their garden with flowers, \(\frac{1}{3}\) with berries, and \(\frac{1}{3}\) with vegetables. The vegetable section has equal parts of carrots, onions, peppers, and tomatoes. What fraction of the garden is planted with carrots? Solve this problem any way you choose.
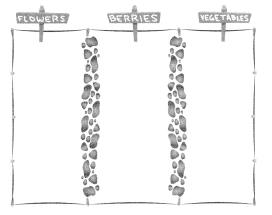
How can you show an equal share of each vegetable?

Look Back! Model with Math Write an equation that models this problem. Explain your reasoning.
Visual Learning Bridge
Essential Question How Can You Divide with Unit Fractions and Whole Numbers?
A.
A utility company is planning to install wind turbines on 4 square miles of land. Each turbine requires \(\frac{1}{6}\) square mile of land. How many turbines can be installed?

Model the problem with a picture or an equation to help you.

B.
One Way
Use an area model to show 4 square miles. Divide each square mile into 6 equal parts to represent \(\frac{1}{6}\) square mile.
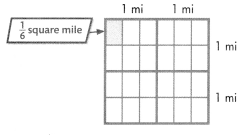
There are 24 parts.
So, 24 wind turbines will fit on the land.
C.
Another Way
Use a number line to show 4 wholes.
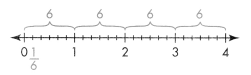
There are 6\(\frac{1}{6}\)s in each whole.
So, there are 24\(\frac{1}{6}\)s in 4 wholes.
4 ÷ \(\frac{1}{6}\) = 24
24 wind turbines will fit on the land.
Convince Me! Reasoning Use an area model to find 2 ÷ \(\frac{1}{4}\). Then use multiplication to check your answer.
Another Example
Use a number line to find \(\frac{1}{4}\) ÷ 6.
If you partition \(\frac{1}{4}\) into 6 equal segments, how long is each segment?
\(\frac{1}{4}\) ÷ 6 = \(\frac{1}{24}\)
Check your answer using multiplication: \(\frac{1}{24}\) × 6 = \(\frac{1}{4}\).
Guided Practice
Do You Understand?
Question 1.
When you divide a whole number by a fraction less than 1, will the quotient be greater than or less than the whole number?
Answer:
The quotient will be less than 1.
Explanation:
The quotient will be less than 1. Because, if we take example a fraction which is less than 1 which is \(\frac{2}{3}\) and a whole number 4 which is greater than 1. So when we divide \(\frac{2}{3}\) with 4 which is \(\frac{2}{3}\) ÷ 4 on solving we will get \(\frac{1}{6}\) which is less than 1.
Question 2.
4 square miles of land is separated into sections that each have an area of \(\frac{1}{2}\) square mile. How many sections are there?

Answer:
Do You Know How?
In 3-6, find each quotient. 3. 2-1
Question 3.
2 ÷ \(\frac{1}{4}\)
Answer:
The quotient will be \(\frac{1}{8}\).
Explanation:
Given that the expression is \(\frac{1}{4}\) ÷ 2, so the quotient will be \(\frac{1}{8}\).
Question 4.
3 ÷ \(\frac{1}{4}\)
Answer:
The quotient will be \(\frac{1}{12}\).
Explanation:
Given that the expression is \(\frac{1}{4}\) ÷ 3, so the quotient will be \(\frac{1}{12}\).
Question 5.
\(\frac{1}{6}\) ÷ 2
Answer:
The quotient will be \(\frac{1}{12}\).
Explanation:
Given that the expression is \(\frac{1}{6}\) ÷ 2, so the quotient will be \(\frac{1}{12}\).
Question 6.
2 ÷ \(\frac{1}{3}\)
Answer:
The quotient will be \(\frac{1}{6}\).
Explanation:
Given that the expression is \(\frac{1}{3}\) ÷ 2, so the quotient will be \(\frac{1}{6}\).
Draw a number line or use a model to help you find the answers!

Independent Practice
Leveled Practice In 7-10, find each quotient. Use a model or number line to help.
Question 7.
5 ÷ \(\frac{1}{2}\)
![]()
Answer:
The quotient will be 10.
Explanation:
Given that the expression is 5 ÷ \(\frac{1}{2}\), so the quotient will be 10.
Question 8.
\(\frac{1}{2}\) ÷ 5
![]()
Answer:
The quotient will be \(\frac{1}{10}\).
Explanation:
Given that the expression is \(\frac{1}{2}\) ÷ 5, so the quotient will be \(\frac{1}{10}\).
Question 9.
6 ÷ \(\frac{1}{3}\)

Answer:
The quotient will be 18.
Explanation:
Given that the expression is 6 ÷ \(\frac{1}{3}\), so the quotient will be 18.
Question 10.
\(\frac{1}{3}\) ÷ 6
Answer:
The quotient will be \(\frac{1}{18}\).
Explanation:
Given that the expression is \(\frac{1}{3}\) ÷ 6, so the quotient will be \(\frac{1}{18}\).
Problem Solving
Question 11.
Keiko divided 5 cups of milk into \(\frac{1}{4}\)-cup portions. How many \(\frac{1}{4}\)-cup portions did Keiko have? Complete the picture to show your solution.
Answer:
The number of portions did Keiko have is \(\frac{1}{20}\).
Explanation:
Given that Keiko divided 5 cups of milk into \(\frac{1}{4}\)-cup portions. So the number of portions did Keiko have is \(\frac{1}{4}\) ÷ 5 which is \(\frac{1}{20}\).
Question 12.
Algebra Ms. Allen has \(\frac{1}{8}\) of a pan of brownies left to divide between 2 children. Draw a picture to find what fraction, f, of the original pan of brownies each child gets. Write an equation for f that models the solution.
Answer:
The fraction equation will be \(\frac{1}{8}\) ÷ 2 = \(\frac{1}{16}\).
Explanation:
Given that Ms. Allen has \(\frac{1}{8}\) of a pan of brownies left to divide between 2 children. So the fraction equation will be \(\frac{1}{8}\) ÷ 2 which is \(\frac{1}{16}\).
Question 13.
Make Sense and Persevere A regular polygon has a perimeter of 2 feet. If each side measures \(\frac{1}{3}\) foot, what is the name of the polygon?
Answer:
A regular polygon has equal side lengths and equal angle measures.

Answer:
The name of the polygon is Hexagon.
Explanation:
The name of the polygon is Hexagon. As \(\frac{1}{3}\) fits into two 6 times. That means there are 6 sides.
Question 14.
Higher Order Thinking Mr. Brent uses \(\frac{1}{4}\) cup of blue paint and \(\frac{1}{4}\) cup of yellow paint to make each batch of green paint. How many batches of green paint can he make with the amount of paint he has left? Explain how you found your answer.

Answer:
Mr. Brent makes 12 batches of green paint.
Explanation:
Given that Mr. Brent uses \(\frac{1}{4}\) cup of blue paint and \(\frac{1}{4}\) cup of yellow paint to make each batch of green paint. Here, every \(\frac{1}{2}\) cup yellow paint combined with \(\frac{3}{4}\) cup of blue paint would make 1 + \(\frac{1}{4}\) cup which is \(\frac{4+1}{4}\) which is \(\frac{5}{4}\). As we can make a total of 15 cups of green paint, so 15 ÷ 1.25 which is 12 batches of paint.
Assessment Practice
Question 15.
Jordan says that 6 ÷ \(\frac{1}{2}\) = 3. Is he correct? If not, justify your reasoning and give the correct quotient.
Answer:
Jordan is wrong.
Explanation:
Given that Jordan says that 6 ÷ \(\frac{1}{2}\) = 3, Jordan is not correct. Because 6+1 = 7 and 7 ÷ 2 which is 3.5. So Jordan is wrong.
Lesson 9.7 Solve Problems Using Division
Solve & Share
Organizers of an architectural tour need to set up information tables every \(\frac{1}{8}\) mile along the 6-mile tour, beginning \(\frac{1}{8}\) mile from the start of the tour. Each table needs 2 signs. How many signs do the organizers need? Solve this problem any way you choose.

Make Sense and Persevere What steps do you need to do to solve this problem? Show your work!

Look Back! How does the number line help you solve this problem?
Visual Learning Bridge
Essential Question How Can You Solve Division Home Problems with Unit Fractions?
A.
John plans to buy sheets of plywood like the ones shown to make boxes with lids. Each box is a cube that has \(\frac{1}{3}\)foot edges. How many sheets of plywood does John need in order to make 5 boxes with lids?
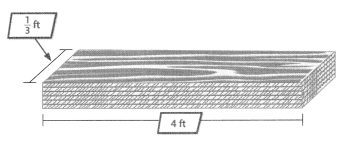
Remember, a cube has 6 identical faces.

B.
What do you know?
Six pieces of plywood are needed for each of the 5 boxes.
Boxes are \(\frac{1}{3}\)-foot cubes. Each sheet of plywood is \(\frac{1}{3}\) foot wide and 4 feet long.
What are you asked to find?
The number of sheets of plywood John needs to buy
C.
Write an equation to help answer each question.
1. How many pieces of plywood are needed boxes for 5 boxes with lids?
2. How many pieces can be cut from 1 sheet of plywood?
4 ÷ \(\frac{1}{3}\) = 12
3. How many sheets of plywood does John need for 5 boxes with lids? 30 ÷ 12 = 2 R6
John needs 3 sheets of plywood.
Convince Me! Reasoning Write a real-world problem that can be solved by first adding 24 and 36 and then dividing by \(\frac{1}{4}\). Find the solution to your problem and explain your answer.
Guided Practice
Do You Understand?
Question 1.
In the example on page 410, why were additional questions answered to help solve the problem?
Answer:
Question 2.
What equations were used to solve the example on page 410?
Answer:
Do You Know How?
Question 3.
Tamara needs tiles to make a border for her bathroom wall. The border will be 9 feet long and \(\frac{1}{3}\) foot wide. Each tile measures \(\frac{1}{3}\) foot by \(\frac{1}{3}\) foot. Each box of tiles contains 6 tiles. How many boxes of tiles does Tamara need? Write two equations that can be used to solve the problem.
Answer:
Tamara needs 5 boxes of tiles.
Explanation:
Given that each tile measures \(\frac{1}{3}\) foot by \(\frac{1}{3}\) foot and each box of tiles contains 6 tiles which is 6X × \(\frac{1}{3}\) × \(\frac{1}{3}\) = 9 × \(\frac{1}{3}\). Therefore X = 4.5. Since X is an integer, the smallest integer such that X = 5.
Independent Practice
Write the equations needed to solve each problem. Then solve.
Question 4.
Robert wants to use all the ingredients listed in the table at the right to make trail mix. How many \(\frac{1}{2}\)-pound packages can he make?

Equations: _______________
Answer: _______________
Answer:
Total number of pounds Robert can make is 8 pounds.
Explanation:
Robert makes a package of 2\(\frac{1}{2}\) + 4 + 1\(\frac{1}{2}\) which is \(\frac{5+8+3}{2}\) which is \(\frac{16}{2}\) = 8.
Question 5.
Rachel used \(\frac{2}{3}\) of a package of cornbread mix. She will use equal parts of the leftover mix to make 2 batches of cornbread. What fraction of the original package will she use for each batch?
Equations: _________
Answer: ____________
Answer:
The fraction of the original package will she use for each batch is \(\frac{1}{3}\).
Explanation:
Given that Rachel used \(\frac{2}{3}\) of a package of cornbread mix and she will use equal parts of the leftover mix to make 2 batches of cornbread. So the fraction of the original package will she use for each batch is \(\frac{2}{3}\) ÷ 2 which is \(\frac{1}{3}\).
Problem Solving
Question 6.
Make Sense and Persevere Sandra is making vegetable soup. If she makes 12 cups of soup, how many cups of onions does she need? Use the data table on the right. Write the equations needed to solve the problem. Then solve.

Answer:
The number of cups of onions does she need is \(\frac{1}{2}\) cups.
Explanation:
Given that Sandra is making vegetable soup and if she makes 12 cups of soup, so the number of cups of onions does she need is, as \(\frac{1}{8}\) cup of onions needed for 3 cups. So for 12 cups Sandra needed \(\frac{1}{8}\) × 4 which is \(\frac{1}{2}\) cups.
Question 7.
Emily needs to buy fabric to make curtain panels for her windows. Each panel will be 4 feet long and \(\frac{1}{2}\) foot wide. Each piece of fabric that she can buy is 4 feet long and 2 feet wide. How many panels can she make from 1 piece of fabric?
Answer:
The number of panels can she make from 1 piece of fabric is 8 .
Explanation:
Here, each panel is 4 ft long and \(\frac{1}{2}\) foot wide and the piece of fabric is 4 ft long and 2 ft wide. So she can fit 4 panels and calculate this area which is
4 × \(\frac{1}{2}\) = 2ft^2
4 × 2 = 8ft^2
So 4 × 2 = 8.
Question 8.
Algebra Barry buys a package of pasta for $2.39 and a jar of tomato sauce for $3.09. He uses a $0.75 coupon and a $0.50 coupon. What is the total cost of Barry’s purchase? Write an expression to show your work.
Answer:
The expression will be $5.48 – $1.25 = $4.23.
Explanation:
Given that Barry buys a package of pasta for $2.39 and a jar of tomato sauce for $3.09, so the total cost is $2.39 + $3.09 which is $5.48 and he uses a $0.75 coupon and a $0.50 coupon and the coupons is $0.75+$0.50 = $1.25. So the expression will be $5.48 – $1.25 which is $4.23.
Question 9.
Higher Order Thinking Mr. Moss had 4 gallons of paint. He painted 8 doors. How many benches can he paint with the paint that is left? Show your work.

Answer:
Mr. Moss can paint 6 benches.
Explanation:
Given that Mr. Moss had 4 gallons of paint and he painted 8 doors. So the number of benches can he paint with the paint that is left is
8 doors/2 = 4,
4 × \(\frac{1}{2}\) = 2 gallons.
He used 2 gallons remaining for the benches.
By dividing remaining paint by paint per bench, so 2 ÷ \(\frac{1}{3}\) on solving we will get 6.
So he can paint 6 benches.
Assessment Practice
Question 10.
Sophia uses \(\frac{1}{2}\) pound of white flour to make one loaf of bread and \(\frac{1}{4}\) pound of cake flour to make one cake. Which shows how many cakes and loaves of bread Sophia can make with the amount of flour that she has?
A. 12 cakes, 4 loaves of bread
B. 6 cakes, 8 loaves of bread
C. 8 cakes, 6 loaves of bread
D. 4 cakes, 12 loaves of bread
Answer:
Sophia can make 12 cakes, 4 loaves of bread.
Explanation:
Given that white flour used for one loaf of bread is \(\frac{1}{2}\) pounds and white flour available is 2 pounds. And cake flour used to make one cake is \(\frac{1}{4}\) pounds and cake flour available is 3 pounds. Now we will divide the available amount by amount used for one.
Number of loaves of bread is 2 × \(\frac{1}{2}\) = 2 × 2 which is 4.
So, the number of loaves of bread is 4.
Number of cakes is 3 × \(\frac{1}{4}\) = 3 × 4 = 12.
So Sophia can make 12 cakes, 4 loaves of bread.
Lesson 9.8 Repeated Reasoning
Activity
Solve & Share
What do you notice about the calculations below? Make a generalization about what you notice. Complete the remaining examples.
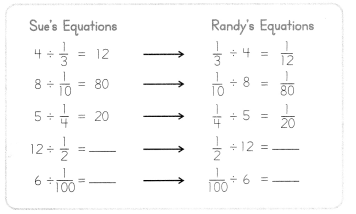
Thinking Habits
Be a good thinker! These questions can help you.
• Are any calculations repeated?
• Can I generalize from examples?
• What shortcuts do I notice?
Look Back! Generalize Test your general method by writing another pair of equations like Sue’s and Randy’s equations.
Visual Learning Bridge
Essential Question How Do You Use Repeated Reasoning When Dividing Whole Numbers and Unit Fractions?
A.
Ali partitioned a 4-foot board into \(\frac{1}{2}\)-foot pieces. She counted 8 pieces.
Then she partitioned a \(\frac{1}{2}\)-foot board into 4 equal pieces. Each piece was \(\frac{1}{8}\) of a foot.
Study the equations below. What generalizations can you make? Explain.
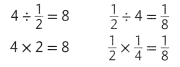
What do I need to do?
I need to understand the equations and make generalizations about them.
B.
How can I make a generalization from repeated reasoning?
I can
• look for things that repeat in a problem.
• test whether my generalization works for other numbers.
Here’s my thinking..

C.
I see that
4 ÷ 2 = 4 × 2 and \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{2}\) × \(\frac{1}{4}\)
Check if the same relationship applies to other numbers.
10 ÷ \(\frac{1}{3}\) = 30 and 10 × 3 = 30
\(\frac{1}{3}\) ÷ 10 = 30 and \(\frac{1}{3}\) × \(\frac{1}{10}\) = \(\frac{1}{30}\)
Dividing a whole number by a unit fraction is the same as multiplying a whole number by the denominator of the unit fraction.
Dividing a unit fraction by a whole number other than zero is the same as multiplying the unit fraction by a unit fraction with the whole number as the denominator.
Convince Me! Generalize Marcus made the following generalization: 12 ÷ \(\frac{1}{5}\) = \(\frac{1}{12}\) × \(\frac{1}{5}\). Is he correct? Explain.
Guided Practice
Generalize
Nathan has two 8-foot boards. He cuts one board into \(\frac{1}{4}\)-foot pieces. He cuts the other board into \(\frac{1}{2}\)-foot pieces.
Repeated reasoning can help you find a general method for solving problems that are same type.

Question 1.
Write and solve a division equation to find how many \(\frac{1}{4}\)-ft pieces can be cut from an 8-foot board. Explain your reasoning.
Answer:
Question 2.
Find how many \(\frac{1}{2}\)-ft pieces can be cut from the 8-foot board. Can you repeat the method you used in Exercise 1 to solve this problem? Explain.
Answer:
Independent Practice
Remember, the method for dividing a whole number by a unit fraction is different from the method for dividing a unit fraction by a whole number.

Generalize
A landscaper’s truck is filled with \(\frac{1}{2}\) ton of gravel. The gravel is shared equally among 3 projects.
Question 3.
Write and solve a division equation to find how much gravel each project will get. Explain your reasoning.
Answer:
Question 4.
Suppose another truck is filled with \(\frac{1}{2}\) ton of gravel. Find how much gravel each project will get if the \(\frac{1}{2}\) ton of gravel is shared equally among 8 projects. Can you repeat the method you used in Exercise 3 to solve this problem? Explain.
Answer:
Problem Solving
Performance Task
Pet Food
Pet Food Karl has a cat and a dog. He buys one bag of cat food and one bag of dog food. How many \(\frac{1}{4}\)-lb servings of cat food can he get from one bag? How many \(\frac{1}{2}\)-lb servings of dog food can he get from one bag?

Question 5.
Reasoning Karl thinks that he will be able to get more servings of dog food than cat food because the bag of dog food weighs more than the bag of cat food. Do you agree with his reasoning? Explain.
Answer:
Question 6.
Model with Math Write a division and a multiplication equation that Karl could use to find the number of servings of cat food in one bag.
Answer:
When you use repeated reasoning, you notice repetition in calculations.

Question 7.
Generalize What generalization can you make that relates the division equation to the multiplication equation you wrote in Exercise 6?
Answer:
Question 8.
Generalize Find how many servings of dog food are in one bag. Can you repeat the method you used in Exercise 6 to solve this problem? Explain.
Answer:
Topic 9 Fluency Practice
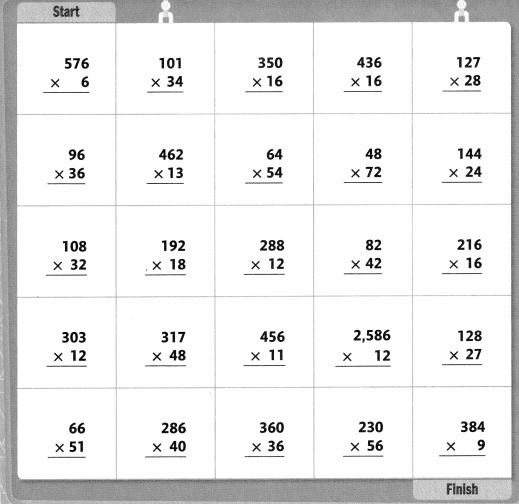
Activity
Follow the Path
Solve each problem. Follow problems with an answer of 3,456 to shade a path from START to FINISH. You can only move up, down, right, or left.

Topic 9 Vocabulary Review
Glossary
Understand Vocabulary
Write always, sometimes, or never.
Word List
• dividend
• divisor
• factor
• inverse operations
• product
• quotient
• unit fraction
Question 1.
A whole number divided by a fraction less than 1 is a mixed number. ____
Answer:
A whole number divided by a fraction less than 1 is a mixed number
Question 2.
The answer to a division problem is greater than the dividend. ___
Answer:
The answer to a division problem is greater than the dividend.
Question 3.
A fraction less than 1 divided by a whole number is a whole number. ____
Answer:
Question 4.
Dividing by \(\frac{1}{2}\) means you are finding how many halves are in the dividend. ____
Answer:
Question 5.
The dividend is the greatest number in a division problem. ____
Answer:
Question 6.
A whole number can be written as a fraction with 1 as the denominator. ____
Answer:
Draw a line from each number in Column A to the correct answer in Column B.

Answer:
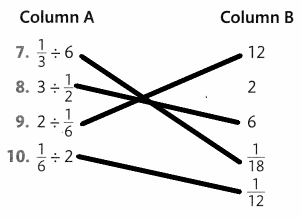
Use Vocabulary in Writing
Question 11.
Explain how to use what you know about whole number division to check your work when you divide with fractions. Use at least three terms from the Word List in your explanation.
Answer:
Topic 9 Reteaching
Set A
pages 385-388, 389-392
You can represent the fraction \(\frac{3}{4}\) as division.
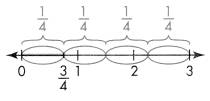
Think: \(\frac{1}{4}\) of 3 wholes.
So, \(\frac{3}{4}\) = 3 ÷ 4.
Remember that any fraction can be represented as division of the numerator by the denominator.
Write a division expression for each fraction.
Question 1.
\(\frac{7}{9}\)
Answer:
The division expression is 7 ÷ 9.
Explanation:
Given that the expression is \(\frac{7}{9}\) and the division expression is 7 ÷ 9.
Question 2.
\(\frac{11}{17}\)
Answer:
The division expression is 11 ÷ 17.
Explanation:
Given that the expression is \(\frac{11}{17}\) and the division expression is 11 ÷ 17.
Question 3.
\(\frac{10}{3}\)
Answer:
The division expression is 10 ÷ 3.
Explanation:
Given that the expression is \(\frac{10}{3}\) and the division expression is 10 ÷ 3.
Write each expression as a fraction or mixed number.
Question 4.
7 ÷ 12
Answer:
The fraction is \(\frac{7}{12}\).
Explanation:
Given that the division expression is 7 ÷ 12 and the fraction is \(\frac{7}{12}\).
Question 5.
13 ÷ 20
Answer:
The fraction is \(\frac{13}{20}\).
Explanation:
Given that the division expression is 7 ÷ 12 and the fraction is \(\frac{13}{20}\).
Question 6.
9 ÷ 5
Answer:
The fraction is 1\(\frac{4}{5}\).
Explanation:
Given that the division expression is 9 ÷ 5 and the fraction is \(\frac{9}{5}\) which is 1\(\frac{4}{5}\).
Question 7.
17 ÷ 7
Answer:
The fraction is 2\(\frac{3}{7}\).
Explanation:
Given that the division expression is 17 ÷ 7 and the fraction is \(\frac{9}{5}\) which is 2\(\frac{3}{7}\).
Set B
pages 393-396, 397-400
A 4-foot board is cut into pieces that are \(\frac{1}{2}\) foot in length. How many pieces are there?
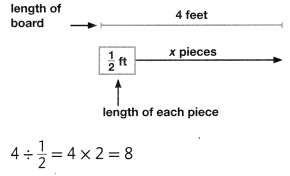
There are 8 pieces.
Remember that you can use multiplication to check your answer.
Question 1.
A 12-foot-long playground is marked off into \(\frac{1}{5}\)-foot-long sections for a game. How many sections are there?
Answer:
The number of sections will be about 2.
Explanation:
Given that a 12-foot-long playground is marked off into \(\frac{1}{5}\)-foot-long sections for a game. So the number of sections are \(\frac{1}{5}\) ÷ 12 which is 2.4.
Question 2.
A 4-pound package of peanuts is divided into \(\frac{1}{4}\)-pound packages. How many \(\frac{1}{4}\)-pound packages are there?
Answer:
Set C
pages 401-404, 405-408
Find \(\frac{1}{2}\) ÷ 4.
Use a number line. Partition \(\frac{1}{2}\) into 4 equal parts.
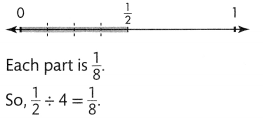
Remember that you can use objects or a number line to help you divide.
Question 1.
\(\frac{1}{3}\) ÷ 2
Answer:
Question 2.
\(\frac{1}{7}\) ÷ 7
Answer:
Question 3.
\(\frac{1}{2}\) ÷ 8
Answer:
Question 4.
\(\frac{1}{8}\) ÷ 2
Answer:
Question 5.
7 ÷ \(\frac{1}{2}\)
Answer:
Question 6.
25 ÷ \(\frac{1}{6}\)
Answer:
Set D
pages 409-412
Helen has $97 in quarters and half dollars combined. She has $13 in quarters. How many half dollars does she have? How much does Helen have in half dollars?

$97 – $13 = $84
How many \(\frac{1}{2}\) dollars are in $84?
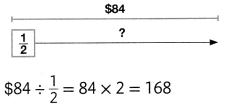
Helen has 168 half dollars.
Remember to read the problem carefully and make sure that you answer the right question and that your answer makes sense.
Question 1.
Ana participated in a charity walk. She raised $0.25 for each \(\frac{1}{2}\) mile that she walked. The first day, Āna walked 11 miles. The second day, she walked 14 miles. How much money did Ana raise?
Answer:
Question 2.
Mr. Holms used \(\frac{4}{5}\) of a carton of orange juice. He used equal amounts of the leftover juice for 2 servings. What fraction of the whole carton of juice did he use for each serving?
Answer:
Set E
pages 413-416
Think about these questions to help you use repeated reasoning when solving division problems.
Thinking Habits
• Are any calculations repeated?
• Can I generalize from examples?
• What shortcuts do I notice?

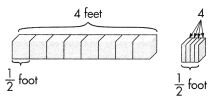
Remember that repeated reasoning can help you find a general method for solving problems that are the same type. Teresa has two 6-foot pieces of ribbon. One piece she cuts into \(\frac{1}{4}\)-foot pieces. The other piece she cuts into \(\frac{1}{2}\)-foot pieces.
Question 1.
How many \(\frac{1}{4}\)-foot pieces can she cut from one piece of ribbon? Explain.
Answer:
Question 2.
How many \(\frac{1}{2}\)-foot pieces can be cut from the 6-foot ribbon? Repeat the method you used in Exercise 1 to solve this problem.
Answer:
Topic 9 Assessment Practice
Question 1.
If the diameter of a tree trunk is growing \(\frac{1}{4}\) inch each year, how many years will it take for the diameter to grow 8 inches? Explain how you found your answer.
Answer:
Question 2.
Select all the equations that the number 4 will make true.
![]() 1 ÷ 4=?
1 ÷ 4=?
![]() 5 ÷ ? = \(\frac{4}{5}\)
5 ÷ ? = \(\frac{4}{5}\)
![]() ? ÷ = \(\frac{1}{2}\)
? ÷ = \(\frac{1}{2}\)
![]() 4 ÷ ? = 16
4 ÷ ? = 16
Answer:
Question 3.
Mrs. Webster wants to divide 6 pints of water into \(\frac{1}{3}\)-pint servings. How many servings are possible? Explain how you found your answer.
Answer:
Question 4.
How many \(\frac{1}{8}\)s are in 25? What multiplication equation can you use to check your answer?
Answer:
Question 5.
Raven is making pillows. She needs \(\frac{1}{5}\) yard of fabric for each pillow. If she has 6 yards of fabric, how many pillows can she make? Use the number line. Choose the equation that represents the problem.
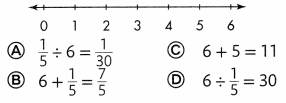
Answer:
Question 6.
A farmer owns 24 acres of land. He plans to use 6 acres for an entrance into the farm and partition the remaining land into \(\frac{1}{3}\)-acre lots. How many \(\frac{1}{3}\)-acre lots will he have?
A. 6 lots
B. 54 lots
C. 18 lots
D. 72 lots
Answer:
Question 7.
One half of a cantaloupe was shared equally among 3 people. What fraction of the whole cantaloupe did each person get? Explain how you found your answer.
Answer:
Question 8.
Cecil and three friends ran a 15-mile relay race. Each friend ran an equal distance. Use an equation to find the distance each friend ran.
Answer:
Question 9.
Match each expression to its quotient.
Answer:
Question 10.
A. Select all the expressions that are equal to \(\frac{1}{6}\).
![]() 6 ÷ 1
6 ÷ 1
![]() 1 ÷ 6
1 ÷ 6
![]() 3 ÷ 18
3 ÷ 18
![]() \(\frac{1}{3}\) ÷ 2
\(\frac{1}{3}\) ÷ 2
![]() 2 ÷ \(\frac{1}{3}\)
2 ÷ \(\frac{1}{3}\)
B. How can you check your answer?
Answer:
Question 11.
Josie has a rug with an area of 18 square feet that is 6 feet long and 3 feet wide. She will put the rug on a floor that is covered in \(\frac{1}{3}\)-square-foot tiles. How many tiles will the rug cover? What equation can you use to check your answer?
Answer:
Question 12.
Ellen says that 1\(\frac{2}{5}\) equals 5 ÷ 7. Is she correct? Explain.
Answer:
Question 13.
Corey has a piece of fabric that is \(\frac{1}{4}\) yard long. He cuts the length of the fabric into 2 equal pieces. Write an expression for the length, in yards, of each piece of fabric and solve.
Answer:
Question 14.
Look at the equations below.

A. Write numbers in the boxes above to make each equation true.
B. What generalization can you make about the equations? Explain.
Answer:
Topic 9 Performance Task
Making Cloth Dolls
Julie and Erin are making cloth dolls for the craft fair. The figure below shows some of the materials they need for each doll.
Question 1.
The Julie and Erin’s Supplies table shows the amounts they have of some of the materials they need.
Part A
If Julie and Erin use the brown yarn they have to make 4 dolls, how much yarn can they use for each doll? Show your work.
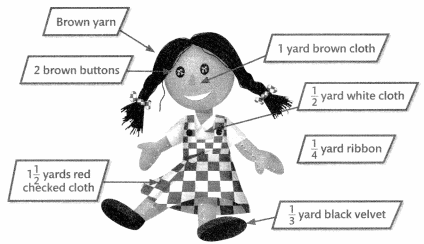
Part B
How many dolls can Julie and Erin make with the amount of black velvet they have? Complete the model to represent the problem.

Part C
How many dolls can Julie and Erin make with the amount of white cloth they have? Write an equation to represent the problem. Use multiplication to check your answer.
Part D
The ribbon used for each doll is divided into 3 equal pieces. What is the length in yards of each piece? Complete the number line to solve.
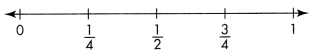
Answer:
Question 2.
Julie and Erin have 6\(\frac{1}{3}\) yards of red checked cloth. After making dresses for 4 dolls, they use the remaining cloth to make bows for the dolls’ hair. They need 8 bows for 4 dolls.
Part A
How much cloth do Julie and Erin have for each bow? Explain.
Part B
Julie wrote the equations shown. What is the pattern in her equations? Explain how to use the pattern to find the quotient you found in Part A.

Answer: