Practice with the help of enVision Math Common Core Grade 6 Answer Key Topic 1 Use Positive Rational Numbers regularly and improve your accuracy in solving questions.
enVision Math Common Core 6th Grade Answers Key Topic 1 Use Positive, Rational Numbers
Topic Essential Question How can you fluently add, subtract, multiply, and divide decimals? How can you multiply and divide fractions?
Answer:
The steps to add, subtract, multiply, and divide decimals are:
a. Write the numbers vertically with the decimals lined up (if the number is a whole number then the decimal goes on the right end of the number)
b. Add zeros to make sure there is the same number of digits in each number.
c. Add or subtract as normal.
d. Multiply just as you would if the numbers were all whole numbers and add at the end.
e. After that count how many decimals places the two factors have (start at the far right of each number) and then give the answer that the total number of decimal places.
f. To divide decimals, always use long division.
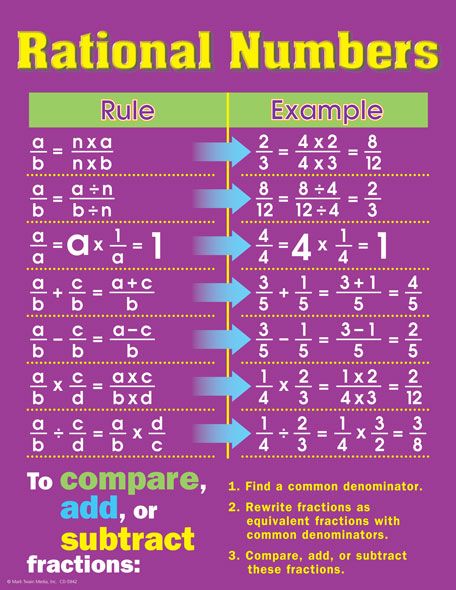
The process to multiply and divide fractions is:
a. Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
b. The first step to dividing fractions is to find the reciprocal (reverse the numerator and denominator) of the second fraction.
c. Next, multiply the two numerators. Then, multiply the two denominators.
enVision STEM Project
VIDEO
Did You Know?
Engineers design equipment to make you safer.
Engineering is the application of math and science to solve problems.
Engineers solve problems by designing and building products, materials, machinery, structures, transportation vehicles, and so many other things.

Engineers work in nearly every area from chemical and electrical engineering to biomedical and oceanographic engineering.

Engineers help keep you healthy.

Engineers find ways to improve and enhance performance of all kinds of products.

Your Task: Improve Your School
Think like an engineer! Take a walk around the inside and the outside of your school building. Make a list of specific things or areas that need improvement. Then choose one idea and do some background research to gain an understanding of factors that might impact improvement efforts. In the next topic, you and your classmates will learn about and implement the engineering design process to propose possible ways to make the improvements.
Topic 1 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
compatible numbers
decimal
divisor
estimate
quotient
Question 1.
Numbers that are easy to compute mentally are ____
Answer:
We know that,
Numbers that are easy to compute mentally are called “Compatible numbers”
Hence, from the above,
We can conclude that the best term to complete the given definition is: Compatible numbers
Question 2.
The number used to be divided is the _____
Answer:
We know that,
The number used to be divided is the “Divisor”
Hence, from the above,
We can conclude that the best term to complete the given definition is: Divisor

Question 3.
A(n) _____ is an approximate answer.
Answer:
We know that,
An “Estimate” is an approximate answer
Hence, from the above,
We can conclude that the best term to complete the given definition is: Estimate
Question 4.
The result of a division problem is a(n) ____
Answer:
We know that,
The result of a division problem is a “Quotient”
Hence, from the above,
We can conclude that the best term to complete the given definition is: Quotient
Whole Number Operations
Calculate each value.
Question 5.
![]()
Answer:
The given division problem is: 348 ÷ 4
Now,
By using the Long Division method,

Hence, from the above,
We can conclude that
The value of the quotient for the given division problem is: 87
Question 6.
9,007 – 3,128
Answer:
The given subtraction problem is: 9,007 – 3,128
So,
9,007 – 3,128 = 5,879
Hence, from the above,
We can conclude that
The result for the given subtraction problem is: 5,879
Question 7.
35 × 17
Answer:
The given multiplication problem is: 35 × 17
Now,
By using the Partial Products method,
35 × 17
= (30 + 5) × (10 + 7)
= (30 × 10) + (30 × 7) + (5 × 10) + (5 × 7)
= 300 + 210 + 50 + 35
= 595
Hence, from the above,
We can conclude that
The value of product for the given multiplication problem is: 595
Question 8.
7,964 + 3,872
Answer:
The given addition problem is: 7,964 + 3,872
So,
7,964 + 3,872 = 11,836
Hence, from the above,
We can conclude that
The result for the given addition problem is: 11,836
Question 9.
![]()
Answer:
The given division problem is: 4,638 ÷ 22
Now,
By using the Long Division method,
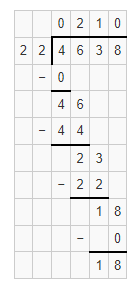
Hence, from the above,
We can conclude that
The value of quotient for the given division problem is: 210
Question 10.
181 × 42
Answer:
The given multiplication problem is: 181 × 42
Now,
By using the Partial Products method,
181 × 42
= (100 + 80 + 1) × (40 + 2)
= (100 ×40) + (100 × 2) + (80 × 40) + (80 × 2) + (1 × 40) + (1 × 2)
= 4,000 + 200 + 3,200 + 160 + 40 + 2
= 7,602
Hence, from the above,
We can conclude that
The value of the product for the given multiplication problem is: 7,602
Mixed Numbers and Fractions
Write each mixed number as a fraction. Write each fraction as a mixed number.
Question 11.
8\(\frac{1}{3}\)
Answer:
The given mixed number is: 8\(\frac{1}{3}\)
So,
To convert the given mixed number into a fraction,
8\(\frac{1}{3}\)
= \(\frac{3 × 8 + 1}{3}\)
= \(\frac{24 + 1}{3}\)
= \(\frac{25}{3}\)
Hence, from the above,
We can conclude that
The representation of the given mixed number into a fraction is: \(\frac{25}{3}\)
Question 12.
5\(\frac{3}{5}\)
Answer:
The given mixed number is: 5\(\frac{3}{5}\)
So,
To convert the given mixed number into a fraction,
5\(\frac{3}{5}\)
= \(\frac{5 × 5 + 3}{5}\)
= \(\frac{25 + 3}{5}\)
= \(\frac{28}{5}\)
Hence, from the above,
We can conclude that
The representation of the given mixed number into a fraction is: \(\frac{28}{5}\)
Question 13.
2\(\frac{5}{8}\)
Answer:
The given mixed number is: 2\(\frac{5}{8}\)
So,
To convert the given mixed number into a fraction,
2\(\frac{5}{8}\)
= \(\frac{2 × 8 + 5}{8}\)
= \(\frac{16 + 5}{8}\)
= \(\frac{21}{8}\)
Hence, from the above,
We can conclude that
The representation of the given mixed number into a fraction is: \(\frac{21}{8}\)
Question 14.
3\(\frac{4}{9}\)
Answer:
The given mixed number is: 3\(\frac{4}{9}\)
So,
To convert the given mixed number into a fraction,
3\(\frac{4}{9}\)
= \(\frac{3 × 9 + 4}{9}\)
= \(\frac{27 + 4}{9}\)
= \(\frac{31}{9}\)
Hence, from the above,
We can conclude that
The representation of the given mixed number into a fraction is: \(\frac{31}{9}\)
Question 15.
\(\frac{24}{7}\)
Answer:
The given fraction is: \(\frac{24}{7}\)
So,
To convert the given fraction into a mixed number,
Quotient\(\frac{Remainder}{Divisor}\)
So,
\(\frac{24}{7}\) = 3\(\frac{3}{7}\)
Hence, from the above,
We can conclude that
The representation of the given fraction into a mixed number is: 3\(\frac{3}{7}\)
Question 16.
\(\frac{43}{9}\)
Answer:
The given fraction is: \(\frac{43}{9}\)
So,
To convert the given fraction into a mixed number,
Quotient\(\frac{Remainder}{Divisor}\)
So,
\(\frac{43}{9}\) = 4\(\frac{7}{9}\)
Hence, from the above,
We can conclude that
The representation of the given fraction into a mixed number is: 4\(\frac{7}{9}\)
Question 17.
\(\frac{59}{8}\)
Answer:
The given fraction is: \(\frac{59}{8}\)
So,
To convert the given fraction into a mixed number,
Quotient\(\frac{Remainder}{Divisor}\)
So,
\(\frac{59}{8}\) = 7\(\frac{3}{8}\)
Hence, from the above,
We can conclude that
The representation of the given fraction into a mixed number is: 7\(\frac{3}{8}\)
Question 18.
\(\frac{32}{5}\)
Answer:
The given fraction is: \(\frac{32}{5}\)
So,
To convert the given fraction into a mixed number,
Quotient\(\frac{Remainder}{Divisor}\)
So,
\(\frac{32}{5}\) = 6\(\frac{2}{5}\)
Hence, from the above,
We can conclude that
The representation of the given fraction into a mixed number is: 6\(\frac{2}{5}\)
Verbal Expressions
Question 19.
How are the expressions “\(\frac{1}{4}\) of 12″ and “12 divided by 4” related?
Answer:
The given expressions are: \(\frac{1}{4}\) × 12 and 12 ÷ 4
So,
We can write
12 ÷ 4
= \(\frac{12}{4}\)
= 12 × \(\frac{1}{4}\)
Hence,f rom the above,
We can conclude that the given expressions 12 × \(\frac{1}{4}\) and 12 ÷ 4 are the same
Decimals
Question 20.
What decimal does this model represent? Explain.

Answer:
The given model is:

Now,
From the given model,
We can observe that
The total number of parts are: 100
The number of shaded parts is: 73
So,
The fraction of the shaded part in the given model = \(\frac{Shaded parts}{Total parts}\)
= \(\frac{73}{100}\)
= 0.73
Hence, from the above,
We can conclude that
The decimal number that the given model represents is: 0.73
Language Development
Fill in the boxes with terms and phrases related to Decimals and Fractions from the given bank. Include illustrations or examples.
annex zeroes (1-1)
compatible numbers (1-1)
decimal point (1-1)
estimate (1-1)
hundredths (1-1)
line up place value (1-1)
rounding (1-1)
tenths (1-1)
algorithm (1-2)
the denominator (1-3)
mixed number (1-3)
the numerator (1-3)
unit fraction (1-3)
reciprocal (1-4)
rewrite (1-4)
multistep problems (1-7)

Topic 1 PICK A PROJECT
PROJECT 1A
What is the most challenging board game you have ever played?
PROJECT: MAKE YOUR OWN BOARD GAME

PROJECT 1B
What is your favorite party food?
PROJECT: PLAN THE MENU FOR A SCHOOL FUNDRAISER

PROJECT 1C
If you planted a garden, what would be in it?
PROJECT: DESIGN A VEGETABLE AND HERB GARDEN

PROJECT 10D
How much food does a tiger eat?
PROJECT: PRESENT A PROPOSAL FOR A TIGER EXHIBIT

Lesson 1.1 Fluently Add, Subtract and Multiply Decimals
ACTIVITY
Solve & Discuss It!
Maxine is making a model windmill for a science fair. She is connecting 4 cardboard tubes together vertically. Each tube is 0.28 meters in length. What is the combined measure of the connected tubes?
Use Appropriate Tools You can use decimal grids to calculate with decimals.


Answer:
It is given that
Maxine is making a model windmill for a science fair. She is connecting 4 cardboard tubes together vertically. Each tube is 0.28 meters in length
So,
The combined measure of the connected tubes = (The number of cardboard tubes) × (The length of each tube)
= 4 × 0.28
= 4 × (0.20 + 0.08)
= (4 × 0.20) + (4 × 0.08)
= 0.8 + 0.32
= 1.12 meters
So,
The representation of the length of 4 cardboard tubes in the decimal grid is:
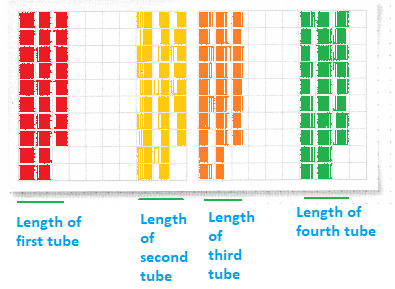
Hence, from the above,
We can conclude that
The combined measure of the 4 connected tubes is: 1.12 meters
Focus on math practices Look for Relationships Suppose that Maxine made another windmill model by connecting 4 cardboard tubes that are each 2.8 meters long. What is the combined measure of this model? What relationships do you see in the factors you used here and above? Explain how this helps you solve the problem.
Answer:
It is given that
Maxine made another windmill model by connecting 4 cardboard tubes that are each 2.8 meters long
So,
The combined measure of another model made by Maxine = (The number of cardboard tubes of another model) × (The length of each tube)
= 4 × 2.8
= 4 × (2 + 0.8)
= (4 × 2) + (4 × 0.8)
= 8 + 3.2
= 11.2 meters
Now,
From the above problem,
We can observe that
The combined measure of 4 connected tubes is: 1.12 meters
So,
When we multiply 1.12 meters by 10,
We will get the combined measure of the other model made by Maxine
Hence, from the above,
We can conclude that
The relationship do you see in the factors you used in this problem and the above problem is:
(The combined measure of 4 connected tubes of the above problem) × 10 = (The combined measure of the 4 connected tubes of this problem)
? Essential Question How can you add, subtract, and multiply with decimals?
Answer:
The steps to add, subtract, multiply, and divide decimals are:
a. Write the numbers vertically with the decimals lined up (if the number is a whole number then the decimal goes on the right end of the number)
b. Add zeros to make sure there is the same number of digits in each number.
c. Add or subtract as normal.
d. Multiply just as you would if the numbers were all whole numbers and add at the end.
e. After that count how many decimals places the two factors have (start at the far right of each number) and then give the answer that the total number of decimal places.
f. To divide decimals, always use long division.
Try It!
Suppose that Martin finished the race 0.47 seconds after Kim. What was Martin’s time in the race? Use an estimate to check that your answer is reasonable.
Answer:
It is given that
Martin finished the race 0.47 seconds after Kim
Now,
We know that,
The time Kim took to complete the race is: 50.9 seconds
So,
The time took by Martin in the race = (The time took by Kim to complete the race) + (The more time taken by Martin to finish the race more than Kim)
= 50.9 + 0.47
= 50.90 + 0.47
= 51.37 seconds
Now,
Estimate:
The time took by Kim to complete the race is: 51 seconds
The more time taken by Martin to finish the race more than Kim is: 0.50 seconds
So,
The time took by Martin to complete the race = (The time took by Kim in the race) + (The more time taken by Martin to finish the race more than Kim)
= 51 + 0.50
= 51.50 seconds
Hence, from the above,
We can conclude that
The time took by Martin in the race is: 51.37 seconds
Since the estimated time and the exact time is near, your answer is reasonable
Convince Me! If Martin finished the race 0.267 seconds after Kim, you would need to add 0.267 to 50.9 to solve the problem. How is adding 0.267 to 50.9 different from adding 0.26 to 50.9?
Answer:
It is given that
If Martin finished the race 0.267 seconds after Kim, you would need to add 0.267 to 50.9 to solve the problem
So,
The time took by Martin in the race = (The time took by Kim in the race) + (The more time taken by Martin to finish the race more than Kim)
= 50.9 + 0.267
= 50.900 + 0.267
= 51.167 seconds ——(1)
So,
The time took by Martin in the race = (The time took by Kim in the race) + (The more time taken by Martin to finish the race more than Kim)
= 50.9 + 0.26
= 50.90 + 0.26
= 51.16 seconds —— (2)
So,
When we compare eq (1) and eq (2),
We can observe that
eq (1) gives the more accurate time when compared to eq (2)
Hence, from the above,
We can conclude that
The difference between the results of eq(1) and eq (2) is the accuracy and precision
Try It!
Suppose that Katie finished the race 0.13 seconds before Amy. What was Katie’s time in the race? Use an estimate to check that your answer is reasonable.
Answer:
It is given that
Katie finished the race 0.13 seconds before Amy
Now,
We know that,
The time Amy took to complete the race is: 20.7 seconds
So,
The time took by Katie in the race = (The time took by Amy to complete the race) – (The time taken by Katie to finish the race before Amy)
= 20.7 – 0.13
= 20.70 – 0.13
= 20.57 seconds
Now,
Estimate:
The time took by Amy to complete the race is: 21 seconds
The time is taken by Katie to finish the race before Amy is: 0.10 seconds
So,
The time took by Katie to complete the race = (The time took by Amy in the race) + (The time taken by Katie to finish the race before Amy)
= 21 – 0.10
= 21.00 – 0.10
= 20.90 seconds
Hence, from the above,
We can conclude that
The time took by Martin in the race is: 20.57 seconds
Since the estimated time and the exact time is near, your answer is reasonable
Try It!
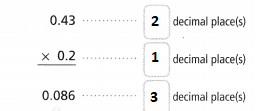
How do you determine where to place the decimal point in the product?
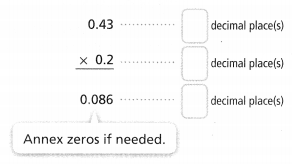
Answer:
We know that,
Decimals are multiplied as if they were whole numbers, and then the decimal point is placed in the product. To find out where the decimal point should be placed, count the number of decimal places after the decimal point in each factor.
Hence,
The representation of the decimal point in the given product is:
KEY CONCEPT

Do You Understand?
Question 1.
? Essential Question How can you add, subtract, and multiply with decimals?
Answer:
The steps to add, subtract, multiply, and divide decimals are:
a. Write the numbers vertically with the decimals lined up (if the number is a whole number then the decimal goes on the right end of the number)
b. Add zeros to make sure there is the same number of digits in each number.
c. Add or subtract as normal.
d. Multiply just as you would if the numbers were all whole numbers and add at the end.
e. After that count how many decimals places the two factors have (start at the far right of each number) and then give the answer that the total number of decimal places.
f. To divide decimals, always use long division.
Question 2.
Generalize How is adding and subtracting decimals similar to and different from adding and subtracting whole numbers?
Answer:
We know that,
Adding and subtracting decimal numbers, numbers with a decimal point is just like adding and subtracting whole numbers.
The only difference is that we line up the numbers according to the decimal point.
For subtraction, the number we are subtracting goes to the bottom.
Question 3.
What can you do if a decimal product has final zeros to the right of the decimal point?
Answer:
We can drop the zeros on the right once the decimal point has been placed in the product. If the number of decimal places is greater than the number of digits in the product, you can insert zeros in front of the product.
Question 4.
Critique Reasoning Diego says that the product of 0.51 × 2.427 will have five decimal places. Is Diego correct? Explain.
Answer:
It is given that
Diego says that the product of 0.51 × 2.427 will have five decimal places
Now,
We know that,
Decimals are multiplied as if they were whole numbers, and then the decimal point is placed in the product. To find out where the decimal point should be placed, count the number of decimal places after the decimal point in each factor.
So,
In
0.51 × 2.427,
We can observe that
There are 2 decimal places in 0.51
There are 3 decimal places in 2.427
So,
In 0.51 × 2,427,
There are 5 decimal places
Hence, from the above,
We can conclude that Diego is correct
Do You Know How?
In 5-10, find each sum or difference.
Question 5.
5.9 + 2.7
Answer:
The given addition problem is: 5.9 + 2.7
So,
By using the Long Addition,
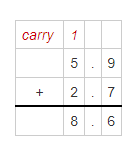
Hence, from the above,
We can conclude that the value of the given addition problem is: 8.6
Question 6.
4.01 – 2.95
Answer:
The given subtraction problem is: 4.01 – 2.95
So,
By using the Long Subtraction,

Hence, from the above,
We can conclude that the value of the given subtraction problem is: 1.06
Question 7.
6.8 – 1.45
Answer:
The given subtraction problem is: 6.8 – 1.45
So,
By using the Long Subtraction,
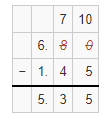
Hence, from the above,
We can conclude that the value of the given subtraction problem is: 5.35
Question 8.
9.62 – 0.3
Answer:
The given subtraction problem is: 9.62 – 0.3
So,
By using the Long Subtraction,
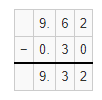
Hence, from the above,
We can conclude that the value of the given subtraction problem is: 9.32
Question 9.
2.57 + 7.706
Answer:
The given addition problem is: 2.57 + 7.706
So,
By using the Long Addition,
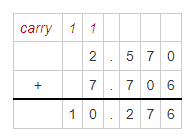
Hence, from the above,
We can conclude that the value of the given addition problem is: 10.276
Question 10.
15 – 6.108
Answer:
The given subtraction problem is: 15 – 6.108
So,
By using the Long Subtraction,
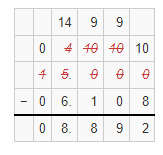
Hence, from the above,
We can conclude that the value of the given subtraction problem is: 8.892
In 11-16, place the decimal point in the correct location in the product.
Question 11.
4 × 0.94 = 376
Answer:

Hence, from the above,
We can conclude that
4 × 0.94 = 3.76
Question 12.
5 × 0.487 = 2435
Answer:

Hence, from the above,
We can conclude that
5 × 0.487 = 2.435
Question 13.
3.4 × 6.8 = 2312
Answer:

Hence, from the above,
We can conclude that
3.4 × 6.8 = 23.12
Question 14.
3.9 × 0.08 = 312
Answer:

Hence, from the above,
We can conclude that
3.9 × 0.08 = 0.312
Question 15.
0.9 × 0.22 = 198
Answer:

Hence, from the above,
We can conclude that
0.9 × 0.22 = 0.198
Question 16.
9 × 1.2 = 108
Answer:

Hence, from the above,
We can conclude that
9 × 1.2 = 10.8
In 17 and 18, find each product.
Question 17.
5.3 × 2.7
Answer:
The given multiplication equation is: 5.3 × 2.7
So,
By using the Long Multiplication method,

Hence, from the above,
We can conclude that
The value of the product for the given multiplication equation is: 14.31
Question 18.
8 × 4.09
Answer:
The given multiplication is: 8 × 4.09
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
The value of the product for the given multiplication equation is: 32.72
Practice & Problem Solving
Scan for Multimedia
In 19-27, find each sum or difference.
Question 19.
2.17 – 0.8
Answer:
The given subtraction equation is: 2.17 – 0.8
So,
By using the Long subtraction,
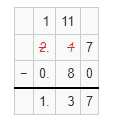
Hence, from the above,
We can conclude that
2.17 – 0.8 = 1.37
Question 20.
4.3 + 4.16
Answer:
The given addition equation is: 4.3 + 4.16
So,
By using the Long Addition,
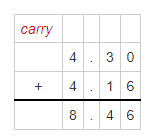
Hence, from the above,
We can conclude that
4.3 + 4.16 = 8.46
Question 21.
46.91 – 28.7
Answer:
The given subtraction equation is: 46.91 – 28.7
So,
By using the Long subtraction,
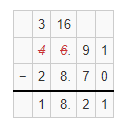
Hence, from the above,
We can conclude that
46.91 – 28.7 = 18.21
Question 22.
4.815 + 2.17
Answer:
The given addition equation is: 4.815 + 2.17
So,
By using the Long Addition,
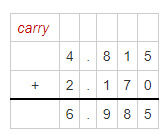
Hence, from the above,
We can conclude that
4.815 + 2.17 = 6.985
Question 23.
5.1 – 0.48
Answer:
The given subtraction equation is: 5.1 – 0.48
So,
By using the Long subtraction,

Hence, from the above,
We can conclude that
5.1 – 0.48 = 4.62
Question 24.
27 + 0.185
Answer:
The given addition equation is: 27 + 0.185
So,
By using the Long Addition,

Hence, from the above,
We can conclude that
27 + 0.185 = 27.185
Question 25.
9.501 – 9.45
Answer:
The given subtraction equation is: 9.501 – 9.45
So,
By using the Long subtraction,
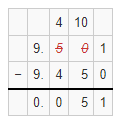
Hence, from the above,
We can conclude that
9.501 – 9.45 = 0.051
Question 26.
14 + 9.8
Answer:
The given addition equation is: 14 + 9.8
So,
By using the Long Addition,
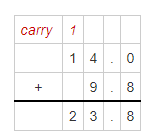
Hence, from the above,
We can conclude that
14 + 9.8 = 23.8
Question 27.
12.65 + 14.24
Answer:
The given addition equation is: 12.65 + 14.24
So,
By using the Long Addition,
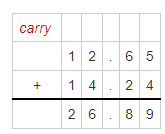
Hence, from the above,
We can conclude that
12.65 + 14.24 = 26.89
In 28-33, find each product.
Question 28.
7 × 0.5
Answer:
The given multiplication equation is: 7 × 0.5
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
7 × 0.5 = 3.5
Question 29.
12 × 0.08
Answer:
The given multiplication equation is: 12 × 0.08
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
12 × 0.08 = 0.96
Question 30.
24 × 0.17
Answer:
The given multiplication equation is: 24 × 0.17
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
24 × 0.17 = 4.08
Question 31.
0.4 × 0.17
Answer:
The given multiplication equation is: 0.4 × 0.17
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
0.4 × 0.17 = 0.068
Question 32.
1.9 × 0.46
Answer:
The given multiplication is: 1.9 × 0.46
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
1.9 × 0.46 = 0.874
Question 33.
3.42 × 5.15
Answer:
The given multiplication is: 3.42 × 5.15
So,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
3.42 × 5.15 = 17.6130
Question 34.
Write an equation that illustrates the following: A number with two decimal places multiplied by a number with one decimal place. The product has only two nonzero digits.
Answer:
It is given that
A number with two decimal places is multiplied by a number with one decimal place. The product has only two nonzero digits.
Now,
Let the number with two decimal places be: 2.55
Let the number with one decimal be: 1.6
So,
We have to find the product of 2.55 × 1.6
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
The multiplication equation with the product value that has only two non-zero digits is: 2.55 × 1.6
Question 35.
The Bright-o Shampoo Factory includes 1.078 ounces of vanilla oil in a 6.35-ounce bottle of shampoo. How much of the bottle of shampoo is NOT vanilla oil?
Answer:
It is given that
The Bright-o Shampoo Factory includes 1.078 ounces of vanilla oil in a 6.35-ounce bottle of shampoo.
So,
The total content present in Bright-o-Shampoo = (The amount of vanilla oil) + (The amount of other content)
Now,
Let the amount of other content be: x
So,
6.35 = 1.078 + x
So,
x = 6.35 – 1.078
Now,
By using the Long Subtraction,
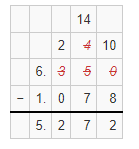
Hence, from the above,
We can conclude that
The amount of the bottle of a shampoo that is not vanilla oil is: 5.272 ounces
In 36-38, use the graph to solve.
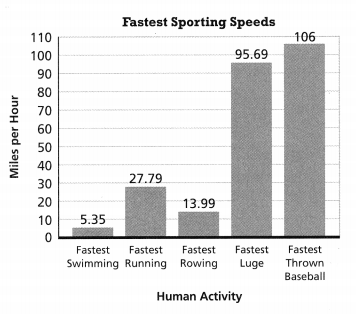
Question 36.
The fastest speed a table tennis ball has been hit is about 13.07 times as fast as the speed for the fastest swimming. What is the speed of the table tennis ball?
Answer:
It is given that
The fastest speed a table tennis ball has been hit is about 13.07 times as fast as the speed for the fastest swimming.
Now,
The given graph is:

Now,
The speed of the table tennis ball = 13.07 × (The speed for the fastest swimming)
= 13.07 × 5.35
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that the speed of the tennis ball is about 70 miles per hour
Question 37.
Look for Relationships How fast would 1.5 times the fastest rowing speed be? Before you solve, tell the number of decimal places in your answer.
Answer:
The given graph is:

Now,
From the given graph,
We can observe that
The fastest rowing speed is: 13.99 miles per hour
So,
The speed of 1.5 times the fastest rowing speed = 1.5 × 13.99
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
1.5 times of the fastest rowing speed is: 209.85 miles per hour
Question 38.
Which activity has a recorded speed about 7 times as fast as the fastest rowing speed?
Answer:
The given graph is:

Now,
From the given graph,
We can observe that
The fastest rowing speed is: 13.99 miles per hour
Now,
7 times of the fastest rowing speed is: 7 × 13.99
Now,
By using the Long Multiplication,
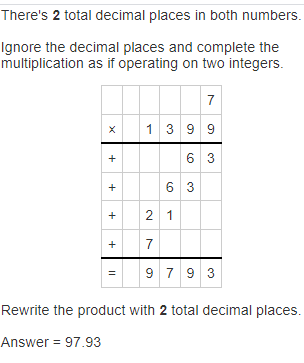
So,
The fastest rowing speed is about: 98 miles per hour
Now,
From the given graph,
We can observe that
The fastest Luge is: 95.69 miles per hour
Hence, from the above,
We can conclude that
“Fastest Luge” has a recorded speed about 7 times as fast as the fastest rowing speed
Question 39.
Matthew a pennant, and a hat. He paid with a $50 bill and some money he borrowed from his friend. If Matthew got $6.01 in change from the cashier, how much did he borrow from his friend to pay for all the items?

Answer:
It is given that
Matthew a pennant, and a hat. He paid with a $50 bill and some money he borrowed from his friend. If Matthew got $6.01 in change from the cashier
Now,
Let the amount Matthew borrowed from his friend be: x
So,
According to the given information,
The amount Matthew borrowed from his friend = (The amount of bill) – (The amount Matthew got in change from the cashier)
x = $50 – $6.01
Now,
By using the Long Subtraction,
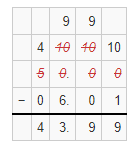
Hence, from the above,
We can conclude that
The amount Matthew borrowed from his friend is: $43.99
Question 40.
Anna’s running time for a race was 23.1 seconds. Another runner’s time was 5.86 seconds faster. Find the other runner’s time.
Answer:
It is given that
Anna’s running time for a race was 23.1 seconds. Another runner’s time was 5.86 seconds faster
So,
The time took by another runner = 5.86 + (Anna’s running time)
= 5.86 + 23.1
Now,
By using the Long Addition,
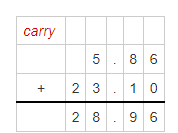
Hence, from the above,
We can conclude that
The time took by another runner is: 28.96 seconds
Question 41.
Higher-Order Thinking Explain why 0.25 × 0.4 has only one decimal place in the product.
Answer:
The given multiplication equation is: 0.25 × 0.4
Now,
By using the Long Multiplication,

Now,
We know that,
In the decimal numbers,
If there are zeros on the right side, then we can neglect those zeros
So,
0.100 can become 0.1
Hence, from the above,
We can conclude that
0.25 × 0.4 has only one decimal place in the product because of the following property:
In the decimal numbers,
If there are zeros on the right side, then we can neglect those zeros
Question 42.
The wings of some hummingbirds beat 52 times per second when hovering. If a hummingbird hovers for 35.5 seconds, how many times do its wings beat?
Answer:
It is given that
The wings of some hummingbirds beat 52 times per second when hovering and a hummingbird hovers for 35.5 seconds
So,
The number of times the wings of a hummingbird beat in 35.5 seconds = (The time a hummingbird hovers) × (The number of times the wings of a hummingbird beat)
= 35.5 × 52
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
The number of times the wings of a hummingbird beat in 35.5 seconds is: 1,846 times
Question 43.
The students at Walden Middle School are selling tins of popcorn to raise money for new uniforms. They sold 42 tins in the first week. How much money did they make in the first week?

Answer:
It is given that
The students at Walden Middle School are selling tins of popcorn to raise money for new uniforms. They sold 42 tins in the first week
Now,
The given figure is:

So,
The money did the students at Walden Middle School made in the first week = (The number of tins) × (The cost of each tin)
= 42 × $9.25
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
The money did the students at Walden Middle School made in the first week is: $388.50
Assessment Practice
Question 44.
Use the information in the table to solve each problem.
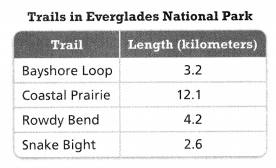
PART A
What is the combined length in kilometers of the Bayshore Loop trail and the Rowdy Bend trail?
Answer:
The given information is:

So,
The combined length of the Bayshore Loop trail and the Rowdy Bend trail = 3.2 + 4.2
Now,
By using the Long Addition,
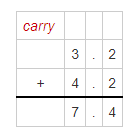
Hence, from the above,
We can conclude that
The combined length of the Bayshore Loop trail and the Rowdy Bend trail is: 7.4 Kilometers
PART B
How many kilometers longer is the Coastal Prairie trail than the Snake Bight trail?
Answer:
The given information is:

So,
The difference between the length of the Coastal Prairie trail and the Snake Bight trail = 12.1 – 2.6
Now,
By using the Long Subtraction,
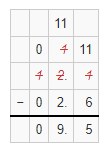
Hence, from the above,
We can conclude that
The Coastal Prairie trail is 9.5 Kilometers longer than the Snake Bight trail
Lesson 1.2 Fluently Divide Whole Numbers and Decimals
Solve & Discuss It!
Some friends went to lunch and split the bill equally. If each person paid $6.75, how many people went to lunch? Use a diagram or equation to explain your thinking.

Answer:
Some friends went to lunch and split the bill equally and each person paid $6.75
Now,
The given figure is:

So,
The number of people that went for lunch – (The total bill) ÷ (The amount paid by each person)
= \(\frac{$27}{$6.75}\)
Now,
By using the Long Division,
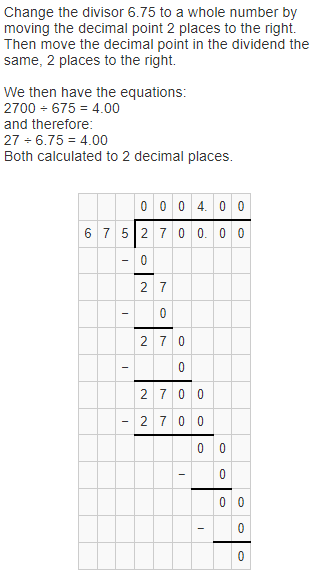
Hence, from the above,
We can conclude that
The number of people that went for lunch is: 4 people
Reasoning How can you use reasoning to create a representation of the problem?
Answer:
Reasoning in maths is the process of applying logical thinking to a situation to derive the correct problem-solving strategy for a given question and using this method to develop and describe a solution. Put more simply, mathematical reasoning is the bridge between fluency and problem-solving.
Focus on math practices
Reasoning Suppose $7.00 was added to the bill for a dessert that everyone shared. How much more does each person have to pay?
Answer:
It is given that
Suppose $7.00 was added to the bill for a dessert that everyone shared
So,
The total bill = $27 + $7
= $34
So,
The amount each person has to pay = (The total bill) ÷ (The number of people that the bill was split)
= \(\frac{$34}{4}\)
Now,
By using the Long Division,
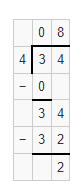
Hence, from the above,
We can conclude that
The amount that each person has to pay is about $8
? Essential Question How can you divide whole numbers and decimals?
Answer:
The steps to divide decimals by Whole Numbers are:
a. Bring down the next digit from the dividend. Continue dividing.
b. Place the decimal point in the quotient.
c. Check your answer: Multiply the divisor by the quotient to see if you get the dividend.
Scan for Multimedia
Try It!
Workers at an electronics company pack 2,610 smartphones in the boxes. Each box holds 9 smartphones. How many boxes do they fill?
Answer:
It is given that
Workers at an electronics company pack 2,610 smartphones in the boxes. Each box holds 9 smartphones
So,
The number of boxes does the workers fill = (The total number of smartphones in the box) ÷ (The number of smartphones each box holds)
= \(\frac{2,610}{9}\)
Now,
By using the Long Division,
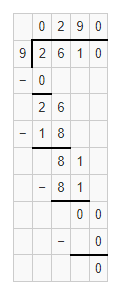
Hence, from the above,
We can conclude that
The number of boxes does the workers fill are: 290 boxes
Convince Me! Why is the first digit of the quotient in the Try It! not in the same place as the first digit of the quotient in Example 1?
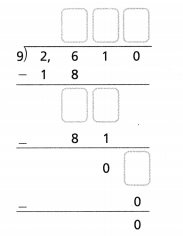
Answer:
We know that,
Use place value to place the first digit. Look at the first digit. If the first digit is less than the divisor, then the first digit of the quotient will be in the hundreds place. If the first digit is greater than or equal to the divisor, then the first digit of the quotient will be in the thousands place
Hence, from the above,
We can conclude that the first digit of the quotient in the Try It! is not in the same place as the first digit of the quotient in Example 1
Try It!
Divide.
a. 65 ÷ 8
Answer:
The given division equation is: 65 ÷ 8
Now,
By using the Long Division,
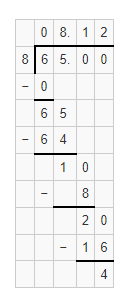
Hence, from the above,
We can conclude that
65 ÷ 8 = 8.12
b. 14.4 ÷ 8
Answer:
The given division equation is: 14.4 ÷ 8
Now,
By using the Long Division,
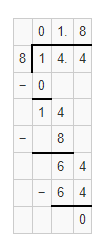
Hence, from the above,
We can conclude that
14.4 ÷ 8 = 1.8
c. 128.8 ÷ 1.4
Answer:
The given division equation is: 128.8 ÷ 1.4
Now,
By using the Long Division,
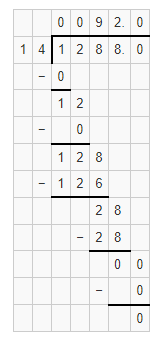
Hence, from the above,
We can conclude that
128.8 ÷ 1.4 = 92
KEY CONCEPT
To divide by a decimal, rewrite the decimal so that you are dividing by a whole number. Multiply both the divisor and the dividend by the same power of 10. Then divide as you would with whole numbers.
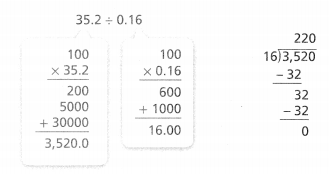
Do You Understand?
Question 1.
? Essential Question How can you divide whole numbers and decimals?
Answer:
The steps to divide decimals by Whole Numbers are:
a. Bring down the next digit from the dividend. Continue dividing.
b. Place the decimal point in the quotient.
c. Check your answer: Multiply the divisor by the quotient to see if you get the dividend.
Question 2.
When dividing with decimals, why is it necessary to multiply both the divisor and the dividend by the same power of 10?
Answer:
In cases like this, you can use powers of 10 to help create an easier problem to solve.
Example:
In this case, you can multiply the divisor, 0.3, by 10 to move the decimal point 1 place to the right. If you multiply the divisor by 10, then you also have to multiply the dividend by 10 to keep the quotient the same.
Question 3.
Use Structure Explain how you can decide where to place the first digit of the quotient for 6,139 ÷ 153.
Answer:
We know that,
Use place value to place the first digit. Look at the first digit. If the first digit is less than the divisor, then the first digit of the quotient will be in the hundreds place. If the first digit is greater than or equal to the divisor, then the first digit of the quotient will be in the thousands place
Hence, from the above,
We can conclude that
For 6,139 ÷ 153,
The first digit of the quotient will be in the hundred’s place
Question 4.
Use Structure How do you know where to place the decimal point in the quotient when dividing a decimal by a whole number?
Answer:
We know that,
The decimal point in the quotient is directly above the decimal point in the dividend. To divide a decimal by a whole number, we place the decimal point in the quotient above the decimal point in the dividend and then divide as usual.
Do You Know How?
Question 5.
Answer:
The given division equation is: 9,853 ÷ 48
So,
By using the Long Division,
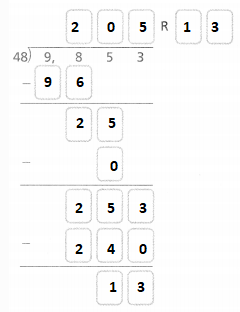
Hence, from the above,
We can conclude that
9,853 ÷ 48 = 205 R 13
In 6 and 7, divide. Record remainders.
Question 6.
2,789 ÷ 36
Answer:
The given division equation is: 2,789 ÷ 36
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
2,879 ÷ 36 = 77 R 17
The remainder for the given division equation is: 17
Question 7.
![]()
Answer:
The given division equation is: 153 ÷ 18
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
153 ÷ 18 = 8 R 8
The remainder for the given division equation is: 8
In 8 and 9, divide. Write remainders as decimals.
Question 8.
![]()
Answer:
The given division equation is: 139 ÷ 4
Now,
By using the Long Division,
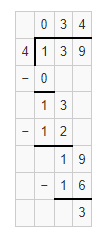
Hence, from the above,
We can conclude that
139 ÷ 4 = 34 R 3
The remainder for the given division equation is: 3
Question 9.
215 ÷ 2
Answer:
The given division equation is: 215 ÷ 2
Now,
By using the Long Division,
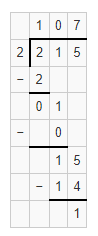
Hence, from the above,
We can conclude that
215 ÷ 2 = 107 R 1
The remainder for the given division equation is: 1
In 10 and 11, divide.
Question 10.
![]()
Answer:
The given division equation is: 34.75 ÷ 5
Now,
By using the Long Division,
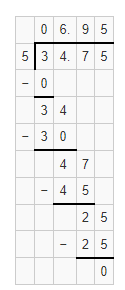
Hence, from the above,
We can conclude that
34.75 ÷ 5 = 6.95
Question 11.
215.25 ÷ 5
Answer:
The given division equation is: 215.25 ÷ 5
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
215.25 ÷ 5 = 43.05
In 12 and 13, divide. Annex zeros if needed to write remainders as decimals.
Question 12.
5.3 ÷ 0.2
Answer:
The given division equation is: 5.3 ÷ 0.2
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
5.3 ÷ 0.2 = 26.5
Question 13.
![]()
Answer:
The given division equation is: 8.9 ÷ 0.4
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
8.9 ÷ 0.4 = 22.2
Practice & Problem Solving
Scan for Multimedia
Leveled Practice
In 14 and 15, divide.
Question 14.
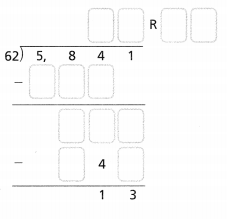
Answer:
The given division equation is: 5,841 ÷ 62
Now,
By using the Long Division,
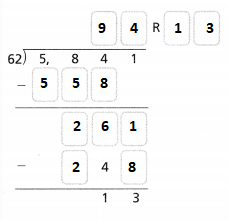
Hence, from the above,
We can conclude that
5,841 ÷ 62 = 94 R 13
Question 15.
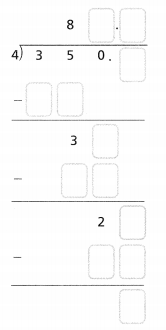
Answer:
The given division equation is: 350 ÷ 4
Now,
By using the Long Division,
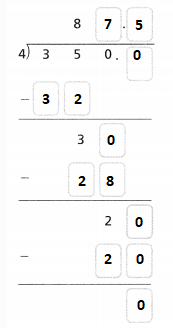
Hence, from the above,
We can conclude that
350 ÷ 4 = 87.5
In 16-19, divide. Record remainders.
Question 16.
2,593 ÷ 21
Answer:
The given division equation is: 2,593 ÷ 21
Now,
By using the Long Division,
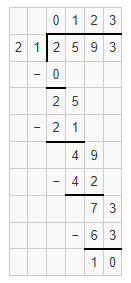
Hence, from the above,
We can conclude that
2,593 ÷ 21 = 123 R 10
The remainder for the given division equation is: 10
Question 17.
![]()
Answer:
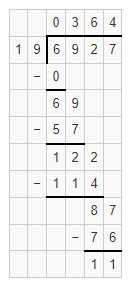
The given division equation is: 6,927 ÷ 19
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
6,927 ÷ 19 = 364 R 11
The remainder for the given division equation is: 11
Question 18.
![]()
Answer:
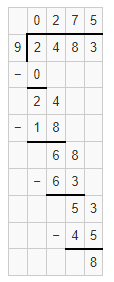
The given division equation is: 2,483 ÷ 9
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
2,483 ÷ 9 = 276 R 8
The remainder for the given division equation is: 8
Question 19.
968 ÷ 38
Answer:
The given division equation is: 968 ÷ 38
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
968 ÷ 38 = 25 R 18
The remainder for the given division equation is: 25 R 18
In 20-23, divide. Write remainders as decimals.
Question 20.
![]()
Answer:
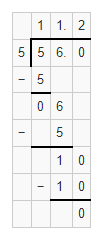
The given division equation is: 56 ÷ 5
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
56 ÷ 5 = 11.2
Question 21.
232 ÷ 40
Answer:
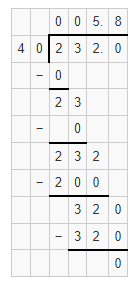
The given division equation is: 232 ÷ 40
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
232 ÷ 40 = 5.8
Question 22.
44 ÷ 10
Answer:
The given division equation is: 44 ÷ 10
Now,
By using the Long Division,
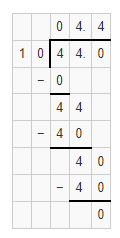
Hence, from the above,
We can conclude that
44 ÷ 10 = 4.4
Question 23.
![]()
Answer:
The given division equation is: 2,626 ÷ 4
Now,
By using the Long Division,
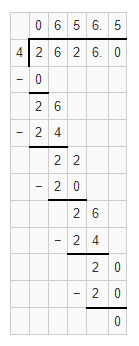
Hence, from the above,
We can conclude that
2,626 ÷ 4 = 656.5
In 24-27, divide.
Question 24.
![]()
Answer:
The given division equation is: $54.18 ÷ 6
Now,
By using the Long Division,
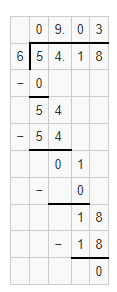
Hence, from the above,
We can conclude that
$54.18 ÷ 6 = $9.03
Question 25.
187.2 ÷ 8
Answer:
The given division equation is: 187.2 ÷ 8
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
187.2 ÷ 8 = 23.4
Question 26.
![]()
Answer:
The given division equation is: 6.3 ÷ 7
Now,
By using the Long Division,
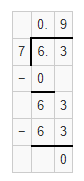
Hence, from the above,
We can conclude that
6.3 ÷ 7 = 0.9
Question 27.
137.5 ÷ 5
Answer:
The given division equation is: 137.5 ÷ 5
Now,
By using the Long Division,
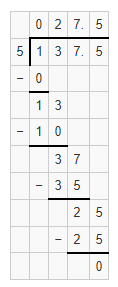
Hence, from the above,
We can conclude that
137.5 ÷ 5 = 27.5
In 28-31, divide. Annex zeros if needed to write remainders as decimals.
Question 28.
6.4 ÷ 0.8
Answer:
The given division equation is: 6.4 ÷ 0.8
Now,
By using the Long Division,
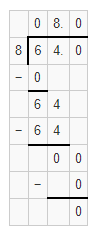
Hence, from the above,
We can conclude that
6.4 ÷ 0.8 = 8
Question 29.
![]()
Answer:
The given division equation is: 0.2430 ÷ 0.6
Now,
By using the Long Division,
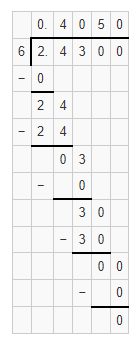
Hence, from the above,
We can conclude that
0.2430 ÷ 0.6 = 0.405
Question 30.
52.056 ÷ 7.23
Answer:
The given division equation is: 52.056 ÷ 7.23
Now,
By using the Long Division,
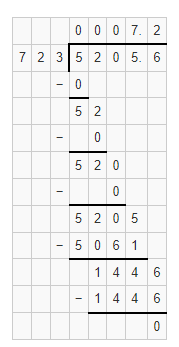
Hence, from the above,
We can conclude that
52.056 ÷ 7.23 = 7.2
Question 31.
![]()
Answer:
The given division equation is: 9.089 ÷ 0.745
Now,
By using the Long Division,
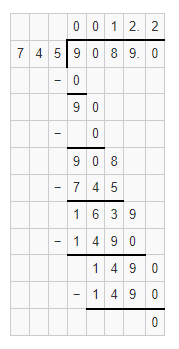
Hence, from the above,
We can conclude that
9.089 ÷ 0.745 = 12.2
Question 32.
Ants are one of the Thorny Devil lizard’s favorite foods. It can eat 45 ants per minute. How long would it take this lizard to eat 1,080 ants? Express your answer in minutes.
Answer:
It is given that
Ants are one of the Thorny Devil lizard’s favorite foods. It can eat 45 ants per minute.
So,
The time it will take for Thorny Devil lizard to eat 1,080 ants = (The total number of ants) ÷ (The number of ants Thorny Devil lizard eat per minute)
= 1,080 ÷ 45
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
The time it will take for Thorny Devil lizard to eat 1,080 ants is: 24 minutes
Question 33.
Critique Reasoning Henrieta divided 0.80 by 20 as shown. Is her work correct? If not, explain why and give a correct response.
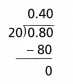
Answer:
It is given that
Henrieta divided 0.80 by 20 as shown
So,
The representation of the division equation Henrieta divided is: 0.80 ÷ 20
Now,
By using the Long Division,
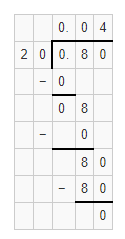
So,
From the above,
We can observe that
0.80 ÷ 20 = 0.04
Hence, from the above,
We can conclude that Henrieta’s work is not correct
Question 34.
Which brand of fruit snacks costs less per pound? How much less?

Answer:
The given figure is:

Now,
The cost per pound of Brand A’s fruit snacks = (The cost of Brand A fruit snacks) ÷ (The amount of Brand A fruit snacks)
= $16.20 ÷ 15
Now,
By using the Long Division,
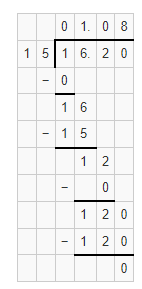
So,
The cost per pound of Brand A’s fruit snacks is: $1.08
Now,
The cost per pound of Brand B’s fruit snacks = (The cost of Brand B fruit snacks) ÷ (The amount of Brand B fruit snacks)
= $22.25 ÷ 25
Now,
By using the Long Division,
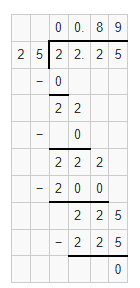
So,
The cost per pound of Brand B’s fruit snacks is: $0.89
So,
The difference between the cost per pound of two brands = $1.08 – $0.89
Now,
By using the Long Subtraction,

So,
The difference between the cost per pound of two brands is: $0.19
Hence, from the above,
We can conclude that
The cost per pound of Brand B’s fruit snacks is: $0.89
The difference between the cost per pound of two brands is: $0.19
Question 35.
Be Precise How many times as much does each item cost in 2010 as in 1960?
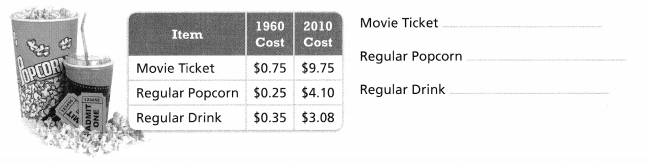
Answer:
The given data is:
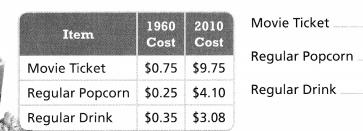
Now,
Let the number of times as much does each item cost in 2010 as in 1960 be x
So,
For the Movie Ticket,
x = $9.75 ÷ $0.75
Now,
By using the Long Division,
So,
For Regular popcorn,
x = $4.10 ÷ $0.25
Now,
By using the Long Division,
So,
For Regular Drink,
x = $3.08 ÷ $0.35
Now,
By using the Long Division,
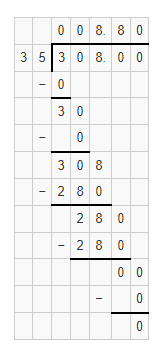
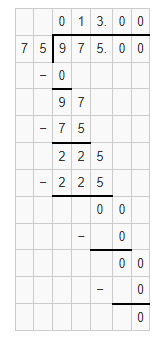
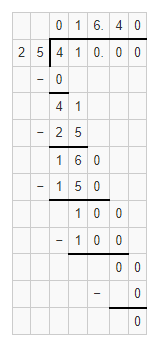
Hence, from the above,
We can conclude that
The number of times as much does the movie ticket cost in 2010 as in 1960 is: 13 times
The number of times as much does the regular ticket cost in 2010 as in 1960 is: 16.40 times
The number of times as much does the regular drink cost in 2010 as in 1960 is: 8.80 times
Question 36.
Higher-Order Thinking Kendra has 5.5 pounds of popcorn and wants to package it equally in 50 bags. How can she use place-value reasoning to find the amount of popcorn to put in each bag?
Answer:
It is given that
Kendra has 5.5 pounds of popcorn and wants to package it equally in 50 bags.
Now,
We know that,
Use place value to place the first digit. Look at the first digit. If the first digit is less than the divisor, then the first digit of the quotient will be in the hundreds place. If the first digit is greater than or equal to the divisor, then the first digit of the quotient will be in the thousands place
So,
The amount of popcorn Kendra put in each bag = (The total number of pounds of popcorn Kendra has) ÷ (The number of bags Kendra wants to package the popcorn equally)
= 5.5 ÷ 50
Now,
By using the Long Division,
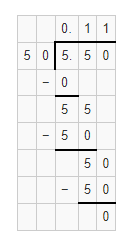
Hence, from the above,
We can conclude that
The amount of popcorn Kendra put in each bag is: 0.11 pounds
Question 37.
You and a friend are paid $38.25 for doing yard work. You worked 2.5 hours and your friend worked 2 hours. You split the money according to the amount of time each of you worked. How much is your share of the money? Explain.
Answer:
It is given that
You and a friend are paid $38.25 for doing yard work. You worked 2.5 hours and your friend worked 2 hours. You split the money according to the amount of time each of you worked
So,
The amount of money that is your share = (The amount of money you and your friend are paid for doing yard work) ÷ (The number of hours you worked)
= $38.25 ÷ 2.5
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
The amount of money that is your share is: $15.30
Assessment Practice
Question 38.
What is the value of the expression 1,248 ÷ 25?
A. 49
B. 49 R9
C. 49.9
D. 49 R 23
Answer:
The given division equation is: 1,248 ÷ 25
Now,
By using the Long Division,
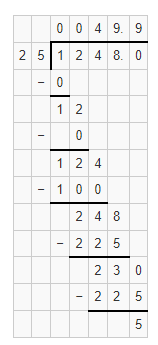
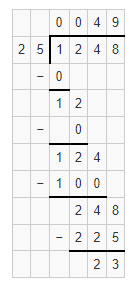
Hence, from the above,
We can conclude that
The value of the expression 1,248 ÷ 25 is:

Question 39.
Which expression has the same solution as 3,157 ÷ 41?
A. 1,852 ÷ 24
B. 1,928 ÷ 25
C. 2,079 ÷ 27
D. 2,184 ÷ 28
Answer:
The given division equation is: 3,157 ÷ 41
Now,
By using the Long Division,
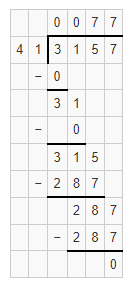
Now,
The expressions that have the same value as the given expression by using the Long Division are:
A. 1,852 ÷ 24

B. 1,928 ÷ 25
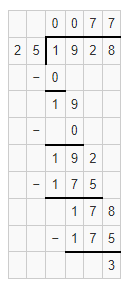
C. 2,079 ÷ 27
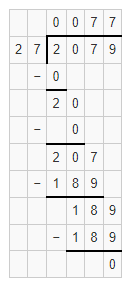
D. 2,184 ÷ 28

Hence, from the above,
We can conclude that
The expressions that have the same value as the given expression are:
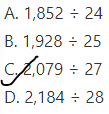
Lesson 1-3 Multiply Fractions
Solve & Discuss It!
ACTIVITY
The art teacher gave each student half of a sheet of paper. Then she asked the students to color one-fourth of their pieces of paper. What part of the original sheet did the students color?
Answer:
It is given that
The art teacher gave each student half of a sheet of paper. Then she asked the students to color one-fourth of their pieces of paper
So,
The part of the original sheet did the students color = (The piece of paper the art teacher gave to each student) × (The part of the paper the are teacher asked the students to color)
= \(\frac{1}{2}\) × \(\frac{1}{4}\)
= \(\frac{1 × 1}{2 × 4}\)
= \(\frac{1}{8}\) of the piece of paper
Hence, from the above,
We can conclude that
The part of the original sheet did the students color is: \(\frac{1}{8}\) of the piece of paper
A model with Math
How can you use a picture to represent the problem?
Answer:
By representing units of measurement and other objects visually, students can begin to think about the problem mathematically. Pictures and diagrams are also good ways of describing solutions to problems; therefore they are an important part of mathematical communication.
Focus on math practices
Reasoning Should your answer be less than or greater than 1? Explain.
Answer:
From the above problem,
We can observe that
The part of the original sheet did the students color is: \(\frac{1}{8}\) of the piece of paper
Now,
By using the Long Division,
The value of \(\frac{1}{8}\) is:
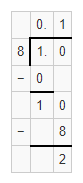
Hence, from the above,
We can conclude that
Your answer is less than 1
? Essential Question How can you multiply fractions and mixed numbers?
Answer:
The steps that are used to multiply mixed numbers and fractions are:
a. Convert the given mixed fraction to an improper fraction.
b. Write the whole number in the form of a fraction with denominator 1.
c. Multiply the numerators of both the fractions.
d. Multiply the denominators of both the fractions.
e. Combine them and simplify the fraction to its lowest form.
Try It!
Find \(\frac{1}{4}\) × \(\frac{1}{5}\) using the area model. Explain.
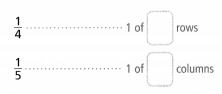
Answer:
The given multiplication equation is:
\(\frac{1}{4}\) × \(\frac{1}{5}\)
Now,
By using the Area model,
So,

So,
\(\frac{1}{4}\) × \(\frac{1}{5}\)
= \(\frac{1 × 1}{4 × 5}\)
= \(\frac{1}{20}\)
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) × \(\frac{1}{5}\) = \(\frac{1}{20}\)
Convince Me! Why is the product of \(\frac{1}{4}\) × \(\frac{1}{5}\) less than each factor?

Answer:
The given multiplication equation is:
\(\frac{1}{4}\) × \(\frac{1}{5}\)
So,
\(\frac{1}{4}\) × \(\frac{1}{5}\)
= \(\frac{1}{20}\)
Now,
When we compare the denominators,
4 < 5 and 5 < 20
So,
20 > 5 > 4 —- (1)
But,
When we compare the denominators,
The same relationship of eq (1) will be reversed
So,
20 < 5 < 4
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) × \(\frac{1}{5}\) is less than each factor
Try It!
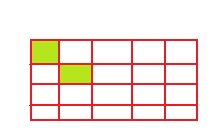
Find \(\frac{3}{4}\) × \(\frac{4}{6}\) using the number line. Explain.
Answer:
The given multiplication equation is:
\(\frac{3}{4}\) × \(\frac{4}{6}\)
So,
\(\frac{3}{4}\) × \(\frac{4}{6}\)
= \(\frac{3 × 4}{4 × 6}\)
= \(\frac{12}{24}\)
= \(\frac{3}{6}\)
So,
The representation of the product of \(\frac{3}{4}\) × \(\frac{4}{6}\) in the number line is:

Hence, from the above,
We can concldue that
\(\frac{3}{4}\) × \(\frac{4}{6}\) = \(\frac{3}{6}\)
Try It!
A clothing factory makes T-shirts. If each machine makes 3\(\frac{1}{3}\) T-shirts per hour, how many T-shirts does one machine make in 4\(\frac{1}{2}\) hours? Write and solve an equation.

Answer:
It is given that
A clothing factory makes T-shirts. If each machine makes 3\(\frac{1}{3}\) T-shirts per hour
So,
The number of T-shirts does 1 machine makes in 4\(\frac{1}{2}\) hours = (The number of T-shirts made by each machine in a hour) × 4\(\frac{1}{2}\) hours
Now,
The representation of 3\(\frac{1}{3}\) into a fraction is: \(\frac{10}{3}\)
The representation of 4\(\frac{1}{2}\) into a fraction is: \(\frac{9}{2}\)
So,
The number of T-shirts does 1 machine makes in 4\(\frac{1}{2}\) hours = \(\frac{10}{3}\) × \(\frac{9}{2}\)
= \(\frac{10 ×9}{3 ×2}\)
= \(\frac{90}{6}\)
= 15 T-shirts
Hence, from the above,
We can conclude that
The number of T-shirts does 1 machine makes in 4\(\frac{1}{2}\) hours is: 15 T-shirts
KEY CONCEPT
You can find the product of fractions or mixed numbers.
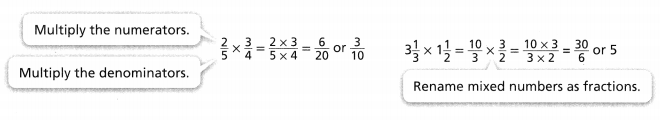
Do You Understand?
Question 1.
? Essential Question How can you multiply fractions and mixed numbers?
Answer:
The steps that are used to multiply mixed numbers and fractions are:
a. Convert the given mixed fraction to an improper fraction.
b. Write the whole number in the form of a fraction with denominator 1.
c. Multiply the numerators of both the fractions.
d. Multiply the denominators of both the fractions.
e. Combine them and simplify the fraction to its lowest form.
Question 2.
Reasoning Is the product of \(\frac{3}{6}\) × \(\frac{5}{4}\) equal to the product of \(\frac{3}{6}\) × \(\frac{5}{6}\)? Explain.
Answer:
The given multiplication equations are:
\(\frac{3}{6}\) × \(\frac{5}{4}\)
\(\frac{3}{6}\) × \(\frac{5}{6}\)
Now,
By using the Long Multiplication,
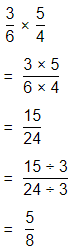
Now,
By using the Long Multiplication,
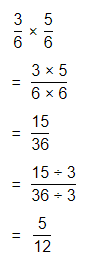
Hence, from the above,
We can conclude that
The product of \(\frac{3}{6}\) × \(\frac{5}{4}\) is not equal to the product of \(\frac{3}{6}\) × \(\frac{5}{6}\)
Question 3.
Construct Arguments Why is adding \(\frac{3}{9}\) and \(\frac{6}{9}\) different from multiplying the two fractions?
Answer:
Question 4.
Tina has \(\frac{1}{2}\) of a pan of cornbread left from a dinner party. She eats \(\frac{1}{2}\) of the leftover part the next night. How much of the whole pan does Tina eat? Write and solve an equation.
Answer:
It is given that
Tina has \(\frac{1}{2}\) of a pan of cornbread left from a dinner party. She eats \(\frac{1}{2}\) of the leftover part the next night
So,
The amount of the whole pan of cornbread does Tina eat = (The amount of a pan of cornbread left from a dinner party) × (The amount of the leftover from a dinner party that Tine eat the next night)
= \(\frac{1}{2}\) × \(\frac{1}{2}\)
Now,
By using the Long Multiplication,
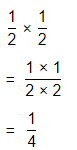
Hence, from the above,
We can conclude that
The amount of the whole pan of cornbread does Tina eat is: \(\frac{1}{4}\) of a pan of cornbread
Question 5.
Construct Arguments Explain how you would multiply 5 × 2\(\frac{1}{2}\).
Answer:
The given multiplication is: 5 × 2\(\frac{1}{2}\)
So,
The representation of 2\(\frac{1}{2}\) into a fraction is:
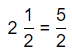
Now,
By using the Long Multiplication,
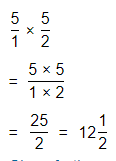
Hence, from the above,
We can conclude that
5 × 2\(\frac{1}{2}\) = \(\frac{25}{2}\)
Question 6.
In Example 1, find the fraction of a whole pan of lasagna that Tom ate if he started with \(\frac{7}{8}\) of a pan.
Answer:
It is given that
Tom has a \(\frac{7}{8}\) of a pan of lasagna left and Tom ate \(\frac{1}{3}\) of this amount
So,
The fraction of a whole pan of lasagna that Tom ate = (The amount of a pan of lasagna left) × (The amount that Tom ate from the amount of lasagna that is left)
= \(\frac{7}{8}\) × \(\frac{1}{3}\)
Now,
By using the Long Multiplication,
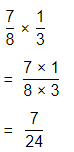
Hence, from the above,
We can conclude that
The fraction of a whole pan of lasagna that Tom ate is: \(\frac{7}{24}\) of a pan of lasagna
Do You Know How?
Question 7.
Find \(\frac{5}{6}\) × \(\frac{1}{2}\). Use the model to help solve.
Answer:
The given multiplication equation is:
\(\frac{5}{6}\) × \(\frac{1}{2}\)
Now,
By using the Area model,
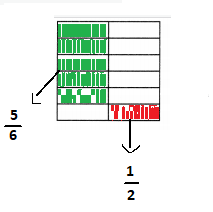
Now,
By using the Long Multiplication,
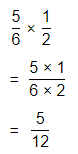
Hence, from the above,
We can conclude that
\(\frac{5}{6}\) × \(\frac{1}{2}\) = \(\frac{5}{12}\)
Question 8.
Find \(\frac{3}{4}\) × \(\frac{4}{9}\).
Answer:
The given multiplication equation is:
\(\frac{3}{4}\) × \(\frac{4}{9}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
\(\frac{3}{4}\) × \(\frac{4}{9}\) = \(\frac{1}{3}\)
In 9-16, find each product.
Question 9.
\(\frac{2}{3}\) × \(\frac{1}{2}\)
Answer:
The given multiplication equation is:
\(\frac{2}{3}\) × \(\frac{1}{2}\)
Now,
By using the Long Multiplication,
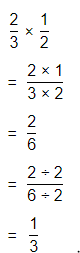
Hence, from the above,
We can conclude that
\(\frac{2}{3}\) × \(\frac{1}{2}\) = \(\frac{1}{3}\)
Question 10.
\(\frac{5}{9}\) × \(\frac{1}{9}\)
Answer:
The given multiplication equation is:
\(\frac{5}{9}\) × \(\frac{1}{9}\)
Now,
By using the Long Division,
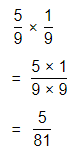
Hence, from the above,
We can conclude that
\(\frac{5}{9}\) × \(\frac{1}{9}\) = \(\frac{5}{81}\)
Question 11.
\(\frac{7}{10}\) × \(\frac{3}{4}\)
Answer:
The given multiplication equation is:
\(\frac{7}{10}\) × \(\frac{3}{4}\)
Now,
By using the Long Division,
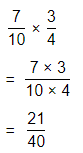
Hence, from the above,
We can conclude that
\(\frac{7}{10}\) × \(\frac{3}{4}\) = \(\frac{21}{40}\)
Question 12.
\(\frac{1}{3}\) × \(\frac{1}{4}\)
Answer:
The given multiplication equation is:
\(\frac{1}{3}\) × \(\frac{1}{4}\)
Now,
By using the Long Multiplication,
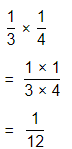
Hence, from the above,
We can conclude that
\(\frac{1}{3}\) × \(\frac{1}{4}\) = \(\frac{1}{12}\)
Question 13.
\(\frac{5}{6}\) × \(\frac{3}{7}\)
Answer:
The given multiplication equation is:
\(\frac{5}{6}\) × \(\frac{3}{7}\)
Now,
By using the Long Division,
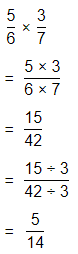
Hence, from the above,
We can conclude that
\(\frac{5}{6}\) × \(\frac{3}{7}\) = \(\frac{5}{14}\)
Question 14.
\(\frac{3}{5}\) × \(\frac{11}{12}\)
Answer:
The give multiplication equation is:
\(\frac{3}{5}\) × \(\frac{11}{12}\)
Now,
By using the Long Multiplication,

Hence, fro the above,
We can conclude that
\(\frac{3}{5}\) × \(\frac{11}{12}\) = \(\frac{11}{20}\)
Question 15.
\(\frac{4}{10}\) × \(\frac{2}{5}\)
Answer:
The given multiplication equation is:
\(\frac{4}{10}\) × \(\frac{2}{5}\)
Now,
By using the Long Multiplication,
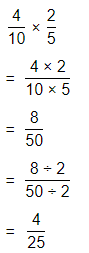
Hence, from the above,
We can conclude that
\(\frac{4}{10}\) × \(\frac{2}{5}\) = \(\frac{4}{25}\)
Question 16.
\(\frac{3}{4}\) × \(\frac{2}{9}\)
Answer:
The given multiplication equation is:
\(\frac{3}{4}\) × \(\frac{2}{9}\)
Now,
By using the Long Multiplication,
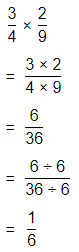
Hence, from the above,
We can conclude that
\(\frac{3}{4}\) × \(\frac{2}{9}\) = \(\frac{1}{6}\)
In 17 and 18, estimate the product. Then complete the multiplication.
Question 17.

Answer:
The given multiplication equation is:
2\(\frac{3}{4}\) × 8
Now,
The representation of 2\(\frac{3}{4}\) into a fraction is:
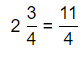
So,
By using the Long Multiplication,
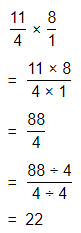
Hence, from the above,
We can conclude that
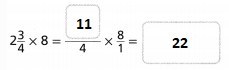
Question 18.
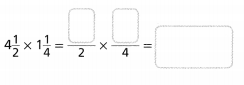
Answer:
The given multiplication equation is:
4\(\frac{1}{2}\) × 1\(\frac{1}{4}\)
Now,
The representation of 4\(\frac{1}{2}\) into a fraction is:
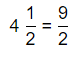
The representation of 1\(\frac{1}{4}\) into a fraction is:
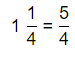
So,
By using the Long Multiplication,
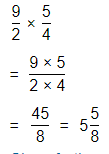
Hence, from the above,
We can conclude that
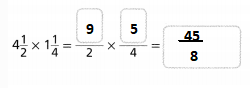
Practice & Problem Solving
Scan for Multimedia
In 19 and 20, find each product. Shade the model to help solve.
Question 19.
\(\frac{1}{3}\) × \(\frac{5}{6}\)

Answer:
The given multiplication equation is:
\(\frac{1}{3}\) × \(\frac{5}{6}\)
Now,
The representation of the given multiplication equation in the form of a model is:
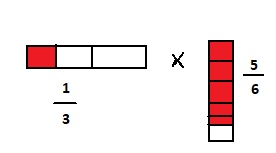
So,
By using the Long Multiplication,
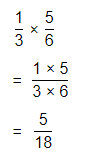
Hence, from the above,
We can conclude that
\(\frac{1}{3}\) × \(\frac{5}{6}\) = \(\frac{5}{18}\)
Question 20.
\(\frac{2}{3}\) × \(\frac{1}{12}\)

Answer:
The given multiplication equation is:
\(\frac{2}{3}\) × \(\frac{1}{12}\)
So,
The representation of the given multiplication equation in the form of a model is:

So,
By using the Long Multiplication,
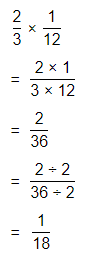
Hence, from the above,
We can conclude that
\(\frac{2}{3}\) × \(\frac{1}{12}\) = \(\frac{1}{18}\)
In 21-28, find each product.
Question 21.
\(\frac{7}{8}\) × \(\frac{1}{2}\)
Answer:
The given multiplication equation is:
\(\frac{7}{8}\) × \(\frac{1}{2}\)
Now,
By using the Long Multiplication,
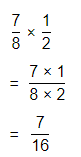
Hence, from the above,
We can conclude that
\(\frac{7}{8}\) × \(\frac{1}{2}\) = \(\frac{7}{16}\)
Question 22.
\(\frac{2}{5}\) × \(\frac{1}{12}\)
Answer:
The given multiplication equation is:
\(\frac{2}{5}\) × \(\frac{1}{12}\)
Now,
By using the Long Multiplication,
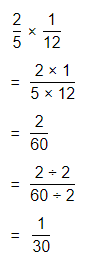
Hence, from the above,
We can conclude that
\(\frac{2}{5}\) × \(\frac{1}{12}\) = \(\frac{1}{30}\)
Question 23.
\(\frac{5}{7}\) × \(\frac{7}{9}\)
Answer:
The given multiplication equation is:
\(\frac{5}{7}\) × \(\frac{7}{9}\)
Now,
By using the Long Multiplication,
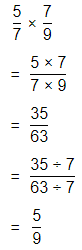
Hence, from the above,
We can conclude that
\(\frac{5}{7}\) × \(\frac{7}{9}\) = \(\frac{5}{9}\)
Question 24.
\(\frac{1}{2}\) × \(\frac{3}{4}\)
Answer:
The given multiplication equation is:
\(\frac{1}{2}\) × \(\frac{3}{4}\)
Now,
By using the Long Multiplication,
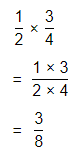
Hence, from the above,
We can conclude that
\(\frac{1}{2}\) × \(\frac{3}{4}\) = \(\frac{3}{8}\)
Question 25.
\(\frac{1}{4}\) × \(\frac{7}{8}\)
Answer:
The given multiplication equation is:
\(\frac{1}{4}\) × \(\frac{7}{8}\)
Now,
By using the Long Multiplication,
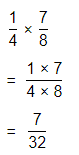
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) × \(\frac{7}{8}\) = \(\frac{7}{32}\)
Question 26.
\(\frac{5}{6}\) × \(\frac{9}{10}\)
Answer:
The given multiplication equation is:
\(\frac{5}{6}\) × \(\frac{9}{10}\)
Now,
By using the Long Multiplication,
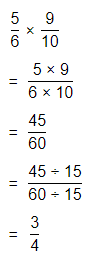
Hence, from the above,
We can conclude that
\(\frac{5}{6}\) × \(\frac{9}{10}\) = \(\frac{3}{4}\)
Question 27.
\(\frac{1}{4}\) × \(\frac{1}{8}\)
Answer:
The given multiplication equation is:
\(\frac{1}{4}\) × \(\frac{1}{8}\)
Now,
By using the Long Multiplication,
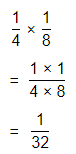
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) × \(\frac{1}{8}\) = \(\frac{1}{32}\)
Question 28.
\(\frac{1}{3}\) × \(\frac{3}{7}\)
Answer:
The given multiplication equation is:
\(\frac{1}{3}\) × \(\frac{3}{7}\)
Now,
By using the Long Multiplication,
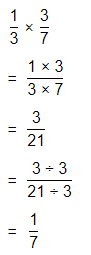
Hence, from the above,
We can conclude that
\(\frac{1}{3}\) × \(\frac{3}{7}\) = \(\frac{1}{7}\)
In 29-36, estimate the product. Then find each product.
Question 29.
2\(\frac{1}{6}\) × 4\(\frac{2}{9}\)
Answer:
The given multiplication equation is:
2\(\frac{1}{6}\) × 4\(\frac{2}{9}\)
Now,
By using the Long Multiplication,
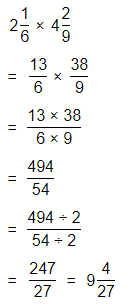
Hence, from the above,
We can conclude that
2\(\frac{1}{6}\) × 4\(\frac{2}{9}\) = \(\frac{247}{27}\)
Question 30.
\(\frac{3}{4}\) × 8\(\frac{1}{2}\)
Answer:
The given multiplication equation is:
\(\frac{3}{4}\) × 8\(\frac{1}{2}\)
Now,
The representation of 8\(\frac{1}{2}\) into a fraction is:
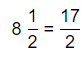
So,
By using the Long Division,
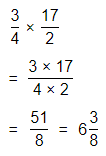
Hence, from the above,
We can conclude that
\(\frac{3}{4}\) × 8\(\frac{1}{2}\) = \(\frac{51}{8}\)
Question 31.
1\(\frac{1}{8}\) × 3\(\frac{1}{3}\)
Answer:
The given multiplication equation is:
1\(\frac{1}{8}\) × 3\(\frac{1}{3}\)
Now,
By using the Long Multiplication,
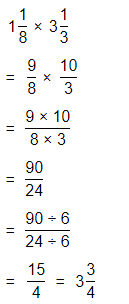
Hence, from the above,
We can conclude that
1\(\frac{1}{8}\) × 3\(\frac{1}{3}\) = \(\frac{15}{4}\)
Question 32.
3\(\frac{1}{2}\) × \(\frac{2}{3}\)
Answer:
The given multiplication equation is:
3\(\frac{1}{2}\) × \(\frac{2}{3}\)
Now,
The representation of 3\(\frac{1}{2}\) into a fraction is:
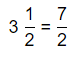
So,
By using the Long Division,
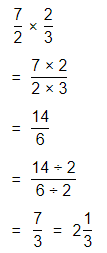
Hence, from the above,
We can conclude that
3\(\frac{1}{2}\) × \(\frac{2}{3}\) = \(\frac{7}{3}\)
Question 33.
3\(\frac{1}{4}\) × 6
Answer:
The given multiplication equation is:
3\(\frac{1}{4}\) × 6
Now,
The representation of 3\(\frac{1}{4}\) into a fraction is:
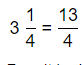
So,
By using the Long Multiplication,
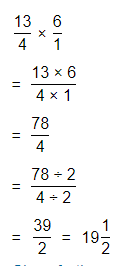
Hence, from the above,
We can conclude that
3\(\frac{1}{4}\) × 6 = \(\frac{39}{2}\)
Question 34.
5\(\frac{1}{3}\) × 3
Answer:
The given multiplication equation is:
5\(\frac{1}{3}\) × 3
Now,
The representation of 5\(\frac{1}{3}\) into a fraction is:
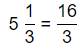
So,
By using the Long Multiplication,
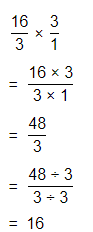
Hence, from the above,
We can conclude that
5\(\frac{1}{3}\) × 3 = 16
Question 35.
2\(\frac{3}{8}\) × 4
Answer:
The given multiplication equation is:
2\(\frac{3}{8}\) × 4
Now,
The representation of 2\(\frac{3}{8}\) into a fraction is:

So,
By using the Long Multiplication,
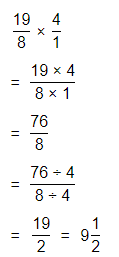
Hence, from the above,
We can conclude that
2\(\frac{3}{8}\) × 4 = \(\frac{19}{2}\)
Question 36.
4\(\frac{1}{8}\) × 5\(\frac{1}{2}\)
Answer:
The given multiplication equation is:
4\(\frac{1}{8}\) × 5\(\frac{1}{2}\)
Now,
By using the Long Multiplication,
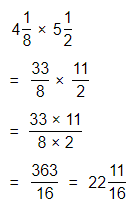
Hence, from the above,
We can conclude that
4\(\frac{1}{8}\) × 5\(\frac{1}{2}\) = \(\frac{363}{16}\)
In 37 and 38, use the diagram at the right.
Question 37.
Linda walked \(\frac{3}{4}\) of the length of the Tremont Trail before stopping for a rest. How far had Linda walked on the trail?

Answer:
It is given that
Linda walked \(\frac{3}{4}\) of the length of the Tremont Trail before stopping for a rest
Now,
The given information is:

So,
The distance covered by Linda on the trail = (The distance Linda walked of the Tremont trail) × (The length of the Tremont trail)
= \(\frac{3}{4}\) × 3\(\frac{1}{2}\)
Now,
The representation of 3\(\frac{1}{2}\) into a fraction is:
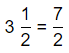
So,
By using the Long Multiplication,
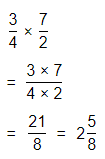
Hence, from the above,
We can conclude that
The distance covered by Linda on the trail is: \(\frac{25}{8}\) miles
Question 38.
The city plans to extend the Wildflower Trail to make it 2\(\frac{1}{2}\) times its current length in the next 5 years. How long will the Wildflower Trail be at the end of 5 years?
Answer:
It is given that
The city plans to extend the Wildflower Trail to make it 2\(\frac{1}{2}\) times its current length in the next 5 years
Now,
The given information is:

So,
The length of the Wildflower trail at the end of 5 years = (The extended length of the Wildflower trail at the end of 5 years) × (The current length of the Wildflower trail)
= 2\(\frac{1}{2}\) × 2\(\frac{3}{8}\)
Now,
By using the Long Multiplication,
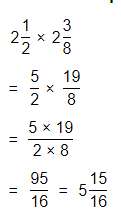
Hence, from the above,
We can conclude that
The length of the Wildflower trail at the end of 5 years will be: \(\frac{95}{16}\) miles
Question 39.
The world’s smallest gecko is \(\frac{3}{4}\) inch long. An adult male Western Banded Gecko is 7\(\frac{1}{3}\) times as long. How long is an adult male Western Banded Gecko?
Answer:
It is given that
The world’s smallest gecko is \(\frac{3}{4}\) inch long. An adult male Western Banded Gecko is 7\(\frac{1}{3}\) times as long
So,
The length of an adult male Western Banded Gecko = (The length of the world’s small gecko) × (The number of times an adult male western banded gecko is as larger than the world’s smallest gecko)
= \(\frac{3}{4}\) × 7\(\frac{1}{3}\)
Now,
The representation of 7\(\frac{1}{3}\) into a fraction is:
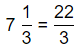
So,
By using the Long Multiplication,
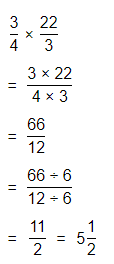
Hence, from the above,
We can conclude that
The length of an adult male Western Banded Gecko is: \(\frac{11}{2}\) inches
Question 40.
Higher-Order Thinking In Ms. Barclay’s classroom, \(\frac{2}{5}\) of the students play chess. Of the students who play chess, \(\frac{5}{6}\) also play sudoku. If there are 30 students in Ms. Barclay’s class, how many play chess and sudoku?
Answer:
It is given that
In Ms. Barclay’s classroom, \(\frac{2}{5}\) of the students play chess. Of the students who play chess, \(\frac{5}{6}\) also play sudoku. If there are 30 students in Ms. Barclay’s class
So,
The number of students who play chess = (The total number of students) × (The fracti of the students that play chess)
= 30 × \(\frac{2}{5}\)
Now,
By using the Long Multiplication,
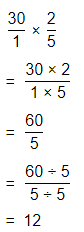
So,
The number of students who play chess are: 12 students
Now,
The number of students who play Sudoku = (The number of students who play chess) × (The fraction of the students who play Sudoku)
= 12 × \(\frac{5}{6}\)
Now,
By using the Long Multiplication,
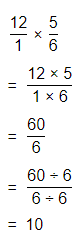
So,
The number of students who play sudoku are: 10 students
Now,
The number of students who play chess and sudoku = (The number of students who play chess) – (The number of students who play sudoku)
= 12 – 10
= 2 students
Hence, from the above,
We can conclude that
The number of students who play chess are: 12 students
The number of students who play sudoku are: 10 students
The number of students who play chess and sudoku are: 2 students
Question 41.
The Boca Grande Causeway in Florida is about 1\(\frac{4}{9}\) times as long as the Golden Gate Bridge in San Francisco. The Golden Gate Bridge is about 9,000 feet long. About how long is the Boca Grande Causeway?
Answer:
It is given that
The Boca Grande Causeway in Florida is about 1\(\frac{4}{9}\) times as long as the Golden Gate Bridge in San Francisco. The Golden Gate Bridge is about 9,000 feet long
So,
The length of the Boca Grande causeway = (The number of times the Boca Grande causeway as long as the Golden Gate Bridge) × (The length of the Golden Gate Bridge)
= 1\(\frac{4}{9}\) × 9,000
Now,
The representation of 1\(\frac{4}{9}\) into a fraction is:

Now,
By using the Long Multiplication,
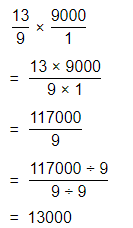
Hence, from the above,
We acn conclude that
The length of the Boca Grande causeway is: 13,000 feet
Question 42.
If \(\frac{7}{8}\) is multiplied by \(\frac{4}{5}\), will the product be greater than either of the two factors? Explain.
Answer:
The given multiplication equation is:
\(\frac{7}{8}\) × \(\frac{4}{5}\)
Now,
The representation of the given multiplication equation in the form of a decimal numbers is:
0.875 × 0.8
Now,
By using the Long Multiplication,
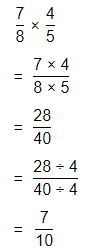
Now,
The representation of the value of the product in the form of a decimal number is: 0.7
Hence, from the above,
We can conclude that
The product would be smaller than either of the two factors
Question 43.
Be Precise To amend the U.S. Constitution, \(\frac{3}{4}\) of the 50 states must approve the amendment. If 35 states approve an amendment, will the Constitution be amended?
Answer:
It is given that
To amend the U.S. Constitution, \(\frac{3}{4}\) of the 50 states must approve the amendment
So,
The number of states that approved the amendment = (The total number of states) × (The number of states who approved the amendment)
= 50 × \(\frac{3}{4}\)
Now,
By using the Long Multiplication,
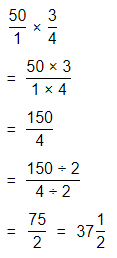
Now,
We can observe that about 37 states approved the amendment from the above Long Multiplication
Hence, from the above,
We can conclude that
If 35 states approve an amendment, the Constitution will be amended
Question 44.
A scientist had \(\frac{3}{4}\) of a bottle of a solution. She used \(\frac{1}{6}\) of the solution in an experiment. How much of the bottle did she use?
Answer:
It is given that
A scientist had \(\frac{3}{4}\) of a bottle of a solution. She used \(\frac{1}{6}\) of the solution in an experiment
So,
The amount of the solution in the bottle did she used = (The total amount of solution in the bottle) × (the amount of solution did she used in an experiment)
= \(\frac{3}{4}\) × \(\frac{1}{6}\)
Now,
By using the Long Multiplication,
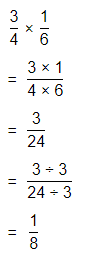
Hence, from the above,
We can conclude that
The amount of the solution in the bottle did she used is: \(\frac{1}{8}\) of the total amount of solution
Question 45.
In the voting for City Council Precinct 5, only \(\frac{1}{2}\) of all eligible voters cast votes. What fraction of all eligible voters voted for Shelley? Morgan? Who received the most votes?

Answer:
It is given that
In the voting for City Council Precinct 5, only \(\frac{1}{2}\) of all eligible voters cast votes
Now,
The given table is:

So,
The fraction of the eligible voters voted for Shelly = (The fraction of the eligible voters voted) × (The fraction of votes received by Shelly)
= \(\frac{1}{2}\) × \(\frac{3}{10}\)
Now,
By using the Long Multiplication,
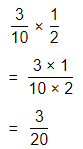
So,
The fraction of the eligible voters voted for Shelly is: \(\frac{3}{20}\) votes
So,
The fraction of the eligible voters voted for Morgan = (The fraction of the eligible voters voted) × (The fraction of votes received by Morgan)
= \(\frac{1}{2}\) × \(\frac{5}{8}\)
Now,
By using the Long Multiplication,

So,
The fraction of the eligible voters voted for Morgan is: \(\frac{5}{16}\) votes
Now,
The representation of \(\frac{3}{20}\) into a decimal number is: 0.15
The representation of \(\frac{5}{16}\) into a decimal number is: 0.3125
Hence, from the above,
We can conclude that
Morgan received the most votes
Assessment Practice
Question 46.
Which of these equations is equivalent to 1\(\frac{1}{2}\) × 3\(\frac{1}{5}\) = 4\(\frac{1}{2}\)?
A. 4\(\frac{1}{2}\) ÷ 3\(\frac{1}{5}\) = 1\(\frac{1}{2}\)
B. 1\(\frac{1}{2}\) ÷ 4\(\frac{1}{2}\) = 3\(\frac{1}{5}\)
C. 1\(\frac{1}{2}\) ÷ 3\(\frac{1}{5}\) = 4\(\frac{1}{2}\)
D. 3\(\frac{1}{5}\) ÷ 4\(\frac{1}{2}\) = 1\(\frac{1}{2}\)
Answer:
The given multiplication equation is:
1\(\frac{1}{2}\) × 3\(\frac{1}{5}\) = 4\(\frac{1}{2}\)
Now,
Divide the above equation with 3\(\frac{1}{5}\)
So,
We will get
4\(\frac{1}{2}\) ÷ 3\(\frac{1}{5}\) = 1\(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The equations that are equivalent to 1\(\frac{1}{2}\) × 3\(\frac{1}{5}\) = 4\(\frac{1}{2}\) are:
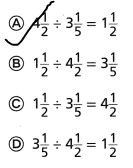
Question 47.
Which of these equations is equivalent to \(\frac{3}{4}\) × 8\(\frac{1}{5}\) = 6\(\frac{3}{20}\)? Select all that apply.
![]() \(\frac{3}{4}\) ÷ 8\(\frac{1}{5}\) = 6\(\frac{3}{20}\)
\(\frac{3}{4}\) ÷ 8\(\frac{1}{5}\) = 6\(\frac{3}{20}\)
![]() 6\(\frac{3}{20}\) ÷ \(\frac{3}{4}\) = 8\(\frac{1}{5}\)
6\(\frac{3}{20}\) ÷ \(\frac{3}{4}\) = 8\(\frac{1}{5}\)
![]() 6\(\frac{3}{20}\) ÷ 8\(\frac{1}{5}\) = \(\frac{3}{4}\)
6\(\frac{3}{20}\) ÷ 8\(\frac{1}{5}\) = \(\frac{3}{4}\)
![]() \(\frac{3}{4}\) ÷ 6\(\frac{3}{20}\) = 8\(\frac{1}{5}\)
\(\frac{3}{4}\) ÷ 6\(\frac{3}{20}\) = 8\(\frac{1}{5}\)
![]() 8\(\frac{1}{5}\) ÷ 6\(\frac{3}{20}\) = \(\frac{3}{4}\)
8\(\frac{1}{5}\) ÷ 6\(\frac{3}{20}\) = \(\frac{3}{4}\)
Answer:
The given multiplication equation is:
\(\frac{3}{4}\) × 8\(\frac{1}{5}\) = 6\(\frac{3}{20}\)
Now,
Divide the above equation with 8\(\frac{1}{5}\)
So,
We will get
6\(\frac{3}{20}\) ÷ 8\(\frac{1}{5}\) = \(\frac{3}{4}\)
Hence, from the above,
We can conclude that
The equations that are equivalent to \(\frac{3}{4}\) × 8\(\frac{1}{5}\) = 6\(\frac{3}{20}\) are:

Topic 1 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary How can you use a compatible number to estimate a quotient when dividing a decimal by a whole number? Lesson 1.2
Answer:
When dividing a decimal by a whole number, we use the following procedure:
a. Estimate the quotient.
b. Perform the division. Remember to place a zero in the quotient when the divisor is larger than the dividend.
c. Compare your estimate with your quotient to verify that the answer makes sense.
Question 2.
Keaton is building a rectangular tabletop and wants to put a metal border around the edge. The length of the tabletop is 1.83 meters and the width is 0.74 meters. Use the formula P = 2l + 2w to find the perimeter of the tabletop. Lesson 1.1
Answer:
It is given that
Keaton is building a rectangular tabletop and wants to put a metal border around the edge. The length of the tabletop is 1.83 meters and the width is 0.74 meters
So,
To find the length of the metal border around the edge,
We have to find the perimeter of the tabletop
Now,
From the give information,
We can observe that
The perimeter of the tabletop (P) = 2l + 2w
Where,
‘l’ is the length of the tabletop
‘w’ is the width of the tabletop
So,
The perimeter of the tabletop (P) = (2 × 1.83) + (2 × 0.74)
= 3.66 + 1.48
= 5.14 meters
Hence, from the above,
We can conclude that
The perimeter of thetabletop is: 5.14 meters
Question 3.
Norbert’s Nursery is having a sale. Flats of flowers are priced as marked, including tax. Jake buys 2 flats of petunias, 3 flats of daisies, and 1 flat of begonias. If he pays with a $50 bill, how much change should Jake receive? Lesson 1.1

Answer:
It is given that
Norbert’s Nursery is having a sale. Flats of flowers are priced as marked, including tax. Jake buys 2 flats of petunias, 3 flats of daisies, and 1 flat of begonias. If he pays with a $50 bill
Now,
The given table is:

Now,
The total price of flats of flowers Jack bought = (2 × The price of each flat of Petunia) + (3 × The price of each flat of daisies) + (1 × The price of each flat of begonias)
= (2 × $5.25) + (3 × $7.65) + (1 × $8.40)
= $10.5 + $22.95 + $8.40
= $41.85
Now,
The amount of change should Jack receive = (The total amount of money Jack gave) – (The total price of the flowers Jack bought)
= $50 – $41.85
= $8.15
Hence, from the above,
We can conclude that
The amount of change should Jack receive is: $8.15
Question 4.
Marguerite is selling space in an advertisement book for a community fund-raising event. Each \(\frac{1}{4}\) page in the book costs $15.50. What is the cost for \(\frac{3}{4}\) page? Lesson 1.1
A. $62.00
B. $46.50
C. $20.67
D. $11.63
Answer:
It is given that
Marguerite is selling space in an advertisement book for a community fund-raising event. Each \(\frac{1}{4}\) page in the book costs $15.50
So,
The cost for \(\frac{3}{4}\) page = 3 × (The cost of \(\frac{1}{4}\) page)
= 3 × $15.50
= $46.50
Hence, from the above,
We can conclude that
The cost for \(\frac{3}{4}\) page is:
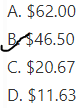
Question 5.
What is the value of 170 ÷ (4 × 5)? Lesson 1.2
Answer:
The given division expression is: 170 ÷ (4 × 5)
So,
170 ÷ (4 × 5)
= 170 ÷ 20
Now,
By using the Long Division,
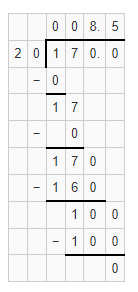
Hence, from the above,
We can conclude that
170 ÷ 20 = 8.5
Question 6.
Lucia walks 2\(\frac{3}{4}\) miles on Monday. On Monday, she walks 1\(\frac{1}{2}\) times farther than on Tuesday. Which equation can be used to find how far Lucia walks on Tuesday? Lesson 1-3
A. 2\(\frac{3}{4}\) × 1\(\frac{1}{2}\) = 4\(\frac{1}{8}\)
B. 2\(\frac{3}{4}\) × 1\(\frac{1}{2}\) = 4\(\frac{1}{4}\)
C. 2\(\frac{3}{4}\) ÷ 1\(\frac{1}{2}\) = 1\(\frac{5}{6}\)
D. 1\(\frac{1}{2}\) ÷ 2\(\frac{3}{4}\) = \(\frac{6}{11}\)
Answer:
It is given that
Lucia walks 2\(\frac{3}{4}\) miles on Monday. On Monday, she walks 1\(\frac{1}{2}\) times farther than on Tuesday
So,
The distance Lucia walked on Tuesday = (The distance Lucia walked on Monday) + 1\(\frac{1}{2}\)
= 2\(\frac{3}{4}\) + 1\(\frac{1}{2}\)
Now,
By using the Long Addition,
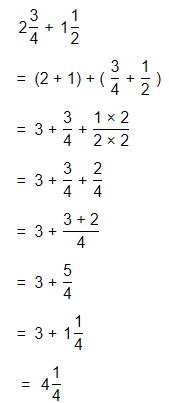
Hence, from the above,
We can conclude that
The equation that can be used to find how far Lucia walks on Tuesday is:

How well did you do on the mid-topic checkpoint? Fill in the stars. 
Topic 1 MID-TOPIC PERFORMANCE TASK
Nyan Robotics Team received their challenge for the year and has to buy parts to build their robot for competitions.

PART A
Team members Eric and Natalia secure a grant for $75.00 to buy beams and channels. If the team needs 3 beams and 6 channels, will the grant cover the cost? If so, how much of the grant will remain?
Answer:
It is given that
Team members Eric and Natalia secure a grant for $75.00 to buy beams and channels and the team needs 3 beams and 6 channels
Now,
The given table is;

So,
The cost of 3 beams and 6 channels = (3 × The cost of each Beam) + (6 × The cost of each Channel)
= (3 × $5.95) + (6 × $8.50)
= $17.85 + $51
= $68.85
So,
The grant received > The cost of 3 beams and 6 channels
Now,
The amount of the grant that will remain = (The total grant granted) – (The cost of 3 beams and 6 channels)
= $75 – $68.85
= $6.15
Hence, from the above,
We can conclude that
The amount of grant that will remain is: $6.15
PART B
Team members Corinne, Kevin, and Tomas decide to share the cost of 2 motor controllers and 4 wheels equally. How much does each member need to contribute?
Answer:
It is given that
Team members Corinne, Kevin, and Tomas decide to share the cost of 2 motor controllers and 4 wheels equally
Now,
The given table is:

So,
The total cost of 2 motor controllers and 4 wheels = (2 × The cost of each motor controller) + (4 × The cost of each wheel)
= (2 × $99.75) + (4 × $18.90)
= $199.5 + $75.6
= $275.1
Now,
The amount of money each member needs to contribute to buy 2 motor controllers and 4 wheels = $275.1 ÷ 3
Now,
By using the Long Division,
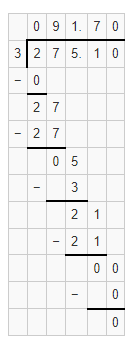
Hence, from the above,
We can conclude that
The amount of money each member needs to contribute to buy 2 motor controllers and 4 wheels is: $91.70
PART C
Nyan Robotics has a budget of $99 to buy sprockets, axles, and gears. If they spend \(\frac{2}{3}\) of the budget on sprockets, how much money from the budget remains to buy axles and gears?
Answer:
It is given that
Nyan Robotics has a budget of $99 to buy sprockets, axles, and gears and they spend \(\frac{2}{3}\) of the budget on sprockets
Now,
The given table is:

Now,
The amount of budget remaining after they spent on sprockets to buy axles and gears = \(\frac{2}{3}\) × $99
Now,
By using the Long Multiplication,
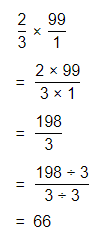
Hence, from the above,
We can conclude that
The amount of budget remaining after they spent on sprockets to buy axles and gears is: $66
3-Act Mathematical Modeling: Stocking Up
3-ACT MATH
Stocking UP
ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.

Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.
Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Reasoning How did you represent the situation using symbols? How did you use those symbols to solve the problem?
Answer:
SEQUEL
Question 15.
Model with Math
The store purchases boxes of pasta for $0.82 and cans of sauce for $1.62. How much profit does the store make from this purchase?
Answer:
Lesson 1.4 Understand Division with Fractions
ACTIVITY
Explore It!
Students are competing in a 4-kilometer relay race. There are 10 runners.
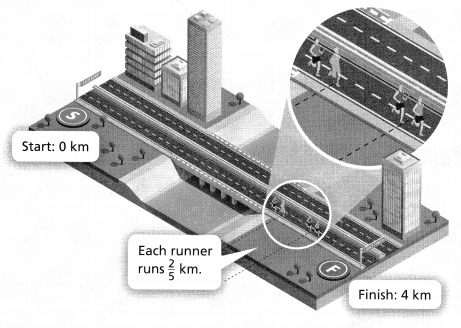
A. Use the number line to represent the data for the race.

Answer:
It is given that
Students are competing in a 4-kilometer relay race. There are 10 runners.
Now,
The given data is:

So,
From the given number line,
We can observe that
There are 10 runners and each runner runs \(\frac{2}{5}\) km and the finish line is at 4 km
Hence,
The representation of the given data in a number line is:
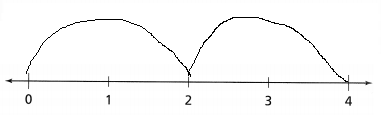
B. Use multiplication or division to describe your work on the number line.
Answer:
It is given that
Students are competing in a 4-kilometer relay race. There are 10 runners.
Now,
The given data is:

Now,
Using Multiplication,
The total distance covered by 10 runners = 10 × (The distance each runner runs)
= 10 × \(\frac{2}{5}\)
Now,
By using the Long Multiplication,
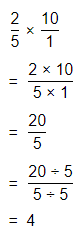
So,
The total distance covered by 10 runners is: 4 km
Focus on math practices
Model with Math
Describe what a number line would look like if there were 10 runners each running; kilometer in a 5-kilometer
race.
Answer:
It is given that
There were 10 runners each running; kilometer in a 5-kilometer race
So,
The total distance covered by 10 runners = 10 × (The distance each runner runs)
= 10 × \(\frac{1}{2}\)
Now,
By using the Long Multiplication,
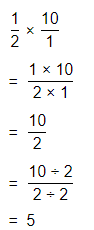
So,
The total distance covered by 10 runners is: 5 km
Hence,
The representation of the given information in a number line is:
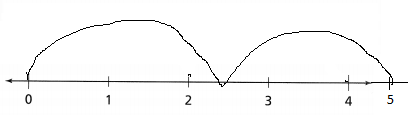
? Essential Question How can you represent the division of fractions?
Answer:
Interpret a fraction as a division of the numerator by the denominator (\(\frac{a}{b}\) = a ÷ b). Solve word problems involving the division of whole numbers leading to answers in the form of fractions or mixed numbers,
Ex: By using visual fraction models or equations to represent the problem.
Try It!
A board is 6 feet long. How many \(\frac{2}{3}\)-foot-long pieces can be cut from the board? Use the number line to show your work.

Answer:
It is given that
A board is 6 feet long
So,
The number of \(\frac{2}{3}\)-foot-long pieces can be cut from the board = (The length of the board) ÷ \(\frac{2}{3}\)
= 6 ÷ \(\frac{2}{3}\)
= 6 × \(\frac{3}{2}\)
Now,
By using the Long Multiplication,
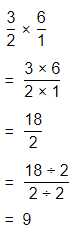
Hence, from the above,
We can conclude that
The number of \(\frac{2}{3}\)-foot-long pieces that can be cut from the board are: 9 pieces
Convince Me! Why is the number of pieces that can be cut from the board greater than the number of feet in the length of the board?
Answer:
Try It!
Make a diagram to find \(\frac{2}{3}\) ÷ 4.
Answer:
The given division expression is: \(\frac{2}{3}\) ÷ 4
Hence,
The representation of the given division expression in the form of an area model is:
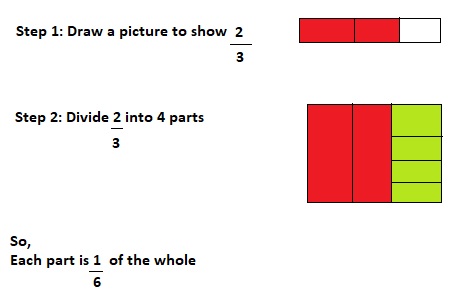
Hence, from the above,
We can conclude that
\(\frac{2}{3}\) ÷ 4 = \(\frac{1}{6}\)
Try It!
Use the pattern in the table above to find 8 ÷ \(\frac{3}{4}\).
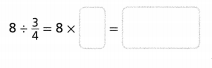
Answer:
The given division expression is: 8 ÷ \(\frac{3}{4}\)
So,
8 ÷ \(\frac{3}{4}\)
= 8 × \(\frac{4}{3}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
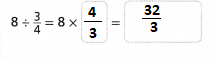
KEY CONCEPT
To divide a whole number by a fraction:

To divide a fraction by a whole number:
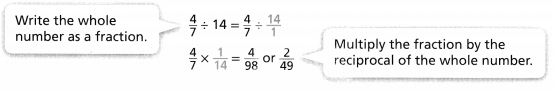
Do You Understand?
Question 1.
? Essential Question How can you represent the division of fractions?
Answer:
Interpret a fraction as a division of the numerator by the denominator (\(\frac{a}{b}\) = a ÷ b). Solve word problems involving the division of whole numbers leading to answers in the form of fractions or mixed numbers,
Ex: By using visual fraction models or equations to represent the problem.
Question 2.
Reasoning Draw a diagram to represent 8 ÷ \(\frac{2}{3}\). Then write an equation to show the solution.
Answer:
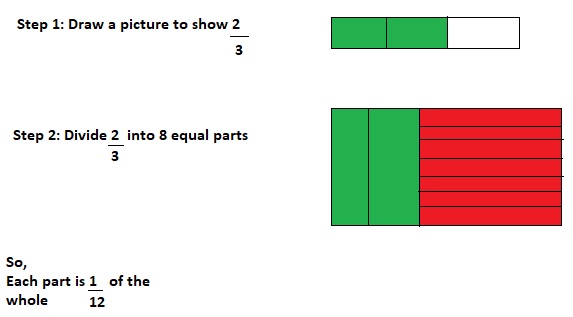
Question 3.
Reasoning is 4 ÷ \(\frac{3}{2}\) the same as 4 ÷ \(\frac{2}{3}\)? Explain.
Answer:
The given division expressions are:
4 ÷ \(\frac{3}{2}\) and 4 ÷ \(\frac{2}{3}\)
So,
4 ÷ \(\frac{3}{2}\)
= 4 × \(\frac{2}{3}\)
So,
4 ÷ \(\frac{2}{3}\)
= 4 × \(\frac{3}{2}\)
Hence, from the above,
We can conclude that
4 ÷ \(\frac{3}{2}\) and 4 ÷ \(\frac{3}{2}\) are not the same
Question 4.
How can you write any nonzero whole number as a fraction?
Answer:
You can multiply the numerator and the denominator of a fraction by any nonzero whole number, as long as you multiply both by the same whole number
Question 5.
Look for Relationships How does the quotient compare to the dividend when the divisor is a fraction less than 1?
Answer:
When the divisor is less than 1, the quotient is larger than the dividend. Decreasing the divisor to \(\frac{1}{2}\) increases the quotient to \(\frac{1}{2}\). When the divisor is smaller than the dividend, the quotient is more than 1.
Question 6.
What division equation is represented by the diagram?

Answer:
The given diagram is:

Now,
From the given diagram,
We can observe that
The total number of equal parts are: 8
The number of shaded parts are: 6
So,
The division equation that is represented by the given diagram = (The number of shaded parts) ÷ (The total number of equal parts)
= \(\frac{6}{8}\)
= \(\frac{6 ÷ 2}{8 ÷ 2}\)
= \(\frac{3}{4}\)
Hence, from the above,
We can conclude that
The division equation that is represented by the given diagram is: \(\frac{3}{4}\)
Do You Know How?
In 7-14, find each reciprocal.
Question 7.
\(\frac{3}{5}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{3}{5}\) is: \(\frac{5}{3}\)
Question 8.
\(\frac{1}{6}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{1}{6}\) is: \(\frac{6}{1}\)
Question 9.
9
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of 9 is: \(\frac{1}{9}\)
Question 10.
\(\frac{7}{4}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{7}{4}\) is: \(\frac{4}{7}\)
Question 11.
\(\frac{5}{8}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{5}{8}\) is: \(\frac{8}{5}\)
Question 12.
16
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of 16 is: \(\frac{1}{16}\)
Question 13.
\(\frac{7}{12}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{7}{12}\) is: \(\frac{12}{7}\)
Question 14.
\(\frac{11}{5}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{11}{5}\) is: \(\frac{5}{11}\)
In 15-22, find each quotient.
Question 15.
6 ÷ \(\frac{2}{3}\)
Answer:
The given division equation is: 6 ÷ \(\frac{2}{3}\)
So,
By using the Long Division,
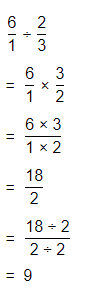
Hence, from the above,
We can conclude that
6 ÷ \(\frac{2}{3}\) = 9
The quotient for the given division equation is: 9
Question 16.
12 ÷ \(\frac{3}{8}\)
Answer:
The given division equation is: 12 ÷ \(\frac{3}{8}\)
So,
By using the Long Division,
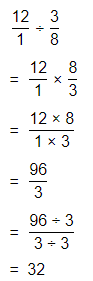
Hence, from the above,
We can conclude that
12 ÷ \(\frac{3}{8}\) = 32
The quotient for the given division equation is: 32
Question 17.
\(\frac{1}{4}\) ÷ 3
Answer:
The given division equation is: \(\frac{1}{4}\) ÷ 3
So,
By using the Long Division,
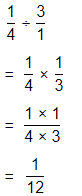
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\)
The quotient for the given division equation is: \(\frac{1}{12}\)
Question 18.
\(\frac{2}{5}\) ÷ 2
Answer:
The given division equation is: \(\frac{2}{5}\) ÷ 2
So,
By using the Long Division,
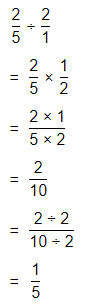
Hence, from the above,
We can conclude that
\(\frac{2}{5}\) ÷ 2 = \(\frac{1}{5}\)
The quotient for the given division equation is: \(\frac{1}{5}\)
Question 19.
2 ÷ \(\frac{1}{2}\)
Answer:
The given division equation is: 2 ÷ \(\frac{1}{2}\)
So,
By using the Long Division,
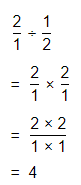
Hence, from the above,
We can conclude that
2 ÷ \(\frac{1}{2}\) = 4
The quotient for the given division equation is: 4
Question 20.
3 ÷ \(\frac{1}{4}\)
Answer:
The given division equation is: 2 ÷ \(\frac{1}{2}\)
So,
By using the Long Division,
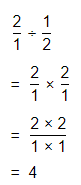
Hence, from the above,
We can conclude that
2 ÷ \(\frac{1}{2}\) = 4
The quotient for the given division equation is: 4
Question 21.
9 ÷ \(\frac{3}{5}\)
Answer:
The given division equation is: 9 ÷ \(\frac{3}{5}\)
So,
By using the Long Division,
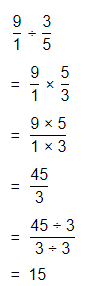
Hence, from the above,
We can conclude that
9 ÷ \(\frac{3}{5}\) = 15
The quotient for the given division equation is: 15
Question 22.
5 ÷ \(\frac{2}{7}\)
Answer:
The given division equation is: 5 ÷ \(\frac{2}{7}\)
So,
By using the Long Division,
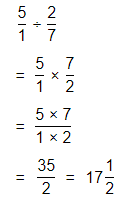
Hence, from the above,
We can conclude that
5 ÷ \(\frac{2}{7}\) = \(\frac{35}{2}\)
The quotient for the given division equation is: \(\frac{35}{2}\)
Practice & Problem Solving
Scan for Multimedia
Leveled Practice In 23 and 24, complete each division sentence.
Question 23.
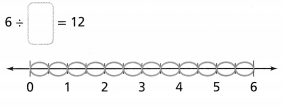
The number line shows 6 wholes.
Answer:
The given number line is:
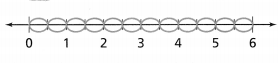
Hence, from the above,
We can conclude that
The completed division sentence is:
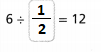
Question 24.
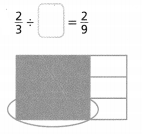
Answer:
The given diagram is:

Hence, from the above,
We can conclude that
The completed division sentence is:
![]()
In 25 and 26, find each quotient. Draw a diagram to help.
Question 25.
\(\frac{3}{5}\) ÷ 3
Answer:
The given division equation is:
\(\frac{3}{5}\) ÷ 3
Now,
The representation of the given division equation in the form of an area model is:
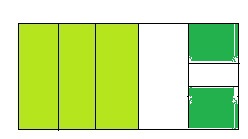
Now,
By using the Long Division,
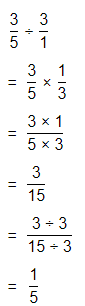
Hence, from the above,
We can conclude that
\(\frac{3}{5}\) ÷ 3 = \(\frac{1}{5}\)
The quotient for the given division equation is: \(\frac{1}{5}\)
Question 26.
2 ÷ \(\frac{2}{5}\)
Answer:
The given division equation is:
2 ÷ \(\frac{2}{5}\)
Now,
The representation of the given division equation in the form of an area model is:

Now,
By using the Long Division,
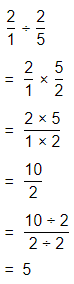
Hence, from the above,
We can conclude that
2 ÷ \(\frac{2}{5}\) = 5
The quotient for the given division equation is: 5
In 27-30, find each reciprocal.
Question 27.
\(\frac{3}{10}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{3}{10}\) is: \(\frac{10}{3}\)
Question 28.
6
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of 6 is: \(\frac{1}{6}\)
Question 29.
\(\frac{1}{15}\)
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of \(\frac{1}{15}\) is: 15
Question 30.
3
Answer:
We know that,
Two numbers whose product is “1” are called “Reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
Hence, from the above,
We can conclude that
The reciprocal of 3 is: \(\frac{1}{3}\)
In 31-38, find each quotient.
Question 31.
36 ÷ \(\frac{3}{4}\)
Answer:
The given division equation is: 36 ÷ \(\frac{3}{4}\)
So,
By using the Long Division,
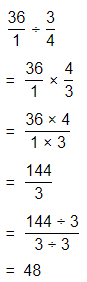
Hence, from the above,
We can conclude that
36 ÷ \(\frac{3}{4}\) = 48
The quotient for the given division equation is: 48
Question 32.
2 ÷ \(\frac{3}{8}\)
Answer:
The given division equation is: 2 ÷ \(\frac{3}{8}\)
So,
By using the Long Division,
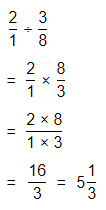
Hence, from the above,
We can conclude that
2 ÷ \(\frac{3}{8}\) = \(\frac{16}{3}\)
The quotient for the given division equation is: \(\frac{16}{3}\)
Question 33.
18 ÷ \(\frac{2}{3}\)
Answer:
The given division equation is: 18 ÷ \(\frac{2}{3}\)
So,
By using the Long Division,
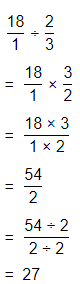
Hence, from the above,
We can conclude that
18 ÷ \(\frac{2}{3}\) = 27
The quotient for the given division equation is: 27
Question 34.
9 ÷ \(\frac{4}{5}\)
Answer:
The given division equation is: 9 ÷ \(\frac{4}{5}\)
So,
By using the Long Division,
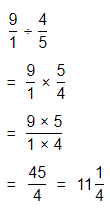
Hence, from the above,
We can conclude that
9 ÷ \(\frac{4}{5}\) = \(\frac{45}{4}\)
The quotient for the given division equation is: \(\frac{45}{4}\)
Question 35.
\(\frac{1}{6}\) ÷ 2
Answer:
The given division equation is: \(\frac{1}{6}\) ÷ 2
So,
By using the Long Division,
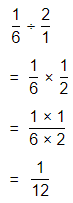
Hence, from the above,
We can conclude that
\(\frac{1}{6}\) ÷ 2 = \(\frac{1}{12}\)
The quotient for the given division equation is: \(\frac{1}{12}\)
Question 36.
\(\frac{2}{3}\) ÷ 3
Answer:
The given division equation is: \(\frac{2}{3}\) ÷ 3
So,
By using the Long Division,

Hence, from the above,
We can conclude that
\(\frac{2}{3}\) ÷ 3 = \(\frac{2}{9}\)
The quotient for the given division equation is: \(\frac{2}{9}\)
Question 37.
\(\frac{3}{5}\) ÷ 2
Answer:
The given division equation is: \(\frac{3}{5}\) ÷ 2
So,
By using the Long Division,
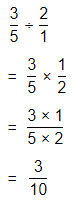
Hence, from the above,
We can conclude that
\(\frac{3}{5}\) ÷ 2 = \(\frac{3}{10}\)
The quotient for the given division equation is: \(\frac{3}{10}\)
Question 38.
\(\frac{1}{4}\) ÷ 4
Answer:
The given division equation is: \(\frac{1}{4}\) ÷ 4
So,
By using the Long Division,
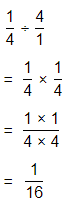
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) ÷ 4 = \(\frac{1}{16}\)
The quotient for the given division equation is: \(\frac{1}{16}\)
Question 39.
A worker is pouring 3 quarts of liquid into \(\frac{3}{8}\)-quart containers. How many of the containers can she fill? Write and solve a division equation.

Answer:
It is given that
A worker is pouring 3 quarts of liquid into \(\frac{3}{8}\)-quart containers
So,
The number of containers she can fill = (The number of quarts of liquid a worker poured) ÷ (The size of each container)
= 3 ÷ \(\frac{3}{8}\)
Now,
By using the Long Division,
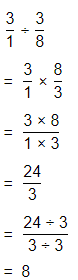
In 40-43, use the given information.

Question 40.
Higher-Order Thinking Without doing any calculations, how can you use the information given to tell which animal moves the fastest?
Answer:
The given information is:

Now,
The distance covered by a snail in 1 hour = 120 ÷ \(\frac{3}{4}\)
So,
By using the Long Division,
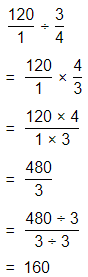
So,
The distance covered by a snail in 1 hour is: 160 ft
Now,
The distance covered by a tortoise in 1 hour = 600 ÷ \(\frac{2}{3}\)
So,
By using the Long Division,
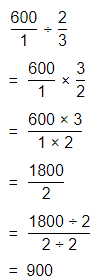
So,
The distance covered by a tortoise in 1 hour is: 900 ft
Now,
The distance covered by a Sloth in 1 hour = 250 ÷ \(\frac{5}{8}\)
So,
By using the Long Division,
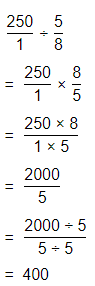
So,
The distance covered by a Sloth in 1 hour is: 400 ft
Hence, from the above,
We can conclude that
The animal which moves the fastest is: Tortoise
Question 41.
Reasoning The quotient 250 ÷ \(\frac{5}{8}\) tells about how far a sloth may move in one hour. How far can a sloth go in 90 minutes? Justify your reasoning.
Answer:
It is given that
The quotient 250 ÷ \(\frac{5}{8}\) tells about how far a sloth may move in one hour
Now,
We know that,
1 hour = 60 minutes
1\(\frac{1}{2}\) hour = 90 minutes
So,
The representation of 1\(\frac{1}{2}\) into a fraction is:
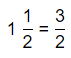
So,
The distance covered by a Sloth in 90 minutes = 250 ÷ \(\frac{3}{2}\)
Now,
By using the Long Division,
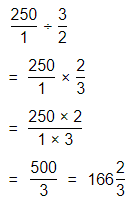
Hence, from the above,
We can conclude that
The distance covered by a Sloth in 90 minutes is: \(\frac{500}{3}\) ft
Question 42.
The quotient 600 ÷ \(\frac{2}{3}\) tells about how far a tortoise may move in one hour. Find that distance.
Answer:
It is given that
The quotient 600 ÷ \(\frac{2}{3}\) tells about how far a tortoise may move in one hour
Now,
According to the given information,
The distance covered by a tortoise in 1 hour = 600 ÷ \(\frac{2}{3}\)
So,
By using the Long Division,
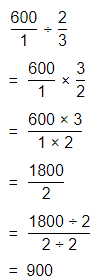
Hence, from the above,
We can conclude that
The distance covered by a tortoise in 1 hour is: 900 ft
Question 43.
Write and solve an equation to find how far a snail can go in one hour.
Answer:
The given information is:

Now,
The distance covered by a snail in 1 hour = 120 ÷ \(\frac{3}{4}\)
So,
By using the Long Division,
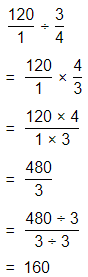
Hence, from the above,
We can conclude that
The distance covered by a snail in 1 hour is: 160 ft
Question 44.
A waitress pours \(\frac{3}{4}\) gallon of orange juice equally into 5 pitchers. What fraction of a gallon of orange juice is in each pitcher? Use the rectangle to represent the problem. Then write an equation to show the solution.

Answer:
It is given that
A waitress pours \(\frac{3}{4}\) gallon of orange juice equally into 5 pitchers.
Now,
The representation of the given information in the form of an Area model is:
Now,
Let the fraction of a gallon of orange juice that is present in each pitcher be x
So,
According to the given information,
5 ÷ x = \(\frac{3}{4}\)
So,
x = 5 ÷ \(\frac{3}{4}\)
Now,
By using the Long Division,
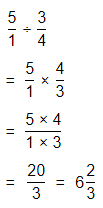
Hence, from the above,
We can conclude that
The fraction of a gallon of orange juice that is present in each pitcher is: \(\frac{20}{3}\) gallons
Assessment Practice
Question 45.
Select all the math statements that have the same quotient.
![]() 12 ÷ \(\frac{2}{3}\)
12 ÷ \(\frac{2}{3}\)
![]() \(\frac{2}{3}\) ÷ \(\frac{1}{27}\)
\(\frac{2}{3}\) ÷ \(\frac{1}{27}\)
![]() 16 ÷ \(\frac{4}{5}\)
16 ÷ \(\frac{4}{5}\)
![]() 12 ÷ \(\frac{3}{2}\)
12 ÷ \(\frac{3}{2}\)
![]() 24 ÷ \(\frac{4}{3}\)
24 ÷ \(\frac{4}{3}\)
Answer:
The given math statements and their quotients are:
a. 12 ÷ \(\frac{2}{3}\)
Now,
By using the Long Division,
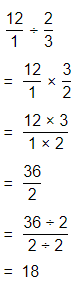
b. \(\frac{2}{3}\) ÷ \(\frac{1}{27}\)
Now,
By using the Long Division,
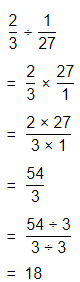
c. 16 ÷ \(\frac{4}{5}\)
Now,
By using the Long Division,

d. 12 ÷ \(\frac{3}{2}\)
Now,
By using the Long Division,
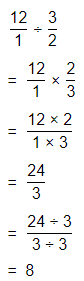
e. 24 ÷ \(\frac{4}{3}\)
Now,
By using the Long Division,
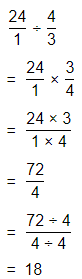
Hence, from the above,
We can conclude that
All the math statements that have the same quotient are:

Question 46.
Select all the math statements that are true.

Answer:
All the math statements that are true are:

Lesson 1.5 Divide Fractions by Fractions
ACTIVITY
Solve & Discuss It!
A granola bar was cut into 6 equal pieces. Someone ate part of the granola bar so that \(\frac{2}{3}\) of the original bar remains. How many \(\frac{1}{6}\) parts are left? Use the picture to draw a model to represent and find \(\frac{2}{3}\) ÷ \(\frac{1}{6}\)

Answer:
It is given that
A granola bar was cut into 6 equal pieces. Someone ate part of the granola bar so that \(\frac{2}{3}\) of the original bar remains
Now,
The given picture is:
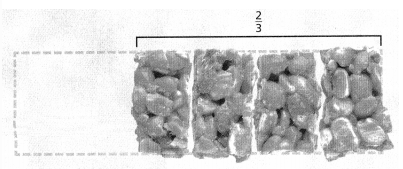
Now,
The representation of the given information in the form of a bar diagram is:
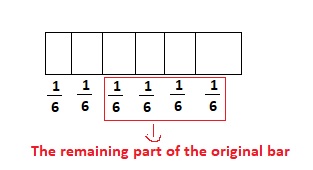
Now,
The number of \(\frac{1}{6}\) parts that are left = (The part that is remained in the original granola bar) ÷ \(\frac{1}{6}\)
= \(\frac{2}{3}\) ÷ \(\frac{1}{6}\)
Now,
By using the Long Division,
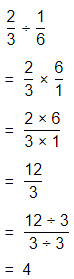
Hence, from the above,
We can conclude that
The number of \(\frac{1}{6}\) parts that are left is: 4
A model with Math
You can model with math by dividing a whole into equal parts.
Answer:
The representation of the above problem in the form of a bar diagram is:

Focus on math practices
Use Structure How can you use multiplication to check your answer?
Answer:
You can use multiplication to check your division answer the following way:
a. Do the division problem.
b. Multiply the quotient times the divisor.
c. If there is a remainder, add it to the multiplication product.
d. Compare this answer to the dividend. They should be the same number
? Essential Question How can you divide a fraction by a fraction?
Answer:
The easiest way to divide fractions is to follow three simple steps:
a. Flip the divisor into a reciprocal.
b. Change the division sign into a multiplication sign and multiply.
c. Simplify if possible.
Try It!
Use the number line below to represent \(\frac{1}{6}\) × 3 = \(\frac{1}{2}\). Then write an equivalent division sentence.
![]()
Answer:
The given multiplication equation is:
\(\frac{1}{6}\) × 3 = \(\frac{1}{2}\)
So,
The representation of the given division equation in the given number line is:
Now,
The representation of the given multiplication equation into division equation is:
\(\frac{1}{2}\) ÷ \(\frac{1}{6}\) = 3
Hence, from the above,
We can conclude that
The equivalent division equation for the given multiplication equation is:
\(\frac{1}{2}\) ÷ \(\frac{1}{6}\) = 3
Convince Me! How are the dividend, divisor, and quotient represented on the number line?
Answer:
In a number line,
The dividend represents the “Product”
The divisor represents the “The division of the dividend into equal parts”
The quotient represents the “The number of times the divisor divided”
Try It!
Find \(\frac{1}{4}\) ÷ \(\frac{3}{8}\). Draw an area model.
Answer:
The given division expression is: \(\frac{1}{4}\) ÷ \(\frac{3}{8}\)
Hence,
The representation of the given division expression by using the area model is:
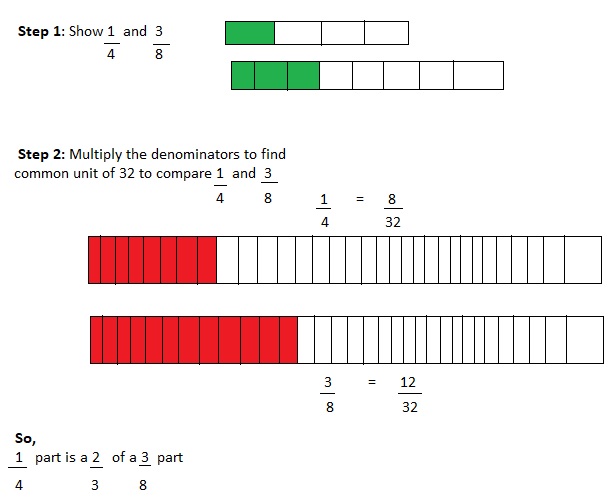
Try It!
How wide is a rectangular strip of land with a length of \(\frac{3}{4}\) mile and an area of \(\frac{1}{2}\) square mile? Use the area formula: A = l × w.

Answer:
It is given that
The length of a rectangular strip is \(\frac{3}{4}\) mile and an area of a rectangular strip is \(\frac{1}{2}\) square mile
Now,
It is given that
Area (A) = Length (L) × Width (W)
So,
\(\frac{1}{2}\) = \(\frac{3}{4}\) × Width (W)
Width (W) = \(\frac{1}{2}\) ÷ \(\frac{3}{4}\)
Now,
By using the Long Division,
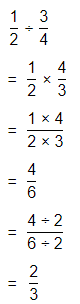
Hence, from the above,
We can conclude that

KEY CONCEPT
To divide a fraction by a fraction, rewrite the division equation as a multiplication equation.
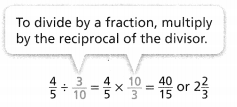
Do You Understand?
Question 1.
?Essential Question How can you divide a fraction by a fraction?
Answer:
The easiest way to divide fractions is to follow three simple steps:
a. Flip the divisor into a reciprocal.
b. Change the division sign into a multiplication sign and multiply.
c. Simplify if possible.
Question 2.
Critique Reasoning To find the quotient of \(\frac{2}{5}\) ÷ \(\frac{8}{5}\), Corey rewrites the problem as \(\frac{5}{2}\) × \(\frac{8}{5}\). Explain Corey’s mistake and how to correct it.
Answer:
It is given that
To find the quotient of \(\frac{2}{5}\) ÷ \(\frac{8}{5}\), Corey rewrites the problem as \(\frac{5}{2}\) × \(\frac{8}{5}\)
Now,
The given division expression is: \(\frac{2}{5}\) ÷ \(\frac{8}{5}\)
Now,
We know that,
We have to find the reciprocal of a fraction that is present to the right side of the division symbol
So,
\(\frac{2}{5}\) ÷ \(\frac{8}{5}\)
= \(\frac{2}{5}\) × \(\frac{5}{8}\)
Hence, from the above,
We can conclude that
Corey’s mistake is: He found the reciprocal of a fraction that is present to the left side of the division symbol instead of the right side of the division symbol
The correct form of the given division expression is:
\(\frac{2}{5}\) × \(\frac{5}{8}\)
Question 3.
Reasoning is the quotient of \(\frac{3}{5}\) ÷ \(\frac{6}{7}\) greater than or less than \(\frac{3}{5}\)? Explain.
Answer:
The given division expression is: \(\frac{3}{5}\) ÷ \(\frac{6}{7}\)
Now,
The representation of the given division expression in the decimal form is:
\(\frac{3}{5}\) ÷ \(\frac{6}{7}\)
= 0.60 ÷ 0.85
Now,
By using the Long Division,
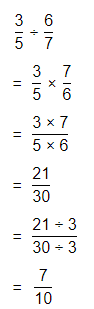
So,
The representation of the quotient value for the given divison expression in the decimal form is: 0.7
Hence, from the above,
We can conclude that
The quotient of \(\frac{3}{5}\) ÷ \(\frac{6}{7}\) is greater than \(\frac{3}{5}\)
Question 4.
How is dividing a whole number by a fraction different from dividing a fraction by a fraction?
Answer:
The steps to divide a fraction by a Whole Number are:
1. Turn the whole number into a fraction.
2. Multiply the fraction by the whole number fraction.
3. Multiply the tops together and the bottoms together
The steps to divide a fraction by a fraction are:
1. Arrange the equation
2. Keep the first fraction
3. Change the sign
4. Flip the fraction
5. Multiply the tops together and the bottoms together
Do You Know How?
In 5–7, write a division sentence to represent each model.
Question 5.
Answer:
The given model is:

Now,
From the given model,
We can observe that
The division sentence to represent the given model is:
\(\frac{4}{5}\) ÷ 4
Now,
By using the Long Division,
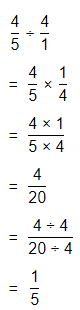
Hence, from the above,
We can conclude that
The division sentence to represent the given model is:
\(\frac{4}{5}\) ÷ 4
Question 6.
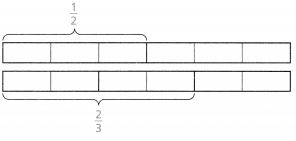
Answer:
The given model is:

Now,
From the given model,
We can observe that
The division sentence to represent the given model is:
\(\frac{1}{2}\) ÷ \(\frac{2}{3}\)
Now,
By using the Long Division,
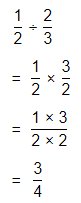
Hence, from the above,
We can conclude that
The division sentence to represent the given model is:
\(\frac{1}{2}\) ÷ \(\frac{2}{3}\)
Question 7.
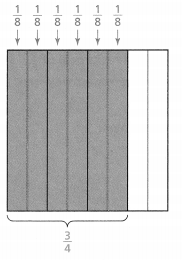
Answer:
The given model is:

Now,
From the given model,
We can observe that
The division sentence for the given model is:
\(\frac{3}{4}\) ÷ \(\frac{1}{8}\)
Now,
By using the Long Division,
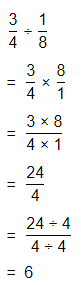
Hence, from the above,
We can conclude that
The division sentence for the given model is:
\(\frac{3}{4}\) ÷ \(\frac{1}{8}\)
In 8-11, find each quotient.
Question 8.
\(\frac{3}{4}\) ÷ \(\frac{2}{3}\)
Answer:
The given division expression is:
\(\frac{3}{4}\) ÷ \(\frac{2}{3}\)
Now,
By using the Long Division,
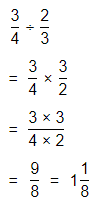
Hence, from the above,
We can conclude that
\(\frac{3}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{9}{8}\)
The quotient for the given division expression is: \(\frac{9}{8}\)
Question 9.
\(\frac{3}{12}\) ÷ \(\frac{1}{8}\)
Answer:
The given division expression is:
\(\frac{3}{12}\) ÷ \(\frac{1}{8}\)
Now,
By using the Long Division,
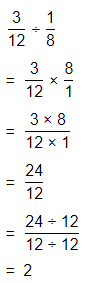
Hence, from the above,
We can conclude that
\(\frac{3}{12}\) ÷ \(\frac{1}{8}\) = 2
The quotient for the given division expression is: 2
Question 10.
\(\frac{1}{2}\) ÷ \(\frac{4}{5}\)
Answer:
The given division expression is:
\(\frac{1}{2}\) ÷ \(\frac{4}{5}\)
Now,
By using the Long Division,
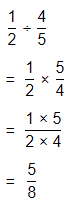
Hence, from the above,
We can conclude that
\(\frac{1}{2}\) ÷ \(\frac{4}{5}\) = \(\frac{5}{8}\)
The quotient for the given division expression is: \(\frac{5}{8}\)
Question 11.
\(\frac{7}{10}\) ÷ \(\frac{2}{5}\)
Answer:
The given division expression is:
\(\frac{7}{10}\) ÷ \(\frac{2}{5}\)
Now,
By using the Long Division,
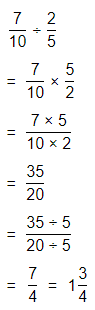
Hence, from the above,
We can conclude that
\(\frac{7}{10}\) ÷ \(\frac{2}{5}\) = \(\frac{7}{4}\)
The quotient for the given division expression is: \(\frac{7}{4}\)
Practice & Problem Solving
Scan for Multimedia
In 12 and 13, complete each division sentence using the models provided.
Question 12.
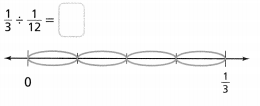
Answer:
The given division expression is:
\(\frac{1}{3}\) ÷ \(\frac{1}{12}\)
Now,
The given model is:
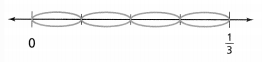
Now,
By using the Long Division,
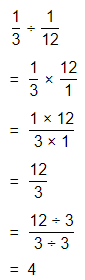
Hence, from the above,
We can conclude that
\(\frac{1}{3}\) ÷ \(\frac{1}{12}\) = 4
Question 13.
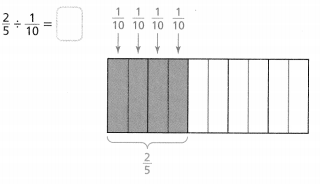
Answer:
The given division expression is:
\(\frac{2}{5}\) ÷ \(\frac{1}{10}\)
Now,
The given model is:
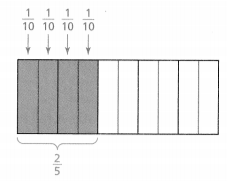
Now,
By using the Long Division,
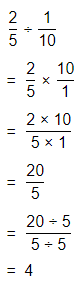
Hence, from the above,
We can conclude that
\(\frac{2}{5}\) ÷ \(\frac{1}{10}\) = 4
In 14-25, find each quotient.
Question 14.
\(\frac{2}{3}\) ÷ \(\frac{1}{3}\)
Answer:
The given division expression is:
\(\frac{2}{3}\) ÷ \(\frac{1}{3}\)
Now,
By using the Long Division,
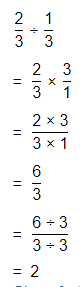
Hence, from the above,
We can conclude that
\(\frac{2}{3}\) ÷ \(\frac{1}{3}\) = 2
The quotient for the given division expresion is: 2
Question 15.
\(\frac{1}{2}\) ÷ \(\frac{1}{16}\)
Answer:
The given division expression is:
\(\frac{1}{2}\) ÷ \(\frac{1}{16}\)
Now,
By using the Long Division,
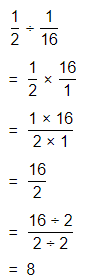
Hence, from the above,
We can conclude that
\(\frac{1}{2}\) ÷ \(\frac{1}{16}\) = 8
The quotient for the given division expresion is: 8
Question 16.
\(\frac{1}{4}\) ÷ \(\frac{1}{12}\)
Answer:
The given division expression is:
\(\frac{1}{4}\) ÷ \(\frac{1}{12}\)
Now,
By using the Long Division,
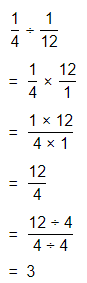
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) ÷ \(\frac{1}{12}\) = 3
The quotient for the given division expresion is: 3
Question 17.
\(\frac{6}{7}\) ÷ \(\frac{3}{7}\)
Answer:
The given division expression is:
\(\frac{6}{7}\) ÷ \(\frac{3}{7}\)
Now,
By using the Long Division,
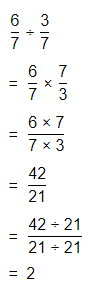
Hence, from the above,
We can conclude that
\(\frac{6}{7}\) ÷ \(\frac{3}{7}\) = 2
The quotient for the given division expresion is: 2
Question 18.
\(\frac{5}{14}\) ÷ \(\frac{4}{7}\)
Answer:
The given division expression is:
\(\frac{5}{14}\) ÷ \(\frac{4}{7}\)
Now,
By using the Long Division,
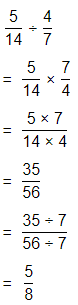
Hence, from the above,
We can conclude that
\(\frac{5}{14}\) ÷ \(\frac{4}{7}\) = \(\frac{5}{8}\)
The quotient for the given division expresion is: \(\frac{5}{8}\)
Question 19.
\(\frac{5}{8}\) ÷ \(\frac{1}{2}\)
Answer:
The given division expression is:
\(\frac{5}{8}\) ÷ \(\frac{1}{2}\)
Now,
By using the Long Division,
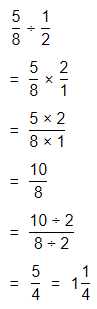
Hence, from the above,
We can conclude that
\(\frac{5}{8}\) ÷ \(\frac{1}{2}\) = \(\frac{5}{4}\)
The quotient for the given division expresion is: \(\frac{5}{4}\)
Question 20.
\(\frac{7}{12}\) ÷ \(\frac{3}{4}\)
Answer:
The given division expression is:
\(\frac{7}{12}\) ÷ \(\frac{3}{4}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
\(\frac{7}{12}\) ÷ \(\frac{3}{4}\) = \(\frac{7}{9}\)
The quotient for the given division expresion is: \(\frac{7}{9}\)
Question 21.
\(\frac{2}{7}\) ÷ \(\frac{1}{2}\)
Answer:
The given division expression is:
\(\frac{2}{7}\) ÷ \(\frac{1}{2}\)
Now,
By using the Long Division,
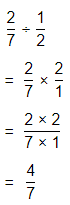
Hence, from the above,
We can conclude that
\(\frac{2}{7}\) ÷ \(\frac{1}{2}\) = \(\frac{4}{7}\)
The quotient for the given division expresion is: \(\frac{4}{7}\)
Question 22.
\(\frac{3}{10}\) ÷ \(\frac{3}{5}\)
Answer:
The given division expression is:
\(\frac{3}{10}\) ÷ \(\frac{3}{5}\)
Now,
By using the Long Division,
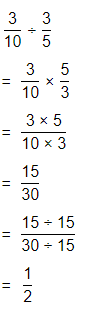
Hence, from the above,
We can conclude that
\(\frac{3}{10}\) ÷ \(\frac{3}{5}\) = \(\frac{1}{2}\)
The quotient for the given division expresion is: \(\frac{1}{2}\)
Question 23.
\(\frac{7}{12}\) ÷ \(\frac{1}{8}\)
Answer:
The given division expression is:
\(\frac{7}{12}\) ÷ \(\frac{1}{8}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
\(\frac{7}{12}\) ÷ \(\frac{1}{8}\) = \(\frac{14}{3}\)
The quotient for the given division expresion is: \(\frac{14}{3}\)
Question 24.
\(\frac{3}{10}\) ÷ \(\frac{3}{5}\)
Answer:
The given division expression is:
\(\frac{3}{10}\) ÷ \(\frac{3}{5}\)
Now,
By using the Long Division,
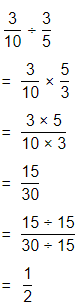
Hence, from the above,
We can conclude that
\(\frac{3}{10}\) ÷ \(\frac{3}{5}\) = \(\frac{1}{2}\)
The quotient for the given division expresion is: \(\frac{1}{2}\)
Question 25.
\(\frac{2}{5}\) ÷ \(\frac{1}{8}\)
Answer:
The given division expression is:
\(\frac{2}{5}\) ÷ \(\frac{1}{8}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
\(\frac{2}{5}\) ÷ \(\frac{1}{8}\) = \(\frac{16}{5}\)
The quotient for the given division expresion is: \(\frac{16}{5}\)
Question 26.
Be Precise A large bag contains \(\frac{12}{15}\) pound of granola. How many \(\frac{1}{3}\) pound bags can be filled with this amount of granola? How much granola is left over?

Answer:
It is given that
A large bag contains \(\frac{12}{15}\) pound of granola
Now,
Let the number of \(\frac{1}{3}\) pound bags that can be filled with the given amount of granola be: x
Now,
According to the given information,
\(\frac{1}{3}\) × x = \(\frac{12}{15}\)
x = \(\frac{12}{15}\) ÷ \(\frac{1}{3}\)
Now,
By using the Long Division,

So,
The number of \(\frac{1}{3}\) pound bags that can be filled with the given amount of granola is about 2 bags
Now,
The amount of granola that is leftover = (The number of \(\frac{1}{3}\) pound bags that can be filled with the given amount of granola) – (The total amount of granola)
= \(\frac{12}{5}\) – \(\frac{12}{15}\)
Now,
By using the Long Subtraction,
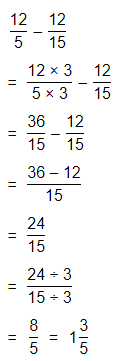
Hence, from the above,
We can conclude that
The amount of granola that is leftover is: \(\frac{8}{5}\) pounds
Question 27.
Higher-Order Thinking Find \(\frac{3}{4}\) ÷ \(\frac{2}{3}\). Then draw a picture and write an explanation describing how to get the answer.
Answer:
The given division expression is:
\(\frac{3}{4}\) ÷ \(\frac{2}{3}\)
Now,
By using the Long Division,
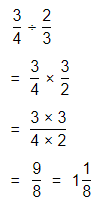
Hence,
The representation of the given division expression in the form of an area model is:

\(\frac{3}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{9}{8}\)
Question 28.
The area of a rectangular painting is \(\frac{1}{6}\) square yard. The width is \(\frac{2}{3}\) yard. What is the length of the painting? Use the formula A = l × w.
Answer:
It is given that
The area of a rectangular painting is \(\frac{1}{6}\) square yard. The width is \(\frac{2}{3}\) yard.
Now,
Let the length of the painting be x yard
Now,
From the given information,
A = l × w
So,
\(\frac{1}{6}\) = x × \(\frac{2}{3}\)
x = \(\frac{1}{6}\) ÷ \(\frac{2}{3}\)
Now,
By using the Long Division,
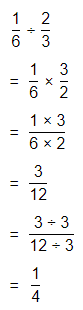
Hence, from the above,
We can conclude that
The length of the painting is: \(\frac{1}{4}\) yard
Question 29.
Solve for n in the equation \(\frac{13}{16}\) ÷ \(\frac{1}{6}\) = n.
Answer:
The given division expression is:
\(\frac{13}{16}\) ÷ \(\frac{1}{6}\) = n
Where,
‘n’ is the quotient for the given division expression
Now,
By using the Long Division,
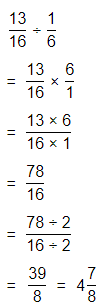
So,
\(\frac{13}{16}\) ÷ \(\frac{1}{6}\) = \(\frac{39}{8}\)
Hence, from the above,
We can conclude that
The value of ‘n’ is: \(\frac{39}{8}\)
Question 30.
Model with Math
A cafeteria uses \(\frac{1}{6}\) pound of coffee to fill a large coffee dispenser. The cafeteria has \(\frac{2}{3}\) pound of coffee to use.
a. Complete the model at the right to find how many coffee dispensers the cafeteria can fill.
b. Write a division sentence that describes the model and tells how many dispensers can be filled.
Answer:
It is given that
A cafeteria uses \(\frac{1}{6}\) pound of coffee to fill a large coffee dispenser. The cafeteria has \(\frac{2}{3}\) pound of coffee to use.
Now,
The representation of the given information in the form of a model is:
Now,
From the given model,
We can observe that
The number of coffee dispensers the cafeteria can fill = (The number of pounds of the coffee cafeteria has to use) ÷ (The number of pounds of the coffee a cafeteria has to use)
= \(\frac{2}{3}\) ÷ \(\frac{1}{6}\)
Now,
By using the Long division,

Hence, from the above,
We can conclude that
a. The model to find how many coffee dispensers the cafeteria can fill is:

b. The division sentence that describes the model and tells how many dispensers can be filled is:
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\)
Question 31.
Model with Math A full load for a small truck to haul is \(\frac{2}{3}\) ton of gravel. The truck is hauling \(\frac{1}{2}\) ton of gravel.

a. Complete the model below to find how much of a full load the truck is hauling.
b. Write a division sentence that describes the model and tells how much of a full load the truck is hauling.
Answer:
It is given that
A full load for a small truck to haul is \(\frac{2}{3}\) ton of gravel. The truck is hauling \(\frac{1}{2}\) ton of gravel.
Now,
The representation of the given information in the form of a model is:
Now,
From the given model,
We can observe that
The amount of a full load the truck is hauling = (The amount of a full load for a small truck to haul) ÷ (The amount of gravel a truck is hauling)
= \(\frac{2}{3}\) ÷ \(\frac{1}{2}\)
Now,
By using the Long Division,
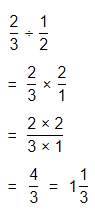
Hence, from the above,
We can conclude that
a. The model below to find how much of a full load the truck is hauling is:

b. The division sentence describes the model and tells how much of a full load the truck is hauling is:
\(\frac{2}{3}\) ÷ \(\frac{1}{2}\)
Question 32.
Use Structure How many \(\frac{1}{4}\)-inch pieces can be cut from a piece of metal \(\frac{5}{4}\) inch long?
Answer:
It is given that
\(\frac{1}{4}\)-inch pieces can be cut from a piece of metal \(\frac{5}{4}\) inch long
So,
The number of \(\frac{1}{4}\)-inch pieces that can be cut from \(\frac{5}{4}\) inch long
= \(\frac{5}{4}\) ÷ \(\frac{1}{4}\)
Now,
By using the Long Division,
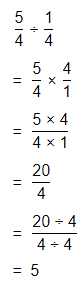
Hence, from the above,
We can conclude that
The number of \(\frac{1}{4}\)-inch pieces that can be cut from \(\frac{5}{4}\) inch long is: 5 pieces
Question 33.
Write a problem that could be solved by finding \(\frac{5}{8}\) ÷ \(\frac{2}{5}\).
Answer:
The given division expression is:
\(\frac{5}{8}\) ÷ \(\frac{2}{5}\)
Now,
By using the Long Division,
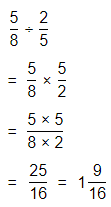
Hence, from the above,
We can conclude that
\(\frac{5}{8}\) ÷ \(\frac{2}{5}\) = \(\frac{25}{16}\)
Assessment Practice
Question 34.
Which division sentence is shown by the model at the right?
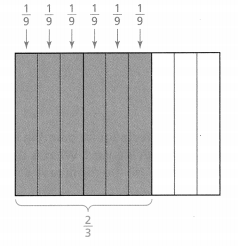
A. \(\frac{2}{3}\) ÷ \(\frac{1}{9}\) = 6
B. \(\frac{1}{9}\) ÷ \(\frac{2}{3}\) = \(\frac{1}{6}\)
C. 6 ÷ \(\frac{1}{9}\) = 54
D. 6 ÷ \(\frac{2}{3}\) = 9
Answer:
The given model is:

Now,
From the given model,
We can observe that
\(\frac{2}{3}\) ÷ \(\frac{1}{9}\)
Now,
By using the Long Division,
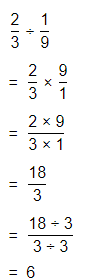
Hence, from the above,
We can conclude that
The division sentence that is shown by the model is:

Lesson 1.6 Divide Mixed Numbers
Solve & Discuss It!
A jeweler has a 5\(\frac{1}{2}\)inch strip of silver wire that she is cutting into 1\(\frac{3}{8}\)-inch pieces. How many pieces can she make?

Answer:
It is given that
A jeweler has a 5\(\frac{1}{2}\)inch strip of silver wire that she is cutting into 1\(\frac{3}{8}\)-inch pieces
So,
The number of pieces of silver wire she can make = (The total length of the silver wire) ÷ (The length of each cutting piece of the silver wire)
= 5\(\frac{1}{2}\) ÷ 1\(\frac{3}{8}\)
Now,
By using the Long Division,
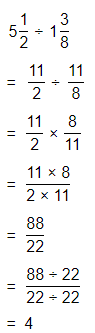
Hence, from the above,
We can conclude that
The number of pieces of silver wire she can make is: 4 pieces
Generalize How can you use what you know about solving problems with fractions to find how many pieces the jeweler can make?
Answer:
The steps to solve problems with fractions with the help of what you know is:
a. Read the problem carefully.
b. Think about what it is asking us to do.
c. Think about the information we need.
d. Solve it.
e Simplify, if necessary.
f. Think about whether our solution makes sense (in order to check it).
Focus on math practices
Generalize Explain how to use estimation to check whether your answer is reasonable.
Answer:
To use estimation, you need to read and understand the problem. There will be clues in the problem to let you know if estimation is a good option for solving that specific problem. Estimating means finding an answer that is an approximate answer
? Essential Question How can you divide with mixed numbers?
Answer:
The steps to divide the mixed numbers are:
Step 1:
Make sure everything is in fraction form (mixed numbers need to be changed to improper fractions).
Step 2:
Flip the second fraction and change the operation to multiply.
Step 3:
Multiply across the top for the new numerator and across the bottom for the new denominator.
Step 4:
Simplify (if needed).
Try It!
How many medium bumper stickers can Damon fit side by side on his car bumper? Find 37\(\frac{1}{2}\) ÷ 10\(\frac{3}{4}\).
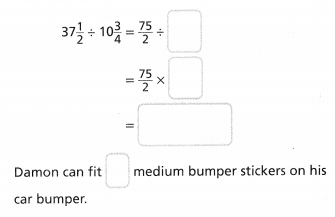
Answer:
The given information is:

Now,
The number of medium bumper stickers can Damon fit side by side on his car bumper = (The total length of the car bumper) ÷ (The length of the medium bumper)
= 37\(\frac{1}{2}\) ÷ 10\(\frac{3}{4}\)
Now,
By using the Long Division,
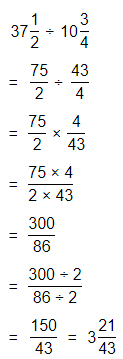
Hence, from the above,
We can conclude that
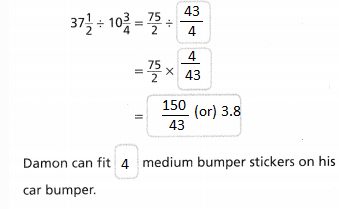
Convince Me! Why do you multiply \(\frac{75}{2}\) by \(\frac{4}{43}\) to divide 37\(\frac{1}{2}\) by 10\(\frac{3}{4}\)?
Answer:
The given division expression is:
37\(\frac{1}{2}\) ÷ 10\(\frac{3}{4}\)
Now,
The representation of the given mixed numbers into a fraction is:
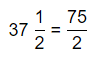

So,
37\(\frac{1}{2}\) ÷ 10\(\frac{3}{4}\)
= \(\frac{75}{2}\) ÷ \(\frac{43}{4}\)
Now,
We know that,
Two numbers whose product is “1” are called “reciprocals” of each other. If a nonzero number is named as a fraction \(\frac{a}{b}\), then its reciprocal is \(\frac{b}{a}\)
So,
\(\frac{75}{2}\) ÷ \(\frac{43}{4}\)
= \(\frac{75}{2}\) × \(\frac{4}{43}\)
Hence, from the above,
We can conclude that
You can multiply \(\frac{75}{2}\) by \(\frac{4}{43}\) to divide 37\(\frac{1}{2}\) by 10\(\frac{3}{4}\) due to the property of “Reciprocals”
Try It!
Divide.
a. 20 ÷ 2\(\frac{2}{3}\)
Answer:
The given division expression is:
20 ÷ 2\(\frac{2}{3}\)
So,
The representtaion of 2\(\frac{2}{3}\) into a fraction is:
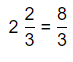
So,
20 ÷ \(\frac{8}{3}\)
Now,
By using the Long Division,
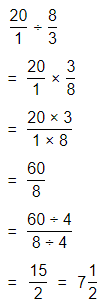
Hence, from the above,
We can conclude that
20 ÷ 2\(\frac{2}{3}\) = \(\frac{15}{2}\)
b. 12\(\frac{1}{2}\) ÷ 6
Answer:
The given division expression is:
12\(\frac{1}{2}\) ÷ 6
So,
The representation of 12\(\frac{1}{2}\) into a fraction is:
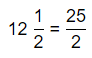
So,
\(\frac{25}{2}\) ÷ 6
Now,
By using the Long Division,
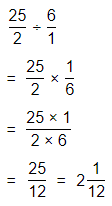
Hence, from the above,
We can conclude that
12\(\frac{1}{2}\) ÷ 6 = \(\frac{25}{12}\)
KEY CONCEPT

Do You Understand?
Question 1.
? Essential Question How can you divide with mixed numbers?
Answer:
The steps to divide the mixed numbers are:
Step 1:
Make sure everything is in fraction form (mixed numbers need to be changed to improper fractions).
Step 2:
Flip the second fraction and change the operation to multiply.
Step 3:
Multiply across the top for the new numerator and across the bottom for the new denominator.
Step 4:
Simplify (if needed).
Question 2.
Generalize When dividing mixed numbers, why is it important to estimate the quotient first?
Answer:
You can estimate to find the approximate quotient of fractions and mixed numbers. Estimating quotients of fractions is similar to estimating products of fractions. To estimate the quotient of two fractions, you will first rewrite the problem as a multiplication problem
Question 3.
Reasoning In Example 1, how many long bumper stickers can Damon fit side by side on his car bumper? Will there be uncovered space? Explain.
Answer:
It is given that
The total length of the bumper is: 37\(\frac{1}{2}\) inches
Now,
The given information is:

Now,
From the given table,
We can observe that
The total length of the bumper = (The length of the short bumper) + (The length of the medium bumper) + (The length of the long bumper)
= 6\(\frac{1}{4}\) + 10\(\frac{3}{4}\) + 15
Now,
By using the Long Addition,
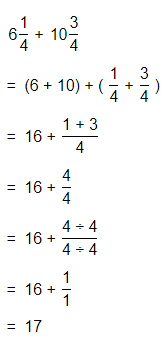
So,
The total length of the bumper = 17 + 15
= 32 inches
Now,
From the answer,
We can observe that
The given total length of the bumper > The calculated total length of the bumper
Hence, from the above,
We can conclude that there will be uncovered space in the bumper
Question 4.
What is the difference between dividing fractions less than 1 and dividing mixed numbers?
Answer:
Dividing mixed numbers is very similar to multiplying mixed numbers. You just add one step i.e., after changing the divisor into an improper fraction, you then find its reciprocal and multiply.
Do You Know How?
In 5–13, find each quotient.
Question 5.

Answer:
The given division expression is:
2\(\frac{5}{8}\) ÷ 2\(\frac{1}{4}\)
Now,
By using the Long Division,
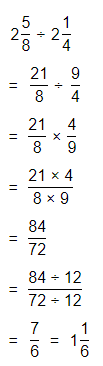
Hence, from the above,
We can conclude that
2\(\frac{5}{8}\) ÷ 2\(\frac{1}{4}\) = \(\frac{7}{8}\)
The quotient for the given division expression is: \(\frac{7}{6}\)
Question 6.
3 ÷ 4\(\frac{1}{2}\)
Answer:
The given division expression is:
3 ÷ 4\(\frac{1}{2}\)
Now,
The representation of 4\(\frac{1}{2}\) into a fraction is:

Now,
By using the Long Division,
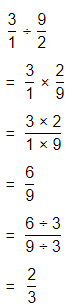
Hence, from the above,
We can conclude that
3 ÷ 4\(\frac{1}{2}\) = \(\frac{2}{3}\)
The quotient for the given division expression is: \(\frac{2}{3}\)
Question 7.
18 ÷ 3\(\frac{2}{3}\)
Answer:
The given division expression is:
18 ÷ 3\(\frac{2}{3}\)
Now,
The representation of 3\(\frac{2}{3}\) into a fraction is:

Now,
By using the Long Division,
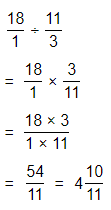
Hence, from the above,
We can conclude that
18 ÷ 3\(\frac{2}{3}\) = \(\frac{54}{11}\)
The quotient for the given division expression is: \(\frac{54}{11}\)
Question 8.
1\(\frac{2}{5}\) ÷ 7
Answer:
The given division expression is:
1\(\frac{2}{5}\) ÷ 7
Now,
The representation of 1\(\frac{2}{5}\) into a fraction is:
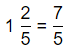
Now,
By using the Long Division,
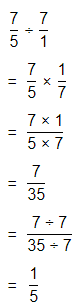
Hence, from the above,
We can conclude that
1\(\frac{2}{5}\) ÷ 7 = \(\frac{1}{5}\)
The quotient for the given division expression is: \(\frac{1}{5}\)
Question 9.
5 ÷ 6\(\frac{2}{5}\)
Answer:
The given division expression is:
5 ÷ 6\(\frac{2}{5}\)
Now,
The representation of 3\(\frac{2}{3}\) into a fraction is:
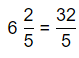
Now,
By using the Long Division,
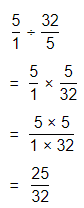
Hence, from the above,
We can conclude that
5 ÷ 6\(\frac{2}{5}\) = \(\frac{25}{32}\)
The quotient for the given division expression is: \(\frac{25}{32}\)
Question 10.
8\(\frac{1}{5}\) ÷ 3\(\frac{3}{4}\)
Answer:
The given division expression is:
8\(\frac{1}{5}\) ÷ 3\(\frac{3}{4}\)
Now,
By using the Long Division,
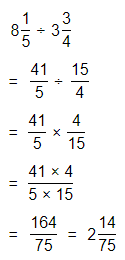
Hence, from the above,
We can conclude that
8\(\frac{1}{5}\) ÷ 3\(\frac{3}{4}\) = \(\frac{164}{75}\)
The quotient for the given division expression is: \(\frac{164}{75}\)
Question 11.
2\(\frac{1}{2}\) ÷ 4\(\frac{1}{10}\)
Answer:
The given division expression is:
2\(\frac{1}{2}\) ÷ 4\(\frac{1}{10}\)
Now,
By using the Long Division,
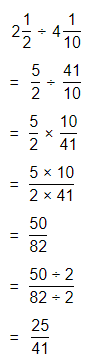
Hence, from the above,
We can conclude that
2\(\frac{1}{2}\) ÷ 4\(\frac{1}{10}\) = \(\frac{25}{41}\)
The quotient for the given division expression is: \(\frac{25}{41}\)
Question 12.
2\(\frac{2}{3}\) ÷ 6
Answer:
The given division expression is:
2\(\frac{2}{3}\) ÷ 6
Now,
The representation of 2\(\frac{2}{3}\) into a fraction is:

Now,
By using the Long Division,
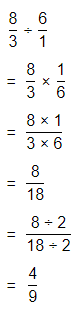
Hence, from the above,
We can conclude that
2\(\frac{2}{3}\) ÷ 6 = \(\frac{4}{9}\)
The quotient for the given division expression is: \(\frac{4}{9}\)
Question 13.
6\(\frac{5}{9}\) ÷ 1\(\frac{7}{9}\)
Answer:
The given division expression is:
6\(\frac{5}{9}\) ÷ 1\(\frac{7}{9}\)
Now,
By using the Long Division,
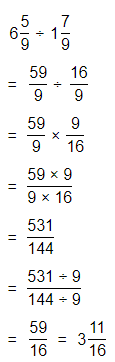
Hence, from the above,
We can conclude that
6\(\frac{5}{9}\) ÷ 1\(\frac{7}{9}\) = \(\frac{59}{16}\)
The quotient for the given division expression is: \(\frac{59}{16}\)
Practice & Problem Solving
Scan for Multimedia
Leveled Practice In 14-25, find each quotient.
Question 14.
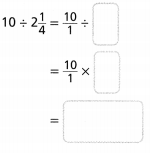
Answer:
The given division expression is:
10 ÷ 2\(\frac{1}{4}\)
Now,
The representation of 2\(\frac{1}{4}\) into a fraction is:
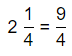
Now,
By using the Long Division,
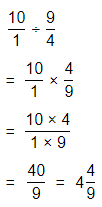
Hence, from the above,
We can conclude that
10 ÷ 2\(\frac{1}{4}\) = \(\frac{40}{9}\)
The quotient for the given division expression is: \(\frac{40}{9}\)
Question 15.
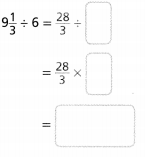
Answer:
The given division expression is:
9\(\frac{1}{3}\) ÷ 6
Now,
The representation of 9\(\frac{1}{3}\) into a fraction is:
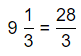
Now,
By using the Long Division,
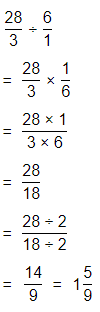
Hence, from the above,
We can conclude that
9\(\frac{1}{3}\) ÷ 6 = \(\frac{14}{9}\)
The quotient for the given division expression is: \(\frac{14}{9}\)
Question 16.
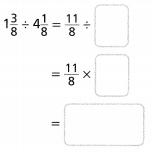
Answer:
The given division expression is:
1\(\frac{3}{8}\) ÷ 4\(\frac{1}{8}\)
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
1\(\frac{3}{8}\) ÷ 4\(\frac{1}{8}\) = \(\frac{1}{3}\)
The quotient for the given division expression is: \(\frac{1}{3}\)
Question 17.
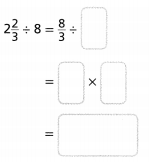
Answer:
The given division expression is:
2\(\frac{2}{3}\) ÷ 8
Now,
The representation of 2\(\frac{2}{3}\) into a fraction is:
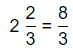
Now,
By using the Long Division,
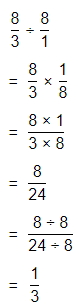
Hence, from the above,
We can conclude that
2\(\frac{2}{3}\) ÷ 8 = \(\frac{1}{3}\)
The quotient for the given division expression is: \(\frac{1}{3}\)
Question 18.
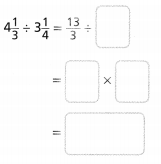
Answer:
The given division expression is:
4\(\frac{1}{3}\) ÷ 3\(\frac{1}{4}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
4\(\frac{1}{3}\) ÷ 3\(\frac{1}{4}\) = \(\frac{4}{3}\)
The quotient for the given division expression is: \(\frac{4}{3}\)
Question 19.

Answer:
The given division expression is:
1 ÷ 8\(\frac{5}{9}\)
Now,
The representation of 8\(\frac{5}{9}\) into a fraction is:
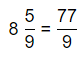
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
1 ÷ 8\(\frac{5}{9}\) = \(\frac{9}{77}\)
The quotient for the given division expression is: \(\frac{9}{77}\)
Question 20.
3\(\frac{5}{6}\) ÷ 9\(\frac{5}{6}\)
Answer:
The given division expression is:
3\(\frac{5}{6}\) ÷ 9\(\frac{5}{6}\)
Now,
By using the Long Division,
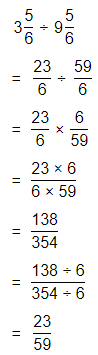
Hence, from the above,
We can conclude that
3\(\frac{5}{6}\) ÷ 9\(\frac{5}{6}\) = \(\frac{23}{59}\)
The quotient for the given division expression is: \(\frac{23}{59}\)
Question 21.
16 ÷ 2\(\frac{2}{3}\)
Answer:
The given division expression is:
16 ÷ 2\(\frac{2}{3}\)
Now,
The representation of 2\(\frac{2}{3}\) into a fraction is:
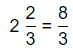
Now,
By using the Long Division,
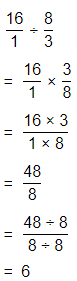
Hence, from the above,
We can conclude that
16 ÷ 2\(\frac{2}{3}\) = 6
The quotient for the given division expression is: 6
Question 22.
2\(\frac{5}{8}\) ÷ 13
Answer:
The given division expression is:
2\(\frac{5}{8}\) ÷ 13
Now,
The representation of 2\(\frac{5}{8}\) into a fraction is:
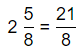
Now,
By using the Long Division,
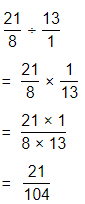
Hence, from the above,
We can conclude that
2\(\frac{5}{8}\) ÷ 13 = \(\frac{21}{104}\)
The quotient for the given division expression is: \(\frac{21}{104}\)
Question 23.
3\(\frac{6}{7}\) ÷ 6\(\frac{3}{4}\)
Answer:
The given division expression is:
3\(\frac{6}{7}\) ÷ 6\(\frac{3}{4}\)
Now,
By using the Long Division,
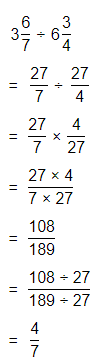
Hence, from the above,
We can conclude that
3\(\frac{6}{7}\) ÷ 6\(\frac{3}{4}\) = \(\frac{4}{7}\)
The quotient for the given division expression is: \(\frac{4}{7}\)
Question 24.
2\(\frac{1}{3}\) ÷ 1\(\frac{1}{3}\)
Answer:
The given division expression is:
2\(\frac{1}{3}\) ÷ 1\(\frac{1}{3}\)
Now,
By using the Long Division,
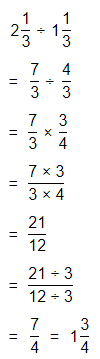
Hence, from the above,
We can conclude that
2\(\frac{1}{3}\) ÷ 1\(\frac{1}{3}\) = \(\frac{7}{4}\)
The quotient for the given division expression is: \(\frac{7}{4}\)
Question 25.
3\(\frac{3}{4}\) ÷ 1\(\frac{1}{2}\)
Answer:
The given division expression is:
3\(\frac{3}{4}\) ÷ 1\(\frac{1}{2}\)
Now,
By using the Long Division,
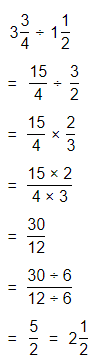
Hence, from the above,
We can conclude that
3\(\frac{3}{4}\) ÷ 1\(\frac{1}{2}\) = \(\frac{5}{2}\)
The quotient for the given division expression is: \(\frac{5}{2}\)
Question 26.
Beth is making a rope ladder. Each step of the ladder is 2\(\frac{1}{3}\), feet wide. Beth has a rope that is 21 feet long. How many steps can she make from the rope?
Answer:
It is given that
Beth is making a rope ladder. Each step of the ladder is 2\(\frac{1}{3}\), feet wide. Beth has a rope that is 21 feet long
So,
The number of steps Berth can make from the rope = (The total length of the rope) ÷ (The length of each step of the ladder)
= 21 ÷ 2\(\frac{1}{3}\)
Now,
The representation of 2\(\frac{1}{3}\) into a fraction form is:
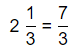
Now,
By using the Long Division,
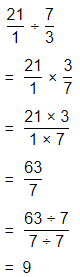
Hence, from the above,
We can conclude that
The number of steps Berth can make from the rope is: 9 steps
Question 27.
The area of this rectangle is 257\(\frac{1}{4}\) in.2. Find side length w.

Answer:
It is given that
The area of this rectangle is 257\(\frac{1}{4}\) in.2
Now,
The given figure is:

Now,
We know that,
The area of a rectangle = Length × Width
So,
257\(\frac{1}{4}\) = 10\(\frac{1}{2}\) × w
w = 257\(\frac{1}{4}\) ÷ 10\(\frac{1}{2}\)
Now,
By using the Long Division,
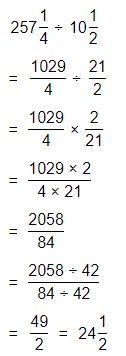
Hence, from the above,
We can conclude that
The side length (w) of the given rectangle is: \(\frac{49}{2}\) in.
In 28 and 29, use the picture.
Question 28.
The larger room is twice as long as the smaller room. How long is the larger room?

Answer:
It is given that
The larger room is twice as long as the smaller room.
Now,
The given figure is:

So,
The length of the larger room = 2 × (The length of the smaller room)
= 2 × 20\(\frac{4}{5}\)
Now,
The representation of 20\(\frac{4}{5}\) into a fraction is:
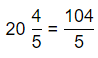
Now,
By using the Long Multiplication,
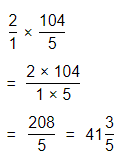
Hence, from the above,
We can conclude that
The length of the larger room is: \(\frac{208}{5}\) feet
Question 29.
If the length of the smaller room is divided into 4 equal parts, how long is each part?
Answer:
It is given that
The length of the smaller room is divided into 4 equal parts
So,
According to the given information,
The length of each part in the smaller room = 20\(\frac{4}{5}\) ÷ 4
Now,
The representation of 20\(\frac{4}{5}\) into a fraction is:
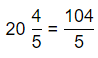
Now,
By using the Long Division,
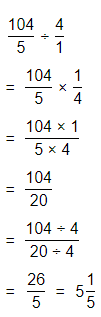
Hence, from the above,
We can conclude that
The length of each part in the smaller room is: [latx]\frac{26}{5}[/latex] feet
Question 30.
Make Sense and Persevere Luis has 3 pounds of ground turkey to make turkey burgers. He uses \(\frac{3}{8}\) pound per burger to make 6 burgers. How many \(\frac{1}{4}\)-pound burgers can Luis make with the remaining turkey?
Answer:
It is given that
Luis has 3 pounds of ground turkey to make turkey burgers. He uses \(\frac{3}{8}\) pound per burger to make 6 burgers
So,
The remaining amount of ground Turkey Luis has = 3 – \(\frac{3}{8}\)
Now,
By using the Long Subtraction,
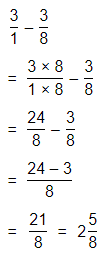
So,
The remaining amount of ground turkey Luis has is: \(\frac{21}{8}\) pounds
Now,
The number of \(\frac{1}{4}\)-pound burgers can Luis make with the remaining turkey =
\(\frac{21}{8}\) ÷ \(\frac{1}{4}\)
Now,
By using the Long Division,
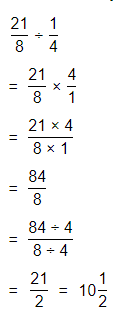
Hence, from the above,
We can conclude that
The number of \(\frac{1}{4}\)-pound burgers can Luis make with the remaining turkey is about 11 burgers
Question 31.
Higher Order Thinking If 9 × \(\frac{n}{5}\) = 9 ÷ \(\frac{n}{5}\), then what does n equal? Explain.
Answer:
It is given that
9 × \(\frac{n}{5}\) = 9 ÷ \(\frac{n}{5}\)
So,
According to the Property of Reciprocals,
9 × \(\frac{n}{5}\) = 9 ÷ \(\frac{n}{5}\)
9 × \(\frac{n}{5}\) = 9 × \(\frac{5}{n}\)
\(\frac{n}{5}\) = \(\frac{5}{n}\)
n × n = 5 × 5
n² = 25
n = \(\sqrt{25}\)
n = 5
Hence, from the above,
We can conclude that
The value of “n” is: 5
Question 32.
Margaret uses 1\(\frac{3}{4}\) teaspoons of key lime zest to make 12 key lime cupcakes. She wants to make 30 cupcakes. How much key lime zest will Margaret use?
Answer:
It is given that
Margaret uses 1\(\frac{3}{4}\) teaspoons of key lime zest to make 1\(\frac{1}{2}\) key lime cupcakes
Now,
Let the number of teaspoons of key lime zest to make 30 cupcakes be x
So,
1\(\frac{3}{4}\) × 12 = x × 30
Now,
The representation of 1\(\frac{3}{4}\) into a fraction is:
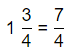
So,
x = \(\frac{7}{4}\) × \(\frac{12}{30}\)
Now,
By using the Long Multiplication,
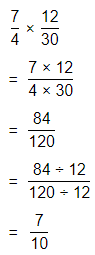
Hence, from the above,
We can conclude that
The number of teaspoons of key lime zest to make 30 cupcakes is: \(\frac{7}{10}\) teaspoons of key lime zest
Question 33.
Use Structure A gem store in Fort Lauderdale received a shipment of 1\(\frac{1}{2}\) pounds of moonstone crystals. If these moonstone crystals were separated into 6 equal bags, how much would each bag weigh?
Answer:
It is given that
A gem store in Fort Lauderdale received a shipment of 1\(\frac{1}{2}\) pounds of moonstone crystals.
So,
The weight of each bag of moonstone crystals = (The total weight of moonstone crystals) ÷ (The number of bags that moonstone crystals equally divided)
= 1\(\frac{1}{2}\) ÷ 6
Now,
The representation of 1\(\frac{1}{2}\) into a fraction is:

Now,
By using the Long Division,
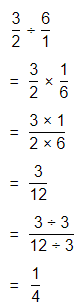
Hence, from the above,
We can conclude that
The weight of each bag of moonstone crystals is: \(\frac{1}{4}\) pounds
Question 34.
The owner of an aquatic store used 17\(\frac{1}{2}\) gallons of water to fill aquariums. He put 5\(\frac{5}{6}\) gallons of water in each aquarium. How many aquariums did he fill?
Answer:
It is given that
The owner of an aquatic store used 17\(\frac{1}{2}\) gallons of water to fill aquariums. He put 5\(\frac{5}{6}\) gallons of water in each aquarium.
So,
The number of aquariums did he fill = (The total amount of water used to fill aquariums) ÷ (The amount of water in each aquarium)
= 17\(\frac{1}{2}\) ÷ 5\(\frac{5}{6}\)
Now,
By using the Long Division,
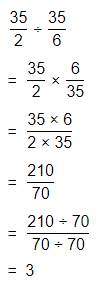
Hence, from the above,
We can conclude that
The number of aquariums did he fill is: 3 aquariums
Question 35.
Write an explanation to a friend about how you would estimate 17\(\frac{1}{5}\) ÷ 3\(\frac{4}{5}\).
Answer:
The given division expression is:
17\(\frac{1}{5}\) ÷ 3\(\frac{4}{5}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
17\(\frac{1}{5}\) ÷ 3\(\frac{4}{5}\) = \(\frac{86}{19}\)
Assessment Practice
Question 36.
A restaurant has 15\(\frac{1}{5}\) pounds of alligator meat to make tasty alligator dishes.
PART A
Each pot of alligator stew requires 2\(\frac{3}{8}\) pounds of alligator meat. Which solution shows how many pots of alligator stew can be made?
A. 36 pots; 15\(\frac{1}{5}\) × 2\(\frac{3}{8}\)
B. \(\frac{5}{32}\) pot; 2\(\frac{3}{8}\) ÷ 15\(\frac{1}{5}\)
C. 7 pots; 15\(\frac{1}{5}\) ÷ 2\(\frac{3}{8}\)
D. 6 pots; 15\(\frac{1}{5}\) ÷ 2\(\frac{3}{8}\)
Answer:
It is given that
A restaurant has 15\(\frac{1}{5}\) pounds of alligator meat to make tasty alligator dishes. Each pot of alligator stew requires 2\(\frac{3}{8}\) pounds of alligator meat
So,
The number of pots of alligator stew can be made = 15\(\frac{1}{5}\) ÷ 2\(\frac{3}{8}\)
Now,
By using the Long Division,
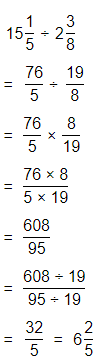
So,
The number of pots of alligator stew that can be made is about 6 pots
Hence, from the above,
We can conclude that
The solution that shows how many pots of alligator stew can be made is:

PART B
The restaurant could make a smaller pot of alligator stew that uses 1\(\frac{3}{5}\) pounds of alligator meat. How many smaller pots of alligator stew can be made than the larger pots?
Answer:
It is given that
The restaurant could make a smaller pot of alligator stew that uses 1\(\frac{3}{5}\) pounds of alligator meat
So,
The number of smaller pots of stew that can be made = 15\(\frac{1}{5}\) ÷ 1\(\frac{3}{5}\)
Now,
By using the Long Division,
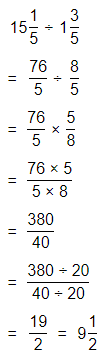
So,
The number of smaller pots of stew that can be made is about 10 pots
Now,
From Part (A),
We can observe that
The number of larger pots of stew that can be made is about 6 pots
So,
The number of smaller pots more than the larger pots = 10 – 6
= 4 pots
Hence, from the above,
We can conclude that
The number of smaller pots more than the larger pots are: 4 pots
Lesson 1.7 Solve Problems with Rational Numbers
ACTIVITY
Explain It!
Jenna feeds her cat twice a day. She gives her cat \(\frac{3}{4}\) can of cat food each time. Jenna is having a friend take care of her cat for 5 days. To prepare, she bought 8 cans of cat food. Did Jenna buy enough cat food?

A. What do you need to know before you can answer the question?
Answer:
It is given that
Jenna feeds her cat twice a day. She gives her cat \(\frac{3}{4}\) can of cat food each time. Jenna is having a friend take care of her cat for 5 days. To prepare, she bought 8 cans of cat food.
Hence,
The hidden question for the given information is:
How much food will be needed for Jenna’s cat for 5 days?
B. How can you determine which operations to use to solve the problem?
Answer:
It is given that
Jenna feeds her cat twice a day. She gives her cat \(\frac{3}{4}\) can of cat food each time. Jenna is having a friend take care of her cat for 5 days. To prepare, she bought 8 cans of cat food.
So,
The operations we will use to solve the given problem is:
a.
To find the total amount of food Jenna gives her cat ——> Multiplication
b.
To find the amount of food Jenna’s cat will need for 5 days ——->Multiplication
c.
To find the amount of food Jenna’s cat will need for 8 days ——-> Multiplication
d.
To know whether Jenna bought enough food or not ——> Comparison
Focus on math practices
Reasoning To find out whether she has enough cat food, Jenna multiplies, divides, and compares. Explain how Jenna may have solved the problem.
Answer:
The steps Jenna took to solve the given problem are:
a.
To find the total amount of food Jenna gives her cat ——> Multiplication
b.
To find the amount of food Jenna’s cat will need for 5 days ——->Multiplication
c.
To find the amount of food Jenna’s cat will need for 8 days ——-> Multiplication
d.
To know whether Jenna bought enough food or not ——> Comparison
?Essential Question How can you solve problems with rational numbers?
Answer:
We know that,
A “Rational number” is a number that can be written as a fraction.
Fractions, integers, and decimals are all rational numbers.
Example:
Fraction to Decimal:
\(\frac{1}{2}\) = 0.5
Decimal to Fraction:
a. 0.15= \(\frac{3}{20}\)
b. 15÷5=3
c. 100÷5=20
Try It!
The farmer decided that he ordered enough planks for an arena that measured 115\(\frac{1}{4}\) ft by 63\(\frac{1}{2}\) ft. Is he correct? Explain.
Answer:
It is given that
The farmer decided that he ordered enough planks for an arena that measured 115\(\frac{1}{4}\) ft by 63\(\frac{1}{2}\) ft.
So,
The perimeter of the arena = 2 × (115\(\frac{1}{4}\) + 63\(\frac{1}{2}\))
Now,
By using the Long Addition,
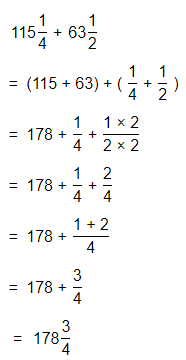
Now,
By using the Long Multiplication,
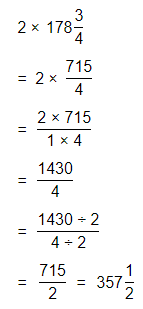
So,
The perimeter of the arena is: \(\frac{715}{2}\) ft
Now,
The number of 8\(\frac{1}{2}\)-foot planks needed = (The perimeter of the arena) ÷ 8\(\frac{1}{2}\)
= \(\frac{715}{2}\) ÷ 8\(\frac{1}{2}\)
Now,
By using the Long Division,
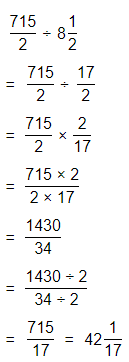
So,
The number of 8\(\frac{1}{2}\)-foot planks needed is about 47 planks
But,
It is given that
A farmer needed 130 8\(\frac{1}{2}\)-foot planks
So,
47 < 130
Hence, from the above,
We can conclude that
The farmer is not correct
Convince Me! What questions do you need to answer to solve the Try It!?
Answer:
The questions you need to answer to solve the Try It is:
a. The perimeter of the arena with the given length and width of the arena
b. The number of 8\(\frac{1}{2}\)-foot planks for the perimeter we find in part (a)
Try It!
The number of runners who finish the marathon is 320. Runners donate $2.50 for each mile they run. How much money is donated? Explain.
Answer:
It is given that
The number of runners who finish the marathon is 320. Runners donate $2.50 for each mile they run
Now,
The total number of miles run by 320 runners = (The total length of the marathon) × 320
= 26.2 × 320
Now,
By using the Long Multiplication,

So,
The total number of miles run by 320 runners is: 8,384 miles
Now,
The amount of money donated = (The total number of miles run by 320 runners) × (The amount of money donated by each runner for each mile)
= 8,384 × $2.50
Now,
By using the Long Multiplication,
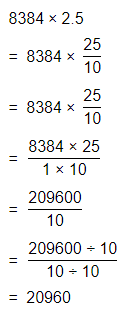
So,
The amount of money donated is: $20,960
Hence, from the above,
We can conclude that
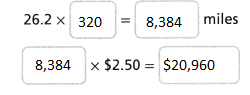
KEY CONCEPT
When solving multistep problems with fractions or decimals:
• decide the steps to use to solve the problem.
• choose the correct operations.
• identify the information you need from the problem.
• correctly use the information.
• calculate accurately.
• interpret solutions and check that the answer is reasonable.
Do You Understand?
Question 1.
?Essential Question How can you solve problems with rational numbers?
Answer:
We know that,
A “Rational number” is a number that can be written as a fraction.
Fractions, integers, and decimals are all rational numbers.
Example:
Fraction to Decimal:
\(\frac{1}{2}\) = 0.5
Decimal to Fraction:
a. 0.15= \(\frac{3}{20}\)
b. 15÷5=3
c. 100÷5=20
Question 2.
Be Precise Meghan has 5\(\frac{1}{4}\) yards of fabric. She plans to use \(\frac{2}{3}\) of the fabric to make 4 identical backpacks. To find how much fabric she will use to make the backpacks, Meghan multiplies 5\(\frac{1}{4}\) by \(\frac{2}{3}\). What else does Meghan need to do to find how much fabric she needs for each backpack?
Answer:
It is given that
Meghan has 5\(\frac{1}{4}\) yards of fabric. She plans to use \(\frac{2}{3}\) of the fabric to make 4 identical backpacks. To find how much fabric she will use to make the backpacks, Meghan multiplies 5\(\frac{1}{4}\) by \(\frac{2}{3}\)
Now,
The amount of fabric needed to make 4 identical backpacks = (The amount of fabric she planned to use to make the backpacks) × (The total length of the fabric) × (The number of identical backpacks)
= \(\frac{2}{3}\) × 5\(\frac{1}{4}\) × 4
So,
Aside From the given information,
Meghan needed to multiply the number of identical backpacks to the result of \(\frac{2}{3}\) × 5\(\frac{1}{4}\)
Hence, from the above,
We can conclude that
To find how much fabric Meghan needs for each backpack,
Meghan needed to multiply the number of identical backpacks to the result of \(\frac{2}{3}\) × 5\(\frac{1}{4}\)
Question 3.
Critique Reasoning Each side of a square patio is 10.5 feet. The patio is made up of 1.5-foot by 1.5-foot square stones. What is the number of stones on the patio? Look at the solution below. Does it include all the steps needed to solve the problem? Explain.

Answer:
It is given that
Each side of a square patio is 10.5 feet. The patio is made up of 1.5-foot by 1.5-foot square stones
Now,
We know that,
The area of a square = Side × Side
So,
The area of a square patio = 10.5 × 10.5
So,
The area of the square stones = 1.5 × 1.5
So,
The number of stones in the patio = (The area of a square patio) ÷ (The area of the square stones)
= (10.5 × 10.5) ÷ (1.5 × 1.5)
= 110.25 ÷ 2.25
Now,
By using the Long Division,
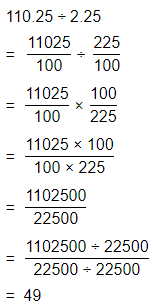
Hence, from the above,
We can conclude that
The given solution did not include all the steps needed to solve the given problem
The number of stones in the patio is: 49 stones
Do You Know How?
Question 4.
Devon records 4 hours of reality shows on her DVR. She records comedy shows for \(\frac{3}{8}\) of that amount of time. Devon watches all the reality and comedy shows in half-hour sittings.
a. Find the number of hours of comedy shows that Devon records.
Answer:
It is given that
Devon records 4 hours of reality shows on her DVR. She records comedy shows for \(\frac{3}{8}\) of that amount of time. Devon watches all the reality and comedy shows in half-hour sittings.
So,
The number of hours of comedy shows that Devon records = \(\frac{3}{8}\) × (The amount of time Devon records the reality shows on her DVR)
= \(\frac{3}{8}\) × 4
Now,
By using the Long Multiplication,
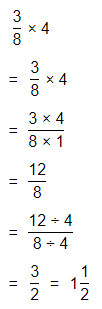
Hence, from the above,
We can conclude that
The number of hours of comedy shows that Devon records are: \(\frac{3}{2}\) hours
b. Find the total number of hours of reality and comedy shows that Devon records.
Answer:
It is given that
Devon records 4 hours of reality shows on her DVR. She records comedy shows for \(\frac{3}{8}\) of that amount of time. Devon watches all the reality and comedy shows in half-hour sittings.
Now,
From part (a),
We can observe that
The number of hours of comedy shows that Devon records are: \(\frac{3}{2}\) hours
So,
The total number of hours of reality and comedy shows that Devon records = (The number of hours of reality shows that Devon records) + (The number of hours of comedy shows that Devon records)
= \(\frac{3}{2}\) + 4
Now,
By using the Long Addition,
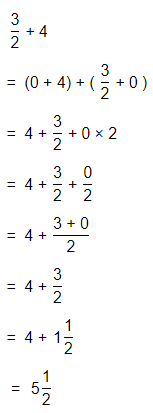
Hence, from the above,
We can conclude that
The total number of hours of reality and comedy shows that Devon records are: 5\(\frac{1}{2}\) hours
c. Find the number of half-hour sittings needed to watch all the shows.
Answer:
It is given that
Devon records 4 hours of reality shows on her DVR. She records comedy shows for \(\frac{3}{8}\) of that amount of time. Devon watches all the reality and comedy shows in half-hour sittings.
Now,
From part (b),
We can observe that
The total number of hours of reality and comedy shows that Devon records are: 5\(\frac{1}{2}\) hours
So,
The number of half-hour sittings needed to watch all the shows = (The total number of hours of reality and comedy shows that Devon records) ÷ \(\frac{1}{2}\)
= 5\(\frac{1}{2}\) ÷ \(\frac{1}{2}\)
Now,
By using the Long Division,
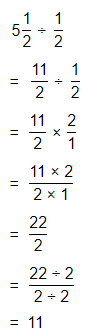
Hence, from the above,
We can conclude that
The number of half-hour sittings needed to watch all the shows is: 11 half-hour sittings
Question 5.
An auto mechanic earns $498.75 in 35 hours during the week. His pay is $2.50 more per hour on weekends. If he works 6 hours on the weekend in addition to 35 hours during the week, how much does he earn?
a. What questions do you need to answer to solve the problem?
Answer:
It is given that
An auto mechanic earns $498.75 in 35 hours during the week. His pay is $2.50 more per hour on weekends. If he works 6 hours on the weekend in addition to 35 hours during the week
Hence,
The questions you need to answer to solve the given problem are:
a. How much does an auto mechanic earn per hour?
b. How much does an auto mechanic earn per hour on weekends?
b. How much does the auto mechanic earn? Explain.
Answer:
It is given that
An auto mechanic earns $498.75 in 35 hours during the week. His pay is $2.50 more per hour on weekends. If he works 6 hours on the weekend in addition to 35 hours during the week
So,
The amount of money does an auto mechanic earn per hour = (The amount an auto mechanic earns during the week) ÷ (Number of hours)
= $498.75 ÷ 35
Now,
By using the Long Division,

So,
The amount of money an auto mechanic earns per hour is: $14.25
Now,
The amount of money an auto mechanic earns on weekends per hour = $2.50 + $14.25
Now,
By using the Long Multiplication,

So,
The amount of money an auto mechanic earns during weekends is: $16.75
Now,
The total amount of money an auto mechanic earns = (The total amount of money an auto mechanic earns during weekdays) + (The total amount of money an auto mechanic earns on weekends)
= $498.75 + (6 × $16.75)
= $498.75 + $100.5
= $599.25
Hence, from the above,
We can conclude that
The total amount of money an auto mechanic earns is: $599.25
Practice & Problem Solving
Scan for Multimedia
In 6-8, use the picture at the right.
Question 6.
You buy 3.17 pounds of apples, 1.25 pounds of pears, and 2.56 pounds of oranges. What is your total bill rounded to the nearest cent?

Answer:
It is given that
You buy 3.17 pounds of apples, 1.25 pounds of pears, and 2.56 pounds of oranges
So,
Your total bill rounded to the nearest cent = [(The total weight of apples) × (The cost of each apple)] + [(The total weight of pears) × (The cost of each pear)] + [(The total weight of oranges) × (The cost of each orange)]
= (3.17 × $0.99) + (1.25 × $1.19) + (2.56 × $1.09)
= $3.13 + $1.48 + 2.79
= $4.61 + $2.79
= $7.40
Hence, from the above,
We can conclude that
Your total bill rounded to the nearest cent is: $7.40
Question 7.
A student pays for 8.9 pounds of apples with a $10 bill. How much change does the student receive?
a. What do you do first to solve the problem?
Answer:
It is given that
A student pays for 8.9 pounds of apples with a $10 bill
Hence,
The hidden question you need to answer for the given problem is:
What is the total bill you have to pay for 8.9 pounds of apples for $0.99 each?
b. What do you do next?
Answer:
After completing the solution in part (a),
The thing you have to do next is:
Subtract the amount of money the student received by subtracting the value of the total bill you have to pay for 8.9 pounds of apples for $0.99 each from $10
Question 8.
A customer pays $3.27 for oranges and $4.76 for pears. How many pounds of fruit does the customer buy?
a. What do you do first to solve the problem?
Answer:
It is given that
A customer pays $3.27 for oranges and $4.76 for pears
Hence,
The hidden question you have to answer for the given problem is:
How many pounds of oranges and pears does the customer can buy?
b. What do you do next?
Answer:
After find the solution to the question present in part (a),
The thing you have to do next is:
Add the number of pounds of oranges and pears to find the total number of pounds of fruit doe the customer bought
Question 9.
Critique Reasoning Students put 2\(\frac{1}{4}\) pounds of trail mix into bags that each weigh \(\frac{3}{8}\) pound. They bring \(\frac{2}{3}\) of the bags of trail mix on a hiking trip. Can you determine how many bags of trail mix are left by completing just one step? Explain.
Answer:
It is given that
Students put 2\(\frac{1}{4}\) pounds of trail mix into bags that each weigh \(\frac{3}{8}\) pound. They bring \(\frac{2}{3}\) of the bags of trail mix on a hiking trip.
So,
The number of bags of trail mix = (The total number of pounds of trail mix) ÷ (The weight of each bag of trail mix)
= 2\(\frac{1}{4}\) ÷ \(\frac{3}{8}\)
Now,
By using the Long Division,
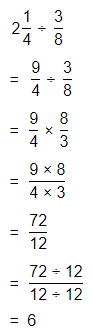
So,
The number of bags of trail mix is: 6 bags
Now,
The \(\frac{2}{3}\) of the bags of trail mix = 6 × \(\frac{2}{3}\)
= \(\frac{6 × 2}{3}\)
= 4 bags
So,
The number of bags of trail mix left = (The total number of bags of trail mix) – (The \(\frac{2}{3}\) of the bags of trail mix)
= 6 – 4
= 2 bags
Hence, from the above,
We can conclude that
The number of bags of trail mix that are left is: 2 bags
We can’t determine the number of bags of trail mix by completing just one step
Question 10.
Three-fifths of the T-shirts in a T-shirt shop are blue. Five-eighths of those T-shirts are on sale. One-third of the blue T-shirts that are on sale are size medium. What fraction of the shop’s T-shirts are blue T-shirts that are on sale and are size medium? Explain.
Answer:
It is given that
Three-fifths of the T-shirts in a T-shirt shop are blue. Five-eighths of those T-shirts are on sale. One-third of the blue T-shirts that are on sale are size medium.
So,
The number of blue T-shirts are: \(\frac{3}{5}\) shirts
The number of blue T-shirts that are on sale = \(\frac{3}{5}\) × \(\frac{5}{8}\)
Now,
By using the Long Multiplication,

So,
The number of blue T-shirts that are on sale is: \(\frac{3}{8}\) shirts
Now,
The number of blue T-shirts that are on sale and are medium size = \(\frac{3}{8}\) × \(\frac{1}{3}\)
Now,
By using the Long Multiplication,
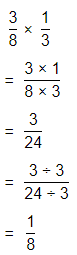
So,
The number of blue shirts that are on sale and are medium size is: \(\frac{1}{8}\) shirts
Hence, from the above,
We can conclude that
The number of blue T-shirts that are on sale is: \(\frac{3}{8}\) shirts
The number of blue shirts that are on sale and are medium size is: \(\frac{1}{8}\) shirts
In 11 and 12, use the diagram.
A community garden is made up of three gardens: a vegetable garden, an herb garden, and a flower garden.
Question 11.
The area of the vegetable garden is 0.4 of the area of the community garden. What is the area of the vegetable garden?

Answer:
It is given that
A community garden is made up of three gardens: a vegetable garden, an herb garden, and a flower garden.
The area of the vegetable garden is 0.4 of the area of the community garden.
Now,
The given figure is:

Now,
From the given figure,
The area of the community garden = (Length of the community garden) × (Width of the community garden)
= 6.2 × 4.5
Now,
By using the Long Multiplication,
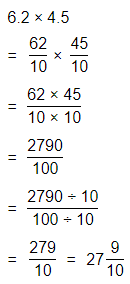
So,
The area of the community garden is: 27.9 m²
Now,
The area of the vegetable garden = 0.4 × (The area of the community garden)
= 0.4 × 27.9
= 11.16 m²
Hence, from the above,
We can conclude that
The area of the vegetable garden is: 11.16 m²
Question 12.
The area of the flower garden is 9.7 square meters greater than the herb garden. What is the area of the flower garden?
Answer:
It is given that
The area of the flower garden is 9.7 square meters greater than the herb garden.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The area of the Herb garden = 2.2 × 1.6
= 3.52 m²
So,
The area of the flower garden = 9.7 + (The area of the flower garden)
= 9.7 + 3.52
= 13.22 m²
Hence, from the above,
We can conclude that
The area of the flower garden is: 13.22 m²
Question 13.
Reasoning At the end of a party, \(\frac{3}{4}\) cup of smoked fish dip is left. Jim divides \(\frac{4}{5}\) of the leftover smoked fish dip equally between 2 friends. How much dip does each friend get?
Answer:
It is given that
At the end of a party, \(\frac{3}{4}\) cup of smoked fish dip is left. Jim divides \(\frac{4}{5}\) of the leftover smoked fish dip equally between 2 friends.
Now,
The \(\frac{4}{5}\) of the leftover smoked fish = \(\frac{4}{5}\) × \(\frac{3}{4}\)
Now,
By using the Long Multiplication,
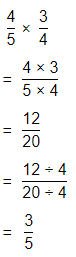
So,
The \(\frac{4}{5}\) of the leftover smoked fish is: \(\frac{3}{5}\)
Now,
The amount of dip each friend get = \(\frac{3}{5}\) ÷ 2
Now,
By using the Long Division,
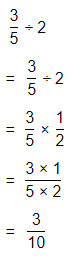
Hence, from the above,
We can conclude that
The amount of dip each friend get is: \(\frac{3}{10}\) of the leftover smoked fish dip
Question 14.
Students are planning a 3-day hiking trip in the Everglades. The hike covers a distance of 18.5 kilometers. The students hike 0.28 of the total distance on the first day. If they split the remaining distance equally between the second and third days, how far will they hike on day 3?
Answer:
It is given that
Students are planning a 3-day hiking trip in the Everglades. The hike covers a distance of 18.5 kilometers. The students hike 0.28 of the total distance on the first day and they split the remaining distance equally between the second and third days
So,
The remaining distance of the hike after the first day = (The total distance of hike) – (The distance of hike on the first day)
= 18.5 – (0.28 × 18.5)
= 18.5 – 5.18
= 13.32 kilometers
Now,
The distance of the hike on the second and the third days which are split equally = (The remaining distance of the hike after the first day) ÷ 2
= 13.32 ÷2
= 6.66 kilometers
So,
The amount of distance the students hiked on the third day is: 6.66 kilometers
Hence, from the above,
We can conclude that
The amount of distance the students hiked on the third day is: 6.66 kilometers
Question 15.
Higher-Order Thinking Kelly buys three containers of potato salad at the deli. She brings \(\frac{4}{5}\) of the potato salad to a picnic. How many pounds of potato salad does Kelly bring to the picnic? Describe two different ways to solve the problem.

Answer:
It is given that
Kelly buys three containers of potato salad at the deli. She brings \(\frac{4}{5}\) of the potato salad to a picnic
Now,
The given figure is:

So,
The total weight of the containers of potato salad = 1.03 + 1.12 + 1.6
= 3.75 pounds
So,
The total weight of potato salad Kelly brought = 3 × (The total weight of the containers of potato salad)
= 3 × 3.75
= 11.25 pounds
Now,
The amount of potato salad Kelly brought to picnic = \(\frac{4}{5}\) × (The total weight of potato salad Kelly brought)
= \(\frac{4}{5}\) × 11.25
= 9 pounds
Hence, from the above,
We can conclude that
The amount of potato salad Kelly brought to the picnic is: 9 pounds
Assessment Practice
Question 16.
Students make 84\(\frac{1}{2}\) ounces of liquid soap for a craft fair. They put the soap in 6\(\frac{1}{2}\)-ounce bottles and sell each bottle for $5.50. Which expression shows how much students earn if they sell all the bottles of liquid soap?
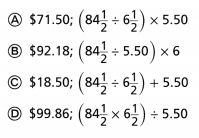
Answer:
It s given that
Students make 84\(\frac{1}{2}\) ounces of liquid soap for a craft fair. They put the soap in 6\(\frac{1}{2}\)-ounce bottles and sell each bottle for $5.50.
So,
The number of bottles of liquid soap = 84\(\frac{1}{2}\) ÷ 6\(\frac{1}{2}\)
Now,
By using the Long Division,

So,
The number of bottles of liquid soap is: 13 bottles
Now,
The cost of the 13 bottles of liquid soap = 13 × (The cost of each liquid soap)
= 13 × $5.50
= $71.5
Hence, from the above,
We can conclude that
The expression shows how much students earn if they sell all the bottles of liquid soap is:
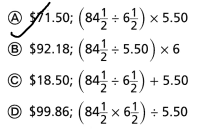
Question 17.
Claire mowed 5 lawns last week. She mowed each lawn in \(\frac{7}{12}\) hour. She mowed the same lawns this week in \(\frac{5}{12}\) hour each using her new lawnmower. How many times longer was Claire’s time to mow all the lawns last week than this week?
Answer:
It is given that
Claire mowed 5 lawns last week. She mowed each lawn in \(\frac{7}{12}\) hour. She mowed the same lawns this week in \(\frac{5}{12}\) hour each using her new lawnmower
So,
The number of hours Claire mowed last week = (The number of lawns) × (The amount of time each lawn was mowed last week)
= 5 × \(\frac{7}{12}\)
Now,
By using the Long Multiplication,

So,
The number of hours Claire mowed last week is: \(\frac{35}{12}\) hours
Now,
The number of hours Claire mowed this week = (The number of lawns) × (The amount of time each lawn was mowed this week)
= 5 × \(\frac{5}{12}\)
Now,
By using the Long Multiplication,

So,
The number of hours Claire mowed this week is: \(\frac{25}{12}\) hours
Now,
The difference between the number of hours Claire mowed the last week and this week = \(\frac{35}{12}\) – \(\frac{25}{12}\)
= \(\frac{35 – 25}{12}\)
= \(\frac{10}{12}\)
= \(\frac{5}{6}\) hours
Hence, from the above,
We can conclude that
Claire’s time to mow all the lawns last week is \(\frac{5}{6}\) times longer than this week
Topic 1 REVIEW
? Topic Essential Question
How can you fluently add, subtract, multiply, and divide decimals? How can you multiply and divide fractions?
Answer:
The steps to add, subtract, multiply, and divide decimals are:
a. Write the numbers vertically with the decimals lined up (if the number is a whole number then the decimal goes on the right end of the number)
b. Add zeros to make sure there is the same number of digits in each number.
c. Add or subtract as normal.
d. Multiply just as you would if the numbers were all whole numbers and add at the end.
e. After that count how many decimals places the two factors have (start at the far right of each number) and then give the answer that the total number of decimal places.
f. To divide decimals, always use long division.
The process to multiply and divide fractions is:
a. Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
b. The first step to dividing fractions is to find the reciprocal (reverse the numerator and denominator) of the second fraction.
c. Next, multiply the two numerators. Then, multiply the two denominators.
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.
Vocabulary
reciprocal
dividend
fraction
product

Answer:

Use Vocabulary in Writing
Explain how to use multiplication to find the value of \(\frac{1}{3}\) ÷ \(\frac{9}{5}\) Use the words multiplication, divisor, quotient, and reciprocal in your explanation.
Answer:
The given division expression is:
\(\frac{1}{3}\) ÷ \(\frac{9}{5}\)
Where,
\(\frac{1}{3}\) is the dividend
\(\frac{9}{5}\) is the divisor
Now,
The “Reciprocal” of \(\frac{9}{5}\) is: \(\frac{5}{9}\)
So,
\(\frac{1}{3}\) ÷ \(\frac{9}{5}\)
= \(\frac{1}{3}\) × \(\frac{5}{9}\)
Now,
By using the Long Multiplication,
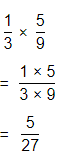
Hence, from the above,
We can conclude that
\(\frac{1}{3}\) ÷ \(\frac{9}{5}\) = \(\frac{5}{27}\)
Concepts and Skills Review
LESSON 1.1 Fluently Add, Subtract and Multiply Decimals
Quick Review
To add or subtract decimals, line up the decimal points so that place-value positions correspond. Add or subtract as you would with whole numbers, and place the decimal point in the answer. To multiply decimals, multiply as you would with whole numbers, then place the decimal point in the product by starting at the right and counting the number of places equal to the sum of the number of decimal places in each factor.
Example
Add, subtract, or multiply.

Practice
Add, subtract, or multiply.
Question 1.
91.2 + 89.9
Answer:
The given Addition expression is: 91.2 + 89.9
Now,
By using the Long Addition,
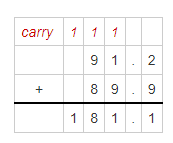
Hence, from the above,
We can conclude that
91.2 + 89.9 = 181.1
Question 2.
902.3 – 8.8
Answer:
The given Subtraction expression is: 902.3 – 8.8
Now,
By using the Long Subtraction,
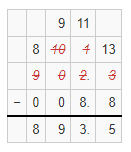
Hence, from the above,
We can conclude that
902.3 – 8.8 = 893.5
Question 3.
5 × 98.2
Answer:
The given Multiplication Expression is: 5 × 98.2
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
5 × 98.2 = 491
Question 4.
4 × 0.21
Answer:
The given Multiplication Expression is: 4 × 0.21
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
4 × 0.21 = 0.84
Question 5.
62.99 – 10.83
Answer:
The given Subtraction Expression is: 62.99 – 10.83
Now,
By using the Long Subtraction,

Hence, from the above,
We can conclude that
62.99 – 10.83 = 52.16
Question 6.
423.22 + 98.30
Answer:
The given Addition Expression is: 423.22 + 98.30
Now,
By using the Long Addition,
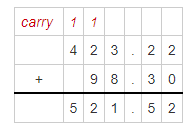
Hence, from the above,
We can conclude that
423.22 + 98.30 = 521.52
Question 7.
4.4 × 6
Answer:
The given Multiplication Expression is: 4.4 × 6
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
4.4 × 6 = 26.4
Question 8.
7 × 21.6
Answer:
The given Multiplication Expression is: 7 × 21.6
Now,
By using the Long Multiplication,
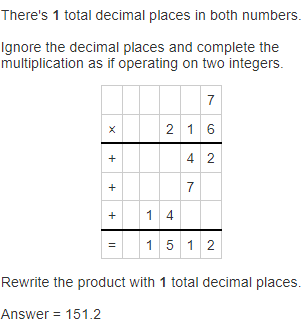
Hence, from the above,
We can conclude that
7 × 21.6 = 151.2
Question 9.
24.52 – 9.6
Answer:
The given Subtraction Expression is: 24.52 – 9.6
Now,
By using the Long Subtraction,
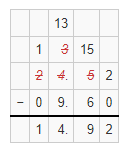
Hence, from the above,
We can conclude that
24.52 – 9.6 = 14.92
Question 10.
369.45 + 32.42
Answer:
The given Addition Expression is: 369.45 + 32.42
Now,
By using the Long Addition,
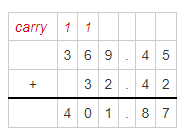
Hence, from the above,
We can conclude that
369.45 + 32.42 = 401.87
Question 11.
12.5 × 163.2
Answer:
The given Multiplication Expression is: 12.5 × 163.2
Now,
By using the Long Multiplication,
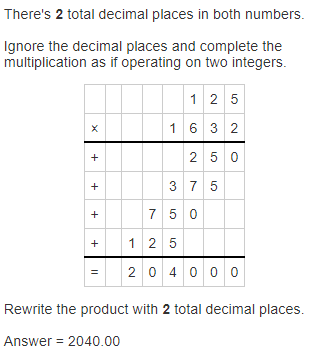
Hence, from the above,
We can conclude that
12.5 × 163.2 = 2,040
Question 12.
16 × 52.3
Answer:
The given Multiplication Expression is: 16 × 52.3
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
16 × 52.3 = 836.8
Question 13.
121.3 + 435.7
Answer:
The given Addition Expression is: 121.3 + 435.7
Now,
By using the Long Addition,
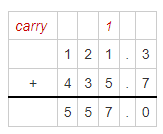
Hence, from the above,
We can conclude that
121.3 + 435.7 = 557
Question 14.
201.7 – 104.6
Answer:
The given Subtraction Expression is: 201.7 – 104.6
Now,
By using the Long Subtraction,
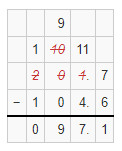
Hence, from the above,
We can conclude that
201.7 – 104.6 = 97.1
LESSON 1.2 Fluently Divide Whole Numbers and Decimals
Quick Review
To divide decimals, multiply the divisor and the dividend by the same power of 10 so that the divisor is a whole number. Then use an algorithm for whole-number division.
Example
Find 2.75 ÷ 0.05.

Practice
Divide.
Question 1.
9.6 ÷ 1.6
Answer:
The given Division Expression is: 9.6 ÷ 1.6
Now,
By using the Long Division,
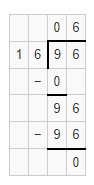
Hence, from the above,
We can conclude that
9.6 ÷ 1.6 = 6
Question 2.
48.4 ÷ 0.4
Answer:
The given Division Expression is: 48.4 ÷ 0.4
Now,
By using the Long Division,
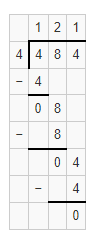
Hence, from the above,
We can conclude that
48.4 ÷ 0.4 = 121
Question 3.
13.2 ÷ 0.006
Answer:
The given Division Expression is: 13.2 ÷ 0.006
Now,
By using the Long Division,
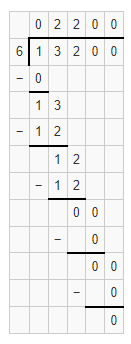
Hence, from the above,
We can conclude that
13.2 ÷ 0.006 = 2,200
Question 4.
10.8 ÷ 0.09
Answer:
The given Division Expression is: 10.8 ÷ 0.09
Now,
By using the Long Division,
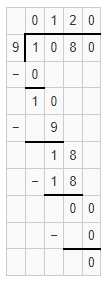
Hence, from the above,
We can conclude that
10.8 ÷ 0.09 = 120
Question 5.
45 ÷ 4.5
Answer:
The given Division expression is: 45 ÷ 4.5
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
45 ÷ 4.5 = 10
Question 6.
1,008 ÷ 1.8
Answer:
The given Division Expression is: 1,008 ÷ 1.8
Now,
By using the Long Division,
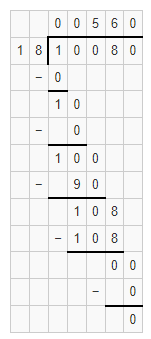
Hence, from the above,
We can conclude that
1,008 ÷ 1.8 = 560
Question 7.
1.26 ÷ 0.2
Answer:
The given Division Expression is: 1.26 ÷ 0.2
Now,
By using the Long Division,
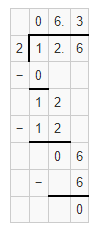
Hence, from the above,
We can conclude that
1.26 ÷ 0.2 = 6.3
Question 8.
2.24 ÷ 3.2
Answer:
The given Division Expression is: 2.24 ÷ 3.2
Now,
By using the Long Division,
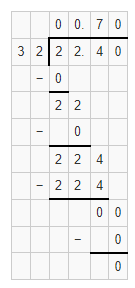
Hence, from the above,
We can conclude that
2.24 ÷ 3.2 = 0.7
Question 9.
35.75 ÷ 55
Answer:
The given Division Expression is: 35.75 ÷ 55
Now,
By using the Long Division,
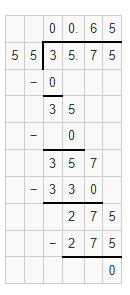
Hence, from the above,
We can conclude that
35.75 ÷ 55 = 0.65
Question 10.
120.4 ÷ 602
Answer:
The given Division Expression is: 120.4 ÷ 602
Now,
By using the Long Division,
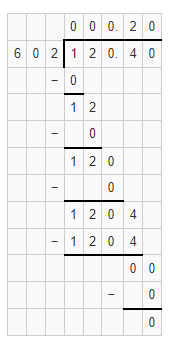
Hence, from the above,
We can conclude that
120.4 ÷ 602 = 0.2
Question 11.
330 ÷ 5.5
Answer:
The given Division Expression is: 330 ÷ 5.5
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
330 ÷ 5.5 = 60
Question 12.
1.08 ÷ 0.027
Answer:
The given Division Expression is: 1.08 ÷ 0.027
Now,
By using the Long Division,
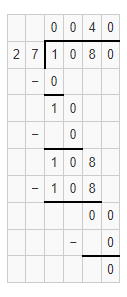
Hence, from the above,
We can conclude that
1.08 ÷ 0.027 = 40
LESSON 1.3 Multiply Fractions
Quick Review
Multiply the numerators to find the numerator of the product. Multiply the denominators to find the denominator of the product.
Example
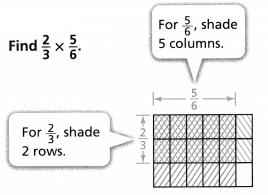
10 of the 18 rectangles are in the overlap area. So, \(\frac{2}{3}\) × \(\frac{5}{6}\) = \(\frac{10}{8}\) or \(\frac{5}{9}\).
Practice
Find each product.
Question 1.
\(\frac{2}{3}\) × \(\frac{3}{8}\)
Answer:
The given Multiplication Expression is:
\(\frac{2}{3}\) × \(\frac{3}{8}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
\(\frac{2}{3}\) × \(\frac{3}{8}\) = \(\frac{1}{4}\)
Question 2.
\(\frac{1}{4}\) × \(\frac{3}{5}\)
Answer:
The given Multiplication Expression is:
\(\frac{1}{4}\) × \(\frac{3}{5}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
\(\frac{1}{4}\) × \(\frac{3}{5}\) = \(\frac{3}{20}\)
Question 3.
\(\frac{1}{6}\) × \(\frac{1}{8}\)
Answer:
The given Multiplication Expression is:
\(\frac{1}{6}\) × \(\frac{1}{8}\)
Now,
By using the Long Multiplication,
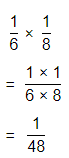
Hence, from the above,
We can conclude that
\(\frac{1}{6}\) × \(\frac{1}{8}\) = \(\frac{1}{48}\)
Question 4.
\(\frac{4}{7}\) × \(\frac{4}{7}\)
Answer:
The given Multiplication Expression is:
\(\frac{4}{7}\) × \(\frac{4}{7}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
\(\frac{4}{7}\) × \(\frac{4}{7}\) = \(\frac{16}{49}\)
Question 5.
\(\frac{6}{7}\) × \(\frac{1}{2}\)
Answer:
The given Multiplication Expression is:
\(\frac{6}{7}\) × \(\frac{1}{2}\)
Now,
By using the Long Multiplication,
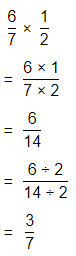
Hence, from the above,
We can conclude that
\(\frac{6}{7}\) × \(\frac{1}{2}\) = \(\frac{3}{7}\)
Question 6.
\(\frac{3}{8}\) × \(\frac{8}{3}\)
Answer:
The given Multiplication Expression is:
\(\frac{3}{8}\) × \(\frac{8}{3}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
\(\frac{3}{8}\) × \(\frac{8}{3}\) = 1
Question 7.
\(\frac{2}{3}\) × \(\frac{1}{3}\)
Answer:
The given Multiplication Expression is:
\(\frac{2}{3}\) × \(\frac{1}{3}\)
Now,
By using the Long Multiplication,
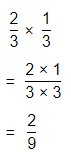
Hence, from the above,
We can conclude that
\(\frac{2}{3}\) × \(\frac{1}{3}\) = \(\frac{2}{9}\)
Question 8.
\(\frac{7}{8}\) × \(\frac{3}{2}\)
Answer:
The given Multiplication Expression is:
\(\frac{7}{8}\) × \(\frac{3}{2}\)
Now,
By using the Long Multiplication,
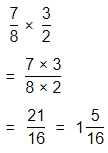
Hence, from the above,
We can conclude that
\(\frac{7}{8}\) × \(\frac{3}{2}\) = \(\frac{21}{16}\)
Question 9.
2\(\frac{1}{3}\) × 4\(\frac{1}{5}\)
Answer:
The given Multiplication Expression is:
2\(\frac{1}{3}\) × 4\(\frac{1}{5}\)
Now,
By using the Long Multiplication,
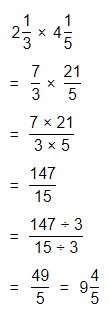
Hence, from the above,
We can conclude that
2\(\frac{1}{3}\) × 4\(\frac{1}{5}\) = \(\frac{49}{5}\)
Question 10.
4\(\frac{1}{2}\) × 6\(\frac{2}{3}\)
Answer:
The given Multiplication Expression is:
4\(\frac{1}{2}\) × 6\(\frac{2}{3}\)
Now,
By using the Long Multiplication,
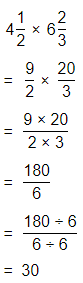
Hence, from the above,
We can conclude that
4\(\frac{1}{2}\) × 6\(\frac{2}{3}\) = 30
Question 11.
3\(\frac{3}{5}\) × 2\(\frac{5}{7}\)
Answer:
The given Multiplication Expression is:
3\(\frac{3}{5}\) × 2\(\frac{5}{7}\)
Now,
By using the Long Multiplication,

Hence, from the above,
We can conclude that
3\(\frac{3}{5}\) × 2\(\frac{5}{7}\) = \(\frac{342}{35}\)
Question 12.
14\(\frac{2}{7}\) × 4\(\frac{3}{10}\)
Answer:
The given Multiplication Expression is:
14\(\frac{2}{7}\) × 4\(\frac{3}{10}\)
Now,
By using the Long Multiplication,
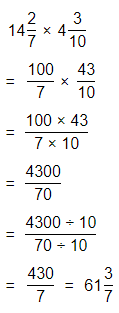
Hence, from the above,
We can conclude that
14\(\frac{2}{7}\) × 4\(\frac{3}{10}\) = \(\frac{430}{7}\)
LESSONS 1.4 AND 1.5 Understand and Divide with Fractions
Quick Review
To divide by a fraction, use the reciprocal of the divisor to rewrite the problem as a multiplication problem.
Practice Find each quotient.
Example
Find 4 ÷ \(\frac{4}{5}\).
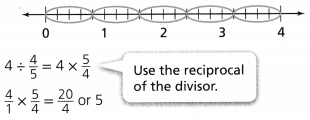
Find \(\frac{3}{4}\) ÷ \(\frac{4}{5}\).
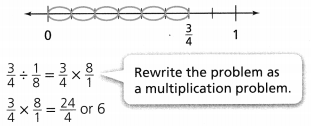
Practice
Find each Quotient
Question 1.
7 ÷ \(\frac{1}{2}\)
Answer:
The given Division Expression is:
7 ÷ \(\frac{1}{2}\)
Now,
By using the Long Division,
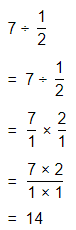
Hence, from the above,
We can conclude that
7 ÷ \(\frac{1}{2}\) = 14
The quotient for the given division expression is: 14
Question 2.
6 ÷ \(\frac{2}{5}\)
Answer:
The given Division Expression is:
6 ÷ \(\frac{2}{5}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
6 ÷ \(\frac{2}{5}\) = 15
The quotient for the given division expression is: 15
Question 3.
2 ÷ \(\frac{1}{8}\)
Answer:
The given Division Expression is:
2 ÷ \(\frac{1}{8}\)
Now,
By using the Long Division,
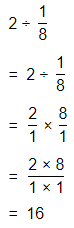
Hence, from the above,
We can conclude that
2 ÷ \(\frac{1}{8}\) = 16
The quotient for the given division expression is: 16
Question 4.
8 ÷ \(\frac{4}{9}\)
Answer:
The given Division Expression is:
8 ÷ \(\frac{4}{9}\)
Now,
By using the Long Division,
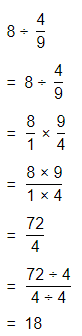
Hence, from the above,
We can conclude that
8 ÷ \(\frac{4}{9}\) = 18
The quotient for the given division expression is: 18
Question 5.
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\)
Answer:
The given Division Expression is:
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\)
Now,
By using the Long Division,
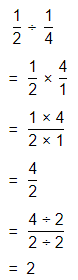
Hence, from the above,
We can conclude that
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\) = 2
The quotient for the given division expression is: 2
Question 6.
\(\frac{8}{10}\) ÷ \(\frac{1}{5}\)
Answer:
The given Division Expression is:
\(\frac{8}{10}\) ÷ \(\frac{1}{5}\)
Now,
By using the Long Division,
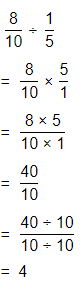
Hence, from the above,
We can conclude that
\(\frac{8}{10}\) ÷ \(\frac{1}{5}\) = 4
The quotient for the given division expression is: 4
Question 7.
\(\frac{5}{6}\) ÷ \(\frac{3}{8}\)
Answer:
The given Division Expression is:
\(\frac{5}{6}\) ÷ \(\frac{3}{8}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
\(\frac{5}{6}\) ÷ \(\frac{3}{8}\) = \(\frac{20}{9}\)
The quotient for the given division expression is: \(\frac{20}{9}\)
Question 8.
\(\frac{1}{3}\) ÷ \(\frac{1}{2}\)
Answer:
The given Division Expression is:
\(\frac{1}{3}\) ÷ \(\frac{1}{2}\)
Now,
By using the Long Division,
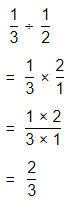
Hence, from the above,
we can conclude that
\(\frac{1}{3}\) ÷ \(\frac{1}{2}\) = \(\frac{2}{3}\)
The quotient for the given division expression is: \(\frac{2}{3}\)
Question 9.
5 ÷ \(\frac{5}{16}\)
Answer:
The given Division Expression is:
5 ÷ \(\frac{5}{16}\)
Now,
By using the Long Division,
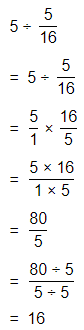
Hence, from the above,
We can conclude that
5 ÷ \(\frac{5}{16}\) = 16
The quotient for the given division expression is: 16
Question 10.
\(\frac{7}{12}\) ÷ \(\frac{3}{4}\)
Answer:
The given Divisio Expression is:
\(\frac{7}{12}\) ÷ \(\frac{3}{4}\)
Now,
By using the Long Division,
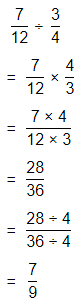
Hence, from the above,
We can conclude that
\(\frac{7}{12}\) ÷ \(\frac{3}{4}\) = \(\frac{7}{9}\)
The quotient for the given division expression is: \(\frac{7}{9}\)
Question 11.
20 ÷ \(\frac{5}{6}\)
Answer;
The given Division Expression is:
20 ÷ \(\frac{5}{6}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
20 ÷ \(\frac{5}{6}\) = 24
The quotient for the given division expression is: 24
Question 12.
16 ÷ \(\frac{1}{4}\)
Answer:
The given Division Expression is:
16 ÷ \(\frac{1}{4}\)
Now,
By using the Long Division,
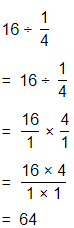
Hence, from the above,
We can conclude that
16 ÷ \(\frac{1}{4}\) = 64
The quotient for the given division expression is: 64
Question 13.
\(\frac{4}{5}\) ÷ \(\frac{1}{8}\)
Answer:
The given Division Expression is:
\(\frac{4}{5}\) ÷ \(\frac{1}{8}\)
Now,
By using the Long Division,
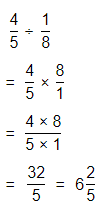
Hence, from the above,
We can conclude that
\(\frac{4}{5}\) ÷ \(\frac{1}{8}\) = \(\frac{32}{5}\)
The quotient for the given division expression is: \(\frac{32}{5}\)
Question 14.
5 ÷ \(\frac{1}{10}\)
Answer:
The given Division Expression is:
5 ÷ \(\frac{1}{10}\)
Now,
By using the Long Division,
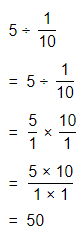
Hence, from the above,
We can conclude that
5 ÷ \(\frac{1}{10}\) = 50
The quotient for the given division expression is: 50
Question 15.
\(\frac{7}{11}\) ÷ \(\frac{1}{11}\)
Answer:
The given Division Expression is:
\(\frac{7}{11}\) ÷ \(\frac{1}{11}\)
Now,
By using the Long Division,
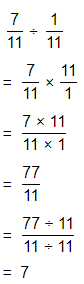
Hence, from the above,
We can conclude that
\(\frac{7}{11}\) ÷ \(\frac{1}{11}\) = 7
The quotient for the given division expression is: 7
Question 16.
4 ÷ \(\frac{2}{8}\)
Answer:
The given Division Expression is:
4 ÷ \(\frac{2}{8}\)
Now,
By using the Long Division,
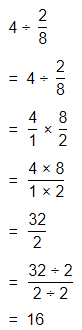
Hence, from the above,
We ca conclude that
4 ÷ \(\frac{2}{8}\) = 16
The quotient for the given division expression is: 16
LESSON 1.6 Divide Mixed Numbers
Quick Review
To divide by a mixed number, rename each mixed number as a fraction. Then use the reciprocal of the divisor to rewrite the problem as a multiplication problem.
Example

Practice
Find each quotient
Question 1.
6\(\frac{3}{8}\) ÷ 4\(\frac{1}{4}\)
Answer:
The given Division Expression is:
6\(\frac{3}{8}\) ÷ 4\(\frac{1}{4}\)
Now,
By using the Long Division,
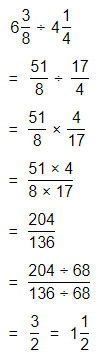
Hence, from the above,
We can conclude that
6\(\frac{3}{8}\) ÷ 4\(\frac{1}{4}\) = \(\frac{3}{2}\)
The quotient for the given division expression is: \(\frac{3}{2}\)
Question 2.
9 ÷ 2\(\frac{2}{7}\)
Answer:
The given Division Expression is:
9 ÷ 2\(\frac{2}{7}\)
Now,
By using the Long Division,
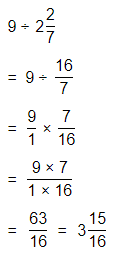
Hence, from the above,
We can conclude that
9 ÷ 2\(\frac{2}{7}\) = \(\frac{63}{16}\)
The quotient for the given division expression is: \(\frac{63}{16}\)
Question 3.
3\(\frac{3}{5}\) ÷ 1\(\frac{1}{5}\)
Answer:
The given Division Expression is:
3\(\frac{3}{5}\) ÷ 1\(\frac{1}{5}\)
Now,
By using the Long Division,
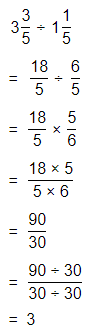
Hence, from the above,
We can conclude that
3\(\frac{3}{5}\) ÷ 1\(\frac{1}{5}\) = 3
The quotient for the given division expression is: 3
Question 4.
5\(\frac{1}{2}\) ÷ 3\(\frac{3}{8}\)
Answer:
The given Division Expression is:
5\(\frac{1}{2}\) ÷ 3\(\frac{3}{8}\)
Now,
By using the Long Division,
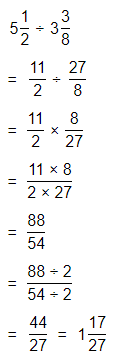
Hence, from the above,
We can conclude that
5\(\frac{1}{2}\) ÷ 3\(\frac{3}{8}\) = \(\frac{44}{27}\)
The quotient for the given division expression is: \(\frac{4}{27}\)
Question 5.
3\(\frac{2}{5}\) ÷1\(\frac{1}{5}\)
Answer:
The given Division Expression is:
3\(\frac{2}{5}\) ÷1\(\frac{1}{5}\)
Now,
By using the Long Division,
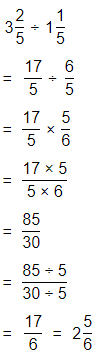
Hence, from the above,
We can conclude that
3\(\frac{2}{5}\) ÷1\(\frac{1}{5}\) = \(\frac{17}{6}\)
The quotient for the given division expression is: \(\frac{17}{6}\)
Question 6.
12\(\frac{1}{6}[/ltex] ÷ 3
Answer:
The given Division Expression is:
12[latex]\frac{1}{6}[/ltex] ÷ 3
Now,
By using the Long Division,

Hence, from the above,
We ca conclude that
12[latex]\frac{1}{6}[/ltex] ÷ 3 = [latex]\frac{73}{18}\)
The quotient for the given division expression is: \(\frac{73}{18}\)
Question 7.
12 ÷ 1\(\frac{1}{2}\)
Answer:
The given Division Expression is:
12 ÷ 1\(\frac{1}{2}\)
Now,
By using the Long Division,
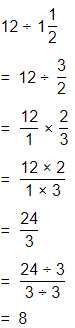
Hence, from the above,
We can conclude that
12 ÷ 1\(\frac{1}{2}\) = 8
The quotient for the given division expression is: 8
Question 8.
3\(\frac{1}{2}\) ÷ 2\(\frac{1}{4}\)
Answer:
The given Division Expression is:
3\(\frac{1}{2}\) ÷ 2\(\frac{1}{4}\)
Now,
By using the Long Division,
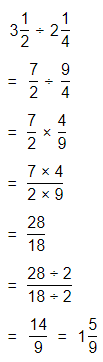
Hence, from the above,
We can conclude that
3\(\frac{1}{2}\) ÷ 2\(\frac{1}{4}\) = \(\frac{14}{9}\)
The quotient for the given division expression is: \(\frac{14}{9}\)
Question 9.
8 ÷ 1\(\frac{1}{4}\)
Answer:
The given Division Expression is:
8 ÷ 1\(\frac{1}{4}\)
Now,
By using the Long Division,
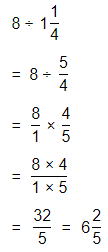
Hence, from the above,
We can conclude that
8 ÷ 1\(\frac{1}{4}\) = \(\frac{32}{5}\)
The quotient for the given division expression is: \(\frac{32}{5}\)
Question 10.
10\(\frac{1}{2}\) ÷ 1\(\frac{3}{4}\)
Answer:
The given Division Expression is:
10\(\frac{1}{2}\) ÷ 1\(\frac{3}{4}\)
Now,
By using the Long Division,
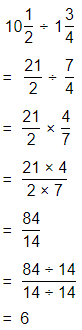
Hence, from the above,
We can conclude that
10\(\frac{1}{2}\) ÷ 1\(\frac{3}{4}\) = 6
The quotient for the given division expression is: 6
Question 11.
3\(\frac{3}{4}\) ÷ 2\(\frac{1}{2}\)
Answer:
The given Division Expression is:
3\(\frac{3}{4}\) ÷ 2\(\frac{1}{2}\)
Now,
By using the Long Division,
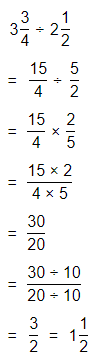
Hence, from the above,
We can conclude that
3\(\frac{3}{4}\) ÷ 2\(\frac{1}{2}\) = \(\frac{3}{2}\)
The quotient for the given division expression is: \(\frac{3}{2}\)
Question 12.
60 ÷ 3\(\frac{1}{3}\)
Answer:
The given Division Expression is:
60 ÷ 3\(\frac{1}{3}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
60 ÷ 3\(\frac{1}{3}\) = 18
The quotient for the given division expression is: 18
LESSON 1.7 Solve Problems with Rational Numbers
Quick Review
When solving multistep problems:
• decide the steps to solve the problem.
• choose the correct operations.
• identify the information you need from the problem.
• correctly use the information.
• calculate accurately.
• check if the answer is reasonable.
Example
Jane’s garden is 3.4 meters by 6.5 meters. If fencing costs $2.25 per meter, how much will it cost to enclose Jane’s garden?
Step 1: Find how much fence is needed.
3.4 + 3.4 + 6.5 + 6.5 = 19.8 meters
Step 2: Multiply to find the cost.
19.8 × 2.25 = $44.55
Step 3: Estimate to check.
3 + 3 + 7 + 7 = 20 meters
20 × 2.00 = $40.00
$40 is close to $44.55, so the answer is reasonable.
Practice
Daisy has one cucumber that is 3 inches long and another cucumber that is 5 inches long. She cuts the cucumbers into \(\frac{3}{8}\)-inch-thick slices and adds them to a salad. How many \(\frac{3}{8}\)-inch-thick slices does Daisy have?
Question 1.
Write division expressions to represent the first steps in the problem.
Answer:
It is given that
Daisy has one cucumber that is 3 inches long and another cucumber that is 5 inches long. She cuts the cucumbers into \(\frac{3}{8}\)-inch-thick slices and adds them to a salad.
So,
The total length of 2 cucumbers = (The length of the first cucumber) + (The length of the second cucumber)
= 3 + 5
= 8 inches
Now,
The number of \(\frac{3}{8}\)-inch-thick slices does Daisy have = (The total length of 2 cucumbers) ÷ \(\frac{3}{8}\)
= 8 ÷ \(\frac{3}{8}\)
Hence, from the above,
We can conclude that
The division expression to represent the given information is:
The number of \(\frac{3}{8}\)-inch-thick slices do Daisy have = 8 ÷ \(\frac{3}{8}\)
Question 2.
Solve. Then explain your answer.
Answer:
From Question 1,
We can observe that
The number of \(\frac{3}{8}\)-inch-thick slices does Daisy have = (The total length of 2 cucumbers) ÷ \(\frac{3}{8}\)
= 8 ÷ \(\frac{3}{8}\)
Now,
By using the Long Division,

Hence, from the above,
We can conclude that
The number of \(\frac{3}{8}\)-inch-thick slices does Daisy have is about 21 pieces
Topic 1 Fluency Practice
Pathfinder
Shade a path from START to FINISH. Follow the solutions in which the digit in the hundredths place is greater than the digit in the tenths place. You can only move up, down, right, or left.
