Practice with the help of enVision Math Common Core Grade 7 Answer Key Topic 2 Analyze and Use Proportional Relationships regularly and improve your accuracy in solving questions.
enVision Math Common Core 7th Grade Answers Key Topic 2 Analyze And Use Proportional Relationships
Topic 2 Essential Question
How can you recognize and represent proportional relationships and use them to solve problems?
3-ACT MATH

Mixin’ It Up Drinking plenty of water each day is important. Water is necessary for everything your body does. Not drinking enough water can lead to health problems. It’s even easier to drink enough water if you like the taste. There are many ways to make water more exciting. You can drink seltzer or filtered water. You can add fruit, vegetables, herbs, or flavor enhancers. You can add more or less based on what you like. Think about this during the 3-Act Mathematical Modeling lesson.
Topic 2 enVision STEM Project
Your Task: An Essential Resource
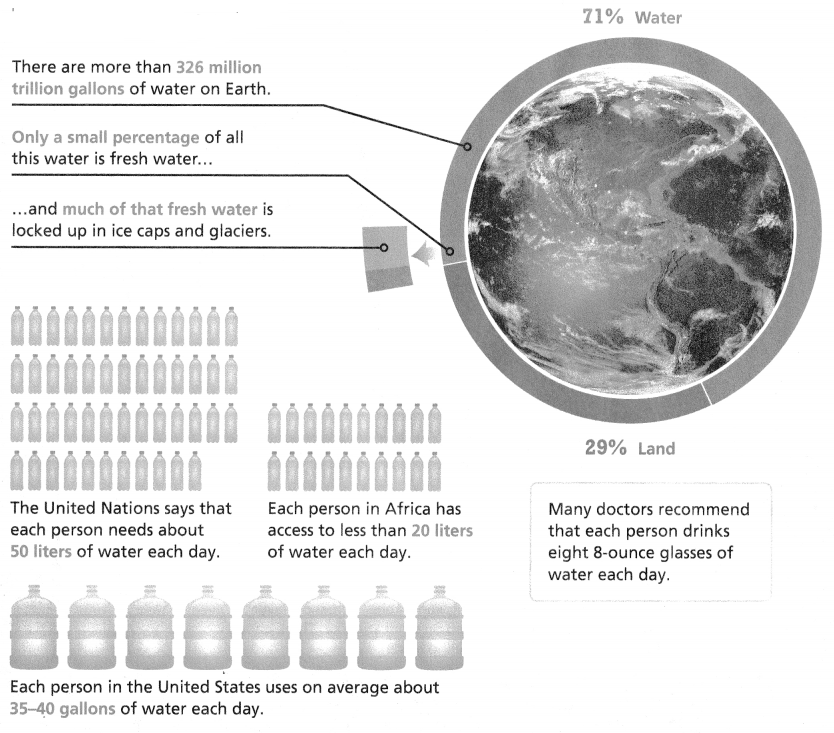
Access to fresh, clean water is important for human survival. You and your classmates will determine how much fresh water is available on Earth for people to use. You will also explore ways in which people have developed access to clean water.

Topic 2 Get Ready!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
- complex fraction
- equivalent ratios
- rate
- ratio
- terms
Question 1.
The quantities x and y in the ratio \(\frac{x}{y}\) are called _________
Answer:
The quantities x and y in the ratio \(\frac{x}{y}\) are called terms.
Explanation:
In the above-given question,
given that,
The quantities x and y in the ratio \(\frac{x}{y}\) are called terms.
for example:
x . y = x/y.
Question 2.
![]() are an example of _________
are an example of _________
Answer:
2dogs/3 cats and 10 dogs/15 cats are an example of Rate.
Explanation:
In the above-given question,
given that,
2 dogs/3 cats and 10 dogs/15 cats are an example of Rate.
for example:
a x c = b x b.
a x 40 = 15 x 15.
a x 40 = 225.
a = 225/40.
Question 3.
A(n) __________ is a type of ratio that has both terms expressed in different units.
Answer:
A(n) ratio is a type of ratio that has both terms expressed in different units.
Explanation:
In the above-given question,
given that,
A(n) ratio is a type of ratio that has both terms expressed in different units.
for example:
2/5 = 2 : 5
Question 4.
A(n) _________ has a fraction in its numerator, denominator, or both.
Answer:
A(n) complex fraction has a fraction in its numerator, denominator, or both.
Explanation:
In the above-given question,
given that,
A(n) complex fraction has a fraction in its numerator, denominator, or both.
for example:
3/5.
where 3 is a numerator.
5 is a denominator.
Equivalent Ratios
Complete each equivalent ratio.
Question 5.
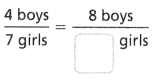
Answer:
The equivalent ratio is 8 boys/14 girls.
Explanation:
In the above-given question,
given that,
4 boys/7 girls = 8 boys/ 14 girls.
4 x 2 = 8.
7 x 2 = 14.
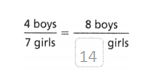
Question 6.
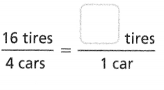
Answer:
The equivalent ratio is 4 tires/ 1 car.
Explanation:
In the above-given question,
given that,
16 tires/ 4 cars.
4 x 1 = 4.
4 x 4 = 16.
so the equivalent ratio is 4 tires/1 car.
Question 7.
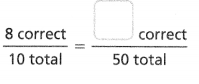
Answer:
The equivalent ratio is 40 correct/50 total.
Explanation:
In the above-given question,
given that,
8 correct/10 total.
8 x 5 = 40.
10 x 5 = 50.
so the equivalent ratio is 40 correct.

Question 8.
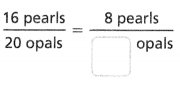
Answer:
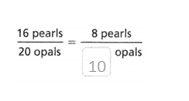
The equivalent ratio is 8 pearls/10 opals.
Explanation:
In the above-given question,
given that,
there are 16 apples and 20 opals.
16 pearls / 20 opals.
2 x 8 = 16.
2 x 10 = 20.
so the equivalent ratio is 10 opals.
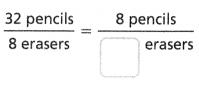
Question 9.
Answer:
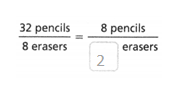
The equivalent ratio is 8 pencils/2 erasers.
Explanation:
In the above-given question,
given that,
32 pencils / 8 erasers.
4 x 8 = 32.
4 x 2 = 8.
32/8 = 8/2.
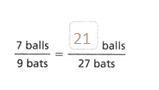
Question 10.

Answer:
The equivalent ratio is 21 balls/ 27 bats.
Explanation:
In the above-given question,
given that,
there are 7 balls and 9 bats.
7 x 3 = 21.
9 x 3 = 27.
so 21/27 is the equivalent ratio.
Rates
Write each situation as a rate.
Question 11.
John travels 150 miles in 3 hours.
Answer:
The rate is 50 miles.
Explanation:
In the above-given question,
given that,
John travels 150 miles in 3 hours.
150 / 3 = 15 miles.
so the rate is 50 miles.
Question 12.
Cameron ate 5 apples in 2 days.
Answer:
The rate is 2.5 apples in a day.
Explanation:
In the above-given question,
given that,
Cameron ate 5 apples in 2 days.
5/2 = 2.5.
so the rate is 2.5 apples in a day.
Equations
Write an equation that represents the pattern in the table.
Question 13.
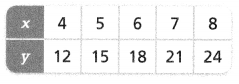
Answer:
The equation is y = 3x.
Explanation:
In the above-given question,
given that,
x = 4 so y = 3 x 4.
x = 5 so y = 5 x 3.
x = 6 so y = 6 x 3.
x = 7 so y = 7 x 3.
x = 8 so y = 8 x 3.
Language Development
Complete the graphic organizer to help you understand new vocabulary terms.

Answer:
When two ratios are equivalent is called proportion.
The constant of proportionality k is the constant value of the ratio of two proportional quantities y and x.
y = kx.
A relationship between two varying quantities where the ratio between the two quantities remains constant.
Explanation:
In the above-given question,
given that,
the proportion is when two ratios are equivalent.
characteristics:
when each ratio is simplified they should be equivalent.
when replacing the variable with the value the equation will balance.
example:
3/5 = a/50.
3 . 50 = a x 5.
150 = 5a.
a = 30.
non-example:
4/6 is not equal to 8/9.
example:
y = kx.
non-example:
y = 3x.
constant ratio is a graph that passes through the origin.
the constant ratio of delta y/delta x.
example:
y = 2x.
y = -2x.
non-example:
y = 2x+3.
y = x X x.
Pick A Project
PROJECT 2A
Who do you think would win a race involving different types of animals?
PROJECT: PREDICTRACE RESULTS

PROJECT 2B
What would it be like to travel to another planet?
PROJECT: CALCULATE THE WEIGHT OF YOUR PACK

PROJECT 2C
What stories can you tell?
PROJECT: WRITE A SHORT STORY

PROJECT 2D
If you could play any musical instrument, what would you play? Why?
PROJECT: PLAY MUSIC

Lesson 2.1 Connect Ratios, Rates, and Unit Rates
Explain It!
In a basketball contest, Elizabeth made 9 out of 25 free throw attempts. Alex made 8 out of 20 free throw attempts. Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.
I can… use ratio concepts and reasoning to solve multi-step problems.

A. Critique Reasoning Do you agree with Janie’s reasoning? Explain.
Answer:
Yes, I agree with Janie’s reasoning.
Explanation:
In the above-given question,
given that,
In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.
Alex made 8 out of 20 free throw attempts.
Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.
9/25 = 8/20.
so I agree with Janie’s reasoning.
B. Construct Arguments Decide who had the better free-throw record. Justify your reasoning using mathematical arguments.
Answer:
Both of them had an equal record.
Explanation:
In the above-given question,
given that,
In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.
Alex made 8 out of 20 free throw attempts.
Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.
9/25 = 8/20.
so both of them had an equal record.
Focus on math practices
Construct Arguments What mathematical model did you use to justify your reasoning? Are there other models you could use to represent the situation?
Answer:
Both of them had an equal record.
Explanation:
In the above-given question,
given that,
In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.
Alex made 8 out of 20 free throw attempts.
Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.
9/25 = 8/20.
so both of them had an equal record.
Essential Question
How are ratios, rates, and unit rates used to solve problems?
Try It!
Jennifer is a lifeguard at the same pool. She earns $137.25 for 15 hours of lifeguarding. How much does Jennifer earn per hour?
Jennifer earns $ ________ per hour.
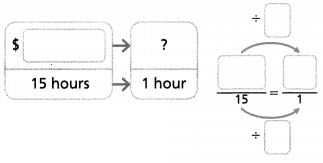
Convince Me! What do you notice about the models used to find how much each lifeguard earns per hour?
Answer:
Jennifer earns per hour = $9.15
Explanation:
In the above-given question,
given that,
Jennifer is a lifeguard at the same pool.
She earns $137.25 for 15 hours of lifeguarding.
$137.25/15.
$9.15.
so Jennifer earns per hour = $9.15.
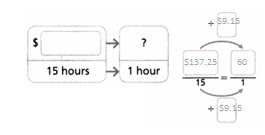
Try It!
A kitchen sink faucet streams 0.5 gallon of water in 10 seconds. A bathroom sink faucet streams 0.75 gallon of water in 18 seconds. Which faucet will fill a 3-gallon container faster?
Answer:
The faucet will fill a 3-gallon container faster = bathroom sink.
Explanation:
In the above-given question,
given that,
A kitchen sink faucet streams 0.5 gallons of water in 10 seconds.
A bathroom sink faucet streams 0.75 gallons of water in 18 seconds.
bathroom sink faucet streams 0.75 gallons of water in 18 seconds.
so the faucet will fill a 3-gallon container faster = bathroom sink.
KEY CONCEPT
You can use equivalent ratios and rates, including unit rates, to compare ratios and to solve problems.
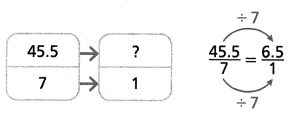
Do You Understand?
Question 1.
Essential Question How are ratios, rates, and unit rates used to solve problems?
Answer:
Yes, the ratios, rates, and units are used to solve problems.
Explanation:
In the above-given question,
given that,
a rate is a ratio that compares two quantities with different units.
unit rate is a rate that has 1 as the denominator.
for example:
24 pencils cost $1.20, how much will 6 pencils cost?
$1.20/24 = $0.05/1 pencil.
5 cents per pencil.
6 pencils will cost = 6 x 5 = 30.
Question 2.
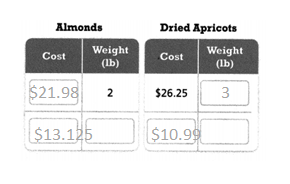
Use Structure Dorian buys 2 pounds of almonds for $21.98 and 3 pounds of dried apricots for $26.25. Which is less expensive per pound? How much less expensive?
Complete the tables of equivalent ratios to help you solve.
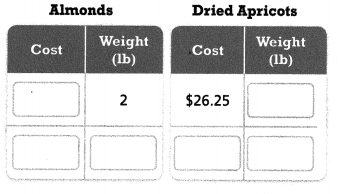
Answer:
The less expensive per pound = $2.135.
Explanation:
In the above-given question,
given that,
Dorian buys 2 pounds of almonds for $21.98 and 3 pounds of dried apricots for $26.25.
$21.98/2 = $10.99.
$26.25/2 = $13.125.
$13.125 – $10.99 = $2.135.
so the less expensive per pound = $2.135.
Question 3.
Generalize How are unit rates and equivalent ratios related?
Answer:
The unit rates and equivalent ratios are related.
Explanation:
In the above-given question,
given that,
A unit rate is a special kind of ratio, where the second number, or the denominator, is equal to one.
for example:
unit rates are miles per gallon.
when two ratios are equivalent, the two-unit rates will always be equal.
for example:
10/4 = 2.50.
Do You Know How?
Question 4.
Krystal is comparing two Internet service plans. Plan 1 costs $34.99 per month. Plan 2 costs $134.97 every 3 months. If Krystal plans to stay with one service plan for 1 year, which should she choose? How much will she save?
Answer:
Krystal will choose plan 1. She will save $20.
Explanation:
In the above-given question,
given that,
Krystal is comparing two Internet service plans.
Plan 1 costs $34.99 per month.
Plan 2 costs $134.97 every 3 months.
$34.99 x 3 = 104.97.
$134.97 – $104.97 = $20.
so Krystal will choose plan 1.
she will save $20.
Question 5.
Pam read 126 pages of her summer reading book in 3 hours. Zack read 180 pages of his summer reading book in 4 hours. If they continue to read at the same speeds, will they both finish the 215-page book after 5 total hours of reading? Explain.
Answer:
Yes, they both will finish the 215-page book after 5 total hours of reading.
Explanation:
In the above-given question,
given that,
Pam read 126 pages of her summer reading book in 3 hours.
Zack read 180 pages of his summer reading book in 4 hours.
180 – 126 = 54.
180 + 54 = 234.
so they both will finish the 215-page book after 5 total hours of reading.
Question 6.
Nora and Eli are making homemade spring rolls for a party. Nora can make 8 spring rolls in 10 minutes. Eli can make 10 spring rolls in 12 minutes. If they each make 40 spring rolls, who will finish first?
Answer:
They both will finish at an equal time.
Explanation:
In the above-given question,
given that,
Nora and Eli are making homemade spring rolls for a party.
Nora can make 8 spring rolls in 10 minutes.
Eli can make 10 spring rolls in 12 minutes.
so both of them will finish at an equal time.
Practice & Problem Solving
Leveled Practice In 7-8, complete the tables of equivalent ratios to solve.
Question 7.
After Megan walked 5 miles, her activity tracker had Meghan’s Steps counted 9,780 steps. David’s activity tracker had counted Miles 11,928 steps after he walked 6 miles. Suppose each person’s step covers about the same distance. Who takes more steps to walk 1 mile? How many more steps?
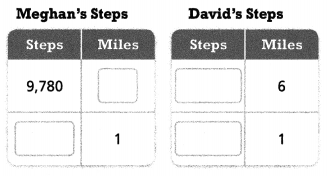
_________ takes more steps to walk 1 mile.
_______ – ________ = _________ more steps for 1 mile
Answer:
David takes more steps to walk 1 mile = 32 steps.
Explanation:
In the above-given question,
given that,
After Megan walked 5 miles, her activity tracker had Meghan’s Steps counted 9,780 miles.
David’s activity tracker had counted Miles 11,928 steps after he walked 6 miles.
9780/5 = 1956 miles.
11928/6 = 1988 miles.
1988 – 1956 = 32.
so David takes more steps to walk 1 mile = 32 steps.

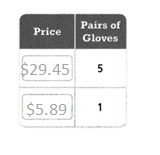
Question 8.
A package of 5 pairs of insulated gloves costs $29.45. What is the cost of a single pair of gloves?

One pair of gloves costs ________.
Answer:
The single pair of gloves = $5.89.
Explanation:
In the above-given question,
given that,
A package of 5 pairs of insulated gloves costs $29.45.
$29.45/5 = $5.89.
$5.89 x 1 = $5.89.
so the single pair of gloves = $5.89.
Question 9.
Which package has the lowest cost per ounce of rice?

Answer:
The lowest cost per ounce of rice = white rice.
Explanation:
In the above-given question,
given that,
the pack of white Rice is 12 ounces = $4.56.
the pack of wheat is 18 ounces = $6.30.
the pack of white rice is 7 ounces = $2.59.
so the lowest cost per ounce of rice = white rice.
Question 10.
A nursery owner buys 5 panes of glass to fix some damage to her greenhouse. The 5 panes cost $14.25. Unfortunately, she breaks 2 more panes while repairing the damage. What is the cost of another 2 panes of glass?
Answer:
The cost of another 2 panes of glass = $5.7.
Explanation:
In the above-given question,
given that,
A nursery owner buys 5 panes of glass to fix some damage to her greenhouse.
The 5 panes cost $14.25.
Unfortunately, she breaks 2 more panes while repairing the damage.
$14.25 / 5 = $2.85.
$2.85 x 2 = 5.7.
so the cost of another 2 panes of glass = $5.7.
Question 11.
Be Precise An arts academy requires there to be 3 teachers for every 75 students and 6 tutors for every 72 students. How many tutors does the academy need if it has 120 students?
Answer:
The tutors do the academy need if it has 120 students = 7 tutors.
Explanation:
In the above-given question,
given that,
An arts academy requires there to be 3 teachers for every 75 students and 6 tutors for every 72 students.
75 + 72 = 147.
3 + 6 = 9.
140/9 = 15.5.
120 / 7 = 17.1.
so the tutors does the academy need if it has 120 students = 7 tutors.
Question 12.
Make Sense and Persevere in large cities, people often take taxis to get from one place to another. What is the cost per mile of a taxi ride? How much is a 47-mile taxi ride?

Answer:
The much is a 47-mile taxi ride = 36.30 fares.
Explanation:
In the above-given question,
given that,
people often take taxis to get from one place to another.
for 36 miles in 25.20 fare.
for 47 miles in 36.30 fare.
so the much is a 47-mile taxi ride = 36.30 fares.
Question 13.
The Largo Middle School track team needs new uniforms. The students plan to sell plush toy tigers (the school mascot) for $5. The students find three companies online that sell stuffed mascots.

a. Which company has the lowest cost per tiger?
Answer:
The company that has the lowest cost per tiger = company C.
Explanation:
In the above-given question,
given that,
The Largo Middle School track team needs new uniforms.
The students plan to sell plush toy tigers (the school mascot) for 5$.
company A- 12 tigers for $33.24.
company B – 14 tigers for $44.80.
company C – 16 tigers for $41.10.
33.24/12 = 2.77.
44.80/14 = 3.2.
41.10/16 = 2.56.
so the company that has the lowest cost per tiger is company C.
b. If they use that company, how much profit will the students make for each tiger sold?
Answer:
The profit will the students make for each tiger sold = $0.84.
Explanation:
In the above-given question,
given that,
The Largo Middle School track team needs new uniforms.
The students plan to sell plush toy tigers (the school mascot) for 5$.
company A- 12 tigers for $33.24.
company B – 14 tigers for $44.80.
company C – 16 tigers for $41.10.
33.24/12 = 2.77.
44.80/14 = 3.2.
41.10/16 = 2.56.
0.21 x 4 = $0.84.
so the profit will the students make for each tiger sold = $0.84.
Question 14.
A contractor purchases 7 dozen pairs of padded work gloves for $103.32. He incorrectly calculates the unit price at $14.76 per pair.
a. What is the correct unit price?
Answer:
The correct unit price = $723.24.
Explanation:
In the above-given question,
given that,
A contractor purchases 7 dozen pairs of padded work gloves for $103.32.
He incorrectly calculates the unit price at $14.76 per pair.
$103.32 x 7 = $723.24.
so the correct unit price = $723.24.
b. Critique Reasoning What error did the contractor likely make?
Answer:
The contractor likely makes the error if he calculated the unit price wrong.
Explanation:
In the above-given question,
given that,
A contractor purchases 7 dozen pairs of padded work gloves for $103.32.
He incorrectly calculates the unit price at $14.76 per pair.
$103.32 x 7 = $723.24.
so the correct unit price = $723.24.
Question 15.
Higher Order Thinking A warehouse store sells 5.5-ounce cans of tuna in packages of 6. A package of 6 cans costs $9.24. The store also sells 6.5-ounce cans of the same tuna in packages of 3 cans for $4.68. It also sells 3.5-ounce cans in packages of 4 cans for $4.48. Which package has the lowest cost per ounce of tuna?
Answer
The package has the lowest cost per ounce of tuna = 6.5 ounces.
Explanation:
In the above-given question,
given that,
A warehouse store sells 5.5-ounce cans of tuna in packages of 6.
A package of 6 cans costs $9.24.
The store also sells 6.5-ounce cans of the same tuna in packages of 3 cans for $4.68.
It also sells 3.5-ounce cans in packages of 4 cans for $4.48.
the package that has the lowest cost per ounce of tuna = 6.5 ounces.
Assessment Practice
Question 16.
Lena is making two dishes for an event. Each batch of her mac-and-cheese recipe calls for 6 ounces of cheese and 2 tablespoons of basil. For every two pizzas, she needs 16 ounces of cheese and 5 tablespoons of basil.
PART A
Lena buys a 32-oz package of cheese. Does she have enough cheese to make 2 batches of mac-and-cheese and 3 pizzas? Explain.
Answer:
Yes, she has enough cheese to make 2 batches of mac-and-cheese and 3 pizzas.
Explanation:
In the above-given question,
given that,
Lena buys a 32-oz package of cheese.
Does she have enough cheese to make 2 batches of mac-and-cheese and 3 pizzas?
Each batch of her mac-and-cheese recipe calls for 6 ounces of cheese and 2 tablespoons of basil.
6 x 2 = 12.
3 x 2 = 6.
so she has enough cheese to make 2 batches of mac-and-cheese and 3 pizzas.
PART B
How many tablespoons of basil does she need? Explain your answer.
Answer:
The number of tablespoons of basil does she need = 6.
Explanation:
In the above-given question,
given that,
Lena buys a 32-oz package of cheese.
Does she have enough cheese to make 2 batches of mac-and-cheese and 3 pizzas?
Each batch of her mac-and-cheese recipe calls for 6 ounces of cheese and 2 tablespoons of basil.
6 x 2 = 12.
3 x 2 = 6.
Question 17.
It cost Irene $58.90 to fill her car’s gas tank with 15 gallons of gas. Select all the rates that are equivalent to $58.90 for 155 gallons of gas.
☐ $41.80 for 11 gallons of gas
☐ $28.80 for 8 gallons of gas
☐ $26.60 for 7 gallons of gas
☐ $8.55 for 2 gallons of gas
☐ $3.80 for 1 gallon of gas
Answer:
Options A, C, and E are correct.
Explanation:
In the above-given question,
given that,
It cost Irene $58.90 to fill her car’s gas tank with 15 gallons of gas.
$58.90/15 = 3.9.
$41.80/11 = 3.8.
28.80/8 = 3.6.
$26.60/7 = 3.8.
$8.55 /2 = 4.27.
$3.80/1 = 3.8.
so options A,C, and E are correct.
Lesson 2.2 Determine Unit Rates with Ratios of Fractions
Solve & Discuss It!
Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did. Allison is video-chatting with Yuki about their class seedlings. Assume that both plants will continue to grow at the same rate. Who should expect to have the taller plant at the end of the school year?
I can… find unit rates with ratios of fractions and use them to solve problems.

Look for Relationships
How can you compare the growth rates of the seedlings?
Focus on math practices
Be Precise What must the students do before they can compare the heights of the plants?
Answer:
The height of Yuki’s class is 5.5 cm in 5 days.
Explanation:
In the above-given question,
given that,
Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did.
the Allison class is 2.5 inches in 5 days.
so the height of Yuki’s class is 5.5 cm in 5 days.
Essential Question
Why is it useful to write a ratio of fractions as a unit rate?
Try It!
Sergio increases his target speed to 30 miles per hour. How many more miles does Sergio need to ride in hour to achieve this target speed?
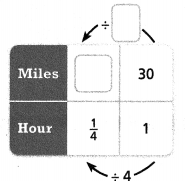
Sergio must ride _______ miles in \(\frac{1}{4}\) hour to achieve this target speed, so he needs to ride an additional ______ mile per \(\frac{1}{4}\) hour.
Answer:
The more miles does Sergio needs to ride in an hour to achieve this target speed = 7.5 miles.
Explanation:
In the above-given question,
given that,
Sergio increases his target speed to 30 miles per hour.
30/4 = 7.5.
so the more does Sergio needs to ride in an hour to achieve this target speed = 7.5 miles.
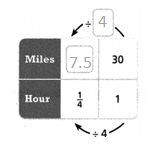
Convince Me! How does the unit rate describe Sergio’s cycling speed? How is the unit rate helpful in determining how much farther Sergio must cycle in a given amount of time each time he increases his target speed?
Try It!
Every other weekend, Bronwyn’s brother Daniel mows the lawn. He can mow 15,000 ft2 in \(\frac{3}{4}\) hour. Who mows the lawn in less time? Explain.
Answer:
The Bronwyn’s brother Daniel mows the lawn in less time = 20000 ft.
Explanation:
In the above-given question,
given that,
Every other weekend, Bronwyn’s brother Daniel mows the lawn.
He can mow 15,000 ft2 in \(\frac{3}{4}\) hour.
15000/0.75 = 20000.
so the Bronwyn,s brother Daniel mows the lawn in less time = 20000 ft.
Try It!
Sonoma bikes 5 miles to Paige’s house. On a map, they measure that distance as \(\frac{5}{6}\) cm. The same map shows that the mall is 3\(\frac{1}{2}\) cm from Paige’s house. What is the actual distance between Paige’s house and the mall?
Answer:
The actual distance between Paige’s house and the mall = 2.67 cm.
Explanation:
In the above-given question,
given that,
Sonoma bikes 5 miles to Paige’s house.
On a map, they measure that distance as \(\frac{5}{6}\) cm.
The same map shows that the mall is 3\(\frac{1}{2}\) cm from Paige’s house.
3(1/2) = 7/2.
7/2 = 3.5.
5/6 = 0.83.
3.5 – 0.83 = 2.67.
so the actual distance between Paige’s house and the mall = 2.67.
KEY CONCEPT
You can use what you know about equivalent ratios and operations with fractions to write a ratio of fractions as a unit rate.
Tia skateboards \(\frac{2}{3}\) mile for every \(\frac{1}{6}\) hour.
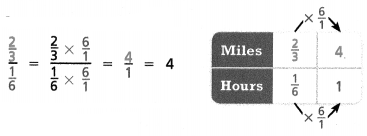
She skateboards 4 miles per hour.
Do You Understand?
Question 1.
Essential Question Why is it useful to write a ratio of fractions as a unit rate?
Answer:
The ratio of fractions as a unit rate = 4 miles per hour.
Explanation:
In the above-given question,
given that,
Tia skateboards \(\frac{2}{3}\) mile for every \(\frac{1}{6}\) hour.
2/3/1/6 = 2/3 x 6/1/1/6 x 6/1.
4/1 = 4.
Question 2.
Use Structure Jacob mixes \(\frac{1}{3}\) cup of yellow paint for every \(\frac{1}{5}\) cup of blue paint to make green paint. How many cups of yellow paint are needed for 1 cup of blue paint? Complete the table below.

Answer:
The number of cups of yellow paint is needed for 1 cup of blue paint = 3.
Explanation:
In the above-given question,
given that,
Use Structure Jacob mixes \(\frac{1}{3}\) cup of yellow paint for every \(\frac{1}{5}\) cup of blue paint to make green paint.
so the cups of yellow paint are 3.
so the number of cups of yellow paint is needed for 1 cup of blue paint = 3.
1/3 x 3.
1/5 x 1.
so the number of cups of yellow paint is needed for 1 cup of blue paint = 3.

Question 3.
Construct Arguments How is making a table of equivalent ratios to find the unit rate similar to finding the unit rate by calculating with fractions? Use a specific example to explain your reasoning.
Answer:
The unit rates and equivalent ratios are related.
Explanation:
In the above-given question,
given that,
A unit rate is a special kind of ratio, where the second number, or the denominator, is equal to one.
for example:
unit rates are miles per gallon.
when two ratios are equivalent, the two-unit rates will always be equal.
for example:
10/4 = 2.50.
Do You Know How?
Question 4.
Claire boarded an airplane in Richmond, VA, and flew 414 miles directly to Charleston, SC. The total flight time was \(\frac{3}{4}\) hour. How fast did Claire’s airplane fly, in miles per hour?
Answer:
The fast did Claire’s airplane fly, in miles per hour = 552 miles.
Explanation:
In the above-given question,
given that,
Claire boarded an airplane in Richmond, VA, and flew 414 miles directly to Charleston, SC.
The total flight time was \(\frac{3}{4}\) hour.
3/4 = 0.75.
414 / 0.75 = 552.
so the fast did Claire’s airplane fly, in miles per hour = 552 miles.
Question 5.
Brad buys two packages of mushrooms. Which mushrooms cost less per pound? Explain.

Answer:
The mushrooms cost less per pound = Cremini.
Explanation:
In the above-given question,
given that,
Brad buys two packages of mushrooms.
Cremini is $11.25 for 2/3 lb.
Chanterelle is $7.99 for 1/2 lb.
$11.25 / 0.6 = 18.75.
$7.99 / 0.5 = 15.98.
so the Cremini cost less pound.
Question 6.
Jed is baking shortbread for a bake sale. The recipe calls for 1\(\frac{1}{4}\) cups of flour and \(\frac{1}{2}\) stick of butter. How many cups of flour will Jed need if he uses 3 sticks of butter?
Answer:
The number of cups of flour will Jed need if he uses 3 sticks of butter = 1.5 cups.
Explanation:
In the above-given question,
given that,
Jed is baking shortbread for a bake sale.
The recipe calls for 1\(\frac{1}{4}\) cups of flour and \(\frac{1}{2}\) stick of butter.
1(1/4) = 5/4.
5/4 = 1.25.
1/2 = 0.5.
3 x 0.5 = 1.5.
so the number of cups of flour will Jed need if he uses 3 sticks of butter = 1.5 cups.
Practice & Problem Solving
Leveled Practice In 7-10, fill in the boxes to find the unit rate.
Question 7.

Answer:
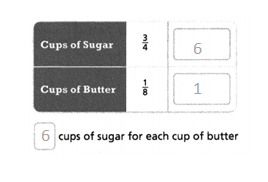
The 6 cups of sugar and 1 cup of butter.
Explanation:
In the above-given question,
given that,
3/4 cups of sugar and 1/8 cups of butter.
3/4/1/8.
3/4 x 8/1.
24/6 = 6/1.
so 6 cups of sugar and 1 cup of butter.
Question 8.

Answer:
The number of miles in an hour = 1.8 miles.
Explanation:
In the above-given question,
given that,
3/5 miles in 1/3 hour.
3/5/1/3.
3/5 x 3/1.
9/5 = 1.8.
so the number of miles in an hour = 1.8 miles.
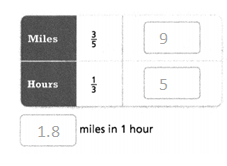
Question 9.
Answer:
The number of miles per gallon = 21 miles.
Explanation:
In the above-given question,
given that,
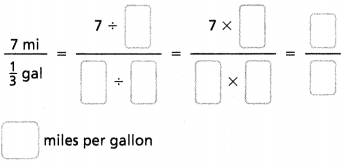
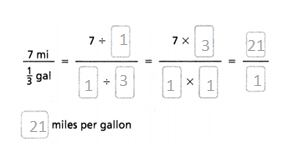
7 miles in 1/3 gallons.
7/1/3 = 7/1 x 3/1.
7/3 = 2.33.
so the number of miles per gallon = 21 miles.
Question 10.
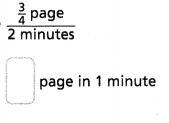
Answer:
The number of pages in 1 minute = 6/4 pages.
Explanation:
In the above-given question,
given that,
3/4 pages in 2 minutes.
3/4/2.
3/4/2/1.
3/4 x 2/1.
6/4.
3/2.
so the number of pages in 1 minute = 3/2 pages.

Question 11.
Hadley paddled a canoe \(\frac{2}{3}\) mile in \(\frac{1}{4}\) hour. How fast did Hadley paddle, in miles per hour?
Answer:
The fast did Hadley paddle, in miles per hour = 2.66 miles.
Explanation:
In the above-given question,
given that,
Hadley paddled a canoe \(\frac{2}{3}\) mile in \(\frac{1}{4}\) hour.
2/3/1/4.
2/3 x 4/1.
8/3 = 2.66.
so the fast did Hadley paddle, in miles per hour = 2.66 miles.
Question 12.
A box of cereal states that there are 90 Calories in a \(\frac{3}{4}\)cup serving. How many Calories are there in 4 cups of the cereal?
Answer:
The number of Calories is there in 4 cups of cereal = 30 calories.
Explanation:
In the above-given question,
given that,
A box of cereal states that there are 90 calories in a 3/4 cup serving.
90/3/4.
90/1 x 4/3.
360/3 = 120.
120/4 = 30.
so the number of Calories is there in 4 cups of cereal = 30 calories.
Question 13.
A robot can complete 8 tasks in \(\frac{5}{6}\) hour. Each task takes the same amount of time.
a. How long does it take the robot to complete one task?
Answer:
The long does it take the robot to complete one task = 9.6 minutes.
Explanation:
In the above-given question,
given that,
A robot can complete 8 tasks in \(\frac{5}{6}\) hour.
8/ 5/6.
8/1 x 6/5.
48/5 = 9.6.
so the long does it take the robot to complete one task = 9.6 minutes.
b. How many tasks can the robot complete in one hour?
Answer:
The tasks can complete in one hour = 576 minutes.
Explanation:
In the above-given question,
given that,
A robot can complete 8 tasks in \(\frac{5}{6}\) hour.
8/ 5/6.
8/1 x 6/5.
48/5 = 9.6.
9.6 x 60 = 576.
so the tasks can complete in one hour = 576 minutes.
Question 14.
You are running a fuel economy study. You want to find out which car can travel a greater distance on 1 gallon of gas.
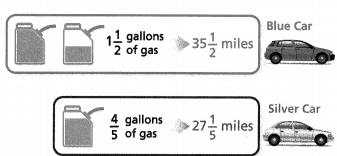
a. What is the gas mileage, in miles per gallon, for the blue car?
Answer:
The gas mileage, in miles per gallon, for the blue car = 0.04 miles.
Explanation:
In the above-given question,
given that,
1(1/2) gallons of gas in 35(1/2).
3/2 / 71/2.
3/2 x 2/71.
6/ 142 = 0.04.
so the gas mileage, in miles per gallon, for the blue car = 0.04 miles.
b. What is the gas mileage, in miles per gallon, for the silver car?
Answer:
The gas mileage, in miles per gallon, for the silver car = 34 miles.
Explanation:
In the above-given question,
given that,
4/5 gallons of gas in 27(1/5) miles.
4/5 / 136/5.
4/5 x 5/136.
4/136 = 34.
so the gas mileage, in miles per gallon, for the silver car = 34 miles.
c. Which car could travel the greater distance on 1 gallon of gas?
Answer:
The silver color car travels a greater distance on 1 gallon of gas.
Explanation:
In the above-given question,
given that,
4/5 gallons of gas in 27(1/5) miles.
4/5 / 136/5.
4/5 x 5/136.
4/136 = 34.
so the gas mileage, in miles per gallon, for the silver car = 34 miles.
Question 15.
Henry incorrectly said the rate \(\frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }} \) can be written as the unit rate 100 pound per quart.
a. What is the correct unit rate?
Answer:
The correct unit rate = 4 pounds.
Explanation:
In the above-given question,
given that,
Henry incorrectly said the rate \(\frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }} \).
1/5 /1/20.
1/5 x 20/1.
4.
so the correct unit rate = 4 pounds.
b. Critique Reasoning What error did Henry likely make?
Answer:
The error did Henry likely make = 4 pounds.
Explanation:
In the above-given question,
given that,
Henry incorrectly said the rate \(\frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }} \).
1/5 /1/20.
1/5 x 20/1.
4.
so the correct unit rate = 4 pounds.
Question 16.
Higher Order Thinking Ari walked 2\(\frac{3}{4}\) miles at a constant speed of 2\(\frac{1}{2}\) miles per hour. Beth walked 1\(\frac{3}{4}\) miles at a constant speed of 1\(\frac{1}{4}\) miles per hour. Cindy walked for 1 hour and 21 minutes at a constant speed of 1\(\frac{1}{8}\) miles per hour. List the three people in order of the times they spent walking from least time to greatest time.
Answer:
The three people in order of the times they spent walking from least time to greatest time = Cindy, Ari, and Beth.
Explanation:
In the above-given question,
given that,
Ari walked 2\(\frac{3}{4}\) miles at a constant speed of 2\(\frac{1}{2}\) miles per hour.
Beth walked 1\(\frac{3}{4}\) miles at a constant speed of 1\(\frac{1}{4}\) miles per hour.
Cindy walked for 1 hour and 21 minutes at a constant speed of 1\(\frac{1}{8}\) miles per hour.
2(3/4) / 2(1/2) = 11/4 / 5/2.
11/4 x 2/5 = 22/20 = 11/10.
1(3/4) / 1(1/4) = 7/4 / 5/4.
7/4 x 4/5 = 28/20 = 7/5.
1/ 21 / 9/8 = 1/21 x 8/9 = 8/189 = 0.04.
so the constant speed from least to great is Cindly, Ari, and Beth.
Assessment Practice
Question 17.
A blueprint shows a house with two fences. Fence A is 1\(\frac{4}{5}\) inches long on the blueprint and is to be 1\(\frac{1}{2}\) feet long. How long is Fence B on the blueprint?
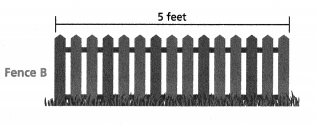
Answer:
The long is Fence B on the blueprint = 2 inches.
Explanation:
In the above-given question,
given that,
A blueprint shows a house with two fences.
Fence A is 1\(\frac{4}{5}\) inches long on the blueprint and is to be 1\(\frac{1}{2}\) feet long.
1(4/5) / 1(1/2).
9/5 / 3/2.
9/5 x 2/3 = 18/15 = 6/3.
so the long is Fence B on the blueprint = 2 inches.
Question 18.
Leo reads 13 pages in \(\frac{1}{3}\) hour. Use the table to find how many pages he reads in one hour.
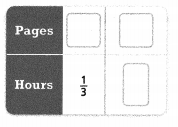
Leo reads _________ pages in one hour.
Answer:
The number of pages he reads in one hour = 39 pages.
Explanation:
In the above-given question,
given that,
Leo reads 13 pages in \(\frac{1}{3}\) hour.
13 /1/3.
13/1 x 3 /1 = 39 /1.
so the number of pages he reads in one hour = 39 pages.
Lesson 2.3 Understand Proportional Relationships: Equivalent Ratios
Solve & Discuss It!
Weight is a measure of force affected by gravity. The Moon’s gravity is less than Earth’s gravity, so objects weigh less on the Moon than on Earth. Using the information provided, how much do you think a cat will weigh on the Moon? Explain your reasoning.
I can… test for equivalent ratios to decide whether quantities are in a proportional relationship.

Make Sense and Persevere
About how much does a cat weigh on Earth?
Focus on math practices
Generalize How could you find the approximate weight of any object on the Moon? Explain your reasoning.
Essential Question
How are proportional quantities described by equivalent ratios?
Try It!
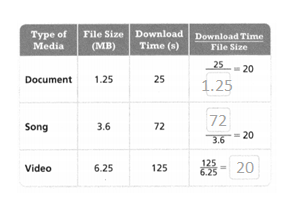
Miles records the time it takes to download a variety of file types. How is the download time related to the file size? Explain.
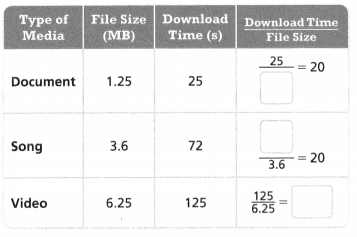
The ratios for each pair of data are ___________, so the download time and the file size are __________.
Answer:
The ratios for each pair of data are the same.
so the download time and the file size are different.
Explanation:
In the above-given question,
given that,
Miles records the time it takes to download a variety of file types.
downloaded time / file size = 25/1.25 = 20.
72/3.6 = 20.
125/6.25 = 20.
so the ratios for each pair of data are the same.
so the download time and the file size are different.
Convince Me!
How can you show that two quantities have a proportional relationship?
Try It!
The table at the right shows information about regular hexagons. Is the relationship between the perimeter and the side length of the hexagons proportional? Explain.
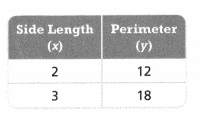
Answer:
Try It!
Ginny’s favorite cookie recipe requires 1\(\frac{1}{3}\) cups of sugar to make 24 cookies. How much sugar does Ginny need to make 36 of these cookies?
Answer:
KEY CONCEPT
Two quantities x and y have a proportional relationship if all the ratios \(\frac{y}{x}\) for related pairs of x and y are equivalent.
A proportion is an equation that states that two ratios are equivalent
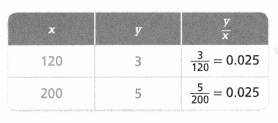
\(\frac{3}{120}\) = \(\frac{5}{200}\)
Do You Understand?
Question 1.
Essential Question How are proportional quantities described by equivalent ratios?
Answer:
Two quantities x and y have a proportional relationship if all the ratios y/x for related pairs of x and y are equivalent.
Explanation:
In the above-given question,
given that,
x = 120 and y = 3.
y/x = 120/3 = 0.025.
x = 200 and y = 5.
y/x = 200/5 = 0.025.
A proportion is an equation that states that two ratios are equivalent.
Question 2.
Look for Relationships How do you know if a relationship between two quantities is NOT proportional?
Answer:
Two quantities x and y have a proportional relationship if all the ratios y/x for related pairs of x and y are equivalent.
Explanation:
In the above-given question,
given that,
x = 120 and y = 3.
y/x = 120/3 = 0.025.
x = 200 and y = 5.
y/x = 200/5 = 0.025.
A proportion is an equation that states that two ratios are equivalent.
Question 3.
Reasoning If the ratio \(\frac{y}{x}\) is the same for all related pairs of x and y, what does that mean about the relationship between x and y?
Answer:
Two quantities x and y have a proportional relationship if all the ratios y/x for related pairs of x and y are equivalent.
Explanation:
In the above-given question,
given that,
x = 120 and y = 3.
y/x = 120/3 = 0.025.
x = 200 and y = 5.
y/x = 200/5 = 0.025.
A proportion is an equation that states that two ratios are equivalent.
Do You Know How?
Question 4.
Use the table below. Do x and y have a proportional relationship? Explain.

Answer:
Yes, they have a proportional relationship.
Explanation:
In the above-given question,
given that,
x = 2, 3, 5, and 8.
y = 5, 7.5, 12.5, and 18.
y/x = 5/2 = 2.5.
y/x = 7.5/3 = 2.5.
y/x = 12.5/5 = 2.5.
y/x = 18/8 = 2.25.
so x and y have a proportioal relationship.
Question 5.
Each triangle is equilateral. Is the relationship between the perimeter and the side length of the equilateral triangles proportional? Explain.
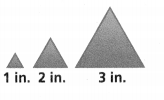
Answer:
Yes, the relationship between the perimeter and the side length of the equilateral triangles are proportional.
Explanation:
In the above-given question,
given that,
there are 3 triangles.
they are 1 in, 2 in, and 3 in.
so the sides of all the sides are equal in every triangle.
so the relationship between the perimeter and the side length of the equilateral triangles are proportional.
Question 6.
Is the relationship between the number of tickets sold and the number of hours proportional? If so, how many tickets were sold in 8 hours?
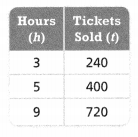
Answer:
The number of tickets was sold in 8 hours = 640 tickets.
Explanation:
In the above-given question,
given that,
the number of tickets sold in the hours.
h = 3, 5, 9.
t = 240, 400, and 720.
t/h = 240/3 = 80.
t/h = 400/5 = 80.
t/h = 720/9 = 80.
80 x 8 = 640.
so the number of tickets was sold in 8 hours = 640 tickets.
Practice & Problem Solving
Question 7.
The amount of seed a landscaper uses and the area of lawn covered have a proportional relationship. Complete the table.
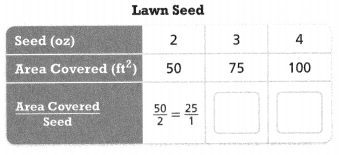
Answer:
Yes, they have a proportional relationship.
Explanation:
In the above-given question,
given that,
the amount of seed a landscaper uses and the area of lawn covered have a proportional relationship.
the area covered is 50, 75, and 100 sq ft.
the seeds are 2, 3, and 4.
area covered/seed = 50/2 = 25/1.
75/3 = 25/1.
100/4 = 25/1.
so they both have a proportional relationship.

Question 8.
Construct Arguments is the relationship between the number of slices of salami in a sandwich and the number of Calories proportional? Explain.
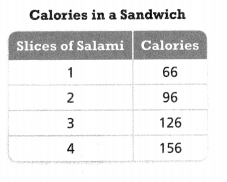
Answer:
No, they don’t have a proportional relationship.
Explanation:
In the above-given question,
given that,
the calories in a sandwich.
slices of salami in calories are given.
66/1 = 66.
96/2 = 48.
126/3 = 42.
156/4 = 39.
so they did not have a proportional relationship.
Question 9.
Look for Relationships A wholesale club sells eggs by the dozen. Does the table show a proportional relationship between the number of dozens of eggs and the cost? Explain.
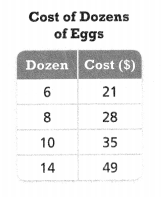
Answer:
The number of dozens of eggs and the cost are proportional.
Explanation:
In the above-given question,
given that,
the cost of dozens of eggs.
cost in dollars is 21, 28, 35, and 49.
dozens are 6, 8, 10, and 14.
cost/dozen = 21/6 =3.5.
28/8 = 3.5
35/10 = 3.5
49/14 = 3.5.
so the number of dozens of eggs and the cost are proportional.
Question 10.
Does the table show a proportional relationship? If so, what is the value of y when x is 11?

Answer:
No, they don’t show a proportional relationship.
Explanation:
In the above-given question,
given that,
the values of x and y are given.
y = 64/4 = 16.
y = 125/5 = 25.
y = 216/6 = 36.
y = 1000/10 = 100.
y =
so they don’t have a proportional relationship.
Question 11.
Does the table show a proportional relationship? If so, what is the value of y when x is 10?
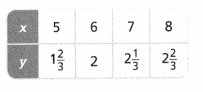
Answer:
The value of y when x is 10 is 3.2.
Explanation:
In the above-given question,
given that,
the value of y is 1(2/3), 2, 2(1/3), and 2(2/3).
the value of x = 5, 6, 7, and 8.
y/x = 1.6/5 = 0.32.
y/x = 2/6 = 0.33.
y/x = 2.3/7 = 0.32.
y/x = 2.6/8 = 0.32.
y/x = 3.2/10 = 0.32.
so the value of y when x is 10 is 3.2.
Question 12.
The height of a building is proportional to the number of floors. The figure shows the height of a building with 9 floors.

a. Reasoning Write the ratio of height of the building to the number of floors. Then find the unit rate, and explain what it means in this situation.
Answer:
The unit rate = 15.
Explanation:
In the above-given question,
given that,
The height of a building is proportional to the number of floors.
the number of floors = 9.
the height of the building = 135 feet.
135/9 = 15.
so the unit rate is 15.
b. How tall would the building be if it had 15 floors?
Answer:
The height of the building is 9.
Explanation:
In the above-given question,
given that,
The height of a building is proportional to the number of floors.
the number of floors = 15.
the height of the building = 135 feet.
135/15 = 9.
so the height of the building is 9.
Question 13.
Higher Order Thinking Do the two tables show the same proportional relationship between x and y? Explain how you know.
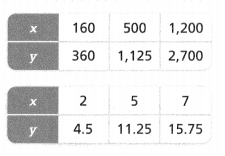
Answer:
Yes, both the tables have the proportional relationship.
Explanation:
In the above-given question,
given that,
the two tables show the same proportional relationship between x and y.
the values of x = 160, 500, and 1200.
the values of y = 360, 1125, and 2700.
y/x = 360/160 = 2.25.
y/x = 1125/500 = 2.25.
y/x = 2500/1200 = 2.08.
y/x = 4.5/2 = 2.25.
y/x = 11.25/5 = 2.25.
y/x = 15.75/7 = 2.25.
so both the tables have a proportional relationship.
Assessment Practice
Question 14.
The table shows the number of cell phone towers a company will build as the number of its customers increases.
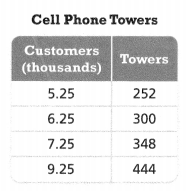
PART A
Is the relationship between the number of towers and the number of customers proportional? Explain.
Answer:
Yes, both of them have a proportional relationship.
Explanation:
In the above-given question,
given that,
the number of cell phone towers a company will build as the number of its customer’s increases.
towers are 252, 300, 348, and 444.
customers(thousands) = 5.25, 6.25, 7.25, and 9.25.
252/5.25 = 48.
300/6.25 = 48.
348/7.25 = 48.
444/9.25 = 48.
so both of them have a proportional relationship.
PART B
If there are 576 towers, how many customers does the company have? Write a proportion you can use to solve.
Answer:
The number of customers does the company has = 56.1.
Explanation:
In the above-given question,
given that,
if there are 576 towers.
the number of customers is 10.25.
576 / 10.25 = 56.1.
so the number of customers does the company have = 56.1.
Question 15.
Select all true statements about the table at the right.

☐ The table shows a proportional relationship.
☐ When x is 20, y is 2.55.
☐ All the ratios \(\frac{y}{x}\) for related pairs of x and y are equivalent to 8.
☐ The unit rate of \(\frac{y}{x}\) for related pairs of x and y is \(\frac{1}{8}\).
☐ If the table continued, when x is 30, y would be 3.75.
Answer:
Options A, B, and E are correct.
Explanation:
In the above-given question,
given that,
the values of x and y are shown.
y/x = 1.5/12 = 0.125.
y/x = 2.25/18 = 0.125.
y/x = 2.75/22 = 0.125.
y/x = 3.25/26 = 0.125.
so options A, B, and E are correct.
Lesson 2.4 Describe Proportional Relationships: Constant of Proportionality
Solve & Discuss It!
Jamal can run 1 mile in 5.05 minutes. If Jamal maintains this pace during a 5-kilometer (5K) race, he expects to break the course record of 15.25 minutes. Is Jamal’s expectation reasonable? Explain.
Answer:
Yes, Jamal’s expectation is reasonable.
Explanation:
In the above-given question,
given that,
Jamal can run 1 mile in 5.05 minutes.
If Jamal maintains this pace during a 5-kilometer (5K) race, he expects to break the course record of 15.25 minutes.
15.25/5 = 3.05.
so Jamal’s expectation is reasonable.
I can… use the constant of proportionality in an equation to represent a proportional relationship

Be Precise How can you convert 5 kilometers to miles?
Focus on math practices
Reasoning Assuming that Jamal runs at a constant rate, how does his pace describe the time it takes him to finish a race of any length?
Essential Question
How can you represent a proportional relationship with an equation?
Answer:
Yes, Jamal’s expectation is reasonable.
Explanation:
In the above-given question,
given that,
Jamal can run 1 mile in 5.05 minutes.
If Jamal maintains this pace during a 5-kilometer (5K) race, he expects to break the course record of 15.25 minutes.
15.25/5 = 3.05.
so Jamal’s expectation is reasonable.
Try It!
Maria made two batches of fruit punch. The table at the right shows how many quarts of juice she used for each batch. Write an equation that relates the proportional quantities.
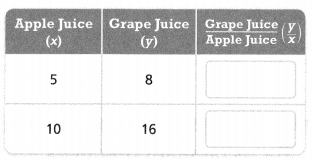
The constant of proportionality is __________.
An equation that represents this proportional relationship is y = ________ x.
Answer:
The constant of proportionality is 1.6.
An equation that represents this proportional relationship is y = kx.
Explanation:
In the above-given question,
given that,
Maria made two batches of fruit punch.
the grape juice contains 8 and 16.
apple juice contains 5 and 10.
y/x = 8/5 = 1.6.
y/x = 16/10 = 1.6.
an equation that represents this proportional relationship is y = kx.
Convince Me! How does the equation change if the amount of grape juice is the independent variable, x, and the amount of apple juice is the dependent variable, y?
Answer:
An equation that represents this proportional relationship is y = kx.
Explanation:
In the above-given question,
given that,
Maria made two batches of fruit punch.
the grape juice contains 8 and 16.
apple juice contains 5 and 10.
y/x = 8/5 = 1.6.
y/x = 16/10 = 1.6.
an equation that represents this proportional relationship is y = kx.
Try It!
A florist sells a dozen roses for $35.40. She sells individual roses for the same unit cost. Write an equation to represent the relationship between the number of roses, x, and the total cost of the roses, y. How much would 18 roses cost?
Answer:
The cost of 18 roses is $1.96.
Explanation:
In the above-given question,
given that,
A florist sells a dozen roses for $35.40.
She sells individual roses for the same unit cost.
$35.40/18 = 1.96.
so the cost of 18 roses is $1.96.
Try It!
Balloon A is released 5 feet above the ground. Balloon B is released at ground level. Both balloons rise at a constant rate.

Which situation can you represent using an equation of the form y = kx? Explain.
Answer:
Balloon A does not have a proportional relationship.
Balloon B has a proportional relationship.
Explanation:
In the above-given question,
given that,
Balloon A is released 5 feet above the ground.
Balloon B is released at ground level.
y = kx.
k = y/x.
k = 9/1 = 9.
k = 13/2 = 6.5.
k = 17/3 = 5.6.
k = 4/1 = 4.
k = 8/2 = 4.
k = 12/3 = 4.
KEY CONCEPT
Two proportional quantities x and y are related by a constant multiple, or the constant of proportionality, k.
You can represent a proportional relationship using the equation y = kx.
Do You Understand?
Question 1.
Essential Question How can you represent a proportional relationship with an equation?
Answer:
Two proportional quantities x and y are related by a constant multiple, or the constant of proportionality, K.
Explanation:
In the above-given question,
given that,
Two proportional quantities x and y are related by a constant multiple, or the constant of proportionality, k.
You can represent a proportional relationship using the equation y = kx.
Question 2.
Generalize How can you use an equation to find an unknown value in a proportional relationship?
Answer:
The unknown value in a proportional relationship is y = kx.
Explanation:
In the above-given question,
given that,
Two proportional quantities x and y are related by a constant multiple, or the constant of proportionality, k.
You can represent a proportional relationship using the equation y = kx.
Question 3.
Reasoning Why does the equation y = 3x + 5 NOT represent a proportional relationship?
Answer:
The equation y = 3x + 5 not represent a proportional relationship.
Explanation:
In the above-given question,
given that,
the equation y = 3x + 5.
where k = 3.
so the equation does not represent a proportional relationship.
Do You Know How?
Question 4.
Determine whether each equation represents a proportional relationship. If it does, identify the constant of proportionality.
a. y = 0.5x – 2
Answer:
The constant of proportionality = 0.5.
Explanation:
In the above-given question,
given that,
the equation is y = 0.5x – 2.
the constant of proportionality = 0.5.
b. y = 1,000x
Answer:
The constant of proportionality = 1000.
Explanation:
In the above-given question,
given that,
the equation is y = kx.
where k = 1000.
so the constant of proportionality = 1000.
c. y = x + 1
Answer:
The constant of proportionality = x.
Explanation:
In the above-given question,
given that,
the equation is y = kx.
where k = x.
so the constant of proportionality = x.
Question 5.
The manager of a concession stand estimates that she needs 3 hot dogs for every 5 people who attend a baseball game. If 1,200 people attend the game, how many hot dogs should the manager order?
Answer:
The number of hot dogs should the manager order = 80.
Explanation:
In the above-given question,
given that,
The manager of a concession stand estimates that she needs 3 hot dogs for every 5 people who attend a baseball game.
y = kx.
y = 5 x 3.
y = 15.
1200 / 15 = 80.
so the number of hot dogs should the manager order = 80.
Question 6.
A half dozen cupcakes cost $15. What constant of proportionality relates the number of cupcakes and total cost? Write an equation that represents this relationship.
Answer:
The equation represents the relationship = $15.
Explanation:
In the above-given question,
given that,
A half dozen cupcakes cost $15.
the constant of proportionality relates to the number of cupcakes and the total cost is y = kx.
y = 15x.
so the equation represents the relationship = $15.
Practice & Problem Solving
Question 7.
What is the constant of proportionality in the equation y = 5x?
Answer:
The constant of proportionality in the equation is 5.
Explanation:
In the above-given question,
given that,
the constant of proportionality in the equation is 5.
y = 5x.
Question 8.
What is the constant of proportionality in the equation y = 0.41x?
Answer:
The constant of proportionality in the equation y = 0.41x.
Explanation:
In the above-given question,
given that,
the equation is y = 0.41x.
k = 0.41.
so the constant of proportionality in the equation y = 0.41x.
Question 9.
The equation P= 3s represents the perimeter P of an equilateral triangle with side length s. Is there a proportional relationship between the perimeter and the side length of an equilateral triangle? Explain.
Answer:
Yes, there is a proportional relationship between the perimeter and the side length of an equilateral triangle.
Explanation:
In the above-given question,
given that,
The equation P= 3s represents the perimeter P of an equilateral triangle with side length s.
the triangle has 3 sides and all the sides has equal length.
p = 3 x s.
so there is a proportional relationship between the perimeter and the side length of an equilateral triangle.
Question 10.
Model with Math In a chemical compound, there are 3 parts zinc for every 16 parts copper, by mass. A piece of the compound contains 320 grams of copper. Write and solve an equation to determine the amount of zinc in the chemical compound.
Answer:
The equation to solve the amount of zinc in the chemical compound is y = 960.
Explanation:
In the above-given question,
given that,
In a chemical compound, there are 3 parts zinc for every 16 parts copper, by mass.
A piece of the compound contains 320 grams of copper.
y = kx.
y = 3 x 320.
y = 960.
so the equation to solve the amount of zinc in the chemical compound is y = 960.
Question 11.
The weight of 3 eggs is shown. Assuming the three eggs are all the same weight, find the constant of proportionality.

Answer:
The constant of proportionality = 40.
Explanation:
In the above-given question,
given that,
The weight of 3 eggs is shown.
the constant of proportionality is:
120/3 = 40.
so the constant of proportionality = 40.
Question 12.
The height of a stack of DVD cases is proportional to the number of cases in the stack. The height of 6 DVD cases is 114 mm.
a. Write an equation that relates the height, y, of a stack of DVD cases and the number of cases, x, in the stack.
Answer:
The equation that relates the height is 19 mm.
Explanation:
In the above-given question,
given that,
The height of a stack of DVD cases is proportional to the number of cases in the stack.
The height of 6 DVD cases is 114 mm.
114/6 = 19.
so the equation that relates the height is 19.
b. What would be the height of 13 DVD cases?
Answer:
The height of 13 DVD cases = 8.769 mm.
Explanation:
In the above-given question,
given that,
The height of a stack of DVD cases is proportional to the number of cases in the stack.
The height of 13 DVD cases is 114 mm.
114/13 = 8.769.
so the height of 13 DVD cases = 8.769 mm.
Question 13.
Ann’s car can travel 228 miles on 6 gallons of gas.
a. Write an equation to represent the distance, y, in miles Ann’s car can travel on x gallons of gas.
Answer:
The equation to represent the distance is 38.
Explanation:
In the above-given question,
given that,
Ann’s car can travel 228 miles on 6 gallons of gas.
y = kx.
228 = k . 6.
k = 228/6.
k = 38.
so the equation to represent the distance is 38.
b. Ann’s car used 7 gallons of gas during a trip. How far did Ann drive?
Answer:
The far did Ann drive = 32.57.
Explanation:
In the above-given question,
given that,
Ann’s car used 7 gallons of gas during a trip.
y = kx.
228/7 = 32.57.
so the far did Ann drive = 32.57.
Question 14.
The value of a baseball player’s rookie card began to increase once the player retired in 1996. The value has increased by $2.52 each year since then.

a. How much was the baseball card worth in 1997? In 1998? In 1999?
Answer:
The baseball card was worth in 1997, 1998, and 1999 is $9.98, $12.50, and $15.02.
Explanation:
In the above-given question,
given that,
The value of a baseball player’s rookie card began to increase once the player retired in 1996.
The value has increased by $2.52 each year since then.
the value is $7.46 in 1996.
$7.46 + $2.52 = $9.98 in 1997.
$9.98 + $2.52 = $12.50 in 1998.
$12.50 + $2.52 = $15.02 in 1999.
b. Construct Arguments Why is there not a proportional relationship between the years since the player retired and the card value? Explain.
Answer:
The value has increased by $2.52 each year.
Explanation:
In the above-given question,
given that,
The value of a baseball player’s rookie card began to increase once the player retired in 1996.
The value has increased by $2.52 each year since then.
the value is $7.46 in 1996.
$7.46 + $2.52 = $9.98 in 1997.
$9.98 + $2.52 = $12.50 in 1998.
$12.50 + $2.52 = $15.02 in 1999.
so there is no proportional relationship.
Question 15.
Higher Order Thinking A car travels 2\(\frac{1}{3}\) miles in 3\(\frac{1}{2}\) minutes at a constant speed.
a. Write an equation to represent the distance the car travels, d, in miles for m minutes.
Answer:
The equation to represent the distance the car travels = 0.6.
Explanation:
In the above-given question,
given that,
A car travels 2\(\frac{1}{3}\) miles in 3\(\frac{1}{2}\) minutes at a constant speed.
2(1/3) in 3(1/2).
7/3 in 7/2.
y = kx.
d = k m.
k = d/m.
k = 7/3 / 7/2.
k = 7/3 x 2/7.
k = 14/21.
k = 0.6.
b. Write an equation to represent the distance the car travels, d, in miles for h hours.
Answer:
The equation to represent the distance the car travels, d, in miles for h hours is k = d/m.
Explanation:
In the above-given question,
given that,
A car travels 2\(\frac{1}{3}\) miles in 3\(\frac{1}{2}\) minutes at a constant speed.
2(1/3) in 3(1/2).
7/3 in 7/2.
y = kx.
d = k m.
k = d/m.
Assessment Practice
Question 16.
For every ten sheets of stickers you buy at a craft store, the total cost increases $20.50.

An equation that relates the number of sheets purchased, x, and the total cost, y, of the stickers is y = _______x.
Use the equation you wrote to complete the table.
Answer:
The number of sheets purchased, x, and the total cost, y, of the stickers is y = kx.
Explanation:
In the above-given question,
given that,
For every ten sheets of stickers, you buy at a craft store, the total cost increases by $20.50.
y = kx.
y = k 2.
$20.50/2 = k.
k = 10.25.
$10.25/7 = 1.46.
$26.65/ 12 = 2.22.

Question 17.
600,000 gallons of water pass through a given point along a river every minute. Which equation represents the amount of water, y, that passes through the point in x minutes?
A. x = 10,000y
B. y = 600,000x
C. y = 10,000x
D. y = 600,000 + x
Answer:
Option B is correct.
Explanation:
In the above-given question,
given that,
The amount of water, y, that passes through the point in x minutes.
y = kx.
where k = 600000.
y = 600000x.
so option B is correct.
Topic 2 Mid-Topic Checkpoint
Question 1.
Vocabulary How do you know if a situation represents a proportional relationship? Lesson 2-3
Answer:
Two proportional quantities x and y are related by a constant multiple, or the constant of proportionality, K.
Explanation:
In the above-given question,
given that,
Two proportional quantities x and y are related by a constant multiple, or the constant of proportionality, k.
You can represent a proportional relationship using the equation y = kx.
Question 2.
Ana runs \(\frac{3}{4}\) mile in 6 minutes. Assuming she runs at a constant rate, what is her speed, in miles per hour? Lessons 2-1 and 2-2

Answer:
The speed in miles per hour = 8.
Explanation:
In the above-given question,
given that,
Ana runs \(\frac{3}{4}\) mile in 6 minutes.
y = kx.
6 = kx 0.75.
k = 6/0.75.
k = 8.
so the speed in miles per hour = 8.

Question 3.
A trail mix recipe includes granola, oats, and almonds. There are 135 Calories in a \(\frac{1}{4}\) cup serving of the trail mix. How many Calories are in 2 cups of trail mix? Lesson 2-2
Answer:
The number of calories is in 2 cups of trail mix = 1080 calories.
Explanation:
In the above-given question,
given that,
A trail mix recipe includes granola, oats, and almonds.
There are 135 Calories in a \(\frac{1}{4}\) cup serving of the trail mix.
135 / 1/4.
135 x 4 = 540.
540 x 2 =
so the number of calories are in 2 cups of trail mix = 1080 calories.
Question 4.
Does this table show a proportional relationship? If so, what is the constant of proportionality? Lessons 2-3 and 2-4

A. Yes; \(\frac{1}{5}\)
B. Yes; 5
C. Yes; 10
D. The quantities are not proportional.
Answer:
Option B is correct.
Explanation:
In the above-given question,
given that,
40/8 = 5.
50/10 = 5.
60/12 = 5.
70/14 = 5.
so option B is correct.
Question 5.
Janet, Rosi, and Tanya buy postcards from their favorite souvenir shop. Janet buys 3 postcards for $1.05. Rosi buys 5 postcards for $1.75. Tanya buys 8 postcards for $2.80. Are the cost, y, in dollars and the number of postcards, x, proportional? Explain your answer. Write an equation to represent this relationship, if possible. Lesson 2-4
Answer:
Yes, they are in a proportional relationship.
Explanation:
In the above-given question,
given that,
Janet, Rosi, and Tanya buy postcards from their favorite souvenir shop.
Janet buys 3 postcards for $1.05. Rosi buys 5 postcards for $1.75. Tanya buys 8 postcards for $2.80.
1.05/3 = 0.35.
1.75/5 = 0.35.
2.80/8 = 0.35.
so they are in a proportional relationship.
Question 6.
Four movie tickets cost $30.00. Five concert tickets cost $36.50. Does the movie or the concert cost less per ticket? How much less? Lesson 2-1
Answer:
The less per ticket = $6.5.
Explanation:
In the above-given question,
given that,
Four movie tickets cost $30.00.
Five concert tickets cost $36.50.
$36.50 – $30.00 = 6.5.
so the cost is less per ticket = $6.5.
Topic 2 Mid-Topic Performance Task
The school’s theater club is building sets that will make ordinary students look like giants. The actors need a door, a table, and a stool that will make them look almost twice as tall.
PART A
The heights of objects in the set are proportional to the actual heights of objects. Complete the table.

The constant of proportionality is _________.
Answer:
PART B
How can the stage manager use the constant of proportionality to find the dimensions of any new props the director requires?
Answer:
PART C
What should the height of a can of fruit juice used as a prop be if its actual height is 7 inches? Show your work.
Answer:
3-ACT MATH
3-Act Mathematical Modeling: Mixin’ It Up

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
When we are drinking first we have to shake it and we have to drink.
Explanation:
In the above-given question,
given that,
Mixin ti up.
that means when we are drinking we have to shake it and we have to use it.
either it is a syrup or any other drink.
Question 2.
Write the Main Question you will answer.
Answer:
When we are drinking first we have to shake it and we have to drink.
Explanation:
In the above-given question,
given that,
Mixin ti up.
that means when we are drinking we have to shake it and we have to use it.
either it is a syrup or any other drink.
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.
Answer:
There is one pineapple and 5 apples.
Explanation:
In the above-given question,
given that,
there are 5 apples and 1 pineapple.
so 1/5 is the unit rate.
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large. Too small

Answer:
The number that is too small is 0.01.
Explanation:
In the above-given question,
given that,
the numbers on the number line are 0.01, 0.02, and …..
the number that is too small is 0.01.
the number that is too large is 1.
so the number that is too small is 0.01.

Question 5.
Plot your prediction on the same number line.
Answer:
The number that is too small is 0.01.
Explanation:
In the above-given question,
given that,
the numbers on the number line are 0.01, 0.02, and …..
the number that is too small is 0.01.
the number that is too large is 1.
so the number that is too small is 0.01.
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Critique Reasoning Choose a classmate’s model. How would you adjust that model?
Answer:
SEQUEL
Question 15.
Use Structure A classmate usually adds 6 drops to 16 ounces of water. Use your updated model to predict the number of drops she would use for the large container.

Answer:
Lesson 2.5 Graph Proportional Relationships
Explore It!
The graph shows the time it takes Jacey to print T-shirts for her school’s math club.
I can… use a graph to determine whether two quantities are proportional.
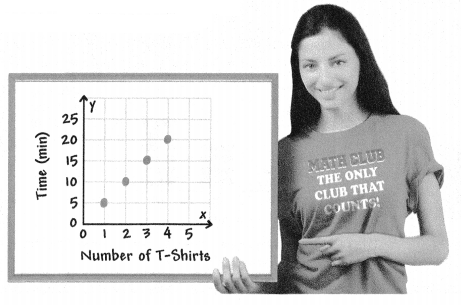
A. Use the points on the graph to complete the table. Are the quantities proportional? Explain.
Answer:
Yes, they are proportional.
Explanation:
In the bove-given question,
given that,
The graph shows the time it takes Jacey to print T-shirts for her school’s math club.
the number of t-shirts is 1 the time in minutes is 5.
2 x 5 = 10.
3 x 5 = 15.
4 x 5 = 20.
5 x 5 = 25.
so they are proportional.

B. Start at (1,5). As you move from one point to the next on the graph, how does the x-coordinate change? How does the y-coordinate change?
Answer:
The x and y coordinates do not change.
Explanation:
In the above-given question,
given that,
Start at (1,5). As you move from one point to the next on the graph.
1 x 5 = 5.
so the coordinates x and y are not changed.
C. Write the points for 0 T-shirts and for 5 T-shirts as ordered pairs. Graph the points and draw the line that passes through all six points.
Answer:
The graph increases.
Explanation:
In the above-given question,
given that,
the points for 0 t-shirts and for 5 T-shirts as ordered pairs.
the point is (0,5).
so the graph increases automatically.
Focus on math practices
Reasoning Suppose that after printing 4 T-shirts it takes Jacey 4 minutes to change the ink cartridge. Would this point for 5 T-shirts lie on the line you drew in Part C? Explain.
Answer:
The point (5,15) lies on the line.
Explanation:
In the above-given question,
given that,
after printing 4 T-shirts it takes Jacey 4 minutes to change the ink cartridge.
5,15 lies on the line.
Essential Question
What does the graph of a proportional relationship look like?
Try It!
Each \(\frac{1}{4}\) cup serving of cereal has 3 grams of protein. How can you use the graph at the right to determine whether the quantities are proportional and to find how many grams of protein are in 1 cup of the cereal?
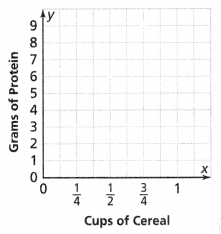
Answer:
The number of grams of protein is in 1 cup of cereal = 9 grams.
Explanation:
In the above-given question,
given that,
Each \(\frac{1}{4}\) cup serving of cereal has 3 grams of protein.
1/4 x 3.
for 1 cup of cereal is 9 grams of protein.
1 x 9 = 9.
so the number of grams of protein is in 1 cup of cereal = 9 grams.
Convince Me! How can you find the constant of proportionality from the coordinates of one point on the graph?
Try It!
Suppose the graph of Mr. Brown’s Road Trip is extended. Find the ordered pair with an x-coordinate of 7. What does this point represent in the situation?
If the graph is extended, it will pass through the point (7, _______). This means
Mr. Brown drives _______ miles in _______ hours.
Answer:
Try It!
Draw two graphs that pass through the point (2, 3), one that represents a proportional relationship and one that does not. Label your graphs as Proportional or NOT Proportional.
Answer:
The point (2,3) passes through the point.
Explanation:
In the above-given question,
given that,
the point (2,3) is a proportional relationship.

KEY CONCEPT
The graph of a proportional relationship is a straight line through the origin.
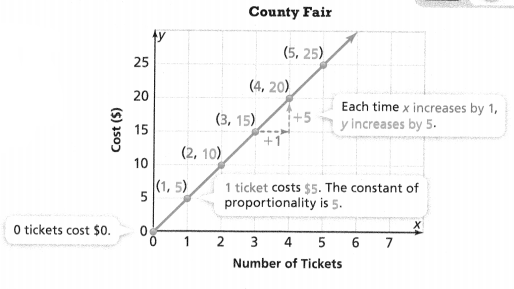
This graph shows that the total cost of tickets at a county fair is proportional to the number of tickets purchased. For each point (x, y) on the line except (0, 0), \(\frac{y}{x}\) = 5, which is the constant of proportionality.
Do You Understand?
Question 1.
Essential Question What does the graph of a proportional relationship look like?
Answer:
The graph shows the proportional relationship.
Explanation:
In the above-given question,
given that,
This graph shows that the total cost of tickets at a county fair is proportional to the number of tickets purchased.
for each point (x,y) except (0,0).
y/x = 5.
so the constant of proportionality is 5.
Question 2.
Reasoning Why will the graph of every proportional relationship include the point (0, 0)?
Answer:
Yes, the graph of every proportional relationship includes the point (0,0).
Explanation:
In the above-given question,
given that,
for every graph, the point (0,0) is included.
the points are (0,0), (1,5), (2, 10), (3, 15).
so the graph of every proportional relationship includes the point (0,0).
Question 3.
Construct Arguments Makayla plotted two points, (0, 0) and (3, 33), on a coordinate grid. Noah says that she is graphing a proportional relationship. Is Noah correct? Explain.
Answer:
Yes, it is a graphing a proportional.
Explanation:
In the above-given question,
given that,
the points are (0,0) and (3, 33).
so it is a graphing a proportional.
Do You Know How?
For 4-7, use the information below.
Martin and Isabelle go bowling. Each game costs $10, and they split that cost. Martin has his own bowling shoes, but Isabelle pays $3 to rent shoes.
Question 4.
Complete the graphs below. Martin’s
Answer:
The points ($3, $10).
Explanation:
In the above-given question,
given that,
Martin and Isabelle go bowling. Each game costs $10, and they split that cost.
Martin has his own bowling shoes, but Isabelle pays $3 to rent shoes.
the point (3, 10) is not a proportional relationship.
Question 5.
Which graph shows a proportional relationship? Explain why.
Answer:
The point (1,5) shows a proportional relationship.
Explanation:
In the above-given question,
given that,
points 1,5, and 2,10 are proportional to each other.
the point (1,5) and (2,10) shows a proportional relationship.
Question 6.
Choose one point on the graph of the proportional relationship and explain what this point means in terms of the situation.
Answer:
The point (1,5) shows a proportional relationship.
Explanation:
In the above-given question,
given that,
points 1,5, and 2,10 are proportional to each other.
the point (1,5) and (2,10) shows a proportional relationship.
Question 7.
What equation represents the proportional relationship?
Answer:
The point (1,5) shows a proportional relationship.
Explanation:
In the above-given question,
given that,
points 1,5, and 2,10 are proportional to each other.
the point (1,5) and (2,10) shows a proportional relationship.
Practice & Problem Solving
Question 8.
For each graph shown, tell whether it shows a proportional relationship. Explain your reasoning.
Answer:
Graph a shows the proportional relationship.
Explanation:
In the above-given question,
given that,
the graph (2,2) and (4,4) shows the proportional relationship.
so graph a shows the proportional relationship.
Question 9.
The graph shows the number of boxes a machine packages over time. Is the relationship proportional? How many boxes does the machine package in 4 minutes?
Answer:
The number of boxes does the machine package in 4 minutes = 100 boxes.
Explanation:
In the above-given question,
given that,
the graph shows the points.
the points are (0,0), (2,50), (4,100).
in 4 minutes the number of boxes that can be package is 100 boxes.
so the number of boxes does the machine package in 4 minutes = 100 boxes.
Question 10.
Does the graph show a proportional relationship? If so, use the graph to find the constant of proportionality.
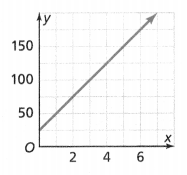
Answer:
Yes, the graph shows a proportional relationship.
The constant of proportionality is 25.
Explanation:
In the above-given question,
given that,
the points (0,25), (1, 50), (2, 75), (3 , 100), (4,125), (5, 175).
so the graph shows a proportional relationship.
so the constant of proportionality is 25.
Question 11.
The graph shows a proportional relationship between the cups of flour a baker uses and the number of cookies made.
a. Use Structure What does the point (0, 0) represent in the situation?
Answer:
The points (0,0) represents a proportional relationship.
Explanation:
In the above-given question,
given that,
the points are (0,0), (1, 18), (2, 35), (3, 50), (4, 75) and (6, 125).
so the points (0,0) represents a proportional relationship.
b. What does the point (1, 18) represent?
Answer:
The point (1, 18) is a proportional relationship.
Explanation:
In the above-given question,
given that,
the points are (0,0), (1, 18), (2, 35), (3, 50), (4, 75) and (6, 125).
so the points (1,18) represents a proportional relationship.
Question 12.
The points (0.5, \(\frac{1}{10}\)) and (7, 1\(\frac{2}{5}\)) are on the graph of a proportional relationship.
a. What is the constant of proportionality?
Answer:
The graph is a proportional relationship.
Explanation:
In the above-given question,
given that,
The points (0.5, \(\frac{1}{10}\)) and (7, 1\(\frac{2}{5}\)).
points (0.5, 0.1) and (7, 1.4).
so the graph shows a proportional relationship.
b. Name one more point on the graph.
Answer:
Point (4,75) is a proportional relationship.
Explanation:
In the above-given question,
given that,
the points are (0.5, 0.1), (7, 1.4), and (4, 75).
the point (4, 75) is a proportional relationship.
c. Write an equation that represents the proportional relationship.
Answer:
The point (3, 50) represents the proportional relationship.
Explanation:
In the above-given question,
given that,
the points are (0.5, 0.1), (7, 1.4), and (4, 75).
the point (3, 50) represents the proportional relationship.
Question 13.
Higher Order Thinking Denmark uses the kroner as its currency. Before a trip to Denmark, Mia wants to exchange $1,700 for kroner.
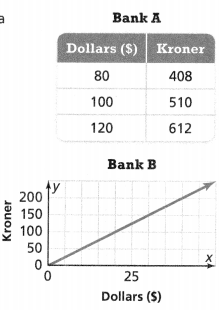
a. Does Bank A or Bank B have the better exchange rate? Explain.
b. How many more kroner would Mia get if she exchanged her $1,700 at the bank with the better exchange rate?
Answer:
Assessment Practice
Question 14.
Does the graph at the right show a proportional relationship between x and y? Explain.

Answer:
No, the graph does not show a proportional relationship.
Explanation:
In the above-given question,
given that,
the points are (0,1), (2, 2), (3, 2), and (4, 5).
the point (2, 2) shows the relationship.
but the graph does not show a proportional relationship.
Question 15.
The graph at the right shows the relationship between rainfall during the growing season and the growth of a type of plant. Which statements about the graph are true?

☐ The point (1, 10) shows the constant of proportionality.
☐ The constant of proportionality is \(\frac{5}{7}\).
☐ The graph does not show a proportional relationship.
☐ The graph is a straight line through the origin.
☐ The point (28, 20) means the type of plant grows 20 mm when it rains 28 cm.
Answer:
The constant of proportionality is (5/7).
Explanation:
In the above-given question,
given that,
the constant of proportionality is 5/7.
2 x 5 = 10, 2 x 7 = 14.
4 x 5 = 20, and 4 x 7 = 28.
6 x 5 = 30, and 6 x 7 = 42.
so the constant of proportionality is (5/7).
Lesson 2.6 Apply Proportional Reasoning to Solve Problems
Solve & Discuss It!
Xander and Pedro are at an ice cream social. For every scoop of ice cream, Xander uses cup of fruit topping. Pedro uses one more tablespoon of fruit topping than the number of scoops. If Xander and Pedro each use the same amount of fruit topping, how many scoops of ice cream does each use?
I can… determine whether a relationship is proportional and use representations to solve problems.
Look for Relationships
There are 2 tablespoons in \(\frac{1}{8}\) cup.
Focus on math practices
Reasoning for which person, Xander or Pedro, is the relationship between the quantities of ice cream and fruit topping proportional? Explain.

Essential Question
How can proportional reasoning help solve a problem?
Answer:
Yes, proportional reasoning help in solving a problem.
Explanation:
In the above-given question,
given that,
There are 2 tablespoons in \(\frac{1}{8}\) cup.
2 x 1/8 = 4.
so the constant of proportionality is 4.
Try It!
After selling half their card collections, DeShawn and Stephanie each buy 9 new cards. What is the ratio of the number of cards DeShawn has to the number Stephanie has?
Answer:
The number of cards DeShawn has to the number Stephanie has = 9 : 2.
Explanation:
In the above-given question,
given that,
After selling half their card collections, DeShawn and Stephanie each buy 9 new cards.
so the ratio is 9 : 2.
so the number of cards DeShawn has to the number Stephanie has = 9 : 2.
Convince Me! Why did the ratio stay the same in the Example but change in the Try It?
Try It!
A florist makes bouquets that include 50 white flowers and 7 red flowers. If the florist orders 1,050 white flowers and 140 red flowers, there will be leftover flowers. How can the florist adjust the order so there are no leftover flowers?
Answer:
The florist adjusts the order so there are no leftover flowers = 20.
Explanation:
In the above-given question,
given that,
A florist makes bouquets that include 50 white flowers and 7 red flowers.
If the florist orders 1,050 white flowers and 140 red flowers.
1050 : 50 = 20.
140 : 7 = 20.
so there are no leftover flowers.
KEY CONCEPT
Think about how two quantities are related before you decide to use proportional reasoning to solve a problem.

You cannot use proportional reasoning to solve this problem because Josh’s age is not a constant multiple of Evie’s age.
Do You Understand?
Question 1.
Essential Question How can proportional reasoning help solve a problem?
Answer:
Proportional reasoning can help in solving a problem.
Explanation:
In the above-given question,
given that,
two quantities are related before you decide to use proportional reasoning to solve a problem.
for example:
Josh is 4 years older than Evie.
Josh is 3 times as old as Evie.
when Evie is 2 years old, Josh is 6 years old.
Question 2.
Use Appropriate Tools How can knowing how to represent proportional relationships in different ways be useful in solving problems?
Answer:
Proportional reasoning can help in solving a problem.
Explanation:
In the above-given question,
given that,
two quantities are related before you decide to use proportional reasoning to solve a problem.
for example:
Josh is 4 years older than Evie.
Josh is 3 times as old as Evie.
when Evie is 2 years old, Josh is 6 years old.
Question 3.
Reasoning How many ways are there to adjust two quantities so that they are in a given proportional relationship? Explain your reasoning.
Answer:
There are 2 ways to adjust two quantities so that they are in given proportional reasoning to solve a problem.
Explanation:
In the above-given question,
given that,
two quantities are related before you decide to use proportional reasoning to solve a problem.
for example:
Josh is 4 years older than Evie.
Josh is 3 times as old as Evie.
when Evie is 2 years old, Josh is 6 years old.
Do You Know How?
Question 4.
A recipe calls for 15 oz of flour for every 8 oz of milk.
a. Is the relationship between ounces of flour and ounces of milk proportional? Explain.
Answer:
No, there is no proportional relationship.
Explanation:
In the above-given question,
given that,
A recipe calls for 15 oz of flour for every 8 oz of milk.
15/8.
so there is no proportional relationship.
b. If you use 15 oz of milk, how much flour should you use?
Answer:
We can use either 3 or 5 oz of flour.
Explanation:
In the above-given question,
given that,
if we use 15 oz of milk, we can use either 3 or 5 oz of flour.
15/3 = 5.
so we can use either 3 or 5 oz of flour.
Question 5.
A food packing company makes a popular fruit cocktail. To ensure a good mixture of fruit, there are 3 cherry halves for every 8 white grapes in a jar. An inspector notices that one jar has 12 cherry halves and 20 white grapes. What can be done to fix the error?
Answer:
The error is 6.6.
Explanation:
In the above-given question,
given that,
A food packing company makes a popular fruit cocktail.
To ensure a good mixture of fruit, there are 3 cherry halves for every 8 white grapes in a jar.
An inspector notices that one jar has 12 cherry halves and 20 white grapes.
12/8 = 3/2.
20/3 = 6.6.
the error is 6.6.
Practice & Problem Solving
Multimedia In 6 and 7, determine whether you can use proportional reasoning and then solve.
Question 6.
If Hector is 8 years old and Mary is 3 years old, how old will Mary be when Hector is 16?
Answer:
Mary is 6 years old.
Explanation:
In the above-given question,
given that,
If Hector is 8 years old and Mary is 3 years old.
8 x 2 = 16.
3 x 2 = 6.
16/2 = 8.
6/2 = 3.
so Mary is 6 years old.
Question 7.
Marco needs to buy some cat food. At the nearest store, 3 bags of cat food cost $15.75. How much would Marco spend on 5 bags of cat food?
Answer:
The Marco spend of 5 bags of cat food = $26.25.
Explanation:
In the above-given question,
given that,
Marco needs to buy some cat food.
At the nearest store, 3 bags of cat food cost $15.75.
$15.75 / 3 = 5.25.
5.25 x 5 = 26.25.
so the Marco spend on 5 bags of cat food = $26.25.
Question 8.
An architect makes a model of a new house with a patio made with pavers. In the model, each paver in the patio is \(\frac{1}{3}\) in. long and a \(\frac{1}{6}\) in. wide. The actual dimensions of the pavers are shown.

a. What is the constant of proportionality that relates the length of a paver in the model and the length of an actual paver?
Answer:
The length of a paper in the model and the length of the actual paver = 0.03125: 0.0528.
Explanation:
In the above-given question,
given that,
An architect makes a model of a new house with a patio made with pavers.
each paver in the patio is \(\frac{1}{3}\) in. long and a \(\frac{1}{6}\) in. wide.
area of the paver = l x b.
area = 1/3 x 1/6.
area = 0.33 x 0.16.
area = 0.0528.
actual paver area = l x b.
area = 1/4 x 1/8.
area = 0.25 x 0.125.
area = 0.03125.
so the ratio is 0.03125 : 0.0528.
b. What is the constant of proportionality that relates the area of a paver in the model and the area of an actual paver? Explain your reasoning.
Answer:
The constant of proportionality is 2.
Explanation:
In the above-given question,
given that,
An architect makes a model of a new house with a patio made with pavers.
each paver in the patio is \(\frac{1}{3}\) in. long and a \(\frac{1}{6}\) in. wide.
area of the paver = l x b.
area = 1/3 x 1/6.
area = 0.33 x 0.16.
area = 0.0528.
actual paver area = l x b.
area = 1/4 x 1/8.
area = 0.25 x 0.125.
area = 0.03125.
2 x 4 = 8.
3 x 2 = 6.
so the proportionality of constant is 2.
Question 9.
Reasoning The table lists recommended amounts of food to order for 25 guests. Nathan is hosting a graduation party for 40 guests. There will also be guests stopping by for a short time. For ordering purposes, Nathan will count each of the 45 “drop-in” guests as half a guest. How much of each food item should Nathan order?

Answer:
The amount of each food item should Nathan order is 24 pieces of fried chicken, 3.66 pounds of Delimeats, and 1.75 pounds of Lasagna.
Explanation:
In the above-given question,
given that,
the table lists recommended amounts of food to order for 25 guests.
24 pieces of fried chicken, 3.66 pounds of Deli meats, and 1.75 pounds of Lasagna.
Question 10.
Emily and Andy each go to a hardware store to buy wire. The table shows the relationship between the cost and the length of wire.
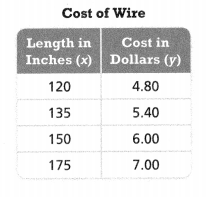
a. Emily needs 24 feet of wire. How much will she spend on wire?
Answer:
The amount she will spend on wire = $5.
Explanation:
In the above-given question,
given that,
Emily needs 24 feet of wire.
580/23.2 = 25.
$25 / 5 = 5.
so the amount she will spend on wire = $5.
b. Andy needs 13 yards of wire. How much will he spend on wire?
Answer:
The amount he will spend on wire = $0.024.
Explanation:
In the above-given question,
given that,
Emily needs 24 feet of wire.
580/23.2 = 25.
1 inch = 0.027 yards.
0.027 x 12 = 0.324.
0.324/13 = 0.024.
Question 11.
Make Sense and Persevere The weights of Michael’s and Brittney’s new puppies are shown in the table and graph. Whose dog gains weight more quickly? Explain.

Answer:
The dog gains weight more quickly = Brittney’s puppy.
Explanation:
In the above-given question,
given that,
The weights of Michael’s and Brittney’s new puppies are shown in the table in the graph.
the weight of 155/1 = 155.
310/2 = 155.
465/3 = 155.
8.6/1 = 8.6.
17.2/2 = 8.6.
so the weight of the Brittney’s puppy weighs more.
Question 12.
Higher Order Thinking Marielle’s painting has the dimensions shown. The school asks her to paint a larger version that will hang in the cafeteria. The larger version will be twice the width and twice the height. Is the area of the original painting proportional to the area of the larger painting? If so, what is the constant of proportionality?
Answer:
The constant of proportionality = 2.
Explanation:
In the above-given question,
given that,
Marielle’s painting has the dimensions shown.
The larger version will be twice the width and twice the height.
area = length x width.
area = 24 x 18.
area = 432 sq inches.
so the constant of proportionality = 2.
Assessment Practice
Question 13.
The ratio of orange juice concentrate to water that Zoe used to make orange juice yesterday was 3: 7. She used 14 ounces of water in the juice yesterday. Today she wants to make twice as much orange juice.
PART A
Is the relationship between the amount of orange juice concentrate c and the amount of water w proportional? Explain.
Answer:
The amount of orange juice concentrate c and the amount of water w is proportional.
Explanation:
In the above-given question,
given that,
The ratio of orange juice concentrate to water that Zoe used to make orange juice yesterday was 3: 7.
She used 14 ounces of water in the juice yesterday.
3 : 7 = 6 : 14.
3 x 2 = 6.
7 x 2 = 14.
so the amount of orange juice concentrate c and the amount of water w is proportional.
PART B
How much orange juice concentrate does she need?
A. 6 ounces
B. 12 ounces
C. 18 ounces
D. 28 ounces
Answer:
Option A is correct.
Explanation:
In the above-given question,
given that,
The ratio of orange juice concentrate to water that Zoe used to make orange juice yesterday was 3: 7.
She used 14 ounces of water in the juice yesterday.
3 : 7 = 6 : 14.
3 x 2 = 6.
7 x 2 = 14.
so option A is correct.
Topic 2 Review
Topic Essential Question
How can you recognize and represent proportional relationships and use them to solve problems?
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.

Answer:
1. Proportional relationship.
2. Constant of proportionality.
3. True proportion.
Explanation:
In the above-given question,
given that,
the definitions of proportional relationship, constant of proportionality, and true proportion.
(1,5), (2, 10), (3, 15) and (4,20) are the examples of proportional relationship.
y x 12.5 = 90.
y = 90/12.5.
y = 72 is the example of constant of proportionality.
2/10 = 1/5.

Use Vocabulary in Writing
A sunflower grows 8 feet in 92 days. Assuming that it grows at a constant rate, explain how you could use this information to find the number of days it took for the sunflower to grow 6 feet. Use vocabulary words in your explanation.
Answer:
The number of days it took for the sunflower to grow 6 feet = 15.3 days.
Explanation:
In the above-given question,
given that,
A sunflower grows 8 feet in 92 days.
y = kx.
6 = k . 92.
k = 92/6.
k = 15.3.
so the number of days it took for the sunflower to grow 6 feet = 15.3 days.
Concepts and Skills Review
Lessons 2.1 And 2.2 Connect Ratios, Rates, and Unit Rates Determine Unit Rates with Ratios of Fractions
Quick Review
A ratio is a relationship in which for every x units of one quantity there are y units of another quantity. A rate is a ratio that relates two quantities with different units. A unit rate relates a quantity to 1 unit of another quantity. You can use what you know about equivalent fractions and calculating with fractions to write a ratio of fractions as a unit rate.
Example
In 3 days, a typical robin can eat up to 42.6 feet of earthworms. Write a rate to relate the number of feet of earthworms to the number of days. Then find the unit rate.
\(\frac{42.6 \text { feet }}{3 \text { days }}=\frac{14.2 \text { feet }}{1 \text { day }}\)
A robin eats 14.2 feet of earthworms per day.
Practice
Question 1.
Mealworms are a healthy food for wild songbirds. Adam buys a 3.5-oz container of mealworms for $8.75. Marco buys a 3.75-oz container of mealworms for $9.75. Which container is the better deal?
Answer:
The better deal = Marco’s deal.
Explanation:
In the above-given question,
given that,
Mealworms are healthy food for wild songbirds.
Adam buys a 3.5-oz container of mealworms for $8.75.
Marco buys a 3.75-oz container of mealworms for $9.75.
8.75 / 3.5 = 2.5.
9.75 / 3.75 = 2.6.
so the Marco container is better.
Question 2.
A painter mixes 2\(\frac{1}{2}\) pints of yellow paint with 4 pints of red paint to make a certain shade of orange paint. How many pints of yellow paint should be mixed with 10 pints of red paint to make this shade of orange?
Answer:
The number of yellow paint should be mixed = 20.
Explanation:
In the above-given question,
given that,
A painter mixes 2\(\frac{1}{2}\) pints of yellow paint with 4 pints of red paint to make a certain shade of orange paint.
2(1/2) = 5/2.
5/2 = 2.5.
2.5 x 2 = 5.
10 x 2 = 20.
so the number of yellow paint should be mixed = 20.
Lesson 2.3 Understand Proportional Relationships: Equivalent Ratios
Quick Review
Two quantities x and y have a proportional relationship if the ratios for every related pair of x and y are equivalent. You can write a proportion to show that two ratios have the same value.
Example
Does the table show a proportional relationship between x and y? Explain.

Because every ratio is equivalent, there is a proportional relationship between x and y.
Practice
In 1 and 2, use the table below that shows information about squares.

Question 1.
Are the perimeter and the side length of squares proportional? Explain.
Answer:
The perimeter and the side length of squares are proportional.
Explanation:
In the above-given question,
given that,
the side lengths are 2, 4, and 6.
the perimeters are 8, 16, and 24.
2 x 4 = 8.
4 x 4 = 16.
6 x 4 = 24.
so the perimeter and the side length of squares are proportional.
Question 2.
Write and solve a proportion to find the perimeter of a square when its side length is 12.
Answer:
The perimeter is 12 cm.
Explanation:
In the above-given question,
given that,
the side length is 12.
12 x 4 = 48.
so the perimeter is 12 cm.
Lesson 2.4 Describe Proportional Relationships: Constant of Proportionality
Quick Review
The equation y = kx describes a proportional relationship between two quantities x and y, where k is the constant of proportionality.k= for any related pair of x and y except when x = 0.
Example
The table shows the wages Roger earned for the hours he worked. What equation relates the wages, w, and the number of hours, h?
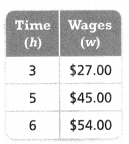
Find the constant of proportionality, k.
\(\frac{27}{3}\) = 9 \(\frac{45}{5}\) = 9 \(\frac{54}{6}\) = 9
Write the equation in the form y = kx.
W = 9h
Practice
Question 1.
Sally is going on vacation with her family. In 2 hours they travel 90.5 miles. If they travel at the same speed, write an equation that represents how far they will travel, d, in h hours.
Answer:
The equation that represents how far they will travel = 45.25 miles.
Explanation:
In the above-given question,
given that,
Sally is going on vacation with her family.
In 2 hours they travel 90.5 miles.
90.5/2 = 45.25 miles.
so the equation that represents how far they will travel = 45.25 miles.
Question 2.
The table shows the weights of bunches of bananas and the price of each bunch. Identify the constant of proportionality. Write an equation to relate weight, w, to the price, p.
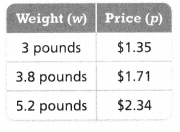
Answer:
The constant of proportionality is 3.
Explanation:
In the above-given question,
given that,
The table shows the weights of bunches of bananas and the price of each bunch.
the price of the bananas is $1.35, $1.71, and $2.34.
the weight of bananas is 3 pounds, 3.8 pounds, and 5.2 pounds.
1.35/3 = 0.45.
1.71/3.8 = 0.45.
2.34/5.2 = 0.45.
so the constant of proportionality = 3.
Lesson 2.5 Graph Proportional Relationships
Quick Review
The graph of a proportional relationship is a straight line through the origin. You can identify the constant of proportionality, k, from the point (1, k) or by dividing for any point (x, y) except the origin.
Example
Is the number of sunny days proportional to the number of rainy days? If so, find the constant of proportionality, and explain its meaning in this situation.
The graph is a straight line through the origin, so it shows a proportional relationship. The constant of proportionality is which means for every1 rainy day, there were 2 sunny days
Practice
Question 1.
Does the graph show a proportional relationship? Explain.

Answer:
The proportional relationship is 1 : 2.
Explanation:
In the above-given question,
given that,
the number of tickets is 4, 8, and 12.
the cost of the tickets = 4, 8, 12, and 14.
the points are (2,4), (4,8), (8, 12), and (12, 16).
2 x 2 = 4, 4 x 2 = 8, 8 x 2 = 16.
so the proportional relationship is 1:2.
Question 2.
Sketch a graph that represents a proportional relationship.
Answer:
The proportional relationship is 1 : 2.
Explanation:
In the above-given question,
given that,
the number of tickets is 4, 8, and 12.
the cost of the tickets = 4, 8, 12, and 14.
the points are (2,4), (4,8), (8, 12), and (12, 16).
2 x 2 = 4, 4 x 2 = 8, 8 x 2 = 16.
so the proportional relationship is 1:2.
Lesson 2.6 Apply Proportional Reasoning to solve Problems
Quick Review
Think about how two quantities are related before you decide to use proportional reasoning to solve a problem.
Example
Ann-Marie makes gift baskets that each contain 3 pounds of gourmet cheese with every 2 boxes of crackers. She ordered 80 pounds of cheese and 50 boxes of crackers. How can she adjust her order to make 25 gift baskets, with no leftover items?
\(\frac{3 \times 25}{2 \times 25}=\frac{75}{50}\)
Ann-Marie can order 5 fewer pounds of cheese so that her order of 75 pounds of cheese and 50 boxes of crackers will make exactly 25 gift baskets.
Practice
Decide which problems can be solved by using proportional reasoning. Select all that apply.
☐ Yani buys 4 dozen flyers for $7.25. What is the cost of 12 dozen?
☐ First-class letters cost $0.49 for the first ounce and $0.22 for each additional ounce. What is the cost of a 5-oz letter?
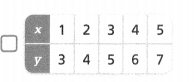
What is the value of y when x = 8?

What is the value of y when x = 5?
Answer:
The value of y is 15 when x = 5.
Explanation:
In the above-given question,
given that,
the values of x and y are given.
x = 1.5, 3, 5.2, 6.5, and 8.
y = 4.5, 9, 15.6, 19.5, and 24.
5 x 3 = 15.
15/3 = 5.
so the value of y is 15 when x = 5.
Topic 2 Fluency Practice
Pathfinder
Shade a path from START to FINISH. Follow the solutions from the least value to the greatest value. You can only move up, down, right, or left.
I can… add, subtract, multiply, and divide integers.

Answer:
3 – 24 = -21, 3 x -13 = -39, 14 x -3 = -42, 44 – 49 = -5, -48/16 = 3, -26 + 7 = -19, -7 – 27 = -34, 13 x -4 = -52, 8 – 19 = -11, -18 / -6 = 3, 3 x -5 = -15, 28/-2 = 14, -35/2 = 17.5 , 4 + – 25 = -21, -68 / 17 = -4, 23 – 46 = -23, -2 – 11 = 13, 15 + -(26) = -11, 17 – 23 = -6, 29 – 38 = -9, -12 / -3 = 4, 18 + (-32) = -14, 11 – 29 = -18, -60/12 = -5, -3 x -2 = 6.
Explanation:
In the above-given question,
given that,
the multiplication, division, addition, and subtraction of numbers.
3 – 24 = -21, 3 x -13 = -39, 14 x -3 = -42, 44 – 49 = -5, -48/16 = 3, -26 + 7 = -19, -7 – 27 = -34, 13 x -4 = -52, 8 – 19 = -11, -18 / -6 = 3, 3 x -5 = -15, 28/-2 = 14, -35/2 = 17.5 , 4 + – 25 = -21, -68 / 17 = -4, 23 – 46 = -23, -2 – 11 = 13, 15 + -(26) = -11, 17 – 23 = -6, 29 – 38 = -9, -12 / -3 = 4, 18 + (-32) = -14, 11 – 29 = -18, -60/12 = -5, -3 x -2 = 6.
