Big Ideas Math Algebra 1 Answers Chapter 1 Solving Linear Equations available here are free of cost. Students can seek homework help and solve the questions covered in the Ch 1 lessons. Also, these solutions of BIM Algebra 1 Ch 1 Answer Book improve their math skills and become math proficient in the future. Choosing the right track during the preparation can change your education life. So, accessing the Big Ideas Math Book Solutions Algebra 1 Ch 1 solving linear equations is a better & fun-learning way for students of high school. Also, it clarifies all your doubts about the concepts of chapter 2 BIM Textbook Solutions.
Big Ideas Math Book Algebra 1 Answer Key Chapter 1 Solving Linear Equations
Get free access to the below available links just by tapping on them and make use of the handy Big Ideas Math Algebra 1 Chapter 1 Solving Linear Equations Solution Key to solve all the questions that appeared in homework, assignments, and yearly exams. Algebra 1 BIM Ch 1 Solving Linear Equations Answer key is explained by the subject experts as per the latest edition of common core standards. So, kids can easily understand the concepts of ch 1 and gain more subject knowledge with the help of the Big Ideas Math Book Solution key of Algebra 1 Chapter 1 Solving Linear Equations.
- Solving Linear Equations Maintaining Mathematical Proficiency – Page 1
- Solving Linear Equations Monitoring Progress – Page 2
- Lesson 1.1 Solving Simple Equations – Page(4-10)
- Solving Simple Equations 1.1 Exercises – Page(8-10)
- Lesson 1.2 Solving Multi-step Equations – Page(12-18)
- Solving Multi-step Equations 1.2 Exercises – Page(16-18)
- Lesson 1.3 Solving Equations with Variables on Both Sides – Page(20-24)
- Solving Equations with Variables on Both Sides 1.3 Exercises – Page(23-24)
- Solving Linear Equations Study Skills: Completing – Page 25
- Solving Linear Equations 1.1-1.3 Quiz – Page 26
- Lesson 1.4 Solving Absolute Value Equations – Page(28-34)
- Solving Absolute Value Equations 1.4 Exercises – Page(32-34)
- Lesson 1.5 Rewriting Equations and Formulas – Page(36-42)
- Rewriting Equations and Formulas 1.5 Exercices – Page(40-42)
- Solving Linear Equations Performance Task: Magic of Mathematics – Page 43
- Solving Linear Equations Chapter Review -Page (44-46)
- Solving Linear Equations Chapter Test – Page 47
- Solving Linear Equations Cumulative Assessment Page(48-49)
Solving Linear Equations Maintaining Mathematical Proficiency
Add or subtract.
Question 1.
-5 + (-2)
Answer:
-5 + (-2 ) = -7
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-5 + ( -2 ) = -5 – 2
= – ( 5 + 2 )
= -7
Hence, from the above,
We can conclude that,
-5 + ( -2 ) = -7
Question 2.
0 + (-13)
Answer:
0 + -13 = -13
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
0 + ( -13 ) = 0 – 13
= -13
Hence, from the above,
We can conclude that,
0 + ( -13 ) = -13
Question 3.
-6 + 14
Answer:
-6 + 14 = 8
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-6 + 14 = +14 – 6
= +8
= 8
Hence, from the above,
We can conclude that
-6 +14 = 8
Question 4.
19 – (-13)
Answer:
19 – ( -13 ) = 32
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
19 – ( -13 ) = 10 + 9 + 10 + 3
= 20 + 12
= 32
Hence, from the above,
We can conclude that,
19 – (-13 ) = 32
Question 5.
-1 – 6
Answer:
-1 -6 = -7
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-1 – 6 = – ( 1 + 6 )
= -7
Hence, from the above,
We can conclude that
-1 -6 = -7
Question 6.
– 5 – (-7)
Answer:
-5 – ( -7 ) = 2
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-5 – ( -7 ) = -5 + 7
= 7 – 5
= 2
Hence, from the above,
We can conclude that
-5 – ( -7 ) = 2
Question 7.
17 + 5
Answer:
17 + 5 = 22
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
17 + 5 = 15 + 2 + 5
= 22
Hence, from the above,
We can conclude that
17 + 5 = 22
Question 8.
8 + (-3)
Answer:
8 + ( -3 ) = 5
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
8 + ( -3 ) = 8 – 3
= 5
Hence, from the above,
We can conclude that
8 + ( -3 ) = 5
Question 9.
11 – 15
Answer:
11 – 15 = -4
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
11 – 15 = -15 + 11
= – ( 15 – 11 )
= -4
Hence, from the above,
We can conclude that,
11 – 15 = -4
Multiply or divide.
Question 10.
-3(8)
Answer:
-3(8) = -3 × 8
= -24
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-3(8) = -3 × +8
= -24
Hence, from the above,
We can conclude that
-3 ( 8 ) = -24
Question 11.
-7 • (-9)
Answer:
-7 . ( -9 ) = -7 × +9
= -63
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-7 . ( 9 ) = -7 × +9
= -63
Hence, from the above,
We can conclude that
-7 . ( 9 ) = -63
Question 12.
4 • (-7)
Answer:
4 . ( -7 ) = 4 × ( -7 )
= -28
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
4. (-7 ) = +4 × -7
= -28
Hence, from the above,
We can conclude that
4 . ( -7 ) = -28
Question 13.
-24 ÷ (-6)
Answer:
-24 ÷ ( -6 ) = 4
Explanation:
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-24 ÷ ( -6 ) = + ( 24 ÷ 6 )
= 4
Hence, from the above,
We can conclude that
-24 ÷ ( -6 ) = 4
Question 14.
-16 ÷ 2
Answer:
-16 ÷ 2 = -8
Explanation:
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-16 ÷ 2 = -8
Hence, from the above,
We can conclude that
-16 ÷ 2 = -8
Question 15.
12 ÷ (-3)
Answer:
12 ÷ ( -3 ) = -4
Explanation:
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
12 ÷ ( -3 )
= 12 ÷ -3
= -4
Hence, from the above,
We can conclude that
12 ÷ ( -3 ) = -4
Question 16.
6 • 8
Answer:
6 . 8 = 6 × 8
= 48
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
6 . 8 = 6 × 8
= 48
Hence, from the above,
We can conclude that
6 . 8 = 48
Question 17.
36 ÷ 6
Answer:
36 ÷ 6 = 6
Explanation:
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
36 ÷ 6 = ( 30 + 6 ) ÷ 6
= ( 30 ÷ 6 ) + ( 6 ÷ 6 )
= 5 + 1
= 6
Hence, from the above,
We can conclude that
36 ÷ 6 = 6
Question 18.
-3(-4)
Answer:
-3 ( -4 ) = -3 × -4
= -12
Explanation:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
We know that,
The result of any mathematical operation follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
So,
-3 ( -4 ) = -3 × -4
= +12
Hence, from the above,
We can conclude that
-3 ( – 4 ) = 12
Question 19.
ABSTRACT REASONING
Summarize the rules for
(a) adding integers,
(b) subtracting integers,
(c) multiplying integers, and
(d) dividing integers.
Give an example of each.
Answer:
a) Adding integers:
We know that,
The result of any mathematical operation i.e., Addition or subtraction follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
Example:
Let take the two numbers -2 and 3
So,
The addition of -2 and 3 is:
-2 + 3 = +1
= 1 ( Since the big number has a positive sign )
b) Subtracting integers:
We know that,
The result of any mathematical operation i.e., Addition or subtraction follows the sign of the big number and if the two numbers have the same sign, then the result of that also operation also follows the same sign and if there is no sign before the number, then we can take that number as positive number i.e., +a
Example:
Let take the two numbers -3 and +8
So,
The subtraction of -3 and +8 is:
-3 – ( +8 ) = -3 – 8
= – ( 3 + 8 )
= -11 ( Since both the numbers have a negative sign )
c) Multiplying integers:
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
Example:
Let take the two numbers +8 and -3
So,
The multiplication of +8 and -3 is:
+8 ( -3 ) = 8 × -3
= -24 ( Since + × – = – )
d) Dividing integers:
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
Example:
Let take the two numbers -12 and -2
So,
The division of -12 and -2 is:
-12 ÷ ( -2 ) = -12 ÷ -2
= ( -10 + -2 ) ÷ -2
= ( -10 ÷ -2 ) + ( -2 ÷ -2 )
= 5 + 1
= 6
Hence, from the above,
We can conclude all the rules for the four basic mathematical operations.
Solving Linear Equations Monitoring Progress
Solve the problem and specify the units of measure.
Question 1.
The population of the United States was about 280 million in 2000 and about 310 million in 2010. What was the annual rate of change in population from 2000 to 2010?
Answer:
The annual rate of change in population from 2000 to 2010 is: 30 million
Explanation:
It is given that the population of the United States was about 280 million in 2000 and about 310 million in 2010.
So,
The annual rate of change in population from 2000 to 2010 = ( The population of United States in 2010 ) – ( The population of United States in 2000 )
= 310 – 280
= 30 million
Hence, from the above,
We can conclude that the annual rate of change in population from 2000 to 2010 is: 30 million
Question 2.
You drive 240 miles and use 8 gallons of gasoline. What was your car’s gas mileage (in miles per gallon)?
Answer:
Your car’s gas mileage ( in miles per gallon ) is: 30
Explanation:
It is given that you drive 240 miles and use 8 gallons of gasoline.
So,
The mileage of your car = ( The total number of miles driven by your car ) ÷ ( The number of gallons of gasoline used by your car )
= 240 ÷ 8
= ( 160 + 80 ) ÷ 8
= ( 160 ÷ 8 ) + ( 80 ÷ 8 )
= 20 + 10
= 30 miles
Hence, from the above,
We can conclude that the mileage of your car is: 30 miles per gallon
Question 3.
A bathtub is in the shape of a rectangular prism. Its dimensions are 5 feet by 3 feet by 18 inches. The bathtub is three-fourths full of water and drains at a rate of 1 cubic foot per minute. About how long does it take for all the water to drain?
Answer:
The total time taken for the water to drain is: 2,430 minutes
Explanation:
It is given that a bathtub is in the shape of a rectangular prism. Its dimensions are 5 feet by 3 feet by 18 inches. The bathtub is three-fourths full of water and drains at a rate of 1 cubic foot per minute.
So,
The volume of the rectangular prism = The dimensions of the rectangular prism
= 5 × 3 × 18 × 12
= 3,240 cubic feet
Now,
The volume of the bathtub which is three-fourths full of water = \(\) {3}{4}[\latex] × 3240
= 2,430 cubic feet
It is also given that that the bathtub drains at a rate of 1 cubic foot per minute.
So,
The time taken to drain 2,430 cubic feet of water in minutes = 2,430 × 1
= 2,430 minutes
Hence, from the above,
We can conclude that the time taken for the water to drain from the bathtub at a rate of 1 cubic foot per minute is: 2,430 minutes
Lesson 1.1 Solving Simple Equations
Essential Question
How can you use simple equations to solve real-life problems?
Exploration 1
Measuring Angles
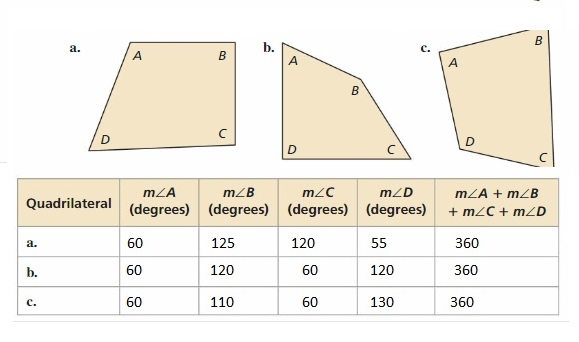
Work with a partner. Use a protractor to measure the angles of each quadrilateral. Copy and complete the table to organize your results. (The notation m∠A denotes the measure of angle A.) How precise are your measurements?

EXPLORATION 2
Making a Conjecture
Work with a partner. Use the completed table in Exploration 1 to write a conjecture about the sum of the angle measures of a quadrilateral. Draw three quadrilaterals that are different from those in Exploration 1 and use them to justify your conjecture.
Answer:
The completed table is:

From the above table,
We can say that the sum of all the angle in any quadrilateral is: 360 degrees
So,
From the above table,
The angles in Quadrilateral a is: 60 degrees, 125 degrees, 120 degrees, and 55 degrees
We know that,
The quadrilateral will have n angles based on the shape.
The shape which has more than 3 sides is called a Quadrilateral.
Ex: Rectangle, Square, Pentagon, Hexagon, etc.
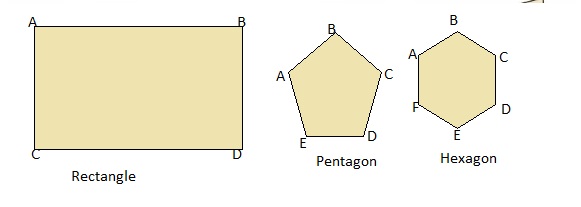
From the above quadrilaterals,
We can say that all the sides in each quadrilateral are equal.
So,
The angles in each quadrilateral are also equal.
So,
In a rectangle, there are 4 sides
So,
By measuring, we can observe that each angle of a rectangle is: 90 degrees
Hence,
The sum of all angles in a rectangle = 90 + 90 + 90 + 90 = 360 degrees
In a pentagon, there are 5 sides
By measuring, we can observe that each rectangle of a pentagon
Hence,
The sum of all the angles in a pentagon = = 72+ 72 + 72 + 72 + 72 = 360 degrees
In a Hexagon, there are 6 sides
So,
By measuring, we can observe that each angle of a hexagon is: 60 degrees
Hence,
The sum of all angle is a Hexagon = 60 + 60 + 60 + 60 + 60 + 60 = 360 degrees
Hence, from the above-drawn quadrilaterals,
We can conclude that our conjecture is proven.
EXPLORATION 3
Applying Your Conjecture
Work with a partner. Use the conjecture you wrote in Exploration 2 to write an equation for each quadrilateral. Then solve the equation to find the value of x. Use a protractor to check the reasonableness of your answer.
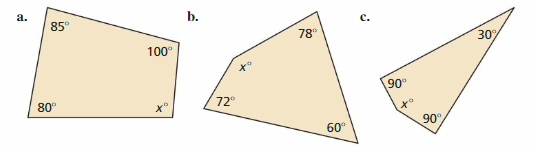
Answer:
The given figure is:

From Exploration 2, the proven conjecture is:
The sum of all angles in a quadrilateral is: 360 degrees
Now,
In Quadrilateral a.,
By using the above-proven conjecture,
85 + 80 + 100 + x = 360 degrees
265 + x = 360 degrees
x = 360 – 265
= 95 degrees
So,
The angle x is: 95 degrees
In Quadrilateral b.,
By using the above-proven conjecture,
72 + 78 + 60 + x = 360 degrees
210 + x = 360 degrees
x = 360 – 210
= 150 degrees
So,
The angle of x is: 150 degrees
In Quadrilateral c.,
By using the above-proven conjecture,
90 + 90 +30 + x = 360 degrees
210 + x = 360 degrees
x = 360 – 210
= 150 degrees
So,
The angle of x is: 150 degrees
Communicate Your Answer
Question 4.
How can you use simple equations to solve real-life problems?
Answer:
Any situation where there is an unknown quantity can be represented by a linear equation like calculating mileage rates and predicting profit.
Example:
Rahul is t years old and Ravi is 3 more than 8 times Rahul’s age. Their combined age is 39. How old is Rahul?
t + (8t + 3) = 39
9t + 3 = 39
9t = 36
t = 36/9
t = 4.
Therefore Rahul is old years old.
Question 5.
Draw your own quadrilateral and cut it out. Tear off the four corners of the quadrilateral and rearrange them to affirm the conjecture you wrote in Exploration 2. Explain how this affirms the conjecture.
Answer:
Your Quadrilateral is:
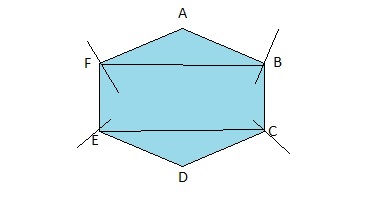
From the above Quadrilateral,
We can observe that the tear-off corners of the quadrilateral are joined and it becomes the triangle.
So,
In the above Quadrilateral, there are two quadrilaterals.
We know that,
The sum of all angles in a triangle is: 180 degrees
So,
The sum of all angles in the two triangles = 180 + 180 = 360 degrees
These two triangles form a quadrilateral.
So,
The sum of all angles in a quadrilateral is: 360 degrees
Hence, from the above,
We can conclude that we can prove Exploration 2’s conjecture by your own example.
1.1 Lesson
Monitoring Progress
Solve the equation. Justify each step. Check your solution.
Question 1.
n + 3 = -7
Answer:
The value of n is: -10
Explanation:
The given equation is:
n + 3 = -7
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
n + 3 = -7
n = -7 – (+3 )
n = -7 – 3
= -10
Hence from the above,
We can conclude that the value of n is: -10
Question 2.
g – \(\frac{1}{3}\) = –\(\frac{2}{3}\)
Answer:
The value of g is: –\(\frac{1}{3}\)
Explanation:
The given equation is:
g – \(\frac{1}{3}\) = –\(\frac{2}{3}\)
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
g – \(\frac{1}{3}\) = –\(\frac{2}{3}\)
g = –\(\frac{2}{3}\) + \(\frac{1}{3}\)
g = \(\frac{-2 + 1}{3}\)
g = \(\frac{-1}{3}\)
g = –\(\frac{1}{3}\)
Hence, fromthe above,
We can conclude that the value of g is: –\(\frac{1}{3}\)
Question 3.
-6.5 = p + 3.9
Answer:
The value of p is: -10.4
Explanation:
The given equation is:
-6.5 = p + 3.9
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-6.5 = p + 3.9
p = -6.5 – 3.9
= – ( 6.5 + 3.9 )
= – 10.4
Hence, from the above,
We can conclude that the value of p is: -10.4
Monitoring Progress
Solve the equation. Justify each step. Check your solution.
Question 4.
\(\frac{y}{3}\) = -6
Answer:
The value of y is: -18
Explanation:
The given equation is:
\(\frac{y}{3}\) = -6
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
\(\frac{y}{3}\) = -6
\(\frac{y}{1}\) × \(\frac{1}{3}\) = -6
\(\frac{y}{1}\) = -6 ÷ \(\frac{1}{3}\)
y = -6 × -3
y = -18
Hence, from the above,
We can conclude that the value of y is: -18
Question 5.
9π = πx
Answer:
The value of x is: 9
Explanation:
The given equation is:
9π = πx
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
9π = πx
9 × π = π × x
x = ( 9 × π ) ÷ π
x = 9
Hence, from the above,
We can conclude that the value of x is: 9
Question 6.
0.05w = 1.4
Answer:
The value of w is: 28
Explanation:
The given equation is:
0.05w = 1.4
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
0.05w = 1.4
0.05 × w = 1.4
\(\frac{5}{100}\) × w = \(\frac{14}{10}\)
w = \(\frac{14}{10}\) ÷ \(\frac{5}{100}\)
w = \(\frac{14}{10}\) × \(\frac{100}{5}\)
w = \(\frac{14 × 100}{10 × 5}\)
w = \(\frac{28}{1}\)
w = 28
Hence, from the above,
We can conclude that the value of w is: 28
Monitoring Progress
Question 7.
Suppose Usain Bolt ran 400 meters at the same average speed that he ran the 200 meters. How long would it take him to run 400 meters? Round your answer to the nearest hundredth of a second.
Answer:
The time it took for him to run 400 meters is: 0.50 seconds
Explanation:
It is given that Usain Bolt ran 400 meters at the same average speed that he ran the 200 meters.
We know that,
Speed = Distance ÷ Time
But, it is given that the average speed is the same.
Hence,
Speed = Constant
So,
Since speed is constant, distance is directly proportional to time.
So,
The time taken by Usain Bolt to run 400 meters = 200 ÷ 400
= ( 2 × 100 ) ÷ ( 4 × 100 )
= 10 ÷ 20
= 0.50 seconds ( 0.5 and 0.50 are the same values Only for the representation purpose, we will add ‘0’ after 5 )
Hence from the above,
We can conclude that the time is taken by Usain Bolt to run 400 meters when rounded-off to the nearest hundredth is: 0.50 seconds
Monitoring Progress
Question 8.
You thought the balance in your checking account was $68. When your bank statement arrives, you realize that you forgot to record a check. The bank statement lists your balance as $26. Write and solve an equation to find the amount of the check that you forgot to record.
Answer:
The amount of the check that you forgot to record is: $42
Explanation:
It is given that you thought the balance in your checking account was $68 and when your bank statement arrives, you realize that you forgot to record a check and the bank statement lists your balance as $26.
Now,
Let the amount you forgot to record be: x
So,
The total balance in your checking account = ( The listed balance ) + ( The amount that you forgot to record a check )
68 = 26 + x
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
68 = 26 + x
x = 68 – 26
x = $42
Hence, from the above,
We can conclude that the amount that forgot to record is: $42
Solving Simple Equations 1.1 Exercises
Monitoring Progress and Modeling with Mathematics
In Exercises 5–14, solve the equation. Justify each step. Check your solution.
Question 1.
VOCABULARY Which of the operations +, -, ×, and ÷ are inverses of each other?
Answer:
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
Hence, from the above,
We can conclude that,
+ is inverse of – and vice-versa
× is inverse of ÷ and vice-versa
Question 2.
VOCABULARY Are the equations -2x = 10 and -5x = 25 equivalent? Explain.
Answer:
The equations -2x = 10 and -5x = 25 are equivalent
Explanation:
The given equations are:
-2x = 10 and -5x = 25
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
So,
From -2x = 10,
x = 10 ÷ ( -2 )
x = -10 ÷ 2
x = -5
From -5x = 25,
x = 25 ÷ ( -5 )
x = -25 ÷ 5
x = -5
Hence, from the above,
We can conclude that the equations -2x = 10 and -5x = 25 are equivalent
Question 3.
WRITING Which property of equality would you use to solve the equation 14x = 56? Explain.
Answer:
The given equation is:
14x = 56
So,
It can be re-written as
14 × x = 56
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x = 56 ÷ 14
x = 4
Hence, from the above,
We can conclude that the value of x is: 4
Question 4.
WHICH ONE DOESN’T BELONG? Which expression does not belong with the other three? Explain your reasoning.

Answer:
The equation C) does not belong to the other three
Explanation:
Let the given equations be named as A), B), C), and D)
So,
The given equations are:
A) 8 = x ÷ 2
B) 3 = x ÷ 4
C) x – 6 = 5
D) x ÷ 3 = 9
So,
From the above equations,
The equations A, B), and D) are dividing the numbers whereas equation C) subtracting the numbers
Hence, from the above,
We can conclude that,
The equation C) does not belong to the other three.
Question 5.
x + 5 = 8
Answer:

Question 6.
m + 9 = 2
Answer:
The value of m is: -5
Explanation:

Question 7.
y – 4 = 3
Answer:
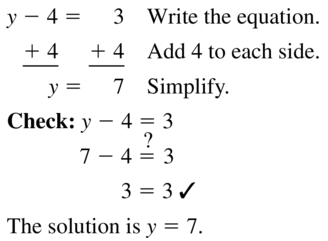
Question 8.
s – 2 = 1
Answer:
The value of s is: 3
Explanation;

Question 9.
w + 3 = -4
Answer:

Question 10.
n – 6 = -7
Answer:
The value of n is: -1
Explanation:

Question 11.
-14 = p – 11
Answer:
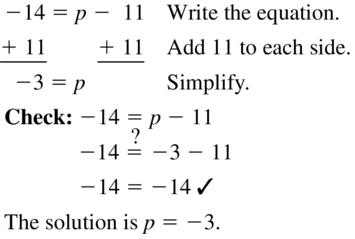
Question 12.
0 = 4 + q
Answer:
The value of q is: -4
Explanation;

Question 13.
r + (-8) = 10
Answer:

Question 14.
t – (-5) = 9
Answer:
The value of t is: 4
Explanation;

Question 15.
MODELING WITH MATHEMATICS
A discounted amusement park ticket costs $12.95 less than the original price p. Write and solve an equation to find the original price.

Answer:
The equation for the original price is:
p = x + $12.95
Explanation:
It is given that a discounted amusement park ticket costs $12.95 less than the original price p.
So,
Let the discounted amusement park ticket be: x
The given original price is: p
So,
The discounted amusement park ticket cost = p – $12.95
x = p – 12.95
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
p = x + $12.95
Hence, from the above,
We can conclude that the equation for the original price is:
p = x + $12.95
Question 16.
MODELING WITH MATHEMATICS
You and a friend are playing a board game. Your final score x is 12 points less than your friend’s final score. Write and solve an equation to find your final score.
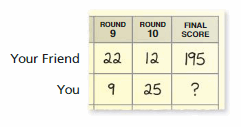
Answer:
Your final score is:
x = ( The score of your friend ) – 12
Explanation:
It is given that you and a friend are playing a board game. Your final score x is 12 points less than your friend’s final score.
So,
The scores table is shown below:

From the above table,
The final score of your friend is: 195
Let the final score of yours is: x
So,
x = ( The final score of your friend ) – 12
= 195 – 12
= 183 points
Hence, from the above,
We can conclude that the final score of yours is: 183 points
USING TOOLS
The sum of the angle measures of a quadrilateral is 360°. In Exercises 17–20, write and solve an equation to find the value of x. Use a protractor to check the reasonableness of your answer.
Question 17.
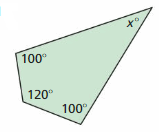
Answer:
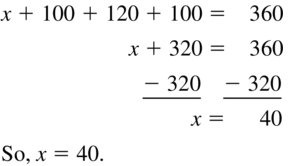
Question 18.
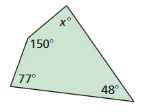
Answer:
The value of x is: 85 degrees
Explanation:
We know that,
The sum of angles in a quadrilateral is: 360 degrees
So,
150 + 48 + 77 + x = 360
275 + x = 360
x = 360 – 275
x = 85 degrees
Hence, from the above,
We can conclude that the value of x is: 85 degrees
Question 19.
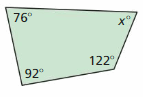
Answer:
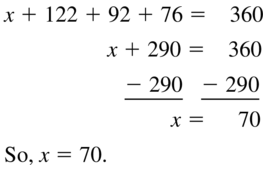
Question 20.
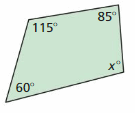
Answer:
The value of x is: 100 degrees
Explanation:
We know that,
The sum of all angles in a quadrilateral is: 360 degrees
So,
115 + 85 + 60 + x = 360
260 + x = 360
x = 360 – 260
x = 100 degrees
Hence, from the above,
We can conclude that the value of x is: 100 degrees
In Exercises 21–30, solve the equation. Justify each step. Check your solution.
Question 21.
5g = 20
Answer:
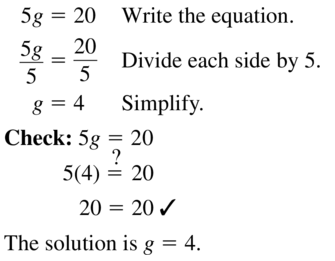
Question 22.
4q = 52
Answer:
The value of g is: 13
Explanation:
The given equation is:
4g = 52
4 × g = 52
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
g = 52 ÷ 4
= ( 44 + 8 ) ÷ 4
= ( 44 ÷ 4 ) + ( 8 ÷ 4 )
= 11 + 2
= 13
Hence, from the above,
We can conclude that the value of g is: 13
Question 23.
p ÷ 5 = 3
Answer:
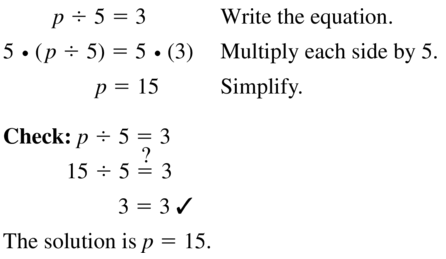
Question 24.
y ÷ 7 = 1
Answer:
The value of y is: 7
Explanation:
The given equation is:
y ÷ 7 = 1
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
y = 1 × 7
y = 7
Hence, from the above,
We can conclude that the value of y is: 7
Question 25.
-8r = 64
Answer:

Question 26.
x ÷(-2) = 8
Answer:
The value of x is: -16
Explanation:
The given equation is:
x ÷ ( -2 ) = 8
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x ÷ ( -2 ) = 8
x = 8 × ( -2 )
x = -16
Hence, from the above,
We can conclude that the value of x is: -16
Question 27.
\(\frac{x}{6}\) = 8
Answer:
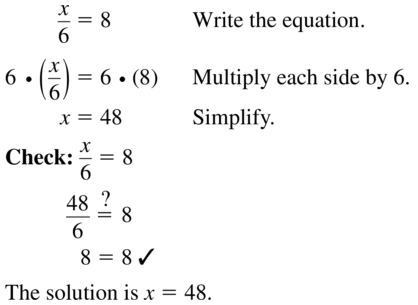
Question 28.
\(\frac{w}{-3}\) = 6
Answer:
The value of w is: -18
Explanation:
The given equation is:
\(\frac{w}{-3}\) = 6
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
\(\frac{w}{-3}\) = 6
w = 6 × ( -3 )
w = -18
Hence, from the above,
We can conclude that the value of w is: -18
Question 29.
-54 = 9s
Answer:
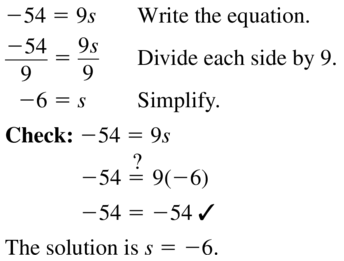
Question 30.
-7 = \(\frac{t}{7}\)
Answer:
The value of t is: -49
Explanation:
The given equation is:
-7 = \(\frac{t}{7}\)
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-7 = \(\frac{t}{7}\)
t = -7 × 7
t = -49
Hence, from the above
We can conclude that the value of t is: -49
In Exercises 31– 38, solve the equation. Check your solution.
Question 31.
\(\frac{3}{2}\) + t = \(\frac{1}{2}\)
Answer:
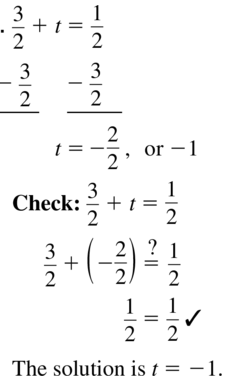
Question 32.
b – \(\frac{3}{16}\) = \(\frac{5}{16}\)
Answer:
The value of b is: \(\frac{1}{2}\)
Explanation:
The given equation is:
b – \(\frac{3}{16}\) = \(\frac{5}{16}\)
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
b = \(\frac{5}{16}\) + \(\frac{3}{16}\)
Since the denominators of both the numerators are equal, add the numerators making the denominator common
So,
b = \(\frac{5 + 3}{16}\)
b = \(\frac{8}{16}\)
b = \(\frac{1}{2}\)
Hence, from the above,
We can conclude that the value of b is: \(\frac{1}{2}\)
Question 33.
\(\frac{3}{7}\)m = 6
Answer:
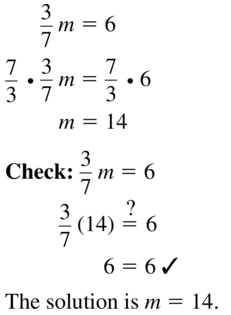
Question 34.
–\(\frac{2}{5}\)y = 4
Answer:
The value of y is: 10
Explanation:
The given equation is:
–\(\frac{2}{5}\)y = 4
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
–\(\frac{2}{5}\)y = 4
–\(\frac{2}{5}\) × y = 4
y = 4 ÷ –\(\frac{2}{5}\)
y = 4 × –\(\frac{5}{2}\)
y = -4 × –\(\frac{5}{2}\)
y = –\(\frac{4}{1}\) × –\(\frac{5}{2}\)
y = –\(\frac{4 × 5}{1 × 2}\)
y = 10
Hence, from the above,
We can conclude that the value of y is: 10
Question 35.
5.2 = a – 0.4
Answer:

Question 36.
f + 3π = 7π
Answer:
The value of f is: 4π
Explanation:
The given equation is:
f + 3π = 7π
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
f + 3π = 7π
f = 7π – 3π
f = π ( 7 – 3 )
f = π ( 4 )
f = 4π
Hence, from the above,
We can conclude that the value of f is: 4π
Question 37.
– 108π = 6πj
Answer:

Question 38.
x ÷ (-2) = 1.4
Answer:
The value of x is: –\(\frac{14}{5}\)
Explanation:
The given equation is:
x ÷ ( -2 ) = 1.4
We know that,
A) – ÷ – = +
B) + ÷ – = –
C) + ÷ + = +
D) – ÷ + = –
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x ÷ ( -2 ) = 1.4
x ÷ ( -2 ) = \(\frac{14}{10}\)
x ÷ ( -2 ) = \(\frac{7}{5}\)
x = \(\frac{7}{5}\) × ( -2 )
x = – \(\frac{7}{5}\) × \(\frac{2}{1}\)
x = –\(\frac{14}{5}\)
Hence, from the above,
We can conclude that the value of x is: –\(\frac{14}{5}\)
ERROR ANALYSIS
In Exercises 39 and 40, describe and correct the error in solving the equation.
Question 39.
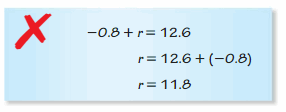
Answer:
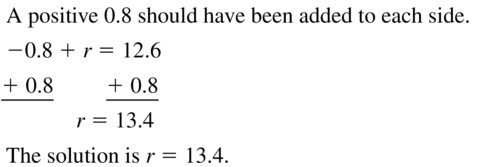
Question 40.
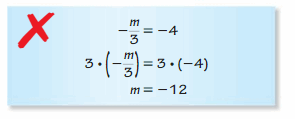
Answer:
A negative 3 should have been multiplied to each side.
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
So,
-(\(\frac{m}{3}\) ) =-4
-3 ( \(\frac{m}{3}\) ) = -4 ( -3 )
3 ( \(\frac{m}{3}\) ) = -4 ( -3 )
3 ( \(\frac{m}{3}\) ) = 12
\(\frac{m}{3}\) × \(\frac{3}{1}\) = 12
m = 12
Hence, from the above,
We can conclude that the value of m is: 12
Question 41.
ANALYZING RELATIONSHIPS
A baker orders 162 eggs. Each carton contains 18 eggs. Which equation can you use to find the number x of cartons? Explain your reasoning and solve the equation.
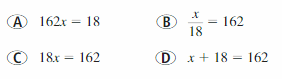
Answer:

MODELING WITH MATHEMATICS
In Exercises 42– 44, write and solve an equation to answer the question.
Question 42.
The temperature at 5 P.M. is 20°F. The temperature at 10 P.M. is -5°F. How many degrees did the temperature fall?
Answer:
The fall in temperature is: 25 degrees Fahrenheit
Explanation:
It is given that the temperature at 5 P.M. is 20°F and the temperature at 10 P.M. is -5°F.
So,
The fall in temperature = ( The temperature at 5 P.M ) – ( The temperature at 10 P.M )
We know that,
A) – × – = +
B) + × – = –
C) + × + = +
D) – × + = –
So,
The fall in temperature = 20 – ( -5 )
= 20 + 5
= 25 degrees Fahrenheit
Hence, from the above,
We can conclude that the fall in temperature is: 25 degrees Fahrenheit
Question 43.
The length of an American flag is 1.9 times its width. What is the width of the flag?

Answer:

Question 44.
The balance of an investment account is $308 more than the balance 4 years ago. The current balance of the account is $4708. What was the balance 4 years ago?
Answer:
The balance 4 years ago is: $4,400
Explanation:
It is given that the balance of an investment account is $308 more than the balance 4 years ago. The current balance of the account is $4708.
So,
The current balance of the account = ( The balance of an investment account 4 years ago ) + $308
Let the balance of an investment account four years ago be x.
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
$4,708 = x + $308
x = 4,708 – 308
x = $4,400
Hence, from the above,
We can conclude that the balance of an investment account four years ago is: $4,400
Question 45.
REASONING
Identify the property of equality that makes Equation 1 and Equation 2 equivalent.
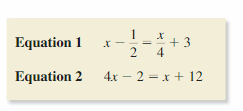
Answer:
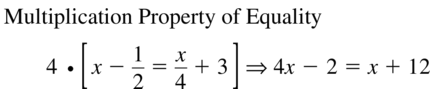
PROBLEM-SOLVING
Question 46.
Tatami mats are used as a floor covering in Japan. One possible layout uses four identical rectangular mats and one square mat, as shown. The area of the square mat is half the area of one of the rectangular mats.
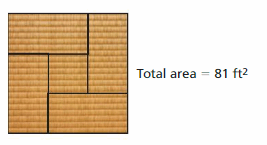
a. Write and solve an equation to find the area of one rectangular mat.
Answer:
The area of one rectangular mat is: 18 ft²
Explanation:
It is given that the tatami mats are used as a floor covering in Japan and for that, one layout of tatami mats requires the four identical rectangular mats and the one square mat
So,
The total area of the tatami mats = ( The area of the four rectangular mats ) + ( The area of the one square mat )
The give tatami mat layout is:

From the layout,
We can observe that
The total area of the layout is: 81 ft²
So,
The total area of tatami mats = 81 ft²
( The area of the four rectangular mats ) + ( The area of the one square mat ) = 81 ft²
It is also given that
The area of a square mat is half of one of the rectangular mats
So,
Area of the square mat = ( Area of the rectangular mat ) ÷ 2
So,
( The area of the four rectangular mats ) + \(\frac{Area of the rectangular mat}{2}\) = 81 ft²
4 ( The area of the rectangular mat ) + \(\frac{Area of the rectangular mat}{2}\) = 81 ft²
\(\frac{8}{2}\) ( The area of the rectangular mat ) + \(\frac{1}{2}\) ( The area of the rectangular mat ) = 81 ft²
( The area of the rectangular mat ) [ \(\frac{8}{2}\) + \(\frac{1}{2}\) ] = 81 ft²
\(\frac{9}{2}\) ( The area of the rectangular mat ) = 81 ft²
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
The area of the rectangular mat = 81 ÷ \(\frac{9}{2}\)
= 81 × \(\frac{2}{9}\)
= \(\frac{81}{1}\) × \(\frac{2}{9}\)
= \(\frac{81 × 2}{9 × 1}\)
= 18 ft²
Hence, from the above,
We can conclude that the area of one rectangular mat is: 18 ft²
b. The length of a rectangular mat is twice the width. Use Guess, Check, and Revise to find the dimensions of one rectangular mat.
Answer:
The dimensions of the rectangular mat are:
Length: 6 ft
Width: 3 ft
Explanation:
From the above problem,
The area of the rectangular mat = 18 ft²
It is given that the length of a rectangular mat is twice the width.
We know that the area of the rectangle = ( Length ) × ( Width )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
It is also given that the length of a rectangular mat is twice the width
So,
Length of a rectangular mat = 2 × Width
Now,
The area of the rectangular mat = Length × Width
18 = 2 × Width × Width
Width × Width = 18 ÷ 2
Width × Width = 9
From guessing,
We can say that
Width of the rectangular mat = 3 ft
Now,
The length of the rectangular mat = 2 × 3
= 6 ft
Hence, from the above,
We can conclude that the dimensions of the rectangular mat are:
Length: 6 ft
Width: 3 ft
Question 47.
PROBLEM-SOLVING
You spend $30.40 on 4 CDs. Each CD costs the same amount and is on sale for 80% of the original price.
a. Write and solve an equation to find how much you spend on each CD.
b. The next day, the CDs are no longer on sale. You have $25. Will you be able to buy 3 more CDs? Explain your reasoning.

Answer:

Question 48.
ANALYZING RELATIONSHIPS
As c increases, does the value of x increase, decrease, or stay the same for each equation? Assume c is positive.
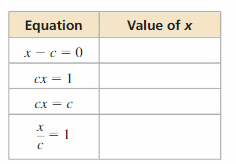
Answer:
Let assume the values of c be: 0,1,2,3
So,
The completed table by taking the values of c is:
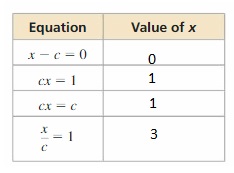
By taking the values of c positive i.e., 0, 1, 2, 3
We can observe that as the value of c increases, the values of x sometimes increasing and sometimes stays the same but not decreasing.
Question 49.
USING STRUCTURE
Use the values -2, 5, 9, and 10 to complete each statement about the equation ax = b – 5.
a. When a = ___ and b = ___, x is a positive integer.
b. When a = ___ and b = ___, x is a negative integer.
Answer:
Question 50.
HOW DO YOU SEE IT?
The circle graph shows the percents of different animals sold at a local pet store in 1 year.
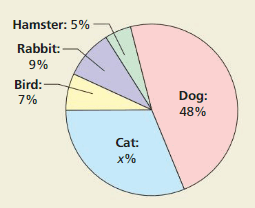
a. What percent is represented by the entire circle?
Answer:
The percent represented by the entire circle is = 69 % + x %
Explanation:
It is given that the circle represents the percent of different animals sold at a local store for 1 year
Now,
The given circle is:

We know that,
In terms of percentages, any circle represents 100%
So,
The equation representing the circle is:
The percentage of different animals in the circle = 48 + 5 + 9 + 7 +x
The percentage of different animals in the circle= 69% + x%
b. How does the equation 7 + 9 + 5 + 48 + x = 100 relate to the circle graph? How can you use this equation to find the percent of cats sold?
Answer:
The percent of cats sold is: 31%
Explanation:
We know that,
In terms of percentages, any circle represents 100%
So,
The total percent of animals = The percent of animals that are represented by the circle
100% = 69% + x%
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x% = 100% – 69%
x% = 31%
Hence, from the above,
We can conclude that the percent of cats is: 31%
Question 51.
REASONING
One-sixth of the girls and two-sevenths of the boys in a school marching band are in the percussion section. The percussion section has 6 girls and 10 boys. How many students are in the marching band? Explain.
Answer:
Question 52.
THOUGHT-PROVOKING
Write a real-life problem that can be modeled by an equation equivalent to the equation 5x = 30. Then solve the equation and write the answer in the context of your real-life problem.
Answer:
Let suppose there is some number of boys. The number of girls is five times of the boys and the total number of girls is 30. Find the number of boys?
Ans:
Let,
The number of boys is x.
It is given that the number of girls is five times of boys.
So,
The number of girls = 5x
It is also given that
The number of girls = 30
So,
5x = 30
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5 × x = 30
x = 30 ÷ 5
x = 6
Hence, from the above,
We can conclude that the number of boys is: 6
MATHEMATICAL CONNECTIONS
In Exercises 53–56, find the height h or the area of the base B of the solid.
Question 53.
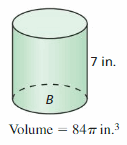
Answer:

Question 54.
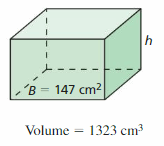
Answer:
The height of the cuboid is: 9 cm
Explanation:
The given figure is:

We know that,
The volume of a cuboid = L × B × H
We know that,
The cuboid is made from a rectangle
We know that,
The area of a rectangle = L × H
So,
The volume of a cuboid = A × B
From the above figure,
The given volume is: 1323 cm³
The given Area is: 147 cm²
So,
1323 = 147 × H
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
H = 1323 ÷ 147
H = 9
Hence, from the above,
We can conclude that the height of the cuboid is: 9 cm
Question 55.
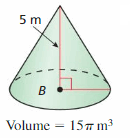
Answer:
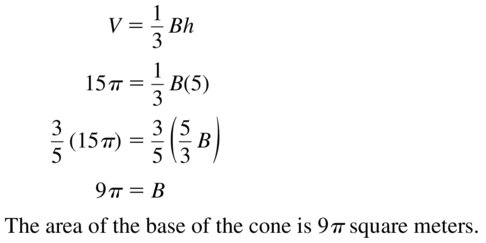
Question 56.
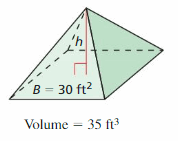
Answer:
The height of the prism is: \(\frac{5}{6}\) ft
Explanation:
The given figure is:

We know that,
The volume of the prism = Area × Height
From the above figure,
The volume of the prism = 35 ft³
The area of the prism = 30 ft²
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
35 = 30 × H
H = 35 ÷ 30
H = \(\frac{5}{6}\) ft
Hence, from the above,
We can conclude that the height of the prism is: \(\frac{5}{6}\) ft
Question 57.
MAKING AN ARGUMENT
In baseball, a player’s batting average is calculated by dividing the number of hits by the number of at-bats. The table shows Player A’s batting average and the number of at-bats for three regular seasons.
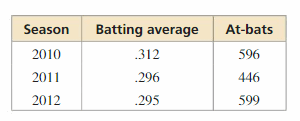
a. How many hits did Player A have in the 2011 regular season? Round your answer to the nearest whole number.
b. Player B had 33 fewer hits in the 2011 season than Player A but had a greater batting average. Your friend concludes that Player B had more at-bats in the 2011 season than Player A. Is your friend correct? Explain. Maintaining
Answer:

Maintaining Mathematical Proficiency
Use the Distributive Property to simplify the expression.
Question 58.
8(y + 3)
Answer:
8 ( y + 3 ) = 8y + 24
Explanation:
The given expression is: 8 ( y + 3 )
We know that,
By using the Distributive Property,
a ( b + c ) = ( a × b ) + ( a × c )
So,
By using the above Property,
8 ( y + 3 ) = ( 8 × y ) + ( 8 × 3 )
= 8y + 24
Hence, from the above,
We can conclude that
8 ( y + 3 ) = 8y + 24
Question 59.
![]()
Answer:
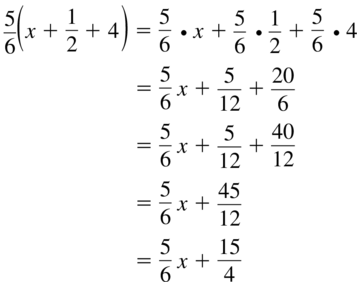
Question 60.
5(m + 3 + n)
Answer:
5 ( m + 3 + n ) = 5m + 5n + 15
Explanation:
The given expression is: 5 ( m + 3 + n )
By using the Distributive Property,
a ( b + c ) = ( a × b ) + ( a × c )
So,
By using the above Property,
5 ( m + 3 + n ) = ( 5 × m ) + ( 5 × 3 ) + ( 5 × n )
= 5m + 15 + 5n
Hence, from the above,
We can conclude that,
5 ( m + 3 + n ) = 5m + 15 + 5n
Question 61.
4(2p + 4q + 6)
Answer:
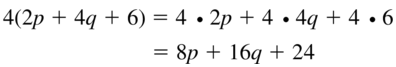
Copy and complete the statement. Round to the nearest hundredth, if necessary.
Question 62.
![]()
Answer:
The missing number is: \(\frac{1}{12}\)
Explanation:
Let the missing number be: x
So,
The given equation is:
\(\frac{5L}{min}\) = \(\frac{x L}{h}\)
We know that,
1 hour = 60 minutes
So,
1 min = \(\frac{1}{60}\) hour
So,
\(\frac{5 L}{min}\) = \(\frac{5 L × 1}{60h}\)
\(\frac{5 L}{min}\) = \(\frac{1 L }{12h}\)
So,
x = \(\frac{1}{12}\)
Hence, from the above,
We can conclude that,
The missing number is: \(\frac{1}{12}\)
Question 63.

Answer:
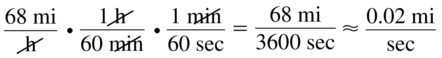
Question 64.
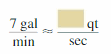
Answer:
The missing number is: \(\frac{1}{12}\)
Explanation:
Let the missing number be: x
So,
The given equation is:
\(\frac{7 gal}{min}\) = \(\frac{x qin}{sec}\)
We know that,
1 min = 60 seconds
1 quintal = 100 kg
1 gallon = 3.78 kg = 4 kg
So,
1 gallon = 0.04 quintal
1 sec = \(\frac{1}{60}\) min
So,
\(\frac{7 gal}{min}\) = \(\frac{x qin × 1}{60min}\)
\(\frac{7 gal}{min}\) = \(\frac{1 L }{12h}\)
So,
x = \(\frac{1}{12}\)
Hence, from the above,
We can conclude that,
The missing number is: \(\frac{1}{12}\)
Question 65.

Answer:
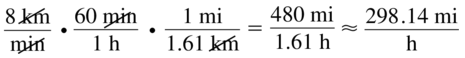
Lesson 1.2 Solving Multi-step Equations
Essential Question
How can you use multi-step equations to solve real-life problems?
EXPLORATION 1
Solving for the Angle Measures of a Polygon
Work with a partner. The sum S of the angle measures of a polygon with n sides can be found using the formula S = 180(n – 2). Write and solve an equation to find each value of x. Justify the steps in your solution. Then find the angle measures of each polygon. How can you check the reasonableness of your answers?
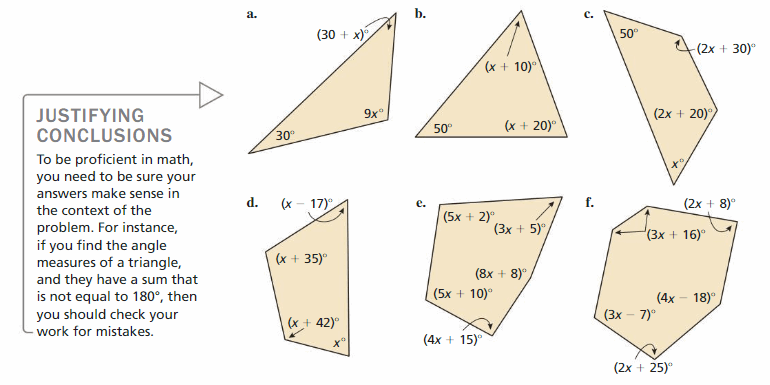
Answer:
The given polygons are:
It is given that,
The sum S of the angle measures of a polygon with n sides can be found using the formula S = 180(n – 2).
a)
The number of sides (n ) = 3
So,
The sum of angles ( S ) = 180 ( n – 2 )
= 180 ( 3 – 2 )
= 180 ( 1 )
= 180
Now,
The given sides of a polygon are: 30, 9x, (30 + x )
So,
30 + 9x + 30 + x = 180
60 + 10x = 180
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
10x = 180 – 60
10x = 120
x = 120 ÷ 10
x = 12
Hence, from the above,
The angle measures of the given polygon are:
30, 9 × 12, 30 + 12
= 30, 108, 45 degrees
b)
The number of sides (n ) = 3
So,
The sum of angles ( S ) = 180 ( n – 2 )
= 180 ( 3 – 2 )
= 180 ( 1 )
= 180
Now,
The given sides of a polygon are: 30, 9x, (30 + x )
So,
50 + x + 10 + 20 + x = 180
80 + 2x = 180
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2x = 180 – 80
2x = 100
x = 100 ÷ 2
x = 50
Hence, from the above,
The angle measures of the given polygon are:
50, 50 + 10, 50 + 20
= 50, 60, 70 degrees
c)
The number of sides (n ) = 4
So,
The sum of angles ( S ) = 180 ( n – 2 )
= 180 ( 4 – 2 )
= 180 ( 2 )
= 360
Now,
The given sides of a polygon are: 50, x, ( 2x + 20), ( 2x + 30 )
So,
50 + x + 2x + 20 + 2x + 30 = 360
100 + 5x = 360
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5x = 360 – 100
5x = 260
x = 260 ÷ 5
x = 52
Hence, from the above,
The angle measures of the given polygon are:
50,52, 2 (52) + 20, 2(52) + 30
= 50, 52, 124, 134 degrees
d)
The number of sides (n ) = 4
So,
The sum of angles ( S ) = 180 ( n – 2 )
= 180 ( 4 – 2 )
= 180 ( 2 )
= 360
Now,
The given sides of a polygon are: x, x + 42, x + 35, x – 17
So,
x + x + 42 + x + 35 + x – 17 = 360
60 + 4x = 360
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4x = 360 – 60
4x = 300
x = 300 ÷ 4
x = 75
Hence, from the above,
The angle measures of the given polygon are:
75, 75 + 42, 75 + 35 , 75 – 17
= 75, 117, 110, 58 degrees
e)
The number of sides (n ) = 5
So,
The sum of angles ( S ) = 180 ( n – 2 )
= 180 ( 5 – 2 )
= 180 ( 3 )
= 540
Now,
The given sides of a polygon are: (4x + 15), (5x + 10), (8x + 8), (3x + 5), (5x + 2)
So,
(4x + 15)+ (5x + 10)+ (8x + 8)+ (3x + 5)+ (5x + 2) = 540
40 + 25x = 540
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
25x = 540 – 40
25x = 500
x = 500 ÷ 25
x = 20
Hence, from the above,
The angle measures of the given polygon are:
(4. 20 + 15)+ (5. 20 + 10)+ (8.20 + 8)+ (3. 20 + 5)+ (5. 20 + 2)
= 95, 110, 168, 65, 102 degrees
f)
The number of sides (n ) = 5
So,
The sum of angles ( S ) = 180 ( n – 2 )
= 180 ( 5 – 2 )
= 180 ( 3 )
= 540
Now,
The given sides of a polygon are: (2x + 25), (3x + 16), (2x + 8), (4x – 18), (3x – 7)
So,
(2x + 25) + (3x + 16) + (2x + 8) + (4x – 18) + (3x – 7) = 540
24 + 14x = 540
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
14x = 540 – 24
14x = 516
x = 540 ÷ 14
x = 38.5
x = 39
Hence, from the above,
The angle measures of the given polygon are:
(2. 39 + 25), (3.39 + 16), (2.39 + 8), (4.39 – 18), (3.39 – 7)
= 103, 133, 86, 138, 110 degrees
EXPLORATION 2
Work with a partner.
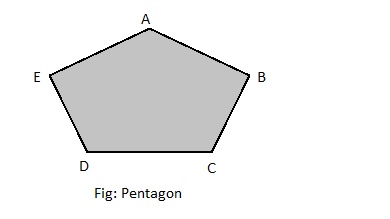
a. Draw an irregular polygon.
Answer:
b. Measure the angles of the polygon. Record the measurements on a separate sheet of paper.
Answer:
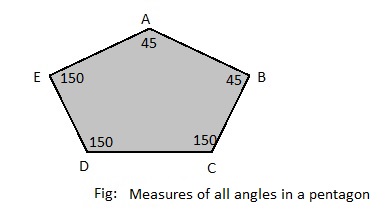
c. Choose a value for x. Then, using this value, work backward to assign a variable expression to each angle measure, as in Exploration 1.
d. Trade polygons with your partner.
e. Solve an equation to find the angle measures of the polygon your partner drew. Do your answers seem reasonable? Explain.
Communicate Your Answer
Question 3.
How can you use multi-step equations to solve real-life problems?
Answer: A multi-step equation is an equation that takes two or more steps to solve. These problems can have a mix of addition, subtraction, multiplication, or division. We also might have to combine like terms or use the distributive property to properly solve our equations
Question 4.
In Exploration 1, you were given the formula for the sum S of the angle measures of a polygon with n sides. Explain why this formula works.
Answer:
We know that,
The sum of the angles in a triangle is: 180 degrees
The triangle is also a quadrilateral
So,
A quadrilateral can be formed by the minimum of the three lines
So,
The minimum sum of all the angles in a quadrilateral is: 180 degrees
Now,
Let suppose we form a quadrilateral with 4 sides.
So,
The sum of all the angles in a quadrilateral = 360 degrees = 180 degrees × 2
= 180 degrees ( 4 sides -2 )
Let suppose we form a quadrilateral with 5 sides
So,
The sum of all the angles in a quadrilateral = 540 degrees = 180 degrees × 3
= 180 degrees ( 5 -2 )
Hence, in general,
We can conclude that the sum of all the angles with n sides in a quadrilateral = 180 degrees ( n-2 )
Question 5.
The sum of the angle measures of a polygon is 1080º. How many sides does the polygon have? Explain how you found your answer.
Answer:
The number of sides the polygon with 1080° have: 6
Explanation:
It is given that the sum of all angle measures of a polygon is: 1080°
We know that,
The sum of angle measures with n sides in a polygon = 180° ( n – 2 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
1080° =180° ( n – 2 )
n – 2 = 1080 ÷ 180
n – 2 = 6
n = 6 + 2
n = 8
Hence, from the above,
We can conclude that the number of sides of the polygon with sum of the angles 1080° is: 6
1.2 Lesson
Monitoring Progress
Solve the equation. Check your solution.
Question 1.
-2n + 3 = 9
Answer:
The value of n is: -3
Explanation:
The given equation is:
-2n + 3 = 9
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-2n + 3 = 9
-2n = 9 – (+3 )
n = 6 ÷ ( -2 )
= -3
Hence from the above,
We can conclude that the value of n is: -3
Question 2.
-21 = \(\frac{1}{2}\) – 11
Question 3.
-2x – 10x + 12 = 18
Answer:
The value of x is: –\(\frac{1}{2}\)
Explanation:
The given equation is:
-2x – 10x + 12 = 18
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-( 2x + 10x ) = 18 – 12
-12x = 6
x = 6 ÷ ( -12 )
x = –\(\frac{1}{2}\)
Hence, from the above,
We can conclude that the value of x is: –\(\frac{1}{2}\)
Monitoring Progress
Solve the equation. Check your solution.
Question 4.
3(x + 1) + 6 = -9
Answer:
The value of x is: -6
Explanation:
The given equation is:
3 ( x + 1 ) + 6 = -9
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
3 ( x + 1 ) = -9 – (+6 )
By using the Distributive property,
3 ( x + 1 ) = 3x + 3
So,
3x + 3 = -15
3x = -15 – ( +3 )
3x = -18
x = -18 ÷ 3
x = -6
Hence, from the above,
We can conclude that the value of x is: -6
Question 5.
15 = 5 + 4(2d – 3)
Answer:
The value of d is:\(\frac{11}{4}\)
Explanation:
The given equation is:
15 = 5 + 4 ( 2d – 3 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
4 ( 2d – 3 ) = 15 -5
4 ( 2d – 3 ) = 10
By using the Distributive property,
4 ( 2d – 3 ) = 4 (2d ) -4 (3 )
= 8d – 12
So,
8d – 12 = 10
8d = 10 + 12
8d = 22
d = 22 ÷ 8
d = \(\frac{11}{4}\)
Hence, from the above,
We can conclude that the value of d is: \(\frac{11}{4}\)
Question 6.
13 = -2(y – 4) + 3y
Answer:
The value of y is: 5
Explanation:
The given equation is:
13 = -2 ( y – 4 ) + 3y
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
By using the Distributive Property,
-2 ( y – 4 ) = -2y + 8
So,
13 = -2y + 8 + 3y
13 = y + 8
y = 13 – 8
y = 5
Hence, from the above,
We can conclude that the value of y is: 5
Question 7.
2x(5 – 3) – 3x = 5
Answer:
The value of x is: 5
Explanation:
The given equation is:
2x ( 5 – 3 ) – 3x = 5
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2x ( 2 ) – 3x = 5
4x – 3x = 5
x = 5
Hence, from the above,
We can conclude that the value of y is: 5
Question 8.
-4(2m + 5) – 3m = 35
Answer:
The value of m is: -5
Explanation:
The given equation is:
-4 ( 2m + 5 ) – 3m = 35
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
Now,
By using the Distributive Property,
-4 ( 2m + 5 ) = -4 (2m ) + 5 ( -4 )
= -8m -20
So,
-8m -20 -3m = 35
-11m – 20 = 35
-11m = 35 + 20
-11m = 55
m = 55 ÷ ( -11 )
m = -5
Hence, from the above,
We can conclude that the value of m is: -5
Question 9.
5(3 – x) + 2(3 – x) = 14
Answer:
The value of x is: 1
Explanation:
The given equation is:
5 ( 3 – x ) + 2 ( 3 – x ) = 14
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
Now,
By using the Distributive property,
5 ( 3 – x ) = 5 (3 ) -5 (x)
= 15 – 5x
2 ( 3 – x ) = 2 (3) – 2 ( x)
= 6 – 2x
So,
15 – 5x + 6 – 2x = 14
21 – 7x = 14
7x = 21 – 14
7x = 7
x = 7 ÷ 7
x = 1
Hence, from the above,
We can conclude that the value of x is: 1
Monitoring Progress
Question 10.
The formula d = \(\frac{1}{2}\)n + 26 relates the nozzle pressure n (in pounds per square inch) of a fire hose and the maximum horizontal distance the water reaches d (in feet). How much pressure is needed to reach a fire 50 feet away?
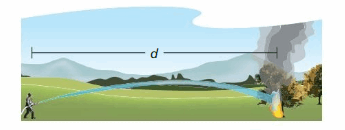
Answer:
The pressure needed to reach a fire 50 feet away (n ) is: 48 pounds per square inch
Explanation:
It is given that the formula
d = \(\frac{1}{2}\)n + 26
relates the nozzle pressure n (in pounds per square inch) of a fire hose and the maximum horizontal distance the water reaches d (in feet).
So,
The given equation is:
d = \(\frac{1}{2}\)n + 26
Where,
d is the maximum horizontal distance
n is the pressure
It is also given that the maximum horizontal distance is: 50 feet
So,
50 = \(\frac{1}{2}\)n + 26
\(\frac{1}{2}\)n = 50 – 26
\(\frac{1}{2}\)n = 24
\(\frac{1}{2}\) × n = 24
n = 24 × 2
n = 48 pounds per square inch
Hence, from the above
We can conclude that the pressure needed to reach 50 feet away is: 48 pounds per square inch
Question 11.
Monitoring Progress
You have 96 feet of fencing to enclose a rectangular pen for your dog. To provide sufficient running space for your dog to exercise, the pen should be three times as long as it is wide. Find the dimensions of the pen.

Answer:
The dimensions of the pen are:
length of the pen: 12 feet
Width of the pen: 36 feet
Explanation;
It is given that you have 96 feet of fencing to enclose a rectangular pen for your dog. To provide sufficient running space for your dog to exercise, the pen should be three times as long as it is wide.
So,
The perimeter of the rectangular pen is: 96 feet
We know that,
The perimeter of the rectangle = 2 (Length + Width )
It is also given that the pen is three times as long as it is wide
So,
Width = 3 × Length
So,
The perimeter of the rectangular pen =2 ( Length + ( 3 × Length ) )
96 = 2 ( 4 × Length )
4 × Length = 96 ÷ 2
4 × Length = 48
Length = 48 ÷ 4
Length = 12 feet
So,
Width = 3 × Length
= 3 × 12 = 36 feet
hence, from the above,
We can conclude that
The dimensions of the rectangular pen are:
Length of the pen is: 12 feet
Width of the pen is: 36 feet
Solving Multi-step Equations 1.2 Exercises
Monitoring Progress and Modeling with Mathematics
In Exercises 3−14, solve the equation. Check your solution.
Vocabulary and Core ConceptCheck
Question 1.
COMPLETE THE SENTENCE To solve the equation 2x + 3x = 20, first combine 2x and 3x because they are _________.
Answer:
The given equation is:
2x + 3x = 20
As 2x and 3x are combined by the symbol “+”, add 2x and 3x
So,
2x + 3x = 5x
So,
5x = 20
x = 20 ÷ 4
x = 5
Question 2.
WRITING Describe two ways to solve the equation 2(4x – 11) = 10.
Answer:
The given equation is:
2 (4x – 11) = 10
Way-1:
2 × (4x – 11) = 10
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4x – 11 = 10 ÷ 2
4x – 11 = 5
4x = 5 + 11
4x = 16
x = 16 ÷ 4
x = 4
Hence,
The value of x is: 4
Way-2:
By using the Distributive Property,
2 (4x – 11) = 2 (4x) – 2 (11)
= 8x – 22
So,
8x – 22 = 10
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
8x = 10 + 22
8x = 32
x = 32 ÷ 8
x = 4
Hence,
The value of x is: 4
Question 3.
3w + 7 = 19
Answer:
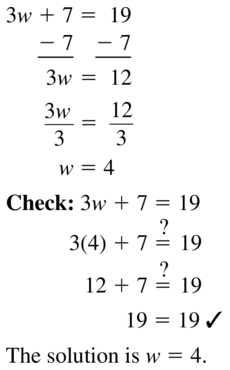
Question 4.
2g – 13 = 3
Answer:
The value of g is: 8
Explanation:
The given equation is:
2g – 13 = 3
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2g = 3 + 13
2g = 16
2 × g = 16
g = 16 ÷ 2
g = 8
Hence, from the above,
We can conclude that the value of g is: 8
Question 5.
11 = 12 – q
Answer:

Question 6.
10 = 7 – m
Answer:
The value of m is: -3
Explanation:
The given equation is:
10 = 7 – m
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-m = 10 – 7
-m = 3
Multiply with “-” on both sides
– (-m ) = -3
m = -3
Hence, from the above,
We can conclude that the value of m is: -3
Question 7.
5 = \(\frac{z}{-4}\) – 3
Answer:
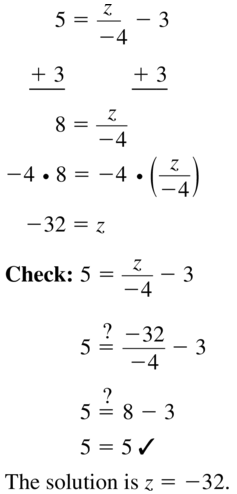
Question 8.
\(\frac{a}{3}\) + 4 = 6
Answer:
The value of a is: 6
Explanation:
The given equation is:
\(\frac{a}{3}\) + 4 = 6
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
\(\frac{a}{3}\) = 6 – 4
\(\frac{a}{3}\) = 2
a = 2 × 3
a = 6
Hence, from the above,
We can conclude that the value of a is: 6
Question 9.
\(\frac{h + 6}{5}\) = 2
Answer:
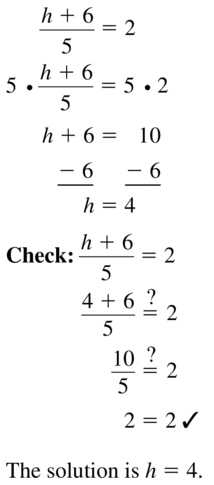
Question 10.
\(\frac{d – 8}{-2}\) = 12
Answer:
The value of d is: -16
Explanation:
The given equation is:
\(\frac{d – 8}{-2}\) = 12
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
d – 8 = 12 × (-2)
d – 8 = -24
d = -24 + 8
d = -16
Hence, from the above,
We can conclude that the value of d is: -16
Question 11.
8y + 3y = 44
Answer:

Question 12.
36 = 13n – 4n
Answer:
The value of n is: 4
Explanation:
The given equation is:
36 = 13n – 4n
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
36 = 9n
9n = 36
n = 36 ÷ 9
n = 4
Hence, from the above,
We can conclude that the value of n is: 4
Question 13.
12v + 10v + 14 = 80
Answer:

Question 14.
6c – 8 – 2c = -16
Answer:
The value of c is: -2
Explanation:
The given equation is:
6c – 8 – 2c = -16
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4c – 8 = -16
4c = -16 + 8
4 × c = -8
c = -8 ÷ 4
c = -2
Hence, from the above,
We can conclude that the value of c is: -2
Question 15.
MODELING WITH MATHEMATICS
The altitude a (in feet) of a plane in minutes after liftoff is given by a = 3400t + 600. How many minutes after liftoff is the plane at an altitude of 21,000 feet?

Answer:

Question 16.
MODELING WITH MATHEMATICS
A repair bill for your car is $553. The parts cost $265. The labor cost is $48 per hour. Write and solve an equation to find the number of hours of labor spent repairing the car.
Answer:
The number of hours of labor spent repairing the car is: 6 hours
Explanation:
It is given that a repair bill for your car is $553. The parts cost $265. The labor cost is $48 per hour.
Let the number of hours of labor spent repairing the car be: x
So,
The total bill to repair your car = ( The labor cost per hour ) × ( The number of hours of labor spent repairing the car ) + (The cost of the parts )
553 = 48x + 265
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
48x = 553 – 265
48x = 288
48 × x = 288
x = 288 ÷ 48
x = 6
Hence, from the above,
We can conclude that the number of hours of labor spent repairing the car is: 6 hours
In Exercises 17−24, solve the equation. Check your solution.
Question 17.
4(z + 5) = 32
Answer:
Question 18.
-2(4g – 3) = 3018.
Answer:
The value of g is: 378
Explanation:
The given equation is:
-2 (4g – 3) = 3018
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-2 × ( 4g – 3 ) = 3018
4g – 3 = 3018 ÷ 2
4g – 3 = 1,509
4g = 1,509 +3
4 × g = 1,512
g = 1,512 ÷ 4
g = 378
Hence, from the above,
We can conclude that the value of g is: 378
Question 19.
6 + 5(m + 1) = 26
Answer:
Question 20.
5h+ 2(11 – h) = -5
Answer:
The value of h is: -9
Explanation:
The given equation is:
5h + 2 ( 11-h ) = -5
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
By using the Distributive Property of Multiplication,
2 ( 11 – h ) = 2 (11 ) – 2 ( h )
= 22 – 2h
So,
5h + 22 – 2h = -5
3h + 22 = -5
3h = -5 – (+22)
3h = -5 -22
3h = -27
h = -27 ÷ 3
h = -9
Hence, from the above,
We can conclude that the value of h is: -9
Question 21.
27 = 3c – 3(6 – 2c)
Answer:

Question 22.
-3 = 12y – 5(2y – 7)
Answer:
The value of y is: -19
Explanation:
The given equation is:
-3 = 12y – 5 (2y – 7)
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
12y – 5 (2y – 7) = -3
By using the Distributive Property of Multiplication,
5 ( 2y – 7 ) = 5 (2y ) – 5 (7 )
= 10y – 35
So,
12y – ( 10y – 35 ) = -3
12y – 10y + 35 = -3
2y + 35 = -3
2y = -3 – (+35 )
2y = -3 – 35
2y = -38
y = -38 ÷ 2
y = -19
Hence, from the above,
We can conclude that the value of y is: -19
Question 23.
-3(3 + x) + 4(x – 6) = -4
Answer:
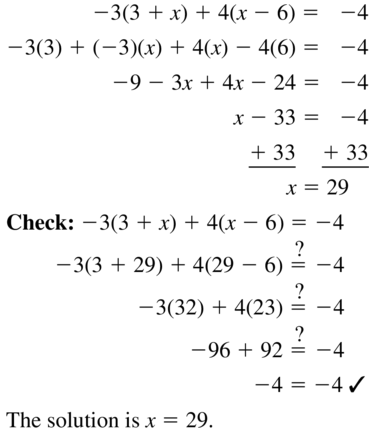
Question 24.
5(r + 9) – 2(1 – r) = 1
Answer:
The value of r is: -6
Explanation:
The given equation is:
5 ( r + 9 ) – 2 ( 1 – r ) = 1
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
Now,
By using the Distributive Property of Multiplication,
5 ( r + 9 ) = 5 ( r ) + 5 ( 9 )
= 5r + 45
2 ( 1 – r ) = 2 ( 1 ) – 2 ( r )
= 2 – 2r
So,
5r + 45 – ( 2 – 2r ) = 1
5r + 45 – 2 + 2r = 1
7r + 43 = 1
7r = 1 – 43
7r = -42
r = -42 ÷ 7
r = -6
Hence, from the above,
We can conclude that the value of r is: -6
USING TOOLS
In Exercises 25−28, find the value of the variable. Then find the angle measures of the polygon. Use a protractor to check the reasonableness of your answer.
Question 25.
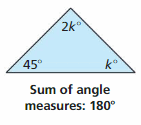
Answer:
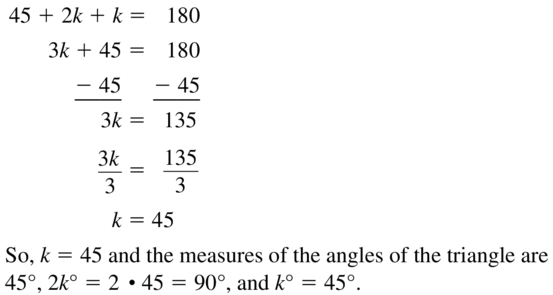
Question 26.
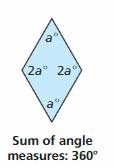
Answer:
The angle measures of the rhombus are:
60°, 60°, 120°, 120°
Explanation:
The given figure is:

From the above figure,
The angle measures of the rhombus are: a°, 2a°, a°, 2a°
It is also given that the sum of all the angle measures is: 360°
So,
a° + 2a° + a° + 2a° = 360°
6a° = 360°
a = 360° ÷ 6
a = 60°
Hence, from the above,
We can conclude that the angle measures of the rhombus are:
a°, 2a°, a°, 2a° = 60°, 2 ( 60° ), 60°, 2 ( 60° )
= 60°, 60°, 120°, 120°
Question 27.
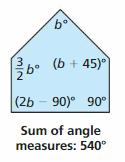
Answer:

Question 28.
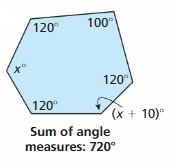
Answer:
The angle measures of the hexagon are:
120°, 120°, 100°, 120°, 250°, 260°
Explanation:
The given figure is:

From the given figure,
The angle measures of the hexagon are:
120°, 120°, 100°, 120°, x°, (x + 10)°
It is also given that the sum of the angle measures of the hexagon is: 720°
So,
120° + 120° + 100° + 120° + x° + (x + 10)° = 720°
470° + x = 720°
x = 720° – 470°
x = 250°
Hence, from the above,
We can conclude that the angle measures of the hexagon are:
120°, 120°, 100°, 120°, x°, (x + 10)° = 120°, 120°, 100°, 120°, 250°, (250 + 10)°
= 120°, 120°, 100°, 120°, 250°, 260°
In Exercises 29−34, write and solve an equation to find the number.
Question 29.
The sum of twice a number and 13 is 75.
Answer:
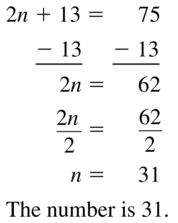
Question 30.
The difference of three times a number and 4 is -19.
Answer:
The number is: -5
Explanation:
It is given that the difference of three times of a number and 4 is -19
Now,
Let the number be x
So,
The three times of a number = 3 (x) = 3x
So,
3x – 4 = -19
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
3x = -19 + 4
3x = -15
x = -15 ÷ 3
x = -5
Hence, from the above,
We can conclude that the number is: -5
Question 31.
Eight plus the quotient of a number and 3 is -2.
Answer:
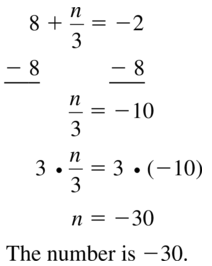
Question 32.
The sum of twice a number and half the number is 10.
Answer:
The number is: 4
Explanation:
It is given that the sum of twice of a number and half the number is 10.
Let the number be x.
So,
The twice of a number = 2 (x ) = 2x
Half of the number = x ÷ 2 = \(\frac{x}{2}\)
So,
2x + \(\frac{x}{2}\) = 10
2x can be rewritten as: \(\frac{4x}{2}\)
So,
\(\frac{4x}{2}\) + \(\frac{x}{2}\) = 10
\(\frac{4x + x}{2}\) = 10
\(\frac{5x}{2}\) = 10
5x = 10 × 2
5x = 20
x = 20 ÷ 5
x = 4
Hence, from the above,
We can conclude that the numebr is: 4
Question 33.
Six times the sum of a number and 15 is -42.
Answer:
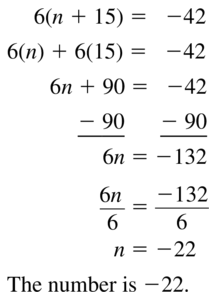
Question 34.
Four times the difference of a number and 7 is 12.
Answer:
The number is: 4
Explanation:
It is given that the four times the difference of a number and 7 is 12
Let the number be x
So,
Four times of the number = 4 ( x ) = 4x
So,
4x – x = 12
3x = 12
x = 12 ÷ 3
x = 4
Hence, from the above,
We can conclude that the number is: 4
USING EQUATIONS
In Exercises 35−37, write and solve an equation to answer the question. Check that the units on each side of the equation balance.
Question 35.
During the summer, you work 30 hours per week at a gas station and earn $8.75 per hour. You also work as a landscaper for $11 per hour and can work as many hours as you want. You want to earn a total of $400 per week. How many hours must you work as a landscaper?
Answer:

Question 36.
The area of the surface of the swimming pool is 210 square feet. What is the length d of the deep end (in feet)?
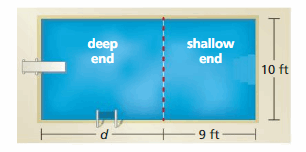
Answer:
The length d of the deep end is: 12 feet
Explanation:
The given figure is:

It is given that the area of the surface of the swimming pool is 210 square feet
From the above figure,
We can observe that the shape of the swimming pool is a rectangle.
So,
Length of the swimming pool = 10 ft
Width of the swimming pool = d + 9 ft
So,
The area of the swimming pool = Length × Width
= 10 × ( d + 9 )
Now,
210 = 10 × ( d + 9 )
d + 9 = 210 ÷ 10
d + 9 = 21
d = 21 – 9
d = 12 feet
Hence, from the above,
We can conclude that the length d of the deep end is: 12 feet
Question 37.
You order two tacos and a salad. The salad costs $2.50. You pay 8% sales tax and leave a $3 tip. You pay a total of $13.80. How much does one taco cost?
Answer:

JUSTIFYING STEPS
In Exercises 38 and 39, justify each step of the solution.
Question 38.
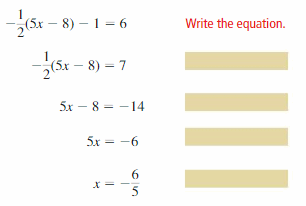
Answer:
–\(\frac{1}{2}\) ( 5x – 8 ) – 1 = 6 Write the equation
–\(\frac{1}{2}\) ( 5x – 8 ) = 6 + 1 Arrange the similar terms
–\(\frac{1}{2}\) ( 5x – 8 ) = 7 Simplify
– ( 5x – 8 ) = 7 × 2 Divide by 2 on both sides
– ( 5x – 8 ) = 14 Simplify
5x – 8 = -14 Multiply with “-” on both sides
5x = -14 + 8 Arrange the similar terms
5x = -6 Divide by 6 on both sides
x = –\(\frac{6}{5}\) The result
Hence,
The solution is: x = –\(\frac{6}{5}\)
Question 39.
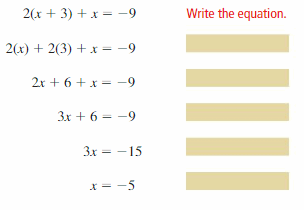
Answer:

ERROR ANALYSIS
In Exercises 40 and 41, describe and correct the error in solving the equation.
Question 40.
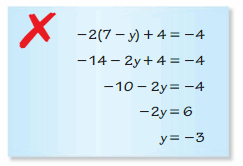
Answer:
The given equation is:
-2 ( 7 – y ) + 4 = -4
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-2 ( 7 – y ) = -4 – (+4 )
-2 ( 7 – y ) = -4 – 4
-2 ( 7 – y ) = -8
Now,
By using the Distributive Property of Multiplication,
2 ( 7 – y ) = 2 ( 7 ) – 2 ( y )
= 14 – 2y
So,
– ( 14 – 2y ) = -8
2y – 14 = -8
2y = -8 + 14
2y = 6
y = 6 ÷ 2
y = 3
Hence,
The value of y is: 3
Question 41.
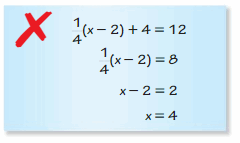
Answer:

MATHEMATICAL CONNECTIONS
In Exercises 42−44, write and solve an equation to answer the question.
Question 42.
The perimeter of the tennis court is 228 feet. What are the dimensions of the court?
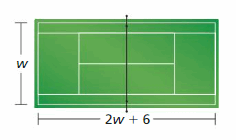
Answer:
The dimensions of the court are:
The Length of the court is: 36 feet
The width of the court is: 78 feet
Explanation:
The given figure is:

It is given that the perimeter of the tennis court is: 228 feet
From the above figure,
We can observe that the shape of the tennis court is the rectangle
So,
The length of the tennis court = w feet
The width of the tennis court = (2w + 6 ) feet
We know that,
The perimeter of the rectangle = 2 ( Length + Width )
So,
The perimeter of the tennis court = 2 ( Length + Width )
228 = 2 ( w + 2w + 6 )
By using the Distributive Property of Multiplication,
2 ( w + 2w + 6 ) = 2 ( 3w + 6 )
= 2 ( 3w ) + 2 ( 6 )
= 6w + 12
So,
228 = 6w + 12
6w = 228 – 12
6w = 216
w = 216 ÷ 6
w = 36
Hence, from the above,
We can conclude that
The length of the tennis court is: 36 feet
The width of the tennis court is: 2w + 6 = 2 ( 36 ) + 6 = 78 feet
Question 43.
The perimeter of the Norwegian flag is 190 inches. What are the dimensions of the flag?
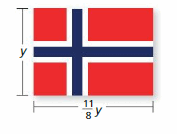
Answer:
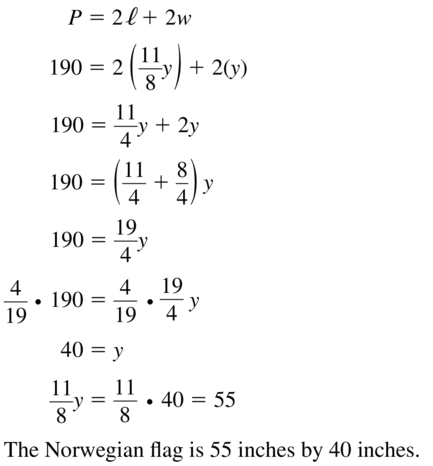
Question 44.
The perimeter of the school crossing sign is 102 inches. What is the length of each side?
Answer:
The length of each side is: 15 inches
Explanation:
The given figure is:

It is given that the perimeter of the crossing sign is 102 inches
We know that,
The perimeter of any polygon is the sum of all the sides of that polygon
So,
The perimeter of the crossing sign = s + ( s + 6 ) + ( s + 6 ) + s + 2s
102 = 6s + 12
102 – 12 = 6s
6s = 90
s = 90 ÷ 6
s = 15 inches
Hence, from the above,
We can conclude that the length of each side is: 15 inches
Question 45.
COMPARING METHODS
Solve the equation 2(4 – 8x) + 6 = -1 using (a) Method 1 from Example 3 and (b) Method 2 from Example 3. Which method do you prefer? Explain.
Answer:
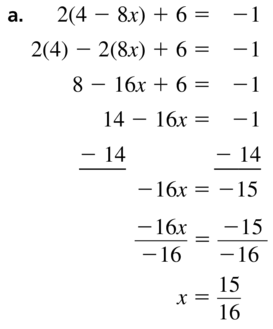

Question 46.
PROBLEM – SOLVING
An online ticket agency charges the amounts shown for basketball tickets. The total cost for an order is $220.70. How many tickets are purchased?
Answer:
Given that,
The total cost for a football ticket order is $220.70
The cost of 1 ticket is $32.50.
The convenience charge is $3.30 per ticket.
The processing charge is 5.90 per ticket.
The total price per 1 ticket = $32.50 + $3.30 + $5.90 = $41.7.
For $220.70 number of tickets is $220.70/$41.7 = $5.2925.
Therefore the number of tickets purchased is 5.
Question 47.
MAKING AN ARGUMENT
You have quarters and dimes that total $2.80. Your friend says it is possible that the number of quarters is 8 more than the number of dimes. Is your friend correct? Explain.
Answer:
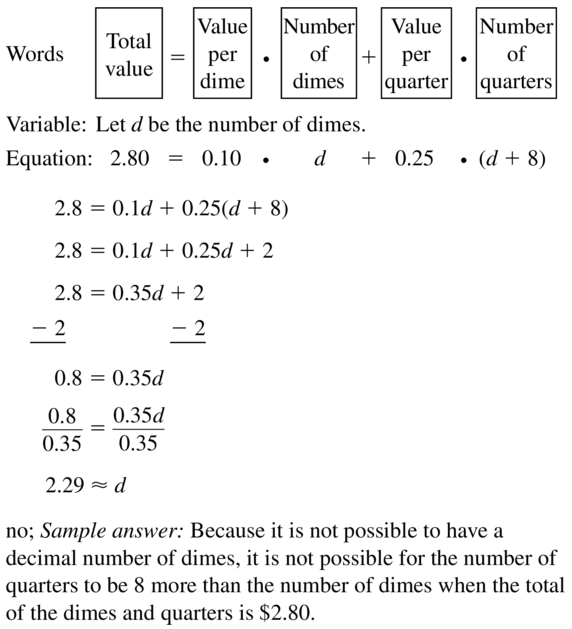
Question 48.
THOUGHT-PROVOKING
You teach a math class and assign a weight to each component of the class. You determine final grades by totaling the products of the weights and the component scores. Choose values for the remaining weights and find the necessary score on the final exam for a student to earn an A (90%) in the class, if possible. Explain your reasoning.
Answer:
The completed table is:
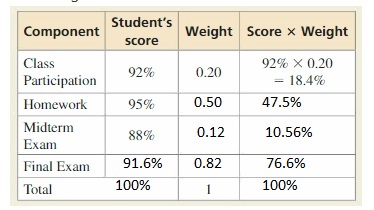
From the above table,
The weights can be calculated by the difference between the total participation and the class participation and divide the total value by 100.
So,
The weight of homework = [ ( 100 – 95 ) ÷ 100]
= 5 ÷ 100
= 0.50
The weight of midterm exam = ( 100 – 88 ) ÷ 100
= 12 ÷ 100
= 0.12
So,
The necessary score of the final exam = ( 92 + 95 + 88 ) % ÷ 3
= 275 % ÷ 3
= 91.6 %
Question 49.
REASONING
An even integer can be represented by the expression 2n, where n is an integer. Find three consecutive even integers that have a sum of 54. Explain your reasoning.
Answer:
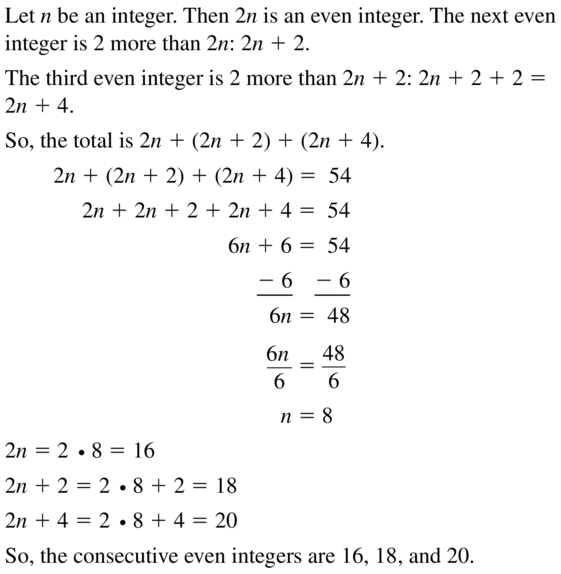
Question 50.
HOW DO YOU SEE IT?
The scatter plot shows the attendance for each meeting of a gaming club.
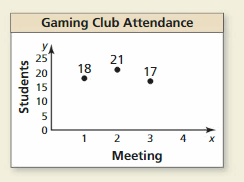
a. The mean attendance for the first four meetings is 20. Is the number of students who attended the fourth meeting greater than or less than 20? Explain.
Answer:
The number of students who attended the fourth meeting is greater than 20
Explanation:
The given graph is:

We know that
The mean = ( Sum of the given numbers ) ÷ (The total number of the numbers)
From the above graph,
The attendance of the 1st meeting = 18
The attendance of the 2nd meeting = 21
The attendance of the 3rd meeting = 17
Let the attendance of the 4th meeting be: x
So,
The mean attendance of the first four meetings = ( The attendance of the 4 meetings ) ÷ ( The total number of meetings )
= ( 18 + 21 + 17 + x ) ÷ 4
It is given that the mean attendance of the first four meetings is: 20
So,
20 = ( 18 + 21 + 17 + x ) ÷ 4
( 56 + x ) ÷ 4 = 20
56 + x = 20 × 4
56 + x = 80
x = 80 – 56
x = 24
Hence, from the above,
We can conclude that the attendance of the 4th meeting is greater than 20
b. Estimate the number of students who attended the fourth meeting.
Answer:
The number of students who attended the fourth meeting is: 24
Explanation:
The mean attendance of the first four meetings = ( The attendance of the 4 meetings ) ÷ ( The total number of meetings )
= ( 18 + 21 + 17 + x ) ÷ 4
It is given that the mean attendance of the first four meetings is: 20
So,
20 = ( 18 + 21 + 17 + x ) ÷ 4
( 56 + x ) ÷ 4 = 20
56 + x = 20 × 4
56 + x = 80
x = 80 – 56
x = 24
Hence, from the above,
We can conclude that the number of students who attended the 4th meeting is: 24
c. Describe a way you can check your estimate in part (b).
Answer:
The estimate in part (b) can be checked by using the property of the mean
So,
The mean attendance of the four meetings = ( The attendance of the four meetings ) ÷ ( The total number of meetings )
= ( 18 + 21 + 17 + 24 ) ÷ 4
= 80 ÷ 4
= 20
Hence, from the above,
We can conclude that the mean attendance of the four meetings is the same as given above.
REASONING
In Exercises 51−56, the letters a, b, and c represent nonzero constants. Solve the equation for x.
Question 51.
bx = -7
Answer:
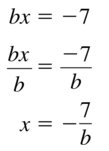
Question 52.
x + a = \(\frac{3}{4}\)
Answer:
The value of x is: \(\frac{3}{4}\) – a
Explanation:
The given equation is:
x + a = \(\frac{3}{4}\)
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x = \(\frac{3}{4}\) – a
Hence, from the above,
We can conclude that the value of a is: \(\frac{3}{4}\) – a
Question 53.
ax – b = 12.5
Answer:
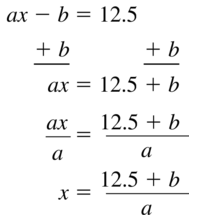
Question 54.
ax + b = c
Answer:
The value of x is: \(\frac{c – b}{a}\)
Explanation:
The given equation is:
ax + b = c
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
ax = c – b
x = \(\frac{c – b}{a}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{c – b}{a}\)
Question 55.
2bx – bx = -8
Answer:
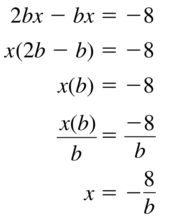
Question 56.
cx – 4b = 5b
Answer
The value of x is: \(\frac{9b}{c}\)
Explanation:
The given equation is:
cx – 4b = 5b
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
cx = 5b + 4b
cx = 9b
x = \(\frac{9b}{c}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{9b}{c}\)
Maintaining Mathematical Proficiency
Simplify the expression.
Question 57.
4m + 5 – 3m
Answer:
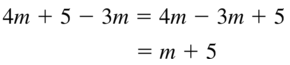
Question 58.
9 – 8b + 6b
Answer:
9 – 8b + 6b
= 9 – (8b – 6b )
= 9 – 2b
Question 59.
6t + 3(1 – 2t) – 5
Answer:
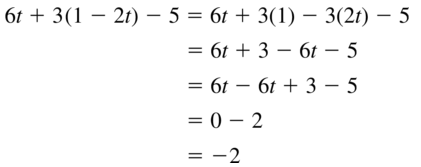
Determine whether (a) x = −1 or (b) x = 2 is a solution of the equation.
Question 60.
x – 8 = -9
Answer:
x = -1 is a solution to the given equation
Explanation:
The given equation is:
x – 8 = -9
a) Let x = -1
So,
-1 – 8 = -9
-9 = -9
As LHS is equal to RHS
x = -1 is a solution of the given equation
b) Let x = 2
So,
2 – 8 = -9
-6 = -9
As LHS is not equal to RHS,
x = 2 is not a solution of the given equation
Question 61.
x + 1.5 = 3.5
Answer:

Question 62.
2x – 1 = 3
Answer:
x = 2 is a solution to the given equation
Explanation:
The given equation is:
2x – 1 = 3
a) Let x = -1
So,
2 ( -1 ) – 1 = 3
-2 – 1 = 3
-3 = 3
As LHS is not equal to RHS
x = -1 is not a solution to the given equation
b) Let x = 2
So,
2 ( 2 ) -1 = 3
4 – 1 = 3
3 = 3
As LHS is equal to RHS,
x = 2 is a solution to the given equation
Question 63.
3x + 4 = 1
Answer:

Question 64.
x + 4 = 3x
Answer:
x = 2 is a solution to the given equation
Explanation:
The given equation is:
x + 4 = 3x
a) Let x = -1
So,
-1 + 4 = 3 ( -1 )
= 3 = -3
As LHS is not equal to RHS,
x = -1 is not a solution to the given equation
b) Let x = 2
So,
2 + 4 = 3 ( 2 )
6 = 6
As LHS is equal to RHS,
x = 2 is a solution to the given equation.
Question 65.
-2(x – 1) = 1 – 3x
Answer:
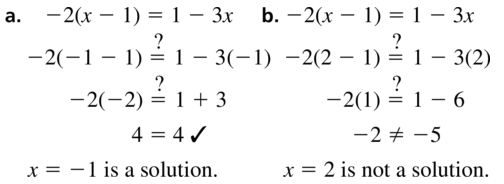
Lesson 1.3 Solving Equations with Variables on Both Sides
EXPLORATION 1
Perimeter
Work with a partner. The two polygons have the same perimeter. Use this information to write and solve an equation involving x. Explain the process you used to find the solution. Then find the perimeter of each polygon.
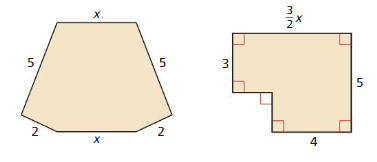
Answer:
The perimeter of the hexagon is: 6
The perimeter of the square is: 6
Explanation:
The given figures are:

Based on the number of sides (n) in the polygon,
We can say the name of that polygon
So,
In the first figure,
The number of sides is: 6
So,
It is Hexagon
In the second figure,
The number of sides is: 4
So,
It is square ( As all the angles are 90° )
It is given that the two polygons have the same perimeter
We know that,
“Perimeter” of a polygon is defined as the sum of all the sides in the polygon
So,
The sum of all sides in the hexagon = 5 + 2 + 5 + 2 + x + x
= 14 + 2x
The sum of all sides in the square = \(\frac{3x}{2}\) + 3 + 4 + 5
= \(\frac{3x}{2}\) + 12
It is given that the perimeter of both the polygons are equal
So,
14 + 2x = \(\frac{3x}{2}\) + 12
14 – 12 = \(\frac{3x}{2}\) – 2x
\(\frac{3x}{2}\) – 2x = 2
We can write 2x as \(\frac{4x}{2}\)
So,
\(\frac{3x}{2}\) – \(\frac{4x}{2}\) = 2
\(\frac{3x – 4x}{2}\) = 2
\(\frac{-x}{2}\) = 2
– \(\frac{x}{2}\) = 2
-x = 2 × 2
-x = 4
x = -4
Hence,
The perimeter of the Hexagon = 14 + 2x = 14 + 2 ( -4 )
= 14 – 8 = 6
The perimeter of the square = \(\frac{3x}{2}\) + 12
\(\frac{3 × -4}{2}\) + 12
= \(\frac{-12}{2}\) + 12
= \(\frac{-12}{2}\) + \(\frac{24}{2}\)
= \(\frac{24 – 12}{2}\)
= \(\frac{12}{2}\)
= 6
Hence, from the above,
We can conclude that
The perimeter of the Hexagon is: 6
The perimeter of the square is: 6
EXPLORATION 2
Perimeter and Area
Work with a partner.
- Each figure has the unusual property that the value of its perimeter (in feet) is equal to the value of its area (in square feet). Use this information to write an equation for each figure.
- Solve each equation for x. Explain the process you used to find the solution.
- Find the perimeter and area of each figure.
Question 3.
How can you solve an equation that has variables on both sides?
Answer:
If the variable is the same on both sides in an equation, then rearrange the like terms
So,
Separate the variables and the numbers and simplify the variables and the numbers
In this way,
We can solve an equation with a single variable
Question 4.
Write three equations that have the variable x on both sides. The equations should be different from those you wrote in Explorations 1 and 2. Have your partner solve the equations.
Answer:
Let the three equations that have variable x on both sides and different from Explorations 1 and 2 are:
a) 6x + 2 = 5x-6
b) 16x = 18x – 2
c) 12x = 15x + 63
Now,
a)
The given equation is:
6x + 2 = 5x – 6
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
6x – 5x = -6 – 2
x = -8
Hence,
The value of x is: -8
b) The given equation is:
9x = 18x – 2
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
18x – 16x = 2
2x = 2
x = 2 ÷ 2
x = 1
Hence,
The value of x is: 1
c) The given equation is:
12x = 15x + 63
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
12x -15x = 63
-3x = 63
x = 63 ÷ ( -3 )
x = -63 ÷ 3
x = -21
Hence,
The value of x is: -21
1.3 Lesson
Monitoring Progress
Solve the equation. Check your solution.
Question 1.
-2x = 3x + 10
Answer:
The value of x is: -2
Explanation:
The given equation is:
-2x = 3x + 10
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-2x – 3x = 10
-5x = 10
x = 10 ÷ (-5)
x = -10 ÷ 5
x = -2
Hence, from the above,
We can conclude that the value of x is: -2
Question 2.
\(\frac{1}{2}\)(6h – 4) = -5h + 1
Answer:
The value of h is: \(\frac{3}{8}\)
Explanation:
The given equation is:
\(\frac{1}{2}\) ( 6h – 4 ) = -5h + 1
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
6h – 4 = 2 ( -5h + 1 )
6h – 4 = 2 ( -5h ) + 2 ( 1 ) [ By using the Distributive Property of Multiplication )
6h – 4 = -10h + 2
6h + 10h = 2 + 4
16h = 6
h = \(\frac{6}{16}\)
h= \(\frac{3}{8}\)
Hence, from the above,
We can conclude that the value of h is: \(\frac{3}{8}\)
Question 3.
–\(\frac{3}{4}\)(8n + 12) = 3(n – 3)
Answer:
The value of n is: 0
Explanation:
The given equation is:
–\(\frac{3}{4}\) ( 8n + 12 ) = 3 ( n – 3 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
8n + 12 = –\(\frac{4}{3}\) × 3 ( n – 3 )
8n + 12 = –\(\frac{4}{3}\) \(\frac{3}{1}\) ( n – 3 )
8n + 12 = –\(\frac{3 × 4}{3 × 1}\) ( n – 3 )
8n + 12 = -4 ( n – 3 )
8n + 12 = -4n – 4 ( -3 )
8n + 12 = -4n + 12
8n + 4n =12 – 12
12n = 0
n = 0
Hence, from the above,
We can conclude that the value of n is: 0
Monitoring Progress
Solve the equation.
Question 4.
4(1 – p) = 4p – 4
Answer:
The value of p is: 1
Explanation:
The given equation is:
4 ( 1 -p ) = 4p – 4
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4 ( 1 ) – 4 ( p ) = 4p – 4
4 – 4p = 4p – 4
4p + 4p = 4 + 4
8p = 8
p = 8 ÷ 8
p = 1
Hence, from the above,
We can conclude that the value of p is: 1
Question 5.
6m – m = –\(\frac{5}{6}\)(6m – 10)
Answer:
The value of m is: \(\frac{5}{6}\)
Explanation:
The given equation is:
6m – m = –\(\frac{5}{6}\) ( 6m – 10 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5m = –\(\frac{5}{6}\) ( 6m – 10 )
5m = –\(\frac{5}{6}\) ( 6m ) – ( –\(\frac{5}{6}\) ( 10 ) )
5m = –\(\frac{5}{6}\) × \(\frac{6m}{1}\) + \(\frac{5}{6}\) \(\frac{10}{1}\)
5m = –\(\frac{5 × 6m}{6 × 1}\) + \(\frac{5 × 10}{6 × 1}\)
5m = -5m + \(\frac{25}{3}\)
5m + 5m = \(\frac{25}{3}\)
10m = \(\frac{25}{3}\)
m = \(\frac{25}{3}\) ÷ \(\frac{10}{1}\)
m = \(\frac{25}{3}\) × \(\frac{1}{10}\)
m = \(\frac{25}{30}\)
m = \(\frac{5}{6}\)
Hence, from the above,
We can conclude that the value of m is: \(\frac{5}{6}\)
Question 6.
10k + 7 = -3 – 10k
Answer:
The value of k is: –\(\frac{1}{2}\)
Explanation:
The given equation is:
10k + 7 = -3 – 10k
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
10k + 10k = -3 – ( +7 )
20k = -3 –
20k = -10
k = -10 ÷ 20
k = –\(\frac{1}{2}\)
Hence, from the above,
We can conclude that the value of k is: –\(\frac{1}{2}\)
Question 7.
3(2a – 2) = -2(3a – 3)
Answer:
The value of a is: 1
Explanation:
The given equation is:
3 ( 2a – 2 ) = -2 ( 3a – 3 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
By using the Distributive Property of Multiplication,
3 ( 2a ) – 3 ( 2 ) = -2 ( 3a ) + 2 ( 3 )
6a – 6 = -6a + 6
6a + 6a = 6 + 6
12a = 12
a = 12 ÷ 12
a = 1
Hence, from the above,
We can conclude that the value of a is: 1
Concept Summary
Steps for Solving Linear Equations
Here are several steps you can use to solve a linear equation. Depending on the equation, you may not need to use some steps.

Step 1
Use the Distributive Property to remove any grouping symbols.
Step 2
Simplify the expression on each side of the equation.
Step 3
Collect the variable terms on one side of the equation and the constant terms on the other side.
Step 4
Isolate the variable.
Step 5
Check your solution.
Monitoring Progress
Question 8.
A boat travels upstream on the Mississippi River for 3.5 hours. The return trip only takes 2.5 hours because the boat travels 2 miles per hour faster downstream due to the current. How far does the boat travel upstream? Answer:
The distance the boat travel upstream is: 17.5 miles
Explanation:
It is given that a boat travels upstream on the Mississippi River for 3.5 hours. The return trip only takes 2.5 hours because the boat travels 2 miles per hour faster downstream due to the current.
Now,
Let x be the speed of the boat traveled upstream
We know that,
Speed = Distance ÷ Time
Distance = Speed × Time
It is given that the time taken by the boat traveled upstream is: 3.5 hours
So,
Distance traveled upstream = 3.5 × x = 3.5x
Now,
It is also given that the speed of the boat is 2 miles per hour faster downstream
So,
Distance traveled downstream by boat = 2.5 ( x + 2 )
SO,
As both the distances are the same,
3.5x = 2.5 ( x + 2 )
By using the Distributive Property of Multiplication,
3.5x = 2.5 ( x) + 2.5 ( 2 )
3.5x = 2.5x + 5
3.5x – 2.5x = 5
x = 5
So,
The distance traveled upstream by boat = 3.5x = 3.5 ( 5 )
= 17.5 miles per hour
Hence, from the above,
We can conclude that the distance traveled upstream by boat is: 17.5 miles per hour
Solving Equations with Variables on Both Sides 1.3 Exercises
Monitoring Progress and Modeling with Mathematics
In Exercises 3–16, solve the equation. Check your solution.
Question 1.
VOCABULARY Is the equation -2(4 – x) = 2x + 8 an identity? Explain your reasoning.
Answer:
-2 ( 4 – x ) = 2x + 8 is not an identity
Explanation:
The given equation is:
-2 ( 4 – x ) = 2x + 8
By using the Distributive Property of Multiplication,
-2 ( 4 ) + 2 ( x ) = 2x + 8
-8 + 2x = 2x + 8
2x – 8 = 2x + 8
As
LHS ≠ RHS
-2 ( 4 – x ) = 2x + 8 is not an identity
Question 2.
WRITING Describe the steps in solving the linear equation 3(3x – 8) = 4x + 6
Answer:
The value of x is: 6
Explanation:
The given equation is:
3 ( 3x – 8 ) = 4x + 6
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
Now,
By using the Distributive Property of Multiplication,
3 ( 3x ) – 3 ( 8 ) = 4x + 6
9x – 24 = 4x + 6
9x – 4x = 6 + 24
5x = 30
x = 30 ÷ 5
x = 6
Hence, from the above,
We can conclude that the value of x is: 6
Question 3.
15 – 2x = 3x
Answer:

Question 4.
26 – 4s = 9s
Answer:
The value of s is: 2
Explanation:
The given equation is:
26 – 4s = 9s
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
26 = 9s + 4s
13s = 26
s = 26 ÷ 13
s = 2
Hence, from the above,
We can conclude that the value of s is: 2
Question 5.
5p – 9 = 2p + 12
Answer:
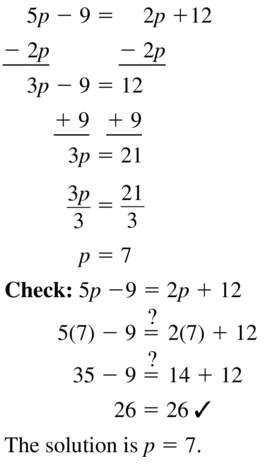
Question 6.
8g + 10 = 35 + 3g
Answer:
The value of g is: 5
Explanation:
The given equation is:
8g + 10 = 35 + 3g
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
8g – 3g = 35 – 10
5g = 25
g = 25 ÷ 5
g = 5
Hence, from the above,
We can conclude that the value of g is: 5
Question 7.
5t + 16 = 6 – 5t
Answer:
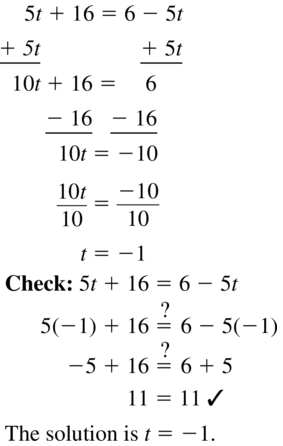
Question 8.
-3r + 10 = 15r – 8
Answer:
The value of r is: 1
Explanation:
The given equation is:
-3r + 10 = 15r – 8
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-3r – 15r = -10 – 8
-18r = -18
r = -18 ÷ ( -18 )
r = 1 [ since – ÷ – = + ]
Hence, from the above,
We can conclude that the value of r is: 1
Question 9.
7 + 3x – 12x = 3x + 1
Answer:

Question 10.
w – 2 + 2w = 6 + 5w
Answer:
The value of w is: -4
Explanation:
The given equation is:
w – 2 + 2w = 6 + 5w
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
w + 2w -5w =6 + 2
-2w = 8
w = -8 ÷ 2
w = -4
Hence, from the above,
We can conclude that the value of w is: -4
Question 11.
10(g + 5) = 2(g + 9)
Answer:

Question 12.
-9(t – 2) = 4(t – 15)
Answer:
The value of t is: 6
Explanation:
The given equation is:
-9 ( t – 2 ) = 4 ( t – 15 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
Now,
By using the Distributive Property of Multiplication,
-9 ( t ) + 9 ( 2 ) = 4 ( t ) – 4 ( 15 )
-9t + 18 = 4t – 60
-9t – 4t = -60 – 18
-13t = -78
t = -78 ÷ ( -13 )
t = 6 [ Since -÷ – = + ]
Hence, from the above,
We can conclude that the value of t is: 6
Question 13.
\(\frac{2}{3}\)(3x + 9) = -2(2x + 6)
Answer:
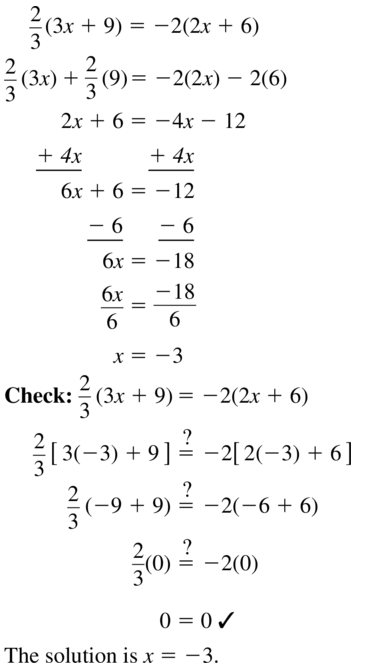
Question 14.
2(2t + 4) = \(\frac{3}{4}\)(24 – 8t)
Answer:
The value of t is: 1
Explanation:
The given equation is:
2 ( 2t + 4 ) = \(\frac{3}{4}\) ( 24 – 8t )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
By using the Distributive Property of Multiplication,
2 ( 2t ) + 2 ( 4 ) = \(\frac{3}{4}\) ( 24 ) – 8t (\(\frac{3}{4}\) )
4t + 8 = \(\frac{3}{4}\) × \(\frac{24}{1}\) – \(\frac{8t}{1}\) × \(\frac{3}{4}\)
4t + 8 = \(\frac{3 × 24}{4 × 1}\) – \(\frac{3 × 8t}{4 × 1}\)
4t + 8 = \(\frac{18}{1}\) – \(\frac{6t}{1}\)
4t + 8 = 18 – 6t
4t + 6t = 18 – 8
10t = 10
t = 10 ÷ 10
t = 1
Hence, from the above,
We can conclude that the value of t is: 1
Question 15.
10(2y + 2) – y = 2(8y – 8)
Answer:

Question 16.
2(4x + 2) = 4x – 12(x – 1)
Answer:
The value of x is: \(\frac{1}{2}\)
Explanation:
The given equation is:
2 ( 4x + 2 ) = 4x – 12 ( x – 1 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
Now,
By using the Distributive Property of Multiplication,
2 ( 4x ) + 2 ( 2 ) = 4x – 12 ( x ) + 12 ( 1 ) [ Since – × – = + ]
8x + 4 = 4x – 12x + 12
8x + 4 =12 – 8x
8x + 8x = 12 – 4
16x = 8
x = 8 ÷ 16
x = \(\frac{1}{2}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{1}{2}\)
Question 17.
MODELING WITH MATHEMATICS
You and your friend drive toward each other. The equation 50h = 190 – 45h represents the number h of hours until you and your friend meet. When will you meet?
Answer:

Question 18.
MODELING WITH MATHEMATICS
The equation 1.5r + 15 = 2.25r represents the number r of movies you must rent to spend the same amount at each movie store. How many movies must you rent to spend the same amount at each movie store?

Answer:
The number of movies you rent to spend the same amount at each movie store is: 20
Explanation:
It is given that
The equation 1.5r + 15 = 2.25r represents the number r of movies you must rent to spend the same amount at each movie store.
Now,
We have to find the value of r to find the number f movies you must rent to spend the same amount at each movie store
So,
The given equation is:
1.5r + 15 = 2.25r
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2.25r – 1.5r = 15
0.75r = 15
\(\frac{75}{100}\)r = 15
r = 15 × \(\frac{100}{75}\)
r = \(\frac{15}{1}\) × \(\frac{100}{75}\)
r = \(\frac{15 × 100}{1 × 75}\)
r = 20
Hence, from the above,
We can conclude that the number of movies you rent to spend the same amount at each movie store is: 20
In Exercises 19–24, solve the equation. Determine whether the equation has one solution, no solution, or infinitely many solutions.
Question 19.
3t + 4 = 12 + 3t
Answer:

Question 20.
6d + 8 = 14 + 3d
Answer:
The value of d is: 2
Explanation:
The given equation is:
6d + 8 = 14 + 3d
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
6d – 3d = 14 – 8
3d = 6
d = 6 ÷ 3
d = 2
Hence, from the above,
We can conclude that the value of d is: 2
Question 21.
2(h + 1) = 5h – 7
Answer:
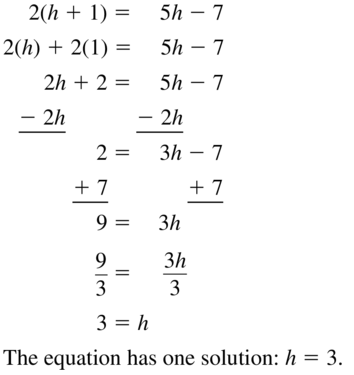
Question 22.
12y + 6 = -6(2y + 1)
Answer:
The value of y is: –\(\frac{1}{2}\)
Explanation:
The given equation is:
12y + 6 = -6 ( 2y + 1 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
By using the Distributive Property of Multiplication,
12y + 6 = -6 ( 2y ) – 6 ( 1 )
12y + 6 = -12y – 6
12y + 12y = -6 – ( +6 )
24y = -6 – 6
24y = -12
y = -12 ÷ 24
y = –\(\frac{1}{2}\)
Hence, from the above,
We can conclude that the value of y is: –\(\frac{1}{2}\)
Question 23.
3(4g + 6) = 2(6g + 9)
Answer:
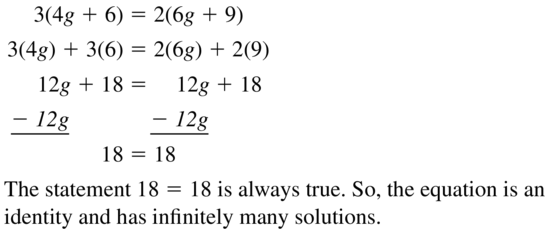
Question 24.
5(1 + 2m) = \(\frac{1}{2}\)(8 + 20m)
Answer:
m has indefinite solutions
Explanation:
The given equation is:
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
By using the Distributive Property of Multiplication,
5 ( 1 ) + 5 ( 2m ) = \(\frac{1}{2}\) ( 8 ) + \(\frac{1}{2}\) ( 20m )
2 ( 5 + 10m ) = 8 + 20m
2 ( 5 ) + 2 ( 10m ) = 8 + 20m
10 + 20m = 8 + 20m
20m – 20m = 8 – 10
20m – 20m = -2
As m has the same coefficients and have the opposite signs, m has indefinite solutions
Hence, from the above,
We can conclude that the equation has the indefinite solutions
ERROR ANALYSIS
In Exercises 25 and 26, describe and correct the error in solving the equation.
Question 25.
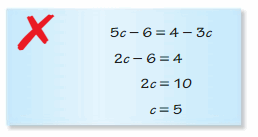
Answer:

Question 26.
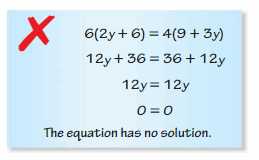
Answer:
The given equation is:
6 ( 2y + 6 ) = 4 ( 9 + 3y )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
Now,
By using the Distributive Property of Multiplication,
6 ( 2y ) + 6 ( 6 ) = 4 ( 9 ) + 4 ( 3y )
12y + 36 = 36 + 12y
12y – 12y = 36 – 36
0 = 0
As the coefficients of y are zero, the equation has no solution
Hence, from the above,
We can conclude that there is no error in the analysis of the equation.
Question 27.
MODELING WITH MATHEMATICS
Write and solve an equation to find the month when you would pay the same total amount for each Internet service.

Answer:

Question 28.
PROBLEM-SOLVING
One serving of granola provides 4% of the protein you need daily. You must get the remaining 48 grams of protein from other sources. How many grams of protein do you need daily?
Answer:
The number of grams of protein you need daily is: 50 grams
Explanation:
It is given that one serving of granola provides 4% of the protein you need daily. You must get the remaining 48 grams of protein from other sources.
So,
Let the number of grams of protein you need daily be: x
So,
The number of grams of protein you need daily = 4 % of x + 48
We know that,
100% = 1
So,
4 % = 0.04
So,
The number of grams of protein you need daily = 0.04x + 48
x = 0.04x + 48
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x – 0.04x = 48
0.96x = 48
\(\frac{96}{100}\)x = 48
x = 48 × \(\frac{100}{96}\)
x = \(\frac{48}{1}\) × \(\frac{100}{96}\)
x = \(\frac{48 × 100}{1 × 96}\)
x = \(\frac{50}{1}\)
x = 50 grams
Hence, from the above,
We can conclude that the number of proteins you need daily is: 50 grams
USING STRUCTURE
In Exercises 29 and 30, find the value of r.
Question 29.
8(x + 6) – 10 + r = 3(x + 12) + 5x
Answer:
Question 30.
4(x – 3) – r + 2x = 5(3x – 7) – 9x
Answer:
The value of r is: 23
Explanation:
The given equation is:
4 ( x – 3 ) – r + 2x = 5 ( 3x – 7 ) – 9x
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
By using the Distributive Property of Multiplication,
4x – 4 ( 3 ) – r + 2x = 5 ( 3x ) – 5 ( 7 ) – 9x
4x – 12 – r + 2x = 15x – 35 – 9x
6x – 12 – r = 6x – 35
r = 6x – 6x – 12 + 35
r = 23
Hence, from the above,
We can conclude that the value of r is: 23
MATHEMATICAL CONNECTIONS
In Exercises 31 and 32, the value of the surface area of the cylinder is equal to the value of the volume of the cylinder. Find the value of x. Then find the surface area and volume of the cylinder.
Question 31.
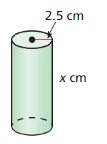
Answer:

Question 32.
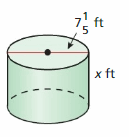
Answer:
The Surface Area of the cylinder is: 461.49 cm²
The volume of the cylinder is: 488.58 cm³
Explanation:
The given figure is:

From the above figure,
The radius of the cylinder is: 7\(\frac{1}{5}\) feet
The height of the cylinder is: x feet
It is given that the Total Surface Area of the cylinder and the volume of the cylinder are equal.
We know that,
The Surface Area of the cylinder = 2πr² + 2πrh
The volume of the cylinder = πr²h
The value of π is: 3.1416
Now,
The representation of 7\(\frac{1}{5}\) in the improper fraction form is: \(\frac{36}{5}\)
So,
2πr² + 2πrh = πr²h
[ 2 × 3.1416 × \(\frac{36}{5}\) × \(\frac{36}{5}\) ] + [ 2 × 3.1416 × \(\frac{36}{5}\) × x ] = [3.1416 × latex]\frac{36}{5}[/latex] × \(\frac{36}{5}\) × x ]
325.72 + 45.23x = 162.86x
162.86x – 45.23x = 325.72
117.63x = 325.72
x = 2.76
x = 3
So,
The Surface Area of the cylinder = 2πr² + 2πrh
= [ 2 × 3.1416 × \(\frac{36}{5}\) × \(\frac{36}{5}\) ] + [ 2 × 3.1416 × \(\frac{36}{5}\) × x ]
= 325.72 + 45.23x
= 325.72 + 45.23 ( 3 )
= 461.49 cm²
The volume of the cylinder = πr²h
= [3.1416 × latex]\frac{36}{5}[/latex] × \(\frac{36}{5}\) × x ]
= 162.86x
= 162.86 ( 3 )
= 488.58 cm³
Hence, from the above,
We can conclude that
The Surface Area of the cylinder is: 461.49 cm²
The volume of the cylinder is: 488.58 cm³
Question 33.
MODELING WITH MATHEMATICS
A cheetah that is running 90 feet per second is 120 feet behind an antelope that is running 60 feet per second. How long will it take the cheetah to catch up to the antelope?
Answer:

Question 34.
MAKING AN ARGUMENT
A cheetah can run at top speed for only about 20 seconds. If an antelope is too far away for a cheetah to catch it in 20 seconds, the antelope is probably safe. Your friend claims the antelope in Exercise 33 will not be safe if the cheetah starts running 650 feet behind it. Is your friend correct? Explain.
Answer:
Your friend is not correct
Explanation:
It is given that a cheetah can run at top speed for only about 20 seconds. If an antelope is too far away for a cheetah to catch it in 20 seconds, the antelope is probably safe. Your friend claims the antelope in Exercise 33 will not be safe if the cheetah starts running 650 feet behind it.
Let the distance of running antelope be x.
Let ‘t’ be the time taken
So,
The distance of running Antelope is:
x = 650 + 60t
The cheetah must arrive at the same position to catch the antelope
So,
x = 90t
Now,
90t = 650 + 60t
90t – 60t = 650
30t = 650
t = 650 ÷ 30
t = 21.7 seconds
But it is given that the cheetah has to reach the same position as the antelope in 20 seconds
But according to the calculation, it takes 21.7 seconds
So,
According to your friend, the antelope is not safe if the cheetah is running 650 meters behind it.
Hence, from the above,
We can conclude that your friend is not correct.
REASONING
In Exercises 35 and 36, for what value of a is the equation an identity? Explain your reasoning.
Question 35.
a(2x + 3) = 9x + 15 + x
Answer:

Question 36.
8x – 8 + 3ax = 5ax – 2a
Answer:
The given equation becomes an identity at a = 4
Explanation:
The given equation is:
8x – 8 + 3ax = 5ax – 2a
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5ax – 3ax = 8x – 8 – 2a
2ax = 8 ( x – 1 ) – 2a
2ax + 2a = 8x – 8
Equate the like coefficients of x and the like constants in both LHS and RHS
So,
2ax = 8x 2a = -8
a = 8x ÷ 2x a = -8 ÷ 2
a = 4 a = -4
Now,
At a = 4,
The equation becomes
8x – 8 + 3ax = 5ax – 2a
8x – 8 + 3x ( 4 ) = 5x ( 4 ) -2 ( 4 )
8x – 8 + 12x = 20x – 8
20x – 8 = 20x – 8
Hence,
At a =4,
The given equation is an Identity
At a = -4,
The equation becomes
8x – 8 + 3ax = 5ax – 2a
8x – 8 + 3x ( -4 ) = 5x ( -4 ) -2 ( -4 )
8x – 8 – 12x = -20x + 8
-4x – 8 = -20x + 8
Hence,
At a = -4, the given equation is not an Identity
Hence, from the above,
We can conclude that the given equation is an Identity at a = 4
Question 37.
REASONING
Two times the greater of two consecutive integers is 9 less than three times the lesser integer. What are the integers?
Answer:

Question 38.
HOW DO YOU SEE IT?
The table and the graph show information about students enrolled in Spanish and French classes at a high school.

a. Use the graph to determine after how many years there will be equal enrollment in Spanish and French classes.
Answer:
The year where there will be equal enrollment in Spanish and French classes is: 6
Explanation:
The given table and the graph of the students for the Spanish and French classes are:

So,
From the above table,
To find the year where there is equal enrollment in both Spanish and French, we have to find the point in the graph that the two points of Spanish and French intersect
So,
From the above graph,
The point that is intersecting is at 6th year
Hence, from the above,
We can conclude that there is an equal enrollment of students in the 6th year in both Spanish and French classes
b. How does the equation 355 – 9x = 229 + 12x relate to the table and the graph? How can you use this equation to determine whether your answer in part (a) is reasonable?
Answer:
The given equation
355 – 9x = 229 + 12x
represents the total number of students enrolled in the different years in both Spanish and French classes
Now,
In part (a),
We observed that there is an equal enrollment of the students at 6th year in both Spanish and French classes
So,
Here,
x is: The number of years
So,
In part (a),
x = 6
Now,
Substitute x = 6 in the given equation.
Now,
355 – 9x = 229 + 12x
355 – 9 ( 6 ) = 229 + 12 ( 6 )
355 – 54 = 229 + 72
301 = 301
As
LHS = RHS
We can say that the answer is reasonable in part (a)
Question 39.
WRITING EQUATIONS
Give an example of a linear equation that has (a) no solution and (b) infinitely many solutions. Justify your answers.
Answer:

Question 40.
THOUGHT-PROVOKING
Draw a different figure that has the same perimeter as the triangle shown. Explain why your figure has the same perimeter.
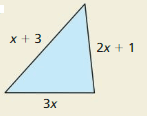
Answer:
x + 3 + 2x + 1 + 3x
6x + 3 = 3(2x + 1)
So, the perimeter is 3(2x + 1)
Maintaining Mathematical Proficiency
Order the values from least to greatest.
Question 41.
9, | -4|, -4, 5, | 2 |
Answer:
![]()
Question 42.
| -32 |, 22, -16, -| 21 |, | -10 |
Answer:
We know that,
| -x | = x
| x | = x
So,
| -32 | = 32
| 21 | = 21
| -10 | = 10
Hence,
The order of the values from the least to the greatest is:
-21, -16, 10, 22, 32
Question 43.
-18, | -24 |, -19, | -18 |, | 22 |
Answer:
![]()
Question 44.
-| – 3 |, | 0 |, -1, | 2 |, -2
Answer:
We know that,
| -x | = x
| x | = x
So,
| -3 | = 3
| 0 | = 0
| 2 | = 2
Hence,
The order of the numbers from the least to the greatest is:
-3, -2, -1, 0, 2
Solving Linear Equations Study Skills: Completing
1.1-1.3 What Did You Learn
Core Vocabulary

Core Concepts
Section 1.1

Section 1.2
![]()
Section 1.3
![]()
Mathematical Practices
Question 1.
How did you make sense of the relationships between the quantities in Exercise 46 on page 9?
Answer:
In Exercise 46 on page 9,
There is a layout of the tatami mat which comprises the four identical rectangular mats and the one square mat.
it is also given that the area of the square mat is half of one of the rectangular mats
Now,
We know that,
The area of the square mat = Area² [ Since all the sides of the square are equal ]
The area of the rectangular mat = Length × Width
So,
According to the given condition,
The relation between the area of the square mat and one of the rectangular mat is:
Area of the square mat = \(\frac{1}{2}\) Area of one of the rectangular mat
Side² = \(\frac{1}{2}\) ( Length × Width )
Question 2.
What is the limitation of the tool you used in Exercises 25–28 on page 16?
Answer:
The limitations of the tool you used in Exercises 25 – 28 on page 16 are:
A) The calculated values and the values measured using the tool will be different
B) We won’t get the exact values of the angle measures using the tool
Question 3.
What definition did you use in your reasoning in Exercises 35 and 36 on page 24?
Answer:
The definition you used in your reasoning in Exercises 35 and 36 on page 24 is:
Make the like coefficients of the same variable in both LHS and RHS equal so that we get the value of the variable.
Study Skills
Completing Homework Efficiently
Before doing homework, review the Core Concepts and examples. Use the tutorials at BigIdeasMath.com for additional help.
Complete homework as though you are also preparing for a quiz. Memorize different types of problems, vocabulary, rules, and so on.

Solving Linear Equations 1.1-1.3 Quiz
Solve the equation. Justify each step. Check your solution. (Section 1.1)
Question 1.
x + 9 = 7
Answer:
The value of x is -2
Explanation:
The given equation is:
x + 9 = 7
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x = 7 – ( +9 )
x = 7 – 9
x = -2
Hence, from the above,
We can conclude that the value of x is: -2
Question 2.
8.6 = z – 3.8
Answer:
The value of z is: 12.4
Explanation:
The given equation is:
8.6 = z – 3.8
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
z = 8.6 + 3.8
z = 12.4
Hence, from the above,
We can conclude that the value of z is: 12.4
Question 3.
60 = -12r
Answer:
The value of r is: -5
Explanation:
The given equation is:
60 = -12r
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
r = 60 ÷ ( -12 )
r = -60 ÷ 12
r = -5
Hence, from the above,
We can conclude that the value of r is: -5
Question 4.
\(\frac{3}{4}\)p = 18
Answer:
The value of p is: 24
Explanation:
The given equation is:
\(\frac{3}{4}\)p = 18
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
p = 18 × \(\frac{4}{3}\)
p = \(\frac{18}{1}\) × \(\frac{4}{3}\)
p = \(\frac{18 × 4}{1 × 3}\)
p = \(\frac{24}{1}\)
p = 24
Hence, from the above,
We can conclude that the value of p is: 24
Solve the equation. Check your solution. (Section 1.2)
Question 5.
2m – 3 = 13
Answer:
The value of m is: 8
Explanation:
The given equation is:
2m – 3 = 13
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2m = 13 + 3
2m = 16
m = 16 ÷ 2
m = 8
Hence, from the above,
We can conclude that the value of m is: 8
Question 6.
5 = 10 – v
Answer:
The value of v is: 5
Explanation:
The given equation is:
5 = 10 – v
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
v= 10 – 5
v = 5
Hence, from the above,
We can conclude that the value of v is: 5
Question 7.
5 = 7w + 8w + 2
Answer:
The value of w is: \(\frac{1}{5}\)
Explanation:
The given equation is:
5 = 7w + 8w + 2
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5 – 2 = 7w + 8w
15w = 3
w = 3 ÷ 15
w = \(\frac{1}{5}\)
Hence, from the above,
We can conclude that the value of w is: \(\frac{1}{5}\)
Question 8.
-21a + 28a – 6 = -10.2
Answer:
The value of a is: –\(\frac{3}{5}\)
Explanation:
The given equation is:
-21a + 28a – 6 = -10.2
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-21a + 28a = -10.2 + 6
7a = -4.2
a = -4.2 ÷ 7
a= –\(\frac{42}{10}\) ÷ 7
a = –\(\frac{42}{10}\) × \(\frac{1}{7}\)
a = –\(\frac{42 × 1}{10 × 7}\)
a = – \(\frac{6}{10}\)
a = –\(\frac{3}{5}\)
Hence, from the above,
We can conclude that the value of a is: –\(\frac{3}{5}\)
Question 9.
2k – 3(2k – 3) = 45
Answer:
The value of k is: -9
Explanation:
The given equation is:
2k – 3 ( 2k – 3 ) = 45
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
SO,
2k – 3 ( 2k ) + 3 ( 3 ) = 45
2k – 6k + 9 = 45
2k – 6k = 45 – 9
-4k = 36
k = 36 ÷ -4
k = -9
Hence, from the above,
We can conclude that the value of k is: -9
Question 10.
68 = \(\frac{1}{5}\)(20x + 50) + 2
Answer:
The value of x is: 14
Explanation:
The given equation is:
68 = \(\frac{1}{5}\) [ 20x + 50 ] + 2
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
68 – 2 = \(\frac{1}{5}\) [ 20x + 50 ]
66 = \(\frac{1}{5}\) [ 20x + 50 ]
66 × 5 = 20x + 50
330 = 20x + 50
20x = 330 – 50
20x = 280
x = 280 ÷ 20
x = 14
Hence, from the above,
We can conclude that the value of x is: 14
Solve the equation. (Section 1.3)
Question 11.
3c + 1 = c + 1
Answer:
The value of c is: 0
Explanation:
The given equation is:
3c + 1 = c + 1
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
3c – c = 1 – 1
2c = 0
c = 0
Hence, from the above,
We can conclude that the value of c is: 0
Question 12.
-8 – 5n = 64 + 3n
Answer:
The value of n is: -9
Explanation:
The given equation is:
-8 – 5n = 64 + 3n
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-8 – 64 = 3n + 5n
-72 = 8n
n = -72 ÷ 8
n = -9
Hence, from the above,
We can conclude that the value of n is: -9
Question 13.
2(8q – 5) = 4q
Answer:
The value of q is: \(\frac{5}{6}\)
Explanation:
Te given equation is:
2 ( 8q – 5 ) = 4q
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2 ( 8q ) – 2 ( 5 ) = 4q
16q – 10 = 4q
16q – 4q = 10
12q = 10
q = 10 ÷ 12
q = \(\frac{5}{6}\)
Hence, from the above,
We can conclude that the value of q is: \(\frac{5}{6}\)
Question 14.
9(y – 4) – 7y = 5(3y – 2)
Answer:
The value of y is: -2
Explanation:
The given equation is:
9 ( y – 4 ) – 7y = 5 ( 3y – 2 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
9 ( y ) – 9 ( 4 ) – 7y = 5 ( 3y ) – 5 ( 2 )
9y – 36 – 7y = 15y – 10
2y – 36 = 15y – 10
15y – 2y = 10 – 36
13y = -26
y = -26 ÷ 13
y = -2
Hence, from the above,
We can conclude that the value of y is: -2
Question 15.
4(g + 8) = 7 + 4g
Answer:
The given equation has no solution
Explanation:
The given equation is:
4 ( g + 8 ) = 7 + 4g
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,the given equation has no solution
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4 ( g ) + 4 ( 8 ) = 7 + 4g
4g + 32 = 7 + 4g
4g – 4g + 7 = 32
7 = 32
Hence, from the above,
We can conclude that the given equation has no solution.
Question 16.
-4(-5h – 4) = 2(10h + 8)
Answer:
The value of h is: 0
Explanation:
The given equation is:
-4 ( 5h – 4 ) = 2 ( 10h + 8 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-4 ( 5h ) + 4 ( 4 ) = 2 ( 10h ) + 2 ( 8 )
-20h + 16 = 20h + 16
-20h – 20h = 1 – 16
-40h =0
h = 0
Hence, from the above,
We can conclude that the value of h is: 0
Question 17.
To estimate how many miles you are from a thunderstorm, count the seconds between when you see lightning and when you hear thunder. Then divide by 5. Write and solve an equation to determine how many seconds you would count for a thunderstorm that is 2 miles away. (Section 1.1)
Answer:
Given,
To estimate how many miles you are from a thunderstorm, count the seconds between when you see lightning and when you hear thunder. Then divide by 5.
x/5 = 2
x = 2 × 5
x = 10
Question 18.
You want to hang three equally-sized travel posters on a wall so that the posters on the ends are each 3 feet from the end of the wall. You want the spacing between posters to be equal. Write and solve an equation to determine how much space you should leave between the posters. (Section 1.2)
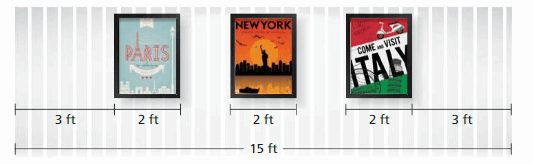
Answer:
The space you should leave between the posters is: \(\frac{3}{2}\) ft
Explanation:
The given figure is:

It is given that you want to hang three equally-sized travel posters on a wall so that the posters on the ends are each 3 feet from the end of the wall. You want the spacing between posters to be equal.
So,
From the figure,
The total space = 15 ft
The total spacing covered at the ends = 3 + 3 = 6 ft
Let the space between the equally spaced posters be x
So,
The total spacing between the travel posters = 2x + 2x + 2x = 6x ft
SO,
The total space = ( The total spacing covered at the ends ) + ( The total spacing between the travel posters )
15 = 6 + 6x
6x = 15 – 6
6x = 9
x = 9 ÷ 6
x = \(\frac{3}{2}\) ft
Hence, from the above,
We can conclude that the spacing between the travel posters is: \(\frac{3}{2}\) ft
Question 19.
You want to paint a piece of pottery at an art studio. The total cost is the cost of the piece plus an hourly studio fee. There are two studios to choose from. (Section 1.3)
a. After how many hours of the painting are the total costs the same at both studios? Justify your answer.
b. Studio B increases the hourly studio fee by $2. How does this affect your answer in part (a)? Explain.

Answer:
a)
It is given that,
The total cost = Cost of the vase + The hourly studio fee
Let the number of hours be x
So,
The total cost for studio A = 10 + 8x
The total cost of studio B = 16 + 6x
It is given that the total costs are the same
So,
10 + 8x = 16 + 6x
8x – 6x = 16 – 10
2x = 6
x = 6 ÷ 2
x = 3
Hence, from the above,
We can conclude that the total cost will be the same after 3 hours for both the studios
b)
It is given that the studio B increases the hourly studio fee by $2
So,
The total hourly studio fee for studio B = 6 + 2 = $8
So,
Now,
As in part (a), the same process will be repeated but in the studio B’s hourly fee of $6, we have to put $8
So,
10 + 8x = 16 + 8x
8x – 8x = 6 – 10
10 = 16
Hence, from the above,
We can conclude that the value of x has no solutions
Lesson 1.4 Solving Absolute Value Equations
Essential Question
How can you solve an absolute value equation?
EXPLORATION 1
Solving an Absolute Value Equation Algebraically
Work with a partner. Consider the absolute value equation
| x + 2 | = 3.

a. Describe the values of x + 2 that make the equation true. Use your description to write two linear equations that represent the solutions of the absolute value equation.
Answer:
We know that,
| x | = x
-| x | = -x
So,
| x + 2 | = 3
x + 2 = 3
x = 3 – 2
x = 1
Now,
-| x + 2 | = 3
| x + 2 | = -3
-x – 2 = -3
-x = -3 + 2
-x = -1
x = 1
So,
The values of x + 2 that make the equation true is: 3 and 3
The value of x is: 1 and 1
b. Use the linear equations you wrote in part (a) to find the solutions of the absolute value equation.
Answer:
We know that,
| x | = x
-| x | = -x
So,
| x + 2 | = 3
x + 2 = 3
x = 3 – 2
x = 1
Now,
-| x + 2 | = 3
-| x + 2 | = -3
-x – 2 = -3
-x = -3 + 2
-x = -1
x = 1
So,
The solutions of | x + 2 | are: 1 and 1
c. How can you use linear equations to solve an absolute value equation?
Answer:
We use linear equations to solve an absolute value equation by using the following properties. They are:
A) | x | = x
B) -| x | = -x
EXPLORATION 2
Solving an Absolute Value Equation Graphically
Work with a partner. Consider the absolute value equation
| x + 2 | = 3.
a. On a real number line, locate the point for which x + 2 = 0.
![]()
Answer:
The given equation is:
x + 2 = 0
x = 0 – 2
x = -2
So,
On a real number line, we have to locate the point x = -2
Hence,
The point we have to locate on the real number line is:
![]()
b. Locate the points that are 3 units from the point you found in part (a). What do you notice about these points?
Answer:
From part (a).
We found that x = -2
Now,
To locate the points that are 3 units away or 3 units behind from the point you found in part (a), i.e., x = -2
We know that,
3 units away imply ” Add 3 ”
3 units behind imply ” Subtract 3 ”
Now,
We have to add 3 and subtract 3 to the point we obtained in part (a)
So,
When we add 3 to x = -2,
x = -2 + 3
x =1
When we subtract 3 from x = -2,
x = -2 – 3
x = -5
Hence,
The points we have to locate in the real number line are: 1 and -5
So,
The real number line with the located points is:
![]()
c. How can you use a number line to solve an absolute value equation?
Answer:
The given absolute value equation is:
| x + 2 | = 3
We know that,
| x | = x
-| x | = -x
So,
| x + 2 | = 3
x + 2 = 3
x = 3 – 2
x = 1
– | x + 2 | = -3
-x – 2 = -3
-x = -3 + 2
-x = -1
x = 1
So,
The values we have to locate in the number line is:
![]()
EXPLORATION 3
Solving an Absolute Value Equation Numerically
Work with a partner. Consider the absolute value equation
| x + 2 | = 3.
a. Use a spreadsheet, as shown, to solve the absolute value equation.
b. Compare the solutions you found using the spreadsheet with those you found in Explorations 1 and 2. What do you notice?
c. How can you use a spreadsheet to solve an absolute value equation?
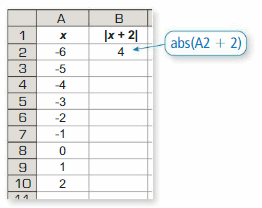
Answer:
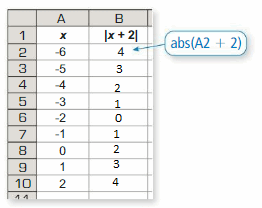
Communicate Your Answer
Question 4.
How can you solve an absolute value equation?
Answer:
We can solve the absolute equation by using the following properties. They are:
A) | x| = x
B) – | x | = -x
Question 5.
What do you like or dislike about the algebraic, graphical, and numerical methods for solving an absolute value equation? Give reasons for your answers.
Answer:
The algebraic, numerical, and graphical methods have their own advantages in their own perspective.
The algebraic methods used to solve the linear equations whereas the graphical method used to indicate the linear equations.
The numerical method is applicable for mathematical operations
1.4 Lesson
Monitoring Progress
Solve the equation. Graph the solutions, if possible.
Question 1.
| x | = 10
Answer:
The value of x is: 10
Explanation:
The given absolute value equation is:
| x | = 10
We know that,
| x | = x
So,
x = 10
Hence, from the above,
We can conclude that the value of x is: 10
Question 2.
| x – 1 | = 4
Answer:
The value of x is: 5
Explanation:
The given absolute value equation is:
| x – 1 | = 4
We know that,
| x | = x
So,
x – 1 = 4
x = 4 + 1
x = 5
Hence, from the above,
We can conclude that the value of x is: 5
Question 3.
| 3 + x | = -3
Answer:
The value of x is: -6
Explanation:
The given absolute value equation is:
| 3 + x | = -3
We know that,
| x | = x
So,
x + 3 = -3
x = -3 – 3
x = -6
Hence, from the above,
We can conclude that the value of x is: -6
Solve the equation. Check your solutions.
Question 4.
| x – 2 | + 5 = 9
Answer:
The value of x is: 6
Explanation:
The given absolute value equation is:
| x – 2 | + 5 = 9
| x – 2 | = 9 – 5
| x – 2 | = 4
We know that,
| x | = x
So,
x – 2 = 4
x = 4 + 2
x = 6
Hence, from the above,
We can conclude that the value of x is: 6
Question 5.
4 | 2x + 7 | = 16
Answer:
The value of x is: –\(\frac{3}{2}\)
Explanation:
The given absolute value equation is:
4 | 2x + 7 | = 16
| 2x + 7 | = 16 ÷ 4
| 2x + 7| = 4
We know that,
| x | = x
So,
2x + 7 = 4
2x = 4 – 7
2x = -3
x = –\(\frac{3}{2}\)
Hence, from the above,
We can conclude that the value of x is: –\(\frac{3}{2}\)
Question 6.
-2 | 5x – 1 | – 3 = -11
Answer:
The value of x is: 1
Explanation:
The given absolute value equation is:
-2 | 5x – 1 | – 3 = -11
-2 | 5x – 1 | = -11 + 3
-2 | 5x – 1 | = -8
| 5x – 1 | = -8 ÷ ( -2 )
| 5x – 1 | = 4
We know that,
| x | = x
So,
5x – 1 = 4
5x = 4 + 1
5x = 5
x = 5 ÷ 5
x = 1
Hence, from the above,
We can conclude that the value of x is: 1
Question 7.
For a poetry contest, the minimum length of a poem is 16 lines. The maximum length is 32 lines. Write an absolute value equation that represents the minimum and maximum lengths.
Answer:
The minimum value length is: 16
The maximum length is: 32
Explanation:
It is given that for a poetry contest, the minimum length of a poem is 16 lines. The maximum length is 32 lines.
So,
The absolute value equation that represents the minimum length of a poem = | The minimum length of a poem |
= | 16 |
= 16
The absolute value equation that represents the maximum length of a poem = | The maximum length of a poem |
= | 32 |
= 32
Hence, from the above,
We can conclude that
The minimum value length is: 16
The maximum length is: 32
Solve the equation. Check your solutions.
Question 8.
| x + 8 | = | 2x + 1 |
Answer:
The value of x is: 7
Explanation:
The given absolute value equation is:
| x + 8 | = | 2x + 1 |
We know that,
| x | = x
So,
x + 8 = 2x + 1
2x – x = 8 – 1
x = 7
Hence from the above,
We can conclude that the value of x is: 7
Question 9.
3 | x – 4 | = | 2x + 5 |
Answer:
The value of x is: 17
Explanation:
The given absolute equation is:
3 | x – 4 | = | 2x + 5 |
We know that,
| x | = x
So,
3 ( x – 4 ) = 2x + 5
3 ( x ) – 3 ( 4 ) = 2x + 5
3x – 12 = 2x + 5
3x – 2x = 5 + 12
x = 17
Hence, from the above,
We can conclude that the value of x is: 17
Solve the equation. Check your solutions.
Question 10.
| x + 6 | = 2x
Answer:
The value of x is: 6
Explanation:
The absolute value equation is:
| x + 6 | = 2x
We know that,
| x | = x
So,
x + 6 = 2x
2x – x = 6
x = 6
Hence, from the above,
We can conclude that the value of x is: 6
Question 11.
| 3x – 2 | = x
Answer:
The value of x is: 1
Explanation:
The given absolute value equation is:
| 3x – 2 | = x
We know that,
| x | = x
So,
3x – 2 = x
Soo,
3x – x = 2
2x = 2
x = 2 ÷ 2
x = 1
Hence, from the above,
We can conclude that the value of x is: 1
Question 12.
| 2 + x | = | x – 8 |
Answer:
The given absolute value equation has no solution
Explanation:
The given absolute value equation is:
| 2 + x | = | x – 8 |
We know that,
| x | = x
So,
2 + x = x – 8
2 = x – x – 8
2 = -8
Hence, from the above,
We can conclude that the given absolute value equation has no solution
Question 13.
| 5x – 2 | = | 5x + 4 |
Answer:
The given absolute value equation has no solution
Explanation:
The given absolute value equation is:
| 5x – 2 | = | 5x + 4 |
We know that,
| x | = x
So,
5x – 2 = 5x + 4
5x – 5x – 2 = 4
-2 = 4
Hence, from the above,
We can conclude that the given absolute value equation has no solution
Solving Absolute Value Equations 1.4 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What is an extraneous solution?
Answer:
Extraneous solutions are values that we get when solving equations that are not really solutions to the equation.
Example for extraneous solution:
| 5x – 2 | = | 5x + 4 |
Question 2.
WRITING
Without calculating, how do you know that the equation | 4x – 7 | = -1 has no solution?
Answer:
The given absolute value equation is:
| 4x – 7 | = -1
We know that,
An absolute value can never equal a negative number.
So,
By the above,
We can say that
| 4x – 7 | must not equal to a negative number.
Hence, from the above,
We can conclude that | 4x – 7 | = -1 has no solution without calculating its solution
Monitoring Progress and Modeling with Mathematics
In Exercises 3−10, simplify the expression.
Question 3.
| -9 |
Answer:
![]()
Question 4.
– | 15 |
Answer:
The value of -| 15 | is: -15
Explanation:
The given absolute value is: -| 15 |
We know that,
| x | = x
| -x | = x
-| x | = -x
So,
-| 15 | = -15
Hence, from the above,
We can conclude that the value of -| 15 | is: -15
Question 5.
| 14 | – | -14 |
Answer:
![]()
Question 6.
| -3 | + | 3 |
Answer:
The value of | -3 | + | 3 | is: 6
Explanation:
The given absolute value expression is:
| -3 | + | 3 |
We know that,
| x | = x
| -x | = x
-| x | = -x
So,
| -3 | + | 3 |
= 3 + 3
= 6
Hence, from the above,
We can conclude that the value of | -3 | + | 3 | is: 6
Question 7.
– | -5 • (-7) |
Answer:
![]()
Question 8.
| -0.8 • 10 |
Answer:
The value of | -0.8 ⋅ 10 | is: 8
Explanation:
The given absolute value expression is:
| -0.8 ⋅ 10 |
We know that,
| x | = x
| -x | = x
-| x | = -x
So,
| -0.8 ⋅ 10 |
= | – ( 8 ⁄ 10 ) ⋅ ( 10 ⁄ 1 ) |
= | – ( 8 × 10 ) ⁄ ( 10 × 1 ) |
= | -8 |
= 8
hence, from the above,
We can conclude that the value of | -0.8 ⋅ 10 | is: 8
Question 9.
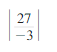
Answer:
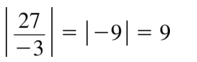
Question 10.
![]()
Answer:
The value of | -12 ⁄ 4 | is: 3
Explanation:
The given absolute value expression is: | -12 ⁄ 4 |
We know that,
| x | = x
| -x | = x
– | x | = -x
So,
| -12 ⁄ 4 | = | -3 |
= 3
Hence, from the above,
We can conclude that the value of | -12 ⁄ 4 | is: 3
In Exercises 11−24, solve the equation. Graph the solution(s), if possible.
Question 11.
| w | = 6
Answer:
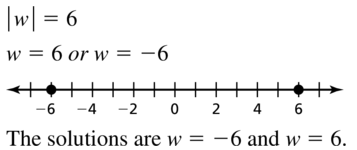
Question 12.
| r | = -2
Answer:
The absolute value of a number must be greater than or equal to 0 and can not be equal to -2.
Hence,
The given absolute eqution has no solution
Question 13.
| y | = -18
Answer:

Question 14.
| x | = 13
Answer:
The value of x is: 13 or -13
Explanation:
The given absolute value equation is:
| x | = 13
We know that,
|x | = x
– | x | = -x
So,
| x | = 13 or – 13
Hence, from the above,
We can conclude that the value of x is: 13 or -13
Question 15.
| m + 3 | = 7
Answer:

Question 16.
| q – 8 | = 14
Answer:
The value of q is: 22 or -6
Explanation:
The given absolute value equation is:
| q – 8 | = 14
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
q – 8 = 14 q – 8 = -14
q = 14 + 8 q = -14 + 8
q = 22 q = -6
Hence, from the above,
We can conclude that the value of q is: 22 or -6
Question 17.
| -3d | = 15
Answer:
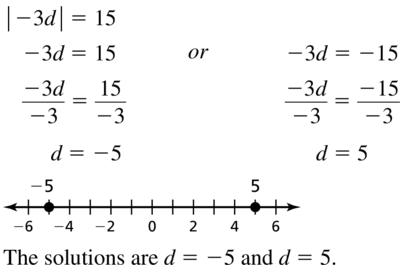
Question 18.
![]()
Answer:
The value of t is: 12 or -12
Explanation:
The given absolute value equation is:
| t / 2 | = 12
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
t / 2 = 6 t / 2 = -6
t = 6 × 2 t = 6 × -2
t = 12 t = -12
Hence, from the above,
We can conclude that the value of t is: 12 or -12
Question 19.
| 4b – 5 | = 19
Answer:

Question 20.
| x – 1 | + 5 = 2
Answer:
The given absolute value equation has no solution
Explanation:
The given absolute value equation is:
| x – 1 | + 5 = 2
| x – 1 | = 2 – 5
| x – 1 | = -3
We know that,
The absolute value of an equation must be greater than or equal to zero
So,
| x – 1 | = -3 has no solution
Hence, from the above,
We can conclude that the given absolute value equation has no solution
Question 21.
-4 | 8 – 5n | = 13
Answer:

Question 22.
![]()
Answer:
The value of y is: -3 or 6
Explanation:
The given absolute value equation is:
-3 | 1 – ( 2 / 3 ) y | = -9
| 1 – (2 / 3 ) y | = -9 ÷ ( -3 )
| 1 – ( 2 / 3 ) y | = 3
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
1 – ( 2 / 3 ) y = 3 1 – ( 2 /3 ) y = -3
2/3 y = 1 – 3 2/3 y = 1 + 3
2 / 3 y = -2 2 / 3 y = 4
2y = -2 × 3 2y = 4 × 3
2y = -6 2y = 12
y = -6 ÷ 2 y = 12 ÷ 2
y = -3 y = 6
Hence, from the above,
We can conclude that the value of y is: -3 or 6
Question 23.
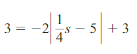
Answer:
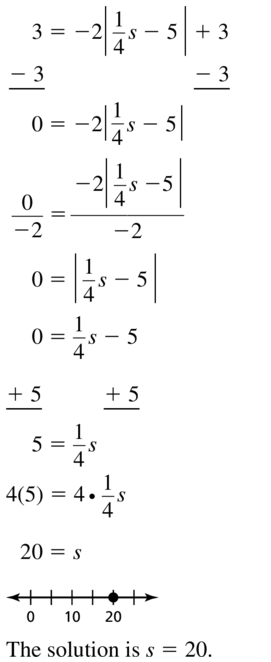
Question 24.
9 | 4p + 2 | + 8 = 35
Answer:
The value of p is: 1 / 4 or -5 / 4
Explanation:
The given absolute value equation is:
9 | 4p + 2 | + 8 = 35
9 | 4p + 2 | = 35 – 8
9 | 4p + 2 | = 27
| 4p + 2 | = 27 ÷ 9
| 4p + 2 | = 3
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
4p + 2 = 3 4p + 2 = -3
4p = 3 – 2 4p = -3 – 2
4p = 1 4p = -5
p = 1 / 4 p = -5 / 4
Hence, from the above,
We can conclude that the value of p is: 1 / 4 or -5 / 4
Question 25.
WRITING EQUATIONS
The minimum distance from Earth to the Sun is 91.4 million miles. The maximum distance is 94.5 million miles.
a. Represent these two distances on a number line.
b. Write an absolute value equation that represents the minimum and maximum distances.
Answer:

Question 26.
WRITING EQUATIONS
The shoulder heights of the shortest and tallest miniature poodles are shown.

a. Represent these two heights on a number line.
b. Write an absolute value equation that represents these heights.
Answer:
a)
The number line that represents the two heights on a number line is:
b)
The minimum shoulder height = ( 15 – 10 ) / 2
= 5 / 2
= 2.5 inches
The maximum shoulder height = 10 + 2.5
= 12.5 inches
Now,
Let the heights between poodles be x.
Hence,
The absolute value equation is:
| x – 12.5 | = 2.5
USING STRUCTURE In Exercises 27−30, match the absolute value equation with its graph without solving the equation.
Question 27.
| x + 2 | = 4
Answer:
Question 28.
| x + 4 | = 2
Answer:
The given absolute value equation is:
| x + 4 | = 2
To find the halfway point, made the absolute value equation equal to 0.
So,
| x + 4 | = 0
So,
x = -4
From the given absolute value equation,
We can say that the distance from the halfway point to the minimum and maximum points is: 2
Question 29.
| x – 2 | = 4
Answer:
Question 30.
| x + 4 | = 2
Answer: A is correct
In Exercises 31−34, write an absolute value equation that has the given solutions.
Question 31.
x = 8 and x = 18
Answer:
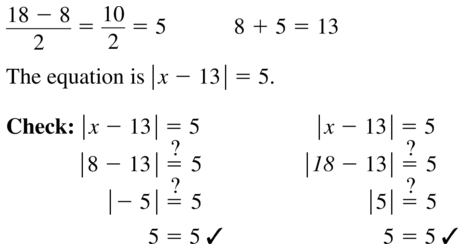
Question 32.
x = -6 and x = 10
Answer:
The given absolute value equation is:
| x – 2 | = 8
Explanation:
The given values of x are:
x = -6 and x = 10
Now,
The halfway point between 10 and -6 = [ 10 – ( -6 ) ] / 2
= [ 10 + 6 ] / 2
= 16 / 2
= 8
The minimum distance from the halfway point = 8 – 6 = 2
Hence,
The absolute value equation is:
| x – 2 | = 5
Question 33.
x = 2 and x = 9
Answer:
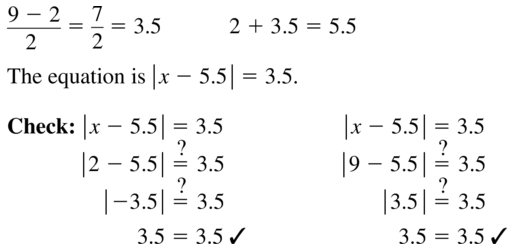
Question 34.
x = -10 and x = -5
Answer:
The given values of x are:
x = -10 and x = -5
Now,
The halfway point between -10 and -5 = [ 10 – ( 5 ) ] / 2
= [ 10 – 5 ] / 2
= 5 / 2
= 2.5
So,
The minimum value from the half-point = 2.5 + ( -10 )
= 2.5 – 10
= -7.5
Hence,
The absolute value equation is:
| x – ( -7.5 ) | = 2.5
| x + 7.5 | = 2.5
In Exercises 35−44, solve the equation. Check your solutions.
Question 35.
| 4n – 15 | = | n |
Answer:

Question 36.
| 2c + 8 | = | 10c |
Answer:
The values of c are: 1 and 2 / 3
Explanation:
The given absolute value equation is:
| 2c + 8 | = | 10c |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
Now,
2c + 8 = 10c 2c + 8 = -10c
10c – 2c = 8 2c + 10c = 8
8c = 8 12c = 8
c = 8 / 8 c = 8 / 12
c = 1 c = 2 /3
Hence, from the above,
We can conclude that the values of c are: 1 and 2 / 3
Question 37.
| 2b – 9 | = | b – 6 |
Answer:

Question 38.
| 3k – 2 | = 2 | k + 2 |
Answer:
The values of k are: 6 and -2 / 5
Explanation:
The given absolute equation is:
| 3k – 2 | = 2 | k + 2 |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
2 ( k + 2 ) = 3k – 2 2 ( k + 2 ) = – ( 3k – 2 )
2k + 4 = 3k – 2 2k + 4 = -3k + 2
3k – 2k = 4 + 2 2k + 3k = 2 – 4
k = 6 5k = -2
k = 6 k = -2 / 5
Hence, from the above,
We can conclude that the values of k are: 6 and -2 / 5
Question 39.
4 | p – 3 | = | 2p + 8 |
Answer:

Question 40.
2 | 4w – 1 | = 3 | 4w + 2 |
Answer:
The value of w is: -2
Explanation:
The given absolute value equation is:
2 | 4w – 1 | = 3 | 4w+ 2 |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
2 ( 4w – 1 ) = 3 ( 4w + 2 ) -2 ( 4w – 1 ) = -3 ( 4w + 2 )
8w – 2 = 12w + 6 -8w + 2 = -12w -6
12w – 8w = -6 – 2 -12w + 8w = 6 + 2
4w = -8 -4w = 8
w = -8 / 4 w = 8 / -4
w = -2 w = -2
Hence, from the above,
We can conclude that the value of w is: -2
Question 41.
| 3h + 1 | = 7h
Answer:

Question 42.
| 6a – 5 | = 4a
Answer:
The value of a is: 5 / 2 and 1 / 2
Explanation:
The given absolute value equation is:
| 6a – 5 | = 4a
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
6a – 5 = 4a 6a – 5 = -4a
6a – 4a = 5 6a + 4a = 5
2a = 5 10a = 5
a = 5 / 2 a = 5 / 10
a = 5 / 2 a = 1 / 2
Hence, from the above,
We can conclude that the values of a are: 5 / 2 and 1 / 2
Question 43.
| f – 6 | = | f + 8 |
Answer:

Question 44.
| 3x – 4 | = | 3x – 5 |
Answer:
The given absolute value equation has no solution
Explanation:
The given absolute value equation is:
| 3x – 4 | = | 3x – 5 |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
3x – 4 = 3x – 5 – ( 3x – 4 ) = – ( 3x – 5 )
4 = 5 4 = 5
Hence, from the above,
We can conclude that the given absolute value equation has no solution
Question 45.
MODELING WITH MATHEMATICS
Starting from 300 feet away, a car drives toward you. It then passes by you at a speed of 48 feet per second. The distance d (in feet) of the car from you after t seconds is given by the equation d = | 300 – 48t |. At what times is the car 60 feet from you?
Answer:

Question 46.
MAKING AN ARGUMENT
Your friend says that the absolute value equation | 3x + 8 | – 9 = -5 has no solution because the constant on the right side of the equation is negative. Is your friend correct? Explain.
Answer:
Yes, your friend is correct
Explanation:
The given absolute value equation is:
| 3x + 8 | – 9 = -5
We know that,
The absolute value equation value must have greater than or equal to 0
But here
The value of the absolute value equation is less than 0
Hence,
The given absolute value equation has no solution.
Hence, from the above,
We can conclude that your friend is correct.
Question 47.
MODELING WITH MATHEMATICS
You randomly survey students about year-round school. The results are shown in the graph.
The error given in the graph means that the actual percentage could be 5% more or 5% less than the percent reported by the survey.
a. Write and solve an absolute value equation to find the least and greatest percents of students who could be in favor of the year-round school.
b. A classmate claims that \(\frac{1}{3}\) of the student body is actually in favor of the year-round school. Does this conflict with the survey data? Explain.
Answer:

Question 48.
MODELING WITH MATHEMATICS
The recommended weight of a soccer ball is 430 grams. The actual weight is allowed to vary by up to 20 grams.
a. Write and solve an absolute value equation to find the minimum and maximum acceptable soccer ball weights.
Answer:
It is given that the recommended weight of a soccer ball is 430 grams and the actual weight is allowed to vary up to 20 grams
Hence,
The absolute value equation that represents the minimum and maximum acceptable soccer ball weights is:
| x – 430 | = 20
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x – 430 = 20 x – 430 = -20
x = 20 + 430 x = -20 + 430
x = 460 grams x = 410 grams
Hence, from the above,
We can conclude that the maximum and minimum acceptable soccer weights respectively are: 460 grams and 410 grams
b. A soccer ball weighs 423 grams. Due to wear and tear, the weight of the ball decreases by 16 grams. Is the weight acceptable? Explain.
Answer:
The weight that caused due to wear and tear is not acceptable
Explanation:
From the above problem,
We get the maximum weight of the soccer ball to be 460 grams with 20 grams increase or decreased to the weight of the ball
Now,
It is given that the weight of the ball is decreased by 16 grams due to wear and tear
So,
The weight of the ball now = 460 – 16 = 444 grams
But it is given that the weight of the ball becomes 423 grams due to wear and tear.
Hence, from the above,
We can conclude that the weight is not acceptable
ERROR ANALYSIS
In Exercises 49 and 50, describe and correct the error in solving the equation.
Question 49.
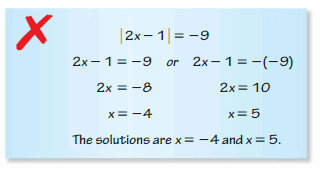
Answer:
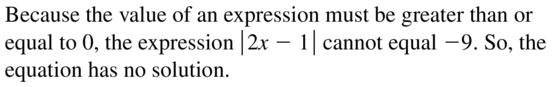
Question 50.

Answer:
The values of x are: -2 and -4 / 3
Explanation:
The given absolute value equation is:
| 5x + 8 | = x
We know that,
| x | = x for x > 0
| x | = – x for x < 0
So,
5x + 8 = x 5x + 8 = -x
5x – x = -8 5x + x = -8
4x = -8 6x = -8
x = -8 / 4 x = -8 / 6
x = -2 x = -4 / 3
Hence, from the above,
We can conclude that the values of x are: -2 and -4 / 3
Question 51.
ANALYZING EQUATIONS
Without solving completely, place each equation into one of the three categories.
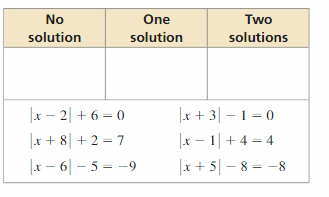
Answer:

Question 52.
USING STRUCTURE
Fill in the equation ![]() with a, b, c, or d so that the equation is graphed correctly.
with a, b, c, or d so that the equation is graphed correctly.
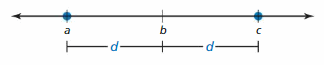
Answer:
ABSTRACT REASONING
In Exercises 53−56, complete the statement with always, sometimes, or never. Explain your reasoning.
Question 53.
If x2 = a2, then | x | is ________ equal to | a |.
Answer:

Question 54.
If a and b are real numbers, then | a – b | is _________ equal to | b – a |.
Answer:
If a and b are real numbers, then
| a – b | is equal to | b – a |
Explanation:
Let,
| a | = 5 and | b | = 9
We know that,
| x | =x for x > 0
| x | = -x for x < 0
So,
| a – b | = | 5 – 9 |
= | -4 | = 4
| b – a | = | 9 – 5 |
= | 4 |
= 4
Hence, from the above,
We can conclude that value of
| a – b | is equal to | b – a | if a and b are real numbers
Question 55.
For any real number p, the equation | x – 4 | = p will ________ have two solutions.
Answer:

Question 56.
For any real number p, the equation | x – p | = 4 will ________ have two solutions.
Answer:
For any real number,
| x – p | = 4 will have two solutions
Explanation:
The given absolute value equation is:
| x – p | = 4
Let the value of p be 1
We know that,
| x | = x for x > 0
| x | = – x for x < 0
So,
| x – 1 | = 4
| x – 1 | = 4 | x – 1 | = -4
x = 4 + 1 x = -4 + 1
x = 5 x = -3
Hence, from the above,
We can conclude that
| x – p | = 4 will have two solutions for any real number p
Question 57.
WRITING
Explain why absolute value equations can have no solution, one solution, or two solutions. Give an example of each case.
Answer:

Question 58.
THOUGHT-PROVOKING
Describe a real-life situation that can be modeled by an absolute value equation with the solutions x = 62 and x = 72.
Answer:
Suppose in a school, an exam is conducted. In that examination, 67% of the students are passed. If the error of the pass percentage is 5 %, then what are the minimum and the maximum number of students passed in the examination?
Now,
The absolute value equation for the given real-life situation is:
| x – 67 | = 5
We know that,
| x | = x for x> 0
| x | =-x for x < 0
So,
x – 67 = 5 x – 67 = -5
x = 5 + 67 x = -5 + 67
x = 72 x = 62
Hence, from the above,
We can conclude that the minimum and maximum number of students passed in the examination respectively are: 72 and 67
Question 59.
CRITICAL THINKING
Solve the equation shown. Explain how you found your solution(s).
8 | x + 2 | – 6 = 5 | x + 2 | + 3
Answer:
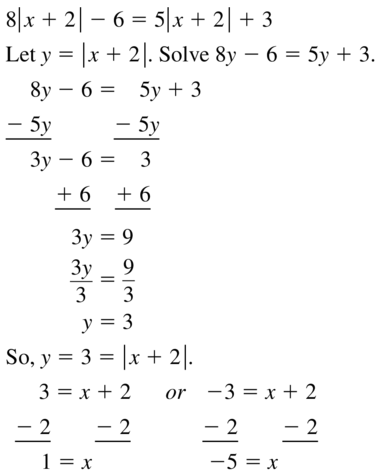
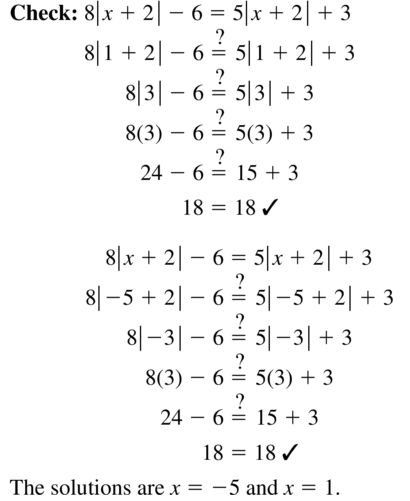
Question 60.
HOW DO YOU SEE IT?
The circle graph shows the results of a survey of registered voters on the day of an election.
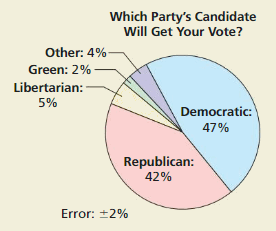
The error given in the graph means that the actual percentage could be 2% more or 2% less than the percent reported by the survey.
a. What are the minimum and maximum percents of voters who could vote Republican?
Answer:
The minimum percentage of voters for Republicans is: 40%
The maximum percentage of voters for Republicans is: 44 %
Explanation:
The given graph is:

From the graph,
The vote percentage for Republicans is: 42 %
The error percentage is: ±2%
So,
The absolute value equation for the maximum and the minimum number of voters is:
| x – 42 | = 2
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x – 42 = 2 x – 42 = -2
x = 2 + 42 x = -2 + 42
x = 44 x = 40
Hence, from the above,
We can conclude that
The minimum percentage of voters for Republicans is: 40%
The maximum percentage of voters for Republicans is: 44 %
b. How can you use absolute value equations to represent your answers in part (a)?
Answer:
From the property of absolute values,
We know that,
| x | = x for x > 0
| x | = -x for x < 0
From the part ( a ),
The absolute value equation is:
| x – 42 | = 2
So,
x – 42 = 2 x – 42 = -2
x = 2 + 42 x = -2 + 42
x = 44 x = 40
Hence, from the above,
We can conclude that we can use absolute values in the above way to represent the answers
c. One candidate receives 44% of the vote. Which party does the candidate belong to? Explain.
Answer:
The candidate of the Republican party receives 44 % of the vote.
Explanation:
The given graph is:

From the above graph,
We can say that,
The percentage of the vote received by the candidate of the Republican party = 42 %
The error percentage = ± 2 %
So,
Now,
The percentage of the vote received by the Republicans = 42 + 2 ( or ) 42 – 2
= 44 ( or ) 40
Hence, from the above,
We can conclude that the candidate of the Republican party received the 44 % of the vote
Question 61.
ABSTRACT REASONING
How many solutions does the equation a | x + b | + c = d have when a > 0 and c = d? when a < 0 and c > d? Explain your reasoning.
Answer:
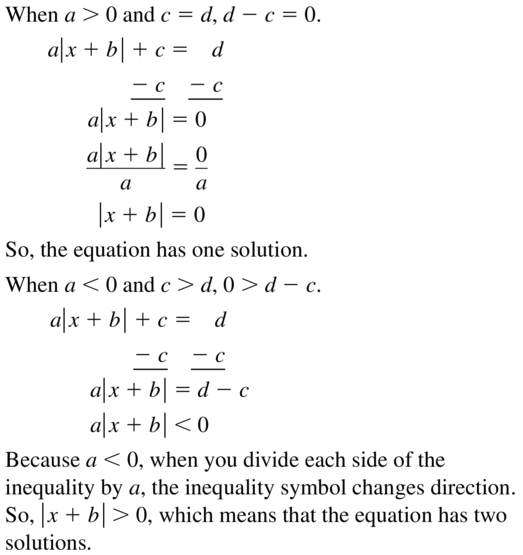
Maintaining Mathematical Proficiency
Identify the property of equality that makes Equation 1 and Equation 2 equivalent. (Section 1.1)
Question 62.

Answer:
The given equations are:
Equation 1: 3x + 8 = x – 1
Equation 2: 3x + 9= x
From Equation 1,
3x + 8 = x – 1
3x + 8 + 1 = x
3x + 9 = x
Hence, from the above,
We can conclude that we can get Equation2 by rearranging the Equation 1
Question 63.

Answer:
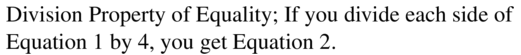
Use a geometric formula to solve the problem.
Question 64.
A square has an area of 81 square meters. Find the side length.
Answer:
The side length of the square is: 9 meters
Explanation:
The given area of the square is: 81 square meters
We know that,
Area of the square = Side × Side
81 = Side × Side
Side² = 81
Apply square root on both sides
√Side² = √81
Side = 9 meters
Hence, from the above,
We can conclude that the side of the square is: 9 meters
Question 65.
A circle has an area of 36π square inches. Find the radius.
Answer:
Question 66.
A triangle has a height of 8 feet and an area of 48 square feet. Find the base.
Answer:
The base of the triangle is: 12 feet
Explanation:
It is given that a triangle has a height of 8 feet and an area of 48 square feet
We know that,
The area of the triangle = ( 1 / 2 ) × Base × Height
48 = ( 1 / 2 ) × Base × 8
Base × 8 = 48 × 2
Base = ( 48 × 2 ) ÷ 8
Base = 96 ÷ 8
Base = 12 feet
Hence, from the above,
We can conclude that the base of the triangle is: 12 feet
Question 67.
A rectangle has a width of 4 centimeters and a perimeter of 26 centimeters. Find the length.
Answer:
Lesson 1.5 Rewriting Equations and Formulas
Essential Question
How can you use a formula for one measurement to write a formula for a different measurement?
Answer:
Write the formula for one measurement and then solve the formula for the different measurement you want to find and use this new formula to find that measurement
Hence, in the above way,
We can use a formula for one measurement to write a formula for a different measurement
EXPLORATION 1
Using an Area Formula
Work with a partner.
a. Write a formula for the area A of a parallelogram.
Answer:
We know that,
The area of the parallelogram ( A) = Base × Height
b. Substitute the given values into the formula. Then solve the equation for b. Justify each step.
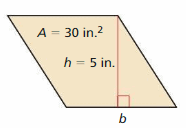
Answer:
The value of b is: 6 in
Explanation:
The given figure is:

From the given figure,
Area ( A) = 30 in²
Height ( h ) = 5 in
Base = b
From part ( a),
Area of the parallelogram = Base × Height
30 = 5 × b
b = 30 ÷ 5
b = 6 in
Hence, from the above,
We can conclude that the value of b is: 6 in
c. Solve the formula in part (a) for b without first substituting values into the formula. Justify each step.
Answer:
From part ( a ),
Area of the parallelogram = Base × Height
Base = ( Area of the parallelogram ) ÷ Height of the parallelogram
From the given figure,
Base = b
So,
b = ( Area of the parallelogram ) ÷ Height of the parallelogram
d. Compare how you solved the equations in parts (b) and (c). How are the processes similar? How are they different?

Answer:
We know that,
The area of the parallelogram = Base × Height
Using the above formula,
We solved parts (b ) and ( c )
EXPLORATION 2
Using Area, Circumference, and Volume Formulas
Work with a partner. Write the indicated formula for each figure. Then write a new formula by solving for the variable whose value is not given. Use the new formula to find the value of the variable.
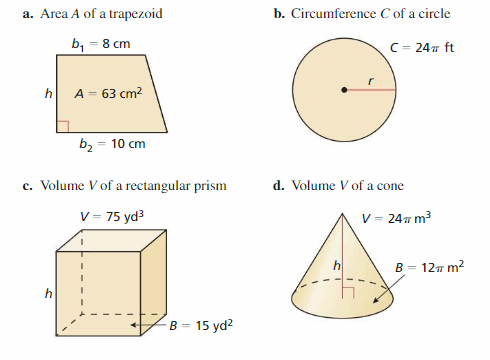
Answer:
The given geometrical figures are:

Now,
a)
The given figure is:
We know that,
Area of the trapezoid = h ( a + b ) / 2
Where,
h is the height between the two sides
a + b is the sum of the parallel sides [ Here, b1 and b2 ]
From the given figure,
Area of the trapezoid = 63 cm²
1st parallel side ( b1 ) = 8 cm
2nd parallel side ( b2 ) = 10 cm
So,
Area of the trapezoid = h ( 8 + 10 ) / 2
63 = h ( 18 ) / 2
63 × 2 = h × 18
h = ( 63 × 2 ) ÷ ( 18 × 1 )
h = 7 cm
Hence, from the above,
We can conclude that the value of h is: 7 cm
b)
The given figure is:
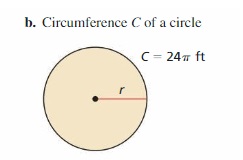
We know that,
Circumference of a circle = 2πr
Where
r is the radius of the circle
From the above figure,
Circumference of the circle ( C ) = 24π ft
So,
24π = 2πr
r = ( 24π ) ÷ ( 2π )
r = 12 ft
Hence, from the above,
We can conclude that the value of r is: 12 ft
c)
The given figure is:
We know that,
The volume of the rectangular prism ( V ) = Length × Width × Height
The area of the rectangle ( B) = Length × Width
So,
The volume of the rectangular prism (V ) = B × Height
From the above figure,
The volume of the rectangular prism ( V ) = 75 yd³
The area of the rectangle ( B ) = 15 yd²
So,
75 = 15 × Height
Height = 75 ÷ 15
Height = 15 yd
Hence, from the above,
We can conclude that the value of h is: 15 yd
d)
The given figure is:
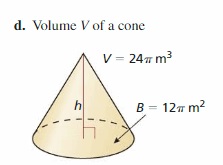
We know that,
The volume of cone ( V ) = πr²h / 3
The area of the circle ( B ) = πr²
Where,
r is the radius of the circle
h is the height of the cone
So,
The volume of the cone ( V ) = Bh / 3
From the above figure,
V = 24π m³
B = 12π m³
So,
24π = 12π × h / 3
h / 3 = 24π ÷ 12π
h / 3 = 2
h = 2 × 3
h = 6 m
Hence, from the above,
We can conclude that the height of the cone is: 6 m
Communicate Your Answer
Question 3.
How can you use a formula for one measurement to write a formula for a different measurement? Give an example that is different from those given in Explorations 1 and 2.
Answer:
Write the formula for one measurement and then solve the formula for the different measurement you want to find and use this new formula to find that measurement
Example:
The given figure is:
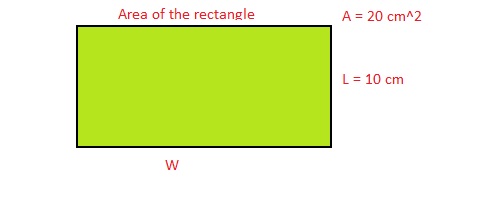
We know that,
The area of the rectangle ( A ) = Length × Width
From the above figure,
A = 20 cm²
L = 10 cm
Let,
W be the width of the rectangle
So,
20 = 10 × W
W = 20 ÷ 10
W = 2 cm
Hence, from the above,
We can conclude that the value of W is: 2 cm
1.5 Lesson
Monitoring Progress
Solve the literal equation for y.
Question 1.
3y – x = 9
Answer:
The value of y is: ( x + 9 ) / 3
Explanation:
The given equation is:
3y – x = 9
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
3y = 9 + x
y = ( x + 9 ) / 3
Hence, from the above,
We can conclude that the value of y is: ( x + 9 ) / 3
Question 2.
2x – 2y = 5
Answer:
The value of y is: ( 2x – 5 ) / 2
Explanation:
The given equation is:
2x – 2y = 5
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
2y = 2x – 5
y = ( 2x – 5 ) / 2
Hence, from the above,
We can conclude that the value of y is: ( 2x – 5 ) / 2
Question 3.
20 = 8x + 4y
Answer:
The value of y is: 5 – 2x
Explanation:
The given equation is:
20 = 8x + 4y
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4y = 20 – 8x
y = ( 20 – 8x ) / 4
y = ( 20 ÷ 4 ) – ( 8x ÷ 4 )
y = 5 – 2x
Hence, from the above,
We can conclude that the value of y is: 5 – 2x
Solve the literal equation for x.
Question 4.
y = 5x – 4x
Answer:
The value of x is: y
Explanation:
The given equation is:
y = 5x – 4x
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x = y
Hence, from the above,
We can conclude that the value of x is: y
Question 5.
2x + kx = m
Answer:
The value of x is: m / ( k + 2 )
Explanation:
The given equation is:
2x + kx = m
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
x ( k + 2 ) = m
x = m / ( k + 2 )
Hence, from the above,
We can conclude that the value of x is: m / ( k + 2 )
Question 6.
3 + 5x – kx = y
Answer:
The value of x is: ( y – 3 ) / ( 5 – k )
Explanation:
The given equation is:
3 + 5x – kx = y
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5x – kx = y – 3
x ( 5 – k ) = y – 3
x = ( y – 3 ) / ( 5 – k )
Hence, from the above,
We can conclude that the value of x is: ( y – 3 ) / ( 5 – k )
Solve the formula for the indicated variable.
Question 7.
Area of a triangle: A = \(\frac{1}{2}\)bh; Solve for h.
Answer:
The value of h is: \(\frac{2A}{b}\)
Explanation:
The given area of a triangle is:
A = \(\frac{1}{2}\) bh
bh = 2A
h = \(\frac{2A}{b}\)
Hence, from the above,
We can onclude that the value of h is: \(\frac{2A}{b}\)
Question 8.
The surface area of a cone: S = πr2 + πrℓ; Solve for ℓ.
Answer:
The value of l is: \(\frac{S}{πr}\) – r
Explanation:
The given surface area of a cone is:
S = πr² + πrl
S= πr ( r + l )
r + l = \(\frac{S}{πr}\)
l = \(\frac{S}{πr}\) – r
Hence, from the above,
We can conclude that the value of l is: \(\frac{S}{πr}\) – r
Monitoring Progress
Question 9.
A fever is generally considered to be a body temperature greater than 100°F. Your friend has a temperature of 37°C. Does your friend have a fever?
Answer:
Your friend does not have a fever
Explanation:
It is given that a fever is generally considered to be a body temperature greater than 100°F.
We know that,
To convert Fahrenheit into Celsius,
°C = ( °F – 32 ) × \(\frac{5}{9}\)
°C = ( 100 – 32 ) × \(\frac{5}{9}\)
°C = 68 × \(\frac{5}{9}\)
°C = 37.7°
But it is given that your friend has a temperature of 37°C
So, for fever, the temperature has to be 37.7°C
Hence, from the above,
We can conclude that your friend does not have a fever
Question 10.
How much money must you deposit in a simple interest account to earn $500 in interest in 5 years at 4% annual interest?
Answer:
The money you deposit in simple interest is: $2,500
Explanation:
It is given that you earned $500 in a simple interest to earn in 5 years at 4% annual interest
Let,
The money you deposited be: $x
We know that,
Simple interest = ( Principle × Time × Rate ) / 100
The principle is the money you deposited
So,
500 = ( x × 5 × 4 ) / 100
( x × 5 × 4 ) = 500 × 100
x × 20 = 500 × 100
x = ( 500 × 100 ) ÷ 20
x = $2,500
Hence, from the above,
We can conclude that the money you deposited is: $2,500
Question 11.
A truck driver averages 60 miles per hour while delivering freight and 45 miles per hour on the return trip. The total driving time is 7 hours. How long does each trip take?
Answer:
The time taken for each trip is: 3 hours and 4 hours respectively
Explanation:
It is given that a truck driver averages 60 miles per hour while delivering freight and 45 miles per hour on the return trip. The total driving time is 7 hours.
We know that,
Speed = \(\frac{Distance}{Time}\)
Time = \(\frac{Distance}{Speed}\)
Let the distance be D
It is given that the total driving time is: 7 hours
So,
7 = \(\frac{D}{60}\) + \(\frac{D}{45}\)
7 / D = \(\frac{60 + 45}{60 × 45}\)
7 / D = \(\frac{105}{2,700}\)
D = 7 / \(\frac{105}{2,700}\)
D = 7 × \(\frac{2,700}{105}\)
D = \(\frac{7}{1}\) × \(\frac{2,700}{105}\)
D = \(\frac{7 × 2,700}{1 × 105}\)
D = 180 miles
So,
The time taken to deliver = \(\frac{180}{60}\) = 3 hours
The time taken to return = \(\frac{180}{45}\) = 4 hours
Hence, from the above,
We can conclude that the time taken for each trip is: 3 hours and 4 hours respectively
Rewriting Equations and Formulas 1.5 Exercices
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Is ![]() a literal equation? Explain.
a literal equation? Explain.
Answer:
The ” Literal equation” is an equation that contains only letters
Now,
The given equation is:
9r + 16 = π / 5
From the above definition,
We can say that the given equation is a ” Literal equation ”
Question 2.
DIFFERENT WORDS, SAME QUESTION?
Which is different? Find “both” answers.
Answer:
The given problems are:
a) Solve 3x + 6y = 24 for x
b) Solve 24 – 3x = 6y for x
c) Solve 6y = 24 – 3x in terms of x
d) Solve 24 – 6y = 3x for x in terms of y
So,
From the above-given problems,
We can observe that d) is different as we have to find x in terms of y whereas in the remaining three problems, we have to find x
Monitoring Progress and Modeling with Mathematics
In Exercises 3–12, solve the literal equation for y.
Question 3.
y – 3x = 13
Answer:
Question 4.
2x + y = 7
Answer:
The value of y is: 7 – 2x
Explanation:
The given literal equation is:
2x + y = 7
Now,
y = 7 – 2x
Hence, from the above,
We can conclude that the value of y is: 7 – 2x
Question 5.
2y – 18x = -26
Answer:
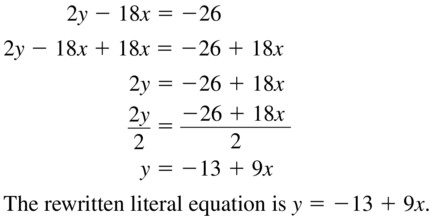
Question 6.
20x + 5y = 15
Answer:
The value of y is: 3 – 4x
Explanation:
The given literal equation is:
20x + 5y = 15
Now,
5y = 15 – 20x
y = ( 15 – 20x ) / 5
y = ( 15 / 5 ) – ( 20x / 5 )
y = 3 – 4x
Hence, from the above,
We can conclude that the value of y is: 3 – 4x
Question 7.
9x – y = 45
Answer:
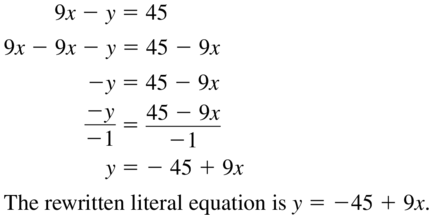
Question 8.
6 – 3y = -6
Answer:
The value of y is: 4
Explanation:
The given literal equation is:
6 – 3y = -6
-3y = -6 – ( +6 )
-3y = -6 -6
-3y = -12
y = -12 ÷ ( -3 )
y = 12 ÷ 3
y = 4
Hence, from the above,
We can conclude that the value of y is: 4
Question 9.
4x – 5 = 7 + 4y
Answer:
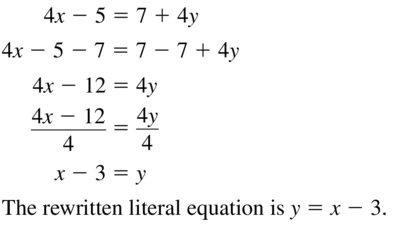
Question 10.
16x + 9 = 9y – 2x
Answer:
The value of y is: 18x + 9
Explanation:
The given literal equation is:
16x + 9 = y – 2x
So,
16x + 2x + 9 = y
18x + 9 = y
y = 18x + 9
Hence, from the above,
We can conclude that the value of y is: 18x + 9
Question 11.
2 +\(\frac{1}{6}\)y = 3x + 4
Answer:

Question 12.
11 – \(\frac{1}{2}\)y = 3 + 6x
Answer:
The value of y is: 16 – 12x
Explanation:
The given literal equation is:
11 – \(\frac{1}{2}\)y = 3 + 6x
So,
–\(\frac{1}{2}\)y = 3 + 6x – 11
-y = 2 ( 3 + 6x – 11 )
y = -2 ( 3 + 6x – 11 )
y = -2 ( 3 ) -2 ( 6x ) + 2 ( 11 )
y = -6 – 12x + 22
y = 16 – 12x
Hence, from the above,
We can conclude that the value of y is: 16 – 12x
In Exercises 13–22, solve the literal equation for x.
Question 13.
y = 4x + 8x
Answer:

Question 14.
m = 10x – x
Answer:
The value of x is: m / 9
Explanation:
The given literal equation is:
m = 10x – x
m = 9x
x = m / 9
Hence, from the above,
We can conclude that the value of x is: m / 9
Question 15.
a = 2x + 6xz
Answer:
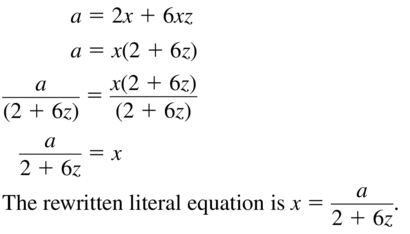
Question 16.
y = 3bx – 7x
Answer:
The value of x is: y / ( 3b – 7 )
Explanation:
The given literal equation is:
y = 3bx – 7x
So,
y = x ( 3b – 7 )
x = y / ( 3b – 7 )
Hence, from the above,
We can conclude that the value of x is: y / ( 3b – 7 )
Question 17.
y = 4x + rx + 6
Answer:
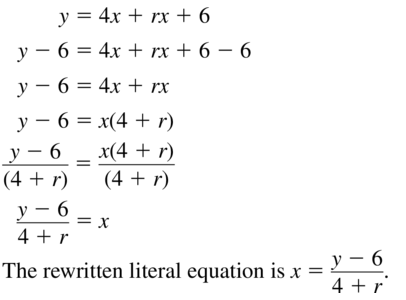
Question 18.
z = 8 + 6x – px
Answer:
The value of x is: ( z – 8 ) / ( 6 – p )
Explanation:
The given literal equation is:
z = 8 + 6x – px
So,
z – 8 = 6x – px
z – 8 = x ( 6 – p )
x = ( z – 8 ) / ( 6 – p )
Hence, from the above,
We can conclude that the value of x is: ( z – 8 ) / ( 6 – p )
Question 19.
sx + tx = r
Answer:
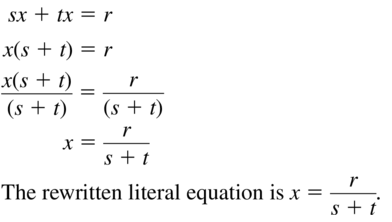
Question 20.
a = bx + cx + d
Answer:
The value of x is: ( a – d ) / ( b + c )
Explanation:
The given literal equation is:
a = bx + cx + d
a – d = bx + cx
a – d = x ( b + c )
x = ( a – d ) / ( b + c )
Hence, from the above,
We can conclude that the value of x is: ( a – d ) / ( b + c )
Question 21.
12 – 5x – 4kx = y
Answer:
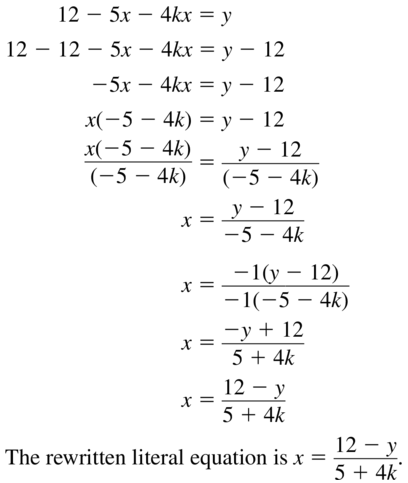
Question 22.
x – 9 + 2wx = y
Answer:
The value of x is: ( y – 9 ) / ( 1 – 2w )
Explanation:
The given literal equation is:
x – 9 + 2wx = y
x – 2wx = y + 9
x ( 1 – 2w ) = y + 9
x = ( y – 9 ) / ( 1 – 2w )
Hence, from the above,
We can conclude that the value of x is: ( y – 9 ) / ( 1 – 2w )
Question 23.
MODELING WITH MATHEMATICS
The total cost C (in dollars) to participate in a ski club is given by the literal equation C = 85x + 60, where x is the number of ski trips you take.
a. Solve the equation for x.
b. How many ski trips do you take if you spend a total of $315? $485?

Answer:

Question 24.
MODELING WITH MATHEMATICS
The penny size of a nail indicates the length of the nail. The penny size d is given by the literal equation d = 4n – 2, where n is the length (in inches) of the nail.
a. Solve the equation for n.
b. Use the equation from part (a) to find the lengths of nails with the following penny sizes: 3, 6, and 10.
Answer:
a)
The given literal equation is:
d = 4n – 2
Where,
n is the length ( in inches ) of the nail
So,
4n = d + 2
n = ( d + 2 ) / 4
b)
It is given that,
The penny sizes ( d ) are: 3, 6, and 10
From part ( a ),
The literal equation is:
n = ( d + 2 ) / 4
Put, d= 3, 6 and 10
So,
n = ( 3 + 2 ) /4 = 5 / 4 inches
n = ( 6 + 2 ) / 4 = 2 inches
n = ( 10 + 2 ) / 4 = 3 inches
ERROR ANALYSIS
In Exercises 25 and 26, describe and correct the error in solving the equation for x.
Question 25.
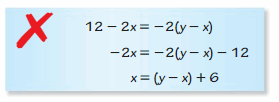
Answer:

Question 26.
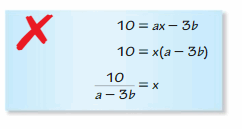
Answer:
The given literal equation is:
10 = ax – 3b
So,
ax = 10 + 3b
x = ( 10 + 3b ) / a
In Exercises 27–30, solve the formula for the indicated variable.
Question 27.
Profit: P = R – C; Solve for C.
Answer:

Question 28.
Surface area of a cylinder: S = 2πr2 + 2πrh; Solve for h.
Answer:
The given Surface area of a cylinder is:
S = 2πr² + 2πrh
So,
S = 2πr ( r + h )
S / 2πr = r + h
h = S / 2πr – r
Hence, from the above,
We can conclude that the value of h is: S / ( 2π
Question 29.
Area of a trapezoid: A = \(\frac{1}{2}\)h(b1 + b2); Solve for b2.
Answer:

Question 30.
The average acceleration of an object: ![]() ; Solve for v1.
; Solve for v1.
Answer:
The given average acceleration of an object is:
a = ( v1 – v0 ) / t
So,
at = v1 – v0
v1 = at + v0
Hence, from the above,
We can conclude that the value of v1 is: at + v0
Question 31.
REWRITING A FORMULA
A common statistic used in professional football is the quarterback rating. This rating is made up of four major factors. One factor is the completion rating given by the formula
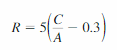
where C is the number of completed passes and A is the number of attempted passes. Solve the formula for C.
Answer:

Question 32.
REWRITING A FORMULA
Newton’s law of gravitation is given by the formula
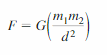
where F is the force between two objects of masses m1 and m2, G is the gravitational constant, and d is the distance between the two objects. Solve the formula for m1.
Answer:
The value of m1 is: Fd² / Gm2
Explanation:
The given Newton’s law of gravitation is given by:
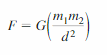
where
F is the force between two objects of masses m1 and m2
G is the gravitational constant
d is the distance between the two objects.
Now,
( m1m2 ) = Fd² / G
m1 = Fd² / Gm2
Hence, from the above,
We can conclude that the value of m1 is: Fd² / Gm2
Question 33.
MODELING WITH MATHEMATICS
The sale price S (in dollars) of an item is given by the formula S = L – rL, where L is the list price (in dollars) and r is the discount rate (in decimal form).
a. Solve the formula for r.

b. The list price of the shirt is $30. What is the discount rate?
Answer:

Question 34.
MODELING WITH MATHEMATICS
The density d of a substance is given by the formula d = \(\frac{m}{V}\), where m is its mass and V is its volume.

a. Solve the formula for m?
Answer:
The given density d of a substance is given by:
d = \(\frac{m}{V}\)
So,
d × V = m
Hence, from the above,
We can conclude that the value of m is: d × V
b. Find the mass of the pyrite sample.
Answer:
The mass of the pyrite sample is: 6.012 gm
Explanation:
The given figure is:

From the above figure,
The density of Pyrite = 5.01 g/cm³
The volume of Pyrite = 1.2 cm³
From part (a),
The mass of Pyrite = Density × Volume
So,
The mass of Pyrite ( m ) = 5.01 × 1.2
= 6.012 gm
Hence, from the above,
We can conclude that the mass of Pyrite is: 6.012 gm
Question 35.
PROBLEM-SOLVING
You deposit $2000 in an account that earns simple interest at an annual rate of 4%. How long must you leave the money in the account to earn $500 in interest?
Answer:

Question 36.
PROBLEM-SOLVING
A flight averages 460 miles per hour. The return flight averages 500 miles per hour due to a tailwind. The total flying time is 4.8 hours. How long is each flight? Explain.

Answer:
The time taken for flight is: 2.5 hours
The time taken for return is: 2.3 hours
Explanation:
It is given that a flight averages 460 miles per hour. The return flight averages 500 miles per hour due to a tailwind. The total flying time is 4.8 hours.
We know that,
Speed = Distance / Time
Time = Distance / Speed
It is also given that the total flying time is 4.8 hours
Let the distance be D
So,
\(\frac{D}{460}\) + \(\frac{D}{500}\) = 4.8
\(\frac{460 + 500}{230,000}\) = 4.8 / D
\(\frac{960}{230,000}\) = 4.8 / D
D = 4.8 × \(\frac{230,000}{960}\)
D = 1,150 miles
Hence,
The time taken for flight = 1,150 ÷ 460 = 2.5 hpurs
The time taken for return = 1,150 ÷ 500 = 2.3 hours
Question 37.
USING STRUCTURE
An athletic facility is building an indoor track. The track is composed of a rectangle and two semicircles, as shown.
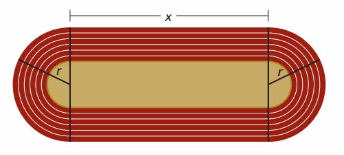
a. Write a formula for the perimeter of the indoor track.
b. Solve the formula for x.
c. The perimeter of the track is 660 feet, and r is 50 feet. Find x. Round your answer to the nearest foot.
Answer:
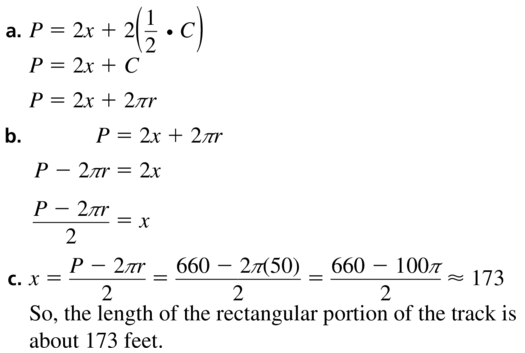
Question 38.
MODELING WITH MATHEMATICS
The distance d (in miles) you travel in a car is given by the two equations shown, where t is the time (in hours) and g is the number of gallons of gasoline the car uses.
a. Write an equation that relates g and t.
Answer:
The given equations are:
d = 55t ——————— (1)
d = 20g ——————— (2)
By the law of Equality,
55t = 20g [ As the LHS for both the equations are equal, make the RHS equal ]
t / g = 20 / 55
t / g = 4 / 11
b. Solve the equation for g.
Answer:
From the given figure,
d = 20g
d = 55t
From part (a),
t / g = 4 / 11
11t = 4g
g = 11t / 4
Hence, from the above,
We can conclude that the value of g is: 11t / 4
c. You travel for 6 hours. How many gallons of gasoline does the car use? How far do you travel? Explain.
Answer:
From part (b),
g = 11t / 4
Where,
g is the number of gallons of gasoline
It is given that you travel for 6 hours
So,
t = 6 hours
Now,
g = ( 11 × 6 ) / 4
g = 66/4 gallons
Hence, from the above,
We can conclude that the number of gallons of gasoline is: 66 / 4 gallons
Question 39.
MODELING WITH MATHEMATICS
One type of stone formation found in Carlsbad Caverns in New Mexico is called a column. This cylindrical stone formation connects to the ceiling and the floor of a cave.

a. Rewrite the formula for the circumference of a circle, so that you can easily calculate the radius of a column given its circumference.
b. What is the radius (to the nearest tenth of a foot) of a column that has a circumference of 7 feet? 8 feet? 9 feet?
c. Explain how you can find the area of a cross-section of a column when you know its circumference.
Answer:

Question 40.
HOW DO YOU SEE IT?
The rectangular prism shown has bases’ with equal side lengths.
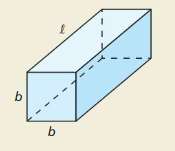
a. Use the figure to write a formula for the surface area S of the rectangular prism.
Answer:
The given figure is:

From the above figure,
The surface area of the rectangular prism ( S) = 2 ( lb + bh + lh )
Where,
l is the length of the rectangular prism
b is the Width of the rectangular prism
h is the height of the rectangular prism
b. Your teacher asks you to rewrite the formula by solving for one of the side lengths, b or ℓ. Which side length would you choose? Explain your reasoning.
Answer:
From part (a),
The surface area of the rectangular prism ( S ) = 2 ( lb + bh + lh )
S / 2 = lb + bh + lh
S / 2 = b ( l + h ) + bh
S / 2 = b ( l + b + h )
b = S / 2 ( l + b + h )
Hence, from the above,
We can conclude that the value of b is: S / 2 ( l + b + h )
Question 41.
MAKING AN ARGUMENT
Your friend claims that Thermometer A displays a greater temperature than Thermometer B. Is your friend correct? Explain your reasoning.

Answer:

Question 42.
THOUGHT-PROVOKING
Give a possible value for h. Justify your answer. Draw and label the figure using your chosen value of h.
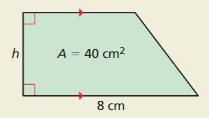
Answer:
The completed figure is:
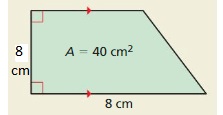
The value of h is: 5 cm
Explanation:
The given figure is:

From the given figure,
We can say that the geometrical figure is the parallelogram
We know that,
Area of the parallelogram = Base × Height
From the given figure,
Area of the parallelogram = 40 cm²
The base of the parallelogram = 8 cm
So,
40 = 8 × Height
Height = 40 ÷ 8
Height = 5 cm
Hence, from the above,
We can conclude that
The completed figure is:

The value of h is: 5 cm
MATHEMATICAL CONNECTIONS
In Exercises 43 and 44, write a formula for the area of the regular polygon. Solve the formula for the height h.
Question 43.
Answer:
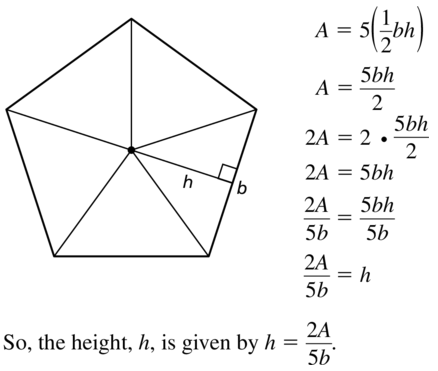
Question 44.
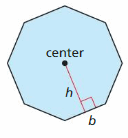
Answer:
The value of h is: A / 3b
Explanation:
The given figure is:

From the above figure,
We can say that the figure is Hexagon
Now,
The Hexagon with the six triangles is:
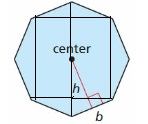
So,
From the figure,
There are 6 triangles
We know that,
The area of a triangle = \(\frac{1}{2}\) × Base × Height
So,
The area of the Hexagon = The area of the 6 triangles
= 6 ( \(\frac{1}{2}\) ) × Base × Height
Let,
The area of the Hexagon be A
The height of the hexagon be h
The Base of the hexagon be b
So,
A = 6 ( \(\frac{1}{2}\) ) × Base × Height
A = 3 × Base × Height
Base × Height = A / 3
Height = A / ( 3 × Base )
So,
h = A / 3b
Hence, from the above,
We can conclude that the value of h is: A / 3b
REASONING
In Exercises 45 and 46, solve the literal equation for a.
Question 45.
![]()
Answer:

Question 46.
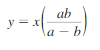
Answer:
The value of a is: \(\frac{by}{y – bx}\)
Explanation:
The given literal equation is:
y = x [ \(\frac{ab}{a – b}\)
\(\frac{ab}{a – b}\) = y / x
x ( ab ) = y ( a – b )
abx = ay – by
by = ay – abx
by = a ( y – bx )
a = \(\frac{by}{y – bx}\)
Hence, from the above,
We can conclude that the value of a is: \(\frac{by}{y – bx}\)
Maintaining Mathematical Proficiency
Evaluate the expression.
Question 47.
15 – 5 + 52
Answer:
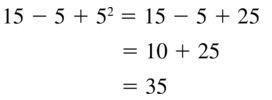
Question 48.
18 • 2 – 42 ÷ 8
Answer:
The given expression is:
18 ⋅ 2 – 4² ÷ 8
We have to remember that,
When there is an expression to solve with multiple mathematical symbols, we have to follow the BODMAS rule
BODMAS indicates the hierarchy we have to follow when we will solve mathematical symbols
In BODMAS,
B – Brackets
O – Of
D – Division
M – Multiplication
A – Addition
S – Subtraction
So,
18 ⋅ 2 – 4² ÷ 8 = 18 ⋅ 2 – ( 4 × 4 ) ÷ 8
= 18 ⋅ 2 – 2
= 36 – 2
= 34
Question 49.
33 + 12 ÷ 3 • 5
Answer:
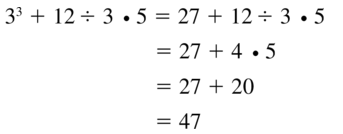
Question 50.
25(5 – 6) + 9 ÷ 3
Answer:
The given expression is:
25(5 – 6) + 9 ÷ 3
We have to remember that,
When there is an expression to solve with multiple mathematical symbols, we have to follow the BODMAS rule
BODMAS indicates the hierarchy we have to follow when we will solve mathematical symbols
In BODMAS,
B – Brackets
O – Of
D – Division
M – Multiplication
A – Addition
S – Subtraction
So,
25(5 – 6) + 9 ÷ 3 = ( 2 × 2 × 2 × 2 × 2 ) ( 5 – 6 ) + ( 9 ÷ 3 )
= ( 2 × 2 × 2 × 2 × 2 ) ( 5 – 6 ) + 3
= ( 2 × 2 × 2 × 2 × 2 ) ( -1 ) + 3
= -( 2 × 2 × 2 × 2 × 2 ) + 3
= -32 + 3
= -29
Solve the equation. Graph the solutions, if possible. (Section 1.4)
Question 51.
| x – 3 | + 4 = 9
Answer:
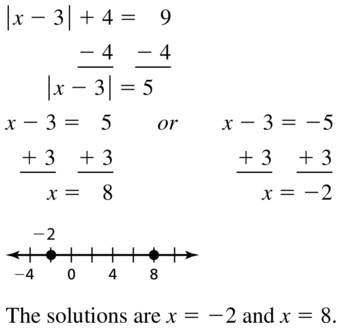
Question 52.
| 3y – 12 | – 7 = 2
Answer:
The values of y are: 7 and 1
Explanation:
The given absolute value equation is:
| 3y – 12 | – 7 = 2
| 3y – 12 | = 2 + 7
| 3y – 12 | = 9
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
3y – 12 = 9 3y – 12 = -9
3y = 9 + 12 3y = -9 + 12
3y = 21 3y = 3
y = 21 / 3 y = 3 / 3
y = 7 y = 1
Hence, from the above,
We can conclude that the values of y are: 7 and 1
Question 53.
2 | 2r + 4 | = -16
Answer:

Question 54.
-4 | s + 9 | = -24
Answer:
The value of s is: -3 and -15
Explanation:
The given absolute value equation is:
-4 | s + 9 | = -24
| s + 9 | = -24 ÷ ( -4 )
| s + 9 | = 6 [ Since – ÷ – = + ]
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
s + 9 = 6 s + 9 = -6
s = 6 – 9 s = -6 – 9
s = -3 s = -15
Hence, from the above,
We can conclude that the values of s are: -3 and -15
Solving Linear Equations Performance Task: Magic of Mathematics
1.4–1.5 What Did You Learn?
Core Vocabulary

Core Concepts
Section 1.4
Section 1.5
![]()
Mathematical Practices
Question 1.
How did you decide whether your friend’s argument in Exercise 46 on page 33 made sense?
Answer:
On page 33 in Exercise 46,
The given absolute equation is:
| 3x + 8 | – 9 = -5
| 3x + 8 | = -5 + 9
| 3x + 8 | = 4
So, from the absolute equation,
We can say that the given absolute value equation has a solution
But, according to your friend,
The argument is that the absolute value equation has no solution
Question 2.
How did you use the structure of the equation in Exercise 59 on page 34 to rewrite the equation?
Answer:
The given absolute value equation in Exercise 59 on page 34 is:
8 | x + 2 | – 6 = 5 | x + 2 | + 3
The above equation can be re-written as:
8 | x + 2 | – 5 | x + 2 | = 3 + 6
3 | x + 2 | = 9
Hence, from the above,
We can conclude that the re-written form of the given absolute value equation is:
3 | x + 2 | = 9
Question 3.
What entry points did you use to answer Exercises 43 and 44 on page 42?
Answer:
In Exercises 43 and 44 on page 42,
We used the triangles as an entry point
In Exercise 43,
The given figure is a pentagon
Using the above entry point,
We divided the pentagon into 5 triangles
In Exercise 44,
The given figure is a Hexagon
Using the above entry point,
We divided the hexagon into 6 triangles.
Performance Task
Magic of Mathematics
Have you ever watched a magician perform a number trick? You can use algebra to explain how these types of tricks work.

To explore the answers to these questions and more, go to 
Solving Linear Equations Chapter Review
1.1 Solving Simple Equations (pp. 3–10)
a. Solve x − 5 = −9. Justify each step.
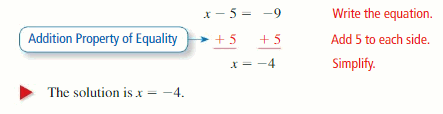
b. Solve 4x = 12. Justify each step.
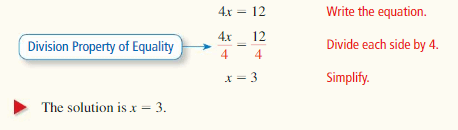
Solve the equation. Justify each step. Check your solution.
Question 1.
z + 3 = -6
Answer:
The value of z is: -9
Explanation:
The given equation is:
z + 3 = -6
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
z = -6 – ( +3 )
z = -6 – 3
z = -9
Hence, from the above,
We can conclude that the value of z is: -9
Question 2.
2.6 = -0.2t
Answer:
The value of t is: -13
Explanation:
The given equation is:
2.6 = -0.2t
\(\frac{26}{10}\) = –\(\frac{2}{10}\)t
t = \(\frac{26}{10}\) ÷ ( –\(\frac{2}{10}\) )
t = – \(\frac{26}{10}\) × \(\frac{10}{2}\)
t = -13
Hence, from the above,
We can conclude that the value of t is: -13
Question 3.
– \(\frac{n}{5}\) = -2
Answer:
The value of n is: 10
Explanation:
The given equation is:
–\(\frac{n}{5}\) = -2
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-n = -2 × 5
-n = -10
n = 10
Hence, from the above,
We can conclude that the value of n is: 10
1.2 Solving Multi-Step Equations (pp. 11–18)
Solve −6x + 23 + 2x = 15.

Solve the equation. Check your Solution.
Question 4.
3y + 11 = -16
Answer:
The value of y is: -9
Explanation:
The given equation is:
3y + 11 = -16
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
3y = -16 – 11
3y = -27
y = -27 ÷ 3
y = -9
Hence, from the above,
We can conclude that the value of y is: -9
Question 5.
6 = 1 – b
Answer:
The value of b is: -5
Explanation:
The given equation is:
6 = 1 – b
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
b = 1 – 6
b = -5
Hence, from the above,
We can conclude that the value of b is: -5
Question 6.
n + 5n + 7 = 43
Answer:
The value of n is: 6
Explanation:
The given equation is:
n + 5n + 7 = 43
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
6n + 7 = 43
6n = 43 – 7
6n = 36
n = 36 ÷ 6
n = 6
Hence, from the above,
We can conclude that the value of n is: 6
Question 7.
-4(2z + 6) – 12 = 4
Answer:
The value of z is: -5
Explanation:
The given equation is:
-4 ( 2z + 6 ) – 12 = 4
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
-4 ( 2z + 6 ) = 4 + 12
-4 ( 2z + 6 ) = 16
-4 ( 2z ) – 4 ( 6 ) = 16
-8z – 24 = 16
-8z = 16 + 24
-8z = 40
z = 40 ÷ ( -8 )
z = -5
Hence, from the above,
We can conclude that the value of z is: -5
Question 8.
\(\frac{3}{2}\)(x – 2) – 5 = 19
Answer:
The value of x is: 18
Explanation:
The given equation is:
\(\frac{3}{2}\) ( x – 2 ) – 5 = 19
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
\(\frac{3}{2}\) ( x – 2 ) = 19 + 5
\(\frac{3}{2}\) ( x – 2 ) = 24
x – 2 = 24 × \(\frac{2}{3}\)
x – 2 = \(\frac{24}{1}\) × \(\frac{2}{3}\)
x – 2 = 16
x = 16 + 2
x = 18
Hence, from the above,
We can conclude that the value of x is: 18
Question 9.
6 = \(\frac{1}{5}\)w + \(\frac{7}{5}\)w – 4
Answer:
The value of w is: \(\frac{25}{4}\)
Explanation:
The given equation is:
6 = \(\frac{1}{5}\)w + \(\frac{7}{5}\)w – 4
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
6 + 4 = \(\frac{1}{5}\)w + \(\frac{7}{5}\)w
10 = w [ \(\frac{1 + 7}{5}\) ]
10 = \(\frac{8}{5}\)w
w = 10 × \(\frac{5}{8}\)
w = \(\frac{10}{1}\) × \(\frac{5}{8}\)
w = \(\frac{25}{4}\)
Hence, from the above,
We can conclude that the value of w is: \(\frac{25}{4}\)
Find the value of x. Then find the angle measures of the polygon.
Question 10.
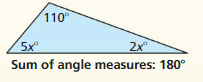
Answer:
The angle measures of the given polygon are: 110°, 50°, 20°
Explanation:
The given figure is:

From the above figure,
The angle measures are: 110°, 5x°, 2x°
It is also given that
The sum of the angle measures = 180°
So,
110 + 5x + 2x = 180°
7x = 180 – 110
7x = 70°
x = 70 / 7
x = 10°
Hence, from the above,
We can conclude that the angle measures of the given polygon are: 110°, 50°, 20°
Question 11.
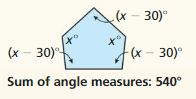
Answer:
The angle measures of the given polygon are: 126°, 126°, 96°, 96°, 96°
Explanation:
The given figure is:

From the above figure,
The angle measures of the given polygon are: ( x – 30 )°, x°, x°, ( x – 30 )°, ( x – 30 )°
It is also given that,
The sum of the angle measures of the given polygon = 540°
So,
( x – 30 )° + x° + x° + ( x – 30 )° + ( x – 30 )° = 540°
5x – 90° = 540°
5x = 540° + 90°
5x = 630°
x = 630 / 5
x = 126°
Hence,f rom the above,
We can conclude that the angle measures of the given polygon are: 126°, 126°, 96°, 96°, 96°
1.3 Solving Equations with Variables on Both Sides (pp. 19–24)
Solve 2( y − 4) = −4( y + 8).
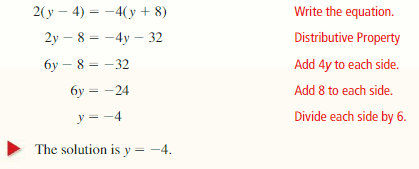
Solve the equation.
Question 12.
3n – 3 = 4n + 1
Answer:
The value of n is: -4
Explanation:
The given equation is:
3n – 3 = 4n + 1
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4n – 3n = -1 – 3
n = -4
Hence, from the above,
We can conclude that the value of n is: -4
Question 13.
5(1 + x) = 5x + 5
Answer:
The given equation has no solution
Explanation:
The given equation is:
5 ( 1 + x ) = 5x + 5
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
5 ( 1 ) + 5 ( x ) = 5x + 5
5 + 5x = 5x + 5
5 = 5x – 5x + 5
5 = 5
Hence, from the above,
We can conclude that the given equation has no solution
Question 14.
3(n + 4) = \(\frac{1}{2}\)(6n + 4)
Answer:
The given equation has no solution
Explanation:
The given equation is:
3 ( n + 4 ) = \(\frac{1}{2}\) ( 6n + 4 )
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
3 ( n ) + 3 ( 4 ) = \(\frac{1}{2}\) ( 6n + 4 )
3n + 12 = \(\frac{1}{2}\) ( 6n + 4 )
2 ( 3n + 12 ) = 6n + 4
2 ( 3n ) + 2 ( 12 ) = 6n + 4
6n + 24 = 6n + 4
24 = 6n – 6n + 4
24 = 4
Hence, from the above,
We can conclude that the given equation has no solution
1.4 Solving Absolute Value Equations (pp. 27–34)
a. Solve | x − 5 | = 3.
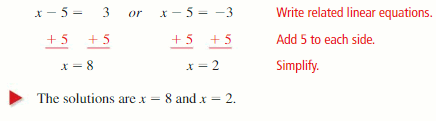
b. Solve | 2x + 6 | = 4x. Check your solutions.


Check the apparent solutions to see if either is extraneous.
The solution is x = 3. Reject x = -1 because it is extraneous.
Solve the equation. Check your solutions.
Question 15.
| y + 3 | = 17
Answer:
The value of y is: 14 or -20
Explaantion:
The given absolute value equation is:
| y + 3 | = 17
We know that,
| x | = x for x 0
| x | = -x for x < 0
So,
y + 3 = 17 y + 3 = -17
y = 17 – 3 y = -17 – 3
y = 14 y = -20
Hence, from the above,
We can conclude that the value of y is: 14 or -20
Question 16.
-2 | 5w – 7 | + 9 = -7
Answer:
The value of w is: 3 or –\(\frac{1}{5}\)
Explanation:
The given absolute value equation is:
-2 | 5w – 7 | + 9 = -7
-2 | 5w – 7 | = -7 – 9
-2 | 5w – 7 | = -16
| 5w – 7 | = -16 / ( -2 )
| 5w – 7 | = 8
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
5w – 7 = 8 5w – 7 = -8
5w = 8 + 7 5w = -8 + 7
5w = 15 5w = -1
w = 15 ÷ 5 w = –\(\frac{1}{5}\)
w = 3 w =-\(\frac{1}{5}\)
Hence, from the above,
We can conclude that the value of w is: 3 or –\(\frac{1}{5}\)
Question 17.
| x – 2 | = | 4 + x |
Answer:
The given absolute equation has no solution
Explanation:
The given absolute value equation is:
| x – 2 | = | 4 + x |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x – 2 = 4 + x – ( x – 2 ) = – ( 4 + x )
-2 = 4 2 = -4
Hence, from the above,
We can conclude that the given absolute equation has no solution
Question 18.
The minimum sustained wind speed of a Category 1 hurricane is 74 miles per hour. The maximum sustained wind speed is 95 miles per hour. Write an absolute value equation that represents the minimum and maximum speeds.
Answer:
The absolute value equation that represents the minimum and maximum speeds is:
| x – 84.5 | = 9.5
Explanation:
It is given that the minimum sustained wind speed of a Category 1 hurricane is 74 miles per hour. The maximum sustained wind speed is 95 miles per hour.
So,
The average wind speed sustained = ( 74 + 95 ) /2
= 169 / 2
= 84.5 miles per hour
Now,
The minimum wind speed from the average speed point = 84.5 – 74
= 9.5 miles per hour
So,
The absolute value equation that represents the minimum and maximum wind speed is:
| x – 84.5 | = 9.5
1.5 Rewriting Equations and Formulas (pp. 35–42)
a. The slope-intercept form of a linear equation is y = mx + b. Solve the equation for m.

b. The formula for the surface area S of a cylinder is S = 2πr2 + 2πrh. Solve the formula for the height h.

Solve the literal equation for y.
Question 19.
2x – 4y = 20
Answer:
The value of y is: ( x / 2 ) – 5
Explanation:
The given literal equation is:
2x – 4y = 20
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4y = 2x – 20
y = ( 2x – 20 ) / 4
y = ( 2x / 4 ) – ( 20 / 4 )
y = ( x / 2 ) – 5
Hence, from the above,
We can conclude that the value of y is: ( x / 2 ) – 5
Question 20.
8x – 3 = 5 + 4y
Answer:
The value of y is: 2x – 2
Explanation:
The given literal equation is:
8x – 3 = 5 + 4y
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
4y = 8x – 3 – 5
4y = 8x – 8
y = ( 8x – 8 ) / 4
y = ( 8x / 4 ) – ( 8 – 4 )
y = 2x – 2
Hence, from the above,
We can conclude that the value of y is: 2x – 2
Question 21.
a a = 9y + 3yx
Answer:
The value of y is: a² / ( 3x + 9 )
Explanation:
The given literal equation is:
a² = 9y + 3yx
When we convert any sign from LHS, then the sign will be converted into the opposite sign in RHS,
So,
+ in LHS is converted into – in RHS and vice-versa
× in LHS is converted into ÷ in RHS and vice-versa
So,
a² = y ( 3x + 9 )
y = a² / ( 3x + 9 )
Hence, from the above,
We can conclude that the value of y is: a² / ( 3x + 9 )
Question 22.
The volume V of a pyramid is given by the formula V = \(\frac{1}{3}\)Bh, where B is the area of the base and h is the height.
a. Solve the formula for h.
b. Find the height h of the pyramid.
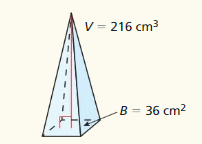
Answer:
a)
The value of h is: \(\frac{3V}{B}\)
Explanation:
The given formula is:
V = \(\frac{1}{3}\)Bh
Where,
B is the area of the base
h is the height
Now,
3V = Bh
h = \(\frac{3V}{B}\)
Hence, from the above,
We can conclude that the value of h is: \(\frac{3V}{B}\)
b)
The value of h is: 18 cm
Explanation:
From the given figure,
Area of the base ( B ) = 36 cm²
Volume of the base ( V ) = 216 cm³
From part (a),
h = \(\frac{3V}{B}\)
h = \(\frac{3 × 216}{36}\)
h = \(\frac{3 × 216}{36 × 1}\)
h = 18 cm
Hence, from the above,
We can conclud ethat the value of h is: 18 cm
Question 23.
The formula F = \(\frac{9}{5}\)(K – 273.15) + 32 converts a temperature from kelvin K to degrees Fahrenheit F.
a. Solve the formula for K.
b. Convert 180°F to kelvin K. Round your answer to the nearest hundredth.
Answer:
a)
The formula for K is:
K = \(\frac{5}{9}\) ( F – 32 ) + 273.15
Explanation:
The given formula for F is:
F = \(\frac{9}{5}\) ( K – 273.15 ) + 32
Now,
F – 32 = \(\frac{9}{5}\) ( K – 273.15 )
\(\frac{5}{9}\) ( F – 32 ) = K – 273.15
K = \(\frac{5}{9}\) ( F – 32 ) + 273.15
Hence, from the above,
We can conclude that the value of K is: \(\frac{5}{9}\) ( F – 32 ) + 273.15
Solving Linear Equations Chapter Test
Solve the equation. Justify each step. Check your solution.
Question 1.
x – 7 = 15
Answer:
The value of x is: 22
Explanation:
The given equation is:
x – 7 = 15
Now,
x = 15 + 7
x = 22
Hence, from the above,
We can conclude that the value of x is: 22
Question 2.
\(\frac{2}{3}\)x = 5
Answer:
The value of x is: \(\frac{15}{2}\)
Explanation:
The given equation is:
\(\frac{2}{3}\) x = 5
Now,
x = 5 × \(\frac{3}{2}\)
x = \(\frac{5}{1}\) × \(\frac{3}{2}\)
x = \(\frac{15}{2}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{15}{2}\)
Question 3
11x + 1 = -1 + x
Answer:
The value of x is: –\(\frac{1}{5}\)
Explanation:
The given equation is:
11x + 1 = -1 + x
Now,
11x – x = -1 – 1
10x = -2
x = –\(\frac{2}{10}\)
x = –\(\frac{1}{5}\)
Hence, from the above,
We can conclude that the value of x is: –\(\frac{1}{2}\)
Solve the equation.
Question 4.
2 | x – 3 | – 5 = 7
Answer:
The value of x is: 9 or -3
Explanation:
The given absolute value equation is:
2 | x – 3 | – 5 = 7
2 | x – 3 | = 7 + 5
2 | x – 3 | = 12
| x – 3 | = \(\frac{12}{2}\)
| x – 3 | = 6
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x – 3 = 6 x – 3 = -6
x = 6 + 3 x = -6 + 3
x = 9 x = -3
Hence, from the above,
We can conclude that the value of x is: 9 or -3
Question 5.
| 2x – 19 | = 4x + 1
Answer:
The value of x is: -10 or 3
Explanation:
The given absolute value equation is:
| 2x – 19 | = 4x + 1
We know that,
| x | = x for x > 0
| x | = -x for x < 0
4x + 1 = 2x – 19 4x + 1 = – ( 2x – 19 )
4x – 2x = -19 – 1 4x + 2x = 19 – 1
2x = -20 6x = 18
x = \(\frac{-20}{2}\) x = \(\frac{18}{6}\)
x = -10 x = 3
Hence, from the above,
We can conclude that the value of x is: -10 or 3
Question 6.
-2 + 5x – 7 = 3x – 9 + 2x
Answer:
The given absolute equation has no solution
Explanation:
The given equation is:
-2 + 5x – 7 = 3x – 9 + 2x
5x – 9 = 5x – 9
Hence, from the above,
We can conclude that the given absolute value equation has no solution
Question 7.
3(x + 4) – 1 = -7
Answer:
The value of x is: -6
Explanation:
The given equation is:
3 ( x + 4 ) – 1 = -7
So,
3 ( x ) + 3 ( 4 ) = -7 + 1
3x + 12 = -6
3x = -6 – 12
3x = -18
x = –\(\frac{18}{3}\)
x = -6
Hence, from the above,
We can conclude that the value of x is: -6
Question 8.
| 20 + 2x | = | 4x + 4 |
Answer:
The value of x is: 8
Explanation:
The given absolute value equation is:
| 20 + 2x | = | 4x + 4 |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
20 + 2x = 4x + 4
4x – 2x = 20 – 4
2x = 16
x = \(\frac{16}{2}\)
x = 8
Hence, from the above,
We can conclude that the value of x is: 8
Question 9.
\(\frac{1}{3}\)(6x + 12) – 2(x – 7) = 19
Answer:
The given equation has no solution
Explanation:
The given equation is:
\(\frac{1}{3}\) ( 6x + 12 ) – 2 ( x – 7 ) = 19
Now,
\(\frac{1}{3}\) ( 6x – 12 ) = 19 + 2 ( x – 7 )
\(\frac{1}{3}\) ( 6x – 12 ) = 19 + 2x – 14
\(\frac{1}{3}\) ( 6x – 12 ) = 2x + 5
1 ( 6x – 12 ) = 3 ( 2x + 5 )
6x – 12 = 6x + 15
6x – 6x = 15 + 12
15 = -12
Hence, from the above,
We can conclude that the given equation has no solution
Describe the values of c for which the equation has no solution. Explain your reasoning.
Question 10.
3x – 5 = 3x – c
Answer:
The value of c is: 5
Explanation:
The given equation is:
3x – 5 = 3x – c
It is given that the equation has no solution
So,
3x – 3x – 5 =-c
-c = -5
c = 5
Hence, from the above,
We can conclude that the value of c is: 5
Question 11.
| x – 7 | = c
Answer:
The value of c is: -7
Explanation:
The given absolute value equation is:
| x – 7 | = c
It is given that the equation has no solution i.e., x = 0
So,
0 – 7 = c
c = -7
Hence, from the above,
We can conclude that the value of c is: -7
Question 12.
A safety regulation states that the minimum height of a handrail is 30 inches. The maximum height is 38 inches. Write an absolute value equation that represents the minimum and maximum heights.
Answer:
The absolute value expression that represents the minimum and maximum heights is:
| x – 64 | = 34
Explanation:
It is given that a safety regulation states that the minimum height of a handrail is 30 inches. The maximum height is 38 inches.
So,
The average height of a handrail = ( 30 + 38 ) / 2
= 68 / 2
= 34 inches
Now,
The minimum height from the average height of a handrail = 34 + 30
= 64 inches
Hence,
The absolute value equation that represents the minimum and maximum height of a handrail is:
| x – 64 | = 34
Question 13.
The perimeter P (in yards) of a soccer field is represented by the formula P = 2ℓ + 2w, where ℓ is the length (in yards) and w is the width (in yards).
a. Solve the formula for w.
Answer:
The given formula is:
P = 2l + 2w
Where,
P is perimeter ( in yards )
l is the length ( in yards )
w is the width ( in yards )
So,
2w = P – 2l
w = ( P – 2l ) / 2
Hence, from the above,
We can conclude that the formula for w is:
w = ( P – 2l ) / 2
b. Find the width of the field.
Answer:
The given figure is:
From the above figure,
Perimeter ( P ) = 330 yd
Length ( l) = 100 yd
From part (a),
w = ( P – 2l ) /2
w = ( 330 – 100 ) / 2
w = 230 / 2
w = 115 yd
Hence, from the above,
We can conclude that the width of the field is: 115 yd
c. About what percent of the field is inside the circle?

Answer:
Given that,
The radius of the circle = 10 yds.
Field in side the circle = diameter.
The diameter of the circle = 2r = 2(10) = 20 yds.
Therefore The field of the circle is 20 yds.
Question 14.
Your car needs new brakes. You call a dealership and a local mechanic for prices.
a. After how many hours are the total costs the same at both places? Justify your answer.
Answer:
From the given table,
Let the total labor hours be x
So,
The total cost at the Dealership = ( Cost of parts ) + ( Labor cost per hour ) × ( Total labor hours )
= 24 + 99x
The total cost at the local mechanic = ( Cost of parts ) + ( Labor cost per hour ) × ( Total labor hours )
= 45 + 89x
It is given that the total cost is the same in both places
So,
24 + 99x = 45 + 89x
99x – 89x = 45 – 24
10x = 21
x = 21 / 10
x = 2.1 hours
Hence, from the above,
We can conclude that after 2.1 hours, the total cost will be the same in both places
b. When do the repairs cost less at the dealership? at the local mechanic? Explain.
Answer:
The given table is:

From the above table,
Compare the labor cost per hour
By comparison,
We can say that the labor cost per hour is less at the local mechanic
Hence, from the above,
We can conclude that the repair cost less at the local mechanic
Question 15.
Consider the equation | 4x + 20 | = 6x. Without calculating, how do you know that x = -2 is an extraneous solution?
Answer:
We know that,
The absolute value equations only accept the values greater than or equal to 0
Hence,
For the given absolute value equation,
| 4x + 20 | = 6x
x = -2 is an extraneous solution
Question 16.
Your friend was solving the equation shown and was confused by the result “-8 = -8.” Explain what this result means.
4(y – 2) – 2y = 6y – 8 – 4y
4y – 8 – 2y = 6y – 8 – 4y
2y – 8 = 2y – 8
-8 = -8
Answer:
The result ” -8 = -8 ” means that the solved equation has no solution
Solving Linear Equations Cumulative Assessment
Question 1.
A mountain biking park has 48 trails, 37.5% of which are beginner trails. The rest are divided evenly between intermediate and expert trails. How many of each kind of trail are there?
A. 12 beginner, 18 intermediate, 18 expert
B. 18 beginner, 15 intermediate, 15 expert
C. 18 beginner, 12 intermediate, 18 expert
D. 30 beginner, 9 intermediate, 9 expert
Answer:
The correct option is: B
The number of beginner trials is: 18
The number of intermediate trials is: 15
The number of expert trials is: 15
Explanation:
It is given that a mountain biking park has 48 trails, 37.5% of which are beginner trails. The rest are divided evenly between intermediate and expert trials.
So,
The number of beginner trials is 3.5 % of the total number of trials
It is given that the total number of trials is: 48
We know that,
The value of 37.5 % is: \(\frac{3}{8}\) [ 37.5 % = 50 % – 12.5 % ]
So,
The number of beginner trials = \(\frac{3}{8}\) × 48
= \(\frac{3}{8}\) × \(\frac{48}{1}\)
= \(\frac{3 × 48}{8 × 1}\)
= 18
So,
The number of intermediate and expert trials = ( The total number of trials ) – ( The number of beginner trials )
= 48 – 18
= 30 trials
It is also given that the intermediate trials and expert trails are divided evenly
So,
30 ÷ 2 = 15 trials each
Hence, from the above,
We can conclude that
The number of beginner trials is: 18
The number of intermediate trials is: 15
The number of expert trials is: 15
Question 2.
Which of the equations are equivalent to cx – a = b?
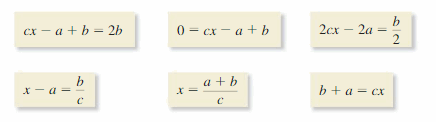
Answer:
The given equations are:
a) cx – a + b = 2b
b) 0 = cx – a + b
c) 2cx – 2a = b / 2
d) x – a = b / 2
e) x = ( a + b ) / c
f) b + a = cx
Now,
We have to find the equations from above that is equivalent to the given equation cx – a = b
Now,
a)
The given equation is:
cx – a + b = 2b
So,
cx – a = b – b
cx – a = b
b)
The given equation is:
0 = cx – a + b
So,
cx – a = -b
c)
The given equation is:
2cx – 2a = b / 2
So,
cx – a = b / 4
d )
The given equation is:
cx – a = b / 2
So,
2 ( cx – a ) = b
e)
The given equation is:
x = ( a + b ) / c
So,
cx = a + b
cx – a = b
f)
The given equation is:
b + a = cx
So,
cx – a = b
Hence, from the above,
We can conclude that the equations that are equivalent to cx – a = b is: a, e, f
Question 3.
Let N represent the number of solutions of the equation 3(x – a) = 3x – 6. Complete each statement with the symbol <, >, or =.
a. When a = 3, N ____ 1.
b. When a = -3, N ____ 1.
c. When a = 2, N ____ 1.
d. When a = -2, N ____ 1.
e. When a = x, N ____ 1.
f. When a = -x, N ____ 1.
Answer:
The given equation is:
3 ( x – a ) = 3x – 6
So,
3x – 3a = 3x – 6
Now,
a) When a = 3,
3x – 3 ( 3 ) = 3x – 6
3x – 9 = 3x – 6
9 = 6
Hence,
When a = 3 there is no solution
Hence,
N < 1
b) When a = -3
3x + 3 ( 3 ) =3 x – 6
9 = -6
Hence,
When a = -3, there is no solution
Hence,
N < 1
c) When a = 2
3x – 3 ( 2 ) = 3x – 6
3x – 6 =3x –
6 = 6
Hence,
When a= 2, there is no solution
Hence,
N < 1
d) When a = -2
3x + 3 ( 2 ) = 3x – 6
3x + 6 = 3x – 6
6 = -6
Hence,
When a = -2, thereis no solution
Hence,
N < 1
e) When a = x
3x – 3 ( x ) = 3x – 6
3x = 6
x = 6 / 3
x = 2
Hence,
When a x, theer is 1 solution
Hence,
N = 1
f) When a = -x
3x + 3 ( x ) = 3x – 6
6x – 3x = -6
3x = -6
x = -6 / 3
x = -2
Hence,
When a = -x, there is 1 solution
Hence,
N = 1
Question 4.
You are painting your dining room white and your living room blue. You spend $132 on 5 cans of paint. The white paint costs $24 per can, and the blue paint costs $28 per can.
a. Use the numbers and symbols to write an equation that represents how many cans of each color you bought.
Answer:
The number of cans of white paint is: 2
The number of cans of blue paint is: 3
Explanation:
It is given that you spend $132 on 5 cans of paint
It is also given that the white paint costs $24 per can and the blue paint costs $28 per can
Now,
Let
The number of white cans is: x
The number of blue cans be: 5 – x
So,
The total cost of paint = ( The number of white cans ) × ( The cost of white paint per can ) + ( The number of blue cans ) × ( The cost of blue paint per can )
132 = 24x + 28 ( 5 – x )
24x + 28 ( 5 ) – 28x = 132
140 – 4x = 132
4x = 140 – 132
4x = 8
x = 8 ÷ 4
x = 2
Hence, from the above,
We can conclude that
The number of cans of white paint is: 2
The number of cans of blue paint is: 3
b. How much would you have saved by switching the colors of the dining room and living room? Explain.
Answer:
The money you have saved by switching the colors of the dining room and living room is: $0
Explanation:
From part (a),
The number of white cans is: 2
The number of blue cans is: 3
It is given that white color is used in the dining room and the blue color is used in the living room
So,
The cost of white paint after interchanging the color in the living room = 24 × 2
= $48
The cost of blue paint after interchanging the color in the dining room = 28 × 3
= $84
So,
The total cost of paint after interchanging the colors = 48 + 84
= $132
Hence,
The amount of money saved = ( The money you paid for the paint before interchanging ) – ( The money you paid for the paint after interchanging )
= 132 – 132
=$0
Question 5.
Which of the equations are equivalent?
Answer:
The given equations are:
a ) 6x + 6 = -14
b ) 8x + 6 = -2x – 14
c ) 5x + 3 = -7
d ) 7x + 3 = 2x – 13
Now,
To find the equivalent equations, find the value of x
So,
a)
The given equation is:
6x + 6 = -14
6x = -14 – 6
6x = -20
x = -20 / 6
x = -10 / 3
b)
The given equation is:
8x + 6 = -2x – 14
8x + 2x = -14 – 6
10x = -20
x = -20 / 10
x = -2
c)
The given equation is:
5x + 3 = -7
5x = -7 -3
5x = -10
x= -10 / 5
x = -2
d)
The given equation is:
7x + 3 = 2x – 13
7x – 2x = -13 – 3
5x = -16
x = -16 / 5
Hence, from the above,
We can conclude that the equations c) and d) are equivalent
Question 6.
The perimeter of the triangle is 13 inches. What is the length of the shortest side?
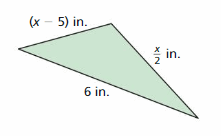
Answer:
The length of the shortest side is: 3 inches
Explanation:
We know that,
The perimeter is the sum of all the sides of the given figure
It is given that the perimeter of the triangle is: 13 inches
So,
The perimeter of the triangle = ( x – 5 ) + ( x / 2 ) + 6
13 = x + 1 + ( x / 2 )
13 = ( 2x / 2 ) + ( x / 2 ) + 1
3x / 2 = 13 – 1
3x / 2 = 12
3x = 12 × 2
3x = 24
x = 24 / 3
x = 8
So,
The lengths of all sides are: ( 8 – 5 ), 6, ( 8 / 2 ) = 3 inches, 6 inches, 4 inches
Hence, from the above,
We can conclude that the length of the shortest side is: 3 inches
Question 7.
You pay $45 per month for cable TV. Your friend buys a satellite TV receiver for $99 and pays $36 per month for satellite TV. Your friend claims that the expenses for a year of satellite TV are less than the expenses for a year of cable.
a. Write and solve an equation to determine when you and your friend will have paid the same amount for TV services.
Answer:
It is given that you pay $45 per month for cable TV. Your friend buys a satellite TV receiver for $99 and pays $36 per month for satellite TV
So,
Let the number of months be x
Now,
The time they paid the same amount for TV services is:
45x = 99 + 36x
45x – 36x = 99
9x= 99
x = 99 / 9
x = 11
Hence, from the above,
We can conclude that after 11 months, you and your friend will pay the same amount for TV services
b. Is your friend correct? Explain.
Answer:
Your friend is correct
Explanation:
We know that,
1 year = 12 months
So,
The expenses paid by you for TV services = 45x = 45 × 12 = $540
The expenses paid by your friend for TV services = 99 + 36x
= 99 + 36 ( 12 )
= 99 + 432
= $531
By comparing the expenses of you and your friend,
We can conclude that your friend is correct
Question 8.
Place each equation into one of the four categories.
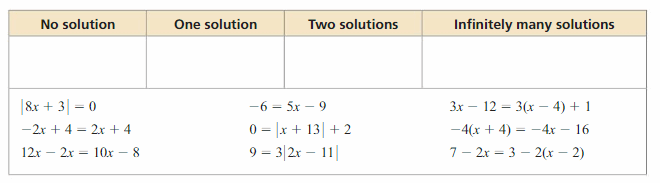
Answer:
|8x + 3| = 0
8x + 3 = 0
8x = -3
x = -3/8
Therefore, this equation has one solution.
-2x + 4 = 2x + 4
-2x = 2x
x = 0
12 – 2x = 10x – 8
20 = 12x
x = 20/12
Therefore, this equation has one solution.
-6 = 5x – 9
3 = 5x
x = 3/5
0 = |x + 13| + 2
|x + 13| = -2
9 = 3|2x – 11|
|2x – 11| = 3
2x – 11 = 3
2x – 11 = -3
Thus the equations has two solutions.
3x – 12 = 3(x – 4) + 1
3x – 12 = 3(x – 4) + 1
3x – 12 = 3x – 12 + 1
3x – 12 = 3x – 11
12 = 11
Since this equation is false, it has no solution.
-4(x + 4) = -4x – 16
-4x – 16 = -4x – 16
7 – 2x = 3 – 2(x – 2)
7 – 2x = 3 – 2x + 4
7 – 2x = 7 – 2x
Since this equation is true, it has infinitely many solutions.
Question 9.
A car travels 1000 feet in 12.5 seconds. Which of the expressions do not represent the average speed of the car?

Answer:
We know that,
Average speed = ( Distance ) ÷ ( Time )
It is given that a car travels 1000 feet in 12.5 seconds
So,
Average speed = 1000 / 12.5
= 80\(\frac{feet}{second}\)
Now,
The given options are:
A) 80\(\frac{second}{feet}\) B) 80\(\frac{feet}{second}\) C) \(\frac{80 feet}{second}\)
D) \(\frac{second}{ 80 feet}\)
Hence, from the above,
We can conclude that option B) represents the average speed