Want to master in Algebra 2 Ch 6 Concepts like Exponential Growth and Decay Functions, Natural Base e, Logarithms, and its functions, properties of logarithms, etc.? Then, accessing this guide is the perfect solution for your concerns. Big Ideas Math Algebra 2 Answers Chapter 6 Exponential and Logarithmic Functions make you understand the topics quickly and clear all your subject queries. Moreover, the BIM Algebra 2 Ch 6 Solutions prevailing are written by the subject experts based on the guidelines of the latest common core curriculum. Hence, download the Big Ideas Math Algebra 2 Ch 6 Exponential and Logarithmic Functions & enhance your maths skills.
Big Ideas Math Book Algebra 2 Answer Key Chapter 6 Exponential and Logarithmic Functions
BIM Algebra 2 Ch 6 Exponential and Logarithmic Functions covers Questions from Exercises 6.1 to 6.7, Review Tests, Chapter Tests, Cumulative Assessments, etc. With the help of this ultimate preparation guide provided performance task test, students can check their knowledge on Chapter 6 Exponential and Logarithmic Functions concepts. Tap on the link directly and practice each & every lesson in Ch 6 Big Ideas Math Algebra 2 Solution Key Pdf. Access online Big Ideas Math Book Algebra 2 Ch 6 Exponential and Logarithmic Functions Answers pdf without paying a single penny.
- Exponential and Logarithmic Functions Maintaining Mathematical Proficiency – Page 293
- Exponential and Logarithmic Functions Mathematical Practices – Page 294
- Lesson 6.1 Exponential Growth and Decay Functions – Page(295-302)
- Exponential Growth and Decay Functions 6.1 Exercises – Page(300-302)
- Lesson 6.2 The Natural Base e – Page(303-308)
- The Natural Base e 6.2 Exercises – Page(307-308)
- Lesson 6.3 Logarithms and Logarithmic Functions – Page(309-316)
- Logarithms and Logarithmic Functions 6.3 Exercises – Page(314-316)
- Lesson 6.4 Transformations of Exponential and Logarithmic Functions – Page(317-324)
- Transformations of Exponential and Logarithmic Functions 6.4 Exercises – Page(322-324)
- Exponential and Logarithmic Functions Study Skills: Forming a Weekly Study Group – Page 325
- Exponential and Logarithmic Functions 6.1–6.4 Quiz – Page 326
- Lesson 6.5 Properties of Logarithms – Page(327-332)
- Properties of Logarithms 6.5 Exercises -Page(331-332)
- Lesson 6.6 Solving Exponential and Logarithmic Equations -Page(333-340)
- Solving Exponential and Logarithmic Equations 6.6 Exercises – Page(338-340)
- Lesson 6.7 Modeling with Exponential and Logarithmic Functions – Page(341-348)
- Modeling with Exponential and Logarithmic Functions 6.7 Exercises – Page(346-348)
- Exponential and Logarithmic Functions Performance Task: Measuring Natural Disasters – Page 349
- Exponential and Logarithmic Functions Chapter Review – Page(350-352)
- Exponential and Logarithmic Functions Chapter Test – Page 353
- Exponential and Logarithmic Functions Cumulative Assessment – Page(354-355)
Exponential and Logarithmic Functions Maintaining Mathematical Proficiency
Evaluate the expression.
Question 1.
3 • 24
Answer:
3 • 24
3 × 2 × 2 × 2 × 2
3 × 16
48
Question 2.
(−2)5
Answer:
(−2)5
-2 × -2 × -2 × -2 × -2
= -32
Question 3.
−(\(\frac{5}{6}\))2
Answer:
−(\(\frac{5}{6}\))2
–\(\frac{25}{36}\)
Question 4.
(\(\frac{3}{4}\))3
Answer:
(\(\frac{3}{4}\))3
\(\frac{27}{64}\)
Find the domain and range of the function represented by the graph.
Question 5.
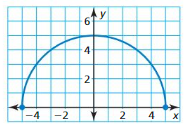
Answer:
The domain of the function is -5 ≤ x ≤ 5
The range of the function is 0 ≤ y ≤ 5
Question 6.
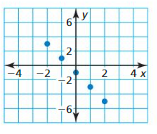
Answer:
The domain of the function is -2 ≤ x ≤ 2
The range of the function is -5 ≤ y ≤ 3
Question 7.
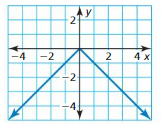
Answer:
The domain of the function is -4 ≤ x ≤ 4
The range of the function is 0 ≤ y ≤ -4
Question 8.
ABSTRACT REASONING
Consider the expressions −4n and (−4)n, where n is an integer. For what values of n is each expression negative? positive? Explain your reasoning.
Answer:
For the expressions −4n put n is equal to odd and even integers 1, 2, 3, 4, 5, 6, 7…
n = 1 then the expression will be -41 = -4
n = 2 then the expression will be -42 = -16
n = 3 then the expression will be -43 = -64 and so on
From the above explanation, it is clear that the expression −4n will be negative for both of odd and even integer.
The expression −4n will be negative for both of odd and even values of n and the expression (-4)n the expression will be negative for every odd integral and positive for every negative integral value of n.
Exponential and Logarithmic Functions Mathematical Practices
Mathematically proficient students know when it is appropriate to use general methods and shortcuts.
Monitoring Progress
Determine whether the data can be modeled by an exponential or linear function. Explain your reasoning. Then write the appropriate model and find y when x = 10
Question 1.
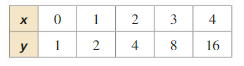
Answer:
Question 2.
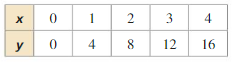
Answer:
Question 3.
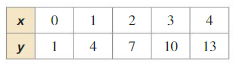
Answer:
Question 4.
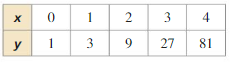
Answer:
Lesson 6.1 Exponential Growth and Decay Functions
Essential Question What are some of the characteristics of the graph of an exponential function?You can use a graphing calculator to evaluate an exponential function. For example, consider the exponential function f(x) = 2x

EXPLORATION 1
Identifying Graphs of Exponential Functions
Work with a partner. Match each exponential function with its graph. Use a table of values to sketch the graph of the function, if necessary.
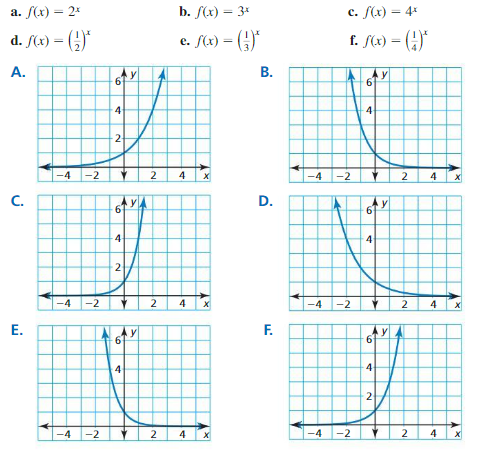
EXPLORATION 2
Characteristics of Graphs of Exponential Functions
Work with a partner. Use the graphs in Exploration 1 to determine the domain, range, and y-intercept of the graph of f(x) = bx, where b is a positive real number other than 1. Explain your reasoning.

Communicate Your Answer
Question 3.
What are some of the characteristics of the graph of an exponential function?
Answer:
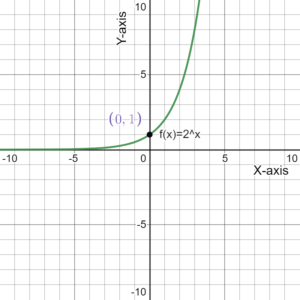
- The graph passes through the point (0,1)
- The domain is all real numbers.
- The range is y>0.
- The graph is increasing.
- The graph is asymptotic to the x-axis as x approaches negative infinity.
- The graph increases without bound as x approaches positive infinity.
- The graph is continuous.
Question 4.
In Exploration 2, is it possible for the graph of f (x) =b x to have an x-intercept? Explain your reasoning.
Answer:
Monitoring Progress
Tell whether the function represents exponential growth or exponential decay. Then graph the function.
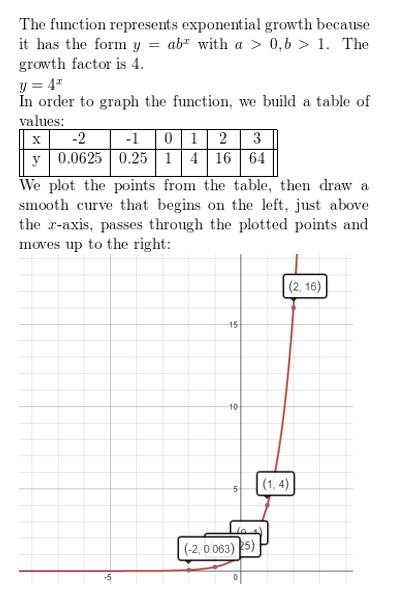
Question 1.
y = 4x
Answer:
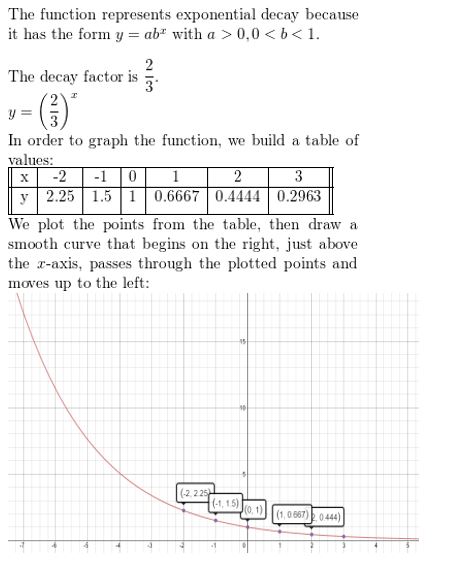
Question 2.
y = (\(\frac{2}{3}\))x
Answer:
Question 3.
f(x) = (0.25)x
Answer:

Question 4.
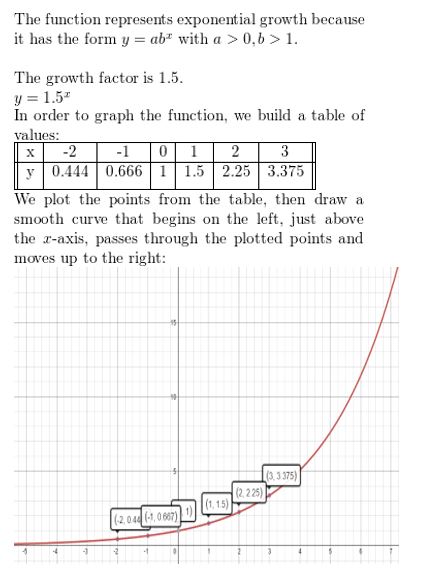
f(x) = (1.5)x
Answer:
Question 5.
WHAT IF?
In Example 2, the value of the car can be approximated by the model y = 25(0.9)t. Identify the annual percent decrease in the value of the car. Estimate when the value of the car will be $8000.
Answer:

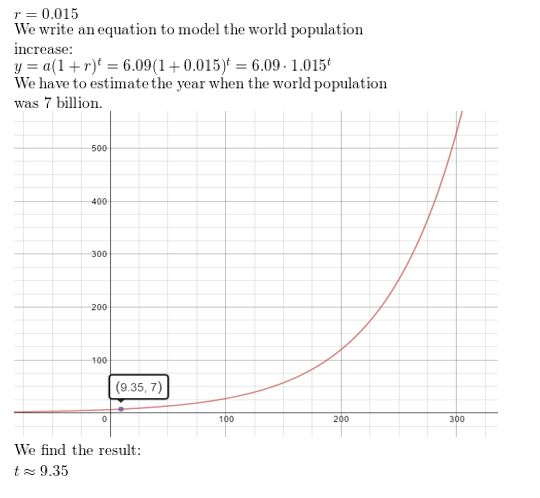
Question 6.
WHAT IF?
In Example 3, assume the world population increased by 1.5% each year. Write an equation to model this situation. Estimate the year when the world population was 7 billion.
Answer:
Question 7.
The amount y (in grams) of the radioactive isotope iodine-123 remaining after t hours is y = a(0.5)t/13, where a is the initial amount (in grams). What percent of the iodine-123 decays each hour?
Answer:

Question 8.
WHAT IF?
In Example 5, find the balance after 3 years when the interest is compounded daily.
Answer:
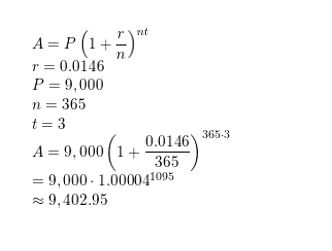
Exponential Growth and Decay Functions 6.1 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
In the exponential growth model y = 2.4(1.5)x, identify the initial amount, the growth factor, and the percent increase.
Answer:
![]()
Question 2.
WHICH ONE DOESN’T BELONG?
Which characteristic of an exponential decay function does not belong with the other three? Explain your reasoning

Answer:
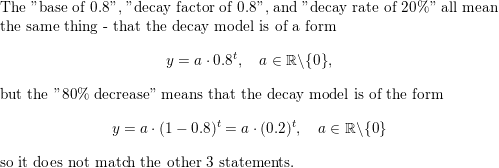
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, evaluate the expression for (a) x = -2 and (b) x = 3.
Question 3.
2x
Answer:
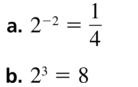
Question 4.
4x
Answer:
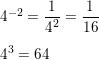
Question 5.
8 • 3x
Answer:

Question 6.
6 • 2x
Answer:
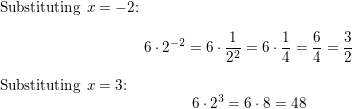
Question 7.
5 + 3x
Answer:
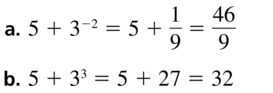
Question 8.
2x − 2
Answer:
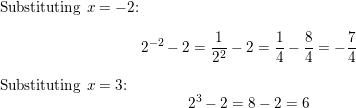
In Exercises 9–18, tell whether the function represents exponential growth or exponential decay. Then graph the function.
Question 9.
y = 6x
Answer:
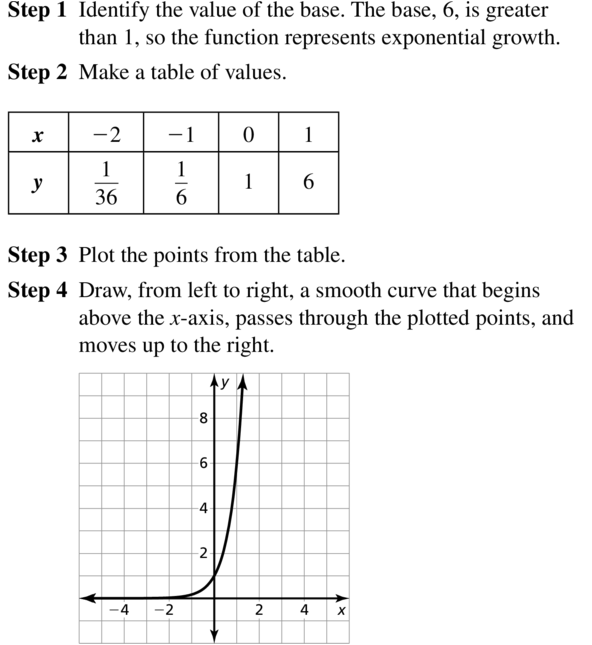
Question 10.
y = 7x
Answer:

Question 11.
y =(\(\frac{1}{6}\))x
Answer:
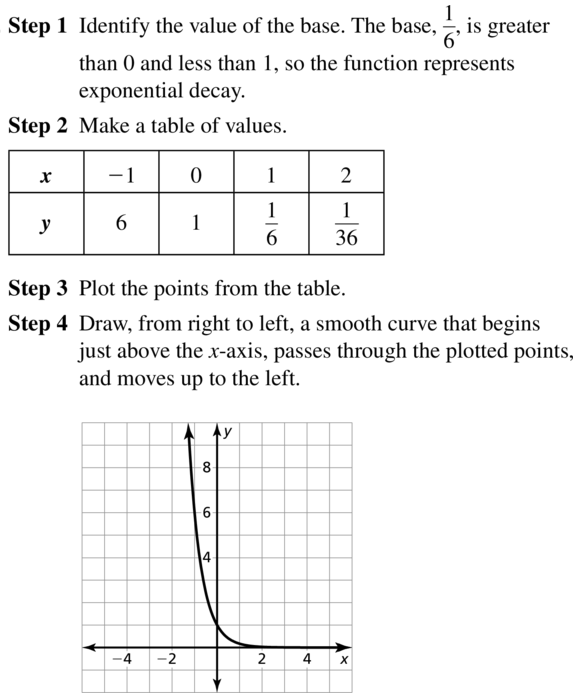
Question 12.
y =(\(\frac{1}{8}\))x
Answer:
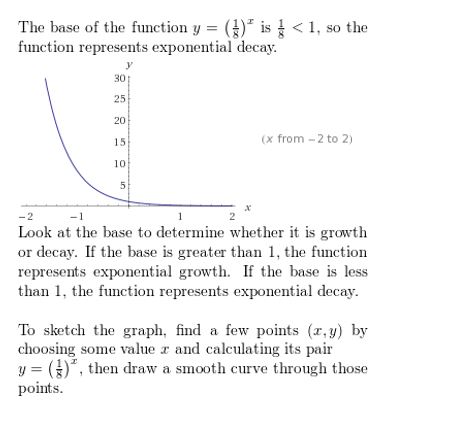
Question 13.
y = (\(\frac{4}{3}\))x
Answer:
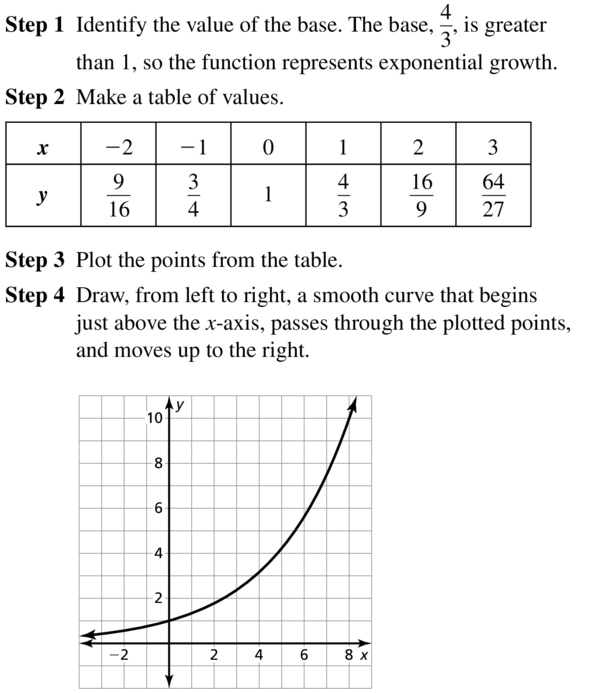
Question 14.
y = (\(\frac{2}{5}\))x
Answer:
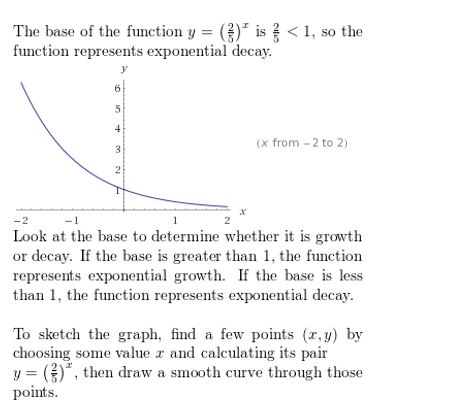
Question 15.
y = (1.2)x
Answer:
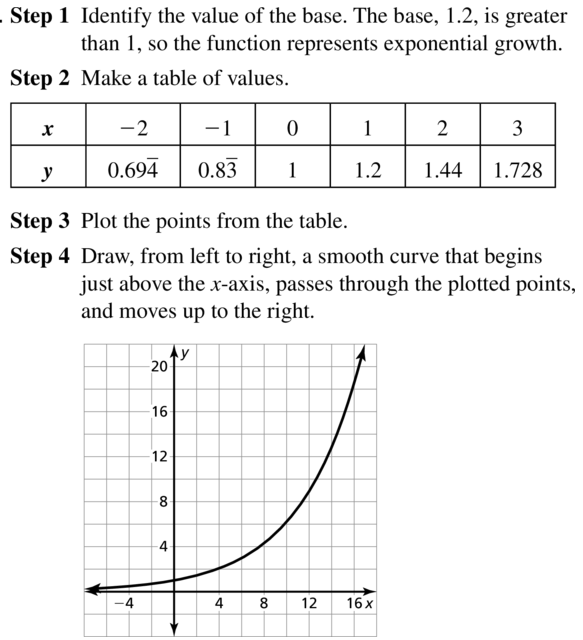
Question 16.
y = (0.75)x
Answer:
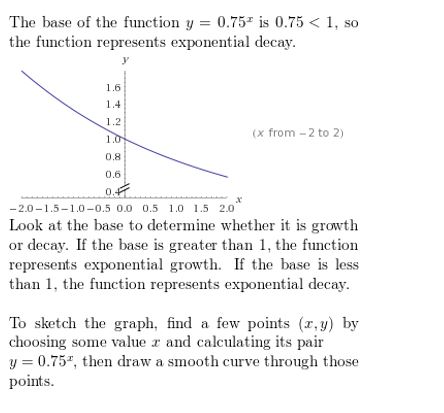
Question 17.
y = (0.6)x
Answer:
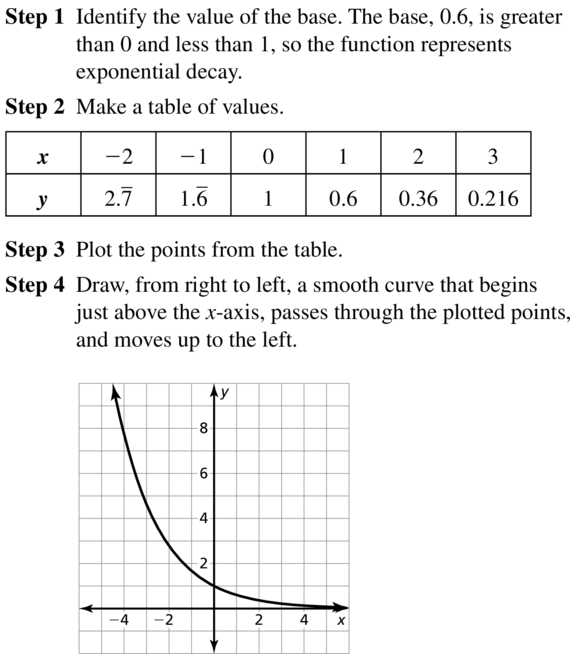
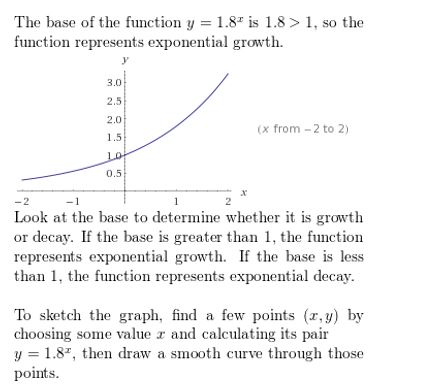
Question 18.
y = (1.8)x
Answer:
ANALYZING RELATIONSHIPS In Exercises 19 and 20, use the graph of f(x) = bx to identify the value of the base b.
Question 19.
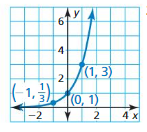
Answer:
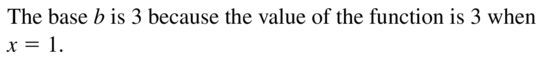
Question 20.
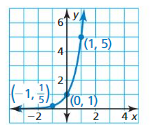
Answer:
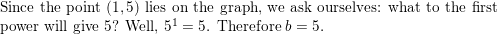
Question 21.
MODELING WITH MATHEMATICS
The value of a mountain bike y (in dollars) can be approximated by the model y = 200(0.75)t, where t is the number of years since the bike was new.
a. Tell whether the model represents exponential growth or exponential decay.
b. Identify the annual percent increase or decrease in the value of the bike.
c. Estimate when the value of the bike will be $50.
Answer:
Question 22.
MODELING WITH MATHEMATICS
The population P(in thousands) of Austin, Texas, during a recent decade can be approximated by y = 494.29(1.03)t, where t is the number of years since the beginning of the decade.
a. Tell whether the model represents exponential growth or exponential decay.
b. Identify the annual percent increase or decrease in population.
c. Estimate when the population was about 590,000.
Answer:

Question 23.
MODELING WITH MATHEMATICS
In 2006, there were approximately 233 million cell phone subscribers in the United States. During the next 4 years, the number of cell phone subscribers increased by about 6% each year.
a. Write an exponential growth model giving the number of cell phone subscribers y (in millions) t years after 2006. Estimate the number of cell phone subscribers in 2008.
b. Estimate the year when the number of cell phone subscribers was about 278 million.
Answer:

Question 24.
MODELING WITH MATHEMATICS
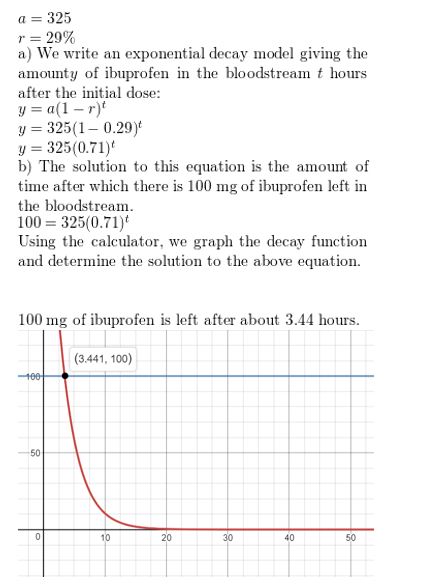
You take a 325 milligram dosage of ibuprofen. During each subsequent hour, the amount of medication in your bloodstream decreases by about 29% each hour.
a. Write an exponential decay model giving the amount y (in milligrams) of ibuprofen in your bloodstream t hours after the initial dose.
b. Estimate how long it takes for you to have 100milligrams of ibuprofen in your bloodstream.
Answer:
JUSTIFYING STEPS In Exercises 25 and 26, justify each step in rewriting the exponential function.
Question 25.

Answer:

Question 26.

Answer:

Question 27.
PROBLEM SOLVING
When a plant or animal dies, it stops acquiring carbon-14 from the atmosphere. The amount y (in grams) of carbon-14 in the body of an organism after t years is y = a(0.5)t/5730, where a is the initial amount (in grams). What percent of the carbon-14 is released each year?
Answer:
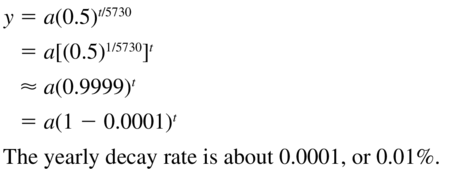
Question 28.
PROBLEM SOLVING
The number y of duckweed fronds in a pond after t days is y = a(1230.25)t/16, where a is the initial number of fronds. By what percent does the duckweed increase each day?

Answer:
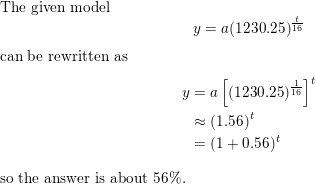
In Exercises 29–36, rewrite the function in the form y = a(1 + r)t or y = a(1 – r)t. Then state the growth or decay rate.
Question 29.
y = a(2)t/3
Answer:

Question 30.
y = a(4)t/6
Answer:

Question 31.
y = a(0.5)t/12
Answer:
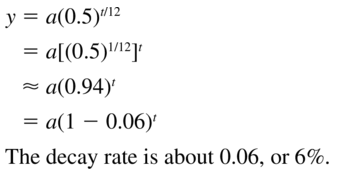
Question 32.
y = a(0.25)t/9
Answer:
y = a(0.25)t/9
y = [a(0.25)1/9]t
y ≈ a(0.86)t
y = a(1 – 0.14)t
y = a(1 – r)t
So, the decay rate is r = 0.14
Question 33.
y = a(\(\frac{2}{3}\))t/10
Answer:
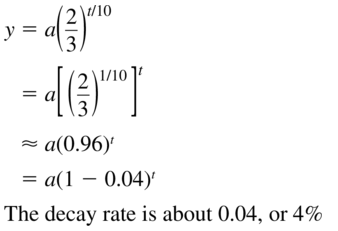
Question 34.
y = a(\(\frac{5}{4}\))t/22
Answer:
Question 35.
y = a(2)8t
Answer:

Question 36.
y = a(\(\frac{1}{3}\))3t
Answer:

Question 37.
PROBLEM SOLVING
You deposit $5000 in an account that pays 2.25% annual interest. Find the balance after 5 years when the interest is compounded quarterly.
Answer:
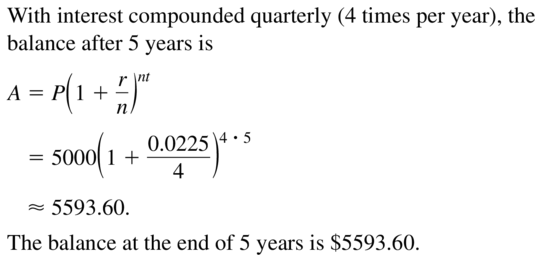
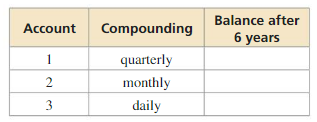
Question 38.
DRAWING CONCLUSIONS
You deposit $2200 into three separate bank accounts that each pay 3% annual interest. How much interest does each account earn after 6 years?
Answer:

Question 39.
ERROR ANALYSIS
You invest $500 in the stock of a company. The value of the stock decreases 2% each year. Describe and correct the error in writing a model for the value of the stock after t years.

Answer:

Question 40.
ERROR ANALYSIS
You deposit $250 in an account that pays 1.25% annual interest. Describe and correct the error in finding the balance after 3 years when the interest is compounded quarterly.
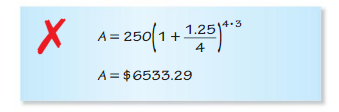
Answer:

In Exercises 41– 44, use the given information to find the amount A in the account earning compound interest after 6 years when the principal is $3500.
Question 41.
r = 2.16%, compounded quarterly
Answer:
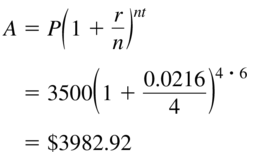
Question 42.
r = 2.29%, compounded monthly
Answer:

Question 43.
r = 1.83%, compounded daily
Answer:
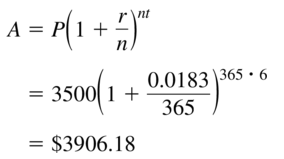
Question 44.
r = 1.26%, compounded monthly
Answer:

Question 45.
USING STRUCTURE
A website recorded the number y of referrals it received from social media websites over a 10-year period. The results can be modeled by y = 2500(1.50)t, where t is the year and 0 ≤ t≤ 9. Interpret the values of a and b in this situation. What is the annual percent increase? Explain.
Answer:

Question 46.
HOW DO YOU SEE IT?
Consider the graph of an exponential function of the form f (x) = abx.
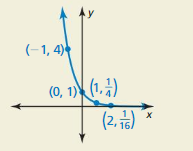
a. Determine whether the graph of f represents exponential growth or exponential decay.
b. What are the domain and range of the function? Explain.
Answer:

Question 47.
MAKING AN ARGUMENT
Your friend says the graph of f(x) = 2x increases at a faster rate than the graph of g (x) = x2 when x ≥ 0. Is your friend correct? Explain your reasoning.
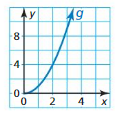
Answer:

Question 48.
THOUGHT PROVOKING
The function f(x) = bx represents an exponential decay function. Write a second exponential decay function in terms of b and x.
Answer:

Question 49.
PROBLEM SOLVING
The population p of a small town after x years can be modeled by the function p = 6850(1.03)x. What is the average rate of change in the population over the first 6 years? Justify your answer.
Answer:
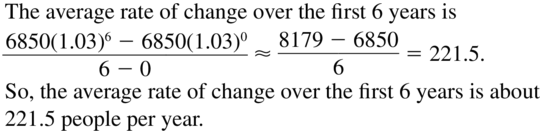
Question 50.
REASONING
Consider the exponential function f(x) = abx.
a. Show that \(\frac{f(x+1)}{f(x)}\) = b.
b. Use the equation in part (a) to explain why there is no exponential function of the form f(x) = abx whose graph passes through the points in the table below.
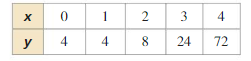
Answer:

Question 51.
PROBLEM SOLVING
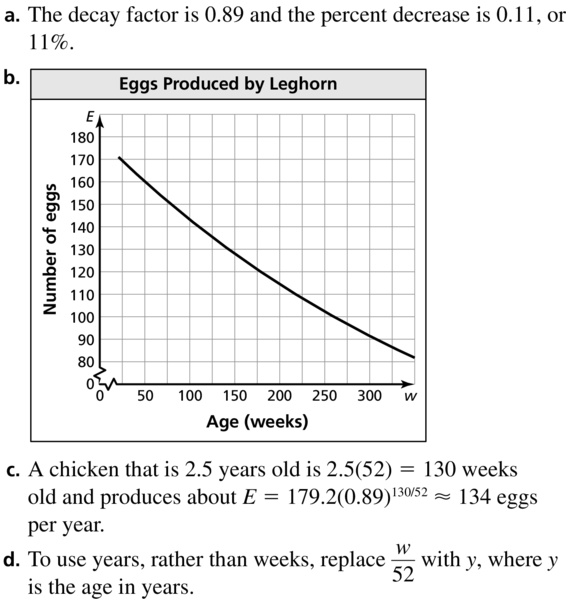
The number E of eggs a Leghorn chicken produces per year can be modeled by the equation E = 179.2(0.89)w/52, where w is the age (in weeks) of the chicken and w ≥ 22.

a. Identify the decay factor and the percent decrease.
b. Graph the model.
c. Estimate the egg production of a chicken that is 2.5 years old.d. Explain how you can rewrite the given equation so that time is measured in years rather than in weeks.
Answer:
Question 52.
CRITICAL THINKING
You buy a new stereo for $1300 and are able to sell it 4 years later for $275. Assume that the resale value of the stereo decays exponentially with time. Write an equation giving the resale value V(in dollars) of the stereo as a function of the time t (in years) since you bought it.
Answer:

Maintaining Mathematical Proficiency
Simplify the expression.
Question 53.
x9 • x2
Answer:
![]()
Question 54.
\(\frac{x^{4}}{x^{3}}\)
Answer:
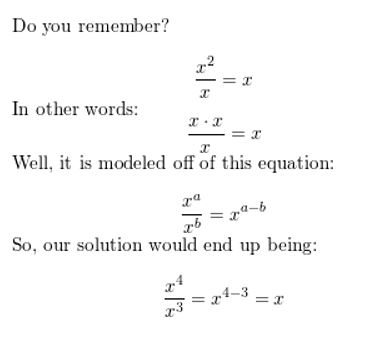
Question 55.
4x • 6x
Answer:
![]()
Question 56.
\(\left(\frac{4 x^{8}}{2 x^{6}}\right)4\)
Answer:

Question 57.
\(\frac{x+3 x}{2}\)
Answer:
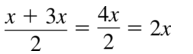
Question 58.
\(\frac{6x}{2}\) + 4x
Answer:
\(\frac{6x}{2}\) + 4x
(6x + 8x)/2 = 14x/2 = 7x
Question 59.
\(\frac{12x}{4x}\) + 5x
Answer:
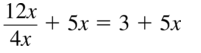
Question 60.
(2x • 3x5)3
Answer:
(6x6)³
= 216x18
Lesson 6.2 The Natural Base e
Essential Question What is the natural base e?
So far in your study of mathematics, you have worked with special numbers such as π and i. Another special number is called the natural base and is denoted by e. The natural base e is irrational, so you cannot find its exact value.
EXPLORATION 1
Approximating the Natural Base e
Work with a partner. One way to approximate the natural base e is to approximate the sum
1 + \(\frac{1}{1}+\frac{1}{1 \cdot 2}+\frac{1}{1 \cdot 2 \cdot 3}+\frac{1}{1 \cdot 2 \cdot 3 \cdot 4}+\cdots\)
Use a spreadsheet or a graphing calculator to approximate this sum. Explain the steps you used. How many decimal places did you use in your approximation?

EXPLORATION 2
Approximating the Natural Base e
Work with a partner. Another way to approximate the natural base e is to consider the expression(1 + \(\frac{1}{x}\))x .
As x increases, the value of this expression approaches the value of e. Copy and complete the table. Then use the results in the table to approximate e. Compare this approximation to the one you obtained in Exploration 1.

EXPLORATION 3
Graphing a Natural Base Function
Work with a partner. Use your approximate value of e in Exploration 1 or 2 to complete the table. Then sketch the graph of the natural base exponential function y =ex. You can use a graphing calculator and the ex key to check your graph. What are the domain and range of y = ex? Justify your answers.

Communicate Your Answer
Question 4.
What is the natural base e?
Answer:
Given,
The natural base e.
To find: What the natural base e is
The natural base, e, is sometime referred as the natural exponent. It is the base for natural log lb, which is written as loge(x).
Approximate value of e is 2.71828 and it is used for calculating growth and decay problems.
The expression (1 + 1/x)^x approaches to e as x increases.
Question 5.
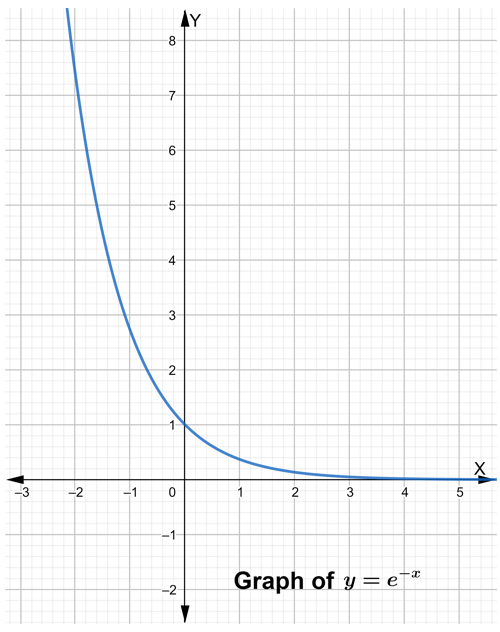
Repeat Exploration 3 for the natural base exponential function y = e-x. Then compare the graph of y = ex to the graph of y = e-x.
Answer:
Question 6.
The natural base e is used in a wide variety of real-life applications. Use the Internet or some other reference to research some of the real-life applications of e.
Answer:
Monitoring Progress
Simplify the expression.
Question 1.
e7 • e4
Answer:

Question 2.
\(\frac{24 e^{8}}{8 e^{5}}\)
Answer:

Question 3.
(10e-3x)3
Answer:

Tell whether the function represents exponential growth or exponential decay. Then graph the function.
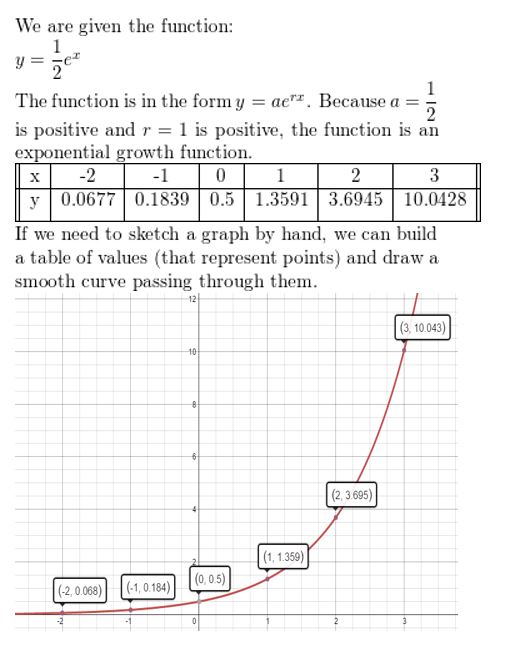
Question 4.
y = \(\frac{1}{2}\)ex
Answer:
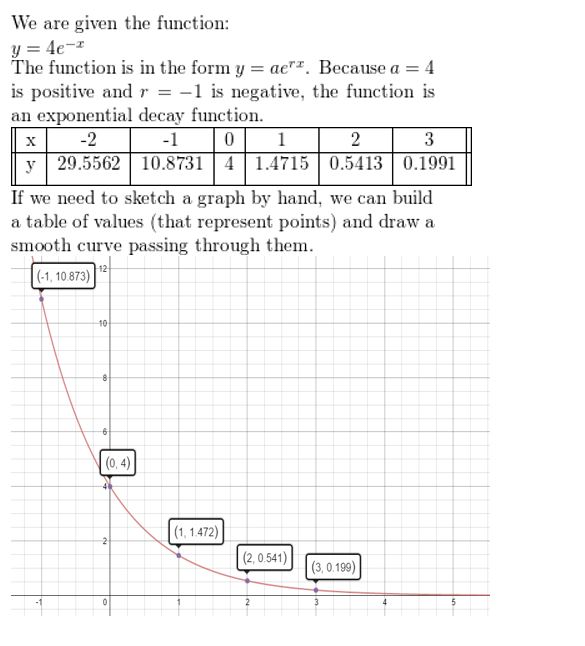
Question 5.
y = 4e-x
Answer:
Question 6.
f(x) = 2e2x
Answer:
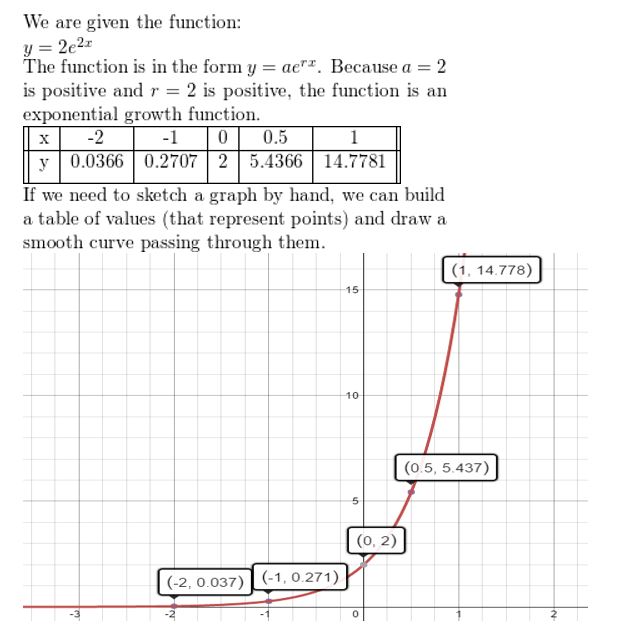
Question 7.
You deposit $4250 in an account that earns 5% annual interest compounded continuously. Compare the balance after 10 years with the accounts in Example 3.
Answer:

The Natural Base e 6.2 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What is the natural base e?
Answer:
![]()
Question 2.
WRITING
Tell whether the function f(x) = \(\frac{1}{3}\)e4x represents exponential growth or exponential decay. Explain.
Answer:
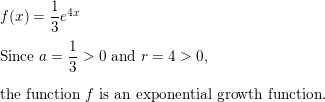
Monitoring Progress and Modeling with Mathematics
In Exercises 3–12, simplify the expression.
Question 3.
e3 • e5
Answer:
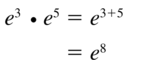
Question 4.
e-4 • e6
Answer:

Question 5.
\(\frac{11 e^{9}}{22 e^{10}}\)
Answer:
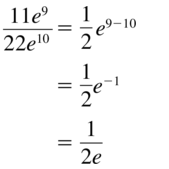
Question 6.
\(\frac{27 e^{7}}{3 e^{4}}\)
Answer:
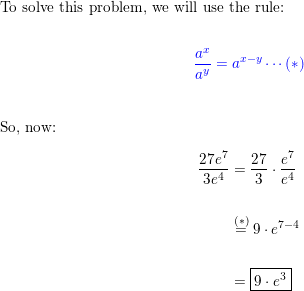
Question 7.
(5e7x)4
Answer:
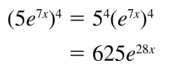
Question 8.
(4e-2x)3
Answer:
(4e^-2x)^3
Apply exponent rule: (a . b)^n = a ^ n b ^n
4^3(e^-2x)^3
Apply exponent rule: (a ^ b)^c = a ^bc
(e^-2x)^3 : e^-6x
put the parts together
4^3e^-6x
64e^-6x
Question 9.
\(\sqrt{9 e^{6 x}}\)
Answer:
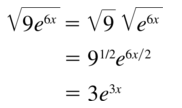
Question 10.
\(\sqrt[3]{8 e^{12 x}}\)
Answer:

Question 11.
ex • e-6x • e8
Answer:
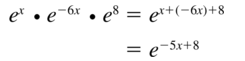
Question 12.
ex • e4 • ex+3
Answer:
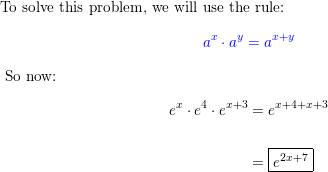
ERROR ANALYSIS In Exercises 13 and 14, describe and correct the error in simplifying the expression.
Question 13.
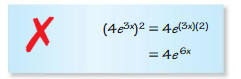
Answer:
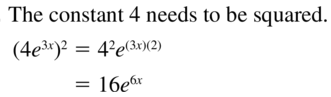
Question 14.
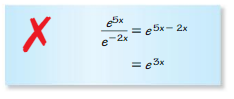
Answer:
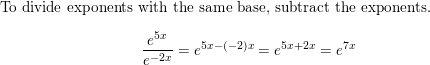
In Exercises 15–22, tell whether the function represents exponential growth or exponential decay. Then graph the function.
Question 15.
y = e3x
Answer:
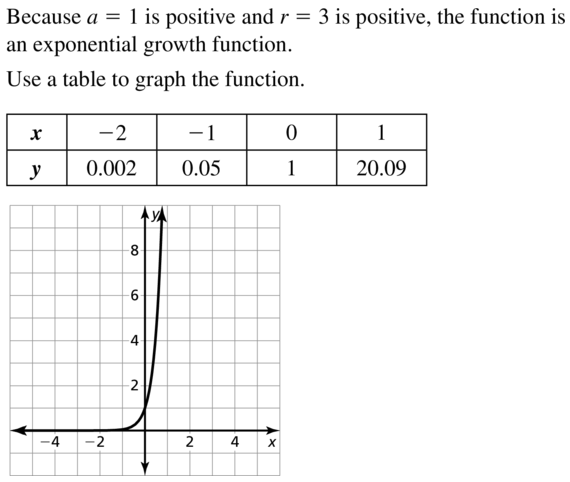
Question 16.
y = e-2x
Answer:
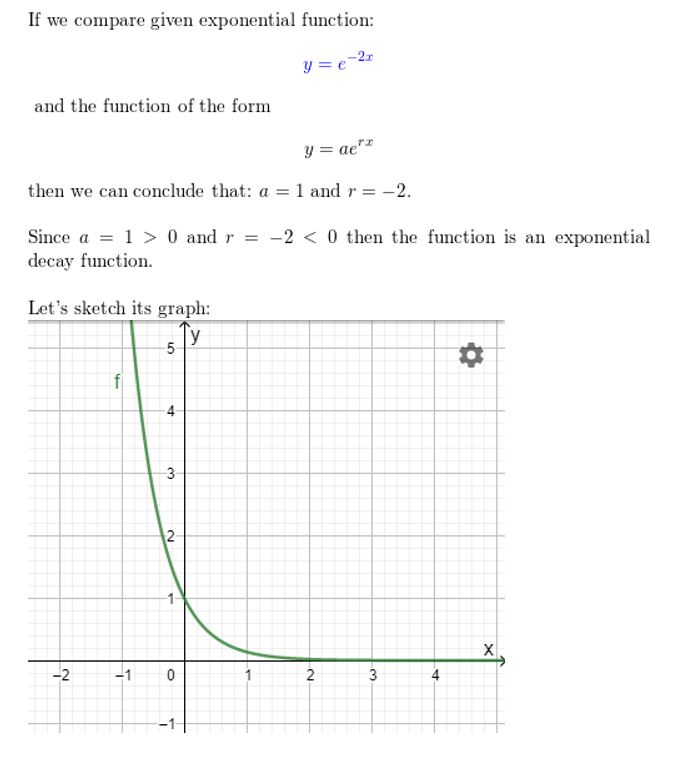
Question 17.
y = 2e-x
Answer:
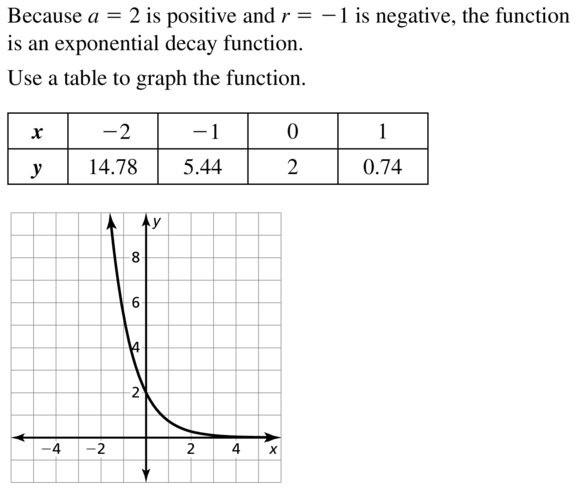
Question 18.
y = 3e2x
Answer:
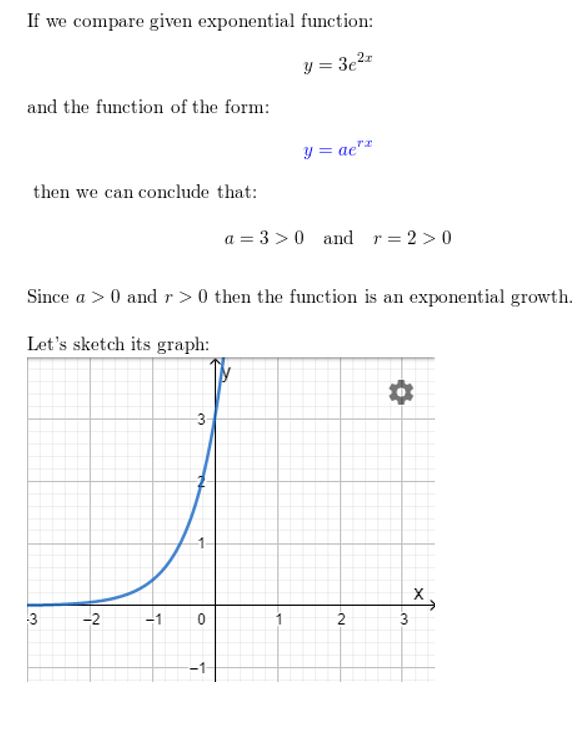
Question 19.
y = 0.5ex
Answer:
Question 20.
y = 0.25e-3x
Answer:

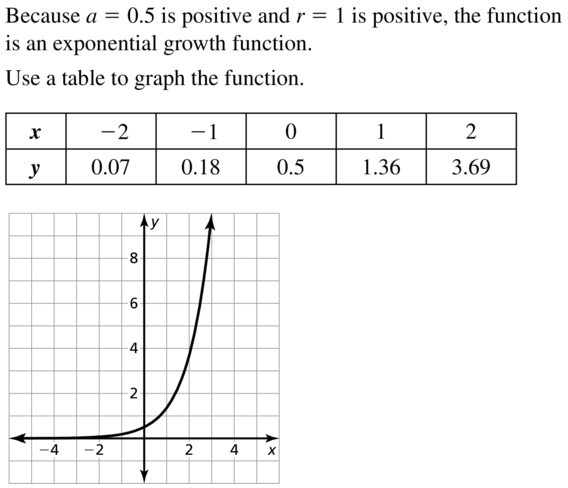
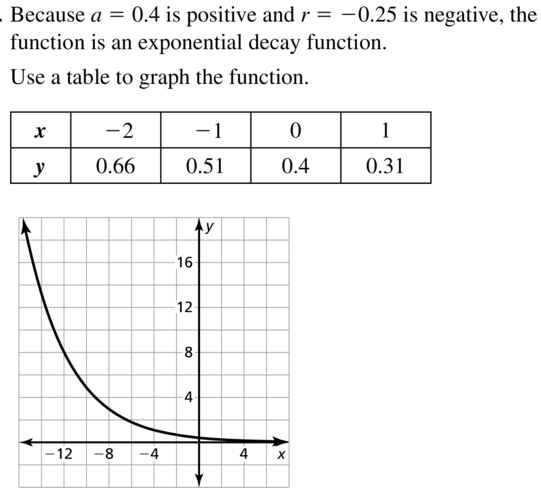
Question 21.
y = 0.4e-0.25x
Answer:
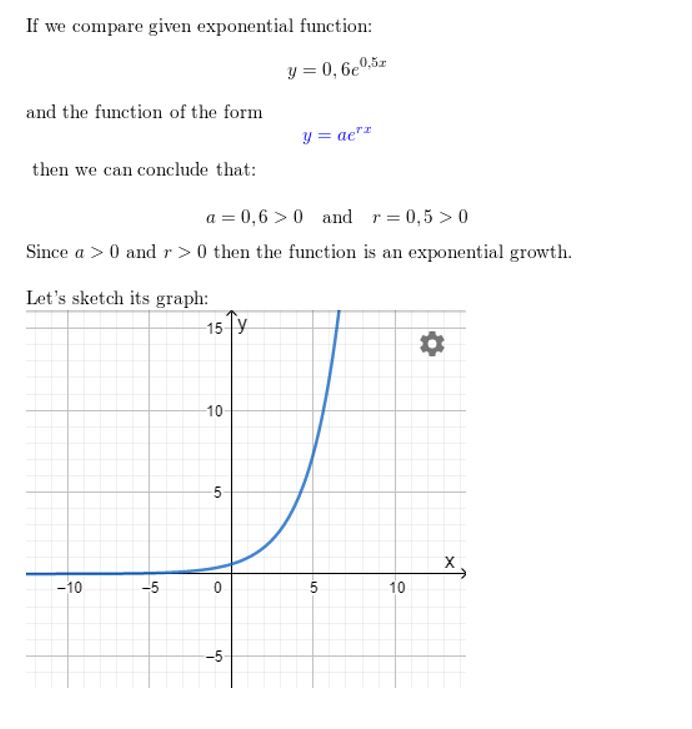
Question 22.
y = 0.6e0.5x
Answer:
ANALYZING EQUATIONS In Exercises 23–26, match the function with its graph. Explain your reasoning.
Question 23.
y = e2x
Answer:

Question 24.
y = e-2x
Answer:

Question 25.
y = 4e-0.5x
Answer:

Question 26.
y = 0.75ex
Answer:
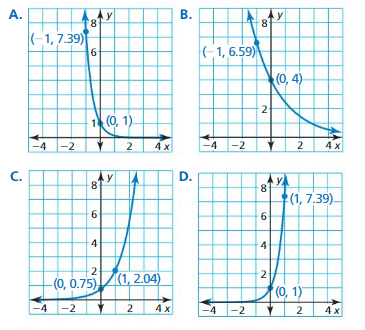
USING STRUCTURE In Exercises 27–30, use the properties of exponents to rewrite the function in the form y = a(1 + r)t or y = a(1 – r)t. Then find the percent rate of change.
Question 27.
y = e-0.25t
Answer:
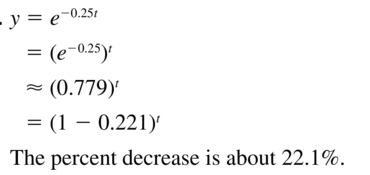
Question 28.
y = e-0.75t
Answer:

Question 29.
y = 2e0.4t
Answer:

Question 30.
y = 0.5e0.8t
Answer:
USING TOOLS In Exercises 31–34, use a table of values or a graphing calculator to graph the function. Then identify the domain and range.
Question 31.
y = ex-2
Answer:

Question 32.
y = ex+1
Answer:
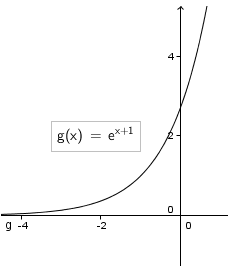
Question 33.
y = 2ex + 1
Answer:

Question 34.
y = 3ex − 5
Answer:

Question 35.
MODELING WITH MATHEMATICS
Investment accounts for a house and education earn annual interest compounded continuously. The balance H(in dollars) of the house fund after t years can be modeled by H = 3224e0.05t. The graph shows the balance in the education fund over time. Which account has the greater principal? Which account has a greater balance after 10 years?
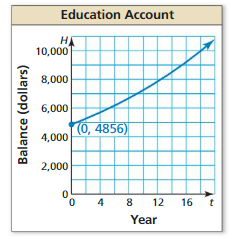
Answer:

Question 36.
MODELING WITH MATHEMATICS
Tritium and sodium-22 decay over time. In a sample of tritium, the amount y (in milligrams) remaining after t years is given by y = 10e−0.0562t. The graph shows the amount of sodium-22 in a sample over time. Which sample started with a greater amount? Which has a greater amount after 10 years?
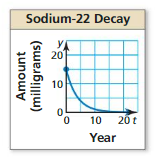
Answer:
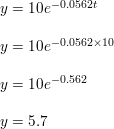
Tritium has greater.
Question 37.
OPEN-ENDED
Find values of a, b, r, and q such that f(x) = aerx and g(x) = beqx are exponential decay functions, but \(\frac{f(x)}{g(x)}\) represents exponential growth.
Answer:
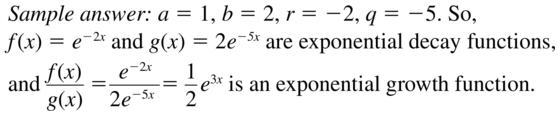
Question 38.
THOUGHT PROVOKING
Explain why A = P(1 + \(\frac{r}{n}\))nt approximates A =Pert as n approaches positive infinity.
Answer:
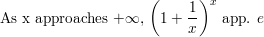
Question 39.
WRITING
Can the natural base e be written as a ratio of two integers? Explain.
Answer:
Question 40.
MAKING AN ARGUMENT
Your friend evaluates f(x) = e-x when x = 1000 and concludes that the graph of y = fx) has an x-intercept at (1000, 0). Is your friend correct? Explain your reasoning.
Answer:

Question 41.
DRAWING CONCLUSIONS
You invest $2500 in an account to save for college. Account 1 pays 6% annual interest compounded quarterly. Account 2 pays 4% annual interest compounded continuously. Which account should you choose to obtain the greater amount in 10 years? Justify your answer.
Answer:

Question 42.
HOW DO YOU SEE IT?
Use the graph to complete each statement.
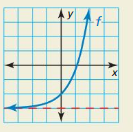
a. f(x) approaches ____ as x approaches +∞.
b. f(x) approaches ____ as x approaches −∞.
Answer:
a) + ∞
b) – 3
Question 43.
PROBLEM SOLVING
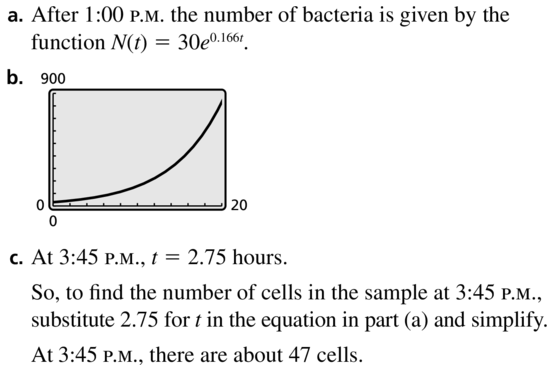
The growth of Mycobacterium tuberculosis bacteria can be modeled by the function N(t) = ae0.166t, where N is the number of cells after t hours and a is the number of cells when t = 0.
a. At 1:00 P.M., there are 30 M. tuberculosis bacteria in a sample. Write a function that gives the number of bacteria after 1:00 P.M.
b. Use a graphing calculator to graph the function in part (a).
c. Describe how to find the number of cells in the sample at 3:45 P.M.
Answer:
Maintaining Mathematical Proficiency
Write the number in scientific notation.
Question 44.
0.006
Answer:

Question 45.
5000
Answer:
![]()
Question 46.
26,000,000
Answer:

Question 47.
0.000000047
Answer:
![]()
Find the inverse of the function. Then graph the function and its inverse.
Question 48.
y = 3x + 5
Answer:
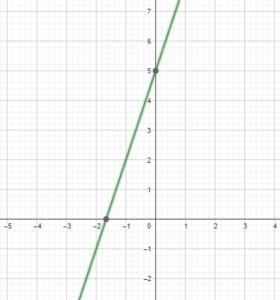
Question 49.
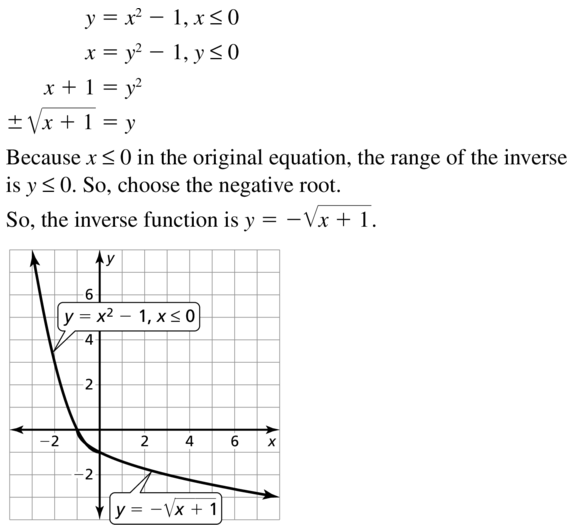
y = x2 − 1, x ≤ 0
Answer:
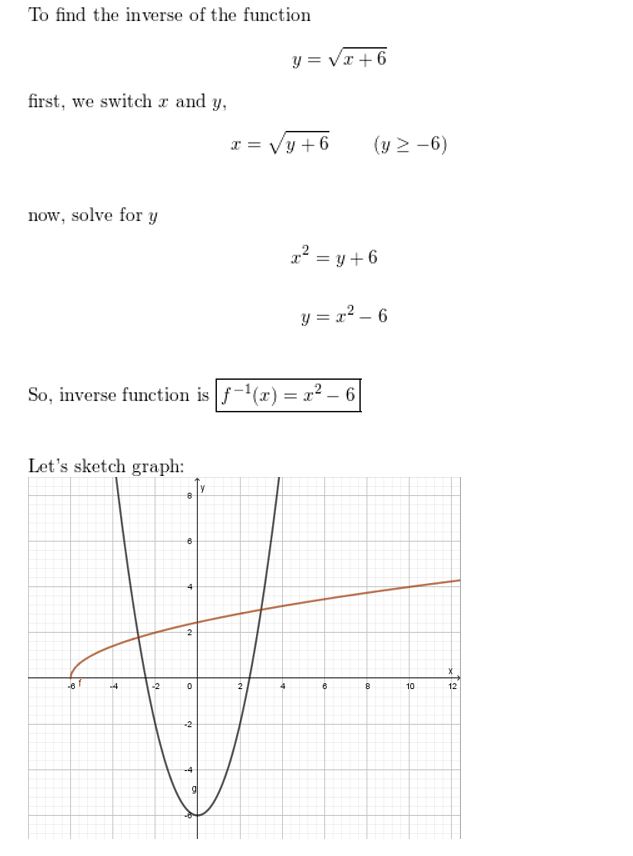
Question 50.
y = \(\sqrt{x+6}\)
Answer:
Question 51.
y = x3 − 2
Answer:

Lesson 6.3 Logarithms and Logarithmic Functions
Essential Question What are some of the characteristics of the graph of a logarithmic function?
Every exponential function of the form f(x) = bx, where b is a positive real number other than 1, has an inverse function that you can denote by g(x) = logbx. This inverse function is called a logarithmic function with base b.
EXPLORATION 1
Rewriting Exponential Equations
Work with a partner. Find the value of x in each exponential equation. Explain your reasoning. Then use the value of x to rewrite the exponential equation in its equivalent logarithmic form, x = logby.
a. 2x = 8
b. 3x = 9
c. 4x = 2
d. 5x = 1
e. 5x = \(\frac{1}{5}\)
f. 8x = 4
EXPLORATION 2
Graphing Exponential and Logarithmic Functions
Work with a partner. Complete each table for the given exponential function. Use the results to complete the table for the given logarithmic function. Explain your reasoning. Then sketch the graphs of f and g in the same coordinate plane.
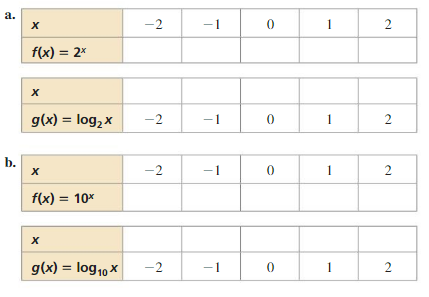
EXPLORATION 3
Characteristics of Graphs of LogarithmicFunctions

Work with a partner. Use the graphs you sketched in Exploration 2 to determine the domain, range, x-intercept, and asymptote of the graph of g(x) = logbx, where b is a positive real number other than 1. Explain your reasoning.
Communicate Your Answer
Question 4.
What are some of the characteristics of the graph of a logarithmic function?
Answer:
1. The graph has a horizontal intercept at (1, 0)
2. The graph is increasing if the base is greater than 1, b > 1
3. The domain of the function is from zero to infinity.
4. The range of the function is (-∞, +∞)
5. The graph is decreasing if the base is in the range 0 < b < 1.
Question 5.
How can you use the graph of an exponential function to obtain the graph of a logarithmic function?
Answer:
We can use the graph of an exponential function to graph the corresponding logarithmic function by swapping the x and y coordinates of the points. Or we can use the reflection of the exponential function in the y = x line to graph the logarithmic function.
Monitoring Progress
Rewrite the equation in exponential form.
Question 1.
log3 81 = 4
Answer:
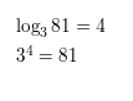
Question 2.
log7 7 = 1
Answer:
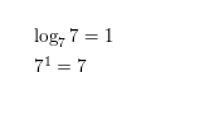
Question 3.
log14 1 = 0
Answer:
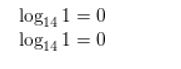
Question 4.
log1/2 32 = −5
Answer:
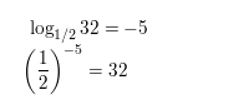
Rewrite the equation in logarithmic form.
Question 5.
72 = 49
Answer:

Question 6.
500 = 1
Answer:
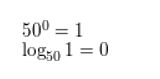
Question 7.
4-1 = \(\frac{1}{4}\)
Answer:
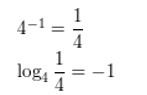
Question 8.
2561/8 = 2
Answer:
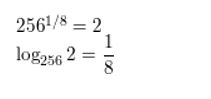
Evaluate the logarithm. If necessary, use a calculator and round your answer to three decimal places.
Question 9.
log2 32
Answer:
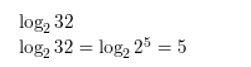
Question 10.
log27 3
Answer:
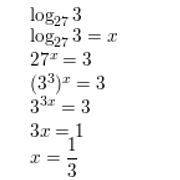
Question 11.
log 12
Answer:
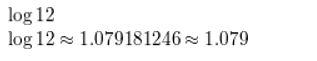
Question 12.
ln 0.75
Answer:
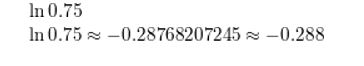
Simplify the expression.
Question 13.
8log8 x
Answer:
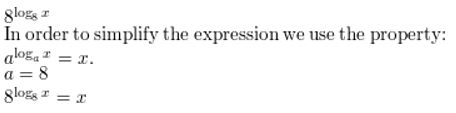
Question 14.
log7 7−3x
Answer:
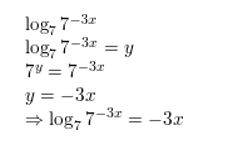
Question 15.
log2 64x
Answer:
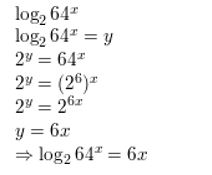
Question 16.
eln 20
Answer:

Question 17.
Find the inverse of y = 4x.
Answer:

Question 18.
Find the inverse of y = ln(x− 5).
Answer:
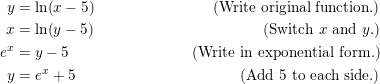
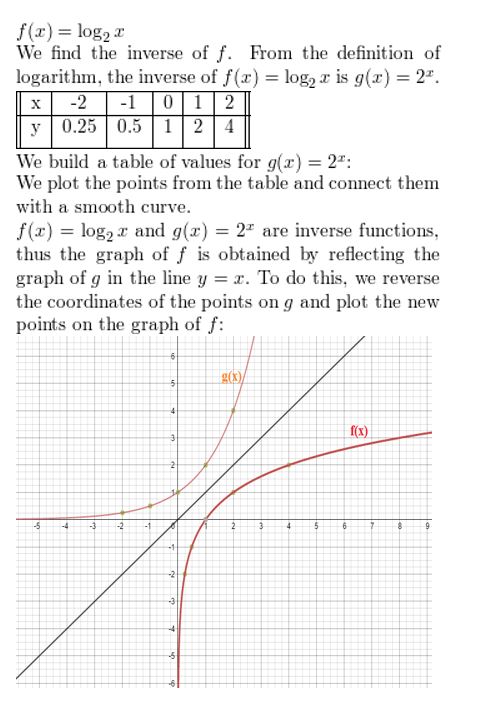
Graph the function.
Question 19.
y = log2 x
Answer:
Question 20.
f(x) = log5 x
Answer:
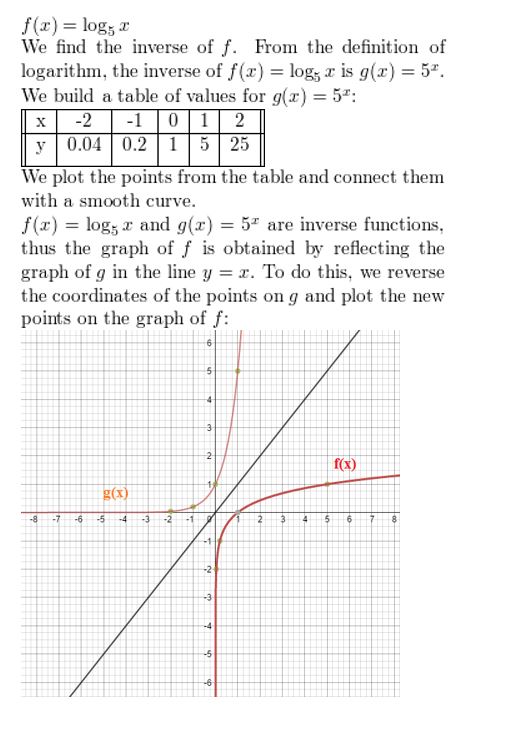
Question 21.
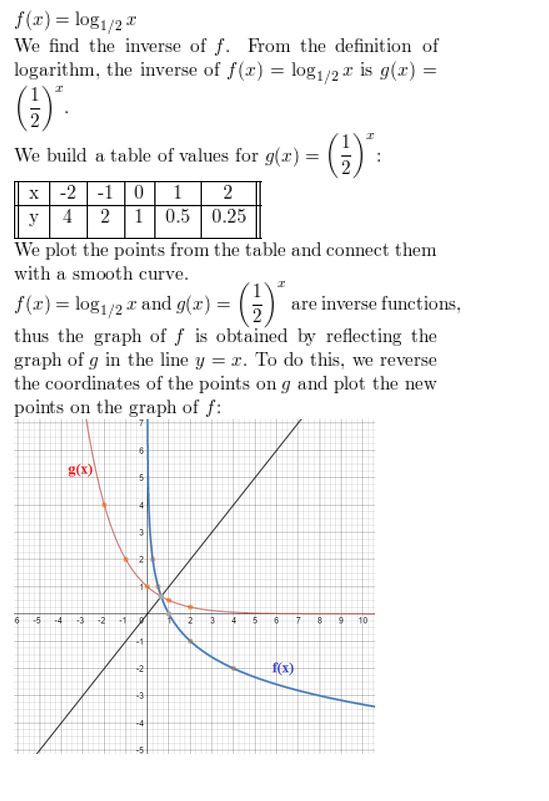
y = log1/2 x
Answer:
Logarithms and Logarithmic Functions 6.3 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A logarithm with base 10 is called a(n) ___________ logarithm.
Answer:
![]()
Question 2.
COMPLETE THE SENTENCE
The expression log3 9 is read as ______________.
Answer: The expression log3 9 is read as Log 9 base 3.
Question 3.
WRITING
Describe the relationship between y = 7x and y = log7 x.
Answer:
![]()
Question 4.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 5–10, rewrite the equation in exponential form.
Question 5.
log3 9 = 2
Answer:
![]()
Question 6.
log4 4 = 1
Answer:

Question 7.
log6 1 = 0
Answer:
![]()
Question 8.
log7 343 = 3
Answer:

Question 9.
log1/2 16 =−4
Answer:
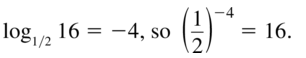
Question 10.
log3 \(\frac{1}{3}\) = −1
Answer:

In Exercises 11–16, rewrite the equation in logarithmic form.
Question 11.
62 = 36
Answer:
![]()
Question 12.
120 = 1
Answer:

Question 13.
16-1 = \(\frac{1}{16}\)
Answer:
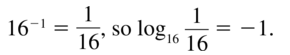
Question 14.
5-2 = \(\frac{1}{25}\)
Answer:
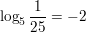
Question 15.
1252/3 = 25
Answer:
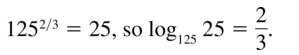
Question 16.
491/2 = 7
Answer:

In Exercises 17–24, evaluate the logarithm.
Question 17.
log3 81
Answer:
![]()
Question 18.
log7 49
Answer:
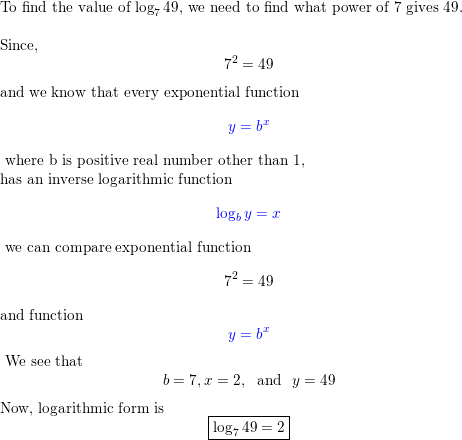
Question 19.
log3 3
Answer:
![]()
Question 20.
log1/2 1
Answer:

Question 21.
log5 \(\frac{1}{625}\)
Answer:
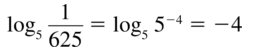
Question 22.
log8 \(\frac{1}{512}\)
Answer:

Question 23.
log4 0.25
Answer:
![]()
Question 24.
log10 0.001
Answer:
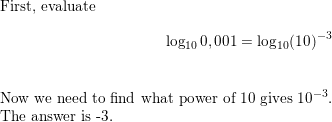
Question 25.
NUMBER SENSE
Order the logarithms from least value to greatest value.
![]()
Answer:
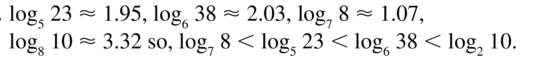
Question 26.
WRITING
Explain why the expressions log2(−1) and log1 1 are not defined.
Answer:

In Exercises 27–32, evaluate the logarithm using a calculator. Round your answer to three decimal places.
Question 27.
log 6
Answer:
![]()
Question 28.
ln 12
Answer:
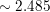
Question 29.
ln \(\frac{1}{3}\)
Answer:
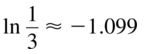
Question 30.
log \(\frac{2}{7}\)
Answer:
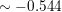
Question 31.
3 ln 0.5
Answer:
![]()
Question 32.
log 0.6 + 1
Answer: log(1.6)
Question 33.
MODELING WITH MATHEMATICS
Skydivers use an instrument called an altimeter to track their altitude as they fall. The altimeter determines altitude by measuring air pressure. The altitude h (in meters) above sea level is related to the air pressure P(in pascals) by the function shown in the diagram. What is the altitude above sea level when the air pressure is 57,000 pascals?
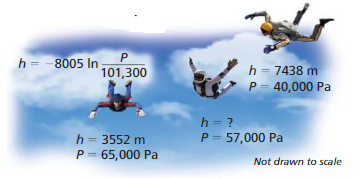
Answer:
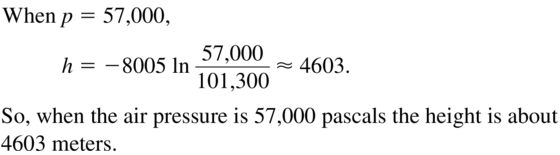
Question 34.
MODELING WITH MATHEMATICS
The pH value for a substance measures how acidic or alkaline the substance is. It is given by the formula pH = −log[H+], where H+ is the hydrogen ion concentration (in moles per liter). Find the pH of each substance.
a. baking soda: [H+] = 10-8 moles per liter
b. vinegar: [H+] = 10-3 moles per liter
Answer:
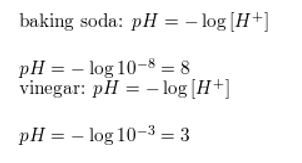
In Exercises 35–40, simplify the expression.
Question 35.
7log7x
Answer:
![]()
Question 36.
3log3 5x
Answer:
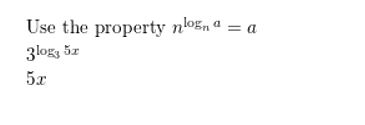
Question 37.
eln4
Answer:
![]()
Question 38.
10log 15
Answer: 15
Question 39.
log3 32x
Answer:
![]()
Question 40.
ln ex + 1
Answer:

Question 41.
ERROR ANALYSIS
Describe and correct the error in rewriting 4−3 = \(\frac{1}{64}\) in logarithmic form.
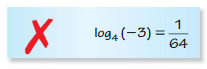
Answer:

Question 42.
ERROR ANALYSIS
Describe and correct the error in simplifying the expression log4 64x.

Answer:
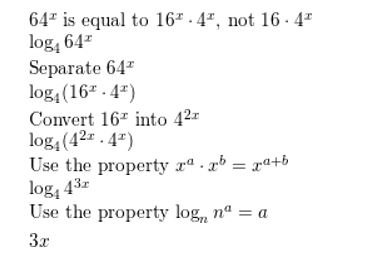
In Exercises 43–52, find the inverse of the function.
Question 43.
y = 0.3x
Answer:
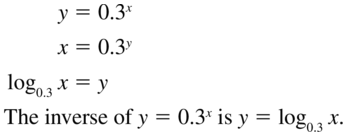
Question 44.
y = 11x
Answer:

Question 45.
y = log2 x
Answer:
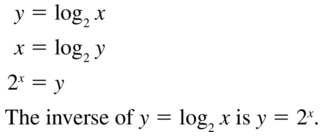
Question 46.
y = log1/5 x
Answer:

Question 47.
y = ln(x − 1)
Answer:
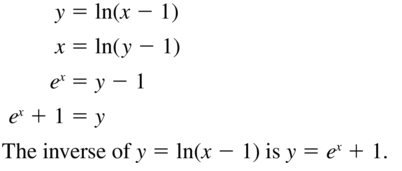
Question 48.
y = ln 2x
Answer:

Question 49.
y = e3x
Answer:
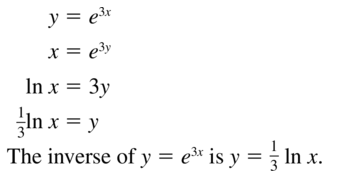
Question 50.
y = ex-4
Answer:
y= x+ 4
Question 51.
y = 5x − 9
Answer:
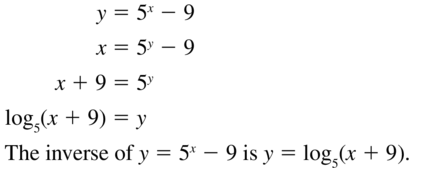
Question 52.
y = 13 + log x
Answer:

Question 53.
PROBLEM SOLVING
The wind speed s (in miles per hour) near the center of a tornado can be modeled by s = 93 log d + 65, where d is the distance (in miles) that the tornado travels.

a. In 1925, a tornado traveled 220 miles through three states. Estimate the wind speed near the center of the tornado.
b. Find the inverse of the given function. Describe what the inverse represents.
Answer:

Question 54.
MODELING WITH MATHEMATICS
The energy magnitude M of an earthquake can be modeled by M = \(\frac{2}{3}\)log E − 9.9, where E is the amount of energy released (in ergs).
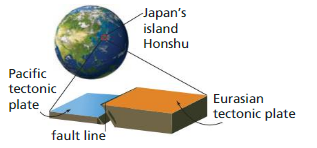
a. In 2011, a powerful earthquake in Japan, caused by the slippage of two tectonic plates along a fault, released 2.24 × 1028 ergs. What was the energy magnitude of the earthquake?
b. Find the inverse of the given function. Describe what the inverse represents.
Answer:

In Exercises 55–60, graph the function.
Question 55.
y = log4 x
Answer:

Question 56.
y = log6 x
Answer:
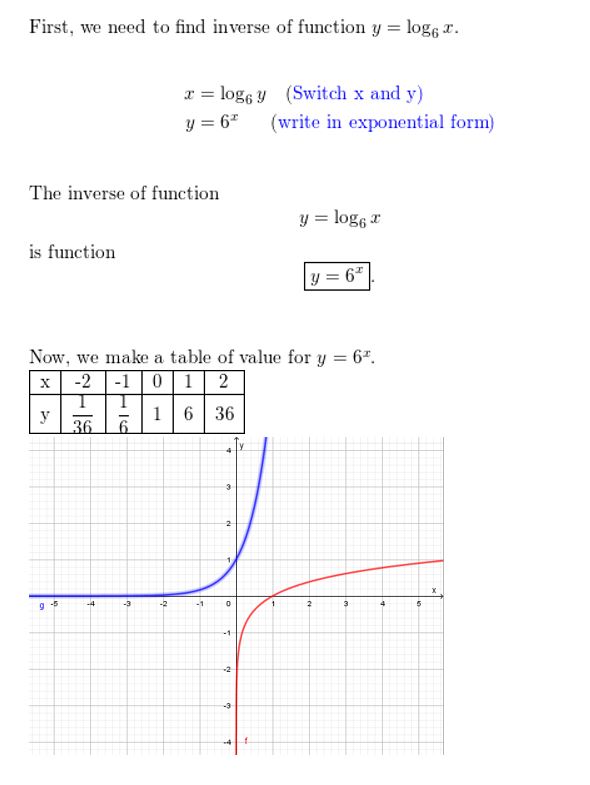
Question 57.
y = log1/3 x
Answer:

Question 58.
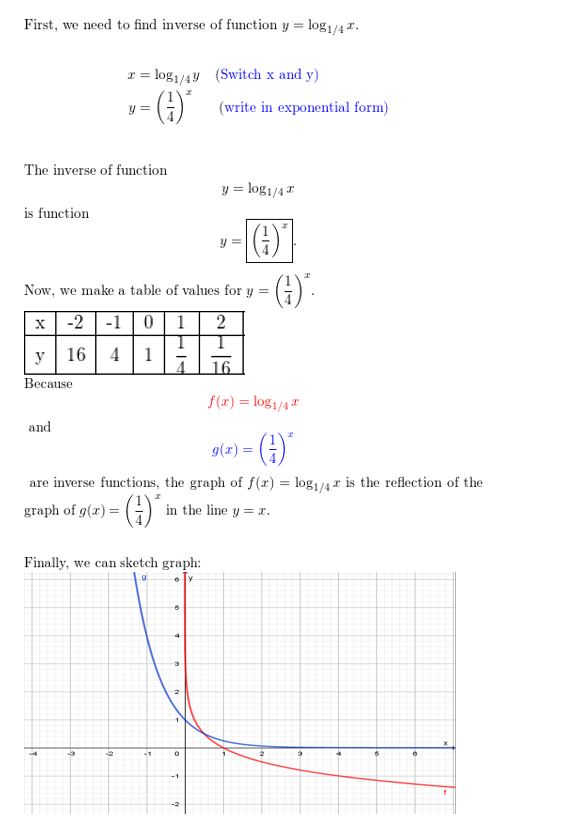
y = log1/4 x
Answer:
Question 59.
y = log2 x − 1
Answer:
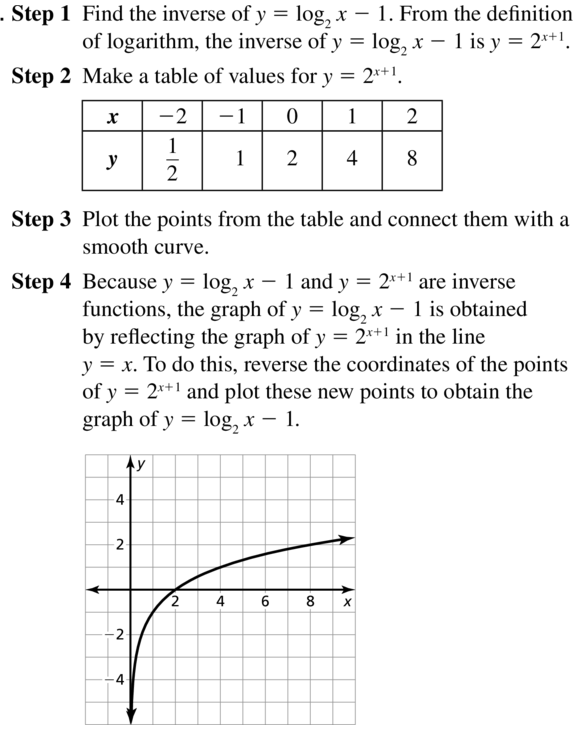
Question 60.
y = log3(x + 2)
Answer:
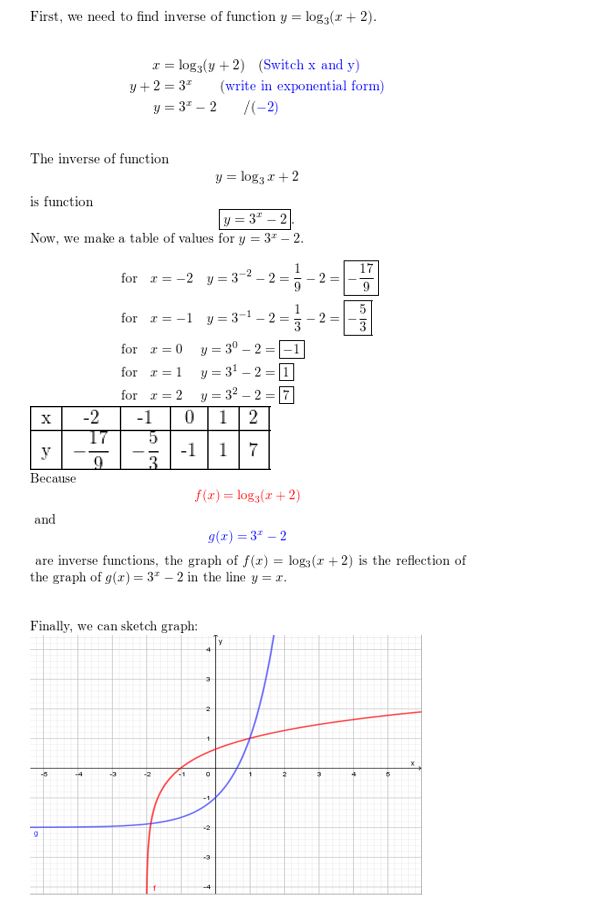
USING TOOLS In Exercises 61–64, use a graphing calculator to graph the function. Determine the domain, range, and asymptote of the function.
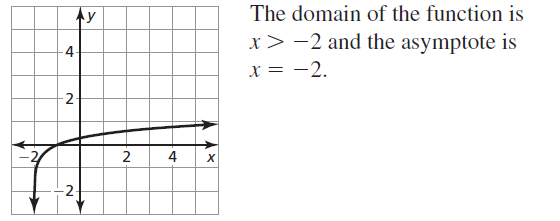
Question 61.
y = log(x+ 2)
Answer:
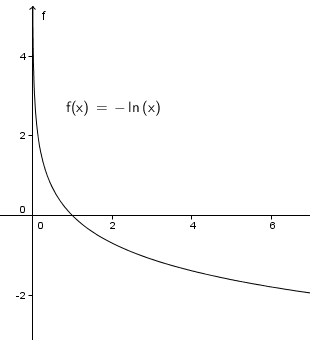
Question 62.
y = −ln x
Answer:
Question 63.
y = ln(−x)
Answer:
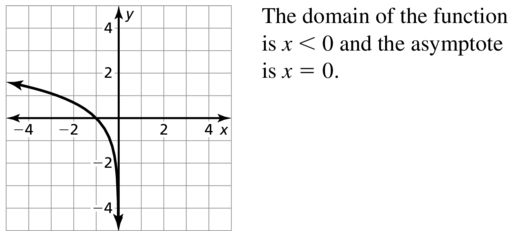
Question 64.
y = 3 − log x
Answer:

Question 65.
MAKING AN ARGUMENT
Your friend states that every logarithmic function will pass through the point (1, 0). Is your friend correct? Explain your reasoning.
Answer:
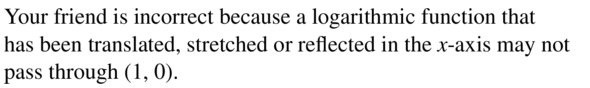
Question 66.
ANALYZING RELATIONSHIPS
Rank the functions in order from the least average rate of change to the greatest average rate of change over the interval 1 ≤ x ≤ 10.
a. y = log6 x
b. y = log3/5 x
Answer:

Question 67.
PROBLEM SOLVING
Biologists have found that the length ℓ (in inches) of an alligator and its weight w (in pounds) are related by the function ℓ = 27.1 ln w − 32.8.

a. Use a graphing calculator to graph the function.
b. Use your graph to estimate the weight of an alligator that is 10 feet long.
c. Use the zero feature to find the x-intercept of the graph of the function. Does this x-value make sense in the context of the situation? Explain.
Answer:

Question 68.
HOW DO YOU SEE IT?
The figure shows the graphs of the two functions f and g.
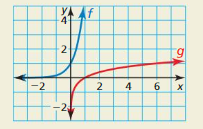
a. Compare the end behavior of the logarithmic function g to that of the exponential function f.
b. Determine whether the functions are inverse functions. Explain.
c. What is the base of each function? Explain.
Answer:

Question 69.
PROBLEM SOLVING
A study in Florida found that the number s of fish species in a pool or lake can be modeled by the function s = 30.6 − 20.5 log A + 3.8(log A)2
where A is the area (in square meters) of the pool or lake.

a. Use a graphing calculator to graph the function on the domain 200 ≤ A ≤ 35,000.
b. Use your graph to estimate the number of species in a lake with an area of 30,000 square meters.
c. Use your graph to estimate the area of a lake that contains six species of fish.
d. Describe what happens to the number of fish species as the area of a pool or lake increases. Explain why your answer makes sense.
Answer:

Question 70.
THOUGHT PROVOKING
Write a logarithmic function that has an output of −4. Then sketch the graph of your function.
Answer:
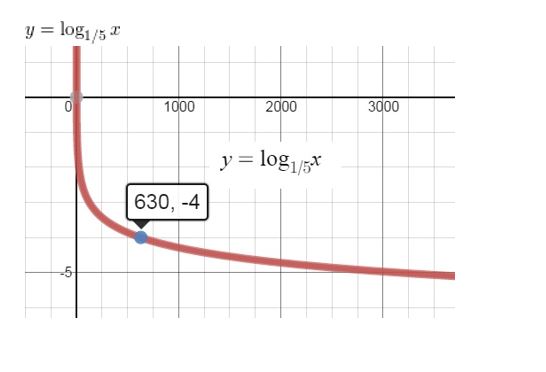
Question 71.
CRITICAL THINKING
Evaluate each logarithm. (Hint: For each logarithm logb x, rewrite b and x as powers of the same base.)
a. log125 25
b. log8 32
c. log27 81
d. log4 128
Answer:

Maintaining Mathematical Proficiency
Let f(x) = \(\sqrt [ 3 ]{ x }\). Write a rule for g that represents the indicated transformation of the graph of f.
Question 72.
g(x) = −f(x)
Answer:

Question 73.
g(x) = f (\(\frac{1}{2}\)x )
Answer:
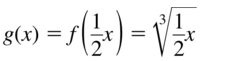
Question 74.
g(x) = f(−x) + 3
Answer:
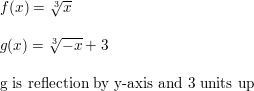
Question 75.
g(x) = f(x+ 2)
Answer:
![]()
Identify the function family to which f belongs. Compare the graph of f to the graph of its parent.
Question 76.
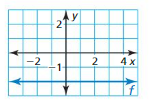
Answer:
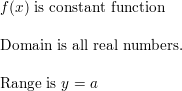
Question 77.
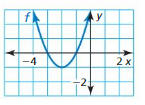
Answer:

Question 78.
Answer:

Lesson 6.4 Transformations of Exponential and Logarithmic Functions
Essential Question How can you transform the graphs of exponential and logarithmic functions?
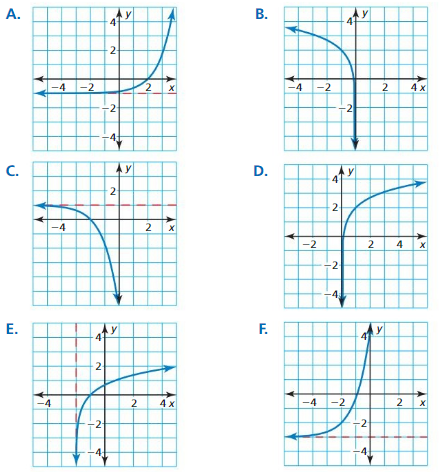
EXPLORATION 1
Identifying Transformations
Work with a partner. Each graph shown is a transformation of the parent function
f(x) = ex or f(x) = ln x.
Match each function with its graph. Explain your reasoning. Then describe the transformation of f represented by g.
a. g(x) = ex+2 − 3
b. g(x) = −ex+2 + 1
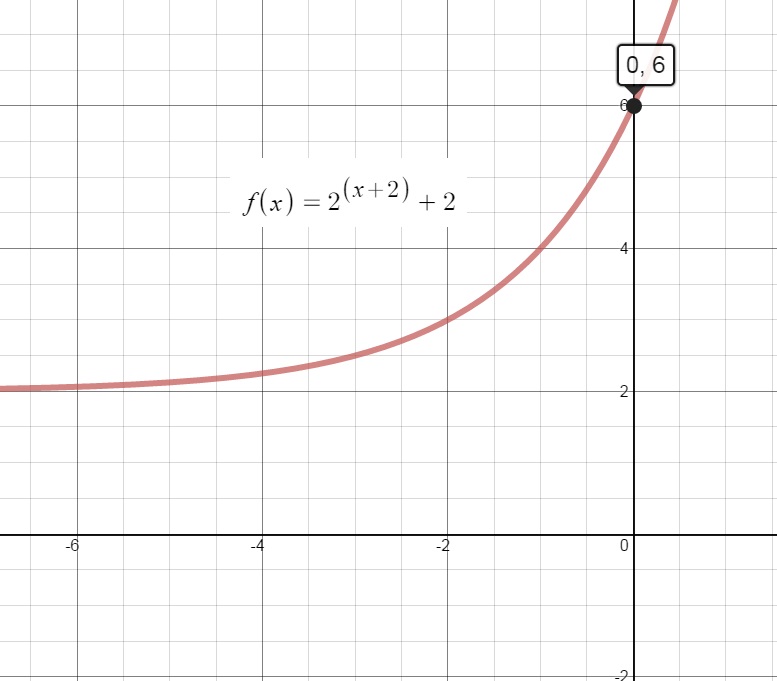
c. g(x) = ex-2 − 1
d. g(x) = ln(x + 2)
e. g(x) = 2 + ln x
f. g(x) = 2 + ln(−x)
EXPLORATION 2
Characteristics of Graphs
Work with a partner. Determine the domain, range, and asymptote of each function in Exploration 1. Justify your answers.
Communicate Your Answer
Question 3.
How can you transform the graphs of exponential and logarithmic functions?
Answer:
Graphing logarithmic functions can be done by locating points on the curve either manually or with a calculator.
When graphing without a calculator, we use the fact that the inverse of a logarithmic function is an exponential function.
When graphing with a calculator,
we use the fact that the calculator can compute only common logarithms.
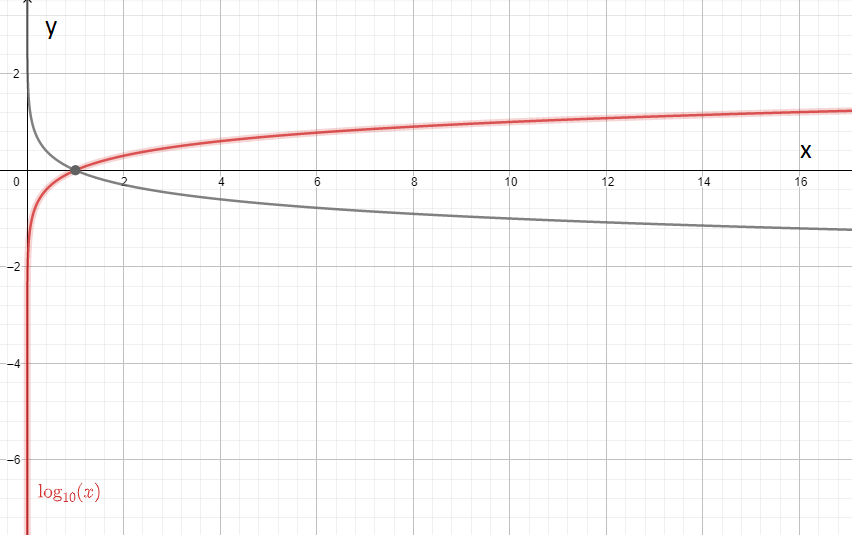
Question 4.
Find the inverse of each function in Exploration 1. Then check your answer by using a graphing calculator to graph each function and its inverse in the same viewing window.

Answer:
Monitoring Progress
Describe the transformation of f represented by g. Then graph each function.
Question 1.
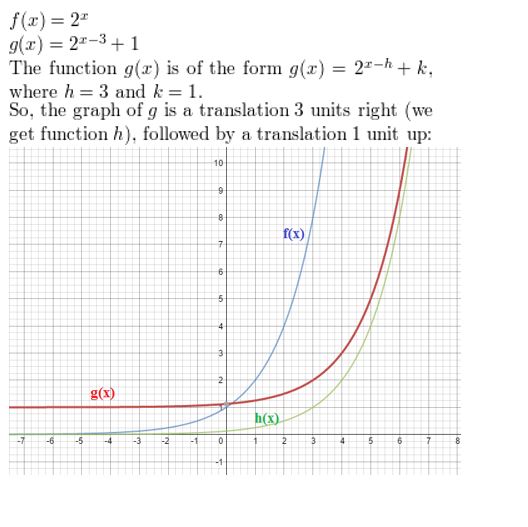
f(x) = 2x, g(x) = 2x-3 + 1
Answer:
Question 2.
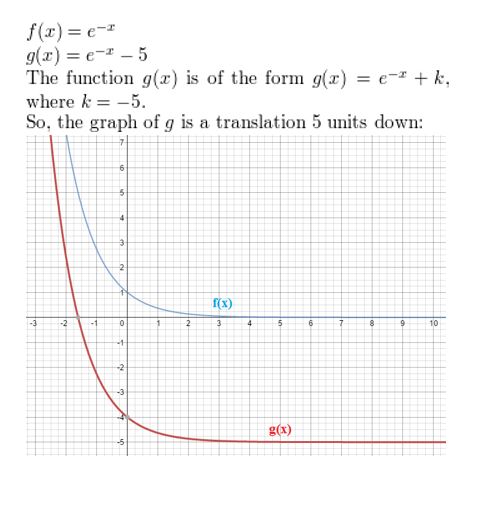
f(x) = e-x, g(x) = e-x − 5
Answer:
Question 3.
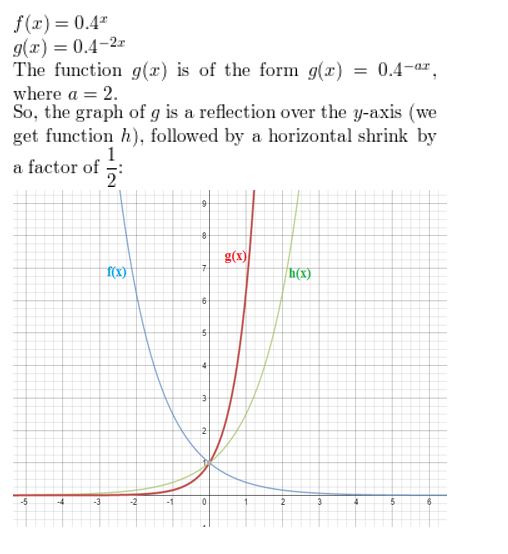
f(x) = 0.4x, g(x) = 0.4-2x
Answer:
Question 4.
f(x) = ex, g(x) = −ex+6
Answer:
Describe the transformation of f represented by g. Then graph each function.
Question 5.
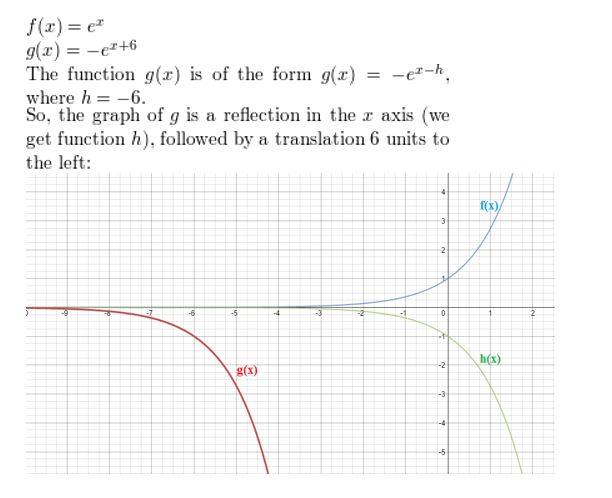
f(x) = log2x, g(x) = −3 log2x
Answer:
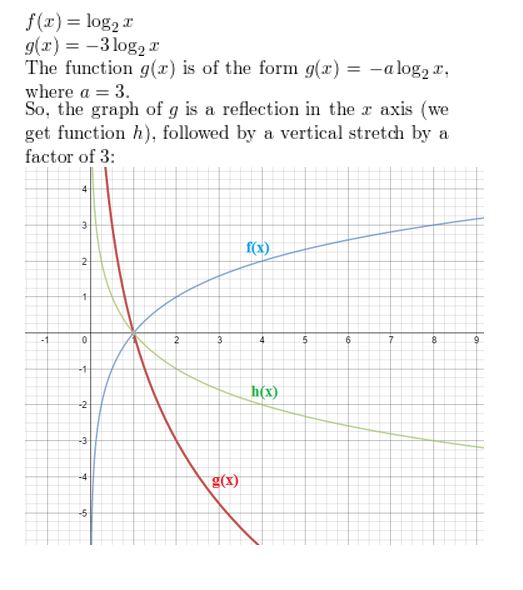
Question 6.
f(x) = log1/4x, g(x) = log1/4(4x) − 5
Answer:
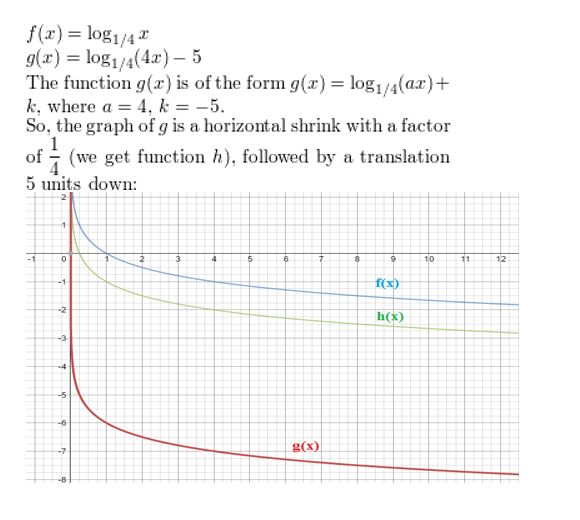
Question 7.
Let the graph of g be a horizontal stretch by a factor of 3, followed by a translation 2 units up of the graph of f(x) = e-x. Write a rule for g.
Answer:
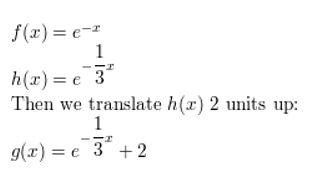
Question 8.
Let the graph of g be a reflection in the y-axis, followed by a translation 4 units to the left of the graph of f(x) = log x. Write a rule for g.
Answer:

Transformations of Exponential and Logarithmic Functions 6.4 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Given the function f(x) = abx-h + k, describe the effects of a, h, and k on the graph of the function.
Answer:

Question 2.
COMPLETE THE SENTENCE
The graph of g(x) = log4(−x) is a reflection in the __________ of the graph of f(x) = log4x,
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3–6, match the function with its graph. Explain your reasoning.
Question 3.
f(x) = 2x+2 − 2
Answer:
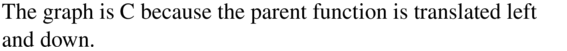
Question 4.
g(x) = 2x+2 + 2
Answer:
Question 5.
h(x) = 2x-2 − 2
Answer:
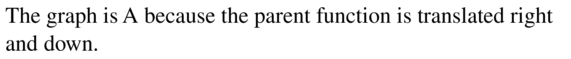
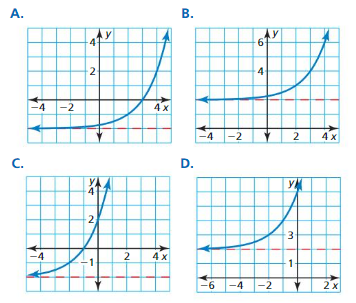
Question 6.
k(x) = 2x-2 + 2
Answer:
In Exercises 7–16, describe the transformation of f represented by g. Then graph each function.
Question 7.
f(x) = 3x, g(x) = 3x + 5
Answer:
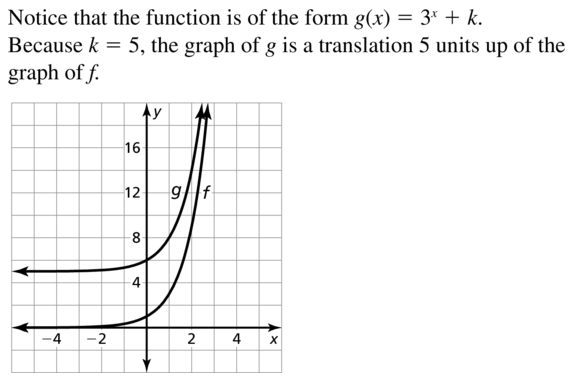
Question 8.
f(x) = 4x, g(x) = 4x − 8
Answer:
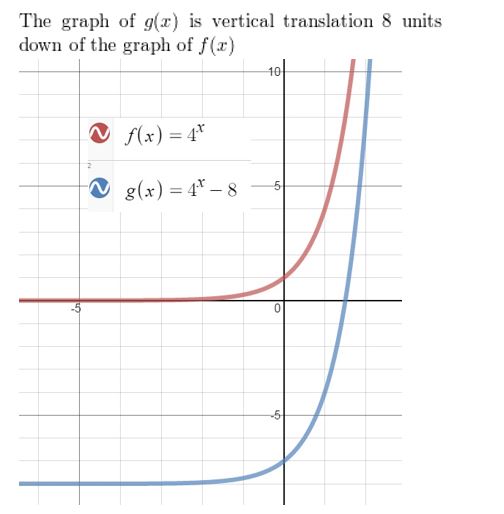
Question 9.
f(x) = ex, g(x) = ex − 1
Answer:

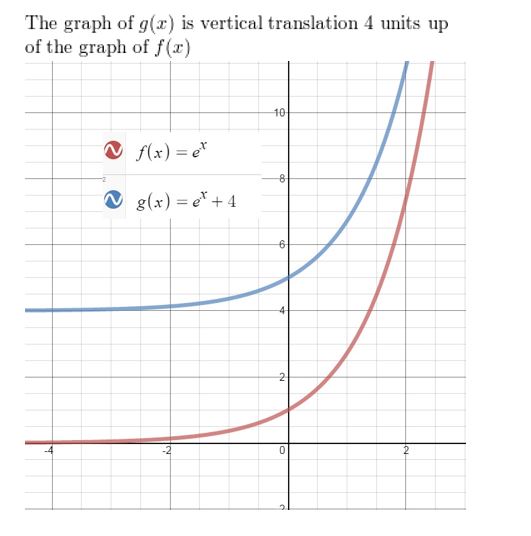
Question 10.
f(x) = ex, g(x) = ex + 4
Answer:
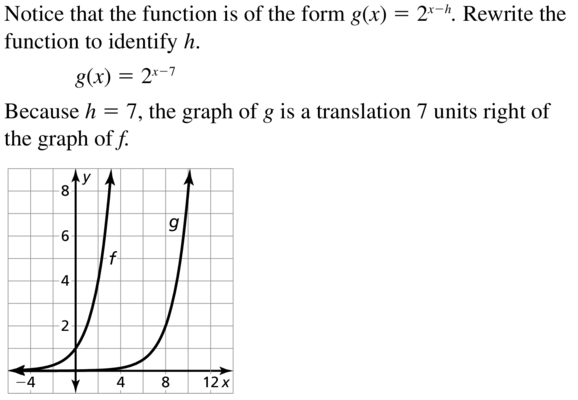
Question 11.
f(x) = 2x, g(x) = 2x-7
Answer:
Question 12.
f(x) = 5x, g(x) = 5x+1
Answer:
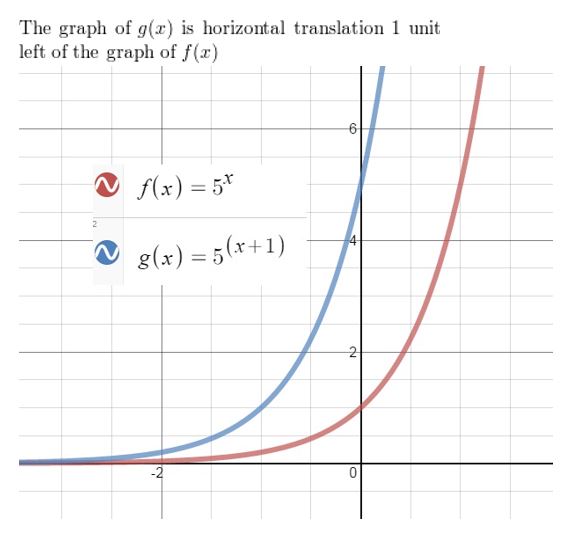
Question 13.
f(x) = e-x, g(x) = e-x + 6
Answer:
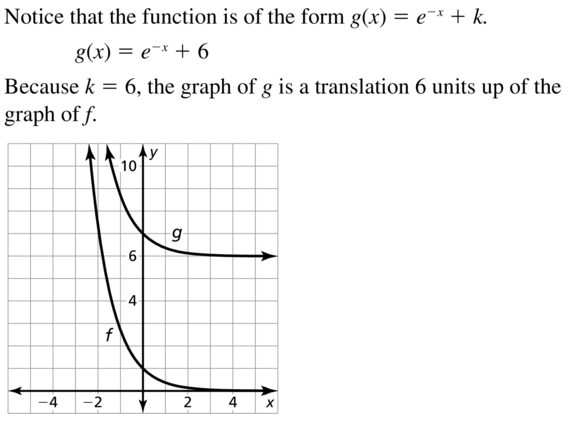
Question 14.
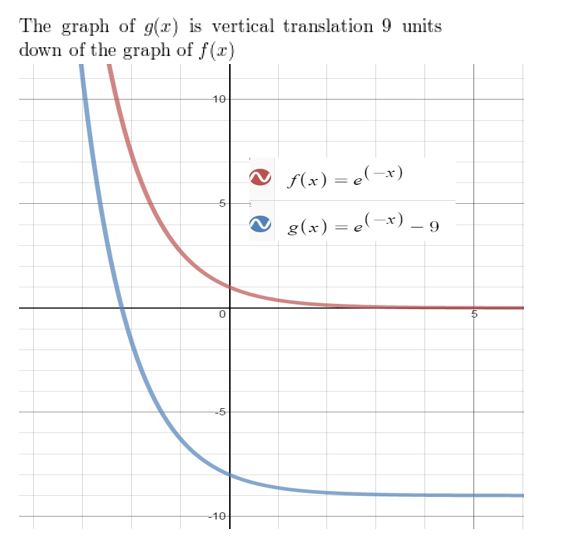
f(x) = e-x, g(x) = e-x − 9
Answer:
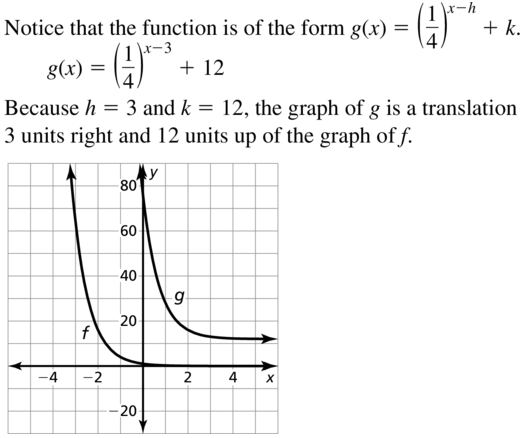
Question 15.
f(x) = (\(\frac{1}{4}\))x, g (x) = (\(\frac{1}{4}\))x-3 + 12
Answer:
Question 16.
f(x) = (\(\frac{1}{3}\))x, g(x) = (\(\frac{1}{3}\))x+2 − \(\frac{2}{3}\)
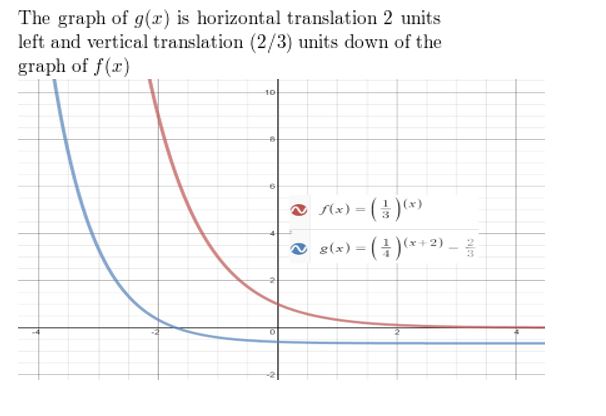
Answer:
In Exercises 17–24, describe the transformation of f represented by g. Then graph each function.
Question 17.
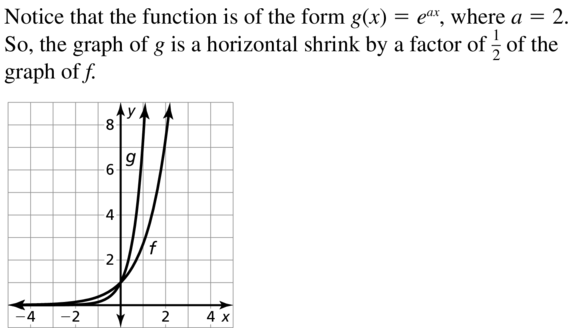
f(x) = ex, g(x) = e2x
Answer:
Question 18.
f(x) = ex, g (x) =4—3 ex
Answer:

Question 19.
f(x) = 2x, g(x) = −2x-3
Answer:
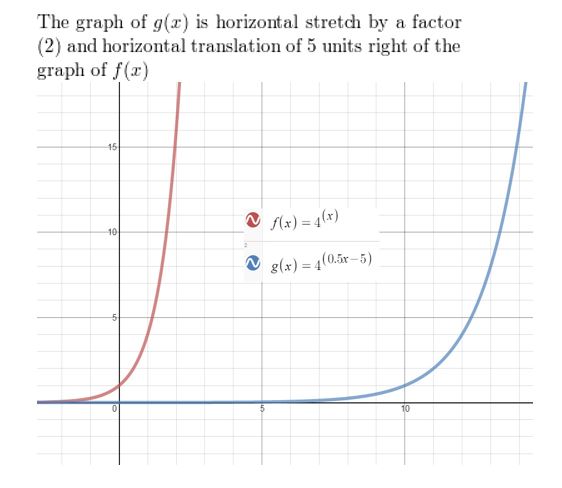
Question 20.
f(x) = 4x, g(x) = 40.5x-5
Answer:
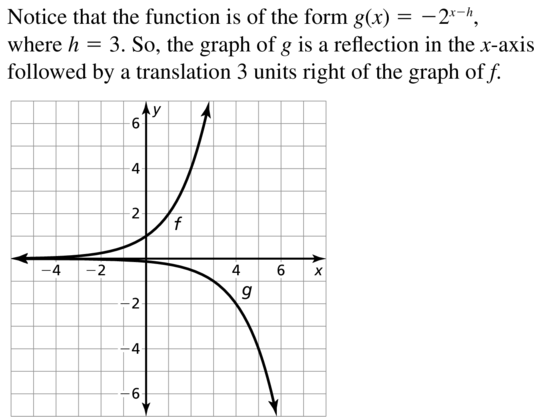
Question 21.
f(x) = e-x, g(x) = 3e-6x
Answer:
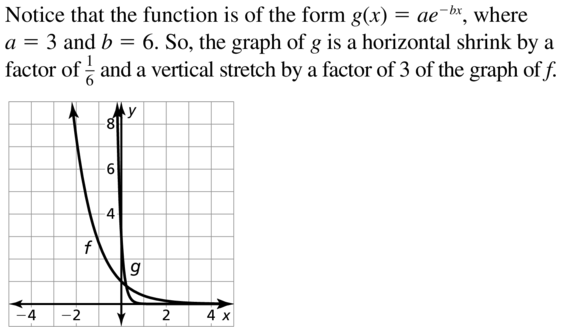
Question 22.
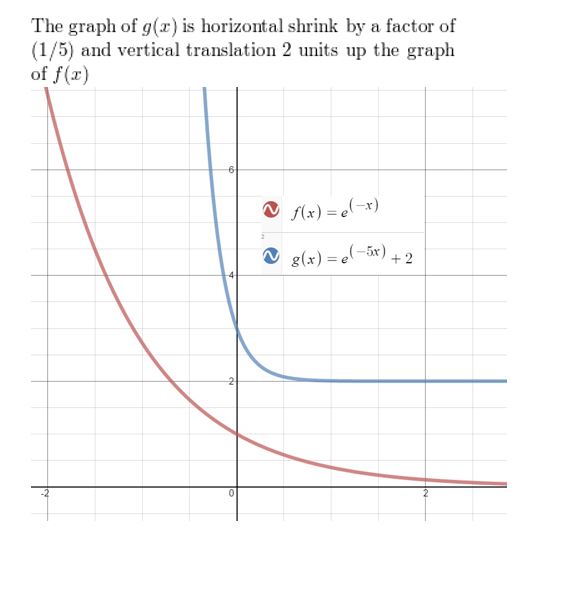
f(x) = e-x, g(x) = e-5x + 2
Answer:
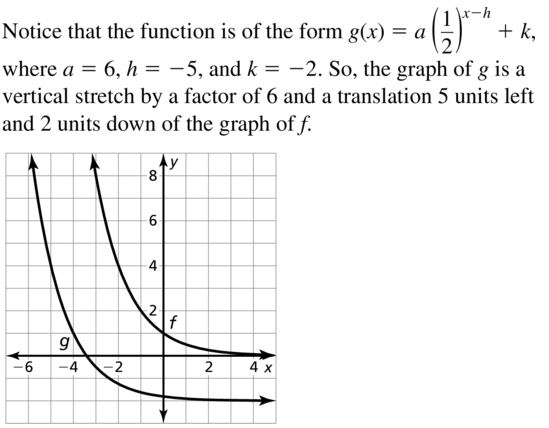
Question 23.
f(x) = (\(\frac{1}{2}\))x, g(x) = 6 (\(\frac{1}{2}\))x+5 − 2
Answer:
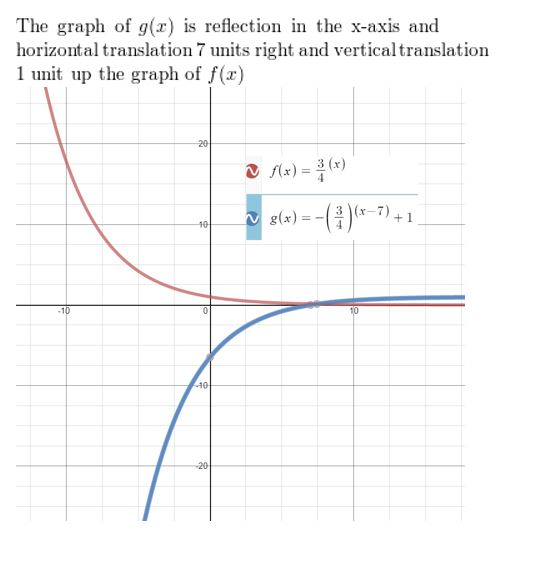
Question 24.
f(x) = (\(\frac{3}{4}\))x, g(x) = −(\(\frac{3}{4}\)) -7 + 1
Answer:
ERROR ANALYSIS In Exercises 25 and 26, describe and correct the error in graphing the function.
Question 25.
f(x) = 2x + 3
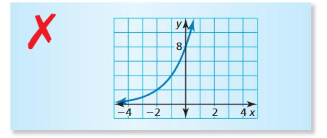
Answer:
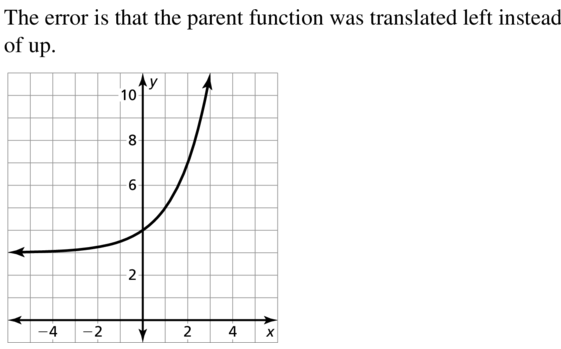
Question 26.
f(x) = 3-x
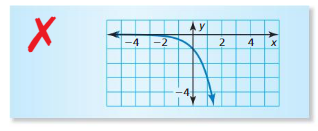
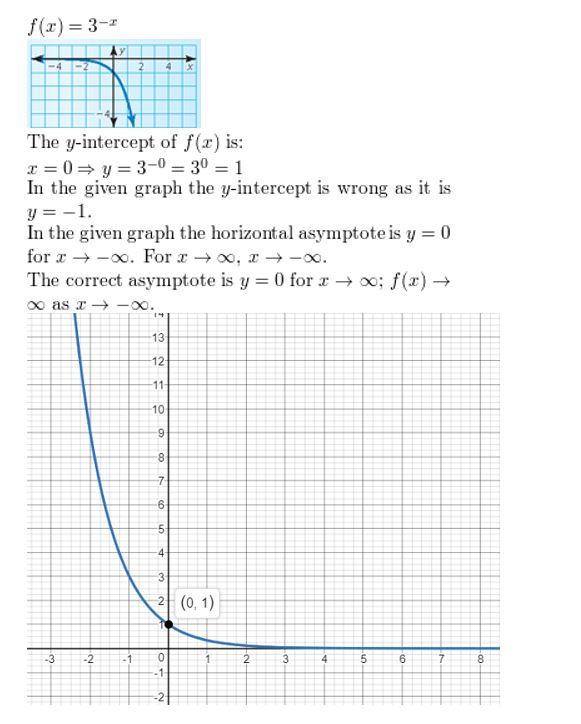
Answer:
In Exercises 27–30, describe the transformation of f represented by g. Then graph each function.
Question 27.
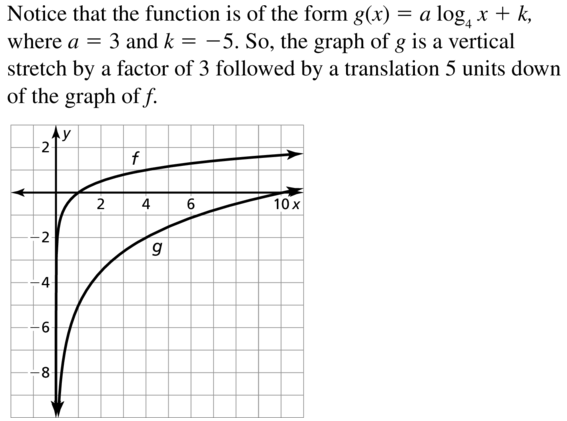
f(x) = log4 x, g(x) = 3 log4 x − 5
Answer:
Question 28.
f(x) = log1/3 x, g(x) = log1/3(−x) + 6
Answer:
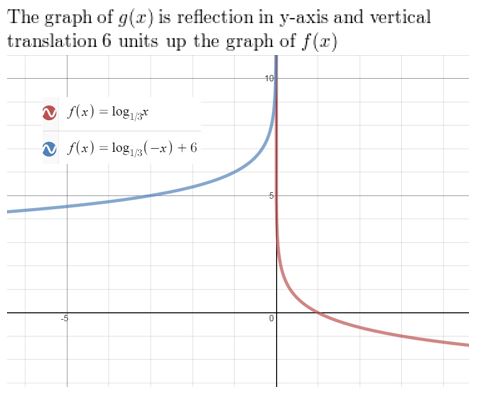
Question 29.
f(x) = log1/5 x, g(x) = − log1/5(x − 7)
Answer:
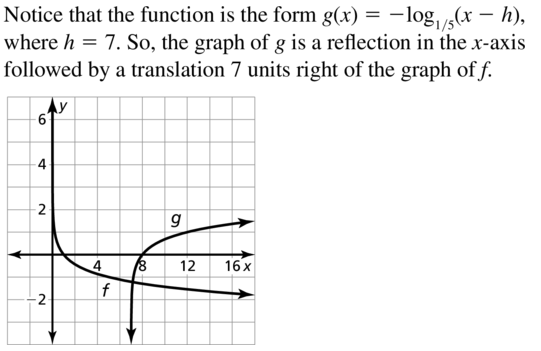
Question 30.
f(x) = log2 x, g(x) = log2(x + 2) − 3
Answer:
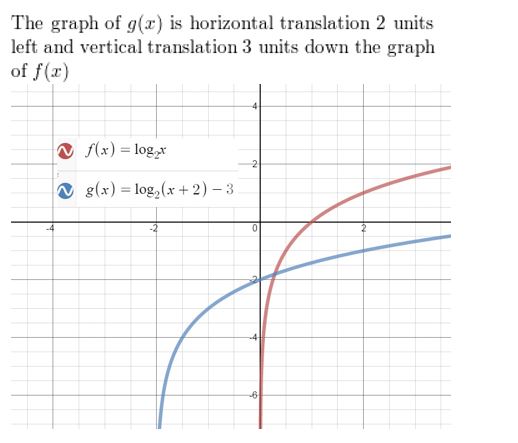
ANALYZING RELATIONSHIPS In Exercises 31–34, match the function with the correct transformation of the graph of f. Explain your reasoning.
Question 31.
y = f(x− 2)
Answer:
Question 32.
y = f(x + 2)
Answer:

Question 33.
y = 2f(x)
Answer:
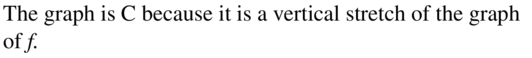
Question 34.
y = f(2x)
Answer:
In Exercises 35–38, write a rule for g that represents the indicated transformations of the graph of f.
Question 35.
f(x) = 5x; translation 2 units down, followed by a reflection in the y-axis
Answer:

Question 36.
f(x) = (\(\frac{2}{3}\))x; reflection in the x-axis, followed by a vertical stretch by a factor of 6 and a translation 4 units left
Answer:
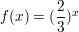
Question 37.
f(x) = ex; horizontal shrink by a factor of \(\frac{1}{2}\), followed by a translation 5 units up
Answer:

Question 38.
f(x) =e-x; translation 4 units right and 1 unit down, followed by a vertical shrink by a factor of \(\frac{1}{3}\)
Answer:
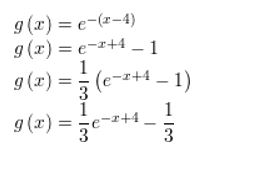
In Exercises 39–42, write a rule for g that represents the indicated transformation of the graph of f.
Question 39.
f(x) = log6 x; vertical stretch by a factor of 6, followed by a translation 5 units down
Answer:

Question 40.
f(x) = log2 x; reflection in the x-axis, followed by a translation 9 units left
Answer:
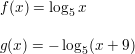
Question 41.
f(x) = log1/2 x; translation 3 units left and 2 units up, followed by a reflection in the y-axis
Answer:

Question 42.
f(x) = ln x; translation 3 units right and 1 unit up, followed by a horizontal stretch by a factor of 8
Answer:

JUSTIFYING STEPS In Exercises 43 and 44, justify each step in writing a rule for g that represents the indicated transformations of the graph of f.
Question 43.
f(x) = log7 x; reflection in the x-axis, followed by a translation 6 units down
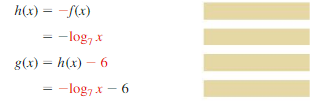
Answer:

Question 44.
f(x) = 8x; vertical stretch by a factor of 4, followed by a translation 1 unit up and 3 units left
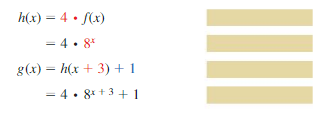
Answer:
USING STRUCTURE In Exercises 45–48, describe the transformation of the graph of f represented by the graph of g. Then give an equation of the asymptote.
Question 45.
f(x) = ex, g(x) = ex + 4
Answer:
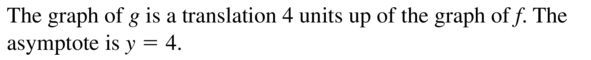
Question 46.
f(x) = 3x, g(x) = 3x-9
Answer:
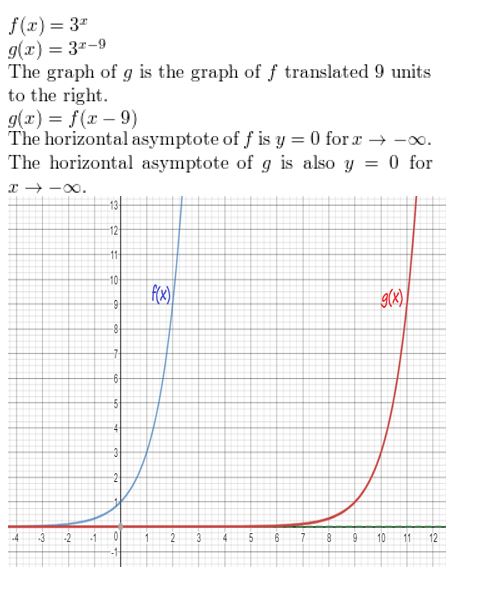
Question 47.
f(x) = ln x, g(x) = ln(x + 6)
Answer:
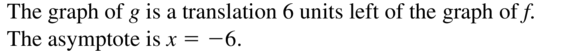
Question 48.
f(x) = log1/5 x, g(x) = log1/5 x + 13
Answer:
Question 49.
MODELING WITH MATHEMATICS
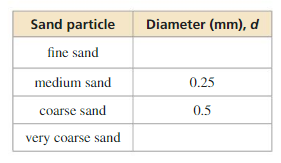
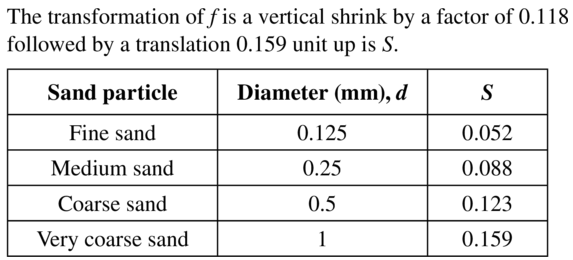
The slope Sof a beach is related to the average diameter d(in millimeters) of the sand particles on the beach by the equation S = 0.159 + 0.118 log d. Describe the transformation of f(d ) = log d represented by S. Then use the function to determine the slope of a beach for each sand type below.
Answer:
Question 50.
HOW DO YOU SEE IT?
The graphs of f(x) = bx and g(x) = (\(\frac{1}{b}\))x are shown for b = 2.
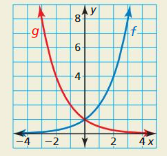
a. Use the graph to describe a transformation of the graph of f that results in the graph of g.
b. Does your answer in part (a) change when 0 < b < 1? Explain.
Answer:
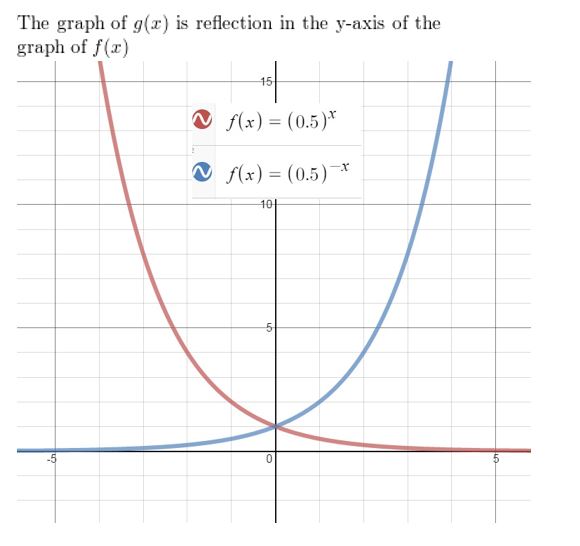
Question 51.
MAKING AN ARGUMENT
Your friend claims a single transformation of f(x) = log x can result in a function g whose graph never intersects the graph of f. Is your friend correct? Explain your reasoning.
Answer:

Question 52.
THOUGHT PROVOKING
Is it possible to transform the graph of f(x) = ex to obtain the graph of g(x) = ln x? Explain your reasoning.
Answer:
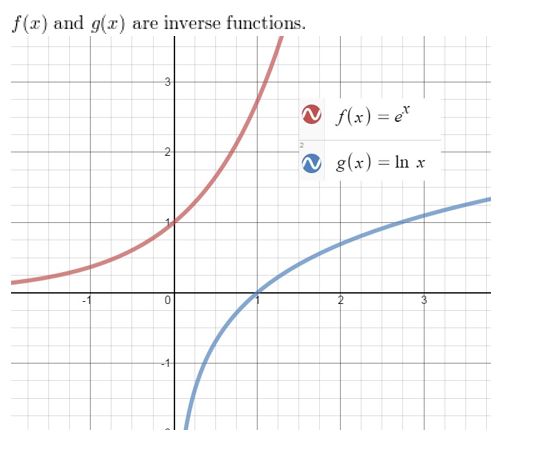
Question 53.
ABSTRACT REASONING
Determine whether each statement is always, sometimes, or never true. Explain your reasoning.
a. A vertical translation of the graph of f(x) = log x changes the equation of the asymptote.
b. A vertical translation of the graph of f(x) = ex changes the equation of the asymptote.
c. A horizontal shrink of the graph of f(x) = log x does not change the domain.
d. The graph of g(x) = abx-h + k does not intersect the x-axis.
Answer:

Question 54.
PROBLEM SOLVING
The amount P (in grams) of 100 grams of plutonium-239 that remains after t years can be modeled by P= 100(0.99997)t.
a. Describe the domain and range of the function.
b. How much plutonium-239 is present after 12,000 years?
c. Describe the transformation of the function if the initial amount of plutonium were 550 grams.
d. Does the transformation in part (c) affect the domain and range of the function? Explain your reasoning.
Answer:

Question 55.
CRITICAL THINKING
Consider the graph of the function h(x) = e-x-2. Describe the transformation of the graph of f(x) = e-x represented by the graph of h. Then describe the transformation of the graph of g(x) = ex represented by the graph of h. Justify your answers.
Answer:

Question 56.
OPEN-ENDED
Write a function of the form y = abx-h + k whose graph has a y-intercept of 5 and an asymptote of y = 2.
Answer:
y=3(2^-x)+2
Maintaining Mathematical Proficiency
Perform the indicated operation.
Question 57.
Let f(x) = x4 and g(x) = x2. Find ( fg)(x). Then evaluate the product when x = 3.
Answer:
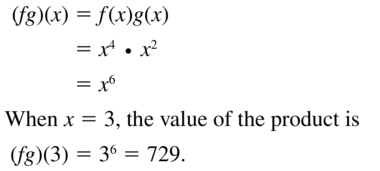
Question 58.
Let f(x) = 4x6 and g(x) = 2x3. Find (\(\frac{f}{g}\)) (x). Then evaluate the quotient when x = 5.
Answer:
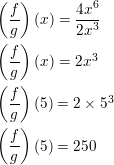
Question 59.
Let f(x) = 6x3 and g(x) = 8x3. Find ( f + g)(x). Then evaluate the sum when x = 2.
Answer:
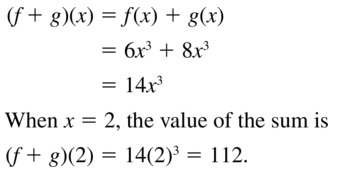
Question 60.
Let f(x) = 2xx and g(x) = 3xx. Find ( f – g)(x). Then evaluate the difference when x = 6.
Answer:
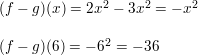
Exponential and Logarithmic Functions Study Skills: Forming a Weekly Study Group
6.1–6.4 What Did You Learn?
Core Vocabulary

Core Concepts

Mathematical Practices
Question 1.
How did you check to make sure your answer was reasonable in Exercise 23 on page 300?
Answer:
Question 2.
How can you justify your conclusions in Exercises 23–26 on page 307?
Answer:
Question 3.
How did you monitor and evaluate your progress in Exercise 66 on page 315?
Answer:
Study Skills: Forming a Weekly Study Group
- Select students who are just as dedicated to doing well in the math class as you are.
- ind a regular meeting place that has minimal distractions.
- Compare schedules and plan at least one time a week to meet, allowing at least 1.5 hours for study time.

Exponential and Logarithmic Functions 6.1–6.4 Quiz
Tell whether the function represents exponential growth or exponential decay. Explain your reasoning.
Question 1.
f(x) = (4.25)x
Answer:
f(x) = (4.25)x
The base b is 4.25
where a ≠ 0
4.25 is greater than 1 (b >1)
The function represents exponential growth.
Question 2.
y = (\(\frac{3}{8}\))x
Answer:
3/8 = number less than one
Question 3.
y = e0.6x
Answer:

Question 4.
f(x) = 5e-2x
Answer:

Simplify the expression.
Question 5.
e8 • e4
Answer:
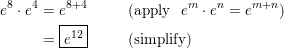
Question 6.
\(\frac{15 e^{3}}{3 e}\)
Answer:

Question 7.
(5e4x)3
Answer:
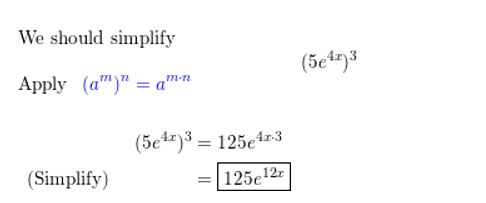
Question 8.
elln 9
Answer:
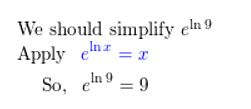
Question 9.
log7 49x
Answer:
Question 10.
log3 81-2x
Answer:
Rewrite the expression in exponential or logarithmic form.
Question 11.
log4 1024 = 5
Answer:
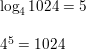
Question 12.
log1/3 27 = −3
Answer:

Question 13.
74 = 2401
Answer:

Question 14.
4-2 = 0.0625
Answer:

Evaluate the logarithm. If necessary, use a calculator and round your answer to three decimal places.
Question 15.
log 45
Answer:
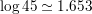
Question 16.
ln 1.4
Answer:
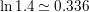
Question 17.
log2 32
Answer:
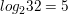
Graph the function and its inverse.
Question 18.
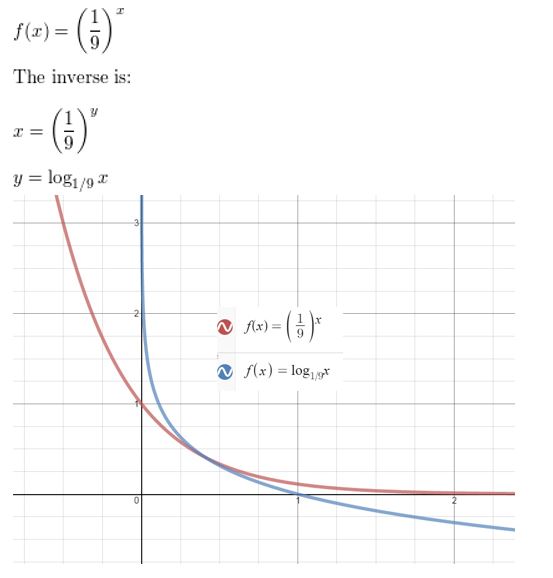
f(x) = (\(\frac{1}{9}\))x
Answer:
Question 19.
y = ln(x − 7)
Answer:

Question 20.
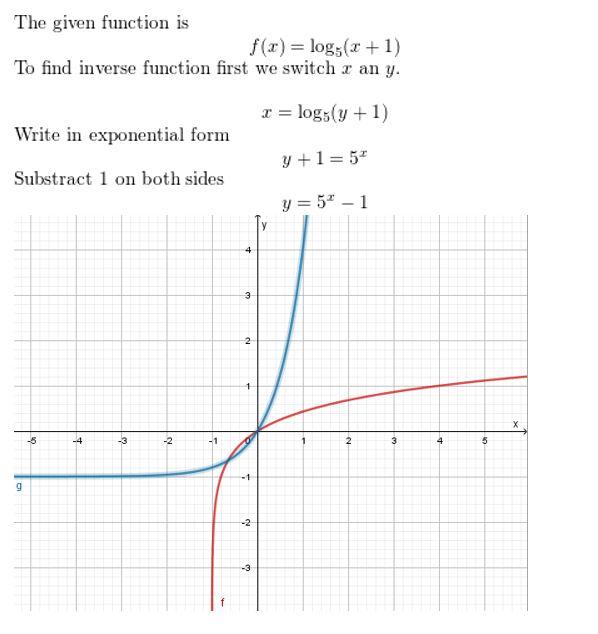
f(x) = log5 (x+ 1)
Answer:
The graph of g is a transformation of the graph of f. Write a rule for g.
Question 21.
f(x) = log3 x
Answer:

Question 22.
f(x) = 3x
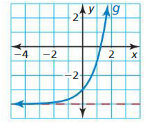
Answer:
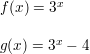
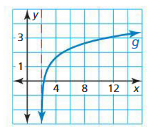
Question 23.
f(x)= log1/2 x
Answer:
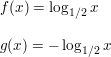
Question 24.
You purchase an antique lamp for $150. The value of the lamp increases by 2.15% each year. Write an exponential model that gives the value y (in dollars) of the lamp t years after you purchased it.
Answer:
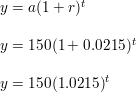
Question 25.
A local bank advertises two certificate of deposit (CD) accounts that you can use to save money and earn interest. The interest is compounded monthly for both accounts.

a. You deposit the minimum required amounts in each CD account. How much money is in each account at the end of its term? How much interest does each account earn? Justify your answers.
b. Describe the benefits and drawbacks of each account.
Answer:
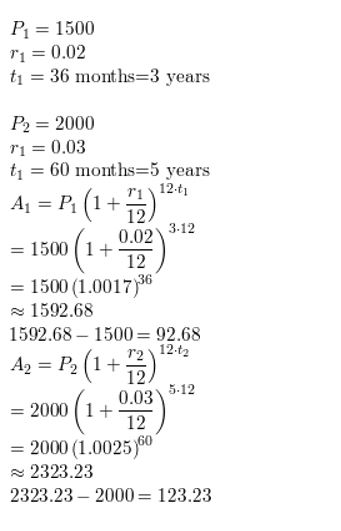
Question 26.
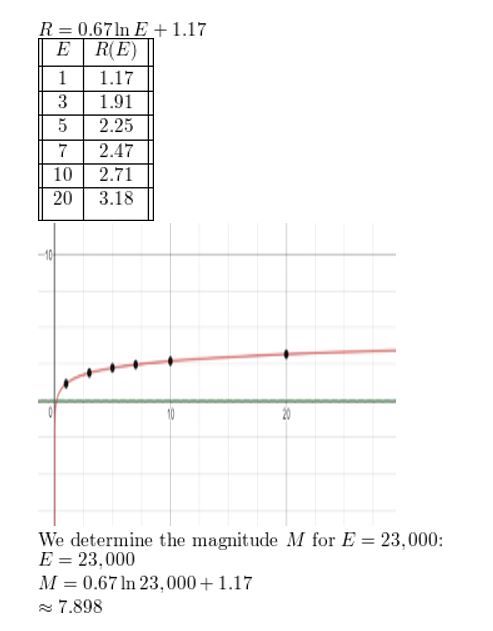
The Richter scale is used for measuring the magnitude of an earthquake. The Richter magnitude R is given by R = 0.67 ln E + 1.17, where E is the energy (in kilowatt-hours) released by the earthquake. Graph the model. What is the Richter magnitude for an earthquake that releases 23,000 kilowatt-hours of energy?
Answer:
Lesson 6.5 Properties of Logarithms
Essential Question How can you use properties of exponents to derive properties of logarithms?
Let x = logb m and y = logb n.
The corresponding exponential forms of these two equations are
bx = m and by = n.
EXPLORATION 1
Product Property of Logarithms
Work with a partner. To derive the Product Property, multiply m and n to obtain mn =bxby = bx+y.
The corresponding logarithmic form of mn = bx+y is logb mn = x + y. So,
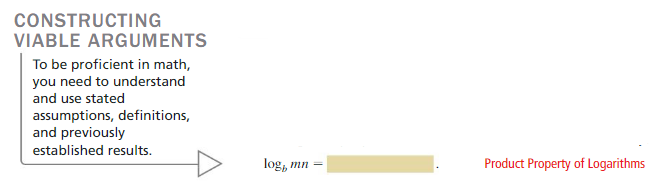
EXPLORATION 2
Quotient Property of Logarithms
Work with a partner. To derive the Quotient Property, divide m by n to obtain
\(\frac{m}{n}=\frac{b^{x}}{b^{y}}\) = bx-y.
The corresponding logarithmic form of \(\frac{m}{n}\) = bx-y is logb \(\frac{m}{n}\) = x − y. So,

EXPLORATION 3
Power Property of Logarithms
Work with a partner. To derive the Power Property, substitute bx for m in the expression logb mn, as follows.

Communicate Your Answer
Question 4.
How can you use properties of exponents to derive properties of logarithms?
Answer:
Question 5.
Use the properties of logarithms that you derived in Explorations 1–3 to evaluate each logarithmic expression.
a. log4 163
b. log3 81-3
c. ln e2 + ln e5
d. 2 ln e6 − ln e5
e. log5 75 − log5 3
f. log4 2 + log4 32
Answer:
Monitoring Progress
Use log6 5 ≈ 0.898 and log6 8 ≈ 1.161 to evaluate the logarithm.
Question 1.
log6 \(\frac{5}{8}\)
Answer:

Question 2.
log6 40
Answer:

Question 3.
log6 64
Answer:
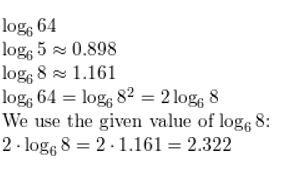
Question 4.
log6 125
Answer:
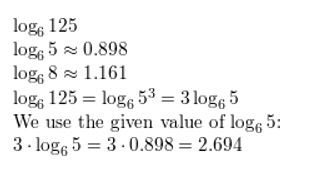
Expand the logarithmic expression.
Question 5.
log6 3x4
Answer:
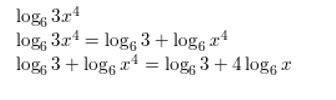
Question 6.
ln \(\frac{5}{12x}\)
Answer:

Condense the logarithmic expression.
Question 7.
log x − log 9
Answer:
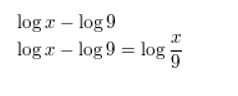
Question 8.
ln 4 + 3 ln 3 − ln 12
Answer:
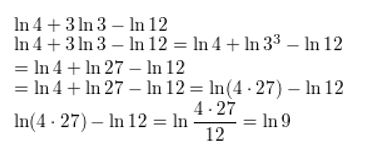
Use the change-of-base formula to evaluate the logarithm.
Question 9.
log5 8
Answer:

Question 10.
log8 14
Answer:
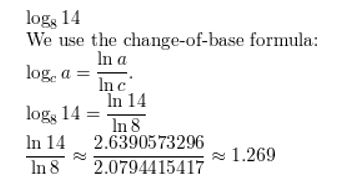
Question 11.
log26 9
Answer:

Question 12.
log12 30
Answer:

Question 13.
WHAT IF?
In Example 6, the artist turns up the volume so that the intensity of the sound triples. By how many decibels does the loudness increase?
Answer:

Properties of Logarithms 6.5 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
To condense the expression log3 2x + log3 y, you need to use the __________ Property of Logarithms.
Answer:
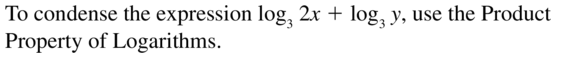
Question 2.
WRITING
Describe two ways to evaluate log7 12 using a calculator.
Answer:
The two ways to evaluate log7 12 using a calculator is
i. By changing its base to a natural base.
ii. By changing its base to a common base.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, use log7 4 ≈ 0.712 and log7 12 ≈ 1.277 to evaluate the logarithm.
Question 3.
log7 3
Answer:

Question 4.
log7 48
Answer:
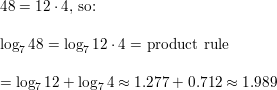
Question 5.
log7 16
Answer:
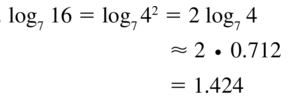
Question 6.
log7 64
Answer:

Question 7.
log7 \(\frac{1}{4}\)
Answer:
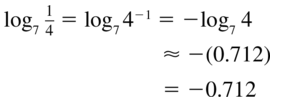
Question 8.
log7 \(\frac{1}{3}\)
Answer:

In Exercises 9–12, match the expression with the logarithm that has the same value. Justify your answer.
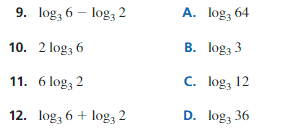
Answer:
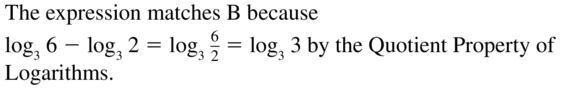

In Exercises 13–20, expand the logarithmic expression.
Question 13.
log3 4x
Answer:
![]()
Question 14.
log8 3x
Answer:
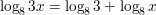
Question 15.
log 10x5
Answer:
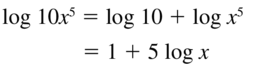
Question 16.
ln 3x4
Answer:
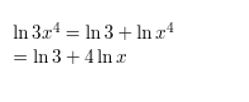
Question 17.
ln \(\frac{x}{3 y}\)
Answer:
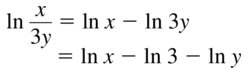
Question 18.
ln \(\frac{6 x^{2}}{y^{4}}\)
Answer:

Question 19.
log7 5\(\sqrt{x}\)
Answer:
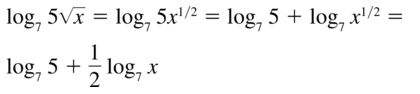
Question 20.
log5 \(\sqrt[3]{x^{2} y}\)
Answer:

ERROR ANALYSIS In Exercises 21 and 22, describe and correct the error in expanding the logarithmic expression.
Question 21.
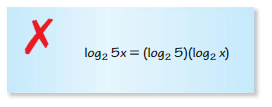
Answer:

Question 22.
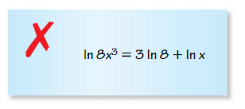
Answer:
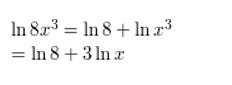
In Exercises 23–30, condense the logarithmic expression.
Question 23.
log4 7 − log4 10
Answer:
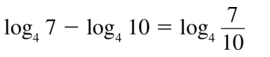
Question 24.
ln 12 − ln 4
Answer:
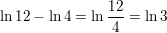
Question 25.
6 ln x+ 4 ln y
Answer:
![]()
Question 26.
2 log x+ log 11
Answer:
2 log x + log 11
log x^2 + log 11
log 11x^2
Question 27.
log5 4 + \(\frac{1}{3}\) log5 x
Answer:
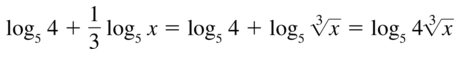
Question 28.
6 ln 2 − 4 ln y
Answer:

Question 29.
5 ln 2 + 7 ln x + 4 ln y
Answer:
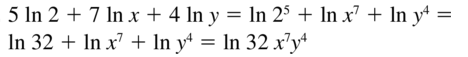
Question 30.
log3 4 + 2 log3 \(\frac{1}{2}\) + log3 x
Answer:
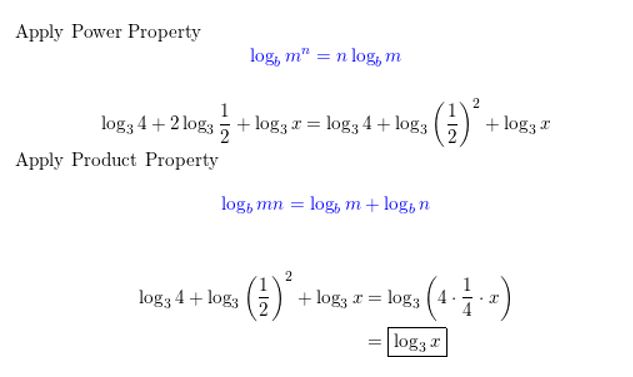
Question 31.
REASONING
Which of the following is not equivalent to log3 \(\frac{y^{4}}{3 x}\)? Justify your answer.
A. 4 log5 y − log5 3x
B. 4 log5 y − log5 3 + log5 x
C. 4 log5 y− log5 3 − log5 x
D. log5 y4 − log5 3 − log5 x
Answer:
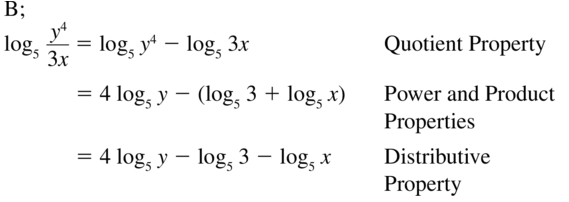
Question 32.
REASONING
Which of the following equations is correct? Justify your answer.
A. log7 x + 2 log7 y = log7 (x + y2)
B. 9 log x − 2 log y = log \(\frac{x^{9}}{y^{2}}\)
C. 5 log4 x + 7 log2 y = log6x5y7
D. log9x − 5 log9 y = log9 \(\frac{x}{5 y}\)
Answer:

In Exercises 33–40, use the change-of-base formula to evaluate the logarithm.
Question 33.
log4 7
Answer:
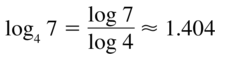
Question 34.
log5 13
Answer:

Question 35.
log9 15
Answer:
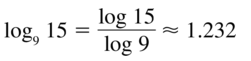
Question 36.
log8 22
Answer:

Question 37.
log6 17
Answer:
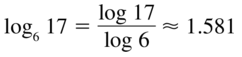
Question 38.
log2 28
Answer:

Question 39.
log7 \(\frac{3}{16}\)
Answer:
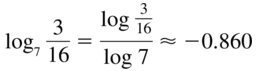
Question 40.
log3 \(\frac{9}{40}\)
Answer:

Question 41.
MAKING AN ARGUMENT
Your friend claims you can use the change-of-base formula to graph y = log3x using a graphing calculator. Is your friend correct? Explain your reasoning.
Answer:
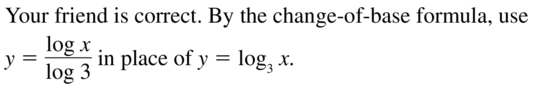
Question 42.
HOW DO YOU SEE IT?
Use the graph to determine the value of \(\frac{\log 8}{\log 2}\).
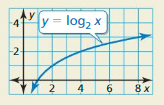
Answer:

MODELING WITH MATHEMATICS In Exercises 43 and 44, use the function L(I ) given in Example 6.
Question 43.
The blue whale can produce sound with an intensity that is 1 million times greater than the intensity of the loudest sound a human can make. Find the difference in the decibel levels of the sounds made by a blue whale and a human.

Answer:

Question 44.
The intensity of the sound of a certain television advertisement is 10 times greater than the intensity of the television program. By how many decibels does the loudness increase?

Answer:
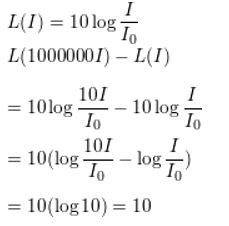
Question 45.
REWRITING A FORMULA
Under certain conditions, the wind speed s (in knots) at an altitude of h meters above a grassy plain can be modeled by the function s(h) = 2 ln 100h.
a. By what amount does the wind speed increase when the altitude doubles?
b. Show that the given function can be written in terms of common logarithms as
s(h) = \(\frac{2}{\log e}\)(log h+ 2).
Answer:

Question 46.
THOUGHT PROVOKING
Determine whether the formula
logb (M + N) = logb M + logbN
is true for all positive, real values of M, N, and b(with b≠ 1). Justify your answer.
Answer:
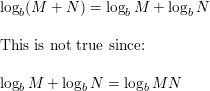
Question 47.
USING STRUCTURE
Use the properties of exponents to prove the change-of-base formula. (Hint: Let x= logb a, y = logb c, and z = logb a.)
Answer:
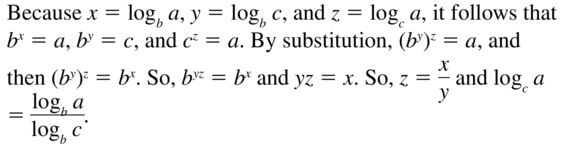
Question 48.
CRITICAL THINKING
Describe three ways to transform the graph of f(x) = log x to obtain the graph of g(x) = log 100x − 1. Justify your answers.
Answer:

Maintaining Mathematical Proficiency
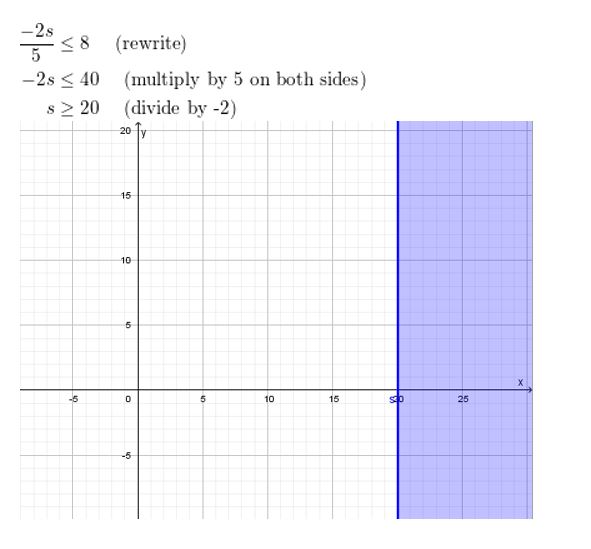
Solve the inequality by graphing.
Question 49.
x2 − 4 > 0
Answer:
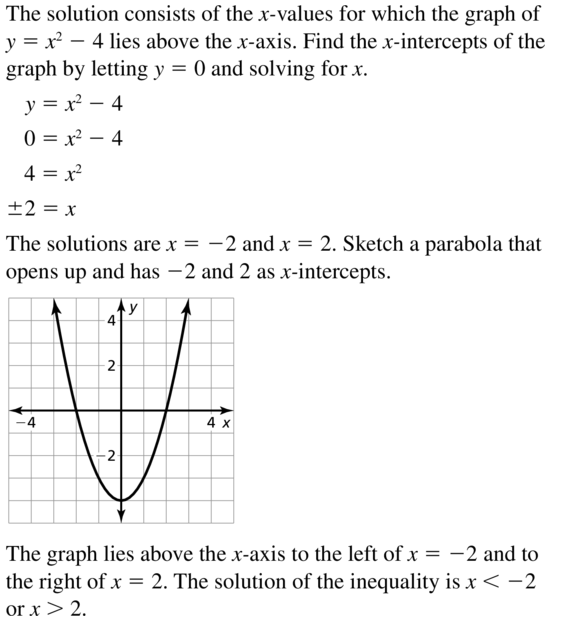
Question 50.
2(x − 6)2 − 5 ≥ 37
Answer:

Question 51.
x2 + 13x + 42 < 0
Answer:
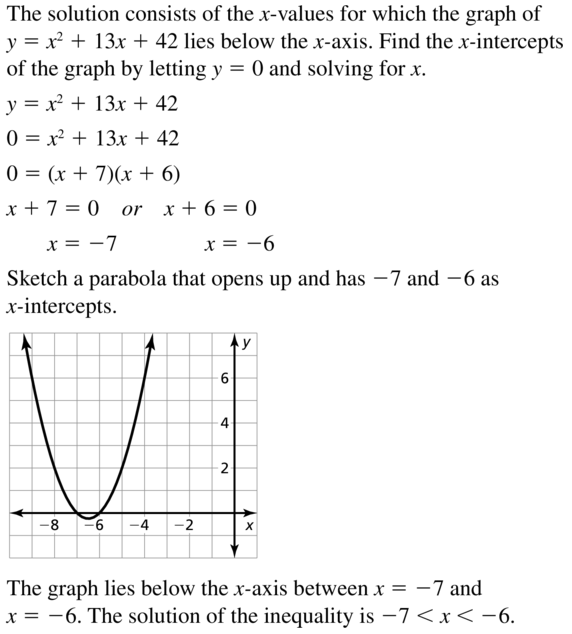
Question 52.
−x2 − 4x + 6 ≤ −6
Answer:
Solve the equation by graphing the related system of equations.
Question 53.
4x2 − 3x − 6 = −x2 + 5x + 3
Answer:

Question 54.
−(x + 3)(x − 2) = x2 − 6x
Answer:
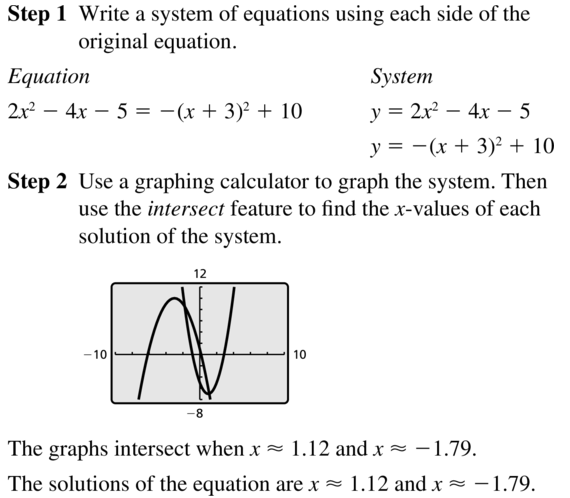
Question 55.
2x2 − 4x − 5 = −(x + 3)2 + 10
Answer:
Question 56.
−(x + 7)2 + 5 = (x + 10)2 − 3
Answer:
Lesson 6.6 Solving Exponential and Logarithmic Equations
Essential Question How can you solve exponential and logarithmic equations?
EXPLORATION 1
Solving Exponential and Logarithmic Equations
Work with a partner. Match each equation with the graph of its related system of equations. Explain your reasoning. Then use the graph to solve the equation.
a. ex = 2
b. ln x = −1
c. 2x = 3-x
d. log4x = 1
e. log5 x = \(\frac{1}{2}\)
f. 4x = 2
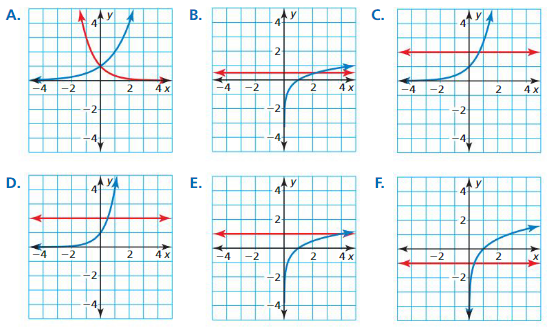
EXPLORATION 2
Solving Exponential and Logarithmic Equations
Work with a partner. Look back at the equations in Explorations 1(a) and 1(b). Suppose you want a more accurate way to solve the equations than using a graphical approach.
a. Show how you could use a numerical approach by creating a table. For instance, you might use a spreadsheet to solve the equations.

b. Show how you could use an analytical approach. For instance, you might try solving the equations by using the inverse properties of exponents and logarithms.
Communicate Your Answer
Question 3.
How can you solve exponential and logarithmic equations?
Answer:
Question 4.
Solve each equation using any method. Explain your choice of method.
a. 16x = 2
b. 2x = 42x+1
c. 2x = 3x+1
d. log x = \(\frac{1}{2}\)
e. ln x = 2
f. log3 x = \(\frac{3}{2}\)
Answer:
Monitoring Progress
Solve the equation.
Question 1.
2x = 5
Answer:
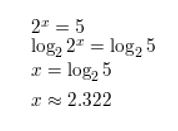
Question 2.
79x = 15
Answer:
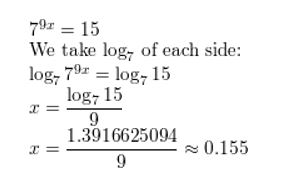
Question 3.
4e-0.3x − 7 = 13
Answer:

Question 4.
WHAT IF?
In Example 2, how long will it take to cool the stew to 100ºF when the room temperature is 75ºF?
Answer:
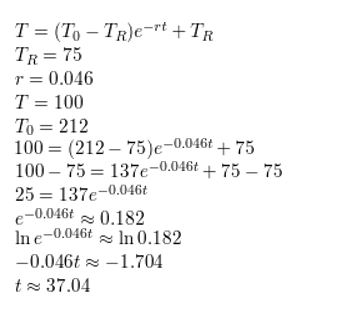
Solve the equation. Check for extraneous solutions.
Question 5.
ln(7x − 4) = ln(2x + 11)
Answer:
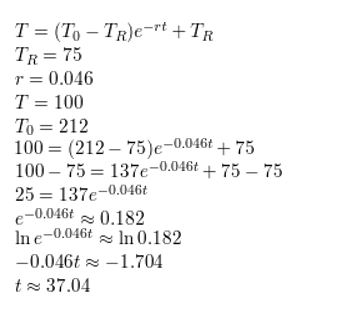
Question 6.
log2(x − 6) = 5
Answer:
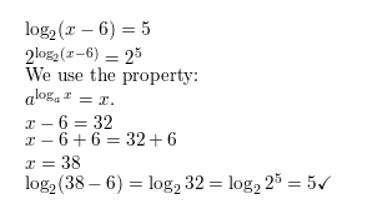
Question 7.
log 5x + log(x − 1) = 2
Answer:
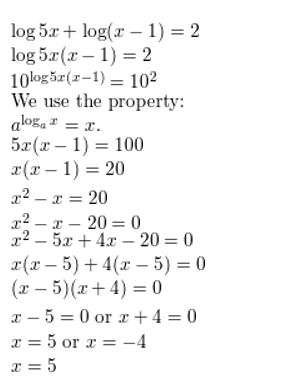
Question 8.
log4 (x + 12) + log4 x = 3
Answer:
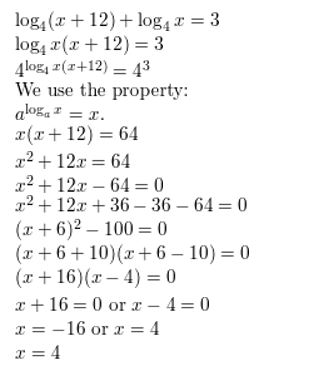
Solve the inequality.
Question 9.
ex < 2
Answer:
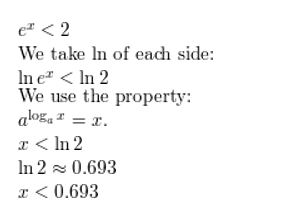
Question 10.
102x-6 > 3
Answer:

Question 11.
log x + 9 < 45 Answer: Question 12. 2 ln x − 1 > 4
Answer:
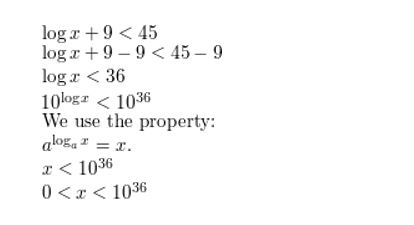
Solving Exponential and Logarithmic Equations 6.6 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The equation 3x-1 = 34 is an example of a(n) ___________ equation.
Answer:
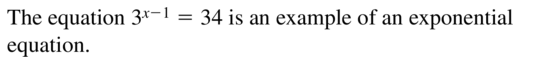
Question 2.
WRITING
Compare the methods for solving exponential and logarithmic equations.
Answer: There are several strategies that can be used to solve equations involving exponents and logarithms. Taking logarithms of both sides is helpful with exponential equations. Rewriting a logarithmic equation as an exponential equation is a useful strategy. Using properties of logarithms is helpful to combine many logarithms into a single one.
Question 3.
WRITING
When do logarithmic equations have extraneous solutions?
Answer:

Question 4.
COMPLETE THE SENTENCE
If b is a positive real number other than 1, then bx = by if and only if _________
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 5–16, solve the equation.
Question 5.
73x+5 = 71-x
Answer:
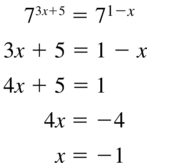
Question 6.
e2x = e3x-1
Answer:
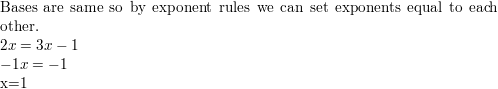
Question 7.
5x-3 = 25x-5
Answer:

Question 8.
62x-6 = 363x-5
Answer:

Question 9.
3x = 7
Answer:
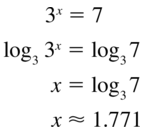
Question 10.
5x = 33
Answer:

Question 11.
495x+2 = (\(\frac{1}{7}\))11-x
Answer:
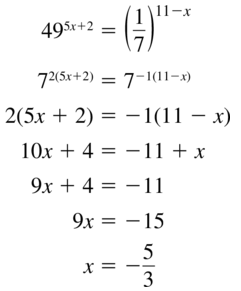
Question 12.
5125x-1 = (\(\frac{1}{8}\))-4-x
Answer:
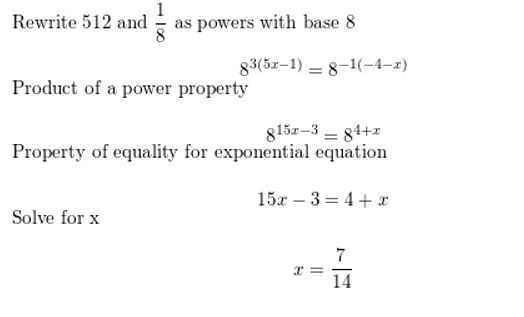
Question 13.
75x = 12
Answer:
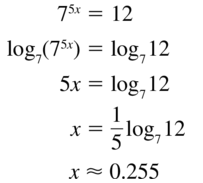
Question 14.
116x = 38
Answer:

Question 15.
3e4x+9 = 15
Answer:
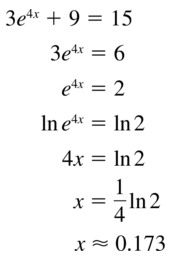
Question 16.
2e2x − 7 = 5
Answer:

Question 17.
MODELING WITH MATHEMATICS
The length ℓ(in centimeters) of a scalloped hammerhead shark can be modeled by the function ℓ = 266 − 219-0.05t
where t is the age (in years) of the shark. How old is a shark that is 175 centimeters long?

Answer:
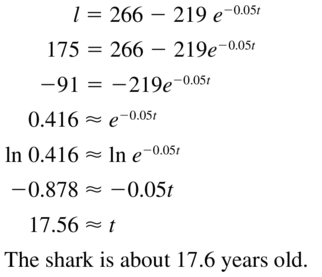
Question 18.
MODELING WITH MATHEMATICS
One hundred grams of radium are stored in a container. The amount R(in grams) of radium present after t years can be modeled by R= 100e−0.00043t. After how many years will only 5 grams of radium be present?
Answer:
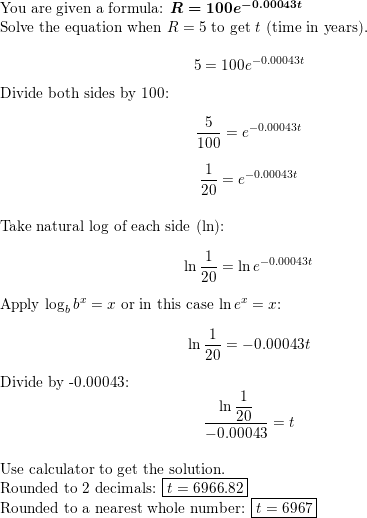
In Exercises 19 and 20, use Newton’s Law of Cooling to solve the problem.
Question 19.
You are driving on a hot day when your car overheats and stops running. The car overheats at 280°F and can be driven again at 230°F. When it is 80°F outside, the cooling rate of the car is r = 0.0058. How long do you have to wait until you can continue driving?

Answer:

Question 20.
You cook a turkey until the internal temperature reaches 180°F. The turkey is placed on the table until the internal temperature reaches 100°F and it can be carved. When the room temperature is 72°F, the cooling rate of the turkey is r = 0.067. How long do you have to wait until you can carve the turkey?
Answer:

In Exercises 21–32, solve the equation.
Question 21.
ln(4x − 7) = ln(x + 11)
Answer:

Question 22.
ln(2x − 4) = ln(x + 6)
Answer:

Question 23.
log2(3x − 4) = log2 5
Answer:

Question 24.
log(7x + 3) = log 38
Answer:

Question 25.
log2(4x + 8) = 5
Answer:

Question 26.
log3(2x + 1) = 2
Answer:
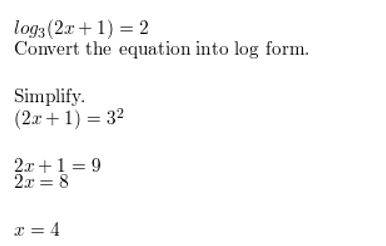
Question 27.
log7(4x + 9) = 2
Answer:

Question 28.
log5(5x + 10) = 4
Answer:
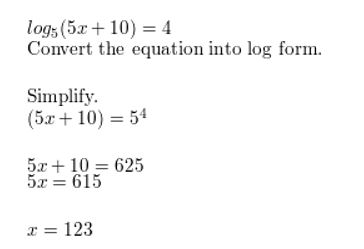
Question 29.
log(12x − 9) = log 3x
Answer:

Question 30.
log6(5x + 9) = log6 6x
Answer:
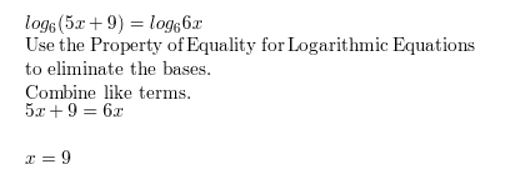
Question 31.
log2(x2 − x − 6) = 2
Answer:

Question 32.
log3(x2 + 9x + 27) = 2
Answer:
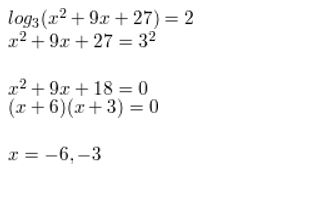
In Exercises 33–40, solve the equation. Check for extraneous solutions.
Question 33.
log2 x + log2 (x − 2) = 3
Answer:

Question 34.
log6 3x + log6 (x − 1) = 3
Answer:

Question 35.
ln x + ln(x + 3) = 4
Answer:

Question 36.
ln x + ln(x − 2) = 5
Answer:

Question 37.
log3 3x2 + log3 3 = 2
Answer:

Question 38.
log4 (−x) + log4 (x + 10) = 2
Answer:

Question 39.
log3(x − 9) + log3(x − 3) = 2
Answer:

Question 40.
log5 (x + 4) + log5 (x + 1) = 2
Answer:
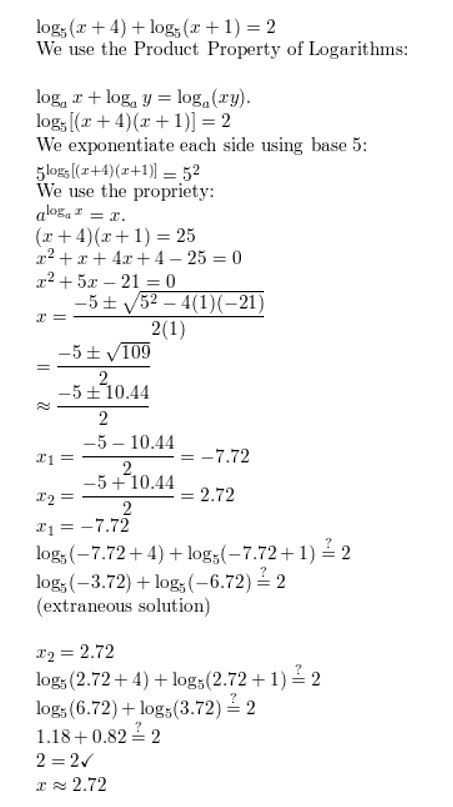
ERROR ANALYSIS In Exercises 41 and 42, describe and correct the error in solving the equation.
Question 41.
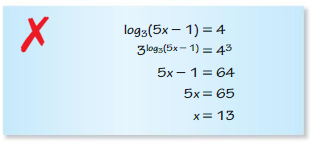
Answer:

Question 42.
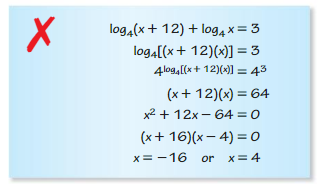
Answer:
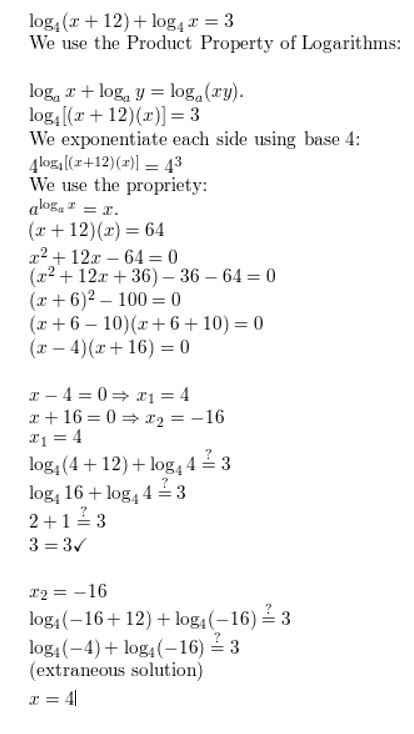
Question 43.
PROBLEM SOLVING
You deposit $100 in an account that pays 6% annual interest. How long will it take for the balance to reach $1000 for each frequency of compounding?
a. annual
b. quarterly
c. daily
d. continuously
Answer:
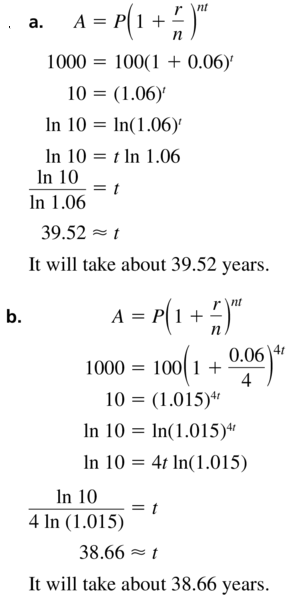
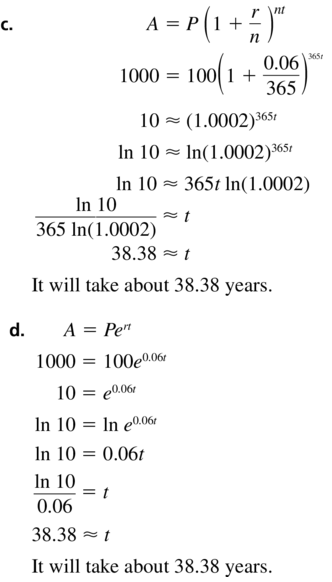
Question 44.
MODELING WITH MATHEMATICS
The apparent magnitude of a star is a measure of the brightness of the star as it appears to observers on Earth. The apparent magnitude M of the dimmest star that can be seen with a telescope is M = 5 log D+ 2, where D is the diameter (in millimeters) of the telescope’s objective lens. What is the diameter of the objective lens of a telescope that can reveal stars with a magnitude of 12?
Answer:

Question 45.
ANALYZING RELATIONSHIPS
Approximate the solution of each equation using the graph.
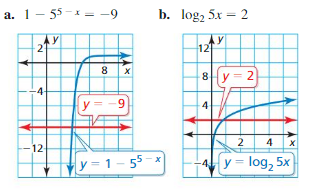
Answer:
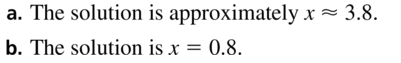
Question 46.
MAKING AN ARGUMENT
Your friend states that a logarithmic equation cannot have a negative solution because logarithmic functions are not defined for negative numbers. Is your friend correct? Justify your answer.
Answer: The statement stated by my friend “A logarithmic equation cannot have a negative solution because functions are not defined for negative numbers” is incorrect.
In Exercises 47–54, solve the inequality.
Question 47.
9x > 54
Answer:

Question 48.
4x ≤ 36
Answer:

Question 49.
ln x ≥ 3
Answer:
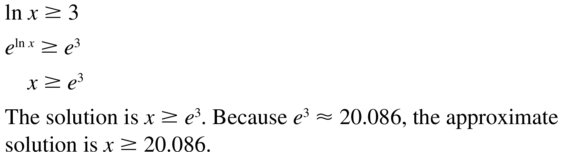
Question 50.
log4 x< 4
Answer:

Question 51.
34x-5 < 8
Answer:
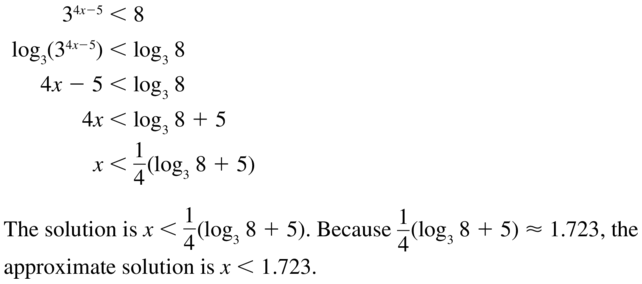
Question 52.
e3x+4 > 11
Answer:

Question 53.
−3 log5 x + 6 ≤ 9
Answer:
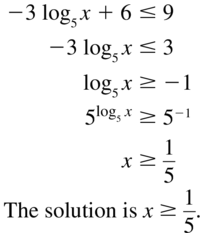
Question 54.
−4 log5 x − 5 ≥ 3
Answer:

Question 55.
COMPARING METHODS
Solve log5 x< 2 algebraically and graphically. Which method do you prefer? Explain your reasoning.
Answer:

Question 56.
PROBLEM SOLVING
You deposit $1000 in an account that pays 3.5% annual interest compounded monthly. When is your balance at least $1200? $3500?
Answer:

Question 57.
PROBLEM SOLVING
An investment that earns a rate of return r doubles in value in t years, where t = \(\frac{\ln 2}{\ln (1+r)}\) and r is expressed as a decimal. What rates of return will double the value of an investment in less than 10 years?
Answer:
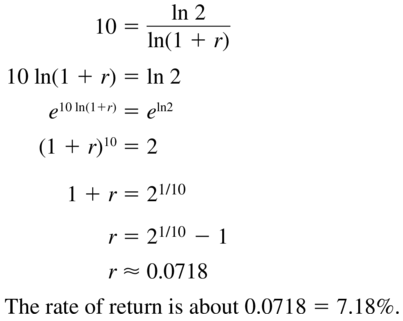
Question 58.
PROBLEM SOLVING
Your family purchases a new car for $20,000. Its value decreases by 15% each year. During what interval does the car’s value exceed $10,000?
Answer:
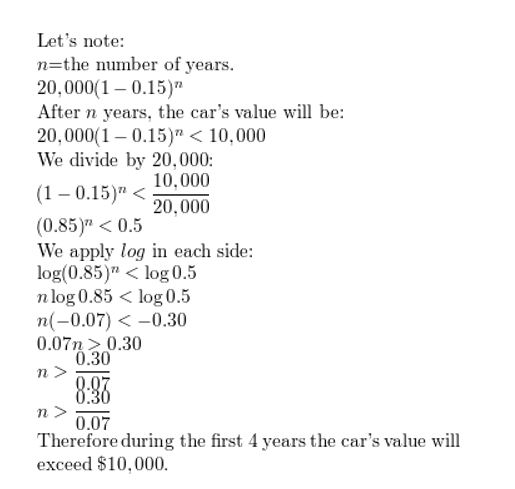
USING TOOLS In Exercises 59–62, use a graphing calculator to solve the equation.
Question 59.
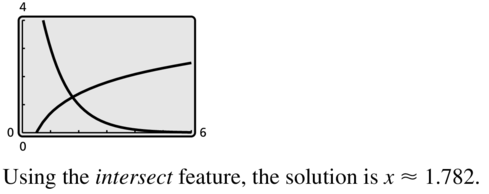
ln 2x = 3-x+2
Answer:
Question 60.
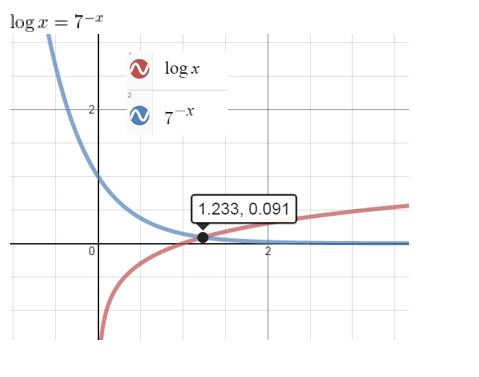
log x = 7-x
Answer:
Question 61.
log x = 3x-3
Answer:
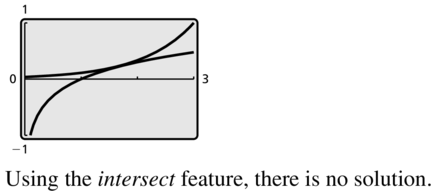
Question 62.
ln 2x = ex-3
Answer:
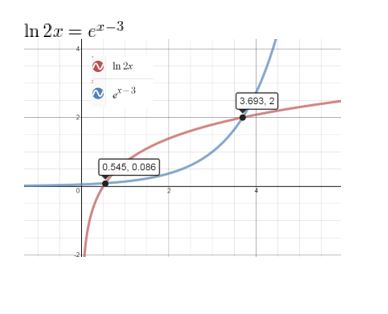
Question 63.
REWRITING A FORMULA
A biologist can estimate the age of an African elephant by measuring the length of its footprint and using the equation ℓ = 45 − 25.7e−0.09a, where ℓis the length (in centimeters) of the footprint and a is the age (in years).

a. Rewrite the equation, solving for a in terms of ℓ.
b. Use the equation in part (a) to find the ages of the elephants whose footprints are shown.
Answer:
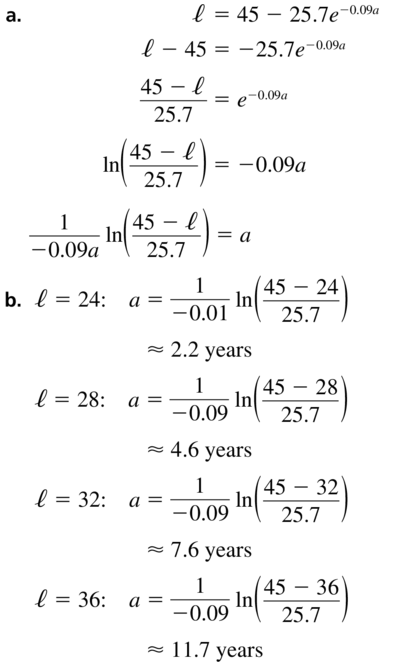
Question 64.
HOW DO YOU SEE IT?
Use the graph to solve the inequality 4 ln x + 6 > 9. Explain your reasoning.
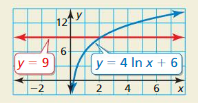
Answer:

Question 65.
OPEN-ENDED
Write an exponential equation that has a solution of x = 4. Then write a logarithmic equation that has a solution of x = −3.
Answer:

Question 66.
THOUGHT PROVOKING
Give examples of logarithmic or exponential equations that have one solution, two solutions, and no solutions.
Answer:
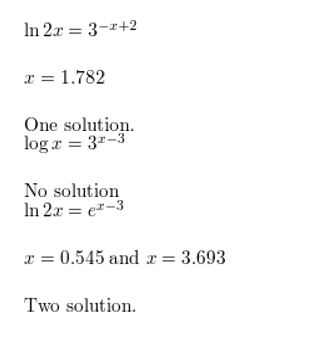
CRITICAL THINKING In Exercises 67–72, solve the equation.
Question 67.
2x+3 = 53x-1
Answer:
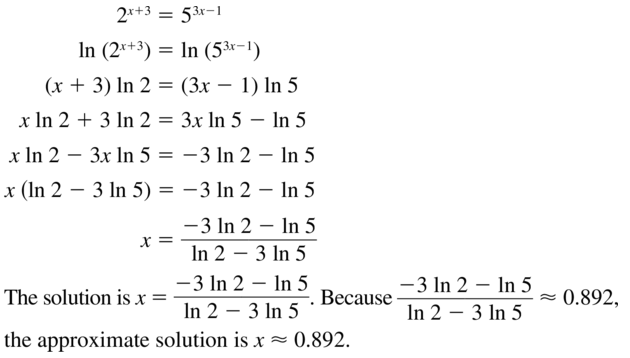
Question 68.
103x-8 = 25-x
Answer:

Question 69.
log3 (x − 6) = log9 2x
Answer:
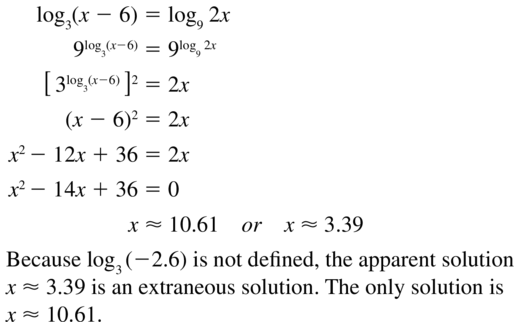
Question 70.
log4 x = log8 4x
Answer:
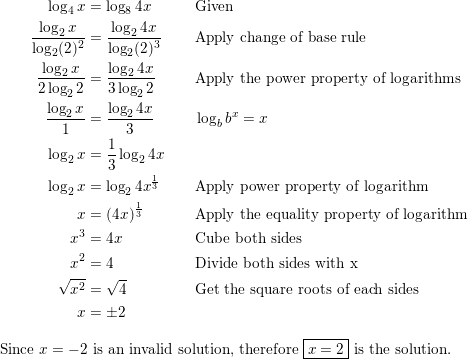
Question 71.
22x − 12 • 2x + 32 = 0
Answer:

Question 72.
52x + 20 • 5x − 125 = 0
Answer:
Question 73.
WRITING
In Exercises 67–70, you solved exponential and logarithmic equations with different bases. Describe general methods for solving such equations.
Answer:

Question 74.
PROBLEM SOLVING
When X-rays of a fixed wavelength strike a material x centimeters thick, the intensity I(x) of the X-rays transmitted through the material is given by I(x) = I0e−μx, where I0 is the initial intensity and μ is a value that depends on the type of material and the wavelength of the X-rays. The table shows the values of μ for various materials and X-rays of medium wavelength.
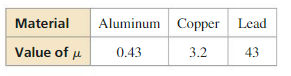
a. Find the thickness of aluminum shielding that reduces the intensity of X-rays to 30% of their initial intensity. (Hint: Find the value of x for which I(x) = 0.3I0.)
b. Repeat part (a) for the copper shielding.
c. Repeat part (a) for the lead shielding.
d. Your dentist puts a lead apron on you before taking X-rays of your teeth to protect you from harmful radiation. Based on your results from parts (a)–(c), explain why lead is a better material to use than aluminum or copper.
Answer:

Maintaining Mathematical Proficiency
Write an equation in point-slope form of the line that passes through the given point and has the given slope.
Question 75.
(1, −2); m = 4
Answer:
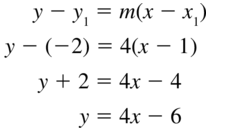
Question 76.
(3, 2); m = −2
Answer:
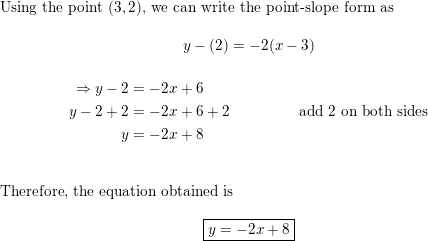
Question 77.
(3, −8); m = − \(\frac{1}{3}\)
Answer:
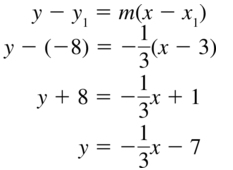
Question 78.
(2, 5); m = 2
Answer:
Use finite differences to determine the degree of the polynomial function that fits the data. Then use technology to find the polynomial function.
Question 79.
(−3, −50), (−2, −13), (−1, 0), (0, 1), (1, 2), (2, 15), (3, 52), (4, 125)
Answer:

Question 80.
(−3, 139), (−2, 32), (−1, 1), (0, −2), (1, −1), (2, 4), (3, 37), (4, 146)
Answer:
Question 81.
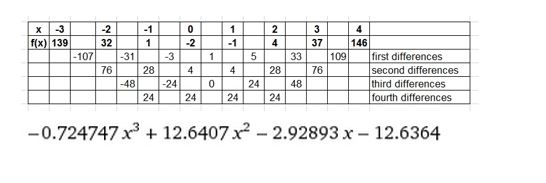
(−3, −327), (−2, −84), (−1, −17), (0, −6), (1, −3), (2, −32), (3, −189), (4, −642)
Answer:

Lesson 6.7 Modeling with Exponential and Logarithmic Functions
Essential Question How can you recognize polynomial, exponential, and logarithmic models?
EXPLORATION 1
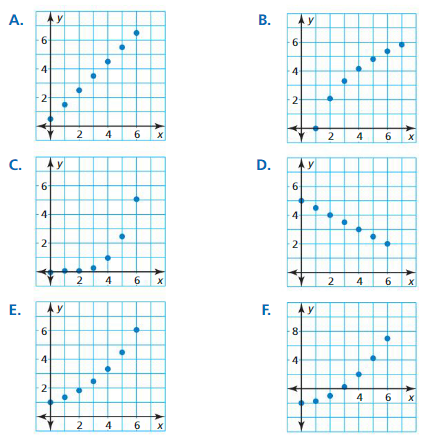
Recognizing Different Types of Models
Work with a partner. Match each type of model with the appropriate scatter plot. Use a regression program to find a model that fits the scatter plot.
a. linear (positive slope)
b. linear (negative slope)
c. quadratic
d. cubic
e. exponential
f. logarithmic
EXPLORATION 2
Exploring Gaussian and Logistic Models

Work with a partner. Two common types of functions that are related to exponential functions are given. Use a graphing calculator to graph each function. Then determine the domain, range, intercept, and asymptote(s) of the function.
a. Gaussian Function: f(x) = e−x2
b. Logistic Function: f(x) = \(\frac{1}{1+e^{-x}}\)
Communicate Your Answer
Question 3.
How can you recognize polynomial, exponential, and logarithmic models?
Answer:
Question4.
Use the Internet or some other reference to find real-life data that can be modeled using one of the types given in Exploration 1. Create a table and a scatter plot of the data. Then use a regression program to find a model that fits the data.
Answer:
Monitoring Progress
Determine the type of function represented by the table. Explain your reasoning.
Question 1.
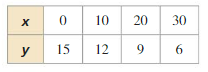
Answer:
Question 2.
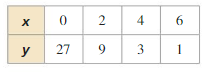
Answer:
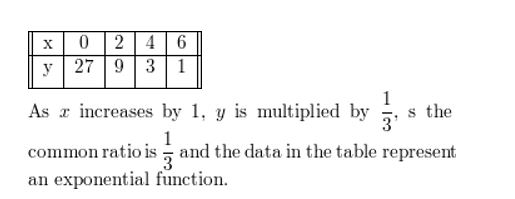
Write an exponential function y = abx whose graph passes through the given points.
Question 3.
(2, 12), (3, 24)
Answer:

Question 4.
(1, 2), (3, 32)
Answer:
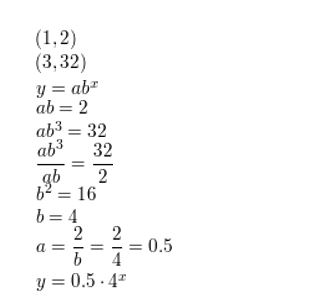
Question 5.
(2, 16), (5, 2)
Answer:
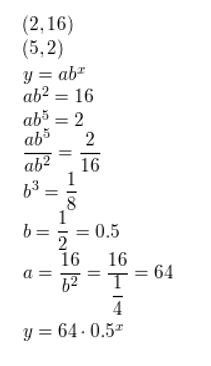
Question 6.
WHAT IF?
Repeat Examples 3 and 4 using the sales data from another store.

Answer:
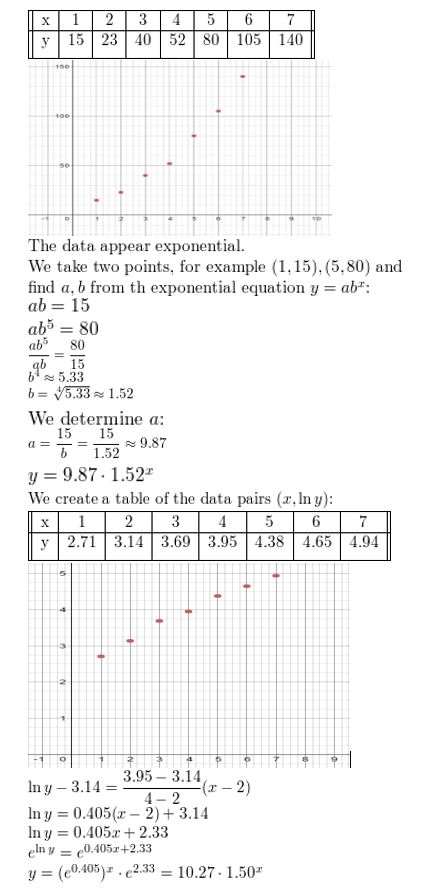
Question 7.
Use a graphing calculator to find an exponential model for the data in Monitoring Progress Question 6.
Answer:

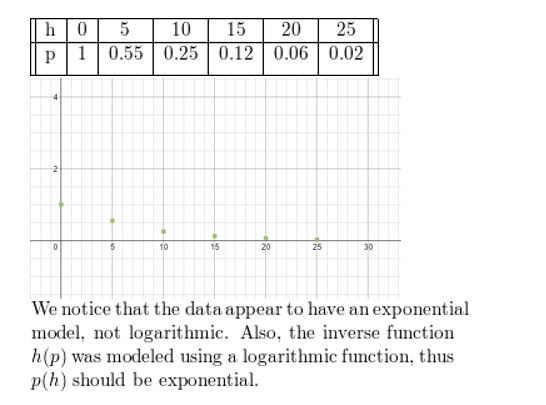
Question 8.
Use a graphing calculator to find a logarithmic model of the form p = a + b ln h for the data in Example 6. Explain why the result is an error message.
Answer:
Modeling with Exponential and Logarithmic Functions 6.7 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Given a set of more than two data pairs (x, y), you can decide whether a(n) __________ function fits the data well by making a scatter plot of the points (x, ln y).
Answer:

Question 2.
WRITING
Given a table of values, explain how you can determine whether an exponential function is a good model for a set of data pairs (x, y).
Answer: For exponential data with equally-spaced inputs, the outputs are multiplied by a constant factor. So, consecutive outputs form a constant ratio.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–6, determine the type of function represented by the table. Explain your reasoning.
Question 3.
Answer:
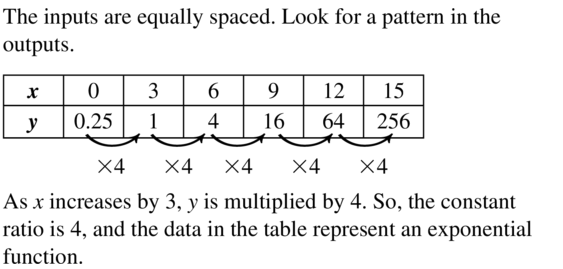
Question 4.
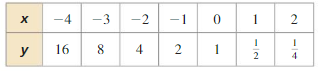
Answer:

Question 5.
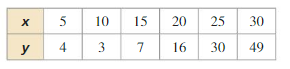
Answer:

Question 6.
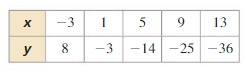
Answer:

In Exercises 7–16, write an exponential function y = abx whose graph passes through the given points.
Question 7.
(1, 3), (2, 12)
Answer:

Question 8.
(2, 24), (3, 144)
Answer:
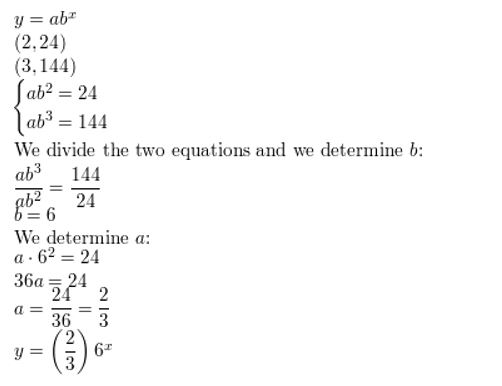
Question 9.
(3, 1), (5, 4)
Answer:

Question 10.
(3, 27), (5, 243)
Answer:

Question 11.
(1, 2), (3, 50)
Answer:

Question 12.
(1, 40), (3, 640)
Answer:
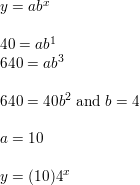
Question 13.
(−1, 10), (4, 0.31)
Answer:

Question 14.
(2, 6.4), (5, 409.6)
Answer:

Question 15.
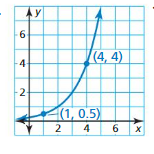
Answer:

Question 16.
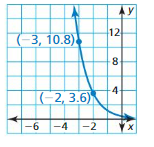
Answer:

ERROR ANALYSIS In Exercises 17 and 18, describe and correct the error in determining the type of function represented by the data.
Question 17.
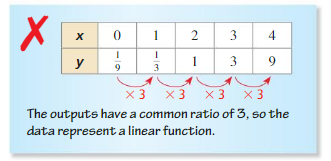
Answer:
Question 18.

Answer:
Question 19.
MODELING WITH MATHEMATICS
A store sells motorized scooters. The table shows the numbers y of scooters sold during the xth year that the store has been open. Write a function that models the data.
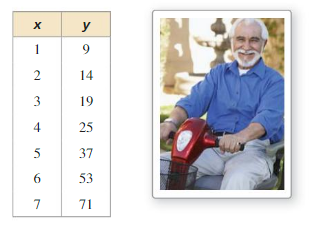
Answer:
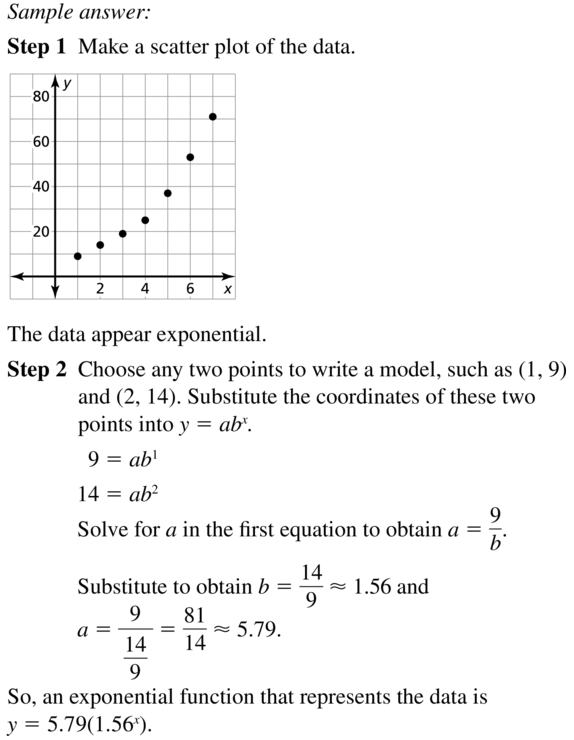
Question 20.
MODELING WITH MATHEMATICS
The table shows the numbers y of visits to a website during the xth month. Write a function that models the data. Then use your model to predict the number of visits after 1 year.

Answer:
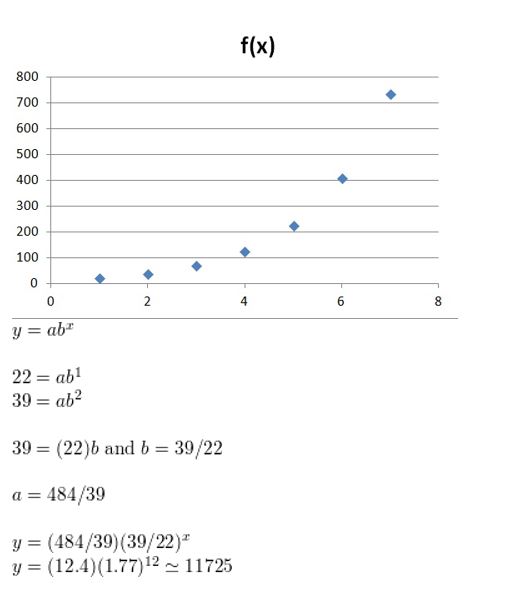
In Exercises 21–24, determine whether the data show an exponential relationship. Then write a function that models the data.
Question 21.
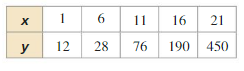
Answer:
Question 22.
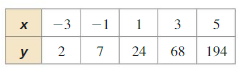
Answer:
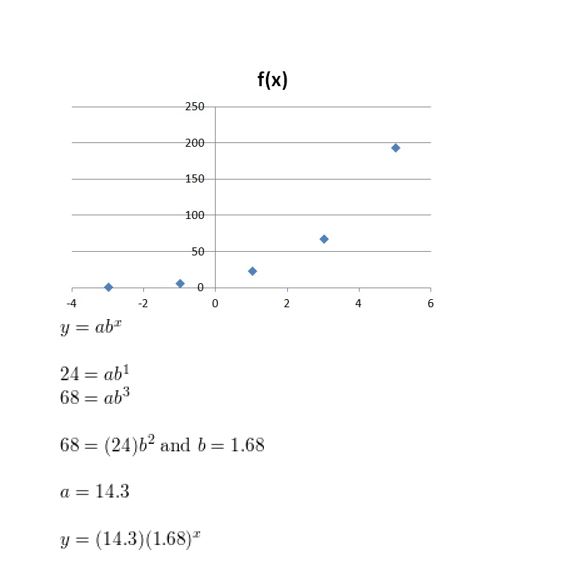
Question 23.
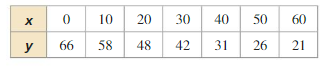
Answer:
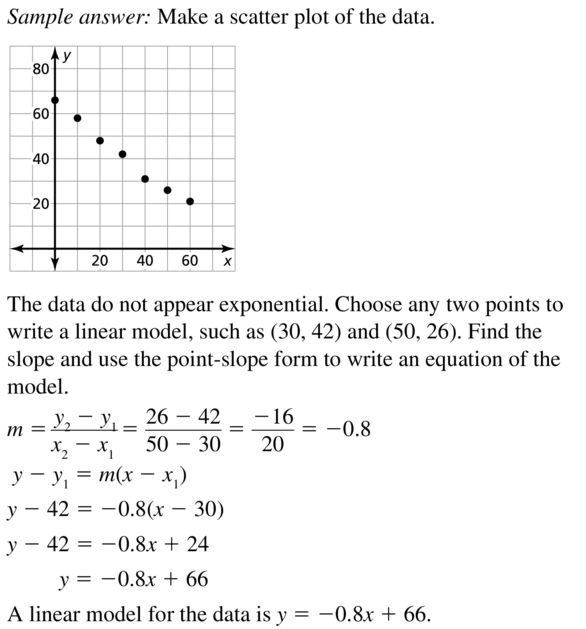
Question 24.
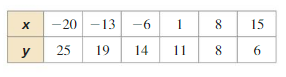
Answer:
Question 25.
MODELING WITH MATHEMATICS
Your visual near point is the closest point at which your eyes can see an object distinctly. The diagram shows the near point y (in centimeters) at age x (in years). Create a scatter plot of the data pairs (x, ln y) to show that an exponential model should be a good fit for the original data pairs (x, y). Then write an exponential model for the original data.
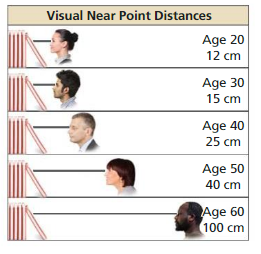
Answer:
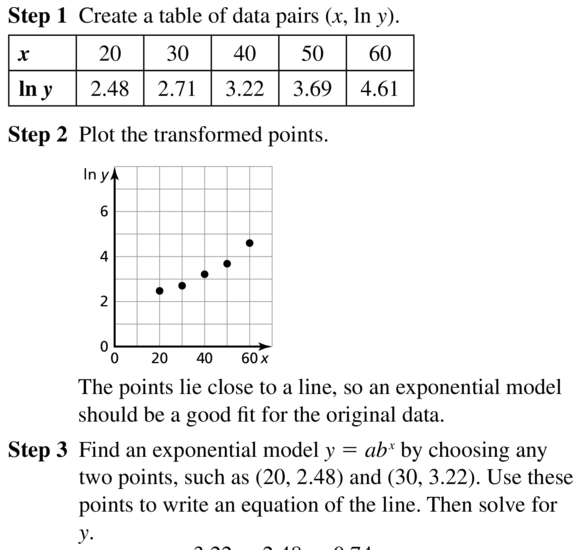

Question 26.
MODELING WITH MATHEMATICS
Use the data from Exercise 19. Create a scatter plot of the data pairs (x, ln y) to show that an exponential model should be a good fit for the original data pairs (x, y). Then write an exponential model for the original data.
Answer:
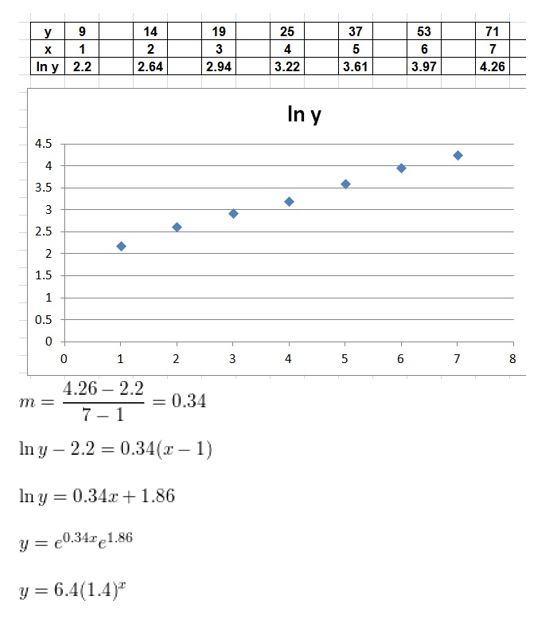
In Exercises 27–30, create a scatter plot of the points (x, ln y) to determine whether an exponential model fits the data. If so, find an exponential model for the data.
Question 27.
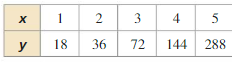
Answer:
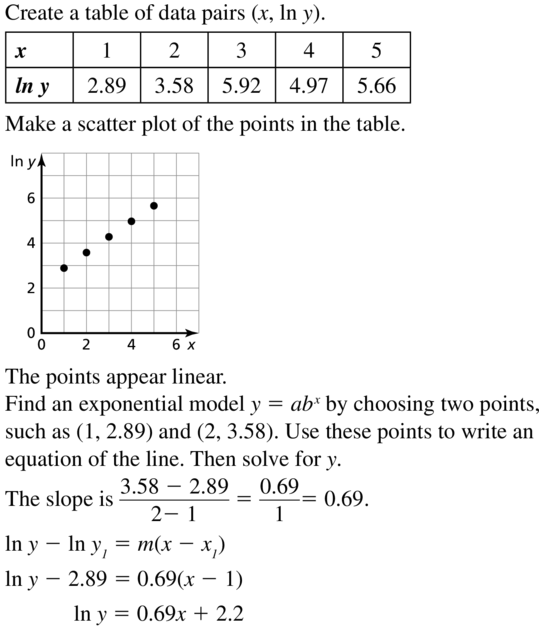

Question 28.
Answer:
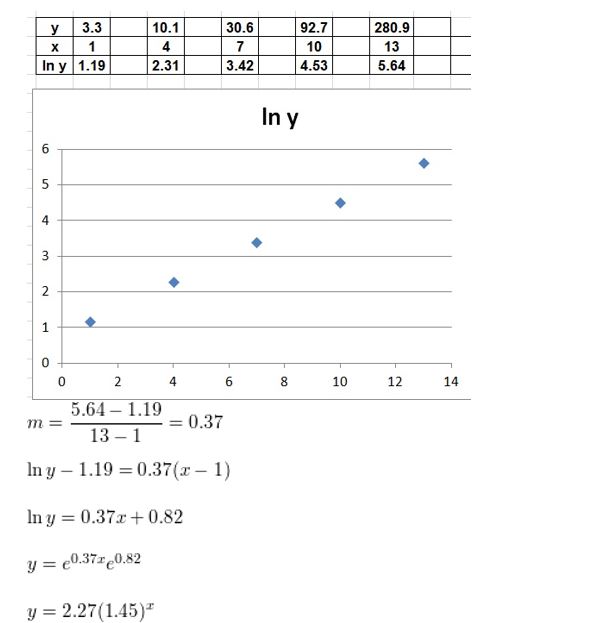
Question 29.
Answer:

Question 30.
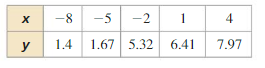
Answer:
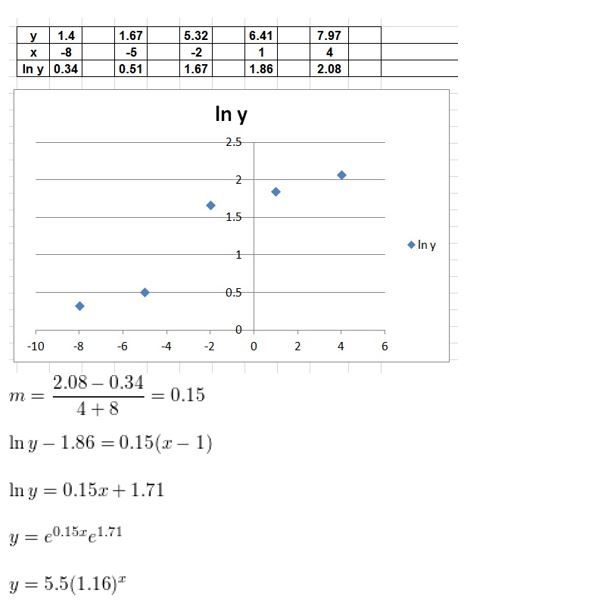
Question 31.
USING TOOLS
Use a graphing calculator to find an exponential model for the data in Exercise 19. Then use the model to predict the number of motorized scooters sold in the tenth year.
Answer:

Question 32.
USING TOOLS
A doctor measures an astronaut’s pulse rate y (in beats per minute) at various times x(in minutes) after the astronaut has finished exercising. The results are shown in the table. Use a graphing calculator to find an exponential model for the data. Then use the model to predict the astronaut’s pulse rate after 16 minutes.

Answer:

Question 33.
USING TOOLS
An object at a temperature of 160°C is removed from a furnace and placed in a room at 20°C. The table shows the temperatures d (in degrees Celsius) at selected times t (in hours) after the object was removed from the furnace. Use a graphing calculator to find a logarithmic model of the form t = a +b ln d that represents the data. Estimate how long it takes for the object to cool to 50°C.

Answer:

Question 34.
USING TOOLS
The f-stops on a camera control the amount of light that enters the camera. Let s be a measure of the amount of light that strikes the film and let f be the f-stop. The table shows several f-stops on a 35-millimeter camera. Use a graphing calculator to find a logarithmic model of the form s = a + b ln f that represents the data. Estimate the amount of light that strikes the film when f = 5.657.

Answer:
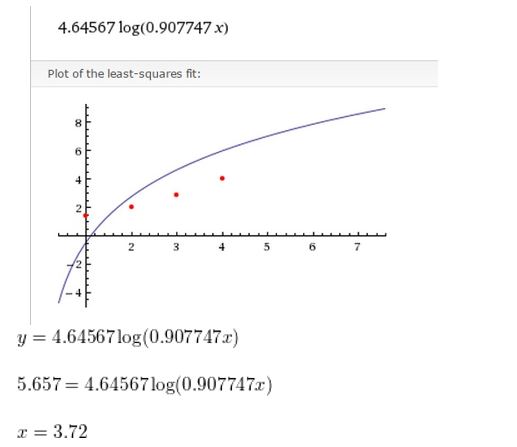
Question 35.
DRAWING CONCLUSIONS
The table shows the average weight (in kilograms) of an Atlantic cod that is x years old from the Gulf of Maine.
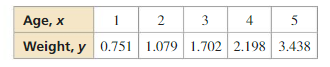
a. Show that an exponential model fits the data. Then find an exponential model for the data.
b. By what percent does the weight of an Atlantic cod increase each year in this period of time? Explain.
Answer:

Question 36.
HOW DO YOU SEE IT?
The graph shows a set of data points (x, ln y). Do the data pairs (x, y) fit an exponential pattern? Explain your reasoning.
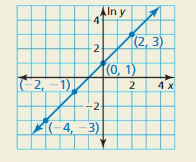
Answer:

Question 37.
MAKING AN ARGUMENT
Your friend says it is possible to find a logarithmic model of the form d = a + b ln t for the data in Exercise 33. Is your friend correct? Explain.
Answer:
Question 38.
THOUGHT PROVOKING
Is it possible to write y as an exponential function of x? Explain your reasoning. (Assume p is positive.)
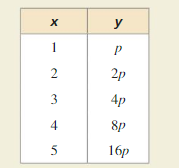
Answer:
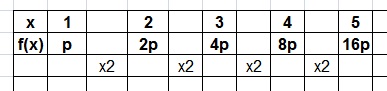
Question 39.
CRITICAL THINKING
You plant a sunflower seedling in your garden. The height h (in centimeters) of the seedling after t weeks can be modeled by the logistic function
h(t) = \(\frac{256}{1+13 e^{-0.65 t}}\)
a. Find the time it takes the sunflower seedling to reach a height of 200 centimeters.
b. Use a graphing calculator to graph the function. Interpret the meaning of the asymptote in the context of this situation.
Answer:
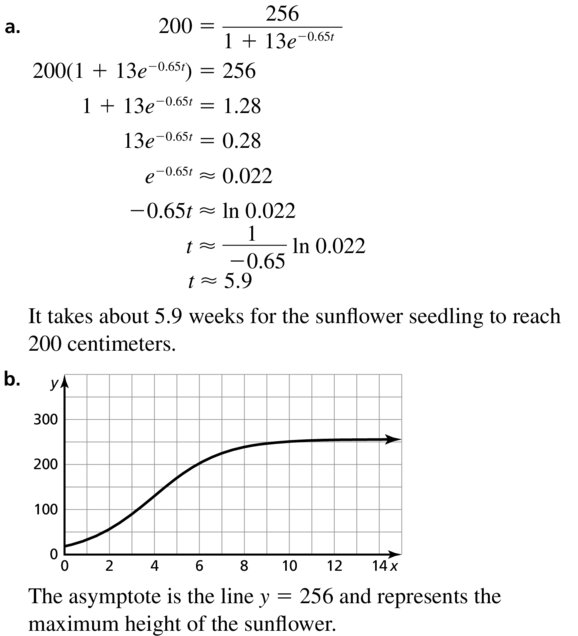
Maintaining Mathematical Proficiency
Tell whether x and y are in a proportional relationship. Explain your reasoning.
Question 40.
y = \(\frac{x}{2}\)
Answer:

Question 41.
y = 3x − 12
Answer:

Question 42.
y = \(\frac{5}{x}\)
Answer:

Question 43.
y = −2x
Answer:
Identify the focus, directrix, and axis of symmetry of the parabola. Then graph the equation.
Question 44.
x = \(\frac{1}{8}\)y2
Answer:
Question 45.
y = 4x2
Answer:
Question 46.
x2 = 3y
Answer:
Question 47.
y2 = \(\frac{2}{5}\)x
Answer:

Exponential and Logarithmic Functions Performance Task: Measuring Natural Disasters
6.5–6.7 What Did You Learn?
Core Vocabulary
exponential equations, p. 334
logarithmic equations, p. 335
Core Concepts
Section 6.5
Properties of Logarithms, p. 328
Change-of-Base Formula, p. 329
Section 6.6
Property of Equality for Exponential Equations, p. 334
Property of Equality for Logarithmic Equations, p. 335
Section 6.7
Classifying Data, p. 342
Writing Exponential Functions, p. 343
Using Exponential and Logarithmic Regression, p. 345
Mathematical Practices
Question 1.
Explain how you used properties of logarithms to rewrite the function in part (b) of Exercise 45 on page 332.
Answer:
Question 2.
How can you use cases to analyze the argument given in Exercise 46 on page 339?
Answer:
Performance Task Measuring Natural Disasters
In 2005, an earthquake measuring 4.1 on the Richter scale barely shook the city of Ocotillo, California, leaving virtually no damage. But in 1906, an earthquake with an estimated 8.2 on the same scale devastated the city of San Francisco. Does twice the measurement on the Richter scale mean twice the intensity of the earthquake?
To explore the answers to these questions and more, go to BigIdeasMath.com.

Exponential and Logarithmic Functions Chapter Review
6.1 Exponential Growth and Decay Functions (pp. 295–302)
Tell whether the function represents exponential growth or exponential decay. Identify the percent increase or decrease. Then graph the function.
Question 1.
f (x) = (\(\frac{1}{3}\))x
Answer:
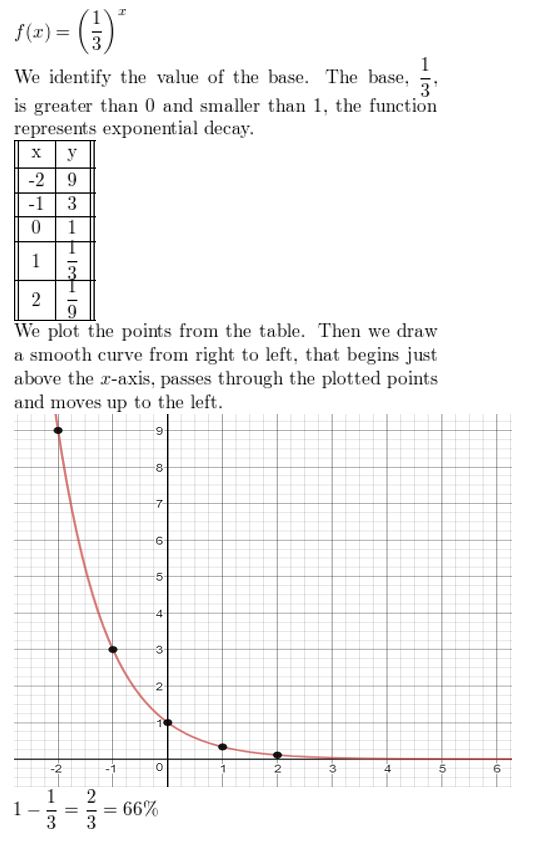
Question 2.
y = 5x
Answer:
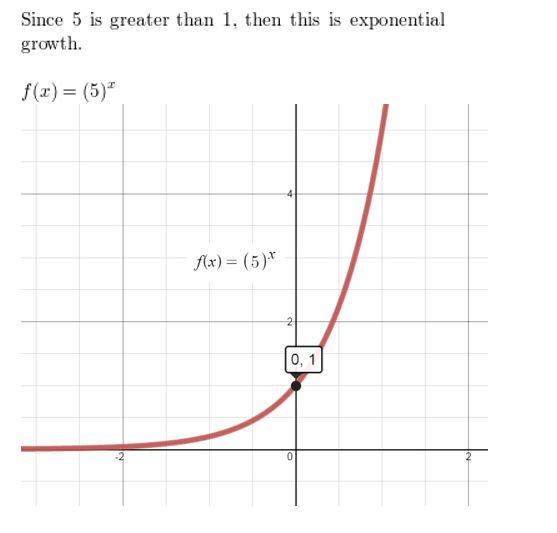
Question 3.
f(x) = (0.2)x
Answer:
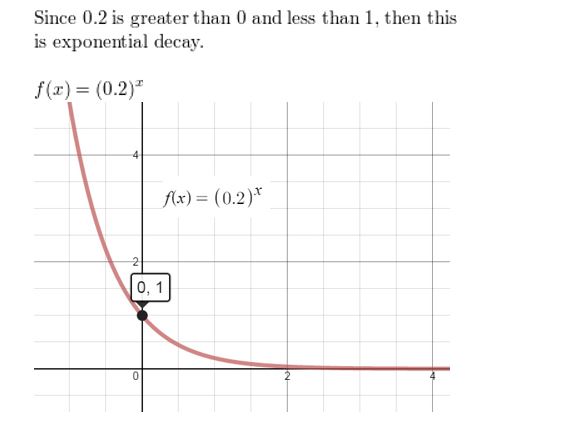
Question 4.
You deposit $1500 in an account that pays 7% annual interest. Find the balance after 2 years when the interest is compounded daily.
Answer:
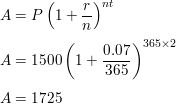
6.2 The Natural Base e (pp. 303–308)
Simplify the expression.
Question 5.
e4 • e11
Answer:
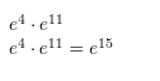
Question 6.
\(\frac{20 e^{3}}{10 e^{6}}\)
Answer:
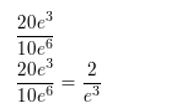
Question 7.
(−3e-5x)2
Answer:
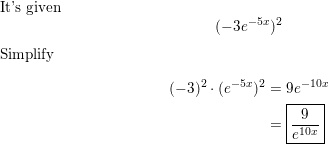
Tell whether the function represents exponential growth or exponential decay. Then graph the function.
Question 8.
f(x) = \(\frac{1}{3}\)ex
Answer:
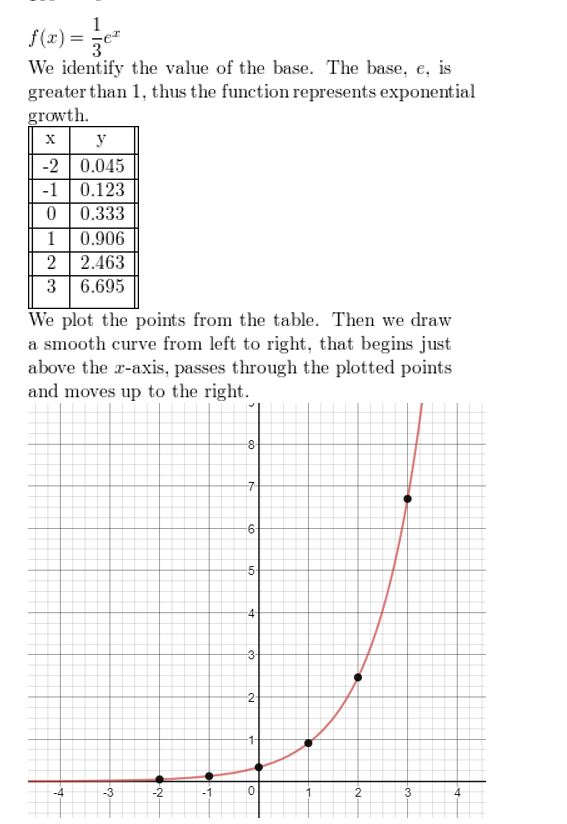
Question 9.
y = 6e-x
Answer:
Question 10.
y = 3e-0.75x
Answer:
6.3 Logarithms and Logarithmic Functions (pp. 309–316)
Evaluate the logarithm.
Question 11.
log2 8
Answer:
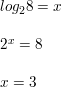
Question 12.
log6 \(\frac{1}{36}\)
Answer:
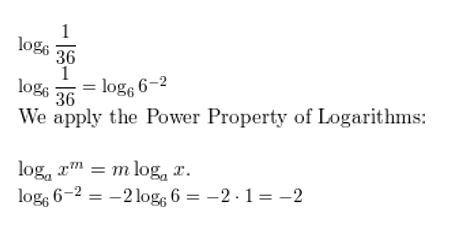
Question 13.
log2 1
Answer:
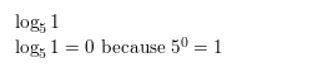
Find the inverse of the function.
Question 14.
f(x) = 8x
Answer:

Question 15.
y = ln(x − 4)
Answer:
Question 16.
y = log(x+ 9)
Answer:
Question 17.
Graph y = log1/5 x.
Answer:
6.4 Transformations of Exponential and Logarithmic Functions (pp. 317–324)
Describe the transformation of f represented by g. Then graph each function.
Question 18.
f(x) = e-x, g(x) = -5x − 8
Answer:
Question 19.
f(x) = log4 x, g(x) = \(\frac{1}{2}\)log4 (x + 5)
Answer:
Write a rule for g.
Question 20.
Let the graph of g be a vertical stretch by a factor of 3, followed by a translation 6 units left and 3 units up of the graph of f(x) = ex.
Answer:
Question 21.
Let the graph of g be a translation 2 units down, followed by a reflection in the y-axis of the graph of f(x) = log x.
Answer:
6.5 Properties of Logarithms (pp. 327–332)
Expand or condense the logarithmic expression.
Question 22.
log8 3xy
Answer:
Question 23.
log 10x3y
Answer:
Question 24.
ln \(\frac{3 y}{x^{5}}\)
Answer:
Question 25.
3 log7 4 + log7 6
Answer:
Question 26.
log2 12 − 2 log2 x
Answer:
Question 27.
2 ln x + 5 ln 2 − ln 8
Answer:
Use the change-of-base formula to evaluate the logarithm.
Question 28.
log2 10
Answer:
Question 29.
log7 9
Answer:
Question 30.
log23 42
Answer:
6.6 Solving Exponential and Logarithmic Equations (pp. 333–340)
Solve the equation. Check for extraneous solutions.
Question 31.
5x = 8
Answer:
Question 32.
log3 (2x − 5) = 2
Answer:
Question 33.
ln x + ln(x + 2) = 3
Answer:
Solve the inequality.
Question 34.
6x > 12
Answer:
Question 35.
ln x ≤ 9
Answer:
Question 36.
e4x-2 ≥ 16
Answer:
6.7 Modeling with Exponential and Logarithmic Functions (pp. 341–348)
Write an exponential model for the data pairs (x, y).
Question 37.
(3, 8), (5, 2)
Answer:
Question 38.
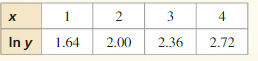
Answer:
Question 39.
A shoe store sells a new type of basketball shoe. The table shows the pairs sold s over time t (in weeks). Use a graphing calculator to find a logarithmic model of the form s = a +b ln t that represents the data. Estimate how many pairs of shoes are sold after 6 weeks.
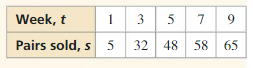
Answer:
Exponential and Logarithmic Functions Chapter Test
Graph the equation. State the domain, range, and asymptote.
Question 1.
y = (\(\frac{1}{2}\))x
Answer:
Question 2.
y = log1/5 x
Answer:
Question 3.
y = 4e-2x
Answer:
Describe the transformation of f represented by g. Then write a rule for g.
Question 4.
f(x) = log x
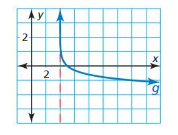
Answer:
Question 5.
f(x) = ex
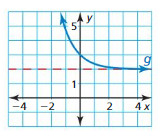
Answer:
Question 6.
f(x) = \(\frac{1}{4}\))x
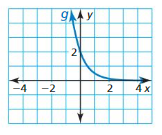
Answer:
Evaluate the logarithm. Use log3 4 ≈ 1.262 and log3 13 ≈ 2.335, if necessary.
Question 7.
log2 52
Answer:
Question 8.
log3 \(\frac{13}{9}\)
Answer:
Question 9.
log3 16
Answer:
Question 10.
log3 8 + log3 \(\frac{1}{2}\)
Answer:
Question 11.
Describe the similarities and differences in solving the equations 45x-2 = 16 and log4(10x + 6) = 1. Then solve each equation.
Answer:
Question 12.
Without calculating, determine whether log511, \(\frac{\log 11}{\log 5}\), and \(\frac{\ln 11}{\ln 5}\) are equivalent expressions. Explain your reasoning.
Answer:
Question 13.
The amount y of oil collected by a petroleum company drilling on the U.S. continental shelf can be modeled by y = 12.263 ln x − 45.381, where y is measured in billions of barrels and x is the number of wells drilled. About how many barrels of oil would you expect to collect after drilling 1000 wells? Find the inverse function and describe the information you obtain from finding the inverse.
Answer:
Question 14.
The percent L of surface light that filters down through bodies of water can be modeled by the exponential function L(x) = 100ekx, where k is a measure of the murkiness of the water and x is the depth (in meters) below the surface.
a. A recreational submersible is traveling in clear water with a k-value of about −0.02. Write a function that gives the percent of surface light that filters down through clear water as a function of depth.
b. Tell whether your function in part (a) represents exponential growth or exponential decay. Explain your reasoning.
c. Estimate the percent of surface light available at a depth of 40 meters.
Answer:
Question 15.
The table shows the values y (in dollars) of a new snowmobile after x years of ownership. Describe three different ways to find an exponential model that represents the data. Then write and use a model to find the year when the snowmobile is worth $2500.

Answer:
Exponential and Logarithmic Functions Cumulative Assessment
Question 1.
Select every value of b for the equation y = bx that could result in the graph shown.
Answer:
Question 2.
Your friend claims more interest is earned when an account pays interest compounded continuously than when it pays interest compounded daily. Do you agree with your friend? Justify your answer.
Answer:
Question 3.
You are designing a rectangular picnic cooler with a length four times its width and height twice its width. The cooler has insulation that is 1 inch thick on each of the four sides and 2 inches thick on the top and bottom.
a. Let x represent the width of the cooler. Write a polynomial function T that gives the volume of the rectangular prism formed by the outer surfaces of the cooler.
b.Write a polynomial function C for the volume of the inside of the cooler.
c. Let I be a polynomial function that represents the volume of the insulation. How is I related to T and C?
d. Write I in standard form. What is the volume of the insulation when the width of the cooler is 8 inches?
Answer:
Question 4.
What is the solution to the logarithmic inequality −4 log2 x ≥ −20?
A. x ≤ 32
B. 0 ≤ x ≤ 32
C. 0 < x ≤ 32
D. x ≥ 32
Answer:
Question 5.
Describe the transformation of f(x) = log2 x represented by the graph of g.
Answer:
Question 6.
Let f(x) = 2x3 − 4x2 + 8x− 1, g(x) = 2x − 3x4 − 6x3+ 5, and h(x) = −7 + x2 + x. Order the following functions from least degree to greatest degree.
A. (f + g)(x)
B. (hg)(x)
C. (h − f)(x)
D. (fh)(x)
Answer:
Question 7.
Write an exponential model that represents each data set. Compare the two models.
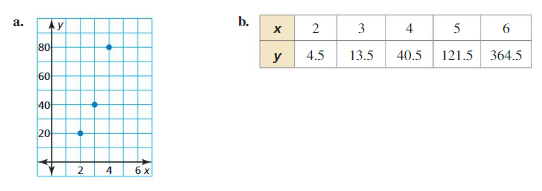
Answer:
Question 8.
Choose a method to solve each quadratic equation. Explain your choice of method.
a. x2 + 4x = 10
b. x2 = −12
c. 4(x − 1)2 = 6x + 2
d. xx − 3x − 18 = 0
Answer:
Question 9.
At the annual pumpkin-tossing contest, contestants compete to see whose catapult will send pumpkins the longest distance. The table shows the horizontal distances y (in feet) a pumpkin travels when launched at different angles x (in degrees). Create a scatter plot of the data. Do the data show a linear, quadratic, or exponential relationship? Use technology to find a model for the data. Find the angle(s) at which a launched pumpkin travels 500 feet.
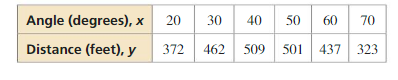
Answer:
