Check out all the topics covered in the Big Ideas Math Answers Grade 4 Chapter 4 Multiply by Two-Digit Numbers from the below section. You can guide your students by making our Big Ideas Math Book 4th Grade Solution Key Chapter 4 Multiply by Two-Digit Numbers as reference. Students who are seriously practicing to score good marks in exams are suggested to practice the problems given in our Big Ideas Math Answers Grade 4 Chapter 4 Answer Key. Access the links given below and Download Big Ideas 4th Grade Solution Key pdf.
Big Ideas 4th Grade Chapter 4 Multiply by Two-Digit Numbers Solution Key
Students can easily understand the concepts in-depth with the help of Big Ideas Math Answers Grade 4 Chapter 4 Multiply by Two-Digit Numbers. We have provided all the questions, answers, along with explanations. Also, most of the explanations are given with images for the best learning for students. In order to become a math expert, you must refer to the Big Ideas Multiply by Two-Digit Numbers chapter. Verify the step-by-step procedure to solve a problem to make your preparation easy.
Lesson 1: Multiply by Tens
Lesson 2: Estimate Products
Lesson 3: Use Area Models to Multiply Two-Digit Numbers
- Lesson 4.3 Use Area Models to Multiply Two-Digit Numbers
- Use Area Models to Multiply Two-Digit Numbers Homework & Practice 4.3
Lesson 4: Use the Distributive Property to Multiply Two-Digit Numbers
- Lesson 4.4 Use the Distributive Property to Multiply Two-Digit Numbers
- Use the Distributive Property to Multiply Two-Digit Numbers Homework & Practice 4.4
Lesson 5: Use Partial Products to Multiply Two-Digit Numbers
- Lesson 4.5 Use Partial Products to Multiply Two-Digit Numbers
- Use Partial Products to Multiply Two-Digit Numbers Homework & Practice 4.5
Lesson 6: Multiply Two-Digit Numbers
Lesson 7: Practice Multiplication Strategies
- Lesson 4.7 Practice Multiplication Strategies
- Practice Multiplication Strategies Homework & Practice 4.7
Lesson 8: Problem Solving: Multiplication with Two-Digit Numbers
- Lesson 4.8 Problem Solving: Multiplication with Two-Digit Numbers
- Problem Solving: Multiplication with Two-Digit Numbers Homework & Practice 4.8
Performance Task
- Multiply by Two-Digit Numbers Performance Task
- Multiply by Two-Digit Numbers Activity
- Multiply by Two-Digit Numbers Chapter Practice
- 4.3 Use Area Models to Multiply Two-Digit Numbers
- 4.4 Use Distributive Property to Multiply Two-Digit Numbers
- 4.5 Use Partial Products to Multiply Two-Digit Numbers
- 4.6 Multiply Two-Digit Numbers
- 4.7 Practice Multiplication Strategies
Lesson 4.1 Multiply by Tens
Explore and Grow
Model each product. Draw each model.
What pattern do you notice in the products?
Answer:
The Place- value method. From the above pattern, we can conclude that the result has different place-values of 6
Explanation:
The position of 3 is different in the given 4 multiplications.
So,
2 × 3 = 6
2 × 30 = 60
2 × 300 = 600
2 × 3000 = 6,000
From the above pattern, we can conclude that the result has different place-values of 6
Repeated Reasoning
How can the pattern above help you find 20 × 30?
Answer:
20 × 30 = 600
Explanation:
You can think of 20 as two tens and 30 as Three tens.
So,
20 × 30 = 2 × 1 ten × 3 × 1 ten = 2 tens × 2 × 3 = 6 × 2 tens = 600
Think and Grow: Multiply by Multiples of Tens
You can use place value and properties to multiply two-digit numbers by multiples of ten.
Example
Find 40 × 20.
One Way: Use place value.
40 × 20 = 40 × ____ tens
= ____ tens
= _____
So, 40 × 20 = _____.
Answer:
800
Explanation:
By using the Place-value method,
40 × 20 = 40 × 2 tens
= 80 tens
= 800
So, 40 × 20 = 800
Another Way: Use the Associative Property of Multiplication.
40 × 20 = 40 × (2 × 10) Rewrite 20 as 2 × 10.
= (40 × 2) × 10 Associative Property of Multiplication
= ____ × 10
= ____
So, 40 × 20 = _____.
Answer:
800
Explanation:
By using the Associative Property of Multiplication,
40 × 20 = 40 × (2 × 10)
= (40 × 2) × 10
= 80 × 10
= 800
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Find 12 × 30.
One Way: Use place value
12 × 30 = 12 × _____ tens
= ____ tens
= _____
So, 12 × 30 = _____.
Answer:
360
Explanation:
Using the Place-value method,
12 × 30 = 12 × 3 tens
= 36 tens
= 360
So, 12 × 30 = 360
Another Way: Use the Associative Property of Multiplication
12 × 30 = 12 × (3 × 10) Rewrite 30 as 3 × 10.
= (12 × 3) × 10 Associative Property of Multiplication
= ____ × 10
= _____
So, 12 × 30 = ____.
Answer: 360
Explanation:
By using the Associative Property of Multiplication,
12 × 30 = 12 × (3 × 10)
= (12 × 3) × 10
= 36 × 10
= 360
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Show and Grow
Find the product.
Question 1.
70 × 40 = _____
Answer:
2800
Explanation:
By using the Associative Property of Multiplication,
70 × 40 = 70 × (4 × 10)
= (70 × 4) × 10
= 280 × 10
= 2800
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 2.
50 × 80 = ____
Answer:
4,000
Explanation:
By using the Associative Property of Multiplication,
50 × 80 = 50 × (8 × 10)
= (50 × 8) × 10
= 400 × 10
= 4000
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 3.
24 × 90 = _____
Answer:
2160
Explanation:
By using the Associative Property of Multiplication,
24 × 90 = 24 × (9 × 10)
= (24 × 9) × 10
= (8 × 3 × 9) × 10
= 216 × 10
= 2160
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 4.
45 × 60 = _____
Answer:
2700
Explanation:
By using the Associative Property of Multiplication,
45 × 60 = 45 × (6 × 10)
= (45 × 6) × 10
= (5 × 9 × 6) × 10
= 270 × 10
= 2700
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Apply and Grow: Practice
Find the product.
Question 5.
90 × 10 = _____
Answer:
900
Explanation:
By using the place-value method,
90 × 10 = 10 × 9 tens
= 90 tens
= 900
So,
90 × 10 = 900
Question 6.
40 × 60 = ____
Answer:
2400
Explaination:
By using the place-value method,
40 × 60 = 40 × 6 tens
= 4 tens × 6 tens
= 24 × tens × tens
= 2400
So,
40 × 60 = 2400
Question 7.
20 × 70 = _____
Answer: 1400
Explanation:
By using the place-value method,
70 × 20 = 70 × 2 tens
= 7 tens × 2 tens
= 14 × tens × tens
= 1400
So,
70 × 20 = 1400
Question 8.
11 × 30 = ____
Answer: 330
Explanation:
By using the place-value method,
11 × 30 = 11 × 3 tens
= 33 tens
= 330
So,
11 × 30 = 330
Question 9.
12 × 40 = ____
Answer: 480
Explanation:
By using the place-value method,
12 × 40 = 12 × 4 tens
= 48 tens
= 480
So,
12 × 40 = 480
Question 10.
15 × 50 = _____
Answer: 750
Explanation:
By using the place-value method,
15 ×50 = 15 × 5 tens
= 75 tens
= 750
So,
15 × 50 = 750
Question 11.
30 × 13 = _____
Answer: 390
Explanation:
By using the place-value method,
13 × 30 = 13 × 3 tens
= 39 tens
= 390
So,
13 × 30 = 390
Question 12.
10 × 76 = _____
Answer: 760
Explanation:
By using the place-value method,
10 × 76 = 76 × 1 ten
= 76 tens
= 760
So,
76 × 10 = 760
Question 13.
40 × 25 = ____
Answer: 1,000
Explanation:
By using the place-value method,
25 × 40 = 25 × 4 tens
= 5 × 5× 4 tens
= 100 tens
= 1,000
So,
25 × 40 = 1,000
Find the missing factor.
Question 14.
50 × ____ = 1,500
Answer: 30
Explanation;
Let the missing number be X
So, 50 × X = 1,500
X = 1,500 / 50 = 30
Hence, the value of X is: 30
Question 15.
20 × ____ = 1,800
Answer: 90
Explanation;
Let the missing number be X
So, 20 × X = 1,800
X = 1,800 /20 = 90
Hence, the value of X is: 90
Question 16.
60 × ___ = 4,200
Answer: 70
Explanation;
Let the missing number be X
So, 60 × X = 4,200
X = 4,200 / 60 = 70
Hence, the value of X is: 70
Question 17.
____ × 80 = 6,400
Answer: 80
Explanation;
Let the missing number be X
So, X × 80 = 6,400
X = 6,400 / 80 = 80
Hence, the value of X is: 80
Question 18.
____ × 90 = 3,600
Answer: 40
Explanation;
Let the missing number be X
So, X × 90 = 3,600
X = 3,600 / 90 = 40
Hence, the value of X is: 40
Question 19.
____ × 70 = 3,500
Answer: 50
Explanation;
Let the missing number be X
So, X × 70 = 3,500
X = 3,500 / 70 = 50
Hence, the value of X is: 50
Compare.
Question 20.
Answer: 60 × 30 is equal to 1,800
Explanation:
60 × 30 = 1,800
Given numbers are: 1,800 and 1,800
By comparing 2 values, we can conclude that 1,800 is equal to 1,800
Question 21.
Answer: 480 is greater than 460
Explanation:
40 × 12 = 480
Given numbers are: 480 and 460
By comparing 2 values, we can conclude that480 is greater than 460
Question 22.
Answer: 2,250 is less than 2,340
Explanation:
25 × 90 = 2,250
Given numbers are 2,250 and 2,340
By comparing 2 values, we can conclude that 2,250 is less than 2,340
Question 23.
It takes 10 days to film 1 episode of a television show. How many days will it take to film a 20-episode season?
Answer: 200 days
Explanation:
Given that it takes 10 days to film 1 episode of a Television show.
So,
The number of days it will take to film a 20-episode season is: 20 × 10 = 200 days
Question 24.
Reasoning
What is Descartes’s number? Explain.
Answer:
Question 25.
YOU BE THE TEACHER
Newton says that the product of two multiples of ten will always have exactly two zeros. Is he correct? Explain.
Answer: He is correct
Explanation:
Let us suppose 2 numbers 10 and 20 which are the two multiples of 10.
Now,
10 × 20 = 200
According to Newton, the product of two multiples of ten will always have exactly two zeroes.
So, from the above multiplication, we can say that Newton is correct.
Think and Grow: Modeling Real Life
Example
Food drive volunteers collect 1,328 cans of food. The volunteers have50 boxes. Each box holds 20 cans. How many cans will fit in the boxes?
Multiply to find how many cans will fit in the boxes.
20 × 50 = 50 × (5 × 10)
Rewrite 50 as 5 × 10.
= (20 × 5) × 10 Associative Property of Multiplication
= 100 × 10
= 1,000
So, 1,000 cans fit in the boxes.
Subtract the number of cans that will fit in the boxes from the total number of cans collected.
The cans that can not fit in the boxes = 1,328 – 1,000 = 328
So,
328 cans will not fit in the boxes.
Show and Grow
Question 26
A library has 2,124 new books. The library has 40 empty shelves. Each shelf holds 35 books. How many not books
will fit on the empty shelves?
Answer: 724
Explanation:
Multiply to find how many books will hold on the shelves.
40 × 35 = 35 × (4 × 10)
Rewrite 40 as 5 × 10.
= (35 × 4) × 10 Associative Property of Multiplication
= 140 × 10
= 1,400
So, 1,400 cans fit in the boxes.
Subtract the number of books that will hold on the shelves from the total number of books collected.
The number of books that will not hold on the shelves = 2,124 – 1,400 = 724
So,
724 books will not hold on the shelves
Question 27.
An apartment building has 15 floors. Each floor is 10 feet tall. An office building has 30 floors. Each floor is 13 feet tall. How much taller is the office building than the apartment building?
Answer: 240 feet
Explanation:
Given that an apartment has 15 floors and in that, each floor is 10 feet tall.
So, the height of the apartment = 15 × 10 = 150 feet
Given that an office building has 30 floors and in that, each floor is 13 feet tall.
So, the height of the office building = 30 × 13 = 390 feet
Now, to calculate how much taller an office building than the apartment, we have to subtract both the heights of the apartment and the office building.
So,
The difference in height between the office building and the apartment = 390 feet – 150 feet = 240 feet.
From the above, we can conclude that the office building is 240 feet taller than the apartment.
Question 28.
You burn 35 calories each hour you spend reading and 50 calories each hour you spend playing board games. In 2
weeks, you spend14 hours reading and 28 hours playing board games. How many calories do you burn reading
and playing board games?
Answer:
The calories burned during reading in 2 weeks = 490 calories
The calories burned during playing board games = 1400 calories
Explanation:
Given that,
The calories burned during reading is: 35 calories each hour
The calories burned during playing board games is: 50 calories each hour
It is also given that In 2 weeks,
the time spend on reading and Playing Board Games are 14 hours and 28 hours
So, to calculate the calorie consumption in these 2 weeks, we have to multiply the number of hours and the number of calories.
So,
The calories burned during reading in 2 weeks = 490 calories
The calories burned during playing board games in 2 weeks = 1400 calories
Multiply by Tens Homework & Practice 4.1
Find the product.
Question 1.
30 × 10 = _____
Answer: 300
Explanation:
The product of multiply by tens can be done in 2 ways. They are:
A) The place-value method B) The Associative Property of Multiplication
A) By using the place-value method:
30 × 10 = 10 × 3 tens
= 1 ten × 3 tens
= 3 × 1 ten × 1 ten
= 3 × 100
= 300
B) The Associative Property of Multiplication:
30 × 10 = 3 × (10 × 10)
= (3 × 10) × 10
= 30 × 10
= 300
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 2.
20 × 90 = _____
Answer: 1800
Explanation:
The product of multiply by tens can be done in 2 ways. They are:
A) The place-value method B) The Associative Property of Multiplication
A) By using the place-value method:
20 × 90 = 20 × 9 tens
= 2 tens × 9 tens
= 18 × 1 ten × 1 ten
= 18 × 100
= 1800
B) The Associative Property of Multiplication:
20 × 90 = 20 × (9 × 10)
= (20 × 9) × 10
=(5 × 4 × 9) × 10
= 180 × 10
= 1800
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 3.
50 × 70 = _____
Answer: 3500
Explanation:
The product of multiply by tens can be done in 2 ways. They are:
A) The place-value method B) The Associative Property of Multiplication
A) By using the place-value method:
50 × 70 = 50 × 7 tens
= 5 tens × 7 tens
= 35 × 1 ten × 1 ten
= 35 × 100
= 3500
B) The Associative Property of Multiplication:
50 × 70 = 50 × (7 × 10)
= (50 × 7) × 10
=(5 × 10 × 7) × 10
= 350 × 10
= 3500
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 4.
40 × 13 = ______
Answer: 520
Explanation:
The product of multiply by tens can be done in 2 ways. They are:
A) The place-value method B) The Associative Property of Multiplication
A) By using the place-value method:
40 × 13 = 13 × 4 tens
= 13 × 4 tens
= 52 × 1 ten
= 52 × 10
= 520
B) The Associative Property of Multiplication:
40 × 13 = 13 × (4 × 10)
= (13 × 4) × 10
=(13 ×2× 2) × 10
= 54 × 10
= 540
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 5.
27 × 60 = _____
Answer: 1620
Explanation:
The product of multiply by tens can be done in 2 ways. They are:
A) The place-value method B) The Associative Property of Multiplication
A) By using the place-value method:
27 × 60 = 27 × 6 tens
= 3 × 9 × 6 tens
= 162 × 1 ten
= 162 × 10
= 1620
B) The Associative Property of Multiplication:
27 × 60 = 27 × (6 × 10)
= (27 × 6) × 10
=(6 × 3 × 9) × 10
= 162 × 10
= 1620
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 6.
80 × 56 = _____
Answer: 4480
Explanation:
The product of multiply by tens can be done in 2 ways. They are:
A) The place-value method B) The Associative Property of Multiplication
A) By using the place-value method:
80 × 56 = 56 × 8 tens
= 7 × 8 × 8 tens
= 448 × 1 ten
= 448 × 10
= 4480
B) The Associative Property of Multiplication:
56 × 80 = 56 × (8 × 10)
= (56 × 8) × 10
=(8 × 7 × 8) × 10
= 448 × 10
= 4480
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Find the missing factor.
Question 7.
70 × ____ = 2,100
Answer: 30
Explanation:
Let the missing number be X
So, 70 × X = 2,100
X = 2,100 / 70 = 30
Hence, the value of X is: 30
Question 8.
____ × 10 = 900
Answer: 90
Let the missing number be X
So, X × 10 = 900
X = 900 / 10 =90
Hence, the value of X is: 90
Question 9.
40 × ____ = 1,600
Answer: 40
Let the missing number be X
So, 40 × X = 1,600
X = 1,600 / 40 = 40
Hence, the value of X is: 40
Question 10.
____ × 20 = 1,600
Answer: 80
Let the missing number be X
So, X× 20 = 1,600
X = 1,600 / 20 = 80
Hence, the value of X is: 80
Question 11.
30 × ____ = 1,800
Answer: 60
Let the missing number be X
So, 30 × X = 1,800
X = 1,800 / 30 = 60
Hence, the value of X is: 60
Question 12.
____ × 50 = 3,000
Answer: 60
Let the missing number be X
So, X × 50 = 3,000
X = 3,000 / 50 = 60
Hence, the value of X is: 60
Compare.
Question 13.
Answer: 7,200 is less than 8,100
Explanation:
90 × 80 = 7,200
Given numbers are: 7,200 and 8,100
By comparing 2 values, we can conclude that 7,200 is less than 8,100
Question 14.
Answer: 1,200 is greater than 1,020
Explanation:
60 ×17 = 1,020
Given numbers are: 1,200 and 1,020
By comparing 2 values, we can conclude that 1,200 is greater than 1,020
Question 15.
Answer: 2,380 is equal to 2,380
Explanation:
34 × 70 = 2,380
Given numbers are:2,380 and 2,380
By comparing the 2 values, we can conclude that 2,380 is equal to2,380
Question 16.
A shallow moonquake occurs 20 kilometers below the moon’s surface. A deep moonquake occurs 35 times deeper than a shallow moonquake. How many kilometers below the surface does the deep moonquake occur?
Answer: 15 kilometers
Explanation:
Given that a shallow moonquake occurred 20 kilometers below the moon’s surface and a deep moonquake occurs 35 meters deeper than a shallow moonquake.
Now, to calculate how much distance the deep moonquake occurred from the surface, we have to subtract the distance that a shallow moonquake occurred from the deep moonquake occurred.
Hence,
The distance below the surface the deep moonquake occurred = 30 – 25 = 15 kilometers
Question 17.
Structure
Write the multiplication equation represented by the number line.
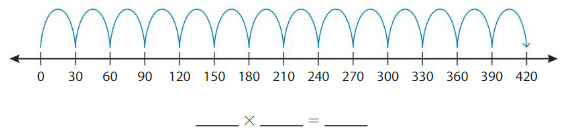
Answer:
Question 18.
Writing
Explain how you can use 20 × 10 = 200 to find 20 × 12.
Answer: By using the Associative Property of Multiplication,
20 × 10 = 10 × (2 × 10)
= (10 × 2) × 10
= 20 × 10
= 200
By using the same method, we can also find the value of 20 × 12.
Now,
By using the Associative Property of Multiplication,
20 × 12 = 12 × (2 × 10)
= (12 × 2) × 10
= 24 × 10
= 240
Note: Associative Property of Multiplication
Take 3 numbers a, b, c.
By using Associative Property, we can write
a × (b × c) = (a × b) × c
Question 19.
DIG DEEPER!
The product of a number and twice that number is 800. What are the numbers?
Answer: 20, 40
Explanation:
Let the number be X
Given that,
X × 2X = 800
Take X as a common multiple.
Hence,
X × X ( 1 × 2) = 800
X × X × 2 = 800
X × X = 800/2 = 400
X × X = 20 × 20
From the above, we can conclude that the value of X is 20
Hence, the value of twice the X is 20 × 2 = 40
So,
The numbers that can give the product 800 are 20, 40
Question 20.
Modeling Real Life
There are 506 new plants in a greenhouse. A worker programs a robot to arrange the plants into14 rows with 30 plants in each row. How many plants will fit in the rows?
Answer: 420
Explanation:
Given that there are 506 new plants in a greenhouse and a robot can arrange the plants into 14 rows with 30 plants each.
So, to find how many plants will fit in the row, we have to multiply 14 and 30( Since the robot arranges the plants in rows)
Now, By using the Associative Property of Multiplication,
14 × 30 = 14 × (3 × 10)
= (14 × 3) × 10
= (2 × 7 × 3) × 10
= 42 × 10
= 420
From the above, we can conclude that 420 plants will fit in the row.
Question 21.
Modeling Real Life
The world’s largest pool is 13 meters longer than the total length of 20 Olympic pools. An Olympic pool is 50 meters long. How long is the world’s largest pool?
Answer: 1013 meters
Explanation: Given that an Olympic pool has a length of 50 meters. But, there are 20 Olympic pools.
So, to find the total length of the Olympic Pool, we have to multiply the number of pools and the length of each pool.
By using the Associative Property of Multiplication,
50 × 20 = 50 × (2 × 10)
= (50 × 2) × 10
= ( 5 × 10 × 2) × 10
= 100 × 10
= 1,000 meters
So, the total length of the 20 Olympic pools = 1,000 meters
The
Question also mentions that the world’s largest pool is 13 meters longer than the total length of 20 Olympic pools.
Hence,
The length of the World’s largest pool = 1,000 + 13 = 1,013 meters.
So, the length of the World’s largest pool is 1,013 meters
Review & Refresh
Find the value of the underlined digit.
Question 22.
52,618
Answer: The place-value of 8 in the given number is: 8
Explanation:
We can find the position of any given number by using the place- value method.
From this, we can conclude that the place-value of 8 is: 8
Question 23.
379,021
Answer: The place-value of 7 in the given number is: 70,000
Explanation:
We can find the position of any given number by using the place- value method.
From this, we can conclude that the place-value of 7 in the given number is: 70,000
Explanation:
Question 24.
203,557
Answer: The place-value of 2 in the given number is: 200,000
Explanation:
We can find the position of any given number by using the place- value method.
From this, we can conclude that the place-value of 2 in the given number is: 200,000
Question 25.
497,384
Answer: The place-value of 3 in the given number is: 300
Explanation:
We can find the position of any given number by using the place- value method.
From this, we can conclude that the place-value of 3 in the given number is: 300
Lesson 4.2 Estimate Products
Explore and Grow
Choose an expression to estimate each product. Write the expression. You may use an expression more than once.
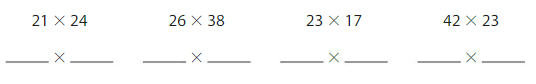
Compare your answers with a partner. Did you choose the same expressions?
Answer:
Let your Expression be 20 ×25.
The given Partner Expressions are:
A) 21 × 24 B) 26 × 38 C) 23 × 17 D) 42 × 23
By Comparing your Expression and your Partner Expression,
A) 500 is less than 504.
Explanation:
Let your Expression be 20 ×25.
By using the Associative Property of Multiplication,
20 × 25 = 25 × ( 2 × 10)
= (25 × 2) × 10
= (5 × 5 × 2) × 10
= 50 × 10
= 500
The given Partner Expressions are:
A) 21 × 24 B) 26 × 38 C) 23 × 17 D) 42 × 23
We can calculate the partner Expressions by Simplifying the given Expressions.
A)
21 × 24 = 3 × 7 × 3 × 8
= 9 × 56
= 504
By comparing your Expression with your Partner Expression, 500 is less than 504.
B)
26 × 38 = 13 × 2 × 19 × 2
= 4× 247
= 988
By comparing your Expression with your Partner Expression, 500 is less than 988.
C)
23 × 17
=391
By comparing your Expression with your Partner Expression, 500 is greater than 391.
D)
42 × 23 = 7 × 2 ×3 × 23
= 966
By comparing your Expression with your Partner Expression, 500 is less than 966.
Construct Arguments
Which estimated product do you think will be closer to the product of 29 and 37? Explain your reasoning.
Answer: 1,000 will be closer to 1,073
Explanation:
Given Product is
29 × 37 = 1,073
Given Expressions are:
25 × 40 = 1,000
30 × 40 = 1,200
Compare the given Product and the Expressions.
By comparison, we can conclude that 1,073 is close to 1,000.
Think and Grow: Estimate Products
You can estimate products using rounding or compatible numbers. Compatible numbers are numbers that are easy to multiply and are close to the actual numbers.
Example
Use rounding to estimate 57 × 38.
Step 1: Round each factor to the nearest ten.
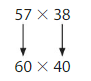
Step 2: Multiply.
60 × 40 = 60 × 4 tens
= 240 tens
= 2400
So, 57 × 38 is about 2400.
Example
Use compatible numbers to estimate 24 × 31.
Step 1: Choose compatible numbers.
Step 2: Multiply.
25 × 30 = 25 × 3 tens
= 75 tens
= 750
So, 24 × 31 is about 750.
Show and Grow
Use rounding to estimate the product.
Question 1.
27 × 50
Answer: 1500
Explanation:
Let 27 be Rounded to 30.
Now, we have to find the result of 30 × 50.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
30 × 50 = 30 × (5 × 10)
= (30 × 5) × 10
= ( 3 × 10 × 5) × 10
= 150 × 10
= 1,500
B) By using the place-value method,
30 × 50 = 30 × 5 tens
= 3 tens × 5 tens
= 15 × 1 ten × 1ten
= 15 × 10 × 10
= 1500
So,
27 × 50 can be rounded to 1,500
Question 2.
42 × 14
Answer: 600
Explanation:
Let 42 be Rounded to 40
Let 14 be Rounded to 15
Now, we have to find the result of 40 × 15.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
40 × 15 = 15 × (4 × 10)
= (15 × 4) × 10
= ( 3 × 4 × 5) × 10
= 60 × 10
= 600
B) By using the place-value method,
40 × 15 = 15 × 4 tens
= 60 tens
= 60 × 10
= 600
So,
42 × 16 can be rounded to 600
Question 3.
61 × 73
Answer: 4,200
Explanation:
Let 61 be Rounded to 60
Let 73 be Rounded to 70
Now, we have to find the result of 60 × 70.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
60 × 70 = 60 × (7 × 10)
= (60 × 7) × 10
= ( 6 × 10 × 7) × 10
= 420 × 10
= 4,200
B) By using the place-value method,
60 × 70 = 60 × 7 tens
= 6 tens ×7 tens
= 42 × 1 ten × 1ten
= 42 × 10 × 10
= 4,200
So,
61 ×73 can be rounded to 4,200
Use compatible numbers to estimate the product.
Question 4.
19 × 26
Answer: 500
Explanation:
Let 19 be Rounded to 20
Let 26 be Rounded to 25
Now, we have to find the result of 20 × 25.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
20 × 25 = 25 × (2 × 10)
= (25 × 2) × 10
= ( 5 × 5 ×2) × 10
= 50 × 10
= 500
B) By using the place-value method,
20 × 25 = 25 × 2 tens
= 50 tens
= 50 × 1 ten
= 50 × 10
= 500
So,
19 ×26 can be rounded to 500
Question 5.
23 × 78
Answer: 2,000
Explanation:
Let 23 be Rounded to 25
Let 78 be Rounded to 80
Now, we have to find the result of 25 × 80.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
25 × 80 = 25 × (8 × 10)
= (25 × 8) × 10
= ( 5× 5 × 8) × 10
= 200 × 10
= 2,000
B) By using the place-value method,
25 × 80 = 25 × 8 tens
= 200 tens
= 200 × 10
= 2,000
So,
23 ×78 can be rounded to 2,000
Question 6.
74 × 20
Answer: 1,500
Explanation:
Let 74 be Rounded to 75
Now, we have to find the result of 75 × 20.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
75 × 20 = 75 × (2 × 10)
= (75 × 2) × 10
= ( 5 × 5 × 3 × 2) × 10
= 150 × 10
= 1,500
B) By using the place-value method,
75× 20 = 75 ×2 tens
= 150 tens
= 150× 10
= 1,500
So,
74 ×20 can be rounded to 1,500
Apply and Grow: Practice
Estimate the product.
Question 7.
41 × 73
Answer: 2,800
Explanation:
Let 41 be Rounded to 40
Let 73 be Rounded to 70
Now, we have to find the result of 40 × 70.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
40 × 70 = 40 × (7 × 10)
= (40 × 7) × 10
= ( 4 × 10 × 7) × 10
= 280 × 10
= 2,800
B) By using the place-value method,
40 × 70 = 40 × 7 tens
= 4 tens ×7 tens
= 28 × 1 ten × 1ten
= 28 × 10 × 10
= 2,800
So,
41 ×73 can be rounded to 2,800
Question 8.
52 × 84
Answer: 4,250
Explanation:
Let 52 be Rounded to 50
Let 84 be Rounded to 85
Now, we have to find the result of 50 × 85.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
50 × 85 = 85 × (5× 10)
= (85 × 5) × 10
= ( 17× 5 × 5) × 10
= 425 × 10
= 4,250
B) By using the place-value method,
50 × 85 = 85 × 5 tens
= 425 tens
= 425 × 10
= 4,250
So,
52 ×84 can be rounded to 4,250
Question 9.
26 × 68
Answer: 1,750
Explanation:
Let 26 be Rounded to 25
Let 68 be Rounded to 70
Now, we have to find the result of 25 × 70.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
25 × 70 = 25 × (7 × 10)
= (25 × 7) × 10
= ( 5 × 5 × 7) × 10
= 175 × 10
= 1,750
B) By using the place-value method,
25 × 70 = 25 × 7 tens
= 175 tens
= 175 × 10
= 1,750
So,
26 ×68 can be rounded to 1,750
Question 10.
38 × 17
Answer: 600
Explanation:
Let 38 be Rounded to 40
Let 17 be Rounded to 15
Now, we have to find the result of 40 × 15.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
15 × 40 = 15 × (4× 10)
= (15 × 4) × 10
= ( 5 × 3 × 4) × 10
= 60 × 10
= 600
B) By using the place-value method,
15 × 40 = 15 × 4 tens
= 60 tens
= 60 × 10
= 600
So,
38 ×17 can be rounded to 600
Question 11.
75 × 24
Answer: 1,875
Explanation:
Let 24 be Rounded to 25
Now, we have to find the result of 25 × 75.
We can find the Product by using the simplification method.
25 × 75
= 5 × 5 × 25 × 3
= 5 × 5× 5 × 5 × 3
= 25 × 25 × 3
= 625 × 3
= 1,875
So,
38 × 17 can be Rounded to 1,875
Question 12.
93 × 53
Answer: 4,500
Explanation:
Let 93 be Rounded to 90
Let 53 be Rounded to 50
Now, we have to find the result of 90 × 50.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
90 × 50 = 90 × (5 × 10)
= (90 × 5) × 10
= ( 5 × 2 × 9 × 5) × 10
= 450 × 10
= 4,500
B) By using the place-value method,
90 × 50 = 90 × 5 tens
= 9 tens × 5 tens
= 45 × 1 ten × 1 ten
= 45 × 10 × 10
= 4,500
So,
93 ×53 can be rounded to 4,500
Question 13.
44 × 78
Answer: 3,600
Explanation:
Let 44 be Rounded to 45
Let 78 be Rounded to 80
Now, we have to find the result of 45 × 80.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
45 × 80 = 45 × (8 × 10)
= (45 × 8) × 10
= ( 5 × 2 × 9 × 4) × 10
= 360 × 10
= 3,600
B) By using the place-value method,
45 × 80 = 45 × 8 tens
= 5 × 9 × 8 tens
= 45 × 8 × 10
= 360 × 10
= 3,600
So,
44 ×78 can be rounded to 4,500
Question 14.
21 × 33
Answer: 600
Explanation:
Let 21 be Rounded to 20
Let 33 be Rounded to 30
Now, we have to find the result of 20 × 30.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
20 × 30 = 20 × (3× 10)
= (20 × 3) × 10
= ( 5× 4 × 3) × 10
= 60 × 10
= 600
B) By using the place-value method,
20 × 30 = 30 × 2 tens
= 3 tens × 2 tens
= 6 × 10 × 10
= 600
So,
21 ×33 can be rounded to 600
Question 15.
45 × 45
Answer: 2,500
Explanation:
Let 45 be Rounded to 50
Now, we have to find the result of 50 × 50.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
50 × 50 = 50 × (5× 10)
= (50 × 5) × 10
= ( 10× 5 × 5) × 10
= 250 × 10
= 2,500
B) By using the place-value method,
50 × 50 = 50 × 5 tens
= 250 tens
= 25 × 10 × 10
= 2,500
So,
45 ×45 can be rounded to 2,500
Open-Ended
Write two possible factors that can be estimated as shown.
Question 16.
2,400
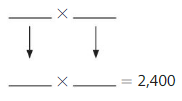
Answer: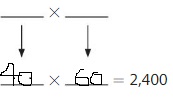 
Explanation:
The given number is: 2,400
The Products of 24 are:
4 × 6 = 24
6 × 4 =24
From the above two products, we can conclude that the two possible numbers that can give the product 2,400 are: 40, 60
Question 17.
1,200
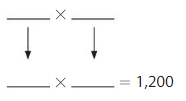
Answer: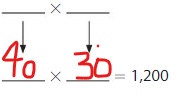 
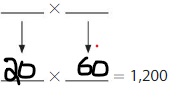
Explanation:
Explanation:
The given number is: 1,200
The Products of 12 are:
3 × 4 =12
4 × 3 =12
6 ×2 =12
2 ×6 =12
From the above two products, we can conclude that the two possible numbers that can give the product 2,400 are: 40, 30, and 20, 60
Question 18.
DIG DEEPER!
You use 50 × 30 to estimate 46 × 29. Will your estimate be greater than or less than the actual product? Explain.
Answer: We will Estimate the Product greater than the actual Product
Explanation:
Given Product is: 46 × 29
Explanation:
Let 46 be Rounded to 50
Let 29 be Rounded to 30
Now, we have to find the result of 50 × 30.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
50 × 30 = 50 × (3 × 10)
= (50 × 3) × 10
= ( 5 × 10 × 3) × 10
= 150 × 10
= 1,500
B) By using the place-value method,
50 × 30 = 30 × 5 tens
= 150 tens
= 150× 10
= 1,500
So,
46 ×29 can be rounded to 1,500
Question 19.
YOU BE THE TEACHER
Your friend uses rounding to estimate 15 × 72. She gets a product of 700. Is your friend’s estimate correct?
Explain.
Answer: No
Explanation:
Your friend is going to estimate 15 × 72 and she gets a product 700.
So, According to her Product, the Possible rounded off numbers to get the product 700 are 10 and 70
So, your Friend’s estimate is not correct.
Now,
Let 72 be Rounded to 70
Now, we have to find the result of 15 × 70.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
15 × 70 = 15 × (7 × 10)
= (15 × 7) × 10
= (3 × 5 × 7) × 10
= 105 × 10
= 1,050
B) By using the place-value method,
15 × 70 = 15 × 7 tens
= 105 tens
= 105 × 10
= 1,050
So,
15 ×72 can be rounded to 1,050
Think and Grow: Modeling Real Life
Example
About how much does 1 year of phone service cost?
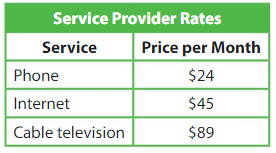
Think: What do you know? What do you need to find? How will you solve it?
There are 12 months in 1 year, so multiply the price per month by 12.
12 × 24 = 288
Estimate the product.
Answer: 
Show and Grow
Question 20.
Use the table above. About how much does 1 year of Internet service cost? About how much does 1 year of cable television service cost?
Answer:
Internet Service cost: $540
Cable television service cost: $1068
Explanation:
In the given table,
The Internet cost and cable television service costs are given per month.
For 1 year, there are 12 months.
So,
The cost of Internet service for a year is: 12 × $45 = $ 540
The cost of cable television service for a year is: 12 × $89 = 1068
Question 21.
A giant panda eats 28 pounds of food each day. An orca eats 17 times as much food as the panda eats each day. About how much food does the orca eat each day?
Answer: 476 Pounds
Explanation:
Given that a giant panda eats 28 pounds of food each day and an Orca eats 17 times as much food as the panda eats each day.
So,
The amount of food eaten by an Orca = 17 × The amount of food eaten by panda
= 17 × 28 = 476 pounds
Estimate Products Homework & Practice 4.2
Use rounding to estimate the product.
Question 1.
42 × 13
Answer: 600
Explanation:
Let 42 be Rounded to 40
Let 13 be Rounded to 15
Now, we have to find the result of 40 × 15.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
40 × 15 = 15 × (4 × 10)
= (15 × 4) × 10
= ( 3 × 4 × 5) × 10
= 60 × 10
= 600
B) By using the place-value method,
40 × 15 = 15 × 4 tens
= 60 tens
= 60 × 10
= 600
So,
42 × 13 can be rounded to 600
Question 2.
56 × 59
Answer: 3,300
Explanation:
Let 56 be Rounded to 55
Let 59 be Rounded to 60
Now, we have to find the result of 55 × 60.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
55 × 60 = 55 × (6 × 10)
= (55 × 6) × 10
= ( 5 × 11 × 6) × 10
= 330 × 10
= 3,300
B) By using the place-value method,
55 × 60 = 55 × 6 tens
= 330 tens
= 330 × 10
= 3,300
So,
42 × 16 can be rounded to 600
Question 3.
19 × 91
Answer: 1,800
Explanation:
Let 19 be Rounded to 20
Let91 be Rounded to 90
Now, we have to find the result of 20 × 90.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
20 × 90 = 20 × (9× 10)
= (20 × 9) × 10
= ( 5 × 4 × 9) × 10
= 180 × 10
= 1,800
B) By using the place-value method,
20 × 90 = 20 × 9 tens
= 2 tens × 9 tens
= 18 × 1 ten × 1 ten
=18 × 10 × 10
= 18 × 100
= 1,800
So,
19 × 91 can be rounded to 1,800
Use compatible numbers to estimate the product.
Question 4.
23 × 78
Answer: 2,000
Explanation:
Let 23 be Rounded to 25
Let 78 be Rounded to 80
Now, we have to find the result of 25 × 80.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
25 × 80 = 25 × (8 × 10)
= (25 × 8) × 10
= ( 5 × 5 × 8) × 10
= 200 × 10
= 2,000
B) By using the place-value method,
25 × 80 = 25 × 8 tens
= 200 tens
= 200 × 10
= 2,000
So,
23 × 78 can be rounded to 2,000
Question 5.
67 × 45
Answer:3,150
Explanation:
Let 67 be Rounded to 70
Now, we have to find the result of 70 × 45.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
45 × 70 = 45 × (7 × 10)
= (45 × 7) × 10
= ( 5 × 9 × 7) × 10
= 315 × 10
= 3,150
B) By using the place-value method,
45 × 70 = 45 × 7 tens
= 315 tens
= 315 × 10
= 3,150
So,
67 × 45 can be rounded to 3,150
Question 6.
19 × 24
Answer: 500
Explanation;
Let 19 be Rounded to 20
Let 24 be Rounded to 25
Now, we have to find the result of 25 × 20.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
20 × 25 =25 × (2 × 10)
= (25 × 2) × 10
= ( 5 × 5 × 2) × 10
= 50 × 10
= 500
B) By using the place-value method,
25 × 20 = 25 × 2 tens
= 50 tens
= 50 × 10
= 500
So,
19 × 24 can be rounded to 500
Estimate the product.
Question 7.
84 × 78
Answer: 6,800
Explanation:
Let 84 be Rounded to 85
Let 78 be Rounded to 80
Now, we have to find the result of 85 × 80.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
85 × 80 = 85 × (8 × 10)
= (85 × 8) × 10
= ( 5 × 17 × 8) × 10
= 680 × 10
= 6,800
B) By using the place-value method,
85 × 80 = 85 × 8 tens
= 680 tens
= 680 × 10
= 6,800
So,
84 × 78 can be rounded to 600
Question 8.
92 × 34
Answer: 3,150
Explanation:
Let 92 be Rounded to 90
Let 34 be Rounded to 35
Now, we have to find the result of 90 × 35.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
90 × 35 = 35 × (9 × 10)
= (35 × 9) × 10
= ( 5 × 7 × 9) × 10
= 315 × 10
= 3,150
B) By using the place-value method,
90 × 35 = 35 × 9 tens
= 315 tens
= 315 × 10
= 3,150
So,
92 × 34 can be rounded to 3,150
Question 9.
57 × 81
Answer: 4,800
Explanation:
Let 57 be Rounded to 60
Let 81 be Rounded to 80
Now, we have to find the result of 80 × 60.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
80 × 60 = 80 × (6 × 10)
= (80 × 6) × 10
= ( 8 × 10 × 6) × 10
= 480 × 10
= 4,800
B) By using the place-value method,
80 × 60 = 80 × 6 tens
= 480 tens
= 480 × 10
= 4,800
So,
57 × 81 can be rounded to 600
Open-Ended
Write two possible factors that could be estimated as shown.
Question 10.
6,400
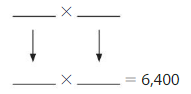
Answer: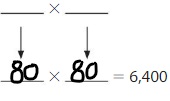 
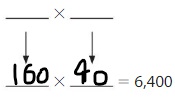
Explanation:
The Products of 64 are:
8 × 8 = 64
16 × 4 =64
From the above two products, we can conclude that the two possible numbers that can give the product 6,400 are: 80,80 and. 160,40
Question 11.
1,600
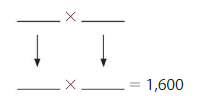
Answer: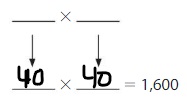
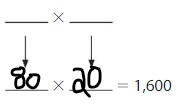
Explanation:
The Products of 16 are:
4 × 4 = 16
8 × 2 =16
From the above two products, we can conclude that the two possible numbers that can give the product 1,600 are: 40, 40 and, 80,20
Question 12.
Reasoning
Are both Newton’s and Descartes’s estimates reasonable? Explain.
Answer: Both Newton’s and Descartes’s estimates are reasonable
Explanation:
According to Newton,
The estimated values of 27 and 68 are 30 and 70
According to Descartes,
The estimated values of 27 and 68 are 25 and 70
According to Newton:
27 × 68 = 2,100
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
30 × 70 = 30 × (7 × 10)
= (30 × 7) × 10
= ( 3 × 10 × 7) × 10
= 210 × 10
= 2,100
B) By using the place-value method,
30× 70 = 30 ×7 tens
= 210 tens
= 210 × 10
= 2,100
So,
27 × 68 can be rounded to 2,100 ( According to Newton)
According to Descartes:
27 × 68 = 1,750
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
25 × 70 = 25 × (7 × 10)
= (25 × 7) × 10
= ( 5 × 5 × 7) × 10
= 175 × 10
= 1,750
B) By using the place-value method,
25× 70 = 25 ×7 tens
= 175 tens
= 175 × 10
= 1,750
So,
27 × 68 can be rounded to 1,750 ( According to Descartes)
Question 13.
DIG DEEPER!
You use 90 × 30 to estimate 92 × 34. Will your estimate be greater than or less than the actual product? Explain.
Answer: No
Your friend is going to estimate 92 × 34 and she gets a product 2,700.
So, your Friend’s estimate is not correct.
Now,
Let 34 be Rounded to 35
Let 92 be Rounded to 90
Now, we have to find the result of 35 × 90.
We can find the product of multiples of ten by using two methods. They are:
A) The place-value method B) Associative Property of Multiplication
A) By using the Associative Property of Multiplication,
35 × 90 = 35 × (9 × 10)
= (35 × 9) × 10
= (9× 5 × 7) × 10
= 315 × 10
= 3,150
B) By using the place-value method,
35 × 90 = 35 × 9 tens
= 315 tens
= 315 × 10
= 3,150
So,
92 ×34 can be rounded to 3,150
Question 14.
Modeling Real Life
About how many hours of darkness does Barrow, Alaska have in December?
Answer: 744 hours
Explanation:
From the above table,
The days of darkness in Barrow, Alaska are 31 days.
We know that there are 24 hours in a day.
So,
The number of hours of darkness does Barrow, Alaska have in December = 31 × 24 = 744 hours
Review & Refresh
Question 15.
Round 253,490 to the nearest ten thousand.
Answer: 250,000
Explanation;
The position of a given number is dependent on the place-value of that number.
So,
When 253,490 rounded off to the nearest ten thousand, the result ts 250,000
Question 16.
Round 628,496 to the nearest hundred thousand.
Answer: 630,000
Explanation;
The position of a given number is dependent on the place-value of that number.
So,
When 628,496 rounded off to the nearest ten thousand, the result ts 630,000
Lesson 4.3 Use Area Models to Multiply Two-Digit Numbers
Explore and Grow
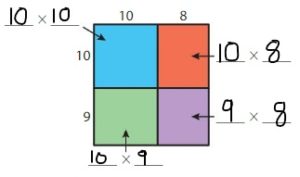
Draw an area model that represents 15 × 18. Then break apart your model into smaller rectangles.
What is the total area of your model? Explain how you found your answer.
Answer: The Total Area of your Model = 400
Explanation:
Count the number of boxes in both the vertical and horizontal directions.
Since all the sides of the figure look the same, take any 1 row in the vertical direction and horizontal direction and count the number of boxes in it.
After counting, you get
The number of boxes in a row present in the vertical direction is: 20
The number of boxes in a row present in the horizontal direction is: 20
So, we can find the total area of your model by multiplying the number of boxes in both the vertical and horizontal directions. ( Remember, there is no need to count all the boxes in both directions since the figure has an equal number of boxes on all sides)
So,
The total area of your model = 20 × 20 = 400
Reasoning
Compare with a partner. Do you get the same answer? Explain.
Answer: Yes
Explanation:
My Partner counted the number of boxes in the middle of the model in both vertical and horizontal directions.
He got,
The number of boxes in a row present in the vertical direction is: 20
The number of boxes in a row present in the horizontal direction is: 20
So,
The total area of my partner’s model = 20 × 20 = 400
So,
My partner and I got the same answer.
Think and Grow: Use Area Models to Multiply
Example
Use an area model and partial products to find 12 × 14.
Model the expression. Break apart 12 as 10 + 2 and 14 as 10 + 4.
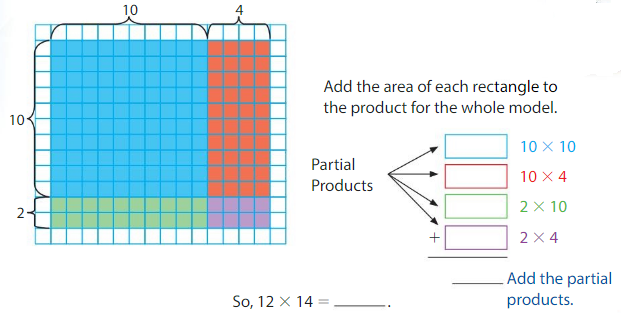
Answer: 168
Explanation:
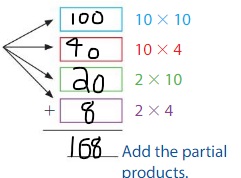So, 12 × 14 = 168
Show and Grow
Use the area model to find the product.
Question 1.
17 × 15 = _____
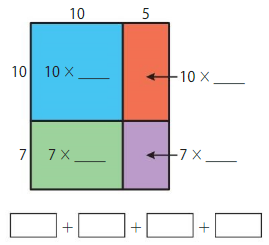
Answer: 255
Explanation:
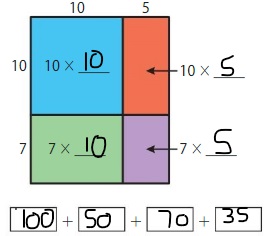So, 17 × 15 = 255
Question 2.
34 × 22 = _____
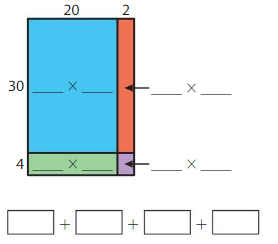
Answer: 748
Explanation:
So, 34 × 22 = 748
Apply and Grow: Practice
Use the area model to find the product.
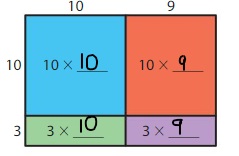
Question 3.
13 × 19 = _____
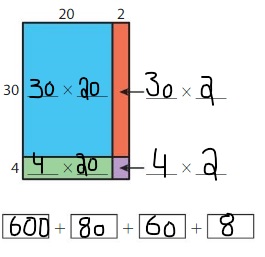
Answer: 247
Explanation:
So, 13 × 19 = 247
Now,
100 + 90 + 30 + 27 = 247
So,
13 × 19 = 247
Question 4.
25 × 39 = ____
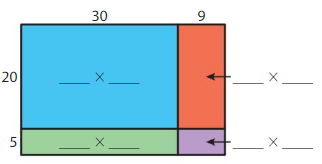
Answer: 975
Explanation:
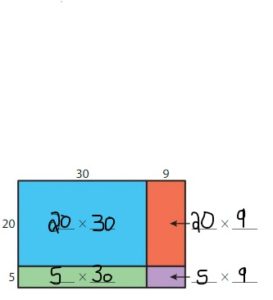
Now,
600 + 150 + 180 + 45 = 975
So,
25 × 39 = 975
Draw an area model to find the product.
Question 5.
11 × 13 = ______
Answer: 143
Explanation: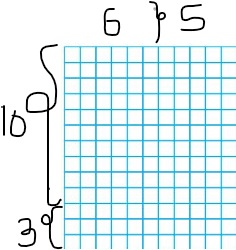 
By using the Partial Products method,
10 × 6 + 3 × 6 + 10 × 5 + 3 × 5
= 60 + 18 + 50 + 15 = 143
So,
11 × 13 = 143
Question 6.
23 × 26 = ______
Answer: 598
Explanation:
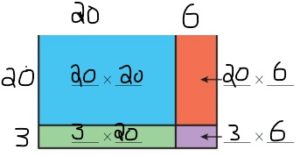
By using the Partial products method,
20 × 20 + 3 × 20 + 20 × 6 + 3 × 6
= 400 + 60 + 120 + 18 = 598
So, 23 × 26 = 598
Question 7.
27 × 45 = ______
Answer: 1,215
Explanation:
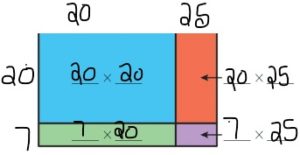
By using the partial products method,
20 × 20 + 7 × 20 + 20 × 25 + 7 ×25
= 400 + 140 +500 + 175 = 1,215
So, 27 × 45 = 1,215
Question 8. Perseid meteors travel 59 kilometers each second. How far does a perseid meteor travel in 15 seconds?
Answer: 885 kilometers
Explanation:
Given that the Perseid meteors travel 59 kilometers each second.
So,
The distance traveled by the Perseid meteors in 15 seconds = 59 × 15 = 885 kilometers
From the above,
We can conclude that the Perseid meteors travel 885 kilometers in 15 seconds.
Question 9.
DIG DEEPER!
Write the multiplication equation represented by the area model.
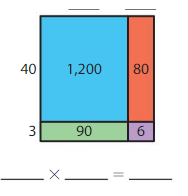
Answer: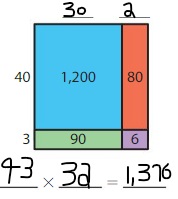 
Explanation:
Using the Partial Products Model,
40 × 30 + 40 × 2 + 3 × 30 + 3 × 2
= 1,200 + 80 + 90 + 6 = 1,376
So, the multiplication equation represented by area model = 43 × 32
Think and Grow: Modeling Real Life
Example
A wind farm has 8 rows of new wind turbines and 3 rows of old wind turbines. Each row has 16 turbines. How many turbines does the wind farm have?
Answer: Add the number of rows of new turbines to the number of rows of old turbines
8 + 3 =11
So,
There are11 rows of turbines.
Multiply the number of rows by the number in each row.
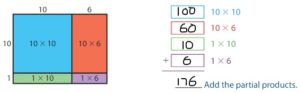
So, the wind farm has 176 turbines.
Show and Grow
Question 10.
You can type 19 words per minute. Your cousin can type 33 words per minute. How many more words can your cousin type in 15 minutes than you?
Answer: 210 words
Explanation:
Given that you can type 19 words per minute and your cousin can type 33 words per minute.
So,
The number of words you can type in 15 minutes = 19 × 15 = 285
The number of words your cousin can type in 15 minutes = 495
Hence,
The number of words you have to type more than your cousin in 15 minutes = 495 – 285 = 310 words
Question 11.
A store owner buys 24 packs of solar eclipse glasses. Each pack has 12 glasses. The store did not sell 18 of the glasses. How many of the glasses did the store sell?
Answer: 270 glasses
Explanation:
Given that a store Owner buys 24 packs of solar eclipse glasses and each pack has 12 glasses.
So,
the total number of glasses that a store owner buy = 24 × 12 = 288 glasses
But,
It is also given that the store owner did not sell 18 glasses.
Hence, the total number of glasses the store owner sold = 288 – 18 = 270 glasses
Use Area Models to Multiply Two-Digit Numbers Homework & Practice 4.3
Use the area model to find the product.
Question 1.
12 × 13 = ______
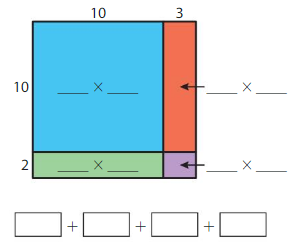
Answer: 156
Explanation: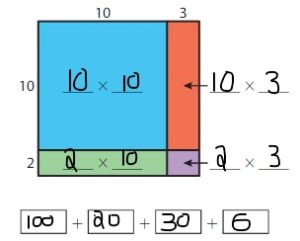 
By using the partial products method,
10 × 10 + 2 ×10 + 10 × 3 + 2 ×3
= 100 + 20 +30 + 6 = 156
So, 12 × 13 = 156
Question 2.
38 × 24 = _____
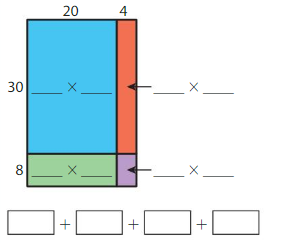
Answer: 912
Explanation: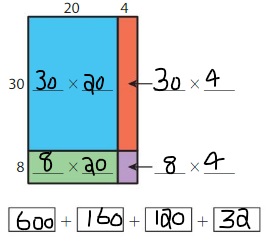 
By using the Partial products method,
30 × 20 + 8 × 20 + 30 × 4 + 8 × 4
= 600 + 160 + 120 + 32 = 912
So, 38 × 24 = 912
Use the area model to find the product.
Question 3.
19 × 18 = ____
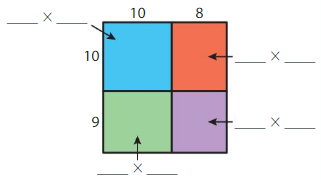
Answer: 342
Explanation:
By using the partial products method,
10 × 10 +8 × 10 + 10 × 9 +9 ×8
= 100 + 80 +90 + 72 = 342
So, 19 × 18 = 342
Question 4.
23 × 25 = _____
Answer: 575
Explanation:
By using the partial products method,
20 × 20 +5 × 20 + 3 × 20 +3 ×5
= 400 + 100 +60 + 15 = 575
So, 23 × 25 = 575
Draw an area model to find the product.
Question 5.
26 × 31 = _____
Answer: 806
Explanation:
By using the partial products method,
20 × 30 +6× 30 + 1 × 20 +6 ×1
= 600 + 180 +20 + 6 = 806
So, 26 × 31 = 806
Question 6.
22 × 47 = ______
Answer: 1,034
Explanation:
By using the partial products method,
20 × 40 +2×40 + 7 × 20 +2 ×7
= 800 + 80 +140 + 14 = 1,034
So, 22 × 47 = 1,034
Question 7.
YOU BE THE TEACHER
Your friend finds 12 × 42. Is your friend correct? Explain.
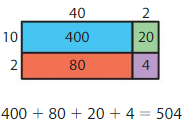
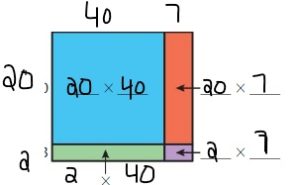
Answer: Yes, your friend is correct.
Explanation:
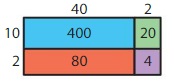
By using the partial products method,
10 × 40 +2×10 + 2 × 40 +2 ×2
= 400 + 20 +80 + 4 = 504
So, 12 × 42 = 504
Question 8.
Writing
Explain how to use an area model and partial products to multiply two-digit numbers.
Answer: 
Let the Partial Products are: a, b, c, d
By using the Partial Products method,
a × c + b × c + a × d + b × d
= ac + bc + ad + bd
So, by using the above method, we can find the product of 2- digit numbers.
Question 9.
Modeling Real Life
A mega-arcade has 9 rows of single-player games and 5 rows of multi-player games. Each row has 24 games. How many games does the arcade have?
Answer: The arcade has 336 games
Explanation:
Given that a mega arcade has 9 rows of single-player games and 5 rows of multi-player games.
So,
Total number of rows present in the arcade = 9 + 5 = 14
It is also given that each row has 24 games.
So,
The total number of games present in the arcade = 14 × 24 = 336
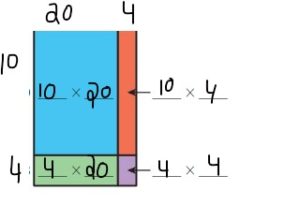
By using the partial products method,
10 × 20 +4 × 20 + 10 × 4 + 4 ×4
= 200 + 80 +40 + 16 = 336
So, 14 × 24 = 336
Review & Refresh
Find the sum. Check whether your answer is reasonable.
Question 10.
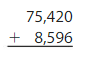
Answer: 84,016
Explanation: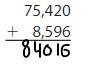 
To find the sum, add the digits starting from the Right-most position. If there is “Carry”, then add that carry to the result of the next Position value.
Question 11.
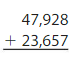
Answer: 71,585
Explanation: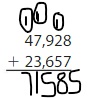
To find the sum, add the digits starting from the Right-most position. If there is “Carry”, then add that carry to the result of the next Position value. (As shown in the above figure)
Question 12.
Answer: 569,821
Explanation:
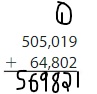
To find the sum, add the digits starting from the Right-most position. If there is “Carry”, then add that carry to the result of the next Position value. (As shown in the above figure)
Lesson 4.4 Use the Distributive Property to Multiply Two-Digit Numbers
Explore and Grow
Use as few base ten blocks as possible to create an area model for 13 × 24. Draw to show your model.
Color your model to show four smaller rectangles. Label the partial products.
Answer: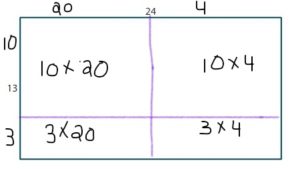 
By using the partial products method,
10 × 20 +3 × 20 + 4 × 3 + 10 ×4
= 200 + 60 +12 + 40 = 312
So, 13 × 24 = 312
Reasoning
How do you think the Distributive Property relates to your area model? Explain.
Answer:
Distributive Property of Multiplication:
Let there are 3 numbers a, b, c.
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
SO, by using the above property, we can conclude that the Distributive Property relates to your area model.
Think and Grow: Use the Distributive Property to Multiply
Example
Find 17 × 25.
One Way: Use an area model and partial products.
Show and Grow
Question 1.
Use the area model and the Distributive Property to find 32 × 19.
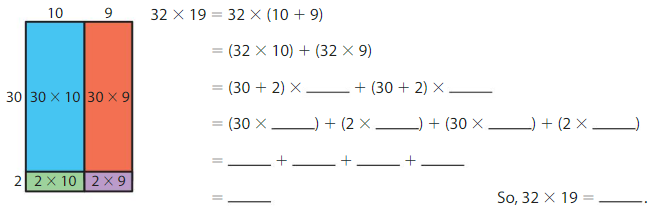
Answer: 608
Explanation:
Using the Distributive Property, we can find the product of 32 × 19
32 × 19 = 32 × ( 10 + 9)
= ( 32 × 10 ) + ( 32 × 9)
= ( 30 + 2 ) × 10 + ( 30 + 2 ) × 9
= ( 30 × 10 ) + ( 2 × 10 ) + ( 30 × 9 ) + ( 2 × 9)
= 300 + 20 + 270 + 18
= 608
So, 32 × 19 = 608
Apply and Grow: Practice
Question 2.
Use the area model and the Distributive Property to find 34 × 26.
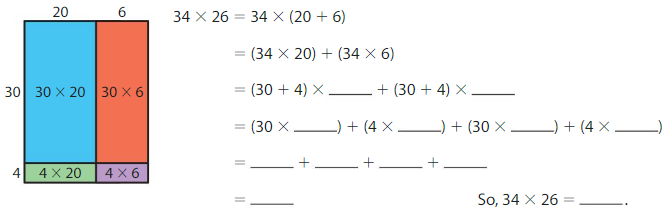
Answer: 884
Explanation:
Using the Distributive Property, we can find the product of 34 × 26
34 × 26 = 34 × ( 20 + 6)
= ( 34 × 20 ) + ( 34 × 6)
= ( 30 + 4 ) × 20 + ( 30 + 4 ) × 6
= ( 30 × 20 ) + ( 4 × 20 ) + ( 30 × 6 ) + ( 4 × 6)
= 600 + 80 + 180 + 24
= 884
So, 34 × 26 = 884
Use the Distributive Property to find the product.
Question 3.
28 × 47 = 28 × (40 + 7)
= (28 × 40) + (28 × 7)
= (20 + 8) × 40 + (20 + 8) × 7
= (20 × 40) + (8 × 40) + (20 × 7) + (8 × 7)
= 800 + 320 + 140 + 56
=1,316
So, 28 × 47 = 1,316
Answer: 28 × 47 = 1,316
Question 4.
39 × 41 = _____
Answer:
39 × 41 = 39 × (40 + 1)
= (39 × 40) + (39 × 1)
= (30 + 9) × 40 + (30 + 9) × 1
= (30 × 40) + (9 × 40) + (30 × 1) + (9 ×1)
=1,200 + 360 + 30 + 9
=1,599
So, 39 × 41 = 1,599
Question 5.
74 × 12 = ______
Answer:
74 × 12 = 74 × (10 + 2)
= (74 × 10) + (74 × 2)
= (70 + 4) × 10 + (70 + 4) × 2
= (70 × 10) + (4 × 10) + (70 × 2) + (4 ×2)
=700 + 40 + 140 + 8
=888
So, 74 × 12 = 888
Question 6.
83 × 65 = _____
Answer:
83 × 65 = 83 × (60 + 5)
= (83 × 60) + (83 × 5)
= (80 + 3) × 60 + (80 + 3) ×5
= (80 × 60) + (3 × 60) + (80 × 5) + (3 ×5)
=4,800 + 180 + 400 + 15
=5,395
So, 83 × 65 = 5,395
Question 7.
Which One Doesn’t Belong?
Which expression does not belong with the other three?
Answer:
Let the given Expressions be ordered as A), B), C) and D)
From the Order, we can say that Expression C) does not belong to the other three.
Explanation:
The given Expressions are:
A) ( 40 + 7) × 52
B) ( 40 + 7) × (50 + 2)
C) ( 40 × 7) × ( 50 × 2)
D) 47 × ( 50 + 2)
The given Expressions are written using the Distributive Property of Multiplication.
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
So, from the above Property, we can conclude that Expression C) does not belong to the other three.
Think and Grow: Modeling Real Life
Example
The dunk tank at a school fair needs 350 gallons of water. There are 27 students in a class. Each student pours13 gallons of water into the tank. Is there enough water in the dunk tank?
Find how many gallons of water the students put in the dunk tank.
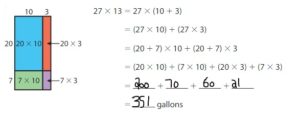
Given that there are 350 gallons at a school fair.
But, we got 351 gallons of water.
So, there is 1 gallon enough water in the dunk tank.
Show and Grow
Question 8.
An event coordinator orders 35 boxes of T-shirts to give away at a baseball game. There are 48 T-shirts in each box. If 2,134 fans attend the game, will each fan get a T-shirt?
Answer: No, each fan will not get a T-shirt.
Explanation:
Given that an event coordinator orders 35 boxes of T-shirts to give away at a baseball game and there are 48 T-shirts in each box.
So, we will get the total number of T-shirts due to the Product of 35 × 48.
We will get the product by using the Distributive Property of Multiplication.
35 × 48 = 35 × (40 + 8)
= (35 × 40) + (35 × 8)
= (30 + 5) × 40 + (30 + 5) × 8
= (30 × 40) + (5 × 40) + (30 × 8) + (8 ×5)
=1,200 + 20 + 240 + 40
=1,680
So, 35× 48 = 1,680
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 9.
A horse owner must provide 4,046 square meters of pasture for each horse. Is the pasture large enough for 2 horses? Explain.
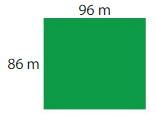
Answer: Yes, the pasture is large enough for 2 horses.
Explanation:
Given that a horse owner must provide 4,046 square meters for each horse.
But, it is also given that the area of pasture is 86 × 96 square meters.
We have to find the Product of 86 × 96 by using the Distributive Property of Multiplication..
86 × 96 = 86 × (90 + 6)
= (86 × 90) + (86 × 6)
= (80 + 6) × 90 + (80 + 6) × 6
= (80 × 90) + (6 × 90) + (80 × 6) + (6 ×6)
=7,200 + 540 + 480 + 36
=8,256
So, 86× 96 = 8,256
By comparing the area of the pasture of each horse and the Product, we can conclude that the pasture is large enough for the 2 horses.
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Use the Distributive Property to Multiply Two-Digit Numbers Homework & Practice 4.4
Question 1.
Use the area model and the Distributive Property to find 45 × 21.
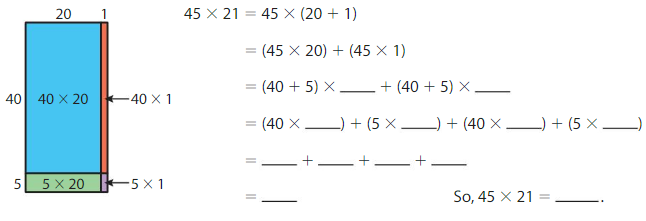
Answer: 945
Explanation: By using the Distributive Property of Multiplication,
45 × 21 = 45 × (20 + 1)
= (45 × 20) + (45 × 1)
= (40 + 5) × 20 + (40 + 5) ×1
= (20 × 40) + (5 × 20) + (40 × 1) + (1 ×5)
=800 + 100 + 40 + 5
=945
So, 45× 21 = 945
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 2.
Use the Distributive Property to find the product.
34 × 49 = 34 × (40 + 9)
= (34 × 40) + (34 × 9)
= (30 + 4) × 40 + (30 + 4) × 9
= (30 × 40) + (4 × 40) + (30 × 9) + (4 × 9)
= 1,200 +160 + 270 + 36
= 1,666
So, 34 × 49 =1,666
Question 3.
14 × 27 = ______
Answer: 378
Explanation: Using the Distributive Property of Multiplication,
14 × 27 = 14 × (20 + 7)
= (14 × 20) + (14 × 7)
= (10 + 4) × 20 + (10 + 4) × 7
= (10 × 20) + (4 × 20) + (10 × 7) + (4 ×7)
=200 + 80 + 70 + 28
=378
So, 14× 27 = 378
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 4.
38 × 31 = ______
Answer: 1,178
Explanation: Using the Distributive Property of Multiplication,
38 × 31 = 38 × (30 + 1)
= (38 × 30) + (38 × 1)
= (30 + 8) × 30 + (30 + 8) ×1
= (30 × 30) + (8× 30) + (30 × 1) + (8 ×1)
=900 + 240 + 30 + 8
=1,178
So, 38× 31 = 1,178
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 5.
58 × 26 = ______
Answer: 1,508
Explanation: Using the Distributive Property of Multiplication,
58 × 26 = 58 × (20 + 6)
= (58 × 20) + (58 × 6)
= (50 + 8) × 20 + (50 + 8) × 6
= (50 × 20) + (8 × 20) + (50 × 6) + (8 ×6)
=1,000 + 160 + 300 + 48
=1,508
So, 58× 26 = 1,508
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 6.
56 × 32 = ______
Answer: 1,792
Explanation: Using the Distributive Property of Multiplication,
56 × 32 = 56 × (30 + 2)
= (56 × 30) + (56× 2)
= (50 + 6) × 30 + (50 + 6) × 2
= (30 × 50) + (6 × 30) + (50 × 2) + (6 ×2)
=1,500 + 180 + 100 + 12
=1,792
So, 56× 32 = 1,792
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 7.
87 × 23 = ______
Answer: 2,001
Explanation: Using the Distributive Property of Multiplication,
87 × 23 = 87 × (20 + 3)
= (87 × 20) + (87 × 3)
= (80 + 7) × 20 + (80 + 7) × 3
= (80 × 20) + (7 × 20) + (3 × 80) + (7 ×3)
=1,600 + 140 + 240 + 21
=2,001
So, 87× 23 = 2,001
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 8.
95 × 81 = ______
Answer: 7,695
Explanation: Using the Distributive Property of Multiplication,
95 × 81 = 95 × (80 + 1)
= (95 × 80) + (95 × 1)
= (90 + 5) × 80 + (90 + 5) × 1
= (90 × 80) + (5 × 80) + (90 × 1) + (1 ×5)
=7,200 + 400 + 90 + 5
=7,695
So, 95× 81 = 7,695
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 9.
DIG DEEPER!
Find 42 × 78 by breaking apart 42 first.
Answer: 3,276
Explanation: Using the Distributive Property of Multiplication,
42 × 78 = 78 × (40 + 2)
= (78 × 40) + (78 × 2)
= (70 + 8) × 40 + (70 + 8) × 2
= (70 × 40) + (8 × 40) + (70 × 8) + (8 ×2)
=2,800 + 320 + 560 + 16
=3,276
So, 42× 78 = 3,276
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Question 10.
Modeling Real Life
The Elephant Building is 335 feet high. A real Asian elephant is 12 feet tall. If 29 real elephants could stand on top of each other, would they reach the top of the building?
Answer: The 29 real elephants would reach the top of the building even when they stand on top of each other.
Explanation:
Give that the Elephant Building is 335 feet high. It is also given that a real Asian Elephant is 12 feet tall and there are 29 real elephants.
So, we have to find the height of 29 real elephants. We can find it using the product of 29 × 12.
We find the product by using the Distributive Property of Multiplication.
29 × 12 = 12 × (20 + 9)
= (12 × 20) + (12 × 9)
= (10 + 2) × 20 + (10 + 2) × 9
= (10 × 20) + (2 × 20) + (10 × 9) + (2 ×9)
=200 + 40 + 90 + 18
=348
So, 29× 12 = 348
We get the result of the Product as 348 feet but given that the Elephant Building is 335 feet high.
From this, we can conclude that if 29 real elephants could stand on top of each other, they would reach the top of the building
Note:
The Distributive property is given as:
a × (b + c) = ( a × b) + ( a × c)
Review & Refresh
Find the difference. Then check your answer.
Question 11.
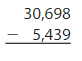
Answer: 25,259
Explanation:
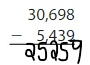
The difference between the multi-digit numbers can be found by the difference taken from the left-most digit. If the number we want to subtract is less than the number to be subtracted, then we will take the carry from the Previous digit and the Previous digit contains 1 less number.
Question 12.
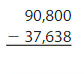
Answer: 53,162
Explanation: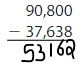 
The difference between the multi-digit numbers can be found by the difference taken from the left-most digit. If the number we want to subtract is less than the number to be subtracted, then we will take the carry from the Previous digit and the Previous digit contains 1 less number.
Question 13.
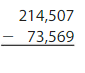
Answer: 140,938
Explanation: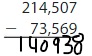 
The difference between the multi-digit numbers can be found by the difference taken from the left-most digit. If the number we want to subtract is less than the number to be subtracted, then we will take the carry from the Previous digit and the Previous digit contains 1 less number.
Lesson 4.5 Use Partial Products to Multiply Two-Digit Numbers
Explore and Grow
How can you use the rectangles to find 24 × 53? Complete the equation.
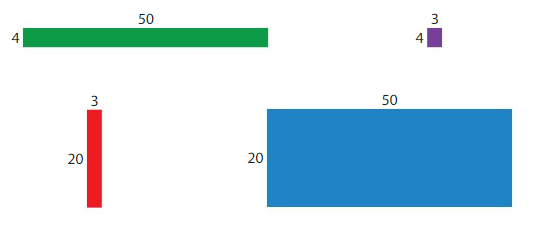
24 × 53 = _____
Answer: 1,272
Explanation: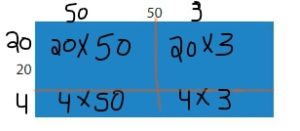 
By using the partial products method,
24 × 53 = 50 × 20 +3 × 20 + 4 × 3 + 50 ×4
= 1,000 + 60 +12 + 200 = 1,272
So, 53 × 24 = 1,272
Reasoning
What does the area of each rectangle represent.
Answer:
Think and Grow: Use Partial Products to Multiply Two-DigitNumbers
Example
Use place value and partial products to find 27 × 48.
Estimate: 30 × 50 = 1,500
So, 27 × 48 =1296
Check: Because 1,296 is close to the estimate, 1,500, the answer is reasonable.
Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
Estimate: ______
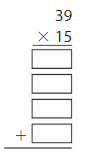
Answer: 585
Explanation:
Using the Partial Products method,
39 × 15 = ( 30 + 9) × ( 10 + 5)
= 30 × 10 + 9 × 10 + 30 × 5 + 9 × 5
= 300 + 90 + 150 + 45
= 585
Estimate:
Let 39 be Rounded to 40.
So, 40 × 15 = 600
As the Estimate and the actual answer are near, the answer is reasonable.
Question 2.
Estimate: ______
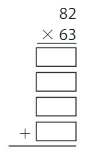
Answer: 5,166
Explanation:
Using the Partial Products method,
82 × 63 = ( 80 + 2) × ( 60 + 3)
= 80 × 60 + 2 × 60 + 80 × 3 + 2 × 3
= 4,800 + 120 + 240 + 6
= 5,166
Estimate:
Let 82 be Rounded to 80.
Let 63 be Rounded to 65.
So, 80 × 65 = 5,200
As the Estimate and the actual answer are near, the answer is reasonable.
Question 3.
Estimate: _______
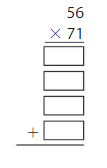
Answer: 3,976
Explanation:
Using the Partial Products method,
56 × 71 = ( 50 + 6) × ( 70 + 1)
= 50 × 70 + 1 × 50 + 70 × 6 + 6 × 1
= 3,500 + 50 + 420 + 6
= 3,976
Estimate:
Let 56 be Rounded to 55.
Let 71 be Rounded to 70.
So, 55 × 70 = 3,850
As the Estimate and the actual answer are not near, the answer is not reasonable.
Apply and Grow: Practice
Find the product. Check whether your answer is reasonable.
Question 4.
Estimate: _____
Answer: 364
Explanation:
Using the Partial Products method,
14 × 26 = ( 10 + 4) × ( 20 + 6)
= 10 × 20 + 10 × 6 + 20 × 4 + 4 × 6
= 200 + 60 + 80 + 24
= 364
Estimate:
Let 26 be Rounded to 25.
Let 14 be Rounded to 15.
So, 25 × 15 = 375
As the Estimate and the actual answer are near, the answer is reasonable.
Question 5.
Estimate: _____
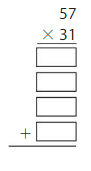
Answer: 1,767
Explanation:
Using the Partial Products method,
57 × 31 = ( 50 + 7) × ( 30 + 1)
= 50 × 30 + 1 × 50 + 30 × 7 + 7 ×1
= 1,500 + 50 + 210 + 7
= 1,767
Estimate:
Let 57 be Rounded to 55. (or) Let 57 be Rounded to 60.
Let 31 be Rounded to 30.
So, 30 × 55 = 1,650 (or) 30 × 60 = 1,800
As the Estimate and the actual answer are near, the answer is reasonable. ( Depending on the Estimate value).
Question 6.
Estimate: _______
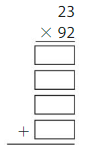
Answer: 2,116
Explanation:
Using the Partial Products method,
23 × 92 = ( 20 +3) × ( 90 + 2)
= 20 × 90 + 2 × 20 + 90 × 3 + 3 ×2
= 1,800 + 40 + 270 + 6
= 2,116
Estimate:
Let 23 be Rounded to 25.
Let 92 be Rounded to 90.
So, 90 × 25 = 2,250
As the Estimate and the actual answer are near, the answer is reasonable.
Question 7.
Estimate: ______
13 × 98 = ______
Answer: 1,274
Explanation:
Using the Partial Products method,
13 × 98 = ( 10 + 3) × ( 90 +8)
= 10 × 90 + 3 × 90 + 10 × 8 + 3 ×8
= 900 + 270 + 80 + 24
= 1,274
Estimate:
Let 13 be Rounded to 15.
Let 98 be Rounded to 100.
So, 15 × 100 = 1,500
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 8.
Estimate: ______
65 × 22 = ______
Answer: 1,430
Explanation:
Using the Partial Products method,
65 × 22 = ( 60 + 5) × ( 20 + 2)
= 60 × 20 + 60 × 2 + 20 × 5 + 5 ×2
= 1,200 + 120 + 100 + 10
= 1,430
Estimate:
Let 22 be Rounded to 20.
So, 20 × 65 = 1,300
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 9.
Estimate: ______
72 × 81 = _____
Answer: 5,832
Explanation:
Using the Partial Products method,
72 × 81 = ( 70 + 2) × (80 + 1)
= 70 × 80 + 1 × 70 + 80 × 2 + 2 ×1
= 5,600 + 70 + 160 + 2
= 5,832
Estimate:
Let 72 be Rounded to 70.
Let 81 be Rounded to 80.
So, 70 × 80 = 5,600
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 10.
A farmer has 58 cows. Each cow produces 29 liters of milk. How many liters of milk do the cows produce in all?
Answer: 1,682 liters
Explanation:
Given that a farmer has 58 cows and each cow gives 29 liters of milk.
So, to find the total quantity of milk, we have to find the Product of 58 × 29 by using the Partial Products method.
Now,
Using the Partial Products method,
58 × 29 = ( 50 + 8) × ( 20 + 9)
= 50 × 20 + 9 × 50 + 20 ×8 + 8 ×9
= 1,000 + 450 + 160 + 72
= 1,682
From the above value, we can conclude that the total quantity of milk produces is 1,682 liters.
Question 11.
Number Sense
How much greater is the product of 12 and 82 than the product of 11 and 82? Explain how you know without multiplying.
Answer: The product of 12 and 82 is greater than 82 than the product of 11 and 82.
Explanation:
The given Products are
A) product of 12 and 82 B) product of 11 and 82
From the above, we can see that both the products have “82” as a Common number. So, find the difference between the remaining 2 numbers and we find that difference as ‘1’.
From this, we can conclude that the product of 12 and 82 is greater than 82 than the product of 11 and 82.
To verify this, we can find the products using the Partial Products method.
Now,
12 × 82 = ( 10 + 2) × ( 80 +2)
= 10 × 80 + 10 × 2 + 80 × 2 + 2 ×2
= 800 + 20 + 160 + 4
= 984
11 × 82 = ( 10 + 1) × ( 80 + 2)
= 10 × 80 + 10 × 2 + 80 ×1 + 2 × 1
= 800 + 20 + 80 + 2
= 902
Now, 984 – 902 = 82
By multiplication also, we can conclude that the product of 12 and 82 is greater than 82 than the product of 11 and 82.
Question 12.
DIG DEEPER!
Write the multiplication equation shown by the partial products.
200 + 60 + 50 + 15
Answer: 13 × 25
Explanation:
By using the Partial Products method,
200 + 60 + 50 + 15
= 20 × 10 + 20 × 3 + 5 ×10 + 5 × 3
= ( 10 + 3) × 20 +( 10 + 3) × 5
= ( 10 + 3) × ( 20 + 5)
= 13 × 25
Think and Grow: Modeling Real Life
Example
How many hours does a koala sleep in 2 weeks?
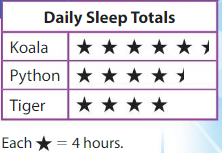
Find how many hours a koala sleeps each day.
We know that,
1 week = 7 days
So,
2 weeks = 2 × 7 days = 14 days
Hence,
A koala sleeps 308 hours in 2 weeks.
Show and Grow
Question 13.
Use the table above. How many hours does a python sleep in 3 weeks?
Answer: 378 hours
Explanation:
From the above table, we can conclude that the python sleeps for 18 hours a day.
We know that,
1 week = 7 days
So,
3 weeks = 3 × 7 = 21 days
Hence, to find how many hours a python sleep in 3 weeks, we have to find the product of 18 × 21.
Using the Partial Products method,
18 × 21 = ( 10 + 8) × ( 20 +1)
= 10 × 20 + 10 × 1 + 20 × 8 + 8 ×1
= 200 + 10 + 160 + 8
= 378
Hence, from the above,
we can conclude that the python sleeps for 378 hours in 3 weeks.
Question 14.
You have 12 packets of pea seeds and23 packets of cucumber seeds. How many fewer pea seeds do you have than cucumber seeds?
Answer: 102 pea seeds are less than cucumber seeds
Explanation:
Given that there are 12 packets of pea seeds and 23 packets of cucumber seeds.
From the table,
The number of seeds in each packet of pea seeds = 12 × 6 = 72
The number of seeds in each packet of cucumber = 12 × 3 = 36 + 6 = 42
So,
The total number of seeds in pea = 72 × 12
The total number of seeds in cucumber = 42 × 23
By using the Partial Products method,
72 × 12 = ( 10 + 2) × ( 70 +2)
= 10 × 70 + 10 × 2 + 2 × 70 + 2 ×2
= 700 + 20 + 140 + 4
= 864
42 × 23 = ( 40 + 2) × ( 20 +3)
= 40 × 20 + 40 × 3 + 20 × 2 + 2 ×3
= 800 + 120 + 40 + 6
= 966
So,
The number of pea seeds less than the cucumber seeds = 966 – 864 = 102 seeds
Use Partial Products to Multiply Two-Digit Numbers Homework & Practice 4.5
Find the product. Check whether your answer is reasonable.
Question 1.
Estimate: _______
Answer: 442
Explanation:
Using the Partial Products method,
17 × 26 = ( 10 + 7) × ( 20 + 6)
= 10 × 20 + 10 × 6 + 20 × 7 + 7 × 6
= 200 + 140 + 60 + 24
= 424
Estimate:
Let 17 be Rounded to 15.
Let 26 be Rounded to 25.
So, 25 × 15 = 375
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 2.
Estimate: _____
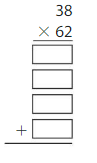
Answer: 2,356
Explanation:
Using the Partial Products method,
38 × 62 = ( 30 + 8) × ( 60 + 2)
= 30 × 60 + 30 × 2 + 60 × 8 + 8 × 2
= 1,800 + 60 + 480 + 16
= 2,356
Estimate:
Let 38 be Rounded to 40.
Let 62 be Rounded to 60.
So, 40 × 60 = 2,400
As the Estimate and the actual answer are near, the answer is reasonable.
Question 3.
Estimate: ______
Answer: 3,913
Explanation:
Using the Partial Products method,
91 × 43 = ( 90 + 1) × ( 40 + 3)
= 90 × 40 + 90 × 3 + 40 × 1 + 3 × 1
= 3,600 + 270 + 40 + 3
= 3,913
Estimate:
Let 91 be Rounded to 90.
Let 43 be Rounded to 45.
So, 90 × 45 = 4,050
As the Estimate and the actual answer are not near, the answer is not reasonable.
Find the product. Check whether your answer is reasonable.
Question 4.
Estimate: _____
Answer: 3,774
Explanation:
Using the Partial Products method,
51 × 74 = ( 50 + 1) × ( 70 + 4)
= 50 × 70 + 50 × 4 + 70 × 1 + 4 × 1
= 3,500 + 200 + 70 + 4
= 3,774
Estimate:
Let 51 be Rounded to 50.
Let 74 be Rounded to 75.
So, 50 × 75 = 3,750
As the Estimate and the actual answer are near, the answer is reasonable.
Question 5.
Estimate: ______
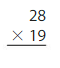
Answer: 532
Explanation:
Using the Partial Products method,
28 × 19 = ( 20 + 8) × ( 10 + 9)
= 10 × 20 + 20 × 9 + 10 × 8 + 9 × 8
= 200 + 180 + 80 + 72
= 532
Estimate:
Let 28 be Rounded to 30.
Let 19 be Rounded to 20.
So, 30 × 15 = 600
As the Estimate and the actual answer are near, the answer is reasonable.
Question 6.
Estimate: ______
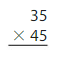
Answer: 1,575
Explanation:
Using the Partial Products method,
35 × 45 = ( 30 + 5) × ( 40 + 5)
= 30 × 40 + 30 × 5 + 40 × 5 + 5 × 5
= 1,200 + 150 + 200 + 25
= 1,575
There is no need for Estimate because they are already rounded numbers. So, the answer is reasonable.
Question 7.
Estimate: ______
82 × 63 = ______
Answer: 5,166
Explanation:
Using the Partial Products method,
82 × 63 = ( 80 + 2) × ( 60 + 3)
= 80 × 60 + 80 × 3 + 60 × 2 + 2 × 3
= 4,800 + 240 + 120 + 6
= 5,166
Estimate:
Let 82 be Rounded to 80.
Let 63 be Rounded to 65.
So, 80 × 65 = 5,200
As the Estimate and the actual answer are near, the answer is reasonable.
Question 8.
Estimate: ______
36 × 93 = ______
Answer: 3,348
Explanation:
Using the Partial Products method,
36 × 93 = ( 30 + 6) × ( 90 + 3)
= 30 × 90 + 30 × 3 + 90 × 6 + 3 × 6
= 2,700 + 90 + 540 + 18
= 3,348
Estimate:
Let 36 be Rounded to 35.
Let 93 be Rounded to 95.
So, 35 × 95 = 3,325
As the Estimate and the actual answer are near, the answer is reasonable.
Question 9.
Estimate: _______
57 × 22 = ______
Answer: 1,254
Explanation:
Using the Partial Products method,
57 × 22 = ( 50 + 7) × ( 20 + 2)
= 50 × 20 + 50 × 2 + 20 × 7 + 7 × 2
= 1,000 + 100 + 140 + 14
= 1,254
Estimate:
Let 57 be Rounded to 55.
Let 22 be Rounded to 20.
So, 55 × 20 = 1,100
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 10.
DIG DEEPER!
Find the missing digits. Then find the product.
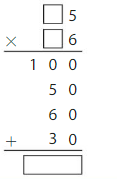
Answer: The missing digits are 1, 1
Explanation:
Using the Partial Products method,
100 + 50 + 60 + 30
= 10 × 10 + 10 × 5 + 10 × 6 + 5 × 6
= 10( 10 + 5) + 6( 10 + 5)
= ( 10 + 5) × ( 10 + 6)
= 15 × 16
So,
From the above, we can conclude that the missing digits are: 1, 1
Question 11.
Modeling Real Life
If Newton meets his goal each month, how many liters of water will he drink in 1 year?
Answer: 396 liters of water
Explanation;
Given,
Each ♦ = 6 liters
From this,
Half ♦ = 3 liters
From the above table,
Monthly water Intake by Newton = 6 × 5 + 3 = 33 liters
So, The yearly intake by Newton can find out by the product of 33 × 12. ( Since a year has 12 months)
Using the Partial Products method,
33 × 12 = ( 30 + 3) × ( 10 + 2)
= 30 × 10 + 30 × 2 + 10 × 3 + 3 × 2
= 300 + 60 + 30 + 6
= 396 liters
From the above,
we can conclude that the yearly intake by Newton is: 396 liters
Question 12.
Modeling Real Life
Use the table in Exercise 11. If you and Descartes each meet your goal each month, how many more liters will you drink in 1 year than Descartes?
Answer: 468 liters
Explanation;
From the above table,
Given that,
The monthly intake of water by you = 6 × 7 + 3 = 45 liters
The monthly intake of water by Descartes = 6 liters
We know that 1 year consists of 12 months.
So,
The yearly intake of water by Descartes = 12 × 6 = 72 liters
The yearly intake of water by you = 45 × 12
We have to find 45 × 12 using the Partial Products method.
45 × 12 = ( 40 + 5) × ( 10 +2)
= 10 × 40 + 40 × 2 + 5 × 10 + 5 ×2
= 400 + 80 + 50 + 10
= 540 liters
Hence,
The amount of water you drink more than Descartes = 540 – 72 = 468 liters
Review & Refresh
Add or subtract. Then check your answer.
Question 13.
512,006 + 318,071 = ______
Answer: 830,077
Explanation:
To find the sum, add the digits starting from the Right-most position. If there is “Carry”, then add that carry to the result of the next Position value.
Question 14.
746,620 – 529,706 = ______
Answer: 216,914
Explanation:
The difference between the multi-digit numbers can be found by the difference taken from the left-most digit. If the number we want to subtract is less than the number to be subtracted, then we will take the carry from the Previous digit and the Previous digit contains 1 less number.
Lesson 4.6 Multiply Two-Digit Numbers
Explore and Grow
Use base ten blocks to model each product. Draw each model.
Answer: 
Reasoning
How are the models related to the product 17 × 13?
Answer:
The above model shows the pattern of the Partial Products method.
According to the Partial Products method,
(10 +7) × (10 + 3 ) ( As in the above model)
= 17 × 13
Think and Grow: Multiply Two-Digit Numbers
Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
Estimate: ______
Answer: 1,312
Explanation: Using the Partial Products method,
41 × 32 = ( 40 + 1) × ( 30 +2)
= 30 × 40 + 40 × 2 + 1 × 30 + 1 ×2
= 1,200 + 80 + 30 + 2
= 1,312
Estimate:
Let 41 be Rounded to 40.
Let 32 be Rounded to 30.
So, 40 × 30 = 1,200
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 2.
Estimate: _____
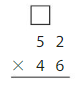
Answer: 2,392
Explanation: Using the Partial Products method,
52 × 46 = ( 50 + 2) × ( 40 +6)
= 50 × 40 + 50 × 6 +2 × 40 + 6 ×2
= 2,000 + 300 + 80 + 12
= 2,392
Estimate:
Let 52 be Rounded to 50.
Let 46 be Rounded to 45.
So, 45 × 50 = 2,250
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 3.
Estimate: ______
Answer: 2,730
Explanation: Using the Partial Products method,
78 × 35 = ( 70 + 8) × ( 30 +5)
= 30 × 70 + 70 × 5 + 8 × 30 + 8 ×5
= 2,100 + 350 + 240 + 40
= 2,730
Estimate:
Let 78 be Rounded to 80.
So, 35 × 80 = 2,800
As the Estimate and the actual answer are near, the answer is reasonable.
Apply and Grow: Practice
Find the product. Check whether your answer is reasonable.
Question 4.
Estimate: _____
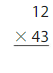
Answer: 516
Explanation: Using the Partial Products method,
12 × 43 = ( 10 + 2) × ( 40 +3)
= 10 × 40 + 10 × 3 + 2 × 40 + 3 ×2
= 400 + 30 + 80 + 6
= 516
Estimate:
Let 12 be Rounded to 10.
Let 43 be Rounded to 45.
So, 45 × 10 = 450
As the Estimate and the actual answer are near, the answer is reasonable.
Question 5.
Estimate: ______
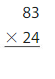
Answer: 1,992
Explanation: Using the Partial Products method,
83 × 24 = ( 80 + 3) × ( 20 +4)
= 80 × 20 + 80 × 4 + 3 × 20 + 3 ×4
= 1,600 + 320 + 60 + 12
= 1,992
Estimate:
Let 83 be Rounded to 85.
Let 24 be Rounded to 25.
So, 85 × 25 = 2,152
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 6.
Estimate: _____
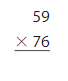
Answer: 4,484
Explanation: Using the Partial Products method,
59 × 76 = ( 50 + 9) × ( 70 +6)
= 50 × 70 + 50 × 6 + 9 × 70 + 9 ×6
= 3,500 + 300 + 630 + 54
= 4,484
EStimate:
Let 59 be Rounded to 60.
Let 76 be Rounded to 75.
So, 60 × 75 = 4,500
As the Estimate and the actual answer are near, the answer is reasonable.
Question 7.
Estimate: ______
22 × 41 = ______
Answer: 902
Explanation: Using the Partial Products method,
41 × 22 = ( 40 + 1) × ( 20 +2)
= 20 × 40 + 40 × 2 + 1 × 20 + 1 ×2
= 800 + 80 + 20 + 2
= 902
Estimate:
Let 41 be Rounded to 40.
Let 22 be Rounded to 20.
So, 40 × 20 = 800
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 8.
Estimate: _____
94 × 32 = ______
Answer: 3,008
Explanation: Using the Partial Products method,
94 × 32 = ( 90 + 4) × ( 30 +2)
= 30 × 90 + 90 × 2 + 4 × 30 + 4 ×2
= 2,700 + 180 + 120 + 8
= 3,008
Estimate:
Let 94 be Rounded to 95.
Let 32 be Rounded to 30.
So, 95 × 30 = 2,850
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 9.
Estimate: _____
63 × 54 = _____
Answer: 3,402
Explanation: Using the Partial Products method,
63 × 54 = ( 60 + 3) × ( 50 +4)
= 60 × 50 + 60 × 4 + 3 × 50 + 3 ×4
= 3,000 + 240 + 150 + 12
= 3,402
Estimate:
Let 63 be Rounded to 65.
Let 54 be Rounded to 55.
So, 55 × 65 = 3,575
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 10.
Newton eats 14 treats each week. Each treat has 33 calories. How many treat calories does Newton eat each week?
Answer: 462 treat calories
Explanation:
Given that Newton eats 14 treats each week and each treat has 33 calories.
So, to find the total number of treat calories, we have to find the product of 14 × 33 by using the Partial Products method.
14 × 33 = ( 10 + 4) × ( 30 +3)
= 10 × 30 + 10 × 3 + 30 × 4 + 3 ×4
= 300 + 30 + 120 + 12
= 462
From the above,
we can conclude that Newton eats 462 treat calories each week.
Question 11.
YOU BE THE TEACHER
Your friend finds 43 × 26. Is he correct? Explain.
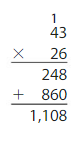
Answer: Your friend is not correct.
Explanation:
First, we will find 43 × 26 by using the Partial Products method.
43 × 26 = ( 40 + 3) × ( 20 +6)
= 40 × 20 + 40 × 6 + 20 × 3 + 3 ×6
= 800 + 240 + 60 + 18
= 860 + 258
= 1,118
Fro the above, we can conclude that 258 must be placed instead of 248
Question 12.
Open-Ended
Use 4 cards to write 2 two-digit numbers that have a product that is close to, but not greater than, 1,200.
_______ × ______
Answer:
Think and Grow: Modeling Real Life
Example
There are 16 hours in 1 day on Neptune. There are 88 times as many hours in 1 day on Mercury as 1 day on Neptune. There are 5,832 hours in 1 day on Venus. Are there more hours in 1 day on Mercury or 1 day on Venus?
Multiply to find how many hours Compare if there are in 1 day on Mercury.
Using the Multiplication method,
So, there are 1,408 hours on Mercury in 1 day
It is also given that there are 5,832 hours on venus in 1 day.
So, to compare how many hours are more on Mercury when compared to venus = 5,832 – 1,408 = 4,424 hours.
So, there are more hours in 1 day on Venus.
Show and Grow
Question 13.
A ninja lantern-shark is 18 inches longer than a whale. A whale-shark is 16 times as long as the ninja lantern-shark. A hammerhead shark is 228 inches long. Is the whale shark ? or the hammerhead shark longer?
Answer: The whale-shark is longer when compared to the hammerhead shark.
Explanation:
Given that a ninja lantern-shark is 18 inches long and a whale shark is 16 times longer than the ninja lantern-shark
So, to find the total length of a whale shark, we have to find the product of 18 × 16 using the Partial Products method.
18 × 16 = ( 10 + 8) × ( 10 +6)
= 10 × 10 + 10 × 6 + 10 × 8 + 8 ×6
= 100 + 60 + 80 + 48
= 288 inches
It is also given that the hammerhead shark is 228 inches long.
From the above, we can conclude that the whale shark is longer than the hammerhead shark.
Question 14.
There are 24 science classrooms in a school district. Each classroom receives 3 hot plates. Each hot plate costs $56. How much do all of the hot plates cost?
Answer: $4,032
Explanation:
Given that there are 24 science classrooms in a school district and each classroom receives 3 hot plates.
So, the total number of hot plates received in a school district = 24 × 3 = 72 hot plates
It is also given that each hot plate costs $56.
So, to find the total cost of the hot plates we have to find the product of 56 × 72 using the Partial Products method.
56 × 72 = (50 + 6) × ( 70 +2)
= 50 × 70 + 50 × 2 + 70 × 6 + 2 ×6
= 3,500 + 100 + 420 + 12
= $4,032
From the above, we can conclude that the cost of all the hotplates in a school district is: $4,032
Question 15.
Fourteen adults and 68 students visit the art museum. What is the total cost of admission?
Answer: $1,656
Explanation:
From the above table,
we can see that
the admission price of an adult is: $26
the admission price of a student is: $19
It is also given that there are 14 adults and 68 students.
So,
the total admission cost of the adults is: 14 × 26
the total admission cost of the children is: 68 × 19
Using the Partial Products method,
14 × 26 = (20 + 6) × ( 10 +4)
= 20 × 10 + 20 × 4 + 10 × 6 + 4 ×6
= 200 + 80 + 60 + 24
= $364
Using the Partial Products method,
68 × 19 = (60 + 8) × ( 10 +9)
= 60 × 10 + 60 × 9 + 10 × 8 + 8 ×9
= 600 + 540 + 80 + 72
= $1,292
Hence,
The total cost of admission (Both adults and children) = 364 + 1,292 = $1,656
Multiply Two-Digit Numbers Homework & Practice 4.6
Find the product. Check whether your answer is reasonable.
Question 1.
Estimate: ______
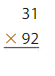
Answer: 1,196
Explanation: Using the Partial Products method,
31 × 92 = ( 30 + 1) × ( 90 +2)
= 30 × 90 + 30 × 2 + 1 × 90 + 1 ×2
= 2,700 + 60 + 90 + 2
= 2,852
Estimate:
Let 31 be Rounded to 30.
Let 92 be Rounded to 90.
So, 30 × 90 = 2,700
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 2.
Estimate: ______
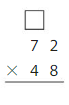
Answer: 3,456
Explanation: Using the Partial Products method,
48 × 72 = ( 40 + 8) × ( 70 +2)
= 70 × 40 + 40 × 2 + 8 × 70 + 8 ×2
= 2,800 + 80 + 560 + 16
= 3,456
Estimate:
Let 48 be Rounded to 50.
Let 72 be Rounded to 70.
So, 50 × 70 = 3,500
As the Estimate and the actual answer are near, the answer is reasonable.
Question 3.
Estimate: _____
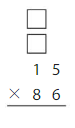
Answer: 1,290
Explanation: Using the Partial Products method,
15 × 86 = ( 10 + 5) × ( 80 +6)
= 10 × 80 + 10 × 6 + 5 × 80 + 5 × 6
= 800 + 60 + 400 + 30
= 1,290
Estimate:
Let 86 be Rounded to 85.
So, 85 × 15 = 1,275
As the Estimate and the actual answer are near, the answer is reasonable.
Question 4.
Estimate: ______
Answer: 4,374
Explanation: Using the Partial Products method,
81 × 54 = ( 80 + 1) × ( 50 +4)
= 80 × 50 + 80 × 4 + 1 × 50 + 1 × 4
= 4,000 + 320 + 50 + 4
= 4,374
Estimate:
Let 81 be Rounded to 80.
Let 54 be Rounded to 55.
So, 55 × 80 = 4,400
As the Estimate and the actual answer are near, the answer is reasonable.
Question 5.
Estimate: ______
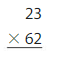
Answer: 1,426
Explanation: Using the Partial Products method,
23 × 62 = ( 20 + 3) × ( 60 +2)
= 20 × 60 + 20 × 2 + 3 × 60 + 3 ×2
= 1,200 + 40 + 180 + 6
= 1,426
Estimate:
Let 23 be Rounded to 25.
Let 62 be Rounded to 60.
So, 25 × 60 = 1,500
As the Estimate and the actual answer are near, the answer is reasonable.
Question 6.
Estimate: _____
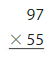
Answer: 5,335
Explanation: Using the Partial Products method,
97 × 55 = ( 90 + 7) × ( 50 +5)
= 90 × 50 + 90 × 5 + 7 × 50 + 7 × 5
= 4,500 + 450 + 350 + 35
= 5,335
Estimate:
Let 97 be Rounded to 95.
So, 55 × 95 = 5,225
As the Estimate and the actual answer are near, the answer is reasonable.
Find the product. Check whether your answer is reasonable.
Question 7.
Estimate: ______
51 × 62 = ______
Answer: 3,162
Explanation: Using the Partial Products method,
51 × 62 = ( 50 +1) × ( 60 +2)
= 60 × 50 + 50 × 2 + 1 × 60 + 1 × 2
= 3,000 + 100 + 60 + 2
= 3,162
Estimate:
Let 51 be Rounded to 50.
Let 62 be Rounded to 60.
So, 50 × 60 = 3,000
As the Estimate and the actual answer are near, the answer is reasonable.
Question 8.
Estimate: ______
37 × 13 = ______
Answer: 481
Explanation: Using the Partial Products method,
37 × 13 = ( 10 +3) × ( 30 +7)
= 10 × 30 + 10 × 7 + 3 × 30 + 3 × 7
= 300 + 70 + 90 + 21
= 481
Estimate:
Let 37 be Rounded to 40.
Let 13 be Rounded to 15.
So, 40 × 15= 600
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 9.
Estimate: _______
49 × 78 = ______
Answer: 3,822
Explanation: Using the Partial Products method,
49 × 78 = ( 40 +9) × ( 70 +8)
= 40 × 70 + 40 × 8 + 9 × 70 + 9 × 8
= 2,800 + 320 + 630 + 72
= 3,822
Estimate:
Let 49 be Rounded to 50.
Let 78 be Rounded to 80.
So, 50 × 80 = 4,000
As the Estimate and the actual answer are near, the answer is reasonable.
Question 10.
Newton plays 21 basketball games. He scores 12 points each game. How many points does he score in all?
Answer: He scored 252 points.
Explanation:
Given that Newton plays 21 basketball games and he scores 12 points each game.
So, to find the total number of points in all games, we have to find the product of 21 × 12
By using the Partial Products method,
21 × 12 = ( 20 +1) × ( 10 + 2)
= 20 × 10 + 20 × 2 + 1 × 10 + 1 × 2
= 200 + 40 + 10 + 2
= 252 points
Hence,
From the above, we can conclude that Newton had scored 252 points in 21 basketball games.
Question 11.
DIG DEEPER!
When you use regrouping to multiply two-digit numbers, why does the second partial product always end in 0?
Answer: Because we divide the partial Products in terms of 10 only.
Ex:
13 × 15 = ( 10 + 3) × (10 + 5)
Question 12.
Number Sense
Find the missing digits.
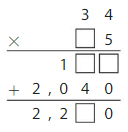
Answer: The missing numbers are: 6, 7, 0 and 1
Explanation:
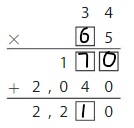
By using the Partial Products method,
34 × 65 = ( 30 +4) × ( 60 + 5)
= 30 × 60 + 30 × 5 + 4 × 60 + 4 × 5
= 1,800 + 150 + 240 + 20
= 2,040 + 170
= 2,210
So,
From the above, we can conclude that the missing numbers are: 6, 7, 0 and 1
Question 13.
Modeling Real Life
A tiger dives 12 feet underwater. An otter dives 25 times deeper than the tiger. A walrus dives 262 feet underwater. Does the otter or walrus dive deeper?
Answer: Otter drives deeper than the Walrus.
Explanation:
Given that a tiger dives 12 feet underwater and an otter dives 25 times deeper than the tiger.
So,
The total distance dived by otter = 25 × 12 feet
By using the Partial Products method,
25 × 12 = ( 20 +5) × ( 10 + 2)
= 20 × 10 + 20 × 2 + 5 × 10 + 2 × 5
= 200 + 40 + 50 + 10
= 300
It is also given that a walrus dives 262 feet underwater.
From the above,
we can conclude that the otter dives deeper than the walrus.
Review & Refresh
Question 14.
Complete the table.
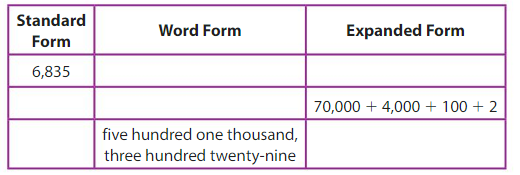
Answer:
A) 6,835
Word Form: Six thousand, eight hundred thirty-five
Expanded Form: 6,000 + 800 + 30 + 5
Explanation:
Any number can be written in 3 forms. They are:
A) Standard Form B) Word Form C) Expanded Form
So, we can write the given form in the remaining 2 forms.
B) 70,000 + 4,000 + 100 + 2
Standard Form: 74,102
Word Form: Seventy-four thousand, One hundred two
Explanation:
Any number can be written in 3 forms. They are:
A) Standard Form B) Word Form C) Expanded Form
So, we can write the given form in the remaining 2 forms.
C) Five hundred one thousand, three hundred twenty-nine
Standard Form: 501,329
Expanded Form: 500,000 +0 + 1,000 + 100 + 0 + 2
Explanation:
Any number can be written in 3 forms. They are:
A) Standard Form B) Word Form C) Expanded Form
So, we can write the given form in the remaining 2 forms.
Lesson 4.7 Practice Multiplication Strategies
Explore and Grow
Choose any strategy to find 60 × 80.
Answer: The strategy to find 60 × 80 is: Associative Property of Multiplication
Explanation: By using the Associative Property of Multiplication,
60 ×80 =60 × (8 × 10)
= (60 × 8) × 10
= (6 × 10 × 8) × 10
= 480 × 10
= 4,800
Choose any strategy to find 72 × 13.
Answer: The strategy to find 72 × 13 is: Distributive Property
Explanation:
72 × 13 = 72 × ( 10 + 3)
= ( 72 × 10 ) + ( 72 ×3)
= ( 70 + 2 ) × 10 + ( 70 + 2 ) × 3
= ( 70 × 10 ) + ( 2 × 10 ) + ( 70 × 3 ) + ( 2 × 3)
= 700 + 20 + 210 + 6
= 936
So, 72 × 13 = 936
Reasoning
Explain why you chose your strategies. Compare your strategies to your partner’s strategies. How are they the same or different?
Answer:
Think and Grow: Practice Multiplication Strategies
Example
Find 62 × 40.
One Way: Use place value.
62 × 40 = 62 × 4 tens
=248 tens
= 248 × 10
= 2,480
So, 62 × 40 = 2,480.
Another Way: Use an area model and partial products.
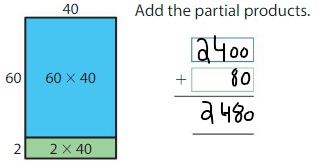
So, 62 × 40 =2,480 .
Example
Find 56 × 83.
One Way: Use place value and partial products.
So, 56 × 83 = 4,648.
Another Way: Use regrouping
Multiply 56 by 3 ones. Then multiply 56 by 8 tens. Regroup if necessary.
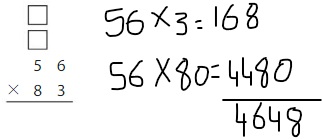
So, 56 × 83 = 4,648.
Show and Grow
Find the product.
Question 1.
90 × 37 = _____
Answer: 3,330
Explanation: Using the Associative Property of Multiplication,
37 × 90 = 37 × (9 × 10)
= (37 × 9) × 10
= (3 × 3 × 37) × 10
= 333 × 10
= 3,330
Question 2.
78 × 21 = ______
Answer: 1,638
Explanation: Using the Distributive Property,
78 × 21 = 78 × ( 20 + 1)
= ( 78 × 20 ) + ( 78 × 1)
= ( 70 + 8 ) × 20 + ( 70 + 8 ) × 1
= ( 70 × 20 ) + ( 8 × 20 ) + ( 70 × 1 ) + ( 8 × 1)
= 1,400 + 160 + 70 + 8
= 1,638
So, 78 × 21 = 1,638
Question 3.
14 × 49 = _____
Answer: 686
Explanation: Using the Associative Property of Multiplication,
14 × 49 = 14 × ( 40 + 9)
= ( 14 × 40 ) + ( 14 × 9)
= ( 10 + 4 ) × 40 + ( 10 + 4 ) × 9
= ( 40 × 10 ) + ( 4 × 40 ) + ( 10 × 9 ) + ( 4 × 9)
= 400 + 160 + 90 + 36
= 686
So, 14 × 49 = 686
Apply and Grow: Practice
Find the product.
Question 4.
74 × 30 = _____
Answer: 2,220
Explanation: Using the Associative Property of Multiplication,
74 × 30 = 74 ( 3 × 10)
= ( 74 × 3) × 10
= 222 × 10
= 2,220
So, 74 × 30 = 2,220
Question 5.
51 × 86 = _____
Answer: 4,386
Explanation: Using the Distributive Property ,
51 × 86 = 51 × ( 80 + 6)
= ( 51 × 80 ) + ( 51 × 6)
= ( 50 + 1 ) × 80 + ( 50 + 1 ) × 6
= ( 50 × 80 ) + ( 1 × 80 ) + ( 50 × 6 ) + ( 1 × 6)
= 4,000 + 80 + 300 + 6
= 4,386
So, 51 × 86 = 4,386
Question 6.
40 × 29 = ______
Answer: 1,160
Explanation: Using the Associative Property of Multiplication,
40 × 29 = 29 × (4 × 10)
= (29 × 4) × 10
= (29× 2 × 2) × 10
= 116 × 10
= 1,160
Question 7.
92 × 80 = _____
Answer: 7,360
Explanation: Using the Associative Property of Multiplication,
92 × 80 = 92 × (8 × 10)
= (92 × 8) × 10
= (92 × 2 × 4) × 10
= 736 × 10
= 7,360
Question 8.
41 × 17 = ______
Answer: 697
Explanation: Using the Distributive Property,
41 × 17 = 41 × ( 10 + 7)
= ( 41 × 10 ) + ( 41 × 7)
= ( 40 + 1 ) × 10 + ( 40 + 1 ) × 7
= ( 40 × 10 ) + ( 1 × 10 ) + ( 40 × 7 ) + ( 1 × 7)
= 400 + 10 + 280 + 7
= 697
So, 41 × 17 = 697
Question 9.
60 × 53 = _____
Answer: 3,180
Explanation: By using the Associative Property of Multiplication,
60 × 53 = 53 × (6 × 10)
= (53 × 6) × 10
= (53× 3 × 2) × 10
= 318 × 10
= 3,180
Logic
Find the missing factor.
Question 10.
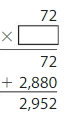
Answer: The missing number is: 41
Explanation:
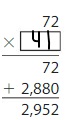
In the given figure, the partial fractions are given.
The 1st partial fraction represents the multiplication with the unit digit and the 2nd partial fraction represents the multiplication with the tens digit.
The first partial fraction will come when 72 is multiplied with 1 and the 2nd partial fraction will come when 72 is multiplied with 4.
So, the missing number is: 41
Question 11.
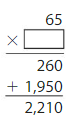
Answer: The missing number is: 34
Explanation:
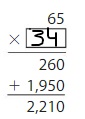
In the given figure, the partial fractions are given.
The 1st partial fraction represents the multiplication with the unit digit and the 2nd partial fraction represents the multiplication with the tens digit.
The first partial fraction will come when 65 is multiplied with 4 and the 2nd partial fraction will come when 65 is multiplied with 3.
So, the missing number is: 34
Question 12.
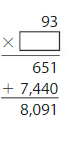
Answer: The missing number is: 87
Explanation:
In the given figure, the partial fractions are given.
The 1st partial fraction represents the multiplication with the unit digit and the 2nd partial fraction represents the multiplication with the tens digit.
The first partial fraction will come when 93 is multiplied with 7 and the 2nd partial fraction will come when 93 is multiplied with 8.
So, the missing number is: 87
Question 13.
Writing
Explain why you start multiplying with the one’s place when using regrouping to multiply.
Answer: When using ” Regrouping” to multiply, we start multiplying from the rightmost position i.e.., one’s position because the place value of that position is 1.
Question 14.
DIG DEEPER!
Find the missing digit so that both products are the same.
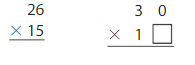
Answer: The missing digit so that both products are the same is: 3
Explanation:
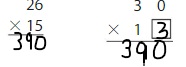
The product of 26 × 15 is:
26 × 15 = 26 × ( 10 + 5)
= ( 26 × 10 ) + ( 26 × 5)
= ( 20 + 6 ) × 10 + ( 20 + 6 ) × 5
= ( 20 × 10 ) + ( 6 × 10 ) + ( 20 × 5 ) + ( 6 × 5)
= 200 + 60 + 100 + 30
= 390
So, 26 × 15 = 390
To get the same result in the next product, we have to find the missing number.
So, 390 / 30 = 13
Hence, the missing digit so that both products are the same is: 3
Think and Grow: Modeling Real Life
Example
A swinging ship ride runs 50 times each afternoon. The ship has 10 rows of benches with 4 seats in each bench. If the ship is full each time it runs, how many people will ride the swinging ship in 1 afternoon?
Multiply to find how many people will ride the swinging ship ride each time.
10 × 4 = 40
So,
40 people will ride the swinging ship ride each time.
Multiply to find how many people will ride the swinging ship in 1 afternoon.
40 × 50 = 40 × (5 × 10) (Rewrite 50 as 5 × 10)
= (40 × 5) × 10 ( By using Associative Property of Multiplication)
= 200 × 10
= 2,000
Hence,
2,000 people will ride the swinging ship in 1 afternoon.
Show and Grow
Question 15.
A teacher orders 25 rock classification kits. Each kit has 4 rows with 9 rocks in each row. How many rocks are there in all?
Answer: 900 rocks
Explanation:
Given that a teacher orders 25 rock classification kits and each kit has 4 rows with 9 rocks in each row.
So,
The total number of rows present in 25 rock classification kits = 25 × 4 = 100 rows
We have to find the number of rocks in 100 rows by multiplying 100 × 9.
Now, 100 × 9 = 900 rocks.
From the above,
We can conclude that there are 900 total rocks.
Question 16.
A hotel has 12 floors with 34 rooms on each floor. 239 rooms are in use. How many rooms are not in use?
Answer: The total number of rooms that are not in use: 169
Explanation:
Given that a hotel has 12 floors with 34 rooms on each floor.
So, the total number of rooms in a hotel = 34 × 12
By using the Distributive method,
34 × 12 = 34 ( 10 + 2 )
= ( 34 × 10 ) + ( 34 × 2 )
= ( 30 + 4 ) × 10 + ( 30 + 4 ) × 2
= ( 30 × 10 ) + ( 4 × 10 ) + ( 30 × 2 ) + ( 4 × 2)
= 300 + 40 + 60 + 8
= 408
But, it is also given that 239 rooms are in use.
So, the number of rooms that are not in use = 408 – 239 = 169 rooms
Question 17.
A child ticket for a natural history museum costs $13. An adult ticket costs twice as much as a child ticket. How much does it cost for 21 children and 14 adults to go to the museum?
Answer: $637
Explanation:
Given that a child ticket for a natural history museum costs $13 and an adult ticket costs twice as much as a child ticket.
So, the cost of an adult ticket = 2 × $13 = $26
So, to find the total cost for 21 children and 14 adults in a museum, we have to find
21 × $13 and 14 × $26
Now,
21 × 13 = 21 ( 10 + 3 )
= ( 21 × 10 ) + ( 21 × 3 )
= ( 20 + 1 ) × 10 + ( 20 +1 ) × 3
= ( 20 × 10 ) + ( 1 × 10 ) + ( 20 × 3 ) + ( 1 × 3)
= 200 + 10 + 60 + 3
= 273
14 × 26 = 14 ( 20 + 6 )
= ( 14 × 20 ) + ( 14 × 6 )
= ( 10 + 4 ) × 20 + ( 10 +4 ) × 6
= ( 10 × 20 ) + ( 4 × 20 ) + ( 10 × 6 ) + ( 4 × 6)
= 200 + 80 + 60 + 24
= 364
Hence,
The total cost for children and adults in a museum = 273 + 364 = $637
Practice Multiplication Strategies Homework & Practice 4.7
Find the product.
Question 1.
16 × 13 = _____
Answer: 208
Explanation: By using the Distributive method,
16 × 13 = 16 ( 10 + 3 )
= ( 16 × 10 ) + ( 16 × 3 )
= ( 10 + 6 ) × 10 + ( 10 + 6 ) × 3
= ( 10 × 10 ) + ( 6 × 10 ) + ( 10 × 3 ) + ( 6 × 3)
= 100 + 30 + 60 + 18
= 208
Question 2.
29 × 50 = _____
Answer: 1,450
Explanation: By using the Associative Property of Multiplication,
29 × 50 = 29 × ( 5 × 10 )
= ( 29 × 5 ) × 10
= 145 × 10
= 1,450
Question 3.
78 × 45 = _____
Answer: 3,510
Explanation: By using the Distributive method,
78 × 45 = 78 ( 40 + 5 )
= ( 78 × 40 ) + ( 78 × 5 )
= ( 70 + 8 ) × 40 + ( 70 + 8 ) × 5
= ( 70 × 40 ) + ( 8 × 40 ) + ( 70 × 5 ) + ( 8 × 5)
= 2,800 + 320 + 350 + 40
= 3,510
Question 4.
30 × 71 = ______
Answer: 2,130
Explanation: By using the Associative Property of Multiplication,
30 × 71 = 71 × ( 3 × 10 )
= ( 71 × 3 ) × 10
= 213 × 10
= 2,130
Question 5.
62 × 14 = _____
Answer: 868
Explanation: By using the Distributive method,
62 × 14 = 62 ( 10 + 4 )
= ( 62 × 10 ) + ( 62 × 4 )
= ( 60 + 2 ) × 10 + ( 60 + 2 ) × 4
= ( 60 × 10 ) + ( 2 × 10 ) + ( 60 × 4 ) + ( 2 × 4)
= 600 + 20 + 240 + 8
= 868
Question 6.
80 × 90 = _____
Answer: 7,200
Explanation: By using the Associative Property of Multiplication,
80 × 90 = 80 × ( 9 × 10 )
= ( 80 × 9 ) × 10
= 720 × 10
= 7,200
Find the product.
Question 7.
70 × 18 = _____
Answer: 1,260
Explanation: By using the Associative Property of Multiplication,
70 × 18 = 18 × ( 7 × 10 )
= ( 18 × 7 ) × 10
= 126 × 10
= 1,260
Question 8.
32 × 59 = _____
Answer: 1,888
Explanation: By using the Distributive method,
32 × 59 = 59 ( 30 + 2 )
= ( 59 × 30 ) + ( 59 × 2 )
= (50 + 9 ) × 30 + ( 50 + 9 ) × 2
= ( 50 × 30 ) + ( 9 × 30 ) + ( 50 × 2 ) + ( 2 × 9)
= 1,500 + 270 + 100 + 18
= 1,888
Question 9.
67 × 20 = ____
Answer: 1,340
Explanation: By using the Associative Property of Multiplication,
67 × 20 = 67 × ( 2 × 10 )
= ( 67 × 2 ) × 10
= 134 × 10
= 1,340
Question 10.
51 × 84 = _____
Answer: 4,284
Explanation: By using the Distributive method,
51 × 84 = 51 ( 80 + 4 )
= ( 51 × 80 ) + ( 51 × 4 )
= (50 + 1 ) × 80 + ( 50 + 1 ) × 4
= ( 50 × 80 ) + ( 1 × 80 ) + ( 50 × 4 ) + ( 1 × 4)
= 4,000 + 80 + 200 + 4
= 4,284
Question 11.
40 × 40 = _____
Answer: 1,600
Explanation: By using the Associative Property of Multiplication,
40 × 40 = 40 × ( 4 × 10 )
= ( 40 × 4 ) × 10
= 160 × 10
= 1,600
Question 12.
23 × 97 = ______
Answer: 2,231
Explanation: By using the Distributive method,
23 × 97 = 97 ( 20 + 3 )
= ( 97 × 20 ) + ( 97 × 3 )
= (90 + 7 ) × 20 + ( 90 + 7 ) × 3
= ( 90 × 20 ) + ( 7 × 20 ) + ( 90 × 3 ) + ( 7 × 3)
= 1,800 + 140 + 270 + 21
= 2,231
Question 13.
Writing
Which strategy do you prefer to use when multiplying two-digit numbers? Explain.
Answer: The strategy you have to prepare when multiplying 2-digit numbers must depend on the numbers.
some strategies to multiply 2-digit numbers are:
A) The place-value method B) The Associative Property of Multiplication C) Distributive Property D) Partial Products method E) Regrouping method
Question 14.
Patterns
What number can you multiply the number of tires by to find the total weight? Use this pattern to complete the table.
Answer: The number you can multiply the number of tires by to find the total weight is: 20
Explanation:
From the above table,
to find the multiple of total weight, divide the number of tires by the total weight. ( Take any 2 values)
So, 80 /4 = 20 ( Multiple of total weight)
From the above,
We can conclude that the number you can multiply the number of tires by to find the total weight is: 20
Question 15.
Modeling Real Life
Each bag of popcorn makes 13 cups. A school has a movie day, and the principal brings 15 boxes of popcorn. Each box has 3 bags of popcorn. How many cups of popcorn does the principal bring?
Answer: 585 cups of popcorn
Explanation:
Given that each bag of popcorn makes 13 cups and the principal brings 15 boxes of popcorn. It is also given that each box has 3 bags of popcorn.
So, to find the total number of cups of popcorn the principal bring = 13 × 15 × 3
Now,
By using the Distributive method,
13 × 45 = 45 ( 10 + 3 )
= (45 × 10 ) + ( 45 × 3 )
= (40 +5 ) × 10 + ( 40 + 5 ) × 3
= ( 40 × 10 ) + ( 5 × 10 ) + ( 40 × 3 ) + ( 5 × 3)
= 400 + 50 + 120 + 15
= 585
From the above,
we can conclude that the number of cups the principal bring is: 585 cups of popcorn
Review & Refresh
Find the product.
Question 16.
8 × 200 = _____
Answer: 1,600
Explanation: By using the Associative Property of Multiplication,
8 × 200 = 8 × (20 × 10)
= (8 × 20) × 10
= (8× 5 × 4) × 10
= 160 × 10
= 1,600
Question 17.
7 × 300 = _____
Answer: 2,100
Explanation: By using the Associative Property of Multiplication,
7 × 300 = 7 × (30 × 10)
= (7 × 30) × 10
= (7× 5 × 6) × 10
= 210 × 10
= 2,100
Question 18.
6,000 × 5 = _____
Answer: 30,000
Explanation: By using the Associative Property of Multiplication,
5 × 6,000 = 5 × (600 × 10)
= (5 × 600) × 10
= (6× 5 × 100) × 10
= 300 × 10
= 3,000
Question 19.
9 × 90 = ____
Answer: 810
Explanation: By using the Associative Property of Multiplication,
9 × 90 = 9 × (9 × 10)
= (9 × 9) × 10
= 81 × 10
= 810
Question 20.
3,000 × 6 = _____
Answer: 18,000
Explanation: By using the Associative Property of Multiplication,
6 × 3,000 = 6 × (300 × 10)
= (6 × 300) × 10
= (6× 3 × 100) × 10
= 1800 × 10
= 18,000
Question 21.
5 × 500 = _____
Answer: 2,500
Explanation: By using the Associative Property of Multiplication,
5 × 500 = 5 × (50 × 10)
= (5 × 50) × 10
= (5× 5 × 10) × 10
= 250 × 10
= 2,500
Lesson 4.8 Problem Solving: Multiplication with Two-Digit Numbers
Explore & Grow
Explain, in your own words, what the problem below is asking. Then explain how you can use multiplication to solve the problem.
A ferry can transport 64 cars each time it leaves a port. The ferry leaves a port 22 times in 1 day. How many cars can the ferry transport in 1 day?
Answer: 1,408 cars can ferry transport in 1 day
Explanation:
Given that a ferry can transport 64 cars each time it leaves a port and the ferry leaves a port 22 times in 1 day.
From this, the total number of cars that can ferry transport in 1 day is: 64 × 22
By using the Distributive method,
64 × 22 = 64 ( 20 + 2 )
= (64 × 20 ) + ( 64 × 2 )
= (60 + 4 ) × 20 + ( 60 + 4 ) × 2
= ( 60 × 20 ) + ( 4 × 20 ) + ( 60 × 2 ) + ( 4 × 2)
= 1,200 + 80 + 120 + 8
= 1,408
From the above,
we can conclude that the total number of cars that ferry transport in 1 day is 1,408 cars.
Construct Arguments
Make a plan to find how many cars the ferry can transport in 1 week.
Answer: 9,856 cars
Explanation:
From the above problem, we know that the total number of cars a ferry can transport in 1 day is: 1,408 cars
We know that,
1 week = 7 days
First, we have to find the total number of cars the ferry can transport in 1 day using the Product 64 × 22.
By using the Distributive method,
64 × 22 = 64 ( 20 + 2 )
= (64 × 20 ) + ( 64 × 2 )
= (60 + 4 ) × 20 + ( 60 + 4 ) × 2
= ( 60 × 20 ) + ( 4 × 20 ) + ( 60 × 2 ) + ( 4 × 2)
= 1,200 + 80 + 120 + 8
= 1,408
Now,
the total number of cars a ferry can transport in 1 week = 1,408 × 7 = 9,856 cars
Think and Grow: Problem Solving: Multiplication with Two-Digit Numbers
Example
A pet store receives a shipment of 8 boxes of dog treats. Each box is 2 feet high and has 18 bags of dog treats. How many ounces of dog treats does the pet store receive in the shipment?
Understand the Problem
What do you know?
• The store receives 8 boxes.
• Each box is 2 feet high.
• Each box has 18 bags of dog treats.
• Each bag weighs 32 ounces.
What do you need to find?
• You need to find how many ounces of dog treats the pet store receives in the shipment.
Make a Plan
How will you solve it?
• Multiply 32 by 18 to find how many ounces of dog treats are in each box.
• Then multiply the product by 8 to find how many ounces of dog treats the pet store receives in the shipment.
• The height of each box is unnecessary information.
Solve
Answer: 4,608 ounces
Explanation:
Given that the store receives 8 boxes and Each box has 18 bags of dog treats. It is also given that each bag weighs 32 ounces.
The number of ounces of dog treats the pet store receives in the shipment = 18 × 8 × 32
It is also given that each box is 2 feet high. But it is not necessary for the calculation of a total number of ounces.
First, we will find the weight of 1 box = 18 × 32
By using the Distributive method,
18 × 32 = 18 ( 30 + 2 )
= (18 × 30 ) + ( 18 × 2 )
= (10 + 8 ) × 30 + ( 10 + 8 ) × 2
= ( 10 ×30 ) + ( 8 × 30 ) + ( 10 × 2 ) + ( 8 × 2)
= 300 + 240 + 20 + 16
= 576
So,
The total weight of dog treats the pet store receives in the shipment = 576 × 8 = 4,608 ounces
Hence,
The pet store receives 4,608 ounces of dog treats.
Show and Grow
Question 1.
Show how to solve the problem above using one equation.
Answer: 18 × 32 × 8
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
Thirteen students create a petition for longer recess. They need 5,000 signatures in all. So far, each student has 99 signatures. How many more signatures do they need?
Answer: 3,713 signatures
Explanation:
Given that there are 13 students that create a petition for longer recess and they need 5,000 signatures in all.
It is also given that each student has 99 signatures.
So, the total number of signatures that 13 students have are: 13 × 99
By using the Distributive method,
13 × 99 = 13 ( 90 + 9 )
= (13 × 90 ) + ( 13 × 9 )
= (10 +3 ) × 90 + ( 10 + 3 ) × 9
= ( 90 × 10 ) + ( 3 × 90 ) + ( 10 × 9 ) + ( 9 × 3)
= 900 + 270 + 90 + 27
= 1,287
But, the students required 5000 signatures in total.
So,
The remainin number of signatures required by students = 5,000 – 1,287 = 3,713 signatures
Question 3.
An activity book has 35 pages and costs $7. Each page has 4 puzzles. You have completed all of the puzzles on 16 of the pages. How many puzzles do you have left to complete?
Answer: 76 puzzles
Explanation:
Given that an activity book has 35 pages and each page has 4 puzzles.
So,
The total number of puzzles = 35 × 4 = 140 puzzles
But, it is also given that the puzzles completed in all of the 16 pages and we know that each page has 4 puzzles.
So,
The number of puzzles in 16 pages = 16 × 4 = 64 puzzles
Now,
The remaining number of puzzles in the remaining pages = 140 – 64 = 76 puzzles
Understand the problem. Then make a plan. How will you solve it? Explain.
Question 4.
Twelve classes provide items for a time capsule. There are 23 students in each class. Each student puts 2 small items in the time capsule. How many items are in the time capsule?
Answer: 552 items
Explanation:
Given that there are 12 classes that provide items for a time capsule and there are 23 students in each class and each student puts 2 small items in the time capsule.
First, we have to find the total number of students by the product 23 × 12
By using the Distributive method,
12 × 23 = 23( 10 + 2 )
= (23 × 10 ) + ( 23 × 2 )
= (20 +3 ) × 10 + ( 20 + 3 ) × 3
= ( 20 × 10 ) + ( 3 × 10 ) + ( 20 × 3 ) + ( 3 × 3)
= 200 + 30 + 60 + 9
= 296 students
Now,
The total number of small items put by the total number of students = 296 × 2 = 552 small items
Question 5.
A craftsman cuts letters and numbers from license plates to make signs. He has 15 Florida plates and 25 Georgia plates. Each plate has a total of 7 letters and numbers. How many letters and numbers does the craftsman cut in all?
Answer: 280 letters and numbers
Explanation;
Given that a craftsman has 15 Florida plates and 25 Georgia plates and each plate has a total of 7 letters and numbers.
Hence,
The total number of plates that a craftsman have = 25 + 15 = 40 plates
The total number of letters and numbers each plate has = 40 × 7 = 280 letters and numbers
Question 6.
DIG DEEPER!
In 1 month, the solar panel and the wind turbine can produce the kilowatt-hours of electricity shown. How much electricity can 28 solar panels and1 small wind turbine produce each month?
Answer: 1,673 kilowatt-hours of electricity
Explanation;
Given that each solar panel produces 30 kilowatt-hours and a wind turbine produces 833 kilowatt-hours.
Now, the electricity produced by 28 solar panels = 28 × 30
By using the Associative Property of Multiplication,
28 × 30 = 28 × (3 × 10)
= (28 × 3) × 10
= (7× 4 × 3) × 10
= 84 × 10
= 840 kilowatt-hours
Hence,
The total electricity produced by 28 solar panels and 1 wind turbine = 840 + 833 = 1,673 kilowatt-hours
Think and Grow: Modeling Real Life
Example
An adult ticket for a zip line course costs $48.A child ticket costs $19 less than an adult ticket. In 1 day, 86 adults and 42 children ride the zipline. How much more money was earned from adult tickets than from child tickets?
Think: What do you know? What do you need to find? How will you solve?
Step 1: How much money was earned from adult tickets?
$48 × 86 = ‘a’
‘a’ is an unknown product.
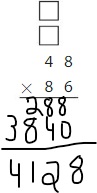
So,
a = 4,128
Step 2: How much money was earned from child tickets?
A child ticket costs $48 – $19 = $29.
$29 × 42 = c
c is the unknown product.
So,
c = 1,218
Step 3: Use m to represent how much more money was earned from adult tickets.
So, $ 2910 more was earned from adult tickets.
Show and Grow
Question 7.
A theater has 45 rows of 72 seats on the floor level and 22 rows of 36 seats in the balcony. How many seats are there in all?
How many more seats are on the floor level than on the balcony?
Answer: 4,032 seats
Explanation;
Given that a theater has 45 rows of 72 seats on the floor level and 22 rows of 36 seats in the balcony.
So,
The total number of seats on the floor level = 45 × 72
The total number of seats on the balcony = 22 × 36
By using the Distributive method,
72 × 45 = 45 ( 70 + 2 )
= (45 × 70 ) + ( 45 × 2 )
= (40 +5 ) × 70 + ( 40 + 5 ) × 2
= ( 40 × 70 ) + ( 5 × 70 ) + ( 40 × 2 ) + ( 5 × 2)
= 2,800 + 350 + 80 + 6
= 3,240
By using the Distributive method,
22 × 36 = 36 ( 20 + 2 )
= (36 × 20 ) + ( 36× 2 )
= (30 +6 ) × 20 + ( 30 + 6) × 2
= ( 30 × 20 ) + ( 6 × 20 ) + ( 30 × 2 ) + ( 6 × 2)
= 600 + 120 + 60 + 12
= 792
So,
The total number of seats ( Floor level and balcony) = 3,240 + 792 = 4,032 seats
Problem Solving: Multiplication with Two-Digit Numbers Homework & Practice 4.8
Understand the problem. Then make a plan. How will you solve it? Explain.
Question 1.
Seventy-two mushers compete in a sled-dog race. Each musher has 16 dogs. How many dogs compete in the race than mushers?
Answer: 1,152 dogs
Explanation:
Given that there are 72 mushers compete in a sled-dog race and each musher has 16 dogs.
So,
The total number of dogs that compete in the race = 16 × 72
By using the Distributive method,
16 × 72 = 72 ( 10 + 6 )
= (72 × 10 ) + ( 72× 6 )
= (70 +2 ) × 10 + ( 70 + 2) × 6
= ( 70 × 10 ) + ( 2 × 10 ) + ( 70 × 6 ) + ( 6 × 2)
= 700 + 20 + 420 + 12
= 1,152
Hence,
The total number of dogs that compete in the race are: 1,152 dogs
Question 2.
A photographer buys 3 USB drives that each cost $5. She puts 16 folders on each drive. Each folder has 75 photographs. How many photographs does the photographer put on the USB drives in all?
Answer: 3,600 photographs
Explanation;
Given that a photographer has 3 USB drives and there are 16 folders and 75 photographers on each drive.
So,
The total number of photographs on all the USB drives = 16 × 3 × 75 = 48 × 75
By using the Distributive method,
48 × 75 = 75 (40 + 8 )
= (75 × 40 ) + ( 75 × 8 )
= (70 +5 ) × 40 + ( 70 + 5) × 8
= ( 70 × 40 ) + ( 5 × 40 ) + ( 70 × 8 ) + ( 5 × 8)
= 2,800 + 200 + 560 + 40
= 3,600 photographs
Hence,
The total number of photographs on all the USB drives are: 3,600 photographs
Question 3.
A teacher has 68 students take 25
Question test. The teacher checks the answers for 9 of the tests. How many answers does the teacher have left to check?
Answer: 1,475 answers
Explanation:
Given that a teacher has 68 students take 25
Question test.
So,
The total number of answers the teacher have to check = 68 × 25
By using the Distributive method,
68 × 25 = 68 ( 20 + 5 )
= (68 × 20 ) + ( 68× 5 )
= (60 +8 ) × 20 + ( 60 + 8) × 5
= ( 60 × 20 ) + ( 8 × 20 ) + ( 60 × 5 ) + ( 8 × 5)
= 1,200 + 160 + 300 + 40
= 1,700
It is also given that the teacher checked 9 papers only.
So.
The number of answers checked = 9 × 25 = 225
Hence,
The number of answers remained unchecked = 1,700 – 225 = 1,475 answers
Question 4.
Each day, a cyclist bikes uphill for 17 miles and downhill for 18 miles. She drinks 32 fluid ounces of water after each bike ride. How many miles does the cyclist bike in 2 weeks?
Answer: 490 miles
Explanation;
Given that a cyclist bikes uphill for 17 miles and downhill for 18 miles.
SO,
The total distance that cyclist bikes each day = 17 + 18 = 35 miles
We know that,
1 week = 7 days
S0, 2 weeks = 2 × 7 = 14 days.
So, the distance traveled by a cyclist in 2 weeks = 35 × 14
By using the Distributive method,
35 × 14 = 35 ( 10 + 4 )
= (35 × 10 ) + ( 35× 4 )
= (30 +5 ) × 10 + ( 30 + 5) × 4
= ( 30 × 10 ) + ( 5 × 10 ) + ( 30 × 4 ) + ( 5 × 4)
= 300 + 50 + 120 + 20
= 490 miles
Hence,
The distance traveled by a cyclist in 2 weeks is: 490 miles
Question 5.
Precision
Which expressions can be used to solve the problem?
Twelve friends play a game that has 308 cards. Each player receives 16 cards. How many cards are left?
(308 – 12) × 16
308 – (16 × 12)
308 – (12 × 16)
(308 – 16) – 12
Answer: Let the Expressions be named as A), B), C) and D)
Either B) or C) can be used to solve the problem.
Explanation:
The given Expressions are;
A) (308 – 12) × 16
B) 308 – (16 × 12)
C) 308 – (12 × 16)
D) (308 – 16) – 12
It is given that there are 12 friends that have 16 cards each and there are 308 cards in total.
So,
The number of cards that have left = 308 – ( 16 × 12 ) (or) 308 – ( 12 × 16 )
Hence,
From the above,
we can conclude that either B) or C) can be used to solve the problem.
Question 6.
Modeling Real Life
A child ticket costs $14 less than an adult ticket. What is the total ticket cost for 18 adults and 37 children?
Answer: The total ticket cost is: $2,617
Explanation:
The given cost of an Adult ticket = $57
It is also given that a child ticket costs $14 less than an adult ticket.
So,
The given cost of a child ticket = 57 – 14 = $43
Now,
The cost for 18 adults = 18 × 57
The cost for 37 children = 37 × 43
By using the Distributive method,
18 × 57 = 57 ( 10 + 8 )
= (57 × 10 ) + ( 57× 8 )
= (50 + 7 ) × 10 + ( 50 + 7) × 8
= ( 50 × 10 ) + ( 7 × 10 ) + ( 50 × 8 ) + ( 7 × 8)
= 500 + 70 + 400 + 56
= 1,026
By using the Distributive method,
37 × 43 = 37 ( 40 + 3 )
= (37 × 40 ) + ( 37× 3 )
= (30 +7 ) × 40 + ( 30 + 7) × 3
= ( 30 × 40 ) + ( 7 × 40 ) + ( 30 × 3 ) + ( 7 × 3)
= 1,200 + 280 + 90 + 21
= 1,591
Hence,
The total cost of tickets = 1,591 + 1,026 = $2,617
Question 7.
Modeling Real Life
An artist creates a pattern by alternating square and rectangular tiles. The pattern has 14 square tiles and 13 rectangular tiles. How long is the pattern?
Answer: 1,680 cm
Explanation:
Given that an artist creates a pattern by alternating square and rectangular tiles and the pattern 14 square tiles and 13 rectangular tiles.
From the given fig.,
Area of Square = 8 × 8 = 64 square cm
Area of Rectangle = 8 × 14 = 112 square cm
So,
Area of 14 squares = 14 × 64
Area of 13 rectangles = 112 × 13
By using the Distributive method,
14 × 64 = 64 ( 10 + 4 )
= (64 × 10 ) + ( 64× 4 )
= (60 +4 ) × 10 + ( 60 + 4) × 4
= ( 60 × 10 ) + ( 4 × 10 ) + ( 60 × 4 ) + ( 4 × 4)
= 600 + 40 + 240 + 16
= 896
By using the Distributive method,
112 × 13 = 13 ( 100 + 12 )
= (13 × 100 ) + ( 13× 12 )
= (10 +3 ) × 100 + ( 10 + 3) × 12
= ( 10 × 100 ) + ( 3× 100 ) + ( 10 × 12 ) + ( 12 × 3)
= 1,000 + 300 + 120 + 36
= 1,456
Hence,
The total length of the Pattern = 896 + 1,456 = 2,352 square cm
Question 8.
Modeling Real Life
A cargo ship has go ship has 34 rows of crates. Each row has 16 stacks of crates. There are 5 crates in each stack. The ship workers unload 862 crates. How many crates are still on the ship?
Answer: 1,858 crates are still on the ship.
Explanation:
Given that a cargo ship has a go ship has 34 rows of crates and each row has 16 stacks of crates. It is also given that there are 5 crates in each stack.
So,
The total number of crates = 34 × 16 × 5 = 34 × 80
By using the Associative Property of Multiplication,
34 × 80 = 34 × (8 × 10)
= (34 × 8) × 10
= (17× 2 × 8) × 10
= 272 × 10
= 2,720
It is also given that the ship workers unload 862 crates.
Hence,
The number of crates that the ship had = 2,720 – 862 = 1,858 crates
Review & Refresh
Estimate the product.
Question 1.
4 × 85
Answer: 340
Explanation:
By using the partial products method,
4 × 85 = ( 80 + 5 ) × ( 2 + 2 )
= ( 80 × 2 ) + (80 × 2 ) + ( 5 × 2 ) + ( 5 × 2 )
= 160 + 160 + 10 + 10
= 340
Question 2.
6 × 705
Answer: 4,230
Explanation:
By using the partial products method,
6 × 705 = ( 700 + 5 ) × ( 2 + 4 )
= ( 700 × 2 ) + (700 × 4 ) + ( 5 × 2 ) + ( 5 × 4 )
= 1,400 + 2,800 + 10 + 20
= 4,230
Question 3.
8 × 7,923
Answer: 63,384
Multiply by Two-Digit Numbers Performance Task
Wind turbines convert wind to energy. Most wind or turbines have 3 blades. The blades rotate slower or faster depending on the speed of the wind. More energy is generated when the blades spin faster.
Question 1.
A wind turbine rotates between 15 and 40 times in 1 minute.
a.What is the least number of times the turbine rotates in 1 hour?
b.What is the greatest number of times the turbine rotates in 1 hour?
Answer:
a) 900 times
b) 2,400 times
Explanation:
Given that a wind turbine rotates between 15 and 40 times in 1 minute.
We know that,
1 hour = 60 minutes
The wind turbine rotates minimum 15 times and maximum 40 times in a minute.
So,
The minimum number of times a wind turbine rotate in 1 hour = 15 × 60
The maximum number of times a wind turbine rotate in 1 hour = 40 × 60
Using the Associative Property of Multiplication,
15 × 60 = 15 ( 6 × 10)
= ( 15 × 6) × 10
= 90 × 10
= 900
Using the Associative Property of Multiplication,
40 × 60 = 40 ( 6 × 10)
= ( 40 × 6) × 10
= 240 × 10
= 2,400
Hence,
The minimum number of times a wind turbine rotate in 1 hour = 900 times
The maximum number of times a wind turbine rotate in 1 hour = 2,400 times
Question 2.
The tips of the turbine blades spin 5 times faster than the speed of the wind. The speed of the wind is 22 miles per hour. How fast do the blade tips spin?
Answer: 110 miles per hour
Explanation;
Given that the tips of the turbine blades spin 5 times faster than the speed of the wind. It is also given that the speed of the wind is 22 miles per hour.
So,
The speed of the blade tips = 22 × 5 = 110 miles per hour
Question 3.
A turbine farm has 7 large wind turbines. Each wind turbine can generate enough energy to power 1,485 houses. How many houses can the turbine farm power in all?
Answer: 10,395 houses
Explanation:
Given that a turbine farm has 7 large wind turbines and each wind turbine can generate enough energy to power 1,485 houses.
So,
The total number of houses that a turbine farm generates enough energy = 1,485 × 7 = 10,395 houses
Question 4.
Use the chart.
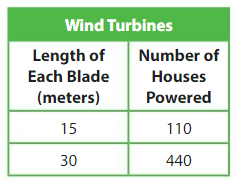
a. How many times more houses are powered when the length of each blade is doubled?
b. A wind turbine has blades that are each 60 meters long. How many houses can the wind turbine power?
Answer:
a) 2 times
b) 33,000 houses
Explanation;
a) The given original length of each blade is 15 meters and 30 meters. It is also given that some houses are powered.
Now,
It is also given that the length of each blade is doubled.
So, 15 meters becomes 30 meters and 30 meters becomes 60 meters.
From this, we have to observe that the change in length also changes the energy powered in a directly proportional way.
From this, we can conclude that
The number of times more houses are powered when the length of each blade is doubled is: 2 times
b) Given that the length f each wind turbine is 60 meters long.
So, the number of houses that can be powered up = 60 × 550
Using the Associative Property of Multiplication,
550 × 60 = 550 × ( 10 × 6)
= ( 550 × 6 ) × 10
= 3300 × 10
= 33,000
Hence,
The number of houses can the wind turbine power is: 33,000 houses
Multiply by Two-Digit Numbers Activity
Multiplication Boss
Directions:
1. Each player flips 4 Number Cards and uses them in any order to create a multiplication problem with two-digit factors.
2. Each player finds the product of the two factors.
3. Players compare products. The player with the greater product takes all 8 cards.
4. If the products are equal, each player flips 4 more cards and plays again. The player with the greater product takes all 16 cards.
5. The player with the most cards at the end of the round wins
Multiply by Two-Digit Numbers Chapter Practice
4.1 Multiply by Tens
Find the product.
Question 1.
50 × 20 = _____
Answer: 1,000
Explanation:
By using the Place-value method,
50 × 20 = 50 × 2 tens
= 5 tens × 2 tens
= 10 × 10 × 10
= 1,000
So, 50 × 20 = 1,000
Question 2.
30 × 60 = _____
Answer: 1,800
Explanation:
By using the Place-value method,
30 × 60 = 30 × 6 tens
= 3 tens × 6 tens
= 18 × 10 × 10
= 1,800
So, 30 × 60 = 1,800
Question 3.
80 × 10 = _____
Answer: 800
Explanation:
By using the Place-value method,
80 × 10 = 10 × 8 tens
= 1 ten × 8 tens
= 8 × 10 × 10
= 800
So, 80 × 10 = 800
Question 4.
40 × 70 = _____
Answer: 2,800
Explanation:
By using the Place-value method,
70 × 40 = 70 × 4 tens
= 7 tens × 4 tens
= 28 × 10 × 10
= 2,800
So, 70 × 40 = 2,800
Question 5.
60 × 50 = _____
Answer: 3,000
Explanation:
By using the Place-value method,
50 × 60 = 50 × 6 tens
= 5 tens × 6 tens
= 30 × 10 × 10
= 3,000
So, 50 × 60 = 3,000
Question 6.
90 × 90 = _____
Answer: 8,100
Explanation:
By using the Place-value method,
90 × 90 = 90 × 9 tens
= 9 tens × 9 tens
= 81 × 10 × 10
= 8,100
So, 90 × 90 = 8,100
Question 7.
70 × 11 = _____
Answer: 770
Explanation:
By using the Place-value method,
70 × 11 = 11 × 7 tens
= 77 tens
= 77 × 10
= 770
So, 70 × 11 = 770
Question 8.
18 × 30 = _____
Answer: 540
Explanation:
By using the Place-value method,
30 × 18 = 18 × 3 tens
= 54 tens
= 54 × 10
= 540
So, 30 × 18 = 540
Question 9.
20 × 75 = _____
Answer: 1,500
Explanation:
By using the Place-value method,
20 × 75 = 75 × 2 tens
= 150 tens
= 150 × 10
= 1,500
So, 20 × 75 = 1,500
Find the missing factor.
Question 10.
40 × ____ = 3,200
Answer: The missing number is: 80
Explanation;
Let the missing number be X
So, 40 × X = 3,200
X = 3,200 /40 = 80
Hence, the value of X is: 80
Question 11.
_____ × 20 = 1,200
Answer:
The missing number is: 60
Explanation;
Let the missing number be X
So, 20 × X = 1,200
X = 1,200 /20 = 60
Hence, the value of X is: 60
Question 12.
30 × ____ = 2,100
Answer:
The missing number is: 70
Explanation;
Let the missing number be X
So, 30 × X = 2,100
X = 2,100 /30 = 70
Hence, the value of X is: 70
4.2 Estimate Products
Estimate the product.
Question 13.
25 × 74
Answer: 1,850
Explanation:
Let 74 be rounded to 75
By using the Partial Fraction method,
25 × 75 = ( 20 + 5) × ( 70 + 5)
= ( 20 × 70) + ( 20 × 5) + ( 5 × 70) + ( 5 × 5)
= 1,400 + 100 + 350 + 25
= 1,875
So,
25 × 74 = 1,875
Question 14.
16 × 28
Answer: 448
Explanation:
Let 16 be rounded to 15
Let 28 be rounded to 30
By using the Partial Fraction method,
15 × 30 = ( 10 + 5) × ( 25 + 5)
= ( 10 × 25) + ( 10 × 5) + ( 5 × 25) + ( 5 × 5)
= 200 + 50 + 125 + 25
= 400
So,
16 × 28 = 400
Question 15.
42 × 81
Answer: 3,402
Explanation:
Let 42 be rounded to 40
Let 81 be rounded to 80
By using the tens method,
40 × 80 = 40 × 8 tens
= 4 tens × 8 tens
= 32 × 1 ten × 1 ten
= 32 × 10 × 10
= 3,200
So,
42 × 81 = 3,200
Open-Ended
Write two possible factors that can be estimated as shown.
Question 16.
8,100
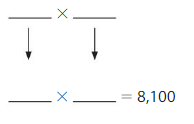
Answer: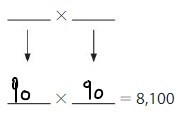 
Explanation:
The Products of 81 are:
9 × 9 = 81
From the above two products, we can conclude that the two possible numbers that can give the product 6,400 are: 90,90
Question 17.
400
Answer: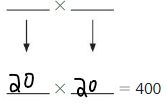 
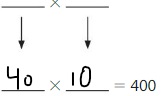
Explanation:
The Products of 64 are:
2 × 2 = 4
4 × 1 =4
From the above two products, we can conclude that the two possible numbers that can give the product 400 are: 20,20 and. 10,40
4.3 Use Area Models to Multiply Two-Digit Numbers
Draw an area model to find the product.
Question 18.
13 × 19 = _____
Answer: 247
Explanation:
By using the Partial Products method,
13 × 19 = ( 10 + 3) × ( 10 + 9)
10 × 10 + 10× 9 + 10 × 3 + 3 × 9
= 100 + 90 + 30 + 27
= 247
So,
19 × 13 = 247
Question 19.
21 × 36 = _____
Answer: 756
Explanation:
By using the Partial Products method,
21 × 36 = ( 20 + 1) × ( 30 + 6)
= 20 × 30 + 20× 6 + 30 × 1 + 1 × 6
= 600 + 120 + 30 + 6
= 756
So,
21 × 36 = 756
Question 20.
YOU BE THE TEACHER
Your friend finds 28 × 24. Is your friend correct? Explain.
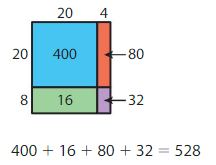
Answer: Your friend is not correct.
Explanation;
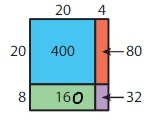
By using the partial Products method,
400 + 160 +80 + 32 = 672
From the above,
we can conclude that in place of 16, 160 must be placed.
4.4 Use Distributive Property to Multiply Two-Digit Numbers
Use Distributive Property to find a product.
Question 21.
27 × 34 = 27 × (30 + 4)
= (27 × 30) + (27 × 4)
= (20 + 7) × 30 + (20 + 7) × 4
= (20 ×30) + (7 × 30) + (20 ×4) + (7 × 4)
= 600 + 210 + 80 + 28
= 918
So, 27 × 34 = 918.
Question 22.
43 × 18 = _____
Answer: 774
Explanation: Using the Partial Products method,
43 × 18 = 43× (10 + 8)
= (43 × 10) + (43 × 8)
= (40 + 3) × 10 + (40 + 3) × 8
= (40 ×10) + (3 × 10) + (40 ×8) + (3 × 8)
= 400 + 30 + 320 + 24
= 774
So, 43 × 18 = 774
Question 23.
35 × 57 = _____
Answer: 1,995
Explanation: Using the Partial products method,
35 × 57 = 35 × (50 + 7)
= (35 × 50) + (35 × 7)
= (30 + 5) × 50 + (30 + 5) × 7
= (50 ×30) + (5 × 50) + (30 ×7) + (7 × 5)
= 1,500 + 250 + 210 + 35
= 1,995
So, 35 × 57 = 1,995
Question 24.
81 × 76 = _____
Answer: 6,156
81 × 76 = 81 × (70 + 6)
= (81 × 70) + (81 × 6)
= (80 + 1) × 70 + (80 + 1) × 6
= (80 ×70) + (70 × 1) + (80 ×6) + (1 × 6)
= 5,600 + 70 + 480 + 6
= 6,156
So, 81 × 76 = 6,156
4.5 Use Partial Products to Multiply Two-Digit Numbers
Find the product. Check whether your answer is reasonable.
Question 25.
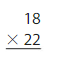
Answer: 396
Explanation: Using the Partial Products method,
18 × 22 = 22 × (10 + 8)
= (22 × 10) + (22 × 8)
= (20 + 2) × 10 + (20 + 2) × 8
= (20 ×10) + (2 × 10) + (20 ×8) + (2 × 8)
= 200 + 20 + 160 + 16
= 396
So, 18 × 22 = 396
Question 26.
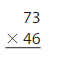
Answer: 3,358
Explanation: Using the Partial Products method,
73 × 46 = 73 × (40 + 6)
= (73 × 40) + (73 × 6)
= (70 + 3) × 40 + (70 + 3) × 6
= (70 ×40) + (3 × 40) + (70 ×6) + (3 × 6)
= 2,800 + 120 + 420 + 18
= 3,358
So, 73 × 46 = 3,358.
Question 27.
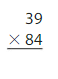
Answer: 3,276
Explanation: By using the Partial Products method,
39 × 84 = 39 × (80 + 4)
= (39 × 80) + (39 × 4)
= (30 + 9) × 80 + (30 + 9) × 4
= (80 ×30) + (9 × 80) + (30 ×4) + (9 × 4)
= 2,400 + 720 + 120 + 36
= 3,276
So, 39 × 84 = 3,276
Question 28.
57 × 19 = _____
Answer: 1,083
Explanation: By using the Partial Products method,
57 × 19 = 57 × (10 + 9)
= (57 × 10) + (57 × 9)
= (50 + 7) × 10 + (50 + 7) × 9
= (50 ×10) + (7 × 10) + (50 ×9) + (7 × 9)
= 500 + 70 + 450 + 63
= 1,083
So, 57 × 19 = 1,083
Question 29.
38 × 65 = _____
Answer: 2,470
Explanation: By using the Partial Products method,
38 × 65 = 65 × (30 + 8)
= (65 × 30) + (65 × 8)
= (60 + 5) × 30 + (60 + 5) × 8
= (60 ×30) + (5 × 30) + (60 ×8) + (5 × 8)
= 1,800 + 150 + 480 + 40
= 2,470
So, 38 × 65 = 2,470
Question 30.
94 × 26 = _____
Answer: 2,444
Explanation: By using the Partial Products method,
94 ×26 = 94 × (20 + 6)
= (94 × 20) + (94 × 6)
= (90 + 4) × 20 + (90 + 4) × 6
= (90 ×20) + (4 × 20) + (90 ×6) + (4 × 6)
= 1,800 + 80 + 540 + 24
= 2,444
So, 94 × 26 = 2,444
Reasoning
Find the missing digits. Then find the product.
Question 31.
Answer:
Question 32.
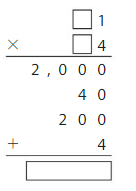
Answer:
4.6 Multiply Two-Digit Numbers
Find the product. Check whether your answer is reasonable.
Question 33.
Estimate: _____
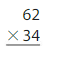
Answer: 2,108
Explanation:
Using the Partial Products method,
34 × 62 = ( 60 + 2) × ( 30 + 4)
= 30 × 60 + 4 × 60 + 30 × 2 + 2 × 4
= 1,800 + 240 + 60 + 8
= 2,108
Estimate:
Let 62 be Rounded to 60.
Let 34 be Rounded to 35.
So, 60 × 35 = 2,100
As the Estimate and the actual answer are near, the answer is reasonable.
Question 34.
Estimate: ____
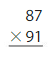
Answer: 7,917
Explanation:
Using the Partial Products method,
87 × 91 = ( 80 + 7) × ( 90 + 1)
= 80 × 90 + 7 × 90 + 80 × 1 + 7 × 1
= 7,200 + 630 + 80 + 7
= 7,917
Estimate:
Let 87 be Rounded to 85.
Let 91 be Rounded to 90.
So, 90 × 85 = 7,650
As the Estimate and the actual answer are not near, the answer is not reasonable.
Question 35.
Estimate: _____
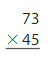
Answer: 3,285
Explanation:
Using the Partial Products method,
73 × 45 = ( 70 + 3) × ( 40 + 5)
= 70 × 40 + 3 × 40 + 70 × 5 + 5 × 3
= 2,800 + 120 + 350 + 15
= 3,285
Estimate:
Let 73 be Rounded to 75.
So, 45 × 75 = 3,375
As the Estimate and the actual answer are near, the answer is reasonable.
Question 36.
Estimate: ____
13 × 21 = ______
Answer: 273
Explanation:
Using the Partial Products method,
13 × 21 = ( 20 + 1) × ( 10 + 3)
= 20 × 10 + 20 × 3 + 10 × 1 + 1 × 3
= 200 + 60 + 10 + 3
= 273
Estimate:
Let 13 be Rounded to 15.
Let 21 be Rounded to 20.
So, 20 × 15 = 300
As the Estimate and the actual answer are near, the answer is reasonable.
Question 37.
Estimate: _____
42 × 53 = _____
Answer: 2,226
Explanation:
Using the Partial Products method,
42 × 53 = ( 40 + 2) × ( 50 + 3)
= 40 × 50 + 3 × 40 + 50 × 2 + 2 × 3
= 2,000 + 120 + 100 + 6
= 2,226
Estimate:
Let 42 be Rounded to 40.
Let 53 be Rounded to 55.
So, 40 × 55 = 2,200
As the Estimate and the actual answer are near, the answer is reasonable.
Question 38.
Estimate: _____
29 × 66 = _____
Answer: 1,914
Explanation:
Using the Partial Products method,
29 × 66 = ( 20 + 9) × ( 60 + 6)
= 20 × 60 + 9 × 60 + 20 × 6 + 9 × 6
= 1,200 + 540 + 120 + 54
= 1,914
Estimate:
Let 29 be Rounded to 30.
Let 66 be Rounded to 65.
So, 30 × 65 = 1,950
As the Estimate and the actual answer are near, the answer is reasonable.
4.7 Practice Multiplication Strategies
Find the product.
Question 39.
80 × 30 = _____
Answer: 2,400
Explanation: Using the Place-value method,
80 × 30 = 80 × 3 tens
= 240 tens
= 2,400
So, 80 × 30 = 2,400
Question 40.
26 × 51 = _____
Answer: 1,326
Explanation: Using the Partial Products method,
26 × 51 = ( 20 + 6) × ( 50 + 1)
= ( 20 × 50) + ( 20 × 1) + ( 6 × 50) + (6 × 1)
= 1,000 + 20 + 300 + 6
= 1,326
Question 41.
94 × 70 = _____
Answer: 6,580
Explanation: Using the Place-value method,
94 × 70 = 94 × 7 tens
= 658 tens
= 6,580
So, 94 × 70 = 6,580
Question 42.
15 × 67 = _____
Answer: 1,005
Explanation: Using the Partial Products method,
15 × 67 = ( 10 + 5) × ( 60 + 7)
= ( 10 × 60) + ( 10 × 7) + ( 5 × 60) + ( 5 × 7)
= 600 + 70 + 300 + 35
=1,005
Question 43.
40 × 38 = _____
Answer: 1,520
Explanation: Using the Place-value method,
38 × 40 = 38 × 4 tens
= 152 tens
= 1,520
So, 38 × 40 = 1,520
Question 44.
29 × 92 = _____
Answer: 2,668
Explanation: Using the partial products method,
29 × 92 = ( 20 + 9) × ( 90 + 2)
= ( 20 × 90 ) + ( 20 × 2) + ( 9 × 90) + ( 9 × 2)
= 1,800 + 40 + 810 + 18
= 2,668
Question 45.
Modeling Real Life
A Ferris wheel runs 40 times each day. It has 16 cars with 4 seats in each car. If the Ferris wheel is full each time it runs, how many people will ride it in 1 day?
Answer: 2,560 people will ride the Ferris wheel in 1 day
Explanation:
Given that a Ferris wheel runs 40 times each day and it has 16 cars with 4 seats in each car.
So, the total number of people that can ride a Ferris wheel = 40 × 16 × 4 = 40 × 64
By using the place-value method,
64 × 40 = 64 × 4 tens
= 256 tens
= 2,560
From the above,
We can conclude that there are 2,560 people who will ride the Ferris wheel in 1 day
4.8 Problem Solving: Multiplication with Two-Digit Numbers
Question 46.
A music fan memorizes 59 songs for a concert. Her goal is to memorize all of the songs from 13 albums. There are 15 songs on each album. How many more songs does the music fan still need to memorize?
Answer: 136 songs
Explanation:
Given that a music fan has to memorize all of the songs from 13 albums and there are 15 songs on each album.
So, the total number of songs the music fan has to memorize = 13 × 15
By using the Partial Products method,
13 × 15 = ( 10 + 3) × ( 10 + 5)
= ( 10 × 10 ) + ( 10 × 5) + ( 3 × 10 ) + ( 3 × 5)
= 100 + 50 + 30 + 15
= 195
It is also given that the music fan memorized 59 songs for the Concert.
Hence,
The number of songs that has to memorize by the music fan = 195 – 59 = 136 songs
Question 47.
Find the area of the Jamaican flag.
Answer: 2,592 inches
Explanation;
The given Jamaican flag is in the shape of a rectangle.
We know that,
Area of the rectangle = length × breadth
So,
Area of the Jamaican flag = 36 × ( 36 + 36) = 36 × 72
Using the Partial Products method,
36 × 72 = ( 30 + 6) × ( 70 + 2)
= ( 30 × 70 ) + ( 30 × 2 ) + ( 6 × 70) + ( 6 × 2)
= 2,100 + 60 + 720 + 12
= 2,592 inches
From this,
We can conclude that the area of the Jamaican flag is: 2,592 inches
Final Words:
We believe that the details provided in Big Ideas Math Answers Grade 4 Chapter 4 Multiply by Two-Digit Numbers are beneficial for you to overcome the difficulties in this chapter. Share this pdf link with your friends to help them to score good marks in the exams. Stay with us to get the latest updates regarding the solutions with explanations of all the BIM Grade 3 chapters.