Get the free pdf of Big Ideas Math Answers Grade 5 Chapter 4 Multiply Whole Numbers. Every problem is explained with the solution and explanation on Big Ideas Multiply Whole Numbers Grade 5 Chapter 4 Math Answers. Our highly trained experts are provided the concepts in a simple way where every student can understand the solving methods. Also, various methods are included to solve the math problems. Therefore, practice all problems and score good marks in the exam. Every explanation is mainly explained with images, graphs, tables, and, etc. So, students will not face any problems to solve the basic questions too difficult questions.
Big Ideas 5th Grade Chapter 4 Multiply Whole NumbersMath Book Answer Key
Save your time by finding every concept and its related problems individually. Quickly go through the below links and check out all the topics with problems. Mainly, concentrate on concepts to prepare and solve the questions on your own. If you understand the concept, it becomes easier to solve difficult problems easily. Download Big Ideas Math Book 5th Grade Answers Chapter 4 Multiply Whole Numbers pdf and start your practice now. We have also included exercises for the better practice of students.
Lesson: 1 Multiplication Patterns
Lesson: 2 Estimate Products
Lesson: 3 Multiply by One-Digit Numbers
Lesson: 4 Multiply by Two-Digit Numbers
Lesson: 5 Multiply by Multi-Digit Whole Numbers
- Lesson 4.5 Multiply by Multi-Digit Whole Numbers
- Multiply by Multi-Digit Whole Numbers Homework & Practice 4.5
Performance Task
- Multiply Whole Numbers Performance Task
- Multiply Whole Numbers Activity
- Multiply Whole Numbers Chapter Practice
Lesson 4.1 Multiplication Patterns
Explore and Grow
Complete the table. Find the value of each expression.
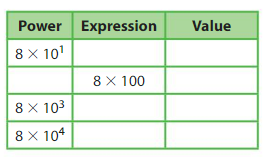
What patterns do you notice?
Answer:
| Power | Expression | Value |
| 8 x 101 | 8 x 10 | 80 |
| 8 x 102 | 8 x 100 | 800 |
| 8 x 103 | 8 x 1,000 | 8,000 |
| 8 x 104 | 8 x 10,000 | 80,000 |
Explanation:
In each product, the number of zeros after 8 is the same as the exponent.
Patterns
Explain how to multiply any number by a power of 10.
Answer:
By multiplying the given number with the 10 as many times as to its the given power value.
Explanation :
Example 4 x 102 we take as 4 x 10 x 10 means 10 is multiplied twice
means as the power of 10 is 2 so we multiply the number 4 with 10 twice,
if it 4 x 103 we take it as 4 x 10 x 10 x 10 means we take 10 by 3 times as power is 3
Think and Grow: Use Patterns to Find Products
Example
Find 46 × 103.
One Way:
Use powers and look for a pattern

46,000
Another Way:
Use place value.
46 × 103 = 46 × 1,000
= 46 thousands
= ___46,000___

So, 46 × 103.
Notice the pattern: In each product, the number of zeros after 46 is the same as the exponent.
Example
Find 40 × 600.
Use a multiplication fact and look for a pattern.
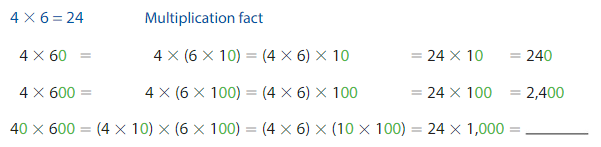
So, 40 × 600 = __24,000____.
Notice the pattern: In each product, the number of zeros after 24 is equal to the number of zeros in the factors.
Show and Grow
Find the product.
Question 1.
78 × 104
Answer:
The product of 78 × 104 = 78 x 10,000 = 780,000
Explanation: As 78 is multiplied by 104 we get the result as 780,000
Question 2.
20 × 400 = ______
Answer:
The product of 20 x 400 = 2x 10 x 4 x 100 = 2 x 4 x 10 x 100 = 8,000
Explanation:
As 20 X 400 has 3 zeros we have 20 x 400 as 8,000
Apply and Grow: Practice
Find the product
Question 3.
11 × 103 = _______
Answer:
The product of 11 × 103 = 11 x 1,000=11,000
Explanation :
The result of 11 × 103 is 11,000
Question 4.
40 × 70 = _______
Answer:
The product of 40 x 70 = 4 x 10 x 7 x 10 =4 x 7 x 10 x 10 = 2,800
Explanation :
When 40 is multiplied by 70 the result is 2,800
Question 5.
300 × 90 = ________
Answer:
The product of 300 x 90 = 3 x 100 x 9 x 10 = 3 x 9 x 100 x 10 = 27,000
Explanation :
When 300 is multiplied by 90 the result is 27,000
Question 6.
104 × 60 = _______
Answer:
The product of 104 × 60 = 10 x 10 x 10 x 10 x 60 = 6,00,000
Explanation :
When 104 is multiplied by 60 the result is 6,00,000
Question 7.
206 × 102 = _______
Answer:
The product of 206 × 102 = 206 x 10 x 10 = 20,600
Explanation :
When 206 is multiplied by 102 the result is 20,600
Question 8.
15 × 200 = _________
Answer:
The product of 15 x 200 = 15 x 2 x 10 x 10 = 3,000
Explanation :
When 15 is multiplied by 200 the result is 3,000
Find the missing factor.
Question 9.
30 × ______ = 15,000
Answer:
30 x ____= 15,000,15,000/30 = 500
Explanation:
So when 15,000 is divided by 30 we get 500 the missing factor is 500
Question 10.
_____ × 103 = 54,000
Answer:
_____ × 103 = 54,000
the missing factor is 54
Explanation :
When 54,000 is divided by 103 or 1000
we get 54,000 x 1/ 1000= 54
Question 11.
500 × ______ =40,000
Answer:
500 × ______ =40,000
the missing factor is 8,000
Explanation:
so when 40,000 is dived by 500 its is equal to
40,000 x 1/500=8,000
Question 12.
A heart pumps about 2,000 gallons of blood each day. How many gallons of blood does the heart pump in 7 days?
Answer:
Given that heart pumps about 2,000 gallons of blood each day and for 7 days it is
2,000 x 7 = 14,000 gallons
Explanation :
So we multiply 2000 by 7 for 7 days and the result is 14,000 gallons
Question 13.
Number Sense
Which expressions are equal to 24,000?

Answer:
240 x 100= 24 x 10 x 10 x 10 = 24,000 so it is equal
30 x 800 = 3 x 10 x 8 x 10 x 10 = 24,000 so this is also equal
400 x 600= 4 x 10 x 10 x 6 x 10 x 10 =24,000 so this also equal
and 24 x 1,000 = 24 x 10 x 10 x 10 = 24,000 which is also equal
so all the given expressions are equal to 24,000
Explanation :
When 
these numbers are multiplied all results are equal to 24,000
Question 14.
Logic
When you multiply any whole number by 100, what do you know about the digits in the product?
Answer:
When we multiply any whole number by 100, it becomes the digit with two zeros in the right , number x 100= number x 102 =number,00
or we get the whole number with additional 2 zeros in the right
Explanation:
For example if the number is 5 it becomes as 5 x 100 = 5 x 102= 500, 2 zeros after 5
Question 15.
DIG DEEPER!
Show how to find 20 × 103 using the Associative Property of Multiplication.
Answer:
The Associative Property of Multiplication of 20 × 103 is
(20 x 10) x 10 x 10 = 20 x ( 10 x 10 ) x 10
(200) x 10 x 10 = 20 x (100) x 10
20,000 = 20,000
Explanation:
Both sides are equal by using the Associative Property of Multiplication Law.
Think and Grow: Modeling Real Life
Example
A black bear consumes 12,000 calories each day for 30 days. A grizzly bear consumes 400,000 calories in 30 days. Which bear consumes more calories in 30 days?
Multiply 12,000 and 30 to find the number of calories the black bear consumes in 30 days. Use a multiplication fact and a pattern.
12 × 3 = ____36____ Multiplication fact
The multiplication fact is 12 × 3 = 36. The factors 12,000 and 30 have a total of _____4_ zeros. So, the product has __4___ zeros after 36.
12,000 × 30 = ___3,60,000______ calories
The black bear consumes 3,60,000 calories in 30 days. Compare the numbers of calories the bears consume in 30 days.
A grizzly bear consumes 4,00,000 x 30 = 120,00,000
So grizzly bear consumes more calories than black bear
The ___grizzly ___ bear consumes more calories in 30 days.
Show and Grow
Question 16.
The attendance at a theme park is about 300,000 guests each month. The attendance at a water park is 2,280,000 guests in 1 year. Which park has a greater attendance in 1 year?
Answer:
The theme park has a greater attendance in 1 year.
Explanation:
The attendance at theme park is about 3,00,000 guests in one month so in a year it is 3,00,000 x 12 = 36,00,000 guests.
and given water park has 22,80,000 guests= 228 x 104 in 1 year
so as compared between the two parks 36,00,000 guests = 360 x104 is greater than 22,80,000 guests= 228 x 104 means the theme park has a greater attendance in 1 year.
Question 17.
Your heart beats 120,000 times each day. In 1 week, a professional athlete’s heart beats 607,000 times. How many more times does your heart beat in 1 week compared to the athlete?
Answer:
Our heart beats 233,000 times more compared to the athlete in 1 week
Explanation :
Each day our heart beats 120,000 times each day
so in 1 week it is 120,000 x 7 = 840,000 times our heart beats in 1 week given athlete’s heart beats in 1 week is 607,000 times so compared to both it is
840,000 – 607,000 = 233,000 times
So our heart beats 233,000 times more compared to the athlete in 1 week
Question 18.
A whale’s brain weighs 103 times as much as a platypus’s brain. The whale’s brain weighs 9,000 grams. How many grams does the platypus’s brain weigh?

Answer:
platypus’s brain weighs 9 grams
Explanation:
Given whale’ brain weighs 103 times as much as a platypus’s brain and also given that whale’s brain weighs 9,000 grams
so platypus’s brain weighs 9,000 x 1/ 103 times = 9,000x 1/1000 = 9 grams.
Multiplication Patterns Homework & Practice 4.1
Find the product
Question 1.
37 × 104
Answer:
37 × 104 = 370,000
Explanation:
The product of 37 × 104 = 37 x 10 x 10 x 10 x 10= 370,000
Question 2.
400 × 90 = ______
Answer:
400 × 90 = 36,000
Explanation:
The product of 400 × 90 = 4 x 10 x 10 x 9 x 10 = 4 x 9 x 103 = 36,000
Question 3.
100 × 900 = _____
Answer:
100 x 900 = 90,000
Explanation:
The product of 100 x 900 = 10 x 10 x 9 x 10 x 10 = 9 x 104 = 90,000
Question 4.
800 × 700 = _____
Answer:
800 x 700 = 560,000
Explanation:
The product of 800 x 700 = 8 x 10 x 10 x 7 x 10 x 10 = 8 x 7 x 104 =560,000
Question 5.
867 × 103 = ______
Answer:
867 × 103 =867,000
Explanation:
The product of 867 × 103 = 867 x 10 x 10 x 10 = 867,000
Question 6.
12 × 6,000 = _______
Answer:
12 x 6,000 = 72,000
Explanation:
The product of 12 x 6,000 = 12 x 6 x 10 x 10 x 10= 12 x 6 x 103 = 72,000
Find the missing factor.
Question 7.
____ × 102 = 3,000
Answer:
30 x 102 = 3,000
Explanation:
The missing factor of ____ × 102 = 3,000 is 3,000 x 1/100= 3 x 103 / 102 =30
Question 8.
______ × 500 = 450,000
Answer:
900 x 500 = 450,000
Explanation:
The missing factor of ______ × 500 = 450,000 is 450,000 x 1/500= 450,000/500=
45 x 104 / 5 x 102 = 9 x 102 = 900
Question 9.
80 × _____ = 640,000
Answer:
80 x 8000 = 640,000
Explanation:
The missing factor of 80 × _____ = 640,000 is 640,000 x 1/80 = 64 x 104 / 8 x 10=
8 x 103 =8,000
Question 10.
Reasoning
Do 50 × 8,000 and 50 × 9,000 have the same number of zeros in their products? Explain.
Answer:
Yes, 50 × 8,000 and 50 × 9,000 have the same number of zeros in their products
Explanation:
Why because 50 x 8,000 = 5 x 10 x 8 x 10 x 10 x 10 = 5 x 8 x 104
and 50 x 9,000 = 5 x 10 x 9 x 10 x 10 x 10 = 5 x 9 x 104
so when compared between 5 x 8 x 104 and 5 x 9 x 104 we have 4 zeros in both the products.
Question 11.
DIG DEEPER!
The product of a number and twice that number is 180,000. Write the multiplication equation.
Answer:
2 n2 = 18 x 104
Explanation:
let the number be n and its twice is 2 n is 180,000
n x 2n = 18 x 10 x 10 x 10 x 10
2 n2 = 18 x (10 x 10) x (10 x 10)
so the multiplication equation is 2 n2 = 18 x 104
Question 12.
Modeling Real Life
A hummingbird flutters its wings 80 times in 1 second. A bumblebee flutters its wings 7,800 times in 1 minute. Which animal flutters its wings more times in 1 minute?

Answer:
bumblebee flutters more
Explanation:
Given humming bird flutters its wings 80 times in 1 second equals to 8 x 10,
bumblebee flutters its wings 7,800 times in 1 second equals to 78 x 102
as 78 x 102 > 8 x 10 means bumblebee flutters its wings more than humming bird in 1 minute.
Question 13.
DIG DEEPER!
In 1 day, the blood in your body travels a total of 12,000 miles. This is about 4 times the distance across the United States from coast to coast. About how many miles is the distance across the United States?
Answer:
The distance across the United States is 3,000 miles.
Explanation:
Given in 1 day the blood in our body travels a total of 12,000 miles which is equal to 4 times the distance across the United States from coast to coast.
so the number of miles in the distance across the United States is
12,000 miles / 4=3,000 miles.
Review & Refresh
Classify the triangle by its sides.
Question 14.

Answer:
Equilateral Triangle
Explanation:
In the given figure it is showing all the 3 sides are equal so we call the triangle as Equilateral Triangle.
Question 15.
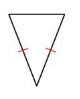
Answer:
Isosceles Triangle
Explanation:
In the above figure it is showing only 2 sides are equal so we call the given triangle as Isosceles Triangle.
Question 16.
Answer:
Scalene Triangle
Explanation:
In the above figure it is showing no side is equal so we call the given triangle as
Scalene Triangle.
Lesson 4.2 Estimate Products
Explore and Grow
Choose an expression to estimate each product. Write the expression. You may use an expression more than once.

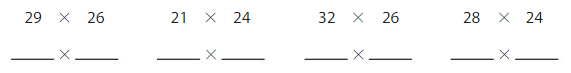
Compare your answers with a partner’s. Did you choose the same expressions?
Answer:
29 x 26
30 x 25
Explanation:
so for 29 x 26 i am choosing the expression 30 x 25 as 29 is near to 30 and 26 is near to 26 i have selected the expression 30 x 25
21 x 24
20 x 25
Explanation :
for 21 x 24 i am choosing the expression 20 x 25 as 21 is near to 20 and 24 is near to 25 i have selected the expression 20 x 25
32 x 26
30 x 25
Explanation :
for 32 x 26 i am choosing the expression 30 x 25 as in the given expressions only 32 is near to 30 and 26 is near to 25 i have selected the expression 30 x 25
28 x 24
30 x 25
Explanation :
for 28 x 24 also i am choosing the expression 30 x 25 why because 28 is near to 30 and 24 is near to 25 so i am selecting the expression 30 x 25
Yes i have selected the same expression 30 x 25 for all the three products 29 x 26, 32 x 26,28 x 24 because for all the given three products the nearest expression we are getting is 30 x 25
Construct Arguments
You estimate the product of 23 and 26 using the expression 25 × 30. Without multiplying, determine whether the estimate is greater than or less than the actual product. Explain.
Answer:
Given the product 23 x 26 as 25 x 30
So the result of given estimate is greater than the actual value
Explanation:
Because as 25 is greater than 23 and 30 is greater than 26 so obviously the expression 25 x 30 has greater value than that of the product of 23 X 26
Think and Grow: Estimate Products
An overestimate is greater than the actual value, and an underestimate is less than the actual value. When you estimate a product, your answer will be an overestimate when both numbers are greater than the original factors. Your answer will be an underestimate when both numbers are less than the original factors.
Example
Use rounding to estimate 204 × 61. Explain whether your estimate is an overestimate or an underestimate.
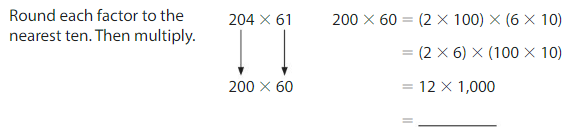
12 x 1,000 = 12,000
So, 204 × 61 is about __12,444___. This is an __underestimate______ because about both rounded numbers are ___200___, __60____ the original factors.
Example
Use compatible numbers to estimate 23 × 194. Explain whether your estimate is an overestimate or an underestimate.
Choose compatible numbers. Then multiply.
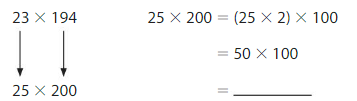
50 x100 = 5,000
So, 23 × 194 is about __4,462____. This is an __overestimate_____ because both compatible numbers are __25____ __200____ the original factors.
Show and Grow
Estimate the product. Explain whether your estimate is an overestimate or an underestimate.
Question 1.
387 × 29
Answer:
387 x 29 =11,223
400 X 30 = 12,000 is overestimate
Explanation :
As our estimate after rounding each factor becomes 387 as 400 nearest hundred and 29 as 30 to nearest ten so it is 400 x 30 = 12 x 1,000=12,000 as 387 x 29 < 400 x 30 as the estimate result is greater than the given product results our estimate is an overestimate
Question 2.
52 × 913
Answer:
52 x 913 = 47,476
50 x 900 = 45,000 is underestimate
Explanation:
As our estimate after rounding each factor becomes 52 as 50 to nearest ten and 913 as 900 nearest hundred so it is 50 X 900 = 45,000
as 52 x 913 > 50 x 900 as the estimate result is less than the given product results
our estimate is an underestimate.
Apply and Grow: Practice
Estimate the product. Explain whether your estimate is an overestimate or an underestimate.
Question 3.
45 × 98
Answer:
45 x 98 = 4,410
50 x 100 = 5,000 is overestimate
Explanation:
As our estimate after rounding each factor becomes 45 as 50 to nearest ten and 98 as 100 to nearest hundred so it is 50 X 100 = 5,000
as 45 x 98 < 50 x 100 as the estimate result is greater than the given product results our estimate is an overestimate
Question 4.
21 × 404
Answer:
21 x 404 = 8,484
20 x 400 = 8,000 is underestimate
Explanation:
As our estimate after rounding each factor becomes 21 as 20 nearest ten and 404 as 400 to nearest hundred so it is 20 X 400 = 8,000
as 21 x 404 > 20 x 400 as the estimate result is less than the given product results our estimate is an underestimate.
Question 5.
394 × 285
Answer:
394 x 285 = 112,290
400 x 300 = 120,000 is overestimate
Explanation:
our estimate after rounding each factor becomes 394 as 400 to nearest hundred and 285 as 300 to nearest hundred so it is 400 X 300 = 120,000
as 394 x 285 < 400 x 300 as the estimate result is greater than the given product results our estimate is an overestimate
Question 6.
596 × 488
Answer:
596 x 488 = 290,848
600 x 500 = 300,000 is overestimate
Explanation:
As our estimate after rounding each factor becomes 596 as 600 to nearest hundred and 488 as 500 to nearest hundred so it is 600 X 500 = 300,000
as 596 x 488 < 600 x 500 as the estimate result is greater than the given product results our estimate is an overestimate
Question 7.
194 × 46
Answer:
194 x 46=8,924
200 x 50 = 10,000 overestimate
Explanation:
As our estimate after rounding each factor becomes 194 as 200 to nearest hundred and 46 as 50 to nearest ten so it is 200 X 50 = 10,000
as 194 x 46 < 600 x 500 as the estimate result is greater than the given product results our estimate is an overestimate
Question 8.
22 × 221
Answer:
22 x 221 =4,862
20 x 200 = 4,000 underestimate
Explanation :
As our estimate after rounding each factor becomes 22 as 20 to nearest ten and 221 as 200 to nearest hundred so it is 20 X 200 = 4,000
as 22 x 221 > 20 x 200 as the estimate result is less than the given product results our estimate is an underestimate.
Question 9.
Number Sense
You estimate 27 × 408 by rounding each number to the nearest ten. Your friend estimates the product using the compatible numbers 25 and 400. Without multiplying, determine which answer is an overestimate and which answer is an underestimate. Explain.
Answer:
27 x 408
30 x 410 Mine is overestimate and
27 x 408
25 x 400 Friend is underestimate
Explanation:
Given my estimate as 27 x 408 by rounding the number to the nearest ten it becomes 27 as 30 and 408 as 410 as 27 is less than 30 and 408 is also less than 410 so the product 27 x 408 is less than 30 x 410
27 x 408
30 x 410
as 27 x 408 < 30 x 410 mine is overestimate.
Now 27 x 408
as 25 x 400
my friend estimates the product using the compatible numbers 25 and 400 as 25 is less than 27 and 400 is less than 408 obviously the product results 25 X 400 <27 x 408 so my friend results are underestimate.
therefore mine is overestimate and friends is underestimate
Question 10.
Writing
Explain two different methods to estimate 49 × 305. Which do you prefer?
Answer:
I prefer 50 x 300
Explanation:
49 x 305 by rounding each number to the nearest ten it is 50 x 310 ,
49 x 305
50 x 310
49 x 305=14,945 and 50 x 310 = 15,500
49 as 50 and 305 as 310 product so 49 is less than 50 and 305 is also less than 310 so the product 49 x 305 is less than 50 x 310
49 x 305 < 50 x 310 which is overestimate
now 49 x 305
50 x 300
49 x 305 compatible numbers are 50 and 300 the results 49 x 305 = 14,945 and 50 x 300 = 15,000 means 49 x 305 < 50 x 300 which is also overestimate,
as both the results are overestimate but i prefer 50,300 compatible numbers only as these number results are very near to the given product 49 x 305 as compared to the rounding the numbers to nearest ten.
so i prefer 50 x 300
Question 11.
DIG DEEPER!
You estimate 9 × 26 using the compatible numbers 10 and 25. Is your estimate an overestimate or an underestimate? Explain.
Answer:
My estimate is underestimate.
Explanation:
My estimate is given as 9 x 26 = 234
and compatible numbers result is 10 x 25 = 250,
as 9 x26 < 10 x 25 as my estimate results is less than the compatible numbers result so my estimate is underestimate
Think and Grow: Modeling Real Life
Example
Earth travels about 1,118 miles in 1 minute. About how far does Earth travel in 1 hour?
Think: What do you know? What do you need to find? How will you solve?

There are 60 minutes in 1 hour, so multiply the distance by 60.
60 × 1,118 = ?
Use rounding to estimate the product.

So, Earth travels about _60,000_____ miles in 1 hour.
Show and Grow
Question 12.
Old Faithful erupts about 19 times in 1 day. Each eruption sprays about 6,050 gallons of water. About how many gallons of water does Old Faithful spray in 1 day?

Answer:
Old faithful spray in 1 day19 x 6,000= 114,000 gallons of water
Explanation :
Given Old Faithful erupts about 19 times in 1 day and each eruption sprays about 6,050 gallons of water, so Old faithful sprays about 19 x 6,050=114,950 gallons of water in 1 day.
Now using rounding to estimate the product it becomes 19 as 20 and 6,050 as 6,000
so Old faithful sprays about 19 x 6,000=114,000 gallons of water in 1 day.
Question 13.
Workers place a foam finger on every seat in a stadium for an upcoming football game. There are 29 sections in the stadium and about 245 seats in each section. About how many foam fingers are needed? Is it better to have an overestimate or an underestimate? Explain.

Answer:
Needed are 7,105 number of foam fingers and It is better to have overestimate
Explanation:
Given there are total 29 sections in the stadium
and 245 seats in each section.
The number of foam fingers needed would be 29 x 245 = 7,105 foam fingers
So we need 7,105 number of foam fingers
So now by using rounding 29 becomes 30 and 245 as 250 so it becomes
30 x 250=7,500 foam fingers.
Now on comparing 29 x 245 < 30 x 350 so the results is overestimate.
So it is better to have overestimate only
Question 14.
DIG DEEPER!
One acre of land is equal to the area of a rectangular piece of land that is 22 yards wide and 220 yards long. Central Park in New York City is 843 acres. What is the approximate area of Central Park in square yards?
Answer:
Central Park in New York City has 22 x 220 x 843 square yards
Explanation:
Given one acre of land is equal to 22 yards wide and 220 yards long
means one acre is 22 x 220 square yards
So Central Park in New York City has 22 x 220 x 843 square yards.
Estimate Products Homework & Practice 4.2
Use rounding to estimate the product. Explain whether your estimate is an overestimate or an underestimate.
Question 1.
85 × 96
Answer:
After rounding 90x 100= 9,000, overestimate
Explanation:
85 x 96=8,160 after rounding it becomes 90 x 100 =9,000
as 85 is less than 90 and 96 is less than 100 so it is overestimate
Question 2.
41 × 21
Answer:
After rounding 40 x 20=800, underestimate
Explanation:
41 x 21 = 861 after rounding it becomes 40 x 20 = 800
as 41 is greater than 40 and 21 is also greater than 20 so it becomes underestimate
Use compatible numbers to estimate the product. Explain whether your estimate is an overestimate or an underestimate.
Question 3.
56 × 106
Answer:
56 x 106 = 5,936 and 55 x 100 = 5,500
as 5,936 > 5,500 ,So my estimate is overestimate
Explanation:
For 56 x 106 compatible numbers are 55 and 100 and its product is 5,500,
56 is greater than 55 and 106 is greater than 100,so the product of given numbers is greater than the product of compatible numbers, so my estimate is overestimate
Question 4.
23 × 597
Answer:
23 x 597 = 13,731 and 25 x 600 = 15,000
as 13,731 < 15,000, So my estimate is underestimate
Explanation:
For 23 x 597 compatible numbers are 25 and 600
56 is greater than 55 and 106 is greater than 100,so the product of given numbers is lesser than the products of compatible numbers, so my estimate is underestimate
Estimate the product
Question 5.
203 × 85
Answer:
203 x 85 = 17,255 and 200 x 90 = 18,000
as 17,255 < 18,000 So my estimate is underestimate
Explanation:
For 203 x 85 compatible numbers are 200 and 90
203 is greater than 200 and 85 is lesser than 90,But the product of given numbers is lesser than the product of compatible numbers so my estimate is underestimate
Question 6.
67 × 405
Answer:
67 x 405 = 27,135 and 70 x 400 = 28,000
as 27,135 < 28,000 So my estimate is underestimate
Explanation:
For 67 x 405 compatible numbers are 70 and 400
As 67 is less than 70 and 405 is greater than 400,but the product of given numbers is lesser than the product of compatible numbers, so my estimate is underestimate
Question 7.
Number Sense
Estimate 426 × 2,045. Is your answer an overestimate or an underestimate? Explain.
Answer:
426 x 2,045=871,170 and 430 x 2,000= 860,000
as 871,170 > 860,000 so mine is overestimate
Explanation:
For 426 x 2,045 compatible numbers are 430 and 2000
As 426 is less than and 430 and 2,045 is greater than 2,000 but the product of given numbers is greater than the product of compatible numbers, so my estimate is overestimate
Question 8.
Open-Ended
Write 2 three-digit numbers. Then estimate their product by rounding so that the answer is an underestimate.
Answer:
188 x 478 = 89,864
200 x 500 = 100,000
as 89,864 < 100,000 , so 188 x 478 is underestimate
Explanation:
To make the product as an underestimate let us take the 2 three-digit numbers as 188 and 478 and their compatible numbers 200 and 500,
As 188 is lesser than 200 and 478 is also less than 500 obviously the product becomes lesser than the product of compatible numbers and their product becomes underestimate.
Question 9.
Reasoning
Without multiplying, determine which estimate is closer to the actual product. Explain.

Answer:
The closer product to 21 x 372 is 20 x 400
Explanation :
If we compare 21 x 372 with 20 x 400 we see 20 is less than 21 which is very close and 372 is near to 400 and the result is much closer than when compared to the result of product of 25 x 400 as 25 is greater than to 21 and even 400 is greater than 372, so obviously the product is much far, So the closer product is 20 x 400
Question 10.
Modeling Real Life
Your cousin sells jars of jam at a farmers’ market. He sells 48 jars in 1 day for $12 each. About how much money does he earn in sales in 1 day?
Answer:
48 x $12 = $ 576 in 1 day
Explanation:
Given that cousin sells 48 jars in 1 day, each jar cost $12 , so the total cost per 1 day is product of number of jars X cost of 1 jar =48 x $12 = $ 576 in 1 day
So my cousin sells $ 576 in 1 day
Question 11.
DIG DEEPER!
SupersaurusA weighed 45 tons. About how many more pounds did an Argentinosaurus weigh than a Supersaurus?

Answer:
Argentinosaurus weighs 72,000 pounds more than a Supersaurus
Explanation:
As we know 1 ton = 2000 pounds, given Supersaurus weighed 45 tons = 45 x 2000=90,000 pounds and Argentinosaurus weighs 81 tons = 81 x 2000= 162,000 pounds, So 162,000 – 90,000= 72,000 means Argentinosaurus weigh 72,000 more than a Supersaurus
Review & Refresh
Use the figure.
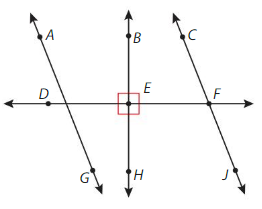
Question 12.
Name a pair of lines that appear to be parallel.
Answer:
( A,G ) and ( C,J) appear as parallel
Explanation:
In geometry, parallel lines can be defined as two lines in the same plane that are at equal distance from each other and never meet so ( A,G ) and ( C,J) appear as parallel
Question 13.
Name two lines that are perpendicular.
Answer:
( D, F ) and ( B, H ) are perpendicular
Explanation:
In geometry,
Two distinct lines intersecting each other at 90° or a right angle are called perpendicular lines
Question 14.
Name two intersecting lines.
Answer:
(D,F) and (C,J) are two intersecting lines
Explanation:
As the line DF are CJ are intersecting at point F so DF,CJ are called as intersecting lines
Lesson 4.3 Multiply by One-Digit Numbers
Explore and Grow
Use the area model and partial products to find 1,985 × 4.
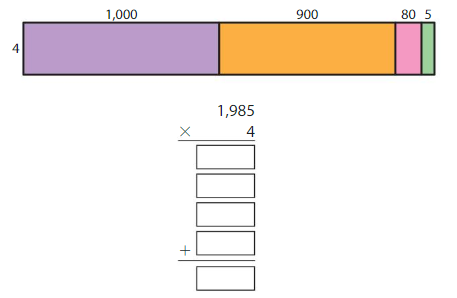
Answer:
1,985 x 4 = 7,940
Reasonable 7,940 is close to 8,000
Explanation :
Step 1: Multiply the ones. Regroup
4 x 5 ones = 20 ones, Regroup 20 ones as 2 tens and 0 ones
2
1985
x 4
0
Step 2 : Multiply the tens. Regroup
4 x 8 tens = 32 tens, 32 tens + 2 tens = 34 tens, Regroup 34 tens as
3 hundreds and 4 tens
3
1985
x 4
40
Step 3 : Multiply the hundreds. Regroup hundreds
4 x 9 hundreds = 36 hundreds, 36 hundreds + 3 hundreds = 39 hundreds
Regroup 39 hundreds as 3 thousands and 9 hundred
3
1985
x 4
940
Step 4 : Multiply the thousands. Add the regrouped thousands
4 x 1 thousands = 4 thousands,4 thousands +3 thousands=7 thousands
3
1985
x 4
7,940
1,985 x 4 = 7,940 Reasonable 7,940 is close to 8,000
Structure
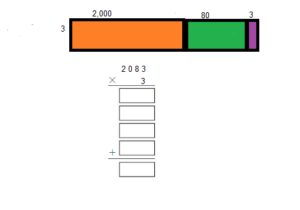
Explain how you can use an area model and partial products to find 2,083 × 3.
Answer:
2,083 x 3 = 6,249
Reasonable 6,249 is close to 6,000 or 6,300
Explanation:
Step 1: Multiply the ones.
3 x 3 ones = 9 ones,
2083
x 3
9
Step 2 : Multiply the tens. Regroup
3 x 8 tens = 24 tens, Regroup 24 tens as 2 hundreds and 4 tens
2
2083
x 3
49
Step 3 : Multiply the hundreds.
3 x 0 hundreds = 0 hundred, 0 hundred + 2 hundreds = 2 hundreds
2083
x 3
249
Step 4 : Multiply the thousands.
3 x 2 thousands = 6 thousands
2083
x 3
6,249
2,083 x 3 = 6,249 Reasonable 6,249 is close to 6,000 or 6,300
Think and Grow: Multiply by One-Digit a Number
Example
Find 8,902 × 4. Estimate ___35,608___

So 8,902 x 4 = 35,608. Reasonable 35,608 is close to 35,600
Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
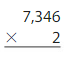
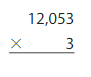
Answer:
1. 7,346 x 2= 14,692 Reasonable 14,692 and is close to 15,000
2. 12,053 x 3 = 36,159 Reasonable 36,159 and is close to 36,000
Explanation:
1.7,346 x 2=14,692
Step 1: Multiply the ones. Regroup
2 x 6 ones = 12 ones, Regroup 12 ones as 1 tens and 2 ones
1
7,346
x 2
2
Step 2 : Multiply the tens.
2 x 4 tens = 8 tens, 8 tens + 1 tens = 9 tens
7,346
x 2
92
Step 3 : Multiply the hundreds.
2 x 3 hundreds = 6 hundreds
7,346
x 2
692
Step 4 : Multiply the thousands.
2 x 7 thousands = 14 thousands
7,346
x 2
14,692
So 7,346 x 2 = 14,692 Reasonable 14,692 and is close to 15,000
2. 12,053 x 3 =36,159
Step 1: Multiply the ones.
3 x 3 ones = 9 ones
12,053
x 3
9
Step 2 : Multiply the tens. Regroup
3 x 5 tens = 15 tens, Regroup 15 tens as 1 hundred and 5 tens
1
12,053
x 3
59
Step 3 : Multiply the hundreds. Regroup
3 x 0 hundreds = 0 hundreds, Regroup 0 hundred +1 hundred = 1 hundred
12,053
x 3
159
Step 4 : Multiply the thousands.
3 x 2 thousands = 6 thousands
12,053
x 3
6,159
Step 5 : Multiply the ten thousands.
3 x 1 ten thousands = 3 ten thousands
12,053
x 3
36,159
12,053 x 3 = 36,159 Reasonable 36,159 is close to 36,000
Apply and Grow: Practice
Find the product. Check whether your answer is reasonable.
Question 3.
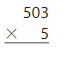
Answer:
503 x 5 = 2,515 Reasonable as 2,515 is close to 2,500
Explanation:
Step 1: Multiply the ones.
5 x 3 ones = 15 ones, Regroup 15 ones as 1 tens and 5 ones
1
503
x 5
5
Step 2 : Multiply the tens. Regroup
5 x 0 tens = 0 tens, 0 tens + 1 tens = 1 tens
503
x 5
15
Step 3 : Multiply the hundreds.
5 x 5 hundreds = 25 hundreds
503
x 5
2,515
503 x 5 = 2,515 Reasonable 2,515 is close to 2,500
Question 4.
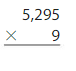
Answer:
5,295 x 9 = 47,655 Reasonable 47,655 is close to 48,000
Explanation:
Step 1: Multiply the ones. Regroup
9 x 5 ones = 45 ones, Regroup 45 ones as 4 tens and 5 ones
4
5,295
x 9
5
Step 2 : Multiply the tens. Regroup
9 x 9 tens = 81 tens, Regroup 81 tens+ 4 tens = 85 tens as 8 hundred and 5 tens
8
5,295
x 9
55
Step 3 : Multiply the hundreds. Regroup
9 x 2 hundreds = 18 hundreds, Regroup 18 hundred +8 hundred =
26 hundreds as 2 thousand and 6 hundreds
2
5,295
x 9
655
Step 4 : Multiply the thousands.
9 x 5 thousands = 45 thousands, Regroup 45 thousands+2 thousand=47 thousand
2
5,295
x 9
47,655
5,295 x 9 =47,655 Reasonable 47,655 is close to 48,000
Question 5.
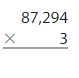
Answer:
87,294 x 3 = 2,61,882 Reasonable 2,61,888 is close to 2,60,000
Explanation:
Step 1: Multiply the ones. Regroup
3 x 4 ones = 12 ones, Regroup 12 ones as 1 ten and 2 ones
1
87,294
x 3
2
Step 2 : Multiply the tens. Regroup
3 x 9 tens = 27 tens, Regroup 27 tens + 1 ten = 28 tens as 2 hundred and 8 tens
2
87,294
x 3
82
Step 3 : Multiply the hundreds. Regroup
3 x 2 hundreds = 6 hundreds, Regroup 6 hundred +2 hundred = 8 hundreds
87,294
x 3
882
Step 4 : Multiply the thousands. Regroup
3 x 7 thousands = 21 thousands, Regroup as 2 ten thousands and 1 thousand
2
87,294
x 3
1882
Step 5 : Multiply the ten thousands.
3 x 8 ten thousands = 24 ten thousands,24 ten thousands+ 2 ten thousands
=26 ten thousands, regroup as 2 hundred thousand and 6 ten thousand
2
87,294
x 3
2,61,882
87,294 x 3 =2,61,882 Reasonable 2,61,888 is close to 2,60,000
Question 6.
399 × 2 = _____
Answer:
399 x 2 = 798 Reasonable 798 is close to 800
Explanation:
Step 1: Multiply the ones.
2 x 9 ones = 18 ones, Regroup 1 ones as 1 tens and 8 ones
1
399
x 2
8
Step 2 : Multiply the tens. Regroup
2 x 9 tens = 18 tens, 18 tens + 1 tens = 19 tens, Regroup 19 tens as 1 hundred and 9 tens
1
399
x 2
98
Step 3 : Multiply the hundreds.
2 x 3 hundreds = 6 hundreds, Regroup 6 hundreds+1 hundreds= 7 hundreds
399
x 2
798
So 399 x 2 = 798 Reasonable 798 is close to 800
Question 7.
33,184 × 2 = _____
Answer:
33,184 x 2 =66,368 Reasonable 66,368 is close to 66,000
Explanation:
Step 1: Multiply the ones.
2 x 4 ones =8 ones
33,184
x 2
8
Step 2 : Multiply the tens. Regroup
2 x 8 tens = 16 tens, Regroup 16 tens as 1 hundred and 6 tens
1
33,184
x 2
68
Step 3 : Multiply the hundreds. Regroup
2 x 1 hundreds = 2 hundreds, Regroup 2 hundreds +1 hundred = 3 hundreds
33,184
x 2
368
Step 4 : Multiply the thousands.
2 x 3 thousands = 6 thousands
33,184
x 2
6368
Step 5 : Multiply the ten thousands.
2 x 3 ten thousands = 6 ten thousands
33184
x 2
66,368
66,368 x 2 = 66,368 Reasonable 66,368 is close to 66,000
Question 8.
60,759 × 4 = _______
Answer:
60,759 x 4 = 2,43,036 Reasonable 2,43,036 is close to 2,40,000
Explanation:
Step 1: Multiply the ones.
4 x 9 ones =36 ones, Regroup 36 ones as 3 tens and 6 ones
3
60759
x 4
6
Step 2 : Multiply the tens. Regroup
4 x 5 tens = 20 tens, Regroup 20 tens + 3 tens = 23 tens as 2 hundred and 3 tens
2
60759
x 4
36
Step 3 : Multiply the hundreds. Regroup
4 x 7 hundreds = 28 hundreds, Regroup 28 hundred +2 hundred =30 hundreds as 3 thousand and 0 hundreds
3
60759
x 4
036
Step 4 : Multiply the thousands.
4 x 0 thousands = 0 thousands , Regroup 0 thousands + 3 thousands=3 thousands
60759
x 4
3036
Step 5 : Multiply the ten thousands.
4 x 6 ten thousands =24 ten thousands
60759
x 4
243068
60,759 x 4 = 2,43,036 Reasonable 2,43,036 is close to 2,40,000
Question 9.
A multiplex has 9 different movie theaters. Each theater has 455 seats. How many seats are in the multiplex?
Answer:
9 x 455 = 4,095 seats
Explanation:
Given a multiplex has 9 different movie theaters, and each theater has 455 seats , so total number of seats in the multiplex is 9 x 455=4,095
there are total 4,095 seats available.
Question 10.
An interstellar object travels 85,700 miles in 1 hour. How far does the object travel in 5 hours?
Answer:
85,770 x 5 = 428,850 miles
Explanation:
Given interstellar object travels 85,700 miles in 1 hour, in 5 hours the interstellar object will travel 85,770 x 5 = 428,850 miles
Question 11.
Without multiplying, determine how much greater 4,395 × 7 is than 4,395 × 6. Explain.
Answer:
it is more by 4,395
Explanation:
Comparing the values both the sides 4,395 is same and as 7 is one time more than 6 we multiply the value by one more time,
so the value of 4,395 x 7 to 4,395 x 6 is one time greater by 4,395
Question 12.
DIG DEEPER!
Find the missing digits.

Answer:
40,716 ÷ 3 = 13572 , Missing digits are 1 , 5, 2
Explanation:
To get the missing digits we divide 40,716 by 3
3)40716(13572
3 3x 1=3
4-3 =1 , we take next digit 0 so it becomes10
——
10 3 x 3=9
09 10- 9=1 , we take next digit 7 becomes 17
——
17 3x 5 = 15
15 17-15=2, we take next digit 1 becomes 21
——
21 3 x 7 = 21
21 21-21 = 0,then we take next digit becomes 6
——–
06 3 x 2 =6
6 6-6=0 and we ends as next no number
——
0
If 40,716 is divided by 3 we will get results as 13572 and missing digits are 1 , 5, 2
Think and Grow: Modeling Real Life
Example
A Cuvier’s beaked whale can dive 1,324 feet deeper than 4 times the depth a beluga whale can dive. How deep can a Cuvier’s beaked whale dive?

Write and solve an equation to find the depth.
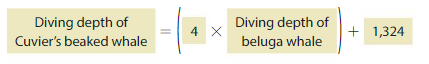
Let d represent the diving depth of a Cuvier’s beaked whale.
d = (4 × 2,123) + 1,324
= __8,492___ + 1,324
= __9,816___
A Cuvier’s beaked whale can dive 9,816 feet.
Show and Grow
Question 13.
The height of Chicago’s Willis Tower is 469 feet more than 2 times the height of the Gateway Arch. How tall is Willis Tower?

Answer:
The height of Chicago’s Willis Tower is 1,729 feet
Explanation:
Willis Tower = ( 2 X height of the Gateway Arch) +469 feet
Given the height of the Gateway Arch in St.Louis as 630 feet
Willis Tower = ( 2 X 630 feet ) + 469 feet
Willis Tower = 1,260 + 469 = 1,729 feet
Question 14.
DIG DEEPER!
The Amazon River is 350 miles shorter than 3 times the length of the Colorado River. How much longer is the Amazon River than the Mississippi River?
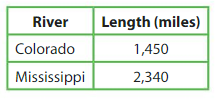
Answer:
Amazon River is 1,660 miles longer than the Mississippi River
Explanation:
Given Amazon River is = ( 3 x Colorado River )- 350 miles
Amazon River = (3 x 1,450)-350 miles
Amazon River = 4,350 – 350 = 4,000 miles
Now comparing Amazon River with Mississippi River = Mississippi River – Amazon River = 4,000-2,340=1,660 miles
So Amazon River is 1,660 miles longer than the Mississippi River
Multiply by One-Digit Numbers Homework & Practice 4.3
Find the product. Check whether your answer is reasonable.
Question 1.
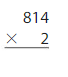
Answer:
814 x 2=1,628 Reasonable 1,624 is close to 1,600 or 2,000
Explanation:
Step 1: Multiply the ones.
2 x 4 ones = 8 ones.
814
x 2
8
Step 2 : Multiply the tens.
2 x 1 tens = 2 tens,
814
x 2
28
Step 3 : Multiply the hundreds.
2 x 8 hundreds = 16 hundreds
814
x 2
1,628
814 x 2=1,628 Reasonable 1,624 is close to 2,000 or 1,600
Question 2.
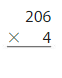
Answer:
206 x 4 = 824 Reasonable 824 is close to 1,000
Step 1: Multiply the ones.
4 x 6 ones = 24 ones. Regroup 24 ones as 2 tens and 4 ones
2
206
x 4
4
Step 2 : Multiply the tens. Regroup
4 x 0 tens = 0 tens, Regroup 0 tens + 2 tens = 2 tens
206
x 4
24
Step 3 : Multiply the hundreds.
4 x 2 hundreds = 8 hundreds
206
x 4
824
206 x 4=824 Reasonable 824 is close to 1,000
Question 3.
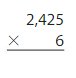
Answer:
2,425 x 6 = 14,550 Reasonable 14,550 is close to 14,500
Explanation:
Step 1: Multiply the ones. Regroup
6 x 5 ones = 30 ones, Regroup 30 ones as 3 tens and 0 ones
3
2,425
x 6
0
Step 2 : Multiply the tens. Regroup
6 x 2 tens = 12 tens, Regroup 12 tens+ 3 tens = 15 tens as 1 hundred and 5 tens
1
2425
x 6
50
Step 3 : Multiply the hundreds. Regroup
6 x 4 hundreds = 24 hundreds, Regroup 24 hundred +1 hundred = 25 hundreds as 2 thousand and 5 hundreds
2
2425
x 6
550
Step 4 : Multiply the thousands.
6 x 2 thousands = 12 thousands, Regroup 12 thousands+2 thousands as
14 thousand
2425
x 6
14,550
2,425 x 6 = 14,550 Reasonable 14,550 is close to 14,500
Question 4.
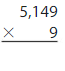
Answer:
5,149 x 9 = 46,341 Reasonable 46,341 is close to 46,000
Explanation:
Step 1: Multiply the ones. Regroup
9 x 9 ones = 81 ones, Regroup 81 ones as 8 tens and 1 ones
8
5149
x 9
1
Step 2 : Multiply the tens. Regroup
9 x 4 tens = 36 tens, Regroup 36 tens+ 8 tens =44 tens as 4 hundred and 4 tens
4
5149
x 9
41
Step 3 : Multiply the hundreds. Regroup
9 x 1 hundreds = 9 hundreds, Regroup 9 hundred +4 hundred =13 hundreds as
1 thousand and 3 hundreds
1
5149
x 9
341
Step 4 : Multiply the thousands.
9 x 5 thousands = 45 thousands, Regroup 45 thousands+1 thousand as 46 thousand
5149
x 9
46,341
5,149 x 9 = 46,341 Reasonable 46,341 is close to 46,000
Question 5.
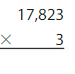
Answer:
17,823 x 3 = 53,469 Reasonable 53,469 is close to 50,000 or 53,000
Explanation:
Step 1: Multiply the ones.
3 x 3 ones = 9 ones
17,823
x 3
9
Step 2 : Multiply the tens.
3 x 2 tens = 6 tens
17,823
x 3
69
Step 3 : Multiply the hundreds. Regroup
3 x 8 hundreds = 24 hundreds, Regroup as 2 thousands and 4 hundreds
2
17823
x 3
469
Step 4 : Multiply the thousands. Regroup
3 x 7 thousands = 21 thousands, Regroup 21 thousands+ 2 thousands= 23 thousands as 2 ten thousands and 3 thousands
2
17823
x 3
3,469
Step 5 : Multiply the ten thousands.
3 x 1 ten thousands = 3 ten thousands ,Regroup 3 ten thousands + 2 ten thousands = 5 ten thousands
17823
x 3
53,469
17823 x 3 = 53,469 Reasonable 53,469 is close to 50,000 or 53,000
Question 6.
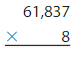
Answer:
61,837 x 8 = 494,696 Reasonable 494,696 is close to 500,000
Explanation:
Step 1: Multiply the ones.
8 x 7 ones =56 ones, Regroup 56 ones as 5 tens and 6 ones
5
61,837
x 8
6
Step 2 : Multiply the tens. Regroup
8 x 3 tens = 24 tens, Regroup 24 tens + 5 tens = 29 tens as 2 hundred and 9 tens
2
61,837
x 8
96
Step 3 : Multiply the hundreds. Regroup
8 x 8 hundreds = 64 hundreds, Regroup 64 hundred +2 hundred =66 hundreds as 6 thousand and 6 hundreds
6
61837
x 8
696
Step 4 : Multiply the thousands. Regroup
8 x 1 thousands = 8 thousands , Regroup 8 thousands + 6 thousands=
14 thousands as 1 ten thousand and 4 thousands
1
61837
x 8
4,696
Step 5 : Multiply the ten thousands. Regroup
8 x 6 ten thousands =48 ten thousands, Regroup 48 ten thousands +1 ten thousand = 49 ten thousands
61837
x 8
494,696
61,837 x 8 = 494,696 Reasonable 494,696 is close to 500,000
Find the product. Check whether your answer is reasonable.
Question 7.
4,257 × 5 = _______
Answer:
4,257 x 5 = 21,285 Reasonable 21,285 is close to 20,000
Explanation:
Step 1: Multiply the ones. Regroup
5 x 7 ones = 35 ones, Regroup 35 ones as 3 tens and 5 ones
3
4257
x 5
5
Step 2 : Multiply the tens. Regroup
5 x 5 tens = 25 tens, Regroup 25 tens+ 3 tens =28 tens as 2 hundreds and 8 tens
2
4257
x 5
85
Step 3 : Multiply the hundreds. Regroup
5 x 2 hundreds = 10 hundreds, Regroup 10 hundreds + 2 hundreds = 12 hundreds as 1 thousand and 2 hundreds
1
4257
x 5
285
Step 4 : Multiply the thousands.
5 x 4 thousands = 20 thousands, Regroup 20 thousands + 1 thousand =21 thousands
4257
x 5
21,285
4,257 x 5 = 21,285 Reasonable 21,285 is close to 20,000
Question 8.
6,702 × 6 = _____
Answer:
6,702 x 6 = 40,212 Reasonable 40,212 is close to 40,000
Explanation:
Step 1: Multiply the ones. Regroup
6 x 2 ones = 12 ones, Regroup 12 ones as 1 ten and 2 ones
1
6702
x 6
2
Step 2 : Multiply the tens. Regroup
6 x 0 tens = 0 tens, Regroup 0 tens+ 1 tens =1 tens
6702
x 6
12
Step 3 : Multiply the hundreds. Regroup
6 x 7 hundreds = 42 hundreds, Regroup 42 hundreds as 4 thousands and 2 hundreds
4
6702
x 6
212
Step 4 : Multiply the thousands.
6 x 6 thousands = 36 thousands, Regroup 36 thousands+ 4 thousand = 40 thousands
6702
x 6
40,212
6,702 x 6 = 40,212 Reasonable 40,212 is close to 40,000
Question 9.
28,956 × 7 = ______
Answer:
28,956 x 7 = 2,02,692 Reasonable 2,02,692 is close to 2,00,000
Explanation:
Step 1: Multiply the ones.
7 x 6 ones =42 ones, Regroup 42 ones as 4 tens and 2 ones
4
28,956
x 7
2
Step 2 : Multiply the tens. Regroup
7 x 5 tens = 35 tens, Regroup 35 tens + 4 tens = 39 tens as 3 hundreds and 9 tens
3
28956
x 7
92
Step 3 : Multiply the hundreds. Regroup
7 x 9 hundreds = 63 hundreds, Regroup 63 hundreds +3 hundred =
66 hundreds as 6 thousand and 6 hundreds
6
28956
x 7
692
Step 4 : Multiply the thousands. Regroup
7 x 8 thousands = 56 thousands , Regroup 56 thousands + 6 thousands=
62 thousands as 6 ten thousand and 2 thousands
6
28956
x 7
2692
Step 5 : Multiply the ten thousands. Regroup
7 x 2 ten thousands = 14 ten thousands, Regroup 14 ten thousands +
6 ten thousands = 20 ten thousands
28956
x 7
20,2692
28,956 x 7 = 2,02,692 Reasonable 2,02,692 is close to 2,00,000
Question 10.
A parking garage has 8 levels. There are 194 parking spots on each level. How many parking spots does the garage have?
Answer:
194 x 8 =1,552 parking spots
Explanation:
Given a parking garage has 8 levels and each level has 194 parking spots so total number of parking spots are 194 is multiplied by 8 ,194 x 8 =1,552 , there are total
1,552 parking spots available in the garage.
Question 11.
YOU BE THE TEACHER
Newton finds 16,041 × 8. Is Newton correct? Explain.
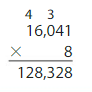
Answer:
Yes, Newton is correct
Explanation:
Step 1: Multiply the ones.
8 x 1 ones = 8 ones
16,041
x 8
8
Step 2 : Multiply the tens. Regroup
8 x 4 tens = 32 tens, Regroup 3 hundreds and 2 tens
3
16,041
x 8
28
Step 3 : Multiply the hundreds. Regroup
8 x 0 hundreds = 0 hundreds, Regroup 0 hundreds +3 hundreds = 3 hundreds
16,041
x 8
328
Step 4 : Multiply the thousands. Regroup
8 x 6 thousands = 48 thousands , Regroup 48 thousands as 4 ten thousand and 8 thousands
4
16,041
x 8
8328
Step 5 : Multiply the ten thousands. Regroup
8 x 1 ten thousands = 8 ten thousands, Regroup 8 ten thousands + 4 ten thousands = 12 ten thousands
16,041
x 8
128,328
As the value of 16,041 x 8 = 128,328, Yes Newton is correct
Question 12.
DIG DEEPER!
Write a different multiplication problem that has the same product as 726 × 5.
Answer:
726 x 5 =3,630
605 x 6 =3,630
Explanation:
we divide the product 3630 by 6

we get Quotient as 605 means when we multiply 605 x 6 we get the same product result 3,630 similarly when 726 x 5 is multiplied,
So 726 x 5 = 605 x 6
Question 13.
Modeling Real Life
The land area of Florida is 8,056 square miles more than 5 times the land area of Vermont. What is the land area of Florida?
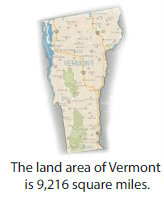
Answer:
The land area of Florida is 49,496 square miles
Explanation:
Given land area of Florida is 8,056 square miles more than 5 times the land area of Vermont and land area of Vermont is 9,216 square miles
land area of Florida = ( 5 x land area of Vermont ) + 9,216 square miles
land area of Florida = ( 5 x 8056 ) + 9,216 square miles
land area of Florida =40280+9,216 = 49,496 square miles
So the land area of Florida is 49,496 square miles.
Question 14.
DIG DEEPER!
A solar farm has 6 rectangular arrays of solar panels. Each array has 105 rows with 8 panels in each row. How many solar panels are on the solar farm?
Answer:
6 x 105 x 8 = 5,040 panels
Explanation:
Given a solar farm has 6 rectangular arrays of solar panels and each array has 105 rows with 8 panels in each row so there are 105 x 8 = 840 panels and we have total 6 rectangular arrays
So total number of solar panels available are 6 x 840 =5,040 panels
Review & Refresh
Multiply.
Question 15.
2 × \(\frac{1}{4}\)
Answer:
2 x 1/4=1/2 or 1 by 2
Explanation:
When 2 is multiplied by fraction of 1,4 we get 2 x 1/4 as 1/2 or 1 by 2
Question 16.
3 × \(\frac{2}{6}\)
Answer:
3 x 2/6 = 6/6 =1
Explanation:
When 3 is multiplied by fraction of 2,6 we get 3 x 2/6 as 6/6 equals to 1
Question 17.
1 × \(\frac{7}{10}\)
Answer:
1 x 7/10 = 7/10 or 0.7
Explanation:
When 1 is multiplied by fraction of 7,10 we get 1 x 7/10 as 7/10 or 0.7
Lesson 4.4 Multiply by Two-Digit Numbers
Explore and Grow
Use the area model and partial products to find 28 × 13.
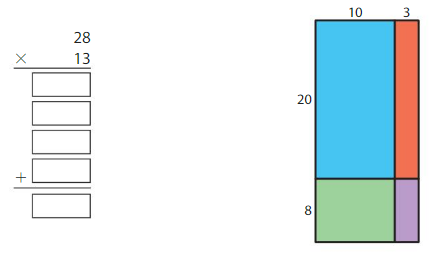
Answer:
28 x 13 = 364 Reasonable 364 is close to 400
Explanation:
Step 1: Multiply 28 by 3 ones. Regroup
3 ones x 28 = 84 ones
2
28
x 13
84
Step 2: Multiply 28 by 1 tens or 10, Regroup
1 tens x 28 =28 tens =280 ones
28
x 13
84
280
Step 3 : Add the partial products.
28
x 13
84
+280
364
28 x 13 =364 Reasonable 364 is close to 400
Repeated Reasoning
Explain how you can use an area model and partial products to find 128 × 13.
Answer:
128 x 13 =1,664 Reasonable 1,664 is close to 1,600
Explanation:
Step 1: Multiply 128 by 3 ones. Regroup
3 ones x 128 = 384 ones
2
128
x 13
384
Step 2: Multiply 128 by 1 tens or 10, Regroup
1 tens x 128 =128 tens =1280 ones
128
x 13
384
1280
Step 3 : Add the partial products.
128
x 13
384
+ 1280
1664
128 x 13 =1,664 Reasonable 1,664 is close to 1,600
Think and Grow: Multiply by a Two-Digit Number
Example
Find 312 × 82. Estimate _______

So 312 x 82= 25,584 Reasonable 25,584 is close to 25,500
Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
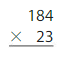
Answer:
184 x 23 = 4,232 Reasonable 4,232 is close to 4,000
Explanation:
Step 1: Multiply 184 by 3 ones. Regroup
3 ones x 184 = 552 ones
21
184
x 23
552
Step 2: Multiply 184 by 2 tens or 20, Regroup
2 tens x 184 =368 tens =3680 ones
1
184
x 23
552
3680
Step 3 : Add the partial products.
184
x 23
552
+3680
4232
184 x 23 =4,232 Reasonable 4,232 is close to 4,000
Question 2.
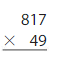
Answer:
817 x 49 = 40,033 Reasonable 40,033 is close to 40,000
Explanation:
Step 1: Multiply 817 by 9 ones. Regroup
9 ones x 817 = 7353 ones
1 6
817
x 49
7353
Step 2: Multiply 817 by 4 tens or 40, Regroup
4 tens x 817 =3,268 tens =32680 ones
2
817
x 49
7353
32680
Step 3 : Add the partial products.
817
x 49
7353
+32680
40033
817 x 49 =40,033 Reasonable 40,033 is close to 40,000
Question 3.
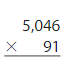
Answer:
5046 x 91 = 4,59,186 Reasonable 4,59,186 is close to 4,60,000
Explanation:
Step 1: Multiply 5046 by 1 ones. Regroup
1 ones x = 5046 ones
5046
x 91
5046
Step 2: Multiply 5046 by 9 tens or 90, Regroup
9 tens x 5046 =45,414 tens =45,4140 ones
45
5046
x 91
5046
454140
Step 3 : Add the partial products.
5046
x 91
5046
+ 454140
4,59,186
5046 x 91 = 4,59,186 Reasonable 4,59,186 is close to 4,60,000
Apply and Grow: Practice
Find the product. Check whether your answer is reasonable.
Question 4.
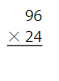
Answer:
96 x 24 = 2,304 Reasonable 2,304 is close to 2,300
Explanation:
Step 1: Multiply 96 by 4 ones. Regroup
4 ones x 96 = ones
2
96
x 24
384
Step 2: Multiply 96 by 2 tens or 20, Regroup
2 tens x 96 =192 tens =1920 ones
1
96
x 24
384
1920
Step 3 : Add the partial products.
96
x 24
384
+1920
2,304
96 x 24 = 2,304 Reasonable 2,304 is close to 2,300
Question 5.
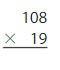
Answer:
108 x 19 = 2,052 Reasonable 2,052 is close to 2,000
Explanation:
Step 1: Multiply 108 by 9 ones. Regroup
9 ones x 108 = 972 ones
7
108
x 19
972
Step 2: Multiply 108 by 1 tens or 10, Regroup
1 tens x 108 =108 tens =1080 ones
108
x 19
972
1080
Step 3 : Add the partial products.
108
x 19
972
+1080
2,052
108 x 19 = 2,052 Reasonable 2,052 is close to 2,000
Question 6.
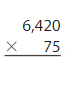
Answer:
6420 x 75 = 4,81,500 Reasonable 4,81,500 is close to 5,00,000
Explanation:
Step 1: Multiply 6420 by 5 ones. Regroup
5 ones x 6420 = 32100 ones
21
6420
x 75
32,100
Step 2: Multiply 6420 by 7 tens or 70, Regroup
7 tens x 6420 =44,940 tens =449400 ones
6420
x 75
32100
449400
Step 3 : Add the partial products.
6420
x 75
32100
+449400
481500
6420 x 75 = 4,81,500 Reasonable 4,81,500 is close to 5,00,000
Question 7.
802 × 41 = ______
Answer:
802 x 41 = 32,882 Reasonable 32,882 is close to 33,000
Explanation:
Step 1: Multiply 802 by 1 ones. Regroup
1 ones x 802 = 802 ones
802
x 41
802
Step 2: Multiply 802 by 4 tens or 40, Regroup
4 tens x 802 =3208 tens =32080 ones
802
x 41
802
32080
Step 3 : Add the partial products.
802
x 41
802
+32080
32,882
802 x 41 = 32,882 Reasonable 32,882 is close to 33,000
Question 8.
577 × 86 = _____
Answer:
577 x 86 = 49,622 Reasonable 49,622 is close to 50,000
Explanation:
Step 1: Multiply 577 by 6 ones. Regroup
6 ones x 577 =3,462 ones
4 4
577
x 86
3462
Step 2: Multiply 577 by 8 tens or 80, Regroup
8 tens x 577 =4616 tens =46160 ones
577
x 86
3462
46160
Step 3 : Add the partial products.
577
x 86
3462
+46160
49622
577 x 86 = 49,622 Reasonable 49,622 is close to 50,000
Question 9.
9,513 × 67 = _____
Answer:
9513 x 67 = 6,37,371 Reasonable 6,37,371 is close to 6,50,000
Explanation:
Step 1: Multiply 9513 by 7 ones. Regroup
7 ones x 9513 =66,591 ones
2
9513
x 67
66,591
Step 2: Multiply 9513 by 6 tens or 60, Regroup
6 tens x 9513 =57078 tens = 570780 ones
9513
x 67
66591
570780
Step 3 : Add the partial products.
9513
x 67
66591
+570780
637371
9513 x 67 = 6,37,371 Reasonable 6,37,371 is close to 6,50,000
Question 10.
Is 6,364 a reasonable product for 706 × 45? Explain your reasoning.
Answer:
No 6,344 is not a reasonable product for 706 x 45 as 706 x 45 = 31,770
Explanation:
When we multiply 706 x 45 we get result as 31,770
as 6,364 is not at all close to 31,770, So 6,344 is not reasonable product for 706 x 45
Question 11.
DIG DEEPER!
Which two-digit number when multiplied by itself has a product of 625?
Answer:
25, because 25 x 25 = 625
Explanation:
Given that a two-digit number when multiplied by itself has a product of 625
lets take the two digit number as X and X x X = 625
X2=625 so X = square root of 625 = √625= √25 x 25, X = 25
So 25 when multiplied by itself we get 625
Think and Grow: Modeling Real Life
Example
A blood bank receives 58 donors in 1 day. Each person donates 1 pint, or about 473 milliliters of blood. About how many milliliters of blood are donated that day?

Multiply the number of people by the amount of blood each person donates to find the total amount of blood donated.
Multiply 473 and 58.
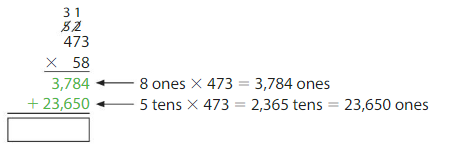
So, about _27,434_ milliliters of blood are donated that day.
Show and Grow
Question 12.
A store sells 15 drones. How much money does the store collect?

Answer:
248 x 15 = $3,720
Explanation:
Given the cost of drone as $248 and the store sells 15 drones, total money collected in the store is $248 x 15=$3,720
Step 1: Multiply 248 by 5 ones. Regroup
5 ones x 248 = 1240 ones
4
248
x15
1240
Step 2: Multiply 248 by 1 tens or 10, Regroup
1 tens x 248 =248 tens = 2480 ones
248
x 15
1240
2480
Step 3 : Add the partial products.
248
x 15
1240
+2480
3720
The store collected total amount is $3,720
Question 13.
What is the area of the soccer field?
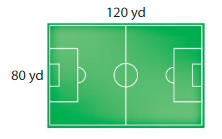
Answer:
The area of the soccer field is 120 x 80 =9,600 square yards
Explanation:
Step 1: Multiply 120 by 0 ones.
0 ones x 120 =120 ones
120
x 80
000
Step 2: Multiply 120 by 8 tens or 80, Regroup
8 tens x 120 =960 tens = 9600 ones
120
x 80
000
9600
Step 3 : Add the partial products.
120
x 80
000
+9600
9600
The total area of the soccer field is 120 x 80 =9,600 square yards
Question 14.
The Cassini spacecraft orbited Saturn for 13 years and 77 days. Three of those years were leap years. For how many days did the Cassini spacecraft orbit Saturn? Justify your answer.
Answer:
Cassini spacecraft orbited Saturn for total 4,825 days
Explanation:
Given the Cassini spacecraft orbited Saturn for 13 years and 77 days and three of those years were leap, First we need to convert years to days and add to 77 days, we know each year has 365 days so first we multiply 365 with 13= 365 x 13 = 4,745 days,
365
x 13
4,745
And we know leap year has 366 days and in 13 years we have 3 leap years so we will add 3 more days to 4,745+3=4,748 days or
adding 3 days as it is saying in 13 years leap years 3 years are leap to 4,745 days=4,745+3=4,748 days
3 days as 3 are leap years
4745
+ 3
4,748
Now adding 4,748 and 77 days
4,748
+ 77
4,825
Cassini spacecraft orbited Saturn for total 4,825 days
Multiply by Two-Digit Numbers Homework & Practice 4.4
Find the product. Check whether your answer is reasonable.
Question 1.
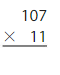
Answer:
107 x 11 =1,177 reasonable 1,177 is close to 1,000 or 12,00
Explanation:
Step 1: Multiply 107 by 1 ones.
1 ones x 107 =107 ones
107
x 11
107
Step 2: Multiply 107 by 1 tens or 10, Regroup
1 tens x 107 =107 tens = 1070 ones
107
x 11
107
1070
Step 3 : Add the partial products.
107
x 11
107
+1070
1,177
107 x 11 =1,177 reasonable 1,177 is close to 1,000 or 12,00
Question 2.
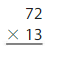
Answer:
72 x 13 = 936 reasonable 936 is close to 1,000
Explanation:
Step 1: Multiply 72 by 3 ones.
3 ones x 72 =216 ones
72
x 13
216
Step 2: Multiply 72 by 1 tens or 10, Regroup
1 tens x 72 =72 tens = 720 ones
72
x 13
216
720
Step 3 : Add the partial products.
72
x 13
216
+720
936
72 x 13 =936 reasonable 936 is close to 1,000
Question 3.
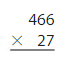
Answer:
466 x 27 = 12,582 reasonable 12,582 is close to 13000 or 12,600
Explanation:
Step 1: Multiply 466 by 7 ones.
7 ones x 466 = 3262 ones
44
466
x 27
3262
Step 2: Multiply 466 by 2 tens or 20, Regroup
2 tens x 466 =932 tens = 9320 ones
466
x 27
3262
9320
Step 3 : Add the partial products.
466
x 27
3262
+9320
12,582
466 x 27 = 12,582 reasonable 12,582 is close to 13000 or 12,600
Find the product. Check whether your answer is reasonable.
Question 4.
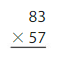
Answer:
83 x 57 = 4,731 reasonable 4731 is close to 5,000
Explanation:
Step 1: Multiply 83 by 7 ones.
7 ones x 83 = 581 ones
2
83
x 57
581
Step 2: Multiply 83 by 5 tens or 50, Regroup
5 tens x 83 =415 tens = 4150 ones
83
x 57
518
4150
Step 3 : Add the partial products.
83
x 57
581
+4150
4731
83 x 57 = 4,731 reasonable 4731 is close to 5,000
Question 5.
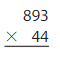
Answer:
893 x 44 = 39,292 reasonable 39,292 is close to 40,000
Explanation:
Step 1: Multiply 893 by 4 ones.
4 ones x 893 = 3,572 ones
3 1
893
x 44
3572
Step 2: Multiply 893 by 4 tens or 40, Regroup
4 tens x 893 =3572 tens = 35720 ones
893
x 44
3572
35720
Step 3 : Add the partial products.
893
x 44
3572
+35720
39292
893 x 44 = 39,292 reasonable 39,292 is close to 40,000
Question 6.
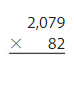
Answer:
2079 x 82 = 170,478 reasonable 170,478 is close to 170,000
Explanation:
Step 1: Multiply 2079 by 2 ones.
2 ones x 2079 = 4,158 ones
11
2079
x 82
4158
Step 2: Multiply 2079 by 8 tens or 80, Regroup
8 tens x 2079 = 16,632 tens = 16,6320 ones
2079
x 82
4158
16,6320
Step 3 : Add the partial products.
2079
x 82
4158
+16,6320
170478
2079 x 82 = 170,478 reasonable 170,478 is close to 170,000
Question 7.
6,082 × 25 = ______
Answer:
6,082 x 25 = 152,050 reasonable 152,050 is close to 150,000
Explanation:
Step 1: Multiply by 5 ones.
5 ones x 6082 = 30,410 ones
41
6082
x 25
30410
Step 2: Multiply 6082 by 2 tens or 20, Regroup
2 tens x 6082 = 12164 tens = 121640 ones
6082
x 25
30410
12,1640
Step 3 : Add the partial products.
6082
x 25
30410
+121640
15,2050
6,082 x 25 = 152,050 reasonable 152,050 is close to 150,000
Question 8.
158 × 96 = ______
Answer:
158 x 96 = 15,168 reasonable 15168 is close to 15,000
Explanation:
Step 1: Multiply 158 by 96 ones.
6 ones x 158 = 948 ones
34
158
x 96
948
Step 2: Multiply 158 by 9 tens or 90, Regroup
9 tens x 158 =1422 tens = 14220 ones
57
158
x 96
948
14220
Step 3 : Add the partial products.
158
x 96
948
+14220
15,168
158 x 96 = 15,168 reasonable 15168 is close to 15,000
Question 9.
98 × 74 = ______
Answer:
98 x 74 = 7252 reasonable 7252 is close to 7000
Explanation:
Step 1: Multiply 98 by 4 ones.
4 ones x 98 = 392 ones
3
98
x74
392
Step 2: Multiply 98 by 7 tens or 70, Regroup
7 tens x 98 = 686 tens = 6860 ones
98
x74
392
6860
Step 3 : Add the partial products.
98
x 74
392
+6860
7252
98 x 74 = 7252 Reasonable 7252 is close to 7000
Question 10.
Writing
Why is one partial product always greater than the other partial product when multiplying by a two-digit number?
Answer:
The first partial product cannot have a multiplicand greater than 9.
The second partial product cannot have a multiplicand less than 10.
So one partial product is always greater than the other partial product when multiplying by a two-digit number
Explanation:
Lets multiply 315 with 26 a two digit number(26)
The multiplicand 26 can be decomposed to (20 + 6). The first partial product is the product of 315 x 6= 1890. The second partial product is the product of 315 x 20 = 6300.
Here the first partial product cannot have a multiplicand greater than 9 which is 6 and the second partial product cannot have a multiplicand less than 10 which is 20,therefore one partial product always greater than the other partial product when multiplying by a two-digit number.
Question 11.
DIG DEEPER!
Use the numbers 2, 4, 6, and 8 once to form the greatest product.
Answer:
The greatest product is 806 x 42 = 33,852
Explanation:
Given numbers are 2,4,6,8 , first greatest number among given numbers are 8 and next is 6 then 4 and then 2 we have the pattern given as 3 digit number multiplied by 2 digit number, so first 3 great digits numbers are 8,6,0 in these the biggest is 8 then 6 but the middle digit is already given as 0 so the first three digits are 806,
Now the left two digits are 2,4 now to make the greatest 2 digit number we take from the combination of 2 and 4 ,in these the greatest number is 4 first then 2 making it as 42 as second greatest two digit number,
therefore the product is 806 X 42 =33,852 making it as the greatest product.
806
x 42
33,852
Question 12.
Modeling Real Life
A store sells 79 virtual reality headsets. How much money does the store collect?

Answer:
$125 X 79 = $9,875
Explanation:
Given that the virtual reality headset cost as $ 79 and the store sells 79 virtual reality headsets, Total money collected by the store is $125 x 79=$9,875
125
x 79
9,875
Question 13.
Modeling Real Life
Your friend needs a trumpet for 12 months. She can rent a trumpet for $42 each month and pay a yearly fee of $25, or she can buy a trumpet for $550. Should she buy or rent the trumpet? Explain.
Answer:
Friend should take the trumpet for rent because it is costing less than buying it.
Rent for 12 months is $529
Buying costs to $550.
Explanation:
Friend needs a trumpet for 12 months and rent of trumpet is $42 for each month, so for 12 months it costs as $42 x 12= $504 and also has to pay a yearly fee of $25 means total cost for entire 12 months is $504+$25= $529.
Given that if she buys its cost to $550, now comparing between rent and buy as $529<$550 ,as rent is less than buying she has to take it for rent so that she can save $21
Review & Refresh
Use a place value chart to answer the question.
Question 14.
4,000 is 10 times as great as what number?
Answer:
4,000 is 10 times as great as 400
Explanation:
Lets us take the number as X,
Given 4,000 is 10 times as great as X means X x 10= 4,000
the value of X equals to 4000 x 1/10= 4000/10=400
X=400 therefore 4,000 is 10 times as great as 400
Question 15.
50 is \(\frac{1}{10}\) of what number?
Answer:
50 is \(\frac{1}{10}\) of 500
Explanation:
Let the number be X and given 50 = 1/10 x X, so X = 50 x 10 = 500
Lesson 4.5 Multiply by Multi-Digit Whole Numbers
Explore and Grow
Use any strategy to find each product.
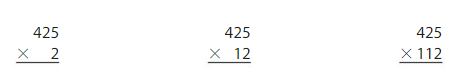
Answer:
425 x 2 = 850 , 425 x 12 =5,100 , 425 x 112 = 47,600
Explanation:
1) 425 x 2 =850, multiply 425 by 2 ones or 2
1
425
x 2
850
2) 425 x 12 = 51,00
Explanation:
Step 1 : Multiply 425 by 2 ones or 2
1
425
x 12
850
Step 2 : Multiply 425 by 1 tens or 10.
425
x 12
850
4250
Step 3: Add the partial products.
425
x 12
850
+4250
5100
3) 425 x 112 = 47,600
Explanation:
Step 1 : Multiply 425 by 2 ones or 2
1
425
x112
850
Step 2 :Multiply 425 by 1 tens or 10.
425
x 112
850
4250
Step 3 : Multiply 425 by 1 hundred or 100. Regroup
425
x 112
850
4250
42500
Step 4: Add the partial products.
425
x 112
850
4250
+ 42500
47,600
Structure
How can you use the first product to find the second product? How can you use the second product to find the third product?
Answer:
Yes we can use the first product to find the second product and use the second product to find the third product.
Explanation:
For example let the numbers be 324 x 125 = 40,500
First product result will be product of 324 is first multiplied by last digit 5 at ones place as 324 x 5=1620
Second product result will be the first product results in addition to multiple of 324 with the second digit which is at tens place as 324 x 20 and add to first product results, so here we have used the first product result to find the second product results
324
x25
1620
6480
8100
Third product result will be the second product results and we add it to the multiple of product of third digit which is at hundreds place as 324 x 100 and add to second product results, so here we have used the second product result to find the third product results
324
x125
8100
32400
40,500
Think and Grow: Multiply Multi-Digit Whole Numbers
Example
Find 2,043 × 132. Estimate __2,69,676_____

2,043 x 132 = 2,69,676 reasonable 2,69,676 is close to 2,70,000
Show and Grow
Find the product. Check whether your answer is reasonable.
Question 1.
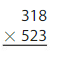
Answer:
318 x 523 =166,314 reasonable 1,66,314 is close to 1,70,000
Explanation:
Step 1 : Multiply 318 by 3 ones or 3
2
318
x 523
954
Step 2 :Multiply 318 by 2 tens or 20.
1
318
x 523
954
6360
Step 3 : Multiply 318 by 5 hundred or 500. Regroup
318
x 523
954
6360
159000
Step 4: Add the partial products.
318
x 523
954
6360
+159000
166314
So 318 x 523 =166,314 reasonable 1,66,314 is close to 1,70,000
Question 2.
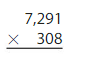
Answer:
7291 x 308 = 2,245,628 reasonable 2,245,628 is close to 2,300,000
Explanation:
Step 1 : Multiply 7291 by 8 ones or 8
27
7291
x 308
58328
Step 2 :Multiply 7219 by 0 tens .
7291
x 308
58328
00000
Step 3 : Multiply 7219 by 3 hundred or 300. Regroup
2
7291
x 308
58328
00000
2187300
Step 4: Add the partial products.
7291
x 308__
58328
00000
+2187300
2245628
7291 x 308 = 2,245,628 Reasonable 2,245,628 is close to 2,300,000
Apply and Grow: Practice
Find the product. Check whether your answer is reasonable.
Question 3.
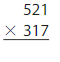
Answer:
521 x 317 = 1,65,157 Reasonable 165,157 is close to 1,700,00
Explanation:
Step 1 : Multiply 521 by 7 ones or 7
1
521
x 317
3647
Step 2 :Multiply 521 by 1 tens or 10 .
521
x 317
3647
5210
Step 3 : Multiply 521 by 3 hundred or 300. Regroup
521
x 317
3647
5210
156300
Step 4: Add the partial products.
521
x 317
3647
5210
+156300
165157
521 x 317 = 1,65,157 Reasonable 165,157 is close to 1,700,00
Question 4.
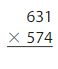
Answer:
631 x 574 = 3,62,194 Reasonable 3,62,194 is close to 3,60,000
Explanation:
Step 1 : Multiply 631 by 4 ones or 4
631
x 574
2524
Step 2 :Multiply 631 by 7 tens or 70 .
631
x 574
2524
44170
Step 3 : Multiply 631 by 5 hundred or 500. Regroup
631
x 574
2524
44170
315500
Step 4: Add the partial products.
631
x 574
2524
44170
+315500
362194
631 x 574 = 3,62,194 Reasonable 3,62,194 is close to 3,60,000
Question 5.
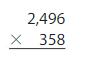
Answer:
2496 x 358 =8,93,568 Reasonable 8,93,568 is close to 9,00,000
Explanation:
Step 1 : Multiply 2496 by 8 ones or 8
374
2496
x 358
19,968
Step 2 :Multiply 2496 by 5 tens or 50 .
243
2496
x 358
19968
124800
Step 3 : Multiply 2496 by 3 hundred or 300. Regroup
2496
x 358
19968
124800
748800
Step 4: Add the partial products.
2496
x 358
19968
124800
748800
893568
2496 x 358 =8,93,568 Reasonable 8,93,568 is close to 9,00,000
Question 6.
155 × 956 = ______
Answer:
155 x 956 = 1,48,180 Reasonable 1,48,180 is close to 1,50,000
Explanation:
Step 1 : Multiply 155 by 6 ones or 6
33
155
x 956
930
Step 2 :Multiply 155 by 5 tens or 50 .
22
155
x 956
930
7750
Step 3 : Multiply 155 by 9 hundred or 900. Regroup
155
x 956
930
7750
139500
Step 4: Add the partial products.
155
x 956
930
7750
139500
148180
155 x 956 = 1,48,180 Reasonable 1,48,180 is close to 1,50,000
Question 7.
748 × 239 = ______
Answer:
748 x 239 = 1,78,772 Reasonable 1,78,772 is close to or 1,80,000 or 2,00,000
Explanation:
Step 1 : Multiply 748 by 9 ones or 9
47
748
x239
6732
Step 2 :Multiply 748 by 3 tens or 30 .
12
748
x 239
6732
22440
Step 3 : Multiply 748 by 2 hundred or 200. Regroup
1
748
x 239
6732
22440
149600
Step 4: Add the partial products.
748
x 239___
6732
22440
+149600
178772
748 x 239 = 1,78,772 Reasonable 1,78,772 is close to or 1,80,000 or 2,00,000
Question 8.
1,907 × 218 = ______
Answer:
1907 x 218 = 415,726 Reasonable 4,15,726 is close to 4,20,000
Explanation:
Step 1 : Multiply 1907 by 8 ones or 8
7 5
1907
x 218
15256
Step 2 :Multiply 1907 by 1 tens or 10 .
1907
x 218
15256
19070
Step 3 : Multiply 1907 by 2 hundred or 200. Regroup
1 1
1907
x 218
15256
19070
381400
Step 4 :Add the partial products.
1907
x 218
15256
19070
+381400
415726
1907 x 218 = 415,726 Reasonable 4,15,726 is close to 4,20,000
Question 9.
The delta of the Nile River is about 150 miles wide. How many feet wide is the delta?
Answer:
5280 x 150 = 7,92,000 feet
Explanation:
Given the delta of the Nile River is about 150 miles wide and 1 mile is equal to 5,280 feet so total feet of Nile River is product of 5280 and 150 , 5280 x 150 = 7,92,000 feet
Question 10.
Reasoning
When you multiply a three-digit number by a four-digit number, what is the greatest number of digits the product can have? Explain.
Answer:
999 x 9999 = 9,989,001 the product will have 7 greatest number of digits.
Explanation:
We know 9 is the greatest digit, so the greatest three-digit number is 999 and the greatest four-digit number is 9999 when 999 x 9999 we get the results as 999 x 9999 = 9,989,001 which consists of total 7 digits in it, therefore when we multiply a three-digit number by a four-digit number, we get 7 greatest number of digits in the results.
Question 11.
DIG DEEPER!
Find the missing digit so that both products are the same.
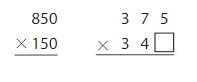
Answer:
The missing digit is 0, as 850 x 150= 1,27,500 and 375 x 340 = 1,27,500 are same
Explanation:
To find the missing digit first we multiply 850 X 150 we get 1,27,500 and it is mentioned that the products are same means
850 x 150= 1,27,500 = 375 x 34___. So to find the missing digit from 34___, we divide 1,27,500 by 375 and the result is 340. So obviously the missing digit is 0.
Think and Grow: Modeling Real Life
Example
The employees at a baseball bat factory need to make 350,000 bats in 6 months. They make 2,750 bats each day and work 127 days in the 6 months. Do the employees make enough bats?

Multiply the number of bats produced each day by the number of days.
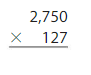
Compare the number of bats produced to the number of bats needed.
2750 x 127 = 3,49,250 bats as 3,49,250 < 3,50,000
The employees does not___ make enough bats.
Explanation:
Each day the employees make 2750 bats and has worked 127 days in 6 months , so in 6 months the employees have made
2750 x 127 =3,49,250 bats, given that the employees at a baseball bat factory need to make 350,000 bats in 6 months, now comparing we are getting difference as the employees made to the required number of bats.
We are getting employees made is less when compared to the needed number of bats as 3,49,250 < 3,50,000. Both are not matching so employees have not made enough bats.
Show and Grow
Question 12.
The drivers at a warehouse need to deliver 40,000 packages each day. The warehouse has 128 trucks. Each truck has 350 packages. The drivers deliver all of the packages on the trucks. Do the warehouse drivers deliver enough packages?
Answer:
350 x 128= 44,800 and required is 40,000 as compared it is less,
Yes, the warehouse drivers can deliver enough packages each day.
Explanation:
Each truck has 350 packages and the ware house has 128 trucks, so the total number of packages in a day are 350 x 128 = 44,800 packages. Now comparing the drivers need only 40,000 packages each day as 44,800 is greater than 40,000, 44,800>40,000.Easily the drivers can deliver the packages each day.
Question 13.
A school buys 5 tablets and 5 laptops. Each tablet costs $379. Each laptop costs $449. How much more does the school pay for laptops than it pays for tablets?
Answer:
Tablets costs = $379 x 5= $1,895
Laptop costs = $449 x 5 = $2,245, Laptop to Tablets = $ 2,245-$1,895=$350, School pays $350 more.
Explanation:
School buys 5 tablets and 5 laptops and each tablet costs $379 and laptop costs $449,the total amount for tablets costs = $379 x 5= $1,895 and for laptop costs = $449 x 5 = $2,245,Now comparing the costs of laptops to tablets $2,245 to $1895 we are getting a difference of $350 among them. So the school pays $379
Question 14.
DIG DEEPER!
A koala sleeps 18 hours each day. How many minutes does the koala sleep in 1 year?

Answer:
The koala sleeps 3,94,200 minutes in 1 year.
Explanation:
We know that in 1 hour equals to 60 minutes and in 1 year we have total 365 days a koala sleep 18 hours each day means
18 x 60 =1,080 minutes in each day, so in 1 year koala sleeps 1080 minutes x 365= 3,94,200 minutes in 1 year.
Multiply by Multi-Digit Whole Numbers Homework & Practice 4.5
Find the product. Check whether your answer is reasonable.
Question 1.
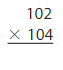
Answer:
102 x 104 =10,608 Reasonable 10,608 is close to 10,000
Explanation:
Step 1 : Multiply 102 by 4 ones or 4
102
x 104
408
Step 2 : Multiply 102 by 0 tens .
102
x 104
408
000
Step 3 : Multiply 102 by 1 hundred or 100. Regroup
102
x 104
408
000
10200
Step 4 : Add the partial products.
102
x 104
408
000
+ 10200
10608
102 x 104 =10,608 Reasonable 10,608 is close to 10,000
Question 2.
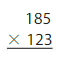
Answer:
185 x 123 = 22,755 Reasonable 22,755 is close to 20,000
Explanation:
Step 1 : Multiply 18 by 3 ones or 3
21
185
x 123
555
Step 2 : Multiply 185 by 2 tens or 20
11
185
x 123
555
3700
Step 3 : Multiply 185 by 1 hundred or 100. Regroup
185
x 123
555
3700
18500
Step 4 : Add the partial products.
185
x 123
555
3700
+ 18500
22755
185 x 123 = 22,755 Reasonable 22,755 is close to 20,000
Question 3.
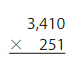
Answer:
3410 x 251 = 855,910 Reasonable 855,910 is close to 8,60,000
Explanation:
Step 1 : Multiply 3410 by 1 ones or 1
3410
x 251
3410
Step 2 : Multiply 3410 by 5 tens or 50
2
3410
x 251
3410
170500
Step 3 : Multiply 3410 by 2 hundred or 200. Regroup
3410
x 251
3410
170500
682000
Step 4 : Add the partial products.
3410
x 251
3410
170500
+682000
855910
3410 x 251 = 855,910 Reasonable 855,910 is close to 8,60,000
Find the product. Check whether your answer is reasonable.
Question 4.
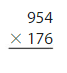
Answer:
954 x 176 = 1,67,904 Reasonable 1,67,904 is close to 1,68,000 or 1,70,000
Explanation:
Step 1 : Multiply 954 by 6 ones or 6
32
954
x 176
5724
Step 2 : Multiply 954 by 7 tens or 70
32
954
x 176
5724
66780
Step 3 : Multiply 954 by 1 hundred or 100. Regroup
954
x 176
5724
66780
95400
Step 4 : Add the partial products.
954
x 176
5724
66780
+95400
167904
954 x 176 = 1,67,904 Reasonable 1,67,904 is close to 1,68,000 or 1,70,000
Question 5.
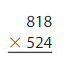
Answer:
818 x 524 = 428,632 Reasonable 4,28,632 is close to 4,30,000 or 4,00,000
Explanation:
Step 1 : Multiply 818 by 4 ones or 4
3
818
x 524
3272
Step 2 : Multiply 818 by 2 tens or 20
1
818
x 524
3272
16360
Step 3 : Multiply 818 by 5 hundred or 500. Regroup
4
818
x 524
3272
16360
409000
Step 4 : Add the partial products.
818
x 524
3272
16360
+ 409000
428632
818 x 524 = 428,632 Reasonable 4,28,632 is close to 4,30,000 or 4,00,000
Question 6.
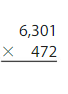
Answer:
6301 x 472 =2,974,072 Reasonable 2,974,072 is close to 3,000,000
Explanation:
Step 1 : Multiply 6301 by 2 ones or 2
6301
x 472
12602
Step 2 : Multiply 6301 by 7 tens or 70
2
6301
x 472
12602
441070
Step 3 : Multiply 6301 by 4 hundred or 400. Regroup
6301
x 472
12602
441070
2520400
Step 4 : Add the partial products.
6301
x 472
12602
441070
+2520400
2974072
6301 x 472 =2,974,072 Reasonable 2,974,072 is close to 3,000,000
Question 7.
999 × 186 = ______
Answer:
999 x 186 = 185,814 Reasonable 185,814 is close to 2,00,000
Explanation:
Step 1 : Multiply 999 by 6 ones or 6
55
999
x 186
5994
Step 2 : Multiply 999 by 8 tens or 80
77
999
x 186
5994
79920
Step 3 : Multiply 999 by 1 hundred or 100. Regroup
999
x 186
5994
79920
99900
Step 4 : Add the partial products.
999
x 186
5994
79920
+99900
185814
999 x 186 = 185,814 Reasonable 185,814 is close to 2,00,000
Question 8.
2,445 × 356 = ______
Answer:
2445 x 356 = 870420 Reasonable 870420 is close to 8,70,000
Explanation:
Step 1 : Multiply 2445 by 6 ones or 6
223
2445
x 356
14670
Step 2 : Multiply 2445 by 5 tens or 50
222
2445
x 356
14670
122250
Step 3 : Multiply 2445 by 3 hundred or 300. Regroup
111
2445
x 356
14670
122250
733500
Step 4 : Add the partial products.
2445
x 356
14670
122250
+733500
870420
2445 x 356 = 870420 Reasonable 870420 is close to 8,70,000
Question 9.
1,564 × 389 = ______
Answer:
1564 x 389 = 608396 Reasonable 6,08,396 is close to 6,00,000
Step 1 : Multiply 1564 by 9 ones or 9
553
1564
x 389
14076
Step 2 : Multiply 1564 by 8 tens or 80
453
1564
x 389
14076
125120
Step 3 : Multiply 1564 by 3 hundred or 300. Regroup
111
1564
x 389
14076
125120
469200
Step 4 : Add the partial products.
1564
x 389
14076
125120
+469200
608396
1564 x 389 = 608396 Reasonable 6,08,396 is close to 6,00,000
Question 10.
Reasoning
Your friend says the product of 4,164 and 137 is 70,460. How will finding an estimate help your friend realize the answer is not reasonable?
Answer:
4164 X 137 = 570,468, 5,70,468 is not equal to 70,460.
Explanation:
Friend says product of 4,164 and 137 is 70,460 , Now finding the estimate the product of 4,164 x 137 = 5,70,468 but friend says it is 70,460. So after finding friend realize the answer is not reasonable and not even close.
Question 11.
YOU BE THE TEACHER
Your friend says that when multiplying 300 by 126, she can multiply 3 × 126 and write two zeros after the product. Is your friend correct? Explain.
Answer:
Yes, Friend is correct
Explanation:
When first we multiply 300 x 126 we get the product as 37,800 and when we multiply 3 x 126 we get result as 378 and if we write two zeros after the product it becomes 37800 which is similar to the result of 300 x 126, so friend is correct.
We can write 300 x 126 as 3 x 102 x 126= (3 x 126 ) x 102 , We know that if any whole number is multiplied by 10 with powers we get the product whole number with the given number of power value additional number of zeros in the right.
as (3 x 126 ) x 102 has 2 as power to 10 we write the result with 2 zeros after the product which is equal to 300 x 126,So friend is correct.
Question 12.
Modeling Real Life
Your friend starts a video channel and wants to have 50,000 subscribers by the end of 1 year. She gets 140 new subscribers each day for 365 days. Does she meet her goal?
Answer:
140 x 365 = 51,100 as 51,100 > 50,000, Yes friend meets her goal.
Explanation:
As friend starts a video channel and wants to have 50,000 subscribers by the end of 1 year, and each day friend gets 140 new subscribers for 365 days , So total number of subscribers for 365 days or 1 year is 140 x 365= 51,100.
As 51,100 is greater than 50,000 means friend can easily meets her goal.
Review & Refresh
Evaluate the expression.
Question 13.
(5 + 8) × 4
Answer:
(5+8) x 4 = 13 x 4 = 52
Explanation:
Expressions inside parentheses are evaluated first from left to right, i.e (5+8) and then we proceed with multiplication.
So first we add the values inside the parentheses or values of bracket (5+8) x 4 ,5+8=13 and multiply by 4= 13 x 4 = 52,
(5 + 8) × 4 = 52
Question 14.
16 + (9 ÷ 3)
Answer:
16 + (9 ÷ 3) = 16 + 3 = 19
Explanation:
First we take expressions inside parentheses (9 ÷ 3) and evaluate then we proceed with addition,
When 9 ÷ 3 we get 3 , Now we go with addition so 16 + 3 = 19.
16 + (9 ÷ 3) = 19
Question 15.
7 × (4 + 6)
Answer:
7 x (4 +6) = 7 x 10 = 70
Explanation:
First we take expressions inside parentheses ( 4 + 6)=10 and proceed with multiplication, 7 x 10 = 70,
7 x (4 +6) = 70
Multiply Whole Numbers Performance Task
The Grand Coulee Dam is located on the Columbia River in Washington. The dam is used to control flood waters, provide irrigation, and generate power.

Question 1.
The dam has 12 pumps that each transfer the same amount of water through pipes from Lake Roosevelt to Banks Lake. Together, the pumps can transfer about 12,000 gallons of water each second.
a. About how many gallons of water can each pump transfer in 1 second?
b. About how many gallons of water can each pump transfer in 1 hour? Explain.
Answer:
a. 12,000 ÷ 12 = 1,000 gallons of water can each pump transfer in 1 second.
b. 1000 x 3,600 seconds = 3,600,000 gallons of water can each pump transfer in 1 hour.
Explanation :
a. Given a dam has 12 pumps that each transfer the same amount of water through pipes from Lake Roosevelt to Banks Lake, and together, the pumps can transfer about 12,000 gallons of water each second.
12 pumps = 12,000 gallons of water each second, Each pump transfer in 1 second is equal to 12,000 divided by 12= 12,000 ÷ 12 =
1,000 gallons of water can each pump transfer in 1 second.
b. Now number of gallons of water can each pump transfer in 1 hour, we know in 1 hour we have 60 minutes and 1 minute has 60 seconds so making it as 3,600 seconds in an hour.1 hour equals to 3,600 seconds. If in 1 second each pump can transfer 1000 gallons of water then in hour it will transfer 1000 x 3,600= 3,600,000 gallons of water can each pump transfer in 1 hour.
Question 2.
The dam generates power Capacity of Power at the Grand Coulee Dam using 33 generators located in 4 different powerhouses.
a. What is the total Power for the Grand Coulee Dam?
b. Only about one-third of the capacity of power for each powerhouse is actually generated each year. About how many megawatts does the Third Powerhouse actually generate in 1 year?
c. There are 106 watts in 1 megawatt. Without calculating, how can you find about how many watts the Third Powerhouse actually generates in 1 year?
Answer:
a. The total Power for the Grand Coulee Dam is 6,701 megawatts.
b. The Third Powerhouse actually generates only 1/3 in 1 year is 1800 x 1/3 = 1800/3=1800 ÷ 1/3 = 600 megawatts
c. The number of watts the Third Powerhouse actually generates in 1 year =600 x 106 watts.
Explanation:
a. First we calculate the total capacity of the power house in each power house with the capacity of power from each generator with the number of generators as per the powerhouse, Total Capacity of the power house = capacity of powerhouse from each generator multiply by number of generators separately. Then adding all capacities we get the total Power for the Grand Coulee Dam as shown in the below table, So total Power for the Grand Coulee Dam is 6,701 megawatts.
b. We have Third Powerhouse has total capacity as 1,800 megawatts as calculated in that only about one-third of the capacity of power for each powerhouse is actually generated each year means total capacity in third powerhouse multiply by 1/3= 1800 x 1/3 = 1800/3=1800 ÷ 1/3 = 600 megawatts.
Third Powerhouse actually generates 600 megawatts in 1 year.
c. Given 1 mega watt equals to 106 watts , We have Third Powerhouse generates 600 megawatts in 1 year, so to convert megawatts into watts we multiply it by 106 watts =600 x 106 watts, Third Powerhouse actually generates 600 x 106 watts in 1 year.
Multiply Whole Numbers Activity
Multiplication Adventure
Directions:
1. Players take turns rolling a die. Players solve problems on their boards to race the explorers to their destinations.
2. On your turn, solve the next multiplication problem in the row of your roll.
3. The first player to get an explorer to a destination wins!
Answer:
Multiply Whole Numbers Chapter Practice
4.1 Multiplication Patterns
Find the product.
Question 1.
72 × 103 = ______
Answer:
72 × 103 = 72,000
Explanation :
72 × 103 = 72 x 10 x 10 x 10 =72,000 , we multiply 72 with 10 three times as 10 power is 3.
Question 2.
30 × 900 = ______
Answer:
30 × 900 =27,000
Explanation:
When we multiply 30 by 900 we get 27,000 or 30 × 900 = 3 x 10 x 9 x 10 x 10 = 3 x 9 x 103= 27 x 103= 27,000
Question 3.
40 × 500 = ______
Answer:
40 × 500 = 20,000
Explanation:
When we multiply 40 by 500 we get 20,000 or 40 × 500 = 4 x 10 x 5 x 10 x 10 = 4 x 5 x 103= 20 x 103=20,000
Question 4.
60 × 800 = ______
Answer:
60 x 800 = 48,000
Explanation:
When we multiply 60 by 800 we get 48,000 or 60 × 800 = 6 x 10 x 8 x 10 x 10 = 6 x 8 x 103= 48 x 103=48,000
Question 5.
20 × 90 = ______
Answer:
20 x 90 = 1800
Explanation:
When we multiply 20 by 90 we get 1800 or 20 × 90 = 2 x 10 x 9 x 10 = 2 x 9 x 102= 18 x 102=1800
Question 6.
102 × 41 = _____
Answer:
102 × 41 =4100
Explanation:
When we multiply 102 × 41 =10 x 10 x 41 = 100 x 41 = 41,00
Find the missing factor.
Question 7.
_____ × 103 = 26,000
Answer:
The missing factor is 26
Explanation:
To get the missing factor, let us take it as X ,So X x 103 = 26,000, therefore X = 26,000 / 103 =26,000/1000=26
Question 8.
600 × ____ = 24,000
Answer:
The missing factor is 40
Explanation:
To get the missing factor, let us take it as X , So 600 x X = 24,000, therefore X = 24,000/600 = 40
Question 9.
5,000 × _____ = 250,000
Answer:
The missing factor is 50
Explanation:
To get the missing factor, let us take it as X , So 5,000 x X = 250,000, therefore X = 250,000/5000 = 50
Question 10.
Logic
The product of a number and twice that number is 320,000. Write the multiplication equation.
Answer:
Let the number be X the multiplication equation is X x 2X =320,000
Explanation:
Let us take the number as X given the product of a number and twice that number equals to 320,000 so the equation becomes as x X x 2X = 320,000 means X multiplied by 2X result is 320,000.
4.2 Estimate Products
Estimate the product. Explain whether your estimate is an overestimate or an underestimate.
Question 11.
44 × 81
Answer:
44 x 81 = 3,564
50 x 80 = 4,000 is overestimate
Explanation :
As our estimate after rounding each factor becomes as 44 as 50 to nearest ten and 81 as 80 to nearest ten as 44 x 81 < 50 x 80 as the estimate result is greater than the given product results our estimate is an overestimate
Question 12.
29 × 67
Answer:
29 x 67 = 1,943
30 x 70 = 2,100 is overestimate
Explanation :
As our estimate after rounding each factor becomes 29 as 30 to nearest ten and 67 as 70 to nearest ten as 29 x 67 < 30 x 70 as the estimate result is greater than the given product results our estimate is an overestimate.
Question 13.
504 × 302
Answer:
504 x 302 = 152,208
500 x 300 = 150,000 is underestimate
Explanation :
As our estimate after rounding each factor becomes 504 as 500 to nearest hundred and 302 as 300 to nearest hundred as 504 x 302 > 500 x 300 as the estimate result is lesser than the given product results our estimate is an underestimate.
Question 14.
797 × 29
Answer:
792 x 29 = 22,968
800 x 30 = 24,000 is overestimate
Explanation :
As our estimate after rounding each factor becomes 792 as 800 to nearest hundred and 29 as 30 to nearest ten as 792 x 29 < 800 x 30 as the estimate result is greater than the given product results our estimate is an overestimate.
4.3 Multiply by One-Digit Numbers
Find the product. Check whether your answer is reasonable.
Question 15.
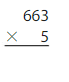
Answer:
663 x 5 = 3,315 Reasonable 3,315 is close to 3,300
Explanation:
Step 1: Multiply the ones. Regroup
5 x 3 ones = 15 ones, Regroup 15 ones as 1 tens and 5 ones
1
663
x 5
5
Step 2 : Multiply the tens. Regroup
5 x 6 tens = 30 tens, 30 tens + 1 tens = 31 tens, Regroup 31 tens as
3 hundreds and 1 tens
3
663
x 5
15
Step 3 : Multiply the hundreds. Regroup hundreds
5 x 6 hundreds = 30 hundreds, 30 hundreds + 3 hundreds = 33 hundreds
Regroup 33 hundreds as 3 thousands and 3 hundred
663
x 5
3315
663 x 5 = 3,315 Reasonable 3,315 is close to 3,300
Question 16.
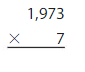
Answer:
1973 x 7 = 13,811 Reasonable 13,811 is close to 14,000
Explanation:
Step 1: Multiply the ones. Regroup
7 x 3 ones = 21 ones, Regroup 21 ones as 2 tens and 1 ones
2
1973
x 7
1
Step 2 : Multiply the tens. Regroup
7 x 7 tens = 49 tens, 49 tens + 2 tens = 51 tens, Regroup 51 tens as
5 hundreds and 1 tens
5
1973
x 7
11
Step 3 : Multiply the hundreds. Regroup hundreds
7 x 9 hundreds = 63 hundreds, 63 hundreds + 5 hundreds = 68 hundreds
Regroup 68 hundreds as 6 thousands and 8 hundreds
6
1973
x 7
811
Step 4 : Multiply the thousands. Add the regrouped thousands
7 x 1 thousands = 7 thousands,7 thousands +6 thousands=13 thousands
1973
x 7
13811
1973 x 7 = 13,811 Reasonable 13,811 is close to 14,000
Question 17.
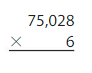
Answer:
75,028 x 6 = 450,168 Reasonable 4,50,168 is close to 4,50,000
Explanation:
Step 1: Multiply the ones. Regroup
6 x 8 ones = 48 ones, Regroup 48 ones as 4 tens and 8 ones
4
75028
x 6
8
Step 2 : Multiply the tens. Regroup
6 x 2 tens = 12 tens, 12 tens + 4 tens = 16 tens, Regroup 16 tens as
1 hundreds and 6 tens
1
75028
x 6
68
Step 3 : Multiply the hundreds. Regroup hundreds
6 x 0 hundreds = 0 hundreds, 0 hundreds + 1 hundreds = 1 hundred
75028
x 6
168
Step 4 : Multiply the thousands. Regroup
6 x 5 thousands = 30 thousands, Regroup 30 thousands as 3 ten thousands and 0 thousands
3
75028
x 6
0168
Step 5 : Multiply the ten thousands.
6 x 7 ten thousands = 42 ten thousands,42 ten thousands+ 3 ten thousands
=45 ten thousands, regroup as 4 hundred thousand and 5 ten thousand
75028
x 6
450168
75,028 x 6 = 4,50,168 Reasonable 4,50,168 is close to 4,50,000
Question 18.
Modeling Real Life
The Great Western Trail is 355 miles longer than 4 times the length of the Iditarod Trail. The Iditarod Trail is 1,025 miles long. How long is the Great Western Trail?
Answer:
The Great Western Trail = 355 + ( 4 x 1,025)= 355 + 4,100 = 4,455 miles
Explanation :
Given that The Great Western Trail is 355 miles longer than 4 times the length of the Iditarod Trail,
The Great Western Trail= 355 + ( 4 x the Iditarod Trail),
and the Iditarod Trail is 1,025 miles ,
The Great Western Trail = 355 + ( 4 x 1025) = 355 + 4100 = 4,455 miles, The Great Western Trail is 4,455 miles long.
4.4 Multiply by Two-Digit Numbers
Find the product. Check whether your answer is reasonable.
Question 19.
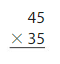
Answer:
45 x 35 = 1575 Reasonable 1575 is close to 1500
Explanation:
Step 1: Multiply 45 by 5 ones. Regroup
5 ones x 45 = 225 ones
2
45
x 35
225
Step 2: Multiply 45 by 3 tens or 30, Regroup
3 tens x 45 =135 tens =1350 ones
45
x 35
225
1350
Step 3 : Add the partial products.
45
x 35
225
+1350
1575
45 x 35 = 1575 Reasonable 1575 is close to 1500
Question 20.
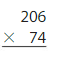
Answer:
206 x 74 = 15,244 Reasonable 15,244 is close to 15,000
Explanation:
Step 1: Multiply 206 by 4 ones. Regroup
4 ones x 206 = 824 ones
2
206
x 74
824
Step 2: Multiply 206 by 7 tens or by 70, Regroup
7 tens x 206 =1442 tens =14420 ones
206
x 74
824
14420
Step 3 : Add the partial products.
206
x 74
824
+ 14420
15244
206 x 74 = 15,244 Reasonable 15,244 is close to 15,000
Question 21.
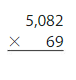
Answer:
5,082 x 69 = 350,658 Reasonable 3,50,658 is close to 3,50,000
Explanation:
Step 1: Multiply 5082 by 9 ones. Regroup
9 ones x 5082 = 45,738 ones
71
5082
x 69
45,738
Step 2: Multiply 5082 by 6 tens or 60, Regroup
6 tens x 5082 = 30492 tens =304920 ones
5082
x 69
45738
304920
Step 3 : Add the partial products.
5082
x 69
45738
+304920
350658
5,082 x 69 = 350,658 Reasonable 3,50,658 is close to 3,50,000
4.5 Multiply by Multi-Digit Whole Numbers
Find the product. Check whether your answer is reasonable.
Question 22.
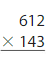
Answer:
612 x 143 = 87,516 Reasonable 87,516 is close to 90,000
Explanation:
Step 1 : Multiply 612 by 3 ones or 3
612
x 143
1836
Step 2 :Multiply 612 by 4 tens or 40.
612
x 143
1836
24480
Step 3 : Multiply 612 by 1 hundred or 100. Regroup
612
x 143
1836
24480
61200
Step 4: Add the partial products.
612
x 143
1836
24480
+61200
87516
612 x 143 = 87,516 Reasonable 87,516 is close to 90,000
Question 23.
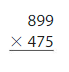
Answer:
899 x 475 = 427,025 Reasonable 4,27,025 is close to 4,30,000
Explanation:
Step 1 : Multiply 899 by 5 ones or 5
44
899
x 475
4495
Step 2 :Multiply 899 by 7 tens or 70.
66
899
x 475
4495
62930
Step 3 : Multiply 899 by 4 hundred or 400. Regroup
33
899
x 475
4495
62930
359600
Step 4: Add the partial products.
899
x 475
4495
62930
+359600
427025
899 x 475 = 427,025 Reasonable 4,27,025 is close to 4,30,000
Question 24.
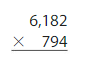
Answer:
6182 x 794 = 4,908,508 Reasonable 4,908,508 is close to 5,000,000
Explanation:
Step 1 : Multiply 6182 by 4 ones or 4
3
6182
x 794
24728
Step 2 :Multiply 6182 by 9 tens or 90.
71
6182
x 794
24728
556380
Step 3 : Multiply 6182 by 7 hundred or 700. Regroup
51
6182
x 794
24728
556380
4327400
Step 4: Add the partial products.
6182
x 794
24728
556380
4327400
4908508
6182 x 794 = 4,908,508 Reasonable 4,908,508 is close to 5,000,000
Conclusion:
We wish the Big Ideas Math Grade 5 Answer Key Chapter 4 Multiply Whole Numbers is beneficial for you all. There are different methods to solve the problems in multiply whole numbers. Prepare the questions on your own and solve the problems. Students are notified to improve their math skills by referring to the Big Ideas Math Answers Grade 5 Chapter 4 Multiply Whole Numbers.