Big Ideas Math Answers Grade 6 Advanced Chapter 1 Numerical Expressions and Factors

Do you want to become proficient in Math and get a good hold of the Big Ideas Math Book Grade 6 Advanced? If so, this is the one-stop destination for all your needs. You can access the Topicwise BIM Grade 6 Advanced Ch 1 Numerical Expressions and Factors Solutions PDF available as a part of your preparation. Test your knowledge of the concepts by solving from the Big Ideas Math Answers Grade 6 Advanced Chapter 1 and identify the knowledge gap accordingly.

Big Ideas Math Book 6th Grade Advanced Answer Key Chapter 1 Numerical Expressions and Factors

Use the ultimate guide over here for all your doubts on Big Ideas Math 6th Grade Advanced Ch 1 Numerical Expressions and Factors Concepts. Big Ideas Math Book 6th Grade Advanced Solutions provided here covers questions from Chapter 1 aligned as per the BIm Textbooks.  All you have to do is simply tap on the quick links available to avail the respective topic in no time. Begin your preparation right away taking the help of the Numerical Expressions and Factors Big Ideas Math Grade 6 Solutions and clear the exam with flying colors.

• Numerical Expressions and Factors STEAM Video/ Performance Task – Page 1
• Numerical Expressions and Factors Vocabulary – Page 2
• Section 1.1 Powers and Exponents – Page(3-8)
• Lesson 1.1 Powers and Exponents – Page(4-6)
• Powers and Exponents Practice 1.1 – Page(7-8)
• Section 1.2 Order of Operations – Page(9-14)
• Lesson 1.2 Order of Operations – Page(10-12)
• Order of Operations Practice 1.2 – Page(13-14)
• Section 1.3 Prime Factorization – Page(15-20)
• Lesson 1.3 Prime Factorization – Page(16-18)
• Prime Factorization Practice 1.3 – Page(19-20)
• Section 1.4 Greatest Common Factor – Page(21-26)
• Lesson 1.4 Greatest Common Factor – Page(22-24)
• Greatest Common Factor Practice 1.4 – Page(25-26)
• Section 1.5 Least Common Multiple – Page(27-32)
• Lesson 1.5 Least Common Multiple – Page(28-30)
• Least Common Multiple Practice 1.5 – Page(31-32)
• Numerical Expressions and Factors Connecting Concepts – Page 33
• Numerical Expressions and Factors Chapter Review – Page(34-37)
• Powers and Exponents Homework & Practice 1.1 – Page 35
• Order of Operations Homework & Practice 1.2 – Page 35
• Prime Factorization Homework & Practice 1.3 – Page 36
• Greatest Common Factor Homework & Practice 1.4 – Page 36
• Least Common Multiple Homework & Practice 1.5 – Page 37
• Numerical Expressions and Factors Practice Test – Page 38
• Numerical Expressions and Factors Cumulative Practice – Page(39-41)

Numerical Expressions and Factors STEAM Video/ Performance Task

STEAM Video

Filling Piñatas

Common factors can be used to make identical groups of objects. Can you think of any situations in which you would want to separate objects into equal groups? Are there any common factors that may be more useful than others? Can you think of any other ways to use common factors?

Watch the STEAM Video “Filling Piñatas.” Then answer the following questions. The table below shows the numbers of party favors that Alex and Enid use to make piñatas

Question 1.
When finding the number of identical piñatas that can be made, why is it helpful for Alex and Enid to list the factors of each number given in the table?
Answer:

Question 2.
You raIt to create 6 identical piñatas. How can you change the numbers of party favors in the table to make this happen? Can you do this without changing the total number of party favors?
Answer:

Performance Task

Setting the Table

After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be asked to plan a fundraising event with the items below.

72 chairs
48 balloons
24 flowers
32 candles

You will find the greatest number of identical tables that can be prepared, and what will be in each centerpiece.When making arrangements for a party, should a part planner always use the greatest number of identical tables possible? Explain why or why not.
Answer:

Getting Ready for Numerical Expressions and Factors

Chapter Exploration

Work with a partner. In Exercises 1 and 2, use the table.

Eratosthenes
(c. 276 – c. 194 B.c.)
This table is called the Sieve of Eratosthenes. Eratosthenes was a Greek mathematician who was the chief librarian at theLibrary of Alexandria in Egypt. He was the first person to calculate the circumference of Earth.

Question 1.
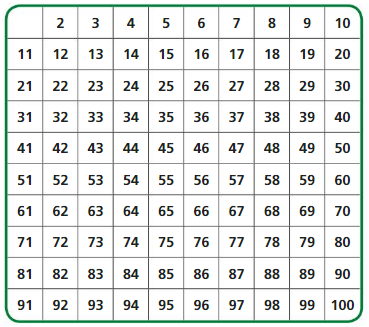
Cross out the multiples of 2 that are greater than 2. Do the same for 3, 5, and 7.
Answer:

Question 2.
The numbers that are not crossed out are called prime numbers. ‘The numbers that are crossed out are called composite numbers. In your own words, describe the characteristics of prime numbers and composite numbers.
Answer:

Question 3.
MODELING REAL LIFE
Work with a partner. Cicadas are insects that live underground and emerge from the ground after x or x + 4 years. Is it possible that both x and x + 4 are prime? Give some examples.
Answer:

Numerical Expressions and Factors Vocabulary

The following vocabulary terms are defined in this chapter. think about what each term might rucan and record your thoughts.
exponent                                                common factors                               common multiples
numerical expression                             greatest common factor                   least common multiple
order of operations
Answer:

Section 1.1 Powers and Exponents

Exploration 1

Writing Expressions Using Exponents

Work with a partner. Copy and complete the table.

Repeated Factors	Using an Exponent	Value
a. 10 × 10
b. 4 × 4
c. 6 × 6
d. 10 × 10 × 10
e. 100 × 100 × 100
f. 3 × 3 × 3 × 3
g. 4 × 4 × 4 × 4 × 4
h. 2 × 2 × 2 × 2 × 2 × 2

Answer:

Math Practice
Repeat Calculations
What patterns do you notice in the expressions? How does this help you write exponents?
Answer:

i. In your own words, describe what the two numbers in the expression 3⁵ mean.
Answer:

Exploration 2

Using a Calculator to Find a Pattern

Work with a partner. Copy the diagram. Use a calculator to find each value. Write one digit of the value in each box. Describe the pattern in the digits of the values.

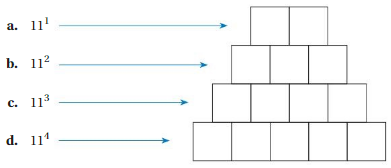
Answer:

Lesson 1.1 Powers and Exponents

Try It Write the product as a power.

Question 1.
2 × 2 × 2
Answer:

Question 2.
6 • 6 • 6 • 6 • 6 • 6
Answer:

Question 3.
15 × 15 × 15 × 15
Answer:

Question 4.
20 • 20 • 20 • 20 • 20 • 20 • 20
Answer:

Try It Find the value of the power.

Question 5.
6³
Answer:

Question 6.
9²
Answer:

Question 7.
3⁴
Answer:

Question 8.
18²
Answer:

Try It Determine whether the number is a perfect square.

Question 9.
25
Answer:

Question 10.
2
Answer:

Question 11.
99
Answer:

Question 12.
36
Answer:

FINDING VALUES OF POWERS
Find the value of the power.
Question 13.
8²
Answer:

Question 14.
3⁵
Answer:

Question 15.
11³
Answer:

Question 16.
VOCABULARY
How are exponents and powers different
Answer:

Question 17.
VOCABULARY
Is 10 a perfect square? Is 100 a perfect square? Explain.
Answer:

Question 18.
WHICH ONE DOESN’T BELONG?
Which one does not belong with the other three? Explain your reasoning.
2⁴ = 2 × 2 × 2 × 2
3² = 3 × 3
3 + 3 + 3 + 3 = 3 × 4
5 • 5 • 5 = 5³
Answer:

Self-Assessment for Problem Solving

Solve each exercise. Then rate your understanding of the success criteria in your journal.

Question 19.
A square solar panel has an area of 16 square feet. Write the area as a power. Then find the side lengths of the Panel.
Answer:

Question 20.
The four-square court shown is a square made up of four identical smaller squares. What is the area of the court?

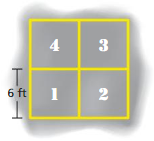
Answer:

Question 21.
DIG DEEPER!
Each face of a number cube is a square with a side length of 16 millimeters. What is the total area of all of the faces of the number cube?
Answer:

Powers and Exponents Practice 1.1

Review & Refresh

Multiply

Question 1.
150 × 2
Answer:

Question 2.
175 × 8
Answer:

Question 3.
123 × 3
Answer:

Question 4.
151 × 9
Answer:

Write the sentence as a numerical expression.

Question 5.
Add 5 and 8, then multiply by 4.
Answer:

Question 6.
Subtract 7 from 11, then divide by 2.
Answer:

Round the number to the indicated place value.

Question 7.
4.03785 to the tenths
Answer:

Question 8.
12.89503 to the hundredths
Answer:

Complete the sentence.

Question 9.
\(\frac{1}{10}\) of 30 is .
Answer:

Question 10.
\(\frac{4}{5}\) of 25 is .
Answer:

Concepts, Skills, & Problem Solving

WRITING EXPRESSIONS USING EXPONENTS
Copy and complete the table. (See Exploration 1 Page.No 3)

Repeated Factors	Using an Exponent	Value
11. 8 × 8
12. 4 × 4 × 4
13. 9 × 9 × 9 × 9
14. 12 × 12 × 12 × 12 × 12

Answer:

WRITING EXPRESSIONS AS POWERS
Write the product as a power.

Question 15.
9 × 9
Answer:

Question 16.
13 × 13
Answer:

Question 17.
15 × 15 × 15
Answer:

Question 18.
2 • 2 • 2 • 2 • 2
Answer:

Question 19.
14 × 14 × 14
Answer:

Question 20.
8 • 8 • 8 • 8
Answer:

Question 21.
11 × 11 × 11 × 11 × 11
Answer:

Question 22.
7 • 7 • 7 • 7 • 7 • 7
Answer:

Question 23.
16 • 16 • 16 • 16
Answer:

Question 24.
43 × 43 × 43 × 43 × 43
Answer:

Question 25.
167 • 167 • 167
Answer:

Question 26.
245 • 245 • 245 • 245
Answer:

FINDING VALUES OF POWERS
Find the value of the power.

Question 27.
5²
Answer:

Question 28.
4³
Answer:

Question 29.
6²
Answer:

Question 30.
1⁷
Answer:

Question 31.
0³
Answer:

Question 32.
8⁴
Answer:

Question 33.
2⁴
Answer:

Question 34.
12²
Answer:

Question 35.
7³
Answer:

Question 36.
5⁴
Answer:

Question 37.
2⁵
Answer:

Question 38.
14²
Answer:

USING TOOLS
Use a calculator to find the value of the power.

Question 39.
7⁶
Answer:

Question 40.
4⁸
Answer:

Question 41.
12⁴
Answer:

Question 42.
17⁵
Answer:

Question 43.
YOU BE THE TEACLIER
Your friend finds the value of 8. Is your friend correct? Explain your reasoning.

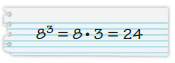
Answer:

IDENTIFYING PERFECT SQUARES
Determine whether the number is a perfect square.

Question 44.
8
Answer:

Question 45.
4
Answer:

Question 46.
81
Answer:

Question 47.
44
Answer:

Question 48.
49
Answer:

Question 49.
125
Answer:

Question 50.
150
Answer:

Question 51.
144
Answer:

Question 52.
MODELING REAL LIFE
On each square centimeter of a person’s skin, there are about 39² bacteria. How many bacteria does this expression represent?
Answer:

Question 53.
MP REPEATED REASONING
The smallest figurine in a gift shop is 2 inches tall. The height of each figurine is twice the height of the previous figurine. What is the height of the tallest figurine?
Answer:

Question 54.
MODELING REAL LIFE
A square painting measures 2 meters on each side. What is the area of the painting in square centimeters?

Answer:

Question 55.
MP NUMBER SENSE
Write three powers that have values greater than 120 and less than 130.
Answer:

Question 56.
DIG DEEPER!
A landscaper has 125 tiles to build a square patio. the patio must have an area of at least 80 square feet.

a. What arc the Possible arrangements for the patio?
b. How many tiles are not used in each arrangement?
Answer:

Question 57.
MP PATTERNS
Copy and complete the table. Describe what happens to the value of the power as the exponent decreases.
Use this pattern to find the value 0f 4⁰.

Answer:

Question 58.
MP REPEATED REASONING
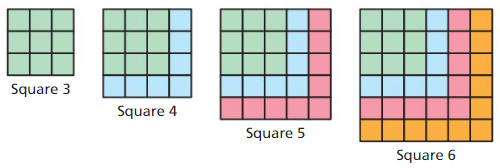
How many blocks do you need to add to Square 6 to get Square 7? to Square 9 to get Square 10? to Square 19 to get Square 20? Explain.

Answer:

Section 1.2 Order of Operations

Exploration 1

Comparing Different Orders

Work with a partner. Find the value of each expression by using different orders of operations. Are your answers the same?

a. Add, then multiply.                  Multiply, then add.
3 + 2 × 2                                      3 + 2 × 2

b. Subtract then multiply.             Multiply, then subtract.
18 – 3 • 3                                       18 – 3 • 3

c. Multiply, then subtract              Subtract, then multiply.
8 × 8 – 2                                        8 × 8 – 2

d. Multiply, then add.                    Add, then multiply.
6 • 6 + 2                                         6 • 6 + 2

Exploration 2

Determining Order of Operations

Work with a partner.

a. Scientific calculators use a standard order of operations when evaluating expressions. Why is a standard order of operations needed?
Answer:

b. Lise a scientific calculator to evaluate each expression in Exploration 1. Enter each expression exactly as written. For each expression, which order of operations is correct?
Answer:

c. What order of operations should be used to evaluate 3 + 2², 18 – 3², 8² – 2, and 6² + 2?
Answer:

d. Do 18 ÷ 3 • 3 and 18 ÷ 3² have the same value? Justify your answer.
Answer:

e. How does evaluating powers fit into the order of operations?
Answer:

Math Practice
Use Technology to Explore
How does a scientific calculator help you explore order of operations?
Answer:

Lesson 1.2 Order of Operations

Try It Evaluate the expression.

Question 1.
7 • 5 + 3
Answer:

Question 2.
(28 – 20) ÷ 4
Answer:

Question 3.
[6 + (15 – 10)] × 5
Answer:

Try It Evaluate the expression.

Question 4.
6 + 2⁴ – 1
Answer:

Question 5.
4 • 3² + 18 – 9
Answer:

Question 6.
16 + (5² – 7) ÷ 3
Answer:

Try It Evaluate the expression.

Question 7.
50 + 6(12 ÷ 4) – 8²
Answer:

Question 8.
5² – \(\frac{1}{5}\)(10 – 5)
Answer:

Question 9.
\(\frac{8(2+5)}{7}\)
Answer:

USING ORDER OF OPERATIONS
Evaluate the expression.

Question 10.
7 + 2 • 4
Answer:

Question 11.
8 ÷ 4 × 2
Answer:

Question 12.
3(5 + 1) ÷ 3²
Answer:

Question 13.
WRITING
Why does 12 – 8 ÷ 2 = 8, hut(12 – 8) ÷ 2 = 2?
Answer:

Question 14.
MP REASONING
Describe the steps ¡n evaluating the expression
8 ÷ (6 – 1) + 3².
Answer:

Question 15.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.
5² – 8 × 2
5² – (8 × 2)
5² – 2 × 8
(5² – 8) × 2
Answer:

Self-Assessment for problem solving

Solve each exercise. Then rate your understanding of the success criteria in your journal.

Question 16.
A square plot of land has side lengths of 10 meters. An archaeologist divides the land into 64 equal parts. What is the area of each part?

Answer:

Question 17.
A glass block window is made of two different-sized glass squares. The window has side lengths of 40 inches. The large glass squares have side lengths of 10 inches. Find the total area of the small glass squares.

Answer:

Question 18.
DIG DEEPER!
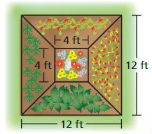
A square vegetable garden has side lengths of 12 feel You plant flowers in the center portion as shown. You divide the remaining space into 1 equal sections and plant tomatoes, onions, zucchini, and peppers. What is the area of the onion section?

Answer:

Order of Operations Practice 1.2

Review & Refresh

Write the product as a power.

Question 1.
11 × 11 × 11 × 11
Answer:

Question 2.
13 × 13 × 13 × 13 × 13
Answer:

Find the missing dimension of the rectangular prism.

Question 3.

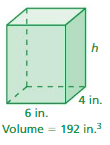
Answer:

Question 4.

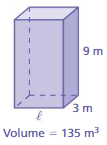
Answer:

Tell whether the number is prime or composite.

Question 5.
9
Answer:

Question 6.
11
Answer:

Question 7.
23
Answer:

Concepts, skills, & Problem Solving

COMPARING DIFFERENT ORDERS
Find the value of the expression by using different orders of operations. Are your answers the saine? (See Exploration 1 Page.No 9)

Question 8.
Add, then multiply. Multiply, then add.
4 + 6 × 6 4 + 6 × 6
Answer:

Question 9.
Subtract, then multiply. MuItiply then subtract.
5 × 5 – 3 5 × 5 – 3
Answer:

USING ORDER OF OPERATIONS
Evaluate the expression.

Question 10.
5 + 8 ÷ 6
Answer:

Question 11.
(11 – 3) ÷ 2 + 1
Answer:

Question 12.
45 ÷ 9 × 12
Answer:

Question 13.
6² – 3 • 4
Answer:

Question 14.
42 ÷ (15 – 2³)
Answer:

Question 15.
4² • 2 + 8 • 7
Answer:

Question 16.
(5² – 2) × 1⁵ + 4
Answer:

Question 17.
4 + 2 × 3² – 9
Answer:

Question 18.
8 ÷ 2 × 3 + 4² ÷ 4
Answer:

Question 19.
3² + 12 ÷ (6 – 3) × 8
Answer:

Question 20.
(10 + 4) ÷ (26 – 19)
Answer:

Question 21.
(5² – 4) • 2 – 18
Answer:

Question 22.
2 × [(16 – 8) × 2]
Answer:

Question 23.
12 + 8 × 3² – 24
Answer:

Question 24.
6² ÷ [(2 + 4) × 2³]
Answer:

YOU BE THE TEACHER
Your friend evaluates the expression. Is your friend correct? Explain your reasoning.
Question 25.

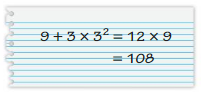
Answer:

Question 26.

Answer:

Question 27.
MP PROBLEM SOLVING
You need to read 20 poems in 5 days for an English project. Each poem is 2 pages long. Evaluate the expression 20 × 2 ÷ 5 to find how many pages you need to read each day.
Answer:

USING ORDER OF OPERATIONS
Evaluate the expression.

Question 28.
12 – 2(7 – 4)
Answer:

Question 29.
4(3 + 5) – 3(6 – 2)
Answer:

Question 30.
6 + \(\frac{1}{4}\) (12 – 8)
Answer:

Question 31.
9² – 8(6 + 2)
Answer:

Question 32.
4(3 – 1)³ + 7(6) – 5²
Answer:

Question 33.
\(8\left[\left(1 \frac{1}{6}+\frac{5}{6}\right) \div 4\right]\)
Answer:

Question 34.
7² – 2\(\left(\frac{11}{8}-\frac{3}{8}\right)\)
Answer:

Question 35.
8(7.3 + 3.7 – 8) ÷ 2
Answer:

Question 36.
2⁴(5.2 – 3.2) ÷ 4
Answer:

Question 37.
\(\frac{6^{2}(3+5)}{4}\)
Answer:

Question 38.
\(\frac{12^{2}-4(6)+1}{11^{2}}\)
Answer:

Question 39.
\(\frac{26 \div 2+5}{3^{2}-3}\)
Answer:

Question 40.
MP PROBLEM SOLVING
Before a show, there arc 8 people in a theater. Five groups of 4 people enter; and then three groups of 2 PeoPle leave. Evaluate the expression 8 5(4) – 3(2) to find how many people arc in the theater.
Answer:

Question 41.
MODELING REAL LIFE
The front door of a house is painted white and blue. Each window is a square with a side length of 7 inches. What is the area of the door that is painted blue?

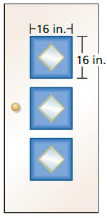
Answer:

Question 42.
MP PROBLEM SOLVING
You buy 6 notebooks, 10 folders, 1 pack of pencils, and 1 lunch box for school. After using a $10 gift card, how much do you owe? Explain how you solved the problem.

Answer:

Question 43.
OPEN-ENDED
Use all four operations and at least one exponent to write an expression that has a value of 100.
Answer:

Question 44.
MP REPEATED REASONING
A Petri dish contains 35 cells. Every day, each cell in the Petri dish divides into 2 cells in a process called mitosis. How many cells are there after 11 days? Justify your answer.
Answer:

Question 45.
MP REASONING
Two groups collect litter along the
side of a road. It takes each group 5 minutes to clean up a 200-yard section. 1 low long does it take both groups working together to clean up 2 miles? Explain how you solved the problem.

Answer:

Question 46.
MP NUMBER SENSE
Copy each statement Insert +, -, ×, or ÷ symbols to make each statement true.

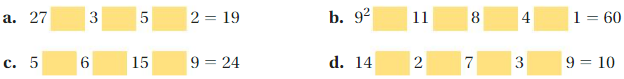
Answer:

Section 1.3 Prime Factorization

Exploration 1

Rewriting Numbers as Products of Factors

Work with a partner. Two students use factor trees to write 108 as a product of factors, as shown below.

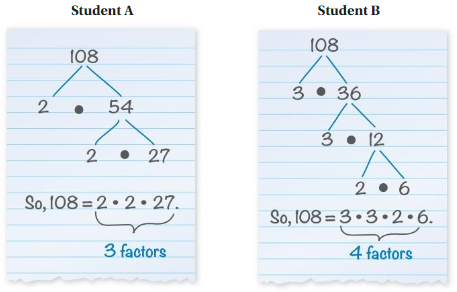
a. Without using 1 as a factor, can you write 108 as a product with more factors than each student used? Justify your answer.
Answer:

b. Use factor trees to Write 80, 162, and 300 as products of as many factors as possible. Do not use 1 as a factor.

Answer:

c. Compare your results in parts (a) and (b) with other groups. For each number, identify the product with the greatest number of factors. What do these factors have in common?
Answer:

Math Practice
Interpret Results
How do you know your answer makes sense?
Answer:

Lesson 1.3 Prime Factorization

Try It List the factor pairs of the number.

Question 1.
18
Answer:

Question 2.
24
Answer:

Question 3.
51
Answer:

Question 4.
WHAT IF?
The woodwinds section of the marching hand has 38 members. Which has more possible arrangements, the brass section or the woodwinds section? Explain.
Answer:

Try It Write the prime factorization of the number.

Question 5.
20
Answer:

Question 6.
88
Answer:

Question 7.
90
Answer:

Question 8.
462
Answer:

Self-Assessment for Concepts & Skills

Solve each exercise. Then rare your understanding of the success criteria in your journal.

WRITING A PRIME FACTORIZATION
Write the prime factorization of the number.
Question 9.
14
Answer:

Question 10.
86
Answer:

Question 11.
10
Answer:

Question 12.
516
Answer:

Question 13.
WRITING
Explain the difference between prime numbers and composite numbers.
Answer:

Question 14.
MP STRUCTURE
Your friend lists the following factor pairs and concludes that there arc 6 factor pairs of 12. Explain why your friend incorrect.
1,12   2,6     3,4
12,1   6,2     4,3
Answer:

Question 15.
WHICH ONE DOESN’T BELONG?
Which factor pair does not belong with the other three? Explain your reasoning.
2, 28   4, 14    6, 9   7, 8
Answer:

Self-Assessment for Problem Solving

Solve each exercise. Then rate your understanding of the Success criteria in your journal

Question 16.
A group of 20 friends plays a card game. ‘The game can be played with 2 or more teams of equal size. Each team must have at least 2 members. List the possible numbers and sizes of teams.

Answer:

Question 17.
You arrange 150 chairs in rows for a school play. You want each row to have the same number of chairs. how many possible arrangements arc there? Are all of the possible arrangements appropriate for the play? Explain.
Answer:

Question 18.
What is the least perfect square that is a factor of 4536? What is the greatest perfect square that is a factor of 4536?
Answer:

Question 19.
DIG DEEPER!
The prime factorization of a number is 2⁴ × 3⁴ × 5⁴ × 7² Is the number a Perfect square? Explain your reasoning.
Answer:

Prime Factorization Practice 1.3

Review & Refresh

Evaluate the expression.

Question 1.
2 + 4² (5 – 3)
Answer:

Question 2.
2³ + 4 × 3²
Answer:

Question 3.
9 × 5 – 2⁴\(\left(\frac{5}{2}-\frac{1}{2}\right)\)
Answer:

Plot the points in a coordinate plane. Draw a line segment connecting the points.

Question 4.
(1, 1) and (4, 3)
Answer:

Question 5.
(2, 3) and (5, 9)
Answer:

Question 6.
(2, 5) and (4, 8)
Answer:

Use the Distributive Property to find the quotient. Justify your answer.

Question 7.
408 ÷ 4
Answer:

Question 8.
628 ÷ 2
Answer:

Question 9.
969 ÷ 3
Answer:

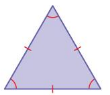
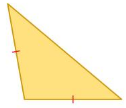
Classify the triangle in as many ways as possible.

Question 10.

Answer:

Question 11.

Answer:

Question 12.

Answer:

Concepts, Skills, & Problem Solving

REWRITING A NUMBER
Write the number as a product of as many factors as possible. (See Exploration 1 Page.No 15)
Question 13.
60
Answer:

Question 14.
63
Answer:

Question 15.
120
Answer:

Question 16.
150
Answer:

FINDING FACTOR PAIRS
List the factor pairs of the number.
Question 17.
15
Answer:

Question 18.
22
Answer:

Question 19.
31
Answer:

Question 20.
39
Answer:

Question 21.
45
Answer:

Question 22.
54
Answer:

Question 23.
59
Answer:

Question 24.
61
Answer:

Question 25.
100
Answer:

Question 26.
58
Answer:

Question 27.
25
Answer:

Question 28.
76
Answer:

Question 29.
52
Answer:

Question 30.
88
Answer:

Question 31.
71
Answer:

Question 32.
91
Answer:

WRITING A PRIME FACTORIZATION
Write the prime factorization of the number.
Question 33.
16
Answer:

Question 34.
25
Answer:

Question 35.
30
Answer:

Question 36.
26
Answer:

Question 37.
84
Answer:

Question 38.
54
Answer:

Question 39.
65
Answer:

Question 40.
77
Answer:

Question 41.
46
Answer:

Question 42.
39
Answer:

Question 43.
99
Answer:

Question 44.
Answer:

Question 45.
315
Answer:

Question 46.
190
Answer:

Question 47.
110
Answer:

Question 48.
640
Answer:

USING A PRIME FACTORIZATION
Find the number represented by the prime factorization.
Question 49.
2² • 3² • 5
Answer:

Question 50.
3² • 5² • 7
Answer:

Question 51.
2³ • 11² • 13
Answer:

Question 52.
YOU BE THE TEACHER
Your friend finds the prime factorization of 72. Is your friend correct? Explain your reasoning.

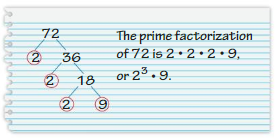
Answer:

USING A PRIME FACTORIZATION
Find the greatest perfect square that is a factor of the number.
Question 53.
250
Answer:

Question 54.
275
Answer:

Question 55.
392
Answer:

Question 56.
338
Answer:

Question 57.
244
Answer:

Question 58.
650
Answer:

Question 59.
756
Answer:

Question 60.
1290
Answer:

Question 61.
2205
Answer:

Question 62.
1890
Answer:

Question 63.
495
Answer:

Question 64.
4725
Answer:

Question 65.
VOCABULARY
A botanist separates plants into equal groups of 5 for an experiment. Is the total number of plants in the experiment prime or composite? Explain.

Answer:

Question 66.
MP REASONING
A teacher divides 36 students into equal groups for a scavenger hunt. Each group should have at least 1 students hut no more than 8 students. What are the possible group sizes?
Answer:

Question 67.
CRITICAL THINKING
Is 2 the only even prime number? Explain.
Answer:

Question 68.
MP LOGIC
One topic at a back saic has 75 cookies. Another table has 60 cupcakes. Which table allows for more rectangular arrangements? Explain.
Answer:

Question 69.
PERFECT NUMBERS
A perfect number is a number that equals the sum of its factors, not including itself. Ëor example, the factors of 28 arc 1, 2, 1, 7, 14, and 28. Because 1 + 2 + 4 + 7 + 14 = 28, 28 is a perfect number. What are the perfect numbers between 1 and 27?
Answer:

Question 70.
MP REPEATED REASONING
Choose any two perfect squares and find their product. ‘Then multiply your answer by another perfect square. Continue this process. Are any of the products perfect squares? What can you conclude?
Answer:

Question 71.
MP PROBLEM SOLVING
The stage manager of a school play creates a rectangular stage that has whole number dimensions and an area of 42 square yards. String lights will outline the stage. What is the least number of yards of string lights needed to enclose the stage?
Answer:

Question 72.
DIG DEEPER!
Consider the rectangular prism shown. Using only whole number dimensions, how many different prisms are possible? Explain.

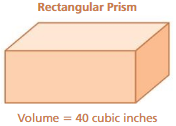
Answer:

Section 1.4 Greatest Common Factor

Exploration 1

Identifying Common Factors

Work with a partner. in parts (a) – (d), create a Venn diagram that represents the factors of each number and identify any common factors.
a. 36 and 18
b. 16 and 56
c. 30 and 75
d. 54 and 90
e. Look at the Venn diagrams in parts (a) – (d). Explain how to identify the greatest common factor of each pair of numbers. Then circle it in each diagram.
Answer:

Exploration 2

Using Prime Factors

Work with a partner.

a. Each Venn diagram represents the prime factorizations of two numbers. Identify each pair of numbers. Explain your reasoning.

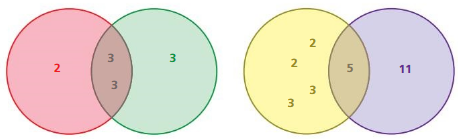
Answer:

b. Create a Venn diagram that represents the prime factorizations of 36 and 18.
Answer:

c. Repeat part (b) for the remaining number pairs in Exploration 1.
Answer:

d. MP STRUCTURE
Make a conjecture about the relationship between the greatest common factors you found in Exploration 1 and the numbers in the overlaps of the Venn diagrams you just created.
Answer:

Math Practice
Interpret a Solution
What does the diagram representing the prime factorizations mean?
Answer:

Lesson 1.4 Greatest Common Factor

Try It Find the GCF of the numbers using lists of factors.

Question 1.
8, 36
Answer:

Question 2.
18, 72
Answer:

Question 3.
14, 28, 49
Answer:

Try It Find the GCF of the numbers using prime factorizations.

Question 4.
20, 15
Answer:

Question 5.
32, 90
Answer:

Question 6.
45, 75, 120
Answer:

Try It

Question 7.
Write a pair of numbers whose greatest common factor is 10.
Answer:

Self-Assessment for concept & Skills

Solve each exercise. ‘Then rate your understanding of the success criteria in your journal.
FINDING THE GCF
Find the GCF of the numbers.
Question 8.
16, 40
Answer:

Question 9.
35, 63
Answer:

Question 10.
18, 72, 141
Answer:

Question 11.
MULTIPLE CHOICE
Which number is not a factor of 10? Explain.
A. 1
B. 2
C. 4
D. 5
Answer:

Question 12.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
What is the greatest common factor of 24 and 32?
What is the greatest common divisor of 24 and 32?
What is the greatest common prime factor of 24 and 32?
What is the product of the common prime factors of 24 and 32?
Answer:

Self-Assessment for Problem Solving

Solve each exercise. Then rate your understanding of the success criteria in your journal.

Question 13.
You usc 30 sandwiches and 42 granola bars to make identical picnic baskets. You make thc greatest number of picnic baskets with no food left over. How many sandwiches and how many granola bars are in each basket?

Answer:

Question 14.
You fill bags with cookies to give to your friends. You bake 45 chocolate chip cookies, 30 peanut butter cookies, and
15 oatmeal cookies. You want identical groups of cookies in each hag with no cookies left over. What is the greatest number of bags you can make?
Answer:

Greatest Common Factor Practice 1.4

Review & Refresh

List the factor pairs of the number.
Question 1.
20
Answer:

Question 2.
16
Answer:

Question 3.
56
Answer:

Question 4.
87
Answer:

Tell whether the statement is always, sometimes, or sever true.

Question 5.
A rectangle is a rhombus.
Answer:

Question 6.
A rhombus is a square.
Answer:

Question 7.
A square is a rectangle.
Answer:

Question 8.
A trapezoid is a parallelogram.
Answer:

Concepts, Skills, & Problem Solving

USING A VENN DIAGRAM
Use a Venn diagram to find the greatest common factor of the numbers. (See Exploration 1 Page.No 21)

Question 9.
12, 30
Answer:

Question 10.
32, 54
Answer:

Question 11.
24, 108
Answer:

FINDING THE GCF
Find the GCF of the numbers using lists of factors
Question 12.
6, 15
Answer:

Question 13.
14, 84
Answer:

Question 14.
45, 76
Answer:

Question 15.
39, 65
Answer:

Question 16.
51, 85
Answer:

Question 17.
40, 63
Answer:

Question 18.
12, 48
Answer:

Question 19.
24, 52
Answer:

Question 20.
30, 58
Answer:

FINDING THE GCF
Find the GCF of the numbers using lists of factors prime factorizations.

Question 21.
45, 60
Answer:

Question 22.
27, 63
Answer:

Question 23.
36, 81
Answer:

Question 24.
72, 84
Answer:

Question 25.
61, 73
Answer:

Question 26.
38, 95
Answer:

Question 27.
60, 75
Answer:

Question 28.
42, 60
Answer:

Question 29.
42, 63
Answer:

Question 30.
24, 96
Answer:

Question 31.
189, 200
Answer:

Question 32.
90, 108
Answer:

OPEN-ENDED
write a pair of numbers with the indicated GCF.

Question 33.
5
Answer:

Question 34.
12
Answer:

Question 35.
37
Answer:

Question 36.
MODELING REAL LIFE
A teacher is making identical activity packets using 92 crayons and 23 sheets of paper. What is the greatest number of packets the teacher can make with no items left over?
Answer:

Question 37.
MODELING REAL LIFE
You arc making balloon arrangements for a birthday party. ‘there are 16 white balloons and 24 red balloons Each arrangement must he identical. What is the greatest number of arrangements you can make using every balloon?

Answer:

YOU BE THE TEACHER
Your friend finds the CCI of the two numbers. Is your friend correct? Explain your reasoning.

Question 38.

Answer:

Question 39.

Answer:

FINDING THE GCF
Find the GCF of the numbers.
Question 40.
35, 56, 63
Answer:

Question 41.
30, 60, 78
Answer:

Question 42.
42, 70, 84
Answer:

Question 43.
40, 55, 72
Answer:

Question 44.
18, 54, 90
Answer:

Question 45.
16, 18, 88
Answer:

Question 46.
52, 78, 101
Answer:

Question 47.
96, 120, 156
Answer:

Question 48.
280, 300, 380
Answer:

Question 49.
OPEN-ENDED
Write three numbers that have a GCF of 16. What method did you use to find your answer?
Answer:

CRITICAL THINKING
Tell whether the statement ¡s always, someUmes, or never true. Explain your reasoning.
Question 50.
The GCF of two even numbers is 2.
Answer:

Question 51.
The GCF of two prime numbers is 1.
Answer:

Question 52.
When one number is a multiple of another, the GCF of the numbers is the greater of the numbers.
Answer:

Question 53.
PROBLEM SOLVING
A science museum makes gift bags for students using 168 magnets, 48 robot figurines, and 24 packs of freeze-dried ice cream. What is the greatest number of gift bags that can be made using all of the items? How many of each item are in each gift bag?

Answer:

Question 54.
VENN DIAGRAM
Consider the numbers 252, 270, and 300.
a. Create a Venn diagram using the prime factors of the numbers.
Answer:

b. Use the Venn diagram to find the GCF of 252, 270, and 300.
Answer:

c. What is the GCF of 252 and 270? 252 and 300? 270 and 300? Explain how you found your answers.
Answer:

Question 55.
MP REASONING
You are making fruit baskets using 54 apples, 36 oranges, and 73 bananas.
a. Explain why you cannot make identical fruit baskets without leftover fruit.
Answer:

b. What is the greatest number of identical fruit baskets you can make with the least amount of fruit left over? Explain how you found your answer
Answer:

Question 56.
DIG DEEPER!
Two rectangular, adjacent rooms share a wall. One-foot-by-one-foot tiles cover the floor of each room. Describe how the greatest possible length of the adjoining wall is related to the total number of tiles in each room. Draw a diagram that represents one possibility.

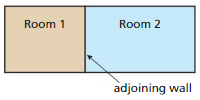
Answer:

Section 1.5 Least Common Multiple

Exploration 1

Identifying Common Multiples

Work with a partner. In paris (a) – (d), create a Venn diagram that represents the first several multiples of each number and identify any common multiples.
a. 8 and 12
Answer:

b. 4 and 14
Answer:

c. 10 and 15
Answer:

d. 20 and 35
Answer:

e. Look at the Venn diagrams in parts (a) – (d). Explain how to identify the least common multiple of each pair of numbers. Then circle it in each diagram.
Answer:

Exploration 2

Using Prime Factors

Work with a partner.

a. Create a Venn diagram that represents the prime factorizations of 8 and 12.

b. Repeat part (a) for the remaining number pairs in Exploration 1.

c. MP STRUCTURE
Make a conjecture about the relationship between the least common multiples you found in Exploration 1 and the numbers in the Venn diagrams you just created.

d. The Venn diagram shows the prime factors of two numbers.

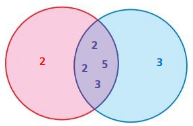
Use the diagram to complete the following tasks.

• Identify the two numbers.
• Find the greatest common factor.
• Find the least common multiple.

Answer:

Math Practice.
Analyze Conjectures
How can you test your conjecture in part (c)?
Answer:

Lesson 1.5 Least Common Multiple

Try It Find the LCM of the numbers using lists of multiples.
Question 1.
3, 8
Answer:

Question 2.
9, 12
Answer:

Question 3.
6, 10
Answer:

Try It Find the LCM of the numbers using prime factorizations.

Question 4.
14, 18
Answer:

Question 5.
28, 36
Answer:

Question 6.
24, 90
Answer:

Try It Find the LCM of the numbers.
Question 7.
2, 5, 8
Answer:

Question 8.
6, 10, 12
Answer:

Question 9.
Write three numbers that have a least common multiple of 100.
Answer:

Self-Assessment for Concepts & Skills

Solve each exercise. Then rare your understanding of the success criteria in your journal

FINDING THE LCM
Find the LCM of the numbers.

Question 10.
6, 9
Answer:

Question 11.
30, 10
Answer:

Question 12.
5, 11
Answer:

Question 13.
MP REASONING
Write two numbers such that 18 and 30 are multiples of the numbers. justify your answer.
Answer:

Question 14.
MP REASONING
You need to find the LCM of 13 and 14. Would you rather list their multiples or use their prime factorizations? Explain.
Answer:

Question 15.
MP CHOOSE TOOLS
A student writes the prime factorizations of 8 and 12 in a table as shown. She claims she can use the table to find the greatest common factor and the least common multiple 8 and 12. How is this possible?


Answer:

Question 16.
CRITICAL THINKING
How can you use least common multiples to add or subtract fractions with different denominators?
Answer:

Self-Assessment for Problem Solving

Solve each exercise. Then rate your understanding of the success criteria in your journal.

Question 17.
A geyser erupts every fourth day. Another geyser erupts every sixth day. Today both geysers erupted. In how many days will b0th geysers erupt on the same day again?

Answer:

Question 18.
A water park has two large buckets that slowly fill with water. One bucket dumps water every 12 minutes. The other bucket dumps water every 10 minutes. Five minutes ago, b0th buckets dumped water. When will both buckets dump water at the same time again?

Answer:

Question 19.
DIG DEEPER!
You purchase disposable plates, cups, and forks for a cookout. Plates are sold in packages of 24, cups in packages of 32, and forks in packages of 18. What are the least numbers of packages you should buy in order to have the same number of plates, cups, and forks?
Answer:

Least Common Multiple Practice 1.5

Review & Refresh

Find the GCF of the numbers.

Question 1.
18, 42
Answer:

Question 2.
72, 96
Answer:

Question 3.
38, 76, 111
Answer:

Divide.
Question 4.
900 ÷ 6
Answer:

Question 5.
1941 ÷ 9
Answer:

Question 6.
672 ÷ 12
Answer:

Write an ordered pair that corresponds to the point.

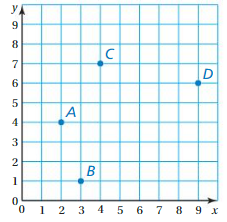
Question 7.
Point A
Answer:

Question 8.
Point B
Answer:

Question 9.
Point C
Answer:

Question 10.
Point D
Answer:

Concepts, Skills, & Problem Solving

USING A VENN DIAGRAM
Use a Venn diagram to find the least common multiple of the numbers. (See Exploration 1 Page.No 27)
Question 11.
3, 7
Answer:

Question 12.
6, 8
Answer:

Question 13.
1, 5
Answer:

FINDING THE LCM
Find the LCM of the numbers using lists of multiplies.
Question 14.
1, 5
Answer:

Question 15.
2, 6
Answer:

Question 16.
2, 3
Answer:

Question 17.
2, 9
Answer:

Question 18.
3, 4
Answer:

Question 19.
8, 9
Answer:

20.
5, 8
Answer:

Question 21.
11, 12
Answer:

Question 22.
12, 18
Answer:

FINDING THE LCM
Find the LCM of the numbers using prime factorizations.
Question 23.
7, 12
Answer:

Question 24.
5, 9
Answer:

Question 25.
4, 11
Answer:

Question 26.
9, 10
Answer:

Question 27.
12, 27
Answer:

Question 28.
18, 45
Answer:

Question 29.
22, 33
Answer:

Question 30.
36, 60
Answer:

Question 31.
35, 50
Answer:

Question 32.
YOU BE THE TEACHER
Your friend finds the LCM of 6 and 9. Is your friend correct? Explain your reasoning.

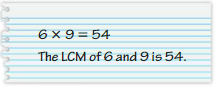
Answer:

Question 33.
MODELING REAL LIFE
You have diving lessons every fifth day and swimming lessons every third day. Today you have both lessons. In how many days will you have both lessons on the same day again?
Answer:

Question 34.
MP REASONING
Which model represents an LCM that is different from the other three? Explain your reasoning.

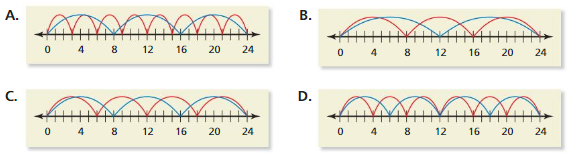
Answer:

FINDING THE LCM
Find the LCM of the numbers.
Question 35.
2, 3, 7
Answer:

Question 36.
3, 5, 11
Answer:

Question 37.
4, 9, 12
Answer:

Question 38.
6, 8, 15
Answer:

Question 39.
7, 18, 21
Answer:

Question 40.
9, 10, 28
Answer:

Question 41.
MP PROBLEM SOLVING
At Union Station, you notice that three subway lines just arrived at the same time. How long must you wait until all three lines arrive at Union Station at the same time again?

Subway Line	Arrival Time
A	Every 10 min
B	Every 12 min
C	Every 15 min

Answer:

Question 42.
DIG DEEPER!
A radio station gives away $15 to every 15th caller, $25 to every 25th caller, and a free concert ticket to every 100th caller. When will the station first give away all three prizes to one caller? When this happens, how much money and how many tickets are given away?
Answer:

Question 43.
MP LOGIC
You and a friend are running on treadmills. You run 0.5 mile every 3 minutes, and your friend runs 2 miles every 14 minutes. You both start and stop running at the same time and run a whole number of miles. What are the least possible numbers of miles you and your friend can run?
Answer:

Question 44.
VENN DIAGRAM
Refer to the Venn diagram.

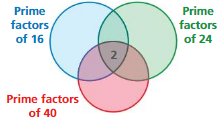
a. Copy and complete the Venn diagram.
Answer:

b. What is the LCM of 16, 24, and 40?
Answer:

c. What is the LCM of 16 and 40? 24 and 40? 16 and 21? Explain how you found your answers.
Answer:

CRITICAL THINKING
Tell whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 45.
The LCM of two different prime numbers is their Product.
Answer:

Question 46.
The LCM of a set of numbers is equal to one of the numbers in the set.
Answer:

Question 47.
The GCF of two different numbers is the LCM of the numbers.
Answer:

Numerical Expressions and Factors Connecting Concepts

Using the Problem-Solving Plan

Question 1.
A sports team gives away shirts at the stadium. There arc 60 large shirts, 1.6 times as many small shirts as large shirts, and 1.5 times as many medium shirts as small shirts. The team wants to divide the shirts into identical groups to he distributed throughout the stadium. What is the greatest number of groups that can be formed using every shirt?

Understand the problem: You know the number of large shirts and two relationships among the numbers of small, medium, and large shirts. You are asked to find the greatest number of identical groups that can be formed using every shirt.

Make a plan: Break the problem into parts. First use multiplication to find the number of each size shirt. Then find the GCF of these numbers.

Solve and check: Lise the plan to solve the problem. Then check your solution.
Answer:

Question 2.
An escape artist fills the tank shown with water. Find the number of cubic feet of water needed to fill the tank. Then find the number of cubic yards of water that are needed to fill the tank. justify your answer.

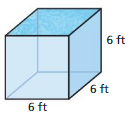
Answer:

Numerical Expressions and Factors Chapter Review

Powers and Exponents Homework & Practice 1.1

Write the product as a power.

Question 1.
3 × 3 × 3 × 3 × 3 × 3
Answer:

Question 2.
5 × 5 × 5
Answer:

Question 3.
17 • 17 • 17 • 17 • 17
Answer:

Find the value of the power.
Question 4.
3³
Answer:

Question 5.
2⁶
Answer:

Question 6.
4⁴
Answer:

Question 7.
Write a power that has a value greater than 2³ and less than 3³.
Answer:

Question 8.
Without evaluating, determine whether 2⁵ or 2² is greater. Explain.
Answer:

Question 9.
The bases on a softball field arc square. What is the area of each base?


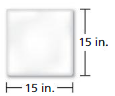
Answer:

Order of Operations Homework & Practice 1.2

Evaluate the expression.

Question 10.
3 × 6 – 12 ÷ 6
Answer:

Question 11.
30 ÷(14 – 2²) × 5
Answer:

Question 12.
\(\frac{5(2.3+3.7)}{2}\)
Answer:

Question 13.
4³ – \(\frac{1}{2}\)(7² + 5)
Answer:

Question 14.
20 × (3² – 4) ÷ 50
Answer:

Question 15.
5 + 3 (4² – 2) ÷ 6
Answer:

Question 16.
Use grouping symbols and at least one exponent to write a numerical expression that has a value of 80.
Answer:

Prime Factorization Homework & Practice 1.3

List the factor Pairs of the number.

Question 17.
28
Answer:

Question 18.
44
Answer:

Question 19.
96
Answer:

Question 20.
There arc 36 graduated cylinders to put away on a shelf after science class. The shelf can fit a maximum of 20 cylinders across and 4 cylinders deep. The teacher wants each row to have the same number of cylinders. List the possible arrangements of the graduated cylinders on the shelf.

Answer:

Write the prime factorization of the number.

Question 21.
12
Answer:

Question 22.
50
Answer:

Question 23.
66
Answer:

Greatest Common Factor Homework & Practice 1.4

Find the GCF of the numbers using lists of factors.
Question 24.
27, 45
Answer:

Question 25.
30, 48
Answer:

Question 26.
28, 48
Answer:

Find the GCF of the numbers using prime factorizations.
Question 27.
24, 80
Answer:

Question 28.
52, 68
Answer:

Question 29.
32, 56
Answer:

Question 30.
Write a pair of numbers that have a GCF of 20.
Answer:

Question 31.
What is the greatest number of friends you can invite to an arcade using the coupon such that the tokens and slices of pizza are equally split between you and your friends with none left over? How many slices of pizza and tokens will each person receive?

Answer:

Least Common Multiple Homework & Practice 1.5

Find the LCM of the numbers using lists of multiples.
Question 32.
4, 14
Answer:

Question 33.
6, 20
Answer:

Question 34.
12, 28
Answer:

Find the LCM of the numbers using prime factorbations.
Question 35.
6, 15
Answer:

Question 36.
10, 12
Answer:

Question 37.
18, 27
Answer:

Question 38.
Find the LCM of 8, 12, and 18.
Answer:

Question 39.
Write a pair of numbers that have an LCM of 84.
Answer:

Question 40.
Write three numbers that have an LCM of 45.
Answer:

Question 41.
You water your roses every sixth day and your hydrangeas every fifth day. Today you water both plants. In how man days will you water both plants on the same day again

Answer:

Question 42.
Hamburgers are sold in packages of 20, while buns are sold in packages of 12. What are the least numbers of packages you should buy in order to have the same number of hamburgers and buns?
Answer:

Question 43.
A science museum is giving away a magnetic liquid kit to every 50th guest and a plasma ball to every 35th guest until someone receives both prizes.

a. Which numbered guest will receive both a magnetic liquid kit and a plasma ball?
Answer:

b. How many people will receive a plasma ball?
Answer:

Numerical Expressions and Factors Practice Test

Question 1.
Find the value of 2³.
Answer:

Question 2.
Evaluate \(\frac{5+4(12-2)}{3^{2}}\)
Answer:

Question 3.
Write 261 • 264 • 264 as a power.
Answer:

Question 4.
List the factor pairs of 66.
Answer:

Question 5.
Write the prime factorization of 56.
Answer:

Find the GCF of the numbers.
Question 6.
24, 54
Answer:

Question 7.
16, 32, 72
Answer:

Question 8.
52, 65
Answer:

Find the LCM of the numbers.
Question 9.
9, 24
Answer:

Question 10.
26, 39
Answer:

Question 11.
6, 12, 11
Answer:

Question 12.
You have 16 yellow beads, 20 red heads, and 21 orange beads to make identical bracelets. What is the greatest number of bracelets that you can make using all of the beads?
Answer:

Question 13.
A bag contains equal numbers of green marbles and blue marbles. You can divide all of the green marbles into groups of 12 and all the blue marbles into groups of 16. What is the least number of each color of marble that can be in the bag?
Answer:

Question 14.
The ages of the members of a family are 65, 58, 27, 25, 5, and 2 years old. What is the total admission price for the family to visit the zoo?

Answer:

Question 15.
A competition awards prizes for fourth, third, second, and first place. The fourth place winner receives $5. Each place above that receives a prize that is five times the amount of the previous prize. How much prize money is awarded?
Answer:

Question 16.
You buy tealight candles and mints as party favors for a baby shower. The tealight candles come in packs of 12 for $3.50. The mints come in packs of 50 for $6.25. What is the least amount of money you can spend to buy the same number of candles and mints?

Answer:

Numerical Expressions and Factors Cumulative Practice

Question 1.
What is the value of 8 × 135?
Answer:

Question 2.
Which number is equivalent to the expression below?
3 • 2³ – 8 ÷ 4
A. 0
B. 4
C. 22
D. 214
Answer:

Question 3.
The top of an end table is a square with a side length of 16 inches. What is the area of the tabletop?

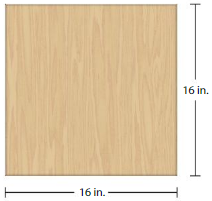
F. 16 in.²
G. 32 in.²
H. 64 in.²
I. 256 in.²
Answer:

Question 4.
You are filling baskets using 18 green eggs, 36 red eggs, and 54 blue eggs. What is the greatest number of baskets that you can fill so that the baskets are identical and there are no eggs left over?
A. 3
B. 6
C. 9
D. 18
Answer:

Question 5.
What is the value of 2² • 3² • 5?
Answer:

Question 6.
You hang the two strands of decorative lights shown below.

Strand 1: changes between red and blue every 15 seconds

Strand 2: changes between green and gold every 18 seconds
Both strands just changed color. After how many seconds will the strands change color at the same time again?
F. 3 seconds
G. 30 seconds
H. 90 seconds
I. 270 seconds
Answer:

Question 7.
Point p is plotted in the coordinate plane below.

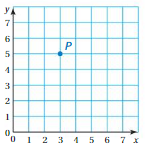
What arc the coordinates of Point p?
A. (5, 3)
B. (4, 3)
C. (3, 5)
D. (3, 4)
Answer:

Question 8.
What is the prime factorization 1100?
F. 2 × 5 × 11
G. 2² × 5² × 11
H. 4 × 5² × 11
I. 2² × 5 × 55
Answer:

Question 9.
What is the least common multiple of 3, 8, and 10?
A. 21
B. 30
C. 80
D. 120
Answer:

Question 10.
What is the area of the shaded region of the figure below?

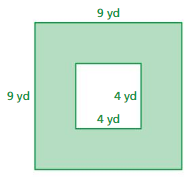
F. 16yd²
G. 65yd²
H. 81 yd²
I. 97 yd²
Answer:

Question 11.
Which expression represents a prime factorization?
A. 4 × 4 × 7
B. 2² × 21 × 23
C. 3⁴ × 5 × 7
D. 5 × 5 × 9 × 11
Answer:

Question 12.
Find the greatest common factor for each pair of numbers.
Think
Solve
Explain
10 and 15      10 and 21     15 and 21
What can you conclude about the greatest common factor of 10, 15, and 21?
Explain your reasoning.
Answer: