Big Ideas Math Answers Grade 6 Chapter 1 Numerical Expressions and Factors: Before knowing the numerical expressions, Grade 6 students must be familiar with composite numbers, factor pairs, and prime numbers. Refer to the concept of vocabulary terms, subtracting and adding the fractions, mixed fractions in the below sections.
Know the various terms like what is exponent, perfect square, power, composite numbers, prime numbers with the help of Big Ideas Math Answers Grade 6 Chapter 1 Numerical Expressions and Factors. You can also get all the answers to the questions which are available in the Big Ideas Math Answers Grade 6 Chapter 1 Numerical Expressions and Factors pdf format. Scroll to the below sections to check example problems, answer PDFs, etc.
Big Ideas Math Book 6th Grade Answer Key Chapter 1 Numerical Expressions and Factors
BIM 6th Grade Chapter 1 Numerical Expression and Factors Answer key helps you in easy and quick learning. Download Big Ideas Math Book 6th Grade Answer Key Chapter 1 Numerical Expressions and Factors pdf to kickstart your preparation. Get the solutions for all the questions in this article. There are various topics included in numerical expressions like Least Common Multiple, Prime Factorisation, Powers and Exponents, Order of Operations, Greatest Common Factor, Exponents and Powers. Click on the below links and prepare for the exam as per the topics.
Performance Task
- Numerical Expressions and Factors Steam Video/Performance Task
- Numerical Expressions and Factors Getting Ready for Chapter 1
Lesson 1: Powers and Exponents
Lesson 2: Order of Operations
Lesson 3: Prime Factorization
Lesson 4: Greatest Common Factor
Lesson 5: Least Common Multiple
Chapter: 1 – Numerical Expressions and Factors
- Numerical Expressions and Factors Connecting Concepts
- Numerical Expressions and Factors Chapter Review
- Numerical Expressions and Factors Practice Test
- Numerical Expressions and Factors Cumulative Practice
Numerical Expressions and Factors Steam Video/Performance Task
Filling Piñatas
Common factors can be used to make identical groups of objects. Can you think of any situations in which you would want to separate objects into equal groups? Are there any common factors that may be more useful than others? Can you think of any other ways to use common factors?
watch the STEAM Video “Filling Piñatas.” Then answer the following questions. The table below shows the numbers of party favors that Alex and Enid use to make piñatas.


Question 1.
When finding the number of identical piñatas that can be made, why is it helpful for Alex and Enid to list the factors of each number given in the table?
Answer: By using the list of the factors of all the numbers Alex and Enid can make identical groups of the objects.
Question 2.
You want to create 6 identical piñatas. How can you change the numbers of party favors in the table to make this happen? Can you do this without changing the total number of party favors?
Answer: You can change the number of party favors to create 6 identical pinatas.
There are 100 Mints. So divide it into two identical groups.
Change the number of mints to 50. And add 50 to new identical pinatas.
Performance Task
Setting the Table
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be asked to plan a fundraising event with the items below.
72 chairs
48 balloons
24 flowers
36 candles

You will find the greatest number of identical tables that can be prepared, and what will be in each centerpiece. When making arrangements for a party, should a party planner always use the greatest number of identical tables possible? Explain why or why not.
Answer:
72 chairs = 2 × 36
= 2 × 2 × 18
= 2 × 2 × 2 × 9
= 2 × 2 × 2 × 3 × 3
2, 2, 2, 3, 3
Therefore, 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72 are the factors of 72.
48 balloons = 2 × 24
= 2 × 2 × 12
= 2 × 2 × 2 × 6
= 2 × 2 × 2 × 2 × 3
The positive Integer factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
The factors of number 24 are 1, 2, 3, 4, 6, 8, 12, 24.
The factors of number 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36
The greatest number of identical tables possible are 1, 2, 3, 4, 6, 12.
Numerical Expressions and Factors Getting Ready for Chapter 1
Chapter Exploration
Work with a partner. In Exercises 1–3, use the table.
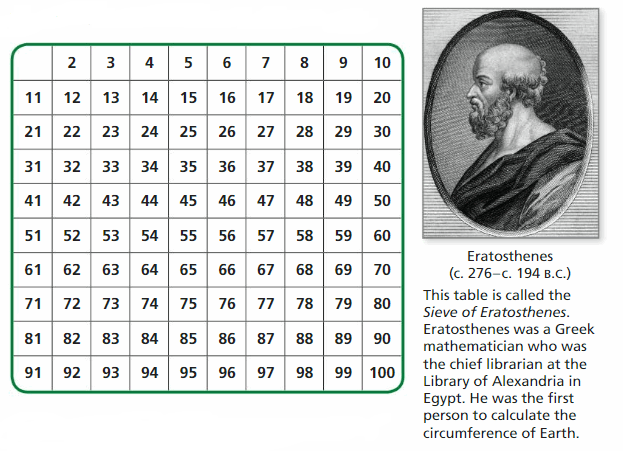
- Cross out the multiples of 2 that are greater than 2. Do the same for 3, 5, and 7.
- The numbers that are not crossed out are called prime numbers. The numbers that are crossed out are called composite numbers. In your own words, describe the characteristics of prime numbers and composite numbers.
- MODELING REAL LIFE Work with a partner. Cicadas are insects that live underground and emerge from the ground after x or x + 4 years. Is it possible that both x and x +4 are prime? Give some examples.
Answer:

The numbers that are not crossed are 2, 3, 5, 7, 9, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,61, 67, 71, 73, 79, 83, 89, 97.
These are not multiples of any numbers. So, the above numbers are the prime numbers.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
Answer:
i. First, we solve any operations inside of parentheses or brackets. Second, we solve any exponents. Third, we solve all multiplication and division from left to right. Fourth, we solve all addition and subtraction from left to right.
ii. “Factors” are numbers we can multiply together to get another number. When we find the factors of two or more numbers, and then find some factors are the same, then they are the “common factors”.
iii. A common multiple is a whole number that is a shared multiple of each set of numbers. The multiples that are common to two or more numbers are called the common multiples of those numbers. The smallest positive number is a multiple of two or more numbers.
Lesson 1.1 Powers and Exponents
Exploration 1
Writing Expressions Using Exponents
Work with a partner. Copy and complete the table.
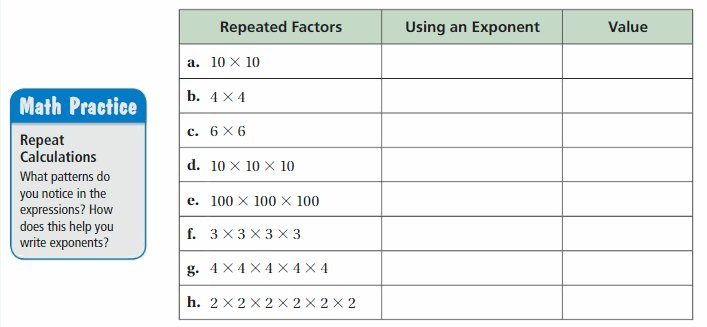
Answer:
i. In your own words, describe what the two numbers in the expression 35 mean.
Answer: 35 means the number 3 repeats 5 times.
3 × 3 × 3 × 3 × 3 = 243
EXPLORATION 2
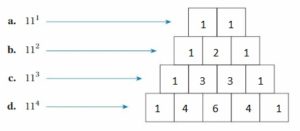
Using a Calculator to Find a Pattern
Work with a partner. Copy the diagram. Use a calculator to find each value. Write one digit of the value in each box. Describe the pattern in the digits of the values.
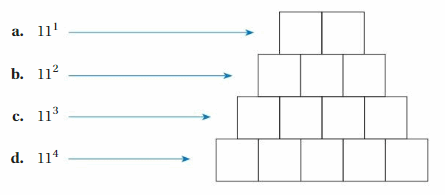
Answer:
1.1 Lesson
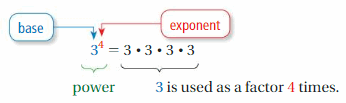
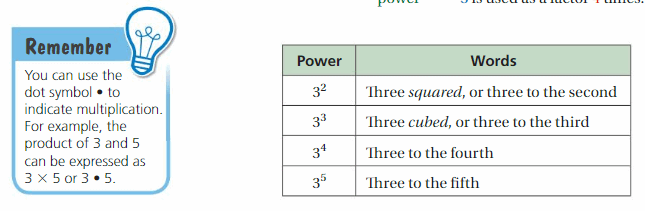
A power is a product of repeated factors. The base of a power is the repeated factor. The exponent of a power indicates the number of times the base is used as a factor.
Try It
Write the product as a power.
Question 1.
2 × 2 × 2
Answer: 2³ = 8
Two cubed or three to the two. Here 2 is repeated three times.
Question 2.
![]()
Answer: 46656 = 66
Six to the six. Here 6 is repeated six times.
Question 3.
15 × 15 × 15 × 15
Answer: 56025 = 154
15 to the power 4. Here 15 is repeated four times.
Question 4.
![]()
Answer: 1280000000 = 207
20 to the power 7. Here 20 is repeated seven times.
Try It
Find the value of the power.
Question 5.
63
Answer: 6 × 6 × 6 = 216
The value of the power 63 is 216.
Question 6.
92
Answer: 9 × 9 = 81
The value of the power 92 is 81
Question 7.
34
Answer: 3 × 3 × 3 × 3
The value of the power 34 is 81.
Question 8.
182
Answer: 18 × 18
The value of the power 182 is 324.
Try It
Determine whether the number is a perfect square.
Question 9.
25
Answer: 5²
Yes, 25 is the perfect square.
A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.
Question 10.
2
Answer: 2 is not a perfect square. 2 cannot be expressed as the square of a number from the same number system.
Question 11.
99
Answer: 99 is not a perfect square. 99 cannot be expressed as the square of a number from the same number system.
Question 12.
36
Answer: 6²
36 is a perfect square
A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING VALUES OF POWERS
Find the value of the power.
Question 13.
82
Answer: 8 × 8 = 64
The value of the power 82 is 64.
Question 14.
35
Answer: 3 × 3 × 3 × 3 × 3 = 243
The value of the power 35 is 243.
Question 15.
113
Answer: 11 × 11 × 11 = 1331
The value of the power 113 is 1331.
Question 16.
VOCABULARY
How are exponents and powers different?
Answer:
An expression that represents repeated multiplication of the same factor is called a power. The number 5 is called the base, and the number 2 is called the exponent. The exponent corresponds to the number of times the base is used as a factor.
Question 17.
VOCABULARY
Is 10 a perfect square? Is 100 a perfect square? Explain.
Answer: 10 is not a perfect square.
A perfect square is a number that is generated by multiplying two equal integers by each other.
100 is a perfect square. Because 10 × 10 = 100.
Question 18.
WHICH ONE DOESN’T BELONG?
Which one does not belong with the other three? Explain your reasoning.
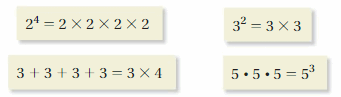
Answer:
24 = 2 × 2 × 2 × 2 = 16
32 = 3 × 3 = 9
3 + 3 + 3 + 3 = 3 × 4
5.5.5 = 125
The 3rd option does not belong to the other three expressions.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 19.
A square solar panel has an area of 16 square feet. Write the area as a power. Then find the side lengths of the panel.
Answer: 4 feet
Explanation:
Given that,
A square solar panel has an area of 16 square feet.
A = s × s
16 = s²
4² = s²
s = 4
Thus the side length of the panel is 4 feet.
Question 20.
The four-square court shown is a square made up of four identical smaller squares. What is the area of the court?
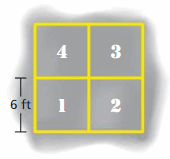
Answer:
Given,
The four-square court shown is a square made up of four identical smaller squares.
The side of each square is 6 feet.
6 + 6 = 12 feet
The area of the court is 12 ft × 12 ft
A = 144 square feet
Thus the area of the court is 144 square feet.
Question 21.
DIG DEEPER!
Each face of a number cube is a square with a side length of 16 millimeters. What is the total area of all of the faces of the number cube?
Answer:
Given that,
Each face of a number cube is a square with a side length of 16 millimeters.
Area of the cube = 6 a²
A = 6 × 16 × 16
A = 1536 sq. mm
Powers and Exponents Practice 1.1
Review & Refresh
Multiply.
Question 1.
150 × 2
Answer: 300
Explanation:
Multiply the two numbers 150 and 2.
First multiply 2 with ones place 2 × 0 = 0
Next multiply with tens place 2 × 50 = 100
Next multiply with hundreds place 2 × 100 = 200
200 + 100 = 300
Question 2.
175 × 8
Answer: 1400
Explanation:
Multiply the two numbers 175 and 8.
First, multiply 2 with ones place 8 × 5 = 40
Next multiply with tens place 8 × 70= 560
Next multiply with hundreds place 8 × 100 = 800
800 + 560 + 40 = 1400
Question 3.
123 × 3
Answer: 369
Explanation:
Multiply the two numbers 123 and 3.
First multiply 2 with ones place 3 × 3 = 9
Next multiply with tens place 3 × 20 = 60
Next multiply with hundreds place 3 ×100 = 300
300 + 60 + 9 = 369
Question 4.
151 × 9
Answer: 1359
Explanation:
Multiply the two numbers 151 and 9.
First multiply 2 with ones place 9 × 1 = 9
Next multiply with tens place 9 × 50 = 450
Next multiply with hundreds place 9 × 100 = 900
900 + 450 + 9 = 1359
Write the sentence as a numerical expression.
Question 5.
Add 5 and 8, then multiply by 4.
Answer: The numerical expression for the above sentence is 5 + 8 × 4
Question 6.
Subtract 7 from 11, then divide by 2.
Answer: The numerical expression for the above sentence is 11 – 7 ÷ 2
Round the number to the indicated place value.
Question 7.
4.03785 to the tenths
Answer: The number 4.03785 nearest to the tenths is 4.0
Question 8.
12.89503 to the hundredths
Answer: The number 12.89503 nearest to the hundredths is 12.90
Complete the sentence.
Question 9.
![]()
Answer: 3
Explanation:
(1/10) × 30 = 30/10 = 3
The product of 1/10 and 30 is 3.
Question 10.

Answer: 20
Explanation:
(4/5) × 25 = 4 × 5 = 20
The product of 4/5 and 25 is 20.
Concepts, Skills, & Problem Solving
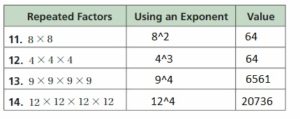
WRITING EXPRESSIONS USING EXPONENTS
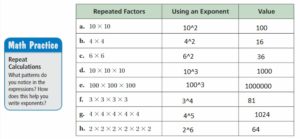
Copy and complete the table. (See Exploration 1, p. 3.)
Answer:
WRITING EXPRESSIONS AS POWERS
Write the product as a power.
Question 15.
9 × 9
Answer: The exponential form of the given expression is 9²
Question 16.
13 × 13
Answer: The exponential form of the given expression is 13²
Question 17.
15 × 15 × 15
Answer: The exponential form of the given expression is 15³
Question 18.
2.2.2.2.2
Answer: The exponential form of the given expression is 25
Question 19.
14 × 14 × 14
Answer: The exponential form of the given expression is 14³
Question 20.
8.8.8.8
Answer: The exponential form of the given expression is 84
Question 21.
11 × 11 × 11 × 11 × 11
Answer: The exponential form of the given expression is 115
Question 22.
7.7.7.7.7.7
Answer: The exponential form of the given expression is 76
Question 23.
16.16.16.16
Answer: The exponential form of the given expression is 164
Question 24.
43 × 43 × 43 × 43 × 43
Answer: The exponential form of the given expression is 435
Question 25.
167 × 167 × 167
Answer: The exponential form of the given expression is 167³
Question 26.
245.245.245.245
Answer: The exponential form of the given expression is 2454
FINDING VALUES OF POWERS
Find the value of the power.
Question 27.
52
Answer: The value of the powers 52 is 5 × 5 = 25
Question 28.
43
Answer: The value of the powers 43 is 4 × 4 × 4 = 64
Question 29.
62
Answer: The value of the powers 62 is 6 × 6 = 36
Question 30.
17
Answer: The value of the powers 17 is 1 × 1 × 1 × 1 × 1 × 1 × 1 = 1
Question 31.
03
Answer: The value of the powers 03 is 0 × 0 × 0 = 0
Question 32.
84
Answer: The value of the powers 84 is 8 × 8 × 8 × 8 = 4096
Question 33.
24
Answer: The value of the powers 24 is 2 × 2 × 2 × 2 = 64
Question 34.
122
Answer: The value of the powers 122 is 12 × 12 = 144
Question 35.
73
Answer: The value of the powers 73 is 7 × 7 × 7 = 343
Question 36.
54
Answer: The value of the powers 54 is 5 × 5 × 5 × 5 = 625
Question 37.
25
Answer: The value of the powers 25 is 2 × 2 × 2 × 2 × 2 = 32
Question 38.
142
Answer: The value of the powers 142 is 14 × 14 = 196
USING TOOLS
Use a calculator to find the value of the power.
Question 39.
76
Answer: 7 × 7 × 7 × 7 × 7 × 7 = 117649
Question 40.
48
Answer: 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 = 256
Question 41.
124
Answer: 12 × 12 × 12 × 12 = 20736
Question 42.
175
Answer: 17 × 17 × 17 × 17 × 17 = 1419857
Question 43.
YOU BE THE TEACHER
Your friend finds the value of 83. Is your friend correct? Explain your reasoning.
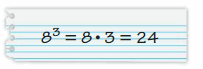
Answer: Your friend is incorrect
83 is nothing but 8 repeats 3 times.
83 = 8 × 8 × 8 = 512
IDENTIFYING PERFECT SQUARES
Determine whether the number is a perfect square.
Question 44.
8
Answer: 8 is not the perfect square. 8 cannot be expressed as the square of a number from the same number system.
Question 45.
4
Answer: 4 is a perfect square.
A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.
Question 46.
81
Answer: 81 perfect square
A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.
Question 47.
44
Answer: 44 is not the perfect square. 44 cannot be expressed as the square of a number from the same number system
Question 48.
49
Answer: 49 is a perfect square
A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.
Question 49.
125
Answer: 125 is not the perfect square. 125 cannot be expressed as the square of a number from the same number system
Question 50.
150
Answer: 150 is not the perfect square. 150 cannot be expressed as the square of a number from the same number system
Question 51.
144
Answer: 144 is the perfect square
A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.
Question 52.
MODELING REAL LIFE
On each square centimeter of a person’s skin, there are about 392 bacteria. How many bacteria does this expression represent?
Answer:
Given,
On each square centimeter of a person’s skin, there are about 392 bacteria.
392 = 39 × 39 = 1521 centimeters
Thus the bacteria represents 1521 centimeters.
Question 53.
REPEATED REASONING
The smallest figurine in a gift shop is 2 inches tall. The height of each figurine is twice the height of the previous figurine. What is the height of the tallest figurine?

Answer:
Given that,
The smallest figurine in a gift shop is 2 inches tall. The height of each figurine is twice the height of the previous figurine.
The second figurine is twice that of the first figurine = 2 × 2 = 4 inches
The third figurine is twice that of the second figurine = 4 × 4 = 16 inches
The fourth figurine is twice that of the third figurine = 16 × 16 = 256 inches
Thus the height of the tallest figurine is 256 inches.
Question 54.
MODELING REAL LIFE
A square painting measures 2 meters on each side. What is the area of the painting in square centimeters?
Answer:
Given that,
A square painting measures 2 meters on each side.
Area of the square = s × s
A = 2 m × 2 m = 4 sq. meters
Thus the area of the painting in square centimeters is 4.
Question 55.
NUMBER SENSE
Write three powers that have values greater than 120 and less than 130.
Answer:
11² = 11(11) = 121; this is between 120 and 130.
5³ = 5(5)(5) = 25(5) = 125; this is between 120 and 130.
2⁷ = 2(2)(2)(2)(2)(2)(2) = 4(2)(2)(2)(2)(2) = 8(2)(2)(2)(2) = 16(2)(2)(2) = 32(2)(2) = 64(2) = 128; this is between 120 and 130.
Question 56.
DIG DEEPER!
A landscaper has 125 tiles to build a square patio. The patio must have an area of at least 80 square feet.
a. What are the possible arrangements for the patio?
Answer:
Given that a square patio of at least 80 square feet is to be built from 125 tiles of length 12 inches or 1 foot.
Since there are 125 tiles and the patio has a shape of a square of at least 80 square feet, then the possible dimensions of the patio are
9 ft × 9 ft = 81 ft
10 ft × 10 ft = 100 ft, and
11 ft × 11 ft = 121 ft.
b. How many tiles are not used in each arrangement?
Answer:
For a patio of dimensions, 9ft by 9ft, the number of tiles that will not be used is given by 125 – 81 = 44
For a patio of dimensions, 10ft by 10ft, the number of tiles that will not be used is given by 125 – 100 = 25
For a patio of dimensions, 11ft by 11ft, the number of tiles that will not be used is given by 125 – 121 = 4
Question 57.
PATTERNS
Copy and complete the table. Describe what happens to the value of the power as the exponent decreases. Use this pattern to find the value of 40.
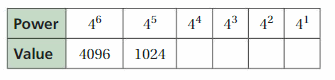
Answer:
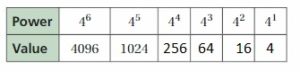
40 = 1
Thus the value of 40 is 1.
Question 58.
REPEATED REASONING
How many blocks do you need to add to Square 6 to get Square 7? to Square 9 to get Square 10? to Square 19 to get Square 20? Explain.
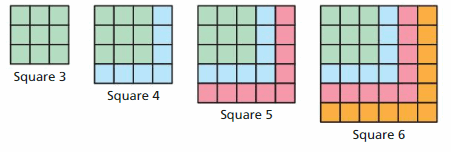
Answer:
You need to add 14 blocks to get square 7. The square 7 contains 7 × 7 = 49 blocks
You need to add 32 blocks to get square 9. The square 9 contains 9 × 9 = 81 blocks
You need to add 19 blocks to get square 10. The square 10 contains 10 × 10 = 100 blocks
You need to add 261 blocks to get square 19. The square 19 contains 19 × 19 = 361 blocks
You need to add 39 blocks to get square 20. The square 20 contains 20 × 20 = 400 blocks
Lesson 1.2 Order of Operations
Order of Operations
EXPLORATION 1
Comparing Different Orders
Work with a partner. Find the value of each expression by using different orders of operations. Are your answers the same?

Answer:
The answers for all the expressions are not the same. The values of each expression will change if you change the order of operations.
a. 3 + 2 × 2
5 × 2 = 10
Multiply, then add
3 + 2 × 2
3 + 4 = 7
b. Subtract then multiply
18 – 3 × 3
15 × 3 = 45
Multiply, then subtract
18 – 3 × 3
18 – 9 = 9
c. Multiply, then subtract
8 × 8 – 2
64 – 2 = 62
Subtract, then Multiply
8 × 8 – 2
8 × 6 = 48
d. Multiply, then add
6 × 6 + 2
36 + 2 = 38
Add, then multiply
6 × 6 + 2
6 × 8 = 48
EXPLORATION 2
Determining Order of Operations
Work with a partner.
a. Scientific calculators use a standard order of operations when evaluating expressions. Why is a standard order of operations needed?
Answer: The order of operations is a rule that tells you the right order in which to solve different parts of a math problem. The order of operations is important because it guarantees that people can all read and solve a problem in the same way.
b. Use a scientific calculator to evaluate each expression in Exploration 1. Enter each expression exactly as written. For each expression, which order of operations is correct?
Answer:
a. 3 + 2 × 2 – Multiply, then add
b. 18 – 3 × 3 – Multiply, then subtract
c. 8 × 8 – 2 – Multiply, then subtract
d. 6 × 6 + 2 – Multiply, then add
c. What order of operations should be used to evaluate 3 + 22, 18 − 32, 82 − 2, and 62 + 2?

Answer:
Solve the expressions by using the calculator.
a. 3 + 2 × 2
3 + 4 = 7
b. 18 – 3 × 3
18 – 9 = 9
c. 8 × 8 – 2
64 – 2 = 62
d. 6 × 6 + 2
36 + 2 = 38
d. Do 18 ÷ 3.3 and 18 ÷ 32 have the same value? Justify your answer.

Answer: No
Explanation:
18 ÷ 3.3
(18 ÷ 3) × 3
6 × 3 = 18
18 ÷ 32 = 2
By using the calculator you can find the difference.
e. How does evaluating powers fit into the order of operations?
Answer:
When an expression has parentheses and powers, evaluate it in the following order: contents of parentheses, powers from left to right, multiplication and division from left to right, and addition and subtraction from left to right.
1.2 Lesson
A numerical expression is an expression that contains numbers and operations. To evaluate, or find the value of, a numerical expression, use a set of rules called the order of operations.
Key Idea
order of operations
- Perform operations in grouping symbols.
- Evaluate numbers with exponents.
- Multiply and divide from left to right.
- Add and subtract from left to right.
Try It
a. Evaluate the expression.
Question 1.
7.5 + 3
Answer: 56
Explanation:
You have to evaluate the expression from left to right.
7(5 + 3) = 7 × 8
= 56
Question 2.
(28 – 20) ÷ 4
Answer: 2
Explanation:
You have to evaluate the expression from left to right.
28 – 20 = 8
8 ÷ 4 = 2
Question 3.
[6 + (15 – 10)] × 5
Answer: 55
Explanation:
You have to evaluate the expression from left to right.
[6 + (15 – 10)] × 5
[6 + 5] × 5
11 × 5 = 55
Try It
Evaluate the expression.
Question 4.
6 + 24 – 1
Answer: 21
Explanation:
You have to evaluate the expression from left to right.
6 + 24 – 1
6 + (16 – 1)
6 + 15 = 21
6 + 24 – 1 = 21
Question 5.
4.32 + 18 – 9
Answer: 45
Explanation:
You have to evaluate the expression from left to right.
4.32 + (18 – 9)
4.32 + 9
4 × 9 + 9
36 + 9 = 45
Question 6.
16 + (52 – 7) ÷ 3
Answer:
Explanation:
You have to evaluate the expression from left to right.
16 + (52 – 7) ÷ 3
16 + (25 – 7) ÷ 3
16 + (18) ÷ 3
16 + (18 ÷ 3)
16 + 6 = 22
Thee symbols × and . are used to indicate multiplication. You can also use parentheses to indicate multiplication. For example, 3(2 +7) is the same as 3 × (2 + 7).
Try It
Evaluate the expression.
Question 7.
50 + 6(12 ÷ 4) – 82
Answer: 4
Explanation:
You have to evaluate the expression from left to right.
50 + 6(12 ÷ 4) – 82
50 + 6(3) – 82
50 + 18 – 82
50 + 18 – 64
68 – 64
4
Question 8.
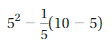
Answer: 24
Explanation:
You have to evaluate the expression from left to right.
5² – 1/5 (10 – 5)
5² – 1/5 (5)
5² – 1
25 – 1
24
Question 9.
![]()
Answer:
Explanation:
You have to evaluate the expression from left to right.
8(2+5) = 8 × 7
(8 × 7)/7 = 8
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
USING ORDER OF OPERATIONS
Evaluate the expression.
Question 10.
7 + 2.4
Answer: 15
Explanation:
You have to evaluate the expression from left to right.
7 + 2 × 4 = 7 + 8 = 15
Question 11.
8 ÷ 4 × 2
Answer: 4
Explanation:
You have to evaluate the expression from left to right.
8 ÷ 4 = 2
2 × 2 = 4
Question 12.
3(5 + 1) ÷ 32
Answer: 2
Explanation:
You have to evaluate the expression from left to right.
3(5 + 1) ÷ 32
3 × 6 ÷ 32
18 ÷ 9 =2
Question 13.
WRITING
Why does 12 − 8 ÷ 2 = 2?
Answer:
12 − 8 ÷ 2
4 ÷ 2 = 2
Question 14.
REASONING
Describe the steps in evaluating the expression 8 ÷ (6 − 4) + 32.
Answer:
8 ÷ (6 − 4) + 32
8 ÷ 2 + 32
4 + 9 = 13
Question 15.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.

Answer: (52 – 8) × 2 does not belong to the other three. Because the order of operations and expressions are different for the fourth option.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
A square plot of land has side lengths of 40 meters. An archaeologist divides the land into 64 equal parts. What is the area of each part?
Answer:
Given that,
A square plot of land has side lengths of 40 meters.
An archaeologist divides the land into 64 equal parts.
Side of the square field = 40m
Area of the square field = s × s
A = 40m × 40m
A = 1600 sq.m
Area of each part of the square = 1600/64 = 25 sq.m
Question 17.
A glass block window is made of two different-sized glass squares. The window has side lengths of 40 inches. The large glass squares have side lengths of 10 inches. Find the total area of the small glass squares.

Answer:
Given,
A glass block window is made of two different-sized glass squares.
The window has side lengths of 40 inches. The large glass squares have side lengths of 10 inches.
40 × 10 = 400
Question 18.
DIG DEEPER!
A square vegetable garden has side lengths of 12 feet. You plant flowers in the center portion as shown. You divide the remaining space into 4 equal sections and plant tomatoes, onions, zucchini, and peppers. What is the area of the onion section?
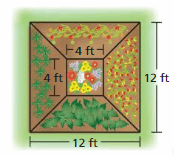
Answer:
A square vegetable garden has side lengths of 12 feet.
You plant flowers in the center portion of the garden, a square that has side lengths of 4 feet.
You divide the remaining space into 4 equal sections and plant tomatoes, onions, zucchini, and peppers.
Given that,
→ side of the square vegetable garden is = 12 feet.
So,
→ Area of square vegetable garden = (side)² = (12)² = 144 feet².
Now, given that, inside this area, there is a square of side 4 feet reserved for flowers.
So,
→ The area of the flower section = (side)² = (4)² = 16 feet².
Therefore,
→ The rest of the garden that is intended for vegetables is = The total garden area – The flower section area = 144 – 16 = 128 feet².
Now, this remaining area is to be divided into four equal sections.
So,
→ The area of the onion section = (1/4) of remaining area = (1/4) × 128 = 32 feet².
Order of Operations Practice 1.2
Review & Refresh
Write the product as a power.
Question 1.
11 × 11 × 11 × 11
Answer: The exponent for the product 11 × 11 × 11 × 11 is 114
Question 2.
13 × 13 × 13 × 13 × 13
Answer: The exponent for the product 13 × 13 × 13 × 13 × 13 is 135
Find the missing dimension of the rectangular prism.
Question 3.
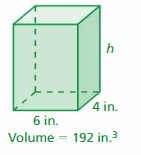
Answer:
Given that,
l = 6 in.
b = 4 in.
h = ?
v = 192 cu. in
Volume of the rectangular prism = lbh
192 = 6 × 4 × h
h = 192/24
h = 8
Thus the height of the rectangular prism is 8 inches.
Question 4.
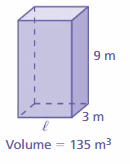
Answer:
Given that,
h = 9m
b = 3m
v = 135 cu. m
l = ?
The volume of the rectangular prism = lbh
135 = l × 3 × 9
135 = l × 27
l = 5m
Tell whether the number is prime or composite.
Question 5.
9
Answer: Composite Number
A natural number greater than 1 that is not prime is called a composite number.
Question 6.
11
Answer: Prime Number
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
Question 7.
23
Answer: Prime Number
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
Concepts, Skills, & Problem Solving
COMPARING DIFFERENT ORDERS
Find the value of the expression by using different orders of operations. Are your answers the same? (See Exploration 1, p. 9.)
Question 8.
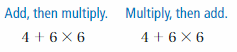
Answer:
4 + 6 × 6
10 × 6 = 60
4 + 6 × 6
4 + 36 = 40
Question 9.
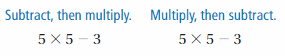
Answer:
5 × 5 – 3
5 × 2 = 10
5 × 5 – 3
25 – 3 = 22
USING ORDER OF OPERATIONS
Evaluate the expression.
Question 10.
5 + 18 ÷ 6
Answer: 8
Explanation:
First, divide then divide.
5 + 3 = 8
Question 11.
(11 – 3) ÷ 2 + 1
Answer:
Explanation:
First, subtract and divide.
(11 – 3) ÷ 2 + 1
8 ÷ 2 + 1
4 + 1 = 5
Question 12.
45 ÷ 9 × 2
Answer: 10
Explanation:
The first divide then multiply.
45 ÷ 9 × 2
5 × 2 = 10
Question 13.
62 – 3.4
Answer: 24
Explanation:
Multiply then subtract
62 – 3.4
36 – 12
24
Question 14.
42 ÷ (15 – 23)
Answer: 6
Explanation:
Subtract then divide.
42 ÷ (15 – 8)
42 ÷ 7
6
Question 15.
42.2 + 8.7
Answer: 88
Explanation:
Multiply then add
42.2 + 8.7
16 × 2 + 56
32 + 56 = 88
Question 16.
(52 – 2) × 15 + 4
Answer: 27
Explanation:
(52 – 2) × 15 + 4
(25 – 2) × 1 + 4
Add, subtract then multiply
23 + 4 = 27
Question 17.
4 + 2 × 32 – 9
Answer: 13
Explanation:
4 + 2 × 32 – 9
4 + 18 – 9
4 + 9 = 13
Question 18.
8 ÷ 2 × 3 + 42 ÷ 4
Answer: 16
Explanation:
8 ÷ 2 × 3 + 42 ÷ 4
(4 × 3) + (16 ÷ 4)
12 + 4
16
Question 19.
32 + 12 ÷ (6 – 3) × 8
Answer: 41
Explanation:
32 + 12 ÷ (6 – 3) × 8
9 + (12 ÷ (6 – 3)) × 8
9 + (12 ÷ 3) × 8
9 + 4 × 8
9 + 32
41
Question 20.
(10 + 4) ÷ (26 – 19)
Answer: 2
Explanation:
Add, subtract then divide
(10 + 4) ÷ (26 – 19)
14 ÷ 7
2
Question 21.
(52 – 4).2 – 18
Answer: 24
Explanation:
((52 – 4).2) – 18
((25 – 4) × 2) – 18
(21 × 2) – 18
42 – 18
24
Question 22.
2 × [(16 – 8) × 2]
Answer: 32
Explanation:
2 × [(16 – 8) × 2]
2 × [8 × 2]
2 × 16
32
Question 23.
12 + 8 × 33 – 24
Answer: 204
Explanation:
12 + 8 × 33 – 24
12 + (8 × 27) – 24
12 + 216 – 24
12 + 192 = 204
Question 24.
62 ÷ [(2 + 4) × 23]
Answer: 48
Explanation:
62 ÷ [(2 + 4) × 23]
36 ÷ [(2 + 4) × 23]
36 ÷ 6 × 8
6 × 8
48
YOU BE THE TEACHER
Your friend evaluates the expression. Is your friend correct? Explain your reasoning.
Question 25.
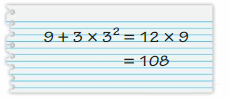
Answer: Your friend is incorrect.
9 + 3 × 3²
9 + (27)
36
Question 26.
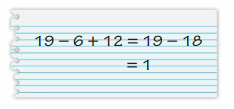
Answer:
19 – 6 + 12
13 + 12
25
Question 27.
PROBLEM SOLVING
You need to read 20 poems in 5 days for an English project. Each poem is 2 pages long. Evaluate the expression 20 × 2 ÷ 5 to find how many pages you need to read each day.
Answer:
Given,
You need to read 20 poems in 5 days for an English project. Each poem is 2 pages long.
20 × 2 ÷ 5
40 ÷ 5 = 8
Thus you need to read 8 pages each day.
USING ORDER OF OPERATIONS
Evaluate the expression.
Question 28.
12 – 2(7 – 4)
Answer:
12 -(2 × (7 – 4))
12 – (2 × 3)
12 – 6 = 6
Question 29.
4(3 + 5) – 3(6 -2)
Answer:
4(3 + 5) – 3(6 -2)
4 × 8 – 3 × 4
32 – 12
20
Question 30.
![]()
Answer:
6 + 1/4 (12 -8)
6 + 1/4(4)
6 + 1
7
Question 31.
92 – 8(6 + 2)
Answer:
81 – (8(6 + 2))
81 – (8 × 8)
81 – 64
17
Question 32.
4(3 – 1)3 + 7(6) – 52
Answer:
4(3 – 1)3 + 7(6) – 52
4(2)3 + 7(6) – 52
4 × 8 + 42 – 25
32 + 42 – 25 = 49
Question 33.
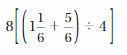
Answer:
8[(1 1/6 + 5/6) ÷ 4]
[8[7/6 + 5/6] ÷ 4]
8[12/6] ÷ 4
8[2 ÷ 4]
8(1/2)
4
Question 34.
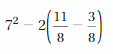
Answer:
49 – 2((11-3)/8)
49 – 2 (8/8)
49 – 2
47
Question 35.
8(7.3 + 3.7 – 8) ÷ 2
Answer:
8(7.3 + 3.7 – 8) ÷ 2
(8(7.3 + 3.7 – 8)) ÷ 2
8 (11 – 8) ÷ 2
8 × 3 ÷ 2
24 ÷ 2
12
Question 36.
24(5.2 – 3.2) ÷ 4
Answer:
24(5.2 – 3.2) ÷ 4
16 (5.2 – 3.2) ÷ 4
16 (2) ÷ 4
32 ÷ 4
8
Question 37.
![]()
Answer:
36(3+5)/4
36 × 8/4
36 × 2
72
Question 38.
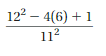
Answer:
(144 – 24 + 1)/121
121/121
1
Question 39.
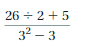
Answer:
26 ÷ 2 + 5 = 18
18/6 = 3
Question 40.
PROBLEM SOLVING
Before a show, there are 8 people in a theater. Five groups of 4 people enter, and then three groups of 2 people leave. Evaluate the expression 8 + 5(4) − 3(2) to find how many people are in the theater.
Answer:
Given,
Before a show, there are 8 people in a theater. Five groups of 4 people enter, and then three groups of 2 people leave.
8 + (5 × 4) – (3 × 2)
8 + 20 – 6
28 – 6
22
Question 41.
MODELING REAL LIFE
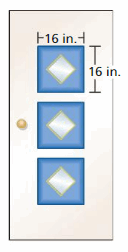
The front door of a house is painted white and blue. Each window is a square with a side length of 7 inches. What is the area of the door that is painted blue?
Answer:
Given,
The front door of a house is painted white and blue. Each window is a square with a side length of 7 inches.
Area of the square = s × s
A = 7 in × 7 in
A = 49 sq. inches
Therefore the area of the door that is painted blue is 49 sq. inches.
Question 42.
PROBLEM SOLVING
You buy 6 notebooks, 10 folders, 1 pack of pencils, and 1 lunch box for school. After using a $10 gift card, how much do you owe? Explain how you solved the problem.

Answer:
Given,
You buy 6 notebooks, 10 folders, 1 pack of pencils, and 1 lunch box for school.
Cost of 1 notebook = $2
6 notebooks = 6 × $2 = $12
Cost of 1 folder = $1
10 folders = 10 × $1 = $10
Cost of 1 pack of pencils = $3
Cost of 1 lunch box = $8
So the total cost is $11 + $10 + $3 + $8 = $31
You used $10 gift card.
$31 – $10 = $21
Thus you ow $21.
Question 43.
OPEN-ENDED
Use all four operations and at least one exponent to write an expression that has a value of 100.
Answer: You need to use +, -, ×, ÷ operations to write the expressions that have the value of 100.
(34 – 1) × 3 + 3² ÷ 9 = 100
Question 44.
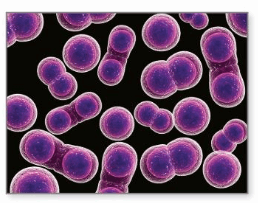
REPEATED REASONING
A Petri dish contains 35 cells. Every day, each cell in the Petri dish divides into 2 cells in a process called mitosis. How many cells are there after 14 days? Justify your answer.
Answer:
Given,
A Petri dish contains 35 cells. Every day, each cell in the Petri dish divides into 2 cells in a process called mitosis
35 ÷ 2 = 17.5
1 day = 0.5 + 0.5 cells
14 days = 14 × 1 = 14 cells
17.5 – 14 = 3.5
Thus there are 3.5 cells after 14 days.
Question 45.
REASONING
Two groups collect litter along the side of a road. It takes each group 5 minutes to clean up a 200-yard section. How long does it take both groups working together to clean up 2 miles? Explain how you solved the problem.
Answer:
Given,
Two groups collect litter along the side of a road. It takes each group 5 minutes to clean up a 200-yard section.
To convert 2 miles to yards, you have to multiply 2 by 1760, because 1 mile equals to 1760 yards:
2 × 1760 = 3520 yards.
If you would like to know how long does it take to clean up 2 miles, you can calculate this using the following steps:
5 × 3520 = 200 × x
17600 = 200 × x /200
x = 17600 / 200
x = 88 minutes
Question 46.
NUMBER SENSE
Copy each statement. Insert +, −, ×, or ÷ symbols to make each statement true.
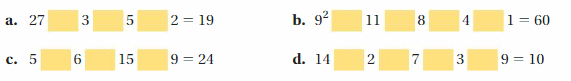
Answer:
You can find the value by using the calculator by inserting the suitable operations.
![]()
Lesson 1.3 Prime Factorization
Prime Factorization
EXPLORATION 1
Rewriting Numbers as Products of Factors
Work with a partner. Two students use factor trees to write 108 as a product of factors, as shown below.
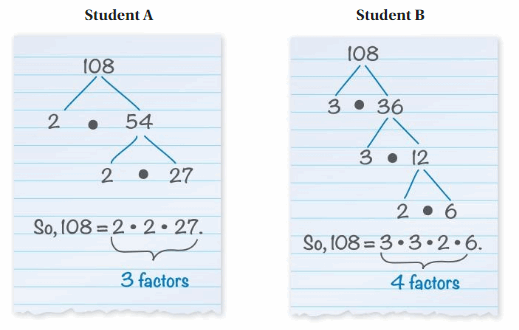
a. Without using 1 as a factor, can you write 108 as a product with more factors than each student used? Justify your answer. Math Practice

Answer: Yes you can find the factors by using the prime factorization.
108 = 2 × 54
= 2 × 2 × 27
= 2 × 2 × 3 × 9
= 2 × 2 × 3 × 3 × 3
b. Use factor trees to write 80, 162, and 300 as products of as many factors as possible. Do not use 1 as a factor.

Answer:
80 = 2 × 40
= 2 × 2 × 20
= 2 × 2 × 2 × 10
= 2 × 2 × 2 × 2 × 5
162 = 2 × 81
= 2 × 3 × 27
= 2 × 3 × 3 × 9
= 2 × 3 × 3 × 3 × 3
300 = 2 × 150
= 2 × 2 × 75
= 2 × 2 × 3 × 25
= 2 × 2 × 3 × 5 × 5
c. Compare your results in parts (a) and (b) with other groups. For each number, identify the product with the greatest number of factors. What do these factors have in common?
Answer: 300 contains the greatest number of factors. (2, 2, 3, 5, 5)
1.3 Lesson
Because 2 is a factor of 10 and 2 . 5 =10, 5 is also a factor of 10. The pair 2, 5 is called a factor pair of 10.
Try It
List the factor pairs of the number.
Question 1.
18
Answer: The factor pairs of 18 are 1, 2, 3, 6, 9, 18
Explanation:
1 × 18 = 18
2 × 9 = 18
3 × 6 = 18
6 × 3 = 18
9 × 2 = 18
18 × 1 = 18
Question 2.
24
Answer: The factor pairs of 1, 2, 3, 4, 6, 8, 12, 24
Explanation:
1 × 24 = 24
2 × 12 = 24
3 × 8 = 24
4 × 6 = 24
6 × 4 = 24
8 × 3 = 24
12 × 2 = 24
24 × 1 = 24
Question 3.
51
Answer: The factor pairs of 1, 3, 17, 51
Explanation:
1 × 51 = 51
3 × 17 = 51
17 × 3 = 51
51 × 1 = 15
Question 4.
WHAT IF?
The woodwinds section of the marching band has 38 members. Which has more possible arrangements, the brass section or the woodwinds section? Explain.
Answer: Brass section. 38 has only two-factor pairs.
38 = 1 × 38
= 2 × 19
Key Idea
Prime Factorization
The prime factorization of a composite number is the number written as a product of its prime factors.
You can use factor pairs and a factor tree to help find the prime factorization of a number. The factor tree is complete when only prime factors appear in the product. A factor tree for 60 is shown.
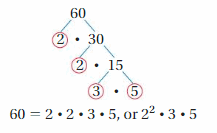

Try It
Write the prime factorization of the number.
Question 5.
20
Answer:
The Prime Factorization is:
2 x 2 x 5
In Exponential Form:
2² x 51
CSV Format:
2, 2, 5
Question 6.
88
Answer:
88 = 2 × 44
= 2 × 2 × 22
= 2 × 2 × 2 × 11
The Prime Factorization is: 2 × 2 × 2 × 11
Question 7.
90
Answer:
90 = 2 × 45
= 2 × 3 × 15
= 2 × 3 × 3 × 5
The Prime Factorization is: 2 × 3 × 3 × 5
Question 8.
462
Answer:
= 2 × 231
= 2 × 3 × 77
= 2 × 3 × 7 × 11
The Prime Factorization is: 2 × 3 × 7 × 11
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING A PRIME FACTORIZATION
Write the prime factorization of the number.
Question 9.
14
Answer:
14 = 2 × 7
The Prime Factorization is: 2 × 7
Question 10.
86
Answer:
86 = 2 × 43
The Prime Factorization is: 2 × 43
Question 11.
40
Answer:
40 = 2 × 20
= 2 × 2 × 10
= 2 × 2 × 2 × 5
The Prime Factorization is: 2 × 2 × 2 × 5
Question 12.
516
Answer:
516 = 2 × 258
= 2 × 2 × 129
= 2 × 2 × 3 × 43
The Prime Factorization is: 2 × 2 × 3 × 43
Question 13.
WRITING
Explain the difference between prime numbers and composite numbers.
Answer:
A prime number is a number that has exactly two factors i.e. ‘1’ and the number itself. A composite number has more than two factors, which means apart from getting divided by number 1 and itself, it can also be divided by at least one integer or number.
Question 14.
STRUCTURE
Your friend lists the following factor pairs and concludes that there are 6 factor pairs of 12. Explain why your friend is incorrect.

Answer: Your friend is incorrect. Because there are 5-factor pairs of 12.
The factor pairs of 12 are
1 × 12 =12
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
Question 15.
WHICH ONE DOESN’T BELONG?
Which factor pair does not belong with the other three? Explain your reasoning.
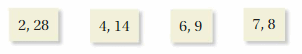
Answer:
2, 28 = 2 × 28 = 56
4, 14 = 4 × 14 = 56
6, 9 = 6 × 9 = 54
7, 8 = 7 × 56
By this we can say that 6, 9 does not belong to the other three expressions.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
A group of 20 friends plays a card game. The game can be played with 2 or more teams of equal size. Each team must have atleast 2 members. List the possible numbers and sizes of teams.

Answer:
Given,
A group of 20 friends plays a card game. The game can be played with 2 or more teams of equal size. Each team must have at least 2 members.
20 = 1 × 20
2 × 10
4 × 5
5 × 4
10 × 2
Thus there are 5 possible numbers and size of teams.
Question 17.

You arrange 150 chairs in rows for a school play. You want each row to have the same number of chairs. How many possible arrangements are there? Are all of the possible arrangements appropriate for the play? Explain.
Answer:
You arrange 150 chairs in rows for a school play. You want each row to have the same number of chairs.
150 = 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Thus there are 12 possible arrangements appropriate for the play.
Question 18.
What is the least perfect square that is a factor of 4536? What is the greatest perfect square that is a factor of 4536?
Answer: least perfect square that is a factor of 4536
Explanation:
What is the last number of 4,536? It is this number: 4536. The answer is 6. Is 6 in the list of numbers that are never perfect squares (2, 3, 7 or 8)?
Answer: No, 6 is not in the list of numbers that are never perfect squares. Let’s continue to the next step.
Step 2:
We now need to obtain the digital root of the number. Here’s how you do it:
Split the number up and add each digit together:
4 + 5 + 3 + 6 = 18
If the answer is more than one digit, you would add each digit of the answer together again:
1 + 8 = 9
1 x 4,5362 x 2,2683 x 1,5124 x 1,1346 x 7567 x 6488 x 5679 x 50412 x 37814 x 32418 x 25221 x 21624 x 18927 x 16828 x 16236 x 12642 x 10854 x 8456 x 8163 x 72
We’re looking for a factor combination with equal numbers for X and Y (like 3×3) above. Notice there isn’t an equal factor combination, that when multiplied together, produce the number 4,536. That means 4,536 is NOT a perfect square.
Question 19.
DIG DEEPER!
The prime factorization of a number is 24 × 34 × 54 × 72. Is the number a perfect square? Explain your reasoning.
Answer:
The prime factorization of a number is 24 × 34 × 54 × 72.
16 × 81 × 625 × 49 = 39690000
Yes, 39690000 is a perfect square.
Prime Factorization Practice 1.3
Review & Refresh
Evaluate the expression.
Question 1.
2 + 42(5 – 3)
Answer: 34
Explanation:
2 + 42(5 – 3)
2 + 42(2)
2 + 16(2) = 2 + 32 = 34
Question 2.
23 + 4 × 32
Answer: 44
Explanation:
23 + 4 × 32
8 + 4 × 9
8 + 36
44
Question 3.
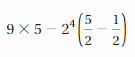
Answer:
Explanation:
9 × 5 – 16(5/2 – 1/2)
9 × 5 – 16(4/2)
45 – 16(2)
45 – 32
13
Plot the points in a coordinate plane. Draw a line segment connecting the points.
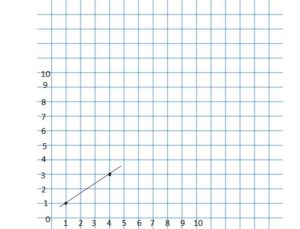
Question 4.
(1, 1) and (4, 3)
Answer:
Question 5.
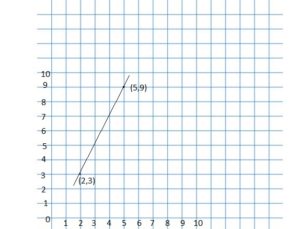
(2, 3) and (5, 9)
Answer:
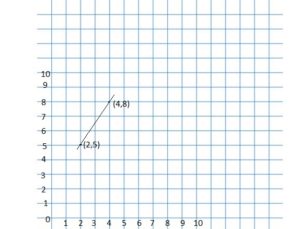
Question 6.
(2, 5) and (4, 8)
Answer:
Use the Distributive Property to find the quotient. Justify your answer.
Question 7.
408 ÷ 4
Answer: 120
Write 408 as 204 and 204
204 ÷ 4 = 51
204 ÷ 4 = 51
51 + 51 = 102
408 ÷ 4 = 102
Question 8.
628 ÷ 2
Answer: 314
608 can be written as 314 and 314
314 ÷ 2 = 157
314 ÷ 2 = 157
157 + 157 = 314
628 ÷ 2 = 314
Question 9.
969 ÷ 3
Answer: 323
969 can be written as 900 and 69
900 ÷ 3 = 300
69 ÷ 3 = 23
300 + 23 = 323
969 ÷ 3 = 323
Classify the triangle in as many ways as possible.
Question 10.
Answer: Acute
Acute angles measure less than 90 degrees. Right angles measure 90 degrees. Obtuse angles measure more than 90 degrees.
Question 11.
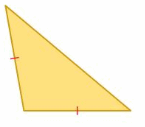
Answer: Obtuse
An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees. However, A reflex angle measures more than 180 degrees but less than 360 degrees.
Question 12.
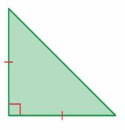
Answer: Right angle
In geometry and trigonometry, a right angle is an angle of exactly 90° (degrees), corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles.
Concepts, Skills, & Problem Solving
REWRITING A NUMBER
Write the number as a product of as many factors as possible. (See Exploration 1, p. 15.)
Question 13.
60
Answer: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
The factors of 60 are:
1 × 60 = 60
2 × 30 = 60
3 × 20 = 60
4 × 15 = 60
5 × 12 = 60
6 × 10 = 60
10 × 6 = 60
12 × 5 = 60
15 × 4 = 60
20 × 3 = 60
30 × 2 = 60
60 × 1 = 60
Question 14.
63
Answer: The factors of 63 are 1, 3, 7, 9, 21, 63
The factors of 63 are:
1 × 63 = 63
3 × 21 = 63
7 × 9 = 63
9 × 7 = 63
21 × 3 = 63
63 × 1 = 63
Question 15.
120
Answer: The factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
The factors of 120 are:
1 × 120 = 120
2 × 60 = 120
3 × 40 = 120
4 × 30 = 120
5 × 24 = 120
6 × 20 = 120
8 × 15 = 120
10 × 12 = 120
12 × 10 = 120
15 × 8 = 120
20 × 6 = 120
24 × 5 = 120
30 × 4 = 120
40 × 3 = 120
60 × 2 = 120
120 × 1 = 120
Question 16.
150
Answer: The factors of 150 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
The factors of 150 are:
1 × 150 = 150
2 × 75 = 150
3 × 50 = 150
5 × 30 = 150
6 × 25 = 150
10 × 15 = 150
FINDING FACTOR PAIRS
List the factor pairs of the number.
Question 17.
15
Answer: The factor pairs of 15 are (1, 15), (3, 5)
1 × 15 = 15
3 × 5 = 15
5 × 3 = 15
15 × 1 = 15
Question 18.
22
Answer: The factor pairs of 22 are (1, 22) (2, 11)
1 × 22 = 22
2 × 11 = 22
11 × 2 = 22
22 × 1 = 22
Question 19.
34
Answer: (1, 34) (2,17)
The factor pairs of 34 are
1 × 34 = 34
2 × 17 = 34
17 × 2 = 34
34 × 1 = 34
Question 20.
39
Answer: (1, 39) (3, 13)
The factor pairs of 39 are
1 × 39 = 39
3 × 13 = 39
13 × 3 = 39
39 × 1 = 39
Question 21.
45
Answer: (1, 45) (3, 15) (5, 9)
The factor pairs of 45 are
1 × 45 = 45
3 × 15 = 45
5 × 9 = 45
Question 22.
54
Answer: (1, 54) (2, 27) (3, 18) (6, 9)
The factor pairs of 54 are
1 × 54 = 54
2 × 27 = 54
3 × 18 = 54
6 × 9 = 54
Question 23.
59
Answer: (1, 59)
The factor pairs of 59 are
1 × 59 = 59
59 × 1 = 59
Question 24.
61
Answer: (1, 61)
The factor pairs of 61 are
1 × 61 = 61
61 × 1 = 61
Question 25.
100
Answer: (1, 100) (2, 50) (4, 25) (5, 20) (10, 10)
The factor pairs of 100 are
1 × 100 = 100
2 × 50 = 100
4 × 25 = 100
5 × 20 = 100
10 × 10 = 100
Question 26.
58
Answer: (1, 58) (2, 29)
The factor pairs of 58 are
1 × 58 = 58
2 × 29 = 58
Question 27.
25
Answer: (1, 25) (5, 5)
The factor pairs of 25 are
1 × 25 = 25
5 × 5 = 25
Question 28.
76
Answer: (1, 76) (2, 38) (4, 19)
The factor pairs of 76 are
1 × 76 = 76
2 × 38 = 76
4 × 19 = 76
Question 29.
52
Answer: (1, 52) (2, 26) (4, 13)
The factor pairs of 52 are
1 × 52 = 52
2 × 26 = 52
4 × 13 = 52
Question 30.
88
Answer: (1,88) (2,44) (4, 22) (8, 11)
The factor pairs of 88 are
1 × 88 = 88
2 × 44 = 88
4 × 22 = 88
8 × 11 = 88
Question 31.
71
Answer: (1,71)
The factor pairs of 71 are
1 × 71 = 71
Question 32.
91
Answer: (1, 91) (7, 13)
The factor pairs of 91 are
1 × 91 = 91
7 × 13 = 91
WRITING A PRIME FACTORIZATION
Write the prime factorization of the number.
Question 33.
16
Answer:
16 = 2 × 8
2 × 2 × 4
2 × 2 × 2 × 2
Question 34.
25
Answer:
25 = 5 × 5
Question 35.
30
Answer:
30 = 2 × 15
= 2 × 3 × 5
Question 36.
26
Answer:
26 = 2 × 13
Question 37.
84
Answer:
84 = 2 × 42
2 × 2 × 21
2 × 2 × 3 × 7
Question 38.
54
Answer:
54 = 2 × 27
2 × 3 × 9
2 × 3 × 3 × 3
Question 39.
65
Answer:
65 = 5 × 13
Question 40.
77
Answer:
77 = 7 × 11
Question 41.
46
Answer:
46 = 2 × 23
Question 42.
39
Answer:
39 = 3 × 13
Question 43.
99
Answer:
99 = 3 × 33
3 × 3 × 11
Question 44.
24
Answer:
24 = 2 × 12
2 × 2 × 6
2 × 2 × 2 × 3
Question 45.
315
Answer:
315 = 3 × 105
3 × 3 × 35
3 × 3 × 5 × 7
Question 46.
490
Answer:
490 = 2 × 245
2 × 5 × 49
2 × 5 × 7 × 7
Question 47.
140
Answer:
2 × 70
2 × 2 × 35
2 × 2 × 5 × 7
Question 48.
640
Answer:
640 = 2 × 320
2 × 2 × 160
2 × 2 × 2 × 80
2 × 2 × 2 × 2 × 40
2 × 2 × 2 × 2 × 2 × 20
2 × 2 × 2 × 2 × 2 × 2 × 10
2 × 2 × 2 × 2 × 2 × 2 × 2 × 5
USING A PRIME FACTORIZATION
Find the number represented by the prime factorization.
Question 49.
22.32.5
Answer:
4 × 9 × 5 = 180
We have to find the prime factorization for 180.
180 = 2 × 90
2 × 2 × 45
2 × 2× 3 × 15
2 × 2 × 3 × 3 × 5
Question 50.
32.52.7
Answer:
9 × 25 × 7 = 1575
We have to find the prime factorization for 1575.
1575 = 3 × 525
3 × 3 × 175
3 × 3 × 5 × 35
3 × 3 × 5 × 5 × 7
Question 51.
23.112.13
Answer:
8 × 11 × 13 = 1144
We have to find the prime factorization for 1144.
1144 = 2 × 572
2 × 2 × 286
2 × 2 × 2 × 143
2 × 2 × 2 × 11 × 13
Question 52.
YOU BE THE TEACHER
Your friend finds the prime factorization of 72. Is your friend correct? Explain your reasoning.

Answer:
72 = 2 × 36
2 × 2 × 18
2 × 2 × 2 × 9
2 × 2 × 2 × 3 × 3
Your friend is incorrect because you have to write the prime factorization for 9 also.
Thus the prime factorization for 72 is 2 × 2 × 2 × 3 × 3
USING A PRIME FACTORIZATION
Find the greatest perfect square that is a factor of the number.
Question 53.
250
Answer:
A = Calculate the square root of the greatest perfect square from the list of all factors of 250. The factors of 250 are 1, 2, 5, 10, 25, 50, 125, and 250. Furthermore, the greatest perfect square on this list is 25 and the square root of 25 is 5. Therefore, A equals 5.
B = Calculate 250 divided by the greatest perfect square from the list of all factors of 250. We determined above that the greatest perfect square from the list of all factors of 250 is 25. Furthermore, 250 divided by 25 is 10, therefore B equals 10.
Now we have A and B and can get our answer to 250 in its simplest radical form as follows:
√250 = A√B
√250 = 5√10
Question 54.
275
Answer:
A = Calculate the square root of the greatest perfect square from the list of all factors of 275. The factors of 275 are 1, 5, 11, 25, 55, and 275. Furthermore, the greatest perfect square on this list is 25 and the square root of 25 is 5. Therefore, A equals 5.
B = Calculate 275 divided by the greatest perfect square from the list of all factors of 275. We determined above that the greatest perfect square from the list of all factors of 275 is 25. Furthermore, 275 divided by 25 is 11, therefore B equals 11.
Now we have A and B and can get our answer to 275 in its simplest radical form as follows:
√275 = A√B
√275 = 5√11
Question 55.
392
Answer:
A = Calculate the square root of the greatest perfect square from the list of all factors of 392. The factors of 392 are 1, 2, 4, 7, 8, 14, 28, 49, 56, 98, 196, and 392. Furthermore, the greatest perfect square on this list is 196 and the square root of 196 is 14. Therefore, A equals 14.
B = Calculate 392 divided by the greatest perfect square from the list of all factors of 392. We determined above that the greatest perfect square from the list of all factors of 392 is 196. Furthermore, 392 divided by 196 is 2, therefore B equals 2.
Now we have A and B and can get our answer to 392 in its simplest radical form as follows:
√392 = A√B
√392 = 14√2
Question 56.
338
Answer:
A = Calculate the square root of the greatest perfect square from the list of all factors of 338. The factors of 338 are 1, 2, 13, 26, 169, 338. Furthermore, the greatest perfect square on this list is 324 and the square root of 324 is 18. Therefore, A equals 18.
B = Calculate 338 divided by the greatest perfect square from the list of all factors of 338. We determined above that the greatest perfect square from the list of all factors of 338 is 324.
Now we have A and B and can get our answer to 338 in its simplest radical form as follows:
√338= A√B
√392 = 18√14
Question 57.
244
Answer:
Our first step would be to find out all the factors of 244
Since this is an even number, we divide 2 we get the factors as 244/2 = 122
Next, we again divide by 2 we get the factor as 122/2 = 61
We cannot go down any further since 61 is a prime number
Since we divided by 2, 2 is itself a factor.
Lastly, we divided by 2, twice; hence 2*2 = 4 is also a factor
The factors of 244 are 2,4,61 and 122
Out of 2,4,61 and 122, the only perfect square is 4
So, the greatest perfect square that is a factor of the number 244 should be 4
Therefore, the answer is: 4
Question 58.
650
Answer:
factor 650 and find the pairs
650=2×5×5×13
the pair is 5×5 which is 5² or 25
the greatest perfect square that is a factor of 650 is 25.
Question 59.
756
Answer:
A = Calculate the square root of the greatest perfect square from the list of all factors of 756. The factors of 756 are 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 27, 28, 36, 42, 54, 63, 84, 108, 126, 189, 252, 378, and 756. Furthermore, the greatest perfect square on this list is 36 and the square root of 36 is 6. Therefore, A equals 6.
B = Calculate 756 divided by the greatest perfect square from the list of all factors of 756. We determined above that the greatest perfect square from the list of all factors of 756 is 36. Furthermore, 756 divided by 36 is 21, therefore B equals 21.
Now we have A and B and can get our answer to 756 in its simplest radical form as follows:
√756 = A√B
√756 = 6√21
Question 60.
1290
Answer:
There is no greatest perfect square that is a factor of 1290.
The factors of 1290 are 1, 2, 3, 5, 6, 10, 15, 30, 43, 86, 129, 215, 258, 430, 645, 1290. There are no perfect squares as factors.
Question 61.
2205
Answer: No, the number 2,205 is not a perfect square.
The factors of 2205 are 1, 3, 5, 7, 9, 15, 21, 35, 45, 49, 63, 105, 147, 245, 315, 441, 735. There are no perfect squares as factors.
Question 62.
1890
Answer: 1890 is not the perfect square.
The factors of 1890 are 1, 3, 9, 27, 67, 201, 603, 1809. There are no perfect squares as factors.
Question 63.
495
Answer: 495 is not the perfect square.
The factors 495 are 1, 3, 5, 9, 11, 15, 33, 45, 55, 99, 165, 495. There are no perfect squares as factors.
Question 64.
4725
Answer: 4725 is not the perfect square.
The factors of 4725 are 1, 3, 5, 7, 9, 15, 21, 25, 27, 35, 45, 63, 75, 105, 135, 175, 189, 225, 315, 525, 675, 945, 1575, 4725. There are no perfect squares as factors.
Question 65.
VOCABULARY
A botanist separates plants into equal groups of 5 for an experiment. Is the total number of plants in the experiment prime or composite? Explain.
Answer: The total number of plants will be a composite.
Explanation:
She is separating them into equal groups of five. So the total number will be a multiple of 5. Five is a prime number. Multiples of prime numbers are composite numbers.
Question 66.
REASONING
A teacher divides 36 students into equal groups for a scavenger hunt. Each group should have at least 4 students but no more than 8 students. What are the possible group sizes?

Answer:
Given,
A teacher divides 36 students into equal groups for a scavenger hunt.
Each group should have at least 4 students but no more than 8 students.
The factors of 36 are 1, 2, 3, 4, 6, 9
So, there are 6 groups of 6, 9 groups of 4.
Question 67.
CRITICAL THINKING
Is 2 the only even prime number? Explain.
Answer:
The definition of a prime number is a positive integer that has exactly two distinct divisors. Since the divisors of 2 are 1 and 2, there are exactly two distinct divisors, so 2 is prime.
Question 68.
LOGIC
One table at a bake sale has 75 cookies. Another table has 60 cupcakes. Which table allows for more rectangular arrangements? Explain.
Answer:
Given,
One table at a bake sale has 75 cookies. Another table has 60 cupcakes.
75 = 3·5², so has 6 divisors. 6 rectangles are possible if you make the distinction between 1×75 and 75×1.
60 = 2²·3·5, so has 12 divisors. 12 rectangles are possible under the same conditions.
Question 69.
PERFECT NUMBERS
A perfect number is a number that equals the sum of its factors, not including itself. For example, the factors of 28 are 1, 2, 4, 7, 14, and 28. Because 1 + 2 + 4 + 7 + 14 = 28, 28 is a perfect number. What are the perfect numbers between 1 and 27?
Answer: Perfect number, a positive integer that is equal to the sum of its proper divisors. The smallest perfect number is 6, which is the sum of 1, 2, and 3. Other perfect numbers are 28, 496, and 8,128.
Question 70.
REPEATED REASONING
Choose any two perfect squares and find their product. Then multiply your answer by another perfect square. Continue this process. Are any of the products perfect squares? What can you conclude?
Answer:
2² × 3² = 4×9=36, which is a square number
Question 71.
PROBLEM SOLVING
The stage manager of a school play creates a rectangular stage that has whole number dimensions and an area of 42 square yards. String lights will outline the stage. What is the least number of yards of string lights needed to enclose the stage?
Answer:
Given that the stage manager of a school play creates a rectangular acting area of 42 square yards.
Let the length of the rectangular acting area be x, then the width is given by 42 / x.
The number of yards of string lights that the manager needs to enclose the area is given by the perimeter of the rectangular area.
Recall that the perimeter of a rectangle is given by
P = 2(length + width) = 2(x + 42/x) = 2x + 84/x
The perimeter is minimum when the differentiation of 2x + 84/x is equal to 0.
Therefore, the minimum number of yards of string lights the manager need to enclose in this area is given by
2x – 84/x = 0
2x² – 84 = 0
2x² = 84
x² = 84/2
x² = 42
x ≈ 6.48
Question 72.
DIG DEEPER!
Consider the rectangular prism shown. Using only whole number dimensions, how many different prisms are possible? Explain.
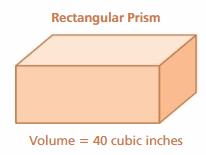
Answer:
The volume of the rectangular prism is lbh
v = 40 cubic inches
Let the length be 5 inches
breadth be 2 inches
height be 4 inches
V = 5 × 2 × 4
V = 40 cu. inches
Lesson 1.4 Greatest Common Factor
A Venn diagram uses circles to describe relationships between two or more sets. The Venn diagram shows the factors of 12 and 15. Numbers that are factors of both 12 and 15 are represented by the overlap of the two circles.
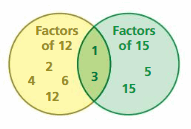
Answer: 1 and 3 are overlapped between the two circles.
So, 1 and 3 are the greatest common factors of 12 and 15.
The factors of 12 are 1, 2, 3, 4, 6, 12
The factors of 15 are 1, 3, 5, 15.
EXPLORATION 1
Identifying Common Factors
Work with a partner. In parts (a) – (d), create a Venn diagram that represents the factors of each number and identify any common factors.
a. 36 and 48
b. 16 and 56
c. 30 and 75
d. 54 and 90
e. Look at the Venn diagrams in parts (a)–(d). Explain how to identify the greatest common factor of each pair of numbers. Then circle it in each diagram.
Answer:
a. 
b. 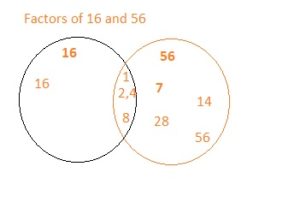
c. 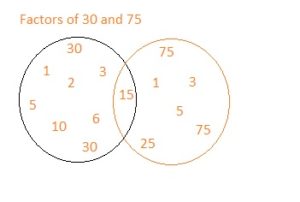
d. 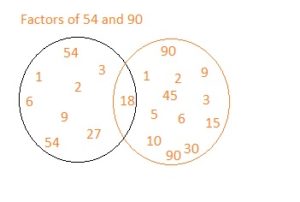
e. 36 and 48 have the greatest common factors.
EXPLORATION 2
Using Prime Factors
Work with a partner
a. Each Venn diagram represents the prime factorizations of two numbers. Identify each pair of numbers. Explain your reasoning.
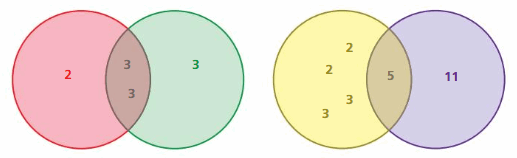
Answer:
i. Red 2 × 3 × 3 = 18
Green 3 × 3 × 3 = 27
GCF = 9
ii. Yellow – 2 × 2 × 3 × 3 × 5 = 180
Purple – 5 × 11 = 55
GCF = 5
b. Create a Venn diagram that represents the prime factorizations of 36 and 48.
Answer:

c. Repeat part(b) for the remaining number pairs in Exploration 1.
Answer:

d. STRUCTURE
Make a conjecture about the relationship between the greatest common factors you found in Exploration 1 and the numbers in the overlaps of the Venn diagrams you just created.

Answer:
a.
The GCF between the two numbers 36 and 48 are 1,2,3,4,6,12
b.
The GCF between the two numbers 16 and 56 are 1,2,4,8
c. 
The GCF between the two numbers 30 and 75 is 15.
d. 
1.4 Lesson
Try It
Find the GCF of the numbers using lists of factors.
Question 1.
8, 36
Answer:
The factors of 8 are: 1, 2, 4, 8
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36
Then the greatest common factor is 4.
Question 2.
18, 72
Answer:
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Then the greatest common factor is 18.
Question 3.
14, 28, 49
Answer:
The factors of 14 are: 1, 2, 7, 14
The factors of 28 are: 1, 2, 4, 7, 14, 28
The factors of 49 are: 1, 7, 49
Then the greatest common factor is 7.
Another way to find the GCF of two or more numbers is by using prime factors. The GCF is the product of the common prime factors of the numbers.
Try It
Find the GCF of the numbers using prime factorizations.
Question 4.
20,45
Answer:
Find the prime factorization of 20
20 = 2 × 2 × 5
Find the prime factorization of 45
45 = 3 × 3 × 5
To find the GCF, multiply all the prime factors common to both numbers:
Therefore, GCF = 5
Question 5.
32,90
Answer:
Find the prime factorization of 32
32 = 2 × 2 × 2 × 2 × 2
Find the prime factorization of 90
90 = 2 × 3 × 3 × 5
To find the GCF, multiply all the prime factors common to both numbers:
Therefore, GCF = 2
Question 6.
45,75,120
Answer:
45= 1,3,5,9,15,45
75= 1,3,5,15,25,75
120=1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120
GCF is 15
Try It
Question 7.
Write a pair of numbers whose greatest common factor is 10.
Answer:
Let’s first find the greatest common factor (GCF) of two whole numbers. The GCF of two numbers is the greatest number that is a factor of both of the numbers. Take the numbers 50 and 30.
50 = 10 × 5
30 = 10 × 3
Their greatest common factor is 10. since 10 is the greatest factor that both numbers have in common.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING THE GCF
Find the GCF of the numbers.
Question 8.
16, 40
Answer:
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, 40
Then the greatest common factor is 8.
Question 9.
35, 63
Answer:
The factors of 35 are: 1, 5, 7, 35
The factors of 63 are: 1, 3, 7, 9, 21, 63
Then the greatest common factor is 7.
Question 10.
18, 72, 144
Answer:
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
The factors of 144 are: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
Then the greatest common factor is 18.
Question 11.
MULTIPLE CHOICE
Which number is not a factor of 10? Explain.
A. 1
B. 2
C. 4
D. 5
Answer: 4
Explanation:
Factors of 10 are: 1, 2, 5, 10
Thus the correct answer is option C.
Question 12.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
The Greatest Common Factor of 24 and 32 is 8
The Greatest Common Divisor of 24 and 32 is 4
The Greatest Common Prime Factor of 24 and 32 is 8
The product of common prime factors of 24 and 32 is 8.
The Greatest Common Divisor of 24 and 32 are different from others.
Self – Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
You use 30 sandwiches and 42 granola bars to make identical picnic baskets. You make the greatest number of picnic baskets with no food left over. How many sandwiches and how many granola bars are in each basket?

Answer: 5 sandwiches and 7 granola in each basket
Explanation:
Given
Represent Sandwiches with S and Granola with G
S = 30
G = 42
To do this, we simply need to determine the ratio of S to G
S:G = 30:42
S:G = 5:7
Question 14.
You fill bags with cookies to give to your friends. You bake 45 chocolate chip cookies, 30 peanut butter cookies, and 15 oatmeal cookies. You want identical groups of cookies in each bag with no cookies left over. What is the greatest number of bags you can make?
Answer: 15 bags
Explanation:
Given,
You fill bags with cookies to give to your friends. You bake 45 chocolate chip cookies, 30 peanut butter cookies, and 15 oatmeal cookies.
You want identical groups of cookies in each bag with no cookies leftover.
45 chocolate chip cookies
30 peanut butter cookies
15 oatmeal cookies
So, the GCF is 15.
Greatest Common Factor Practice 1.4
Review & Refresh
List the factor pairs of the number.
Question 1.
20
Answer: The factor pairs of 20 are (1, 20) (4,5) (2,10)
Explanation:
1 × 20 = 20
4 × 5 = 20
2 × 10 = 20
Question 2.
16
Answer: The factor pairs of 16 are (1,16), (2, 8) (4,4)
Explanation:
1 × 16 = 16
2 × 8 = 16
4 × 4 = 16
Question 3.
56
Answer: The factor pairs of 56 are (1,56) (7,8) (28,2) (14,4)
Explanation:
1 × 56 = 56
7 × 8 = 56
28 × 2 = 56
14 × 4 = 56
Question 4.
87
Answer: The factor pairs of 87 are (1,87) (3,29)
Explanation:
1 × 87 = 87
3 × 29 = 87
Tell whether the statement is always, sometimes, or never true.
Question 5.
A rectangle is a rhombus.
Answer: sometimes
No, because all four sides of a rectangle don’t have to be equal. However, the sets of rectangles and rhombuses do intersect, and their intersection is the set of square all squares are both a rectangle and a rhombus.
Question 6.
A rhombus is a square.
Answer: true
A square is a special case of a rhombus because it has four equal-length sides and goes above and beyond that to also have four right angles. Every square you see will be a rhombus, but not every rhombus you meet will be a square.
Question 7.
A square is a rectangle.
Answer: not always
A square also fits the definition of a rectangle.
Question 8.
A trapezoid is a parallelogram.
Answer: never true
A trapezoid has one pair of parallel sides and a parallelogram has two pairs of parallel sides. So a parallelogram is also a trapezoid.
Concepts, Skills, & Problem Solving
USING A VENN DIAGRAM
Use a Venn diagram to find the greatest common factor of the numbers. (See Exploration 1, p. 21.)
Question 9.
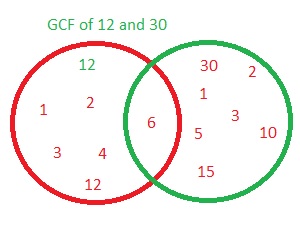
12,30
Answer: 6
Question 10.
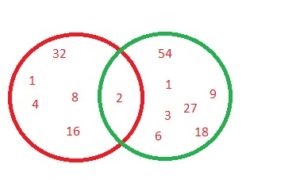
32,54
Answer: 2
Question 11.
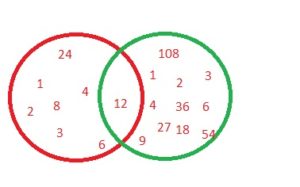
24,108
Answer: 12
FINDING THE GCF
Find the GCF of the numbers using lists of factors.
Question 12.
6, 15
Answer: GCF is 3
Explanation:
The factors of 6 are: 1,2,3,6
The factors of 15 are: 1,3,5,15
The common Factors in 6 and 15 is 3.
Thus the greatest common factor is 3.
Question 13.
14, 84
Answer: GCF is 14
Explanation:
The factors of 14 are: 1,2,7,14
The factors of 84 are: 1,2,3,4,6,7,12,14,21,28,42 84
The greatest common factor is 14.
Question 14.
45, 108
Answer: GCF is 9
Explanation:
The factors of 45 are: 1,3,5,9,15,45
The factors of 108 are: 1,2,3,4,6,9,12,18,27,36,54,108
The greatest common factor is 9.
Question 15.
39, 65
Answer: GCF is 13
Explanation:
The factors of 39 are: 1,3,13,39
The factors of 65 are: 1,5,13,65
Thus the greatest common factor is 13.
Question 16.
51, 85
Answer: GCF is 17
Explanation:
The factors of 51 are: 1,3,17,51
The factors of 1,5,17,85
Thus the greatest common factor is 17
Question 17.
40, 63
Answer: GCF is 1
Explanation:
The factors of 40 are: 1,2,4,5,8,10,20,40
The factors of 63 are: 1,3,7,9,21,63
Thus the greatest common factor is 1.
Question 18.
12, 48
Answer: GCF is 12
Explanation:
The factors of 12 are: 1,2,3,4,6,12
The factors of 48 are: 1,2,3,4,6,8,12,16,24,48
Thus the greatest common factor is 12.
Question 19.
24, 52
Answer: GCF is 4
Explanation:
The factors of 24 are: 1,2,3,4,6,8,12,24
The factors of 1,2,4,13,36,52
Thus the greatest common factor is 4.
Question 20.
30, 58
Answer: GCF is 2
Explanation:
The factors of 30 are: 1,2,3,5,6,10,15,30
The factors of 58 are: 1,2,29,58
Thus the greatest common factor is 2.
FINDING THE GCF
Find the GCF of the numbers using prime factorizations.
Question 21.
45, 60
Answer:
The prime factorization of 45 is 3 x 3 x 5
The prime factorization 60 is 2 x 2 x 3 x 5
GCF of 45, 60 is 3 × 5 = 15
Question 22.
27, 63
Answer: 9
The prime factorization of 27 is 3 x 3 x 3
The prime factorization of 63 is 3 x 3 x 7
Thus GCF of 27, 63 is 9
Question 23.
36, 81
Answer: 9
The prime factorization of 36 is 2 x 2 x 3 x 3
The prime factorization of 81 is 3 x 3 x 3 x 3
Thus the GCF of 36, 81 is 9.
Question 24.
72, 84
Answer: 12
The prime factorization of 72 is 2 x 2 x 2 x 3 x 3
The prime factorization of 84 is 2 x 2 x 3 x 7
Thus the GCF of 72, 84 is 12.
Question 25.
61, 73
Answer: 1
The prime factorization of 61 is 1 × 61
The prime factorization 73 is 1 × 73
Thus the GCF of 61, 73 is 1
Question 26.
38, 95
Answer: 19
The prime factorization of 38 is 2 x 19
The prime factorization of 95 is 5 x 19
Thus the GCF of 38, 95 is 19
Question 27.
60, 75
Answer: 15
The prime factorization of 60 is 2 x 2 x 3 x 5
The prime factorization of 75 is 3 x 5 x 5
Thus the GCF of 60, 75 is 15.
Question 28.
42, 60
Answer: 6
The prime factorization 42 is 2 × 3 × 7
The prime factorization 60 is 2 × 2 × 3 × 5
Thus the GCF of 42, 60 is 6
Question 29.
42, 63
Answer: 21
The prime factorization of 42 is 2 × 3 × 7
The prime factorization of 63 is 3 × 3 ×7
Thus the GCF of 42, 63 is 21
Question 30.
24, 96
Answer: 24
The prime factorization of 24 is 2 × 2 × 2 × 3
The prime factorization of 96 is 2 x 2 x 2 x 2 x 2 x 3
Thus the GCF of 24, 96 is 24.
Question 31.
189, 200
Answer: 24
The prime factorization of 189 is 3 x 3 x 3 x 7
The prime factorization of 200 is 2 x 2 x 2 x 5 x 5
Thus the GCF of 189, 200 is 24.
Question 32.
90, 108
Answer: 18
The prime factorization of 90 is 2 x 3 x 3 x 5
The prime factorization of 108 is 2 x 2 x 3 x 3 x 3
Thus the GCF of 90, 108 is 18.
OPEN-ENDED
Write a pair of numbers with the indicated GCF.
Question 33.
5
Answer: 10, 15
The factors of 10 are: 1,2,5,10
The factors of 15 are: 1,3,5,15
Thus 10, 15 are pairs of numbers with the indicated GCF 5.
Question 34.
12
Answer: 72, 84
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
The factors of 84 are: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Then the greatest common factor is 12.
Question 35.
37
Answer: 37,74
The factors of 37 are: 1,37
The factors of 74 are: 1,2,37,74
Thus 37,74 are pairs of numbers with the indicated GCF 37.
Question 36.
MODELING REAL LIFE
A teacher is making identical activity packets using 92 crayons and 23 sheets of paper. What is the greatest number of packets the teacher can make with no items left over?
Answer: 23 packets
Explanation:
Factor both numbers:
1. 92=2·46=2·2·23;
2. 23 is a prime number.
Then the greatest common factor GCF (92, 23)=23.
This means that teacher can make 23 packets, each of them will contain 4 crayons and 1 sheet.
Question 37.
MODELING REAL LIFE
You are making balloon arrangements for a birthday party. There are 16 white balloons and 24 red balloons. Each arrangement must be identical. What is the greatest number of arrangements you can make using every balloon?

Answer:
This is a GCF problem. To find the GCF, list the factors.
24
1×24, 2×12, 4×6, 8×3 …
16
1×16, 2×8, 4×4, …
The greatest common factor is 8 because it is the greatest factor of both numbers.
so 8 arrangements, 2 white balloons and 3 red balloons each.
Because- 8 is the number of groups, and 8×3 =24 so 3 reds, and 2 whites because 8×2=16
YOU BE THE TEACHER
Your friend finds the GCF of the two numbers. Is your friend correct? Explain your reasoning.
Question 38.

Answer:
No, your friend is incorrect.
42 = 2 × 3 × 7
154 = 2 × 7 × 11
Thus the GCF is 14.
Question 39.

Answer: Yes your friend is correct.
Thus the GCF of 36 and 60 is 12.
FINDING THE GCF
Find the GCF of the numbers.
Question 40.
35, 56, 63
Answer: GCF is 7
Explanation:
The factors of 35 are: 1,5,7,35
The factors of 56 are: 1,2,4,7,8,14,28,56
The factors of 63 are: 1,3,7,9,21,63
Thus the greatest common factor is 7.
Question 41.
30, 60, 78
Answer: GCF is 6
Explanation:
The factors of 30 are: 1,2,3,5,6,10,15,30
The factors of 60 are: 1,2,3,4,5,6,10,12,15,20,30,60
The factors of 78 are: 1,2,3,6,13,26,39,78
Thus the greatest common factor is 6.
Question 42.
42, 70, 84
Answer: GCF is 14
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
The factors of 70 are: 1, 2, 5, 7, 10, 14, 35, 70
The factors of 84 are: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Then the greatest common factor is 14.
Question 43.
40, 55, 72
Answer: GCF is 1
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, 40
The factors of 55 are: 1, 5, 11, 55
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Then the greatest common factor is 1.
Question 44.
18, 54, 90
Answer: GCF is 18
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54
The factors of 90 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Then the greatest common factor is 18.
Question 45.
16, 48, 88
Answer: GCF is 8
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 88 are: 1, 2, 4, 8, 11, 22, 44, 88
Then the greatest common factor is 8.
Question 46.
52, 78, 104
Answer: GCF is 26
The factors of 52 are: 1, 2, 4, 13, 26, 52
The factors of 78 are: 1, 2, 3, 6, 13, 26, 39, 78
The factors of 104 are: 1, 2, 4, 8, 13, 26, 52, 104
Then the greatest common factor is 26.
Question 47.
96, 120, 156
Answer: GCF is 12
The factors of 96 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
The factors of 120 are: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
The factors of 156 are: 1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78, 156
Then the greatest common factor is 12.
Question 48.
280, 300, 380
Answer: GCF is 20
The factors of 280 are: 1, 2, 4, 5, 7, 8, 10, 14, 20, 28, 35, 40, 56, 70, 140, 280
The factors of 300 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300
The factors of 380 are: 1, 2, 4, 5, 10, 19, 20, 38, 76, 95, 190, 380
Then the greatest common factor is 20.
Question 49.
OPEN-ENDED
Write three numbers that have a GCF of 16. What method did you use to find your answer?
Answer: 16, 32, 48
The factors of 16 are: 2 × 2 × 2 × 2
The factors of 32 are : 2 × 2 × 2 × 2 × 2
The factors of 48 are: 3 × 2 × 2 × 2 × 2
CRITICAL THINKING
Tell whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 50.
The GCF of two even numbers is 2.
Answer: Always
Explanation:
Example:
The factors of 14 are: 1, 2, 7, 14
The factors of 16 are: 1, 2, 4, 8, 16
Then the greatest common factor is 2.
Question 51.
The GCF of two prime numbers is 1.
Answer: Always
Explanation:
Example:
The factors of 3 are: 1, 3
The factors of 5 are: 1, 5
Then the greatest common factor is 1.
Question 52.
When one number is a multiple of another, the GCF of the numbers is the greater of the numbers.
Answer:
When one number is a multiple of another, the GCF of the numbers is the greater of the numbers. This is never true since the GCF is a factor of both numbers. So the GCF is the smaller of the two numbers.
Question 53.
PROBLEM SOLVING
A science museum makes gift bags for students using 168 magnets, 48 robot figurines, and 24 packs of freeze-dried ice cream. What is the greatest number of gift bags that can be made using all of the items? How many of each item are in each gift bag?

Answer:
The greatest common factor of 24, 48, and 168 is 24, so 24 gift bags can be made. Each will have 1/24 of the number of gift items of each type that are available.
In each bag are
1/24 × 168 magnets = 7 magnets
1/24 × 48 robot figurines = 2 robot figurines
1/24 × 24 packs of ice cream = 1 pack of ice cream
Question 54.
VENN DIAGRAM
Consider the numbers 252, 270, and 300.
a. Create a Venn diagram using the prime factors of the numbers.
Answer:
b. Use the Venn diagram to find the GCF of 252, 270, and 300.
Answer:
The factors of 252 are: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252
The factors of 270 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270
The factors of 300 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300
Then the greatest common factor is 6.
c. What is the GCF of 252 and 270? 252 and 300? 270 and 300? Explain how you found your answers.
Answer:
The factors of 252 are: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252
The factors of 270 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270
The GCF of 252 and 270 is 18.
252 and 300:
The factors of 252 are: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252
The factors of 300 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300
Then the greatest common factor is 12.
270 and 300:
The factors of 270 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270
The factors of 300 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300
Then the greatest common factor is 30.
Question 55.
REASONING
You are making fruit baskets using 54 apples, 36 oranges, and 73 bananas.
a. Explain why you cannot make identical fruit baskets without leftover fruit.
Answer: 73 is a prime number. It can only be divided by 1 and by itself.
b. What is the greatest number of identical fruit baskets you can make with the least amount of fruit left over? Explain how you found your answer.
Answer:
The GCF of the three numbers:
54 36 73
1×54 1×36 1×73
2×27 2×18
3×18 3×12
6×9 4×9
6×6
GCF of 54, 36, and 73 is 1
GCF of 54 and 36 is 18
If we divide 54 apples into 18 baskets, we have 3 apples in each basket
If we divide 36 oranges into 18 baskets, we have 2 oranges in each basket
If we divide 73 bananas into 18 baskets, we have 4 bananas in each basket + one banana left over.
So the greatest number of identical fruit baskets we can make with the least amount of fruit left over is 18 baskets
Question 56.
DIG DEEPER!
Two rectangular, adjacent rooms share a wall. One-foot-by-one-foot tiles cover the floor of each room. Describe how the greatest possible length of the adjoining wall is related to the total number of tiles in each room. Draw a diagram that represents one possibility.
Answer:
Consider two adjacent rectangular rooms having Length=L, and, Breadth = B
Now Suppose the wall which is in between two rooms has a height or length =H.
The breadth of wall = B [ if the wall doesn’t exceed the breadth of the room]
Considering two rooms to be identical,
Area of each room= L × B square unit
Area of each tile = 1×1=1 square unit
Number of tiles required= L B ÷ 1= LB tiles( product of length and breadth of the room is the number of tiles required)
Suppose if,LB= N
B= N/LArea of the wall(W) = B×H= B H square unit
B =W/H
Equating (1) and (2)
N/L = W/ H
H = WL/N
H = WL/LB
H = W/B
H = Area of wall/Breadth of room or wall
Lesson 1.5 Least Common Multiple
EXPLORATION 1
Identifying Common Multiples
Work with a partner. In parts (a)–(d), create a Venn diagram that represents the first several multiples of each number and identify any common multiples.
a. 8 and 12
b. 4 and 14
c. 10 and 15
d. 20 and 35
e. Look at the Venn diagrams in parts (a)–(d). Explain how to identify the least common multiple of each pair of numbers. Then circle it in each diagram.
Answer:
a. 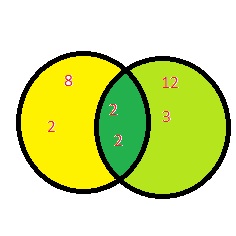
b. 
c.
d. 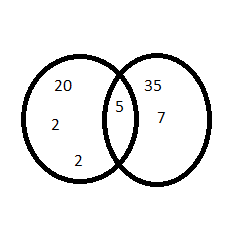
EXPLORATION 2
Using Prime Factors
Work with a partner.
a. Create a Venn diagram that represents the prime factorizations of 8 and 12.

Answer:

b. Repeat part (a) for the remaining number pairs in Exploration 1.
Answer:
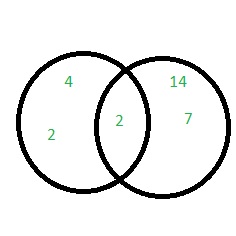
c. STRUCTURE
Make a conjecture about the relationship between the least common multiples you found in Exploration 1 and the numbers in the Venn diagrams you just created.
Answer:
The numbers which are overlapped are the least common multiples of the numbers.
d. The Venn diagram shows the prime factors of two numbers.
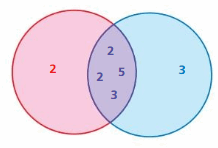
Use the diagram to complete the following tasks.
- Identify the two numbers.
- Find the greatest common factor.
- Find the least common multiple
Answer:
- 120, 180
- The factors of 120 are: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120The factors of 180 are: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180Then the greatest common factor is 60.
- Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 120:
120, 240, 360, 480, 600
Multiples of 180:
180, 360, 540, 720
Therefore,
LCM(120, 180) = 360
1.5 Lesson
Try It
Find the LCM of the numbers using lists of multiples.
Question 1.
3, 8
Answer: 24
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Multiples of 8:
8, 16, 24, 32, 40
Therefore,
LCM(3, 8) = 24
Question 2.
9, 12
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 9:
9, 18, 27, 36, 45, 54
Multiples of 12:
12, 24, 36, 48, 60
Therefore,
LCM(9, 12) = 36
Question 3.
6, 10
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 6:
6, 12, 18, 24, 30, 36, 42
Multiples of 10:
10, 20, 30, 40, 50
Therefore,
LCM(6, 10) = 30
Try It
Find the LCM of the numbers using prime factorizations.
Question 4.
14, 18
Answer:
List all prime factors for each number.
Prime Factorization of 14 is:
2 x 7
Prime Factorization of 18 is:
2 x 3 x 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 3, 3, 7
Multiply these factors together to find the LCM.
LCM = 2 x 3 x 3 x 7 = 126
LCM(14, 18) = 126
Question 5.
28, 36
Answer:
List all prime factors for each number.
Prime Factorization of 28 is:
2 x 2 x 7
Prime Factorization of 36 is:
2 x 2 x 3 x 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 3, 3, 7
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 3 x 3 x 7 = 252
LCM = 252
Therefore,
LCM(28, 36) = 252
Question 6.
24, 90
Answer:
List all prime factors for each number.
Prime Factorization of 24 is:
2 x 2 x 2 x 3
Prime Factorization of 90 is:
2 x 3 x 3 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 2, 3, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 2 x 3 x 3 x 5 = 360
LCM = 360
Therefore,
LCM(24, 90) = 360
Try It
Find the LCM of the numbers.
Question 7.
2, 5, 8
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 2:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44
Multiples of 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50
Multiples of 8:
8, 16, 24, 32, 40, 48, 56
Therefore,
LCM(2, 5, 8) = 40
Question 8.
6, 10, 12
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72
Multiples of 10:
10, 20, 30, 40, 50, 60, 70, 80
Multiples of 12:
12, 24, 36, 48, 60, 72, 84
Therefore,
LCM(6, 10, 12) = 60
Question 9.
Write three numbers that have a least common multiple of 100.
Answer: 1, 10, 100
Explanation:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 1:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102
Multiples of 10:
10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120
Multiples of 100:
100, 200, 300
Therefore,
LCM(1, 10, 100) = 100
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING THE LCM
Find the LCM of the numbers.
Question 10.
6, 9
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 6:
6, 12, 18, 24, 30
Multiples of 9:
9, 18, 27, 36
Therefore,
LCM(6, 9) = 18
Question 11.
30, 40
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 30:
30, 60, 90, 120, 150, 180
Multiples of 40:
40, 80, 120, 160, 200
Therefore,
LCM(30, 40) = 120
Question 12.
5, 11
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65
Multiples of 11:
11, 22, 33, 44, 55, 66, 77
Therefore,
LCM(5, 11) = 55
Question 13.
Reasoning
Write two numbers such that 18 and 30 are multiples of the numbers. Justify your answer.
Answer: 3, 6
Explanation:
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Multiples of 6: 6,12,18,24,30,36,42,48
Thus 18 and 30 are the multiples of 3 and 6.
Question 14.
REASONING
You need to find the LCM of 13 and 14. Would you rather list their multiples or use their prime factorizations? Explain.
Answer:
List all prime factors for each number.
Prime Factorization of 13 shows:
13 is prime = 13
Prime Factorization of 14 is:
2 x 7
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 7, 13
Multiply these factors together to find the LCM.
LCM = 2 x 7 x 13 = 182
In exponential form:
LCM = 2 x 7 x 13 = 182
LCM = 182
Therefore,
LCM(13, 14) = 182
Question 15.
CHOOSE TOOLS
A student writes the prime factorizations of 8 and 12 in a table as shown. She claims she can use the table to find the greatest common factor and the least common multiple of 8 and 12. How is this possible?
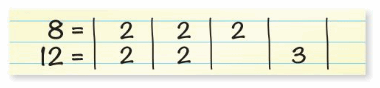

Answer:
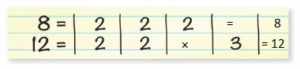
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 2, 3
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 2 x 3 = 24
The least common multiple of 8 and 12 is 24.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
A geyser erupts every fourth day. Another geyser erupts every sixth day. Today both geysers erupted. In how many days will both geysers erupt on the same day again?
Answer:
Given,
A geyser erupts every fourth day. Another geyser erupts every sixth day. Today both geysers erupted.
The geyser erupts on the same day after 12 days.
Question 18.
A water park has two large buckets that slowly fill with water. One bucket dumps water every 12 minutes. The other bucket dumps water every 10 minutes. Five minutes ago, both buckets dumped water. When will both buckets dump water at the same time again?

Answer:
Given,
A water park has two large buckets that slowly fill with water.
One bucket dumps water every 12 minutes.
The other bucket dumps water every 10 minutes.
Five minutes ago, both buckets dumped water.
Both buckets will dump again at the same time in 60 minutes (1 hour.)
Question 19.
DIG DEEPER!
You purchase disposable plates, cups, and forks for a cookout. Plates are sold in packages of 24, cups in packages of 32, and forks in packages of 48. What are the least numbers of packages you should buy in order to have the same number of plates, cups, and forks?
Answer:
Given,
You purchase disposable plates, cups, and forks for a cookout. Plates are sold in packages of 24, cups in packages of 32, and forks in packages of 48.
We solve this question using the Lowest Common Multiple (LCM) method/
Step 1
We list multiples of each number until the first common multiple is found. This is referred to as the lowest common multiple.
Plates are sold in packages of 24
Cups in packages of 32
Forks in packages of 48
Multiples of 24:
24, 48, 72, 96, 120, 144
Multiples of 32:
32, 64, 96, 128, 160
Multiples of 48:
48, 96, 144, 192
Therefore,
LCM(24, 32, 48) = 96
Hence, the least numbers of packages you should buy in order to have the same number of plates, cups, and forks is 96 packages
Least Common Multiple Practice 1.5
Review & Refresh
Find the GCF of the numbers.
Question 1.
18, 42
Answer:
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
Then the greatest common factor is 6.
Question 2.
72, 96
Answer:
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
The factors of 96 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Then the greatest common factor is 24.
Question 3.
38, 76, 114
Answer:
The factors of 38 are: 1, 2, 19, 38
The factors of 76 are: 1, 2, 4, 19, 38, 76
The factors of 114 are: 1, 2, 3, 6, 19, 38, 57, 114
Then the greatest common factor is 38.
Divide.
Question 4.
900 ÷ 6
Answer: 150
Explanation:
Divide the two numbers 900 and 6.
900/6 = 150
It means 6 divides 900 150 times.
Thus the quotient is 150.
Question 5.
1944 ÷ 9
Answer: 216
Explanation:
Divide the two numbers 1944 and 9
1944/9 = 216
It means that 9 divides 1944 216 times.
Thus the quotient is 216
Question 6.
672 ÷ 12
Answer: 56
Explanation:
Divide the two numbers 672 and 12.
672/12 = 56
It means 12 divides 672 56 times.
Thus the quotient is 56.
Write an ordered pair that corresponds to the point.
Question 7.
Point A
Answer: (2,4)
By seeing the below graph we can find the ordered pairs.
2 lies on the x-axis and 4 lies on the y-axis.
So, the ordered pairs to the point A is (2,4)
Question 8.
Point B
Answer: (3,1)
By seeing the below graph we can find the ordered pairs.
3 lies on the x-axis and 1 lies on the y-axis.
So, the ordered pairs to the point A is (3,1)
Question 9.
Point C
Answer: (4,7)
By seeing the below graph we can find the ordered pairs.
4 lies on the x-axis and 7 lies on the y-axis.
So, the ordered pairs to the point A is (4,7)
Question 10.
Point D
Answer: (9,6)
By seeing the below graph we can find the ordered pairs.
9 lies on the x-axis and 6 lies on the y-axis.
So, the ordered pairs to the point A is (9,6)
Concepts, Skills, & Problem Solving
USING A VENN DIAGRAM
Use a Venn diagram to find the least common multiple of the numbers. (See Exploration 1, p. 27.)
Question 11.
3, 7
Answer: 21
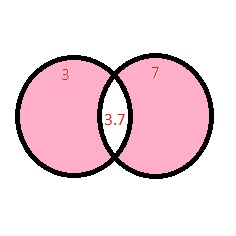
Question 12.
6, 8
Answer: 24
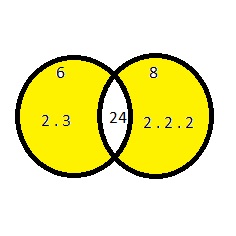
Question 13.
4, 5
Answer:
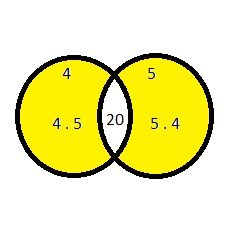
FINDING THE LCM
Find the LCM of the numbers using lists of multiples.
Question 14.
1, 5
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 1:
1, 2, 3, 4, 5, 6, 7
Multiples of 5:
5, 10, 15
Therefore,
LCM(1, 5) = 5
Question 15.
2, 6
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 2:
2, 4, 6, 8, 10
Multiples of 6:
6, 12, 18
Therefore,
LCM(2, 6) = 6
Question 16.
2, 3
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 2:
2, 4, 6, 8, 10
Multiples of 3:
3, 6, 9, 12
Therefore,
LCM(2, 3) = 6
Question 17.
2, 9
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 2:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22
Multiples of 9:
9, 18, 27, 36
Therefore,
LCM(2, 9) = 18
Question 18.
3, 4
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 3:
3, 6, 9, 12, 15, 18
Multiples of 4:
4, 8, 12, 16, 20
Therefore,
LCM(3, 4) = 12
Question 19.
8, 9
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 8:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88
Multiples of 9:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Therefore,
LCM(8, 9) = 72
Question 20.
5, 8
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50
Multiples of 8:
8, 16, 24, 32, 40, 48, 56
Therefore,
LCM(5, 8) = 40
Question 21.
11, 12
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 11:
11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156
Therefore,
LCM(11, 12) = 132
Question 22.
12, 18
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 12:
12, 24, 36, 48, 60
Multiples of 18:
18, 36, 54, 72
Therefore,
LCM(12, 18) = 36
FINDING THE LCM
Find the LCM of the numbers using prime factorizations.
Question 23.
7, 12
Answer:
List all prime factors for each number.
Prime Factorization of 7 shows:
7 is prime
Prime Factorization of 12 is:
2 x 2 x 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 3, 7
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 3 x 7 = 84
LCM = 84
Therefore,
LCM(7, 12) = 84
Question 24.
5, 9 4
Answer:
List all prime factors for each number.
Prime Factorization of 4 is:
2 x 2
Prime Factorization of 5 shows:
5 is prime
Prime Factorization of 9 is:
3 x 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 3, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 3 x 3 x 5 = 180
LCM = 180
Therefore,
LCM(4, 5, 9) = 180
Question 25.
4, 11
Answer:
List all prime factors for each number.
Prime Factorization of 4 is:
2 x 2
Prime Factorization of 11 shows:
11 is prime
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 11
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 11 = 44
LCM = 44
Therefore,
LCM(4, 11) = 44
Question 26.
9, 10
Answer:
List all prime factors for each number.
Prime Factorization of 9 is:
3 x 3
Prime Factorization of 10 is:
2 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 3, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 3 x 3 x 5 = 90
LCM = 90
Therefore,
LCM(9, 10) = 90
Question 27.
12, 27
Answer:
List all prime factors for each number.
Prime Factorization of 12 is:
2 x 2 x 3
Prime Factorization of 27 is:
3 x 3 x 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 3, 3, 3
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 3 x 3 x 3 = 108
LCM = 108
Therefore,
LCM(12, 27) = 108
Question 28.
18, 45
Answer:
List all prime factors for each number.
Prime Factorization of 18 is:
2 x 3 x 3
Prime Factorization of 45 is:
3 x 3 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 3, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 3 x 3 x 5 = 90
LCM = 90
Therefore,
LCM(18, 45) = 90
Question 29.
22, 23
Answer:
List all prime factors for each number.
Prime Factorization of 22 is:
2 x 11
Prime Factorization of 23 shows:
23 is prime
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 11, 23
Multiply these factors together to find the LCM.
LCM = 2 x 11 x 23 = 506
LCM = 506
Therefore,
LCM(22, 23) = 506
Question 30.
36, 60
Answer:
List all prime factors for each number.
Prime Factorization of 36 is:
2 x 2 x 3 x 3
Prime Factorization of 60 is:
2 x 2 x 3 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 2, 3, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 3 x 3 x 5 = 180
LCM = 180
Therefore,
LCM(36, 60) = 180
Question 31.
35, 50
Answer:
List all prime factors for each number.
Prime Factorization of 35 is:
5 x 7
Prime Factorization of 50 is:
2 x 5 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 5, 5, 7
Multiply these factors together to find the LCM.
LCM = 2 x 5 x 5 x 7 = 350
LCM = 350
Therefore,
LCM(35, 50) = 350
Question 32.
YOU BE THE TEACHER
Your friend finds the LCM of 6 and 9. Is your friend correct? Explain your reasoning.

Answer: No friend is incorrect.
List all prime factors for each number.
Prime Factorization of 6 is:
2 x 3
Prime Factorization of 9 is:
3 x 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 3, 3
Multiply these factors together to find the LCM.
LCM = 2 x 3 x 3 = 18
LCM = 18
Therefore,
LCM(6, 9) = 18
Question 33.
MODELING REAL LIFE
You have diving lessons every fifth day and swimming lessons every third day. Today you have both lessons. In how many days will you have both lessons on the same day again?
Answer:
After 15 days
diving is on 0 , 5 , 10 , 15 , 20 , … days
swimming is on 0 , 3, 6 , 9, 12 , 15 , 18 , … days
Thus the next will be in 15 days
Question 34.
REASONING
Which model represents an LCM that is different from the other three? Explain your reasoning.
Answer: The number line B is different from the other three number lines.
FINDING THE LCM
Find the LCM of the numbers.
Question 35.
2, 3, 7
Answer:
LCM(2,3) = (2 × 3) / GCF(2,3)
= (2 × 3) / 1
= 6 / 1
= 6
LCM(6,7) = (6 × 7) / GCF(6,7)
= (6 × 7) / 1
= 42 / 1
= 42
Therefore,
LCM(2, 3, 7) = 42
Question 36.
3, 5, 11
Answer:
LCM(3,5) = (3 × 5) / GCF(3,5)
= (3 × 5) / 1
= 15 / 1
= 15
LCM(15,11) = (15 × 11) / GCF(15,11)
= (15 × 11) / 1
= 165 / 1
= 165
Therefore,
LCM(3, 5, 11) = 165
Question 37.
4, 9, 12
Answer:
LCM(4,9) = (4 × 9) / GCF(4,9)
= (4 × 9) / 1
= 36 / 1
= 36
LCM(36,12) = (36 × 12) / GCF(36,12)
= (36 × 12) / 12
= 432 / 12
= 36
Therefore,
LCM(4, 9, 12) = 36
Question 38.
6, 8, 15
Answer:
LCM(6,8) = (6 × 8) / GCF(6,8)
= (6 × 8) / 2
= 48 / 2
= 24
LCM(24,15) = (24 × 15) / GCF(24,15)
= (24 × 15) / 3
= 360 / 3
= 120
Therefore,
LCM(6, 8, 15) = 120
Question 39.
7, 18, 21
Answer:
LCM(7,18) = (7 × 18) / GCF(7,18)
= (7 × 18) / 1
= 126 / 1
= 126
LCM(126,21) = (126 × 21) / GCF(126,21)
= (126 × 21) / 21
= 2646 / 21
= 126
Therefore,
LCM(7, 18, 21) = 126
Question 40.
9, 10, 28
Answer:
LCM(9,10) = (9 × 10) / GCF(9,10)
= (9 × 10) / 1
= 90 / 1
= 90
LCM(90,28) = (90 × 28) / GCF(90,28)
= (90 × 28) / 2
= 2520 / 2
= 1260
Therefore,
LCM(9, 10, 28) = 1260
Question 41.
PROBLEM SOLVING
At Union Station, you notice that three subway lines just arrived at the same time. How long must you wait until all three lines arrive at Union Station at the same time again?
Answer: 60 minutes
Explanation:
The complete question in the attached figure
Step 1
Find the least common multiple (LCM) of the three numbers
List the prime factors of each number
10 = 2 × 5
12 = 2 × 2 × 3
15 = 3 × 5
Multiply each factor the greatest number of times it occurs in any of the numbers to find out the LCM
The LCM is equal to
4 × 3 × 5 = 60
Thus You must wait 60 minutes for all three lines to arrive at Union Station at the same time again.
Question 42.
DIG DEEPER!
A radio station gives away $15 to every 15th caller, $25 to every 25th caller, and a free concert ticket to every 100th caller. When will the station first give away all three prizes to one caller? When this happens, how much money and how many tickets are given away?
Answer:
Given,
Radio Station gives :
1st prize: $15 to 15th caller
2nd prize: $25 to 25th caller
3rd prize: free concert tickets to 100th caller
So, in order to get all three prizes the caller must be 15th, 25th, and 100th caller at the same time. But to find when the radio station will give first all three prizes we calculate L.C.M. of ( 15, 25, 100 ) that is 300
Hence, the station first gives away all three prizes to the 300th caller.
Question 43.
LOGIC
You and a friend are running on treadmills. You run 0.5 mile every 3 minutes, and your friend runs 2 miles every 14 minutes. You both start and stop running at the same time and run a whole number of miles. What are the least possible numbers of miles you and your friend can run?
Answer:
If you run 0.5 miles every 3 minutes then you run 1 mile every 6 minutes.
If your friend runs 2 miles every 14 minutes then your friend runs 1 mile every 7 minutes.
You will both then both run a whole number of minutes for a time that is a multiple of 6 and 7.
The least common multiple of 6 and 7 is 42 so the least possible time you and your friend could run for and both run a whole number of miles is then 42 minutes.
Since you run 1 mile every 6 minutes, in 42 minutes you will run 42/6=7 miles.
Since your friend runs 1 mile every 7 minutes, in 42 minutes your friend will run 42/7=6 miles.
Question 44.
VENN DIAGRAM
Refer to the Venn diagram.
a. Copy and complete the Venn diagram.
b. What is the LCM of 16, 24, and 40?
c. What is the LCM of 16 and 40? 24 and 40? 16 and 24? Explain how you found your answers.
Answer:
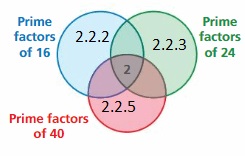
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
LCM of 16, 40:
Multiples of 16:
16, 32, 48, 64, 80, 96, 112
Multiples of 40:
40, 80, 120, 160
Therefore,
LCM(16, 40) = 80
LCM of 24, 40:
Multiples of 24:
24, 48, 72, 96, 120, 144, 168
Multiples of 40:
40, 80, 120, 160, 200
Therefore,
LCM(24, 40) = 120
LCM of 16, 24:
Multiples of 16:
16, 32, 48, 64, 80
Multiples of 24:
24, 48, 72, 96
Therefore,
LCM(16, 24) = 48
CRITICAL THINKING
Tell whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 45.
The LCM of two different prime numbers is their product.
Answer: Always true
Example:
3 × 5 = 15
Question 46.
The LCM of a set of numbers is equal to one of the numbers in the set.
Answer:
The LCM of a set of numbers is equal to one of the numbers in the set. Always Sometimes Never true. Question 909193: The LCM of a set of numbers is equal to one of the numbers in the set. This is sometimes true.
Question 47.
The GCF of two different numbers is the LCM of the numbers.
Answer:
Another way to find the LCM of two numbers is to divide their product by their greatest common factor ( GCF ). Example 2: Find the least common multiple of 18 and 20. The common factors are 2 and 3 .
Numerical Expressions and Factors Connecting Concepts
Getting Ready for Chapter Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A sports team gives away shirts at the stadium. There are 60 large shirts, 1.6 times as many small shirts as large shirts, and 1.5 times as many medium shirts as small shirts. The team wants to divide the shirts into identical groups to be distributed throughout the stadium. What is the greatest number of groups that can be formed using every shirt?
Understand the Problem
You know the number of large shirts and two relationships among the numbers of small, medium, and large shirts. You are asked to find the greatest number of identical groups that can be formed using every shirt.
Make a plan
Break the problem into parts. First use multiplication to find the number of each size shirt. Then find the GCF of these numbers.
Solve and Check
Use the plan to solve the problem. Then check your solution.
Answer:
Given,
A sports team gives away shirts at the stadium.
There are 60 large shirts, 1.6 times as many small shirts as large shirts, and 1.5 times as many medium shirts as small shirts. The team wants to divide the shirts into identical groups to be distributed throughout the stadium.
60 × 1.6 = 96
60 × 1.5 = 90
The factors of 90 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
The factors of 96 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Then the greatest common factor is 6.
Question 2.
An escape artist fills the tank shown with water. Find the number of cubic feet of water needed to fill the tank. Then find the number of cubic yards of water that are needed to fill the tank. Justify your answer.
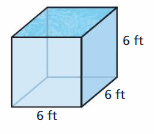
Answer:
Given,
An escape artist fills the tank shown with water.
side = 6 ft
We know that
The volume of the cube = s³
V = 6ft × 6ft × 6ft
V = 216 cubic ft.
Performance Task
Setting the Table
At the beginning of this chapter, you watched a STEAM video called “Filling Piñatas.” You are now ready to complete the performance task for this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Answer:
Factors of 50 – 1, 2, 5, 10, 25, and 50
Factors of 12 – 1, 2, 3, 4, 6, 12
Factors of 16 – 1, 2, 4, 8, 16
The factors of number 24 are 1, 2, 3, 4, 6, 8, 12, 24.
The factors of 100 are 1,2,4,5,10,20,25,50 and 100.
Numerical Expressions and Factors Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use an Information Frame to organize and remember concepts. Here is an example of an Information Frame for the vocabulary term power.
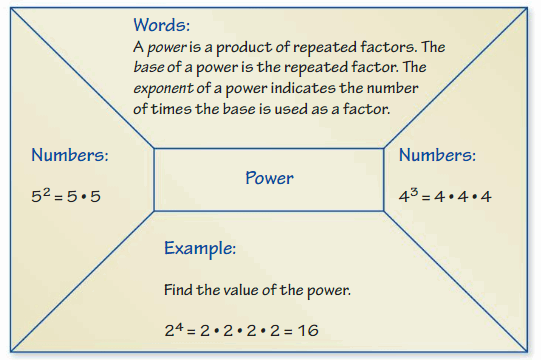
Choose and complete a graphic organizer to help you study the concept.

- perfect square
- numerical expression
- order of operations
- prime factorization
- greatest common factor (GCF)
- least common multiple (LCM)
Answer:
1. A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system. Examples of Numbers that are Perfect Squares. 25 is a perfect square.
2. A numerical expression is a mathematical sentence involving only numbers and one or more operation symbols. Examples of operation symbols are the ones for addition, subtraction, multiplication, and division.
3. Order of operations refers to which operations should be performed in what order, but it’s just convention.
4. “Prime Factorization” is finding which prime numbers multiply together to make the original number.
5. Greatest Common Factor. The highest number that divides exactly into two or more numbers.
6. Least Common Multiple. The smallest positive number that is a multiple of two or more numbers.
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

1.1 Powers and Exponents (pp. 3-8)
Write the product as a power.
Question 1.
3 × 3 × 3 × 3 × 3 × 3
Answer: The product of 3 × 3 × 3 × 3 × 3 × 3 is 36
Question 2.
5 × 5 × 5
Answer: The product of 5 × 5 × 5 is 53
Question 3.
17 . 17 . 17 . 17 . 17
Answer: The product of 17 . 17 . 17 . 17 . 17 is 175
Question 4.
33
Answer: 3 × 3 × 3
Question 5.
26
Answer: 2 × 2 × 2 × 2 × 2 × 2
Question 6.
44
Answer: 4 × 4 × 4 × 4
Question 7.
Write a power that has a value greater than 23 and less than 33.
Answer: The power that has a value greater than 23 and less than 33 is 4²
Question 8.
Without evaluating, determine whether 25 or 42 is greater. Explain.
Answer: 25 > 42
Explanation:
The exponent with the highest number will be greater.
Question 9.
The bases on a softball field are square. What is the area of each base?

Answer:
Given,
The bases on a softball field are square.
s = 15 inches
We know that,
Area of the square = s × s
A = 15 × 15
A = 225 sq. in
Thus the area of each base is 225 sq. in.
1.2 Order of Operations (pp. 9–14)
Evaluate the expression.
Question 10.
3 × 6 – 12 ÷ 6
Answer: 16
Explanation:
You have to evaluate from left to right.
(3 × 6) – (12 ÷ 6)
18 – 2 = 16
Question 11.
30 ÷ (14 – 22) × 5
Answer: 15
Explanation:
You have to evaluate from left to right.
30 ÷ (14 – 4) × 5
30 ÷ 10 × 5
3 × 5 = 15
Question 12.
![]()
Answer: 15
Explanation:
You have to evaluate from left to right.
2.3 + 3.7 = 6
5(6)/2 = 30/2 = 15
Question 13.
![]()
Answer: 37
Explanation:
You have to evaluate from left to right.
7² + 5 = 49 + 5 = 54
1/2 × 54 = 27
4³ – 27 = 64 – 27 = 37
Question 14.
20 (32 – 4) ÷ 50
Answer: 2
Explanation:
You have to evaluate from left to right.
(32 – 4) = 9 – 4 = 5
20 × 5 ÷ 50
100 ÷ 50 = 2
Question 15.
5 + 3(42 – 2) ÷ 6
Answer: 12
Explanation:
You have to evaluate from left to right.
(42 – 2) = 16 – 2 = 14
5 + 3(14) ÷ 6
5 + 42 ÷ 6
5 + 7 = 12
Question 16.
Use grouping symbols and at least one exponent to write a numerical expression that has a value of 80.
Answer: 6 + (9² – 7) = 80
1.3 Prime Factorization (pp. 15–20)
List the factor pairs of the number.
Question 17.
28
Answer: The factor pairs of the number 28 are 1, 2, 4, 7, 14, 28
Explanation:
28 = 1 × 28
2 × 14
4 × 7
7 × 4
14 × 2
28 × 1
Question 18.
44
Answer: The factor pairs of the number 44 are 1, 2, 4, 11, 44.
Explanation:
44 = 1 × 44
2 × 22
4 × 11
11 × 4
44 × 1
Question 19.
96
Answer: The factor pairs of the number 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Explanation:
1 and 96 are a factor pair of 96 since 1 x 96= 96
2 and 48 are a factor pair of 96 since 2 x 48= 96
3 and 32 are a factor pair of 96 since 3 x 32= 96
4 and 24 are a factor pair of 96 since 4 x 24= 96
6 and 16 are a factor pair of 96 since 6 x 16= 96
8 and 12 are a factor pair of 96 since 8 x 12= 96
12 and 8 are a factor pair of 96 since 12 x 8= 96
16 and 6 are a factor pair of 96 since 16 x 6= 96
24 and 4 are a factor pair of 96 since 24 x 4= 96
32 and 3 are a factor pair of 96 since 32 x 3= 96
48 and 2 are a factor pair of 96 since 48 x 2= 96
96 and 1 are a factor pair of 96 since 96 x 1= 96
Question 20.
There are 36 graduated cylinders to put away on a shelf after science class. The shelf can fit a maximum of 20 cylinders across and 4 cylinders deep. The teacher wants each row to have the same number of cylinders. List the possible arrangements of the graduated cylinders on the shelf.

Answer:
Given,
There are 36 graduated cylinders to put away on a shelf after science class.
The shelf can fit a maximum of 20 cylinders across and 4 cylinders deep.
The teacher wants each row to have the same number of cylinders.
There are three possible arrangements of the graduated cylinders on the shelf.
1. 4 rows of 9 graduated cylinders
2. 3 rows of 12 graduated cylinders.
3. 2 rows of 18 graduated cylinders.
Write the prime factorization of the number.
Question 21.
42
Answer: The prime factorization of the number 42 is 2 × 3 × 7
Explanation:
42 = 2 × 21
= 2 × 3 × 7
Question 22.
50
Answer: The prime factorization of the number 2 × 5 × 5
Explanation:
50 = 2 × 25
= 2 × 5 × 5
Question 23.
66
Answer: The prime factorization of the number 2 × 3 × 11
Explanation:
66 = 2 × 33
= 2 × 3 × 11
1.4 Greatest Common Factor (pp. 21–26)
Find the GCF of the numbers using lists of factors.
Question 24.
27, 45
Answer: GCF is 9
Explanation:
The factors of 27 are: 1, 3, 9, 27
The factors of 45 are: 1, 3, 5, 9, 15, 45
Then the greatest common factor is 9.
Question 25.
30, 48
Answer: GCF is 6
Explanation:
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Then the greatest common factor is 6.
Question 26.
28, 48
Answer: GCF is 4
Explanation:
The factors of 28 are: 1, 2, 4, 7, 14, 28
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Then the greatest common factor is 4.
Find the GCF of the numbers using prime factorizations.
Question 27.
24, 80
Answer:
The prime factorization is the product of the circled primes. So the prime factorization of 24 is 24 = 2 · 2 · 2 · 3 = 2³ . 3
The prime factorization is the product of the circled primes. So the prime factorization of 80 is 80 = 2 x 2 x 2 x 2 x 5 = 2² . 2² . 5
Question 28.
52, 68
Answer:
The prime factorization is the product of the circled primes. So the prime factorization of 52 is 2 x 2 x 13 = 2² . 13
The prime factorization is the product of the circled primes. So the prime factorization of 68 is 2 × 2 × 17 = 2². 17
Question 29.
32, 56
Answer:
The prime factorization is the product of the circled primes. So the prime factorization of 32 is 2 x 2 x 2 x 2 x 2 = 25
The prime factorization is the product of the circled primes. So the prime factorization of 56 is 2 x 2 x 2 x 7 = 2³ . 7
Question 30.
Write a pair of numbers that have a GCF of 20.
Answer: The prime factors of 20 are 2 x 2 x 5. The GCF of 20 is 5.
Question 31.
What is the greatest number of friends you can invite to an arcade using the coupon such that the tokens and slices of pizza are equally split between you and your friends with none left over? How many slices of pizza and tokens will each person receive?

Answer: (n/4)-1
Explanation:
Total slices = n
Total number of people =4
Each people may be eat = n/4 slices
Here Harris eats 1 slice fewer
Then Harris eats (n/4)-1 slices
1.5 Least Common Multiple (pp. 27–32)
Find the LCM of the numbers using lists of multiples.
Question 32.
4, 14
Answer: 28
Explanation:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, 36
Multiples of 14:
14, 28, 42, 56
Therefore,
LCM(4, 14) = 28
Question 33.
6, 20
Answer: 60
Explanation:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
Multiples of 20:
20, 40, 60, 80, 100
The LCM of 6, 20 is 60
Question 34.
12, 28
Answer: 84
Explanation:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96
Multiples of 28:
28, 56, 84, 112, 140, 168, 196
LCM of 12, 28 is 84
Find the LCM of the numbers using prime factorizations.
Question 35.
6, 45
Answer:
Prime Factorisation of 6: 2 × 3
Prime Factorisation of 45: 3 × 3 × 5
LCM is 2 × 3 × 3 × 3 × 5 = 60
Question 36.
10, 12
Answer: 60
Prime factorization of 10: 2 × 5
Prime factorization of 12: 2 × 2 × 3
LCM is 5 × 2 × 2 × 3 = 60
Question 37.
18, 27
Answer:
Prime factorization of 18: 2 × 3 × 3
Prime factorization of 27: 3 × 3 × 3
LCM is 2 × 3 × 3 × 3 = 54
Question 38.
Find the LCM of 8, 12, and 18.
Answer: 72
Prime Factorisation of 8: 2 × 2 × 2
Prime Factorisation of 12: 2 × 2 × 3
Prime factorization of 18: 2 × 3 × 3
LCM = 72
Question 39.
Write a pair of numbers that have an LCM of 84.
Answer: 84 and 12
Explanation:
The LCM of 84 and 12 is 84.
Prime factorization of 12: 2 × 2 × 3
Prime factorization of 84: 2 × 2 × 3 × 7
The Least Common Multiple is 2 × 2 × 3 × 7 = 84
Question 40.
Write three numbers that have an LCM of 45.
Answer: 3, 15, 45
Explanation:
The prime factorization of 15: 3 × 5
The prime factorization of 45: 3 × 3 × 5
The LCM of 3, 15, 45 is 45.
Question 41.
You water your roses every sixth day and your hydrangeas every fifth day. Today you water both plants. In how many days will you water both plants on the same day again?

Answer: 30
Explanation:
Given,
You water your roses every sixth day and your hydrangeas every fifth day. Today you water both plants.
6 × 5 = 30
You water both plants for 30 days on the same day again.
Question 42.
Hamburgers are sold in packages of 20, while buns are sold in packages of 12. What are the least numbers of packages you should buy in order to have the same number of hamburgers and buns?
Answer:
Given,
Hamburgers are sold in packages of 20, while buns are sold in packages of 12.
At least 5 packages of buns and 3 packages of hamburgers.
20×3=60
12×5=60
So that is how you get the answer by seeing if they have any integers in common.
Question 43.
A science museum is giving away a magnetic liquid kit to every 50th guest and a plasma ball to every 35th guest until someone receives both prizes.

a. Which numbered guest will receive both a magnetic liquid kit and a plasma ball?
Answer:
A magnetic liquid kit prize every 50 guests and a plasma ball every 35 guests.
1.Guest 50th
2.Guest 100th
3.Guest 150th
4.Guest 200th
5.Guest 250th
6.Guest 300th
7.Guest 350th
8.Guest 400th and so on, in case no coincidence would happen.
b. How many people will receive a plasma ball?
Answer:
1.Guest 35th
2.Guest 70th
3.Guest 105th
4.Guest 140th
5.Guest 175th
6.Guest 210th
7.Guest 245th
8.Guest 280th
9.Guest 315th
10.Guest 350th.
As you can see, Guest 350th will be the first one to receive both prizes, and including him or her, a total of ten guests will receive the plasma ball until that moment. There wasn’t any coincidence before Guest 350th.
Numerical Expressions and Factors Practice Test
Question 1.
Find the value of 23.
Answer:
23 can be written as 2 × 2 × 2 = 8
Thus the value of 23 is 8.
Question 2.
Evaluate ![]()
Answer:
5 + 4(12 – 2) = 5 + 4(10) = 5 + 40
(5 + 40)/3² = 45/9 = 5
Thus the value of ![]() is 5.
is 5.
Question 3.
Write 264.264.264 as a power
Answer: 264.264.264 can be written as 264³
Question 4.
List the factor pairs of 66.
Answer: The factor pairs of 66 are (1,66) (2, 33) (6, 11)
66 = 1 × 66
66 = 2 × 33
66 = 6 × 11
Question 5.
Write the prime factorization of 56.
Answer:
56 = 2 × 28
= 2 × 2 × 14
= 2 × 2 × 2 × 7
Thus the prime factorization of 56 is 2 × 2 × 2 × 7
Find the GCF of the numbers.
Question 6.
24, 54
Answer: GCF is 6
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54
Then the greatest common factor is 6.
Question 7.
16, 32, 72
Answer: GCF is 8
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 32 are: 1, 2, 4, 8, 16, 32
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Then the greatest common factor is 8.
Question 8.
52, 65
Answer: GCF is 13
The factors of 52 are: 1, 2, 4, 13, 26, 52
The factors of 65 are: 1, 5, 13, 65
Then the greatest common factor is 13.
Find the LCM of the numbers.
Question 9.
9, 24
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 9:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Multiples of 24:
24, 48, 72, 96, 120
Therefore,
LCM(9, 24) = 72
Question 10.
26, 39
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 26:
26, 52, 78, 104, 130
Multiples of 39:
39, 78, 117, 156
Therefore,
LCM(26, 39) = 78
Question 11.
6, 12, 14
Answer:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108
Multiples of 14:
14, 28, 42, 56, 70, 84, 98, 112
Therefore,
LCM(6, 12, 14) = 84
Question 12.
You have 16 yellow beads, 20 red beads, and 24 orange beads to make identical bracelets. What is the greatest number of bracelets that you can make using all of the beads?
Answer:
To find how many identical bracelets you can make, you need to find a common denominator.
In this case, all three numbers; 16, 20, and 24, can be divided by four.
So you now know you can have four bracelets.
Then you take your numbers of each color beads and divide them by four so you know how many of each color will be on the bracelets.
In the end, you have four bracelets, each with 4 yellow beads, 5 red beads and 6 orange beads
Question 13.
A bag contains equal numbers of green marbles and blue marbles. You can divide all of the green marbles into groups of 12 and all the blue marbles into groups of 16. What is the least number of each color of marble that can be in the bag?
Answer:
Given,
A bag contains equal numbers of green marbles and blue marbles.
You can divide all of the green marbles into groups of 12 and all the blue marbles into groups of 16.
To solve this problem, we need to find for the LCM of each number. That is:
12: 12, 24, 36, 48, 60
16: 16, 32, 48, 64, 80
So we can see that the LCM is 48.
Therefore the least number of each color of marble must be 48.
Question 14.
The ages of the members of a family are 65, 58, 27, 25, 5, and 2 years old. What is the total admission price for the family to visit the zoo?

Answer:
The ages of the members of a family are 65, 58, 27, 25, 5, and 2 years old.
We can find the total admission price for the family to visit the zoo by following the above table.
$10 + $12 + $27 + $12 + $8 + $8 = $77
Question 15.
A competition awards prizes for fourth, third, second, and first place. The fourth place winner receives $5. Each place above that receives a prize that is five times the amount of the previous prize. How much prize money is awarded?
Answer:
A competition awards prizes for fourth, third, second, and first place. The fourth place winner receives $5. Each place above that receives a prize that is five times the amount of the previous prize.
Each place above that receives a prize that is five times the amount of the previous prize
So we can say that;
Pn = 5 × P(n+1)
Where n ⇒ Number Place
Pn = Price received by Number place
Substituting the values of n as 3,2,1 to find the price of third second first place winner.
P3 = 5 × P(3+1) = 5 × P4 = 5 × 5 = 25
P2 = 5 × P(2+1) = 5 × P3 = 5 × 25 = 125
P1 = 5 × P(1+1) = 5 × P2 = 5 × 125 = 625
Now We will find the Total Prize money awarded.
Total Prize money awarded = 625 + 125 + 25 + 5 = 780
Hence A total of $780 price money was awarded.
Question 16.
You buy tealight candles and mints as party favors for a baby shower. The tealight candles come in packs of 12 for $3.50. The mints come in packs of 50 for $6.25. What is the least amount of money you can spend to buy the same number of candles and mints?

Answer: The least amount of money it can be spent is $125.
Explanation:
First, we write the prime factorization of each number:
12= 2·2·3
15= 2·5·5
Then, we search for each different factor which appears the greater number of times. The factor 2 appears in both factorizations so the least common multiple is:
LCM= 2·2·3·5·5=300
Hence, the total quantity of packs of each thing is:
Candles: 300÷12=25
Mints: 300÷50=6
The least amount of money it can be spent is:
T=25×$3.50 + 6×$6.25= $87.5 + $37.5= $125
Numerical Expressions and Factors Cumulative Practice
Question 1.
Find the value of 8 × 135?


Answer: Multiply the two numbers 8 and 135
8 × 135 = 1080
Question 2.
Which number is equivalent to the expression blow?
3.23 – 8 ÷ 4
Answer: 22
Explanation:
Given the expression 3.23 – 8 ÷ 4
3 × 8 -(8÷4)
24 – (2)
24 – 2 = 22
Question 3.
The top of an end table is a square with a side length of 16 inches. What is the area of the tabletop?
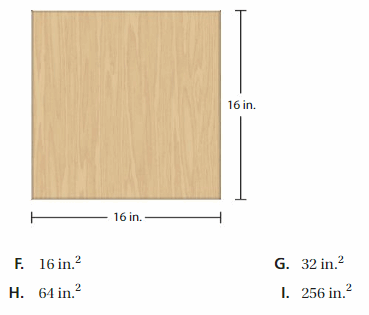
Answer: I
Explanation:
Given that
The top of an end table is a square with a side length of 16 inches.
Area of the square = s × s
A = 16 × 16
A = 256 in²
Thus the correct answer is option I.
Question 4.
You are filling baskets using 18 green eggs, 36 red eggs, and 54 blue eggs. What is the greatest number of baskets that you can fill so that the baskets are identical and there are no eggs left over?
A. 3
B. 6
C. 9
D. 18
Answer: D
Explanation:
Given,
You are filling baskets using 18 green eggs, 36 red eggs, and 54 blue eggs.
18/n = 36/n = 54/n
Factors of 18 are 2,3,6,9,18
Factors of 36 are 2,3,4,6,9,12,18.
Factors of 54 are 2,3,6,9,18,27,54.
The common multiples of 18,36 and 54 are 2,3,6,9,18.
Thus the greatest among them is 18.
Thus the correct answer is option D.
Question 5.
What is the value of 23.32.5?

Answer:
23.32.5
2³ = 8
3² = 9
8 × 9 × 5 = 360
Question 6.
You hang the two strands of decorative lights shown below.

Both strands just changed color. After how many seconds will the strands change color at the same time again?
F. 3 seconds
G. 30 seconds
H. 90 seconds
I. 270 seconds
Answer: 3 seconds
Explanation:
Strand I: Changes between red and blue every 15 seconds
Strand II: Changes between green and gold every 18 seconds
18 – 15 = 3 seconds
Thus the correct answer is option F.
Question 7.
Point P is plotted in the coordinate plane below.
What are the coordinates of Point P ?
A. (5, 3)
B. (4, 3)
C. (3, 5)
D. (3, 4)
Answer: C
By seeing the above graph we can find the coordinates of point p.
The X-axis is on 3 and Y-axis is on 5.
Thus the correct answer is option c.
Question 8.
What is the prime factorization of 1100?
F. 2 × 5 × 11
G. 22 × 52 × 11
H. 4 × 52 × 11
I. 22 × 5 × 55
Answer: G
Prime factorization of 1100: 2 × 550
2 × 2 × 275
2 × 2 × 5 × 55
2 × 2 × 5 × 5 × 11
Thus the correct answer is option b.
Question 9.
What is the least common multiple of 3, 8, and 10?
A. 24
B. 30
C. 80
D. 120
Answer: D
Multiples of 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120, 123, 126
Multiples of 8:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136
Multiples of 10:
10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140.
The common multiple among the three is 120.
Thus the correct answer is option D.
Question 10.
What is the area of the shaded region of the figure below?
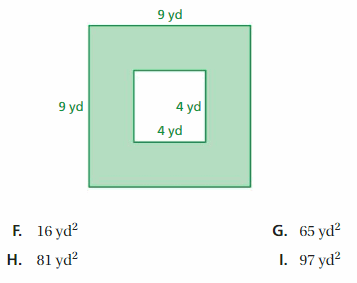
Answer:
The above figure is square.
s = 4 yd
Area of the square = s × s
A = 4 yd × 4 yd
A = 16 sq. yd
The area of the outer box.
s = 9 yd
Area of the square = s × s
A = 9 yd × 9 yd
A = 81 sq. yd
The area of the shaded region is 81 – 16 = 65 sq. yd
Thus the correct answer is option G.
Question 11.
Which expression represents a prime factorization?
A. 4 × 4 × 7
B. 22 × 21 × 23
C. 34 × 5 × 7
D. 5 × 5 × 9 × 11
Answer: B
Prime factorization:
22 × 21 × 23
2, 21, 23 is a prime number.
Thus the correct answer is option B.
Question 12.
Find the greatest common factor for each pair of numbers.

What can you conclude about the greatest common factor of 10, 15, and 21? Explain your reasoning.
Answer: 1
Explanation:
The factors of 10 are: 1, 2, 5, 10
The factors of 15 are: 1, 3, 5, 15
The factors of 21 are: 1, 3, 7, 21
Then the greatest common factor is 1.
Final Words:
I wish that the details prevailed in this article regarding Big Ideas Math Grade 6 Chapter 1 Numerical Expressions and Factors Answer Key is helpful for all the students and also teachers. Make use of the solutions and score good marks in the exams. Best Of Luck!!
