For the best practice, the Big Ideas Math Grade 7 Chapter 5 Ratios and Proportions Answer Sheet is given here. A detailed explanation of solutions prepared by great math experts which are included in the below sections. Click on the Big Ideas Math Book Grade 7 Answer Key Chapter 5 Ratios and Proportions link on our website and start your preparation. Get the free pdfs here in the following sections.
Big Ideas Math Answers Grade 7 Chapter 5 Ratios and Proportions preparation material is here. Candidates can quickly get this material without much search because we are giving the lesson-wise information in detail here. This will act as a guide for your complete preparation. Get a clear idea of ratios and their tables. Follow the below sections and know more about Ratios and Proportions.
Big Ideas Math Book 7th Grade Answer Key Chapter 5 Ratios and Proportions
Feeling difficult to get the best solutions for all the math problems? If you get a guide with clear explanations and short solutions, then you will feel it easy and fun learning. Therefore, check out Big Ideas Math Book 7th Grade Answer Key Chapter 5 Ratios and Proportions Pdf here which is given with a clear explanation. Know the various topics involved in ratios and proportions.
Various topics like graphs of proportional relationships, rates, and unit rates, identifying proportional relationships, writing and solving proportions, ratios, and ratio tables, scale drawings, and so on. Check Big Ideas Math Answers Grade 7 Chapter 5 Ratios and Proportions solved examples in the next sections.
Performance Task
- Ratios and Proportions STEAM Video/ Performance Task
- Ratios and Proportions Getting Ready for Chapter 5
Lesson: 1 Ratios and Ratio Tables
Lesson: 2 Rates and Unit Rates
Lesson: 3 Identifying Proportional Relationships
- Lesson 5.3 Identifying Proportional Relationships
- Identifying Proportional Relationships Homework & Practice 5.3
Lesson: 4 Writing and Solving Proportions
Lesson: 5 Graphs of Proportional Relationships
- Lesson 5.5 Graphs of Proportional Relationships
- Graphs of Proportional Relationships Homework & Practice 5.5
Lesson: 6 Scale Drawings
Chapter: 5 – Ratios and Proportions
- Ratios and Proportions Connecting Concepts
- Ratios and Proportions Chapter Review
- Ratios and Proportions Practice Test
- Ratios and Proportions Cumulative Practice
Ratios and Proportions STEAM Video/ Performance Task
STEAM Video
Painting a Large Room
Shades of paint can be made by mixing other paints. What colors of paints can you mix to make green paint?

Watch the STEAM Video “Painting a Large Room.” Then answer the following questions.
1. Enid estimates that they need 2 gallons of paint to apply two coats to the wall shown. How many square feet does she expect \(\frac{1}{2}\) gallon of paint will cover?

Answer:
1/2 gallon of paint will cover 60 sq feet.
Explanation:
Enid estimates that they need 2 gallons of paint to apply two coats to the wall of 240 sq ft
The area of the shown figure = 24 x 10
= 240 square feet
To know how many sq feet does 1/2 gallon of paint will cover (240 . 1/2) . 1/2
= 240 . 1/4
= 60
So, 1/2 gallon of paint will cover 60 sq feet.
2. Describe a room that requires 5\(\frac{1}{2}\) gallons of paint to apply one coat of paint to each of the four walls.
Answer:
The room has 4 walls each wall is 330 sq feet.
Explanation:
A room requires 5(1/2) gallons of paint to apply one coat of paint to each of the four walls.
Enid estimates that they need 2 gallons of paint to apply two coats to the wall of 240 sq ft
If they coat only once, she would require 1 gallon of paint for a wall of 240 sq feet.
If she wants to use 5(1/2) = 11/2 gallons of paint, then the area of walls will be
= 240 . (11/2)
= 120 . 11 = 1320 Square feet
Each wall = 1320/4 =330 sq feet
The room has 4 walls each wall is 330 sq feet.
Performance Task
Mixing Paint
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the amounts of each tint used to make different colors of paint. For example:

You will be asked to solve various ratio problems about mixing paint. Given any color of paint, how can you make the paint slightly lighter in color?
Ratios and Proportions Getting Ready for Chapter 5
Chapter Exploration
The Meaning of a Word Rate
When you rent snorkel gear at the beach, rate you should pay attention to the rental. The rental rate is in dollars per hour.

1. Work with a partner. Complete each step.
• Match each description with a rate.
• Match each rate with a fraction.
• Give a reasonable value for each fraction. Then give an unreasonable value.

2. Work with a partner Describe a situation to which the given fraction can apply. Show how to rewrite each expression as a division problem. Then simplify and interpret your result.

Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
proportional
constant of proportionality
scale drawing
Lesson 5.1 Ratios and Ratio Tables
EXPLORATION 1
Describing Ratio Relationships
Work with a partner. Use the recipe shown.

a. Identify several ratios in the recipe.
b. You halve the recipe. Describe your ratio relationships in part (a) using the new quantities. Is the relationship between the ingredients the same as in part(a)? Explain.
Answer:
a. Stewed tomatoes : chicken broth = 9 ounces : 15 ounces
Stewed tomatoes : Chopped Spinach = 9 ounces : 9 ounces = 1 : 1
Chopped Spinach : chicken broth = 9 ounces : 15 ounces
Chopped Chicken : grated parmesan = 1 cup : 5 tablespoons
Chicken broth : Chopped Chicken = 15 ounces : 1 cup
Stewed tomatoes : chopped chicken = 9 ounces : 1 cup = Chopped Spinach : chopped chicken
Stewed tomatoes : grated parmesan = 9 ounces : 5 tablespoons = Chopped Spinach : grated parmesan
chicken broth : grated parmesan = 15 ounces : 5 tablespoons = 5 ounces : 1 tablespoon
b. The relationship between the ingredients the same as in part(a).
Explanation:
a. The several ratios of the recipe are Stewed tomatoes : chicken broth = 9 ounces : 15 ounces
Stewed tomatoes : Chopped Spinach = 9 ounces : 9 ounces = 1 : 1
Chopped Spinach : chicken broth = 9 ounces : 15 ounces
Chopped Chicken : grated parmesan = 1 cup : 5 tablespoons
Chicken broth : Chopped Chicken = 15 ounces : 1 cup
Stewed tomatoes : chopped chicken = 9 ounces : 1 cup = Chopped Spinach : chopped chicken
Stewed tomatoes : grated parmesan = 9 ounces : 5 tablespoons = Chopped Spinach : grated parmesan
chicken broth : grated parmesan = 15 ounces : 5 tablespoons = 5 ounces : 1 tablespoon
b. The relationship between the ingredients the same as in part(a).
EXPLORATION 2
Completing Ratio Tables
Work with a partner. Use the ratio tables shown.
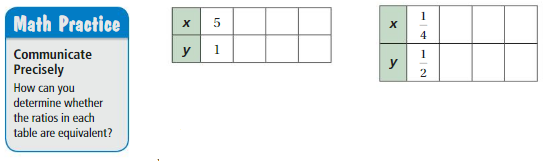
a. Complete the first ratio table using multiple operations. Use the same operations to complete the second ratio table.
b. Are the ratios in the first table equivalent? the second table? Explain.
c. Do the strategies for completing ratio tables of whole numbers work for completing ratio tables of fractions? Explain your reasoning.
Answer:
a. 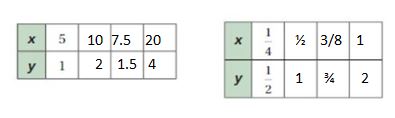
b. Yes
Explanation:
a. 5 x 2 = 10, 1 x 2 = 2, 1/4 x 2 = 1/2, 1/2 x 2 = 1
5 x 1.5 = 7.5, 1 x 1.5 = 1.5, 1/4 x 3/2 = 3/8, 1/2 x 3/2 = 3/4
5 x 4 = 20, 1 x 4 = 4, 1/4 x 4 = 1, 1/2 x 4= 2
b. Yes the ratios in the first table are equivalent to the second table.

Try It
Question 1.
You mix \(\frac{2}{3}\) teaspoon of baking soda with 3 teaspoons of salt. Find and interpret the value of the ratio of baking soda to salt.
Answer:
The ratio of baking soda to salt is 2 : 1.
Explanation:
Given that,
You mix \(\frac{2}{3}\) teaspoon of baking soda with 3 teaspoons of salt.
The ratio of baking soda to salt = 2/3 to 3 = 2/3 : 3
= 2/3 / 3 = 2/3 . 3/1 = 2/1 = 2 : 1
The ratio of baking soda to salt is 2 : 1.
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 2.
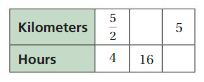
Answer:
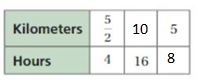
Explanation:
The missing values in the ratio table are
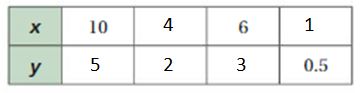
4 x 4 = 16. So, 5/2 x 4 = 10
5/2 . x = 5
x = 2
So, 4 . 2 = 8
The equivalent ratios are 5/2 : 4, 10 : 16, 5 : 8.
Question 3.
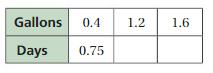
Answer:
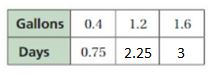
Explanation:
0.4 . x = 1.2
x = 1.2/0.4 = 3
So, 0.75 . 3 = 2.25
0.4 . y = 1.6
y = 1.6/0.4 = 4
So, 0.75 . 4 = 3
The equivalent ratios are 0.4 : 0.75, 1.2 : 2.25, 1.6 : 3
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
WRITING AND INTERPRETING RATIOS
You include \(\frac{1}{2}\) tablespoon of essential oils in a solution for every 12 tablespoons of jojoba oil. Find and interpret the value of the ratio of jojoba oil to essential oils.

Answer:
The amount of jojoba oil in the solution is the 24th amount of essential oil.
Explanation:
You include \(\frac{1}{2}\) tablespoon of essential oils in a solution for every 12 tablespoons of jojoba oil
The ratio of jojoba oil to essential oil = 12 : 1/2
= 12 ÷ 1/2
= 12 . 2/1
= 24
The amount of jojoba oil in the solution is the 24th amount of essential oil.
Question 5.
NUMBER SENSE
Find the missing values in the ratio table. Then write the equivalent ratios.
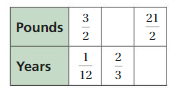
Answer:
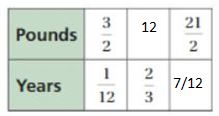
Explanation:
1/12 . x = 2/3
x = 2/3 . 12
x = 8
So, Pounds = 3/2 . 8 = 12
3/2 . 7 = 21/2
1/12 . 7 = 7/12
The equivalent ratios are 3/2 : 1/12, 12 : 2/3, 21/2 : 7/12
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
DIG DEEPER!
A satellite orbiting Earth travels 14\(\frac{1}{2}\) miles every 3 seconds. How far does the satellite travel in \(\frac{3}{4}\) minute?

Answer:
The satellite travels 217(1/2) miles in 3/4 minutes.
Explanation:
A satellite orbiting Earth travels 14\(\frac{1}{2}\) miles every 3 seconds.
So, it travels 14.5/3 miles = 29/6 miles in every 1 second
3/4 minutes = 3/4 . 60
= 45 seconds
Therefore, it travels 45 . 29/6 miles in 3/4 minutes
= 217(1/2) miles in 3/4 minutes.
Hence, the satellite travels 217(1/2) miles in 3/4 minutes.
Question 7.
An engine runs on a mixture of 0.1 quart of oil for every 3.5 quarts of gasoline. You make 3 quarts of the mixture. How much oil and how much gasoline do you use?
Answer:
We use 0.083 quarts of oil and 2.917 quarts of gasoline.
Explanation:
The ratio of oil to gasoline = 0.1 : 3.5 = 1 : 35
use the ratio table to find an equivalent ratio in which the total mixture is 3 quarts.
For 3 quarts mixture
Oil required is 1/36 * 3 = 3/36
= 1/12 = 0.083 quarts
Gasoline required is
35/36 * 3 = 35/12 = 2.917 quarts
We use 0.083 quarts of oil and 2.917 quarts of gasoline.
Ratios and Ratio Tables Homework & Practice 5.1
Review & Refresh
Solve the inequality. Graph the solution.
Question 1.
4p + 7 ≥ 19
Answer:
p ≥ 3

Explanation:
Given that,
4p + 7 ≥ 19
Subtract 7 from both sides
4p + 7 – 7 ≥ 19 – 7
4p ≥ 12
Divide both sides by 4
4p/4 ≥ 12/4
p ≥ 3
Question 2.
14 < – 6n – 10
Answer:
-4 > n
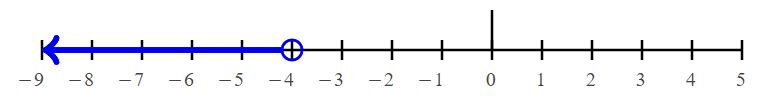
Explanation:
Given that,
14 < – 6n – 10
Add 10 to both sides
14 + 10 < -6n – 10 + 10
24 < -6n
Divide both sides by -6
24/-6 > -6n/-6
-4 > n
Question 3.
– 3(2 + d) ≤ 15
Answer:
d ≥ -7

Explanation:
Given that,
– 3(2 + d) ≤ 15
Divide both sides by -3
– 3(2 + d)/-3 ≥ 15/-3
2 + d ≥ -5
d ≥ -5 – 2
d ≥ -7
Find the quotient. Write fractions in simplest form.
Question 4.
\(\frac{2}{9}\) ÷ \(\frac{4}{3}\)
Answer:
\(\frac{2}{9}\) ÷ \(\frac{4}{3}\) = 1/6 = 0.166
Explanation:
\(\frac{2}{9}\) ÷ \(\frac{4}{3}\) = 2/9 . 3/4
= (2 . 3) / (9 . 4)
= 1/6
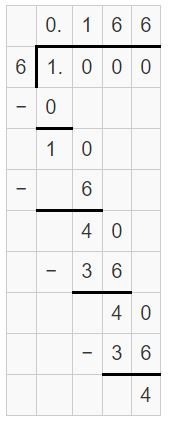
Question 5.
10.08 ÷ 12
Answer:
10.08 ÷ 12 = 3024/25 = 120.96
Explanation:
10.08 ÷ 12 = 1008/100 ÷ 12
= 1008/100 . 12/1
= (1008 . 12)/100
= (100.8 . 3)/25
= 3024/25 = 120.96
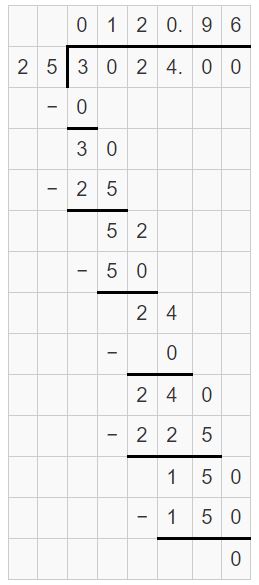
Question 6.
– \(\frac{5}{6}\) ÷ \(\frac{3}{10}\) = -25/9 = -2.7777
Answer:
– \(\frac{5}{6}\) ÷ \(\frac{3}{10}\)
Explanation:
– \(\frac{5}{6}\) ÷ \(\frac{3}{10}\) = -5/6 . 10/3
= (-5 . 10)/(3 . 6)
= -25/9 = -2.7777
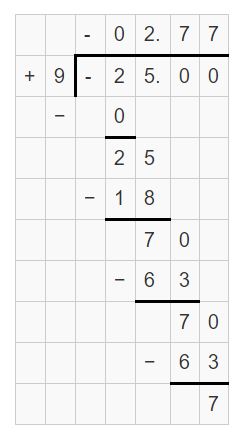
Question 7.
Which ratio can be represented by the tape diagram?
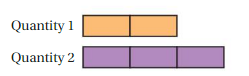
A. 3 : 4
B. 4 : 5
C. 4 : 9
D. 8 : 12
Answer:
D. 8 : 12
Explanation:
Quantity 1 has 2 boxes, quantity 2 has 3 boxes.
Out of all given ratios, 8 : 12 satisfy the condition
The ratio of given quantity = 2 : 3
2 * 4 : 3 * 4 = 8 : 12
Concepts, Skills, & Problem Solving
OPEN-ENDED Complete the ratio table using multiple operations. Are the ratios in the table equivalent? Explain. (See Exploration 2, p. 183.)
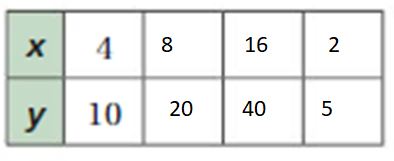
Question 8.
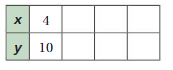
Answer:
Explanation:
4 x 2 = 8, 10 2 = 20
8 x 2 = 16, 20 x 2 = 40
16/8 = 2, 40/8 = 5
The equivalent ratios are 4:10, 8:20, 16:40, 2:5.
Question 9.
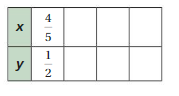
Answer:
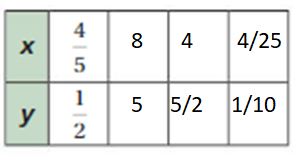
Explanation:
4/5 x 10 = 8, 1/2 x 10 = 5
4/5 x 5 = 4, 1/2 x 5 = 5/2
4 x 1/25 = 4/25, 5/2 x 1/25 = 1/10
WRITING AND INTERPRETING RATIOS Find the ratio. Then find and interpret the value of the ratio.

Question 10.
club soda : white grape juice
Answer:
club soda : white grape juice = 2 : 1
Explanation:
Club soda = 4 cups
white grape juice = 2 cups
club soda : white grape juice = 4 : 2
= 2 : 1
Question 11.
mint leaves : chopped watermelon
Answer:
mint leaves : chopped watermelon = 1 : 6
Explanation:
mint leaves = 1/2 cup
chopped watermelon = 3 cups
mint leaves : chopped watermelon = 1/2 : 3
= 1 : 3 x 2
= 1 : 6
Question 12.
white grape juice to sugar
Answer:
white grape juice : sugar = 8 : 3
Explanation:
white grape juice = 2 cups
sugar=3/4 cup
white grape juice : sugar = 2 : 3/4
= 2 x 4: 3
= 8 : 3
Question 13.
lime juice to mint leaves
Answer:
lime juice to mint leaves is 3 : 2
Explanation:
lime juice = 3/4 cup
mint leaves = 1/2 cup
lime juice to mint leaves = 3/4 : 1/2
= 3/2 : 1
= 3 : 2
Question 14.
You have blue ribbon and red ribbon in the ratio \(\frac{1}{2}\) : \(\frac{1}{5}\) . Your friend finds the value of the ratio. Is your friend correct? Explain your reasoning.

Answer:
Wrong.
Explanation:
1/2 : 1/5 = 1/2 ÷ 1/5
= 1/2 . 5/1 = 5/2
COMPLETING A RATIO TABLE Find the missing values in the ratio table. Then write the equivalent ratios.
Question 15.
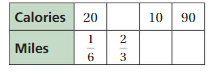
Answer:
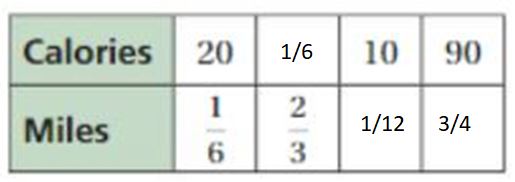
Explanation:
To find the missing values,
1/6 . x = 2/3
x = 2/3 . 6
x = 4
So, calories = 20 . 4 = 80
20 . y = 10
y = 10/20 = 1/2
Miles = 1/6 . 1/2 = 1/12
10 . z = 90
z = 90/10
z = 9
Miles = 1/12 . 9 = 3/4
The equivalent ratios are 20 : 1/6, 80 : 2/3, 10 : 1/12, 90 : 3/4
Question 16.
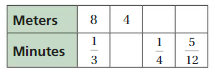
Answer:
Explanation:
To find the missing values,
8/2 = 4
Minutes = 1/3/2 = 1/3 . 2 = 1/6
1/3 . x = 1/4
x = 1/4 . 3 = 3/4
Meters = 8 . 3/4 = 6
1/3 . y = 5/12
y = 5/12 . 3 = 5/4
Meters = 8 . 5/4 = 10
The equivalent ratios are 8 : 1/3, 4 : 2/3, 6 : 1/4, 10 : 5/12
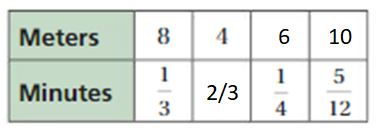
Question 17.
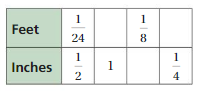
Answer:
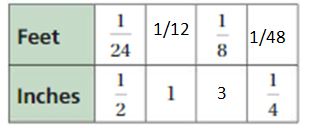
Explanation:
To find the missing values,
1/2 . x = 1
x = 2
1/24 . 2 = 1/12 = Feet
1/24 . y = 1/8
y = 1/8 . 24 = 3
Inches = 1/2 . 3 = 3/2
1/2 . z = 1/4
z = 1/4 . 2 = 1/2
Feet = 1/24 . 1/2 = 1/48
The equivalent ratios are 1/24 : 1/2, 1/12 : 1, 1/8 : 3, 1/48 : 1/4
Question 18.
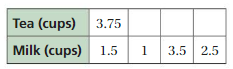
Answer:
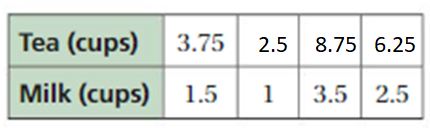
Explanation:
To find missing values,
1.5 . x = 1
x = 1/1.5 = 2/3
Tea = 3.75 . 2/3 = 2.5
1.5 . y = 3.5
y = 35/15 = 7/3
Tea = 3.75 . 7/3 = 8.75
1.5 . z = 2.5
z = 5/3
3.75 . 5/3 = 6.25
Question 19.
CRITICAL THINKING
Are the two statements equivalent? Explain your reasoning.
The ratio of boys to girls is 2 to 3.
The ratio of girls to boys is 3 to 2.
Answer:
Yes, both the statements are equivalent.
Explanation:
The ratio of boys to girls is 2 to 3.
boys : girls = 2 : 3
The ratio of girls to boys is 3 to 2.
girls : boys = 3 : 2
Question 20.
MODELING REAL LIFE
A city dumps plastic shade balls into a reservoir to prevent water from evaporating during a drought. It costs $5760 for 16,000 shade balls. How much does it cost for 12,000 shade balls?

Answer:
The cost for 12,000 shade balls is $4320
Explanation:
It costs $5760 for 16,000 shade balls.
The cost for 12,000 shade balls = (5760 x 12,000)/16000
= 69120/16
= 4320
So, the The cost for 12,000 shade balls is $4320
Question 21.
MODELING REAL LIFE
An oil spill spreads 25 square meters every \(\frac{1}{6}\) hour. What is the area of the oil spill after 2 hours?
Answer:
The area that the oil spill covers after 2 hours is 300 sq meters.
Explanation:
An oil spill spreads 25 square meters every 1/6 hour
The unit rate = 25 ÷ 1/6
= 25 x 6 = 150 square meters per hour
Every 1 hour spreads 150 square meters
The area that the oil spill covers after 2 hours = 2 x 150 = 300 sq meters
Question 22.
MODELING REAL LIFE
You mix 0.25 cup of juice concentrate for every 2 cups of water to make 18 cups of juice. How much juice concentrate do you use? How much water do you use?

Answer:
To make 18 cups of juice we use 16 cups of water and 2 cups of juice concentrate
Explanation:
The ratio between cups of water and cups of juice concentration is 2 to 1/4
The unit rate = 2 / 1/4
= 2 x 4 = 8 cups of water per cup of juice concentrate
So, to make 9 cups of juice we use 8 cups of water and 1 cup of juice concentrate
To make 18 cups of juice we use 16 cups of water and 2 cups of juice concentrate
Question 23.
A store sells 2\(\frac{1}{4}\) pounds of mulch for every 1\(\frac{1}{2}\) pounds of gravel sold. The store sells 180 pounds of mulch and gravel combined. How many pounds of each item does the store sell?
Answer:
Mulch = 108 pounds, gravel = 72 pounds
Explanation:
Let 2(1/4)x = 9/4 x be the amount of mulch so that 1(1/2)x = 3x/2 is the amount of gravel the store sell, both in pounds.
Given that thestore sells a total of 180 pounds of mulch and gravel, we can write
9x/4 + 3x/2 = 180
9x + 6x = 180 x 4
15x = 720
x = 720/15
x = 48
So, the store sells 9/4(48) = 108 pounds of mulch and 3/2(48) = 72 pounds of gravel.
Question 24.
DIG DEEPER!
You mix \(\frac{1}{4}\) cup of red paint for every \(\frac{1}{2}\) cup of blue paint to make 3 gallons of purple paint.
a. How much red paint do you use? How much blue paint do you use?
b. You decide that you want to make a lighter purple paint. You make the new mixture by adding \(\frac{1}{4}\) cup of white paint for every \(\frac{1}{4}\) cup of red paint and \(\frac{1}{2}\) cup of blue paint. How much red paint, blue paint, and white paint do you use to make 1\(\frac{1}{2}\) gallons of the lighter purple paint?
Answer:
a. We use 12 cups of red paint, 24 cups of blue paint
b. white paint = 6 cups, red paint = 6 cups, blue paint = 12 cups.
Explanation:
You mix \(\frac{1}{4}\) cup of red paint for every \(\frac{1}{2}\) cup of blue paint to make 3 gallons of purple paint.
a. The ratio of red paint to blue paint = 1/4 : 1/2
1/4x + 1/2x = (x + 2x)/4 = 3x/4
3x/4 = 3
x = 3 . 4/3
x = 4 cups
1 cup = 1/16 gallons
So, 4 cups = 4/16 = 1/4 gallons
12 . 4 = 48 cups = 1/4 . 12 = 3 gallons
So, 1/4(48) = 12 cups of red paint and 1/2(48) = 24 cups of blue paint is required to make 3 gallons
b. You make the new mixture by adding \(\frac{1}{4}\) cup of white paint for every \(\frac{1}{4}\) cup of red paint and \(\frac{1}{2}\) cup of blue paint.
(1/4 + 1/4 +1/2) = 1
1 cup = 1/16 gallons
The total lighter purple paint = 1(1/2) = 3/2 gallons
Total number of cups = (3/2) 16
= 24
white paint = 1/4 (24) = 6 cups
red paint = 1/4 (24) = 6 cups
blue paint = 1/2 (24) = 12 cups
Lesson 5.2 Rates and Unit Rates
EXPLORATION 1
Writing Rates
Work with a partner.
a. How many degrees does the minute hand on a clock move every 15 minutes? Write a rate that compares the number of degrees moved by the minute hand to the number of hours elapsed.

b. Can you use the rate in part(a) to determine how many degrees the minute hand moves in \(\frac{1}{2}\) hour? Explain your reasoning.
c. Write a rate that represents the number of degrees moved by the minute hand every hour. How can you use this rate to find the number of degrees moved by the minute hand in 2\(\frac{1}{2}\) hours?
d. Draw a clock with hour and minute hands. Draw another clock that shows the time after the minute hand moves 900°. How many degrees does the hour hand move in this time? in one hour? Explain your reasoning.
Try It
Question 1.
There is \(\frac{1}{4}\) gram of fat for every \(\frac{1}{3}\) tablespoon of powdered peanut butter. How many grams of fat are there for every tablespoon of the powder?
Answer:
We have 3/4 grams of fat for every tablespoon of the powder.
Explanation:
There is \(\frac{1}{4}\) gram of fat for every \(\frac{1}{3}\) tablespoon of powdered peanut butter.
There are 1/4 / 1/3 = 1/4. 3 = 3/4 grams of fat for every tablespoon of the powder.
Question 2.
WHAT IF?
The scientist later states that the iron travels 3 feet every 10 minutes. Does this change your answer in Example 2? Explain.
Answer:
The liquid iron travels about 432 feet in 1 day.
Explanation:
The iron travels 3 feet for every 10 minutes
The ratio of feet to minutes is 3 : 10
Divide the quantity by 10 to get the unit rate per minute. Then multiply each quantity by 1440 to find the distance traveled in 24 hours.

So, the liquid iron travels about 432 feet in 1 day.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
VOCABULARY
How can you tell when a rate is a unit rate?
Answer:
A unit rate is described as hoe many units of the first type of quantity corresponds to one unit of the second type of quantity. When the denominator is 1, then you can say that that rate is a unit rate. Few examples of unit rate are m/sec, feet/hour.
Question 4.
WRITING
Explain why rates are usually written as unit rates.
Answer:
Generally, a rate is a ratio of two quantities. Rates are usually written as unit rates because they are easier to read, easier to understand and easier to compare.
Find the unit rate.
Question 5.
$1.32 for 12 ounces
Answer:
$0.11 for 1 ounce
Explanation:
$1.32 for 12 ounces = 1.32 : 12
= 1.32/12 : 12/12
= 0.11 : 1
Question 6.
\(\frac{1}{4}\) gallon for every \(\frac{3}{10}\) mile
Answer:
5/6 gallon for every 1 mile
Explanation:
\(\frac{1}{4}\) gallon for every \(\frac{3}{10}\) mile = 1/4 : 3/10
= 1/4 x 10/3 : 3/10 x 10/3
= 5/6 : 1
Question 7.
USING TOOLS
Find the missing values in the ratio table. Then write the unit rate of grams per cup and the unit rate of cups per gram.
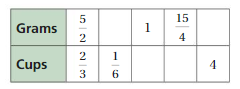
Answer:
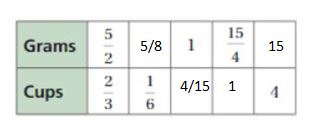
The unit rate of grams per cup = 15/4 : 1
The unit rate of cups per gram = 1 : 4/15
Explanation:
2/3 . x = 1/6
x = 1/6 . 3/2 = 1/4
1/4 . 5/2 = 5/8 = grams
5/2 . y = 1
y = 1 . 2/5 = 2/5
2/3 . 2/5 = 4/15 = cups
5/2 . 3/2 = 15/4
So, 2/3 . 3/2 = 1 = cups
2/3 . z = 4
z = 4 . 3/2 = 6
So, 5/2 . 6 = 15
grams: cups = 5/2 : 2/3
The unit rate of grams per cup = 5/2 . 3/2 : 1 = 15/4 : 1
cups : grams = 4/15 : 1
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
Two people compete in a five-mile go-kart race. Person A travels \(\frac{1}{10}\) mile every 15 seconds. Person B travels \(\frac{3}{8}\) mile every 48 seconds. Who wins the race? What is the difference of the finish times of the competitors?

Answer:
Person B wins the race.
The difference of the finish times of the competitors = 1.833 minutes
Explanation:
Two people compete in a five-mile go-kart race.
Person A travels 1/10 miles for 15 seconds = 1/10 : 15
Person A unit rate = 1/150 : 1
It means, A travels 1/150 miles per1 second
So, person A completes the race in 5 x 150 = 750 seconds = 750/60 = 12.5 minutes
Person B travels 3/8 mile for 48 seconds = 3/8 : 48
Person B unit rate = 3/384 : 1
It means B travels 3/384 miles in 1 second.
So, person B completes the race in 5 . (384/3) = 1920/3 = 640
= 640/60 = 10.666 minutes
Hence, person B wins the race.
The difference of the finish times of the competitors = 12.5 – 10.66 = 1.8333 minutes
Question 9.
DIG DEEPER!
A bus travels 0.8 mile east every 45 seconds. A second bus travels 0.55 mile west every 30 seconds. The buses start at the same location. Use two methods to determine how far apart the buses are after 15 minutes. Explain your reasoning.
Answer:
Two buses are 1/2 mile apart after 15 minutes.
Explanation:
A bus travels 0.8 mile east every 45 seconds = 0.8 : 45
The unit rate = 0.8/45 : 1
A second bus travels 0.55 mile west every 30 seconds = 0.55 : 30
The unit rate = 0.55/30 : 1
Find how much distance, busses travelled after 15 minutes = 15 x 60 = 900 seconds
First bus travels (0.8/45) x 900 = 16 miles
Second bus travels (0.55/30) x 900 = 16.5 miles
The difference in their distances = 16.5 – 16 = 1/2 mile
Rates and Unit Rates Homework & Practice 5.2
Review & Refresh
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 1.
Answer:
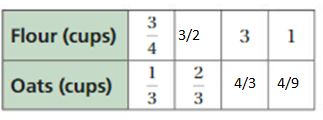
The equivalent ratios are 3/4 : 1/3, 3/2 : 2/3, 3 : 3/4, 1 : 4/9
Explanation:
To find the missing values,
1/3 . x = 2/3
x = 2
3/4 . 2 = 3/2 = flour
3/4 . y = 3
y = 4
1/3 . 4 = 4/3 = oats1
3/4 . z = 1
z = 4/3
4/3 . 1/3 = 4/9 = oats2
The equivalent ratios are 3/4 : 1/3, 3/2 : 2/3, 3 : 3/4, 1 : 4/9
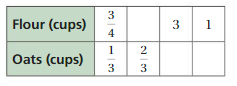
Question 2.
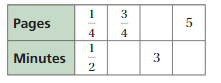
Answer:
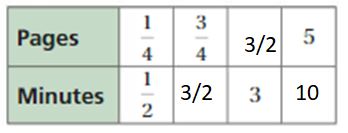
The equivalent ratios are 1/4 : 1/2, 3/4 : 3/2, 3/2 : 3, 5 : 10
Explanation:
To find the missing values,
1/4 . x = 3/4
x = 3
1/2 . 3 = 3/2 = minutes1
1/2 . y = 3
y = 6
1/4 . 6 = 3/2 = pages
1/4 . z = 5
z = 20
1/2 . 20 = 10 = minutes 2
The equivalent ratios are 1/4 : 1/2, 3/4 : 3/2, 3/2 : 3, 5 : 10
Copy and complete the statement using <, >, or =.
Question 3.
![]()
Answer:
9/2 > 8/3
Explanation:
9/2 = 4.5
8/3 = 2.6666
So, 9/2 > 8/3
Question 4.
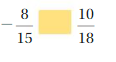
Answer:
-8/15 < 10/18
Explanation:
-8/15 = -0.5333
10/18 = 0.555
So, -8/15 < 10/18
Question 5.
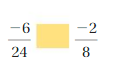
Answer:
-6/24 = -2/8
Explanation:
-6/24 = -0.25
-2/8 = -0.25
So, -6/24 = -2/8
Concepts, Skills, & Problem Solving
WRITING RATES Find the number of degrees moved by the minute hand of a clock in the given amount of time. Explain your reasoning. (See Exploration 1, p. 189.)
Question 6.
\(\frac{2}{3}\) hour
Answer:
240 degrees.
Explanation:
The minute hand passes through 60 minutes ( = 360 degrees) in 1 hour.
In 2/3 hours it passes through 2/3 * 360 = 240 degrees.
Question 7.
\(\frac{7}{12}\) hour
Answer:
210 degrees
Explanation:
The minute hand passes through 60 minutes ( = 360 degrees) in 1 hour.
In 7/12 hours it passes through 7/12 * 360 = 210 degrees
Question 8.
1\(\frac{1}{4}\) hours
Answer:
450 degrees = (360 + 90) degrees
Explanation:
The minute hand passes through 60 minutes ( = 360 degrees) in 1 hour.
In 1(1/4) = 5/4 hours it passes through 5/4 * 360 = 450 degrees
FINDING UNIT RATES Find the unit rate.
Question 9.
180 miles in 3 hours
Answer:
6 miles per 1 hour
Explanation:
180 miles in 3 hours = 18 : 3
The unit rate is 18/3 : 1 = 6 : 1
Question 10.
256 miles per 8 gallons
Answer:
32 miles per 1 gallon
Explanation:
256 miles per 8 gallons = 256 : 8
The unit rate is 256/8 : 1 = 32 : 1
Question 11.
\(\frac{1}{2}\) pound : 5 days
Answer:
1/10 pounds for 1 day
Explanation:
\(\frac{1}{2}\) pound : 5 days = 1/2 : 5
The unit rate is 1/2/5 : 1
= 1/10 : 1
Question 12.
4 grams for every \(\frac{3}{4}\) serving
Answer:
16/3 grams per serving
Explanation:
4 grams for every \(\frac{3}{4}\) serving = 4 : 3/4
The unit rate is = 4 x (4/3) : 1
= 16/3 : 1
Question 13.
$9.60 for 4 pounds
Answer:
$2.4 per 1 pound
Explanation:
$9.60 for 4 pounds = 9.60 : 4
The unit rate is 9.60/4 : 1
= 2.4 : 1
Question 14.
$4.80 for 6 cans
Answer:
$0.8 per 1 can
Explanation:
$4.80 for 6 cans = 4.80 : 6
The unit rate is 4.80/6 : 1
= 0.8 : 1
Question 15.
297 words in 5.5 minutes
Answer:
54 words in 1 minute
Explanation:
297 words in 5.5 minutes = 297 : 5.5
The unit rate is 297/5.5 : 1
= 54 : 1
Question 16.
\(\frac{1}{3}\) kilogram: \(\frac{2}{3}\) foot
Answer:
1/2 kilogram per 1 foot
Explanation:
\(\frac{1}{3}\) kilogram: \(\frac{2}{3}\) foot = 1/3 : 2/3
The unit rate is 1/3 x (3/2) : 1
= 1/2 : 1
Question 17.
\(\frac{5}{8}\) ounce per \(\frac{1}{4}\) pint
Answer:
5/2 ounce per 1 pint
Explanation:
\(\frac{5}{8}\) ounce per \(\frac{1}{4}\) pint = 5/8 : 1/4
The unit rate is 5/8 x 4 : 1
= 5/2 : 1
Question 18.
21\(\frac{3}{4}\) meters in 2\(\frac{1}{2}\) hours
Answer:
87 meters in 1 hour
Explanation:
21\(\frac{3}{4}\) meters in 2\(\frac{1}{2}\) hours = 21(3/4) : 2(1/2)
= 87/4 : 5/2
The unit rate is 87/4 x (2/5) : 1
= 87/10 : 1
USING TOOLS Find the missing values in the ratio table. Then write the equivalent ratios.
Question 19.
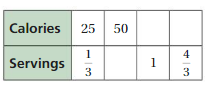
Answer:
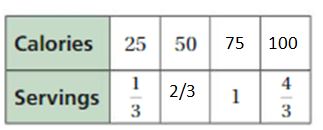
The equivalent ratios are 25 : 1/3, 50 : 2/3, 75 : 1, 100 : 4/3
Explanation:
To find the missing values,
25 . x = 50
x = 50/25 = 2
1/3 . 2 = 2/3 = servings
1/3 . y = 1
y = 3
25 . 3 = 75 = calories1
1/3 . z = 4/3
z = 4
25 . 4 = 100 = calories2
The equivalent ratios are 25 : 1/3, 50 : 2/3, 75 : 1, 100 : 4/3
Question 20.
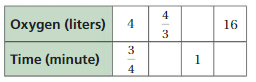
Answer:
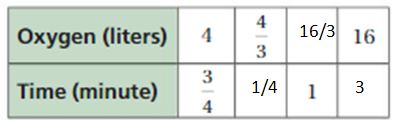
The equivalent ratios are 4 : 3/4, 4/3 : 1/4, 16/3 : 1, 16 : 3
Explanation:
To find the missing values,
4x = 4/3
x = 1/3
3/4 . 1/3 = 1/4 = time1
3/4 y = 1
y = 4/3
4 . 4/3 = 16/3 = oxygen
4z = 16
z = 16/4 = 4
3/4 . 4 = 3 = time2
The equivalent ratios are 4 : 3/4, 4/3 : 1/4, 16/3 : 1, 16 : 3
Question 21.
PROBLEM SOLVING
In January 2012, the U.S.population was about 313 million people. In January 2017, it was about 324 million. What was the average rate of population change per year?
Answer:
The average rate of population change per year = 2.2 million
Explanation:
In January 2012, the U.S.population was about 313 million people
In January 2017, it was about 324 million
After 5 years, the population change = 324 – 313 = 11 million
The average rate of population change per year = 11/5 = 2.2 million
Question 22.
MODELING REAL LIFE
You can sand \(\frac{4}{9}\) square yard of wood in \(\frac{1}{2}\) hour. How many square yards can you sand in 3.2 hours? Justify your answer.
Answer:
128/45 square yards can you sand in 3.2 hours.
Explanation:
You can sand \(\frac{4}{9}\) square yard of wood in \(\frac{1}{2}\) hour
In 3.2 hours, you can sand 4/9 x 3.2 x 2 sq yads
= 25.6/9 = 128/45
So, 128/45 square yards can you sand in 3.2 hours.
Question 23.
REASONING
Tell whether the rates are equivalent. Justify your answer.
Question 23.
75 pounds per 1.5 years
38.4 ounces per 0.75 year
Answer:
Rates are not equivalent.
Explanation:
75 pounds per 1.5 years = 75 : 1.5
= 750/15 = 50
38.4 ounces per 0.75 year = 38.4 : 0.75
= 384 : 7.5 = 51.2
So, rates are not equivalent
Question 24.
7\(\frac{1}{2}\) miles for every \(\frac{3}{4}\) hour
\(\frac{1}{2}\) mile for every 3 minutes
Answer:
Rates are not equivalent.
Explanation:
7\(\frac{1}{2}\) miles for every \(\frac{3}{4}\) hour = 7(1/2) : 3/4
= 15/2 : 3/4
= 15/2 . 4/3 = 10
\(\frac{1}{2}\) mile for every 3 minutes = 1/2 : 3
= 1 : 6
So, rates are not equivalent
Question 25.
PROBLEM SOLVING
The table shows nutritional information for three beverages.
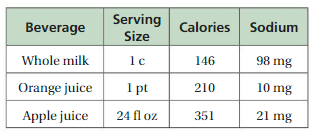
a. Which has the most calories per fluid ounce?
b. Which has the least sodium per fluid ounce?
Answer:
a. whole milk has the most calories per fluid ounce
b. Oange juice has the least sodium per fluid ounce.
Explanation:
a.
Convert serving size to fluid ounce
Whole Milk = 1 c = 8 fl oz
Orange juice = 1 pt = 16 fl oz
Whole milk = 146 : 8 = 146/8 : 1
= 18.25
There are 18.25 calories in 1 fluid ounce of Whole Milk.
Orange juice = 210 : 16 = 210/16 : 1
= 13.125
There are 13.125 calories in 1 fluid ounce of Orange Juice.
Apple juice = 351 : 24
= 351/24 : 1
There are 14.625 calories in 1 fluid ounce of Apple Juice.
So, whole milk has the most calories per fluid ounce
b. Whole milk = 98 : 8
= 98/8 : 1
= 12.25
Orange juice = 10 : 16
= 10/16 : 1
= 0.625
Apple juice = 21 : 24
= 21/24 : 1
= 0.875
So, orange juice has the least sodium per fluid ounce.
Question 26.
MODELING REAL LIFE
A shuttle leaving Earth’s atmosphere travels 15 miles every 2 seconds. When entering the Earth’s atmosphere, the shuttle travels 2\(\frac{3}{8}\) miles per \(\frac{1}{2}\) second. Find the difference in the distances traveled after 15 seconds when leaving and entering the atmosphere.
Answer:
The difference in the distances traveled is 2503 miles.
Explanation:
A shuttle leaving Earth’s atmosphere travels 15 miles every 2 seconds. = 15 : 2
= 15/2 : 1
= 7.5 miles for every second
When entering the Earth’s atmosphere, the shuttle travels 2\(\frac{3}{8}\) miles per \(\frac{1}{2}\) second = 2(3/8) : /2
= 19/8 : 1/2
= 19/8 . 2 = 19/4
= 4.75 miles per second
After 15 minutes = 15 x 60 = 900 seconds,
A shuttle leaving Earth’s atmosphere travels = 7.5 x 900
= 6750 miles
When entering the Earth’s atmosphere, the shuttle travels = 4.75 x 900
= 4247 miles
The difference in the distances traveled = 6750 – 4247
= 2503 miles
Question 27.
RESEARCH
Fire hydrants are one of four different colors to indicate the rate at which water comes from the hydrant.
a. Use the Internet to find the ranges of rates indicated by each color.
b. Research why a fire fighter needs to know the rate at which water comes out of a hydrant.
Answer:
a. Blue – 1500 or more gallons per minute
Green – 1000 to 1499 gallons per minute
Red – Less than 500 gallons per minute
Orange – 500 to 999 gallons per minute
b. Fire hydrants are flow-tested at a residual pressure of 20 psi. Therefore, firefighters should understand the typical flow rates of fire hydrants at a pressure. They should not expect that the fire hydrant will be supplied at an increased pressure, resulting in a greater flow rate.
Explanation:
a. Blue – 1500 or more gallons per minute
Green – 1000 to 1499 gallons per minute
Red – Less than 500 gallons per minute
Orange – 500 to 999 gallons per minute
Question 28.
DIG DEEPER!
You and a friend start riding bikes toward each other from opposite ends of a 24-mile biking route. You ride 2\(\frac{1}{6}\) miles every \(\frac{1}{4}\) hour. Your friend rides 7\(\frac{1}{3}\) miles per hour.

a. After how many hours do you meet?
b. When you meet, who has traveled farther? How much farther?
Answer:
a. They meet after 1(1/2) hour.
b. You have traveled farther 2 miles.
Explanation:
You ride 2\(\frac{1}{6}\) miles every \(\frac{1}{4}\) hour.
= 2(1/6) : 1/4
= 13/6 : 1/4
= 13/6 . 4 = (13 . 2)/3 = 26/3 : 1
Your friend rides 7\(\frac{1}{3}\) miles per hour.
= 7(1/3) : 1
= 22/3 : 1
After 1 hour, you traveled = 26/3 miles, your friend traveled 22/3 miles
= 26/3 + 22/3 = 48/3
= 16 miles
Since you and your friend moving towards each other at 16 miles per hour
we can write 24/16 = 3/2 = 1.5 hours.
So, they meet after 1(1/2) hour.
b. You have traveled 26/3 (1.5) = 13 miles at the time of the meeting
Your friend has traveled 22/3 (1.5) = 11 miles at the time of the meeting.
You have traveled farther 2 miles.
Lesson 5.3 Identifying Proportional Relationships
EXPLORATION 1
Determining Proportional Relationships
Work with a partner.
a. You can paint 50 square feet of a surface every 40 minutes. How long does it take you to paint the mural shown? Explain how you found your answer.

b. The number of square feet you paint is proportional to the number of minutes it takes you. What do you think it means for a quantity to be proportional to another quantity?
c. Assume your friends paint at the same rate as you. The table shows how long it takes you and different numbers of friends to paint a fence. Is x proportional to y in the table? Explain.

d. How long will it take you and four friends to paint the fence? Explain how you found your answer.
Answer:
a. It takes 3 hours to paint the mural.
b. It means if the number of squares feet increases or decreases then the number of minutes to paint also increases or decreases respectively.
c. x is not proportional to y.
Explanation:
a. The area of mural = 25 x 9 = 225 sq ft
You can paint 50 square feet of a surface every 40 minutes
To paint the given mural it takes (40 x 225)/50 = 180 minutes = 3 hours
b. The number of square feet you paint is proportional to the number of minutes it takes you.
It means if the number of squares feet increases or decreases then the number of minutes to paint also increases or decreases respectively.
c. x : y = 1 : 4, 2 : 2 = 1 : 1
3 : 4/3 = 9 : 4, 4 : 1
All those are not equa so, x is not proportional to y.

Try It
Tell whether the ratios form a proportion.
Question 1.
1 : 2 and 5 : 10
Answer:
1 : 2 and 5 : 10 form a proportion.
Explanation:
Compare the values of the ratios
1/2
5/10 = (5 ÷ 5) / (10 ÷ 5) = 1/2
The values of the ratios are equivalent
So, 1 : 2 and 5 : 10 form a proportion.
Question 2.
4 : 6 and 18 : 24
Answer:
4 : 6 and 18 : 24 do not form a proportion.
Explanation:
Compare the values of the ratios
4/6 = (4 ÷ 2)/(6 ÷ 2) = 2/3
18/24 = (18 ÷ 6)/(24 ÷ 6) = 3/4
The values of the ratios are not equivalent
So, 4 : 6 and 18 : 24 do not form a proportion.
Question 3.
4.5 to 3 and 6 to 9
Answer:
4.5 to 3 and 6 to 9 do not form a proportion.
Explanation:
Compare the values of the ratios
4.5/3 = 45/30
= (45 ÷ 15) / (30 ÷ 15) =3/2
6/9 = (6 ÷ 3) / (9 ÷ 3)
= 2/3
The values of the ratios are not equivalent
So, 4.5 to 3 and 6 to 9 do not form a proportion.
Question 4.
\(\frac{1}{2}\) to \(\frac{1}{4}\) and 8 to 4
Answer:
\(\frac{1}{2}\) to \(\frac{1}{4}\) and 8 to 4 form a proportion
Explanation:
Compare the values of the ratios
1/2 : 1/4 = (1/2) / (1/4)
= 1/2 . 4 = 2 : 1
8 : 4 = (8 ÷ 4) / (4 ÷ 4) = 2 : 1
The values of the ratios are equivalent
So, \(\frac{1}{2}\) to \(\frac{1}{4}\) and 8 to 4 form a proportion
Tell whether the ratios form a proportion.
Question 5.
6 : 2 and 12 : 1
Answer:
6 : 2 and 12 : 1 do not form a proportion.
Explanation:
Compare the values of the ratios
6 : 2 = (6 ÷ 2) : (2 ÷ 2) = 3 : 1
12 : 1 = (12 ÷ 1) : (1 ÷ 1) = 12 : 1
The values of the ratios are not equivalent
So, 6 : 2 and 12 : 1 do not form a proportion.
Question 6.
8 : 12 and \(\frac{2}{3}\) : 1
Answer:
8 : 12 and \(\frac{2}{3}\) : 1 form a proportion
Explanation:
Use the cross product property to determine whether the ratios form a proportion.
8/12 = 2/3 : 1
8/12 = 2/3
8 . 3 = 12 . 2
24 = 24
The cross productsare equal.
So, 8 : 12 and \(\frac{2}{3}\) : 1 form a proportion
Tell whether x and y are proportional.
Question 7.
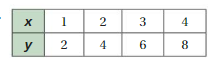
Answer:
x and y are proportional.
Explanation:
Compare the values of ratios x to y
1/2, 2/4 = 1/2, 3/6 = 1/2, 4/8 = 1/2
The values of the ratios are equivalent.
So, x and y are proportional.
Question 8.
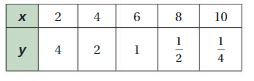
Answer:
x and y are not proportional.
Explanation:
Compare the values of ratios x to y
2/4 = 1/2, 4/2 = 2, 6/1 = 6, 8/1/2 = 16, 10/1/4 = 40
The values of the ratios are not equivalent.
So, x and y are not proportional.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
PROPORTIONS Tell whether the ratios form a proportion.
Question 9.
4 : 14 and 12 : 40
Answer:
4 : 14 and 12 : 40 do not form a proportion.
Explanation:
Use the cross product property to determine whether the ratios form a proportion.
4/14 = 12/40
Cross multiply
4 . 40 = 12 . 14
160 ≠ 168
The cross products are not equal
So, 4 : 14 and 12 : 40 do not form a proportion
Question 10.
9 : 3 and 45 : 15
Answer:
9 : 3 and 45 : 15 form a proportion.
Explanation:
Compare the values of the ratios
9/3 = (9 ÷ 3) / (3 ÷ 3) = 3/1
45/15 = (45 ÷ 15) / (15 ÷ 15) = 3/1
The ratios are equivalent
So, 9 : 3 and 45 : 15 form a proportion
Question 11.
VOCABULARY
Explain how to determine whether two quantities are proportional.
Answer:
The two quantities are proportional means they are having equivalent ratios.
Question 12.
WHICH ONE DOESN’T BELONG?
Which ratio does not belong with the other three? Explain your reasoning.

Answer:
3/5 does not belong with the other three.
Explanation:
4/10 = 2/5
2/5
3/5
6/15 = 2/5
So, 3/5 does not belong with the other three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
After making 20 servings of pasta, a chef has used 30 cloves of garlic. The chef used 6 cloves to make the first 4 servings. How many cloves of garlic are used to make 10 servings? Justify your answer.

Answer:
15 cloves of garlic are used to make 10 servings?
Explanation:
After making 20 servings of pasta, a chef has used 30 cloves of garlic.
The ratio of garlic cloves to serving of pasta = 30 : 20
= 30/20 : 1
= 3/2 : 1
The chef used 6 cloves to make the first 4 servings
The ratio of garlic cloves to serving of pasta = 6 : 4
= 6/4 : 1
= 3/2 : 1
It means 1.5 garlic cloves are used to make 1 serving.
The ratios are proportional
So, to make 10 servings, multiply 1.5 by 10
= 1.5 x 10 = 15 cloves
Therefore, 15 cloves of garlic are used to make 10 servings.
Question 14.
DIG DEEPER!
A runner completes a 25-mile race in 5 hours. The runner completes the first 7.5 miles in 1.5 hours.
a. Do these rates form a proportion? Justify your answer.
b. Can you determine, with certainty, the time it took the runner to complete 10 miles? Explain your reasoning.
Answer:
a. Yes, these form a proportion
b. It takes 2 hours for the runner to complete 10 miles.
Explanation:
a. A runner completes a 25-mile race in 5 hours.
The ratio of miles to hours = 25 : 5
= 25/5 : 1
= 5 : 1
The runner completes the first 7.5 miles in 1.5 hours.
The ratio of miles to hours = 7.5/1.5
= 75/15 : 1
= 5 : 1
It means the runner completes 5 miles in 1 hour
The ratios are proportional
b. So, it takes 10/5 = 2 hours for the runner to complete 10 miles.
Identifying Proportional Relationships Homework & Practice 5.3
Review & Refresh
Find the unit rate.
Question 1.
30 inches per 5 years
Answer:
6 inches per 1 year
Explanation:
30 inches per 5 years = 30 : 5
= 30/5 : 1
= 6 : 1
6 inches per 1 year
Question 2.
486 games every 3 seasons
Answer:
162 games every season
Explanation:
486 games every 3 seasons = 486 : 3
= 486/3 : 1
= 162 : 1
162 games every season
Question 3.
8750 steps every 1.25 hours
Answer:
7000 steps every hour
Explanation:
8750 steps every 1.25 hours = 8750 : 1.25
= 8750/1.25 : 1
= 7000 : 1
7000 steps every hour
Question 4.
3.75 pints out of every 5 gallons
Answer:
0.75 prints out of every gallon
Explanation:
3.75 pints out of every 5 gallons = 3.75 : 5
= 3.75/5 : 1
= 3/4 : 1
0.75 prints out of every gallon
Add or subtract.
Question 5.
– 28 + 15
Answer:
– 28 + 15 = -13
Explanation:
– 28 + 15 = -13
Question 6.
– 6 + (- 11)
Answer:
– 6 + (- 11) = -17
Explanation:
– 6 + (- 11) = -6 – 11
= -17
Question 7.
– 10 – 8
Answer:
– 10 – 8 = -18
Explanation:
– 10 – 8 = -18
Question 8.
– 17 – (- 14)
Answer:
– 17 – (- 14) = -3
Explanation:
– 17 – (- 14) = -17 + 14
= -3
Solve the equation.
Question 9.
\(\frac{x}{6}\) = 25
Answer:
x = 150
Explanation:
\(\frac{x}{6}\) = 25
Multiply both sides by 6
x/6 • 6 = 25 • 6
x = 150
Question 10.
8x = 72
Answer:
x = 9
Explanation:
8x = 72
Divide both sides by 8
8x/8 = 72/8
x = 9
Question 11.
150 = 2x
Answer:
x = 75
Explanation:
150 = 2x
Divide both sides by 2
150/2 = 2x/2
75 = x
Question 12.
35 = \(\frac{x}{4}\)
Answer:
x = 140
Explanation:
35 = \(\frac{x}{4}\)
Multiply both sides by 4
35 • 4 = x/4 • 4
140 = x
Concepts, Skills, & Problem Solving
REASONING You can paint 75 square feet of a surface every 45 minutes. Determine how long it takes you to paint a wall with the given dimensions. (See Exploration 1, p. 195.)
Question 13.
8 ft × 5 ft
Answer:
24 minutes
Explanation:
You can paint 75 square feet of a surface every 45 minutes
= 75 : 45
= 75/45 : 1
= 5/3 : 1
So, you can paint 5/3 sq feet of a surface in 1 minute.
The given area is 8 ft × 5 ft = 40 sq ft
Divide 40 by 5/3
= 40 / 5/3
= 40 . 3/5
= 24 minutes
Question 14.
7 ft × 6 ft
Answer:
25 minutes 12 seconds
Explanation:
The given area is 7 ft × 6 ft = 42 sq ft
Divide 42 by 5/3
= 42/5/3
= 42 . 3/5
= 126/5
= 25(1/5)
= 25 minutes 12 seconds
Question 15.
9 ft × 9 ft
Answer:
48 minutes 36 seconds
Explanation:
The given area is 9 ft × 9 ft = 81 sq ft
Divide 81 by 5/3
= 81/5/3
= 81 . 3/5
= 243/5
= 48(3/5)
= 48 minutes 36 seconds
PROPORTIONS Tell whether the ratios form a proportion.
Question 16.
1 to 3 and 7 to 21
Answer:
1 to 3 and 7 to 21 form a proportion.
Explanation:
Compare the values of the ratios
1 to 3 = 1 : 3
7 to 21 = 7 : 21
= (7 ÷ 7) : (21 ÷ 7)
= 1 : 3
The ratios are equivalent
So, 1 to 3 and 7 to 21 form a proportion.
Question 17.
1 : 5 and 6 : 30
Answer:
1 : 5 and 6 : 30 form a proportion
Explanation:
Compare the values of the ratios
1 : 5 = 1/5
6 : 30 = (6 ÷ 6) : (30 ÷ 6)
= 1/5
The ratios are equivalent
So, 1 : 5 and 6 : 30 form a proportion
Question 18.
3 to 4 and 24 to 18
Answer:
3 to 4 and 24 to 18 do not form a proportion
Explanation:
Compare the values of the ratios
3 to 24 = 3 : 24
= (3 ÷ 3) : (24 ÷ 3)
= 1 : 8
24 to 18 = 24 : 18
= (24 ÷ 6) : (18 ÷ 6)
= 4 : 3
The ratios are not equivalent
So, 3 to 4 and 24 to 18 do not form a proportion
Question 19.
3.5 : 2 and 14 : 8
Answer:
3.5 : 2 and 14 : 8 do not form a proportion
Explanation:
Compare the values of the ratios
35 : 2 = 35/2
14 : 8 = (14 ÷ 2) : (8 ÷ 2)
= 7 : 4 = 7/4
The ratios are not equivalent
So, 3.5 : 2 and 14 : 8 do not form a proportion
Question 20.
24: 30 and 3 : \(\frac{7}{2}\)
Answer:
24: 30 and 3 : \(\frac{7}{2}\) do not form a proportion.
Explanation:
Compare the values of the ratios
24 : 30 = 24/30
= (24 ÷ 2)/(30 ÷ 2)
= 12/15
3 : 7/2 = 6 : 7
= 6/7
The ratios are not equivalent
So, 24: 30 and 3 : \(\frac{7}{2}\) do not form a proportion.
Question 21.
\(\frac{21}{2}\) : 3 and 16 : 6
Answer:
\(\frac{21}{2}\) : 3 and 16 : 6 do not form a proportion.
Explanation:
21/2 : 3 = 21 : 6
= (21 ÷ 3) : (6 ÷ 3)
= 7 : 2
16 : 6 = (16 ÷ 2) : (6 ÷ 2)
= 8 : 3
The ratios are not equivalent
So, \(\frac{21}{2}\) : 3 and 16 : 6 do not form a proportion.
Question 22.
0.6 : 0.5 and 12 : 10
Answer:
0.6 : 0.5 and 12 : 10 form a proportion
Explanation:
Compare the values of the ratios
0.6 : 0.5 = 6/5
12 : 10 = (12 ÷ 2) : (10 ÷ 2)
= 6 : 5
The ratios are equivalent
So, 0.6 : 0.5 and 12 : 10 form a proportion
Question 23.
2 to 4 and 11 to \(\frac{11}{2}\)
Answer:
2 to 4 and 11 to \(\frac{11}{2}\) do not form a proportion.
Explanation:
Compare the values of the ratios
2 to 4 = 2 : 4
= (2 ÷ 2) : (4 ÷ 2)
= 1 : 2
11 to \(\frac{11}{2}\) = 11 : 11/2
= 22 : 11
= (22 ÷ 11) : (11 ÷ 11)
= 2 : 1
The ratios are not equivalent
So, 2 to 4 and 11 to \(\frac{11}{2}\) do not form a proportion.
Question 24
\(\frac{5}{8}\) : \(\frac{2}{3}\) and \(\frac{1}{4}\) : \(\frac{1}{3}\)
Answer:
\(\frac{5}{8}\) : \(\frac{2}{3}\) and \(\frac{1}{4}\) : \(\frac{1}{3}\) do not form a proportion.
Explanation:
Compare the values of the ratios
\(\frac{5}{8}\) : \(\frac{2}{3}\) = 5/8 / 2/3
= 5/8 . 3/2
= 15/16
\(\frac{1}{4}\) : \(\frac{1}{3}\) = 1/4 / 1/3
= 1/4 . 3 = 3/4
The ratios are not equivalent
So, \(\frac{5}{8}\) : \(\frac{2}{3}\) and \(\frac{1}{4}\) : \(\frac{1}{3}\) do not form proportion
IDENTIFYING PROPORTIONAL RELATIONSHIPS Tell whether x and y are proportional.
Question 25.
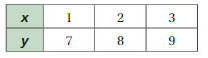
Answer:
x and y are not proportional.
Explanation:
Compare the values of the ratios x to y.
1/7, 2/8 = 1/4, 3/9 = 1/3
The values of the ratios are not equivalent.
So, x and y are not proportional.
Question 26.
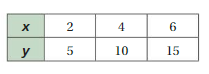
Answer:
x and y are proportional.
Explanation:
Compare the values of the ratios x to y.
2/5, 4/10 = 2/5, 6/15 = 2/5
The values of the ratios are equivalent
So, x and y are proportional.
Question 27.
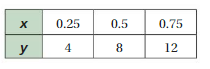
Answer:
x and y are proportional.
Explanation:
Compare the values of the ratios x to y.
0.25/4 = 1/16, 0.5/8 = 1/6, 0.75/12 = 1/16
The values of the ratios are equivalent
So, x and y are proportional.
Question 28.
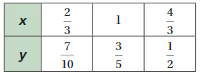
Answer:
x and y are not proportional.
Explanation:
Compare the values of the ratios x to y.
2/3 / 7/10 = 2/3 . 10/7 = 20/21, 1/3/5 = 1/3 . 5 = 5/3
4/3 / 1/2 = 4/3 . 2 = 8/3
The values of the ratios are not equivalent
So, x and y are not proportional.
YOU BE THE TEACHER Your friend determines whether x and y are proportional. Is your friend correct? Explain your reasoning.
Question 29.

Answer:
Correct.
Explanation:
Compare the values of the ratios x to y.
8 + 1 = 9
3 + 1 = 4
The values of the ratios x to y are equal.
So, x and y are proportional.
Question 30.

Answer:
Wrong
Explanation:
Compare the values of the ratios x to y.
2/6 = 1/3
4/12 = 1/3
8/18 = 4/9
The values of the ratios x to y are not equal.
So, x and y are not proportional.
PROPORTIONS Tell whether the rates form a proportion.
Question 31.
7 inches in 9 hours;
42 inches in 54 hours
Answer:
Ratios form a proportion.
Explanation:
7 inches in 9 hours = 7 : 9
42 inches in 54 hours = 42 : 54
= (42 ÷ 6) : (54 ÷ 6)
= 7 : 9
The ratios are equivalent
So, ratios form a proportion.
Question 32.
12 players from 21 teams;
15 players from 24 teams
Answer:
The ratios do not form a proportion.
Explanation:
12 players from 21 teams; = 12 : 21
= (12 ÷ 3) : (21 ÷ 3)
= 4 : 7
15 players from 24 teams = 15 : 24
= (15 ÷ 3) : (24 ÷ 3)
= 5 : 8
The ratios are not equivalent
So, ratios do not form a proportion.
Question 33.
385 calories in 3.5 servings; 300 calories in 3 servings
Answer:
385 calories in 3.5 servings; 300 calories in 3 servings do not form a proportion.
Explanation:
385 calories in 3.5 servings = 385 : 3.5
= 110
300 calories in 3 servings = 300 : 3
= 100
The ratios are not equivalent
So, 385 calories in 3.5 servings; 300 calories in 3 servings do not form a proportion.
Question 34.
4.8 laps every 8 minutes; 3.6 laps every 6 minutes
Answer:
4.8 laps every 8 minutes; 3.6 laps every 6 minutes form a proportion.
Explanation:
4.8 laps every 8 minutes = 4.8 : 8
= (4.8 ÷ 8) : (8 ÷ 8)
= 3/5 : 1
3.6 laps every 6 minutes = 3.6 : 6
= (3.6 ÷ 6) : (6 ÷ 6)
= 3/5 : 1
The ratios are equivalent
So, 4.8 laps every 8 minutes; 3.6 laps every 6 minutes form a proportion.
Question 35.
\(\frac{3}{4}\) pound for every 5 gallons; \(\frac{4}{5}\) pound for every 5\(\frac{1}{3}\) gallons
Answer:
\(\frac{3}{4}\) pound for every 5 gallons; \(\frac{4}{5}\) pound for every 5\(\frac{1}{3}\) gallons do not form a proportion.
Explanation:
\(\frac{3}{4}\) pound for every 5 gallons = 3/4 : 5
= 3 : 20
\(\frac{4}{5}\) pound for every 5\(\frac{1}{3}\) gallons = 4/5 : 5(1/3)
= 4/5 : 16/3
= 4/5 . 3/16
= 15/16
The ratios are not equivalent
So, \(\frac{3}{4}\) pound for every 5 gallons; \(\frac{4}{5}\) pound for every 5\(\frac{1}{3}\) gallons do not form a proportion.
Question 36.
MODELING REAL LIFE
You do 90 sit-ups in 2 minutes. Your friend does 126 sit-ups in 2.8 minutes. Do these rates form a proportion? Explain.

Answer:
The rates form a proportion
Explanation:
You do 90 sit-ups in 2 minutes = 90/2
= 45 sit-ups in 1 minute
Your friend does 126 sit-ups in 2.8 minutes = 126/2.8
= 45 sit-ups in 1 minute
They are equivalent.
So, the rates form a proportion
Question 37.
MODELING REAL LIFE
Find the heart rates of you and your friend. Do these rates form a proportion? Explain.
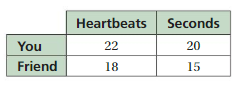
Answer:
The rates do not form a proportion
Explanation:
Your heart rate = 22/20
= 11/10
Your friend heat rate = 18/15 = 6/5
The ratios are not equivalent
So, the rates do not form a proportion
Question 38.
PROBLEM SOLVING
You earn $56 walking your neighbor’s dog for 8 hours. Your friend earns $36 painting your neighbor’s fence for 4 hours. Are the pay rates equivalent? Explain.
Answer:
The pay rates are not equivalent.
Explanation:
You earn $56 walking your neighbor’s dog for 8 hours.
= 56 : 8
= 7
Your friend earns $36 painting your neighbor’s fence for 4 hours
= 36 : 4
= 9
So, the pay rates are not equivalent.
Question 39.
GEOMETRY
Are the heights and bases of the two triangles proportional? Explain.
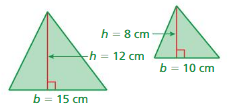
Answer:
The heights and bases of the two triangles proportional
Explanation:
Height to base of first triangle = 12 : 15
= (12 ÷ 3) : (15 ÷ 3)
= 4 : 5
Height to base of second triangle = 8 : 10
= (8 ÷ 2) : (10 ÷ 5)
= 4 : 5
The ratios are equivalent
So, the heights and bases of the two triangles proportional
Question 40.
REASONING
A pitcher coming back from an injury limits the number of pitches thrown in bullpen sessions as shown.
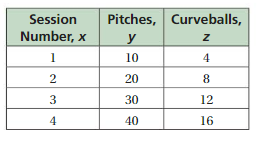
a. Which quantities are proportional?
b. How many pitches that are not curveballs will the pitcher likely throw in Session 5?
Answer:
a. None of the quantities are proportional.
b. Curveballs are 20, pitches are 50.
Explanation:
a. By observing the table we can say that,
None of the quantities are proportional.
b. In session 5, the pitches are 5 . 10 = 50
curveballs are 5 . 4 = 20
Question 41.
STRUCTURE
You add the same numbers of pennies and dimes to the coins shown. Is the new ratio of pennies to dimes proportional to the original ratio of pennies to dimes? If so, illustrate your answer with an example. If not, show why with a counterexample.
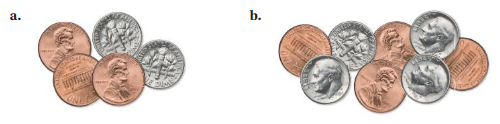
Answer:
The new ratio of pennies to dimes is not proportional to the original ratio of pennies to dimes.
Explanation:
Number of pennies to dimes in image a = 3 : 2
Number of pennies to dimes in image b = 4 : 4
= 1 : 1
The ratios are not equivalent
So, the new ratio of pennies to dimes is not proportional to the original ratio of pennies to dimes.
Question 42.
REASONING
You are 13 years old, and your cousin is 19 years old. As you grow older, is your age proportional to your cousin’s age? Explain your reasoning.
Answer:
Your age is not proportional to your cousin’s age
Explanation:
You are 13 years old, and your cousin is 19 years old.
= 13 : 19
As you grow older
Suppose after 3 years the ratio is (13 + 3) / (19 + 3) = 16/21
13/19≠ 16/21
So, your age is not proportional to your cousin’s age
Question 43.
MODELING REAL LIFE
The shadow of the moon during a solar eclipse travels 2300 miles in 1 hour. In the first 20 minutes, the shadow traveled 766\(\frac{2}{3}\) miles. How long does it take for the shadow to travel 1150 miles? Justify your answer.

Answer:
It takes 30 minutes for the shadow to travel 1150 miles
Explanation:
The shadow of the moon during a solar eclipse travels 2300 miles in 1 hour
= 2300 : 1
In the first 20 minutes, the shadow traveled 766\(\frac{2}{3}\) miles.
= 766(2/3) : 20
= 2300/3 : 20
So, it travels 2300/3 miles in 20 minutes
The time taken for the shadow to travel 1150 miles is 1150 . 20 x (3/2300)
= 69000/2300
= 30
Therefore, The time taken for the shadow to travel 1150 miles is 30 minutes
Question 44.
MODELING REAL LIFE
In 60 seconds, a car in a parade travels 0.2 mile. The car traveled the last 0.05 mile in 12 seconds. How long did it take for the car to travel 0.1 mile? Justify your answer.
Answer:
It takes 32 seconds for the car to travel 0.1 mile.
Explanation:
In 60 seconds, a car in a parade travels 0.2 mile.
Car travels to time = 0.2 : 60
The car traveled the last 0.05 mile in 12 seconds
= 0.05 : 12
So, the car travels (0.2 – 0.05 = 0.15 miles) in (60 – 12 = 48 seconds)
The time taken to travel 0.1 mile = (48 x 0.1)/0.15 = 32 seconds.
Question 45.
OPEN-ENDED
Describe (a) a real-life situation where you expect two quantities to be proportional and (b) a real-life situation where you do not expect two quantities to be proportional. Explain your reasoning.
Answer:
(a) We will the real-life situation as the relationship between the number of gallons of fuel that we put in the tank and the amount of money we have to pay.
(b) The real-life situation is 2 persons buy different items at a store and pay amount.
Explanation:
(a) Let us take two people to put fuel their cars. Person 1 puts 5 gallons of fuel and pays 20 dollars.
Person 2 puts 8 gallons of fuel pays 32 dollars.
The ratio to the number of gallons to dollars is 5 : 20, 8 : 32
= 1 : 4, 1 : 4
So, the ratios are proportional.
(b) Let us assume 2 persons buy different products at the store and pays the bill.
Person 1 buys 2 items per 15 dollars and person 2 buys 4 items for 32 dollars.
Question 46.
PROBLEM SOLVING
A specific shade of red nail polish requires 7 parts red to 2 parts yellow. A mixture contains 35 quarts of red and 8 quarts of yellow. Is the mixture the correct shade? If so, justify your answer. If not, explain how you can fix the mixture to make the correct shade of red.

Answer:
To fix the mixture add 2 more quarts of yellow.
Explanation:
The ratio of nail polish = 7/2 = (7 . 5) / (2 . 5) = 35/10 red/yellow
The ratio of mixture = 35/8 red/yellow
To fix the mixture make the two ratios 35/10 and 35/8 equivalent
Add 2 more quarts of yellow to the mixture
35/10 = 35/(8 + 2)
To fix the mixture add 2 more quarts of yellow.
Question 47.
LOGIC
The quantities x and y are proportional. Use each of the integers 1–5 to complete the table. Justify your answer.
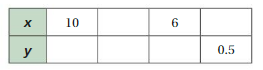
Answer:
Explanation:
The quantities x and y are proportional.
Let us take x/2 = y
So, 10/2 = 5
6/2 = 3
0.5 x 2 = 1
4/2 = 2
Question 48.
CRITICAL THINKING
Ratio A and Ratio B form a proportion. Ratio B and Ratio C also form a proportion. Do Ratio A and Ratio C form a proportion? Justify your answer.
Answer:
Ratio A and Ratio C form a proportion.
Explanation:
Ratio A and Ratio B form a proportion
Ratio B and Ratio C also form a proportion
So, Ratio A : Ratio B = Ratio B : Ratio C
Ratio A = (Ratio B)/Ratio C x Ratio B
Ratio C = (Ratio B x Ratio B)/Ratio A
Ratio A : Ratio C = [(Ratio B)/Ratio C x Ratio B] : [(Ratio B x Ratio B)/Ratio A]
= 1/Ratio C : 1/Ratio A
= Ratio A : Ratio C
So, Ratio A and Ratio C form a proportion
Lesson 5.4 Writing and Solving Proportions
EXPLORATION 1
Solving a Ratio Problem
Work with a partner. A train travels 50 miles every 40 minutes. To determine the number of miles the train travels in 90 minutes, your friend creates the following table.
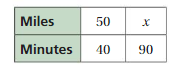
a. Explain how you can find the value of x.
b. Can you use the information in the table to write a proportion? If so, explain how you can use the proportion to find the value of x. If not, explain why not.
c. How far does the train below travel in 2 hours?

d. Share your results in part(c) with other groups. Compare and contrast methods used to solve the problem.
Answer:
a. x = 112.5
b. yes
c. 120 miles
Explanation:
a. 50/40 = x/90
(50/40) . 90 = x
4500/40 = x
x = 112.5
b. We can use information in the table to write a proportion.
c. The train travels 30 miles in 1/2 hour.
The distance traveled in 2 hours is 30. 2 . 2 = 120 miles
Try It
Solve the proportion.
Question 1.
\(\frac{5}{8}=\frac{20}{d}\)
Answer:
d = 32
Explanation:
\(\frac{5}{8}=\frac{20}{d}\)
cross multiply the fractions
5d = 20 . 8
5d = 160
d = 160/5
d = 32
Question 2.
\(\frac{7}{z}=\frac{14}{10}\)
Answer:
z = 5
Explanation:
\(\frac{7}{z}=\frac{14}{10}\)
cross multiply the fractions
7 . 10 = 14 . z
70 = 14z
70/14 = z
5 = z
Question 3.
\(\frac{21}{24}=\frac{x}{8}\)
Answer:
x = 7
Explanation:
\(\frac{21}{24}=\frac{x}{8}\)
cross multiply the fractions
21 . 8 = 24x
168 = 24x
168/24 = x
x = 7
Solve the proportion.
Question 4.
\(\frac{w}{6}=\frac{6}{9}\)
Answer:
w = 4
Explanation:
\(\frac{w}{6}=\frac{6}{9}\)
cross multiply the fractions
9w = 6 . 6
9w = 36
w = 36/9
w = 4
Question 5.
\(\frac{12}{10}=\frac{a}{15}\)
Answer:
a = 18
Explanation:
\(\frac{12}{10}=\frac{a}{15}\)
cross multiply the fractions
12 . 15 = 10a
180 = 10a
a = 180/10
a = 18
Question 6.
\(\frac{y}{10}=\frac{3}{5}\)
Answer:
y = 6
Explanation:
\(\frac{y}{10}=\frac{3}{5}\)
cross multiply the fractions
5y = 3 . 10
5y = 30
y = 30/5
y = 6
Solve the proportion.
Question 7.
\(\frac{2}{7}=\frac{x}{28}\)
Answer:
x = 8
Explanation:
\(\frac{2}{7}=\frac{x}{28}\)
cross multiply the fractions
2 . 28 = 7x
56 = 7x
x = 56/7
x = 8
Question 8.
\(\frac{12}{5}=\frac{6}{y}\)
Answer:
y = 5/2
Explanation:
\(\frac{12}{5}=\frac{6}{y}\)
cross multiply the fractions
12y = 6 . 5
12y = 30
y = 30/12
y = 5/2
Question 9.
\(\frac{40}{z+1}=\frac{15}{6}\)
Answer:
z = 15
Explanation:
\(\frac{40}{z+1}=\frac{15}{6}\)
cross multiply the fractions
40 . 6 = 15(z + 1)
240 = 15z + 15
240 – 15 = 15z
225 = 15z
z = 225/15
z = 15
Find the value of x so that the ratios are equivalent.
Question 10.
2 : 4 and x : 6
Answer:
x = 3
Explanation:
2/4 = x/6
cross multiply the fractions
2 . 6 = 4x
12 = 4x
x = 12/4
x = 3
Question 11.
x : 5 and 8 : 2
Answer:
x = 20
Explanation:
x/5 = 8/2
x/5 = 4
x = 4 . 5
x = 20
Question 12.
4 to 3 and 10 to x
Answer:
x = 15/2
Explanation:
4/3 = 10/x
cross multiply the fractions
4x = 3 . 10
4x = 30
x = 30/4
x = 15/2
Question 13.
Write a proportion that can be used to find the number of tomatoes in the new recipe.
Answer:
The number of tomatoes in the new recipe are 4.
Explanation:
In the original recipe, the ratio of the black beans to the number of tomatoes is 1.5 : 1
For the new recipe to be proportional to the original recipe, these ratios must be equivalent.
So the vales of the ratios must be equal
1.5/1 = 6/x
1.5 = 6/x
1.5x = 6
x = 6/1.5
x = 4
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING A PROPORTION Solve the proportion.
Question 14.
\(\frac{5}{12}=\frac{b}{36}\)
Answer:
b = 15
Explanation:
\(\frac{5}{12}=\frac{b}{36}\)
Cross multiply the fractions
(5 x 36) = 12b
180 = 12b
b = 180/12
b = 15
Question 15.
\(\frac{6}{p}=\frac{42}{35}\)
Answer:
p = 5
Explanation:
\(\frac{6}{p}=\frac{42}{35}\)
Cross multiply the fractions
6 x 35 = 42p
210 = 42p
p = 210/42
p = 5
Question 16.
WRITING AND SOLVING A PROPORTION
Find the value of x so that the ratios x : 9 and 5 : 6 are equivalent.
Answer:
x = 15/2
Explanation:
The ratios x : 9 and 5 : 6 are equivalent.
x/9 = 5/6
Cross multiply the fractionsx
6x = 9 . 5
6x = 45
x = 45/6
x = 15/2
Question 17.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
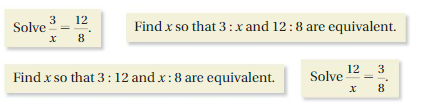
Answer:
Solve 12/x = 3/8 is different, x = 32
For remaining x = 2
Explanation:
3/x = 12/8
3 • 8 = 12x
24 = 12x
x = 2
3 : x and 12 : 8 are equivalent
3/x = 12/8
So, x = 2
3 : 12 and x : 8 are equivalent
3/12 = x/8
3 • 8 = 12x
x = 2
12/x = 3/8
12 • 8 = 3x
3x= 96
x = 96/3 = 32
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
You burn 35 calories every 3 minutes running on a treadmill. You want to run for at least 15 minutes, but no more than 30 minutes. What are the possible numbers of calories that you will burn? Justify your answer.
Answer:
The possible number of calories burned in between 560/3 and 350.
Explanation:
You burn 35 calories every 3 minutes running on a treadmill.
35 : 3
= 35/3 : 1
You want to run for at least 15 minutes, but no more than 30 minutes means you want to run in between 16 and 30 minutes
If you run for 16 minutes then, the number of calories burn = (35/3) x 16
= 560/3
If you run for 30 minutes, then the number of calories burn = (35/3) x 30
= 1050/3 = 350
So, the possible number of calories burned in between 560/3 and 350.
Question 19.
DIG DEEPER!
Two boats travel at the same speed to different destinations. Boat A reaches its destination in 12 minutes. Boat B reaches its destination in 18 minutes. Boat B travels 3 miles farther than Boat A. How fast do the boats travel? Justify your answer.

Answer:
The boat travels with 1/2 mile/hr.
Explanation:
Boat A reaches its destination in 12 minutes
Boat B reaches its destination in 18 minutes
Let us take the speed as x miles/minute
So, Boat A travels 12x miles
Boat B travels 18x miles
Boat B travels 3 miles farther than Boat A
18x + 3 = 12x
18x – 12x = -3
6x = -3
x = 3/6
x = 1/2 mile/hr
So, the boat travels with 1/2 mile/hr
Writing and Solving Proportions Homework & Practice 5.4
Review & Refresh
Tell whether and are proportional.
Question 1.
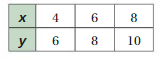
Answer:
x and y are not proportional.
Explanation:
Compare the values of the ratios x to y
4/6 = 2/3
6/8 = 3/4
8/10 = 4/5
The values of the ratios are not equivalent
So, x and y are not proportional.
Question 2.
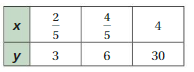
Answer:
x and y are proportional.
Explanation:
Compare the values of the ratios x to y
2/5/3 = 2/15
4/5/6 = 2/15
4/30 = 2/15
The values of the ratios are equivalent
So, x and y are proportional.
Plot the ordered pair in a coordinate plane.
Question 3.
A (- 5, – 2)
Answer:

Explanation:
In point A (- 5, – 2)
The x coordinate and y coordinate values are negative.
so, the point lies in 3rd quadrant.
Take 5 units on the x-axis, 2 units on the y-axis, and locate the point.
Question 4.
B (- 3, 0)
Answer:
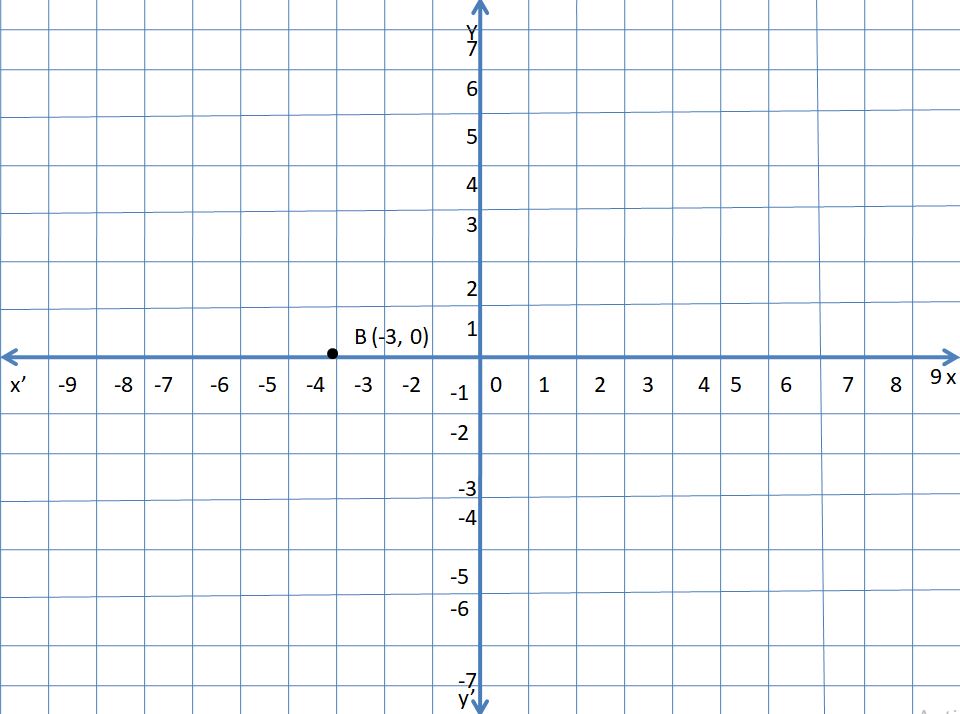
Explanation:
In the point B (- 3, 0)
The x coordinate, y coordinates are negative and zero.
So, the point lies in the x-axis.
Question 5.
C (- 1, 2)
Answer:

Explanation:
In point C (- 1, 2) has x coordinate negative value and y coordinate positive value.
so, the point lies in the 2nd quadrant.
Take -1 units on the x-axis, 2 units on the y-axis, and mark the point.
Question 6.
D (1, 4)
Answer:
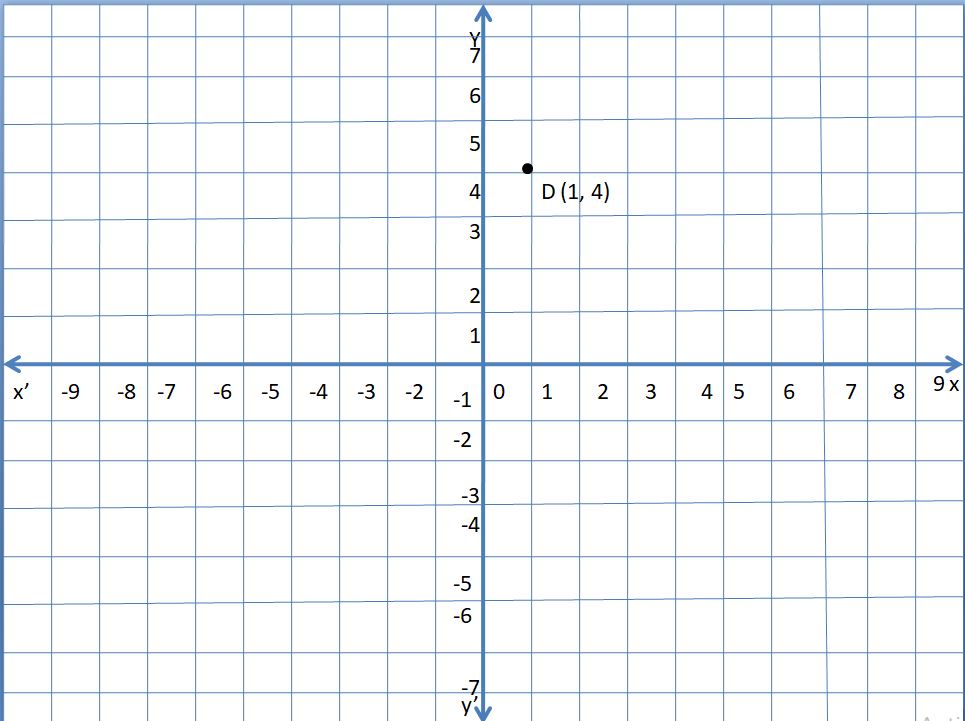
Explanation:
In point D (1, 4) the x, y coordinates are positive.
So, the point lies in quadrant 1.
Take 1 unit on the x-axis, 4 units on the y-axis, and mark the point.
Question 7.
Which expression is equivalent to (3w – 8) – 4(2w + 3)?
A. 11w + 4
B. – 5w – 5
C. – 5w + 4
D. – 5w – 20
Answer:
D. – 5w – 20
Explanation:
(3w – 8) – 4(2w + 3) = 3w – 8 – 8w – 12
= -5w -20
Concepts, Skills, & Problem Solving
SOLVING A RATIO PROBLEM Determine how far the vehicle travels in 3 hours. (See Exploration 1, p. 203.)
Question 8.
A helicopter travels 240 miles every 2 hours.
Answer:
The helicopter travels 360 miles in 3 hours.
Explanation:
A helicopter travels 240 miles every 2 hours = 240 : 2
= 240/2 : 1
= 120 : 1
The helicopter travels 120 miles in 1 hour
The distance traveled by the vehicle in 3 hours = 120 * 3
= 360 miles
Question 9.
A motorcycle travels 25 miles every 0.5 hour.
Answer:
A motorcycle travels 150 miles in 3 hours.
Explanation:
A motorcycle travels 25 miles every 0.5 hour = 25 : 0.5
= 25/0.5 : 1
= 50 : 1
The motorcycle travels 50 miles in 1 hour
So, the distance traveled by the vehicle in 3 hours = 50 * 3 = 150 miles
Question 10.
A train travels 10 miles every \(\frac{1}{4}\) hour.
Answer:
A train travels 120 miles in 3 hours.
Explanation:
A train travels 10 miles every \(\frac{1}{4}\) hour = 10 : 1/4
= 4 * 10 : 1
= 40 : 1
A train travels 40 miles in 1 hour
So, the distance traveled by the vehicle in 3 hours = 40 * 3 = 120 miles
Question 11.
A ferry travels 45 miles every 1\(\frac{1}{2}\) hours.
Answer:
A ferry travels 90 miles in 3 hours
Explanation:
A ferry travels 45 miles every 1\(\frac{1}{2}\) hours = 45 : 1(1/2)
= 45 : 3/2
= 45 * 2 : 3
= 90 : 3
= 30 : 1
A ferry travels 30 miles in 1 hour
So, the distance traveled by the vehicle in 3 hours = 30 * 3 = 90
SOLVING A PROPORTION Solve the proportion. Explain your choice of method.
Question 12.
\(\frac{1}{4}=\frac{z}{20}\)
Answer:
z = 5
Explanation:
\(\frac{1}{4}=\frac{z}{20}\)
Cross multiply the fractions
20 = 4z
z = 20/4
z = 5
Question 13.
\(\frac{3}{4}=\frac{12}{y}\)
Answer:
y = 16
Explanation:
\(\frac{3}{4}=\frac{12}{y}\)
The product of 3 and waht number is 12?
Because the product pf 3 and 4 is 12, multiply the denominator by 4 to find y
4 * 4 = 16
So, y = 16
Question 14.
\(\frac{35}{k}=\frac{7}{3}\)
Answer:
k = 15
Explanation:
\(\frac{35}{k}=\frac{7}{3}\)
Divide both sides by 35
(35/k)/35 = (7/3)/35
1/k = 1/15
k = 15
Question 15.
\(\frac{b}{36}=\frac{5}{9}\)
Answer:
b = 20
Explanation:
\(\frac{b}{36}=\frac{5}{9}\)
Cross multiply the proportions
9b = 5 * 36
9b = 180
b = 180/9
b = 20
Question 16.
\(\frac{x}{8}=\frac{3}{12}\)
Answer:
x = 2
Explanation:
\(\frac{x}{8}=\frac{3}{12}\)
Cross multiply the fractions
12x = 3 * 8
12x = 24
x = 24/12
x = 2
Question 17.
\(\frac{3}{4}=\frac{v}{14}\)
Answer:
v = 21/2
Explanation:
\(\frac{3}{4}=\frac{v}{14}\)
Cross multiply the fractions
3 * 14 = 4v
42 = 4v
v = 42/4
v = 21/2
Question 18.
\(\frac{15}{8}=\frac{45}{c}\)
Answer:
c = 24
Explanation:
\(\frac{15}{8}=\frac{45}{c}\)
Cross multiply the fractions
15c = 45 * 8
15c = 360
c = 360/15
c = 24
Question 19.
\(\frac{35}{28}=\frac{n}{12}\)
Answer:
n = 15
Explanation:
\(\frac{35}{28}=\frac{n}{12}\)
Cross multiply the fractions
35 * 12 = 28n
420 = 28n
n = 420/28
n = 15
Question 20.
\(\frac{a}{6}=\frac{15}{2}\)
Answer:
a = 45
Explanation:
\(\frac{a}{6}=\frac{15}{2}\)
Cross multiply the fractions
2a = 15 * 6
2a = 90
a = 90/2
a = 45
Question 21.
\(\frac{y}{9}=\frac{44}{54}\)
Answer:
y = 22/3
Explanation:
\(\frac{y}{9}=\frac{44}{54}\)
Cross multiply the fractions
54y = 44 * 9
54y = 396
y = 396/54
y = 22/3
Question 22.
\(\frac{4}{24}=\frac{c}{36}\)
Answer:
c = 6
Explanation:
\(\frac{4}{24}=\frac{c}{36}\)
Cross multiply the fractions
4 * 36 = 24c
144 = 24c
c = 144/24
c = 6
Question 23.
\(\frac{20}{16}=\frac{d}{12}\)
Answer:
d = 15
Explanation:
\(\frac{20}{16}=\frac{d}{12}\)
Cross multiply the fractions
20 * 12 = 16d
240 = 16d
d = 240/16
d = 15
Question 24.
\(\frac{10}{7}=\frac{8}{k}\)
Answer:
k = 5.6
Explanation:
Cross multiply the fractions
10k = 8 * 7
10k = 56
k = 56/10
k = 5.6
Question 25.
\(\frac{5}{n}=\frac{16}{32}\)
Answer:
n = 10
Explanation:
\(\frac{5}{n}=\frac{16}{32}\)
Cross multiply the fractions
5 * 32 = 16n
160 = 16n
n = 160/16
n = 10
Question 26.
\(\frac{9}{10}=\frac{d}{6.4}\)
Answer:
d = 5.76
Explanation:
\(\frac{9}{10}=\frac{d}{6.4}\)
Cross multiply the fractions
10d = 6.4 * 9
10d = 57.6
d = 57.6/10
d = 5.76
Question 27.
\(\frac{2.4}{1.8}=\frac{7.2}{k}\)
Answer:
k = 5.4
Explanation:
\(\frac{2.4}{1.8}=\frac{7.2}{k}\)
Cross multiply the fractions
2.4k = 7.2 * 1.8
2.4k = 12.96
k = 12.96/2.4
k = 5.4
Question 28.
YOU BE THE TEACHER
Your friend solves the proportion \(\frac{m}{8}=\frac{15}{24}\). Is your friend correct? Explain your reasoning.

Answer:
Correct
Explanation:
m/8 = 15/24
Cross multiply the fractions
24m = 15 * 8
24m = 120
m = 120/24
m = 5
Question 29.
NUMBER SENSE
Without solving, determine whether \(\frac{x}{4}=\frac{15}{3}\) and \(\frac{x}{15}=\frac{4}{3}\) have the same solution. Explain your reasoning.
Answer:
Both have same solution.
Explanation:
\(\frac{x}{4}=\frac{15}{3}[/latex
Cross multiply the fractions
3x = 15 * 4
[latex]\frac{x}{15}=\frac{4}{3}\)
Cross multiply the fractions
3x = 4 * 15
We got same equation
So, both have same solution.
WRITING A PROPORTION Use the table to write a proportion.
Question 30.
Answer:
6/7 = 18/w, w = 6
Explanation:
12/14 = 18/w
Cross multiply the fractions
12w = 18 * 4
w = 72/12
w = 6
12/14 = 18/w
6/7 = 18/w
Question 31.
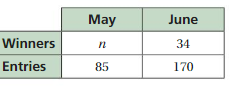
Answer:
n/85 = 1/5, n = 17
Explanation:
n/85 = 34/170
n/85 = 1/5
Cross multiply the fractions
5n = 85
n = 85/5
n = 17
Question 32.
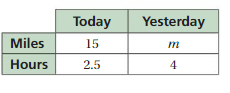
Answer:
15/2.5 = m/4, m = 24
Explanation:
15/2.5 = m/4
Cross multiply the fractions
15 * 4 = 2.5m
60 = 2.5m
m = 60/2.5
m = 24
Question 33.
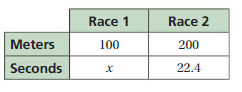
Answer:
x = 11.2
Explanation:
100/x = 200/22.4
Cross multiply the fractions
100 * 22.4 = 200x
2240 = 200x
x = 2240/200
x = 11.2
WRITING AND SOLVING A PROPORTION Find the value of x so that the ratios are equivalent.
Question 34.
1 : 8 and 4 : x
Answer:
x = 32
Explanation:
1/8 = 4/x
Cross multiply the fractions
x = 8 * 4
x = 32
Question 35.
4 to 5 and x to 20
Answer:
x = 16
Explanation:
4/5 = x/20
Cross multiply the fractions
20 * 4 = 5x
80 = 5x
x = 80/5
x = 16
Question 36.
3 : x and 12 : 40
Answer:
x = 10
Explanation:
3/x = 12/40
Cross multiply the fractions
3 * 40 = 12x
120 = 12x
x = 120/12
x = 10
Question 37.
x to 0.25 and 6 to 1.5
Answer:
x = 1
Explanation:
x/0.25 = 6/1.5
Cross multiply the fractions
1.5x = 6 * 0.25
1.5x = 1.5
x = 1.5/1.5
x = 1
Question 38.
x : \(\frac{5}{2}\) and 8 : 10
Answer:
x = 2
Explanation:
x : 5/2 = 8 : 10
Cross multiply the fractions
10x = 8 * 5/2
10x = 20
x = 20/10
x = 2
Question 39.
\(\frac{7}{4}\) to 14 and x to 32
Answer:
x = 4
Explanation:
7/4 : 14 = x : 32
Cross multiply the fractions
14x = 32 * (7/4)
14x = 56
x = 56/14
x = 4
Question 40.
WRITING A PROPORTION
Your science teacher has a photograph of the space shuttle Atlantis. Every 1 centimeter in the photograph represents 200 centimeters on the actual shuttle. Which of the proportions can you use to find the actual length x of Atlantis? Explain.

Answer:
1/200 = x/19.5
Explanation:
Every 1 centimeter in the photograph represents 200 centimeters on the actual shuttle
= 1 : 200
Length of atlantis on model = 19.5
The actual length on Atlantis = x
Scale 1:200
When length on model = 1
Actual length = 200
When actual length = x
Length on model = 19.5
Scale = x : 19.5
Equating both scales
1/200 = x/19.5
Question 41.
MODELING REAL LIFE
In an orchestra, the ratio of trombones to violas is 1 to 3. There are 9 violas. How many trombones are in the orchestra?
Answer:
There are 3 trombones in the orchestra.
Explanation:
t/9 = 1/3
3t = 9
t = 9/3
t = 3
There are 3 trombones in the orchestra.
Question 42.
MODELING REAL LIFE
A dance team has 80 dancers. The ratio of seventh-grade dancers to all dancers is 5:16. Find the number of seventh-grade dancers on the team.
Answer:
The number of seventh-grade dancers on the team is 25.
Explanation:
A dance team has 80 dancers
Let us take the seventh-grade dancers as x
The ratio of seventh-grade dancers to all dancers is 5:16
x : 80 = 5 : 16
x/80 = 5/16
Cross multiply the fractions
16x = 5 *80
16x = 400
x = 400/16
x = 25
The number of seventh-grade dancers on the team is 25.
Question 43.
MODELING REAL LIFE
There are 144 people in an audience. The ratio of adults to children is 5 to 3. How many are adults?
Answer:
The number of adults in the audience are 18.
Explanation:
The ratio of adults to children is 5 to 3
adults : children = 5 : 3
There are 144 people in an audience.
5x + 3x = 144
8x = 144
x = 144/8
x = 18
So, the number of adults in the audience are 18.
Question 44.
PROBLEM SOLVING
You have $50 to buy T-shirts. You can buy 3 T-shirts for $24. Do you have enough money to buy 7 T-shirts? Justify your answer.
Answer:
No.
Explanation:
You can buy 3 T-shirts for $24
= 24 : 3
= 24/3 : 1
= 8 : 1
So, you can buy 1 T-shirt per $8.
The money required to buy 7 T-shirts = 7 * 8 = $56
The remaining money after buying 3 T-shirts is 50 – 24 = $26
$26 is not enough to buy 7 T-shirts.
Question 45.
PROBLEM SOLVING
You buy 10 vegetarian pizzas and pay with $100. How much change do you receive?

Answer:
The change you receive = $15
Explanation:
3 vegetarian pizzas for $25.50 = 25.50 : 3
= 25.50/3 : 1
= 8.5 : 1
So, you have to pay $8.5 for 1 vegetarian pizza
If you buy 10 vegetarian pizzas, then amount is 10 * 8.5 = $85
The change you receive = 100 – 85 = 15
Question 46.
MODELING REAL LIFE
A person who weighs 120 pounds on Earth weighs 20 pounds on the Moon. How much does a 93-pound person weigh on the Moon?
Answer:
The weight of a 93-pound person weigh on the Moon is 15.5 pounds
Explanation:
The ratio of a person weight on earth to moon = 120 : 20
= 120/20 : 1
= 6 : 1
The weight of a 93-pound person weigh on the Moon is 93/6 = 31/2 = 15.5 pounds.
Question 47.
PROBLEM SOLVING
Three pounds of lawn seed covers 1800 square feet. How many bags are needed to cover 8400 square feet?

Answer:
The number of bags required to cover 8400 sq ft is 14.
Explanation:
Three pounds of lawn seed covers 1800 square feet.
The ratio of lawn to seed cover = 1800 : 3
= 1800/3 : 1
= 600 : 1
So, 1 seed bag covers 600 sq ft
The number of bags required to cover 8400 sq ft is 8400/600
= 14 bags
Question 48.
MODELING REAL LIFE
There are 180 white lockers in a school. There are 3 white lockers for every 5 blue lockers. How many lockers are in the school?
Answer:
There are 480 lockers in the school.
Explanation:
There are 3 white lockers for every 5 blue lockers
= 3 : 5
Let b be the number of blue lockers
3/5 = 180/b
3b = 180 * 5
3b = 900
b = 900/3
b = 300
300 + 180 = 400
So, there are 480 lockers in the school.
CONVERTING MEASURES Use a proportion to complete the statement. Round to the nearest hundredth if necessary.
Question 49.
![]()
Answer:
3.73 miles
Explanation:
1 km = 0.621371
6 km = 6 * 0.621371
= 3.72823 miles
= 3.73 miles
Question 50.
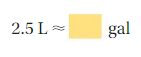
Answer:
0.66 gal
Explanation:
1 L = 0.264172 gal
2.5 L = 0.264172 * 2.5
= 0.66043
2.5 L = 0.66 gal
Question 51.

Answer:
40.82 kg
Explanation:
1 lb = 0.453592 kgs
90 lb = 0.453592 * 90
= 40.8233
90 lb = 40.82 kg
SOLVING A PROPORTION Solve the proportion.
Question 52.
![]()
Answer:
x = 3/2
Explanation:
2x/5 = 9/15
Cross-multiply the fractions
15 * 2x = 9 * 5
30x = 45
x = 45/30
x = 3/2
Question 53.
![]()
Answer:
d = 12
Explanation:
5/2 = (d – 2)/4
Cross-multiply the fractions
20 = 2(d – 2)
20 = 2d – 4
20 + 4 = 2d
24 = 2d
d = 24/2
d = 12
Question 54.
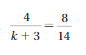
Answer:
k = 4
Explanation:
4/(k + 3) = 8/14
Cross-multiply the fractions
14 * 4 = 8(k + 3)
56 = 8k + 24
56 – 24 = 8k
32 = 8k
k = 32/8
k = 4
Question 55.
LOGIC
It takes 6 hours for 2 people to build a swing set. Can you use the proportion \(\frac{2}{6}=\frac{5}{h}\) to determine the number of hours h it will take 5 people h6to build the swing set? Explain.
Answer:
It will take 15 hours for 5 people to build the swing set.
Explanation:
It takes 6 hours for 2 people to build a swing set
2 people – 6 hours
5 people – ?
We have a proportion,
2/6 = 5/h
2h = 6 * 5
2h = 30
h = 30/2
h = 15
It will take 15 hours for 5 people to build the swing set.
Question 56.
STRUCTURE
The ratios a : b and c : d are equivalent. Which of the following equations are proportions? Explain your reasoning.

Answer:
a/d = c/b is not equivalent proportion.
Explanation:
a/b = c/d
ad = bc
b/a = d/c
bc = ad
a/c = b/d
ad = bc
a/d = c/b
ab = cd
c/a = d/b
bc = ad
So, a/d = c/b is not equivalent proportion.
Question 57.
CRITICAL THINKING
Consider the proportions \(\frac{m}{n}=\frac{1}{2}\) and \(\frac{n}{k}=\frac{2}{5}\). What is \(\frac{m}{k}\) ? Explain your reasoning.
Answer:
m/k = 1/5
Explanation:
m/n = 1/2
So m = x, n = 2x
n/k = 2/5
n = 2x, k = 5x
So, m/k = x/5x
= 1/5
Lesson 5.5 Graphs of Proportional Relationships
EXPLORATION 1
Representing Relationships Graphically
Work with a partner. The tables represent two different ways that red and blue food coloring are mixed.
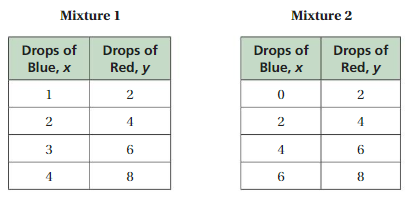
a. Represent each table in the same coordinate plane. Which graph represents a proportional relationship? How do you know?

b. Find the unit rate of the proportional relationship. How is the unit rate shown on the graph?
c. What is the multiplicative relationship between x and y for the proportional relationship? How can you use this value to write an equation that relates y and x?
Answer:
Mixture 1
a. 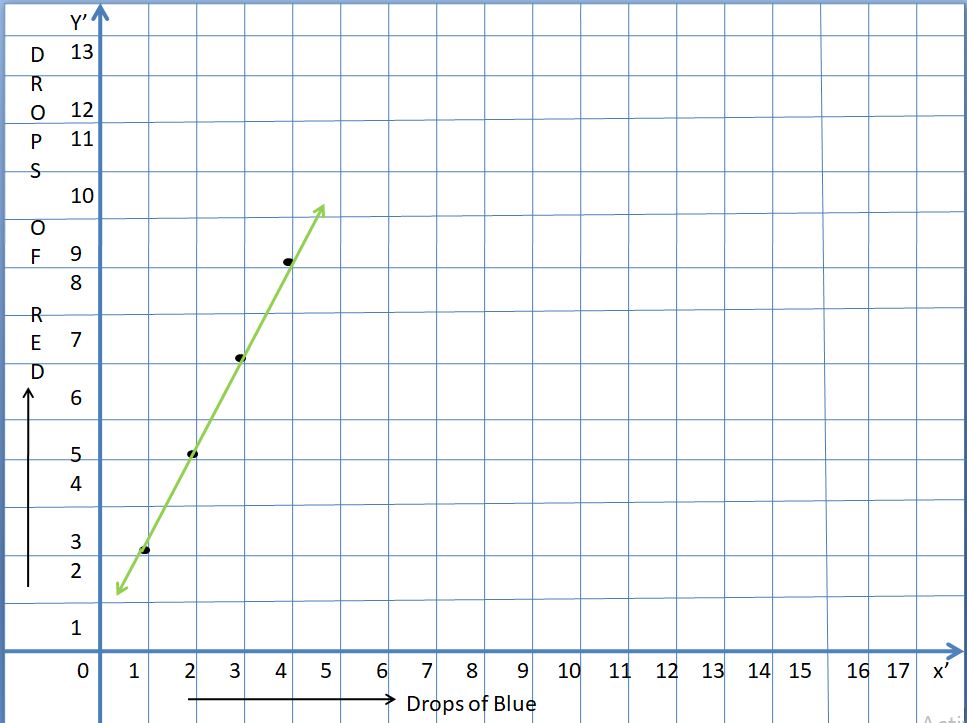
Mixture 2
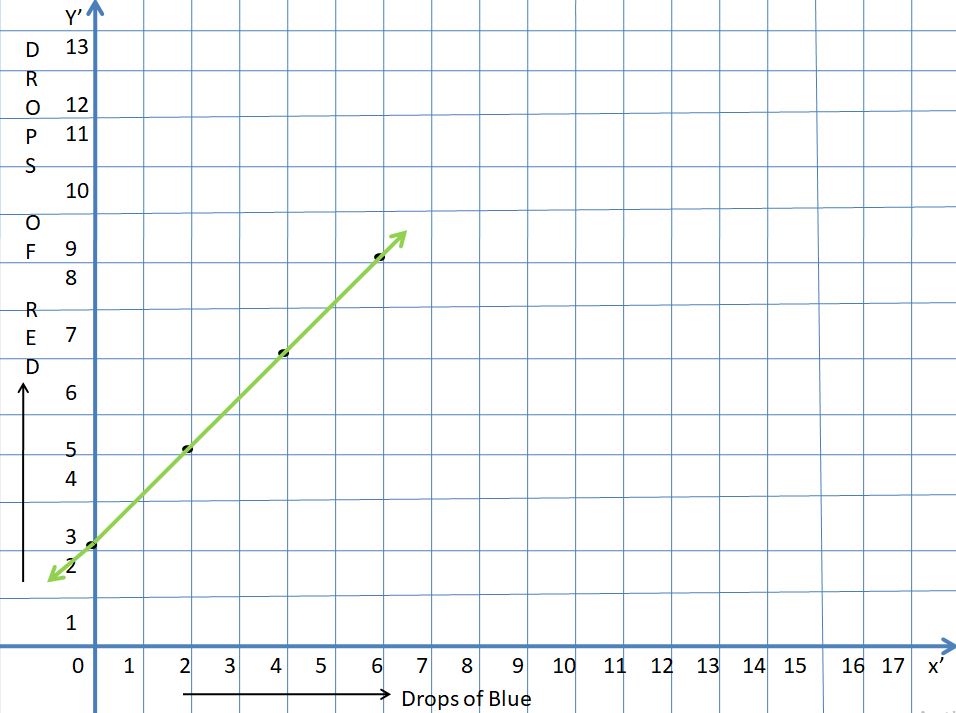
b. If the line passes through the origin, then x and y are proportional.
Explanation:
a.The points in mixture 1 are A (1, 2), B (2, 4), C (3, 6), D (4, 8)
The points in mixture 2 are E (0, 2), F (2, 4), G (4, 6), H (6, 8)
b. If the line passes through the origin, then x and y are proportional.

Try It
Tell whether x and y are proportional. Explain your reasoning.
Question 1.
Answer:
The line does not pass through the origin. So, x and y are not proportional.
Explanation:
The line does not pass through the origin. So, x and y are not proportional.
Question 2.
Answer:
x and y are not proportional.
Explanation:
The line pass through the origin. So, x and y are not proportional.
Question 3.
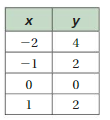
Answer:
x and y are not proportional.
Explanation:
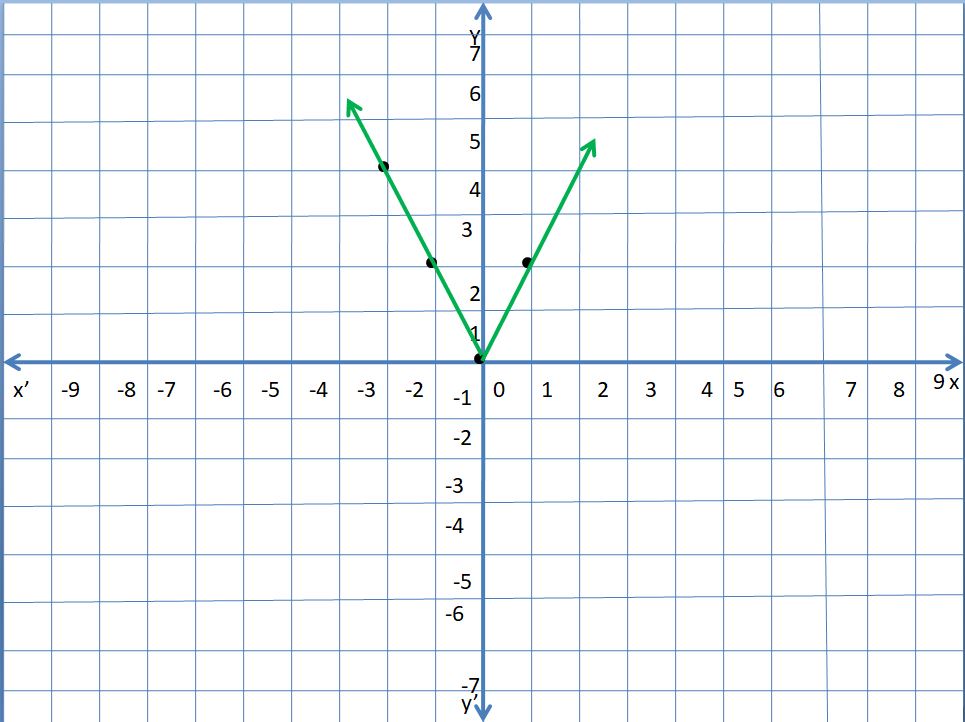
The line pass through the origin. So, x and y are not proportional.
Question 4.
WHAT IF
Does your answer change when you use the point (\(\frac{1}{2}\), \(\frac{1}{4}\))to find the speed of the subway car? Explain your reasoning.
Answer:
No.
Explanation:
The point (1/2, 1/4) indicates that the subway car travels 1/4 mile every 1/2 minutes.
1/4 : 1/2
= 2/4 : 1
= 1/2 : 1
So, the unit rate is 1/2 mile per minute
The speed of the subway car is 1/2 mile per minute.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
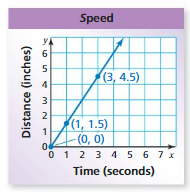
Question 5.
IDENTIFYING A PROPORTIONAL RELATIONSHIP Use the graph shown to tell whether x and y are proportional. Explain your reasoning.
Answer:
x and y are proportional.
Explanation:
x/y = 0/0
1.5/1 = 15/10 = 3/2
4.5/3 = 45/30 = 3/2
As the line pass through the origin, so, x and y are proportional.
Question 6.
FINDING A UNIT RATE
Interpret each plotted point in the graph. Then identify the unit rate, if possible.
Answer:
The unit rate is 1.5
Explanation:
time : distance = 1.5/1
= 15/10 = 3/2
The unit rate is 1.5
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
The table shows the temperature (in degrees Fahrenheit), hours after midnight.

a. Describe a proportional relationship between time and temperature shown by the table. Explain your reasoning.
b. Find the temperature 3.5 hours after midnight.
Answer:
b. 161 degrees Fahrenheit
Explanation:
a. The table shows the proportional relationship between hours and temperature.
0.5/44 = 1/88
1/46
1.5/48 = 1/32
The temperature after 3.5 hours, is 3.5 * 46 = 161 degrees Fahrenheit
Question 8.
DIG DEEPER!
Show how you can use a proportional relationship to plan the heights of the vertical supports of a waterskiing ramp. Then explain how increasing the steepness of the ramp affects the proportional relationship.
Answer:
The vertical supports tell the height of the ramp. As the height of the ramp increases the distance from the ramp is increases.
Graphs of Proportional Relationships Homework & Practice 5.5
Review & Refresh
Find the value of x so that the ratios are equivalent.
Question 1.
2 : 7 and 8 : x
Answer:
x = 28
Explanation:
2/7 = 8/x
Cross multiply the fractions
2x = 8 * 7
2x = 56
x = 56/2
x = 28
Question 2.
3 to 2 and x to 18
Answer:
x = 27
Explanation:
3/2 = x/18
Cross multiply the fractions
3 * 18 = 2x
54 = 2x
x = 54/2
x = 27
Question 3.
9 : x and 54 : 8
Answer:
x = 4/3
Explanation:
9/x = 54/8
Cross multiply the fractions
54x = 9 * 8
54x = 72
x = 72/54
x = 4/3
Find the quotient, if possible.
Question 4.
36 ÷ 4
Answer:
36 ÷ 4 = 9
Explanation:
The quotient of two integers of the same sign is positive.
36 ÷ 4 = 9
Question 5.
42 ÷ (- 6)
Answer:
42 ÷ (- 6) = -7
Explanation:
The quotient of two integers of the different signs is negative.
42 ÷ (- 6) = -7
Question 6.
– 39 ÷ 3
Answer:
– 39 ÷ 3 = -13
Explanation:
The quotient of two integers of the different signs is negative.
– 39 ÷ 3 = -13
Question 7.
– 44 ÷ (- 4)
Answer:
– 44 ÷ (- 4) = 11
Explanation:
The quotient of two integers of the same sign is positive.
– 44 ÷ (- 4) = 11
Solve the inequality. Graph the solution.
Question 8.
– \(\frac{x}{3}\) < 2
Answer:
x > -6

Explanation:
– \(\frac{x}{3}\) < 2
Multiply each side by 3
-x/3 . 3 < 2 . 3
-x < 6
x > -6
Question 9.
\(\frac{1}{3}\)p ≥ 4
Answer:
p ≥ 12
Explanation:
\(\frac{1}{3}\)p ≥ 4
Multiply each side by 3
\(\frac{1}{3}\)3p ≥ 4 . 3
p ≥ 12
Question 10.
– 8 < \(\frac{2}{3}\)n
Answer:
-24 < n
Explanation:
– 8 < \(\frac{2}{3}\)n
Multiply each side by 3/2
-8 x (3/2) < 2n/3 x (3/2)
-24 < n
Question 11.
– 2w ≤ 10
Answer:
w ≥ 5

Explanation:
– 2w ≤ 10
Divide each side by 2
– 2w/2 ≤ 10/2
-w ≤ 5
w ≥ 5
Concepts, Skills, & Problem Solving
REPRESENTING RELATIONSHIPS GRAPHICALLY Represent the table graphically. Does the graph represent a proportional relationship? How do you know? (See Exploration 1, p. 211.)
Question 12.
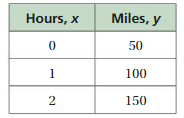
Answer:
x and y are not proportional.
Explanation:
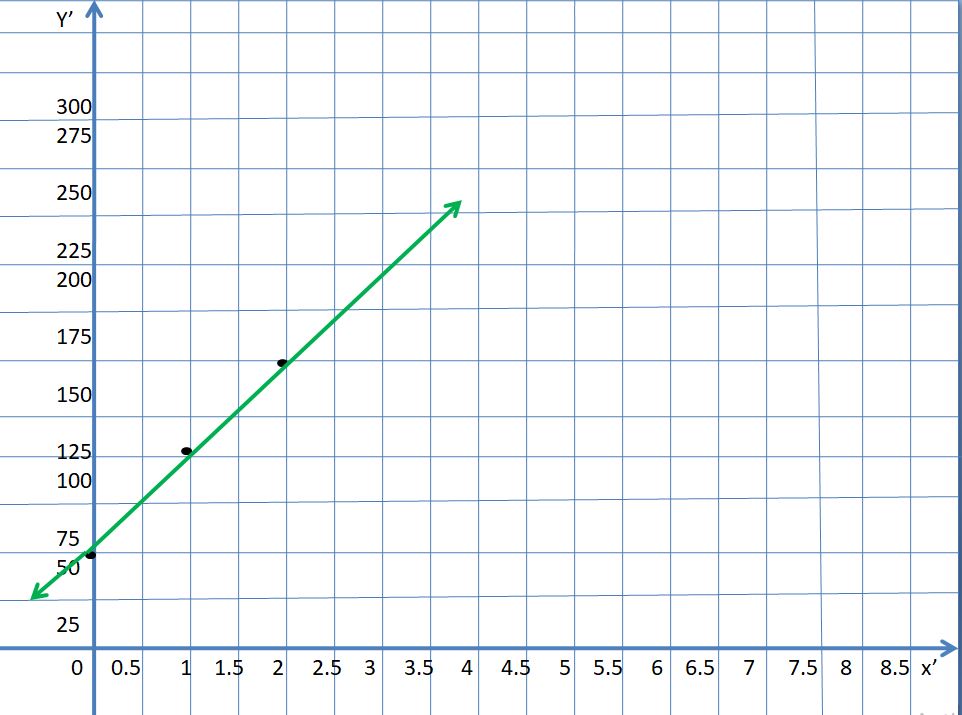
The line does not pass through the origin.
So, x and y are not proportional.
Question 13.
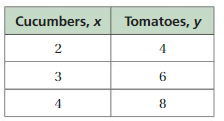
Answer:
x and y are proportional.
Explanation:
The line pass through the origin.
So, x and y are proportional.
IDENTIFYING A PROPORTIONAL RELATIONSHIP Tell whether x and y are proportional. Explain your reasoning.
Question 14.
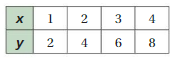
Answer:
x and y are proportional.
Explanation:
Compare the values of ratios x to y
x/y = 1/2
2/4 = 1/2
3/6 = 1/2
4/8 = 1/2
The ratios are equivalent.
So, x and y are proportional.
Question 15.
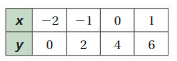
Answer:
x and y are not proportional.
Explanation:
Compare the values of ratios x to y
x/y = -2/0 = 0
-1/2
0/4 = 0
1/6
The ratios are not equivalent
So, x and y are not proportional.
Question 16.
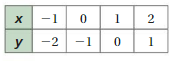
Answer:
x and y are not proportional.
Explanation:
Compare the values of ratios x to y
x/y = -1/-2 = 1/2
0/-1 = 0
1/0 = 0
2/1
All the ratios are not equivalent
So, x and y are not proportional.
Question 17.
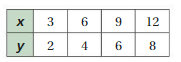
Answer:
x and y are proportional.
Explanation:
Compare the values of ratios x to y
x/y = 3/2
6/4 = 3/2
9/6 = 3/2
12/8 = 3/2
All the ratios are equivalent
So, x and y are proportional.
Question 18.
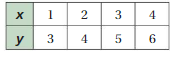
Answer:
x and y are not proportional.
Explanation:
Compare the values of ratios x to y
x/y = 1/3
2/4 = 1/2
3/5
4/6 = 2/3
All the ratios are not equivalent
So, x and y are not proportional.
Question 19.
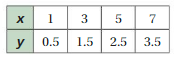
Answer:
x and y are proportional.
Explanation:
Compare the values of ratios x to y
x/y = 1/0.5 = 2
3/1.5 = 2
5/2.5 = 2
7/3.5 = 2
The ratios are equivalent
So, x and y are proportional.
Question 20.
YOU BE THE TEACHER
Your friend uses the graph to determine whether x and y are proportional. Is your friend correct? Explain your reasoning.
Answer:
The line does not pass through the origin.
so, x and y are not proportional.
FINDING A UNIT RATE Interpret each plotted point in the graph. Then identify the unit rate.
Question 21.
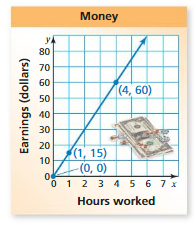
Answer:
Tnit rate is 1/15
Explanation:
The points are (1, 15), (4, 60)
x/y = 1/15
4/60 = (4 ÷ 4)/(60 ÷ 4)
= 1/15
So, unit rate is 1/15
Question 22.
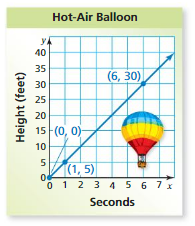
Answer:
The unit rate is 0.2 seconds per feet.
Explanation:
The points are (1, 5), (6, 30)
x/y = 1/5
6/30 = 1/5
The unit rate is 0.2 seconds per feet.
IDENTIFYING A PROPORTIONAL RELATIONSHIP Tell whether x and y are proportional. If so, identify the constant of proportionality. Explain your reasoning.
Question 23.
x – y = 0
Answer:
x and y are proportional.
Explanation:
x – y = 0
x = 0 + y
x = y

So, x and y are proportional.
Question 24.
\(\frac{x}{y}\) = 2
Answer:
x and y are proportional.
Explanation:
\(\frac{x}{y}\) = 2
x = 2y
If y = 0, then x = 2(0) = 0
If y = 1, then x = 2(1) = 2
If y = 2, then x = 2(2) = 4

So, x and y are proportional.
Question 25.
8 = xy
Answer:
x and y are proportional.
Explanation:
8 = xy
y = 8/x
If x = 0, then y = 8/0 = 0
If x = 1, then y = 8/1 = 8
If x = 2, then y = 8/2 = 4

So, x and y are proportional.
Question 26.
x2 = y
Answer:
x and y are proportional.
Explanation:
x2 = y
If x = 0, then y = 0
If x = 1, then y = 1
If x = 2, then y = 4

So, x and y are proportional.
WRITING AN EQUATION The variables and are proportional. Use the values to find the constant of proportionality. Then write an equation that relates x and y.
Question 27.
When y = 72, x = 3.
Answer:
y = 24x
Explanation:
y/x = 72/3
y/x = 24
y = 24x
Question 28.
When y = 20, x = 12.
Answer:
5x = 3y
Explanation:
y/x = 20/12
y/x = 5/3
Cross multiply the fractions
3y = 5x
Question 29.
When y = 45, x = 40.
Answer:
9x = 8y
Explanation:
y/x = 45/40
y/x = 9/8
Cross multiply the fractions
8y = 9x
Question 30.
MODELING REAL LIFE
The table shows the profit y for recycling x pounds of aluminum. Find the profit for recycling 75 pounds of aluminum.
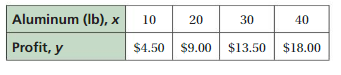
Answer:
The profit for recycling 75 pounds of aluminum is $33.75
Explanation:
The profit is $4.50 for recycling 10 pounds of aluminum
= 4.50 : 10
= 4.50/10 : 1
= 0.45 : 1
The profit is 40.45 for recycling 1 pound of aluminum.
The profit for recycling 75 pounds of aluminum is $135/4
Question 31.
MODELING REAL LIFE
The graph shows the cost of buying concert tickets. Tell whether x and y are proportional. If so, find and interpret the constant of proportionality. Then find the cost of 14 tickets.
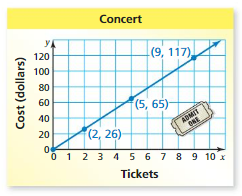
Answer:
x and y are proportional.
The cost for buying 14 tickets is $182
13x = y
Explanation:
The line in the graph passes through the origin. so, x and y are proportional.
The cost for buying 2 tickets is 26
= 26 : 2
=13 : 1
The cost for buying 1 ticket is $13.
So, the cost for buying 14 tickets is 14 * 13 = $182
x/y = 2/26
x/y = 1/13
Cross multiply the fractions
13x = y
Question 32.
REASONING
The graph of a proportional relationship passes through (12, 16) and (1, y) Find y.
Answer:
y = 4/3
Explanation:
12/16 = 1/y
3/4 = 1/y
Cross multiply the fractions
3y = 4
y = 4/3
Question 33.
PROBLEM SOLVING
The amount of chlorine in a swimming pool is proportional to the volume of water. The pool has 2.5 milligrams of chlorine per liter of water. How much chlorine is in the pool?

Answer:
The amount of chlorine in the pool is 75708.225 milligrams.
Explanation:
The amount of chlorine in a swimming pool varies directly with the volume of water. The pool has 2.5 milligrams of chlorine per liter of water.
1 gallon = 3.78541 litre
8000 gallons = 8000 * 3.78541 = 30283.29 litres
The amount of chlorine in the pool = 30283.29 * 2.5
= 75708.225 milligrams.
Question 34.
DIG DEEPER!
A vehicle travels 250 feet every 3 seconds. Find the value of the ratio, the unit rate, and the constant of proportionality. How are they related?
Answer:
The ratio is 250 : 3
The unit rate is 250/3 : 1
3x = 250y
Explanation:
A vehicle travels 250 feet every 3 seconds
= 250 : 3
= 250/3 : 1
The unit rate is 250/3 : 1
x/y = 250/3
Cross multiply the proportions
3x = 250y
Lesson 5.6 Scale Drawings
EXPLORATION 1
Creating a Scale Drawing
Work with a partner. Several sections in a zoo are drawn on 1-centimeter grid paper as shown. Each centimeter in the drawing represents 4 meters.
a. Describe the relationship between the lengths of the fences in the drawing and the actual side lengths of the fences.
b. Describe the relationship between the areas of the sections in the drawing and the actual areas of the sections.
c. Are the relationships in parts (a) and (b) the same? Explain your reasoning.
d. Choose a different distance to represent each centimeter on a piece of 1-centimeter grid paper. Then create a new drawing of the sections in the zoo using the distance you chose. Describe any similarities or differences in the drawings.

Try It
Question 1.
What is the actual distance between Traverse City and Marquette?
Answer:
The distance between Traverse City and Marquette is 150 miles
Explanation:
Use the centimeter ruler to find the distance on the map between traverse city and Marquette.
the map distance is about 3 centimeters
Use the scale 1 cm : 50 mi and the ratio 3 cm : d mi to write and solve a proportion
1/50 = 3/d
d = 50 * 3
d = 150
So, the distance between Traverse City and Marquette is 150 miles
Question 2.
A drawing has a scale of 1 mm : 20 cm. What is the scale factor of the drawing?
Answer:
The scale factor is 1/200
Explanation:
Write the scale with the same units. Use the factor 1 cm = 10 mm
1 mm : 20 cm = 1 mm : (20 • 10) mm
= 1 : 200
So, the scale factor is 1/200
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
VOCABULARY
In your own words, explain the meaning of the scale and scale factor of a drawing or model.
Answer:
A scale factor is a number that multiplies times a given quantity to produce a smaller or longer version of the original number. It is also defined as the ratio of a drawing or blueprint to the actual object or distance.
The measurements in scale drawings are proportional to the measurements of the actual object. The scale is the ratio that compares the measurements of the drawings with the actual measurements.
Question 4.
FINDING AN ACTUAL DISTANCE
Consider the scale drawing of Balanced Rock in Arches National Park. What is the actual height of the structure?

Answer:
h = 1/975.36
Explanation:
scale drawing is 1 cm : 32 ft
1 foot = 30.48 cm
So, 32 ft = 975.36 cm
1 cm : 32 ft = 1 : 975.36
h = 1/975.36
Question 5.
FINDING A SCALE FACTOR
A drawing has a scale of 3 in. : 2 ft. What is the scale factor of the drawing?
Answer:
The scale factor is 1/8
Explanation:
3 in. : 2 ft
1 foot = 12 inches
2 ft = 24 inches
The scale is 3 : 24 inches = 1/8
Question 6.
REASONING
Describe the scale factor of a model that is (a) larger than the actual object and (b) smaller than the actual object.
Answer:
If the scale of the factor is larger than the actual object, then every point is considered larger in the image. It means we represent a lion in a smaller box.
If the scale of the factor is less than the actual object, it means we represent the pen as a larger box.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
A scale drawing of the Parthenon is shown. Find the actual perimeter and area of the rectangular face of the Parthenon. Then recreate the scale drawing with a scale factor of 0.2. Find the perimeter and area of the rectangular face in your drawing.

Answer:
The actual perimeter of the rectangular face of the Parthenon is 26 ft
The actual area of the rectangular face of the Parthenon is 36 sq ft
the perimeter of the rectangular face in your drawing is 5.2 ft
area of the rectangular face in your drawing is 1.44 sq ft.
Explanation:
Perimeter of the rectangular face of the Parthenon = 2(l + b)
= 2(4 + 9) = 13 * 2
= 26 ft
Area of the rectangular face of the Parthenon = l * b
= 4 * 9
= 36 sq ft
Scale factor = 0.2
The length of the rectangular face in your drawing = 0.2 * 9
= 1.8
The breadth of the rectangular face in your drawing = 4 * 0.2
= 0.8
Perimeter is 2(1.8 + 0.8) = 5.2
Area is 0.8 * 1.8 = 1.44
Question 8.
DIG DEEPER!
You are in charge of creating a billboard advertisement that is 16 feet long and 8 feet tall. Choose a product. Create a scale drawing of the billboard using words and a picture. What is the scale factor of your design?
Answer:
The scale factor is 2
Explanation:
The details of the billboard advertisement is 16 : 8
= 2 : 1
1 unit is 4 units on the scale
So, the billboard advertisement is 16 * 4 : 8 * 4
= 64 : 32
= 2 : 1
So, the scale factor is 2
Scale Drawings Homework & Practice 5.6
Review & Refresh
Tell whether x and y are proportional. Explain your reasoning.
Question 1.
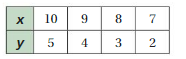
Answer:
x and y are not proportional
Explanation:
Compare the values of ratios x to y
10/5 = 2
9/4 = 2.25
8/3 = 2.6666
7/2 = 3.5
The ratios are not equivalent
So, x and y are not proportional
Question 2.
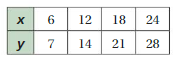
Answer:
x and y are proportional
Explanation:
Compare the values of ratios x to y
6/7
12/14 = 6/7
18/21 = 6/7
24/28 = 6/7
The ratios are equivalent
So, x and y are proportional
Simplify the expression.
Question 3.
7p + 6p
Answer:
7p + 6p = 13p
Explanation:
The given expression is 7p + 6p
= 13p
Question 4.
8 + 3d – 17
Answer:
8 + 3d – 17 = 3d – 9
Explanation:
The given expression is 8 + 3d – 17
= 3d – 9
Question 5.
– 2 + \(\frac{2}{5}\)b – \(\frac{1}{4}\)b + 6
Answer:
– 2 + \(\frac{2}{5}\)b – \(\frac{1}{4}\)b + 6 = 4 + 3b/20
Explanation:
The given expression is – 2 + \(\frac{2}{5}\)b – \(\frac{1}{4}\)b + 6
= 4 + (8b – 5b)/20
= 4 + 3b/20
Write the word sentence as an inequality.
Question 6.
A number is less than – 3.
Answer:
n < -3
Explanation:
Let us the number as n
n < -3
Question 7.
7 plus a number z is more than 5.
Answer:
7 + z > 5, z > -2
Explanation:
more than means > symbol
7 + z > 5
z > 5 – 7
z > -2
Question 8.
The product of a number m and 6 is no less than 30.
Answer:
6m > 30
Explanation:
No less than means >
m . 6 > 30
6m > 30
Divide both sides by 6
6m/6 > 30/6
m > 30/6
Concepts, Skills, & Problem Solving
CREATING A SCALE DRAWING Each centimeter on the 1-centimeter grid paper represents 8 inches. Create a proportional drawing of the figure that is larger or smaller than the figure shown. (See Exploration 1, p. 217.)
Question 9.
Answer:
The base of the traingle is 16 inches
Explanation:
1 cm = 8 inches
The base of triangle = 2 cm
= 2 * 8 = 16 inches
Actually, 1 cm = 0.393701 inches
The size of drawing/real size = 1/8
2/real size = 1/8
16 = real size
Question 10.
Answer:
The bottom surface is 24 inches, the height is 24 inches, the top surface is 8 inches.
Explanation:
1 cm = 8 inches
Bottom surface is 3 cm
= 3 * 8 = 24 inches
Height is 3 cm
= 3 * 8 = 24 inches
Top surface = 1 cm
= 1 * 8 = 8 inches
FINDING AN ACTUAL DISTANCE Use the map in Example 1 to find the actual distance between the cities.
Question 11.
Kalamazoo and Ann Arbor
Answer:
The distance between Kalamazoo and Ann Arbor is 100 miles.
Explanation:
Use the centimeter ruler to find the distance on the map between Kalamazoo and Ann Arbor
The map distance is about 2 cm
Use the scale 1 cm : 50 mi and the ratio 2 cm : d mi to write and solve a proportion
1/50 = 2/d
d = 50 * 2
d = 100
So, the distance between Kalamazoo and Ann Arbor is 100 miles.
Question 12.
Lansing and Flint
Answer:
The distance between Lansing and Flint is 50 miles.
Explanation:
Use the centimeter ruler to find the distance on the map between Lansing and Flint
The map distance is about 1 cm
Use the scale 1 cm : 50 mi and the ratio 1 cm : d mi to write and solve a proportion
1/50 = 1/d
d = 50 * 1
d = 50
So, the distance between Lansing and Flint is 50 miles.
Question 13.
Grand Rapids and Escanaba
Answer:
The distance between Grand Rapids and Escanaba is 200 miles.
Explanation:
Use the centimeter ruler to find the distance on the map between Grand Rapids and Escanaba
The map distance is about 4 cm
Use the scale 1 cm : 50 mi and the ratio 4 cm : d mi to write and solve a proportion
1/50 = 1/d
d = 50 * 4
d = 200
So, the distance between Grand Rapids and Escanaba is 200 miles.
Question 14.
Saginaw and Alpena
Answer:
The distance between Saginaw and Alpena is 150 miles.
Explanation:
Use the centimeter ruler to find the distance on the map between Saginaw and Alpena
The map distance is about 3 cm
Use the scale 1 cm : 50 mi and the ratio 4 cm : d mi to write and solve a proportion
1/50 = 1/d
d = 50 * 3
d = 150
So, the distance between Saginaw and Alpena is 150 miles.
USING A SCALE Find the missing dimension. Use the scale 1 : 12.
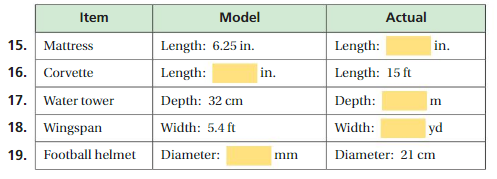
Answer:
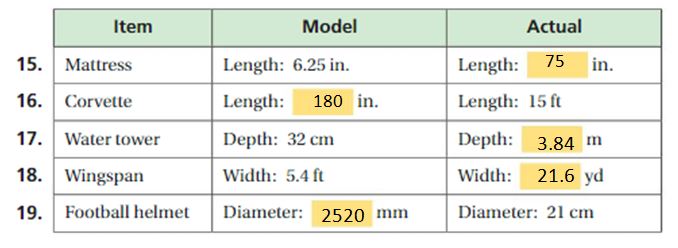
Explanation:
15. 1 inch = 12 inches
So, 6.25 x 12 = 75 inches
16. 1 ft = 12 inches
x in = 15 * 12
x in = 180 inches
17. 1 m = 100 cm
32 cm = 0.32 m
32 * 1 = .32 * 12
= 3.84 m
18. 1 ft = 0.333333 yard
5.4 ft = 5.4 * 0.333333
= 1.8 yard * 12 = 21.6 yard
19. 1 cm = 10 mm
21 cm = 210 mm
210 * 12 = 2520 mm
FINDING A SCALE FACTOR Use a centimeter ruler to find the scale and the scale factor of the drawing.
Question 20.
Answer:
1 cm = 30 m
Explanation:
Using the centimeter ruler, the length is 4 cm
So, 4 cm = 120 m
1 cm = 120/4
1 cm = 30 m
Question 21.
Answer:
1 cm = 8 mm
Explanation:
Using the centimeter ruler, the length is 3 cm
So, 3 cm = 24 mm
1 cm = 24/3
= 8 mm
Question 22.
CRITICAL THINKING
You know the length and the width of a scale model. What additional information do you need to know to find the scale of the model? Explain.
Answer:
You need to know the scale factor to know the scale of the model.
Question 23.
MODELING REAL LIFE
Central Park is a rectangular park in New YorkCity.
a. Find the perimeter and the area of the scale drawing of Central Park.
b. Find the actual perimeter and area of Central Park.
Answer:
a. The perimeter of the scale drawing of Central Park = 26 cm
The area of the scale drawing of Central Park = 30 sq cm
b. The perimeter of the scale drawing of Central Park = 8320 cm
The area of the scale drawing of Central Park = 3072000 sq cm
Explanation:
a. The length of the central park is 10 cm
The breadth of the central park is 3 cm
The perimeter of the scale drawing of Central Park = 2(10 + 3)
= 2(13)
= 26 cm
The area of the scale drawing of Central Park = 10 * 3
= 30 sq cm
b. 1 cm = 320 m
The length of the central park is 10 * 320 = 3200
The breadth of the central park is 3 * 320 = 960
The perimeter of the scale drawing of Central Park = 2(3200 + 960)
= 8320 cm
The area of the scale drawing of Central Park = 3200 * 960
= 3072000 sq cm
Question 24.
PROBLEM SOLVING
In a blueprint,each square has a side length of \(\frac{1}{4}\) inch.
a. Ceramic tile costs $5 per square foot. How much does it cost to tile the bathroom?
b. Carpet costs $18 per square yard. How much does it cost to carpet the bedroom and living room?
Answer:
a. The cost to the bathroom = $0.06075
b. The cost to carpet the bedroom and living room = $0.02430
Explanation:
Square side length = 1/4 inch
1 feet = 12 inch
1 inch : 16 ft = 1 : 16 * 12 = 1 : 192
a. one square side length is 1/4
1 foot = 12 inch
So, the length of the bathroom = 4(1/4) = 1 = 1 * 0.0833333
= 0.0833333
The breadth of the bathroom = 7(1/4) = 7/4
= (7 * 0.0833333)/4
= 0.583333/4
= 0.14583325
The area of bathroom = 0.0833333 * 0.14583325
= 0.01215 sq in
Ceramic tile costs $5 per square foot
The cost to the bathroom = 0.01215 * 5 = $0.06075
b. 1 inch = 0.0277778 yard
length of bathroom + living room = 1 * 0.0277778 = 0.0277778
breadth of bathroom + living room = 7/4 (0.0277778)
= 0.04861115
The area of bathroom + living room = 0.0277778 * 0.04861115
= 0.00135031080247
Carpet costs $18 per square yard.
The cost to carpet the bedroom and living room = 0.00135031080247 * 18 = $0.02430
REPRODUCING A SCALE DRAWING Recreate the scale drawing so that it has a scale of 1 cm : 4 m.
Question 25.
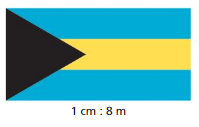
Answer:

Explanation:
1 m = 100 cm
Actual length = 1 cm * (1 cm / 400 cm)
= 1/400 cm
Actual breadth = 8 m * (1 cm / 4 m)
= 2 cm
Question 26.
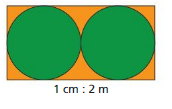
Answer:

Explanation:
1 cm = 100 m
Actual length = 1 cm * (1 cm / 400 cm)
= 1/400 cm
Actual breadth = 2 m * ( 1 cm / 4 m)
= 1/2 cm
Question 27.
DIG DEEPER!
Make a conjecture about the relationship between the scale factor of a drawing and the quotients ![]() . Explain your reasoning.
. Explain your reasoning.
Answer:
drawing perimeter/ actual perimeter = scale factor
drawing area/actual area = scale factor
Ratios and Proportions Connecting Concepts
Using the Problem-Solving Plan
Question 1.
The table shows the toll y(in dollars) for traveling x miles on a turnpike. You have $8.25 to pay your toll. How far can you travel on the turnpike?

Understand the problem.
The table shows the tolls for traveling several different distances on a turnpike. You have $8.25 to pay the toll. You are asked to find how far you can travel on the turnpike with $8.25 for tolls.
Make a plan.
First, determine the relationship between x and y and write an equation to represent the relationship. Then use the equation to determine the distance you can travel.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
You can travel 55 miles with $8.25 for tolls.
Explanation:
x : y = 40 : 6
= 40/6 : 1
= 20/3 : 1
You need to pay $1 for 20/3 miles
So, 20/3 : 1 = x : 8.25
8.25 (20/3) = x
55 = x
So, you can travel 55 miles with $8.25 for tolls.
Question 2.
A company uses a silo in the shape of a rectangular prism to store bird seed. The base of the silo is a square with side lengths of 20 feet. Are the height and the volume of the silo proportional? Justify your answer.
Answer:
The height and the volume of the silo proportional
Explanation:
The base of the silo is a square with side lengths of 20 feet.
The area of silo = side² = 20²
= 400 sq ft
Height = h
Volume = lwh
= 400h
h : 400h = 1 : 400
The height and the volume of the silo proportional
Question 3.
A rectangle is drawn in a coordinate plane as shown. In the same coordinate plane, create a scale drawing of the rectangle that has a vertex at (0, 0) and a scale factor of 3.
Answer:
The length of rectangle = 2/3
Breadth = 1/3
Explanation:
The length of rectangle = 2 units
The breadth of rectangle = 1 unit
length : breadth = 2 : 1
length = 2breadth
The scale factor = 3
The length of rectangle = 2/3
Breadth = 1/3
Performance Task
Mixing Paint
At the beginning of this chapter, you watched a STEAM Video called “Painting a Large Room.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Ratios and Proportions Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
Graphic Organizers
You can use an Example and Non-Example Chart to list examples and non-examples of a concept. Here is an Example and Non-Example Chart for scale factor.
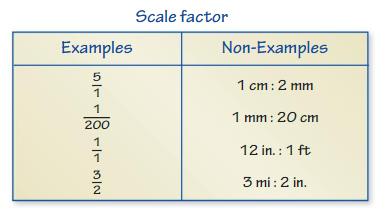
Choose and complete a graphic organizer to help you study the concept.

1. ratio
2. equivalent ratios
3. rate
4. unit rate
5. equivalent rates
6. proportion
7. cross products
8. proportional
9. scale
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

5.1 Ratios and Ratio Tables (pp. 183–188)
Learning Target: Understand ratios of rational numbers and use ratio tables to represent equivalent ratios.
Write the ratio. Then find and interpret the value of the ratio.
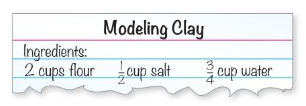
Question 1.
salt: flour
Answer:
1/2 : 2
Explanation:
salt : flour = 1/2 cup : 2 cups
Question 2.
water to flour
Answer:
3/4 cup : 2 cups
Explanation:
water to flour = 3/4 : 2
Question 3.
salt to water
Answer:
1/2 cup : 3/4 cup
Explanation:
salt to water = 1/2 cup : 3/4 cup
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 4.
Answer:
The equivalent ratios are 3/2 : 1/2, 3 : 1, 9/2 : 3/2, 6 : 2
Explanation:
The missing values in the ratio table are
3/2 • x = 3
x = 3 • 2/3
x = 2
Milk1 = 2 • 1/2 = 1
1/2 • y = 3/2
y = 3
Flour1 = 3/2 • 3
= 9/2
1/2 • z = 2
z = 4
Flour2 = 3/2 • 4
= 6
The equivalent ratios are 3/2 : 1/2, 3 : 1, 9/2 : 3/2, 6 : 2
Question 5.
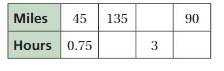
Answer:
The equivalent ratios are 45 : 0.75, 135 : 2.25, 180 : 3, 90 : 1.5
Explanation:
The missing values in the ratio table are
45 • x = 135
x = 135/45
x = 3
Hours1 = 0.75 • 3
= 2.25
0.75 • y = 3
y = 3/0.75
y = 4
Miles1 = 45 • 4 = 180
45 • z = 90
z = 90/45 = 2
Hours2 = 0.75 • 2 = 1.5
The equivalent ratios are 45 : 0.75, 135 : 2.25, 180 : 3, 90 : 1.5
Question 6.
The cost for 16 ounces of cheese is $3.20. What is the cost for 20 ounces of cheese?
Answer:
The cost for 20 ounces of cheese is $3.95
Explanation:
The cost for 16 ounces of cheese is $3.20
The cost for 1 ounce of cheese is 3.20/16
The cost for 20 ounces of cheese is 20(3.20/16)
= 63.2/16
= 3.95
5.2 Rates and Unit Rates (pp. 189–194)
Learning Target: Understand rates involving fractions and use unit rates to solve problems.
Find the unit rate.
Question 7.
289 miles on 10 gallons
Answer:
28.9 miles per 1 gallon
Explanation:
289 miles on 10 gallons
= 289 : 10
= 289/10 : 1
= 28.9 : 1
Question 8.
6 \(\frac{2}{5}\) revolutions in 2\(\frac{2}{3}\) seconds
Answer:
2.4 revolutions in 1 second
Explanation:
6 \(\frac{2}{5}\) revolutions in 2\(\frac{2}{3}\) seconds = 32/5 : 8/3
= 32/5 • 3/8 : 1
= 12/5 : 1
Question 9.
You can mow 23,760 square feet in \(\frac{1}{2}\) hour. How many square feet can you mow in 2 hours? Justify your answer.
Answer:
95040 sq ft you can mow in 2 hours.
Explanation:
You can mow 23,760 square feet in \(\frac{1}{2}\) hour
= 23760 : 1/2
= 23760 • 2 : 1
= 47520 : 1
So you can mow 47520 sq ft in 1 hour
The number of sq ft you can mow in 2 hours = 47520 • 2
= 95040
Tell whether the rates are equivalent. Justify your answer.
Question 10.
60 centimeters every 2.5 years
30 centimeters every 15 months
Answer:
The rates are equivalent.
Explanation:
60 centimeters every 2.5 years = 60 : 2.5
= 600 : 25
= 24 : 1
24 cm every year
= 24 : 12
= 2 : 1
2 cm every month
30 centimeters every 15 months = 30 : 15
= 2 : 1
So, The rates are equivalent.
Question 11.
2.56 per \(\frac{1}{2}\) pound
$0.48 per 6 ounces
Answer:
The ratios are not equivalent.
Explanation:
2.56 per \(\frac{1}{2}\) pound = 2.56 : 1/2
= 2.56 * 2 : 1
= 5.12 : 1
1 pound = 16 ounces
$0.48 per 6 ounces = 0.48 : 6
= 0.48 : 6 * 16
= 0.48 : 96
= 1 : 200
So, the ratios are not equivalent.
5.3 Identifying Proportional Relationships (pp. 195–202)
Learning Target: Determine whether two quantities are in a proportional relationship.
Tell whether the ratios form a proportion.
Question 12.
4 to 9 and 2 to 3
Answer:
The rates do not form a proportion.
Explanation:
4 to 9 = 4 : 9
2 to 3 = 2 : 3
So, the rates do not form a proportion.
Question 13.
12 : 22 and 18 : 33
Answer:
The rates form a proportion.
Explanation:
12 : 22 = 12 : 22
= 6 : 11
18 : 33 = 18 : 33
= 6 : 11
So, the rates form a proportion.
Question 14.
\(\frac{1}{2}\) : 2 and \(\frac{1}{4}\) : \(\frac{1}{10}\)
Answer:
The rates do not form a proportion
Explanation:
\(\frac{1}{2}\) : 2 = 1 : 4
\(\frac{1}{4}\) : \(\frac{1}{10}\) = 1/4 : 1/10
= 10 : 4
= 5 : 2
So, the rates do not form a proportion.
Question 15.
3.2 to 8 and 1.2 to 3
Answer:
The ratios are equivalent.
Explanation:
3.2 to 8 = 3.2 : 8
= 2/5
1.2 to 3 = 1.2 : 3
= 2/5
So, the ratios are equivalent.
Question 16.
Tell whether x and y are proportional.
Answer:
The x and y are proportional
Explanation:
x/y = 1/4
3/12 = (3 • 1)/(4 • 3) = 1/4
6/24 = (6 • 1)/(6 • 4) = 1/4
8/32 = (8 • 1)/(8 • 4) = 1/4
So, the x and y are proportional.
Question 17.
You can type 250 characters in 60 seconds. Your friend can type 375 characters in 90 seconds. Do these rates form a proportion? Explain.
Answer:
The rates form a proportion.
Explanation:
You can type 250 characters in 60 seconds = 250 : 60
= (25 • 10) : (6 • 10) = 25 : 6
Your friend can type 375 characters in 90 seconds = 375 : 90
= (25 • 15) : (6 • 15)
= 25 : 6
So, the rates form a proportion.
5.4 Writing and Solving Proportions (pp. 203–210)
Learning Target: Use proportions to solve ratio problems.
Solve the proportion. Explain your choice of method.
Question 18.
\(\frac{3}{8}=\frac{9}{x}\)
Answer:
x = 24
Explanation:
\(\frac{3}{8}=\frac{9}{x}\)
Cross multiply the fractions
3x = 9 * 8
x = 3 * 8
x = 24
Question 19.
\(\frac{x}{4}=\frac{2}{5}\)
Answer:
x = 8/5
Explanation:
\(\frac{x}{4}=\frac{2}{5}\)
Cross multiply the fractions
5x = 2 * 4
5x = 8
x = 8/5
Question 20.
\(\frac{5}{12}=\frac{y}{15}\)
Answer:
y = 75/12
Explanation:
\(\frac{5}{12}=\frac{y}{15}\)
Cross multiply the fractions
15 * 5 = 12y
75 = 12y
y = 75/12
Question 21.
\(\frac{s+1}{4}=\frac{4}{8}\)
Answer:
s = 1
Explanation:
\(\frac{s+1}{4}=\frac{4}{8}\)
Cross multiply the fractions
8(s + 1) = 4 * 4
8s + 8 = 16
8s = 16 – 8
8s = 8
s = 1
Use the table to write a proportion.
Question 22.
Answer:
6/12 = 8/m, m = 12
Explanation:
The ratios are proportional.
6/12 = 8/m
Cross multiply the fractions
6m = 8 * 12
6m = 96
m = 96/8
m = 12
Question 23.
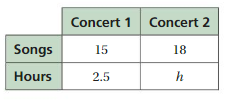
Answer:
15/h = 18/2.5
Explanation:
The ratios are proportional.
So, 15/h = 18/2.5
Question 24.
Find the value of x so that the ratios 8 : 20 and 6 : x are equivalent.
Answer:
x = 15
Explanation:
8/20 = 6/x
Cross multiply the fractions
8x = 6 * 20
8x = 120
x = 120/8
x = 15
Question 25.
Swamp gas consists primarily of methane, a chemical compound consisting of a 1 : 4 ratio of carbon to hydrogen atoms. If a sample of methane contains 1564 hydrogen atoms, how many carbon atoms are present in the sample?

Answer:
The number of carbon atoms present in the sample is 391.
Explanation:
Swamp gas consists primarily of methane, a chemical compound consisting of a 1 : 4 ratio of carbon to hydrogen atoms
The number of carbon atoms present in the sample is 1564/4
= 391
5.5 Graphs of Proportional Relationships (pp. 211–216)
Learning Target: Represent proportional relationships using graphs and equations.
Question 26.
Tell whether x and y are proportional. Explain your reasoning.
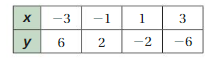
Answer:
x and y are proportional
Explanation:
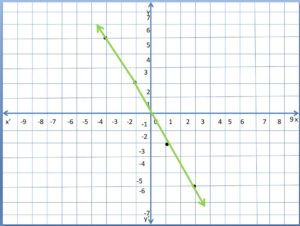
The line passes through origin.
So, x and y are proportional
Question 27.
The graph shows the number of visits your website received over the past 6 months. Interpret each plotted point in the graph. Then identify the unit rate.
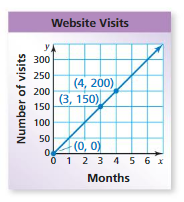
Answer:
50 : 1
Explanation:
Number of visitors : months = 150 : 3
= 150/3 : 1
= 50 : 1
Tell whether x and y are proportional. If so, identify the constant of proportionality. Explain your reasoning.
Question 28.
x + y = 6
Answer:
x and y are not proportional.
Explanation:
x + y = 6
y = 6 – x
If x = 1, then y = 6 – 1 = 5
If x = 2, then y = 6 – 2 = 4
If x = 3, y = 6 – 3 = 3
1/5, 2/4, 3/3 are not equivalent ratios
So, x and y are not proportional.
Question 29.
y – x = 0
Answer:
x and y are proportional.
Explanation:
y – x = 0
y = x
If x = 1, then y = 1
If x = 2, then y = 2
If x = 3, then y = 3
1/2, 2/2, 3/3 are equivalent ratios
So, x and y are proportional.
Question 30.
\(\frac{x}{y}\) = 20
Answer:
x and y are proportional.
Explanation:
\(\frac{x}{y}\) = 20
x = 20y
If y = 1, then x = 20(1) = 20
If y = 2, then x = 20(2) = 40
If y = 3, then x = 20(3) = 60
20/1, 40/2, 60/3 are equivalent ratios
So, x and y are proportional.
Question 31.
x = y + 2
Answer:
x and are not proportional.
Explanation:
x = y + 2
If y = 1, then x = 1 + 2 = 3
If y = 2, then x = 2 + 2 = 4
If y = 3, then x = 3 + 2 = 6
3/1, 4/2, 6/3 are not equivalent
So, x and are not proportional.
Question 32.
The variables x and y are proportional. When y = 4, x = \(\frac{1}{2}\). Find the constant of proportionality. Then write an equation that relates x and y.
Answer:
x = 8y
Explanation:
x/y = k
(1/2)/4 = k
k = 1/8
x/y = 8
x = 8y
5.6 Scale Drawings (pp. 217–222)
Learning Target: Solve problems involving scale drawings.
Find the missing dimension. Use the scale factor 1 : 20.
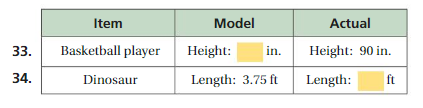
Answer:
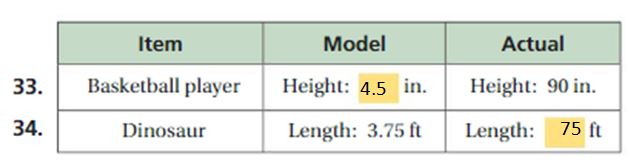
Explanation:
33. Scale factor = 1/20
Use the scale 1 : 20
90(1/20) = 9/2 = 4.5
34. x/20 = 3.75
x = 3.75 * 20
x = 75
Actual legth = 75 ft
Use a centimeter ruler to find the scale and the scale factor of the drawing.
Question 35.

Answer:
The scale is 7.62, scale factor is 39.3701 in
Explanation:
The length of drawing = 10 cm
10 cm = 30 in
1 cm = 0.393701
10 cm = 39.3701 in
10 cm : 30 in = 1 cm : 3 in
3 inch = 7.62
The actual length is 39.3701 inch
So, the scale is 7.62, scale factor is 39.3701 in
Question 36

Answer:
The scale is 19.05, scale factor is 19.05
Explanation:
Uisng the centimeter ruler, length is 4 cm
4 cm = 7.5 in
1 cm = 0.393701
4 cm = 1.5748 in
4 cm : 7.5 in
7.5 inch = 19.05
4 cm : 7.5 inch = 4 cm : 19.05 cm
the scale is 19.05, scale factor is 19.05
Question 37.
A scale model of a lighthouse has a scale of 1 in.: 8ft. The scale model is 20 inches tall. How tall is the lighthouse?
Answer:
Explanation:
A scale model of a lighthouse has a scale of 1 in.: 8ft
The scale model is 20 inches tall
Ratios and Proportions Practice Test
Find the unit rate.
Question 1.
84 miles in 12 days
Answer:
7 miles in 1 day
Explanation:
84 miles in 12 days
= 84 : 12
= 84/12 : 1
= 7 : 1
Question 2.
2 \(\frac{2}{5}\) kilometers in 3\(\frac{3}{4}\) minutes
Answer:
48 kilometers in 75 minutes.
Explanation:
2 \(\frac{2}{5}\) kilometers in 3\(\frac{3}{4}\) minutes = 12/5 : 15/4
= 12/5 • 4/15 : 1
= 48/75 : 1
Tell whether the ratios form a proportion.
Question 3.
1 to 0.4 and 9 to 3.6
Answer:
The ratios form a proportion.
Explanation:
1 to 0.4 = 1 : 0.4
= 5/2
9 to 3.6 = 9 : 3.6
= 5/2
So, the ratios form a proportion.
Question 4.
2 : \(\frac{8}{3}\) and \(\frac{2}{3}\) : 6
Answer:
The ratios do not form a proportion.
Explanation:
2 : \(\frac{8}{3}\) = 6 : 8
= 3/4
\(\frac{2}{3}\) : 6 = 2 : 18
= 1/9
So, the ratios do not form a proportion.
Tell whether and are proportional. Explain your reasoning.
Question 5.
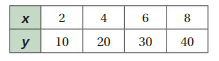
Answer:
x and y are proportional
Explanation:
x/y = 2/10 = 1/5
4/20 = 1/5
6/30 = 1/5
8/40 = 1/5
So, x and y are proportional
Question 6.
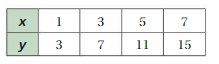
Answer:
x and y are not proportional.
Explanation:
x/y = 1/3, 3/7, 5/11, 7/15
So, x and y are not proportional.
Question 7.
Use the table to write a proportion.
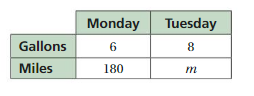
Answer:
1/30 = 8/m
Explanation:
the ratios are proportional
so, 6/180 = 8/m
1/30 = 8/m
Solve the proportion.
Question 8.
\(\frac{x}{8}=\frac{9}{4}\)
Answer:
x = 18
Explanation:
\(\frac{x}{8}=\frac{9}{4}\)
Cross multiply the fractions
4x = 9 * 8
4x = 72
x = 72/4
x = 18
Question 9.
\(\frac{17}{4}=\frac{y}{6}\)
Answer:
y = 51/2
Explanation:
\(\frac{17}{4}=\frac{y}{6}\)
Cross multiply the fractions
17 * 6 = 4y
102 = 4y
y = 102/4
y = 51/2
Tell whether and are proportional. If so, identify the constant of proportionality. Explain your reasoning.
Question 10.
xy – 11 = 5
Answer:
x, y are not proportional.
Explanation:
xy – 11 = 5
xy = 5 + 11
xy = 16
x = 16/y
Question 11.
\(\frac{y}{x}\) = 8
Answer:
x and y are proportional
Explanation:
\(\frac{y}{x}\) = 8
y = 8x
So, x and y are proportional
Question 12.
A recipe calls for \(\frac{2}{3}\) cup flour for every cup sugar. Write the ratio of sugar to flour. Then find and interpret the value of the ratio.
Answer:
The ratio of sugar to flour is 3 : 2.
Explanation:
A recipe calls for \(\frac{2}{3}\) cup flour for every cup sugar
Flour : sugar = 2/3 : 1
Sugar to flour = 1 : 2/3
= 3 : 2
Question 13.
The graph shows the number of cycles of a crosswalk signal during the day and during the night.
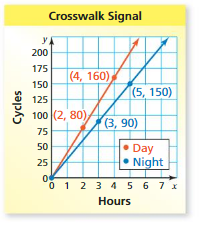
a. Write equations that relate x and y for both the day and night periods.
b. Find how many more cycles occur during the day than during the night for a six-hour period.
Answer:
a. The equation for day is 40 x = y
the equation for night is 30x = y
b. 60 more cycles occur during the day than during the night for a six-hour period.
Explanation:
a. For day, 2 hours is 80 cycles
x/y = 2/80 = 1/40
40x = y
For night, 3 hours is 90
x/y = 3/90 = 1/30
30x = y
a. For day, the number of cycles for 3 hours is 90
90 : 3 = 30 : 1
So, 30 cycles per 1 hour
The number of cycles per 6 hours is 30 * 6 = 180
For night,
the number of cycles is 80 for 2 hours
80 : 2 = 40 : 1
The number of cycles for 6 hours is 40 * 6 = 240
240 – 180 = 60
Question 14.
An engineer is using computer-aided design (CAD) software to design a component for a space shuttle. The scale of the drawing is 1 cm : 60 in. The actual length of the component is 12.75 feet. What is the length of the component in the drawing?
Answer:
The length of the component in the drawing is 25 cm
Explanation:
Write the proportion relating the model length to the actual length. the scale has inches for the actual length units so you must use 12.5 feet = 15 inches in the proportion
model/actual = 1 cm/60 in = x cm/150 in
60x = 150
x = 150/6
= 25
Question 15.
A specific shade of green glaze is made of 5 parts blue glaze to 3 parts yellow glaze. A glaze mixture contains 25 quarts of blue glaze and 9 quarts of yellow glaze. How can you fix the mixture to make the specific shade of green glaze?
Answer:
25 parts blue to 15 parts yellow
Explanation:
25 blue to 9 yellow
The rate is not equal to the specific rate, 5 parts blue to 3 parts yellow
25 parts blue to 15 parts yellow
Ratios and Proportions Cumulative Practice

Question 1.
The school store sells 4 pencils for $0.80. What is the unit cost of a pencil?
A. $0.20
B. $0.80
C. $3.20
D. $5.00
Answer:
A. $0.20
Explanation:
The school store sells 4 pencils for $0.80
= 0.80 : 4
= 0.80/4 : 1
= 0.2 : 1
Question 2.
What is the simplified form of the expression?
3x – (2x – 5)
F. x – 5
G. x + 5
H. 5x – 5
I. – x – 5
Answer:
G. x + 5
Explanation:
The given expression is 3x – (2x – 5)
= 3x – 2x + 5
= x + 5
Question 3.
Which fraction is equivalent to – 1.25?”

Answer:
B.
Explanation:
-1.25 = -125/100
= -5/4
-1(1/4) = -5/4
Question 4.
What is the value of for the proportion \(\frac{8}{12}=\frac{x}{18}\)?

Answer:
x = 12
Explanation:
\(\frac{8}{12}=\frac{x}{18}\)
Cross multiply the fractions
8 * 18 = 12x
144 = 12x
x = 144/12
x = 12
Question 5.
What inequality is represented by the graph?
![]()
F. x – 3 < 7
G. x + 6 ≤ 10
H. – 5 + x < – 1 I. x – 8 > – 4
Answer:
G. x + 6 ≤ 10
Explanation:
the graph represents x ≤ 4.
Solve all the given options
x – 3 < 7
x < 7 + 3
x < 10
G. x + 6 ≤ 10
x ≤ 10 – 6
x ≤ 4
H. – 5 + x < – 1
x < -1 + 5
x < 4
I. x – 8 > – 4
x > -4 + 8
x > 4
Question 6.
What is the missing value in the ratio table?
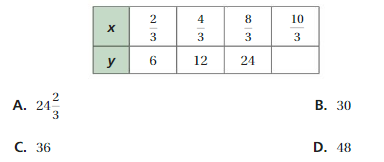
Answer:
B. 30
Explanation:
2/3 • x = 10/3
x = 10/3 • 3/2
x = 5
6 • 5 = 30
Question 7.
Which expression shows factoring 12x + 54 using the GCF?
F. 2(6x + 27)
G. 3(4x + 18)
H. 6(2x + 9)
I. 12(x + \(\frac{9}{2}\))
Answer:
H. 6(2x + 9)
Explanation:
12x = 3 • 2 • 2 • x
54 = 2 • 3 • 9
The common prime factors are 3 • 2 = 6
So, the GCF of 12x + 54 is 6
12x + 54 = 6(2x) + 6(9)
= 6(2x + 9)
Question 8.
The distance traveled by a high-speed train is proportional to the number of hours traveled. Which of the following is not a valid interpretation of the graph?
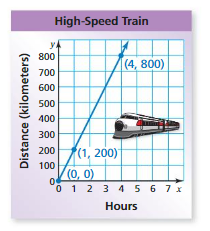
A. The train travels 0 kilometers in 0 hours.
B. The unit rate is 200 kilometers per hour.
C. After 4 hours, the train is traveling 800 kilometers per hour.
D. The train travels 800 kilometers in 4 hours.
Answer:
B. The unit rate is 200 kilometers per hour.
Explanation:
The distance traveled by a high-speed train is proportional to the number of hours traveled
200 proportional to 1 = 200 : 1
Question 9.
Which graph represents a number that is at most – 2?
Answer:
H.
Explanation:
At most means less than or equal to
x ≤ -2
Question 10.
A map of the state where your friend lives has the scale \(\frac{1}{2}\) in. : 10 mi.

Part A Your friend measured the distance between her town and the state capital on the map. Her measurement was 4\(\frac{1}{2}\) inches. Based on your friend’s measurement, what is the actual distance (in miles) between her town and the state capital? Show your work and explain your reasoning.
Part B Your friend wants to mark her favorite campsite on the map. She knows that the campsite is 65 miles north of her town. What distance on the map (in inches) represents an actual distance of 65 miles? Show your work and explain your reasoning.
Answer:
A. 90 miles
B. 3(1/4) inch
Explanation:
A. Write the proportion relating the model distance on the map to the actual distance where x is the actual distance. Then solve the proportion by cross multiplying
model/actual = 1/2/10 = 4(1/2)/x
0.5/10 = 4.5/x
0.5x = 45
x = 45/0.5
x = 90 miles
B. Write the proportion relating the model distance to the actual distance where y is the model distance.
0.5/10 = y/65
cross multiply
10y = 0.5 * 65
10y = 32.5
y = 32.5/10
y = 3.25
= 3(1/4) inch
Question 11.
What is the value of the expression – 56 ÷ (- 8)?

Answer:
– 56 ÷ (- 8) = 7
Explanation:
– 56 ÷ (- 8)
The quotient of two negative integers is positive
56 ÷ 8 = 7
Question 12.
The quantities and are proportional. What is the missing value in the table?
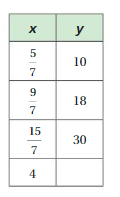
A. 38
B. 42
C. 46
D. 56
Answer:
D. 56
Explanation:
Two quantities are proportional
5/7x = 4
x = 4 (7/5)
x = 28/5
Missing value = 10(28/5) = 2(28) = 56
Question 13.
To begin a board game, you place a playing piece at START. On your first three turns, you move ahead 8 spaces, move back 3 spaces, and then move ahead 2 spaces. How many spaces are you from START?
F. 2
G. 3
H. 7
I. 13
Answer:
H. 7
Explanation:
For the first three turns, you move ahead 8 spaces and move back 3 spaces
= 8 – 3 = 5
move ahead 2 spaces
5 + 2 = 7
Final Words:
Big Ideas Math Answers Grade 7 Chapter 5 Ratios and Proportions detailed pdf is here. Check Big Ideas Math Book Grade 7 Chapter 5 Ratios and proportions and make the learning easy. Therefore collect Big Ideas Math 7th Grade Chapter 5 Ratios and Proportions Answer Key and complete your preparation. Stay tuned to our website to know the trending information regarding Ratios and Proportions. Bookmark our page to know all the details of Grade 7. We wish all the best for all students.
