Middle School Students who are struggling with the concepts of Big Ideas Math Grade 8 Ch 3 Angles and Triangles need not worry anymore. Big Ideas Math Book 8th Grade Chapter 3 Angles and Triangles help you finish your homework in time and gives you assistance whenever you need it. Detailed Solutions provided in Big Ideas Math Grade 8 Answers Chapter 3 make it easy for you to attain knowledge regarding the particular topic in a matter of seconds. Access the BIM Book Grade 8 Ch 3 Angles and Triangles Answer Key via direct links and prepare effectively.
Big Ideas Math Book 8th Grade Answer Key Chapter 3 Angles and Triangles
Access the Big Ideas Math Grade 8 Ch 3 Angles and Triangles Answers includes questions from the Lessons, Chapter Tests, Assessment Tests, Cumulative Practice, etc. Kick start your preparation and attempt the exam with confidence and stand out from the rest of the crowd. Refer to the direct links available for Grade 8 BIM Book Chapter 3 Angles and Triangles Solution Key and prepare the respective topic accordingly in no time.
Performance
Lesson: 1 Parallel Lines and Transversals
Lesson: 2 Angles of Triangles
Lesson: 3 Angles of Polygons
Lesson: 4 Using Similar Triangles
Chapter 3 – Angles and Triangles
- Angles and Triangles Connecting Concepts
- Angles and Triangles Chapter Review
- Angles and Triangles Practice Test
- Angles and Triangles Cumulative Practice
Angles and Triangles STEAM Video/Performance
STEAM Video
Each cell in a honeycomb is in the shape of a regular hexagon. Why might bees use this shape?

Watch the STEAM Video “Honeycombs.” Then answer the following questions.
Question 1.
Enid and Tony show regular tilings made out of squares, equilateral triangles, and regular hexagons. What is the sum of the interior angle measures of the tiling made from equilateral triangles, outlined below in yellow?
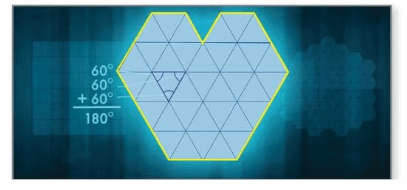
Answer:
The sum of interior angles of the equilateral triangle = 180°
x + x + x = 180°
3x° = 180°
x = 180/3
x° = 60°
Question 2.
The cells in a honeycomb use a tiling pattern of the regular hexagon shown. A cell is 10 millimeters deep. About how much honey can one cell hold? Explain.
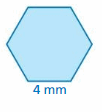
Performance Task
Turtle Shells
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given angle measures of shapes seen on a turtle shell.
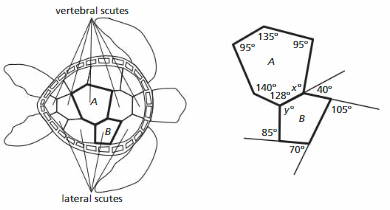

You will be asked to find angle sums and missing angle measures. What other animals have features that resemble geometric shapes?
Angles and Triangles Getting Ready for Chapter 3
Chapter Exploration
When an object is transverse, it is lying or extending across something. In the drawing, the fallen tree lying across the railroad track is transverse to the track.

1. Work with a partner.
• Discuss what it means for two lines to be parallel. Decide on a strategy for drawing parallel lines. Then draw two parallel lines.

• Draw a third line that intersects the parallel lines. This line is called a transversal
a. How many angles are formed by the parallel lines and the transversal? Label each angle.
Answer: 8 angles are formed by the parallel lines and the transversal
b. Which of these angles have equal measures? Explain your reasoning.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what the terms might mean and record your thoughts.

Lesson 3.1 Parallel Lines and Transversals
EXPLORATION 1
Work with a partner. Use geometry software and the lines A and B shown.
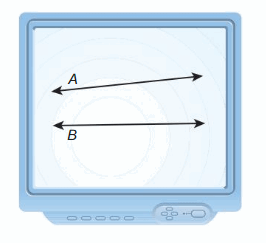
a. Are line A and B line parallel? Explain your reasoning.
b. Draw a line that intersects both line A and line B. What do you notice about the measures of the angles that are created?

c. Rotate line A or line B until the angles created by the intersection of line A and line C are congruent to the angles created by the intersection of line B and line C. What do you notice about line A and line B?
d. Rotate line to create different angle measures. Are the angles that were congruent in part(c) still congruent?
e. Make a conjecture about the measures of the angles created when a line intersects two parallel lines.
3.1 Lesson
Try It
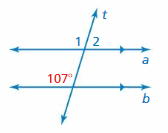
Use the figure to find the measure of the angle. Explain your reasoning
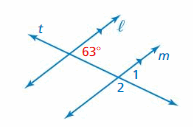
Question 1.
∠1
Answer: 63°
Explanation:
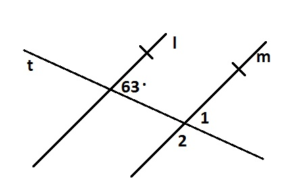
∠1 and 63° angle are corresponding angles are formed by transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠1 is 63°
Question 2.
∠2
Answer: 117°
Explanation:
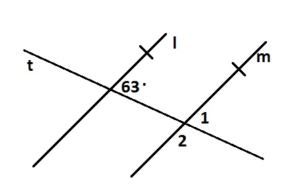
∠1 and ∠2 are supplementary angle.
∠1 + ∠2 = 180°
63° + ∠2 = 180°
∠2 = 180° – 63°
∠2 = 117°
So, the measure of ∠2 = 117°
Try It
Question 3.
Use the figureto find the measures of the numbered angles.
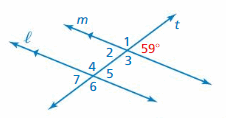
Answer:
∠1 and 59° are the supplementary angles
∠1 + 59° = 180°
∠1 = 180° – 59°
∠1 = 121°
∠2 and 59° are vertical angles. They are congruent.
So, the measure of ∠1 is 121°
∠3 and 59° are supplementary angles.
∠3 + 59° = 180°
∠3 = 180° – 59°
∠3 = 121°
∠4, ∠5, ∠6, ∠7 corresponding angles are congruent because they are formed by a transversal intersecting parallel side.
the measure of ∠4 is 121°
the measure of ∠5 is 59°
the measure of ∠6 is 121°
the measure of ∠7 is 59°
Try It
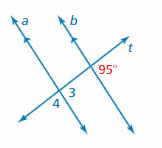
In Example 3, the measure of ∠4 is 84°. Find the measure of the angle. Explain your reasoning.
Question 4.
∠3
Answer:
The measure of ∠4 is 84°.
∠3 and ∠4 are supplementary angles.
∠3 + ∠4 = 180°
∠3 + 84° = 180°
∠3 = 180° – 84°
∠3 = 96°
Question 5.
∠5
Answer:
∠4 and ∠5 are alternate interior angles formed by transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠5 is 84°
Question 6.
∠6
Answer:
∠3 and ∠6 are alternate exterior angles formed by transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠6 is 96°
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
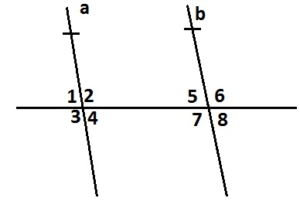
FINDING ANGLE MEASURES
Use the figure to find the measures of the numbered angles.
Question 7.
Answer:
∠1 and 120° are the supplementary angles.
∠1 + 120° = 180°
∠1 = 180 – 120
∠1 = 60°
Thus the measure of ∠1 is 60°
∠2 and 120° are the vertical angles. They are congruent.
Thus the measure of ∠2 is 120°
∠3 and 120° are the supplementary angles.
∠3 + 120° = 180°
∠3 = 180 – 120
∠3 = 60°
∠4, ∠5, ∠6, ∠7 are corresponding angles are formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠4 is 60°
Thus the measure of ∠5 is 120°
Thus the measure of ∠6 is 120°
Thus the measure of ∠7 is 60°
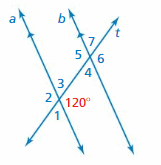
Question 8.
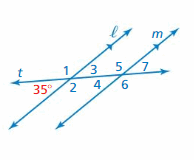
Answer:
∠1 and 35° are the supplementary angles.
∠1 + 35° = 180°
∠1 = 180 – 35
∠1 = 145°
Thus the measure of ∠1 is 145°
∠2 and 35° are the supplementary angles.
∠2 + 35° = 180°
∠2 = 180 – 35
∠2 = 145°
Thus the measure of ∠2 is 145°
∠3 and 35° are the vertical angles. They are congruent.
Thus the measure of ∠3 is 35°
∠4, ∠5, ∠6, ∠7 are corresponding angles are formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠4 is 35°
Thus the measure of ∠5 is 145°
Thus the measure of ∠6 is 145°
Thus the measure of ∠7 is 35°
Question 9.
WHICH ONE DOESN’T BELONG?
Which angle measure does not belong with the other three? Explain your reasoning.

Answer:
∠2, ∠6 are corresponding angles are formed by transversal intersecting parallel lines.
∠6, ∠8 are vertical angles are formed by transversal intersecting parallel lines.
∠5 does not belong to the other three because all the other three measure are equal.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
A cross section of a pier is shown. Find the value of a. Justify your answer.
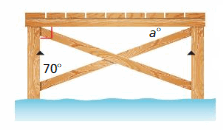
Answer:
The angle a and the angle of 70 degrees are complementary angles because they belong to a right triangle, where the third angle is the right angle.
∠a + 70 = 90
∠a = 90 – 70
∠a = 20°
Question 11.
The head tube angle of a bike determines how easy the bike is to steer. A bike frame with angle approximations is shown. What is the head tube angle of the bike?
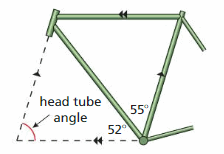
Answer:
The lines AB and CD are parallel.
ABC and BCD are the corresponding angles formed by transversal intersecting parallel lines.
∠BCD = 55°
∠BAC + ∠ABC + ∠ACB = 180°
The sum of the angles in a triangle is 180°
∠BAC + 55°+ 52° = 180°
∠BAC + 107° = 180°
∠BAC = 180° – 107°
∠BAC = 73°
So, the head tube angle of a bike is 73°
Parallel Lines and Transversals Homework & Practice 3.1
Review & Refresh
Find the values of the ratios (red to blue) of the perimeters and areas of the similar figures.
Question 1.
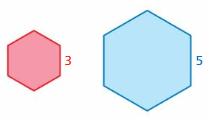
Answer:
perimeter of red hexagon/perimeter of blue hexagon = \(\frac{3}{5}\)
The values of the ratios of the perimeter is \(\frac{3}{5}\)
Area of red hexagon/Area of blue hexagon = (\(\frac{3}{5}\))² = \(\frac{9}{25}\)
The values of the ratios of the area is \(\frac{9}{25}\)
Question 2.
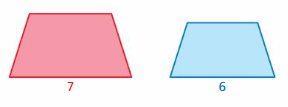
Answer:
perimeter of red trapezium /perimeter of blue trapezium = \(\frac{7}{6}\)
The values of the ratios of the perimeter is \(\frac{7}{6}\)
Area of red hexagon/Area of blue hexagon = (\(\frac{7}{6}\))² = \(\frac{49}{36}\)
The values of the ratios of the area is \(\frac{49}{36}\)
Evaluate the expression.
Question 3.
4 + 32
Answer:
4 + 9 = 13
Question 4.
5(2)2 – 6
Answer:
5(4) – 6
20 – 6 = 14
Question 5.
11 + (-7)2 – 9
Answer:
11 + 49 – 9
11 + 40 = 50
Concepts, Skills, & Problem Solving
EXPLORING INTERSECTIONS OF LINES
Use a protractor to determine whether lines a and b are parallel. (See Exploration 1, p. 103.)
Question 6.
Answer:
Use a protractor to measure ∠1 and ∠2
∠1 ≈ 60°
∠2 ≈ 60°
∠1 and ∠2, it means the two angles are congruent. The angles are exterior alternate angles.
According to the converse of the exterior alternate angles theorem, the two lines are parallel.
a || b
Question 7.
Answer:
Use a protractor to measure ∠1 and ∠2
∠1 ≈ 50°
∠2 ≈ 60°
∠1 and ∠2, it means the two angles are not congruent. The angles are exterior alternate angles.
According to the converse of the exterior alternate angles theorem, the two lines are not parallel.
FINDING ANGLE MEASURES
Use the figure to find the measures of the numbered angles. Explain your reasoning.
Question 8.
Answer:
∠1 and 107° are corresponding angles. They are congruent.
So, the measure of ∠1 is 107°.
∠1 and ∠2 are supplementary angles.
∠1 + ∠2 = 180°
107° + ∠2 = 180°
∠2 = 180° – 107°
∠2 = 73°
So, the measure of ∠2 is 73°
Question 9.
Answer:
∠3 and 95° are corresponding angles. They are congruent.
Thus the measure of ∠3 is 95°
∠3 and ∠4 are supplementary angles.
∠3 + ∠4 = 180°
95° + ∠4 = 180°
∠4 = 180 – 95
∠4 = 85°
So the measure of ∠4 is 85°
Question 10.
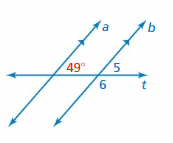
Answer:
∠5 and 49° are corresponding angles. They are congruent.
So, the measure of ∠5 is 49°
∠5 and ∠6 are supplementary angles.
∠5 + ∠6 = 180°
49° + ∠6 = 180°
∠6 = 180° – 49°
∠6 = 131°
So, the measure of ∠6 is 131°
Question 11.
YOU BE THE TEACHER
Your friend describes a relationship between the angles shown. Is your friend correct? Explain your reasoning.

Answer:
Since the two lines are not parallel. Hence ∠5 is not congruent to ∠6.
By this, we can say that your friend is not correct.
Question 12.
PROBLEM SOLVING
The painted lines that separate parking spaces are parallel. The measure of ∠1 is 60°. What is the measure of ∠2? Explain.
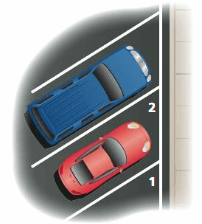
Answer:
∠1 and ∠2 are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
The measure of ∠1 is 60° so the measure of ∠2 is 60°
Question 13.
OPEN-ENDED
Describe two real-life situations that use parallel lines.
Answer:
Example 1: The railroad tracks and the tram tracks are parallel lines.
Example 2: The shelves of a bookcase.
USING CORRESPONDING ANGLES
Use the figure to find the measures of the numbered angles.
Question 14.
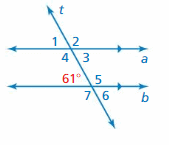
Answer:
∠1 and 60° are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
∠1 and ∠2 are supplementary angles.
∠1 + ∠2 = 180°
60° + ∠2 = 180°
∠2 = 180° – 60°
∠2 = 119°
So, the measure of ∠2 is 119°
∠3 and ∠1 are vertical angles. They are congruent.
So, the measure of ∠3 is 61°
∠4 and ∠2 are vertical angles. They are congruent.
∠5, ∠6, ∠7 corresponding angles are congruent because they are formed by a transversal intersecting parallel lines.
So, the measure of ∠5 is 119°
So, the measure of ∠6 is 61°
So, the measure of ∠7 is 119°
Question 15.
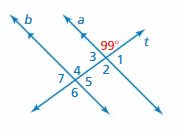
Answer:
∠1 and 99° are supplementary angles.
∠1 + 99° = 180°
∠1 = 180° – 99°
∠1 = 81°
Thus the measure of ∠1 is 81°
∠2 and 99° are vertical angles. They are congruent.
The measure of ∠2 is 99°
∠3 and ∠1 are vertical angles. They are congruent.
So, the measure of ∠3 is 81°
∠4, ∠5, ∠6, ∠7 corresponding angles are congruent because they are formed by a transversal intersecting parallel lines.
So, the measure of ∠4 is 99°
So, the measure of ∠5 is 81°
So, the measure of ∠6 is 99°
So, the measure of ∠7 is 81°
Question 16.
Answer:
∠1 and 90° are supplementary angles.
∠1 + 90° = 180°
∠1 = 180° – 90°
∠1 = 90°
Thus the measure of ∠1 is 90°
∠2 and 90° are vertical angles. They are congruent.
Thus the measure of ∠2 is 90°
∠3 and ∠1 are vertical angles. They are congruent.
So, the measure of ∠3 is 90°
∠4, ∠5, ∠6, ∠7 corresponding angles are congruent because they are formed by a transversal intersecting parallel lines.
So, the measure of ∠4 is 90°
So, the measure of ∠5 is 90°
So, the measure of ∠6 is 90°
So, the measure of ∠7 is 90°
USING CORRESPONDING ANGLES
Complete the statement. Explain your reasoning.
Question 17.
If the measure of ∠1 = 124°, then the measure of ![]()
Answer:
∠1 and ∠8 are corresponding angles. They are congruent.
The measure of ∠1 = 124°, then the measure of ∠8 is 124°
∠8 and ∠4 are supplementary angles.
∠8 + ∠4 = 180°
124° + ∠4 = 180°
∠4 = 180° – 124°
∠4 = 56°
So, the measure of ∠4 is 56°
Question 18.
If the measure of ∠2 = 48°, then the measure of ![]()
Answer:
∠2 and ∠7 are corresponding angles. They are congruent.
The measure of ∠2 = 48°, then the measure of ∠7 is 48°
∠7 and ∠3 are supplementary angles.
∠7 + ∠3 = 180°
48° + ∠3 = 180°
∠3 = 180° – 48°
∠3 = 132°
Thus the measure of ∠3 = 132°
Question 19.
If the measure of ∠4 = 55°, then the measure of ![]()
Answer:
∠4 and ∠2 are alternate interior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠2 is 55°
Question 20.
If the measure of ∠6 = 120°, then the measure of ![]()
Answer:
∠6 and ∠8 are alternate exterior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠8 is 120°
Question 21.
If the measure of ∠7 = 50.5°, then the measure of ![]()
Answer:
∠7 and ∠2 are corresponding angles. They are congruent.
The measure of ∠7 is 50.5°, so the measure of ∠2 is 50.5°
∠2 and ∠6 are supplementary angle.
∠2 + ∠6 = 180°
50.5° + ∠6 = 180°
∠6 = 180° – 50.5°
∠6 = 129.5°
So, the measure of ∠6 is 129.5°
Question 22.
If the measure of ∠3 = 118.7°, then the measure of ![]()
Answer:
∠3 and ∠6 are corresponding angles. They are congruent.
The measure of ∠3 is 118.7°
So, the measure of ∠6 is 118.7°
∠6 and ∠2 are supplementary angles.
∠6 + ∠2 = 180°
118.7° + ∠2 = 180°
∠2 = 180° – 118.7°
∠2 = 61.3°
So, the measure of ∠2 is 61.3°
Question 23.
MODELING REAL LIFE
A rainbow forms when sunlight reflects of raindrops at different angles. For blue light, the measure ∠2 is 40°. What is the measure of ∠1?
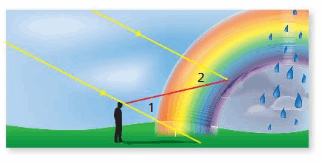
Answer:
∠4 and ∠5 are alternate interior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠1 is 40°
Question 24.
REASONING
Is there a relationship between exterior angles that lie on the same side of a transversal? interior angles that lie on the same side of a transversal? Explain.
Answer:
∠7 and ∠8 are Exterior angles that lie on the same side of the transversal. Hence ∠7 and ∠8 are supplementary angles.
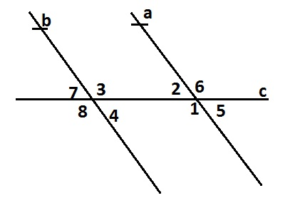
∠3 and ∠4 are interior angles that lie on the same side of the transversal. Hence ∠3 and ∠4 are supplementary angles.
Question 25.
REASONING
When a transversal is perpendicular to two parallel lines, all the angles formed measure 90°. Explain why.
Answer:
When a transversal is perpendicular to two parallel lines, all the angles formed measure 90°.
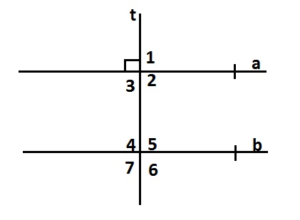
All the angles formed are 90 degrees because perpendicular lines form 90 degree angles.
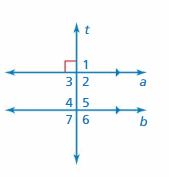
Question 26.
REASONING
Two horizontal lines are cut by a transversal. What is the least number of angle measures you need to know to find the measure of every angle? Explain your reasoning.
Answer:
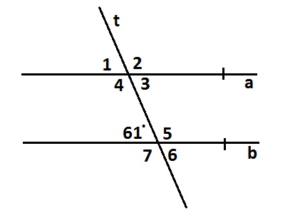
In the below example two horizontal lines a and b are cut by a transversal line t, we know only one angle 61 the measure of all the angles are find with the help of one known measure, 61°
∠1 and 61° are corresponding angles formed by a transversal intersecting parallel lines. the angles are congruent.
Thus the measure of ∠1 is 61°
∠1 and ∠2 are supplementary angles.
∠1 + ∠2 = 180°
61° + ∠2 = 180°
∠2 = 180° – 61°
∠2 = 119°
Thus the measure of ∠2 is 119°
∠3 and ∠1 are vertical angles. They are congruent.
Thus the measure of ∠3 is 61°
∠4 and ∠2 are vertical angles. They are congruent.
Thus the measure of ∠4 is 119°
∠5, ∠6, ∠7 corresponding angles are formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠5 is 119°
Thus the measure of ∠6 is 61°
Thus the measure of ∠7 is 119°
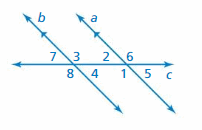
Question 27.
LOGIC
Describe two ways you can show that ∠1 is congruent to ∠7.
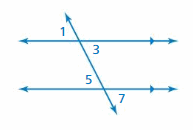
Answer:
∠1 and ∠7 are alternate exterior angles formed by a transeversal intersecting parallel lines. So, ∠1 and ∠7 are congruent.
∠1 and ∠5 are corresponding angles formed by a transeversal intersecting parallel lines. So, ∠1 and ∠5 are congruent.
∠5 and ∠7 are vertical angles so they are congruent.
Hence ∠1 and ∠7 are congruent.
FINDING A VALUE
Find the value of x.
Question 28.
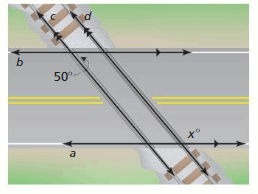
Answer:
∠1 and 50° are alternate interior angles. They are congruent.
So, the measure of ∠1 is 50°
∠2 and ∠1 are corresponding angles. They are congruent.
So, the measure of ∠2 is 50°
∠2 and x are supplementary angle.
∠2 + x = 180°
50° + x = 180°
x = 180° – 50°
x = 130°
So, the measure of x is 130°
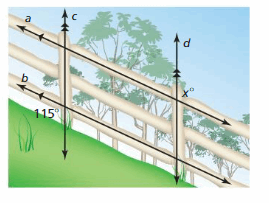
Question 29.
Answer:
∠1 and 115° are corresponding angles. They are congruent.
So, the measure of ∠1 is 115°
∠1 and x are alternate exterior angles. They are congruent.
So, the measure of x is 115°
Question 30.
PROJECT
Trace line p and line t on a piece of paper. Label ∠1. Move the paper so that ∠1 aligns with ∠8. Describe the transformations that you used to show that ∠1 is congruent to ∠8.
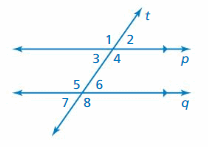
Answer: 180° rotation, translation about line t.
Question 31.
OPEN-ENDED
Refer to the figure.
a. Do the horizontal lines appear to be parallel? Explain.
Answer: The three horizontal lines seem to spread apart, even though in reality they are parallel.
b. Draw your own optical illusion using parallel lines.
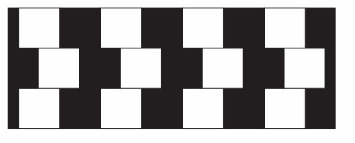
Answer:

Question 32.
DIG DEEPER!
The figure shows the angles used to make a shot on an air hockey table.
a. Find the value of x.
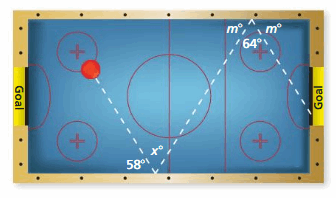
Answer:
As the lines AB and CD are parallel and ∠BCD are alternate interior angles transversal BC, they are congruent.
∠ABC ≅ ∠BCD
x = 64
b. How does the angle the puck hits the edge of the table relate to the angle it leaves the edge of the table?
Answer:
m∠MBA + m∠ABC + m∠CBN = 180°
58 ° + 64° + m∠CBN = 180°
122 ° + m∠CBN = 180°
m∠CBN = 180° – 122 °
m∠CBN = 58°
Lesson 3.2 Angles of Triangles
EXPLORATION 1
Exploring Interior and Exterior Angles of Triangles
Work with a partner.
a. Draw several triangles using geometry software. What can you conclude about the sums of the angle measures?
b. You can extend one side of a triangle to form an exterior angle as shown.
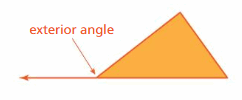
Use geometry software to draw a triangle and an exterior angle. Compare the measure of the exterior angle with the measures of the interior angles. Repeat this process for several different triangles. What can you conclude?
Answer:
EXPLORATION 2
Using Parallel Lines and Transversals
Work with a partner. Describe what is shown in the figure below. Then use what you know about parallel lines and transversals to justify your conclusions in Exploration 1.
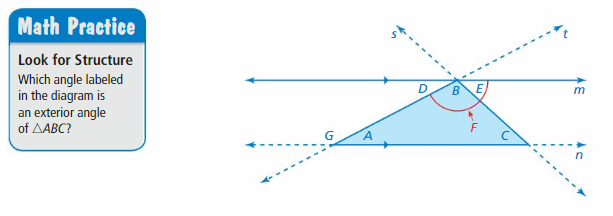
Answer:
3.2 Lesson
Try It
Find the measures of the interior angles of the triangle.
Question 1.
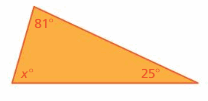
Answer: 81°, 25°, 74°
Explanation:
Sum of all the angles in a triangle = 180°
x° + 81° + 25° = 180°
x° = 180° – 81° – 25°
x = 74°
Thus the measure of the interior angle is 74°
Question 2.
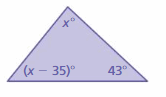
Answer: 43°, 51°, 86°
Explanation:
Sum of all the angles in a triangle = 180°
x° + (x – 35)° + 43° = 180°
x° + x° – 35° + 43° = 180°
2x° + 8° = 180°
2x° = 180° – 8°
2x° = 172°
x° = 172°/2
x° = 86°
The measure of the interior angle of the triangle
(x – 35)° = 86 – 35
(x – 35)° = 51°
x° = 51° + 35°
x° = 86°
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
VOCABULARY
How many exterior angles does a triangle have at each vertex? Explain.
Answer:
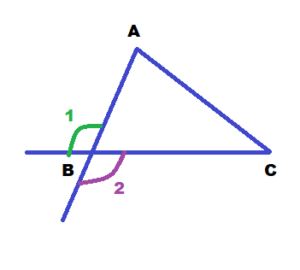
At each vertex of a triangle, there are two exterior angles, which are congruent.
FINDING ANGLE MEASURES
Find the value of x.
Question 5.
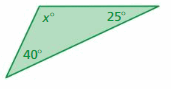
Answer:
Sum of all the angles in a triangle = 180°
x° + 25° + 40° = 180°
x° + 65° = 180°
x° = 180°
x° = 180° – 65°
x° = 115°
Thus the value of x is 115°
Question 6.
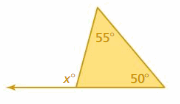
Answer:
x° = 50° + 55°
x° = 105°
Thus the value of x is 105°
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
The Historic Triangle in Virginia connects Jamestown, Williamsburg, and Yorktown. The interior angle at Williamsburg is 120°. The interior angle at Jamestown is twice the measure of the interior angle at Yorktown. Find the measures of the interior angles at Jamestown and Yorktown. Explain your reasoning.
Answer:
The interior angle at Williamsburg is 120°.
Let the interior angles at Jamestown be x°
Let the interior angles at Yorktown be 2x°
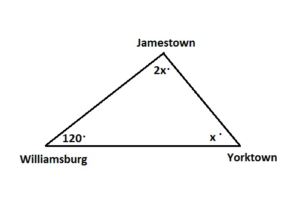
Sum of all the angles in a triangle = 180°
x° + 2x° + 120° = 180°
3x° + 120° = 180°
3x° = 180° – 120°
3x° = 60°
x° = 60/3
x° = 20°
The interior angles at Jamestown be x° = 20°
The interior angles at Yorktown be 2x° = 2(20)° = 40°
Question 8.
A helicopter travels from point C to point A to perform a medical supply drop. The helicopter then needs to land at point B. How many degrees should the helicopter turn at point A to travel towards point B? Justify your answer.
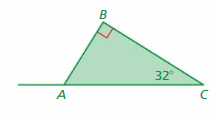
Answer:
Given,
A helicopter travels from point C to point A to perform a medical supply drop.
The helicopter then needs to land at point B.
A = 90° + 32°
A = 122°
Thus the helicopter should turn 122° at point A to travel towards point B.
Angles of Triangles Homework & Practice 3.2
Review & Refresh
Use the figure to find the measure of the angle. Explain your reasoning.
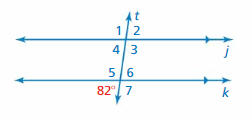
Question 1.
∠2
Answer: 82°
∠2 and 82° are alternate exterior angles formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠2 is 82°
Question 2.
∠6
Answer: 82°
∠6 and 82° are vertical angles formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠6 is 82°
Question 3.
∠4
Answer: 82°
∠4 and 82° are corresponding angles formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠4 is 82°
Question 4.
∠1
Answer: 98°
∠4 and 82° are corresponding angles formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠4 is 82°
∠4 and ∠1 are supplementary angles
∠4 + ∠1 = 180°
82° + ∠1 = 180°
∠1 = 180° – 82°
∠1 = 98°
You spin the spinner shown.
Question 5.
What are the favorable outcomes of spinning a number less than 4?
Answer: 1, 2, 3
Explanation:
The favorable outcome of spinning a number less than 4 is 1, 2, and 3.
Question 6.
In how many ways can spinning an odd number occur?
Answer: two ways
Odd numbers = 1 and 3
So, in two ways spinning an odd number can occur.
Concepts, Skills, & Problem Solving
USING PARALLEL LINES AND TRANSVERSALS
Consider the figure below. (See Exploration 2, p. 111.)
Question 7.
Use a protractor to find the measures of the labeled angles.
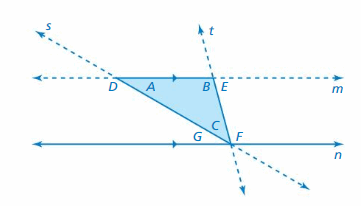
Answer:
Use a protractor to determine the measures of the angles A, B, C.
m∠A = 30°
m∠B = 105°
m∠C = 45°
m∠D = 150°
m∠E = 75°
m∠F = 105°
m∠G = 30°
Question 8.
Is ∠F an exterior angle of Triangle ABC ? Justify your answer.
Answer:
An exterior angle is the angle between one side of a triangle and the extension of an adjacent side. ∠F is not an exterior angle of triangle ABC because it has a side of triangle ABC, but not the extension of the adjacent side DF.
USING INTERIOR ANGLE MEASURES
Find the measures of the interior angles of the triangle.
Question 9.
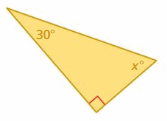
Answer:
Sum of all the angles in a triangle = 180°
x° + 90° + 30° = 180°
x° + 120° = 180°
x° = 180° – 120°
x° = 60°
Question 10.
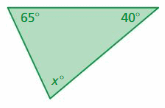
Answer:
Sum of all the angles in a triangle = 180°
x° + 65° + 40° = 180°
x° + 105° = 180°
x° = 180° – 105°
x° = 75°
Question 11.
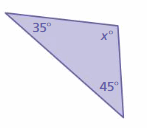
Answer:
Sum of all the angles in a triangle = 180°
x° + 35° + 45° = 180°
x° + 80° = 180°
x° = 180° – 80°
x° = 100°
Question 12.

Answer:
Sum of all the angles in a triangle = 180°
x° + (x + 65)° + 25° = 180°
x° + x° + 65° + 25° = 180°
2x° + 90° = 180°
2x° = 180° – 90°
2x° = 90°
x° = 90°/2
x° = 45°
(x + 65)° = 45 + 65 = 110
x° = 25°
Question 13.
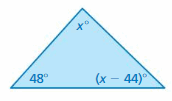
Answer:
Sum of all the angles in a triangle = 180°
x° + (x – 44)° + 48° = 180°
x° + x° – 44° + 48° = 180°
2x° + 4° = 180°
2x° = 180° – 4°
2x° = 176°
x° = 176°/2
x° = 88°
(x – 44)° = 88 – 44 = 44
x° = 44°
Question 14.
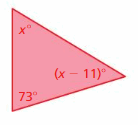
Answer:
Sum of all the angles in a triangle = 180°
x° + (x – 11)° + 73° = 180°
x° + x° – 11° + 73° = 180°
2x° + 62° = 180°
2x° = 180° – 62°
2x° = 118°
x° = 118°/2
x° = 59°
(x – 11)° = 59 – 11 = 48
x° = 48°
FINDING EXTERIOR ANGLE MEASURES
Find the measure of the exterior angle.
Question 15.
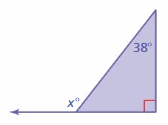
Answer:
x° = 38° + 90°
x° = 128°
The measure of exterior angle is 128°
Question 16.
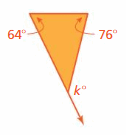
Answer:
k° = 64° + 76°
k° = 140°
The measure of an exterior angle is 140°
Question 17.
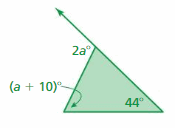
Answer:
2a° = (a + 10°) + 44°
2a° = a + 54°
2a° – a° = 54
a° = 54
The measure of the exterior angle = 2a = 2(54°) = 108°
Question 18.
MODELING REAL LIFE
A tornado is located between city hall and a cell phone tower and is heading towards the cell phone tower. By what angle does the tornado’s direction need to change so that it passes over the radar station instead? Justify your answer.
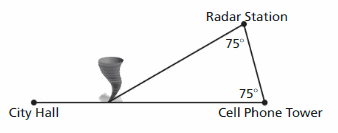
Answer:
Sum of all the angles in a triangle = 180°
x° + 75° + 75° = 180°
x° + 150° – 150° = 180° – 150°
x° = 30°
Thus the angle that tornado direction needs to change is 30°.
Question 19.
YOU BE THE TEACHER
Your friend finds the measure of the exterior angle shown. Is your friend correct? Explain your reasoning.

Answer:
Your friend is not correct because the measure of the exterior angle is equal to the sum of two non-adjacent interior angles.
Question 20.
REASONING
The ratio of the interior angle measures of a triangle is 2 : 3 : 5. What are the angle measures?
Answer:
Sum of all the angles in a triangle = 180°
2x° + 3x° + 5x° = 180°
10x° = 180°
x = 180/10
x = 18°
2x° = 2(18°) = 36°
3x° = 3(18) = 54°
5x° = 5(18) = 90°
Question 21.
PROBLEM SOLVING
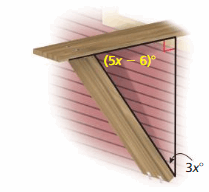
The support for a window air-conditioning unit forms a triangle and an exterior angle. What is the measure of the exterior angle?
Answer:
The measure of the exterior angle DBC is
m∠DBC = m∠ABC + m∠ACB
m∠ABC + m∠ACB = 90°
5x – 6 + 3x = 90
8x – 6 = 90
8x = 90 + 6
8x = 96
x = 96/8
x = 12
m∠DBC = m∠BAC+ m∠ACB
= 90° + 3(12)°
= 126°
Question 22.
REASONING
A triangle has an exterior angle with a measure of 120°. Can you determine the measures of the interior angles? Explain.
Answer:
A triangle has an exterior angle with a measure of 120°
m∠ACB = m∠A + m∠B
m∠A + m∠B = 120°
According to the exterior angles
We have
m∠C + m∠ACD = 180°
m∠C + 120° = 180°
m∠C = 180° – 120°
m∠C = 60°
ANGLES OF TRIANGLES
Determine whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 23.
Given three angle measures, you can construct a triangle.
Answer:
We can construct a triangle if the sum of the measure of the 3 angles is 180°.
As a matter of fact, if the sum of the measures of the 3 angles is 180°
We can build an infinity of triangles that are similar.
Question 24.
The acute interior angles of a right triangle are complementary.
Answer:
Let A, B, C be the angles of a right triangle with m∠A = 90°
m∠A + m∠B + m∠C = 180°
90° + m∠B + m∠C = 180°
m∠B + m∠C = 180° – 90°
m∠B + m∠C = 90°
This means ∠B and ∠C are complementary.
Question 25.
A triangle has more than one vertex with an acute exterior angle.
Answer:
An exterior angle of a triangle and the adjacent triangle’s angle are complementary. If an exterior angle is acute, it means the adjacent triangle’s angle is obtuse.
Since we are given that more than one exterior angle is acute, it means the triangle would have more than one obtuse angle, which is impossible.
The statement is never true.
Question 26.
DIG DEEPER!
Using the figure at the right, show that z = x + y. (Hint: Find two equations involving w.)
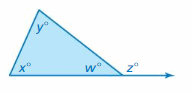
Answer:
The angles z and w are supplementary
z + w = 180°
The sum of a triangle is 180°
x + y + w = 180°
z = 180° – w
x + y = 180° – w
z = x + y
Lesson 3.3 Angles of Polygons
EXPLORATION 1
Work with a partner. In parts (a)-(f), use what you know about the interior angle measures of triangles to find the sum of the interior angle measures of each figure.
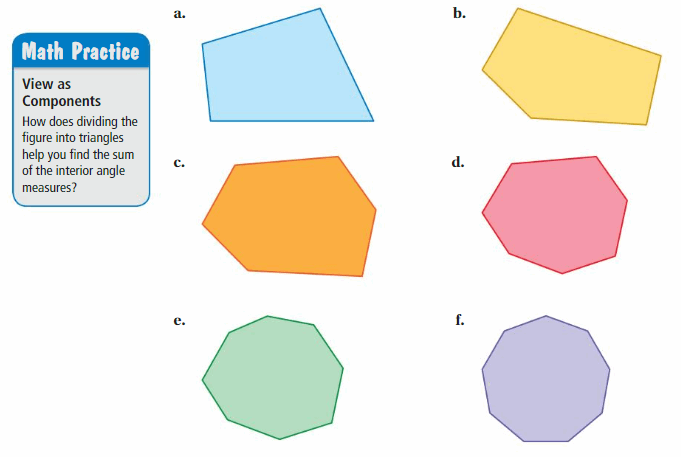
g. REPEATED REASONING
Use your results in parts (a)–(f) to complete the table. Then write an equation that represents the sum of the interior angle measures of a polygon with n sides.
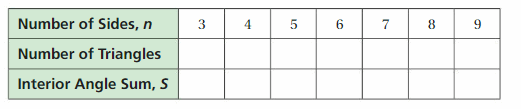
Answer:
3.3 Lesson
Try It
Find the sum of the interior angle measures of the green polygon.
Question 1.

Answer:
S = (n – 2) . 180°
S = (7 – 2) . 180°
S = 5 . 180°
S = 900°
Thus the sum of the interior angle measure is 900°
Question 2.

Answer:
S = (n – 2) . 180°
S = (6 – 2) . 180°
S = 4 . 180°
S = 720°
Thus the sum of the interior angle measure is 720°
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
WRITING
Explain how to find the sum of the interior measures of a polygon.

Answer:
Steps to find the sum of the interior measurements of the polygon:
1. Count the number of sides of the polygon.
2. Subtract the number of sides by 2.
3. Multiply the result of the subtraction by 180°
Question 6.
FINDING THE SUM OF INTERIOR ANGLE MEASURES
Find the sum of the interior angle measures of the green polygon.
Answer:
S = (n – 2) . 180°
S = (4 – 2) . 180°
S = 2 . 180°
S = 360°
Thus the sum of the interior angle measure is 360°
FINDING AN INTERIOR ANGLE MEASURE
Find the value of x.
Question 7.
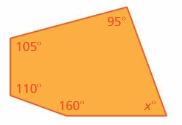
Answer:
S = (n – 2) . 180°
S = (5 – 2) . 180°
S = 3 . 180°
S = 540°
Thus the sum of the interior angle measure is 540°
x° + 160° + 110° + 105° + 95° = 540°
x° + 470° = 540°
x° = 540° – 470°
x° = 70°
Thus the value of x is 70°.
Question 8.
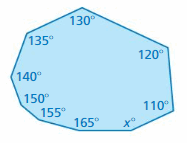
Answer:
S = (n – 2) . 180°
S = (9 – 2) . 180°
S = 7 . 180°
S = 1260°
Thus the sum of the interior angle measure is 1260°
x° + 165° + 155° + 150° + 140° + 135° + 130° + 125° + 110° = 1260°
x° + 1105° = 1260°
x° = 1260° – 1105°
x° = 155°
Thus the value of x is 155°
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
A company installs an octagonal swimming pool.
a. Find the value of a for the pool shown at the left.
Answer:
S = (n – 2) . 180°
S = (8 – 2) . 180°
S = 6 . 180°
S = 1080°
Thus the sum of the interior angle measure is 1080°
a° + 120° + a° + 120° + a° + 120° + a° + 120° = 1080°
4a° + 480° = 1080°
4a° = 1080° – 480°
4a° = 600°
a° = 600/4
a° = 150°
Thus the value of x is 150°.
b. The company installs a different pool that is also in the shape of an octagon. The second pool has twice the length and one-third the width of the first pool. Are the sums of the interior angles of the pools different? Justify your answer.
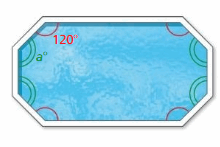
Answer:
No for any octagon the sum of the interior angles is 1080 degrees.
Question 10.
DIG DEEPER!
A Bronze Star Medal A is shown.
a. How many interior angles are there?
Answer: 10 interior angles are there
b. What is the sum of the interior angle measures?

Answer:
S = (n – 2) . 180°
S = (10 – 2) . 180°
S = 8 . 180°
S = 1440°
Thus the sum of the interior angle measure is 1440°
Angles of Polygons Homework & Practice 3.3
Find the value of x.
Question 1.
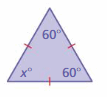
Answer: 60°
Explanation:
Sum of all the angles = 180°
x° + 60° + 60° = 180°
x° + 120° = 180°
x° = 180° – 120°
x° = 60°
Question 2.
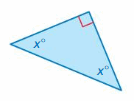
Answer: 45°
Explanation:
Sum of all the angles = 180°
x° + x° + 90° = 180°
2x° + 90° = 180°
2x° = 180° – 90°
2x° = 90°
x° = 45°
Question 3.
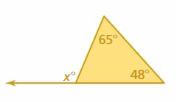
Answer: 113°
Explanation:
x° = 65° + 48°
x° = 113°
Thus the measure of an exterior angle is 113°
Solve the proportion.
Question 4.
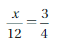
Answer: 9
Explanation:
\(\frac{x}{12}\) = \(\frac{3}{4}\)
12 . \(\frac{x}{12}\) = \(\frac{3}{4}\) . 12
x = 3 . 3
x = 9
Question 5.
![]()
Answer: 2
Explanation:
\(\frac{14}{21}\) = \(\frac{x}{3}\)
3 . \(\frac{14}{21}\) = \(\frac{x}{3}\) . 3
x = 2
Question 6.
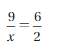
Answer: 3
Explanation:
\(\frac{9}{x}\) = \(\frac{6}{2}\)
2. \(\frac{9}{x}\) = 6
18 = 6x
x = 3
Concepts, Skills, & Problem Solving
EXPLORING INTERIOR ANGLES OF POLYGONS
Use triangles to find the sum of the interior angle measures of the polygon. (See Exploration 1, p. 117.)
Question 7.

Answer: 360°
Explanation:
Number of sides = 4
Number of interior triangles in the given figure = 2
The Sum of the measures of the interior angles using triangle = 2 . 180° = 360°
Question 8.

Answer: 1260°
Explanation:
Number of sides = 9
Number of interior triangles in the given figure = 7
The Sum of the measures of the interior angles using triangle = 7 . 180° = 1260°
Question 9.

Answer: 540°
Explanation:
Number of sides = 5
Number of interior triangles in the given figure = 3
The Sum of the measures of the interior angles using triangle = 3 . 180° = 540°
FINDING THE SUM OF INTERIOR ANGLE MEASURES
Find the sum of the interior angle measures of the polygon.
Question 10.
Answer: 360°
Explanation:
S = (n – 2) . 180°
S = (4- 2) . 180°
S = 2 . 180°
S = 360°
Thus the sum of the interior angle measure is 360°
Question 11.
Answer: 1080°
Explanation:
S = (n – 2) . 180°
S = (8- 2) . 180°
S = 6 . 180°
S = 1080°
Thus the sum of the interior angle measure is 1080°
Question 12.
Answer: 1260°
Explanation:
S = (n – 2) . 180°
S = (9- 2) . 180°
S = 7 . 180°
S = 1260°
Thus the sum of the interior angle measure is 1260°
Question 13.
YOU BE THE TEACHER
Your friend finds the sum of the interior angle measures of a 13-gon. Is your friend correct? Explain your reasoning.
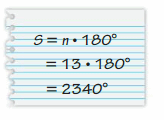
Answer:
To find the sum of the interior angle measures he should subtract 2 from the number of sides of the polygon and then multiply by 180°
S = (n – 2) . 180°
By this, we can say that your friend is not correct.
FINDING AN INTERIOR ANGLE MEASURE
Find the value of x.
Question 14.
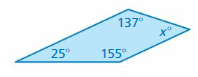
Answer:
S = (n – 2) . 180°
S = (4- 2) . 180°
S = 2 . 180°
S = 360°
Thus the sum of the interior angle measure is 360°
x° + 155° + 25° + 137° = 360°
x° + 317° = 360°
x° = 360° – 317°
x° = 43°
Question 15.
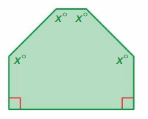
Answer:
S = (n – 2) . 180°
S = (6- 2) . 180°
S = 4 . 180°
S = 720°
Thus the sum of the interior angle measure is 720°
x° + x° + x° + x° + 90° + 90° = 720°
4x° + 180° = 720°
4x° = 720° – 180°
4x° = 540°
x° = 540/4
x° = 135°
Question 16.
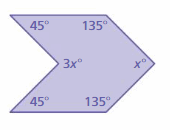
Answer:
S = (n – 2) . 180°
S = (6- 2) . 180°
S = 4 . 180°
S = 720°
Thus the sum of the interior angle measure is 720°
3x° + 45° + 135° + x° + 135° + 45° = 720°
4x° + 360° = 720°
4x° = 720° – 360°
4x° = 360°
x° = 360/4
x° = 90°
FINDING A MEASURE
Find the measure of each interior angle of the regular polygon.
Question 17.

Answer:
S = (n – 2) . 180°
S = (3- 2) . 180°
S = 1 . 180°
S = 180°
Thus the sum of the interior angle measure is 180°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 3.
180 ÷ 3 = 60°
Question 18.

Answer:
S = (n – 2) . 180°
S = (9 – 2) . 180°
S = 7 . 180°
S = 1260°
Thus the sum of the interior angle measure is 1260°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 9.
1260 ÷ 9 = 140°
Question 19.

Answer:
S = (n – 2) . 180°
S = (12 – 2) . 180°
S = 10 . 180°
S = 1800°
Thus the sum of the interior angle measure is 1800°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 12.
1800 ÷ 12 = 150°
Question 20.
YOU BE THE TEACHER
Your friend finds the measure of each interior angle of a regular 20-gon. Is your friend correct? Explain your reasoning.

Answer:
No, my friend is not correct because to find the measure of each interior angle of a regular 20-gon, he should divide the sum of the measured interior angles by the number of interior angles, in this case, 20 but your friend divide it by 18 so he is not correct.
Question 21.
MODELING REAL LIFE
A firehydrant bolt is in the shape of a regular pentagon.

a. What is the measure of each interior angle?
Answer:
S = (n – 2) . 180°
S = (5- 2) . 180°
S = 3 . 180°
S = 540°
Thus the sum of the interior angle measure is 540°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 5.
540÷ 5 = 108°
b. RESEARCH
Why are firehydrants made this way?
Question 22.
PROBLEM SOLVING
The interior angles of a regular polygon each measure 165°. How many sides does the polygon have?
Answer:
(n – 2) . 180 = 165 . n
180n – 360 = 165n
180n – 360 + 360 – 165n = 165n + 360 – 165n
15n = 360
n = 360/15
n = 24
Therefore the polygon has 24 sides
Question 23.
STRUCTURE
A molecule can be represented by a polygon with interior angles that each measure 120°. What polygon represents the molecule? Does the polygon have to be regular? Justify your answers.
Answer:
(n – 2) . 180 = 120 . n
180n – 360 = 120n
180n – 120n = 360
60n = 360
n = 6
Question 24.
PROBLEM SOLVING
The border of a Susan B. Anthony dollar is in the shape of a regular polygon.
a. How many sides does the polygon have?
Answer: The polygon has 11 sides.
b. What is the measure of each interior angle of the border? Round your answer to the nearest degree.

Answer:
S = (n – 2) . 180°
S = (11 – 2) . 180°
S = 9 . 180°
S = 1620°
Thus the sum of the interior angle measure is 1620°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 11.
1620 ÷ 11 = 147°
Question 25.
REASONING
The center of the stained glass window is in the shape of a regular polygon. What are the measures of the interior angles of the green triangle?
Answer:
(n-2)180°/n = (8-2)180°/8 = 135°
m∠OAB = m∠OBA = 135/2 = 67.5°
m∠AOB + m∠OAB + m∠OBA = 180°
m∠AOB + 67.5° + 67.5° = 180°
m∠AOB + 135° = 180°
m∠AOB = 180° – 135°
m∠AOB = 45°
Question 26.
GEOMETRY
Draw a pentagon that has two right interior angles, two 45° interior angles, and one 270° interior angle.

Answer:
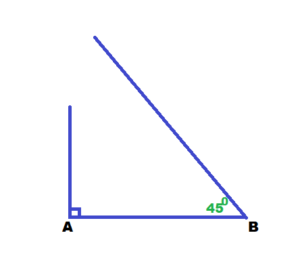
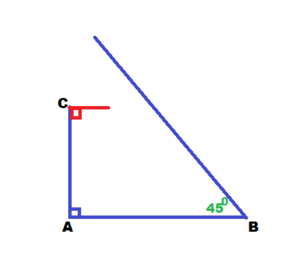
Question 27.
DIG DEEPER!
The floor of a gazebo is in the shape of a heptagon, a seven-sided polygon. Four of the interior angles measure 135°. The other interior angles have equal measures. Find their measures.

Answer:
The given polygon has 7 sides.
S = (n – 2) . 180°
S = (7 – 2) . 180°
S = 5 . 180°
S = 900°
Thus the sum of the interior angle measure is 900°
4 . 135° + 3 . x° = 900°
540° + 3x° = 900°
3x° = 900° – 540°
3x° = 360°
x° = 360/3
x° = 120°
Lesson 3.4 Using Similar Triangles
Using Similar Triangles
EXPLORATION 1
Work with a partner. Use geometry software.
a. Draw a triangle that has a 50° angle and a 30° angle. Then draw a triangle that is either larger or smaller that has the same two angle measures. Are the triangles congruent? similar? Explain your reasoning.
a. Choose any two angle measures whose sum is less than 180°. Repeat part(a) using the angle measures you chose.
c. Compare your results in parts (a) and (b) with other pairs of students. Make a conjecture about two triangles that have two pairs of congruent angles.
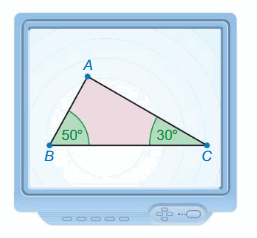
Answer:
EXPLORATION 2
Using Indirect Measurement
Work with a partner. Use the fact that two rays from the Sun are parallel to make a plan for how to find the height of the flagpole. Explain your reasoning.
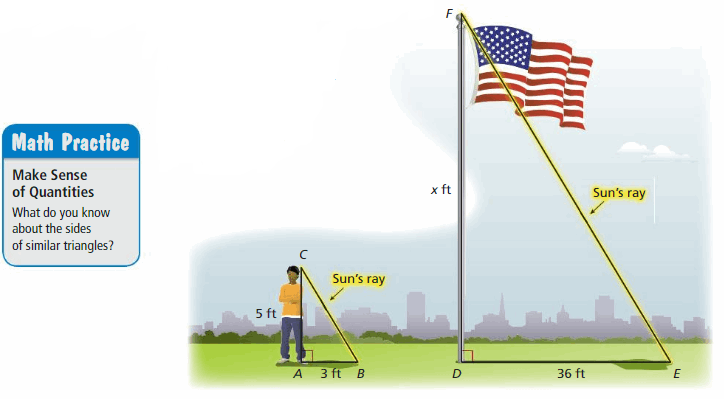
Answer:
3.4 Lesson
Try It
Tell whether the triangles are similar. Explain.
Question 1.
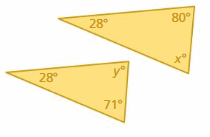
Answer: No
Explanation:
x° + 28° + 80° = 180°
x° + 108° = 180°
x° = 180° – 108°
x° = 72°
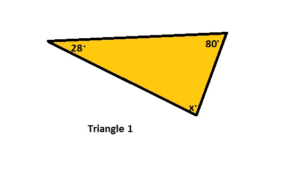
y° + 28° + 71° = 180°
y° + 99° = 180°
y° = 180° – 99°
y° = 81°
The triangles do not have two pairs of congruent angles.
So, the triangles are not similar.
Question 2.
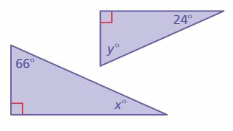
Answer: Yes
Explanation:
x° + 66° + 90° = 180°
x° + 156° = 180°
x° = 180° – 156°
x° = 24°
y° + 24° + 90° = 180°
y° + 114° = 180°
y° = 180° – 114°
y° = 66°
The triangles have two pairs of congruent angles.
Thus the triangles are similar.
Try It
Question 3.
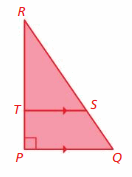
Can you determine whether △PQR and △TSRand are similar? Explain.
Answer: No
Explanation:
We are not given any information about the lengths of the sides either, therefore with only a pair of congruent angles, we cannot tell whether the triangles are similar.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
IDENTIFYING SIMILAR TRIANGLES
Tell whether the triangles are similar. Explain.
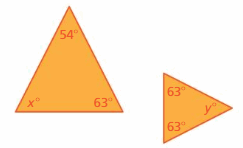
Answer: Yes
Explanation:
x° + 54° + 63° = 180°
x° + 107° = 180°
x° = 180° – 107°
x° = 63°
Question 5.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
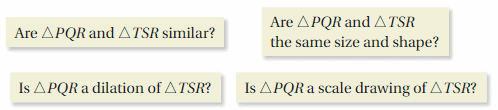
Answer: Option B
Explanation:
ΔPQR and ΔTSR are congruent as TS || PQ leads to two pairs of correspondent congruent angles.
ΔPQR is a dilation of ΔTSR because their sides are proportional, the constant of proportionality being greater than 1.
ΔPQR is a scale drawing of ΔTSR because their sides are proportional.
The question that does not fit is
“Are ΔPQR and ΔTSR the same size and shape?”
because the triangles do not have the same size, but they have the same shape.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
DIG DEEPER!
Engineers plan to construct an aqueduct to transport water from the top of a ridge to farmland. A portion of the project is complete. Find the length of the entire aqueduct.
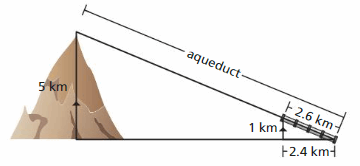

Answer:
Aqueduct/2.6 = 5/1
Aqueduct = 5 × 2.6
Aqueduct = 13
Thus the length of the Aqueduct is 13 km.
Question 7.
You want to go on a swamp tour. How long does it take a swamp vehicle that travels at 3.2 miles per hour to travel across the swamp, from point Z to point Y? Justify your answer.
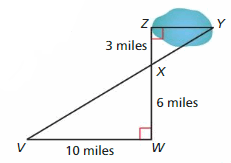
Answer:
a/10 = 3/6
6 × a = 3 × 10
6a = 30
a = 30/6
a = 5
The length from point Z to point Y is 5 miles.
Time to travel from point Z to point Y = 5/3.5 = 1.56 hour
Using Similar Triangles Homework & Practice 3.4
Review & Refresh
Find the measure of each interior angle of the regular polygon.
Question 1.
octagon
Answer: The measure of each interior angle is 135°
Explanation:
S = (n – 2) . 180°
S = (8- 2) . 180°
S = 6 . 180°
S = 1080°
Thus the sum of the interior angle measure is 1080°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 8.
1080÷ 8= 135°
Question 2.
decagon
Answer: The measure of each exterior angle is 144°
Explanation:
S = (n – 2) . 180°
S = (10 – 2) . 180°
S = 8 . 180°
S = 1440°
Thus the sum of the interior angle measure is 1440°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 10.
1440÷ 10= 144°
Question 3.
18-gon
Answer: The measure of each interior angle is 160°
Explanation:
S = (n – 2) . 180°
S = (18- 2) . 180°
S = 16 . 180°
S = 2880°
Thus the sum of the interior angle measure is 2880°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 18.
2880 ÷ 18= 160°
Solve the equation. Check your solution.
Question 4.
3.5 + y = -1
Answer:
Given the equation
3.5 + y = -1
y = -1 – 3.5
y = -4.5
Question 5.
9x = 54
Answer:
Given the equation
9x = 54
x = 54/9
x = 6
Question 6.
-4 = \(\frac{2}{7}\)p
Answer:
Given the equation
-4 = \(\frac{2}{7}\)p
-4 × 7 = 2p
2p = -28
p = -28/2
p = -14
Concepts, Skills, & Problem Solving
CREATING SIMILAR TRIANGLES
Draw a triangle that is either larger or smaller than the one given and has two of the same angle measures. Explain why the new triangle is similar to the original triangle. (See Exploration 1, p. 123.)
Question 7.
Answer:
The above triangle and the given triangle are similar because the two angles in both the triangles are the same so the third angle is also the same.
Question 8.
Answer:

The above triangle and the given triangle are similar because the two angles in both the triangles are the same so the third angle is also the same.
IDENTIFYING SIMILAR TRIANGLES
Tell whether the triangles are similar. Explain.
Question 9.
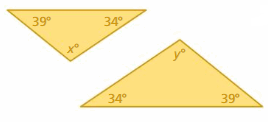
Answer: The triangles have two pairs of congruent angles.
So, the third angles are congruent, and the triangles are similar.
Question 10.
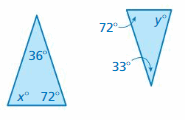
Answer:
x° + 36° + 72° = 180°
x° + 108° = 180°
x° = 180° – 108°
x° = 72°
y° + 33° + 72° = 180°
y° + 105° = 180°
y° = 180° – 105°
y° = 72°
The triangles do not have two pairs of congruent angles.
Therefore the triangles are not similar.
Question 11.
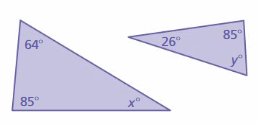
Answer:
x° + 64° + 85° = 180°
x° + 149° = 180°
x° = 180° – 149°
x° = 31°
y° + 26° + 85° = 180°
y° + 111° = 180°
y° = 180° – 111°
y° = 69°
The triangles do not have two pairs of congruent angles.
Therefore the triangles are not similar.
Question 12.
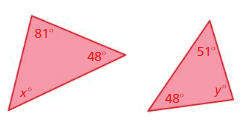
Answer:
x° + 48° + 81° = 180°
x° + 129° = 180°
x° = 180° – 129°
x° = 51°
y° + 48° + 51° = 180°
y° + 99° = 180°
y° = 180° – 99°
y° = 81°
The triangles have two pairs of congruent angles.
Therefore the triangles are similar.
Question 13.
GEOMETRY
Which of the rulers are similar in shape? Explain.
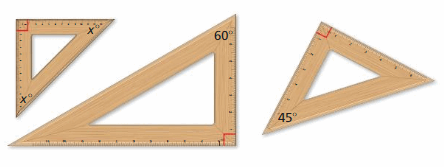
Answer:
2x + 90 = 180°
2x = 180 – 90°
2x = 90°
x = 90/2
x = 45°
The ruler on the left and the ruler on the right both have the shape of a right triangle with 45° angles, therefore they are similar in shape, while the middle ruler has 60°, 30° angles.
STRUCTURE
Tell whether the triangles are similar. Explain.
Question 14.
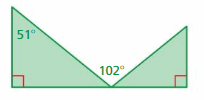
Answer:
m∠APB + m∠B = 90°
m∠APB + 51° = 90°
m∠APB = 90° – 51°
m∠APB = 39°
m∠APB + m∠BPD + m∠DPC = 180°
39° + 102° + m∠DPC = 180°
m∠DPC + 141° = 180
m∠DPC = 180 – 141°
m∠DPC = 39°
m∠A = m∠C
m∠APB = m∠DPC
Question 15.
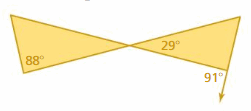
Answer:
∠APB ≅ ∠CPD
m∠APB = m∠CPD
m∠APB = 29°
m∠A + m∠B + m∠APB = 180°
m∠A + 88° + 29° = 180°
m∠A + 117° = 180°
m∠A = 180° – 117°
m∠A = 63°
m∠PDC + m∠PDE = 180°
m∠PDC + 91° = 180°
m∠PDC = 180° – 91°
m∠PDC = 89°
IDENTIFYING SIMILAR TRIANGLES
Can you determine whether the triangles are similar? Explain.
Question 16.
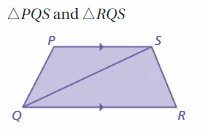
Answer:
PS || QR
∠PSQ and ∠SQR are interior angles using the transversal QS, thus they are congruent.
∠PSQ ≅ ∠SQR
Question 17.

Answer:
As AB || DE there are two pairs of congruent alternate interior angles, using the transversals AE and BD.
∠A≅ ∠E
∠B≅ ∠D
The two pairs of congruent angles are enough to prove that the triangles are similar.
ΔABC ∼ ΔEDC
Question 18.
PROBLEM SOLVING
A water sample must be taken from water atleast 20 feet deep. Find the depth of the water 50 feet from shore. Is this an appropriate location for a water sample?
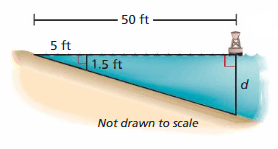
Answer:
ΔAMN ∼ ΔABC
MN/BC = AM/AB
1.5/d = 5/50
d = 1.5 × 10
d = 15 feet
Therefore 15 feet is not an appropriate location.
Question 19.
MODELING REAL LIFE
A map shows the number of steps you must take to get to a treasure. However, the map is old, and the last dimension is unreadable. Explain why the triangles are similar. How many steps do you take from the pyramids to the treasure?
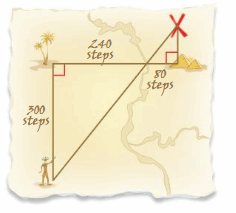
Answer:
The two triangles are similar because they are right triangles and ∠AXB ≅ ∠PXQ because they are vertical angles.
PQ/300 = 80/240
240PQ = 24000
PQ = 24000/240
PQ = 100 steps
Question 20.
PROBLEM SOLVING
A person who is 6 feet tall casts a 3-foot-long shadow. A nearby pine tree casts a 15-foot-long shadow. What is the height h of the pine tree?
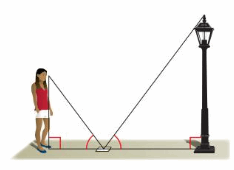
Answer:
Given,
A person who is 6 feet tall casts a 3-foot-long shadow.
A nearby pine tree casts a 15-foot-long shadow.
ΔXAB ∼ ΔXPQ
AB/PQ = XB/XQ
6/PQ = 3/15
PQ = 30 ft
Question 21.
OPEN-ENDED
You place a mirror on the ground 6 feet from the lamppost. You move back 3 feet and see the top of the lamppost in the mirror. What is the height of the lamppost?
Answer:
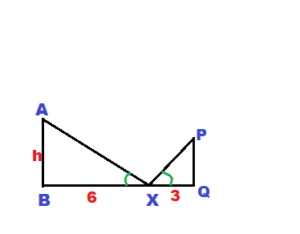
ΔXAB ∼ ΔXPQ
AB/PQ = XB/XQ
h/PQ = 6/3
h = 2PQ
Question 22.
DIG DEEPER!
In each of two right triangles, one angle measure is two times another angle measure. Can you determine that the triangles are similar? Explain your reasoning.
Answer:
We are given the right triangle ABC
m∠A = 2m∠B
Case 1:
m∠A = 90°
90° = 2m∠B
m∠B = 45°
m∠C = 180° – 90° – 45° = 45°
Case 2:
m∠B = 90°
m∠A = 2 × 90° = 180°
Case 3:
m∠C = 90°
m∠A + m∠B = 180 – m∠C = 180° – 90° = 90°
2m∠B + m∠B = 90°
3m∠B = 90°
m∠B = 30°
m∠A = 2 . 30° = 60°
Question 23.
GEOMETRY
In the diagram, \(\overline{B G}\), \(\overline{C F}\) and \(\overline{D E}\) are parallel. The length of \(\overline{B D}\) is 6.32 feet, and the length of \(\overline{D E}\) is 6 feet. Name all pairs of similar triangles in the diagram. Then find the lengths of \(\overline{B G}\) and \(\overline{C F}\)
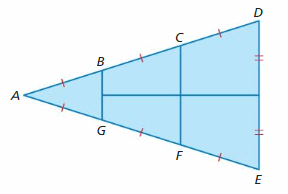
Answer:
ΔABG ∼ ΔACF
ΔACF ∼ ΔADE
ΔABG ∼ ΔADE
AB = BC = CD = BD/2 = 6.32/2 = 3.16
AB/CD = BG/DE
3BG = 6
BG = 2 feet
ΔACF ∼ ΔADE
AC/AD = CF/DE
2/3 = CF/6
3CF = 2(6)
CF = 4 feet
Angles and Triangles Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A dog park is divided into sections for large and small dogs. The ratio of the perimeter of the small dog section to the perimeter of the entire dog park is 7 : 12. Find the area of each section.
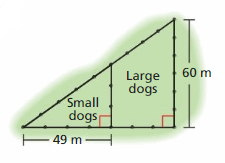
Understand the problem
You know two dimensions of a dog park and the ratio of the perimeter of the small dog section to the perimeter of the entire park. You are asked to find the area of each section.
Make a plan
Verify that the small triangle and the large triangle are similar. Then use the ratio of the perimeters to find the base or the height of each triangle and calculate the areas.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Question 2.
You rotate lines m and t 180° about point P. The image of line m is parallel to the original line. Use the diagram to show that when a transversal intersects parallel lines, each of the following pairs of angles are congruent. Explain your reasoning.
a. alternate interior angles
b. alternate exterior angles
c. corresponding angles
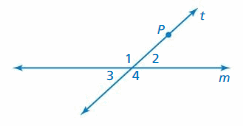
Answer:
Performance Task
Turtle Shells
At the beginning of this chapter, you watched a STEAM Video called “Honeycombs.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Angles and Triangles Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
Graphic Organizers
You can use an Example and Non-Example to list examples and non-examples of a concept. Here is an Example and Non-Example Chart for transversals.
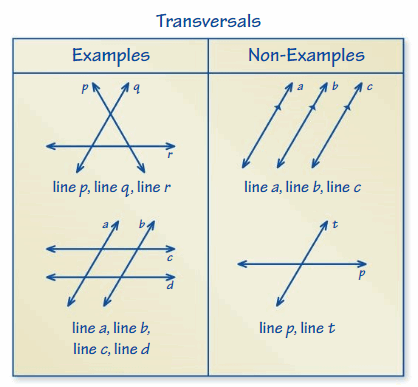
Choose and complete a graphic organizer to help you study the concept.
- interior angles formed by parallel lines and a transversal
- exterior angles formed by parallel lines and a transversal
- interior angles of a triangle
- exterior angles of a triangle
- polygons
- similar triangles

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

3.1 Parallel Lines and Transversals (pp. 103–110)
Use the figure to find the measure of the angle. Explain your reasoning.
Question 1.
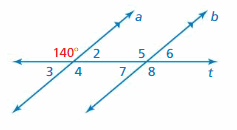
∠8
Answer: 140°
Explanation:
∠8 and 140 degrees angle are alternate exterior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠8 is 140°
Question 2.
∠5
Answer: 140°
Explanation:
∠5 and 140 degrees angle are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠5 is 140°
Question 3.
∠7
Answer: 40°
Explanation:
∠5 and 140 degrees angle are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠5 is 140°
∠5 and ∠7 are supplementary angle.
∠5 + ∠7 = 180°
140° + ∠7 = 180°
∠7 = 180° – 140°
∠7 = 40°
So, the measure of ∠7 is 40°
Question 4.
∠2
Answer: 40°
Explanation:
140 and ∠2 are supplementary angle.
140° + ∠2 = 180°
∠2 = 180° – 140°
∠2 = 40°
So, the measure of ∠2 is 40°
Question 5.
∠6
Answer: 40°
Explanation:
∠5 and 140 degrees angle are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠5 is 140°
∠5 and ∠6 are supplementary angle.
140° + ∠6 = 180°
∠6 = 180° – 140°
∠6 = 40°
So, the measure of ∠6 is 40°
Complete the statement. Explain your reasoning.
Question 6.
If the measure of ∠1 = 123°, then the measure of ∠7 = ![]()
Answer: 123°
Explanation:
∠1 and ∠7 are alternate exterior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠7 is 123°
Question 7.
If the measure of ∠2 = 58°, then the measure of ![]()
Answer: 122°
Explanation:
∠2 and ∠6 are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠6 is 58°
∠5 and ∠6 are supplementary angle.
∠5 + ∠6 = 180°
58° + ∠5 = 180°
∠5 = 180° – 58°
∠5 = 122°
So, the measure of ∠5 is 122°
Question 8.
If the measure of ∠5 = 119°, then the measure of ![]()
Answer: 119°
Explanation:
∠3 and ∠5 are alternate interior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠3 is 119°
Question 9.
If the measure of ∠4 = 60°, then the measure of ![]()
Answer: 60°
Explanation:
∠4 and ∠6 are alternate exterior angles formed by a transversal intersecting parallel lines. The angles are congruent.
So, the measure of ∠4 is 60°
Question 10.
In Exercises 6–9, describe the relationship between ∠2 and ∠8.
Answer: ∠2 ≅ ∠8
Question 11.
In a park, a bike path and a horse riding path are parallel. In one part of the park, a hiking trail intersects the two paths. Find the measures of ∠1 and ∠2. Explain your reasoning.
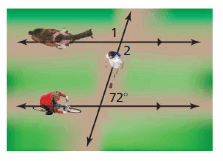
Answer: ∠1 = 108°, ∠2 = 108°
Explanation:
∠3 and 72° are alternate interior angles. They are congruent.
So, the measure of ∠3 is 72°
∠3 + ∠1 = 180°
72° + ∠1 = 180°
∠1 = 180° – 72°
∠1 = 108°
So, the measure of ∠1 is 108°
∠1 and ∠2 are alternating interior angles. They are congruent.
3.2 Angles of Triangles (pp. 111 – 116)
Find the measures of the interior angles of the triangle.
Question 12.
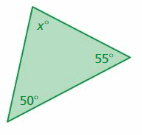
Answer:
Sum of all the angles in a triangle = 180°
x° + 50° + 55° = 180°
x° + 105° = 180°
x° = 180° – 105°
x° = 75°
Question 13.
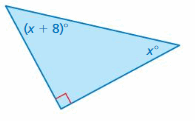
Answer:
Sum of all the angles in a triangle = 180°
x° + (x + 8)° + 90° = 180°
2x° + 8° + 90° = 180°
2x° + 98° = 180°
2x° = 180° – 98°
2x° = 82
x° = 82/2
x° = 41°
(x + 8)° = (41 + 8)° = 49°
Find the measure of the exterior angle.
Question 14.
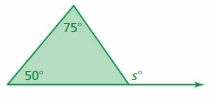
Answer:
s° = 50° + 75°
s° = 125°
Thus the measure of the exterior angle is 125°
Question 15.
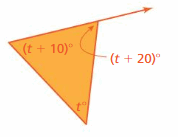
Answer:
Sum of all the angles in a triangle = 180°
t° + (t + 10)° + (t + 20)° = 180°
3t° + 10° + 20° = 180°
3t° + 30° = 180°
3t° = 180° – 30°
3t° = 150°
t° = 150/3
t° = 50°
Exterior angle:
t° + (t + 10)°
t° + t° + 10°
2t° + 10°
2(50)° + 10°
= 100° + 10°
= 110°
Thus the measure of the exterior angle is 110°.
Question 16.
What is the measure of each interior angle of an equilateral triangle? Explain.
Answer:
S = (n – 2) . 180°
S = (3- 2) . 180°
S = 1 . 180°
S = 180°
Thus the sum of the interior angle measure is 180°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 3.
180 ÷ 3 = 60°
Question 17.
You draw the Leo constellation. You notice that the three stars Denebola, Zosma, and Chertan form a triangle. In your drawing, you find the measure of the interior angle at Denebola is 30° and the measure of the interior angle of the triangle at Zosma is 56°. What is the measure of the interior angle of the triangle at Chertan?
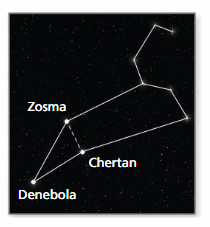
Answer:
Sum of all the angles in a triangle = 180°
x° + 30° + 56° = 180°
x° + 86° = 180°
x° = 180° – 86°
x° = 94°
Thus the measure of the interior angle of the triangle at Chertan = 94°
3.3 Angles of Polygons (pp. 117–122)
Find the sum of the interior angle measures of the polygon.
Question 18.

Answer:
The polygon has 13 sides
S = (n – 2) . 180°
S = (13- 2) . 180°
S = 11 . 180°
S = 1980°
Thus the sum of the interior angle measure is 1980°
Question 19.
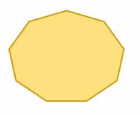
Answer:
The polygon has 9 sides
S = (n – 2) . 180°
S = (9- 2) . 180°
S = 7 . 180°
S = 1260°
Thus the sum of the interior angle measure is 1260°
Find the value of x.
Question 20.
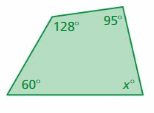
Answer:
S = (n – 2) . 180°
S = (4 – 2) . 180°
S = 2 . 180°
S = 360°
Thus the sum of the interior angle measure is 360°
x° + 60° + 128° + 95° = 360°
x° + 283° = 360°
x° = 360° – 283°
x° = 77°
Thus the value of x is 77°.
Question 21.
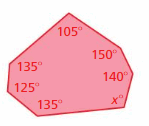
Answer:
S = (n – 2) . 180°
S = (7 – 2) . 180°
S = 5 . 180°
S = 900°
Thus the sum of the interior angle measure is 900°
x° + 135° + 125° + 135° + 105° + 150° + 140° = 900°
x° + 790° = 900°
x° = 900° – 790°
x° = 110°
Question 22.
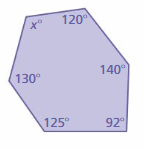
Answer:
S = (n – 2) . 180°
S = (6 – 2) . 180°
S = 4 . 180°
S = 720°
Thus the sum of the interior angle measure is 720°
x° + 120° + 140° + 92° + 125° + 130° = 720°
x° + 607° = 720°
x° = 720° – 607°
x° = 113°
The value of x° is 113°
Question 23.
Find the measure of each interior angle of the regular polygon.

Answer:
The given polygon is an octagon. It has 8 sides.
S = (n – 2) . 180°
S = (8 – 2) . 180°
S = 6 . 180°
S = 1080°
Thus the sum of the interior angle measure is 1080°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 8.
1080 ÷ 3 = 135°
3.4 Using Similar Triangles (pp. 123–128)
Tell whether the triangles are similar. Explain.
Question 24.
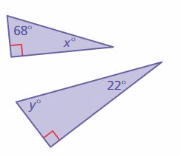
Answer:
x° + 68° + 90° = 180°
x° = 180° – 158°
x° = 22°
y° + 22° + 90° = 180°
y° + 112° = 180°
y° = 180° – 112°
y° = 68°
The triangles have two pairs of congruent angles.
So, the triangles are similar.
Question 25.
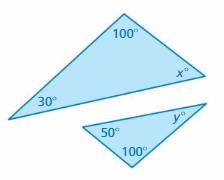
Answer:
x° + 100° + 30° = 180°
x° + 130° = 180°
x° = 180° – 130°
x° = 50°
y° + 100° + 50° = 180°
y° + 150° = 180°
y° = 180° – 150°
y° = 30°
The triangles have two pairs of congruent angles.
So, the triangles are similar.
Question 26.
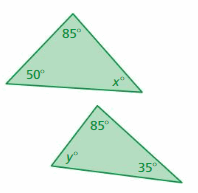
Answer:
x° + 50° + 85° = 180°
x° + 135° = 180°
x° = 180° – 135°
x° = 45°
y° + 85° + 35° = 180°
y° + 120° = 180°
y° = 180° – 120°
y° = 60°
The triangles do not have two pairs of congruent angles.
So, the triangles are not similar.
Question 27.
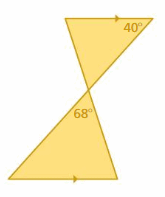
Answer:
∠B ≅ ∠D
∠A ≅ ∠C
∠AXB ≅ ∠CXD
∠AXB and ∠CXD are vertical angles.
ΔAXB ∼ ΔCXD
Question 28.
A person who is 5 feet tall casts a shadow that is 4 feet long. A nearby building casts a shadow that is 24 feet long. What is the height of the building?
Answer:
Given,
A person who is 5 feet tall casts a shadow that is 4 feet long.
A nearby building casts a shadow that is 24 feet long.
Let the height of the building = x ft
x/24 = 5/4
24 . x/24 = 5/4 . 24
x = 30
Thus the height of the building is 30 ft.
Angles and Triangles Practice Test
Practice Test
Use the figure to find the measure of the angle. Explain your reasoning.
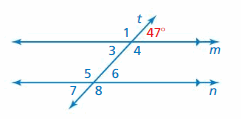
Question 1.
∠7
Answer: 47°
Explanation:
∠7 and 47° angles are alternate exterior angles formed by a transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠7 is 47°
Question 2.
∠6
Answer: 47°
Explanation:
∠6 and 47° angles are corresponding angles formed by a transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠6 is 47°
Question 3.
∠4
Answer: 133°
Explanation:
∠4 and 47° are supplementary angles.
47° + ∠4 = 180°
∠4 = 180° – 47°
∠4 = 133°
Thus the measure of ∠4 = 133°
Question 4.
∠5
Answer: 133°
Explanation:
∠6 and 47° angles are corresponding angles formed by transversal intersecting parallel lines. The angles are congruent.
Thus the measure of ∠6 is 47°
∠6 + ∠5 = 180°
47° + ∠5 = 180°
∠5 = 180° – 47°
∠5 = 133°
Thus the measure of ∠5 = 133°
Question 5.
Find the value of x.
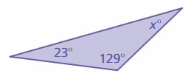
Answer: 28°
Explanation:
Sum of all the angles in a triangle = 180°
x° + 129° + 23° = 180°
x° + 152° = 180°
x° = 180° – 152°
x° = 28°
Thus the value of x° is 28°
Question 6.
Find the measures of the interior angles.
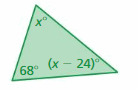
Answer: 68°
Explanation:
Sum of all the angles in a triangle = 180°
x° + (x – 24)° + 68° = 180°
x° + x° – 24° + 68° = 180°
2x° + 44° = 180°
2x° = 180° – 44°
2x° = 136°
x° = 68°
(x – 24)° = (68 – 24)° = 44°
Question 7.
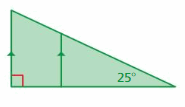
Find the measure of the exterior angle.
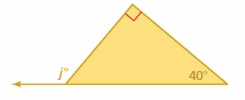
Answer:
j° = 40° + 90°
j° = 130°
The measure of an exterior angle is 130°.
Question 8.
Find the measure of the interior angle measures of the border of the coin.

Answer:
The coin has 7 sides.
S = (n – 2) . 180°
S = (7 – 2) . 180°
S = 5 . 180°
S = 900°
Thus the sum of the interior angle measure is 900°
Question 9.
Find the value of x.
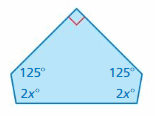
Answer:
S = (n – 2) . 180°
S = (5 – 2) . 180°
S = 3 . 180°
S = 540°
Thus the sum of the interior angle measure is 540°
2x° + 125° + 90° + 2x° + 125° = 540°
4x° + 340° = 540°
4x° = 540° – 340°
4x° = 200°
x° = 200/4
x° = 50°
The value of x° is 50°
Question 10.
Find the measure of each interior angle of the regular polygon.

Answer:
S = (n – 2) . 180°
S = (6 – 2) . 180°
S = 4 . 180°
S = 720°
Thus the sum of the interior angle measure is 720°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 6.
720 ÷ 6 = 120°
Tell whether the triangles are similar. Explain.
Question 11.
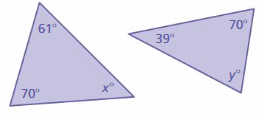
Answer:
To find x°:
x° + 61° + 70° = 180°
x° + 131° = 180°
x° = 180° – 131°
x° = 49°
To find y°:
x° + 39° + 70° = 180°
x° + 109° = 180°
x° = 180° – 109°
x° = 71°
The triangles do not have two pairs of congruent angles.
So, the triangles are not similar.
Question 12.
Answer:
∠A ≅ ∠QPB
∠C ≅ ∠PQB
ΔBPQ ∼ ΔBAC
Question 13.
Describe two ways you can find the measure of ∠5.
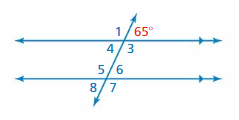
Answer:
One way: ∠3 and 65° are supplementary angles. ∠5 and ∠3 are alternate interior angles.
Another way: ∠8 and 65° are alternate exterior angles. ∠5 and ∠8 are supplementary angles.
Question 14.
You swim 3.6 kilometers per hour. How long (in minutes) will it take you to swim the distance d across the pond?
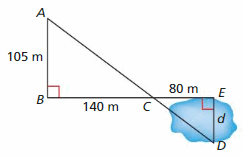
Answer:
Given,
You swim 3.6 kilometers per hour.
d/105 = 80/140
105 . d/105 = 80/140 . 105
d = 60
The length of the pond is 60 m.
Speed = 3.6 km per hour = 1 m sec
Distance = d = 60m
Time it will take to swim across the pond
= distance/speed
= 60/1
= 60 sec = 1 min
Angles and Triangles Cumulative Practice
Question 1.
The border of a Canadian one-dollar coin is shaped like an 11-sided regular polygon. The shape was chosen to help visually impaired people identify the coin. How many degrees are in each interior angle along the border? Round your answer to the nearest degree.

Answer:
S = (n – 2) . 180°
S = (11 – 2) . 180°
S = 9 . 180°
S = 1620°
Thus the sum of the interior angle measure is 1620°
In a regular polygon, each interior angle is congruent. So, divide the sum of the interior angle measures by the number of interior angles, 11.
1620 ÷ 11 = 147°
Question 2.
A public utility charges its residential customers for natural gas based on the number of therms used each month. The formula shows how the monthly cost tin dollars is related to the number of terms used.
C = 11 + 1.6t
Solve this formula for t.

Answer:
C = 11 + 1.6t
C – 11 = 1.6t
1.6t = C – 11
t = (C – 11)/1.6
Thus the correct answer is option B.
Question 3.
What is the value of x?
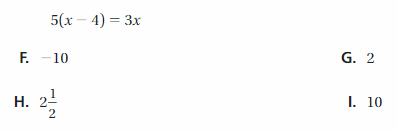
Answer:
5(x – 4) = 3x
5x – 20 = 3x
5x – 3x = 20
2x = 20
x = 20/2
x = 10
Thus the correct answer is option I.
Question 4.
In the figures, △PQR is similar to △STU. What is the value of x?
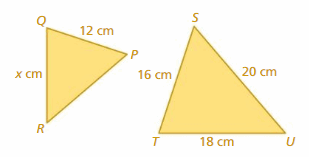
A. 9.6
B. 10\(\frac{2}{3}\)
C. 13.5
D. 15
Answer:
△PQR is similar to △STU
PQ = 12
ST = 16
SU = 20
TU = 18
PQ/ST = QR/TU
12/16 = X/18
16X = 12 × 18
X = 216/16
X = 13.5 cm
Thus the correct answer is option C.
Question 5.
What is the value of x?
Answer:
∠y and 125° are supplementary angles.
125° + ∠y = 180°
∠y = 180° – 125°
∠y = 55°
So, the measure of ∠y = 55°
∠x and ∠y are alternate interior angles. They are congruent.
So, the measure of ∠x = 55°
Question 6.
Your friend was solving an equation in the box shown.
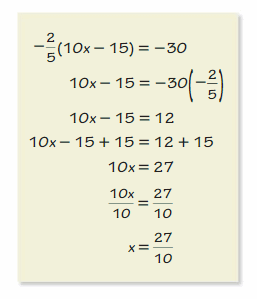
What should your friend do to correct the error that she made?
F. Multiply both sides by –\(\frac{5}{2}\) instead of –\(\frac{2}{5}\).
G. Multiply both sides by \(\frac{2}{5}\) instead of –\(\frac{2}{5}\).
H. Distribute –\(\frac{2}{5}\) to get 4x – 6.
I. Add 15 to -30.
Answer:
My friend made the error by multiplying both sides by –\(\frac{2}{5}\).
To correct the error she should multiply both sides by –\(\frac{5}{2}\) instead of –\(\frac{2}{5}\)
Thus the correct answer is option F.
Question 7.
In the coordinate plane below, ∆XYZ is plotted and its vertices are labeled.
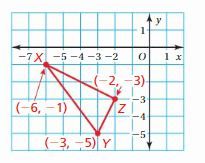
Which of the following shows ∆X’Y’Z’, the image of ∆XYZ after it is reflected in the y-axis?
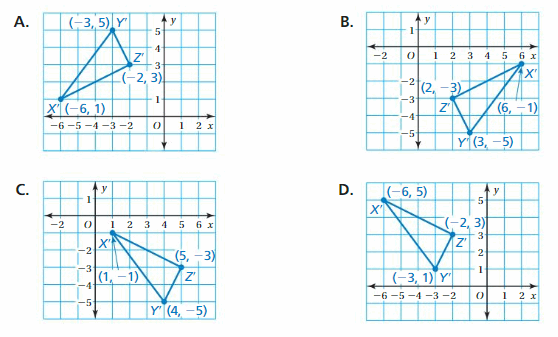
Answer:
Given,
X(-6,-1)
Y(-3,-5)
X(-2,-3)
Reflecting a point (x,y) in the y-axis.
(x, y) = (-x, y)
X(-6,-1) = X'(6, -1)
Y(-3,-5) = Y'(3, -5)
X(-2,-3) = Z'(2, -3)
Thus the correct answer is option B.
Question 8.
The sum S of the interior angle measures of a polygon with n sides can be found by using a formula.

Part A
Write the formula.
Answer:
S = (n – 2) . 180°
Part B
A quadrilateral has angles measuring 100°, 90°, and 90°. Find the measure of its fourth angle. Show your work and explain your reasoning.
Answer:
The quadrilateral has 4 sides
S = (n – 2) . 180°
S = (4 – 2) . 180°
S = 2 . 180°
S = 360 °
Thus the sum of the interior angles is 360 °
x° + 100° + 90° + 90° = 360°
x° + 280° = 360°
x° = 360° – 280°
x° = 80°
Thus the value of x° is 80°
Part C
The sum of the measures of the angles of the pentagon shown is 540°. Divide the pentagon into triangles to show why this must be true. Show your work and explain your reasoning.
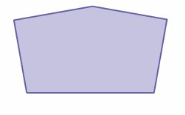
Answer:
Number of sides = 3
The number of interior triangles in the given figure = 3
Sum of the interior angles measure using triangle = 3 × 180° = 540
Conclusion:
I wish the details prevailed in the above article is beneficial for all the 8th grade students. Hope our Big Ideas Math Answers Grade 8 Chapter 3 Angles and Triangles helped you a lot to overcome the difficulties in this chapter. Feel free to post your comments in the comment box. Stay tuned to our ccssmathanswers.com to get step by step explanation for all the Grade 8 chapters.
