Gain more subject knowledge on Circles concepts with the help of Big Ideas Math Geometry Answers Chapter 10 Circles guide. Shared guide of BIM Textbook Solutions Geometry Ch 10 Circles helps students understand the concepts quickly and concentrate on other math concepts too. Want to get a good grip on the high school-related circle topics? Then, make use of this BigIdeas Math Geometry Answers Ch 10 Circles Pdf for free. Subject experts provided this BIM geometry 10th chapter solution key based on the latest syllabus and common core standards curriculum guidelines.
Big Ideas Math Book Geometry Answer Key Chapter 10 Circles
Presented Geometry Chapter 10 Circles Big Ideas Math Answers are easy to understand and free to access at any time and anywhere. So, students are advised to access online or download the lesson-wise BIM Textbook Answers of Geometry Ch 10 Circles in Pdf format. Check out each and every lesson of circles as a part of your preparation and clear your queries within no time.
Common Core Curriculum High School Big Ideas Math Book Geometry Ch 10 Solution Key are prepared as per the latest textbooks. Questions included in the BIM Modeling Real Life Geometry Answers are from Exercises, Chapter Tests, Review Tests, Cumulative Practice, Assessment Tests, etc.
Circles Maintaining Mathematical Proficiency
Find the Product.
Question 1.
(x + 7) (x + 4)
Answer:
(x + 7) (x + 4) = x² + 14x + 28
Explanation:
(x + 7) (x + 4) = x(x + 7) + 7(x + 4)
= x² + 7x + 7x + 28
= x² + 14x + 28
Question 2.
(a + 1) (a – 5)
Answer:
(a + 1) (a – 5) = a² – 4a – 5
Explanation:
(a + 1) (a – 5) = a(a – 5) + 1(a – 5)
= a² – 5a + a – 5
= a² – 4a – 5
Question 3.
(q – 9) (3q – 4)
Answer:
(q – 9) (3q – 4) = 3q² – 31q + 32
Explanation:
(q – 9) (3q – 4) = q(3q – 4) – 9(3q – 4)Exercise 10.3 Using Chords
= 3q² – 4q – 27q + 32
= 3q² – 31q + 32
Question 4.
(2v – 7) (5v + 1)
Answer:
(2v – 7) (5v + 1) = 10v² – 33v – 7
Explanation:
(2v – 7) (5v + 1) = 2v(5v + 1)- 7(5v + 1)
= 10v² + 2v – 35v – 7
= 10v² – 33v – 7
Question 5.
(4h + 3) (2 + h)
Answer:
(4h + 3) (2 + h) = 4h² + 11h + 6
Explanation:
(4h + 3) (2 + h) = 4h(2 + h) + 3(2 + h)
= 8h + 4h² + 6 + 3h
= 4h² + 11h + 6
Question 6.
(8 – 6b) (5 – 3b)
Answer:
(8 – 6b) (5 – 3b) = 18b² – 54b + 40
Explanation:
(8 – 6b) (5 – 3b) = 8(5 – 3b) – 6b(5 – 3b)
= 40 – 24b – 30b + 18b²
= 18b² – 54b + 40
Solve the equation by completing the square. Round your answer to the nearest hundredth, if necessary.
Question 7.
x2 – 2x = 5
Answer:
The solutions are x = √6 + 1, x = 1 – √6
Explanation:
x² – 2x = 5
x² – 2x + 1² = 5 + 1²
(x – 1)² = 6
x – 1 = ±√6
x = ±√6 + 1
The solutions are x = √6 + 1, x = -√6 + 1
Question 8.
r2 + 10r = -7
Answer:
The solutions are r = √18 – 5, r = 5 – √18
Explanation:
r2 + 10r = -7
r² + 10r + 5² = -7 + 5²
(r + 5)² = -7 + 25 = 18
r + 5 = ±√18
r = ±√18 – 5
The solutions are r = √18 – 5, r = 5 – √18
Question 9.
w2 – 8w = 9
Answer:
The solutions are w = 9, w = -1
Explanation:
w2 – 8w = 9
w2 – 8w + 4² = 9 + 4²
(w – 4)² = 9 + 16 = 25
w – 4 = ±5
w = 5 + 4, w = -5 + 4
w = 9, w = -1
The solutions are w = 9, w = -1
Question 10.
p2 + 10p – 4 = 0
Answer:
The solutions are p = √29 – 5, p = 5 – √29
Explanation:
p2 + 10p = 4
p² + 10p + 5² = 4 + 5²
(p + 5)² = 4 + 25
(p + 5)² = 29
p + 5 = ±√29
p = ±√29 – 5
The solutions are p = √29 – 5, p = 5 – √29
Question 11.
k2 – 4k – 7 = 0
Answer:
The solutions are k = √11 + 2, k = 2 – √11
Explanation:
k² – 4k= 7
k² – 4k + 2² = 7 + 4
(k – 2)² = 11
k – 2 = ±√11
k = √11 + 2, k = 2 – √11
The solutions are k = √11 + 2, k = 2 – √11
Question 12.
– z2 + 2z = 1
Answer:
The solutions are z = 1
Explanation:
-z² + 2z = 1
z² – 2z = -1
z² – 2z + 1 = -1 + 1
(z – 1)² = 0
z = 1
The solutions are z = 1
Question 13.
ABSTRACT REASONING
write an expression that represents the product of two consecutive positive odd integers. Explain your reasoning.
Answer:
Let us take two consecutive odd integers are x and (x + 2)
The product of two consecutive odd integers is x • (x + 2)
x(x + 2) = x² + 2x
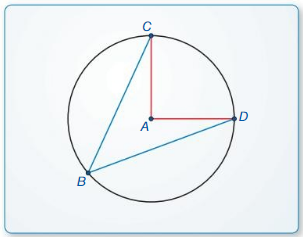
Circles Mathematical Practices
Monitoring progress
Let ⊙A, ⊙B, and ⊙C consist of points that are 3 units from the centers.
Question 1.
Draw ⊙C so that it passes through points A and B in the figure at the right. Explain your reasoning.
Answer:
Question 2.
Draw ⊙A, ⊙B, and OC so that each is tangent to the other two. Draw a larger circle, ⊙D, that is tangent to each of the other three circles. Is the distance from point D to a point on ⊙D less than, greater than, or equal to 6? Explain.
Answer:
10.1 Lines and Segments that Intersect Circles
Exploration 1
Lines and Line Segments That Intersect Circles
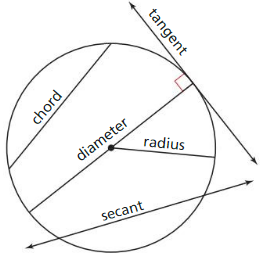
Work with a partner: The drawing at the right shows five lines or segments that intersect a circle. Use the relationships shown to write a definition for each type of line or segment. Then use the Internet or some other resource to verify your definitions.
Chord: _________________
Secant: _________________
Tangent: _________________
Radius: _________________
Diameter: _________________
Answer:
Chord: A chord of a circle is a straight line segment whose endpoints both lie on a circular arc.
Secant: A straight line that intersects a circle in two points is called a secant line.
Tangent: Tangent line is a line that intersects a curved line at exactly one point.
Radius: It is the distance from the centre of the circle to any point on the circle.
Diameter: It the straight that joins two points on the circle and passes through the centre of the circle.
Exploration 2
Using String to Draw a Circle
Work with a partner: Use two pencils, a piece of string, and a piece of paper.
a. Tie the two ends of the piece of string loosely around the two pencils.
Answer:
Using string draw a circle with a partner with two pencils. We are using a piece of string and a piece of paper.
The condition to draw is that the two ends of the piece of string are tied loosely around the two pencils. We get the following circle.
From the diagram, the circle is improper because the two ends of the piece of string are tied loosely around the two pencils.
b. Anchor one pencil of the paper at the center of the circle. Use the other pencil to draw a circle around the anchor point while using slight pressure to keep the string taut. Do not let the string wind around either pencil.

Answer:
To draw a circle we swing the piece of string and piece of paper. In the condition one pencil on the paper at the centre of the circle and using the other pencil.
Draw a circle around the anchor point while using slight pressure to keep the string and don’t let the string wind around either.

Constructed the circle with the pencil with the given conditions we got the proper circle.
c. Explain how the distance between the two pencil points as you draw the circle is related to two of the lines or line segments you defined in Exploration 1.
REASONING ABSTRACTLY
To be proficient in math, you need to know and flexibly use different properties of operations and objects.
Answer:
Draw the circle with two pencils, a piece of string, and a piece of paper. The distance between the two pencil points we can draw the circle is the radius of the circle which is defined as a segment whose endpoints are the center and any point on a circle is the radius.
Communicate Your Answer
Question 3.
What are the definitions of the lines and segments that intersect a circle?
Answer: The lines and segments that intersect a circle are a diameter.
The Diameter is a straight line passing from one side of a circle to its other side through the center of the circle.
Question 4.
Of the five types of lines and segments in Exploration 1, which one is a subset of another? Explain.
Answer: The Diameter of a circle can be considered as a subset of the chord. The diameter is a chord that passes through the circle from one side to the other side through the centre of the circle.
Question 5.
Explain how to draw a circle with a diameter of 8 inches.
Answer:
Given that,
The diameter of the circle is 8cm.
So, the radius of the circle is 4cm.
Using a compass you can draw a circle.
Then join the radius and get a diameter of 8cm.
Lesson 10.1 Lines and Segments that Intersect Circles
Monitoring progress
Question 1.
In Example 1, What word best describes \(\overline{A G}\)? \(\overline{C B}\)?
Answer:
\(\overline{A G}\) is secant because it is a line that intersects the circle at two points.
\(\overline{C B}\) is the radius as it is the distance from the centre to the point of a circle.
Question 2.
In Example 1, name a tangent and a tangent segment.
Answer:
\(\overline{D E}\) is the tangent of the circle
\(\overline{D E}\) is the tangent segment of the circle.
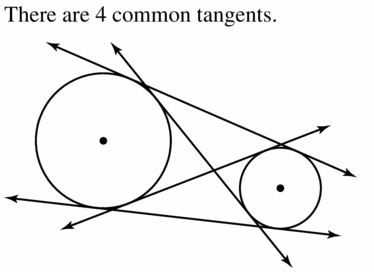
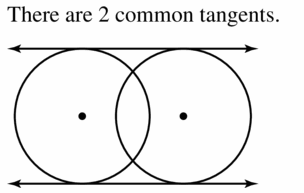
Tell how many common tangents the circles have and draw them. State whether the tangents are external tangents or internal tangents.
Question 3.
Answer:
4 tangents.
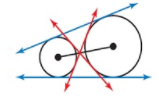
A tangent is a line segment that intersects the circle at exactly one point. Internal tangents are the lines that intersect the segments joining the centres of two circles. External tangents are the lines that do not cross the segment joining the centres of the circles.
Blue lines represent the external tangents and red lines represent the internal tangents.
Question 4.

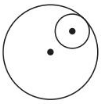
Answer:
One tangent.
One external tangent.
Question 5.

Answer:
No tangent.
It is not possible to draw a common tangent for this type of circle.
Question 6.
Is \(\overline{D E}\) tangent to ⊙C?
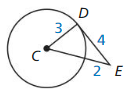
Answer:
Use the converse of Pythagorean theorem i.e 2² = 3² + 4²
4 = 9 + 16
By the tangent line to the circle theorem, \(\overline{D E}\) is not a tangent to ⊙C
Question 7.
\(\overline{S T}\) is tangent to ⊙Q.
Find the radius of ⊙Q.
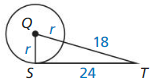
Answer:
The radius of ⊙Q is 7 units.
Explanation:
By using the Pythagorean theorem
(18 + r)² = r² + 24²
324 + 36r + r² = r² + 576
36r = 576 – 324
36r = 252
r = 7
Question 8.
Points M and N are points of tangency. Find the value(s) of x.
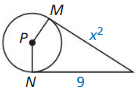
Answer:
The values of x are 3 or -3.
Explanation:
x² = 9
x = ±3
Exercise 10.1 Lines and Segments that Intersect Circles
Vocabulary and Core Concept Check
Question 1.
WRITING
How are chords and secants alike? How are they different?
Answer:

Question 2.
WRITING
Explain how you can determine from the context whether the words radius and diameter are referring to segments or lengths.
Answer:
Radius and diameter are the lengths of the line segments that pass through the centre of a circle. Radius is half of the diameter.
Question 3.
COMPLETE THE SENTENCE
Coplanar circles that have a common center are called ____________ .
Answer:
Question 4.
WHICH ONE DOESNT BELONG?
Which segment does not belong with the other three? Explain your reasoning.
chord radius tangent diameter
Answer:
A chord, a radius and a diamter are segments and they intersect a circle in two points. A tangent is a line that intersects a circle at one point.
Monitoring Progress and Modeling with Mathematics
In Exercises 5 – 10, use the diagram.
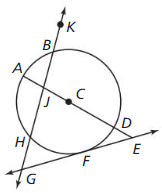
Question 5.
Name the circle.
Answer:
![]()
Question 6.
Name two radii.
Answer:
The name of the two radii is CD and AC.
Question 7.
Name two chords.
Answer:
![]()
Question 8.
Name a diameter.
Answer:
The name of diameter is AD
Question 9.
Name a secant.
Answer:
![]()
Question 10.
Name a tangent and a point of tangency
Answer:
GE is the tangent and F is the point of tangency.
In Exercises 11 – 14, copy the diagram. Tell how many common tangents the circles have and draw them.
Question 11.
Answer:
Question 12.
Answer:
No common tangent because two circles do not intersect at one point.
Question 13.
Answer:
Question 14.
Answer:
One common tangent.

In Exercises 15 – 18, tell whether the common tangent is internal or external.
Question 15.
Answer:

Question 16.
Answer:
The common tangent is the internal tangent because it intersects the segment that joins the centres of two circles.
Question 17.
Answer:

Question 18.
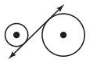
Answer:
The common tangent is the internal tangent because it intersects the segment that joins the centres of two circles.
In Exercises 19 – 22, tell whether \(\overline{A B}\) is tangent to ⊙C. Explain your reasoning.
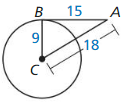
Question 19.
Answer:

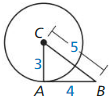
Question 20.
Answer:
Use the converse of the Pythagorean theorem
18² _____________ 15² + 9²
324 _____________ 225 + 81
324 ≠ 304
△ ACB is not a right angled triangle.
So, \(\overline{A B}\) is not tangent to ⊙C at B.
Question 21.
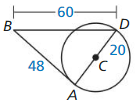
Answer:

Question 22.
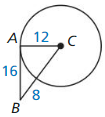
Answer:
Use the converse of the Pythagorean theorem
8² _____________ 12² + 16²
64 _____________ 144 + 256
64 ≠ 400
△ ACB is not a right angled triangle.
So, \(\overline{A B}\) is not tangent to ⊙C at B.
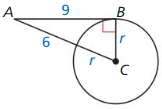
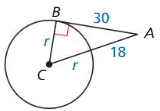
In Exercises 23 – 26, point B is a point of tangency. Find the radius r of ⊙C.
Question 23.
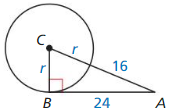
Answer:
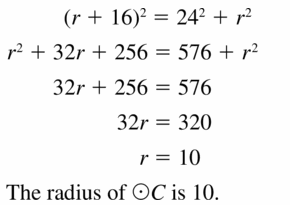
Question 24.
Answer:
(r + 6)² = r² + 9²
r² + 12r + 36 = r² + 81
12r = 81 – 36
12r = 45
r = \(\frac { 15 }{ 4 } \)
Therefore, the radius of ⊙C is \(\frac { 15 }{ 4 } \)
Question 25.
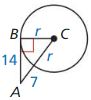
Answer:
Question 26.
Answer:
(r + 18)² = r² + 30²
r² + 36r + 324 = r² + 900
36r = 900 – 324
36r = 576
r = 16
Therefore, the radius of ⊙C is 16
CONSTRUCTION
In Exercises 27 and 28. construct ⊙C with the given radius and point A outside of ⊙C. Then construct a line tangent to ⊙C that passes through A.
Question 27.
r = 2 in.
Answer:
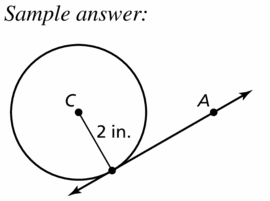
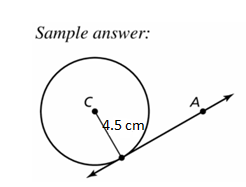
Question 28.
r = 4.5 cm
Answer:
In Exercises 29 – 32, points B and D are points of tangency. Find the value(s) of x.
Question 29.
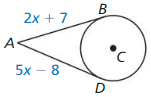
Answer:
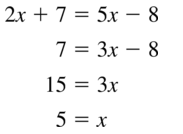
Question 30.
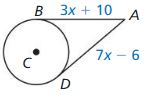
Answer:
3x + 10 = 7x – 6
7x – 3x = 10 + 6
4x = 16
x = 4
Question 31.
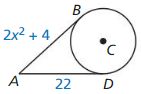
Answer:
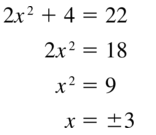
Question 32.
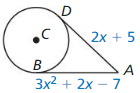
Answer:
2x + 5 = 3x² + 2x – 7
3x² = 5 + 7
3x² = 12
x² = 4
x = ±2
Question 33.
ERROR ANALYSIS
Describe and correct the error in determining whether \(\overline{X Y}\) is tangent to ⊙Z.
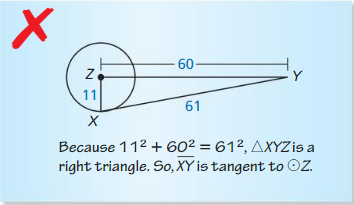
Answer:
![]()
Question 34.
ERROR ANALYSIS
Describe and correct the error in finding the radius of ⊙T.
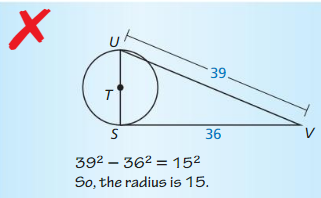
Answer:
39² = 36² + 15²
So, 15 is the diameter.
The radius is \(\frac { 15 }{ 2 } \).
Question 35.
ABSTRACT REASONING
For a point outside of a circle, how many lines exist tangent to the circle that pass through the point? How many such lines exist for a point on the circle? inside the circle? Explain your reasoning.
Answer:
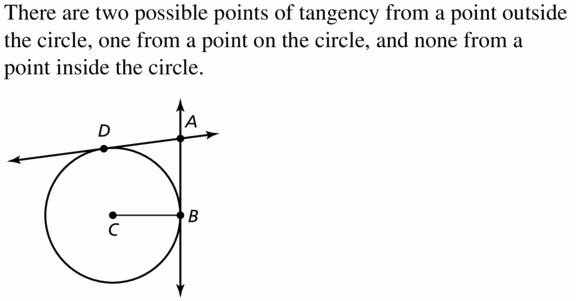
Question 36.
CRITICAL THINKING
When will two lines tangent to the same circle not intersect? Justify your answer.
Answer:
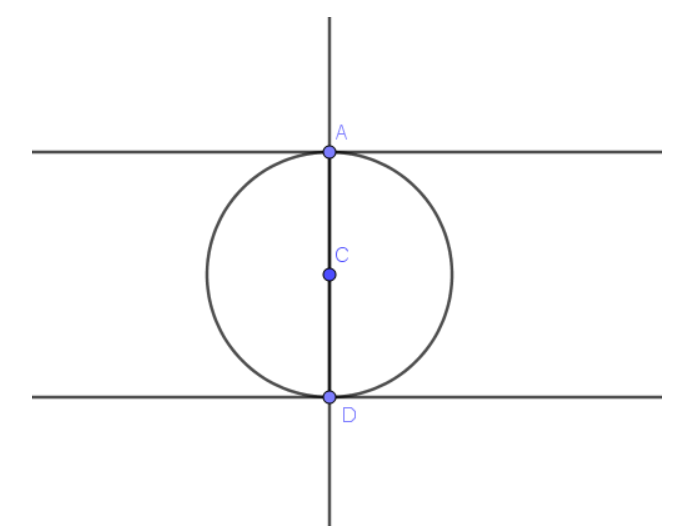
Using tangent line to circle theorem, it follow that the angle between tangent and radius is a right angle. Let’s draw these tangents at the two ends of the same diameter. We can observe a diameter AD like a transverzal of these tangents.
Question 37.
USING STRUCTURE
Each side of quadrilateral TVWX is tangent to ⊙Y. Find the perimeter of the quadrilateral.
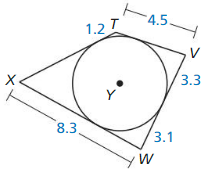
Answer:
Question 38.
LOGIC
In ⊙C, radii \(\overline{C A}\) and \(\overline{C B}\) are perpendicular. ![]() are tangent to ⊙C.
are tangent to ⊙C.
a. Sketch ⊙C, \(\overline{C A}\), \(\overline{C B}\), ![]() .
.
Answer:
b. What type of quadrilateral is CADB? Explain your reasoning.
Answer:
Question 39.
MAKING AN ARGUMENT
Two hike paths are tangent to an approximately circular pond. Your class is building a nature trail that begins at the intersection B of the bike paths and runs between the bike paths and over a bridge through the center P of the pond. Your classmate uses the Converse of the Angle Bisector Theorem (Theorem 6.4) to conclude that the trail must bisect the angle formed by the bike paths. Is your classmate correct? Explain your reasoning.
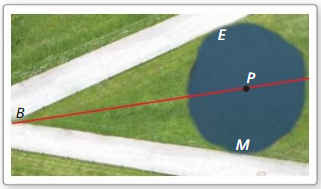
Answer:

Question 40.
MODELING WITH MATHEMATICS
A bicycle chain is pulled tightly so that \(\overline{M N}\) is a common tangent of the gears. Find the distance between the centers of the gears.

Answer:
height h = 4.3 – 1.8
h = 2.5
x² = MN² + h²
x² = 17.6² + 2.5²
x² = 316.01
x = 17.8
Therefore, the distance between the centre of the gear is 17.8 in.
Question 41.
WRITING
Explain why the diameter of a circle is the longest chord of the circle.
Answer:

Question 42.
HOW DO YOU SEE IT?
In the figure, \(\vec{P}\)A is tangent to the dime. \(\vec{P}\)C is tangent to the quarter, and \(\vec{P}\)B is a common internal tangent. How do you know that \(\overline{P A} \cong \overline{P B} \cong \overline{P C}\)
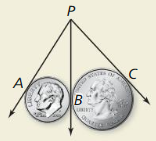
Answer:
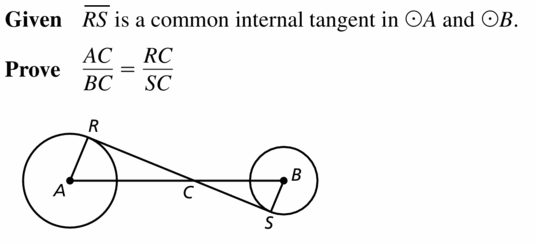
Question 43.
PROOF
In the diagram, \(\overline{R S}\) is a common internal tangent to ⊙A and ⊙B. Prove that \(\frac{\Lambda C}{B C}=\frac{R C}{S C}\)
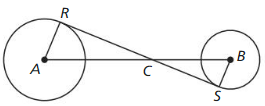
Answer:

Question 44.
THOUGHT PROVOKING
A polygon is circumscribed about a circle when every side of the polygon is tangent to the circle. In the diagram. quadrilateral ABCD is circumscribed about ⊙Q. Is it always true that AB + CD = AD + BC? Justify your answer.
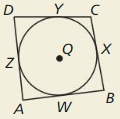
Answer:
Question 45.
MATHEMATICAL CONNECTIONS
Find the values of x and y. Justify your answer.
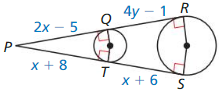
Answer:
Question 46.
PROVING A THEOREM
Prove the External Tangent Congruence Theorem (Theorem 10.2).
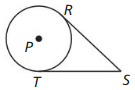
Given \(\overline{S R}\) and \(\overline{S T}\) are tangent to ⊙P.
Prove \(\overline{S R} \cong \overline{S T}\)
Answer:
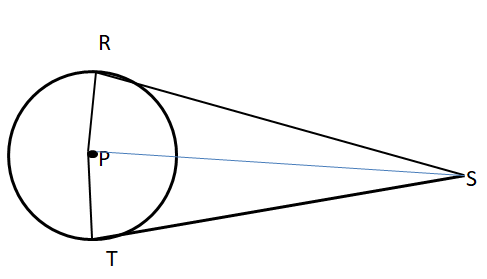
∠PRS and ∠PTS are the right angles. So the legs of circles are congruent.
Therefore, \(\overline{S R} \cong \overline{S T}\)
Question 47.
PROVING A THEOREM
Use the diagram to prove each part of the biconditional in the Tangent Line to Circle Theorem (Theorem 10.1 ).
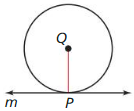
a. Prove indirectly that if a line is tangent to a circle, then it is perpendicular to a radius. (Hint: If you assume line m is not perpendicular to \(\overline{Q P}\), then the perpendicular segment from point Q to line m must intersect line m at some other point R.)
Ghen Line m is tangent to ⊙Q at point P.
Prove m ⊥ \(\overline{Q P}\)
b. Prove indirectly that if a line is perpendicular to a radius at its endpoint, then the line is tangent to the circle.
Gien m ⊥ \(\overline{Q P}\)
Prove Line m is tangent to ⊙Q.
Answer:
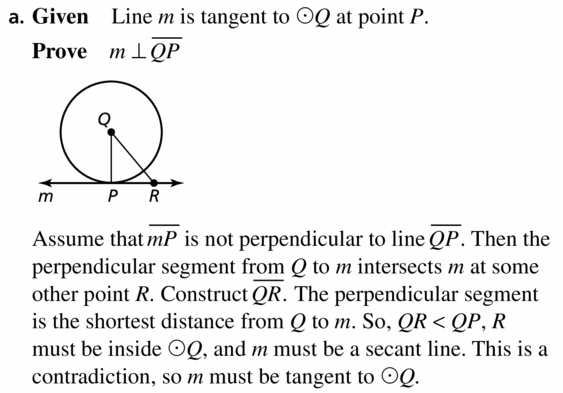

Question 48.
REASONING
In the diagram, AB = AC = 12, BC = 8, and all three segments are Langent to ⊙P. What is the radius of ⊙P? Justify your answer.
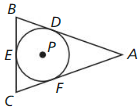
Answer:
Given,
AB = AC = 12, BC = 8
Perimeter of ABC = 12 +12 + 8 = 32 units
AE is the height so AE by Pythagorean theorem is
√(12)² – (8/2)² = 8√2 units
Area of the triangle = 1/2 × 8 × 8√2 = 32√2 sq. units
Area of triangle APC = 1/2 × 12 × r = 6r sq. units
Area of triangle APB = 1/2 × 12 × r = 6r sq. units
Area of triangle BPC = 1/2 × 8 × r = 4r sq. units
Total area of this triangle is 32√2 sq. units
6r + 6r + 4r + = 32√2 sq. units
16r = 32√2
r = 2√2
So, the radius of the inscribed circle is 2√2 units.
Maintaining Mathematical Proficiency
Find the indicated measure.
Question 49.
m∠JKM
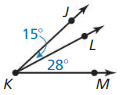
Answer:

Question 50.
AB
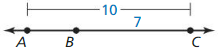
Answer:
AC = AB + BC
10 = AB + 7
AB = 10 – 7
AB = 3
10.2 Finding Arc Measures
Exploration 1
Measuring Circular Arcs
Work with a partner: Use dynamic geometry software to find the measure of \(\widehat{B C}\). Verify your answers using trigonometry.
a.
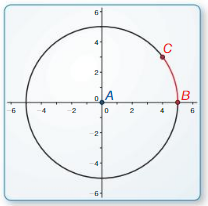
Points
A(0, 0)
B(5, 0)
C(4, 3)
Answer:
30 degrees
b.
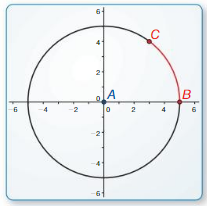
Points
A(0, 0)
B(5, 0)
C(3, 4)
Answer:
60 degrees
c.
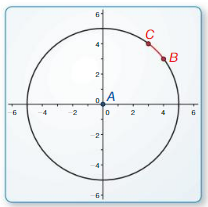
Points
A(0, 0)
B(4, 3)
C(3, 4)
Answer:
15 degrees
d.
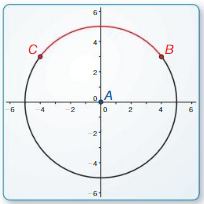
Points
A(0, 0)
B(4, 3)
C(- 4, 3)
Answer:
90 degrees
Communicate Your Answer
Question 2.
How are circular arcs measured?
Answer:
Circular arcs are measured using the formula.
The formula for the arc length L = θ x r.
Where θ is in radian then L = θ x (π/180) x r.
Where θ in degree L = length of an arc.
Question 3.
Use dynamic geometry software to draw a circular arc with the given measure.
USING TOOLS STRATEGICALLY
To be proficient in math, you need to use technological tools to explore and deepen your understanding of concepts.
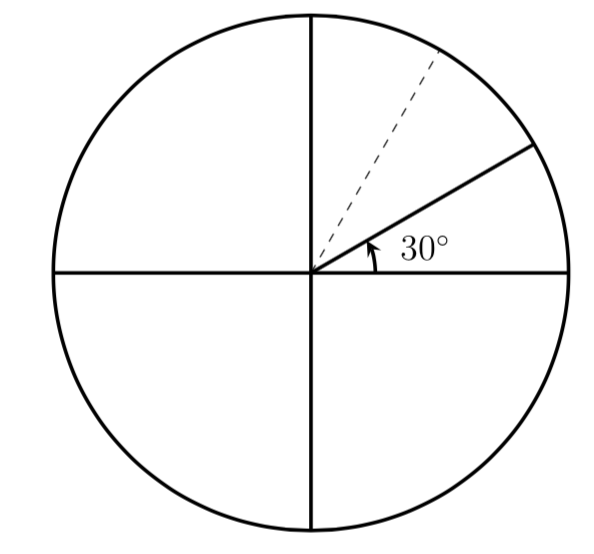
a. 30°
Answer:
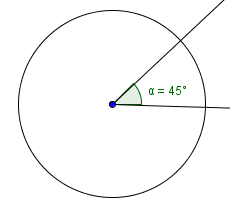
b. 45°
Answer:
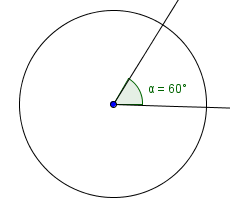
c. 60°
Answer:
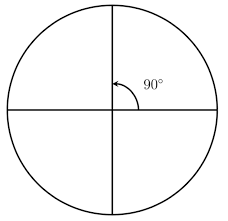
d. 90°
Answer:
Lesson 10.2 Finding Arc Measures
Monitoring Progress
Identify the given arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.
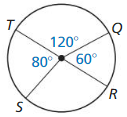
Question 1.
\(\widehat{T Q}\)
Answer:
\(\widehat{T Q}\) is a minor arc.
\(\widehat{T Q}\) = 120°
Question 2.
\(\widehat{Q R T}\)
Answer:
\(\widehat{Q R T}\)
Question 3.
\(\widehat{T Q R}\) is a major arc.
\(\widehat{Q R T}\) = QR + RS + ST
RS = 360° – (60 + 120 + 80)
= 360 – 260 = 100°
So, \(\widehat{Q R T}\) = 60° + 100° + 80°
\(\widehat{Q R T}\) = 240°
Answer:
Question 4.
\(\widehat{Q S}\)
Answer:
\(\widehat{Q S}\) = QR + RS
= 60 + 100 = 160°
Therefore, \(\widehat{Q S}\) = 160° and it is a minor arc.
Question 5.
\(\widehat{T S}\)
Answer:
\(\widehat{T S}\) = 80° and it is a minor arc.
Question 6.
\(\widehat{R S T}\)
Answer:
\(\widehat{R S T}\) = 100 + 80 = 180
Therefore, \(\widehat{R S T}\) = 180° and it is a minor arc.
Tell whether the red arcs are congruent. Explain why or why not.
Question 7.
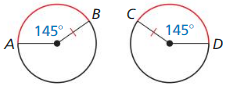
Answer:
\(\widehat{A B}\), \(\widehat{C D}\) are congruent as they measure same radius and same arc length.
Question 8.
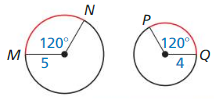
Answer:
\(\widehat{M N}\), \(\widehat{P Q}\) are not congruent as they measure different radius.
Exercise 10.2 Finding Arc Measures
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Copy and complele:
If ∠ACB and ∠DCE are congruent central angles of ⊙C, then \(\widehat{A B}\) and \(\widehat{D E}\) arc.
Answer:

Question 2.
WHICH ONE DOESNT BELONG?
Which circle does not belong with the other three? Explain your reasoning.
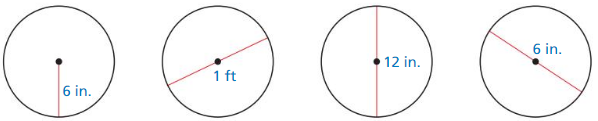
Answer:
We know that 1 ft = 12 in
So, the fourth circle does not belong to the other three as its diameter is different.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, name the red minor arc and find its measure. Then name the blue major arc and find its measure.
Question 3.
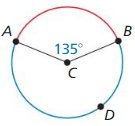
Answer:

Question 4.
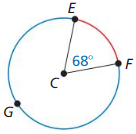
Answer:
The minor arc \(\widehat{E F}\) = 68° and major arc \(\widehat{F G E}\) = 360° – 68° = 292°.
Question 5.
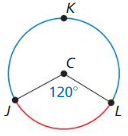
Answer:

Question 6.
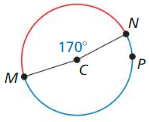
Answer:
The minor arc is \(\widehat{M N}\) = 170°, major arc \(\widehat{N P M}\) = 360° – 170° = 190°.
In Exercises 7 – 14. identify the given arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.

Question 7.
\(\widehat{B C}\)
Answer:
![]()
Question 8.
\(\widehat{D C}\)
Answer:
\(\widehat{D C}\) is a minor arc and it has a measure of 65°.
Question 9.
\(\widehat{E D}\)
Answer:
![]()
Question 10.
\(\widehat{A E}\)
Answer:
\(\widehat{A E}\) is a minor arc and it has a measure of 70°.
Question 11.
\(\widehat{E A B}\)
Answer:
![]()
Question 12.
\(\widehat{A B C}\)
Answer:
\(\widehat{A B C}\) is a semicircle and it has a measure of 180°.
Question 13.
\(\widehat{B A C}\)
Answer:
![]()
Question 14.
\(\widehat{E B D}\)
Answer:
\(\widehat{E B D}\) is a major arc and it has a measure of 315°.
In Exercises 15 and 16, find the measure of each arc.
Question 15.
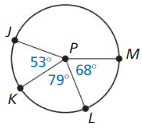
a. \(\widehat{J L}\)
b. \(\widehat{K M}\)
c. \(\widehat{J L M}\)
d. \(\widehat{J M}\)
Answer:
Question 16.
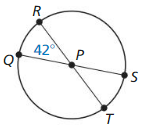
a. \(\widehat{R S}\)
Answer:
\(\widehat{R S}\) = \(\widehat{Q R S}\) – \(\widehat{Q R}\)
= 180 – 42
= 138°
So, \(\widehat{R S}\) = 138°
b. \(\widehat{Q R S}\)
Answer:
\(\widehat{Q R S}\) = 180°
c. \(\widehat{Q S T}\)
Answer:
\(\widehat{Q S T}\) = \(\widehat{Q R S}\) + \(\widehat{S T}\)
= 180 + 42 = 222
So, \(\widehat{Q S T}\) = 222°
d. \(\widehat{Q T}\)
Answer:
\(\widehat{Q T}\) = 360 – (42 + 138 + 42)
= 360 – (222)
= 138°
\(\widehat{Q T}\) = 138°
Question 17.
MODELING WITH MATHEMATICS
A recent survey asked high school students their favorite type of music. The results are shown in the circle graph. Find each indicated arc measure.
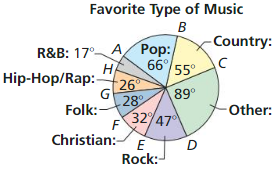
a. m\(\widehat{A E}\)
b. m\(\widehat{A C E}\)
c. m\(\widehat{G D C}\)
d. m\(\widehat{B H C}\)
e. m\(\widehat{F D}\)
f. m\(\widehat{F B D}\)
Answer:
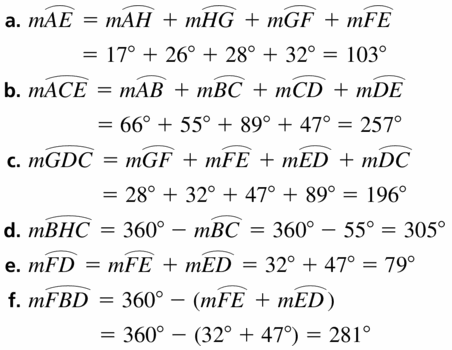
Question 18.
ABSTRACT REASONING
The circle graph shows the percentages of students enrolled in fall Sports at a high school. Is it possible to find the measure of each minor arc? If so, find the measure 0f the arc for each category shown. If not, explain why it is not possible.
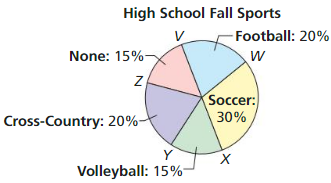
Answer:
Soccer angle = 30% of 360 = 108°
Volleyball angle = 15% of 360 = 54°
Cross-country angle = 20% of 360 = 72°
None angle = 15% of 360 = 54°
Football angle = 20% of 360 = 72°
In Exercises 19 – 22, tell whether the red arcs are congruent. Explain why or why not.
Question 19.

Answer:
![]()
Question 20.
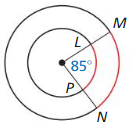
Answer:
\(\widehat{L P}\) and \(\widehat{M N}\) are not congruet because they are not in the same circle.
Question 21.
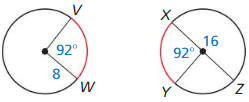
Answer:
![]()
Question 22.
Answer:
\(\widehat{R S Q}\), \(\widehat{F G H}\) are not congruent because those two circles have different radii.
MATHEMATICAL CONNECTIONS
In Exercises 23 and 24. find the value of x. Then find the measure of the red arc.
Question 23.
Answer:
Question 24.
Answer:
4x + 6x + 7x + 7x = 360
24x = 360
x = 15
m\(\widehat{R S T}\) = 6(15) + 7(15)
= 90 + 105 = 195°
So, m\(\widehat{R S T}\) = 195°
Question 25.
MAKING AN ARGUMENT
Your friend claims that any two arcs with the same measure are similar. Your cousin claims that an two arcs with the same measure are congruent. Who is correct? Explain.
Answer:
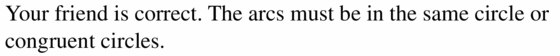
Question 26.
MAKING AN ARGUMENT
Your friend claims that there is not enough information given to find the value of x. Is your friend correct? Explain your reasoning.

Answer:
My friend is wrong.
4x + x + x + 4x = 360
10x = 360
x = 36°
Question 27.
ERROR ANALYSIS
Describe and correct the error in naming the red arc.
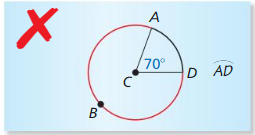
Answer:
![]()
Question 28.
ERROR ANALYSIS
Describe and correct the error in naming congruent arc.

Answer:
\(\widehat{J K}\), \(\widehat{N P}\) are not congruent because those two arcs are from different circles.
Question 29.
ATTENDING TO PRECISION
Two diameters of ⊙P are \(\widehat{A B}\) and \(\widehat{C D}\). Find m\(\widehat{A C D}\) and m\(\widehat{A C}\) when m\(\widehat{A D}\) = 20°.
Answer:
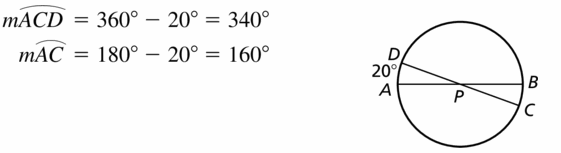
Question 30.
REASONING
In ⊙R, m\(\widehat{A B}\) = 60°, m\(\widehat{B C}\) = 25°. m\(\widehat{C D}\) = 70°, and m\(\widehat{D E}\) = 20°. Find two possible measures of \(\widehat{A E}\).
Answer:
\(\widehat{A E}\) = 360 – (\(\widehat{A B}\) + \(\widehat{B C}\) + \(\widehat{C D}\) + \(\widehat{D E}\))
= 360 – (60 + 25 + 70 + 20)
= 360 – (175)
= 185
\(\widehat{A E}\) = \(\widehat{A B}\) + \(\widehat{B C}\) + \(\widehat{C D}\) + \(\widehat{D E}\)
= 60 + 25 + 70 + 20 = 175
So, the two possibilities of \(\widehat{A E}\) are 185°, 175°
Question 31.
MODELING WITH MATHEMATICS
On a regulation dartboard, the outermost circle is divided into twenty congruent sections. What is the measure of each arc in this circle?

Answer:
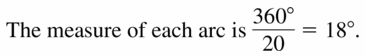
Question 32.
MODELING WITH MATHEMATICS
You can use the time zone wheel to find the time in different locations across the world. For example, to find the time in Tokyo when it is 4 P.M. in San Francisco, rotate the small wheel until 4 P.M. and San Francisco line up, as shown. Then look at Tokyo to see that it is 9 A.M. there.
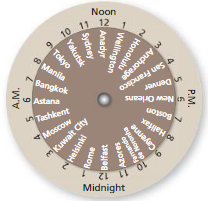
a. What is the arc measure between each time zone 0n the wheel?
Answer:
As the circle is divided into 24 sectors, each time zone angle = \(\frac { 360 }{ 24 } \) = 15°
b. What is the measure of the minor arc from the Tokyo zone to the Anchorage zone?
Answer:
The measure of the minor arc from the Tokyo zone to the Anchorage zone = 15 + 15 + 15 + 15 + 15 + 15
= 90°
c. If two locations differ by 180° on the wheel, then it is 3 P.M. at one location when it is _________ at the other location.
Answer:
Kuwaiti city.
Question 33.
PROVING A THEOREM
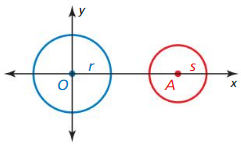
Write a coordinate proof of the Similar Circles Theorem (Theorem 10.5).
Given ⊙O with center O(0, 0) and radius r.
⊙A with center A(a, 0) and radius s
Prove ⊙O ~ ⊙A
Answer:
Question 34.
ABSTRACT REASONING
Is there enough information to tell whether ⊙C ≅ ⊙D? Explain your reasoning.
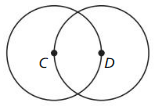
Answer:
Both circles ⊙C and ⊙D have the same radius so those circles are congruent.
Question 35.
PROVING A THEOREM
Use the diagram to prove each part of the biconditional in the Congruent Circles Theorem (Theorem 10.3).
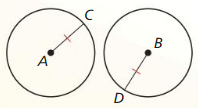
a. Given \(\overline{A C} \cong \overline{B D}\)
Prove ⊙A ≅ ⊙B
b. Given ⊙A ≅ ⊙B
prove \(\overline{A C} \cong \overline{B D}\)
Answer:
Question 36.
HOW DO YOU SEE IT?
Are the circles on the target similar or congruent? Explain your reasoning.
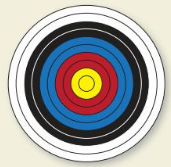
Answer:
Given that the radius of different circles shown the different colors is different. It is adding as we are moving outwards.
The circles on the target are not congruent as they have diameters and radii but they are similar as they have a common center.
Question 37.
PROVING A THEOREM
Use the diagram to prove each part of the biconditional in the Congruent Central Angles Theorem (Theorem 10.4).
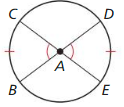
a. Given ∠ABC ≅ ∠DAE
Prove \(\widehat{B C}\) ≅ \(\widehat{D E}\)
b. Given \(\widehat{B C}\) ≅ \(\widehat{D E}\)
Prove ∠ABC ≅ ∠DAE
Answer:
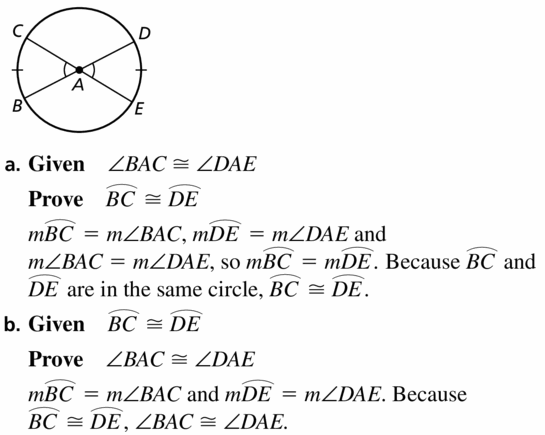
Question 38.
THOUGHT PROVOKING
Write a formula for the length of a circular arc. Justify your answer.
Answer:
The formula to find the length of a circular arc is radius x angle.
Maintaining Mathematical Proficiency
Find the value of x. Tell whether the side lengths form a Pythagorean triple.
Question 39.
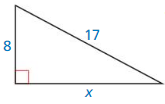
Answer:

Question 40.
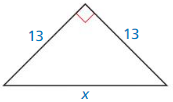
Answer:
x² = 13² + 13²
= 169 + 169
= 338
x = 13√2
Question 41
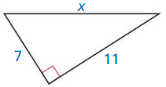
Answer:

Question 42.
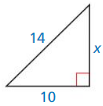
Answer:
14² = x² + 10²
196 = x² + 100
x² = 196 – 100
x² = 96
x = 4√6
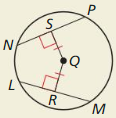
10.3 Using Chords
Exploration 1
Drawing Diameters
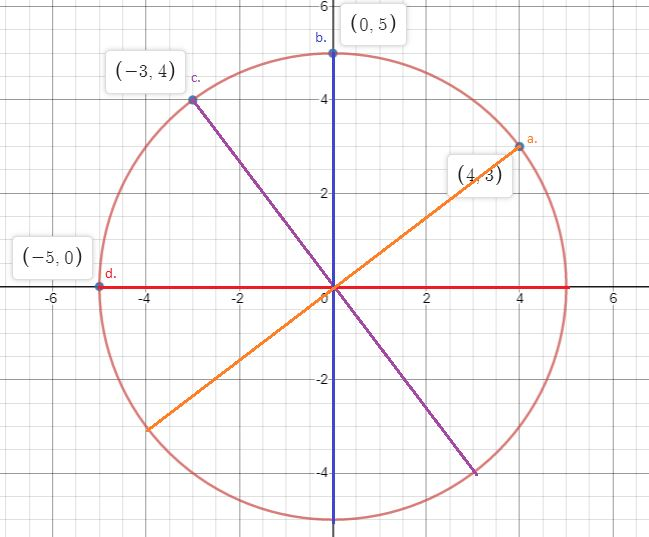
Work with a partner: Use dynamic geometry software to construct a circle of radius 5 with center at the origin. Draw a diameter that has the given point as an endpoint. Explain how you know that the chord you drew is a diameter.
a. (4, 3)
b. (0, 5)
c. (-3, 4)
d. (-5, 0)
Answer:
Exploration 2
Writing a Conjecture about Chords
Work with a partner. Use dynamic geometry software to construct a chord \(\overline{B C}\) of a circle A. Construct a chord on the perpendicular bisector of \(\overline{B C}\). What do you notice? Change the original chord and the circle several times. Are your results always the same? Use your results to write a conjecture.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
Exploration 3
A Chord Perpendicular to a Diameter
Work with a partner. Use dynamic geometry software to construct a diameter \(\overline{B C}\) of a circle A. Then construct a chord \(\overline{D E}\) perpendicular to \(\overline{B C}\) at point F. Find the lengths DF and EF. What do you notice? Change the chord perpendicular to \(\overline{B C}\) and the circle several times. Do you always get the same results? Write a conjecture about a chord that is perpendicular to a diameter of a circle.
Answer:
Communicate Your Answer
Question 4.
What are two ways to determine when a chord is a diameter of a circle?
Answer:
If a chord passes through the centre of the circle, then it is the diameter of a circle.
The longest chord of the circle is the diameter of a circle.
Lesson 10.3 Using Chords
Monitoring Progress
In Exercises 1 and 2, use the diagram of ⊙D.
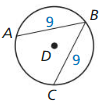
Question 1.
If m\(\widehat{A B}\) = 110°. find m\(\widehat{B C}\).
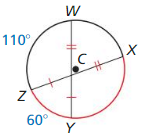
Answer:
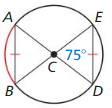
Because AB and BC are congruent chords in congruent circles, the corresponding minor arcs \(\widehat{A B}\), \(\widehat{B C}\) are congruent by the congruent corresponding chords theorem.
So, \(\widehat{A B}\) = \(\widehat{B C}\)
\(\widehat{B C}\) = 110°
Question 2.
If m\(\widehat{A C}\) = 150° find m\(\widehat{A B}\).
Answer:
\(\widehat{A C}\) = 360 – (\(\widehat{A B}\) + \(\widehat{B C}\))
150 = 360 – 2(\(\widehat{A B}\))
2(\(\widehat{A B}\)) = 360 – 150 = 210
\(\widehat{A B}\) = 105°
In Exercises 3 and 4. find the indicated length or arc measure.
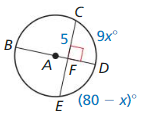
Question 3.
CE
Answer:
CE = 5 + 5
= 10 units
Question 4.
m\(\widehat{C E}\)
Answer:
m\(\widehat{C E}\) = 9x + 180 – x = 180 – 8x
m\(\widehat{C E}\) = 180 – 8x
Question 5.
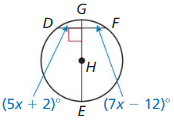
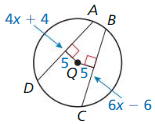
In the diagram, JK = LM = 24, NP = 3x, and NQ = 7x – 12. Find the radius of ⊙N
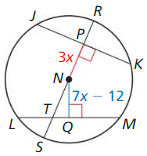
Answer:
Given,
In the diagram, JK = LM = 24, NP = 3x, and NQ = 7x – 12.
JK = LM
NP = NQ
3x = 7x – 12
4x = 12
x = 3
NP = 3x
NP = 3 × 3 = 9
JK = 24
PK = 1/2(24) = 12
PK = 12
NK = √(NP)² + (PK)²
NK = √(9)² + (12)²
NK = √81 + 144
NK = √225 = 15
Thus the radius of the circle is 15.
Exercise 10.3 Using Chords
Vocabulary and Core Concept Check
Question 1.
WRITING
Describe what it means to bisect a chord.
Answer:

Question 2.
WRITING
Two chords of a circle are perpendicular and congruent. Does one of them have to be a diameter? Explain your reasoning.
Answer:
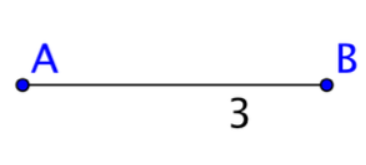
Imagine a line segment of length 3 units, AB.
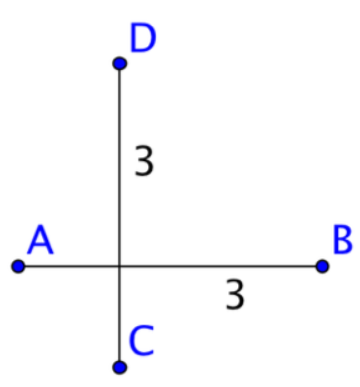
A second congruent segment of length 3 that is perpendicular to AB called CD.
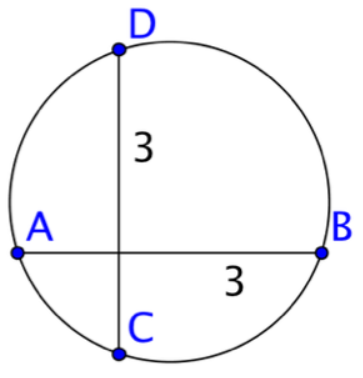
Circumscribe both these line segments and note that AB and CD are now chords.
While both chords are perpendicular and congruent, neither chord is a diameter. Thus, it is possible to have two chords of this type with neither one diameter of the circle.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, find the measure of the red arc or chord in ⊙C.
Question 3.
Answer:
Question 4.
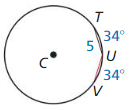
Answer:
Arc length = radius x angle
= 5 x 34 = 170
Question 5.
Answer:
Question 6.
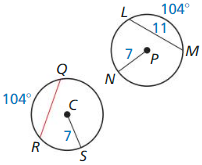
Answer:
As the two circles radius is the same and the angle is the same so the chord length is 11 units.
In Exercise 7-10, find the value of x.
Question 7.
Answer:
Question 8.
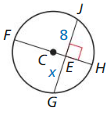
Answer:
By the perpendicular bisector theorem RS = ST
x = 40°
Question 9.
Answer:

Question 10.
Answer:
5x + 2 = 7x – 12
7x – 5x = 2 + 12
2x = 14
x = 7
Question 11.
ERROR ANALYSIS
Describe and correct the error in reasoning.
Answer:
![]()
Question 12.
PROBLEM SOLVING
In the cross section of the submarine shown, the control panels are parallel and the same length. Describe a method you can use to find the center of the cross section. Justify your method.

Answer:
In Exercises 13 and 14, determine whether \(\overline{A B}\) is a diameter of the circle. Explain your reasoning.
Question 13.
Answer:
Question 14.
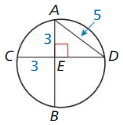
Answer:
5² = 3² + x²
25 = 9 + x²
x² = 25 – 9
x = 4
So, AB is not diameter of the circle.
In Exercises 15 and 16, find the radius of ⊙Q.
Question 15.
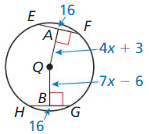
Answer:
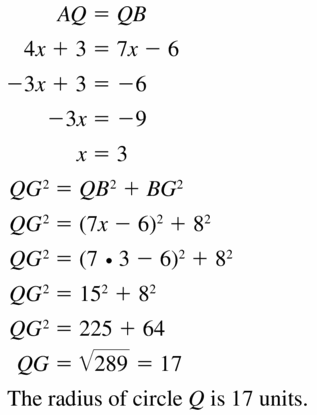
Question 16.
Answer:
AD = BC
4x + 4 = 6x – 6
6x – 4x = 4 + 6
2x = 10
x = 5
BC = 6(5) – 6 = 30 – 6 = 24
QC² = 5² + 12²
= 25 + 144 = 169
QC = 13
Therefore, the radius is 13.
Question 17.
PROBLEM SOLVING
An archaeologist finds part of a circular plate. What was the diameter of the plate to the nearest tenth of an inch? Justify your answer.
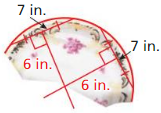
Answer:

Question 18.
HOW DO YOU SEE IT?
What can you conclude from each diagram? Name a theorem that justifies your answer.
a.
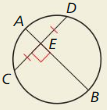
Answer:
Perpendicular chord bisector converse theorem.
b.
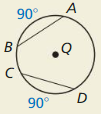
Answer:
Congruent Corresponding Chords theorem
c.
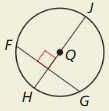
Answer:
Perpendicular chord bisector theorem
d.
Answer:
Equidistant chords theorem
Question 19.
PROVING A THEOREM
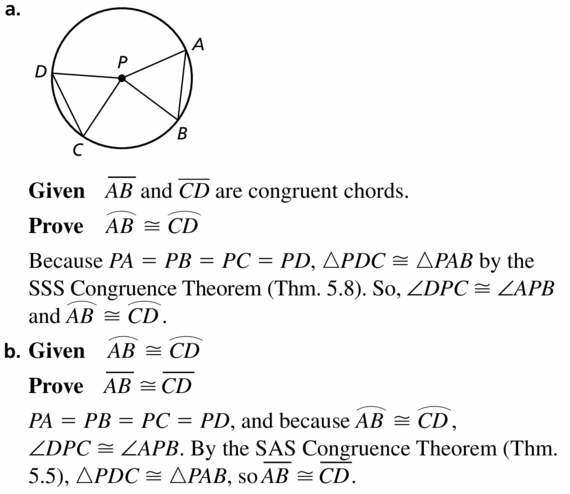
Use the diagram to prove each part of the biconditional in the Congruent Corresponding Chords Theorem (Theorem 10.6).
a. Given \(\overline{A B}\) and \(\overline{C D}\) are congruent chords.
Prove \(\widehat{A B} \cong \widehat{C D}\)
b. Given \(\widehat{A B} \cong \widehat{C D}\)
Prove \(\overline{A B}\) ≅ \(\overline{C D}\)
Answer:
Question 20.
MATHEMATICAL CONNECTIONS
In ⊙P, all the arcs shown have integer measures. Show that x must be even.
Answer:
Using congruent corresponding chords theorem
m arcAB = m arcBC
x = 2(180 – m arcAB)
Thus the value of x must be a even integer.
Question 21.
REASONING
In ⊙P. the lengths of the parallel chords are 20, 16, and 12. Find m\(\widehat{A B}\). Explain your reasoning.
Answer:
Question 22.
PROVING A THEOREM
Use congruent triangles to prove the Perpendicular Chord Bisector Theorem (Theorem 10.7).
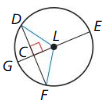
Given \(\overline{E G}\) is a diameter of ⊙L.
\(\overline{E G}\) ⊥ \(\overline{D F}\)
Prove \(\overline{D C}\) ≅ \(\overline{F C}\), \(\widehat{D G} \cong \widehat{F G}\)
Answer:
Let L be the centre of the circle
draw any chord DF on the circle
As DF passes through LG.
The length of DC is the same as FC.
Question 23.
PROVING A THEOREM
Write a proof of the Perpendicular Chord Bisector Converse (Theorem 10.8).
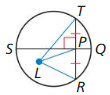
Given \(\overline{Q S}\) is a perpendicular bisector of \(\overline{R T}\).
Prove \(\overline{Q S}\) is a diameter of the circle L.
(Hint: Plot the center L and draw △LPT and △LPR.)
Answer:

Question 24.
THOUGHT PROVOKING
Consider two chords that intersect at point P. Do you think that \(\frac{A P}{B P}=\frac{C P}{D P}\)? Justify your answer.
Answer:
Question 25.
PROVING A THEOREM
Use the diagram with the Equidistant Chords Theorem (Theorem 10.9) to prove both parts of the biconditional of this theorem.
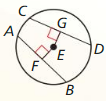
\(\overline{A B}\) ≅ \(\overline{C D}\) if and only if EF = EG
Answer:
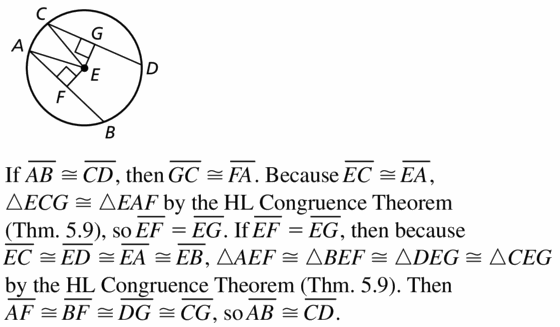
Question 26.
MAKING AN ARGUMENT
A car is designed so that the rear wheel is only partially visible below the body of the car. The bottom edge of the panel is parallel [o the ground. Your friend claims that the point where the tire touches the ground bisects \(\widehat{A B}\). Is your friend correct? Explain your reasoning.

Answer:
Maintaining Mathematical Proficiency
Find the missing interior angle measure.
Question 27.
Quadrilateral JKLW has angle measures m∠J = 32°, m∠K = 25°, and m∠L = 44°. Find m∠M.
Answer:
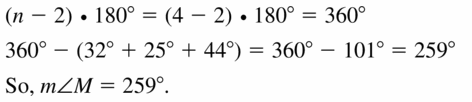
Question 28.
Pentagon PQRST has angle measures m∠P = 85°, m∠Q = 134°, m∠R = 97°, and m∠S =102°.
Find m∠T.
Answer:
The sum of interior angles of a pentagon = 540°
m∠T = 540 – (85 + 134 + 97 + 102)
= 540 – 418 = 122
m∠T = 122°.
10.1 – 10.3 Quiz
In Exercises 1 – 6, use the diagram. (Section 10.1)
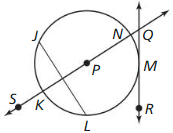
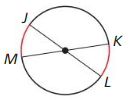
Question 1.
Name the circle.
Answer:
The circle has a chord, diameter and tangent.
Question 2.
Name a radius.
Answer:
NP is the radius of the circle.
Question 3.
Name a diameter.
Answer:
KN is the diameter of the circle.
Question 4.
Name a chord.
Answer:
JL is the chord
Question 5.
Name a secant.
Answer:
SN is the secant
Question 6.
Name a tangent.
Answer:
QR is the tangent.
Find the value of x.
Question 7.
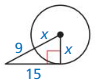
Answer:
(9 + x)² = x² + 15²
81 + 18x + x² = x² + 225
18x = 225 – 81
18x = 144
x = 8
Question 8.
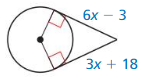
Answer:
6x – 3 = 3x + 18
6x – 3x = 18 + 3
3x = 21
x = 7
Identify the given arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.
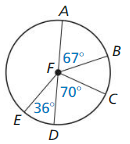
Question 9.
\(\widehat{A E}\)
Answer:
\(\widehat{A E}\) = 180 – 36
= 144
So, \(\widehat{A E}\) = 144°
Question 10.
\(\widehat{B C}\)
Answer:
\(\widehat{B C}\) = 180 – (67 + 70)
= 180 – 137 = 43
So, \(\widehat{B C}\) = 43°
Question 11.
\(\widehat{A C}\)
Answer:
\(\widehat{A C}\) = 43 + 67 = 110°
Question 12.
\(\widehat{A C D}\)
Answer:
\(\widehat{A C D}\) = 180°
Question 13.
\(\widehat{A C E}\)
Answer:
\(\widehat{A C E}\) = 180 + 36 = 216°
Question 14.
\(\widehat{B E C}\)
Answer:
\(\widehat{B E C}\) = 70 + 36 + 43 = 149°
Tell whether the red arcs are congruent. Explain why or why not.
Question 15.
Answer:
As two chords pass through the centre of the circle. Those two red arcs are congruent.
Question 16.
Answer:
Red arcs are not congruent because the radius of the two circles is different.
Question 17.
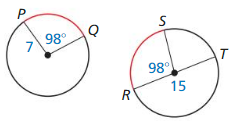
Find the measure of the red arc in ⊙Q.
Answer:
BE and EG are congruent chords of the same circle.
Therefore by the congruent corresponding chords theorem, BD and EG are congruent.
m arcBD = m arcEG
m arcBD = 360 (150 + 110)
= 360 – 260 = 100
So, m arcEG = 100 degrees
Question 18.
In the diagram. AC = FD = 30, PG = x + 5, and PJ = 3x – 1. Find the radius of ⊙P.
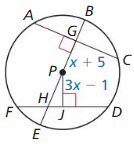
Answer:
As AC and FD are congruent, they are at equidistance from the center P.
PG = PJ
x + 5 = 3x – 1
2x = 6
x = 3
x + 5 = 3 + 5 = 8
PG = 8 units
GC = 1/2 × AC
GC = 1/2 × 30 = 15
GC = 15
PC² = PG² + GC²
PC² = 8² + 15²
PC² = 64+ 225
PC² = 289
PC = 17
Thus PC is the radius of the circle.
Question 19.
A circular clock can be divided into 12 congruent sections.

a. Find the measure of each arc in this circle.
Answer:
The measure of each arc = \(\frac { 360 }{ 12 } \) = 30°
b. Find the measure of the minor arc formed by the hour and minute hands when the times is 7:00.
Answer:
When the time is 7:00 the minute hand is at 12 and hour hand is at 7 and so the minor arc is subtended by 12 – 7 = 5 of these sections and so the angle subtended is 30 x 5 = 150°
c. Find a time at which the hour and minute hands form an arc that is congruent to the arc in part (b).
Answer:
A minor arc is equal to 150° can be formed by multiple placements of the hour and the minute hand. One of them can be the time 5:00 when the minute hand is at 12 and the hour hand is at 5.
10.4 Inscribed Angles and Polygons
Exploration 1
Inscribed Angles and Central Angles
work with a partner: Use dynamic geometry software.
Sample
a. Construct an inscribed angle in a circle. Then construct the corresponding central angle.
Answer: An Inscribed point in a cycle is established in such a form that its pair views/rays are working as the chord to the circle and the top of the angle is located on the edge of the circle. In geometry, an inscribed side is the angle created in the center of a circle when pair majors meet on the circle
b. Measure both angles. How is the inscribed angle related to its intercepted arc?
Answer: The inscribed site is half in size as the area of the interior phase of the division of the round arc subtended by it at the middle of the circle.
An Inscribed point in a cycle is established in such a form that its pair views/rays are working as the chord to the circle and the top of the angle is located on the edge of the circle
c. Repeat parts (a) and (b) several times. Record your results in a table. Write a conjecture about how an inscribed angle is related to its intercepted arc.
ATTENDING TO PRECISION
To be proficient in math, you need to communicate precisely with others.
Answer: An Inscribed point in a cycle is established in such a form that its pair views/rays are working as the chord to the circle and the top of the angle is located on the edge of the circle. In geometry, an inscribed side is the angle created in the center of a circle when pair of majors meet on the circle
It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
Exploration 2
A Quadrilateral with Inscribed Angles
work with a partner: Use dynamic geometry software.
Sample
a. Construct a quadrilateral with each vertex on a circle.
Answer:
b. Measure all four angles. What relationships do you notice?
Answer:
c. Repeat parts (a) and (b) several times. Record your results in a table. Then write a conjecture that summarizes the data.
Answer:
Communicate Your Answer
Question 3.
How are inscribed angles related to their intercepted arcs? How are the angles of an inscribed quadrilateral related to each other?
Answer:
The inscribed angle is always half in size as the central angle formed at the center of the circle by the intercepted arc.
In an inscribed quadrilateral, each pair of interior opposite angles are supplementary in nature and always add up to 180 degrees.
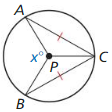
Question 4.
Quadrilateral EFGH is inscribed in ⊙C. and m ∠ E = 80°. What is m ∠ G? Explain.
Answer:
m ∠ E + m ∠ H = 80 + 80 = 160°
m ∠ E + m ∠ H + m ∠ G + m ∠ F = 360
160° + m ∠ G + m ∠ F = 360
m ∠ G + m ∠ F = 360 – 160 = 200
m ∠ G = 100°
Lesson 10.4 Inscribed Angles and Polygons
Monitoring Progress
Find the measure of the red arc or angle.
Question 1.
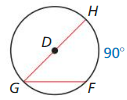
Answer:
m∠G = \(\frac { 90 }{ 2 } \) = 45°
Question 2.
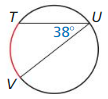
Answer:
\(\widehat{T V}\) = 2 • 38 = 76°
Question 3.
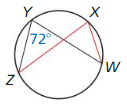
Answer:
m∠W = 72°
Find the value of each variable.
Question 4.
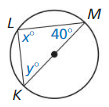
Answer:
x° = 90°
y° = 180 – (40 + 90) = 180 – 130
y° = 50°
Question 5.
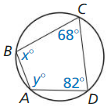
Answer:
∠B + ∠D = 180
∠B + 82 = 180
x° = 98°
∠C + ∠A = 180
68 + y° = 180
y° = 112°
Question 6.
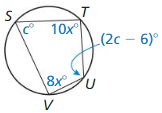
Answer:
∠S + ∠U = 180°
c + 2c – 6 = 180
3c = 186
c = 62°
∠T + ∠V = 180°
10x + 8x = 180
18x = 180
x = 10°
Question 7.
In Example 5, explain how to find locations where the left side of the statue is all that appears in your camera’s field of vision.
Answer:
As we know, according to the inscribed right angle theorem, if a right angle is inscribed in a circle, then the hypotenuse of the triangle is considered as the diameter of the circle.
So, draw the circle that has the left half of the statue as diameter.
Hence the left side of the statue perfectly fits within the camera 90 degrees field of vision from any point on that semicircle.
Exercise 10.4 Inscribed Angles and Polygons
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
If a circle is circumscribed about a polygon, then the polygon is an ___________ .
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different?
Find “both” answers.
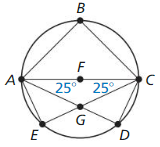
Find m∠ABC.
Answer:
m∠ABC = 60°
Find m∠AGC.
Answer:
m∠AGC = 180 – (25 + 25)
= 180 – 50 = 130°
Find m∠AEC.
Answer:
m∠AEC = 180 – (50 + 50)
= 180 – 100 = 80°
Find m∠ADC.
Answer:
m∠ADC = 180 – (25 + 50)
= 180 – 75 = 105°
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 8, find the indicated measure.
Question 3.
m∠A
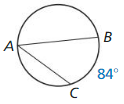
Answer:
Question 4.
m∠G
Answer:
m∠G = 360 – (70 + 120)
= 360 – 190 = 170°
Question 5.
m ∠ N
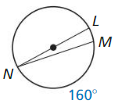
Answer:
Question 6.
m\(\widehat{R S}\)
Answer:
m\(\widehat{R S}\) = 2 • 67 = 134°
Question 7.
m\(\widehat{V U}\)
Answer:
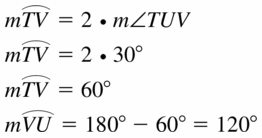
Question 8.
m\(\widehat{W X}\)
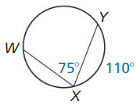
Answer:
m\(\widehat{W X}\) = \(\frac { 75 }{ 2 } \) = 37.5
In Exercises 9 and 10, name two pairs of congruent angles.
Question 9.
Answer:
Question 10.
Answer:
m∠W = m∠Z, m∠X = m∠Y
In Exercises 11 and 12, find the measure of the red arc or angle.
Question 11.
Answer:
Question 12.
Answer:
\(\widehat{P S}\) = 2 • 40 = 80
In Exercises 13 – 16, find the value of each variable.
Question 13.
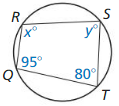
Answer:

Question 14.
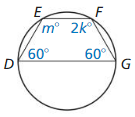
Answer:
m∠E + m∠G = 180
m + 60 = 180
m = 120°
m∠D + m∠F = 180
60 + 2k = 180
k = 60°
Question 15.
Answer:
Question 16.
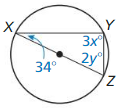
Answer:
3x° = 90°
x° = 30°
2y° + 90° + 34° = 180°
2y° + 124° = 180°
2y° = 56°
y° = 28°
Question 17.
ERROR ANALYSIS
Describe and correct the error in finding m\(\widehat{B C}\).
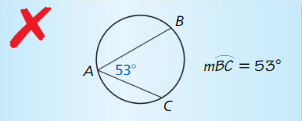
Answer:
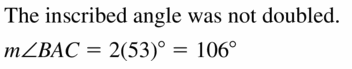
Question 18.
MODELING WITH MATHEMATICS
A carpenter’s square is an L-shaped tool used to draw right angles. You need to cut a circular piece of wood into two semicircles. How can you use the carpenter’s square to draw a diameter on the circular piece of wood?

Answer:
Recall that when a right triangle is inscribed in a circle, then the hypotenuse is the diameter of the circle. Simply use the carpenter’s square to inscribe it into the circle. The hypotenuse formed by both legs of the square should provide a diameter for the circle.
MATHEMATICAL CONNECTIONS
In Exercises 19 – 21, find the values of x and y. Then find the measures of the interior angles of the polygon.
Question 19.
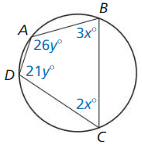
Answer:
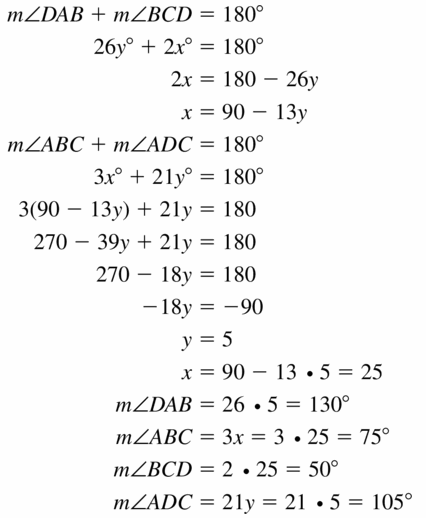
Question 20.
Answer:
∠B + ∠C = 180
14x + 4x = 180
18x = 180°
x = 10°
∠A + ∠D = 180
9y + 24y = 180
33y = 180°
y = 5.45°
∠A = 130.9°, ∠B = 40°, ∠C = 140°, ∠D = 49°
Question 21.
Answer:
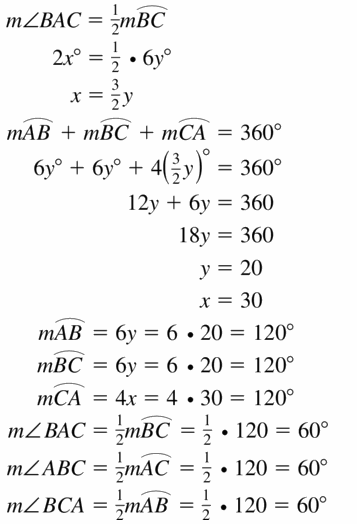
Question 22.
MAKING AN ARGUMENT
Your friend claims that ∠PTQ ≅ ∠PSQ ≅ ∠PRQ. Is our friend correct? Explain your reasoning.
Answer:
Yes, my friend is correct.
∠PTQ ≅ ∠PSQ ≅ ∠PRQ is correct according to the inscribed angles of a circle theorem.
Question 23.
CONSTRUCTION
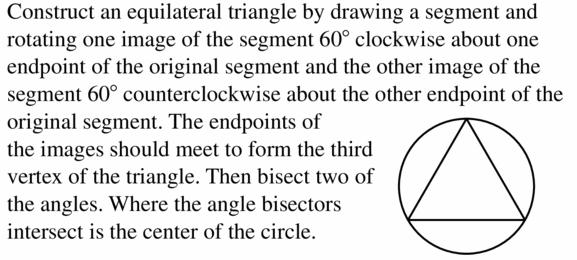
Construct an equilateral triangle inscribed in a circle.
Answer:
Question 24.
CONSTRUTION
The side length of an inscribed regular hexagon is equal to the radius of the circumscribed circle. Use this fact to construct a regular hexagon inscribed in a circle.
Answer:
As the side length is equal to the radius. Draw a line representing the radius and draw a chord different chords in the form of hexagons of the radius of the circle.
REASONING
In Exercises 25 – 30, determine whether a quadrilateral of the given type can always be inscribed inside a circle. Explain your reasoning.
Question 25.
Square
Answer:
![]()
Question 26.
rectangle
Answer:
yes, angles are right angles.
Question 27.
parallelogram
Answer:
![]()
Question 28.
kite
Answer:
No.
Question 29.
rhombus
Answer:
![]()
Question 30.
isosceles trapezoid
Answer:
Yes, the opposite angles are always supplementary.
Question 31.
MODELING WITH MATHEMATICS
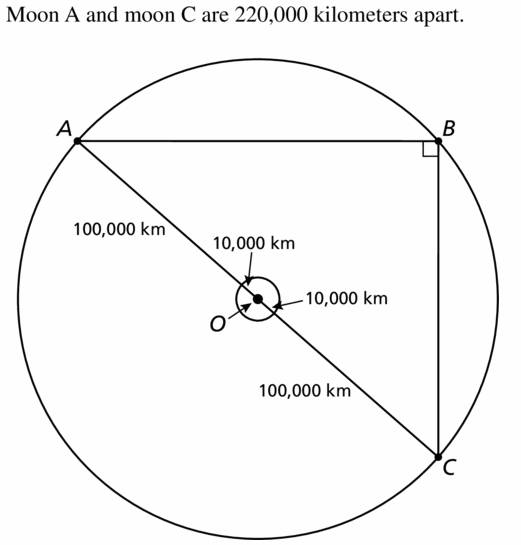
Three moons, A, B, and C, are in the same circular orbit 1,00,000 kilometers above the surface of a planet. The planet is 20,000 kilometers in diameter and m∠ABC = 90°. Draw a diagram of the situation. How far is moon A from moon C?
Answer:
Question 32.
MODELING WITH MATHEMATICS
At the movie theater. you want to choose a seat that has the best viewing angle, so that you can be close to the screen and still see the whole screen without moving your eyes. You previously decided that seat F7 has the best viewing angle, but this time someone else is already sitting there. Where else can you sit so that your seat has the same viewing angle as seat F7? Explain.
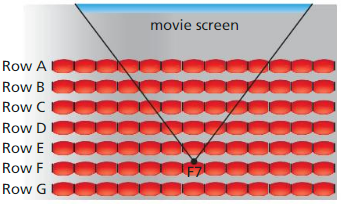
Answer:
First circumscribe the circle about the triangle that the seat F7 makes with the movie screen. Now, by the inscribed angles of a circle theorem, any angle (seat) that intercept the same arc as angle at the seat F7 will have the same viewing angle.
Therefore, use the inscribed angles of a circle theorem to find the seat.
Question 33.
WRITING
A right triangle is inscribed in a circle, and the radius of the circle is given. Explain how to find the length of the hypotenuse.
Answer:
Question 34.
HOW DO YOU SEE IT?
Let point Y represent your location on the soccer field below. What type of angle is ∠AYB if you stand anywhere on the circle except at point A or point B?
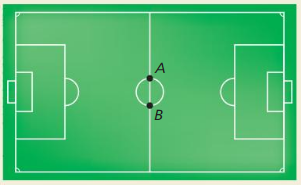
Answer:
Question 35.
WRITING
Explain why the diagonals of a rectangle inscribed in a circle are diameters of the circle.
Answer:

Question 36.
THOUGHT PROVOKING
The figure shows a circle that is circumscribed about ∆ABC. Is it possible to circumscribe a circle about any triangle? Justify your answer.
Answer:
Yes.
Question 37.
PROVING A THEOREM
If an angle is inscribed in ⊙Q. the center Q can be on a side of the inscribed angle, inside the inscribed angle, or outside the inscribed angle. Prove each case of the Measure of an Inscribed Angle Theorem (Theorem 10. 10).
a. Case 1
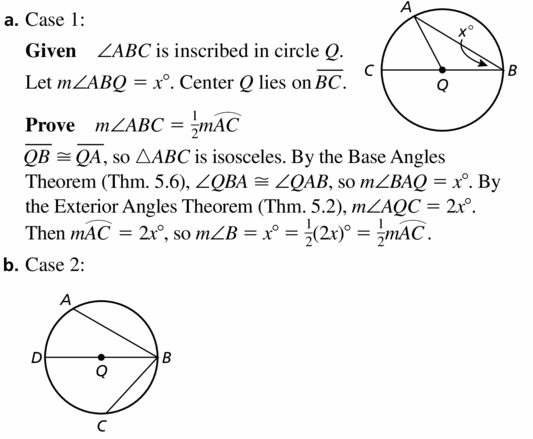
Given ∠ABC is inscribed in ⊙Q
Let m∠B = x°
Center Q lies on \(\overline{B C}\).
Prove m∠ABC = \(\frac{1}{2}\)m\(\widehat{A C}\)
(Hint: Show that ∆AQB is isosceles. Then write m\(\widehat{A C}\) in terms of x.)
b. Case 2
Use the diagram and auxiliary line to write Given and Prove statements for Case 2. Then write a proof
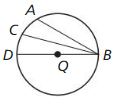
c. Case 3
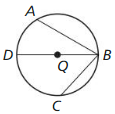
Use the diagram and auxiliary line to write Given and Prove statements for Case 3. Then write a proof.
Answer:

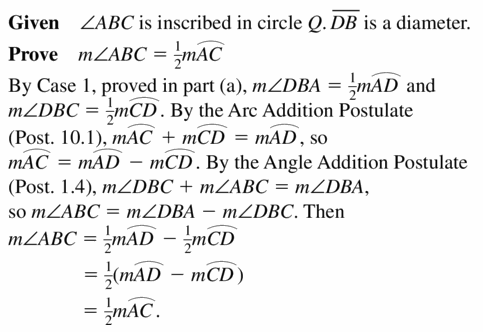
Question 38.
PROVING A THEOREM
Write a paragraph proof of the Inscribed Angles of a Circle Theorem (Theorem 10.11). First, draw a diagram and write Given and Prove statements.
Answer:
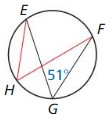
If two inscribed angles of a circle intercept the same arc, then the angles are congruent.
Question 39.
PROVING A THEOREM
The Inscribed Right Triangle Theorem (Theorem 10.12) is written as a conditional statement and its converse. Write a plan for proof for each statement.
Answer:

Question 40.
PROVING A THEOREM
Copy and complete the paragraph proof for one part of the Inscribed Quadrilateral Theorem (Theorem 10. 13).
Given ⊙C with inscribed quadrilateral DEFG
Prove m ∠ D + m ∠ F = 180°,
m ∠ E + m ∠ G = 180°
By the Arc Addition Postulate (Postulate 10. 1),
m\(\widehat{E F G}\) + ________ = 360° and m\(\widehat{F G D}\) + m\(\widehat{D E F}\) = 360°.
Using the ___________ Theorem. m\(\widehat{E D G}\) = 2m ∠ F, m\(\widehat{E F G}\) = 2m∠D, m\(\widehat{D E F}\) = 2m∠G, and m\(\widehat{F G D}\) = 2m ∠ E. By the Substitution Property of Equality, 2m∠D + ________ = 360°, So _________ . Similarly, __________ .
Answer:
m\(\widehat{E F G}\) + m\(\widehat{E D F}\) = 360° and m\(\widehat{F G D}\) + m\(\widehat{D E F}\) = 360°.
Using the the measure of an inscribed angle Theorem. m\(\widehat{E D G}\) = 2m ∠ F, m\(\widehat{E F G}\) = 2m∠D, m\(\widehat{D E F}\) = 2m∠G, and m\(\widehat{F G D}\) = 2m ∠ E. By the Substitution Property of Equality, 2m∠D + 2m∠G = 360°.
Question 41.
CRITICAL THINKING
In the diagram, ∠C is a right angle. If you draw the smallest possible circle through C tangent to \(\overline{A B}\), the circle will intersect \(\overline{A C}\) at J and \(\overline{B C}\) at K. Find the exact length of \(\overline{J K}\).
Answer:

Question 42.
CRITICAL THINKING
You are making a circular cutting board. To begin, you glue eight 1-inch boards together, as shown. Then you draw and cut a circle with an 8-inch diameter from the boards.
a. \(\overline{F H}\) is a diameter of the circular cutting board. Write a proportion relating GJ and JH. State a theorem in to justify your answer.
Answer:
Each board is 1 inch and FJ spans 6 boards.
\(\overline{F H}\) = 6 inches
b. Find FJ, JH, and GJ. What is the length of the cutting board seam labeled \(\overline{G K}\)?
Answer:
Each board is 1 inch and JH spans 2 boards.
JH = 2 inches
Equation is \(\frac { JH }{ GJ } \) = \(\frac { GJ }{ FJ } \)
\(\frac { 2 }{ GJ } \) = \(\frac { GJ }{ 6 } \)
12 = GJ²
GJ = 2√3
GK = 2(GJ)
GK = 4√3
So, FJ = 6, JH = 2, JG = 2√3, GK = 4√3
Maintaining Mathematical Proficiency
Solve the equation. Check your solution.
Question 43.
3x = 145
Answer:
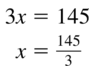
Question 44.
\(\frac{1}{2}\)x = 63
Answer:
x = 63 • 2
x = 126
Question 45.
240 = 2x
Answer:
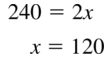
Question 46.
75 = \(\frac{1}{2}\)(x – 30)
Answer:
75 • 2 = x – 30
150 + 30 = x
x = 180
10.5 Angle Relationships in Circles
Exploration 1
Angles Formed by a Chord and Tangent Line
Work with a partner: Use dynamic geometry software.
Sample
a. Construct a chord in a circle. At one of the endpoints of the chord. construct a tangent line to the circle.
Answer:
b. Find the measures of the two angles formed by the chord and the tangent line.
Answer:
c. Find the measures of the two circular arcs determined by the chord.
Answer:
d. Repeat parts (a) – (c) several times. Record your results in a table. Then write a conjecture that summarizes the data.
Answer:
Exploration 2
Angles Formed by Intersecting Chords
Work with a partner: Use dynamic geometry software.
sample
a. Construct two chords that intersect inside a circle.
Answer:
b. Find the measure of one of the angles formed by the intersecting chords.
Answer:
c. Find the measures of the arcs intercepted h the angle in part (b) and its vertical angle. What do you observe?
Answer:
d. Repeat parts (a) – (c) several times. Record your results in a table. Then write a conjecture that summarizes the data.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results.
Answer:
Communicate Your Answer
Question 3.
When a chord intersects a tangent line or another chord, what relationships exist among the angles and arcs formed?
Answer: When a chord intersects a tangent line or another chord then the angle formed between the chord also the tangent is equal to the half of angle subtended by the chord at the centre of the circle.
Question 4.
Line m is tangent to the circle in the figure at the left. Find the measure of ∠1.
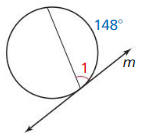
Answer:
m∠1 = \(\frac { 1 }{ 2 } \) • 148
m∠1 = 74°
Question 5.
Two chords intersect inside a circle to form a pair of vertical angles with measures of 55°. Find the sum of the measures of the arcs intercepted by the two angles.
Answer:
The sum of the measures of the arcs intercepted by the two angles = \(\frac { 1 }{ 2 } \) • 55
= 27.5
Lesson 10.5 Angle Relationships in Circles
Monitoring Progress
Line m is tangent to the circle. Find the indicated measure.
Question 1.
m ∠ 1
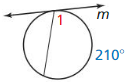
Answer:
m ∠ 1 = \(\frac { 1 }{ 2 } \) • 210
m ∠ 1 = 105°
Question 2.
m\(\widehat{R S T}\)
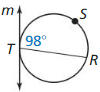
Answer:
m\(\widehat{R S T}\) = 2 • 98 = 196°
m\(\widehat{R S T}\) = 196°
Question 3.
m\(\widehat{X Y}\)
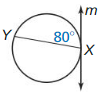
Answer:
m\(\widehat{X Y}\) = \(\frac { 1 }{ 2 } \) • 80
m\(\widehat{X Y}\) = 40°
Find the value of the variable.
Question 4.
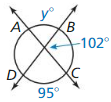
Answer:
y° = \(\frac { 1 }{ 2 } \) • (102 + 95)
= 98.5°
Question 5.
Answer:
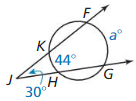
a° = 2 • 30° + 44°
= 60° + 44° = 104°
So, a° = 104°.
Find the value of x.
Question 6.
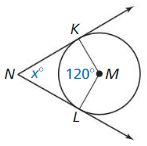
Answer:
x° = 180° – 120°
x° = 60°
Question 7.
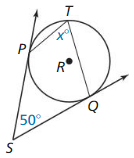
Answer:
50° = 180° – x°
x° = 180° – 50°
x° = 130°
Question 8.
You are on top of Mount Rainier on a clear day. You are about 2.73 miles above sea level at point B. Find m\(\widehat{C D}\), which represents the part of Earth that you can see.
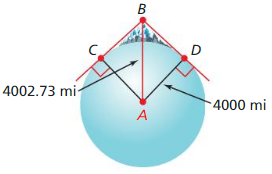
Answer:
CB and BD are tangents, CB is perpendicular to AB and CD is perpendicular to AD by the tangent line to circle theorem.
△ABC is similar to △ABD by the hypotenuese leg congruence theorem.
∠CBA is similar to ∠ABD. So, m∠CBA = 74.5°, m∠CBD = 2 • 74.5° = 149°
m∠CBD = 180° – m∠CAD
m∠CBD = 180° – CD
149° = 180° – CD
CD = 31°
The part of earth you can see
Exercise 10.5 Angle Relationships in Circles
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Points A, B, C, and D are on a circle, and ![]() intersects
intersects ![]() at point P.
at point P.
If m∠APC = \(\frac{1}{2}\)(m\(\widehat{B D}\) – m\(\widehat{A C}\)). then point P is _________ the circle.
Answer:
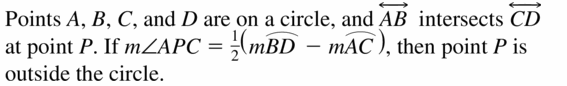
Question 2.
WRITING
Explain how to find the measure of a circumscribed angle.
Answer:
A circumscribed angle is the angle made by two intersecting tangent lines to a circle. Draw lines from the circle centre to the point of tangency. The angle between the radius and tangent line is 90°. The sum of angles of a quadrilateral is 360°. Angles between radii and tangent lines is 180°. The angle at two tangent lines meet is circumscribed angle.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, line t is tangent to the circle. Find the indicated measure.
Question 3.
m\(\widehat{A B}\)
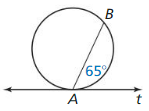
Answer:
![]()
Question 4.
m\(\widehat{D E F}\)
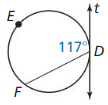
Answer:
m\(\widehat{D E F}\) = 2(117°) = 234°
Question 5.
m < 1
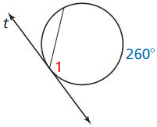
Answer:
![]()
Question 6.
m ∠ 3
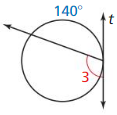
Answer:
m ∠ 3 = ½ • 140 = 70°
In Exercises 7 – 14, find the value of x.
Question 7.
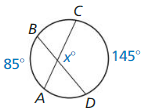
Answer:
Question 8.
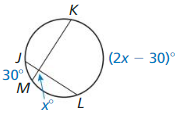
Answer:
x° = ½ • (30 + 2x – 30)
Question 9.
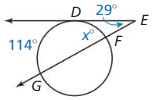
Answer:
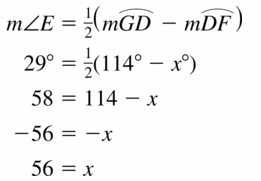
Question 10.
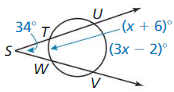
Answer:
34° = ½ (3x – 2 – (x + 6))
34° = ½ (3x – 2 – x – 6)
34° = ½ (2x – 8)
34° = x – 4
x° = 34 + 4
x° = 38°
Question 11.
Answer:
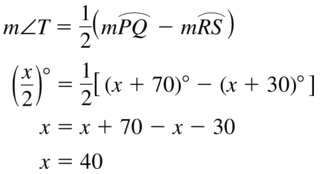
Question 12.
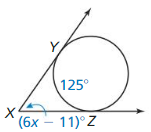
Answer:
6x – 11 = 2 • 125
6x = 250 + 11
6x = 261
x° = 43.5°
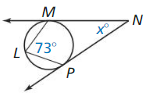
Question 13.
Answer:
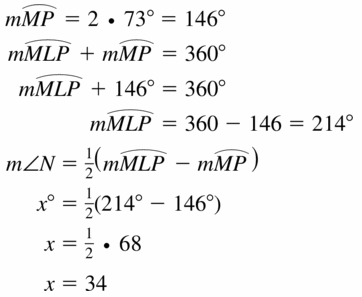
Question 14.
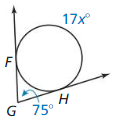
Answer:
17x° = 75°
x° = 4.41°
ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error in finding the angle measure.
Question 15.
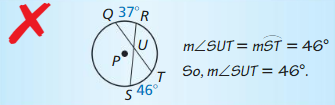
Answer:
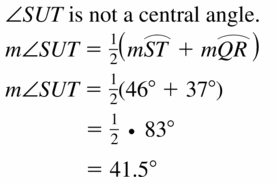
Question 16.
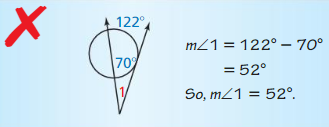
Answer:
m∠1 = ½ (122 – 70)
= ½ (52) = 26
So, m∠1 = 26°
In Exercises 17 – 22, find the indicated angle measure. justify your answer.
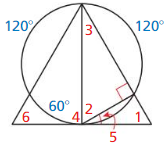
Question 17.
m ∠ 1
Answer:

Question 18.
m ∠ 2
Answer:
m ∠ 2 = 60°
Explanation:
m ∠ 3 =30°, So, m ∠ 2 = 180° – (90° + 30°)
= 180° – 120° = 60°
Therefore, m ∠ 2 = 60°
Question 19.
m ∠ 3
Answer:
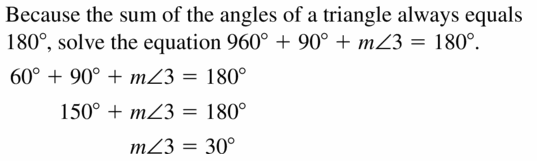
Question 20.
m ∠ 4
Answer:
m ∠ 4 = 90°
Question 21.
m ∠ 5
Answer:
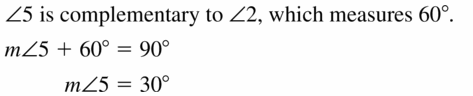
Question 22.
m ∠ 6
Answer:
m ∠ 6 = 180° – (60° + 30° + 30°) = 180° – 120°
m ∠ 6 = 60°
Question 23.
PROBLEM SOLVING
You are flying in a hot air balloon about 1.2 miles above the ground. Find the measure of the arc that represents the part of Earth you can see. The radius of Earth is about 4000 miles.
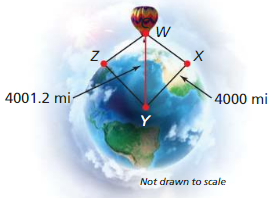
Answer:
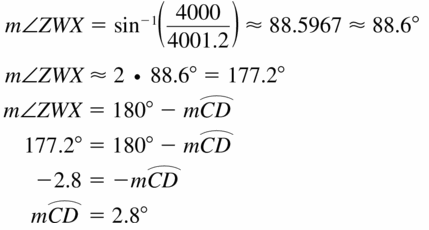
Question 24.
PROBLEM SOLVING
You are watching fireworks over San Diego Bay S as you sail away in a boat. The highest point the fireworks reach F is about 0.2 mile above the bay. Your eyes E are about 0.01 mile above the water. At point B you can no longer see the fireworks because of the curvature of Earth. The radius of Earth is about 4000 miles, and \(\overline{F E}\) is tangent to Earth at point T. Find m\(\widehat{s B}\). Round your answer to the nearest tenth.
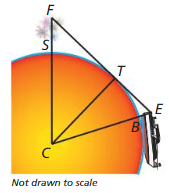
Answer:
We know that,
In geometry, a tangent is also referred to as a tangent line and it can be defined as a straight line that touches a plane curve at a specific point.
From the diagram.
You should apply the cosine function to determine the measure of the angle formed by the hypotenuse side of the triangle. It represents the radius of the earth.
m<SB = cos^-1 (4000/4000 + 0.2) + cos^-1 (4000/4000 + 0.001)
m<SB = cos^-1 (4000/4000.2) + cos^-1 (4000/4000.01)
m<SB = cos^-1 (0.99995) + cos^-1(0.9999975)
m<SB = 0.573 + 0.128
m<SB = 0.701 approximately equal to 0.70 degrees.
Therefore the measure of angle m<SB rounded to the nearest tenth is equal to 0.70 degrees.
Question 25.
MATHEMATICAL CONNECTIONS
In the diagram, \(\vec{B}\)A is tangent to ⊙E. Write an algebraic expression for m\(\widehat{C D}\) in terms of x. Then find m\(\widehat{C D}\).
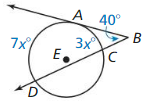
Answer:
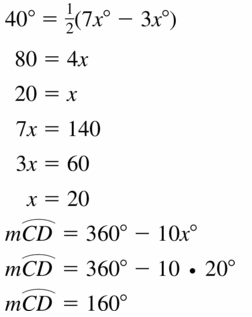
Question 26.
MATHEMATICAL CONNECTIONS
The circles in the diagram are concentric. Write an algebraic expression for c in terms of a and b.
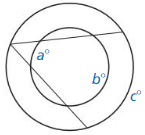
Answer:
a° = ½(c° – b°)
Question 27.
ABSTRACT REASONING
In the diagram. \(\vec{P}\)L is tangent to the circle, and \(\overline{K J}\) is a diameter. What is the range of possible angle measures of ∠LPJ? Explain your reasoning.
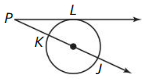
Answer:
Question 28.
ABSTRACT REASONING
In the diagram, \(\overline{A B}\) is an chord that is not a diameter of the circle. Line in is tangent to the circle at point A. What is the range of possible values of x? Explain your reasoning. (The diagram is not drawn to scale.)
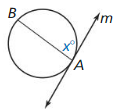
Answer:
The possible values of x are less than 180°.
Question 29.
PROOF
In the diagram ![]() and
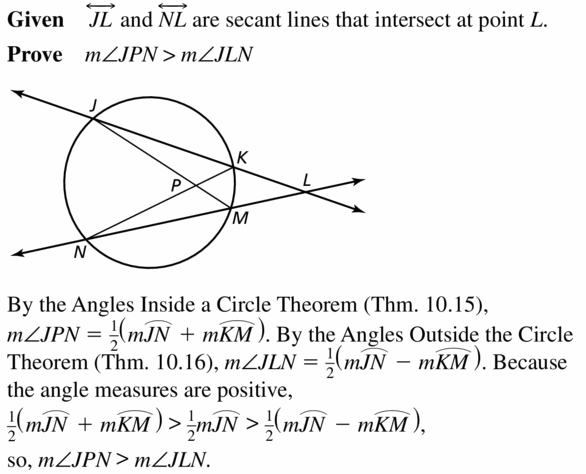
and ![]() are secant lines that intersect at point L. Prove that m∠JPN > m∠JLN.
are secant lines that intersect at point L. Prove that m∠JPN > m∠JLN.
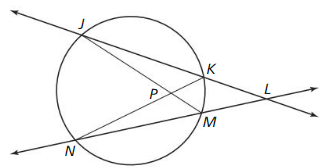
Answer:
Question 30.
MAKING AN ARGUMENT
Your friend claims that it is possible for a circumscribed angle to have the same measure as its intercepted arc. Is your friend correct? Explain your reasoning.
Answer:
Yes, when the circumscribed angle measures 90°, the central angle measures 90°, so the intercepted arc also measures 90°.
Question 31.
REASONING
Points A and B are on a circle, and t is a tangent line containing A and another point C.
a. Draw two diagrams that illustrate this situation.
b. Write an equation for m\(\widehat{A B}\) in terms of m∠BAC for each diagram.
c. For what measure of ∠BAC can you use either equation to find m\(\widehat{A B}\)? Explain.
Answer:
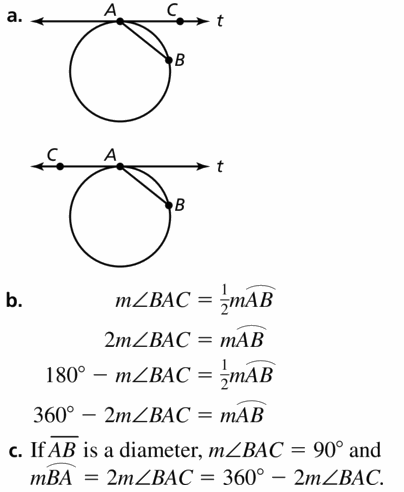
Question 32.
REASONING
∆XYZ is an equilateral triangle inscribed in ⊙P. AB is tangent to ⊙P at point X, \(\overline{B C}\) is tangent to ⊙P at point Y. and \(\overline{A C}\) is tangent to ⊙P at point Z. Draw a diagram that illustrates this situation. Then classify ∆ABC by its angles and sides. Justify your answer.
Answer:
∆XYZ is an equilateral triangle
m∠X = m∠Y
m∠Z = 60
By the measure of an inscribed angle theorem, m arcXY = 2m∠Z
2m∠Z = 120
for YZ, m arcYZ = 2m∠X
2m∠X = 120
for XZ, m arcXZ = 2m∠Y
2m∠Y = 120
m∠A = 1/2(XYZ – m XZ)
= 1/2(240 – 120)
1/2 × 120 = 60
m∠B = 60
m∠C = 60
∠A ≅ ∠B
∠B ≅ ∠C
So, ABC is equilateral and equiangular.
Question 33.
PROVING A THEOREM
To prove the Tangent and Intersected Chord Theorem (Theorem 10. 14), you must prove three cases.
a. The diagram shows the case where \(\overline{A B}\) contains the center of the circle. Use the Tangent Line to Circle Theorem (Theorem 10.1) to write a paragraph proof for this case.
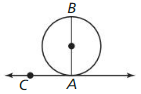
b. Draw a diagram and write a proof for the case where the center of the circle is in the interior of ∠CAB.
c. Draw a diagram and write a proof for the case where the center of the circle is in the exterior of ∠CAB.
Answer:
Question 34.
HOW DO YOU SEE IT?
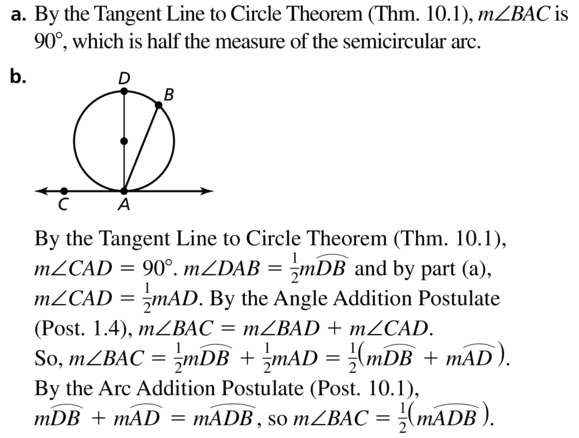
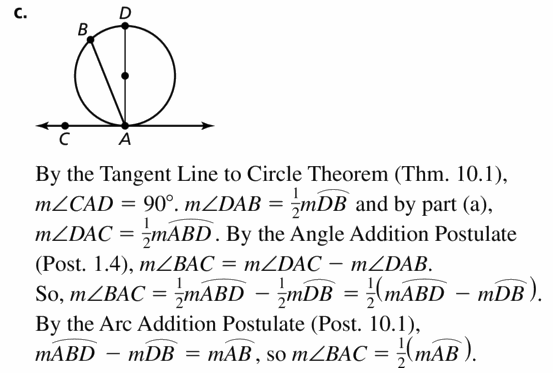
In the diagram, television cameras are Positioned at A and B to record what happens on stage. The stage is an arc of ⊙A. You would like the camera at B to have a 30° view of the stage. Should you move the camera closer or farther away? Explain your reasoning.
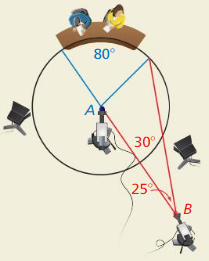
Answer:
25° = ½(80° – 30°) = ½(50°)
So, you should move the camera closer.
Question 35.
PROVING A THEOREM
Write a proof of the Angles Inside the Circle Theorem (Theorem 10.15).
Given Chords \(\overline{A C}\) and \(\overline{B D}\) intersect inside a circle.
Prove m ∠ 1 = \(\frac{1}{2}\)(m\(\widehat{D C}\) + m\(\widehat{A B}\))
Answer:

Question 36.
THOUGHT PROVOKING
In the figure, ![]() and
and ![]() are tangent to the circle. Point A is any point on the major are formed by the endpoints of the chord \(\overline{B C}\). Label all congruent angles in the figure. Justify your reasoning.
are tangent to the circle. Point A is any point on the major are formed by the endpoints of the chord \(\overline{B C}\). Label all congruent angles in the figure. Justify your reasoning.
Answer:
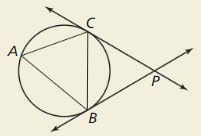
m∠CPB = ½(CAB – CB)
Question 37.
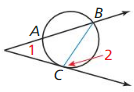
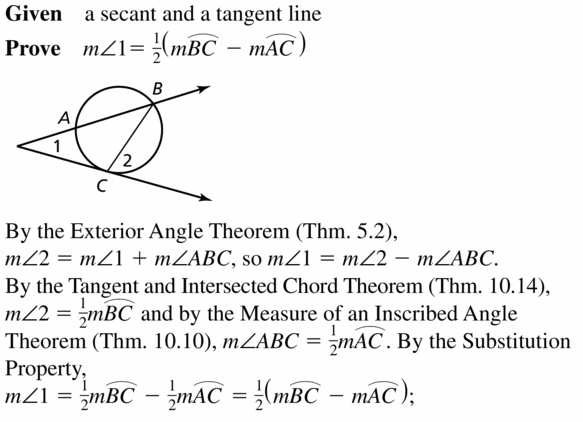
PROVING A THEOREM
Use the diagram below to prove the Angles Outside the Circle Theorem (Theorem 10.16) for the case of a tangent and a secant. Then copy the diagrams for the other two cases on page 563 and draw appropriate auxiliary segments. Use your diagrams to prove each case.
Answer:

Question 38.
PROVING A THEOREM
Prove that the Circumscribed Angle Theorem (Theorem 10.17) follows from the Angles Outside the Circle Theorem (Theorem 10.16).
Answer:
In Exercises 39 and 40, find the indicated measure(s). justify your answer
Question 39.
Find m ∠ P when m\(\widehat{W Z Y}\) = 200°
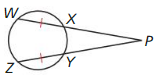
Answer:
Question 40.
Find m\(\widehat{A B}\) and m\(\widehat{E D}\)
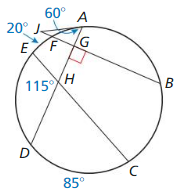
Answer:
m\(\widehat{E D}\) = ½ (115°) = 57.5°
∠GJA = 30°
Maintaining Mathematical Proficiency
Solve the equation.
Question 41.
x2 + x = 12
Answer:
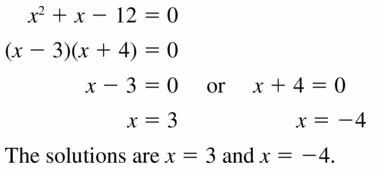
Question 42.
x2 = 12x + 35
Answer:
x² = 12x + 35
x = \(\frac { 12 ± √(144 + 140) }{ 2 } \)
x = \(\frac { 12 ± √284 }{ 2 } \)
x = \(\frac { 12 + √284 }{ 2 } \), \(\frac { 12 – √284 }{ 2 } \)
Question 43.
– 3 = x2 + 4x
Answer:
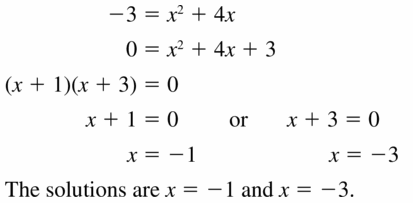
10.6 Segment Relationships in Circles
Exploration 1
Segments Formed by Two Intersecting Chords
Work with a partner: Use dynamic geometry software.
Sample
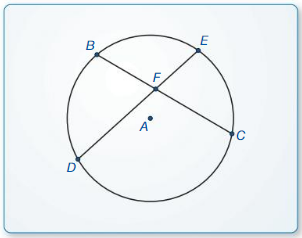
a.
Construct two chords \(\overline{B C}\) and \(\overline{D E}\) that intersect in the interior of a circle at a point F.
Answer:
b.
Find the segment lengths BE, CF, DF, and EF and complete the table. What do you observe?
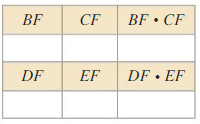
Answer:
c. Repeat parts (a) and (b) several times. Write a conjecture about your results.
REASONING ABSTRACTLY
To be proficient in math, you need to make sense of quantities and their relationships in problem situations.
Answer:
Exploration 2
Secants Intersecting Outside a Circle
Work with a partner: Use dynamic geometry software.
Sample
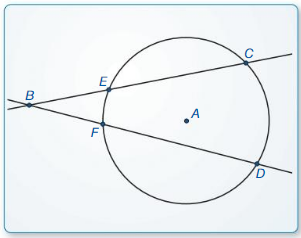
a. Construct two secant ![]() and
and ![]() that intersect at a point B outside a circle, as shown.
that intersect at a point B outside a circle, as shown.
Answer:
b. Find the segment lengths BE, BC, BF, and BD. and complete the table. What do you observe?
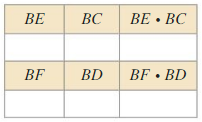
Answer:
c. Repeat parts (a) and (b) several times. Write a conjecture about your results.
Answer:
Communicate Your Answer
Question 3.
What relationships exist among the segments formed by two intersecting chords or among segments of two secants that intersect outside a circle?
Answer:
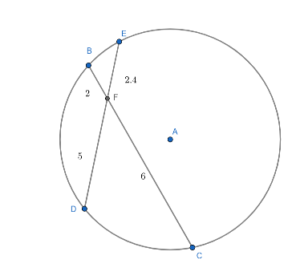
BF = 2
CF = 6
DF = 5
EF = 2.4
BF . CF = 2 × 6 = 12
DF . EF = 5 × 2.4 = 12
Thus the product of DF, EF is obtained as 12 units.
Therefore, the relationship that exists between the segments formed by two intersecting chords is that the product of segments of one chord is equal to the product of the segments of the other chord.
While the relationship that exists among the segments of two secants that intersect outside the circle is that the product of the length of the segment of one secant with its external segment is equal to the product of the lengths segment of another secant with its external segment which was solved using assumption and basic mathematical operations.
Question 4.
Find the segment length AF in the figure at the left.
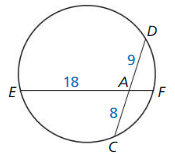
Answer:
EA • AF = AD • AC
18 • AF = 9 • 8
AF = 4
Lesson 10.6 Segment Relationships in Circles
Monitoring Progress
Find the value of x.
Question 1.
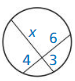
Answer:
x = 8
Explanation:
4 • 6 = 3 • x
3x = 24
x = 8
Question 2.
Answer:
x = 5
Explanation:
2 • x + 1 = 4 • 3
x + 1 = 6
x = 5
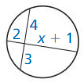
Question 3.
Answer:
x = \(\frac { 54 }{ 5 } \)
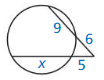
Explanation:
6 • 9 = 5 • x
54 = 5x
x = \(\frac { 54 }{ 5 } \)
Question 4.
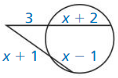
Answer:
x = \(\frac { 3 ± √37 }{ 2 } \)
Explanation:
3 • x + 2 = x + 1 • x – 1
3x + 6 = x² – 1
x² – 3x – 7 = 0
x = \(\frac { 3 ± √(9 + 28) }{ 2 } \)
x = \(\frac { 3 ± √37 }{ 2 } \)
Question 5.
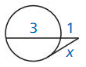
Answer:
x = ±√3
Explanation:
x² = 3 • 1
x² = 3
x = ±√3
Question 6.
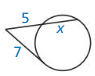
Answer:
x = \(\frac { 49 }{ 5 } \)
Explanation:
7² = 5 • x
49 = 5x
x = \(\frac { 49 }{ 5 } \)
Question 7.
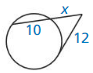
Answer:
x = 14.4
Explanation:
12² = 10x
144 = 10x
x = 14.4
Question 8.
WHAT IF?
In Example 4, CB = 35 feet and CE = 14 feet. Find the radius of the tank.
Answer:
The radius of the tank is 36.75
Explanation:
CB² = CE ⋅ CD
35² = 14 ⋅ (2r + 14)
1225 = 28r + 196
28r = 1029
r = 36.75
Exercise 10.6 Segment Relationships in Circles
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
The part of the secant segment that is outside the circle is called a(n) ______________ .
Answer:

Question 2.
WRITING
Explain the difference between a tangent segment and a secant segment.
Answer:
A tangent segment intersects the circle at only one point. It actually doesn’t go through the circle. If a ball is rolling on a table top, then it would be the tangent. A secant segment intersects the circle in two points. It goes through the circle. In a tangent, no part is in the interior of the circle. In a secant, there is a part in the interior called a chord.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6, find the value of x.
Question 3.
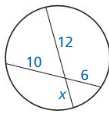
Answer:
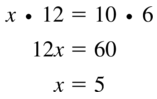
Question 4.
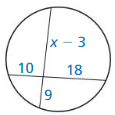
Answer:
x = 23
Explanation:
10 • 18 = 9 • (x – 3)
20 = x – 3
x = 23
Question 5.
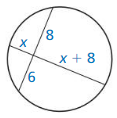
Answer:
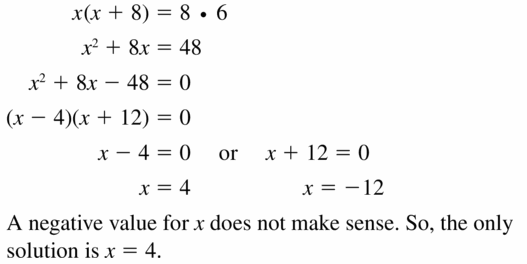
Question 6.
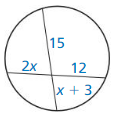
Answer:
x = 5
Explanation:
2x • 12 = 15 • (x + 3)
24x = 15x + 45
9x = 45
x = 5
In Exercises 7 – 10, find the value of x.
Question 7.
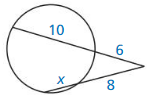
Answer:
Question 8.
Answer:
x = \(\frac { 35 }{ 4 } \)
Explanation:
5 • 7 = 4 • x
4x = 35
x = \(\frac { 35 }{ 4 } \)
Question 9.
Answer:
Question 10.
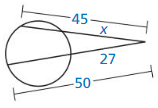
Answer:
x = 30
Explanation:
45 • x = 50 • 27
45x = 1350
x = 30
In Exercises 11 – 14. find the value of x.
Question 11.
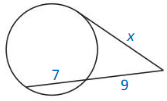
Answer:

Question 12.
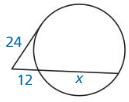
Answer:
x = 48
Explanation:
24² = 12x
576 = 12x
x = 48
Question 13.
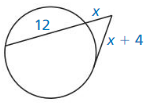
Answer:
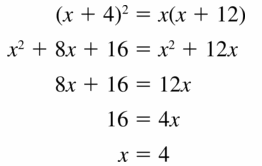
Question 14.
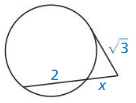
Answer:
x = 1.5
Explanation:
3 = 2x
x = 1.5
Question 15.
ERROR ANALYSIS
Describe and correct the error in finding CD.
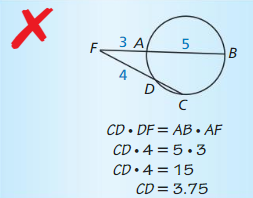
Answer:

Question 16.
MODELING WITH MATHEMATICS
The Cassini spacecraft is on a mission in orbit around Saturn until September 2017. Three of Saturn’s moons. Tethys. Calypso, and Teleslo. have nearly circular orbits of radius 2,95,000 kilometers. The diagram shows the positions of the moons and the spacecraft on one of Cassini’s missions. Find the distance DB from Cassini to Tethys when \(\overline{A D}\) is tangent to the circular orbit.
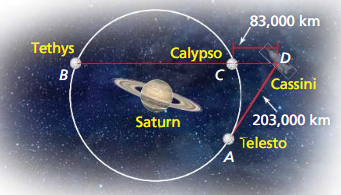
Answer:
BD = 579493 km
Explanation:
(203,000)² = 83000x
x = 496493
BC = 496493
BD = 496493 + 83000 = 579493
Question 17.
MODELING WITH MATHEMATICS
The circular stone mound in Ireland called Newgrange has a diameter of 250 feet. A passage 62 feet long leads toward the center of the mound. Find the perpendicular distance x from the end of the passage to either side of the mound.
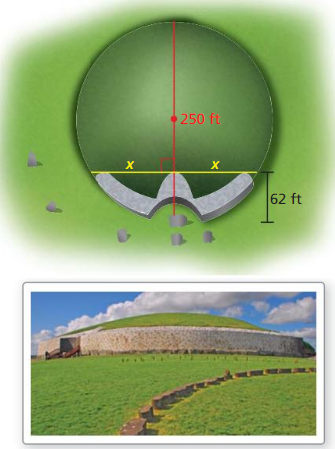
Answer:

Question 18.
MODELING WITH MATHEMATICS
You are designing an animated logo for our website. Sparkles leave point C and move to the Outer circle along the segments shown so that all of the sparkles reach the outer circle at the same time. Sparkles travel from point C to point D at 2 centimeters per second. How fast should sparkles move from point C to point N? Explain.
Answer:
5.33 should sparkles move from point C to point N.
Explanation:
4 • 8 = 6 • x
x = 5.33
Question 19.
PROVING A THEOREM
Write a two-column proof of the Segments of Chords Theorem (Theorem 10.18).
Plan for Proof:
Use the diagram to draw \(\overline{A C}\) and \(\overline{D B}\). Show that ∆EAC and ∆EDB are similar. Use the fact that corresponding side lengths in similar triangles are proportional.
Answer:
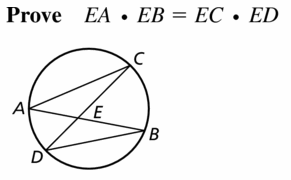

Question 20.
PROVING A THEOREM
Prove the Segments of Secants Theorem (Theorem 10.19). (Hint: Draw a diagram and add auxiliary line segments to form similar triangles.)
Answer:
Question 21.
PROVING A THEOREM
Use the Tangent Line to Circle Theorem (Theorem 10. 1) to prove the Segments of Secants and Tangents Theorem (Theorem 10.20) for the special case when the secant segment Contains the center of the circle.
Answer:

Question 22.
PROVING A THEOREM
Prove the Segments of Secants and Tangents Theorem (Theorem 10.20). (Hint: Draw a diagram and add auxiliary line segments to form similar triangles.)
Answer:
Question 23.
WRITING EQUATIONS
In the diagram of the water well, AB, AD, and DE are known. Write an equation for BC using these three measurements.
Answer:
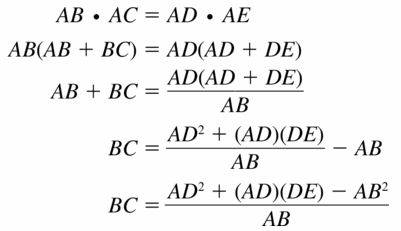
Question 24.
HOW DO YOU SEE IT?
Which two theorems would you need to use to tind PQ? Explain your reasoning.
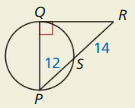
Answer:
The two theorems that can be used are
First, you use the tangent line to circle theorem to conclude that QR is a tangent to the circle.
Then you use the segments of secants and tangents theorem to find QR
QR² = SR. PR
By the Pythagorean theorem, PQ² = PR² – QR²
Question 25.
CRITICAL THINKING
In the figure, AB = 12, BC = 8, DE = 6, PD = 4, and a is a point of tangency. Find the radius of ⊙P.
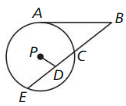
Answer:

Question 26.
THOUGHT PROVOKING
Circumscribe a triangle about a circle. Then, using the points of tangency, inscribe a triangle in the circle. Must it be true that the two triangles are similar? Explain your reasoning.
Answer:
Maintaining Mathematical Proficiency
Solve the equation by completing the square.
Question 27.
x2 + 4x = 45
Answer:
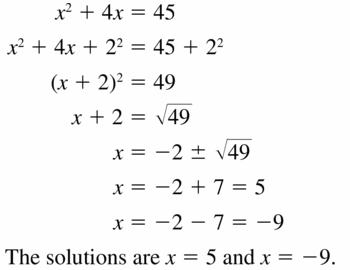
Question 28.
x2 – 2x – 1 = 8
Answer:
x = 1 + √10, x = 1 – √10
Explanation:
x² – 2x – 1 = 8
x² – 2x – 9 = 0
x = \(\frac { 2 ± √(4 + 36) }{ 2 } \)
x = \(\frac { 2 ± √40 }{ 2 } \)
x = 1 + √10, x = 1 – √10
Question 29.
2x2 + 12x + 20 = 34
Answer:
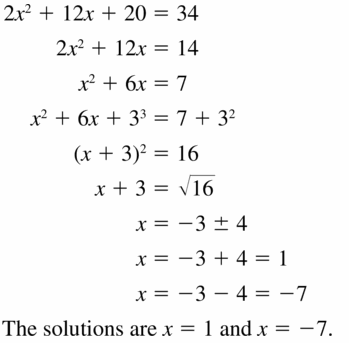
Question 30.
– 4x2 + 8x + 44 = 16
Answer:
x = 1 + √8, x = 1 – √8
Explanation:
– 4x² + 8x + 44 = 16
4x² – 8x – 28 =0
x² – 2x – 7 = 0
x = \(\frac { 2 ± √(4 + 28) }{ 2 } \)
x = \(\frac { 2 ± √32 }{ 2 } \)
x = 1 ± √8
10.7 Circles in the Coordinate Plane
Exploration 1
The Equation of a Circle with Center at the Origin
Work with a partner: Use dynamic geometry software to Construct and determine the equations of circles centered at (0, 0) in the coordinate plane, as described below.
a. Complete the first two rows of the table for circles with the given radii. Complete the other rows for circles with radii of your choice.
Answer:

b. Write an equation of a circle with center (0, 0) and radius r.
Answer:
x² + y² = r²
Explanation:
(x – 0)² + (y – 0)² = r²
x² + y² = r²
Exploration 2
The Equation of a Circle with Center (h, k)
Work with a partner: Use dynamic geometry software to construct and determine the equations of circles of radius 2 in the coordinate plane, as described below.
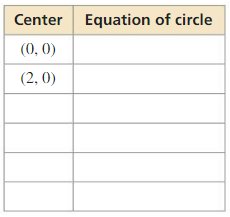
a. Complete the first two rows of the table for circles with the given centers. Complete the other rows for circles with centers of your choice.
Answer:

b. Write an equation of a circle with center (h, k) and radius 2.
Answer:
(x – h)² + (y – k)² = 4
c. Write an equation of a circle with center (h, k) and radius r.
Answer:
(x – h)² + (y – k)² = r²
Exploration 3
Deriving the Standard Equation of a Circle
Work with a partner. Consider a circle with radius r and center (h, k).
Write the Distance Formula to represent the distance d between a point (x, y) on the circle and the center (h, k) of the circle. Then square each side of the Distance Formula equation.
How does your result compare with the equation you wrote in part (c) of Exploration 2?
MAKING SENSE OF PROBLEMS
To be proficient in math, you need to explain correspondences between equations and graphs.
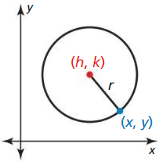
Answer:
(x – h)² + (y – k)² = r²
Communicate Your Answer
Question 4.
What is the equation of a circle with center (h, k) and radius r in the coordinate plane?
Answer:
(x – h)² + (y – k)² = r²
Question 5.
Write an equation of the circle with center (4, – 1) and radius 3.
Answer:
x² + y² – 8x + 2y + 8 = 0
Explanation:
(x – 4)² + (y + 1)² = 9
x² – 8x + 16 + y² + 2y + 1 = 9
x² + y² – 8x + 2y = 9 – 17
x² + y² – 8x + 2y + 8 = 0
Lesson 10.7 Circles in the Coordinate Plane
Monitoring Progress
Write the standard equation of the circle with the given center and radius.
Question 1.
center: (0, 0), radius: 2.5
Answer:
x² + y² = 6.25
Explanation:
(x – 0)² + (y – 0)² = 2.5²
x² + y² = 6.25
Question 2.
center: (- 2, 5), radius: 7
Answer:
(x + 2)² + (y – 5)² = 49
Explanation:
(x + 2)² + (y – 5)² = 7²
(x + 2)² + (y – 5)² = 49
Question 3.
The point (3, 4) is on a circle with center (1, 4). Write the standard equation of the circle.
Answer:
(x – 1)² + (y – 4)² = 4
Explanation:
r = √(3 – 1)² + (4 – 4)²
= √(2)²
r = 2
(x – 1)² + (y – 4)² = 2²
(x – 1)² + (y – 4)² = 4
Question 4.
The equation of a circle is x2 + y2 – 8x + 6y + 9 = 0. Find the center and the radius of the circle. Then graph the circle.
Answer:
The center of the circle (4, -3) and radius is 4.
Explanation:
x² + y² – 8x + 6y + 9 = 0
x² – 8x + 16 + y² + 6y + 9 = 16
(x – 4)² + (y + 3)² = 4²
The center of the circle (4, -3) and radius is 4.
Question 5.
Prove or disprove that the point (1, √5 ) lies on the circle centered at the origin and containing the point (0, 1).
Answer:
Disproved.
Explanation:
We consider the circle centred at the origin and containing the point (0, 1).
Therefore, we can conclude that the radius of the circle r = 1, let O (0, 0) and B (1, √5). So the distance between two points is
OB = √(1 – 0) + (√5 – 0)² = √(1 + 5) = √6
As the radius of the given circle is 1 and distance of the point B from its centre is √6. So we can conclude that point does lie on the given circle.
Question 6.
why are three seismographs needed to locate an earthquake’s epicentre?
Answer: During an earthquake, seismic waves are transferred each over the globe. Though they may weaken with distance, seismographs are sensitive enough to still descry these waves. In order to determine the position of an earthquake center seismographs from at least three different places are demanded a particular event.
Exercise 10.7 Circles in the Coordinate Plane
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What is the standard equation of a circle?
Answer:
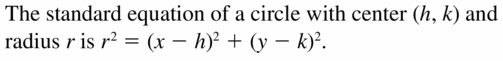
Question 2.
WRITING
Explain why knowing the location of the center and one point on a circle is enough to graph the circle.
Answer:
If we know the location of the center and one point on the circle, we can graph a circle because the distance from the center to the point is called the radius.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 8, write the standard equation of the circle.
Question 3.
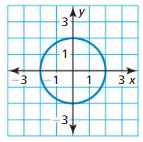
Answer:
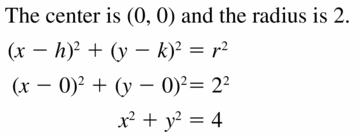
Question 4.
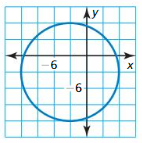
Answer:
x² + y² = 36
Explanation:
The center is (0, 0) and the radius is 6
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 6²
x² + y² = 36
Question 5.
a circle with center (0, 0) and radius 7
Answer:
Question 6.
a circle with center (4, 1) and radius 5
Answer:
(x – 4)² + (y – 1)² = 25
Explanation:
(x – h)² + (y – k)² = r²
(x – 4)² + (y – 1)² = 5²
(x – 4)² + (y – 1)² = 25
Question 7.
a circle with center (- 3, 4) and radius 1
Answer:
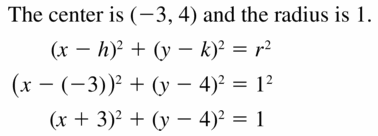
Question 8.
a circle with center (3, – 5) and radius 7
Answer:
(x – 3)² + (y + 5)² = 49
Explanation:
(x – h)² + (y – k)² = r²
(x – 3)² + (y + 5)² = 7²
(x – 3)² + (y + 5)² = 49
In Exercises 9 – 11, use the given information to write the standard equation of the circle.
Question 9.
The center is (0, 0), and a point on the circle is (0, 6).
Answer:
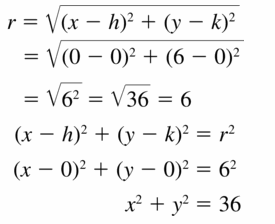
Question 10.
The center is (1, 2), and a point on the circle is (4, 2).
Answer:
x² + y² = 9
Explanation:
r = √(x – h)² + (y – k)²
= √(4 – 1)² + (2 – 2)²
= √3²
r = 3
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 3²
x² + y² = 9
Question 11.
The center is (0, 0). and a point on the circle is (3, – 7).
Answer:
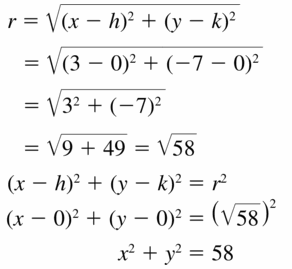
Question 12.
ERROR ANALYSIS
Describe and correct the error in writing the standard equation of a circle.

Answer:
(x – h)² + (y – k)² = r²
(x + 3)² + (y + 5)² = 3²
(x + 3)² + (y + 5)² = 9
In Exercises 13 – 18, find the center and radius of the circle. Then graph the circle.
Question 13.
x2 + y2 = 49
Answer:
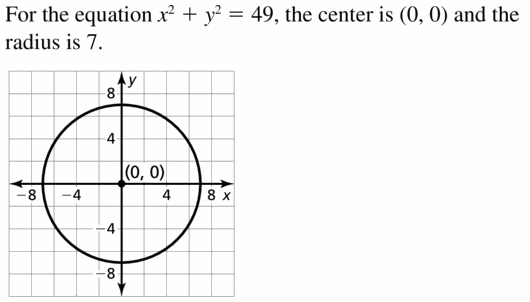
Question 14.
(x + 5)2 + (y – 3)2 = 9
Answer:
Center is (-5, 3) and rdaius is 3.
Explanation:
For the equation (x + 5)2 + (y – 3)2 = 9, center is (-5, 3) and rdaius is 3.
Question 15.
x2 + y2 – 6x = 7
Answer:
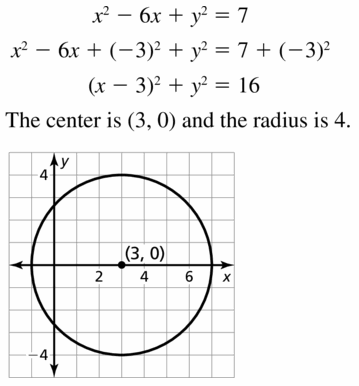
Question 16.
x2 + y2 + 4y = 32
Answer:
The center is (0, -2) and radius is 6
Explanation:
x2 + y2 + 4y = 32
x² + y² + 4y + 4 = 32 + 4
x² + (y + 2)² = 36
(x – 0)² + (y – (-2))² = 6²
The center is (0, -2) and radius is 6
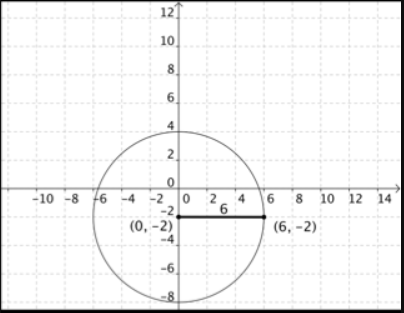
Question 17.
x2 + y2 – 8x – 2y = – 16
Answer:

Question 18.
x2 + y2 + 4x + 12y = – 15
Answer:
The center is (-2, -6) and radius is 5
Explanation:
x2 + y2 + 4x + 12y = – 15
x² + 4x + 4 + y² + 12y + 36 = -15 + 36 + 4
(x + 2)² + (y + 6)² = 5²
The center is (-2, -6) and radius is 5
In Exercises 19 – 22, prove or disprove the statement.
Question 19.
The point (2, 3) lies on the circle centered at the origin with radius 8.
Answer:

Question 20.
The point (4, √5) lies on the circle centered at the origin with radius 3.
Answer:
The point (4, √5) does not lie on the circle.
Explanation:
r² = (x – h)² + (y – k)²
3² ______________ (4 – 0)² + (√5 – 0)²
9 ______________ 16 + 5
9 ≠ 21
Because the radius is 3 and the distance between center and the point is more than the radius. So the point does not lie on the circle.
Question 21.
The point (√6, 2) lies on the circle centered at the origin and containing the point (3, – 1).
Answer:

Question 22.
The point (√7, 5) lies on the circle centered at the origin and containing the point (5, 2).
Answer:
The point (√7, 5) does not lie on the circle.
Explanation:
r² = (x – h)² + (y – k)²
= (√7 – 0)² + (5 – 0)² = 7 + 25 = 32
r = 5.65
(5.65)² ______________ (5 – 0)² + (2 – 0)²
32 ______________ 25 + 4
32 ≠ 29
Because the radius is 3 and the distance between center and the point is more than the radius. So the point does not lie on the circle.
Question 23.
MODELING WITH MATHEMATICS
A City’s commuter system has three zones. Zone I serves people living within 3 miles of the city’s center. Zone 2 serves those between 3 and 7 miles from the center. Zone 3 serves those over 7 miles from the center.
a. Graph this Situation on a coordinate plane where each unit corresponds to 1 mile. Locate the city’s center at the origin.
b. Determine which zone serves people whose homes are represented by the points (3, 4), (6, 5), (1, 2), (0.3). and (1, 6).
Answer:
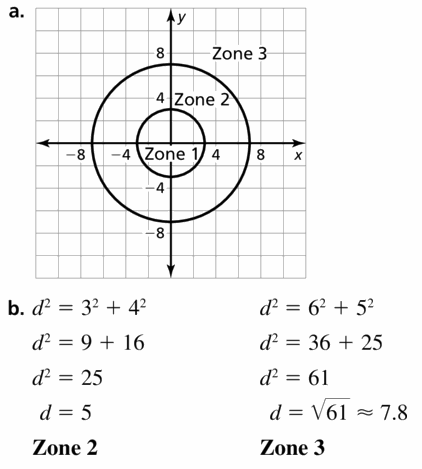
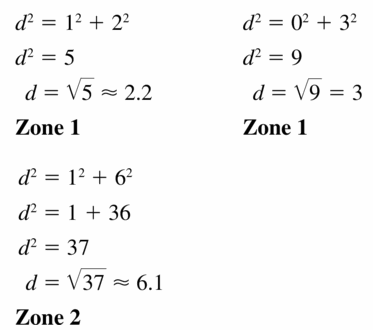
Question 24.
MODELING WITH MATHEMATICS
Telecommunication towers can be used to transmit cellular phone calls. A graph with units measured in kilometers shows towers at points (0, 0), (0, 5), and (6, 3). These towers have a range of about 3 kilometers.
a. Sketch a graph and locate the towers. Are there any locations that may receive calls from more than one tower? Explain your reasoning.
Answer:
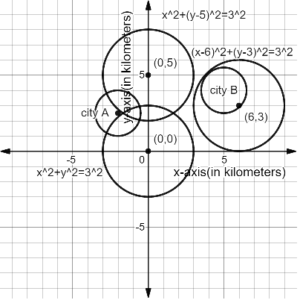
b. The center of City A is located at (- 2, 2.5), and the center of City B is located at (5, 4). Each city has a radius of 1.5 kilometers. Which city seems to have better cell phone coverage? Explain your reasoning.
Answer:
There are three towers at points (0, 0), (0, 5) and (6, 3) with range of about 3 km
a. Let’s sketch the graph to locate towers. Draw the points (0, 0), (0, 5) and (6, 3). Then draw three circles with centers at these points and radii 3.
There are locations that can receive calls from more that one tower because circles with centers (0, 0) and (0, 5) overlap. Locations in their intersection can receive calls from two towers.
The city A has a center located at (-2, 2.5) and city B has a center located at (5, 4). Both cities have radius 1.5 km
Let’s draw the city A as a circle with center (-2, 2.5) and radius 1.5 and city B with center (5, 4) and radius 1.5.
From the graph we can conclude that the city B has better cell phone coverage because parts of city A do not have coverage.
Question 25.
REASONING
Sketch the graph of the circle whose equation is x2 + y2 = 16. Then sketch the graph of the circle after the translation (x, y) → (x – 2, y – 4). What is the equation of the image? Make a conjecture about the equation of the image of a circle centered at the origin after a translation m units to the left and n units down.
Answer:
Question 26.
HOW DO YOU SEE IT?
Match each graph with its equation.
a.  |
A. x2 + (y + 3) 2 = 4 |
b.  |
B. (x – 3) 2 + y2 = 4 |
c.  |
C. (x + 3) 2 + y2 = 4 |
d.  |
D. x2 + (y – 3) 2 = 4 |
Answer:
a ➝ C, b ➝ A, c ➝ D, d ➝ B
Question 27.
USING STRUCTURE
The vertices of ∆XYZ are X(4, 5), Y(4, 13), and Z(8, 9). Find the equation of the circle circumscribed about ∆XYZ. Justify your answer.
Answer:

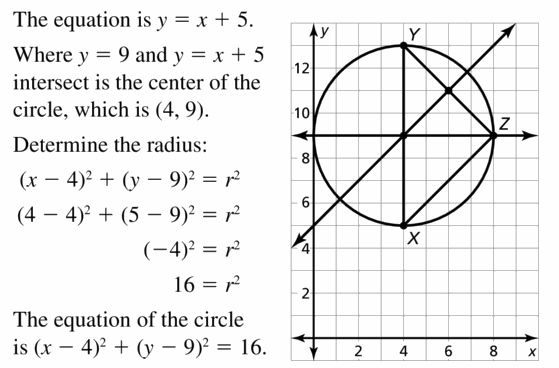
Question 28.
THOUGHT PROVOKING
A circle has center (h, k) and contains point (a, b). Write the equation of the line tangent to the circle at point (a, b).
Answer:
y – b = \(\frac { h – a }{ b – k } \)(x – a)
Explanation:
It is given a circle with center C(h, k. A circle with point A(a, b). We have to write the equation of a tangent that intersects the circle at point A
By the tangent line to circle theorem, a tangent is perpendicular to the radius. Two lines are perpendicular if and only if their slopes are negative reciprocals. So, find the equation of the line AC to know its slope.
The equation of the line which has two points (a, b), (c, d) is y – b = \(\frac { b – c }{ a – d } \)(x – a)
The equation of the line which has two points A(a, b) and C(h, k) is
y – b = \(\frac { b – k }{ a – h } \)(x – a)
Therefore, the slope of the line through A nad C is \(\frac { b – k }{ a – h } \)
Hence the slope of the tangent is –\(\frac { a – h }{ b – k } \) = \(\frac { h – a }{ b – k } \)
Use the equation of the line y = kx + n through the point (a, b)
y – b = k(x – a) to find the equation of the tangent
The equation of the tangent with slope \(\frac { h – a }{ b – k } \) and through the point A(a, b) is y – b = \(\frac { h – a }{ b – k } \)(x – a)
MATHEMATICAL CONNECTIONS
In Exercises 29 – 32, use the equations to determine whether the line is a tangent, a secant a secant that contains the diameter, or name of these. Explain your reasoning.
Question 29.
Circle: (x – 4)2 + (y – 3)2 = 9
Line: y = 6
Answer:
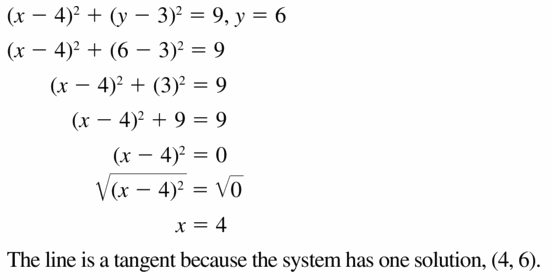
Question 30.
Circle: (x + 2)2 + (y – 2)2 = 16
Line: y = 2x – 4
Answer:
The line is a secant line.
Explanation:
(x + 2)2 + (y – 2)2 = 16, y = 2x – 4
(x + 2)2 + (2x – 4 – 2)2 = 16
x² + 4x + 4 + (2x – 6)² = 16
x² + 4x + 4 + 4x² – 24x + 36 = 16
5x² – 20x + 40 – 16 = 0
5x² – 20x + 24 = 0
x = \(\frac { 20 ±√-80 }{ 10 } \)
x = 2, y = 2 • 2 – 4 = 0, (2, 0)
The system has two solutions and point does not lie on the line. So the line is a secant line.
Question 31.
Circle: (x – 5)2 + (y + 1)2 = 4
Line: y = \(\frac{1}{5}\)x – 3\
Answer:
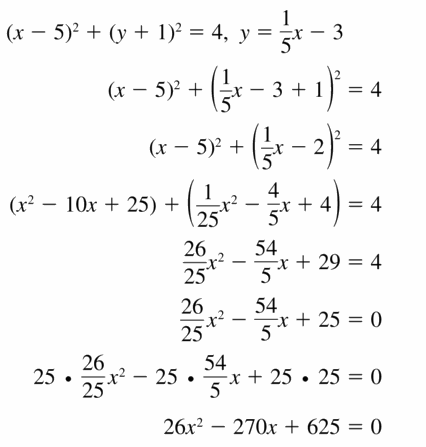


Question 32.
Circle: (x + 3)2 + (y – 6)2 = 25
Line: y = –\(\frac{4}{3}\)x + 2
Answer:
The line is a secant line.
Explanation:
(x + 3)2 + (y – 6)2 = 25, y = –\(\frac{4}{3}\)x + 2
(x + 3)2 + (-\(\frac{4}{3}\)x + 2 – 6)2 = 25
x² + 6x + 9 + \(\frac { 16x² }{ 9 } \) + \(\frac { 32x }{ 3 } \) + 16 = 25
\(\frac { 25x² }{ 9 } \) + \(\frac { 50x }{ 3 } \) = 0
x(25x + 150) = 0
x = 0 or x = -6
y = 2, y = 10
(0, 2) and (-6, 10)
d = √(0 + 6)² + (2 – 10)²
= √(36 + 64)
= 10 ≠ 5
The system has two solutions and point does not lie on the line. So the line is a secant line.
MAKING AN ARGUMENT
Question 33.
Your friend claims that the equation of a circle passing through the points (- 1, 0) and (1, 0) is x2 – 2yk + y2 = 1 with center (0, k). Is your friend correct? Explain your reasoning.
Answer:

Question 34.
REASONING
Four tangent circles are centered on the x-axis. The radius of ⊙A is twice the radius of ⊙O, The radius of ⊙B is three times the radius of ⊙O, The radius of ⊙C is four times the radius of ⊙O, All circles have integer radii, and the point (63, 16) is On ⊙C. What is the equation of ⊙A? Explain your reasoning.
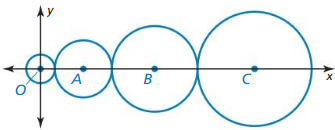
Answer:
We know that,
The general form of the circle equation is (x – h)² + (y – k)² = r²
The radius of the circle C = 4.7
Where,
R = radius of the circle O.
The point on the circle C = (63, 16)
From the equation
(63 – h)² + (16 – k)² = (4 x r)²
K = y coordinates of the center of circle C.
K = 0
H = r + 4r + 6r + 4r = 15r
(63-15r)² + (16 – 0)² = (4r)²
209r² – 1890r + 4225 = 0
(5r) x (209r – 845) = 0
R = 5
Or
R = 845/209
The radius of circle A, rA = 2r.
rA = 2 x 5 = 10.
x = coordinates of the centre of circle A = 3r
Therefore the centre of circle A = (3×5, 0) = (15,0).
The standard equation of circle A is (x – 15)² + y² = 10²
Where r = 845/209
rA = 2 x 845/209 = 1690/209
Coordinates of A = (3 x 845/209, 0); (2535/209, 0)
The other standard equation of circle a is (x – 2535/209)² + y² = (1690/209)².
Maintaining Mathematical Proficiency
Identify the arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.
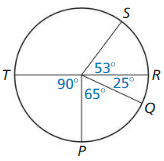
Question 35.
\(\widehat{R S}\)
Answer:
![]()
Question 36.
\(\widehat{P R}\)
Answer:
\(\widehat{P R}\) is a right angle
\(\widehat{P R}\) = 25 + 65 = 90°
Question 37.
\(\widehat{P R T}\)
Answer:
Question 38.
\(\widehat{S T}\)
Answer:
\(\widehat{S T}\) is a major arc
\(\widehat{S T}\) = 360 – (90 + 65 +25 + 53) = 127°
Question 39.
\(\widehat{R S T}\)
Answer:
![]()
Question 40.
\(\widehat{Q S}\)
Answer:
\(\widehat{Q S}\) is a minor arc
\(\widehat{Q S}\) = 25 + 53 = 78°
Circles Review
10.1 Lines and Segments That Intersect Circles
Tell whether the line, ray, or segment is best described as a radius, chord, diameter, secant, or tangent of ⊙P.
Question 1.
\(\overline{P K}\)
Answer:
\(\overline{P K}\) is radius
Question 2.
\(\overline{N M}\)
Answer:
\(\overline{N M}\) is chord
Question 3.
\(\vec{J}\)L
Answer:
\(\vec{J}\)L is tangent
Question 4.
\(\overline{K N}\)
Answer:
\(\overline{K N}\) is diameter
Question 5.
![]()
Answer:
NL is secant
Question 6.
\(\overline{P N}\)
Answer:
\(\overline{P N}\) is radius
Tell whether the common tangent is internal or external.
Question 7.
Answer:
Internal common tangent
Question 8.
Answer:
External common tangent
Points Y and Z are points of tangency. Find the value of the variable.
Question 9.

Answer:
a = \(\frac { 3 ± 33 }{ 18 } \)
Explanation:
3a = 9a² – 30
9a² – 3a – 30 = 0
a = \(\frac { 3 ± 33 }{ 18 } \)
Question 10.
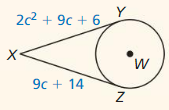
Answer:
c = 2
Explanation:
2c² + 9c + 6 = 9c + 14
2c² – 8 = 0
c² – 4 = 0
c = 2
Question 11.
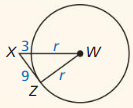
Answer:
r = 12
Explanation:
(3 + r)² = r² + 9²
9 + 6r + r² = r² + 81
6r = 72
r = 12
Question 12.
Tell whether \(\overline{B D}\) is tangent to ⊙C. Explain.
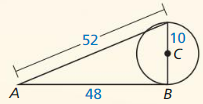
Answer:
\(\overline{B D}\) is not tangent to ⊙C
Explanation:
52² = 10² + 48²
2704 = 100 + 2304
So, \(\overline{B D}\) is not tangent to ⊙C
10.2 Finding Arc Measures
Use the diagram above to find the measure of the indicated arc.
Question 13.
\(\widehat{K L}\)
Answer:
\(\widehat{K L}\) = 100°
Explanation:
\(\widehat{K L}\) = ∠KPL = 100°
Question 14.
\(\widehat{L M}\)
Answer:
\(\widehat{L M}\) = 60°
Explanation:
\(\widehat{L M}\) = 180° – 120°
= 60°
Question 15.
\(\widehat{K M}\)
Answer:
\(\widehat{K M}\) = 160°
Explanation:
\(\widehat{K M}\) = 100° + 60°
= 160°
Question 16.
\(\widehat{K N}\)
Answer:
\(\widehat{K N}\) = 80°
Explanation:
\(\widehat{K N}\) = 360 – (120 + 100 + 60)
= 360 – 280 = 80°
Tell whether the red arcs are congruent. Explain why or why not.
Question 17.
Answer:
\(\widehat{S T}\), \(\widehat{Y Z}\) are not congruent.
Explanation:
\(\widehat{S T}\), \(\widehat{Y Z}\) are not congruent. Because both arcs are from different circles and having different radii.
Question 18.
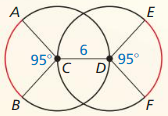
Answer:
\(\widehat{A B}\), \(\widehat{E F}\) are congruent.
Explanation:
\(\widehat{A B}\), \(\widehat{E F}\) are congruent. Because those circles have same radii.
10.3 Using Chords
Find the measure of \(\widehat{A B}\).
Question 19.
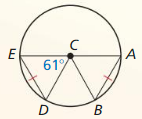
Answer:
\(\widehat{A B}\) = 61°
Explanation:
\(\widehat{A B}\) = 61°
If ED = AB, then \(\widehat{A B}\) = \(\widehat{E D}\)
Question 20.
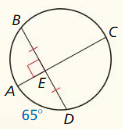
Answer:
\(\widehat{A B}\) = 65°
Explanation:
\(\widehat{A B}\) = \(\widehat{A D}\)
So, \(\widehat{A B}\) = 65°
Question 21.
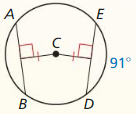
Answer:
\(\widehat{A B}\) = 91°
Explanation:
\(\widehat{A B}\) = \(\widehat{E D}\)
So, \(\widehat{A B}\) = 91°
Question 22.
In the diagram. QN = QP = 10, JK = 4x, and LM = 6x – 24. Find the radius of ⊙Q.
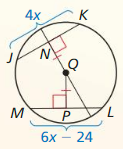
Answer:
The radius of ⊙Q is 26.
Explanation:
6x – 24 = 4x
6x – 4x = 24
2x = 24
x = 12
ML = 6(12) – 24 = 48
JN = \(\frac { 48 }{ 2 } \) = 24
JQ² = JN² + NQ²
= 24² + 10² = 576 + 100
JQ = 26
Therefore, the radius of ⊙Q is 26
10.4 Inscribed Angles and Polygons
Find the value(s) of the variable(s).
Question 23.
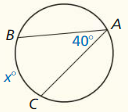
Answer:
x° = 80°
Explanation:
x° = 2 • 40° = 80°
Question 24.
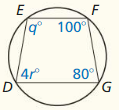
Answer:
q° = 100°, r° = 20°
Explanation:
q° + 80° = 180°
q° = 100°
4r° + 100 = 180°
4r° = 80°
r° = 20°
Question 25.
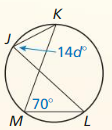
Answer:
d° = 5°
Explanation:
14d° = 70°
d° = 5°
Question 26.
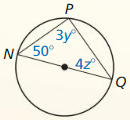
Answer:
y° = 30°, z° = 10°
Explanation:
3y° = 90°
y° = 30°
50° + 90° + 4z° = 180°
4z° = 40°
z° = 10°
Question 27.
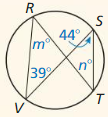
Answer:
m° = 44°
n° = 39°
Explanation:
m° = 44°
n° = 39°
Question 28.
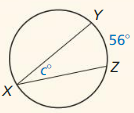
Answer:
c° = 28°
Explanation:
c° = ½ • 56 = 28
10.5 Angle Relationships in Circles
Find the value of x.
Question 29.
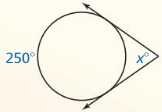
Answer:
x° = 250°
Explanation:
x° = 250°
Question 30.
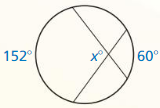
Answer:
x° = 106°
Explanation:
x° = ½(152 + 60)
= ½(212) = 106°
Question 31.
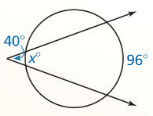
Answer:
x° = 28°
Explanation:
x° = ½(96 – 40)
= ½(56) = 28°
Question 32.
Line l is tangent to the circle. Find m\(\widehat{X Y Z}\).
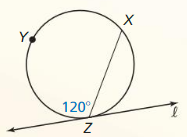
Answer:
m\(\widehat{X Y Z}\) = 240°
Explanation:
m\(\widehat{X Y Z}\) = 2(120)
= 240°
10.6 Segment Relationships in Circles
Find the value of x.
Question 33.
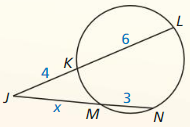
Answer:
x = 8
Explanation:
3 • x = 4 • 6
x = 8
Question 34.
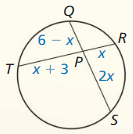
Answer:
x = 3
Explanation:
(x + 3) • x = (6 – x) • 2x
x + 3 = 12 – 2x
3x = 9
x = 3
Question 35.
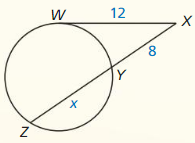
Answer:
x = 18
Explanation:
12² = 8 • x
144 = 8x
x = 18
Question 36.
A local park has a circular ice skating rink. You are standing at point A, about 12 feet from the edge of the rink. The distance from you to a point of tangency on the rink is about 20 feet. Estimate the radius of the rink.
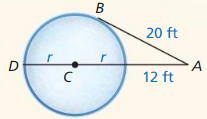
Answer:
Estimated radius of the rink is 10 ft
Explanation:
20² = 12 • (2r + 12)
400 = 24r + 144
256 = 24r
r = 10.66
Therefore, estimated radius of the rink is 10 ft
10.7 Circles in the Coordinate Plane
Write the standard equation of the circle shown.
Question 37.
Answer:
(x – 4)² + (y + 1)² = 12.25
Explanation:
(x – 4)² + (y + 1)² = 3.5²
(x – 4)² + (y + 1)² = 12.25
Question 38.
Answer:
(x – 8)² + (y – 5)² = 36
Explanation:
(x – 8)² + (y – 5)² = 6²
(x – 8)² + (y – 5)² = 36
Question 39.
Answer:
x² + y² = 4
Explanation:
(x – 0)² + (y – 0)² = 2²
x² + y² = 4
Write the standard equation of the circle with the given center and radius.
Question 40.
center: (0,0), radius: 9
Answer:
x² + y² = 81
Explanation:
(x – 0)² + (y – 0)² = 9²
x² + y² = 81
Question 41.
center: (- 5, 2), radius: 1.3
Answer:
(x + 5)² + (y – 2)² = 1.69
Explanation:
(x + 5)² + (y – 2)² = 1.3²
(x + 5)² + (y – 2)² = 1.69
Question 42.
center: (6, 21), radius: 4
Answer:
(x – 6)² + (y – 21)² = 16
Explanation:
(x – 6)² + (y – 21)² = 4²
(x – 6)² + (y – 21)² = 16
Question 43.
center: (- 3, 2), radius: 16
Answer:
(x + 3)² + (y – 2)² = 256
Explanation:
(x + 3)² + (y – 2)² = 16²
(x + 3)² + (y – 2)² = 256
Question 44.
center: (10, 7), radius: 3.5
Answer:
(x – 10)² + (y – 7)² = 12.25
Explanation:
(x – 10)² + (y – 7)² = 3.5²
(x – 10)² + (y – 7)² = 12.25
Question 45.
center: (0, 0), radius: 5.2
Answer:
x² + y² = 27.04
Explanation:
(x – 0)² + (y – 0)² = 5.2²
x² + y² = 27.04
Question 46.
The point (- 7, 1) is on a circle with center (- 7, 6). Write the standard equation of the circle.
Answer:
(x + 7)² + (y – 6)² = 25
Explanation:
r² = (-7 + 7)² + (6 – 1)²
= 5²
r = 5
And, centre is (-7, 6)
The standard equation of a circle is (x – (-7))² + (y – 6)² = 5²
(x + 7)² + (y – 6)² = 25
Question 47.
The equation of a circle is x2 + y2 – 12x + 8y + 48 = 0. Find the center and the radius of the circle. Then graph the circle.
Answer:
The radius of the circle is 2, the centre is (6, -4)
Explanation:
x2 + y2 – 12x + 8y + 48 = 0
x² – 12x + 36 + y² + 8y + 16 = 4
(x – 6)² + (y + 4)² = 2²
So, the radius of the circle is 2, the centre is (6, -4)
Question 48.
Prove or disprove that the point (4, – 3) lies on the circle centred at the origin and containing
the point (- 5, 0).
Answer:
The point (4, – 3) lies on the circle.
Explanation:
Use the distance formula to find the radius of the circle with cente (0, 0) and a point (-5, 0)
r = √(-5 – 0)² + (0 – 0)² = 5
The distance from the point (4, -3) to the center (0, 0)
d = √(4 – 0)² + (-3 – 0)² = √(16 +9) = 5
Since the radius of the circle is 5, the point lies on the circle.
Circles Chapter Test
Find the measure of each numbered angle in ⊙P. Justify your answer.
Question 1.
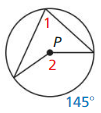
Answer:
m∠1 = 72.5°
m∠2 = 145°
Explanation:
m∠1 = \(\frac { 145 }{ 2 } \)
= 72.5°
m∠2 = 145°
Question 2.
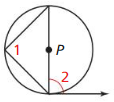
Answer:
m∠1 = 60°, m∠2 = 90°
Explanation:
A tangent is perpendicualr to diameter. So, m∠2 = 90°
m∠1 = 60°
Question 3.
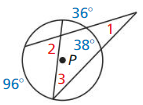
Answer:
m∠1 = 48°
Explanation:
m∠1 = \(\frac { 96 }{ 2 } \) = 48°
Question 4.
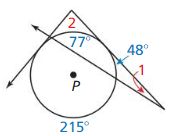
Answer:
Use the diagram.
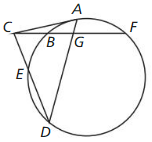
Question 5.
AG = 2, GD = 9, and BG = 3. Find GF.
Answer:
Given that,
AG = 2
GD = 9
BG = 3
The two chords AD and BF intersects each other at point G.
The value of segment GF is
AG x GD = BG x GF
2 x 9 = 3 x GF
GF = 2 x 9/3
GF = 6
Therefore the value of segment GF is 6.
Question 6.
CF = 12, CB = 3, and CD = 9. Find CE.
Answer:
CF = 12, CB = 3, and CD = 9
CE × CD = CB × CF
CE × 9 = 12 × 3
CE = 36/9
CE = 4
Thus the value of CE is 4.
Question 7.
BF = 9 and CB = 3. Find CA
Answer:
CA² = CB × CF
CF = CB + BF
CF = 3 + 9 = 12
CA² = CB × CF
CA² = 3 × 12
CA² = 36
CA = 6
Thus the value of CA is 6.
Question 8.
Sketch a pentagon inscribed in a circle. Label the pentagon ABCDE. Describe the relationship between each pair of angles. Explain your reasoning.
a. ∠CDE and ∠CAE
Answer:
b. ∠CBE and ∠CAE
Answer:
Find the value of the variable. Justify your answer.
Question 9.
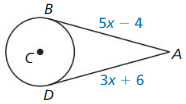
Answer:
x = 5
Explanation:
5x – 4 = 3x + 6
5x – 3x = 6 + 4
2x = 10
x = 5
Question 10.
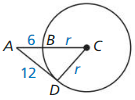
Answer:
r = 9
Explanation:
(6 + r)² = 12² + r²
36 + 12r + r² = 144 + r²
12r = 108
r = 9
Question 11.
Prove or disprove that the point (2√2, – 1) lies on the circle centered at (0, 2) and containing the point (- 1, 4).
Answer:
Disproved
Explanation:
We consider the circle centred at the A(0, 2) and containing the point B(-1, 4).
AB = √(-1 – 0)² + (4 – 2)² = √1 + 4 = √5
The distance between centre A(0, 2) and P(2√2, – 1) is
AP = √(2√2 – 0)² + (-1 – 2)² = √8 + 9 = √17
AB ≠ AP
So, the point (2√2, – 1) dies not lie on the circle.
Prove the given statement.
Question 12.
\(\widehat{S T} \cong \widehat{R Q}\)
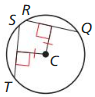
Answer:
Question 13.
\(\widehat{J M} \cong \widehat{L M}\)
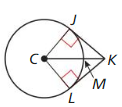
Answer:
Question 14.
\(\widehat{D G} \cong \widehat{F G}\)
Answer:
Question 15.
A bank of lighting hangs over a stage. Each light illuminates a circular region on the stage. A coordinate plane is used to arrange the lights, using a corner of the stage as the origin. The equation (x – 13)2 + (y – 4)2 = 16 represents the boundary of the region illuminated by one of the lights. Three actors stand at the points A(11, 4), B(8, 5), and C(15, 5). Graph the given equation. Then determine which actors are illuminated by the light.
Answer:
The equation (x – 13)² + (y – 4)²= 16 represents the standard equation of the circle with center (13, 4) and radius 4
Graph the circle with center S(13, 4), radius 4. Then graph the points A(11,4), B (8, 5), C(15,5) which represents the places where the actors stand.
From the graph, we can see that points A and C inside the circle and point B is outside the circle. Therefore, actors who stand at points A and C are illuminated by the light
Question 16.
If a car goes around a turn too quickly, it can leave tracks that form an arc of a circle. By finding the radius of the circle, accident investigators can estimate the speed of the car.
Answer:
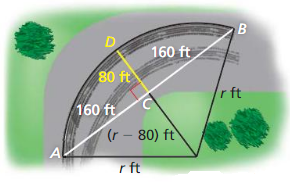
a. To find the radius, accident investigators choose points A and B on the tire marks. Then the investigators find the midpoint C of \(\overline{A B}\). Use the diagram to find the radius r of the circle. Explain why this method works.
Answer:
The radius r of the circle = 155.71 ft
Explanation:
Given that,
AC = 130 ft, CD = 70 ft
CE = (r – 70) ft
r² = a² + b²
r²= 130²+ (r – 70)²
r² = 16900 + r² – 140r + 4900
140r = 21,800
r = 155.71 ft
b. The formula S = 3.87√fr can be used to estimate a car’s speed in miles per hour, where f is the coefficient of friction and r is the radius of the circle in feet. If f = 0.7, estimate the car’s speed in part (a).
Answer:
The estimated car’s speed is 39.67 miles per hour
Explanation:
S = 3.87√fr
S = 3.8 √(0.7 x 155.71)
S = 3.8 √108.997
S = 3.8 x 10.44
S = 39.67
Circles Cumulative Assessment
Question 1.
Classify each segment as specifically as possible.
a. \(\overline{B G}\)
Answer:
\(\overline{B G}\) is a chord
b. \(\overline{C D}\)
Answer:
\(\overline{C D}\) is radius.
c. \(\overline{A D}\)
Answer:
\(\overline{A D}\) is diameter.
d. \(\overline{F E}\)
Answer:
\(\overline{F E}\) is a chord
Question 2.
Copy and complete the paragraph proof.
Given Circle C with center (2, 1) and radius 1,
Circle D with center (0, 3) and radius 4
Prove Circle C is similar to Circle D.
Map Circle C to Circle C’ by using the _________ (x, y) → _________ so that Circle C’ and Circle D have the same center at (____, _____). Dilate Circle C’ using a cellIer of dilation (_____, _____) and a scale factor of _____ . Because there is a _________ transformation that maps Circle C to Circle D, Circle C is __________ Circle D.
Answer:
Map Circle C to Circle C’ by using the scale factor (x, y) → (0, 3) so that Circle C’ and Circle D have the same center at (2, 1). Dilate Circle C’ using a cellIer of dilation (2, 1) and a scale factor of circles. Because there is a transformation that maps Circle C to Circle D, Circle C is similar to Circle D.
Question 3.
Use the diagram to write a proof.
Given ∆JPL ≅ ∆NPL
\(\overline{P K}\) is an altitude of ∆JPL
\(\overline{P M}\) is an altitude ∆NPL
Prove ∆PKL ~ ∆NMP
Answer:
∆JPL is similar to ∆NPL and PK is the altitude of ∆JPL and PM is an altitude of ∆NPL
Altitude is a line drawn from one vertex to the opposite site. It is perpendicular to the side.
So, ∆PKL is similar to ∆NMP
Question 4.
The equation of a circle is x² + y² + 14x – 16y + 77 = 0. What are the center and radius of the circle?
(A) center: (14, – 16). radius: 8.8
(B) center: (- 7, 8), radius: 6
(C) center (- 14, 16), radius: 8.8
(D) center: (7, – 8), radius: 5.2
Answer:
(B) center: (- 7, 8), radius: 6
Explanation:
x² + y² + 14x – 16y + 77 = 0
x² + 14x + 49 + y² – 16y + 64 = 36
(x + 7)² + (y – 8)² = 6²
So, the centre is (-7, 8) and radius is 6.
Question 5.
The coordinates of the vertices of a quadrilateral are W(- 7, – 6), X(1, – 2), Y(3, – 6) and Z(- 5, – 10). Prove that quadrilateral WXYZ is a rectangle.
Answer:
Proved
Explanation:
Find the distance of WY and ZX
WY = √(-7 – 3)² + (-6 + 6)² = √(-10)² = 10
ZX = √(1 + 5)² + (-2 + 10)² = √6² + 8² = 10
WY = ZX, the diagonals are congruent
Use the slope formula to find the slopes of diagonals
Slope of WY = \(\frac { -6 + 6 }{ -7 – 3 } \) = 0
Slope of ZX = \(\frac { -2 + 10 }{ 1 + 5 } \) = \(\frac { 4 }{ 3 } \)
Because the product of slopes of diagonals is 0, the diagonals are not perpendicular
Therefore, the quadrilateral WXYZ is a rectangle.
Question 6.
Which angles have the same measure as ∠ACB? Select all that apply.
im – 295
∠DEF ∠JGK ∠KGL ∠LGM ∠MGJ
∠QNR ∠STV ∠SWV ∠VWU ∠XYZ
Answer:
∠VWU
Question 7.
Classify each related conditional statement based on the conditional statement
“If you are a soccer player. then you are an athlete.”
a. If you are not a soccer player, then you are not an athlete.
Answer:
False
b. If you are an athlete, then you are a soccer player.
Answer:
False
c. You are a soccer player if and only if you are an athlete.
Answer:
True
d. If you are not an athlete, then you are not a soccer player.
Answer:
False
Question 8.
Your friend claims that the quadrilateral shown can be inscribed in a circle. Is your friend correct? Explain our reasoning.
Answer:
If the sum of any two angles is 180°, then the quadrilateral is inscribed in a circle.
So, 70° + 110° = 180°, 110° + 70°= 180°
So, my friend is correct.
