Practice with the help of enVision Math Common Core Grade 7 Answer Key Topic 3 Analyze and Solve Percent Problems regularly and improve your accuracy in solving questions.
enVision Math Common Core 7th Grade Answers Key Topic 3 Analyze And Solve Percent Problems
Topic 3 Essential Question
How can percent show proportional relationships between quantities and be used to solve problems?
3-ACT MATH

The Smart Shopper
Why do stores and manufacturers print coupons? It seems like they lose money every time you use one. Well, some coupons are designed to steer you toward a specific brand and gain your loyalty. Stores also offer coupons to get you into the store, counting on you buying other items while you are there. If you’re clever, you can use multiple coupons. Think about this during the 3-Act Mathematical Modeling lesson.3

Topic 3 enVision STEM Project
Did You Know?
One of the first popular activity trackers was a pedometer, which measures number of steps taken. Some sources trace the history of the pedometer back to Leonardo da Vinci.

A pedometer called Manpo-kei (10,000 steps meter) was introduced in Japan in the mid1960s. Research led by Dr. Yoshiro Hatano indicated that 10,000 steps a day is the ideal energy output to maintain health.

Today, most activity trackers are electronic devices that can sync to a computer or a smartphone.
Many activity trackers are wearable technology. Some common places to wear activity trackers are on the wrist, arm, or chest. There are even collar-mounted activity trackers for dogs.

Your Task: Analyze Activity Tracker Data
Activity trackers, also called fitness trackers, have become quite popular in recent years. But is the data collected actually helpful to the user? You and your classmates will explore the types of data that an activity tracker collects, and how that data can help users reach their activity and fitness goals.

Topic 3 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box. Write it on the blank.
- percent
- proportion
- rate
- ratio
Question 1.
A ________is a ratio in which the first term is compared to 100.
Answer:
A percent is a ratio in which the first term is compared to 100.
Explanation:
In the above-given question,
given that,
A percent is a ratio in which the first term is compared to 100.
for example:
38/100 = x/100.
x = 38%.
38/100 = 38.
Question 2.
A ratio that relates two quantities with different units of measure is a _________.
Answer:
A ratio that relates two quantities with different units of measure is a rate.
Explanation:
In the above-given question,
given that,
A ratio that relates two quantities with different units of measure is a rate.
for example:
34mi/2 gal.
we can convert any rate to a unit rate.
Question 3.
A statement that two ratios are equal is called a _________.
Answer:
A statement that two ratios are equal is called a proportion.
Explanation:
In the above-given question,
given that,
A statement that two ratios are equal is called a proportion.
for example:
5/10 = 1/2.
Question 4.
The relationship “3 students out of 5 students” is an example of a _________.
Answer:
The relationship “3 students out of 5 students” is an example of a ratio.
Explanation:
In the above-given question,
given that,
The relationship “3 students out of 5 students” is an example of a ratio.
Fractions, Decimals, and Percents
Write each number in two equivalent forms as a fraction, decimal, or percent.
Question 5.
0.29
Answer:
The number infraction is 29/100.
decimal = 0.29.
percent = 29%.
Explanation:
In the above-given question,
given that,
the number is 0.29.
decimal = 0.29.
percent = 29%.
fraction = 29/100.
Question 6.
35%
Answer:
The number of fraction is 35/100.
decimal = 0.35.
percent = 35%.
Explanation:
In the above-given question,
given that,
the number is 35%.
decimal = 0.35.
percent = 35%.
fraction = 35/100.

Question 7.
\(\frac{2}{5}\)
Answer:
The number infraction is 2/5.
decimal = 40.0..
percent = 0.4%.
Explanation:
In the above-given question,
given that,
the number is 2/5.
decimal = 40.0.
percent = 0.4%.
fraction = 2/5.
Proportions
Find the unknown number in each proportion.
Question 8.
\(\frac{x \text { days }}{4 \text { years }}=\frac{365.25 \text { days }}{1 \text { year }}\)
Answer:
x = 1461.
Explanation:
In the above-given question,
given that,
x/4 = 365.25.
x = 365.25 x 4.
x = 1461.
Question 9.
\(\frac{33,264 \text { feet }}{x \text { miles }}=\frac{5,280 \text { feet }}{1 \text { mile }}\)
Answer:
x = 1.569.
Explanation:
In the above-given question,
given that,
3364/x = 5280/1.
x = 5280/3364.
x = 1.569.
Question 10.
A cooking magazine shows a photo of a main dish on the front cover of 5 out of the 12 issues it publishes each year. Write and solve a proportion to determine how many times a photo of a main dish will be on the front cover during the next 5 years.
Answer:
The number of times a photo of a main dish will be on the front cover during the next 5 years = 3 times.
Explanation:
In the above-given question,
given that,
A cooking magazine shows a photo of a main dish on the front cover of 5 out of the 12 issues it publishes each year.
5/100 x 12.
0.05 x 12.
0.6.
0.6 x 5 = 3.
so the number of times a photo of the main dish will be on the front cover during the next 5 years = 3 times.
Language Development
Fill in the spider map by writing new vocabulary terms on each diagonal and related ideas.
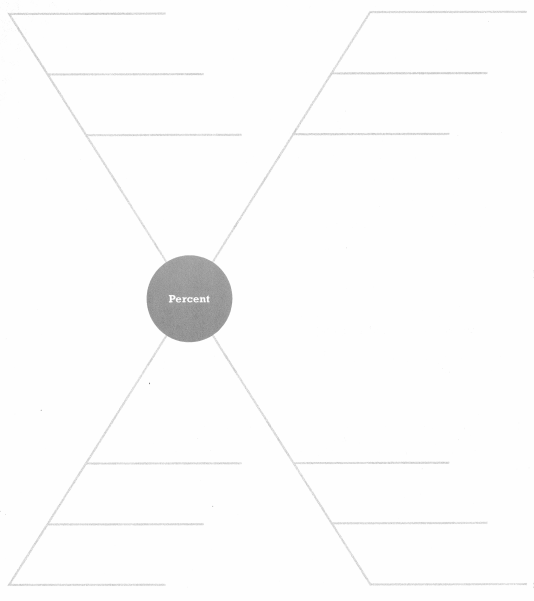
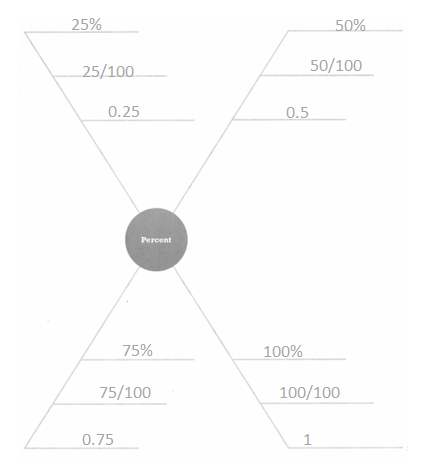
Answer:
25/100 = 0.25.
50/100 = 0.5.
75/100 = 0.75.
100/100 = 1.
Explanation:
In the above-given question,
given that,
the percent of all the terms in problem.
the four terms are 25, 50, 75, and 100.
25/100 = 0.25.
50/100 = 0.5.
75/100 = 0.75.
100/100 = 1.
Pick A Project
PROJECT 3A
How can you make sure you are getting the best deal?
PROJECT: SEARCH FOR BARGAINS

Answer:
Yes, I am getting the best deal.
Explanation:
In the above-given question,
given that,
they kept the discount of 50% on summer sale.
50/100 = 0.5.
so I am getting the best deal.
PROJECT 3B
What makes a song’s lyrics easy to remember?
PROJECT: WRITE AND PERFORM A CHEER OR A RAP
PROJECT 3C
If you were to play basketball, what strategies would you practice?
PROJECT: ESTIMATE BASKETS

PROJECT 3D
What are some elements of your favorite app?
PROJECT: DESIGN AN APP ICON

Lesson 3.1 Analyze Percents of Numbers
Solve & Discuss It!
Jaime’s older brother and his three friends want to split the cost of lunch. They also want to leave a 15%-20% tip. How much should each person pay?
I can… understand, find, and analyze percents of numbers.

Reasoning Which line on the receipt will you use to calculate the tip?
Answer:
The amount should each person pay = 30%
Explanation:
In the above-given question,
given that,
Jaime’s older brother and his three friends want to split the cost of lunch.
They also want to leave a 15%-20% tip.
15/100 – 20/100.
50/100 = 0.5.
20/100 = 0.2.
0.5 – 0.2 = 0.3.
30/100.
so the amount should each person pay = 30%.
Focus on math practices
Reasoning How would the amount each person pays change if the tip is determined before or after the bill is split?
Essential Question
How do percents show the relationship between quantities?
Try It!
Kita’s phone had a fully charged battery. With normal usage, her phone will last 18 hours. How much time is left on Kita’s phone battery with 12% charge remaining?
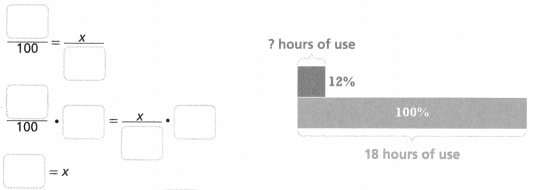
Kita’s phone battery has __________ hours remaining.
Answer:
The time left on Kita’s phone battery with 12% charge remaining = 3 hours.
Explanation:
In the above-given question,
given that,
Kita’s phone had a fully charged battery.
With normal usage, her phone will last 18 hours.
21/100 = x/18.
0.21 = x/18.
x/18 x 0.21.
x = 3.78.
so the time left on Kita’s phone battery with 12% charge remaining = 3 hours.
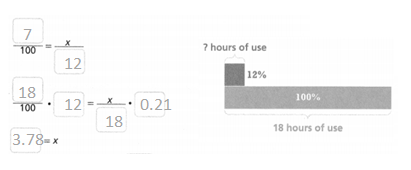
Convince Me! Why is 51% of a number more than half of the number?
Try It!
a. Find 0.08% of 720.
Answer:
0.576.
Explanation:
In the above-given question,
given that,
0.08% of 720.
0.08/100 x 720.
0.0008 x 720 = 0.576.
b. Find 162.5% of 200.
Answer:
162.5.
Explanation:
In the above-given question,
given that,
162.5% of 200.
162.5/100 x 200.
1.625 x 100 = 162.5.

c. Find 0.3% of 60.
Answer:
0.18.
Explanation:
In the above-given question,
given that,
0.3% of 60.
0.3/100 x 60.
0.003 x 60 = 0.18.
KEY CONCEPT
A percent is one way to represent the relationship between two quantities, generally that of a part to the whole.

Do You Understand?
Question 1.
Essential Question How do percents show the relationship between quantities?
Answer:
x = 9.
Explanation:
In the above-given question,
given that,
60/100 = x/15.
0.6 = x/15.
0.6 x 15 = x.
x = 9.
Question 2.
Reasoning How does a value that is greater than 100% of the original value or less than 1% of the original value compare to the original value?.
Answer:
The original value is greater than 1%.
Explanation:
In the above-given question,
given that,
the original value is 9%.
9/100 = 0.09.
1/100 = 0.01.
0.01 is greater than 0.09.
so the original value is greater than 1%.
Question 3.
Construct Arguments Gene stated that finding 25% of a number is the same as dividing the number by \(\frac{1}{4}\). Is Gene correct? Explain.
Answer:
Yes, Gene was correct.
Explanation:
In the above-given question,
given that,
Gene stated that finding 25% of a number is the same as dividing the number by \(\frac{1}{4}\).
25/100 = 0.25.
1/4 of 100.
so Gene was correct.
Do You Know How?
Question 4.
An 8-ounce serving of apples contains 8% of your daily vitamin C. How many ounces of apples would you need to get 100% of your daily vitamin C?
Answer:
The number of ounces of apples would you need to get 100% of your daily vitamin C = 100-ounce.
Explanation:
In the above-given question,
given that,
An 8-ounce serving of apples contains 8% of your daily vitamin C.
for 8-ounce it will get 8%.
for 100 ounces it will get 100%.
so 100 ounces of apples would you need to get 100% of your daily vitamin C.
Question 5.
Find the percent of each number.
a. 59% of 640
Answer:
377.6.
Explanation:
In the above-given question,
given that,
59% of 640.
59/100 x 640.
0.59 x 640.
377.6.
b. 0.20% of 3,542
Answer:
7.084.
Explanation:
In the above-given question,
given that,
0.20% of 3542.
0.20/100 x 3542.
0.002 x 3542.
7.084.
c. 195% of 568
Answer:
1107.6.
Explanation:
In the above-given question,
given that,
195% of 568.
195/100 x 568.
1.95 x 568.
1107.6.
d. 74% of 920
Answer:
680.8.
Explanation:
In the above-given question,
given that,
74% of 920.
74/100 x 920.
0.74 x 920.
680.8.
Question 6.
Water is 2 parts hydrogen and 1 part oxygen (H2O). For one molecule of water, each atom has the atomic mass unit, u, shown. What percent of the mass of a water molecule is hydrogen?
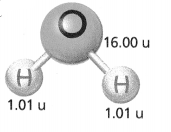
Answer:
The mass of a water molecule in hydrogen = 2.02.
Explanation:
In the above-given question,
given that,
Water is 2 parts hydrogen and 1 part oxygen (H2O).
For one molecule of water, each atom has an atomic mass unit.
the mass of hydrogen is 1.01.
1.01 x 2 = 2.02.
so the mass of a water molecule in hydrogen is 2.02.
Practice & Problem Solving
Leveled Practice In 7-8, fill in the boxes to solve.
Question 7.
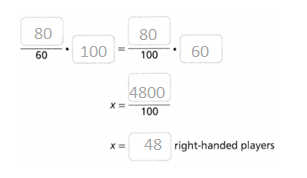
A local Little League has a total of 60 players, 80% of whom are right-handed. How many right-handed players are there?
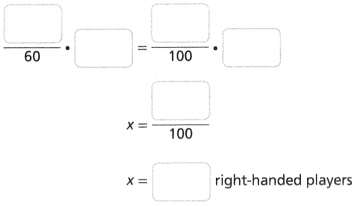
Answer:
The number of right-handed players is there = 48.
Explanation:
In the above-given question,
given that,
A local Little League has a total of 60 players,
80% of whom are right-handed.
80/100 x 60.
0.8 x 60.
48.
so the number of right-handed players is there = 48.
Question 8.
Sandra’s volleyball team has a total of 20 uniforms. 20% are medium-sized uniforms. How many uniforms are medium-sized?
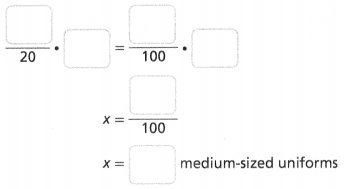
Answer:
The number of uniforms is medium-sized = 4.
Explanation:
In the above-given question,
given that,
Sandra’s volleyball team has a total of 20 uniforms.
20% are medium-sized uniforms.
20/100 = 0.20.
0.20 x 20 = 4.
so the number of uniforms are medium-sized = 4.

Question 9.
Meg is a veterinarian. In a given week, 50% of the 16 dogs she saw were Boxers. Steve is also a veterinarian. In the same week, 7 of the 35 dogs he saw this week were Boxers. Each wants to record the part, the whole, and the percent.
a. Does Meg need to find the part, the whole, or the percent?
Answer:
Meg needs to find the whole = 8.
Explanation:
In the above-given question,
given that,
Meg is a veterinarian. In a given week, 50% of the 16 dogs she saw were boxers.
Steve is also a veterinarian.
In the same week, 7 of the 35 dogs he saw this week were Boxers.
50/100 x 16.
0.5 x 16 = 8.
7/35 x 100.
0.2 x 100 = 20.
b. Does Steve need to find the part, the whole, or the percent?
Answer:
Steve needs to find the part.
Explanation:
In the above-given question,
given that,
Steve is also a veterinarian.
In the same week, 7 of the 35 dogs he saw this week were Boxers.
50/100 x 16.
0.5 x 16 = 8.
7/35 x 100.
0.2 x 100 = 20.
so steve needs to find the part.
Question 10.
Olivia is a stockbroker. She makes 4% of her sales in commission. Last week, she sold $7,200 worth of stocks.
a. How much commission did she make last week?
Answer:
The much commission did she make last week = $288.
Explanation:
In the above-given question,
given that,
Olivia is a stockbroker.
She makes 4% of her sales in commission.
Last week, she sold $7,200 worth of stocks.
4/100 x 7200.
0.04 x 7200 = 288.
so the much commission did she make last week = $288.
b. If she were to average that same commission each week, how much would she make in commissions in a year, treating a year as having exactly 52 weeks?
Answer:
The much would she make in commissions in a year, treating a year as having exactly 52 weeks = $3744.
Explanation:
In the above-given question,
given that,
If she were to average that same commission each week.
52/100 = 0.52.
0.52 x 7200 = 3744.
so the much she make in commission is $3744.
Question 11.
The registration fee for a used car is 0.8% of the sale price of $5,700. How much is the fee?
Answer:
The fee is $45.6.
Explanation:
In the above-given question,
given that,
The registration fee for a used car is 0.8% of the sale price of $5,700.
0.8/100 x 5700.
0.008 x 5700.
45.6.
so the fee is $45.6.
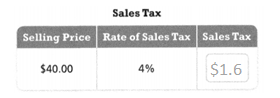
Question 12.
The total cost of an item is the price plus the sales tax.
Find the sales tax to complete the table. Then find the total cost of the item.

Answer:
The total cost of the item = $1.6.
Explanation:
In the above-given question,
given that,
The total cost of an item is the price plus the sales tax.
4/100 x 40.
0.04 x 40.
1.6.
Question 13.
Is 700% of 5 less than 10, greater than 10 but less than 100, or greater than 100? Explain your reasoning.
Answer:
35 is greater than 10 but less than 100.
Explanation:
In the above-given question,
given that,
700/100 x 5.
7 x 5.
35.
35 is greater than 10 but less than 100.
Question 14.
Is 250% of 44 less than 100, greater than 100 but less than 150, or greater than 150? Explain your reasoning.
Answer:
110 is greater than 100 but less than 150.
Explanation:
In the above-given question,
given that,
250% of 44.
250/100 x 44.
2.5 x 44.
110.
Question 15.
The seed and skin of a typical avocado is about 30%-40% of the avocado’s weight. For an 8-ounce avocado, how many ounces of edible fruit does it have?
Answer:
The number of ounces of edible fruit does it have = 5.6 ounces.
Explanation:
In the above-given question,
given that,
The seed and skin of a typical avocado is about 30%-40% of the avocado’s weight.
30/100 – 40/100.
30 + 40 = 70.
70/100 = 0.7.
0.7 x 8 = 5.6.
so the number of ounces of edible fruit does it have = 5.6 ounces.
Question 16.
A new health drink has 130% of the recommended daily allowance (RDA) for a certain vitamin. The RDA for this vitamin is 45 mg. How many milligrams of the vitamin are in the drink?
Answer:
The milligrams of the vitamin is in the drink = 60.75 mg.
Explanation:
In the above-given question,
given that,
A new health drink has 130% of the recommended daily allowance (RDA) for a certain vitamin.
The RDA for this vitamin is 45 mg.
135/100 x 45.
1.35 x 45.
60.75.
so the milligrams of the vitamin is in the drink = 60.75 mg.
Question 17.
Make Sense and Persevere 153 is 0.9% of what number? Tell which equivalent ratios you used to find the solution.
Answer:
The equivalent ratios used to find the solution = 1.377.
Explanation:
In the above-given question,
given that,
153 is 0.9%.
153 x 0.9/100.
153 x 0.009.
1.377.
so the equivalent ratio used to find the solution is 1.377.
Question 18.
Construct Arguments Brad says that if a second number is 125% of the first number, then the first number must be 75% of the second number. Is he correct? Justify your answer.
Answer:
Yes, Brad was correct.
Explanation:
In the above-given question,
given that,
Brad says that if a second number is 125% of the first number.
the first number must be 75%of the second number.
125/100 = 1.25.
75/100 = 0.75.
so he was correct.
Question 19.
Higher-Order Thinking Mark and Joe work as jewelers. Mark has an hourly wage of $24 and gets overtime for every hour he works over 40 hours. The overtime pay rate is 150% of the normal rate. Joe makes 5% commission on all jewelry he sells. Who earns more money in a week if Mark works 60 hours and Joe sells $21,000 worth of jewelry? Explain.
Answer:
Joe earns more money than the mark.
Explanation:
In the above-given question,
given that,
Mark and Joe work as jewelers.
Mark has an hourly wage of $24 and gets overtime for every hour he works over 40 hours.
The overtime pay rate is 150% of the normal rate.
5/100 = 0.05.
40 x 60 = 2400.
so Joe earns more money than the mark.
Assessment Practice
Question 20.
Pamela and John work as tutors at two different test-prep companies. Pamela earns $20 per hour. John earns $65 per pupil. Pamela works 40 hours each week. John has 11 pupils. Who earns more money in a week? Explain.
Answer:
The more money earns in a week = Pamela.
Explanation:
In the above-given question,
given that,
Pamela and John work as tutors at two different test-prep companies.
Pamela earns $20 per hour.
John earns $65 per pupil.
Pamela works 40 hours each week.
John has 11 pupils.
40 x $20 = $800.
$65 x 11 = $715.
so pamela earns more than john.
Question 21.
An Olympic-sized pool, which holds 660,000 gallons of water, is only 63% full. The pool maintenance company adds more water, filling the pool to 90% full. How many gallons of water did they add?
A. 244,200
B. 594,000
C. 178,200
D. 415,800
Answer:
The number of gallons of water they add = 178,200 gallons.
Explanation:
In the above-given question,
given that,
An Olympic-sized pool, which holds 660,000 gallons of water, is only 63% full.
The pool maintenance company adds more water, filling the pool to 90% full.
63 – 90 = 27.
27 x 660,000 = 178,200.
Lesson 3.2 Connect Percent and Proportion
Solve & Discuss It!
A florist is making flower arrangements for a party. He uses purple and white flowers in a ratio of 3 purple flowers to 1 white flower. How many flowers will he need in order to make 30 identical arrangements?
I can… use proportions to solve percent problems.
Look for Relationships
How are the number of purple flowers related to the number of white flowers?
Answer:
The ratio of purple flowers to the number of white flowers = 1: 3.
Explanation:
In the above-given question,
given that,
A florist is making flower arrangements for a party.
He uses purple and white flowers in a ratio of 3 purple flowers to 1 white flower.
the ratio is 1 : 3.
so the ratio of purple flowers to the number of white flowers = 1: 3.
Focus on math practices
Make Sense and Persevere If the florist can only buy white flowers in groups of flowers that have 3 white flowers and 2 red flowers, how many red flowers will the florist have to purchase? Explain your answer.
Answer:
The ratio of white flowers to the number of red flowers = 12.
Explanation:
In the above-given question,
given that,
If the florist can only buy white flowers in groups of flowers that have 3 white flowers and 2 red flowers.
2 + 3 = 5.
5 x 6 = 30.
2 + 2 + 2 + 2 + 2 = 12.
so the ratio of white flowers to the number of red flowers = 12.
Essential Question
How does proportional reasoning relate to percent?
Try It!
Camila makes 2 of her 5 shots attempted. Is the percent of shots she made more than, less than, or the same as Emily’s percent of shots?
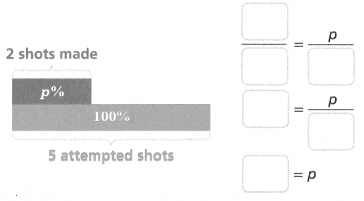
Camila made _______% of her shots.
Camila’s percent of the shots made is _______ Emily’s.
Answer:
Camila made 2/5% of her shots.
Camila’s percent of the sots made is 40 Emily’s.
Explanation:
In the above-given question,
given that,
Camila makes 2 of her 5 shots attempted.
2/5 = p/100.
p = 2/5 x 100.
p = 0.4 x 100.
p = 40.

Convince Me! A hockey goalie stops 37 out of 40 shots. What percent of attempted goals did she stop?
Answer:
The percent of attempted goals did she stop = 14.8%
Explanation:
In the above-given question,
given that,
A hockey goalie stops 37 out of 40 shots.
37/100 x 40.
0.37 x 40.
14.8 %.
so the percent of attempted goals did she stop = 14.8%.
Try It!
a. Megan’s room is expanded so the width is 150% of 3 meters. What is the new width?
Answer:
The new width = 4.5 meters.
Explanation:
In the above-given question,
Megan’s room is expanded so the width is 150% of 3 meters.
150/100 x 3.
15/10 x 3.
1.5 x 3.
4.5 meters.
b. Use the soy milk label in Example 3. What is the recommended amount of iron needed each day? Round your answer to the nearest mg.
Answer:
The recommended amount of iron needed each day =
Explanation:
In the above-given question,
given that,
KEY CONCEPT
Percent problems represent a kind of proportional relationship. You can use proportional reasoning to solve percent problems.
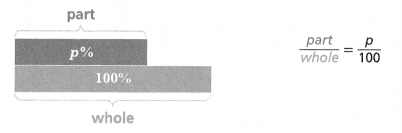
Do You Understand?
Question 1.
Essential Question How does proportional reasoning relate to percent?
Answer:
part/whole = p/100.
Explanation:
In the above-given question,
given that,
Percent problems represent a kind of proportional relationship.
if the whole is 100%.
part is p.
part/whole = p/100.
Question 2.
Reasoning Why does one of the ratios in a percent proportion always have a denominator of 100?
Answer:
The proportion always has a denominator of 100.
Explanation:
In the above-given question,
given that,
the whole is always 100%.
so part /whole = p/100.
so the proportion always has a denominator of 100.
Question 3.
Construct Arguments The proportion \(\frac{75}{W}=\frac{150}{100}\) can be used to find the whole, w. Use the language of percent to explain whether w is less than or greater than 75.
Answer:
The weight is greater than 75.
Explanation:
In the above-given question,
given that,
The proportion \(\frac{75}{W}=\frac{150}{100}\) can be used to find the whole, w.
75/w = 150/100.
75/w = 1.5.
w = 1.5 x 75.
w = 112.5.
the weight is greater than 75.
Do You Know How?
Question 4.
Write a percent proportion for the bar diagram shown.
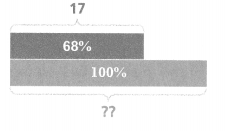
Answer:
The percent proportion for the bar diagram is 11.56
Explanation:
In the above-given question,
given that,
68/100 = 17/p.
0.68 = 17/p.
0.68 x 17 = p.
11.56 = p.
Question 5.
Use a proportion to find each value.
a. 2% of 180
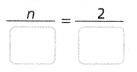
Answer:
n = 3.6.
Explanation:
In the above-given question,
given that,
2% of 180.
2/100 = n/180.
0.02 = n/180.
n = 0.02 x 180.
n = 3.6.
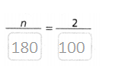
b. What percent is 17 out of 40?
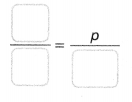
Answer:
p = 6.8.
Explanation:
In the above-given question,
given that,
17/100 = p/40.
0.17 = p/40.
p = 0.17 x 40.
p = 6.8.
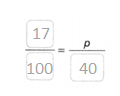
Question 6.
Construct Arguments Gia researches online that her car is worth $3,000. She hopes to sell it for 85% of that value, but she wants to get at least 70%. She ends up selling it for $1,800. Did she get what she wanted? Justify your answer.
Answer:
Yes, she gets what she wanted.
Explanation:
In the above-given question,
given that,
Gia researches online that her car is worth $3,000.
she hopes to sell it for 85% of that value, but she wants to get at least 70%.
She ends up selling it for $1,800.
85/100 x 3000.
0.85 x 3000.
70/100 x 1800.
0.7 x 1800.
Practice & Problem Solving
Leveled Practice In 7-8, fill in the boxes to solve.
Question 7.
The rabbit population in a certain area is 200% of last year’s population. There are 1,100 rabbits this year. How many were there last year?
\(\frac{1,100}{w}\) = \(\frac{}{}\)
There were _______ rabbits last year.
Answer:
The number of rabbits last year = 2200.
Explanation:
In the above-given question,
given that,
The rabbit population in a certain area is 200% of last year’s population.
There are 1,100 rabbits this year.
1100/w = 200/100.
1100/w = 2.
w = 2 x 1100.
w = 2200.
so the number of rabbits last year = 2200.
Question 8.
A company that makes hair-care products had 3,000 people try a new shampoo. Of the 3,000 people, 9 had a mild allergic reaction. What percent of the people had a mild allergic reaction?
\(\frac{9}{3,200}\) = \(\frac{p}{}\)
Percent = _________%
Answer:
The percent of the people who had a mild allergic reaction = 8.4%.
Explanation:
In the above-given question,
given that,
A company that makes hair-care products had 3,000 people try a new shampoo.
Of the 3,000 people, 9 had a mild allergic reaction.
9/3200 = p/3000.
0.0028 = p/3000.
p = 3000 x 0.0028.
p = 8.4%.
so the percent of the people had a mild allergic reaction = 8.4%.
Question 9.
A survey was given to people who owned a certain type of car. What percent of the people surveyed were completely satisfied with the car?
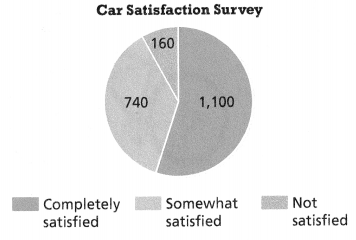
Answer:
The percent of the people surveyed were completely satisfied with the car = 1100.
Explanation:
In the above-given question,
given that,
A survey was given to people who owned a certain type of car.
completely satisfied = 1100.
somewhat satisfied = 740%.
not satisfied = 160%.
so the percent of the people surveyed were completely satisfied with thw car = 1100%.
Question 10.
The Washingtons buy a studio apartment for $240,000. They pay a down payment of $60,000
a. Their down payment is what percent of the purchase price?
Answer:
The down payment is 0.4.
Explanation:
In the above-given question,
given that,
The Washingtons buy a studio apartment for $240,000.
They pay a down payment of $60,000.
240000/60000 = 0.4.
b. What percent of the purchase price would a $12,000 down payment be?
Answer:
The percent of the purchase price would be a $12000 down payment = $20.
Explanation:
In the above-given question,
given that,
The Washingtons buy a studio apartment for $240,000.
240000/12000 = 20.
so the percent of the purchase price would be a $120000 down payment = $20.
Question 11.
A restaurant customer left $3.50 as a tip. The tax on the meal was 7% and the tip was 20% of the cost including tax.

a. What piece of information is not needed to compute the bill after tax and tip?
Answer:
The piece of information is not needed to compute the bill after tax and tip = $0.455.
Explanation:
In the above-given question,
given that,
A restaurant customer left $3.50 as a tip.
The tax on the meal was 7% and the tip was 20% of the cost including tax.
20% – 7% = 13%.
13/100 = 0.13.
3.50 x 0.13 = 0.455.
so the piece of information is not needed to compute the bill after tax and tip = $0.455.
b. Make Sense and Persevere What was the total bill?
Answer:
Question 12.
Reasoning What is a good estimate for 380% of 60? Explain.
Answer:
The good estimate is 228.
Explanation:
In the above-given question,
given that,
380% of 60.
380/100 x 60.
3.8 x 60 = 228.
so the good estimate is 228.
Question 13.
Critique Reasoning Marna thinks that about 35% of her mail is junk mail. She gets about twice as much regular mail as junk mail. Is she correct? Explain.
Answer:
Yes, she was correct.
Explanation:
In the above-given question,
given that,
Marna thinks that about 35% of her mail is junk mail.
She gets about twice as much regular mail as junk mail.
35% + 35%.
70%.
70/100 = 0.7.
so she was correct.
Question 14.
Hypatia has read 13 chapters of a 22-chapter book. What percent of the chapters has she read?
Answer:
The chapters she has read = 9%.
Explanation:
In the above-given question,
given that,
Hypatia has read 13 chapters of a 22-chapter book.
22 – 13 = 9.
9 percent = 9/100.
so 9% of the chapters has she read.
Question 15.
A school year has 4 quarters. What percent of a school year is 7 quarters?
Answer:
The percent of a school year = 28%.
Explanation:
In the above-given question,
given that,
A school year has 4 quarters.
4/100 = 7/q.
0.04 = 7/q.
q = 0.04 x 7.
q = 0.28.
so the percent of a school year = 28%.
Question 16.
Construct Arguments A survey found that 27% of high school students and 94% of teachers and school employees drive to school. The ratio of students to employees is about 10 to 1. Roger states that the number of students who drive to school is greater than the number of teachers and employees who drive to school. Explain how Roger’s statement could be correct.
Answer:
The ratio of students to employees is about 10 to 1.
Explanation:
In the above-given question,
given that,
A survey found that 27% of high school students and 94% of teachers and school employees.
The ratio of students to employees is about 10 to 1.
27/100 = 0.27.
94/100 = 0.94.
so the ratio of students to employees is about 10 to 1.
Question 17.
Higher Order Thinking Stefan sells Jin a bicycle for $114 and a helmet for $18. The total cost for Jin is 120% of what Stefan spent originally to buy the bike and helmet. How much did Stefan spend originally? How much money did he make by selling the bicycle and helmet to Jin?

Answer:
The money did he make by selling the bicycle and helmet to Jin = $132.
Explanation:
In the above-given question,
given that,
Stefan sells Jin a bicycle for $114 and a helmet for $18.
The total cost for Jin is 120% of what Stefan spent originally to buy the bike and helmet.
$114 + $18 = $132.
so the money did he make by selling the bicycle and helmet to Jin = $132.
Assessment Practice
Question 18.
Last month Nicole spent $30. This month she spent 140% of what she spent last month. Write a proportional equation to represent the situation. How much did Nicole spend this month?
Answer:
The amount did Nicole spend this month = $42.
Explanation:
In the above-given question,
given that,
Last month Nicole spent $30.
This month she spent 140% of what she spent last month.
140/100 x $30.
1.4 x $30.
$42.
so the amount did Nicole spend this month = $42.
Question 19.
Mr. Jones, the owner of a small store buys kayak paddles for $50.00 each, and sells them for 180% of the purchase price.
PART A
A customer buys a paddle for $97.65, which includes the selling price and sales tax. What is the sales tax rate?
A 7.65%
B. 4.7%
C. 9.75%
D. 8.5%
Answer:
Option C was correct.
Explanation:
In the above-given question,
given that,
Mr. Jones, the owner of a small store buys kayak paddles for $50.00 each and sells them for 180% of the purchase price.
A customer buys a paddle for $97.65, which includes the selling price and sales tax.
180/100 = 1.8.
1.8 x 50.
90.
so option C was correct.
PART B
If Mr. Jones buys paddles for $35 instead of $50, and uses the same percent increase on price, how many paddles must Mr. Jones sell for the total paddle sales, before tax, to be at least $250? Explain your answer.
Answer:
Mr. Jones sells for the total paddle sales = $40.
Explanation:
In the above-given question,
given that,
If Mr. Jones buys paddles for $35 instead of $50 and uses the same percent increase on the price.
$250/$50.
$.5.
$35 + $5 = $40.
Lesson 3.3 Represent and Use the Percent Equation
Solve & Discuss It!
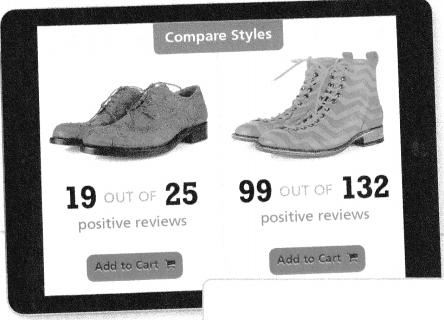
Fran is shopping for a new pair of shoes. She did some research and has narrowed the options to the two pairs she likes the most. Based on buyers’ reviews, which pair do you recommend that she buy? Explain your thinking.
I can.. represent and solve percent problems using equations.
Model with Math
How can you use what you know about ratios to compare the reviews?
Focus on math practices
Model with Math Describe another situation in which you could use ratios to make a decision.
Essential Question
How are percent problems related to proportional reasoning?
Try It!
An elephant weighs 15,000 pounds on Earth and 2,500 pounds on the Moon. Assuming the weights are proportional, what percent of its weight on Earth is its weight on the Moon?
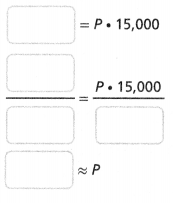
The elephant’s weight on the Moon is about __________% of its weight on Earth.
Answer:
The elephant’s weight on the Moon is about 6% of its weight on Earth.
Explanation:
In the above-given question,
given that,
An elephant weighs 15,000 pounds on Earth and 2,500 pounds on the Moon.
Assuming the weights are proportional.
2500 = p x 15000.
p = 15000/2500.
p = 6.
so the elephant’s weight on the Moon is about 6% of its weight on Earth.

Convince Me! How does the percent describe how the weights are related?
Try It!
To make a profit, a clothing store sells board shorts at 115% of the amount they paid for them. How much did the store pay for the board shorts shown?

Answer:
The store pays for the board shorts = $32.2.
Explanation:
In the above-given question,
given that,
To make a profit, a clothing store sells board shorts at 115% of the amount they paid for them.
the cost of the short is $28.
115/100 x $28.
1.15 x $28 = $32.2.
so the store pay for the board shorts = $32.2.
KEY CONCEPT
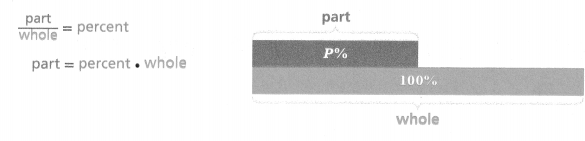
The percent equation shows how a percent relates proportional quantities. The percent is a constant of proportionality and the equation has the same form as y = mx.
Do You Understand?
Question 1.
Essential Question How are percent problems related to proportional reasoning?
Answer:
The percent problem related to proportional reasoning is y = mx.
Explanation:
In the above-given question,
given that,
The percent equation shows how a percent relates to proportional quantities.
The percent is a constant of proportionality and the equation has the same form as y = mx.
part/whole = percent.
part = percent x whole.
Question 2.
Reasoning A waiter at a restaurant receives $11 as a tip on a $47.20 bill. He usually receives tips that are 20% of the total bill. Is the tip amount what the waiter typically receives? Explain.
Answer:
The tip amount is the waiter typically receives = $11.64.
Explanation:
In the above-given question,
given that,
A waiter at a restaurant receives $11 as a tip on a $47.20 bill.
He usually receives tips that are 20% of the total bill.
$47.20 + $11.
$58.2.
20/100 x $58.2.
0.2 x $58.2 = $11.64.
Question 3.
Construct Arguments Sara used an equation to solve the problem below. Justify each step of her work. About 11% of people are left-handed. How many people would you expect to be left-handed in a class of 30 students?
l = 0.11 • 30
ļ = 3.3
about 3 students
Answer:
The number of people would you accept to be left-handed = 3 students.
Explanation:
In the above-given question,
given that,
11% of people are left-handed.
11/100 x 30.
0.11 x 30 = 3.3.
so the number of people would you accept to be left-handed = 3 students.
Do You Know How?
Question 4.
An auto insurance company pays 12% commission to its agents for each new insurance policy they sell. How much commission does an agent make on a $1,000 policy?
Answer:
The commission does an agent makes on a $1000 policy = $10.
Explanation:
In the above-given question,
given that,
An auto insurance company pays a 12% commission to its agents for each new insurance policy they sell.
12/100 x $1000.
0.12 x $1000.
$10.
so the commission does an agent make on a $1000 policy = $10.
Question 5.
Curt and Melanie are mixing blue and yellow paint to make seafoam green paint. Use the percent equation to find how much yellow paint they should use.

Answer:
The quantity of yellow paint they should use = 1.5.
Explanation:
In the above-given question,
given that,
Curt and Melanie are mixing blue and yellow paint to make seafoam green paint.
70% = 70/100.
70/100 = 0.7.
30/100 = 30%.
30% = 0.3.
0.3 + 0.7 = 1.
1 x 1.5 = 1.5.
so the quantity of yellow paint they should use = 1.5.
Question 6.
Bill paid $35.99 in tax on a laptop that cost $449.99. About what percent sales tax did Bill pay?
Answer:
The percent sales tax did Bill pay = 4.8%.
Explanation:
In the above-given question,
given that,
Bill paid $35.99 in tax on a laptop that cost $449.99
$449.99 + $35.99.
$485.98.
so the percent of sales tax did Bill pay = 4.8%.
Practice & Problem Solving
Leveled Practice In 7 and 8, solve each percent problem.
Question 7.
In a survey of 500 voters, 430 said they would vote for the same candidate again. What percent of the voters would vote the same way again?
part = percent. whole
_______ = p% • ________
_______ = p%
Answer:
The percent of the votes would vote the same way again = 0.086.
Explanation:
In the above-given question,
given that,
In a survey of 500 voters, 430 said they would vote for the same candidate again.
500 = p% x 430.
p% = 430/500.
p% = 0.86.
p = 0.086.
so the percent of the votes would vote the same way again = 0.086.
Question 8.
The local newspaper has letters to the editor from 40 people. If this number represents 5% of all of the newspaper’s readers, how many readers, r, does the newspaper have?
part = percent. whole
______ = ______ • r
______ = r
Answer:
The number of readers r does the newspaper have = 0.00125.
Explanation:
In the above-given question,
given that,
The local newspaper has letters to the editor from 40 people.
If this number represents 5% of all of the newspaper’s readers.
5% = 40 x r.
5/100 = 40 x r.
0.05 = 40r.
r = 0.05/40.
r = 0.00125.
so the number of readers r does the newspaper have = 0.00125.
Question 9.
Make Sense and Persevere What percent of the 16-gigabyte hard drive shown is used for photos?

Answer:
The percent of the 16-gigabyte hard drive shown is used for photos = 0.002075.
Explanation:
In the above-given question,
given that,
percent = part/whole.
percent = 3.32/16.
percent = 0.2075.
0.2075% = 0.002075.
so the percent of the 16-gigabyte hard drive shown is used for photos = 0.002075.
Question 10.
A shirt that normally costs $30 is on sale for $21.75. What percent of the regular price is the sale price?
Answer:
The percent of the regular price = 0.0825.
Explanation:
In the above-given question,
given that,
A shirt that normally costs $30 is on sale for $21.75.
$30 – $21.75 = $8.25.
$8.25% = 0.0825.
so the percent of the regular price = 0.0825.
Question 11.
Complete the table.
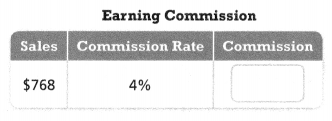
Answer:
The commission = $30.72.
Explanation:
In the above-given question,
given that,
the sales of the earning commission = $768.
the commission rate = 4%.
4/100 = 768/c.
0.04 = 768/c.
c = 0.04 x 768.
c = $30.72.

Question 12.
Complete the table.
Answer:
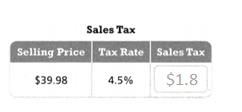
The sales tax = $1.7991.
Explanation:
In the above-given question,
given that,
the selling price is $39.98.
the tax rate is 4.5%.
4.5 /100 x $39.98.
0.045 x $39.98.
$1.7991.
so the sales tax = $1.7991.
Question 13.
A restaurant automatically charges a 20% gratuity if a party has 6 or more people. How much gratuity is added to a party of 6 on a $141 bill?
Answer:
The much gratuity is added to a party of 6 on a $141 bill = $169.2.
Explanation:
In the above-given question,
given that,
A restaurant automatically charges a 20% gratuity if a party has 6 or more people.
20/100 = 0.2.
0.2 x 6 = 1.2.
1.2 x $141 = 169.2.
Question 14.
Make Sense and Persevere A large university accepts 70% of the students who apply. Of the students the university accepts, 25% actually enroll. If 20,000 students apply, how many enroll?
Answer:
The number of students that enroll = 200 students.
Explanation:
In the above-given question,
given that,
A large university accepts 70% of the students who apply.
Of the students the university accepts, 25% actually enroll.
70 + 25 = 95.
95/100 x 20000.
0.95 x 20000.
200.
so the number of students that enroll = 200 students.
Question 15.
Model with Math There are 4,000 books in the town’s library. Of these, 2,600 are fiction. Write a percent equation that you can use to find the percent of the books that are fiction. Then solve your equation.
Answer:
The percent of the books that are fiction = 0.01538.
Explanation:
In the above-given question,
given that,
There are 4,000 books in the town’s library.
Of these, 2,600 are fiction.
4000/2600 = 1.538.
1.538% = 0.01538.
Question 16.
A salesperson earns 4% commission on furnace sales.
a. What is the commission that the salesperson earns on the sale of $33,000 worth of furnaces?
Answer:
The salesperson earns on the sale of $33000 = $1320.
Explanation:
In the above-given question,
given that,
A salesperson earns a 4% commission on furnace sales.
4/100 x $33000.
0.04 x $33000.
$1320.
so the salesperson earns on the sale of $33000 = $1320.
b. Suppose the salesperson doubles his sales of furnaces. What would be true about the commission? Explain without using any calculations.
Answer:
The salesperson doubles his sales of furnaces = $2640.
Explanation:
In the above-given question,
given that,
A salesperson earns a 4% commission on furnace sales.
4/100 x $33000.
0.04 x $33000.
$1320.
1320 x $2 = $2640.
so the salesperson doubles his sales of furnaces = $2640.
Question 17.
Heidi earns 3% commission on the jewelry she sells each week. Last week, she sold the pieces of jewelry shown.

a. How much did she make in commission?
Answer:
She makes in commission is 21.9%.
Explanation:
In the above-given question,
given that,
Heidi earns 3% commission on the jewelry she sells each week.
$110 + $275 + $200 + $145.
$730.
3% of $730.
3/100 x 730.
0.03 x 730.
21.9.
b. Reasoning How much did the jewelry store take in from her sales? How do you know?
Answer:
The jewelry store takes in from her sales 29.2%.
Explanation:
In the above-given question,
given that,
Heidi earns 3% commission on the jewelry she sells each week.
$110 + $275 + $200 + $145.
$730.
4% of $730.
4/100 x 730.
0.04 x 730.
29.2.
Question 18.
Higher Order Thinking in a company, 60% of the workers are men. If 1,380 women work for the company, how many workers are there in all? Show two different ways that you can solve this problem.
Answer:
The number of workers in all = 828 workers.
Explanation:
In the above-given question,
given that,
In a company, 60% of the workers are men.
If 1,380 women work for the company.
60% of 1380.
60/100 x 1380.
6/10 x 1380.
0.6 x 1380.
828.
so the number of workers in all = 828 workers.
Assessment Practice
Question 19.
A salesperson starts working 40 hours per week at a job with two options for being paid. Option A is an hourly wage of $19. Option B is a commission rate of 8% on weekly sales. How much does the salesperson need to sell in a given week to earn the same amount with each option?
A. $9,500
B. $4,750
C. $760
D. $320
Answer:
The salesperson needs to sell in a given week to earn the same amount with each option = $320.
Explanation:
In the above-given question,
given that,
A salesperson starts working 40 hours per week at a job with two options for being paid.
Option A is an hourly wage of $19. Option B is a commission rate of 8% on weekly sales.
8/100 x 40.
0.08 x 40.
3.2.
so the salesperson needs to sell in a given week to earn the same amount with each option = $320.
Question 20.
At a real estate agency, an agent sold a house for $382,000. The commission rate is 5.5% for the real estate agency. The commission for the agent is 30% of the amount the real estate agency gets. How much did the agent earn in commission? Explain your answer.
Answer:
The agent earn in commission = $114600.
Explanation:
In the above-given question,
given that,
At a real estate agency, an agent sold a house for $382,000.
The commission rate is 5.5% for the real estate agency.
The commission for the agent is 30% of the amount the real estate agency gets.
30/100 x $382000.
0.3 x $382000.
114600.
so the agent earn in commission = $114600.
Topic 3 Mid-Topic Checkpoint
Question 1.
Vocabulary Explain how the percent equation relates proportional quantities. Lesson 3-3
Answer:
The percent equation shows how a percent relates to proportional quantities.
y = mx.
Explanation:
In the above-given question,
given that,
The percent equation shows how a percent relates proportional quantities.
The percent is a constant of proportionality and the equation has the same form as y = mx.
part/whole = percent.
part = percent x whole.
Question 2.
Colleen buys a movie for $20 and pays 7% sales tax. Her cousin, Brad, lives in another state. Brad buys the same movie for $22 and pays 6% sales tax. Who pays more sales tax? How much more? Lessons 3-1 and 3-3
Answer:
Brad pays more sales tax = $0.1.
Explanation:
In the above-given question,
given that,
Colleen buys a movie for $20 and pays 7% sales tax.
Her cousin, Brad, lives in another state.
Brad buys the same movie for $22 and pays 6% sales tax.
7/100 x $20.
0.07 x 20 = $1.4.
6/100 x $22.
0.06 x 22 = $1.3.
Brad pays more sales tax = $0.1.
Question 3.
Kamesh and Paolo each read 40 books in one year. Kamesh read 12 nonfiction books. Thirty-five percent of the books Paolo read were nonfiction. Who read more nonfiction books? How many more? Lesson 3-2
Answer:
Kamesh read more notifications.
Explanation:
In the above-given question,
given that,
Kamesh and Paolo each read 40 books in one year.
Kamesh read 12 nonfiction books.
Thirty-five percent of the books Paolo read were nonfiction.
35% x 40.
0.35 x 40 = $14.
35% x 12.
0.35 x 12 = $4.2.
so Kamesh read more notifications.
Question 4.
Val buys a computer for $920. If this is 115% of what the store paid for the same computer, how much did the store earn on the sale? Lesson 3-3
Answer:
The much did the store earn on the sale = $1058.
Explanation:
In the above-given question,
given that,
Val buys a computer for $920.
If this is 115% of what the store paid for the same computer.
115/100 x $920.
1.15 x $920 = $1058.
so the much did the store earn on the sale = $1058.
Question 5.
For each situation, select the percent to answer the question. Lessons 3-1, 3-2, and 3-3
Answer:
25%, 5%, and 5%
Explanation:
In the above-given question,
given that,
In an auto repair shop, 14 of the 56 cars received oil changes.
14/56 = 0.25.
0.25 x 100 = 25%.
Harry pays $3.50 sales tax on a $70 item.
In a box of 250 paperclips, 50 are red.
250/50 = 5%.

Question 6.
Explain how you can use proportional reasoning to determine the whole if you know that 21 is 60% of the whole. Lesson 3-2
Answer:
12.6%.
Explanation:
In the above-given question,
given that,
21 is 60%.
60/100 x 21.
0.6 x 21.
12.6.

Topic 3 Mid-Topic Performance Task
The coach of a women’s basketball team wants each of her starting players to make at least 75% of the free throws attempted during regular season games. The table shows the statistics for the starting players after the first 15 games.
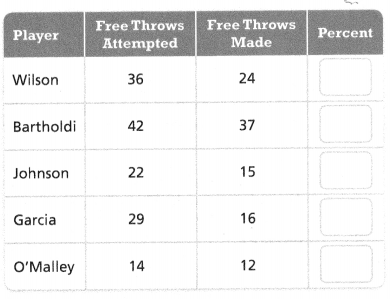
PART A
Use the table. Find the percentage of free throws made by each player. Round to the nearest whole percent.
Answer:
The percentage of free throws made by each player = 1.5%, 1.1%, 1.4%, 1.8%, and 0.7%.
Explanation:
In the above-given question,
given that,
Wilson free throws attempted = 36/24 = 1.5.
Bartholdi free throws attempted = 42/37 = 1.1.
Jhonson free throws attempted = 22/15 = 1.4.
Garcia free throws attempted = 29/16 = 1.8.
O’Malley free throws attempted = 14/12 = 0.7.
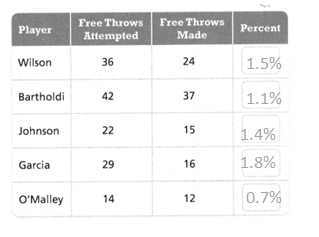
PART B
Choose one of the players with a free-throw percentage less than 75%. Determine a number of free throws the player could attempt and make during the next 10 games to increase her free-throw percentage to at least 75%.
Answer:
PART C
Choose one of the players with a free-throw percentage greater than 75%. Determine the number of free throws that the player could miss during the next 10 games and still maintain an overall percentage of at least 75%.
Answer:
Lesson 3.4 Solve Percent Change and Percent Error Problems
Explain It!
Nadia lives in the town of Bayville. Quinn lives in the town of Portside. Nadia and Quinn each claim that her respective town’s population is growing more rapidly.
I can… solve problems involving percent change and percent error.
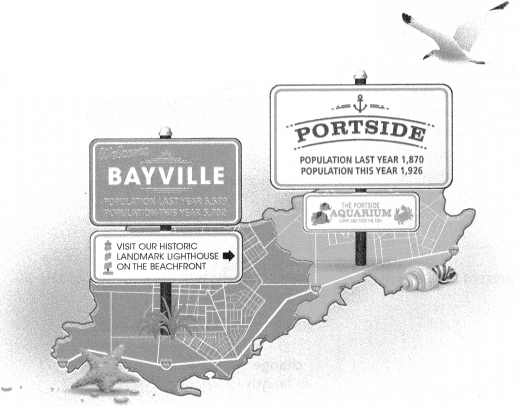
A. Write an argument to support Nadia. Why might she argue that Bayville’s population is growing more rapidly?
Answer:
The population is growing more rapidly because they have the Historic place, LightHouse, and Beachfront.
Explanation:
In the above-given question,
given that,
Nadia lives in the town of Bayville.
Quinn lives in the town of Portside.
Nadia’s population has last year 3399.
Quinn has population has 1870.
Nadia population has this year 3702.
Quinn’s population has 1926.
Nadia has a Historic place, LightHouse, and Beachfront.
so the population is growing more rapidly.
B. Write an argument to support Quinn. Why might she argue that Portside’s population is growing more rapidly?
Answer:
The population is growing more rapidly because they have the Aquarium.
Explanation:
In the above-given question,
given that,
Nadia lives in the town of Bayville.
Quinn lives in the town of Portside.
Nadia’s population has last year 3399.
Quinn has population has 1870.
Nadia population has this year 3702.
Quinn’s population has 1926.
Quinn has a Historic place, LightHouse, and Beachfront.
so the population is growing more rapidly.
c. Whose reasoning is more logical? Explain why.
Answer:
Nadia’s reasoning is more logical.
Explanation:
In the above-given question,
given that,
Nadia lives in the town of Bayville.
Quinn lives in the town of Portside.
Nadia’s population has last year 3399.
Quinn has population has 1870.
Nadia population has this year 3702.
Quinn’s population has 1926.
the population of Nadia is very high.
so Nadia’s reasoning is more logical.
Focus on math practices
Critique Reasoning Suppose Bayville’s population is expected to grow 3% next year. Nadia says that means the population will increase by 300 people. Is Nadia’s reasoning correct? Explain.
Answer:
Yes, Nadia was correct.
Explanation:
In the above-given question,
given that,
Bayville’s population is expected to grow 3% next year.
3/100 = 0.03.
300.
so Nadia was correct.
Essential Question
How is finding percent error similar to finding percent change?
Try It!
What will be the length of the alligator next year if its length changes by the same percent as it changed this year?
percent change • length this year = change in length
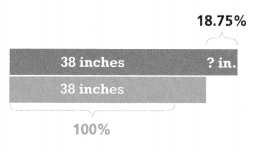
0.1875 • ________ = ________
_______ + _______ = ________
Next year, the length of the alligator will be ________ inches long.
Answer:
Next year, the length of the alligator will be 45 inches long.
Explanation:
In the above-given question,
given that,
percent change • length this year = change in length.
0.1875 x 38 = 7.125.
7.125 + 38 = 45.125.
so next year, the length of the alligator will be 45 inches long.
Convince Me! Why is the increase in the alligator’s length different from year to year, even though the percent change stayed the same?
Try It!
The specification for the length of a bolt is 4.75 inches. A machinist makes a bolt that is 4.769 inches long. What is the percent error of the bolt’s length?

Answer:
The percent error of the bolt’s = 0.019.
Explanation:
In the above-given question,
given that,
The specification for the length of a bolt is 4.75 inches.
A machinist makes a bolt that is 4.769 inches long.
4.769 – 4.75 = 0.019.
so the percent error of the bolt’s = 0.019.
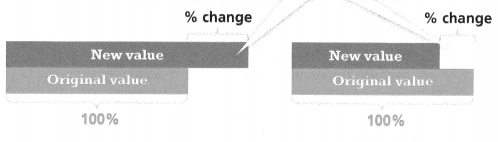
KEY CONCEPT
Percent change and percent error problems are kinds of percent problems. You can use the percent equation to solve them.
amount of change = percent change • original amount
The amount of change is the difference between original and new values
Do You Understand?
Question 1.
Essential Question How is finding percent error similar to finding percent change?
Answer:
Yes, percent error and percent change problems are the same.
Explanation:
In the above-given question,
given that,
Percent change and percent error problems are kinds of percent problems.
amount of change = percent change • original amount.
The amount of change is the difference between original and new values.
Question 2.
Reasoning Give an example of a problem in which the percent error is greater than 20%, but less than 50%. Explain how you determined the percent error.
Answer:
The percent error is less than 20% but less than 50%.
Explanation:
In the above-given question,
given that,
percent error = percent change x original amount.
percent error = 5% x 3%.
percent error = 15%.
so the percent error is less than 20% but less than 50%.
Question 3.
Construct Arguments A store manager marked up a $10 flash drive by 20%. She then marked it down by 20%. Explain why the new price of the flash drive is not $10.
Answer:
The new price of the flash drives is $2.
Explanation:
In the above-given question,
given that,
A store manager marked up a $10 flash drive by 20%.
She then marked it down by 20%.
20/100 x 10.
0.2 x 10 = 2.
so the new price of the flash drives is $2.
Do You Know How?
Question 4.
Lita’s softball team won 8 games last month and 10 this month. What was the percent change in games the team won? Was it an increase or decrease?
Answer:
The percent change in games the team won = 80.
Explanation:
In the above-given question,
given that,
Lita’s softball team won 8 games last month and 10 this month.
percent change = percent change x original amount.
percent change = 8 x 10.
percent change = 80.
Question 5.
What is the percent change in the price of a gallon of gas, to the nearest whole percent? Is it an increase or a decrease?

Answer:
The percent change in the price of a gallon of gas = 42.
Explanation:
In the above-given question,
given that,
3.499 last year.
3.079 this year.
3.499 – 3.079 = 0.42.
42/100 = 42.
so the percent change in the price of a gallon of gas = 42.
Question 6.
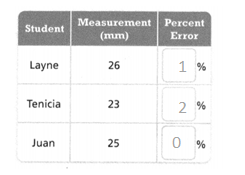
Several students measured a 25-mm-long nail and wrote the measurements shown in the table below. Whose measurement had the greatest percent error? Round to the nearest percent.
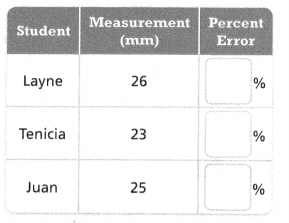
Answer:
Tenicia has the greatest percent error.
Explanation:
In the above-given question,
given that,
Several students measured a 25-mm-long nail and wrote the measurements.
26 – 25 = 1.
25 – 23 = 2.
25 – 25 = 0.
so Tenicia had the greatest measurement.
Practice & Problem Solving
Leveled Practice In 7-8, use the bar diagram and fill in the boxes to solve.
Question 7.
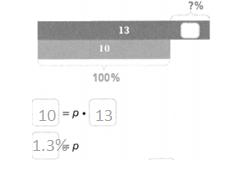
The original quantity is 10 and the new quantity is 13. What is the percent change? Is it an increase or decrease?
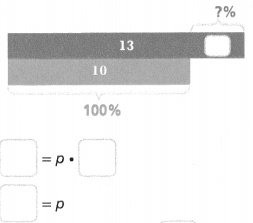
The percent decrease is _______ %.
Answer:
The percent decrease is 1.3%.
Explanation:
In the above-given question,
given that,
The original quantity is 10 and the new quantity is 13.
percent change = 10 x 13.
percent change = 130.
130/100 = 1.3.
so the percent decrease is 1.3%.
Question 8.
The original quantity is 5 and the new quantity is 3. What is the percent change? Is it an increase or decrease?
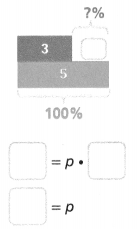
The percent increase is _______%.
Answer:
The percent increase is 0.006%.
Explanation:
In the above-given question,
given that,
The original quantity is 10 and the new quantity is 13.
3 = p x 5.
percent change = 3/5.
0.6/100 = 0.006..
so the percent increase is 0.006%.
Question 9.
At noon, a tank contained 10 cm of water. After several hours, it contained 7 cm of water. What is the percent decrease of water in the tank?
Answer:
The percent decrease of water in the tank = 3%.
Explanation:
In the above-given question,
given that,
At noon, a tank contained 10 cm of water. After several hours, it contained 7 cm of water.
percent change = 10 – 7.
percent change = 3.
so the percent decrease of water in the tank = 3%.
Question 10.
Craig likes to collect vinyl records. Last year he had 10 records in his collection. Now he has 12 records. What is the percent increase of his collection?
Answer:
The percent increase of his collection = 2%.
Explanation:
In the above-given question,
given that,
Craig likes to collect vinyl records. Last year he had 10 records in his collection.
Now he has 12 records.
percent increase = 12 – 10.
percent increase = 2.
so the percent increase of his collection = 2%.
Question 11.
Carl bought an airline ticket. Two weeks ago, the cost of this flight was $300.

What is the percent increase?
Answer:
The percent increase = 75%.
Explanation:
In the above-given question,
given that,
Carl bought an airline ticket. Two weeks ago, the cost of this flight was $300.
percent increase = 375 – 300.
percent increase = 75.
so the percent increase = 75%.
Question 12.
On Monday, a museum had 150 visitors. On Tuesday, it had 260 visitors.
a. Estimate the percent change in the number of visitors to the museum.
Answer:
The percent change in the number of visitors to the museum = 39000.
Explanation:
In the above-given question,
given that,
On Monday, a museum had 150 visitors. On Tuesday, it had 260 visitors.
percent change = 150 x 260.
percent change = 39000.
so the percent change in the number of visitors to the museum = 39000.
b. About how many people would have to visit the museum on Wednesday to have the same percent change from Tuesday to Wednesday as from Monday to Tuesday? Explain your answer.
Answer:
The percent change from Tuesday to Wednesday = 110.
Explanation:
In the above-given question,
given that,
On Monday, a museum had 150 visitors. On Tuesday, it had 260 visitors.
percent change = 150 – 260.
percent change = 110.
so the percent change from Tuesday to Wednesday = 110.
Question 13.
Rihanna has a container with a volume of 1.5 liters. She estimates the volume to be 2.1 liters. What is the percent error?
Answer:
The percent error = 0.6.
Explanation:
In the above-given question,
given that,
Rihanna has a container with a volume of 1.5 liters.
She estimates the volume to be 2.1 liters.
percent error is similar to the percent change.
percent change = 2.1 – 1.5.
percent change = 0.6.
so the percent error = 0.6.
Question 14.
The label on a package of bolts says each bolt has a diameter of 0.35 inch. To be in the package, the percent error of the diameter must be less than 5%. One bolt has a diameter of 0.33 inch. Should it go in the package? Why or why not?
Answer:
Yes, it would go in the package.
Explanation:
In the above-given question,
given that,
The label on a package of bolts says each bolt has a diameter of 0.35 inches.
To be in the package, the percent error of the diameter must be less than 5%. One bolt has a diameter of 0.33 inches.
percent error = 0.35 – 0.33.
percent error = 0.02.
5/100 x 0.02 = 0.05 x 0.02.
0.001.
it would go in the package.
Question 15.
A band expects to have 16 songs on their next album. The band writes and records 62.5% more songs than they expect to have in the album. During the editing process, 50% of the songs are removed. How many songs will there be in the final album?
Answer:
The number of songs will there be in the final album = 200.
Explanation:
In the above-given question,
given that,
A band expects to have 16 songs on their next album.
The band writes and records 62.5% more songs than they expect to have in the album.
During the editing process, 50% of the songs are removed.
50% – 62.5% = 12.5%.
12.5% x 16.
200.
so the number of songs will there be in the final album = 200.
Question 16.
Make Sense and Persevere in the first week of July, a record 1,060 people went to the local swimming pool. In the second week, 105 fewer people went to the pool. In the third week, 135 more people went to the pool than in the second week. In the fourth week, 136 fewer people went to the pool than in the third week.
What is the percent change in the number of people who went to the pool between the first and last weeks?
Answer:
The percent change in the number of people who went to the pool between the first and last weeks = 924.
Explanation:
In the above-given question,
given that,
Persevere in the first week of July, a record 1,060 people went to the local swimming pool.
In the second week, 105 fewer people went to the pool. In the third week, 135 more people went to the pool than in the second week.
In the fourth week, 136 fewer people went to the pool than in the third week.
percent change =1060 – 136.
percent change = 924.
so the percent change in the number of people between first and last weeks = 924.
Question 17.
Be Precise You have 20 quarters. You find 40% more quarters in your room. Then you go shopping and spend 50% of the total number of quarters.
a. Write an expression that represents the total number of quarters you take with you when you go shopping.
Answer:
The total number of quarters you take with you when you go shopping = 2 quarters.
Explanation:
In the above-given question,
given that,
You have 20 quarters. You find 40% more quarters in your room.
Then you go shopping and spend 50% of the total number of quarters.
50 – 40 = 10%.
20 x 10/100.
20 x 0.1.
2.
so the total number of quarters you take with you and go shopping = 2 quarters.
b. How much money do you have left?
Answer:
The money I have left = 18 quarters.
Explanation:
In the above-given question,
given that,
You have 20 quarters. You find 40% more quarters in your room.
Then you go shopping and spend 50% of the total number of quarters.
20 – 2 = 18.
so the money I have left = 18 quarters.
Question 18.
Higher Order Thinking The dot plot shows predictions for the winning time in a 200-meter sprint. The winner finished the race in 22.3 seconds. Find the greatest percent error for a prediction to the nearest tenth of a percent. Justify your answer.
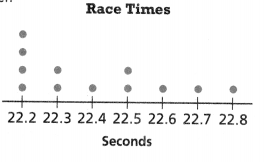
Answer:
The greatest percent error for a prediction to the nearest tenth of a percent = 22.2 seconds.
Explanation:
In the above-given question,
given that,
The dot plot shows predictions for the winning time in a 200-meter sprint.
The winner finished the race in 22.3 seconds.
200/100 = 0.02%.
22.3 – 0.02 = 22.2 seconds.
Assessment Practice
Question 19.
The amount of money in a savings account increases from $250 to $270 in one month. If the percent increase is the same for every month, how much money will be in the account at the end of the next month?
A. $291.60
B. $295
C. $289.60
D. $300
Answer:
The much money will be in the account at the end of the next month = 0.2.
Explanation:
In the above-given question,
given that,
The amount of money in the savings account increases from $250 to $270 in one month.
270 – 250 = 20.
20% = 20/100.
20/100 = 0.2.
Question 20.
A meteorologist predicted that there would be 1.0 inches of rainfall from a storm. Instead, there were 2.2 inches of rainfall. Which statements are true?
☐ The prediction was off by 35%.
☐ If the percent error should be less than 60%, the prediction was acceptable.
☐ The percent error of the prediction was about 55%.
☐ If the percent error should be less than 20%, the prediction was acceptable.
☐ The difference between the predicted and actual rainfall was 1.2 inches.
Answer:
The statements are true is the difference between the predicted and actual rainfall was 1.2 inches.
Explanation:
In the above-given question,
given that,
A meteorologist predicted that there would be 1.0 inches of rainfall from a storm.
Instead, there were 2.2 inches of rainfall.
2.2 – 1.0 = 1.2.
so the difference between predicted and actual rainfall = 1.2 inches.
3-ACT MATH
3-Act Mathematical Modeling:
The Smart Shopper

АСТ 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Make a prediction to answer this Main Question. Explain how you arrived at your prediction.

Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.

Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.

Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
ACT 3
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Be Precise Describe how you would tell the friends to use their coupons.
Answer:
SEQUEL
Question 15.
Make Sense and Persevere Suppose the $20 coupon requires a purchase of $100 or more. How would that affect your solution?
Answer:
They affect the solution = $80.
Explanation:
In the above-given question,
given that,
Suppose the $20 coupon requires a purchase of $100 or more.
$100 – $20 = $80.
so they affect the solution = $80.
Lesson 3.5 Solve Markup and Markdown Problems
Solve & Discuss It!
Clare subscribes to an online music streaming service for a yearly fee of $96. Starting next month, there will be a 12% increase in the fee.
The ad for another music streaming service is shown below. Should Clare switch? Explain.
I can… solve problems involving percent markup and markdown.

Model with Math
You can use the percent equation to determine the percent increase.
Focus on math practices
Make Sense and Persevere What is another problem-solving method you could use to check that your solution makes sense?
Essential Question
How are the concepts of percent markup and percent markdown related to the percent equation?
Try It!
What is the percent markup on a $300 phone sold for $465?
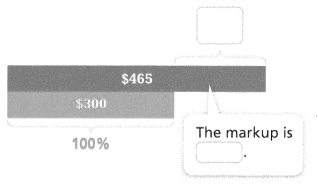
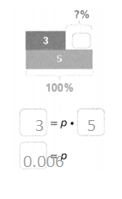
markup = percent markup • cost
________ = p • 300
________ = p
The percent markup on the phone is _________%.
Answer:
The percent markup on the phone is 1.55%.
Explanation:
In the above-given question,
given that,
the percent markup on a $300 phone sold for $465.
markup = percent markup x cost.
markup = p x 300.
465/300 = p.
p = 1.55.
so the percent markup on the phone is 1.55%.
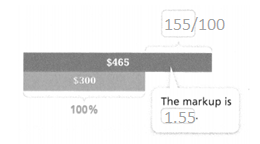
Convince Me! How does the percent equation help solve markup problems?
Try It!
What is the selling price for a $45 pair of shoes with a 15% markup?
Answer:
The markup = 0.003.
Explanation:
In the above-given question,
given that,
the selling price = $45.
markup = 15%.
markup = percent markup x cost.
15% = p x $45.
0.15 = p x $45.
p = 0.15/45.
p = 0.003.
Try It!
Find the percent markdown for an $80 jacket that is on sale for $48.
Answer:
The markup = $32.
Explanation:
In the above-given question,
given that,
the selling price = $45.
markup = 15%.
markdown = $80 – $48.
markdown = $32.
KEY CONCEPT
You can solve markup and markdown problems using the percent equation.

Do You Understand?
Question 1.
Essential Question How are the concepts of markup and markdown related to the percent equation?
Answer:
markup and markdown are proportional to each other.
Explanation:
In the above-given question,
given that,
markup = percent markup x original value.
markdown = percent markdown x original value.
markup = new value is greater than the original value.
markdown = new value is less than the original value.
Question 2.
Reasoning What does the amount of the markup or markdown represent in the percent equation?
Answer:
The amount of the markup or markdown is proportional to each other.
Explanation:
In the above-given question,
given that,
markup = percent markup x original value.
markdown = percent markdown x original value.
so the amount of the markup or markdown is proportional to each other.
Question 3.
Generalize When an item is marked up by a certain percent and then marked down by the same percent, is the sale price equal to the price before the markup and markdown?
Answer:
markup = percent markup x original value.
markdown = percent markdown x original value.
Explanation:
In the above-given question,
given that,
When an item is marked up by a certain percent and then marked down by the same percent.
markup = percent markup x original value.
markdown = percent markdown x original value.
Do You Know How?
Question 4.
An item costs $4 before tax and $4.32 after sales tax. What is the sales tax rate?
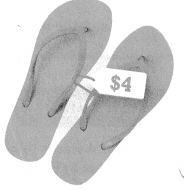
Answer:
The sales tax rate = $8.32.
Explanation:
In the above-given question,
given that,
An item costs $4 before tax and $4.32 after sales tax.
$4 + $4.32.
$8.32.
so the sales tax rate = $8.32.
Question 5.
Sheila buys two concert tickets from her friend. She pays $90 for the two tickets. She looks at the tickets and sees that each ticket has a face value of $52.50.
a. How much of a markdown did her friend give Sheila? Explain how you know.
Answer:
The percent markdown = $1.174.
Explanation:
In the above-given question,
given that,
Sheila buys two concert tickets from her friend. She pays $90 for the two tickets.
She looks at the tickets and sees that each ticket has a face value of $52.50.
markdown = percent markdown x original value.
$52.50 = percent markdown x $90.
percent markdown = $90/$52.50.
percent markdown = $1.714.
b. What was the percent markdown, rounded to the nearest whole percent?
Answer:
The percent markdown rounded to the nearest whole percent = $2.
Explanation:
In the above-given question,
given that,
Sheila buys two concert tickets from her friend. She pays $90 for the two tickets.
She looks at the tickets and sees that each ticket has a face value of $52.50.
markdown = percent markdown x original value.
$52.50 = percent markdown x $90.
percent markdown = $90/$52.50.
percent markdown = $1.714.
$2.
Question 6.
Find the sale prices.
a. $4,200 with a 35% markdown
Answer:
The sale price = $1470.
Explanation:
In the above-given question,
given that,
the sales price = percent markdown x original value.
sales price = 35% x $4200.
sales price = 0.35 x $4200.
sales price = $1470.
b. $5,000 with a 44% markdown
Answer:
The sale price = $2200.
Explanation:
In the above-given question,
given that,
the sales price = percent markdown x original value.
sales price = 44% x $5000.
sales price = 0.44 x $5000.
sales price = $2200.
Practice & Problem Solving
Leveled Practice In 7-8, fill in the boxes to solve.
Question 7.
A $300 suit is marked down by 20%. Find the sale price rounded to the nearest dollar.
markdown = percent markdown • original price
markdown = $_________
original price – markdown = sale price
$ _______ – $ ______
sale price = $ ________
Answer:
The sale price = $300.
Explanation:
In the above-given question,
given that,
A $300 suit is marked down by 20%.
sale price = original price – markdown.
sale price = $300 – 20%.
sale price = $300 – 0.2.
sale price = $299.8.
Question 8.
The selling price of an item is $650 marked up from the wholesale cost of $450. Find the percent markup from wholesale cost to selling price.
selling price – markup = wholesale cost
$ _______ – $ ______ = $ _______
markup = percent markup × wholesale cost
_______ = _______ × _______
The percent markup is about ________.
Answer:
The markup = $250.
Explanation:
In the above-given question,
given that,
The selling price of an item is $650 marked up from the wholesale cost of $450.
wholesale cost = selling price – markup.
$450 = $650 – markup.
markup = $250.
Question 9.
Karen purchased the DVD player shown in the sign on the right. Find the percent markdown rounded to the nearest percent.

Answer:
The markdown = 27,048.143.
Explanation:
In the above-given question,
given that,
Karen purchased the DVD player shown in the sign on the right.
markdown = percent markdown x original value.
markdown = $175.90 x $153.77.
markdown = 27,048.143.
Question 10.
A store manager instructs his employees to mark up all items by 30%. A store clerk puts a price tag of $30 on an item that the store bought for $27. As an employee, you notice that this selling price is incorrect.
a. Find the correct selling price. Round to the nearest dollar.
Answer:
The correct selling price is $3.
Explanation:
In the above-given question,
given that,
A store manager instructs his employees to mark up all items by 30%.
A store clerk puts a price tag of $30 on an item that the store-bought for $27.
selling price = original price – mark up.
selling price = $30 – $27.
selling price = $3.
so the correct selling price = $3.
b. What was the clerk’s likely error?
Answer:
The clerk’s likely error is he said his employees to mark up all items by 30%.
Explanation:
In the above-given question,
given that,
A store clerk puts a price tag of $30 on an item that the store-bought for $27.
selling price = original price – mark up.
selling price = $30 – $27.
selling price = $3.
so the correct selling price = $3.
Question 11.
Nate has $50 to spend at the grocery store. He fills his shopping cart with items totaling $46. At checkout he will have to pay 6% sales tax on all items in the cart. Does he have enough money to buy everything in his cart? Explain.
Answer:
Enough money to buy everything in his cart = $96.
Explanation:
In the above-given question,
given that,
Nate has $50 to spend at the grocery store.
He fills his shopping cart with items totaling $46.
$50 + $46.
$96.
enough money to buy everything in his cart = $96.
Question 12.
A department store buys 300 shirts at a cost of $1,800 and sells them for $10 each. Find the percent markup rounded to the nearest percent.
Answer:
The percent markup = $180.
Explanation:
In the above-given question,
given that,
A department store buys 300 shirts at a cost of $1,800 and sells them for $10 each.
markup = percent markup x original price.
$10 = p x $1800.
p = $180.
so the percent markup rounded to the nearest percent = $180.
Question 13.
Make Sense and Persevere A computer store buys a computer system at a cost of $465.60. The selling price was first at $776, but then the store advertised a 30% markdown on the system.
a. Find the current sale price. Round to the nearest cent if necessary.
Answer:
The sales price nearest cent = $310.
Explanation:
In the above-given question,
given that,
A computer store buys a computer system at a cost of $465.60.
The selling price was first at $776, but then the store advertised a 30% markdown on the system.
sales price = original price – markdown.
sales price = $465.60 – $776.
sales price = 310.4.
so the sales price nearest cent = $310.
b. Members of the store’s loyalty club get an additional 10% off their computer purchases. How much do club members pay for the computer with their discount?
Answer:
Explanation:
In the above-given question,
given that,
Members of the store’s loyalty club get an additional 10% off their computer purchases.
Question 14.
Higher Order Thinking A sporting goods store manager was selling a kayak set for a certain price. The manager offered the markdowns shown on the right, making the one-day sale price of the kayak set $328. Find the original selling price of the kayak set.

Answer:
The selling price = $312.2.
Explanation:
In the above-given question,
given that,
A sporting goods store manager was selling a kayak set for a certain price.
The manager offered the markdowns shown on the right, making the one-day sale price of the kayak set $328.
original selling price = markdown x 40%.
selling price = $328 x 0.4.
selling price = $131.2.
Assessment Practice
Question 15.
Eliza cannot decide which of two bicycles to buy. The original price of each is $380. The first is marked down by 50%. The second is marked down by 30% with an additional 20% off. Which bicycle should Eliza buy if the bicycles are the same except for the selling price? Explain your answer.
Answer:
The selling price = 0.16.
Explanation:
In the above-given question,
given that,
Eliza cannot decide which of two bicycles to buy.
The original price of each is $380.
The first is marked down by 50%.
The second is marked down by 30% with an additional 20% off.
original selling price = markdown x 20%.
selling price = 80% x 0.2.
selling price = 0.16.
Question 16.
A shoe store uses a 50% markup for all of the shoes it sells. The store also charges a 10% sales tax on all purchases. What would be the purchase price, including sales tax, of a pair of shoes that has a wholesale cost of $57?
Answer:
The purchase price, including sales tax, of a pair of shoes that has a wholesale cost = $2.28.
Explanation:
In the above-given question,
given that,
A shoe store uses a 50% markup for all of the shoes it sells.
The store also charges a 10% sales tax on all purchases.
wholesale cost = 40% x $57.
wholesale cost = 0.04 x 57.
wholesale cost = $2.28.
Lesson 3.6 Solve Simple Interest Problems
Explore It!
Gerard compares the offers at two different banks to decide where he should open a savings account.
I can… apply percent reasoning to solve simple interest problems.

A. Draw a representation to show how much would be in the first savings account if Gerard’s initial deposit were d dollars.
Answer:
B. Draw a representation to show how much would be in the second savings account if Gerard’s initial deposit were d dollars.
Answer:
C. Use the two representations you drew to explain how the offers at the two banks are similar and how they are different.
Answer:
Focus on math practices
Construct Arguments Gerard’s first deposit is $500. Which bank should he choose? Explain.
Essential Question
How does simple interest show proportional reasoning and relate to the percent equation?
Try It!
Victoria has another account at the bank that pays 2\(\frac{1}{2}\)% simple interest. How much interest will she earn in 8 years on an initial deposit of $250 assuming she neither adds to nor withdraws from the account?
2\(\frac{1}{2}\)% interest expressed as a decimal is ________.
Interest after 1 year: s = _______ • $ _______
= $ _______
Interest after 8 years: $ ______ • _______
= $ ______
Victoria will earn $ _______ in interest over 8 years.
Answer:
The victoria will earn $2000 in 8 years.
Explanation:
In the above-given question,
given that,
Victoria has another account at the bank that pays 2\(\frac{1}{2}\)% simple interest.
Interest after 1 year = 1 x 250.
Interest after 8 years = 8 x 250.
2000.
so victoria will earn $2000 in 8 years.
Convince Me! Would the interest for the second year be the same if it were calculated on the total after the first year? Why or why not?
Try It!
Another company will lend Maya’s older sister $4,000. Every month, she will pay $11.88 in interest. What is the interest rate, rounded to the nearest tenth of a percent, for 1 year?
Answer:
The interest rate rounded to the nearest tenth of a percent = $3857.44.
Explanation:
In the above-given question,
given that,
Another company will lend Maya’s older sister $4,000.
Every month, she will pay $11.88 in interest.
1 year = 12 months.
$11.88 x 12 = $142.56.
4000 – $142.56 = 3857.44.
so the interest rate rounded to the nearest tenth of a percent = $3857.44.
Try It!
Katelyn’s older brother borrowed money for school. He took out a loan that charges 6% simple interest. He will end up paying $720 in interest after 6 years. How much did Katelyn’s brother borrow for school?
Answer:
Katelyn’s brother borrows for school = $120.
Explanation:
In the above-given question,
given that,
Katelyn’s older brother borrowed money for school.
He took out a loan that charges 6% simple interest.
He will end up paying $720 in interest after 6 years.
$720/6 = 120.
so Katelyn’s brother borrows for school = $120.
KEY CONCEPT
Simple interest represents a proportional relationship between the yearly interest and the principal, or initial amount. The ratio of yearly interest to principal is the interest rate.
Do You Understand?
Question 1.
Essential Question How does simple interest show proportional reasoning and relate to the percent equation?
Answer:
Simple interest represents a proportional relationship between the yearly interest and the principal or initial amount.
Explanation:
In the above-given question,
given that,
Simple interest represents a proportional relationship between the yearly interest and the principal or initial amount.
the ratio of yearly interest to principal to the interest rate.
Question 2.
Reasoning If the interest earned on an account after 2 years is $15, how much would it be after 10 years? Why?
Answer:
The interest earned on an account after 10 years = $60.
Explanation:
In the above-given question,
given that,
If the interest earned on an account after 2 years is $15.
2 years = $15.
10 years = $15 x $5.
10 years = $60.
so the interest earned on an account after 10 years = $60.
Question 3.
Be Precise Angelina is deciding which bank would give her the best simple interest rate on a $300 deposit. One bank says that she will have $320 in her account if she leaves the principal for 2 years. Is this enough information for Angelina to find the interest rate? Explain.
Answer:
Yes, it is enough information for Angelina to find the interest rate.
Explanation:
In the above-given question,
given that,
Angelina is deciding which bank would give her the best simple interest rate on a $300 deposit.
One bank says that she will have $320 in her account if she leaves the principal for 2 years.
2 years = 24 months.
for 1 month = 1 rs.
do this is enough information.
Do You Know How?
Question 4.
Find the missing value in each row. Use the percent equation.
Answer:
$15.
4 years.
$50.
1%.
Explanation:
In the above-given question,
given that,
100 x 5/100 x 3 = $15.
$500 x 4/100 x 4 = $20.
$50 x 10/100 x 7 = $35.
$200 x 1/100 x 2 = $6.
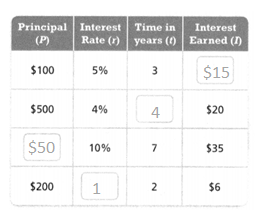
Question 5.
Annika’s older cousin borrowed $800 to repair her car. She will pay off the loan after 2 years by paying back the principal plus 4.5% simple interest for each year.
a. How much will she pay in interest? Show your work.
Answer:
She will pay = $72.
Explanation:
In the above-given question,
given that,
Annika’s older cousin borrowed $800 to repair her car.
She will pay off the loan after 2 years by paying back the principal plus 4.5% simple interest for each year.
800 x 2 x 4.5%.
8 x 2 x 4.5.
$72.
so she will pay = $72.
b. How much will she pay back altogether?
Answer:
She will pay back = $72.
Explanation:
In the above-given question,
given that,
Annika’s older cousin borrowed $800 to repair her car.
She will pay off the loan after 2 years by paying back the principal plus 4.5% simple interest for each year.
800 x 2 x 4.5%.
8 x 2 x 4.5.
$72.
so she will pay back = $72.
Question 6.
J.D. opened a savings account with $425. After 2 years, the total interest he earned was $10.20. What was the annual interest rate?
Answer:
The annual interest rate = $870.4.
Explanation:
In the above-given question,
given that,
J.D. opened a savings account with $425.
After 2 years, the total interest he earned was $10.20.
$10.20 + $425 = $435.20.
$435.20 x 2 = $870.4.
Practice & Problem Solving
Leveled Practice In 7-8, fill in the boxes to solve.
Question 7.
Edward deposited $6,000 into a savings account 4 years ago. The simple interest rate is 3%. How much money did Edward earn in interest?
Interest = $ ______ • ______ • ______ years
Edward earned $ _______ in interest
Answer:
Edward earned = $720.
Explanation:
In the above-given question,
given that,
Edward deposited $6,000 into a savings account 4 years ago.
The simple interest rate is 3%.
interest = $6000 x 4 x 3/100.
interest = $60 x 4 x 3.
interest = $720.
so Edward earned = $720.
Question 8.
The interest on $2,000 for 2 years is $320. What is the simple interest rate?
$ ______ = $2,000 • r • ______
$ _____ = $ _____ • r
______ = r
_______% = r
Answer:
The simple interest rate = 8%.
Explanation:
In the above-given question,
given that,
The interest on $2,000 for 2 years is $320.
$320 = $2000 x r x 2.
$320 x 2 = $640.
$640 x $2000 = 8.
Question 9.
Suppose you deposited $100 in a savings account 4 years ago with a simple interest rate of 2.2%. The interest that you earned in those 4 years is $8.80. Which of the following is true? Select all that apply.
☐ The interest rate is 0.022.
☐ The principal was $100.
☐ The interest earned is $4.
☐ The account was opened 8 years and 8 months ago
Answer:
Option B, C, and D are correct.
Explanation:
In the above-given question,
given that,
Suppose you deposited $100 in a savings account 4 years ago with a simple interest rate of 2.2%.
The interest that you earned in those 4 years is $8.80.
the principal was $100.
the interest earned is $4.
the account was opened 8 years and 8 months ago.
Question 10.
A new bank customer with $3,000 wants to open a money market account. The bank is offering a simple interest rate of 1.1%.
a. How much interest will the customer earn in 20 years?
Answer:
The interest will the customer earn in 20 years = $660.
Explanation:
In the above-given question,
given that,
A new bank customer with $3,000 wants to open a money market account.
The bank is offering a simple interest rate of 1.1%.
3000 x 11/1000 x 20.
60 x 11 = 660.
so the interest will the customer earn in 20 years = 660.
b. What will be the account balance after 20 years?
Answer:
The interest will the customer earn in 20 years = $660.
Explanation:
In the above-given question,
given that,
A new bank customer with $3,000 wants to open a money market account.
The bank is offering a simple interest rate of 1.1%.
3000 x 11/1000 x 20.
60 x 11 = 660.
so the interest will the customer earn in 20 years = 660.
Question 11.
Boden’s account has a principal of $500 and a simple interest rate of 3.3%. Complete the double number line. How much money will be in the account after 4 years, assuming Boden does not add or take out any money?
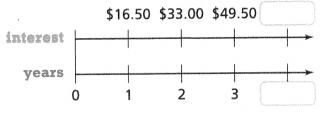
Answer:
The money will be in the account after 4 years = $66.
Explanation:
In the above-given question,
given that,
Boden’s account has a principal of $500 and a simple interest rate of 3.3%.
$500 x 4 x 3.3.
500 x 4 x 33/1000.
20 x 3.3 = $66.
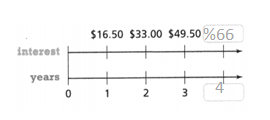
Question 12.
Critique Reasoning Monica deposits $100 into a savings account that pays a simple interest rate of 3.4%. Paul deposits $200 into a savings account that pays a simple interest rate of 2.2%. Monica says that she will earn more interest in one year because her interest rate is higher. Do you agree? Justify your response.
Answer:
Monica says that she will earn more interest in one year because her interest is higher.
Explanation:
In the above-given question,
given that,
Monica deposits $100 into a savings account that pays a simple interest rate of 3.4%.
Paul deposits $200 into a savings account that pays a simple interest rate of 2.2%.
100 x 3.4 =
34.
200 x 2.2 = 8.8.
Question 13.
Construct Argument Tommy earned $76.00 in interest after 5 years on a principal of $400. Jane earned $82.00 in interest after 2 years on a principal of $1,000. Which bank would you rather use, Tommy’s or Jane’s? Why?
Answer:
I will use Jane’s bank.
Explanation:
In the above-given question,
given that,
Tommy earned $76.00 in interest after 5 years on a principal of $400.
Jane earned $82.00 in interest after 2 years on a principal of $1,000.
400 x 5 x $76 = $152000.
1000 x 82 x 2 = $164000.
Jane’s bank will get the higher principal.
Question 14.
Reasoning A bank manager wants to encourage new customers to open accounts with initial deposits of at least $3,000. He has posters made for the promotion.

a. Under the new promotion, what is the minimum amount of interest a new account would make in one year if there were no withdrawls from the account?
Answer:
There were no withdrawals from the account = $144.
Explanation:
In the above-given question,
given that,
A bank manager wants to encourage new customers to open accounts with initial deposits of at least $3,000.
simple interest of 4.8%.
4.8 x 1 x 3000.
3000 x 48/1000 x 1.
$144.
b. The manager wants to add the sentence, “Open an account with $3,000 and earn at least $120 interest each year!” to the poster. Do you agree? Explain.
Answer:
Yes, the sentence was correct.
Explanation:
In the above-given question,
given that,
The manager wants to add the sentence, “Open an account with $3,000 and earn at least $120 interest each year!.
4.8 x 1 x 3000.
3000 x 48/1000 x 1.
$144.
so 144 is greater than $120.
the sentence was correct.
Question 15.
Suppose you deposit $100 in Account A with a simple interest rate of 3.4%, and $300 in Account B with a simple interest rate of 1.8%. One year later, you get a bank statement that shows the interest for Account A is $3.40 and the interest for Account B is $540.00.
a. Which account statement is incorrect?
Answer:
Yes, the account B statement is incorrect.
Explanation:
In the above-given question,
given that,
Suppose you deposit $100 in Account A with a simple interest rate of 3.4%, and $300 in Account B with a simple interest rate of 1.8%.
One year later, you get a bank statement that shows the interest for Account A is $3.40 and the interest for Account B is $540.00.
3.4 x 100.
34/1000 x 100.
3.4 x 1.
3.4.
1.8% x 300.
18/1000 x 300.
1.8 x 3.
5.4.
so the bank statement is incorrect for Account B.
b. What may have been the bank’s error?
Answer:
The error is account B.
Explanation:
In the above-given question,
given that,
Suppose you deposit $100 in Account A with a simple interest rate of 3.4%, and $300 in Account B with a simple interest rate of 1.8%.
One year later, you get a bank statement that shows the interest for Account A is $3.40 and the interest for Account B is $540.00.
3.4 x 100.
34/1000 x 100.
3.4 x 1.
3.4.
1.8% x 300.
18/1000 x 300.
1.8 x 3.
5.4.
Question 16.
Higher Order Thinking You have two different savings accounts. For Account A, the interest earned after 18 months is $12.00. For Account B, the interest earned after 27 months is $27.00.
a. If the interest rate is 3.2% for Account A, how much is the principal?
Answer:
The principle is $6.912.
Explanation:
In the above-given question,
given that,
You have two different savings accounts.
For Account A, the interest earned after 18 months is $12.00.
For Account B, the interest earned after 27 months is $27.00.
$12 x 18 x 3.2%.
$12 x 18 x 0.032.
$12 x 0.576.
$6.912.
b. If the interest rate is 2.4% for Account B, how much is the principal?
Answer:
The principle is $17.496.
Explanation:
In the above-given question,
given that,
You have two different savings accounts.
For Account A, the interest earned after 18 months is $12.00.
For Account B, the interest earned after 27 months is $27.00.
27 x $27 x 0.024.
$27 x 0.648.
17.496.
c. Which account earned you the most interest in the first year? Explain.
Answer:
Account B has earned the most interest in the first year.
Explanation:
In the above-given question,
given that,
You have two different savings accounts.
For Account A, the interest earned after 18 months is $12.00.
For Account B, the interest earned after 27 months is $27.00.
27 x $27 x 0.024.
$27 x 0.648.
17.496.
Assessment Practice
Question 17.
A certificate of deposit with principal $150 earns 4% annual interest for 2 years. Select all the options that would earn the same amount of interest.
☐ $300 at 2% for 2 years
☐ $150 at 6% for 18 months
☐ $400 at 3% for 1 year
☐ $100 at 1% for 8 years
☐ $50 at 48% for 6 months
Answer:
Option A and option C are correct.
Explanation:
In the above-given given question,
given that,
A certificate of deposit with a principal of $150 earns 4% annual interest for 2 years.
$150 x 4% x 2.
$150 x 4/100 x 2.
$15 x 0.4 x 2.
$12.
so option A and option C are correct.
Question 18.
Dakota earned $15.75 in interest in Account A and $28.00 in interest in Account B after 21 months. If the simple interest rate is for 3.0% for Account A and 4.0% for Account B, which account had the greater principal? Explain.
Answer:
Account B had the greater principal.
Explanation:
In the above-given question,
given that,
Dakota earned $15.75 in interest in Account A and $28.00 in interest in Account B after 21 months.
If the simple interest rate is 3.0% for Account A and 4.0% for Account B, which account had the greater principal.
$15.75 x 3% x 21.
15.75 x 0.003 x 21.
0.99225.
$28 x 21 x 4%.
$28 x 21 x 0.04.
$23.52.
so account B had the greater principal.
Topic 3 Review
Topic Essential Question
How can percents show proportional relationships between quantities and be used to solve problems?
Vocabulary Review
Complete each definition and then provide an example of each word.

Answer:
1: Markup simple interest.
2: Percent change.
3: Markup principal.
4: Vocabulary.
Explanation:
In the above-given question,
given that,
the markup simple interest is the decrease from the original price of an item to its sale price.
the accuracy of a measured or estimated value compared to its actual value is described as the percent change.
an initial amount of money that is deposited in an account is called the markup principal.
the vocabulary describes how much a quantity has changed relative to its original amount.
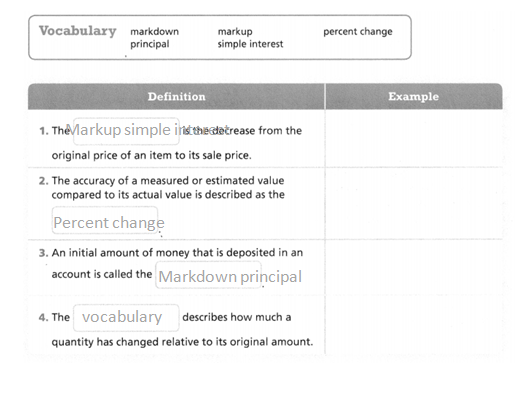
Use Vocabulary in Writing
Birute deposits $500 in a savings account with a simple interest rate of 1.3%. How could you use this information to find the interest she would earn in 4 years and determine the percent change in her savings account?
Answer:
The percent change in her savings account.
Explanation:
In the above-given question,
given that,
Birute deposits $500 in savings account with a simple interest rate of 1.3%
How could you use this information to find the interest she would earn in 4 years and determine the percent change.
$500 x 1.3% x 4.
$500 x 13/1000 x 4.
5 x 1.3 x 4.
26.
so the percent change in her savings account.
Concepts and Skills Review
Lesson 3.1 Analyze Percents of Numbers
Quick Review
You can use equivalent ratios to find the percent of a number. Remember that a percent is a ratio that relates a number to 100.
Example
Find 57% of 690.
\(\frac{57}{100}=\frac{x}{690}\)
\(\frac{57}{100} \cdot 690=\frac{x}{690} \cdot 690\)
393.3 = x
Practice
Question 1.
Find 0.8% of 1,046.
Answer:
8.368.
Explanation:
In the above-given question,
given that,
0.8% of 1046.
0.8/100 x 1046.
0.008 x 1046.
8.368.
Question 2.
Find 160% of 98.
Answer:
156.8.
Explanation:
In the above-given question,
given that,
160% of 98.
160/100 x 98.
1.6 x 98.
156.8.
Question 3.
A company charges a shipping fee that is 4.5% of the purchase price for all items it ships. What is the fee to ship an item that costs $56?
Answer:
The fee to ship an item that costs = $2.52.
Explanation:
In the above-given question,
given that,
company charges a shipping fee that is 4.5% of the purchase price for all items it ships.
$56 x 4.5%.
56 x 45/1000.
$56 x 0.045.
$2.52.
Lesson 3.2 Connect Percent and Proportion
Quick Review
You can use proportions to solve different types of percent problems. There are three values in a percent problem–the percent, the part, and the whole. If you know two of these values, you can set up a proportion to find the third value.
Example
What percent of 19 is 4.75?
The whole is 19 and the part is 4.75. Write a proportion, and solve for the percent, p.
\(\frac{\text { part }}{\text { whole }}=\frac{p}{100}\)
\(\frac{4.75}{19}=\frac{p}{100}\)
\(\frac{4.75}{19} \cdot 100=\frac{p}{100} \cdot 100\)
25 = p
So, 4.75 is 25% of 19.
Practice
Question 1.
24.94 is 29% of what number?
Answer:
The number is 7.3.
Explanation:
In the above-given question,
given that,
24.94 is 29% of what number.
24.94 / p = 29/100.
p = 0.29 x 24.94.
p = 7.3.
Question 2.
On Thursday, a restaurant serves iced tea to 35 of its 140 customers. What percent of the customers order iced tea?
Answer:
The percent of the customers who order iced tea = 25%.
Explanation:
In the above-given question,
given that,
On Thursday, a restaurant serves iced tea to 35 of its 140 customers.
35/140 = p/100.
0.25 x 100 = p.
p = 25%.
Question 3.
Liam puts $40 in savings in March and 175% of this amount in savings in April. How much does Liam put in savings in April?
Answer:
whole = 100
4,75 = 100 4,175. 100 = 70100
Lesson 3.3 Represent and Use the Percent Equation
Quick Review
You can use the percent equation to solve percent problems.
part = percent • whole
Substitute two of the three values to solve for the unknown value.
Example
Michael earns a 6% commission on each house he sells. If he sells a house for $180,000, how much does he earn in commission, c?
c = 0.06. 180,000
c = 10,800
Michael earns $10,800 in commission.
Practice
Question 1.
Sharon paid $78 sales tax on a new camera. If the sales tax rate is 6.5%, what was the cost of the camera?
Answer:
Question 2.
There are 45 students who play a woodwind instrument in the school band. Of these, 18 play the saxophone. What percent of these students play the saxophone?
Answer:
Lesson 3.4 Solve Percent Change and Percent Error Problems
Quick Review
A percent change can be an increase or a decrease. You can use an equation to find a percent change.
change = percent change • original amount
A percent error is always a nonnegative value. You can use an equation to find a percent error.
difference = percent error • actual
Example
Juan’s puppy weighed 16 pounds at the age of 2 months. The puppy weighed 60 pounds at the age of 8 months. What is the percent change in the puppy’s weight?
change in pounds = 60 – 16 = 44
44 = P • 16
\(\frac{44}{16}\) = P
2.75 = P
The puppy’s weight increased by 275%.
Practice
Question 1.
In 2014, the attendance at Jefferson School’s Fall Festival was 650. In 2015, the attendance was 575. What was the percent change in attendance from 2014 to 2015? Round to the nearest whole percent.
Answer:
Question 2.
Melissa estimated that she would read 250 pages last week. She read 290 pages. What is the percent error of Melissa’s estimate? Round to the nearest whole percent.
Answer:
Lesson 3.5 Solve Markup and Markdown Problems
Quick Review
You can use the percent equation to solve markup and markdown problems.
markup = percent markup • cost
markdown = percent markdown • selling price
Example
Bree buys a purse for $90. She sells it at her store for $135. What is the percent markup on the purse?
markup = $135 – $90 = $45
45 = P • 90
45 = P
0.5 =P The decimal 0.5 is equivalent to 50%.
The percent markup on the purse is 50%.
Practice
Question 1.
Hank buys a used car for $7,200 and plans to sell it on his used car lot. What is the price of the car after a markup of 15%?
Answer:
The price of the car after a markup of 15% =
Explanation:
In the above-given question,
given that,
Hank buys a used car for $7,200 and plans to sell it on his used car lot.
part = percent x whole.
part = 15 x 7200.
part = 15/100 x 7200.
part = 1080.
so the price of the car after a markup of 15% = 1080.
Question 2.
Nya wants to buy a sweater that had an original price of $55. The sweater is now discounted 20% and the sales tax rate is 5.5%. How much will Nya pay for the sweater?
Answer:
Nya pays for the sweater.
Explanation:
In the above-given question,
given that,
Nya wants to buy a sweater that had an original price of $55.
The sweater is now discounted 20% and the sales tax rate is 5.5%.
$55 x 20/100 x 5.5%.
55 x 0.2 x 55/1000.
55 x 0.2 x 0.055.
0.605.
so Nya pays for the sweater = 0.605.
Lesson 3.6 Solve Simple Interest Problems
Quick Review
You consider four quantities when solving problems involving simple interest.
initial amount, or principal, p
interest rate, r
time, t amount of simple interest, I
Example
Yuni loaned $400 to her brother. He will repay the loan by paying 2.5% simple interest for 3 years. How much will he pay in interest?
I = 400 • 0.025 • 3 = $30
He will pay $30 in interest.
Practice
Question 1.
Ethan put $700 into a Certificate of Deposit (CD) account that earns 1.8% interest each year. What will the interest of the CD account be after 6 years?
Answer:
The interest of the CD account is after 6 years = $75.6.
Explanation:
In the above-given question,
given that,
Ethan put $700 into a Certificate of Deposit (CD) account that earns 1.8% interest each year.
$700 x 1.8% x 6.
$700 x 1.8/100 x 6.
$700 x 0.018 x 6.
$75.6.
Question 2.
Kelly opened a bank account that earns 1.2% simple interest each year. After 7 years, Kelly will earn $126 in interest. How much did Kelly deposit when she opened the account?
Answer:
The kelly deposit when she opened the account = $10.584.
Explanation:
In the above-given question,
given that,
Kelly opened a bank account that earns 1.2% simple interest each year.
After 7 years, Kelly will earn $126 in interest.
$126 x 7 x 1.2%.
$126 x 7 x 1.2/100.
$126 x 7 x 0.012.
$126 x 0.084.
$10.584.
so the kelly deposit when she opened the account = $10.584.
Topic 3 Fluency Practice
Riddle Rearranging
Find the value of x in each unit rate. Then arrange the answers in order from least to greatest. The letters will spell out the answer to the riddle below.
I can… find unit rates with ratios of fractions.

Answer:
0.75 xc = 0.3h, 0.4 min = 0.6 ml, and 0.25 mi = 0.625 h.
Explanation:
In the above-given question,
given that,
3/4c/1/3h = xc/1h.
0.75c/0.3h = xc/h.
0.75c x xc = 0.3h x h.
0.75xc = 0.3h.
3/5ml/2/5 min = x ml /1min.
0.6ml/0.4 min = x ml / 1 min.
0.4 x 1 min = x ml x 0.6 ml.
0.4 min = 0.6ml.
1/4mi/5/8 h = x mi / 1h.
0.25 mi/ 0.625 h = x mi / 1h.
x mi /1 h = 0.25 mi/0.625 h.