Practice with the help of enVision Math Common Core Grade 8 Answer Key Topic 1 Real Numbers regularly and improve your accuracy in solving questions.
enVision Math Common Core 8th Grade Answers Key Topic 1 Real Numbers
enVision STEM Project
Did You Know?
Natural resources are materials that occur in nature, such as water, fossil fuels, wood, and minerals. Natural resources not only meet basic human needs, but also support industry and economy.

Minerals are used in the manufacturing of all types of common objects, including cell phones, computers, light bulbs, and medicines.
Water, oil, and forests are some of the natural resources that are in danger of someday being depleted.
70% of available fresh water is used in agriculture…

…and 10% for human consumption.
Each person in the United States needs over 48,000 pounds of minerals each year.
About 18 million acres of forest are lost to deforestation each year.

Solar power, wind power and other renewable energy sources are helping to lessen the dependency on oil and fossil fuels.

Fossil fuels are expected to supply almost 80% of world energy use through 2040.

Your Task: Going, Going, Gone?
Natural resource depletion is an important issue facing the world. Suppose a natural resource is being depleted at the rate of 1.333% per year. If there were 300 million tons of this resource in 2005, and there are no new discoveries, how much will be left in the year 2045? You and your classmates will explore the depletion of this resource over time.

Answer:
It is given that
A natural resource is being depleted at the rate of 1.333% per year and there were 300 million tons of this resource in 2005, and there are no new discoveries
So,
The number of resources left in 2045 = The number of resources present in 2005 – The decrease of the number of resources from 2005 to 2045
So,
The number of resources left in 2045 = 300 million – 1.33% of 300 million × (2045 – 2005)
The number of resources left in 2045 = 300 million – 159.6 million
The number of resources left in 2045 = 140.4 million
Hence, from the above,
We can conclude that the number of resources left in 2045 is: 140.4 million
Topic 1 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box. Write it on the blank.
Question 1.
A(n) ____ is a decimal that ends in repeating zeros.
Answer:
A “Terminating decimal” is a decimal that ends in repeating zeros
Hence, from the above,
We can conclude that the best term from the box for this definition is “Terminating decimal”
Question 2.
A(n) ____ is a decimal in which a digit or digits repeat
Answer:
A “Repeating decimal” is a decimal in which a digit or digits repeat
Hence, from the above,
We can conclude that the best term from the box for this definition is “Repeating decimal”
Question 3.
A(n) ____ is either a counting number, the opposite of a counting number, or zero
Answer:
An “Integer” is either a counting number, the opposite of a counting number, or zero
Hence, from the above,
We can conclude that the best term from the box for this definition is “Integer”
Question 4.
A(n) ___ is a number that can be used to describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.
Answer:
A “Fraction” is a number that can be used to describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.
Hence, from the above,
We can conclude that the best term from the box for this definition is “Fraction”
Terminating and Repeating Decimals
Determine whether each decimal is terminating or repeating.
Question 5.
5.692
Answer:
The given decimal is: 5.692
We know that,
A terminating decimal is usually defined as a decimal number that contains a finite number of digits after the decimal point
Hence, from the above,
We can conclude that the given decimal is a terminating decimal
Question 6.
-0.222222…
Answer:
The given decimal is -0.222222….
We know that,
A repeating decimal or recurring decimal is the decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero
Hence, from the above,
We can conclude that the given decimal is a repeating decimal
Question 7.
7.0001
Answer:
The given decimal is: 7.0001
We know that,
A terminating decimal is usually defined as a decimal number that contains a finite number of digits after the decimal point
Hence, from the above,
We can conclude that the given decimal is a terminating decimal
Question 8.
7.2\(\overline{8}\)
Answer:
The given decimal is: 7.2\(\overline{8}\)
We know that,
A repeating decimal or recurring decimal is the decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero
Hence, from the above,
We can conclude that the given decimal is a repeating decimal
Question 9.
1.\(\overline{178}\)
Answer:
The given decimal is: 1.\(\overline{178}\)
We know that,
A repeating decimal or recurring decimal is the decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero
Hence, from the above,
We can conclude that the given decimal is a repeating decimal
Question 10.
-4.03479
Answer:
The given decimal is: -4.03479
We know that,
A terminating decimal is usually defined as a decimal number that contains a finite number of digits after the decimal point
Hence, from the above,
We can conclude that the given decimal is a terminating decimal
Multiplying Integers
Find each product.
Question 11.
2.2
Answer:
The given expression is: 2 × 2
Hence,
2 × 2 = 4
Question 12.
-5. (-5)
Answer:
The given expression is: -5 × -5
We know that,
– × – = +
Hence,
-5 × -5 = 25
Question 13.
7.7
Answer:
The given expression is: 7 × 7
Hence,
7 × 7 = 49
Question 14.
-6 ∙ (-6) ∙ (-6)
Answer:
The given expression is: -6 × -6 × -6
We know that,
– × – × –
= + × –
= –
Hence,
-6 × -6 × -6
= 36 × -6
= -216
Question 15.
10 ∙ 10 ∙ 10
Answer:
The given expression is: 10 × 10 × 10
Hence,
10 × 10 × 10 = 1,000
Question 16.
-9 ∙ (-9) ∙ (-9)
Answer:
The given expression is: -9 × -9 × -9
We know that,
– × – × –
= + × –
= –
Hence,
-9 × -9 × -9
= 81 × -9
= -729
Simplifying Expressions
Simplify each expression.
Question 17.
(4 ∙ 10) + (5 ∙ 100)
Answer:
The given expression is:
(4 × 10) + (5 × 100)
So,
(4 × 10) + (5 × 100)
= 40 + 500
= 540
Hence, from the above,
We can conclude that the value of the expression is: 540
Question 18.
(2100) + (7.10)
Answer:
The given expression is:
2100 + (7 × 10)
So,
2100 + (7 × 10)
= 2100 + 70
= 2170
Hence, from the above,
We can conclude that the value of the given expression is: 2170
Question 19.
(6 · 100) – (1 · 10)
Answer:
The given expression is:
(6 × 100) – (1 × 10)
So,
(6 × 100) – (1 × 10)
= 600 – 10
= 590
Hence, from the above,
We can conclude that the value of the given expression is: 590
Question 20.
(9 ∙ 1,000) + (4 ∙ 10)
Answer:
The given expression is:
(9 × 1,000) + (4 × 10)
So,
(9 × 1,000) + (4 × 10)
= 9,000 + 40
= 9,040
Hence, from the above,
We can conclude that the value of the given expression is: 9,040
Question 21.
(3 · 1,000) – (2 ∙ 100)
Answer:
The given expression is:
(3 × 1,000) – (2 × 100)
So,
(3 × 1,000) – (2 × 100)
= 3,000 – 200
= 2,800
Hence, from the above,
We can conclude that the value of the given expression is: 2,800
Question 22.
(2 ∙ 10) + (7 · 100)
Answer:
The given expression is:
(2 × 10) + (7 × 100)
So,
(2 × 10) + (7 × 100)
= 20 + 700
= 720
Hence, from the above,
we can conclude that the value of the given expression is: 720
Language Development
Fill in the word map with new terms, definitions, and supporting examples or illustrations.

Topic 1 PICK A PROJECT
PROJECT 1A
Who is your favorite poet, and why?
PROJECT: WRITE A POEM

PROJECT 1B
If you moved to a tiny house, what would you bring with you?
PROJECT: DESIGN A TINY HOUSE

PROJECT 1C
If you could travel anywhere in space, where would you go?
PROJECT: PLAN A TOUR OF THE MILKY WAY

PROJECT 1D
Why do you think people tell stories around a campfire?
PROJECT: TELL A FOLK STORY

Lesson 1.1 Rational Numbers as Decimals
Solve & Discuss It!
Jaylon has a wrench labeled 0.1875 inches and bolts labeled in fractions of an inch. Which size bolt will fit best with the wrench? Explain.

Answer:
It is given that
Jaylon has a wrench labeled 0.1875 inches and bolts labeled in fractions of an inch.
Now,
We know that,
The bolt will be fit in a wrench only when
The size of the bolt (inches) = The size of the wrench (inches)
Now,
The representation of the bolts in the decimal numbers is:
\(\frac{3}{8}\) = 0.375 inches
\(\frac{1}{8}\) = 0.046 inches
\(\frac{3}{16}\) = 0.1875 inches
\(\frac{1}{4}\) = 0.25 inches
Hence, from the above,
We can conclude that the bolt which has the size \(\frac{3}{16}\) inches will fit best with the wrench
Reasoning
How can you write these numbers in the same form?
Answer:
The representation of the sizes of bolts in the decimal form is by using the properties of place values
We know that,
A terminating decimal can be written as a fraction by using properties of place value.
Example:
3.75 = three and seventy-five hundredths or \(\frac{375}{100}\), which is equal to the improper fraction
Focus on math practices
Reasoning Why is it useful to write a rational number as a fraction or as a decimal?
Answer:
Rational numbers are whole numbers, fractions, and decimals – the numbers we use in our daily lives. They can be written as a ratio of two integers. … The definition says that a number is rational if you can write it in the form \(\frac{a}{b}\) where a and b are integers, and b is not zero.
? Essential Question
How can you write repeating decimals as fractions?
Answer:
Because repeating decimals are rational numbers, you can write them in fraction form.
STEP 1
Assign a variable to represent the repeating decimal.
STEP 2
Write an equation: variable = decimal.
STEP 3
Multiply each side of the equation by 10d, where d is the number of repeating digits in the repeating decimal.
STEP 4
Subtract equivalent expressions of the variable and the repeating decimal from each side of the equation.
STEP 5
Solve for the variable. Write an equivalent fraction so that the numerator and denominator are integers, if necessary.
Try It!
In another baseball division, one team had a winning percentage of 0.444…. What fraction of their games did this team win?
The team won their games.
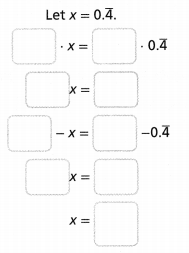
Answer:
It is given that
In another baseball division, one team had a winning percentage of 0.444…
Since only 1 number is repeated,
The repeating decimal can be written as 0.\(\overline{4}\)
Now,
According to the steps of converting a repeating decimal to a fraction (Essential Question),
Step 1:
Let x = 0.\(\overline{4}\)
Step 2:
Multiply with 10 on both sides since only 1 number is repeating
So,
10x = 10 (0.\(\overline{4}\))
10x = 4.\(\overline{4}\)
Step 3:
10x – x = 4.\(\overline{4}\) – 0.\(\overline{4}\)
9x = 4
x = \(\frac{4}{9}\)
Hence, from the above,
We can conclude that the team won \(\frac{4}{9}\) of their games
Convince Me!
How do you know what power of ten to multiply by in the second step at the right?
Answer:
Let x be the repeating portion.
Multiply this equation by a power of 10 to move the repeating digits immediately to the left of the decimal point (in other words, to eliminate any zeros preceding the repeating digits).
Try It!
Write the repeating decimal 0.63333… as a fraction.
Answer:
The given repeating decimal is: 0.6333333
Now,
According to the steps of converting a repeating decimal to a fraction (Essential Question),
Step 1:
Let x = 0.6\(\overline{3}\)
Step 2:
Multiply with 10 on both sides since only 1 number is repeating
So,
10x = 10 (0.6\(\overline{3}\))
10x = 6.\(\overline{3}\)
Step 3:
10x – x = 6.\(\overline{3}\) – 0.6\(\overline{3}\)
9x = 6.33 – 0.63
9x = 5.7
Divide by 9 into both sides
So,
\(\frac{9}{9}\)x = \(\frac{5.7}{9}\)
x = \(\frac{57}{90}\)
Hence, from the above,
We can conclude that the value of the given repeating decimal in the fraction form is: \(\frac{57}{90}\)
Try It!
Write the repeating decimal 4.1363636… as a fraction.
Answer:
The given repeating decimal is 4.1363636…..
Now,
According to the steps of converting a repeating decimal to a fraction (Essential Question),
Step 1:
Let x = 4.1\(\overline{36}\)
Step 2:
Multiply with 100 on both sides since 2 numbers are repeating
So,
100x = 100 (4.1\(\overline{36}\))
100x = 41.\(\overline{36}\)
Step 3:
100x – x = 41.\(\overline{36}\) – 4.1\(\overline{36}\)
99x = 413.636 – 4.136
99x = 409.5
Divide by 99 into both sides
So,
\(\frac{99}{99}\)x = \(\frac{409.5}{99}\)
x = \(\frac{4095}{990}\)
Hence, from the above,
We can conclude that the value of the given repeating decimal in the fraction form is: \(\frac{4095}{990}\)
KEY CONCEPT
Because repeating decimals are rational numbers, you can write them in fraction form.
STEP 1
Assign a variable to represent the repeating decimal.
STEP 2
Write an equation: variable = decimal.
STEP 3
Multiply each side of the equation by 10d, where d is the number of repeating digits in the repeating decimal.
STEP 4
Subtract equivalent expressions of the variable and the repeating decimal from each side of the equation.
STEP 5
Solve for the variable. Write an equivalent fraction so that the numerator and denominator are integers, if necessary.
Do You Understand?
Question 1.
? Essential Question
How can you write repeating decimals as fractions?
Answer:
Because repeating decimals are rational numbers, you can write them in fraction form.
STEP 1
Assign a variable to represent the repeating decimal.
STEP 2
Write an equation: variable = decimal.
STEP 3
Multiply each side of the equation by 10d, where d is the number of repeating digits in the repeating decimal.
STEP 4
Subtract equivalent expressions of the variable and the repeating decimal from each side of the equation.
STEP 5
Solve for the variable. Write an equivalent fraction so that the numerator and denominator are integers, if necessary.
Question 2.
Use Structure Why do you multiply by a power of 10 when writing a repeating decimal as a rational number?
Answer:
The idea is to multiply by some number (10, 100, 1000, etc.) so that when we subtract the original number from the multiple, the repeating part cancels out.
Question 3.
Be Precise How do you decide by which power of 10 to multiply an equation when writing a decimal with repeating digits as a fraction?
Answer:
The idea is to multiply by some number (10, 100, 1000, etc.) so that when we subtract the original number from the multiple, the repeating part cancels out.
Do You Know How?
Question 4.
A survey reported that 63.63% of moviegoers prefer action films. This percent represents a repeating decimal. Write it as a fraction.
Answer:
It is given that
A survey reported that 63.63% of moviegoers prefer action films. This percent represents a repeating decimal
So,
The given repeating decimal is 63.6363…..%
Now,
According to the steps of converting a repeating decimal to a fraction (Essential Question),
Step 1:
Let x = 63.\(\overline{63}\)
Step 2:
Multiply with 100 on both sides since 2 numbers are repeating
So,
100x = 100 (63.\(\overline{63}\))
100x = 6363.\(\overline{63}\)
Step 3:
100x – x = 6363.\(\overline{63}\) – 63.\(\overline{63}\)
99x = 6,300
Divide by 99 into both sides
So,
\(\frac{99}{99}\)x = \(\frac{6,300}{99}\)
x = \(\frac{6,300}{99}\)
Hence, from the above,
We can conclude that the value of the given repeating decimal in the fraction form is: \(\frac{6,300}{99}\)
Question 5.
A student estimates the weight of astronauts on the Moon by multiplying their weight by the decimal 0.16666… What fraction can be used for the same estimation?

Answer:
It is given that
A student estimates the weight of astronauts on the Moon by multiplying their weight by the decimal 0.16666…
Now,

Hence, from the above,
We can conclude that the fraction that can be used for the same estimation is: \(\frac{1}{6}\)
Question 6.
Write 2.3181818… as a mixed number.
Answer:
The given repeating decimal is 2.3181818…
Now,
According to the steps of converting a repeating decimal to a fraction (Essential Question),
Step 1:
Let x = 2.3\(\overline{18}\)
Step 2:
Multiply with 100 on both sides since 2 numbers are repeating
So,
100x = 100 (2.3\(\overline{18}\))
100x = 23.\(\overline{18}\)
Step 3:
100x – x = 23.\(\overline{18}\) – 2.3\(\overline{18}\)
99x = 231.818 – 2.318
99x = 229.5
Divide by 99 into both sides
So,
\(\frac{99}{99}\)x = \(\frac{229.5}{99}\)
x = \(\frac{2295}{990}\)
x = \(\frac{51}{22}\)
So,
The representation of the above fraction in the mixed form is: 2\(\frac{7}{22}\)
Hence, from the above,
We can conclude that the value of the given repeating decimal in the mixed fraction form is: 2\(\frac{7}{22}\)
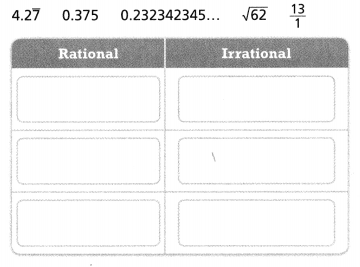
Practice & Problem Solving
Leveled Practice In 7 and 8, write the decimal as a fraction or mixed number.
Question 7.
Write the number 0.21212121… as a fraction.
Let x = ![]()
100x = ![]()
100x – x = ![]() –
– ![]()
99x = ![]()
x = ![]()
So 0.2121… is equal to
Answer:
The given repeating decimal is: 0.212121….
Now,

Hence, from the above,
We can conclude that the value of the repeating decimal in the fraction form is: \(\frac{21}{99}\)
Question 8.
Write 3.7 as a mixed number.
Let x = ![]()
10x = ![]()
9x = ![]()
x = ![]()
So 3.\(\overline{7}\) is equal to ![]()
Answer:
The given repeating decimal is: 3.\(\overline{7}\)
Now,
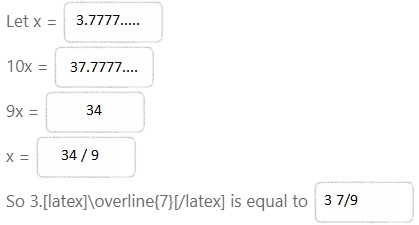
Hence, from the above,
We can conclude that the representation of the given repeating decimal in the mixed fraction form is: 3\(\frac{7}{9}\)
Question 9.
Write the number shown on the scale as a fraction.

Answer
The number that is shown on the scale is: 0.233333
Now,
From the: above number,
We can observe that the number is a repeating decimal
Now,

So,
The simplified form of \(\frac{2.1}{9}\) is: \(\frac{7}{30}\)
Hence, from the above,
We can conclude that the representation of the number that is shown on the scale as a fraction is: \(\frac{7}{30}\)
Question 10.
Tomas asked 15 students whether summer break should be longer. He used his calculator to divide the number of students who said yes by the total number of students. His calculator showed the result as 0.9333…
a. Write this number as a fraction.
Answer:
The given repeating decimal is 0.93333…
Now,

So,
The simplified form of \(\frac{8.4}{9}\) is: \(\frac{14}{15}\)
Hence, from the above,
We can conclude that the representation of the repeating number in the form of the fraction is: \(\frac{14}{15}\)
b. How many students said that summer break should be longer?
Answer:
It is given that
Tomas asked 15 students whether summer break should be longer. He used his calculator to divide the number of students who said yes by the total number of students.
So,
The number of students that said summer break should be longer = \(\frac{The number of students that said yes that summer break is longer}{The total number of students}
Now,
From part (a),
The fraction form of his calculated result from part (a) is: 14 / 15
Hence, from the above,
We can conclude that the number of students that said the summer break should be longer is: 14 students
Question 11.
Write 0.[latex]\overline{87}\) as a fraction.
Answer:
The given repeating decimal is 0.\(\overline{87}\)
Now,

Hence, from the above,
We can conclude that the representation of the repeating decimal in the fraction form in the simplest form is: \(\frac{29}{33}\)
Question 12.
Write 0.\(\overline{8}\) as a fraction.
Answer:
The given repeating decimal is 0.\(\overline{8}\)
Now,

Hence, from the above,
We can conclude that the representation of the given repeating decimal in the fraction form is: \(\frac{8}{9}\)
Question 13.
Write 1.\(\overline{48}\) as a mixed number.
Answer:
The given repeating decimal number is 1.\(\overline{48}\)
Now,
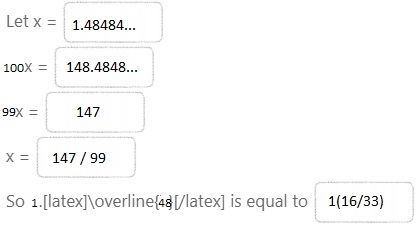
Hence, from the above,
We can conclude that the representation of the given repeating decimal in the mixed fraction form is: 1\(\frac{16}{33}\)
Question 14.
Write 0.\(\overline{6}\) as a fraction.
Answer:
The given repeating decimal is 0.\(\overline{6}\)
Now,

Hence, from the above,
We can conclude that the representation of the given repeating decimal in the fraction form is: \(\frac{2}{3}\)
Question 15.
A manufacturer determines that the cost of making a computer component is $2.161616. Write the cost as a fraction and as a mixed number.

Answer:
It is given that
A manufacturer determines that the cost of making a computer component is $2.161616
So,
The given repeating decimal is 2.161616…
Now,
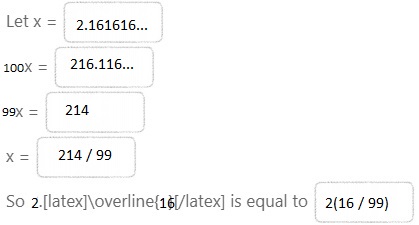
Hence, from the above,
We can conclude that
The cost of a computer component in a fraction form is: \(\frac{214}{99}\)
The cost of a computer component in a mixed fraction form is: 2\(\frac{16}{99}\)
Question 16.
Reasoning When writing a repeating decimal as a fraction, does the number of repeating digits you use matter? Explain.
Answer:
No. Even if the number of different digits in the cycle is 1 or 1 million, the method of finding the fraction is the same
Question 17.
Higher Order Thinking When writing a repeating decimal as a fraction, why does the fraction always have only 9s or 9s and 0s as digits in the denominator?
Answer:
When writing a repeating decimal as a fraction, the fraction always has only 9s or 9s and 0s as digits in the denominator because we are talking here about a geometric series and they are decimals, so the right side i.e., after the decimal point, the digits are in tenths, hundredths and so on
Assessment Practice
Question 18.
Which decimal is equivalent to \(\frac{188}{11}\)?
A. 17.\(\overline{09}\)
B. 17.0\(\overline{09}\)
C. 17.\(\overline{1709}\)
D. 17.\(\overline{1709}\)0
Answer:
The given fraction is: \(\frac{188}{11}\)
So,
The representation of the given fraction in the decimal form is:
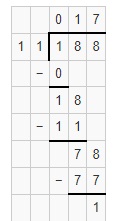
we know that,
\(\frac{1}{11}\) = 0.090909…..
So,
\(\frac{188}{11}\) = 17.090909….
= 17.\(\overline{09}\)
Hence, from the above,
We can conclude that option A matches the representation of the repeating decimal for the given fraction
Question 19.
Choose the repeating decimal that is equal to the fraction on the left.
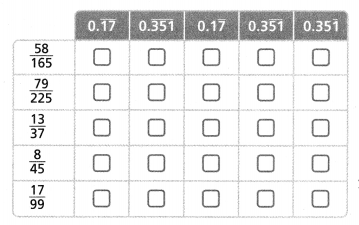
Answer:
Follow the process that is mentioned below to solve the given repeating decimals in the fraction form
Now,
STEP 1
Assign a variable to represent the repeating decimal.
STEP 2
Write an equation: variable = decimal.
STEP 3
Multiply each side of the equation by 10d, where d is the number of repeating digits in the repeating decimal.
STEP 4
Subtract equivalent expressions of the variable and the repeating decimal from each side of the equation.
STEP 5
Solve for the variable. Write an equivalent fraction so that the numerator and denominator are integers, if necessary.
Hence,

Lesson 1.2 Understand Irrational Numbers
Explain It!
Sofia wrote a decimal as a fraction. Her classmate Nora says that her method and answer are not correct. Sofia disagrees and says that this is the method she learned.

A. Construct Arguments Is Nora or Sofia correct? Explain your reasoning.
Answer:
The given number is 0.121121112111112…..
Now,
From the given number,
We can observe that the given decimal is not a repeating decimal because there are other numbers other than the repeating numbers in the given decimal or a terminating decimal because the decimal is not finite
So,
Since the given decimal is not a repeating decimal,
The method that we used to convert the repeating decimal into a fraction is not applicable
Hence, from the above,
We can conclude that Nora is correct
B. Use Structure What is a nonterminating decimal number that can not be written as a fraction.
Answer:
A non-terminating, non-repeating decimal is a decimal number that continues endlessly, with no group of digits repeating endlessly. Decimals of this type cannot be represented as fractions, and as a result, are irrational numbers
Focus on math practices
Construct Arguments is 0.12112111211112… a rational number? Explain.
Answer:
0.12112111211112… can’t be represented in the form of \(\frac{p}{q}\) and it has non terminating non-repeating decimal expansion
Hence, from the above,
We can conclude that 0.12112111211112… is not a rational number
? Essential Question
How is an irrational number different from a rational number?
Answer:
Numbers that can be expressed in \(\frac{a}{b}\) or fraction form are rational numbers where a is an integer and b is a non-zero integer and the irrational numbers are the numbers that cannot be written in \(\frac{a}{b}\) form
Try It!
Classify each number as rational or irrational.

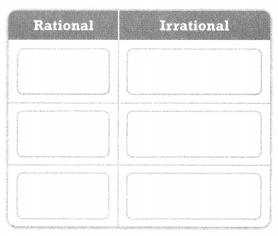
Answer:
The given numbers are:

Now,
We know that,
Numbers that can be expressed in \(\frac{a}{b}\) or fraction form are rational numbers where a is an integer and b is a non-zero integer and the irrational numbers are the numbers that cannot be written in \(\frac{a}{b}\) form
Hence,
The representation of the rational and irrational numbers are:
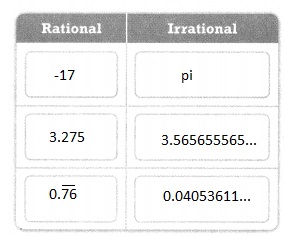
Convince Me!
Construct Arguments Jen classifies the number 4.567 as irrational because it does not repeat. Is Jen correct? Explain.
Answer:
The given decimal is: 4.567
We know that,
A rational number is a number that can be written in the form of \(\frac{a}{b}\)
A terminating decimal has the finite number of digits without repeating and it is also a rational number
So,
We can observe that we can write 4.567 as a rational number
Hence, from the above,
We can conclude that Jen is not correct
Try It!
Classify each number as rational or irrational and explain.
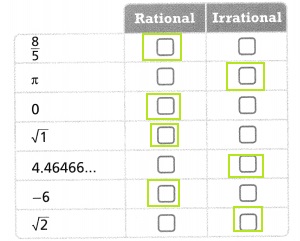
A) \(\frac{2}{3}\)
B) \(\sqrt{25}\)
C) -0.7\(\overline{5}\)
D) \(\sqrt{2}\)
E) 7,548,123
Answer:
The given numbers are:
A) \(\frac{2}{3}\)
B) \(\sqrt{25}\)
C) -0.7\(\overline{5}\)
D) \(\sqrt{2}\)
E) 7,548,123
Now,
We know that,
A “Rational number” is a number that can be written in the form of \(\frac{a}{b}\)
Ex: Terminating decimals, perfect squares, etc
An “Irrational number” is a number that can not be written in the form of \(\frac{a}{b}\)
Ex: Non-terminating decimals
So,
From the given numbers,
Rational numbers ——> A, B, E
Irrational numbers ——> C, D
KEY CONCEPT
Numbers that are not rational are called irrational numbers.
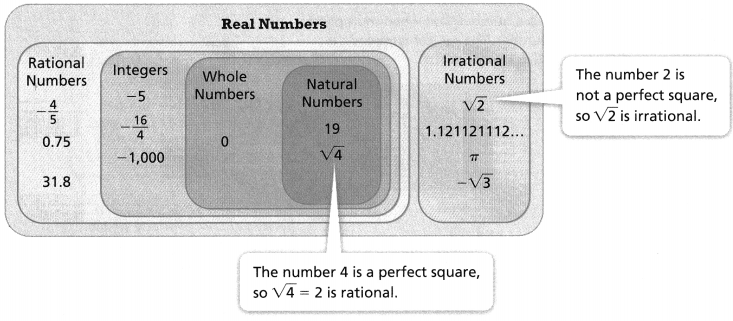
Do You Understand?
Question 1.
? Essential Question How is an irrational number different from a rational number?
Answer:
Numbers that can be expressed in \(\frac{a}{b}\) or fraction form are rational numbers where a is an integer and b is a non-zero integer and the irrational numbers are the numbers that cannot be written in \(\frac{a}{b}\) form
Question 2.
Reasoning How can you tell whether a square root of a whole number is rational or irrational?
Answer:
If the square root of an integer is itself an integer (Ex: √4 = 2), then by definition it is rational – If the square root is not an integer (Ex: √2 = 1.41414…), then it must be irrational. Put another way the only integers for which the square root of an integer can be rational is if is a perfect square – that is where x is an integer
Question 3.
Construct Arguments Could a number ever be both rational and irrational? Explain.
Answer:
No. A rational number is a number that can be expressed as the quotient of two integers. An irrational number is a number that cannot be expressed as a quotient of two integers. So if a number is either rational or irrational, it cannot also be the other.
Do You Know How?
Question 4.
Is the number 65.4349224… rational or irrational? Explain.
Answer:
The given number is 65.4349224…
From the given number,
We can observe that the given number is a non-repeating and non-terminating decimal number
Hence, from the above,
We can conclude that the given number is an irrational number
Question 5.
Is the number \(\sqrt{2,500}\) rational or irrational? Explain.
Answer:
The given number is: \(\sqrt{2,500}\)
We know that,
A perfect square number is a rational number
So,
\(\sqrt{2,500}\) = 50
Hence, from the above,
We can conclude that the given number is a rational number
Question 6.
Classify each number as rational or irrational.
Answer:
We know that,
A “Rational number” is a number that can be written in the form of \(\frac{a}{b}\)
Ex: Perfect squares
An “Irrational number” is a number that can not be written in the form of \(\frac{a}{b}\)
Ex: Non-terminating decimal numbers
Hence,
The representation of the rational and irrational numbers from the given numbers are:

Practice & Problem Solving
Question 7.
Is 5.787787778… a rational or irrational number? Explain.
Answer:
The given number is 5.787787778…
From the given number,
We can observe that the given number is a non-repeating and non-terminating decimal number
Hence, from the above,
We can conclude that the given number is an irrational number
Question 8.
Is \(\sqrt{42}\) rational or irrational? Explain.
Answer:
The given number is \(\sqrt{42}\)
From the given number,
We can observe that the given number is not a perfect square
Hence, from the above,
We can conclude that the given number is an irrational number
Question 9.
A teacher places seven cards, lettered A-G, on a table. Which cards show irrational numbers?

Answer:
The given cards are:

We know that,
An “Irrational number” is a number that can not be written in the form of \(\frac{a}{b}\)
Hence, from the above,
We can conclude that from the given cards,
The irrational numbers are:
A) π
B) 8.25635…,
C) 6.\(\overline{31}\)
Question 10.
Circle the irrational number in the list below.
A) 7.\(\overline{27}\)
B) \(\frac{5}{9}\)
C) \(\sqrt{15}\)
D) \(\sqrt{196}\)
Answer:
The given numbers are:
A) 7.\(\overline{27}\)
B) \(\frac{5}{9}\)
C) \(\sqrt{15}\)
D) \(\sqrt{196}\)
Now,
We know that,
A “Rational number” is a number that can be written in the form of \(\frac{a}{b}\)
Ex: Perfect squares
An “Irrational number” is a number that can not be written in the form of \(\frac{a}{b}\)
Ex: Non-terminating decimal numbers
Hence, from the above,
We can conclude that
From the given numbers,
The irrational numbers are A) and C)
Question 11.
Lisa writes the following list of numbers.
5.737737773…, 26, \(\sqrt{45}\), –\(\frac{3}{2}\), 0, 9
Answer:
The given numbers are:
A) 5.7377377737… B) 26 C) \(\sqrt{45}\)
D) –\(\frac{3}{2}\) E) 0 F) 9
Now,
We know that,
A “Rational number” is a number that can be written in the form of \(\frac{a}{b}\)
Ex: Perfect squares
An “Irrational number” is a number that can not be written in the form of \(\frac{a}{b}\)
Ex: Non-terminating decimal numbers
a. Which numbers are rational?
Answer:
From the given numbers,
The rational numbers are: B, D, E, and F
b. Which numbers are irrational?
Answer:
From the given numbers,
The irrational numbers are: A and C
Question 12.
Construct Arguments Deena says that 9.565565556… is a rational number because it has a repeating pattern. Do you agree? Explain.
Answer:
The given number is 9.565565556…
From the given number,
We can observe that the number is a non-repeating and a non-terminating decimal
So,
The given number is an irrational number
Hence, from the above,
We can conclude that we don’t have to agree with Deena
Question 13.
Is \(\sqrt{1,815}\) rational? Explain.
Answer:
The given number is: \(\sqrt{1,815}\)
We know that,
A “Rational number” is a number that can be written in the form of \(\frac{a}{b}\)
Ex: Perfect squares
Now,
From the given square root,
We can observe that it won’t form a perfect square
Hence, from the above,
We can conclude that the given number is an irrational number
Question 14.
Is the decimal form of \(\frac{13}{3}\) Explain.
Answer:
The given number is: \(\frac{13}{3}\)
We know that,
\(\frac{13}{3}\) = 4.3333…..
We know that,
An “Irrational number” is a number that can not be written in the form of \(\frac{a}{b}\)
Hence, from the above,
We can conclude that the decimal form of \(\frac{13}{3}\) is an irrational number
Question 15.
Write the side length of the square rug as a square root. Is the side length a rational or irrational number? Explain.

Answer:
The given figure is:

From the given figure,
We can observe that the given figure depicts the shape of a square
Now,
Let the side length of a square be x
We know that,
Area = (Side length)²
x² = 100
x = \(\sqrt{100}\)
We know that,
A “Perfect square” is a rational number
Hence, from the above,
We can conclude that a side length is a rational number
Question 16.
Reasoning The numbers 2.888… and 2.999… are both rational numbers. What is an irrational number that is between the two rational numbers?
Answer:
A rational number is a number which is can be represented as the quotient of two numbers without having any remainder i.e., having remainder 0. For example 2.45, 2, 3 etc.
An irrational number has a non-zero remainder and has a nonterminating quotient.
Hence,
The numbers between 2.888… and 2.999… are 2.8889………, 2.8890…….., 2.8891…… etc
Question 17.
Higher Order Thinking You are given the expressions \(\sqrt{76+n}\) and \(\sqrt{2 n+26}\). What is the smallest value of n that will make each number rational?
Answer:
The given expressions are: \(\sqrt{76+n}\) and \(\sqrt{2 n+26}\)
Now,
To find the smallest value of n so that each expression will be a rational number,
\(\sqrt{76+n}\) = \(\sqrt{2 n+26}\)
Squaring on both sides
So,
76 + n = 2n + 26
2n – n = 76 – 26
n = 50
Hence, from the above,
We can conclude that the smallest value of n so that the given expressions will become a rational number is: 5
Assessment Practice
Question 18.
Which numbers are rational?
I. 1.1111111…
II. 1.567
III. 1.101101110…
A. II and III
B. III only
C. II only
D. I and II
E I only
F. None of the above
Answer:
The given numbers are:
I. 1.1111111…
II. 1.567
III. 1.101101110…
We know that,
A “Rational number” is a number that can be written in the form of \(\frac{a}{b}\)
So,
From the given numbers,
1 and 2 are the rational numbers
Hence, from the above,
we can conclude that option D matches with the given situation
Question 19.
Determine whether the following numbers are rational or irrational.

Answer:
The representation of the given numbers as rational and irrational numbers is:
Lesson 1.3 Compare and Order Real Numbers
Solve & Discuss It!
Courtney and Malik are buying a rug to fit in a 50-square-foot space. Which rug should they purchase? Explain.

Answer:
It is given that
Courtney and Malik are buying a rug to fit in a 50-square-foot space
Now,
The given figure is:

Now,
From the above figure,
We can observe that
The rugs are in different shapes i.e., a square, a circle, and a rectangle
Now,
The area of a square rug = The side length of a square rug × The side length of a square rug
= 7 × 7
= 49 ft²
Now,
The area of a circular rug = π × \(\frac{Diameter of a circular rug²}{4}\)
= 3.14 × \(\frac{8 ×8}{4}\)
= 3.14 ×16
= 50.24 ft²
Now,
The area of a rectangular rug = Length × Width
= 6 × 8\(\frac{1}{2}\)
= 6 × \(\frac{17}{2}\)
= \(\frac{6 ×17}{2}\)
= 51 ft²
Now,
When we compare the area of the rugs,
The area of the square rug is less than 50 ft²
Hence, from the above,
We can conclude that
Courtney and Malik should buy the square rug
Focus on math practices
Make Sense and Persevere How did you decide which rug Courtney and Malik should purchase?
Answer:
It is given that
Courtney and Malik are buying a rug to fit in a 50 ft² space
So,
To fit in a 50 ft² space,
The area of any type of rug should be less than 50 ft²
Now,
From the above problem,
We can observe that
The area of the square rug is the only area that is less than 50 ft²
Hence, from the above,
We can conclude that
Courtney and Mali should purchase the rugs based on the areas of the rugs
?Essential Question
How can you compare and order rational and irrational numbers?
Answer:
In the given numbers, one of them is rational while other one is irrational. To make the comparison, let us first make the given irrational number into rational number and then carry out the comparison. So, let us square both the given numbers
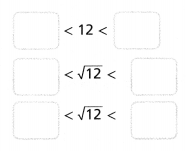
Try It!
Between which two whole numbers is \(\sqrt{12}\)?
Answer:
The given number is: \(\sqrt{12}\)
Now,
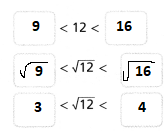
Hence, from the above,
We can conclude that
\(\sqrt{12}\) is in between 3 and 4
Convince Me!
Which of the two numbers is a better estimate for \(\sqrt{12}\)? Explain.
Answer:
The given number is: \(\sqrt{12}\)
Now,
We know that,
12 will be 3² and 4²
So,
\(\sqrt{12}\) will be between 3 and 4
Now,
When we observe the numbers between 3 and 4
The value of \(\frac{12}\) will be near to 3.4
Hence, from the above,
We can conclude that
The two numbers that are better estimate for \(\sqrt{12}\) is: 3 and 4
Try It!
Compare and order the following numbers:
\(\sqrt{11}\), 2\(\frac{1}{4}\), -2.5, 3.\(\overline{6}\), -3.97621 …
Answer:
The given numbers are:
\(\sqrt{11}\), 2\(\frac{1}{4}\), -2.5, 3.\(\overline{6}\), -3.97621 …
So,
\(\sqrt{11}\) ≅ 3.3
2\(\frac{1}{4}\) = 2.25
3.\(\overline{6}\) = 3.666……
So,
The order of the numbers from the least to the greatest is:
-3.97621…….. < -2.5 < 2.25 < \(\sqrt{11}\) < 3.\(\overline{6}\)
KEY CONCEPT
To compare rational and irrational numbers, you must first find rational approximations of the irrational numbers. You can approximate irrational numbers using perfect squares or by rounding.
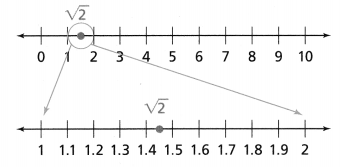
Do You Understand?
Question 1.
? Essential Question How can you compare and order rational and irrational numbers?
Answer:
In the given numbers, one of them is rational while other one is irrational. To make the comparison, let us first make the given irrational number into rational number and then carry out the comparison. So, let us square both the given numbers
Question 2.
Reasoning
The “leech” is a technical term for the slanted edge of a sail. Is the length of the leech shown closer to 5 meters or 6 meters? Explain.
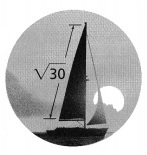
Answer:
It is given that
The “leech” is a technical term for the slanted edge of a sail
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The length of the leech is: \(\sqrt{30}\) meters
Now,
We know that,
5² < 30 < 6²
5 < \(\sqrt{30}\) < 6
Now,
We know that,
\(\sqrt{30}\) ≅ 5.4
So,
\(\sqrt{30}\) is close to 5
Hence, from the above,
We can conclude that
The length of the leech shown above is close to 5 meters
Question 3.
Construct Arguments which is a better approximation of \(\sqrt{20}\), 4.5 or 4.47? Explain.
Answer:
The given number is: \(\sqrt{20}\)
Now,
We know that,
4² < 20 < 5²
4 < \(\sqrt{20}\) < 5
Now,
We know that,
4.5² = 20.25
So,
The value of \(\sqrt{20}\) is close to 4.4
Hence, from the above,
We can conclude that
The better approximation of \(\sqrt{20}\) is: 4.4
Do You Know How?
Question 4.
Approximate \(\sqrt{39}\) to the nearest whole number.
Answer:
The given number is: \(\sqrt{39}\)
Now,
We know that,
6² < 39 < 7²
6 < \(\sqrt{39}\) < 7
Now,
We know that,
6.5² = 42.25
So,
The value of \(\sqrt{39}\) is close to 6.2
So,
The value of \(\sqrt{39}\) is closes to 6 that is the nearest whole number
Hence, from the above,
We can conclude that
The better approximation of \(\sqrt{39}\) that is the closest to the whole number is: 6
Question 5.
Approximate \(\sqrt{18}\) to the nearest tenth and plot the number on a number line.
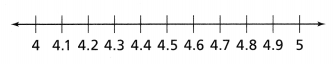
Answer:
The given number is: \(\sqrt{18}\)
Now,
We know that,
4² < 18 < 5²
4 < \(\sqrt{18}\) < 5
Now,
We know that,
4.5² = 20.25
4.2² = 17.69
So,
\(\sqrt{18}\) is close to 4.2
Hence, from the above,
We can conclude that
The representation of the approximate value of \(\sqrt{18}\) on the given number line is:

The approximate value of \(\sqrt{18}\) is: 4.2
Question 6.
Compare 5.7145… and \(\sqrt{29}\). Show your work.
Answer:
The given numbers are: 5.7145…… and \(\sqrt{29}\)
Now,
We know that,
5² < 29 < 6²
So,
5 < \(\sqrt{29}\) < 6
Now,
We know that,
5.5² = 30.25
5.3² = 28.09
So,
The approximate value of \(\sqrt{29}\) is: 5.3
Now,
When we compare the given numbers,
We can observ ethat
5.7145….. > 5.3
Hence, from the above,
We can conclude that
The order of the given numbers is:
5.7145……….. > \(\sqrt{29}\)
Question 7.
Compare and order the following numbers
5.2, -5.\(\overline{6}\), 3\(\frac{9}{10}\), \(\sqrt{21}\)
Answer:
The given numbers are:
5.2, -5.\(\overline{6}\), 3\(\frac{9}{10}\), \(\sqrt{21}\)
Now,
We know that,
-5.\(\overline{6}\) = -5.666666…..
3\(\frac{9}{10}\) = 3.9
\(\sqrt{21}\) ≅ 4.58
So,
The order of the given numbers from the least to the greatest is:
-5.\(\overline{6}\) < 3\(\frac{9}{10}\) < \(\sqrt{21}\) < 5.2
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is:
-5.\(\overline{6}\) < 3\(\frac{9}{10}\) < \(\sqrt{21}\) < 5.2
Practice & Problem Solving
Question 8.
Leveled Practice Find the rational approximation of \(\sqrt{15}\).
a. Approximate using perfect squares.
![]() < 15 <
< 15 < ![]()
![]() = < \(\sqrt{15}\) <
= < \(\sqrt{15}\) < ![]()
![]() < \(\sqrt{15}\) <
< \(\sqrt{15}\) < ![]()
Answer:
The given number is: \(\sqrt{15}\)
Now,
We know that,
By using the approximation using the perfect squares,
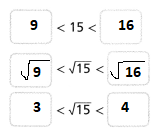
Hence, from the above,
We can conclude that
The approximate numbers that are between \(\sqrt{15}\) are: 3 and 4
b. Locate and plot \(\sqrt{15}\) on a number line. Find a better approximation using decimals.
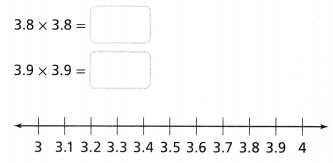
Answer:
From Part (a),
We know that,
The approximate numbers that are between \(\sqrt{15}\) are: 3 and 4
Now,
We know that,
3.5 ² = 12.25
Now,
So,
The approximate number that is the closest to \(\sqrt{15}\) is: 3.8
Hence, from the above,
We can conclude that
The representation of the approximation of \(\sqrt{15}\) in the given number line is:

The approximate number that is close to \(\sqrt{15}\) is: 3.8
Question 9.
Compare – 1.96312… and –\(\sqrt{5}\). Show your work.
Answer:
The given numbers are: -1.96312…… and –\(\sqrt{5}\)
Now,
We know that,
2² < 5 < 3²
2 < \(\sqrt{5}\) < 3
Now,
We know that,
2.5² = 6.25
2.2² = 4.84
So,
The approximate value of –\(\sqrt{5}\) is: -2.2
So,
The order of the given numbers from the least to the greatest is:
-1.96312……. > –\(\sqrt{5}\)
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is:
-1.96312……. > –\(\sqrt{5}\)
Question 10.
Does \(\frac{1}{6}\), -3, \(\sqrt{7}\), –\(\frac{6}{5}\), or 4.5 come first when the numbers are listed from least to greatest? Explain.
Answer:
The given numbers are: \(\frac{1}{6}\), -3, \(\sqrt{7}\), –\(\frac{6}{5}\), and 4.5
Now,
\(\frac{1}{6}\) = 0.166
\(\sqrt{7}\) = 2.64
–\(\frac{6}{5}\) = -1.2
So,
The order of the given numbers from the least to the greatest is:
-3 < –\(\frac{6}{5}\) < \(\frac{1}{6}\) < \(\sqrt{7}\) < 4.5
Hence, from the above,
We can conclude that
“-3” will come first when the given numbers will be arranged from the least to the greatest
Question 11.
A museum director wants to hang the painting on a wall. To the nearest foot, how tall does the wall need to be?

Answer:
It is given that
A museum director wants to hang the painting on a wall
Now,
The given figure is:

Now,
From the given figure,
We can obsere that
The painting on a wall is about \(\sqrt{90}\) ft
Now,
We know that,
9² < 90 < 10²
9 < \(\sqrt{90}\) < 10
Now,
We know that,
9.5² = 90.25
So,
The approximate value of \(\sqrt{90}\) is: 9.4 ft
Hence, from the above,
We can conclude that
The height of the wall needed to hang a painting is about 9.4 ft
Question 12.
Dina has several small clay pots. She wants to display them in order of height, from shortest to tallest. What will be the order of the pots?
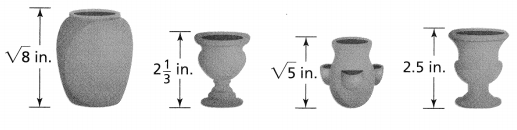
Answer:
It is given that
Dina has several small clay pots. She wants to display them in order of height, from shortest to tallest
Now,
The given heights are:
\(\sqrt{8}\), 2\(\frac{1}{3}\), \(\sqrt{5}\), and 2.5
Now,
We now that,
\(\sqrt{8}\) ≅ 2.82 in.
2\(\frac{1}{3}\) = 2.033 in.
\(\sqrt{5}\) ≅ 2.23 in.
So,
The order of the heights from the shortest to the tallest is:
2\(\frac{1}{3}\) in. < \(\sqrt{5}\) in. < 2.5 in. < \(\sqrt{8}\) in.
Hence, from the above,
We can conclude that
The order of the pots is:
2\(\frac{1}{3}\) in. < \(\sqrt{5}\) in. < 2.5 in. < \(\sqrt{8}\) in.
Question 13.
Rosie is comparing \(\sqrt{7}\) and 3.44444…. She says that \(\sqrt{7}\) > 3.44444… because \(\sqrt{7}\) = 3.5.
a. What is the correct comparison?
Answer:
It is given that
Rosie is comparing \(\sqrt{7}\) and 3.44444…. She says that \(\sqrt{7}\) > 3.44444… because \(\sqrt{7}\) = 3.5.
Now,
We know that,
2² < 7 < 3²
2 < \(\sqrt{7}\) < 3
Now,
We know that,
2.6² = 6.76
2.7² = 7.29
So,
The approximate value of \(\sqrt{7}\) is: 2.6
So,
The order of the given numbers is:
\(\sqrt{7}\) < 3.44444…..
Hence, from the above,
We can conclude that
The correct comparison of the given numbers is:
\(\sqrt{7}\) < 3.44444…..
b. Critique Reasoning What mistake did Rosie likely make?
Answer:
The given numbers are: \(\sqrt{7}\) and 3.44444…..
Now,
It is also given that
\(\sqrt{7}\) = 3.5
But, 3.5 = \(\frac{7}{2}\)
Hence, from the above,
We can conclude that
The mistake Rosie likely make is:
She considered \(\sqrt{7}\) = \(\frac{7}{2}\)
Question 14.
Model with Math Approximate – √23 to the nearest tenth. Draw the point on the number line.
Answer:
The given number is: –\(\sqrt{23}\)
Now,
We know that,
4² < 23 < 5²
4 < \(\sqrt{23}\) < 5
Now,
We know that,
4.5² = 20.25
4.7² = 22.09
So,
The approximate value of –\(\sqrt{23}\) is: -4.7
Hence,
The representtaion of the approximate value of –\(\sqrt{23}\) on the given number line is:
![]()
Question 15.
Higher Order Thinking The length of a rectangle is twice the width. The area of the rectangle is 90 square units. Note that you can divide the rectangle into two squares.

a. Which irrational number represents the length of each side of the squares?
Answer:
It is given that
The length of a rectangle is twice the width. The area of the rectangle is 90 square units. Note that you can divide the rectangle into two squares.
Now,
The given figure is:

Now,
According to the given information,
The area of each square = \(\frac{90}{2}\)
= 45 square units
Now,
We know that,
The area of a square = Side²
So,
Side of a squre = \(\sqrt{The area of a square}\)
So,
The side length of each square = \(\sqrt{45}\) units
Hence, from the above,
We can conclude that
The irrational number that represents the length of each side of the squares is: \(\sqrt{45}\) units
b. Estimate the length and width of the rectangle.
Answer:
It is given that
The length of a rectangle is twice the width. The area of the rectangle is 90 square units. Note that you can divide the rectangle into two squares.
Now,
The given figure is:

Now,
Let the width of the rectangle be x units
So,
The length of the rectangle = 2 (Width) = 2x units
Now,
We know that,
The length of a rectangle = Length × Width
So,
According to the given information,
90 = 2x × x
90 = 2x²
x² = \(\frac{90}{2}\)
x = \(\sqrt{45}\)
Hence, from the above,
We can conclude that
The length of the rectangle is: 2\(\sqrt{45}\) units
The width of the rectangle is: \(\sqrt{45}\) units
Assessment Practice
Question 16.
Which list shows the numbers in order from least to greatest?
A. -4, –\(\frac{9}{4}\), \(\frac{1}{2}\), 3.7, \(\sqrt{5}\)
B. -4, –\(\frac{9}{4}\), \(\frac{1}{2}\), \(\sqrt{5}\), 3.7
C. –\(\frac{9}{4}\), \(\frac{1}{2}\), 3.7, \(\sqrt{5}\), -4
D. –\(\frac{9}{4}\), -4, \(\frac{1}{2}\), 3.7, \(\sqrt{5}\)
Answer:
The given list of numbers are:
-4, –\(\frac{9}{4}\), \(\frac{1}{2}\), 3.7, \(\sqrt{5}\)
Now,
We know that,
–\(\frac{9}{4}\) = -2.25
\(\frac{1}{2}\) = 0.5
\(\sqrt{5}\) ≅ 2.23
So,
The order of the given list of numbers from the least to the greatest is:
-4 < –\(\frac{9}{4}\) < \(\frac{1}{2}\) < \(\sqrt{5}\) < 3.7
Hence, from the above,
We can conclude that
The list that shows the numbers from the least to the greatest is:

Question 17.
The area of a square poster is 31 square inches. Find the length of one side of the poster. Explain.
PART A
To the nearest whole inch
Answer:
It is given that
The area of a square poster is 31 square inches
Now,
We know that,
The area of a square = Side²
Side = \(\sqrt{Area of a square}\)
So,
According to the given information,
The length of one side of the poster = \(\sqrt{31}\) inches
Now,
We know that,
5² < 31 < 6²
5 < \(\sqrt{31}\) < 6
Now,
We know that,
5.5² = 30.25
5.6² = 31.36
So,
The approximate value of \(\sqrt{31}\) is: 5.5
Hence, from the above,
We can conclude that
The length of one side of the poster to the nearest whole inch is: 6 inches
PART B
To the nearest tenth of an inch
Answer:
It is given that
The area of a square poster is 31 square inches
Now,
We know that,
The area of a square = Side²
Side = \(\sqrt{Area of a square}\)
So,
According to the given information,
The length of one side of the poster = \(\sqrt{31}\) inches
Now,
We know that,
5² < 31 < 6²
5 < \(\sqrt{31}\) < 6
Now,
We know that,
5.5² = 30.25
5.6² = 31.36
So,
The approximate value of \(\sqrt{31}\) is: 5.5
Hence, from the above,
We can conclude that
The length of one side of the poster to the nearest tenth of an inch is: 5.5 inches
Lesson 1.4 Evaluate Square Roots and Cube Roots
Solve & Discuss It!
ACTIVITY
Matt and his dad are building a tree house. They buy enough flooring material to cover an area of 36 square feet. What are all possible dimensions of the floor?

Answer:
It is given that
Matt and his dad are building a tree house. They buy enough flooring material to cover an area of 36 square feet
Now,
To find the length and width of the floor, find the multiples of 36
So,
The multiples of 36 are:
36 = 1 × 36, 2 × 18, 3 × 12, 4 × 9, 9 ×4, 12 × 3, 18 × 2, 36 × 1
So,
All the possible dimensions of the floor are:
1 × 36, 2 × 18, 3 × 12, 4 × 9, 9 ×4, 12 × 3, 18 × 2, 36 × 1
Hence, from the above,
We can conclude that
All the possible dimensions of the floor are:
1 × 36, 2 × 18, 3 × 12, 4 × 9, 9 ×4, 12 × 3, 18 × 2, 36 × 1
Look for Relationships
Can different floor dimensions result in the same area?
Answer:
From the above problem,
We can observe that
All the possible dimensions of the floor are:
1 × 36, 2 × 18, 3 × 12, 4 × 9, 9 ×4, 12 × 3, 18 × 2, 36 × 1
Now,
When we find the area by using all the different dimensions of the floor,
We can observe that the area of the floor is the same
Hence, from the above
We can conclude that
The different floor dimensions result in the same area
Focus on math practices
Reasoning Why is there only one set of dimensions for a square floor when there are more sets for a rectangular floor? Are all the dimensions reasonable? Explain.
Answer:
From the above problem,
We can observe that
All the possible dimensions of the floor are:
1 × 36, 2 × 18, 3 × 12, 4 × 9, 9 ×4, 12 × 3, 18 × 2, 36 × 1
Now,
We know that,
A square has the same side lengths
A square has the same parallel side lengths
Hence,
The square floor has only one set of dimensions whereas the rectangular floor has more sets and all the dimensions will be reasonable
? Essential Question
How do you evaluate cube roots and square roots?
Answer:
Let the number be: p
Now,
The square of a number is: p²
The cube of a number is: p³
The square root of a number is: \(\sqrt{p}\)
The cube root of a number is: \(\sqrt[3]{p}\)
Try It!
A cube-shaped art sculpture has a volume of 64 cubic feet. What is the length of each edge of the cube?
The length of each edge is ![]() feet.
feet.
Answer:
It is given that
A cube-shaped art sculpture has a volume of 64 cubic feet.
Now,
We know that,
A cube has all the same side lengths
Now,
Let the side length of a cube be: s
So,
The volume of a cube (V) = s³
So,
Side = \(\sqrt[3]{V}\)
Now,
So,
![]()
Hence, from the above,
We can conclude that
The length of each edge of the cube is: 4 feet
Convince Me!
How can you find the cube root of 64?
Answer:
Let the number be: p
Now,
The cube root of a number is: \(\sqrt[3]{p}\)
So,
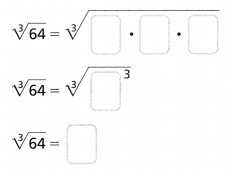
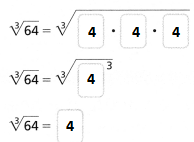
The cube root of 64 = \(\sqrt[3]{64}\)
= \(\sqrt[3]{4 × 4 × 4}\)
= 4
Hence, from the above,
We can conclude that
The cube root of 64 is: 4
Try It!
Evaluate.
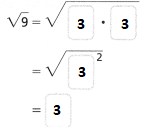
a. \(\sqrt[3]{27}\)
Answer:
The given number is: \(\sqrt[3]{27}\)
Now,
![]()
Hence, from the above,
We can conclude that
The cube root of the given number is: 3
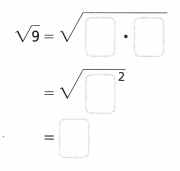
b. \(\sqrt{25}\)
Answer:
The given number is: \(\sqrt{25}\)
Now,
![]()
Hence, from the above,
We can conclude that
The square root of the given number is: 5
c. \(\sqrt{81}\)
Answer:
The given number is: \(\sqrt{81}\)
Now,
![]()
Hence, from the above,
We can conclude that
The square root of the given number is: 9
d. \(\sqrt[3]{1}\)
Answer:
The given number is: \(\sqrt[3]{1}\)
Now,
![]()
Hence, from the above,
We can conclude that
The cube root of the given number is: 1
Try It!
Emily wants to buy a tablecloth to cover a square card table. She knows the tabletop has an area of 9 square feet. What are the minimum dimensions of the tablecloth Emily needs?
Emily should buy a tablecloth that measures at least
![]() feet by
feet by ![]() feet.
feet.
Answer:
It is given that
Emily wants to buy a tablecloth to cover a square card table. She knows the tabletop has an area of 9 square feet.
Now,
We know that,
The area of a square = Side²
So,
According to the given information,
The area of a square table = Side²
Side² = 9
Now,
So,

Hence, from the above,
We can conclude that
The minimum dimensions of the table cloth Emily needs is: 3 feet × 3 feet
KEY CONCEPT
The cube root of a number is a number whose cube is equal to that number.
Cubing a number and taking the cube root of the number are inverse operations.
The square root of a number is a number whose square is equal to that number.
Squaring a number and taking the square root of the number are inverse operations.
Do You Understand?
Question 1.
? Essential Question How do you evaluate cube roots and square roots?
Answer:
Let the number be: p
Now,
The square of a number is: p²
The cube of a number is: p³
The square root of a number is: \(\sqrt{p}\)
The cube root of a number is: \(\sqrt[3]{p}\)
Question 2.
Generalize A certain number is both a perfect square and a perfect cube. Will its square root and its cube root always be different numbers? Explain.
Answer:
We know that,
A perfect square is a number whose square root is an integer; and a perfect cube is a number whose cube root is an integer.
A number that is a perfect square and perfect cube will not always have different numbers as its square root and cube root.
Question 3.
Critique Reasoning A cube-shaped box has a volume of 27 cubic inches. Bethany says each side of the cube measures 9 inches because 9 × 3 = 27. Is Bethany correct? Explain your reasoning.
Answer:
It is given that
A cube-shaped box has a volume of 27 cubic inches. Bethany says each side of the cube measures 9 inches because 9 × 3 = 27
Now,
We know that,
A “Cube” has the equal side lengths
Now,
We know that,
The volume of a cube (V) = Side³
So,
Side = \(\sqrt[3]{V}\)
Now,
For the volume of 27 cubic inches,
Side = \(\sqrt[3]{27}\)
= \(\sqrt[3]{3 × 3 ×3}\)
= 3 inches
So,
Each side of the cube measures 3 inches
Hence, from the above,
We can conclude that
Bethany is not correct
Do You Know How?
Question 4.
A cube has a volume of 8 cubic inches. What is the length of each edge of the cube?
Answer:
It is given that
A cube has a volume of 8 cubic inches
Now,
We know that,
A “Cube” has the equal side lengths
Now,
We know that,
The volume of a cube (V) = Side³
So,
Side = \(\sqrt[3]{V}\)
Now,
For the volume of 8 cubic inches,
Side = \(\sqrt[3]{8}\)
= \(\sqrt[3]{2 × 2 ×2}\)
= 2 inches
Hence, from the above,
We can conclude that
The length of each edge of the given cube is: 2 inches
Question 5.
Below is a model of the infield of a baseball stadium. How long is each side of the infield?
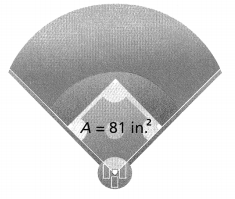
Answer:
It is given that
Below is a model of the infield of a baseball stadium
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The infield is in the form of a square
Now,
We know that,
The area of a square = Side²
So,
Each Side of the infield =\(\sqrt{The area of the infield}\)
= \(\sqrt{81}\)
Now,
![]()
Hence, from the above,
We can conclude that
The length of each side of the infield is: 9 inches
Question 6.
Julio cubes a number and then takes the cube root of the result. He ends up with 20. What number did Julio start with?
Answer:
It is given that
Julio cubes a number and then takes the cube root of the result. He ends up with 20
Now,
Let us say that the number is x.
So
The first step that Julio do is to cube the number so that the number will become: x³
Then,
The next he did was take cube root of the number, so that the result will become: \(\sqrt[3]{x³}\)
Now,
By solving the above expression,
\(\sqrt[3]{x³}\) = x
Now,
It is given that
The end result is 20
So,
x = 20
So,
Julio started and ended with the same number which is 20.
Hence, from the above,
We can conclude that
The number did Julio start with is: 20
Practice & Problem Solving
Leveled Practice
In 7 and 8, evaluate the cube root or square root.
Question 7.
Relate the volume of the cube to the length
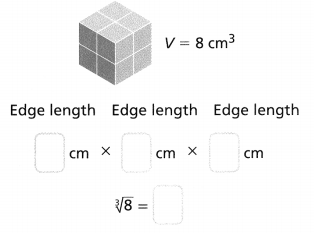
Answer:
The given figure is:

Now,
We know that,
The volume of a cube (V) = Side³
So,
Side = \(\sqrt[3]{V}\)
So,
Side = \(\sqrt[3]{8}\)
Now,

Hence, from the above,
We can conclude that
The length of each edge of the cube is: 2 cm
Question 8.
Relate the area of the square to the length of each edge.
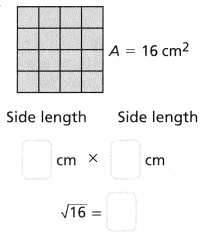
Answer:
The given figure is:
Now,
We know that,
The area of a square (V) = Side²
So,
Side = \(\sqrt{V}\)
So,
Side = \(\sqrt{16}\)
Now,

Hence, from the above,
We can conclude that
The length of each side of the square is: 4 cm
Question 9.
Would you classify the number 169 as a perfect square, a perfect cube, both, or neither? Explain.
Answer:
The given number is: 169
Now,
We know that,
A perfect cube is a number that can be expressed as the product of three equal integers
A perfect square is a number that can be expressed as the product of two equal integers
Now,
169 can be written as:
169 = 13 × 13
Hence, from the above,
We can conclude that
169 would be classified as a perfect square
Question 10.
The volume of a cube is 512 cubic inches. What is the length of each side of the cube?
Answer:
It is given that
The volume of a cube is 512 cubic inches
Now,
We know that,
The volume of a cube (V) = Side³
So,
Side = \(\sqrt[3]{V}\)
So,
Side = \(\sqrt[3]{512}\)
So,
![]()
Hence, from the above,
We can conclude that
The length of each edge of the cube is: 8 inches
Question 11.
A square technology chip has an area of 25 square cm. How long is each side of the chip?
Answer:
It is given that
A square technology chip has an area of 25 square cm.
Now,
We know that,
The area of a square = Side²
So,
Side = \(\sqrt{The area of a square}\)
So,
Side = \(\sqrt{25}\)
So,
![]()
Hence, from the above,
We can conclude that
The length of each side of the chip is: 5 cm
Question 12.
Would you classify the number 200 as a perfect square, a perfect cube, both, or neither? Explain.
Answer:
The given number is: 200
Now,
We know that,
A perfect cube is a number that can be expressed as the product of three equal integers
A perfect square is a number that can be expressed as the product of two equal integers
Now,
200 can be written as:
200 = 100 × 2
= 10 × 10 × 2
Hence, from the above,
We can conclude that
200 would not be classified neither as a perfect square nor a perfect cube
Question 13.
A company is making building blocks. What is the length of each side of the block?

Answer:
It is given that
A company is making building blocks
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The building blocks is in the form of a cube
Now,
We know that,
The volume of a cube (V) = Side³
So,
Side = \(\sqrt[3]{V}\)
So,
Side = \(\sqrt[3]{1}\)
Now,
![]()
Hence, from the above,
We can conclude that
The length of each side of the block is: 1 ft
Question 14.
Mrs. Drew wants to build a square sandbox with an area of 121 square feet. What is the total length of wood Mrs. Drew needs to make the sides of the sandbox?
Answer:
It is given that
Mrs. Drew wants to build a square sandbox with an area of 121 square feet
Now,
We know that,
The area of a square (A) = Side²
So,
Side = \(\sqrt{A}\)
So,
Side = \(\sqrt{121}\)
Now,
![]()
So,
The side of the sandbox is: 11 feet
Now,
To find the total length of wood Mrs. Drew needs to make the sides of the sandbox = 4 × (The length of the side of the sandbox)
= 4 × 11
= 44 feet
Hence, from the above,
We can conclude that
The total length of wood Mrs. Drew needs to make the sides of the sandbox is: 44 feet
Question 15.
Construct Arguments Diego says that if you cube the number 4 and then take the cube root of the result, you end up with 8. Is Diego correct? Explain.
Answer:
It is given that
Diego says that if you cube the number 4 and then take the cube root of the result, you end up with 8
Now,
According to the given information,
Step 1:
4³ = 4 × 4 × 4
= 64
Step 2:
\(\sqrt[3]{64}\)
= \(\sqrt[3]{4 × 4 ×4}\)
= 4
But,
It is given that
The end result is 8 and we got 4
Hence,f rom the above,
We can conclude that
Diego is not correct
Question 16.
Higher Order Thinking Talia is packing a moving box. She has a square-framed poster with an area of 9 square feet. The cube-shaped box has a volume of 30 cubic feet. Will the poster lie flat in the box? Explain.
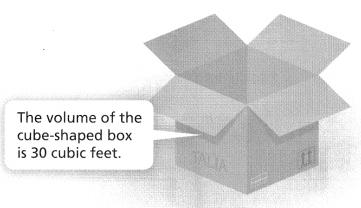
Answer:
It is given that
Talia is packing a moving box. She has a square-framed poster with an area of 9 square feet. The cube-shaped box has a volume of 30 cubic feet
Now,
The given figure is:

Now,
To make the square-framed poster fit into a cube-shaped box,
The side of square-framed poster < The side of each edge of the cube-shaped box
Now,
We know that,
The area of a square = Side²
The volume of a cube = Side³
So,
\(\sqrt{9}\) = 3 feet
\(\sqrt[3]{30}\) = 3.10 feet
So,
3 < 3.10
So,
The side of square-framed poster < The side of each edge of the cube-shaped box
Hence, from the above,
We can conclude that
The poster lie flat in the box
Assessment Practice
Question 17.
Which expression has the greatest value?
A. \(\sqrt{49}\) . 2
B. \(\sqrt{49}\) – \(\sqrt{16}\)
C. \(\sqrt{25}\) + \(\sqrt{16}\)
D. \(\sqrt{25}\).3
Answer:
The given expressions are:
a.
The given expression is: \(\sqrt{49}\) . 2
Now,
We know that,
\(\sqrt{49}\) = 7
So,
The value of the given expression is: 14
b.
The given expression is:
\(\sqrt{49}\) – \(\sqrt{16}\)
Now,
We know that,
\(\sqrt{49}\) = 7
\(\sqrt{16}\) = 4
So,
The value of the given expression is: 3
c.
The given expression is:
\(\sqrt{25}\) + \(\sqrt{16}\)
Now,
We know that,
\(\sqrt{25}\) = 5
\(\sqrt{16}\) = 4
So,
The value of the given expression is: 9
d.
The given expression is:
\(\sqrt{25}\).3
Now,
We know that,
\(\sqrt{25}\) = 5
So,
The value of the given expression is: 15
Hence, from the above,
We can conclude that
The expression that has the greatest value is:

Question 18.
A toy has various shaped objects that a child can push through matching holes. The area of the square hole is 8 square cm. The volume of a cube-shaped block is 64 cubic cm
PART A
Which edge length can you find? Explain.
Answer:
It is given that
A toy has various shaped objects that a child can push through matching holes. The area of the square hole is 8 square cm. The volume of a cube-shaped block is 64 cubic cm
Now,
We know that,
The area of a square (A) = Side²
The volume of a cube (V) = Side³
So,
\(\sqrt{8}\) = 2.82 cm
\(\sqrt[3]{64}\) = 4 cm
Hence, from the above,
We can conclude that
The value of the edge lengths you found are:
The side of a square-shaped hole is: 2.82 cm
The side of a cube-shaped block is: 4 cm
PART B
Will the block fit in the square hole? Explain.
Answer:
Now,
From Part A,
We can observe that
The side of a square-shaped hole is: 2.82 cm
The side of a cube-shaped block is: 4 cm
Now,
For the block to fit in the square hole,
The side of the block < The side of the hole
But,
4 cm > 2.82 cm
Hence, from the above,
We can conclude that
The block will not fit in the square hole
Lesson 1.5 Solve Equations Using Square Roots and Cube Roots
Solve & Discuss It!
Janine can use up to 150 one-inch blocks to build a solid, cube-shaped model. What are the dimensions of the possible models that she can build? How many blocks would Janine use for each model? Explain.
Answer:
It is given that
Janine can use up to 150 one-inch blocks to build a solid, cube-shaped model
Now,
The given figure is:

Now,
We know that,
The volume of a cube = Length × Width × Height
Now,
To find the dimensions of the possible models that Janine can model,
We have to find the multiples of 150 in terms of three
So,
150 = 25 × 6
150 = 5 × 5 × 6
So,
The total number of blocks Janine would use for each model = The sum of the above three multiples of 150
= 5 + 5 + 6
= 16 blocks
Hence, from the above,
We can conclude that
The dimensions of the possible model that Janine can build is: 5 × 5 × 6
The total number of blocks Janine would use for each model is: 16 blocks
Look for Relationships
How are the dimensions of a solid related to its volume?
Answer:
The volume, V , of any rectangular solid is the product of the length, width, and height. We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, B , is equal to length × Width.
Focus on math practices
Reasoning Janine wants to build a model using \(\frac{1}{2}\)-inch cubes. How many \(\frac{1}{2}\)-inch cubes would she use to build a solid, cube-shaped model with side lengths of 4 inches? Show your work.
Answer:
It is given that
Janine wants to build a model using \(\frac{1}{2}\)-inch cubes and a cube-shaped model with side lengths of 4 inches
Now,
According to the given information,
The number of \(\frac{1}{2}\)-inch cubes would Janine used to build a solid = \(\frac{1}{2}\) × 8 blocks
Hence, from the above,
We can conclude that
The number of \(\frac{1}{2}\)-inch cubes would she use to build a solid, cube-shaped model with side lengths of 4 inches is: 8 blocks
? Essential Question
How can you solve equations with squares and cubes?
Answer:
The steps to solve equations with squares are:
Step 1:
Divide all terms by a (the coefficient of x2).
Step 2:
Move the number term (c/a) to the right side of the equation.
Step 3:
Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.
The steps to solve equations with cubes are:
Step 1:
Divide all terms by a (the coefficient of x³).
Step 2:
Move the number term (\(\frac{d}{a}\)) to the right side of the equation.
Step 3:
Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.
Try It!
What is the side length, s, of the square below?

Each side of the square measures ![]() meters.
meters.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
It is a square
Now,
We know that,
The area of a square = Side²
Now,
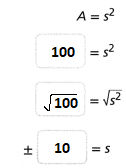
So,
![]()
Hence, from the above,
We can conclude that
Each side of the square measures 10 meters
Convince Me!
Why are there two possible solutions to the equation s2 = 100? Explain why only one of the solutions is valid in this situation.
Answer:
The given equation is: s²
Now,
We know that,
The square of a positive number or a negative number is always positive and the square root of a number must always be positive
So,
s² = 100
s = \(\sqrt{100}\)
s = ± 10
Now,
We know that,
The side of any figure will always be positive
Hence, from the above,
We can conclude that
Only one of the solutions is valid in this situation because of the property of sides of the geometrical figures
Try It!
Solve x3 = 64.
Answer:
The given equation is:
x³ = 64
So,
x = \(\sqrt[3]{64}\)
x = \(\sqrt[3]{4 × 4 × 4}\)
x = 4
Hence, from the above,
We can conclude that
The value of x for the given equation is: 4
Try It!
a. Solve a3 = 11.
Answer:
The given equation is:
a³ = 11
So,
a = \(\sqrt[3]{11}\)
Now,
We know that,
The cube of a number will always be positive
Hence, from the above,
We can conclude that
The possible solution for the given equation is: \(\sqrt[3]{11}\)
b. Solve c2 = 27.
Answer:
The given equation is:
c² = 27
So,
c = ±\(\sqrt{27}\)
Hence, from the above,
We can conclude that
The possible solutions for the given equation is: \(\sqrt{27}\), –\(\sqrt{27}\)
KEY CONCEPT
You can use square roots to solve equations involving squares.
x2 = a
\(\sqrt{x^{2}}\) = \(\sqrt{a}\)
x = + \(\sqrt{a}\), –\(\sqrt{a}\)
You can use cube roots to solve equations involving cubes. x2 = b Vx3 = xb
x3 = b
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{b}\)
x = \(\sqrt[3]{b}\)
Do You Understand?
Question 1.
? Essential Question
How can you solve equations with squares and cubes?
Answer:
The steps to solve equations with squares are:
Step 1:
Divide all terms by a (the coefficient of x2).
Step 2:
Move the number term (c/a) to the right side of the equation.
Step 3:
Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.
The steps to solve equations with cubes are:
Step 1:
Divide all terms by a (the coefficient of x³).
Step 2:
Move the number term (\(\frac{d}{a}\)) to the right side of the equation.
Step 3:
Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.
Question 2.
Be Precise Suri solved the equation x2 = 49 and found that x = 7. What error did Suri make?
Answer:
It is given that
Suri solved the equation x2 = 49 and found that x = 7.
Now,
The given equation is:
x² = 49
Now,
We know that,
The square of a number is always positive but the square root of a number can either be positive or negative
So,
x = \(\sqrt{49}\)
x = ±7
x = 7, -7
Hence, from the above,
We can conclude that
The error did Suri made is that he did not consider the negative square root of 49
Question 3.
Construct Arguments There is an error in the work shown below. Explain the error and provide a correct solution.
x3 = 125
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{125}\)
x = 5 and x = -5
Answer:
The given equation is:
x³ = 125
Now,
We know that,
The cube root of a number will always be positive
So,
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{125}\)
x = \(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{5 × 5 × 5}\)
x = 5
Hence, from the above,
We can conclude that
The error is not considering that the cube root of a number will always be positive
The correct solution is:
x = 5
Question 4.
Why are the solutions to x2 = 17 irrational?
Answer:
The given equation is:
x² = 17
So,
x = ±\(\sqrt{17}\)
Now,
We know that,
The perfect square will be an integer and we know that an integer is a rational number
Now,
When we look at 17,
It is not a perfect square
Hence, from the above,
We can conclude that
The solutions of the given equation are irrational
Do You Know How?
Question 5.
If a cube has a volume of 27 cubic cm, what is the length of each edge? Use the volume formula, V = s3, and show your work.
Answer:
It is given that
A cube has a volume of 27 cubic cm
Now,
We know that,
The volume of a cube (V) = Side³
So,
Side = \(\sqrt[3]{V}\)
Now,
According to the given information,
Side = \(\sqrt[3]{27}\)
Side = \(\sqrt[3]{3 × 3 × 3}\)
Side = 3 cm
Hence, from the above,
We can conclude that
The length of each edge of the give cube is: 3 cm
Question 6.
Darius is building a square launch pad for a rocket project. If the area of the launch pad is 121 square cm, what is its side length? Use the area formula, A = s2, and show your work.
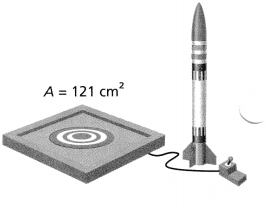
Answer:
It is given that
Darius is building a square launch pad for a rocket project. If the area of the launch pad is 121 square cm,
Now,
We know that,
The area of a square (A) = Side²
So,
Side = \(\sqrt{A}\)
Now,
According to the given information,
Side = \(\sqrt{121}\)
Side = \(\sqrt{11 × 11}\)
Side = 11 cm
Hence, from the above,
We can conclude that
The side length of the launch pad is: 1 cm
Question 7.
Solve the equation x3 = -215.
Answer:
The given equation is:
x³ = -215
Now,
We know that,
The square root won’t accept negative values but the cube root will accept both positive and negative values
So,
x = \(\sqrt[3]{-215}\)
Now,
![]()
Hence, from the above,
We can conclude that
The solution for the given equation is: -5.99
Practice & Problem Solving
Leveled Practice
In 8 and 9, solve.
Question 8.
z2 = 1
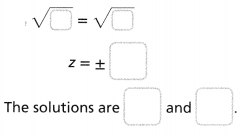
Answer:
The given equation is:
z² = 1
Now,
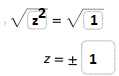
Hence, from the above,
We can conclude that
![]()
Question 9.
a3 = 216
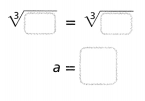
Answer:
The given equation is:
a³ = 216
Now,
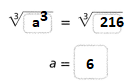
Hence, from the above,
We can conclude that
The solution for the given equation is: 6
Question 10.
Solve v2 = 47.
Answer:
The give equation is:
v² = 47
Now,
\(\sqrt{v²}\) = \(\sqrt{47}\)
v = ±\(\sqrt{47}\)
Now,
![]()
Hence, from the above,
We can conclude that
The solutions for the given equation are: 6.85, and -6.85
Question 11.
The area of a square photo is 9 square inches. How long is each side of the photo?
Answer:
It is given that
The area of a square photo is 9 square inches
Now,
We know that,
The area of a square (A) = Side² (s)
So,
s² = 9
\(\sqrt{s²}\) = \(\sqrt{9}\)
s = 3 inches [Because the length of the side will never be negative]
Hence, from the above,
We can conclude that
The length of each side of the photo is: 3 inches
Question 12.
Solve the equation y2 = 81.
Answer:
The given equation is:
y² = 81
Now,
\(\sqrt{y²}\) = ±\(\sqrt{81}\)
y = ±9
Hence, from the above,
We can conclude that
The solutions for the given equation are: 9, and -9
Question 13.
Solve the equation w3 = 1,000.
Answer:
The given equation is:
w³ = 1,000
Now,
\(\sqrt[3]{w³}\) = \(\sqrt[3]{1,000}\)
w = \(\sqrt[3]{10 × 10 × 10}\)
w = 10
Hence, from the above,
We can conclude that
The solution for the given equation is: 10
Question 14.
The area of a square garden is shown. How long is each side of the garden?
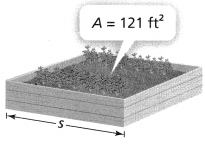
Answer:
It is given that
The area of a square garden is shown.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The area of the square garden is: 121 ft²
Now,
We know that,
The area of a square (A) = s²
So,
According to the given information,
s² = 121
\(\sqrt{s²}\) = \(\sqrt{121}\)
s = 11 ft [Since the length of the side will never be negative]
Hence, from the above,
We can conclude that
The length of each side of the garden is: 11 ft
Question 15.
Solve b2 = 77.
Answer:
The given equation is:
b² = 77
Now,
\(\sqrt{b²}\) = ±\(\sqrt{77}\)
Now,
![]()
Hence, from the above,
We can conclude that
The solutions for the givene quation are: 8.77, and -8.77
Question 16.
Find the value of c in the equation c3 = 1,728.
Answer:
The given equation is:
c³ = 1,728
Now,
\(\sqrt[3]{c³}\) = \(\sqrt[3]{1,728}\)
c = 12
Hence, from the above,
We can conclude that
The value of c for the given equation is: 12
Question 17.
Solve the equation v3 = 12.
Answer:
The given equation is:
v³ = 12
Now,
\(\sqrt[3]{v³}\) = \(\sqrt[3]{12}\)
Now,
![]()
Hence, from the above,
We can conclude that
The solution for the given equation is: 2.28
Question 18.
Higher Order Thinking Explain why
\(\sqrt[3]{-\frac{8}{27}}\) is –\(\frac{2}{3}\)
Answer:
The given equation is:
\(\sqrt[3]{-\frac{8}{27}}\)
Now,
We know that,
\(\sqrt[3]{\frac{a}{b}}\) = \(\frac{\sqrt[3]{a}}{\sqrt[3]{b}}\)
So,
\(\sqrt[3]{-\frac{8}{27}}\) = –\(\frac{\sqrt[8]{a}}{\sqrt[3]{27}}\)
= –\(\frac{\sqrt[2 × 2 ×2]{a}}{\sqrt[3]{3 ×3 × 3}}\)
= –\(\frac{2}{3}\)
Hence, from the above,
We can conclude that
\(\sqrt[3]{-\frac{8}{27}}\) is –\(\frac{2}{3}\) due to the below property of Exponents:
\(\sqrt[3]{\frac{a}{b}}\) = \(\frac{\sqrt[3]{a}}{\sqrt[3]{b}}\)
Question 19.
Critique Reasoning Manolo says that the solution of the equation g2 = 36 is g = 6 because 6 × 6 = 36. Is Manolo’s reasoning complete? Explain.
Answer:
It is given that
Manolo says that the solution of the equation g2 = 36 is g = 6 because 6 × 6 = 36
Now,
The given equation is:
g² = 36
Now,
We know that,
The square of a number will always be positive but the square root of a number will either be positive or negative
So,
\(\sqrt{g²}\) = ±\(\sqrt{36}\)
g = ±6
So,
The solutions for the given equation are: 6, -6
Hence, from the above,
We can conclude that
Manolo’s reasoning is not complete
Question 20.
Evaluate \(\sqrt[3]{-512}\).
a. Write your answer as an integer.
Answer:
The given equation is:
\(\sqrt[3]{-512}\)
Now,
\(\sqrt[3]{-512}\) = \(\sqrt[3]{(-8) × (-8) × (-8)}\)
= -8
Hence, from the above,
We can conclude that
The value of \(\sqrt[3]{-512}\) as an integer is: -8
b. Explain how you can check that your result is correct.
Answer:
The given equation is:
\(\sqrt[3]{-512}\)
Now,
From part (a),
We get the value of the given equation is: 8
Now,
\(\sqrt[3]{(-8) × (-8) × (-8)}\)
= \(\sqrt[3]{64 × (-8)}\)
= \(\sqrt[3]{-512}\)
Hence, from the above,
We can conclude that
The result is correct because the givene quation and the result are the same
Question 21.
Yael has a square-shaped garage with 228 square feet of floor space. She plans to build an addition that will increase the floor space by 50%. What will be the length, to the nearest tenth, of one side of the new garage?
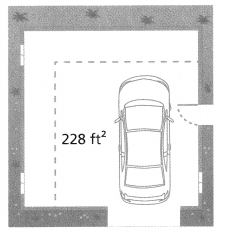
Answer:
It is given that
Yael has a square-shaped garage with 228 square feet of floor space. She plans to build an addition that will increase the floor space by 50%.
Now,
According to the given information,
50% of 228 = \(\frac{50}{100}\) × 228
= \(\frac{50 × 228}{100}\)
= 114 square feet
So,
The area of the new garage = 228 + 114
= 342 square feet
Now,
We know that,
The area of a square (A) = Side (s)²
So,
s² = 342
\(\sqrt{s²}\) = \(\sqrt{342}\)
Now,
![]()
Hence, from the above,
We can conclude that
The length of one side of the new garage is: 18.5 feet
Assessment Practice
Question 22.
The Traverses are adding a new room to their house. The room will be a cube with a volume of 6,859 cubic feet. They are going to put in hardwood floors, which costs $10 per square foot. How much will the hardwood floors cost?
Answer:
It is given that
The Traverses are adding a new room to their house. The room will be a cube with a volume of 6,859 cubic feet. They are going to put in hardwood floors, which costs $10 per square foot
Now,
We know that,
The volume of a cube (V) = s³
So,
According to the given information,
s³ = 6,859
\(\sqrt[3]{s³}\) = \(\sqrt[3]{6,859}\)
s = 19 feet
So,
The length of each edge of the new room is: 19 feet
Now,
To find the total cost of hardwood floors, find the perimeter of the room and multiply the result with the cost per square foot
Now,
We know that,
The perimeter of a cube = 6s
So,
The perimeter of the cube (p) = 6 × 19
= 114 feet
Now,
The total cost of hardwood floors = 114 × $10
= $1,140
Hence, from the above,
We can conclude that
The total cost of hardwood floors is: $1,140
Question 23.
While packing for their cross-country move, the Chen family uses a crate that has the shape of a cube.
PART A
If the crate has the volume V = 64 cubic feet, what is the length of one edge?
It is given that
While packing for their cross-country move, the Chen family uses a crate that has the shape of a cube and the crate has the volume V = 64 cubic feet
Now,
We know that,
The volume of a cube (V) = s³
So,
According to the given information,
s³ = 64
\(\sqrt[3]{s³}\) = \(\sqrt[3]{64}\)
s = 4 feet
Hence, from the above,
We can conclude that
The length of each edge of the crate is: 4 feet
PART B
The Chens want to pack a large, framed painting. If the framed painting has the shape of a square with an area of 12 square feet, will the painting fit flat against a side of the crate? Explain.
Answer:
It is given that
The Chens want to pack a large, framed painting. If the framed painting has the shape of a square with an area of 12 square feet
Now,
We know that,
The area of a square (A) = s²
So,
According to the given information,
s² = 12
Now,
\(\sqrt{s²}\) = \(\sqrt{12}\)
Now,
![]()
So,
According to the given information,
The side of the crate > The side of the painting
4 > 2.28
Hence, from the above,
We can conclude that
The painting will fit flat against a side of the crate
Topic 1 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary How can you show that a number is a rational number? Lesson 1.2
Answer:
A rational number is a number that can be written as a ratio. That means it can be written as a fraction, in which both the numerator (the number on top) and the denominator (the number on the bottom) are whole numbers
Question 2.
Which shows 0.2\(\overline{3}\) as a fraction? Lesson 1.1
A. \(\frac{2}{33}\)
B. \(\frac{7}{33}\)
C. \(\frac{23}{99}\)
D. \(\frac{7}{30}\)
Answer:
The given expression is: 0.2\(\overline{3}\)
Hence, from the above,
We can conclude that
The options that show 0.2\(\overline{3}[/latex as a fraction is:
Question 3.
Approximate [latex]\sqrt{8}\) to the nearest hundredth. Show your work. Lesson 1.3
Answer:
The given expression is: \(\sqrt{8}\)
Now,
![]()
Hence, from the above,
We can conclude that
The approximate value of the given expression to the nearest hundredth is: 2.82
Question 4.
Solve the equation m2 = 14. Lesson 1.5
Answer:
The given equation is:
m² = 14
Now,
\(\sqrt{m²}\) = ±\(\sqrt{14}\)
Now,
![]()
Hence, from the above,
We can conclude that
The solutions for the given equation are: 3.74, -3.74
Question 5.
A fish tank is in the shape of a cube. Its volume is 125 ft3. What is the area of one face of the tank? Lessons 1.4 and 1.5
Answer:
It is given that
A fish tank is in the shape of a cube. Its volume is 125 ft3.
Now,
We know that,
The volume of a cube (V) = s³
So,
s³= 125
Now,
\(\sqrt[3]{s³}\) = \(\sqrt[3]{125}\)
s = \(\sqrt[3]{5 × 5 × 5}\)
s = 5 ft
Now,
We know that,
The surface area of a cube = 4s²
So,
The area of one face of the tank = 4 × 5²
= 4 × 25
= 100 ft²
Hence, from the above,
We can conclude that
The area of one face of the tank is: 100 ft²
Question 6.
Write 1.\(\overline{12}\) as a mixed number. Show your work. Lesson 1.1
Answer:
The given expression is: 1.\(\overline{12}\)
Now,
The representation of the given expression in the form of a fraction is: \(\frac{28}{25}\)
Now,
The representation of \(\frac{28}{25}\) into a mixed number is: 1\(\frac{3}{25}\)
Hence, from the above,
We can conclude that
The representation of 1.\(\overline{12}\) as a mixed number is: 1\(\frac{3}{25}\)
How well did you do on the mid-topic checkpoint? Fill in the stars. 
Topic 1 MID-TOPIC PERFORMANCE TASK
Six members of the math club are forming two teams for a contest. The teams will be determined by having each student draw a number from a box.
PART A
The table shows the results of the draw. The students who drew rational numbers will form the team called the Tigers. The students who drew irrational numbers will form the team called the Lions. List the members of each team.
Answer:
It is given that
Six members of the math club are forming two teams for a contest. The teams will be determined by having each student draw a number from a box.
Now,
The given table is:

Now,
We know that,
The numbers that can be written in the form of \(\frac{p}{q}\) are “Rational numbers”
The numbers that can not be written in the form of \(\frac{p}{q}\) are “Irrational numbers”
Now,
From the given table,
The list of rational numbers are:
6.\(\overline{34}\), \(\sqrt{36}\), 6.3\(\overline{4}\)
The list of Irrational numbers are:
\(\sqrt{38}\), 6.343443444….,, \(\sqrt{34}\)
Hence, from the above,
We can conclude that
The students present in the Tigers Team are:
6.\(\overline{34}\), \(\sqrt{36}\), 6.3\(\overline{4}\)
The students present in the Lions Team are:
\(\sqrt{38}\), 6.343443444….,, \(\sqrt{34}\)
PART B
The student on each team who drew the greatest number will be the captain of that team. Who will be the captain of the Tigers? Show your work.
Answer:
From Part A,
We can observe that
The students present in the Tigers Team are:
6.\(\overline{34}\), \(\sqrt{36}\), 6.3\(\overline{4}\)
Now,
From the above list of numbers,
We can observe that
6.\(\overline{34}\) is the greater number
Hence, from the above,
We can conclude that
The captain of the Tigers Team is: Anya
PART C
Who will be the captain of the Lions? Show your work.
Answer:
The students present in the Lions Team are:
\(\sqrt{38}\), 6.343443444….,, \(\sqrt{34}\)
Now,
From the above list of numbers,
We can observe that
6.343443444…., is the greater number
Hence, from the above,
We can conclude that
The captain of the Lions Team is: Ryan
Lesson 1.6 Use Properties of Integer Exponents
Solve & Discuss It!
One band’s streaming video concert to benefit a global charity costs $1.00 to view.
The first day, the concert got 2,187 views. The second day, it got about three times as many views. On the third day, it got 3 times as many views as on the second day. If the trend continues, how much money will the band raise on Day 7?

Answer:
It is given that
One band’s streaming video concert to benefit a global charity costs $1.00 to view.
The first day, the concert got 2,187 views. The second day, it got about three times as many views. On the third day, it got 3 times as many views as on the second day
So,
According to the given information,
The amount of money got on the first day of concert = (The total number of views) × $1
= 2,187 × $1
= $2,187
The amount of money got on the second day of concert = (The amount of money got on the first day of concert) × 3
= $2,187 × 3
= $6,561
The amount of money got on the third day of concert = (The amount of money got on the second day of concert) × 3
= $6,561 × 3
= $19,683
The amount of money got on the fourth day of concert = (The amount of money got on the third day of concert) × 3
= $19,683 × 3
= $59,049
The amount of money got on the fifth day of concert = (The amount of money got on the fourth day of concert) × 3
= $59,049 × 3
= $1,77,147
The amount of money got on the sixth day of concert = (The amount of money got on the fifth day of concert) × 3
= $1,77,147 × 3
= $5,31,441
The amount of money got on the seventh day of concert = (The amount of money got on the sixth day of concert) × 3
= $5,31,441 × 3
= $15,94,323
Hence, from the above,
We can conclude that
The amount of money the Band raise on Day 7 is: $15,94,323
Focus on math practices
Use Structure Use prime factorization to write an expression equivalent to the amount of money raised by the band on the last day of the week.
Answer:
From the above,
We can observe that
The amount of money got on the last day of the wee is: $15,94,323
Now,
By using the Prime factorisation method,

Hence, from the above,
We can conclude that
The prime factorisation of 15,94,323 is: 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3
? Essential Question
How do properties of integer exponents help you write equivalent expressions?
Answer:
The properties of integer exponents can be used to write equivalent expressions by combining numeric or algebraic expressions that have a common base, distributing exponents to products and quotients, and simplifying powers of powers.
The local zoo welcomed a newborn African elephant that weighed 34 kg. It is expected that at adulthood, the newborn elephant will weigh approximately 34 times as much as its birth weight. What expression represents the expected adult weight of the newborn elephant?
Answer:
It is given that
The local zoo welcomed a newborn African elephant that weighed 34 kg. It is expected that at adulthood, the newborn elephant will weigh approximately 34 times as much as its birth weight
Now,
According to the given information,
The expected adult weight of the newborn elephant = (The actual weight of the newborn elephant) × (The number of times the expected weight will be as much as its birth weight)
= 34 × 34
Now,
According to the “Product of Powers Property”,
When multiplying two powers with the same bases, add the exponents
So,
The expected adult weight of the newborn elephant = 34 + 4
= 38 kg
Hence, from the above,
We can conclude that
The expected adult weight of the newborn elephant is: 38 kg
Convince Me!
Explain why the Product of Powers Property makes mathematical sense.
Answer:
The Power of a Product rule states that a term raised to a power is equal to the product of its factors raised to the same power
Try It!
Write equivalent expressions using the properties of exponents.
a. (73)2
Answer:
The given expression is: (7³)²
Now,
We know that,
The “Power of Powers Property” states that to find the power of a power, multiply the exponents
So,
(7³)² = 73 × 2
= 76
Hence, from the above,
We can conclude that
The value of the given expression is: 76
b. (45)3
Answer:
The given expression is: (45)3
Now,
We know that,
The “Power of Powers Property” states that to find the power of a power, multiply the exponents
So,
(45)3 = 43 × 5
= 415
Hence, from the above,
We can conclude that
The value of the given expression is: 415
c. 94 × 84
Answer:
The given expression is: 94 × 84
Now,
We know that,
By using the “Power of Products Property”, when multiplying two exponential expressions with the same exponent and different powers, multiply the bases and keep the exponents the same
So,
94 × 84 = (9 × 8)4
= 724
Hence, from the above,
We can conclude that
The value of the given expression is: 724
d. 89 ÷ 83
Answer:
The given expression is: 89 ÷ 83
Now,
We know that,
The “Quotient of powers Property” states that when dividing two exponential expressions with the same base, subtract the exponents
So,
89 ÷ 83 = 89 – 3
= 86
Hence, from the above,
We can conclude that
The value of the given expression is: 86
KEY CONCEPT
Use these properties when simplifying expressions with exponents (when a, m, and n ≠ 0).

Do You Understand?
Question 1.
Essential Question How do properties of integer exponents help you write equivalent expressions?
Answer:
The properties of integer exponents can be used to write equivalent expressions by combining numeric or algebraic expressions that have a common base, distributing exponents to products and quotients, and simplifying powers of powers.
Question 2.
Look for Relationships If you are writing an equivalent expression for 23 × 24, how many times would you write 2 as a factor?
Answer:
It is given that
you are writing an equivalent expression for 23 × 24
Now,
The given expression is: 23 × 24
Now,
We know that,
The “Power of Powers Property” states that to find the power of a power, multiply the exponents
So,
23 × 24 = 23 + 4
= 27
= 2 × 2 × 2 × 2 × 2 × 2 × 2
Hence, from the above,
We can conclude that
We would write 2 as a factor 7 times
Question 3.
Construct Arguments Kristen wrote 58 as an expression equivalent to (52)4. Her math partner writes 56. Who is correct?
Answer:
It is given that
Kristen wrote 58 as an expression equivalent to (52)4. Her math partner writes 56
Now,
The given expression is: 58
Now,
We know that,
(am)n = amn
Now,
According to the above Property,
58 = 54 × 2
= (54)2
= (52)4
Hence, from the above,
We can conclude that
Kristen is correct
Question 4.
Critique Reasoning Tyler says that an equivalent expression for 23 × 53 is 109. Is he correct? Explain.
Answer:
It is given that
Tyler says that an equivalent expression for 23 × 53 is 109
Now,
The given expression is: 23 × 53
Now,
We know that,
am × bm = (a × b)m
So,
23 × 53 = (2 × 5)3
= 103
So,
The equivalent expression for 23 × 53 is: 103
Hence, from the above,
We can conclude that
Tyler is not correct
Do You Know How?
Question 5.
Write an equivalent expression for 712 × 74.
Answer:
The given expression is: 712 × 74
Now,
We know that,
am × an = am + n
So,
712 × 74 = (7)12 + 4
= 716
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 716
Question 6.
Write an equivalent expression for (82)4.
Answer:
The given expression is: (82)4
Now,
We know that,
(am)n = amn
So,
(82)4 = 82 × 4
= 88
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 88
Question 7.
A billboard has the given dimensions.
Using exponents, write two equivalent expressions for the area of the rectangle.
Answer:
It is given that
A billboard has the given dimensions.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The billboard is in the form of a rectangle.
Now,
From the given figure,
We can observe that
The length of the billboard is: 7² ft
The width of the billboard is: 4² ft
Now,
We know that,
We know that,
am × bm = (a × b)m
So,
The area of the rectangle (A) = 7² × 4²
= (7 × 4)²
= 28² ft²
Hence, from the above,
We can conclude that
The two equivalent expressions for the area of the rectangle is: 7² × 4² and 28² ft²
Question 8.
Write an equivalent expression for 189 – 184.
Answer:
The given expression is: 189 – 184
Now,
189 – 184 = 184 (185 – 1)
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 184 (185 – 1)
Practice & Problem Solving
Leveled Practice
In 9-12, use the properties of exponents to write an equivalent expression for each given expression.
Question 9.
28 × 24
Answer:
The given expression is: 28 × 24
Now,
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 212
Question 10.
\(\frac{8^{7}}{8^{3}}\)
Answer:
The given expression is: \(\frac{87}{83}\)
Now,
We know that,
\(\frac{am}{an}\) = am – n
So,
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 84
Question 11.
(34)5
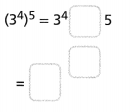
Answer:
The given expression is: (34)5
Now,
We know that,
(am)n = amn
Now,
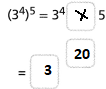
Hence, from the above,
We can conclude that
The equivalent expression for thegiven expression is: 320
Question 12.
39 × 29
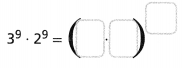
Answer:
The given expression is: 39 × 29
Now,
We know that,
am × bm = (a × b)m
Now,
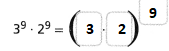
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: (3 × 2)9
Question 13.
a. How do you multiply powers that have the same base?
Answer:
If the two exponential expressions have the same base and different exponents and both are multiplying each other, then add the exponents by keeping the bases same
b. How do you divide powers that have the same base?
Answer:
If the two exponential expressions have the same base and different exponents and both are dividing each other, then subtract the exponents by keeping the bases same
c. How do you find the power of a power?
Answer:
When an exponential expression contains the power of a power, we will multiply both the powers by keeping the base constant
d. How do you multiply powers with different bases but the same exponent?
Answer:
If the two exponential expressions have the same exponent and different bases and both are multiplying each other, then multiply the bases by keeping the exponents same
Question 14.
Which expressions are equivalent to 211?
Select all that apply.
![]() \(\frac{2^{23}}{2^{12}}\)
\(\frac{2^{23}}{2^{12}}\)
![]() 27 ∙ 24
27 ∙ 24
![]() \(\frac{2^{9}}{2^{2}}\)
\(\frac{2^{9}}{2^{2}}\)
![]() 22 ∙ 29
22 ∙ 29
Answer:
The given expression is: 211
Hence, from the above,
We can conclude that
The expressions that are equivalent to 211 are:

In 15-18, use the properties of exponents to write an equivalent expression for each given expression.
Question 15.
(44)3
Answer:
The given expression is: (44)3
Now,
We know that,
(am)n = am × n
So,
(44)3 = 44 × 3
= 412
Hence, from the above,
We can conclude that
(44)3 = 412
Question 16.
\(\frac{3^{12}}{3^{3}}\)
Answer:
The given expression is: \(\frac{3^{12}}{3^{3}}\)
Now,
We know that,
\(\frac{am}{an}\) = am – n
So,
\(\frac{3^{12}}{3^{3}}\) = 312 – 3
= 39
Hence, from the above,
We can conclude that
\(\frac{3^{12}}{3^{3}}\) = 39
Question 17.
45 × 42
Answer:
The given expression is: 45 × 42
Now,
We know that,
am × an = am + n
So,
45 × 42 = 45 + 2
= 47
Hence, from the above,
We can conclude that
45 × 42 = 47
Question 18.
64 × 24
Answer:
The given expression is: 64 × 24
Now,
We know that,
am × bm = (a × b)m
So,
64 × 24 = (6 × 2)4
= 124
Hence, from the above,
We can conclude that
64 × 24 = 124
Question 19.
Critique Reasoning Alberto incorrectly stated that \(\frac{5^{7}}{5^{4}}\) = 13. What was Alberto’s error? Explain your reasoning and find the correct answer.
Answer:
It is given that
Alberto incorrectly stated that \(\frac{5^{7}}{5^{4}}\) = 13
Now,
The given expression is: \(\frac{5^{7}}{5^{4}}\)
Now,
We know that,
\(\frac{am}{an}\) = am – n>
So,
\(\frac{5^{7}}{5^{4}}\) = 5 7 – 4
= 53
So,
From the above,
We can observe that
Alberto applied the “Quotient of Powers Property” incorrectly
Hence, from the above,
We can conclude that
Alberto’s error is: Alberto applied the “Quotient of Powers Property” incorrectly
Question 20.
Is the expression 8 × 85 equivalent to (8 × 8)5? Explain.
Answer:
Question 21.
Is the expression (32)-3 equivalent to (33)-2? Explain.
Answer:
Question 22.
Is the expression 32 ∙ 3-3 equivalent to 33 ∙ 3-2? Explain.
Answer:
Question 23.
Model with Math What is the width of the rectangle written as an exponential expression?
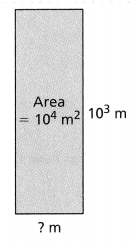
Answer:
Question 24.
Simplify the expression \(\left(\left(\frac{1}{2}\right)^{3}\right)^{3}\).
Answer:
Question 25.
Higher Order Thinking Use a property of exponents to write (3b)5 as a product of powers.
Answer:
Assessment Practice
Question 26.
Select all the expressions equivalent to 45 ∙ 410
![]() 45 + 410
45 + 410
![]() 43 ∙ 45
43 ∙ 45
![]() 43 ∙ 412
43 ∙ 412
![]() 43 + 412
43 + 412
![]() 418 – 43
418 – 43
![]() 415
415
Question 27.
Your teacher asks the class to evaluate the expression (23)1. Your classmate gives an incorrect answer of 16.
PART A
Evaluate the expression.
PART B
What was the likely error?
A. Your classmate divided the exponents.
B. Your classmate multiplied the exponents.
C. Your classmate added the exponents.
D. Your classmate subtracted the exponents.
Answer:
Lesson 1.7 More Properties of Integer Exponents
ACTIVITY
Explore It!
Calvin and Mike do sit-ups when they work out. They start with 64 sit-ups for the first set and do half as many each subsequent set.

Look for Relationships
Determine whether the relationship shown for Set 1 is also true for Sets 2-5.
A. What representation can you use to show the relationship between the set number and the number of sit-ups?
B. What conclusion can you make about the relationship between the number of sit-ups in each set?
Focus on math practices
Use Structure How could you determine the number of sit-up sets Calvin and Mike do?
? Essential Question
What do the Zero Exponent and Negative Exponent Properties mean?
Try It!
Evaluate
a. (-7)0
b. (43)0
c. 10
d. (0.50)
Convince Me!
Why is 2(70) = 2?
Try It!
Write each expression using positive exponents.
a. 8-2
b. 2-4
c. 3-5
Answer:
Try It!
Write each expression using positive exponents.
a. \(\frac{1}{5^{-3}}\)
b. \(\frac{1}{2^{-6}}\)
KEY CONCEPT
Use these additional properties when simplifying or generating equivalent expressions with exponents (when a ≠ 0 and n ≠ 0).
Zero Exponent Property
a0 = 1
Negative Exponent Property
a-n = \(\frac{1}{a^{n}}\)
Do You Understand?
Question 1.
Essential Question What do the Zero Exponent and Negative Exponent Properties mean?
Question 2.
Reasoning In the expression 9-12, what does the negative exponent mean?
Question 3.
Reasoning in the expression 3(20), what is the order of operations? Explain how you would evaluate the expression.
Do You Know How?
Question 4.
Simplify 1,999,9990.
Answer:
Question 5.
a. Write 7-6 using a positive exponent.
b. Rewrite \(\frac{1}{10^{-3}}\) using a positive exponent.
Answer:
Question 6.
Evaluate 27xoy-2 for x = 4 and y = 3.
Answer:
Practice & Problem Solving
Leveled Practice In 7-8, complete each table to find the value of a nonzero number raised to the power of 0.
Question 7.
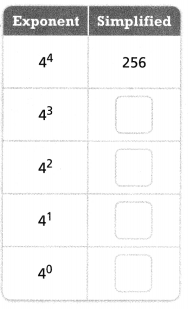
Answer:
Question 8.

Answer:
Question 9.
Given: (-3.2)0
a. Simplify the given expression.
b. Write two expressions equivalent to the given expression. Explain why the three expressions are equivalent.
Answer:
Question 10.
Simplify each expression for x = 6.
a. 12x0(x-4)
b. 14(x-2)
In 11 and 12, compare the values using >,<, or =.
Question 11.
3-2 ![]() 1
1
Answer:
Question 12.
\(\left(\frac{1}{4}\right)^{0}\) ![]() 1
1
In 13 and 14, rewrite each expression using a positive exponent.
Question 13.
9-4
Answer:
Question 14.
\(\frac{1}{2^{-6}}\)
Answer:
Question 15.
Given: 9y0
a. Simplify the expression for y = 3.
b. Construct Arguments Will the value of the given expression vary depending on y? Explain.
Answer:
Question 16.
Simplify each expression for x = 4.
a. -5x-4
b. 7x-3
Answer:
Question 17.
Evaluate each pair of expressions.
a. (-3)-8 and -3-8
b. (-3)-9 and -3-9
Answer:
Question 18.
Be Precise To win a math game, Lamar has to pick a card with an expression that has a value greater than 1. The card Lamar chooses reads \(\left(\frac{1}{2}\right)^{-4}\). Does Lamar win the game? Explain.
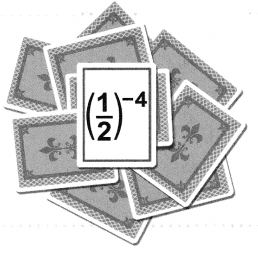
Answer:
Question 19.
Simplify the expression. Assume that x is nonzero. Your answer should have only positive exponents. x-10 ∙ x6
Answer:
Question 20.
Higher Order Thinking
a. Is the value of the expression \(\left(\frac{1}{4^{-3}}\right)^{-2}\) greater than 1, equal to 1, or less than 1?
b. If the value of the expression is greater than 1, show how you can change one sign to make the value less than 1. If the value is less than 1, show how you can change one sign to make the value greater than 1. If the value is equal to 1, show how you can make one change to make the value not equal to 1.
Assessment Practice
Question 21.
Which expressions are equal to 5-3? Select all
that apply.
![]() 125
125
![]() 125-1
125-1
![]() 53
53
![]() \(\frac{1}{5^{3}}\)
\(\frac{1}{5^{3}}\)
![]() \(\frac{1}{125}\)
\(\frac{1}{125}\)
Answer:
Question 22.
Which expressions have a value less than 1 when x = 4? Select all that apply.
![]() \(\left(\frac{3}{x^{2}}\right)^{0}\)
\(\left(\frac{3}{x^{2}}\right)^{0}\)
![]() \(\frac{x^{0}}{3^{2}}\)
\(\frac{x^{0}}{3^{2}}\)
![]() \(\frac{1}{6^{-x}}\)
\(\frac{1}{6^{-x}}\)
![]() \(\frac{1}{x^{-3}}\)
\(\frac{1}{x^{-3}}\)
![]() 3x-4
3x-4
Lesson 1.8 Use Powers of 10 to Estimate Quantities
ACTIVITY
Explain It!
Keegan and Jeff did some research and found that there are approximately 7,492,000,000,000,000,000 grains of sand on Earth. Jeff says that it is about 7 × 1015 grains of sand. Keegan says that this is about 7 × 1018 grains of sand.

A. How might Jeff have determined his estimate? How might Keegan have determined his estimate?
B. Whose estimate, Jeff’s or Keegan’s, is more logical? Explain.
Focus on math practices
Be Precise Do you think the two estimates are close in value? Explain your reasoning.
? Essential Question
when would you use a power of 10 to estimate a quantity?
Try It!
Light travels 299,792,458 meters per second. Sound travels at 332 meters per second. Use a power of 10 to compare the speed of light to the speed of sound.
299,792,458 rounded to the greatest place value is ![]()
There are ![]() zeros in the rounded number.
zeros in the rounded number.
The estimated speed of light is ![]() × 10
× 10![]() meters per second.
meters per second.
3 × 10![]() > 3 × 10
> 3 × 10![]() , so the speed of light is faster than the speed of sound.
, so the speed of light is faster than the speed of sound.
322 rounded to the greatest place value is ![]()
There are ![]() zeros in the rounded number. The estimated speed of sound is
zeros in the rounded number. The estimated speed of sound is ![]() × 10
× 10![]() meters per second.
meters per second.
Convince Me!
Country A has a population of 1,238,682,005 and Country B has a population of 1,106,487,394. How would you compare these populations?
Try It!
There are approximately 1,020,000,000 cars in the world. The number of cars in the United States is approximately 239,800,000.
Compare the number of cars in the world to that in the United States.
KEY CONCEPT
You can estimate a very large or very small number by rounding the number to its greatest place value, and then writing that number as a single digit times a power of 10.

Do You Understand?
Question 1.
? Essential Question when would you use powers of 10 to estimate a quantity?
Answer:
Question 2.
Construct Arguments Kim writes an estimate for the number 0.00436 as 4 × 103. Explain why this cannot be correct.
Answer:
Question 3.
Be Precise Raquel estimated 304,900,000,000 as 3 × 108. What error did she make?
Answer:
Do You Know How?
Question 4.
Use a single digit times a power of 10 to estimate the height of Mt. Everest to the nearest ten thousand feet.

Answer:
Question 5.
A scientist records the mass of a proton as 0.0000000000000000000000016726231 gram. Use a single digit times a power of 10 to estimate the mass.
Answer:
Question 6.
The tanks at the Georgia Aquarium hold approximately 8.4 × 106 gallons of water. The tanks at the Audubon Aquarium of the Americas hold about 400,000 gallons of water. Use a single digit times a power of 10 to estimate how many times greater the amount of water is at the Georgia Aquarium.
Answer:
Practice & Problem Solving
Leveled Practice in 7-9, use powers of 10 to estimate quantities.
Question 7.
A city has a population of 2,549,786 people. Estimate this population to the nearest million. Express your answer as the product of a single digit and a power of 10. Rounded to the nearest million, the population is about ![]()
Written as the product of a single digit and a power of ten, this number is ![]()
Answer:
Question 8.
Use a single digit times a power of 10 to estimate the number 0.00002468. Rounded to the nearest hundred thousandth, the number is about ![]()
Written as a single digit times a power of ten, the estimate is ![]()
Answer:
Question 9.
The approximate circumferences of Earth and Saturn are shown. How many times greater is the circumference of Saturn than the circumference of Earth?
The circumference of Saturn is
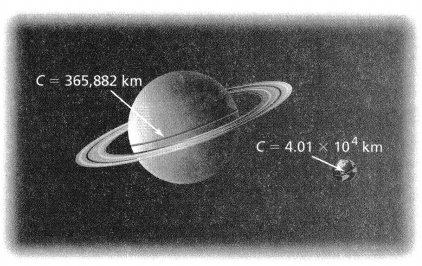
Saturn’s circumference is about![]() times greater than the circumference of Earth.
times greater than the circumference of Earth.
Answer:
Question 10.
Estimate 0.037854921 to the nearest hundredth. Express your answer as a single digit times a power of ten.
Answer:
Question 11.
Compare the numbers 6 × 10-6 and 2 × 10-8.
a. Which number has the greater value?
b. Which number has the lesser value?
c. How many times greater is the greater number?
Answer:
Question 12.
Taylor made $43,785 last year. Use a single digit times a power of ten to express this value rounded to the nearest ten thousand.
Answer:
Question 13.
The length of plant cell A is 8 × 10-5 meter. The length of plant cell B is 0.000004 meter. How many times greater is plant cell A’s length than plant cell B’s length?
Answer:
Question 14.
Critique Reasoning The diameter of one species of bacteria is shown. Bonnie approximates this measure as 3 × 10-11 meter. Is she correct? Explain.
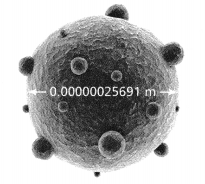
Answer:
Question 15.
The populations of Cities A and B are 2.6 × 105 and 1,560,000, respectively. The population of City C is twice the population of City B. The population of City C is how many times the population of City A?
Answer:
Assessment Practice
Question 16.
Earth is approximately 5 × 109 years old. For which of these ages could this be an approximation?
A. 4,762,100,000 years
B. 48,000,000,000 years
C. 4.45 × 109 years
D. 4.249999999 × 109 years
Answer:
Question 17.
PART A
Express 0.000000298 as a single digit times a power of ten rounded to the nearest ten millionth.
PART B
Explain how negative powers of 10 can be helpful when writing and comparing small numbers.
Answer:
Lesson 1.9 Understand Scientific Notation
ACTIVITY
Solve & Discuss It!
Scientists often write very large or very small numbers using exponents. How might a scientist write the number shown using exponents?

Use Structure
How can you use your knowledge of powers of 10 to rewrite the number?
Focus on math practices
Look for Relationships What does the exponent in 1015 tell you about the value of the number?
? Essential Question
What is scientific notation and why is it used?
Try It!
The height of Angel Falls, the tallest waterfall in the world, is 3,212 feet. How do you write this number in scientific notation?
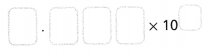
Convince Me!
Why do very large numbers have positive exponents when written in scientific notation? Explain.
Try It!
A common mechanical pencil lead measures about 0.005 meter in diameter. How can you express this measurement using scientific notation ?
Try It!
Write the numbers in standard form.
a. 9.225 × 1018
b. 6.3 × 10-8
Answer:
KEY CONCEPT
Scientific notation is a way to write very large numbers or very small numbers. Scientists use scientific notation as a more efficient and convenient way of writing such numbers.
A number in scientific notation is the product of two factors. The first factor must be greater than or equal to 1 and less than 10. The second factor is a power of 10.

To write a number in scientific notation in standard form, multiply the decimal number by the power of 10.
Do You Understand?
Question 1.
?Essential Question What is scientific notation and why is it used?
Answer:
Question 2.
Critique Reasoning Taylor states that 2,800,000 in scientific notation is 2.8 × 10-6 because the number has six places to the right of the 2. Is Taylor’s reasoning correct?
Answer:
Question 3.
Construct Arguments Sam will write 0.000032 in scientific notation. Sam thinks that the exponent of 10 will be positive. Do you agree? Construct an argument to support your response.
Answer:
Do You Know How?
Question 4.
Express 586,400,000 in scientific notation.
Answer:
Question 5.
The genetic information of almost every living thing is stored in a tiny strand called DNA. Human DNA is 3.4 × 10-8 meter long. Write the length in standard form.
Answer:
Question 6.
The largest virus known to man is the Megavirus, which measures 0.00000044 meter across. Express this number in scientific notation.
Answer:
Question 7.
How would you write the number displayed on the calculator screen in standard form?

Answer:
Practice & Problem Solving
Leveled Practice In 8 and 9, write the numbers in the correct format.
Question 8.
The Sun is 1.5 × 108 kilometers from Earth. 1.5 × 108 is written as ![]() in standard form.
in standard form.
Answer:
Question 9.
Brenna wants an easier way to write 0.0000000000000000587.
0.0000000000000000587 is written as ![]() × 10
× 10![]() in scientific notation.
in scientific notation.
Answer:
Question 10.
Is 23 × 10-8 written in scientific notation? Justify your response.
Answer:
Question 11.
Is 8.6 × 107 written in scientific notation? Justify your response.
Answer:
Question 12.
Simone evaluates an expression using her calculator. The calculator display is shown at the right. Express the number in standard form.

Answer:
Question 13.
Express the number 0.00001038 in scientific notation.
Answer:
Question 14.
Express the number 80,000 in scientific notation.
Answer:
Question 15.
Peter evaluates an expression using his calculator. The calculator display is shown at the right. Express the number in standard form.

Answer:
Question 16.
a. What should you do first to write 5.871 × 10-7 in standard form?
b. Express the number in standard form
Answer:
Question 17.
Express 2.58 × 10-2 in standard form.
Answer:
Question 18.
At a certain point, the Grand Canyon is approximately 1,600,000 centimeters across. Express this number in scientific notation.

Answer:
Question 19.
The length of a bacterial cell is 5.2 × 10-6 meter. Express the length of the cell in standard form.
Answer:
Question 20.
Higher Order Thinking Express the distance 4,300,000 meters using scientific notation in meters, and then in millimeters.
Answer:
Assessment Practice
Question 21.
Which of the following numbers are written in scientific notation?
![]() 12 × 106
12 × 106
![]() 12
12
![]() 6.89 × 106
6.89 × 106
![]() 6.89
6.89
![]() 0.4
0.4
![]() 4 × 10-1
4 × 10-1
Answer:
Question 22.
Jeana’s calculator display shows the number to the right.
PART A
Express this number in scientific notation.
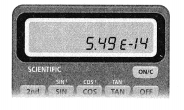
PART B
Express this number in standard form.
3-Act Mathematical Modeling: Hard-Working Organs
3-ACT MATH

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.

Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
АСТ 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.

Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it greater or less than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer;
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
ACT 3
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Generalize What pattern did you notice in your calculations? How did that pattern help you solve the problem?
Answer:
SEQUEL
Question 15.
Use Structure How many times does a heart beat in a lifetime? Use your solution to the Main Question to help you solve.

Answer:
Lesson 1.10 Operations with Numbers in Scientific Notation
Solve & Discuss It!
The homecoming committee wants to fly an aerial banner over the football game. The banner is 1,280 inches long and 780 inches tall. How many different ways can the area of the banner be expressed?

Focus on math practices
Be Precise Which of the solutions is easiest to manipulate?
? Essential Question
How does using scientific notation help when computing with very large or very small numbers?
Try It!
The planet Venus is on average 2.5 × 107 kilometers from Earth. The planet Mars is on average 2.25 × 108 kilometers from Earth. When Venus, Earth, and Mars are aligned, what is the average distance from Venus to Mars?
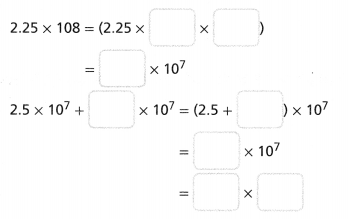
Answer:
Convince Me!
In Example 1 and the Try it, why did you move the decimal point to get the final answer?
Try It!
There are 1 × 1014 good bacteria in the human body. There are 2.6 x 1018 good bacteria among the spectators in a soccer stadium. About how many spectators are in the stadium? Express your answer in scientific notation.
KEY CONCEPT
Operations with very large or very small numbers can be carried out more efficiently using scientific notation. The properties of exponents apply when carrying out operations.

Do You Understand?
Question 1.
? Essential Question
How does using scientific notation help when computing with very small or very large numbers?
Question 2.
Use Structure When multiplying and dividing two numbers in scientific notation, why do you sometimes have to rewrite one factor?
Answer:
Question 3.
Use Structure For the sum of (5.2 × 104) and (6.95 × 104) in scientific notation, why will the power of 10 be 105?
Answer:
Do You Know How?
Question 4.
A bacteriologist estimates that there are 5.2 × 104 bacteria growing in each of 20 petri dishes. About how many bacteria in total are growing in the petri dishes? Express your answer in scientific notation.
Answer:
Question 5.
The distance from Earth to the Moon is approximately 1.2 × 109 feet. The Apollo 11 spacecraft was approximately 360 feet long. About how many spacecraft of that length would fit end to end from Earth to the Moon? Express your answer in scientific notation.

Answer:
Question 6.
The mass of Mars is 6.42 × 1023 kilograms. The mass of Mercury is 3.3 × 1023 kilograms.
a. What is the combined mass of Mars and Mercury expressed in scientific notation?
b. What is the difference in the mass of the two planets expressed in scientific notation?
Answer:
Practice & Problem Solving
Leveled Practice In 7 and 8, perform the operation and express your answer in scientific notation.
Question 7.
(7 × 10-6)(7 × 10-6)
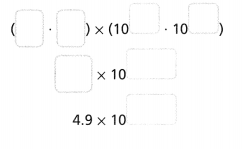
Answer:
Question 8.
(3.76 × 105) + (7.44 × 105)
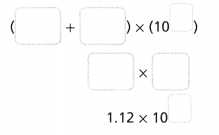
Answer:
Question 9.
What is the value of n in the equation
1.9 × 107 = (1 × 105)(1.9 × 10n)?
Answer:
Question 10.
Find (5.3 × 103) – (8 × 102).
Express your answer in scientific notation.
Answer:
Question 11.
What is the mass of 30,000 molecules? Express your answer in scientific notation.
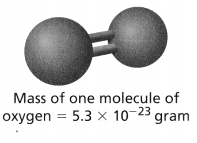
Answer:
Question 12.
Critique Reasoning Your friend says that the product of 4.8 × 108 and 2 × 10-3 is 9.6 × 10-5. Is this answer correct? Explain.
Answer:
Question 13.
Find \(\frac{7.2 \times 10^{-8}}{3 \times 10^{-2}}\). Write your answer in scientific white notation.
Answer:
Question 14.
A certain star is 4.3 × 102 light years from Earth. One light year is about 5.9 × 1012 miles. How far from Earth (in miles) is the star? Express your answer in scientific notation.
Question 15.
The total consumption of fruit juice in a particular country in 2006 was about 2.28 × 109 gallons. The population of that country that year was 3 × 108. What was the average number of gallons consumed per person in the country in 2006?
Answer:
Question 16.
The greatest distance between the Sun and Jupiter is about 8.166 × 108 kilometers. The greatest distance between the Sun and Saturn is about 1.515 × 109 kilometers. What is the difference between these two distances?
Answer:
Question 17.
What was the approximate number of pounds of garbage produced per person in the country in one year? Express your answer in scientific notation.

Answer:
Question 18.
Higher Order Thinking
a. What is the value of n in the equation
1.5 × 1012 = (5 × 105)(3 × 10n)?
b. Explain why the exponent on the left side of the equation is not equal to the sum of the exponents on the right side.
Assessment Practice
Question 19.
Find (2.2 × 105) ÷ (4.4 × 10-3). When you regroup the factors, what do you notice about the quotient of the decimal factors? How does this affect the exponent of the quotient?
Answer:
Question 20.
Which expression has the least value?
A. (4.7 × 104) + (8 × 104)
B. (7.08 × 103) + (2.21 × 103)
C. (5.43 × 108) – (2.33 × 108)
D. (9.35 × 106) – (6.7 × 106)
Answer:
Topic 1 Review
? Topic Essential Question
What are real numbers? How are real numbers used to solve problems?
Vocabulary Review


Use Vocabulary in Writing
Use vocabulary words to explain how to find the length of each side of a square garden with an area of 196 square inches.
Concepts and Skills Review
LESSON 1.1 Rational Numbers as Decimals
Quick Review
You can write repeating decimals in fraction form by writing two equations. You multiply each side of one equation by a power of 10. Then you subtract the equations to eliminate the repeating decimal.
Practice
Write each number as a fraction or a mixed number.
Question 1.
0.\(\overline{7}\)
Answer:
Question 2.
0.0\(\overline{4}\)
Answer:
Question 3.
4.\(\overline{45}\)
Question 4.
2.191919….
Answer:
LESSON 1.2 Understand Irrational Numbers
Quick Review
An irrational number is a number that cannot be written in the form \(\frac{a}{b}\), where a and b are integers and b ≠ 0. Rational and irrational numbers together make up the real number system.

Practice
Question 1.
Determine which numbers are irrational. Select all that apply.
![]() \(\sqrt{36}\)
\(\sqrt{36}\)
![]() \(\sqrt{23}\)
\(\sqrt{23}\)
![]() -4.232323….
-4.232323….
![]() 0.151551555….
0.151551555….
![]() 0.3\(\overline{5}\)
0.3\(\overline{5}\)
![]() π
π
Question 2.
Classify -0.\(\overline{25}\) as rational or irrational. Explain.
Answer:
LESSON 1.3 Compare and Order Real Numbers
Quick Review
To compare and order real numbers, it helps to first write each number in decimal form.
Practice
Question 1.
Between which two whole numbers does \(\sqrt{89}\) lie?
\(\sqrt{89}\) is between ![]() and
and ![]()
Answer:
Question 2.
Compare and order the following numbers. Locate each number on a number line. 2.\(\overline{3}\), \(\sqrt{8}\), 2.5, 2\(\frac{1}{4}\)
Answer:
LESSON 1.4 Evaluate Square Roots and Cube Roots
Quick Review
Remember that a perfect square is the square of an integer. A square root of a number is a number that when multiplied by itself is equal to the original number. Similarly, a perfect cube is the cube of an integer. A cube root of a number is a number that when cubed is equal to the original number.
Practice
Classify each number as a perfect square, a perfect cube, both, or neither.
Question 1.
27
Answer:
Question 2.
100
Answer:
Question 3.
64
Answer:
Question 4.
24
Answer:
Question 5.
A gift box is a cube with a volume of 512 cubic inches. What is the length of each edge of the box?
Answer:
LESSON 1.5 Solve Equations Using Square Roots and Cube Roots
Quick Review
You can use square roots to solve equations involving squares. You can use cube roots to solve equations involving cubes. Equations with square roots often have two solutions. Look at the context to see whether both solutions are valid.
Practice Solve for x.
Question 1.
x3 = 64
Answer:
Question 2.
x2 = 49
Answer:
Question 3.
x3 = 25
Answer:
Question 4.
x2 = 125
Answer:
Question 5.
A container has a cube shape. It has a volume of 216 cubic inches. What are the dimensions of one face of the container?
LESSON 1.6 Use Properties of Integer Exponents
Quick Review
These properties can help you write equivalent expressions that contain exponents.
Product of Powers Property
am.an = am+n
Power of Powers Property
(am)n = amn
Power of Products Property
an ∙ bn = (a ∙ b)n
Quotient of Powers Property
am ÷ an = am-n, when a ≠ 0
Practice
Use the properties of exponents to write an equivalent expression for each given expression.
Question 1.
64 ∙ 63
Answer:
Question 2.
(36)-2
Answer:
Question 3.
73 ∙ 23
Answer:
Question 4.
410 ÷ 44
Answer:
LESSON 1.7 More Properties of Integer Exponents
Quick Review
The Zero Exponent Property states that any nonzero number raised to the power of 0 is equal to 1. The Negative Exponent Property states that for any nonzero rational number a and integer n, a-n = \(\frac{1}{a^{n}}\)
Practice
Write each expression using positive exponents.
Question 1.
9-4
Answer:
Question 2.
\(\frac{1}{3^{-5}}\)
Answer:
Evaluate each expression for x = 2 and y = 5
Question 3.
-4x-2 + 3y0
Answer:
Question 4.
2x0y-2
Answer:
LESSON 1.8 Use Powers of 10 to Estimate Quantities
Quick Review
You can estimate very large and very small quantities by writing the number as a single digit times a power of 10.
Practice
Question 1.
In the year 2013 the population of California was about 38,332,521 people. Write the estimated population as a single digit times a power of 10.
Answer:
Question 2.
The wavelength of green light is about 0.00000051 meter. What is this estimated wavelength as a single digit times a power of 10?
Answer:
Question 3.
The land area of Connecticut is about 12,549,000,000 square meters. The land area of Rhode Island is about 2,707,000,000 square meters. How many times greater is the land area of Connecticut than the land area of Rhode Island?
Answer:
LESSON 1.9 Understand Scientific Notation
Quick Review
A number in scientific notation is written as a product of two factors, one greater than or equal to 1 and less than 10, and the other a power of 10.
Practice
Question 1.
Write 803,000,000 in scientific notation.
Answer:
Question 2.
Write 0.0000000068 in scientific notation.
Answer:
Question 3.
Write 1.359 × 105 in standard form.
Answer:
Question 4.
The radius of a hydrogen atom is 0.000000000025 meter. How would you express this radius in scientific notation?
LESSON 1.10 Operations with Numbers in Scientific Notation
Quick Review
When multiplying and dividing numbers in scientific notation, multiply or divide the first factors. Then multiply or divide the powers of 10. When adding and subtracting numbers in scientific notation, first write the numbers with the same power of 10. Then add or subtract the first factors, and keep the same power of 10.
If the decimal part of the result is not greater than or equal to 1 and less than 10, move the decimal point and adjust the exponent.
Practice
Perform each operation. Express your answers in scientific notation.
Question 1.
(2.8 × 104) × (4 × 105)
Answer:
Question 2.
(6 × 109) ÷ (2.4 × 103)
Question 3.
(4.1 × 104) + (5.6 × 106)
Answer:
Question 4.
The population of Town A is 1.26 × 105 people. The population of Town B is 2.8 × 104 people. How many times greater is the population of Town A than the population of Town B?
Answer:
Topic 1 Fluency Practice
Crisscrossed
Solve each equation. Write your answers in the cross-number puzzle below. Each digit, negative sign, and decimal point of
your answer goes in its own box.
Across
A -377 = x – 1,000
B x3 = 1,000
C x3 = -8
D x + 7 = -209
F x + 19 = -9
J 14 + x = -9
L m – 2.02 = -0.58
M -3.09 + x = -0.7
N -2.49 = -5 + x
Q x – 3.5 = -3.1
T q – 0.63 = 1.16
V 8.3 + x = 12.1
Down
A y – 11 = 49
B x + 8 = 20
C z3 = -1,331
D 11 + x = 3
E x – 14 -7.96
F 14 + x = -19
G d + 200 = 95
H x2 = 144
K -12 = t – 15.95
P 0.3 + x = 11
R x – 3 = -21
S – 7 = -70 + y