We have infinite points in the coordinate plane. A line passes through a point (x, y). The different forms of equations of straight lines are equations of horizontal and vertical lines, Point-slope form, two-point form, slope-intercept form, intercept form, and normal form. Get to know more about the Equation of a Line Parallel to the x-axis in the following sections of this page.
Also, Read:
Equation of a Line Parallel to X-Axis
A line can be defined as a straight one-dimensional geometric figure that doesn’t have the thickness and extends endlessly in both directions. A straight line on the coordinate plane can be described by an equation is called the equation of a line. If all the points the straight line having the same y-coordinate or ordinate values, then it is called the equation of a line parallel to the x-axis.
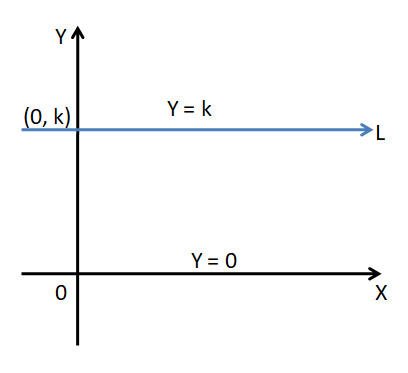
The general form of the equation of a line that is parallel to the x-ais is y = k. Here, k is the distance between the x-axis and the line. If a point P(x, y) lies on the line, then y = b. The equation of x-ais is y = 0 as the x-axis is parallel to itself at a distance of 0 from it.
Different Forms of the Equation of Line
The various forms of the equations of a straight line are long the lines.
Slope Intercept Form
The equation of a slope-intercept form of a straight line is y = mx + b.
Here, m is the slope,
b is the y-intercept.
Point Slope Form
The point-slope form of a line is y – y₁ = m(x – x₁)
Here, m is the slope of the line
(x₁, y₁) is a point on the line.
Two Point Form
The two points form of a line is \(\frac { y – y₁ }{ y₂ – y₁ } = \frac { x – x₁ }{ x₂ – x₁ }\)
Here, (x₁, y₁), (x₂, y₂) are the two points on the line
Slope of the line = \(\frac { y₂ – y₁ }{ x₂ – x₁ } \)
Intercept Form
Intercept form of a line is \(\frac { x }{ a } +\frac { y }{ b }\) = 1
Here, a is the x-intercept
b is the y-intercept
Equation of x-axis
The equation of x-axis is y = 0. Because the value of “ordinate” in all the points on the x-axis is zero.
Equation of y-axis
The equation of y-axis is x = 0. Why because the value of abscissa in all points on the y-axis is zero.
General Equation
The general equation of a straight line is ax + by + c = 0.
Equation of a Line Parallel to X-Axis Examples
Example 1:
Find the equation of a line parallel to the x-axis at a distance of 7 units above the x-axis?
Solution:
We know that the equation of a line parallel to the x-axis at a distance b from it is y = b.
Therefore, the equation of a straight line parallel to the x-axis at a distance 7 units above the x-axis is y = 7.
Example 2:
Find the equation of a line parallel to the x-axis at a distance of 5 units below the x-axis?
Solution:
We know that If a straight line is parallel and below to x-axis at a distance b, then its equation is y = -b.
Therefore, the equation of a line parallel to the x-axis at a distance of 5 units below the x-axis is y = -5.
Example 3:
Find the equation of a straight line parallel to the x-axis at a distance of 10 units above the x-axis?
Solution:
We know that the equation of a line parallel to the x-axis at a distance b from it is y = b.
Therefore, the equation of a straight line parallel to the x-axis at a distance 10 units above the x-axis is y = 10.
FAQs on Equation of Line Parallel to X-Axis
1. How do you find the equation of a line?
The general form of equation of a line is ax + by + c = 0. Any equation in this form is called the equation of a straight line.
2. What is the equation of the line parallel to the x-axis?
The equation of a straight line parallel to the x-axis is y = b as all the points on that line have y-coordinate values as zero’s. Here, b is the distance between the line and the x-axis.
3. How do you write an equation of a line parallel to a line?
The slope-intercept form of a line is y = mx + c. If two lines are parallel, then their slopes are equal and the y-intercept depends on the line points. So, if you know one line, then it is easy to find the equation of a line parallel to the given line and passes through one point.