Engage NY Eureka Math 4th Grade Module 3 Lesson 11 Answer Key
Eureka Math Grade 4 Module 3 Lesson 11 Problem Set Answer Key
Question 1.
Solve the following expressions using the standard algorithm, the partial products method, and the area model.
a. 4 2 5 × 4
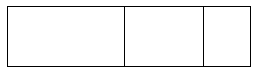
4 (400 + 20 + 5)
(4 × __400___ ) + (4 × _20____ ) + (4 × __5___ )
Answer:
425 X 4 =
Standard Algorithm =
1,2
425
X 4
1,700
Partial Products =
425
X 4
20
80
+ 1600
1,700
Area Model =

425 X 4 = 1,700,
Explanation:
Solved the following expression 425 X 4 using
the standard algorithm =
we add same time of multiplying
1,2
425
X 4
1,700
(4 X 5 ones = 20 ones )+ (4 X 2 tens = 8 tens) +
(4 X 4 hundreds = 16 hundreds) = 20 + 80 + 1,600 = 1,700,
partial products =
425
X 4
20— 4 X 5
80—-4 X 20
+ 1600–4 X 400
1,700
and the area model is as shown in the picture above,
So 425 X 4 = 1,700.
b. 5 3 4 × 7

7 ( __500_ + _30___ + _4___ )
( _7_ × __500___ ) + ( 7__ × __30___ ) + ( 7__ × _4___ )
Answer:
534 X 7 =
Standard Algorithm =
2,2
534
X 7
3,738
Partial Products =
534
X 7
28
210
+3500
3,738
Area Model =

534 X 7 = 3,738,
Explanation:
Solved the following expression 534 X 7 using
the standard algorithm =
we add same time of multiplying
2,2
534
X 7
3,738
(7 X 4 ones = 28 ones )+ (7 X 3 tens = 21 tens) +
(7 X 5 hundreds = 35 hundreds) = 28 + 210 + 3,500 = 3,738,
partial products =
534
X 7
28— 7 X 4
210—-7 X 30
+3500–7 X 500
3,738
and the area model is as shown in the picture above
So 534 X 7 = 3,738.
c. 2 0 9 × 8

8__ ( _200___ + _9___ )
( _8_ × _200____ ) + ( _8_ × __9___ )
Answer:
209 X 8 =
Standard Algorithm =
7,
209
X 8
1,672
Partial Products =
209
X 8
72
0000
+1600
1,672
Area Model =
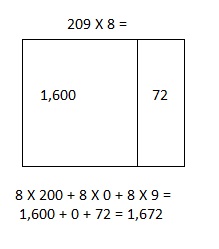
209 X 8 = 1,672,
Explanation:
Solved the following expression 209 X 8 using
the standard algorithm =
we add same time of multiplying
7
209
X 8
1,672
(8 X 9 ones = 72 ones )+ (8 X 0 tens = 0 tens) +
(8 X 2 hundreds = 16 hundreds) = 72 + 0 + 1,600 = 1,672,
partial products =
209
X 8
72— 8 X 9
000—-8 X 0
+1600–8 X 200
1,672
and the area model is as shown in the picture above
So 209 X 8 = 1,672.
Question 2.
Solve using the partial products method.
Cayla’s school has 258 students. Janet’s school has 3 times as many students as Cayla’s. How many students are in Janet’s school?
Answer:
There are in Janet’s school are 774 students,
Explanation:
Given Cayla’s school has 258 students. Janet’s school has
3 times as many students as Cayla’s.
So there are number of students in Janet’s school are
3 X 258 students =
Partial Products =
258
X 3
024
150
+600
774
So there are in Janet’s school are 774 students.
Question 3.
Model with a tape diagram and solve.
4 times as much as 467
Answer:
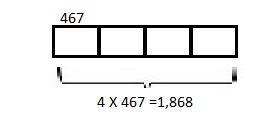
4 X 467 = 1,868,
Explanation:
Modeled with a tape diagram as shown above and
4 times as much as 467 is 4 X 467 =
2,2
467
X 4
1,868
So, 4 X 467 = 1,868.
Solve using the standard algorithm, the area model, the distributive property, or the partial products method.
Question 4.
5,131 × 7
Answer:
Standard algorithm:
5,131
X 7
35,917
Explanation:
Given expression as 5,131 X 7 solving using standard algorithm
method as
2
5,131
X 7
35,917
First we multiply (7 X 1 one = 7 ones) + (7 X 3 tens = 21 tens) +
(7 X 1 hundred = 7 hundreds) + (7 X 5 thousands = 35 thousands),
So 7 X 5,131 = 35,917.
Question 5.
3 times as many as 2,805,
Answer:
3 X 2,805 = 8,415,
Explanation:
Given to find 3 times as many as 2,805 using the
distributive property as shown below
3 X 2,000 + 3 X 800 + 3 X 0 + 3 X 5 =
6,000 + 2,400 + 0 + 15 = 8,415,
So 3 times as many as 2,805 = 8,415.
Question 6.
A restaurant sells 1,725 pounds of spaghetti and
925 pounds of linguini every month. After 9 months,
how many pounds of pasta does the restaurant sell?
Answer:
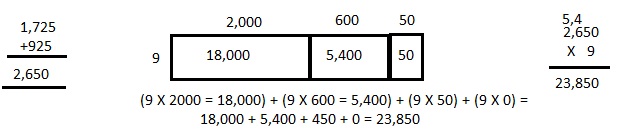
23,850 pounds of pasta the restaurant saled in 9 months,
Explanation:
Given a restaurant sells 1,725 pounds of spaghetti and
925 pounds of linguini every month. After 9 months,
number of pounds of pasta does the restaurant sell is
9 X (1,725 +925) pounds = 9 X 2,650 =
5,4
2,650
X 9
23,850
Solved using the area model as shown above.
Eureka Math Grade 4 Module 3 Lesson 11 Exit Ticket Answer Key
Question 1.
Solve using the standard algorithm, the area model, the distributive property, or the partial products method.
2,809 × 4
Answer:
2,809
X 4
11,236
2,809 X 4 = 11,236,
Explanation:
Solved using the distributive property as shown below
(4 X 2,000) + (4 X 800) + (4 X 0) + (4 X 9) =
8,000 + 3,200 + 0 + 36 =11,236,
So, 2,809 X 4 = 11,236.
Question 2.
The monthly school newspaper is 9 pages long.
Mrs. Smith needs to print 675 copies.
What will be the total number of pages printed?
Answer:
Total number of pages printed are 6,075,
Explanation:
Given the monthly school newspaper is 9 pages long.
and Mrs. Smith needs to print 675 copies,
So the total number of pages printed are 9 X 6,075,
Solving using Partial Products as shown below
6,075
X 9
45—9 X 5
630–9 X 7
000– 9 X 0
5400–9 X 6
6,075
therefore, total number of pages printed are 6,075.
Eureka Math Grade 4 Module 3 Lesson 11 Homework Answer Key
Question 1.
Solve the following expressions using the standard algorithm, the partial products method, and the area model.
a. 3 0 2 × 8

8 (300 + 2)
(8 × _300____ ) + (8 × __2___ )
Answer:
302 X 8 =
Standard Algorithm =
1
302
X 8
2,416
Partial Products =
302
X 8
16
00
+2400
2,416
Area Model =

302 X 8 = 2,416,
Explanation:
Solved the following expression 302 X 8 using
the standard algorithm =
we add same time of multiplying
1
302
X 8
2,416
(8 X 2 ones = 16 ones )+ (8 X 0 tens = 0 tens) +
(8 X 3 hundreds = 24 hundreds) = 16 + 0 + 2,400 = 2,416,
partial products =
302
X 8
16
00
+2400
2,416
and the area model is as shown in the picture above,
So 302 X 8 = 2,416.
b. 2 1 6 × 5
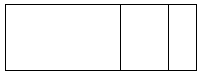
5 ( _200___ + _10___ + _6___ )
( 5__ × __200___ ) + ( _5_ × __10___ ) + ( 5__ × _6___ )
Answer:
216 X 5 =
Standard Algorithm =
3
216
X 5
1,080
Partial Products =
216
X 5
30
50
+1000
1,080
Area Model =

216 X 5 = 1,080,
Explanation:
Solved the following expression 302 X 8 using
the standard algorithm =
we add same time of multiplying
3
216
X 5
1,080
(5 X 6 ones = 30 ones )+ (5 X 1 tens = 5 tens) +
(5 X 2 hundreds = 10 hundreds) = 30 + 50 + 1,000 = 1,080,
partial products =
216
X 5
30
50
+1000
1,080
and the area model is as shown in the picture above,
So 216 X 5 = 1,080.
c. 5 9 3 × 9
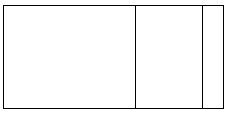
_9_ ( _500___ + _90___ + _3___ )
( _9_ × __500___ ) + ( _9_ × __90___ ) + ( _9_ × __3__ )
Answer:
593 X 9 =
Standard Algorithm =
8,2
593
X 9
5,337
Partial Products =
593
X 9
27
810
+4500
5,337
Area Model =

593 X 9 = 5,337,
Explanation:
Solved the following expression 593 X 9 using
the standard algorithm =
we add same time of multiplying
8,2
593
X 9
5,337
(9 X 3 ones = 27 ones )+ (9 X 9 tens = 81 tens) +
(9 X 5 hundreds = 45 hundreds)= 27 + 810 + 4,500 = 5,337,
partial products =
593
X 9
27
810
+4500
5,337
and the area model is as shown in the picture above,
So 593 X 9 = 5,337.
Question 2.
Solve using the partial products method.
On Monday, 475 people visited the museum.
On Saturday, there were 4 times as many visitors
as there were on Monday. How many people
visited the museum on Saturday?
Answer:
Number of people visited the museum on
Saturday are 1,900,
Partial Products =
475
X 4
20
280
+1600
1,900
Explanation:
Given to solve using the partial products method.
On Monday, 475 people visited the museum.
On Saturday, there were 4 times as many visitors
as there were on Monday.
475
X 4
20
280
+1600
1,900
Number of people visited the museum on Saturday are 1,900.
Question 3.
Model with a tape diagram and solve.
6 times as much as 384
Answer:
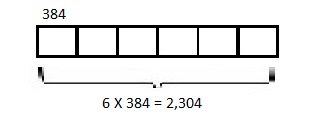
6 X 384 = 2,304,
Explanation:
Modeled with a tape diagram as shown above and
6 times as much as 384 is 4 X 467 =
5,2
384
X 6
2,304
So, 4 X 467 = 2,304.
Solve using the standard algorithm, the area model,
the distributive property, or the partial products method.
Question 4.
6,253 × 3
Answer:
6,253 X 3 = 18,759,
Explanation:
Given expression 6,253 X 3 using the distributive property method
we solve
6000 X 3 + 200 X 3 + 50 X 3 + 3 X 3 =
18,000 + 600 + 150 + 9 = 18,759,
theerfore 6,253 X 3 = 18,759.
Question 5.
7 times as many as 3,073
Answer:
7 times as many as 3,073 is 21,511,
Explanation:
We solve 7 times as many as 3,073 the partial products method as
3,073
X 7
21—- 7 x 3
490—–7 X 70
0000—- 7 X 0
21000—-7 X 3,000
21,511
So, 7 times as many as 3,073 is 21,511.
Question 6.
A cafeteria makes 2,516 pounds of white rice and
608 pounds of brown rice every month. After 6 months,
how many pounds of rice does the cafeteria make?
Answer:
After 6 months 18,744 pounds of rice the cafeteria make,
Explanation:
Given a cafeteria makes 2,516 pounds of white rice and
608 pounds of brown rice every month. Total number of
pounds of rice every month is 2,516 + 608 = 3,124 pounds,
Now number of pounds of rice does the cafeteria make after
6 months is 6 X 3,124 using the standard algorithm we solve as
1,2
3,124
X 6
18,744
First we multiply 6 X 4 ones = 24 ones, 6 X 2 tens = 12 tens,
6 X 1 hundred = 6 hundreds, 6 X 3 thousands = 18 thousands,
24 + 120 + 600 + 1,8000 = 18,744,
therefore, after 6 months 18,744 pounds of rice the cafeteria make.