Engage NY Eureka Math 5th Grade Module 6 Lesson 10 Answer Key
Eureka Math Grade 5 Module 6 Lesson 10 Problem Set Answer Key
Question 1.
Use the coordinate plane below to complete the following tasks.
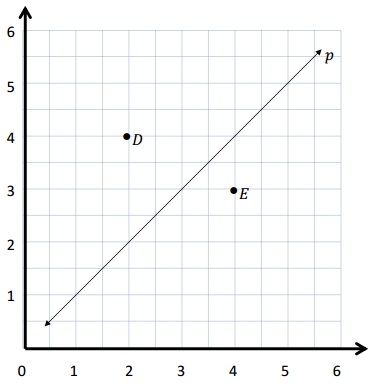
a. Line p represents the rule x and y are equal.
b. Construct a line, d, that is parallel to line p and contains point D.
c. Name 3 coordinate pairs on line d.
d. Identify a rule to describe line d.
e. Construct a line, e, that is parallel to line p and contains point E.
f. Name 3 points on line e.
g. Identify a rule to describe line e.
h. Compare and contrast lines d and e in terms of their relationship to line p.
Answer:
a. Yes, Line p represents the rule x and y are equal because all x and y coordinates are equal .
Some of the coordinate points on line p are ( 1, 1) , (2, 2) .
b. A line, d, that is parallel to line p and contains point D is shown in below graph with coordinate points (1, 3) and (3, 5)
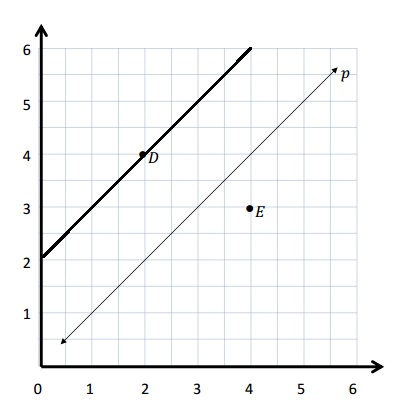
c. The 3 coordinate pairs on line d are (1, 3) , (1\(\frac{1}{2}\), 3\(\frac{1}{2}\)) and (3\(\frac{1}{2}\), 5\(\frac{1}{2}\)) .
d. A rule for line d, is y is 2 more than x .
e. A line, e, that is parallel to line p and contains point E .
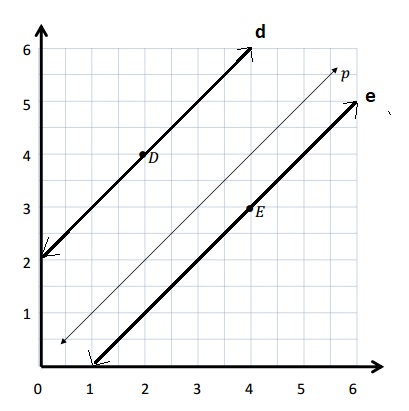
f . 3 points that are on line e are (2, 1) , ( 3, 2) and (5, 4).
g. A rule for line e, is y is 1 less than x .
h. Line p is parallel to line d and line p is parallel to line e .
Question 2.
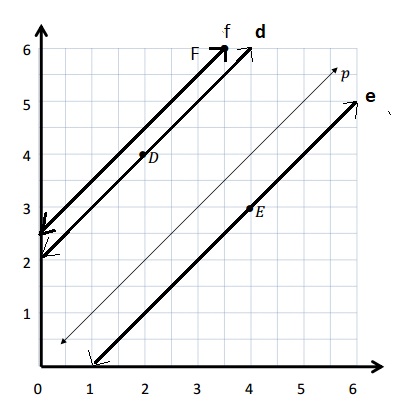
Write a rule for a fourth line that would be parallel to those above and would contain the point (3\(\frac{1}{2}\), 6). Explain how you know.
Answer:
First plot the point F (3\(\frac{1}{2}\), 6) and draw a line that is parallel to line p , d and e.
Question 3.
Use the coordinate plane below to complete the following tasks.
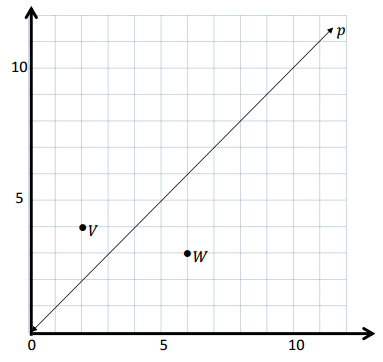
a. Line p represents the rule x and y are equal.
b. Construct a line, v, that contains the origin and point V.
c. Name 3 points on line v.
d. Identify a rule to describe line v.
e. Construct a line, w, that contains the origin and point W.
f. Name 3 points on line w.
g. Identify a rule to describe line w.
h. Compare and contrast lines v and w in terms of their relationship to line p.
i. What patterns do you see in lines that are generated by multiplication rules?
Answer:
a. Yes , Line p represents the rule x and y are equal because the coordinates of x and y are equal .
two coordinate points on line p are (1, 1) and (8, 8)
b.
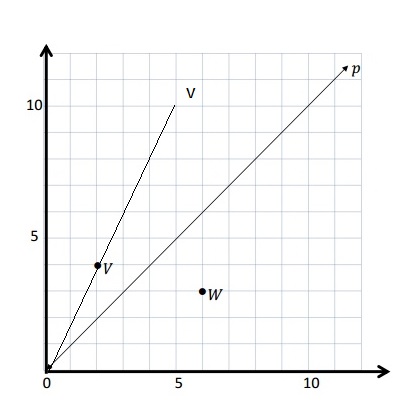
c. The 3 points on line v are ( 2, 4) , (3,6) and ( 4, 8).
d. The rule to describe line v is the y coordinate is double the x coordinate .
e.
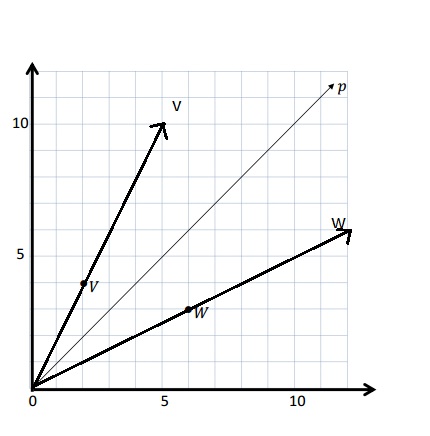
f. The 3 points on line w are (2, 1), (4, 2) and ( 10, 5)
g. The rule to describe line w is the y coordinate is half of x coordinate .
h. The line v is steeper and line w is shallower than p . The rule used is multiplication of x but line v multiplies by a greater number .
i. They are not parallel lines because in line p the x and y coordinates are equal . The v and w lines are stepper and shallower respectively .
Question 4.
Circle the rules that generate lines that are parallel to each other.
add 5 to x
multiply x by \(\frac{2}{3}\)
x plus \(\frac{1}{2}\)
x times 1\(\frac{1}{2}\)
Answer:

Eureka Math Grade 5 Module 6 Lesson 10 Exit Ticket Answer Key
Use the coordinate plane below to complete the following tasks.
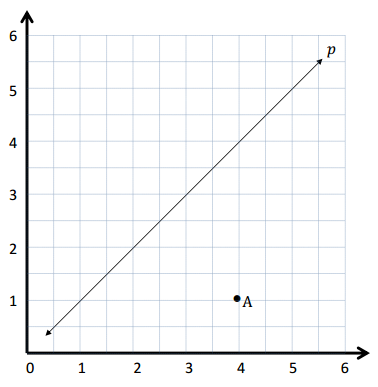
a. Line p represents the rule x and y are equal.
b. Construct a line, a, that is parallel to line p and contains point A.
c. Name 3 points on line a.
d. Identify a rule to describe line a.
Answer:
b.
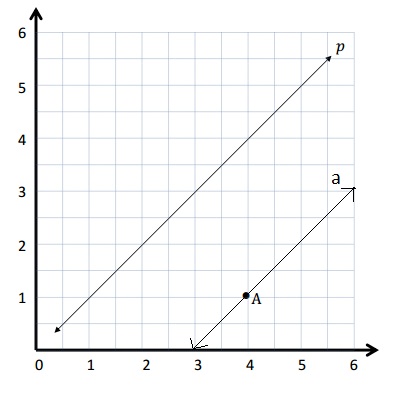
c. The 3 points on line a are (4, 1) , ( 5, 2) and (6, 3)
d. The rule to describe line a is the y coordinate is 3 less than x coordinate .
Eureka Math Grade 5 Module 6 Lesson 10 Homework Answer Key
Question 1.
Use the coordinate plane to complete the following tasks.
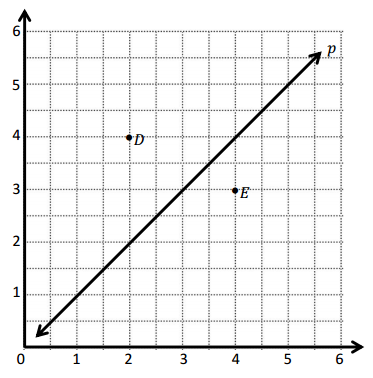
a. Line p represents the rule x and y are equal.
b. Construct a line, d, that is parallel to line p and contains point D.
c. Name 3 coordinate pairs on line d.
d. Identify a rule to describe line d.
e. Construct a line, e, that is parallel to line p and contains point E.
f. Name 3 points on line e.
g. Identify a rule to describe line e.
h. Compare and contrast lines d and e in terms of their relationship to line p.
Answer:
b.
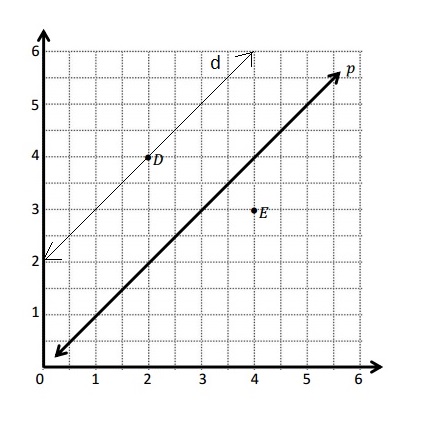
c. The 3 coordinates pairs of line d are (1, 3) , (2, 4) and (3, 5).
d. The rule to describe line d is the y coordinate is 2 more than the x coordinate .
e.
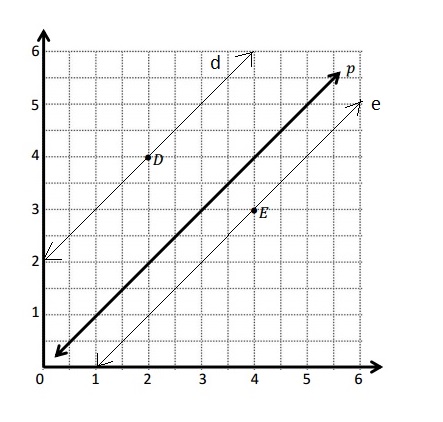
f. The 3 points on line e are (2, 1) , (3, 2) and (5, 4) .
g. The rule to describe line e is the y coordinate is 1 less than the x coordinate .
h. Line d and Line e are both parallel to line p .
Question 2.
Write a rule for a fourth line that would be parallel to those above and that would contain the point (5\(\frac{1}{2}\), 2). Explain how you know.
Answer:
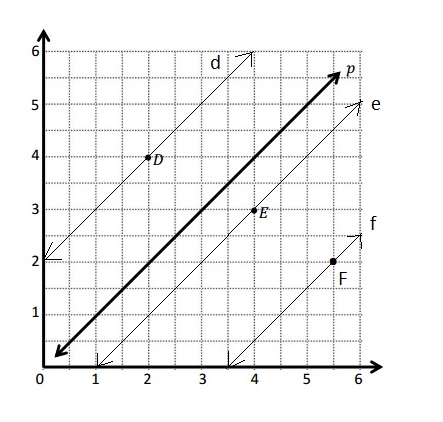
Explanation :
First mark the point F ((5\(\frac{1}{2}\), 2)) and then draw a line that is parallel to line p .
The 3 coordinate points on line f are (4, \(\frac{1}{2}\)) , (4 \(\frac{1}{2}\), 1 ) and (6 , 2\(\frac{1}{2}\)).
The rule for line f is the y coordinate is 3\(\frac{1}{2}\) less than the x coordinate .
Question 3.
Use the coordinate plane below to complete the following tasks.
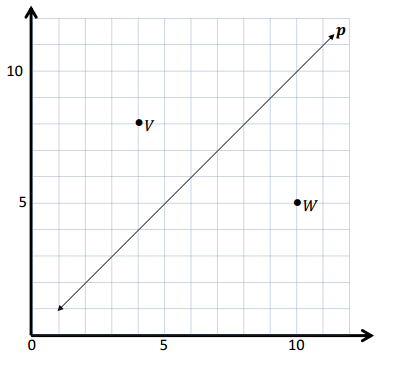
a. Line p represents the rule x and y are equal.
b. Construct a line, v, that contains the origin and point V.
c. Name 3 points on line v.
d. Identify a rule to describe line v.
e. Construct a line, w, that contains the origin and point W.
f. Name 3 points on line w.
g. Identify a rule to describe line w.
h. Compare and contrast lines v and w in terms of their relationship to line p.
i. What patterns do you see in lines that are generated by multiplication rules?
Answer:
b.
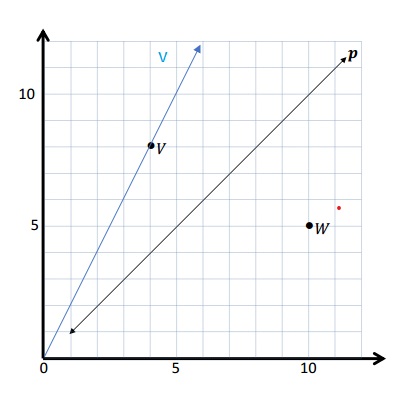
c. The 3 points on line v are (1, 2) , ( 2, 4) and (5, 10) .
d. The rule to describe the line v is the y coordinate is double the x coordinate .
e.
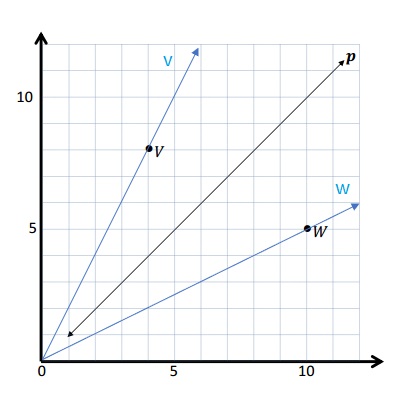
f. The 3 coordinate points on line w are ( 2, 1), (4, 2) and (6, 3) .
g. The rule to describe the line w is the y coordinate is half of x coordinate .
h. The line v is steeper and line w is shallower than p . The rule used is multiplication of x but line v multiplies by a greater number .
i. They are not parallel lines because in line p the x and y coordinates are equal . The v and w lines are stepper and shallower respectively .