Engage NY Eureka Math 6th Grade Module 4 Lesson 8 Answer Key
Eureka Math Grade 6 Module 4 Lesson 8 Example Answer Key
Example 1.
Additive Identity Property of Zero
g + 0 = g
Remember a letter in a mathematical expression represents a number. Can we replace g with any number?
Answer:
Yes
Choose a value for g, and replace g with that number in the equation. What do you observe?
Answer:
The value of g does not change when 0 is added to g.
Repeat this process several times, each time choosing a different number for g.
Will all values of result in a true number sentence?
Answer:
Yes
Write the mathematical language for this property below:
Answer:
g + 0 = g, additive identity property of zero. Any number added to zero equals itself.
Example 2.
Multiplicative Identity Property of One
g × 1 = g
Remember a letter in a mathematical expression represents a number. Can we replace g with any number?
Answer:
Yes
Choose a value for g, and replace g with that number in the equation. What do you observe?
Answer:
The value of g does not change when g is multiplied by 1.
Will all values of result in a true number sentence? Experiment with different values before making your claim.
Answer:
Yes
Write the mathematical language for this property below:
Answer:
g × 1 = g, multiplicative identity property of one. Any number multiplied by one equals itself.
Example 3.
Commutative Property of Addition and Multiplication
3 + 4 = 4 + 3
3 × 4 = 4 × 3
Replace the 3’s in these number sentences with the letter
Answer:
a + 4 = 4 + a
a × 4 = 4 × a
Choose a value for a, and replace with that number in each of the equations. What do you observe?
Answer:
The result is a true number sentence.
Will all values of result in a true number sentence? Experiment with different values before making your claim.
Answer:
Yes, any number, even zero, can be used in place of the variable
Now, write the equations again, this time replacing the number 4 with a variable, b.
Answer:
a + b = b + a
a × b = b × a
Will all values of and result in true number sentences for the first two equations? Experiment with different values before making your claim.
Answer:
Yes
Write the mathematical language for this property below:
Answer:
a + b = b + a commutative property of addition. Order does not matter when adding.
a × b = b × a commutative property of multiplication. Order does not matter when multiplying.
Example 4.
3 + 3 + 3 + 3 = 4 × 3
3 ÷ 4 = \(\frac{3}{4}\)
Replace the 3’s in these number sentences with the letter
Answer:
a + a + a + a = 4 × a
a ÷ 4 = \(\frac{a}{4}\)
Choose a value for a, and replace a with that number in each of the equations. What do you observe?
Answer:
The result is a true number sentence.
Will all values of a result in a true number sentence? Experiment with different values before making your claim.
Answer:
Yes, any number, even zero, can be used in place of the variable
Now, write the equations again, this time replacing the number 4 with a variable, b.
Answer:
a + a + a + a = b × a
a ÷ b = \(\frac{a}{b}\), b ≠ 0
Will all values of and result in true number sentences for the equations? Experiment with different values before making your claim.
Answer:
In the equation a + a + a + a = b × a, any value can be substituted for the variable a, but only 4 can be used for b since there are exactly 4 copies of a in the equation.
It is true for all values of and all values of b ≠ 0.
Eureka Math Grade 6 Module 4 Lesson 8 Problem Set Answer Key
Question 1.
State the commutative property of addition using the variables a and b.
Answer:
a + b = b + a
Question 2.
State the commutative property of multiplication using the variables a and b.
Answer:
a × b = b × a
Question 3.
State the additive property of zero using the variable b.
Answer:
b + 0 = b
Question 4.
State the multiplicative identity property of one using the variable b.
Answer:
b × 1 = b
Question 5.
Demonstrate the property listed in the first column by filling in the third column of the table.

Answer:
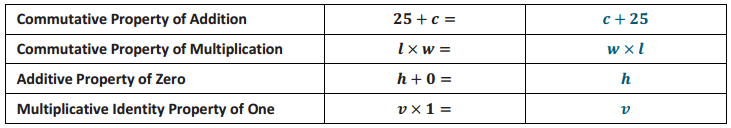
Question 6.
Why is there no commutative property for subtraction or division? Show examples.
Answer:
Answers will vary. Examples should show reasoning and proof that the commutative property does not work for subtraction and division. An example would be 8 ÷ 2 and 2 ÷ 8. 8 ÷ 2 = 4, but 2 ÷ 8 = \(\frac{1}{4}\).
Eureka Math Grade 6 Module 4 Lesson 8 Exit Ticket Answer Key
Question 1.
State the commutative property of addition, and provide an example using two different numbers.
Answer:
Any two different addends can be chosen, such as 5 + 6 = 6 + 5.
Question 2.
State the commutative property of multiplication, and provide an example using two different numbers.
Answer:
Any two different factors can be chosen, such as 4 × 9 = 9 × 4.
Question 3.
State the additive property of zero, and provide an example using any other number.
Answer:
Any nonzero addend can be chosen, such as 3 + 0 = 3.
Question 4.
State the multiplicative identity property of one, and provide an example using any other number.
Answer:
Any nonzero factor can be chosen, such as 12 × 1 = 12.
Eureka Math Grade 6 Module 4 Lesson 8 Opening Exercise Answer Key
4 + 0 = 4
4 × 1 = 4
4 ÷ 1 = 4
4 × 0 = 0
1 ÷ 4 = \(\frac{1}{4}\)
How many of these statements are true?
Answer:
All of them
How many of those statements would be true if the number was replaced with the number in each of the number sentences?
Answer:
All of them
Would the number sentences be true if we were to replace the number with any other number?
What if we replaced the number 4 with the number 0? Would each of the number sentences be true?
Answer:
No. The first four are true, but the last one, dividing by zero, is not true.
What if we replace the number 4 with a letter g? Please write all 4 expressions below, replacing each 4 with a g.
Answer:
g + 0 = g
g × 1 = g
g ÷ 1 = g
g × 0 = 0
1 ÷ g = \(\frac{1}{g}\)
Are these all true (except for g= 0) when dividing?
Answer:
Yes
Eureka Math Grade 6 Module 4 Lesson 8 Division of Fractions II Answer Key
Division of Fractions II – Round 1
Directions: Determine the quotient of the fractions and simplify.
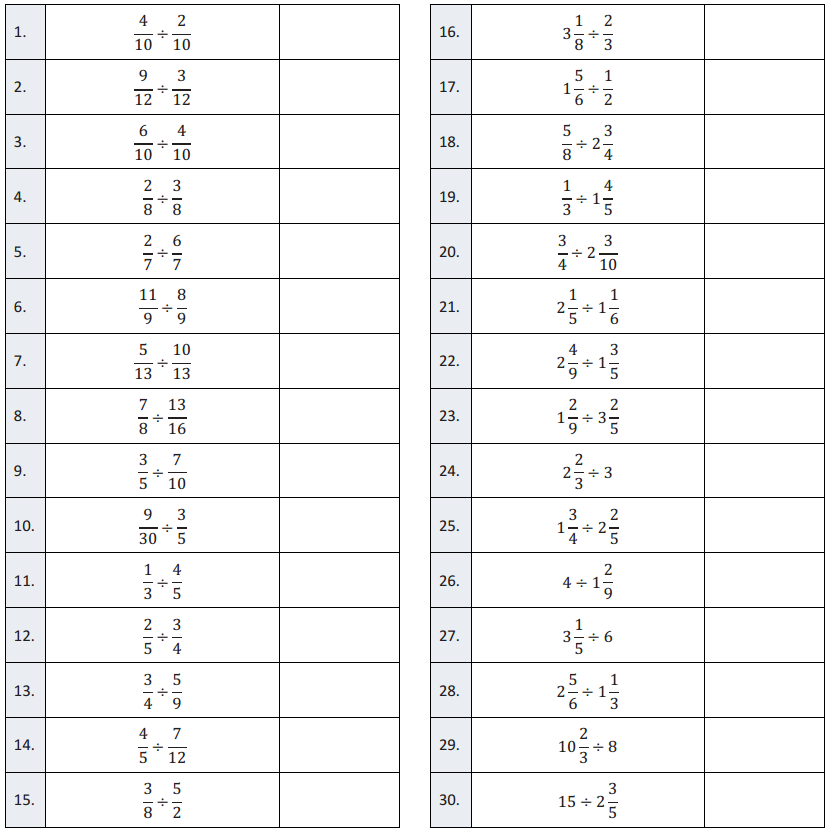
Question 1.
\(\frac{4}{10} \div \frac{2}{10}\)
Answer:
\(\frac{4}{2}\) = 2
Question 2.
\(\frac{9}{12} \div \frac{3}{12}\)
Answer:
\(\frac{9}{3}\) = 3
Question 3.
\(\frac{6}{10} \div \frac{4}{10}\)
Answer:
\(\frac{6}{4}=\frac{3}{2}=1 \frac{1}{2}\)
Question 4.
\(\frac{2}{8} \div \frac{3}{8}\)
Answer:
\(\frac{2}{3}\)
Question 5.
\(\frac{2}{7} \div \frac{6}{7}\)
Answer:
\(\frac{2}{6}=\frac{1}{3}\)
Question 6.
\(\frac{11}{9} \div \frac{8}{9}\)
Answer:
\(\frac{11}{8}=1 \frac{3}{8}\)
Question 7.
\(\frac{5}{13} \div \frac{10}{13}\)
Answer:
\(\frac{5}{10}=\frac{1}{2}\)
Question 8.
\(\frac{7}{8} \div \frac{13}{16}\)
Answer:
\(\frac{14}{13}=1 \frac{1}{13}\)
Question 9.
\(\frac{3}{5} \div \frac{7}{10}\)
Answer:
\(\frac{6}{7}\)
Question 10.
\(\frac{9}{30} \div \frac{3}{5}\)
Answer:
\(\frac{9}{18}=\frac{1}{2}\)
Question 11.
\(\frac{1}{3} \div \frac{4}{5}\)
Answer:
\(\frac{5}{12}\)
Question 12.
\(\frac{2}{5} \div \frac{3}{4}\)
Answer:
\(\frac{8}{15}\)
Question 13.
\(\frac{3}{4} \div \frac{5}{9}\)
Answer:
\(\frac{27}{20}=1 \frac{7}{20}\)
Question 14.
\(\frac{4}{5} \div \frac{7}{12}\)
Answer:
\(\frac{48}{35}=1 \frac{13}{35}\)
Question 15.
\(\frac{3}{8} \div \frac{5}{2}\)
Answer:
\(\frac{6}{40}=\frac{3}{20}\)
Question 16.
\(3 \frac{1}{8} \div \frac{2}{3}\)
Answer:
\(\frac{75}{16}=4 \frac{11}{16}\)
Question 17.
\(1 \frac{5}{6} \div \frac{1}{2}\)
Answer:
\(\frac{22}{6}=\frac{11}{3}=3 \frac{2}{3}\)
Question 18.
\(\frac{5}{8} \div 2 \frac{3}{4}\)
Answer:
\(\frac{20}{88}=\frac{5}{22}\)
Question 19.
\(\frac{1}{3} \div 1 \frac{4}{5}\)
Answer:
\(\frac{5}{27}\)
Question 20.
\(\frac{3}{4} \div 2 \frac{3}{10}\)
Answer:
\(\frac{30}{92}=\frac{15}{46}\)
Question 21.
\(2 \frac{1}{5} \div 1 \frac{1}{6}\)
Answer:
\(\frac{66}{35}=1 \frac{31}{35}\)
Question 22.
\(2 \frac{4}{9} \div 1 \frac{3}{5}\)
Answer:
\(\frac{110}{72}=\frac{55}{36}=1 \frac{19}{36}\)
Question 23.
\(1 \frac{2}{9} \div 3 \frac{2}{5}\)
Answer:
\(\frac{55}{153}\)
Question 24.
\(2 \frac{2}{3} \div 3\)
Answer:
\(\frac{8}{9}\)
Question 25.
\(1 \frac{3}{4} \div 2 \frac{2}{5}\)
Answer:
\(\frac{35}{48}\)
Question 26.
\(4 \div 1 \frac{2}{9}\)
Answer:
\(\frac{36}{11}=3 \frac{3}{11}\)
Question 27.
\(3 \frac{1}{5} \div 6\)
Answer:
\(\frac{16}{30}=\frac{8}{15}\)
Question 28.
\(2 \frac{5}{6} \div 1 \frac{1}{3}\)
Answer:
\(\frac{51}{24}=2 \frac{3}{24}=2 \frac{1}{8}\)
Question 29.
\(10 \frac{2}{3} \div 8\)
Answer:
\(\frac{32}{24}=\frac{4}{3}=1 \frac{1}{3}\)
Question 30.
\(15 \div 2 \frac{3}{5}\)
Answer:
\(\frac{75}{13}=5 \frac{10}{13}\)
Division of Fractions II – Round 2
Directions: Determine the quotient of the fractions and simplify.
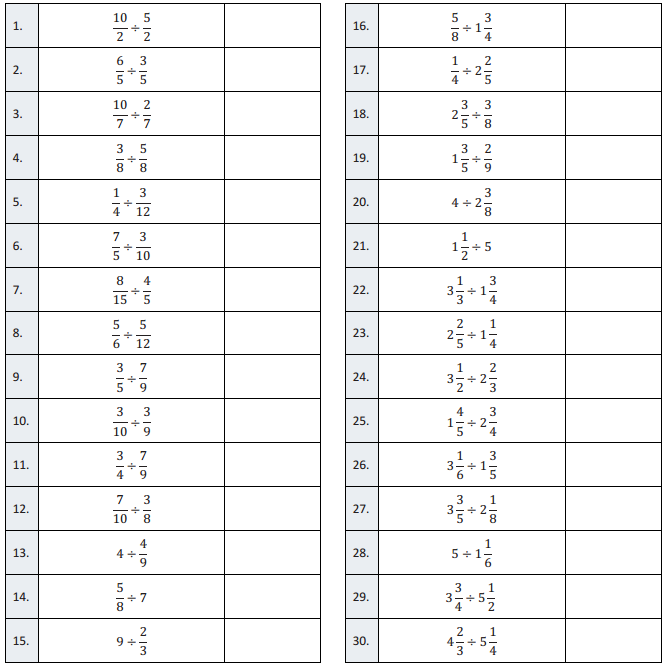
Question 1.
\(\frac{10}{2} \div \frac{5}{2}\)
Answer:
\(\frac{10}{5}\) = 2
Question 2.
\(\frac{6}{5} \div \frac{3}{5}\)
Answer:
\(\frac{6}{3}\) = 2
Question 3.
\(\frac{10}{7} \div \frac{2}{7}\)
Answer:
\(\frac{10}{2}\) = 5
Question 4.
\(\frac{3}{8} \div \frac{5}{8}\)
Answer:
\(\frac{3}{5}\)
Question 5.
\(\frac{1}{4} \div \frac{3}{12}\)
Answer:
\(\frac{3}{3}\) = 1
Question 6.
\(\frac{1}{4} \div \frac{3}{12}\)
Answer:
\(\frac{14}{3}=4 \frac{2}{3}\)
Question 7.
\(\frac{8}{15} \div \frac{4}{5}\)
Answer:
\(\frac{8}{12}=\frac{2}{3}\)
Question 8.
\(\frac{5}{6} \div \frac{5}{12}\)
Answer:
\(\frac{10}{5}\) = 2
Question 9.
\(\frac{3}{5} \div \frac{7}{9}\)
Answer:
\(\frac{27}{35}\)
Question 10.
\(\frac{3}{10} \div \frac{3}{9}\)
Answer:
\(\frac{27}{30}=\frac{9}{10}\)
Question 11.
\(\frac{3}{4} \div \frac{7}{9}\)
Answer:
\(\frac{27}{28}\)
Question 12.
\(\frac{7}{10} \div \frac{3}{8}\)
Answer:
\(\frac{56}{30}=\frac{28}{15}=1 \frac{13}{15}\)
Question 13.
\(4 \div \frac{4}{9}\)
Answer:
\(\frac{36}{4}\) = 9
Question 14.
\(\frac{5}{8} \div 7\)
Answer:
\(\frac{5}{56}\)
Question 15.
\(9 \div \frac{2}{3}\)
Answer:
\(\frac{27}{2}=13 \frac{1}{2}\)
Question 16.
\(\frac{5}{8} \div 1 \frac{3}{4}\)
Answer:
\(\frac{20}{56}=\frac{5}{14}\)
Question 17.
\(\frac{1}{4} \div 2 \frac{2}{5}\)
Answer:
\(\frac{5}{48}\)
Question 18.
\(2 \frac{3}{5} \div \frac{3}{8}\)
Answer:
\(\frac{104}{15}=6 \frac{14}{15}\)
Question 19.
\(1 \frac{3}{5} \div \frac{2}{9}\)
Answer:
\(\frac{72}{10}=7 \frac{2}{10}=7 \frac{1}{5}\)
Question 20.
\(4 \div 2 \frac{3}{8}\)
Answer:
\(\frac{32}{19}=1 \frac{13}{19}\)
Question 21.
\(1 \frac{1}{2} \div 5\)
Answer:
\(\frac{3}{10}\)
Question 22.
\(3 \frac{1}{3} \div 1 \frac{3}{4}\)
Answer:
\(\frac{40}{21}=1 \frac{19}{21}\)
Question 23.
\(2 \frac{2}{5} \div 1 \frac{1}{4}\)
Answer:
\(\frac{48}{25}=1 \frac{23}{25}\)
Question 24.
\(3 \frac{1}{2} \div 2 \frac{2}{3}\)
Answer:
\(\frac{21}{16}=1 \frac{5}{16}\)
Question 25.
\(1 \frac{4}{5} \div 2 \frac{3}{4}\)
Answer:
\(\frac{36}{55}\)
Question 26.
\(3 \frac{1}{6} \div 1 \frac{3}{5}\)
Answer:
\(\frac{95}{48}=1 \frac{47}{48}\)
Question 27.
\(3 \frac{3}{5} \div 2 \frac{1}{8}\)
Answer:
\(\frac{144}{85}=1 \frac{59}{85}\)
Question 28.
\(5 \div 1 \frac{1}{6}\)
Answer:
\(\frac{30}{7}=4 \frac{2}{7}\)
Question 29.
\(3 \frac{3}{4} \div 5 \frac{1}{2}\)
Answer:
\(\frac{30}{44}=\frac{15}{22}\)
Question 30.
\(4 \frac{2}{3} \div 5 \frac{1}{4}\)
Answer:
\(\frac{56}{63}=\frac{8}{9}\)