Gain Complete Knowledge required on the Concept Divide Fractions by accessing our Go Math Grade 5 Answer Key Chapter 8. You will have Questions belonging to practice problems, mid-chapter, and review tests along with detailed explanations. Those, who are in search of Go Math Grade 5 Answer Key can download them free of cost.
We have compiled HMH 5th Grade Go Math Answer Key Ch 8 Dividing Fractions with Step by Step Solutions making it easy to grab the concepts within easily. Tap on the direct links available for Lessons of Ch 8 Dividing Fractions to get the problems related to them instantly.
Go Math Grade 5 Answer Key Chapter 8 Divide Fractions
Score better grades in your exams by practicing from the HMH Go Math 5th Grade Solution Key. Firstly, solve the problems on your own and later cross-check them with the Solutions Provided and improve your Math Skills. You will have topics like Divide Fractions and Whole Numbers, Interpret Division with Fractions and Fraction, Connect Fractions to Division, and Whole-Number Division.
Lesson 1: Investigate • Divide Fractions and Whole Numbers
Lesson 2: Problem Solving • Use Multiplication
Lesson 3: Connect Fractions to Division
Mid-Chapter Checkpoint
Lesson 4: Fraction and Whole-Number Division
Lesson 5: Interpret Division with Fractions
Chapter 8: Review/Test
- Chapter Review/Test – Page No. 361
- Chapter Review/Test – Page No. 362
- Chapter Review/Test – Page No. 363
- Chapter Review/Test – Page No. 364
Share and Show – Page No. 341
Divide and check the quotient.
Question 1.

3 ÷ \(\frac{1}{3}\) = _____ because _____ × \(\frac{1}{3}\) = 3
Answer: 3 ÷ \(\frac{1}{3}\) = 9 because 9 × \(\frac{1}{3}\) = 3
Explanation:
Step 1: Place a \(\frac{1}{3}\) strip under a three 1 whole strip to show the \(\frac{1}{3}\).
Step 2: Find 9 fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{3}\) strip.
Each piece is \(\frac{1}{3}\) of the whole.
Step 3: Record and check the quotient.
3 ÷ \(\frac{1}{3}\) = 9 because 9 × \(\frac{1}{3}\) = 3
Question 2.

Think: What label should I write for each tick mark?
3 ÷ \(\frac{1}{6}\) = _____ because _____ × \(\frac{1}{6}\) = 3
Answer: 18, 18
Explanation:
Step 1: Skip count by sixths from 0 to 3 find 3 ÷ \(\frac{1}{6}\).
Step 2: There are 18 one-sixths in 3 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Now record and check the quotient.
3 ÷ \(\frac{1}{6}\) = 18 because 18 × \(\frac{1}{6}\) = 3
Question 3.

\(\frac{1}{4}\) ÷ 2 = \(\frac{□}{□}\)
Answer: \(\frac{1}{8}\)
Explanation:
Step 1: Place a \(\frac{1}{4}\) strip under a 1 whole strip to show the \(\frac{1}{4}\) on the strip.
Step 2: Find 2 \(\frac{1}{8}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{4}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\)
Divide. Draw a number line or use fraction strips.
Question 4.
1 ÷ \(\frac{1}{3}\) = _____
Answer: 3
Explanation:
Step 1: Skip count by thirds from 0 to 1 find 1 ÷ \(\frac{1}{3}\).
Step 2: There are 3 \(\frac{1}{3}\) in 1 whole.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Now record and check the quotient.
1 ÷ \(\frac{1}{3}\) = 3
Question 5.
3 ÷ \(\frac{1}{4}\) = _____
Answer: 12
Explanation:
Step 1: Skip count by fourths from 0 to 3 find 3 ÷ \(\frac{1}{4}\).
Step 2: There are 12 one-fourths in 3 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Now record and check the quotient.
3 ÷ \(\frac{1}{4}\) = 12 because 12 × \(\frac{1}{4}\) = 3
Question 6.
\(\frac{1}{5}\) ÷ 2 = _____
Answer: \(\frac{1}{10}\)
Explanation:
Step 1: Place a \(\frac{1}{5}\) strip under a 2 whole strip to show the \(\frac{1}{5}\) on the strip.
Step 2: Find 2 \(\frac{1}{10}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{5}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{5}\) ÷ 2 = \(\frac{1}{10}\)

Question 7.
2 ÷ \(\frac{1}{2}\) = _____
Answer: 4
Explanation:
Step 1: Skip count by halves from 0 to 2 find 2 ÷ \(\frac{1}{2}\).
Step 2: There are 4 halves in 2 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
2 ÷ \(\frac{1}{2}\) = 4 because 4 × \(\frac{1}{2}\) = 2
Question 8.
\(\frac{1}{4}\) ÷ 3 = _____
Answer: \(\frac{1}{12}\)
Explanation:
Step 1: Place a \(\frac{1}{4}\) strip under a 3 whole strip to show the \(\frac{1}{4}\) on the strip.
Step 2: Find 3 \(\frac{1}{12}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{4}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\)
Question 9.
5 ÷ \(\frac{1}{2}\) = _____
Answer: 10
Explanation:
Step 1: Skip count by halves from 0 to 5 find 5 ÷ \(\frac{1}{2}\).
Step 2: There are 10 halves in 5 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
5 ÷ \(\frac{1}{2}\) = 10 because 10 × \(\frac{1}{2}\) = 5
Question 10.
4 ÷ \(\frac{1}{2}\) = _____
Answer: 8
Explanation:
Step 1: Skip count by halves from 0 to 4 find 4 ÷ \(\frac{1}{2}\).
Step 2: There are 8 halves in 4 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
4 ÷ \(\frac{1}{2}\) = 8 because 8 × \(\frac{1}{2}\) = 4
Question 11.
\(\frac{1}{6}\) ÷ 2 = _____
Answer: \(\frac{1}{12}\)
Explanation:
Step 1: Place a \(\frac{1}{6}\) strip under a 2 whole strip to show the \(\frac{1}{6}\) on the strip.
Step 2: Find 2 \(\frac{1}{12}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{6}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{6}\) ÷ 2 = \(\frac{1}{12}\)
Question 12.
3 ÷ \(\frac{1}{5}\) = _____
Answer: 15
Explanation:
Step 1: Skip count by fifths from 0 to 3 find 3 ÷ \(\frac{1}{5}\).
Step 2: There are 15 one fifths in 3 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
3 ÷ \(\frac{1}{5}\) = 15 because 15 × \(\frac{1}{5}\) = 3
Problem Solving – Page No. 342
Sense or Nonsense?
Question 13.
Emilio and Julia used different ways to find \(\frac{1}{2}\) ÷ 4. Emilio used a model to find the quotient. Julia used a related multiplication equation to find the quotient. Whose answer makes sense? Whose answer is nonsense? Explain your reasoning.
Emilio’s Work
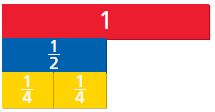
\(\frac{1}{2}\) ÷ 4
Julia’s Work
If \(\frac{1}{2}\) ÷ 4 = ■, then ■ × 4 = \(\frac{1}{2}\)
I know that \(\frac{1}{8}\) ÷ 4 = \(\frac{1}{2}\)
So, \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\) because \(\frac{1}{8}\) × 4 = \(\frac{1}{2}\)
Type below:
____________
Answer:
Julia’s Work is sense.
Emilio’s work is nonsense.
Question 13.
• For the answer that is nonsense, describe how to find the correct answer.
Type below:
____________
Answer:
Emilio’s work is nonsense becuase she divided \(\frac{1}{2}\) into two parts i.e., \(\frac{1}{4}\) and \(\frac{1}{4}\).
\(\frac{1}{2}\)/4 = \(\frac{1}{2}\) × \(\frac{1}{4}\)
Emilio must multiply the whole number with the denominator.
\(\frac{1}{2}\) × \(\frac{1}{4}\) = \(\frac{1}{8}\)
Question 13.
If you were going to find \(\frac{1}{2}\) ÷ 5, explain how you would find the quotient using fraction strips.
Type below:
____________
Answer: \(\frac{1}{10}\)
Explanation:
Step 1: Place a \(\frac{1}{2}\) strip under a 5 whole strip to show the \(\frac{1}{2}\) on the strip.
Step 2: Find 2 \(\frac{1}{10}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{2}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{2}\) ÷ 5 = \(\frac{1}{10}\)

Share and Show – Page No. 345
Question 1.
A chef has 5 blocks of butter. Each block weighs 1 pound.
She cuts each block into fourths. How many \(\frac{1}{4}\)-pound pieces of butter does the chef have?
First, draw rectangles to represent the blocks of butter.
Then, divide each rectangle into fourths.
Finally, multiply the number of fourths in each block by the number of blocks.
So, the chef has ______ one-fourth-pound pieces of butter.
______ one-fourth-pound
Answer: 20
Explanation:
Step 1: First form 5 rectangles to represent the blocks of butter. And then divide each rectangle into fourths.
Step 2: Now we will multiply the number of fourths in each block by the number of blocks.
Multiply the fourths with the whole number.
4 × 5 = 20
Thus the chef has 20 one fourth pound pieces of butter.
Question 2.
What if the chef had 3 blocks of butter and cut the blocks into thirds? How many \(\frac{1}{3}\)-pound pieces of butter would the chef have?
______ \(\frac{1}{3}\)-pound
Answer: 9
Explanation:
Multiply the number of thirds in each block with the number of blocks.
3 × thirds = 3 × 3 = 9
Thus the chef has 9 one third pound pieces of butter.
Question 3.
Jason has 2 pizzas that he cuts into fourths. How many \(\frac{1}{4}\)-size pizza slices does he have?
______ \(\frac{1}{4}\)-size pizza slices
Answer: 8
Explanation:
Step 1: First, draw 2 circles to represent pizzas. Then divide each circle into fourths.
Step 2: Now multiply the number of fourths in each circle by the number of circles.
4 × 2 = 8
So, Jason has 8 one fourth size pizza slices.
Question 4.
Thomas makes 5 sandwiches that he cuts into thirds. How many \(\frac{1}{3}\)-size sandwich pieces does he have?
______ \(\frac{1}{3}\)-size sandwich pieces
Answer: 15
Explanation:
Step 1: First, draw 5 rectangles to represent sandwiches. Then divide each rectangle into thirds.
Step 2: Multiply one third with the number of sandwiches.
3 × 5 = 15
Thomas has 15 one-third sandwich pieces.
Question 5.
Holly cuts 3 pans of brownies into eighths. How many \(\frac{1}{8}\)-size brownie pieces does she have?
______ \(\frac{1}{8}\)-size brownie pieces
Answer: 24
Explanation:
Step 1: First draw 3 rectangles to represent the ribbons. Then divide each rectangle into the pieces.
Step 2: Now multiply the Number of eights with the number of ribbons.
8 × 3 = 24
Thus Holy has 24 one eighths pieces of ribbon.
On Your Own – Page No. 346
Question 6.
Julie wants to make a drawing that is \(\frac{1}{4}\) the size of the original. If a tree in the original drawing is 8 inches tall, how tall will the tree in Julie’s drawing be?
______ inches
Answer: 2
Explanation:
Given, Julie wants to make a drawing that is \(\frac{1}{4}\) the size of the original.
The tree is 8 inches tall.
8 × \(\frac{1}{4}\) = 2
The height of the tree in Julie’s drawing is 2 inches.
Question 7.
Three friends go to a book fair. Allen spends $2.60. Maria spends 4 times as much as Allen. Akio spends $3.45 less than Maria. How much does Akio spend?
$ ______
Answer: $ 6.95
Explanation:
To find how much Akio spends for first we will find how much Maria spends, and then subtract 3.45 dollars from that value.
Allen spends 2.60 dollars.
Maris spends 4 times as much as Allen.
4 × 2.60 = 10.4
So, Maria spends 10.4 dollars.
Akio spends for 3.45 dollars less than Maria.
10.4 – 3.45 = 6.95
So, Akio spends 6.95 dollars.
Question 8.
Brianna has a sheet of paper that is 6 feet long. She cuts the length of paper into sixths and then cuts the length of each of these \(\frac{1}{6}\) pieces into thirds. How many pieces does she have? How many inches long is each piece?
______ pieces , each ______ inches long
Answer: 18 pieces, each 0.33 inches long
Explanation:
Brianna has a sheet of paper that is 6 feet long.
She cuts the length of paper into sixths and then cuts the length of each of these \(\frac{1}{6}\) pieces into thirds.
Then we will count the one-third pieces to find how many pieces she has.
6 feet ÷18 = 0.33 feet
So, each piece is 0.33 feet long.

Question 9.
Pose a Problem Look back at Problem 8. Write a similar problem by changing the length of the paper and the size of the pieces.
Type below:
____________
Answer:
Explanation:
John has a tree that is 10 feet long. She cuts the length of the tree into tenth and then cuts the length of each of these 1/10 pieces into fourth. How many pieces does he have? How many feet long is each piece?
Answer:
First, draw one rectangle to represent the tree. Then divide this rectangle into tenths, and then we will divide each 1/10 piece into fourths.
Then we will count the one-fourth pieces to find how many pieces he has.
1 tree = 10 feet
10 feet ÷ 40 = 0.4 feet
So, each piece is 0.4 feet long.
Question 10.
Test Prep Adrian made 3 carrot cakes. He cut each cake into fourths. How many \(\frac{1}{4}\)-size cake pieces does he have?
Options:
a. 16
b. 12
c. 1 \(\frac{1}{3}\)
d. 1
Answer: 12
Explanation:
Test Prep Adrian made 3 carrot cakes.
He cut each cake into fourths.

By seeing the above figure we can say that Adrian has 12 one-quarter-size pieces of a granola bar.
Share and Show – Page No. 349
Draw lines on the model to complete the number sentence.
Question 1.
Six friends share 4 pizzas equally.
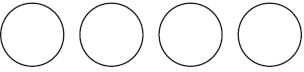
4 ÷ 6 =
Each friend’s share is _____ of a pizza.
\(\frac{□}{□}\) of a pizza.
Answer: \(\frac{2}{3}\)
Explanation:
Draw lines to divide each pizza into 4 equal pieces.
Each friend gets \(\frac{2}{3}\) of a pizza.
4 ÷ 6 = \(\frac{2}{3}\)
Each friend’s share is \(\frac{2}{3}\) of a pizza.
Question 2.
Four brothers share 5 sandwiches equally.

5 ÷ 4 =
Each brother’s share is ____ sandwiches.
\(\frac{□}{□}\) sandwiches
Answer: \(\frac{5}{4}\)
Explanation:
Draw lines to divide each sandwich into 4 equal pieces.
Divide the number of brothers by the total number of sandwiches.
5 ÷ 4 = \(\frac{5}{4}\)
Each brother’s share is \(\frac{5}{4}\) sandwiches.
Complete the number sentence to solve.
Question 3.
Twelve friends share 3 pies equally. What fraction of a pie does each friend get?
3 ÷ 12 =
Each friend’s share is _____ of a pie.
\(\frac{□}{□}\) of a pie
Answer: \(\frac{1}{4}\)
Explanation:
Twelve friends share 3 pies equally.
3 ÷ 12 = \(\frac{1}{4}\)
Each friend’s share is \(\frac{1}{4}\) of a pie.
Question 4.
Three students share 8 blocks of clay equally. How much clay does each student get?
8 ÷ 3 =
Each student’s share is ____ blocks of clay.
\(\frac{□}{□}\) blocks of clay
Answer: 2 \(\frac{2}{3}\)
Explanation:
Three students share 8 blocks of clay equally.
Divide the number of blocks by three students.
8 ÷ 3 = \(\frac{8}{3}\)
\(\frac{8}{3}\) = 2 \(\frac{2}{3}\)
Each student’s share is 2 \(\frac{2}{3}\) blocks of clay.
On Your Own
Complete the number sentence to solve.
Question 5.
Four students share 7 oranges equally. How many oranges does each student get?
7 ÷ 4 =
Each student’s share is _____ oranges.
_____ \(\frac{□}{□}\) oranges
Answer: 1 \(\frac{3}{4}\)
Explanation:
Four students share 7 oranges equally.
Draw lines to divide each orange into 4 equal pieces.
7 ÷ 4 = \(\frac{7}{4}\)
Convert the improper fraction to the mixed fraction.
\(\frac{7}{4}\) = 1 \(\frac{3}{4}\)
Each student’s share is 1 \(\frac{3}{4}\) oranges.
Question 6.
Eight girls share 5 fruit bars equally. What fraction of a fruit bar does each girl get?
5 ÷ 8 =
Each girl’s share is _____ of a fruit bar.
\(\frac{□}{□}\) of a fruit bar
Answer: \(\frac{5}{8}\)
Explanation:
Given that,
Eight girls share 5 fruit bars equally.
5 ÷ 8 = \(\frac{5}{8}\)
Thus the fraction of the fruit bar each friend gets is \(\frac{5}{8}\).
Question 7.
Nine friends share 6 pizzas equally. What fraction of a pizza does each friend get?
6 ÷ 9 =
Each friend’s share is _ of a pizza.
\(\frac{□}{□}\) of a pizza
Answer: \(\frac{2}{3}\)
Explanation:
Nine friends share 6 pizzas equally.
Draw lines to divide each pizza into 9 pieces.
6 ÷ 9 = \(\frac{2}{3}\)
Thus each friend’s share is \(\frac{2}{3}\) of a pizza.
Question 8.
Two boys share 9 feet of rope equally. How many feet of rope does each boy get?
9 ÷ 2 =
Each boy’s share is ____ feet of rope.
______ \(\frac{□}{□}\) feet of rope
Answer: 4 \(\frac{1}{2}\)
Explanation:
Two boys share 9 feet of rope equally.
Divide nine into halves.
9 ÷ 2 = \(\frac{9}{2}\)
\(\frac{9}{2}\) = 4 \(\frac{1}{2}\)
Problem Solving – Page No. 350
Question 9.
Shawna has 3 adults and 2 children coming over for dessert. She is going to serve 2 small apple pies. If she plans to give each person, including herself, an equal amount of pie, how much pie will each person get?

\(\frac{□}{□}\) pie
Answer: \(\frac{1}{3}\) pie
Explanation:
To find how much pie each person will get, we will find when 2 small apple pies we will divide by 6 persons.
2 ÷ 6 = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Therefore each person will get \(\frac{1}{3}\) pie.
Question 10.
There are 36 members in the math club. Addison brought 81 brownies to share with all the members. How many brownies does each member get?
______ \(\frac{□}{□}\) brownies
Answer: 2 \(\frac{1}{4}\)
Explanation:
Given that, There are 36 members in the math club.
Addison brought 81 brownies to share with all the members.
Dividing the number of brownies by members in the math club.
81 ÷ 36 = \(\frac{81}{36}\) = \(\frac{9}{4}\)
The mixed fraction of \(\frac{9}{4}\) is 2 \(\frac{1}{4}\)
Thus each member gets 2 \(\frac{1}{4}\) brownies.
Question 11.
Eight students share 12 oatmeal muffins equally and 6 students share 15 apple muffins equally. Carmine is in both groups of students. What is the total number of muffins Carmine gets?
______ muffins
Answer: 4 muffins
Explanation:
Since Carmine is in both groups of students, for first we will find out how many each student of each group gets.
Now we will find how many oatmeal muffins each of the 8 students get, we will divide the 12 oatmeal muffins by the 8 students.
12 ÷ 8 = \(\frac{12}{8}\) = \(\frac{3}{2}\)
\(\frac{3}{2}\) = 1 \(\frac{1}{2}\)
So, each student shares 1 \(\frac{1}{2}\) oatmeal muffins.
To find how many apple muffins each of the 6 students get we will divide the 15 apple muffins by the 6 students.
15 ÷ 6 = \(\frac{15}{6}\) = \(\frac{5}{2}\)
\(\frac{5}{2}\) = 2 \(\frac{1}{2}\)
As Carmine is in both groups we need to add the total number of muffins
1 \(\frac{1}{2}\) + 2 \(\frac{1}{2}\) = 4
Therefore the total number of muffins Carmine gets is 4.
Question 12.
Nine friends order 4 large pizzas. Four of the friends share 2 pizzas equally and the other 5 friends share 2 pizzas equally. In which group does each member get a greater amount of pizza? Explain your reasoning.
Type below:
____________
Answer:
To find in which group each member get a greater amount of pizza, for first, we will find how many each of the friends gets.
Given that 4 friends share 2 pizzas equally, so to find how many pizzas each of the 4 students get, we will find when dividing the 2 pizzas among 4 friends.
2 ÷ 4 = 2/4 = \(\frac{1}{2}\)
In this group, each student’s share is \(\frac{1}{2}\) of the pizza.
The other 5 friends share 2 pizzas equally, so to find out how many pizzas each of the 5 students get, we will find when we divide the 2 pizza among 5 friends.
2 ÷ 5 = \(\frac{2}{5}\)
In this group, each student’s share is \(\frac{2}{5}\) of the pizza.
\(\frac{1}{2}\) > \(\frac{2}{5}\) so as a group with four members get a greater amount of pizza.
Question 13.
Test Prep Jason baked 5 cherry pies. He wants to share them equally among 3 of his neighbors. How many pies will each neighbor get?
Options:
a. \(\frac{3}{8}\)
b. \(\frac{3}{5}\)
c. 1 \(\frac{2}{3}\)
d. 2 \(\frac{2}{3}\)
Answer: 1 \(\frac{2}{3}\)
Explanation:
To find how many pies each neighbor we have to divide number of cherry pies by number of neighbor.
5 ÷ 3 = \(\frac{5}{3}\)
Convert the improper fraction to the mixed fraction.
\(\frac{5}{3}\) = 1 \(\frac{2}{3}\)
Mid-Chapter Checkpoint – Page No. 351
Concepts and Skills
Question 1.
Explain how you can tell, without computing, whether the quotient \(\frac{1}{2}\) ÷ 6 is greater than 1 or less than 1.
Type below:
____________
Answer:
\(\frac{1}{2}\) ÷ 6 = \(\frac{1}{12}\)
\(\frac{1}{12}\) is less than 1.
Divide. Draw a number line or use fraction strips.
Question 2.
3 ÷ \(\frac{1}{2}\)
______
Answer: 6
Explanation:
Step 1: Draw a number line from 0 to 3. Label each half on your number line.
Step 2: Skip count by halves from 0 to 3 to find 3 ÷ \(\frac{1}{2}\).
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
3 ÷ \(\frac{1}{2}\) = 6 because 6 × \(\frac{1}{2}\) = 3
Question 3.
1 ÷ \(\frac{1}{4}\)
______
Answer: 4
Explanation:
Step 1: Draw a number line from 0 to 1. Label each fourth on your number line.
Step 2: Skip count by fourths from 0 to 1 to find 1 ÷ \(\frac{1}{4}\).
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
1 ÷ \(\frac{1}{4}\) = 4 because 4 × \(\frac{1}{4}\) = 1
Question 4.
\(\frac{1}{2}\) ÷ 2
\(\frac{□}{□}\)
Answer: \(\frac{1}{4}\)
Explanation:
Step 1: Place a \(\frac{1}{2}\) strip under a 2 whole strip to show the \(\frac{1}{2}\) on the strip.
Step 2: Find 4 \(\frac{1}{2}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{2}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{2}\) ÷ 2 = \(\frac{1}{4}\)
Question 5.
\(\frac{1}{3}\) ÷ 4
_____ \(\frac{□}{□}\)
Answer: \(\frac{1}{12}\)
Explanation:
Step 1: Place a \(\frac{1}{3}\) strip under a 4 whole strip to show the \(\frac{1}{3}\) on the strip.
Step 2: Find 12 \(\frac{1}{3}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{3}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{3}\) ÷ 4 = \(\frac{1}{12}\)
Question 6.
2 ÷ \(\frac{1}{6}\)
______
Answer: 12
Explanation:
Step 1: Draw a number line from 0 to 2. Label each sixth on your number line.
Step 2: Skip count by fourths from 0 to 2 to find 2 ÷ \(\frac{1}{6}\).
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
2 ÷ \(\frac{1}{6}\) = 12 because 12 × \(\frac{1}{6}\) = 2
Question 7.
\(\frac{1}{4}\) ÷ 3
\(\frac{□}{□}\)
Answer: \(\frac{1}{12}\)
Explanation:
Step 1: Place a \(\frac{1}{4}\) strip under a 3 whole strip to show the \(\frac{1}{4}\) on the strip.
Step 2: Find 12 \(\frac{1}{4}\) fraction strips, all with the same denominator, that fit exactly under the \(\frac{1}{4}\) strip.
Step 3: Record and check the quotient.
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\)
Complete the number sentence to solve.
Question 8.
Two students share 3 granola bars equally. How many granola bars does each student get?
3 ÷ 2 = ______
Each student’s share is ______ granola bars.
_____ \(\frac{□}{□}\) granola bars
Answer: 1 \(\frac{1}{2}\)
Explanation:
Given that Two students share 3 granola bars equally.
Divide the number of granola bars by 2.
3 ÷ 2 = \(\frac{3}{2}\)
Convert the improper fraction into the mixed fraction.
\(\frac{3}{2}\) = 1 \(\frac{1}{2}\)
Thus each student’s share is 1 \(\frac{1}{2}\) granola bars.
Question 9.
Five girls share 4 sandwiches equally. What fraction of a sandwich does each girl get?
4 ÷ 5 = _____
Each girl’s share is ______ of a sandwich.
\(\frac{□}{□}\) of a sandwich
Answer: \(\frac{4}{5}\)
Explanation:
Given that, Five girls share 4 sandwiches equally.
Dividing the number of sandwiches by five girls.
4 ÷ 5 = \(\frac{4}{5}\)
Each girl’s share is \(\frac{4}{5}\) of a sandwich.
Question 10.
Nine boys share 4 pizzas equally. What fraction of a pizza does each boy get?
4 ÷ 9 = _____
Each boy’s share is _____ of a pizza.
\(\frac{□}{□}\) of a pizza
Answer: \(\frac{4}{9}\)
Explanation:
Given, Nine boys share 4 pizzas equally.
Dividing 4 pizzas by number of nine boys
4 ÷ 9 = \(\frac{4}{9}\)
Each boy’s share is \(\frac{4}{9}\) of a pizza.
Question 11.
Four friends share 10 fruit bars equally. How many fruit bars does each friend get?
10 ÷ 4 = _____
Each friend’s share is _____ fruit bars.
_____ \(\frac{□}{□}\) fruit bars
Answer: 2 \(\frac{1}{2}\)
Explanation:
Given, Four friends share 10 fruit bars equally.
Dividing the number of fruit bars by the number of friends.
10 ÷ 4 = \(\frac{10}{4}\) = \(\frac{5}{2}\)
Convert the improper fraction into the mixed fraction.
\(\frac{5}{2}\) = 2 \(\frac{1}{2}\)
Mid-Chapter Checkpoint – Page No. 352
Question 12.
Mateo has 8 liters of punch for a party. Each glass holds \(\frac{1}{5}\) liter of punch. How many glasses can Mateo fill with punch?
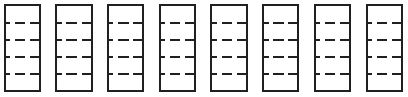
______ glasses
Answer: 40
Explanation:
Draw the rectangle that represents the number of liters.
Each rectangle is equal to 1 liter.
Each rectangle contains a one-fifth liter of punch.
Now multiply the fifths with the number of liters.
8 × 5 = 40
40 glasses can Mateo fill with a punch.
Question 13.
Four friends share 3 sheets of construction paper equally. What fraction of a sheet of paper does each friend get?
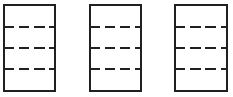
\(\frac{□}{□}\)
Answer: \(\frac{3}{4}\)
Explanation:
The rectangle represents the sheet of the construction paper.
Divide each rectangle into fourths.
3 × \(\frac{1}{4}\) = \(\frac{3}{4}\)
Each friend gets \(\frac{3}{4}\) sheet of paper.
Question 14.
Caleb and 2 friends are sharing \(\frac{1}{2}\) quart of milk equally. What fraction of a quart of milk does each of the 3 friends get?
\(\frac{□}{□}\) quart of milk
Answer: \(\frac{1}{6}\) quart of milk
Explanation:
Caleb and 2 friends are sharing \(\frac{1}{2}\) quart of milk equally.
\(\frac{1}{2}\) ÷ 3 = \(\frac{1}{6}\)
Therefore each of 3 friend gets \(\frac{1}{6}\) quart of milk.
Question 15.
Toni and Makayla are working on a craft project. Makayla has 3 yards of ribbon and Toni has 4 yards of ribbon. They cut all the ribbon into pieces that are \(\frac{1}{4}\) yard long. How many pieces of ribbon do they have?
Makayla: __________ pieces of ribbon
Toni: __________ pieces of ribbon
Answer:
Makayla: 12 pieces of ribbon
Toni: 16 pieces of ribbon
Explanation:
Toni and Makayla are working on a craft project.
Makayla has 3 yards of ribbon and Toni has 4 yards of ribbon.
They cut all the ribbon into pieces that are \(\frac{1}{4}\) yard long.
Now multiply the number of yards of ribbon that Makayla has with \(\frac{1}{4}\)
3 ÷ \(\frac{1}{4}\) = 12 pieces of ribbon
Multiply the number of yards of ribbon that Toni has with \(\frac{1}{4}\)
4 ÷ \(\frac{1}{4}\) = 16 pieces of ribbon
Share and Show – Page No. 355
Question 1.
Use the model to complete the number sentence.
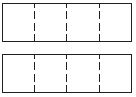
2 ÷ \(\frac{1}{4}\) = 2 × ______ = ______
Answer: 2 × 4 = 8
Explanation:
- Draw 2 rectangles and divide each rectangle into fourths.
- When you divide 1 rectangle into fourths you are finding the number of fourths in 2 rectangles.
- There are 2 groups of rectangles. There are 8 fourths
- Complete the number sentence.
Question 2.
Use the model to complete the number sentence.
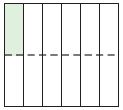
\(\frac{1}{6}\) ÷ 2 = _ × \(\frac{1}{6}\) = _
Type below:
__________
Answer: \(\frac{1}{12}\)
Explanation:
- Draw the rectangle and divide the rectangle into sixths.
- The rectangle is divided into 2 equal parts. You can find 12 sixths.
- In the figure, you can see one shaded part in the rectangle.
- Complete the number sentence.
\(\frac{1}{6}\) × \(\frac{1}{2}\) = \(\frac{1}{12}\)
Write a related multiplication sentence to solve.
Question 3.
3 ÷ \(\frac{1}{4}\)
______
Answer: 12
Explanation:
- Draw 3 rectangles and divide each rectangle into fourths.
- When you divide 1 rectangle into fourths you are finding the number of fourths in 3 rectangles.
- There are 3 groups of rectangles. There are 12 fourths
- Complete the number sentence.
3 × 4 = 12
3 ÷ \(\frac{1}{4}\) = 12
Question 4.
\(\frac{1}{5}\) ÷ 4
\(\frac{□}{□}\)
Answer: \(\frac{1}{20}\)
Explanation:
- Draw the rectangle and divide the rectangle into fifths.
- The rectangle is divided into 4 equal parts. You can find 20 fifths.
- Complete the number sentence.
\(\frac{1}{5}\) × \(\frac{1}{4}\) = \(\frac{1}{20}\)
\(\frac{1}{5}\) ÷ 4 = \(\frac{1}{20}\)
Question 5.
\(\frac{1}{9}\) ÷ 3
\(\frac{□}{□}\)
Answer: \(\frac{1}{27}\)
Explanation:
- Draw 3 rectangle and divide the rectangle into ninths.
- The rectangle is divided into 3 equal parts. You can find 27 ninths.
- Complete the number sentence.
\(\frac{1}{9}\) × \(\frac{1}{3}\) = \(\frac{1}{27}\)
\(\frac{1}{9}\) ÷ 3 = \(\frac{1}{27}\)
Question 6.
7 ÷ \(\frac{1}{2}\)
______
Answer: 14
Explanation:
- Draw 7 rectangles and divide each rectangle into halves.
- When you divide 7 rectangles into halves you are finding the number of halves in 7 rectangles.
- There are 7 groups of rectangles. There are 14 halves.
- Complete the number sentence.
7 × 2 = 14
7 ÷ \(\frac{1}{2}\) = 14
On Your Own
Write a related multiplication sentence to solve.
Question 7.
5 ÷ \(\frac{1}{3}\)
______
Answer: 15
Explanation:
- Draw 5 rectangles and divide each rectangle into thirds.
- When you divide 5 rectangles into halves you are finding the number of thirds in 5 rectangles.
- There are 5 groups of rectangles. There are 15 thirds.
- Complete the number sentence.
5 × 3 = 15
5 ÷ \(\frac{1}{3}\) = 15
Question 8.
8 ÷ \(\frac{1}{2}\)
______
Answer: 16
Explanation:
- Draw 8 rectangles and divide each rectangle into halves.
- When you divide 8 rectangles into halves you are finding the number of thirds in 8 rectangles.
- There are 8 groups of rectangles. There are 16 halves.
- Complete the number sentence.
8 × 2 = 16
8 ÷ \(\frac{1}{2}\) = 16
Question 9.
\(\frac{1}{7}\) ÷ 4
\(\frac{□}{□}\)
Answer: \(\frac{1}{28}\)
Explanation:
\(\frac{1}{7}\) ÷ 4
- Draw 4 rectangles and divide the rectangle into sevenths.
- The rectangle is divided into 4 equal parts. You can find 28 sevenths.
- Complete the number sentence.
\(\frac{1}{7}\) × \(\frac{1}{4}\) = \(\frac{1}{28}\)
Thus, \(\frac{1}{7}\) ÷ 4 = \(\frac{1}{28}\)
Question 10.
\(\frac{1}{2}\) ÷ 9
\(\frac{□}{□}\)
Answer: \(\frac{1}{18}\)
Explanation:
\(\frac{1}{2}\) ÷ 9
- Draw 9 rectangles and divide the rectangle into halves.
- The rectangle is divided into 9 equal parts. You can find 18 halves.
- Complete the number sentence.
\(\frac{1}{2}\) × \(\frac{1}{9}\) = \(\frac{1}{18}\)
\(\frac{1}{2}\) ÷ 9 = \(\frac{1}{18}\)
Question 11.
\(\frac{1}{3}\) ÷ 4
\(\frac{□}{□}\)
Answer: \(\frac{1}{12}\)
Explanation:
\(\frac{1}{3}\) ÷ 4
- Draw 4 rectangles and divide the rectangle into thirds.
- The rectangle is divided into 4 equal parts. You can find 12 thirds.
- Complete the number sentence.
\(\frac{1}{3}\) × \(\frac{1}{4}\) = \(\frac{1}{12}\)
\(\frac{1}{3}\) ÷ 4 = \(\frac{1}{12}\)
Question 12.
\(\frac{1}{4}\) ÷ 12
\(\frac{□}{□}\)
Answer: \(\frac{1}{48}\)
Explanation:
- Draw 12 rectangles and divide the rectangle into fourths.
- The rectangle is divided into 12 equal parts. You can find 48 thirds.
- Complete the number sentence.
\(\frac{1}{4}\) ÷ 12 = \(\frac{1}{4}\) × \(\frac{1}{12}\) = \(\frac{1}{48}\)
Question 13.
6 ÷ \(\frac{1}{5}\)
______
Answer: 30
Explanation:
- Draw 6 rectangles and divide each rectangle into fifths.
- When you divide 6 rectangles into fifths you are finding the number of fifths in 6 rectangles.
- There are 6 groups of rectangles. There are 30 fifths.
- Complete the number sentence.
6 × 5 = 30
6 ÷ \(\frac{1}{5}\) = 30
Question 14.
\(\frac{2}{3}\) ÷ 3
\(\frac{□}{□}\)
Answer: \(\frac{2}{9}\)
Explanation:
\(\frac{2}{3}\) ÷ 3
- Draw 3 rectangles and divide the rectangle into two thirds.
- The rectangle is divided into 3 equal parts.
- Complete the number sentence.
\(\frac{2}{3}\) ÷ 3 = \(\frac{2}{3}\) × \(\frac{1}{3}\) = \(\frac{2}{9}\)
UNLOCK the Problem – Page No. 356
Question 15.
The slowest mammal is the three-toed sloth. The top speed of a three-toed sloth on the ground is about \(\frac{1}{4}\) foot per second. The top speed of a giant tortoise on the ground is about \(\frac{1}{3}\) foot per second. How much longer would it take a three-toed sloth than a giant tortoise to travel 10 feet on the ground?

a. What do you need to find?
Type below:
__________
Answer: We Need to find How much longer would it take a three-toed sloth than a giant tortoise to travel 10 feet on the ground.
Question 15.
b. What operations will you use to solve the problem?
Type below:
__________
Answer:
The operations which we will use is:
Multiplication to find how many seconds three-toed sloth tortoise need to travel 10 feet.
Subtraction to finds how second longer need three-toed to travel 10 feet.
Question 15.
c. Show the steps you used to solve the problem.
Type below:
__________
Answer:
To find how much longer would it take a three-toed sloth than a giant tortoise to travel 10 feet on the ground, for first we will find how much seconds a three-toed sloth and giant tortoise need to travel 10 feet.
The top speed of a three-toed sloth on the ground is about 1/4 foot per second, so to find how much seconds need a three-toed sloth to travel 10 feet we will find as:
10 feet ÷ 1/4 foot per second = 10 × 4 = 40 seconds
The top speed of a giant tortoise on the ground is about 1/3 foot per second, so to find how much seconds need a giant tortoise to travel 10 feet we will find as:
10 feet ÷ 1/3 foot per second = 10 × 3 = 30 seconds
Question 15.
d. Complete the sentences.
A three-toed sloth would travel 10 feet in _____ seconds.
A giant tortoise would travel 10 feet in _____ seconds.
Since _____ – _____ = _____, it would take a three-toed sloth _____ seconds longer to travel 10 feet.
Type below:
__________
Answer:
A three-toed sloth would travel 10 feet in 40 seconds.
A giant tortoise would travel 10 feet in 30 seconds.
Since 40 – 30 = 10, it would take a three-toed sloth 10 seconds longer to travel 10 feet.
Question 15.
e. Fill in the bubble for the correct answer choice.
Options:
a. 10 seconds
b. 30 seconds
c. 40 seconds
d. 70 seconds
Answer: 10 seconds
Explanation:
A three-toed sloth would travel 10 feet in 40 seconds.
A giant tortoise would travel 10 feet in 30 seconds.
Since 40 – 30 = 10, it would take a three-toed sloth 10 seconds longer to travel 10 feet.
The correct answer is option A.
Question 16.
Robert divides 8 cups of almonds into \(\frac{1}{8}\)-cup servings. How many servings does he have?
Options:
a. 1
b. 16
c. 8
d. 64
Answer: 64
Explanation:
Robert divides 8 cups of almonds into \(\frac{1}{8}\)-cup servings.
8 × \(\frac{1}{8}\)
8 × 8 = 64
Thus robert has 64 servings.
The correct answer is option D.
Question 17.
Tina cuts \(\frac{1}{3}\) yard of fabric into 4 equal parts. What is the length of each part?
Options:
a. 12 yards
b. 1 \(\frac{1}{3}\) yards
c. \(\frac{3}{4}\) yards
d. \(\frac{1}{12}\) yards
Answer: \(\frac{1}{12}\) yards
Explanation:
\(\frac{1}{3}\) ÷ 4
\(\frac{1}{3}\) × \(\frac{1}{4}\) = \(\frac{1}{12}\) yards
The correct answer is option D.
Share and Show – Page No. 359
Question 1.
Complete the story problem to represent 3 ÷ \(\frac{1}{4}\).
Carmen has a roll of paper that is ______ feet long. She cuts the paper into pieces that are each ______ foot long. How many pieces of paper does Carmen have?
Type below:
__________
Answer:
3 ÷ \(\frac{1}{4}\)
3 × 4 = 12
Carmen has a roll of paper that is 3 feet long.
She cuts the paper into pieces that are each \(\frac{1}{4}\) foot long.
Question 2.
Draw a diagram to represent the problem. Then solve. April has 6 fruit bars. She cuts the bars into halves. How many \(\frac{1}{2}\)-size bar pieces does she have?
_____ \(\frac{1}{2}\)-size bar pieces
Answer:
First, draw 6 rectangles that represent fruit bars.
Now divide each fruit bar into halves.
Dividing 6 fruit bards by halves.
6 ÷ \(\frac{1}{2}\) = 12
Thus she has 12 \(\frac{1}{2}\)-size bar pieces
Question 3.
Write an equation to represent the problem. Then solve. Two friends share \(\frac{1}{4}\) of a large peach pie. What fraction of the whole pie does each friend get?
\(\frac{□}{□}\)
Answer: \(\frac{1}{8}\)
Explanation:
Given that, Two friends share \(\frac{1}{4}\) of a large peach pie.
\(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\)
Thus the fraction of the whole pie each friend gets is \(\frac{1}{8}\).
On Your Own
Question 4.
Write an equation to represent the problem. Then solve.
Benito has \(\frac{1}{3}\) -kilogram of grapes. He divides the grapes equally into 3 bags. What fraction of a kilogram of grapes is in each bag?
\(\frac{□}{□}\)
Answer: \(\frac{1}{9}\)
Explanation:
Given:
Benito has \(\frac{1}{3}\) -kilogram of grapes. He divides the grapes equally into 3 bags.
The equation for the division is,
\(\frac{1}{3}\) ÷ 3 = \(\frac{1}{9}\)
\(\frac{1}{9}\) of a kilogram of grapes is in each bag.
Question 5.
Draw a diagram to represent the problem. Then solve.
Sonya has 5 sandwiches. She cuts each sandwich into fourths. How many \(\frac{1}{4}\)-size sandwich pieces does she have?
_____ \(\frac{1}{4}\)-size sandwich pieces
Answer: 20
Explanation:
Given,
Sonya has 5 sandwiches. She cuts each sandwich into fourths.
Dividing the number of sandwiches by fourths.
5 ÷ \(\frac{1}{4}\) = 5 × 4 = 20
Thus she has 20 \(\frac{1}{4}\)-size sandwich pieces.
Question 6.
Write a story problem to represent 2 ÷ \(\frac{1}{8}\). Then solve.
Type below:
__________
Answer:
Erica makes 2 sandwiches and cuts each sandwich into eighths. How many \(\frac{1}{8}\) size sandwich pieces does she have?
Answer: 2 ÷ \(\frac{1}{8}\)
2 ÷ \(\frac{1}{8}\) = 16 because 16 × \(\frac{1}{8}\) = 2
Problem Solving – Page No. 360
Pose a Problem
Question 7.
Amy wrote the following problem to represent 4 ÷ \(\frac{1}{6}\) .

Jacob has a board that is 4 feet long. He cuts the board into pieces that are each \(\frac{1}{6}\) foot long. How many pieces does Jacob have now?
Then Amy drew this diagram to solve her problem.
![]()
So, Jacob has 24 pieces.
Write a new problem using a different item to be divided and different fractional pieces. Then draw a diagram to solve your problem.
Pose a problem. Draw a diagram to solve your problem.
Type below:
__________
Question 8.
Test Prep Melvin has \(\frac{1}{4}\) of a gallon of fruit punch. He shares the punch equally with each of 2 friends and himself. Which equation represents the fraction of a gallon of punch that each of the friends get?
Options:
a. \(\frac{1}{4}\) ÷ \(\frac{1}{3}\) = n
b. \(\frac{1}{4}\) ÷ 3 = n
c. 3 ÷ \(\frac{1}{4}\) = n
d. 3 ÷ 4 = n
Answer: \(\frac{1}{4}\) ÷ 3 = n
Explanation:
Melvin has \(\frac{1}{4}\) of a gallon of fruit punch.
He shares the punch equally with each of 2 friends and himself.
The expressions which represents this are \(\frac{1}{4}\) ÷ 3 or \(\frac{1}{4}\) × \(\frac{1}{3}\).
So, the correct answers \(\frac{1}{4}\) ÷ 3 = n i.e., option B.
Chapter Review/Test – Page No. 361
Concepts and Skills
Divide. Draw a number line or use fraction strips.
Question 1.
2 ÷ \(\frac{1}{3}\) = ______
Answer: 6
Explanation:
Step 1: Draw a number line from 0 to 2. Divide the number line into thirds. Label each third on your number line.
Step 2: Skip count by thirds from 0 to 2 to find 2 ÷ \(\frac{1}{3}\).
There are 6 thirds in 2 wholes.
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
2 ÷ \(\frac{1}{3}\) = 6 because 6 × \(\frac{1}{3}\) = 2
Question 2.
1 ÷ \(\frac{1}{5}\) = ______
Answer: 5
Explanation:
Step 1: Draw a number line from 0 to 1. Divide the number line into fifths. Label each fifth on your number line.
Step 2: Skip count by fifths from 0 to 1 to find 1 ÷ \(\frac{1}{5}\).
You can use the relationship between multiplication and division to explain and check your solution.
Step 3: Record and check the quotient.
1 ÷ \(\frac{1}{5}\) = 5 because 5 × \(\frac{1}{5}\) = 1
Question 3.
\(\frac{1}{4}\) ÷ 3 = \(\frac{□}{□}\)
Answer: \(\frac{1}{12}\)
Explanation:
Step 1: Draw a number line from 0 to 3. Divide the number line into fourths. Label each fourth on your number line.
Step 2: Skip count by fourth from 0 to 3 to find 3 ÷ \(\frac{1}{4}\).
You can use the relationship between multiplication and division to explain and check your solution.
3 ÷ \(\frac{1}{4}\) = \(\frac{1}{12}\)
Thus \(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\)
Complete the number sentence to solve.
Question 4.
Three students share 4 sandwiches equally. How many sandwiches does each student get?
4 ÷ 3 = ______ \(\frac{□}{□}\)
Answer: 1 \(\frac{1}{3}\)
Explanation:
To find what fraction of sandwich each student gets we have to divide the number of sandwiches by the number of students.
4 ÷ 3 = \(\frac{4}{3}\)
Now convert the improper fraction to the mixed fraction.
\(\frac{4}{3}\) = 1 \(\frac{1}{3}\)
Question 5.
Six girls share 5 pints of milk equally. What fraction of a pint of milk does each girl get?
5 ÷ 6 = \(\frac{□}{□}\)
Answer: \(\frac{5}{6}\)
Explanation:
Given that, Six girls share 5 pints of milk equally.
To find the fraction of a pint of milk each girl gets, we have to divide the pints of milk by the number of girls.
5 ÷ 6 = \(\frac{5}{6}\)
Thus each girl get \(\frac{5}{6}\) pint of milk.
Write a related multiplication sentence to solve.
Question 6.
\(\frac{1}{4}\) ÷ 5
Type below:
__________
Answer: \(\frac{1}{20}\)
Explanation:
\(\frac{1}{4}\) ÷ 5
\(\frac{1}{4}\) × \(\frac{1}{5}\) = \(\frac{1}{20}\)
\(\frac{1}{4}\) ÷ 5 = \(\frac{1}{20}\)
Question 7.
\(\frac{1}{3}\) ÷ 9
Type below:
__________
Answer: \(\frac{1}{27}\)
Explanation:
\(\frac{1}{3}\) ÷ 9
\(\frac{1}{3}\) × \(\frac{1}{9}\) = \(\frac{1}{27}\)
\(\frac{1}{3}\) ÷ 9 = \(\frac{1}{27}\)
Question 8.
8 ÷ \(\frac{1}{2}\)
Type below:
__________
Answer: 16
Explanation:
8 ÷ \(\frac{1}{2}\)
8 × 2 = 16
Question 9.
5 ÷ \(\frac{1}{6}\)
Type below:
__________
Answer: 30
Explanation:
5 ÷ \(\frac{1}{6}\)
5 × 6 = 30
Question 10.
Write a story problem to represent \(\frac{1}{2}\) ÷ 3. Then solve.
Type below:
__________
Answer: \(\frac{1}{6}\)
Explanation:
\(\frac{1}{2}\) ÷ 3
\(\frac{1}{2}\) × \(\frac{1}{3}\) = \(\frac{1}{6}\)
Question 11.
Write a story problem to represent 3 ÷ \(\frac{1}{2}\). Then solve.
Type below:
__________
Answer: 6
Explanation:
3 ÷ \(\frac{1}{2}\)
3 × 2 = 6
Chapter Review/Test – Page No. 362
Fill in the bubble completely to show your answer.
Question 12.
Michelle cuts \(\frac{1}{4}\) yard of ribbon into 4 equal pieces. What is the length of each piece?
Options:
a. \(\frac{1}{16}\) yard
b. \(\frac{1}{8}\) yard
c. 1 yard
d. 16 yard
Answer: \(\frac{1}{16}\) yard
Explanation:
Michelle cuts \(\frac{1}{4}\) yard of ribbon into 4 equal pieces.
\(\frac{1}{4}\) ÷ 4
\(\frac{1}{4}\) × \(\frac{1}{4}\) = \(\frac{1}{16}\)
Thus the correct answer is option A.
Question 13.
Ashton picked 6 pounds of pecans. He wants to share the pecans equally among 5 of his neighbors. How many pounds of pecans will each neighbor get?
Options:
a. \(\frac{5}{11}\) pound
b. \(\frac{5}{6}\) pound
c. 1 \(\frac{1}{5}\) pounds
d. 2 \(\frac{1}{5}\) pounds
Answer: 1 \(\frac{1}{5}\) pounds
Explanation:
Ashton picked 6 pounds of pecans.
He wants to share the pecans equally among 5 of his neighbors.
Divide the number of pounds by the number of neighbors.
= \(\frac{6}{5}\)
Now convert the improper fraction to the mixed fraction.
\(\frac{6}{5}\) = 1 \(\frac{1}{5}\) pounds
Thus the correct answer is option C.
Question 14.
Isabella has 5 pounds of trail mix. She divides the mix into \(\frac{1}{4}\)-pound servings. How many \(\frac{1}{4}\)-pound servings does she have?
Options:
a. 1 \(\frac{1}{4}\)
b. 9
c. 16
d. 20
Answer: 1 \(\frac{1}{4}\)
Explanation:
Given,
Isabella has 5 pounds of trail mix.
She divides the mix into \(\frac{1}{4}\)-pound servings.
5 × \(\frac{1}{4}\) = \(\frac{5}{4}\)
Now convert the improper fraction to the mixed fraction.
\(\frac{5}{4}\) = 1 \(\frac{1}{4}\)
Thus the correct answer is option A.
Question 15.
Melvin has \(\frac{1}{2}\) of a cake. He shares the cake equally with each of 2 friends and himself. Which equation represents the fraction of the whole cake that each of the friends get?
Options:
a. \(\frac{1}{2}\) ÷ \(\frac{1}{3}\) = n
b. \(\frac{1}{2}\) ÷ 3 = n
c. 2 ÷ \(\frac{1}{3}\) = n
d. 2 ÷ 3 = n
Answer: \(\frac{1}{2}\) ÷ 3 = n
Explanation:
Melvin has \(\frac{1}{2}\) of a cake.
He shares the cake equally with each of 2 friends and himself.
\(\frac{1}{2}\) divided by 3.
\(\frac{1}{2}\) ÷ 3 = n
Thus the correct answer is option B.
Chapter Review/Test – Page No. 363
Fill in the bubble completely to show your answer.
Question 16.
Camille has 8 feet of rope. She cuts the rope into \(\frac{1}{3}\)-foot pieces for a science project. How many \(\frac{1}{3}\)-foot pieces of rope does she have?
Options:
a. 24
b. 8
c. 3
d. 2 \(\frac{2}{3}\)
Answer: 24
Explanation:
Given,
Camille has 8 feet of rope.
She cuts the rope into \(\frac{1}{3}\)-foot pieces for a science project.
8 ÷ \(\frac{1}{3}\) = 8 × 3 = 24
Thus the correct answer is option A.
Question 17.
Awan makes 3 sandwiches and cuts each sandwich into sixths. How many \(\frac{1}{6}\)-size sandwich pieces does he have?
Options:
a. \(\frac{1}{2}\)
b. 2
c. 9
d. 18
Answer: 18
Explanation:
Given that, Awan makes 3 sandwiches and cuts each sandwich into sixths.
3 ÷ \(\frac{1}{6}\)
3/ \(\frac{1}{6}\) = 3 × 6 = 18
The correct answer is option D.
Question 18.
Eight students share 5 blocks of modeling clay equally. What fraction of one block of modeling clay does each student get?
Options:
a. \(\frac{1}{40}\)
b. \(\frac{1}{8}\)
c. \(\frac{5}{8}\)
d. 1 \(\frac{3}{5}\)
Answer: 1 \(\frac{3}{5}\)
Explanation:
Eight students share 5 blocks of modeling clay equally.
Divide number of students by the number of blocks.
8 ÷ 5 = \(\frac{8}{5}\)
Convert the fraction to the mixed fraction.
\(\frac{8}{5}\) = 1 \(\frac{3}{5}\)
So, the correct answer is option D.
Question 19.
The diagram below represents which division problem?
![]()
Options:
a. 5 ÷ \(\frac{1}{3}\)
b. \(\frac{1}{3}\) ÷ 5
c. 5 ÷ \(\frac{1}{4}\)
d. \(\frac{1}{4}\) ÷ 5
Answer: 5 ÷ \(\frac{1}{3}\)
Explanation:
The figure above shows that there are 5 rectangles. Each rectangle is divided into three parts.
So, the fraction is one third.
Divide number of blocks by the number of thirds.
5 ÷ \(\frac{1}{3}\)
Thus the correct answer is option A.
Chapter Review/Test – Page No. 364
Constructed Response
Question 20.
Dora buys one package each of the 1-pound, 2-pound, and 4-pound packages of ground beef to make hamburgers. How many \(\frac{1}{4}\)-pound hamburgers can she make? Show your work using words, pictures, or numbers.
Explain how you found your answer.
______ hamburgers
Answer: 28 hamburgers
Explanation:
Given:
Dora buys one package each of the 1-pound, 2-pound, and 4-pound packages of ground beef to make hamburgers.
Total number of pounds = 1 + 2 + 4 = 7 pounds
Now divide number of pounds by \(\frac{1}{4}\)
7 ÷ \(\frac{1}{4}\) = 28
Thus Dora can make 28 Hamburgers.
Performance Task
Question 21.
Suppose your teacher gives you the division problem 6 ÷ \(\frac{1}{5}\).
A). In the space below, draw a diagram to represent 6 ÷ \(\frac{1}{5}\).
Type below:
__________
Answer:
Draw 6 rectangles and divide each whole by one-fifths fractions.
Question 21.
B). Write a story problem to represent 6 ÷ \(\frac{1}{5}\).
Type below:
__________
Answer:
Kyra has 6 feet of rope. If she cuts the rope into \(\frac{1}{5}\) foot pieces for a project. How many \(\frac{1}{5}\)-foot pieces of rope does she have?
Question 21.
C). Use a related multiplication expression to solve your story problem.
Show your work.
Type below:
__________
Answer:
The multiplication expression to solve the above problem is
6 ÷ \(\frac{1}{5}\) = 6/\(\frac{1}{5}\) = 6 × 5 = 30
Question 21.
D). Write a division problem that shows a unit fraction divided by a whole number. Write a story problem to represent your division problem. Then solve.
Type below:
__________
Answer:
Isabella has 7 pounds of trail mix. She divides the mix into \(\frac{1}{4}\)-pound servings. How many \(\frac{1}{4}\)-pound servings does she have?
Conclusion
Hoping that Go Math Grade 5 Answer Chapter 8 Divide Fractions has helped you to resolve your queries on time. Get a good hold of the concepts and attempt the final exams with confidence. To know more about such related concepts stay connected to our site on a regular basis.
