Big Ideas Math Answers Grade 4 Chapter 5 Divide Multi-Digit Numbers by One-Digit Numbers are included here to help the students to improve their preparation level. You must practice every question given on Big Ideas Math Answers Grade 4 to aware of the different questions impose in the exam. Practice all the problems and verify the solution and explanation to find out the easy method to solve problems. Students are suggested to learn the in-depth concept of Divide Multi-Digit Numbers into One-Digit Numbers and start practicing the below questions.
Big Ideas Grade 4 Answer Key Chapter 5 Divide Multi-Digit Numbers by One-Digit Numbers
Learn from basics using Big Ideas Grade 4 Solution Key pdf. Click on the below attached links and start solving all the problems. Tips and tricks are also given to help the students to remember the process to solve different problems. So, by referring to our bigideasmathanswer.com students can get a complete grip on the concepts as well as they will become math experts easily. Find out various methods to solve problems and choose the best out of one that makes your learning easy.
Lesson: 1 Divide Tens, Hundreds, and Thousands
- Lesson 5.1 Divide Tens, Hundreds, and Thousands
- Divide Tens, Hundreds and Thousands Homework & Practice 5.1
Lesson: 2 Estimate Quotients
Lesson: 3 Understand Division and Remainder
- Lesson 5.3 Understand Division and Remainder
- Understand Division and Remainder Homework & Practice 5.3
Lesson: 4 Use Partial Quotients
Lesson: 5 Use Partial Quotients with a Remainder
- Lesson 5.5 Use Partial Quotients with a Remainder
- Use Partial Quotients with a Remainder Homework & Practice 5.5
Lesson: 6 Divide Two-Digit Numbers by One-Digit Numbers
- Lesson 5.6 Divide Two-Digit Numbers by One-Digit Numbers
- Divide Two-Digit Numbers by One-Digit Numbers Homework & Practice 5.6
Lesson: 7 Divide Multi-Digit Numbers by One-Digit Numbers
- Lesson 5.7 Divide Multi-Digit Numbers by One-Digit Numbers
- Divide Multi-Digit Numbers by One-Digit Numbers Homework & Practice 5.7
Lesson: 8 Divide by One-Digit Numbers
Lesson: 9 Problem Solving: Division
Performance Task
- Divide Multi-Digit Numbers by One-Digit Numbers Performance Task
- Divide Multi-Digit Numbers by One-Digit Numbers Activity
- Divide Multi-Digit Numbers by One-Digit Numbers Chapter Practice
Lesson 5.1 Divide Tens, Hundreds, and Thousands
Explore and Grow
Use a model to find each missing factor. Draw each model. Then write the related division equation.

What pattern do you notice?
Answer: The pattern follows the multiplication of 4 with ones, tens, hundreds, and thousands.

Explanation:
Let the missing number be X.
Now,
The given Expressions are:
A) X × 2 = 8
So, X can be calculated by
X= 8 ÷ 2 = 4
B) X × 2 = 80
So, X can be calculated by
X= 80 ÷ 2 = 40
C) X × 2 = 800
So, X can be calculated by
X= 800 ÷ 2 = 400
D) X × 2 = 8,000
So, X can be calculated by
X= 8,000 ÷ 2 = 4,000
Hence, from the above,
We can conclude that the pattern follows the multiplication of 4 with ones, tens, hundreds, and thousands.
Repeated Reasoning
Explain how 12 ÷ 4 can help you find 1,200 ÷ 4
Answer: 1,200 ÷ 4 is 100 times the value of 12 ÷ 4.
Explanation:
The value of 12 ÷ 4 = 3
Now,
we know that 1,200 times is 100 times the value of 12. ( From the place-value Concept)
So,
1,200 ÷ 4 = 120 tens ÷ 4
=30 tens
= 300
Hence, from the values of 3 and 300,
We can conclude that the value of 300 is 100 times the value of 3.
Think and Grow: Divide Tens, Hundreds and Thousands
You can use place value and basic division facts to divide tens, hundreds, or thousands by one-digit numbers.
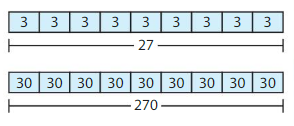
Example
Find 270 ÷ 9
Think: 27 ÷ 9
270 ÷ 9 = 27 tens ÷ 9
= 3 tens
= 30
So, 270 ÷ 9 = 30

Example
Find 5,600 ÷ 8.
Think: 56 ÷ 8
5,600 ÷ 8 = 56 hundreds ÷ 8
= 7 hundreds
= 700
So, 5,600 ÷ 8 = 700
Show and Grow
Question 1.
Find 2,400 ÷ 6.
Think: 24 ÷ 6 = 3
2,400 ÷ 6 = 24 hundreds ÷ 6
= 3 hundreds
=300
So, 2,400 ÷ 6 = 300.
Question 2.
Find each quotient.
49 ÷ 7 =_____
490 ÷ 7 = ______
4,900 ÷ 7 = ______
Answer: Let the Expressions be A), B) and C)
So,
The quotients of A), B) and C) are:
A) 7
B) 70
C) 700
Explanation:
Let the given Expressions be A), B) and C)
So, the given Expressions are:
A) 49 ÷ 7
B) 490 ÷ 7
C) 4,900 ÷ 7
So,
A) 49 ÷ 7 = 7
B) 490 ÷ 7 = 49 tens ÷ 7
= 7 tens
=70
So, 490 ÷ 7 = 70
C) 4,900 ÷ 7 = 49 hundreds ÷ 7
= 7 hundred
= 700
So, 4,900 ÷ 7 = 700
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Apply and Grow: Practice
Find the quotient
Question 3.
50 ÷ 5 = _____
Answer: 10
Explanation:
The given Expression is:
50 ÷ 5 = 5 tens ÷ 5
= 1 ten
=10
So, 50 ÷ 5 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 4.
360 ÷ 6 = _____
Answer: 60
Explanation:
The given Expression is:
360 ÷ 6 = 36 tens ÷ 6
= 6 tens
=60
So, 360 ÷ 6 = 60
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 5.
7,200 ÷ 8 = ______
Answer: 900
Explanation:
The given Expression is:
7,200 ÷ 8 = 72 hundreds ÷ 8
= 9 hundred
=900
So, 7,200 ÷ 8 = 900
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 6.
180 ÷ 2 = ______
Answer: 90
Explanation:
The given Expression is:
180 ÷ 2 = 18 tens ÷ 2
= 9 tens
=90
So, 180 ÷ 2 = 90
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 7.
4,200 ÷ 7 = _____
Answer: 600
Explanation:
The given Expression is:
4,200 ÷ 7 = 42 hundreds ÷ 7
= 6 hundred
=600
So, 4,200 ÷ 7 = 600
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 8.
20 ÷ 2 = ____
Answer: 10
Explanation:
The given Expression is:
20 ÷ 2 = 2 tens ÷ 2
= 1 ten
=10
So, 20 ÷ 2 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 9.
2,000 ÷ 5 = _____
Answer: 400
Explanation:
The given Expression is:
2,000 ÷ 5 = 20 hundreds ÷ 5
= 4 hundred
=400
So, 2,000 ÷ 5 = 400
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 10.
30 ÷ 3 = _____
Answer: 10
Explanation:
The given Expression is:
30 ÷ 3 = 3 tens ÷ 3
= 1 ten
=10
So, 30 ÷ 3 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 11.
320 ÷ 4 = ______
Answer: 80
Explanation:
The given Expression is:
320 ÷ 4 = 32 tens ÷ 4
= 8 tens
=80
So, 320 ÷ 4 = 80
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 12.
140 ÷ 2 = _____
Answer: 70
Explanation:
The given Expression is:
140 ÷ 2 = 14 tens ÷ 2
= 7 tens
=70
So, 140 ÷ 2 = 70
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 13.
5,400 ÷ 9 = ____
Answer: 600
Explanation:
The given Expression is:
5,400 ÷ 9 = 54 hundreds ÷ 9
= 6 hundred
=600
So, 5,400 ÷ 9 = 600
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 14.
180 ÷ 6 = _____
Answer: 30
Explanation:
The given Expression is:
180 ÷ 6 = 18 tens ÷ 6
= 3 tens
=30
So, 180 ÷ 6 = 30
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
DIG DEEPER!
Find the missing number.
Question 15.
70 ÷ ____ = 10
Answer: The missing number is: 7
Explanation:
Let the missing number be X.
The given Expression is:
70 ÷ X = 10
So, X can be calculated by
X= 70 ÷ 10 = 70
Question 16.
4,000 ÷ _____ = 800
Answer: The missing number is: 20
Explanation:
Let the missing number be X.
The given Expression is:
4,000 ÷ X = 800
So, X can be calculated by
X= 4,000 ÷ 800 = 20
Question 17.
160 ÷ _____ = 40
Answer: The missing number is: 4
Explanation:
Let the missing number be X.
The given Expression is:
160 ÷ X = 40
So, X can be calculated by
X= 160 ÷ 40 = 4
Question 18.
_____ ÷ 7 = 300
Answer: The missing number is: 2,100
Explanation:
Let the missing number be X.
The given Expression is:
X ÷ 7 = 300
So, X can be calculated by
X= 70 × 300 = 2,100
Question 19.
_____ ÷ 5 = 70
Answer: The missing number is: 350
Explanation:
Let the missing number be X.
The given Expression is:
X ÷ 5 = 70
So, X can be calculated by
X= 70 × 5 = 350
Question 20.
_____ ÷ 6 = 10
Answer: The missing number is: 60
Explanation:
Let the missing number be X.
The given Expression is:
X ÷ 6 = 10
So, X can be calculated by
X= 6 × 10 = 60
Compare
Question 21.
![]()
Answer: 10 is equal to 10
Explanation:
Let the given Expressions be A) and B)
The given Expressions are:
A) 40 ÷ 4 = 4 tens ÷ 4
= 1 ten
= 10
B) 1 × 10 = 10
So, from the above,
We can conclude that 10 is equal to 10
Question 22.
![]()
Answer: 20 is less than 200
Explanation:
Let the given Expressions be A) and B)
The given Expressions are:
A) 160 ÷ 8 = 16 tens ÷ 8
= 2 tens
= 20
B) 2 × 100 = 200
So, from the above,
We can conclude that 20 is less than 200
Question 23.
![]()
Answer: 900 is greater than 90
Explanation:
Let the given Expressions be A) and B)
The given Expressions are:
A) 8,100 ÷ 9 = 81 hundreds ÷ 9
= 9 hundreds
= 900
B) 9 × 10 = 90
So, from the above,
We can conclude that 900 is equal to 90
Question 24.
There are 240 students visiting a fair. They are divided equally among 8 barns. How many students are in each barn?

Answer: There are 30 students in each barn.
Explanation:
Given that there are 240 students visiting a fair and these students are divided equally among 8 barns.
So,
The number of students in each barn can be calculated by dividing the number of students by the number of barns.
Hence,
The number of students in each barn is:
240 ÷ 8 = 24 tens ÷ 8
= 3 tens
= 30
So, 240 ÷ 8 = 30 students
Question 25.
YOU BE THE TEACHER
Is Descartes correct? Explain.

Answer: Descartes is not correct.
Explanation:
Given Expression is 2,500 ÷ 5
The value of 2,500 ÷ 5 is:
2,500 ÷ 5 = 25 hundreds ÷ 5
= 5 hundreds
= 500
So, 2,500 ÷ 5 = 500
But, According to Descartes,
2,500 ÷ 5 = 5,000
But, up on calculation, we get the result as 500.
So, Descartes is not correct.
Think and Grow: Modeling Real Life
Example
A lobster lays 5,400 eggs. It lays 9 times as many eggs as a seahorse. How many eggs does the seahorse lay?

Draw a model.

Show and Grow
Question 26.
A coach has 350 career wins. He has 7 times as many careers wins as wins this season. How many wins does the coach have this season?

Answer: 50 wins
Explanation:
Given that a coach has 350 career wins and he has 7 times as many careers wins as this season.
So,
The number of wins that the coach has in this season can be calculated by dividing the total career wins by the number of times the career wins of this season.
Hence,
The number of career wins in this season is:
350 ÷ 7 = 35 tens ÷ 7
= 5 tens
= 50
So, from the above,
We can conclude that the career wins of this season are: 50
Question 27.
There are 160 shareable bicycles in a city. There are 8 bicycle-sharing stations. Each station has the same number of bicycles. How many bicycles are at each station?
Answer: 20 bicycles are at each station.
Explanation:
Given that there are 160 shareable bicycles in a city and there are 8 bicycle-sharing stations.
It is also given that each station has the same number of bicycles.
So, the number of bicycles in each station are:
160 ÷ 8 = 16 tens ÷ 8
= 2 tens
= 20
So, 160 ÷ 8 = 20
Hence, from the above,
We can conclude that there are 20 bicycles at each station.
Question 28.
A charity has 637 adult volunteers and 563 teenage volunteers. All of the volunteers are divided, into 6 equal groups. How many volunteers are in each group?
Answer: There are 200 volunteers in each group.
Explanation;
Given that a charity has 637 adult volunteers and 563 teenage volunteers.
So,
The total number of Volunteers = Number of adult volunteers + Number of teenage volunteers
= 637 + 563
= 1,200 volunteers
It is also given that the volunteers are divided into 6 equal groups.
So, the number of volunteers in each group are 1,200 ÷ 6.
Now,
1,200 ÷ 6 = 12 hundreds ÷ 6
= 2 hundred
= 200
Hence, from the above,
We can conclude that there are 200 volunteers in each group.
Divide Tens, Hundreds and Thousands Homework & Practice 5.1
Question 1.
Find 150 ÷ 3.
Think: 15 ÷ 3 = 5
150 ÷ 3 = 15 tens ÷ 3
= 5 tens
= 50
So, 150 ÷ 3 = 50
Question 2.
Find 6,300 ÷ 7
Think: 63 ÷ 7 = 9
6,300 ÷ 7 = 63 hundreds ÷ 7
= 9 hundreds
= 900
So, 6300 ÷ 7 = 900
Find the quotient.
Question 3.
12 ÷ 2 = _____
120 ÷ 2 = ______
1,200 ÷ 2 = ______
Answer:
Let the Expressions be A), B) and C)
So,
The quotients of A), B) and C) are:
A) 6
B) 60
C) 600
Explanation:
Let the given Expressions be A), B) and C)
So, the given Expressions are:
A) 12 ÷ 2
B) 120 ÷ 2
C) 1,200 ÷ 2
So,
A) 12 ÷ 2 = 6
B) 120 ÷ 2 = 12 tens ÷ 2
= 6 tens
=60
So, 120 ÷ 2 = 60
C) 1,200 ÷ 2 = 12 hundreds ÷ 2
= 6 hundred
= 600
So, 1,200 ÷ 2 = 600
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 4.
40 ÷ 8 = _____
400 ÷ 8 = ______
4,000 ÷ 8 = ______
Answer:
Let the Expressions be A), B) and C)
So,
The quotients of A), B) and C) are:
A) 5
B) 50
C) 500
Explanation:
Let the given Expressions be A), B) and C)
So, the given Expressions are:
A) 40 ÷ 8
B) 400 ÷ 8
C) 4,000 ÷ 8
So,
A) 40 ÷ 8 = 5
B) 400 ÷ 8 = 40 tens ÷ 8
= 5 tens
=50
So, 400 ÷ 8 = 50
C) 4,000 ÷ 8 = 40 hundreds ÷ 8
= 5 hundred
= 500
So, 4,000 ÷ 8 = 500
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Find the quotient.
Question 5.
80 ÷ 8 = ______
Answer: 10
Explanation:
The given Expression is:
80 ÷ 8 = 8 tens ÷ 8
= 1 ten
=10
So, 80 ÷ 8 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 6.
300 ÷ 6 = _____
Answer: 50
Explanation:
The given Expression is:
300 ÷ 6 = 30 tens ÷ 6
= 5 tens
=50
So, 300 ÷ 6 = 50
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 7.
1,000 ÷ 5 = _____
Answer: 200
Explanation:
The given Expression is:
1,000 ÷ 5 = 10 hundreds ÷ 5
= 2 hundred
=200
So, 1,000 ÷ 5 = 200
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Find the quotient.
Question 8.
40 ÷ 8 = ______
Answer: 5
Explanation:
The given Expression is:
40 ÷ 8 = 4 tens ÷ 8
=5
So, 40 ÷ 8 = 5
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 9.
6,400 ÷ 8 = _____
Answer: 800
Explanation:
The given Expression is:
6,400 ÷ 8 = 64 hundred ÷ 8
= 8 hundred
=800
So, 6,400 ÷ 8 = 800
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 10.
350 ÷ 5 = ______
Answer: 70
Explanation:
The given Expression is:
350 ÷ 5 = 35 tens ÷ 5
= 7 tens
=70
So, 350 ÷ 5 = 70
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 11.
2,100 ÷ 7 = ____
Answer: 300
Explanation:
The given Expression is:
2,100 ÷ 7 = 21 hundreds ÷ 7
= 3 hundred
=300
So, 2,100 ÷ 7 = 300
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 12.
240 ÷ 3 = ______
Answer: 80
Explanation:
The given Expression is:
240 ÷ 3 = 24 tens ÷ 3
= 8 tens
=80
So, 240 ÷ 3 = 80
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 13.
90 ÷ 9 = _____
Answer: 10
Explanation:
The given Expression is:
90 ÷ 9 = 9 tens ÷ 9
= 1 ten
=10
So, 90 ÷ 9 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
DIG DEEPER!
Find the missing number.
Question 14.
50 ÷ ______ = 10
Answer: The missing number is: 5
Explanation:
Let the missing Expression be X.
The given Expression is:
50 ÷ X = 10
So, X can be calculated by
X= 160 ÷ 40 = 4
Question 15.
_____ ÷ 7 = 600
Answer: The missing number is: 4,200
Explanation:
Let the missing Expression be X.
The given Expression is:
X ÷ 7 = 600
So, X can be calculated by
X= 600 × 7 = 4,200
Question 16.
320 ÷ ______ = 40
Answer: The missing number is: 8
Explanation:
Let the missing number be X.
The given Expression is:
320 ÷ X = 40
So, X can be calculated by
X= 3200 ÷ 40 = 8
Compare
Question 17.
![]()
Answer: 10 is equal to 10
Explanation:
Let the given Expressions be A) and B)
The given Expressions are:
A) 30 ÷ 3 = 3 tens ÷ 3
= 1 ten
= 10
B) 1 × 10 = 10
So, from the above,
We can conclude that 10 is equal to 10
Question 18.

Answer: 70 is less than 700
Explanation:
Let the given Expressions be A) and B)
The given Expressions are:
A)560 ÷ 8 = 56 tens ÷ 8
= 7 tens
= 70
B) 9 × 100 = 700
So, from the above,
We can conclude that 70 is less than 700
Question 19.

Answer: 700 is less than 7,000
Explanation:
Let the given Expressions be A) and B)
The given Expressions are:
A) 4,900 ÷ 7 = 49 hundreds ÷ 7
= 7 hundreds
= 700
B) 7 × 1,000 = 7,000
So, from the above,
We can conclude that 700 is equal to 7,000
Question 20.
A movie theater has 180 seats. The seats are divided into 9 equal rows. How many seats are in each row?
Answer: There are 20 seats in each row.
Explanation:
Given that a model theater has 180 seats and the seats are divided into 9 equal rows.
Now, to find the number of seats in each row, we have to divide the total number of seats by the number of rows.
So,
180 ÷ 9 = 18 tens ÷ 9
= 2 tens
= 20 seats
So, from the above,
We can conclude that the number of seats in each row is: 20 seats
Question 21.
Number Sense
What is Newton’s number?

Answer:
Question 22.
Modeling Real Life
A gorilla understands 2,000 words. She understands 4 times as many words as a toddler. How many words does the toddler understand?

Answer: The toddler understands 500 words.
Explanation:
Given that a gorilla understands 2,000 words.
It is also given that the gorilla understands 4 times as many words as a toddler.
So,
The words understand by a toddler = The words understand by a gorilla ÷ 4
So,
2,000 ÷ 4 = 20 hundreds ÷ 4
= 5 hundred
= 500
Hence, from the above,
We can conclude that the words understand by a toddler are: 500 words
Review & Refresh
Compare
Question 23.
![]()
Answer: 1,834 is greater than 1,796
Explanation:
Given numbers are 1,834 and 1,796.
Hence, from these 2 numbers,
We can conclude that 1,834 is greater than 1,796
Question 24.
![]()
Answer: 62,905 is greater than 62,081
Explanation:
Given numbers are 62,905 and 62,081.
Hence, from these 2 numbers,
We can conclude that 62,905 is greater than 62,081
Question 25.
![]()
Answer: 9,142 is less than 9,146
Explanation:
Given numbers are 9,142 and 9,146
Hence, from these 2 numbers,
We can conclude that 9,142 is less than 9,146.
Question 26.
![]()
Answer: 52,048 is less than 52,071
Explanation:
Given numbers are 52,048 and 52,071
Hence, from these 2 numbers,
We can conclude that 52,048 is less than 52,071
Question 27.
![]()
Answer: 402,157 is equal to 402,157
Explanation:
Given numbers are 402,157 and 402,157
Hence, from these 2 numbers,
We can conclude that 402,157 is equal to 402,157
Question 28.
![]()
Answer: 387,402 is less than 384,927
Explanation:
Given numbers are 387,402 and 384,927
Hence, from these 2 numbers,
We can conclude that 387,402 is less than 384,927
Lesson 5.2 Estimate Quotients
Explore and Grow
Explain how you can use the table to estimate 740 ÷ 8.

740 ÷ 8 is about ______.
Answer: 90
Explanation:
Let 740 be Estimated to 720.
So, now we have to find the value of 720 ÷ 8
Now,
720 ÷ 8 = 72 tens ÷ 8
= 9 tens
= 90
Hence, from the above,
We can conclude that 740 ÷ 8 is about 90.
Reasoning
Why did you choose your estimate? Compare your results with your partner.
Answer: We choose the Estimate to round off the Result because the quotient must be the Integer.
Think and Grow: Estimate Quotients
You can use division facts and compatible numbers to estimate a quotient.
Example
Estimate 154 ÷ 4.

Look at the first two digits of the dividend and use basic division facts. and are close to the actual numbers.
Think: What number close to 154 is easily divided by 4?
Try 120. 12 ÷ 4 = 3, so 120 ÷ 4 =30.
Try 160. 16 ÷ 4 , = 4, so 160 ÷ 4 = 140.
Choose 160 because 154 is closer to 160.
So, 154 ÷ 4 is about 40.
When solving division problems, you can check whether an answer is reasonable by finding two numbers that a quotient is between.
Example
Find two numbers that the quotient 6,427 ÷ 7 is between.

Think: What numbers close to 6,427 are easily divided by7?
Use 6,300. 63 ÷ 7 = 9, so 6,300 ÷ 7 = 900.
Use 7,000. 70 ÷ 7 = 10, so 7,000 ÷ 7 = 1,000 .
6,427 is between 6,300 and 7,000.
So, the quotient 6,427 ÷ 7 is between 900 and 1,000.
Show and Grow
Estimate the quotient.
Question 1.
61 ÷ 3
Answer: 20
Explanation;
Let 61 be rounded off to 60.
So, now we have to find 60 ÷ 3
Now,
60 ÷ 3 = 6 tens ÷ 3
= 2 tens
= 20
Hence, from the above,
We can conclude that 61 ÷ 3 can be rounded off to 20.
Question 2.
465 ÷ 9
Answer: 50
Explanation:
Let 465 be rounded off to 450.
So, now we have to find 450 ÷ 9
Now,
450 ÷ 9 = 45 tens ÷ 9
= 5 tens
= 50
Hence, from the above,
We can conclude that 465 ÷ 9 can be rounded off to 50..
Find two numbers that the quotient is between.
Question 3.
477 ÷ 8
Answer: The Quotient of 477 ÷ 8 is between 50 and 60.
Explanation:
Use 400. 40 ÷ 8 = 5, so 400 ÷ 8 = 50.
Use 480. 48 ÷ 8 = 6, so 480 ÷ 8 = 60 .
477 is between 400 and 480.
So, the quotient of 477 ÷ 8 is between 50 and 60.
Question 4.
5,194 ÷ 6
Answer: The Quotient of 5,194 ÷ 6 is between 800 and 900
Explanation:
Use 4,800. 48 ÷ 6 = 8, so 4,800 ÷ 6 = 800.
Use 5,400. 54 ÷ 6 = 9, so 5,400 ÷ 6 = 900 .
5,194 is between 4,800 and 5,400.
So, the quotient of 5,194 ÷ 6 is between 800 and 900
Apply and Grow: Practice
Estimate the quotient
Question 5.
29 ÷ 5
Answer: 6
Explanation;
Let 29 be rounded off to 30.
So, now we have to find 30 ÷ 5
Now,
30 ÷ 5 = 3 tens ÷ 5
= 6
Hence, from the above,
We can conclude that 29 ÷ 5 can be rounded off to 6.
Question 6.
571 ÷ 8
Answer: 70
Explanation;
Let 571 be rounded off to 560.
So, now we have to find 560 ÷ 8
Now,
560 ÷ 8 = 56 tens ÷ 8
= 7 tens
= 70
Hence, from the above,
We can conclude that 571 ÷ 8 can be rounded off to 70.
Question 7.
202 ÷ 6
Answer: 30
Explanation;
Let 202 be rounded off to 180.
So, now we have to find 180 ÷ 6
Now,
180 ÷ 6 = 18 tens ÷ 6
= 3 tens
= 30
Hence, from the above,
We can conclude that 202 ÷ 6 can be rounded off to 30.
Question 8.
3,384 ÷ 7
Answer: 500
Explanation;
Let 3,384 be rounded off to 3,500.
So, now we have to find 3,500 ÷ 7
Now,
3,500 ÷ 7 = 35 hundreds ÷ 7
= 5 hundred
= 500
Hence, from the above,
We can conclude that 3,384 ÷ 7 can be rounded off to 500.
Find two estimates that the quotient is between.
Question 9.
22 ÷ 3
Answer: The Quotient of 22 ÷ 3 is between 7 and 8.
Explanation:
Use 21. , so 21 ÷ 3 = 7.
Use 24. so 24 ÷ 3 = 8 .
22 is between 21 and 24.
So, the quotient of 22 ÷ 3 is between 7 and 8.
Question 10.
165 ÷ 9
Answer: The Quotient of 165 ÷ 9 is between 10 and 20
Explanation:
Use 90. 9 ÷ 9 = 1, so 90 ÷ 9 = 10.
Use 180. 18 ÷ 9 = 2, so 180 ÷ 9 = 20 .
165 is between 90 and 180.
So, the quotient of 165 ÷ 9 is between 10 and 20
Question 11.
2,387 ÷ 5
Answer: The Quotient of 2,387 ÷ 5 is between 400 and 500.
Explanation:
Use 2,000. 20 ÷ 5 = 4, so 2,000 ÷ 5 = 400.
Use 2,500. 25 ÷ 5 = 5, so 2,500 ÷ 5 = 500 .
2,387 is between 2,000 and 2,500.
So, the quotient of 2,387 ÷ 5 is between 400 and 500.
Question 12.
3,813 ÷ 4
Answer: The Quotient of 3,813 ÷ 4 is between 900 and 1,000
Explanation:
Use 3,600. 36 ÷ 4 = 9, so 3,600 ÷ 4 = 900.
Use 4,000. 40 ÷ 4 = 10, so 4,000 ÷ 4 = 1,000 .
3,813 is between 3,600 and 4,000.
So, the quotient of 2,387 ÷ 5 is between 400 and 500.
DIG DEEPER!
Estimate to compare.
Question 13.
![]()
Answer: 3 is greater than 2
Explanation;
Given Expressions are 26 ÷ 9 and 2
Let 26 be rounded to 27.
Now,
27 ÷ 9 = 3
Hence, from the above values,
We can conclude that 3 is greater than 2
Question 14.
![]()
Answer: 50 is equal to 50.
Explanation;
Given Expressions are 142 ÷ 3 and 50
Let 142 be rounded to 150.
Now,
150 ÷ 3 = 15 tens ÷ 3
= 5 tens
= 50
Hence, from the above values,
We can conclude that 50 is equal to 50.
Question 15.
![]()
Answer: 80 is less than 90
Explanation;
Given Expressions are 645 ÷ 8 and 816 ÷ 9
Let 645 be rounded to 640.
Now,
640 ÷ 8 = 64 tens ÷ 8
= 8 tens
= 80
Let 816 be rounded to 810.
Now,
810 ÷ 9 = 81 tens ÷ 9
= 9 tens
= 90
Hence, from the above results,
We can conclude that 80 is less than 90
Question 16.
![]()
Answer: 200 is equal to 200
Explanation;
Given Expressions are 1,200 ÷ 6 and 800 ÷ 4
Now,
1,200 ÷ 6 = 12 hundreds ÷ 6
= 2 hundred
= 200
Now,
800 ÷ 4 = 80 tens ÷ 4
= 20 tens
= 200
Hence, from the above results,
We can conclude that 200 is equal to 200
Question 17.
A pizza shop owner has 2,532 coupons in pamphlets of 4 coupons each. He wants to determine whether he has enough pamphlets to give one to each of his first 600 customers. Can he use an estimate, or is an exact answer required? Explain.

Answer: He has to use an Estimate.
Explanation:
Given that a pizza owner has 2,532 coupons in pamphlets of 4 coupons each and he wants to give one to each of his first 600 customers.
So, we have to first find the total number of coupons he has.
But, there are 2,532 coupons in pamphlets for 4 coupons each. The coupons are in such a way that we can cot divide all the coupons equally.
So, we have to find the estimate of 2,532
Let 2,532 be rounded to 2,400 ( Since the coupons are to be divided into 4 coupons each)
Hence,
2,400 ÷ 4 = 24 hundreds ÷ 4
= 6 hundred
= 600
From this,
We can conclude that the pizza owner has to use an Estimate.
YOU BE THE TEACHER
Your friend finds a quotient. Is his answer reasonable? Estimate to check.
Question 18.
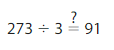
Answer: His answer is reasonable
Explanation:
Given Expression is 273 ÷ 3
Let 273 be rounded to 270
Now,
270 ÷ 3 = 27 tens ÷ 3
= 9 tens
= 90
Since there is not much difference between the Estimate quotient and the quotient of your friend, his answer is reasonable.
Question 19.
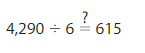
Answer: His answer is not reasonable.
Explanation:
Given Expression is 4,290 ÷ 6
Let 4,290 be rounded to 4,200
Now,
4,200 ÷ 6 = 42 hundreds ÷ 6
= 7 hundred
= 700
Since the Estimate quotient and the quotient of your friend has large difference, the answer of your friend is not reasonable.
Think and Grow: Modeling Real Life
Example
Mount Nantai is 2,486 meters above sea level. It is about 8 times as many meters above sea level as the Taal Volcano. About how many meters above sea level is the Taal Volcano?

Mount Nantai is about 8 times as many meters above sea level as the Taal Volcano, so estimate 2,486 ÷ 8.
Think: What number close to 2,486 is easily divided by 8?
Try 2,400. 24 ÷ 8 = 3, so 2,400 ÷ 8 = 300.
Try 3,200. 32 ÷ 8 = 4, so 3,200 ÷ 8 = 400.
Choose 2,400 because 2,486 is closer to 2,400.
So, the Taal Volcano is about 400 meters above sea level.
Show and Grow
Question 20.
There are about 3,785 milliliters in 1 gallon. There are 4 times as many milliliters in 1 gallon as there are in 1 quart. About how many milliliters are in 1 quart?
Answer: 900 milliliters
Explanation:
Given that there are about 3,785 milliliters in 1 gallon and there are 4 times as many milliliters in 1 gallon as there are in 1 quart.
So,
The number of milliliters in 1 gallon = the number of milliliters in 1 quant
So, we have to find 3,785 ÷ 4
Now,
Let 3,785 be rounded to 3,600
So,
3,600 ÷ 4 = 36 hundreds ÷ 4
= 9 hundred
= 900
Hence, from the above,
We can conclude that the number of milliliters in 1 quant is: 900 milliliters.
Question 21.
A teenager works at an amusement park for 3 months and earns $2,178. She earns the same amount each month. About how much money does she earn each month?
Answer: $700
Explanation:
Given that a teenager works at an amusement park for 3 months ad earns $2,178 and she earns the same amount each month.
So, the amount of money she earns each month = $2,178 ÷ 3
Now,
Let 2,178 be rounded to 2,100 (Since the amount of money is the same each month)
Now,
2,100 ÷ 3 = 21 hundreds ÷ 3
= 7 hundred
=700
Hence, from the above,
We can conclude that she earns $700 each month.
Question 22.
An animal shelter has a bin filled with 456 pounds of dog food. There are 4 large dogs at the shelter who each eat 2 pounds of dog food each day. For about how many days can the dogs eat from the bin of food?

Answer: The dogs eat food from the bin of food for about 60 days.
Explanation:
Given that an animal shelter has a bin filled with 456 pounds of dog food.
It is also given that there are 4 large dogs at the shelter who each eat 2 pounds of dog food each day.
So,
The total amount of food dogs eat = 4 × 2 = 8 pounds
So,
The number of days the total amount of food the dogs eat = Total amount of food ÷ Total amount of food dogs eat per each day
= 456 ÷ 8
Let,
456 be rounded to 480
Now,
480 ÷ 8 = 48 tens ÷ 8
= 6 tens
= 60
Hence, from the above,
We can conclude that the dogs complete the total food in about 60 days.
Estimate Quotients Homework & Practice 5.2
Estimate the quotient.
Question 1.
33 ÷ 4.
Answer: 8
Explanation;
Let 33 be rounded off to 32.
So, now we have to find 32 ÷ 4
Now,
32 ÷ 4 = 8
Hence, from the above,
We can conclude that 33 ÷ 4 can be rounded off to 8.
Question 2.
527 ÷ 9
Answer: 60
Explanation;
Let 527 be rounded off to 540.
So, now we have to find 540 ÷ 9
Now,
540 ÷ 9 = 54 tens ÷ 9
= 6 tens
= 60
Hence, from the above,
We can conclude that 527 ÷ 9 can be rounded off to 60.
Find two estimates that the quotient is between.
Question 3.
308 ÷ 7
Answer: The Quotient of 308 ÷ 7 is between 40 and 50
Explanation:
Use 280. 28 ÷ 7 = 4, so 280 ÷ 7 = 40.
Use 350. 35 ÷ 7 = 5, so 350 ÷ 7 = 50 .
308 is between 280 and 350.
So, the quotient of 308÷ 7 is between 40 and 50.
Question 4.
3,421 ÷ 6
Answer: The Quotient of 3,421 ÷ 6 is between 500 and 600
Explanation:
Use 3,000. 30 ÷ 6 = 5, so 3,000 ÷ 6 = 500.
Use 3,600. 36 ÷ 6 = 6, so 3,600 ÷ 6 = 600 .
3,421 is between 3,000 and 3,600.
So, the quotient of 3,421 ÷ 6 is between 500 and 600.
DIG DEEPER!
Estimate to compare
Question 5.
![]()
Answer: 30 is less than 40
Explanation;
Given Expressions are 97 ÷ 3 and 40
Let 97 be rounded to 90.
Now,
90 ÷ 3 = 30
Hence, from the above values,
We can conclude that 30 is greater than 40
Question 6.
![]()
Answer: 80 is greater than 20
Explanation;
Given Expressions are 425 ÷ 5 and 182 ÷7
Let 425 be rounded to 400.
Now,
400 ÷ 5 = 40 tens ÷ 5
= 8 tens
= 80
Let 182 be rounded to 140.
Now,
140 ÷ 7 =14 tens ÷ 7
= 2 tens
= 20
Hence, from the above results,
We can conclude that 80 is greater than 20
Question 7.
Three friends want to share 261 tickets equally. They want to determine whether they can each have at least 87 tickets. Can they use an estimate, or is an exact answer required? Explain.

Answer: The three friends don’t have to use an Estimate and they needed an exact answer.
Explanation:
Given that 3 friends want to share 261 tickets equally and they want to determine whether they each have at least 87 tickets.
By using Estimate:
Let 261 be rounded to 270.
So, 270 tickets have to be shared among 3 friends.
Now,
270 ÷ 3 = 27 tens ÷ 3
= 9 tens
= 90
So, each friend have 90 tickets.
Now,
The given actual value is 261 tickets.
So,
261 ÷ 3 = ( 240 + 21 ) ÷ 3 ( Divide 261 into multiples of 3 so that all the partitioned numbers can be divided exactly)
= ( 240 ÷ 3) + ( 21 ÷ 3)
= 80 + 7
= 87 tickets.
Hence, from the above,
We can conclude that the 3 friends required an exact number.
Question 8.
Reasoning
Explain how to find a better estimate for 462 ÷ 5 than the one shown.
Round 462 to 500. Estimate 500 ÷ 5. 500 ÷ 5 = 100, so 462 ÷ 5 is about 100.
Answer: The better estimate to find 462 ÷ 5 is to round off 462 to 450.
Explanation:
Given Expression is 462 ÷ 5
Let 462 be rounded to 450
So,
450 ÷ 5 = 45 tens ÷ 5
= 9 tens
= 90
Now,
Let 462 be rounded to 500.
So,
500 ÷ 5 = 5 hundreds ÷ 5
= 1 hundred
=100
But, 462 is near to 450 when compared to 450.
So,
We can conclude that
462 ÷ 5 = 90
Question 9.
Modeling Real Life
A machine that makes toy spinners is in operation for 8 hours each day. The machine makes 7,829 toy spinners in 1 day. About how many toy spinners does the machine make each hour?
Answer: About 1,000 toy spinners the machine make each hour.
Explanation:
Given that a machine that makes toy spinners is in operation for 8 hours each day and the machine makes 7,829 toy spinners in 1 day.
So, to find the number of toy spinners the machine make each hour, we have to find the value of 7,829 ÷ 8
Now,
Let 7,829 be rounded to 8,000
So, 8,000 ÷ 8 = 80 hundreds ÷ 8
= 10 hundred
=1,000
So, from the above
We can conclude that about 1,000 toy spinners the machine make each hour.
Question 10.
Modeling Real Life
A little penguin has 10,235 feathers. The penguin has about 3 times as many feathers as a blue jay. About how many feathers does the blue jay have?

Answer: The blue jay have about 3,412 feathers.
Explanation;
Given that a penguin has 10,235 feathers and it has about 3 times as many feathers as a blue jay.
So,
The feathers of a blue jay = 10,235 ÷ 3
Now,
Let 10,235 be rounded to 10,236
So,
10,236 ÷ 3 = ( 9,000 + 1,236) ÷ 3
=( 9,000 ÷ 3 )+ ( 1,236 ÷ 3)
= 3,000 + 412
= 3,412 feathers
Hence, from the above,
We can conclude that there are about 3,412 feathers in a blue jay.
Review & Refresh
Write an equation for the comparison sentence.
Question 11.
15 is 9 more than 6.
Answer:
Question 12.
56 is 7 times as many as 8.
Answer: 7 ×8 = 56
Explanation:
Given that 56 is 7 times as many as 8
That means 8 + 8 + 8+ 8 + 8 +8 + 8 = 56
= 7 ×8 = 56
Lesson 5.3 Understand Division and Remainder
Explore and Grow
Use base ten blocks to determine whether 14 can be divided equally among 2, 3, 4, or 5 groups. Draw and describe your models.

Answer: 
Structure
Explain why the units that are leftover cannot be put into a group.
Answer: The leftover units of the above group can not be put into a group because it is clearly mentioned that the blocks will have to be divided into equal parts.
Think and Grow: Find and Interpret Remainder
Sometimes you cannot divide a number evenly and there is an amount left over.
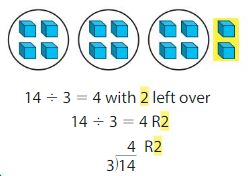
The amount left over is called the remainder. Use an R to represent the remainder.
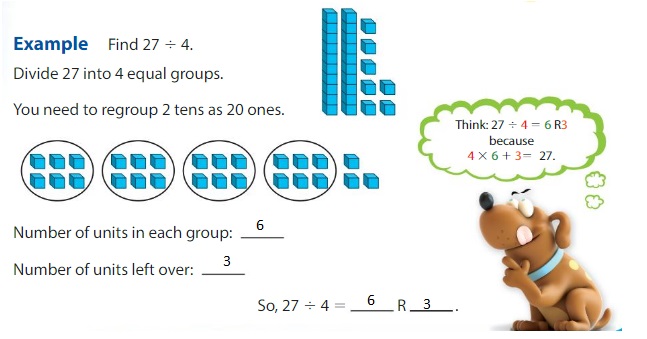
Show and Grow
Use a model to find the quotient and the remainder.
Question 1.
19 ÷ 6 = _____ R _____
Answer: 6 R 1
Explanation:
Number of Units in each group = 6
Number of units leftover = 1
So,
19 ÷ 6 = 6 R 1
Where R is the Remainder (or) the number of units leftover
Question 2.
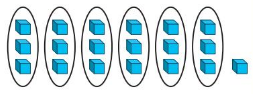
34 ÷ 5 = _____ R ______
Answer: 6 R 4
Explanation:
Number of Units in each group = 6
Number of units leftover = 4
So,
34 ÷ 5 = 6 R 4
Where R is the Remainder (or) the number of units leftover
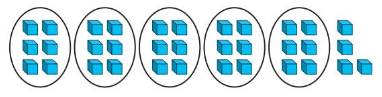
Question 3.
26 ÷ 3 = _____ R _____
Answer: 8 R 2
Explanation:
Divide 26 into 3 equal parts.
So, we will get
Number of Units in each group = 8
Number of units leftover = 2
Hence,
26 ÷ 3 = 8 R 2
Where R is the Remainder (or) the number of units leftover
Question 4.
20 ÷ 7 = ______ R _____
Answer: 14 R 6
Explanation:
Divide 20 into 7 equal parts.
So, we will get
Number of Units in each group = 2
Number of units leftover = 6
Hence,
20 ÷ 7 = 14 R 6
Where R is the Remainder (or) the number of units leftover
Apply and Grow: Practice
Use a model to find the quotient and the remainder.
Question 5.
13 ÷ 2 = _____ R _____
Answer: 6 R 1
Explanation:
Divide 13 into 2 equal parts.
So, we will get
Number of Units in each group = 6
Number of units leftover = 1
Hence,
13 ÷ 2 = 6 R 1
Where R is the Remainder (or) the number of units leftover
Question 6.
25 ÷ 9 = ____ R ____
Answer: 2 R 7
Explanation:
Divide 25 into 9 equal parts.
So, we will get
Number of Units in each group = 2
Number of units leftover = 7
Hence,
25 ÷ 9 = 2 R 7
Where R is the Remainder (or) the number of units leftover
Question 7.
28 ÷ 8 = _______ R _____
Answer: 3 R 4
Explanation:
Divide 28 into 8 equal parts.
So, we will get
Number of Units in each group = 3
Number of units leftover = 4
Hence,
28 ÷ 8 = 3 R 4
Where R is the Remainder (or) the number of units leftover
Question 8.
15 ÷ 4 = _____ R _____
Answer: 3 R 3
Explanation:
Divide 15 into 4 equal parts.
So, we will get
Number of Units in each group = 3
Number of units leftover = 3
Hence,
15 ÷ 4 = 3 R 3
Where R is the Remainder (or) the number of units leftover
Question 9.
29 ÷ 6 = _____ R ______
Answer: 4 R 5
Explanation:
Divide 29 into 6 equal parts.
So, we will get
Number of Units in each group = 4
Number of units leftover = 5
Hence,
29 ÷ 6 = 4 R 5
Where R is the Remainder (or) the number of units leftover
Question 10.
11 ÷ 5 = ______ R ______
Answer: 2 R 1
Explanation:
Divide 11 into 5 equal parts.
So, we will get
Number of Units in each group = 2
Number of units leftover = 1
Hence,
11 ÷ 5 = 2 R 1
Where R is the Remainder (or) the number of units leftover
Question 11.
Descartes has 23 cat treats to divide equally among 4 friends. How many treats does he give each friend? How many treats are left over?
Answer:
The number of treats he gives to each friend = 5
The number of treats leftover = 3
Explanation:
Given that Descartes has 23 cat treats to divide equally among 4 friends.
So,
We have to find 23 ÷ 4 to find the number of treats he gives to each friend and the number of treats leftover
Now,
Divide 23 into 4 equal parts.
So, we will get
Number of Units in each group = 5
Number of units leftover = 3
So,
23 ÷ 4 = 5 R 3
Where R is the Remainder (or) the number of units leftover
Hence, from the above,
We can conclude that,
The number of treats he gives to each friend = 5
The number of treats leftover = 3
Question 12.
You have 26 markers. How many groups of 3 markers can you make? How many markers are left over?
Answer:
The number of markers can you make = 8
The number of markers leftover = 2
Explanation:
Given that you have 26 markers and you have to make a group of 3 markers each.
So, we have to find 26 ÷ 3 so that we can find the number of markers that you make and the number of markers leftover.
Now,
Divide 26 into 3 equal parts.
So, we will get
Number of Units in each group = 8
Number of units leftover = 2
So,
26 ÷ 3 = 8 R 2
Where R is the Remainder (or) the number of units leftover
Hence, from the above,
We can conclude that,
The number of markers can you make = 8
The number of markers leftover = 2
Question 13.
Structure
Write a division equation represented by the model.
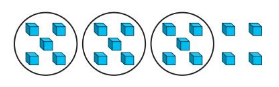
Answer: 19 ÷ 3 = 5 R 4
Explanation:
Given model is

So, from the above model, we can see that
The number of groups = 3
The number of units in each group = 5
The number of units leftover = 4
So, to find the total number of units,
Total number of units = (The number of groups × The number of units in each group ) + ( The number of units leftover)
= (5 × 3) + 4 = 15 + 4 = 19
Hence, from the above, the division equation represented by the model is:
19 ÷ 3 = 5 R 4
Question 14.
YOU BE THE TEACHER
Is Newton correct? Draw a model to support your answer.
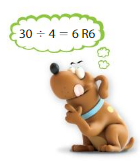
Answer: Yes, Newton is correct.
Explanation:
The given division equation is:
30 ÷ 4
From the division equation, we can see that
The number of units in each group = 6
The number of units leftover = 6
So, we can write
30 ÷ 4 = 6 R 6
Newton has also given the same division equation as we got above.
Hence, Newton is correct.
Think and Grow: Modeling Real Life
Example
A water taxi transports passengers to an island. The taxi holds no more than 8 passengers at a time. There are 53 people in line to ride the water taxi.

• How many trips to the island are full?
• How many trips to the island are needed?
• How many passengers are on the last trip?
Use a model to find 53 ÷ 8.

The quotient is 6. The remainder is 5.
Interpret the quotient and the remainder.
How many trips to the island are full?
“6” is the number of trips that have 8 passengers.
So, 6 trips to the island are full.
How many trips to the island are needed?
6 trips are full and 1 trip is not full.
So, 7 trips are needed.
How many passengers are on the last trip?
“5” is the number of passengers that are on the last trip.
So, 5 passengers are on their last trip.
Show and Grow
Question 15.
Tours of a crayon factory have no more than 9 guests. There are 87 guests in line to tour the factory.
• How many tours are full?
• How many tours are needed?
• How many guests are on the last tour?

Answer:
a) 9 Tours are full.
b) 10 Tours are needed.
c) 6 guests are on the last tour.
Explanation:
Given that there are 87 guests in line to tour a crayon factory It is also given that there are no more than 9 guests in the tours of a crayon factory.
We have to observe that to make all the guests full on all the trips without leftovers, we will need 10 trips. i.e.., 90 guests.
So, now we have to find the number of guests in each tour of a crayon factory by finding the quotient and remainder of 87 ÷ 9.
Now,
87 ÷ 9
From this, we can see
The number of guests in each tour that are full = 9
The number of guests leftover on the last trip = 6
Hence, from the above,
We can conclude that
a) 9 Tours are full.
b) 10 Tours are needed.
c) 6 guests are on the last tour.
Understand Division and Remainder Homework & Practice 5.3
Use a model to find the quotient and the remainder.
Question 1.
25 ÷ 7 = _____ R _____
Answer: 3 R 4
Explanation:
Divide 25 into 7 equal parts.
So, we will get
Number of Units in each group = 3
Number of units leftover = 4
Hence,
25 ÷ 7 = 3 R 4
Where R is the Remainder (or) the number of units leftover
Question 2.
19 ÷ 2 = ______ R ______
Answer: 9 R 1
Explanation:
Divide 19 into 2 equal parts.
So, we will get
Number of Units in each group = 9
Number of units leftover = 1
Hence,
19 ÷ 2 = 9 R 1
Where R is the Remainder (or) the number of units leftover
Question 3.
27 ÷ 6 = _____ R ______
Answer: 4 R 3
Explanation:
Divide 27 into 6 equal parts.
So, we will get
Number of Units in each group = 4
Number of units leftover = 3
Hence,
27 ÷ 6 = 4 R 3
Where R is the Remainder (or) the number of units leftover
Question 4.
26 ÷ 4 = ______ R ______
Answer: 6 R 2
Explanation:
Divide 26 into 4 equal parts.
So, we will get
Number of Units in each group = 6
Number of units leftover = 2
Hence,
26 ÷ 4 = 6 R 2
Where R is the Remainder (or) the number of units leftover
Use a model to find the quotient and the remainder.
Question 5.
29 ÷ 8 = _____ R _____
Answer: 3 R 5
Explanation:
Divide 29 into 8 equal parts.
So, we will get
Number of Units in each group = 3
Number of units leftover = 5
Hence,
29 ÷ 8 = 3 R 5
Where R is the Remainder (or) the number of units leftover
Question 6.
11 ÷ 2 = _____ R ______
Answer: 5 R 1
Explanation:
Divide 11 into 2 equal parts.
So, we will get
Number of Units in each group = 5
Number of units leftover = 1
Hence,
11 ÷ 2 = 5 R 1
Where R is the Remainder (or) the number of units leftover
Question 7.
DIG DEEPER!
A number divided by 4 has a remainder. What numbers might the remainder be? Explain.
Answer:
Question 8.
Modeling Real Life
Tours of a space center can have no more than 7 guests. There are 31 guests in line to tour the space center.
• How many tours are full?
• How many tours are needed?
• How many guests are on the last tour?
Answer:
a) 4 Tours are full.
b) 5 Tours are needed.
c) 3 guests are on the last tour.
Explanation:
Given that there are 31 guests in line to tour the space center. It is also given that there are no more than 7 guests in the tours of a space center.
We have to observe that to make all the guests full on all the trips without leftovers, we will need 5 trips. i.e.., 35 guests.
So, now we have to find the number of guests in each tour of a crayon factory by finding the quotient and remainder of 31 ÷ 7.
Now,
31 ÷ 7
From this, we can see
The number of guests in each tour that are full = 4
The number of guests leftover on the last trip = 3
Hence, from the above,
We can conclude that
a) 4 Tours are full.
b) 5 Tours are needed.
c) 3 guests are on the last tour.
Question 9.
Modeling Real Life
You need 3 googly eyes to make one monster puppet. You have 28 googly eyes. How many monster puppets can you make?

Answer: You can make 9 monster puppets.
Explanation:
Given that you need 3 googly eyes to make 1 monster puppet.
It is also given that you have 28 googly eyes.
So, to find the number of monster puppets that you can make with the given googly eyes, we have to find the quotient and remainder of 28 ÷ 3.
The quotient of 28 ÷ 3.is the number of monster puppets that you can make with the help of given googly eyes.
Now,
28 ÷ 3
From this, we can find
The number of units in each group = 9
The number of units leftover = 1
Now, we have to observe that “The number of units in each group” is the “Quotient”
Hence, from the above,
We can conclude that You can make 9 monster puppets with 1 leftover.
Question 10.
Modeling Real Life
Forty-one students attend tryouts for a debate league. Each team can have 6 students. How many students will not be on a team?
Answer: 5 students will not be on a team
Explanation:
Given that 41 students attend tryouts for a debate league and each team can have 6 students.
So, to find the number of students that can not form a team, we have to find the quotient and remainder of 41 ÷6
Now,
41 ÷ 6
From this, we can observe that
The number of students in each team = 6
The number of students that can not form a team = 5
Hence, from the above,
We can conclude that 5 students will not be on a team.
Question 11.
Modeling Real Life
A book has 37 pages. You read 7 pages each day. How many days will it take you to finish the book?
Answer: About 5 days
Explanation:
Given that a book has 37 pages and you read 7 pages each day.
To find the number of days it will take to finish the book, we have to find the quotient of 37 ÷ 7.
Now,
37 ÷ 7
From this,
The number of groups that can be filled = 5
The number of groups that are leftover = 2
Hence, from the above,
We can conclude that the book will be finished in about 5 days.
Review & Refresh
Estimate the sum or difference.
Question 12.
50,917 – 23,846 = _____
Answer: 27,071
Question 13.
499,042 + 181,765 = ______
Answer: 680,807
5.4 Use Partial Quotients
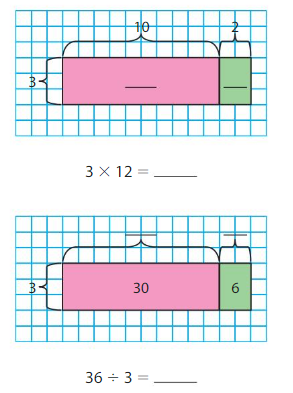
Explore and Grow
Use the area models to find 3 × 12 and 36 ÷ 3.
Answer: 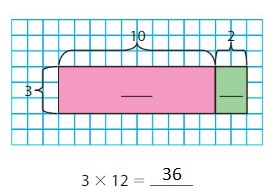
Reasoning
How does the Distributive Property relate to each of the area models? Explain.
Answer: The “Distributive Property for Partial Quotients” works in a similar way to ” The Distributive Property of Partial Products”
Explanation:
Take the above 2 Area models as examples.
In the 1st Area model, we have to find 3 × 12.
Now, by using the Distributive Property of Partial Products,
3 × 12 = 3 × (10 + 2)
= ( 3 ×10 ) + ( 3 × 2 )
= 30 + 6
= 36
Hence, 3 × 12 = 36
In the 2ndArea model, we have to find 36 ÷ 3
Now, by using the Distributive Property for Partial Quotients,
36 ÷ 3 = ( 30 + 6 ) ÷ 3
= ( 30 ÷ 3 ) + ( 6 ÷ 3 )
= 10 + 2
= 12
Hence, 36 ÷ 3 = 12
Note: When the quotient has to divide into Partial quotients, the partial quotients has to be the multiples of the number that has to divide the quotient.
Think and Grow: Use Partial Quotients to Divide
To divide using partial quotients, subtract a multiple of the divisor that is less than the dividend. Continue to subtract multiples until the remainder is less than the divisor. The factors that are multiplied by the divisor are called partial quotients. Their sum is the quotient.
Example
Use an area model and partial quotients to find 235 ÷ 5.
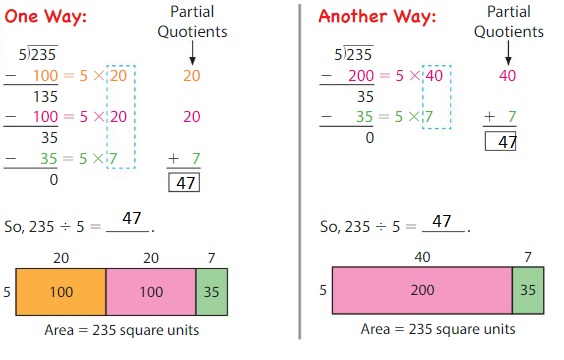
Show and Grow
Use an area model and partial quotients to divide.
Question 1.
60 ÷ 4 = _____
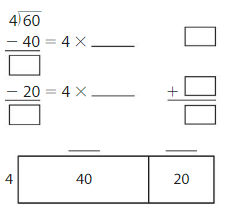
Answer: 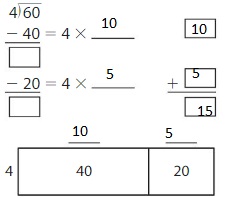
Explanation:
By using the Distributive Property for Partial Quotients,
60 ÷ 4 = ( 40 + 20 ) ÷ 4
= ( 40 ÷ 4 ) + ( 20 ÷ 4 )
= 10 + 5
= 15
Hence, 60 ÷ 4 = 15
Question 2.
192 ÷ 3 = _____
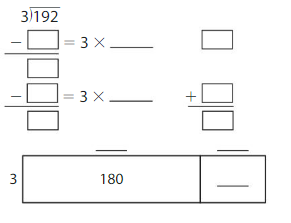
Answer: 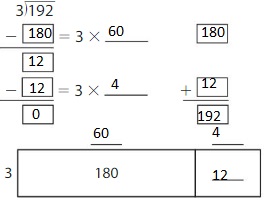
Explanation:
By using the Distributive Property for Partial Quotients,
192 ÷ 3 = ( 180 + 12 ) ÷ 3
= ( 180 ÷ 3 ) + ( 12 ÷ 3 )
= 60 + 4
= 64
Hence, 192 ÷ 3 = 64
Apply and Grow: Practice
Question 3.
Use an area model and partial quotients to find 264 ÷ 8.
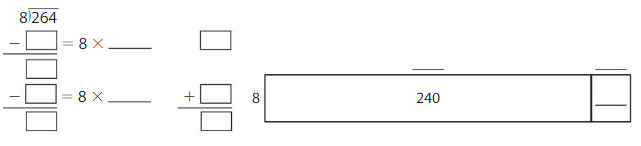
Answer: 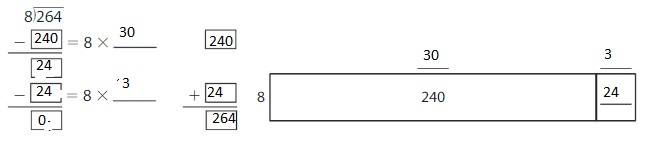
Explanation:
By using the Distributive Property for Partial Quotients,
264 ÷ 8 = ( 240 + 24 ) ÷ 8
= ( 240 ÷ 8 ) + ( 24 ÷ 8 )
= 30 + 3
= 33
Hence, 264 ÷ 8 = 33
Use partial quotients to divide
Question 4.
\(\sqrt [ 4 ]{ 96 } \)
Answer: 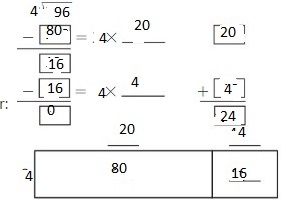
Explanation:
By using the Distributive Property for Partial Quotients,
96 ÷ 4 = ( 80 + 16 ) ÷ 4
= ( 80 ÷ 4 ) + ( 16 ÷ 4 )
= 20 + 4
= 24
Hence, 96 ÷ 4 = 24
Question 5.
\(\sqrt [ 9 ]{ 405 } \)
Answer: 
Explanation:
By using the Distributive Property for Partial Quotients,
405 ÷ 9 = ( 360 + 45 ) ÷ 9
= ( 360 ÷ 9 ) + ( 45 ÷ 9 )
= 40 + 5
= 45
Hence, 405 ÷ 9 = 45
Question 6.
\(\sqrt [ 6 ]{ 378 } \)
Answer: 
Explanation:
By using the Distributive Property for Partial Quotients,
378 ÷ 6 = ( 360 + 18 ) ÷ 6
= ( 360 ÷ 6 ) + ( 18 ÷ 6 )
= 60 + 3
= 63
Hence, 378 ÷ 6 = 63
Question 7.
\(\sqrt [ 7 ]{ 84 } \)
Answer: 
Explanation:
By using the Distributive Property for Partial Quotients,
84 ÷ 7 = ( 70 + 14 ) ÷ 7
= ( 70 ÷ 7 ) + ( 14 ÷ 7 )
= 10 +2
= 12
Hence, 84 ÷ 7 = 12
Question 8.
\(\sqrt [ 5 ]{ 735 } \)
Answer: 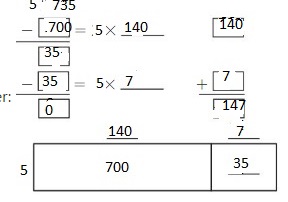
Explanation:
By using the Distributive Property for Partial Quotients,
735 ÷ 5 = ( 700 + 35 ) ÷ 5
= ( 700 ÷ 5 ) + ( 35 ÷ 5 )
= 140 + 7
= 147
Hence, 735 ÷ 5 = 147
Question 9.
Structure
Find the missing numbers.
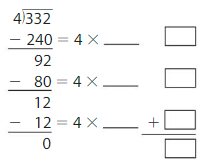
Answer: The missing numbers are: 60, 20, and 3.
Explanation:
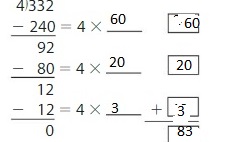
By using the Distributive Property for Partial Quotients,
332 ÷ 4 = ( 240 + 80 + 12 ) ÷ 4
= ( 240 ÷ 4 ) + ( 80 ÷ 4 ) + ( 12 ÷ 4 )
= 60 + 20 + 3
= 83
Hence, 332 ÷ 4 = 63
Think and Grow: Modeling Real Life
Example
There are 8 students on each tug-of-war team. How many tug-of-war teams are there?
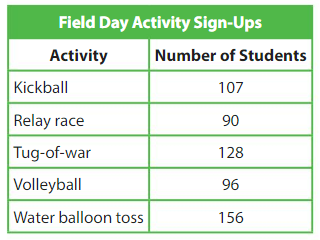
Use an area model and partial quotients to find 128 ÷ 8.
Show and Grow
Use the table above.
Question 10.
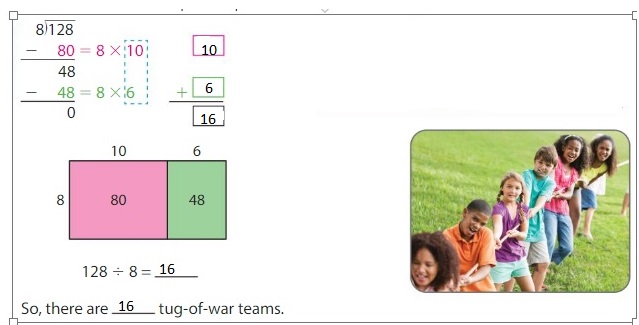
There are 5 students on each relay race team. How many relay race teams are there?
Answer: 18 relay race teams
Explanation:
The given number of students in relay race = 90
Given that there are 5 students on each relay race team.
SO, to find the number of relay race teams, we have to find the value of 90 ÷ 5.
Hence, from the above,
We can conclude that there are 18 relay race teams.
Question 11.
DIG DEEPER!
There are 6 students on beach volleyball team. There are 4 fewer students on each water balloon toss team than each volleyball team. How many of each team are there?
Answer: There are 78 teams of water balloon toss team.
Explanation:
Given that,
The total number of students in the volleyball team = 96
The total number of students in the water balloon toss team = 156
It is also given that,
There are 6 students on each volleyball team and there are 4 fewer students on each water balloon toss team.
So,
The number of students on water balloon toss team = 6 – 4 = 2 students.
Hence, to find the number of students on each water balloon toss team, we have to find the value of 156 ÷ 2 by using the Distributive Property of Partial quotients.
Using the Distributive Property of Partial quotients,
156 ÷ 2 = ( 140 + 16 ) ÷ 2
= ( 140 ÷ 2 ) + ( 16 ÷ 2 )
= 70 + 8
= 78
Hence, from the above,
We can conclude that there are 78 students on each water balloon toss team.
Question 12.
Twenty-seven students were absent on the day of sign-ups. They all decide to play kickball. There are 9 students on each kickball team. How many kickball teams are there?
Answer: There are 3 kickball teams
Explanation:
Given that there are 27 students who were absent on the day of sign-ups and they all decide to play kickball. It is also given that there are 9 students on each kickball team.
So, to find the number of kickball teams, we have to find the value of 27 ÷ 9
Now, by using the Distributive Property of partial quotients,
27 ÷ 9 = ( 18 + 9 ) ÷ 9
= ( 18 ÷ 9 ) + ( 9 ÷ 9 )
= 2 + 1
= 3
Hence, from the above,
We can conclude that there are 3 kickball teams.
Use Partial Quotients Homework & Practice 5.4
Question 1.
Use an area model and partial quotients to find 345 ÷ 5.
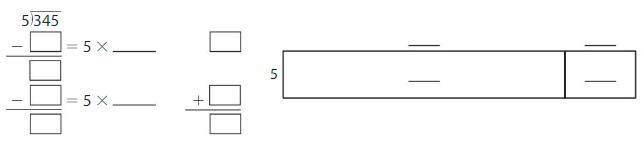
Answer: 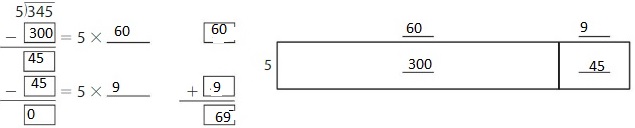
Explanation:
Using the Distributive Property of Partial quotients,
345 ÷ 5 = ( 300 + 45 ) ÷ 5
= ( 300 ÷ 5 ) + ( 45 ÷ 5 )
= 60 + 9
= 69
Hence, 345 ÷ 5 = 63
Use partial quotients to divide.
Question 2.
\(\sqrt [ 6 ]{ 90 } \)
Answer: 15
Explanation:
Using the Distributive Property of Partial quotients,
90 ÷ 6 = ( 60 + 30 ) ÷ 6
= ( 60 ÷ 6 ) + ( 30 ÷ 6 )
= 10 + 5
= 15
Hence, 90 ÷ 6 = 15
Question 3.
\(\sqrt [ 3 ]{ 48 } \)
Answer: 16
Explanation:
Using the Distributive Property of Partial quotients,
48 ÷ 3 = ( 18 + 30 ) ÷ 3
= ( 30 ÷ 3 ) + ( 18 ÷ 3 )
= 10 + 6
= 16
Hence, 48 ÷ 3 = 16
Question 4.
\(\sqrt [ 8 ]{ 200 } \)
Answer: 25
Explanation:
Using the Distributive Property of Partial quotients,
200 ÷ 8 = ( 160 + 40 ) ÷ 8
= ( 160 ÷ 8 ) + ( 40 ÷ 8 )
= 20 + 5
= 25
Hence, 200 ÷ 8 = 25
Use partial quotients to divide.
Question 5.
\(\sqrt [ 4 ]{ 56 } \)
Answer: 14
Explanation:
Using the Distributive Property of Partial quotients,
56 ÷ 4 = ( 40 + 16 ) ÷ 4
= ( 40 ÷ 4 ) + ( 16 ÷ 4 )
= 10 + 4
= 14
Hence, 56 ÷ 4 = 14
Question 6.
\(\sqrt [ 7 ]{ 511 } \)
Answer: 73
Explanation:
Using the Distributive Property of Partial quotients,
511 ÷ 7 = ( 490 + 21 ) ÷ 7
= ( 490 ÷ 7 ) + ( 21 ÷ 7 )
= 70 + 3
= 73
Hence, 511 ÷ 7 = 73
Question 7.
\(\sqrt [ 9 ]{ 423 } \)
Answer: 47
Explanation;
Using the Distributive Property of Partial quotients,
423 ÷ 9 = ( 360 + 63 ) ÷ 9
= ( 360 ÷ 9 ) + ( 63 ÷ 9 )
= 40 + 7
= 47
Hence, 423 ÷ 9 = 47
Question 8.
YOU BE THE TEACHER
Descartes finds 952 ÷ 8. Is he correct? Explain.
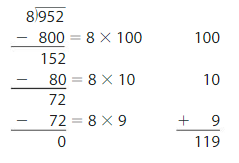
Answer: Descartes is correct.
Explanation:
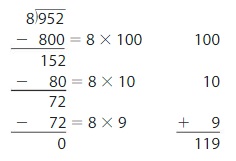
By using the Distributive Property for Partial Quotients,
952 ÷ 8 = ( 800 + 80 + 72 ) ÷ 8
= ( 800 ÷ 8 ) + ( 80 ÷ 8 ) + ( 72 ÷ 8 )
= 100 + 10 + 9
= 119
Hence, 952 ÷ 8 = 119
Question 9.
Writing
Explain how you can solve a division problem in more than one-way using partial quotients.
Answer: We can solve partial quotients in more than one-way by dividing the partial quotients in more than 2 multiples.
Explanation:
Take an example of 952 ÷ 8.
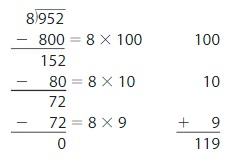
From the above, we can see that the partial quotients are divided in to 3 quotients which are the multiples of 8.
Question 10.
Modeling Real Life
Each shelter animal gets 3 toys. How many shelter animals are there?
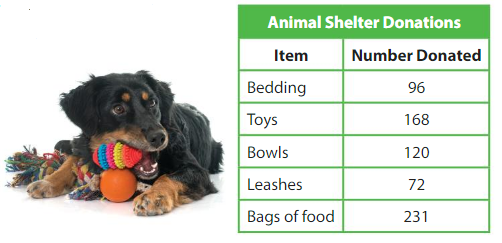
Answer: There are 56 shelter animals.
Explanation:
From the given table,
The number of toys donated = 168
It is also given that each shelter animal gets 3 toys.
So,
The number of shelter animals = The number of toys donated ÷ The number of toys that each shelter animal gets
= 168 ÷ 3
By using the Distributive property of quotients,
168 ÷ 3 = ( 150 + 18 ) ÷ 3
= ( 150 ÷ 3 ) + ( 18 ÷ 3 )
= 50 + 6
= 56
Hence, from the above,
We can conclude that there are 56 shelter animals.
Review & Refresh
Find the product.
Question 11.
40 × 70 = _____
Answer: 2,800
Explanation:
Using the Place-value method,
40 × 70 = 40 × 7 tens
= 4 tens × 7 tens
= 28 × 1 ten × 1 ten
= 28 × 10 × 10
= 2,800
Hence, 40 × 70 = 2,800
Question 12.
30 × 58 = ______
Answer: 1740
Explanation:
Using the Distributive Property of partial products,
30 × 58 = 30 × ( 50 + 8 )
= ( 30 × 50 ) + ( 30 × 8 )
= 1,500 + 240
= 1,740
Hence, 30 × 58 = 1,740
Question 13.
62 × 90 = ______
Answer: 5580
Explanation:
Using the place-value method,
62 × 90 = 62 × 9 tens
= 558 tens
= 558 × 10
= 5,580
Hence,62 × 90 = 5,580
Lesson 5.5 Use Partial Quotients with a Remainder
Explore and Grow
Use an area model to find 125 ÷ 5.
Answer: 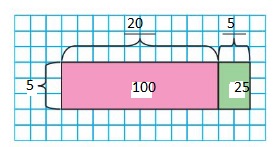
Explanation:
Using the Distributive Property of partial quotients,
125 ÷ 5 = ( 100 + 25 ) ÷ 5
= ( 100 ÷ 5 ) + ( 25 ÷ 5 )
= 20 + 5
= 25
Hence, 125 ÷ 5 = 25
Can you use an area model to find 128 ÷ 5? Explain your reasoning.
Answer: We can’t use an area model to find 128 ÷ 5 because 128 can’t be divided by 5 as 128 leaves a remainder.
Explanation:
Given division Expression is 128 ÷ 5
From this Expression, we can say that 128 can’t be divided by 5
When 128 is divided by 5, it leaves a remainder of 3.
So,
128 ÷ 5
From this,
The number of units in each group = 25
The number of units that are leftover = 3
Hence,
128 ÷ 5 = 25 R 3
Construct Arguments
Explain to your partner how your model shows that 5 does not divide evenly into 128.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Like the above arrangement, do the remaining 20 times.
Hence, we arranged 125 models in to a group and there are 3 models that are not fit in the group.
In this way, 128 will not be divided by 5 evenly.
Think and Grow: Practice
Example
Use partial quotients to find 2,918 ÷ 4.

So, 2,918 ÷ 4 = 2,916 R 2.
Show and Grow
Use partial quotients to divide.
Question 1.
82 ÷ 3 = _____
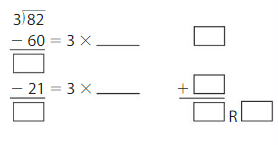
Answer: 27 R 1
Explanation:
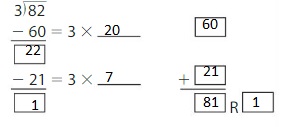
Using Distributive property of partial quotients,
82 ÷ 3 = ( 60 + 21 ) ÷ 3
= ( 60 ÷ 3 ) + ( 21 ÷ 3)
= 20 + 7
= 27 R 1
Hence, 82 ÷ 3 = 27 R 1
Question 2.
754 ÷ 9 = _____
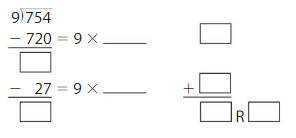
Answer: 83 R 7
Explanation:
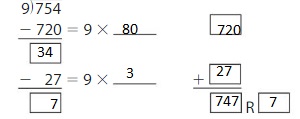
Using Distributive property of partial quotients,
754 ÷ 9 = ( 720 + 27 ) ÷ 9
= ( 720 ÷ 9 ) + ( 27 ÷ 9 )
= 80 + 3
= 83 R 7
Hence, 754 ÷ 9 = 83 R 7
Question 3.
\(\sqrt [ 8 ]{ 460 } \)
Answer: 57 R 4
Explanation:
Using Distributive property of partial quotients,
460 ÷ 8 = ( 400 + 56 ) ÷ 8
= ( 400 ÷ 8 ) + ( 56 ÷ 8 )
= 50 + 7
= 57 R 4
Hence, 460 ÷ 8 = 57 R 4
Question 4.
\(\sqrt [ 5 ]{ 3,242 } \)
Answer: 648 R 2
Explanation:
Using Distributive property of partial quotients,
3,242 ÷ 5 = ( 3,000 + 200 + 40 ) ÷ 5
= ( 3,000 ÷ 5 ) + ( 200 ÷ 5 ) + ( 40 ÷ 5 )
= 600 + 40 + 8
= 648 R 2
Hence, 3,242 ÷ 5 = 648 R 2
Question 5.
\(\sqrt [ 6 ]{ 5,850 } \)
Answer: 975 R 0
Explanation:
Using Distributive property of partial quotients,
5,850 ÷ 6 = ( 5,400 + 420 + 30 ) ÷ 6
= ( 5,400 ÷ 6 ) + ( 420 ÷ 6 ) + ( 30 ÷ 6 )
= 900 + 70 + 5
Hence, 5,850 ÷ 6 = 975 R 0
Apply and Grow: Practice
Use partial quotients to divide.
Question 6.
\(\sqrt [ 5 ]{ 63 } \)
Answer: 12 R 3
Explanation:
Using Distributive property of partial quotients,
63 ÷ 5 = ( 50 + 10 ) ÷ 5
= ( 50 ÷ 5 ) + ( 10 ÷ 5 )
= 10 + 2
= 12 R 3
Hence, 63 ÷ 5 = 12 R 3
Question 7.
\(\sqrt [ 7 ]{ 401 } \)
Answer: 57 R 2
Explanation:
Using Distributive property of partial quotients,
401 ÷ 7 = ( 350 + 49 ) ÷ 7
= ( 350 ÷ 7 ) + ( 49 ÷ 7 )
= 50 + 7
= 57 R 2
Hence, 401 ÷ 7 = 57 R 2
Question 8.
\(\sqrt [ 4 ]{ 5,237 } \)
Answer: 1,309 R 1
Explanation:
Using Distributive property of partial quotients,
5,237 ÷ 4 = ( 5,200 + 36 ) ÷ 4
= ( 5,200 ÷ 4 ) + ( 36 ÷ 4 )
= 1,300 + 9
= 1,309 R 1
Hence, 5,237 ÷ 4 = 1,309 R 1
Question 9.
\(\sqrt [ 9 ]{ 256 } \)
Answer: 28 R 4
Explanation:
Using Distributive property of partial quotients,
256 ÷ 9 = ( 180 + 72 ) ÷ 9
= ( 180 ÷ 9 ) + ( 72 ÷ 9 )
= 20 + 8
= 28 R 4
Hence, 256 ÷ 9 = 28 R 4
Question 10.
\(\sqrt [ 8 ]{ 945 } \)
Answer: 118 R 1
Explanation:
Using Distributive property of partial quotients,
945 ÷ 8 = ( 880 + 64 ) ÷ 8
= ( 880 ÷ 8 ) + ( 64 ÷ 8 )
= 110 + 8
= 118 R 1
Hence, 945 ÷ 8 = 118 R 1
Question 11.
\(\sqrt [ 2 ]{ 7,043 } \)
Answer: 3521 R 1
Explanation:
Using Distributive property of partial quotients,
7,043 ÷ 2 = ( 7,000 + 42 ) ÷ 2
= ( 7,000 ÷ 2 ) + ( 42 ÷ 2 )
= 3,500 + 21
= 3,521 R 1
Hence, 7,043 ÷ 2 = 3,521 R 1
Question 12.
The third, fourth, and fifth grades make 146 science projects for a fair. Did each grade make the same number of projects? Explain.

Answer: No, each grade did not make the same number of projects.
Explanation:
It is given that the third, fourth, and fifth grades make 146 science projects for a fair.
From this,
The total number of grades = 3
Now, to find whether each grade makes the same number of projects or not, we can find out by knowing the value of 146 ÷ 3.
Now,
Using Distributive property of partial quotients,
146 ÷ 3 = ( 120 + 24 ) ÷ 3
= ( 120 ÷ 3 ) + ( 24 ÷ 3 )
= 40 + 8
= 48 R 2
Hence, 146 ÷ 3 = 48 R 2
Question 13.
Structure
Newton found 315 ÷ 6. Explain how the steps would be different if he had used 50 as the first partial quotient?
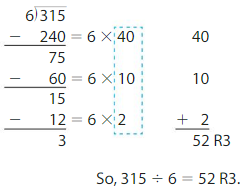
Answer:
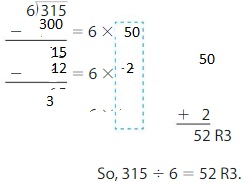
By changing the first partial quotient to 50, the number of partial quotients reduced to 2, and hence the calculation of the division becomes easy.
Think and Grow: Modeling Real Life
Example
There are 1,862 people attending a mud run. Each wave of runners can have8 people. How many waves of runners are needed?

Use partial quotients to find 1,862 ÷ 8.
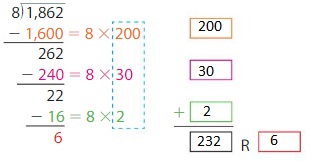
1,862 ÷ 8 = 232 R 6
Interpret the quotient and the remainder.
The quotient is 232. This means that 232 waves of runners will have 8 people.
The remainder is 6. This means that 1 wave of runners will have 6 people.
So, 1864 waves of runners are needed.
Show and Grow
Question 14.
A juice factory has 768 fluid ounces of juice for guests to sample. A worker pours the juice into 5-fluid ounce cups. How many cups does the worker fill?
Answer: The number of cups that the worker fill = 153 cups
Explanation:
Given that a juice factory has 78 fluid ounces of juice for guests to sample and a worker pours the juice into 5- fluid ounce cups.
To find the number of cups that the worker fill, we have to find the quotient of 768 ÷ 5
Now,
768 ÷ 5 = ( 700 + 60 + 5 ) ÷ 5
= ( 700 ÷ 5 ) + ( 60 ÷ 5 ) + ( 5 ÷ 5 )
= 140 + 12 + 1
= 153 R 3
Hence,
The number of cups that the worker fill = 153 cups
Question 15.
A toy company designs 214 collectible figures. The company releases 6 of the figures each month. How many months will it take the company to release all of the collectible figures? How many years will it take?

Answer:
The number of months that the company released all the toys = About 35 years
The number of years that the company released all the toys = About 3 years
Explanation:
Given that a toy company designs 214 collectible figures and the company releases 6 of the figures each month.
Now,
The number of months that the company released all toys = 214 ÷ 6
Now,
214 ÷ 6 = ( 180 + 30 ) ÷ 6
= ( 180 ÷ 6 ) + ( 30 ÷ 6 )
= 30 + 5
= 35 R 4
We know that,
1 year = 12 months
It is given that 6 figures released each month.
So, for 1 year, 72 toys will be released.
Now,
The number of years that the company released all the toys = 214 ÷ 72
Now,
214 ÷ 72 = 2 R 70
Hence, from the above,
We can conclude that
The number of months that the company released all the toys = About 35 years
The number of years that the company released all the toys = About 3 years
Use Partial Quotients with a Remainder Homework & Practice 5.5
Use partial quotients to divide.
Question 1.
\(\sqrt [ 4 ]{ 67 } \)
Answer: 16 R 3
Explanation:
Using Distributive property of partial quotients,
67 ÷ 4 = ( 60 + 4 ) ÷ 4
= ( 60 ÷ 4 ) + ( 4 ÷ 4 )
= 15 + 1
= 16 R 3
Hence, 67 ÷ 4 = 16 R 3
Question 2.
\(\sqrt [ 2 ]{ 715 } \)
Answer: 357 R 1
Explanation:
Using Distributive property of partial quotients,
715 ÷ 2 = ( 700 + 14 ) ÷ 2
= ( 700 ÷ 2 ) + ( 14 ÷ 2 )
= 350 + 7
= 357 R 1
Hence, 715 ÷ 2 = 357 R 1
Question 3.
\(\sqrt [ 5 ]{ 1,308 } \)
Answer: 261 R 3
Explanation:
Using Distributive property of partial quotients,
1,308 ÷ 5 = ( 1,000 + 300 + 5 ) ÷ 5
= ( 1,000 ÷ 5 ) + ( 300 ÷ 5 ) + ( 5 ÷ 5 )
= 200 + 60 + 1
= 261 R 3
Hence, 1,308 ÷ 5 = 261 R 3
Question 4.
\(\sqrt [ 3 ]{ 516 } \)
Answer: 172 R 0
Explanation:
Using Distributive property of partial quotients,
516 ÷ 3 = ( 510 + 6 ) ÷ 3
= ( 510 ÷ 3 ) + ( 6 ÷ 3 )
= 170 + 2
= 172 R 0
Hence, 516 ÷ 3 = 172 R 0
Question 5.
\(\sqrt [ 9 ]{ 2,497 } \)
Answer: 277 R 4
Explanation:
Using Distributive property of partial quotients,
2,497 ÷ 9 = ( 1,800 + 630 + 36 + 27 ) ÷ 9
= ( 1,800 ÷ 9 ) + ( 630 ÷ 9 ) + ( 36 ÷ 9 ) + ( 27 ÷ 9 )
= 200 + 70 + 4 + 3
= 277 R 4
Hence, 2,497 ÷ 9 = 277 R 4
Question 6.
\(\sqrt [ 6 ]{ 831 } \)
Answer: 138 R 3
Explanation:
Using Distributive property of partial quotients,
831 ÷ 6 = ( 780 + 48 ) ÷ 6
= (780 ÷ 6 ) + ( 48 ÷ 6 )
= 130 + 8
= 138 R 3
Hence, 831 ÷ 6 = 138 R 3
Use partial quotients to divide.
Question 7.
\(\sqrt [ 9 ]{ 476 } \)
Answer: 52 R 8
Explanation:
Using Distributive property of partial quotients,
476 ÷ 9 = ( 450 + 18 ) ÷ 9
= ( 450 ÷ 9 ) + ( 18 ÷ 9 )
= 50 + 2
= 52 R 8
Hence, 476 ÷ 9 = 52 R 8
Question 8.
\(\sqrt [ 7 ]{ 2,254 } \)
Answer: 322 R 0
Explanation:
Using Distributive property of partial quotients,
2,254 ÷ 7 = ( 2,100 + 140 + 14 ) ÷ 7
= ( 2,100 ÷ 7 ) + ( 140 ÷ 7 ) + ( 14 ÷ 7 )
= 300 + 20 + 2
= 322 R 0
Hence, 2,254 ÷ 7 = 322 R 0
Question 9.
\(\sqrt [ 4 ]{ 3,018 } \)
Answer: 754 R 2
Explanation:
Using Distributive property of partial quotients,
3,018 ÷ 4 = ( 2,800 + 200 + 16 ) ÷ 4
= ( 2,800 ÷ 4 ) + ( 200 ÷ 4 ) + ( 16 ÷ 4 )
= 700 + 50 + 4
= 754 R 2
Hence, 3,018 ÷ 4 = 754 R 2
Question 10.
Reasoning
Show how to use the least number of partial quotients to find 3,526 ÷ 4
Answer:
By using the Distributive property of partial quotients,
3,526 ÷ 4 = ( 3,520 + 4) ÷ 4
= ( 3,520 ÷ 4 ) + ( 4 ÷ 4 )
= 880 + 1
= 881 R 2
Hence, 3,526 ÷ 4 = 881 R 2
Hence, from the above,
We can conclude that the least number of partial quotients are “2” in 3,526 ÷ 4
Question 11.
Modeling Real Life
A gardening center has 1,582 pots to fill. Each bag of soil can fill 4 pots. How many bags of soil are needed?

Answer: The number of bags of soil needed = 395 R 2
Explanation:
Given that a gardening center has 1,582 pots to fill and each bag of soil can fill 4 pots.
So, the number of bags of soil needed = Number of pots ÷ Number of pots that each bag of soil fill
= 1,582 ÷ 4
By using the Distributive property of quotients,
1,582 ÷ 4 = ( 1,200 + 360 + 20 ) ÷ 4
= ( 1,200 ÷ 4 ) + ( 360 ÷ 4 ) + ( 20 ÷ 4 )
= 300 + 90 + 5
= 395 R 2
Hence, from the above,
We can conclude that the number of bags of soil needed are: 395 R 2
Question 12.
DIG DEEPER!
You have 178 photos. You put 3 photos on each page of an album. Your friend has 354 photos. She puts 6 photos on each page of an album. Who uses more pages? Explain.
Answer: The one who has 178 photos uses more pages.
Explanation:
Given that you 178 photos and you put 3 photos on each page of an album.
Hence, The number of pages used by you = The number of photos ÷ The number of photos on each page of an album
= 178 ÷ 3
By using the Distributive property of quotients,
178 ÷ 3 = ( 150 + 27 ) ÷ 3
= ( 150 ÷ 3 ) + ( 27 ÷ 3 )
= 50 + 9
= 59 R 1 pages
It is also given that your friend has 354 photos and she puts 6 photos on each page of an album.
Hence, The number of pages used by your friend = The number of photos ÷ The number of photos on each page of an album
= 354 ÷ 6
By using the Distributie property of quotients,
354 ÷ 6 = ( 300 + 48 + 6 ) ÷ 6
= ( 300 ÷ 6 ) + ( 48 ÷ 6 ) + ( 6 ÷ 6 )
= 50 + 8 + 1
= 59 pages
Hence, from the above,
we can conclude that you have more pages wh0 have 60 pages.
Review & Refresh
Question 13.
An Olympic swimmer wants to eat 10,000 calories each day. He eats 3,142 calories at breakfast and 3,269 calories at lunch. How many more calories must the swimmer eat to reach his goal?
Answer: The swimmer must eat 3,589 calories to reach his goal.
Explanation:
Given that an Olympic swimmer wants to eat 10,000 calories each day.
It is also given that he eats 3,142 calories at breakfast and 3,269 calories at lunch.
So,
The total calories he eat = 3,142 + 3,269 = 6,411 calories
Hence,
The number of calories he wants to eat more to reach his goal = Total number of calories – The number of calories he eats
= 10,000 – 6,411
= 3,589 calories
Hence, from the above,
We can conclude that the swimmer must eat 3,589 calories to reach his goal.
Lesson 5.6 Divide Two-Digit Numbers by One-Digit Numbers
Explore and Grow
Use a model to find each quotient. Draw each model.
84 ÷ 4
85 ÷ 5
Answer:
84 ÷ 4 = 21
85 ÷ 5 = 17
Explanation:
Let the given Expressions be marked as A) and B)
So,
A) 84 ÷4 B) 85 ÷ 5
Now,
By using the Distributive property of partial quotients,
84 ÷ 4 = ( 80 + 4 ) ÷ 4
= ( 80 ÷ 4 ) + ( 4 ÷ 4 )
= 20 + 1
= 21
Hence, 84 ÷ 4 = 21
By using the Distributive property of partial quotients,
85 ÷ 5 = ( 80 + 5 0 ÷ 5
= ( 80 ÷ 5 ) + ( 5 ÷ 5 )
= 16 + 1
= 17
Hence, 85 ÷ 5 = 17
Construct Arguments
Explain to your partner how your methods for finding the quotients above are the same. Then explain how they are different.
Answer: Let you and your partner are finding the value of 70 ÷ 5.
You want to use the Partial quotients method and your partner wants to use the area model method.
Even though the methods of your’s and your partner are different, the answer will be the same.
Now,
By using the Distributive Property of partial quotients,
70 ÷ 5 = ( 65 + 5) ÷ 5
= ( 65 ÷ 5 ) + ( 5 ÷ 5 )
= 13 + 1
= 14
So, 70 ÷ 5 = 14
Now,
By using the Area Model,
70 ÷ 5
From this,
The number of units that are grouped together = 14
The number of units that are leftover = 0
So, 70 ÷ 5 = 14 R 0
Think and Grow: Use Regrouping to Divide

Show and Grow
Divide. Then check your answer.
Question 1.
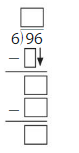
Answer: 96 ÷ 6 = 16
Explanation:
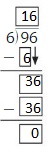
By using the partial quotients method,
96 ÷ 6 = ( 90 + 6 ) ÷ 6
= ( 90 ÷ 6 ) + ( 6 ÷ 6 )
= 15 + 1
= 16
Hence, 96 ÷ 6 = 16
Question 2.
Answer: 88 ÷ 2 = 44
Explanation:
By using the partial quotients method,
88 ÷ 2 = ( 80 + 8 ) ÷ 2
= ( 80 ÷ 2 ) + ( 8 ÷ 2 )
= 40 + 4
= 44
So, 88 ÷ 2 = 44
Question 3.

Answer: 74 ÷ 5 = 14 R 4
Explanation:
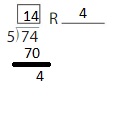
By using the partial quotients method,
74 ÷ 5 = ( 65 + 5 ) ÷ 5
= ( 65 ÷ 5 ) + ( 5 ÷ 5 )
= 13 + 1
= 14
So, 74 ÷ 5 = 14 R 4
Apply and Grow: Practice
Divide. Then check your answer.
Question 4.
\(\sqrt [ 5 ]{ 60 } \)
Answer: 60 ÷ 5 = 12
Explanation:
By using the partial quotients method,
60 ÷ 5 = ( 55 + 5 ) ÷ 5
= ( 55 ÷ 5 ) + ( 5 ÷ 5 )
= 11 + 1
= 12
Hence, 60 ÷ 5 = 12
Question 5.
\(\sqrt [ 6 ]{ 70 } \)
Answer: 70 ÷ 6 = 11 R 4
Explanation:
70 ÷ 6 = ( 60 + 6 ) ÷ 6
= ( 60 ÷ 6 ) + ( 6 ÷ 6 )
= 10 + 1
= 11
Hence, 70 ÷ 6 = 11 R 4
Question 6.
\(\sqrt [ 8 ]{ 90 } \)
Answer: 90 ÷ 8 = 11 R 2
Explanation:
By using the partial quotients method,
90 ÷ 8 = ( 80 + 8 ) ÷ 8
= ( 80 ÷ 8 ) + ( 8 ÷ 8 )
= 10 + 1
= 11
Hence, 90 ÷ 8 = 11 R 2
Question 7.
\(\sqrt [ 3 ]{ 93 } \)
Answer: 93 ÷ 3 = 31 R 0
Explanation:
By using the partial quotients method,
93 ÷ 3 = ( 90 + 3 ) ÷ 3
= ( 90 ÷ 3 ) + ( 3 ÷ 3 )
= 30 + 1
= 31
Hence, 93 ÷ 3 = 31 R 0
Question 8.
\(\sqrt [ 2 ]{ 45 } \)
Answer: 45 ÷ 2 = 22 R 1
Explanation:
By using the partila quotients method,
45 ÷ 2 = ( 40 + 4 ) ÷ 2
= ( 40 ÷ 2 ) + ( 4 ÷ 2 )
= 20 + 2
= 22
Hence, 45 ÷ 2 = 22 R 1
Question 9.
\(\sqrt [ 3 ]{ 64 } \)
Answer: 64 ÷ 3 = 21 R 1
Explanation:
By using the partial quotients method,
64 ÷ 3 = ( 60 + 3 ) ÷ 3
= ( 60 ÷ 3 ) + ( 3 ÷ 3 )
= 20 + 1
= 21
Hence, 64 ÷ 3 = 21 R 1
Question 10.
\(\sqrt [ 6 ]{ 42} \)
Answer: 42 ÷ 6 = 7
Explanation:
By using the partial quotients method,
42 ÷ 6 = ( 36 + 6 ) ÷ 6
= ( 36 ÷ 6 ) + ( 6 ÷ 6 )
= 6 + 1
= 7
Hence, 42 ÷ 6 = 7
Question 11.
\(\sqrt [ 8 ]{ 36 } \)
Answer: 36 ÷ 8 = 4 R 4
Explanantion:
By using the partial quotients method,
36 ÷ 8 = ( 24 + 8 ) ÷ 8
= ( 24 ÷ 8 ) + ( 8 ÷ 8 )
= 3 + 1
= 4 R 4
Hence, 36 ÷ 8 = 4 R 4
Question 12.
\(\sqrt [ 7 ]{ 50 } \)
Answer: 50 ÷ 7 = 7 R 1
Explanation:
By using the partial quotients method,
50 ÷ 7 = ( 42 + 7 ) ÷ 7
= ( 42 ÷ 7 ) + ( 7 ÷ 7 )
= 6 + 1
= 7
Hence, 50 ÷ 7 = 7 R 1
Question 13.
Writing
Explain how you can use estimation to check the reasonableness of your answer when dividing a two-digit number by a one-digit number.
Answer: We can check the estimation to check the reasonableness of the answer when dividing a two-digit number by a one-digit number by 2 methods. They are:
A) The partial quotients method B) Regrouping C) Area model method
Question 14.
Structure
Find the missing numbers.
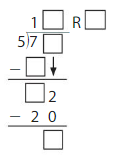
Answer: The missing numbers are: 4, 2, 5, 2, and 2 ( The order of numbers is from top to bottom)
Explanation:
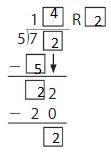
By using the partial quotients method,
72 ÷ 5 = ( 65 + 5 ) ÷ 5
= ( 65 ÷ 5 ) + ( 5 ÷ 5 )
= 13 + 1
= 14
Hence, 72 ÷ 5 = 14 R 2
Think and Grow: Modeling Real Life
Example
A house cat has 64 muscles in its ears. It has the same number of muscles in each ear. How many muscles does the house cat have in each ear?

The house cat has 2 ears, so find 64 ÷ 2.
Think: 64 is 6 tens and 4 ones.
Divide the tens.

Show and Grow
Question 15.
You earn 5 cents for each plastic bottle you recycle. You recycle some bottles and earn 75 cents. How many bottles did you recycle?
Answer: 75 ÷ 5 = 15 bottles
Explanation:
Given,
The cost of each plastic bottle you recycle = 5 cents
The total money earned by recycling plastic bottles = 75 cents
So,
The number of plastic bottles = The total money earned by recycling plastic bottles ÷ The cost of each plastic bottle you recycle
=75 ÷ 5
Now,
By using the partial quotients method,
75 ÷ 5 = ( 70 + 5 ) ÷ 5
= ( 70 ÷ 5 ) + ( 5 ÷ 5 )
= 14 + 1
= 15
Hence, from the above,
We can conclude that there are 15 plastic bottles that are recycled.
Question 16.
DIG DEEPER!
A cross-country runner must run 80 miles in 1 week. He wants to run about the same number of miles each day. How many miles should he run each day? How can you interpret the remainder?
Answer: 80 ÷ 7 = 11 R 3
Explanation:
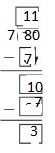
By using the partial quotients method,
80 ÷ 7 = ( 70 + 7 ) ÷ 7
= ( 70 ÷ 7 ) + ( 7 ÷ 7 )
= 10 + 1
= 11
Hence, 80 ÷ 7 = 11 R 3
Question 17.
Admission to a go-kart park costs a total of $78 for 3 adults and 3 children. The price is the same for all ages. What is the cost of admission for each person?

Answer: 78 ÷ 6 = $13
Explanation:
Given that admission to a go-kart, park costs a total of $78 for 3 adults and 3 children and it is also given that the price is the same for all ages.
Hence, the price for children and adults are the same.
Hence, total number of people = 3 adults + 3 children = 6 people
To find the cost of admission for each person, we have to find the value of 78 ÷ 6
Now,
By using the partial products method,
78 ÷ 6 = ( 60 + 18 ) ÷ 6
= ( 60 ÷ 6 ) + ( 18 ÷ 6 )
= 10 + 3
= 13
Hence, from the above,
We can conclude that the cost of admission for each person is: $13.
Divide Two-Digit Numbers by One-Digit Numbers Homework & Practice 5.6
Divide. Then check your answer.
Question 1.
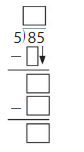
Answer: 85 ÷ 5 = 17
Explanation:
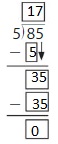
By using the partial quotients method,
85 ÷ 5 = ( 80 + 5 ) ÷ 5
= ( 80 ÷ 5 ) + ( 5 ÷ 5 )
= 16 + 1
= 17
Hence, 85 ÷ 5 = 17
Question 2.

Answer: 63 ÷ 3 = 21
Explanation:
![]()
By using the partial quotients method,
63 ÷ 3 = ( 60 + 3 ) ÷ 3
= ( 60 ÷ 3 ) + ( 3 ÷ 3 )
=20 + 1
= 21
Hence, 63 ÷ 3 = 21
Question 3.
Answer: 94 ÷ 7 =13 R 3
Explanation:
By using the partial quotients method,
94 ÷7 = ( 84 + 7 ) ÷ 7
= ( 84 ÷ 7 ) + ( 7 ÷ 7 )
= 12 + 1
= 13 R 3
Hence, 94 ÷ 7 = 13 R 3
Divide. Then check your answer.
Question 4.
\(\sqrt [ 6 ]{ 74 } \)
Answer: 74 ÷ 6 = 12 R 2
Explanation:
By using the partial products method,
74 ÷ 6 = ( 60 + 12 ) ÷ 6
= ( 60 ÷ 6 ) + ( 12 ÷ 6 )
= 10 + 2
= 12 R 2
Hence, 74 ÷ 6 = 12 R 2
Question 5.
\(\sqrt [ 8 ]{ 92 } \)
Answer: 92 ÷ 8 = 11 R 4
Explanation:
By using the partial products method,
92 ÷ 8 = ( 80 + 8 ) ÷ 8
= ( 80 ÷ 8 ) + ( 8 ÷ 8 )
= 10 + 1
= 11 R 4
Hence, 92 ÷ 8 = 11 R 4
Question 6.
\(\sqrt [ 3 ]{ 50 } \)
Answer: 50 ÷ 3 = 16 R 2
Explanation:
By using the partial quotients method,
50 ÷ 3 = ( 42 + 6 ) ÷ 3
= ( 42 ÷ 3 ) + ( 6 ÷ 3 )
= 14 + 2
= 16 R 2
Hence, 50 ÷ 3 = 16 R 2
Question 7.
\(\sqrt [ 2 ]{ 83 } \)
Answer: 83 ÷ 2 = 41 R 1
Explanation:
By using the partial quotients method,
83 ÷ 2 = ( 80 + 2 ) ÷ 2
= ( 80 ÷ 2 ) + ( 2 ÷ 2 )
= 40 + 1
= 41 R 1
Hence, 83 ÷ 2 = 41 R 1
Question 8.
\(\sqrt [ 9 ]{ 72 } \)
Answer: 72 ÷ 9 = 8 R 0
Explanation:
By using the partial quotients method,
72 ÷ 9 = ( 63 + 9 ) ÷ 9
= ( 63 ÷ 9 ) + ( 9 ÷ 9 )
= 7 + 1
= 8 R 0
Hence, 72 ÷ 9 = 8 R 0
Question 9.
\(\sqrt [ 7 ]{ 65 } \)
Answer: 65 ÷ 7 = 9 R 2
Explanation:
By using the artial products method,
65 ÷ 7 = ( 56 + 7 ) ÷ 7
= ( 56 ÷ 7 ) + ( 7 ÷ 7 )
= 8 + 1
= 9 R 2
Hence, 65 ÷ 7 = 9 R 2
Question 10.
Which One Doesn’t Belong?
Which problem does not require regrouping not to solve?
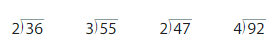
Answer: Let the given Expressions be named as A), B), C), and D)
Hence,
A) 36 ÷ 2
B) 55 ÷ 2
C) 47 ÷ 2
D) 92 ÷ 2
From the above Expressions, we can conclude that Expression A) does not require Regrouping to solve.
Explanation:
Let the given Expressions be named as A), B), C), and D)
Hence,
A) 36 ÷ 2
B) 55 ÷ 2
C) 47 ÷ 2
D) 92 ÷ 2
A) 36 ÷ 2 = ( 3 tens + 6 ones ) ÷ 2
= ( 3 tens ÷ 2 ) + ( 6 ones ÷ 2 )
= 15 + 3
= 18
Here, as there are no tens left to regroup, there is no need for Regrouping again.
B) 55 ÷ 2 = ( 5 tens + 5 ones ) ÷ 2
= ( 5 tens ÷ 2 ) + ( 5 ones ÷ 2 )
It can’t be solved further and there is need for us for further Regrouping.
Hence, the remaining two will also be the same.
Hence, from the above,
We can conclude that Expression A) does not require Regrouping.
Question 11.
Modeling Real Life
A team of 6 students finishes an obstacle course in 66 minutes. Each student spends the same number of minutes on the course. How many minutes is each student on the course?

Answer: Each student takes 11 minutes to finish an obstacle course.
Explanation:
Given that a team of 6 students finishes an obstacle course in 66 minutes and it is also given that each student spends the same number of minutes on the course.
So,
The number of minutes each student takes on the course = The number of total minutes taken to complete an obstacle course ÷ The number of members on each team
= 66 ÷ 6
Now,
By using the partial quotients method,
66 ÷ 6 = ( 60 + 6 ) ÷ 6
= ( 60 ÷ 6 ) + ( 6 ÷ 6 )
= 10 + 1
= 11 minutes
Hence, from the above,
We can conclude that each student takes 11 minutes to finish an obstacle race.
Question 12.
DIG DEEPER!
You want to make 40 origami animals in 3 days. You want to make about the same number of animals each day. How many animals should you make each day? How can you interpret the remainder?

Answer: You should make 13 animals each day.
Explanation:
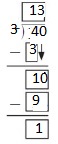
Given that you want to make 40 origami animals in 3 days and you want to make about the same number of animals each day.
So,
The number of animals you want to make on each day = Total number of animals ÷ 3
= 40 ÷ 3
Now,
By using the partial quotients method,
40 ÷ 3 = ( 30 + 9 ) ÷ 3
= ( 30 ÷ 3 ) + ( 9 ÷ 3 )
= 10 + 3
= 13 R 1
Hence, from the above,
We can conclude that you have to make 13 animals each day with one remaining at last.
Review & Refresh
Estimate the product.
Question 13.
32 × 67
Answer: 32 × 67 = 2,144
Explanation:
By using the partial products method,
32 × 6 = ( 30 + 2 ) × ( 60 + 7 )
= ( 30 × 60 ) + ( 2 × 60 ) + ( 30 × 7 ) + ( 2 × 7 )
= 1,800 + 120 + 210 + 14
= 2,144
Hence, 32 × 67 = 2,144
Question 14.
24 × 51
Answer: 24 × 51 = 1,224
Explanation:
By using the partial products method,
24 × 51 = ( 20 + 4 ) × ( 50 + 1 )
= ( 20 × 50 ) + ( 20 × 1 ) + ( 4 × 50 ) + ( 4 × 1 )
= 1,000 + 20 + 200 + 4
= 1,244
Hence, 24 × 51 = 1,244
Question 15.
96 × 75
Answer: 96 × 75 = 7,200
Explanation:
By using the partial products method,
96 × 75 = ( 90 + 6 ) × ( 70 + 5 )
= ( 90 × 70 ) + ( 90 × 5 ) + ( 6 × 70 ) + ( 6 × 5 )
= 6,300 + 450 + 420 + 30
= 7,200
Hence, 96 × 75 = 7,200
Lesson 5.7 Divide Multi-Digit Numbers by One-Digit Numbers
Explore and Grow
Use a model to divide. Draw each model.
348 ÷ 3
148 ÷ 3
Answer:
348 ÷ 3 = 116
148 ÷ 3 = 49 R 1
Explanation:
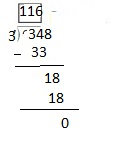
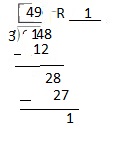
By using the partial quotients method,
348 ÷ 3 = ( 330+ 18 ) ÷ 3
= ( 330 ÷ 3 ) + ( 18 ÷ 3 )
= 110 + 6
= 116
Hence, 348 ÷ 3 = 116
148 ÷ 3 = ( 120 + 27 ) ÷ 3
= ( 120 ÷ 3 ) + ( 27 ÷ 3 )
= 40 + 9
= 49 R 1
Hence, 148 ÷ 3 = 49 R 1
Reasoning
Explain why the quotient of 148 ÷ 3 does not have a digit in the hundreds place.
Answer:
When 148 is divided by 3, the hundreds place in 148 won’t be divided by 3. This is the reason why the quotient of 148 ÷ 3 does not have the hundreds place.
Think and Grow: Practice
Example
Find 907 ÷ 5.
Estimate: 1,000 ÷ 5 = 200 R 0

So, 907 ÷ 5 = 181 R 2.
Check: Because 181 R 2 is close to the estimate, the answer is reasonable.
Show and Grow
Divide. Then check your answer.
Question 1.
Answer: 531 ÷ 4 = 132 R 3
Explanation:
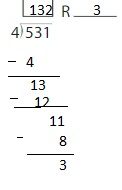
By using the partial quotients method,
531 ÷ 4 = ( 480 +48 ) ÷ 4
= ( 480 ÷ 4 ) + ( 48 ÷ 4 )
= 120 + 12
= 132 R 3
Hence, 531 ÷ 4 = 132 R 3
Question 2.

Answer: 7,180 ÷ 5 = 1,436
Explanation:
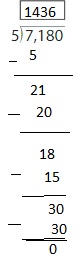
By using the partial quotients method,
7,180 ÷ 5 = ( 7,000 + 150 + 30 ) ÷ 5
= ( 7,000 ÷ 5 ) + ( 150 ÷ 5 ) + ( 30 ÷ 5 )
= 1,400 + 10 + 30 + 6
= 1,436
Hence, 7,180 ÷ 5 = 1,436
Question 3.
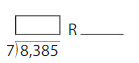
Answer: 8,385 ÷ 7 = 1,197 R 6
Explanation:

By using the partial quotients method,
8,385 ÷ 7 = ( 7,700 + 630 + 49 ) ÷ 7
= ( 7,700 ÷ 7 ) + ( 630 ÷ 7 ) + ( 49 ÷ 7 )
= 1,100 + 90 + 7
=1,197 R 6
Hence, 8,385 ÷ 7 = 1,197 R 6
Apply and Grow: Practice
Divide. Then check your answer.
Question 4.
\(\sqrt [ 5 ]{ 6,381 } \)
Answer: 6,381 ÷ 5 = 1,276 R 1
Explanation:
By using the partial quotients method,
6,381 ÷ 5 = ( 6,000 + 350 + 30 ) ÷ 5
= ( 6,000 ÷ 5 ) + ( 350 ÷ 5 ) + ( 30 ÷ 5 )
=1,200 + 70 + 6
=1,276 R 1
Hence, 6,381 ÷ 5 = 1,276 R 1
Question 5.
\(\sqrt [ 3 ]{ 4,605 } \)
Answer: 4,605 ÷ 3 = 1,535 R 0
Explanation:
4,605 ÷ 3 = ( 4,500 + 105 ) ÷ 3
= ( 4,500 ÷ 3 ) + ( 105 ÷ 3 )
= 1,500 + 35
= 1,535 R 0
Hence, 4,605 ÷ 3 = 1,535 R 0
Question 6.
\(\sqrt [ 6 ]{ 820 } \)
Answer: 820 ÷ 6 = 136 R 4
Explanation:
By using the partial quotients method,
820 ÷ 6 = ( 720 + 90 + 6 ) ÷ 6
= ( 720 ÷ 6 ) + ( 90 ÷ 6 ) + ( 6 ÷ 6 )
= 120 + 15 + 1
= 136 R 4
Hence, 820 ÷ 6 = 136 R 4
Question 7.
\(\sqrt [ 6 ]{ 7,039 } \)
Answer: 7,039 ÷ 6 = 1,173 R 1
Explanation:
By using the partial quotients method,
7,039 ÷ 6 = ( 6,600 + 420 + 18 ) ÷ 6
= ( 6,600 ÷ 6 ) + ( 420 ÷ 6 ) + ( 18 ÷ 6 )
= 1,100 + 70 + 3
= 1,173 R 1
Hence,
7,039 ÷ 6 = 1,173 R 1
Question 8.
\(\sqrt [ 4 ]{ 855 } \)
Answer: 855 ÷ 4 = 213 R 3
Explanation:
By using the partial quotients method,
855 ÷ 4 = ( 800 + 52 ) ÷ 4
= ( 800 ÷ 4 ) + ( 52 ÷ 4 )
= 200 + 13
= 213 R 3
Hence, 855 ÷ 4 = 213 R 3
Question 9.
\(\sqrt [ 2 ]{ 367 } \)
Answer: 367 ÷ 2 = 183 R 1
Explanation:
By using the partial quotients method,
367 ÷ 2 = ( 360 + 6 ) ÷ 2
= ( 360 ÷ 2 ) + ( 6 ÷ 2 )
= 180 + 3
= 183 R 1
Hence, 367 ÷ 2 = 183 R 1
Question 10.
\(\sqrt [ 8 ]{ 9,692 } \)
Answer: 9,692 ÷ 8 = 1,211 R 4
Explanation:
By using the partial quotients method,
9,692 ÷ 8 = ( 9,600 + 88 ) ÷ 8
= ( 9,600 ÷ 8 ) + ( 88 ÷ 8 )
= 1,200 + 11
= 1,211 R 4
Hence, 9,692 ÷ 8 = 1,211 R 4
Question 11.
\(\sqrt [ 7 ]{ 8,345 } \)
Answer: 8,345 ÷ 7 = 1,192 R 1
Explanation:
By using the partial quotients method,
8,345 ÷ 7 = ( 7,700 +630 +14 ) ÷ 7
= ( 7,700 ÷ 7 ) + ( 630 ÷ 7 ) + ( 14 ÷ 7 )
= 1,100 + 90 + 2
=1,192 R 1
Hence, 8,345 ÷ 7 = 1,192 R 1
Question 12.
\(\sqrt [ 7 ]{ 971 } \)
Answer: 971 ÷ 7 = 138 R 5
Explanation:
By using the partial quotients method,
971 ÷ 7 = ( 910 + 56 ) ÷ 7
= ( 910 ÷ 7 ) + ( 56 ÷ 7 )
= 130 + 8
= 138 R 5
Hence, 971 ÷ 7 = 138 R 5
Question 13.
There are 8,274 people at an air show. The people are divided into equally 6 sections. How many people are in each section?

Answer: There are 1,379 people in each section.
Explanation:
Given that there are 8,274 people at an air show and the people are divided equally into 6 sections.
So,
The number of people in each section = Total number of people ÷ Number of sections
= 8,274 ÷ 6
Now,
By using the partial quotients method,
8,274 ÷ 6 = ( 7,800 + 420 + 54 ) ÷ 6
= ( 7,800 ÷ 6 ) + ( 420 ÷ 6 ) + ( 54 ÷ 6 )
= 1,300 + 70 + 9
= 1,379
Hence, from the above,
We can conclude that there are 1,379 people in each section.
Question 14.
YOU BE THE TEACHER
Newton finds 120 ÷ 5. Is he correct? Explain.
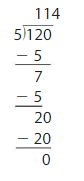
Answer: Newton is not correct.
Explanation:
According to Newton,
For 120 ÷ 5,
Quotient = 114 and Remainder = 0
But,
By using the partial quotients method,
120 ÷ 5 = ( 100 + 20 ) ÷ 5
= ( 100 ÷ 5 ) + ( 20 ÷ 5 )
= 20 + 4 )
= 24
Hence,
According to the partial quotients method,
For 120 ÷ 5,
Quotient = 24 and Remainder = 0
Hence, from the above,
We can conclude that Newton is not correct.
Think and Grow: Modeling Real Life
Example
There are 1,014 toy car tires at a factory. Each car needs 4 tires. How many toy cars can the factory workers make with the tires?
Each car needs 4 tires, so find 1,014 ÷ 4.
1 thousand cannot be shared among 4 groups without regrouping. So, regroup 1 thousand as 10 hundreds.
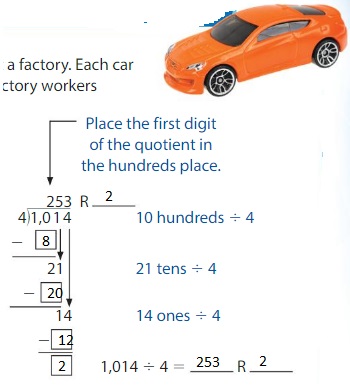
Interpret the quotient and the remainder.
The quotient is 253. The factory workers can make 253 toy cars.
The remainder is 2. There are 2 tires left over.
Show and Grow
Question 15.
A principal orders 750 tablets. The distributor can fit 8 tablets in each box. How many boxes are needed to ship all of the tablets?
Answer:
The number of boxes needed to ship all of the tablets= 93 boxes with 6 leftovers = 93 R 6
Explanation:
Given that a principal orders 750 tablets and the distributor can fit 8 tablets in each box.
So,
The number of boxes needed to ship all of the tablets = The number of tablets ordered ÷ The number of tablets that fits into each box
= 750 ÷ 8
Now,
By using the partial quotients method,
750 ÷ 8 = ( 720 + 24 ) ÷ 8
= ( 720 ÷ 8 ) + ( 24 ÷ 8 )
= 90 + 3
= 93 R 6
Hence, from the above,
We can conclude that
The number of boxes needed to ship all the tablets = 93 boxes with 6 leftovers
Question 16.
An athlete’s heart rate after a 5-mile run is 171 beats per minute, which is 3 times as fast as her resting heart rate. What is the athlete’s resting heart rate?

Answer: The athlete’s resting heart rate is 57 beats per minute.
Explanation:
Given that an athlete’s heart rate after a 5-mile run is 171 beats per minute. It is also given that 171 beats per minute which are 3 times as fast as her resting heart rate.
So,
The athlete’s heart rating rate = Athlete’s heart rate after a 5-mile run ÷ 3
= 171 ÷ 3
Now,
By using the partial quotients method,
171 ÷ 3 = ( 150 + 21 ) ÷ 3
= ( 150 ÷ 3 ) + ( 21 ÷ 3 )
= 50 + 7
= 57 beats per minute.
Hence, from the above,
We can conclude that the athlete’s resting heart rate is 57 beats per minute.
Question 17.
A car costs $5,749. The taxes and fees for the car cost an additional $496. A customer uses a 5-year interest-free loan to buy the car. How much money will the customer pay for the car each year?
Answer: The customer will pay $1,249 for the car each year
Explanation:
Given that a car costs $5,749 and the taxes and fees for the car cost an additional $496.
So,
The total cost of the car = 5,749 + 496 = $6,245
It is also given that the customer uses a 5-year interest – free loan to buy the car.
So,
The money that the customer will pay each year = The total cost of the car ÷ 5
= 6,245 ÷ 5
Now,
By using the partial quotients method,
6,245 ÷ 5 = ( 6,000 + 200 + 45 ) ÷ 5
= ( 6,000 ÷ 5 ) + ( 200 ÷ 5 ) + ( 45 ÷ 5 )
= 1,200 + 40 + 9
= $1,249
Hence, from the above,
We can conclude that
The money that the customer pay each year = $1,249
Divide Multi-Digit Numbers by One-Digit Numbers Homework & Practice 5.7
Divide. Then check your answer.
Question 1.
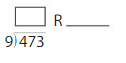
Answer: 473 ÷ 9 = 52 R 5
Explanation:
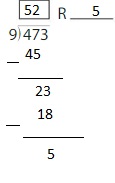
By using the partial quotients method,
473 ÷ 9 = ( 450 ÷ 9) + ( 18 ÷ 9)
= 50 + 2
= 52 R 5
Hence, 473 ÷ 9 = 52 R 5
Question 2.

Answer: 3,904 ÷ 2 = 1,952
Explanation:
By using the partial quotients method,
3,904 ÷ 2 = ( 3,000 + 900 + 4 ) ÷ 2
= ( 3,000 ÷ 2 ) + ( 900 ÷ 2 ) + ( 4 ÷ 2 )
= 1,500 + 450 +2
= 1,902
Hence, 3,904 ÷ 2 = 1,902
Question 3.
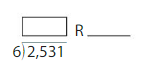
Answer: 2,531 ÷6 = 421 R 5
Explanation:
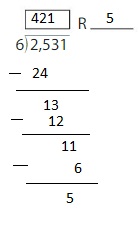
By using the partial quotients method,
2,531 ÷ 6 = ( 2,400 + 120 + 6 ) ÷ 6
= ( 2,400 ÷ 6 ) + ( 120 ÷ 6 ) + ( 6 ÷ 6 )
= 400 + 20 + 1
= 421 R 5
Hence, 2,531 ÷ 6 = 421 R 5
Question 4.
\(\sqrt [ 5 ]{ 8,271 } \)
Answer: 8,271 ÷ 5 = 1,654 R 1
Explanation:
By using the partial quotients method,
8,271 ÷ 5 = ( 8,000 + 250 + 20 ) ÷ 5
= ( 8,000 ÷ 5 ) + ( 250 ÷ 5 ) + (20 ÷ 5 )
= 1,600 + 50 + 4
= 1,654 R 1
Hence, 8,271 ÷ 5 = 1,654 R 1
Question 5.
\(\sqrt [ 7 ]{ 952 } \)
Answer: 952 ÷ 7 = 136
Explanation:
By using the partial quotients method,
952 ÷ 7 = ( 910 + 42 ) ÷ 7
= (910 ÷ 7 ) + ( 42 ÷ 7 )
= 130 + 6
= 136
Hence, 952 ÷ 7 = 136
Question 6.
\(\sqrt [ 8 ]{ 9,107 } \)
Answer: 9,107 ÷ 8 = 1,138 R 3
Explanation:
9,107 ÷ 8 = ( 8,800 + 240 + 56 +8 ) ÷ 8
= ( 8,800 ÷ 8 ) + ( 240 ÷ 8 ) + ( 56 ÷ 8 ) + ( 8 ÷ 8 )
= 1,100 + 30 + 7 + 1
= 1,138 R 3
Hence, 9,107 ÷ 8 = 1,138 R 3
Divide. Then check your answer.
Question 7.
\(\sqrt [ 3 ]{ 509 } \)
Answer: 509 ÷ 3 = 169 R 2
Explanation:
By using the partial quotients method,
509 ÷ 3 = ( 480 + 27 ) ÷ 3
= ( 480 ÷ 3 ) + ( 27 ÷ 3 )
= 160 + 9
= 169 R 2
Hence, 509 ÷ 3 = 169 R 2
Question 8.
\(\sqrt [ 4 ]{ 7,150 } \)
Answer: 7,150 ÷ 4 = 1,787 R 2
Explanation:
7,150 ÷ 4 = ( 6,800 + 320 + 28 ) ÷ 4
= ( 6,800 ÷ 4 ) + ( 320 ÷ 4 ) + ( 28 ÷ 4 )
= 1,700 + 80 + 7
= 1,787 R 2
Hence, 7,150 ÷ 4 = 1,787 R 2
Question 9.
\(\sqrt [ 2 ]{ 5,547 } \)
Answer: 5,547 ÷ 2 = 2,773 R 1
Explanation:
5,547 ÷ 2 = ( 5,000 + 500 +46 ) ÷ 2
= ( 5,000 ÷ 2 ) + ( 500 ÷ 2 ) + ( 46 ÷ 2 )
= 2,500 + 250 + 23
= 2,273 R 1
Hence, 5,547 ÷ 2 = 2,273 R 1
Question 10.
\(\sqrt [ 3 ]{ 756 } \)
Answer: 756 ÷ 3 = 252 R 0
Explanation:
756 ÷ 3 = ( 720 +36 ) ÷ 3
= ( 720 ÷ 3 ) + ( 36 ÷ 3 )
= 240 + 12
= 252
Hence, 756 ÷ 3 = 252 R 0
Question 11.
\(\sqrt [ 4 ]{ 6,871 } \)
Answer: 6,871 ÷ 4 = 1,717 R 3
Explanation:
6,871 ÷ 4 = ( 6,000 + 800 + 64 + 4 ) ÷ 4
= ( 6,000 ÷ 4 ) + ( 800 ÷ 4 ) + ( 64 ÷ 4 ) + ( 4 ÷ 4 )
= 1,500 + 200 + 16 +1
= 1,717 R 3
Hence, 6,871 ÷ 4 = 1,717 R 3
Question 12.
\(\sqrt [ 5 ]{ 108 } \)
Answer: 108 ÷ 5 = 21 R 3
Explanation:
108 ÷ 5 = ( 100 +5 ) ÷ 5
= ( 100 ÷ 5 ) + ( 5 ÷ 5 )
= 20 + 1
= 21 R 3
Hence, 108 ÷ 5 = 21 R 3
Question 13.
A deli sells 203 pretzel roll sandwiches. Each bag has 7 pretzel rolls. How many bags of pretzel rolls are used?

Answer: The number of pretzel rolls is used = 29 rolls
Explanation:
Given that a deli sells 203 pretzel roll sandwiches and each bag has 7 pretzel rolls.
So,
The number of pretzel rolls used = Total number of pretzel roll sandwiches ÷ 7
= 203 ÷ 7
Now,
By using the partial quotients method,
203 ÷ 7 = ( 140 + 63 ) ÷ 7
= ( 140 ÷ 7 ) + ( 63 ÷ 7 )
= 20 + 9
= 29 bags
Hence, from the above,
We can conclude that there are 29 bags of pretzel rolls of sandwiches
Question 14.
DIG DEEPER!
Which expression does have a 4-digit quotient? Explain not how you know without solving.
6,197 ÷ 2
3, 261 ÷ 5
5,240 ÷ 4
9,045 ÷ 8
Answer:
Let the Expressions be named as A), B), C), and D)
So,
A) 6,197 ÷ 2
B) 3, 261 ÷ 5
C) 5,240 ÷ 4
D) 9,045 ÷ 8
From the above,
Expression C) does have a 4- digit quotient without leaving a remainder.
Explanation;
Let the Expressions be named as A), B), C), and D)
So,
A) 6,197 ÷ 2
B) 3, 261 ÷ 5
C) 5,240 ÷ 4
D) 9,045 ÷ 8
A) 6,197 ÷ 2
By using the partial quotients method,
6,197 ÷ 2 = ( 6,000 + 196 ) ÷ 2
= ( 6,000 + 196 ) ÷ 2
= 3,000 + 98
=3,098 R 1
Hence, 6,197 ÷ 2 = 3,098 R 1
B) 3,261 ÷ 5 = ( 3,000 + 250 + 10 ) ÷ 5
= ( 3,000 ÷ 5 ) + ( 250 ÷ 5 ) + ( 10 ÷ 5 )
= 600 + 50 + 2
= 652 R 1
Hence, 3,261 ÷ 5 = 652 R 1
C) 5,240 ÷ 4 = ( 5,200 + 40 ) ÷ 4
= ( 5,200 ÷ 4 ) + ( 40 ÷ 4 )
= 1,300 + 10
= 1,310 R 0
Hence, 5,240 ÷ 4 = 1,310
D) 9,045 ÷ 8 = ( 9,000 + 40 ) ÷ 8
= ( 9,000 ÷ 8 ) + ( 40 ÷ 8 )
= 1,125 + 5
= 1,130 R 5
Hence, from all the 4 Expressions,
We can conclude that the Expression C) has 4-digit quotient having remainder 0
Question 15.
Modeling Real Life
There are 505 pieces of chalk donated for a community event. The chalk is bundled into groups of 7 pieces. How many bundles can be made?

Answer: The number of bundles that can be made = 72 R 1
Explanation:
Given that there are 505 pieces of chalk donated for a community event and the chalk is bundled into groups of 7 pieces.
So,
The number of bundles that can be made = 505 ÷ 7
Now,
By using the partial quotients method,
505 ÷ 7 = ( 490 + 14 ) ÷ 7
= ( 490 ÷ 7 ) + ( 14 ÷ 7 )
= 70 + 2
= 72 R 1
Hence, from the above,
We can conclude that
The number of bundles that can be made = 72 bundles with 1 leftover
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 16.
Estimate: _____
61 × 3 = _____
Answer: 61 × 3 =183
Explanation:
By using theDistributive Property,
61 × 3 = ( 60 + 1 ) × 3
= ( 60 × 3 ) + ( 1 × 3 )
= 180 + 3
= 183
So, 61 × 3 = 183
Estimate:
Let 61 be rounded to 60.
So, by using the place-value method,
60 × 3 = 6 tens × 3
= 18 tens
= 18 × 10
= 180
So, 60 × 3 = 180
Hence, from the above,
We can conclude that the actual answer is near to the Estimate. So, the answer is reasonable.
Question 17.
Estimate: ______
54 × 9 = ______
Answer: 54 × 9 = 486
Explanation:
By using the Distributive Property,
54 × 9 = ( 50 + 4 ) × 9
= ( 50 × 9 ) + ( 4 × 9 )
= 450 + 36
= 486
So, 54 × 9 = 486
Estimate:
Let 54 be rounded to 55.
Let 9 be rounded to 10
So, by using the place-value method,
10 × 55 = 1 ten × 55
= 55 tens
= 55 × 10
= 550
So, 55 × 10 = 550
Hence, from the above,
We can conclude that the actual answer is not near to the Estimate. So, the answer is not reasonable.
Question 18.
Estimate: _______
82 × 7 = ______
Answer: 82 × 7 = 574
Explanation:
By using the Distributive Property,
82 × 7 = ( 80 + 2 ) × 7
= ( 80 × 7 ) + ( 2 × 7 )
= 560 + 14
= 574
So, 82 × 7 = 574
Estimate:
Let 82 be rounded to 80.
Let 7 be rounded to 5.
So, by using the place-value method,
80 × 5 = 8 tens × 5
= 40 tens
= 40 × 10
= 400
So, 80 × 5 = 400
Hence, from the above,
We can conclude that the actual answer is not near to the Estimate. So, the answer is not reasonable.
Lesson 5.8 Divide by One-Digit Numbers
Explore and Grow
Use a model to find each quotient. Draw each model.
312 ÷ 3
312 ÷ 4
Answer:
312 ÷ 3 = 104
312 ÷ 4 = 78
Explanation:
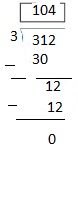
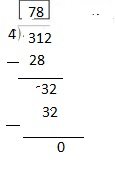
By using the partial quotients method,
312 ÷ 3 = ( 300 + 12 )÷ 3
= ( 300 ÷ 3 ) + ( 12 ÷ 3 )
= 100 + 4
= 104
Hence, 312 ÷ 3 = 104
By using the partial quotients method,
312 ÷ 4 = ( 280 + 20 + 12 ) ÷ 4
= ( 280 ÷ 4 ) + ( 20 ÷ 4 ) + ( 12 ÷ 4 )
= 70 + 5 + 3
= 78
Hence, 312 ÷ 4 = 78
Structure
Compare your models for each quotient. What is the same? What is different? What do you think this means when using regrouping to divide?
Answer: The Divisor for both the models is the same and the quotient is different for both Expressions.
Think and Grow: Divide by One-Digit Numbers
Example
Find 4,829 ÷ 8.
4 thousand cannot be shared among 8 groups without regrouping. So, regroup 4 thousands as 40 hundred and combine with 8 hundred.

Show and Grow
Divide. Then check your answer.
Question 1.

Answer: 756 ÷ 7 = 108
Explanation:
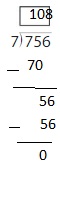
By using the partial quotients method,
756 ÷ 7 = ( 700 + 56 ) ÷ 7
= ( 700 ÷ 7 ) + ( 56 v 7 )
= 100 + 8
= 108
Hence, 756 ÷ 7 = 108
Question 2.
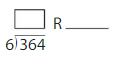
Answer: 364 ÷ 6 = 6 R 4
Explanation:
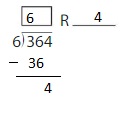
By using the partial quotients method,
364 ÷ 6 = ( 300 + 60 ) ÷ 6
= ( 300 ÷ 6 ) + ( 60 ÷ 6 )
= 50 + 10
= 60 R 4
Hence, 364 ÷ 6 = 60 R 4
Question 3.
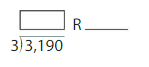
Answer: 3,190 ÷ 3 = 1,063 R 1
Explanation:
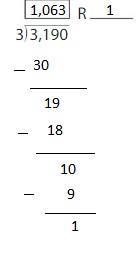
By using the partial quotients method,
3,190 ÷ 3 = ( 3,000 + 180 + 9 ) ÷ 3
= ( 3,000 ÷ 3 ) + ( 180 ÷ 3 ) + ( 9 ÷ 3 )
= 1,000 + 60 + 3
= 1,063 R 1
Hence, 3,190 ÷ 3 = 1,063 R 1
Apply and Grow: Practice
Divide. Then check your answer.
Question 4.
\(\sqrt [ 2 ]{ 81 } \)
Answer: 81 ÷ 2 = 40 R 1
Explanation:
By using the partial quotients method,
81 ÷ 2 = ( 60 + 20 ) ÷ 2
= ( 60 ÷ 2 ) + ( 20 ÷ 2 )
= 30 + 10
= 40 R 1
Hence, 81 ÷ 2 = 40 R 1
Question 5.
\(\sqrt [ 4 ]{ 428 } \)
Answer: 428 ÷ 4 = 107
Explanation:
By using the partial quotients method,
428 ÷ 4 = ( 400 + 28 ) ÷ 4
= ( 400 ÷ 4 ) + ( 28 ÷ 4 )
= 100 + 7
= 107
Hence, 428 ÷ 4 = 107
Question 6.
\(\sqrt [ 6 ]{ 842 } \)
Answer: 842 ÷ 6 = 140 R 2
Explanation:
By using the partial quotients method,
842 ÷ 6 = ( 780 + 60 ) ÷ 6
= ( 780 ÷ 6 ) + ( 60 ÷ 6 )
= 130 + 10
= 140 R 2
Hence, 842 ÷ 6 = 140 R 2
Question 7.
\(\sqrt [ 3 ]{ 2,724 } \)
Answer: 2,724 ÷ 3 = 908
Explanation:
By using partial quotients method,
2,724 ÷ 3 = ( 2,700 + 24 ) ÷ 3
= ( 2,700 ÷ 3 ) + ( 24 ÷ 3 )
= 900 + 8
= 908
Hence, 2,724 ÷ 3 = 908
Question 8.
\(\sqrt [ 9 ]{ 635 } \)
Answer: 635 ÷ 9 = 70 R 5
Explanation:
By using partial products method,
635 ÷ 9 = ( 540 + 90 ) ÷ 9
= ( 540 ÷ 9 ) + ( 90 ÷ 9 )
= 60 + 10
= 70 R 5
Hence, 635 ÷ 9 = 70 R 5
Question 9.
\(\sqrt [ 6 ]{ 1,442 } \)
Answer: 1,442 ÷ 6 = 240 R 2
Explanation:
By using partial quotients method,
1,442 ÷ 6 = ( 1,200 +240 ) ÷ 6
= ( 1,200 ÷ 6 ) + ( 240 ÷ 6 )
= 200 +40
= 240 R 2
Hence, 1,442 ÷ 6 = 240 R 2
Question 10.
\(\sqrt [ 6 ]{ 303 } \)
Answer: 303 ÷ 6 = 50 R 3
Explanation:
By using partial quotients method,
303 ÷ 6 = ( 240 + 60 ) ÷ 6
= ( 240 ÷ 6 ) + ( 60 ÷ 6 )
= 40 + 10
= 50 R 3
Hence, 303 ÷ 6 = 50 R 3
Question 11.
\(\sqrt [ 5 ]{ 2,530 } \)
Answer: 2,530 ÷ 5 = 506
Explanation:
By using partial quotients method,
2,530 ÷ 5 = ( 2,500 + 30 ) ÷ 5
= ( 2,500 ÷ 5 ) + ( 30 ÷ 5 )
= 500 + 6
= 506
Hence, 2,530 ÷ 5 = 506
Question 12.
\(\sqrt [ 8 ]{ 7,209 } \)
Answer: 7,209 ÷ 8 = 900 R 9
Explanation:
By using partial quotients method,
7,209 ÷ 8 = ( 6,400 + 800 ) ÷ 8
= ( 6,400 ÷ 8 ) + ( 800 ÷ 8 )
= 800 + 100
= 900 R 9
Hence, 7,209 ÷ 8 = 900 R 9
Question 13.
The 5 developers of a phone app earn a profit of $4,535 this month. They divide the profit equally. How much money does each developer get?

Answer: Each developer gets the money of $907
Explanation:
Given that the 5 developers of a phone app earn a profit of $4,535 this month and it is also given that they divide the profit equally.
So,
The money each developer get = The total profit earned by 5 developers ÷ 5
= $4,535 ÷ 5
Now,
By using the partial quotients method,
4,535 ÷ 5 = ( 4,500 + 35 ) ÷ 5
= ( 4,500 ÷ 5 ) + ( 35 ÷ 5 )
= 900 + 7
= 907
Hence, from the above,
We can conclude that the money got by each developer is $907.
Question 14.
Newton finds 817 ÷ 4. Is he correct? Explain.
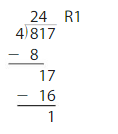
Answer: Newton is not correct.
Explanation;
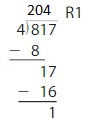
By using the partial quotients method,
817 ÷ 4 = ( 800 + 16 ) ÷ 4
= ( 800 ÷ 4 ) + ( 16 ÷ 4 )
= 200 + 4
= 204 R 1
According to Newton,
817 ÷ 4 = 24 R 1
But according to the partial quotients method,
817 ÷ 4 = 204 R 1
Hence, from the above,
We can conclude that Newton is not correct.
Think and Grow: Modeling Real Life
Example
Seven players are placed on each basketball team. Remaining basketball players are added to the teams, so some of the teams have 8 players. How many basketball teams have 7 players? 8 players?
There are 1,839 players signed up for basketball, so find 1,839 ÷ 7.
1 thousand be shared cannot among 7 groups without regrouping. So, regroup 1 thousand as 10 hundreds and combine with 8 hundreds.

Interpret the quotient and the remainder.
The quotient is262. So, there are 262 basketball teams in all.
The remainder is 5. So, 5 basketball teams have 8 players.
Subtract to find how many teams have 7 players. 262 −5 = 257
So, 257 basketball teams have 7 players and 5 have 8 players.
Show and Grow
Use the table above.
Question 15.
Nine players are placed on each ball hockey team. Remaining players are added to the teams, so some of the teams have 10 players. How many ball hockey teams have9 players? 10 players?
Answer:
Given that there are 9 players on each ball hockey team.
So, the quotient represents the ball hockey teams who have 9 players and the remainder represents the ball hockey teams who have 10 players.
Now,
By using the partial quotients method,
952 ÷ 9 = ( 900 + 45 ) ÷ 9
= ( 900 ÷ 9 ) + ( 45 ÷ 9 )
= 100 + 5
= 105 R 7
The quotient is 105. So, there are 105 ball hockey teams in all.
The remainder is 7. So, 7 ball hockey teams have 10 players.
Subtract to find the number of teams has 9 players. 105 −7 = 98
So, 98 basketball teams have 9 players and 7 have 10 players.
Question 16.
Eighty-four players who signed up to play soccer decide not to play. Eight players are placed on each soccer team. How many soccer teams are there?
Answer: There are 299 soccer teams
Explanation:
Given that 84 players who signed up to play soccer decide not to play and it is also given that 8 players are placed on each soccer team.
It is also given that,
The total number of players who play soccer = 2,476 players
So,
The number of players who played soccer = 2,476 – 84 = 2,392 players
Now,
The number of soccer teams = 2,392 ÷ 8
Now,
By using the partial quotients method,
2,392 ÷ 8 = ( 1,600 + 720 + 72 ) ÷ 8
= ( 1,600 ÷ 8 ) + ( 720 ÷ 8 ) + ( 72 ÷ 8 )
= 200 + 90 + 9
= 299
Hence, from the above,
we can conclude that there are 299 soccer teams.
Divide by One-Digit Numbers Homework & Practice 5.8
Divide. Then check your answer.
Question 1.

Answer: 832 ÷ 8 = 104
Explanation:
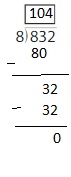
By using the partial quotients method,
832 ÷ 8 = ( 800 + 32 ) ÷ 8
= ( 800 ÷ 8 ) + ( 32 ÷ 8 )
= 100 + 4
= 104
Hence, 832 ÷ 8 = 104
Question 2.
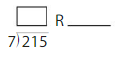
Answer: 215 ÷ 7 = 30 R 5
Explanation:
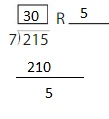
By using the partial quotients method,
215 ÷ 7 = ( 140 + 70 ) ÷7
( 140 ÷ 7 ) + ( 70 ÷ 7 )
= 20 + 10
= 30 R 5
Hence, 215 ÷7 = 30 R 5
Question 3.
Answer: 5,078 ÷ 5 = 1,015 R 3
Explanation:
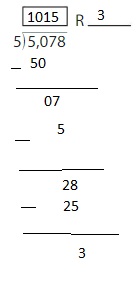
By using the partial quotients method,
5,078 ÷ 5 = ( 5,000 + 75 ) ÷ 5
= ( 5,000 ÷5 ) + ( 75 ÷ 5 )
= 1,000 + 15
= 1,015 R 3
Hence, 5,078 ÷ 5 = 1,015 R 3
Question 4.
\(\sqrt [ 7 ]{ 94 } \)
Answer: 94 ÷ 7 = 13 R 3
Explanation:
By using the partial quotients method,
94 ÷ 7 = ( 84 + 7 ) ÷ 7
= ( 84 ÷ 7 ) + ( 7 ÷ 7 )
= 12 + 1
= 13 R 1
Hence, 94 ÷ 7 = 13 R 1
Question 5.
\(\sqrt [ 6 ]{ 731 } \)
Answer: 731 ÷ 6 = 121 R 5
Explanation:
By using the partial quotients method,
731 ÷ 6 = ( 720 + 6 ) ÷ 6
= ( 720 ÷ 6 ) + ( 6 ÷ 6 )
= 120 + 1
= 121 R 5
Hence, 731 ÷ 6 = 121 R 5
Question 6.
\(\sqrt [ 4 ]{ 6,514 } \)
Answer: 6,514 ÷ 4 = 1,628 R 2
Explanation:
By using the partial quotients method,
6,514 ÷ 4 = ( 6,000 + 480 + 32 ) ÷ 4
= ( 6,000 ÷ 4 ) + ( 480 ÷ 4 ) + ( 32 ÷ 4 )
= 1,500 + 120 + 8
= 1,628 R 2
Hence, 6,514 ÷ 4 = 1,628 R 2
Question 7.
\(\sqrt [ 3 ]{ 62 } \)
Answer: 62 ÷ 3 = 20 R 2
Explanation:
By using the partial quotients method,
62 ÷3 = ( 33 + 27 ) ÷ 3
= ( 33 ÷ 3 ) + ( 27 ÷ 3 )
= 11 + 9
= 20 R 2
Hence, 62 ÷ 3 = 20 R 2
Question 8.
\(\sqrt [ 5 ]{ 548 } \)
Answer: 548 ÷ 5 = 109 R 3
Explanation:
By using the partial quotients method,
548 ÷ 5 = ( 500 + 45 ) ÷ 5
= ( 500 ÷ 5 ) + ( 45 ÷ 5 )
= 100 + 9
= 109 R 3
Hence, 548 ÷ 5 = 109 R 3
Question 9.
\(\sqrt [ 2 ]{ 4,136 } \)
Answer: 4,136 ÷ 2 = 2,068
Explanation:
By using the partial quotients method,
4,136 ÷ 2 = ( 4,000 + 100 + 36 ) ÷ 2
= ( 4,000 ÷ 2 ) + ( 100 ÷ 2 ) + ( 36 ÷ 2 )
= 2,000 + 50 + 18
= 2,068
Hence, 4,136 ÷ 2 = 2,068
Divide. Then check your answer.
Question 10.
\(\sqrt [ 7 ]{ 214 } \)
Answer: 214 ÷ 7 = 30 R 4
Explanation:
By using the partial quotients method,
214 ÷ 7 = ( 140 + 70 ) ÷ 7
= ( 140 ÷ 7 ) + ( 70 ÷ 7 )
= 20 + 10
= 30 R 4
Hence, 214 ÷ 7 = 30 R 4
Question 11.
\(\sqrt [ 4 ]{ 321 } \)
Answer: 321 ÷ 4 = 80 R 1
Explanation:
By usng the partial quotients method,
321 ÷ 4 = ( 280 + 40 ) ÷ 4
= ( 280 ÷ 4 ) + ( 40 ÷ 4 )
= 70 + 10
= 80 R 1
Hence, 321 ÷ 4 = 80 R 1
Question 12.
\(\sqrt [ 6 ]{ 5,162 } \)
Answer: 5,162 ÷6 = 860 R 2
Explanation:
By using the partial quotients method,
5,162 ÷ 6 = ( 4,800 + 300 + 60 ) ÷ 6
= ( 4,800 ÷ 6 ) + ( 300 ÷ 6 ) + ( 60 ÷ 6 )
= 800 + 50 + 10
= 860 R 2
Hence, 5,162 ÷ 6 = 860 R 2
Question 13.
\(\sqrt [ 2 ]{ 7,301 } \)
Answer: 7,301 ÷ 2 = 3,650 R 1
Explanation:
By using the partial quotients method,
7,301 ÷ 2 = ( 7,000 + 300 ) ÷ 2
= ( 7,000 ÷ 2 ) + ( 300 ÷ 2 )
= 3,500 + 150
= 3,650 R 1
Hence, 7,301 ÷ 2 = 3,650 R 1
Question 14.
\(\sqrt [ 5 ]{ 603 } \)
Answer: 603 ÷ 5 = 120 R 3
Explanation:
By using the partial products method,
603 ÷ 5 = ( 550 + 50 ) ÷ 5
= ( 550 ÷ 5 ) + ( 50 ÷ 5 )
= 110 + 10
= 120 R 3
Hence, 603 ÷ 5 = 120 R 3
Question 15.
\(\sqrt [ 3 ]{ 6,082 } \)
Answer: 6,082 ÷ 3 = 2,027 R 1
Explanation:
By using the partial quotients method,
6,082 ÷ 3 = ( 6,000 + 81 ) ÷ 3
= ( 6,000 ÷ 3 ) + ( 81 ÷ 3 )
= 2,000 + 27
= 2,027 R 1
Hence, 6,082 ÷ 3 = 2,027 R 1
Question 16.
There are 450 pounds of grapes for a grape stomping contest. They are divided equally into 5 barrels. How many pounds of grapes are in each barrel?

Answer: There are 90 pounds of grapes in each barrel.
Explanation:
Given that there are 450 pounds of grapes for a grape stomping contest and they are divided equally into 5 barrels.
So,
The number of pounds of grapes in each barrel = Total number of pounds of groups ÷ 5
= 450 ÷ 5
Now,
By using the partial quotients method,
450 ÷ 5 = ( 400 + 50 ) ÷ 5
= ( 400 ÷ 5 ) + ( 50 ÷ 5 )
= 80 + 10
= 90 pounds
Hence, from the above,
We can conclude that there are 90 pounds of grapes in each barrel.
Question 17.
DIG DEEPER!
How could you change the dividend in Exercise 11 so that there would be no remainder? Explain.
Answer: The dividend given in Exercise 11 is 321 and leaves the remainder 1 when the dividend is divided by 4.
So, to make the dividend a number in such a way that it is divisible by 4 and leaves the remainder 0
By observing the given number 321, we can say that it is close to 320 which is divisible by 4 and leaves the remainder 0.
Hence, the number which we have to change so that the remainder will be 0 is: 320
Question 18.
Modeling Real Life
Five actresses are placed on each team. Remaining actresses are added to the teams, so some of the teams have 6 actresses. How many teams have 5 actresses? 6 actresses?
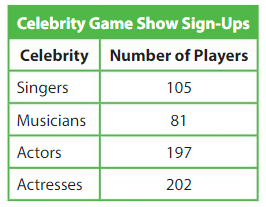
Answer:
The number of teams that have 5 actresses = 40
The number of teams that have 6 actresses = 2
Explanation:
Given that actresses are placed on each team and the remaining actresses are added to the teams.
So, from the table, we can see that
The total number of actresses = 202
Now, to find the number of teams that have 5 actresses, we have to find the value of 202 ÷ 5
The remainder of 202 ÷ 5 gives the number of teams that have 6 actresses
Now,
By using the partial quotients method,
202 ÷ 5 = ( 150 + 50 ) ÷ 5
= ( 150 ÷ 5 ) + ( 50 ÷ 5 )
= 30 + 10
= 40 R 2
Hence, from the above,
We can conclude that
The number of teams that have 5 actresses = 40 teams
The number of teams that have 6 actresses = 2 teams
Review & Refresh
Write the value of the underlined digit.
Question 19.
86,109
Answer: The place- value of 6 in 86,109 is: 6,000
Explanation:
We know that the position of a given digit in any number depends on the place-value of that number.
So,
The place-value of 6 in 86,109 is: 6,000
Question 20.
15,327
Answer: The place-value of 1 in 15,327 is: 10,000
Explanation:
We know that the position of a given digit in any number depends on the place-value of that number.
So,
The place-value of 1 in 15,327 is: 10,000
Question 21.
914,263
Answer: The place-value of 9 in 914,263 is: 900,000
Explanation:
We know that the position of a given digit in any number depends on the place-value of that number.
So,
The place-value of 9 in 914,263 is: 900,000
Question 22.
284,505
Answer: The place-value of 0 in 284,505 is: 0 ( Since 0 × 10 = 0 )
Explanation:
We know that the position of a given digit in any number depends on the place-value of that number.
So,
The place-value of 0 in 284,505 is: 0 ( Since 0 × 10 = 0 )
Lesson 5.9 Problem Solving: Division
Explore & Grow
Make a plan to solve the problem.
A fruit vendor has 352 green apples and 424 red apples. The vendor uses all of the apples to make fruit baskets. He puts 8 apples in each basket. How many fruit baskets does the vendor make?

Answer: The fruit vendor makes 97 fruit baskets
Explanation:
Given that a fruit vendor has 352 green apples and 424 red apples.
So,
Total number of apples = Number of red apples + Number of green apples
= 352 + 424
= 776 apples.
It is also given that the vendor uses all of the apples to make fruit baskets and he puts 8 apples in each basket.
Hence,
The number of fruit baskets that the vendor makes = Total number of apples ÷ Number of apples the vendor puts in each basket
= 776 ÷ 8
Now,
By using the partial quotients method,
776 ÷ 8 = ( 720 + 56 ) ÷ 8
= ( 720 ÷ 8 ) + ( 56 ÷ 8 )
= 90 + 7
= 97 baskets
Hence, from the above,
We can conclude that there are 97 fruit baskets that the vendor made.
Make Sense of Problems
The vendor decides that each basket should have 8 of the same colored apples. Does this change your plan to solve the problem? Will this change the answer? Explain.
Answer: Yes, you have to change your plan to solve the problem but this way will not change the answer as we will get the same answer as above.
Explanation:
Given that the vendor decides that each basket should have 8 of the same colored apples.
So,
The number of fruit baskets that have red apples = 424 ÷ 8
Now,
By using the partial quotients method,
424 ÷ 8 = ( 400 + 24 ) ÷ 8
= ( 400 ÷ 8 ) + ( 24 ÷ 8 )
= 50 + 3
= 53 fruit baskets ( for every 8 red apples)
Now,
The number of fruit baskets that have green apples = 352 ÷ 8
Now,
By using the partial quotients method,
352 ÷ 8 = ( 320 + 32 ) ÷ 8
= ( 320 ÷ 8 ) + ( 32 ÷ 8 )
= 40 + 4
= 44 fruit baskets ( for every 8 green apples)
So,
Total number of fruit baskets that a vendor make = Number of fruit baskets that have red apples + Number of fruit baskets that have green apples
= 44 + 53 = 97 fruit baskets
Hence, from the above,
We can conclude that we change the plan of solving the problem but the answer remains the same.
Think and Grow: Problem Solving: Division
Example
The speed of sound in water is 1,484 meters per second. Sound travels 112 more than 4 times as many meters per second in water as it does in air. What is the speed of sound in air?

Understand the Problem
What do you know?
• The speed of sound in water is sound 1,484 meters per second.
• Sound travels 112 more than 4 times as many meters per second in water as it does in air.
What do you need to find?
• You need to find the speed in the air.
Make a Plan
How will you solve it?
• Subtract 112 from 1,484 to find 4 times the speed of sound in the air.
• Then divide the difference by 4 to find the speed of sound in the air.
Solve

So,
The speed of sound in air is 343 meters per second.
Show and Grow
Question 1.
Explain how you can check whether your answer above is reasonable.
Answer:
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
A surf shop owner divides 635 stickers evenly among all of her surfboards. Each surfboard has 3 tiki stickers and 2 turtle stickers. How many surfboards does she have?
Answer: She has 127 surfboards
Explanation:
Given that a surf shop owner divides 635 stickers evenly among all of her surfboards and each surfboard has 3 tiki stickers and 2 turtle stickers.
So,
The total number of stickers on each surfboard = Number of tiki stickers + Number of turtle stickers
= 3 + 2
= 5 stickers
So,
Total number of surfboards = Total number of stickers ÷ The number of stickers on each surfboard
= 635 ÷ 5
By using the partial quotients method,
635 ÷ 5 = ( 600 + 35 ) ÷ 5
= ( 600 ÷ 5 ) + ( 35 ÷ 5 )
= 120 + 7
= 127 surfboards
Hence, from the above,
We can conclude that there are 127 surfboards.
Question 3.
There are 1,008 projects in a science fair. The projects are divided into equally 9 rooms. Each room has 8 equal rows of projects. How many projects are in each row?

Answer: There are 14 projects in each row.
Explanation:
Given that there are 1,008 projects in a science fair and the projects are divided into equally 9 rooms. It is also given that each room has 8 equal rows of projects.
So,
Total number of rooms = 9 × 8 =72 rooms
Now,
Number of projects in each row = Total number of projects ÷ Total number of rooms
= 1,008 ÷ 72
Now,
By using the partial quotients method,
1,008 ÷ 72 = ( 720 + 288 )÷ 72
= ( 720 ÷ 72 ) + ( 288 ÷ 72 )
= 10 + 4
= 14 projects in each row
Hence, from the above,
We can conclude that there are 14 projects in each row.
Understand the problem. Then make a plan. How will you solve it? Explain.
Question 4.
Of 78 students who work on a mural, 22 students design it, and the rest of the students paint it. The painters are divided equally among 4 areas of the mural. How many painters are assigned to each area?
Answer: 14 painters are assigned to each area.
Explanation:
Given that there are 78 students who work on a mural and 22 students designed the mural and the remaining students painted it.
So,
The students who painted the mural = Total number of students – The students who designed the mural
= 78 – 22
= 56 students
It is also given that the painters are divided equally among 4 areas of the mural.
So,
The number of painters divided = The number of students who painted the mural ÷ 4
= 56 ÷ 4
Now,
By using the partial quotients method,
56 ÷ 4 = ( 40 + 16 ) ÷ 4
= ( 40 ÷ 4 ) + ( 16 ÷ 4 )
= 10 + 4
= 14 students
Hence, from the above,
we can conclude that there are 14 students are assigned to each area.
Question 5.
The Winter Olympics occur twice every 8 years. How many times will the Winter Olympics occur in 200 years?
Answer: 50 times
Explanation:
Given that the Winter Olympics occur twice every 8 years.
So, the Winter Olympics occur every 4 years. ( 8 ÷ 2 = 4 )
So,
The number of times Winter Olympics occur in 200 years = 200 ÷ 4
Now,
By using the partial quotients method,
200 ÷ 4 = ( 160 + 40 ) ÷ 4
= ( 160 ÷ 4 ) + ( 40 ÷ 4 )
= 40 + 10
= 50 times
Hence, from the above,
We can conclude that the Winter Olympics occur 50 times in 200 years.
Question 6.
A party planner wants to put 12 balloons at each of 15 tables. The balloons come in packages of 8. How many packages of balloons must the party planner buy?
Answer: The party planner buy 176 packages of balloons with 4 leftover balloons
Explanation:
Given that a part planner wants to put 12 balloons at each of 15 tables.
So,
Total number of balloons = 15 × 12
Now,
By using the partial products method,
12 × 15 = ( 10 + 2 ) × ( 10 + 5 )
= ( 10 × 10 ) + ( 10 × 5 ) + ( 2 × 10 ) + ( 2 × 5 )
= 100 + 50 + 20 +10
= 180 balloons
It is also given that the balloons come in packages of 8.
So,
The number of balloons that each package contain = Total number of balloons ÷ 8
= 180 ÷ 8
Now,
By using the partial quotients method,
180 ÷ 8 = ( 160 + 16 ) ÷ 8
= ( 160 ÷ 8 ) + ( 16 ÷ 8 )
= 20 + 2
= 22 R 4
Hence, from the above,
We can conclude that the number of balloons that each package contain is: 22 with 4 leftovers
Question 7.
An art teacher has 8 boxes of craft sticks. Each box has 235 sticks. The students use the sticks to make as many hexagons as possible. How many sticks are used?

Answer: The number of sticks used is: 313 with 2 leftover
Explanation:
Given that an art teacher has 8 boxes of craft sticks and each box has 235 sticks.
So,
Total number of sticks = 235 × 8
Now,
By using the partial products method,
235 × 8 = ( 200 + 35 ) × 8
= ( 200 × 8 ) + ( 35 × 8 )
= 1,600 + 280
= 1,880 sticks
It is also given the sticks are used to make hexagons.
We know that,
The number of sides of Hexagon = 6
So,
The number of sticks used to make hexagons = 1,880 ÷ 6
Now,
By using the partial quotients method,
1,880 ÷ 6 = ( 1,800 + 60 + 18 ) ÷ 6
= ( 1,800 ÷ 6 ) + ( 60 ÷ 6 ) + ( 18 ÷ 6 )
= 300 + 10 + 3
= 313 R 2
Hence, from the above,
We can conclude that the number of sticks used for making hexagons is: 313 with 2 leftover
Think and Grow: Modeling Real Life
Example
A book enthusiast has $200 to buy an e-reader and e-books. He uses a $20 off coupon and buys the e-reader shown. Each e-book costs $6. How many e-books can the book enthusiast buy?
Think: What do you know? What do you need to find? How will you solve it?

Step 1: How much money does the book enthusiast pay for the e-reader?
Subtract $20 from $119.
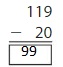
Step 2: Subtract to find how much money he has left to spend on e-books.
$200 – _____ = d
d is the unknown difference.
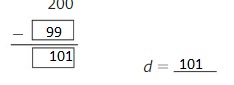
Step 3: Use to find the number of e-books the book enthusiast can buy.

So, the book enthusiast can buy 16 e-books.
Show and Grow
Question 8.
You run 17 laps around a track. Newton runs 5 times as many laps as you. Descartes runs 35 more laps than Newton. Eight laps around the track are equal to 1 mile. How many miles does Descartes run?

Answer: Descartes runs 15 miles
Explanation:
Given that you run 17 laps around a track and Newton runs 5 times as many laps as you.
So,
The number of laps covered by Newton = 17 × 5 = 85 laps
It is also given that Descartes runs 35 more laps than Newton.
So,
The number of laps covered by Descartes = 35 + Number of laps covered by Newton
= 35 + 85
= 120 laps
Given that,
8 laps = 1 mile
So,
The number of miles covered by Descartes = The number of laps covered by Descartes ÷ 8
= 120 ÷ 8
Now,
By using the partial quotients method,
120 ÷ 8 = ( 80 + 40 ) ÷ 8
= ( 80 ÷ 8 ) + ( 40 ÷ 8 )
= 10 + 5
= 15 miles
Hence, from the above,
We can conclude that Descartes covers 15 miles.
Problem Solving: Division Homework & Practice 5.9
Understand the problem. Then make a plan. How will you solve it? Explain.
Question 1.
You borrow a 235-page book from the library. You read 190 pages. You have 3 days left until you have to return the book. You want to read the same number of pages each day to finish the book. How many pages should you read each day?
Answer: The number of pages you should read each day is: 15 pages
Explanation:
Given that you borrow a 235-page book and you read 190 pages. It is also given that you have only 3 days left until you have to return the book.
So,
The number of remaining pages = 235 – 190 = 45 pages
So,
The number of pages you should read each day = 45 ÷ 3
Now,
By using the partial quotients method,
45 ÷ 3 = ( 30 + 15 ) ÷ 3
= ( 30 ÷ 3 ) + ( 15 ÷ 3 )
= 10 + 5
= 15
Hence, from the above,
We can conclude that the number of pages you should read each day is: 15 pages
Question 2.
There are 24 fourth-graders and 38 fifth graders traveling to a math competition. If 8 students can fit into each van, how many vans are needed?
Answer: The number of vans needed is: 7 R 6
Explanation:
Given that there are 24 fourth-graders and 38 fifth-graders traveling to a math competition.
So,
The total number of students who are traveling to a math competition = Number of fourth-graders + Number of fifth-graders
= 24 + 38
= 62 students
It is also given that 8 students can fit into each van.
So,
The number of vans needed = Total number of students ÷ Number of students fit into each van
= 62 ÷ 8
Now,
By using the partial quotients method,
62 ÷ 8 = ( 40 + 16 ) ÷ 8
= ( 40 ÷ 8 ) + ( 16 ÷ 8 )
= 5 + 2
= 7 vans with 6 students leftover
= 7 R 6
Hence, from the above,
We can conclude that the number of vans needed is: 7 vans with 6 students leftover
Question 3.
Your class has 3 bags of buttons to make riding horses for a relay race. Each bag has 54 buttons. What is the greatest number of horses your class can make?

Answer: The greatest number of horses your class can make = 40 horses
Explanation:
Given that your class has 3 bags of buttons to make riding horses for a relay race and each bag contains 54 buttons
So,
The total number of buttons present = 54 × 3
Now,
By using the Distributive Property of multiplication,
54 × 3 = ( 50 + 4 ) × 3
( 50 × 3 ) + ( 4 × 3 )
= 150 + 12
= 162 buttons
It is also given that each horse needs 4 buttons.
So,
The greatest number of horses you can make = Total number of buttons ÷ 4
= 162 ÷ 4
NOw,
By using the partial quotients method,
162 ÷ 4 = ( 120 + 40 ) ÷ 4
= ( 120 ÷ 4 ) + ( 40 ÷ 4 )
= 30 + 10
= 40 horses with 2 buttons leftover
= 40 R 2
Hence, from the above,
We can conclude that the greatest number of horses you can make = 40 horses
Question 4.
Factory workers make 2,597 small, 2,597 medium, and 2,597 large plush toys. The workers pack the toys into boxes with 4 toys in each box. How many toys are left over?
Answer: The number of toys leftover are: 3 toys
Explanation:
Given that factory workers make 2,597 small, 2,597 medium, and 2,597 large plush toys.
So,
Total number of toys that factory workers can made = 2,597 + 2,597 + 2,597
= 7,791 toys
It is also given that the workers pack the toys into boxes with 4 toys in each box.
So,
The number of toys in each box = Total number of toys that the factory workers can make ÷ 4
= 7,791 ÷ 4
Now,
By using the partial quotients method,
7,791 ÷ 4 = ( 7,200 + 520 + 68 ) ÷ 4
= ( 7,200 ÷ 4 ) + ( 520 ÷ 4 ) + ( 68 ÷ 4 )
= 1,200 + 130 + 17
=1,347 R 3
Hence, from the above,
We can conclude that there are 3 leftovers after all the toys packed into group of 4.
Question 5.
Writing
Write and solve a two-step word problem that can be solved using division.
Answer:
Question 6.
Modeling Real Life
You exercise for 300 minutes this week. Outside of jogging, you divide your exercising time equally among 3 other activities. How many minutes do you spend on each of your other 3 activities?
Answer: You spend 100 minutes on each of your other 3 activities.
Explanation:
Given that you exercise for 300 minutes this week.
It is also given that outside of jogging, you divide your exercising time equally among 3 other activities.
So,
The number of minutes you spend on each of your 3 other activities = Total minutes of exercising ÷ Total number of activities outside jogging
= 300 ÷ 3
Now,
By using the partial quotients method,
300 ÷ 3 = ( 270 + 30 ) ÷ 3
= ( 270 ÷ 3 ) + ( 30 ÷ 3 )
= 90 + 10
= 100 minutes.
Hence, from the above,
we can conclude that you spent 100 minutes on each of the 3 other activities outside of jogging.
Question 7.
Modeling Real Life
Drones are used to help protect orangutans and their habitats. A drone takes a picture every 2 seconds. How many pictures does the drone take in 30 minutes?

Answer: The drone makes 900 pictures in 30 minutes.
Explanation:
Given that the drones are used to help protect orangutans and their habitats
It is also given that a drone takes a picture every 2 seconds.
We know that,
1 minute = 60 seconds
So,
30 minutes = 30 × 60 seconds
Now,
By using the place-value method,
30 × 60 = 3 tens × 60
= 3 tens × 6 tens
= 18 × 10 × 10
= 1,800 seconds
So,
The number of pictures does the drone takes in 30 minutes = 1,800 ÷ 2
Now,
By using the partial quotients method,
1,800 ÷ 2 = ( 1,000 +800 ) ÷ 2
= ( 1,000 ÷ 2 ) + ( 800 ÷ 2 )
= 500 + 400
= 900 pictures
Hence, from the above,
we can conclude that the drone takes 900 pictures in 30 minutes.
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 8.
Estimate: _____
41 × 22 = _____
Answer: 41 × 22 = 902
Explanation:
By using the partial products method,
41 × 22 = ( 40 + 1 ) × ( 20 + 2 )
=( 40 × 20 ) + ( 1 × 20 ) + ( 40 × 2 ) + ( 1 × 2 )
= 800 + 20 + 80 + 2
= 902
So, 41 × 22 = 902
Estimate:
Let 41 be rounded to 40.
Let 22 be rounded to 20.
So, by using the place-value method,
40 × 20 = 4 tens × 20
= 80 tens
= 80 × 10
= 800
So, 40 × 20 = 400
Hence, from the above,
We can conclude that the actual answer is not near to the Estimate. So, the answer is not reasonable.
Question 9.
Estimate: ______
87 × 19 = ______
Answer: 87 × 19 = 1,653
Explanation:
By using the partial products method,
87 × 19 = ( 80 + 17 ) × ( 10 + 9 )
=( 80 × 10 ) + ( 80 × 9 ) + ( 17 × 10 ) + ( 17 × 9 )
= 800 + 720 + 170 + 153
= 1,653
So, 87 × 19 = 1,653
Estimate:
Let 87 be rounded to 85.
Let 19 be rounded to 20.
So, by using the place-value method,
85 × 20 = 2 tens × 85
= 170 tens
= 170 × 10
= 1,700
So, 85 × 20 = 1,700
Hence, from the above,
We can conclude that the actual answer is near to the Estimate. So, the answer is reasonable.
Question 10.
Estimate: _____
36 × 59 = ______
Answer: 36 × 59 = 2,124
Explanation:
By using the partial products method,
36 × 59 = ( 30 + 6 ) × ( 50 + 9 )
=( 30 × 50 ) + ( 30 × 9 ) + ( 6 × 50 ) + ( 6 × 9 )
= 1,500 + 270 + 300 + 54
= 2,124
So, 36 × 59 = 2,124
Estimate:
Let 36 be rounded to 35.
Let 59 be rounded to 60.
So, by using the place-value method,
35 × 60 = 6 tens × 35
= 210 tens
= 210 × 10
= 2,100
So, 35 × 60 = 2,100
Hence, from the above,
We can conclude that the actual answer is near to the Estimate. So, the answer is reasonable.
Divide Multi-Digit Numbers by One-Digit Numbers Performance Task
The students in fourth grade go on a field trip to a planetarium.
Question 1.
The teachers have $760 to buy all of the tickets for the teachers and students. They receive less than $6 in change.
a. Each ticket costs $6. How many tickets do the teachers buy?
b. Exactly how much money is left over?

c. There are 6 groups on the field trip. Each group has 1 teacher. There is an equal number of students in each group. How many students are in each group?
d. Two groups can be in the planetarium for each show. The planetarium has 7 rows of seats with 8 seats in each row. How many seats are empty during each show?
Answer:
a) The teachers buy 126 tickets.
b) The money that is leftover: $4
c) The number of students in each group: 20
d) The number of seats empty during each show is: 0
Explanation:
Given that the teachers have $760 to buy all of the tickets for the teachers and students and they received less than $6 change.
a) Given that each ticket cost $6
So,
The number of tickets that the teachers can buy = 760 ÷ 6
Now,
By using the partial quotients method,
760 ÷ 6 = ( 600 + 120 + 36 ) ÷ 6
= ( 600 ÷ 6 ) + ( 120 ÷ 6 ) + ( 36 ÷ 6 )
= 100 + 20 + 6
= 126 tickets with 4 leftover as change=
= 126 R 4
b) From the above,
The money that is leftover = $4
c) Given that there are 6 groups on the field trip and each group has 1 teacher.
It is also given that there is an equal number of students in each group.
From the number of tickets, we can conclude that there are 126 students.
So,
The number of groups of students = 126 ÷ 6
Now,
By using the partial quotients method,
126 ÷ 6 = ( 60 + 60 ) ÷ 6
= ( 60 ÷ 6 ) + ( 60 ÷ 6 )
= 10 + 10
= 20 R 6
Hence, from the above,
we can conclude that there are 20 student groups.
d) Given that there are two groups in the planetarium for each show and the planetarium has 7 rows of seats with 8 seats in each row.
So,
The total number of seats = 7 × 8 = 56 seats
So,
The number of seats that are empty during each show = 56 ÷ 2 = 28
Hence, there are no empty seats left in each show.
Question 2.
The groups will be at the planetarium from 11:00 A.M. until 2:30 P.M. During that time they will rotate through 7 events: the planetarium show, 5 activities, and lunch. The planetarium show lasts 45 minutes. Each activity lasts 22 minutes. Students have 5 minutes between each event. How long does each group have to eat lunch?

Answer: Each group has 10 minutes to eat lunch.
Explanation:
Given that,
The groups will be at the planetarium from 11:00 A.M. until 2:30 P.M.
The number of events = 7
The number of activities = 5
The time of planetarium show = 45 minutes
The time each activity lasts = 22 minutes
So,
The time at which 5 activities lasts = 22 × 5 = 110 minutes
The time for which students have time between each event = 5 minutes
Now,
The total time that the groups will be at the planetarium = From 11:00 A.M. until 2:30 P.M.
= 3 hours 30 minutes
= 210 minutes
The time taken by the groups for the activities and events = 45 + 110 =155 minutes
So,
The remaining time = 210 – 155 = 55 minutes
The time is taken by all the students between the events = 5 × 7 = 35 minutes
So, the remaining time = 55 – 35 = 20 minutes
Given that there are 2 groups in the above Exercise.
So, The time is taken for lunch by each group = 20 ÷ 2 = 10 minutes.
Hence, from the above,
we can conclude that there are 10 minutes for each group to eat lunch.
Question 3.
You learn that the distance around Mars is about twice the distance around the moon. The distance around Mars is 13,263 miles. To find the distance around the moon, do you think an estimate or an exact answer is needed? Explain.
Answer: We need an Estimate.
Explanation:
Given that the distance around Mars is about twice the distance around the moon and the distance around Mars is 13,263 miles.
So,
The distance of Moon = The distance around Mars ÷ 2
= 13,263 ÷ 2
If we find the value of 13,263 ÷ 2, we will get the answer with decimals.
So, we have to take an Estimate to calculate the distance around the Moon.
Estimate:
let 13,263 be rounded to 13,262
Now,
By using the partial quotients method,
13,262 ÷ 2 = ( 12,000 + 1,000 + 260 + 2 ) ÷ 2
= ( 12,000 ÷ 2 ) + ( 1,000 ÷ 2 ) + ( 260 ÷ 2 ) + ( 2 ÷ 2 )
= 6,000 + 500 + 130 +1
= 6,631 miles.
Hence, from the above,
We can conclude that the estimated distance around the Moon = 6,631 miles
Divide Multi-Digit Numbers by One-Digit Numbers Activity
Division Dots
Directions:
1. Players take turns connecting two dots, each using a different color.
2. On your turn, connect two dots, vertically or horizontally. If you close a square around a division problem, find and write the quotient and the remainder. If you do not close a square, your turn is over.
3. Continue playing until all division problems are solved.
4. The player with the most completed squares wins!

Answer:
Divide Multi-Digit Numbers by One-Digit Numbers Chapter Practice
5.1 Divide Tens, Hundreds, and Thousands
Find the quotient.
Question 1.
90 ÷ 9 = _____
Answer: The quotient is: 10
Explanation:
The given Expression is:
90 ÷ 9 =9 tens ÷ 9
= 1 ten
=10
So, 90 ÷ 9 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 2.
560 ÷ 7 = _____
Answer: The quotient is: 80
Explanation:
The given Expression is:
560 ÷ 7 = 56 tens ÷ 7
= 8 tens
=80
So, 560 ÷ 7 = 80
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 3.
2,700 ÷ 9 = _____
Answer: The quotient is: 300
Explanation:
The given Expression is:
2,700 ÷ 9 = 27 hundreds ÷ 9
= 3 hundred
=300
So, 2,700 ÷ 9 = 300
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 4.
240 ÷ 4 = ______
Answer: The quotient is: 60
Explanation:
The given Expression is:
240 ÷ 4 = 24 tens ÷ 4
= 6 tens
=60
So, 240 ÷ 4 = 60
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 5.
4,500 ÷ 5 = _____
Answer: The quotient is: 900
Explanation:
The given Expression is:
4,500 ÷ 5 = 45 hundreds ÷ 5
= 9 hundred
=900
So, 4,500 ÷ 5 = 900
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 6.
60 ÷ 6 = _____
Answer: The quotient is: 10
Explanation:
The given Expression is:
60 ÷ 6 = 6 tens ÷ 6
= 1 ten
=10
So, 60 ÷ 6 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 7.
1,600 ÷ 8 = _____
Answer: The quotient is: 200
Explanation:
The given Expression is:
1,600 ÷ 8 = 16 hundreds ÷ 8
= 2 hundred
=200
So, 1,600 ÷ 8 = 200
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 8.
30 ÷ 3 = ______
Answer: The quotient is: 10
Explanation:
The given Expression is:
30 ÷ 3 = 3 tens ÷ 3
= 1 ten
=10
So, 30 ÷ 3 = 10
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Question 9.
540 ÷ 9 = _____
Answer: The quotient is: 60
Explanation:
The given Expression is:
540 ÷ 9 = 54 tens ÷ 9
= 6 tens
=60
So, 540 ÷ 9 = 60
Note: The “Quotient” of an Expression is defined as a number that divides the Dividend and the quotient should be an Integer.
Find the missing number.
Question 10.
720 ÷ _____ = 80
Answer: The missing number is: 9
Explanation:
Let the missing number be X.
The given Expression is:
720 ÷ X = 80
So, X can be calculated by
X= 720 ÷ 80 = 9
Question 11.
_____ ÷ 7 = 10
Answer: 70
Explanation:
Let the missing number be X.
The given Expression is:
X ÷ 7 = 10
So, X can be calculated by
X= 7 × 10 = 70
Question 12.
1,800 ÷ _____ = 600
Answer: The missing number is: 3
Explanation:
Let the missing number be X.
The given Expression is:
1,800 ÷ X = 600
So, X can be calculated by
X= 1,800 ÷ 600 = 3
5.2 Estimate Quotients
Question 13.
47 ÷ 7
Answer: The estimated quotient is: 7
Explanation;
Let 47 be rounded off to 49.
So, now we have to find 49 ÷ 7
Now,
49 ÷ 7 = ( 42 + 7 ) ÷ 7
= ( 42 ÷ 7 ) + ( 7 ÷ 7 )
= 6 + 1
= 7
Hence, from the above,
We can conclude that 47 ÷ 7 can be rounded off to 7.
Question 14.
593 ÷ 6
Answer: The estimated quotient is: 99
Explanation;
Let 593 be rounded off to 594.
So, now we have to find 594 ÷ 6
Now,
594 ÷ 6 = ( 540 + 54 ) ÷ 6
= ( 540 ÷ 6 ) + ( 54 ÷ 6 )
= 90 + 19
= 99
Hence, from the above,
We can conclude that 593 ÷ 6 can be rounded off to 99
Find two estimates that the quotient is between.
Question 15.
261 ÷ 8
Answer: The quotient of 261 ÷ 8 is between 30 and 40.
Explanation:
Use 240. 24 ÷ 8 = 3, so 240 ÷ 8 = 30.
Use 320. 32 ÷ 8 = 4, so 320 ÷ 8 = 40 .
261 is between 240 and 320.
So, the quotient of 261 ÷ 8 is between 30 and 40.
Question 16.
7,012 ÷ 9
Answer: The quotient of 7,012 ÷ 9 is between 700 and 800.
Explanation:
Use 6,300. 63 ÷ 9 = 7, so 6,300 ÷ 9 = 700.
Use 7,200. 72 ÷ 9 = 8, so 7,200 ÷ 9 = 800 .
7,012 is between 6,300 and 7,200.
So, the quotient of 7,012 ÷ 9 is between 700 and 800.
Question 17.
Reasoning
Explain how to find a better estimate for 2,589 ÷ 6 than the one shown.
Round 2,589 to 3,000. Estimate 3,000 ÷ 6.
3,000 ÷ 6 = 500, so 2,589 ÷ 6 is about 500.
Answer: The better Estimate to find 2,589 ÷ 6 is to round off 2,589 to 2,580
Explanation:
Given Expression is 2,589 ÷ 6
Let 2,589 be rounded to 3,000
So,
3,000 ÷ 6 = 300 tens ÷ 6
= 50 tens
= 500
Now,
Let 2,589 be rounded to 2,580.
So,
2,580 ÷ 6 = 258 tens ÷ 6
= 43 tens
=430
But, 2,589 is near to 2,580 when compared to 3,000.
So,
We can conclude that
2,580 ÷ 6 = 43
5.3 Understand Division and Remainder
Use a model to find the quotient and the remainder.
Question 18.
14 ÷ 4 = _____ R _____
Answer: 3 R 2
Explanation:
Divide 14 into 4 equal parts.
So, we will get
Number of Units in each group = 3
Number of units leftover = 2
Hence,
26 ÷ 3 = 3 R 2
Where R is the Remainder (or) the number of units leftover
Question 19.
28 ÷ 6 = _____ R ______
Answer: 4 R 4
Explanation:
Divide 28 into 6 equal parts.
So, we will get
Number of Units in each group = 4
Number of units leftover = 4
Hence,
28 ÷ 6 = 4 R 4
Where R is the Remainder (or) the number of units leftover
Question 20.
18 ÷ 7 = _____ R ______
Answer: 2 R 4
Explanation:
Divide 18 into 7 equal parts.
So, we will get
Number of Units in each group = 2
Number of units leftover = 4
Hence,
18 ÷ 7 = 2 R 4
Where R is the Remainder (or) the number of units leftover
Question 21.
23 ÷ 3 = _____ R _______
Answer: 7 R 2
Explanation:
Divide 23 into 3 equal parts.
So, we will get
Number of Units in each group = 7
Number of units leftover = 2
Hence,
23 ÷ 3 = 7 R 2
Where R is the Remainder (or) the number of units leftover
Question 22.
Modeling Real Life
Tours of a factory can have no more than 9 guests. There are 76 guests in line to tour the factory.
• How many tours are full?
• How many tours are needed?
• How many guests are on the last tour?

Answer:
a) The number of tours that are full = 8 tours
b) The number of tours needed = 9 tours
c) The number of guests on the last tour = 4 guests
Explanation:
Given that there are 76 guests in line to tour a factory It is also given that there are no more than 9 guests on the tours of a factory.
We have to observe that to make all the guests full on all the trips without leftovers, we will need 9 trips. i.e.., 81 guests.
So, now we have to find the number of guests in each tour of a crayon factory by finding the quotient and remainder of 76 ÷ 9.
Now,
76 ÷ 9
From this, we can see
The number of guests in each tour that are full = 8
The number of guests leftover on the last trip = 4
Hence, from the above,
We can conclude that
a) 8 Tours are full.
b) 9 Tours are needed.
c) 4 guests are on the last tour.
5.4 Use Partial Quotients
Use partial quotients to divide.
Question 23.
\(\sqrt [ 8 ]{ 504 } \)
Answer: 504 ÷ 8 = 63
Explanation:
By using the partial quotients method,
504 ÷ 8 = ( 480 + 24 ) ÷ 8
( 480 ÷ 8 ) + ( 24 ÷ 8 )
= 60 + 3
= 63
Hence, 504 ÷ 8 = 63
Question 24.
\(\sqrt [ 4 ]{ 52 } \)
Answer: 52 ÷ 4 = 13
Explanation:
By using the partial quotients method,
52 ÷ 4 = ( 40 + 12 ) ÷ 4
= ( 40 ÷ 4 ) + ( 12 ÷ 4 )
= 10 + 3
= 13
Hence, 52 ÷ 4 = 13
Question 25.
\(\sqrt [ 7 ]{ 119 } \)
Answer: 119 ÷ 7 = 17
Explanation:
By using the partial quotients method,
119 ÷ 7 = ( 105 + 14 ) ÷ 7
= ( 105 ÷ 7 ) + ( 14 ÷ 7 )
= 15 + 2
= 17
Hence, 119 ÷ 7 = 17
5.5 Use Partial Quotients with an Remainder
Use partial quotients to divide.
Question 26.
\(\sqrt [ 5 ]{ 82 } \)
Answer: 82 ÷ 5 = 16 R 2
Explanation:
By using the partial quotients method,
82 ÷ 5 = ( 75 + 5 ) ÷ 5
= ( 75 ÷ 5 ) + ( 5 ÷ 5 )
= 15 + 1
= 16 R 2
Hence, 82 ÷ 5 = 16 R 2
Question 27.
\(\sqrt [ 8 ]{ 759 } \)
Answer: 759 ÷ 8 = 94 R 7
Explanation:
By using the partial quotients method,
759 ÷ 8 = ( 720 + 32 ) ÷ 8
= ( 720 ÷ 8 ) + ( 32 ÷ 8 )
= 90 + 4
= 94 R 7
Hence, 759 ÷ 8 = 94 R 7
Question 28.
\(\sqrt [ 3]{ 5,468 } \)
Answer: 5,468 ÷ 3 = 1,822 R 2
Explanation:
By using the partial quotients method,
5,468 ÷ 3 = ( 5,400 + 66 ) ÷ 3
= ( 5,400 ÷ 3 ) + ( 66 ÷ 3 )
= 1,800 + 22
= 1,822 R 2
Hence, 5,468 ÷ 3 = 1,822 R 2
5.6 Divide Two-Digit Numbers by One-Digit Numbers
Divide. Then check your answer.
Question 29.
\(\sqrt [ 3 ]{ 58 } \)
Answer: 58 ÷ 3 = 19 R 1
Explanation:
By using the partial quotients method,
58 ÷ 3 = ( 48 + 9 ) ÷ 3
= ( 48 ÷ 3 ) + ( 9 ÷ 3 )
= 16 + 3
= 19 R 1
Hence, 58 ÷ 3 = 19 R 1
Question 30.
\(\sqrt [ 4 ]{ 90 } \)
Answer: 90 ÷ 4 = 22 R 2
Explanation:
By using the partial quotients method,
90 ÷ 4 = ( 80 + 8 ) ÷ 4
= ( 80 ÷ 4 ) + ( 8 ÷ 4 )
= 20 + 2
= 22 R 2
Hence, 90 ÷ 4 = 22 R 2
Question 31.
\(\sqrt [ 2 ]{ 67 } \)
Answer: 67 ÷ 2 = 33 R 1
Explanation:
By using the partial quotients method,
67 ÷ 2 = ( 60 + 6 ) ÷ 2
= ( 60 ÷ 2 ) + ( 6 ÷ 2 )
= 30 + 3
= 33 R 1
Hence, 67 ÷ 2 = 33 R 1
5.7 Divide Multi-Digit Numbers by One-Digit Numbers
Divide. Then check your answer.
Question 32.
\(\sqrt [ 5 ]{ 865 } \)
Answer: 865 ÷ 5 = 173
Explanation:
By using the partial quotients method,
865 ÷ 5 = ( 800 + 65 )÷ 5
= ( 800 ÷ 5 ) + ( 65 ÷ 5 )
= 160 + 13
= 173
Hnece, 865 ÷ 5 = 173
Question 33.
\(\sqrt [ 2 ]{ 7,532 } \)
Answer: 7,532 ÷ 2 = 3,766
Explanation:
By using the partial quotients method,
7,532 ÷ 2 = ( 7,000 + 500 + 3 ) ÷ 2
= ( 7,000 ÷ 2 ) + ( 500 ÷ 2 ) + ( 32 ÷ 2 )
= 3,500 + 250 + 16
= 3,766
Hence, 7,532 ÷ 2 = 3,766
Question 34.
\(\sqrt [ 4 ]{ 507 } \)
Answer: 507 ÷ 4 = 126 R 3
Explanation:
By using the partial quotients method,
507 ÷ 4 = ( 480 + 24 ) ÷ 4
= ( 480 ÷ 4 ) + ( 24 ÷ 4 )
= 120 + 6
= 126 R 3
Hence, 507 ÷ 4 = 126 R 3
Question 35.
\(\sqrt [ 6 ]{ 9,127 } \)
Answer: 9,127 ÷ 6 = 1,521 R 1
Explanation:
By using the partial quotients method,
9,127 ÷ 6 = ( 9,000 + 126 ) ÷ 6
= ( 9,000 ÷ 6 ) + ( 126 ÷ 6 )
= 1,500 + 21
= 1,521 R 1
Question 36.
\(\sqrt [ 8 ]{ 253 } \)
Answer: 253 ÷ 8 = 31 R 5
Explanation:
By using the partial quotients method,
253 ÷ 8 = ( 240 + 8 ) ÷ 8
= ( 240 ÷ 8 ) + ( 8 v 8 )
= 30 + 1
= 31 R 5
Hence,253 ÷ 8 = 31 R 5
Question 37.
\(\sqrt [ 6 ]{ 429 } \)
Answer: 429 ÷ 6 = 71 R 3
Explanation:
By using the partial quotients,
429 ÷ 6 = ( 420 + 6 ) ÷ 6
= ( 420 ÷ 6 ) + ( 6 ÷ 6 )
= 70 + 1
= 71 R 3
Hence, 429 ÷ 6 = 71 R 3
5.8 Divide by One-Digit Numbers
Divide. Then check your answer.
Question 38.
\(\sqrt [ 3 ]{ 91 } \)
Answer: 91 ÷ 3 = 30 R 1
Explanation:
By using the partial quotients method,
91 ÷ 3 = ( 60 + 30 ) ÷ 3
= ( 60 ÷ 3 ) + ( 30 ÷ 3 )
= 20 + 10
= 30 R 1
Hence, 91 ÷ 3 = 30 R 1
Question 39.
\(\sqrt [ 7 ]{ 914 } \)
Answer: 914 ÷ 7 = 130 R 4
Explanation:
By using the partial quotients method,
914 ÷ 7 = ( 840 + 70 ) ÷ 7
= ( 840 ÷ 7 ) + ( 70 ÷ 7 )
= 120 + 10
= 130 R 4
Hence, 914 ÷ 7 = 130 R 4
Question 40.
\(\sqrt [ 2 ]{ 6,075 } \)
Answer: 6,075 ÷ 2 = 3,037 R 1
Explanation:
By using the partial quotients method,
6,075 ÷ 2 = ( 6,000 + 74 ) ÷ 2
= ( 6,000 ÷ 2 ) + ( 74 ÷ 2 )
= 3,000 + 37
= 3,037 R 1
Hence, 6,075 ÷ 2 = 3,037 R 1
5.9 Problem Solving: Division
Question 41.
A young snake sheds its skin every 2 weeks. How many times will the snake shed its skin in 3 years?


Answer: A young snake sheds its skin 78 times in 3 years.
Explanation:
Given that a young snake sheds its skin every 2 weeks
We know that,
1 year = 52 weeks
So,
3 years = 3 × 52 = 156 weeks
So,
The number of times the young snake sheds its skin in 3 years = 156 ÷ 2
Now,
By using the partial quotients method,
156 ÷ 2 = ( 100 + 56 ) ÷ 2
= ( 100 ÷ 2 ) + ( 56 ÷ 2 )
= 50 + 28
= 78 times
Hence, from the above,
We can conclude that the young snake will shed its skin 78 times in 3 years
Conclusion:
After your preparation please test your knowledge by solving the problems provided at the end of the chapter. You can also prepare the questions on your own and solve the problems if you learn the concepts in depth. Prepare well and secure highest marks in the exams. All the Best!!!
