Do you want to overcome the difficult Grade 5 Chapter 6 Divide Whole Numbers math learning? Then, get connected to this page. Learn every part of this page to get the best learning way. We have provided Big Ideas Math Answers Grade 5 Chapter 6 Divide Whole Numbers on this page. Download Big Ideas Math Answers Grade 5 Chapter 6 Divide Whole Numbers PDF without paying ay amount. Check out topic-wise questions and solutions along with explanations of Big Ideas Math Answers Grade 5 Chapter 6 to solve difficult questions easily. The different concepts with different methods are included on this page for the students.
Big Ideas Math Book 5th Grade Chapter 6 Divide Whole Numbers Answer Key
All topics of the division of whole numbers such as Relate Multiplication and Division, Estimate Quotients, Division Patterns, Divide by One-Digit Numbers, Use Partial Quotients with a Remainder, Use Partial Quotients to Divide by Two-Digit Numbers, Divide Four-Digit Numbers by Two-Digit Numbers, and Divide Three-Digit Numbers by Two-Digit Numbers on this page. Click on the below links and start learning the concepts now. Make the most out of the below links and score better grades in your exams.
Lesson: 1 Relate Multiplication and Division
- Lesson 6.1 Relate Multiplication and Division
- Relate Multiplication and Division Homework & Practice 6.1
Lesson: 2 Division Patterns
Lesson: 3 Estimate Quotients
Lesson: 4 Divide by One-Digit Numbers
Lesson: 5 Use Partial Quotients to Divide by Two-Digit Numbers
- Lesson 6.5 Use Partial Quotients to Divide by Two-Digit Numbers
- Use Partial Quotients to Divide by Two-Digit Numbers Homework & Practice 6.5
Lesson: 6 Use Partial Quotients with a Remainder
- Lesson 6.6 Use Partial Quotients with a Remainder
- Use Partial Quotients with a Remainder Homework & Practice 6.6
Lesson: 7 Divide Three-Digit Numbers by Two-Digit Numbers
- Lesson 6.7 Divide Three-Digit Numbers by Two-Digit Numbers
- Divide Three-Digit Numbers by Two-Digit Numbers Homework & Practice 6.7
Lesson: 8 Divide Four-Digit Numbers by Two-Digit Numbers
- Lesson 6.8 Divide Four-Digit Numbers by Two-Digit Numbers
- Divide Four-Digit Numbers by Two-Digit Numbers Homework & Practice 6.8
Lesson: 9 Problem Solving: Division
Chapter: 6 – Divide Whole Numbers
- Divide Whole Numbers Performance Task
- Divide Whole Numbers Activity
- Divide Whole Numbers Chapter Practice
Lesson 6.1 Relate Multiplication and Division
Explore and Grow
Use the area models to find 6 × 19 and 114 ÷ 6.

Answer:
6 x 19 = 114
114 ÷ 6 = 19
Explanation:
First, multiply 6 and 19 to get the product 114. Here 6, 19 are the factors and 114 is the product. When you divide the product by anyone factor, you will automatically get the quotient as another factor. Here, 144 is the dividend, 6 is the divisor and 19 is the quotient.
114 = 60 + 54
= (6 x _) + (6 x _)
Find the sum of unknown factors of the smaller areas: 10 + 9 = 19.
The related multiplication equation is 6 x 19 = 114. So, 114 ÷ 6 = 19.
Reasoning
How do you think you can use multiplication to solve a division problem?
Answer:
Think and Grow: Relate Multiplication and Division
Key Idea
Inverse operations are operations that “undo” each other. Just as addition and subtraction are inverse operations, multiplication and division are also inverse operations.
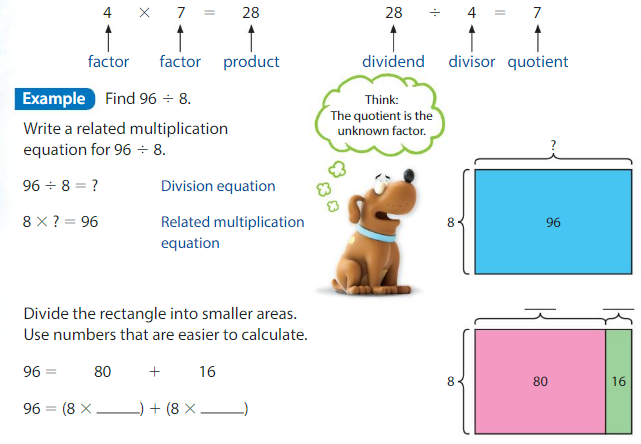
Find the sum of the unknown factors of the smaller areas: _____ + ______ = _______ .
The related multiplication equation is 8 × ______ = 96. So, 96 ÷ 8 = ______ .
Show and Grow
Use multiplication to find the quotient.
Question 1.
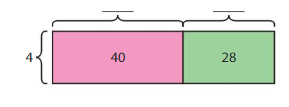
68 ÷ 4 = _____
Answer:
17.
Explanation:
68 = 40 + 28
= (4 x _) + (4 x _)
Sum of unknown factors of the smallest areas: 10 + 7 = 17
The related multiplication equation is 4 x 17 = 68. So, 68 ÷ 4 = 17.
Question 2.
138 ÷ 6 = _____
Answer:
138 ÷ 6 = 23
Explanation:
138 = 60 + 78
= (6 x _) + 6 x _)
Sum of unknown factors of the smallest areas: 10 + 13 = 23
The related multiplication equation is 23 x 6 = 138. So, 138 ÷ 6 = 23.
Apply and Grow: Practice
Use multiplication to find the quotient.
Question 3.
24 ÷ 2 = _____
Answer:
24 ÷ 2 = 12
Explanation:
24 = 20 + 4
= (2 x _) + (2 x _)
Sum of unknown factors of the smallest areas: 10 + 2 = 12
The related multiplication equation is 2 x 12 = 24. So 24 ÷ 2 = 12.
Question 4.
48 ÷ 3 = _____
Answer:
48 ÷ 3 = 16.
Explanation:
48 = 30 + 18
= (3 x _) + (3 x _)
Sum of unknown factors of the smallest areas: 10 + 6 = 16
The related multiplication equation is 3 x 16 = 48. So, 48 ÷ 3 = 16.
Question 5.
98 ÷ 7 = _____
Answer:
14.
Explanation:
98 = 35 + 63
= (7 x _) + (7 x _)
The sum of unknown factors is 5 + 9 = 14.
The multiplication equation for 98 ÷ 7 is 7 x 14 = 98. So, 98 ÷ 7 = 14.
Question 6.
125 ÷ 5 = _____
Answer:
25.
Explanation:
125 = 100 + 25
= (5 x _) + (5 x _)
The sum of unknown factors of 5 is 20 + 5 = 25
The multiplication equation for 125 ÷ 5 is 25 x 5 = 125. So, 125 ÷ 5 = 25.
Question 7.
243 ÷ 9 = _____
Answer:
27.
Explanation:
243 = 162 + 81
= (9 x _) + (9 x _)
The sum of unknown factors of 9 is 18 + 9 = 27.
The related multiplication equation is 27 x 9 = 243. So, 243 ÷ 9 = 27.
Question 8.
132 ÷ 4 = _____
Answer:
33.
Explanation:
132 = 72 + 60
= (4 x _) + (4 x _)
The sum of unknown factors of 4 is 18 + 15 = 33
The related multiplication equation is 33 x 4 = 132. So, 132 ÷ 4 = 33.
Question 9.
Structure
Draw two different ways to divide the rectangle for 112 ÷ 8. Write each product using the Distributive Property.

Answer:
112 ÷ 8 = 14.
Explanation:
Method 1 is to divide the 112 by 8 to get the quotient. Here dividend is 8 divisor is 8 and quotient is 14.
112 = 64 + 48
= (8 x _) + (8 x _)
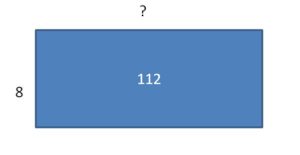
The sum of unknown areas are 8 + 6 = 14.
The relative multiplication equation is 14 x 8 = 112. So, 112 ÷ 8 = 14.
Method 2 is by dividing the divisor into two parts. And dividing each part by divisor. Get the sum of quotients to get the result.
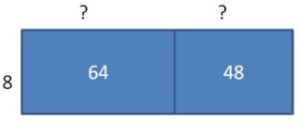
112 = 64 + 48
= (8 x _) + (8 x _)
= 8 x (_ + _)
The sum of unknown areas is 8 + 16 = 14.
The relative multiplication equation is 14 x 8 = 112. So, 112 ÷ 8 = 14.
Number Sense
Compare
Question 10.
![]()
Answer:
90 ÷ 6 = 80 ÷ 5.
Explanation:
When you divide 90 with 6, you will get remainder 0 and quotient as 16.
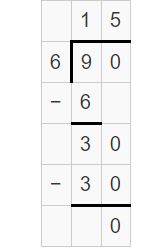
In the same way, when you divide 80 with 5, you will also get the quotient is 16, and the remainder as 0. Therefore, both expressions are equal.
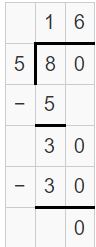
Question 11.
![]()
Answer:
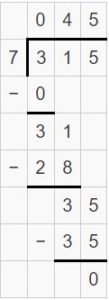
405 ÷ 9 = 315 ÷ 7
Explanation:
If you divide 405 with divisor 9, you can see quotient 45, remainder 0.
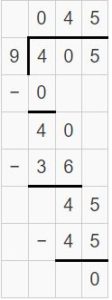
And when you divide divisor 315 by dividend 7, you can see remainder zero and quotient 45. Hence, both expressions are equal to one other.
Think and Grow: Modeling Real Life
Example
An employee has 4 boxes with 36 sticky hands in each box. He divides the sticky hands equally among 6 vending machines. How many sticky hands are in each vending machine?

Multiply the number of boxes by the number of sticky hands in each box to find the total number of sticky hands.
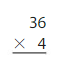
Divide the total number of sticky hands by the number of vending machines to find the number of sticky hands in each vending machine.
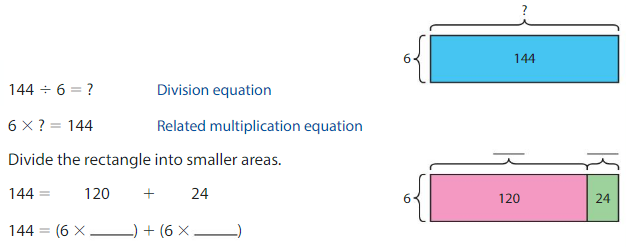
Find the sum of the unknown factors of the smaller areas:
____ + ______ = ______
The related multiplication equation is 6 × _____ = 144.
So, 144 ÷ 6 = ______.
There are ________ sticky hands in each vending machine.
Show and Grow
Question 12.
There are 6 fifth-grade classes with 21 students in each class. The students are divided equally into 7 groups. How many students are in each group?
Answer:
18 students are there in each group.
Explanation:
Here, we need to multiply the number of students in each class to get the total number of students in the fifth-grade class. i.e 6 x 21 = 126.
Divide the total number of groups in the fifth grade by the total number of students in the fifth grade to find the number of students in each group.
126 ÷ 7 = ? Division Equation
7 x ? = 126 Related Multiplication Equation
Divide the rectangles into two parts.
126 = 70 + 56
126 = (7 x _) + (7 x _)
Find the sum of the unknown factors of the part: 10 + 8 = 18.
The related multiplication equation is 7 x 18 = 126. So, 126 ÷ 7 = 18.
There are 18 students in each group.
Question 13.
Newton makes 11 clay bowls each month for 1 year. He takes an equal number of bowls to each of the 3 craft fairs. How many bowls does Newton take to each craft fair?
Answer:
Newton can take 44 bowls to each craft fair.
Explanation:
Newton makes 11 clay bowls each month for 1 year means. He can make 11 x 12 = 132 clay bowls.
Divide the total clay bowls by the number of craft fairs to get the number of bowls to each craft fair.
132 ÷ 3 = ? Division Equation
3 x ? = 132 Related Multiplication Equation
Divide the rectangle into two smaller areas.
132 = 66 + 66
132 = (3 x _) + (3 x _)
The sum of unknown factors of 11 are 22 + 22 = 44.
The related multiplication equation for 132 ÷ 3 is 3 x 44 = 132. So, 132 ÷ 3 = 44.
Newton can take 44 bowls to each craft fair.
Relate Multiplication and Division Homework & Practice 6.1
Use multiplication to find the quotient.
Question 1.
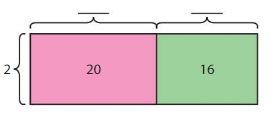
36 ÷ 2 = ______
Answer:
36 ÷ 2 = 18.
Explanation:
36 = 20 + 16
36 = (2 x 10) + (2 x 8)
The sum of factors of 2 are 10 + 8 = 18.
The related multiplication equation is 2 x 18 = 36.
So, 36 ÷ 2 = 18.
Question 2.
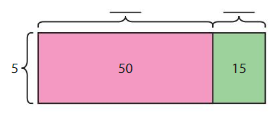
65 ÷ 5 = _____
Answer:
65 ÷ 5 = 13.
Explanation:
65 can be written as the sum of 50 and 15.
65 = 50 + 15
65 = (5 x 10) + (5 x 3)
The sum of smallest areas is 10 + 3 = 13.
The related multiplication equation is 5 x 13 = 65.
So, 65 ÷ 5 = 13.
Use multiplication to find the quotient.
Question 3.
57 ÷ 3 = ______
Answer:
57 ÷ 3 = 19.
Explanation:
57 = 39 + 18
57 = (3 x 13) + (3 x 6)
The sum of smallest areas is 13 + 6 = 19.
The related multiplication equation is 19 x 3 = 57.
So, 57 ÷ 3 = 19.
Question 4.
64 ÷ 4 = ______
Answer:
64 ÷ 4 = 16.
Explanation:
64 = 40 + 24
64 = (4 x 10) + (4 x 6)
The sum of smallest areas is 10 + 6 = 16
The related multiplication equation is 16 x 4 = 64.
So, 64 ÷ 4 = 16.
Question 5.
207 ÷ 9 = _____
Answer:
207 ÷ 9 = 23.
Explanation:
207 = 108 + 99
207 = (9 x 12) + (9 x 11)
The sum of smallest areas of the rectangles is 12 + 11 = 23
The related multiplication equation is 23 x 9 = 207.
So, 207 ÷ 9 = 23.
Question 6.
147 ÷ 7 = _____
Answer:
147 ÷ 7 = 21.
Explanation:
147 = 105 + 42
147 = (7 x 15) + (7 x 6)
The sum of smallest areas of the rectangles is 15 + 6 = 21
The related multiplication equation is 21 x 7 = 147.
So, 147 ÷ 7 = 21.
Question 7.
YOU BE THE TEACHER
Your friend finds 192 ÷ 6 by writing (6 × 30) + (6 × 2). She says the quotient is 12. Is your friend correct? Explain.
Answer:
Wrong.
Explanation:
We can write 192 as the sum of 180 and 12.
192 = 180 + 12
192 = (6 x 30) + (6 x 2)
The sum of factors of 6 is 30 + 2 = 32
The related multiplication equation for 192 ÷ 6 is 32 x 6 = 192.
So, when you multiply 192 by 6, it leaves remainder 0 and quotient 32.
Therefore, 192 ÷ 6 = 32.
Question 8.
Writing
Explain how you can use multiplication to solve a division problem.
Answer:
The condition to use multiplication to solve the division problems is the division of numbers should leave the remainder 0. When you divide the divisor by dividend, you will get a quotient as the answer. The product of quotient and divisor gives the result as a dividend. So, here quotient, the divisor is called the factors, and the dividend is called the product. Here, you need to split the dividend into two sections using addition property and multiply each part by the divisor. Add those factors to get the quotient value.
Question 9.
Modeling Real Life
A music teacher has 6 fifth-grade classes with 16 students in each class. She places the students into 4 equal rows for a chorus concert. How many students are in each row?
Answer:
There are 24 students in each row at the chorus concert.
Explanation:
The total number students = 16 x 6 = 96
The number of fifth-grade classes = 6
The music teacher arranges students into 4 equal rows for a chorus concert.
The number of students in each row = 96 / 4 = 24.
Question 10.
Modeling Real Life
You win 50 tickets, 12 tickets, and 16 tickets at an arcade. You are able to buy 3 of the same item with no tickets left over. How many tickets does 1 item cost?

Answer:
The cost of 1 item is 26 tickets.
Explanation:
The total number of tickets won at an arcade = 50 + 12 + 16 = 78 tickets
As given in the questions, you are able to buy 3 of the same item with no tickets left over. So, divide total tickets by the number of items to get one item cost.
The cost of 1 item = 78 / 3 = 26 tickets.
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 11.
31.4 × 9.2 = _____
Answer:
31.4 × 9.2 = 288.88
Explanation:

Add a dot to the second digit.
The product is reasonable.
Question 12.
67.3 × 4.2 = ______
Answer:
67.3 × 4.2 = 282.66
Explanation:

Add dot before two digits from the left side.
Product is reasonable.
Question 13.
0.8 × 5.98 = ______
Answer:
0.8 × 5.98 = 4.784
Explanation:

Add dot after 3 digits from the left side.
The Product is reasonable.
Lesson 6.2 Division Patterns
Explore and Grow
Use any strategy to find each missing factor. Then write a related division equation.

What pattern do you notice?
Answer:
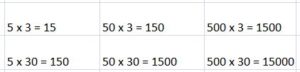
Explanation:
The factors of 15 which satisfy the condition are 5, 3. So, the missing factor is 5. The related multiplication equation is 5 x 3 = 15.
The factors of 150 that satisfy the condition are 50, 3. So, the missing factor is 50. The related multiplication equation is 50 x 3 = 150.
The factors of 1500 that satisfy the condition are 500, 3. So, the missing factor is 500. Related multiplication equation is 500 x 3 = 1500.
The factors of 150 that satisfy the condition are 5, 30. So, the missing factor is 5. Related multiplication equation is 5 x 30 = 150.
The factors of 1500 that satisfy the condition are 50, 30. So, the missing factor is 50. Related multiplication equation is 50 x 30 = 1500.
The factors of 15000 that satisfy the condition are 500, 30. So, the missing factor is 500. Related multiplication equation is 500 x 30 = 15000.
Repeated Reasoning
Explain how finding 35 ÷ 7 can help you find 350 ÷ 70.
Answer:
Canceling zeros in 350 ÷ 70 will get 35 ÷ 7.
35 ÷ 7 = 5.
Explanation:
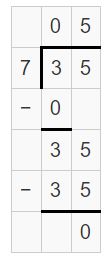
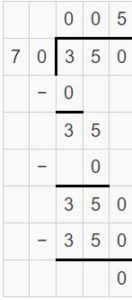
Here both 35 ÷ 7, 350 ÷ 70 give the same answer 5.
Think and Grow: Division Patterns
You can use place value and basic division facts to divide tens, hundreds, or thousands by one-digit numbers or multiples of ten.
Example
Find 63,00 ÷ 7.
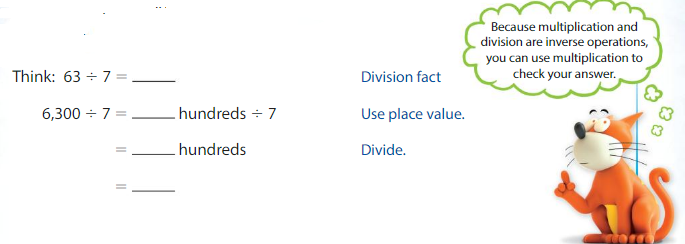
So, 6,300 ÷ 7 = 900.
Example
Find 1,200 ÷ 40.
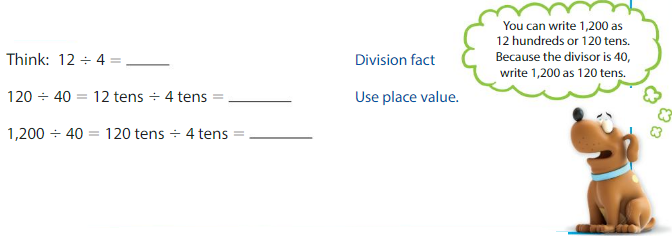
So, 1,200 ÷ 40 = 30.
Show and Grow
Find the quotient.
Question 1.
2,500 ÷ 5 = ________
Think: _____ ÷ _____ = _____
Answer:
2,500 ÷ 5 = 500
Think: 25 hundreds ÷ 5 = (25 ÷ 5) hundreds = 5 hundreds.
Explanation:
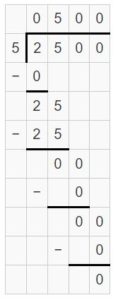
Question 2.
420 ÷ 60 = ______
Think: _____ ÷ _____ = ______
Answer:
420 ÷ 60 = 7
Think: 420 ÷ 60 = 42 tens ÷ 6 tens = 42 ÷ 6 = 7
Explanation:
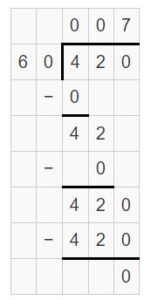
Question 3.
5,400 ÷ 90 = ______
Answer:
5,400 ÷ 90 = 60
5,400 ÷ 90 = 54 hundreds ÷ 9 tens = 54 tens ÷ 9 = (54 ÷ 9) tens = 6 tens
Explanation:
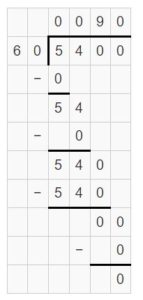
Question 4.
8,000 ÷ 20 = ______
Answer:
8,000 ÷ 20 = 400
8,000 ÷ 20 = 8 thousands ÷ 2 tens = 8 hundreds ÷ 2 = (8 ÷ 2) hundreds = 4 hundreds
Explanation:
Apply and Grow: Practice
Find the quotient.
Question 5.
800 ÷ 4 = ______
Answer:
800 ÷ 4 = 200
800 ÷ 4 = 8 hundreds ÷ 4 = (8 ÷ 4) hundreds = 2 hundreds
Explanation:
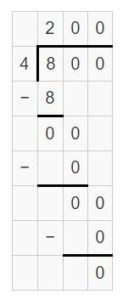
Question 6.
120 ÷ 60 = ______
Answer:
120 ÷ 60 = 2
120 ÷ 60 = 12 tens ÷ 6 tens = 12 ÷ 6 = 2
Explanation:
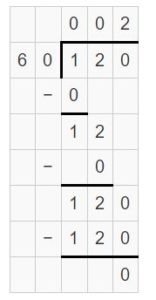
Question 7.
5,600 ÷ 7 = _____
Answer:
5,600 ÷ 7 = 800
5,600 ÷ 7 = 56 hundreds ÷ 7 = (56 ÷7) hundreds = 8 hundreds
Explanation:
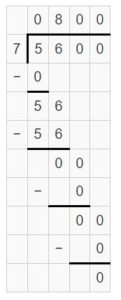
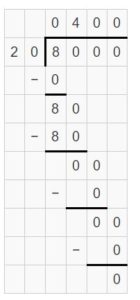
Question 8.
300 ÷ 50 = _____
Answer:
300 ÷ 50 = 7
300 ÷ 50 = 3 hundreds ÷ 5 tens = 3 tens ÷ 5 = 30 ÷ 5 = 7
Explanation:
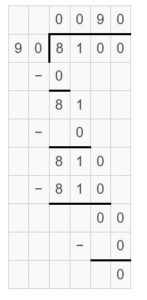
Question 9.
8,100 ÷ 90 = ______
Answer:
8,100 ÷ 90 = 90
8,100 ÷ 90 = 81 hundreds ÷ 9 tens = 81 tens ÷ 9 = (81 ÷ 9) tens = 9 tens
Explanation:
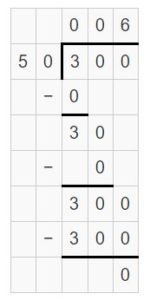
Question 10.
3,000 ÷ 30 = ______
Answer:
3,000 ÷ 30 = 100
3,000 ÷ 30 = 3 thousands ÷ 3 tens = 3 hundreds ÷ 3 = (3 ÷ 3) hundreds = 1 hundreds
Explanation:
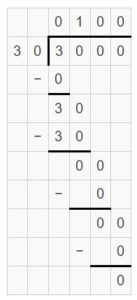
Question 11.
1,000 divided by 20 is _____.
Answer:
1,000 divided by 20 is 50.
Explanation:
1 thousand divided by 2 tens = 1 hundred ÷ 2 = (10 ÷ 2) tens = 5 tens.
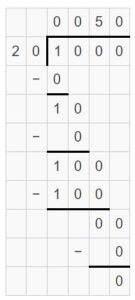
Question 12.
900 divided by 10 is ______.
Answer:
900 divided by 10 is 90.
Explanation:
9 hundred ÷ 1 ten = 9 tens ÷ 1 = 9 tens
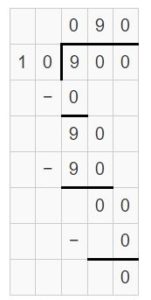
Question 13.
1,800 divided by 60 is _____.
Answer:
1,800 divided by 60 is 30.
Explanation:
18 hundred ÷ 6 tens = 18 tens ÷ 6 = (18 ÷ 6) tens = 3 tens
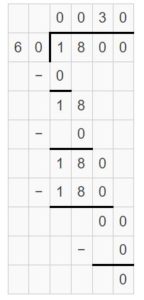
Find the missing factor.
Question 14.
_____ ÷ 40 = 8
Answer:
320 ÷ 40 = 8
Explanation:
Take the unknown value as x tens because the denominator has tens and the quotient does not have tens. Find which number divides by 4 gives 8. So, 32 divided by 4 gives 8.
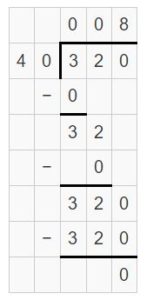
Question 15.
360 ÷ ____ = 6
Answer:
360 ÷ 60 = 6
Explanation:
We know that numerator number has tens so denominator number must also have tens to get the quotient in ones. Then, check 36 divided by which number gives the quotient 6. So, the answer is 6 tens.
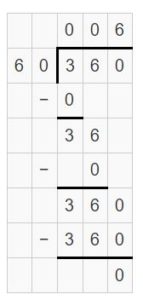
Question 16.
7,200 ÷ _____ = 90
Answer:
7,200 ÷ 80 = 90
Explanation:
Here, the numerator has hundred and the quotient has tens. So, the denominator will have tens. Check 72 divided by which number gives 9. Hence, the denominator is 8 tens.
Compare
Question 17.
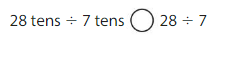
Answer:
28 tens ÷ 7 tens = 28 ÷ 7
Explanation:
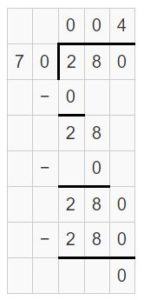
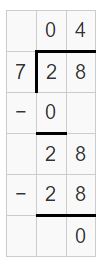
So, 28 tens ÷ 7 tens = 28 ÷ 7
Question 18.
![]()
Answer:
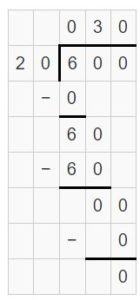
2700 ÷ 90 ≠ 24 tens ÷ 8 tens
Explanation:
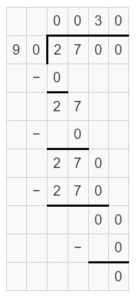
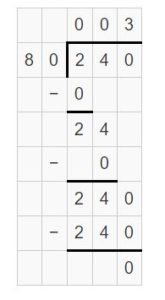
Question 19.
A jeweler has 600 rings. He displays 20 rings in each ring cushion. How many ring cushions does he use?
Answer:
A jeweler uses 30 ring cushions to display rings.
Explanation:
The number of rings = 600
Number of rings in each ring cushion = 20
Number of ring cushions required to display rings = 600 ÷ 20 = 6 hundred ÷ 2 tens = 6 tens ÷ 2 = 3 tens
Question 20.
Writing
Explain how to use 45 ÷ 9 to find 4,500 ÷ 90.
Answer:
45 ÷ 9 and 4500 ÷ 90 gives the same answer with different units. Because, in 4500 ÷ 90, we have 45 hundred ÷ 9 tens. We can write it as (45 ÷ 9) tens. So, solve 45 ÷ 9 and substitute the value in (45 ÷ 9) tens to get the answer. Actually, 45 ÷ 9 = 5, 4,500 ÷ 90 = (45 ÷ 9) tens = 5 tens
Question 21.
Number Sense
Which number cards have a quotient of 70?

Answer:
2800 ÷ 40 have a quotient of 70.
Explanation:
From the given divisions we can say that the quotient should be 70. Out of all the above 4 questions, 2800 ÷ 40 only gives the quotient in tens and 28 ÷ 4 is 7. So, 2800 ÷ 40 has a quotient of 70.
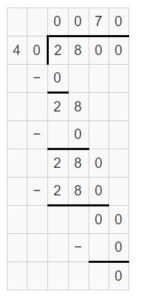
Think and Grow: Modeling Real Life
Example
A blue whale’s heart beats once every 10 seconds. How many times does the blue whale’s heart beat in 1 hour?

Think: How many seconds are in 1 hour? There are 60 seconds in 1 minute, and 60 minutes in 1 hour. So, multiply 60 by 60 to find how many seconds are in 1 hour.
60 × 60 = 3,600
Divide 3,600 by 10 to find how many times the blue whale’s heart beats in 1 hour.
Think: 36 ÷ 1 = _______ Division fact
360 ÷ 10 = 36 tens ÷ 1 ten = _________ Use place value.
3,600 ÷ 10 = 360 tens ÷ 1 ten = _____
So, the blue whale’s heart beats _______ times in 1 hour.
Show and Grow
Question 22.
A box of tennis balls weighs 3 kilograms. Each tennis ball weighs about 60 grams. How many tennis balls are in the box?

Answer:
The number of tennis balls in the box is 3000 grams ÷ 60 grams = 50.
Explanation:
The weight of tennis balls box = 3 kilograms = 3000 grams
The weight of each tennis ball = 60 grams
The number of tennis balls in the box = 3000 grams ÷ 60 grams = 3 thousand ÷ 6 tens = 3 hundreds ÷ 6 = 30 tens ÷ 6 = 5 tens
Question 23.
DIG DEEPER!
An automated teller machine, or ATM, has only $20 bills. At the start of the day, it has $10,000. One hundred eighty $20 bills are withdrawn throughout the day. How many $20 bills does the ATM have left?

Answer:
The ATM has 320 $20 bills left after counting the withdrawn amount.
Explanation:
The amount at the ATM at the start of the day = $10,000
The number of bills at the start of the day = $10,000 ÷ $20 = 10 thousand ÷ 2 tens = (10 ÷ 2) hundred = 5 hundred
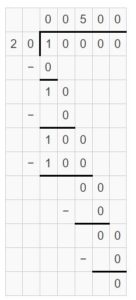
The withdrawn amount throughout the day = One hundred eighty $20 bills
The left amount in the ATM = 500 bills – 180 bills = 320 $20 bills
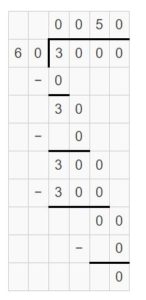
Question 24.
DIG DEEPER!
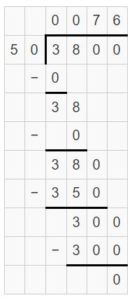
A cargo van can hold up to 2 tons. The driver weighs 200 pounds. He needs to transport as many 50-pound bags of dog food as possible. How many bags of dog food can the van hold?

Answer:
A cargo van can transport 76-pound bags of dog food.
Explanation:
The weight can hold by a cargo van = 2 tons = 2 x 2000 pounds = 4000 pounds
Driver weight = 200 pounds
Weight of each dog food bag = 50-pounds
The remaining weight can be left for the dog food bags = 4000 – 200 = 3800 pounds
The number of bags van can transport = 3800 ÷ 50 = 38 hundred ÷ 5 tens = (38 ÷ 5) ten = 7.6 ten = 76
Division Patterns Homework & Practice 6.2
Find the quotient.
Question 1.
180 ÷ 2 = ______
Think: ____ ÷ _____ = _______
Answer:
180 ÷ 2 = 90
Think: 18 tens ÷ 2 = 9 tens
Explanation:
Question 2.
4,200 ÷ 70 = _____
Think: _____ ÷ _____ = _____
Answer:
4,200 ÷ 70 = 60
Think: 42 hundred ÷ 7 tens = (42 ÷ 7) tens = 6 tens
Explanation:
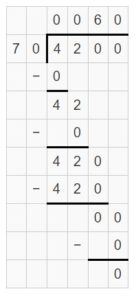
Question 3.
4,000 ÷ 5 = _____
Answer:
4,000 ÷ 5 = 800.
Explanation:
4 thousands ÷ 5 = 40 hundreds ÷ 5 = 8 hundreds.
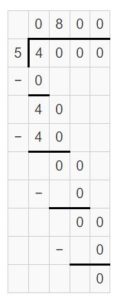
Question 4.
270 ÷ 30 = _______
Answer:
270 ÷ 30 = 9.
Explanation:
27 tens ÷ 3 tens = 27 ÷ 3 = 9.
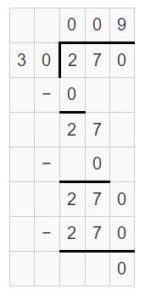
Question 5.
2,400 ÷ 60 = ______
Answer:
2,400 ÷ 60 = 40.
Explanation:
24 hundreds ÷ 6 tens = 4 tens.
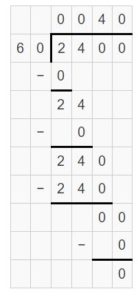
Question 6.
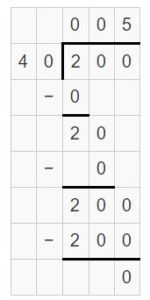
200 divided by 40 is ______.
Answer:
200 divided by 40 is 5.
Explanation:
2 hundreds ÷ 4 tens = 20 tens ÷ 4 tens = 20 ÷ 4 = 5
Question 7.
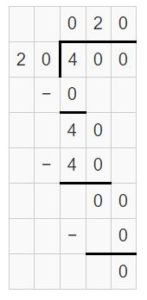
400 divided by 20 is ______.
Answer:
400 divided by 20 is 20.
Explanation:
4 hundreds ÷ 2 tens = 4 tens ÷ 2 = 2 tens.
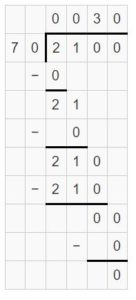
Question 8.
2,100 divided by 70 is ______.
Answer:
2,100 divided by 70 is 30.
Explanation:
21 hundreds ÷ 7 tens = 21 tens ÷ 7 = 3 tens
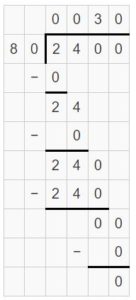
Find the missing factor.
Question 9.
2,400 ÷ ____ = 30
Answer:
2,400 ÷ 80 = 30.
Explanation:
Check which number divided by 24 gives quotient 3. So, 24 ÷ 8 = 3. That means 24 hundreds ÷ tens = 3 tens
(24 ÷ _) tens = 3 tens
24 ÷ 8 tens = 3 tens
Question 10.
______ ÷ 60 = 50
Answer:
3,000 ÷ 60 = 50.
Explanation:
_ thousands ÷ 6 tens = 5 tens
_ ÷ 6 hundreds = 5 tens
So, 3,000 ÷ 60 = 50
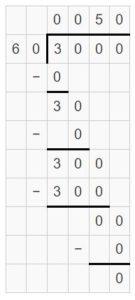
Question 11.
700 ÷ ____ = 70
Answer:
700 ÷ 10 = 70.
Explanation:
7 hundreds ÷ ___ = 7 tens
So, 7 hundreds ÷ ten = 7 tens
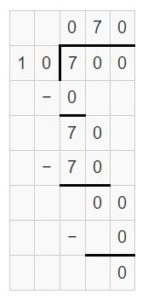
Compare
Question 12.
![]()
Answer:
45 hundreds ÷ 9 > 450 ÷ 90
Explanation:
45 hundreds ÷ 9 = 5 hundreds
450 ÷ 90 = 5
So, 45 hundreds ÷ 9 > 450 ÷ 90
Question 13.
![]()
Answer:
3600 ÷ 60 < 140 ÷ 2
Explanation:
3600 ÷ 60 = 36 hundreds ÷ 6 tens = 36 ÷ 6 tens = 6 tens
140 ÷ 2 = 14 tens ÷ 2 = (14 ÷ 2) tens = 7 tens
So, 3600 ÷ 60 < 140 ÷ 2
Question 14.
The elevator to the Top of the Rock Observation Deck in New York City travels 1,200 feet each minute. How many feet does the elevator travel each second?

Answer:
The elevator to the Top of the Rock Observation Deck in New York City travels 20 feet in each second.
Explanation:
The elevator to the Top of the Rock Observation Deck in New York City travels 1,200 feet each minute.
1 minute has 60 seconds.
So, the elevator travels 1200 feet ÷ 60 in each second.
= 12 hundreds feet ÷ 6 tens = 12 tens ÷ 6 = 2 tens feet.
Question 15.
Reasoning
Why is 640 ÷ 80 equal to 64 ÷ 8?
Answer:
640 ÷ 80 = 64 tens ÷ 8 tens = 64 ÷ 8.
We can say that in 640 ÷ 80 both numerator and denominator have tens. By canceling those tens, we will get 64 ÷ 8.
So, 640 ÷ 80 = 64 ÷ 8
Question 16.
Modeling Real Life
A black bear in a zoo eats 8 kilograms of food each day. He eats 4 equal-sized meals each day. How many grams of food are in each meal?
Answer:
A black bear in a zoo eats 2000 grand of food are in each meal.
Explanation:
The weight of food a black bear in a zoo eats a day = 8 kilograms = 8 x 1000 grams = 8000 grams
Number of meals in a day = 4 equal-sized meals
The weight of food black bear eat in each meal = 8000 ÷ 4 = 8 thousand ÷ 4 = (8 ÷ 4) thousand = 2 thound grams.
Question 17.
DIG DEEPER!
How many times faster does a grizzly bear’s heart beat each minute outside of hibernation than during hibernation?
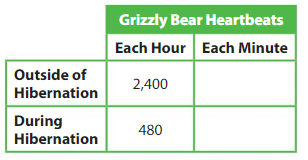
Answer:
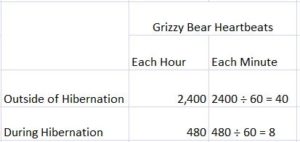
Explanation:
1 Hour = 60 Minutes
So, outside of hibernation = 2400 ÷ 60 = 24 hundreds ÷ 6 tens = 24 ÷ 6 tens = 4 tens
During hibernation = 480 ÷ 60 = 48 tens ÷ 6 tens = 48 ÷ 6 = 8.
Review & Refresh
Compare.
Question 18.
![]()
Answer:
7.829 > 7.851
Explanation:
7.829 is greater than 7.851. Because the digits after point will have lesser value.
Question 19.
![]()
Answer:
0.65 = 0.650
Explanation:
In 0.650, 0 after 65 will have no value. So, 0.65 = 0.650.
Question 20.
![]()
Answer:
2.816 < 2.814
Explanation:
2.816 is less than 2.814. Because the digits after point will have lesser value.
Lesson 6.3 Estimate Quotients
Explore and Grow
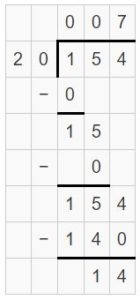
Complete the table. Explain how you can use the table to estimate 154 ÷ 20.

154 ÷ 20 is about ______.
Answer:
154 ÷ 20 = 7
Explanation:
154 is greater than 160 and less than 140. So, the quotient lies between 7 and 8. Dividing 154 by 20 gives quotient 7, and remainder not zero.
Reasoning
Why did you choose your estimate? Compare your results with your partner’s.
Answer:
I have chosen estimate to get the result for division of two numbers. It may not give accurate result, but it gives appropriate value of quotient with easy and quick process. when compared with partners result, i will find the quotient fastly and appropriate answer.To estimate your result, you need to find the nearest numbers those are exactly divided by the divisor.
Think and Grow: Estimate Quotients
You can use division facts and compatible numbers to estimate a quotient.
Example
Estimate 4,139 ÷ 6.
Look at the first two digits of the dividend and use basic division facts.
Think: What numbers close to 4,139 are easily divided by 6?
Use 3,600. 36 ÷ 6 = 6, so 3,600 ÷ 6 = 600 .
Use 4,200. 42 ÷ 6 = 7, so 4,200 ÷ 6 = 700.
Choose 4,200 because 4,139 is closer to 4,200.
So, 4,139 ÷ 6 is about 700.

Example
Estimate 2,805 ÷ 30.
Think: What numbers close to 2,805 are easily divided by 30?
Use 2,700. 27 ÷ 3 = 9
270 ÷ 30 = 9
2,700 ÷ 30 = 90
Use 3,000. 30 ÷ 3 = 10
300 ÷ 30 = 10
3,000 ÷ 30 = 100
Choose 2,700 because 2,805 is closer to 2,700.
So, 2,805 ÷ 30 is about 90.
Show and Grow
Find two numbers that the quotient is between.
Question 1.
5,482 ÷ 7
4,900 ÷ 7 = _____
5,600 ÷ 7 = ______
Answer:
5,482 ÷ 7 = 800
4,900 ÷ 7 = 49 hundreds ÷ 7 = 7 hundreds
5,600 ÷ 7 = 56 hundreds ÷ 7 = 8 hundreds
Explanation:
As the given dividend 5,482 is near to 5,600 and 5,600 ÷ 7 is 800. So, the answer is 800.
Question 2.
176 ÷ 52
150 ÷ 50 = ______
200 ÷ 50 = _______
Answer:
176 ÷ 52 is about 4.
150 ÷ 50 = 15 tens ÷ 5 tens = 3
200 ÷ 50 = 20 tens ÷ 5 tens = 4
Explanation:
Choose 200 because 176 is closer to 200.
So, 176 ÷ 52 is about 4
Question 3.
2,620 ÷ 67
Answer:
2,620 ÷ 67 is
Explanation:
What numbers close to 2,620 are easily divided by 67?
2620 ÷ 70 = 26 hundreds ÷ 7 tens = 26 tens ÷ 7 =
Use 3,600. 36 ÷ 6 = 6, so 3,600 ÷ 6 = 600 .
Use 4,200. 42 ÷ 6 = 7, so 4,200 ÷ 6 = 700.
Choose 4,200 because 4,139 is closer to 4,200.
Estimate the quotients
Question 4.
1,471 ÷ 5
Answer:
1,471 ÷ 5 is about 300.
Explanation:
Choose what numbers close to 1471 and easily divided by 5.
1500 ÷ 5 = 15 hundreds ÷ 5 = 3 hundreds = 300
1000 ÷ 5 = 10 hundreds ÷ 5 = 2 hundreds = 200
So, choose 1500 because 1471 is nearer to 1500.
Question 5.
280 ÷ 41
Answer:
280 ÷ 41 is about 7.
Explanation:
What numbers close to 280 and easily divisible by 40.
280 ÷ 40 = 28 tens ÷ 4 tens = 7
So, choose 280.
Question 6.
4,750 ÷ 88
Answer:
4,750 ÷ 88 is about 50.
Explanation:
Choose what numbers are closer to 4750 and divisible by 90.
4500 ÷ 90 = 45 hundreds ÷ 9 tens = 5 tens = 50
5400 ÷ 90 = 54 hundreds ÷ 9 tens = 6 tens = 60
So, choose 4500 which is the nearest number to 4750.
Apply and Grow: Practice
Estimate the quotients
Question 7.
557 ÷ 6
Answer:
557 ÷ 6 is about 90.
Explanation:
What numbers close to 557 and are easily divided by 6.
540 ÷ 6 = 54 tens ÷ 6 = 9 tens = 90
600 ÷ 6 = 60 tens ÷ 6 = 10 tens = 100
So, choose the number 540 is near to 557.
Question 8.
3,231 ÷ 5
Answer:
3,231 ÷ 5 is about 600.
Explanation:
What numbers close to 3231 and easily divided by 5.
3000 ÷ 5 = 30 hundreds ÷ 5 = 6 hundreds = 600
3500 ÷ 5 = 35 hundreds ÷ 5 = 7 hundreds = 700
So, choose 3000 which is near to 3231.
Question 9.
896 ÷ 11
Answer:
896 ÷ 11 is about 90.
Explanation:
Choose the numbers that are near to 896 and divisible by 11.
880 ÷ 11 = 88 tens ÷ 11 = 88
990 ÷ 11 = 99 tens ÷ 11 = 99
So, select 880 that is near to 896.
Question 10.
\(\sqrt [ 39 ]{ 7,610 } \)
Answer:
\(\sqrt [ 39 ]{ 7,610 } \) is about 200.
Explanation:
Choose the numbers that are near to 7610 and divisible by 40.
8000 ÷ 40 = 8 thousands ÷ 4 tens = 8 hundreds ÷ 4 = 2 hundreds = 200
4000 ÷ 40 = 4 thousands ÷ 4 tens = 1 hundred = 100
So, choose 8000 which is near to 7610 and divisible by 40 that is near to 39.
Question 11.
\(\sqrt [ 94 ]{ 6,287 } \)
Answer:
\(\sqrt [ 94 ]{ 6,287 } \) is about 70.
Explanation:
Choose the numbers those are close to 6287 and divisible by 90 that is near to 94.
6300 ÷ 90 = 63 hundreds ÷ 9 tens = 7 tens = 70
5400 ÷ 90 = 54 hundreds÷ 9 tens = 6 ten = 60
So, choose 6300 that is close to 6287 and divisible 90 that is near to 94.
Question 12.
\(\sqrt [ 79 ]{ 6,297 } \)
Answer:
\(\sqrt [ 79 ]{ 6,297 } \) is about
Explanation:
Choose the numbers those are close to 6297 and divisible by 80 that is near to 79.
6400 ÷ 80 = 64 hundreds ÷ 8 tens = 8 tens = 80
5600 ÷ 80 = 56 hundreds ÷ 8 tens = 7 tens = 70
So, choose 6400 that is close to 6297 and divisible 80 that is near to 79.
Question 13.
In 1 hour, toll bridge attendants collect $4,873 from cars. About how many cars cross the bridge that hour?

Answer:
Number of cars cross the bridge in one hour is 500 approximately.
Explanation:
Toll bridge attendants collection from cars in 1 hour = $4,873
One car cost = $11
Choose the number that is near to $4,873 and divisible by 10 which is near to 11.
4000 ÷ 10 = 4 thousands ÷ ten = 4 hundreds
5000 ÷ 10 = 5 thousands ÷ ten = 5 hundreds
So, choose 5000 which is near to 4873.
Question 14.
Reasoning
Newton has $415 to spend during a 15-day trip. He does not want to run out of money, so he plans to spend about the same amount each day. He estimates that the amount he can spend each day is $450 ÷ 15 = $30 or $300 ÷ 15 = $20. Which estimate should he choose? Explain.
Answer:
Newton should choose $300 ÷ 15 = $20.
Explanation:
Newton is spending $415 each day on a 15-day trip.
He can’t choose $450 ÷ 15 = $30 plan, because here the amount spend on a day is more than 415 so if he follow this he will be run out of money at the ending days of the trip.
So, he must choose $300 ÷ 15 estimate to spend the money without issues.
Question 15.
Writing
Without calculating, explain how you know whether the quotient of 176 and 62 is closer to 2 or 3.
Answer:
We can easily say that the quotient of 176 and 62 is 3. The reason is for your easy calculation, make 62 as 60 and the multiple of 60 which is nearest to 176 is 180.
Think and Grow: Modeling Real Life
Example
The Eiffel Tower is about 2 times as tall as the Washington Monument. About how tall is the Washington Monument?

Because the Eiffel Tower is about 2 times as tall as the Washington Monument, estimate 1,063 ÷ 2.
Think: What numbers close to 1,063 are easily divided by2?
Use 1,000. 10 ÷ 2 = 5, so 1,000 ÷ 2 = 500.
Use 1,200. 12 ÷ 2 = 6, so, 1,200 ÷ 2 = 600.
Choose 1,000 because 1,063 is closer to 1,000.
So, the Washington Monument is about 500 feet tall.
Show and Grow
Question 16.
The Pacific Crest Trail is 2,650 miles long. It is about 7 times as long as the Bigfoot Trail. About how long is the Bigfoot Trail?
Answer:
The length of bigfoot trail is about 400 miles.
Explanation:
Pacific Crest Trail = 7 times Bigfoot trail
2650 miles = 7 Bigfoot tail
Bigfoot tail = 2650 ÷ 7
2800 ÷ 7 = 28 hundreds ÷ 7 = 4 hundreds
2100 ÷ 7 = 21 hundreds ÷ 7 = 3 hundreds
So, the length of bigfoot trail is 400 miles.
Question 17.
A family spends $2,473 each year for cell phone service. About how much does the family spend each month for cell phone service?
Answer:
The amount spend by a family for cell phone service in a month is 200.
Explanation:
The amount spend by a family for cell phone service in a year = $2,473
The amount spend by a family for cell phone service in a month = $2,473 ÷ 12
2400 ÷ 12 = 24 hundreds ÷ 12 = 2 hundreds
3600 ÷ 12 = 36 hundreds ÷ 12 = 3 hundreds
So, choose 2400 that is near to 2473.
Question 18.
DIG DEEPER!
You have 31 days to read a book with 138 pages and another book with 160 pages. You want to read an equal number of pages each day. About how many pages do you read each day?
Answer:
The number of pages read each day are 10.
Explanation:
The total number of pages in two books = 138 + 160 = 298
Number of days to read books = 31
If you read an equal number of pages each day, then number of pages read in a day = 298 ÷ 31
Choose the numbers near to 298 and divisible by 30 near to 31.
300 ÷ 30 = 3 hundreds ÷ 3 tens = 3 ÷ 3 tens = 1 ten
270 ÷ 30 = 27 tens ÷ 3 tens = 9
Estimate Quotients Homework & Practice 6.3
Find two numbers that the quotient is between.
Question 1.
1,306 ÷ 3
1,200 ÷ 3 = _____
1,500 ÷ 3 = _____
Answer:
1,306 ÷ 3 is about 400.
1,200 ÷ 3 = 12 hundreds ÷ 3 = 4 hundreds
1,500 ÷ 3 = 15 hundreds ÷ 3 = 5 hundreds
Explanation:
The number 1200 is near to 1306.
Question 2.
435 ÷ 80
400 ÷ 80 = ______
480 ÷ 80 = ______
Answer:
435 ÷ 80 is about 5.
400 ÷ 80 = 4 hundreds ÷ 8 tens = 40 tens ÷ 8 tens = 5
480 ÷ 80 = 48 tens ÷ 8 tens = 6
Explanation:
Number 400 is close to 435 and divisible by 80.
Question 3.
5,691 ÷ 68
Answer:
5,691 ÷ 68 is about 80.
Explanation:
What numbers are closer to 5691 and divisible by 70 which is near to 68.
5600 ÷ 70 = 56 hundreds ÷ 7 tens = 8 tens
4900 ÷ 70 = 49 hundreds ÷ 7 tens = 7 tens
So, choose 5600 which is near to 5691 and divisible by 70 which is near to 68.
Estimate the quotient.
Question 4.
2,506 ÷ 2
Answer:
2,506 ÷ 2 is about 1300
Explanation:
What numbers are near to 2506, divisible by 2.
2400 ÷ 2 = 24 hundreds ÷ 2 = 12 hundreds
2600 ÷ 2 = 26 hundreds ÷ 2 = 13 hundreds
So, choose 2600 which is near to 2506.
Question 5.
4,392 ÷ 88
Answer:
4,392 ÷ 88 is 50.
Explanation:
What numbers are near to 4392 and divided by 90 near to 88.
4500 ÷ 90 = 45 hundreds ÷ 9 tens = 5 tens
3600 ÷ 90 = 36 hundreds ÷ 9 tens = 4 tens
So, choose 4500 near to 4392.
Question 6.
2,416 ÷ 6
Answer:
2,416 ÷ 6 is 400.
Explanation:
What numbers are close to 2416 and divided by 6.
2400 ÷ 6 = 24 hundreds ÷ 6 = 4 hundreds
3000 ÷ 6 = 30 hundreds ÷ 6 = 5 hundreds
So, choose 2400 near to 2416.
Question 7.
\(\sqrt [ 52 ]{ 386 } \)
Answer:
\(\sqrt [ 52 ]{ 386 } \) is 8.
Explanation:
What numbers are near to 386 and divided by 50 which is near to 52.
350 ÷ 50 = 35 tens ÷ 5 tens = 7
400 ÷ 50 = 40 tens ÷ 5 tens = 8
So choose 400 near to 386.
Question 8.
\(\sqrt [ 21 ]{ 1,495 } \)
Answer:
\(\sqrt [ 21 ]{ 1,495 } \) is 70.
Explanation:
What numbers are close to 1495 and divided by 21 which is near to 20.
1400 ÷ 20 = 14 hundreds ÷ 2 tens = 7 tens
1600 ÷ 20 = 16 hundreds ÷ 2 tens = 8 tens
So, choose 1400 near to 1495.
Question 9.
\(\sqrt [ 43 ]{ 3,509 } \)
Answer:
\(\sqrt [ 43 ]{ 3,509 } \) is 90.
Explanation:
What numbers are near to 3509 and divisible by 40 near to 43.
3200 ÷ 40 = 32 hundreds ÷ 4 tens = 8 tens
3600 ÷ 40 = 36 hundreds ÷ 4 tens = 9 tens
So, choose 3600 close to 3509.
Question 10.
The length of 1 year on Uranus is a little more than 84 years on Earth. About how many Uranus years are equal to 175 Earth years?

Answer:
2 Uranus years are equal to 175 earth years.
Explanation:
Given that,
The length of 1 year on Uranus is a little more than 84 years on Earth.
175 earth years = 175 ÷ 84 years
160 ÷ 80 = 16 tens ÷ 8 tens = 2
240 ÷ 80 = 24 tens ÷ 8 tens = 3
So, 160 is near to 175.
Question 11.
YOU BE THE TEACHER
Your friend finds a quotient. Estimate to check whether your friend’s answer is reasonable.
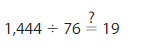
Answer:
Yes, the answer is reasonable.
Explanation:
What numbers are close to 1444 and divided by 76 which is near to 80.
1600 ÷ 80 = 16 hundreds ÷ 8 tens = 2 tens
800 ÷ 80 = 8 hundreds ÷ 8 tens = 1 tens
So, choose 1600 near to 1444.
Question 12.
Reasoning
A florist has 336 roses and 28 vases. He wants to determine how many flowers he can put into each vase without any left over. Should he use an estimate or an exact answer? Explain.
Answer:
He will get an exact answer i.e in each vase there are 12 roses.
Explanation:
The florist has 336 roses and 28 vases.
The number of flowers in each vase = 336 ÷ 28 = 12
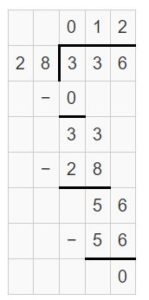
Question 13.
Modeling Real Life
A train ride from Chicago to Emeryville, California, is 2,438 miles. It is about 8 times as long as a train ride from Chicago to PortHuron, Michigan. About how long is the train ride from Chicago to Port Huron?
Answer:
The train ride from Chicago to Port Huron is about 300 miles long.
Explanation:
A train ride from Chicago to Emeryville, California = 8 x a train ride from Chicago to PortHuron, Michigan
2,438 = 8 x a train ride from Chicago to PortHuron, Michigan
A train ride from Chicago to PortHuron, Michigan = 2438 ÷ 8
Choose the numbers close to 2438, divided by 8.
2400 ÷ 8 = 24 hundreds ÷ 8 = 3 hundreds
3200 ÷ 8 = 32 hundreds ÷ 8 = 4 hundreds
So, choose 2400 is near to 2438.
Question 14.
Modeling Real Life
You are reading a book that has 784 pages. You have 18 days to read the entire book. About how many pages should you read each day?
Answer:
You can read 40 pages each day to complete the book in 18 days.
Explanation:
The number of pages of the book = 784
Number days to read book = 18
Number of pages should be read each day = 784 ÷ 18
Select the numbers which are near 784 and divided by 20 near 18.
600 ÷ 20 = 6 hundreds ÷ 2 tens = 3 tens
800 ÷ 20 = 8 hundreds ÷ 2 tens = 4 tens
So, choose 800 which is closer to 784 and divided by 20.
Review & Refresh
Write the decimal as a fraction.
Question 15.
0.61
Answer:
0.61 = (61 / 100)
Explanation:
Rewrite the decimal number as a fraction having a denominator 1.
0.61 = 0.61 / 1
Multiply the numerator and denominator of the fraction by 100 to remove 2 decimal places.
( 0.61 / 1) x (100 / 100) = 61 / 100
Question 16.
0.084
Answer:
0.084 = (84 / 1000)
Explanation:
Represent the given decimal number as a fraction with denominator 1.
0.084 = 0.084 / 1
Multiply the denominator and numerator of the fraction by the same number to remove 3 decimal places. Here, you can multiply by 10³ = 1000.
(0.084 / 1) x (1000 / 1000) = 84 / 1000
Question 17.
0.709
Answer:
0.709 = 709 / 1000
Explanation:
Mention the given decimal number as a fraction by keeping 1 in the denominator.
0.709 = 0.709 / 1
Multiply the fraction to eliminate 3 decimal places. Here, you can multiply both top and bottom by 10³ = 1000.
(0.709 / 1) x (1000 / 1000) = (709 / 1000)
Question 18.
0.5
Answer:
0.5 = 5 / 10
Explanation:
Keep 1 at the bottom and write the decimal number as a fraction.
0.5 = 0.5 / 1
Multiply both top and bottom by 10¹ = 10 to eliminate the decimal places.
(0.5 / 1) x (10 / 10) = 5 / 10
Lesson 6.4 Divide by One-Digit Numbers
Explore and Grow
Complete all three models to find 248 ÷ 8.
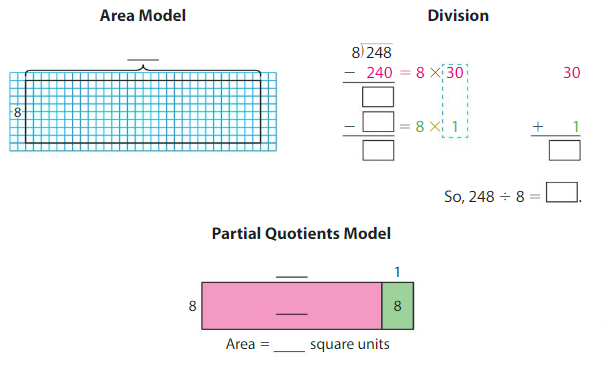
Answer:
248 ÷ 8 = 31.
Structure
How would the models be the same for 3,069 ÷ 5? How would they be different?
Answer:
By using the Estimate Quotients process, we can just find the nearest possible value of the quotient. But this model gives the exact quotient value along with the remainder.
Think and Grow: Divide by One-Digit Numbers
Example
Find 3,069 ÷ 5. Estimate _______

So, 3,069 ÷ 5 = 613 R 4
Check: Because 613 R 4 is close to the estimate, the answer is reasonable.
Show and Grow
Divide. Then check your answer.
Question 1.
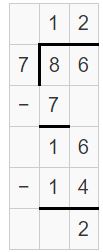
\(\sqrt [ 7 ]{ 86 } \)
Answer:
\(\sqrt [ 7 ]{ 86 } \) = 12 R 2
Explanation:
Question 2.
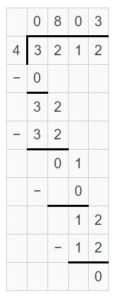
\(\sqrt [ 4 ]{ 3,212 } \)
Answer:
\(\sqrt [ 4 ]{ 3,212 } \) = 803 R 0
Explanation:
Question 3.
\(\sqrt [ 6 ]{ 1,759 } \)
Answer:
\(\sqrt [ 6 ]{ 1,759 } \) = 293 R 1
Explanation:
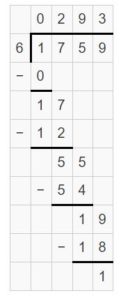
Apply and Grow: Practice
Divide. Then check your answer.
Question 4.
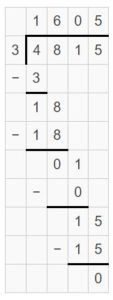
\(\sqrt [ 3 ]{ 4,185 } \)
Answer:
\(\sqrt [ 3 ]{ 4,185 } \) = 1605 R 0
Explanation:
Question 5.
\(\sqrt [ 6 ]{ 730 } \)
Answer:
\(\sqrt [ 6 ]{ 730 } \) = 121 R 4
Explanation:
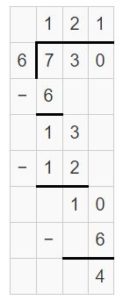
Question 6.
\(\sqrt [ 8 ]{ 7,106 } \)
Answer:
\(\sqrt [ 8 ]{ 7,106 } \) = 888 R 2
Explanation:
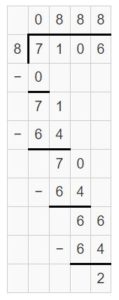
Question 7.
824 ÷ 4 = ______
Answer:
824 ÷ 4 = 206 R 0
Explanation:
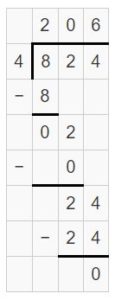
Question 8.
4,526 ÷ 2 = ______
Answer:
4,526 ÷ 2 = 2263
Explanation:
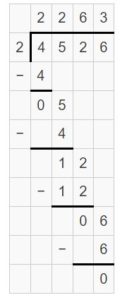
Question 9.
9,364 ÷ 9 = _______
Answer:
9,364 ÷ 9 = 1040 R 9
Explanation:
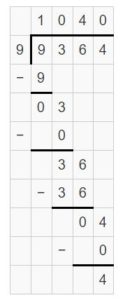
Question 10.
Your cousin babysits for 5 days and earns a total of $375. How much money does your cousin earn each day?
Answer:
Your cousin earns $75 on babysits daily.
Explanation:
Cousin earnings on babysits = $375
Number of days cousin babysits = 5
Amount she earns each day = $375 ÷ 5 = $75
Question 11.
Number Sense
Without calculating, determine whether you place the first digit of the quotient in the hundreds place or the thousands place. Explain.
6,529 ÷ 8
Answer:
I will place the first digit of the quotient on the hundreds place.
6,529 ÷ 8 = 816 R 1
Explanation:
Generally, we place the quotients on the top of the dividend one by one. Here, we can easily say that we are putting the first digit of the quotient on hundreds of places by seeing the numbers. The strategy here is if the first digit of the divided is greater than the divisor, then the quotient will have (dividend – 1) numbers.
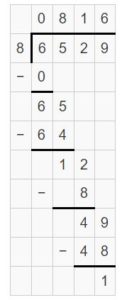
Question 12.
DIG DEEPER!
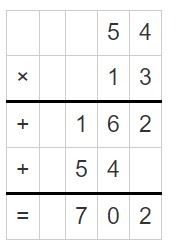
Complete the multiplication problem to check the division work. Then use the word cards to label each part of the multiplication problem.
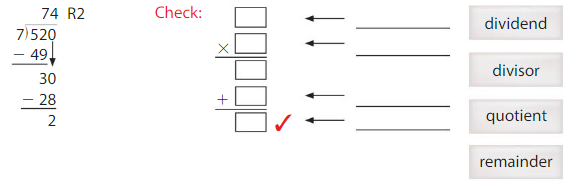
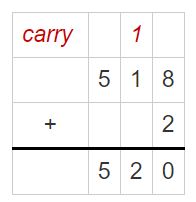
Answer:
dividend = divisor × quotient + remainder
520 = 7 x 74 + 2
= 518 + 2
Explanation:

Think and Grow: Modeling Real Life
Example
There are 118 elements in the periodic table. There are 6 groups of students in a class. Each group is assigned about the same number of elements to study. How many elements does each group study?
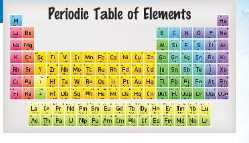
Divide 118 by 6 to find how many elements each group studies.
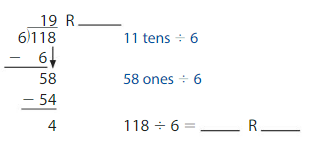
Interpret the quotient and the remainder.
The quotient is 19. So, each group studies at least 19 elements.
The remainder is 4. There are 4 elements not assigned to a group.
So, 6 groups must study 1 more element.
Subtract to find how many groups study 19 elements. 6 − 2 = 4
So, 2 groups study 21 elements, and 4 groups study 19 elements.
Show and Grow
Question 13.
A total of 243 students take a field trip on 5 buses. Each bus must have about the same number of students. How many students must ride on each bus?
Answer:
At least 48 students must ride on each bus.
Explanation:
Divide 243 by 5 to get how many students must ride on each bus.
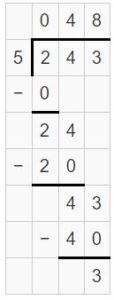
The quotient is 48. So, each bus has at least 48 students.
The remainder is 3. There are 3 students who are not on buses.
Subtract to find how many buses have 48 students. 5 – 3 = 2
So, 3 buses have 147, and 2 buses have 96 students.
Question 14.
DIG DEEPER!
The boiling point of tungsten is 5,660 degrees Celsius. This is 160 degrees hotter than 2 times the boiling point of iron. What is the boiling point of iron?
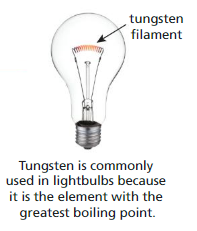
Answer:
The boiling point of iron is 2750 degrees Celsius.
Explanation:
The boiling point of tungsten = 5660 degrees Celsius
= 160 degrees + 2 times the boiling point of the iron.
2 times the boiling point of the iron = 5660 – 160 = 5500
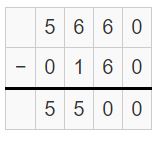
Thus boiling point of the iron = 5500 ÷ 2

So, the boiling point of the iron = 2750 degrees Celsius.
Divide by One-Digit Numbers Homework & Practice 6.4
Divide. Then Check your answer.
Question 1.
\(\sqrt [ 6 ]{ 834 } \)
Answer:
\(\sqrt [ 6 ]{ 834 } \) = 139 R 0
Explanation:
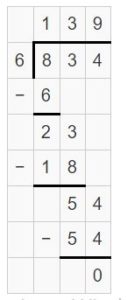
Question 2.
\(\sqrt [ 4 ]{ 881 } \)
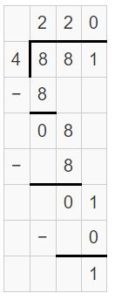
Answer:
\(\sqrt [ 4 ]{ 881 } \) = 220 R 1
Explanation:
Question 3.
\(\sqrt [ 2 ]{ 4,135 } \)
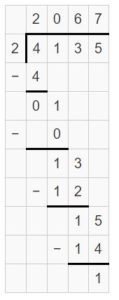
Answer:
\(\sqrt [ 2 ]{ 4,135 } \) = 2067 R 1
Explanation:
Question 4.
215 ÷ 7 = ______
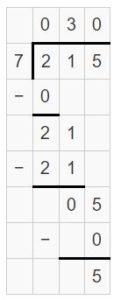
Answer:
215 ÷ 7 = 30 R 5
Explanation:
Question 5.
6,517 ÷ 4 = _____
Answer:
6,517 ÷ 4 = 1629 R 1
Explanation:
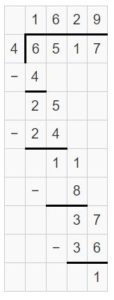
Question 6.
3,155 ÷ 5 = _____
Answer:
3,155 ÷ 5 = 631
Explanation:
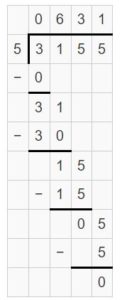
Question 7.
Your friend makes care packages with 9 items in each package. She has 1,350 items. How many care packages can she make?
Answer:
Your friend can make 150 care packages.
Explanation:
Divide 1350 by 9 to get the number of care packages made by your friend.
 So, 150 care packages made by your friend.
So, 150 care packages made by your friend.
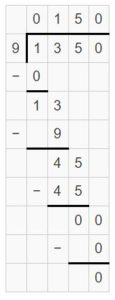
Question 8.
Number Sense
What is the dividend when the divisor is 8 and the quotient is 96 with remainder 3? Explain how you found the dividend.
Answer:
The dividend is 771.
Explanation:
Dividend = Divisor × Quotient + Remainder
Dividend = 8 x 96 + 3
= 768 + 3 = 771
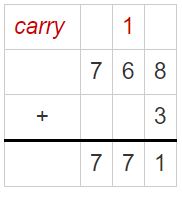
Question 9.
Reasoning
Your friend says the quotient of 3,627 and 9 is 43. Is your friend’s answer reasonable? Explain.
Answer:
Not reasonable. why because, when we divide 3627 by 9, we can see the quotient as 403 and the remainder 0.
Explanation:
We can see that the quotient of 3627 by 9 is 403. So, it is not reasonable.
Question 10.
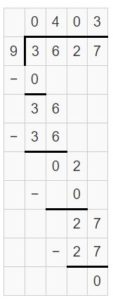
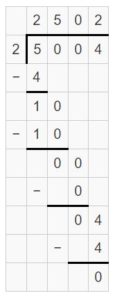
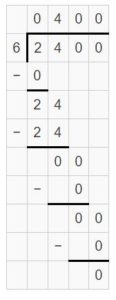
DIG DEEPER!
Choose two numbers to write a division expression that has the greatest quotient. Then evaluate.

Answer:
5004 ÷ 2 = 2502 is the division expression that has the greatest quotient.
Explanation:
5004 ÷ 2 = 2502
2400 ÷ 6 = 400
6378 ÷ 3 = 2126
Out of all 5004 ÷ 2 has the greatest quotient.
Question 11.
Modeling Real Life
A principal invites 138 students to a reward breakfast. Nine students sit at each table. How many tables are there?
Answer:
There are 15 tables.
Explanation:
Divide 138 by 9 to find how many tables are there.
There are 15 tables.
Question 12.
Modeling Real Life
A class makes origami cubes. Each cube requires 6 sheets of paper. The class makes as many cubes as possible with 550 sheets of paper. How many more sheets of paper does the class need to make one more cube?

Answer:
2 more sheets are needed to make one more cube.
Explanation:
Divide 550 by 6 to get how many more sheets of paper does the class need to make one more cube.
The remainder is 4. So, 2 more sheets of paper are required to make one more cube.
Review & Refresh
Estimate the product.
Question 13.
0.9 × 82
Answer:
0.9 × 82 = 80
Explanation:
To multiply the numbers, round them to the nearest greatest value.
0.9 x 82 = 1 x 80
= 1 x 8 tens = 8 tens
Question 14.
36 × 2.71
Answer:
36 × 2.71 = 120
Explanation:
36 × 2.71 = 40 x 3 = 4 tens x 3
= 12 tens = 120
Lesson 6.5 Use Partial Quotients to Divide by Two-Digit Numbers
Explore and Grow
How can you use an area model to find 168 ÷ 14?
Answer:
168 ÷ 14 = 12
Explanation:
168 = 140 + 28

Area = 168 sq units
so, 168 ÷ 14 = 12
Reasoning
Explain how your model shows the quotient.
Answer:
Think and Grow: Use Partial Quotients to Divide
Example
Use an area model and partial quotients to find 180÷ 12.

Example
Use an area model and partial quotients to find 396 ÷ 18.
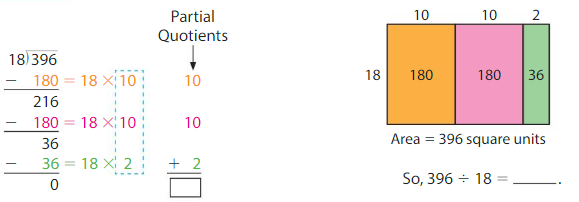
Show and Grow
Use an area model and partial quotients to divide.
Question 1.
176 ÷ 16 = _____
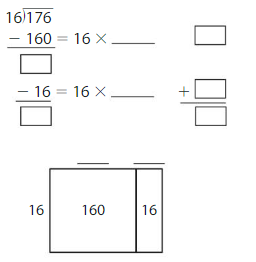
Answer:
176 ÷ 16 = 11
Explanation:
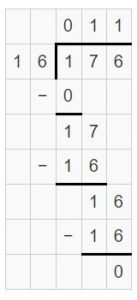
Partial quotients 10 + 1 = 11
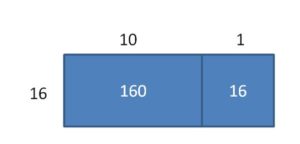
Area = 160 + 16 = 176
So, 176 ÷ 16 = 11
Question 2.
182 ÷ 13 = _____
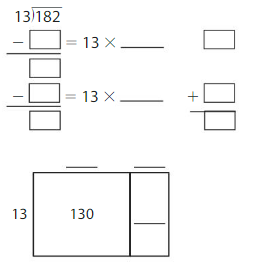
Answer:
182 ÷ 13 = 14
Explanation:
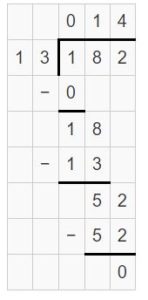
Partial Quotients = 10 + 4 = 14
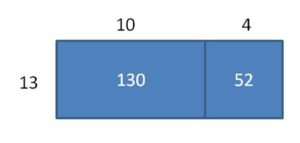
Area = 130 + 52 = 182
So, 182 ÷ 13 = 14
Apply and Grow: Practice
Use an area model and partial quotients to divide.
Question 3.
154 ÷ 14 = _____
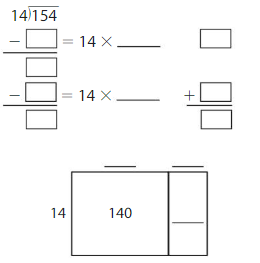
Answer:
154 ÷ 14 = 11
Explanation:
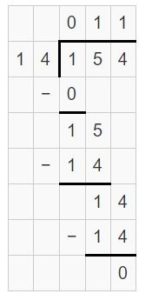
Partial Quotient = 10 + 1 = 11
Area = 140 + 14 = 154
So, 154 ÷ 14 = 11.
Question 4.
224 ÷ 16 = _____
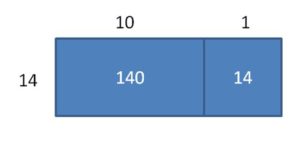
Answer:
224 ÷ 16 = 14
Explanation:
Partial quotients = 10 + 4 = 14
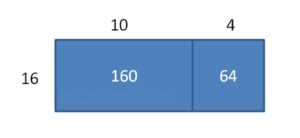
Area = 160 + 64 = 224
so, 224 ÷ 16 = 14.
Use partial quotients to divide.
Question 5.
204 ÷ 17
Answer:
204 ÷ 17 = 12
Explanation:
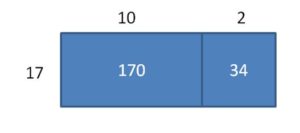
Area = 170 + 34 = 204
So, 204 ÷ 17 = 10 + 2 = 12
Question 6.
225 ÷ 15
Answer:
225 ÷ 15 = 15
Explanation:
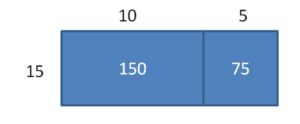
Area = 150 + 75 = 225
So, 225 ÷ 15 = 10 + 5 = 15
Question 7.
Writing
Explain why there is more than one way to draw an area model to find a quotient.
Answer:
Area model or box model is a rectangular diagram used for division or multiplication problems. Here the quotient or factors and divisor define the length and width of the rectangle. You can break the area of a rectangle into several smaller boxes using number bonds to make calculations easier. So, there are several ways to draw an areal model to find the quotient.
Question 8.
A puma jumps 132 inches up onto a rock. How many feet does the puma jump?

Answer:
11 foot the puma jumps up on the rock.
Explanation:
We already know that 1 foot = 12 inches
Divide 132 ÷ 12 to get how many feet does the puma jump.
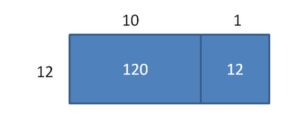
Area = 120 + 12 = 132
So, 132 ÷ 12 = 10 + 1 = 11
Question 9.
DIG DEEPER!
Write two related division equations represented by the model.
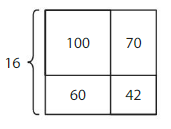
Answer:
160 ÷ 16, 112 ÷ 16.
Explanation:
Add the first column and second columns separately to get the dividends of the division equation. And the width of the rectangle is the divisor of the division equations.
So, first equation is (100 + 60) ÷ 16 = 160 ÷ 16
Second equation is (70 + 42) ÷ 16 = 112 ÷ 16
Think and Grow: Modeling Real Life
Example
A zookeeper cleans the rectangular floor of a baboon enclosure. The floor of the enclosure has an area of 156 square feet and a width of 12 feet. What is the length of the enclosure?

Use the area of a rectangle formula. Write the related division equation to find the length of the enclosure.
ℓ × w = A Area formula
ℓ × 12 = 156
156 ÷ 12 = ℓ
Use an area model and partial quotients to find 156 ÷ 12.
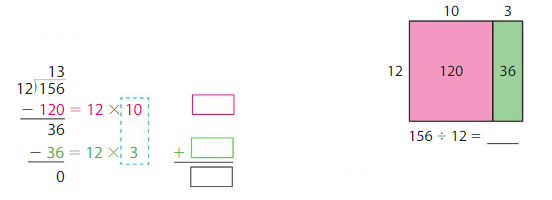
So, the length of the enclosure is 10 + 3 = 13.
Show and Grow
Question 10.
A bakery owner tiles the rectangular floor. What is the length of the floor?
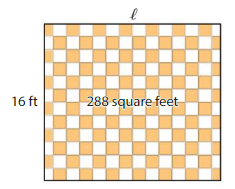
Answer:
The length of the rectangular floor is 18 feet.
Explanation:
Length x Width = Area
l x 16 = 288
l = 288 ÷ 16
Here, we are using partial quotients to find 288 ÷ 16
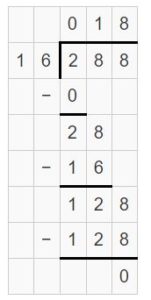
So, 288 ÷ 16 = 10 + 8 = 18
Question 11.
There are 176 fifth graders and 198 sixth graders signed up for soccer. Each soccer team has 11 players. How many more sixth-grade teams are there than fifth-grade teams?
Answer:
Number of fifth-grade teams = 16
Number of six-grade teams = 18
So, 18 – 16 = 2 sixth-grade teams are more than fifth-grade teams.
Explanation:
Number of fifth-grade teams = 176 ÷ 11
Using the area model to find 176 ÷ 11
Area = 110 + 66 = 176
So, 176 ÷ 11 = 10 + 6 = 16
Number of six-grade teams = 198 ÷ 11
Using partial quotients to find 198 ÷ 11
So, 198 ÷ 11 = 10 + 8 = 18
Therefore, 18 – 16 = 2 sixth-grade teams are more than fifth-grade teams.
Question 12.
DIG DEEPER!
Newton earns $195 for working 15 hours as a radio host. How much money does Newton earn in 3 hours?
Answer:
Newton can earn $39 in 3 hours for working as a radio host.
Explanation:
Divide 195 ÷ 15 to get how much money does newton earn in one hour.
Use the area model to find 195 ÷ 15.

Area = 150 + 45 = 195
So, 195 ÷ 15 = 10 + 3 = 13
Newton earns $13 in one hour.
So, the money earned in 3 hours = 13 x 3 = $39
Use Partial Quotients to Divide by Two-Digit Numbers Homework & Practice 6.5
Use an area model and partial quotients to divide.
Question 1.
165 ÷ 11 = ______
Answer:
165 ÷ 11 = 55
Explanation:
Area = 110 + 55 = 165
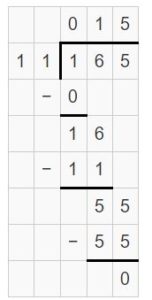
Partial Quotients = 10 + 5 = 15
So, 165 ÷ 11 = 55
Question 2.
192 ÷ 12 = ______
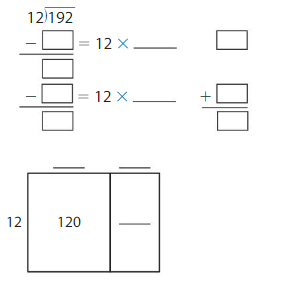
Answer:
192 ÷ 12 = 16
Explanation:
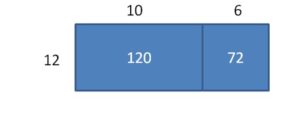
Area = 120 + 72 = 192
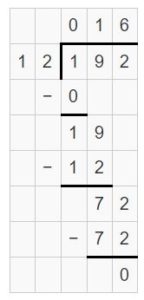
Partial Quotients = 10 + 6 = 16
So, 192 ÷ 12 = 16
Use partial products to divide.
Question 3.
156 ÷ 13
Answer:
156 ÷ 13 = 12
Explanation:
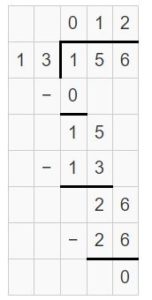
Partial Quotients = 10 + 2 = 12
So, 156 ÷ 13 = 12
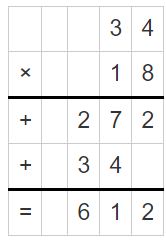
Question 4.
121 ÷ 11
Answer:
121 ÷ 11 = 11
Explanation:
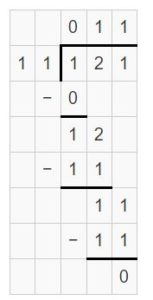
Partial Quotients = 10 + 1 = 11
So, 121 ÷ 11 = 11.
Question 5.
There are 143 players in a football league. The director divides the players into13 teams. How many players are on each team?
Answer:
There are 11 players on each team.
Explanation:
Divide 143 ÷ 13 to get the number of players on each team.
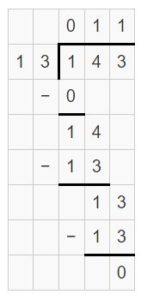
Partial Quotients = 10 + 1 = 11
So, 143 ÷ 13 = 11
Question 6.
Open-Ended
Write a division expression that has a 3-digit dividend, a divisor between 15 and 20, and no remainder. Use base ten blocks to find the quotient.
Answer:
112 ÷ 16 = 7.
Explanation:
The value of each block is written there.
Question 7.
Structure
Newton finds 506 ÷ 22. Explain how his steps change if he uses 20 as the first partial quotient.
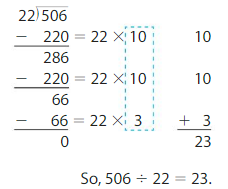
Answer:
If he uses 20 x 22 = 440 as the first partial quotient. Then 506 – 440 = 66. And the second partial quotient will be 22 x 3 = 66. Then 66 – 66 = 0. So the remainder is 0. Partial quotients = 20 + 3 = 23.
Question 8.
Modeling Real Life
A rectangular Olympic gymnastics floor has an area of 144 square meters. What is the length of the floor?
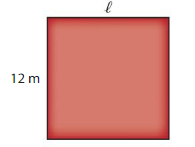
Answer:
The length of the floor is 12 m.
Explanation:
l x w = A
l x 12 = 144
l = 144 ÷ 12
Using the area model, find 144 ÷ 12.
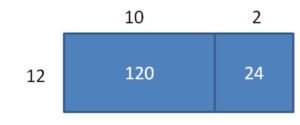
Area = 120 + 24 = 144
So, 144 ÷ 12 = 10 + 2 = 12.
Question 9.
Modeling Real Life
A vending machine worker has 78 bags of cherry fruit snacks and 91 bags of strawberry fruit snacks. Each row of the vending machine holds 13 items from front to back. How many rows does the worker fill with fruit snacks?
Answer:
The worker fills the fruit snacks on 13 rows.
Explanation:
The total number of fruit bags = 78 + 91 = 169
Divide 169 ÷ 13 to get how many rows does the worker fill with fruit snacks.
Use the area model to calculate 169 ÷ 13.

Area = 130 + 39 = 169
So, 169 ÷ 13 = 10 + 3 = 13
So, the worker fills the fruit snacks on 13 rows.
Review & Refresh
Evaluate the expression.
Question 10.
24 ÷ (6 + 2) + 14
Answer:
24 ÷ (6 + 2) + 14 = 17
Explanation:
24 ÷ (6 + 2) + 14 = 24 ÷ 8 + 14
24 ÷ 8 = 3
3 + 14 = 17
Question 11.
5 + 10 × 7 – 9
Answer:
5 + 10 × 7 – 9 = 66
Explanation:
Based on the arithmetical operator included between the numbers, it has given some preference to evaluate first.
5 + 10 × 7 – 9 = 5 + (10 x 7) – 9
= (5 + 70) – 9
= 75 – 9 = 66.
Question 12.
(135 + 96 + 165) × 10
Answer:
(135 + 96 + 165) × 10 = 3960
Explanation:
(135 + 96 + 165) × 10 = 396 x 10 = 3960
Lesson 6.6 Use Partial Quotients with a Remainder
Explore and Grow
Use an area model to find 240 ÷ 15.
Answer:
240 ÷ 15 = 16.
Explanation:
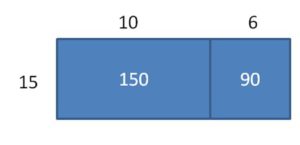
Area = 150 + 90 = 240
So, 240 ÷ 15 = 10 + 6 = 16
Can you use an area model to find 190 ÷ 15? Explain your reasoning.

Answer:
We can’t use the area model to find 190 ÷ 15. Why because 15 does not divide evenly into 190.
Construct Arguments
Explain to your partner how you know that 15 does not divide evenly into 190.
Answer:
First, we need to find the first partial quotient i.e 15 x 10 = 150. Then 190 – 150 = 40. 40 is not divisible by 15. So, we can say that 15 does not divide evenly into 190.
Think and Grow: Use Partial Quotients
Example
Use an area model and partial quotients to find 475 ÷ 19.
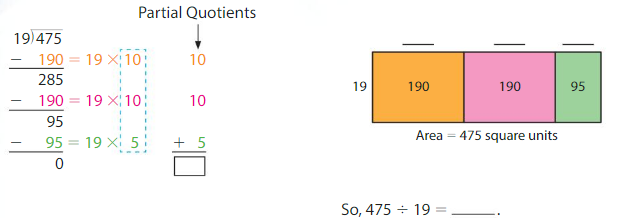
Answer:
475 ÷ 19 = 10 + 10 + 5 = 25
Example
Use partial quotients to find 1,890 ÷ 52.
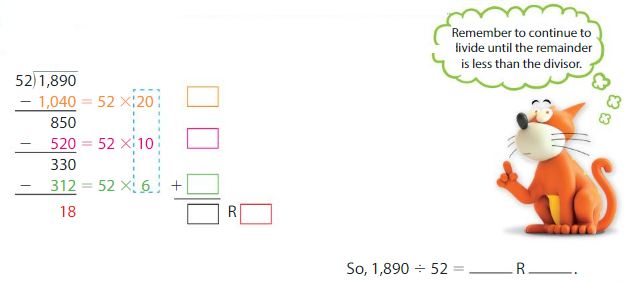
Answer:
1,890 ÷ 52 = (20 + 10 + 6) R 18 = 36 R 18.
Show and Grow
Use partial quotients to divide.
Question 1.
523 ÷ 41 = _____ R ____
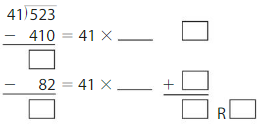
Answer:
523 ÷ 41 = 12 R 31.
Explanation:
Partial quotient = 10 + 2 = 12
So, 523 ÷ 41 = 12 R 31
Question 2.
2,760 ÷ 87 = ____ R ____
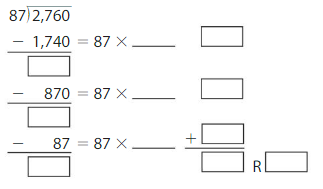
Answer:
2,760 ÷ 87 = 31 R 63
Explanation:
Partial quotient = 30 + 1 = 31
So, 2,760 ÷ 87 = 31 R 63
Apply and Grow: Practice
Use partial quotients to divide.
Question 3.
\(\sqrt [ 28 ]{ 476 } \)
Answer:
\(\sqrt [ 28 ]{ 476 } \) = 17 R 28
Explanation:
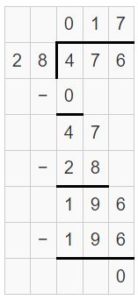
Partial quotient = 10 + 7 = 17
So, \(\sqrt [ 28 ]{ 476 } \) = 17 R 28
Question 4.
\(\sqrt [ 31 ]{ 605 } \)
Answer:
\(\sqrt [ 31 ]{ 605 } \) = 19 R 16
Explanation:
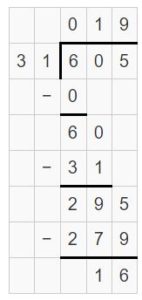
Partial quotient = 10 + 9 = 19
So, \(\sqrt [ 31 ]{ 605 } \) = 19 R 19
Question 5.
\(\sqrt [ 47 ]{ 1,833 } \)
Answer:
\(\sqrt [ 47 ]{ 1,833 } \) = 39
Explanation:
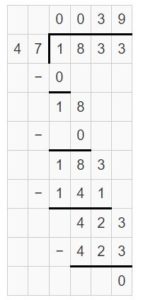
Partial quotient = 30 + 9 = 39
So, \(\sqrt [ 47 ]{ 1,833 } \) = 39 R 0
Question 6.
846 ÷ 93 = ______
Answer:
846 ÷ 93 = 9 R 9
Explanation:
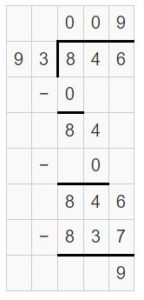
Partial quotient = 9
So, 846 ÷ 93 = 9 R 9
Question 7.
6,305 ÷ 65 = _______
Answer:
6,305 ÷ 65 = 97 R 0
Explanation:
Partial quotient = 90 + 7 = 97
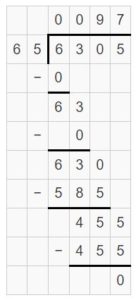
So, 6,305 ÷ 65 = 97 R 0
Question 8.
5,603 ÷ 72 = _____
Answer:
5,603 ÷ 72 = 77 R 59
Explanation:
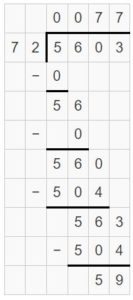
Partial quotient = 70 + 7 = 77
So, 5,603 ÷ 72 = 77 R 59
Question 9.
A punching bag weighs 960 ounces. There are 16 ounces in 1 pound. What is the weight of the punching bag in pounds?

Answer:
The weight of the punching bag in pounds is 60.
Explanation:
Divide 960 by 16 to get the weight of the punching bag in pounds.
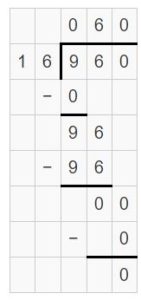
Partial quotients = 60
So, 960 ÷ 16 = 60
Question 10.
Reasoning
Your friend wants to divide 2,561 by 34. She multiplies 34 by 100 for her first partial quotient. Is this reasonable? Explain.
Answer:
The first partial quotient is 34 x 70 = 2380. So, it is not reasonable.
Question 11.
DIG DEEPER!
A division problem has 56 as its divisor. The partial quotients are 10 and 8. The remainder is 2. What is the dividend?
Answer:
The dividend is 1010.
Explanation:
Partial Quotients = 10 + 8 = 18
Dividend = Divisor x Quotient + Remainder.
Dividend = 56 x 18 + 2
= 1008 + 2 = 1010.
Think and Grow: Modeling Real Life
Example
You have 214 seeds. You want to plant all of the seeds by putting 1 seed in each section of a 12-section egg carton. How many egg cartons do you need?

Divide 214 by 12 to find how many egg cartons you need.
Use partial quotients.
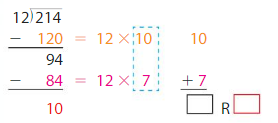
214 ÷ 12 = 17 R 10
Interpret the quotient and the remainder.
The quotient is 17. So, 17 cartons will be full.
The remainder is 10. So, 1 carton will have 10 seeds.
So, you need 18 egg cartons.
Show and Grow
Question 12.
A screen printing shop makes 736 T-shirts. A shipping box can hold 28 T-shirts. How many boxes are needed to ship all of the T-shirts?
Answer:
27 shipping boxes are required to ship all of the T-shirts.
Explanation:
Divide 736 by 28 to find how many boxes are needed to ship all of the T-shirts
Use partial quotients.
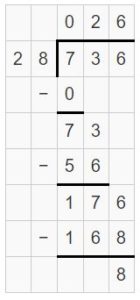
Interpret the quotient and the remainder.
The quotient is 26. So, 26 shipping boxes will be full.
The remainder is 8. So, 1 shipping box will have 8 T-shirts.
So, you need 27 shipping boxes.
Question 13.
The owner of a popcorn stand makes 2,568 ounces of popcorn in 1 day. How many 64-ounce bags of popcorn can the owner fill completely?
Answer:
The owner can fill 41, 64-ounce bags of popcorn.
Explanation:
Divide 2,568 by 64 to find how many 64-ounce bags of popcorn can the owner fill completely.
Use partial quotient.
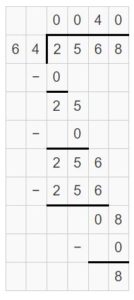
Interpret the quotient and the remainder.
The quotient is 40. So, 40-ounce bags of popcorn are full.
The remainder is 8. So, 1 bag of popcorn will have 8-ounce.
So, the owner can fill 41, 64-ounce bags of popcorn.
Question 14.
DIG DEEPER!
A fruit bouquet worker needs 24 strawberries, 40 grapes, 16 raspberries, and 16 blackberries to make 1 fruit bouquet. How many fruit bouquets can the worker make with the amount of fruit in stock? Explain?
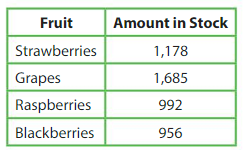
Answer:
The worker can make 51 fruit bouquets with the amount of fruit in stock.
Explanation:
The total amount of fruits in stock = 1178 + 1685 + 992 + 956 = 4811
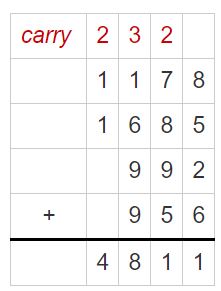
Number of fruits in the bouqet = 24 + 40 + 16 + 16 = 96
Divide 4811 by 96 to find how many fruit bouquets can the worker make with the amount of fruit in stock
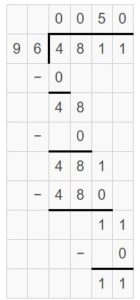
Partial quotient = 50
So, 4811 ÷ 96 = 50 R 11.
Use Partial Quotients with a Remainder Homework & Practice 6.6
Use partial quotients to divide.
Question 1.
426 ÷ 21 = _____ R _____
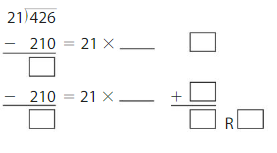
Answer:
426 ÷ 21 = 20 R 6
Explanation:
Partial quotient = 20
So, 426 ÷ 21 = 20 R 6
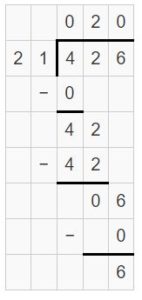
Question 2.
1,832 ÷ 32 = ______ R _____
Answer:
1,832 ÷ 32 = 57 R 8
Explanation:
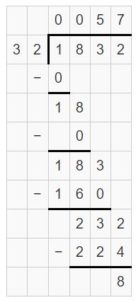
Partial quotient = 50 + 7 = 57
So, 1,832 ÷ 32 = 57 R 8
Question 3.
\(\sqrt [ 16 ]{ 279 } \)
Answer:
\(\sqrt [ 16 ]{ 279 } \) = 17 R 7
Explanation:
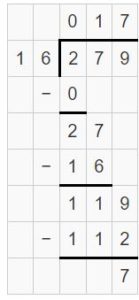
Partial quotient = 10 + 7 = 17
So, \(\sqrt [ 16 ]{ 279 } \) = 17 R 7
Question 4.
\(\sqrt [ 95 ]{ 970 } \)
Answer:
\(\sqrt [ 95 ]{ 970 } \) = 10 R 20
Explanation:
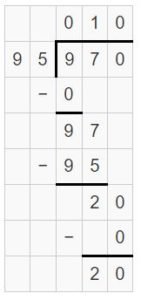
Partial quotient = 10
So, \(\sqrt [ 95 ]{ 970 } \) = 10 R 20
Question 5.
\(\sqrt [ 43 ]{ 2,451 } \)
Answer:
\(\sqrt [ 43 ]{ 2,451 } \) = 57
Explanation:
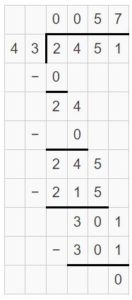
Partial quotient = 50 + 7 = 57
So, \(\sqrt [ 43 ]{ 2,451 } \) = 57
Use partial quotients to divide.
Question 6.
504 ÷ 18 = ______
Answer:
504 ÷ 18 = 28
Explanation:
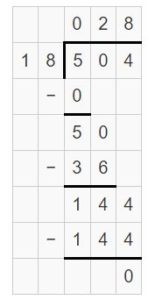
Partial quotient = 20 + 8 = 28
So, 504 ÷ 18 = 28
Question 7.
3,740 ÷ 64 = _____
Answer:
3,740 ÷ 64 = 58 R 28
Explanation:
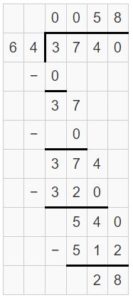
Partial quotient = 50 + 8 = 58
So, 3,740 ÷ 64 = 58 R 28
Question 8.
9,261 ÷ 57 = ______
Answer:
9,261 ÷ 57 = 162 R 27
Explanation:
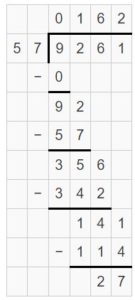
Partial quotients = 100 + 60 + 2 = 162
So, 9,261 ÷ 57 = 162 R 27
Question 9.
A teacher has 1,025 books. She places an equal number of books into each of 30 bins. How many books are in each bin?

Answer:
35 books are in each bin.
Explanation:
Divide 1025 by 30 to find how many books are in each bin.
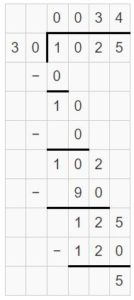
Interpret the quotient and the remainder.
The quotient is 34. So, 34 bins are required to fill books.
The remainder is 5. So, 1 bin will have 5 books.
So, 35 books are there in each bin.
Question 10.
Number Sense
What is the greatest possible whole number remainder when you divide a number by 75? Explain.
Answer:
74 is the greatest possible whole number divided obtained after dividing a number by 75. This remainder is obtained by dividing 149 by 75.
Question 11.
Structure
Solve 4,123 ÷ 78 two different ways using partial quotients.
Answer:
4,123 ÷ 78 = 52 R 67
Explanation:
Method 1:
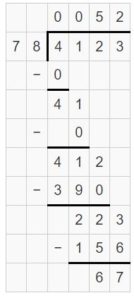
Partial Quotients = 50 + 2 = 52
Method 2:
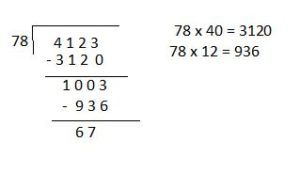
Partial Quotients = 40 + 12 = 52
So, 4,123 ÷ 78 = 52 R 67
Question 12.
Modeling Real Life
One study shows that American adults eat about 31 pounds of cheese each year. How many years does it take for an adult to eat 1,500 pounds of cheese?
Answer:
It takes a total of 49 years for an adult to eat 1500 pounds of cheese.
Explanation:
Divide 1500 pounds by 31 pounds.
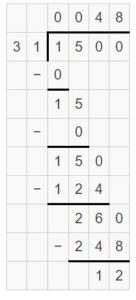
Interpret the quotient and the remainder.
The quotient is 48. So, it takes 48 years for an adult to eat cheese.
The remainder is 12. So, an adult will eat 12 pounds of cheese in 1 year.
So, it takes a total of 49 years for an adult to eat 1,500 pounds of cheese.
Question 13.
Modeling Real Life
There are 212 students and 89 teachers attending a leadership conference. One table can seat 16 people. How many tables are needed?
Answer:
A total of 19 tables are needed.
Explanation:
Number of people attending conference = 212 + 89 = 301
One can table can seat 16 people.
So, divide 301 by 16 to find how many tables are needed.
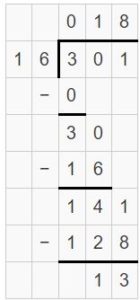
Partial quotients = 10 + 8
Interpret the quotient and the remainder.
The quotient is 18. So, 18 tables are required.
The remainder is 13. So, 1 more table having 13 people.
So, the number of tables required is 19.
Review & Refresh
Estimate the product.
Question 14.
487 × 92
Answer:
487 × 92 = 45000
Explanation:
Round up the given numbers to the nearest hundreds and tens.
487 can be rounded to 500 and 92 can be rounded to 90.
So, 500 x 90 = 5 hundreds x 9 tens = 45 thousands.
Question 15.
24 × 211
Answer:
24 × 211 = 4000
Explanation:
Round up the given numbers to the nearest hundreds and tens.
24 can be rounded to 20 and 211 can be rounded to 200.
So, 200 x 20 = 2 hundreds x 2 tens = 4 thousands.
Question 16.
49 × 657
Answer:
49 × 657 = 35000
Explanation:
Round up the given numbers to the nearest hundreds and tens.
49 can be rounded to 50 and 657 can be rounded to 700.
So, 50 x 700 = 5 tens x 7 hundreds = 35 thousands.
Lesson 6.7 Divide Three-Digit Numbers by Two-Digit Numbers
Explore and Grow
All of the division problems have no remainders. Which problems have one-digit quotients? Which problems have two-digit quotients? How do you know without calculating?

Answer:
The division problems have one-digit quotients are 344 ÷ 43, 340 ÷ 68, 711 ÷ 79. And the division problems which have two-digit quotients are 312 ÷ 18, 840 ÷ 24, 407 ÷ 11.
Explanation:
All the divisors are two digits, so we can take the first two digits or three digits of the dividend for calculation. If the dividend starting digits are greater than divisor numbers, then it has a two-digit quotient. If the divided starting digits is less than the divisor, then it has a one-digit quotient.
Reasoning
Explain how estimation can help you determine the number of digits in a quotient.
Answer:
The simple strategy is, the starting digits of the dividend is greater than the divisor, then it has a one-digit quotient. And if the starting digits of the divisor is greater than the divisor, then it has the two-digit quotient.
Think and Grow: Divide Three-Digit Numbers by Two-DigitNumbers
Example
Find 368 ÷ 16. Estimate ______
Use the estimate to place the first digit in the quotient.

Answer:
368 ÷ 16 = 23.
Show and Grow
Divide. Then check your answer.
Question 1.
\(\sqrt [ 18 ]{ 612 } \)
Answer:
\(\sqrt [ 18 ]{ 612 } \) = 34
Explanation:
The digit is in the hundreds place.
Divide the tens.
61 tens ÷ 18
3 tens x 18
61 tens – 54 tens
There are 7 tens left over.
Divide the ones.
72 ones ÷ 18
4 ones x 18
72 ones – 72 ones
There are 0 ones left over.
Regroup 3 tens and 4 ones.
So, 612 ÷ 18 = 34.
Use multiplication to check your answer.
Question 2.
\(\sqrt [ 42 ]{ 294 } \)
Answer:
\(\sqrt [ 42 ]{ 294 } \) = 7
Explanation:
The digit is in the hundreds place.
Divide the hundreds.
29 hundreds ÷ 42
7 ones x 42
294 – 294 = 0
So, \(\sqrt [ 42 ]{ 294 } \) = 7.
Use multiplication to check your answer.
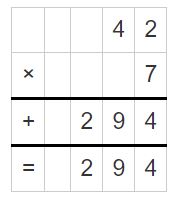
Question 3.
\(\sqrt [ 30 ]{ 580 } \)
Answer:
\(\sqrt [ 30 ]{ 580 } \) = 19
Explanation:
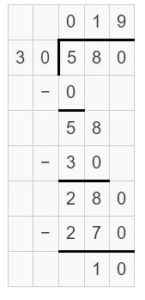
Apply and Grow: Practice
Divide. Then check your answer.
Question 4.
\(\sqrt [ 16 ]{ 293 } \)
Answer:
\(\sqrt [ 16 ]{ 293 } \) = 18.
Explanation:
The first digit is in the hundreds place.
Divide the tens.
29 tens ÷ 16.
1 ten x 16
29 tens – 16 tens = 13 tens
divide the ones.
133 ÷ 16
16 x 8 ones = 128
133 – 128 = 5
Regroup 10 tens and 8 ones = 10 + 8 = 18.
So, \(\sqrt [ 16 ]{ 293 } \) = 18.
Use multiplication to check your answer.
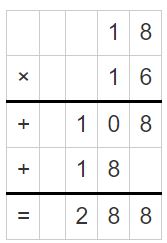
Question 5.
\(\sqrt [ 35 ]{ 375 } \)
Answer:
\(\sqrt [ 35 ]{ 375 } \) = 10
Explanation:
The first digit is in the hundreds place.
Divide the tens.
37 tens ÷ 35
1 ten x 35 = 35 tens
37 tens – 35 tens = 2 tens
Divide the ones.
25 ÷ 35
So, \(\sqrt [ 35 ]{ 375 } \) = 10
Use multiplication to check your answer.
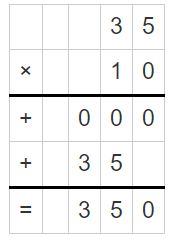
Question 6.
\(\sqrt [ 77 ]{ 847 } \)
Answer:
\(\sqrt [ 77 ]{ 847 } \) = 11
Explanation:
The first digit is in the hundreds place.
Divide the tens.
84 tens ÷ 77
1 ten x 77 = 770
84 tens – 77 tens = 7 tens
Divide the ones.
77 one ÷ 77 = 1
Regroup 1 ten and 1.
So, \(\sqrt [ 77 ]{ 847 } \) = 11.
Use multiplication to check your answer.
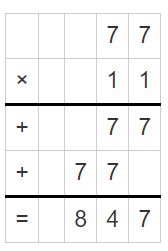
Question 7.
564 ÷ 94 = ______
Answer:
564 ÷ 94 = 6
Explanation:
The first digit is in the hundreds place.
564 ÷ 94 = 6
Use multiplication to check your answer.

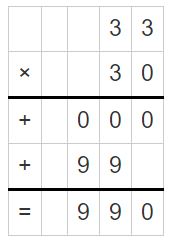
Question 8.
998 ÷ 33 = _______
Answer:
998 ÷ 33 = 30
Explanation:
The first digit is in the hundreds place.
Divide the tens.
3 tens x 33 = 99 tens
99 tens – 99 tens = 0
So, 998 ÷ 33 = 30
Use multiplication to check your answer.
Question 9.
702 ÷ 54 = ________
Answer:
702 ÷ 54 = 13
Explanation:
The first digit is in the hundreds place.
Divide the tens.
70 tens ÷ 54
1 ten x 54 = 54 tens
70 tens – 54 tens = 16 tens
divide the ones.
162 ÷ 54
54 x 3 ones = 162
162 – 162 = 0
Regroup 1 ten and 3 ones.
So, 702 ÷ 54 = 13
Use multiplication to check your answer.
Question 10.
A period of 20 years is called a score. It takes about 460 years for a score plastic bottle to decompose in a landfill. How many scores does it take for a plastic bottle to decompose?

Answer:
It requires 23 scores for a plastic bottle to decompose.
Explanation:
Divide 460 by 20 to get how many scores does it take for a plastic bottle to decompose.
Divide the ten.
46 tens ÷ 20
2 tens x 20 = 40 tens
46 tens – 40 tens = 6 tens
Divide the ones.
60 ÷ 20
20 x 3 ones = 60
60 – 60 = 0
Regroup 2 tens and 3 ones.
So, 460 ÷ 20 = 23
Therefore, 23 scores are required for a plastic bottle to decompose.
Question 11.
Number Sense
Can you have a remainder that is greater than the divisor?
Answer:
No, remainder of a division problem is not greater than the divisor.
Explanation:
If a remainder is greater than divisor, latter can go one more time and hence division is not complete. Even if remainder is equal to divisor, it can still go one more time. Hence remainder has to be less than the divisor.
Question 12.
Structure
Find 304 ÷ 16 using two different methods. Which method do you prefer? Why?
Answer:
I prefer to solve 304 ÷ 16 by using the actual division method. Because actual division method gives the exact answer easily.
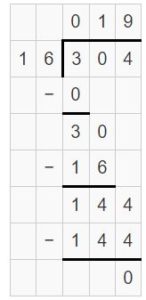
So, 304 ÷ 16 = 19.
Think and Grow: Modeling Real Life
Example
Tours of a television studio have no more than 45 guests. There are 589 guests in line to tour the studio. How many tours are full?

Divide the total number of guests by the number of guests in each tour to find how many tours are full.
Divide the tens. Then divide the ones.
589 ÷ 45 = 13 R 4
Interpret the quotient and the remainder.
The quotient is 13. So, 13 tours are full with 45 guests each.
The remainder is 4. There are 4 guests left. So, the last tour is not full and has 4 guests.
So, 13 tours are full.
Show and Grow
Question 13.
A farmer has 918 eggs to sell at a farmer’s market. She packs 12 eggs in each carton. How many cartons are full?
Answer:
76 Cartons are full.
Explanation:
Divide the total number of eggs by number of eggs in each carton to get how many cartons are full.
Divide the tens. Then divide the ones.
918 ÷ 12 = 76 R 6
Interpret the quotient and the remainder.
The quotient is 76. So, 12 cartons are full with 12 eggs each.
The remainder is 6. There are 6 eggs left.
So the last carton is not fill and has 6 eggs.
So, 76 cartons are full.
Question 14.
Descartes makes 770 cups of apple cider. He pours 16 cups of cider into each container. How many containers does Descartes need?
Answer:
Descartes need 49 containers to fill 770 cups of apple cider.
Explanation:
Divide number of cups of aplicider by the number of cups of cider in each container to get how many containers are required.
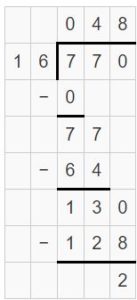
Divide the tens. Then divide the ones.
770 ÷ 16 = 48 R 2
Interpret the quotient and the remainder.
The quotient is 48. So, 48 containers are full with 16 cups of apple cider.
The remainder is 2. There are 2 cups of cider is left.
So the last container is not full and has 2 cups of cider.
So, 49 containers are required.
Question 15.
DIG DEEPER!
Six teachers and 144 students attend a glassblowing demonstration. An auditorium has 10 rows with 23 seats in each row. Students begin filling in the front row and do not leave any empty seats. The remaining students and teachers sit in the last row. How many students sit with the teachers?

Answer:
6 students sit with the teachers in the last row of the auditorium.
Explanation:
Divide 144 by 23.
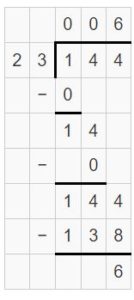 1
1
144 ÷ 23 = 6 R 6
Interpret the quotient and the remainder.
The quotient is 6. So, 6 rows are filled with the students.
The remainder is 6. So, 6 more students are left to sit with teachers.
Divide Three-Digit Numbers by Two-Digit Numbers Homework & Practice 6.7
Divide. Then check your answer.
Question 1.
\(\sqrt [ 21 ]{ 735 } \)
Answer:
\(\sqrt [ 21 ]{ 735 } \) = 35
Explanation:
The first digit is in the hundreds place.
Divide the tens.
73 tens ÷ 21
3 tens x 21 = 63 tens
73 tens – 63 tens = 10 tens
Divide the ones.
105 one ÷ 21
21 x 5 one = 105 ones
105 ones – 105 ones = 0
Regroup 3 tens and 5 ones.
So, \(\sqrt [ 21 ]{ 735 } \) = 35
Use multiplication to check your answer.

Question 2.
\(\sqrt [ 64 ]{ 802 } \)
Answer:
\(\sqrt [ 64 ]{ 802 } \) = 12 R 34.
Explanation:
The first digit is in the hundreds place.
Divide the tens. Then divide the ones.
80 tens ÷ 64
64 x 1 ten = 64 tens
80 tens – 64 tens = 16 tens
162 ones ÷ 64
64 x 2 ones = 128 ones
162 ones – 128 ones = 34 ones
Regroup 1 ten and 2 ones
So, \(\sqrt [ 64 ]{ 802 } \) = 12 R 34.
Use multiplication to check your answer.
64 x 12 = 768
786 + 34 = 802
Question 3.
\(\sqrt [ 40 ]{ 901 } \)
Answer:
\(\sqrt [ 40 ]{ 901 } \) = 22 R 21
Explanation:
Divide the tens. Then divide the ones.
90 tens ÷ 40
2 tens x 40 = 80 tens
90 tens – 80 tens = 10 tens
101 one ÷ 40
40 x 2 = 80 ones
101 one – 80 one = 21 one
Regroup 2 tens and 2 ones.
So, \(\sqrt [ 40 ]{ 901 } \) = 22 R 21
Use multiplication to check your answer.
22 x 40 = 880
880 + 21 = 101.
Question 4.
486 ÷ 18 = ______
Answer:
486 ÷ 18 = 24 R 14
Explanation:
Divide the tens. Then divide the ones.
48 tens ÷ 18
2 tens x 18 tens = 36 tens
48 tens – 36 tens = 8 tens
86 ones ÷ 18
18 x 4 ones = 72 ones
86 ones – 72 ones = 14 ones
Regroup 2 tens and 4 ones.
So, 486 ÷ 18 = 24 R 14
Use multiplication to check your answer.
24 x 18 = 432
432 + 14 = 486
Question 5.
266 ÷ 19 = ______
Answer:
266 ÷ 19 = 14
Explanation:
Divide the tens. Then divide the ones.
26 tens ÷ 19
1 ten x 19 = 19 tens
26 tens – 19 tens = 7 tens
76 ones ÷ 19
19 x 4 ones = 76 ones
76 ones – 76 ones = 0
Regroup 1 ten and 4 ones.
So, 266 ÷ 19 = 14.
Use multiplication to check your answer.

Question 6.
284 ÷ 37 = _______
Answer:
284 ÷ 37 = 8 R 12
Explanation:
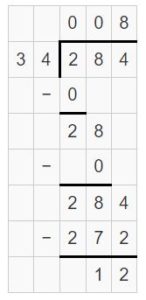
Use multiplication to check your answer.
34 x 8 = 2872
284 – 272 = 12.
Question 7.
A factory packages identical bags of nails into a box and ships them to a store. The store receives 960 nails in the box. How many bags of nails does the store receive?

Answer:
The store receives 40 nails of bags.
Explanation:
Divide 960 by 24 to get how many bags of nails does the store receive.
Divide the tens. Then divide the ones.
96 tens ÷ 24
24 x 4 tens = 96 tens
96 tens – 96 tens = 0
So, 960 ÷ 24 = 40
Therefore, store receives 40 nails of bags.
Question 8.
Logic
Find the missing digits.
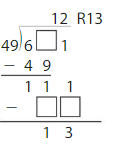
Answer:
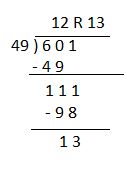
The first missing digit is 0. Second missing digts are 98 = 49 x 2.
Question 9.
DIG DEEPER!
Change the dividend in the equation to another three-digit number so that there is no remainder.
893 ÷ 61 = 14 R 39
Answer:
854 ÷ 61 = 14
Explanation:
14 x 61 = 893
Question 10.
Modeling Real Life
An amusement park ride seats 12 people. There are 458 people in line. How many times does the ride run full?
Answer:
38 times the ride run full.
Explanation:
Divide 458 by 12 to get how many times does the ride run full.
Divide the tens. Then divide the ones.
45 tens ÷ 12
12 x 3 tens = 36 tens
45 tens – 36 tens = 9 tens
98 ones ÷ 12
12 x 8 ones = 69 ones
98 ones – 96 ines = 2 ones
Regroup 3 tens and 8 ones.
So, 458 ÷ 12 = 38 R 2.
Interpret the quotient and the remainder.
The quotient is 38. So, 38 times the ride is full.
The remainder is 2. There are 2 more people to ride.
So, the last ride run is not full and has 2 people.
So, 38 times the ride is full.
Question 11.
DIG DEEPER!
A city mayor receives 990 new garbage cans. She gives half of the garbage cans to the city’s residents. She divides the rest of the cans into 16 equal groups for the city’s parks and streets. How many garbage cans are left over?

Answer:
15 more garbage cans are left over.
Explanation:
990 ÷ 2 = 495 garbage cans are handed over to city students
Divide 495 by 16.
Divide the tens. Then divide the ones.
495 ÷ 16 = 30 R 15.
Interpret the quotient and the remainder.
The quotient is 30. So, 30 groups of cans are given to parks.
the remainder is 15.. So, 15 more cans are remaining.
Review & Refresh
Question 12.
Round 18.692.
Nearest whole number: ________
Nearest tenth: _______
Nearest hundredth: _______
Answer:
Nearest whole number: 19
Nearest tenth: 18.7
Nearest hundredth: 18.69
Explanation:
In the number 18.692, digit at decimal place is 6. So, nearest tenths is 18.7, the digit at the units place is 8. So, the nearest whole number is 20. And the digit at hundredth place is 9 so, the nearest hundredth is 18.69.
Question 13.
Round 5.153.
Nearest whole number: ______
Nearest tenth: _______
Nearest hundredth: _______
Answer:
Nearest whole number: 5
Nearest tenth: 5.1
Nearest hundredth: 5.15
Explanation:
In the given number 5.153 the number at units place is 5 so nearest whole number is also 5. The number at tenths place is 1, so the nearest 10th is 5.1, The number at hundredth place is 5 so the nearest 100th is 5.15.
Lesson 6.8 Divide Four-Digit Numbers by Two-Digit Numbers
Explore and Grow
All of the division problems have no remainders. Which problems have two-digit quotients? Which problems have three-digit quotients? How do you know without calculating?
Answer:
The division problems which have two digit quotients are 4774 ÷ 62, 1050 ÷ 25, and 1995 ÷21. The problems that have three digit quotients are 1890 ÷18, 8200 ÷40, and 6138 ÷ 33.
Explanation:
We can simply say that in each problem the denominator is a two digit number and numerator is a four digit number. Here, if the first two digits of the numerator are greater than or equal to the denominator, then it has three digit quotient. If the first two digits of the numerator are less than the denominator, then it has two digit quotient.
Reasoning
Can a four-digit whole number divided by a two-digit whole number have a whole number quotient with four digits? Explain your reasoning.
Answer:
No, a four digit whole number divided by a two digit whole number have a whole number quotient with four digits. Because, the division process will reduce the number of digits of the dividend by at least 1.
Think and Grow: Divide Four-Digit Numbers by Two-Digit Numbers
Example
Find 3,290 ÷ 31.
Estimate _______
Use the estimate to place the first digit in the quotient.
\(\sqrt [ 31 ]{ 3,290 } \)
The first digit is in the ______ place.
Divide the hundreds.

Show and Grow
Divide. Then check your answer.
Question 1.
\(\sqrt [ 28 ]{ 1,148 } \)
Answer:
\(\sqrt [ 28 ]{ 1,148 } \) = 41
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
11 hundreds ÷ 28
11 hundreds cannot be shared among 28 groups without regrouping.
So, add next number.
Divide the tens.
114 tens ÷ 28
28 x 4 tens = 112 tens
114 tens – 112 tens = 2 tens
There are 2 tens left over.
Divide thee ones.
28 ones ÷ 28
28 x 1 one = 28 ones
28 ones – 28 ones = 0
So, 1148 ÷ 28 = 41
Use multiplication to check your answer.

Question 2.
\(\sqrt [ 13 ]{ 1,596 } \)
Answer:
\(\sqrt [ 13 ]{ 1,596 } \) = 122 R 10
Explanation:
the first digit is in the thousands place.
divide the hundred.
15 hundreds ÷ 13
13 x 1 hundred = 13 hundreds
15 hundreds – 13 hundreds = 2 hundreds.
There are 2 hundreds left over.
Divide the tens
29 tens ÷ 13
13 x 2 tens = 26 tens
29 tens – 26 tens = 3 tens
Divide the ones.
36 ones ÷ 13
13 x 2 ones = 26 ones.
36 ones – 26 ones = 10
So, 1596 ÷ 13 = 122 R 10
Use multiplication to check your answer.
1586 + 10 = 1596.
Apply and Grow: Practice
Divide. Then check your answer.
Question 3.
\(\sqrt [ 16 ]{ 9,640 } \)
Answer:
\(\sqrt [ 16 ]{ 9,640 } \) = 602 R 8.
Explanation:
The first digit is in the thousands place.
divide the hundreds.
96 hundreds ÷ 16
16 x 6 hundreds = 96 hundreds.
96 hundreds – 96 hundreds = 0
Divide the tens.
4 tens ÷ 16
40 ÷ 16
16 x 2 = 32
40 – 32 = 8
So 9640 ÷ 16 = 602 R 8
Use multiplication to check your answer.
9632 + 8 = 9640
Question 4.
\(\sqrt [ 26 ]{ 5,460 } \)
Answer:
\(\sqrt [ 26 ]{ 5,460 } \) = 210
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
54 hundreds ÷ 26
26 x 2 hundreds = 52 hundreds
54 hundreds – 52 hundreds = 2 hundreds
Divide the tens.
26 tens ÷ 26
26 x 1 ten = 26 tens
26 tens – 26 tens = 0
So, 5460 ÷ 26 = 210
Use multiplication to check your answer.
Question 5.
\(\sqrt [ 37 ]{ 3,885 } \)
Answer:
\(\sqrt [ 37 ]{ 3,885 } \) = 105
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
38 hundreds ÷ 37
37 x 1 hundreds = 37 hundreds
38 hundreds – 37 hundreds = 1 hundred
Divide the tens.
18 tens ÷ 37
As 18 can’t be shared among 37 groups. So place 0 and add next number.
Divide ones.
185 ones ÷ 37
37 x 5 ones = 185 ones
185 ones – 185 ones = 0
So, \(\sqrt [ 37 ]{ 3,885 } \) = 105
Use multiplication to check your answer.
Question 6.
2,784 ÷ 72 = _______
Answer:
2,784 ÷ 72 = 38 R 48
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
27 hundreds ÷ 72
As the 27 can’t be shared among 72 groups. add next number.
Divide the tens.
278 tens ÷ 72
72 x 3 tens = 216 tens
278 tens – 216 tens = 62 tens
Divide the ones
624 ones ÷ 72
72 x 8 ones = 576 ones
624 ones – 576 ones = 48 ones.
So, 2,784 ÷ 72 = 38 R 48
Use multiplication to check your answer.

2736 + 48 = 2784.
Question 7.
8,047 ÷ 83 = _______
Answer:
8,047 ÷ 83 = 96 R 79
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
80 hundreds ÷ 83
As the 80 can’t be shared among 83 groups. add next number.
Divide the tens.
804 tens ÷ 83
83 x 9 tens = 747 tens
804 tens – 747 tens = 57 tens
Divide the ones
577 ones ÷ 83
83 x 6 ones = 498
577 ones – 498 ones = 79 ones.
So, 8,047 ÷ 83 = 96 R 79
Use multiplication to check your answer.

7968 + 79 = 8047
Question 8.
9,504 ÷ 96 = ________
Answer:
9,504 ÷ 96 = 99
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
As the 95 can’t be shared among 96 groups. add next number.
Divide the tens.
950 tens ÷ 96
96 x 9 tens = 864 tens
950 tens – 864 tens = 86 tens
Divide the ones.
864 ones ÷ 96
96 x 9 ones = 864 ones
864 ones – 864 ones = 0
So, 9,504 ÷ 96 = 99
Use multiplication to check your answer.
Question 9.
A rectangular section of the flame trench on Launch Pad 39A at NASA’s Kennedy Space Center was damaged during the launch of the space shuttle. The area of the Discovery section damaged was 1,500 square feet. The section was 75 feet long. How wide was the section?

Answer:
The section was 20 feet wide.
Explanation:
Divide 1500 by 75 to get the section wide area.
75 x 2 tens = 150 tens
So, 1500 ÷ 75 = 20.
Question 10.
Reasoning
Your friend finds 6,408 ÷ 51 and gets an answer of 124 R 84. Explain your friend’s mistake.
Answer:
6,408 ÷ 51 = 125 R 33. My friend made mistake at the one’s division.
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
64 hundreds ÷ 51
51 x 1 hundred = 51 hundreds
64 hundreds – 51 hundreds = 13 hundreds
Divide the tens
130 tens ÷ 51
51 x 2 tens = 102 tens
130 tens – 102 tens = 28 tens
Divide the ones.
288 ones ÷ 51
51 x 5 ones = 255 ones
288 ones – 255 ones = 33 ones
So, 6,408 ÷ 51 = 125 R 33
Question 11.
Writing
Explain why you can use multiplication to check your answer to a division problem.
Answer:
Multiplication and division are the inverse operations. For example when you divide 20 by 5, the quotient is 4. And multiply 4 x 5 = 20. So, it is proved that multiplication is helpful to check whether the division is correct or not.
Think and Grow: Modeling Real Life
Example
The Great Barrier Reef is 2,300 kilometers long. A marine biologist studies the entire reef. He can explore no more than 75 kilometers of the reef each week. How many kilometers of the reef does the biologist explore the last week?

Divide the total length by the length he can explore each week to find how many weeks he explores the reef.
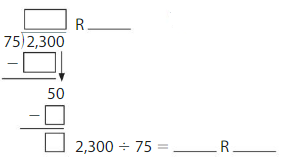
Interpret the quotient and the remainder.
The quotient is ______. So, the biologist explores 75 kilometers of the reef each week for ______ weeks.
The remainder is ______. There are _____ kilometers left.
So, the biologist explores ______ kilometers of the reef the last week.
Show and Grow
Question 12.
A librarian has 1,048 books to shelve. Each shelf can hold 32 books. The librarian fills each shelf before moving to another shelf. How many books are on the last shelf?
Answer:
There are 24 books on the last shelf.
Explanation:
Divide 1048 by 32 to get how many books are there on the last shelf.
So, 1048 ÷ 32 = 32 R 24
Interpret the quotient and the remainder.
The quotient is 32. So, 32 shelfs are filled with books.
The remainder is 24. There are 24 books to be filled in the shelfs.
So, there are 4 books on the last shelf.
Question 13.
A banker receives 2,215 nickels. A standard roll of nickels contains 40 nickels. How many standard rolls of nickels can the banker make?
Answer:
The banker can make 55 standard rolls of nickels.
Explanation:
Divide 2215 by 40 to get how many standard rolls of nickels can the banker make.
2215 ÷ 40 = 55 R 15
Interpret the quotient and the remainder.
The quotient is 55. So, banker can make 55 standard roll of nickels.
Question 14.
DIG DEEPER!
A recreation director prepares the course of a 3-mile race by posting a motivational sign every 85 yards along the course. How many signs does the director use? Explain.

Answer:
The director uses 65 signs.
Explanation:
Divide 3 miles by 85 yards to get how many signs does the director use.
3 miles = 3 x 1760 = 5280 yards
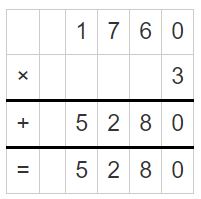
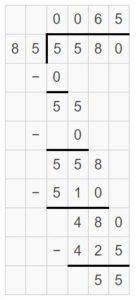
The quotient is 65.
So, the director use 65 signs.
Divide Four-Digit Numbers by Two-Digit Numbers Homework & Practice 6.8
Divide. Then Check you answer.
Question 1.
\(\sqrt [ 13 ]{ 5,343 } \)
Answer:
\(\sqrt [ 13 ]{ 5,343 } \) = 411
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
53 hundreds ÷ 13
13 x 4 hundreds = 52 hundreds
53 hundreds – 52 hundreds = 1 hundred
Divide the tens.
14 tens ÷ 13
13 x 1 ten = 13 tens
14 tens – 13 tens = 1 ten
divide the ones.
13 ones ÷ 13
13 x 1 = 13 one
13 ones – 13 ones = 0
So, \(\sqrt [ 13 ]{ 5,343 } \) = 411
Use multiplication to check your answer.
Question 2.
\(\sqrt [ 23 ]{ 32,96 } \)
Answer:
\(\sqrt [ 23 ]{ 32,96 } \) = 143 R 7
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
32 hundreds ÷ 23
23 x 1 hundred = 23 hundreds
32 hundreds – 23 hundreds = 9 hundreds
Divide the tens
99 tens ÷ 23
23 x 4 tens = 92 tens
99 tens – 92 tens = 7 tens
Divide the ones
76 ones ÷ 23
76 ones – 69 ones = 7 ones.
So, \(\sqrt [ 23 ]{ 32,96 } \) = 143 R 7
Use multiplication to check your answer.

3289 + 7 = 3296
Question 3.
\(\sqrt [ 48 ]{ 1,414 } \)
Answer:
\(\sqrt [ 48 ]{ 1,414 } \) = 29 R 22
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
14 hundreds ÷ 48
As 14 can’t be shared among 48 groups. Add next number.
Divide the tens.
141 tens ÷ 48
48 x 2 tens = 96 tens
141 tens – 96 tens = 45 tens
Divide the ones.
454 ones ÷ 48
48 x 9 ones = 432 ones
454 ones – 432 ones = 22 ones.
So, \(\sqrt [ 48 ]{ 1,414 } \) = 29 R 22
Use multiplication to check your answer.
1392 + 22 = 1414
Question 4.
3,300 ÷ 15 = _____
Answer:
3,300 ÷ 15 = 220
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
33 hundreds ÷ 15
15 x 2 hundreds = 30 hundreds
33 hundreds – 30 hundreds = 3 hundreds
Divide the tens.
30 tens ÷ 15
15 x 2 tens = 30 tens
30 tens – 30 tens = 0
So, 3,300 ÷ 15 = 220
Use multiplication to check your answer.
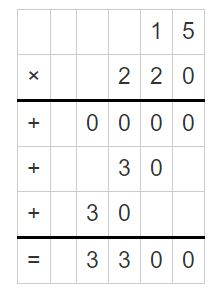
Question 5.
4,592 ÷ 82 = _____
Answer:
4,592 ÷ 82 = 56
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
45 ÷ 82
As, 45 can’t be shared among the 82 groups. So add next digit.
Divide the tens.
459 tens ÷ 82
82 x 5 tens = 410 tens
459 tens – 410 tens = 49 tens
Divide the ones.
492 ones ÷ 82
82 x 6 ones = 492 ones
492 ones – 492 ones = 0
So, 4,592 ÷ 82 = 56
Use multiplication to check your answer.

Question 6.
8,751 ÷ 64 = _______
Answer:
8,751 ÷ 64 = 136 R 47
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
87 ÷ 64
64 x 1 hundred = 64 hundreds
87 hundreds – 64 hundreds = 23 hundreds
Divide the tens.
235 tens ÷ 64
64 x 3 tens = 192 tens
235 tens – 192 tens = 43 tens
Divide the ones.
431 ones ÷ 64
64 x 6 ones = 384 ones
431 ones – 384 ones = 47
so, 8,751 ÷ 64 = 136 R 47
Use multiplication to check your answer.

8704 + 47 = 8751
Question 7.
A hot-air balloon travels 2,016 miles in 96 hours. The balloon travels the same number of miles each hour. How many miles does the balloon travel in 1 hour?
Answer:
The balloon travels 21 miles in 1 hour.
Explanation:
Divide 2016 by 96 to get how many miles does the balloon travel in 1 hour.
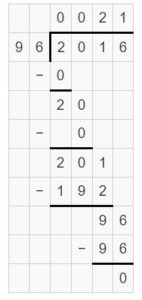
So, the balloon travels 21 miles in 1 hour.
Question 8.
The area of the rectangle is 1,875 square feet. What is the width of the rectangle?
Answer:
The width of the rectangle is 25 feet.
Explanation:
Divide 1875 by 75 to get the width of the rectangle.
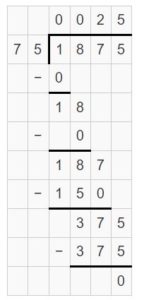
So, the rectangle width is 25 feet.
Question 9.
Which One Doesn’t Belong?
Which expression does not have a two-digit quotient?
1,955 ÷ 85
6,701 ÷ 36
1,699 ÷ 54
2,754 ÷ 71
Answer:
6701 ÷ 36 does not have a two-digit quotient.
Explanation:
The reason is The first two digit numbers of the dividend 67 is greater than the divisor 36.
Question 10.
YOU BE THE TEACHER
Is your friend correct? Explain. Show how to check your friend’s answer in two different ways.
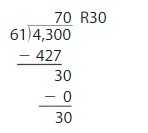
Answer:
Yes, my friend is correct.
The method is just divide 4300 by 61.
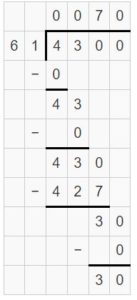
Second method is using multiplication.
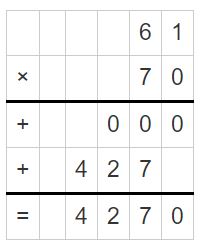
4270 + 30 = 4300.
Question 11.
Modeling Real Life
A recycling company has 2,609 pounds of materials to sort. For efficiency, it divides all of the materials into boxes that each hold 20 pounds of materials. How many pounds of materials are in the last box?
Answer:
The last box has 9 pounds of the material.
Explanation:
Divide 2609 by 20 to get how many pounds of materials are in the last box.
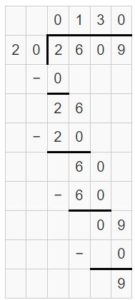
So, 2609 ÷ 20 = 130 R 9
Interpret the quotient and the remainder.
The quotient is 130. So, 130 boxes are full of the materials.
The remainder is 9. So the last box has 9 pounds of materials.
Question 12.
Modeling Real Life
An art museum has 1,025 paintings to divide equally among 20 rooms. How many more paintings does it need so that every room has the same number of paintings?
Answer:
15 more paintings are required so that all the rooms have same number of paintings.
Explanation:
Divide 1025 by 20.
Interpret the quotient and the remainder.
The quotient is 51. So, 51 rooms are full.
The remainder is 5.
So, you need 20 – 5 = 15 more paintings.
Review & Refresh
Find the difference. Then check your answer.
Question 14.
145.92 – 15.78 = _____
Answer:
145.92 – 15.78 = 130.14
Explanation:
Add 130.14 + 15.78 = 145.92
Question 15.
3.63 – 0.48 = ______
Answer:
3.63 – 0.48 = 3.15
Explanation:
3.15 + 0.48 = 3.63
Lesson 6.9 Problem Solving: Division
Explore and Grow
Make a plan to solve the problem.
A mother giraffe weighs 11 times as much as a new born giraffe. The combined weight of the giraffes is 1,800 pounds. What is the weight of each giraffe?

Answer:
The weight of the mother giraffe is 1650 pounds and the weight of the newborn giraffe is 150 pounds.
Explanation:
The weight of mother giraffe = 11 x weight of a newborn giraffe
Mother giraffe weight + newborn giraffe weight = 1800 pounds
11 x weight of newborn giraffe + new born giraffe weight = 1800 pounds
12 weight of newborn giraffe = 1800
Weight of newborn giraffe = 1800 ÷ 12 = 150
The weight of mother giraffe = 11 x 150 = 1650
Make Sense of Problems
How does your plan change if the combined weight of the giraffes is 1,752 pounds? Explain.
Answer:
The weight of mother giraffe = 11 x weight of a newborn giraffe
Mother giraffe weight + newborn giraffe weight = 1752 pounds
11 x weight of newborn giraffe + new born giraffe weight = 1752 pounds
12 weight of newborn giraffe = 1752
Weight of newborn giraffe = 1752 ÷ 12 = 146
The weight of mother giraffe = 146 x 11 = 1606.
So, the weight of the newborn giraffe = 146 pounds, and the mother giraffe’s weight = 1606 pounds.
Think and Grow: Problem Solving: Division
Example
The length of an oil tanker is 15 times the length of a tugboat. The combined length of the boats is 304 meters. What is the length of each boat?
Understand the Problem
What do you know?
• You need to find the length of each boat.
What do you need to find?
• The length of the oil tanker is 15 times the length of the tugboat.
• The combined length of the boats is 304 meters.
Make a Plan
How will you solve?
• Draw and use tape diagrams to help write a division problem that gives the length of the tugboat.
• Multiply the length of the tugboat by 15 to find the length of the oil tanker.
Solve
Step 1:Draw ______ part for the length of the tugboat and _____ parts for the length of the oil tanker.
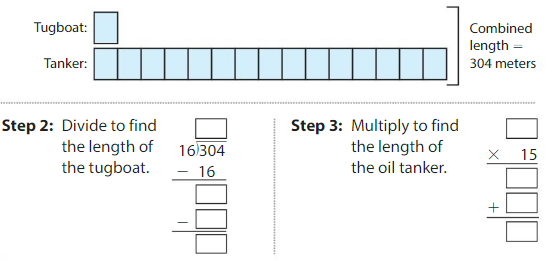
The tugboat is _______ meters long, and the oil tanker is _____ meters long.
Show and Grow
Question 1.
Explain how you can check your answer above.
Answer:
The length of tugboat = 304 ÷ 16 = 19
Multiply to find the length of oil tanker.
285 + 19 = 304
The tugboat is 19 meters long, and the oil tanker is 304 meters long.
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
A lion weighs 7 times as much as a leopard. The combined weight of the cats is 480 pounds. What is the weight of each cat?
Answer:
The leopard weight is 68 pounds and the lion weight is 408 pounds.
Explanation:
Draw 1 part the weight of the leopard and 7 parts the weight of the lion.
Divide to find the weight of the leopard.
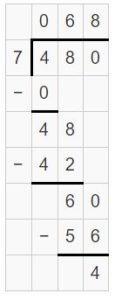
Multiply to get the weight of the lion.

The leopard weight is 68 pounds and the lion weight is 408 pounds.
Question 3.
A fifth-grade class raises $1,040 for a field trip to a museum. One admission ticket costs $8 and one lunch costs $5. How many people can attend the field trip?
Answer:
80 people can attend the trip.
Explanation:
The cost of trip for one person = 8 + 5 = 13
Divide 1040 by 13 to get how many people can attend the field trip.
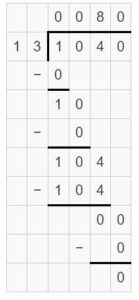
A total of 80 people can attend the trip.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 4.
A photo album has 15 pages. Each page can hold 6 photographs. How many of these albums do you need for 1,025 photographs?
Answer:
12 albums are needed for 1025 photographs.
Explanation:
Multiply 15 and 6 to get how many photos can hold an album.
Number of photos in the album = 15 x 6 = 90
Divide 1025 by 90 to get how many albums required.
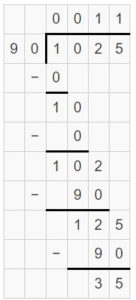
Interpret the quotient and the remainder.
The quotient is 11. So, 11 albums have 90 photos.
The remainder is 35. So, the last album has 35 photos.
So, a total of 12 albums are required for 1025 photographs.
Question 5.
You, Newton, and Descartes play a video game. You have 5 times as many points as Newton. Descartes has 9 times as many points as Newton. You, Newton, and Descartes have 1,320 points in all. How many points do you have?
Answer:
You have 264 points.
Explanation:
Draw 1 part of newton, 5 parts of me, and 9 parts of Descartes.
Divide 1320 by 5 to get the points you have.
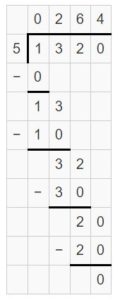
Question 6.
DIG DEEPER!
The Amazon River is 4,000 miles long. It is 1,688 miles shorter than 3 times the length of the Rio Grande. How long is the Rio Grande?

Answer:
The length of the Rio Grande is 17064 miles.
Explanation:
The length of Amazon river = 4000 miles
The Rio Grande river length = 3 (4000 + 1688)
= 3 x 5688
So, the length of the Rio Grande is 17064 miles.
Think and Grow: Modeling Real Life
Example
A chemist mixes 1,530 milliliters of a solution. The solution must be divided equally among 12 beakers. How much solution should be poured into each beaker?

Divide 1,530 by 12 to find how much can be poured into each beaker.
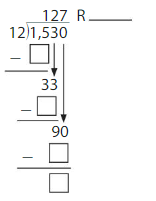
Interpret the quotient and the remainder.
The quotient is ______. So, ______ milliliters of solution can be poured into each beaker.
The remainder is ______. So, ______ milliliters of solution are left over.
The leftover solution can also be divided equally among the 12 beakers. The number of milliliters of leftover solution poured into each beaker can be written as a fraction.
So, ______ milliliters should be poured into each beaker.
Show and Grow
Question 7.
A great white shark migrates a total of 2,210 miles in 52 days. The shark travels the same number of miles each day. How many miles does the shark travel each day?
Answer:
The shark travels 42 (26 / 52) miles each day.
Explanation:
Divide 2210 by 52 to know how many miles does the shark travel each day.
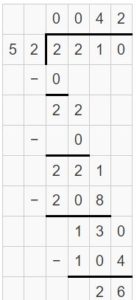
Interpret the quotient and the remainder.
The quotient is 42. So, the shark travels 42 miles in each day.
The remainder is 26. So, the shark travels must travel 26 miles.
The leftover miles can also be divided equally among 52 days. It can be expressed as a fraction.
So, 42 (26 / 52) miles should be traveled in each day.
Question 8.
Newton has 2,480 baseball cards and 1,235 football cards in his collection. He wants to put all of the cards into an album. Each page holds 18 cards. How many pages does he need for all of his cards? Explain.
Answer:
The number of pages required for all cards is 206 (7/18)
Explanation:
The number of cards = 2480 + 1235 = 3715
Divide 3715 by 18 to get how many pages does he need for all of his cards.
Interpret the quotient and the remainder.
The quotient is 206. So, 206 pages are required for all his cards.
The remainder is 7. So, 7 more are leftover.
So, The number of pages required for all cards is 206 (7/18).
Question 9.
Descartes has 6 large boxes with 48 party favors in each box and 5 small boxes with 16 party favors in each box. He puts 15 favors in each gift basket. How many baskets does he make? Explain.
Answer:
The number of boxes made are 24 (8/15).
Explanation:
Multiply boxes and party favors to get the number of party favors.
48 x 6 = 288, 5 x 16 = 80
Party favors at Descartes = 288 + 80 = 368
Divide 368 by 15 to get how many baskets does he make.
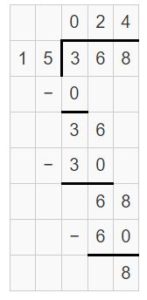
Interpret the quotient and the remainder.
The quotient is 24. The remainder is 8.
So, the number of boxes made are 24 (8/15).
Question 10.
DIG DEEPER!
Write and solve a word problem involving division in which the remainder can be written as a fraction.
Answer:
The question is a person spends a total of $160 on his food for 30 days. The person spends the same amount each day. How much does the person spend money each day?
Explanation:
Divide 160 by 30.
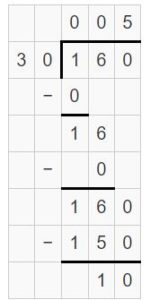
Interpret the quotient and the remainder.
The quotient is 5 and the remainder is 10.
So, the person spends 5(10 / 30) = 5(1/3) on each day.
Problem Solving: Division Homework & Practice 6.9
Understand the problem. What do you know? What do you need to find? Explain.
Question 1.
A DVD storage tower has 8 shelves. Each shelf can display 12 DVDs. How many storage towers does a worker need to display 1,440 DVDs?
Answer:
15 storage towers are required to display 1,440 DVDs.
Explanation:
Number of DVDs at storage tower = 12 x 8 = 96
Divide 1440 by 96
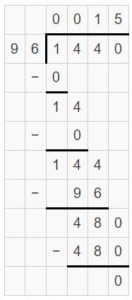
So, 15 storage towers are required to display 1,440 DVDs.
Question 2.
The Eastern Continental Trail is 15 times longer than the Erie Canalway Trail. The combined length of the hiking trails is 5,760 miles. What is the length of each hiking trail?
Answer:
The length of Erie Canalway Trail is 360 and the length of Eastern Continental Trail is 5400.
Explanation:
Draw 15 parts for the length of Eastern Continental Trail and 1 part for Erie Canalway Trail.

Divide 5760 by 16 to find the length of Erie Canalway Trail
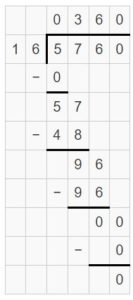
Multiply to find the length of the Eastern Continental Trail.
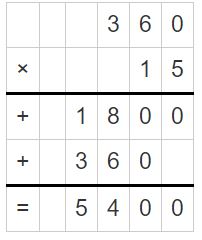
The length of the Erie Canalway Trail is 360 and the length of the Eastern Continental Trail is 5400.
Understand the problem. Then make a plan. How will you solve? Explain.
Question 3.
A runner finished a total of 1,500 kilometers in races before retiring. She finished thirty-two15-kilometer races. The rest of her races were10-kilometer races. How many of her races were10-kilometer races?
Answer:
Her 10-kilometer races are 102.
Explanation:
The total number of kilometers = 1500
15-kilometer races = 32
10-kilometer races = ?
Total number of kilometers of 15 kilometer races = 15 x 32 = 480
Total number of kilometers of 10-kilometer races = 1500 – 480 = 150 tens – 48 tens = 102 tens
10-kilometer races = 1020 ÷ 10
= 102 tens ÷ ten = 102.
Question 4.
You, Newton, and Descartes volunteer this summer. You have 2 times as many volunteer minutes as Newton. Descartes has 3 times as many volunteer minutes as Newton. You, Newton, and Descartes have 5,040 volunteer minutes altogether. How many minutes do you volunteer?
Answer:
I will volunteer for 1680 minutes.
Explanation:
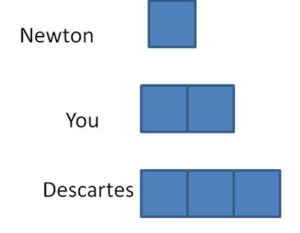
Divide 5040 by 6 to know how many minutes do newton volunteer.
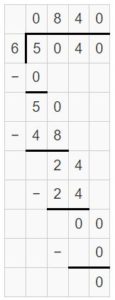
So, newton volunteer 840 minutes.
Multiply 840 x 2 to get how many minutes you volunteer.
I will volunteer for 1680 minutes.
Question 5.
A factory packs boxes with glitter pens. One box can hold 36 glitter pens. The factory produces 5,982 glitter pens. The factory fills as many boxes as possible. How many glitter pens will not fit into the boxes?
Answer:
30 glitter pens will not fit into the boxes.
Explanation:
Divide 5982 by 36
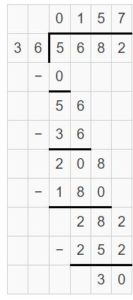
The remainder is 30. So, 30 glitter pens will not fit into the boxes.
Question 6.
DIG DEEPER!
The Burj Khalifa in Dubai is the tallest building in the world, at 2,717 feet. It is 217 feet taller than 5 times the height that the Dubai Fountain reaches. How high does the Dubai Fountain reach?

Answer:
Dubai Fountain should reach 500 feet high.
Explanation:
The height of Burj Khalifa in Dubai = 2717 feet
2717 – 217 = 2500
Divide 2500 by 5 to get how high does the Dubai Fountain reach.
25 hundreds ÷ 5 = 5 hundreds.
So, Dubai Fountain should reach 500 feet high.
Question 7.
Modeling Real Life
A woodworker spends a total of 162 hours making 24 birdhouses. He spends the same amount of time on each birdhouse. How many hours does he spend on each birdhouse?
Answer:
He spends 6(3/4) hours on each birdhouse.
Explanation:
Divide 162 by 24.

The quotient is 6 and the remainder is 18.
So, he spends 6 (18/24) = 6(3/4) hours on each birdhouse.
Question 8.
Modeling Real Life
A truck driver drives 2,580 miles in 40 hours. He drives the same number of miles each hour. How many miles does he drive each hour?
Answer:
He drives 64 (/2) miles each hour.
Explanation:
Divide 2580 by 40 to find how many miles does he drive each hour.
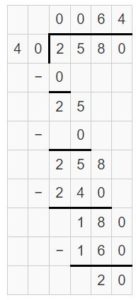
Interpret the quotient and the remainder.
The quotient is 64. The remainder is 20
So, He drives 64 (20/40) = 64 (1/2) miles each hour.
Review & Refresh
Find the product.
Question 9.
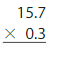
Answer:
4.71
Explanation:
Question 10.
Answer:
111.696
Explanation:

Question 11.
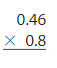
Answer:
0.368
Explanation:

Divide Whole Numbers Performance Task
You are planning a family road trip to see your cousin 448 miles away.

Question 1.
Your family will drive about 55 miles each hour during the trip.
a.About how many hours will your family spend driving?
b.You plan to leave at 8:00 A.M. and make two equal-length stops. You want to reach your cousin’s home by 5:30 P.M. How many minutes can you spend at each stop?
c.The roads will be under construction on the return trip home, so you will travel fewer than 55 miles each hour. Will the driving time be longer than or shorter than 8 hours? Use an example to justify your answer.
Answer:
a. My family spends 8(8/55) on driving.
b. I can spend 90 minutes at each stop.
c. The driving times is longer than 8 hours.
Explanation:
a. Divide 448 by 55
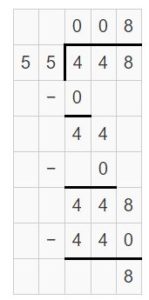
The quotient is 8 and the remainder is 8.
So, my family spends 8(8/55) on driving.
b. As it takes 8 hours. Without taking any stops you will reach the destination by 4:00 PM. 5:30 – 4:00 = 1:30. So, 180 minutes / 2 = 90 minutes. So, i can spend 90 minutes at each stop.
c. As the driving time per one hour is more than 55 miles. So, the driving times is longer than 8 hours.
Question 2.
You want to estimate the amount of money your family will spend on gasoline during your road trip.

a. On a previous road trip, your family drove 150 miles using about 5 gallons of gasoline. About how many miles did your family drive using 1 gallon of gasoline?
b. Research the price of 1 gallon of gasoline in your area. Estimate the amount of money your family will spend on gasoline to drive to your cousin’s home and back.
c. Your aunt offers to let your family borrow her hybrid car. Your aunt drives about 47 miles using 1 gallon of gasoline. About how much money will your family save on gasoline if they borrow your aunt’s hybrid car Most hybrid cars use gasoline and for the trip?
Answer:
a. My family drives 30 miles using 1 gallon of gasoline.
b. My family spends $10 on gasoline
c. you can save $28 on the trip.
Explanation:
a. Divide 150 by 5.
15 tens ÷ 5 = 3 tens = 30
So, My family drives 30 miles using 1 gallon of gasoline.
b. 1 gallon of gasoline = $2
Divide 896 by 150
The quantity of gasoline required = 5 (146/150)
Amount = 5 x 2= 10
c. Divide 896 by 47
896 ÷ 47 = 19
Amount = 19 x 2 = 38
38 – 10 = 28
Divide Whole Numbers Activity
Division Dot
Directions:
1. Players take turns connecting two dots, each using a different color.
2. On your turn, connect two dots, vertically or horizontally. If you close a square around a division problem, then find and write the quotient and the remainder. If you do not close a square,then your turn is over.
3. Continue playing until all division problems are solved.
4. The player with the most completed squares wins!

Answer:
9623 ÷ 54 = 178 R 11
758 ÷ 11 = 68 R 10
8484 ÷ 21 = 404 R 0
945 ÷ 15 = 63 R 0
160 ÷ 38 = 4 R 8
4500 ÷ 20 = 225 R 0
548 ÷ 47 = 11 R 31
1344 ÷ 48 = 28 R 0
3947 ÷33 = 119 R 20
832 ÷ 64 = 13 R 0
7313 ÷71 = 103 R 0
394 ÷ 27 = 14 R 16
476 ÷53 = 8 R 52
5208 ÷ 93 = 56 R 0
216 ÷18 = 12 R 0
6378 ÷ 24 = 265 R 18
Divide Whole Numbers Chapter Practice
6.1 Relate Multiplication and Division
Use multiplication to find the quotient.
Question 1.
78 ÷ 6 = _____
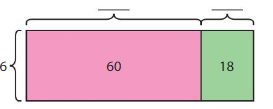
Answer:
78 ÷ 6 = 13.
Explanation:
78 = 60 + 18
78 = (6 x _) + (6 x _)
Sum of unknown factors of the smallest areas: 10 + 3 = 13
The related multiplication equation is 6 x 13 = 78. So, 78 ÷ 6 = 13.
Question 2.
76 ÷ 4 = ______
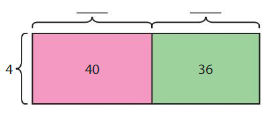
Answer:
76 ÷ 4 = 19.
Explanation:
76 = 40 + 36
76 = (4 x _) + (4 x _)
Sum of unknown factors of the smallest areas: 10 + 9 = 19
The related multiplication equation is 4 x 19 = 76
Question 3.
105 ÷ 5 = _____
Answer:
105 ÷ 5 = 21.
Explanation:
105 = 50 + 55
105 = (5 x _) + (5 x _)
Sum of unknown factors of the smallest areas: 10 + 11 = 21
The related multiplication equation is 5 x 21 = 105
Question 4.
288 ÷ 8 = _____
Answer:
288 ÷ 8 = 36.
Explanation:
288 = 160 + 128
288 = (8 x _) + (8 x _)
Sum of unknown factors of the smallest areas: 20 + 16 = 36
The related multiplication equation is 8 x 36 = 288
6.2 Division Patterns
Find the quotient.
Question 5.
4,500 ÷ 5 = ______
Answer:
4,500 ÷ 5 = 900.
Explanation:
4,500 ÷ 5 = 45 hundreds ÷ 5
= 9 hundreds = 900.
Question 6.
140 ÷ 70 = _____
Answer:
140 ÷ 70 = 2.
Explanation:
140 ÷ 70 = 14 tens ÷ 7 tens
= 14 ÷ 7 = 2.
Question 7.
160 ÷ 20 = _____
Answer:
160 ÷ 20 = 8.
Explanation:
160 ÷ 20 = 16 tens ÷ 2 tens
= 16 ÷ 2 = 8
Question 8.
720 ÷ 9 = ______
Answer:
720 ÷ 9 = 80.
Explanation:
720 ÷ 9 = 72 tens ÷ 9
= 8 tens = 80.
Question 9.
4,900 ÷ 70 = ______
Answer:
4,900 ÷ 70 = 70.
Explanation:
4,900 ÷ 70 = 49 hundreds ÷ 7 tens
= 49 tens ÷ 7 = 7 tens = 70
Question 10.
10,000 ÷ 5 = ______
Answer:
10,000 ÷ 5 = 2000.
Explanation:
10,000 ÷ 5 = 10 thousands ÷ 5
= 2 thousands = 2000.
6.3 Estimate Quotients
Find two numbers that the quotient is between.
Question 11.
604 ÷ 19
600 ÷ 20 = _____
800 ÷ 20 = _____
Answer:
600 ÷ 20 = 30
800 ÷ 20 = 40
Explanation:
600 ÷ 20 = 6 hundreds ÷ 2 tens
= 6 tens ÷ 2 = 3 tens = 30
800 ÷ 20 = 8 hundreds ÷ 2 tens
= 8 tens ÷ 2 = 4 tens = 40
Question 12.
1,732 ÷ 40
1,600 ÷ 40 = ______
2,000 ÷ 40 = _______
Answer:
1,600 ÷ 40 = 40
2,000 ÷ 40 = 50
Explanation:
1,600 ÷ 40 = 16 hundreds ÷ 4 tens
= 16 tens ÷ 4 = 4 tens = 40
2,000 ÷ 40 = 20 hundreds ÷ 4 tens
= 20 tens ÷ 4 = 5 tens = 50
Question 13.
4,096 ÷ 61
Answer:
3600 ÷ 60 = 60
4200 ÷ 60 = 70.
Explanation:
Choose What numbers close to 4069 are easily divided by 60?
4200 ÷ 60 = 42 hundreds ÷ 6 tens
= 42 tens ÷ 6 = 7 tens = 70
3600 ÷ 60 = 36 hundreds ÷ 6 tens
= 36 tens ÷ 6 = 6 tens = 60
Estimate the quotient.
Question 14.
3,411 ÷ 53
Answer:
3,411 ÷ 53 = 70.
Explanation:
Choose What numbers close to 3411 are easily divided by 50?
3500 ÷ 50 = 35 hundreds ÷ 5 tens = 35 tens ÷ 5 = 7 tens
3000 ÷ 50 = 30 hundreds ÷ 5 tens = 30 tens ÷ 5 = 6 tens
So, choose 3500 is near to 3411 and divided by 50.
Question 15.
1,678 ÷ 92
Answer:
1,678 ÷ 92 = 20
Explanation:
Choose What numbers close to 1678 are easily divided by 90?
900 ÷ 90 = 9 hundreds ÷ 9 tens = 9 tens ÷ 9 = 1 ten
1800 ÷ 90 = 18 hundreds ÷ 9 tens = 18 tens ÷ 9 = 2 tens
So, select 1800 near to 1678 and divided by 90.
Question 16.
6,581 ÷ 77
Answer:
6,581 ÷ 77 = 80.
Explanation:
Choose what numbers are near to 581 and are easily divided by 80 near to 77.
6400 ÷ 80 = 64 hundreds ÷ 8 tens = 64 tens ÷ 8 = 8 tens
7200 ÷ 80 = 72 hundreds ÷ 8 tens = 72 tens ÷ 8 = 9 tens
So, choose 6400 close to 6581 which is divided by 80 close to 77.
Question 17.
YOU BE THE TEACHER
Your friend finds the quotient. Estimate to check whether your friend’s answer is reasonable?
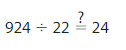
Answer:
Not reasonable.
Explanation:
Choose what numbers are close to 924 and divided by 20 near to 22.
800 ÷ 20 = 8 hundreds ÷ 2 tens = 8 tens ÷ 2 = 4 tens
1000 ÷ 20 = 10 hundreds ÷ 2 tens = 10 tens ÷ 2 = 5 tens
So, select 1000 near to 924 and divided by 20.
6.4 Divide by One-Digit Numbers
Divide. Then check your answer.
Question 18.
\(\sqrt [ 5 ]{ 415 } \)
Answer:
\(\sqrt [ 5 ]{ 415 } \) = 83.
Explanation:
Divide the tens
41 tens ÷ 5
8 tens x 5
41 tens – 40 tens
there is 1 ten leftover.
Divide the ones.
15 ones ÷ 5
3 ones x 5
15 ones – 15 ones
There are 0 ones left over.
So, 415 ÷ 5 = 83
Question 19.
\(\sqrt [ 6 ]{ 6,432 } \)
Answer:
\(\sqrt [ 6 ]{ 6,432 } \) = 1072
Explanation:
Divide the thousands.
6 thousands ÷ 6
6 x 1 thousand
6 thousands – 6 thousands
There is 0 thousand left over.
Divide the tens.
43 tens ÷ 6
6 x 7 tens
43 tens – 42 tens
There is 1 ten left over.
So, \(\sqrt [ 6 ]{ 6,432 } \) = 1072
Question 20.
\(\sqrt [ 9 ]{ 5,628 } \)
Answer:
\(\sqrt [ 9 ]{ 5,628 } \) = 625 R 3
Explanation:
Divide the hundreds.
56 hundreds ÷ 9
9 x 4 hundreds
56 hundreds – 54 hundreds
There are 2 hundreds left over
Divide the tens
22 tens ÷ 9
9 x 2 tens
22 tens – 18 tens
There are 4 tens left over
Divide the ones
48 ones ÷ 9
9 x 5 ones
48 ones – 45 ones
There are 3 ones left.
So, \(\sqrt [ 9 ]{ 5,628 } \) = 625 R 3
Question 21.
8,021 ÷ 7 = ______
Answer:
8,021 ÷ 7 = 1145 R 6
Explanation:
Divide the thousands
8 hundreds ÷ 7
7 x 10 hundreds
80 hundreds – 70 hundreds
There are 10 hundreds eft over.
divide the tens.
102 tens ÷ 7
7 x 14 tens
102 tens – 98 tens
There are 4 tens left over.
41 ones ÷ 7
7 x 5 ones
41 ones – 35 ones
There are 6 ones left over.
So, 8,021 ÷ 7 = 1145 R 6
Question 22.
817 ÷ 8 = ______
Answer:
817 ÷ 8 = 102 R 1
Explanation:
Divide the hundreds
8 hundreds ÷ 8
8 x 1 hundred
8 hundreds – 8 hundreds
There are 0 hundreds left over
Divide the ones.
17 ones ÷ 8
8 x 2 ones
17 ones – 16 ones
There are 1 one left over
So, 817 ÷ 8 = 102 R 1
Question 23.
3,007 ÷ 3 = ______
Answer:
3,007 ÷ 3 = 1002 R 1
Explanation:
Divide the thousand
3 thousand ÷ 3
3 thousand x 1
3 thousand – 3 thousand
there are 0 thousand left over.
Divide the ones.
7 ones ÷ 3
3 x 2 ones
7 ones – 6 ones
There are 1 one leftover.
So, 3,007 ÷ 3 = 1002 R 1
6.5 Use Partial Quotients to Divide by Two-Digit Numbers
Use partial quotients to divide.
Question 24.
156 ÷ 13
Answer:
156 ÷ 13 = 43
Explanation:
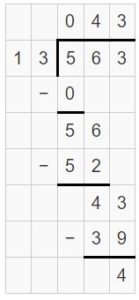
Partial quotients = 40 + 3 = 43
Question 25.
208 ÷ 16
Answer:
208 ÷ 16 = 13
Explanation:
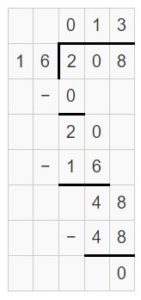
Partial quotients = 10 + 3 = 13
6.6 Use Partial Quotients with a Remainder
Use partial quotients to divide.
Question 26.
\(\sqrt [ 50 ]{ 805 } \)
Answer:
\(\sqrt [ 50 ]{ 805 } \) = 53 R 10
Explanation:
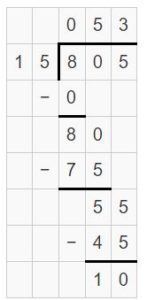
Partial quotients = 50 + 3
So, \(\sqrt [ 50 ]{ 805 } \) = 53 R 10
Question 27.
\(\sqrt [ 18 ]{ 741 } \)
Answer:
\(\sqrt [ 18 ]{ 741 } \) = 41 R 3
Explanation:
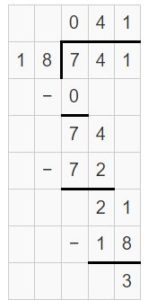
Partial qo=uotients = 40 + 1 = 41
So, \(\sqrt [ 18 ]{ 741 } \) = 41 R 3.
Question 28.
\(\sqrt [ 48 ]{ 2,500 } \)
Answer:
\(\sqrt [ 48 ]{ 2,500 } \) = 52 R 4
Explanation:
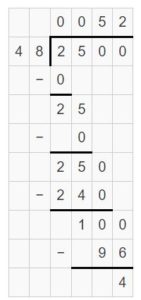
Partial quotients = 50 + 2 = 52
So, \(\sqrt [ 48 ]{ 2,500 } \) = 52 R 4
Question 29.
792 ÷ 13 = ______
Answer:
792 ÷ 13 = 60 R 12
Explanation:
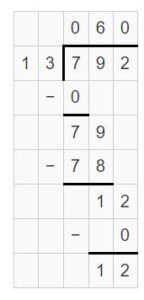
Partial quotients = 60
So, 792 ÷ 13 = 60 R 12
Question 30.
3,982 ÷ 25 = _____
Answer:
3,982 ÷ 25 = 159 R 7
Explanation:

Partial quotients = 100 + 50 + 9 = 159
So, 3,982 ÷ 25 = 159 R 7
Question 31.
6,927 ÷ 68 = ____
Answer:
6,927 ÷ 68 = 101 R 59
Explanation:
Partial quotients = 100 + 1 = 101
So, 6,927 ÷ 68 = 101 R 59
Question 32.
Modeling Real Life
There are 405 projects in a science fair. The coordinator displays the projects in rows of 42. How many rows have exactly 42 projects?
Answer:
9 rows have exactly 42 projects.
Explanation:
Divide 405 by 42.
9 rows have exactly 42 projects.
6.7 Divide Three-Digit Numbers by Two-Digit Numbers
Divide. Then check your answer.
Question 33.
\(\sqrt [ 31 ]{ 961 } \)
Answer:
\(\sqrt [ 31 ]{ 961 } \) = 31
Explanation:
The first digit is in the hundreds place.
Divide the tens.
96 tens ÷ 31
3 tens x 31 = 93 tens
96 tens – 93 tens = 3 tens
Divide the ones.
31 one ÷ 31
31 x 1 one = 31 ones
31 ones – 31 ones = 0
There are 0 ones leftover.
So, \(\sqrt [ 31 ]{ 961 } \) = 31
Use multiplication to check your answer.
Question 34.
\(\sqrt [ 27 ]{ 803 } \)
Answer:
\(\sqrt [ 27 ]{ 803 } \) = 28 R 47
Explanation:
The first digit is in the hundreds place.
Divide the tens.
80 tens ÷ 27
2 tens x 27 = 54 tens
80 tens – 54 tens = 26 tens
Divide the ones.
263 one ÷ 27
27 x 8 one = 216 ones
263 one – 216 ones = 47
Regroup 2 tens and 8 ones.
So, \(\sqrt [ 27 ]{ 803 } \) = 28 R 47
Use multiplication to check your answer.
756 + 47 = 803.
Question 35.
\(\sqrt [ 19 ]{ 245 } \)
Answer:
\(\sqrt [ 19 ]{ 245 } \) = 12 R 17
Explanation:
The first digit is in the hundreds place.
Divide the tens.
24 tens ÷ 19
1 ten x 19 = 19 tens
24 tens – 19 tens = 5 tens
Divide the ones.
55 one ÷ 19
19 x 2 one = 38 ones
55 one – 38 ones = 17 ones
Regroup 1 tens and 2 ones.
So, \(\sqrt [ 19 ]{ 245 } \) = 12 R 17
Use multiplication to check your answer.
12 x 19 = 228
228 + 17 = 245.
6.8 Divide Four-Digit Numbers by Two-Digit Numbers
Divide. Then check your answer.
Question 36.
6,636 ÷ 84 = _____
Answer:
6,636 ÷ 84 = 79
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
66 hundreds ÷ 84
66 hundreds cannot be shared among 84 groups without regrouping.
So, add next number.
Divide the tens.
663 tens ÷ 84
84 x 7 tens = 588 tens
663 tens – 588 tens = 75 tens
There are 75 tens left over.
Divide the ones.
756 ones ÷ 84
84 x 9 one = 756 ones
756 ones – 756 ones = 0
So, 6,636 ÷ 84 = 79
Use multiplication to check your answer.

Question 37.
2,418 ÷ 21 = ______
Answer:
2,418 ÷ 21 = 115 R 3
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
24 hundreds ÷ 21
21 x 1 hundred
24 hundreds – 21 hundreds
There are 3 hundreds left over.
Divide the tens.
31 tens ÷ 21
21 x 1 tens = 21 tens
31 tens – 21 tens = 10 tens
There are 10 tens left over.
Divide the ones.
108 ones ÷ 21
21 x 5 one = 105 ones
108 ones – 105 ones = 3
So, 2,418 ÷ 21 = 115 R 3
Use multiplication to check your answer.
115 x 21 = 2415
2415 + 3 = 2418.
Question 38.
4,960 ÷ 62 = _____
Answer:
4,960 ÷ 62 = 80
Explanation:
The first digit is in the thousands place.
Divide the hundreds.
49 hundreds ÷ 62
49 hundreds cannot be shared among 62 groups without regrouping.
So, add next number.
Divide the tens.
496 tens ÷ 62
62 x 8 tens = 496 tens
496 tens – 496 tens = 0 tens
There are 0 tens left over.
So, 4,960 ÷ 62 = 80
Use multiplication to check your answer.
62 x 80 = 4960.
6.9 Problem Solving: Division
Question 39.
The weight of a giant panda is 10 times the weight of a red panda. The combined weight of the pandas is 220 pounds. What is the weight of each panda?

Answer:
The weight of red panda is 20. The weight of gaint panda is 200.
Explanation:
The weight of giant panda = 10 x weight of red panda
The weight of giant panda + weight of red panda = 220
10 x weight of red panda + weight of red panda = 220
11 x weight of red panda = 220
divide 220 by 11
22 tens ÷ 11 = 2 tens
The weight of a red panda is 20.
The weight of gaint panda = 10 x 20 = 200.
Question 40.
A company fills claw arcade machines with stuffed animals. One machine can hold 50 stuffed animals. The company has 2,357 stuffed animals. The company fills as many machines as possible. How many stuffed animals do not fit into the machines?
Answer:
There are 25 stuffed animals do not fit into machines.
Explanation:
Divide 2375 by 50.
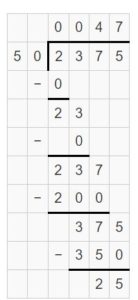
The quotient is 47 and the remainder is 25.
So there are 25 stuffed animals do not fit into machine.
Conclusion:
Before going to start the preparation learn the topics covered here and learn. We have also included a short and crisp explanation for the questions. Make use of Go Math Grade 5 Chapter 6 Solution Key and score better grades in your exams. Bookmark our site to get detailed solutions for all the Big Ideas Math Grade 5 Chapters.
