Do you face any difficulties in the concepts of Big Ideas Math Grade 8 Exponents and Scientific Notation Chapter? If So, you have come the right way and we will provide you the complete Big Ideas Math Grade 8 Answers Chapter 8 Exponents and Scientific Notation Solutions all in one place. Look no further and begin your preparation taking the help of the quick resources and stand out from the rest of the crowd. Consistent practice is the only key to achieve success in your journey of learning math.
Big Ideas Math Book 8th Grade Answer Key Chapter 8 Exponents and Scientific Notation
Middle School Students are advised to go through the Topicwise BIM Grade 8 Chapter 8 Exponents and Scientific Notation Answers provided to resolve their queries at the soonest. All the Concepts here are given by subject experts in a simple and easy-to-understand language. Big Ideas Math Textbook Solution Key is given via direct links and you can download the respective topic and prepare anywhere and anytime.
Performance Task
- Exponents and Scientific Notation STEAM Video/ Performance Task
- Exponents and Scientific Notation Getting Ready for Chapter 8
Lesson: 1 Exponents
Lesson: 2 Product of Powers Property
Lesson: 3 Quotient of Powers Property
Lesson: 4 Zero and Negative Exponents
Lesson: 5 Estimating Quantities
Lesson: 6 Scientific Notation
Lesson: 7 Operations in Scientific Notation
- Lesson 8.7 Operations in Scientific Notation
- Operations in Scientific Notation Homework & Practice 8.7
Chapter: 8 – Exponents and Scientific Notation
- Exponents and Scientific Notation Connecting Concepts
- Exponents and Scientific Notation Chapter Review
- Exponents and Scientific Notation Practice Test
- Exponents and Scientific Notation Cumulative Practice
Exponents and Scientific Notation STEAM Video/ Performance Task
STEAM Video
Carbon Atoms
Carbon is one of the four main elements of life. The number of carbon atoms in a compound can be represented using exponents. In what other real-life situations are exponents used?

Watch the STEAM Video “Carbon Atoms.” Then answer the following questions.
1. The table shows the percent carbon by weight for humans and plants. How many pounds of carbon are in a 130-pound person? a 25-pound plant?
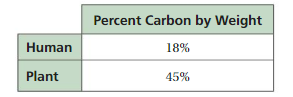
a. Pounds of Carbon in 130-pound person is 2.57 X 1021.
b. Pounds of Carbon in 25 -pound plant is 1.23975 X 1021.
Explanation:
Given 1 carbon atoms consists of 5 X 1022,
a. So 1 person has 18% of carbon means 18 ÷ 100 X 5 × 1022 =
18 X 5 X 1022-2 = 90 X 1020 = 9 X 10 X 1020 = 9 X 1021 now,
We know 1 gram is equal to 0.00220462 pound
So 0.00220462 X 9 X 1021 as 0.00220462 approximately equal to ≈
2.204 X 10-3 X 9 X 1021 = 19.836 X 1021-3 = 19.836 X 1018 = 1.9836 X 1019 now
in 130-pound person is 130 X 1.9836 X 1019 = 257.868 X 1019 = 2.57 X 1021.
b. So 1 plant has 45% of carbon means 45 ÷ 100 X 5 × 1022 =
45 X 5 X 1022-2 = 225 X 1020 = 2.25 X 100 X 1020 = 2.25 X 1022 now,
We know 1 gram is equal to 0.00220462 pound
So 0.00220462 X 2.25 X 1022 as 0.00220462 approximately equal to ≈
2.204 X 10-3 X 2.25 X 1022 = 4.959 X 1022-3 = 4.959 X 1019 = 4.959 X 1019 now
in 25-pound plant is 25 X 4.959 X 1019 =123.975 X 1019 = 1.23975 X 1021.
2. Steven says 5 × 1022, carbon atoms are in 1 gram of carbon. How many carbon atoms are in 3 grams of carbon?
In 3 grams of carbon = 3 X (5 x1022) = 15 x 1022 carbon atoms are available
Explanation:
Given Steven says 5 x1022 ,carbon atoms are in 1 gram of carbon,
in 3 grams of carbon it will be (5 x 1022) X 3 = 5 X 3 X (1022)=
15 x 1022 carbon atoms are available.
Performance Task
Elements in the Universe
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given information about the atomic masses of the four most common elements in the universe: oxygen, hydrogen, helium, and carbon.

You will be asked to solve problems about the amounts of carbon dioxide in Earth’s atmosphere for several years. What might cause the amount of carbon dioxide in the atmosphere to increase over time?
Exponents and Scientific Notation Getting Ready for Chapter 8
Chapter Exploration
1. Work with a partner. Write each distance as a whole number. Which numbers do you know how to write in words? For instance, in words, 102 is equal to one hundred.

a. 1027 meters diameter of the observable universe is
10000000 0000000000 0000000000 is equal to
octillion ( quadrilliard )
b. 1021 meters diameter of the Milky Way galaxy is
10 0000000000 0000000000 is equal to
sextillion (trilliard)
c. 1016 meters diameter of the solar system is
10 0000000000 00000 is equal to
10 quadrillion or 10 thousand trillion
d. 107 meters diameter of Earth is 10000000
is equal to ten million (crore (India))
e. 104 meters diameter of Halley’s Comet is 10000
is equal to ten thousand
f. 103 meters diameter of a meteor crater is
1000 is equal to thousand.
Explanation:
a. 1027 meters diameter of the observable universe,
we call the number 10 is called the base
and the number 27 is called the exponent, we multiply 10 by 27 times,
we write 10 to the 27th power as 1,000,000,000,000,000,000,000,000,000
is equal to octillion ( quadrilliard )
b. 1021 meters diameter of the Milky Way galaxy,
we call the number 10 is called the base
and the number 21 is called the exponent, we multiply 10 by 21 times,
we write 10 to the 21th power as 1,000,000,000,000,000,000,000
is equal to sextillion (trilliard)
c. 1016 meters diameter of the solar system
we call the number 10 is called the base
and the number 16 is called the exponent, we multiply 10 by 16 times,
we write 10 to the 16th power as 10,000,000,000,000,000 is equal to
10 quadrillion or 10 thousand trillion
d. 107 meters diameter of Earth
we call the number 10 is called the base
and the number 7 is called the exponent, we multiply 10 by 7 times,
we write 10 to the 7th power as 10,000,000 is equal to ten million (crore (India))
e. 104 meters diameter of Halley’s Comet we call the number 10 is called the base
and the number 4 is called the exponent, we multiply 10 by 4 times,
we write 10 to the 4th power as 10,000 is equal to ten thousand
f. 103 meters diameter of a meteor crater we call the number 10 is called the base
and the number 27 is called the exponent, we multiply 10 by 3 times
we write 10 to the 3th power as 1,000 is equal to thousand.
2. Work with a partner. Write the numbers of wives, sacks, cats, and kits as powers.

Man ,wives are 70 + 71 = 1 + 7 = 8,
Man, wives, sacks are 70 + 72 = 1 + 49 = 50
Man, wives, sacks, cats are 70 + 73 = 1 + 343 = 344,
Man, wives, sacks, cats , kits are 70 + 74 = 1 + 2401 = 2402
Total 2402 are going to St. Ives.
Explanation:
Given I met a man with seven wives so
writing as powers man and seven wives means 1 + 71 = 8,
man, each wives had seven sacks means 1 + 72 = 49,
man, wives, each sack had seven cats are 1+ 73 = 1 + 343 = 344,
man, wives, sacks , Each cat had seven kits are 1+ 74 = 1 + 2401 = 2402,
So in total kits, cats, sacks, wives and man are 2402 are going to St. Ives.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
power
exponent of a power
base of a power
scientific notation
Lesson 8.1 Exponents
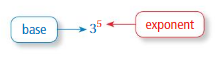
The expression 35 is called a power. The base is 3. The exponent is 5.
EXPLORATION 1
Using Exponent Notation
Work with a partner.
a. Copy and complete the table.
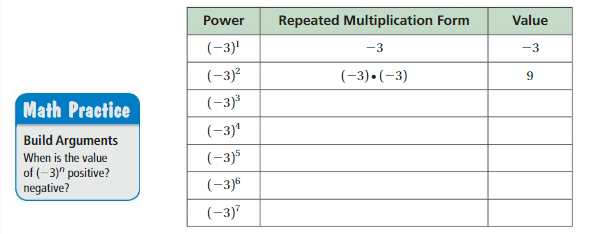
Explanation:
Given Powers wrote repeated multiplication form and value as
(-3)3= (-3).(-3).(-3)= -27, multiplied -3 three times as power is 3
(-3)4= (-3).(-3).(-3).(-3)= 81,multiplied -3 four times as power is 4
(-3)5= (-3).(-3).(-3).(-3).(-3)= -243,multiplied -3 five times as power is 5
(-3)6= (-3).(-3).(-3).(-3).(-3).(-3)= 729,multiplied -3 five times as power is 6
(-3)7= (-3).(-3).(-3).(-3).(-3).(-3).(-3)= 2187,multiplied -3 five times as power is 7
b. Describe what is meant by the expression (- 3)n. How can you find the value of (- 3)n?
Answer:
The expression (-3)n is called a power. The base is -3. The exponent is n.
We find the value of (- 3)n we multiply -3 with n number of times.
Explanation:
An expression that represents repeated multiplication
of the same factor is called a power. Here the expression
(-3)n is called a power of n and the number -3 is called the base,
and the number n is called the exponent. The exponent corresponds
to the number of times the base is used as a factor.
EXPLORATION 2
Using Exponent Notation
Work with a partner. On a game show, each small cube is worth $3. The small cubes are arranged to form a large cube. Show how you can use a power to find the total value of the large cube. Then write an explanation to convince a friend that your answer is correct.

Answer:

The total value of the large cube is =$3 X (320)320
My answer is correct as given base as 320 and exponent is 320.
Explanation:
Given small cubes are arranged to form large cube,
and power is 320, base is 320 and exponent is 320,
each small cube is worth $3 so the total value of the large
cube is $3 multiplied by 320 and multiplied $3 with 320 by 320 times is
$3 X (320)320 as my answer is correct I say my friend because
given base is 320 and exponent is 320 we write as (320)320 and
multiply by $3 to get the value of the large cube.
Try It
Write the product using exponents.
Question 1.
\(\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}\)
Answer:
\(\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}\) = (\(\frac{1}{4}\))5
Explanation:
As \(\frac{1}{4}\) is multiplied by 5 times,
the expression is (\(\frac{1}{4}\))5.
The base is \(\frac{1}{4}\) and the exponent is 5.
Question 2.
0.3 • 0.3 • 0.3 • 0.3 • x • x
Answer:
0.3 • 0.3 • 0.3 • 0.3 • x • x = (0.3)4 X (x)2
Explanation:
As 0.3 is multiplied 4 times we write as (0.3)4 and x
is multiplied twice so (x)2
so the expression is (0.3)4 X (x)2.
Evaluate the expression.
Question 3.
122
Answer:
122 = 144
Explanation:
Given 122 means 12 is multiplied twice
as 12 X 12 we get 144.
here base is 12 and exponent is 2.
Question 4.
(- 2)6
Answer:
(- 2)6 = 64
Explanation:
Given (- 2)6 we multiply -2 by 6 times as
-2 X -2 X -2 X -2 X -2 X -2 we get 64
here base is -2 and exponent is 6.
Question 5.
– 54
Answer:
– 54 =625
Explanation:
Given – 54 we multiply -5 by 4 times as
-5 X -5 X -5 X -5 = 625,
here base is -5 and 4 is exponent.
Question 6.
\(\left(-\frac{1}{6}\right)^{3}\)
Answer:
\(\left(-\frac{1}{6}\right)^{3}\) = –\(\frac{1}{216}\)
Explanation:
Given \(\left(-\frac{1}{6}\right)^{3}\) we multiply
– \(\frac{1}{6}\) by 3 times as –\(\frac{1}{6}\) X
– \(\frac{1}{6}\) X –\(\frac{1}{6}\) we get
– \(\frac{1}{216}\) here base is –\(\frac{1}{6}\)
and 3 is exponent.
Evaluate the expression.
Question 7.
9 – 25 . 0.5
Answer:
9 – 25 . 0.5 = -7
Explanation:
Given 9 – 25 . 0.5 = First we solve 25 . 0.5
25 X 0.5 as 0.5 can be written as \(\frac{1}{2}\),
= 32 X \(\frac{1}{2}\) = 16 now we subtract 16 from 9
9-16 = -7
Question 8.
|- 33 ÷ 27|
Answer:
|- 33 ÷ 27| = -1
Explanation:
First we calculate – 33 we multiply -3 by 3 times as
-3 X -3 X -3 = -27 now we divide -27 by 27 we get -1.
Question 9.
(7 . 4 – 43) ÷ 6
Answer:
(7 . 4 – 43) ÷ 6 = -6
Explanation:
First we calculate the value of 43
we multiply 4 by 3 times as 4 X 4 X 4 = 64,
Now we multiply 7 X 4 = 28 now we subtract 64 from 28
we get (7 . 4 – 43) =(28 – 64) = -36 now we divide this by 6 we get
-36 ÷ 6 = -6, So (7 . 4 – 43) ÷ 6 = -6.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING EXPRESSIONS USING EXPONENTS Write the product using exponents.
Question 10.
(- 0.9) • (- 0.9) • (- 0.9)
Answer:
(- 0.9) • (- 0.9) • (- 0.9 )= (-0.9)3
Explanation:
As -0.9 is multiplied by 3 times we write as
(-0.9)3 here -0.9 is base and 3 is exponent.
Question 11.
\(\frac{1}{8}\) • \(\frac{1}{8}\) • y • y • y
Answer:
\(\frac{1}{8}\) • \(\frac{1}{8}\) • y • y • y =
(\(\frac{1}{8}\))2 X (y)3
Explanation:
As \(\frac{1}{8}\) is multiplied by 2 times we write as
(\(\frac{1}{8}\))2
and y is multiplied 3 times we write as (y)3,
So \(\frac{1}{8}\) • \(\frac{1}{8}\) • y • y • y =
(\(\frac{1}{8}\))2 X (y)3.
EVALUATING EXPRESSIONS Evaluate the expression.
Question 12.
112
Answer:
112 = 121
Explanation:
Given 112 means 11 is multiplied twice
as 11 X 11 = 121.
Question 13.
– 63
Answer:
– 63 = – 216
Explanation:
Given – 6 is multiplied by 3 times as
– 6 X -6 X -6 = -216
Question 14.
(- 0.3)4
Answer:
(- 0.3)4 = 0.0081
Explanation:
As (-0.3) is multiplied by 4 times we get
-0.3 X -0.3 X -0.3 X -0.3 = 0.0081
USING ORDER OF OPERATIONS Evaluate the expression.
Question 15.
|- 24 ÷ 22|
Answer:
|- 24 ÷ 22|= -6
Explanation:
First we calculate 22 we get 4,
now we divide -24 by 4 we get -6.
Question 16.
(33 – 6 • 8) ÷ 7
Answer:
(33 – 6 • 8) ÷ 7 = -3
Explanation:
First we calculate 6 X 8 we get 48 Now we subtract
48 from 33 as 33 is 3 X 3 X 3 = 27 we get (27 – 48 )= -21
now we divide -21 by 7 we get -3 therefore
(33 – 6 • 8) ÷ 7 = -3 .
Question 17.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.
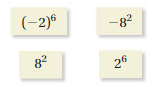
Answer:
The expression – 82 does not belongs to other three.
Explanation:
Given expressions (-2)6,- 82 ,-82 and 26
the values are (-2)6= -2 X -2 X -2 X -2 X -2 X -2 = 64,
– 82 =- ( 8 X 8) = -64,
82 = 8 X 8 = 64 and 26 = 2 X 2 X 2 X 2 X 2 X 2 = 64
as (-2)6,-82 and 26 have same value 64 only – 82 =-64 is different,
so the expression – 82 does not belongs to other three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
DIG DEEPER!
Consider the diameters of three planets.
Planet A: 109m
Planet B: 107n
Planet C: 108m
a. Write each diameter as a whole number.
b. A dwarf planet is discovered with a radius that is \(\frac{1}{100}\) the radius Planet C. Write the diameter of the dwarf planet as a power.
Answer:
a. Planet A: 109m = 1000000000m
Planet B: 107n = 10000000n
Planet C: 108m = 100000000m
b. diameter = 2 X 106m
Explanation:
The diameters of three planets are given as
Planet A: 109m, Planet B: 107n, Planet C: 108m
in part a,we write whole for Planet A as 10 is multiplied by 9 times
so 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 =1000000000m
Planet B as 10 is multiplied by 7 times therefore it is
10 X 10 X 10 X 10 X 10 X 10 X 10 =10000000n and Planet C
as 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 =100000000m and
in part b, Given a dwarf planet is discovered with a radius that is
\(\frac{1}{100}\) the radius Planet C and
we know diameter = 2 X radius so diameter is
2 X 100000000 X \(\frac{1}{100}\) = 2 X 1000000,
therfore the diameter of the dwarf planet as a power is 2 X 106m.
Question 19.
A fish jumps out of the water at a speed of 12 feet per second. The height y (in feet) of the fish above the surface of the water is represented by the equation y = – 16x2 + 12x, where x is the time (in seconds) since the jump began. The fish reaches its highest point above the surface of the water after 0.375 second. How far above the surface is the fish at this time?

Answer:
The fish is 2.25 feet above the surface at 0.375 second.
Explanation:
The height y (in feet) of the fish above the surface of the water
is represented by the equation y = – 16x2 + 12x,
where x is the time (in seconds) since the jump began.
The fish reaches its highest point above the surface
of the water after 0.375 second, So X = 0.375 second
we substitute In the equation as
y=- 16 (0.375 X 0.375 ) + 12 (0.375)= – 16 ( 0.140625) + 4.5
= -2.25 + 4.5 = 2.25
The fish is 2.25 feet above the surface at 0.375 second.
Exponents Homework & Practice 8.1
Review & Refresh
Sketch a graph that represents the situation.
Question 1.
A trading card becomes more valuable over time. The value increases at a constant rate, and then at a faster and faster rate.
Answer:
Sketch is
Explanation:
We represent the graph Trading card as
on X axis Time and on Y axis Value,
Given the value increases at a constant rate,
so first we draw a straight Line with positive slope,
and increase rate is represented by exponential growth as
shown in the figure above.
Question 2.
The water level of a river remains constant, and then decreases at a constant rate.
Answer:
Explanation:
Given the water level of a river remains constant
and then decreases at a constant rate so in the graph
we draw a straight Line with positive slope as constant,
and decrease rate is represented as decay shown in the figure above.
The vertices of a figure are given. Rotate the figure as described. Find the coordinates of the image.
Question 3.
A(0, – 4), B(0, – 1), C(2, – 1)
90° clockwise about the origin
Answer:
A/(-4,0)
B/(-1,0)
C/(-1,-2)
Explanation:
When we rotate a figure of 90 degrees clockwise about the origin,
each point of the given figure has to be changed from (x, y) to (y, -x).
So A(0,-4) becomes A/(-4,-0)= A/(-4,0) ,
B(0,-1) becomes B/(-1,-0)= B/(-1,0) and
C(2, – 1) becomes C/(-1,-2)
Question 4.
E(1, 2), F(1, 3), G(4, 3), H(4, 2)
180° about the origin
Answer:
E/(-1,-2)
F/(-1,-3)
G/(-4,-3)
H/(-4,-2)
Explanation:
Rotation of a point through 180°, about the origin when a point A (x, y)
is rotated about the origin O through 180° in anticlockwise
or clockwise direction, it takes the new position A’ (-x, -y)
So E(1,2) becomes E/(-1,-2), F(1,3) becomes F/(-1,-3), G(4,3)
becomes G/(-4,-3) and H(4,2) becomes H/(-4,-2).
Concepts, Skills, & Problem Solving
USING EXPONENT NOTATION Write the power in repeated multiplication form. Then find the value of the power.(See Exploration 1, p. 319.)
Question 5.
44
Answer:
4 X 4 X 4 X 4, 256
Explanation:
First we write 44 in repeated multiplication form as
power is 4 times 4 X 4 X 4 X 4 and the value is 256.
Question 6.
(- 8)2
Answer:
-8 X -8 , 64
Explanation:
First we write (- 8)2 in repeated multiplication form as
– 8 X -8 as power is 2 times and the value is 64.
Question 7.
(- 2)3
Answer:
– 2 X -2 X -2 , -8
Explanation:
First we write (- 2)3 in repeated multiplication form as
– 2 X -2 X -2 as power is 3 times and the value is -8.
WRITING EXPRESSIONS USING EXPONENTS Write the product using exponents.
Question 8.
3 • 3 • 3 • 3
Answer:
3 • 3 • 3 • 3 = (3)4
Explanation:
We write the product 3 • 3 • 3 • 3 in exponents as (3)4
because 3 is multiplied by 4 times.
Question 9.
(- 6) • (- 6)
Answer:
(- 6) • (- 6) = (-6)2
Explanation:
We write the product (-6) X (-6) in exponents as (-6)2
because -6 is multiplied by 2 times.
Question 10.
(- \(\frac{1}{2}\)) • (- \(\frac{1}{2}\)) • (- \(\frac{1}{2}\))
Answer:
(- \(\frac{1}{2}\)) • (- \(\frac{1}{2}\)) • (- \(\frac{1}{2}\))=
(- \(\frac{1}{2}\))3
Explanation:
We write the product (- \(\frac{1}{2}\)) X(- \(\frac{1}{2}\))
X (- \(\frac{1}{2}\)) in exponent as (- \(\frac{1}{2}\))3
here – \(\frac{1}{2}\) is multiplied by 3 times.
Question 11.
\(\frac{1}{3}\) • \(\frac{1}{3}\) • \(\frac{1}{3}\)
Answer:
\(\frac{1}{3}\) • \(\frac{1}{3}\) • \(\frac{1}{3}\)=
(\(\frac{1}{3}\))3
Explanation:
We write the product ( \(\frac{1}{3}\)) X ( \(\frac{1}{3}\)) X
(\(\frac{1}{3}\)) in exponent as (\(\frac{1}{3}\))3
here \(\frac{1}{3}\) is multiplied by 3 times.
Question 12.
π • π • π • x • x • x • x
Answer:
π • π • π • x • x • x • x = (π)3 X (x)4
Explanation:
We write the product π • π • π • x • x • x • x
in exponent as (π)3 X (x)4 here π is multiplied by
3 times and X is multiplied 4 times.
Question 13.
(- 4) • (- 4) • (- 4) • y • y
Answer:
(- 4) • (- 4) • (- 4) • y • y = (-4)3 X (y)2
Explanation:
Here we write the product (- 4) • (- 4) • (- 4) • y • y
as (-4)3 X (y)2,-4 is multiplied three times and y is
multiplied by 2 times
Question 14.
6.4 • 6.4 • 6.4 • 6.4 • b • b • b
Answer:
6.4 • 6.4 • 6.4 • 6.4 • b • b • b = (6.4)4 X (b)3
Explanation:
Here we write the product 6.4 • 6.4 • 6.4 • 6.4 • b • b • b
as (6.4)4 X (b)3,6.4 is multiplied four times and b is
multiplied by 3 times.
Question 15.
(- t) • (- t) • (- t) • (- t) • (- t)
Answer:
(- t) • (- t) • (- t) • (- t) • (- t ) = (-t)5
Explanation:
Here we write the given product (- t) • (- t) • (- t) • (- t) • (- t)
as (-t)5 because – t is multiplied by 5 times.
Question 16.
– (7 • 7 • 7 • 7 • 7)
Answer:
– (7 • 7 • 7 • 7 • 7) = -(7)5
Explanation:
We write the given product as – (7 • 7 • 7 • 7 • 7)
= -(7)5 here -(7) is multiplied by 5 times.
Question 17.
\(-\left(\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}\right)\)
Answer:
\(-\left(\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}\right)\)= – (\(\frac{1}{4}\))4
Explanation:
We write the given product as
\(-\left(\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}\right)\)
as – (\(\frac{1}{4}\))4 because \(\frac{1}{4}\)
is multiplied by 4 times.
EVALUATING EXPRESSIONS Evaluate the expression.
Question 18.
52
Answer:
52 = 5 X 5 = 25
Explanation:
Given 52 we write the expression as 5 X 5
and the value is 25
Question 19.
– 113
Answer:
– 113 = (-11 X -11 X -11) = -1331
Explanation:
Given – 113 we write it as (-11 X -11 X -11)
we get -1331.
Question 20.
(- 1)6
Answer:
(- 1)6= (-1 X -1 X -1 X -1 X -1 X -1) = 1
Explanation:
Given (- 1)6 as power is 6 we multiply -1 by
6 times as (-1 X -1 X -1 X -1 X -1 X -1) we get 1.
Question 21.
(\(\frac{1}{6}\))6
Answer:
(\(\frac{1}{6}\))6
= \(\frac{1}{6}\) X \(\frac{1}{6}\) X
\(\frac{1}{6}\) X \(\frac{1}{6}\) X
\(\frac{1}{6}\) X \(\frac{1}{6}\) = \(\frac{1}{46656}\)
Explanation:
Given (\(\frac{1}{6}\))6 here power is 6 we multiply
\(\frac{1}{6}\) by 6 times as \(\frac{1}{6}\) X \(\frac{1}{6}\) X
\(\frac{1}{6}\) X \(\frac{1}{6}\) X
\(\frac{1}{6}\) X \(\frac{1}{6}\) we get \(\frac{1}{46656}\)
Question 22.
(- \(\frac{1}{12}\))2
Answer:
(- \(\frac{1}{12}\))2 = –\(\frac{1}{12}\) X –\(\frac{1}{12}\) = \(\frac{1}{144}\)
Explanation:
Given (- \(\frac{1}{12}\))2
the expression has power 2 we write it as –\(\frac{1}{12}\) X –\(\frac{1}{12}\)
we get \(\frac{1}{144}\)
Question 23.
– (\(\frac{1}{9}\))3
Answer:
– (\(\frac{1}{9}\))3 = – \(\frac{1}{9}\) X – \(\frac{1}{9}\) X –\(\frac{1}{9}\)=
– \(\frac{1}{729}\)
Explanation:
Given – (\(\frac{1}{9}\))3 as in the expression we have power 3 we multiply
– \(\frac{1}{9}\) by three times as – \(\frac{1}{9}\) X – \(\frac{1}{9}\) X –\(\frac{1}{9}\) we get –\(\frac{1}{729}\)
Question 24.
YOU BE THE TEACHER
Your friend evaluates the power – 62. Is your friend correct? Explain your reasoning.
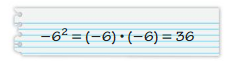
Answer:
Yes friend is correct,
Explanation:
Given friend evaluates the power – 62 as -6 X -6 = 36,
as given -6 has power 2 we multiply -6 twice so we get 36,
which is similar to what friend has evaluated so friend is correct.
STRUCTURE Write the prime factorization of the number using exponents.
Question 25.
675
Answer:
675 = 33 X 52
Explanation:
The number 675 is a composite number so, it is possible to factorize it.
In other words, 675 can be divided by 1, by itself and at least by 3 and 5.
A composite number is a positive integer that has at least one positive divisor
other than one or the number itself.
In other words, a composite number is any integer greater than one that is not a prime number.
The prime factorization of 675 = 33 X 52.
The prime factors of 675 are 3 and 5.

Question 26.
280
Answer:
280 = 23 X 5 X 7
Explanation:
The number 280 is a composite number so, it is possible to factorize it.
In other words, 280 can be divided by 1, by itself and at least by 2, 5 and 7.
A composite number is a positive integer that has at least one
positive divisor other than one or the number itself.
In other words, a composite number is any integer greater than
one that is not a prime number.
The prime factorization of 280 = 23 X 5 X 7.
The prime factors of 280 are 2, 5 and 7.

Question 27.
363
Answer:
363 = 3 X 112
Explanation:
The number 363 is a composite number so, it is possible to factorize it.
In other words, 363 can be divided by 1, by itself and at least by 3 and 11.
A composite number is a positive integer that has at least one
positive divisor other than one or the number itself.
In other words, a composite number is any integer greater than
one that is not a prime number.
The prime factorization of 363 = 3 X 112.
The prime factors of 363 are 3 and 11.

Question 28.
PATTERNS
The largest doll is 12 inches tall. The height of each of the other dolls is \(\frac{7}{10}\) the height of the next larger doll. Write an expression involving a power that represents the height of the smallest doll. What is the height of the smallest doll?

Answer:
The height of the smallest doll is 4.116 inches.
Explanation:
Given the largest doll is 12 inches tall, The height of each of the other dolls is
\(\frac{7}{10}\) the height of the next larger doll, There are 4 dolls
So 12 X \(\frac{7}{10}\) X \(\frac{7}{10}\) X \(\frac{7}{10}\) =
\(\frac{4116}{1000}\) = 4.116 inches, therefore the height of the smallest doll is 4.116 inches.
USING ORDER OF OPERATIONS Evaluate the expression.
Question 29.
5 + 2 • 23
Answer:
5 + 2 • 23 = 21
Explanation:
Given 5 + 2 • 23 we first simplify 23 and multiply with 2
we get 2 X 2 X 2 X 2 = 16 and add 5, 16 + 5 = 21,
therefore 5 + 2 • 23 = 21
Question 30.
2 + 7 • (- 3)2
Answer:
2 + 7 • (- 3)2 = 65
Explanation:
Given expression as 2 + 7 • (- 3)2 we first simplify 7 • (- 3)2
we multiply – 3 twice as – 3 X -3 = 9 and multiply with 7 we get
7 X 9 = 63 now we add 2 to 63 now we get 2 + 63 = 65,
therefore 2 + 7 • (- 3)2 = 65.
Question 31.
(132 – 122) ÷ 5
Answer:
(132 – 122) ÷ 5= 5.
Explanation:
We have expression as (132 – 122) ÷ 5 first
we calculate (132 – 122) so 13 X 13 = 169 and
12 X 12 = 144 we subtract 144 from 169 we get
169 – 144 = 25 now we divide 25 by 5 we get 5,
therefore (132 – 122) ÷ 5= 5.
Question 32.
\(\frac{1}{2}\)(43 – 6 • 32)
Answer:
\(\frac{1}{2}\)(43 – 6 • 32) = 5
Explanation:
Given expression as \(\frac{1}{2}\)(43 – 6 • 32) First we evaluate
(43 – 6 • 32) as 32) as 3 X 3 = 9 now multiply by 6 we get 6 X 9 = 54,
43 = 4 x 4 X 4 = 64, So 64 – 54 =10 Now we multiply 10 with \(\frac{1}{2}\)
we get 5, therefore \(\frac{1}{2}\)(43 – 6 • 32) = 5.
Question 33.
|\(\frac{1}{2}\)(7 + 53)|
Answer:
|\(\frac{1}{2}\)(7 + 53)| = 66
Explanation:
given expression is |\(\frac{1}{2}\)(7 + 53)| so first we evaluate
(7 + 53) = 7 + 5 X 5 X 5 = 7 + 125 = 132 now we multiply 132 with \(\frac{1}{2}\)
we get \(\frac{1}{2}\) X 132 = 66. So |\(\frac{1}{2}\)(7 + 53)| = 66.
Question 34.
|(- \(\frac{1}{2}\))3 ÷ (\(\frac{1}{4}\))2|
Answer:
|(- \(\frac{1}{2}\))3 ÷ (\(\frac{1}{4}\))2| = -2
Explanation:
Given expression as |(- \(\frac{1}{2}\))3 ÷ (\(\frac{1}{4}\))2|
first we evaluate (- \(\frac{1}{2}\))3= – \(\frac{1}{2}\) X – \(\frac{1}{2}\) X
– \(\frac{1}{2}\) = – \(\frac{1}{8}\), Now (\(\frac{1}{4}\))2
= \(\frac{1}{4}\) X \(\frac{1}{4}\) = \(\frac{1}{16}\),
now we multiply – \(\frac{1}{8}\) with \(\frac{1}{16}\) = -2.
Question 35.
(92 – 15 • 2) ÷ 17
Answer:
(92 – 15 • 2) ÷ 17 = 3
Explanation:
The expression is (92 – 15 • 2) ÷ 17 we evaluate first (92 – 15 • 2) as
9 X 9 = 81 and 15 X 2 = 30 so 81 – 30 = 51 now we divide 51 by 17
we get 3 as 17 x 3 = 51 therefore (92 – 15 • 2) ÷ 17 = 3.
Question 36.
– 6 • (- 52 + 20)
Answer:
– 6 • (- 52 + 20) = 30
Explanation:
The given expression is – 6 • (- 52 + 20) we first find
(- 52 + 20) = – 5 X -5 = -25 + 20 = -5 now we multiply -5 with -6
we get – 5 X -6 = 30, So – 6 • (- 52 + 20) = 30.
Question 37.
(- 4 + 12 – 62) ÷ 7
Answer:
(- 4 + 12 – 62) ÷ 7 = – 4
Explanation:
Given expression is (- 4 + 12 – 62) ÷ 7 we calculate first (- 4 + 12 – 62) as
-4 +12 – (6 X 6)= -4 +12 -36 = -40 + 12 = – 28 now we divide -28 by 7 we
get -4, therefore (- 4 + 12 – 62) ÷ 7 = – 4
Question 38.
STRUCTURE
Copy and complete the table. Compare the values of 2h – 1 with the values of 2h – 1. When are the values the same?
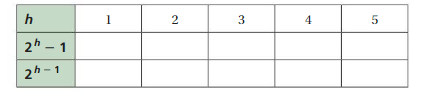
Answer:
Comparing the values of 2h – 1 with the values of 2h – 1 both do not
have any same values.
Explanation:
First we calculate 2h -1 we substitute h as 1,2,3,4,5
we get If h is 1 , 21 -1= 2 – 1 = 2, if h is 2 we get 22 -1= 4 -1 = 3,
now h = 3, 23 -1 = 8 – 1 = 7, if h =4 , 24 -1= 16 – 1 = 15 and
h=5, 25 -1= 32 – 1 = 31. So for h =1,2,3,4,5 we get 2h -1 = 2,3,7,15,31 respectively
Now we substitute for h= 1, 2h-1 = 21-1= 20= 1, for h = 2 it is 22-1 = 21 = 2, now h = 3
23-1 = 22 = 2 X 2 = 4 , if h is 4 we get 24-1 = 23 = 2 X 2 X = 8 and if h is 5
we get 25-1 = 24 = 2 X 2 X 2 X 2 = 16, So for h = 1,2,3,4,5, we get 2h-1 = 1,
2,4,8,16 respectively. As comparing the values of 2h – 1 with the values of 2h – 1
both do not have any same values. Hence no common values.
Question 39.
MODELING REAL LIFE
Scientists use carbon-14 dating to determine the age of a sample of organic material.
a. The amount C(in grams) of carbon-14 remaining after t years of a
sample of organic material is represented by the equation C = 100(0.99988)t. Find the amount of carbon-14 remaining after 4 years.
b. What percent of the carbon-14 remains after 4 years?
Answer:
a. The amount of carbon – 14 remaining after 4 years is 99.95 grams.
b. The percent of the carbon – 14 remains after 4 years is 99.95%.
Explanation:
a. Given the amount C(in grams) of carbon-14 remaining
after t years of a sample of organic material is represented
by the equation C = 100(0.99988)t we the amount of carbon-14 remaining
after 4 years as t = 4 we substitute C = 100(0.99988)4 we get C =
100 X 0.99988 X 0.99988 X 0.99988 X 0.99988 = 99.95 grams,
therefore The amount of carbon – 14 remaining after 4 years is 99.95 grams.
b. Now the percent of the carbon – 14 remains after 4 years , we have the amount
of carbon after 4 years is 99.95 grams,
So Percentage is 100 X 99.95 by 100 = 99.95 %.
Question 40.
DIG DEEPER!
The frequency (in vibrations per second) of a note on a piano is represented by the equation F = 440(1.0595)n, where n is the number of notes above A440. Each black or white key represents one note.

a. How many notes do you take to travel from A440 to A?
b. What is the frequency of A?
c. Compare the frequency of A to the frequency of A440.
Answer:
a. There are 12 notes to travel from A440 to A.
b. The frequency of A is 880 vibrations.
c. The frequency of A is twice to the frequency of A440.
Explanation:
a. As each black or white key represents one note, to reach
from A 440 to A if we count there are 12 notes to travel.
b. The frequency (in vibrations per second) of a note on a piano
is represented by the equation F = 440(1.0595)n, For note A, n =12
F = 440(1.0595)12, F = 440 X 1.0595 X 1.0595 X 1.0595 X 1.0595 X
1.0595 X 1.0595 X 1.0595 X 1.0595 X 1.0595 X 1.0595 X 1.0595 X 1.0595 =
F=880.37 therefore the frequency of A is 880 vibrations.
c. The frequency of A to the frequency of A440 is 880 by 440(1.0595)0,
we get approximately 2, So the frequency of A is twice to the frequency of A440.
Lesson 8.2 Product of Powers Property
EXPLORATION 1
Finding Products of Powers
Work with a partner.
a. Copy and complete the table. Use your results to write a general rule for finding am • an, a product of two powers with the same base.
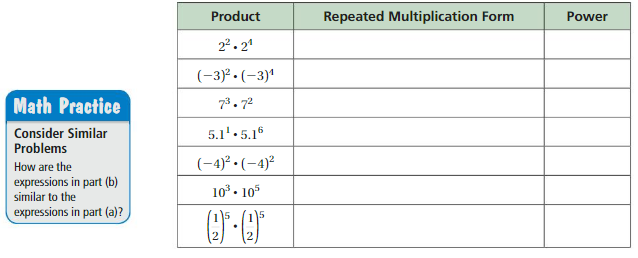
b. Show how to use your rule in part(a) to write each expression below as a single power. Then write a general rule for finding (am)n, a power of a power.
![]()
Answer:
a.
General rule for am • an = am+n a product of two powers with the same base
then powers are added.
b.
(73)2 = 73×2 = 76,
(62)2 = 62×2 = 64,
(32)3 = 32×3 = 36,
(22 )4= 22×4 = 28,
((\(\frac{1}{2}\))2)5 = (\(\frac{1}{2}\))2 x 5 = (\(\frac{1}{2}\))10
General rule for finding (am)n power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n .
Explanation:
a. Completed the table as shown above as Product,
Repeated Multiplication Form and Power as
(22 X 24) = 22+4 = 2 X 2 X 2 X 2 X 2 X 2 = 26
(-3)2 X (-3)4 = (-3)2+4 = -3 X -3 X -3 X -3 X -3 X -3 = (-3)6
73 X 72 = (7)3+2 = 7 X 7 X 7 X 7 X 7 = 75
5.11 X 5.16 = (5.1)1+6 = 5.1 X 5.1 X 5.1 X 5.1 X 5.1 X 5.1 X5.1 =(5.1)7
(-4)2 X (-4)2 = (-4)2+2 = -4 X -4 X -4 X -4 = (-4)4
103 X 105= 103+5 = 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 = 108
(\(\frac{1}{2}\))5 X (\(\frac{1}{2}\))5=(\(\frac{1}{2}\))5+5
=\(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) = (\(\frac{1}{2}\))10
General rule for am • an = am+n a product of two powers with the same base,
powers are added. If two powers have the same base
then we can multiply the powers.
When we multiply two powers we add their exponents.
b. We write (73)2 as 73×2 = 76,
(62)2 as 62×2 = 64,
(32)3 as 32×3 = 36,
(22 )4 as 22×4 = 28,
((\(\frac{1}{2}\))2)5 = (\(\frac{1}{2}\))2 x 5 = (\(\frac{1}{2}\))10
wrote each expression as a single power above,
General rule for finding (am)n a power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n .
EXPLORATION 2
Finding Powers of Products
Work with a partner. Copy and complete the table. Use your results to general rule write a for finding (ab)m, a power of a product.
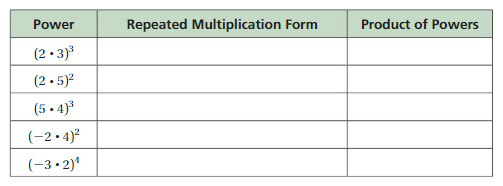
Answer:
Explanation:
Completed the table as shown above as first
Repeated Multiplication Form and Product of Powers as
(2 X 3)3 = 2 X 2 X 2 X 3 X 3 X 3 = 23 X 33
(2 X 5)2 = 2 X 2 X 5 X 5 = 22 X 52
(5 X 4)3 = 5 X 5 X 5 X 4 X 4 X 4 = 53 X 43
(-2 X 4)2 = -2 X -2 X 4 X 4 = -22 X 42
(-3 X 2)4 = -3 X -3 X -3 X -3 X 2 X 2 X 2 X 2 = -34 X 24
We know general rule to write (ab)m power of a product is am X bm
Try It
Simplify the expression. Write your answer as a power.
Question 1.
62 • 64
Answer:
62 • 64 = 66
Explanation:
Given 62 • 64 we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added. As both base are 6 so 62 • 64 = 62+4 = 66
Question 2.
(- \(\frac{1}{2}\))3 • (- \(\frac{1}{2}\))6
Answer:
(- \(\frac{1}{2}\))3 • (- \(\frac{1}{2}\))6 =(- \(\frac{1}{2}\))9
Given (- \(\frac{1}{2}\))3 • (- \(\frac{1}{2}\))6 we have general rule for
am • an = am+n If product of two powers with the same base
then powers are added as both bases are same so (- \(\frac{1}{2}\))3 • (- \(\frac{1}{2}\))6 =
(- \(\frac{1}{2}\))3+6 =(- \(\frac{1}{2}\))9
Question 3.
z • z12
Answer:
z • z12 = z13
Explanation:
Given z • z12 we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, here both bases are z so z • z12 = z1+12= z13
Simplify the expression. Write your answer as a power.
Question 4.
(43)5
Answer:
(43)5 =(4)15
Explanation:
Given (43)5 we have general rule for finding (am)n a power of a power,
If two powers have the same base then we can multiply the
powers as (am)n = am x n . Here both base is 4 so (43)5 =(43x5) = (4)15
Question 5.
(y2)4
Answer:
(y2)4 =(y)8
Explanation:
Given (y2)4 we have general rule for finding (am)n a power of a power,
If two powers have the same base then we can multiply the
powers as (am)n = am x n . Here both base is y so (y2)4 =(y2x4) = (y)8
Question 6.
((- 4)3)2
Answer:
((- 4)3)2 = (-4)6
Explanation:
Given ((- 4)3)2 we use general rule for finding (am)n a power of a power,
If two powers have the same base then we can multiply the
powers as (am)n = am x n . Here both base is 4 so ((- 4)3)2 =(- 4)3x2 = (-4)6
Simplify the expression.
Question 7.
(5y)4
Answer:
(5y)4 = 54 X y4
Explanation:
Given (5y)4 to simplify the expression we use general rule to
write (ab)m power of a product as am X bm ,So (5y)4 = 54 X y4
Question 8.
(ab)5
Answer:
(ab)5= a5 X b5
Explanation:
Given (ab)5 to simplify the expression we use general rule to
write (ab)m power of a product as am X bm ,So (ab)5= a5 X b5
Question 9.
(0.5 mn)2
Answer:
(0.5 mn)2= 0.52 X m2 X n2
Explanation:
Given (0.5 mn)2 to simplify the expression we use general rule to
write (abc)m power of a product as am X bm X cm , So (0.5 mn)2= 0.52 X m2 X n2
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING POWERS Simplify the expression. Write your answer as a power.
Question 10.
47 • 44
Answer:
47 • 44= 411
Explanation:
Given 47 • 44 we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added. So 47 • 44 = 47+4 = 411
Question 11.
(g6)3
Answer:
(g6)3=g18
Explanation:
Given (g6)3 we have general rule for finding (am)n a power of a power,
If two powers have the same base then we can multiply the
powers as (am)n = am x n . So (g6)3= g6x3= g18
Question 12.
(- \(\frac{1}{3}\))5 • (- \(\frac{1}{3}\))7
Answer:
(- \(\frac{1}{3}\))5 • (- \(\frac{1}{3}\))7= (- \(\frac{1}{3}\))12
Explanation:
Given (- \(\frac{1}{3}\))5 • (- \(\frac{1}{3}\))7
we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, here both bases are – \(\frac{1}{3}\) so
(- \(\frac{1}{3}\))5 • (- \(\frac{1}{3}\))7= (- \(\frac{1}{3}\))5+7 = (- \(\frac{1}{3}\))12
FINDING A POWER OF A PRODUCT Simplify the expression.
Question 13.
(8t)4
Answer:
(8t)4 = 84 X t4
Explanation:
Given (8t)4 we have general rule to write (ab)m
power of a product as am X bm therefore (8t)4 = 84 X t4
Question 14.
(yz)6
Answer:
(yz)6= y6 X z6
Explanation:
Given (yz)6 we have general rule to write (ab)m
power of a product as am X bm therefore (yz)6= y6 X z6
Question 15.
(\(\frac{1}{4}\)gh)3
Answer:
(\(\frac{1}{4}\)gh)3= (\(\frac{1}{4}\))3 X g3 X h3
Explanation:
Given (\(\frac{1}{4}\)gh)3 to simplify the expression we use general rule to
write (abc)m power of a product as am X bm X cm , So (\(\frac{1}{4}\)gh)3= (\(\frac{1}{4}\))3 X g3 X h3
Question 16.
CRITICAL THINKING
Can you use the Product of Powers Property to simplify 52 • 64? Explain.
Answer:
No, we can not use the Product of Powers Property to simplify 52 • 64
Explanation:
Given to simplify 52 • 64 as both bases are different
and Product of Powers Property is in general,
for all real numbers we multiply two powers having
the same base we add the exponents but here the bases are different
5,6 so no, we can not use the Product of Powers Property to simplify 52 • 64
Question 17.
OPEN-ENDED
Write an expression that simplifies to x12 using the Product of Powers Property.
Answer:
The expression is x2 X x10 simplifies to x12
Explanation:
Given an expression that simplifies to x12 by
using the Product of Powers Property we write as x12 = x2 X x10
as we know Product of Powers Property is for am • an = am+n
If product of two powers with the same base then
powers are added. As base is x here we have m + n = 12,
so we can take powers (m , n) as (2,10) or (6,6) or (1,11) or (3,9) or
(4,8) or (5,7) or (7,5) or (8,4) or (9,3) or (10,2) or (11,1). So I took (2,10)
as m, n and wrote expression as x2 X x10 = x12 .
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
A newborn blue whale weighs 37 kilograms. An adult blue whale weighs 81 times the weight of the newborn. How many kilograms does the adult blue whale weigh?

Answer:
The adult blue whale weighs 81 X 37 kilograms = 311 kilograms
Explanation:
Given A newborn blue whale weighs 37 kilograms.
An adult blue whale weighs 81 times the weight of the newborn.
So the adult blue whale weighs 81 X 37 kilograms , we write 81 as
multiple of 3 we get 81 = 3 X 3 X 3 X 3, 81 = 34 therefore
81 X 37 kilograms = 34 X 37 kilograms,
when bases are same powers are added
34 X 37 kilograms = 34+7 = 311 kilograms,
therefore the adult blue whale weighs
81 X 37 kilograms = 311 kilograms.
Question 19.
One megabyte of cell phone storage space is 220 bytes. An app uses 44 megabytes of storage space. How many bytes of storage space does the app use?
Answer:
The app used 228 bytes of storage space.
Explanation:
Given One megabyte of cell phone storage space is 220 bytes.
and an app uses 44 megabytes of storage space.
the number of bytes of storage space does the app use is
44 X 220 bytes as 4 we can write as 2 X 2 = 22 (22)4 X 220
44 X 220 = (22)4 X 220 = 28 X 220= 28+20 = 228 bytes.
Question 19.
DIG DEEPER!
The diagram shows the area of a small circular rug. The radius of a large circular rug is 3 times the radius of the small rug. Write an expression for the area of the large rug in terms of x. Justify your answer.

Answer:
The area of the large rug in terms of x is 9πx2 X \(\frac{1}{4}\)
Explanation:
We have area of small circular rug as
A= \(\frac{1}{4}\) X πx2
A = π X (\(\frac{x}{2}\))2
hence the radius of small rug is \(\frac{x}{2}\) and radius
of large rug is \(\frac{3x}{2}\), therefore the area of the
large rug is π X (\(\frac{3x}{2}\))2= 9πx2 X \(\frac{1}{4}\),
therefore the area of the large rug in terms of x is 9πx2 X \(\frac{1}{4}\).
Product of Powers Property Homework & Practice 8.2
Review & Refresh
Write the product using exponents.
Question 1.
11 • 11 • 11 • 11 • 11
Answer:
11 • 11 • 11 • 11 • 11 = 115
Explanation:
Given 11 • 11 • 11 • 11 • 11 as 11 is multiplied by 5 times
we write as 11 • 11 • 11 • 11 • 11 = 115
Question 2.
(- 6) • (- 6) • (- 6) • z • z
Answer:
(- 6) • (- 6) • (- 6) • z • z = (-6)3 X z2
Explanation:
Given (- 6) • (- 6) • (- 6) • z • z we have -6 multiplied
by 3 times and z twice so write the product as
(- 6) • (- 6) • (- 6) • z • z = (-6)3 X z2
Find the value of for the given value of x.
Question 3.
y = – 4x; x = 7
Answer:
y= -28
Explanation:
Given y = -4x and value of x as 7,
we substitute x as y = -4 X 7, So y = -28.
Question 4.
y = 5x + 6; x = – 2
Answer:
y= -4
Explanation:
Given y= 5x + 6 and value of x as -2,
we substitute x as y= 5 X -2 + 6 = -10 + 6 = -4,
therefore y = -4.
Question 5.
y = 10 – 3x ; x = 3
Answer:
y=1
Explanation:
Given y= 10 – 3x and value of x as 3,
we substitute x as y= 10 – 3 X 3 = 10 – 9 = 1,
therefore y =1.
Question 6.
What is the measure of each interior angle of the regular polygon?
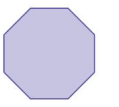
A. 45°
B. 135°
C. 1080°
D. 1440°
Answer:
The measure of each interior angle of the
regular polygon given is B.135°.
Explanation:
We know each Angle (of a Regular Polygon) =
(n−2) × 180° / n where n is number of sides
in the given figure we 8 sides so n is 8,
the measure of each interior angle is (8-2) X 180° / 8=
6 X 180° / 8 = 135° . So the measure of each
interior angle of the regular polygon given is B.135°.
Concepts, Skills, &Problem Solving
FINDING PRODUCTS OF POWERS Write the expression in repeated multiplication form. Then write the expression as a power. (See Exploration 1, p. 325.)
Question 7.
56 • 53
Answer:
56 • 53 = 5 X 5 X 5 X 5 X 5 X 5 X 5 X 5 X 5 = 59
Explanation:
Given 56 • 53 the expression in repeated multiplication form is
5 X 5 X 5 X 5 X 5 X 5 X 5 X 5 X 5 and expression as power
is 56 • 53= 56+3 = 59
Question 8.
(64)2
Answer:
(64)2 = 6 X 6 X 6 X 6 X 6 X 6 X 6X 6 = 68
Explanation:
Given (64)2 the expression in repeated multiplication form is
6 X 6 X 6 X 6 X 6 X 6 X 6 X 6 and expression as power
is (64)2 = 64×2 = 68
Question 9.
(- 8)3 • (- 8)4
Answer:
(- 8)3 • (- 8)4= (- 8)7
Explanation:
Given (- 8)3 • (- 8)4 the expression in repeated multiplication form is
-8 X -8 X -8 X -8 X -8 X -8 X -8 and expression as power
is (- 8)3 • (- 8)4= (- 8)3+4 = (- 8)7
FINDING POWERS Simplify the expression. Write your answer as a power.
Question 10.
32 • 32
Answer:
32 • 32 = 34
Explanation:
We write the given 32 • 32 expression as a power,
so 32 • 32 as bases are same 3 powers are added 32+2 = 34
Question 11.
810 • 84
Answer:
810 • 84 = 814
Explanation:
We write the given 810 • 84 expression as a power,
here 810 • 84 has same bases 8 so same powers are
added as 810+4 = 814
Question 12.
(54)3
Answer:
(54)3 = (5)12
Explanation:
We write the given expression (54)3 as a power,
so (54)3 has powers of powers therefore powers
are multiplied as (5)4 x 3 = 512
Question 13.
((- 3)2)4
Answer:
((- 3)2)4 = (- 3)8
Explanation:
We write the given expression ((- 3)2)4 as a power,
so ((- 32)4 has powers of powers therefore powers
are multiplied as (-3)2 x 4 = (-3)8
Question 14.
(- 4)5 • (- 4)7
Answer:
(- 4)5 • (- 4)7= (- 4)12
Explanation:
We write the given expression (- 4)5 • (- 4)7 as a power,
here (- 4)5 • (- 4)7 has same bases -4 so same powers are
added as (- 4)5+7 = (- 4)12.
Question 15.
h6 • h
Answer:
h6 • h = h7
Explanation:
We write the given expression h6 • h as a power,
here h6 • h has same bases h so same powers are
added as (h)6+1 = (h)7.
Question 16.
(b12)3
Answer:
(b12)3 = (b)36
Explanation:
We write the given expression (b12)3 as a power,
so (b12)3 has powers of powers therefore powers
are multiplied as (b)12 x 3 = (b)36
Question 17.
(\(\frac{2}{3}\))2 • (\(\frac{2}{3}\))6
Answer:
(\(\frac{2}{3}\))2 • (\(\frac{2}{3}\))6= (\(\frac{2}{3}\))8
Explanation:
We write the given expression (\(\frac{2}{3}\))2 • (\(\frac{2}{3}\))6
as a power, here (\(\frac{2}{3}\))2 • (\(\frac{2}{3}\))6
has same bases so same powers are added as (\(\frac{2}{3}\))2+6
= (\(\frac{2}{3}\))8
Question 18.
(3.83)4
Answer:
(3.83)4= (3.8)12
Explanation:
We write the given expression (3.83)4 as a power,
so (3.83)4 has powers of powers therefore powers
are multiplied as (3.8)3 x 4 = (3.8)12
Question 19.
(n3)5
Answer:
(n3)5 = (n)15
Explanation:
We write the given expression (n3)5 as a power,
so (n3)5 has powers of powers therefore powers
are multiplied as (n)3 X 5= (n)15
Question 20.
((- \(\frac{3}{4}\))5)2
Answer:
((- \(\frac{3}{4}\))5)2= (- \(\frac{3}{4}\))10
Explanation:
We write the given expression ((- \(\frac{3}{4}\))5)2 as a power,
so ((- \(\frac{3}{4}\))5)2 has powers of powers therefore powers
are multiplied as (- \(\frac{3}{4}\))5 x 2= (- \(\frac{3}{4}\))10
Question 21.
(- \(\frac{1}{2}\))8 • (- \(\frac{1}{2}\))9
Answer:
(- \(\frac{1}{2}\))8 • (- \(\frac{1}{2}\))9= (- \(\frac{1}{2}\))17
Explanation:
We write the given expression (-\(\frac{1}{2}\))8 • (- \(\frac{1}{2}\))9
as a power, here (-\(\frac{1}{2}\))8 • (- \(\frac{1}{2}\))9
has same bases so same powers are added as (-\(\frac{1}{2}\))8+9
= (-\(\frac{1}{2}\))17
YOU BE THE TEACHER Your friend simplifies the expression.
Is your friend correct? Explain your reasoning.
Question 22.
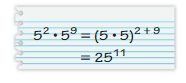
Answer:
No, Friend is in correct as 52 X 59 = 511 not 2511
Explanation:
Given expression is 52 X 52
here as base is same 5 we add powers
as 52+9 we get 511 not 2511
Question 23.
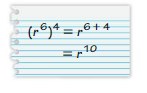
Answer:
No, friend is In correct as (r6)4= (r)6 x 4 = (r)24 not r10
Explanation:
Given expression is (r6)4 here we have
powers of powers therefore powers
are multiplied not added so (r6)4= (r)6 x 4 = (r)24
not r10 therefore friend is incorrect.
FINDING A POWER OF A PRODUCT Simplify the expression.
Question 24.
(6g)3
Answer:
(6g)3 = 216 g3
Explanation:
Given (6g)3 we simplify as 63 X g3= 6 X 6 X 6 X g X g X g
= 216 g3 here we multiplied 6 by 3 times and g by
3 times as both has power 3.
Question 25.
(- 3v)5
Answer:
(- 3v)5 = -243v5
Explanation:
Given (-3v)5 we simplify as
– 3 X -3 X -3 X -3 X -3 X v X v X v X v X v = -243v5,
here we multiplied -3 and v by
5 times as power for both is 5.
Question 26.
(\(\frac{1}{5}\)k)2
Answer:
(\(\frac{1}{5}\)k)2 = \(\frac{1}{25}\)k2
Explanation:
Given expression (\(\frac{1}{5}\)k)2 we simplify as
\(\frac{1}{5}\) X \(\frac{1}{5}\) X k X k = \(\frac{1}{25}\)k2
here we multiply \(\frac{1}{5}\) and k
by 2 times as power for both is 2.
Question 27.
(1.2 m)4
Answer:
(1.2 m)4 = 2.0736m4
Explanation:
Given expression as (1.2 m)4 we simplify as
1.2 X 1.2 X 1.2 X m X m X m X m is 2.0736m4
here we multiply 1.2 and m by 4 times as
power for both is 4.
Question 28.
(rt)12
Answer:
(rt)12 = r12 X t12
Explanation:
Given expression as (rt)12 we simplify as
r X r X r X r X r X r X r X r X r X r X r X r X
t X t X t X t X t X t X t X t X t X t X t X t is r12 X t12
here we multiply r and t by 12 times as
power for both is 12.
Question 29.
(- \(\frac{3}{4}\)p)3
Answer:
(- \(\frac{3}{4}\)p)3 = –\(\frac{27}{64}\)p3
Explanation:
Given expression as (- \(\frac{3}{4}\)p)3 we simplify as
– \(\frac{3}{4}\) X – \(\frac{3}{4}\) X – \(\frac{3}{4}\) X p X p X p is
–\(\frac{27}{64}\)p3
here we multiply –\(\frac{3}{4}\) and p by 3 times as
power for both is 3.
Question 30.
PRECISION
Is 32 + 33 equal to 35? Explain.
Answer:
No,32 + 33 is not equal to 35
Explanation:
Given expression is 32 + 33 first we solve
32 as 3 X 3 = 9 and 33 = 3 X 3 X 3 = 27 so
32 + 33= 9 + 27 = 36 now we have 35 which is
equal to 3 X 3 X 3 X 3 X 3 = 243 as 36 ≠ 243 so
no, 32 + 33 ≠ 35
Question 31.
PROBLEM SOLVING
A display case for the artifact shown is in the shape of a cube. Each side of the display case is three times longer than the width w of the artifact.

a. Write a power that represents the volume of the case.
b. Simplify your expression in part(a).
Answer:
a. The volume of the case is (3w)3.
b. Simplified form is 27w3.
Explanation:
Given a display case for the artifact shown
is in the shape of a cube. Each side of the display
case is three times longer than the width w of the artifact.
a. we have volume of cube as (edge)3
So the volume of the case = 3w X 3w X 3w = (3w)3.
b. Simplified form of (3w)3= 3 X 3 X 3 X w X w X w = 27w3.
Question 32.
LOGIC
Show that (3 • 8 • x)7 = 67 • 47 • x7.
Answer:
(3 • 8 • x)7 = ( 37 X 27) X 47 X x7 = 67 x 47 x x7
Explanation:
Given expression is (3 • 8 • x)7 we write 8 as
multiple of 2 X 4 so (3 X 2 X 4 X x)7
and now we multiply first 3 and 2 as (6 X 4 X x)7
we simplify we get 67 x 47 x x7
So (3 • 8 • x)7 = 67 • 47 • x7.
Question 33.
MODELING REAL LIFE
The lowest altitude of an altocumulus cloud is about 38 feet. The highest altitude of an altocumulus cloud is about 3 times the lowest altitude. What is the highest altitude of an altocumulus cloud? Write your answer as a power.
Answer:
The highest altitude of an altocumulus cloud is
3 X 38= 39 feet.
Explanation:
Given The lowest altitude of an altocumulus cloud is
about 38 feet. The highest altitude of an altocumulus cloud is
about 3 times the lowest altitude. So the highest altitude
of an altocumulus cloud is 3 X 38 as bases are same
powers are added 31+8 = 39 feet.
Question 34.
GEOMETRY
A square pyramid has a height h and a base with side lengths. The side lengths of the base increase by 50%. Write a formula for the volume of the new pyramid in terms of s and h.
Answer:
The formula for the volume of the
new pyramid is terms of s and h is 3s2h by 4.
Explanation:
Given a square pyramid has a height h and
a base with side lengths. The side lengths
of the base increase by 50%. So volume is
s2\(\frac{h}{3}\) and side length s
increases by 50%, so s + 50%s = s + \(\frac{50}{100}\)s
= s + \(\frac{1}{2}\)s = \(\frac{3s}{2}\).
The new volume is (\(\frac{3s}{2}\))2 X \(\frac{h}{3}\)
= 9s2 X \(\frac{h}{12}\) = 3s2h by 4
therefore the formula for the volume of the
new pyramid is terms of s and h is 3s2h by 4.
Question 35.
MODELING REAL LIFE
The United States Postal Service delivers about 24 • 3 • 53 pieces of mail each second. There are 28 • 34 • 52 seconds in 6 days. How many pieces of mail does the United States Postal Service deliver in 6 days? Write your answer as an expression involving three powers.

Answer:
Number of pieces of mails does the United States Postal Service
deliver in 6 days is 212 X 35 X 55 .
Explanation:
Given the United States Postal Service delivers about
24 • 3 • 53 pieces of mail each second. There are 28 • 34 • 52
seconds in 6 days. so number of pieces of mail does
the United States Postal Service deliver in 6 days is
24 X 3 X 53 X 28 X 34 X 52 we add the same bases power we get
24 X 28 X 3 X 34 X 53 X 52 as 24+8 X 31+4 X 53+2
= 212 X 35 X 55 therefore number of pieces of mails
does the United States Postal Service
deliver in 6 days is 212 X 35 X 55 .
Question 36.
REASONING
The row numbers y and column numbers x of a chessboard are shown. Each position on the chessboard has a stack of pennies. (Only the first row is shown.) The number of pennies in each stack is 2x • 2y.

a. Which locations have 32 pennies in their stacks?
b. How much money (in dollars) is in the location with the tallest stack?
c. A penny is about 0.06 inch thick. About how tall is the tallest stack?
Answer:
a. The locations are the combinations of (x,y)=
(1,4),(2,3),(3,2),(4,1).
b. $655.36 is the money in the location with the tallest stack.
c. The tallest stack is 3932.16 inches.
Explanation:
The row numbers y and column numbers x,
The number of pennies in each stack is 2x • 2y
a. The locations that have 32 pennies in their stacks is
2x • 2y = 32 we write 32 as power of 2 we get
2x • 2y = 25 we write 2x • 2y (bases are same powers are added)
as 2x+y = 25 therefore x + y = 5, So the locations
are the combinations of (x, y)= (1,4),(2,3),(3,2),(4,1).
b. The tallest stack will be in the location of (8,8)
so the maximum combination is 28 X 28 = 28+8 = 216
= 65536 pennies. Now converting pennies into dollar
1 penny = 0.01 dollar so 65536 X 0.01 = $655.36,
therefore $655.36 is the money in the location
with the tallest stack.
c. Given each penny is about 0.06 inch thick
the tallest stack is 65536 X 0.06 = 3932.16 inches.
Question 37.
CRITICAL THINKING
Find the value of x in the equation without evaluating the power.
![]()
Answer:
a. x = 3
b. x = 4
Explanation:
a. Given 25 X 2x = 256, we write 256 as 28,
so 25 X 2x = 25 + x = 28 , 5 + x = 8 so x = 8 – 5,
therefore x = 3.
b. Given (\(\frac{1}{3}\))2 X (\(\frac{1}{3}\))x = \(\frac{1}{729}\)
\(\frac{1}{729}\) as multiple of \(\frac{1}{3}\) we get
\(\frac{1}{729}\) as (\(\frac{1}{3}\)))6 so (\(\frac{1}{3}\))2 X (\(\frac{1}{3}\))x = (\(\frac{1}{3}\)))6 as bases are same
we equate powers as 2 + x = 6 therefore x = 6 – 2 = 4, So X = 4.
Lesson 8.3 Quotient of Powers Property
EXPLORATION 1
Finding Quotients of Powers
Work with a partner.
a. Copy and complete the table. Use your results to write a general rule for finding \(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base.
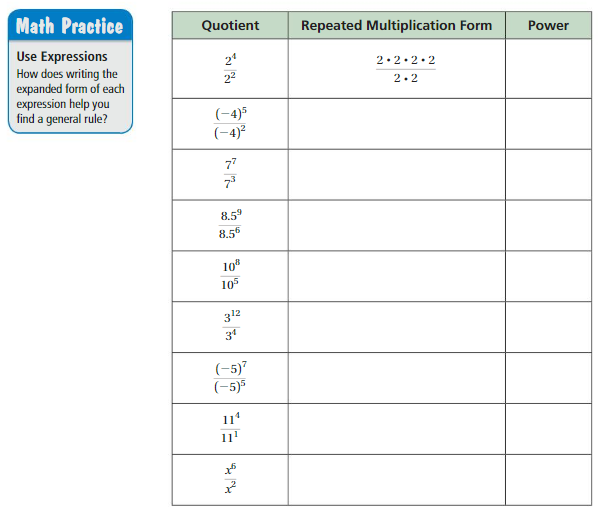
b. Use your rule in part(a) to simplify the quotients in the first column of the table above. Does your rule give the results in the third column?
Answer:
a. 
The general rule for finding \(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base is am-n
b. Yes my rule gives the result in third column.
Explanation:
a. Completed the given table as shown above.
We use the general rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base is am-n .
b. We use part(a) rule to simplify the quotients in
the first column of the table above
and rule gives the results in the third column as
\(\frac{2^{4}}{2^{2}}\) =24-2 = 22
\(\frac{-4^{5}}{-4^{2}}\) = (-4)5-2 = (-4)3
\(\frac{7^{7}}{7^{3}}\) = 77-3 = 74
\(\frac{8.5^{9}}{8.5^{6}}\) = (8.5)9-6 = (8.5)3
\(\frac{10^{8}}{10^{5}}\) = 108-5 = 103
\(\frac{3^{12}}{3^{4}}\) = 312-4 = 38
\(\frac{-5^{7}}{-5^{5}}\) = (-5)7-2 =(-5)2
\(\frac{11^{4}}{11^{1}}\) = 114-1 =113
\(\frac{x^{6}}{x^{2}}\) = x6 – 2= x4
Try It
Simplify the expression. Write your answer as a power.
Question 1.
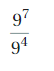
Answer:
\(\frac{9^{7}}{9^{4}}\) = 97-4 = 93
Explanation:
Given \(\frac{9^{7}}{9^{4}}\) we use rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base as am-n
so \(\frac{9^{7}}{9^{4}}\) = 97-4 = 93
Question 2.
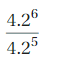
Answer:
\(\frac{4.2^{6}}{4.2^{5}}\) = 4.26-5 = 4.21 = 4.2
Explanation:
Given \(\frac{4.2^{6}}{4.2^{5}}\) we use rule for finding \(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
so \(\frac{4.2^{6}}{4.2^{5}}\) = 4.26-5 = 4.21 = 4.2
Question 3.
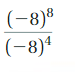
Answer:
\(\frac{-8^{8}}{-8^{4}}\) = (-8)8-4 = (-8)4
Explanation:
Given \(\frac{-8^{8}}{-8^{4}}\) we use rule for finding \(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
so \(\frac{-8^{8}}{-8^{4}}\) = (-8)8-4 = (-8)4
Question 4.
![]()
Answer:
\(\frac{x^{8}}{x^{3}}\) = (x)8-3 = (x)5
Explanation:
Given \(\frac{x^{8}}{x^{3}}\) we use rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base as am-n
so \(\frac{x^{8}}{x^{3}}\) = (x)8-3 = (x)5
Simplify the expression. Write your answer as a power.
Question 5.
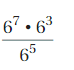
Answer:
\(\frac{6^{7}}{6^{5}}\) X 63 = 65
Explanation:
Given \(\frac{6^{7}}{6^{5}}\) X 63 we use rule for finding \(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
first we solve \(\frac{6^{7}}{6^{5}}\) = = 67-5 = 62
and now we multiply by = 62 X 63 as bases are same 6 now
we add powers as = 62+3 = 65
therefore \(\frac{6^{7}}{6^{5}}\) X 63 = 65
Question 6.
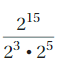
Answer:
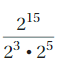 = 27
= 27
Explanation:
First we multiply denominators as bases are same
we add powers so 23 X 25 = 23+5 = 28
now we solve \(\frac{2^{15}}{2^{8}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{2^{15}}{2^{8}}\) = 215-8 = 27
therefore 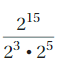 = 27
= 27
Question 7.
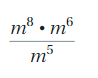
Answer:
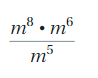 = m9
= m9
Explanation:
First we multiply numerators as bases are same
we add powers so m8 X m6 = m8+6 = m14
now we solve \(\frac{m^{14}}{m^{5}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{m^{14}}{m^{5}}\) = m14-5 = m9
Simplify the expression. Write your answer as a power.
Question 8.
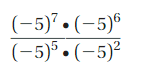
Answer:
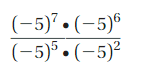 = (-5)6
= (-5)6
Explanation:
First we calculate separately values of numerators
and denominators then divide , we have numerator (-5)7 X (-5)6
we have same bases as -5 so we add powers as (-5)7+6 = (-5)13
we have denominator (-5)5 X (-5)2
we have same base as -5 so we add powers as (-5)5+2 = (-5)7
Now we have \(\frac{-5^{13}}{-5^{7}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\), a quotient of
two powers with the same base as am-n
\(\frac{-5^{13}}{-5^{7}}\) = (-5)13-7 = (-5)6
Question 9.
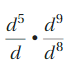
Answer:
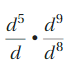 = d5
= d5
Explanation:
First we calculate separately values of numerators
and denominators then divide , we have numerator (d)5 X (d)9
we have same bases as d so we add powers as (d)5+9 = (d)14
we have denominator (d) X (d)8
we have same base as d so we add powers as (d)1+8 = (d)9
Now we have \(\frac{d^{14}}{d^{9}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\), a quotient of
two powers with the same base as am-n
\(\frac{d^{14}}{d^{9}}\) = (d)14-9 = d5
Question 10.
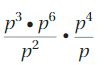
Answer:
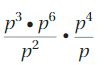 = p10
= p10
Explanation:
First we calculate separately values of numerators
and denominators then divide , we have numerator (p)3 X (p)6 X (p)4
we have same bases as p so we add powers as (p)3+6+4 = (d)13
we have denominator (p)2 X (p)
we have same bases as p so we add powers as (p)2+1 = (p)3
Now we have \(\frac{p^{13}}{p^{3}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{p^{13}}{p^{3}}\) = (p)13-3 = p10
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SIMPLIFYING EXPRESSIONS Simplify the expression. Write your answer as a power.
Question 11.
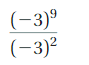
Answer:
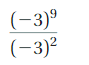 = (-3)7
= (-3)7
Explanation:
Given \(\frac{-3^{9}}{-3^{2}}\) we use rule for
finding \(\frac{a^{m}}{a^{n}}\), a quotient of two
powers with the same base as am-n
so \(\frac{-3^{9}}{-3^{2}}\) = (-3)9-2 = (-3)7
Question 12.
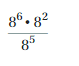
Answer:
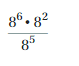 = (8)3
= (8)3
Explanation:
First we calculate separately values of numerators
and denominators then divide , we have numerator (8)6 X (8)2
we have same bases as d so we add powers as (8)6+2 = (8)8
\(\frac{8^{8}}{8^{5}}\) we use rule for
finding \(\frac{a^{m}}{a^{n}}\), a quotient of two
powers with the same base as am-n
so \(\frac{8^{8}}{8^{5}}\) = (8)8-5 = (8)3
Question 13.
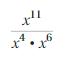
Answer:
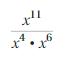 = x
= x
Explanation:
First we multiply denominators as bases are same
we add powers so x4 X x6 = x4+6 = x10
now we solve \(\frac{x^{11}}{x^{10}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{x^{11}}{x^{10}}\) = x11-10 = x
Question 14.
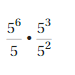
Answer:
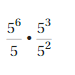 = 56
= 56
Explanation:
First we calculate separately values of numerators
and denominators then divide , we have numerator (5)6 X (5)3
we have same bases as 5 so we add powers as (5)6+3 = (5)9
we have denominator 5 X (5)2
we have same bases as 5 so we add powers as (5)1+2 = (5)3
Now we have \(\frac{5^{9}}{5^{3}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{5^{9}}{5^{3}}\) = (5)9-3 = 56
Question 15.
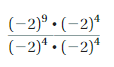
Answer:
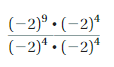 = (-2)5
= (-2)5
Explanation:
First we calculate separately values of numerators
and denominators then divide , we have numerator (-2)9 X (-2)4
we have same bases as -2 so we add powers as (-2)9+4 = (-2)13
we have denominator (-2)4 X (-2)4
we have same base as -2 so we add powers as (-2)4+4 = (-2)8
Now we have \(\frac{-2^{13}}{-2^{8}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\), a quotient of two
powers with the same base as am-n
\(\frac{-2^{13}}{-2^{8}}\) = (-2)13-8 = (-2)5
Question 16.
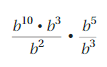
Answer:
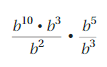 = b13
= b13
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (b)10 X (b)3 X (b)5
we have same bases as b so we add powers as (b)10+3+5 = (b)18
we have denominator (b)2 X (b)3
we have same base as b so we add powers as (b)2+3 = (b)5
Now we have \(\frac{b^{18}}{b^{5}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{b^{18}}{b^{5}}\) = (b)18-5 = b13
Question 17.
WHICH ONE DOESN’T BELONG?
Which quotient does not belong with the other three? Explain your reasoning.
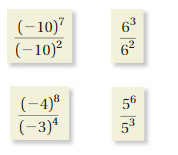
Answer:
\(\frac{-4^{8}}{-3^{4}}\) does not belongs with the other three.
Explanation:
Given \(\frac{-10^{7}}{-10^{2}}\) have same base -10,
\(\frac{6^{3}}{6^{2}}\) have same base 6,
\(\frac{5^{6}}{5^{3}}\) have same base 5 but
\(\frac{-4^{8}}{-3^{4}}\) has different bases -4 and -3,
So, \(\frac{-4^{8}}{-3^{4}}\) does not belongs with the other three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
You want to purchase a cat tracker. Tracker A detects your cat within a radius of 4 • 102 feet of your home. Tracker B detects your cat within a radius of 104 feet of your home. Which tracker has a greater radius? How many times greater?

Answer:
Tracker B has greater radius than Tracker A and
Tracker B is greater by radius of 9,600 feet.
Explanation:
Given Tracker A detects your cat within a radius of 4 • 102 feet of your home.
Tracker B detects your cat within a radius of 104 feet of your home,
Tracker A = 4 X 102 = 4 X 100 = 400 feet
Tracker B = 104 feet = 10 X 10 X 10 X 10 = 10,000 feet as
comparing Tracker A and Tracker B,Tracker B is greater than Tracker A,
by 10,000 – 400 = 9,600 feet, therfore Tracker B
has greater radius than Tracker A and
Tracker B is greater by radius of 9,600 feet.
Question 19.
DIG DEEPER!
An earthquake of magnitude 3.0 is 102 times stronger than an earthquake of magnitude 1.0. An earthquake of magnitude 8.0 is 107 times stronger than an earthquake of magnitude 1.0. How many times stronger is an earthquake of magnitude 8.0 than an earthquake of magnitude 3.0?
Answer:
105 times stronger is an earthquake of magnitude 8.0
more than an earthquake of magnitude 3.0.
Explanation:
Given an earthquake of magnitude 3.0 is 102 times
stronger than an earthquake of magnitude 1.0 and
an earthquake of magnitude 8.0 is 107 times stronger
than an earthquake of magnitude 1.0. So how many times
stronger is an earthquake of magnitude 8.0 than an
earthquake of magnitude 3.0 is \(\frac{10^{7}}{10^{2}}\) ,
so we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
as \(\frac{10^{7}}{10^{2}}\) = 107-2 = 105
therefore 105 times stronger is an earthquake of magnitude 8.0
more than an earthquake of magnitude 3.0.
Question 20.
The edge length of a cube-shaped crate is the square of the edge length of a cube-shaped box. Write an expression for the number of boxes that can fit in the crate. Justify your answer.
Answer:
The number of boxes that fit in the crate is x3
Explanation:
Let the edge be x, So the volume of box is V = x3
Given the edge length of a cube-shaped crate is the square of the
edge length of a cube-shaped box so
the volume crate with side equal to the side of the box x2 = ( x2)3
we use general rule for finding (am)n a power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n so ( x2)3 = x2 x 3=( x)6
The number of boxes that fit in crate is
\(\frac{x^{6}}{x^{3}}\) now we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
therefore \(\frac{x^{6}}{x^{3}}\) = x6-3 = x3
so the number of boxes that fit in the crate is x3
Quotient of Powers Property Homework & Practice 8.3
Review & Refresh
Simplify the expression. Write your answer as a power.
Question 1.
42 • 43
Answer:
42 • 43 = 45
Explanation:
Given expression as 42 • 43
we use general rule for am • an = am+n a product of
two powers with the same base then powers are added.
So 42 • 43 = 42+3 = 45
Question 2.
(a5)5
Answer:
(a5)5 = a25
Explanation:
Given expression is (a5)5 we have general rule for
finding (am)n a power of a power, If two powers have the
same base then we can multiply the
powers as (am)n = am x n . So (a5)5 = a5X5 = a25 .
Question 3.
(xy)7
Answer:
(xy)7= x7 X y7 = x7 y7
Explanation:
Given expression as (xy)7as both as same
power 7 we write as x7 X y7 = x7 y7
The red figure is similar to the blue figure. Describe a similarity transformation between the figures.
Question 4.
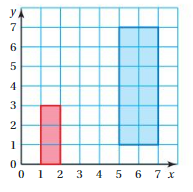
Answer:
Similarity between two figures is
dilate the red figure using a scale factor of 2:3
and then reflect the image in the x- axis.
Explanation:
By comparing the side lengths, we can see that
the blue figure is 2:3 the size of red figure,
Similarity between two figures is dilate the red figure
using a scale factor of 2:3 and then reflect the image in the x- axis.
Question 5.
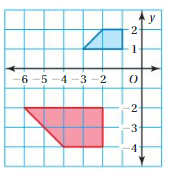
Answer:
Similarity between two figures is
dilate the red figure using a scale factor of 1/2
and then reflect the image in the x- axis.
Explanation:
By comparing the side lengths, we can see that
the blue figure is one-half the size of red figure,
Similarity between two figures is dilate the red figure
using a scale factor of 1/2 and then reflect the image in the x- axis.
Concepts, Skills, & Problem Solving
FINDING QUOTIENTS OF POWERS Write the quotient as repeated multiplication. Then write the quotient as a power.(See Exploration 1, p. 331.)
Question 6.
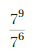
Answer:
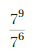 = \(\frac{7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7}{7 X 7 X 7 X 7 X 7 X 7}\) = 73
= \(\frac{7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7}{7 X 7 X 7 X 7 X 7 X 7}\) = 73
Explanation:
Given \(\frac{7^{9}}{7^{6}}\) the repeated multiplication is
\(\frac{7 X 7 X 7 X 7 X 7 X 7 X 7 X 7 X 7}{7 X 7 X 7 X 7 X 7 X 7}\) and
the quotient as a power we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n,so \(\frac{7^{9}}{7^{6}}\) is 79-6 = 73
Question 7.
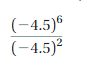
Answer:
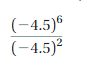 = \(\frac{-4.5 X -4.5 X -4.5 X -4.5 X -4.5 X -4.5}{-4.5 X -4.5}\) = (-4.5)4.
= \(\frac{-4.5 X -4.5 X -4.5 X -4.5 X -4.5 X -4.5}{-4.5 X -4.5}\) = (-4.5)4.
Explanation:
Given \(\frac{-4.5^{6}}{-4.5^{2}}\) the repeated multiplication is
\(\frac{-4.5 X -4.5 X -4.5 X -4.5 X -4.5 X -4.5}{-4.5 X -4.5}\) and
the quotient as a power we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n ,so \(\frac{-4.5^{6}}{-4.5^{2}}\)
is (-4.5)6-2 = (-4.5)4.
Question 8.
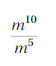
Answer:
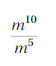 = \(\frac{m X m X m X m X m X m X m X m X m X m}{m X m X m X m X m }\) = m5
= \(\frac{m X m X m X m X m X m X m X m X m X m}{m X m X m X m X m }\) = m5
Explanation:
Given \(\frac{m^{10}}{m^{5}}\) the repeated multiplication is
and \(\frac{m X m X m X m X m X m X m X m X m X m}{m X m X m X m X m }\)
the quotient as a power we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{m^{10}}{m^{5}}\)
is (m)10-5 = m5.
DIVIDING POWERS WITH THE SAME BASE Simplify the expression. Write your answer as a power.
Question 9.
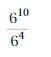
Answer:
\(\frac{6^{10}}{6^{4}}\) = 66.
Explanation:
As given expression is \(\frac{6^{10}}{6^{4}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{6^{10}}{6^{4}}\) =
(6)10-4 = 66.
Question 10.
![]()
Answer:
\(\frac{8^{9}}{8^{7}}\) = 82.
Explanation:
As given expression is \(\frac{8^{9}}{8^{7}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{8^{9}}{8^{7}}\) =
(8)9-7 = 82.
Question 11.
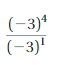
Answer:
\(\frac{-3^{4}}{-3^{1}}\) = -33.
Explanation:
As given expression is \(\frac{-3^{4}}{-3^{1}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{-3^{4}}{-3^{1}}\) =
(-3)4-1 = -33.
Question 12.
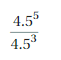
Answer:
\(\frac{4.5^{5}}{4.5^{3}}\) = 4.52.
Explanation:
As given expression is \(\frac{4.5^{5}}{4.5^{3}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{4.5^{5}}{4.5^{3}}\) =
(4.5)5-3 = 4.52.
Question 13.
![]()
Answer:
\(\frac{64^{4}}{64^{3}}\) = 64.
Explanation:
As given expression is \(\frac{64^{4}}{64^{3}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{64^{4}}{64^{3}}\) =
(64)4-3 = 64.
Question 14.
Answer:
\(\frac{-17^{5}}{-17^{2}}\) = (-17)3.
Explanation:
As given expression is \(\frac{-17^{5}}{-17^{2}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{-17^{5}}{-17^{2}}\) =
(-17)5-2 = (-17)3.
Question 15.
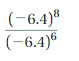
Answer:
\(\frac{-6.4^{8}}{-6.4^{6}}\) = (-6.4)2.
Explanation:
As given expression is \(\frac{-6.4^{8}}{-6.4^{6}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{-6.4^{8}}{-6.4^{6}}\) =
(-6.4)8-6 = (-6.4)2.
Question 16.
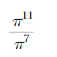
Answer:
\(\frac{π^{11}}{π^{7}}\) = π4.
Explanation:
As given expression is \(\frac{π^{11}}{π^{7}}\) we use
rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{π^{11}}{π^{7}}\)=
(π)11-7 = π4.
Question 17.
YOU BE THE TEACHER
Your friend simplifies the quotient. Is your friend correct? Explain your reasoning.

Answer:
No, friend is incorrect as \(\frac{6^{15}}{6^{5}}\) = 610 ≠ 63
Explanation:
Given \(\frac{6^{15}}{6^{5}}\) as per rule finding
\(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{6^{15}}{6^{5}}\) = 615-5
= 610 but friend says \(\frac{6^{15}}{6^{5}}\) = 615/5= 63
which is incorrect therefore \(\frac{6^{15}}{6^{5}}\) = 610 ≠ 63
exponents should be subtracted not divided.
SIMPLIFYING AN EXPRESSION Simplify the expression. Write your answer as a power.
Question 18.
\(\frac{7^{5} \cdot 7^{3}}{7^{2}}\)
Answer:
\(\frac{7^{5} \cdot 7^{3}}{7^{2}}\) = 76.
Explanation:
Given Expression as \(\frac{7^{5} \cdot 7^{3}}{7^{2}}\)
first we calculate separately values of numerators
then divide with denominator, we have numerator (7)5 X (7)3
we have same bases as 7 so we add powers as (7)5+3 = (7)8
Now we have \(\frac{7^{8}}{7^{2}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{7^{8}}{7^{2}}\) = (7)8-2 = 76
Question 19.
\(\frac{6^{13}}{6^{4} \cdot 6^{2}}\)
Answer:
\(\frac{6^{13}}{6^{4} \cdot 6^{2}}\) = 67
Explanation:
Given expression \(\frac{6^{13}}{6^{4} \cdot 6^{2}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator (6)4 X (6)2
we have same bases as 6 so we add powers as (6)4+2 = (6)6
Now we have \(\frac{6^{13}}{6^{6}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{6^{13}}{6^{6}}\) = (6)13-6 = 67
Question 20.
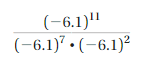
Answer:
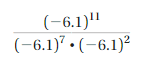 = = (-6.1)2
= = (-6.1)2
Explanation:
Given expression \(\frac{-6.1^{11}}{-6.1^{7} \cdot -6.1^{2}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator (-6.1)7 X (-6.1)2
we have same bases as -6.1 so we add powers as (-6.1)7+2 = (-6.1)9
Now we have \(\frac{-6.1^{11}}{-6.1^{9}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{-6.1^{11}}{-6.1^{9}}\) = (-6.1)11-9 = (-6.1)2
Question 21.
\(\frac{\pi^{30}}{\pi^{18} \cdot \pi^{4}}\)
Answer:
\(\frac{\pi^{30}}{\pi^{18} \cdot \pi^{4}}\) = (π)8
Explanation:
Given expression is \(\frac{\pi^{30}}{\pi^{18} \cdot \pi^{4}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator (π)18 X (π)4
we have same bases as π so we add powers as (π)18+4 = (π)22
Now we have \(\frac{\pi^{30}}{\pi^{22} \) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{\pi^{30}}{\pi^{22} \) = (π)30-22 = π8
Question 22.
\(\frac{c^{22}}{c^{8} \cdot c^{9}}\)
Answer:
\(\frac{c^{22}}{c^{8} \cdot c^{9}}\) = c5
Explanation:
Given expression is \(\frac{c^{22}}{c^{8} \cdot c^{9}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator c8 X c9
we have same bases as c so we add powers as c8+9 = c17
Now we have \(\frac{c^{22}} {c^{17}} \) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{c^{22}} {c^{17}} \) = c22-17 = c5
Question 23.
\(\frac{z^{8} \cdot z^{6}}{z^{8}}\)
Answer:
\(\frac{z^{8} \cdot z^{6}}{z^{8}}\) = z6
Explanation:
Given expression is \(\frac{z^{8} \cdot z^{6}}{z^{8}}\)
first we calculate separately values of numerators
then divide with denominator, we have numerator z6 X z8
we have same bases as z so we add powers as z6+8 = z14
Now we have \(\frac{z^{14}}{z^{8}} \) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{z^{14}}{z^{8}} \) = z14-8 = z6
Question 24.
MODELING REAL LIFE
The sound intensity of a normal conversation is 106 times greater than the quietest noise a person can hear. The sound intensity of a jet at takeoff is 1014 times greater than the quietest noise a person can hear. How many times more intense is the sound of a jet at takeoff than the sound of a normal conversation?

Answer:
108 times more intense is the sound of a jet at takeoff than
the sound of a normal conversation.
Explanation:
Given the sound intensity of a normal conversation is 106 times
greater than the quietest noise a person can hear.
The sound intensity of a jet at takeoff is 1014 times
greater than the quietest noise a person can hear.
Therefore more intense is the sound of a jet at takeoff than
the sound of a normal conversation is \(\frac{10^{14}}{10^{6}} \)
so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{10^{14}}{10^{6}} \) = 1014-6= 108
therefore 108 times more intense is the sound of a jet at
takeoff than the sound of a normal conversation.
SIMPLIFYING AN EXPRESSION Simplify the expression. Write your answer as a power.
Question 25.
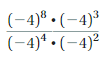
Answer:
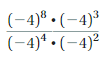 = (-4)5
= (-4)5
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (-4)8 X (-4)3
we have same bases as -4 so we add powers as (-4)8+3 = (-4)11
we have denominator (-4)4 X (-4)2
we have same base as -4 so we add powers as (-4)4+2 = (-4)6
Now we have \(\frac{-4^{11}}{-4^{6}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{-4^{11}}{-4^{6}}\) = (-4)11-6 = (-4)5
Question 26.
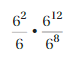
Answer:
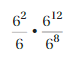 = 65
= 65
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (6)2 X (6)12
we have same bases as 6 so we add powers as (6)2+12 = (6)14
we have denominator (6)1 X (6)8
we have same base as 6 so we add powers as (6)1+8 = (6)9
Now we have \(\frac{6^{14}}{6^{9}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{6^{14}}{6^{9}}\) = (6)14-9 = 65
Question 27.
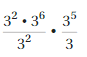
Answer:
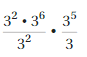 = 310
= 310
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (3)2 X (3)6 X (3)5
we have same bases as 3 so we add powers as (3)2+6+5 = (3)13
we have denominator (3)2 X (3)1
we have same base as 3 so we add powers as (3)2+1 = (3)3
Now we have \(\frac{3^{13}}{3^{3}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{3^{13}}{3^{3}}\) = (3)13-3 = 310
Question 28.
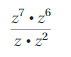
Answer:
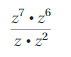 = z10
= z10
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (z)7 X (z)6
we have same bases as z so we add powers as z7+6 = z13
we have denominator (z)1 X (z)2
we have same base as z so we add powers as (z)1+2 = (z)3
Now we have \(\frac{3^{13}}{3^{3}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{z^{13}}{z^{3}}\) = (z)13-3 = z10
Question 29.
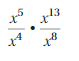
Answer:
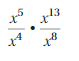 = x6
= x6
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (x)5 X (x)13
we have same bases as x so we add powers as x5+13 = x18
we have denominator (x)4 X (x)8
we have same base as x so we add powers as (x)4+8 = (x)12
Now we have \(\frac{x^{18}}{x^{12}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{x^{18}}{x^{12}}\) = (x)18-12 = x6
Question 30.
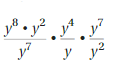
Answer:
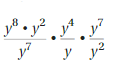 = y11
= y11
Explanation:
First we calculate separately all multiple values of numerators
and denominators then divide, we have numerator (y)8 X (y)2 X (y)4 X (y)7
we have same bases as y so we add powers as y8+2+4+7 = y21
we have denominator (y)7 X (y)1 X (y)2 we have same base
as y so we add powers as (y)7+1+2 = (y)10
Now we have \(\frac{y^{21}}{y^{10}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{y^{21}}{y^{10}}\) = (y)21-10 = y11
Question 31.
REASONING
The storage capacities and prices of five devices are shown in the table.
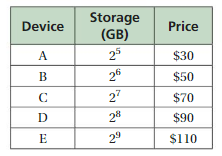
a. How many times more storage does Device D have than Device B?
b. Do storage and price have a linear relationship? Explain.
Answer:
a. 4 times more storage capacity Device D have than Device B.
b. No, as the price increases by $20 storage capacity doubles.
Explanation:
Given the storage capacities and prices of five devices are
as shown above in the table,
a. Storage Device D has capacity of 28 GB and Device B has
capacity of 28 GB as Device D has more capacity by
\(\frac{2^{8}}{2^{6}}\) = (2)8-6 = 22= 4,
therefore 4 times more storage capacity Device D
have than Device B.
b. As seen the price increases by $20 storage capacity doubles so
there is no linear relationship between storage and price.
Question 32.
DIG DEEPER!
Consider the equation \(\frac{9^{m}}{9^{n}}\) = 92
a. Find two numbers m and n that satisfy the equation.
b. Describe the number of solutions that satisfy the equation. Explain your reasoning.
Answer:
a. The two numbers m and n are 3,1.
b. We have more number of solutions that satisfy the equation as
explained below
Explanation:
Given the equation \(\frac{9^{m}}{9^{n}}\) = 92
a. We have rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n so \(\frac{9^{m}}{9^{n}}\)= 9m-n= 92 so
m-n=2, m=2+n we can take n=1 we get m= 2 + 1 = 3 so m,n is 3,1.
the equation is \(\frac{9^{3}}{9^{1}}\)= 93-1= 92
b. As m=2 + n we can take n any natural number from 1 to infinity,
as if n=1 m will be 2+1=3, if n=2 , m will be 2+2 = 4 and so on.
therefore (m, n)=(n+2,n) or (m,m-2)=(3,1)….(5,3),(∞,∞-2) are the
(infinity, infinity minus 2) numbers of solutions that satisfy the equation.
Question 33.
MODELING REAL LIFE
A scientist estimates that there are about 1024 stars in the universe and that each galaxy has, on average, approximately the same number of stars as the Milky Way galaxy. About how many galaxies are in the universe?

Answer:
1013 galaxies are there in the universe.
Explanation:
A scientist estimates that there are about 1024 stars in the
universe and that each galaxy has, on average, approximately
the same number of stars as the Milky Way galaxy.
so number of galaxies in the universe are \(\frac{10^{24}}{10^{1} \cdot 10^{10}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator (10)1 X (10)10
we have same bases as 10 so we add powers as (10)1+10 = (10)11
Now we have \(\frac{10^{24}}{10^{11}} \) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{10^{24}}{10^{11}} \) = (10)24-11 = 1013
therefore 1013 galaxies are there in the universe.
Question 34.
NUMBER SENSE
Find the value of x that makes c = 89 true. Explain how you found your answer.
Answer:
The value of x is 10,
Explanation:
Given \(\frac{8^{3 x}}{8^{2 x}+1}\) = 89 is true,
so we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
as bases are same 8 so 83x-(2x+1) = 89 now we equate powers we have
3x-(2x+1)= 9, means x-1=9 therefore x = 9 + 1 = 10.
Lesson 8.4 Zero and Negative Exponents
EXPLORATION 1
Understanding Zero Exponents
Work with a partner.
a. Copy and complete the table.
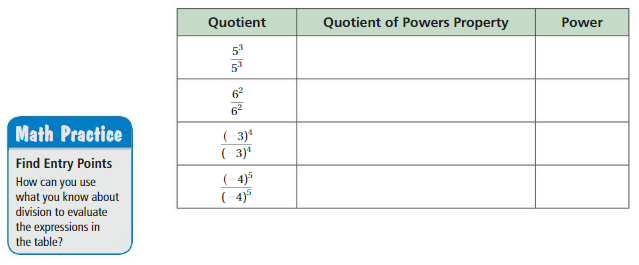
b. Evaluate each expression in the first column of the table in part(a). How can you use these results to define a0, where a ≠ 0?
Answer:
a.
b. We define a0
Explanation:
a. We completed the table by using quotient of powers of property,
as \(\frac{a^{m}}{a^{n}}\) = am-n
then by the quotient rule for exponents we can write this as
an-n =\(\frac{a^{n}}{a^{n}}\) Then this becomes a problem about
dividing fractions. Since the numerator and denominator
are both the same this becomes .
EXPLORATION 2
Understanding Negative Exponents
Work with a partner.
a. Copy and complete the table.
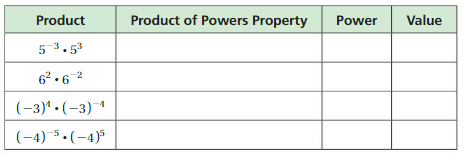
b. How can you use the Multiplicative Inverse Property to rewrite the powers containing negative exponents in the first column of the table?
c. Use your results in parts (a) and (b) to define a-n, where a ≠ 0 and n is an integer.
Answer:
a.
b. We rewrite the powers containing negative exponents in the first column of the table as
5-3 X 53 as 62X 6-2 as 4 X 3-4 as -4-5 X -45 as =
c. a-n, where a ≠ 0 we write a-n as \(\frac{1}{a^{n}}\)
Explanation:
a. To complete the table first we write Product of Powers Property
then write their power and value.
As here we use Product of Powers Property
for am • an = am+n If product of two powers with the same base then
powers are added. So 5-3 X 53 = 5-3+3 = 50 = 1, 62X 6-2 = 62-2 = 60 = 1,
4 X 3-4 = 4-4 =0 = 1 and -4-5 X -45 = -4-5+5 =-40 = 1.
b. The inverse property of multiplication states that if you
multiply a number by its reciprocal, also called the multiplicative inverse,
the product will be 1. (a/b)*(b/a)=1,so we rewrite the powers
containing negative exponents in the first column of the table as
5-3 X 53 as 62X 6-2 as 4 X 3-4 as -4-5 X -45 as =
Try It
Evaluate the expression.
Question 1.
4-2
Answer:
4-2 =
Explanation:
Given expression as 4-2 so we write as
Question 2.
(- 2)– 5
Answer:
(- 2)– 5=
Explanation:
Given expression as (-2)-5 so we write as
Question 3.
6-8 • 68
Answer:
6-8 • 68 = 1
Explanation:
we write the given expression 6-8 X 68 as Product of Powers Property
for am • an = am+n If product of two powers with the same base then
powers are added. So 6-8 X 68 = 6-8+8 = 60 = 1.
Question 4.
\(\frac{(-3)^{5}}{(-3)^{6}}\)
Answer:
\(\frac{(-3)^{5}}{(-3)^{6}}\) = – \(\frac{1}{3}\) or -3-1
Explanation:
Given expression as \(\frac{(-3)^{5}}{(-3)^{6}}\) we use
the quotient rule for exponents we can write this as \(\frac{a^{n}}{a^{n}}\) = am-n ,
so (-3)5-6 ,= (-3)-1 or – \(\frac{1}{3}\).
Question 5.
\(\frac{1}{5^{7}} \cdot \frac{1}{5^{4}}\)
Answer:
\(\frac{1}{5^{7}} \cdot \frac{1}{5^{4}}\) = \(\frac{1}{5^{11}}\)
Explanation:
Given expression is \(\frac{1}{5^{7}} \cdot \frac{1}{5^{4}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator 57 X 54
we have same bases as 5 so we add powers as 57+4 = 511
as numerator is 1 we write as \(\frac{1}{5^{11}}\).
Question 6.
\(\frac{4^{5} \cdot 4^{3}}{4^{2}}\)
Answer:
\(\frac{4^{5} \cdot 4^{3}}{4^{2}}\) = 46
Explanation:
Given Expression as \(\frac{4^{5} \cdot 4^{3}}{4^{2}}\)
first we calculate separately values of numerators
then divide with denominator, we have numerator (4)5 X (4)3
we have same bases as 4 so we add powers as (4)5+3 = (4)8
Now we have \(\frac{4^{8}}{4^{2}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{4^{8}}{4^{2}}\) = (4)8-2 = 46
Simplify. Write the expression using only positive exponents.
Question 7.
8x-2
Answer:
8x-2 = \(\frac{8}{x^{2}}\)
Explanation:
Given 8x-2 we write the expression as positive exponents by using
so 8 X \(\frac{1}{x^{2}}\) or \(\frac{8}{x^{2}}\)
Question 8.
b0 • b-10
Answer:
b0 • b-10 = \(\frac{1}{b^{10}}\)
Explanation:
Given b0 • b-10 we write the expression as positive exponents by using
so b0 X \(\frac{1}{b^{10}}\) as we know b0 =1,
b0 X \(\frac{1}{b^{10}}\)=1 X \(\frac{1}{b^{10}}\) or \(\frac{1}{b^{10}}\).
Question 9.
\(\frac{z^{6}}{15 z^{9}}\)
Answer:
\(\frac{z^{6}}{15 z^{9}}\) = \(\frac{1}{15 z^{3}}\)
Explanation:
Given expression as \(\frac{z^{6}}{15 z^{9}}\) first we write it as
\(\frac{1}{15}\) X \(\frac{z^{6}}{z^{9}}\) now we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
as \(\frac{1}{15}\) X z6-9 we get \(\frac{1}{15}\) X z-3
= \(\frac{1}{15 z^{3}}\).
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
EVALUATING EXPRESSIONS Evaluate the expression.
Question 10.
7-2
Answer:
7-2= \(\frac{1}{49}\)
Explanation:
Given 7-2 we write the expression as positive exponents by using
so \(\frac{1}{7^{2}}\)= \(\frac{1}{49}\)
Question 11.
4-3 • 40
Answer:
4-3 • 40 = \(\frac{1}{64}\)
Explanation:
Given 4-3 X 40 we write the expression as positive exponents by using
so \(\frac{1}{4^{3}}\) X 40 as we know 40 =1,
\(\frac{1}{4^{3}}\) X 40 =\(\frac{1}{4^{3}}\) x 1 = \(\frac{1}{64}\).
Question 12.
\(\frac{(-9)^{5}}{(-9)^{7}}\)
Answer:
\(\frac{(-9)^{5}}{(-9)^{7}}\) = \(\frac{1}{-9^{2}}\) = \(\frac{1}{81}\)
Explanation:
Given expression as \(\frac{-9^{5}}{-9^{7}}\) now we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
as -95-7 we get -9-2 we write as \(\frac{1}{-9^{2}}\) = \(\frac{1}{81}\).
SIMPLIFYING EXPRESSIONS Simplify. Write the expression using only positive exponents.
Question 13.
10t-5
Answer:
10t-5 = \(\frac{10}{t^{5}}\)
Explanation:
Given 10t-5 we write as 10 X t-5 = now we write t-5 as tSo 10 X t-5 = 10 X
Question 14.
w3 • w-9
Answer:
w3 • w-9 =
Explanation:
Given expression is w3 • w-9 first we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, so we add powers as w3-9 = w-6,
So w-6 =
Question 15.
\(\frac{r^{8} \cdot r^{8}}{4}\)
Answer:
\(\frac{r^{8} \cdot r^{8}}{4}\) = \(\frac{r^{16}}{4}\)
Explanation:
Given expression is \(\frac{r^{8} \cdot r^{8}}{4}\) first we
solve numerator by using general rule for am • an = am+n
If product of two powers with the same base then
powers are added, so we add powers as r8+8 = r16,
now we write as r16 X \(\frac{1}{4}\) = \(\frac{r^{16}}{4}\).
Question 16.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
d bit is different because writing (-3) X (-3) X (-3) as a power
with an integer base is (-3)3 no negative exponent.
one more answer is all a,b,c bits have fractions but only d bit
is not in fraction form.
Explanation:
a. Writing \(\frac{1}{3 X 3 X 3}\) using negative exponent is 3-3.
b. Writing 3 to the negative third is 3-3.
c. Writing \(\frac{1^{3}}{3^{3}}\) is 3-3.
d. Writing (-3) X (-3) X (-3) as a power with an integer base is (-3)3.
As a, b, c has value 3-3only bit d has (-3)3.
Therefore d bit is different because writing (-3) X (-3) X (-3) as a power
with an integer base is (-3)3 we don not have a negative exponent.
one more answer is all a,b,c bits have fractions but only d bit
is not in fraction form.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
The mass of a grain of sand is about 10-3 gram. About how many grains of sand are in a 10-kilogram bag of sand?
Answer:
There are about 10,000,000 grains of sand.
Explanation:
Given the mass of a grain of sand is about 10-3 gram.
We know 1 kg = 1000 grams ,10 kg = 10 X 1000 = 10,000 grams,
therefore one grain of sand is 10,000 X 1000 = 10,000,000 grains of sand.
Question 18.
A one-celled, aquatic organism called a dinoflagellate is 1000 micrometers long. A microscope magnifies the dinoflagellate 100 times. What is the magnified length of the dinoflagellate in meters? (1 micrometer is 10-6; meter.)
Answer:
The magnified length of the dinoflagellate in meters10-1 meters
Explanation:
Given one-celled, aquatic organism called a dinoflagellate is
1000 micrometers long. A microscope magnifies the
dinoflagellate 100 times, the magnified length in meters is
1 micrometer is 10-6 meter now dinoflagellate is 1000 X 10-6 X 100 =
103 X 10-6 X 102 we use general rule for am • an = am+n
If product of two powers with the same base then
powers are added so all have base 10 we add powers as
103-6+2 = 10-1 meters therefore the magnified length of
the dinoflagellate in meters10-1 meters.
Question 19.
DIG DEEPER!
A garden is 12 yards long. Assuming the snail moves at a constant speed, how many minutes does it take the snail to travel the length of the garden? Justify your answer.

Answer:
Snail takes 15 minutes to travel the length of the garden
Explanation:
Given a garden is 12 yards long and the constant speed of snail is
5-2 foot per second. We know 1 yard is equal to 3 foot and
speed = distance by time ,So 5-2 = 12 X 3 by time
therefore time = 12 X 3 X 52 seconds = 36 X 25 seconds = 900 seconds,
converting seconds in minutes 900 divide by 60 or \(\frac{900}{60}\)= 15 minutes, therefore snail takes 15 minutes to travel the length of the garden.
Zero and Negative Exponents Homework & Practice 8.4
Review & Refresh
Simplify the expression. Write your answer as a power.
Question 1.
\(\frac{10^{8}}{10^{4}}\)
Answer:
\(\frac{10^{8}}{10^{4}}\) = 104
Explanation:
Given expression \(\frac{10^{8}}{10^{4}}\) so
now we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base has am-n
So \(\frac{10^{8}}{10^{4}}\) = 108-4 = 104
Question 2.
\(\frac{y^{9}}{y^{7}}\)
Answer:
\(\frac{y^{9}}{y^{7}}\) = y2
Explanation:
Given expression \(\frac{y^{9}}{y^{7}}\) so
now we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base has am-n
So \(\frac{y^{9}}{y^{7}}\) = y9-7 = y2
Question 3.
\(\frac{(-3)^{8} \cdot(-3)^{3}}{(-3)^{2}}\)
Answer:
\(\frac{(-3)^{8} \cdot(-3)^{3}}{(-3)^{2}}\) = (-3)9
Explanation:
Given Expression as \(\frac{-3^{8} \cdot -3^{3}}{-3^{2}}\)
first we calculate separately values of numerators
then divide with denominator, we have numerator (-3)8 X (-3)3
we have same bases as -3 so we add powers as (-3)8+3 = (-3)11
Now we have \(\frac{-3^{11}}{-3^{2}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
So \(\frac{-3^{11}}{-3^{2}}\) = (-3)11-2 = (-3)9
Tell whether the triangles are similar. Explain.
Question 4.
Answer:
Yes, The triangles are similar.
Explanation:
Given two triangles in figure to know if they are similar we have
two triangles are said to be similar if their corresponding angles
are congruent and the corresponding sides are in proportion.
In the above two figures the triangles have the same angle measures,
and the corresponding sides are in proportion. So triangles are similar.
Question 5.
Answer:
Yes, The triangles are similar.
Explanation:
Given two triangles in figure to know if they are similar we have
two triangles are said to be similar if their corresponding angles
are congruent and the corresponding sides are in proportion.
In the above two figures the triangles do not have the same angle measures,
So triangles are not similar.
Question 6.
Which data display best orders numerical data and shows how they are distributed?
A. bar graph
B. line graph
C. scatter plot
D. stem-and-leaf plot
Answer:
D. stem-and-leaf plot
Explanation:
A stem-and-leaf plot best orders numerical data and shows
how the data is distributed since it orders the values from
least to greatest and shows how many values lie under each “stem” in the stem-and leaf plot so you can see how the data is distributed.
Concepts, Skills, &Problem Solving
UNDERSTANDING NEGATIVE EXPONENTS Copy and complete the table. (See Exploration 2, p. 337.)
Answer:
Explanation:
To complete the table first we write Product of Powers Property
then write their power and value.
As here we use Product of Powers Property
for am • an = am+n If product of two powers with the same base then
powers are added. So 7. 7-4 X 74 = 7-4+4 = 70 = 1,
8. (-2)5X (-2)-5 = (-2)5-5 = (-2)0 = 1.
EVALUATING EXPRESSIONS Evaluate the expression.
Question 9.
\(\frac{8^{7}}{8^{7}}\)
Answer:
\(\frac{8^{7}}{8^{7}}\) = 1
Explanation:
Given expression is \(\frac{8^{7}}{8^{7}}\)= 87 X 8-7 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added. So 87 X 8-7 = 87-7 = 80 = 1.
Question 10.
50 • 53
Answer:
50 • 53 = 53 = 125.
Explanation:
Given expression is 50 X 53 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added. So 50 X 53 = 50+3 = 53 = 125.
Question 11.
(- 2)-8 • (- 2)8
Answer:
(- 2)-8 • (- 2)8 = 1
Explanation:
Given expression is -2-8 X -28 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added. So (-2)-8 X (-2)8 = (-2)-8+8 = (-2)0= 1.
Question 12.
94 • 9-4
Answer:
94 • 9-4 = 1
Explanation:
Given expression is 94 X 9-4 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added. So 94 X 9-4 = 94-4 = 90= 1.
Question 13.
6-2
Answer:
6-2= \(\frac{1}{36}\)
Explanation:
Given expression as 6-2 we write the expression as positive exponents by using
so \(\frac{1}{6^{2}}\) = \(\frac{1}{36}\).
Question 14.
1580
Answer:
1580 = 1
Explanation:
Given expression is 1580 it is proven that any number or
expression raised to the power of zero is always equal to 1.
In other words, if the exponent is zero then the result is 1.
So 1580 = 1.
Question 15.
\(\frac{4^{3}}{4^{5}}\)
Answer:
\(\frac{4^{3}}{4^{5}}\) = \(\frac{1}{4^{2}}\) = \(\frac{1}{16}\)
Explanation:
Given expression is \(\frac{4^{3}}{4^{5}}\)
now we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base has am-n So \(\frac{4^{3}}{4^{5}}\) =
43-5 = 4-2 = \(\frac{1}{4^{2}}\) = \(\frac{1}{16}\).
Question 16.
\(\frac{-3}{(-3)^{2}}\)
Answer:
\(\frac{-3}{(-3)^{2}}\) = –\(\frac{1}{3}\)
Explanation:
Given expression is \(\frac{-3}{(-3)^{2}}\)
now we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base has am-n ,so \(\frac{-3}{(-3)^{2}}\) =
(-3)1-2 = (-3)-1 = –\(\frac{1}{3}\).
Question 17.
22 • 2-4
Answer:
22 • 2-4 = \(\frac{1}{4}\)
Explanation:
Given expression is 22 X 2-4 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added so 22-4 = 22 X 2-4 = 2-2 = \(\frac{1}{2^{2}}\) = \(\frac{1}{4}\).
Question 18.
3-3 • 3-2
Answer:
3-3 • 3-2 = \(\frac{1}{243}\)
Explanation:
Given expression is 3-3 • 3-2 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added so 3-3-2 = 3-5 = \(\frac{1}{3^{5}}\) = \(\frac{1}{243}\).
Question 19.
\(\frac{1}{5^{3}} \cdot \frac{1}{5^{6}}\)
Answer:
\(\frac{1}{5^{3}} \cdot \frac{1}{5^{6}}\) = \(\frac{1}{5^{9}}\) =
\(\frac{1}{1953125}\)
Explanation:
Given expression is \(\frac{1}{5^{3}} \cdot \frac{1}{5^{6}}\)
now we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base has am-n ,so \(\frac{1}{5^{3}} \cdot \frac{1}{5^{6}}\) =
(5)-3-6 = (5)-9 = \(\frac{1}{5^{9}}\) =
\(\frac{1}{1953125}\).
Question 20.
\(\frac{(1.5)^{2}}{(1.5)^{2} \cdot(1.5)^{4}}\)
Answer:
\(\frac{(1.5)^{2}}{(1.5)^{2} \cdot(1.5)^{4}}\) = \(\frac{1}{5.0625}\)
Explanation:
Given expression is \(\frac{(1.5)^{2}}{(1.5)^{2} \cdot(1.5)^{4}}\)
First we multiply denominators as bases are same
we add powers so (1.5)2 X (1.5)4 = (1.5)2+4 = (1.5)6
now we solve \(\frac{1.5^{2}}{1.5^{6}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{1.5^{2}}{1.5^{6}}\) = 1.52-6 = 1.5-4 now we use =\(\frac{1}{1.5^{4}}\) =
\(\frac{1}{5.0625}\).
Question 21.
YOU BE THE TEACHER
Your friend evaluates 4-3. Is your friend correct? Explain your reasoning.

Answer:
No, friend is incorrect as 4-3 = \(\frac{1}{64}\) ≠ -64
Explanation:
Given expression is 4-3 we have = \(\frac{1}{4^{3}}\) = \(\frac{1}{64}\),
but friend says = -64 which is in correct as 4-3 = \(\frac{1}{64}\) ≠ -64.
Question 22.
CRITICAL THINKING
How can you write the number 1 as a power with base 2? a power with base 10?
Answer:
21 and 101
Explanation:
Given to write the number 1 as a power with base 2 is 21 and
a power with base 10 is 101.
Question 23.
NUMBER SENSE
Without evaluating, order 50, 54, and 5-5 from least to greatest. Explain your reasoning.
Answer:
Order 50, 54, and 5-5 from least to greatest is 5-5, 50 and 54
Explanation:
Given order 50, 54, and 5-5 from least to greatest as each has base 5,
we take consideration of orders as -5 < 0 < 4 so Order 50, 54, and 5-5
from least to greatest is 5-5, 50 and 54.
SIMPLIFYING EXPRESSIONS Simplify. Write the expression using only positive exponents.
Question 24.
6y-4
Answer:
6y-4 = \(\frac{6}{y^{4}}\)
Explanation:
Given expression as 6y-4 we write the expression using only
positive exponents for 6 X y-4 as we write first y-4 we have
=
\(\frac{1}{y^{4}}\) now 6 X \(\frac{1}{y^{4}}\) = \(\frac{6}{y^{4}}\).
Question 25.
8-2 • a7
Answer:
8-2 • a7 = \(\frac{a^{7}}{64}\)
Explanation:
Given expression as 8-2 X a7 we write the expression using only
positive exponents for 8-2 X a7 as we write first 8-2 we have
=
\(\frac{1}{8^{2}}\), So a7 X \(\frac{1}{8^{2}}\) = \(\frac{a^{7}}{64}\).
Question 26.
\(\frac{9 c^{3}}{c^{4}}\)
Answer:
\(\frac{9 c^{3}}{c^{4}}\) = \(\frac{9}{c}\)
Explanation:
Given expression is \(\frac{9 c^{3}}{c^{4}}\) = 9 X \(\frac{c^{3}}{c^{4}}\)
First we solve \(\frac{c^{3}}{c^{4}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{c^{3}}{c^{4}}\) = c3-4 = c-1
now we use .
Question 27.
\(\frac{5 b^{2}}{b^{3}}\)
Answer:
\(\frac{5 b^{2}}{b^{3}}\) = \(\frac{5}{b}\)
Explanation:
Given expression is \(\frac{5 b^{2}}{b^{3}}\) = 5 X \(\frac{b^{2}}{b^{3}}\)
First we solve \(\frac{b^{2}}{b^{3}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{b^{2}}{b^{3}}\) = b2-3 = b-1
now we use .
Question 28.
\(\frac{8 x^{3}}{2 x^{9}}\)
Answer:
\(\frac{8 x^{3}}{2 x^{9}}\) = \(\frac{4}{x^{6}}\)
Explanation:
Given expression as \(\frac{8 x^{3}}{2 x^{9}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{x^{3}}{x^{9}}\) = x3-9 = x-6 for x-6 we use
Question 29.
3d-4 • 4d4
Answer:
3d-4 • 4d4 = 12
Explanation:
Given expression 3d-4 • 4d4 first we multiply d-4 X d4 ,
here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added, we have same base d so d-4+4 = d0= 1,
Now we multiply 1 with 3,4 as 3 X 4 X 1 we get 12.
Question 30.
m-2 • n3
Answer:
m-2 • n3 =
Explanation:
Given expression is m-2 • n3 so we write m-2 we use
Question 31.
\(\frac{3^{2} \cdot k^{0} \cdot w^{0}}{w^{6}}\)
Answer:
\(\frac{3^{2} \cdot k^{0} \cdot w^{0}}{w^{6}}\) =
Explanation:
Given expression \(\frac{3^{2} \cdot k^{0} \cdot w^{0}}{w^{6}}\) we know
k0 and w0 is 1 now we have \(\frac{3^{2}}{w^{6}}\) X 1 X 1 = \(\frac{9}{w^{6}}\).
Question 32.
OPEN-ENDED
Write two different powers with negative exponents that have the same value. Justify your answer.
Answer:
We write two different powers with negative exponents that
have the same value are 2and the value will be
Explanation:
Let us take two different powers with negative exponents that
have the same value are 2we have .
REASONING In Exercises 33–36, use the table.
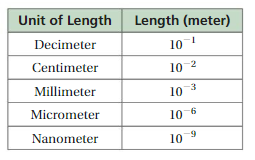
Question 33.
How many millimeters are in a decimeter?
Answer:
100 millimeters are in a decimeter.
Explanation:
Given to find millimeter are in a decimeter we have as per table
millimeters are in a decimeter we write as 10so 100 millimeters are in a decimeter.
Question 34.
How many micrometers are in a centimeter?
Answer:
10000 micrometers are in a centimeter
Explanation:
Given to find micrometers are in a centimeter we have as per table
micrometers are in a centimeter we write as 10so 10000 micrometers are in a centimeter.
Question 35.
How many nanometers are in a millimeter?
Answer:
1,000,000 nanometers are in a millimeter
Explanation:
Given to find nanometers are in a millimeter we have as per table
nanometers are in a millimeter we write as 10so 1,000,000 nanometers are in a millimeter.
Question 36.
How many micrometers are in a meter?
Answer:
1,000,000 micrometers are in a meter
Explanation:
Given to find micrometers are in a meter we have as per table
micrometers are in a meter we write as 10so 1,000,000 micrometers are in a meter.
Question 37.
MODELING REAL LIFE
A bacterium is 100 micrometers long. A virus is 1000 times smaller than the bacterium.
a. Using the table above, find the length of the virus in meters.
b. Is the answer to part (a) less than, greater than, or equal to 1 micrometer?
Answer:
a. The length of the virus in meters is
Explanation:
Given a bacterium is 100 micrometers long. A virus is 1000 times
smaller than the bacterium.
a. The length of the virus in meters is 1 micrometer = 10-6 meters
= 100 X 10-6 by 1000 = 102 X 10-6 X 10-3
we have Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added so = therefore the length of the virus in meters is b. We have 1 micrometer as length of the virus it is So t
Question 38.
DIG DEEPER!
Every 2 seconds, someone in the United States needs blood. A sample blood donation is shown.
a. One cubic millimeter of blood contains about 104 white blood cells. How many white blood cells are in the donation? (1 mm3 = 10-3 mL)
b. One cubic millimeter of blood contains about 5 × 106 red blood cells. How many red blood cells are in the donation?
c. Compare your answers for parts (a) and (b).
Answer:
a. The white blood cells in the donation are 107 white blood cells
and the blood donation contains 500 ml are 5 X 109 white blood cells.
b. The red blood cells in the donation are 5 X 109 red blood cells
and the blood donation contains 500 ml are 25 X 1011 red blood cells.
c. The white blood cells are 500 times more than the red blood cells.
Explanation:
a. One cubic millimeter of blood contains about 104 white blood cells.
(1 mm3 = 10-3 mL),The white blood cells in the donation are
1 mm3 = 10-3 mL,
104 = 10-3 mL,
1 mL= 104+3, therefore 1 mL is 107 white blood cells,
Now the blood donation contains 500 ml = 5 X 102 X 10 7 =
5 X 109 white blood cells.
b.One cubic millimeter of blood contains about 5 × 106 red blood cells,
The red blood cells in the donation are
1 mm3 = 10-3 mL so
5 X 106 = 10-3 mL therefore 1 mL= 5 X 106 X 103
= 5 X 106+3 = 5 X 109 red blood cells
Now the blood donation contains 500 ml = 5 X 102 X 5 X 109 = 25 X 102+9
= 25 X 1011 red blood cells.
c. Now comparison of the white blood cells and the red blood cells are
25 X 1011 divide by 5 X 109 = 5 X 1011-9 = 5 X 102 = 5 X 100 = 500 ,
So the white blood cells are 500 times more than the red blood cells.
Question 39.
PRECISION
Describe how to rewrite a power with a positive exponent as a fraction with a power in the denominator. Use the definition of negative exponents to justify your reasoning.
Answer:
Explanation:
To rewrite a power with a positive exponent as a fraction
with a power in the denominator by using the definition of
negative exponents we write the power as 1 divided by a power
with the same base and a negative exponents , Example
an = a-(-n) =
Question 40.
REASONING
The definition of a negative exponent states that a-n = \(\frac{1}{a^{n^{*}}}\).
Explain why this rule does not apply when a = 0.
Answer:
Explanation:
we have negative exponent states that a-n = \(\frac{1}{a^{n^{*}}}\) but this
rule does not apply when a= 0 as 0-n = 0 or
if we use negative exponent we get =
we could get 0 or 1 so it is undefined.
Lesson 8.5 Estimating Quantities
EXPLORATION 1
Work with a partner. Match each picture with the most appropriate distance. Explain your reasoning.

Answer:

Explanation:
Here we match each picture with the most appropriate distance
a. If we look at the picture it is very away so we take the
least distance in all as 6 X 10-2 m .
b. If we look at the picture it is very far so we take the
far distance in all as 6 X 103 m .
c. If we look at the picture it can jump very little distance so we take
as 2 X 10-1 m.
d. If we look at the picture it is at near distance so we take
as 1 X 101 m.
EXPLORATION 2
Approximating Numbers
Work with a partner. Match each number in List 1 with its closest approximation in List 2. Explain your method.

Answer:
Explanation:
We matched each number in List 1 with its closest
approximation in List 2 as
a. 180,000,000,000,000 is nearly or approximately equal to ≈ 2,00,000,000,000,000,
we have after 2 followed by 14 zeros so we take as 2 X 1014 matches with C.
therefore we match a. to C.
b. 0.0000000011 is nearly or approximately equal to ≈ 1 X 10-9 matches with C,
we have divided 1 by 10 followed by 9 zeros.
therefore we match b. to F.
c. 302,000,000,000 is nearly or approximately equal to ≈ 300,000,000,000,
we have after 3 followed by 11 zeros so we take as 3 X 1011 matches with A.
therefore match c. to A.
d. 0.00000028 is nearly or approximately equal to ≈ 0.0000003,
so 3 X 10-7 matches with E, we have divided 3 by 10 followed by 7 zeros,
therefore we match d. to E.
e. 0.0000097 is nearly or approximately equal to ≈ 0.00001,
so 1 X 10-5 matches with B, we have divided 1 by 10 followed by 5 zeros,
therefore we match e. to B.
f. 330,000,000,000,000 is nearly or approximately equal to ≈ 3,00,000,000,000,000
we have after 3 followed by 14 zeros so we take as 3 X 1014 matches with H.
therefore we match f. to H.
g. 26,000,000,000,000 is nearly or approximately equal to ≈ 30,000,000,000,000
we have after 3 followed by 13 zeros so we take as 3 X 1013 matches with D.
therefore we match g. to D.
h. 0.000023 is nearly or approximately equal to ≈ 0.00002,
so 2 X 10-5 matches with G, we have divided 2 by 10 followed by 5 zeros,
therefore we match h. to G.
Try It
Round the number. Write the result as the product of a single digit and a power of 10.
Question 1.
8,031,426,100
Answer:
8,031,426,100 = 8 X 109
Explanation:
Given number is 8,031,426,100 is nearly or approximately
equal to ≈ 8,000,000,000 so we have 8 followed by 9 zeros,
so we write as 8 X 109.
Question 2.
98,247,836,218
Answer:
98,247,836,218 = 1 X 1011
Explanation:
Given number is 98,247,836,218 is nearly or approximately
equal to ≈ 100,000,000,000 so we have 1 followed by 11 zeros,
so we write as 1 X 1011.
Round the number. Write the result as the product of a single digit and a power of 10.
Question 3.
0.000384509
Answer:
0.000384509 = 4 X 10-4
Explanation:
Given number is 0.000384509 is nearly or approximately
equal to ≈ 0.0004, we have divided 4 by 10 followed
by 4 zeros so we write as 4 X 10-4.
Question 4.
0.00000726
Answer:
0.00000726 = 7 X 10-6
Explanation:
Given number is 0.00000726 is nearly or approximately
equal to ≈ 0.000007, we have divided 7 by 10
followed by zeros so we write as 7 X 10-6.
Question 5.
The distance from Mercury to Mars is about 105,651,744 miles. The distance from Saturn to Jupiter is about 4 times this distance. What is the approximate distance from Saturn to Jupiter?
Answer:
The distance from Saturn to Jupiter is (105,651,744)4 miles
Explanation:
Given the distance from Mercury to Mars is about 105,651,744 miles,
and the distance from Saturn to Jupiter is about 4 times this distance,
so 4 times of 105,651,744 is 105,651,744 X 105,651,744 X
105,651,744 X 105,651,744 = (105,651,744)4 miles.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
APPROXIMATING A NUMBER Round the number. Write the result as the product of a single digit and a power of 10.
Question 6.
899,032,878,300
Answer:
899,032,878,300 = 9 X 1011
Explanation:
Given number is 899,032,878,300 is nearly or approximately
equal to ≈ 900,000,000,000 so we have 9 followed by 11 zeros,
so we write as 9 X 1011.
Question 7.
62,322,118,987
Answer:
62,322,118,987= 6 X 1010
Explanation:
Given number is 62,322,118,987 is nearly or approximately
equal to ≈ 60,000,000,000 so we have 6 followed by 10 zeros,
so we write as 6 X 1010.
Question 8.
0.00000278101
Answer:
0.00000278101 = 3 X 10-6
Explanation:
Given number is 0.00000278101 is nearly or approximately equal to ≈ 0.000003,
we have divided 3 by 10 followed by 6 zeros so we write as
3 X 10-6.
Question 9.
0.000013094
Answer:
0.000013094 = 1 X 10-5.
Explanation:
Given number is 0.000013094 is nearly or approximately
equal to ≈ 0.00001, we have divided 1 by 10
followed by 5 zeros so we write as 1 X 10-5.
Question 10.
APPROXIMATING A QUANTITY
Lake A has a volume of 21,150,427,000 cubic meters. Lake B has a volume that is 2.5 times the volume of Lake A. What is the approximate volume of Lake B?
Answer:
Explanation:
Given Lake A has a volume of 21,150,427,000 cubic meters.
Lake B has a volume that is 2.5 times the volume of Lake A.
The approximate volume of Lake B is 2.5 X 21,150,427,000,
we take 21,150,427,000 is nearly or approximately
equal to ≈ 20,000,000,000 so 2.5 X 20,000,000,000
= 5 X 10,000,000,000 = 5 X 1010.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
On average, a small dog’s heart beats about 530,000,000 times
during its lifetime, and a large dog’s heart beats about 1.4 times this amount.
What is the approximate number of heartbeats in the lifetime of a large dog?
Answer:
The approximate number of heartbeats in the lifetime of a
large dog is 7 X 108 times.
Explanation:
Given on average, a small dog’s heart beats about
530,000,000 times during its lifetime and a large dog’s
heart beats about 1.4 times this amount.
So number of heartbeats in the lifetime of a large dog
= 1.5 X 530,000,000 we take 530,000,000 is nearly or approximately
equal to ≈ 500,000,000 so 1.5 X 500,000,000 = 7.5 X 100,000,000
= 7 X 108 times, therefore the approximate number
of heartbeats in the lifetime of a large dog is 7 X 108 times.
Question 12.
DIG DEEPER!
A physicist observes a gamma ray with a wavelength of 0.00000000135 millimeter and an X-ray with a wavelength of 0.00000012 millimeter. (a) About how many times shorter is the wavelength of the gamma ray than the wavelength of the X-ray? (b) The diagram shows wavelengths of visible light. Which ray has a wavelength closer to the wavelength of dark blue light?
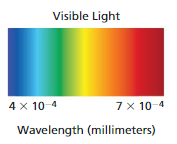
Answer:
a.102 or 100 times shorter is the wavelength of the
gamma ray than the wavelength of the X-ray.
b. X-ray has a wave length closer to the wavelength of dark blue light.
Explanation:
Given a physicist observes a gamma ray with a wavelength
of 0.00000000135 millimeter is nearly or approximately
equal to ≈ 0.000000001 millimeter = 1 X 10-9 millimeters,
and an X-ray with a wavelength 0.00000012 millimeter
is nearly or approximately equal to ≈ 0.0000001 millimeter=
1 X 10-7 millimeters so now comparing wavelength
of the gamma ray with the wavelength of the X-ray,
1 X 10-9 millimeters with 1 X 10-7 millimeters so
we have 102 or 100 times shorter is the wavelength of the
gamma ray than the wavelength of the X-ray.
b. We have dark blue wavelength as 4 X 10-4 millimeters so
it is close to an X-ray with a wavelength 0.00000012 millimeter
is nearly or approximately equal to ≈ 0.0000001 millimeter =
1 X 10-7 millimeters. So X-ray has a wave length closer to the
wavelength of dark blue light.
Estimating Quantities Homework & Practice 8.5
Review & Refresh
Simplify. Write the expression using only positive exponents.
Question 1.
3x-5
Answer:
3x-5= \(\frac{3}{x^{5}}\)
Explanation:
Given expression as 3x-5 we write the expression using only
positive exponents for 3 X x-5 as we write first x-5 we have
=
\(\frac{1}{x^{5}}\) now 3 X \(\frac{1}{x^{5}}\) = \(\frac{3}{x^{5}}\).
Question 2.
d0 • d-4
Answer:
d0 • d-4 = \(\frac{1}{d^{4}}\)
Explanation:
Given d0 • d-4 we write the expression as positive exponents by using
so d0 X \(\frac{1}{d^{4}}\) as we know d0 =1,
d0 X \(\frac{1}{d^{4}}\)=1 X \(\frac{1}{d^{4}}\) or \(\frac{1}{d^{4}}\).
Question 3.
\(\frac{a^{6}}{2 a^{11}}\)
Answer:
\(\frac{a^{6}}{2 a^{11}}\) = \(\frac{1}{2 a^{5}}\)
Explanation:
Given expression as \(\frac{a^{6}}{2 a^{11}}\) we use rule for finding
\(\frac{a^{m}}{a^{n}}\), a quotient of two powers with the same base as am-n
\(\frac{a^{6}}{a^{11}}\) = a6-11 = a-5 for a-5 we use
Write an equation in point-slope form of the line that passes through the given point and has the given slope.
Question 4.
(- 1, 2); m = – \(\frac{1}{3}\)
Answer:
The equation in point-slope form is (y-2)= – \(\frac{1}{3}\) (x+1)
Explanation:
Given (- 1, 2); m = – \(\frac{1}{3}\) we know
for straight-line equations the “point-slope” form with
(x1, y1) and a slope m we have formula y – y1 = m(x – x1)
here we have (x1, y1) are (-1,2) and a slope m is – \(\frac{1}{3}\),
So the equation in point-slope form is (y-2)= – \(\frac{1}{3}\) (x+1).
Question 5.
(3, 4); m = \(\frac{3}{4}\)
Answer:
The equation in point-slope form is (y-4)= \(\frac{3}{4}\) (x-3)
Explanation:
Given (3, 4); m = \(\frac{3}{4}\) we know
for straight-line equations the “point-slope” form with
(x1, y1) and a slope m we have formula y – y1 = m(x – x1)
here we have (x1, y1) are (3,4) and a slope m is \(\frac{3}{4}\),
So the equation in point-slope form is (y-4)= \(\frac{3}{4}\) (x-3).
Question 6.
(1, – 4); m = – 2
Answer:
The equation in point-slope form is (y+4)=-2 (x-1)
Explanation:
Given (1, -4); m = -2 we know
for straight-line equations the “point-slope” form with
(x1, y1) and a slope m we have formula y – y1 = m(x – x1)
here we have (x1, y1) are (1,4) and a slope m is – 2,
So the equation in point-slope form is (y+4)= -2(x-1).
Concepts, Skills, & Problem Solving
APPROXIMATING NUMBERS Match the number with its closest approximation. (See Exploration 2, p. 343.)
Question 7.
0.000618
Answer:
0.000618 ≈ 0.0006 ≈ 6 X 10-4
So we match with B with its closest approximation
Explanation:
0.000618 is nearly or approximately equal to ≈ 0.0006 ≈ 6 X 10-4 ,
we have divided 6 by 10 followed by 4 zeros,
therefore we match B with its closest approximation.
Question 8.
7,257,993,201
Answer:
7,257,993,201 ≈ 7,000,000,000 ≈ 7 X 109
therefore we match D with its closest approximation.
Explanation:
Given number is 7,257,993,201 nearly or approximately
equal to ≈ 7,000,000,000 so we have 7 followed by 9 zeros,
so we write as 7 X 109 therefore we match D with its closest approximation.
Question 9.
0.0006781004
Answer:
0.0006781004 ≈ 0.0007 ≈ 7 X 10-4
So we match with C with its closest approximation
Explanation:
0.000618 is nearly or approximately equal to ≈ 0.0007 ≈ 7 X 10-4 ,
we have divided 7 by 10 followed by 4 zeros,
therefore we match C with its closest approximation.
Question 10.
782,309,441
Answer:
782,309,441≈ 800,000,000 ≈ 8 X 108
therefore we match A with its closest approximation.
Explanation:
Given number is 782,309,441 nearly or approximately
equal to ≈ 800,000,000 so we have 8 followed by 8 zeros,
so we write as 8 X 108 therefore we match A with its closest approximation.
A. 8 × 108
B. 6 × 10-4
C. 7 × 10-4
D. 7 × 109
APPROXIMATING A LARGE NUMBER Round the number. Write the result as a product of a single digit and a power of 10.
Question 11.
414,148,636,008
Answer:
414,148,636,008 ≈ 4 X 1011
Explanation:
Given number is 414,148,636,008 nearly or approximately
equal to ≈ 400,000,000,000 so we have 4 followed by 11 zeros,
so we write as 4 X 1011.
Question 12.
231,210
Answer:
231,210 ≈ 2 X 105
Explanation:
Given number is 231,210 nearly or approximately
equal to ≈ 200,000 so we have 2 followed by 5 zeros,
so we write as 2 X 105.
Question 13.
28,007,806,203
Answer:
28,007,806,203 ≈ 3 X 1010
Explanation:
Given number is 28,007,806,203 nearly or approximately
equal to ≈ 30,000,000,000 so we have 3 followed by 10 zeros,
so we write as 3 X 1010.
Question 14.
38,108,996,999
Answer:
38,108,996,999 ≈ 4 X 1010
Explanation:
Given number is 38,108,996,999 nearly or approximately
equal to ≈ 40,000,000,000 so we have 4 followed by 10 zeros,
so we write as 4 X 1010.
Question 15.
1,003,111,391,008
Answer:
1,003,111,391,008 ≈ 1 X 1012
Explanation:
Given number is 1,003,111,391,008 nearly or approximately
equal to ≈ 1,000,000,000,000 so we have 1 followed by 12 zeros,
so we write as 1 X 1012.
Question 16.
627,638,538
Answer:
627,638,538 ≈ 6 X 108
Explanation:
Given number is 627,638,538 nearly or approximately
equal to ≈ 6,00,000,000 so we have 6 followed by 8 zeros,
so we write as 6 X 108.
Question 17.
APPROXIMATING A LARGE NUMBER
A company earns $518,204,500. Round the number. Write the result as a product of a single digit and a power of 10.

Answer:
$518,204,500 ≈ 5 X 108 dollars
Explanation:
Given number is $518,204,500 nearly or approximately
equal to ≈ 500,000,000 so we have 5 followed by 8 zeros,
so we write as 5 X 108 dollars.
APPROXIMATING A SMALL NUMBER Round the number.
Write the result as a product of a single digit and a power of 10.
Question 18.
0.00000124
Answer:
0.00000124 ≈ 1 X 10-6
Explanation:
As 0.00000124 is nearly or approximately equal to ≈ 0.000001 ≈
1 X 0.000001 = 1 X 10-6 or we have divided 1 by 10 followed by 6 zeros.
Question 19.
0.00003946
Answer:
0.00003946 ≈ 4 X 10-5
Explanation:
As 0.00003946 is nearly or approximately equal to ≈ 0.00004 ≈
4 X 0.00001= 4 X 10-5 or we have divided 4 by 10 followed by 5 zeros.
Question 20.
0.00001726
Answer:
0.00001726 ≈ 2 X 10-5
Explanation:
As 0.00001726 is nearly or approximately equal to ≈ 0.00002 ≈ 2 X 10-5,
or we have divided 2 by 10 followed by 5 zeros.
Question 21.
0.00063718
Answer:
0.00063718 ≈ 6 X 10-4
Explanation:
As 0.00063718 is nearly or approximately equal to ≈ 0.0006 ≈ 6 X 10-4,
or we have divided 6 by 10 followed by 4 zeros.
Question 22.
0.00000000305
Answer:
0.00000000305 ≈ 3 X 10-9
Explanation:
As 0.00000000305 is nearly or approximately
equal to ≈ 0.000000003 ≈ 3 X 10-9,
or we have divided 3 by 10 followed by 9 zeros.
Question 23.
0.000000000994
Answer:
0.000000000994 ≈ 1 X 10-9
Explanation:
As 0.000000000994 is nearly or approximately
equal to ≈ 0.000000001 ≈ 1 X 10-9,
or we have divided 1 by 10 followed by 9 zeros.
Question 24.
YOU BE THE TEACHER
Your friend rounds 0.000468 to the nearest ten thousandth and writes the result as a product of a single digit and a power of 10. Is your friend correct? Explain your reasoning.

Answer:
Yes, Friend is correct as 0.000468 to the nearest ten thousandth is 5 X 10-4
Explanation:
As 0.000468 is nearly or approximately to the nearest
ten thousandth is equal to ≈ 0.0005 ≈ 5 X 0.0001= 5 X 10-4,
which is equal to the value of friend, So Yes, Friend is correct
as 0.000468 to the nearest ten thousandth is 5 X 10-4.
Question 25.
APPROXIMATING A QUANTITY
A series of mystery books contains 2,029,242 words. A series of science fiction books contains about 3.5 times the number of words as the mystery book series. What is the approximate number of words in the science fiction book series?
Answer:
The approximate number of words in the
science fiction book series are 7 X 106 words.
Explanation:
Given a series of mystery books contains 2,029,242 words,
a series of science fiction books contains about 3.5 times the
number of words as the mystery book series.
therefore approximate number of words in the science
fiction book series are 3.5 X 2,029,242 as 2,029,242 is
approximately equal to ≈ 2 X 1000,000 so 3.5 X 2 X 1,000,000
= 7 X 106 words.
Question 26.
APPROXIMATING A QUANTITY
A volcanic eruption ejects about 43,600,000,000 cubic feet of volcanic rock. A smaller volcanic eruption ejects about 75% of this amount. What is the approximate amount of volcanic rock that the smaller volcanic eruption ejects?

Answer:
The approximate amount of volcanic rock that the
smaller volcanic eruption ejects is 3 X 1010 cubic feet.
Explanation:
Given a volcanic eruption ejects about 43,600,000,000 cubic feet
of volcanic rock. A smaller volcanic eruption ejects about 75% of
this amount, So the smaller volcanic eruption is 75% X 43,600,000,000
we get \(\frac{75}{100}\) X 43,600,000,000 = 75 X 43,6000000 =
32,700,000,000 is approximately equal to ≈ 3 X 10,000,000,000 = 3 X 1010 cubic feet.
Question 27.
STRUCTURE
Find a number that is approximately 1.5 times 61,040,000,100.
Write the result as the product of a single digit and a power of 10.
Answer:
The number approximate value of 1.5 times 61,040,000,100 is 9 X 1010
Explanation:
The number approximate value of 1.5 times 61,040,000,100 is
1.5 X 61,040,000,100 = 91,560,000,150 is approximately
equal to ≈ 9 X 10,000,000,000 = 9 X 1010 .
Question 28.
APPROXIMATING A QUANTITY
A mitochondrion has a diameter of about 0.00000031 meter. The diameter of a chloroplast is about 3 times that of the mitochondrion. What is the approximate diameter of the chloroplast?
Answer:
The approximate diameter of the chloroplast is 9 X 10-7 meters.
Explanation:
A mitochondrion has a diameter of about 0.00000031 meter.
The diameter of a chloroplast is about 3 times that of the
mitochondrion. So the approximate diameter of the chloroplast is
3 X 0.00000031 = 0.00000093 is approximately
equal to ≈ 9 X 0.0000001 = 9 X 10-7 meters.
Question 29.
MODELING REAL LIFE
A photo taken with a smartphone has 1,227,104 pixels. A photo taken with a camera has 11,943,936 pixels. Approximately how many times more pixels are in the photo taken with the camera?
Answer:
10 times more pixels are in the photo taken with the camera.
Explanation:
Given a photo taken with a smartphone has 1,227,104 pixels and
A photo taken with a camera has 11,943,936 pixels.
Number of times the pixels are in the photo taken with the camera is
\(\frac{11943936}{1227104}\) = 9.7334341669 is approximately
equal to ≈ 10, So 10 times more pixels are in the photo taken with the camera.
Question 30.
MODELING REAL LIFE
A star has a core temperature of about 115,000,000°F. The temperature of a lightning strike is about 10,300°F. Approximately how many times hotter is the core temperature of the star than the temperature of the lightning strike?
Answer:
11165 times hotter is the core temperature of the star than the
temperature of the lightning strike
Explanation:
Given a star has a core temperature of about 115,000,000°F and
the temperature of a lightning strike is about 10,300°F.
Number of times hotter is the core temperature of the star
more than the temperature of the lightning strike is
\(\frac{115000000}{10300}\) = 11,165.048543689
is approximately equal to ≈ 11165, So 11165 times hotter is the
core temperature of the star than the temperature of the lightning strike.
Question 31.
REASONING
The table shows the diameters of five types of animal hairs.

a. Order the hair types from greatest to least diameter.
b. What unit should be used to represent these data? Explain your reasoning.
Answer:
a. The hair types from greatest to least diameter are
Cow, Buffalo, Camel, Donkey, Rat.
b. Millimeters unit should be used to represent these data.
Explanation:
a. Given the table shows the diameters of five types of animal hairs as
Buffalo = 0.00011 is approximately equal to ≈ 1 X 10-4
Rat = 0.00004 is approximately equal to ≈ 4 X 10-5
Camel = 0.00008 is approximately equal to ≈ 8 X 10-5
Cow = 0.00016 is approximately equal to ≈ 1 X 10-4
Donkey = 0.00005 is approximately equal to ≈ 5 X 10-5,
Now from greatest to least diameters are
1 X 10-4 > 1 X 10-4 > 8 X 10-5 > 5 X 10-5> 4 X 10-5,
therefore the hair types from greatest to least diameter are
Cow, Buffalo, Camel, Donkey, Rat.
b. As the smallest unit of length is millimeter,
Millimeter is the smallest common unit of length that is represented as
‘mm’. The relation between mm and m is 1 meter = 1000 millimeter.
So millimeters unit should be used to represent these data.
Question 32.
PROBLEM SOLVING
The distance between New York City and Princeton is about 68,500 meters. The distance between New York City and San Antonio is about 40 times this distance. What is the approximate distance between New York City and San Antonio? Write the result as the product of a single digit and a power of 10.
Answer:
The approximate distance between New York City and San Antonio is
3 X 106 meters.
Explanation:
Given the distance between New York City and Princeton
is about 68,500 meters. The distance between New York City
and San Antonio is about 40 times this distance.
So the approximate distance between New York City and San Antonio is
40 X 68500 = 2,740,000 is approximately equal to ≈ 3 X 1,000,000 = 3 X 106 meters.
Question 33.
REASONING
Is 5 × 106 a better approximation of 5,447,040 or 5,305,004? Explain.
Answer:
5 × 106 a better approximation of 5,305,004
Explanation:
We have 5,447,040 or 5,305,004 we take approximate values ,
now 5 × 106 is approximately equal to ≈ 5,000,000 now if
we see for 5,000,000 the more near value is 5,305,004 than the
5,447,040. So 5 × 106 a better approximation of 5,305,004.
Question 34.
DIG DEEPER!
A proton weighs 0.00000000000167 nanogram. About how much do 8 protons weigh? Write the result as the product of a single digit and a power of 10. Is your answer an overestimate or an underestimate?
Answer:
The weight of 8 protons is 1 × 10-11
My answer is overestimate.
Explanation:
A proton weighs 0.00000000000167 nanogram.
So 8 protons weighs is 8 X 0.00000000000167 =1.336 X 10-11
is approximately equal to ≈ 1 X 10-11.
My answer is overestimate given proton weighs
0.00000000000167 nanogram is approximately equal to ≈ 1 X 10-12
and the weight of 8 protons is 1 × 10-11 if we see 1 X 10-11 > 1 X 10-12 ,
So my answer is overestimate.
Lesson 8.6 Scientific Notation
EXPLORATION 1
Work with a partner. Use a graphing calculator.
a. Experiment with multiplying very large numbers until your calculator displays an answer that is not in standard form. What do you think the answer means?
b. Enter the function y = 10x into your graphing calculator. Use the table feature to evaluate the function for positive integer values of x until the calculator displays a y-value that is not in standard form. Do the results support your answer in part(a)? Explain.
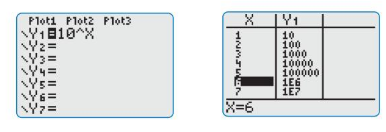
c. Repeat part(a) with very small numbers.
d. Enter the function y = (\(\frac{1}{10}\))x into your graphing calculator. Use the table feature to evaluate the function for positive integer values of x until the calculator displays a y-value that is not in standard form. Do the results support your answer in part(c)? Explain.
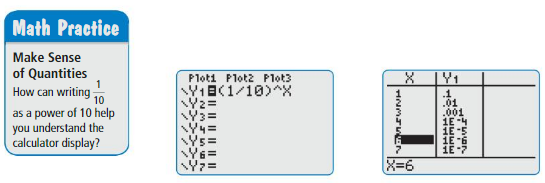
a. Means the answer is big so answer is not in standard form it
will be in scientific notation.
b. Until at x =6 the calculator displays a y-value that is not in
standard form. Yes the results support my answer in part(a),
c. Means the answer is small so answer is not in standard form it
will be in scientific notation.
d. Until at x =6 the calculator displays a y-value that is not in
standard form. Yes the results support my answer in part(c).
Explanation:
a. If multiplying very large numbers until my calculator
displays an answer that is not in standard form. We use
scientific notation it is just a shorthand way of expressing
gigantic numbers also known as an exponential form,
scientific notation has been one of the oldest mathematical approaches.
If numbers are too big to be simply calculated we refer to
scientific notation to handle these circumstances.
For example 4.5 X 109 years or (on a calculator)
4.5E9 years (1 billion in scientific notation means
10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10)
b. Entering the function y = 10x into graphing calculator.
Using the table feature we evaluate the function for positive integer
values of until x =6 the calculator displays a y-value that is not in standard form.
Yes the results support my answer in part(a) as we multiplied
very large number, calculator displays an answer that is not in standard form.
c. If multiplying very small numbers until my calculator
displays an answer that is not in standard form. We use
scientific notation it is just a shorthand way of expressing
numbers also known as an exponential form,
For example 0.000003426
Step 1: Move the decimal so that there is only one digit in front of the decimal.
0.000003.426
Step 2: Count the number of moves from the original decimal to the new position.
0.000003.426, There are 6 moves
Step 3: Write the new number as a product with a power of ten.
3.426 x 10-6 , 3E-6 the number of moves becomes the exponent.
d. Entering the function y = (\(\frac{1}{10}\))x into graphing calculator.
Using the table feature we evaluate the function for positive integer
values of until x =6 the calculator displays a y-value that is not in standard form.
Yes the results support my answer in part(c) as we multiplied
very small number, calculator displays an answer that is not in standard form.

Try It
Write the number in scientific notation.
Question 1.
50,000
Answer:
50,000 = 5 X 104
Explanation:
Given number is 50,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 50,000 = 5 X 10000 = 5 X 104.
Question 2.
25,000,000
Answer:
25,000,000 = 25 X 106
Explanation:
Given number is 25,000,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 25,000,000 = 25 X 1000000 = 25 X 106.
Question 3.
683
Answer:
683 = 6.83 X 102
Explanation:
Given number is 683 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 683 = 6.83 X 100 = 6.83 X 102 .
Question 4.
0.005
Answer:
0.005 = 5 X 10-3
Explanation:
Given number is 0.005 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.005 = 5 X 0.001 = 5 X 10-3.
Question 5.
0.00000033
Answer:
0.00000033 = 3.3 X 10-7
Explanation:
Given number is 0.00000033 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.00000033 = 3.3 X 0.0000001 = 3.3 X 10-7.
Question 6.
0.000506
Answer:
0.000506 = 5.06 X 10-4
Explanation:
Given number is 0.000506 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.000506 = 5.06 X 0.0001 = 5.06 X 10-4.
Write the number in standard form.
Question 7.
6 × 107
Answer:
6 × 107 = 60,000,000
Explanation:
Given 6 × 107 the number in standard form is
6 X 10,000,000 , So 6 × 107 = 60,000,000.
Question 8.
9.9 × 10-5
Answer:
9.9 × 10-5 = 0.000099
Explanation:
Given 9.9 × 10-5 the number in standard form is
1 × 0.000099 = 0.000099.
Question 9.
1.285 × 104
Answer:
1.285 × 104 = 12850
Explanation:
Given 1.285 × 104 the number in standard form is
1.285 X 10,000 , So 1.285 × 104 = 12850.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING NUMBERS IN SCIENTIFIC NOTATION Write the number in scientific notation.
Question 10.
675,000,000
Answer:
675,000,000 = 6.75 X 108
Explanation:
Given number is 675,000,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 675,000,000 = 6.75 X 1,00,000,000 = 6.75 X 108 .
Question 11.
0.000000084
Answer:
0.000000084 = 8.4 X 10-8
Explanation:
Given number is 0.000000084 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.000000084 = 8.4 X 0.00000001 = 8.4 X 10-8.
Question 12.
0.000012001
Answer:
0.000012001 = 1 X 10-5
Explanation:
Given number is 0.000012001 first we write
in approximately equal to ≈0.00001 now in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.00001= 1 X 0.00001 = 1 X 10-5.
WRITING NUMBERS IN STANDARD FORM Write the number in standard form.
Question 13.
8 × 10-7
Answer:
8 × 10-7 = 0.0000008
Explanation:
Given 8 × 10-7 the number in standard form is
8 × 0.0000001 = 0.0000008.
Question 14.
3.876 × 107
Answer:
3.876 × 107 = 38,760,000
Explanation:
Given 3.876 × 107 the number in standard form is
3.876 X 10,000,000 = 38,760,000 so 3.876 × 107 = 38,760,000.
Question 15.
1.11 × 10-5
Answer:
1.11 × 10-5 = 0.0000111
Explanation:
Given 1.11 × 10-5 the number in standard form is
1.11 × 0.00001 = 0.0000111.
Question 16.
WHICH ONE DOESN’T BELONG?
Which number does not belong with the other three? Explain.
![]()
Answer:
d. 10 X 9.2-13 does not belong with the other three
Explanation:
Given 2.8 X 1015 , 4.3 X 10-30 , 1.05 X 1028 all are single digit to
the left of decimal sign and is multiplied by an integer power of 10,
but only 10 X 9.2-13 has power for 9.213 ,so 10 X 9.2-13
does not belong with the other three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
A series of movies is about 3.285 × 104 seconds long.
How long does it take to watch the series twice?
Express your answer using more-appropriate units.
Answer:
The time it takes to watch the series twice is 18.25 hours.
Explanation:
Given a series of movies is about 3.285 × 104 seconds long
and the time it takes to watch the series twice is
2 X 3.285 × 104 seconds = 6.57 X 104 seconds,
now we convert seconds into hours as 1 hour = 3600 seconds,
so \(\frac{6.57}{3600}\) X 104 = 18.25 hours, therefore
the time it takes to watch the series twice is 18.25 hours.
Question 18.
The total power of a space shuttle during launch is the sum of the power from its solid rocket boosters and the power from its main engines. e power from the solid rocket boosters is 9,750,000,000 watts. What is the power from the main engines?

Answer:
The power from the main engines is 1.99 X 109 watts.
Explanation:
Given the power from the solid rocket boosters is
9,750,000,000 watts is approximately equal to ≈9.75 X109 watts
Let the main engine power be x, Total Power =
power from the solid rocket boosters + power from the main engines,
1.174 X 1010 watts = 9.75 X 109 watts + x, So x = (11.74 – 1.99) X 109 watts
= 9.75 X 109 watts, therefore the power from the main engines is 1.99 X 109 watts.
Question 19.
The area of a trampoline is about 1.8 × 104 square inches.
Write this number in standard form. Then represent the area of the
trampoline using more-appropriate units.
Answer:
The area of the trampoline is 125 square feet
Explanation:
Given the area of a trampoline is about 1.8 × 104 square inches,
so we get 1.8 × 104 as 18000 square inches, now we
represent the area of the trampoline using more-appropriate units
in square feet, We know 1 square feet = 144 square inches
= \(\frac{18000}{144}\) = 125 square feet,
so the area of the trampoline is 125 square feet.
Question 20.
DIG DEEPER!
The epidermis, dermis, and hypodermis are layers of your skin. The dermis is about 3.5 millimeters thick. The epidermis is about 1.25 × 10-3 meter thick. The hypodermis is about 0.15 centimeter thick. What is the difference in thickness of the thickest layer and the thinnest layer? Justify your answer.
Answer:
The difference in thickness of the thickest layer and
the thinnest layer is 0.002 meters
Explanation:
Given the epidermis, dermis, and hypodermis are layers of your skin.
The dermis is about 3.5 millimeters thick. The epidermis is about
1.25 × 10-3 meter thick. The hypodermis is about 0.15 centimeter thick.
So the difference in thickness of the thickest layer and the thinnest layer is
1 millimeter = 0.001 meters,
dermis = 3.5 X 0.001 = 0.0035 meters,
epidermis = 1.25 X 10-3 = 0.00125 meters,
hypodermis = 0.15 centimeter, we know 1 centimeter = 0.01 meter,
so 0.15 X 0.01 = 0.0015 meters, we have the thickest as 0.0035 meters and
thinnest is 0.00125 meters , So the difference in thickness of
the thickest layer and the thinnest layer is 0.0035 – 0.00125 =
0.00225 is approximately equal to ≈ 0.002 meters.
Scientific Notation Homework & Practice 8.6
Review & Refresh
Round the number. Write the result as the product of a single digit and a power of 10.
Question 1.
0.00000129
Answer:
0.00000129 ≈ 1 X 10-6
Explanation:
As 0.00000129 is nearly or approximately equal to ≈ 0.000001 ≈
1 X 0.000001 = 1 X 10-6 or we have divided 1 by 10 followed by 6 zeros.
Question 2.
4,241,933,200
Answer:
4,241,933,200 ≈ 4 X 109
Explanation:
Given number is 4,241,933,200 nearly or approximately
equal to ≈ 2,000,000,000 so we have 4 followed by 9 zeros,
so we write as 4 X 109.
Question 3.
0.0000001801
Answer:
0.0000001801≈ 2 X 10-7
Explanation:
As 0.0000001801 is nearly or approximately equal to ≈ 0.0000002 ≈
2 X 0.0000001 = 2 X 10-7 or we have divided 2 by 10 followed by 7 zeros.
Question 4.
879,679,466
Answer:
879,679,466 ≈ 9 X 108
Explanation:
Given number is 879,679,466 nearly or approximately
equal to ≈ 9,00,000,000 so we have 9 followed by 8 zeros,
so we write as 9 X 108.
Write the product using exponents.
Question 5.
4 • 4 • 4 • 4 • 4
Answer:
4 • 4 • 4 • 4 • 4 = (4)5
Explanation:
We write the product 4 • 4 • 4 • 4 • 4 in exponents as (4)5
because 4 is multiplied by 5 times.
Question 6.
3 • 3 • 3 • y • y • y
Answer:
3 • 3 • 3 • y • y • y = 33y3= (3y)3
Explanation:
We write the product 3 • 3 • 3• y • y • y in exponents as (3y)3
because 3 is multiplied by 3 times and y is also multiplied by 3 times.
Question 7.
(- 2) • (- 2) • (- 2)
Answer:
(- 2) • (- 2) • (- 2) = (-2)3
Explanation:
We write the product (-2) • (-2) • (-2) in exponents as (-2)3
because -2 is multiplied by 3 times.
Concepts, Skills, &Problem Solving
USING A GRAPHING CALCULATOR Use a graphing calculator to evaluate x the function when 10. Write the number in standard form. (See Exploration 1, p. 349.)
Question 8.
y = (\(\frac{1}{10}\))x
Answer:
The number in standard form is 0.0000000001
Explanation:
Given y = (\(\frac{1}{10}\))x and x = 10 so
y = (\(\frac{1}{10}\))10 so 1 X 10-10 = 1X 0.0000000001
= 0.0000000001 therefore the number in standard form is 0.0000000001.
Question 9.
y = 20x
Answer:
The number in standard form is 10,240,000,000,000
Explanation:
Given y = 20x and x = 10 so y= (20)10 = 10,240,000,000,000,
therefore the number in standard form is 10,240,000,000,000.
WRITING NUMBERS IN SCIENTIFIC NOTATION Write the number in scientific notation.
Question 10.
0.0021
Answer:
0.0021 = 2.1 X 10-3
Explanation:
Given number is 0.0021 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.0021 = 2.1 X 0.001 = 2.1 X 10-3.
Question 11.
5,430,000
Answer:
5,430,000 = 5.43 X 106
Explanation:
Given number is 5,430,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 5,430,000 = 5.43 X 1,000,000 = 5.43 X 106.
Question 12.
321,000,000
Answer:
321,000,000 = 3.21 X 108
Explanation:
Given number is 321,000,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 321,000,000 = 3.21 X 1,00,000,000 = 3.21 X 108.
Question 13.
0.00000625
Answer:
0.00000625 = 6.25 X 10-6
Explanation:
Given number is 0.00000625 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.00000625 = 6.25 X 0.000001 = 6.25 X 10-6.
Question 14.
0.00004
Answer:
0.00004 = 4 X 10-5
Explanation:
Given number is 0.00004 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.00004 = 4 X 0.00001 = 4 X 10-5.
Question 15.
10,700,000
Answer:
10,700,000 = 1.07 X 107
Explanation:
Given number is 10,700,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 10,700,000 = 1.07 X 10,000,000 = 1.07 X 107.
Question 16.
45,600,000,000
Answer:
45,600,000,000 = 4.56 X 1010
Explanation:
Given number is 45,600,000,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 45,600,000,000 = 4.56 X 10,000,000,000 = 4.56 X 1010.
Question 17.
0.000000000009256
Answer:
0.000000000009256 = 9.256 X 10-12
Explanation:
Given number 0.000000000009256 is in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.000000000009256 = 9.256 X 0.000000000001 = 9.256 X 10-12.
Question 18.
840,000
Answer:
840,000 = 8.4 X 105
Explanation:
Given number is 840,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 840,000 = 8.4 X 100,000 = 8.4 X 105.
WRITING NUMBERS IN STANDARD FORM Write the number in standard form.
Question 19
7 × 107
Answer:
7 × 107 = 70,000,000
Explanation:
Given 7 × 107 the number in standard form is
7 X 10,000,000 =70,000,000.
Question 20.
8 × 10-3
Answer:
8 X 10-3 = 0.008
Explanation:
Given 8 × 10-3 the number in standard form is
8 × 0.001 = 0.008.
Question 21.
5 × 102
Answer:
5 × 102 = 500
Explanation:
Given 5 × 102 the number in standard form is
7 X 100 = 500.
Question 22.
2.7 × 10-4
Answer:
2.7 × 10-4 = 0.00027
Explanation:
Given 2.7 × 10-4 the number in standard form is
2.7 × 0.0001 = 0.00027.
Question 23.
4.4 × 10-5
Answer:
4.4 × 10-5 = 0.000044
Explanation:
Given 4.4 × 10-5 the number in standard form is
4.4 × 0.00001 = 0.000044.
Question 24.
2.1 × 103
Answer:
2.1 × 103= 2,100
Explanation:
Given 2.1 × 103 the number in standard form is
2.1 X 1000 = 2,100.
Question 25.
1.66 × 109
Answer:
1.66 × 109 = 1,660,000,000
Explanation:
Given 1.66 × 109 the number in standard form is
1.66 X 1,000,000,000 = 1,660,000,000.
Question 26.
3.85 × 10-8
Answer:
3.85 × 10-8 = 0.0000000385
Explanation:
Given 3.85 × 10-8 the number in standard form is
3.85 × 0.00000001 = 0.0000000385.
Question 27.
9.725 × 106
Answer:
9.725 × 106 = 9,725,000
Explanation:
Given 9.725 × 106 the number in standard form is
9.725 X 1,000,000 = 9,725,000.
Question 28.
MODELING REAL LIFE
The U.S.Brig Niagara, a warship from the Battle of Lake Erie in 1813, uses about 28,300 feet of rope to operate its sails and spars. Write this number in scientific notation.

Answer:
28,300 feet = 2.83 X 104
Explanation:
Given the U.S.Brig Niagara, a warship from the Battle of
Lake Erie in 1813, uses about 28,300 feet of rope to
operate its sails and spars this number in scientific notation as
we write a number in scientific notation has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 28,300 = 2.83 X 10,000 = 2.83 X 104.
Question 29.
MODELING REAL LIFE
The radius of a fishing line is 2.5 × 10-4 feet. Write this ×number in standard form. Then write your answer using inches.
Answer:
The number in standard form is 0.00025 feet,
In inches it is 0.003 inches.
Explanation:
The radius of a fishing line is 2.5 × 10-4 feet,
The number in standard form is 2.5 X 0.0001 = 0.00025 feet,
Now to convert feet into inches we know 1 foot is 12 inch so
0.00025 X 12 = 0.003 inches.
Question 30.
MODELING REAL LIFE
Platelets are cell-like particles in the blood that help form blood clots.
a. How many platelets are in 3 milliliters of blood? Write your answer in standard form.
b. An adult human body contains about 5 liters of blood. How many platelets are in an adult human body?
Answer:
a. There are 810,000,000 milliliters platelets in 3 milliliters of blood.
b. There are 1,350,000,000,000 milliliters platelets are in an adult human body.
Explanation:
a. Given blood has 2.7 X 108 platelets per milliliters,
So the number of platelets in 3 milliliters of blood is
3 X 2.7 X 108 = 8.1 X 108 = 810,000,000 milliliters.
b. An adult human body contains about 5 liters of blood,
So the number of platelets in an human body are, we know
1 liter = 1000 milliliters so 5 liters is equal to 5,000 milliliters,
5000 X 2.7 X 108 = 1,350,000,000,000 milliliters ,therefore
There are 1,350,000,000,000 milliliters platelets are in an adult human body.
CHOOSING APPROPRIATE UNITS Match each value with the most appropriate unit of measurement.
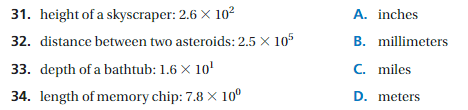
Answer:
We match each value with the most appropriate unit of measurement
as 31. D, 32. C, 33. A , 34. B
Explanation:
Given
a. Height of a skyscraper is : 2.6 X 102 = 2.6 X 100 = 260,
so the most appropriate unit of measurement is meters as
it is used to measure big lengths.
b. Distance between two asteroids : 2.5 X 105 = 2.5 X 100,000 = 250,000
so the most appropriate unit of measurement is miles as
it is used to measure long distances.
c. Depth of bathtub: 1.6 X 101 = 16,
so the most appropriate unit of measurement is inches as
it is used to measure the length of small objects.
d. Length of memory chip : 7.8 X 100 = 7.8 X 1 = 7.8
so the most appropriate unit of measurement is millimeters as
it is used to measure very short lengths or thicknesses.
Question 35.
NUMBER SENSE
Describe how the value of a number written in scientific notation changes when you increase the exponent by 1.
Answer:
The number increases by 10 times
Explanation:
Whenever we increase the exponent by 1
in scientific notation the number becomes 10 times of
previous number. Example we have number 280 we write
number in scientific notation as single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 280 = 2.8 X 100 = 2.8 X 102 now if we increase exponent by 1 we get
2.8 X 103 as 2.8 X 1000 = 2800 here the value has increase by 10 times from
280 to 2800.
Question 36.
PROBLEM SOLVING
The area of the Florida Keys National Marine Sanctuary is about 9600 square kilometers. The area of the Florida Reef Tract is about 16.2% of the area of the sanctuary. What is the area of the Florida Reef Tract? Write your answer in scientific notation.

Answer:
The area of the Florida Reef Tract is 1.5552 X 103 square kilometers
Explanation:
Given the area of the Florida Keys National Marine Sanctuary
is about 9600 square kilometers. The area of the Florida Reef
Tract is about 16.2% of the area of the sanctuary.
So the area of the Florida Reef Tract is \(\frac{16.2}{100}\) X 9600 =
1555.2 square kilometers, Now we convert 1555.2 in scientific notation as
single digit to the left of decimal sign and is multiplied
by an integer power of 10, So 1.552 X 1000 = 1.552 X 103 square kilometers,
therefore the area of the Florida Reef Tract is 1.5552 X 103 square kilometers.
Question 37.
REASONING
A gigameter is 1.0 × 106 kilometers. How many square kilometers
are in 5 square gigameters?
Answer:
There are 5 X 1012 kilometers2 are there in 5 square gigameters
Explanation:
Given a gigameter is 1.0 × 106 kilometers, So 1 Square kilometer =
(1.0 X 106)2 kilometers2 = 1.0 X 1012 kilometers2, So
5 gigameter2= 5 X 1012 kilometers2 therefore there are
5 X 1012 kilometers2 are there in 5 square gigameter.
Question 38.
PROBLEM SOLVING
There are about 1.4 × 109 cubic kilometers of water on Earth.
About 2.5% of the water is freshwater. How much freshwater is on Earth?
Answer:
Fresh water available on earth is 3.5 X 107 kilometers3
Explanation:
Given there are about 1.4 × 109 cubic kilometers of water on Earth
and about 2.5% of the water is freshwater so the amount of
fresh water available is 2.5 % of 1.4 × 109 cubic kilometers
= \(\frac{2.5}{100}\) X 1.4 × 109 = 3.5 X 107 kilometers3 ,
therefore fresh water available on earth is 3.5 X 107 kilometers3 .
Question 39.
CRITICAL THINKING
The table shows the speed of light through each of five media. Determine in which media light travels the fastest and the slowest.
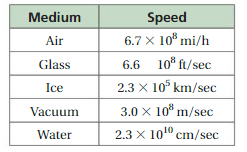
Answer:
Fastest is Vacuum 3.0 X 108 m/sec and slowest is Glass 2.01 X 108 m/sec,
Explanation:
Given the table shows the speed of light through each of five media
Air is 6.7 X 108 mi/sec now convert into meters per second
6.7 X 108 X \(\frac{1609}{3600}\) = 2.99 X 108 m/sec,
Now speed in glass is 6.6 X 108 ft/sec now convert into meters per second
6.6 X 108 X 0.3048 = 2.01 X 108 m/sec,
Now speed in Ice is 2.3 X 105 km/sec now convert into meters per second
2.3 X 105 X 1000 = 2.3 X 108 m/sec, already Vacuum is in m/sec,
so now speed in Water is 2.3 X 1010 cm/sec now
convert into meters per second 2.3 X 1010 X \(\frac{1}{100}\) =
2.3 X 108 m/sec, Now
Medium Speed in m/sec
Air 2.99 X 108 m/sec
Glass 2.01 X 108 m/sec
Ice 2.3 X 108 m/sec
Vacuum 3.0 X 108 m/sec
Water 2.3 X 108 m/sec , So now if we see at speeds the
fastest is Vacuum 3.0 X 108 m/sec and slowest is Glass 2.01 X 108 m/sec.
Question 40.
STRUCTURE
The mass of an atom or molecule is measured in atomic mass units. Which is greater, a carat or a milligram? Explain.

Answer:
A carat is greater unit than milligram,
Explanation:
The mass of an atom or molecule is measured in atomic mass units.
One atomic mass unit(amu) is equivalent to
1 amu = 8.3 X 10-24 carat
1 amu = 1.66 X 10-21 milligram
now 8.3 X 10-24 carat = 1.66 X 10-21 milligram
8.3 carat = 1.66 X 103 milligram
So 1 carat = \(\frac{1660}{8.3}\) = 200 milligrams,
therefore A carat is greater unit than milligram.
Lesson 8.7 Operations in Scientific Notation
EXPLORATION 1
Adding and Subtracting in Scientific Notation
Work with a partner.
a. Complete the table by finding the sum and the difference of Expression 1 and Expression 2. Write your answers in scientific notation. Explain your method.
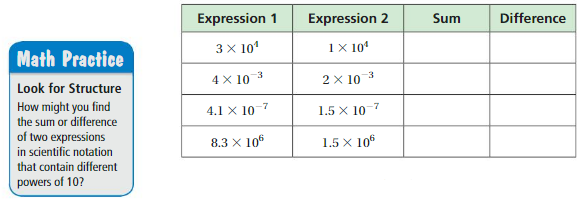
b. Use your results in part(a) to explain how to find (a × 10n) + (b × 10n) and (a × 10n) – (b × 10n).
Answer:
a.
b. (a × 10n) + (b × 10n) = (a + b ) X 10n
(a × 10n) – (b × 10n) = (a-b) X 10n
Explanation:
a. One of the properties of quantities with exponents is that
numbers with exponents can be added and subtracted
only when they have the same base and exponent.
Since all numbers in scientific notation have the same base (10),
we need only worry about the exponents.
To be added or subtracted, two numbers in scientific notation they
must be manipulated so that their bases have the same exponent,
this will ensure that corresponding digits in their coefficients
have the same place value.
So completed the table by finding
the sum and the difference of Expression 1 and Expression 2.
1. Sum = ( 3 X 104) + ( 1 X 104) = ( 3 + 1) X 104 = 4 X 104,
Difference = ( 3 X 104) – ( 1 X 104) = ( 3 – 1) X 104 = 2 X 104,
2. Sum = ( 4 X 10-3) + ( 2 X 10-3) = ( 4 + 2) X 10-3 = 6 X 10-3,
Difference = ( 4 X 10-3) – ( 2 X 10-3) = ( 4 – 2) X 10-3 = 2 X 10-3,
3. Sum=( 4.1 X 10-7) + ( 1.5 X 10-7) = ( 4.1 + 1.5) X 10-7 = 5.6 X 10-7,
Difference = ( 4.1 X 10-7) – ( 1.5 X 10-7) = ( 4.1 – 1.5) X 10-7 = 2.6 X 10-7,
4. Sum = ( 8.3 X 106) + ( 1.5 X 106) = ( 8.3 + 1.5) X 106 = 9.8 X 106,
Difference = ( 8.3 X 106) – ( 1.5 X 106) = ( 8.3 – 1.5) X 106 = 6.8 X 106.
b. (a × 10n) + (b × 10n) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10n
as (a × 10n) + (b × 10n) = (a + b ) X 10n and
(a × 10n) – (b × 10n) can be completed using the distributive property
of multiplication over subtraction, i.e., factor out the common factor 10n
as (a × 10n) – (b × 10n) = (a-b) X 10n.
EXPLORATION 2
Multiplying and Dividing in Scientific Notation
Work with a partner.
a. Complete the table by finding the product and the quotient of
Expression 1 and Expression 2. Write your answers in scientific notation.
Explain your method.
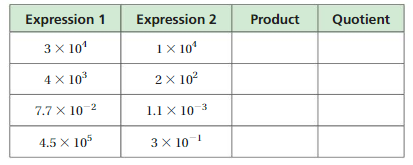
b. Use your results in part(a) to explain how to find (a × 10n) × (b × 10m) and
(a × 10n) ÷ (b ÷ 10m). Describe any properties that you use.
Answer:
b. (a × 10n) × (b × 10m) = (a × b) X (10n × 10m) = (a × b) X (10n+m) ,
Separately we multiply the coefficients and exponents and
we use Product of Powers Property for an • am = an+m
If product of two powers with the same base then
powers are added and (a × 10n) ÷ (b ÷ 10m) = a ÷ b X (10n–m),
Separately we divide the coefficients and exponents.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
We use the general rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base is am-n .
Explanation:
a. To multiply numbers in scientific notation these are the steps:
If the numbers are not in scientific notation, convert them.
Regroup the numbers using the commutative and
associative properties of exponents. Now multiply the two
numbers written in scientific notation, we work out
the coefficients and the exponents separately.
we use the product rule; bm x b n = b(m + n) to multiply the bases.
Join the new coefficient to the new power of 10 to get the answer.
If the product of the coefficients is greater than 9, convert it to
scientific notation and multiply by the new power of 10.
To divide two numbers written in scientific notation, follow the steps below:
Separately we divide the coefficients and exponents.
For the division of bases, use the division rule of exponents,
where the exponents are subtracted.
Combine the result of coefficients by the new power of 10.
If the quotient from division of coefficients is not
less than 10 and greater than 1, convert it to scientific notation
and multiply it by the new power of 10.
Noted that when you dividing exponential terms,
always subtract the denominator from the numerator.
So completed the table by finding the product and the
quotient of Expression 1 and Expression 2.
Now first we do write Products as
1.(3 X 104) X ( 1 X 104) = (3 X 1) X ( 104+4) = 3 X 108 .
2.(4 X 103) X (2 X 102) = (4 X 2 ) X ( 103+2) = 8 X 105.
3.(7.7 X 10-2) X (1.1 X 10-3) = (7.7 X 1.1 ) X (10-2+(-3)) = 8.47 X 10-5.
4.(4.5 X 105) X (3 X 10-1) = (4.5 X 3) X ( 105+(-1)) = 13.5 X 104.
Now we write Quotients as separately and divide the
coefficients and exponents.
For the division of bases, use the division rule of exponents,
where the exponents are subtracted.
1. (3 X 104) ÷ ( 1 X 104) = (3 ÷ 1) X ( 104-4) = 3 X 100 = 3 X 1 = 3.
2. (4 X 103) ÷ (2 X 102) = (4 ÷ 2 ) X ( 103-2) = 2 X 101 = 2 X 10 = 20.
3. (7.7 X 10-2) ÷ (1.1 X 10-3) = (7.7 ÷ 1.1 ) X (10-2-(-3)) =7 X 101 =7 X 10 = 70
4. (4.5 X 105) ÷ (3 X 10-1) = (4.5 ÷ 3) X ( 105-(-1)) = 1.5 X 106.
b. Here we multiply the coefficients separately and
use Product of Powers Property for an • am = an+m
we have rule of product of two powers with the same base then
we add powers, so (a × 10n) × (b × 10m) =
(a × b) X (10n × 10m) = (a × b) X (10n+m).
Separately we divide the coefficients and exponents.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
We use the general rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base is am-n .
So first we divide divide a ÷ b and then divide exponential terms
therefore (a × 10n) ÷ (b ÷ 10m) = a ÷ b X (10n-m).
Try It
Find the sum or difference.
Question 1.
(8.2 × 102) + (3.41 × 10-1)
Answer:
(8.2 × 102) + (3.41 × 10-1) =8203.41 X 10-1= 820.341
Explanation:
Given Expressions as (8.2 × 102) + (3.41 × 10-1)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 102 as 10-1 ·So we take 103 and then grouping the 103 with 8.2.
So 8.2 X 102 becomes 8200 X 10-1 therefore
(8.2 × 102) + (3.41 × 10-1) =(8.2 X 103 × 10-1) + (3.41 × 10-1) =
(8200 X 10-1) + (3.41 × 10-1)
using the distributive property of multiplication over addition,
we get (8200+3.41) X 10-1 =8203.41 X 10-1= 820.341
Question 2.
(7.8 × 10-5) – (4.5 × 10-5)
Answer:
(7.8 × 10-5) – (4.5 × 10-5) = 3.3 X 10-5
Explanation:
Given expressions as (7.8 × 10-5) – (4.5 × 10-5)
using the distributive property of multiplication over subtraction,
we get (7.8 – 4.5 ) X 10-5 = 3.3 X 10-5.
Find the product.
Question 3.
6 × (8 × 10-5)
Answer:
6 × (8 × 10-5) = 48 X 10-5
Explanation:
As given expression is 6 × (8 × 10-5) so we use
associative law of multiplication as a X (b X c) = (a X b ) X c,
So 6 × (8 × 10-5) = (6 × 8) × 10-5 = 48 X 10-5.
Question 4.
(7 × 102) × (3 × 105)
Answer:
(7 × 102) × (3 × 105) = 21 X 107
Explanation:
Given expressions as (7 × 102) × (3 × 105)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (7 × 102) × (3 × 105) = (7 X 3) X (102 × 105) = 21 X (102+5) = 21 X 107 .
Question 5.
(2 × 104) × (6 × 10-7)
Answer:
(2 × 104) × (6 × 10-7) = 12 X 10-3
Explanation:
Given expressions as (2 × 104) × (6 × 10-7)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (2 × 104) × (6 × 10-7) = (2 X 6) X (104 × 10-7) = 12 X (104-7) = 12 X 10-3 .
Question 6.
(3 × 108) × (9 × 103)
Answer:
(3 × 108) × (9 × 103) = 27 X 1011
Explanation:
Given expressions as (3 × 108) × (9 × 103)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (3 × 108) × (9 × 103) = (3 X 9) X (108 × 103) = 27 X (108+3) = 27 X 1011 .
Find the quotient.
Question 7.
(9.2 × 1012) ÷ 4.6
Answer:
(9.2 × 1012) ÷ 4.6 = 2 X 1012
Explanation:
Given expression as (9.2 × 1012) ÷ 4.6,
Separately we divide the coefficients
and multiply exponent with base
so (9.2 ÷ 4.6) X 1012 = 2 X 1012.
Question 8.
(1.5 × 10-3) ÷ (7.5 × 102)
Answer:
(1.5 × 10-3) ÷ (7.5 × 102) = 0.2 X 10-5
Explanation:
Given expressions as (1.5 × 10-3) ÷ (7.5 × 102),
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (1.5 × 10-3) ÷ (7.5 × 102) = (1.5 ÷ 7.5 ) X ( 10-3-2) = 0.2 X 10-5.
Question 9.
(3.75 × 10-8) ÷ (1.25 × 10-7)
Answer:
(3.75 × 10-8) ÷ (1.25 × 10-7) = 3 X 10-1 or 0.3
Explanation:
Given expressions as (3.75 × 10-8) ÷ (1.25 × 10-7),
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (3.75 × 10-8) ÷ (1.25 × 10-7) =
(3.75 ÷ 1.25 ) X ( 10-8-(-7)) = 3 X 10-1= 0.3.
Question 10.
(9.2 × 106) ÷ (2.3 × 1012)
Answer:
(9.2 × 106) ÷ (2.3 × 1012) = 4 X 10-6
Explanation:
Given expressions as (9.2 × 106) ÷ (2.3 × 1012) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (9.2 × 106) ÷ (2.3 × 1012) =
(9.2 ÷ 2.3 ) X ( 106-12) = 4 X 10-6.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
WRITING
Describe how to add or subtract two numbers written in scientific notation with
the same power of 10.
Answer:
Example (a × 10m) + (b × 10m) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10m
as (a × 10m) + (b × 10m) = (a + b ) X 10m , Here we have the same power 10.
Explanation:
One of the properties of quantities with exponents is that
numbers with exponents can be added and subtracted
only when they have the same base and exponent.
Since all numbers in scientific notation have the same base (10),
we need only worry about the exponents.
To be added or subtracted, two numbers in scientific notation they
must be manipulated so that their bases have the same exponent,
this will ensure that corresponding digits in their coefficients
have the same place value.
Question 12.
NUMBER SENSE
Two numbers written in scientific notation have different powers of 10. Do you have to rewrite the numbers so they have the same power of 10 before multiplying or dividing? Explain.
Answer:
No need to rewrite the numbers so that they have
the same power of 10 before multiplying or dividing.
Explanation:
The steps to multiply two numbers in scientific notation is
multiply the coefficients round to the number of
significant figures in the coefficient with the smallest number
of significant figures and we add the exponents.
The steps to divide two numbers in scientific notation is
divide the coefficients–round to the number of significant
figures in the coefficient with the smallest number of significant figures
and we subtract the exponents.
No need to rewrite the numbers so that they have
the same power of 10 before multiplying or dividing.
In multiplication we add exponents with same base and
in division we subtract exponents.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
OPERATIONS IN SCIENTIFIC NOTATION Evaluate the expression. Write your answer in scientific notation.
Question 13.
(7.26 × 104) + (3.4 × 104)
Answer:
(7.26 × 104) + (3.4 × 104) = 10.66 X 104
Explanation:
Given expressions as (7.26 × 104) + (3.4 × 104) as it is
(a × 10n) + (b × 10n) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10n
as (a × 10n) + (b × 10n) = (a + b ) X 10n so (7.26 × 104) + (3.4 × 104) =
(7.26 + 3.4 ) X 104 =10.66 X 104 .
Question 14.
(2.8 × 10-5) – (1.6 × 10-6)
Answer:
(2.8 × 10-5) – (1.6 × 10-6) = 26.4 X 10-6
Explanation:
Given Expressions as (2.8 × 10-5) – (1.6 × 10-6)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 10-5 as 10-6 · So we take 10-5 and then grouping the 10-5 with 2.8.
So 2.8 X 10-5 becomes 28 X 10-6 therefore (2.8 × 10-5) – (1.6 × 10-6)=
(2.8 ×10 X 10-6) – (1.6 × 10-6) = (28 X 10-6) – (1.6 × 10-6)
using the distributive property of multiplication over subtraction,
we get (28-1.6) X 10-6 = 26.4 X 10-6.
Question 15.
(2.4 × 104) × (3.8 × 10-6)
Answer:
(2.4 × 104) × (3.8 × 10-6) = 9.12 X 10-2
Explanation:
Given expressions as (2.4 × 104) × (3.8 × 10-6)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (2.4 × 104) × (3.8 × 10-6) = (2.4 X 3.8) X (104 × 10-6) =
9.12 X (104-6) = 9.12 X 10-2 .
Question 16.
(5.2 × 10-3) ÷ (1.3 × 10-12)
Answer:
(5.2 × 10-3) ÷ (1.3 × 10-12) = 4 X 109
Explanation:
Given expressions as (5.2 × 10-3) ÷ (1.3 × 10-12) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (5.2 × 10-3) ÷ (1.3 × 10-12) =
(5.2 ÷ 1.3 ) X ( 10-3+12) = 4 X 109.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
It takes the Sun about 2.3 × 108 years to orbit the center of the Milky Way. It takes Pluto about 2.5 × 102 years to orbit the Sun. How ×many times does Pluto orbit the Sun while the Sun completes one orbit around the Milky Way?
Answer:
9.2 X 105 times
Explanation:
Given It takes the Sun about 2.3 × 108 years to orbit the
center of the Milky Way. It takes Pluto about 2.5 × 102 years
to orbit the Sun. So number of times does Pluto orbit the Sun
while the Sun completes one orbit around the Milky Way is
dividing the number of years the sun takes by
the number of years Pluto takes. So we divide by dividing the factors and
dividing the powers of 10 then rewrite in scientific notation
as (2.3 × 108 ) ÷ (2.5 × 102) = \(\frac{2.3}{2.5}\) X (108-2) =
0.92 X 106 = 0.92 X 10 X 105 = 9.2 X105 times.
Question 18.
A person typically breathes about 8.64 × 108 liters of air per day.
The life expectancy of a person in the United States at birth is about 29,200 days.
Estimate the total amount of air a person born in the United States breathes over a lifetime.
Answer:
The total amount of air a person born in the United States
breathes over a lifetime is 2.52288 X 1013 liters
Explanation:
A person typically breathes about 8.64 × 108 liters of air per day.
The life expectancy of a person in the United States at birth is
about 29,200 days. The total amount of air a person born in the
United States breathes over a lifetime is 29,200 X 8.64 × 108 =
292 X 102 X 8.64 X 108 =(when bases are same powers are added)
2.92 X 8.64 X 1010 =2522.88 X1010 = 2.522 X 1013 liters.
therefore the total amount of air a person born in the United States
breathes over a lifetime is 2.52288 X 1013 liters.
Question 19.
In one week, about 4100 movie theaters each sold an average of 2200 tickets for Movie A. About 3.6 × 107 total tickets were sold at the theaters during the week. An article claims that about 25% of all tickets sold during the week were for Movie A. Is this claim accurate? Justify your answer.

Answer:
Yes, the claim is accurate.
Explanation:
Given in one week, about 4100 movie theaters each sold
an average of 2200 tickets for Movie A. About 3.6 × 107 total
tickets were sold at the theaters during the week.
Number of tickets for movie A =
4100 X 2200 = 9,020,000= 9.02 X 106 =
is approximately equal to ≈ 9 X 106 tickets.
Now 25% of total movie tickets is \(\frac{25}{100}\) X 3.6 × 107 =
25 X 3.6 X 105 = 90 X 105 = 9 X 10 X 105 =9 X 106 tickets.
Therefore, the claim of 25% of movie tickets sold for movie A
is approximately accurate.
Operations in Scientific Notation Homework & Practice 8.7
Review & Refresh
Write the number in scientific notation.
Question 1.
0.0038
Answer:
0.0038 = 3.8 X 10-3.
Explanation:
Given number is 0.0038 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.0038 = 3.8 X 0.001 = 3.8 X 10-3.
Question 2.
74,000,000
Answer:
74,000,000 = 7.4 X 107
Explanation:
Given number is 74,000,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 74,000,000 = 7.4 X 10,000,000 = 7.4 X 107 .
Question 3.
0.0000475
Answer:
0.0000475 = 4.75 X 10-5
Explanation:
Given number is 0.0000475 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.0000475 = 4.75 X 0.00001 = 4.75 X 10-5.
Find the values of the ratios (red to blue) of the perimeters and areas of the similar figures.
Question 4.
Answer:
Ratios of perimeter is \(\frac{3}{4}\),
Ratios of area is \(\frac{9}{16}\)
Explanation:
The ratios of corresponding sides are 9/12. These all reduce to 3/4.
It is then said that the scale factor of these two similar squares is 3 : 4.
The perimeter of red square is 4 X 9
the perimeter of blue square is 4 X 12
When we compare the ratios of the perimeters of these similar squares,
we get 4 X 9 : 4 X 12= 9 : 12 = 3 : 4
Now Area of square is side square
so the area of red square is 92 = 81
the area of blue square is 122= 144
So the ratio of their areas is 81 : 144 = 9 :16.
Therefore Ratios of perimeter is \(\frac{3}{4}\),
Ratios of area is \(\frac{9}{16}\)
Question 5.
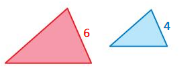
Answer:
Perimeter is \(\frac{3}{2}\),
Area is \(\frac{9}{4}\)
Explanation:
The ratios of corresponding sides are 6/4. These all reduce to 3/2.
It is then said that the scale factor of these two similar triangles is 3 : 2.
The perimeter of red triangle is 6 + 6 + 6 = 18 and
the perimeter of blue triangle is 4 + 4 + 4=12.
When we compare the ratios of the perimeters of these similar triangles,
we get 18 : 12 = 3:2.
We know if two similar triangles have a scale factor of a : b,
then the ratio of their areas is a2 : b2.
We have scale factor as 3 : 2 so the ratio of their areas is 32 : 22= 9 : 4.
Therefore the Perimeter is \(\frac{3}{2}\) and Area is \(\frac{9}{4}\).
Concepts, Skills, & Problem Solving
OPERATIONS IN SCIENTIFIC NOTATION Find the sum, difference, product, and quotient of Expression 1 and Expression 2. Write your answers in scientific notation. (See Explorations 1 and 2, p. 355.)
Question 6.
3 × 103 Expression 1
2 × 103 Expression 2
Answer:
Sum = (3 X 103) + (2 × 103) = 5 X 103,
Difference = (3 X 103) – (2 × 103) = 1 X 103 = 103,
Product = (3 X 103) X (2 × 103) = 6 X 106,
Quotient = (3 X 103) ÷ (2 × 103) = \(\frac{3}{2}\) = 1.5
Explanation:
For sum:
Given expressions as (3 × 103) + (2 × 103) as it is
(a × 10n) + (b × 10n) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10n
as (a × 10n) + (b × 10n) = (a + b ) X 10n so (3× 103) + (2 × 103) =
(3 + 2) X 103 =5 X 103.
For difference:
Given expressions as (3 × 103) – (2 × 103)
using the distributive property of multiplication over subtraction,
we get (3-2) X 103 = 1 X 103 = 103
For product:
Given expressions as (3 × 103) × (2 × 103)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (3 × 103) × (2 × 103) = (3 X 2) X (103 × 103) = 6 X (103+3) = 6 X 106.
For quotient:
Given expressions as (3 × 103) ÷ (2 × 103) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (3×103) ÷ (2 × 103) =
(3 ÷ 2 ) X ( 103-3) = (3 ÷ 2 ) X 100 = (3 ÷ 2 ) X 1 = (3 ÷ 2 ) = \(\frac{3}{2}\) =1.5.
Question 7.
6 × 10-4 Expression 1
1.5 × 10-4 Expression 2
Answer:
Sum = (6 X 10-4) + (1.5 × 10-4) = 7.5 X 10-4,
Difference = (6 X 10-4) – (1.5 × 10-4) = 4.5 X 10-4 ,
Product = (6 X 10-4) X (1.5 × 10-4) = 9 X 10-8,
Quotient = (6 X 10-4) ÷ (1.5 × 10-4) = 4 X 100,
Explanation:
For sum:
Given expressions as (6 × 10-4) + (1.5 × 10-4) as it is
(a × 10n) + (b × 10n) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10n
as (a × 10n) + (b × 10n) = (a + b ) X 10n so (3× 103) + (2 × 103) =
(6 + 1.5) X 10-4 =7.5 X 10-4.
For difference:
Given expressions as (6 × 10-4) – (1.5 × 10-4)
using the distributive property of multiplication over subtraction,
we get (6-1.5) X 10-4 = 4.5 X 10-4.
For product:
Given expressions as (6 × 10-4) × (1.5 × 10-4)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (6 × 10-4) × (1.5 × 10-4) = (6 X 1.5) X (10-4 × 10-4) = 6 X (10-4-4) = 9 X 10-8.
For quotient:
Given expressions as (6 × 10-4) ÷ (1.5 × 10-4) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (6×10-4) ÷ (1.5 × 10-4) =
(6 ÷ 1.5 ) X ( 10-4-(-4)) = (6 ÷ 1.5 ) X 100 = (4) X 100 or 4.
ADDING AND SUBTRACTING IN SCIENTIFIC NOTATION Find the sum or difference. Write your answer in scientific notation.
Question 8.
(2 × 105) + (3.8 × 105)
Answer:
(2 × 105) + (3.8 × 105) = 5.8 X 105.
Explanation:
Given expressions as (2 × 105) + (3.8 × 105) as it is
(a × 10n) + (b × 10n) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10n
as (a × 10n) + (b × 10n) = (a + b ) X 10n so (2× 105) + (3.8 × 105) =
(2 + 3.8) X 105 =5.8 X 105.
Question 9.
(6.33 × 10-9) – (4.5 × 10-9)
Answer:
(6.33 × 10-9) – (4.5 × 10-9) = 1.83 X 10-9.
Explanation:
Given expressions as (6.33 × 10-9) – (4.5 × 10-9)
using the distributive property of multiplication over subtraction,
we get (6.33 – 4.5) X 10-9 = 1.83 X 10-9.
Question 10.
(9.2 × 108) – (4 × 108)
Answer:
(9.2 × 108) – (4 × 108) = 5.2 X 108.
Explanation:
Given expressions as (9.2 × 108) – (4 × 108)
using the distributive property of multiplication over subtraction,
we get (9.2 – 4) X 108 = 5.2 X 108.
Question 11.
(7.2 × 10-6) + (5.44 × 10-6)
Answer:
(7.2 × 10-6) + (5.44 × 10-6) = 12.64 X 10-6 = 1.264 X 10-5
Explanation:
Given expressions as (7.2 × 10-6) + (5.44 × 10-6) as it is
(a × 10n) + (b × 10n) can be completed using the distributive property
of multiplication over addition, i.e., factor out the common factor 10n
as (a × 10n) + (b × 10n) = (a + b ) X 10n so (2× 105) + (3.8 × 105) =
(7.2 + 5.44) X 10-6 =12.64 X 10-6 = 1.264 X 10-5.
Question 12.
(7.8 × 107) – (2.45 × 106)
Answer:
(7.8 × 107) – (2.45 × 106) = 7.55 X 107
Explanation:
Given expressions as (7.8 × 107) – (2.45 × 106)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 106 as 107 · So we take 107 and then grouping the 107 with 2.45.
So 2.45 X 106 becomes 0.245 X 107 therefore (7.8 × 107) – (0.245 × 107)=
(7.8 X 107) – (2.45 X 10-1X 101 X 106) = (7.8 X 107) – (0.245 × 107)
using the distributive property of multiplication over subtraction,
we get (7.8 – 0.245) X 107 = 7.55 X 107.
Question 13.
(5 × 10-5) + (2.46 × 10-3)
Answer:
(5 × 10-5) + (2.46 × 10-3) = 2.51 X 10-5.
Explanation:
Given expressions as (5 × 10-5) + (2.46 × 10-3)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 10-5 as 10-3 · So we take 10-3 and then grouping the 10-3 with 5.
So 5 X 10-5 becomes 0.05 X 10-3 therefore (5 × 10-5) + (2.46 × 10-3)=
(5 X 10-2 X 10-3) + (2.46 X 10-3) = (0.05 X 10-3) + (2.46 × 10-3)
using the distributive property of multiplication over addition,
we get (0.05 + 2.46) X 10-5 = 2.51 X 10-5.
Question 14.
(9.7 × 106) + (6.7 × 105)
Answer:
(9.7 × 106) + (6.7 × 105) = 103.7 X 105 or 1.037 X 107
Explanation:
Given expressions as (9.7 × 106) + (6.7 × 105)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 106 as 105 · So we take 105 and then grouping the 105 with 9.7.
So 9.7 X 106 becomes 97 X 105 therefore (9.7 × 106) + (6.7 × 105)=
(9.7 X 101 X 105) + (6.7 X 105) = (97 X 105) + (6.7 × 105)
using the distributive property of multiplication over addition,
we get (97 + 6.7) X 105 = 103.7 X 105 = 1 .037 X 102 X 105 = 1.037 X 107 .
Question 15.
(2.4 × 10-1) – (5.5 × 10-2)
Answer:
(2.4 × 10-1) – (5.5 × 10-2) = 1.85 X 10-1
Explanation:
Given expressions as (2.4 × 10-1) – (5.5 × 10-2)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 10-2 as 10-1 · So we take 10-1 and then grouping the 10-1 with 5.5.
So 5.5 X 10-2 becomes 0.55 X 10-1 therefore (2.4 × 10-1) – (5.5 × 10-2) =
(2.4 X 10-1) – (5.5 X 10-1X 10-1) = (2.4 X 10-1) – (0.55 × 10-1)
using the distributive property of multiplication over subtraction,
we get (2.4 – 0.55) X 10-1 = 1.85 X 10-1.
Question 16.
YOU BE THE TEACHER
Your friend adds 2.5 × 109 and 5.3 × 108. Is your friend correct? Explain your reasoning.
Answer:
Yes, Friend is correct
Explanation:
Given expressions as 2.5 × 109 and 5.3 × 108
we do sum as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 108 as 109 · So we take 109 and then grouping the 109 with 5.3.
So 5.3 X 109 becomes 0.53 X 109 therefore (2.5 × 109) + (5.3 × 108) =
(2.5 X 109) + (5.3 X 10-1 X 10 X 108) = (2.5 X 109) + (0.53 × 109)
using the distributive property of multiplication over addition,
we get (2.5 + 0.53 ) X 109 = 3.03 X 109.
As the results are same friend is correct.
MULTIPLYING AND DIVIDING IN SCIENTIFIC NOTATION Find the product or quotient. Write your answer in scientific notation.
Question 17.
5 × (7 × 107)
Answer:
5 × (7 × 107) = 3.5 X 108
Explanation:
As given expression is 5 × (7 × 107) so we use
associative law of multiplication as a X (b X c) = (a X b ) X c,
So 5 × (7 × 107) = (5 X 7) × 107 = 35 X 107.= 3.7 X 10 X 107 = 3.7 X 108.
Question 18.
(5.8 × 10-6) ÷ (2 × 10-3)
Answer:
(5.8 × 10-6) ÷ (2 × 10-3) = 2.9 X 10-3.
Explanation:
Given expressions as (5.8 × 10-6) ÷ (2 × 10-3) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (5.8 × 10-6) ÷ (2 × 10-3) = (5.8 ÷ 2 ) X ( 10-6+3) = 2.9 X 10-3.
Question 19.
(1.2 × 10-5) ÷ 4
Answer:
(1.2 × 10-5) ÷ 4 = 3 X 10-6
Explanation:
Given expression is (1.2 × 10-5) ÷ 4 so (1.2 ÷ 4) X 10-5= 0.3 X 10-5=
3 X 10-1X 10-5= 3 X 10-6.
Question 20.
(5 × 10-7) × (3 × 106)
Answer:
(5 × 10-7) × (3 × 106) = 15 X 10-1 = 1.5
Explanation:
Given expressions as (5 × 10-7) × (3 × 106)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (5 × 10-7) × (3 × 106) = (5 X 3) X (10-7 × 106) = 15 X (10-7+6) = 15 X 10-1 = 1.5.
Question 21.
(3.6 × 107) ÷ (7.2 × 107)
Answer:
(3.6 × 107) ÷ (7.2 × 107) = 5 X 10-1
Explanation:
Given expressions as (5.8 × 10-6) ÷ (2 × 10-3) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (3.6 × 107) ÷ (7.2 × 107) = (3.6 ÷ 7.2 ) X ( 10-7+7) = 0.5 X 100 = 5 X 10-1.
Question 22.
(7.2 × 10-1) × (4 × 10-7)
Answer:
(7.2 × 10-1) × (4 × 10-7) = 2.88 X 10-7
Explanation:
Given expressions as (7.2 × 10-1) × (4 × 10-7)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (7.2 × 10-1) × (4 × 10-7) = (7.2 X 4) X (10-1 × 10-7) =
28.8 X (10-1-7) = 28.8 X 10-8 = 2.88 X 10-7.
Question 23.
(6.5 × 108) × (1.4 × 10-5)
Answer:
(6.5 × 108) × (1.4 × 10-5) = 9.1 X 103
Explanation:
Given expressions as (6.5 × 108) × (1.4 × 10-5)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (6.5 × 108) × (1.4 × 10-5) = (6.5 X 1.4) X (108 × 10-5) =
9.1 X (108-5) = 9.1 X 103.
Question 24.
(2.8 × 104) ÷ (2.5 × 106)
Answer:
(2.8 × 104) ÷ (2.5 × 106) = 1.12 X 10-2
Explanation:
Given expressions as (2.8 × 104) ÷ (2.5 × 106) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (2.8 × 104) ÷ (2.5 × 106) = (2.8 ÷ 2.5 ) X ( 104-6) = 1.12 X 10-2.
MATCHING You use technology to find four sums.
Match the sum with its standard form.
Question 25.
4.3E8
Answer:
4.3E8 matches with C. 430,000,000
Explanation:
Given number 4.3E8 here nearly or approximately equals to ≈ 4.3 X 108,
The exponent “8” says to use the 10 by eight times in a multiplication as
4.3 E 8 = 4.3 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 = 430,000,000,
So 4.3E8 we will match with C.
Question 26.
4.3E – 8
Answer:
4.3E – 8 matches with B. 0.000000043
Explanation:
Given number 4.3E – 8 nearly or approximately equals to ≈ 4.3 X 10-8,
The exponent “-8” says to use the 10-1 by eight times in a multiplication as
4.3 E 8 = 4.3 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 = 0.000000043,
so 4.3E -8 we will match with B.
Question 27.
4.3E10
Answer:
4.3E10 matches with D. 43,000,000,000
Explanation:
Given number 4.3E10 nearly or approximately equals to ≈ 4.3 X 1010,
The exponent “10” says to use the 10 by ten times in a multiplication as
4.3 E 10 = 4.3 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 =
43,000,000,000 so 4.3E10 we will match with D.
Question 28.
4.3E – 10
Answer:
4.3E – 10 matches with A.0.00000000043
Explanation:
Given number 4.3E – 10 nearly or approximately equals to ≈ 4.3 X 10-10,
The exponent “-10” says to use the 10-1 by eight times in a multiplication as
4.3 E 8 = 4.3 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1 X 0.1
= 0.00000000043 so 4.3E -10 we will match with A.
A. 0.00000000043
B. 0.000000043
C. 430,000,000
D. 43,000,000,000
Question 29.
MODELING REAL LIFE
How many times greater is the thickness of a dime than the thickness of a dollar bill?

Answer:
The dime is about 12 times thicker than the dollar bill.
Explanation:
Given the thickness of dime is 0.135 = 1.35 X 10-1 and
the thickness of a dollar is 1.0922 X 10-2 divide the thickness of
dime with the thickness of dollar as (1.35 × 10-1) ÷ (1.0922 × 10-2)
now we separately divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (1.35 × 10-1) ÷ (1.0922 × 10-2) = (1.35 ÷ 1.0922 ) X ( 10-1+2) =
1.2360 X 101= 12.36 approximately equals to ≈ 12.
Therefore the dime is about 12 times thicker than the dollar bill.
Question 30.
MULTIPLE CHOICE
On a social media website, Celebrity A has about 8.6 × 106 followers and Celebrity B has about 4.1 × 106 followers. Determine which of the following is the best estimate for the number of followers for Celebrity A compared to the number of followers for Celebrity B.
A. more than 2 times greater
B. less than 2 times greater
C. more than 20 times greater
D. less than 20 times greater
Answer:
The best estimate for the number of followers for Celebrity A
compared to the number of followers for Celebrity B is
A. more than 2 times greater.
Explanation:
Given on a social media website, Celebrity A has about
8.6 × 106 followers and Celebrity B has about 4.1 × 106 followers.
To find the best estimate for the number of followers for Celebrity A
compared to the number of followers for Celebrity B we divide them as
the number of followers for Celebrity A to the number of
followers for Celebrity B as (8.6 × 106) ÷ (4.1× 106)
now we separately divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (8.6× 106) ÷ (4.1 × 106) = (8.6 ÷ 4.1) X ( 106-6) =
2.097 X 100= 2.097 X 1 = 2.097 approximately equals to ≈ 2.
The best estimate for the number of followers for Celebrity A
compared to the number of followers for Celebrity B is
A. more than 2 times greater.
REASONING Evaluate the expression. Write your answer in scientific notation.
Question 31.
5,200,000 × (8.3 × 102) – (3.1 × 108)
Answer:
5,200,000 × (8.3 × 102) – (3.1 × 108) = 4.006 X 109
Explanation:
Given expressions as 5,200,000 × (8.3 × 102) – (3.1 × 108),
So first we solve 5,200,000 × (8.3 × 102) as 5.2 X 106 X (8.3 × 102),
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
(5.2 X 8.3) X (106 X 102) = (43.16) X (106+2) = 43.16 X 108,
now we subtract expressions as (43.16 X 108) – (3.1 × 108) =
using the distributive property of multiplication over subtraction,
we get (43.16 – 3.1) X 108 = 40.06 X 108 = 4.006 X 10 X 108 = 4.006 X 109.
Question 32.
(9 × 10-3) + (2.4 × 10-5) ÷ 0.0012
Answer:
(9 × 10-3) + (2.4 × 10-5) ÷ 0.0012 = 7.52
Explanation:
Given (9 × 10-3) + (2.4 × 10-5) ÷ 0.0012 first we solve
(9 × 10-3) + (2.4 × 10-5) given expressions as 9 × 10-3 and 2.4 × 10-5
we do sum as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 10-5 as 103 · So we take 10-5 and then grouping the 10-5 with 2.4.
So 2.4 X 10-5 becomes 0.024 X 10-3 therefore (9 × 10-3) + (2.4 × 10-5)=
(9X 10-3) + (2.4 X 10-2 X 10-3) = (9 X 10-3) + (0.024 × 10-3)
using the distributive property of multiplication over addition,
we get (9 + 0.024 ) X 10-3 = 9.024 X 10-3.
So (9 × 10-3) + (2.4 × 10-5) = 9.024 X 10-3 now we write 0.0012 as
1.2 X 10-3 therefore we divide (9.024 X 10-3) ÷ (1.2 X 10-3),
now we separately divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (9.024 ÷ 1.2) X (10-3 ÷ 10-3) so 7.52 X 10-3+3 = 7.52 X 100 =
7.52 X 1 = 7.52.
Question 33.
GEOMETRY
Find the perimeter of the rectangle at the right.

Answer:
The perimeter of the rectangle at the right is 1.962 X 108 cm.
Explanation:
Given area of rectangle as 5.612 X 1014cm2 and breadth as
9.2 X 107 cm , We will find the length first we take length as l,
we know area of rectangle is length X breadth so
5.612 X 1014 cm2 = l X 9.2 X 107
so l= (5.612 X 1014 ) ÷ (9.2 X 107) now we separately divide
the coefficients and exponents. We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
(5.612 X 9.2) X (1014 ÷ 107) = 0.61 X (1014-7) = 0.61X 107=0.61 X 107 cm,
therefore length of rectangle is 0.61 X 107 cm now we will calculate
perimeter of rectangle as we know perimeter of rectangle =
2 x ( length + breadth)= 2 X ((0.61 X 107)+(9.2 X 107))cm,
now we calculate first (0.61 X 107)+(9.2 X 107) using the
distributive property of multiplication over addition,
we get (0.61 + 9.2) X 107 = 9.81 X 107 now 2 X (9.81X 107)=
19.62 X 107= 1.962 X 108 cm. Therefore the perimeter of the
rectangle at the right is 1.962 X 108 cm.
Question 34.
DIG DEEPER!
A human heart pumps about 7 × 10-2 liter of blood per heartbeat.
The average human heart beats about 72 times per minute.
How many liters of blood does a heart pump in 1 year? 70 years?
Answer:
2.65 X 106 liters of blood a heart pump in 1 year.
1.855 X 108 liters of blood a heart pump for 70 years.
Explanation:
Given a human heart pumps about 7 × 10-2 liter of blood per heartbeat.
The average human heart beats about 72 times per minute.
The the number of liters per minute multiply the number of
heartbeats per minute by the number of liters per heartbeat as
72 X 7 × 10-2 = 504 × 10-2 =5.04 liters per minute,
now we multiply by 60 to get liters per hour since
there are 60 minutes in 1 hour so 60 X 5.04 = 302.4 liters per hour,
now we multiply by 24 to get liters per day since
there are 24 hours in 1 day so 302.4 X 24 = 7257.6 liters per day,
now we multiply by 365 to get liters per year since
there are 365 days in 1 year and write in scientific notation
and round to two decimal places as 7257.6 X 365 = 2649024 =
2.649024 X 106 approximately equal to ≈ 2.65 X 106 liters per year
Now for 70 years it is 70 X 2.65 X 106 = 185.5 X 106 = 1.855 X 100 X 106 =
1.855 X 102 X 106 =1.855 X 108 liters for 70 years.
Question 35.
MODELING REAL LIFE
Use the Internet or another reference to find the populations and areas (in square miles) of India, China, Argentina, the United States, and Egypt. Round each population to the nearest million and each area to the nearest thousand square miles.
a. Write each population and area in scientific notation.
b. Use your answers to part(a) to find and order the population densities (people per square mile) of each country from least to greatest.
Answer:
a. In India : Population = 1.311 X 109 , Area = 1.269 X 106
In China : Population = 1.371 X 109 , Area = 3.705 X 106
In Argentina : Population = 4.3 X 107 , Area = 1.074 X 106
In United States : Population = 3.21 X 108, Area = 3.797 X 106
In Egypt: Population = 9.2 X 107 , Area = 3.9 X 106
b. The population densities are
India = 1.033 X 103
China = 3.7 X 102
Argentina =4.0 X 101
United States = 8.45 X 101
and in Egypt = 2.36 X 101
Each country from least to greatest is
Egypt, Argentina, United States, China, India.
Explanation:
The following were found by doing a google search :
we write each population and area in scientific notation,
We know 1 billion = 109 and 1 million = 106 ,
a. In India : Population = 1.311 billion= 1.311 X 109
Area = 1.268 million = 1.269 X 106
In China : Population = 1.371 billion = 1.371 X 109
Area =3.705 million= 3.705 X 106
In Argentina : Population= 43 million = 4.3 X 107
Area = 1.074 million = 1.074 X 106
In United States : Population=321 million = 3.21 X 108
Area =3.797 million= 3.797 X 106
In Egypt: Population = 92 million= 9.2 X 107
Area =390,000= 3.9 X 106
b. Divide each country’s population by its area to
get its population density, and we separately divide
the coefficients and exponents. We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
India = ( 1.311 X 109 ) ÷ ( 1.269 X 106) = 1.033 X 103
(1.311 ÷ 1.269) X (109-6) = 1.033 X 103 ,
China = ( 1.371 X 109 ) ÷ ( 3.705 X 106) =
(1.371 ÷ 3.705) X (109-6) = 0.370 X 103 = 3.7 X 102,
Argentina = ( 4.3 X 107 ) ÷ ( 1.074 X 106) =
(4.3 ÷ 1.074) X (107-6) = 4 X 101,
United States = ( 3.21 X 108 ) ÷ ( 3.797 X 106) =
(3.21 ÷ 3.797) X (108-6) = 0.845 X 102 = 8.45X 101,
Egypt = (9.2 X 107 ) ÷ ( 3.9 X 106) =
(9.2 ÷ 3.9) X (107-6) = 2.36 X 101,
Now we write each country from least to greatest density as
2.36 X 101 < 4 X 101 < 8.45X 101< 3.7 X 102,1.033 X 103 so
Egypt, Argentina, United States, China, India.
Exponents and Scientific Notation Connecting Concepts
Using the Problem-Solving Plan
Question 1.
Atoms are made of protons, neutrons, and electrons. The table shows the numbers of protons and the masses of several atoms. Use a line of best fit to estimate the mass (in grams) of an atom that has 29 protons.
Understand the problem.
You know the numbers of protons and the masses of several atoms. You are asked to use the line of best fit to estimate the mass of an atom that has 29 protons.
Make a plan.
Use a graphing calculator to find an equation of the line of best fit.
Then evaluate the equation when x = 29.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Mass of an atom that has 29 protons is 4.843 X 10-23 grams
Explanation:
Given 1 proton has 1.67 X 10-24 grams of mass,
So 29 protons has 29 X 1.67 X 10-24 grams,
48.43 X 10-24 = 4.843 X 10-23 grams.
Question 2.
Modoc Country, California, is 74.9 miles long and 56.2 miles wide. 263A map of the county is drawn using a scale factor of 2.11 × 10-6. What is the perimeter of the county on the map? Express your answer using more appropriate units.
Answer:
The perimeter of the country on the map is 6.66631 X 1011 inches
Explanation:
Given Modoc Country, California, is 74.9 miles long and 56.2 miles wide.
First we calculate perimeter it is 2 X ( 74.9 + 56.2) mile = 2 X 131.1 =
262.2 miles, So perimeter of Modoc Country, California is 262.2 miles.
Now on map we will use in inches , we know 1 mile = 5280 feet and
1 feet is equal to 12 inches so 262.2 we will convert into inches.
262.2 X 5280 X 12 = 1406592 inches. Now we are given with
scaling factor on the map as 2.11 × 10-6 equals to 1 inch on the map,
So now perimeter of the country on the map is
(1406592 ) ÷ 2.11 × 10-6 = 666631.27 X 106 = 6.66631 X 1011 inches.
Question 3.
A research company estimates that in the United States, 7733 about 8.37 × 107 adult males and 6.59 × 107 adult females watch NFL football, while 3.13 × 107 adult males and 5.41 × 107 adult females do not watch NFL football. Organize the results in a two-way table. Include the marginal frequencies.
Answer:
Explanation:
Given A research company estimates that in the United States, 7733 about
8.37 × 107 adult males and 6.59 × 107 adult females watch NFL football,
while 3.13 × 107 adult males and 5.41 × 107 adult females do not watch NFL football.
Organized the results in two-way table above,
Entries in the “Total” row and “Total” column are called
marginal frequencies or the marginal distribution.
Entries in the body of the table are called joint frequencies.
So total adult watched NFL football match are
(8.37 X 107) + (6.59 X 107)=14.96 X 107 and do not
watch NFL football are(3.13 X 107) + (5.41 X 107) = 8.54 X 107.
Performance Task
Elements in the Universe
At the beginning of this chapter, you watched a STEAM Video called “Carbon Atoms.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Answer:
Exponents and Scientific Notation Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Let us take an example : 52 ,
An expression that represents repeated multiplication
of the same factor is called a power.
Here the number 5 is called the base,
and the number 2 is called the exponent.
The exponent corresponds to the number of times
the base is used as a factor.
A method for expressing very large or very small numbers
as a product of decimal less than 10 and multiplied
by a power of 10.
Example: 8 X 107 or 5 X 10-2.
Graphic Organizers
You can use a Definition and Example Chart to organize information about a concept.
Here is an example of a Definition and Example Chart for the vocabulary term power.
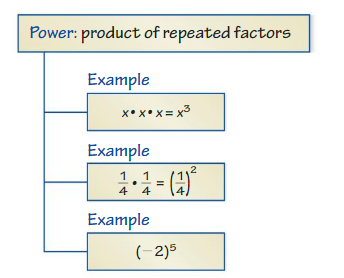
Choose and complete a graphic organizer to help you study the concept.
1. Product of Powers Property
2. Power of a Power Property
3. Power of a Product Property
4. Quotient of Powers Property
5. negative exponents
6. scientific notation
7. adding and subtracting numbers in scientific notation
8. multiplying and dividing numbers in scientific notation
Graphic Organizer:
1. Product of Powers Property
2. Power of a Power Property
3. Power of a Product Property
4. Quotient of Powers Property
5. negative exponents & power of a quotient

6. scientific notation
7. adding and subtracting numbers in scientific notation

8. multiplying and dividing numbers in scientific notation

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

8.1 Exponents (pp. 319–324)
Learning Target: Use exponents to write and evaluate expressions. Write the product using exponents.
Question 1.
(- 9) • (- 9) • (- 9) • (- 9) • (- 9)
Answer:
(- 9) • (- 9) • (- 9) • (- 9) • (- 9) =(-9)5
Explanation:
As -9 is multiplied by 5 times we write as
(-9)5 here -9 is base and 5 is exponent.
Question 2.
2 • 2 • 2 • n • n
Answer:
2 • 2 • 2 • n • n = (2)3 X (n)2
Explanation:
As 2 is multiplied 3 times we write as (2)3 and n
is multiplied twice so (n)2
so the expression is (2)3 X (n)2 .
Evaluate the expression.
Question 3.
113
Answer:
113 = 1331
Explanation:
Given 113 means 11 is multiplied thrice
as 11 X 11 X 11 we get 1331.
here base is 11 and exponent is 3.
Question 4.
-(\(\frac{1}{2}\))4
Answer:
-(\(\frac{1}{2}\))4 = – \(\frac{1}{16}\)
Explanation:
Given -(\(\frac{1}{2}\))4 means \(\frac{1}{2}\) is multiplied four times
as- (\(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) ) = – \(\frac{1}{16}\).
Question 5.
|\(\frac{1}{2}\left(16-6^{3}\right)\)|
Answer:
|\(\frac{1}{2}\left(16-6^{3}\right)\)| = 100
Explanation:
Given expression as |\(\frac{1}{2}\left(16-6^{3}\right)\)|=
first we solve 63 =6 X 6 X 6 = 216 now (16-216) = -200
so |\(\frac{1}{2}\) X -200|= |-100|= 100.
Question 6.
The profit P(in dollars) earned by a local merchant selling x items is 3 represented by the equation P = 0.2x3 – 10. How much more profit does he earn selling 15 items than 5 items?
Answer:
More profits he earn by selling 15 items than 5 items is $650
Explanation:
Given P = 0.2x3 – 10
Profit by selling 5 items is
0.2 X (5)3 – 10 = 0.2 X 125 – 10 = 25 – 10 = $15.
Profit by selling 15 items is
0.2 X (15)3 – 10 = 0.2 X 3375 – 10 = 675 – 10 = $665.
More profits he earn by selling 15 items than 5 items is
$665 -15 = $650.
8.2 Product of Powers Property (pp. 325–330)
Learning Target: Generate equivalent expressions involving products of powers.
Simplify the expression. Write your answer as a power.
Question 7.
p5 • p2
Answer:
p5 • p2 = p7
Explanation:
We write the given p5 • p7 expression as a power,
we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added,
so p5 • p2 as bases are same p powers are added p5+2 = p7.
Question 8.
(n11)2
Answer:
(n11)2 = n22
Explanation:
We write the given expression (n11)2 as a power,
General rule for finding (am)n power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n .
so (n11)2 has powers of powers therefore powers
are multiplied as (n)11 X 2= (n)22
Question 9.
\(\left(-\frac{2}{5}\right)^{3} \cdot\left(-\frac{2}{5}\right)^{2}\)
Answer:
\(\left(-\frac{2}{5}\right)^{3} \cdot\left(-\frac{2}{5}\right)^{2}\) = –
Explanation:
Given expression is \(\left(-\frac{2}{5}\right)^{3} \cdot\left(-\frac{2}{5}\right)^{2}\)
we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, so we add powers as (-\(\frac{2}{5}\))3+2 =
(-\(\frac{2}{5}\))5 So \(\left(-\frac{2}{5}\right)^{3} \cdot\left(-\frac{2}{5}\right)^{2}\) =
Question 10.
Simplify (- 2k)4.
Answer:
(- 2k)4 = (-2)4 X k4
Explanation:
Given to simplify the expression (- 2k)4 we use general rule to
write (ab)m power of a product as am X bm ,So (- 2k)4 = (-2)4 X k4
Question 11.
Write an expression that simplifies to x24 using the Power of a Power Property.
Answer:
x24 = (x12)2
Explanation :
To simplify x24 using the Power of a Power Property,
we use general rule for finding (am)n power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n ,here m X n = 24,
lets take m, n as 12,2 so that 12 X 2 = 24, therefore (x12)2 = x12 x 2 = x24.
therefore x24 = (x12)2 .
Question 12.
You send an email with a file size of 4 kilobytes. One kilobyte is 210 bytes. What is the file size of your email in bytes?

Answer:
The file size of my email in bytes is
Explanation:
Given I send an email with a file size of 4 kilobytes. One kilobyte is 210 bytes.
The file size of my email in bytes is 4 X 210 bytes as 4 can be written as 2 X 2 =22,
So 22 X 210 we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, 22 X 210 = 22+10 = 212 bytes.
Question 13.
Explain how to use properties of powers 2 to simplify the expression 27 • 32.
Answer:
27 • 32 = 33 X 32 = 35
Explanation:
Given expression as 27 • 32 first we write 27 as power of 3,
so 27 = 3 X 3 X 3 = 33 now 27 • 32 = 33 X 32 ,
we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, 33 X 32 = 33+2= 35.
8.3 Quotient of Powers Property (pp. 331–336)
Learning Target: Generate equivalent expressions involving quotients of powers.
Simplify the expression. Write your answer as a power.
Question 14.
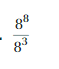
Answer:
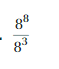 = (8)8-3 = (8)5
= (8)8-3 = (8)5
Explanation:
Given \(\frac{8^{8}}{8^{3}}\) we use rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base as am-n
so \(\frac{8^{8}}{8^{3}}\) = (8)8-3 = (8)5
Question 15.

Answer:
 = 510
= 510
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (5)2 X (5)9
we have same bases as 5 so we add powers as (5)2+9 = (5)11
we have denominator (5)1
Now we have \(\frac{5^{11}}{5^{1}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{5^{11}}{5^{1}}\) = (5)11-1 = 510.
Question 16.
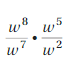
Answer:
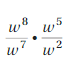 = w4
= w4
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (w)8 X (w)5
we have same bases as w so we add powers as (w)8+5 = (w)13
we have denominator (w)7 X (w)2
we have same base as w so we add powers as (w)7+2 = (w)9
Now we have \(\frac{w^{13}}{w^{9}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{w^{13}}{w^{9}}\) = (w)13-9 = w4.
Question 17.
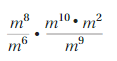
Answer:
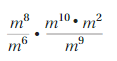 = m5
= m5
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (m)8 X (m)10 X (m)2
we have same bases as m so we add powers as (m)8+10+2 = (m)20
we have denominator (m)6 X (m)9
we have same base as m so we add powers as (m)6+9 = (m)15
Now we have \(\frac{m^{20}}{m^{15}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{m^{20}}{m^{15}}\) = (m)20-15 = m5.
Question 18.
Write an expression that simplifies to x3 using the Quotient of Powers Property.
Answer:
x3 = \(\frac{x^{6}}{x^{3}}\)
Explanation:
To simplify x3 using the Quotient of Powers Property,
we use rule for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n here we have m-n = 3,So lets take
m, n as 6,3 so that 6-3 = 3 therefore \(\frac{x^{6}}{x^{3}}\)= x6-3 = x3.
therefore x3 = \(\frac{x^{6}}{x^{3}}\).
Question 19.
At the end of a fiscal year, a company has made 1.62 × 77 dollars in profit. The company employs 73 people. How much will each person receive if the company divides the profit equally among its employees?
Answer:
Each person will receive $3889.62 if the company divides
the profit equally among its employees.
Explanation:
Given at the end of a fiscal year, a company has made 1.62 × 77 dollars in profit,
The company employs 73 people. To find how much each person
receive if the company divides the profit equally among its employees is
1.62 × 77 ÷ 73 we use the division rule of exponents,
where the exponents are subtracted. 1.62 X ( 77 ÷ 73 ) = 1.62 X ( 77-3) =
1.62 X 74 = 1.62 X 7 X 7 X 7 X 7 = 3889.62, Therefore each person
will receive $3889.62 if the company divides the profit equally among its employees.
8.4 Zero and Negative Exponents (pp. 337–342)
Learning Target: Understand the concepts of zero and negative exponents.
Evaluate the expression.
Question 20.
2-4
Answer:
4-2
Explanation:
Given expression as 2-4 so we write as
Question 21.
950
Answer:
950 = 1
Explanation:
Given expression is 950 it is proven that any number or
expression raised to the power of zero is always equal to 1.
In other words, if the exponent is zero then the result is 1.
So 950 = 1.
Question 22.
\(\frac{8^{2}}{8^{4}}\)
Answer:
\(\frac{8^{2}}{8^{4}}\) = \(\frac{1}{8^{2}}\) = \(\frac{1}{64}\).
Explanation:
Given expression as \(\frac{8^{2}}{8^{4}}\) now we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
as 82-4 we get 8-2 we write as \(\frac{1}{8^{2}}\) = \(\frac{1}{64}\).
Question 23.
(- 12)-7 • (- 12)7
Answer:
(- 12)-7 • (- 12)7= 1
Explanation:
Given expression is -12-7 X -127 ,
Here we use Product of Powers Property for am • an = am+n
if we have product of two powers with the same base then
powers are added. So (12)-7 X (12)7 = (12)-7+7 = (12)0= 1.
Question 24.
\(\frac{1}{7^{9}} \cdot \frac{1}{7^{6}}\)
Answer:
\(\frac{1}{7^{9}} \cdot \frac{1}{7^{6}}\) = \(\frac{1}{7^{15}}\)
Explanation:
Given expression is \(\frac{1}{7^{9}} \cdot \frac{1}{7^{6}}\)
first we calculate separately values of denominators
then divide with numerator, we have denominator 79 X 76
we have same bases as 7 so we add powers as 79+6 = 715
as numerator is 1 we write as \(\frac{1}{7^{15}}\).
Question 25.
\(\frac{9^{4} \cdot 9^{2}}{9^{2}}\)
Answer:
\(\frac{9^{4} \cdot 9^{2}}{9^{2}}\) = 94
Explanation:
Given Expression as \(\frac{9^{4} \cdot 9^{2}}{9^{2}}\)
first we calculate separately values of numerators
then divide with denominator, we have numerator (9)4 X (9)2
we have same bases as 9 so we add powers as (9)4+2 = (9)6
Now we have \(\frac{9^{6}}{9^{2}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n,
So \(\frac{9^{6}}{9^{2}}\) = (9)6-2 = (9)4.
Simplify. Write the expression using only positive exponents.
Question 26.
x-2 • x0
Answer:
x-2 • x0 = \(\frac{1}{x^{2}}\)
Explanation:
Given expression is x-2 • x0 = \(\frac{1}{x^{2}}\).
Question 27.
y-8y3
Answer:
y-8y3 = \(\frac{1}{y^{5}}\)
Explanation:
Given expression is y-8 • y3 = \(\frac{1}{y^{5}}\).
Question 28.
\(\frac{3^{-1} \cdot z^{5}}{z^{-2}}\)
Answer:
\(\frac{3^{-1} \cdot z^{5}}{z^{-2}}\) =
Explanation:
Given expression is \(\frac{3^{-1} \cdot z^{5}}{z^{-2}}\)
we use rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base as am-n
for \(\frac{z^{5}}{z^{-2}}\) as z= z7
now we have 3-1 X z7
Question 29.
Write an expression that simplifies to x-4.
Answer:
x-4 =
Explanation:
To simplify x-4 we use rule for finding \(\frac{a^{m}}{a^{n}}\),
a quotient of two powers with the same base as am-n,So m-n = -4 we take
m, n as 4,8 which makes (4-8) = -4 therefore x-4 =
Question 30.
Water flows from a shower head at a rate of 24-1 gallon per second. How many gallons do you use when taking a 15-minute shower? a 20-minute shower?

Answer:
In 15 minutes we use in 20 minutes shower we use 50
Explanation:
Given water flows from a shower head at a rate of 24-1 gallon per second,
to know how many gallons we used in 15-minutes first
we convert minutes to seconds as 1 minute is equal to 60 seconds,
so 15 minutes is equal to 15 X 60 = 900 seconds now number of gallons we
used in 15 minutes are 900 X 24-1 =
Question 31.
Explain two different methods for simplifying w-2 • w5.
Answer:
One is product of powers = w-2 • w5 = w-2+5 = w3 or
other is quotient of two powers with the same base = w5-2 = w3
Explanation:
To simplify w-2 • w5 first we use
other method is we write as .
8.5 Estimating Quantities (pp. 343–348)
Learning Target: Round numbers and write the results as the product of a single digit and a power of 10.
Round the number. Write the result as a product of a single digit and a power of 10.
Question 32.
29,197,543
Answer:
29,197,543 = 3 X 107
Explanation:
Given number is 29,197,543 is nearly or approximately
equal to ≈ 30,000,000 so we have 3 followed by 11 zeros,
so we write as 3 X 107.
Question 33.
0.000000647
Answer:
0.000000647 = 6 X 10-7
Explanation:
Given number 0.000000647 is nearly or approximately
equal to ≈ 0.0000006, we have divided 6 by 10 followed
by 7 zeros so we write as 6 X 10-7.
Question 34.
The speed of light is 299,792,458 meters per second. About how far can a light beam travel in 3 seconds? Write your answer as a product of a single digit and a power of 10.
Answer:
A light beam can travel 9 X 108 meters in 3 seconds.
Explanation:
Given the speed of light is 299,792,458 meters per second.
to know about how far can a light beam travel in 3 seconds is
3 X 299,792,458 now we write 299,792,458 is nearly or approximately
equal to ≈ 300,000,000 so 3 X 300,000,000 = 900,000,000
so we have 9 followed by 8 zeros so we write as 9 X 108 meters.
Therefore a light beam can travel 9 X 108 meters in 3 seconds.
Question 35.
The population of Albany, New York is about 98,989 and the population of Moscow, Russia is about 12,235,448. Approximately how many times greater is the population of Moscow than the population of Albany?
Answer:
100 times greater is the population of Moscow than the population of Albany.
Explanation:
Given the population of Albany, New York is about 98,989 and
the population of Moscow, Russia is about 12,235,448 if we see the
the population of Moscow is greater than the population of Albany.
So 12,235,448
8.6 Scientific Notation (pp. 349–354)
Learning Target: Understand the concept of scientific notation.
Write the number in scientific notation.
Question 36.
0.00036
Answer:
0.00036= 3.6 X 10-4
Explanation:
Given number is 0.00036 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 0.00036 = 3.6 X 0.0001 = 3.6 X 10-4.
Question 37.
800,000
Answer:
800,000 = 8 X 105
Explanation:
Given number is 800,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 800,000 = 8 X 100000 = 8 X 105.
Question 38.
79,200,000
Answer:
79,200,000 = 7.92 X 107
Explanation:
Given number is 79,200,000 in scientific notation
we write a number so that it has single digit to
the left of decimal sign and is multiplied by an integer power of 10.
So 79,200,000 = 7.29 X 10000000 = 7.29 X 107.
Write the number in standard form.
Question 39.
2 × 107
Answer:
2 X 107 = 20,000,000
Explanation:
Given 2 × 107 the number in standard form is
2 X 10,000,000 = 20,000,000.
So 2 X 107 = 20,000,000.
Question 40.
4.8 × 10-3
Answer:
4.8 × 10-3 = 0.0048
Explanation:
Given 4.8 × 10-3 the number in standard form is
4.8 × 0.001 = 0.0048.
Question 41.
6.25 × 105
Answer:
6.25 × 105 = 6,25,000
Explanation:
Given 6.25 105 the number in standard form is
6.25 X 100,000 = 6,25,000.
So 6.25 X 105 = 6,25,000.
Question 42.
The mass of a single dust particle is 7.52 × 10-10 kilogram. What is the mass of a dust ball made of 100 dust particles? Express your answer using more-appropriate units.
Answer:
The mass of a dust ball made of 100 dust particles is 7.52 10-8 kilogram
Explanation:
Given the mass of a single dust particle is 7.52 × 10-10 kilogram.
So the mass of a dust ball made of 100 dust particles is
7.52 × 10-10 X 100 = 7.52 X 10-10 X 102 = 7.52 × 10-10+2 = 7.52 × 10-8.
Therefore the mass of a dust ball made of 100 dust
particles is 7.52 10-8 kilogram.
8.7 Operations in Scientific Notation (pp. 355–360)
Learning Target: Perform operations with numbers written in scientific notation.
Evaluate the expression. Write your answer in scientific notation.
Question 43.
(4.2 × 108) + (5.9 × 109)
Answer:
(4.2 × 108) + (5.9 × 109) = 6.32 X 109
Explanation:
Given Expressions as (4.2 × 108) + (5.9 × 109)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 108 as 109 ·So we take 109 and then grouping the 109 with 4.2.
So 4.2 X 108 becomes 0.42 X 109 therefore
(4.2 × 108) + (5.9 × 109) =(0.42 X 101X 108) + (5.9 X 109) =
(0.42 X 109) + (5.9 × 109)
using the distributive property of multiplication over addition,
we get (0.42+5.9) X 109 = 6.32 X 109.
Question 44.
(5.9 × 10-4) – (1.8 × 10-4)
Answer:
(5.9 × 10-4) – (1.8 × 10-4) = 4.1 X 10-4
Explanation:
Given expressions as (5.9 × 10-4) – (1.8 × 10-4)
using the distributive property of multiplication over subtraction,
we get (5.9 – 1.8 ) X 10-4 = 4.1 X 10-4.
Question 45.
(7.7 × 108) × (4.9 × 10-5)
Answer:
(7.7 × 108) × (4.9 × 10-5) =3.773 X 104
Explanation:
Given expressions as (7.7 × 108) × (4.9 × 10-5)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (7.7 × 108) × (4.9 × 10-5) = (7.7 X 4.9) X (108 × 10-5) =
37.73 X (108-5) = 3.773 X 10 X 103 = 3.773 X 104.
Question 46.
(3.6 × 105) ÷ (1.8 × 109)
Answer:
(3.6 × 105) ÷ (1.8 × 109) = 2 X 10-4
Explanation:
Given expressions as (3.6 × 105) ÷ (1.8 × 109) ,
Separately we divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (3.6 × 105) ÷ (1.8 × 109) = (3.6 ÷ 1.8 ) X ( 105-9) = 2 X 10-4.
Question 47.
A white blood cell has a diameter of about 0.000012 meter. How many times greater is the diameter of a white blood cell than the diameter of a red blood cell?

Answer:
1.5 times greater is the diameter of a white blood cell
than the diameter of a red blood cell
Explanation:
Given a white blood cell has a diameter of about 0.000012 meter and
red blood cell has a diameter of about 8 X 10-6 meter,
the number of times greater is the diameter of a white blood cell
than the diameter of a red blood cell is 0.000012 ÷ 8 X 10-6 we write
0.000012 approximately equal to ≈ 1.2 X 10-5 now separately we
divide the coefficients and exponents.
We use the division rule of exponents,
where the exponents are subtracted.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
so (1.2 X 10-5) ÷ 8 X 10-6 = (1.2 ÷ 8) X (10-5 ÷ 10-6) =
0.15 X (10-5+6) = 0.15 X 10 = 1.5 therefore 1.5 times greater is
the diameter of a white blood cell than the diameter of a red blood cell.
Exponents and Scientific Notation Practice Test
Write the product using exponents.
Question 1.
(- 15) • (- 15) • (- 15)
Answer:
(- 15) • (- 15) • (- 15) = (-15)3
Explanation:
As -15 is multiplied by 3 times we write as
(-15)3 here -15 is base and 3 is exponent.
Question 2.
4 • 4 • x • x • x
Answer:
4 • 4 • x • x • x = (4)2 X (x)3
Explanation:
As 4 is multiplied 2 times we write as (4)2 and x
is multiplied thrice so (x)3
so the expression is 4 • 4 • x • x • x = (4)2 X (x)3
Evaluate the expression.
Question 3.
10 + 33 ÷ 9
Answer:
10 + 33 ÷ 9 = 13
Explanation:
Given expression 10 + 33 ÷ 9 first we write 9 as
3 X 3 = 32 ÷now we divide 33 ÷ 32 so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n, 33 ÷ 32 = ( 33-2) = 31= 3,
now we add 10 so 10 + 3 = 13.
Question 4.
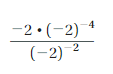
Answer:
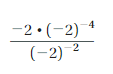 = (-2)-1=
= (-2)-1=
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (-2)1 X (-2)-4
we have same bases as -2 so we add powers as (-2)1-4 = (-2)-3
we have denominator (-2)-2
Now we have \(\frac{-2^{-3}}{-2^{-2}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{-2^{-3}}{-2^{-2}}\) = (-2)-3+2 = (-2)-1n
Simplify the expression. Write your answer as a power.
Question 5.
910 • 9
Answer:
910 • 9 = 911
Explanation:
We write the given 910 • 91 expression as a power,
we have general rule for am • an = am+n
If product of two powers with the same base then
powers are added, so 910 • 91 as bases are same 9
powers are added 910+1 = 911.
Question 6.
(66)5
Answer:
(66)5 = 630
Explanation:
We write the given expression (66)5 as a power,
General rule for finding (am)n power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n .
so (66)5 has powers of powers therefore powers
are multiplied as (6)6 X 5= (6)30
Question 7.
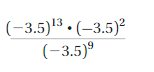
Answer:
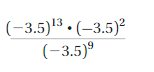 = (-3.5)6
= (-3.5)6
Explanation:
First we calculate separately values of numerators
and denominators then divide, we have numerator (-3.5)13 X (-3.5)2
we have same bases as -3.5 so we add powers as (-3.5)13+2 = (-3.5)15
we have denominator (-3.5)9
Now we have \(\frac{-3.5^{15}}{-3.5^{9}}\) so we use rule
for finding \(\frac{a^{m}}{a^{n}}\) a quotient of
two powers with the same base as am-n
\(\frac{-3.5^{15}}{-3.5^{9}}\) = (-3.5)15-9 = (-3.5)6.
Question 8.
Simplify (2y)7.
Answer:
(2y)7 =(2)7 X y7
Explanation:
Given to simplify the expression (2y)7 we use general rule to
write (ab)m power of a product as am X bm ,So (2y)7 = (2)7 X y7
Round the number. Write the result as a product of a single digit and a power of 10.
Question 9.
4,610,428,970
Answer:
4,610,428,970 = 5 X 109
Explanation:
Given number is 4,610,428,970 is nearly or approximately
equal to ≈ 5,000,000,000 so we have 5 followed by 9 zeros,
so we write as 4,610,428,970 = 5 X 109 .
Question 10.
0.00000572
Answer:
0.00000572 = 5.72 X 10-6
Explanation:
Given number 0.00000572 is nearly or approximately
equal to ≈ 0.000006, we have divided 6 by 10 followed
by 6 zeros so we write as 6 X 10-6.
Write the number in standard form.
Question 11.
3 × 107
Answer:
3 X 107 = 30,000,000
Explanation:
Given 3 × 107 the number in standard form is
3 X 10,000,000 = 30,000,000.
So 3 X 107 = 30,000,000.
Question 12.
9.05 × 10-3
Answer:
9.05 × 10-3 = 0.00905
Explanation:
Given 9.05 × 10-3 the number in standard form is
9.05 × 0.001 = 0.00905.
Evaluate the expression. Write your answer in scientific notation.
Question 13.
(7.8 × 107) + (9.9 × 107)
Answer:
(7.8 × 107) + (9.9 × 107) = 1.77 X 108
Explanation:
Given expressions as (7.8 × 107) + (9.9 × 107)
using the distributive property of multiplication over addition,
we get (7.8 × 107) + (9.9 × 107) = (7.8 + 9.9 ) X 107 = 17.7 X 107 =
1.77 X 10 X 107 =1.77 X 108.
Question 14.
(6.4 × 105) – (5.4 × 104)
Answer:
(6.4 × 105) – (5.4 × 104) = 5.86 X 105
Explanation:
Given expressions as (6.4 × 105) – (5.4 × 104)
as the powers of 10 differ we need to modify before we factor.
We work around this by using our exponent property bm · bn = b (m+n)
to rewrite the 104 as 105 · So we take 104 and then grouping the 104 with 5.4.
So 5.4 X 104 becomes 0.54 X 105 therefore = (6.4 × 105) – (5.4 × 104) =
(6.4 X 105) – (5.4 X 10-1X 10 X 104) = (6.4 X 105) – (0.54 × 105)
using the distributive property of multiplication over subtraction,
we get (6.4 – 0.54) X 105 = 5.86 X 105.
Question 15.
(3.1 × 106) × (2.7 × 10-2)
Ans;
(3.1 × 106) × (2.7 × 10-2) = 8.37 X 104.
Explanation:
Given expressions as (3.1 × 106) × (2.7 × 10-2)
we work out the coefficients and the exponents separately.
and use the product rule; bm x b n = b(m + n) to multiply the bases.
So (3.1 × 106) × (2.7 × 10-2) = (3.1 X 2.7) X (106 × 10-2) =
8.37 X (106-2) = 8.37 X 104.
Question 16.
(9.6 × 107) ÷ (1.2 × 10-4)
Answer:
(9.6 × 107) ÷ (1.2 × 10-4) = 8 X 1011
Explanation:
Given expressions as (9.6 × 107) ÷ (1.2 × 10-4),
Separately we divide the coefficients and exponents.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator.
So (9.6 × 107) ÷ (1.2 × 10-4) = (9.6 ÷ 1.2 ) X ( 107-(-4)) = 8 X 1011.
Question 17.
Is (xy2)3 the same as (xy3)2? Explain.
Answer:
(xy2)3 is not same as (xy3)2
Explanation:
Given expressions (xy2)3 the same as (xy3)2
first we solve the expressions with general rule for
finding (am)n power of a power,
If two powers have the same base then
we can multiply the powers as (am)n = am x n as
(xy2)3 = (x)3 X (y2)3 = (x)3 X (y2x3) = x3 X y6.
Now (xy3)2 = (x)2 X (y3)2 = (x)2 X (y3×2) = x2 X y6.
Now comparing x3 X y6 with x2 X y6 as x powers are not same so
(xy2)3 is not same as (xy3)2.
Question 18.
One scoop of rice weighs about 39 milligrams.
a. Write a linear function that relates the weight of rice to the number of scoops. What is the weight of 5 scoops of rice?
b. A grain of rice weighs about 33 milligrams. About how many grains of rice are in 1 scoop?
Answer:
a. The linear function that relates the weight of rice to the
number of scoops is y= 39x ,The weight of 5 scoops of rice
is 98415 grams,
b. There are 729 grains in 1 scoop of rice
Explanation:
Given One scoop of rice weighs about 39 milligrams.
Let us take x as number of scoops and y represent
the weight of rice,
a.The linear function that relates the
weight of rice to the number of scoops is y= 39x ,
so the weight of 5 scoops of rice = y= 39 X 5 =
19683 X 5 = 98415 grams,
The weight of 5 scoops of rice is 98415 grams,
b. A grain of rice weighs about 33 milligrams the number of
grains of rice are in 1 scoop is 39 ÷ 33,We use the division rule
of exponents, where the exponents are subtracted.
So (39 ÷ 33) = 39-3 = 36 = 3 X 3 X 3 X 3 X 3 X 3 = 729,
therefore there are 729 grains in 1 scoop of rice.
Question 19.
There are about 10,000 taste buds on a human tongue.
Write this number in scientific notation.
Answer:
10,000 = 1 x 104 taste buds are there on a human tongue.
Question 20.
From 1978 to 2008, the amount of lead allowed in the air in the
United States was 1.5 × 10-6 gram per cubic meter.
In 2008, the amount allowed was reduced by 90%.
What is the new amount of lead allowed in the air?

Answer:
1.5 X 10-7 gram per cubic meter is the new amount of lead allowed in the air.
Explanation:
Given from 1978 to 2008, the amount of lead allowed in the air in the
United States was 1.5 × 10-6 gram per cubic meter.
In 2008, the amount allowed was reduced by 90%.
to know the new amount of lead allowed in the air, we see
as it was reduced by 90% then 10% is still allowed, to find 10% of
original amount multiply by 0.1 so 0.1 X 1.5 × 10-6 = 0.15 X 10-6 =
= 1.5 X 10-7 gram per cubic meter, Therefore 1.5 X 10-7 gram per cubic meter
is the new amount of lead allowed in the air.
Exponents and Scientific Notation Cumulative Practice

Answer :
Bit B, 3072 years.
Explanation:
Cats were tamed 3 X 210 years ago in Egypt, So it was
3 X 210 = 3 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 = 3072 Years,
So bit b is matched.
Question 1.
Mercury’s distance from the Sun is approximately 5.79 × 107 kilometers. What is this distance in standard form?
A. 5,790,000 km
B. 57,900,000 km
C. 579,000,000 km
D. 5,790,000,000 km
Answer:
The distance of 5.79 × 107 kilometers in standard form is approximately
equal to ≈ 57,900,000 km so matches with B bit.
Explanation:
Given Mercury’s distance from the Sun is approximately 5.79 × 107 kilometers,
So the distance in standard form is the number in standard form is
5.79 X 10,000,000 = 57,900,000 km. So 5.79 X 107 km matches with B bit
57,900,000 km.
Question 2.
Your friend solves the problem. What should your friend change to correctly answer the question?
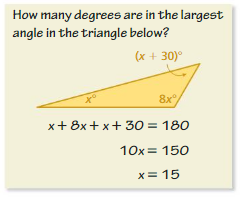
F. The left side of the equation should equal 360° instead of 180°.
G. The sum of the acute angles should equal 90.°
H. Evaluate the smallest angle when x = 15.
I. Evaluate the largest angle when x = 15.
Answer:
I. Evaluate the largest angle when x = 15.
Explanation:
Friend already solved x = 15°,So the largest angle in the triangle
is 8x = 8 X 15°= 120°,So friend needs to
Evaluate the largest angle when x = 15. So bit I is the correct answer.
Question 3.
Which expression is equivalent to the expression 2423?
A. 212
B. 47
C. 48
D. 128
Answer:
2423 = 128, D bit
Explanation:
Given expression is 2423 we know when bases are same
product of powers property says add the powers.
So 2423 = 24 X 23 = 24+3= 27 = 2 X 2 X 2 X 2 X 2 X 2 X 2 = 128,
therefore 2423 =128, so it matches with bit D.
Question 4.
You randomly survey students in your school about whether they have a pet. You display your results in the two-way table. How many female students took the survey?
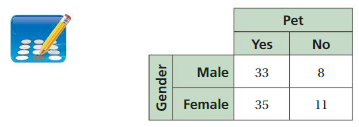
Answer:
Female 46 students took the survey.
Explanation:
As per two-way table it displays number of students in school
about whether they have a pet or not , So yes are 35 and no are 11,
Therefore total number of female students are 35 + 11 = 46,
So 46 female students took the survey.
Question 5.
A bank account pays interest so that the amount in the account doubles every 10 years. The account started with $5,000 in 1940. Which expression represents the amount (in dollars) in the account n decades later?
F. 2n • 5000
G. 5000 (n + 1)
H. 5000n
I. 2n + 5000
Answer:
F. 2n • 5000
Explanation:
Given a bank account pays interest so that the amount in the account
doubles every 10 years. The account started with $5,000 in 1940,
The expression that represents the amount (in dollars) in
the account n decades later is since the amount is getting doubled
every decade, So it will be increasing in multiples of 2,
so the correct answer is 2n X 5000 so bit F.
Question 6.
The formula for the volume V of a pyramid is V = \(\frac{1}{3}\)Bh.
Which equation represents a formula for the height h of the pyramid?
A. h= \(\frac{1}{3}\) VB
B. h = \(\frac{3 V}{B}\)
C. h = \(\frac{V}{3B}\)
D. h = V – \(\frac{1}{3}\)B
Answer:
B. h = \(\frac{3 V}{B}\)
Explanation:
Given the formula for the volume V of a pyramid is V = \(\frac{1}{3}\)Bh,
If we cross multiply 3 with V divide by B we get height,
So the formula for the height h of the pyramid is h = 3 V X \(\frac{1}{B}\).
Therefore the correct answer is bit B, h = \(\frac{3 V}{B}\).
Question 7.
The gross domestic product (GDP) is a way to measure how much a country produces economically in a year. The table below shows the approximate population and GDP for the United States.

Part A Write the population and the GDP using scientific notation.
Part B Find the GDP per person for the United States using your answers from PartA. Write your answer in scientific notation. Show your work and explain your reasoning.
Answer:
Part A : Population is 3.24 X 108,
GDP is $1.86 X 1013
Part B :
The GDP per person for the United States is 5.74 X 105
Explanation:
Part A:
Given the population of United States, 2016 is 324,000,000 the scientific
notation is 3.24 X 100,000,000 = 3.24 X 108 and GDP is
$18,600,000,000,000 in scientific notation is $1.86 X 10,000,000,000,000 =
$1.86 X 1013.
Part B :
The GDP per person is dividing the GDP of a country by its population,
So ($1.86 X 1013) ÷ (3.24 X 108) ,Separately we divide the coefficients and exponents.
Noted that when we are dividing exponential terms,
always subtract the denominator from the numerator,
Therefore (1.86 ÷ 3.24) X (1013 ÷ 108) = 0.574 X (1013-8) =
0.574 X 105 = 0.574 X 10 X 104 = 5.74 X 105.
Question 8.
What is the equation of the line shown in the graph?
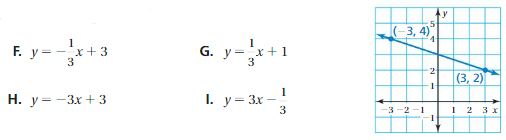
Answer:
F. y = –
Explanation:
The equation of line is y = mx + b, Where m is slope and
b is y – intercept So m= (y2-y1) ÷ (x2 -x1)
from graph we have (x1,y1)= (3,2) and (x2,y2) = (-3,4)
m= (4-2) ÷ (-3-3) = 2 ÷ (-6) = (-1 ÷ 3) = now y-intercept is y value of the point where the line intersects the y- axis.
So here it is 3, Now the equation of the line is y =-y = -(1 ÷
Question 9.
Which graph represents a linear function?
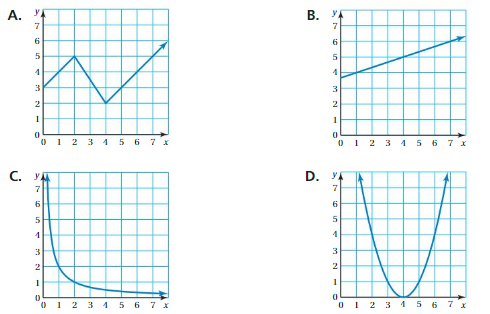
Answer:
Graph In B bit represents a linear function
Explanation:
Linear function is one where if there is a constant rate of change,
If we see all the graphs only in graph B there is constant rate of change,
in graph A it is increasing, decreasing and again increasing,
in graph C it is higher and at a time decreased
in graph D it decreased and again increased,
Therefore only in graph B , therefore only in graph B
it represents a linear function.
Question 10.
Find (- 2.5)-2.

Answer:
(- 2.5)-2 =
Explanation:
Given expression as (- 2.5)-2 we write the expression as
positive exponents by using So (- 2.5)-2 is
Question 11.
Two lines have the same y-intercept. The slope of one line is 1, and
the slope of the other line is – 1. What can you conclude?
F. The lines are parallel.
G. The lines meet at exactly one point.
H. The lines meet at more than one point.
I. The situation described is impossible.
Answer:
G. The lines meet at exactly one point.
Explanation:
If two lines have different slopes, they cannot be the same line.
However, if they share a y-intercept, that means they cross the
y-axis at the same y value. Since the x value is constant on the
y-axis (0), they also share an x-value here. If they share an x value
and corresponding y value, they intersect at that point,
in this case their y-intercept and two lines can’t intersect
at more than one point, So we conclude the lines meet at exactly one point.
Question 12.
Which list of ordered pairs represents the mapping diagram?
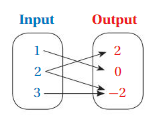
A. (1, 2), (2, 0), (3, – 2)
B. (1, 0), (2, 2), (3, – 2)
C. (1, 0), (2, 2), (2, – 2), (3, – 2)
D. (0, 1), (2, 2), (- 2, 2), (- 2, 3)
Answer:
C. (1, 0), (2, 2), (2, – 2), (3, – 2)
Explanation:
A mapping shows how the elements are paired.
Its like a flow chart for a function, showing the input and output values.
A mapping diagram consists of two parallel columns..
Lines or arrows are drawn from domain to range,
to represent the relation between any two elements.
So by seeing as 1 is related 0, 2 is related to 2, -2 and 3 is related to -2,
therefore the ordered pairs are (1,0),(2,2),(2,-2),(3,-2) matches with
bit C.