Practice with the help of enVision Math Common Core Grade 5 Answer Key Topic 13 Write and Interpret Numerical Expressions regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 13 Write and Interpret Numerical Expressions

enVision STEM Project: Food Chains and Food Webs
Do Research Use the Internet or other sources to find out more about food chains and food webs. Investigate the roles of producers, consumers, and decomposers. Explain how energy from sunlight is transferred to consumers.
Journal: Write a Report Include what you found. Also in your report:
• Draw a food web from an ecosystem near your home.
• Draw arrows on your food web to show how energy moves. Explain why the order is important.
• On one food chain of your food web, label each organism as a producer, consumer, or decomposer.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
• difference
• equation
• product
• sum
• quotient
Question 1.
The answer to a division problem is the ____.
Answer:
The answer to a division problem is the Quotient
Question 2.
The ____ of 5 and 7 is 12.
Answer:
The sum of 5 and 7 is 12
Question 3.
To find the ___ between 16 and 4, you subtract.
Answer:
To find the difference between 16 and 4, you subtract
Question 4.
A number sentence that shows two equivalent values is a(n) ____.
Answer:
A number sentence that shows two equivalent values is an Equation
Mixed Review
Find each answer.
Question 5.
648 ÷ 18
Answer:

Question 6.
35 × 100
Answer:
3500
Question 7.
47.15 + 92.9
Answer:
140.05
Question 8.
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
Answer:
1/4 + 1/4 + 1/4
1/2 + 1/4
3/4
Question 9.
3.4 – 2.7
Answer:
0.7
Question 10.
1.9 + 7
Answer:
8.9
Question 11.
3\(\frac{2}{5}\) + \(\frac{1}{2}\)
Answer:
3 2/5 + 1/2
17/5 + 1/2
39/10
Question 12.
75 ÷ \(\frac{1}{5}\)
Answer:
75 ÷ 1/5
75 / 1/5
75 x 5
= 375
Question 13.
$3.75 + $2.49
Answer:
$6.24
Question 14.
8\(\frac{5}{8}\) – 1\(\frac{2}{8}\)
Answer:
8 5/8 – 1 2/8
69/8 – 10/8
59/8
Question 15.
31.8 × 2.3
Answer:
73.14
Question 16.
9 – 4.6
Answer:
4.4
Question 17.
Jackson bought 2 tickets to the state fair. Each ticket cost $12. He spent $15 on rides and $8.50 on food. How much did Jackson spend in all?
Answer:
Total cost of tickets = $12 x 2 = $24
Total money after spending $15 on rides = $24 + $15 =$39
Total money after spending $8.50 on food = $39 + $8.50 = $47.50
Total money spent = $47.50
Question 18.
A baker has 3 pounds of dried fruit. Each batch of a recipe she is making uses \(\frac{1}{2}\) pound of the fruit. How many batches can she make?
A. 9 batches
B. 6 batches
C. 2 batches
D. 1\(\frac{1}{2}\) batches
Answer:
B. 6 batches
Multiplication
Question 19.
What equation comes next in the pattern below? Explain.
7 × 10 = 70
7 × 100 = 700
7 × 1,000 = 7,000
Answer:
7 × 10,000 = 70,000
pick a Project
PROJECT 13A
What’s been recovered from the wreck of the Atocha?
Project: Write a Treasure Adventure Mystery Story

PROJECT 13B
Do you like to play games?
Project: Design a Game Using Dominos

PROJECT 13C
What happens when a calculation is incorrect?
Project: Program a Robot

3-ACT MATH PREVIEW
Math Modeling
Video

Before watching the video, think:
A conjecture is a statement someone believes is true based on observations. You can usually either prove or disprove a conjecture. Keep an eye out for the conjecture in this video.
Lesson 13.1 Evaluate Expressions
Activity
Solve&Share
Jordan and Annika are working on 15 + 12 ÷ 3 + 5. Jordan says the answer is 14 and Annika says the answer is 24. Who is right?
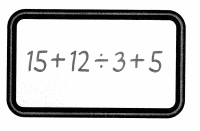
Solve this problem any way you choose.

Look Back! Construct Arguments Do you think two students, who made no computation errors, would get different values for this numerical expression? Explain.
(4 × 35) + (36 × 8)
Visual Learning Bridge
Essential Question What Order Should You Use When You Evaluate an Expression?
A.
Jack evaluated [(7 × 2) – 3] ÷ 8 = 2 × 3.
To avoid getting more than one answer, he used the order of operations given at the right.
Parentheses, brackets, and braces are all used to group numbers in numerical expressions.

Order of Operations
1. Evaluate inside parentheses (), brackets [ ], and braces {}.
2. Multiply and divide from left to right.
3. Add and subtract from left to right,
B.
Step 1
First, do the operations inside the parentheses.

Then, evaluate the terms inside the brackets.
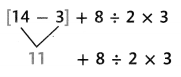
C.
Step 2
Next, multiply and divide in order from left to right.

D.
Step 3
Finally, add and subtract in order from left to right.
11 + 12 = 23
So, the value of the expression is 23.
Convince Me! Construct Arguments Would the value of {2+[(15 – 3) – 6]} ÷ 2 change if the braces were removed? Explain.
Guided Practice
Do You Understand?
Question 1.
Explain the steps involved in evaluating the expression [(4 + 2) – 1] × 3.
Answer:
[(4 + 2) – 1] × 3
[(6) – 1] × 3
[5] × 3
15.
Question 2.
Would the value of (12 – 4) ÷ 4 + 1 change if the parentheses were removed? Explain.
Answer:
(12 – 4) ÷ 4 + 1
(8) ÷ 4 + 1
2 + 1
3.
Do You Know How?
In 3-6, use the order of operations to evaluate the expression.
Question 3.
[7 × (6 – 1)] + 100
Answer:
[7 × (6 – 1)] + 100
[7 × (5)] + 100
[35] + 100
135
Question 4.
17 + 4 × 3
Answer:
17 + 4 × 3
17 + 12
29
Question 5.
(8 + 1) + 9 × 7
Answer:
(8 + 1) + 9 × 7
(9) + 9 × 7
(9) + 63
72
Question 6.
{[(4 × 3) ÷ 2] + 3} × 6
Answer:
{[(4 × 3) ÷ 2] + 3} × 6
{[(12) ÷ 2] + 3} × 6
{6 + 3} × 6
{9} × 6
54.
Independent Practice
Remember to evaluate inside parentheses, brackets, and braces first.

Leveled Practice In 7-21, use the order of operations to evaluate the expression.
Question 7.
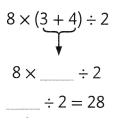
Answer:
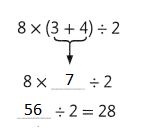
Question 8.
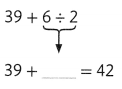
Answer:

Question 9.
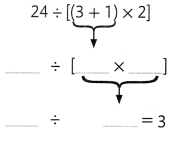
Answer:
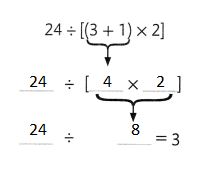
Question 10.
5 ÷ 5 + 4 × 12
Answer:
5 ÷ 5 + 4 × 12
1 + 4 × 12
1 + 48
49
Question 11.
[6 – (3 × 2)] + 4
Answer:
[6 – (3 × 2)] + 4
[6 – (6)] + 4
[0] + 4
4
Question 12.
(4 × 8) ÷ 2 + 8
Answer:
(4 × 8) ÷ 2 + 8
(32) ÷ 2 + 8
16 + 8
24
Question 13.
(18 + 7) × (11 – 7)
Answer:
(18 + 7) × (11 – 7)
(25) × (4)
100
Question 14.
2 + [4 + (5 × 6)]
Answer:
2 + [4 + (5 × 6)]
2 + [4 + (30)]
2 + [34]
36
Question 15.
(9 + 11) ÷ (5 + 4 + 1)
Answer:
(9 + 11) ÷ (5 + 4 + 1)
(20) ÷ (10)
2
Question 16.
90 – 5 × 5 × 2
Answer:
90 – 5 × 5 × 2
90 – 50
40
Question 17.
120 – 40 ÷ 4 × 6
Answer:
120 – 40 ÷ 4 × 6
120 – 10 × 6
120 – 60
60
Question 18.
22 + (96 – 40) ÷ 8
Answer:
22 + (96 – 40) ÷ 8
22 + (56) ÷ 8
22 + 7
29
Question 19.
(7.7 + 0.3) ÷ 0.1 × 4
Answer:
(7.7 + 0.3) ÷ 0.1 × 4
(8) ÷ 0.1 × 4
80 x 4
320
Question 20.
32 ÷ (12 – 4) + 7
Answer:
32 ÷ (12 – 4) + 7
32 ÷ (8) + 7
4 + 7
11
Question 21.
{8 × [1 + (20 – 6)} ÷ \(\frac{1}{2}\)
Answer:
{8 × [1 + (20 – 6)} ÷ \(\frac{1}{2}\)
{8 × [1 + (20 – 6)} ÷ 1/2
{8 × [1 + (14)} ÷ 1/2
{8 × 15} ÷ 1/2
{120} ÷ 1/2
240.
Problem Solving
Question 22.
Dan and his 4 friends want to share the cost of a meal equally. They order 2 large pizzas and 5 small drinks. If they leave a tip of $6.30, how much does each person pay?

Answer:
Given,
They order 2 large pizzas and 5 small drinks.
They leave a tip of $6.30
So,
(2 x 12) + (5 x 1.50) + 6.30
(24) + (7.50) + 6.30
$37.8
Total Number of friends = 5
Each person have to pay = 37.8 ÷ 5
= $7.56
Question 23.
Higher Order Thinking Use the operation signs +, -, ×, and ÷ once each in the expression below to make the number sentence true.
![]()
Answer:
![]()
Question 24.
Be Precise Carlotta needs 12\(\frac{1}{2}\) yards of ribbon for a project. She has 5\(\frac{1}{4}\) yards of ribbon on one spool and 2\(\frac{1}{2}\) yards on another spool. How much more ribbon does she need?
Answer:
Question 25.
Theresa bought three containers of tennis balls at $2.98 each. She had a coupon for $1 off. Her mom paid for half of the remaining cost. How much did Theresa pay? Evaluate the expression [(3 × 2.98) – 1] ÷ 2.
Answer:
[(3 × 2.98) – 1] ÷ 2
[8.94 – 1] ÷ 2
[7.94] ÷ 2
3.97
Question 26.
enVision®STEM Giraffes are herbivores, or plant eaters. A giraffe can eat up to 75 pounds of leaves each day. Write and evaluate an expression to find how many pounds of leaves 5 giraffes can eat in a week.
Evaluate the expression in the parentheses first. Then subtract inside the brackets.

Assessment Practice
Question 27.
Which expression has a value of 8?
A. 11 – 6 – 3
B. 4 + 30 ÷ 6
C. (9 + 7) ÷ 2
D. 1 + 1 × (2 + 2)
Answer:
C. (9 + 7) ÷ 2
D. 1 + 1 × (2 + 2)
Question 28.
Using the order of operations, which operation should you perform last to evaluate this expression?
(1 × 2.5) + (52 ÷ 13) +(6.7 – 5) – (98 + 8)
A. Addition
B. Subtraction
C. Multiplication
D. Division
Answer:
B. Subtraction
Lesson 13.2 Write Numerical Expressions
Activity
Solve & Share
A baker packages 12 cupcakes to a box. Sean orders 5 boxes for his sister’s graduation party and 3.5 boxes for the Variety Show party. Write an expression that shows the calculations you could use to find the number of cupcakes Sean orders.
Model with Math
You can write a numerical expression to model this situation.

Look Back! Write a different expression to model Sean’s order. Evaluate both expressions to check that they are equivalent. How many cupcakes does Sean order?
Visual Learning Bridge
Essential Question How Can You Write a Numerical Expression to Record Calculations?
A.
The school auditorium has 546 seats on the main floor and 102 in the balcony. Every seat is filled for all of the Variety Show performances. Write an expression that shows the calculations you could use to determine how many tickets were sold.

B.
Think about how you would calculate the total number of tickets.
Add 546 + 102 to find the total number of seats.
Then multiply by the number of performances, 4.
So, you need to write a numerical expression that represents:
“Find 4 times the sum of 546 and 102.”
C.
Use numbers and symbols to write the numerical expression.
The sum of 546 and 102: 546 + 102
4 times the sum: 4 × (546 + 102)
Remember, parentheses show which calculation to do first.

The expression 4 × (546 + 102) shows the calculations for the number of tickets sold.
Convince Me! Reasoning Two students wrote different expressions to find the total number of tickets sold. Is their work correct? Explain.
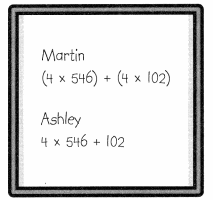
Guided Practice
Do You Understand?
Question 1.
Why do some numerical expressions contain parentheses?
Answer:
Parentheses are symbols that group things together. This becomes very important in numerical expressions because operations inside parentheses are always completed first when evaluating the expression.
Question 2.
Show how to use a property to write an equivalent expression for 9 × (7 + 44). Can you use a different property to write another equivalent expression? Explain.
Answer:
Do You Know How?
In 3-6, write a numerical expression for each calculation.
Question 3.
Add 8 and 7, and then multiply by 2.
Answer:
(8 + 7) x 2
Question 4.
Find triple the difference between 44.75 and 22.8.
Answer:
3 x (44.75 – 22.8)
Question 5.
Multiply 4 times \(\frac{7}{8}\) and then add 12.
Answer:
(4 x 7/8) + 12
Question 6.
Add 49 to the quotient of 125 and 5.
Answer:
49 + (125 ÷ 5)
Independent Practice
In 7-11, write a numerical expression for each calculation.
Question 7.
Add 91, 129, and 16, and then divide by 44.
Answer:
(91 + 129 + 16) ÷ 44
Question 8.
Find 8.5 times the difference between 77 and 13.
Answer:
8.5 x (77 – 13)
Question 9.
Subtract 55 from the sum of 234 and 8.
Answer:
(234 + 8) – 55
Question 10.
Multiply \(\frac{2}{3}\) by 42, and then multiply that product by 10.
Answer:
( 2/3 x 42 ) x 10
Question 11.
Write an expression to show the calculations you could use to determine the total area of the rectangles at the right.

Answer:
3 x ( 18 x 22 )
Problem Solving
Question 12.
Model with Math Ronnie’s Rentals charges $25 plus $15 per hour to rent a chain saw. David rented a chain saw for 5 hours. Write an expression to show how you could calculate the total amount David paid.
Answer:
5 x (25 + 15)
Question 13.
Fourteen students bought their art teacher a new easel for $129 and a set of blank canvases for $46. Sales tax was $10.50. They shared the cost equally. Write an expression to show how you could calculate the amount each student paid.
Answer:
[(129 + 46) + 10.50] ÷ 14
Question 14.
A-Z Vocabulary When evaluating an expression, why is it important to use the order of operations?
Answer:
When evaluating an expression, it is important to use the order of operations. The order of operations is a set of rules for how to evaluate expressions. They make sure everyone gets the same answer.
Question 15.
A storage shed is shaped like a rectangular prism. The width is 8 yards, the height is 4 yards, and the volume is 288 cubic yards. Explain how to find the length of the storage shed.
Answer:
Volume = Length x Breadth x Height
Length = Volume ÷ (Breadth x Height)
Length = 288 ÷ (8 x 4)
Length = 288 ÷ 32
Length = 9 yards
Question 16.
Higher Order Thinking Danielle has a third of the amount needed to pay for her choir trip expenses. Does the expression (77 + 106 +34) ÷ 3 show how you could calculate the amount of money Danielle has? Explain.

Answer:
Yes.
The expression (77 + 106 +34) ÷ 3 show how I could calculate the amount of money Danielle has
(77 + 106 +34) ÷ 3
(217) ÷ 3
$72.3
Assessment Practice
Question 17.
Which expression represents the following phrase?
Subtract 214 from 721 and then divide by 5.
A. (721 ÷ 214) – 5
B. 721 – 214 ÷ 5
C. (721 ÷ 5) – 214
D. (721 – 214) ÷ 5
Answer:
D. (721 – 214) ÷ 5
Question 18.
What is the first step in evaluating this expression?
2 × (47 + 122) – 16
A. Multiply 2 and 47
B. Multiply 2 and 16
C. Add 47 and 122
D. Add 2 and 47
Answer:
C. Add 47 and 122
Lesson 13.3 Interpret Numerical Expressions
Solve & Share
Mrs. Katz is planning her family’s trip to the museum. She made a list of the expenses. Then she wrote the following expression to show how she can calculate the total cost.
6 × (4.20 + 8 + 12 + 3.50)
How many people do you think are in the family? How can you tell?

Use Structure You can interpret the relationships in numerical expressions without doing any calculations.

Look Back! While they are at the museum, the family decides to watch a movie about earthquakes for $2.75 per person. Jana and Kay disagree as to how they should adjust Mrs. Katz’s expression to find the total expenses for the trip. Jana says the expression should be 6 × (4.20 + 8 + 12 + 3.50) + 2.75. Kay says the expression should be 6 × (4.20 + 8 + 12 + 3.50 + 2.75). Who is correct? Explain.
Visual Learning Bridge
Essential Question
How Can You Interpret Numerical Expressions Without Evaluating Them?
A.
Jimmy’s clown costume requires \(\frac{7}{8}\) + \(\frac{1}{2}\) + 1\(\frac{3}{4}\) yards of fabric.
His dad’s matching clown costume requires 3 × (\(\frac{7}{8}\) + \(\frac{1}{2}\) + 1\(\frac{3}{4}\))) yards. How does the amount of fabric needed for the dad’s costume compare to the amount needed for Jimmy’s costume?

You can compare the expressions and solve the problem without doing any calculations.

B.
Interpret the part of each expression that is the same.
\(\frac{7}{8}\) + \(\frac{1}{2}\) + 1\(\frac{3}{4}\)
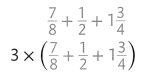
Both expressions contain the sum \(\frac{7}{8}\) + \(\frac{1}{2}\) + 1\(\frac{3}{4}\). This is the amount of fabric needed for Jimmy’s costume.
C.
Interpret the part of each expression that is different.
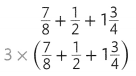
Remember, multiplying by 3 means “3 times as much.”

The second expression shows that the sum is multiplied by 3. So, the dad’s costume requires 3 times as much fabric as Jimmy’s costume.
Convince Me! Reasoning The 7 students in a sewing class equally share the cost of fabric and other supplies. Last month, each student paid ($167.94 + $21.41) ÷ 7. This month, each student paid ($77.23 + $6.49) ÷ 7. Without doing any calculations, in which month did each student pay more? Explain.
Answer:
In the last month each student paid more. Because the value is more compared to this month.
Guided Practice
Do You Understand?
Question 1.
The number of yards of fabric needed for Rob’s costume is ![]() . How does the amount of fabric needed for Rob’s costume compare to the amount needed for Jimmy’s costume? Explain.
. How does the amount of fabric needed for Rob’s costume compare to the amount needed for Jimmy’s costume? Explain.
Answer:
Question 2.
Without doing any calculations, explain why the following number sentence is true.
14 + (413 × 7) > 6+ (413 × 7)
Answer:
Do You Know How?
Without doing any calculations, describe how Expression A compares to Expression B.
Question 3.
A 8 × (41,516 – 987)
B 41,516 – 987
Answer:
In 4 and 5, without doing any calculations, write >, <, or =.
Question 4.
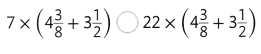
Answer:
Question 5.
![]()
Answer:
Independent Practice
In 6 and 7, without doing any calculations, describe how Expression A compares to Expression B.
Question 6.
A (613 + 15,090) ÷ 4
B 613 + 15,090
Answer:
Question 7.
A (418 × \(\frac{1}{4}\)1) + (418 × \(\frac{1}{2}\))
B 418 × \(\frac{3}{4}\)
Answer:
In 8-11, without doing any calculations, write >, <, or =.
Question 8.
(284 + 910) ÷ 30 img 73 (284 + 7,816) ÷ 30
Answer:
(284 + 910) ÷ 30 < 73 (284 + 7,816) ÷ 30
Question 9.
\(\frac{1}{3}\) × (5,366 – 117) img 735,366 – 117
Answer:
\(\frac{1}{3}\) × (5,366 – 117) < 735,366 – 117
Question 10.
71 +(13,888 – 4,296) img 73 70 + (13,888 – 4,296)
Answer:
71 +(13,888 – 4,296) < 73 70 + (13,888 – 4,296)
Question 11.
15 × (3.6 + 9.44) img 73 (15 × 3.6) + (15 × 9.44)
Answer:
15 × (3.6 + 9.44) < 73 (15 × 3.6) + (15 × 9.44)
Problem Solving
Question 12.
A four-story parking garage has spaces for 240 + 285 + 250 + 267 cars. While one floor is closed for repairs, the garage has spaces for 240 +250 + 267 cars. How many spaces are there on the floor that is closed? Explain.
Answer:
240 + 285 + 250 + 267 > 240 +250 + 267
By comparing,
285 spaces are there on the floor that is closed
Question 13.
Use Structure Peter bought ![]() yards of ribbon. Marilyn bought
yards of ribbon. Marilyn bought ![]() yards of ribbon. Without doing any calculations, determine who bought more ribbon. Explain.
yards of ribbon. Without doing any calculations, determine who bought more ribbon. Explain.
Answer:
Marilyn bought more ribbon.
Question 14.
Brook’s score in a card game is 713 + 102 + 516. On her next turn, she draws one of the cards shown. Now her score is (713 + 102 + 516) ÷ 2. Which card did Brook draw? Explain.

Answer:

Question 15.
Marta bought a 0.25-kilogram box of fish food. She uses 80 grams a week. Is one box of fish food enough for 4 weeks? Explain.
Answer:
No. For 4 weeks, she needs 4 x 80 = 320 grams
But, she bought only 250 grams.
Question 16.
Higher Order Thinking How can you tell that (496 + 77 + 189) × 10 is twice as large as (496 + 77 + 189) × 5 without doing complicated calculations?
Answer:
10 is twice 5. Hence, (496 + 77 + 189) × 10 is twice as large as (496 + 77 + 189) × 5
Assessment Practice
Question 17.
Which statement describes the expression (21 + 1.5) × 12 – 5?
A. The sum of 21 and 1.5 times the difference of 12 and 5
B. Five less than the sum of 21 and 1.5 multiplied by 12
C. Five less than the product of 12 and 1.5 added to 21
D. Subtract the product of 12 and 5 from the sum of 21. and 1.5
Answer:
A. The sum of 21 and 1.5 times the difference of 12 and 5
Lesson 13.4 Reasoning
Activity
Problem Solving
Solve & Share
The camp cook has 6 dozen eggs. He uses 18 eggs to bake some brownies. Then he uses twice as many eggs to make pancakes. How many eggs does the cook have left? Use reasoning to write and evaluate an expression that represents the problem.

Thinking Habits
Be a good thinker! These questions can help you.
• What do the numbers and symbols in the problem mean?
• How are the numbers or quantities related?
• How can I represent a word problem using pictures, numbers, or equations?
Look Back! Reasoning Explain how the numbers, symbols, and operations in your expression represent this problem.
Visual Learning Bridge
Essential Question How Can You Use Reasoning to Solve Problems?
A.
Rose has 3 albums for her soccer cards. She gets 7 more cards for each of her albums for her birthday. How many cards does Rose have in all?

What do I need to do to solve the problem?
I need to find how many cards, including Rose’s new cards, will be in each album. Then I need to multiply to find the number of cards in 3 albums.
You can use tools or draw a diagram to help solve the problem.

B.
How can I use reasoning to solve this problem?
I can
• identify the quantities I know.
• use mathematical properties, symbols, and operations to show relationships.
• use diagrams to help.
Here’s my thinking…

C.
I need to find how many cards Rose has in all.
I can use a diagram to show how the quantities in the problem are related. Then I can write an expression.
There are 22 cards in each of her 3 albums. She gets 7 more cards for each of her 3 albums.
![]()
3 × (22 + 7) = 3 × 29
= 87
Rose has 87 cards.
Convince Me! Reasoning How can you use the Distributive Property to write an expression equivalent to the one given above? Use reasoning to explain how you know the expressions are equivalent.
Guided Practice
Reasoning Todd has 4 baseball card albums like the one pictured. He lets his best friend Franco choose 5 cards from each album. How many cards does Todd have now?
Question 1.
Write an expression to represent the total number of cards in Todd’s albums before he gives some cards to Franco. Explain how your expression represents the quantities and the relationship between the quantities.

Answer:
(4 x 42)
4 represents the number of card albums
42 represents the number of cards in each album
multiplication or ‘x’ gives the total number of cards in 4 albums.
Question 2.
Write an expression to represent the total number of cards in Todd’s albums after he gives some cards to Franco.
Answer:
(4 x 42) – (4 x 5)
Question 3.
How many cards does Todd have after he gives some cards to Franco? Explain how you solved the problem.
Answer:
(4 x 42) – (4 x 5)
168 – 20 = 148
Todd have 148 cards.
Independent Practice
Remember to think about the meaning of each number before solving the problem.

Reasoning
Brandon is filling a flower order for a banquet. He needs 3 large arrangements and 12 small arrangements. The large arrangements each contain 28 roses. The small arrangements each contain 16 roses. How many roses does Brandon need in all?
Question 4.
Write an expression to represent the total number of roses Brandon needs. You can use a diagram to help.
Answer:
(3 x 28) + (12 x 16)
Question 5.
Explain how the numbers, symbols, and operations in your expression represent the problem.
Answer:
the number represents the number of arrangements and number of roses
the operation represents multiplication and addition
symbols represent the separation between the large and small arrangements.
Question 6.
How many roses does Brandon need? Explain how you solved the problem.
Answer:
(3 x 28) + (12 x 16)
84 + 192
276.
Problem Solving
Performance Task
Math Supplies
Ms. Kim is ordering sets of place-value blocks for the 3rd, 4th, and 5th graders. She wants one set for each student, and there are 6 sets of blocks in a carton. How many cartons should Ms. Kim order?

Question 7.
Make Sense and Persevere What information in the problem do you need?
Answer:
Information related to 3rd, 4th, and 5th graders and the number of students.
Question 8.
Reasoning Does this problem require more than one operation? Does the order of the operations matter? Explain.
Answer:
Yes.
As there are 6 sets of blocks are in each carton. We have to divide the whole by 6.
Question 9.
A model with Math Writes an expression to represent the number of cartons Ms. Kim needs to order. You can use a diagram to help.
Answer:
Use reasoning to make sense of the relationship between the numbers.

Question 10.
Construct Arguments Did you use grouping symbols in your expression? If so, explain why they are needed.
Answer:
Question 11.
Be Precise Find the total number of cartons Ms. Kim should order. Explain how you found the answer.
Answer:
Topic 13 Fluency Practice
Activity
Find a Match
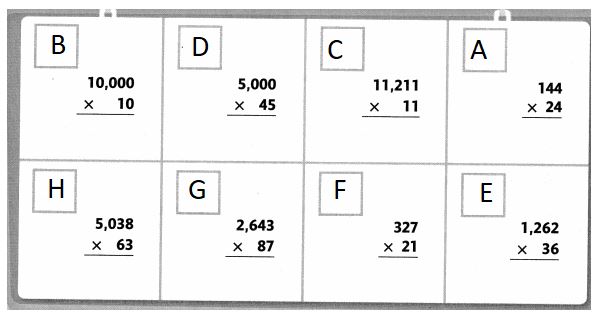
Work with a partner. Point to a clue. Read the clue. Look below the clues to find a match. Write the clue letter in the box next to the match. Find a match for every clue.

Clues

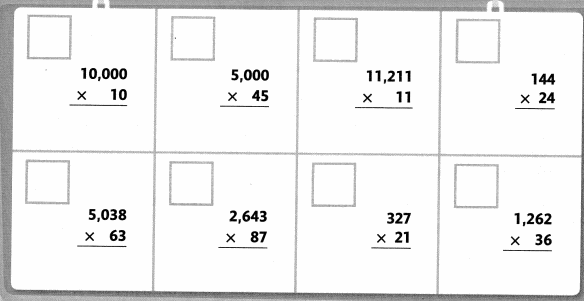
Answer:
Topic 13 Vocabulary Review
Word List
Glossary
Understand Vocabulary
Choose the best term from the Word List. Write it on the blank.
• braces
• brackets
• evaluate
• numerical expression
• order of operations
• parentheses
• variable
Question 1.
A set of rules that describes the order in which calculations are done is known as the ____
Answer:
A set of rules that describes the order in which calculations are done is known as the order of operations
Question 2.
____ , ____ and _____ are symbols used in mathematical expressions to group numbers or variables.
Answer:
braces, brackets, and parentheses are symbols used in mathematical expressions to group numbers or variables.
Question 3.
A(n) ____ is a mathematical phrase that contains numbers and at least one operation.
Answer:
a numerical expression is a mathematical phrase that contains numbers and at least one operation.
For each term, give an example and a non-example.

Answer:
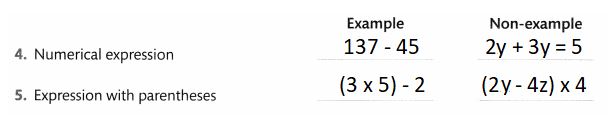
Draw a line from each number in Column A to the correct value in Column B.
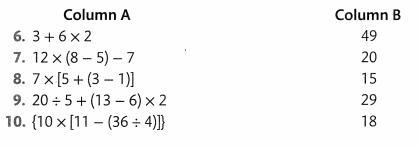
Answer:
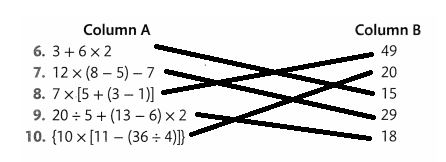
Use Vocabulary in Writing
Question 11.
Explain why the order of operations is important. Use at least three terms from the Word List in your explanation.
Answer:
The order of operations is a rule that tells you the right order in which to solve different parts of a math problem. … Subtraction, multiplication, and division are all examples of operations. The order of operations is important because it guarantees that people can all read and solve a problem in the same way.
Topic 13 ReTeaching
Set A
pages 537-540
Use the order of operations to evaluate 50 + (8 + 2) × (14 – 4).
Order of Operations
1. Calculate inside parentheses, brackets, and braces.
2. Multiply and divide from left to right.
3. Add and subtract from left to right.
Perform the operations inside the parentheses, brackets, and braces.
50 + (8 + 2) × (14 – 4) = 50 + 10 × 10
Multiply and divide in order from left to right.
50 + 10 × 10 = 50 + 100
Add and subtract in order from left to right.
50 + 100 = 150
Remember that if the parentheses are inside brackets or braces, perform the operations inside the parentheses first.
Evaluate each expression.
Question 1.
(78 + 47) ÷ 25
Answer:
(78 + 47) ÷ 25
(125) ÷ 25
5
Question 2.
4 + 8 × 6 ÷ 2 + 3
Answer:
4 + 8 × 6 ÷ 2 + 3
4 + 8 × 3 + 3
4 + 24 + 3
31
Question 3.
[(8 × 25) ÷ 5] + 120
Answer:
[(8 × 25) ÷ 5] + 120
[200 ÷ 5] + 120
[40] + 120
160
Question 4.
312 × (40 + 60) ÷ 60
Answer:
312 × (40 + 60) ÷ 60
312 × (100) ÷ 60
312 × (100) ÷ 60
312 x 5/3
520
Question 5.
80 – (0.4 + 0.2) × 10
Answer:
80 – (0.4 + 0.2) × 10
80 – (0.6) × 10
80 – 6
74
Question 6.
(18 – 3) ÷ 5 + 4
Answer:
(18 – 3) ÷ 5 + 4
(15) ÷ 5 + 4
3 + 4
7
Question 7.
8 × 5 + 7 × 3 – (10 – 5)
Answer:
8 × 5 + 7 × 3 – (10 – 5)
8 × 5 + 7 × 3 – (5)
40 + 21 – (5)
61 – 5
56
Question 8.
22 – {[87 – 32) ÷ 5] × 2}
Answer:
22 – {[87 – 32) ÷ 5] × 2}
22 – {55 ÷ 5] × 2}
22 – 11 × 2
0.
Set B
pages 541-544
Write a numerical expression for the phrase: “Subtract 15 from the product of 12 and 7”.
Think:
Sum → Addition (+)
Difference → Subtraction (-)
Product → Multiplication (×)
Quotient → Division (÷)
Product of 12 and 7: 12 × 7
Subtract 15 from the product: (12 × 7) – 15
So, a numerical expression for the phrase is: (12 × 7) – 15.
Remember that you can use parentheses to show which calculation to do first. Write a numerical expression for each phrase.
Question 1.
Add 15 to the product of \(\frac{3}{4}\) and 12.
Answer:
(3/4 x 12) + 15
Question 2.
Find the difference of 29 and 13, and then divide by 2.
Answer:
(29 – 13) ÷ 2
Question 3.
Add 1\(\frac{1}{2}\) and \(\frac{3}{4}\), and then subtract \(\frac{1}{3}\).
Answer:
( 1 1/2 + 3/4 ) – 1/3
Question 4.
Multiply 1.2 by 5 and then subtract 0.7.
Answer:
( 1.2 x 5 ) – 0.7
Question 5.
Add the quotient of 120 and 3 to the product of 15 and 10.
Answer:
(120 ÷ 3) + (15 x 10)
Set C
pages 545-548
The expressions below show how many miles each student ran this week. How does Alex’s distance compare to Kim’s distance?
Kim: (4 × 3\(\frac{1}{2}\))
Alex: (4 × 3\(\frac{1}{2}\)) + 2\(\frac{1}{2}\)
What is the same about the expressions? Both contain the product 4 × 3\(\frac{1}{2}\).
What is different about the expressions?
2\(\frac{1}{2}\) is added in Alex’s expression.
So, Alex ran 2\(\frac{1}{2}\) miles farther than Kim this week.
Remember that sometimes you can compare numerical expressions without doing any calculations.
Without doing any calculations, write >, <, or =
Question 1.
72 × (37 – 9) ![]() 69 × (37 – 9)
69 × (37 – 9)
Answer:
72 × (37 – 9) > 69 × (37 – 9)
Question 2.
(144 ÷ 12) – 6 ![]() 144 ÷ 12
144 ÷ 12
Answer:
(144 ÷ 12) – 6 < 144 ÷ 12
Question 3.
(4 + \(\frac{1}{2}\) + 3) × 2 ![]() 2 × (4 + \(\frac{1}{2}\) + 3)
2 × (4 + \(\frac{1}{2}\) + 3)
Answer:
(4 + \(\frac{1}{2}\) + 3) × 2 < 2 × (4 + \(\frac{1}{2}\) + 3)
Question 4.
Describe how Expression A compares to Expression B.
A $3.99 + ($9.50 × 2)
B $9.50 × 2
Answer:
Value of A is 3.99 more than Value of B
Set D
pages 549-552
Think about these questions to help you reason abstractly and quantitatively.
Thinking Habits
• What do the numbers and symbols in the problem mean?
• How are the numbers or quantities related?
• How can I represent a word problem using pictures, numbers, or equations?
Remember that you can use diagrams to help solve problems.
Question 1.
Kerry has 5 metal and 3 wood paperweights in her collection. She has twice as many glass paperweights as metal paperweights. Write an expression to represent the total number of paperweights in her collection. Then find the total number of paperweights.
Answer:
Question 2.
Reese had 327 baseball cards. Then he lost 8 of them and gave 15 of them to his brother. Write an expression to represent the number of baseball cards he has left. Then find how many baseball cards he has left.
Answer:
Topic 13 Assessment Practice
Question 1.
Which of the following is equal to 10?
A. 2 × (45 ÷ 9)
B. 24 – (7 × 3)
C. 1 + (4 × 2)
D. (2 × 25) × 5
Answer:
A. 2 × (45 ÷ 9)
Question 2.
Select all of the expressions that are equal to 8 × 65.
![]() 3 + 5 × 60
3 + 5 × 60
![]() 8 × (60 + 5)
8 × (60 + 5)
![]() 8 × (50 + 15)
8 × (50 + 15)
![]() (8 + 60) × (8 + 5)
(8 + 60) × (8 + 5)
![]() (8 × 60) + (8 × 5)
(8 × 60) + (8 × 5)
Answer:
![]() 8 × (60 + 5)
8 × (60 + 5)
![]() 8 × (50 + 15)
8 × (50 + 15)
![]() (8 × 60) + (8 × 5)
(8 × 60) + (8 × 5)
Question 3.
Which is the value of the expression 7 + (3 × 4) – 2?
A. 38
B. 20
C. 17
D. 12
Answer:
C.17
Question 4.
Which expression represents the following calculation?
Add 16 to the quotient of 72 and 8.
A. (72 – 8) + 16
B. (72 ÷ 8) + 16
C. (16 + 72) ÷ 8
D. (16 + 72) + 8
Answer:
B. (72 ÷ 8) + 16
Question 5.
What is the value of
(100 × 15) + (10 × 15)?
Answer:
(100 × 15) + (10 × 15)
(1500) + (150)
1650
Question 6.
Describe how the value of Expression A compares to the value of Expression B.
A. 12 × (54 ÷ \(\frac{2}{5}\))
B. 54 ÷ \(\frac{2}{5}\)
Answer:
Value of A is 12 times the value of B
Question 7.
Write >, <, or = in the circle to make the statement true.
(368 × 19) – 24 img 95 (368 × 19) – 47
Answer:
(368 × 19) – 24 < 95 (368 × 19) – 47
Question 8.
Insert parentheses to make the statement true.
7 + 6 × 14 – 9 = 37
Answer:
Question 9.
Which expression represents the following calculation?
Subtract 2 from the product of 7 and 3.
A. (7 + 3) – 2
B. 7 × (3 – 2)
C. (7 × 3) – 2
D. (7 × 2) – 3
Answer:
C. (7 × 3) – 2
Question 10.
What is the value of the expression (6 + 3) × 2?
Answer:
(6 + 3) × 2
9 × 2
18
Question 11.
Evaluate the expression (6 + 12 ÷ 2) + 4. Show your work.
Answer:
(6 + 12 ÷ 2) + 4
(6 + 6) + 4
12 + 4
16
Question 12.
Write >, <, or = in the circle to make the statement true.
(249 + 1,078) × \(\frac{1}{3}\) img 96 (249 + 1,078) ÷ 3
Answer:
(249 + 1,078) × \(\frac{1}{3}\) < 96 (249 + 1,078) ÷ 3
Question 13.
Write an expression to find the product of 3 and 28 plus the product of 2 and 15. Then solve.
Answer:
(3 x 28) + (2 x 15)
84 + 30
114
Question 14.
Evaluate the expression.
6 + (24 – 4) + 8 ÷ 2
A. What step do you perform first in evaluating this expression?
B. What step do you perform second in evaluating this expression?
C. What is the value of the expression?
Answer:
A. Subtraction 24-4
B. Division 8 ÷ 2
C. 30
Decorating
Jackie is decorating her room. She wants to put a border around the ceiling. She will put wallpaper on one wall and paint the other three walls.
Question 1.
The drawing of Jackie’s Room shows the width of the room. The expression [13.2 – (2 × 2.8)] ÷2 represents the length of her room.
Part A
How much border does Jackie need to go around the entire ceiling of her room? Explain how you can tell from the expression.

Part B.
What is the length of Jackie’s room? Show the steps you use to evaluate the expression.
Answer:
Question 2.
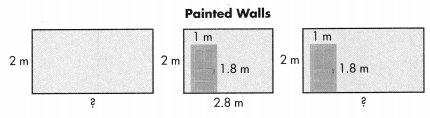
The Painted Walls drawing shows the three walls Jackie wants to paint. One wall is 2.8 meters long. The length of each of the other walls is the answer you found in Question 1, Part B.
Answer:
Part A
Write an expression to represent how many square meters Jackie will paint.
Part B
Evaluate the expression you wrote in Part A to find how many square meters Jackie will paint. Show the steps you used to evaluate the expression.
Answer:
Question 3.
The wall Jackie wants to wallpaper has two windows. The Wallpapered Wall drawing shows the lengths and widths of the wall and the windows. Each roll of wallpaper covers 0.8 square meter.
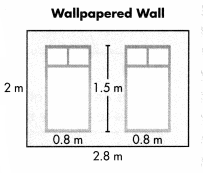
Part A
What does the expression 2 × (1.5 × 0.8) represent? What does the expression (2.8 × 2) – (2 × (1.5 × 0.8)] represent?
Part B
Write an expression to find how many rolls of wallpaper Jackie needs to buy. Show the steps you used to evaluate the expression.
Answer: