Practice with the help of enVision Math Common Core Grade 5 Answer Key Topic 4 Use Models and Strategies to Multiply Decimals regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 4 Use Models and Strategies to Multiply Decimals
Essential Question: What are some common procedures for estimating and finding products involving decimals?

enVision STEM Project: Solar Energy
Do Research Use the Internet or other sources to learn about solar energy. Find at least five ways that we use the Sun’s energy today.
Answer:
To dry your clothes.
To grow your food.
To heat your water.
To power your car.
To generate your electricity.
Explanation:
In the above-given question,
given that,
The sun has gone to a lot of trouble to send us its energy.
we can use solar energy in many ways.
they are:
to dry your clothes.
to grow your food.
to heat your water.
to power your car.
to generate your electricity.
Journal: Write a Report Include what you found. Also in your report:
• Describe at least one way that you could use solar energy. Could it save you money?
• Estimate how much your family pays for energy costs such as lights, gasoline, heating, and cooling.
• Make up and solve problems by multiplying whole numbers and decimals.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
• exponent
• hundredths
• overestimate
• partial products
• power
• round
• tenths
• thousandths
• underestimate
Question 1.
One way to estimate a number is to ____ the number.
Answer:
One way to estimate a number is to round the number.
Explanation:
In the above-given question,
given that,
one way to estimate a number is to round the number.
for example:
2.456 round to tenths.
2.556.

Question 2.
Using 50 for the number of weeks in a year is a(n) _____.
Answer:
Using 50 for the number of weeks in a year is a(n) is exponents.
Explanation:
In the above-given question,
given that,
using 50 for the number of weeks in a year is a(n) is exponents.
for example:
a(n) = 50.
a = 5.
50/5 = 10.
Question 3.
In the number 3.072, the digit 7 is in the ___ place and the digit 2 is in the ____ place.
Answer:
In the number 3.072, the digit 7 is in the hundredths place and the digit 2 is in the thousandths place.
Explanation:
In the above-given question,
given that,
In the number 3.072, the digit 7 is in the hundredths place and the digit 2 is in the thousandths place.
for example:
3.072.
7 is in the hundredths place.
2 is in the thousands place.
Question 4.
10,000 is a(n) ____ of 10 because 10 × 10 × 10 × 10 = 10,000.
Answer:
10,000 is a(n) power of 10 because 10 x 10 x 10 x 10 = 10,000.
Explanation:
In the above-given question,
given that,
for example:
10 x 10 x 10 x 10.
100 x 100 = 10,000.
Whole Number Multiplication Find each product.
Question 5.
64 × 100
Answer:
The product is 6400.
Explanation:
In the above-given question,
given that,
the two numbers are 64 and 100.
multiply the two numbers.
64 x 100 = 6400.
so the product is 6400.
Question 6.
7,823 × 103
Answer:
The product is 7823000.
Explanation:
In the above-given question,
given that,
the two numbers are 7823 and 1000.
multiply the two numbers.
7823 x 1000 = 7823000.
so the product is 7823000.
Question 7.
10 × 1,405
Answer:
The product is 14050.
Explanation:
In the above-given question,
given that,
the two numbers are 10 and 1405.
multiply the two numbers.
10 x 1405 = 14050.
so the product is 14050.
Question 8.
53 × 413
Answer:
The product is 21889.
Explanation:
In the above-given question,
given that,
the two numbers are 53 and 413.
multiply the two numbers.
53 x 413 = 21889.
so the product is 21889.
Question 9.
906 × 57
Answer:
The product is 51,642.
Explanation:
In the above-given question,
given that,
the two numbers are 906 and 57.
multiply the two numbers.
906 x 57 = 51,642.
so the product is 51,642.
Question 10.
1,037 × 80
Answer:
The product is 82,960.
Explanation:
In the above-given question,
given that,
the two numbers are 1037 and 80.
multiply the two numbers.
1037 × 80 = 82,960.
so the product is 82,960.

Round Decimals
Round each number to the nearest tenth.
Question 11.
842.121
Answer:
The number to the nearest tenth = 842.10.
Explanation:
In the above-given question,
given that,
the number is 842.121.
to round a number to the nearest tenth look at the number of ones.
if this is 5 or more round up.
if it is 4 or less round down.
842.10.
so the number to the nearest tenth = 842.10.
Question 12.
10,386.145
Answer:
The number to the nearest tenth = 10386.10.
Explanation:
In the above-given question,
given that,
the number is 10,386.145.
to round a number to the nearest tenth look at the number of ones.
if this is 5 or more round up.
if it is 4 or less round down.
10386.10.
so the number to the nearest tenth = 10386.10.
Question 13.
585.055
Answer:
The number to the nearest tenth = 585.155.
Explanation:
In the above-given question,
given that,
the number is 585.055.
to round a number to the nearest tenth look at the number of ones.
if this is 5 or more round up.
if it is 4 or less round down.
585.055.
so the number to the nearest tenth = 585.155.
Properties of Multiplication
Use the Commutative and Associative Properties of Multiplication to complete each multiplication.
Question 14.
96 × 42 = 4,032 so 42 × 96 = ___
Answer:
42 x 96 = 4032.
Explanation:
In the above-given question,
given that,
the two numbers are 96 and 42.
multiply the two numbers.
96 x 42 = 4032.
42 x 96 = 4032.
Question 15.
4 (58 × 25) = 4 × (25 × ___) = (___ × ___) × 58 = ___
Answer:
4(58 x 25) = 4 x (25 x 58) = (25 x 4) x 58 = 5800.
Explanation:
In the above-given question,
given that,
the two numbers are 58, 4, and 25.
multiply the two numbers.
4 x 25 x 58.
25 x 4 x 8 = 5800.
Question 16.
(293 × 50) × 20 = 293 × (50 × ___) = ___
Answer:
293 x 50 x 20 = 293 x 50 x 20 = 2,93,000.
Explanation:
In the above-given question,
given that,
the two numbers are 293, 50, and 20.
multiply the two numbers.
293 x 50 x 20.
50 x 293 x 20 = 2,93,000.

pick a Project
PROJECT 4A
How can you set up an exercise plan?
Project: Plan an exercise Program
PROJECT 4B
How much does it cost to dress a team?
Project: Budget a Team

PROJECT 4C
How far can a rocket go in 100 seconds?
Project: Make a Poster

Answer:
The rocket can go in 100 sec = 790 km.
Explanation:
The above-given question,
given that,
the rocket can go in 100 sec is:
1 minute = 60 sec.
1 sec = 7.9 km.
100sec = 7.9 x 100.
790 km.
PROJECT 4D
How much extra do you have to pay?
Project: Make a Data Display

Lesson 4.1 Multiply Decimals by Powers of 10
Activity
Solve & Share
Javier is helping his parents put up posters in their movie theater. Each poster has a thickness of 0.012 inch. How thick is a stack of 10 posters? 100 posters? 1,000 posters? Solve this problem any way you choose.
Answer:
The thick is a stack of 10 posters = 0.12.
the thick is a stack of 100 posters = 1.2.
the thick is a stack of 1000 posters = 12.
Explanation:
In the above-given question,
given that,
Javier is helping his parents put up posters in their movie theater.
Each poster has a thickness of 0.012.
0.012 x 10 = 0.12.
0.012 x 100 = 1.2.
0.012 x 1000 = 12.
You can use the structure of our number system and mental math to help you.

Look Back! Use Structure How is your answer for 1,000 posters similar to 0.012? How is it different?
Visual Learning Bridge
Essential Question
What Patterns Can Help You Multiply Decimals by Powers of 10?
A.
You can use place value and what you know about whole numbers to multiply decimals by powers of 10. What patterns can you find?
We already know what happens when a whole number is multiplied by powers of 10.


B.
In a place-value chart, the same pattern appears when a decimal is multiplied by powers of 10.
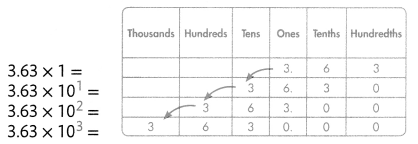
A digit in one place is worth 10 times more when moved to the place on its left. Every time a number is multiplied by 10, the digits of the number shift to the left.
C.
Holding the numbers still, another pattern appears.
3.63 × 1 = 3.63
3.63 × 101 = 36.3
3.63 × 102 = 363.0
3.63 × 103 = 3630.0
It looks like the decimal point moves to the right each time.

Convince Me! Use Structure Complete the chart. What patterns can you use to place the decimal point?

Answer:
1.275 x 10 = 12.75, 1.275 x 100 = 127.5, 1.275 x 1000 = 1275.
26.014 x 10 = 260.14, 26.014 x 100 = 2601.4, 26.014x 1000 = 26014.
0.4 x 10 = 4, 0.4 x 100 = 40, 0.4 x 1000 = 400.
Explanation:
In the above-given question,
given that,
the numbers are 1.275, 26.014, and 0.4.
multiply the numbers by 10, 100, and 1000.
1.275 x 10 = 12.75, 1.275 x 100 = 127.5, 1.275 x 1000 = 1275.
26.014 x 10 = 260.14, 26.014 x 100 = 2601.4, 26.014x 1000 = 26014.
0.4 x 10 = 4, 0.4 x 100 = 40, 0.4 x 1000 = 400.

Guided Practice
Do You Understand?
Question 1.
When multiplying by a power of 10, like 4.58 × 103, how do you know you are moving the decimal in the correct direction?
Answer:
The number is 4580.
Explanation:
In the above-given question,
given that,
4.58 × 103.
4.58 x 10 x 10 x 10.
4.58 x 1000 = 4580.
so the number is 4580.
Do You Know How?
In 2-5, find each product.
Question 2.
0.009 × 10
Answer:
The product is 0.09.
Explanation:
In the above-given question,
given that,
the numbers are 0.009 and 10.
multiply the numbers.
0.009 x 10 = 0.09.
so the product is 0.09.
Question 3.
3.1 × 103
Answer:
The product is 3100.
Explanation:
In the above-given question,
given that,
the numbers are 3.1 and 1000.
multiply the numbers.
3.1 x 1000 = 3100.
so the product is 3100.
Question 4.
0.062 × 102
Answer:
The product is 6.2.
Explanation:
In the above-given question,
given that,
the numbers are 0.062 and 100.
multiply the numbers.
0.062 x 100 = 6.2.
so the product is 6.2.
Question 5.
1.24 × 104
Answer:
The product is 1240.
Explanation:
In the above-given question,
given that,
the numbers are 1.24 and 10000.
multiply the numbers.
1.24 x 10000 = 1240.
so the product is 1240.
Independent Practice
Leveled Practice in 6 and 7, find each product.
Place-value patterns can help you solve these problems.

Question 6.
42.3 ×1 = ___
42.3 × 10 = ___
42.3 × 102 = ___
Answer:
42.3 x 1 = 42.3.
42.3 x 10 = 423.
42.3 x 100 = 4230.
Explanation:
In the above-given question,
given that,
the numbers are 42.3, 42.2 x 10, and 42.3 x 100.
42.3 x 1 = 42.3.
42.3 x 10 = 423.
42.3 x 100 = 4230.
Question 7.
____ = 0.086 × 101
___ = 0.086 × 100
____ = 0.086 × 1,000
Answer:
0.086 x 10 = 0.86.
0.086 x 100 = 8.6.
0.086 x 1000 = 86.
Explanation:
In the above-given question,
given that,
the numbers are 0.086 x 10, 0.086 x 100, and 0.086 x 1000.
0.086 x 10 = 0.86.
0.086 x 100 = 8.6.
0.086 x 1000 = 86.
In 8-15, find each product.
Question 8.
63.7 × 10
Answer:
The product is 637.
Explanation:
In the above-given question,
given that,
the numbers are 63.7 and 10.
multiply the numbers.
63.7 x 10 = 637.
so the product is 637.
Question 9.
563.7 × 102
Answer:
The product is 56370.
Explanation:
In the above-given question,
given that,
the numbers are 563.7 and 100.
multiply the numbers.
563.7 x 100 = 56370.
so the product is 56370.
Question 10.
0.365 × 104
Answer:
The product is 3650.
Explanation:
In the above-given question,
given that,
the numbers are 0.365 and 10000.
multiply the numbers.
0.365 x 10000 = 3650.
so the product is 3650.
Question 11.
5.02 × 100
Answer:
The product is 502.
Explanation:
In the above-given question,
given that,
the numbers are 5.02 and 100.
multiply the numbers.
5.02 x 100 = 502.
so the product is 502.
Question 12.
94.6 × 103
Answer:
The product is 94600.
Explanation:
In the above-given question,
given that,
the numbers are 94.6 and 1000.
multiply the numbers.
94.6 x 1000 = 94600.
so the product is 94600.
Question 13.
0.9463 × 102
Answer:
The product is 94.63.
Explanation:
In the above-given question,
given that,
the numbers are 0.9463 and 100.
multiply the numbers.
0.9463 x 100 = 94.63.
so the product is 94.63.
Question 14.
0.678 × 100
Answer:
The product is 67.8.
Explanation:
In the above-given question,
given that,
the numbers are 0.678 and 100.
multiply the numbers.
0.678 x 100 = 67.8.
so the product is 67.8.
Question 15.
681.7 × 104
Answer:
The product is 6817000.
Explanation:
In the above-given question,
given that,
the numbers are 681.7 and 10000.
multiply the numbers.
681.7 x 10000 = 6817000.
so the product is 6817000.
In 16-18, find the missing exponent.
Question 16.
0.629 × ![]() = 62.9
= 62.9
Answer:
The missing exponent is 2.
Explanation:
In the above-given question,
given that,
0.629 x 10 x 10.
0.629 x 100 = 62.9.
0.629
Question 17.
![]() × 0.056 = 560
× 0.056 = 560
Answer:
The missing exponent is 4.
Explanation:
In the above-given question,
given that,
10 x 10 x 10 x 10 x 0.056.
100 x 100 x 0.056.
10000 x 0.056.
560.
Question 18.
1.23 = ![]() × 0.123
× 0.123
Answer:
The missing exponent is 0.
Explanation:
In the above-given question,
given that,
1.23 x 10.
1.23.
Problem Solving
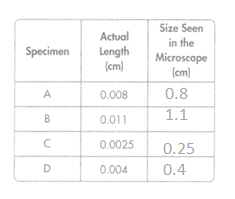
In 19-21, use the table to find the answers.
Question 19.
Monroe uses a microscope to observe specimens in science class. The microscope enlarges objects to 100 times their actual size. Find the size of each specimen as seen in the microscope.
Answer:
The size of each specimen as seen in the microscope = 0.8, 11, 0.25, and 0.4.
Explanation:
In the above-given question,
given that,
Monroe uses a microscope to observe specimens in science class.
The microscope enlarges objects to 100 times their actual size.
0.008 x 100 = 0.8.
0.011 x 100 = 11.
0.0025 x 100 = 0.25.
0.004 x 100 = 0.4.
Question 20.
Monroe’s teacher wants each student to draw a sketch of the longest specimen. Which specimen is the longest?
Answer:
Specimen B is the longest.
Explanation:
In the above-given question,
given that,
Monroe’s teacher wants each student to draw a sketch of the longest specimen.
0.008 x 100 = 0.8.
0.011 x 100 = 11.
0.0025 x 100 = 0.25.
0.004 x 100 = 0.4.
so specimen B is the longest.
Question 21.
Seen through the microscope, a specimen is 0.75 cm long. What is its actual length?
Answer:
The actual length = 75 cm.
Explanation:
In the above-given question,
given that,
a specimen is 0.75 cm long.
0.75 x 100 = 75.
so the actual length of the specimen is 75 cm.
Question 22.
Jon’s binoculars enlarge objects to 10 times their actual size. If the length of an ant is 0.43 inch, what is the length as seen up close through his binoculars?
Answer:
The length as seen up close through his binoculars = 4.3 inches.
Explanation:
In the above-given question,
given that,
Jon’s binoculars enlarge objects to 10 times their actual size.
If the length of an ant is 0.43 inches.
0.43 x 10 = 4.3 inches.
so the length as seen up close through his binoculars = 4.3 inches.
Question 23.
Higher Order Thinking Jefferson drew a line 9.5 inches long. Brittany drew a line 10 times as long. What is the difference in length between the two lines?
Answer:
The difference in length between the two lines = 85.5 inches.
Explanation:
In the above-given question,
given that,
Jefferson drew a line 9.5 inches long.
Brittany drew a line 10 times as long.
9.5 x 10 = 95.
95 – 9.5 = 85.5.
so the difference in length between the two lines = 85.5 inches.
Question 24.
Construct Arguments José ran 2.6 miles. Pavel ran 2.60 miles. Who ran farther? Explain your reasoning.
Answer:
Jose and Pavel ran the same.
Explanation:
In the above-given question,
given that,
José ran 2.6 miles. Pavel ran 2.60 miles.
2.6 is equal to 2.60.
so Jose and Pavel ran the same.
Assessment Practice
Question 25.
Choose all equations that are true.
![]() 4.82 × 1,000 = 482,000
4.82 × 1,000 = 482,000
![]() 4.82 × 102 = 482
4.82 × 102 = 482
![]() 482 × 101 = 48.2
482 × 101 = 48.2
![]() 482 × 103 = 482
482 × 103 = 482
![]() 48.2 × 104 = 4,820
48.2 × 104 = 4,820
Answer:
4.82 x 100 = 482.
Explanation:
In the above-given question,
given that,
The equations are:
4.82 x 1000 = 482000.
4.82 x 10 = 482.
482 x 1000 = 482.
48.2 x 10000 = 4820.
so the equation that is true is 4.82 x 100 = 482.
Question 26.
Choose all equations that are true when 102 is placed in the box.
![]() o 37 =
o 37 = ![]() × 0.37 0
× 0.37 0
![]() 0.37 =
0.37 = ![]() × 0.037
× 0.037
![]() 0370 =
0370 = ![]() × 3.7
× 3.7
![]() 0.37 =
0.37 = ![]() × 3.7
× 3.7
![]() 3.7 =
3.7 = ![]() × 0.037
× 0.037
Answer:
None of the equations are true.
Explanation:
In the above-given question,
given that,
37 x 102 = 0.370.
0.37 x 102 = 0.037.
0370 x 102 = 3.7.
3.7 x 102 = 0.037.
so none of the equations are true.
Lesson 4.2 Estimate the Product of a Decimal and a Whole Number
Activity
Solve & Share
Renee needs 32 strands of twine for an art project. Each strand must be 1.25 centimeters long. About how many centimeters of twine does she need? Solve this problem any way you choose!
Answer:
The centimeters of twine does she need = 40 cm.
Explanation:
In the above-given question,
given that,
Renee needs 32 strands of twine for an art project.
Each strand must be 1.25 centimeters long.
32 x 1.25 = 40.
so the centimeters of twine does she need = 40 cm.
Generalize How can you relate what you know about estimating with whole numbers to estimating with decimals? Show
your work!

Look Back! Is your estimate an overestimate or an underestimate? How can you tell?
Visual Learning Bridge
Essential Question
What Are Some Ways to Estimate Products of Decimals and Whole Numbers?
A.
A wedding planner needs to buy 16 pounds of sliced cheddar cheese. About how much will the cheese cost?

B.
One Way
Round each number to the nearest dollar and nearest ten.
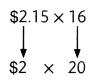
$2 × 20 = $40
The cheese will cost about $40.
C.
Another Way
Use compatible numbers that you can multiply mentally.
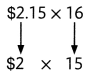
$2 × 15 = $30
The cheese will cost about $30.
Convince Me! Reasoning About how much money would 18 pounds of cheese cost if the price is $3.95 per pound? Use two different ways to estimate the product. Are your estimates overestimates or underestimates? Explain.
Another Example
Manuel walks a total of 0.75 mile to and from school each day. If there have been 105 school days so far this year, about how many miles has he walked in all?
Round to the nearest whole number.

Use compatible numbers.
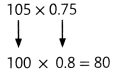
Be sure to place the decimal point correctly.

Both methods provide reasonable estimates of how far Manuel has walked.
Guided Practice
Do You Understand?
Question 1.
Number Sense There are about 20 school days in a month. In the problem above, about how many miles does Manuel walk each month? Write an equation to show your work.
Answer:
The number of miles does Manuel walks each month = 16.
Explanation:
In the above-given question,
given that,
There are about 20 school days in a month.
0.75 x 20.
0.8 x 20 = 16.
so the number of miles does Manuel walks each month = 16.
Question 2.
Without multiplying, which estimate in the Another example do you think is closer to the exact answer? Explain your reasoning
Answer:
The number of miles does Manuel walks each month = 16.
Explanation:
In the above-given question,
given that,
There are about 20 school days in a month.
0.75 x 20.
0.8 x 20 = 16.
so the number of miles does Manuel walks each month = 16.
Do You Know How?
In 3-8, estimate each product using rounding or compatible numbers.
Question 3.
0.87 × 112
Answer:
The product is 112.
Explanation:
In the above-given question,
given that,
the numbers are 0.87 and 112.
0.87 x 112.
0.8 is equal to 1.
112 x 1 = 112.
so the product is 112.
Question 4.
104 × 0.33
Answer:
The product is 52.
Explanation:
In the above-given question,
given that,
the numbers are 104 and 0.33.
104 x 0.33.
0.33 is equal to 0.5.
104 x 0.5 = 52.
so the product is 52.
Question 5.
9.02 × 80
Answer:
The product is 720.
Explanation:
In the above-given question,
given that,
the numbers are 9.02 and 80.
9.02 x 80.
9.02 is equal to 9.
9 x 80 = 720.
so the product is 720.
Question 6.
0.54 × 24
Answer:
The product is 12.
Explanation:
In the above-given question,
given that,
the numbers are 0.54 and 24.
0.54 x 24.
0.54 is equal to 0.5.
0.5 x 24 = 12.
so the product is 12.
Question 7.
33.05 × 200
Answer:
The product is 6600.
Explanation:
In the above-given question,
given that,
the numbers are 33.05 and 200.
33.05 x 200.
33.05 is equal to 33.
33 x 200 = 6600.
so the product is 6600.
Question 8.
0.79 × 51
Answer:
The product is 51.
Explanation:
In the above-given question,
given that,
the numbers are 0.70 and 51.
0.7 x 51.
0.7 is equal to 1.
51 x 1 = 51.
so the product is 51.
Independent Practice
In 9-16, estimate each product.
Question 9.
0.12 × 105
Answer:
The product is 10.5.
Explanation:
In the above-given question,
given that,
the numbers are 0.12 and 105.
0.12 x 105.
0.12 is equal to 0.1.
105 x 0.1 = 10.5.
so the product is 10.5.
Question 10.
45.3 × 4
Answer:
The product is 180.
Explanation:
In the above-given question,
given that,
the numbers are 45.3 and 4.
45.3 x 4.
45.3 is equal to 45.
45 x 4 = 180.
so the product is 180.
Question 11.
99.2 × 82
Answer:
The product is 8118.
Explanation:
In the above-given question,
given that,
the numbers are 99.2 and 82.
99.2 x 82.
99.2 is equal to 99.
99 x 82 = 8118.
so the product is 8118.
Question 12.
37 × 0.93
Answer:
The product is 37.
Explanation:
In the above-given question,
given that,
the numbers are 37 and 0.93.
37 x 0.93.
0.93 is equal to 1.
37 x 1 = 37.
so the product is 37.
Question 13.
1.67 × 4
Answer:
The product is 8.
Explanation:
In the above-given question,
given that,
the numbers are 1.67 and 4.
1.67 x 4.
1.67 is equal to 2.
4 x 2 = 8.
so the product is 8.
Question 14.
3.2 × 184
Answer:
The product is 552.
Explanation:
In the above-given question,
given that,
the numbers are 3.2 and 184.
3.2 x 184.
3.2 is equal to 3.
184 x 3 = 552.
so the product is 552.
Question 15.
12 × 0.37
Answer:
The product is 3.6.
Explanation:
In the above-given question,
given that,
the numbers are 12 and 0.3.
0.3 x 12.
0.3 is equal to 0.3.
12 x 0.3 = 3.6.
so the product is 3.6.
Question 16.
0.904 × 75
Answer:
The product is 75.
Explanation:
In the above-given question,
given that,
the numbers are 0.904 and 75.
0.904 x 75.
0.9 is equal to 1.
75 x 1 = 75.
so the product is 75.
Problem Solving
Question 17.
About how much money does Stan need to buy 5 T-shirts and 10 buttons?
Answer:
The cost to buy 5 T-shirts and 10 buttons = $82.
Explanation:
In the above-given question,
given that,
the cost of a button is $1.95.
the cost of the T-shirt is $12.50.
1.95 x 10 = 19.5.
12.50 x 5 = 62.5.
19.5 + 62.5 = 82.
so the cost to buy 5 T-shirts and 10 buttons = $82.

Question 18.
Joseph buys a pair of shorts for $17.95 and 4 T-shirts. About how much money does he spend?
Answer:
The amount of money he spends = $67.95.
Explanation:
In the above-given question,
given that,
Joseph buys a pair of shorts for $17.95 and 4 T-shirts.
$12.50 x 4 = 50.
$17.95 + 50 = 67.95.
so the money he spend = $67.95.
Question 19.
Marcy picked 18.8 pounds of peaches at the pick-your-own orchard. Each pound costs $1.28. About how much did Marcy pay for the peaches? Write an equation to model your work.
Answer:
The amount did Marcy pay for the peaches = $24.064.
Explanation:
In the above-given question,
given that,
Marcy picked 18.8 pounds of peaches at the pick-your-own orchard.
Each pound costs $1.28.
18.8 x 1.28 = 24.064.
so the amount did Marcy pay for the peaches = $24.064.
Question 20.
Be Precise Joshua had $20. He spent $4.58 on Friday, $7.43 on Saturday, and $3.50 on Sunday. How much money does he have left? Show how you found the answer.
Answer:
The money does he have left = $15.51.
Explanation:
In the above-given question,
given that,
Be Precise Joshua had $20.
He spent $4.58 on Friday.
$7.43 on Saturday, and $3.50 on Sunday.
4.58 + 7.43 + 3.50 = 15.51.
so the money does he have left = $15.51.
Question 21.
Higher Order Thinking Ms. Webster works 4 days a week at her office and 1 day a week at home. The route to Ms. Webster’s office is 23.7 miles. The route home is 21.8 miles. About how many miles does she drive for work each week? Explain how you found your answer.
Answer:
The number of miles does she drive for work each week = $116.6.
Explanation:
In the above-given question,
given that,
Ms. Webster works 4 days a week at her office and 1 day a week at home.
The route to Ms. Webster’s office is 23.7 miles.
The route home is 21.8 miles.
23.7 x 4 = 94.8.
21.8 x 1 = 21.8.
94.8 + 21.8 = 116.6
so the number of miles does she drive for work each week = $116.6.
Assessment Practice
Question 22.
Rounding to the nearest tenth, which of the following give an underestimate?
![]() 39.45 × 1.7
39.45 × 1.7
![]() 27.54 × 0.74
27.54 × 0.74
![]() 9.91 × 8.74
9.91 × 8.74
![]() 78.95 × 1.26
78.95 × 1.26
![]() 18.19 × 2.28
18.19 × 2.28
Answer:
The equations are 39.45 x 1.7 and 27.54 x 0.74.
Explanation:
In the above-given question,
given that,
the equations are:
39.45 x 1.7 = 67.065.
27.54 x 0.74 = 20.3796.
9.91 x 8.74 = 86.6134.
78.95 x 1.26 = 99.477.
18.19 x 2.28 = 41.4732.
Question 23.
Rounding to the nearest whole number, which of the following give an overestimate?
![]() 11.6 × 9.5
11.6 × 9.5
![]() 4.49 × 8.3
4.49 × 8.3
![]() 12.9 × 0.9
12.9 × 0.9
![]() 0.62 × 1.5
0.62 × 1.5
![]() 8.46 × 7.38
8.46 × 7.38
Answer:
The equation is 8.46 x 7.38.
Explanation:
In the above-given question,
given that,
the equations are:
11.6 x 9.5 = 110.2.
4.49 x 8.3 = 37.267.
12.9 x 0.9 = 11.61.
0.62 x 1.5 = 0.93.
8.46 x 7.38 = 62.4348.
Lesson 4.3 Use Models to Multiply a Decimal and a Whole Number
Activity
Solve & Share
Mara has 4 garden plots. Each is 0.7 acre in area. What is the total area of the garden plots? Use objects or the grids below to show your work.
How can you represent multiplying a decimal and a whole number?


Look Back! Critique Reasoning Ed says a decimal grid shows 10 tenths. Monica says a decimal grid shows 100 hundredths. Who is correct? Explain.
Visual Learning Bridge
Essential Question How Can You Model Multiplying a Decimal by a Whole Number?
A.
How can you use models to find 4 × 0.36?
When showing decimals, it is important to establish which type of block represents 1.
You can use place-value blocks to show multiplication of a decimal by a whole number.


B.
Multiplying 4 × 0.36 is like combining 4 groups each containing 0.36.
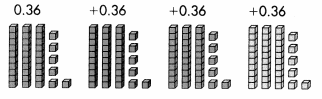
Regrouping after combining the blocks gives:
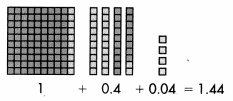

Convince Me! Make Sense and Persevere Bari made a train with 5 cars that are each 1.27 meter long. What is the total length of the train? Use place-value blocks to model the problem. Then find the product using an equation and compare the answers.
Guided Practice
Do You Understand?
Question 1.
Without multiplying, is 4 × 0.36 less than or greater than 4? Explain.
Answer:
4 x 0.36 is greater than 4.
Explanation:
In the above-given question,
given that,
the numbers are 0.36 and 4.
4 x 0.36 = 1.44.
1.44 is greater than 4.
so 4 x 0.36 is greater than 4.
Do You Know How?
In 2-5, find the product. You may use place-value blocks to help.
Question 2.
0.8 × 4
Answer:
The product is 3.2.
Explanation:
In the above-given question,
given that,
the numbers are 0.8 and 4.
multiply the two numbers.
0.8 x 4 = 3.2.
so the product is 3.2.
Question 3.
0.7 × 3
Answer:
The product is 2.1.
Explanation:
In the above-given question,
given that,
the numbers are 0.7 and 3.
multiply the two numbers.
0.7 x 3 = 2.1.
so the product is 2.1.
Question 4.
0.5 × 6
Answer:
The product is 3.0.
Explanation:
In the above-given question,
given that,
the numbers are 0.5 and 6.
multiply the two numbers.
0.5 x 6 = 3.0.
so the product is 3.0.
Question 5.
0.6 × 5
Answer:
The product is 3.0.
Explanation:
In the above-given question,
given that,
the numbers are 0.6 and 5.
multiply the two numbers.
0.6 x 5 = 3.0.
so the product is 3.0.
Independent Practice
Use or draw place-value blocks to help you model the problem.

In 6 and 7, find the product. Use place-value blocks to help.
Question 6.
0.55 × 3 = ___
Answer:
The product is 1.65.
Explanation:
In the above-given question,
given that,
the numbers are 0.55 and 3.
multiply the two numbers.
0.55 x 3 = 1.65.
so the product is 1.65.
Question 7.
___ = 0.45 × 2
Answer:
The product is 0.9.
Explanation:
In the above-given question,
given that,
the numbers are 0.45 and 2.
multiply the two numbers.
0.45 x 2 = 0.9.
so the product is 0.9.
In 8-19, find the product. Use place-value blocks to help.
Question 8.
5 × 0.5
Answer:
The product is 2.5.
Explanation:
In the above-given question,
given that,
the numbers are 0.5 and 5.
multiply the two numbers.
0.5 x 5 = 2.5.
so the product is 2.5.
Question 9.
4 × 0.27
Answer:
The product is 1.08.
Explanation:
In the above-given question,
given that,
the numbers are 0.27 and 4.
multiply the two numbers.
0.27 x 4 = 1.08.
so the product is 1.08.
Question 10.
6 × 0.13
Answer:
The product is 0.78.
Explanation:
In the above-given question,
given that,
the numbers are 0.13 and 6.
multiply the two numbers.
0.13 x 6 = 0.78.
so the product is 0.78.
Question 11.
0.78 × 5
Answer:
The product is 3.9.
Explanation:
In the above-given question,
given that,
the numbers are 0.78 and 5.
multiply the two numbers.
0.78 x 5 = 3.9.
so the product is 3.9.
Question 12.
10 × 0.32
Answer:
The product is 3.2.
Explanation:
In the above-given question,
given that,
the numbers are 0.32 and 10.
multiply the two numbers.
0.32 x 10 = 3.2.
so the product is 3.2.
Question 13.
6 × 2.03
Answer:
The product is 12.18.
Explanation:
In the above-given question,
given that,
the numbers are 6 and 2.03.
multiply the two numbers.
6 x 2.03 = 12.18.
so the product is 12.18.
Question 14.
1.35 × 5
Answer:
The product is 6.75.
Explanation:
In the above-given question,
given that,
the numbers are 1.35 and 5.
multiply the two numbers.
1.35 x 5 = 6.75.
so the product is 6.75.
Question 15.
100 × 0.12
Answer:
The product is 12.
Explanation:
In the above-given question,
given that,
the numbers are 100 and 0.12.
multiply the two numbers.
100 x 0.12 = 12.
so the product is 12.
Question 16.
4 × 0.15
Answer:
The product is 0.6.
Explanation:
In the above-given question,
given that,
the numbers are 0.15 and 4.
multiply the two numbers.
0.15 x 4 = 0.6.
so the product is 0.6.
Question 17.
3 × 2.5
Answer:
The product is 7.5.
Explanation:
In the above-given question,
given that,
the numbers are 3 and 2.5.
multiply the two numbers.
3 x 2.5 = 7.5.
so the product is 7.5.
Question 18.
0.9 × 7
Answer:
The product is 6.3.
Explanation:
In the above-given question,
given that,
the numbers are 0.9 and 7.
multiply the two numbers.
0.9 x 7 = 6.3.
so the product is 6.3.
Question 19.
0.35 × 3
Answer:
The product is 1.05.
Explanation:
In the above-given question,
given that,
the numbers are 0.35 and 3.
multiply the two numbers.
0.35 x 3 = 1.05.
so the product is 1.05.
Problem Solving
Question 20.
A city is building 3 parks in a new subdivision. Each park will be 1.25 acres. How many total acres will the 3 parks be? Use place-value blocks to model the problem if you need help.
Answer:
The total number of acres will the 3 parks be 3.75 acres.
Explanation:
In the above-given question,
given that,
A city is building 3 parks in a new subdivision.
Each park will be 1.25 acres.
1.25 x 3 = 3.75.
so the total number of acres will the 3 parks be 3.75 acres.
How is multiplying with decimals like multiplying whole numbers?

Question 21.
Higher Order Thinking The city acquired more land next to the subdivision. If it decides to make each park 12.5 acres, how many additional acres would the parks occupy?
Answer:
The number of additional acres would the parks occupy = 8.75 acres.
Explanation:
In the above-given question,
given that,
The city acquired more land next to the subdivision.
If it decides to make each park 12.5 acres.
3.75 – 12.5 = 8.75.
so the number of additional acres would the parks occupy = 8.75 acres.
Question 22.
Write a multiplication equation that matches the shading on the grid.

Answer:
2 + 0.4 = 2.4.
Explanation:
In the above-given question,
given that,
there are 2 hundred blocks.
1 + 1 = 2.
there are 4 tens blocks.
0.4.
2 + 0.4 = 2.4
Question 23.
Critique Reasoning Jen multiplied 9 by 0.989 and got an answer of 89.01. How can you use estimation to show that Jen’s answer is wrong? What mistake do you think she made?
Answer:
Yes, the estimation was wrong.
Explanation:
In the above-given question,
given that,
Jen multiplied 9 by 0.989 and got an answer of 89.01.
0.989 x 9 = 8.901.
so the estimation shows that Jen’s answer is wrong.
Assessment Practice
Question 24.
Anita needs 5 pounds of bananas to make banana bread for a bake sale. Each pound of bananas costs $0.50.
Part A
How can Anita use place-value blocks to find the total cost of the bananas? What is the total cost?
Part B
How can Anita use what she knows about whole-number multiplication to check her answer?
Answer:
The total cost of the bananas = $2.5.
Explanation:
In the above-given question,
given that,
Anita needs 5 pounds of bananas to make banana bread for a bake sale.
Each pound of bananas costs $0.50.
$0.50 x 5 = $2.5.
so the total cost of the bananas = $2.5.
Lesson 4.4 Multiply a Decimal and a Whole Number
Solve & Share
A car travels 1.15 kilometers in 1 minute. If it travels at a constant speed, how far will it travel in 3 minutes? in 5 minutes? Solve this problem any way you choose!

Answer:
The far will it travel in 3 minutes = 3.45.
the far will it travel in 5 minutes = 5.75.
Explanation:
In the above-given question,
given that,
A car travels 1.15 kilometers in 1 minute.
If it travels at a constant speed,
1.15 x 3 = 3.45.
1.15 x 5 = 5.75.
Generalize You can connect what you know about whole-number multiplication to multiplying a decimal by a whole number.

Look Back! How can addition be used to answer the questions above?
Visual Learning Bridge
Essential Question How Do You Multiply a Decimal by a Whole Number?
A.
To raise money for a charity, $0.15 was collected from every ticket sold to a Lions baseball game. If you bought 12 tickets, how much money would go to the charity?

You can multiply 0.15 × 12 by thinking about 15 × 12 and using place-value patterns.
B.
One Way
Add 0.15 twelve times.

C.
Another Way
First, multiply as you would with whole numbers.
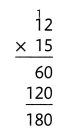
Use number sense to place the decimal point.

Notice the digits are the same.

Convince Me! Generalize Here are two similar problems:
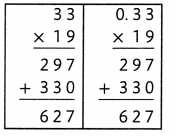
Place the decimal point correctly in each answer. Explain your thinking.
Guided Practice
Do You Understand?
Question 1.
What is the difference between multiplying a whole number by a decimal and multiplying two whole numbers?
Answer:
The answer is the same.
Explanation:
In the above-given question,
given that,
33 x 19 = 627.
0.33 x 19 = 627.
so the answer is the same.
Question 2.
If a group bought 24 tickets, how much money would go to charity? Explain how you found your answer.
Answer:
The money would go to charity = 3.36.
Explanation:
In the above-given question,
given that,
If a group bought 24 tickets.
24 x 0.14 = 3.36.
so the money would go to charity = 3.36.
Do You Know How?
For 3-8, find each product.
Question 3.
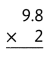
Answer:
The product is 19.6.
Explanation:
In the above-given question,
given that,
the two numbers are 9.8 and 2.
multiply the two numbers.
9.8 x 2 = 19.6.
so the product is 19.6.
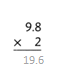
Question 4.
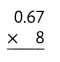
Answer:
The product is 5.36.
Explanation:
In the above-given question,
given that,
the two numbers are 0.67 and 8.
multiply the two numbers.
0.67 x 8 = 5.36.
so the product is 5.36.
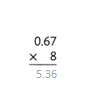
Question 5.
34 × 5.3
Answer:
The product is 180.2.
Explanation:
In the above-given question,
given that,
the two numbers are 34 and 5.3.
multiply the two numbers.
34 x 5.3 = 180.2.
so the product is 19.6.
Question 6.
4.6 × 21
Answer:
The product is 96.6.
Explanation:
In the above-given question,
given that,
the two numbers are 4.6 and 21.
multiply the two numbers.
4.6 x 21 = 96.6.
so the product is 96.6.
Question 7.
0.6 × 15
Answer:
The product is 9.
Explanation:
In the above-given question,
given that,
the two numbers are 0.6 and 15.
multiply the two numbers.
0.6 x 15 = 9.
so the product is 9.
Question 8.
55 × 1.1
Answer:
The product is 60.5.
Explanation:
In the above-given question,
given that,
the two numbers are 55 and 1.1.
multiply the two numbers.
55 x 1.1 = 60.5.
so the product is 60.5.
Independent Practice
For 9-20, find each product.
Use what you know about whole-number multiplication and place value to help you!

Question 9.
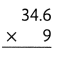
Answer:
The product is 311.4.
Explanation:
In the above-given question,
given that,
the two numbers are 34.6 and 9.
multiply the two numbers.
34.6 x 9 = 311.4.
so the product is 311.4.
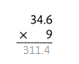
Question 10.
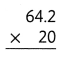
Answer:
The product is 1284.
Explanation:
In the above-given question,
given that,
the two numbers are 64.2 and 20.
multiply the two numbers.
64.2 x 20 = 1284.
so the product is 1284.
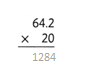
Question 11.
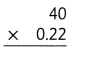
Answer:
The product is 8.8.
Explanation:
In the above-given question,
given that,
the two numbers are 40 and 0.22.
multiply the two numbers.
40 x 0.22 = 8.8.
so the product is 8.8.

Question 12.
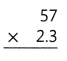
Answer:
The product is 131.1.
Explanation:
In the above-given question,
given that,
the two numbers are 57 and 2.3.
multiply the two numbers.
57 x 2.3 = 131.1.
so the product is 131.1.
Question 13.
5.8 × 11
Answer:
The product is 63.8.
Explanation:
In the above-given question,
given that,
the two numbers are 5.8 and 11.
multiply the two numbers.
5.8 x 11 = 63.8.
so the product is 63.8.
Question 14.
56 × 0.4
Answer:
The product is 22.4.
Explanation:
In the above-given question,
given that,
the two numbers are 56 and 0.4.
multiply the two numbers.
56 x 0.4 = 22.4.
so the product is 22.4.
Question 15.
170 × 0.003
Answer:
The product is 0.51.
Explanation:
In the above-given question,
given that,
the two numbers are 170 and 0.003.
multiply the two numbers.
170 x 0.003 = 0.51.
so the product is 0.51.
Question 16.
0.3 × 99
Answer:
The product is 29.7.
Explanation:
In the above-given question,
given that,
the two numbers are 0.3 and 99.
multiply the two numbers.
0.3 x 99 = 29.7.
so the product is 29.7.
Question 17.
26 × 1.61
Answer:
The product is 41.86.
Explanation:
In the above-given question,
given that,
the two numbers are 26 and 1.61.
multiply the two numbers.
26 x 1.61 = 41.86.
so the product is 41.86.
Question 18.
50 × 0.914
Answer:
The product is 45.7.
Explanation:
In the above-given question,
given that,
the two numbers are 50 and 0.914.
multiply the two numbers.
50 x 0.914 = 45.7.
so the product is 45.7.
Question 19.
10.76 × 100
Answer:
The product is 1076.
Explanation:
In the above-given question,
given that,
the two numbers are 10.76 and 100.
multiply the two numbers.
10.76 x 100 = 1076.
so the product is 1076.
Question 20.
2.54 × 12
Answer:
The product is 30.48.
Explanation:
In the above-given question,
given that,
the two numbers are 2.54 and 12.
multiply the two numbers.
2.54 x 12 = 30.48.
so the product is 30.48.
Problem Solving
Question 21.
enVision® STEM To meet peak energy demand, an electric power cooperative buys back electricity generated locally. They pay $0.07 per solar-powered kWh (kilowatt-hour). How much money does a school make when it sells back 956 kWh to the cooperative?
Round and estimate to check for reasonableness.

Answer:
The money does a school makes when it sells back 956 kWh to the cooperative = $66.92.
Explanation:
In the above-given question,
given that,
an electric power cooperative buys back electricity generated locally.
They pay $0.07 per solar-powered kWh (kilowatt-hour).
956 x 0.07 = 66.92.
so the money doe a school makes when it sells back 956 kWh to the cooperative = $66.92.
Question 22.
The airline that Vince is using has a baggage weight limit of 41 pounds. He has two green bags, each weighing 18.4 pounds, and one blue bag weighing 3.7 pounds. Are his bags within the weight limit? Explain.
Answer:
Yes, the bags within the weight limit.
Explanation:
In the above-given question,
given that,
The airline that Vince is using has a baggage weight limit of 41 pounds.
He has two green bags, each weighing 18.4 pounds.
18.4 + 3.7 = 22.1.
so the bags are within the limit.
Question 23.
Michael keeps track of how much time he uses his family’s computer each week for 10 weeks. He created the frequency table with the data he collected. How many hours did Michael spend on the computer?

Answer:
The number of hours did Michael spend on the computer = 17.
Explanation:
In the above-given question,
given that,
Michael keeps track of how much time he uses his family’s computer each week for 10 weeks.
3.5 + 4 + 4.5 + 5 = 17.
so the number of hours did Micheal spend on the computer = 17.
Question 24.
Critique Reasoning Sara is multiplying two factors, one is a whole number and one has two decimal places. She says the product could have one decimal place. Is she correct? Give an example and explain your reasoning.
Answer:
Yes, she was correct.
Explanation:
In the above-given question,
given that,
23 and 23.4.
23 x 23.4 = 538.2.
so she was correct..
Question 25.
Higher Order Thinking Heather clears a rectangular region in her yard for a garden. If the length is a one-digit whole number and the width is 5.5 meters, what is the least possible area? What is the greatest possible area? Explain how you found your answers.
Answer:
The least possible area = 60.5.
the greatest possible area = 126.5.
Explanation:
In the above-given question,
given that,
Heather clears a rectangular region in her yard for a garden.
If the length is a one-digit whole number and the width is 5.5 meters.
the whole number is 11.
11 x 5.5 = 60.5.
the whole number is 23.
23 x 5.5 = 126.5.
so the least possible area = 60.5.
Assessment Practice
Question 26.
Which of the following equations is NOT true?
A. 75 × 3 = 225
B. 75 × 0.3 = 22.5
C. 7.5 × 3 = 2.25
D. 75 × 0.03 = 2.25
Answer:
Option C is not correct.
Explanation:
In the above-given question,
given that,
7.5 x 3 = 22.5.
they have given that
7.5 x 3 = 2.25.
so option C is not correct.
Question 27.
Which of the following equations is NOT true?
A. 50 × 12 = 600
B. 50 × 0.12 = 6
C. 0.5 × 12 = 60
D. 50 × 1.2 = 60
Answer:
Option C is not correct.
Explanation:
In the above-given question,
given that,
0.5 x 12 = 60.
they have given that
0.5 x 12 = 6.
so option C is not correct.
Lesson 4.5 Use Models to Multiply a Decimal and a Decimal
Activity
Solve & Share
A rectangle has an area of 0.24 square meter. What are some possibilities for the length and width of the rectangle? Tell why. Solve this problem any way you choose. You may use hundredths grids if you like.
Can both dimensions be greater than 1 meter? Can both dimensions be less than 1 meter? Show your work in the space below.

Look Back! Generalize How did you use what you know about whole numbers and place value to find the dimensions that worked?
Visual Learning Bridge
Essential Question
How Can You Model Decimal Multiplication?
A.
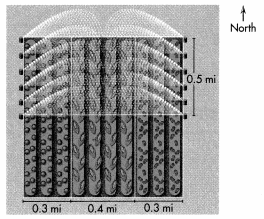
A farmer has a square field that is 1 mile wide by 1 mile long. Her irrigation system can water the northern 0.5 mile of her field. If her tomatoes are planted in a strip 0.3 mile wide, what is the area of her watered tomatoes?
B.
This problem can be shown on a hundredths grid with each side representing 1 mile. The tomato area is 0.3 mile wide, so shade the first 3 columns red. The watered area is the top 0.5 miles, so shade the top 5 rows blue.
The area of the watered tomatoes is the pink area where the shading overlaps.

C.
This area can be written as a product of decimals.
0.3 × 0.5 = 0.15
There is 0.15 square miles of watered tomatoes.
Because both factors are less than 1, the product is less than either factor.
Convince Me! Be Precise Use the double hundredths grid to model 0.7 × 1.6. What does the length of each side of a hundredths grid represent? Explain how to find the product.

Answer:
Each side of the hundredths grid represents = 2.
Explanation:
In the above-given question,
given that,
0.7 x 1.6.
1.12.
so each side of the hundredths grid represents = 2.
Guided Practice
Do You Understand?
Question 1.
Write a multiplication equation to match the model.

Answer:
0.18 x 0.20 = 0.036.
Explanation:
In the above-given question,
the grid represents the
0.18 and 0.20.
0.18 x 0.20 = 0.036.
Question 2.
Explain why 2.7 is not a reasonable answer for 0.3 × 0.9. What is the correct answer?
Answer:
The correct answer is 0.27.
Explanation:
In the above-given question,
given that,
the two numbers are 0.3 and 0.9.
0.3 x 0.9 = 0.27.
so 2.7 is wrong.
Do You Know How?
In 3 and 4, shade the hundredths grids to find the product.
Question 3.
0.7 × 0.8

Answer:
The product is 0.56.
Explanation:
In the above-given question,
given that,
the two numbers are 0.7 and 0.8.
multiply the numbers.
0.7 x 0.8 = 0.56.
so the product is 0.56.
Question 4.
0.1 × 2.1

Answer:
The product is 0.21.
Explanation:
In the above-given question,
given that,
the two numbers are 0.1 and 2.1.
multiply the numbers.
0.1 x 2.1 = 0.21.
so the product is 0.21.
Independent Practice
In 5-8, shade the hundredths grids to find the product.
Remember that the area where the shading overlaps represents the product.

Question 5.
0.4 × 0.5

Answer:
The product is 0.2.
Explanation:
In the above-given question,
given that,
the two numbers are 0.4 and 0.5.
multiply the numbers.
0.4 x 0.5 = 0.2.
so the product is 0.2.
Question 6.
0.3 × 0.7

Answer:
The product is 0.21.
Explanation:
In the above-given question,
given that,
the two numbers are 0.7 and 0.3.
multiply the numbers.
0.7 x 0.3 = 0.21.
so the product is 0.21.
Question 7.
0.5 × 1.7

Answer:
The product is 0.85.
Explanation:
In the above-given question,
given that,
the two numbers are 0.5 and 1.7.
multiply the numbers.
0.5 x 1.7 = 0.85.
so the product is 0.85.
Question 8.
0.6 × 1.2

Answer:
The product is 0.72.
Explanation:
In the above-given question,
given that,
the two numbers are 0.6 and 1.2.
multiply the numbers.
0.6 x 1.2 = 0.72.
so the product is 0.72.
In 9-16, find the product. You may use grids to help.
Question 9.
0.2 × 0.8
Answer:
The product is 0.16.
Explanation:
In the above-given question,
given that,
the two numbers are 0.2 and 0.8.
multiply the numbers.
0.2 x 0.8 = 0.16.
so the product is 0.16.
Question 10.
2.4 × 0.7
Answer:
The product is 1.68.
Explanation:
In the above-given question,
given that,
the two numbers are 2.4 and 0.7.
multiply the numbers.
0.7 x 2.4 = 1.68.
so the product is 1.68.
Question 11.
3.9 × 0.4
Answer:
The product is 1.56.
Explanation:
In the above-given question,
given that,
the two numbers are 3.9 and 0.4.
multiply the numbers.
3.9 x 0.4 = 1.56.
so the product is 1.56.
Question 12.
0.5 × 0.7
Answer:
The product is 0.35.
Explanation:
In the above-given question,
given that,
the two numbers are 0.7 and 0.5.
multiply the numbers.
0.7 x 0.5 = 0.35.
so the product is 0.35.
Question 13.
0.9 × 0.1
Answer:
The product is 0.09.
Explanation:
In the above-given question,
given that,
the two numbers are 0.9 and 0.1.
multiply the numbers.
0.9 x 0.1 = 0.09.
so the product is 0.09.
Question 14.
0.2 × 1.5
Answer:
The product is 0.3.
Explanation:
In the above-given question,
given that,
the two numbers are 0.2 and 1.5.
multiply the numbers.
0.2 x 1.5 = 0.3.
so the product is 0.3.
Question 15.
0.6 × 0.6
Answer:
The product is 0.36.
Explanation:
In the above-given question,
given that,
the two numbers are 0.6 and 0.6.
multiply the numbers.
0.6 x 0.6 = 0.36.
so the product is 0.36.
Question 16.
2.8 × 0.3
Answer:
The product is 0.84.
Explanation:
In the above-given question,
given that,
the two numbers are 2.8 and 0.3.
multiply the numbers.
2.8 x 0.3 = 0.84.
so the product is 0.84.
Problem Solving
Question 17.
Model with Math Write a multiplication equation to represent this decimal model.
Answer:
Question 18.
Higher Order Thinking explain why 3.4 × 0.5 has only one decimal place in the product.
Answer:
Yes, it has only one decimal point.
Explanation:
In the above-given question,
given that,
3.4 and 0.5.
3.4 x 0.5 = 1.7.
so it has only one decimal place in the product.
Question 19.
Jack’s bookshelf has 6 shelves. Each shelf can hold 12 books. He has already placed 54 books on the shelves. How many more books can the bookshelf hold?
Answer:
The number of books can the bookshelf can hold = 9.
Explanation:
In the above-given question,
given that,
Jack’s bookshelf has 6 shelves.
Each shelf can hold 12 books.
He has already placed 54 books on the shelves.
54 / 6 = 9.
so the number of books can the bookshelf can hold = 9.
Question 20.
Number Sense Write a number that has a 6 in the thousandths place, a 5 in the hundredths place, and a 0 in the tenths place. Then write a number less than your number and a number greater than your number.
Answer:
The number is 65302.
Explanation:
In the above-given question,
given that,
Write a number that has a 6 in the thousandths place,
a 5 in the hundredths place, and a 0 in the tenths place.
the number is 65302.
the number is greater than 65322.
the number is less than 65301.
Question 21.
If you multiply two decimals less than 1, can you predict whether the product will be less than or greater than either of the factors? Explain.
Answer:
It is less than the factors.
Explanation:
In the above-given question,
given that,
If you multiply two decimals less than 1.
0.4 x 0.3 = 0.12.
it is less than the factors.
Question 22.
Judy claims that she can find 0.5 × 2.4 by dividing 2.4 into two equal parts. Is she correct? Draw a decimal model to explain your answer.
Answer:
Yes, she was correct.
Explanation:
In the above-given question,
given that,
0.5 and 2.4.
0.5 x 2.4 = 1.2.
1.2 + 1.2 = 2.4.
so she was correct.
Assessment Practice
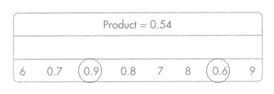
Question 23.
Find two numbers that you can multiply to get a product of 0.54. Write the numbers in the box.

Answer:
The numbers are 0.6 and 0.9.
Explanation:
In the above-given question,
given that,
the product is 0.54.
0.6 x 0.9 = 0.54.
so the numbers are 0.6 and 0.9.
Lesson 4.6 Multiply Decimals Using Partial Products
Activity
Solve & Share
Julie has 0.5 of her backyard set up for growing vegetables. Of the vegetable area, 0.4 has bell peppers in it. What part of the backyard contains bell peppers?

You can use appropriate tools, such as a grid, to model decimal multiplication.
Look Back! What do you notice about the factors and their product in the above problem?
Visual Learning Bridge
Essential Question That How Can You Multiply Decimals Using Partial Products?
A.
June walked 1.7 miles in 1 hour. If she walks at the same rate, how far will she walk in 1.5 hours?
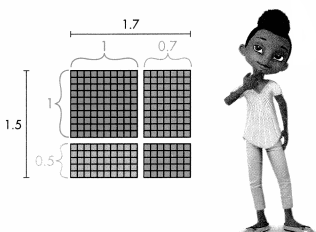
You can use what you know about partial products and whole numbers to model multiplication with decimals.
B.
Estimate first.
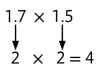
Since 2 is greater than 1.7 and 1.5, 4 is an overestimate.

C.
Like with whole numbers, you can use an area model to help break the problem into parts.
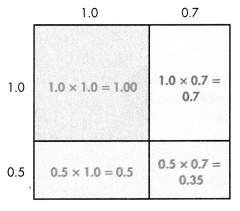
D.
The partial products make up the different pieces of the area model.
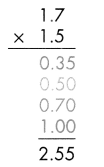
1.7 × 1.5 = 2.55, which is close to the estimate. June will walk 2.55 miles.
Convince Me! Make Sense and Persevere in the example above, how many miles will June walk in 2.8 hours? Estimate first, then compare your answer to the estimate.
Guided Practice
Do You Understand?
Question 1.
Carter is filling 6.5-ounce bottles with salsa. He was able to fill 7.5 bottles. How many ounces of salsa did he have? Draw an area model to show the partial products.
Answer:
The number of ounces
Do You Know How?
In 2-5, estimate first. Then find each product. Check that your answer is reasonable.
Question 2.
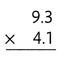
Answer:
The product is 38.13.
Explanation:
In the above-given that,
given that,
the numbers are 9.3 and 4.1.
multiply the numbers.
9.3 x 4.1 = 38.13.
so the product is 38.13.
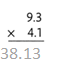
Question 3.
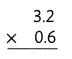
Answer:
The product is 1.92.
Explanation:
In the above-given that,
given that,
the numbers are 3.2 and 0.6.
multiply the numbers.
3.2 x 0.6 = 1.92.
so the product is 1.92.

Question 4.
0.7 × 1.9
Answer:
The product is 1.33.
Explanation:
In the above-given that,
given that,
the numbers are 0.7 and 1.9.
multiply the numbers.
0.7 x 1.9 = 1.33.
so the product is 1.33.
Question 5.
12.6 × 0.2
Answer:
The product is 2.52.
Explanation:
In the above-given that,
given that,
the numbers are 12.6 and 0.2.
multiply the numbers.
12.6 x 0.2 = 2.52
so the product is 2.52.
Independent Practice
Question 6.
Find 7.5 × 1.8 using partial products. Draw an area model to show the partial products.
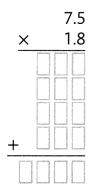
Answer:
The product is 13.5.
Explanation:
In the above-given that,
given that,
the numbers are 7.5 and 1.8.
multiply the numbers.
7.5 x 1.8 = 13.5.
so the product is 13.5.
In 7-14, estimate first. Then multiply using partial products. Then check that your answer is reasonable.
Question 7.
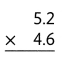
Answer:
5.2 x 4.6 = 23.92.
Explanation:
In the above-given that,
given that,
the numbers are 5.2 and 4.6.
multiply the numbers.
5.2 x 4.6 = 23.92.
so the product is 23.92.
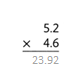
Question 8.

Answer:
19.1 x 8.5 = 162.35
Explanation:
In the above-given that,
given that,
the numbers are 19.1 and 8.5.
multiply the numbers.
19.1 x 8.5 = 162.35.
so the product is 162.35.

Question 9.
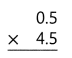
Answer:
0.5 x 4.5 = 2.25.
Explanation:
In the above-given that,
given that,
the numbers are 0.5 and 4.5.
multiply the numbers.
0.5 x 4.5 = 2.25.
so the product is 2.25.
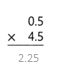
Question 10.
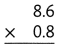
Answer:
8.6 x 0.8 = 6.88.
Explanation:
In the above-given that,
given that,
the numbers are 8.6 and 0.8.
multiply the numbers.
8.6 x 0.8 = 6.88.
so the product is 6.88.

Question 11.
5.5 × 0.6
Answer:
5.5 x 0.6 = 3.3.
Explanation:
In the above-given that,
given that,
the numbers are 5.5 and 0.6.
multiply the numbers.
5.5 x 0.6 = 3.3.
so the product is 3.3.
Question 12.
3.5 × 0.4
Answer:
3.5 x 0.4 = 1.4.
Explanation:
In the above-given that,
given that,
the numbers are 3.5 and 0.4.
multiply the numbers.
3.5 x 0.4 = 1.4.
so the product is 1.4.
Question 13.
6.8 × 7.2
Answer:
6.8 x 7.2 = 48.96.
Explanation:
In the above-given that,
given that,
the numbers are 6.8 and 7.2.
multiply the numbers.
6.8 x 7.2 = 48.96.
so the product is 48.96.
Question 14.
8.3 × 6.4
Answer:
8.3 x 6.4 = 53.12.
Explanation:
In the above-given that,
given that,
the numbers are 8.3 and 6.4.
multiply the numbers.
8.3 x 6.4 = 53.12.
so the product is 53.12.
Problem Solving
Question 15.
enVision® STEM The gravity of Venus is 0.35 times that of Jupiter. What is the gravity of Venus in relation to Earth’s gravity?

Answer:
The gravity of Venus in relation to Earth’s gravity = 0.91.
Explanation:
In the above-given question,
given that,
The gravity of Venus is 0.35 times that of Jupiter.
the gravity of the mercury = 0.39.
the gravity of Neptune = 1.22.
the gravity of Jupiter = 2.6.
2.6 x 0.35 = 0.91.
so the gravity of venus in relation to Earth’s gravity = 0.91.
Question 16.
About how many times as great is Jupiter’s relative surface gravity as Neptune’s relative surface gravity?
Answer:
The number of times as great is Jupiter’s relative surface gravity as Neptune’s relative surface gravity = 1 time.
Explanation:
In the above-given question,
given that,
the gravity of Neptune = 1.22.
the gravity of Jupiter = 2.6.
1.22 – 2.6 = 1.38.
1.38 is equal to 1.
Question 17.
One quart of water weighs about 2.1 pounds. There are 4 quarts in a gallon. How much does a gallon of water weigh?

Answer:
The gallon of water weighs = galloons.
Explanation:
In the above-given question,
given that,
One quart of water weighs about 2.1 pounds.
There are 4 quarts in a gallon.
2.1 x 4 = 9.6.
so the gallon of water weighs = 9.6 galloons.
Question 18.
Isaac bought three packages of nuts. He bought one package of peanuts that weighed 3.07 pounds. He also bought two packages of pecans that weighed 1.46 pounds and 1.5 pounds. Did the peanuts or the pecans weigh more? How much more?
Answer:
The peanuts weigh more.
Explanation:
In the above-given question,
given that,
Isaac bought three packages of nuts.
He bought one package of peanuts that weighed 3.07 pounds.
also bought two packages of pecans that weighed 1.46 pounds and 1.5 pounds.
1.46 + 1.5 = 2.96.
3.07 is greater than 2.96.
so the peanuts weigh more.
Question 19.
Make Sense and Persevere How does estimation help you place the decimal point in a product correctly? Explain your reasoning.
Answer:
Question 20.
Higher Order Thinking The area of Dimitri’s table top is a whole number of square feet. Could the length and width be decimal numbers each with one decimal place? Explain your answer.
Answer:
Yes, the answer is correct.
Explanation:
In the above-given question,
given that,
for example:
2.6 is the length.
3.4 is the width.
area = l x w.
area = 2.6 x 3.4.
area = 8.84.
Assessment Practice
Question 21.
Joy drinks 4.5 bottles of water per day. Each bottle contains 16.5 fluid ounces. How many fluid ounces of water does she drink per day?
A. 20.10 fluid Ounces
B. 64.00 fluid ounces
C. 74.25 fluid Ounces
D. 82.50 fluid Ounces
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
Joy drinks 4.5 bottles of water per day.
Each bottle contains 16.5 fluid ounces.
4.5 x 16.5 = 74.25.
so option C is correct.
Question 22.
One square mile equals 2.6 square kilometers. How many square kilometers are in 14.4 square miles?
A. 11.52 square kilometers
B. 17.00 square kilometers
C. 37.44 square kilometers
D. 86.40 square kilometers
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
One square mile equals 2.6 square kilometers.
14.4 x 2.6 = 37.44.
so the number of square kilometers are in 14.4 is 37.44 miles.
Lesson 4.7 Use Properties to Multiply Decimals
Activity
Solve & Share
The weight of a small bag of raisins is 0.3 times the weight of a large bag. The large bag weighs 0.8 pound. What is the weight of the small bag? Solve this problem any way you choose.
Answer:
The weight of the small bag = 0.24.
Explanation:
In the above-given question,
given that,
The weight of a small bag of raisins is 0.3 times the weight of a large bag.
The large bag weighs 0.8 pounds.
0.8 x 0.3 = 0.24.
so the weight of the small bag = 0.24.
You can estimate whether the answer is greater than or less than 0.5 pound.

Look Back! Look for Relationships How is solving this problem like finding the product of 3 and 8? How is it different?
Visual Learning Bridge
Essential Question How Can You Use Properties to Multiply Decimals?
A.
Entries for a poster contest must be 0.5 m2 or smaller. Can Jemelle enter her poster?

Use what you know about decimals and properties to multiply 0.6 × 0.9.

B.
Step 1
Rewrite the multiplication expression.
0.6 × 0.9 = (6 × 0.1) × (9 × 0.1)
Rearrange the factors using the Associative and Commutative Properties.
(6 × 0.1) × (9 × 0.1) = (6 × 9) × (0.1 × 0.1)
C.
Step 2
Multiply the whole numbers. Multiply the decimals. Write the product.
(6 × 9) × (0.1 × 0.1) = 54 × 0.01 = 0.54
One tenth of one tenth is one hundredth. 0.1 × 0.1 = 0.01.

0.54 > 0.5,
so Jemelle cannot enter her poster.
Convince Me! Use Structure Tyler explained how he multiplies 0.7 × 0.2. “I multiply 7 × 2 = 14. I know that a tenth times a tenth is a hundredth, so I use hundredths to write the product. The product is 0.14.” Use properties to show that Tyler is correct.
Answer:
Yes, Tailor was correct.
Explanation:
In the above-given question,
given that,
Tyler explained how he multiplies 0.7 × 0.2. “I multiply 7 × 2 = 14.
0.7 x 0.2 = 0.14.
so Tailor was correct.
Another example
A slice of bread has 1.25 grams of fat. How many grams of fat are in 1.5 slices?
1.25 × 1.5 =
= (125 × 0.01) (15 × 0.1)
= (125 × 15) × (0.01 × 0.1)
= 1,875 × 0.001
= 1.875
The picture shows that one tenth of one hundredth is one thousandth. 0.1 × 0.01 = 0.001

There are 1.875 grams of fat in 1.5 slices of bread.
Guided Practice
Do You Understand?
Question 1.
Mason is multiplying (3 × 5) × (0.1 × 0.1). What decimal multiplication problem is he solving?
Answer:
3 x 5 x 0.1 x 0.1 = 0.15.
Explanation:
In the above-given question,
given that,
Mason is multiplying (3 x 5) x (0.1 x 0.1).
15 x (0.1 x 0.1).
15 x 0.01.
0.15.
Question 2.
Complete Mason’s work to find the product.
Answer:
3 x 5 x 0.1 x 0.1 = 0.15.
Explanation:
In the above-given question,
given that,
Mason is multiplying (3 x 5) x (0.1 x 0.1).
15 x (0.1 x 0.1).
15 x 0.01.
0.15.
Do You Know How?
In 3-6, use properties to find each product.
Question 3.
0.3 × 0.7
Answer:
0.3 x 0.7 = 0.21.
Explanation:
In the above-given question,
given that,
the two numbers are 0.3 and 0.7.
0.3 x 0.7.
3 x 0.1 = 0.3.
7 x 0.1 = 0.7.
(3 x 7) x (0.1 x 0.1).
(21) x (0.01).
0.21.
Question 4.
0.63 × 2.8
Answer:
0.63 x 2.8 = 17.64.
Explanation:
In the above-given question,
given that,
the two numbers are 0.63 and 2.8.
0.63 x 2.8.
63 x 0.1 = 0.63.
28 x 0.1 = 0.7.
(63 x 28) x (0.1 x 0.1).
(1764) x (0.01).
17.64.
Question 5.
2.6 × 1.4
Answer:
2.6 x 1.4 = 3.64.
Explanation:
In the above-given question,
given that,
the two numbers are 2.6 and 1.4.
2.6 x 1.4.
2.6 x 0.1 = 2.6.
1.4 x 0.1 = 1.4.
(2.6 x 1.4) x (0.1 x 0.1).
(3.64) x (0.01).
3.64.
Question 6.
4.5 × 0.08
Answer:
4.5 x 0.08 = 3.6.
Explanation:
In the above-given question,
given that,
the two numbers are 0.3 and 0.7.
4.5 x 0.08.
45 x 0.1 = 4.5.
8 x 0.01 = 0.08.
(45 x 8) x (0.1 x 0.01).
(360) x (0.01).
3.6.
Independent Practice
In 7-15, find each product.
Question 7.
0.6 × 0.2
Answer:
The product is 0.12.
Explanation:
In the above-given question,
given that,
the numbers are 0.6 and 0.2.
multiply the two numbers.
0.6 x 0.2 = 0.12.
Question 8.
0.33 × 0.8
Answer:
The product is 0.264.
Explanation:
In the above-given question,
given that,
the numbers are 0.33 and 0.8.
multiply the two numbers.
0.33 x 0.8 = 0.264.
Question 9.
1.7 × 0.22
Answer:
The product is 0.374.
Explanation:
In the above-given question,
given that,
the numbers are 1.7 and 0.22.
multiply the two numbers.
1.7 x 0.22 = 0.374.
Question 10.
1.8 × 0.9
Answer:
The product is 1.62.
Explanation:
In the above-given question,
given that,
the numbers are 0.9 and 1.8.
multiply the two numbers.
0.9 x 1.8 = 1.62.
Question 11.
0.03 × 1.6
Answer:
The product is 0.48.
Explanation:
In the above-given question,
given that,
the numbers are 1.6 and 0.03.
multiply the two numbers.
1.6 x 0.03 = 0.48.
Question 12.
4.2 × 4.2
Answer:
The product is 17.64.
Explanation:
In the above-given question,
given that,
the numbers are 4.2 and 4.2.
multiply the two numbers.
4.2 x 4.2 = 17.64.
Question 13.
11.1 × 0.8
Answer:
The product is 8.88.
Explanation:
In the above-given question,
given that,
the numbers are 0.8 and 11.1.
multiply the two numbers.
0.8 x 11.1 = 8.88.
Question 14.
1.16 × 0.4
Answer:
The product is 0.464.
Explanation:
In the above-given question,
given that,
the numbers are 1.16 and 0.4.
multiply the two numbers.
1.16 x 0.4 = 0.464.
Question 15.
1.6 × 0.01
Answer:
The product is 0.016.
Explanation:
In the above-given question,
given that,
the numbers are 1.6 and 0.01.
multiply the two numbers.
1.6 x 0.01 = 0.016.
Problem Solving
Question 16.
The total rainfall in March was 3.6 inches. In April, the total rainfall was 1.4 times as much. What was the total rainfall in April?
Answer:
The total rainfall in April = 5.04.
Explanation:
In the above-given question,
given that,
The total rainfall in March was 3.6 inches.
In April, the total rainfall was 1.4 times as much.
3.6 x 1.4 = 5.04.
so the total rainfall in April = 5.04.
Question 17.
A newly hatched alligator is 0.5 foot long. An adult alligator is 16.4 times as long. How many feet longer is the adult alligator than the newborn alligator?
Answer:
The longer is the adult alligator than the newborn alligator = 8.2 feet.
Explanation:
In the above-given question,
given that,
A newly hatched alligator is 0.5 feet long.
An adult alligator is 16.4 times as long.
16.4 x 0.5 = 8.2.
so the longer is the adult alligator than the newborn alligator = 8.2 feet.
Question 18.
Make Sense and Persevere The Nature Club held a grasshopper jumping contest. The distance Bugmaster jumped is 1.2 times the distance Green Lightning jumped. The distance Top Hopper jumped is 1.5 times the distance Bugmaster jumped. Complete the table to show the distances Bugmaster and Top Hopper jumped.
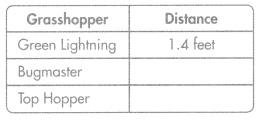
Answer:
The Bugmaster and Top Hopper jumped = 1.68 feet and 2.1 feet.
Explanation:
In the above-given question,
given that,
The Nature Club held a grasshopper jumping contest.
The distance Bugmaster jumped is 1.2 times the distance green Lightning jumped.
The distance Top Hopper jumped is 1.5 times the distance Bugmaster jumped.
1.4 x 1.2 = 1.68.
1.4 x 1.5 = 2.1.
Question 19.
Amanda bought a 6-cup bag of shredded cheese for $6.89. She used 2.25 cups to make lasagna and 1.25 cups to make pizza. How much cheese is left?
Is there any information that you don’t need to solve this problem?

Answer:
The quantity of cheese left = $3.39.
Explanation:
In the above-given question,
given that,
Amanda bought a 6-cup bag of shredded cheese for $6.89.
She used 2.25 cups to make lasagna and 1.25 cups to make pizza.
2.25 + 1.25 = 3.5.
6.89 – 3.5 = 3.39.
so the quantity of cheese left = 3.39.
Question 20.
Higher Order Thinking Jodi drew the Eiffel Tower 6.5 inches tall. She thought it was too tall, so she multiplied its height by 0.8. The second drawing was too short, so she multiplied its height by 1.2. Predict whether her last drawing was shorter, the same as, or taller than her first drawing. Check your prediction by finding the height of the last drawing.
Answer:
The taller than her first drawing = 4.5 inches.
Explanation:
In the above-given question,
given that,
Jodi drew the Eiffel Tower 6.5 inches tall.
She thought it was too tall, so she multiplied its height by 0.8.
The second drawing was too short, so she multiplied its height by 1.2.
0.8 + 1.2 = 2.
6.5 – 2 = 4.5.
so the taller than her first drawing = 4.5 inches.
Assessment Practice
Question 21.
Which expression is equivalent to 0.4 × 0.3?
A. (4 × 0.01) × (3 × 0.01)
B. (4 × 10) × (3 × 10)
C. (4 × 0.1) × (3 × 0.1)
D. (4 × 0.1) × (3 × 0.01)
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
0.4 x 0.3 = 0.12.
4 x 0.1 = 0.4.
3 x 0.1 = 0.3.
0.4 x 0.3 = 0.12.
so option C is correct.
Question 22.
Which expression is equivalent to 0.71 × 2.8?
A. (71 × 28) × (0.01 × 0.1)
B. (71 × 28) × (0.1 × 0.1)
C. (0.71 × 2.8) × (0.01 × 0.1)
D. (71 × 28) × (100 × 10)
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
0.71 x 2.8 = 1.96.
0.71 x 2.8 x 0.01 x 0.1 = 1.96.
so option C is correct.
Lesson 4.8 Use Number Sense to Multiply Decimals
Activity
Solve & Share
Three students in Ms. Cho’s class wrote the following problems on the board. The correct digits in the products are given, but the decimal point isn’t placed yet. Where should the decimal point go in each product?

You can use reasoning to consider the size of each factor when placing the decimal point. Show your work!

Look Back! Generalize If both factors are less than 1, what do you know about their product?
Visual Learning Bridge
Essential Question
How Can You Use Number Sense Question to Multiply Decimals?
A.
You have learned how to estimate when multiplying with decimals. You can also use number sense to reason about the relative size of factors and the product.
You can use number sense to put the decimal point in the correct place.

49.20 × 0.55 = 2706
B.
Think about the relative size of the factors.
Multiplying a number by a decimal less than 1 gives a product less than the other factor. Since 0.55 is less than 1, the product is less than 49.2.
Since 0.55 is about one half, the product is about half of 49.2, or about half of 50. So, the decimal point
1 should be between the 7 and 0.
49.2 × 0.55 = 27.06
C.
Use number sense to reason about the product.
How can you place the decimal point in the product of the equation below?
6.2 × 5.1 is 3162.
Notice that the smallest unit in both factors is a tenth (0.1). Since the product of 0.1 and 0.1 is 0.01, the product of 6.2 and 5.1 will have two decimal places.
So, 6.2 × 5.1 = 31.62.
This makes sense because 6 times 5 equals 30.

Convince Me! Construct Arguments The decimal point is missing in the answer for each of these problems. Use number sense to decide where the decimal point should be placed. Explain your thinking.
54.7 × 0.53 = 28991
54.7 × 5.3 = 28991
Guided Practice
Do You Understand?
Question 1.
Describe the unknown factor.
____ × 5.1 is about 300.
Answer:
The unknown factor is 58.823.
Explanation:
In the above-given question,
given that,
300/5.1 = 58.8.
58.8 x 5.1 = 300.
the unknown factor is 58.823.
Do You Know How?
Question 2.
Number Sense Janelle wrote 23.4 for the product of 7.8 × 0.3. Use number sense to decide if Janelle placed the decimal point in the correct place in the product. If it is incorrect, give the correct product.
Answer:
7.8 x 0.3 = 2.34.
Explanation:
In the above-given question,
given that,
Janelle wrote 23.4 for the product of 7.8 × 0.3.
7.8 x 0.3 = 2.34.
so the product is correct.
Use number sense to decide where the decimal point belongs in the product.
Question 3.
5 × 3.4 = 17
Answer:
5 x 3.4 = 17.
Explanation:
In the above-given question,
given that,
the two numbers are 5 and 3.4.
multiply the two numbers.
5 x 3.4 = 17.
Question 4.
1922 = 3.1 × 6.2
Answer:
3.1 x 6.2 = 19.22.
Explanation:
In the above-given question,
given that,
the two numbers are 3.1 and 6.2.
multiply the two numbers.
3.1 x 6.2 = 19.22.
Question 5.
0.6 × 0.4 = 24
Answer:
0.6 x 0.4 = 0.24.
Explanation:
In the above-given question,
given that,
the two numbers are 0.6 and 0.4.
multiply the two numbers.
0.6 x 0.4 = 0.24.
Independent Practice
In 6-9, the product is shown without the decimal point. Use number sense to place the decimal point correctly.
Question 6.
5.01 × 3 = 1503
Answer:
5.01 x 3 = 15.03.
Explanation:
In the above-given question,
given that,
the two numbers are 5.01 and 3.
multiply the two numbers.
5.01 x 3 = 15.03.
Question 7.
6.22 × 3 = 1866
Answer:
6.22 x 3 = 18.66.
Explanation:
In the above-given question,
given that,
the two numbers are 6.22 and 3.
multiply the two numbers.
6.22 x 3 = 18.66.
Question 8.
81 = 0.9 × 0.9
Answer:
0.9 x 0.9 = 0.81.
Explanation:
In the above-given question,
given that,
the two numbers are 0.9 and 0.9.
multiply the two numbers.
0.9 x 0.9 = 0.81.
Question 9.
1.8 × 1.9 = 342
Answer:
1.8 x 1.9 = 3.42.
Explanation:
In the above-given question,
given that,
the two numbers are 1.8 and 1.9
multiply the two numbers.
1.8 x 1.9 = 3.42.
In 10-15, tell whether or not the decimal point has been placed correctly in the product. If not, rewrite the product with the decimal point correctly placed.
Use number sense or estimation to help you!

Question 10.
12 × 4.8 = 57.6
Answer:
12 x 4.8 = 57.6.
Explanation:
In the above-given question,
given that,
the two numbers are 12 and 4.8.
multiply the two numbers.
12 x 4.8 = 57.6.
Question 11.
5.2 × 6.4 = 3.328
Answer:
5.2 x 6.4 = 33.28.
Explanation:
In the above-given question,
given that,
the two numbers are 5.2 and 6.4.
multiply the two numbers.
5.2 x 6.4 = 33.28.
Question 12.
6.99 × 21 = 14.679
Answer:
6.99 x 21 = 146.79.
Explanation:
In the above-given question,
given that,
the two numbers are 6.99 and 21.
multiply the two numbers.
6.99 x 21 = 146.79.
Question 13.
6.2 = 0.05 × 12.4
Answer:
0.05 x 12.4 = 0.62.
Explanation:
In the above-given question,
given that,
the two numbers are 0.05 and 12.4.
multiply the two numbers.
0.05 x 12.4 = 0.62.
Question 14.
60.84 = 18 × 3.38
Answer:
18 x 3.38 = 60.84.
Explanation:
In the above-given question,
given that,
the two numbers are 18 and 3.38.
multiply the two numbers.
18 x 3.38 = 60.84.
Question 15.
9.01 × 91 = 81.991
Answer:
9.01 x 91 = 819.91.
Explanation:
In the above-given question,
given that,
the two numbers are 9.01 and 91.
multiply the two numbers.
9.01 x 91 = 819.91.
Problem Solving
Question 16.
A pig farmer needs 60 square feet to house a sow. Is the pen pictured to the right large enough? Explain your reasoning
Answer:
The pen is not pictured to the right large enough.
Explanation:
In the above-given question,
given that,
A pig farmer needs 60 square feet to house a sow.
10.5 x 6.4 = 67.2.
so the pen is not pictured to the right large enough.
Question 17.
Critique Reasoning Quincey says that 3 is a good estimate for 3.4 × 0.09. Is he correct? Why?
Answer:
Yes, 3 is a good estimate for 3.4 x 0.09.
Explanation:
In the above-given question,
given that,
3.4 x 0.09 = 0.306.
so 3 is a good estimate for 3.4 x 0.09.
Question 18.
Ron bought 2 DVDs for $12.95 each. He spent $25 on magazines. Did he spend more on DVDs or magazines? How much more? Write equations to show your work.
Answer:
He spends more on DVDs.
Explanation:
In the above-given question,
given that,
Ron bought 2 DVDs for $12.95 each.
He spent $25 on magazines.
he spend more on DVDs.
Question 19.
You can convert gallons to liters by using a factor of 3.79. That is, 1 gallon is about 3.79 liters. About how many liters are in 37 gallons? Is your answer an underestimate or overestimate? Explain.
Answer:
Yes, the answer is an overestimate.
Explanation:
In the above-given question,
given that,
You can convert gallons to liters by using a factor of 3.79.
That is, 1 gallon is about 3.79 liters.
37 x 3.79 = 140.23.
so the answer is overestimated.
Question 20.
Higher Order Thinking Find two factors that would give a product of 0.22.
Answer:
The two factors are 0.11 and 2.
Explanation:
In the above-given question,
given that,
the two factors are 0.11 and 2.
0.11 x 2 = 0.22.
so the factors are 0.11 and 2.
Assessment Practice
Question 21.
Which of the following is the missing factor?
___ × 2.3 = 34.73
A. 0.151
B. 1.51
C. 15.1
D. 151
Answer:
The missing factor is 15.1.
Explanation:
In the above-given question,
given that,
15.1 x 2.3 = 34.73.
34.73 / 2.3 = 15.1.
so the missing factor is 15.1.
Question 22.
Which two factors would give a product of 7.5?
A. 0.3 and 0.25
B. 0.3 and 2.5
C. 3 and 0.25
D. 3 and 2.5
Answer:
Option D is correct.
Explanation:
In the above-given question,
given that,
3 x 2.5 = 7.5.
so option D is correct.
Lesson 4.9 Model with Math
Activity
Problem Solving
Solve&Share
Susan is making sandwiches for a picnic. She needs 1.2 pounds of ham, 1.5 pounds of bologna, and 2 pounds of cheese. How much will she spend in all? Solve this problem any way you choose. Use models to help.
Answer:
The amount he spends in all = 4.7.
Explanation:
In the above-given question,
given that,
Susan is making sandwiches for a picnic.
She needs 1.2 pounds of ham.
1.5 pounds of bologna, and 2 pounds of cheese.
1.2 + 1.5 + 2 = 4.7.
so the amount he spends in all = 4.7.

Thinking Habits
Be a good thinker! These questions can help you.
• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?
Look Back! What math did you use to solve this problem?
Visual Learning Bridge
Essential Question
How Can You Model a Problem with an Equation?
A.
Alex is buying vegetables for dinner. He buys 6 ears of corn, 1.4 pounds of green beans, and 2.5 pounds of potatoes. How much money does he spend?

What do I need to do to solve the problem?
I need to find how much money Alex spends on vegetables.

Here’s my thinking…
B.
How can I model with math?
I can
• use previously learned concepts and skills.
• decide what steps need to be completed to find the final answer
• use an equation to represent and solve this problem.
C.
I will use an equation to represent this situation.
Let t be the total cost.
t = (6 × $0.35) + (1.4 × $1.80) + (2.5 × $0.70)
Multiply with money as you would multiply with decimals.

Now add the subtotals.
$2.10 + $2.52 + $1.75 = $6.37
So, Alex spends $6.37 on vegetables.
Convince Me! Model with Math Beth buys 3.2 pounds of potatoes and gives the clerk a $5 bill. Write an equation that shows how much change she will get back. Explain how your equation represents this problem.
Answer:
The change she will get back = 30.
Explanation:
In the above-given question,
given that,
Beth buys 3.2 pounds of potatoes and gives the clerk a $5 bill.
1 pound = 100.
1 dollar = 70.
3.2 x 100 = 320.
5 x 70 = 350.
350 – 320 = 30.
so the change she will get back = 30.
Guided Practice
Model with Math Jackie downloaded 14 songs priced at $0.99 each and 1 song for $1.29. She had a coupon for $2.50. What was the total amount Jackie paid?
Answer:
The total amount Jackie paid = $2.28.
Explanation:
In the above-given question,
given that,
Jackie downloaded 14 songs priced at $0.99 each and 1 song for $1.29.
she had a coupon for $2.50.
0.99 + 1.29 = 2.28.
so the total amount Jackie paid = $2.28.
You can model with math by writing an equation to show how the quantities in the problem are related.

Question 1.
What do you need to find first?
Answer:
The total amount Jackie paid = $2.28.
Explanation:
In the above-given question,
given that,
Jackie downloaded 14 songs priced at $0.99 each and 1 song for $1.29.
she had a coupon for $2.50.
0.99 + 1.29 = 2.28.
so the total amount Jackie paid = $2.28.
Question 2.
Write an equation to represent the problem.
Answer:
The total amount Jackie paid = $2.28.
Explanation:
In the above-given question,
given that,
Jackie downloaded 14 songs priced at $0.99 each and 1 song for $1.29.
she had a coupon for $2.50.
0.99 + 1.29 = 2.28.
so the total amount Jackie paid = $2.28.
Question 3.
What is the solution to the problem?
Answer:
The total amount Jackie paid = $2.28.
Explanation:
In the above-given question,
given that,
Jackie downloaded 14 songs priced at $0.99 each and 1 song for $1.29.
she had a coupon for $2.50.
0.99 + 1.29 = 2.28.
so the total amount Jackie paid = $2.28.
Independent Practice
Model with Math George bought 2.5 pounds of each type of fruit shown on the sign. What was the total cost of the fruit he bought?

Question 4.
What do you need to find?
Answer:
The total cost of the fruit he bought = $2.635.
Explanation:
In the above-given question,
given that,
George bought 2.5 pounds of each type of fruit shown on the sign.
the cost of Apples is $1.30/lb.
the cost of Grapes is $1.65/lb.
the cost of Bananas is $0.49/lb.
1.30 + 1.65 + 0.49 = 2.635.
so the total cost of the fruit he bought = $2.635.
Question 5.
Write an equation to represent the problem.
Answer:
The total cost of the fruit he bought = $2.635.
Explanation:
In the above-given question,
given that,
George bought 2.5 pounds of each type of fruit shown on the sign.
the cost of Apples is $1.30/lb.
the cost of Grapes is $1.65/lb.
the cost of Bananas is $0.49/lb.
1.30 + 1.65 + 0.49 = 2.635.
so the total cost of the fruit he bought = $2.635.
Question 6.
What is the solution to the problem?
Answer:
The total cost of the fruit he bought = $2.635.
Explanation:
In the above-given question,
given that,
George bought 2.5 pounds of each type of fruit shown on the sign.
the cost of Apples is $1.30/lb.
the cost of Grapes is $1.65/lb.
the cost of Bananas is $0.49/lb.
1.30 + 1.65 + 0.49 = 2.635.
so the total cost of the fruit he bought = $2.635.
Problem Solving
Performance Task
Coin Collection
Tina and Shannon counted the coins in their coin collections. Tina discovered that she had 538 more coins than Shannon. Whose collection is worth more? How much more?
Question 7.
Make Sense and Persevere Do you need all of the information given to solve the problem? Explain.
Answer:
Yes, she was correct.
Explanation:
In the above-given question,
given that,
Tina and Shannon counted the coins in their coin collections.
Tina discovered that she had 538 more coins than Shannon.
917 + 100 + 45 + 19 = 1081.
488 + 23 + 10 + 22 = 543.
1081 – 543 = 538.
Question 8.
Reasoning How is finding the total value of the coins in Tina’s collection similar to finding the total value of coins in Shannon’s collection?
Answer:
The total value of the coins in Tina’s collection is 1081.
Explanation:
In the above-given question,
given that,
Tina and Shannon counted the coins in their coin collections.
Tina discovered that she had 538 more coins than Shannon.
917 + 100 + 45 + 19 = 1081.
488 + 23 + 10 + 22 = 543.
1081 – 543 = 538.
Deciding what steps need to be completed to find the final answer can help you model with math.

Question 9.
Model with Math Write and solve an equation to represent the total value of the coins in Tina’s collection. Then write and solve an equation to represent the total value of the coins in Shannon’s collection.
Answer:
The total value of the coins in Shanno’s collection = 543.
Explanation:
In the above-given question,
given that,
Tina and Shannon counted the coins in their coin collections.
Tina discovered that she had 538 more coins than Shannon.
917 + 100 + 45 + 19 = 1081.
488 + 23 + 10 + 22 = 543.
1081 – 543 = 538.
Question 10.
Be Precise Whose collection is worth more? How much more? Show your work.
Answer:
Tina’s collection is worth more.
Explanation:
In the above-given question,
given that,
Tina and Shannon counted the coins in their coin collections.
Tina discovered that she had 538 more coins than Shannon.
917 + 100 + 45 + 19 = 1081.
488 + 23 + 10 + 22 = 543.
1081 – 543 = 538.
Topic 4 Fluency Practice
Activity
Find a match
Work with a partner. Point to a clue.
Read the clue.
Look below the clues to find a match. Write the clue letter in the box above the match.
Find a match for every clue.

Clues


Answer:
51 x 63 = 3213.
10 x 10 = 100.
42 x 11 = 462.
20 x 12 = 240.
15 x 17 = 255.
40 x 23 = 920.
331 x 29 = 9599.
25 x 16 = 400.
Explanation:
In the above-given question,
given that,
the product 240 is equal to A.
the product 100 is equal to B.
the product 462 is equal to C.
the product 255 is equal to D.
the product 400 is equal to E.
product 9 is equal to F.
product 3 is equal to G.
product 9 is equal to H.
Topic 4 Vocabulary Review
Glossory
Word List
• compatible numbers
• estimate
• exponent
• overestimate
• partial products
• power of 10
• product
• underestimate
Write always, sometimes, or never.
Question 1.
Multiplying a decimal by 104 shifts the decimal point 4 places to the right.
Answer:
104 x 2.1 = 218.4.
Explanation:
In the above-given question,
given that,
104 x 2.1 = 218.4.
we will use compatible numbers.
Question 2.
The product of a whole number and a decimal number is a whole number.
Answer:
The product of a whole number and a decimal number is a whole number.
Explanation:
In the above-given question,
given that,
for example:
if we divide the whole number by decimal number.
we will get decimal numbers.
so the product of a whole number and a decimal number is a whole number.
Question 3.
The product of two decimal numbers less than 1 is greater than either factor.
Answer:
0.1 x 0.2 = 0.02.
Explanation:
In the above-given question,
given that,
0.1 x 0.2.
0.02.
the two decimal numbers is less than 1.
Question 4.
The product of a number multiplied by 0.1 is 10 times as much as multiplying the same number by 0.01.
Answer:
0.1 x 10 = 1.
Explanation:
In the above-given question,
given that,
The product of a number multiplied by 0.1.
0.1 x 10 = 1.
but they have given the 0.01.
so the expression was wrong.
Cross out the numbers that are NOT powers of 10.
Question 5.
106 40 × 103 1 × 0.001 0.55 0.001
Answer:
The numbers that are not powers of 10 are 0.55 and 0.001.
Explanation:
In the above-given question,
given that,
the numbers are 106 40 × 103 1 × 0.001 0.55 0.001.
0.55 and 0.001 are not the powers of 10.
so the numbers that are not powers of 10 are 0.55 and 0.001.
Draw a line from each number in Column A to the same value in Column B. Column A
Answer:
7.2 x 1000 = 7.2 x 10 x 10 x 10.
0.38 x 10000 = 3800.
240 x 0.03 = 7.2.
3.8 x 0.1 = 0.38.
0.08 x 0.9 = 0.072.
Explanation:
In the above-given question,
given that,
the numbers are 7.2 x 1000.
7.2 x 1000 = 7.2 x 10 x 10 x 10.
0.38 x 10000 = 3800.
240 x 0.03 = 7.2.
3.8 x 0.1 = 0.38.
0.08 x 0.9 = 0.072.

Use Vocabulary in Writing
Question 11.
The digits in the product of 0.48 and a decimal number between 350 and 400 are 182136. Explain how to correctly place the decimal point without knowing the other factor. Then place the decimal point in the product.
Answer:
The missing number is 379.
Explanation:
In the above-given question,
given that,
The digits in the product of 0.48 and a decimal number between 350 and 400 are 182136.
182136/0.48 = 379.
so the number between 350 and 400 is 379.
Topic 4 Reteaching
Set A
pages 129-132, 133-136
Use the patterns in this table to find 8.56 × 10 and 0.36 × 100.

Remember you can use rounding or compatible numbers to estimate.
Find each product.
Question 1.
10 × 4.5
Answer:
10 x 4.5 = 45.
Explanation:
In the above-given question,
given that,
the two numbers are 10 and 4.5.
multiply the numbers.
10 x 4.5 = 45.
Question 2.
103 × 3.67
Answer:
3.67 x 1000 = 3670.
Explanation:
In the above-given question,
given that,
the two numbers are 3.67 and 1000.
multiply the numbers.
3.67 x 1000 = 3670.
Question 3.
100 × 4.5
Answer:
100 x 4.5 = 450.
Explanation:
In the above-given question,
given that,
the two numbers are 100 and 4.5.
multiply the numbers.
100 x 4.5 = 450.
Question 4.
0.008 × 102
Answer:
0.08 x 100 = 8.
Explanation:
In the above-given question,
given that,
the two numbers are 100 and 0.08.
multiply the numbers.
0.08 x 100 = 8.
Estimate each product.
Question 5.
0.38 × 99
Answer:
0.38 x 99 = 3.42.
Explanation:
In the above-given question,
given that,
the two numbers are 0.38 and 99.
multiply the numbers.
0.38 x 99 = 3.42.
Question 6.
8 × 56.7
Answer:
8 x 56.7 = 453.6.
Explanation:
In the above-given question,
given that,
the two numbers are 8 and 56.7.
multiply the numbers.
8 x 56.7 = 453.6.
Question 7.
11 × 4.89
Answer:
11 x 4.89 = 53.79.
Explanation:
In the above-given question,
given that,
the two numbers are 11 and 4.8.
multiply the numbers.
11 x 4.89 = 53.79.
Question 8.
24 × 3.9
Answer:
24 x 3.9 = 93.6.
Explanation:
In the above-given question,
given that,
the two numbers are 24 and 3.9.
multiply the numbers.
24 x 3.9 = 93.6.
Set B
pages 137-140, 141-144
Find 3 × 0.15.
Model the multiplication as repeated addition with place-value blocks.
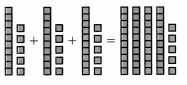
So, 3 × 0.15 = 0.45.
Remember to estimate by rounding or using compatible numbers to check the reasonableness of the answer.
Find each product. Use place-value blocks as necessary
Question 1.
50 × 3.67
Answer:
50 x 3.67 = 183.5.
Explanation:
In the above-given question,
given that,
the two numbers are 50 and 3.67.
multiply the numbers.
50 x 3.67 = 183.5.
Question 2.
5.86 × 5
Answer:
5.86 x 5 = 29.3.
Explanation:
In the above-given question,
given that,
the two numbers are 5 and 5.86.
multiply the numbers.
5.86 x 5 = 29.3.
Question 3.
14 × 9.67
Answer:
14 x 9.67 = 135.38.
Explanation:
In the above-given question,
given that,
the two numbers are 14 and 9.67.
multiply the numbers.
14 x 9.67 = 135.38.
Question 4.
8 × 56.7
Answer:
8 x 56.7 = 453.6.
Explanation:
In the above-given question,
given that,
the two numbers are 8 and 56.7.
multiply the numbers.
8 x 56.7 = 453.6.
Question 5.
11 × 0.06
Answer:
11 x 0.06 = 0.66.
Explanation:
In the above-given question,
given that,
the two numbers are 11 and 0.06.
multiply the numbers.
11 x 0.06 = 0.66.
Question 6.
2.03 × 6
Answer:
2.03 x 6 = 12.18.
Explanation:
In the above-given question,
given that,
the two numbers are 2.03 and 6.
multiply the numbers.
2.03 x 6 = 12.18.
Question 7.
25 × 1.63
Answer:
25 x 1.63 = 40.75.
Explanation:
In the above-given question,
given that,
the two numbers are 25 and 1.63.
multiply the numbers.
25 x 1.63 = 40.75.
Question 8.
5.62 × 75
Answer:
5.62 x 75 = 421.5.
Explanation:
In the above-given question,
given that,
the two numbers are 5.62 and 75.
multiply the numbers.
5.62 x 75 = 421.5.
Set C
pages 145-148, 149-152
Find 0.2 × 1.7.
Model using hundredths grids.

The product is where the shading overlaps. So, 0.2 × 1.7 = 0.34.
Find each product.
Question 1.
1.3 × 0.4
Answer:
The product is 0.52.
Explanation:
In the above-given question,
given that,
the two numbers are 1.3 and 0.4.
multiply the numbers.
1.3 x 0.4 = 0.52.
so the product is 0.52.
Question 2.
5.8 × 5.2
Answer:
The product is 30.16.
Explanation:
In the above-given question,
given that,
the two numbers are 5.8 and 5.2.
multiply the numbers.
5.8 x 5.2 = 30.16.
so the product is 30.16.
Question 3.
8.3 × 10.7
Answer:
The product is 30.16.
Explanation:
In the above-given question,
given that,
the two numbers are 5.8 and 5.2.
multiply the numbers.
5.8 x 5.2 = 30.16.
so the product is 30.16.
Question 4.
3.4 × 0.7
Answer:
The product is 2.38.
Explanation:
In the above-given question,
given that,
the two numbers are 3.4 and 0.7.
multiply the numbers.
3.4 x 0.7 = 2.38.
so the product is 2.38.
Question 5.
2.4 × 3.6
Answer:
The product is 8.64.
Explanation:
In the above-given question,
given that,
the two numbers are 2.4 and 3.6.
multiply the numbers.
2.4 x 3.6 = 8.64.
so the product is 8.64.
Question 6.
9.7 × 11.2
Answer:
The product is 108.64.
Explanation:
In the above-given question,
given that,
the two numbers are 9.7 and 11.2.
multiply the numbers.
9.7 x 11.2 = 108.64.
so the product is 108.64.
Question 7.
1.5 × 0.6
Answer:
The product is 0.9.
Explanation:
In the above-given question,
given that,
the two numbers are 1.5 and 0.6.
multiply the numbers.
1.5 x 0.6 = 0.9.
so the product is 0.9.
Question 8.
67.5 × 9.2
Answer:
The product is 621.
Explanation:
In the above-given question,
given that,
the two numbers are 67.5 and 9.2.
multiply the numbers.
67.5 x 9.2 = 621.
so the product is 621.
Set D
pages 153-156 Use properties to find 0.8 × 0.4.
Rewrite each decimal as a product of a whole number and a decimal. Next, use the Associative and Commutative Properties to rearrange the factors.
0.8 × 0.4 =
= (8 × 0.1) × (4 × 0.1)
= (8 × 4) (0.1 × 0.1)
= 32 × 0.01
= 0.32
So, 0.8 × 0.4 = 0.32
Remember if two factors less than one are multiplied, their product is less than either factor.
Use properties to find each product.
Question 1.
0.6 × 0.3
Answer:
0.6 x 0.3 = 18.
Explanation:
In the above-given question,
given that,
the two numbers are 0.6 and 0.3.
6 x 0.1 = 0.6.
3 x 0.1 = 0.7.
6 x 3 = 18.
18 x 0.1
Question 2.
2.5 × 0.7
Answer:
2.5 x 0.7 = 1.75.
Explanation:
In the above-given question,
given that,
the two numbers are 2.5 and 0.7.
25 x 0.1 = 2.5.
7 x 0.1 = 0.7.
25 x 7 x 0.01 = 1.75.
Question 3.
0.04 × 1.9
Answer:
0.04 x 1.9 = 0.076.
Explanation:
In the above-given question,
given that,
the two numbers are 0.04 and 1.9.
0.04 x 1.9 = 0.076.
Question 4.
0.23 × 0.8
Answer:
0.23 x 0.8 = 0.184.
Explanation:
In the above-given question,
given that,
23 x 0.1 = 0.23.
8 x 0.1 = 0.8.
23 x 8 = 184.
0.1 x 0.1 = 0.01.
0.23 x 0.8 = 0.184.
Question 5.
0.1 × 8.2
Answer:
0.1 x 8.2 = 0.82.
Explanation:
In the above-given question,
given that,
1 x 0.1 = 0.1.
82 x 0.1 = 0.82.
1 x 82 = 82.
0.1 x 0.1 = 0.01.
0.1 x 8.2 = 0.82.
Question 6.
5.7 × 3.6
Answer:
5.7 x 3.6 = 20.52.
Explanation:
In the above-given question,
given that,
57 x 0.1 = 5.7.
36 x 0.1 = 3.6.
57 x 36 x 0.01 = 20.52.
Question 7.
4.2 × 6.5
Answer:
4.2 x 6.5 = 27.3.
Explanation:
In the above-given question,
given that,
42 x 0.1 = 4.2.
65 x 0.1 = 6.5.
4.2 x 6.5 = 27.3.
Question 8.
9.11 × 0.3
Answer:
9.11 x 0.3 = 2.733.
Explanation:
In the above-given question,
given that,
911 x 0.01 = 9.11.
3 x 0.1 = 0.3.
9.11 x 0.3 = 2.733.
Set E
pages 157-160
The decimal is missing in the product below. Use number sense to place the decimal point correctly.
43.5 × 1.7 = 7395
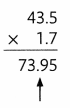
Since 1.7 is greater than 1, the product will be greater than 43.5. Since 43.5 is about 40 and 1.7 is about 2, the answer will be about 80. The decimal point should be between the 3 and the 9.
So, 43.5 × 1.7 = 73.95.
Remember that it may be Reteaching helpful to compare each factor to 1 in order to determine the relative size of the product.
The decimal point is missing in each product. Use number sense to place the decimal point correctly.
Question 1.
4 × 0.21 = 84
Answer:
4 x 0.21 = 0.84.
Explanation:
In the above-given question,
given that,
the two numbers are 4 and 0.21.
multiply the numbers.
4 x 0.21 = 0.84.
Question 2.
4.5 × 6.2 = 279
Answer:
Question 3.
7 × 21.6 = 1512
Answer:
Question 4.
6.4 × 3.2 = 2048
Answer:
Question 5.
31.5 × 0.01 = 315
Answer:
Question 6.
1.4 × 52.3 = 7322
Answer:
Question 7.
0.12 × 0.9 = 108
Answer:
Question 8.
12.5 × 163.2 = 2040
Answer:
Set F
pages 161-164
Think about these questions to help you model with math.
Thinking Habits
• How can I use math I know to help solve this problem?
• How can I use numbers, words, and symbols to solve the problem?
• How can I use pictures, objects, or an equation to represent the problem?

Remember that you can write an equation to show how the quantities in a problem are related.
Mr. Jennings made the stained glass window below with the dimensions shown. What is the total area of the window?
Question 1.
What do you need to find first?
Answer:
Question 2.
Write an equation to model the problem. Then solve the problem.
Answer:
Patti went to the bakery. She bought a loaf of bread for $3.49, 6 muffins that cost $1.25 each, and a bottle of juice for $1.79. She gave the cashier a $20 bill. How much change should Patti receive?
Question 3.
What do you need to find first?
Answer:
The change should Patti receive = $13.47.
Explanation:
In the above-given question,
given that,
Patti went to the bakery.
She bought a loaf of bread for $3.49, 6 muffins that cost $1.25 each, and a bottle of juice for $1.79.
She gave the cashier a $20 bill.
3.49 + 1.25 + 1.79 =
20 – 6.53 = 13.47.
so the change should patti receive = $13.47.
Question 4.
Answer the question. Write equations to show your work.
Answer:
The change should Patti receive = $13.47.
Explanation:
In the above-given question,
given that,
Patti went to the bakery.
She bought a loaf of bread for $3.49, 6 muffins that cost $1.25 each, and a bottle of juice for $1.79.
She gave the cashier a $20 bill.
3.49 + 1.25 + 1.79 =
20 – 6.53 = 13.47.
so the change should patti receive = $13.47
Topic 4 Assessment Practice
Question 1.
A credit card is 0.76 mm thick. How thick is a stack of 103 credit cards? Explain.
Answer:
The thick is a stack of 103 credit cards = 78.28 mm thick.
Explanation:
In the above-given question,
given that,
A credit card is 0.76 mm thick.
103 x 0.76 = 78.28.
so the thick is a stack of 78.28 mm.
Question 2.
Leo has 59 bricks each measuring 0.19 m long. He lines up the bricks to make a row.
A. Estimate the length of Leo’s row of bricks. Write an equation to model your work.
B. Find the actual length of the row of bricks.
Answer:
The actual length of the row of bricks = 11.21 m.
Explanation:
In the above-given question,
given that,
Leo has 59 bricks each measuring 0.19 m long.
He lines up the bricks to make a row.
59 x 0.19 = 11.21 m.
so the actual length of the row of bricks = 11.21 m.
Question 3.
Susan colored in the decimal grid shown below. Write an expression that shows the area she colored. Then evaluate the expression.

Answer:
The area she colored = 0.24.
Explanation:
In the above-given question,
given that,
l = 0.8 and w = 0.3.
0.3 x 0.8 = 0.24.
so the area she colored = 0.24.
Question 4.
Match each expression on the left with its product.
Answer:
5 x 0.08 = 0.4.
0.5 x 0.08 = 0.04.
50 x 0.8 = 40.
5 x 0.8 = 4.
Explanation:
In the above-given question,
given that,
match each expression with its product.
5 x 0.08 = 0.4.
0.5 x 0.08 = 0.04.
50 x 0.8 = 40.
5 x 0.8 = 4.
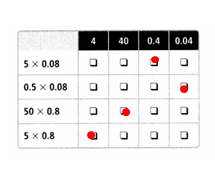
Question 5.
Michelle bought 4.6 yards of fabric. Each yard of fabric cost $4.95. How much did Michelle spend on fabric? Enter your answer in the box.
Answer:
The Michelle spend on fabric = $22.77.
Explanation:
In the above-given question,
given that,
Michelle bought 4.6 yards of fabric.
Each yard of fabric costs $4.95.
4.6 x $4.95 = 22.77.
so the Michelle spend on fabric = $22.77.
Question 6.
Choose all the expressions that are equal to 0.75 × 0.5.
Answer:
The expressions are 5/10 x 75/100 and 75/100 x 5/10.
Explanation:
In the above-given question,
given that,
the expressions are 5/10 x 75/10, 5/10 x 75/100, 5/100 x 75/100, 50/100 x 75/100, and 75/100 x 5/10.
0.75 x 0.5 = 0.375.
5/10 x 75/10 = 0.5 x 7.5 = 3.75.
5/10 x 75/100 = 0.5 x 0.75 = 0.375.
5/100 x 75/100 = 0.05 x 0.75 = 0.0375.
50/100 x 75/100 = 0.75 x 0.05 = 0.0375.
75/100 x 5/10 = 0.75 x 0.5 = 0.375.
Question 7.
Select each equation that the number 102 makes true.
![]() 0.031 ×
0.031 × ![]() = 31
= 31
![]() 0.501 ×
0.501 × ![]() = 501
= 501
![]() 04.08 ×
04.08 × ![]() = 408
= 408
![]() 0.97 ×
0.97 × ![]() = 97
= 97
![]() 55 ×
55 × ![]() = 550
= 550
Answer:
55 x 10 = 550.
Explanation:
In the above-given question that,
given that,
0.031 x 10 = 0.31.
0.501 x 10 = 5.01.
4.08 x 10 = 40.8.
0.97 x 10 = 9.7.
55 x 10 = 550.
Question 8.
Nadia drew a square in her notebook. Each side measured 2.5 centimeters.

A. What is the perimeter of Nadia’s square? Write an equation to model your work.
B. What is the area of Nadia’s square? Write an equation to model your work.
Answer:
A. The perimeter of Nadia’s square = 10 cm.
B. the area of square = 6.25 sq cm.
Explanation:
In the above-given question,
given that,
the side of the square is 2.5 cm.
perimeter of square = 4 x side.
4 x 2.5 = 10 cm.
area of square = side x side.
2.5 x 2.5 = 6.25.
so the area of the square is 6.25 cm.
Question 9.
Match each expression on the left with its product.

Answer:
3.04 x 100 = 304.
0.304 x 10000 = 3040.
3.04 x 10 = 30.4.
0.304 x 10 = 3.04.
Explanation:
In the above-given question,
given that,
match each expression with its product.
3.04 x 100 = 304.
0.304 x 10000 = 3040.
3.04 x 10 = 30.4.
0.304 x 10 = 3.04.
Question 10.
Select all the expressions that are equal to 0.09 × 0.4.

Answer:
That epressions are A and B.
Explanation:
In the above-given question,
given that,
0.09 x 0.4 = 0.036.
9/100 x 4/10 = 0.09 x 0.4 = 0.036.
4/10 x 9/100 = 0.09 x 0.4 = 0.036.
4/100 x 9/100 = 0.9 x 0.4 = 0.36.
40/100 x 9/100 = 0.4 x 0.09 = 0.036.
so the expressions are true is A and B.
Question 11.
One glass of lemonade has 115 calories. How many calories are in 3.5 glasses of lemonade? Write an equation to model your work.
Answer:
The number of calories in 3.5 glasses of lemonade = 402.5.
Explanation:
In the above-given question,
given that,
One glass of lemonade has 115 calories.
3.5 x 115 = 402.5.
so the number of calories in 3.5 glasses of lemonade = 402.5.
Question 12.
Natalie likes to mail lots of postcards when she goes on vacation. In 2014, the cost of a postcard stamp was $0.34.
A. Natalie buys 10 postcard stamps. What is the total cost of the stamps? Explain.
B. Natalie and her friends decide to buy 100 postcard stamps. What will be the total cost of the stamps? Explain.
Answer:
A. The total cost of 10 postcard stamps = 3.4.
B. The total cost of 100 postcard stamps = 34.
Explanation:
In the above-given question,
given that,
Natalie likes to mail lots of postcards when she goes on vacation.
In 2014, the cost of a postcard stamp was $0.34.
10 x 0.34 = 3.4.
100 x 0.34 = 34.
so the total cost of 10 postcard stamps = 3.4.
The total cost of 100 postcard stamps = 34.
Question 13.
Without doing the multiplication, match each expression on the left with the correct product. Use number sense to help you.
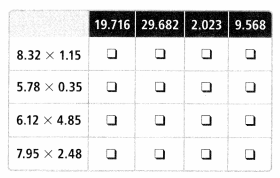
Answer:
8.32 x 1.15 = 9.568.
5.78 x 0.35 = 2.023.
6.12 x 4.85 = 29.682.
7.95 x 2.48 = 19.716.
Explanation:
In the above-given question,
given that,
match each expression with its product.
8.32 x 1.15 = 9.568.
5.78 x 0.35 = 2.023.
6.12 x 4.85 = 29.682.
7.95 x 2.48 = 19.716.
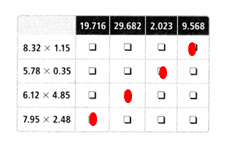
Question 14.
Derrick runs 2.25 miles each day. How many total miles will he have run after 10 days? Explain.
Answer:
The total number of miles will he have run after 10 days = 22.5 miles.
Explanation:
In the above-given question,
given that,
Derrick runs 2.25 miles each day.
2.25 x 10 = 22.5 miles.
so the total number of miles will he have run after 10 days = 22.5 miles.
Question 15.
Select each equation that the decimal 0.65 makes true.
![]() 102 ×
102 × ![]() = 65
= 65
![]() 104 ×
104 × ![]() = 650
= 650
![]() 101×
101× ![]() = 6.5
= 6.5
![]() 103×
103× ![]() = 65
= 65
![]() 101 ×
101 × ![]() = 65
= 65
Answer:
The equation that are true is 100 x 0.65 = 65, 10 x 0.65 = 6.5.
Explanation:
In the above-given question,
given that,
100 x 0.65 = 65.
10000 x 0.65 = 6500.
10 x 0.65 = 6.5.
1000 x 0.65 = 650.
10 x 0.65 = 6.5.
Question 16.
A farmer plants 0.4 of a field with wheat. The field is 2.3 acres.
A. Shade the grids to model the multiplication.

B. How many acres are planted with wheat? Use an equation and the model to explain.
Answer:
The number of acres is planted with wheat = 5.75 acres.
Explanation:
In the above-given question,
given that,
A farmer plants 0.4 of a field with wheat.
The field is 2.3 acres.
2.3 / 0.4 = 5.75.
so the number of acres is planted with wheat = 5.75 acres.
Question 17.
Bradley walks 0.65 mile each Friday to his friend’s house. He takes a different route home that is 1.2 miles. How many miles will Bradley walk to his friend’s house and back in a year? Show your work. Reminder: there are 52 weeks in a year.
Answer:
The number of miles will Bradley walk to his friend’s house and back in a year = 0.78 miles.
Explanation:
In the above-given question,
given that,
Bradley walks 0.65 miles each Friday to his friend’s house.
He takes a different route home that is 1.2 miles.
0.65 x 1.2 = 0.78.
so the number of miles will Bradley walk to his friend’s house and back in a year = 0.78 miles.
Question 18.
Alyssa paints 3 walls blue. Each of the walls is 8.3 feet tall and 7.5 feet wide.
A. Round the length and width to the nearest whole number. Then estimate the area that Alyssa will paint. Write equations to model your work.
B. Find the exact area. Write equations to model your work.
C. Compare your estimate to the exact answer. Why is your answer reasonable?
Answer:
The exact area = 47.4.
Explanation:
In the above-given question,
given that,
Alyssa paints 3 walls blue. Each of the walls is 8.3 feet tall and 7.5 feet wide.
8.3 + 7.5 = 15.8.
15.8 x 3 = 47.4.
so the exact area is 47.4.
Question 19.
Leticia and Jamal go to a bakery.
A. Jamal wants to buy 6 muffins. How much will this cost? Write an equation to model your work.
B. Leticia wants to buy 12 bagels. She uses partial products to find her total. She says “$16.80 is close to my estimate of 12 × $1 = $12, so this total is reasonable.” Do you agree with her? Explain your reasoning
Answer:
A. The cost of 6 muffins = $1.99.
B. No, it is not reasonable.
Explanation:
In the above-given question,
given that,
Leticia and Jamal go to a bakery.
the cost of the bagel is $0.95.
the cost of the Muffin is $1.99.
1.99 x 6 = 11.94.
0.95 x 12 = 11.4.
Question 20.
The area of one fabric square is 4.85 square inches. What is the area of a quilt made with 102 fabric squares? Explain.
Answer:
The area of the quilt made with 100 fabric squares = 485 in.
Explanation:
In the above-given question,
given that,
The area of one fabric square is 4.85 square inches.
4.85 x 100 = 485.
so the area of the quilt made with 100 fabric squares = 485 sq in.
Question 21.
Jen bought 3.72 pounds of apples at a farmer’s market. Andrea bought 4 times as much as Jen.

A. Which expression represents the problem? Use the bar diagram to help.
A. 3.72 × 4
B. 3.72 × 1
C. 3.72 ÷ 4.
D. 3.72 ÷ 1
Answer:
Option C is the correct answer.
Explanation:
In the above-given question,
given that,
Jen bought 3.72 pounds of apples at a farmer’s market.
Andrea bought 4 times as much as Jen.
3.72 / 4 = 0.93.
so option C is the correct answer.
B. How many pounds of apples did Andrea buy?
Answer:
The number of pounds of apples did Andrea buy = 0.93 pounds.
Explanation:
In the above-given question,
given that,
Jen bought 3.72 pounds of apples at a farmer’s market.
Andrea bought 4 times as much as Jen.
3.72 / 4 = 0.93.
so the number of pounds of apples did Andrea buy = 0.93.
Topic 4 Performance Task
An exchange rate is how much of one country’s currency (money) you would get for another country’s currency. The table below shows the recent exchange rate between the U.S. dollar and the currency of some other countries.
For example, if you had $2 (U.S.) dollars, you could exchange that for 26.48 Mexican pesos:
2 × 13.24 = 26.48.

Question 1.
Jade has $10, Julio has $100, and Anna has $1,000. How many Japanese yen would each person get in exchange for their dollars?
Answer:
The Japanese yen would each person get in exchange for their dollars = $1.0182.
Explanation:
In the above-given question,
given that,
Jade has $10, Julio has $100, and Anna has $1,000.
Japanese yen has 101.82.
101.82/10 = 10.182.
101.82/100 = 1.0182.
101.82/1000 = 0.10182.
Question 2.
Ivana has $5.50. Luc has 1.4 times as much money as Ivana.
Part A
How many Indian rupees would Ivana get?
Part B
How many dollars does Luc have? How many rupees can he exchange for that? Round your answer to the nearest hundredth.
Answer:
The number of rupees can he exchange for that = $3.92.
Explanation:
In the above-given question,
given that,
Ivana has $5.50. Luc has 1.4 times as much money as Ivana.
5.50/1.4 = 3.92.
so the number of rupees can he exchange for that = $3.92.
Question 3.
Use estimation to solve. Marcus has $250. About how many Venezuelan bolívares could he obtain? Is your estimate an overestimate or an underestimate? Explain.
Answer:
The number of Venezuelan bolivares could he obtain = $38.
Explanation:
In the above-given question,
given that,
Marcus has $250.
250/6.59 = 37.9.
so the number of Venezuelan bolivares could he obtain = $37.9.
Question 4.
Jorge is traveling to Kenya to photograph wildlife. How many Kenyan shillings will he receive for $500? His friends give him a $50 gift certificate right before he leaves. How many Kenyan shillings can he exchange for that amount?
Answer:
The Kenyan shillings can be exchanged for that amount = 10.
Explanation:
In the above-given question,
given that,
Jorge is traveling to Kenya to photograph wildlife.
His friends give him a $50 gift certificate right before he leaves.
500/50 = 10.
so the Kenyan shillings can be exchanged for that amount = 10.
Question 5.
Kofi is taking a trip to Mexico to see Mayan and Aztec pyramids. He wants to exchange $300 before arriving there. How many Mexican pesos can he receive? Write and solve an equation to show your work.
Answer:
The number of Mexican pesos can he receive = 0.044 pesos.
Explanation:
In the above-given question,
given that,
Kofi is taking a trip to Mexico to see the Mayan and Aztec pyramids.
He wants to exchange $300 before arriving there.
13.24/300 = 0.044.
so the number of Mexican pesos can he receive = 0.044.
Question 6.
Mary is planning a vacation to Europe. The exchange rate for the U.S. dollar to the Euro is 0.73.
Part A
Sketch place-value blocks to model how many Euros Mary will get for 3 U.S. dollars.
Part B
How many Euros can Mary get for $3? Write an equation to show your work.
Part C
How does the model help you find the product?
Answer:
The number of Euros can Mary get for $3 = $0.24.
Explanation:
In the above-given question,
given that,
Mary is planning a vacation to Europe.
The exchange rate for the U.S. dollar to the Euro is 0.73.
0.73/3 = 0.24.
so the number of Euros can Mary get for $3 = $0.24