Practice with the help of enVision Math Common Core Grade 5 Answer Key Topic 8 Apply Understanding of Multiplication to Multiply Fractions regularly and improve your accuracy in solving questions.
Envision Math Common Core 5th Grade Answers Key Topic 8 Apply Understanding of Multiplication to Multiply Fractions

enVision STEM Project: Kitchen Chemistry
Do Research Use the Internet or other sources to learn about physical changes to substances. Look for examples of physical changes that occur in the kitchen. When you condense, freeze, melt, vaporize, or whip air into a substance, you are making physical changes to that substance.
Journal: Write a Report Include what you found. Also in your report:
• Give examples of foods that are commonly condensed, frozen, melted, vaporized, or whipped.
• Write your favorite recipe that involves making physical changes to the food.
• Make up and solve multiplication problems with fractions and mixed numbers.
Review What You Know
Vocabulary
• benchmark fractions
• mixed number
• equivalent fractions
• multiple
• factor
Choose the best term from the box. Write it on the blank.
Question 1.
To estimate the sum of two or more fractions, replace the addends with _____
Answer:
Question 2.
You can find ____ by multiplying both the numerator and the denominator of a fraction by the same nonzero number.
Answer:
Question 3.
A ____ of a number is a product of the number and any nonzero whole number.
Answer:
Multiply and Divide
Find each product or quotient.
Question 4.
108 × 2
Answer:
Question 5.
270 ÷ 30
Answer:
Question 6.
243 × 20
Answer:
Question 7.
288 ÷ 24
Answer:
Question 8.
456 × 11
Answer:
Question 9.
432 ÷ 24
Answer:
Fraction Sums and Differences
Find each answer
Question 10.
\(\frac{5}{9}\) + \(\frac{8}{9}\)
Answer:
Question 11.
2\(\frac{2}{3}\) + 5\(\frac{1}{2}\)
Answer:
Question 12.
\(\frac{11}{12}\) – \(\frac{2}{3}\)
Answer:
Question 13.
6\(\frac{7}{10}\) – 2\(\frac{3}{5}\)
Answer:
Question 14.
At the library, Herb spent \(\frac{1}{6}\) hour looking for a book, \(\frac{1}{4}\) hour reading, and \(\frac{1}{2}\) hour doing research on the computer. How many hours did Herb spend at the library?
Answer:
Common Denominators
Question 15.
Explain how you can find a common denominator for \(\frac{3}{5}\) and \(\frac{5}{8}\).
Answer:
Pick a Project
PROJECT 8A
What story does your quilt tell?
Project: Design a Quilt

PROJECT 8B
Can you make art with just sticky notes?
Project: Create a Mosaic with Sticky Notes

PROJECT 8C
How much calcium does your body need?
Project: Analyze Menus for Calcium-Rich Foods
PROJECT 8D
Have you ever been in a cave?
Project: Create a Scale Model of a Cave

Lesson 8.1 Multiply a Fraction by a Whole Number
Solve & Share
Sasha walked \(\frac{1}{2}\) mile every day for 5 days. How far did she walk? Draw a picture or use any model to help you solve the problem.
Model with Math What are some different ways you can model multiplication problems?

Look Back! How does using a model help you multiply a fraction by a whole number?
Visual Learning Bridge
Essential Question What Are Some Ways to Multiply a on Fraction by a Whole Number?
A.
Joann wants to make 6 batches of fruit punch. How many cups of orange juice does she need?
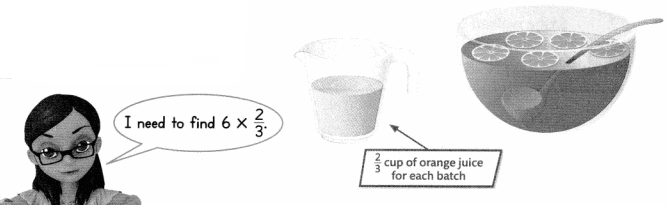
B.
One way to represent 6 × \(\frac{2}{3}\) is to use repeated addition.

C.
You can think of \(\frac{2}{3}\) as 2 times \(\frac{1}{3}\).

\(\frac{2}{3}\) = 2 × \(\frac{1}{3}\)
So, 6 × \(\frac{2}{3}\) = 6 × (2 × \(\frac{1}{3}\)).
Use the Associative Property.
6 × (2 × \(\frac{1}{3}\)) = (6 × 2) × \(\frac{1}{3}\)
= 12 × \(\frac{1}{3}\)
= \(\frac{12}{3}\) = 4
Joann needs 4 cups of orange juice to make 6 batches of punch.
Convince Me! Use Structure Find 10 × \(\frac{3}{5}\). Use repeated addition to check your answer. Show all of your work.
Guided Practice
Do You Understand?
Question 1.
Explain why 8 × \(\frac{3}{4}\) is the same as adding \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\)
Answer:
Question 2.
Find 2 × \(\frac{3}{5}\). Shade the model to help solve.
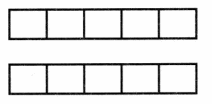
Answer:
Do You Know How?
Question 3.
Find 3 × \(\frac{2}{3}\) using repeated addition.
Answer:
Question 4.
Find 6 × \(\frac{3}{4}\) using the Associative Property.
Answer:
Independent Practice
Leveled Practice In 5-7, complete each equation to find the product.
Question 5.
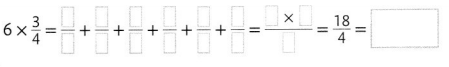
Answer:
Question 6.

Answer:
Question 7.

Answer:
In 8-15, find each product. Use models to help, if necessary.
Question 8.
35 × \(\frac{3}{5}\)
Answer:
Question 9.
7 × \(\frac{5}{12}\)
Answer:
Question 10.
9 × \(\frac{2}{3}\)
Answer:
Question 11.
300 × \(\frac{1}{2}\)
Answer:
Question 12.
64 × \(\frac{3}{8}\)
Answer:
Question 13.
900 × \(\frac{2}{3}\)
Answer:
Question 14.
84 × \(\frac{1}{4}\)
Answer:
Question 15.
42 × \(\frac{2}{7}\)
Answer:
Problem Solving
Question 16.
Higher Order Thinking Explain how you would find 36 × \(\frac{3}{4}\) mentally.
Answer:
Question 17.
Each lap around a track is \(\frac{5}{6}\) kilometer. Samantha drove around the track 24 times. How far did Samantha drive?
Answer:
Question 18.
Drake is making capes. He uses \(\frac{1}{3}\) yard of fabric for each cape he makes. What is the total amount of fabric Drake needs to make 96 capes?
Answer:
Question 19.
Bradley is making fruit salad. For each bowl of fruit salad, he needs \(\frac{3}{4}\) cup of grapes. How many cups of grapes will he use if he makes 24 bowls of fruit salad?
Answer:
Question 20.
Construct Arguments Do you think the difference 1.4 – 0.95 is less than 1 or greater than 1? Explain.
Answer:
Question 21.
Write a multiplication Expression that shows 106.
Answer:
Question 22.
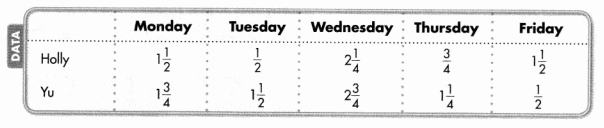
The table shows the number of miles each person ran this week. Who ran more miles by the end of the week? How many more?

Answer:
Assessment Practice
Question 23.
Select all equations that would be made true with the fraction \(\frac{3}{8}\)
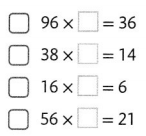
Answer:
Question 24.
Select all equations that would be made true with the number 56.
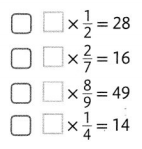
Answer:
Lesson 8.2 Multiply a Whole Number by a Fraction
Solve & Share
Brandon has 6 eggs. He needs \(\frac{2}{3}\) of the eggs to make an omelet. How many eggs does he need?
Model with Math Would a drawing help you picture the situation?

Look Back! Should your answer be less than or greater than 6? How do you know?
Visual Learning Bridge
Essential Question How Can You Multiply a Whole Number by a Fraction?
A.
Claudia has 8 yards of fabric. She needs \(\frac{3}{4}\) of the fabric to make a banner. How many yards of fabric does she need?
You can use models to represent the problem.

You need to find \(\frac{3}{4}\) of 8.
B.
Step 1
Since you are finding \(\frac{3}{4}\) of 8, divide the model into 4 equal parts.
C.
Step 2
Since you are finding \(\frac{3}{4}\) of 8, take 3 of those parts to make 6.

Claudia needs 6 yards of fabric to make a banner.
Convince Me! Model with Math Here is how Lydia found the product \(\frac{4}{5}\) × 10.

Use the model at the right to show that Lydia’s answer is correct.
Another example
Find \(\frac{3}{4}\) × 2.
Divide 2 into 4 equal parts.
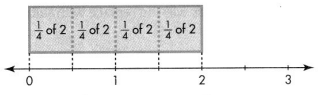
Each part is \(\frac{1}{2}\). So 3 parts make \(\frac{3}{2}\).
So, \(\frac{3}{4}\) × 2 = \(\frac{3}{2}\)
Think three-fourths of 2 wholes.

Guided Practice
Do You Understand?
Question 1.
Explain why the product of 4 × \(\frac{2}{3}\) the same as the product of \(\frac{2}{3}\) × 4.
Answer:
Question 2.
In the problem at the top of page 338, what multiplication equation could be used to find how many yards of fabric Claudia did not use?
Answer:
Do You Know How?
In 3 and 4, use the model to find each product.
Question 3.
\(\frac{2}{3}\) × 6

Answer:
Question 4.
\(\frac{3}{8}\) × 4
Answer:
Independent Practice
In 5-7, find each product. Draw models to help.
Question 5.
\(\frac{2}{3}\) × 15
Answer:
Question 6.
\(\frac{11}{12}\) × 6
Answer:
Question 7.
\(\frac{5}{8}\) × 16
Answer:
Problem Solving
Question 8.
Construct Arguments Janice said that when you multiply a fraction less than 1 by a nonzero whole number, the product is always less than the whole number. Do you agree? Explain.
Answer:
Question 9.
enVision STEM A scientist wants to find out how the properties of water change when salt is added to it. For every cup of water she has, she replaces of it with salt. If she has 24 cups of water, how many cups will she replace with salt?
Answer:
Question 10.
Shanna attends school for 1 week longer than \(\frac{3}{4}\) of the year. How many weeks in a year does Shanna attend school?
Answer:
There are 52 weeks in a year.

Question 11.
Higher Order Thinking Gina has 48 stickers. \(\frac{3}{8}\) of the stickers have pictures of flowers. \(\frac{1}{8}\) of the stickers have pictures of plants. The rest of the stickers have pictures of people. How many stickers have pictures of people? Explain how you found your answer.
Answer:
Question 12.
Two paperback books cost a total of $10. How much change will Stacy get if she buys two hardcover books and two paperback books and gives the clerk three $20 bills?

Answer:
Assessment Practice
Question 13.
Select each Expression that has a product of 12.

Answer:
Question 14.
Select each equation that would be made true with the number 4.

Answer:
Lesson 8.3 Multiply Fractions and Whole Numbers
Activity
Solve & Share
Julie has 10 yards of ribbon. She divides the ribbon into 3 equal pieces and uses 2 of the pieces on gifts. How much ribbon does she use? Solve this problem any way you choose.

Model with Math You can use words, pictures, and equations to solve the problem. Show your work in the space above!

Look Back! Should the answer be less than or greater than 5? How do you know?
Visual Learning Bridge
Essential Question How Can You Multiply Fractions question and Whole Numbers?
A.
Hal spent \(\frac{3}{4}\) hour reading each day for 7 days. How much total time did he spend reading?
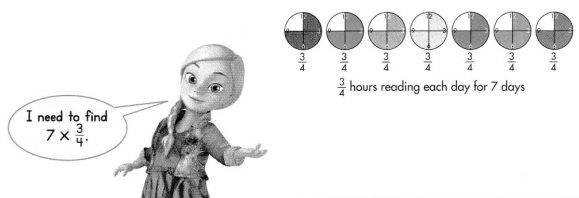
B.
Multiply to find the number of fourths.
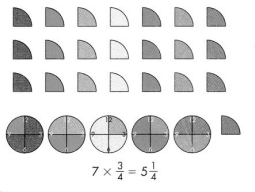
7 × \(\frac{3}{4}\) = 7 × 3 × \(\frac{1}{4}\)
= 21 × \(\frac{1}{4}\)
= \(\frac{21}{4}\)
Rewrite as a mixed number
\(\frac{21}{4}\) = 5\(\frac{1}{4}\)
Hal spent 5\(\frac{1}{4}\) hours reading.
To rename \(\frac{21}{4}\), divide the numerator by the denominator.

Convince Me! Be Precise What are the products \(\frac{4}{9}\) × 6 and 6 × \(\frac{4}{9}\)?
Guided Practice
Do You Understand?
Question 1.
What is \(\frac{3}{4}\) of a ribbon that is 7 feet long?
Answer:
Question 2.
Explain how \(\frac{3}{4}\) × 7, 7, and 3 × \(\frac{7}{4}\) are all related.
Answer:
Do You Know How?
In 3-5, find each product. Write the product as a mixed number.
Question 3.

Answer:
Question 4.
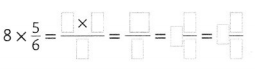
Answer:
Question 5.

Answer:
Independent Practice
Leveled Practice In 6-16, find each product. Write the product as a mixed number.
Remember: You can use division to rename a fraction as a mixed number.

Question 6.

Answer:
Question 7.

Answer:
Question 8.

Answer:
Question 9.
\(\frac{4}{5}\) × 500
Answer:
Question 10.
5 × \(\frac{2}{3}\)
Answer:
Question 11.
17 × \(\frac{6}{8}\)
Answer:
Question 12.
\(\frac{9}{10}\) × 25
Answer:
Question 13.
\(\frac{7}{8}\) × 320
Answer:
Question 14.
28 × \(\frac{7}{12}\)
Answer:
Question 15.
\(\frac{2}{3}\) × 1,287
Answer:
Question 16.
900 × \(\frac{2}{9}\)
Answer:
Problem Solving
Question 17.
About 0.6 of the human body is made up of water. If a person has a mass of 75 kilograms, what is the mass of the water in this person’s body?
Answer:
Question 18.
Number Sense How can you use mental math to find 25 × \(\frac{3}{10}\)?
Answer:
Question 19.
During a nature walk, Jill identified 20 species of animals and plants.
a Construct Arguments Jill said that of the species she identified were animals. Can this be correct? Explain.
b If \(\frac{3}{5}\) of the species Jill identified were animals, how many plants did Jill identify?
Answer:
Question 20.
A rectangular painting is 2 feet long and \(\frac{5}{6}\) a foot wide. What is the area of the painting?

Answer:
Question 21.
Higher Order Thinking An art teacher makes a batch of purple paint by mixing \(\frac{3}{4}\) cup red paint with \(\frac{3}{4}\) cup blue paint. If she mixes 13 batches, how many cups of purple paint will she have?
Answer:
Question 22.
enVision STEM A water molecule is made up of 3 atoms. One third of the atoms are oxygen and the remaining atoms are hydrogen. If there are 114 water molecules, how many hydrogen atoms are there? Show your work.
Answer:
Question 23.
Select all that are true.
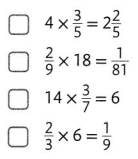
Answer:
Assessment Practice
Question 24.
Select all that are true.
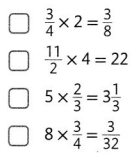
Answer:
Lesson 8.4 Use Models to Multiply Two Fractions
Activity
Solve & Share
The art teacher gave each student half of a sheet of paper. Then she asked the students to color one fourth of their pieces of paper. What part of the original sheet did the students color? Solve this problem any way you choose.
You can draw a picture to represent the problem.

Look Back! Reasoning Should your answer be less than or greater than 1? How do you know?
Visual Learning Bridge
Essential Question How Can You Use a Model to Multiply Fractions?
A.
There was \(\frac{1}{4}\) of a pan of lasagna left. Tom ate of this amount. What fraction of a whole pan of lasagna did he eat?

Find \(\frac{1}{3}\) of \(\frac{1}{4}\) to solve the problem.

B.
One Way
Divide one whole into fourths.
Divide \(\frac{1}{4}\) into 3 equal parts.
Divide the other \(\frac{1}{4}\)s into 3 equal parts.
![]()
12 parts make one whole, so one part is \(\frac{1}{12}\).
\(\frac{1}{3}\) × \(\frac{1}{4}\) = \(\frac{1}{12}\)
C.
Another Way
Shade 1 of the 3 rows yellow to represent \(\frac{1}{3}\).
Shade 1 of the 4 columns red to represent \(\frac{1}{4}\).
The orange overlap shows the product.

1 out of 12 parts are shaded orange.
\(\frac{1}{3}\) × \(\frac{1}{4}\) = \(\frac{1×1}{3×4}\)
Tom ate \(\frac{1}{12}\) of the pan of lasagna.
Convince Me! Reasoning Find \(\frac{1}{4}\) × \(\frac{1}{5}\) using the model. Explain your work.

Another example
Find \(\frac{2}{3}\) × \(\frac{3}{4}\) using a number line.
\(\frac{1}{3}\) means 1 of 3 equal parts, so \(\frac{1}{3}\) of \(\frac{3}{4}\) is \(\frac{1}{4}\)
\(\frac{2}{3}\) means 2 of 3 equal parts, so \(\frac{2}{3}\) of \(\frac{3}{4}\) is 2 times \(\frac{1}{4}\).
\(\frac{2}{3}\) × \(\frac{3}{4}\) = \(\frac{2}{4}\) or \(\frac{1}{2}\)
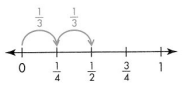
Guided Practice
Do You Understand?
Question 1.
Use the model in box Con page 346 to find \(\frac{2}{3}\) × \(\frac{2}{4}\).
Answer:
Question 2.
Create a story problem for \(\frac{2}{3}\) × \(\frac{2}{4}\).
Answer:
Do You Know How?
Question 3.
Find \(\frac{5}{6}\) × \(\frac{1}{2}\). Shade the model to help solve.

Answer:
Question 4.
Find \(\frac{3}{4}\) of \(\frac{4}{9}\).
Answer:
Independent Practice
In 5-6, find each product. Shade the model to help solve.
Question 5.
\(\frac{1}{3}\) × \(\frac{5}{6}\)
![]()
Answer:
Question 6.
\(\frac{2}{3}\) × \(\frac{1}{12}\)

Answer:
In 7-14, find each product. Use models to help.
Question 7.
\(\frac{7}{8}\) × \(\frac{1}{12}\)
Answer:
Question 8.
\(\frac{2}{5}\) × \(\frac{1}{12}\)
Answer:
Question 9.
\(\frac{5}{7}\) × \(\frac{7}{9}\)
Answer:
Question 10.
\(\frac{1}{2}\) × \(\frac{3}{4}\)
Answer:
Question 11.
\(\frac{1}{4}\) × \(\frac{7}{8}\)
Answer:
Question 12.
\(\frac{5}{6}\) of \(\frac{9}{10}\)
Answer:
Question 13.
\(\frac{1}{4}\) × \(\frac{1}{8}\)
Answer:
Question 14.
\(\frac{1}{3}\) of \(\frac{3}{7}\)
Answer:
Problem Solving
Question 15.
Make Sense and Persevere Will $50 be enough to buy 6 cans of paint? Explain.
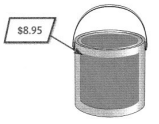
Answer:
Question 16.
A scientist had \(\frac{3}{4}\) of a bottle of a solution. She used \(\frac{1}{6}\) of the solution in an Experiment. How much of the bottle did she use?
Answer:
Question 17.
Algebra What value of n makes the equation \(\frac{2}{3}\) × n = \(\frac{4}{9}\) true?
Answer:
Question 18.
Write an Expression that shows 104.
Answer:
Question 19.
A plumber charges $45 for the first hour and $30 for each additional hour. How much does he charge if it takes him 4 hours to make a repair?
Answer:
Question 20.
Higher Order Thinking If \(\frac{7}{8}\) is multiplied by \(\frac{4}{5}\) will the product be greater than either of the two factors? Explain.
Answer:
Question 21.
In the voting for City Council Precinct 5, only \(\frac{1}{2}\) of all eligible voters cast votes. What fraction of all eligible voters voted for Shelley? Morgan? Who received more votes?

Answer:
Assessment Practice
Question 22.
Majid made the model to show multiplying a fraction by a fraction. Which multiplication equation does the model show?
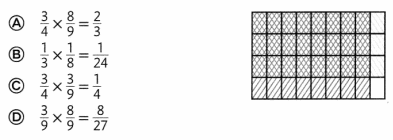
Answer:
Lesson 8.5 Multiply Two Fractions
Activity
Solve & Share
On Dan’s eReader, \(\frac{2}{3}\) of the books are fiction. Of the fiction books, \(\frac{4}{5}\) are mysteries. What fraction of the books on Dan’s eReader are mysteries? Solve this problem any way you choose.
You can model with math by writing a multiplication sentence to solve the problem.

Look Back! What fraction of the books are not mysteries? Explain.
Visual Learning Bridge
Essential Question How Can You Find the Product Question of Two Fractions?
A.
Amelia takes pictures with her smartphone. Of the pictures, \(\frac{5}{6}\) are of animals. What fraction of all her pictures are of dogs?

You need to find \(\frac{3}{4}\) of \(\frac{5}{6}\) to answer the question.

B.
Step 1
Estimate \(\frac{3}{4}\) × \(\frac{5}{6}\).
Since both fractions are less than 1, the product will be less than 1.
C.
Step 2
Multiply the numerators. Then multiply the denominators.
\(\frac{3}{4}\) × \(\frac{5}{6}\) = \(\frac{3 \times 5}{4 \times 6}\)
Since \(\frac{15}{24}\) < 1, the answer is reasonable.
So, \(\frac{15}{24}\) or \(\frac{5}{8}\) of all Amelia’s pictures have dogs in them.
\(\frac{15}{24}\) and \(\frac{5}{8}\) are equivalent fractions.

Convince Me! Model with Math \(\frac{1}{10}\) of the animal pictures on Amelia’s smartphone are of cats. Write and solve an equation to find what fraction of all her pictures have cats in them.
Guided Practice
Do You Understand?
Question 1.
Is the product \(\frac{3}{6}\) × \(\frac{5}{4}\) of equal to the product of \(\frac{3}{4}\) × \(\frac{5}{6}\)? Explain how you know.
Answer:
Question 2.
How is adding \(\frac{3}{9}\) and \(\frac{6}{9}\) different from multiplying the two fractions? Explain.
Answer:
Do You Know How?
In 3-10, find each product.
Question 3.
\(\frac{2}{3}\) × \(\frac{1}{2}\)
Answer:
Question 4.
\(\frac{5}{4}\) of \(\frac{1}{9}\)
Answer:
Question 5.
\(\frac{7}{10}\) × \(\frac{3}{4}\)
Answer:
Question 6.
\(\frac{1}{3}\) × \(\frac{1}{4}\)
Answer:
Question 7.
\(\frac{5}{6}\) of \(\frac{3}{7}\)
Answer:
Question 8.
\(\frac{3}{5}\) × \(\frac{11}{12}\)
Answer:
Question 9.
\(\frac{4}{10}\) × \(\frac{2}{5}\)
Answer:
Question 10.
\(\frac{3}{4}\) × \(\frac{2}{9}\)
Answer:
Independent Practice
In 11-30, find each product.
Question 11.
\(\frac{9}{10}\) × \(\frac{1}{2}\)
Answer:
Question 12.
\(\frac{5}{6}\) × \(\frac{1}{3}\)
Answer:
Question 13.
\(\frac{4}{7}\) of \(\frac{7}{9}\)
Answer:
Question 14.
\(\frac{3}{4}\) × \(\frac{4}{5}\)
Answer:
Question 15.
\(\frac{2}{3}\) × \(\frac{7}{8}\)
Answer:
Question 16.
\(\frac{6}{7}\) × \(\frac{3}{8}\)
Answer:
Question 17.
\(\frac{1}{3}\) of \(\frac{3}{4}\)
Answer:
Question 18.
\(\frac{6}{7}\) × \(\frac{3}{8}\)
Answer:
Question 19.
\(\frac{2}{5}\) of \(\frac{5}{12}\)
Answer:
Question 20.
\(\frac{2}{3}\) × \(\frac{4}{5}\)
Answer:
Question 21.
\(\frac{1}{2}\) × \(\frac{1}{2}\)
Answer:
Question 22.
\(\frac{1}{2}\) of \(\frac{8}{9}\)
Answer:
Question 23.
\(\frac{2}{3}\) × (\(\frac{3}{5}\) + \(\frac{1}{5}\))
Answer:
Question 24.
(\(\frac{3}{7}\) + \(\frac{2}{7}\)) × \(\frac{2}{3}\)
Answer:
Question 25.
\(\frac{1}{2}\) × (\(\frac{1}{3}\) + \(\frac{1}{3}\))
Answer:
Question 26.
(\(\frac{9}{10}\) – \(\frac{3}{10}\)) × \(\frac{1}{4}\)
Answer:
Question 27.
\(\frac{2}{3}\) × (\(\frac{3}{5}\) + \(\frac{1}{5}\))
Answer:
Question 28.
(\(\frac{8}{9}\) – \(\frac{1}{3}\)) × \(\frac{3}{4}\)
Answer:
Question 29.
(\(\frac{5}{12}\) + \(\frac{1}{6}\)) × \(\frac{5}{6}\)
Answer:
Question 30.
\(\frac{11}{12}\) × (\(\frac{3}{4}\) – \(\frac{1}{2}\))
Answer:
Problem Solving
Question 31.
Eduardo runs 6 laps around the track at Lincoln Park School. Then he runs 3\(\frac{1}{2}\) miles to get home. How far will he run in all? Show your work.

Answer:
Question 32.
Be Precise To amend the U.S. Constitution, \(\frac{3}{4}\) of the 50 states must approve the amendment. If 35 states approve an amendment, will the Constitution be amended?
Answer:
Question 33.
Higher Order Thinking In Ms. Barclay’s classroom, \(\frac{2}{5}\) of the students play chess. Of the students who play chess, \(\frac{5}{6}\) also play sudoku. If there are 30 students in her class, how many play chess and sudoku?
Answer:
Question 34.
One sheet of stamps is shown at the right. Emma needs to buy 50 stamps to send out invitations for her graduation party. Will 2 sheets of stamps be enough? How do you know?

Answer:
Assessment Practice
Question 35.
Choose all the Expressions that have \(\frac{3}{4}\) as a product.

Answer:
Question 36.
Choose all the multiplication sentences that have \(\frac{1}{4}\) as the missing part.

Answer:
Lesson 8.6 Area of a Rectangle
Activity
Solve&Share
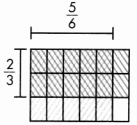
A rectangular poster is \(\frac{1}{4}\) yard wide and \(\frac{3}{4}\) yard tall. What is its area? Solve this problem any way you choose.
You can use appropriate tools, like grid paper, to solve the problem.

Look Back! Is the area of a poster that is \(\frac{3}{4}\) yard wide and \(\frac{1}{4}\) yard tall the same as the area of the poster above? Explain.
Visual Learning Bridge
Essential Question How Can You Find the Area of a Question Rectangle with Fractional Side Lengths?
A.
Jenny has a rectangular garden. What is the area of her garden?
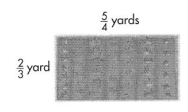
The area of a rectangle is found by multiplying the length by the width.

B.
Step 1
\(\frac{1}{4}\) × \(\frac{1}{3}\) = \(\frac{1}{12}\) because 12 rectangles each \(\frac{1}{4}\) wide and \(\frac{1}{3}\) high fit in a unit square.
C.
Step 2
A rectangle of width \(\frac{5}{4}\) yards and height \(\frac{2}{3}\) yard is tiled with 5 × 2 rectangles of area \(\frac{1}{12}\).

so, \(\frac{5}{4}\) × \(\frac{2}{3}\) = \(\frac{5 \times 2}{4 \times 3}\) = \(\frac{10}{12}\)
The area of Jenny’s garden is \(\frac{10}{12}\) square yard.
Convince Me! Reasoning Mason has a rectangular garden that is \(\frac{2}{3}\) yard wide by \(\frac{7}{4}\) yards long. What is the area of Mason’s garden? Use a drawing to show your work.
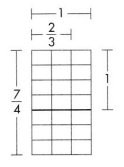
Guided Practice
Do You Understand?
Question 1.
If you do not remember the formula for finding the area of a rectangle, how can you find its area?
Answer:
Question 2.
How could you define area?
Answer:
Do You Know How?
Question 3.
Find the area of a rectangle with side lengths \(\frac{2}{3}\) foot and \(\frac{1}{2}\) foot.
Answer:
Question 4.
Find the area of a square with side lengths of \(\frac{5}{4}\) inches.
Answer:
Independent Practice
In 5-10, find each area.
Question 5.
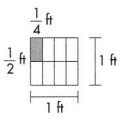
Answer:
Question 6.
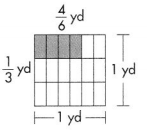
Answer:
Question 7.

Answer:
Question 8.
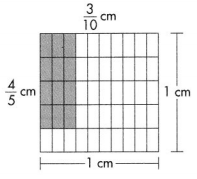
Answer:
Question 9.

Answer:
Question 10.

Answer:
Question 11.
Find the area of a rectangle with side lengths \(\frac{5}{3}\) feet and \(\frac{3}{4}\) foot.
Answer:
Question 12.
Find the area of a square with side lengths of \(\frac{3}{8}\) inch.
Answer:
Question 13.
Find the area of a rectangle with side lengths \(\frac{7}{2}\) centimeters and \(\frac{5}{4}\) centimeters.
Answer:
Problem Solving
Question 14.
Construct Arguments
Roy and Tom are working on a multiplication problem. Roy claims that \(\frac{7}{4}\) × \(\frac{3}{8}\) = \(\frac{21}{32}\). Tom claims that the correct answer is \(\frac{21}{8}\). Who is correct? Explain your
Answer:
Question 15.
Emilio needs to know how much area to clear for his son’s square sandbox. Each side of the sandbox is \(\frac{3}{4}\) yard. Find the area that the sandbox will cover.
Answer:
Question 16.
Margaret purchased a doormat measuring \(\frac{1}{2}\) yard by \(\frac{2}{3}\) yard for her back door step. If the step is square yard, will the mat fit? Explain.
Answer:
Question 17.
Each person on a Ferris wheel pays $6.50 for a ticket. There are 72 passengers. How much money is collected from all the passengers?
Answer:
Question 18.
Higher Order Thinking Kim is installing blue and white tile in her bathroom. She made a diagram of the layout showing the area of both colors. Write two Expressions that describe the area of the blue tile.

Answer:
Question 19.
Wilhelmina has 8.3 ounces of peanut butter. If she makes 5 sandwiches with an equal amount of peanut butter on each, how much peanut butter does she put on each one?
Answer:
Question 20.
Irene buys a talking doll for $10.66 and some batteries for $4.22. She pays with a $20 bill. Estimate how much change she should get, to the nearest dime.
Answer:
Assessment Practice
Question 21.
Juno calculated the area of a square to be \(\frac{4}{9}\) square yard. Which shows the side length of the square?
A. \(\frac{2}{9}\) yard
B. \(\frac{4}{9}\) yard
C. \(\frac{2}{3}\) yard
D. \(\frac{8}{9}\) yard
Answer:
Question 22.
Bo calculated the area of a square to be \(\frac{25}{4}\) square inches. Which shows the side length of the square?
A. \(\frac{25}{2}\) inches
B. \(\frac{25}{8}\) inches
C. \(\frac{5}{2}\) inches
D. \(\frac{5}{4}\) inches
Answer:
Lesson 8.7 Multiply mixed Numbers
Activity
Solve & Share
Look at the ingredients needed to make Josie’s special pancakes. How much pancake mix and milk will you need if you want to double the recipe? To triple the recipe? Solve this problem any way you choose.
Generalize How can you use what you know about multiplying fractions to help you multiply mixed numbers?

Look Back! What number sentence can you write using repeated addition to show how much pancake mix is needed if the recipe is tripled?
Visual Learning Bridge
Essential Question How Can You Find the Product of mixed Numbers?
A.
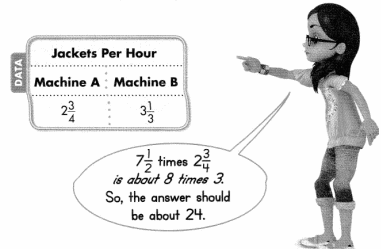
A clothing factory has machines that make jackets. The machines operate for 7\(\frac{1}{2}\) hours each day. How many jackets can Machine A make in one day?
B.
One Way
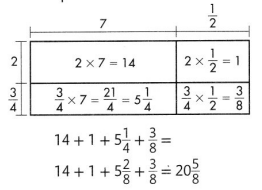
You can use an area model to find the partial products. Then add to find the final product.
C.
Another Way
You can also use an equation to find the product. Rename the mixed numbers, then multiply.
7\(\frac{1}{2}\) × 2\(\frac{3}{4}\) = \(\frac{15}{2}\) × \(\frac{11}{4}\)
= \(\frac{165}{8}\)
= 20\(\frac{5}{8}\)
Machine A makes 20 jackets each day.
Since 20 is close to the estimate of 24, the answer is reasonable.

Convince Me! Model with Math How many jackets can Machine B make in one day? Write an equation to model your work.
Guided Practice
Do You Understand?
Question 1.
Explain how you would multiply 5 × 2\(\frac{1}{2}\)
Answer:
Do You Know How?
In 2 and 3, estimate the product. Then complete the multiplication.
Question 2.
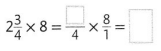
Answer:
Question 3.
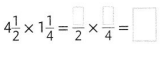
Answer:
Independent Practice
Compare your product against your estimate to check for reasonableness.

In 4-9, estimate the product. Then complete the multiplication.
Question 4.
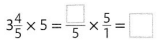
Answer:
Question 5.
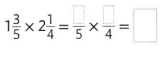
Answer:
Question 6.

Answer:
Question 7.
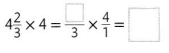
Answer:
Question 8.

Answer:
Question 9.

Answer:
In 10-20, estimate the product. Then find each product.
Question 10.
2\(\frac{1}{2}\) × 4\(\frac{1}{2}\)
Answer:
Question 11.
\(\frac{3}{4}\) × 8\(\frac{1}{2}\)
Answer:
Question 12.
1\(\frac{1}{8}\) × 3\(\frac{1}{3}\)
Answer:
Question 13.
3\(\frac{1}{5}\) × \(\frac{2}{3}\)
Answer:
Question 14.
3\(\frac{1}{4}\) × 6
Answer:
Question 15.
5\(\frac{1}{3}\) × 3
Answer:
Question 16.
2\(\frac{3}{8}\) × 4
Answer:
Question 17.
4\(\frac{1}{8}\) × 5\(\frac{1}{2}\)
Answer:
Question 18.
![]()
Answer:
Question 19.
![]()
Answer:
Question 20.
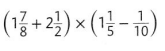
Answer:
Problem Solving
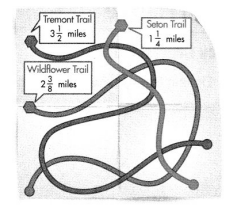
In 21-23, use the diagram at the right.
Question 21.
Make Sense and Persevere Bernie and Chloe hiked the Tremont Trail to the end and back. Then they hiked the Wildflower Trail to the end before stopping to eat lunch. How far did they hike before they ate lunch?
Answer:
Question 22.
Higher Order Thinking In one day, Ricardo hiked 2\(\frac{1}{2}\) times as far as Bernie and Chloe hiked before they ate lunch. How far did he hike?
Answer:
Question 23.
The city plans to Extend the Wildflower Trail 2\(\frac{1}{2}\) times its current length in the next 5 years. How long will the Wildflower Trail be at the end of 5 years?
Answer:
Question 24.
How can you use multiplication to find 3\(\frac{3}{5}\) + 3\(\frac{3}{5}\) + 3\(\frac{3}{5}\) ?
Answer:
Question 25.
The world’s smallest gecko is \(\frac{3}{4}\) inch long. An adult male Western Banded Gecko is 7\(\frac{1}{3}\) times as long. How long is a Western Banded Gecko?
Answer:
Question 26.
The Akashi-Kaikyo Bridge in Japan is about 1\(\frac{5}{8}\) times as long as the Golden Gate Bridge in San Francisco. The Golden Gate Bridge is about 9,000 feet long. About how long is the Akashi-Kaikyo Bridge?
Answer:
Question 27.
Patty spent 3.5 times as much as Sandy on their shopping trip. If Sandy spent $20.50, how much did Patty spend?
Answer:
Assessment Practice
Question 28.
Choose all that are true.
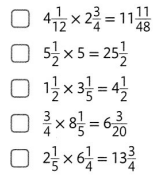
Answer:
Question 29.
Choose all that are true.

Answer:
Lesson 8.8 Multiplication as Scaling
Solve & Share
Without multiplying, circle the problem in each set with the greatest product and underline the problem with the least product. Solve this problem any way you choose.
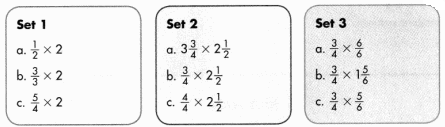
How can you use what you know about multiplying fractions to help you find the problem with the greatest product?

Look Back! Construct Arguments How is \(\frac{3}{2}\) × 2 like 1 × 2?
Visual Learning Bridge
Essential Question How Can You Use Number Sense to Question Evaluate the Size of a Product?
A.
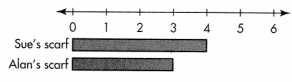
Sue knitted scarves that are 4 feet long for herself and her friends Joe and Alan. After a month, they compared the lengths of their scarves. Some scarves had stretched and some had shrunk. The results are shown in the chart. How had the lengths of Joe’s and Alan’s scarves changed?
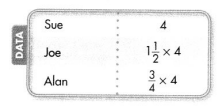
Think of multiplication as scaling or resizing.

B.
Alan’s scarf
Alan’s scarf shrank.
\(\frac{3}{4}\) × 4 < 4 Multiplying a number by a fraction less than 1 results in a product less than the given number.
C.
Joe’s scarf
Joe’s scarf stretched.
\(\frac{3}{4}\) × 4 > 4
Multiplying a number by a fraction greater than 1 results in a product greater than the starting number.

Convince Me! Use Structure Sue knitted a scarf for her friend June that was also 4 feet long. After a month, the length of June’s scarf could be represented by the Expression \(\frac{3}{3}\) × 4. How did the length of June’s scarf change? Explain.
Guided Practice
Do You Understand?
Question 1.
Why does multiplying a number by 3\(\frac{1}{2}\) increase its value?
Answer:
Question 2.
Which of the following are less than 8?
8 × \(\frac{9}{10}\)
8 × \(\frac{7}{6}\)
\(\frac{3}{5}\) × 8
Answer:
Do You Know How?
In 3-5, without multiplying decide which symbol belongs in the box: <, >, or =
Question 3.
![]()
Answer:
Question 4.
![]()
Answer:
Question 5.
![]()
Answer:
Independent Practice
In 6-17, without multiplying, decide which symbol belongs in the box: <, >, or =.
Question 6.
2\(\frac{1}{2}\) × 1\(\frac{2}{3}\) ![]() 1\(\frac{2}{3}\)
1\(\frac{2}{3}\)
Answer:
Question 7.
\(\frac{3}{5}\) × 4\(\frac{4}{5}\) ![]() 4\(\frac{4}{5}\)
4\(\frac{4}{5}\)
Answer:
Question 8.
1\(\frac{2}{7}\) ![]() 1\(\frac{2}{7}\) × \(\frac{5}{5}\)
1\(\frac{2}{7}\) × \(\frac{5}{5}\)
Answer:
Question 9.
\(\frac{1}{3}\) × 2\(\frac{2}{5}\) ![]() 2\(\frac{2}{5}\)
2\(\frac{2}{5}\)
Answer:
Question 10.
3\(\frac{3}{5}\) ![]() 3\(\frac{3}{5}\) × \(\frac{2}{2}\)
3\(\frac{3}{5}\) × \(\frac{2}{2}\)
Answer:
Question 11.
4\(\frac{1}{3}\) × 2\(\frac{2}{7}\) ![]() 2\(\frac{2}{7}\)
2\(\frac{2}{7}\)
Answer:
Question 12.
2\(\frac{1}{5}\) × \(\frac{1}{10}\) ![]() 2\(\frac{1}{5}\)
2\(\frac{1}{5}\)
Answer:
Question 13.
\(\frac{1}{2}\) × 1\(\frac{2}{5}\) ![]() 1\(\frac{2}{5}\)
1\(\frac{2}{5}\)
Answer:
Question 14.
4\(\frac{3}{4}\) × 3\(\frac{1}{4}\) ![]() 4\(\frac{3}{4}\)
4\(\frac{3}{4}\)
Answer:
Question 15.
1\(\frac{3}{4}\) ![]() 1\(\frac{1}{12}\) × 1\(\frac{3}{4}\)
1\(\frac{1}{12}\) × 1\(\frac{3}{4}\)
Answer:
Question 16.
5\(\frac{1}{3}\) × \(\frac{5}{6}\) ![]() 5\(\frac{1}{3}\)
5\(\frac{1}{3}\)
Answer:
Question 17.
\(\frac{5}{5}\) × 4\(\frac{2}{3}\) ![]() 4\(\frac{2}{3}\)
4\(\frac{2}{3}\)
Answer:
In 18 and 19, without multiplying, order the following products from least to greatest.
Question 18.
![]()
Answer:
Question 19.
![]()
Answer:
In 20 and 21, without multiplying, order the following products from greatest to least.
Question 20.
![]()
Answer:
Question 21.
![]()
Answer:
Problem Solving
Question 22.
Who ran farther by the end of the week? How much farther? Use the table below that shows the distances in miles.
Answer:
Question 23.
Be Precise Ethan took a quiz with 15 questions. If he answered of the questions correctly, how many did he get wrong?
Answer:
Question 24.
At a taffy pull, George stretched the taffy to 3 feet. Jose stretched it 1 times as far as George. Maria stretched it as far as George. Sally stretched it, as far. Who stretched it the farthest? the least?
Answer:
Question 25.
Higher Order Thinking Without multiplying, decide which symbol belongs in the box: <, >, or =. Explain how you decided
4\(\frac{3}{4}\) × 3\(\frac{1}{4}\) ![]() 4\(\frac{1}{2}\)
4\(\frac{1}{2}\)
Answer:
Question 26.
Write two decimals with a product close to 6.3.
__.__ × __ .__ ≈ 6.3
≈ is a symbol that means is approximately equal to.

Assessment Practice
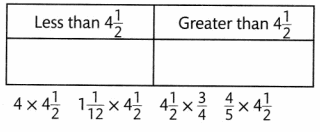
Question 27.
Write each Expression in the correct answer space to show products less than 4\(\frac{1}{2}\) and those greater than 4\(\frac{1}{2}\).
Answer:
Question 28.
Write each Expression in the correct answer space to show products less than 1\(\frac{3}{4}\) and those greater than 1\(\frac{3}{4}\).

Answer:
Lesson 8.9 Make Sense and Persevere
Problem Solving
Solve & Share
A rectangular dog park was built with the dimensions shown. The fencing that completely surrounds the park cost $12 a yard. Each square yard of grass sod that covers the entire park cost $8. What was the total cost for the fencing and the sod? Solve this problem any way you choose.
Thinking Habits
Be a good thinker!
These questions can help you.
• What do I need to find?
• What do I know?
• What’s my plan for solving the problem?
• What else can I try if I get stuck?
• How can I check that my solution makes sense?
Look Back! Make Sense and Persevere Before solving the problem, how do you know that the area of the dog park must be greater than 200 square yards?
Visual Learning Bridge
Essential Question How Can You Make Sense of Problems and Persevere in Solving Them?
A.
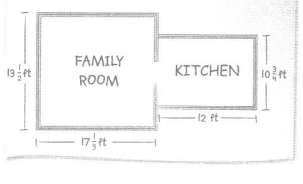
Gwen is planning to tile the entire floor of the family room and kitchen. Tile costs $12 per square foot. What is the total cost of tiling the family room and kitchen floors?
You can make sense of the problem by answering these questions. What do you know? What are you asked to find?

Here’s my thinking…

B.
How can I make sense of and solve the problem?
I can
• identify the quantities given.
• understand how the quantities are related.
• choose and implement an appropriate strategy.
• check to be sure my work and answer make sense.
C.
Find the area of the family room.
A = 17\(\frac{1}{3}\) × 13\(\frac{1}{2}\) = \(\frac{52 \times 27}{3 \times 2}\) = \(\frac{1,404}{6}\) = 234
The area of the family room is 234 square feet.
Find the area of the kitchen.
A = 12 × 10\(\frac{3}{4}\) = \(\frac{12 \times 43}{1 \times 4}\) = \(\frac{516}{4}\) = 129
The area of the kitchen is 129 square feet.
Add to find the total area. 234 + 129 = 363
Calculate the total cost. 363 × 12 = 4,356
The total cost is $4,356.
Convince Me! Make Sense and Persevere How much more does it cost to tile the family room floor than the kitchen floor? Show your work.
Guided Practice
Make Sense and Persevere
A website has a daily trivia contest. On Mondays, Wednesdays, and Fridays, you have 1\(\frac{1}{2}\) hours to submit an answer. On Tuesdays and Thursdays, you have 1\(\frac{1}{4}\) hours. On Saturdays and Sundays, you have only \(\frac{3}{4}\) of an hour. How many hours each week do you have to submit an answer?
Remember to compare your answer to your estimate.

Question 1.
Estimate the total hours each week you have to submit an answer. Write an equation to show your work.
Answer:
Question 2.
Write an equation using multiplication and a variable to represent the problem. Then solve the equation and answer the question.
Answer:
Independent Practice
Make Sense and Persevere
Isabel is buying framing to go around the perimeter of one of her paintings. Each inch of framing costs $0.40. What is the total cost of the framing for the painting?

Question 3.
What is the first step you need to do? What is the answer to the first step? Write an equation to show your work.
Answer:
Question 4.
What is the next step to solve the problem? What is the answer to the problem? Write an equation to show your work.
Answer:
Question 5.
How can you check that your answer makes sense?
Answer:
Problem Solving
Performance Task
Hiking Trails
The Farina family spent a week at the state park. Christine hiked the Evergreen trail twice and the Yellow River trail once. Brian hiked each of the three longest trails once. How many more miles did Brian hike than Christine?

Question 6.
Make Sense and Persevere What do you know? What are you asked to find? What information do you not need?
Answer:
Question 7.
Make Sense and Persevere What information do you need to find before you can answer the final question?
Answer:
Read the problem carefully so you can identify what you know and what you are asked to find.

Question 8.
Model with Math Write equations to represent the information in Exercise 7.
Answer:
Question 9.
Make Sense and Persevere Solve the problem.
Answer:
Question 10.
Construct Arguments Explain why your answer makes sense.
Answer:
Topic 8 Fluency Practice
Activity
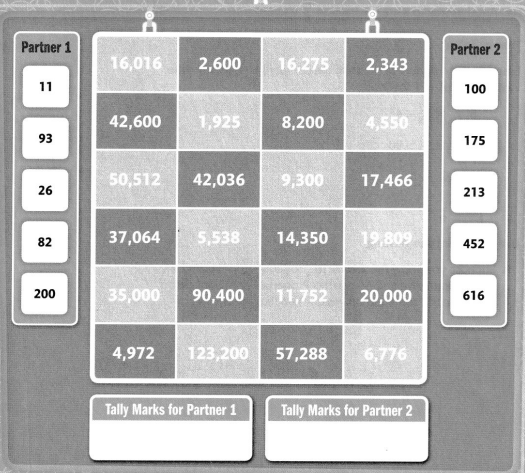
Point & Tally
Work with a partner. Get paper and a pencil. Each partner chooses light blue or dark blue.
At the same time, Partner 1 and Partner 2 each point to one of their black numbers. Both partners find the product of the two numbers.
The partner who chose the color where the product appears gets a tally mark. Work until one partner has seven tally marks.

Topic 8 Vocabulary Review
Glossary
Understand Vocabulary
Choose the best term from the box. Write it on the blank.
Word List
• area model
• Associative Property of Multiplication
• benchmark fractions
• Commutative Property of Multiplication
• mixed number
• round
Question 1.
To estimate the product of two mixed numbers, ____ each factor to the nearest whole number.
Answer:
Question 2.
Using ____ can help make it easier to estimate computations.
Answer:
Question 3.
The product of two fractions can be represented by a(n) ____
Answer:
Question 4.
Another way to write the fraction \(\frac{19}{5}\) is as a ____
Answer:
True or False
Estimate each product to decide if the comparison is true or false. Write T for true or F for false.
____ Question 5.
6\(\frac{3}{5}\) × 5\(\frac{7}{8}\) < 42
Answer:
____ Question 6.
8\(\frac{2}{9}\) × 9\(\frac{1}{4}\) > 90
Answer:
____ Question 7.
\(\frac{2}{7}\) × \(\frac{5}{8}\) < 1
Answer:
___ Question 8.
5\(\frac{1}{10}\) × 3 > 15
Answer:
Use Vocabulary in Writing
Question 9.
Suppose you know the answer to \(\frac{4}{5}\) × (20 × 1\(\frac{7}{8}\)). Explain how the Commutative and Associative Properties of Multiplication can make the computation easier. Then find the answer.
Answer:
Topic 8 Reteaching
Set A
pages 333-336
Find 4 × \(\frac{2}{3}\) using a number line.

Each jump is \(\frac{2}{3}\).
1 × \(\frac{2}{3}\) = \(\frac{2}{3}\)
2 × \(\frac{2}{3}\) = \(\frac{4}{3}\) = 1\(\frac{1}{3}\)
3 × \(\frac{2}{3}\) = \(\frac{6}{3}\) = 2
4 × \(\frac{2}{3}\) = \(\frac{8}{3}\) = 2\(\frac{2}{3}\)
So, 4 × \(\frac{2}{3}\) = 2\(\frac{2}{3}\)
This makes sense because \(\frac{2}{3}\) is less than 1, so 4 × \(\frac{2}{3}\) should be less than 4.
Remember to multiply the numerator of the fraction by the whole number.
Find each product. Use number lines, fraction strips, or drawings to help you.
Question 1.
4 × \(\frac{3}{4}\)
Answer:
Question 2.
7 × \(\frac{1}{4}\)
Answer:
Question 3.
8 × \(\frac{5}{6}\)
Answer:
Question 4.
10 × \(\frac{1}{2}\)
Answer:
Question 5.
9 × \(\frac{1}{3}\)
Answer:
Question 6.
9 × \(\frac{2}{3}\)
Answer:
Question 7.
3 × \(\frac{7}{8}\)
Answer:
Question 8.
7 × \(\frac{3}{8}\)
Answer:
Question 9.
5 × \(\frac{5}{6}\)
Answer:
Question 10.
12 × \(\frac{2}{3}\)
Answer:
Question 11.
15 × \(\frac{4}{5}\)
Answer:
Question 12.
2 × \(\frac{9}{10}\)
Answer:
Set B
pages 337-340, 341-344
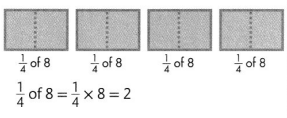
Mary’s clock uses \(\frac{3}{4}\) of the batteries in the package. How many batteries does the clock need?

Find \(\frac{3}{4}\) of 8
\(\frac{1}{4}\) of 8 is 2.
\(\frac{3}{4}\) is three times as much as \(\frac{1}{4}\).
So, \(\frac{3}{4}\) of 8 is three times as much as 2.
\(\frac{3}{4}\) of 8 is 6.
Mary’s clock needs 6 batteries.
Remember that the word of often means to multiply.
Find each product.
Question 1.
4 × \(\frac{1}{2}\)
Answer:
Question 2.
\(\frac{3}{4}\) of 16
Answer:
Question 3.
24 × \(\frac{1}{8}\)
Answer:
Question 4.
\(\frac{4}{7}\) of 28
Answer:
Question 5.
\(\frac{4}{5}\) × 37
Answer:
Question 6.
\(\frac{7}{8}\) × 219
Answer:
Question 7.
Marco weighs 80 pounds. His bones make up about \(\frac{1}{5}\) of his body weight. How much do his bones weigh?
Answer:
Question 8.
Monica bought 12 gallons of paint. She used \(\frac{2}{3}\) of the paint to paint her house. How many gallons of paint did she use?
Answer:
Question 9.
A soccer coach gives each player \(\frac{1}{2}\) liter of water at halftime. If there are 11 players, how many liters does he need?
Answer:
Set C
pages 345-348
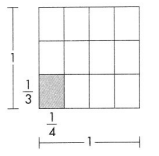
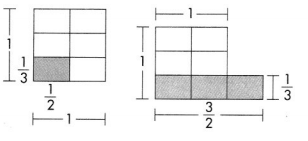
Find \(\frac{2}{3}\) × \(\frac{5}{6}\).
A drawing can show fraction multiplication. Start with a rectangle that has 3 rows and 6 columns. There are 18 sections in all.
For \(\frac{2}{3}\), shade 2 rows.
For \(\frac{5}{6}\), shade 5 columns
Count the sections in the overlap.
10 of the 18 squares are in the overlap area.
so, \(\frac{5}{6}\) × \(\frac{2}{3}\) = \(\frac{10}{18}\) or \(\frac{5}{9}\).
Remember to use each denominator to make the grid.
Find each product. Use models to help.
Question 1.
\(\frac{2}{3}\) × \(\frac{3}{8}\)
Answer:
Question 2.
\(\frac{1}{4}\) × \(\frac{3}{5}\)

Answer:
Question 3.
\(\frac{1}{6}\) × \(\frac{1}{8}\)
Answer:
Question 4.
\(\frac{4}{7}\) × \(\frac{4}{7}\)
Answer:
Set D
pages 349-352
Find \(\frac{4}{5}\) × \(\frac{3}{4}\)
Multiply the numerators to find the numerator of the product. Multiply the denominators to find the denominator of the product.
\(\frac{4}{5}\) × \(\frac{3}{4}\) = \(\frac{4 \times 3}{5 \times 4}\) = \(\frac{12}{20}\) or \(\frac{3}{5}\)
Remember to multiply the numerators together and the denominators together.
Question 1.
\(\frac{6}{7}\) × \(\frac{1}{2}\)
Answer:
Question 2.
\(\frac{3}{8}\) × \(\frac{8}{3}\)
Answer:
Question 3.
\(\frac{2}{3}\) × \(\frac{1}{3}\)
Answer:
Question 4.
\(\frac{7}{8}\) × \(\frac{3}{2}\)
Answer:
Set E
pages 353-356
Find the area of a rectangle with length \(\frac{3}{2}\) and width \(\frac{1}{3}\).
The rectangle of length \(\frac{3}{2}\) and width \(\frac{1}{3}\) is tiled with 3 rectangles of area \(\frac{1}{2 \times 3}\)
So, the area of the rectangle is \(\frac{3}{6}\) or \(\frac{1}{2}\) square unit.
Remember that a unit square can be used to help find areas of rectangles.
Find the area of a rectangle with the given dimensions.
Question 1.
Length: \(\frac{8}{5}\) units
Width: \(\frac{3}{4}\) unit
Answer:
Question 2.
Length: \(\frac{4}{3}\) units
Width: \(\frac{7}{10}\) unit
Answer:
Question 3.
Gabriel has a square canvas that measures \(\frac{5}{4}\) feet on each side. What is the area of Gabriel’s canvas?
Answer:
Set F
pages 357-360 Find 3\(\frac{1}{2}\) × 2\(\frac{7}{8}\)
Estimate: 3\(\frac{1}{2}\) × 2\(\frac{7}{8}\) is about 4 × 3 = 12.
Rename fractions, then multiply.
\(\frac{7}{2}\) × \(\frac{23}{8}\) = \(\frac{161}{16}\) = 10\(\frac{1}{16}\) The product 10\(\frac{1}{16}\) is close to the estimate, 12.
An area model can also represent the product of mixed numbers.
A rectangular field of crops is 4\(\frac{2}{3}\) miles by 2\(\frac{3}{4}\) miles. Calculate 4\(\frac{2}{3}\) × 2\(\frac{3}{4}\) to find the area.
Estimate: 4\(\frac{2}{3}\) × 2\(\frac{3}{4}\) is about 5 × 3 = 15.
Use an area model to find the partial products.
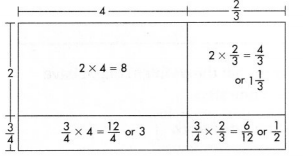
Add the partial products.
8 + 1\(\frac{1}{3}\) + 3 + \(\frac{1}{2}\) =
8 + 1\(\frac{1}{6}\) + 3 + \(\frac{3}{6}\) =
8 + 3 + 1\(\frac{2}{6}\) + \(\frac{3}{6}\) = 12\(\frac{5}{6}\)
So, 4\(\frac{2}{3}\) × 2\(\frac{3}{4}\) = 12\(\frac{5}{6}\)
The area of the field is 12\(\frac{5}{6}\) square miles. The product is close to the estimate of 15, so the answer is reasonable.
Remember to compare your answer with your estimate.
Estimate. Then find each product.
Question 1.
2\(\frac{1}{3}\) × 4\(\frac{1}{5}\)
Answer:
Question 2.
4\(\frac{1}{2}\) × 6\(\frac{2}{3}\)
Answer:
Question 3.
3\(\frac{3}{5}\) × 2\(\frac{5}{7}\)
Answer:
Question 4.
14\(\frac{2}{7}\) × 4\(\frac{3}{10}\)
Answer:
Use the grid. Write the missing labels and find the product.
Question 5.
6\(\frac{2}{3}\) × 3\(\frac{3}{5}\)

Answer:
Question 6.
2\(\frac{5}{12}\) × 3\(\frac{1}{3}\)
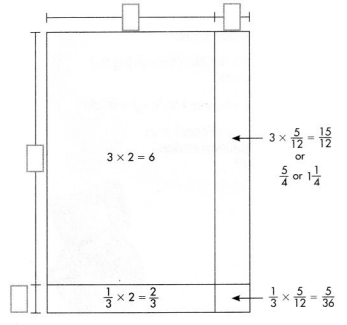
Answer:
Set G
pages 361-364
Multiplication can be thought of as scaling, or resizing, a fraction.
Will the product of 4\(\frac{1}{2}\) × \(\frac{3}{4}\) be greater than or less than 4\(\frac{1}{2}\)? How can you tell without multiplying?
Since \(\frac{3}{4}\) < 1, 4\(\frac{1}{2}\) × \(\frac{3}{4}\) < 4\(\frac{1}{2}\) × 1
Will the product of 4\(\frac{1}{2}\) × 2\(\frac{1}{3}\) be greater than or less than 4\(\frac{1}{2}\)? How can you tell without multiplying?
Since 2\(\frac{1}{3}\) > 1, 4\(\frac{1}{2}\) × 2\(\frac{1}{3}\) > 4\(\frac{1}{2}\) × 1.
So, 4\(\frac{1}{2}\) × 2\(\frac{1}{3}\) will be greater than 4\(\frac{1}{2}\).
Remember that a fraction is equal to 1 if the numerator and denominator are the same.
Without multiplying, decide which symbol belongs in the box: <, >, or =
Question 1.
2\(\frac{1}{10}\) × \(\frac{3}{5}\) ![]() 2\(\frac{1}{10}\)
2\(\frac{1}{10}\)
Answer:
Question 2.
\(\frac{3}{4}\) × \(\frac{5}{5}\) ![]() \(\frac{3}{4}\)
\(\frac{3}{4}\)
Answer:
Question 3.
7\(\frac{1}{2}\) × 1\(\frac{1}{6}\) ![]() 7\(\frac{1}{2}\)
7\(\frac{1}{2}\)
Answer:
Question 4.
\(\frac{8}{3}\) × \(\frac{9}{10}\) ![]() \(\frac{8}{3}\)
\(\frac{8}{3}\)
Answer:
Order each set of numbers from least to greatest.
Question 5.
3\(\frac{1}{5}\), 3\(\frac{1}{5}\) × \(\frac{9}{10}\), 3\(\frac{1}{5}\) × 1\(\frac{1}{2}\)
Answer:
Question 6.
\(\frac{2}{3}\) × \(\frac{3}{4}\), \(\frac{2}{3}\) × \(\frac{5}{4}\), \(\frac{2}{3}\)
Answer:
Question 7.
2\(\frac{1}{3}\) × \(\frac{5}{5}\), 2\(\frac{1}{3}\) × \(\frac{6}{5}\), 2\(\frac{1}{3}\) × \(\frac{1}{5}\)
Answer:
Set H
pages 365-368
Think about these questions to help you make sense and persevere in solving them.
Thinking Habits
• What do I need to find?
• What do I know?
• What’s my plan for solving the problem?
• What else can I try if I get stuck?
• How can I check that my solution makes sense?
Remember that the problem might have more than one step. Solve. Show your work.
Question 1.
John has 1\(\frac{1}{2}\) hours of homework each day from Monday through Thursday and 2\(\frac{3}{4}\) hours over the weekend. How much homework does John have in a week?
Answer:
Question 2.
Elle is buying new flooring for her kitchen and laundry room. She knows that the area of the kitchen is 132 square feet. The laundry room is 8\(\frac{1}{3}\) feet by 6\(\frac{3}{4}\) feet. What is the total area of the two rooms?
Answer:
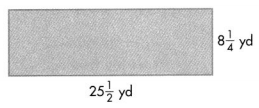
Topic 8 Assessment Practice
Question 1.
Which rectangle has the greater area, a rectangle with length \(\frac{1}{12}\) foot and width \(\frac{3}{4}\) foot or a rectangle with length \(\frac{1}{16}\) foot and width foot?
Answer:
Question 2.
Alberto runs 3\(\frac{1}{2}\) miles each day.

A. Write an equation using the variable n to model how far he runs in 7 days.
B. How far does he run in 7 days?
C. Explain how to estimate how far he would run in 11 days.
Answer:
Question 3.
Is the following equation true? Explain.
\(\frac{5}{6}\) × \(\frac{8}{4}\) = \(\frac{5}{3}\)
Answer:
Question 4.
Complete the equation. Show your work.
16 × \(\frac{5}{8}\) = ?
Answer:
Question 5.
Select all the Expressions that are equal to \(\frac{4}{7}\) × 6.
![]() 4 ÷ 6 × 7 = \(\frac{14}{3}\)
4 ÷ 6 × 7 = \(\frac{14}{3}\)
![]() \(\frac{6}{7}\) × 4 = \(\frac{24}{7}\)
\(\frac{6}{7}\) × 4 = \(\frac{24}{7}\)
![]() 6 ÷ 4 × 7 = 10\(\frac{1}{2}\)
6 ÷ 4 × 7 = 10\(\frac{1}{2}\)
![]() 4 × 6 ÷ 7 = 3\(\frac{3}{7}\)
4 × 6 ÷ 7 = 3\(\frac{3}{7}\)
![]() 7 ÷ 4 × 6 = \(\frac{21}{2}\)
7 ÷ 4 × 6 = \(\frac{21}{2}\)
Answer:
Question 6.
Tracy took a test that had 24 questions. She got \(\frac{5}{6}\) of the questions correct. How many questions did she answer correctly? Write an equation to model your work.
Answer:
Question 7.
Jenna ran 2\(\frac{7}{8}\) kilometers each day for a week. How far did she run in all? Give an estimate, then find the actual amount. Show your work.
Answer:
Question 8.
Eduardo has a recipe that uses \(\frac{2}{3}\) cup of flour for each batch. If he makes 4 batches, how many cups of flour will he need? How many cups of flour will he need in total if he makes 3 more batches? Write your answers as mixed numbers. Use the number line to help.

Answer:
Question 9.
Complete the equation. Explain how you got your answer.
\(\frac{6}{7}\) × \(\frac{2}{5}\) = ?
Answer:
Question 10.
Ted and his friends are rolling out clay for art class. Ted rolled out his clay until it was 2 feet long. Noah rolled out his clay
\(\frac{3}{5}\) as long as Ted’s clay. Jeannine rolled out her clay until it was 1\(\frac{1}{2}\) times as long as Ted’s clay. Miles rolled out his clay \(\frac{5}{5}\) as long as Ted’s clay.
A. Without completing the multiplication, whose clay is longer than Ted’s clay? How can you tell?
B. Without completing the multiplication, whose clay is shorter than Ted’s clay? How can you tell?
C. Whose clay is the same length as Ted’s clay? How can you tell?
Answer:
Question 11.
Find the product of \(\frac{7}{8}\) × \(\frac{9}{10}\). Then write another product with the same answer.
Answer:
Question 12.
Which of the following is equal to \(\frac{4}{7}\) × \(\frac{11}{15}\)?
a. \(\frac{4 \times 7}{11 \times 15}\) = \(\frac{28}{165}\)
b. \(\frac{4 \times 15}{7 \times 11}\) = \(\frac{60}{77}\)
c. \(\frac{4 \times 11}{7 \times 15}\) = \(\frac{44}{105}\)
d. \(\frac{7 \times 15}{4 \times 11}\) = \(\frac{105}{44}\)
Answer:
Question 13.
Members of a landscaping company built a retaining wall. They used brick to make the top \(\frac{2}{3}\) of the wall.
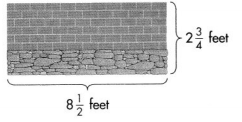
A. What is the height of the brick portion of the wall? Write an equation to model your work.
B. Estimate the area of the whole retaining wall.
C. What is the area of the whole retaining wall? Write an equation to show your work. Compare your answer to your estimate to see if your answer is reasonable.
Answer:
Question 14.
Tyler’s family rented 15 DVDs last month.

A. Of the 15 DVDs, \(\frac{1}{5}\) were comedies. How many movies were comedies? Use the model to help you.
B. Of the 15 DVDs, \(\frac{3}{5}\) were comedies. How many movies were comedies? Use the model to help you.
C. What relationship do you notice between the number of comedies and the number of documentaries?
Answer:
Question 15.
Kristen and Niko buy a canvas for their art studio.
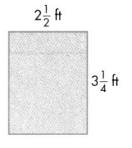
A. Estimate the area of their canvas. Write an equation to model your work.
B. Find the actual area of their canvas. Write your answer as a mixed number.
C. Compare your answer to your estimate to see if your answer is reasonable.
Answer:
Topic 8 Performance Task
What’s for Dinner?
Branden and Ashley are making the casserole in the Tuna Casserole Recipe card.
Question 1.
Branden is trying to decide how much tuna casserole to make.
Part A
How many cups of tuna does Branden need to make 3 times the recipe? Draw a model to show how to solve.

Part B
How many cups of shredded cheddar cheese does Branden need to make \(\frac{2}{3}\) of the recipe? Draw a model to show your work.
Part C
How many cups of fried onion rings does Branden need to make 2\(\frac{1}{2}\) times the recipe? Show how to use a model and partial products to multiply.
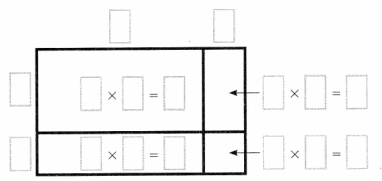
Part D
How many cups of cooked macaroni does Branden need to make 2\(\frac{1}{2}\) times the recipe? Show how to rename fractions, then multiply.
Answer:
Question 2.
Ashley’s casserole dish is shown in Ashley’s Dish drawing.
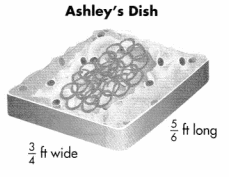
Part A
What is the area of the bottom of Ashley’s dish? Complete the model to show your work.
Part B
Branden’s casserole dish is 1\(\frac{1}{2}\) times as wide and 1\(\frac{4}{5}\) times as long as Ashley’s dish. Is Branden’s dish longer or shorter than Ashley’s dish? Explain your reasoning.
Part C
What is the area of the bottom of Branden’s dish? Show your work.
Answer: