Practice with the help of enVision Math Common Core Grade 7 Answer Key Topic 4 Generate Equivalent Expressions regularly and improve your accuracy in solving questions.
enVision Math Common Core 7th Grade Answers Key Topic 4 Generate Equivalent Expressions
Topic 4 Essential Question
How can properties of operations help to generate equivalent expressions that can be used in solving problems?
3-ACT MATH

Topic 4 enVision STEM Project
Did You Know?
In 2013, just over 30% of American consumers knew about activity trackers. By 2015, about 82% recognized them.
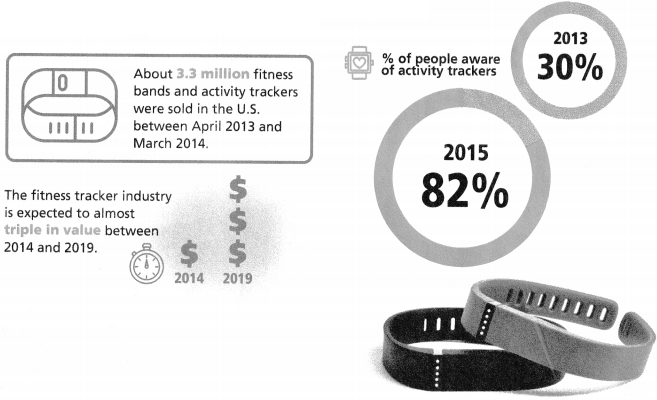
Continued research and development leads to technological advances and breakthroughs, such as the use of biosensing apparel to track activity.

Your Task: Analyze Activity Tracker Data
The ways that data are communicated and presented to the user are just as important as the types of data collected. You and your classmates will continue your exploration of activity trackers and use data to develop models based on individual fitness goals.
Topic 4 Get Ready
Review What You Know
Vocabulary
Choose the best term from the box to complete each definition.
evaluate
expression
factor
order of operations
substitute
term
Question 1.
When you __________ an expression, you replace each variable with a given value.
Answer:
When you evaluate an expression, you replace each variable with a given value.
Explanation:
In the above-given question,
given that,
when we evaluate an expression, we replace each variable with a given value.
for example:
Evaluate 3a-2b.
for a = 6 and b = 4.
3(6) – 2(4).
18 – 8.
10.
Question 2.
To evaluate a + 3 when a = 7, you can _________ 7 for a in the expression.
Answer:
To evaluate a + 3 when a = 7, you can substitute 7 for a in the expression.
Explanation:
In the above-given question,
given that,
if we evaluate a + 3 when a = 7.
we will substitute 7 for a in the expression.
a + 3.
7 + 3.
10.
Question 3
The set of rules used to determine the order in which operations are performed is called the _________
Answer:
The set of rules used to determine the order in which operations are performed is called the order of operations.
Explanation:
In the above-given question,
given that,
The set of rules used to determine the order in which operations are performed is called the order of operations.
for example:
3 + [6(11 + 1 – 4)]/8 x 2.
3+[6(8)]/8 x 2.
3 + 48 / 8 x 2.
3 + 6 x 2.
3 + 12.
15.
Question 4.
Each part of an expression that is separated by a plus or minus sign is a(n) __________.
Answer:
Each part of an expression that is separated by a plus or minus sign is the term.
Explanation:
In the above-given question,
given that,
Each part of an expression that is separated by a plus or minus sign is the term.
for example:
2x + 4y – 9.
where x and y are variables.
9 is the constant.
2 and 4 are coefficients.
terms are 2x, 4y, and 9.
Question 5.
A(n) __________ is a mathematical phrase that can contain numbers, variables, and operation symbols.
Answer:
An expression is a mathematical phrase that can contain numbers, variables, and operation symbols.
Explanation:
In the above-given question,
given that,
An expression is a mathematical phrase that can contain numbers, variables, and operation symbols.
for example:
n + 7 = 10.
x – 5 = 3.
3p = 15.
y/2 = 5.
Question 6.
When two numbers are multiplied to get a product, each number is called a(n) _________.
Answer:
When two numbers are multiplied to get a product, each number is called a factor.
Explanation:
In the above-given question,
given that,
When two numbers are multiplied to get a product, each number is called a factor.
for example:
3 x 5 = 15.
3 and 5 are the factors.
15 is the product.
Order of Operations
Evaluate each expression using the order of operations.
Question 7.
3(18 – 7) + 2
Answer:
3(18 – 7) + 2 = 35.
Explanation:
In the above-given question,
given that,
3(18 – 7) + 2.
3(11) + 2.
33 + 2.
35.
3(18 – 7) + 2 = 35.
Question 8.
(13 + 2) ÷ (9 – 4)
Answer:
(13 + 2) ÷ (9 – 4) = 3.
Explanation:
In the above-given question,
given that,
(13 + 2) ÷ (9 – 4).
(13 + 2) ÷ (9 – 4).
15 / 5.
3.
(13 + 2) ÷ (9 – 4) = 3.
Question 9.
24 ÷ 4 • 2 – 2
Answer:
24 ÷ 4 • 2 – 2 = 10.
Explanation:
In the above-given question,
given that,
24 ÷ 4 • 2 – 2.
6 . 2 – 2.
12 – 2.
10.
24 ÷ 4 • 2 – 2 = 10.
Equivalent Expressions
Evaluate each expression when a = -4 and b = 3.
Question 10.
ab
Answer:
ab = -12.
Explanation:
In the above-given question,
given that,
a = -4 and b = 3.
– 4 x 3.
-12.
ab = -12.
Question 11.
2a + 3b
Answer:
2a + 3b = 1.
Explanation:
In the above-given question,
given that,
a = -4 and b = 3.
2(-4) + 3(3).
-8 + 9.
1.
2a + 3b = 1.
Question 12.
2(a – b)
Answer:
2(a – b) = -14.
Explanation:
In the above-given question,
given that,
a = -4 and b = 3.
2(-4 – 3).
2(-7).
-14.
2(a – b) = -14.
Question 13.
Explain the difference between evaluating 3 • 7 – 4 ÷ 2 and evaluating 3(7 – 4) ÷ 2.
Answer:
The two expressions are different.
Explanation:
In the above-given question,
given that,
3 . 7 – 4 ÷ 2.
3 . 7 – 2.
21 – 2.
19.
3(7 – 4) ÷ 2.
3(3) / 2.
9 / 2.
Language Development
Complete each math statement using the word bank.

To evaluate an algebraic expression, substitute a __________ for the variable in the expression.
Answer:
To evaluate an algebraic expression, substitute properties of operations for the variable in the expression.
Explanation:
In the above-given question,
given that,
To evaluate an algebraic expression, substitute properties of operations for the variable in the expression.
for example:
n + 7 = 10.
x – 5 = 3.
3p = 15.
y/2 = 5.
In the algebraic expression 3(x – 2), 3 and x – 2 are ___________
Answer:
In the algebraic expression 3(x – 2), 3, and x – 2 are coefficients.
Explanation:
In the above-given question,
given that,
In the algebraic expression 3(x – 2), 3 and x – 2 are coefficients.
for example:
3(x – 2).
3 and x-2 are coefficients.
To generate equivalent expressions, you can use the __________
Answer:
To generate equivalent expressions, you can use the order of operations.
Explanation:
In the above-given question,
given that,
To generate equivalent expressions, you can use the order of operations.
for example:
5(x – 1) + 7.
5(x) + 5(-7) + 7.
5x – 5 + 7.
5x + 2.
In the expression 4x + 2x – 6y, you first need to __________
Answer:
In the expression 4x + 2x – 6y, you first need to add.
Explanation:
In the above-given question,
given that,
In the expression 4x + 2x – 6y, you first need to add.
4x + 2y – 6y.
4x – 4y.
You can use the Distributive Property to __________ the algebraic expression 5(x – 7).
Answer:
You can use the Distributive property to find the algebraic expression.
Explanation:
In the above-given question,
given that,
we can use the distributive property to find the algebraic expression.
for example:
5(x – 7).
5x – 35.
In the algebraic expression, 6x + 10, x is the ________ , 6 is the ________ and 10 is the ___________
Answer:
In the algebraic expression 6x + 10, x is the coefficient, 6 is the variable, and 10 is the constant.
Explanation:
In the above-given question,
given that,
In the algebraic expression 6x + 10, x is the coefficient, 6 is the variable, and 10 is the constant.
for example:
6x + 10.
where 6 is the variable.
x is coefficient.
10 is constant.
Four words that describe operations that can be used with expressions are _________, and ________, _________ and __________.
Answer:
The words that describe the operations are constants, terms, variables, and coefficients.
Explanation:
In the above-given question,
given that,
The words that describe the operations are constants, terms, variables, and coefficients.
for example:
2x + 4y – 9.
where x and y are variables.
9 is the constant.
2 and 4 are coefficients.
terms are 2x, 4y, and 9.
In the algebraic expression 5x + 4 + 6x – 3, you use the Commutative Property to _________ like terms next to each other and the Associative Property to _________ like terms together.
Answer:
Pick A Project
PROJECT 4A
Which emojis would you use to tell the story of your day so far?
PROJECT: WRITE AND ILLUSTRATE A CHILDREN’S BOOK

PROJECT 4B
How many different ways can you represent a dollar?
PROJECT: GENERATE EQUIVALENCE

PROJECT 4C
If you wrote a song, what would it sound like?
PROJECT: COMPOSE A SONG

PROJECT 4D
What was your favorite structure at a playground when you were younger?
PROJECT: BUILD A MODEL PLAYGROUND

Lesson 4.1 Write and Evaluate Algebraic Expressions
Solve & Discuss It!
Mr. Ramirez’s class was playing a game in which students need to match sticky notes that have equivalent expressions. How can you sort the expressions into groups?
I can… write and evaluate algebraic expressions.
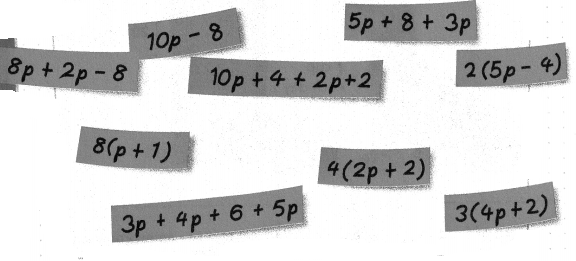
Focus on math practices
Reasoning is there more than one way to group the expressions? Give an example.
Answer:
Yes, there are more than one way to group the expressions.
Explanation:
In the above-given question,
given that,
A numerical expression in mathematics can be a combination of numbers, integers combined using.
for example:
16 is an numerical expression.
Essential Question
How can algebraic expressions be used to represent and solve problems?
Answer:
We can use algebra to solve mathematical problems.
Explanation:
In the above-given question,
given that,
we can also interpret the solution in the context of the original problem.
for example:
2x + 5 = 43.
where 43 is the constant.
always has an equal symbol.
2x + 5 = algebraic expression.
Try It!
Misumi started with $217 in her bank account. She deposits $25.50 each week and never withdraws any money. What expression can Misumi use to determine her account balance after w weeks?
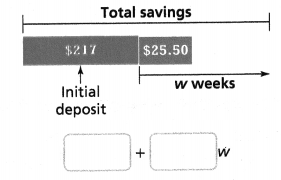
Answer:
The expression can Misumi use to determine her account balance after w weeks = 8.5 weeks.
Explanation:
In the above-given question,
given that,
Misumi started with $217 in her bank account.
She deposits $25.50 each week and never withdraws any money.
$217 / 25.50 = 8.5.
so the expression can Misumi use to determine her account balance after w weeks = 8.5.
Convince Me! How did you determine which value to use for the constant and which value to use for the coefficient?
Answer:
x is coefficient and 3 is constant.
Explanation:
In the above-given question,
given that,
2x + 3 is the expression.
x is the coefficient.
3 is the constant.
Try It!
The cost to rent a scooter is $15.50 per hour and the cost to rent a watercraft is $22.80 per hour. Use the expression 15.5s + 22.8w to determine how much it would cost to rent a scooter for 3\(\frac{1}{2}\) hours and a watercraft for 1\(\frac{3}{4}\) hours.
Answer:
The cost would cost to rent a scooter for 3(1/2) hours and watercraft for 1(3/4) hours = $54.25 and $40.
Explanation:
In the above-given question,
given that,
The cost to rent a scooter is $15.50 per hour and the cost to rent a watercraft is $22.80 per hour.
Use the expression 15.5s + 22.8w to determine how much.
15.5s + 22.8w.
3. 1/2 = 7/2.
1. 3/4 = 7/4.
15.5(7/2) + 22.8(7/4).
108.5/2 + 159.6/4.
54.25 + 39.9.
Try It!
Emelia earns $8.74 per hour plus a gas allowance of $3.50 per day at her job. How much does Emelia’s job pay in a day when she works 5\(\frac{1}{2}\) hours? Write an expression and evaluate for 5\(\frac{1}{2}\) hours.
Answer:
Emelia’s job pay in a day when she works 5(1/2) hours = $67.32.
Explanation:
In the above-given question,
given that,
Emelia earns $8.74 per hour plus a gas allowance of $3.50 per day at her job.
$8.74 + $3.50.
$12.24.
5(1/2) = 5.5.
5.5 x $12.24 = $67.32.
so Emelia’s job pay in a day when she works 5(1/2) hours = $67.32.
KEY CONCEPT
Algebraic expressions can be used to represent problems with unknown or variable values. Values can be substituted for variables to evaluate the expression.
Do You Understand?
Question 1.
Essential Question How are algebraic expressions used to represent and solve problems?
Answer:
Algebraic expressions are used to represent problems with unknowns or variable values.
Explanation:
In the above-given question,
given that,
Algebraic expressions are used to represent problems with unknowns or variable values.
Values can be substituted for variables to evaluate the expression.
for example:
2x + 3y = a.
where x = 2 and y = 3.
2 x 2 + 3 x 3 = a.
4 + 9 = a.
13 = a.
Question 2.
Use Structure How is a constant term different than a variable term for an expression that represents a real-world situation?
Answer:
a = 13.
Explanation:
In the above-given question,
given that,
2x + 3y = a.
where x = 2 and y = 3.
2 x 2 + 3 x 3 = a.
4 + 9 = a.
13 = a.
Question 3.
Look for Relationships Explain why you can have different values when evaluating an algebraic expression.
Answer:
To evaluate an algebraic expression we have to substitute a number for each variable and perform the arithmetic operations.
Explanation:
In the above-given question,
given that,
To evaluate an algebraic expression we have to substitute a number for each variable and perform the arithmetic operations.
for example:
x + 6.
where x = 6.
6 + 6 = 12.
if we know the value of our variables, we can replace the variables with their values and then evaluate the expression.
Do You Know How?
Question 4.
A tank containing 35 gallons of water is leaking at a rate of \(\frac{1}{4}\) gallon per minute. Write an expression to determine the number of gallons left in the tank after m minutes.
Answer:
The number of gallons left in the tank after m minutes = 8.75 gallons.
Explanation:
In the above-given question,
given that,
A tank containing 35 gallons of water is leaking at a rate of \(\frac{1}{4}\) gallon per minute.
35 x 1/4 = 35/4.
8.75.
so the number of gallons left in the tank after m minutes = 8.75 gallons.
Question 5.
Write an algebraic expression that Marshall can use to determine the total cost of buying a watermelon that weighs w pounds and some tomatoes that weigh t pounds. How much will it cost to buy a watermelon that weighs 18\(\frac{1}{2}\) pounds and 5 pounds of tomatoes?
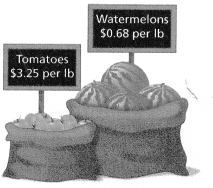
Answer:
The much will it cost to buy a watermelon that weighs 18(1/2) pounds and 5 pounds of tomatoes = $29.25 and $3.4.
Explanation:
In the above-given question,
given that,
the cost of tomatoes is $3.25 per lb.
the cost of watermelons is $0.68 per lb.
18/2 = 9.
$3.25 x 9 = $29.25.
0.68 x 5 = $3.4.
so the much will it cost to buy a watermelon that weighs 18(1/2) pounds and 5 pounds of tomatoes = $29.25 and $3.4.
Question 6.
What is the value of \(\frac{3}{8}\)x – 4.5 when x = 0.4?
Answer:
(3/8)x – 4.5 = 4.35.
Explanation:
In the above-given question,
given that,
(3/8)x – 4.5.
where x = 0.4.
(3/8)0.4 – 4.5.
0.375 x 0.4 – 4.5.
0.15 – 4.5.
4.35.
(3/8)x – 4.5 = 4.35.
Question 7.
What is the value of 8.4n – 3.2p when n = 2 and p = 4?
Answer:
8.4n – 3.2p = 4.
Explanation:
In the above-given question,
given that,
8.4n – 3.2p.
8.4 (2) – 3.2 (4).
16.8 – 12.8.
4.
8.4n – 3.2p = 4.
Practice & Problem Solving
Leveled Practice For 8-10, fill in the boxes to complete the problems.
Question 8.
Evaluate 10.2x + 9.4y when x = 2 and y = 3.
10.2 (_______) + 9.4 (_______)
= _______ + 28.2
= _______
Answer:
10.2 x + 9.4 y = 48.6.
Explanation:
In the above-given question,
given that,
10.2 x + 9.4 y.
where x = 2 and y = 3.
10.2 x 2 + 9.4 x 3.
20.4 + 28.2.
48.6.
10.2 x + 9.4 y = 48.6.
Question 9.
Evaluate \(\frac{1}{2}\)t + \(\frac{3}{8}\) when t = \(\frac{1}{4}\)
\(\frac{1}{2}\)(________) + \(\frac{3}{8}\)
= ______ + \(\frac{3}{8}\)
= ______
Answer:
1/2 x 1/4 + 3/8 = 0.5.
Explanation:
In the above-given question,
given that,
1/2 = 0.5.
1/4 = 0.25.
0.5 x 0.25 + 3/8.
0.125 + 0.375.
0.5.
1/2 x 1/4 + 3/8 = 0.5.
Question 10.
Write an expression that represents the height of a tree that began at 6 feet and increases by 2 feet per year. Let y represent the number of years.
_____ + ______ y
Answer:
6x + 2y.
Explanation:
In the above-given question,
given that,
the height of a tree that began at 6 feet and increases by 2 feet per year.
6x + 2y.
where y represents the number of years.
so the expression is 6x + 2y.
For 11-14, evaluate each expression for the given value of the variable(s).
Question 11.
3d – 4
d = 1.2
Answer:
3d – 4 = 0.4.
Explanation:
In the above-given question,
given that,
3d – 4.
where d = 1.2.
3(1.2) – 4.
3.6 – 4.
0.4.
3d – 4 = 0.4.
Question 12.
0.5f – 2.39
f = 12, 9 = 2
Answer:
0.5f – 2.39 = 3.68.
Explanation:
In the above-given question,
given that,
0.5f – 2.39.
where f = 12 and 9 = 2.
0.5 x 12 – 2.32.
6 – 2.32.
3.68.
0.5f – 2.39 = 3.68.
Question 13.
p + 3
p = \(\frac{3}{5}\)
Answer:
p + 3 = 3.6.
Explanation:
In the above-given question,
given that,
p + 3.
where p = 3/5.
3/5 = 0.6.
0.6 + 3.
3.6.
p + 3 = 3.6.
Question 14.
34 + \(\frac{4}{9}\)w
w = –\(\frac{1}{2}\)
Answer:
34 + 4/9x w = 33.9.
Explanation:
In the above-given question,
given that,
34 + 4/9x w.
where w = -1/2.
34 + 4/9(-1/2).
34 + 0.4(-0.5).
34 – 0.1.
33.9.
Question 15.
Model with Math What expression can be used to determine the total cost of buying g pounds of granola for $3.25 per pound and f pounds of flour for $0.74 per pound?
Answer:
$3.25g and $0.74f.
Explanation:
In the above-given question,
given that,
the total cost of buying g pounds of granola for $3.25 per pound.
f pounds of flour for $0.74 per pound.
$3.25g + $0.74f
Question 16.
Model with Math Which expression can be used to determine the total weight of a box that by itself weighs 0.2 kilogram and contains p plaques that weigh 1.3 kilograms each?
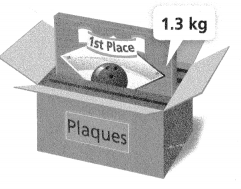
A. 1.3p +0.2
B. 0.2p + 1.3
C. 0.2 – 1.3p
D. 1.2p
Answer:
Option A is correct.
Explanation:
In the above-given question,
given that,
total weight of a box that by itself weighs 0.2 kilogram.
and contains p plaques that weigh 1.3 kilograms each.
0.2 + 1.3p.
so option A is correct.
Question 17.
The expression -120 + 13n represents a submarine that began at a depth of 120 feet below sea level and ascended at a rate of 13 feet per minute. What was the depth of the submarine after 6 minutes?
Answer:
The depth of the submarine after 6 minutes = – 42 feet.
Explanation:
In the above-given question,
given that,
The expression -120 + 13n represents a submarine that began at a depth of 120 feet below sea level.
ascended at a rate of 13 feet per minute.
-120 + 13(6).
-120 + 78.
-42.
so the depth of the submarine after 6 minutes = -42 feet.
Question 18.
Be Precise A full grain silo empties at a constant rate. Write an expression to determine the amount of grain left after s seconds.

Answer:
The amount of grain left after 5 seconds = 2982.5 cubic feet.
Explanation:
In the above-given question,
given that,
A full grain silo empties at a constant rate.
the capacity of food grain is 3000 cubic feet.
3000 – 3.5/s.
3000 – 3.5(5).
3000 – 17.5.
2982.5.
so the amount of grain left after 5 seconds = 2982.5 cubic feet.
Question 19.
Higher Order Thinking For the expression 5 – 5x to have a negative value, what must be true about the value of x?
Answer:
The value of x = 4.
Explanation:
In the above-given question,
given that,
the expression is 5 – 5x.
where x = 4.
5 – 5(4).
5 – 20.
-15.
Assessment Practice
Question 20.
Joe bought g gallons of gasoline for $2.85 per gallon and c cans of oil for $3.15 per can.
PART A
What expression can be used to determine the total amount Joe spent on gasoline and oil?
Answer:
The total amount joe spend on gasoline and oil = $2.85g + $3.15c.
Explanation:
In the above-given question,
given that,
Joe bought g gallons of gasoline for $2.85 per gallon.
c cans of oil for $3.15 per can.
$2.85g + $3.15c.
so the total amount joe spends on gasoline and oil = $2.85g + $3.15c.
PART B
Joe spent $15. He bought 2 cans of oil. About how many gallons of gasoline did he buy?
A. 2.5
B. 3
C. 3.5
D. 4
Answer:
The gallons of gasoline did he buy = 3 gallons.
Explanation:
In the above-given question,
given that,
Joe spent $15. He bought 2 cans of oil.
1.5 x 2.
3.
the gallons of gasoline did he buy = 3.
so option B is correct.
Question 21.
The outside temperature was 73°F at 1 P.M. and decreases at a rate of 1.5°F each hour. What expression can be used to determine the temperature h hours after 1 P.M.?
Answer:
The expression can be used to determine the temperature h hours after 1 P.M = 71.5°F.
Explanation:
In the above-given question,
given that,
The outside temperature was 73°F at 1 P.M. and decreases at a rate of 1.5°F each hour.
73 – 1.5.
71.5°F.
so the expression can be used to determine the temperature h hours after 1 P.M = 71.5°F.
Lesson 4.2 Generate Equivalent Expressions
Explore It!
A shipment of eggs contains some cartons with a dozen eggs and some cartons with a half-dozen eggs.
I can… write equivalent expressions for given expressions.

A. How can you represent the total number of eggs in the shipment using diagrams or images? Explain your diagram.
Answer:
1 dozen + 1/2 dozen eggs.
Explanation:
In the above-given question,
given that,
A shipment of eggs contains some cartons with a dozen eggs and some cartons with a half-dozen eggs.
1 dozen = 12.
1/2 doxen = 12/2.
12/2 = 6.
12 + 1/2 eggs.
B. How can you represent the total number of eggs in the shipment using expressions? What variables do you use? What do they represent?
Answer:
1 dozen + 1/2 dozen eggs.
Explanation:
In the above-given question,
given that,
A shipment of eggs contains some cartons with a dozen eggs and some cartons with a half-dozen eggs.
1 dozen = 12.
1/2 doxen = 12/2.
12/2 = 6.
12 + 1/2 eggs.
Focus on math practices
Construct Arguments How do the two representations compare? How are they different?
Essential Question
What are equivalent expressions?
Try It!
Nancy wrote the expression 3x – 12 to represent the relationship in a table of values. Use properties of operations to write two equivalent expressions.
3(x – _____)
_____ + 3x
Answer:
The two equivalent expressions are 36 + 3x.
Explanation:
In the above-given question,
given that,
3x – 12.
3(x – 12).
3x – 36.
36 + 3x.
Convince Me! What property can you use to write an equivalent expression for -5(x – 2)? Explain.
Answer:
-5(x – 2) = -5x – 10.
Explanation:
In the above-given question,
given that,
-5(x – 2).
-5x – 10.
we can use the distributive property.
-5x -10.
Try It!
Use properties of operations to write two expressions that are equivalent to \(\frac{3}{4}\)n + (8 + \(\frac{1}{3}\)z).
Answer:
3/4n + (8 + {1/3}) = 0.75n + 8.3z.
Explanation:
In the above-given question,
given that,
3/4n + (8 + {1/3})z.
3/4n + 8 + 0.3z.
0.75n + 8.3z.
3/4n + (8 + {1/3}) = 0.75n + 8.3z.
Try It!
Write two expressions that are equivalent to –\(\frac{5}{4}\)x – \(\frac{3}{4}\)
Answer:
-5/4 – 3/4 = 2.
Explanation:
In the above-given question,
given that,
-5/4 – 3/4.
-5/4 = 1.25.
3/4 = 0.75.
-1.25 – 0.75.
2.
KEY CONCEPT
You can use properties of operations to write equivalent expressions.

Do You Understand?
What are equivalent
Question 1.
Essential Question expressions?
Answer:
-1/2(x + 8), -1/2x + (-4) and -4 +(-1/2x) are equivalent.
Explanation:
In the above-given question,
given that,
-1/2(x + 8).
-1/2x + (-1/2) . 8.
-1/2x + (-4).
-4 + (-1/2x).
the three expressions are true.
Question 2.
Make Sense and Persevere For which operations is the Commutative Property true?
Answer:
(-4) + -1/2x.
Explanation:
In the above-given question,
given that,
(-4) + -1/2x.
we can use the commutative property for the expression.
-1/2x + (-4).
Question 3.
How can the Associative Property be applied when writing equivalent expressions with variables?
Answer:
Do You Know How?
Question 4.
Write an expression equivalent to -3 + \(\frac{2}{3}\)y – 4 – \(\frac{1}{3}\)y.
Answer:
-3 + (2/3)y – 4 – (1/3)y.
Explanation:
In the above-given question,
given that,
-3 + \(\frac{2}{3}\)y – 4 – \(\frac{1}{3}\)y.
-3 + (2/3)y – 4 – (1/3)y.
-3 – 4 + (2/3)y – (1/3)y.
-7 + 1/3y.
-3 + (2/3)y – 4 – (1/3)y = -7 + 1/3y.
Question 5.
Complete the tables to determine if the expressions are equivalent. If the expressions are equivalent, name the property or properties that make them equivalent.
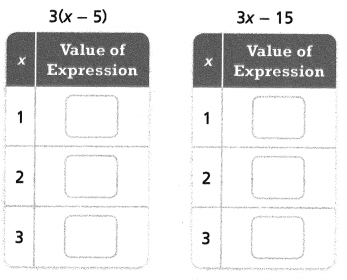
Answer:
3(x – 5) = 3x – 15.
Explanation:
In the above-given question,
given that,
3(x – 5).
3x – 15.
x = 1.
3 – 15 = -12.
x = 2.
6 – 15 = -9.
x = 3.
9 – 15 = -6.
Question 6.
Use the properties of operations to write an expression equivalent to 4x + \(\frac{1}{2}\) + 2x – 3.
Answer:
4x +[{1/2}] + 2x – 3 = 3x -3.
Explanation:
In the above-given question,
given that,
4x + (1/2) + 2x – 3.
4x + 2x + (1/2) – 3.
6x + (1/2) -3.
3x – 3.
4x +[{1/2}] + 2x – 3 = 3x -3.
Practice & Problem Solving
For 7-9, write an equivalent expression.
Question 7.
-3(7 + 5g)
Answer:
-36g.
Explanation:
In the above-given question,
given that,
-3(7 + 5g).
-3 x 7 = -21.
-3 x 5 = 15.
-21 + (-15g).
-36g.
Question 8.
(x + 7) + 3y
Answer:
24xy.
Explanation:
In the above-given question,
given that,
(x + 7) + 3y.
3y x X + 3y x 7.
3xy + 21y.
24xy.
Question 9.
\(\frac{2}{9}\) – \(\frac{1}{5}\) • x
Answer:
2/9 – 1/5 . X =
Explanation:
In the above-given question,
given that,
2/9 x X – (1/5)x.
2/9 x – 1/5 x.
Question 10.
Which expression is equivalent to t + 4 + 3 – 2t?
A. t + 7
B. -t + 7
C. 6t
D. 10t
Answer:
t + 4 + 3 – 2t = -t + 7.
Explanation:
In the above-given question,
given that,
t + 4 + 3 – 2t.
t + 7 – 2t.
t – 2t + 7.
-t + 7.
t + 4 + 3 – 2t = -t + 7.
Question 11.
The distance in feet that Karina swims in a race is represented by 4d – 4, where d is the distance for each lap. What is an expression equivalent to 4d – 4?

Answer:
The expression equal to 4d – 4 = 4(d – 4).
Explanation:
In the above-given question,
given that,
4d – 4.
4(d – 4).
4d – 16.
4d – 4 = 4d – 16.
Question 12.
Use the Associative Property to write an expression equivalent to (w + 9) + 3.
Answer:
The expression is (3 + w) + 9.
Explanation:
In the above-given question,
given that,
the expression is (w + 9) + 3.
(3 + w) + 3.
6 + w.
Question 13.
Nigel is planning his training schedule for a marathon over a 4-day period. He is uncertain how many miles he will run on two d
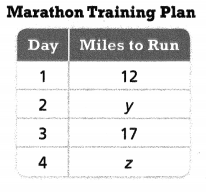
Answer:
The number of miles he will run on two days = 14.5 miles.
Explanation:
In the above-given question,
given that,
Nigel is planning his training schedule for a marathon over a 4-day period.
on day 1 he will run 12 miles.
on day 2 he will run 14.5 miles.
on day 3 he will run 17 miles.
12 + 17 = 29.
29/2 = 14.5.
on day 2 he will run 14.5 miles.
Question 14.
Maria said the expression -4n+ 3 + 9n – 4 is equivalent to 4n. What error did Maria likely make?
Answer:
-4n + 3 + 9n – 4 = 5n – 1.
Explanation:
In the above-given question,
given that,
-4n + 3 + 9n – 4.
-4n + 9n = 5n.
5n + 3 – 4.
5n – 1.
-4n + 3 + 9n – 4 = 5n – 1.
Question 15.
Write an expression equivalent to x – 3y + 4.
Answer:
x – 3y + 4 = 4 + x – 3y.
Explanation:
In the above-given question,
given that,
x – 3y + 4.
4 + x – 3y.
x + 4 – 3y.
Question 16.
Andre wrote the expression -2 + 4x = 3 to represent the relationship shown in the table.

Write two other expressions that also represent the relationship shown in the table.
Answer:
-2 + 4x = 3.
Explanation:
In the above-given question,
given that,
-2 + 4x.
x = 0.
-2 + 0.
-2.
x = 6.
-2 + 4(6).
-2 + 24.
22.
x = 12.
-2 + 4(12).
-2 + 48.
46.
Question 17.
Higher Order Thinking to rent a car for a trip, four friends are combining their money. The group chat shows the amount of money that each puts in. One expression for their total amount of money is 189 plus p plus 224 plus q.

a. Use the Commutative Property to write two equivalent expressions.
Answer:
The expressions are 189 + p + 224q.
Explanation:
In the above-given question,
given that,
189 + p + 224q.
p + 189 + 224q.
224q + p + 189.
b. If they need $500 to rent a car, find at least two different pairs of numbers that p and q could be.
Answer:
$500 + p + 224q.
Explanation:
In the above-given question,
given that,
500 – 224 = 276.
276 + p + 224q.
p + 276 + 224q.
224q + 276 + p.
Assessment Practice
Question 18.
Select all expressions equivalent to \(\frac{3}{5}\)x + 3.

Answer:
The expressions equivalent to (3/5)x + 3 = 1 + 2/5x + 3 and 4/5x – 1/5x + 3.
Explanation:
In the above-given question,
given that,
(3/5)x + 3.
1 + 2/5x + 3.
4/5x – 1/5x + 3.
3/5x + 3.
so the expressions equivalent to (3/5)x + 3 = 1 + 2/5x + 3 and 4/5x – 1/5x + 3.
Lesson 4.3 Simplify Expressions
Solve & Discuss It!
How can the tiles below be sorted?
I can… use properties of operations to simplify expressions.

Focus on math practices
Reasoning Would sorting the tiles with positive coefficients together and tiles with negative coefficients together help to simplify an expression that involves all the tiles? Explain.
Answer:
The positive coefficients are 4.25, 3/5y, 3/8, 1/5, 2.1x, and 1/2x.
The negative coefficients are -0.5, -0.5x, -2.1y, and -2.
Explanation:
In the above-given question,
given that,
the coefficients are 4.25, 3/5y, 3/8, 1/5, 2.1x, -0.5, -0.5x, -2.1y, -2, and 1/2x.
the positive coefficients are 4.25, 3/5y, 3/8, 1/5, 2.1x, and 1/2x.
the negative coefficients are -0.5, -0.5x, -2.1y, and -2.
Essential Question
How are properties of operations used to simplify expressions?
Try It!
Simplify the expression – 6 – 6f + 7 – 3f – 9.
______ – 3f – _____ + 7 – ______
_____ – ______
Answer:
-6 – 6f + 7 – 3f – 9 = -9f – 23.
Explanation:
In the above-given question,
given that,
-6 – 6f + 7 – 3f – 9.
-6f – 3f – 6 + 7 – 9.
-9f – 13 – 9.
-9f – 23.
-6 – 6f + 7 – 3f – 9 = -9f – 23.
Convince Me! How do you decide in what way to reorder the terms of an expression when simplifying it?
Try It!
Simplify each expression.
a. 59.95m – 30 + 7.95m + 45 + 9.49m
Answer:
59.95m – 30 + 7.95m + 45 + 9.49m = 52m – 5.51.
Explanation:
In the above-given question,
given that,
59.95m – 30 + 7.95m + 45 + 9.49.
59.95m + 7.95m – 30 + 45 + 9.49.
52m – 15 + 9.49.
52m – 5.51.
b. -0.5p + \(\frac{1}{2}\)p – 2.75 + \(\frac{2}{3}\)p
Answer:
-0.5p + (1/2)p – 2.75 + (2/3)p = 0.6p – 2.75.
Explanation:
In the above-given question,
given that,
-0.5p + (1/2)p – 2.75 + (2/3)p.
-0.5p + 0.5p – 2.75 + 0.6p.
0.6p – 2.75.
-0.5p + (1/2)p – 2.75 + (2/3)p = 0.6p – 2.75.
Try It!
Simplify the expression -3.7 +59 + 4k + 11.1 – 10g.
(______ – 10g) + 4k + (______ + 11.1)
= _______ + 4k + ______
The simplified expression is ________.
Answer:
-3.7 + 59 + 4k + 11.1 – 10g = 55.3 – 10g.
Explanation:
In the above-given question,
given that,
-3.7 + 59 + 4k + 11.1 – 10g.
-3.7 + 11.1 – 11.1 + 59 – 10g.
-3.7 + 59 – 10g.
55.3 – 10g.
KEY CONCEPT
When simplifying algebraic expressions, use properties of operations to combine like terms.
To simplify the expression below, group like terms.
\(\frac{3}{10}\)y – 3.5x – \(\frac{3}{8}\) +0.53x + 5.25 – 2.75y – 12
(-3.5x + 0.53x) + (\(\frac{3}{10}\)y – 2.75y) + (-\(\frac{3}{8}\) + 5.25 – 12)
Then combine like terms.
-2.97x – 2.45y – 7.125
Do You Understand?
Question 1.
Essential Question How are properties of operations used to simplify expressions?
Answer:
The properties of operations are used to combine like terms.
Explanation:
In the above-given question,
given that,
the properties of operations used to combine like terms.
for example:
\(\frac{3}{10}\)y – 3.5x – \(\frac{3}{8}\) +0.53x + 5.25 – 2.75y – 12
(-3.5x + 0.53x) + (\(\frac{3}{10}\)y – 2.75y) + (-\(\frac{3}{8}\) + 5.25 – 12)
Then combine like terms.
-2.97x – 2.45y – 7.125
Question 2.
Make Sense and Persevere Explain why constant terms expressed as different rational number types can be combined.
Answer:
The constant terms remain the same.
Explanation:
In the above-given question,
given that,
constant terms expressed as different rational number types can be combined.
for example:
\(\frac{3}{10}\)y – 3.5x – \(\frac{3}{8}\) +0.53x + 5.25 – 2.75y – 12
(-3.5x + 0.53x) + (\(\frac{3}{10}\)y – 2.75y) + (-\(\frac{3}{8}\) + 5.25 – 12)
Then combine like terms.
-2.97x – 2.45y – 7.125
Question 3.
Reasoning How do you know when an expression is in its simplest form?
Answer:
The expression is in its simplest form when it has only limited expressions.
Explanation:
In the above-given question,
given that,
for example:
-3.7 + 59 + 4k + 11.1 – 10g.
-3.7 + 11.1 – 11.1 + 59 – 10g.
-3.7 + 59 – 10g.
55.3 – 10g.
Do You Know How?
Question 4.
Simplify -4b + (-9k) – 6 – 3b + 12.
Answer:
-7b – 9k + 6.
Explanation:
In the above-given question,
given that,
-4b + (-9k) – 6 – 3b + 12.
-4b – 3b -9k – 6 + 12.
-7b – 9k + 6.
Question 5.
Simplify -2 + 6.45z – 6+ (-3.25z).
Answer:
-8 + 3.2z.
Explanation:
In the above-given question,
given that,
-2 + 6.45z – 6+ (-3.25z).
-2 + 6.45z – 6 – 3.25z.
-8 + 3.2z.
Question 6.
Simplify –9 + (-\(\frac{1}{3}\)y) +6 – \(\frac{4}{3}\)y.
Answer:
-3 – 5/3y.
Explanation:
In the above-given question,
given that,
–9 + (-\(\frac{1}{3}\)y) +6 – \(\frac{4}{3}\)y.
-9 – 1/3y + 6 – 4/3y.
-9 + 6 – 5/3y.
-3 – 5/3y.
Practice & Problem Solving
In 7-10, simplify each expression.
Question 7.
–2.8f +0.96 – 12 – 4
Answer:
-2.8f + 0.96 – 12 – 4 = -2.8f – 15.04.
Explanation:
In the above-given question,
given that,
-2.8f + 0.96 – 12 – 4.
-2.8f + 0.96 – 16.
-2.8f – 15.04.
-2.8f + 0.96 – 12 – 4 = -2.8f – 15.04.
Question 8.
3.2 – 5.1n – 3n + 5
Answer:
3.2 – 5.1n – 3n + 5 = 8.2 – 8.1n.
Explanation:
In the above-given question,
given that,
3.2 – 5.1n – 3n + 5.
3.2 – 8.1n + 5.
8.2 – 8.1n.
3.2 – 5.1n – 3n + 5 = 8.2 – 8.1n.
Question 9.
2n + 5.5 – 0.9n – 8 + 4.5p
Answer:
2n + 5.5 – 0.9n – 8 + 4.5p = 4.5p – 2.5 + 1.1n.
Explanation:
In the above-given question,
given that,
2n + 5.5 – 0.9n – 8 + 4.5p.
2n – 0.9n + 5.5 – 8 + 4.5p.
1.1n – 2.5 + 4.5p.
4.5p – 2.5 + 1.1n.
2n + 5.5 – 0.9n – 8 + 4.5p = 4.5p – 2.5 + 1.1n.
Question 10.
12 + (-4) – \(\frac{2}{5}\)j – \(\frac{4}{5}\)j + 5
Answer:
12 + (-4) – 2/5j – 4/5j + 5 = 13 – 6/5j.
Explanation:
In the above-given question,
given that,
12 + (-4) – 2/5j – 4/5j + 5.
12 -4 – 6/5j + 5.
8 – 6/5j + 5.
13 – 6/5j.
12 + (-4) – 2/5j – 4/5j + 5 = 13 – 6/5j.
Question 11.
Which expression is equivalent to -5v + (-2) + 1 + (-2v)?
A. -9v
B. -4v
C. -7v – 1
D. -7V + 3
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
-5v + (-2) + 1 + (-2v).
-5v -2 + 1 -2v.
-7v -1.
so option C is correct.
Question 12.
Which expression is equivalent to \(\frac{2}{3}\)x + (-3) + (-2) – \(\frac{1}{3}\)x?
A. x + 5
B. –\(\frac{1}{3}\)x + 5
C. \(\frac{1}{3}\)x – 1
D. \(\frac{1}{3}\)x – 5
Answer:
Option D is correct.
Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\)x + (-3) + (-2) – \(\frac{1}{3}\)x.
2/3x -3 -2 -1/3x.
1/3x -5
so option D is correct.
Question 13.
The dimensions of a garden are shown. Write an expression to find the perimeter.

Answer:
The perimeter of the garden = x – 7.
Explanation:
In the above-given question,
given that,
the length of the garden = x.
the width of the garden = 1/2x – 7.
area of the garden = l x b.
x + 1/2x – 7.
2/2x – 7.
x – 7.
so the perimeter of the garden = x – 7.
Question 14.
Simplify the expression 8h + (-7.3d) – 14 + 5d – 3.2h.
Answer:
8h + (-7.3d) – 14 + 5d – 3.2h = 5.2h – 2.3d – 14.
Explanation:
In the above-given question,
given that,
8h + (-7.3d) – 14 + 5d – 3.2h.
8h – 7.3d – 14 + 5d – 3.2h.
5.2h – 2.3d – 14.
8h + (-7.3d) – 14 + 5d – 3.2h = 5.2h – 2.3d – 14.
Question 15.
Simply 4 – 2y + (-8y) + 6.2.
Answer:
4 – 2y + (-8y) + 6.2 = 10.2 – 10y.
Explanation:
In the above-given question,
given that,
4 – 2y + (-8y) + 6.2.
4 – 2y – 8y + 6.2.
4 – 10y + 6.2.
10.2 – 10y.
4 – 2y + (-8y) + 6.2 = 10.2 – 10y.
Question 16.
Simplify \(\frac{4}{9}\)z – \(\frac{3}{9}\)z + 5 – \(\frac{5}{9}\)z – 8.
Answer:
4/9z – 3/9z + 5 – 5/9z – 8 = -4/9z – 3.
Explanation:
In the above-given question,
given that,
4/9z – 3/9z + 5 – 5/9z – 8.
1/9z + 5 – 5/9z – 8.
-4/9z + 5 – 8.
-4/9z – 3.
4/9z – 3/9z + 5 – 5/9z – 8 = -4/9z – 3.
Question 17.
Construct Arguments Explain whether 11t – 4t is equivalent to 4t – 11t. Support your answer by evaluating the expression for t = 2.
Answer:
The values are the same but 11t – 4t is positive and 4t – 11t is negative.
Explanation:
In the above-given question,
given that,
11t – 4t is equivalent to 4t – 11t.
t = 2.
11(2) – 4(2).
22 – 8.
14.
4t – 11t.
4(2) – 11(2).
8 – 22.
-14.
Question 18.
The signs show the costs of different games at a math festival. How much would it cost n people to play Decimal Decisions and Ratio Rage?

Answer:
The cost would take to n people to play Decimal Decisions and Ratio Rage = 6.6n/4 – 3.
Explanation:
In the above-given question,
given that,
the cost of 1 Game is 5.5n – 3.
the cost of 1 Game is n/4.
5.5n – 3 + n/4.
6.6n/4 – 3.
the cost would take to n people to play Decimal Decisions and Ratio Rage = 6.6n/4 – 3.
Question 19.
Higher Order Thinking in the expression ax + bx, a is a decimal and b is a fraction. How do you decide whether to write a as a fraction or b as a decimal?
Answer:
Yes, we can write an as a fraction and b as a decimal.
Explanation:
In the above-given question,
given that,
in the expression ax + bx, a is a decimal and b is a fraction.
for example:
a = 1.1.
b = 1/2.
ax + bx.
1.1x + 1/2x.
so 1.1 is a decimal and 1/2 is a fraction.
Assessment Practice
Question 20.
Select all expressions equivalent to -6z + (-5.5) + 3.5z + 5y – 2.5.
☐ -8 + 5y + 2.52
☐ -2.5z + 5y – 8
☐ -8 + 5y +(-2.5z)
☐ 2.5y + (-2.5z) – 5.5
☐ 5y – 8 – 2.5z
Answer:
Option B and C are correct.
Explanation:
In the above-given question,
given that,
-6z + (-5.5) + 3.5z + 5y – 2.5.
-6z + 3.5z – 5.5 – 2.5 + 5y.
-2.5z -8 + 5y.
so options B and C are correct.
Lesson 4.4 Expand Expressions
Solve & Discuss It!
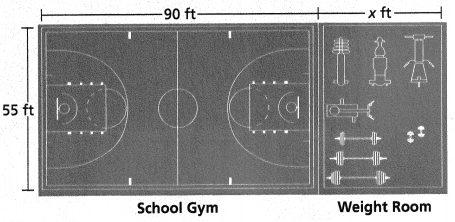
The school is planning to add a weight room to the gym. If the total area of the gym and weight room should stay under 5,500 square feet, what is one possible length for the new weight room? Show your work. Are there other lengths that would work? Why or why not? -90 ft
I can… expand expressions using the Distributive Property.
Look for Relationships
What is the relationship between the areas of the gym and weight room?
Answer:
The relationship between the areas of the gym and weight room = 550 ft.
Explanation:
In the above-given question,
given that,
The school is planning to add a weight room to the gym.
If the total area of the gym and weight room should stay under 5,500 square feet.
the area of the school is l x b.
where l = 90 ft and b = 55 ft.
area = l x b.
area = 90 x 55.
area = 4950.
5500 – 4950 = 550.
so the relationship between the areas of the gym and weight room = 550 ft.
Focus on math practices
Model with Math What is an expression using x that represents the total area of the gym and the weight room?

Answer:
The relationship between the areas of the gym and weight room = 550 ft.
Explanation:
In the above-given question,
given that,
The school is planning to add a weight room to the gym.
If the total area of the gym and weight room should stay under 5,500 square feet.
the area of the school is l x b.
where l = 90 ft and b = 55 ft.
area = l x b.
area = 90 x 55.
area = 4950.
5500 – 4950 = 550.
so the relationship between the areas of the gym and weight room = 550 ft.
Essential Question
How does the value of an expression change when it is expanded?
Try It!
What is the expanded form of the expression 3.6(t + 5)?
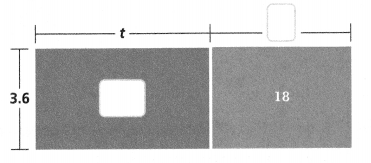
3.6(t + 5)
= ________t + _______ • 5
= _______ + _______
The expanded expression is _______.
Answer:
3.6t + 18.
Explanation:
In the above-given question,
given that,
3.6(t + 5).
3.6 x t = 3.6t.
3.6t + 3.6 x 5.
3.6t + 18.
Convince Me! If you know the value of t, would the evaluated expression be different if you added the known value of t and 5 and then multiplied by 3.6? Explain.
Try It!
Expand the expression t(-1.2w + 3).
Answer:
The expression is -1.2tw + 3t.
Explanation:
In the above-given question,
given that,
the expression is t(-1.2w + 3).
-1.2tw + 3t.
so the expanded expression is -1.2tw + 3t.
Try It!
Simplify the expression –\(\frac{2}{5}\)(10 + 15m – 20n).
Answer:
The expression is -4 -6m – 8n.
Explanation:
In the above-given question,
given that,
–\(\frac{2}{5}\)(10 + 15m – 20n).
-2/5 (10 + 15m – 20n).
-2/5(10 + 15m – 20n).
-20/5 – 30/5m – 40/5n.
-4 – 6m – 8n.
KEY CONCEPT
You can expand an expression using the Distributive Property.
Multiply, or distribute, the factor outside the parentheses with each term inside the parentheses.
-7(3y – 1)
= (-7)(3y) + (-7)(-1)
= -21y + 7
The sign of each term is included in all calculations.
Do You Understand?
Question 1.
Essential Question How does the value of an expression change when it is expanded?
Answer:
The value of an expression change when it is expanded.
Explanation:
In the above-given question,
given that,
the value of an expression change when it is expanded.
for example:
-8(2y – 2).
-8(-2y) + (-8) (-2).
-16y + -16.
Question 2.
Use Structure How does the subtraction part of the expression change when a(b – c) is expanded?
Answer:
The subtraction part of the expression change.
Explanation:
In the above-given question,
given that,
a(b – c).
ax b – a x c.
ab – ac.
the product of in terms is multiplied with outterms.
Question 3.
Make Sense and Persevere When does expanding and simplifying a(b + c) result in a positive value for ac?
Answer:
ab + ac.
Explanation:
In the above-given question,
given that,
the expression is a(b + c).
a x b + a x c.
ab + ac.
the sign is positive.
so the value for ac is also positive.
Do You Know How?
Question 4.
Shoes and hats are on sale. The expression \(\frac{1}{4}\)(s + 24.80) can be used to determine the discount when you buy shoes with a retail price of s dollars and a hat with a retail price of $24.80. Write another expression that can be used to determine the discount.

Answer:
Another expression is $1.55.
Explanation:
In the above-given question,
given that,
Shoes and hats are on sale.
The expression \(\frac{1}{4}\)(s + 24.80).
when you buy shoes with a retail price of s dollars and a hat with a retail price of $24.80.
1/4 (s + 24.80).
s/4 + 24.80/4.
s/4 + 6.2.
s/4 = – 6.2.
s = -6.2/4.
s = 1.55.
so the retail price of the shoes = $1.55.
Question 5.
Expand x(4 – 3.4y).
Answer:
The expression is 4x – 3.4xy.
Explanation:
In the above-given question,
given that,
x(4 – 3.4y).
4x X – 3.4 x X x Y.
4x – 3.4xy.
so the expanded expression is 4x – 3.4xy.
Question 6.
Expand –\(\frac{2}{10}\)(1 – 2x + 2).
Answer:
The expanded expression is -3/5 – 2/5x.
Explanation:
In the above-given question,
given that,
–\(\frac{2}{10}\)(1 – 2x + 2).
-2/10 (1 – 2x + 2).
-1/5 (1 – 2x + 2).
-1/5 – 2/5x – 2/5.
-3/5 – 2/5x.
Practice & Problem Solving
Leveled Practice For 7-8, fill in the boxes to expand each expression.
Question 7.
3(n + 7)
= (3) (_____) + (3) (_____)
= ____ + _____
Answer:
3n + 21.
Explanation:
In the above-given question,
given that,
3(n + 7).
3 x n + 3 x 7.
3n + 21.
Question 8.
4(x – 3)
= ______ x – ______ (3)
= ______ – ______
Answer:
4x – 12.
Explanation:
In the above-given question,
given that,
4(x – 3).
4 x X – 4 x 3.
4x – 12.
For 9-14, write the expanded form of the expression.
Question 9.
y(0.5 + 8)
Answer:
y(0.5 + 8) = 8.5y.
Explanation:
In the above-given question,
given that,
y(0.5 + 8).
0.5y + 8y.
8.5y.
y(0.5 + 8) = 8.5y.
Question 10.
4(3 + 4x – 2)
Answer:
4(3 + 4x – 2) = 4 + 16x.
Explanation:
In the above-given question,
given that,
4(3 + 4x – 2).
4 x 3 + 4x x 4 – 2 x 4.
12 + 16x – 8.
4 + 16x.
4(3 + 4x – 2) = 4 + 16x.
Question 11.
6(y + x)
Answer:
6(y + x) = 6y + 6x.
Explanation:
In the above-given question,
given that,
6(y + x).
6 x y + 6 x x.
6y + 6x.
6(y + x) = 6y + 6x.
Question 12.
-2.5(-3 + 4n + 8)
Answer:
-2.5 (-3 + 4n + 8) = -14.5 – 10n.
Explanation:
In the above-given question,
given that,
-2.5 (-3 + 4n + 8).
-2.5 x -3 – 2.5 x 4n – 2.5 x 8.
-5.5 – 10n – 20.
-14.5 – 10n.
-2.5 (-3 + 4n + 8) = -14.5 – 10n.
Question 13.
–\(\frac{1}{3}\)(y – x)
Answer:
–\(\frac{1}{3}\)(y – x) = -1/3y + x/3.
Explanation:
In the above-given question,
given that,
–\(\frac{1}{3}\)(y – x).
-1/3(y – x).
-1/3y + x/3.
–\(\frac{1}{3}\)(y – x) = -1/3y + x/3.
Question 14.
8(6x – 4)
Answer:
8(6x – 4) = 48x – 32.
Explanation:
In the above-given question,
given that,
8(6x – 4).
8 x 6x – 4 x 8.
48x – 32.
8(6x – 4) = 48x – 32.
Question 15.
Higher Order Thinking A grocery store has a 13%-off sale on all bread. You decide to purchase 6 loaves of bread. Let b be the original price of a loaf of bread. Expand the expression 6(b – 0.13b). Once the expression is expanded, what do the terms represent?
Answer:
6(b – 0.13b) = -5.22b.
Explanation:
In the above-given question,
given that,
A grocery store has a 13%-off sale on all bread.
You decide to purchase 6 loaves of bread.
Let b be the original price of a loaf of bread.
6(b – 0.13b).
6 x b – 0.13b x 6.
6b – 0.78b.
-5.22b.
6(b – 0.13b) = -5.22b.
Question 16.
A gardener plans to extend the length of a rectangular garden. Let x represent the garden’s original length. The expression 4(x + 7) represents the area of the extended garden. When asked for the area of the extended portion, the gardener incorrectly said it was 11 square feet. Describe the error the gardener made.
Answer:
The error the gardener made = 4x + 28.
Explanation:
In the above-given question,
given that,
Let x represent the garden’s original length.
The expression 4(x + 7) represents the area of the extended garden.
4(x + 7).
4 x x + 4 x 7.
4x + 28.
Question 17.
Find a difference equivalent to the product 11(x – y).
Answer:
11(x – y) = 11x – 11y.
Explanation:
In the above-given question,
given that,
11(x – y).
11 x x – 11 x y.
11x – 11y.
11(x – y) = 11x – 11y.
Question 18.
Use the Distributive Property to write an expression equivalent to 0.4(-5 – 7y – 13.8).
Answer:
0.4(-5 – 7y – 13.8) = -10.12 – 2.8y.
Explanation:
In the above-given question,
given that,
the expression is 0.4(-5 – 7y – 13.8).
0.4 x (-5) – 0.4 (7y) – 0.4 (-13.8).
-4.6 – 2.8y – 5.52.
-10.12 – 2.8y.
Question 19.
Make Sense and Persevere Use the Distributive Property to expand 7(7x – 3y) – 6.
Answer:
7(7x – 3y) – 6 = 49x – 21y – 6.
Explanation:
In the above-given question,
given that,
7(7x – 3y) – 6.
7 x 7x – 7 (3y) – 6.
49x – 21y – 6.
7(7x – 3y) – 6 = 49x – 21y – 6.
Question 20.
Use the Distributive Property to write an expression equivalent to y(-3 – 8x).
Answer:
y(-3 – 8x) = -3y – 8xy.
Explanation:
In the above-given question,
given that,
y(-3 – 8x).
-3 x y – 8x (y).
-3y -8xy.
Question 21.
An architect plans to build an extension to Meiling’s rectangular deck. Let x represent the increase, in meters, of her deck’s length. The expression 5(X + 8) represents the area of the deck, where 5 is the width, in meters, and (x + 8) represents the extended length, in meters. Use the Distributive Property to write an expression that represents the total area of Meiling’s new deck.
Answer:
The total area of Meiling’s new deck = 5x + 40.
Explanation:
In the above-given question,
given that,
An architect plans to build an extension to Meiling’s rectangular deck.
Let x represent the increase, in meters, of her deck’s length.
The expression 5(X + 8) represents the area of the deck, where 5 is the width, in meters, and (x + 8) represents the extended length in meters.
5(x + 8).
5 x x + 5 x 8.
5x + 40.
Assessment Practice
Question 22.
Select all expressions equivalent to –\(\frac{1}{2}\)(4 – 2 + 8x).
☐ -4x – 1
☐ 4x – 1
☐ 3x
☐ -2 + 1 – 4x
☐ 2 + 1 – 4x
☐ 4x + 1
Answer:
-4x -1 and -2 + 1 – 4x.
Explanation:
In the above-given question,
given that,
–\(\frac{1}{2}\)(4 – 2 + 8x).
-1/2(4 – 2 + 8x).
-4/2 – 2/2 + 8/2x.
-2 + 1 – 4x.
-1 – 4x.
Question 23.
An expression is shown.
\(\frac{1}{5}\)(5 – 7y + 10) Create an equivalent expression without parentheses.
Answer:
1/5(5 – 7y + 10) = 1 – 7/5y + 2.
Explanation:
In the above-given question,
given that,
1/5(5 – 7y + 10).
5/5 – 7/5y + 10/5.
1 – 7/5y + 2.
Lesson 4.5 Factor Expressions
Explain It!
Tasha is packing gift bags that include the same items. She has 72 glow sticks, 36 markers, and 24 bottles of bubbles. Tasha believes that she can pack no more than 6 bags using all of her supplies.
Answer:
Yes, she can pack 44 bags.
Explanation:
In the above-given question,
given that,
Tasha is packing gift bags that include the same items.
She has 72 glow sticks, 36 markers, and 24 bottles of bubbles.
72 + 36 + 24 = 132.
132/3 = 44.
she can pack 44 bags.
I can… use common factors and the Distributive Property to factor expressions.

Make Sense and Persevere
How can you use what you know about common factors to solve the problem?
A. Critique Reasoning Do you agree with Tasha? Explain.
Answer:
No, Tasha is wrong.
Explanation:
In the above-given question,
given that,
Tasha is packing gift bags that include the same items.
She has 72 glow sticks, 36 markers, and 24 bottles of bubbles.
72 + 36 + 24 = 132.
132/3 = 44.
she can pack 44 bags.
B. If Tasha creates the greatest number of gift bags, how many of each item is in each bag? Explain how you know.
Answer:
Tasha packs 44 bags.
Explanation:
In the above-given question,
given that,
Tasha is packing gift bags that include the same items.
She has 72 glow sticks, 36 markers, and 24 bottles of bubbles.
72 + 36 + 24 = 132.
132/3 = 44.
she can pack 44 bags.
Focus on math practices
Reasoning Tasha added more markers and now has a total of 48 markers. Does this change the possible number of gift bags? Explain.
Essential Question
How does the Distributive Property relate to factoring expressions?
Try It!
Use factoring to write an expression for the length of the pool with the given width.

4x + 20 = _____ (x + _____)
So, the length of the pool is ______ meters.
Answer:
The length of the pool is 4(x + 5) meters.
Explanation:
In the above-given question,
given that,
4x + 20.
4(x + 5).
the length of the pool is 4(x + 5) meters.
Convince Me! How can you use the Distributive Property to check the factored expression? Use the factored expression for Example 1 in your explanation.
Try It!
Show two different ways to factor -(4x – 28).
Answer:
-(4x – 28) = -4(x – 7).
Explanation:
In the above-given question,
given that,
-(4x – 28).
-4x + 28.
-4(x – 7).
Try It!
Write an equivalent expression for the expression above using a negative factor.
Answer:
The equivalent expression for the expression is -4(x – 7).
Explanation:
In the above-given question,
given that,
the equivalent expression for the expression is -4(x – 7).
-(4x – 28).
-4x + 28.
-4(x – 7).
KEY CONCEPT
The greatest common factor (GCF) can be used to factor expressions.
The Distributive Property can be applied to factor an expression. Factoring an expression creates an equivalent expression.

Do You Understand?
Question 1.
Essential Question How does the Distributive Property relate to factoring expressions?
Answer:
2x + 8 = 2(x + 4).
Explanation:
In the above-given question,
given that,
the distributive property can be applied to factor an expression.
factoring an expression creates an equivalent expression.
2x + 8.
2(x + 4).
Question 2.
Susan incorrectly factored the expression below.
12a – 156 + 6
3(4a + 5b + 3)
a. Explain any errors Susan may have made when factoring.
Answer:
12a + 15b + 9.
Explanation:
In the above-given question,
given that,
3(4a + 5b + 3).
(3 x 4a) + (3 x 5b) + (3 x 3).
12a + 15b + 9.
b. Factor the expression correctly.
Answer:
12a + 15b + 9.
Explanation:
In the above-given question,
given that,
3(4a + 5b + 3).
(3 x 4a) + (3 x 5b) + (3 x 3).
12a + 15b + 9.
Do You Know How?
Question 3.
Sahil is putting together supply kits and has 36 packs of x pencils, 12 packs of y crayons, and 24 erasers.
a. Write an expression to show the total number of items.
Answer:
The expression to show the total number of items = 36x + 12y + 24.
Explanation:
In the above-given question,
given that,
Sahil is putting together supply kits and has 36 packs of x pencils, 12 packs of y crayons, and 24 erasers.
36 x X + 12 x Y + 24,
36x + 12y + 24.
so the expression to show the total number of items = 36x + 12y + 24.
b. Use factoring to show many kits Sahil can make while putting every type of item in each kit.
Answer:
The expression to show the total number of items = 36x + 12y + 24.
Explanation:
In the above-given question,
given that,
Sahil is putting together supply kits and has 36 packs of x pencils, 12 packs of y crayons, and 24 erasers.
36 x X + 12 x Y + 24,
36x + 12y + 24.
so the expression to show the total number of items = 36x + 12y + 24.
c. Use the factored expression to find the number of each item in each kit.
Answer:
The expression to show the total number of items = 36x + 12y + 24.
Explanation:
In the above-given question,
given that,
Sahil is putting together supply kits and has 36 packs of x pencils, 12 packs of y crayons, and 24 erasers.
36 x X + 12 x Y + 24,
36x + 12y + 24.
so the expression to show the total number of items = 36x + 12y + 24.
Question 4.
Show two different ways to factor – 12x + 24 – 18y.
Answer:
-12x + 24 – 18y and -2(6x – 12 + 9y).
Explanation:
In the above-given question,
given that,
the expression is – 12x + 24 – 18y.
-2(6x – 12 + 9y).
Question 5.
How can you use the Distributive Property to factor the expression 6x + 15?
Answer:
3(2x + 5).
Explanation:
In the above-given question,
given that,
the given expression is 6x + 15.
3x + 3x +15.
3(2x + 5).
Practice & Problem Solving
Leveled Practice In 6-9, factor the expression.
Question 6.
16a + 10.
The GCF of 16a and 10 is 2.
2 × ______ = 16a
2 × _______ = 10
The factored expression is ________
Answer:
2 x 8a = 16a.
2 x 5 = 10.
The factored expression is 16a + 10.
Explanation:
In the above-given question,
given that,
the expression is 16a + 10.
2(8a + 5).
2 x 8a = 16a.
2 x 5 = 10.
Question 7.
-9y – 3.
The positive GCF of -9y and -3 is 3.
3 × ______ = -9y
3 × ______ = -3
The factored expression is ________
Answer:
3 x -3y = -9y.
3 x 1 = -3.
Explanation:
In the above-given question,
given that,
the expression is -9y – 3.
-3(3y + 1).
-3 x 3y = -9y.
-3 x 1 = -3.
Question 8.
14x + 49
Answer:
7 x 2x = 14x.
7 x 7 = 49.
Explanation:
In the above-given question,
given that,
the expression is 14x + 49.
7(2x + 7).
7 x 2x = 14x.
7 x 7 = 49.
Question 9.
12y – 16
Answer:
2 x 6y = 12y.
2 x 8 = 16.
Explanation:
In the above-given question,
given that,
the expression is 12y – 16.
2(6y – 8).
2 x 6y = 12y.
2 x 8 = 16.
Question 10.
This model shows the area of a garden. Write two expressions that represent the area.

Answer:
The area of the garden = 5x + 10.
Explanation:
In the above-given question,
given that,
the expression is 5x + 10.
5(x + 2).
5 x x = 5x.
5 x 2 = 10.
so the area of the garden = 5x + 10.
Question 11.
Use the GCF to write the factored form of the expression 18x + 24y.
Answer:
The factored form of the expression is 2(9x + 12y).
Explanation:
In the above-given question,
given that,
the expression is 18x + 24y.
2(9x + 12y).
6(3x + 4y).
so the factored form of the expression is 2(9x + 12y).
Question 12.
Find the dimensions of the sports field at the right if the width is at least 60 yards.
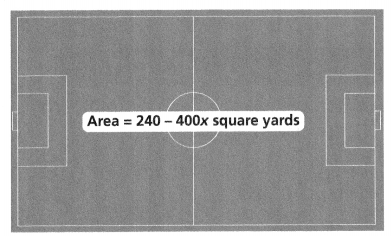
Answer:
The dimensions of the sports field = -160 and 60.
Explanation:
In the above-given question,
given that,
the expression is 240 – 400x.
-160x.
-160(60).
-9600.
so the dimensions of the sports field = -160 and 60.
Question 13.
Your friend incorrectly factors the expression 15x – 20xy as 5x( 3 – 4xy).
a. Factor the expression correctly.
Answer:
The expression correctly = 5(3x – 4xy).
Explanation:
In the above-given question,
given that,
the expression is 15x – 20xy.
5(3x – 4xy).
5 x 3x = 15x.
5 x 4xy = 20xy.
so the expression correctly is 5(3x – 4xy).
b. What error did your friend likely make?
Answer:
The expression correctly = 5(3x – 4xy).
Explanation:
In the above-given question,
given that,
the expression is 15x – 20xy.
5(3x – 4xy).
5 x 3x = 15x.
5 x 4xy = 20xy.
so the expression correctly is 5(3x – 4xy).
Question 14.
You are given the expression 12x + 18y + 26.
a. Make Sense and Persevere What is the first step in factoring the expression?
Answer:
The first step in factoring is 2(6x + 9y + 18).
Explanation:
In the above-given question,
given that,
the expression is 12x + 18y + 26.
2(6x + 9y + 13).
2 x 6x = 12x.
2 x 9y = 18y.
2 x 13 = 26.
b. Factor the expression.
Answer:
The expression is 2(6x + 9y + 18).
Explanation:
In the above-given question,
given that,
the expression is 12x + 18y + 26.
2(6x + 9y + 13).
2 x 6x = 12x.
2 x 9y = 18y.
2 x 13 = 26.
Question 15.
A hotel manager is adding a tile border around the hotel’s rectangular pool. Let x represent the width of the pool, in feet. The length is 3 more than 2 times the width, as shown. Write two expressions that give the perimeter of the pool.

Answer:
The perimeter of the pool = 2XxX + 3x.
Explanation:
In the above-given question,
given that,
Let x represent the width of the pool, in feet.
The length is 3 more than 2 times the width, as shown.
the perimeter of the rectangle = length x width.
perimeter = 2x + 3 x X.
perimeter = 2×2 x 3x.
Question 16.
Higher Order Thinking Use the expressions below.
14m + mn
2y + 2x + 4
–\(\frac{3}{4}\)m + 8m + m
4 – 3p
5.75t + 7.75t – t
8xy – 6xy
a. Circle the expressions that have like terms.
Answer:
The expressions that have the like terms = 14m + mn, 5.75t + 7.75t -t, and 8xy – 6xy.
Explanation:
In the above-given question,
given that,
the expressions are 14m + mn
2y + 2x + 4.
–\(\frac{3}{4}\)m + 8m + m.
4 – 3p.
5.75t + 7.75t – t.
8xy – 6xy.
the like terms are 8xy – 6xy = 2xy.
5.75t + 7.75t – t = 13.5t – t.
12.5 t.
b. Explain why the other expressions do not have like terms.
Answer:
The other expressions that do not have like terms are 4 – 3p, 14m + mn.
Explanation:
In the above-given question,
given that,
the expressions are 14m + mn
2y + 2x + 4.
–\(\frac{3}{4}\)m + 8m + m.
4 – 3p.
5.75t + 7.75t – t.
8xy – 6xy.
the unlike terms are 14m + mn.
2y + 2x + 4.
Question 17.
Construct Arguments Ryan says the expression 3 + 5y cannot be factored using a GCF. Is he correct? Explain why or why not.
Answer:
Yes, Ryan was correct.
Explanation:
In the above-given question,
given that,
the expression is 3 + 5y.
we cannot be factored in using a GCF.
so Ryan was correct.
Assessment Practice
Question 18.
Select all the expressions equivalent to 12 + 30y.
☐ 3(4 + 10y)
☐ 4(3 + 10y)
☐ 6(2 + 5y)
☐ 2(6 + 30y)
☐ 6(3 + 10y)
Answer:
The expressions equivaent to 12 + 30y is 3(4 + 10y), 6(2 + 5y).
Explanation:
In the above-given question,
given that,
the expression is 12 + 30y.
3(4 + 10y).
6(2 + 5y).
3 x 4 = 12 + 3 x 10y = 30y.
6 x 2 = 12 + 6 x 5y = 30y.
Question 19.
Write an expression that is the product of two factors and is equivalent to -2x – 10.
Answer:
The expression is -2(x + 5).
Explanation:
In the above-given question,
given that,
the expression is -2x – 10.
-2(x + 5).
-2x + 10.
Topic 4 Mid-Topic Checkpoint
Question 1.
Vocabulary If you write an expression to represent the following situation, how can you determine which is the constant and which is the coefficient of the variable? Lesson 4-1
The zoo charges the Garcia family an admission fee of $5.25 per person and a one-time fee of $3.50 to rent a wagon for their young children.
Answer:
The admission fee is the coefficient and rents a wagon is constant.
Explanation:
In the above-given question,
given that,
The zoo charges the Garcia family an admission fee of $5.25 per person.
a one-time fee of $3.50 to rent a wagon for their young children.
$5.25x + $3.50.
$5.25 is the coefficient of the variable.
$3.50 is the constant.
Question 2.
An online photo service charges $20 to make a photo book with 16 pages. Each extra page costs $1.75. The cost to ship the completed photo book is $5. Write an expression to determine the total cost in dollars to make and ship a photo book with x extra pages. Lesson 4-1
Answer:
The total cost in dollars to make and ship a photo book with X extra pages is $20x + $5 = $1.75.
Explanation:
In the above-given question,
given that,
An online photo service charges $20 to make a photo book with 16 pages.
Each extra page costs $1.75.
The cost to ship the completed photo book is $5.
$20x + $5 = $1.75.
$25x -$1.75 = $5.
Question 3.
Write an expression equivalent to 2a + (\(\frac{3}{4}\)a + \(\frac{1}{5}\)b) by combining like terms. Lesson 4-3
Answer:
The expression equivalent to 2a + 3/4a + 1/5b is 5/4a + 1/5b.
Explanation:
In the above-given question,
given that,
the given expression is 2a + (\(\frac{3}{4}\)a + \(\frac{1}{5}\)b).
2a + 3/4a + 1/5b.
5/4a + 1/5b.
Question 4.
Which expression is equivalent to 3.2y – \(\frac{1}{3}\) + (-7y) + \(\frac{2}{3}\)? Lesson 4-2
A. -10.2y + \(\frac{1}{3}\)
B. -3.8y + \(\frac{1}{3}\)
C. -3\(\frac{7}{15}\)y
D. -3y
Answer:
Option B is the correct.
Explanation:
In the above-given question,
given that,
the expression is 3.2y – \(\frac{1}{3}\) + (-7y) + \(\frac{2}{3}\).
3.2y – 1/3 -7y + 2/3.
-3.8y + 1/3.
so option B is the correct.
Question 5.
Ray wants to buy a hat that costs $10 and some shirts that cost $12 each. The sales tax rate is 6.5%. Write an expression to determine the amount of sales tax that Ray will pay on his entire purchase. Expand to simplify the expression. Lesson 4-4
Answer:
The expression to determine the amount of sales tax that Ray will pay on his entire purchase = $22 + 6.5%.
Explanation:
In the above-given question,
given that,
Ray wants to buy a hat that costs $10 and some shirts that cost $12 each.
The sales tax rate is 6.5%.
$10 + $12 + 6.5%.
$22 + 6.5%.
Question 6.
Factor the expression 28r + 425 – 35. Lesson 4-5
Answer:
The expression is 7(4r + 61 – 5).
Explanation:
In the above-given question,
given that,
the expression is 28r + 425 – 35.
7(4r + 61 – 5).
7 x 4r = 28r.
61 x 7 = 425.
7 x 5 = 35.
Question 7.
Describe two ways the Distributive Property can be used to write equivalent expressions. Lessons 4-4 and 4-5
Answer:
The two ways the distributive property can be used to write equivalent expressions
Explanation:
In the above-given question,
given that,
-1/2(x + 8), -1/2x + (-4) and -4 +(-1/2x) are equivalent.
-1/2(x + 8).
-1/2x + (-1/2) . 8.
-1/2x + (-4).
-4 + (-1/2x).
the three expressions are true.
Topic 4 Mid-Topic Performance Task
Alison is a buyer for a chain of 6 flower shops. This means that she buys flowers in bulk from a supplier and then distributes them to the 6 flower shops in the chain.
PART A
This week Alison bought 108 bunches of carnations and 96 bunches of roses from the supplier. Let c represent the number of carnations in each bunch, and let r represent the number of roses in each bunch. Write an expression to show the total number of carnations and roses that Alison bought.
Answer:
The total number of carnations and roses that Alison bought = 12(9c + 8r).
Explanation:
In the above-given question,
given that,
This week Alison bought 108 bunches of carnations and 96 bunches of roses from the supplier.
Let c represent the number of carnations in each bunch, and let r represent the number of roses in each bunch.
108c + 96r.
12(9c + 8r).
12 x 9c = 108c.
12 x 8r = 96r.
PART B
Alison wants to distribute the carnations and roses equally among the 6 flower shops. Factor the expression from Part A using 6 as the common factor. How does the factored expression help Alison determine how many carnations and how many roses each flower shop should get?
Answer:
The common factor is 3(c + r).
Explanation:
In the above-given question,
given that,
Alison wants to distribute the carnations and roses equally among the 6 flower shops.
3c + 3r.
3(c + r).
1(3c + 3r).
so the common factor is 3(c + r).
PART C
There are 24 carnations in each bunch and 12 roses in each bunch. Use your answer to Part B to determine the total number of carnations and the total number of roses Alison will distribute to each flower shop this week.
Answer:
The total number of carnations and roses = 6(4c + 2r).
Explanation:
In the above-given question,
given that,
There are 24 carnations in each bunch and 12 roses in each bunch.
24 c + 12 r.
2(12c + 6r).
6(4c + 2r).
6 x 4c = 24c.
6 x 2r = 12r.
PART D
Jake manages one of the flower shops. He wants to use the carnations and roses to make bouquets. He wants each bouquet to have the same combination of carnations and roses, with no flowers left over. Determine a way that Jake can divide the flowers to make the bouquets. How many bouquets will there be?
Answer:
The number of bouquets will there be = 6(c + r).
Explanation:
In the above-given question,
given that,
Jake manages one of the flower shops.
He wants to use the carnations and roses to make bouquets.
He wants each bouquet to have the same combination of carnations and roses, with no flowers left over.
6 and 6.
6 x 6 = 36.
6c + 6r.
6(c + r).
so the number of bouquets will there be = 6(c + 1).
3-Act Mathematical Modeling:
I’ve Got You Covered

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.

Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
The two numbers are 1 and 10.
Explanation:
In the above-given question,
given that,
the number line is 10 cm long.
the short is 1 cm.
the large is 10 cm.
so the two numbers that are too small and too large is 1 and 10.
Question 5.
Plot your prediction on the same number line.
Answer:
The two numbers are 1 and 10.
Explanation:
In the above-given question,
given that,
the number line is 10 cm long.
the short is 1 cm.
the large is 10 cm.
so the two numbers that are too small and too large is 1 and 10.
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
The figure contain 7 objects.
Explanation:
In the above-given question,
given that,
the figure contains 7 objects.
3 objects on the left side.
4 objects on the right side.
so the figure contain 7 objects.
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
The figure contain 7 objects.
Explanation:
In the above-given question,
given that,
the figure contains 7 objects.
3 objects on the left side.
4 objects on the right side.
so the figure contain 7 objects.
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.
Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:
ACT 3
Extension
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Generalize What pattern did you notice in your calculations? How did that pattern help you solve the problem?
Answer:
SEQUEL
Question 15.
Reasoning A classmate says that another object needs 512 tiles. What do you know about the dimensions of the object?
Answer:
The dimensions of the object = 22 and 26.
Explanation:
In the above-given question,
given that,
A classmate says that another object needs 512 tiles.
22 x 26 = 512.
the length = 22.
the width = 26.
area = l x b.
22 x 26.
512.
Lesson 4.6 Add Expressions
Solve & Discuss It!
The Smith family took a 2-day road trip. On the second day, they drove the distance they traveled on the first day. What is a possible distance they could have traveled over the 2 days? Is there more than one possible distance? Justify your response.
I can… add expressions that represent real-world problems.

Make Sense and Persevere
How are the quantities in the problem related?
Answer:
The quantities in the problem are the smith family took a 2-day road trip.
Explanation:
In the above-given question,
given that,
The Smith family took a 2-day road trip.
On the second day, they drove the distance they traveled on the first day.
2 + 2 = 4.
Focus on math practices
Use Structure How can two different expressions be used to represent the total distance?
Essential Question
How can properties of operations be used to add expressions?
Try It!
Sophia and Ollie each deposit $120 to open a joint account. They each make monthly deposits as shown. What expression represents the amount in the account after m months?
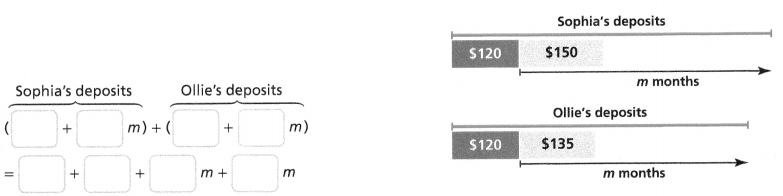
The amount of money in the joint account after m months is ______ + _______.
Answer:
The amount of money in the joint account after m months is 120 + 120 = $525..
Explanation:
In the above-given question,
given that,
Sophia and Ollie each deposit $120 to open a joint account.
120 + 150 = 270.
120 + 135 = 255.
270 + 255 = 525.
so the amount of money in the joint account after m months is $525.
Convince Me! Explain why the initial deposits and monthly deposits are not combined into one term?
Try It!
Find each sum.
a. (9.740 – 250.50) + (-5.48p + 185.70)
Answer:
Te sum is 60.54.
Explanation:
In the above-given question,
given that,
(9.740 – 250.50) + (-5.48p + 185.70).
(-240.76) + (180.22).
60.54.
b. (\(\frac{2}{11}\)x – 3 – 5y) + (-\(\frac{3}{11}\) + 5y + 5.5)
Answer:
-1/11 x + 2.5 + 5y.
Explanation:
In the above-given question,
given that,
(\(\frac{2}{11}\)x – 3 – 5y) + (-\(\frac{3}{11}\) + 5y + 5.5)
(2/11)x – 3 – 5y + (-3/11) + 5y + 5.5.
-1/11x + 2.5 + 5y.
-1/11 x + 2.5 + 5y.
C. (-14.2b – 97.35) + (6.76d – 118.7 – 3.4d)
Answer:
-14.2b – 216.05 + 3.36d.
Explanation:
In the above-given question,
given that,
(-14.2b – 97.35) + (6.76d – 118.7 – 3.4d).
-14.2b – 97.35 + 3.36d – 118.7.
-14.2b – 216.05 + 3.36d.
d. (\(\frac{3}{8}\) – \(\frac{1}{6}\)m + 5t) + (\(\frac{7}{10}\)m + 9t + \(\frac{1}{4}\))
Answer:
1/3 + 3/2m + 14t.
Explanation:
In the above-given question,
given that,
\(\frac{3}{8}\) – \(\frac{1}{6}\)m + 5t) + (\(\frac{7}{10}\)m + 9t + \(\frac{1}{4}\))
3/8 – 1/6 m + 5t + 7/10 m + 9t + 1/4.
3/8 + 1/4 – 1/6 m + 7/10 m + 5t + 9t.
3/8 + 1/4 + 3/2 m + 14 t.
1/3 + 3/2m + 14t.
KEY CONCEPT
Adding expressions may require combining like terms.
Terms with the same variables are added together and constants are added together.
When adding terms with the same variables, the rules for adding rational numbers apply to their coefficients.
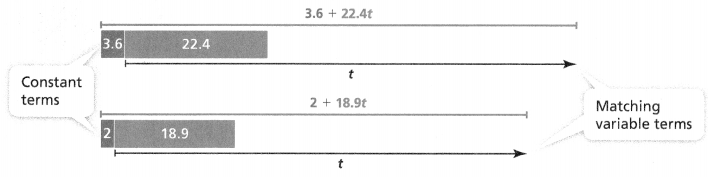
(3.6 + 22.4t) + (2 + 18.9t) = 5.6 + 41.3t
Do You Understand?
Question 1.
Essential Question How can properties of operations be used to add expressions?
Answer:
The properties of operations be used to add expressions with the like terms.
Explanation:
In the above-given question,
given that,
Adding expressions may require combining like terms.
Terms with the same variables are added together and constants are added together.
When adding terms with the same variables, the rules for adding rational numbers apply to their coefficients.
(3.6 + 22.4t) + (2 + 18.9t).
5.6 + 41.3t.
Question 2.
Reasoning Explain whether the coefficients of two terms with different variables can be added to make one new term.
Answer:
Yes the coefficients of two terms with different variables can be added to make the new term.
Explanation:
In the above-given question,
given that,
Adding expressions may require combining like terms.
Terms with the same variables are added together and constants are added together.
When adding terms with the same variables, the rules for adding rational numbers apply to their coefficients.
(3.6 + 22.4t) + (2 + 18.9t).
5.6 + 41.3t.
Question 3.
Be Precise which properties of operations could be used to show that (-5p + 9) + (-2 + p) is equivalent to (-5p) + p + 9 – 2?
Answer:
The equivalent expression is -4p + 7.
Explanation:
In the above-given question,
given that,
the expression is (-5p + 9) + (-2 + p).
-5p + 9 -2 + p.
-4p + 7.
Do You Know How?
Question 4.
Dillon says that 4b and -2b are not like terms because 4b is positive and -2b is negative. Is he correct? Explain.
Answer:
No, they are like terms.
Explanation:
In the above-given question,
given that,
Dillon says that 4b and -2b are not like terms because 4b is positive and -2b is negative.
4b and 2b are same.
4b – 2b = 2b.
so they are like terms.
Question 5.
Joel spent $28 for an Internet data service and pays $14.50 per month. He spent $24.50 to join an online movie streaming site and pays $13.25 per month. Write an expression to represent Joel’s total cost for both memberships after m months.

Answer:
The expression to represent Joel’s total cost for both memberships after m months = $27.75m + $52.50.
Explanation:
In the above-given question,
given that,
Joel spent $28 for an Internet data service and pays $14.50 per month.
He spent $24.50 to join an online movie streaming site and pays $13.25 per month.
$14.50m + $13.25m + $28 + $24.50.
$27.75m + $52.50.
Question 6.
Add \(\frac{1}{3}\)n + \(\frac{2}{3}\) and –\(\frac{1}{6}\)n + \(\frac{1}{6}\)m.
Answer:
-1/3n + 2/3 + 1/6m.
Explanation:
In the above-given question,
given that,
\(\frac{1}{3}\)n + \(\frac{2}{3}\) and –\(\frac{1}{6}\)n + \(\frac{1}{6}\)m.
1/3 n + 2/3 – 1/6 n + 1/6m.
-1/3n + 2/3 + 1/6m.
Question 7.
Find the sum.
(-3.5t – 4s +4.5) + (-7.1 – 0.3s + 4.1t)
Answer:
2.6 + 0.6t – 4.3s.
Explanation:
In the above-given question,
given that,
(-3.5t – 4s +4.5) + (-7.1 – 0.3s + 4.1t).
-3.5t – 4s + 4.5 -7.1 – 0.3s + 4.1t.
0.6 t – 4.3s – 2.6.
2.6 + 0.6t – 4.3s.
Practice & Problem Solving
Leveled Practice For 8-9, fill in the boxes to add the expressions.
Question 8.
(2a + 8) + (4a + 5)
= (2a + ______) + (8 + _____)
= _______ + 13
Answer:
6a + 13.
Explanation:
In the above-given question,
given that,
the expression is (2a + 8) + (4a + 5).
(2a + 4a) + ( 8 + 5).
6a + 13.
Question 9.
(\(\frac{2}{7}\)x – 7) + (\(\frac{1}{7}\)x + 8)
= (_______ + _______) + (-7 + ______)
= ______x + ______
Answer:
3/7 + 1.
Explanation:
In the above-given question,
given that,
(\(\frac{2}{7}\)x – 7) + (\(\frac{1}{7}\)x + 8).
(2/7 + 1/7)x – 7 + 8.
3/7x + 1.
Question 10.
Find the sum.
(8b + 7) + (6x – 4) + (5c + 8)
Answer:
8b + 6x + 11.
Explanation:
In the above-given question,
given that,
(8b + 7) + (6x – 4) + (5c + 8).
8b + 7 + 6x – 4 + 5c + 8.
8b + 3 + 6x + 8.
8b + 6x + 11.
Question 11.
Combine like terms.
(-3y – 5) + (5m + 7y) + (6 + 9m)
Answer:
14m + 4y + 1.
Explanation:
In the above-given question,
given that,
(-3y – 5) + (5m + 7y) + (6 + 9m)
-3y – 5 + 5m + 7y + 6 + 9m.
4y + 1 + 14m.
14m + 4y + 1.
Question 12.
Felipe is going to plant b sunflower seeds in one garden and 5b + 10 sunflower seeds in another. How many seeds is Felipe going to plant altogether?

Answer:
The number of seeds Felipe going to plant altogether = 5bsquare + 10b.
Explanation:
In the above-given question,
given that,
Felipe is going to plant b sunflower seeds in one garden and 5b + 10 sunflower seeds in another.
(5b + 10) b.
5b x b + 10b.
so the number of seeds Felipe goind to plant altogether = 5bsquare + 10b.
Question 13.
An art class is making a mural for the school that has a triangle drawn in the middle. The length of the bottom of the triangle is x. Another side is 1 more than three times the length of the bottom of the triangle. The last side is 2 more than the bottom of the triangle. Write and simplify an expression for the perimeter of the triangle.
Answer:
The perimeter of the triangle =
Explanation:
In the above-given question,
given that,
An art class is making a mural for the school that has a triangle drawn in the middle.
The length of the bottom of the triangle is x.
Another side is 1 more than three times the length of the bottom of the triangle.
The last side is 2 more than the bottom of the triangle.
x + 3x + 2x.
p = x + 2x + 3x.
p = 6x.
so the perimeter of the triangle = 6x.
Question 14.
On a math test, Sarah has to identify all the coefficients and constants of the expression 4 + n + 7m. Sarah identifies the only coefficient as 7 and the only constant as 4.
a. Identify all the coefficients of the expression.
Answer:
The coefficients of the expression is 7.
Explanation:
In the above-given question,
given that,
On a math test, Sarah has to identify all the coefficients and constants of the expression 4 + n + 7m.
Sarah identifies the only coefficient as 7.
so the coefficient is 7.
b. Identify all the constants of the expression.
Answer:
The constants of the expression is n.
Explanation:
In the above-given question,
given that,
On a math test, Sarah has to identify all the coefficients and constants of the expression 4 + n + 7m.
Sarah identifies the only constant as n.
so the constant is n.
c. What error did Sarah likely make?
Answer:
Sarah make the mistake was 4 is the constant.
Explanation:
In the above-given question,
given that,
On a math test, Sarah has to identify all the coefficients and constants of the expression 4 + n + 7m.
Sarah identifies the only constant as 4.
so the constant is 4.
Question 15.
The width of a rectangle is 5x – 2.5 feet and the length is 2.5x + 8 feet. Find the perimeter of the rectangle.
Answer:
The perimeter of the rectangle = 6.25x – 20.
Explanation:
In the above-given question,
given that,
The width of a rectangle is 5x – 2.5 feet and the length is 2.5x + 8 feet.
(5x – 2.5) x (2.5x + 8).
6.25x – 20.
so the perimeter of the rectangle = 6.25x – 20.
Question 16.
Nina has x coins. Clayton has 5 fewer coins than six times the number of coins Nina has. Write an expression for the total number of coins Nina and Clayton have altogether. Then simplify the expression.
Answer:
The expression for the total number of coins Nina and Clayton have altogether = 6x – 30.
Explanation:
In the above-given question,
given that,
Nina has x coins.
Clayton has 5 fewer coins than six times the number of coins Nina has.
x – 5 x 6.
6x – 30.
so the expression for the total number of coins Nina and Clayton have altogether = 6x – 30.
Question 17.
Higher Order Thinking Use the expression (8x + 2) + (-9x + 7).
a. Find the sum.
Answer:
9 – x.
Explanation:
In the above-given question,
given that
(8x + 2) + (-9x + 7).
8x + 2 -9x + 7.
-x + 9.
9 – x.
b. Reasoning Explain how you know when to combine terms with variables.
Answer:
We have to combine the variables when they have like terms.
Explanation:
In the above-given question,
given that
(8x + 2) + (-9x + 7).
8x + 2 -9x + 7.
-x + 9.
9 – x.
Question 18.
Gabe went to the Florida Mall. He bought k model planes and spent $24 on books. Then he spent another $25 at another store.

a. Write an expression that represents the amount Gabe spent at the mall.
Answer:
The expression that represents the amount Gabe = $49k + $14.99.
Explanation:
In the above-given question,
given that,
Gabe went to the Florida Mall.
He bought k model planes and spent $24k on books.
Then he spent another $25k at another store.
each model panel cost $14.99.
$24k + $25k + $14.99.
$49k + $14.99.
b. How much did Gabe spend in all if he bought 3 model planes?
Answer:
The amount did Gabe spend in all if he bought 3 models planes = $93.97.
Explanation:
In the above-given question,
given that,
Gabe went to the Florida Mall.
He bought k model planes and spent $24k on books.
Then he spent another $25k at another store.
each model panel cost $14.99.
3 x $14.99 = 93.97.
so the amount did Gabe spend in all if he bought 3 models planes = $93.97.
Assessment Practice
Question 19.
A middle school with x students conducted a survey to determine students’ Tuesday afternoon activities.
PART A
Write an expression for each activity.
25 more than one-tenth of the students dance.
20 fewer than three-tenths of the students play soccer.
21 more than one-tenth of the students play baseball
Answer:
25 + 1/10, 20 – 3/10, and 21 + 1/10.
Explanation:
In the above-given question,
given that,
25 more than one-tenth of the students dance.
20 fewer than three-tenths of the students play soccer.
21 more than one-tenth of the students play baseball.
25 + 1/10, 20 – 3/10, and 21/10.
PART B
Write a simplified expression to represent the number of students who either dance or play baseball on Tuesday afternoons.
Answer:
The number of students who either dance or play baseball on Tuesday afternoons = 25 + 1/10 and 21/10.
Explanation:
In the above-given question,
given that,
25 more than one-tenth of the students dance.
21 more than one-tenth of the students play baseball.
25 + 1/10 and 21/10.
Lesson 4.7 Subtract Expressions
Explore It!
The East Side Bulldogs and the West Side Bears are playing a football game. A fan is keeping score using T for a touchdown plus extra point, worth 7 points total, and F for a field goal, worth 3 points.
I can… subtract expressions using properties of operations.

A. How can you represent the score of each team using expressions?
Answer:
The score of the each team using expressions = 10 points.
Explanation:
In the above-given question,
given that,
East Side Bulldogs and the West Side Bears are playing a football game.
fan is keeping score using T for a touchdown.
plus extra point, worth 7 points total, and F for a field goal, worth 3 points.
7 + 5 = 12.
B. How can you represent the difference of the teams’ scores using an expression?
Answer:
The difference of the teams scores using an expression is 4.
Explanation:
In the above-given question,
given that,
East Side Bulldogs and the West Side Bears are playing a football game.
fan is keeping score using T for a touchdown.
plus extra point, worth 7 points total, and F for a field goal, worth 3 points.
12 – 1 = 11.
C. How can you determine how many more points the winning team had than the losing team?
Answer:
The number of points the winning team had than the losing team = 1.
Explanation:
In the above-given question,
given that,
East Side Bulldogs and the West Side Bears are playing a football game.
fan is keeping score using T for a touchdown.
plus extra point, worth 7 points total, and F for a field goal, worth 3 points.
12 – 1 = 11.
so the number of points the winning team had than the losing team = 1.
Focus on math practices
Look for Relationships How can looking at the coefficients help you determine which team scored the greater number of points?
Essential Question
How can properties of operations be used to subtract expressions?
Try It!
A frame holds a picture that is 15 inches long and x inches wide. The frame border is 3 inches wide around the picture. What expression represents the area of the frame border?
Area of frame border = Area of entire frame – Area of photo = ________ – ________
The area of the frame is _________ in2
Answer:
The expression represents the area of the frame border =
Explanation:
In the above-given question,
given that,
A frame holds a picture that is 15 inches long and x inches wide.
The frame border is 3 inches wide around the picture.
3 = 15 – x.
x = 15/3.
x = 5.
so the expression represents the area of the frame border is 5 square inches.
Convince Me! Why can you choose to add or subtract when subtracting an expression?
Try It!
Subtract (0.95x – 0.04) – (0.99x – 0.13).
Answer:
0.04x + 0.09.
Explanation:
In the above-given question,
given that,
(0.95x – 0.04) – (0.99x – 0.13).
0.95x – 0.04 – 0.99x + 0.13.
0.04x + 0.09.
0.04x + 0.09.
Try It!
Subtract (17 + 4.5m + 8k) – (7.5m – 9 + 4k).
Answer:
4k – 3m + 26.
Explanation:
In the above-given question,
given that,
(17 + 4.5m + 8k) – (7.5m – 9 + 4k).
17 + 4.5m + 8k – 7.5m + 9 – 4k.
26 – 3m + 4k.
4k – 3m + 26.
KEY CONCEPT
To subtract expressions, you can use properties of operations.
Write the subtraction as addition and use the Distributive Property to multiply – 1 to the terms in the expression being subtracted.
5 – (2x – 7)
= 5 – (-2x – 7)
= 5 +(-1)(-2x – 7)
= 5+ (-1)(-2)x + (-1)(-7)
= 5 + 2x + 7
You can use the Distributive Property to distribute the minus sign to the second expression, which changes the signs of the terms.
5 – (-2x – 7)
= 5 + 2x + 7
Do You Understand?
Question 1.
Essential Question How can properties of operations be used to subtract expressions?
Answer:
The properties be used to subtract expressions are Distributive property.
Explanation:
In the above-given question,
given that,
5 – (2x – 7)
= 5 – (-2x – 7)
= 5 +(-1)(-2x – 7)
= 5+ (-1)(-2)x + (-1)(-7)
= 5 + 2x + 7.
Question 2.
Use Structure How is subtracting – 4x from 9x similar to subtracting -4 from 9?
Answer:
The difference is 5x.
Explanation:
In the above-given question,
given that,
-4x and 9x.
9x – 4x.
5x.
so the difference is 5x.
Question 3.
Is adding the quantity – 12 + 8r to an expression the same as subtracting -8r+ 12 from the same expression? Explain your reasoning.
Answer:
No, the expressions are not equal.
Explanation:
In the above-given question,
given that,
-12 + 8r.
8r – 12.
-8r + 12.
12 – 8r.
so both the expressions are not equal.
Do You Know How?
Question 4.
Subtract.
a. (21x) – (-16 + 7x)
Answer:
28x + 16.
Explanation:
In the above-given question,
given that,
subtract the expressions.
21x – (-16 + 7x).
21x + (-1) (-16 + 7x).
21x + (-1)(-16) + (-1)(-7x).
21x + 16 + 7x.
28x + 16.
b. (-13n) – (17 – 5n)
Answer:
18n – 17.
Explanation:
In the above-given question,
given that,
subtract the expressions.
(-13n) – (17 – 5n).
13n – 17 + 5n.
18n – 17.
c. (4y – 7) – (y – 7)
Answer:
3y.
Explanation:
In the above-given question,
given that,
subtract the expressions.
(4y – 7) – (y – 7).
4y – 7 -y + 7.
3y.
d. (-w + 0.4) – (-w – 0.4)
Answer:
0.8.
Explanation:
In the above-given question,
given that,
subtract the expressions.
(-w + 0.4) – (-w – 0.4).
-w + 0.4 + w + 0.4.
0.8.
Question 5.
Jude has 5 pairs of sunglasses that cost the same in his online shopping cart but then decides to get only 2. Each pair of sunglasses is the same price. Let p represent the cost of each pair. Write an expression for the original cost, the updated cost, and the difference in cost.

Answer:
The expression for the original cost, the updated cost, and the difference in cost = $2.02.
Explanation:
In the above-given question,
given that,
Jude has 5 pairs of sunglasses that cost the same in his online shopping cart but then decides to get only 2.
Each pair of sunglasses is the same price. Let p represent the cost of each pair.
5 – 2 = 3p.
3 x $1.49 = 4.47.
$6.49 – $4.47 = $2.02.
so the difference in cost = $2.02.
Question 6.
Subtract and simplify.
\(\frac{1}{6}\)m – (-\(\frac{5}{8}\)m + \(\frac{1}{3}\))
Answer:
53m + 1/3.
Explanation:
In the above-given question,
given that,
\(\frac{1}{6}\)m – (-\(\frac{5}{8}\)m + \(\frac{1}{3}\)).
1/6m + 5/8m + 1/3.
6 x 8 = 48.
48 + 5 = 53.
53m + 1/3.
Practice & Problem Solving
Multimedia Leveled Practice In 7-9, fill in the missing signs or numbers.
Question 7.
Rewrite the expression 14m – (5 + 8m)
14m ![]() 5
5 ![]() 8m
8m
Answer:
The missing signs are minus.
Explanation:
In the above-given question,
given that,
14m – (5 + 8m).
14m – 5 – 8m.
6m – 5.
Question 8.
Rewrite the expression 13d – (-9d – 4) without parentheses. without parentheses.
13d ![]() 9d
9d ![]() 4
4
Answer:
The expression is 22d + 4.
Explanation:
In the above-given question,
given that,
the expression is 13d – (-9d – 4).
13d + 9d + 4.
22d + 4.
so the expression without parentheses is 22d + 4.
Question 9.
Write an equivalent expression to 8k – (5 + 2k) without parentheses. Then simplify.
8k – (5 + 2k) = 8k ![]() 5
5 ![]() 2k
2k
= 8k ![]() 2k
2k ![]() 5
5
= ![]() k
k ![]() 5
5
Answer:
The equivalent expression is 6k – 5.
Explanation:
In the above-given question,
given that,
8k – (5 + 2k).
8k – 5 – 2k.
6k – 5.
Question 10.
A company has two manufacturing plants with daily production levels of 5x + 11 items and 2x – 3 items, respectively, where x represents a minimum quantity. The first plant produces how many more items daily than the second plant?
Answer:
The first plant produces 3 more items daily than the second plant.
Explanation:
In the above-given question,
given that,
A company has two manufacturing plants with daily production levels of 5x + 11 items and 2x – 3 items.
5x + 11 – 2x – 3.
3x + 8.
so the first plant produces 3 more items daily than the second plant.
Question 11.
Two communications companies offer calling plans. With Company X, it costs 35¢ to connect and then 5¢ for each minute. With Company Y, it costs 15¢ to connect and then 4¢ for each minute.
Write and simplify an expression that represents how much more Company X charges than Company Y, in cents, for n minutes.
Answer:
The expression that represents company X charges than company Y, in cents, for n minutes =
Explanation:
In the above-given question,
given that,
Two communications companies offer calling plans. With Company X, it costs 35¢ to connect and then 5¢ for each minute.
With Company Y, it costs 15¢ to connect and then 4¢ for each minute.
35 + 5 = 40¢.
15 + 4 = 19¢.
40 – 19 = 21¢.
so the expression that represents company x charges than company y, in cents, for n minutes = 21¢.
Question 12.
Make Sense and Persevere The base and height of a triangle are each extended 2 cm. What is the area of the shaded region? How do you know?
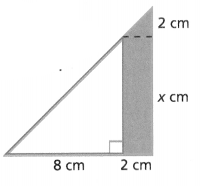
Answer:
The area of the shaded region = x cm.
Explanation:
In the above-given question,
given that,
The base and height of a triangle are each extended 2 cm.
area = 1/2 x b x h.
area = 1/2 x 2 x x.
area = 2/2x.
area = x cm.
so the area of the shaded region is x cm.
Question 13.
Two friends shop for fresh fruit. Jackson buys a watermelon for $7.65 and 5 pounds of cherries. Tim buys a pineapple for $2.45 and 4 pounds of cherries. Use the variable p to represent the price, in dollars, per pound of cherries. Write and simplify an expression to represent how much more Jackson spent.
Answer:
The expression to represent how much more jackson spent = $6.2p.
Explanation:
In the above-given question,
given that,
Two friends shop for fresh fruit.
Jackson buys a watermelon for $7.65 and 5 pounds of cherries.
Tim buys a pineapple for $2.45 and 4 pounds of cherries.
$2.45 + 4 = $6.45.
$7.65 + 5 = $12.65.
$12.65 – $6.45 = $6.2.
so the expression to represent how much more jacson spent = $6.2p.
Question 14.
Yu’s family wants to rent a car to go on vacation. Envocar charges $50.50 and 8¢ per mile. Freedomride charges $70.50 and 12¢ per mile. How much more does Freedomride charge for driving d miles than EnvoCar?
Answer:
The much does Freedomride charge for driving d miles than Envo Car = $20 and 4¢ .
Explanation:
In the above-given question,
given that,
Yu’s family wants to rent a car to go on vacation.
Envocar charges $50.50 and 8¢ per mile.
Freedomride charges $70.50 and 12¢ per mile.
$50.50 and 8¢ .
$70.50 and 12¢ .
70.50 – 50.50 and 12 – 8.
$20 and 4¢ .
Question 15.
A rectangular garden has a walkway around it. Find the area of the walkway.

Answer:
The area of the walkway = 168x + 136.5 sq ft.
Explanation:
In the above-given question,
given that,
the area of the walkway = l x b.
area = (8x + 6.5 ft ) x 21 ft.
area = 168x + 136.5 square ft.
Question 16.
Critique Reasoning Tim incorrectly rewrote the expression \(\frac{1}{2}\)p – (\(\frac{1}{4}\)p + 4) as \(\frac{1}{2}\)p + \(\frac{1}{4}\)p – 4. Rewrite the expression without parentheses. What was Tim’s error?
Answer:
The Tim’s error = 1/2p – 4.
Explanation:
In the above-given question,
given that,
Tim incorrectly rewrote the expression \(\frac{1}{2}\)p – (\(\frac{1}{4}\)p + 4).
\(\frac{1}{2}\)p + \(\frac{1}{4}\)p – 4.
1/2p – 1/4p – 4.
1/2p – 4.
Question 17.
Higher Order Thinking Find the difference.
(7x – 6\(\frac{2}{3}\)) – (-3x +4\(\frac{3}{4}\))
Answer:
The difference is 10x – 7.
Explanation:
In the above-given question,
given that,
(7x – 6\(\frac{2}{3}\)) – (-3x +4\(\frac{3}{4}\))
7x – 6 x 2/3 – (-3x + 4 (3/4).
7x – 6 (2/3) + 3x – 4 (-3/4).
10x -4 – 3.
10x – 7.
Question 18.
Each month, a shopkeeper spends 5x + 11 dollars on rent and electricity. If he spends 2x – 3 dollars on rent, how much does he spend on electricity?
Answer:
The much he spend on electricity = 3x + 8.
Explanation:
In the above-given question,
given that,
Each month, a shopkeeper spends 5x + 11 dollars on rent and electricity.
If he spends 2x – 3 dollars on rent.
5x + 11 – 2x – 3.
3x + 8.
Question 19.
Use the expression \(\frac{1}{4}\)p – (1 – \(\frac{1}{3}\)p).
a. Rewrite the expression without parentheses. Simplify. Show your work.
Answer:
The expression is 1/7p – 1.
Explanation:
In the above-given question,
given that,
\(\frac{1}{4}\)p – (1 – \(\frac{1}{3}\)p).
1/4 p – (1 – 1/3p).
1/4p – 1 + 1/3p.
1/7p – 1.
b. Use a different method to write the expression without parentheses. Do not simplify.
Answer:
The expression is 1/7p – 1.
Explanation:
In the above-given question,
given that,
\(\frac{1}{4}\)p – (1 – \(\frac{1}{3}\)p).
1/4 p – (1 – 1/3p).
1/4p – 1 + 1/3p.
1/7p – 1.
Assessment Practice
Question 20.
An expression is shown.
(0.25n – 0.3) – (0.8n – 0.25)
Create an equivalent expression without parentheses.
Answer:
The equivalent expression without parantheses = 0.05 – 0.55n.
Explanation:
In the above-given question,
given that,
(0.25n – 0.3) – (0.8n – 0.25).
0.25n – 0.3 – 0.8n + 0.25.
-0.55n + 0.05.
Lesson 4.8 Analyze Equivalent Expressions
Solve & Discuss It!
How many toothpicks make a triangle? Two triangles? Write an expression that represents the number of toothpicks needed to make x triangles that appear side-by-side in a single row, as shown. Explain your reasoning.
I can… use an equivalent expression to find new information.

Look for Relationships
What do you notice about the number of toothpicks needed for more than 1 triangle?
Focus on math practices
Reasoning Can there be more than one expression that represents the total number of toothpicks needed to make x triangles in the arrangement shown? Explain.
Essential Question
How can writing equivalent expressions show how quantities are related?
Try It!
Joe is buying gift cards that are on sale for 15% off. He uses c – 0.15c to determine the sale price of gift cards. What is an equivalent expression that Joe could also use to determine the sale price of a gift card?
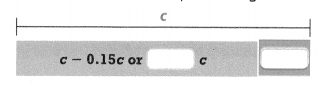
Answer:
The equivalent expression that Joe could use to determine the sale price = 0.15 – 0.15c.
Explanation:
In the above-given question,
given that,
Joe is buying gift cards that are on sale for 15% off.
He uses c – 0.15c to determine the sale price of gift cards.
15/100 – 0.15c.
0.15 – 0.15c.
Convince Me! How do you know if an expression is describing a percent increase or a percent decrease?
Try It!
The total area, in square feet, of a rectangular stage that has been widened by x feet is represented by 1,900 + 76x. Use the Distributive Property to factor the expression. What does each factor in the equivalent expression tell you about the stage?

Answer:
The equivalent expression about the stage = 1900x + 76 x square.
Explanation:
In the above-given question,
given that,
The total area, in square feet, of a rectangular stage that has been widened by x feet is represented by 1,900 + 76x.
1900 + 76x x x.
1900x + 76xsquare.
KEY CONCEPT
Rewriting expressions can clarify relationships among quantities or variables. When you rewrite an expression, you are writing an equivalent expression.
4x + 12 is equivalent to 4(x + 3) is equivalent to x + x + x + x + 3 + 3 + 3 + 3
Do You Understand?
Question 1.
Essential Question How can writing equivalent expressions show how quantities are related?
Answer:
The equivalent expressions are 4x + 12.
Explanation:
In the above-given question,
given that,
4x + 12.
4(x + 3).
x + x + x + x + 3 + 3 + 3 + 3.
Question 2.
Use Structure The total area, in square feet, of a rectangular mural that has been extended by x feet is represented by 5.5(7.5 + x). Expand the expression using the Distributive Property. What do each of the terms in the equivalent expression tell you about the mural?

Answer:
The expressions tell you about the mural = 41.25 + 5.5x.
Explanation:
In the above-given question,
given that,
the expression is 5.5(7.5 + x).
5.5 x 7.5 + 5.5 x x.
41.25 + 5.5x.
so the equivalent expression is 41.25 + 5.5x.
Question 3.
The expression (2x + 6) + x represents the perimeter of an isosceles triangle. If x represents the length of one side of the triangle, explain how you can use the Distributive Property to find the length of each of the two equivalent sides?
Answer:
The Distributive property to find the length of each of the two equivalent sides = 2x square + 6x.
Explanation:
In the above-given question,
given that,
The expression (2x + 6) + x represents the perimeter of an isosceles triangle.
(2x + 6) + x.
2x X x + 6x.
so the distributive property to find the length of each of the two equivalent sides = 2x x x + 6x.
Do You Know How?
Question 4.
Rewrite the expression 12x + 8 to find an equivalent expression. Show three possible expressions. What do the rewritten expressions tell you about the relationships among the quantities?
Answer:
The expression are 2(6x + 4) and 4(3x + 2).
Explanation:
In the above-given question,
given that,
Rewrite the expression 12x + 8 to find an equivalent expression.
2 (6x + 4).
4 (3x + 2).
Question 5.
A rope is used to make a fence in the shape of an equilateral triangle around a newly planted tree. The length of the rope is represented with the expression 9x + 15

a. Rewrite the expression to represent the three side lengths of the rope fence.
Answer:
The length of the rope is represented with the expression =
Explanation:
In the above-given question,
given that,
9x + 15.
3(3x + 5).
3 x 3x = 9x.
3 x 5 = 15.
so the length of the rope is 3(3x + 5).
b. What is the length of one side?
Answer:
The length of one side = 3x.
Explanation:
In the above-given question,
given that,
9x + 15.
3(3x + 5).
so the length of one side = 3x.
Question 6.
The expression (x – 0.35x) represents 35% off the cost of an item x. How is this equivalent to multiplying x by 0.65?
Answer:
The expression equivalent to multiplying = 0.4225.
Explanation:
In the above-given question,
given that,
The expression (x – 0.35x) represents 35% off the cost of an item x.
x = 0.65.
0.65 – 0.35(0.65).
0.65 – 0.2275.
0.4225.
Practice & Problem Solving
Question 7.
Reasoning Eric is planning an event at a hotel. Let g stand for the number of Eric’s guests. The two expressions represent the difference between the cost of the rooms. Expression 1: (326 + 37g) – (287 + 23g). Expression 2: 39 + 14g. What can you tell about Expression 2 and Expression 1?

Answer:
The two expressions are same.
Explanation:
In the above-given question,
given that,
Eric is planning an event at a hotel. Let g stand for the number of Eric’s guests.
The two expressions represent the difference between the cost of the rooms.
Expression 1: (326 + 37g) – (287 + 23g). Expression 2: 39 + 14g.
326 + 37g – 287 – 23g.
39 + 14g.
so the expressions 1 and 2 are same.
Question 8.
A student received a coupon for 17% off the total purchase price at a clothing store. Let b be the original price of the purchase. Use the expression b-0.17b for the new price of the purchase. Write an equivalent expression by combining like terms.
Answer:
The equivalent expression is 0.16b.
Explanation:
In the above-given question,
given that,
A student received a coupon for 17% off the total purchase price at a clothing store.
Let b be the original price of the purchase.
Use the expression b-0.17b for the new price of the purchase.
0.17b – b.
0.16b.
so the equivaent expression is 0.16b.
Question 9.
Kirana buys boxes of crackers that each have the same cost, c. She represents the cost of 3 boxes of cheese crackers, 2 boxes of poppy seed crackers, and 2 boxes of plain crackers using the expression 3c + 2c + 2c. What equivalent expression can represent the cost?
Answer:
The equivalent epression that represent the cost = 7c.
Explanation:
In the above-given question,
given that,
Kirana buys boxes of crackers that each have the same cost c.
She represents the cost of 3 boxes of cheese crackers.
2 boxes of poppy seed crackers, and 2 boxes of plain crackers using the expression 3c + 2c + 2c.
3c + 2c + 2c.
5c + 2c.
7c.
so the equivalent expression that represent the cost = 7c.
Question 10.
A student received a coupon for 14% off the total purchase price at a clothing store. Let c be the original price of the purchase. The expression c – 0.14c represents the new price of the purchase. Write an equivalent expression to show another way to represent the new price.
Answer:
The equivalent expression to show another way to represent the new price = 0.13c.
Explanation:
In the above-given question,
given that,
A student received a coupon for 14% off the total purchase price at a clothing store.
Let c be the original price of the purchase.
The expression c – 0.14c represents the new price of the purchase.
c – 0.14c.
0.13c.
so the equivalent expression to show another way to represent the new price = 0.13c.
Question 11.
A farmer recently sold a large plot of land. The sale decreased his total acreage by 8%. Let v be the original acreage.
a. Find two equivalent expressions that will give the new acreage.
Answer:
The two equivalent expressions that will give the new acreage = v – 0.08v and 0.07v.
Explanation:
In the above-given question,
given that,
A farmer recently sold a large plot of land.
The sale decreased his total acreage by 8%.
v – 0.08v.
0.07v.
b. Use the expressions to describe two ways to find the new acreage.
Answer:
The two equivalent expressions that will give the new acreage = v – 0.08v and 0.07v.
Explanation:
In the above-given question,
given that,
A farmer recently sold a large plot of land.
The sale decreased his total acreage by 8%.
v – 0.08v.
0.07v.
Question 12.
An art teacher enlarged the area of a copy of a painting by 49%. Let d represent the area of the original painting. The expression d + 0.49d is one way to represent the area of the new painting. Write two additional expressions that will give the area of the new painting.
Answer:
The two additional expressions that will give the area of the new painting = d + 0.49d and 0.50d.
Explanation:
In the above-given question,
given that,
An art teacher enlarged the area of a copy of a painting by 49%.
Let d represent the area of the original painting.
The expression d + 0.49d is one way to represent the area of the new painting.
so the expressions are d nd d + 0.49d.
0.50d.
Question 13.
Use Structure The area of a rectangular playground has been extended on one side. The total area of the playground, in square meters, can be written as 352 + 22x. Rewrite the expression to give a possible set of dimensions for the playground.
Answer:
The expression to give a possible set of dimensions for the playground = 22(16 + x).
Explanation:
In the above-given question,
given that,
The area of a rectangular playground has been extended on one side.
The total area of the playground, in square meters, can be written as 352 + 22x.
352 + 22x.
22(16 + x).
22 x 16 = 352.
22 x x = 22x.
Question 14.
The manager of a store increases the price of the bathing suits by 7%. Let t be the original price of a bathing suit. The new price is t + 0.07t. a. Find an expression equivalent to t + 0.07t.
Answer:
The expression equivalent to t + 0.07t = 0.08t.
Explanation:
In the above-given question,
given that,
The manager of a store increases the price of the bathing suits by 7%.
Let t be the original price of a bathing suit.
The new price is t + 0.07t.
0.08t.
b. If the original price of a bathing suit was $19.99, estimate the new price by first rounding the original price to the nearest dollar.
Answer:
The original price to the nearest dollar = $20 + $1.4t.
Explanation:
In the above-given question,
given that,
If the original price of a bathing suit was $19.99.
19.99 = 20.
20 + 0.07 x 20.
20 + 1.4t.
Question 15.
Higher Order Thinking A customer at a clothing store is buying a pair of pants and a shirt. The customer can choose between a sale that offers a discount on pants, or a coupon for a discount on the entire purchase. Let n represent the original price of the pants and s represent the price of the shirt

a. Write two expressions that represent the “15% off sale on all pants” option.
Answer:
The expressions that represents is n – 0.015.
Explanation:
In the above-given question,
given that,
A customer at a clothing store is buying a pair of pants and a shirt.
The customer can choose between a sale that offers a discount on pants, or a coupon for a discount on the entire purchase.
n – 0.015.
b. Write two expressions that represent the “10% off her entire purchase” option.
Answer:
The expressions that represents is n – 0.010.
Explanation:
In the above-given question,
given that,
A customer at a clothing store is buying a pair of pants and a shirt.
The customer can choose between a sale that offers a discount on pants, or a coupon for a discount on the entire purchase.
n – 0.010.
c. If the original cost of the pants is $25 and the shirt is $10, which option should the customer choose? Explain.
Answer:
The customer choose the both pants and shirts = $35.
Explanation:
In the above-given question,
given that,
If the original cost of the pants is $25 and the shirt is $10.
$25 + $10.
$35.
so the customer choose the both pants and shirts = $35.
Assessment Practice
Question 16.
At a college, the cost of tuition increased by 10%. Let b represent the former cost of tuition. Use the expression b + 0.10b for the new cost of tuition.
PART A
Write an equivalent expression for the new cost of tuition.
Answer:
The new cost of tuition is 0.11b.
Explanation:
In the above-given question,
given that,
At a college, the cost of tuition increased by 10%.
Let b represent the former cost of tuition.
b + 0.10b.
0.11b.
so the new cost of tution is 0.11b.
PART B
What does your equivalent expression tell you about how to find the new cost of tuition?
Answer:
250
4-8 Analyze Equivalent Expressions
Topic 4 Review
Topic Essential Question
How can properties of operations help to generate equivalent expressions that can be used in solving problems?
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.
Vocabulary
coefficient
constant
variable
factor
expression

Answer:
A term that contains only a number is constant.
The number part of the term that contains a variable is coefficient.
A variable is a letter that represents an unknown value.
Explanation:
In the above-given question,
given that,
A term that contains only a number is constant.
The number part of the term that contains a variable is coefficient.
A variable is a letter that represents an unknown value.
for example:
2x + 4y – 9.
where 2 and 4 are coefficients.
x and y are variables.
9 is the constant.
Use Vocabulary in Writing
Membership in a digital library has a $5 startup fee and then costs $9.95 per month. Membership in a video streaming service costs $7.99 per month with no startup fee. Use vocabulary words to explain how this information could be used to write an expression for the total cost of both memberships after m months.
Answer:
The total cost of memberships after m months = $49.75 + $7.99m.
Explanation:
In the above-given question,
given that,
Membership in a digital library has a $5 startup fee and then costs $9.95 per month.
Membership in a video streaming service costs $7.99 per month with no startup fee.
5 x $9.95 + $7.99m.
$49.75 + $7.99m.
so the total cost of memberships after m months = $49.75 + $7.99m.
Concepts and Skills Review
Lesson 4.1 Write and Evaluate Algebraic Expressions
Quick Review
You can use an algebraic expression to represent and solve a problem with unknown values. The expression can consist of coefficients, constants, and variables. You can substitute values for variables to evaluate expressions.
Example
A farm charges $1.75 for each pound of strawberries picked and $2 for a basket to hold the strawberries. What is the total cost to pick 5 pounds of strawberries?
Answer:
The total cost to pick 5 pounds of strawberries = $10.75.
Explanation:
In the above-given question,
given that,
A farm charges $1.75 for each pound of strawberries picked and $2 for a basket to hold the strawberries.
($1.75 x $5) + 2.
($8.75) + 2.
$10.75.
Write an expression to represent the total cost in dollars to pick p pounds of strawberries.
1.75p + 2
Substitute 5 for p.
1.75(5) + 2 = 8.75 + 2 = 10.75
It costs $10.75 to pick 5 pounds of strawberries.
Practice
Question 1.
Haddie makes and sells knit scarves. Next week she will pay a $25 fee for the use of a booth at a craft fair. She will charge $12 for each scarf she sells at the fair. Write an expression to determine Haddie’s profit for selling s scarves after paying the fee for the use of the booth.
Answer:
The expression to determine Haddie’s profit for selling scarves = $37.
Explanation:
In the above-given question,
given that,
Haddie makes and sells knit scarves.
Next week she will pay a $25 fee for the use of a booth at a craft fair.
She will charge $12 for each scarf she sells at the fair.
$25 + $12.
$37.
so the expression to determine Haddie’s profit for selling scarves = $37.
Question 2.
The cost to buy p pounds of potatoes at $0.32 per pound and n pounds of onions at $0.48 per pound can be determined by using the expression 0.32p + 0.48n. How much will it cost to buy 4.5 pounds of potatoes and 2.5 pounds of onions?
Answer:
The cost to buy 4.5 pounds of potatoes and 2.5 pounds of onions = 0.4608 + 1.2n.
Explanation:
In the above-given question,
given that,
The cost to buy p pounds of potatoes at $0.32 per pound and
n pounds of onions at $0.48 per pound can be determined by using the expression 0.32p + 0.48n.
0.32 x 4.5p = 0.4608p.
0.48 x 2.5n = 1.2.
0.4608 + 1.2n.
Lessons 4-2 AND 4-3 Generate Equivalent Expressions and Simplify Expressions
Quick Review
You can use properties of operations and combine like terms to simplify expressions. Like terms are terms that have the same variable part.
Example
Simplify the expression below.
-7 + \(\frac{1}{3}\)n – \(\frac{4}{3}\) + 2n
Use the Commutative Property to put like terms together,
\(\frac{1}{3}\)n + 2n – 7 – \(\frac{4}{3}\)
Combine like terms.
2\(\frac{1}{3}\)n – 8\(\frac{1}{3}\)
Practice
Simplify each expression below.
Question 1.
\(\frac{5}{8}\)m + 9 – \(\frac{3}{8}\)m – 15
Answer:
3/8 – 6.
Explanation:
In the above-given question,
given that,
\(\frac{5}{8}\)m + 9 – \(\frac{3}{8}\)m – 15.
Use the Commutative Property to put like terms together,
5/8 – 3/8 + 9 – 15.
combine like terms.
3/8 – 6.
Question 2.
-8w + (-4z) + 2 + 6w + 9z – 7
Answer:
5z – 2w – 5.
Explanation:
In the above-given question,
given that,
-8w + (-4z) + 2 + 6w + 9z – 7.
Use the Commutative Property to put like terms together,
6w – 8w -4z + 9z -7 + 2.
combine like terms.
-2w + 5z -5.
5z – 2w – 5.
Question 3.
-6 + (-2d) + (-4d) + 3d
Answer:
-3(d + 2).
Explanation:
In the above-given question,
given that,
-6 + (-2d) + (-4d) + 3d.
Use the Commutative Property to put like terms together,
-6 – 2d – 4d + 3d.
combine like terms.
3d – 6d -6.
-3d – 6.
-3(d + 2).
Lesson 4.4 Expand Expressions
Quick Review
The Distributive Property allows you to multiply each term inside parentheses by a factor that is outside the parentheses. This means that you can use the Distributive Property to expand expressions.
Example
Expand the expression (6 + 7).
(\(\frac{1}{4}\) × h) + (\(\frac{1}{4}\) × 7) = \(\frac{1}{4}\)h + 1.75
Practice
Question 1.
Expand the expression 3.5(-3n + 4).
Answer:
The expression is -10.5n + 14.
Explanation:
In the above-given question,
given that,
the expression is 3.5(-3n + 4).
3.5 x -3n + 3.5 x 4.
-10.5n + 14.
so the expression is -10.5n + 14.
Question 2.
Simplify the expression –\(\frac{3}{5}\)(-8 + \(\frac{5}{9}\)x – 3).
Answer:
5/9 + 24/5 – 3.
Explanation:
In the above-given question,
given that,
the expression –\(\frac{3}{5}\)(-8 + \(\frac{5}{9}\)x – 3).
-3/5 -8 + 5/9 x – 3.
24/5 + 5/9x – 3.
5/9x + 24/5 – 3.
Lesson 4.5 Factor Expressions
Quick Review
When you factor an expression, you write it as a product of two expressions. The new expression is equivalent to the original expression. The greatest common factor (GCF) and the Distributive Property are tools that you use when you need to factor an expression.
Example
Factor the expression 12x – 9y + 15.
The GCF of 12x, 15, and -9y is 3.
Rewrite each term using 3 as a factor.
12x = 3 • 4x
-9y = 3 • (-3y)
15= 3 • 5
Use the Distributive Property to factor the expression.
3(4x – 3y + 5)
Practice
Factor each expression.
Question 1.
63a – 42b
Answer:
3(21a – 14b).
Explanation:
In the above-given question,
given that,
the expression is 63a – 42b.
3(21a – 14b).
3 x 21a = 63a.
3 x 14b = 42b.
Question 2.
81y + 54
Answer:
9(9y + 6).
Explanation:
In the above-given question,
given that,
the expression is 81y + 54.
9(9y + 6).
9 x 9y = 81y.
9 x 6 = 54.
Question 3.
Which show a way to factor the expression 32t – 48? Select all that apply.
☐ 2(16t – 24)
☐ 4(12t – 48)
☐ 6(26 – 42)
☐ 8(4t – 6)
☐ 16(2t – 3)
Answer:
2(16t – 24) and 8(4t – 6).
Explanation:
In the above-given question,
given that,
the expression is 32t – 48.
2(16t – 24).
2 x 16t = 32t.
2 x 24 = 48.
8(4t – 6).
8 x 4t = 32t.
8 x 6 = 48.
Lessons 4.6 AND 4.7 Add and Subtract Expressions
Quick Review
Adding and subtracting expressions may require combining like terms. This means that you must use the Commutative and Associative Properties to reorder and group terms as needed.
Example
Kerry has n markers. Rachel has 1 marker fewer than twice the number of markers Kerry has. Write and simplify an expression for the total number of markers they have.
Number of markers Kerry has: n
Number of markers Rachel has: 2n – 1
Total number of markers:
n + (2n – 1)
(n + 2n) – 1
3n – 1
Practice
Add the expressions.
Question 1.
5.2C – 7.35) + (-3.9C + 2.65)
Answer:
1.3c – 4.7.
Explanation:
In the above-given question,
given that,
5.2C – 7.35) + (-3.9C + 2.65).
5.2c – 7.35 – 3.9c + 2.65.
5.2c – 3.9c + 2.65 – 7.35.
1.3c – 4.7.
Question 2.
(6x – 2y – 5) – (-5 + 9y – 8x)
Answer:
14x – 11y.
Explanation:
In the above-given question,
given that,
(6x – 2y – 5) – (-5 + 9y – 8x).
6x – 2y – 5 + 5 – 9y + 8x.
14x – 11y.
Question 3.
Last week Jean ran 2 fewer than 4m miles. This week she ran 0.5 miles more than last week. Write and simplify an expression for the total number of miles Jean ran in the two weeks.
Answer:
The total number of miles Jean ran in the two weeks = 2.5m.
Explanation:
In the above-given question,
given that,
Last week Jean ran 2 fewer than 4m miles.
This week she ran 0.5 miles more than last week.
2m + 0.5m.
2.5m.
so the total number of miles Jean ran in the two weeks = 2.5m.
Lesson 4.8 Analyze Equivalent Expressions
Quick Review
Equivalent expressions can help to show new information about a problem. Sometimes the equivalent expression will be an expanded expression. In other cases, it will be a factored expression.
Example
The perimeter of a square is represented with the expression 84 + 44s. What is the length of one side of the square?
A square has 4 sides, so factor 4 out of each term in the expression for the perimeter.
84 + 445 = 4 • 21 + 4 • 11s = 4(21 + 115)
The factor within the parentheses represents the length of one side of the square.
The length of one side is 21 + 11s.
Practice
Question 1.
Hal earns n dollars per hour. Next month he will receive a 2% raise in pay per hour. The expression n + 0.02n is one way to represent Hal’s pay per hour after the raise. Write an equivalent simplified expression that will represent his pay per hour after the raise.
Answer:
The equivalent expression that will represent his pay per hour after the raise = 0.03n.
Explanation:
In the above-given question,
given that,
Hal earns n dollars per hour.
Next month he will receive a 2% raise in pay per hour.
The expression n + 0.02n is one way to represent Hal’s pay per hour after the raise.
n + 0.02n = 0.03n.
Question 2.
The area of a garden plot can be represented by the expression 84z – 54. The garden will be divided into six sections for planting six different vegetables. The sections will be equal in area. Write an expression that represents the area of each section.
Answer:
The expression that represents the area of each section =
Explanati
Topic 4 Fluency Practice
Hidden Clue
For each ordered pair, solve the percent problems to find the coordinates. Then locate and label the corresponding point on the graph. Draw line segments to connect the points in alphabetical order. Use the completed picture to help you answer the riddle below.
I can… represent and solve percent problems.
