Go Math Grade 3 Answer Key Chapter 11 Perimeter and Area helps you prepare for the exams. All the Concepts of Area and Perimeter are clearly explained in our Chapter 11 Perimeter and Area Go Math Grade 3 Answer Key. Go Math Grade 3 Perimeter and Area can be of great help during your preparation. You can get the Homework Help needed by referring to the Go Math Grade 3 Answer Key Chapter 11 Perimeter and Area.
Go Math Grade 3 Chapter 11 Perimeter and Area Answer Key
Enhance your Problem-Solving Skills using the HMH Go Math Grade 3 Ch 11 Perimeter and Area Solution Key. Cross Check the Solutions in the 3rd Grade Go Math Ch 11 Perimeter and Area Answer Key and understand where you went wrong. Get to know the Lessons in Chapter 11 with the quick links available below and solve the problems in it.
Lesson 1: Model Perimeter
Lesson 2: Find Perimeter
Lesson 3: Find Unknown Side Lengths
Lesson 4: Understand Area
Lesson 5: Measure Area
Lesson 6: Use Area Models
Mid -Chapter Checkpoint
Lesson 7: Problem Solving Area of Rectangles
- Problem Solving Area of Rectangles – Page No. 667
- Problem Solving Area of Rectangles Lesson Check – Page No. 668
Lesson 8: Area of Combined Rectangles
Lesson 9: Same Perimeter, Different Areas
- Same Perimeter, Different Areas – Page No. 679
- Same Perimeter, Different Areas Lesson Check – Page No. 680
- Same Perimeter, Different Areas Lesson Check 1 – Page No. 685
- Same Perimeter, Different Areas Lesson Check 2 – Page No. 686
Review/Test
- Review/Test – Page No. 687
- Review/Test – Page No. 688
- Review/Test – Page No. 689
- Review/Test – Page No. 690
- Review/Test – Page No. 691
- Review/Test – Page No. 692
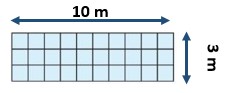
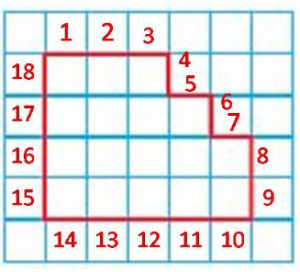
Model Perimeter – Page No. 629
Find the perimeter of the shape. Each unit is 1 centimeter.
Question 1.
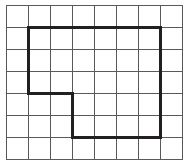
22 centimeters
Answer:
22 centimeters
Explanation:
Each square in the grid is a 1 by 1-centimeter square. So, we have to do is add up the lengths of the dark segments right over the figure. Start the count from the box where 1 is placed. This parameter is 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 centimeters long. So, it is 22 centimeters.
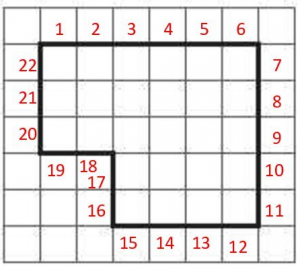
Question 2.
__________ centimeters
Answer:
22 centimeters
Explanation:
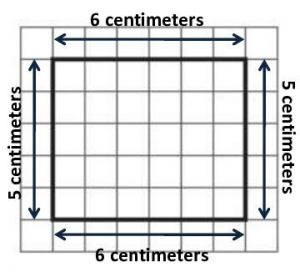
Look at the length of each side. Then, add the length of each side to get the perimeter of the given shape. The lengths of the sides are 6 + 5 + 6 + 5 = 22 centimeters.
Question 3.
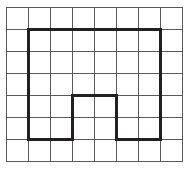
__________ centimeters
Answer:
26 centimeters
Explanation:
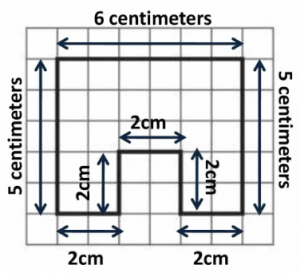
Given that each unit is 1 centimeter. Count the lengths of each box from number 1. So, this parameter is 26 centimeters long. or 6 + 5 + 2 + 2 + 2 + 2 + 2 + 5 = 26.
Question 4.
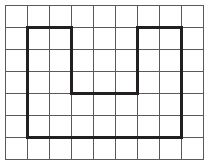
__________ centimeters
Answer:
30 centimeters
Explanation:
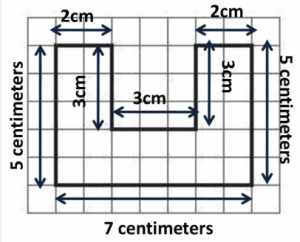
Look at the length of each side. Then, add the length of each side to get the perimeter of the given shape. The lengths of the sides are 2 + 3 + 3+ 3 + 2 + 5 + 7 + 5 = 30 centimeters long.
Problem Solving
Use the drawing for 5–6. Each unit is 1 centimeter.
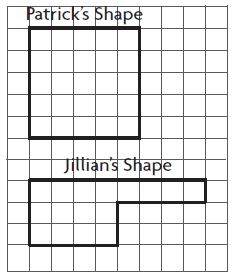
Question 5.
What is the perimeter of Patrick’s shape?
__________ centimeters
Answer:
20 centimeters
Explanation:
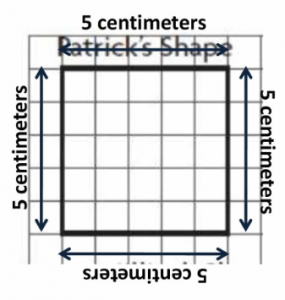
The perimeter of Patrick’s shape = 5 + 5 + 5 + 5 =20 centimeters.
Question 6.
How much greater is the perimeter of Jillian’s shape than the perimeter of Patrick’s shape?
__________ centimeters
Answer:
2 centimeters
Explanation:
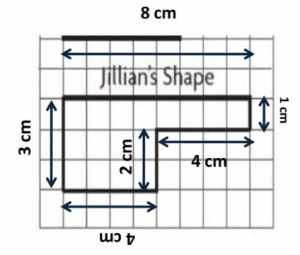
First, the perimeter of Jillian’s shape = 8 + 1 + 4 + 2 + 4 + 3 = 22 centimeters.
Difference = 22 – 20 = 2 centimeters.
The perimeter of Jillian’s shape is 2 centimeters greater than the perimeter of Patrick’s shape.
Model Perimeter – Page No. 630
Lesson Check
Question 1.
Find the perimeter of the shape.
Each unit is 1 centimeter.
Options:
a. 14 centimeters
b. 16 centimeters
c. 18 centimeters
d. 20 centimeters
Answer:
d. 20 centimeters
Explanation:
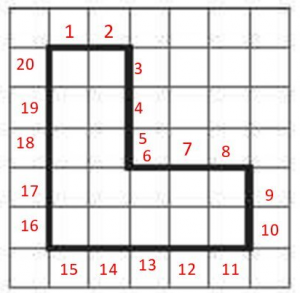
Given that each unit is 1 centimeter. Count the lengths of each box of the dark lines from number 1. So, this parameter is 20 centimeters long.
Question 2.
Find the perimeter of the shape.
Each unit is 1 centimeter.
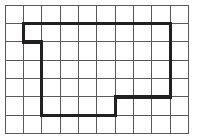
Options:
a. 19 centimeters
b. 26 centimeters
c. 33 centimeters
d. 55 centimeters
Answer:
b. 26 centimeters
Explanation:
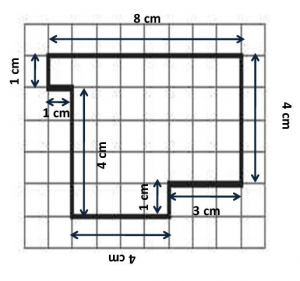
Find the length of each box and add them to find the perimeter of the given shape. The perimeter of the given shape is 8 + 4 +3 + 1 + 4 + 4 + 1 + 1 = 26 centimeters.
Spiral Review
Question 3.
Which lists the fractions in order from least to greatest?
\(\frac{2}{4}, \frac{2}{3}, \frac{2}{6}\)
Options:
a. \(\frac{2}{3}, \frac{2}{4}, \frac{2}{6}\)
b. \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\)
c. \(\frac{2}{4}, \frac{2}{3}, \frac{2}{6}\)
d. \(\frac{2}{3}, \frac{2}{6}, \frac{2}{4}\)
Answer:
b. \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\)
Explanation:
The numerator of the given factors is the same. So, look at the denominators to compare the size of the pieces. As the denominator gets smaller, the fraction gets larger. In the given problem, 3 is the smaller denominator compared to 4 and 6. Then, 4 is the next smaller denominator. So, the fractions in order from least to greatest are 2/6, 2/4, 2/3.
Question 4.
Kasey’s school starts at the time shown on the clock. What time does Kasey’s school start?

Options:
a. 6:40
b. 8:06
c. 8:30
d. 9:30
Answer:
c. 8:30
Explanation:
In the figure, hour-hand is indicating number 8. So, we say it is 8 hours. The minute hand is on 6. To find the minutes, multiply 6 x 5 = 30. So, it indicates 30 minutes. The time is 8 hours 30 minutes.
Question 5.
Michael and Dex are comparing fraction strips. Which statement is NOT correct?
Options:
a. \(\frac{1}{2}<\frac{2}{2}\)
b. \(\frac{2}{3}>\frac{1}{3}\)
c. \(\frac{4}{8}<\frac{3}{8}\)
d. \(\frac{4}{6}>\frac{2}{6}\)
Answer:
c. \(\frac{4}{8}<\frac{3}{8}\)
Explanation:
The denominators of the given fractions are the same. So, look at the numerators to compare the numbers.
1 < 2 is correct.
2 > 1 is correct.
4 < 3 is not correct. So, 4/8 < 3/8 is not correct.
Question 6.
Aiden wants to find the mass of a bowling ball. Which unit should he use?
Options:
a. liter
b. inch
c. gram
d. kilogram
Answer:
d. kilogram
Explanation:
The kilogram is used to find the mass of a bowling ball.
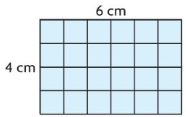
Find Perimeter – Page No. 635
Use a ruler to find the perimeter. (Note: on mobile devices like smart phones or tablets, the measurements will not be accurate.)
Question 1.
12 centimeters
Answer:
12 cm
Explanation:
Add the lengths of the sides measured to the perimeter. 4 + 3 + 2 + 3 = 12 cm.
Question 2.
_________ centimeters
Answer:
13 centimeters
Explanation:
Use a centimeter ruler to measure the length of each side.
Record and add the lengths of the sides measured to the nearest centimeter.
5 cm + 1 cm + 1 cm + 2 cm + 4 cm = 13 centimeters.
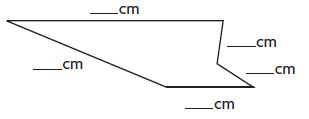
Question 3.
_________ inches
Answer:
8 inches
Explanation:
Use an inch ruler to measure the length of each side to the nearest inch.
Record and add the lengths of the sides measured to the nearest inch.
2 in + 2 in + 2 in + 2 in =8 inches.
Question 4.
_________ inches
Answer:
6 inches
Explanation:
Use an inch ruler to measure the length of each side.
Record and add the lengths of the sides measured to the nearest inch.
2 in + 2 in + 2 in = 6 inches.
Problem Solving
Draw a picture to solve 5–6.
Question 5.
Evan has a square sticker that measures 5 inches on each side. What is the perimeter of the sticker?
_________ inches
Answer:
20 inches
Explanation:
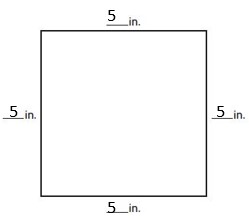
The square has equal sides. Each side has 5 inches. So, the perimeter of the sticker is 5 x 4 = 20 inches.
Question 6.
Sophie draws a shape that has 6 sides. Each side is 3 centimeters. What is the perimeter of the shape?
_________ centimeters
Answer:
18 centimeters
Explanation:
The perimeter of the shape is = Addition of all sides.
Given that Sophie draws a shape that has 6 sides with 3 centimeters. So, the perimeter of the shape = 3 + 3 + 3 + 3 + 3 + 3 = 18 centimeters
Find Perimeter – Page No. 636
Lesson Check
Use an inch ruler for 1–2.
Question 1.
Ty cut a label the size of the shape shown. What is the perimeter, in inches, of Ty’s label?

Options:
a. 4 inches
b. 5 inches
c. 6 inches
d. 7 inches
Answer:
c. 6 inches
Explanation:
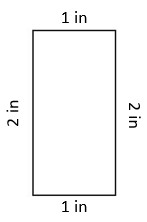
By using an inch ruler, Ty can measure the length of each side of the given shape. Now, find the lengths of each side.
1 in + 2 in + 1 in + 2 in = 6 inches.
Question 2.
Julie drew the shape shown below. What is the perimeter, in inches, of the shape?

Options:
a. 2 inches
b. 4 inches
c. 6 inches
d. 8 inches
Answer:
d. 8 inches
Explanation:
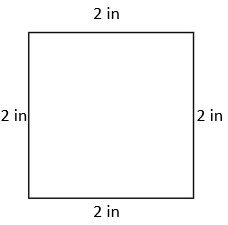
Julie can use an inch ruler to measure the length of each side of the shape. Now, find the lengths of each side. Each side has 2 inches. So, the perimeter of the shape is 2 in + 2 in + 2 in + 2 in = 8 inches.
Spiral Review
Question 3.
What is the perimeter of the shape below?

Options:
a. 8 units
b. 10 units
c. 20 units
d. 22 units
Answer:
c. 20 units
Explanation:
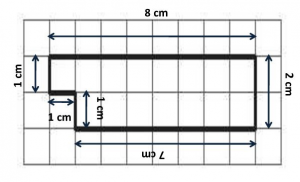
From the figure, each unit is 1 centimeter. Count the lengths of each box from number 1. So, this parameter is 20 units long.
Question 4.
Vince arrives for his trumpet lesson after school at the time shown on the clock. What time does Vince arrive for his trumpet lesson?

Options:
a. 3:26 A.M.
b. 4:26 A.M.
c. 3:26 P.M.
d. 4:26 P.M.
Answer:
c. 3:26 P.M.
Explanation:
Given that Vince arrives for his trumpet lesson after school at the time shown on the clock. As it is mentioned after school time, it is Noon. The times afternoon and before midnight are written with P.M. The hour hand is indicating number 3. So, the answer is 3:26 P.M.
Question 5.
Matthew’s small fish tank holds 12 liters. His large fish tank holds 25 liters. How many more liters does his large fish tank hold?
Options:
a. 12 liters
b. 13 liters
c. 25 liters
d. 37 liters
Answer:
b. 13 liters
Explanation:
To get the more liters, do subtraction of large fish tank liters to small fish tank liters. So, The large fish tank is 25 liters – 12 liters = 13 liters more than Matthew’s small fish tank.
Question 6.
Cecila and Sasha are comparing fraction strips. Which statement is correct?
Options:
a. \(\frac{1}{2}<\frac{1}{3}\)
b. \(\frac{1}{8}>\frac{1}{6}\)
c. \(\frac{1}{4}>\frac{1}{2}\)
d. \(\frac{1}{6}<\frac{1}{4}\)
Answer:
d. \(\frac{1}{6}<\frac{1}{4}\)
Explanation:
Cecila and Sasha are comparing fraction strips. In the given fractions, the numerators are same. So, compare the denominators to find the largest fraction. As the denominator gets smaller, the fraction gets larger.
2 < 3 wrong.
8 > 6 wrong.
4 > 2 wrong.
6 < 4 correct.
So, 1/6 < 1/4 is the correct answer.
Find Unknown Side Lengths – Page No. 641
Find the unknown side lengths.
Question 1.
Perimeter = 33 centimeters
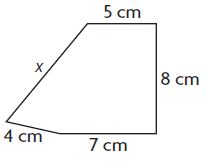
5 + 8 + 7 + 4 + x = 33
24 + x = 33
x = 9
x = ____ 9 _____ centimeters
Answer:
9 centimeters
Explanation:
If I knew the length x, I would add all the side lengths to find the perimeter. Given Perimeter = 33 centimeters.
Add the lengths of the given sides. 5 + 8 + 7 + 4 + x = 33.
24 + x = 33.
x = 33 – 24 =9.
x = 9 centimeters.
Question 2.
Perimeter = 14 feet
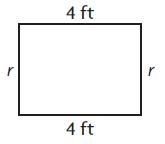
r = ____ feet
Answer:
3 feet
Explanation:
Given Perimeter = 14 feet.
Add the lengths of the given sides to find r.
4 ft + 4 ft + r + r = 14 feet.
If r =1 -> 4 + 4 + 1 + 1 = 10 not equal to 14.
If r = 2 -> 4 + 4 + 2 + 2 = 12 not equal to 14.
If r = 3 -> 4 + 4 + 3 + 3 = 14 equal to 14.
So, r = 3 feet.
Question 3.
Perimeter = 37 meters
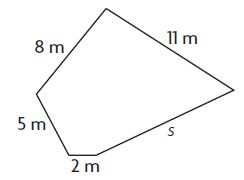
s = ____ meters
Answer:
11 meters
Explanation:
Given that Perimeter = 37 meters.
Add the lengths of the given sides to find s.
8 + 11 + 5 + 2 + s = 37.
26 + s = 37.
s = 37 – 26 = 11.
s = 11 meters.
Question 4.
Perimeter = 92 inches
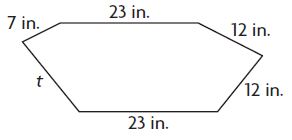
t = ____ inches
Answer:
15 inches
Explanation:
Given that Perimeter = 92 inches.
Add the lengths of the given sides to find t.
7 + 23 + 12 + 12 +23 + t = 92
77 + t = 92.
s = 92 – 77 = 15.
s = 15 inches.
Problem Solving
Question 5.
Steven has a rectangular rug with a perimeter of 16 feet. The width of the rug is 5 feet. What is the length of the rug? ____ feet
Answer:
3 feet
Explanation:

Given that Steven has a rectangular rug with a perimeter of 16 feet. Rectangular has 4 sides with two pairs of opposite sides that are equal in length.
Let the length will be x.
If x = 1 feet -> 5 + x + 5 + x = 5 + 1 + 5 + 1 = 12 feet not equal to 16.
If x = 2 feet -> 5 + x + 5 + x = 5 + 2 + 5 + 2 = 14 feet not equal to 16.
If x = 3 feet -> 5 + x + 5 + x = 5 + 3 + 5 + 3 = 16 feet equal to 16.
So, the length of the blanket is 3 feet.
Question 6.
Kerstin has a square tile. The perimeter of the tile is 32 inches. What is the length of each side of the tile?
____ inches
Answer:
8 inches
Explanation:
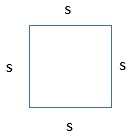
A square has four sides that are equal in length.
So, 4 x s = 32
4 x 8 = 32.
So, the length of each side of the square is 8 inches.
Find Unknown Side Lengths – Page No. 642
Lesson Check
Question 1.
Jesse is putting a ribbon around a square frame. He uses 24 inches of ribbon. How long is each side of the frame? Options:
a. 4 inches
b. 5 inches
c. 6 inches
d. 8 inches
Answer:
c. 6 inches
Explanation:
Jesse is putting a ribbon around a square frame. A square has four sides that are equal in length.
So, 4 x k = 24 inches.
4 x 6 = 24 inches.
Each side of the frame 6 inches.
Question 2.
Davia draws a shape with 5 sides. Two sides are each 5 inches long. Two other sides are each 4 inches long. The perimeter of the shape is 27 inches. What is the length of the fifth side?
Options:
a. 9 inches
b. 13 inches
c. 14 inches
d. 18 inches
Answer:
a. 9 inches
Explanation:
. From the given information, Davia draws a shape with 5 sides.
2 sides = each 5 inches long.
2 sides = each 4 inches long.
Let the other side is k.
The perimeter of the shape = 5 + 5 + 4 + 4 + k = 27 inches.
18 + k = 27 inches.
k = 27 – 18 inches.
k = 9 inches.
Spiral Review
Question 3.
Which of the following represents 7 + 7 + 7 + 7?
Options:
a. 4 × 4
b. 4 × 7
c. 6 × 7
d. 7 × 7
Answer:
b. 4 × 7
Explanation:
7 + 7 + 7 + 7 = 28.
4 x 4 = 16 not equal to 28.
4 x 7 = 28 equal to 28.
7 + 7 + 7 + 7 = 4 × 7.
Question 4.
Bob bought 3 packs of model cars. He gave 4 cars to Ann. Bob has 11 cars left. How many model cars were in each pack?
Options:
a. 18
b. 11
c. 7
d. 5
Answer:
d. 5
Explanation:
If Bob has 11 cars left after he gave 4 to Ann, that means he had 15 cars in total. If Bob had 15 cars in total, and these 15 cars were divided into 3 packs, that means each pack contained 5 cars. The answer is 5 cars in each pack.
Question 5.
Randy looked at his watch when he started and finished reading. How long did Randy read?
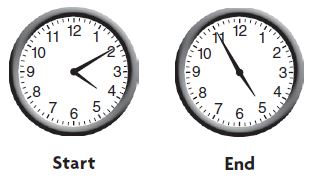
Options:
a. 55 minutes
b. 45 minutes
c. 35 minutes
d. 15 minutes
Answer:
b. 45 minutes
Explanation:
Randy started reading at 4:10.
Randy finished reading at 4:55.
Subtract to find the Randy read time.
4:55 – 4:10 = 45 minutes
So, Randy read 45 minutes.
Question 6.
Which statement does the model represent?
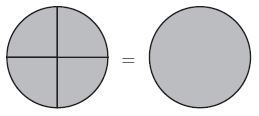
Options:
a. \(\frac{4}{4}\) = 1
b. \(\frac{3}{4}\) = 1
c. \(\frac{2}{4}\) = 1
d. \(\frac{1}{4}\) = 1
Answer:
a. \(\frac{4}{4}\) = 1
Explanation:
The first image represents the whole circle divided into 4 equal parts. So, each part is \(\frac{1}{4}\).
Together, all 4 parts represent \(\frac{4}{4}\) or one whole circle.
The second image represents one whole circle.
\(\frac{4}{4}\) = 1.
Understand Area – Page No. 647
Count to find the area for the shape.
Question 1.
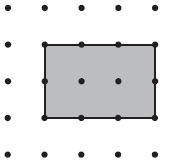
Area = 6 square units
Answer:
6 square units
Explanation:
The area is the measure of the number of unit squares needed to cover a flat surface. A unit square is a square with a side length of 1 unit. It has an area of 1 square unit (sq un). Count the number of Squares to get the answers. 1, 2, 3, 4, 5, 6.
Area = 6 square units.
Question 2.
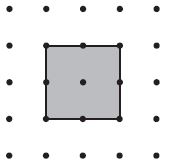
Area = ______ square units
Answer:
4 square units
Explanation:
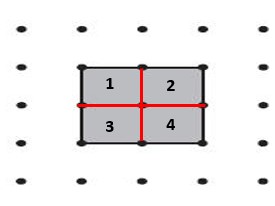
Count the number of Squares to get the answers. 1, 2, 3, 4.
Area = 4 square units.
Question 3.
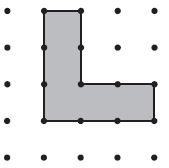
Area = ______ square units
Answer:
5 square units
Explanation:
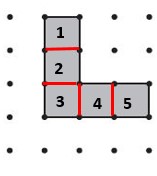
Count the number of Squares to get the answers. 1, 2, 3, 4, 5.
Area = 5 square units.
Question 4.
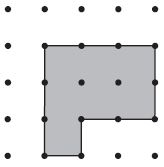
Area = ______ square units
Answer:
7 square units
Explanation:
Count the number of Squares to get the answers. 1, 2, 3, 4, 5, 6, 7.
Area = 7 square units.
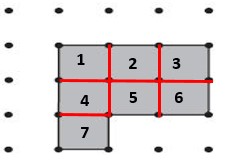
Question 5.
Area = ______ square units
Answer:
8 square units
Explanation:
Count the number of Squares to get the answers. 1, 2, 3, 4, 5, 6, 7, 8.
Area = 8 square units.
Question 6.
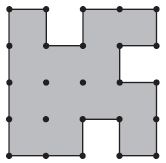
Area = ______ square units
Answer:
13 square units
Explanation:
Count the number of Squares to get the answers. 1, 2, 3, 4, 5, 6, 7, 8,9, 10, 11, 12, 13.
Area = 13 square units.
Write area or perimeter for each situation.
Question 7.
carpeting a floor
_________
Answer:
Area
Question 8.
fencing a garden
_________
Answer:
2. Perimeter
Problem Solving
Use the diagram for 9–10.
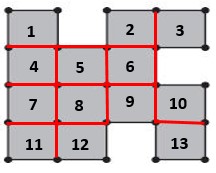
Answer:
12 square units
Explanation:
Count the number of Squares to get the answers. 1, 2, 3, 4, 5, 6, 7, 8,9, 10, 11, 12.
Area = 12 square units.
Question 9.
Rober to is building a platform for his model railroad. What is the area of the platform?
Area = ______ square units
Answer:
12 square units
Explanation:
The area of the platform = Count the total number of Squares to get the answers. 1, 2, 3, 4, 5, 6, 7, 8,9, 10, 11, 12.
Area = 12 square units.
Question 10.
Rober to will put a border around the edges of the platform. How much border will he need?
Border = ______ units
Answer:
16 units
Explanation:
To know the edges of the platform, we need to calculate the perimeter of the given shape. So, we need to add the length of all sides. 2 + 4 + 3 + 2 + 1 + 1 + 2 + 1 = 16 units.
Understand Area – Page No. 648
Lesson Check
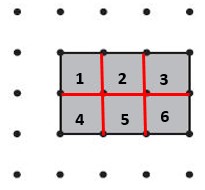
Question 1.
Josh used rubber bands to make the shape below on his geoboard. What is the area of the shape?

Options:
a. 3 square units
b. 4 square units
c. 5 square units
d. 6 square units
Answer:
a. 3 square units
Explanation:
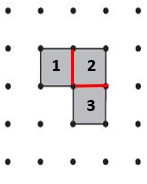
If Josh used rubber bands to make the shape below on his geoboard, he can divide the shape into 2 smaller regular shapes.
The shape 1 marked as square = 1 square unit.
The shape 2 marked as rectangle = 2 square units.
The total area = Shape 1 + Shape 2 = 1 + 2 = 3 square units.
Question 2.
Wilma drew the shape below on dot paper. What is the area of the shape she drew?
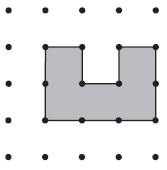
Options:
a. 4 square units
b. 5 square units
c. 6 square units
d. 7 square units
Answer:
b. 5 square units
Explanation:
Wilma drew the shape below on dot paper.
The area of the shape = number of unite square boxes = 1 + 1 + 1 + 1 + 1 = 5 square units.
Spiral Review
Question 3.
Leonardo knows it is 42 days until summer break. How many weeks is it until Leonardo’s summer break? (Hint: There are 7 days in a week.)
Options:
a. 5 weeks
b. 6 weeks
c. 7 weeks
d. 8 weeks
Answer:
b. 6 weeks
Explanation:
Leonardo knows it is 42 days until summer break. There are 7 days in a week. So, by dividing 42 with 7 Leonardo can find summer break in weeks. 42/7 = 6 weeks.
Question 4.
Nan cut a submarine sandwich into 4 equal parts and ate one part. What fraction represents the part of the sandwich Nan ate?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{1}{3}\)
c. \(\frac{4}{4}\)
d. \(\frac{4}{1}\)
Answer:
a. \(\frac{1}{4}\)
Explanation:
Nan cut a submarine sandwich into 4 equal parts and ate one part. So, remaining parts are 3. The fraction of the sandwich Nan ate = \(\frac{1}{4}\).
Question 5.
Wanda is eating breakfast. Which is a reasonable time for Wanda to be eating breakfast?
Options:
a. 7:45 A.M.
b. 7:45 P.M.
c. 2:15 P.M.
d. 2:15 A.M.
Answer:
a. 7:45 A.M.
Explanation:
The reasonable time for Wanda to eat breakfast is 7:45 A.M. Because breakfast will eat in the morning i.e, A.M.
Question 6.
Dick has 2 bags of dog food. Each bag contains 5 kilograms of food. How many kilograms of food does Dick have in all?
Options:
a. 3 kilograms
b. 5 kilograms
c. 7 kilograms
d. 10 kilograms
Answer:
d. 10 kilograms
Explanation:
Dick has 2 x 5 = 10 kilograms of food in total.
Measure Area – Page No. 653
Count to find the area of the shape. Each unit square is 1 square centimeter.
Question 1.
Area 14 square centimeters.
Answer:
14 square centimeters
Explanation:
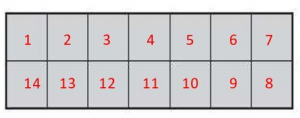
The number of unit square in the given figure is 14. So, the area of the shape = 14 square centimeters.
Question 2.
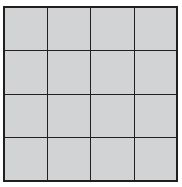
Area = ________ square centimeters
Answer:
16 square centimeters
Explanation:
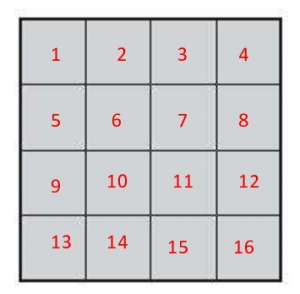
The area of the shape = 16 square centimeters.
Question 3.
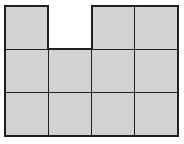
Area = ________ square centimeters
Answer:
11 square centimeters
Explanation:
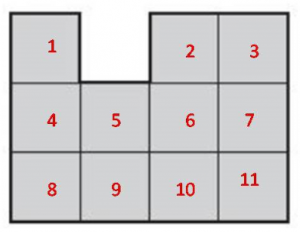
The area of the shape = 11 square centimeters.
Question 4.

Area = ________ square centimeters
Answer:
22 square centimeters
Explanation:
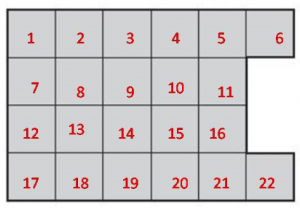
The area of the shape = 22 square centimeters.
Problem Solving
Alan is painting his deck gray. Use the diagram at the right for 5–6. Each unit square is 1 square meter.
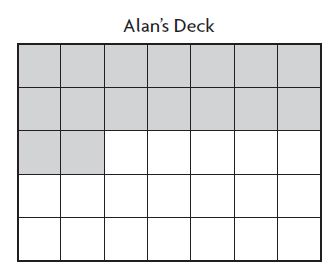
Question 5.
What is the area of the deck that Alan has already painted gray?
_______ square meters
Answer:
16 square meters
Explanation:
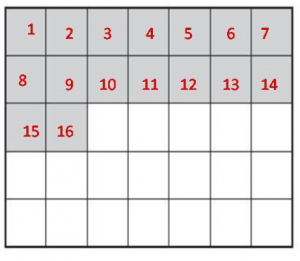
The area of the deck that Alan has already painted gray is 16 square meters.
Question 6.
What is the area of the deck that Alan has left to paint?
_______ square meters
Answer:
19 square meters
Explanation:
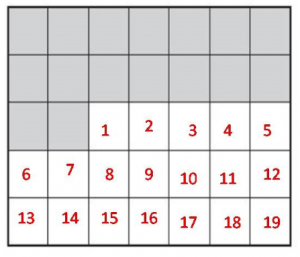
The area of the deck that Alan has left to paint is 19 square meters.
Measure Area – Page No. 654
Lesson Check
Each unit square in the diagram is 1 square foot.
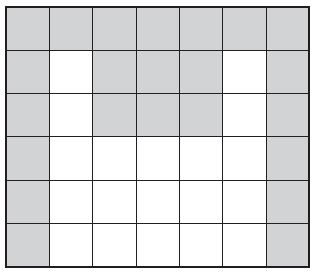
Question 1.
How many square feet are shaded?
Options:
a. 19 square feet
b. 21 square feet
c. 23 square feet
d. 25 square feet
Answer:
c. 23 square feet
Explanation:
Question 2.
What is the area that has NOT been shaded?
Options:
a. 19 square feet
b. 21 square feet
c. 23 square feet
d. 25 square feet
Answer:
a. 19 square feet
Explanation:
Spiral Review
Question 3.
Sonya buys 6 packages of rolls. There are 6 rolls in each package. How many rolls does Sonya buy?
Options:
a. 42
b. 36
c. 24
d. 12
Answer:
b. 36
Explanation:
6 x 6 = 36. Sonya buys 36 rolls.
Question 4.
Charlie mixed 6 liters of juice with 2 liters of soda to make fruit punch. How many liters of fruit punch did Charlie make?
Options:
a. 3 liters
b. 4 liters
c. 8 liters
d. 12 liters
Answer:
c. 8 liters
Explanation:
6 + 2 = 8 liters. Charlie can make 8 liters of fruit punch.
Question 5.
Which drawing shows \(\frac{2}{3}\) of the circle shaded?
Options:
a. 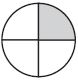
b. 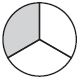
c. 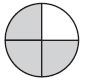
d.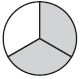
Answer:
d. 
Explanation:
Option d is the correct answer. 2/3 means the whole circle has 3 parts. 2 of the parts are shaded.
Question 6.
Use the models to name a fraction that is equivalent to \(\frac{1}{2}\).
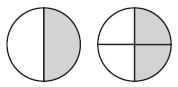
Options:
a. \(\frac{2}{1}\)
b. \(\frac{2}{2}\)
c. \(\frac{2}{4}\)
d. \(\frac{4}{4}\)
Answer:
c. \(\frac{2}{4}\)
Explanation:
\(\frac{2}{4}\) = \(\frac{1}{2}\). So, the answer is \(\frac{2}{4}\)
Use Area Models – Page No. 659
Find the area of each shape. Each unit square is 1 square foot.
Question 1.
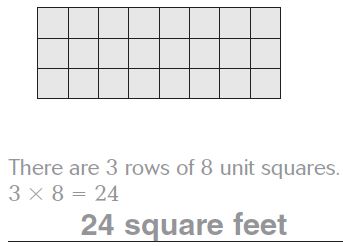
Answer:
24 square feet
Explanation:
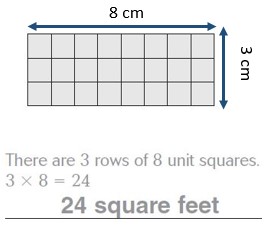
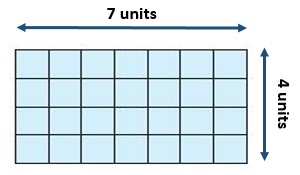
There are 3 rows of 8 unit squares.
3 x 8 = 24.
Question 2.
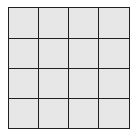
_________ square feet
Find the area of each shape.
Each unit square is 1 square meter.
Answer:
16 square feet
Explanation:
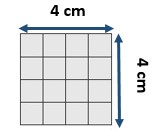
There are 4 rows of 4 unit squares.
4 x 4 = 16 square feet.
Question 3.
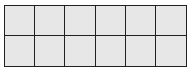
_________ square meters
Answer:
12 square meters
Explanation:
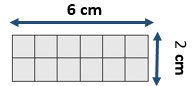
There are 2 rows of 6 unit squares.
2 x 6 = 12 square meters.
Question 4.
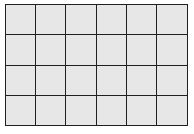
_________ square meters
Answer:
24 square meters
Explanation:
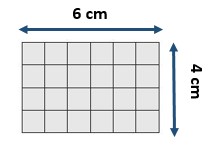
There are 4 rows of 6 unit squares.
4 x 6 = 24 square meters.
Question 5.
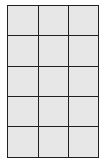
_________ square meters
Answer:
15 square meters
Explanation:
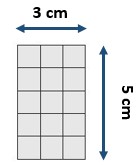
There are 5 rows of 3 unit squares.
5 x 3 = 15 square meters.
Problem Solving
Question 6.
Landon made a rug for the hallway. Each unit square is 1 square foot. What is the area of the rug?
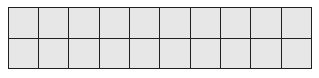
_________ square feet
Answer:
20 square feet
Explanation:
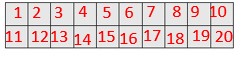
Count the number of unit square boxes = 20 square feet. Or, there are 2 rows of 10 unit squares.
2 x 10 = 20 square feet.
Question 7.
Eva makes a border at the top of a picture frame. Each unit square is 1 square inch. What is the area of the border? ![]()
_________ square feet
Answer:
8 square feet
Explanation:
![]()
Count the number of unit square boxes = 20 square feet. Or, there are 1 rows of 8 unit squares.
1 x 8 = 8 square feet.
Use Area Models – Page No. 660
Lesson Check
Question 1.
The entrance to an office has a tiled floor. Each square tile is 1 square meter. What is the area of the floor?
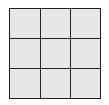
Options:
a. 8 square meters
b. 9 square meters
c. 10 square meters
d. 12 square meters
Answer:
b. 9 square meters
Explanation:

There are 9 square boxes available. So, the area of the floor = 9 square meters.
Question 2.
Ms. Burns buys a new rug. Each unit square is 1 square foot. What is the area of the rug?
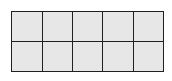
Options:
a. 5 square feet
b. 7 square feet
c. 10 square feet
d. 12 square feet
Answer:
c. 10 square feet
Explanation:
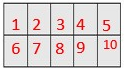
The area of the rug = 10 square feet.
Spiral Review
Question 3.
Ann and Bill are comparing fraction strips. Which statement is correct?
Options:
a. \(\frac{3}{8}>\frac{5}{8}\)
b. \(\frac{3}{4}<\frac{1}{4}\)
c. \(\frac{3}{6}>\frac{4}{6}\)
d. \(\frac{1}{3}<\frac{2}{3}\)
Answer:
d. \(\frac{1}{3}<\frac{2}{3}\)
Explanation:
The denominator of the given fractions are same. So, compare the numerators to find the correct answer.
3 > 5 wrong.
3 < 1 wrong.
3 > 4 wrong.
1 < 2 correct.
The answer is \(\frac{1}{3}<\frac{2}{3}\).
Question 4.
Claire bought 6 packs of baseball cards. Each pack had the same number of cards. If Claire bought 48 baseball cards in all, how many cards were in each pack?
Options:
a. 54
b. 42
c. 8
d. 6
Answer:
c. 8
Explanation:
6 x k = 48. So, k = 48/6 = 8.
8 cards were in each pack.
Question 5.
Austin left for school at 7:35 A.M.. He arrived at school 15 minutes later. What time did Austin arrive at school?
Options:
a. 7:40 A.M.
b. 7:50 A.M.
c. 7:55 A.M.
d. 8:00 A.M.
Answer:
b. 7:50 A.M.
Explanation:
7:35 A.M. + 15 minutes = 7:50 A.M
Question 6.
Wyatt’s room is a rectangle with a perimeter of 40 feet. The width of the room is 8 feet. What is the length of the room?
Options:
a. 5 feet
b. 12 feet
c. 16 feet
d. 32 feet
Answer:
b. 12 feet
Explanation:
The perimeter of rectangle = 40 feet.
The width of the room is 8 feet.
8 + k + 8 + k = 40.
If k = 10 -> 8 + 10 + 8 + 10 = 36.
If k = 11 -> 8 + 11 + 8 + 11 = 38.
If k = 12 -> 8 + 12 + 8 + 12 = 40.
So, the length of the room = 12 feet.
Mid -Chapter Checkpoint – Page No. 661
Vocabulary
Choose the best term from the box.

Question 1.
The distance around a figure is the _____________ .
_____________
Answer:
Perimeter
Question 2.
The measure of the number of unit squares needed to cover a figure with no gaps or overlaps is the _____________ .
_____________
Answer:
Area
Concepts and Skills
Find the perimeter of the figure. Each unit is 1 centimeter.
Question 3.
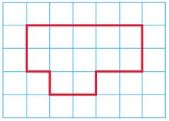
_______ centimeters
Answer:
16 centimeters
Explanation:
5 + 2 + 2 + 1 + 2 + 1 + 1 + 2 = 16 centimeters.
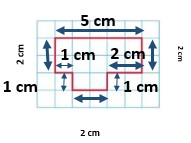
Question 4.
_______ centimeters
Answer:
14 cm
Explanation:
4 + 3 + 4 + 3 = 14 cm.
Find the unknown side lengths.
Question 5.
Perimeter = 33 centimeters
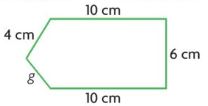
g = ______ centimeters
Answer:
3 centimeters
Explanation:
Given that Perimeter = 33 centimeters.
10 + 6 + 10 + g + 4 = 33 centimeters.
30 + g = 33 centimeters.
g= 33 – 30 centimeters.
g = 3 centimeters.
Question 6.
Perimeter = 32 feet

k = ______ feet
Answer:
4 feet
Explanation:
Perimeter = 32 feet.
12 ft + k + 12 ft + k = 32 feet.
If k = 1 then 12 + 1 + 12 + 1 = 26 feet not equal to 32 feet.
If k = 2 then 12 + 2 + 12 + 2 = 28 feet not equal to 32 feet.
If k = 3 then 12 + 3 + 12 + 3 = 30 feet not equal to 32 feet.
If k = 4 then 12 + 4 + 12 + 4 = 32 feet equal to 32 feet.
So, k = 4 feet.
Find the area of the figure. Each unit square is 1 square meter.
Question 7.
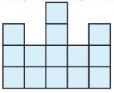
______ square meters
Answer:
14 square meters
Explanation:
Question 8.
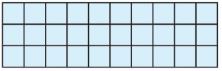
______ square meters
Answer:
30 square meters
Explanation:
10 x 3 = 30 square meters.
Mid -Chapter Checkpoint – Page No. 662
Question 9.
Ramona is making a lid for her rectangular jewelry box. The jewelry box has side lengths of 6 centimeters and 4 centimeters. What is the area of the lid Ramona is making?
______ square meters
Answer:
24 square meters.
Explanation:
The area of the lid = 4 cm x 6 cm = 24 cm.
Ramona making 24 cm lid for her rectangular jewelry box.
Question 10.
Adrienne is decorating a square picture frame. She glued 36 inches of ribbon around the edge of the frame. What is the length of each side of the picture frame?
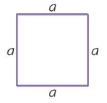
a = ______ inches
Answer:
9 inches
Explanation:
A square has the same lengths.
The length of each side 4 x a = 36 inches.
a = 36/4 = 9 inches.
Question 11.
Margo will sweep a room. A diagram of the floor that she needs to sweep is shown at the right. What is the area of the floor?
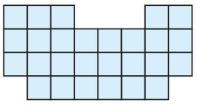
______ square units
Answer:
27 square units
Explanation:
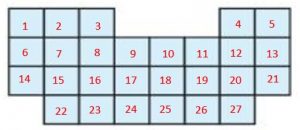
27 square units
Question 12.
Jeff is making a poster for a car wash for the Campout Club. What is the perimeter of the poster?

______ feet
Answer:
8 ft
Explanation:
Perimeter = 3 + 1 + 3 + 1 = 8 ft.
Question 13.
A rectangle has two side lengths of 8 inches and two side lengths of 10 inches. What is the perimeter of the rectangle? What is the area of the rectangle?
Perimeter ______ inches
Area = ______ square inches
Answer:
Perimeter = 36 inches.
Area = 80 square inches.
Explanation:
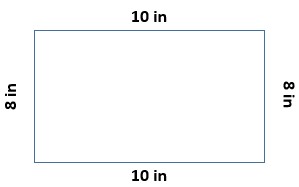
The perimeter of the rectangle = 8 + 10 + 8 + 10 = 36.
Area = 10 x 8 = 80 square inches.
Problem Solving Area of Rectangles – Page No. 667
Use the information for 1–3.
An artist makes rectangular murals in different sizes. Below are the available sizes. Each unit square is 1 square meter.

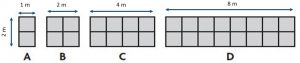
Question 1.
Complete the table to find the area of each mural.
| Mural | Length (in meters) | Width (in meters) | Area (in square meters) |
| A | 2 | 1 | 2 |
| B | 2 | 2 | 4 |
| C | 2 | __4_______ | __8_______ |
| D | 2 | ____8_____ | ___16______ |
Question 2.
Find and describe a pattern of how the length changes and how the width changes for murals A through D.
Type below:
_____________
Answer:
For each mural, the width doubles and the length stays the same.
Question 3.
How do the areas of the murals change when the width changes?
Type below:
_____________
Answer:
For each mural, the area doubles.
Question 4.
Dan built a deck that is 5 feet long and 5 feet wide. He built another deck that is 5 feet long and 7 feet wide. He built a third deck that is 5 feet long and 9 feet wide. How do the areas change?
Type below:
_____________
Answer:
The area of each deck is increased by 10 square feet.
Explanation:
1st deck area = 5 x 5 = 25 feet.
2nd deck area = 5 x 7 = 35 feet.
3rd deck area = 5 x 9 = 45 feet.
The area of each deck is increased by 10 square feet.
Problem Solving Area of Rectangles – Page No. 668
Lesson Check
Question 1.
Lauren drew the designs below. Each unit square is 1 square centimeter. If the pattern continues, what will be the area of the fourth shape?
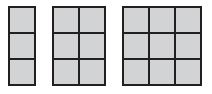
Options:
a. 10 square centimeters
b. 12 square centimeters
c. 14 square centimeters
d. 16 square centimeters
Answer:
b. 12 square centimeters
Explanation:
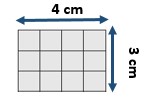
4 x 3 = 12 cm. The area of the fourth shape is 12 square centimeters.
Question 2.
Henry built one garden that is 3 feet wide and 3 feet long. He also built a garden that is 3 feet wide and 6 feet long, and a garden that is 3 feet wide and 9 feet long. How do the areas change?
Options:
a. The areas do not change.
b. The areas double.
c. The areas increase by 3 square feet.
d. The areas increase by 9 square feet.
Answer:
d. The areas increase by 9 square feet.
Explanation:
1st garden = 3 x 3 = 9 feet.
2nd garden = 3 x 6 = 18 feet.
3rd garden = 3 x 9 = 27 feet.
The areas increase by 9 square feet.
Spiral Review
Question 3.
Joe, Jim, and Jack share 27 football cards equally. How many cards does each boy get?
Options:
a. 7
b. 8
c. 9
d. 10
Answer:
c. 9
Explanation:
x + x + x = 27.
3x = 27.
x = 27/3 = 9.
Each boy gets 9 football cards.
Question 4.
Nita uses \(\frac{1}{3}\) of a carton of 12 eggs. How many eggs does she use?

Options:
a. 3
b. 4
c. 6
d. 9
Answer:
b. 4
Explanation:
\(\frac{1}{3}\) of a carton of 12 eggs = \(\frac{1}{3}\) x 12 = 4.
Nita uses 4 eggs.
Question 5.
Brenda made 8 necklaces. Each necklace has 10 large beads. How many large beads did Brenda use to make the necklaces?
Options:
a. 80
b. 85
c. 90
d. 100
Answer:
a. 80
Explanation:
8 x 10 = 80 beads.
Brenda uses 80 beads to make the necklaces
Question 6.
Neal is tiling his kitchen floor. Each square tile is 1 square foot. Neal uses 6 rows of tiles with 9 tiles in each row. What is the area of the floor?
Options:
a. 15 square feet
b. 52 square feet
c. 54 square feet
d. 57 square feet
Answer:
c. 54 square feet
Explanation:
The area of the floor = 6 x 9 = 54 square feet.
Area of Combined Rectangles – Page No. 673
Use the Distributive Property to find the area.
Show your multiplication and addition equations.
Question 1.
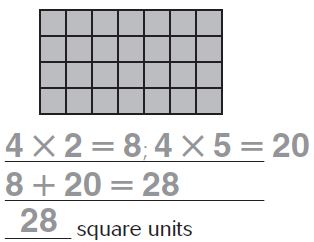
Answer:
28 Square Units
Explanation:
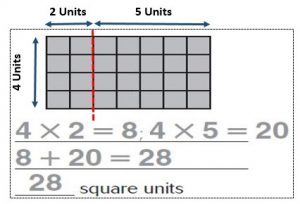
Question 2.

_______ square units
Answer:
27 square units
Explanation:
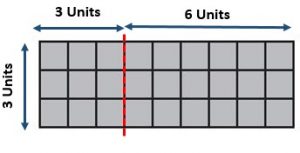
3 x 3 = 9; 3 x 6 = 18.
9 + 18 = 27
27 square units.
Draw a line to break apart the shape into rectangles. Find the area of the shape.
Question 3.
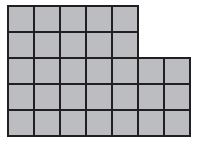
Type below:
_____________
Answer:
31 square units
Explanation:
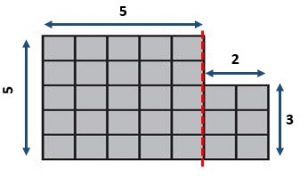
5 x 5 = 25; 2 x 3 = 6
25 + 6 = 31
31 square units
Question 4.
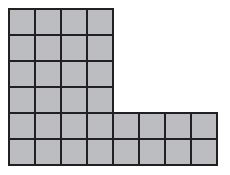
Type below:
_____________
Answer:
32 square units
Explanation:
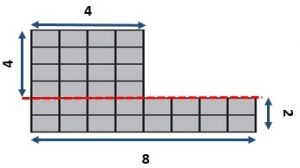
4 x 4 = 16; 2 x 8 = 16.
16 + 16 = 32.
32 square units
Problem Solving
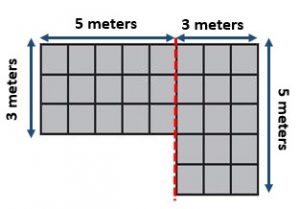
A diagram of Frank’s room is at right. Each unit square is 1 square foot.
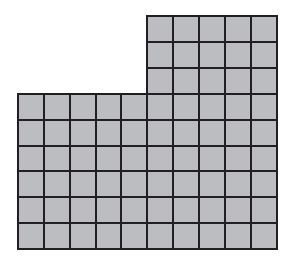
Question 5.
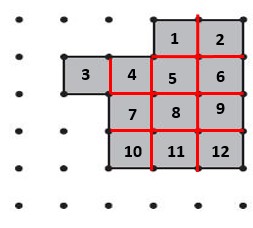
Draw a line to divide the shape of Frank’s room into rectangles.
Answer:
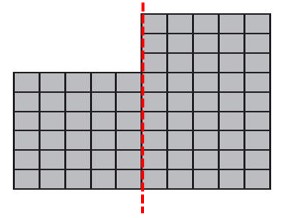
Question 6.
What is the total area of Frank’s room?
_______ square feet
Answer:
75 square feet
Explanation:
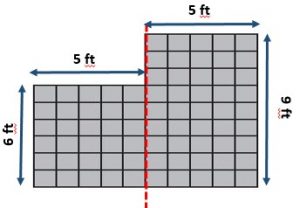
6 x 5 = 30; 5 x 9 = 45
30 + 45 = 75.
75 square feet
Area of Combined Rectangles – Page No. 674
Lesson Check
Question 1.
The diagram shows Ben’s backyard. Each unit square is 1 square yard. What is the area of Ben’s backyard?
Options:
a. 12 square yards
b. 16 square yards
c. 18 square yards
d. 24 square yards
Answer:
b. 16 square yards
Explanation:
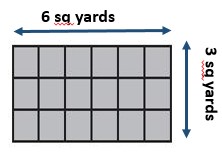
6 x 3 = 18 square yards
Question 2.
The diagram shows a room in an art gallery. Each unit square is 1 square meter. What is the area of the room?
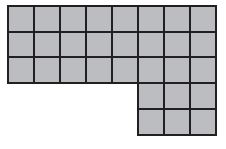
Options:
a. 24 square meters
b. 30 square meters
c. 36 square meters
d. 40 square meters
Answer:
b. 30 square meters
Explanation:
3 x 5 = 15; 3 x 5 = 15
15 + 15 = 30 square meters
Spiral Review
Question 3.
Naomi needs to solve 28 ÷ 7 = ■. What related multiplication fact can she use to find the unknown number?
Options:
a. 3 × 7 = 21
b. 4 × 7 = 28
c. 5 × 7 = 35
d. 6 × 7 = 42
Answer:
b. 4 × 7 = 28
Explanation:
28 ÷ 7 = 4. So, 4 x 7 = 28 is the answer.
Question 4.
Karen drew a triangle with side lengths 3 centimeters, 4 centimeters, and 5 centimeters. What is the perimeter of the triangle?
Options:
a. 7 centimeters
b. 9 centimeters
c. 11 centimeters
d. 12 centimeters
Answer:
d. 12 centimeters
Explanation:
Perimeter = 3 centimeters + 4 centimeters + 5 centimeters = 12 centimeters.
Question 5.
The rectangle is divided into equal parts. What is the name of the equal parts?
![]()
Options:
a. half
b. third
c. fourth
d. sixth
Answer:
c. fourth
Question 6.
Use an inch ruler. To the nearest half inch, how long is this line segment?
![]()
Options:
a. 1
b. 1 \(\frac{1}{2}\)
c. 2
d. 2 \(\frac{1}{2}\)
Answer:
c. 2
Explanation:
The line segment = 2 inches.
Same Perimeter, Different Areas – Page No. 679
Find the perimeter and the area.
Tell which rectangle has a greater area.
Question 1.
A: Perimeter = 12 ;
Area = 9 square units
B: Perimeter = ______ units;
Area = ______ square units;
Rectangle ______ has a greater area.
Answer:
Rectangle A has a greater area.
Explanation:
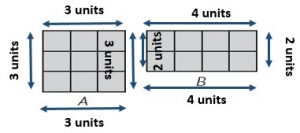
A: Perimeter = 12 ;
Area = 9 square units
B: Perimeter = 2 + 4 + 2 + 4 = 12
Area = 2 x 4 = 8 square units
Rectangle A has a greater area.
Question 2.
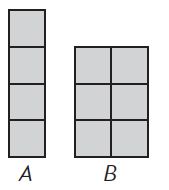
A: Perimeter = ______ units;
Area = ______ square units;
B: Perimeter = ______ units;
Area = ______ square units;
Rectangle ______ has a greater area.
Answer:
Rectangle A has a greater area.
Explanation:
A: Perimeter = 4 + 1 + 4 + 1 = 10
Area = 4 x 1 = 4 square units
B: Perimeter = 3 + 2 + 3 + 2 = 10
Area = 3 x 2 = 6 square units
Rectangle B has a greater area.
Problem Solving
Question 3.
Tara’s and Jody’s bedrooms are shaped like rectangles. Tara’s bedroom is 9 feet long and 8 feet wide. Jody’s bedroom is 7 feet long and 10 feet wide. Whose bedroom has the greater area? Explain.
_________ ‘s bedrooms is greater.
Answer:
Tara’s bedroom has a greater area than Jody’s bedroom area.
Explanation:
Tara’s bedroom area = 9 x 8 = 72 feet.
Jody’s bedroom area = 7 x 10 = 70 feet.
72 feet > 70 feet.
Tara’s bedroom has a greater area than Jody’s bedroom area.
Question 4.
Mr. Sanchez has 16 feet of fencing to put around a rectangular garden. He wants the garden to have the greatest possible area. How long should the sides of the garden be?
Width: ______ Length: ______ feet long
Answer:
All four sides should be 4 feet long.
Explanation:
Mr. Sanchez has 16 feet of fencing to put around a rectangular garden.
Perimeter = 1 + 7 + 1 + 7 = 16 feet. Area = 1 x 7 = 7 feet.
Perimeter = 2 + 6 + 2 + 6 = 16 feet. Area = 2 x 6 = 12 feet.
Perimeter = 3 + 5 + 3 + 5 = 16 feet. Area = 3 x 5 = 15 feet.
perimeter = 4 + 4 + 4 + 4 = 16 feet. Area = 4 x 4 = 16 feet.
The area is maximum when all the four sides are 4 feet long.
Same Perimeter, Different Areas – Page No. 680
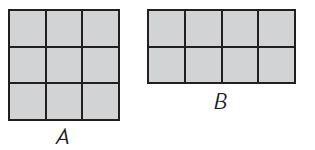
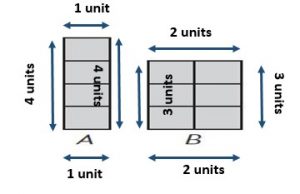
Question 1.
Which shape has a perimeter of 12 units and an area of 8 square units?
Options:
a. 
b. 
c. 
d. ![]()
Answer:
b
Explanation:
Perimeter = 2 + 4 + 2 + 4 = 12 units.
Area = 2 x 4 = 8 square units
Question 2.
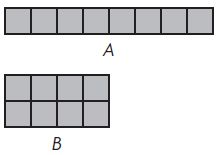
All four rectangles below have the same perimeter. Which rectangle has the greatest area?
Options:
a. 
b. 
c. 
d. 
Answer:
d
Explanation:
a. Area = 2 x 10 = 20.
b. Area = 3 x 9 = 27.
c. Area = 4 x 8 = 32.
d. Area = 5 x 7 = 35.
d has the greatest area.
Spiral Review
Question 3.
Kerrie covers a table with 8 rows of square tiles. There are 7 tiles in each row. What is the area that Kerrie covers in square units?
Options:
a. 15 square units
b. 35 square units
c. 42 square units
d. 56 square units
Answer:
d. 56 square units
Explanation:
Area = 8 x 7 = 56.
Kerrie covers 56 square units area.
Question 4.
Von has a rectangular workroom with a perimeter of 26 feet. The length of the workroom is 6 feet. What is the width of Von’s workroom?
Options:
a. 7 feet
b. 13 feet
c. 20 feet
d. 26 feet
Answer:
a. 7 feet
Explanation:
Perimeter = 26 feet.
Length = 6 feet.
Given Von has a rectangular workroom. So, two lengths and two widths are the same for a rectangle.
Perimeter of a rectangle = Length + Width + Length + Width = 6 + W + 6 + W = 26 feet.
12 + 2W = 26 feet.
2W = 26 – 12 = 14.
W = 14/2 = 7 feet.
Same Perimeter, Different Areas – Page No. 685
Find the perimeter and the area. Tell which rectangle has a greater perimeter.
Question 1.
A: Area = 8 square units ;
Perimeter = 18 units ;
B: Area = _______ square units;
Perimeter = _______ units;
Rectangle _______ has a greater perimeter.
Answer:
Rectangle A has a greater perimeter
Explanation:
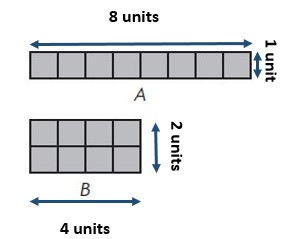
A: Area = 8 square units ;
Perimeter = 18 units ;
B: Area = ___8____ square units;
Perimeter = ____12___ units;
Rectangle ___A____ has a greater perimeter.
Question 2.
A: Area = _______ square units;
Perimeter = _______ units;
Question 2.
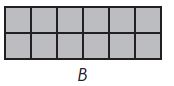
B: Area = _______ square units;
Perimeter = _______ units;
Rectangle _______ has a greater perimeter.
Answer:
Rectangle B has a greater perimeter
Explanation:
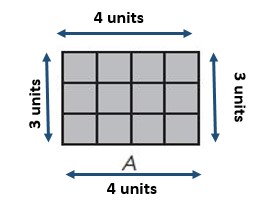
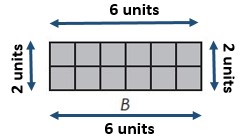
A: Area = 12 square units ;
Perimeter = 14 units ;
B: Area = ___12____ square units;
Perimeter = ____16___ units;
Rectangle ___B____ has a greater perimeter.
Question 3.
A: Area = _______ square units;
Perimeter = _______ units;
Question 3.
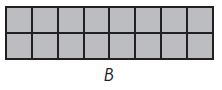
B: Area = _______ square units;
Perimeter = _______ units;
Rectangle _______ has a greater perimeter.
Answer:
Rectangle B has a greater perimeter
Explanation:
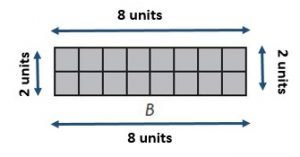
A: Area = 16 square units ;
Perimeter = 16 units ;
B: Area = ___16____ square units;
Perimeter = ____20___ units;
Rectangle ___B____ has a greater perimeter.
Problem Solving
Use the tile designs for 4–5.
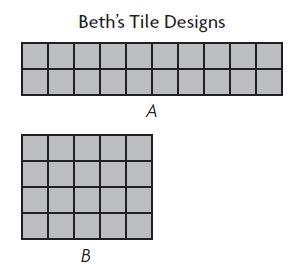
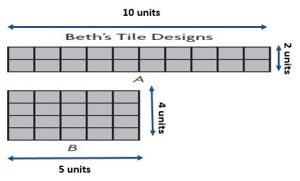
Question 4.
Compare the areas of Design A and Design B.
The area of Design A ________ The area of Design B
Answer:
The area of Rectangle A and Rectangle B are equal.
Explanation:
A: Area = 20 square units ;
B: Area = ___20____ square units;
Question 5.
Compare the perimeters. Which design has the greater perimeter?
The perimeter of A ________ The perimeter of B
Answer:
The perimeter of A Greater than the perimeter of B
Explanation:
A: Perimeter = 24 units ;
B: Perimeter = ____18___ units;
Same Perimeter, Different Areas – Page No. 686
Lesson Check
Question 1.
Jake drew two rectangles. Which statement is true?
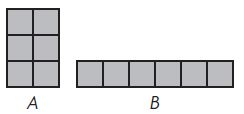
Options:
a. The perimeters are the same.
b. The area of A is greater.
c. The perimeter of A is greater.
d. The perimeter of B is greater
Answer:
d. The perimeter of B is greater
Explanation:
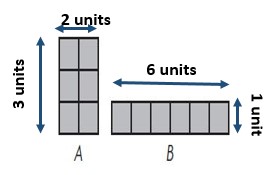
A: Area = 6 square units ;
Perimeter = 10 units ;
B: Area = ___6____ square units;
Perimeter = ____14___ units;
The perimeter of B is greater.
Question 2.
Alyssa drew two rectangles. Which statement is true?
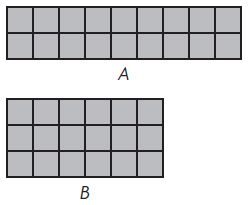
Options:
a. The perimeter of B is greater.
b. The perimeter of A is greater.
c. The area of B is greater.
d. The perimeters are the same.
Answer:
b. The perimeter of A is greater.
Explanation:
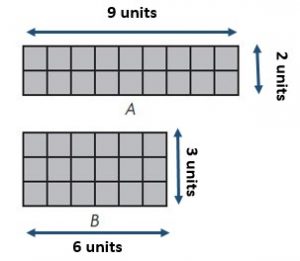
A: Area = 18 square units ;
Perimeter = 22 units ;
B: Area = ___18____ square units;
Perimeter = ____18___ units;
The perimeter of A is greater.
Spiral Review
Question 3.
Marsha was asked to find the value of 8 – 3 x 2. She wrote a wrong answer. Which is the correct answer?
Options:
a. 22
b. 10
c. 4
d. 2
Answer:
d. 2
Explanation:
8 – (3 x 2) = 8 – 6 = 2
Question 4.
What fraction names the point on the number line?

Options:
a. \(\frac{1}{4}\)
b. \(\frac{2}{3}\)
c. \(\frac{3}{4}\)
d. \(\frac{3}{1}\)
Answer:
c. \(\frac{3}{4}\)
Explanation:
From the given figure, we can write the fraction name the point on the number line = \(\frac{3}{4}\)
Question 5.
Kyle drew three line segments with these lengths: \(\frac{2}{4}\) inch, \(\frac{2}{3}\) inch, and \(\frac{2}{6}\) inch. Which list orders the fractions from least to greatest?
Options:
a. \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\)
b. \(\frac{2}{3}, \frac{2}{4}, \frac{2}{6}\)
c. \(\frac{2}{4}, \frac{2}{3}, \frac{2}{6}\)
d. \(\frac{2}{6}, \frac{2}{3}, \frac{2}{4}\)
Answer:
c. \(\frac{3}{4}\)
Explanation:
Given fractions are \(\frac{2}{4}\) inch, \(\frac{2}{3}\) inch, and \(\frac{2}{6}\) inch.
All the fractions have the same numerator. The denominators should compare to find the answer. The smaller denominator represents the larger number. So, \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\) is the answer.
Question 6.
On Monday, \(\frac{3}{8}\) inch of snow fell. On Tuesday, \(\frac{5}{8}\) inch of snow fell. Which statement correctly compares the snow amounts?
Options:
a. \(\frac{3}{8}=\frac{5}{8}\)
b. \(\frac{3}{8}<\frac{5}{8}\)
c. \(\frac{5}{8}<\frac{3}{8}\)
d. \(\frac{3}{8}>\frac{5}{8}\)
Answer:
b. \(\frac{3}{8}<\frac{5}{8}\)
Explanation:
Given fractions are \(\frac{3}{8}\) and \(\frac{5}{8}\).
The denominators are equal for given fractions. So, compare numerators to find the correct equation.
3 < 5. So, \(\frac{3}{8}<\frac{5}{8}\) is the correct answer.
Review/Test – Page No. 687
Question 1.
Find the perimeter of each figure on the grid. Identify the figure that have a perimeter of 14 units. Mark all that apply.
Options:
a. 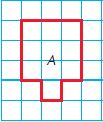
b. 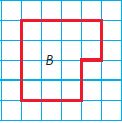
c. 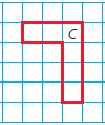
d. 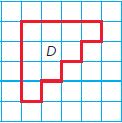
Answer:
a and c have a perimeter of 14 units.
Explanation:
a. The Perimeter of A = 14 units.
b. The perimeter of B = 16 units.
c. The perimeter of C = 14 units.
d. The perimeter of D = 16 units
Question 2.
Kim wants to put trim around a picture she drew. How many centimeters of trim does Kim need for the perimeter of the picture?
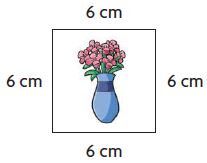
_________ centimeters
Answer:
24 centimeters
Explanation:
Perimeter = 6 + 6 + 6+ 6 = 24 centimeters.
Question 3.
Sophia drew this rectangle on dot paper. What is the area of the rectangle?
_________ square units
Answer:
8 square units
Explanation:
8 square units
Review/Test – Page No. 688
Question 4.
The drawing shows Seth’s plan for a fort in his backyard. Each unit square is 1 square foot.
Which equations can Seth use to find the area of the fort?
Mark all that apply.
Options:
a. 4 + 4 + 4 + 4 = 16
b. 7 + 4 + 7 + 4 = 22
c. 7 + 7 + 7 + 7 = 28
d. 4 × 4 = 16
e. 7 × 7 = 49
f. 4 × 7 = 28
Answer:
b and f are correct.
Explanation:
Area = 4 × 7 = 28
Perimeter = 7 + 4 + 7 + 4 = 22.
Question 5.
Which rectangle has a number of square units for its area equal to the number of units of its perimeter?
Options:
a. ![]()
b. 
c. ![]()
d. 
Answer:
B rectangle has a number of square units for its area equal to the number of units of its perimeter
Explanation:
a. Area = 1 x 7 = 7 units.
Perimeter = 1 + 7 + 1 + 7 = 16 units.
b. a. Area = 4 x 4 = 16 units.
Perimeter = 4 + 4 + 4 + 4 = 16 units.
c. a. Area = 2 x 6 = 12 units.
Perimeter = 2 + 6 + 2 + 6 = 16 units.
d. a. Area = 3 x 5 = 7 units.
Perimeter = 3 + 5 + 3 + 5 = 16 units.
Question 6.
Vanessa uses a ruler to draw a square. The perimeter of the square is 12 centimeters. Select a number to complete the sentence.
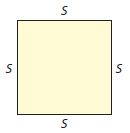
The square has a side length of  centimeters.
centimeters.
_________ centimeters
Answer:
3 centimeters
Explanation:
Perimeter = s + s + s + s = 12 centimeters.
4s = 12 centimeters.
s = 3 centimeters.
Review/Test – Page No. 689
Question 7.
Tomas drew two rectangles on grid paper.
Circle the words that make the sentence true.
Rectangle A has an area that is  the area of Rectangle B, and a perimeter that is
the area of Rectangle B, and a perimeter that is  the perimeter of Rectangle B.
the perimeter of Rectangle B.
Type below:
_____________
Answer:
Rectangle A has an area that is the same as the area of Rectangle B.
A perimeter that is less than the perimeter of Rectangle B.
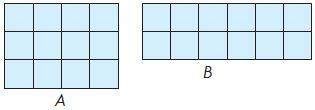
Explanation:
A: Area = 3 x 4 = 12 units.
Perimeter = 3 + 4 + 3 + 4 = 14 units.
B: Area = 2 x 6 = 12 units.
Perimeter = 2 + 6 + 2 + 6 = 16 units.
Question 8.
Yuji drew this figure on grid paper. What is the perimeter of the figure?
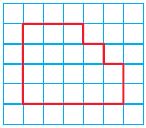
________ units
Answer:
18 units
Explanation:
Question 9.
What is the area of the figure shown? Each unit square is 1 square meter.
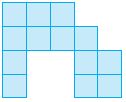
________ square meters
Answer:
13 square meters
Explanation:
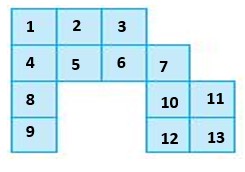
Review/Test – Page No. 690
Question 10.
Shawn drew a rectangle that was 2 units wide and 6 units long. Draw a different rectangle that has the same perimeter but a different area.

Type below:
_____________
Answer:
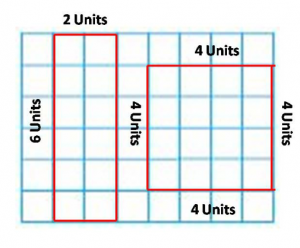
Area = 2 x 6 = 12 Square Units.
Area = 4 x 4 = 16 Square Units.
Question 11.
Mrs. Rios put a wallpaper border around the room shown below. She used 72 feet of wallpaper border. What is the unknown side length? Show your work.
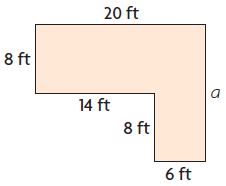
a = ________ ft
Answer:
16 feet
Explanation:
20 + a + 6 + 8 + 14 + 8 = 72 feet.
a + 56 = 72 feet.
a = 72 – 56 feet.
a = 16 feet.
Question 12.
Elizabeth has two gardens in her yard. The first garden is 8 feet long and 6 feet wide. The second garden is half the length of the first garden. The area of the second garden is twice the area of the first garden. For numbers 12a–12d, select True or False.
First garden = 8 x 6 = 48 feet.
Second garden length = Half the length of the first garden = 4 feet.
Second Garden Area = Twice the area of the first garden = 2 x 48 = 96.
Second Garden Area Width = 4 x s = 96.
s = 96/4 = 24
a. The area of the first garden is 48 square feet.
i. True
ii. False
Answer:
i. True
Question 12.
b. The area of the second garden is 24 square feet.
i. True
ii. False
Answer:
ii. False
Question 12.
c. The width of the second garden is 12 feet.
i. True
ii. False
Answer:
ii. False
Explanation:
Question 12.
d. The width of the second garden is 24 feet.
i. True
ii. False
Answer:
i. True
Review/Test – Page No. 691
Question 13.
Marcus bought some postcards. Each postcard had a perimeter of 16 inches. Which could be one of the postcards Marcus bought? Mark all that apply.
Options:
a. 
b. 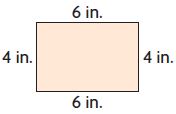
c. 
d. 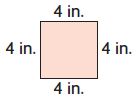
Answer:
a and d options are correct.
Explanation:
3 + 5 + 3 + 5 = 16 inches
4 + 6 + 4 + 6 = 20 inches.
5 + 10 + 5 + 10 = 30 inches.
4 + 4 + 4 + 4 = 16 inches.
Question 14.
Anthony wants to make two different rectangular flowerbeds, each with an area of 24 square feet. He will build a wooden frame around each flowerbed. The flowerbeds will have side lengths that are whole numbers.
Part A
Each unit square on the grid below is 1 square foot. Draw two possible flowerbeds. Label each with a letter.

Type below:
__________
Answer:
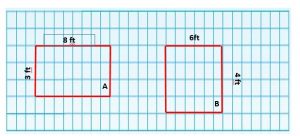
Question 14.
Part B
Which of the flowerbeds will take more wood to the frame?
Explain how you know.
Type below:
__________
Answer:
A Perimeter is greater than B Perimeter.
Explanation:
Area = 24.
3 x 8 = 24; 4 x 6 = 24.
A Perimeter = 8 + 3 + 8 + 3 = 22 feet.
B Perimeter = 4 + 6 + 4 + 6 = 20 feet.
A Perimeter is greater than B Perimeter.
Review/Test – Page No. 692
Question 15.
Keisha draws a sketch of her living room on grid paper. Each unit square is 1 square meter. Write and solve a multiplication equation that can be used to find the area of the living room in square meters.
Type below:
__________
Answer:
40 meter.
Explanation:
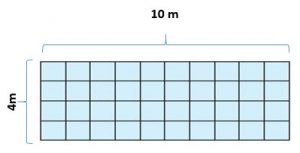
4 x 10 = 40 m.
Question 16.
Mr. Wicks designs houses. He uses grid paper to plan a new house design. The kitchen will have an area between 70 square feet and 85 square feet. The pantry will have an area between 4 square feet and 15 square feet. Draw and label a diagram to show what Mr. Wicks could design. Explain how to find the total area.
Type below:
__________
Answer:
78 square feet
Explanation: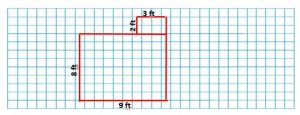
Are of Kitchen = 8 x 9 = 72 square feet. (70 < 72 < 85)
Area of Pantry = 3 x 2 = 6 square feet. (4 < 6 < 15)
Total area of kitchen and pantry = 72 + 6 = 78 square feet.
Conclusion
Go Math Grade 3 Answer Key Chapter 11 Perimeter and Area has step-by-step solutions for all the problems making it easy for you to understand the concepts. Practice problems from the Go Math Grade 3 Answer Key Chapter 11 Perimeter and Area Extra Practice and test your preparation standards.
